CORDIC算法VHDL实现
CORDIC算法原理及实现

图4.1 圆坐标系旋转
CORDIC算法原理 --圆坐标系旋转原理
上面的方程组同样可写成矩阵向量形式:
x2 cos y sin 2 sin x1 y cos 1
例如一个90o相移为:
x2 0 1 x1 - y1 y 1 0 y x 1 1 2
x (i 1) x (i ) y (i ) di 2 i y (i 1) y (i ) x (i ) d i 2 i z (i 1) z (i ) d i e (i )
1
z
(0)
通过设定x(0)=1和z(0)=0来计算tan-1y(0)。向量模式 中,判决算子di 满足下面条件:
d i sign ( x (i ) y (i ) )
因此 我们输入x(0)和y(0)(z(0)=0),并通过迭代使y(0) 取值趋近于0。
CORDIC算法原理 --向量模式
CORDIC算法原理 --圆坐标系旋转原理
前面所示的伪旋转现在可以表示为(对每次迭代):
x (i 1) x (i ) d i (2 i y (i ) )
(4.7) 在这里引入第三个方程,被称为角度累加器,用来在 每次迭代过程中追踪累加的旋转角度: z (i 1) z (i ) d i (i ) (4.8) 这里:di=±1。符号di是一个判决算子,用于确定旋转的方向。 上述三个方程式为圆周坐标系中用于角度旋转的CORDIC算法的 表达式。在本章的后续部分中我们还将看到CORDIC算法被用于其 它的坐标系,通过使用这些坐标系可以执行更大范围的函数计算。
CORDIC算法原理 --圆坐标系旋转原理
CORDIC算法VHDL实现

CORDIC算法VHDL实现LIBRARY ieee;USE ieee.std_logic_1164.all;USE ieee.std_logic_arith.all;USE ieee.STD_LOGIC_UNSIGNED.all;ENTITY cordicCOS_SIN ISPORT(clk :IN std_logic;deg_in :IN std_logic_vector (13 downto 0);cos :OUT std_logic_vector(15 downto 0);sin :OUT std_logic_vector(15 downto 0));END cordicCOS_SIN;architecture rlt_cordicCOS_SIN of cordicCOS_SIN isconstant c1:std_logic_vector(13 downto 0):=CONV_STD_LOGIC_VECTOR(4096,14); constant c2:std_logic_vector(13 downto 0):=CONV_STD_LOGIC_VECTOR(2048,14); constant c3:std_logic_vector(13 downto 0):=CONV_STD_LOGIC_VECTOR(1209,14); --arctan(1/2)constant c4:std_logic_vector(13 downto 0):=CONV_STD_LOGIC_VECTOR(639,14); --arctan(1/4)--constant x0:std_logic_vector(15 downto 0):=CONV_STD_LOGIC_VECTOR(19895,16); signal x0 :std_logic_vector(15 downto 0);signal y1,x1 :std_logic_vector(15 downto 0);signal y2,x2 :std_logic_vector(15 downto 0);signal y3,x3 :std_logic_vector(17 downto 0);signal y4,x4 :std_logic_vector(19 downto 0);signal p1,p2,p3,p4 :std_logic_vector(13 downto 0);beginx0 <= conv_std_logic_vector(26980,16);---------------------------------step 1------------------------------------ process(clk)beginif rising_edge(clk) thenif deg_in(13) ='1' theny1 <= x"0000" -x0;elsey1 <= x0;end if;end if;end process;process(clk)beginif rising_edge(clk) thenx1 <=(others =>'0');end if;end process;process(clk)beginif rising_edge(clk) thenif deg_in(13) ='1' thenp1 <= deg_in + c1;elsep1 <= deg_in - c1;end if;end if;end process;---------------------------------step 2------------------------------------ process(clk)beginif rising_edge(clk) thenif p1(13) ='1' theny2 <= y1 - x1;elsey2 <= y1 + x1;end if;end if;end process;process(clk)beginif rising_edge(clk) thenif p1(13) ='1' thenx2 <= x1 + y1;elsex2 <= x1 - y1;end if;end if;end process;process(clk)beginif rising_edge(clk) thenif p1(13) ='1' thenp2 <= p1 + c2;elsep2 <= p1 - c2;end if;end process;---------------------------------step 3------------------------------------ process(clk)beginif rising_edge(clk) thenif p2(13) ='1' theny3 <= (y2(15) & y2 &'0') -(x2(15) & x2(15) & x2);elsey3 <= (y2(15) & y2 &'0') + (x2(15) & x2(15) & x2);end if;end if;end process;process(clk)beginif rising_edge(clk) thenif p2(13) ='1' thenx3 <= (x2(15) & x2 & '0') + (y2(15) & y2(15) & y2 );elsex3 <= (x2(15) & x2 & '0') - (y2(15) & y2(15) & y2 );end if;end if;end process;process(clk)beginif rising_edge(clk) thenif p2(13) ='1' thenp3 <= p2 + c3;elsep3 <= p2 - c3;end if;end process;---------------------------------step 4------------------------------------ process(clk)beginif rising_edge(clk) thenif p3(13) ='1' theny4 <= (y3 & "00") -(x3(17) & x3(17) & x3);elsey4 <= (y3 & "00") +(x3(17) & x3(17) & x3);end if;end if;end process;process(clk)beginif rising_edge(clk) thenif p3(13) ='1' thenx4 <= (x3 & "00") + (y3(17) & y3(17) & y3 );elsex4 <= (x3 & "00") - (y3(17) & y3(17) & y3 );end if;end if;end process;process(clk)beginif rising_edge(clk) thenif p3(13) ='1' thenp4 <= p3 + c4;elsep4 <= p3 - c4;end if;end if;end process;cos<=x4(19 downto 4); sin<=y4(19 downto 4); end rlt_cordicCOS_SIN;。
正交信号发生器的FPGA设计与仿真

正交信号发生器的FPGA设计与仿真作者:雷能芳来源:《价值工程》2011年第24期摘要:正交信号发生器的FPGA 实现通常都是基于查找表的方法,为了达到高精度要求,需要耗费大量的ROM 资源去建立庞大的查找表。
文中提出了一种基于流水线CORDIC 算法的实现方案,可有效地节省FPGA 的硬件资源。
并根据DSP 开发工具DSP Builder的优点,采用VHDL文本与Simulink 模型图相结合的方法进行了FPGA设计,仿真结果验证了设计的正确性及可行性。
Abstract: The common approach to implement orthogonal signal generator on FPGA is based on look-up tables, which require a huge volume of ROM to achieve high resolution. This paper proposes a pipelined architecture for implementation of orthogonal signal generator on FPGA, which, based on CORDIC algorithm, can save considerable hardware resources and improve the speed performance as well. According to advantages of DSP Builder, the system is designed by utilizing VHDL and Simulink module. The correctness and feasibility of this design is verified by simulation result.关键词:CORDIC算法;FPGA;DSP Builder;正交信号Key words: CORDIC algorithm;FPGA;DSP Builder;orthogonal signal中图分类号:TP391.9文献标识码:A 文章编号:1006-4311(2011)24-0140-020引言正交信号发生器是电子技术领域中最基本的电子仪器,广泛应用于通信系统、电子对抗、电子测量、科研教学等领域。
实验7 Cordic 算法实现

实验七. Cordic 算法实现组长:刘家尚 学号:5100309219 组员:黄钰坤 学号:5100309218一、 实验目的1.掌握VHDL 语言描述数学运算电路的方法。
2. 掌握Cordic 算法,并用该算法实现sin 和cos 函数。
二、 实验内容1. 在初始化的时候数码管显示待计算的角度数据“0000”。
2. 数码管显示的角度数据以4位无符号16进制数的形式显示。
显示的数据p 和角度数值 (单位是弧度)的对应关系如下:265535πθ⨯=p 即:显示“FFFF ”代表2πθ=,“0001”代表2655351πθ⨯=。
3.BTN3、2、1、0分别控制所对应的4个数码管显示的角度内容,每按一下按钮,对应数码管显示的内容加1(加到‘F ’时再按按钮回到‘0’)。
4.SW0和SW1用于选择数码管显示的内容。
任意时刻SW0拨到向下位置时显示角度,SW0拨到向上位置时显示计算结果。
对于计算结果,具体显示sin 还是cos 的值由SW1决定,即:SW1拨到向下位置时显示cos 值,SW1拨到向上位置时显示sin 值。
5.计算结果以4位无符号16进制数的形式显示,显示内容d 和对应的数值v 关系如下:65535dv =即:显示“FFFF ”代表计算结果1=v ,显示“0001”代表655351=v 。
三、 解决方案程序分为7个模块,包括分频模块、按键获取模块、七段数码管显示模块、选择显示模块、获取输入角θ模块、CordicPipeline 模块和外层Cordic 模块1. 分频器模块定义一个整数count 作为计数器计数,当计数器计数到125000时,输出电平翻转,由输入时钟为50MHz ,故有输出的时钟为50M/(2*125000)=200Hz 。
该频率用于数码管扫描和按键扫描。
2. 按键获取模块按键防抖模块同样的采用上述分频器产生的200Hz 的频率进行扫描。
而防抖的关键是利用输入信号与它的延时信号相与的方式产生一个单脉冲。
基于FPGA的CORDIC算法实现

关键词:现场可编程门阵列ꎻ坐标旋转数字计算方法ꎻ平行算法ꎻ正反旋转抵消 中图分类号:TN402 文献标识码:A 文章编号:1005-9490(2018)05-1242-05
在硬件设计中实现三角函数一般有 3 种方法: 查表法ꎬ级数展开法ꎬCORDIC 算法[1] ꎮ 查表法简单 易实现ꎬ但是随着系统对数据精度的提高ꎬ其占用资 源也不断增大ꎮ 级数展开法运算复杂ꎬ不利于硬件 实现ꎮ 自 CORDIC[2] 算法被提出ꎬ人们不断对其进 行研究与改进ꎬ它的优点也愈发明显ꎬ新颖的结构被 提出ꎬ不仅速度快ꎬ消耗硬件资源少ꎬ而且可以达到 很高的精度ꎮ
第5期
蔡权利ꎬ高 博等:基于 FPGA 的 CORDIC 算法实现
{x1 = x0 -y0tanθ y1 = y0 +x0 tanθ
(2)
12 43
图 1 CORDIC 向量旋转示意图
CORDIC 算法思想是利用 2-i 近似 tanθi ꎬ来实现
三角函数的计算ꎮ
当使用 2-i 近似 tanθi ꎬ从而每次的旋转角度为
Abstract:The delay and resources consumption of traditional cordic algorithm are large. For this reasonꎬan opti ̄ mized parallel algorithm based on parallel cordic algorithm is proposedꎬwhich predicts the rotation directions of the lower part and the high part by using the binary ̄to ̄bipolar algorithm and the micro ̄rotation angle codingꎬ and reduces the rotation times by using positive ( negative) rotations to compensate negative ( positive) rotations in the high part rotation. The proposed algorithm is designed and validated by FPGA. The results indicate that the delayꎬ the source consumption and the precision are improved obviously compared with traditional algorithms. Key words:FPGAꎻCORDICꎻparallel algorithmꎻrotation compensation EEACC:0260 doi:10.3969 / j.issn.1005-9490.2018.05.032
cordic算法求角度的verilog实现

cordic算法求角度的verilog实现1. 引言1.1 概述本篇文章旨在探讨并介绍Cordic算法在Verilog中的实现方式。
Cordic算法是一种用于计算三角函数和超越函数的快速算法,它具备较高的精度和计算效率,被广泛应用于数字信号处理、通信系统等领域。
1.2 文章结构文章将按照以下顺序进行介绍:首先,对Cordic算法进行概述,包括原理介绍、应用领域以及优势与局限性。
接着,在第三部分中详细解释了Verilog实现Cordic算法的设计思路和步骤。
随后,在第四部分中对该设计进行功能验证和性能评估,探究其计算准确性和速度。
最后,在第五部分对结果进行总结和讨论,并提出改进之处和未来发展方向建议。
1.3 目的本文主要目的有两个方面:一方面是介绍Cordic算法作为一种高效计算角度的方法,对其原理进行深入剖析并说明其应用范围与局限性;另一方面是通过使用Verilog语言实现Cordic算法,展示其在硬件电路设计中的具体应用,并评估其功能和性能。
通过本文的介绍,读者可以了解Cordic算法的基本原理及其在Verilog中的实现方式,同时对其优势与限制有更深入的认识。
此外,读者也可以通过作者对功能验证和性能评估结果的分析,对该算法在实际应用中的表现有更清晰的认识。
最后,读者可以从结论与展望部分中获得未来改进该算法以及相关硬件电路设计发展方向的建议。
2. Cordic算法概述:2.1 原理介绍:Cordic算法,全称为Coordinate Rotation Digital Computer算法,是一种用于计算各种三角函数(如正弦、余弦、正切)的迭代近似方法。
该算法基于旋转操作,通过一系列迭代步骤逐渐逼近所需的角度值。
Cordic算法最初由Volder在1959年提出,并被广泛应用于计算机领域中需要高效计算三角函数的场景。
其核心思想是将复杂的三角运算转化为一系列简单的位移、加减和比较等基本操作,从而实现了高速且低资源消耗的计算。
流水线CORDIC算法的FPGA实现

流水线CORDIC算法的FPGA实现作者:赵林军来源:《电脑知识与技术·学术交流》2008年第30期摘要:从CORDIC算法的基本原理出发,讨论其工作过程以及旋转角的覆盖范围,在此基础上,给出了具有流水线结构的FPGA实现结构以及增益因子的大小与流水线级数的确定关系,给出了VHDL实现算法,经程序设计与Quartus6.0调试与仿真,结果表明采用FPGA实现的CORDIC算法具有较好的运算精度。
关键词:CORDIC;VHDL;实现;流水线中图分类号:TP391文献标识码:A文章编号:1009-3044(2008)30-0716-02The Implementation of Pipeline CORDIC Algorithm Based on VHDLZHAO Lin-jun(Shanxi University of Technology, Hanzhong 723003, China)Abstract: From the basal principle of CORDIC algorithm, this paper discusses the algorithmic course of work and its coverage range of revolution angle. Based on this, the article gives a pipelined structure which realized by FPGA and a VHDL program. Compiled and simulated by QuartusⅡ6.0, its operational results has a higher precision. Finally, the essential way to improve the CORDIC performance has been pointed out.Key words: CORDIC; VHDL; Implementation; Pipeline1 引言CORDIC(Coordinate Rotation Digital Computer)算法是J.Vocder[1]于1959年在美国航空控制系统的设计中提出来的一种用于计算平面直角坐标系和极坐标系下函数值的循环迭代算法,J.S Walther[2]将其推广了CORDIC算法,将圆周旋转、线性旋转与双曲线旋转均包括到了同一个CORDIC迭代方程之中,由于该算法仅涉及移位与加减运算,便于软硬件实现,因而受到了人们的广泛关注。
针对正弦余弦计算的CORDIC算法优化及其FPGA实现

直接数字频率合成器是现代频率合成的主要工具,它有频率分辨率高,频率转化快等众多优点。这种器件被广泛应用于众多领域。
在CORDIC算法中,对数据的操作只有移位和加/减,易于用硬件实现的。而且CORDIC算法也容易流水线实现,可以在计算系统中的高速进行。
本文链接:/Thesis_Y1325245.aspx
授权使用:武汉大学(whdx),授权号:a42506fa-e993-4c54-b65b-9e4501376a91
下载时间:2010年12月7日
对于Jacobi算法的硬件实现,论文经过分析总结提出了两种大的结构:串行计算机构和并行计算结构。串行计算结构又根据具体计算过程的不同分成了两种方法,一种方法是先寻找矩阵非对角元素的最大元,然后对其相应的行列进行Jacobi旋转;另一种方法是通过遍历的方法来对矩阵的行列依次进行Jacobi旋转。并行计算结构是一种阵列型的结构,它由对角线处理单元和非对角线处理单元通过一定的连接组成,每个处理单元处理四个矩阵元素,在一次处理后跟相邻的单元进行数据交换进行新的一次计算。
2.会议论文肖顺文.陈亚军CORDIC算法的优化设计及其FPGA实现2007
针对采用流水结构实现CORDIC算法存在的不足,从旋转角度范围、旋转角度精度的调整、模校正因子的分解三个方面进行了详细的分析,并给出了相应的优化和改进措施;实现了CORDIC算法的全流水结构,并用CORDIC算法实现信号发生器加以验证。
设计以Altera CycloneⅡ EP2C35F672C8为目标器件,对算法的实现电路进行功能和时序仿真。仿真结果表明,算法电路有较高的转换精度和较高的运算速度,其中坐标转换模块的时钟频率达到130MHz,信号处理模块的时钟频率达到140MHz。最后,在FPGA硬件平台上对数字图像旋转引擎进行了整体验证。图像的输入信号取自 PC机的 VGA信号接口,处理后的图像输出液晶显示器的VGA信号接口。验证的结果显示,数字图像旋转引擎所处理的图像清晰稳定,能设定旋转角度、旋转方向和缩放比例,实现自如流畅的动态画面旋转和缩放。
改进型高速高精度CORDIC算法及其在DDFS中的应用

改进型高速高精度CORDIC算法及其在DDFS中的应用史方显;曾立;陈昱;王淼;占丰【摘要】提出了一种新的选择迭代式高速高精度CORDIC(COrdinate Rotation Digital Computer)算法.基于表驱动法缩小目标旋转角度,通过改进的基本角度选择方法旁路不必要的迭代;并以移位和减法实现幅度校正,减小硬件资源消耗.设定角度误差小于10-5rad时,迭代次数减小至7次以下.在DDFS(Direct Digital Frequency Synthesizer)的应用中,利用区间压缩技术在Xilinx的FPGA中实现20位定点小数电路设计.仿真及实测结果表明,该算法幅度误差小于2×10-5,输出延时不大于43.5ns,同时硬件资源消耗不增加.%A novel optional-iteration high speed and high precision CORDIC algorithm is proposed in this paper.First the rotation is conducted with a corresponding angle based on table-driven method.Then the algorithm bypasses unnecessary iterations using a new basic angle choosing technique.And the correction is achieved by shift and subtraction to reduce hardware consumption.Calculation and simulation indicate that the new algorithm can reduce the iteration number to less than 7 when the phase error is smaller than 10-5 rad.In the application of DDFS,20 fractional binary bits design is implemented in Xilinx FPGA with range reduction method.This design can reduce amplitude error to smaller than 2 x 10-5 for sine and cosine,cut the output delay down to 43.5ns in circuit test,and no hardware consumption increase.【期刊名称】《电子学报》【年(卷),期】2017(045)002【总页数】6页(P446-451)【关键词】坐标旋转数字计算机;直接数字频率合成器;表驱动;现场可编程门阵列【作者】史方显;曾立;陈昱;王淼;占丰【作者单位】北京航空航天大学宇航学院,北京100191;北京航空航天大学宇航学院,北京100191;北京航空航天大学宇航学院,北京100191;北京航空航天大学宇航学院,北京100191;山东航天电子技术研究所,山东烟台264000【正文语种】中文【中图分类】TN431.2直接数字频率合成技术(DDFS)属于第三代频率合成技术,由Tierney J在1971年首先提出[1].传统的DDFS基于查找表(LUT)技术,其主要结构包括相位累加器、查找表、DAC和低通滤波器.累加器在时钟的上升沿对频率控制字进行累加,将结果作为地址在查找表中读出正余弦值,通过DAC后进行低通滤波.在满足Nyquist采样定律的情况下,增大频率控制字可增大合成的频率.这种方法具有快速转换、高频率分辨率、低相位噪声和相位连续等优点[2].但由于有限字长的截断误差,基于查找表的DDFS必须在精度和面积、速度之间折衷.坐标旋转数字计算机(CORDIC)可通过移位和加减计算平方根、正余弦、模长与相位以及坐标变换,易于在FPGA等VLSI 器件中实现,广泛应用于FFT、矩阵分解和DDFS[3].CORDIC算法最早由Volder J E在1959年提出[4],圆周坐标下的CORDIC算法的核心思想是通过一系列的基本角度{θi=arctan2-i}的加减逐渐逼近输入角度,并对结果进行校正,i依次递增.其基本公式为其中x、y为旋转向量端点的横坐标值和纵坐标值.由式(1)可知旋转的过程中剩余未旋转角度zi的绝对值不断趋近于0,δi∈{-1,1}用以指示zi的正负,当δi=-1时逆时针旋转,δi=1时顺时针旋转.设旋转前后的向量长度分别为Ri和Ri+1,则有[4]即每次旋转后向量长度增加,为确保其端点仍在单位圆上,应对式(1)计算结果进行校正,且第i次旋转的校正系数为提高运算速度的主要方法有减小迭代次数、降低关键路径延时等,如文献[5]提出了改进型的并行CORDIC,但其精度只能达到10-4量级.文献[6]在资源利用率上有一定优势,但迭代过程依赖于时钟信号,导致延时较长.传统的CORDIC算法中的i是单调递增的,在|zi|较小的情况下仍可能进行较大角度旋转,致使迭代次数较大.文献[7]等提出了可调整基本角度系数的基4混合CORDIC,但判断系数所用的选择方程比较复杂,硬件资源消耗较大.针对传统算法的这些缺点,本文提出一种新的选择迭代式CORDIC算法,以相对简单的方式跳过不必要的旋转,在减小迭代次数的同时确保硬件资源消耗不增加.3.1 算法说明将[0,π/4]等分为长度为I的区间,第m个区间起点为αm,正余弦值{sinαm}和{cosαm}以及基本角度{θi}均存储在查找表中,其中0≤m≤⎣π/4I」且m为正整数,tanθi=2-i.输入角度φ首先通过由{αm}组成的比较阵列,根据比较结果返回m 的值,查表得x0=cosαm、y0=sinαm做为旋转的起点,此时已经旋转至φ的附近,故实际旋转的目标角度为φ-αm,且满足φ-αm≤φ.后续迭代均采用与zi绝对值最相近的基本角度θi,此时|θi-|zi||取最小值.i在增大的过程中跳过某些值,以此加速|zi|→0的过程,将迭代次数减小至最低.当i→∞时zi→0,此时的xi和yi为cosφ和sinφ的精确值,但实际的迭代次数是有限的,假设迭代次数为N.浮点数格式下忽略舍入误差,CORDIC的精度是由角度误差Δφ确定的.取相同的角度误差Δφ引起的正弦逼近误差为正弦的2阶导数为-sinx,∀x∈(0,π/4]其2阶导数小于0,Φyerr(φ)单调递减,由此可得最大误差出现在Φyerr(0)=sin(Δφ),同理可得∀x∈(0,π/4]余弦函数的最大逼近误差为Φxerr(π/4)= cos(π/4)-cos(π/4+Δφ).设精度要求为误差上限不大于f,且sin(Δφ)> cos(π/4)-cos(π/4+Δφ),由此可确定迭代终止的条件为max(θi)取不大于φ-αm的最大基本角度即可,同时取min(θi)≤Δφ以满足精度要求.3.2 求迭代次数上限由文献[8]可知,对于b位二进制小数下的CORDIC,当i ≥(b-log23)/3时,令θi=arctan2-i≈2-i不影响计算精度.由于实际旋转的目标角度较小,本文选取的i范围满足上述要求.若e满足则迭代次数的首次加1必定发生在[X+2-e,X+2-e+1]区间内,X为基本角度的线性组合.[0,2-e]范围内迭代次数为由0增大到1,[2-e,2-e+1]范围内迭代次数由1增加到2,[2-e+2+2-e,2-e+2+2-e+1]范围内迭代次数由2增大到3.根据规律提出以下假设:当N≥3时,迭代次数由N-1增大到N发生在以下区间上.以归纳法证明.当N=3时已证明成立,假设当N=s(s≥3)时仍成立,且区间A上的最大迭代次数为s.图1中则迭代次数由s-1增大到s发生在区间[L,M]中.由于4H、2H和H均为基本角度{θi≈2-i}中的元素,故角度2H、4H和角度H一样,可由一次旋转得到;且区间B、D长度与A相同,故除第一次旋转外,区间B、D上的剩余旋转与A相同,即区间B、D上的最大迭代次数为s.区间C、D上的迭代关于4H对称,所选基本角度相同,只是δi不同,因此区间C上的最大迭代次数仍为s. 最大迭代次数由s增大到s+1发生在区间[P,Q]上,此时相对于区间[L,M]多了一次旋转4H,且P、Q满足即N=s+1时假设仍成立,故对于N≥3假设均成立.在选定{θi}的情况下,最大迭代次数和区间长度正相关,当满足如下不等式时最大迭代次数为N-1.若将[0,π/4]等分为15个区间,此时αm+1-αm=π/60rad,精度要求在10-6数量级可得Δφ≈10-5rad,据此取5≤i≤18,根据式(6)得出e=15.由式(10)可得此时最大迭代次数为7,当φ-αm单调递增时,最早出现在区间内.3.3 MATLAB仿真验证在MATLAB中对本文提出改进型CORDIC算法和传统的CORDIC算法进行迭代,每隔10-6rad取一个点,可遍历{θi}在[0,π/4]内所有组合结果,并在角度误差不大于Δφ的情况下完成对[0,π/4]内任一角度的迭代.由图2可得本文提出的CORDIC算法迭代次数不超过7次,大部分集中在6次及以下,和式(10)得出的结果相同;传统的CORDIC算法最大迭代次数为16,且N大多集中在10次及以上.图2的下半部分给出了根据计算结果画出的余弦曲线和正弦误差,其幅值误差最大值为9.955×10-6.文献[7]提出的高基混合CORDIC算法达到n位精度需要的迭代次数为「3n/8+1⎣,误差为10-6量级时需要迭代大于9次,误差小于2×10-5时需要迭代大于8次;文献[6]的迭代分三级共24次.故本文提出的CORDIC算法在迭代次数上明显优于文献[6]和[7].MATLAB的计算是基于单精度浮点数,而在FPGA中进行浮点数的运算需要消耗大量的硬件资源;使用定点数会带来额外的舍入误差及其累积和传递,且定点数的乘法消耗的资源也较多.因此需要进行误差计算并重新考虑校正的方法.以下的分析均基于小数位宽为b的定点数.4.1 移位/减法进行校正校正因子{ki}是i的离散单调增函数,当i ≥5时满足0.999512076087079≤ki<1.设其二进制值为其中aj∈{0,1},传统的校正可表示为其中(xi)j表示xi右移j位的结果.由于满足条件的ki非常接近1,故aj=1的个数远大于aj=0的个数,进行乘法校正时部分积数目较大,耗费较多资源的同时也带来很大的延时[9];同理,若以移位/加法进行校正需要加法器的个数接近b.本文采用移位/减法的方式进行校正,取2-l≈1-ki,当满足1≤l<b时将待校正的xi右移l位得(xi)l,xi= xi- (xi)l为校正后的结果;yi同理.若l ≥b则(xi)l视为0,即ki≈1,可不进行校正,此时只需要1个减法器.由表1可知这种近似带来的误差很小.4.2 误差的计算式(12)表示校正后的第n+1次迭代,0≤n≤N-1.设本次迭代所选基本角度为θi,tanθi=2-i,此时校正因子为ki.算法最终计算结果的误差由3部分组成:(1)有限位宽带来的舍入误差Δx0、Δy0及其累积和传递的结果ΔxN、ΔyN;(2)以1-2-l近似ki带来的误差Δki;(3)迭代终止时Δφ带来的逼近误差.在矩阵模式下可表示为由多元函数的系统误差公式可得[10]其中Δxn为n次迭代舍入误差的累积值.同理可得根据文献[11]给出的公式,再考虑校正因子的误差可得舍入误差传递后的上限为其中其行列式的值满足且由式(14)~(18)得迭代最终误差如式(20)所示,将相应数值代入得其最大值不超过2×10-5.4.3 FPGA仿真与实测图3详细描述了本文提出的改进型CORDIC算法运算框图.在复位信号无效的情况下,累加器在时钟上升沿对频率控制字从-π开始进行累加,为保证相位的连续性,当累加结果溢出时将结果减去2π,累加器的输出送至区间压缩模块.将[-π,π]等分为8个区间,按照映射函数将[0,π/4]之外的角度压缩至[0,π/4][12].迭代完成后根据输入角度所在区间和三角函数的变换公式进行输出变换,结果输出到DAC.图4为Modelsim仿真所得输入角度(test-theta)、所在区间(interval)和正弦(sinvalue)余弦(cosvalue)波形,从图中可以看到相位的线性增加和溢出后减去2π再累加,interval信号的变化指示了输入角度所处区间,最后输出两路正交的正余弦信号.为完整表示[-π,π]内的角度,累加器进行运算时使用的是24位数据,包括1位符号位、3位整数位和20位小数位;压缩后的弧度制整数位为0,采用22位数据,包括1位符号位、1位整数位和20位小数位.将Modelsim仿真的数据导出,在Matlab中计算出20位定点小数下的误差如图5所示.由图5可得,误差的变化具有周期性,这是因为第二步旋转的起始角度φ-αm是周期变化的,最大误差均发生在迭代次数最多时,此时Δx0、Δy0累积和传递达到最大.由于Φyerr单调递减,Φxerr单调递增,故正弦的最大误差总体在减小,余弦的最大误差总体在增大,但两者的最大幅度均不超过2×10-5,符合计算结果.在[0,π/4]内φ相同时Δφ对余弦引起的误差总是小于正弦,故余弦函数的误差总体上小于正弦误差. 本设计电路的实现采用VHDL语言描述,FPGA型号为Xilinx公司Virtex5系列XC5VLX30,图6为实际输出波形.表2列出了本文设计与文献[5]和文献[6]的主要性能的对比,其中输出延时为FPGA实测数据.由于减小了迭代次数,本文提出的CORDIC算法精度最高,输出延时基本达到并行CORDIC算法的水平,运算速度比多级迭代的文献[6]有较大提高;且硬件资源消耗和文献[5]相比有所减少.本文提出的改进型CORDIC算法从以下两个方面减小迭代次数:(1)基于表驱动法一次旋转至输入角度附近,减小目标旋转角度的大小;(2)选取和剩余未旋转角度绝对值最相近的基本角度进行迭代,加速z→0的过程.迭代次数的减小降低了输出延迟,提高了速度;同时降低了舍入误差的传递和累积,提高了正余弦幅度精度.并通过移位/减法实现幅度校正,减少校正时加法器的使用数量,控制总的资源消耗.计算和实测结果表明,在硬件消耗未增加的情况下,本文提出的CORDIC算法在迭代次数、精度和速度等方面优于传统设计.史方显(通信作者) 男,1992年10月出生于安徽淮南.北京航空航天大学硕士研究生,研究方向为VHDL数字VLSI设计及FPGA在航天电子系统中的应用.E-mail:******************.cn曾立男,1976年8月出生于湖南邵阳.清华大学博士,北京航空航天大学副教授,研究方向为为空间环境仪器科学与工程.E-mail:**************.cn【相关文献】[1]Tierney J,Rader C M,Gold B.A digital frequency synthesizer[J].IEEE Transactions on Audio and Electroacoustics,1971,19(1):48-57.[2]Yang W,Hao M.A direct digital frequency synthesizer based on CORDIC algorithm implemented with FPGA[A].Proceedings of the 5th International Conference onASIC[C].Beijing,China:IEEE,2003.2:832-835.[3]Han W,Yousi Z,Xiaokang L.A parallel double-step CORDIC algorithm for digital down converter[A].2009 7th Annual Communication Networks and Services Research Conference (CNSR)[C].Moncton,BC,Canada:IEEE,2009.257-261.[4]Volder J E.The CORDIC trigonometric computing technique[J].IRE Transactions on Electronic Computers,1959,Ec-8(3):330-334.[5]祁艳杰,刘章发.基于Parallel-CORDIC的高精度高速度直接数字频率合成器的FPGA实现[J].电子学报,2014,42(7):1392-1397. QI Yan-jie,LIU Zhang-fa.FPGA implementation of high speed and high precision direct digital frequency synthesizer based on parallel-CORDIC[J].Acta Electronica Sinica,2014,42(7):1392-1397.(in Chinese)[6]Xin R,Zhang X,Li H,et al.An area optimized direct digital frequency synthesizer based on improved hybrid CORDIC algorithm[A].3rd International Workshop on Signal Design and Its Applications in Communications[C].Chengdu,China:IEEE,2007.243-246.[7]Shukla R,Ray K C.Low latency hybrid CORDIC algorithm[J].IEEE Transactions on Computers,2014,63(12):3066-3078.[8]Chuang T P,Huang C C,Hsiao S F.Design of a CORDIC-based SIN/COS intellectual property (IP) using predictable sign bits[A].Proceedings of the 27th European Solid-State Circuits Conference[C].Villach,Austria:IEEE,2001.277-280.[9]Han L,Ko S B.High-speed parallel decimal multiplication with redundant internal encodings[J].IEEE Transactions on Computers,2013,62(5):956-968.[10]Fei Yetai.Error Theory and Data Processing[M].Beijing:Higher Education Press,2010.66-74.(in Chinese)[11]Hu Y H.The quantization effects of the CORDIC algorithm[J].IEEE Transactions on Signal Processing,1992,40(4):834-844.[12]Maharatna K,Banerjee S,Grass E,et al.Modified virtually scaling-free adaptive CORDIC rotator algorithm and architecture[J].IEEE Transactions on Circuits and Systems for Video Technology,2005,15(11):1463-1474.。
FM解调及AFC算法的VHDL设计实现

FM解调及AFC算法的VHDL设计实现孙秀睿【摘要】根据遥测中频PCM/FM信号的解调原理,介绍了FM解调及自动频率控制(AFC)设计的理论架构和实现方法,通过理论分析、公式推导和Matlab仿真等手段证明了方法的正确性,在此基础上完成VHDL程序设计,最后进行了仿真测试和实验验证.仿真结果和实验结果证明了该实现方法的可行性.【期刊名称】《电讯技术》【年(卷),期】2010(050)003【总页数】3页(P42-44)【关键词】遥测;PCM/FM;解调算法;自动频率控制;低通滤波器;VHDL【作者】孙秀睿【作者单位】中国工程物理研究院电子工程研究所,四川,绵阳,621900【正文语种】中文【中图分类】TN7631 引言PCM/FM是常用的调制体制之一,传统的调制解调处理以模拟技术为主。
由于数字技术的发展,信号和数据处理能力大大提高,促进了遥测通信系统从模拟终端设备到数字设备的发展。
数字方法的采用可以满足在通用平台上实现多种通信体制下的信号处理工作,避免重复设计,节约成本,提高设计的灵活性。
本文根据全软化解调原理,采用数字方法实现了中频PCM/FM遥测信号的解调,并通过仿真与实验证明了设计的正确性和可行性,获得了较好的解调性能。
2 基本原理FM解调方案设计框图如图1所示。
前端的基带I、Q信号进行数字鉴相,计算出各点相位,经数字鉴频得到频率输出,由于此时的频率值中还包含有载波频偏成分,经过AFC后消除了载波频偏的影响,最后用低通滤波器进行滤波得到FM解调的输出。
图1 FM解调方案设计框图Fig.1 Block diagram of FM demodulation3 软件解调算法的数学模型3.1 数字鉴相数字鉴相采用的是CORDIC算法。
收到前端送来的基带I、Q信号后,首先要完成的就是从每对I、Q样点中获取相位信息。
采用CORDIC算法可以计算出每对I、Q样点对应的幅度和相位。
FPGA中提供了CORDIC算法的I PCORE,通过调用I PCORE,可以较为容易地在FPGA中实现样点相位提取的功能。
FPGA环境下基于cordic运算实现反正切运算(VHDL)

CORDIC 算法实现反正切运算算法1. 前言CORDIC 算法包括圆周系统、线性系统、双曲系统三种旋转系统,每种系统又分别具有旋转模式和向量模式两种运算模式。
其中,运用最为广泛的时圆周系统的两种运算模式,本文也立足与项目应用,仅阐述圆周系统,其余系统可参看相关资料。
2. 算法分析要充分理解圆周系统,我们需先引入其旋转模式的概念,再以旋转模式引申到向量的概念中去。
CORDIC 算法的旋转模式运算的实质就是执行一个平面内旋转,如图1所示,就是从一个坐标点转换到另一个坐标点的过程.iX iY模式运算示意图如图1中所示,原向量i i (Y )X ,的坐标表达式为i i X r cos Y r sin αα=*⎧⎨=*⎩ (1)其中,r 为向量的长度,由于本文的目的是讨论角度的计算,所以,都假定向量旋转过程中的长度是固定不变的,这样,我们可以专注于角度的变化。
所以,目标向量j j (Y )X ,的坐标表达式为j jX r cos()Y r sin()αθαθ=*+⎧⎨=*+⎩ (2)即j i i j i i X r (cos cos sin sin )cos sin Y r sin cos cos sin )Y cos X sin X Y αθαθθθαθαθθθ=*-=+⎧⎨=*+=+⎩(用向量统一表示为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡i i j j Y X Y X θθθθcos sin sin cos (3) 公式1表示由向量i i (Y )X ,到向量j j (Y )X ,的旋转过程,即转过的相角为θ,可以通过迭代运算分多步执行角度旋转,每一步完成旋转的一部分.单步表述为:⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡++n n n n n nn n Y X Y X θθθθcos sin sin cos 11 (4)其中n 1X +表示下一步迭代需要执行的运算。
根据公式2,必须确切知道每单步要旋转的角度n θ,具体计算方法阐述如下: 为方便表示,并简化方程中的参量,方程(4)提取COS 后变成⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡++n n n n n n n Y X Y X 1tan tan 1cos 11θθθ (5)规定每一步所调整的角度为⎪⎭⎫⎝⎛=n n 21arctan θ (6)即单次调整n θ最大为当n=0时调整45︒,其后每次调整值逐步减小,如此多次调整后最终调整角度值即为目标值θ,向量旋转完毕。
CORDIC算法在正余弦函数中的应用及其FPGA实现_常柯阳

{
yi
>> i
zi sign( z i )
θi +/ -
ìx n = cos θ ï 其中设增益 í y n = sin θ , ï z ® 0 î n
+/ xi + 1 xn - 1
>> n - 1
+/ yi + 1 yn - 1
>> n - 1
zi + 1 zn - 1 sign( z n - 1) θn - 1 +/ zn
广东工业大学 自动化学院, 广州 510006 Faculty of Automation, Guangdong University of Technology, Guangzhou 510006, China CHANG Keyang, ZENG Yuenan, CHEN Ping, et al. Application of CORDIC algorithm in sine & cosine function and its implementation on FPGA. Computer Engineering and Applications, 2013, 49 (7) : 140-143. Abstract:Sine & cosine function is used broadly in engineering. Ordinarily, lookup-table algorithm implements easily, but a large amount of memory units are necessary and the contradiction between accuracy and the mount of memory units is acute. Traditional CORDIC (Coordinate Rotation Digital Computer) algorithm can achieve higher accuracy with less memory units, but needs more hardware resource and has long output delay. A new architecture combined with lookup-table and CORDIC algorithm is proposed. The design, simulation and hardware testing based on FPGA of the improved algorithm have been completed which indicates that it can achieve higher accuracy and lower output delay with less hardware resource and few memory units. Key words: CORDIC algorithm; lookup-table; sine & cosine function; Field Programmable Gate Array (FPGA) 摘 要: 正余弦函数在工程实现中应用很广泛。常用的查找表方法实现简单, 但占用存储器资源较多, 计算精度与存储容
一种CORDIC算法优化及32位浮点反正切函数FPGA实现

一种CORDIC算法优化及32位浮点反正切函数FPGA实现鲍宜鹏【摘要】通过对反正切函数实现算法的研究,在传统CORDIC算法的基础上,提出了一种以超前进位加法器为基本单元的迭代结构,双时钟输入,完成了反正切函数的ASIC电路设计。
该算法采用TSMC 55 nm工艺,在Synopsys/syn10.12环境中综合实现。
该算法的关键路径由原来的2.9 ns提升至1.3 ns,最高运算频率可以达到769 MHz,即优化后的CORDIC算法比优化前速率提高了2倍多。
%Through the study of algorithms implements of the arctangent function, proposed a hierarchical carry lookahead adder structure as the basic unit of iterations basing on traditional CORDIC algorithms, double clock input, completed the ASIC circuit design of the arctangent function. The algorithm applied TSMC 55 nm process and achieved a comprehensive in Synopsys/syn 10.12 environment. The key way of the algorithm was reduced from 2.9 ns to 1.3 ns, the highest operation frequency is able to reach 769 MHz, the speed of the whole system was twice more than the original design.【期刊名称】《电子与封装》【年(卷),期】2015(000)003【总页数】4页(P22-25)【关键词】CORDIC算法;分层次超前进位加法;反正切函数【作者】鲍宜鹏【作者单位】中国电子科技集团公司第58研究所,江苏无锡 214035【正文语种】中文【中图分类】TN402在导航通信、数字信号处理等许多领域都会大量使用反正切函数进行必要的计算。
FPGA算法学习(1)--Cordic(Verilog实现)

FPGA算法学习(1)--Cordic(Verilog实现)上两篇博⽂、做了理论分析和实现,但是所⽤到的变量依然是浮点型,⽽cordic真正的⽤处是基于FPGA等只能处理定点的平台。
只需将满⾜精度的浮点数,放⼤2^n倍,取整,再进⾏处理。
1. 旋转模式假设要通过FPGA计算极坐标(55.6767°,1)的直⾓坐标。
⾸先,⾓度值为浮点数,需要进⾏放⼤处理,放⼤10000倍。
则预设的旋转⾓度同样要放⼤10000倍。
实现伪旋转(忽略模长补偿因⼦)的代码如下所⽰,注意,因为是整型运算,起始旋转时x放⼤了215,放⼤倍数决定计算精度,满⾜需求即可。
最后得到的x,y在缩⼩215,即得到伪旋转后的x,y。
最后进⾏模长波长运算(因为是浮点,同样需要放⼤)。
#include <stdio.h>#include <stdlib.h>int cordic_c(int a,int r);int x = 32768, y = 0; //以X轴为旋转起始点,放⼤倍数2^15int main(viod){int remain = cordic_c(556767,1); //极坐标值(极⾓,极径)printf("旋转⾓度误差:%d, 直⾓坐标:x = %d, y = %d\n",remain,x,y);return 0;}int cordic_c(int a,int r){const int theta[] = {450000,265651,140362,71250,35763,17899,8952,4476,2238,1119,560,280,140,70,35,17,9,4,2,1}; //旋转⾓度int i = 0;int x_temp = 0, y_temp = 0;int angle_new = 0; //旋转后终⽌⾓度int angle_remain = a; //旋转后,剩余⾓度char detection; //旋转⽅向for( i=0; i<20;i++){if(angle_remain > 0){angle_new = angle_new + theta[i];angle_remain = a - angle_new;x_temp = (x - (y >>i));y_temp = (y + (x >> i));x = x_temp;y = y_temp;detection = '+';}else{angle_new = angle_new - theta[i];angle_remain = a - angle_new;x_temp = (x + (y>>i));y_temp = (y - (x>>i));x = x_temp;y = y_temp;detection = '-';}printf(" x = %-8d, y = %-8d, 旋转次数 = %-8d 旋转⾓度 = %-12d 旋转⽅向:%-8c 终点⾓度 = %-8d\n", x,y,i+1, theta[i],detection,angle_new);}x = r*x;y = r*y;return angle_remain;}完整的FPGA实现过程,包含预处理和后处理,⽀持{-π,π}的⾓度,采⽤流⽔线⽅式实现,Verilog完整代码如下,注意在移位过程中要⽤算术移位(>>>),才能保证带符号的数正确移位:/****************************************************///预处理module Cordic_Pre(clk,rst_n,phi,phi_pre,quadrant_flag);/****************************************************/input clk;input rst_n;input signed [23:0] phi;output signed [23:0] phi_pre; //预处理后的⾓度值output [1:0] quadrant_flag; //象限标记/****************************************************/parameter ANGLE_P90 = 24'sd90_0000, //输⼊⾓度范围{-pi,pi},⾓度值放⼤了10000倍ANGLE_N90 = -24'sd90_0000,ANGLE_0 = 24'sd00_0000;/****************************************************/reg signed [23:0] phi_pre_r;reg [1:0] quadrant_flag_r;/****************************************************/always @(posedge clk or negedge rst_n)beginif(rst_n == 1'b0)beginphi_pre_r <= 24'sd0;quadrant_flag_r <= 2'b00;endelse if(phi >= ANGLE_0 && phi <= ANGLE_P90) //第⼀象限beginphi_pre_r <= phi;quadrant_flag_r <= 2'b01;endelse if(phi > ANGLE_P90 ) //第⼆象限beginphi_pre_r <= phi - ANGLE_P90;quadrant_flag_r <= 2'b10;endelse if(phi < ANGLE_0 && phi >= ANGLE_N90) //第四象限beginphi_pre_r <= phi;quadrant_flag_r <= 2'b00;endelsebegin //第三象限phi_pre_r <= phi - ANGLE_N90;quadrant_flag_r <= 2'b11;endend/****************************************************/assign phi_pre = phi_pre_r;assign quadrant_flag = quadrant_flag_r;/****************************************************/endmodule我的设计要求精度较⾼,所以采⽤20次旋转,旋转过程的代码如下:/****************************************************/module Cordic_Rotate(clk,rst_n,phi_pre,quadrant_flag,ret_x,ret_y,quadrant);/****************************************************/input clk;input rst_n;input signed [23:0] phi_pre;input [1:0] quadrant_flag;output signed [16:0] ret_x;output signed [16:0] ret_y;output [1:0] quadrant;/****************************************************/parameter X_ORIGN = 17'sd32768; //旋转时x的起始⼤⼩,根据精度要求⽽定。
基于FPGA的Cordic算法实现的设计与验证
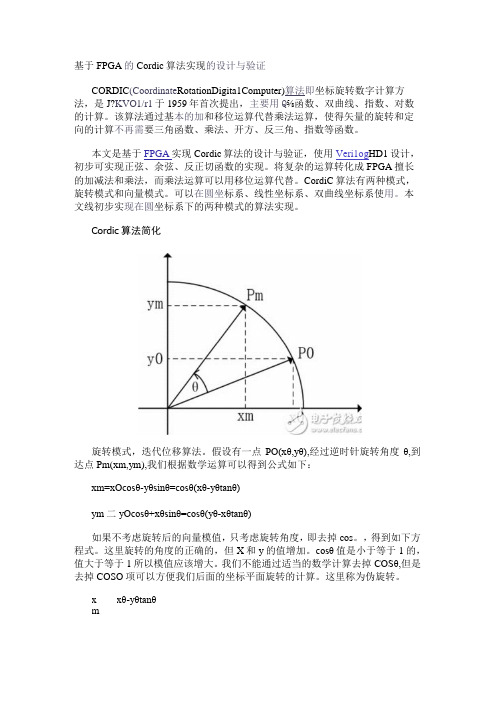
基于FPGA的Cordic算法实现的设计与验证CORDIC(Coordinate RotationDigita1Computer)算法即坐标旋转数字计算方法,是J?KVO1/r1于1959年首次提出,主要用Q⅝函数、双曲线、指数、对数的计算。
该算法通过基本的加和移位运算代替乘法运算,使得矢量的旋转和定向的计算不再需要三角函数、乘法、开方、反三角、指数等函数。
本文是基于FPGA实现Cordic算法的设计与验证,使用Veri1og HD1设计,初步可实现正弦、余弦、反正切函数的实现。
将复杂的运算转化成FPGA擅长的加减法和乘法,而乘法运算可以用移位运算代替。
CordiC算法有两种模式,旋转模式和向量模式。
可以在圆坐标系、线性坐标系、双曲线坐标系使用。
本文线初步实现在圆坐标系下的两种模式的算法实现。
Cordic算法简化旋转模式,迭代位移算法。
假设有一点PO(xθ,yθ),经过逆时针旋转角度θ,到达点Pm(xm,ym),我们根据数学运算可以得到公式如下:xm=xOcosθ-yθsinθ=cosθ(xθ-yθtanθ)ym二yOcosθ+xθsinθ=cosθ(yθ-xθtanθ)如果不考虑旋转后的向量模值,只考虑旋转角度,即去掉cos。
,得到如下方程式。
这里旋转的角度的正确的,但X和y的值增加。
cosθ值是小于等于1的,值大于等于1所以模值应该增大。
我们不能通过适当的数学计算去掉COSθ,但是去掉COSO项可以方便我们后面的坐标平面旋转的计算。
这里称为伪旋转。
xθ-yθtanθxmym-yθ-xθtanθCordic的方法核心就是伪旋转,将旋转角θ细化成若干个大小固定的角度θi,规定满足tanBi=2^-i,通过一系列的迭代旋转,每次旋转θi,i为迭代次数,规定ΣBi的范围即旋转角度θ的范围为[-99.7,99.7]。
如果θ的大于这个范围则可通过三角运算操作转化到该范围的角度。
我们通过事先将所有每次旋转的角度计算出来,由于每次旋转的角度是固定的,所以经过i次旋转的EOi可能会超过O,所以就必须设置一个方向值di,如果旋转角度之和己经小于θ,则di为1下次旋转继续为顺时针旋转,如果旋转角度之和大于。
基于流水线结构的cordic算法的实现

基于流水线结构的cordic算法的实现摘要系统在处理数据的时候,一个指令周期含有多个时钟脉冲,每个脉冲周期由不同的部件完成不同的操作。
非流水线结构是指一个指令周期完成以后再接受下一条处理数据的指令;而流水线结构,每个时钟脉冲都接受下一条处理数据的指令,只是不同的部件做不同的事情,就象生产线流水操作一样,并不是等一个或一批产品做完,再接受下一批生产命令,而是每个工序完成以后,立即接受下一批生产任务。
这样提高了系统处理数据的速度。
随着超大规模集成电路(Very Large Scale Integrated circuits , VLSI)技术的飞速发展,经常需要用硬件快速和精确地进行三角函数值的计算,而坐标旋转算法(Coordinate Rotational Digital Computer, CORDIC)能够将多种难以用硬件电路直接实现的复杂的三角函数运算分解为统一的加减、移位操作,极大地降低了硬件设计的复杂性。
在现代信号处理中,经常会遇到三角函数、超越函数和坐标转化等问题。
传统的实现方法有查找表多项式展开等方法,但是这些方法在精度、速度、简单性和效率方面往往不能兼顾。
CORDIC 算法则可以很好地兼顾这几方面的要求。
CORDIC算法只使用移位和加减运算,硬件实现简单。
使用流水线结构,每级CORDIC使用独立的单元,这样使运算速度非常快。
当流水线填满之后,每个时钟周期就会得到一个结果。
从CORDIC算法的基本原理出发,讨论其工作过程以及旋转角的覆盖范围,在此基础上,给出具有流水线结构的FPGA实现方法以及增益因子的大小与流水线级数的确定关系,给出了verilog实现算法,在Quartus6.0调试与仿真,验证采用FPGA实现的CORDIC算法的有效性。
关键词: CORDIC 算法 旋转 迭代 verilog 语言 流水线一、 CORDIC 算法原理CORDIC ,即坐标旋转算法(Coordinate Rotations Digital Computr ),是由Voider J 等人于1959 年在设计美国航空导航控制系统的过程中提出来的算法。
cordic算法实现

CORDIC 的算法实现CORDIC 运算就是执行一个平面旋转,如下图所示,就是从一个向量转换到另一个向量.向量(Xi,Yi)的平面旋转用矩阵表示为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡i i j j Y X Y X θθθθcos sin sin cos (1)旋转角度可以通过迭代运算分为多步执行,每一步完成旋转的一部分.单步表述为:⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡++n n n n n n n n Y X Y X θθθθcos sin sin cos 11(2)方程(2)提取COS 后变成⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡++n n n n n n n Y X Y X 1tan tan 1cos 11θθθ (3)方程(3)相比于(2)的4次相乘只需要3次,另外乘法可以通过选择如TANGEN 表示为2的次方的角度来消除乘法运算.2的次方的乘法或者除法运算可以用简单的移位来实现. 每一步的角度表示为⎪⎭⎫⎝⎛=n n 21arctan θ (4)旋转的角度:∑∞==0n nn S θθ(5)其中{}1;1+-=n S(6) n θtan 表示为n n n S -=2tan θ(7)结合(3)和(7)得到⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡--++n n nn n n n n n Y X S S Y X 1221cos 11θ (8)削去n θcos 系数,这一运算被简化成少量简单的移位和加法来实现.系数通过预先计算来消YX(Xj, Yj)(Xi, Yi)θ除. 第一步,重建系数 ⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=n n 21arctan cos cos θ (9)第二步,计算方程(9),得所有的’n ’,记为K607253.021arctan cos 10≈⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛==∏∞=n n P K (10)K 是一个常数(给初始向量以及旋转角度的所有值),是一个非离散的常数,派生参数P 的定义也是因为需要经常使用. 用公式表示确却的计算:()()⎩⎨⎧+=-=θθθθsin cos sin cos i i ji i j X Y K Y Y X K X (11)代入K,方程(8)变成⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡--++n n n n n n n n Y X S S Y X 122111 (12)或者⎩⎨⎧+=-=-+-+nnn n n nn n n n X S Y Y Y S X X 212122 (13)此时引入一个新的变量’Z ’,表示未旋转的角度∑=+-=ni i n Z 01θθ(14)Sn 表示Zn 的符号⎩⎨⎧≥+<-=0101n n n Z if Z if S (15)结合(5),(15)可以减少未旋转的角度到0,用伪代码表示为 For n=0 to [inf] If (Z(n) >= 0) then Z(n + 1) := Z(n) – atan(1/2^n); Else Z(n + 1) := Z(n) + atan(1/2^n); End if; End for;Arctan(1/2^i)是一个预先计算好的值,形成一个查找表的形式,[inf]为需要的迭代次数,每一位需要1次(16轮的迭代将产生16位的结果),如果加入X,Y 的计算,用伪代码的表示如下: For n=0 to [inf] If (Z(n) >= 0) then X(n + 1) := X(n) – (Yn/2^n);Y(n + 1) := Y(n) + (Xn/2^n); Z(n + 1) := Z(n) – atan(1/2^n); Else X(n + 1) := X(n) + (Yn/2^n); Y(n + 1) := Y(n) – (Xn/2^n); Z(n + 1) := Z(n) + atan(1/2^n); End if; End for;使Z 趋向于0,[]()()()()()()[]0,sin cos ,sin cos ,,i i i i i i i i j j jZ X Z Y P Z Y Z X P Z Y X+-=存在一种特殊情况:60725.01≈==K PX i 0=i Y θ=i Z[][]0,sin ,cos ,,θθ=j j jZ Y X另一个就是使Y 趋向于0[]⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++=i i i i i j j j X Y Z Y X P Z Y Xarctan ,0,,,22 这存在两种特殊的情况:1)X X i = Y Y i = 0=i Z[]⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=i ii i jj jX Y Y X P Z Y Xarctan ,0,,,22 2)1=i X a Y i = 0=i Z[]()[]a a P Z Y Xj j jarctan ,0,1,,2+=由上面的分析,来讨论SINE,COSINE 的实现.用上面提到的第一种假设[]()()()()()()[]0,sin cos ,sin cos ,,i i i i i i i i j j jZ X Z Y P Z Y Z X P Z Y X+-=使用以下值作为输入60725.06467.111≈==P X i 0=i Y θ=i Z=>[][]0,sin ,cos ,,θθ=j j jZ Y XZ 的值从-180DEG 到+180DEG ,可以将角度表示为0x8000 = –180degrees 0xEFFF = +80degrees其他的输入输出数值范围都是在-1到+1, )(4)(19898215hex DBA dec P Xi ==∙=举例如下: 计算30DEG 的SINE,COSINE:)(1555)(5461303602deg 303602deg 12deg 360161616hex dec =≈∙≡≡≡那么CORDIC 运算就是要计算Z=X ”1555”,的SINE,COSINE.Sin : 16380(dec) = 3FFC(hex) Cos : 28381(dec) = 6EDD(hex)输出范围在-1到+1,可以通过以下计算来得到:4999.01638020.1163800.121515=∙≡≡ 8661.0283812.1283810.121515=∙≡≡ 所以,30度的SINE 值是0.4999,COSINE 值是0.8661,相比于理论值,存在很小的误差.在提供的代码中Ain 就是量化后的角度输入,而输出则是量化后的SINE,COSINE 输出,量化的计算采用上面提供的方法.。
基于VHDL语言的CRC信道编解码电路设计与实现

0 引言
衡量数字通信系统的一个重要指标是误码率,它关系到 通信系统的通信质量,低的误码率就意味着很好的通信质 量。因此,如何降低误码率一直是通信系统设计首先要考虑 的头等大事。通信过程中产生的误码原因主要是由于传输过 程中信道的变化及噪声加入的结果,因此可以在信号传输前 进行信道编码,增加信号的冗余度;在接收端进行纠错检错 减少噪声的影响,从而尽可能的恢复原始信号,达到减少误 码的目的。循环冗余校验码(CRC)就是具有这种强检错功 能的技术,由于它的高效率、高性能,实现起来相对简单, 在 LAN、MODEM 等数字信息传送技术和 ARJ、PKZIP 等数据压 缩和解压缩技术中,CRC 被广泛采用作为检验手段,效果显 著。其中具有 16 个冗余比特的 CRC 编码进入了多个国际通 信标准。研究 CRC 码的实现具有实际意义。
1 CRC 码的原理
一个由若干个“0”或“1”组成 n 位二进制数可以表示 成为( n -1)阶的多项式的各项系数,也就是说,一个 n 位二 进制数可以用( n -1)阶多项式表示。一个8位二进制数可以用
一个7阶二进制码多项式表示[1],例如11000001 可表示为: B ( X) = 1 X7 + 1 X6 + 0 X5 + 0 X4+ 0 X 3+ 0 X 2 + 0 X1+ 1 X 0=
始信息位后添 r 个0后的数据除以生成多项式对应的二进制 数,所得余数即是校验位。
2.2 解码电路的设计思想 一个合法的CRC码的多项式,它应该能被 G(X ) 整除。据
此,现对一个位长为 n 的数据段(可能不是一合法CRC码), 其多项式除以 G(X ) ,若其余数为零,说明该码字是合法的,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LIBRARY ieee;
USE ieee.std_logic_1164.all;
USE ieee.std_logic_arith.all;
USE ieee.STD_LOGIC_UNSIGNED.all;
ENTITY cordicCOS_SIN IS
PORT
(
clk :IN std_logic;
deg_in :IN std_logic_vector (13 downto 0);
cos :OUT std_logic_vector(15 downto 0);
sin :OUT std_logic_vector(15 downto 0)
);
END cordicCOS_SIN;
architecture rlt_cordicCOS_SIN of cordicCOS_SIN is
constant c1:std_logic_vector(13 downto 0):=CONV_STD_LOGIC_VECTOR(4096,14); constant c2:std_logic_vector(13 downto 0):=CONV_STD_LOGIC_VECTOR(2048,14); constant c3:std_logic_vector(13 downto 0):=CONV_STD_LOGIC_VECTOR(1209,14); --arctan(1/2)
constant c4:std_logic_vector(13 downto 0):=CONV_STD_LOGIC_VECTOR(639,14); --arctan(1/4)
--constant x0:std_logic_vector(15 downto 0):=CONV_STD_LOGIC_VECTOR(19895,16); signal x0 :std_logic_vector(15 downto 0);
signal y1,x1 :std_logic_vector(15 downto 0);
signal y2,x2 :std_logic_vector(15 downto 0);
signal y3,x3 :std_logic_vector(17 downto 0);
signal y4,x4 :std_logic_vector(19 downto 0);
signal p1,p2,p3,p4 :std_logic_vector(13 downto 0);
begin
x0 <= conv_std_logic_vector(26980,16);
---------------------------------step 1------------------------------------ process(clk)
begin
if rising_edge(clk) then
if deg_in(13) ='1' then
y1 <= x"0000" -x0;
else
y1 <= x0;
end if;
end if;
end process;
process(clk)
begin
if rising_edge(clk) then
x1 <=(others =>'0');
end if;
end process;
process(clk)
begin
if rising_edge(clk) then
if deg_in(13) ='1' then
p1 <= deg_in + c1;
else
p1 <= deg_in - c1;
end if;
end if;
end process;
---------------------------------step 2------------------------------------ process(clk)
begin
if rising_edge(clk) then
if p1(13) ='1' then
y2 <= y1 - x1;
else
y2 <= y1 + x1;
end if;
end if;
end process;
process(clk)
begin
if rising_edge(clk) then
if p1(13) ='1' then
x2 <= x1 + y1;
else
x2 <= x1 - y1;
end if;
end if;
end process;
process(clk)
begin
if rising_edge(clk) then
if p1(13) ='1' then
p2 <= p1 + c2;
else
p2 <= p1 - c2;
end if;
end if;
end process;
---------------------------------step 3------------------------------------ process(clk)
begin
if rising_edge(clk) then
if p2(13) ='1' then
y3 <= (y2(15) & y2 &'0') -(x2(15) & x2(15) & x2);
else
y3 <= (y2(15) & y2 &'0') + (x2(15) & x2(15) & x2);
end if;
end if;
end process;
process(clk)
begin
if rising_edge(clk) then
if p2(13) ='1' then
x3 <= (x2(15) & x2 & '0') + (y2(15) & y2(15) & y2 );
else
x3 <= (x2(15) & x2 & '0') - (y2(15) & y2(15) & y2 );
end if;
end if;
end process;
process(clk)
begin
if rising_edge(clk) then
if p2(13) ='1' then
p3 <= p2 + c3;
else
p3 <= p2 - c3;
end if;
end if;
end process;
---------------------------------step 4------------------------------------ process(clk)
begin
if rising_edge(clk) then
if p3(13) ='1' then
y4 <= (y3 & "00") -(x3(17) & x3(17) & x3);
else
y4 <= (y3 & "00") +(x3(17) & x3(17) & x3);
end if;
end if;
end process;
process(clk)
begin
if rising_edge(clk) then
if p3(13) ='1' then
x4 <= (x3 & "00") + (y3(17) & y3(17) & y3 );
else
x4 <= (x3 & "00") - (y3(17) & y3(17) & y3 );
end if;
end if;
end process;
process(clk)
begin
if rising_edge(clk) then
if p3(13) ='1' then
p4 <= p3 + c4;
else
p4 <= p3 - c4;
end if;
end if;
end process;
cos<=x4(19 downto 4);
sin<=y4(19 downto 4);
end rlt_cordicCOS_SIN;。
