全排列生成算法-递增进位制数-递减进位制数

合集下载

全排列的几种算法

全排列的⼏种算法全排列，我们⾼中时就学过，数学上很简单，可是⽤计算机的算法实现还是有点味道的，今天我将我碰到的⼏种算法如数奉上，欢迎交流！第⼀种：递归最常见的也是最好理解的⽅法：简单点：⽐如"a" ,"b","c"全排列，可以看做事"a" +"b","c"的全排列及"b"+ "a","c"的全排列及"c" + "a","b"的全排列也就是说，遍历原数组中的每个元素，让剩余的元素全排列，这样就找到规律了。

代码如下：public static void main(String[] args) {char buf[]={'a','b','c','d'};perm(buf,0,buf.length-1);}public static void perm(char[] buf,int start,int end){if(start==end){//当只要求对数组中⼀个字母进⾏全排列时，只要就按该数组输出即可（特殊情况）for(int i=0;i<=end;i++){System.out.print(buf[i]);}System.out.println();}else{//多个字母全排列（普遍情况）for(int i=start;i<=end;i++){//（让指针start分别指向每⼀个数）char temp=buf[start];//交换数组第⼀个元素与后续的元素buf[start]=buf[i];buf[i]=temp;perm(buf,start+1,end);//后续元素递归全排列temp=buf[start];//将交换后的数组还原buf[start]=buf[i];buf[i]=temp;}}}第⼆中⽅法：也是递归，但是和第⼀种有所区别，算法：将数据分为两部分，递归将数据从左侧移右侧实现全排列⽐较抽象，如list abcd，遍历每⼀个数，将每个数放到⼀个新的list中,并将该元素从原list删除，然后将剩下的元素继续遍历每个元素继续放到新的list ⾥，这样，当list的长度为原list长度，或者原list长度为0时打印结果！下⾯是简单的⽰意图：// abcd//bcd a//cd ab//d abc//abcd//c abd//abdc//bd ac//d acb//acbd//b acd//acdb//bc ad ...//acd b ...//abd c ...//abc d ...源代码如下：private static void sort(List datas, List target) {//System.out.println("size="+datas.size());if (datas.size()==0) {for (Object obj : target)System.out.print(obj+" ");System.out.print(" ");return;}for (int i = 0; i < datas.size(); i++) {List newDatas = new ArrayList(datas);List newTarget = new ArrayList(target);newTarget.add(newDatas.get(i));newDatas.remove(i);sort(newDatas, newTarget);}}public static void main(String[] args) {List list = new ArrayList();for(int i=0;i<5;i++){list.add(i+1);}sort(list, new ArrayList());}第三种⽅法：⾮递归直接上代码：public static void main(String[] args) {int[] arr = new int[]{1,2,3,4,5,6};for(int i :arr){System.out.print(i + " ");}System.out.println();int totalnum = 1;while(NextNumber(arr,arr.length)){for(int i :arr){System.out.print(i + " ");}System.out.println();totalnum ++;}System.out.println("Total Num: " + totalnum);}private static Boolean NextNumber(int[] arr, int n){//数组最后⼀个元素位置int lastIndex = n-1;//从右向左确定第⼀个数字（前⾯的数字⽐它⼩）int firstIndex = lastIndex;for(;arr[firstIndex-1]>arr[firstIndex];firstIndex--){if(firstIndex == 1){//已经轮询完毕,此数已经是最⼤的那个数return false;}}//从右向左确定⼀个交换数（此数⽐arr[firstIndex]⼩且⽐arr[firstIndex-1]⼤）int swapIndex = lastIndex;for(;swapIndex > firstIndex;swapIndex--){if(arr[swapIndex] < arr[firstIndex] && arr[swapIndex] > arr[firstIndex-1]){break;}}//交换数字swap(arr,firstIndex-1,swapIndex);//将firstIndex右边的数字排序for(;firstIndex < lastIndex;firstIndex++,lastIndex--){if(arr[firstIndex] > arr[lastIndex]){swap(arr,firstIndex,lastIndex);}}return true;}private static void swap(int[] arr,int i, int j){int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}如果此⽂对你有帮助，请留个⾔，新⼈需要打架的⽀持和⿎励！。

排列组合公式及排列组合算法 ( 2 0 2 0 )

秒杀排列组合（上）————排列篇首先为什么要写排列组合？因为排列组合在数学中占有重要的地位，其与概率论也有密切关系；并且排列组合问题在求职的笔试，面试出现的概率特别高，而我在网上又没有搜到比较全面题型的文章；同时，我觉得编写排列组合程序对学习递归也是很有帮助的；当然，最重要的原因是排列组合本身就很有趣！所以就总结下排列组合的各种问法，分两篇写：上篇写排列，下篇写组合。

首先从各【导师实操追-女孩教-学】大IT公司的题中总结出排列组合的对象都是整形数组或字符数组，排列问题可以按输入数据分为两大类：输入数据【扣扣】有重复和无重复，又可以按输出数据分为两大类：输出数据有【⒈】重复和无重复；而排列问题也偶尔会考非递归。

首先提一【０】下全排列的几种算法：1—【１】—字典序法2——递增进位数制法; 3——递减进位数制法【б】4——邻位交换法5——n进制数法6——递归生成法7——循【⒐】环移位法8——回溯法由于侧【５】重点在输入数据无重复，所以先看输入数据无重复类型：其中又【２】可以分为全排列和分组后排列：首先写基【６】本的全排列：1.输出数组a的全排列(不可重复取)如a={1,2,3}。

输出123，132，213，231，312，321这个是最基本，也是最经典的排列算法思想：可以输出1加上23的全排列，2加13的全排列，3加上12的全排列，运用递归求比如23的全排列.依次递归下去；比如现在要2开头求全排，首先要交换1，2的位置，让a[0]变为2，在用递归求13的所有全排列，前面加个2就是2开头的所有全排列了，最后运用回溯再把1，2调换回来。

代码清单：public class PaiLie {public void runPermutation(int[] a){getAllPermutation(a, 0);-*index用于控制如上述分析中2加上13的所有全列的*-public void getAllPermutation(int[] a,int index){-*与a的元素个数相同则输出*-if(index == a.length-1){for(int i = 0; i a.length; i++){System.out.print(a[i] + " ");System.out.println();return;for(int i = index; i a.length; i++){swap(a ,index, i);getAllPermutation(a, index+1);swap(a ,index, i);public void swap(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;public static void main(String[] args) {PaiLie robot = new PaiLie();int[] a = {1,2,3};robot.runPermutation(a);2.输出数组a的全排列(可重复取)如a={1,2}。

全排列生成算法

全排列的生成算法对于给左的字符集，用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。

字典序法按照字典序求下一个排列的算法广例字符集{1,2,3},较小的数字较先,这样按字典序生成的全排列是：123,132,213,231,312,321o注意一个全排列可看做一个字符串，字符串可有前缀、后缀/生成给泄全排列的下一个排列所谓一个全排列的下一个排列就是这一个排列与下一个排列之间没有其他的排列。

这就要求这一个排列与下一个排列有尽可能长的共同前缀，也即变化限制在尽可能短的后缀上。

广例839647521是1—9的排列。

1—9的排列最前而的是123456789,最后而的是987654321,从右向左扫描若都是增的，就到了987654321,也就没有下一个了。

否则找出第一次出现下降的位置。

算法：由P1P2...Pn生成的下一个排列的算法如下：1求j=max{j| Pj-I<pj}2.求|=max{k| Pi-1<Pk }3.交换Pi-1与PI得到P1P2...PI-1 （P i....Pn ）,将红色部分顺序逆转，得到结果.例求839647521的下一个排列1.确定i,从左到右两两比较找出后一个数比前一个大的组合，在这里有39 47,然后i 取这些组中最到的位宜号（不是最大的数）在这两组数中7的位置号最大为6,所以i=62.确立I.找岀在i （包括i）后面的所有比i前面那一位大的数的最大的位置号，在此例中7, 5都满足要求，则选5, 5的位置号为7,所以1=73.先将4和5交换，然后将5后的四位数倒转得到结果8396574213 839651247以上算法是在数论课上老师给岀的关于字典序全排列的生成算法，以前也经常要用到全排列生成算法来生成一个全排列对所有的情况进行测试，每次都是现到网上找一个算法，然后直接copy代码，修改一下和自己的程序兼容就行了，也不看是怎么来的，不是我不想看，实在是说的很抽象，那一大堆公式来吓人，一个实例都不给，更有甚者连算法都没有，只是在那里说，想看都看不懂，也没那个耐心取理解那些人写出来的那种让人无法忍受的解释。

全排列的生成算法

全排列的生成算法全排列的生成算法就是对于给定的字符集，用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。

任何n 个字符集的排列都可以与1～n的n个数字的排列一一对应，因此在此就以n个数字的排列为例说明排列的生成法。

n个字符的全体排列之间存在一个确定的线性顺序关系。

所有的排列中除最后一个排列外，都有一个后继；除第一个排列外，都有一个前驱。

每个排列的后继都可以从它的前驱经过最少的变化而得到，全排列的生成算法就是从第一个排列开始逐个生成所有的排列的方法。

全排列的生成法通常有以下几种：字典序法递增进位数制法递减进位数制法邻位交换法递归类算法1.字典序法字典序法中，对于数字1、2、3......n的排列，不同排列的先后关系是从左到右逐个比较对应的数字的先后来决定的。

例如对于5个数字的排列12354和12345，排列12345在前，排列12354在后。

按照这样的规定，5个数字的所有的排列中最前面的是12345，最后面的是54321。

字典序算法如下：设P是1～n的一个全排列:p=p1p2......pn=p1p2......pj-1pjpj+1......pk-1pkpk+1......pn1）从排列的右端开始，找出第一个比右边数字小的数字的序号j（j从左端开始计算），即j=max{i|pi<pi+1}2）在pj的右边的数字中，找出所有比pj大的数中最小的数字pk，即 k=max{i|pi>pj}（右边的数从右至左是递增的，因此k是所有大于pj的数字中序号最大者）3）对换pi，pk4）再将pj+1......pk-1pkpk+1pn倒转得到排列p’’=p1p2.....pj-1pjpn.....pk+1pkpk-1.....pj+1，这就是排列p的下一个下一个排列。

例如839647521是数字1～9的一个排列。

从它生成下一个排列的步骤如下：自右至左找出排列中第一个比右边数字小的数字4 839647521在该数字后的数字中找出比4大的数中最小的一个5 839647521将5与4交换 839657421将7421倒转 839651247所以839647521的下一个排列是839651247。

A43计算公式

从四个元素中选三个元素的排列数为:A43=4×3×2=24。

从四个元素中选三个元素的组合数为:C43=4×3×2/(3×2×1)=4。

从n个不同元素中任取m（m≤n）个元素，按照一定的顺序排列起来，叫做从n个不同元素中取出m个元素的一个排列。

当m=n时所有的排列情况叫全排列。

公式：全排列数f(n)=n!(定义0!=1)
以下介绍全排列算法四种：
1、字典序法
2、递增进位制数法
3、递减进位制数法
4、邻位对换法
用具体的例子来理解上面的定义：4种颜色按不同颜色，进行排列，有多少种排列方法，如果是6种颜色呢。

从6种颜色中取出4种进行排列呢。

解：
A(4,4)=4x(4-1)x(4-2)x(4-3)x(4-4+1)=4x1x2x3x1=24。

A(6,6)=6x5x4x3x2x1=720。

A(6,4)=6!/(6-4)!=(6x5x4x3x2x1)/2=360。

组合数学：1-2 排列组合的生成

对上述过程，一般地，对于i，将前一步所得的每一排列重复 i 次，然后将 i 由第一排的最后往前移，至最前列，正好走了 i 次,下一个接着将 i 放在下一排列的最前面，然后依次往后移，一直下去即得 i 元排列。下面我们用较正式的语言来说这件事。
对给定的一个整数k，我们赋其一个方向，即在其上写一个箭头（指向左侧或右侧）
1.2 排列组合生成算法
1. 全排列的生成算法 2. 组合的生成算法
3. 一般排列的生成算法
1. 全排列的生成算法
全排列的生成算法就是对于给定的字符集，用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。
这里介绍4种全排列算法： (A) 直接生成法 (B) 序数法 (C) 字典序法 (D) 换位法
n的p进制表示： n a i p i , 0 a i p
i 1
i 1 k
我们来看另一种表示
n!=((n-1)+1)(n-1)!=(n-1)(n-1)!+(n-1)!, (n-1)!=(n-2)(n-2)!+(n-2)!, …, 故 n!= (n-1)(n-1)!+ (n-2)(n-2)!+…+2×2!+2!
3. 一般排列的生成算法
n中取r的排列生成可以由组合生成和全排列生成结合而得到。
839647521的下一个为839651247。
一般而言，设P是[1,n]的一个全排列。
P=P1P2…Pn=P1P2…Pj-1PjPj+1…Pk-1PkPk+1…Pn
(1) 找出 j=max{ i |Pi<Pi+1}，k=max{ i |Pi>Pj}； (2) 对换 Pj，Pk； (3) 将 Pj+1…Pk-1PjPk+1…Pn翻转， P1P2…Pj-1PkPn…Pk+1PjPk-1…Pj+1即是P的下一个。该算法的优点是排列清晰，而且保持着字典序。缺点是算法较繁琐。

组合数学第一章排列组合5全排列的生成算法合

1.5.2字典序法
[例] 求839647521的下一个排列
找出比右边数字小的标号最大的数4
8397655 72124124517
44><＜2157
大小为于于后44的的缀用用橙绿色色表表示示
在找接后出上即缀其前87中后3缀59比2将861缀4344中此97大、变65找后52的1得5出为缀的标到比对翻7下号84换转一3大2最916个的大5。1数的24数77 5
1.5.2字典序法
对给定的字符集中的字符规定了一个先后关系，在此基础上规定两个全排列的先后是从左到右逐个比较对应的字符的先后。
1.5.2字典序法
[例]字符集{1,2,3},较小的数字较先,这样按字典序生成的全排列是: 123,132,213,231,312,321。
※※ 一个全排列可看做一个字符串，字
规则：令n个元素为1，2,…,n. p p1 p2 pn 是这n个数的任意一个排列，我们可以找到一个序列和它对应，其中ai 可以看作是排列P中数i+1所在位置右边比i+1小的数的个数。
例排列3214，它是元素1，2，3，4的一个排列, 它对应的序列是什么？
例序列311对应的排列是什么？
练习
求839763ห้องสมุดไป่ตู้421的下一个排列
1.5.3邻位对换法
序数法和字典排序法，求下一个排列在不进位的情况下很容易。这就启发我们，能不能设计一种算法，下一个排列总是上一个排列某相邻两位对换得到的。
活动状态
以1←2←3←4←为初始排列，箭头所指一侧，相邻的数比它小时，则称该数组处在活动状态， 1 2 3←4←的←2←，3，4都处于的活动状态。
符串可有前缀、后缀。

全排列生成算法的分析

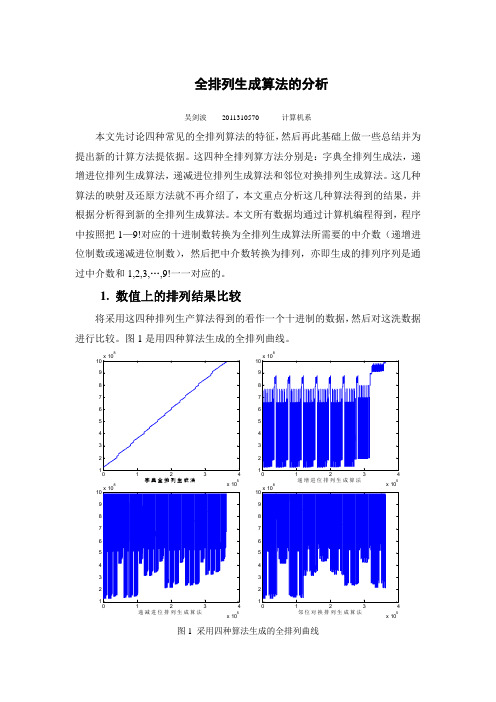
只有三个[0,1,7]。
x 105 2
x 105 2
1.5
1.5
1
1
0.5
0.5
0 0 x 105
4
2
4
6
字典全排列生成法
0
80
2
4
6
8
x 105递增进位排列生成算法
4
3
3
2
2
1
1
0
0
2
4
6
递减进位排列生成算法
0 8
2
4
6
8
邻位对换排列生成算法
图 3. 四种全排列算法生成的相邻排列之间相同的字符个数的直方图
从另一个角度来思考，把生成的排列全部当着一个字符串，然后来比较这些字符串有多少个位是不同的。比如排列"123456789"和"123456879"其中"78"两个字符的位置不一样，则认为它们有 2 个位是不同的。上面的每种算法计算的排列结果分别与上一次计算的排列结果比较，也就是将相邻的两个中介数生成的排列进行对比，看有多少个字符是不同的，这里可以反映出通过该算法得到的排列在字符上的变化的情况。
进行比较。图 1 是用四种算法生成的全排列曲线。
x 108 10
9 8 7 6 5 4 3 2 1
0
8
x 10 10
9 8 7 6 5 4 3 2 1
0
1
2
3
字典全排列生成法
1
2
3
递减进位排列生成算法
4
5
x 10
4
5
x 10
x 108 10
9 8 7 6 5 4 3 2 1

四种权威全排列生成算法

#include <iostream>#include <algorithm>#include <time.h>using namespace std; //全排列生成算法void SpecifiedPrum(int a[],int n,int m);//声明函数，为求给定排列后的某个排列void FullPerm(int a[],int n);//声明函数，为求所有全排列void Example();//程序例子void Zidian1_1(int a[],int n,int m);//声明函数，字典序(基于中介数)下求给定排列后的某个排列void Zidian1_2(int a[],int n);//声明函数，字典序(基于中介数)下求所有全排列void Zidian2_1(int a[],int n,int m);//声明函数，字典序(基于相邻排列特征)下求给定排列后的某个排列void Zidian2_2(int a[],int n);//声明函数，字典序(基于相邻排列特征)下求所有全排列void Dizeng1(int a[],int n,int m);//声明函数，递增进位制数法下求给定排列后的某个排列void Dizeng2(int a[],int n);//声明函数，递增进位制数法下求所有全排列void Dijian1(int a[],int n,int m);//声明函数，递减进位制数法下求给定排列后的某个排列void Dijian2(int a[],int n);//声明函数，递减进位制数法下求所有全排列void Linwei1(int a[],int n,int m);//声明函数，邻位对换法下求给定排列后的某个排列void Linwei2(int a[],int n);//声明函数，邻位对换法下求所有全排列int main(){int a[10];int p,n,m;while(1)//循环，可以多次输入请求{cout<<"请输入所需的算法模式序号："<<endl;cout<<"0.退出程序"<<endl;cout<<"1.求给定排列后的某个排列"<<endl;cout<<"2.求所有全排列"<<endl;cout<<"3.程序输入举例"<<endl;cout<<"请输入序号：";cin>>p;if(p==0)//退出循环，结束程序break;else if (p==1)//求给定排列后的某个排列，调用函数SpecifiedPrum();{cout<<"请输入排列中元素的个数：";cin>>n;cout<<"请输入想要求多少个之后的排列：";cin>>m;cout<<"请输入初始排列：";for(int i=n-1;i>=0;i--)//输入原排列cin>>a[i];cout<<"*****************************************************************************"<<endl;SpecifiedPrum(a,n,m);}else if(p==2)//求所有全排列，调用函数FullPerm();{cout<<"请输入排列的元素个数：";cin>>n;cout<<"******************************************************************** *********"<<endl;FullPerm(a,n);}else if(p==3)//例子Example();//程序例子elsecout<<"Wrong Input!"<<endl;cout<<"******************************************************************** *********"<<endl;}}void SpecifiedPrum(int a[],int n,int m)//求给定排列后的某个排列{Zidian1_1(a,n,m);Zidian2_1(a,n,m);Dizeng1(a,n,m);Dijian1(a, n,m);Linwei1(a,n,m);}void FullPerm(int a[],int n)//求给定排列后的某个排列{Zidian1_2(a,n);Zidian2_2(a,n);Dizeng2(a,n);Dijian2(a, n);Linwei2(a,n);}void Zidian1_1(int a[],int n,int m)//字典序(基于中介数)下求给定排列后的某个排列{int b[10];int d[10];int c[10]={1,2,3,4,5,6,7,8,9};//初始化c数组用于中介数还原int sign=0;//设置溢出标志为零for (int i=n-1;i>0;i--)//生成原排列的中介数{int temp=0;for (int j=i-1;j>=0;j--)if(a[i]>a[j])temp++;b[i-1]=temp;}while(m>0)//原中介数每次加一，循环m次，求新中介数；{for(int i=0;i<n-1;i++){if(b[i]<i+1){b[i]++; break;}elseb[i]=0;if(i==n-2)//中序数相加后溢出，设标志sign为1sign=1;}m--;}for (int i=n-2;i>=0;i--)//由新中介数还原得到所求新排列的1到n-1位{int s=b[i];for (int j=0;;j++){if(c[j]!=0)s--;if (s==-1){d[i+1]=c[j];c[j]=0;break; }}}for (int i=0;i<n;i++)//求出新排列最后一位的元素if(c[i]!=0){d[0]=c[i];break;}cout<<"字典序(基于中介数)：";if(sign==1)//溢出，提示不存在排列cout<<"Not Exist!"<<endl;else//打印出新排列{for (int i=n-1;i>=0;i-- )cout<<d[i]<<' ';cout<<endl;}cout<<endl;}void Zidian1_2(int a[],int n)//字典序(基于中介数)下求所有全排列{clock_t start=clock();int b[10];int m=1;cout<<"字典序(基于中介数)："<<endl;for(int i=0;i<n;i++)//输入原排列并计算全排列的总个数m{a[i]=n-i;m=m*a[i];cout<<i+1<<' ';}cout<<endl;for (int i=n-1;i>0;i--)//生成第一个排列的中介数{int temp=0;for (int j=i-1;j>=0;j--)if(a[i]>a[j])temp++;b[i-1]=temp;}while(m>1)//原中介数每次加一，循环m-1次，求得所有排列；{int c[10]={1,2,3,4,5,6,7,8,9};//初始化c数组用于中介数还原for(int i=0;i<n-1;i++)//中介数加一得新中介数{if(b[i]<i+1){b[i]++; break;}elseb[i]=0;}for (int i=n-2;i>=0;i--)//由新中介数还原得到所求新排列的1到n-1位{int s=b[i];for (int j=0;;j++){if(c[j]!=0)s--;if (s==-1){a[i+1]=c[j];c[j]=0;break; }}}for (int i=0;i<n;i++)//求出新排列最后一位的元素if(c[i]!=0){a[0]=c[i];break;}for (int i=n-1;i>=0;i-- )//打印出新排列cout<<a[i]<<' ';cout<<endl;m--;}clock_t end=clock();cout<<endl<< "Running Time: "<<static_cast<double>(end-start)/CLOCKS_PER_SEC*1000<<"ms"<<endl;//输出运行时间cout<<endl;}void Zidian2_1(int a[],int n,int m)//字典序(基于相邻排列特征)下求给定排列后的某个排列{int b[10];for (int i=0;i<n;i++)//用数列b[]代替a[]，以保证a[]不变b[i]=a[i];int sign=0;//设置溢出标志为零while(m>0)//求下一排列，循环m次，求的所需排列{int s;for(s=1;s<n;s++)//从头到左寻找第一次下降位置，位置用s记录，跳出for循环if (b[s]<b[s-1])break;if(s==n)//溢出，设sign为1，跳出while循环{ sign=1;break;}int t=s-1;while(b[t]>b[s])//找出后缀中比a[s]大的最小数，位置用t记录t--;t=t+1;swap(b[s],b[t]);//交换a[s]和a[t]的值for(int i=0;i<s/2;i++)swap(b[i],b[s-i-1]);//将后缀子序列反转m--;//m--循环}cout<<"字典序(基于相邻排列特征)：";if(sign==1)//溢出，提示不存在排列cout<<"Not Exist!"<<endl;else//打印出新排列{for (int i=n-1;i>=0;i-- )cout<<b[i]<<' ';cout<<endl;}cout<<endl;}void Zidian2_2(int a[],int n)//字典序(基于相邻排列特征)下求所有全排列{clock_t start=clock();int m=1;cout<<"字典序(基于相邻排列特征)："<<endl;for(int i=0;i<n;i++)//输入原排列并计算全排列的总个数m{a[i]=n-i;m=m*a[i];cout<<i+1<<' ';}cout<<endl;while(m>1)//求下一排列，循环m-1次，求的所有排列{int s;for(s=1;s<n;s++)//从头到左寻找第一次下降位置，位置用s记录，跳出for循环if (a[s]<a[s-1])break;int t=s-1;while(a[t]>a[s])//找出后缀中比a[s]大的最小数，位置用t记录t--;t=t+1;swap(a[s],a[t]);//交换a[s]和a[t]的值for(int i=0;i<s/2;i++)swap(a[i],a[s-i-1]);//将后缀子序列反转for (int i=n-1;i>=0;i-- )//打印出新排列cout<<a[i]<<' ';cout<<endl;m--;//m--循环}clock_t end=clock();cout<<endl<< "Running Time: "<<static_cast<double>(end-start)/CLOCKS_PER_SEC*1000<<"ms"<<endl;//输出运行时间cout<<endl;}void Dizeng1(int a[],int n,int m)//递增进位制数法下求给定排列后的某个排列{int b[10];int c[10]={1,1,1,1,1,1,1,1,1,1};//建立数列c[]，并将所有元素初始化为1，用来求新排列int sign=0;//设置溢出标志为零for (int i=n-1;i>=0;i--)//生成原排列的中介数{int temp=0;for(int j=i-1;j>=0&&a[i]!=1;j--)//记录某个数右边比它小的数的个数，存入temp if(a[j]<a[i])temp++;if(a[i]>=2)b[a[i]-2]=temp;//将temp存入数列b[]中相应的位置}while(m>0)//原中介数每次加一，循环m次，求新中介数；{for(int i=0;i<n-1;i++){if(b[i]<i+1){b[i]++; break;}elseb[i]=0;if(i==n-2)//中序数相加后溢出，设标志sign为1sign=1;}m--;//m减一再循环}for (int i=n-2;i>=0;i--)//根据新中介数求新排列{int temp=b[i];//用以统计从低位已经遍历的值为1的个数int s=0;//相应元素应填充的位置为swhile(temp>=0)//查找填充位置s{if(c[s++]==1)temp--;}s=s-1;//s自减一c[s]=i+2;//将元素填入s位置}cout<<"递增进位制数法：";if(sign==1)//溢出，提示不存在排列cout<<"Not Exist!"<<endl;else//打印出新排列{for (int i=n-1;i>=0;i-- )cout<<c[i]<<' ';cout<<endl;}cout<<endl;}void Dizeng2(int a[],int n)//声明函数，递增进位制数法下求所有全排列{int b[10];clock_t start=clock();int m=1;cout<<"递增进位制数法："<<endl;for(int i=0;i<n;i++)//输入原排列并计算全排列的总个数m{a[i]=n-i;m=m*a[i];cout<<i+1<<' ';}cout<<endl;for (int i=n-1;i>=0;i--)//生成第一个排列的中介数{int temp=0;for(int j=i-1;j>=0&&a[i]!=1;j--)//记录某个数右边比它小的数的个数，存入temp if(a[j]<a[i])temp++;if(a[i]>=2)b[a[i]-2]=temp;//将temp存入数列b[]中相应的位置}while(m>1)//原中介数每次加一，循环m-1次，求的所有排列；{int c[10]={1,1,1,1,1,1,1,1,1,1};//建立数列c[]，并将所有元素初始化为1，用来求新排列for(int i=0;i<n-1;i++)//中介数加一{if(b[i]<i+1){b[i]++; break;}elseb[i]=0;}for (int i=n-2;i>=0;i--)//根据新中介数求新排列{int temp=b[i];//用以统计从低位已经遍历的值为0的个数int s=0;//相应元素应填充的位置为swhile(temp>=0)//查找填充位置s{if(c[s++]==1)temp--;}s=s-1;//s自减一c[s]=i+2;//将元素填入s位置}for (int i=n-1;i>=0;i-- )//打印出新排列cout<<c[i]<<' ';cout<<endl;m--;//m减一再循环}clock_t end=clock();cout<<endl<< "Running Time: "<<static_cast<double>(end-start)/CLOCKS_PER_SEC*1000<<"ms"<<endl;//输出运行时间cout<<endl;}void Dijian1(int a[],int n,int m)//递减进位制数法下求给定排列后的某个排列{int b[10];int c[10]={1,1,1,1,1,1,1,1,1,1};//建立数列c[]，并将所有元素初始化为1，用来求新排列int sign=0;//设置溢出标志为零for (int i=n-1;i>=0;i--)//生成原排列的中介数{int temp=0;for(int j=i-1;j>=0&&a[i]!=1;j--)//记录某个数右边比它小的数的个数，存入temp if(a[j]<a[i])temp++;if(a[i]>=2)b[n-a[i]]=temp;//将temp存入数列b[]中相应的位置}while(m>0)//原中介数每次加一，循环m次，求新中介数；{for(int i=0;i<n-1;i++){if(b[i]<n-i-1){b[i]++; break;}elseb[i]=0;if(i==n-2)//中序数相加后溢出，设标志sign为1sign=1;}m--;//m减一再循环}for (int i=0;i<n-1;i++)//根据新中介数求新排列{int temp=b[i];//用以统计从低位已经遍历的值为1的个数int s=0;//相应元素应填充的位置为swhile(temp>=0)//查找填充位置s{if(c[s++]==1)temp--;}s=s-1;//s自减一c[s]=n-i;//将元素填入s位置}cout<<"递减进位制数法：";if(sign==1)//溢出，提示不存在排列cout<<"Not Exist!"<<endl;else//打印出新排列{for (int i=n-1;i>=0;i-- )cout<<c[i]<<' ';cout<<endl;}cout<<endl;}void Dijian2(int a[],int n)//递减进位制数法下求所有全排列{int b[10];clock_t start=clock();int m=1;cout<<"递减进位制数法："<<endl;for(int i=0;i<n;i++)//输入原排列并计算全排列的总个数m{a[i]=n-i;m=m*a[i];cout<<i+1<<' ';}cout<<endl;for (int i=n-1;i>=0;i--)//生成原排列的中介数{int temp=0;for(int j=i-1;j>=0&&a[i]!=1;j--)//记录某个数右边比它小的数的个数，存入temp if(a[j]<a[i])temp++;if(a[i]>=2)b[n-a[i]]=temp;//将temp存入数列b[]中相应的位置}while(m>1)//原中介数每次加一，循环m-1次，求的所有排列；{int c[10]={1,1,1,1,1,1,1,1,1,1};//建立数列c[]，并将所有元素初始化为1，用来求新排列for(int i=0;i<n-1;i++)//中介数加一{if(b[i]<n-i-1){b[i]++; break;}elseb[i]=0;}for (int i=0;i<n-1;i++)//根据新中介数求新排列{int temp=b[i];//用以统计从低位已经遍历的值为0的个数int s=0;//相应元素应填充的位置为swhile(temp>=0)//查找填充位置s{if(c[s++]==1)temp--;}s=s-1;//s自减一c[s]=n-i;//将元素填入s位置}for (int i=n-1;i>=0;i-- )cout<<c[i]<<' ';cout<<endl;m--;//m减一再循环}clock_t end=clock();cout<<endl<< "Running Time: "<<static_cast<double>(end-start)/CLOCKS_PER_SEC*1000<<"ms"<<endl;//输出运行时间cout<<endl;}void Linwei1(int a[],int n,int m)//邻位对换法下求给定排列后的某个排列{int b[10]={0};//建立数列b[]，并初始化所有元素为零，这样可以使求元素2时对应的中介数一般化，不用单独考虑int c[10]={1,1,1,1,1,1,1,1,1,1};//建立数列c[]，并将所有元素初始化为1，用来求新排列int sign=0;//设置溢出标志为零for (int i=2;i<=n;i++)//生成原排列的中介数{int s=0;while(a[s]!=i)//遍历a[]找出i的位置存于ss++;int temp;//方向指示数，奇右偶左if(i%2==0)//i为偶数temp=b[n-i+2]+b[n-i+1];else//i为奇数temp=b[n-i+1];int t=0;//背向i方向上，小于i的数的个数设为tif(temp%2==0)//指示数为偶数{for (int j=0;j<s;j++)//i右边比i小的数的个数if(a[j]<i)t++;}else//指示数为奇数{for (int j=n-1;j>s;j--)//i左边比i小的数的个数if(a[j]<i)t++;}b[n-i]=t;}while(m>0)//原中介数每次加一，循环m次，求新中介数；{for(int i=0;i<n-1;i++){if(b[i]<n-i-1){b[i]++; break;}elseb[i]=0;if(i==n-2)//中序数相加后溢出，设标志sign为1sign=1;}m--;//m减一再循环}for (int i=0;i<n-1;i++)//根据新中介数求新排列{int t;//方向指示数，奇右偶左if ((n-i)%2!=0)t=b[i+1];elset=b[i+1]+b[i+2];int temp=b[i];//用以统计从低位已经遍历的值为1的个数int s;//相应元素应填充的位置为sif(t%2==0)//t为偶，方向向左{s=0;//s为零while(temp>=0)//查找填充位置sif(c[s++]==1)temp--;s=s-1;//s自减一c[s]=n-i;//将元素填入s位置}else//方向向右{s=n-1;while(temp>=0)//查找填充位置sif(c[s--]==1)temp--;s=s+1;//s自减一c[s]=n-i;//将元素填入s位置}}cout<<"邻位对换法：";if(sign==1)//溢出，提示不存在排列cout<<"Not Exist!"<<endl;else//打印出新排列{for (int i=n-1;i>=0;i-- )cout<<c[i]<<' ';cout<<endl;}}void Linwei2(int a[],int n)//声明函数，邻位对换法下求所有全排列{int b[10]={0};//建立数列b[]，并初始化所有元素为零，这样可以使求元素2时对应的中介数一般化，不用单独考虑clock_t start=clock();int m=1;cout<<"邻位对换法："<<endl;for(int i=0;i<n;i++)//输入原排列并计算全排列的总个数m{a[i]=n-i;m=m*a[i];cout<<i+1<<' ';}cout<<endl;for (int i=2;i<=n;i++)//生成原排列的中介数{int s=0;while(a[s]!=i)//遍历a[]找出i的位置存于ss++;int temp;//方向指示数，奇右偶左if(i%2==0)//i为偶数temp=b[n-i+2]+b[n-i+1];else//i为奇数temp=b[n-i+1];int t=0;//背向i方向上，小于i的数的个数设为tif(temp%2==0)//指示数为偶数{for (int j=0;j<s;j++)//i右边比i小的数的个数if(a[j]<i)t++;}else//指示数为奇数{for (int j=n-1;j>s;j--)//i左边比i小的数的个数if(a[j]<i)t++;}b[n-i]=t;}while(m>1)//原中介数每次加一，循环m次，求的所有排列；{int c[10]={1,1,1,1,1,1,1,1,1,1};//建立数列c[]，并将所有元素初始化为1，用来求新排列for(int i=0;i<n-1;i++)//中介数加一{if(b[i]<n-i-1){b[i]++; break;}elseb[i]=0;}for (int i=0;i<n-1;i++)//根据新中介数求新排列{int t;//方向指示数，奇右偶左if ((n-i)%2!=0)t=b[i+1];elset=b[i+1]+b[i+2];int temp=b[i];//用以统计从低位已经遍历的值为1的个数int s;//相应元素应填充的位置为sif(t%2==0)//t为偶，方向向左{s=0;//s为零while(temp>=0)//查找填充位置sif(c[s++]==1)temp--;s=s-1;//s自减一c[s]=n-i;//将元素填入s位置}else//方向向右{s=n-1;while(temp>=0)//查找填充位置sif(c[s--]==1)temp--;s=s+1;//s自减一c[s]=n-i;//将元素填入s位置}}for (int i=n-1;i>=0;i-- )cout<<c[i]<<' ';cout<<endl;m--;//m减一再循环}clock_t end=clock();cout<<endl<< "Running Time: "<<static_cast<double>(end-start)/CLOCKS_PER_SEC*1000<<"ms"<<endl;//输出运行时间}void Example(){cout<<"*Example: "<<endl;cout<<"请输入所需的算法模式序号："<<endl;cout<<"0.退出程序"<<endl;cout<<"1.求给定排列后的某个排列"<<endl;cout<<"2.求所有全排列"<<endl;cout<<"3.程序输入举例"<<endl;cout<<"请输入序号：1"<<endl;cout<<"请输入排列中元素的个数：5"<<endl;cout<<"请输入想要求多少个之后的排列：100"<<endl;cout<<"请输入初始排列：1 2 3 4 5"<<endl;cout<<"******************************************************************** *********"<<endl;cout<<"字典序(基于中介数)：5 1 4 2 3"<<endl<<endl;cout<<"字典序(基于相邻排列特征)：5 1 4 2 3"<<endl<<endl;cout<<"递增进位制数法：5 3 1 2 4"<<endl<<endl;cout<<"递减进位制数法：3 2 1 4 5"<<endl<<endl;cout<<"邻位对换法：4 2 1 3 5"<<endl;}。

组合数学中的全排列生成算法完整版

组合数学全排列生成算法组合数学中的全排列深成算法历来是组合数学考试的重要考察点，因此在这里我简单的介绍一下6种全排列生成算法的详细过程，并借此比较它们之间的优劣之处。

不论是哪种全排列生成算法，都遵循着“原排列”→“原中介数”→“新中介数”→“新排列”的过程。

其中中介数依据算法的不同会的到递增进位制数和递减进位制数。

关于排列和中介数的一一对应性的证明我们不做讨论，这里仅仅给出了排列和中介数的详细映射方法。

相信熟练掌握了方法就可以顺利通过这部分的考察。

递增进位制和递减进位制数所谓递增进位制和递减进位制数字是指数字的进制随着数字位置的不同递增或递减。

通常我们见到的都是固定进制数字，如2进制，10进制等。

m位n进制数可以表示的数字是m*n个。

而m位递增或递减进位制数则可以表示数字m!个。

例如递增进位制数4121，它的进制从右向左依次是2、3、4、5。

即其最高位（就是数字4那位）最大值可能是4；第三高位最大可能是3；第二高位最大可能是2；最末位最大可能是1。

如果将4121加上1的话，会使最末位得到0，同时进位；第二位的2与进位相加，也会得到0，同时进位；第三位的1与进位相加得到2，不再进位。

最终得到结果是4200。

递减进位制的道理是一样的，只不过进制从右向左依次是9、8、7、6……，正好与递增进位制相反。

很明显，递减进位制的一个最大的好处就是加法不易进位，因为它在进行加法最频繁的末几位里（最右边）进制比较大。

接下来要了解的是递增进位制、递减进位制数和其序号的关系。

递增、递减进位制数可以被看作一个有序的数字集合。

如果规定递增进位制和递减进位制数的0的序号是十进制0，递增进位制数的987654321和递减进位制数的123456789对应十进制序号362880（即9!），则可以整理一套对应法则。

其中，递增进位制数（a1 a2 a3 a4 a5 a6 a7 a8 a9）为：a1*9! + a2*8! + ….+ a8*2! + a9*1! =序号例如序号100的递增进位制数就是4020，即4*4！+ 0*3！+ 2*2！+ 0*1！=100。

1.5 组合数学之全排列的生成算法

Yiqiang Wei <weiyiqiang@>
1.5.1字典序法
方法2-1：
由72642321推算出839647521 中介数右端加一个 0扩成0 9位，先定 1，每定 72642321中未出现，1在最右边一位，其左边未定位下加一点，从（位－位下点数=0）的位中选最左的。
=279905
Yiqiang Wei <weiyiqiang@>
1.5.2递增进位制数法由(anan-1…a2)↑求p1p2…pn。
从大到小求出n,n-1,…,2,1的位置 _ ... _ n _ _ …_
\______ ______/ V
an个空格 n的右边有an个空格。 n-1的右边有an-1个空格。 ………… 2的右边有a2个空格。最后一个空格就是1的位置。
83964752 1 726423210
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●
2 的位置 3 4 5 6 7 8 9 定 1
Yiqiang Wei <weiyiqiang@>
1.5.1字典序法
方法2-2：
由72642321推算出839647521 已定出上标‘●’，找左起第一个0，下标‘__’
※※ 两个字符串，相同前缀越长的越靠近。
Yiqiang Wei <weiyiqiang@>
1.5 全排列的生成算法
如何生成给定全排列的下一个排列所谓一个的下一个就是这一个与下一个之间没有其他的。这就要求这一个与下一个有尽可能长的共同前缀，也即变化限制在尽可能短的后缀上。例如 839647521是1--9的排列。1—9的排列最前面的是123456789，最后面的是987654321，从右向左扫描若都是增的，就到了987654321，也就没有下一个了。否则找出第一次出现下降的位置。

排列组合生成算法

《组合数学》第二讲排列组合生成算法1一. 排列生成算法z排列生成有几种典型算法, 这些算法都很有成效. 它们在实际中具有广泛应用价值.1.序数法2.字典序法3.邻位互换法(Johnson-Trotter)4.轮转法31. 序数法z序数法基于一一对应概念.z先在排列和一种特殊的序列之间建立一种一一对应关系, 然后再给出由序列产生排列的方法z因为序列的产生非常方便, 这样我们就可以得到一种利用序列来生成排列的方法.z如何建立这种一一对应?45z 思路类似数的10进制、2进制和p 进制表示.;90,1010≤≤=∑−=k m k k k a a n;10,210≤≤=∑−=k m k k k a a n.10,1−≤≤=∑−=p a p a n k m k kkz这相当于自然数与某种序列之间建立了一一对应关系.z可以利用置换来表示整数:n!=n(n-1)! =(n-1+1)(n-1)!= (n-1)(n-1)!+(n-1)!(n-1)!= (n-2)(n-2)!+(n-2)!n!= (n-1)(n-1)!+ (n-2)(n-2)!+ (n-3)(n-3)!+…+2•2!+1•1!+16z n!-1=(n-1) (n-1)!+(n-2) (n-2)!+(n-3) (n-3)!+ …+2•2!+1•1!z可以证明, 从0到n!-1之间的任何整数m 都可唯一地表示为:m=a n-1 (n-1)!+a n-2 (n-2)!+…+a2•2!+a1•1!其中0≤a≤i, i=1,2, …,n-1.iz m与序列(a n-1,a n-2 ,…a2,a1)一一对应z书中有确定这些系数的方法.z例如：10＝1⋅3!＋2⋅2!＋0⋅1!7z因为满足条件0≤a≤i, 1≤i≤n-1 （2.1）i的序列(a, a n-2, …, a2, a1)n-1共有n!个, 这恰好与0到n!-1的n!个整数一一对应.z需要建立满足条件(2.1)的n!个序列(a, a n-2, …, a2, a1)和n元集合S的n-1全部排列之间的一一对应关系.89z 还需要给出一种办法, 由每个满足条件(2.1)的序列(a n -1,a n -2, …,a 2,a 1)可生成唯一的一个排列.z 这样我们就可以产生出所有的排列. z 怎么样由一个满足条件(2.1)的序列产生一个n 阶排列?z 如何把1,2,…,n 的一个排列与一个满足条件(2.1)的序列建立起直接的关系?10z 行列式定义中有逆序数的概念, 就是一个排列中违反自然顺序的数对: 比如12354的逆序数为1, 而43215的逆序数为6.z 设p 1p 2…p n 是任意一个n 元排列, 则i +1后面比i +1小的数字的个数a i 总不超过i , 即a i ≤i , i =1,2,…,n -1.z 这样自然由一个排列得到一个序列(a n -1,a n -2,…,a 2,a 1), 而且满足条件(2.1).11z 我们可以如下建立序列与排列的对应:z 设序列(a n -1,a n -2, …,a 2,a 1)满足条件(2.1).则它所对应的排列为(p)=p 1p 2…p n , 其中a i 可以看作是排列(p)中数i +1所在位置后面比i +1小的数的个数.z 要说明这种对应的合理性, 必须清楚. 如何由序列产生出它所对应的排列.z 我们通过一个具体的例题说明思想方法.12例2.1(1) 4213→(301)4后面比4小的数的个数a 3=3; 3后面比3小的数的个数a 2=0; 2后面比2小的数的个数a 1=1.(2) (301) →4213由a 3=3知1,2,3都在4的后面; 由a 2=0知1,2都在3前面; 由a 1=1知1在2后面.(3) (4213)↔(a 3a 2a 1)=(301).2. 字典序法对给定的字符集中的字符规定了一个先后关系，在此基础上规定两个全排列的先后是从左到右逐个比较对应的字符的先后。

全排列算法——精选推荐

本文为原创，如需转载，请注明作者和出处，谢谢！全排列是将一组数按一定顺序进行排列，如果这组数有n个，那么全排列数为n!个。

现以{1, 2, 3, 4, 5}为例说明如何编写全排列的递归算法。

1、首先看最后两个数4, 5。

它们的全排列为4 5和5 4, 即以4开头的5的全排列和以5开头的4的全排列。

由于一个数的全排列就是其本身，从而得到以上结果。

2、再看后三个数3, 4, 5。

它们的全排列为3 4 5、3 5 4、 4 3 5、 4 53、 53 4、 54 3 六组数。

即以3开头的和4,5的全排列的组合、以4开头的和3,5的全排列的组合和以5开头的和3,4的全排列的组合.从而可以推断，设一组数p = {r1, r2, r3, ... ,rn}, 全排列为perm(p)，pn = p - {rn}。

因此perm(p) = r1perm(p1), r2perm(p2), r3perm(p3), ... , rnperm(pn)。

当n = 1时perm(p} = r1。

为了更容易理解，将整组数中的所有的数分别与第一个数交换，这样就总是在处理后n-1个数的全排列。

算法如下：#include <stdio.h>int n =0;void swap(int *a, int *b){int m;m = *a;*a = *b;*b = m;}void perm(int list[], int k, int m){int i;if(k > m){for(i =0; i <= m; i++) printf("%d ", list[i]);printf("\n");n++;}else{for(i = k; i <= m; i++){swap(&list[k], &list[i]); perm(list, k +1, m); swap(&list[k], &list[i]);}}}int m ain(){int list[] = {1, 2, 3, 4, 5};perm(list, 0, 4);printf("total:%d\n", n);return0;}谁有更高效的递归和非递归算法，请回贴。

清华大学组合数学课件

Combinatorics第章排列与组合第一章马昱春MA Yuchunmyc@1内容回顾•全排列生成算法(A)字典序法(B)递增进位制数法(C)递减进位制数法(D)邻位对换法•全排列：P是[1,n]的一个全排列。

P=P 1P 2…P n •序号：先于此排列的排列的个数。

–字典序中将先于此排列的排列按前缀分类，得到排列的序号n-1(n-i)!小的数的个数i=1,2,,n-1∑k i (n i)! k i ：P i 的右边比P i 小的数的个数i 1,2,…,n 1i=1•中介数：每个排列对应的中介数即k 1k 2…k n-1–递增/递减进位制数–记录排列的结构全排列序号中介数对应2–全排列，序号，中介数一一对应字典序下的对应关系n-1排列：P=P 1P 2…P n序号：∑k i (n-i)! i=1中介数：k 1k 2…k n-11230(00)()↑1321(01)↑ (321)n!-1=5 (21)………………()↑=2*2!+1*1!=5共有n!个排列0到(n!-1)0到(n!-1)个中介数3中介数的特点：记录当前数字右边比当前数字小的数字的个数•给定一个排列求后面或者前面的某个排列给定个排列求后面或者前面的某个排列–“原排列”→“原中介数”→“新中介数”“新排列”→新排列递增/递减进位制数加减法序号(A)字典序法(B)递增进位制数法(C)递减进位制数法(D)邻位对换法0 123 (00)↑ 123 (00)↑ 123 (00)↓ 123 (00)↓1 132 (01)↑ 213 (01)↑ 132 (01)↓ 132 (01)↓2213(10)132(10)312(02)312(02)2 213 (10)↑ 132 (10)↑ 312 (02)↓ 312 (02)↓3 231 (11)↑ 231 (11)↑ 213 (10)↓ 321 (10)↓4 312 (20)↑ 312 (20)↑ 231 (11)↓ 231 (11)↓5321(21)321(21)321(12)213(12)5 321 (21)↑ 321 (21)↑ 321 (12)↓ 213 (12)↓对中介数的不同解释算法构成了不同的排列顺序4常用排列生成工具_p,•C++标准程序库中有两个函数next permutation, prev_permutation，可以生成字典序排列#include algorithm•#include<algorithm>bool next_permutation( iterator start, iterator end ); bool prev_permutation( iterator start, iterator end ); bool prev permutation(iterator start iterator end);–The next_permutation() function attempts to transform thegiven range of elements [start,end) into the nextgiven range of elements[start end)into the nextlexicographically greater permutation of elements. If itsucceeds, it returns true, otherwise, it returns false.•/blog/stl_next_permutation.html5•Matlab中也支持排列的生成–用命令perms得到排列,用法：perms(vector) 给出向量vector的所有排列，例如perms([2 3 5]) 运行结果：5 3 2，5 2 3，3 5 2，3 2 5结果532523352325，2 3 5，2 5 3–此函数值只能适用于n < 15的情况下。

全排列C编程

全排列C++编程全排列的生成算法全排列的生成算法就是对于给定的字符集，用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。

任何n个字符集的排列都可以与1～n的n个数字的排列一一对应，因此在此就以n个数字的排列为例说明排列的生成法。

n个字符的全体排列之间存在一个确定的线性顺序关系。

所有的排列中除最后一个排列外，都有一个后继；除第一个排列外，都有一个前驱。

每个排列的后继都可以从它的前驱经过最少的变化而得到，全排列的生成算法就是从第一个排列开始逐个生成所有的排列的方法。

例如对于5个数字的排列12354和12345，排列12345在前，排列12354在后。

按照这样的规定，5个数字的所有的排列中最前面的是12345，最后面的是54321。

字典序算法如下：设P是1～n的一个全排列:p=p1p2......pn=p1p2......pj-1pjpj+1......pk-1pkpk+1......pn 1）从排列的右端开始，找出第一个比右边数字小的数字的序号j（j从左端开始计算），即j=max{i|pi<pi+1}2）在pj的右边的数字中，找出所有比pj大的数中最小的数字pk，即k=max{i|pi>pj}（右边的数从右至左是递增的，因此k是所有大于pj的数字中序号最大者）3）对换pi，pk4）再将pj+1......pk-1pkpk+1pn倒转得到排列p''=p1p2.....pj-1pjpn.....pk+1pkpk-1.....pj+1，这就是排列p的下一个下一个排列。

例如839647521是数字1～9的一个排列。

从它生成下一个排列的步骤如下：自右至左找出排列中第一个比右边数字小的数字4 839647521在该数字后的数字中找出比4大的数中最小的一个5 839647521将5与4交换839657421将7421倒转839651247所以839647521的下一个排列是839651247。

全排列生成算法

全排列生成算法
全排列生成算法是指，在计算机算法领域，使用一组有限个数的元素，按照一定的顺序排列出所有可能的排列组合，这种算法的应用非常广泛。

它通常应用在诸如有限的搜索空间有限的排列搜索，模拟和调度系统中，如模拟多核心交叉编程和利用资源安排调度程序等，而在互联网领域，全排列生成算法得到了广泛的运用。

首先，全排列生成算法可以将URL地址和关键词进行排列组合，构建出多种搜索语义，帮助用户更好、更快地获取需要的资料，进而提高搜索效率，极大的提升了用户的搜索体验，也减轻了后端的搜索计算压力。

此外，在互联网推广项目中，也能用全排列生成算法对网站的多元素构建，来减少网站页面广告群体和PV、UV背后被推广页面之间的数量差异，有效提高推广项目的效率、投入产出比，进一步影响经济效益。

总之，全排列生成算法的应用范围很广，在互联网领域得到了广泛的应用和发挥，可以说有着重要的作用。

它可以极大的提高互联网用户的搜索体验和互联网推广的效益，也可以减轻后端的搜索计算压力，同时用户也可以获得更快速、更准确的搜索结果。

组合数学第4章[生成排列与组合]PPT教学课件

2020/12/10
14
§4.2 生成组合
生成组合
4.2.1 基2算法若S是n个元素的集合，元素为{xn-1,...,x1,x0}，则生成组合就是生成S的所有2n个子集。任一子集可以描述成：
(an-1,...,a1,a0)=an-1...a1a0 其中，ai为1或0，表示xi在或不在子集中。
于是S的全部子集可以用0~2n-1的整数来描述，只要生成这些整数，也就得到了所有组合。
其中，0表示空集，2n-1表示S本身。
全排列生成算法
2020/12/10
6
3. 直接生成全排列的算法
全排列生成算法
[定义]对排列中的每个元素k，赋予其一
个方向：k 或 k 。如果一个整数k的箭头指向一个与其相邻但比它小的整数，则
称k是活动的。
例如，对于：263154
只有6、3、5是活动的。
2020/12/10
7
显然：
全排列生成算法
a1+a2+...+an 度量了排列的无序程度。
2020/12/10
11
全排列生
[例]31524的逆序列是1,2,0,1,0。成算法
[结论]对于逆序列，显然有0≤ak≤n-k。且任何一个排列都可确定一个逆序列。
[定理]若b1,b2,...,bn是满足0≤bk≤n-k的整数序列，则存在{1,2,...,n}的唯一的一个排列，其逆序列为b1,b2,...,bn 。
21
2020/12/10
4
{1,2,3}的排列
全排列生
1 2 3 成算法 2 31 31 2 32 1 13 2 2 13
2020/12/10
5

n个数的所有排列

n个数的所有排列如果用P表示n个元素的排列，而Pi表示不包含元素i的排列，(i)Pi表示在排列Pi前加上前缀i的排列，那么，n个元素的排列可递归定义为：如果n=1，则排列P只有一个元素i如果n>1，则排列P由排列(i)Pi构成（i=1、2、....、n-1）。

根据定义，容易看出如果已经生成了k-1个元素的排列，那么，k 个元素的排列可以在每个k-1个元素的排列Pi前添加元素i而生成。

例如2个元素的排列是1 2和2 1，对每个元素而言，p1是2 3和3 2，在每个排列前加上1即生成1 2 3和1 3 2两个新排列，p2和p3则是1 3、3 1和1 2、2 1，按同样方法可生成新排列2 1 3、2 3 1和3 1 2、3 2 1。

主要代码如下：/*函数名称：Permutation函数功能：普通递归算法：输出n个数的所有全排列输入变量：int n：1，2，3，...，n共n个自然数输出变量：无*/void Permutation(int n){int *a = new int[n];//用来存储n个自然数for (int i=0; i<n; i++) //存储全排列的元素值a[i] = i + 1;Recursion(a, n, n-1); //调用递归函数delete []a;}/*函数名称：Recursion函数功能：递归输出n个数的所有全排列输入变量：int a[]：存储了1，2，3，...，n共n个自然数的数组int n：数组a[]的长度int k：正在处理的k个元素所组成的排列输出变量：无*/void Recursion(int a[], int n, int k){if (k == 0) //排列只有一个元素a[k]，直接输出Print(a, n);else{int temp;for (int i=0; i<=k; i++) //穷举，依次让第k个元素与前面的元素交换{temp = a[i];a[i] = a[k];a[k] = temp;Recursion(a, n, k-1); //递归生成k-1个元素的全排列temp = a[i]; //再换回来a[i] = a[k];a[k] = temp;}}void Print(int a[], int n){for (int i=0; i<n; i++)cout << a[i];cout << endl;}循环移位法是一种很容易理解的非有序全排列算法，它的原理是：如果已经生成了k-1个元素的排列，则在每个排列后添加元素k使之成为k个元素的排列，然后将每个排列循环左移（右移），每移动一次就产生一个新的排列。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

{
int count = 0;
int flag = 1;
while(count < media[i])
{
if(result[flag] == 0)
{
count ++;
}
flag ++;
{
cout<<result[i];
}
cout<<endl;
*/
}
finish = clock();
printf("The time was: %f\n", (double)(finish - start) / CLOCKS_PER_SEC);
cout<<"请选择方法（1为递增，2为递减）："<<endl;
cin>>way;
while(way != 1 && way != 2)
{
cout<<"输入错误，请选择方法（1为递增，2为递减）："<<endl;
cin>>way;
}
cout<<"进位递增法"<<endl<<"请输入全排列的长度:"<<endl;
{
cout<<result[i];
}
cout<<endl;
for(int i = length; i > 0; i--)
{
cout<<f[i];
}
cout<<endl<<endl;
*/
}
finish = clock();
}
while(result[flag] != 0)
{
flag ++;
}
result[flag] = i;
f[i] = flag;
}
//输出结果
/*for(int i = length; i > 0; i--)
printf("The time was: %f\n", (double)(finish - start) / CLOCKS_PER_SEC);
}
system("pause");
return 0;
}
result[f[m]] = result[f[m] + 1];
result[f[m] + 1] = t;
f[result[f[m]]] = f[m] ;
f[m] ++;
//输出结果
/*
for(int i = length; i > 0; i--)
for(int i = m+1; i<= length; i++)
{
result[length + 1 - i] = temp[length + 1 - i];
f[result[length + 1 - i]] = length + 1 - i;
}
int t = result[f[m]];
{
int f = 1;
for(int i = m + 1; i <= n; i++)
{
f *= i;
}
return f;
}
int main()
{
int length;
int index = -1;
int way;
clock_t finish,start;
/*****************递增递减算法*****************/
#include <stdio.h>
#include <iostream>
#include <math.h>
#include <time.h>
using namespace std;
int factorial(int n,int m)
int l = length;
while(1)
{
//求中介数
media[2] ++;
int k = 2;
while(media[k] > k - 1)
{
media[k] = 0;
k ++;
media[k] ++;
int *temp = new int[length + 1];
for (int i = 0;i <= length; i ++)
{
f[i] = length + 1 - i;
result[i] = length + 1 - i;
temp[i] = 0;
}
}
else
{
int maxIndex = factorial(length,1) - 1;
int *media = new int[length + 1];
int *result = new int[length + 1];
int *f = new int[length + 1];
cin>>length;
start = clock();
if(way == 1)
{
int maxIndex = factorial(length,1) - 1;
int *media = new int[length + 2];
int *result = new int[length + 1];
while(1)
{
//求对应的排列
int m;
for(m = length; f[m] == m ;m--)
{
temp[length + 1 - m] = m;
}
if(m == 0) break;
if(m < length)
{
for(int i = 1; i <= m; i ++)
{
result[length + 1 - i] = result[m + 1 - i];
f#43; 1 - i;
}
}
}
if(k > length)
break;
l = k;
//求对应的排列
for(int i = 1; i <= l; i++)
{
result[f[i]] = 0;
}
for(int i = l; i > 0; i--)
int *f = new int[length + 1];
for (int i = 0;i <= length; i ++)
{
f[i] = length + 1 - i;
result[i] = length + 1 - i;
media[i] = 0;
}

全排列生成算法-递增进位制数-递减进位制数

全排列的几种算法

排 列 组 合 公 式 及 排 列 组 合 算 法 ( 2 0 2 0 )

全排列生成算法

全排列的生成算法

A43计算公式

组合数学：1-2 排列组合的生成

组合数学 第一章 排列组合5全排列的生成算法合

全排列生成算法的分析

四种权威全排列生成算法

组合数学中的全排列生成算法完整版

1.5 组合数学之全排列的生成算法

排列组合生成算法

最新全排列算法解析(完整版)

全排列算法——精选推荐

清华大学组合数学课件

全排列C编程

全排列生成算法

组合数学第4章[生成排列与组合]PPT教学课件

n个数的所有排列

排列组合公式及排列组合算法 ( 2 0 2 0 )

组合数学第一章排列组合5全排列的生成算法合