多相流传热学1_2
多相流课件

煤燃烧国家重点实验室 SKLCC
单质或纯物质的相图
煤燃烧国家重点实验室 SKLCC
§1-2 多相流的定义和分类
定义: 必须同时考虑物质多相共存且具有明显相 界面的混合物流动力学 的 特殊流动问题称为 多相流。 在多相流动力学中,所谓的相不仅按物质的状
态,而且按化学组成、尺寸和形状等划分。
煤燃烧国家重点实验室 SKLCC
2、气固两相流
气体和固体颗粒混合在一起共同流动。 固体颗粒本身无流动性; 当流体流速足够大, 流体中所含的固体小颗粒 具有类似流体特性; 在某些条件下,可将颗粒相作为流体考虑,在 另一些条件下,必须考虑颗粒相本身的特点。
例:空气中夹带灰粒与尘土,沙漠风沙,飞雪,冰雹, 气力输送,气流干燥,煤粉燃烧,石油催裂化,矿物 的流化床焙烧,气力浮选等
1、气液两相流
气体和液体 物质 混合在一起共同流动。 单工质汽液两相流 ,如水-水蒸汽 汽、液两相均具有相同的化学成份; 在压力和温度发生变化时会发生相变。 双组分工质气液两相流, 如空气-水 两相具有不同的化学成份。
例:蒸发器、冷凝器、反应器、气液混合器、气液分离器 等。
煤燃烧国家重点实验室 SKLCC
煤燃烧国家重点实验室 SKLCC
5、气液液、气液固和液液固多相流
气体、液体和固体颗粒混合在一起共同流动称为气液固三 相流; 气体与两种不能均匀混合、互不相溶的液体混合物在一起 的流动称为气液液三相流; 两种不能均匀混合、互不相溶的液体与固体颗粒混合在一 起的共同流动称为液液固三相流。 例: 油田油井及井口内的原油-水-气-沙粒的三种以上相 态物质的混合物流动,烟气洗涤塔等
空气中夹带灰粒与尘土沙漠风沙飞雪冰雹气力输送气流干燥煤粉燃烧石油催裂化矿物的流化床焙烧气力浮选等煤燃烧国家重点实验室sklcc油田开采与地面集输分离排污中的油水两相流化工过程中的乳浊液流动物质提纯和萃取过程中的液液混合流等煤燃烧国家重点实验室sklcc气体与两种不能均匀混合互不相溶的液体混合物在一起的流动称为气液液三相流
传热学第一二三类边界条件

传热学第一二三类边界条件
本文主要介绍传热学中的第一、二、三类边界条件。
传热学是研究热量传递过程的一门学科,其中边界条件是热传递方程求解的关键之一。
在传热学中,边界条件分为三类。
第一类边界条件是指在热传递过程中,边界上的温度是已知的。
这种情况通常出现在热源/冷源表面或是固体表面。
为了简化计算,
我们通常将边界上的温度视为常数。
第二类边界条件是指在热传递过程中,边界上的热流密度是已知的。
这种情况通常出现在流体内部或是气体内部,因为在这种情况下,温度是不均匀的,而热流密度是更为基本的量。
第三类边界条件是指在热传递过程中,边界上的热通量是已知的。
这种情况通常出现在较为复杂的热传递问题中,如辐射传热问题等。
在这种情况下,我们需要利用热传递方程和能量守恒定律来求解未知的温度分布。
总之,在传热学中,不同类型的边界条件可以帮助我们更好地分析和理解热传递过程,从而得出更为准确的结果。
- 1 -。
多相流体力学介绍及其工程应用

5、多相流体力学在现代工程中的应用
根据换热情况的不同, 多相流还可分为与外界无加热或冷却等热量交换过程的绝热 多相流和有热量交换的多相流。在有热交换的多相流中伴随着流动过程常会发生单组 分工质的相变(即液体汽化成蒸汽或蒸汽凝结成液体)。
3、自然生活中的多相流
多相流在自然界、日常生活中都是广泛存在的。自然界中常见的 夹着灰粒、尘埃或雨滴的风,夹着泥沙的河水以及湖面或海面上带雾 的上升气流等均为多相流的实例。在日常生活中常见的烟雾,啤酒夹 着气泡从瓶中注入杯子的流动过程以及沸腾的水壶中水的循环也都属 于多相流的范畴。严格地说,即使在一般认为是单相流体的液体和气 体中也往往含有另一相的成分在内。例如,当温度降低时,含于气体 中的水蒸汽就会凝结,使气体带有微量水分。又如在水流中几乎也总 含有少量空气。但是,在这些情况下,由于气体或液体中所含另一相 数量微小,所以仍可看作单相流体。
在医药卫生工程中,血清、疫苗、药物乃至眼球等组织器管的低温保存设备 和冷手术刀等的设计和正常操作均与多相流体力学理论有着密切的关系。
在现代叶轮机械工程中,有不少叶轮机械的工质为两相流体或多相流体, 诸如 锅炉排粉机和引风机中的气固两相流体等。
5、多相流体力学在现代工程中的应用
在现代石油工程中,存在一系列复杂的多相流体力学问题。诸如各种垂直和 倾斜油井井筒中的油、气、水、砂四相流动问题, 油气储运中的长距离油气混输问 题和油气分离问题等。
传热学1-2
传热学 Heat Transfer
假设:
(1)稳态过程;(2)将圆管按厚度等于管子壁厚的平板处理。
1/ h1
计算:
1/ h2
三个环节单位面积热阻:
1 水侧换热面积热阻 1 4 2 1.15 10 m K/W 2 h1 8700W/(m K)
1.5 103 mm 3.92 106 m 2 K/W 383W/(m K)
4)GR Kirchhoff
澳大利亚物 理学家。 1879 年用试 验证明了黑 体辐射正比 于其绝对温 度的四次方。
德国物理学家。 德国物理学家。 德国物理学家。 1884 年从热力 1900 年提出 1859年提出 了能量子的概 了确定物体吸 学角度证明了 念,据此建立 收比和发射率 黑体辐射正比 了黑体辐射能 之间关系的定 于其绝对温度 随波长分布的 律。 的四次方。 定律。
Φ Ah1 (t f 1 t w1 )
Φ A
Φ Ah2 (t w2 t f 2 )
(t w1 t w 2 )
在稳态情况下,由上面三个式子计算的热流量应 是相等的。将上述 3 式改写成温差的表示式:
3/29
传热学 Heat Transfer
Φ t f 1 tw1 Ah1 1 Φ 相加 1 tw1 tw2 tf1 tf 2 Φ A Ah1 A Ah2 Φ tw 2 t f 2 Ah2
23/29
传热学 Heat Transfer
3.数值模拟 这种方法随着计算机的进一步发展而会越来越显 出其重要性;本课程中将通过导热问题介绍其基本思 想。
大电流母线中流场的计算结果及与可视化实验的对比
传热学三类边界条件(第一二三类边界条件)

传热学三类边界条件(第一二三类边界条件)文化 2020-05-08 10:38:49 共10个回答【定解条件】使微分方程获得某一特定问题的解的附加条件.1)初始条件:给出初始时刻的温度分布2)边界条件:给出导热物体边界上的温度或换热情况.【第一类边界条件】规定了边界上的温度值.【第二类边界条件】规定了边界上的热流密度值.【第三类边界条件】规定了边界上物体与周围流体间的表面传热系数h及流体温度tf.对稳态问题只需边界条件.通过其表面来分析,其表面能量守恒故应有kdT/dx=h(T-T∞)1.定解条件是初始条件和边界条件的统称.2.温度值热,流密度值,传热系数h及流体温度tf.3.初始条件是指在微分方程中未知函数在初始时刻所需满足的条件.4.边界条件绝热,定壁温和对流条件你好,第一类边界条件:规定了边界上的温度值.第二类边界条件:规定了边界上的热流密度.第三类边界条件:规定了边界上物体与周围流体间表面传热系数h以及周围流体的温度Tf.边界条件有三类第一类,规定了边界上的温度值.第二类,规定了边界上的传热密度值.第三类,规定了物体与周围流体间的表面传热系数h及周围流体的温度.对于稳态导热问题,定解条件中没有初始条件,仅有边界条件.边界条件有:1、第一类边界条件,规定了边界上的温度2、第二类边界条件,规定了边界上的热流密度值3、第三类边界条件,规定了边界上物体与周围流体间的表面传热系数h及周围流体温度tf.至于需要几个独立的边界条件,与所求区域有关,比如圆,只需一个.而长方形区域,则必须明确四条边上的边界条件.传热学问题常壁温边界条件就是第一类边界条件,壁温为常数,常热流边界条件就是第二类边界条件,热流密度为常数边值问题中的边界条件的形式多种多样,在端点处大体上可以写成这样的形式,Ay+By'=C,若B=0,A≠0,则称为第一类边界条件或狄里克莱(Dirichlet)条件;B≠0,A=0,comsol在声学模拟无限边界有三种方法:1.采用平面波辐射,或球面波辐射边界条件.2.采用完美匹配层.3.采用周期性边界条件.。
多相流传热学1_2

冷凝器 再循环锅炉
压力抑制水池 给水泵
循环水泵
Dai C
研究多相流的意义
自然现象: 大气流动,风雨雪砂雾雹,河床、冰川、海洋、 喷泉、泥石流、生物系统等
Dai C
自然界中的多相流
Dai C
一、绪论
1:主要参考资料
1、主要参考资料
教科书(Books) (1) 鲁钟琪 编著:《两相流与沸腾传热》清华大学出版社,2002年 (2) 林宗虎 等编著:《气液两相流和沸腾传热》西安交通大学出版社,2003年 (3) 郭烈锦 编著:《两相与多相流动力学》西安交通大学出版社,2002年 (4) Naterer Greg F.: Heat Transfer in Single and Multiphase Systems, CRC Press, 2003 (5) Kolev N.I. : Multiphase Flow Dynamics, 2002, Springer (6) Collier J.G.:Convective boiling and condensation, McGraw Hill, 1981 期刊(Journals) (7) International Journal of Multiphase Flow (1974 -) (8) ASME Journal of Heat Transfer (9) International Journal of Heat and Mass Transfer
Dai C
一、绪论
多相流的概念
(4) 同时存在两种及两种以上相态的物质混合体的流动就是两相或多 相流。气体和液体属于连续介质也称为连续相或流动相(Continuous phase),固体颗粒、液滴和气泡属于离散介质(Dispersed phase) , 也称分散相或颗粒相。流动相和颗粒相组成的流动叫做两相或多相流 动。[3] 气液两相 气固两相 液固两相 液液两相
传热学第二章

习题平板2-1 用平底锅烧开水,与水相接触的锅底温度为111℃,热流密度为424002/m W 。
使用一段时间后,锅底结了一层平均厚度为3mm 的水垢。
假设此时与水相接触的水垢的表面温度及热流密度分别等于原来的值,试计算水垢与金属锅底接触面的温度。
水垢的导热系数取为1W/(m.K)。
解:由题意得424001003.0111=-=w t q =w/m 2所以t=238.2℃2-2 一冷藏室的墙由钢皮矿渣棉及石棉板三层叠合构成,各层的厚度依次为0.794mm.,152mm 及9.5mm ,导热系数分别为45)./(K m W ,0. 07)./(K m W 及0.1)./(K m W 。
冷藏室的有效换热面积为37.22m ,室内外气温分别为-2℃及30℃,室内外壁面的表面传热系数可分别按1.5)./(2K m W 及2.5)./(2K m W 计算。
为维持冷藏室温度恒定,试确定冷藏室内的冷却排管每小时需带走的热量。
解:由题意得332211212111λδλδλδ++++-⨯=Φh h t t A =2.371.00095.007.0152.045000794.05.215.11)2(30⨯++++--=357.14W357.14×3600=1285.6KJ2-3有一厚为20mm 的平板墙,导热系数为1.3)./(K m W 。
为使每平方米墙的热损失不超过1500W,在外表面上覆盖了一层导热系数为0.12)./(K m W 的保温材料。
已知复合壁两侧的温度分别为750℃及55℃,试确定此时保温层的厚度。
解:依据题意,有150012.03.1020.0557502221121≤+-=+-=δλδλδt t q ,解得:m 05375.02≥δ 2-4 一烘箱的炉门由两种保温材料A 及B 组成,且B A δδ2=(见附图)。
已知)./(1.0K m W A =λ,)./(06.0K m W B =λ,烘箱内空气温度4001=f t ℃,内壁面的总表面传热系数)./(501K m W h =。
华科传热学04-1,2

2016/1/1
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
3 对流换热系数与对流换热微分方程
①对流换热系数(表面传热系数)
h Φ ( A(t w t )) [W (m2 C)]
——当流体与壁面温度相差 1℃ 时、每单位 壁面面积上、单位时间内所传递的热量.
电子器件散热
2016/1/1
4
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
②对流换热的特点: (1) 导热与热对流同时存在的复杂热传递过 程 (2) 必须有直接接触(流体与壁面)和宏观 运动;也必须有温差 (3) 由于流体的粘性和受壁面摩擦阻力的影 响,紧贴壁面处会形成速度梯度很大的边 界层;热边界层 ③特征:以简单的对流换热过程为例,对 对流换热过程的特征进行粗略的分析。
2016/1/1
y
t∞
u∞
qw
tw
x
6
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
1. they will rebound off the solid surface 2. they will be absorbed into the solid surface 3. they will adhere to the solid surface
第四章 对流换热原理
§4-1 对流换热概述 §4-2 层流流动换热的微分方程组 §4-3 对流换热过程的相似理论 §4-4 边界层理论 §4-5 紊流流动换热
(完整版)第四版传热学第一、二章习题解答

传热学习题集第一章思考题1. 试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。
答:导热和对流的区别在于:物体内部依靠微观粒子的热运动而产生的热量传递现象,称为导热;对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。
联系是:在发生对流换热的同时必然伴生有导热。
导热、对流这两种热量传递方式,只有在物质存在的条件下才能实现,而辐射可以在真空中传播,辐射换热时不仅有能 量的转移还伴有能量形式的转换。
2. 以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩-玻耳兹曼定律是应当熟记的传热学公式。
试写出这三个公式并说明其中每一个符号及其意义。
答:① 傅立叶定律:dx dt q λ-=,其中,q -热流密度;λ-导热系数;dx dt-沿x 方向的温度变化率,“-”表示热量传递的方向是沿着温度降低的方向。
② 牛顿冷却公式:)(f w t t h q -=,其中,q -热流密度;h -表面传热系数;wt -固体表面温度;ft -流体的温度。
③ 斯忒藩-玻耳兹曼定律:4T q σ=,其中,q -热流密度;σ-斯忒藩-玻耳兹曼常数;T -辐射物体的热力学温度。
3. 导热系数、表面传热系数及传热系数的单位各是什么?哪些是物性参数,哪些与过程有关?答:① 导热系数的单位是:W/(m.K);② 表面传热系数的单位是:W/(m 2.K);③ 传热系数的单位是:W/(m 2.K)。
这三个参数中,只有导热系数是物性参数,其它均与过程有关。
4. 当热量从壁面一侧的流体穿过壁面传给另一侧的流体时,冷、热流体之间的换热量可以通过其中任何一个环节来计算(过程是稳态的),但本章中又引入了传热方程式,并说它是“换热器热工计算的基本公式”。
试分析引入传热方程式的工程实用意义。
答:因为在许多工业换热设备中,进行热量交换的冷、热流体也常处于固体壁面的两侧,是工程技术中经常遇到的一种典型热量传递过程。
5. 用铝制的水壶烧开水时,尽管炉火很旺,但水壶仍然安然无恙。
传热学课后习题答案(第四版)

第1章1-3 解:电热器的加热功率: kW W tcm QP 95.16.195060)1543(101000101018.4633==-⨯⨯⨯⨯⨯=∆==-ττ15分钟可节省的能量:kJ J t cm Q 4.752752400)1527(15101000101018.4633==-⨯⨯⨯⨯⨯⨯=∆=-1-33 解:W h h t t A w f 7.45601044.02.061)]10(2[6311)(2121=++--⨯=++-=Φλδ如果取K m W h ./3022=,则W h h t t A w f 52.45301044.02.061)]10(2[6311)(2121=++--⨯=++-=Φλδ即随室外风力减弱,散热量减小。
但因墙的热阻主要在绝热层上,室外风力变化对散热量的影响不大。
第2章2-4 解:按热平衡关系有:)(1222121f w BBA A w f t t h h t t -=++-λδλδ,得:)2550(5.906.01.0250150400-=++-B Bδδ,由此得:,0794.0,0397.0m m A B ==δδ 2-9 解:由0)(2121=+=w w m t t t ℃从附录5查得空气层的导热系数为K m W ⋅/0244.0空气λ 双层时:W t t A w w s 95.410244.0008.078.0006.02)]20(20[6.06.02)(21=+⨯--⨯⨯=+-=Φ空气空气玻璃玻璃λδλδ单层时:W t t A w w d 187278.0/006.0)]20(20[6.06.0/)(21=--⨯⨯=-=Φ玻璃玻璃λδ两种情况下的热损失之比:)(6.4495.411872倍==ΦΦs d题2-15解:这是一个通过双层圆筒壁的稳态导热问题。
由附录4可查得煤灰泡沫砖的最高允许温度为300℃。
设矿渣棉与媒灰泡沫砖交界面处的温度为t w ,则有 23212121ln 21ln 21)(d d l d d l t t πλπλ+-=Φ (a ) 23221211ln )(2ln )(2d d t t l d d t t l w w -=-=Φπλπλ (b ) 65110ln )50(12.02565ln )400(11.0:-⨯=-⨯w w t t 即由此可解得:4.167=w t ℃<300℃又由式(a )可知,在其他条件均不变的情况下,增加煤灰泡沫砖的厚度δ2对将使3d 增大,从而损失将减小;又由式(b )左边可知t w 将会升高。
传热学 第一二章49页

A 气体的导热系数 气 体 0.0 ~00W .6 6 (m K)
特点:(a) 气体的导热系数基本不随压力的改变而变化 (b) 随温度的升高而增大 (c) 随分子质量减小而增大
B 液体的导热系数 液 体 0.~ 007.W 7(m C)
特点:(a) 随压力的升高而增大 p
A
A
AA
传热学 (Heat Transfer)
《传热学》杨世铭、陶文铨编著,第三版
《传热学》
《传热学》 一. 序论 二. 导热基本定律及稳态导热 三. 非稳态导热 四. 导热问题的数值算法 五. 对流换热 六. 凝结与沸腾换热 七. 热辐射基本定律及物体的辐射换热 八. 辐射换热的计算 九. 传热过程分析与换热器热计算
hΦ(A (twt))W (m 2K)
—— 当流体与壁面温度相差1度时、每单位壁面面积上、单位时 间内所传递的热量
影响h因素:流速、流体物性、壁面形状大小等
(3) 对流换热热阻 Φ t t qtt
1(h)ARh 1h rh
Rh1(h)A[CW ]
rh1h [m2CW ]
q:热流密度,单位时间通过单位面积的热量[W/m2]
A:垂直于导热方向的截面积[m2]
负号:代表热量传递方向与温度升高方向相反
(2) 导热系数
金 属 非金 属 液 固 体 体 气体
(3) 一维稳态导热及其导热热阻
q 0 d x ttw w 1 2d t q tw 1 tw 2
ΦA dt
dx
Fourier 定律:
(2) 对流换热 A th
Newton 冷却公式:
(3) 热辐射
AT4
Stenfan-Boltzmann 定律:
传热学讲义—第二章

第二章 稳态导热本章重点:具备利用导热微分方程式建立不同边界条件下稳态导热问题的数学模型的能力第一节 通过平壁的导热1-1 第一类边界条件 研究的问题:(1)几何条件:设有一单层平壁,厚度为δ,其宽度、高度远大于其厚度(宽度、高度是厚度的10倍以上)。
这时可认为沿高度与宽度两个方向的温度变化率很小,温度只沿厚度方向发生变化。
(属一维导热问题)(2)物理条件:无内热源,材料的导热系数λ为常数。
(3) 边界条件:假设平壁两侧表面分别保持均匀稳定的温度1w t 和2w t ,21w w t t >。
(为第一类边界条件,同时说明过程是稳态的)求:平壁的温度分布及通过平壁的热流密度值。
方法1 导热微分方程:采用直角坐标系,这是一个常物性、无内热源、一维稳态导热问题(温度只在 x 方向变化)。
导热微分方程式为:022=dxtd (2-1)边界条件为:10w x t t == , 2w x t t ==δ (2-2)对式(2-1)连续积分两次,得其通解: 21c x c t += (2-3)这里1c 、2c 为常数,由边界条件确定 ,解得:⎪⎩⎪⎨⎧=-=11221ww w t c t t c δ (2-4)最后得单层平壁内的温度分布为: x t t t t w w w δ211--= (2-5)由于δ 、1w t 、2w t 均为定值。
所以温度分布成线性关系,即温度分布曲线的斜率是常数(温度梯度),const t t dx dt w w =-=δ12 (2-6)热流密度为:)(21w w t t dx dt q -=-=δλλ2/m W (2-7) 若表面积为 A, 在此条件下 , 通过平壁的导热热流量则为 :t A qA ∆==Φδλ W (2-8)考虑导热系数随温度变化的情况:对于导热系数随温度线形变化,即)1(0bt +=λλ,此时导热微分方程为:0=⎪⎭⎫⎝⎛dx dt dx d λ 解这个方程,最后得:⎥⎦⎤⎢⎣⎡++-+⎪⎭⎫ ⎝⎛+=+)(211212121121122w w w w w w t t b x t t bt t bt t δ 或 x tt t t b b t b t w w w w w δ12211)(21122-⎥⎦⎤⎢⎣⎡+++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+说明:壁内温度不再是直线规律,而是按曲线变化。
流体的多相流动和多相传热

流体的多相流动和多相传热多相流动和多相传热是流体力学和传热学中的重要研究领域,涉及到两种或多种不同相态的流体在相互作用中的行为及其传热特性。
在工程和科学领域中,多相流动和多相传热的研究对于理解和解决现实生活中的许多问题具有重要意义。
一、多相流动的基本概念多相流动是指在同一空间内同时存在着两种或多种不同相态的流体。
常见的多相流动包括气固、液固和气液两相流动。
在多相流动中,流体与固体或另一种流体之间通过界面相互作用并产生各种现象。
多相流动的特点包括相态转换、相分离、相互作用等。
1. 相态转换相态转换是指流体在不同条件下从一种相态转变为另一种相态的过程。
例如,水从液态转变为气态的过程称为蒸发,气体从气态转变为液态的过程称为冷凝。
相态转换会伴随着能量的吸收或释放,对多相流动和多相传热的研究具有重要影响。
2. 相分离相分离是指在两种或多种相态的流体中,不同相态的物质会产生分离现象。
例如,在液固两相流动中,固体颗粒可能会沉积在底部形成固体堆积。
相分离现象对于流体力学和传热学的研究与应用非常重要。
3. 相互作用相互作用是指在多相流动中不同相态的流体之间通过界面相互作用产生的现象。
例如,在两种相态的气体流动中,气泡的生成和破裂是气液两相流动的典型现象。
相互作用对于多相流动的传热特性具有重要影响。
二、多相流动的数学模型多相流动的数学模型在流体力学和传热学的研究中起着重要作用,它描述了不同相态的流体在空间和时间上的分布及其相互作用规律。
常见的多相流动模型包括欧拉模型、拉格朗日模型和欧拉-拉格朗日混合模型。
1. 欧拉模型欧拉模型假设流体处于连续介质的状态,将流体视为宏观量的集合。
欧拉模型通过质量、动量和能量守恒方程来描述流体的运动及其与固体界面的相互作用。
欧拉模型在多相流动的研究和工程应用中被广泛采用。
2. 拉格朗日模型拉格朗日模型将流体视为由大量微观粒子组成的离散系统。
拉格朗日模型通过分析流体粒子的运动轨迹和相互作用来描述流体的运动规律。
传热学1-2
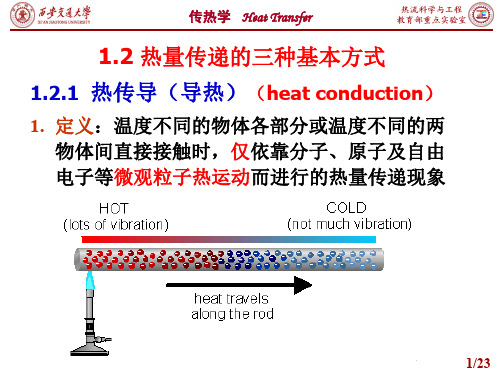
ttw w1 1
tw2 tw 2
分析:
dt q = dx
常数
q dx
0
tw 2
tw1
dt dx dx
6/23
传热学 Heat Transfer
q x 0 t t
故得
tw 2
w1
q
(tw2 tw1 )
(tw1 tw2 )
计算: 将已知数值代入得
300C 100C 2 2 q 0.242W/(m K) 9.68 10 W/m 硅藻土砖: 0.05m
讨论:
由于铜与硅藻土砖导热系数的巨大差别,在相同的条件 下通过铜板的导热量比通过硅藻土砖的导热量大三个数量级; 铜是热的良导体,而硅藻土砖可起到一定的隔热作用。
8/23
16/23
传热学 Heat Transfer
3. 辐射传热的一个计算特例 物体表面间间辐射换热的计算涉及到物体表面的 辐射能力、吸收能力、表面间的几何关系等多方面 的因素,不同情况下计算公式不一样。
最简单的情形之一:一面积为A1小凸物体被包容 在一个面积为A2内很大的空腔内。该物体与空腔表 面的辐射换热量计算式:
Φ 1 A1 (T -T )
4 1 4 2
使用条件:
A1 A2
17/23
传热学 Heat Transfer
1.2.4 实际的热量传递常包含数种方式 室内暖气片的散热:
热水
对流传热
管子内壁
导热
管子外壁
室内环境
对流传热+辐射
注意:最后环节中的对流是暖气片外表面与周围空 气间进行的;而辐射是外表面与四周固体表面间进 行的。各部分之间不发生宏观相对位移
传热学1-2
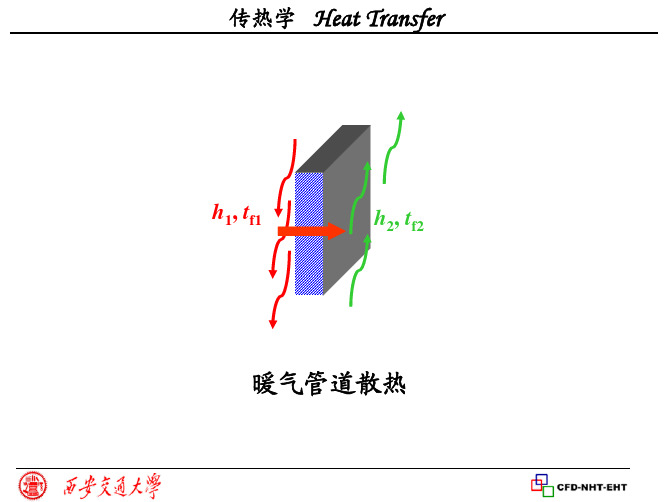
Tf 2
A
B
C
传热学 Heat Transfer
SUMMARY OF CHAP.1
1.Three basic modes of HT
传热学 Heat Transfer
2.HT Process
Φ = kA(t f 1 - tf2 )
h1, tf1 h2, tf2
k=
1 δ 1 + + h1 λ h 2
Φ t f 1 tw1 = Ah1 Φ tw1 tw 2 = ( Aλ δ ) Φ tw 2 t f 2 = Ah2
传热学 Heat Transfer
tf1 tf 2
1 δ 1 = Φ + + Ah1 Aλ Ah2
A(t f 1 t f 2 ) Φ= 1 δ 1 + + h1 λ h2
I R
U
t1
t2
Φ
U I= R
通过平壁导热的热阻
Φ=
t1
δ (λA)
t2
Δt
Rλ = δ (λA)
δ (λA)
传热学 Heat Transfer
A(t f 1 t f 2 ) Φ= 1 δ 1 + + h1 λ h2
tf1 tw1 tw2
1 (h2 A)
h1, tf1
h2, tf2
tf2
δ
1 (h1 A) δ (λA)
1
δ
传热学 Heat Transfer
3.Rate equations of the three modes
传热学 Heat Transfer
本章作业
1-2,1-5,1-7,1-17,1-28
�
传热学 Heat Transfer
第二章 多相流热物性模型及相关物性参数

y 10z 141.5 131.5 o z 3.0324 0.02023 o
式中:μon——地面脱气原油的粘度,mPa.s; t——温度,℃; δo——原油的相对密度,无因次; x、y、z——中间变量。
多相混输技术的研究及其应用 2015-7-3
8
第二章 多相流热物性模型
1、雷萨特给出了求溶解度的相关关系式:
多相混输技术的研究及其应用 2015-7-3 14
第二章 多相流热物性模型
y g 1.33 105 o Rs 0.178 1 y M g o P g y g 0.826lg 118 . 69 0 . 891 T
Z (1 0.34Tr 0.6) Pr 上式的使用范围:0≤Pr<12和1.25≤Tr<1.6。
二、粘度 (一)一般原油粘度 1、缺乏实验数据的情况下所用的计算方法
20
多相混输技术的研究及其应用 2015-7-3 6
2 0.658 20 0.866 2 20
gs Rs (0.00379 o 0.00393 ) 4.08779 o 4.43818
3、天然气相对密度 同一温度、压力下,气体的密度与干空气密度之比为气体相对密度。
多相混输技术的研究及其应用 2015-7-3 2
传热学课件-传热学课件第四版-第一章-32页文档资料

b 微电子: 电子芯片冷却 c 生物医学:肿瘤高温热疗;生物芯片;组织与器
官的冷冻保存 d 军 事:飞机、坦克;激光武器;弹药贮存 e 制 冷:跨临界二氧化碳汽车空调/热泵;高温
水源热泵 f 新 能 源:太阳能;燃料电池
总之,传热学应用可大致归为三大类: 强化传热 削弱传热 温度控制
§1-2 热量传递的三种基本方式
钢: q tw 1 tw 2 3 .4 6 3 1 0 0 1 .4 0 1 6 5 W 0 m 2 0 .05
铬砖:
q tw 1 tw 2 2 .3 3 2 1 0 0 9 .2 0 1 8 3 W 0 m 2 0 .05
硅藻土砖:
q t w 1 t w 2 0 .2 3 4 1 0 2 0 9 .6 0 1 8 2 W 0 m 2 0 .05
(32) 对流换热:传当递流到体另流一过处一的个现物象体。表面时的热量传递
过程,他与单纯的对流不同,具有如下特点:
a 导热与热对流同时存在的复杂热传递过程
b 必须有直接接触(流体与壁面)和宏观运动;也
必须有温差
c 壁面处会形成速度梯度很大的边界层 (3)对流换热的分类
(1)材料为铜,λ=375 w/(mK ); (2)材料为钢, λ=36.4 w/(mK ); (3)材料为铬砖, λ=2.32 w/(mK ); (4)材料为铬藻土砖, λ=0.242 w/(mK )。
解:参见图1-3。 及一维稳态导热公式有:
铜:
q tw 1 tw 2 3 7 3 5 0 1 0 1 .5 1 0 6 W 0 m 2 0 .05
热量传递的三种基本方式:导热(热传导)、对流(热对流) 和热辐射。
1.2.1 导热(热传导)(Conduction)
传热学第一类边界条件和第二类边界条件

传热学第一类边界条件和第二类边界条件
传热学中的第一类边界条件,也称为Dirichlet边界条件,是指在一个传热问题中,确定性地指定了边界上的温度或温度梯度。
这意味着在问题求解过程中,我们已经知道了边界上的温度或温度梯度,而不需要再进行计算。
这种边界条件可以用数学表达式或实验测量来确定。
例如,在一个热传导问题中,我们可能知道一块热板的一个表面的温度为100℃,这就是一个第一类边界条件。
通过这个边界条件,我们可以得出在该边界表面上的温度分布。
第二类边界条件,也称为Neumann边界条件,用于指定边界上的传热速率或热通量。
在这种情况下,我们并不知道边界上的温度或温度梯度,但我们知道边界上的传热速率或热通量。
传热速率是指单位时间内通过单位面积的热量。
以热传导问题为例,我们可能知道一块热板的一个表面的传热速率为200 W/m^2,这就是一个第二类边界条件。
通过这个边界条件,我们可以得出在该边界表面上的热流分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高层烟囱
Feed water
送 水
Power Transmission Tower
输电铁塔
蒸气
Steam Heat Recovery Steam Boiler
余热回收锅炉
Steam Turbine
蒸汽机
发电机
Generator
Condenser
冷凝器
发电机 压缩机 燃气轮机 Generator
Compressor Generator
C
lm t ds lm ds nl (nl ) nl lm dA
C S
nl
ds t
其中:
A Pi Qj Rk P Q R divA i j k x y z j k i x y z i j k z x y
Dai度:Mesoscale (Mesoscope) 晶格(unit cell),流体微团,代表基本单元(REV) A unit cell is used to identify a geometric configuration for a grouping of atoms in the solid. REV stands for Representative Elementary Volume. 宏观:Macroscope: Bulk, Domain, Configuration, Boundary, … 微观:Microscope: Molecular, free path, statistical, interstitial diffusion, …
S
C
A
Dai C
一、绪论
多相流的概念
2、两相流和多相流的概念 (1) 两相流和单相流比较,多出一个相和相间界面,因此,流场的组成, 从宏观方面看,包括三部分。以气液两相流来说,包括气相、液相和气 液界面。[1] (2) 异质物体或系统中,各存在分界面的独立物质称之为相。自然界常见 的物质有三相:固相、液相和气相。因此,由任意两种存在分界面的独 立物质组成的物质或系统称之为两相物体或系统。两相物体的流动称为 两相流。 [2] (3)固相、液相和气相三相同时存在的系统称之为三相或多相系统,多相 物质的流动称为多相流。
Dai C
多相流传热学
2010 年 3 月
Dai C
多相流传热学
一、Preface 二、Twophase Flow and Boiling 三、LBM programming 四、Nonlinear Science and Chaos 五、Interface Science 六、Particulate and its Dynamics 七、Multiphase Flow Measurement 八、Future (Discussion) examination (1.5w) (1.5w) (1.0w) (1.5w) (1.0w) (0.5w) (0.5w) (0.5w)
1:分子自由程 颗粒相特征尺寸 Dl 计算网格单元尺寸 Vol 空间尺寸 H 适合于有微细颗粒的均匀混合多相流系统 2:分子自由程 颗粒相特征尺寸 Dl 计算网格单元尺寸 Vol 空间尺寸 H 适合于有较明显相界面的多相流系统
1 3 1 3
Dai C
一、绪论
Water Intake channel
燃气排气
Combustion Gas
Exhaust Gas
排
气
冷却水入口
Electric Power
电力输出
液化天然气
Water Intake channel
冷却水出口
LNG Plant
Dai C
多相流应用例 (原子能发电机组)
核能发电站
蒸气
变压器
汽轮机
发电机
Dai C
一、绪论
2:研究方法
唯象
宏观现象 宏观结论 例:牛顿冷却定律;傅立叶定律;雷诺定律等 微观现象 宏观统计 宏观结论
例:边界层理论;气化核心说;湍流雷诺应力等
统计
微观统计 微观现象 宏观结论 例:普朗克辐射;量子力学理论
Dai C
一、绪论
•目前仍然以实验研究为主,理论研究为辅
2:研究方法
Continuous phase (m) Wall w Dispersed phase (l)
interface
气液液,气液固,液液固多相流
fine dispersed phase (non-structured, homogeneous) Heterogeneous (structured)
Dai C
冷凝器 再循环锅炉
压力抑制水池 给水泵
循环水泵
Dai C
研究多相流的意义
自然现象: 大气流动,风雨雪砂雾雹,河床、冰川、海洋、 喷泉、泥石流、生物系统等
Dai C
自然界中的多相流
Dai C
一、绪论
1:主要参考资料
1、主要参考资料
教科书(Books) (1) 鲁钟琪 编著:《两相流与沸腾传热》清华大学出版社,2002年 (2) 林宗虎 等编著:《气液两相流和沸腾传热》西安交通大学出版社,2003年 (3) 郭烈锦 编著:《两相与多相流动力学》西安交通大学出版社,2002年 (4) Naterer Greg F.: Heat Transfer in Single and Multiphase Systems, CRC Press, 2003 (5) Kolev N.I. : Multiphase Flow Dynamics, 2002, Springer (6) Collier J.G.:Convective boiling and condensation, McGraw Hill, 1981 期刊(Journals) (7) International Journal of Multiphase Flow (1974 -) (8) ASME Journal of Heat Transfer (9) International Journal of Heat and Mass Transfer
Kn 1 Kn 0.1 ~ 0.01 Kn 1 Kn 1
Dai C
一、绪论
传统计算方法在处理含微小颗粒的多相流时困难
界面压差与表面张力项 其中:
2:研究方法
有关:
表面张力或表面自由能;
H 颗粒表面曲率;
1 H 1 R 1 R1 R2
一般表面张力在 R 0.001m
一、绪论
ndF dV
S V
Π n dF Π dV
S V
扩张黏度 其中: 牛顿流体粘性应力张量
2 Π [V (V ) T ] ( )( V ) 3
:对低密度下的单原子气体和不可压缩流体可以忽略, 但对多原子气体或含气泡的液体或有吸收声音的介质不可忽略。
•主要涉及的研究领域: 流体力学、热力学、传热学、材料学、物理学和数学 •研究的重点和难点: 相界面特性(Interface), 非线性动力系统(Nonlinear dynamics) •研究的尺度(Scale): 微观尺度:Microscale (Microscope) 介观尺度:Mesoscale (Mesoscope) 宏观尺度:Macroscale (Macroscope) 巨观尺度:Megascale (Mesoscope)
Dai C
一、绪论
• 利比尼兹(Leibnitz)积分法则:
3:一些数学基础
一维线性定积分
( )
f ( x, )dx
( )
d d f f dx f ( , ) ( , ) d d ( )
边界条件
( )
f ( x, )
唯象理论和统计理论是相互渗透,相辅相成的。
Dai C
一、绪论
多 多相流 多尺度 多学科 多维 多功能 MultiMulti-phase Multi-scale Multi-disciplined Multi-dimensional Multi-functional
2:研究方法
“20世纪的文明是微观的,我认为21世纪微观和宏观应结合成一 体”“21世纪是越小越好,觉得小的是操纵一切的,而我猜测, 21世纪将要把微观和宏观整体的联系起来,这不光是影响物 理,也影响到生命的发展。……目前,微观和宏观的冲突已经非 常尖锐,靠一个不能解决另一个,把它们联系起来会有一些突 破,这个突破会影响科学的将来。”“仅是基因并不能解开生命 之谜,生命是宏观的” —— 李政道《21世纪的100个科学难题》1998
R
曲平面 球面
R1
R2
时对动量或能量交换影响大,因此要求:
计算网格单元尺寸很小
Dai C
一、绪论
• 高斯(Gauss)定理:
3:一些数学基础
n
n dF div dV dV
S V V
V S
• 高斯-奥斯托格拉德斯基(Gauss-Ostrogradskii)定理:
克努森数(Knudsen) Kn
2:研究方法
Dl
连续相速度
相对马赫数(Mach)
Mrr
Vm Vl am
颗粒相声速 连续相声速
连续介质流 滑移流 过渡流 自由流
Mr / Re 0.01 or 0.01 Mr / Re 0.1 or 0.1 Mr / Re 3 or Mr / Re 3 or
2:研究方法
Dai C
一、绪论
相界面(Interface): 气液界面、液固界面、气固界面
2:研究方法
