实验三-回归分析资料
计量经济学实验三--李子奈
实验三 多元线性回归一 实验目的:(1) 掌握多元线性回归模型的估计方法 (2) 模型方程的F 检验,参数的t 检验 (3) 模型的外推预测与置信区间预测二 实验要求:应用教材P105习题11做多元线性回归模型估计,对回归方程和回归参数进行检验并做出单点预测与置信区间预测 三 实验原理:最小二乘法四 预备知识:最小二乘法估计原理、t 检验、F 检验、点预测和置信区间预测 五 实验内容:在一项对某社区家庭对某种消费品的消费需要调查中,得到书中的表所示的序号对某商品的消费支出Y 商品单价X1 家庭月收入X2 序号对某商品的消费支出Y 商品单价X1 家庭月收入X2 1 591.9 23.56 7620 6 644.4 34.14 12920 2 654.5 24.44 9120 7 680.0 35.3 14340 3 623.6 32.07 10670 8 724.0 38.7 15960 4 647.0 32.46 11160 9 757.1 39.63 18000 5 674.0 31.15 11900 10706.8 46.68 19300 归分析。
(1)估计回归方程的参数及及随机干扰项的方差2,计算2R 及2R 。
(2)对方程进行F 检验,对参数进行t 检验,并构造参数95%的置信区间. (3)如果商品单价变为35元,则某一月收入为20000元的家庭的消费支出估计是多少?构造该估计值的95%的置信区间。
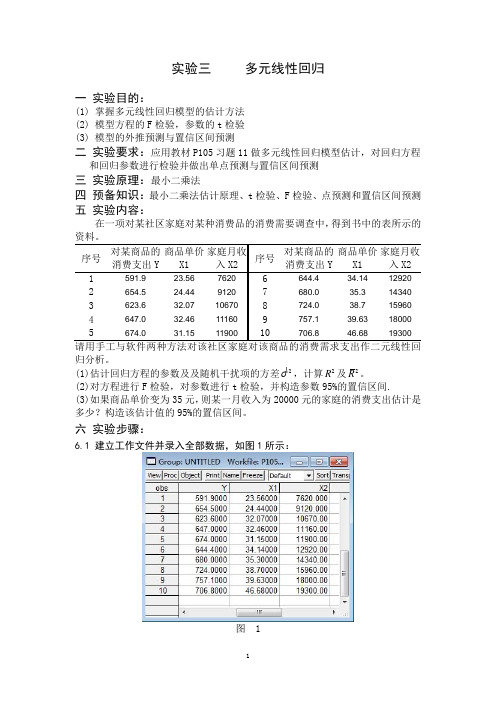
六 实验步骤:6.1 建立工作文件并录入全部数据,如图1所示:图 16.2 建立二元线性回归模型01122Y X X βββ=++点击主界面菜单Quick\Estimate Equation 选项,在弹出的对话框中输入:Y C X1 X2点击确定即可得到回归结果,如图2所示图 2根据图2的信息,得到回归模型的估计结果为:626.51939.790610.02862(15.61)( 3.06)(4.90)Y X X =-+-20.902218R = 20.874281R = .. 1.650804D W =22116.847i e =∑ 32.29408F = (2,7)df =随机干扰项的方差估计值为22116.847302.40677σ∧==6.3 结果的分析与检验 6.3.1 方程的F 检验 回归模型的F 值为:32.29408F =因为在5%的显著性水平下,F 统计量的临界值为0.05(2,7) 4.74F =所以有 0.05(2,7)F F > 所以回归方程通过F 检验,方程显著成立。
实验三回归分析

实验三回归分析一、考察温度对产量的影响,测得10组数据(见表一)2、对其回归方程进行显著性检验;3、预测X=42时产量的估计值及预测区间(置信水平为95%)。
二、根据表二提供的经济数据完成以下问题:1、试画出散点图,判断国民收入(Y)与消费量(X)是否有线性关系;2、求出Y关于X的一元线性回归方程;3、对方程作显著性检验;4、现测得1981年消费量X=3441,试给出1981年国民收入的预测值及相应的区间估计。
(显著性水平为0.05)。
三、某厂生产的一种电器的年销售量Y与竞争对手的价格X1及本厂的价格X2有关。
表三是十个城市中记录的资料。
否显著?并解释回归系数的含义;2、对回归模型进行初步诊断,并指出有无可疑点或异常点?3、已知某城市中本厂电器的售价X2=160元,竞争对手售价X1=170元,使用上述建立的回归模型预测该城市的年销售量;4、能否建立决定系数R2 >0.68,模型中所有回归系数在0.10水平上是显著的回归模型(提示:考虑二次项和交叉项,用逐步回归)。
四、某科学基金会的管理人员欲了解从事研究的工作人员中,高水平的数学家工资额Y与他们的研究成果(论文、著作等)的质量指标X1,从事研究工作的时间X2以及能成功获得资助的指标X3之间的关系,为此按一定的设计方案调查了24位此类型的数学家,数据见表四。
1、假设误差服从2N 分布,建立Y与X1,X2和X3之间的线性回归方程,(0,)并研究相应的统计推断问题,作相应的诊断和检验;2、假设某位数据数学家的关于X1,X2,X3的值为(5.1,20,7.2),试预测他的年工资额,并给出置信水平为95%的置信区间。
线性回归分析实验报告

线性回归分析实验报告实验报告:线性回归分析一、引言线性回归是一种基本的统计分析方法,用于研究自变量与因变量之间的线性关系。
此实验旨在通过一个实际案例对线性回归进行分析,并解释如何使用该方法进行预测和解释。
二、实验方法1.数据收集:从电商网站收集了一份销售量与广告费用的数据集,其中包括了十个月的数据。
该数据集包括两个变量:广告费用(自变量)和销售量(因变量)。
2.数据处理:首先对数据进行清洗,包括处理缺失值和异常值等。
然后进行数据转换,对广告费用进行对数转换,以适应线性回归的假设。
3.构建模型:使用线性回归模型,将广告费用作为自变量,销售量作为因变量,构建一个简单的线性回归模型。
模型的公式为:销售量=β0+β1*广告费用+ε,其中β0和β1是回归系数,ε是误差项。
4.模型评估:通过计算回归系数的置信区间和检验假设以评估模型的拟合程度和相关性。
此外,还使用残差分析来检验模型的合理性和独立性。
5.模型预测:根据模型的回归系数和新的广告费用数据,预测销售量。
三、实验结果1.数据描述:首先对数据进行描述性统计。
数据集的平均广告费用为1000元,标准差为200元。
平均销售量为1000件,标准差为150件。
广告费用和销售量之间的相关系数为0.8,说明两者存在一定的正相关关系。
2. 模型拟合:通过拟合线性回归模型,得到回归系数的估计值。
估计值的标准误差很小,R-square值为0.64,说明模型可以解释63%的销售量变异。
3.置信区间和假设检验:通过计算回归系数的置信区间,发现β1的置信区间不包含零,说明广告费用对销售量有显著影响。
假设检验结果也支持这一结论。
4.残差分析:通过残差分析,发现残差的分布基本符合正态性假设,没有明显的模式或趋势。
这表明模型的合理性和独立性。
四、结论与讨论通过线性回归分析,我们得出以下结论:1.广告费用对销售量有显著影响,且为正相关关系。
随着广告费用的增加,销售量也呈现增加的趋势。
2.线性回归模型可以解释63%的销售量变异,说明模型的拟合程度较好。
《应用回归分析》自相关性的诊断及处理实验报告

《应用回归分析》自相关性的诊断及处理实验报告
二、实验步骤:(只需关键步骤)
1、分析→回归→线性→保存→残差
2、转换→计算变量;分析→回归→线性。
3、转换→计算变量;分析→回归→线性
三、实验结果分析:(提供关键结果截图和分析)
1.用普通最小二乘法建立y与x1和x2的回归方程,用残差图和DW检验诊断序列的自相关性;
由图可知y与x1和x2的回归方程为:
Y=574062+191.098x1+2.045x2
从输出结果中可以看到DW=0.283,查DW表,n=23,k=2,显著性水平由DW<1.26,也说明残差序列存在正的自相关。
自相关系数,也说明误差存在高度的自相关。
分析:从输出结果中可以看到DW=0.745,查DW表,n=52,k=3,显著性水平 =0.05,dL=1.47,dU=1.64.由DW<1.47,也说明残差序列存在正的自相关。
α
625.0745.02
1121-1ˆ=⨯-=≈DW ρ 也说明误差项存在较高度的自相关。
2.用迭代法处理序列相关,并建立回归方程;
回归方程为:y=-178.775+211.110x1+1.436x2
从结果中看到新回归残差的DW=1.716,
查DW 表,n=52,k=3,显著性水平0.5 由此可知DW 落入无自相关性区
域,说明残差序列无自相关
3.用一阶差分法处理序列相关,并建立回归方程;
从结果中看到回归残差的DW=2.042,根据P 104表4-4的DW 的取值范围来诊断 ,误差项。
《应用回归分析》自变量选择与逐步回归实验报告三

《应用回归分析》自变量选择与逐步回归实验报告二、实验步骤:(只需关键步骤)步骤1:建立全模型;步骤2:用前进法选择自变量;步骤3:用后退法选择自变量;步骤4:用逐步回归法选择自变量。
三、实验结果分析:(提供关键结果截图和分析)1.建立全模型回归方程;2.用前进法选择自变量;由图可知,依次引出x5,x1,x2。
由图可知:最有回归模型为有y^=874.583-0.611x1-0.353x2+0.637x5。
由图可知:最优模型的复决定系数R^2=0.996.调整后的复决定系数R a2=0.995. 最优模型的复决定系数R^2=0.989.调整后的复决定系数R a2=0.988. 最优模型的复决定系数R^2=0.992.调整后的复决定系数R a2=0.991.3.用后退法选择自变量;从图上可以看出:依次剔除变量x4,x3,x6。
从上图可知:最优回归模型为y^=874.583-0.611x1-0.353x2+0.637x5。
最优模型的复决定系数R2=0.996; 调整后的复决定系数R2=0.995。
4.用逐步回归法选择自变量;从右图上可以看出:先依次引入变量x6,x3,x4,x1,x5,x2b, 后又剔除了变量x4 X3,x6, 最终得到只包含两个变量x1,x5,x2b的最优模型。
由图知最有回归模型为,y^=874.53-0.611x1-0.353x2+0.637x5。
最优模型的复决定系数R2=0.996; 调整后的复决定系数R2=0.995。
5.根据以上结果分三种方法的差异。
前进法的特点是:自变量一旦被选入,就永远保留在模型中;前进法的缺点:不能反映自变量选进模型后的变化情况。
后退法的特点是:自变量一旦被剔除,就不能再选入模型;后退法的缺点:开始把全部自变量都引入模型,计算量大。
逐步回归的基本思想是有进出的。
具体做法是将变量一个一个的引入,每引入一个自变量后,对已选入的变量要进行逐个检验,当原引入的变量由于后面变量的引入而变得不再显著时要将其剔除引入一个变量或从回归方程中剔除一个变量,为逐步回归的一步,每一步都要进行F检验,以确保每次引入新的变量之前回归方程中只包含显著的变量。
线性回归算法实验分析

线性回归算法实验分析⼀、线性回归实验⽬标 算法推导过程中已经给出了求解⽅法,基于最⼩乘法直接求解,但这并不是机器学习的思想,由此引⼊了梯度下降⽅法。
实验主要内容: (1)线性回归⽅程实现 (2)梯度下降效果 (3)对⽐不同梯度下降测量 (4)建模曲线分析 (5)过拟合与⽋拟合 (6)正则化的作⽤ (7)提前停⽌策略⼆、实验步骤 ⾸先准备环境,配置画图参数,过滤警告。
import numpy as npimport osimport warningsimport matplotlibimport matplotlib.pyplot as plt# 画图参数设置plt.rcParams['belsize'] = 14plt.rcParams['belsize'] = 12plt.rcParams['belsize'] = 12# 过滤警告warnings.filterwarnings('ignore') 构造数据点(样本):# 通过rand函数可以返回⼀个或⼀组服从“0~1”均匀分布的随机样本值。
随机样本取值范围是[0,1),不包括1X = 2 * np.random.rand(100, 1)# 构造线性⽅程,加⼊随机抖动# numpy.random.randn()是从标准正态分布中返回⼀个或多个样本值# 1.当函数括号内没有参数时,返回⼀个浮点数;# 2.当函数括号内有⼀个参数时,返回秩为1的数组,不能表⽰向量和矩阵# 3.当函数括号内有两个及以上参数时,返回对应维度的数组,能表⽰向量或矩阵。
np.random.randn(⾏,列)# 4.np.random.standard_normal()函数与np.random.randn类似,但是输⼊参数为元组(tuple)y = 3*X + 4 + np.random.randn(100, 1)plt.plot(X, y, 'b.') # b指定为蓝⾊,.指定线条格式plt.xlabel('X_1')plt.ylabel('y')# 设置x轴为0-2,y轴为0-15plt.axis([0, 2, 0, 15])plt.show() 执⾏显⽰数据点如下所⽰:1、线性回归⽅程实现"""线性回归⽅程实现"""# numpy.c_:按⾏连接两个矩阵,就是把两矩阵左右相加,要求⾏数相等。
回归分析

图 2-11-1 销售收入与广告费用散点 从散点图可以看出,随着广告费用的增加,销售收入也随之增加,二者的数 据点分布在一条直线的附近,因此二者之间具有正的线性相关关系。 通过散点图观察可以判断两个变量之间有无相关关系, 并对关系形态做出大 致描述,但要准确度量变量间的关系强度,则需要计算相关系数。 Step2 计算相关系数度量关系强度并对相关系数的可靠性进行检验 (显著性 检验) 相关系数(Correlation Coefficient)是度量两个随机变量之间线性关系 强度的统计量,计算相关系数时,假定两个变量是线性关系。样本相关系数记为
p 2.7415E 09 0.05 ,双尾检验的p值接近于0,拒绝 H 0 ,说明销售收入
与广告费用之间存在显著线性相关关系。 Step3 求销售收入与广告费用的估计的回归方程 回归模型中的参数 0 和 1 是未知的,需要利用样本数据去估计它们。当用
ˆ 和 ˆ 估计模型中的参数 和 时,就得到了估计的回归方程 样本统计量 0 1 0 1
显著的线性关系。从表 3-2知 F 116.396 , p 值接近于0,表明销售收入与广告 费用之间的线性关系显著。 回归系数检验( t 检验):它用于检验自变量对因变量的影响是否显著。在 一元线性回归中,由于只有一个自变量,故回归系数检验与线性关系检验等价。 检验统计量是基于回归系数 1 的抽样分布来构造的 t 统计量。从表2-11-2知 1 的 95%的置信区间为 (4.132,6.130) , 0 的95%的置信区间为 (-4.913,554.013) 。 其中 1 的置信区间表示: 广告费用每变动1万元, 销售收入的平均变动量为4.132 万 6.130万元。 实验2 多元线性回归 一家高技术公司人事部为研究软件开发人员的薪金与他们的资历、 管理水平、 教育水平等因素之间的关系, 要建立一个数学模型,以便分析公司人事策略的合 理性, 并作为新聘用人员薪金的参考。他们认为目前公司人员的薪金总体上是合 理的,可以作为建模的依据,于是调查了46名软件开发人员的档案资料,见表 2-11-3, 其中资历一列指从事专业工作的年数, 管理水平一列中1表示管理人员, 0表示非管理人员,教育水平一列中1表示中学水平,2表示大学水平,3表示研究 生水平。 表2-11-3
实验报告用EXCEL进行相关与回归分析

实验报告用EXCEL进行相关与回归分析
一、实验介绍
本实验通过用Excel进行相关和回归分析,以探讨两个变量之间的关系。
二、实验步骤
(1)首先,在Excel中收集数据,并将这些数据编入表格,表格中
的每一列分别表示变量,每一行表示一组观测数据;
(2)进行相关分析,首先,需要在Excel中计算出两个变量之间的
相关系数,然后判断相关系数的绝对值,确定变量之间的相关关系;
(3)接着,进行回归分析,在回归分析中,可以使用线性回归、非
线性回归等方法,用Excel中的函数计算出回归方程,以及回归系数r2,表示变量之间的回归关系;
(4)最后,根据实验结果,利用Excel拟合数据,画出变量之间的
拟合曲线,作出实验结果的图解;
三、实验结果
本次实验使用的数据集是一组实验观测数据,观测数据为抽样数据,
表示其中一种物品同时装入不同重量时的质量损失情况,两个变量分别为
物品的重量和质量损失。
在相关分析中,使用Excel函数计算出来的两个变量之间的相关系数为:0.837、根据结果可以判断,两个变量之间有较强的相关性。
而在回归分析中,使用Excel函数计算出来的线性回归方程为:
y=0.36x-1.27,回归系数r2为:0.701、由此可以看出,两个变量之间有较强的回归关系。
线性回归分析实验报告总结

RUN;
PROC GPLOT DATA=b;
PLOT RESIDUAL*PREDICTED RESIDUAL*x1 RESIDUAL*x2;
SYMBOL V=DOT I=NONE;
RUN;
PROC IML;
N=31;PI=1;
USE two_6;
READ ALL VAR{x1 x2 y} INTO M;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 2 52294 26147 <.0001
Error12
Corrected Total14 53902
由表中的数据可知:SSE(F)=; =15-4=11,而从第(1)问可知SSE(R)=; =15-3=12;所以检验统计量观测值 =[()/1]/[11]=
X=M[,2]#M[,3];
X2=M[,3];
Y=M[,1];
P=Y||X||X2;
CREATE RESOLVE VAR{Y X X2};
APPEND FROM P;
QUIT;
PROC REG DATA=RESOLVE;
MODEL Y=X X2;
RUN;
PROC PRINT;
RUN;(1)<表一>参数估计的sas输出结果为:
(5)对于给定的X1、X2的值为(X01,X02)=(220,2500),由回归方程 =++得到销售量Y的预测值为
从proc reg过程得到矩阵(XTX)-1为:
令X0=(220,2500)T,因为MSE=,利用sas系统中proc iml过程计算可得
实验项目三:多元线性回归模型分析

实验项目三:多元线性回归模型一、实验目的通过上机实验,使学生掌握计量经济学软件包EViews,运用EViews软件进行多元线性回归模型的分析,用最小二乘法估计参数。
二、预备知识(1)Windows操作系统的常用操作;(2)数据库的基础知识;(3)Excel软件的基本操作;(4)多元线性回归模型的相关理论知识。
三、实验内容1、系统的进入、运行;2、从Excel文件导入数据;3、用EViews软件建立多元线性回归模型并做分析。
四、实验步骤(一)、启动软件包Eviews 的启动步骤:进入Windows /双击Eviews 快捷方式,进入EViews 窗口;或点击开始 /程序/ Eviews 3/EViews3.1,进入E Views 窗口。
(二)、创建工作文件具体操作过程。
1、打开新建对象类型对话框,选择工作文件W orkfile,2、打开工作文件时间频率和样本区间对话框,选择数据频率为“Annual”,样本区间为1978年至2000年。
3、点击O K 确认,得新建工作文件窗口。
(三)、把Excel数据导入到EViews1、打开实验二所用到的数据文件(sy2.xls),选定人均居民消费和人均GDP 两列数据后复制(注意:不用选定数据名称),回到Windows桌面或硬盘的任意目录,右击鼠标新建一个文本文件,把刚才从Excel中复制的数据粘贴到新的文本文件。
2、回到EViews的工作文件窗口,点击Procs/Import/Read Text-Lotus-Excel…,选择刚才建设的文本文件后将会出现“ASCII Text Import”窗口,在“Name for series or Numbers of Series if names in file ”栏目,输入两列数据的名称,分析是consp和gdpp,如图3-1所示。
按OK后,将会把数据导入到EViews,如图3-2所示。
(四)、回归分析1、在经济理论指导下,设定如下的理论模型:0121t t t t consp gdpp gdpp βββε-=+++ (3-1)(图3-1)(图3-2)2、对以上理论模型作普通最小二乘法估计:在主菜单选 Q uick \Estimate Equations ,进入输入估计 方程对话框, 输入待估计方程,选择估计方法—普通最小二乘法,如图3-3所示。
市场调查与预测实验——回归分析

残差项
▼回归分析的主要目的:根据样本回归函数, 估计总体回归函数。
注意:这里总体回归函 数可能永远无法知道。
一、 回归模型的构建
❖一元线性回归模型
Y 0 1X
❖一元线性回归模型的基本假设 1. 对模型设定的假设 2. 对解释变量的假设 3. 对随机误差项的假设
二、 回归模型的检验
F检验
F检验是根据平方和分解式,直接从回归效果检验回归方 程的显著性。
F SSR /1 SSE / (n 2)
总平方和SST中,包括能够由自变量解释的部分SSR,以及 不能由自变量解释的部分SSE。回归平方和SSR越大,回归 的效果就越好。
回归分析的内容
线性回归
一元线性回归 多元线性回归 多个因变量与多个自变量的回归
假设1:回归模型是正确设定的。
假设2:解(释1)变模量型X是选确择定了性正变确量的,变不量是;随机变量,在重复抽 样(中2取)固模定型值选。择了正确的函数形式;
假设3:解释变量X在所抽取的样本中具有变异性,而且随着 样本容量的无限增加,解释变量X的样本方差趋于一 个非零的有限常数。
假设4:随机误差项µ具有给定X条件下的零均值、同方差以 及不序列相关性。
❖ 回归分析关心的是根据解释变量的已
知或给定值,考察被解释变量的总体均 值,即当解释变量取某个确定值时,与 之统计相关的被解释变量所有可能出现 的对应值的平均值。
研究过程:将该99户家庭划分为组内收入差不多的10 组,以分析每一收入组的家庭消费支出。
E(Y|X)=f(X)
一、 回归模型的构建
❖总体回归函数 E(Y|X)=f(X)
函数的具体 形式?
3500
每 月 消 费 2000 1500 1000
应用的回归分析报告报告材料实验三多元线性回归

实验三:多元线性回归实验内容习题一(P64例3.1)(1)打开SPSS软件,输入数据如下(部分):选择“分析”中“回归--线性”,以y为应变量,以x1-x9为自变量,点击“确定”得:所以得回归方程为:y=1.465x1+2.575x2+2.005x3+0.891x5+0.67x6+0.28x7+11.405x8-160.711x9-2721.493从回国方程可以看到,x1-x9对居民的消费支出起正影响,x9对居民的消费性支出起负影响。
(2)F检验。
用SPSS软件计算出的方差分析图如下:从输出结果可知,Sig即显著性P值,由P值为0.000可知,此回归方程高度显著。
t检验。
通过定性分析,先剔除x4,用y与其他8个变量做回归分析,计算结果如下图:剔除x4之后,仍然有不显著的自变量,此时最大的P值为p8=0.827,因此进一步剔除x8,用y与其余6个变量作回归,回归系数表如下图:T检验中,依次剔除P值最大的自变量,直到最后所有的自变量在显著性水平为0.05时都显著。
习题二(P93.例4.3)(1)打开SPSS软件,输入数据如下图:(2)建立y对x的普通最小二乘回归,决定系数R2=0.912,回归标准差为247.62.方差分析表和回归系数输出表如下:(3)在原始数据中增加一列变量RES_1,即残差值,如图:然后以x(居民收入)为x轴,残差值为y轴画散点图:从残差图看出,误差项具有明显的异方差性,误差随着x的增加而呈现出增加的趋势。
(4)计算等级相关系数。
先计算出残差的绝对值,如图:然后选择分析中的“相关--双变量”,选择x和e为变量,在相关系数一栏里选择Spearman 打钩,点击确定即得到等级相关系数,如下图所示:从上图可知,相关系数为0.686,P值=2.055E-5,即残差绝对值e与自变量x显著相关,存在异方差。
(5)用加权最小二乘法来消除异方差。
选择“分析”中“回归--权重估计”,以x为自变量,y为因变量,对x进行加权估计,得:然后画出加权最小二乘残差图,如下:比较前后两幅残差图,可以得出,加权最小二乘估计的效果好于普通最小二乘估计效果。
实验数据分析方法_回归分析

0.10
0.9877 0.9000 0.8054 0.7293 0.6694 0.6215 0.5822 0.5494 0.5214 0.4973 0.4762 0.4575 0.4409 0.4259 0.4124 0.4000 0.3887 0.3783 0.3687 0.3598 0.3233 0.2960 0.2746 0.2573 0.2428 0.2306 0.2108 0.1954 0.1829 0.1726 0.1638
上式右边第二项是回归值ŷ与平均值 y 之差的平方和,我们
称它为回归平方和,并记为U: U (y ˆ k y ) 2 ( b 0 b x k b 0 b x ) 2
k
b2 (xkx)2.
— 可以看出,回归平方和U是由于x的变化而引起的。因
此U反映了在y的总的变化中由于x和y的线性关系而引起
解之可得:
b
xkyk
xk yk N
(xk x)(yk y)
xk2N 1( xk)2
(xk x)2
b0N 1( ykb xk)ybx,
实验数据分析方法_Chap.6
8
其中 1 N
1N
xNk1xk,
y Nk1
yk.
在给定参数估计值b, b0后,可得到相应的回归方程 (或回归函数)为: yˆ b0 bx.
0.05
0.9969 0.9500 0.8783 0.8114 0.7545 0.7067 0.6664 0.6319 0.6021 0.5760 0.5529 0.5324 0.5139 0.4973 0.4821 0.4683 0.4555 0.4438 0.4329 0.4227 0.3809 0.3494 0.3246 0.3044 0.2875 0.2732 0.2500 0.2319 0.2172 0.2050 0.1946
计量经济学_三元线性回归模型案例分析

计量经济学_三元线性回归模型案例分析计量经济学课程设计班级:学号:姓名:2011年1⽉⼀,问题设计改⾰开放以来,随着经济体制的改⾰深化和经济的快速增长,中国的财政收⽀状况发⽣了很⼤的变化,中央和地⽅的税收收⼊1978年为519.28亿元到2002年已增长到17636.45亿元25年间增长了33倍。
为了研究中国税收收⼊增长的主要原因,分析中央和地⽅税收收⼊的增长规律,预测中国税收未来的增长趋势,需要建⽴计量经济学模型。
⼆,理论基础影响中国税收收⼊增长的因素很多,但据分析主要的因素可能有:(1)从宏观经济看,经济整体增长是税收增长的基本源泉。
(2)公共财政的需求,税收收⼊是财政的主体,社会经济的发展和社会保障的完善等都对公共财政提出要求,因此对预算指出所表现的公共财政的需求对当年的税收收⼊可能有⼀定的影响。
(3)物价⽔平。
我国的税制结构以流转税为主,以现⾏价格计算的DGP等指标和和经营者收⼊⽔平都与物价⽔平有关。
(4)税收政策因。
我国⾃1978年以来经历了两次⼤的税制改⾰,⼀次是1984—1985年的国有企业利改税,另⼀次是1994年的全国范围内的新税制改⾰。
税制改⾰对税收会产⽣影响,特别是1985年税收陡增215.42%。
但是第⼆次税制改⾰对税收的增长速度的影响不是⾮常⼤。
因此可以从以上⼏个⽅⾯,分析各种因素对中国税收增长的具体影响。
为了反映中国税收增长的全貌,选择包括中央和地⽅税收的‘国家财政收⼊’中的“各项税收”(简称“税收收⼊”)作为被解释变量,以放映国家税收的增长;选择“国内⽣产总值(GDP)”作为经济整体增长⽔平的代表;选择中央和地⽅“财政⽀出”作为公共财政需求的代表;选择“商品零售物价指数”作为物价⽔平的代表。
由于税制改⾰难以量化,⽽且1985年以后财税体制改⾰对税收增长影响不是很⼤,可暂不考虑。
所以解释变量设定为可观测“国内⽣产总值(GDP)”、“财政⽀出”、“商品零售物价指数”三,数理经济学⽅程Y = C(1) + C(2)*XY i=β0+β2X2+β3X3+β4X4四,计量经济学⽅程设定线性回归模型为:Y i=β0+β2X2+β3X3+β4X4+µ五,数据收集从《国家统计局》获取以下数据:年份财政收⼊(亿元)Y 国内⽣产总值(亿元)X2财政⽀出(亿元)X3商品零售价格指数(%)X41985 2040.79 8964.4 2004.25 108.8 1986 2090.73 10202.2 2204.91 106 1987 2140.36 11962.5 2262.18 107.3 1988 2390.47 14928.3 2491.21 118.5 1989 2727.4 16909.2 2823.78 117.81990 2821.86 18547.9 3083.59 102.1 1991 2990.17 21617.8 3386.62 102.9 1992 3296.91 26638.1 3742.2 105.4 1993 4255.3 34636.4 4642.3 113.2 1994 5126.88 46759.4 5792.62 121.7 1995 6038.04 58478.1 6823.72 114.8 1996 6909.82 67884.6 7937.55 106.1 1997 8234.04 74462.6 9233.56 100.8 1998 9262.8 78345.2 10798.18 97.4 1999 10682.58 82067.5 13187.67 97 2000 12581.51 89468.1 15886.5 98.5 2001 15301.38 97314.8 18902.58 99.2 2002 17636.45 104790.6 22053.15 98.7六,参数估计利⽤eviews软件可以得到Y关于X2的散点图:可以看出Y和X2成线性相关关系Y关于X3的散点图:可以看出Y和X3成线性相关关系Y关于X4的散点图:Dependent Variable: YMethod: Least SquaresDate: 01/09/10 Time: 13:16Sample: 1978 2002Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C -2582.755 940.6119 -2.745825 0.0121X2 0.022067 0.005577 3.956633 0.0007X3 0.702104 0.033236 21.12474 0.0000X4 23.98506 8.738296 2.744821 0.0121R-squared 0.997430 Mean dependent var 4848.366Adjusted R-squared 0.997063 S.D. dependent var 4870.971S.E. of regression 263.9591 Akaike info criterion 14.13511Sum squared resid 1463163. Schwarz criterion 14.33013Log likelihood -172.6889 F-statistic 2717.254Durbin-Watson stat 0.948521 Prob(F-statistic) 0.000000模型估计的结果为:Y i=-2582.755+0.022067X2+0.702104X3+23.98506X4(940.6119) (0.0056) (0.0332) (8.7383)t={-2.7458} {3.9567} {21.1247} {2.7449}R2=0.997 R2=0.997 F=2717.254 df=21七,相关检验1.经济意义检验模型估计结果说明,在假定其他变量不变的情况下,当年GDP 每增长1亿元,税收收⼊就会增长0.02207亿元;在假定其他变量不变的情况下,当年财政⽀出每增长1亿元,税收收⼊就会增长0.7021亿元;在假定其他变量不变的情况下,当零售商品物2.统计检验(1)拟合优度:R2=0.997,修正的可决系数为R2=0.997这说明模型对样本拟合的很好。
实验报告简单线性回归分析

西南科技大学Southwest University of Science and Technology经济管理学院计量经济学实验报告——多元线性回归的检验专业班级:姓名: 学号: 任课教师: 成绩:简单线性回归模型的处理实验目的:掌握多元回归参数的估计和检验的处理方法。
实验要求:学会建立模型,估计模型中的未知参数等。
试验用软件:Eviews实验原理:线性回归模型的最小二乘估计、回归系数的估计和检验。
实验内容:1、实验用样本数据:运用Eviews软件,建立1990-2001年中国国内生产总值X和深圳市收入Y的回归模型,做简单线性回归分析,并对回归结果进行检验。
以研究我国国内生产总值对深圳市收入的影响。
经过简单的回归分析后得出表EQ1:Depe ndent Variable: Y Method: Least Squares Date: 11/27/11 Time: 14:02 Sample: 1990 2001 In cluded observati ons: 12 VariableCoefficientStd. Error t-Statistic Prob.C -3.611151 4.161790 -0.867692 0.4059 X0.134582 0.003867 34.80013 0.0000 R-squared0.991810 Mean depe ndent var 119.8793 Adjusted R-squared 0.990991 S.D. dependent var 79.361247.02733 S.E. of regressi on7.532484 Akaike infocriteri on8Sum squared resid 567.3831 Schwarz criteri on 7.1081561211.0490.00000Log likelihood-40.16403F-statisticDurbin-Wats on stat 2.051640 Prob(F-statistic)其中拟合优度为:0.991810有很强的线性关系2、实验步骤: 1、 回归分析:(1) 在 Objects 菜单中点击 New objects ,在 New objects 选择 Group ,并以GROUP01定义文件名,点击 OK 出现数据编辑窗口,, 按顺序键入数据。
实验三相关分析与回归分析

实验三相关分析与回归分析一、实验目的:1.掌握相关分析的概念及意义,并熟练掌握对数据进行相关分析的操作步骤;2.了解相关分析过程中各参数的意义及选择,以及结果阅读;3.充分理解相关与偏相关的涵义;4.掌握常用回归分析原理及操作步骤;5.掌握回归参数的正确选择及回归结果的科学解释二、主要内容:二元定距变量的相关分析(pearson);二元定序变量的相关分析;(spearman, kendall’s tau-b)(注:当资料不服从双变量正态分布,或总体分布型未知,或原始数据是用等级表示时,宜用Spearman 或Kendall 相关)偏相关分析;线性回归分析;曲线估计;逻辑回归分析;三、上机练习:练习1:数据文件3-1,调查了某地1962年~1988年国民收入与城乡居民储蓄存款余额,利用相关分析分析二者的关系。
并尝试用城乡居民储蓄存款余额预测国民收入。
练习2:数据文件3-2,调查了某公司员工当前工资,起始工资,工作经验及受教育年限,试分析四者之间的关系。
尝试建立一个以起始工资,工作经验及受教育年限等为自变量,当前工资为因变量的回归模型。
练习3:数据文件3-3,调查了松柏的生长情况,分析其月生长量与月平均气温、月降雨量、月平均日照时数、月平均湿度这四个气候因素哪个因素有关。
练习4:调用数据文件3-4,分析mpg(每加仑汽油行使里程)与weight(车重)的相互关系,制作观测量数据的散点图,根据分析结果,选择并最终确定最佳回归模型。
练习5:根据某医院对癌症患者的调查数据3-5,其中的变量包括年龄(age)、患病时间(time)、肿瘤扩散等级(pathscat)、肿瘤大小(pathssize)、肿瘤史(histgrad)和癌变部位的淋巴结是否含有癌细胞(ln_yesno),试建立相关模型,对癌变部位的淋巴结是否含有癌细胞的情况进行预测。
统计回归模型实验报告(3篇)

第1篇一、实验背景与目的随着社会科学和自然科学研究的深入,统计分析方法在各个领域得到了广泛应用。
回归分析作为统计学中一种重要的预测和描述方法,在经济学、医学、心理学等领域发挥着重要作用。
本次实验旨在通过EViews软件,对统计回归模型进行实践操作,掌握回归分析的原理和方法,并验证模型在实际问题中的应用效果。
二、实验内容与步骤1. 数据准备(1)收集实验所需数据:选取某地区近五年居民消费支出与居民收入作为实验数据。
(2)数据整理:将数据录入EViews软件,并进行必要的预处理,如剔除异常值、缺失值等。
2. 模型设定(1)根据实验目的,设定回归模型为:消费支出= β0 + β1 居民收入+ ε,其中β0为截距项,β1为居民收入对消费支出的影响系数,ε为误差项。
(2)选择合适的回归模型:根据实验数据特点,选择线性回归模型进行建模。
3. 模型估计(1)在EViews软件中,输入数据并选择线性回归模型。
(2)进行参数估计:利用最小二乘法(OLS)估计模型参数,得到β0和β1的估计值。
4. 模型检验(1)检验模型的整体拟合优度:计算R²、F统计量等指标,判断模型是否显著。
(2)检验参数估计的显著性:进行t检验,判断β0和β1是否显著异于零。
(3)检验误差项的正态性:进行正态性检验,判断误差项是否符合正态分布。
5. 模型应用(1)预测居民消费支出:利用估计出的模型,预测居民收入在一定范围内的消费支出。
(2)分析居民收入对消费支出的影响:根据β1的估计值,分析居民收入对消费支出的影响程度。
三、实验结果与分析1. 模型整体拟合优度根据实验数据,计算R²为0.9,F统计量为35.12,表明模型整体拟合优度较好,可以用于预测和描述居民消费支出与居民收入之间的关系。
2. 参数估计的显著性t检验结果显示,β0和β1的t值分别为2.12和3.45,均大于临界值,表明β0和β1在统计上显著异于零,居民收入对消费支出有显著影响。
计量经济学 实验3 多元回归模型

目录目录 (1)一、建立多元线性回归模型 (3)(一) 建立包括时间变量的三元线性回归模型; (3)1. 建立工作文件:CREATE A 78 94 (3)2. 输入统计资料:DATA Y L K (3)3. 生成时间变量t:GENR T=@TREND(77) (3)4. 建立回归模型:LS Y C T L K (3)(二) 建立剔除时间变量的二元线性回归模型; (4)(三) 建立非线性回归模型——C-D生产函数。
(5)二、比较、选择最佳模型 (8)(一) 回归系数的符号及数值是否合理; (8)(二) 模型的更改是否提高了拟合优度; (8)(三) 模型中各个解释变量是否显著; (8)(四) 残差分布情况 (8)实验三多元回归模型【实验目的】掌握建立多元回归模型和比较、筛选模型的方法。
【实验内容】建立我国国有独立核算工业企业生产函数。
根据生产函数理论,生产函数的基本形式为:()ε,tY=。
其中,L、K分别为生产过程中投入的劳动与资金,fL,K,时间变量t反映技术进步的影响。
表3-1列出了我国1978-1994年期间国有独立核算工业企业的有关统计资料;其中产出Y为工业总产值(可比价),L、K分别为年末职工人数和固定资产净值(可比价)。
资料来源:根据《中国统计年鉴-1995》和《中国工业经济年鉴-1995》计算整理【实验步骤】一、 建立多元线性回归模型(一) 建立包括时间变量的三元线性回归模型;在命令窗口依次键入以下命令即可:1. 建立工作文件: CREATE A 78 942. 输入统计资料: DATA Y L K3. 生成时间变量t : GENR T=@TREND(77)4. 建立回归模型: LS Y C T L K则生产函数的估计结果及有关信息如图3-1所示。
图3-1 我国国有独立核算工业企业生产函数的估计结果 因此,我国国有独立工业企业的生产函数为:K L t y 7764.06667.06789.7732.675ˆ+++-= (模型1)t =(-0.252) (0.672) (0.781) (7.433)9958.02=R 9948.02=R 551.1018=F 模型的计算结果表明,我国国有独立核算工业企业的劳动力边际产出为0.6667,资金的边际产出为0.7764,技术进步的影响使工业总产值平均每年递增77.68亿元。
《应用回归分析 》---多元线性回归分析实验报告

《应用回归分析》---多元线性回归分析实验报告
二、实验步骤:
1、计算出增广的样本相关矩阵
2、给出回归方程
Y=-65.074+2.689*腰围+(-0.078*体重)3、对所得回归方程做拟合优度检验
4、对回归方程做显著性检验
5、对回归系数做显著性检验
三、实验结果分析:
1、计算出增广的样本相关矩阵相关矩阵
2、给出回归方程
回归方程:Y=-65.074+2.689*腰围+(-0.078*体重)
3、对所得回归方程做拟合优度检验
由表可知x与y的决定性系数为r2=0.800,说明模型的你和效果一般,x与y 线性相关系数为R=0.894,说明x与y有较显著的线性关系,当F=33.931,显著性Sig.p=0.000,说明回归方程显著
4、对回归方程做显著性检验
5、对回归系数做显著性检验
Beta的t检验统计量t=-6.254,对应p的值接近0,说明体重和体内脂肪比重对腰围数据有显著影响
6、结合回归方程对该问题做一些基本分析
从上面的分析过程中可以看出腰围和脂肪比重以及腰围和体重的相关性都是很大的,通过检验可以看出回归方程、回归系数也很显著。
其次可以观察到腰围、脂肪比重、体重的数据都是服从正态分布的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 回归分析1.为了分析X 射线的杀菌作用,用200千伏的X 射线来照射细菌,每次照射6分钟用平板计数法估计尚存活的细菌数,照射次数记为 t ,照射后的细菌数y 如表1所示。
表1 X 射线照射次数与残留细菌数试求:①给出y 与t 的二次函数回归模型;②在同一坐标系内做出原始数据与拟合结果的散点图;③预测t=16时残留的细菌数;④根据问题实际意义,你认为选择多项式函数是否合适?⑤给出非线性回归模型,并预测照射16次后细菌残留数目。
解:(1)实验程序: t=1:15;y=[352 211 197 160 142 106 104 60 56 38 36 32 21 19 15];rstool(t',y','purequadratic')结果如图1所示:468101250100150200250300350图1在Matlab 工作区中输入命令:beta ,rmsebeta =347.8967 -51.1394 1.9897 rmse =22.2649所以y 与t 的二次回归模型函数:29897.11394.518967.347t t y +-= (2)画出同一坐标散点图,如图2所示,程序如下: [p,s]=polyfit(t,y,2); Y=polyconf(p,t,y); plot(t,y,'k+',t,Y,'r')05101550100150200250300350400图2 散点图(3)当t=16时,计算程序如下: [p,s]=polyfit(t,y,2); Y=polyconf(p,16); 结果是:Y =39.0396即说明预测残留的细菌数y=39.0396个;(4)用二次函数计算出细菌残留数为39.0396,显然与实际不相符合。
根据实际问题的意义可知:尽管二次多项式拟合效果较好,但是用于预测并不理想。
因此,如何根据原始数据散点图的规律,选择适当的回归曲线是非常重要的,因此有必要研究非线性回归分析。
(5)由(2)散点图可知,可以假设将要拟合的的非线性模型为t /b ae y =对将要拟合的非线性模型t /b ae y =,建立的M-文件volum.m 如下: function yhat=volum(beta,t) yhat=beta(1)*exp(beta(2).*t);%输入数据 t=1:15;y=[352 211 197 160 142 106 104 60 56 38 36 32 21 19 15]; beta0=[150,0]';%求回归系数[beta,r,J]=nlinfit(t',y','volum',beta0); betay=nlpredci('volum',16,beta,r,J)得结果:beta =400.0905 -0.2240,y =11.1014,即回归模型为:t e y 2240.0-0905.400=,那么根据此模型我们可以知道:当t=16时,残留的细菌数y=11.1014,很显然这样的结果会更令人满意!2.某销售公司将库存占用资金情况、广告投入的费用、员工薪酬以及销售额等方面的数据作了汇总(表 2),该公司试图根据这些数据找到销售额与其他变量之间的关系,以便进行销售额预测并为工作决策提供参考依据。
(1)建立销售额的回归模型;(2)如果未来某月库存资金额为150万元,广告投入预算为45万元,员工薪酬总额为27万元,试根据建立的回归模型预测该月的销售额。
表2 库存资金额、广告投入、员工薪酬、销售额汇总表(单位:万元)月份 库存资金额(x1) 广告投入(x2) 员工薪酬总额(x3) 销售额(y)1 75.2 2 77.63 80.74 76.05 79.56 81.87 67.78 98.39 74.0 10 151.0 11 90.8 12 102.3 13 115.6 14 125.0 15 137.8 16 175.6 17 155.2 18 174.3解:首先,作出因变量与各自变量的样本散点图,如图3所示,程序如下:x1=[75.2 77.6 80.7 76.0 79.5 81.8 67.7 98.3 74.0 151.0 90.8 102.3 115.6 125.0 137.8 175.6 155.2 174.3];x2=[30.6 31.3 33.9 29.6 32.5 27.9 24.8 23.6 33.9 27.7 45.5 42.6 40.0 45.8 51.7 67.2 65.0 65.4];x3=[21.1 21.4 22.9 21.4 21.5 21.7 21.5 21.0 22.4 24.7 23.2 24.3 23.1 29.1 24.6 27.5 26.5 26.8];y=[1090.4 1133.0 1242.1 1003.2 1283.2 1012.2 1098.8 826.3 1003.3 1554.6 1199.0 1483.1 1407.1 1551.3 1601.2 2311.7 2126.7 2256.5]; subplot(1,3,1),plot(x1,y,'g*'); subplot(1,3,2),plot(x2,y,'k+'); subplot(1,3,3),plot(x3,y,'ro');21.1 21.4 22.9 21.4 21.5 21.7 21.5 21.0 22.4 24.7 23.2 24.3 23.1 29.1 24.6 27.5 26.5 26.8 1090.4 1133.0 1242.1 1003.2 1283.2 1012.2 1098.8 826.3 1003.3 1554.6 1199.0 1483.1 1407.1 1551.3 1601.2 2311.7 2126.7 2256.530.6 31.3 33.9 29.6 32.5 27.9 24.8 23.6 33.9 27.7 45.5 42.6 40.0 45.8 51.7 67.2 65.0 65.4图3 因变量y 与各自变量的样本散点图从图上可以看出这些点大致分布在一条直线旁边,因此有较好的线性关系,可以采用线性回归。
设回归方程为:3322110ˆˆˆˆˆx x x y ββββ+++=,建立M-文件输入如下程序:x1=[75.2 77.6 80.7 76.0 79.5 81.8 67.7 98.3 74.0 151.0 90.8 102.3 115.6 125.0 137.8 175.6 155.2 174.3];x2=[30.6 31.3 33.9 29.6 32.5 27.9 24.8 23.6 33.9 27.7 45.5 42.6 40.0 45.8 51.7 67.2 65.0 65.4];x3=[21.1 21.4 22.9 21.4 21.5 21.7 21.5 21.0 22.4 24.7 23.2 24.3 23.1 29.1 24.6 27.5 26.5 26.8];y=[1090.4 1133.0 1242.1 1003.2 1283.2 1012.2 1098.8 826.3 1003.3 1554.6 1199.0 1483.1 1407.1 1551.3 1601.2 2311.7 2126.7 2256.5]; n=18;m=3;x=[ones(n,1),x1',x2',x3'];[b,bint,r,rint,s]=regress(y',x,0.05); b,bint,r,rint,s运行后即得到结果如表3所示表3 对初步回归模型的计算结果残差列向量r =[44.0394 59.3264 96.5750 -35.3239 179.3461 -36.4116 180.2202 -244.3408 -99.0812 84.1521 -184.5600 67.5082 -33.4048 -89.1104 -159.6274 69.7451 44.7425 56.2050]T对应残差的)1(α-置信区间rint 如下:[-228.8318,316.9105]、 [-214.8092,333.4620] [-173.5015,366.6515]、 [-311.2066,240.5589] [-75.9312,434.6233]、 [-313.1813, 240.3581] [-69.6357,430.0762]、 [-449.7576,-38.9240] [-365.7729,167.6105]、 [-69.8815,238.1857] [-428.0384,58.9185]、 [-208.3399,343.3563] [-312.3682, 245.5587]、[-199.0870,20.8662] [-415.9094,96.6547]、 [-172.6973,312.1875] [-207.2697,296.7547]、 [-186.8695,299.2794]。
因此得到初步的回归方程为:3215698.92879.157252.59075.53-ˆx x x y+++=,当未来某月库存资金额为150万元,广告投入预算为45万元,员工薪酬总额为27万元,那么根据所建立的回归模型可以预测出该月的销售额为1751.2万元。
3.葛洲坝机组发电耗水率的主要影响因素为库水位、出库流量。
现从数据库中将 2005年10月某天15时-16时06分范围内的出库流量、库水位对应的耗水率读取处理,数据如表4所示,试利用多元线性回归分析方法建立耗水率与出库流量、库水位的模型。
(表4数据来源:余波,多元线性回归分析在机组发电耗水率中的应用,计算机与现代化,2008(2))表4 耗水率与出库流量、库水位数据时间 库水位(米) 出库流量 机组发电耗水率 (年-月-天-时) (立方米) (立方米/万千瓦)解:首先,作出耗水率y 与各自变量的样本散点图,如图4所示,程序如下:x1=[65.08 65.10 65.12 65.17 65.21 65.37 65.38 65.39 65.40 65.43 65.47 65.53 65.62 65.58 65.70 65.84];x2=[15607 15565 15540 15507 15432 15619 15536 15514 15519 15510 15489 15437 16355 14708 14393 14296];y=[60.46 60.28 60.10 59.78 59.44 59.25 58.91 58.76 58.73 58.63 58.48 58.31 57.96 57.06 56.43 55.83]; subplot(1,2,1),plot(x1,y,'g*'); subplot(1,2,2),plot(x2,y,'k+');x 104图4 耗水率y 与库水位、出库量关系散点图65.08 65.10 65.12 65.17 65.21 65.37 65.38 65.39 65.40 65.43 65.47 65.53 65.62 65.58 65.70 65.842005-10-15:00 2005-10-15:02 2005-10-15:04 2005-10-15:06 2005-10-15:08 2005-10-15:10 2005-10-15:12 2005-10-15:14 2005-10-15:16 2005-10-15:18 2005-10-15:20 2005-10-15:22 2005-10-16:00 2005-10-16:02 2005-10-16:04 2005-10-16:0615607 15565 15540 15507 15432 15619 15536 15514 15519 15510 15489 15437 16355 14708 14393 1429660.46 60.28 60.10 59.78 59.44 59.25 58.91 58.76 58.73 58.63 58.48 58.31 57.96 57.06 56.43 55.83从散点图中可以看出机组发电耗水率y 与库水位1x 有较好的线性关系,而与出库流量2x 的关系难以确定,可以采用建立二次函数的回归模型。
