九年级数学下册第二十九章投影与视图292三视图2922由三视图想象出立体图形课时训练.docx
九年级数学下册第二十九章投影与视图29.2三视图2教学课件新版新人教版

导入新课
由于三视图不仅反映了物体的形状,而且反映了 各个方向的尺寸大小,设计人员可以把自己构思的物 体用三视图表示出来,再由工人制造出符合各种要求 的机器、工具、生活用品等,因此三视图在许多行业 有着广泛的应用.
导入新课
前面我们讨论了由立体图形(实物)画出三 视图,那么由三视图能否想象出立体图形(实 物)呢?
新课讲解
【例1】如图,分别根据三视图(1)(2)说出立体 图形的名称.
(1)
(2)
新课讲解
分析:由三视图想象立体图形时,首先分别根 据主视图、俯视图和左视图想象立体图形的前面、 上面和左侧面,然后再综合起来考虑整体图形.
新课讲解
(1)
(1)从三个方向看立体图 形,视图都是矩形,可以想 象这个立体图形是长方体, 如图所示:
x=1或x=2.
主视图
x1 2y 俯视图
y=3.
课堂小结
1.一个视图不能确定物体的空间形状,根据三视 图要描述几何体或实物原型时,必须将各视图对照起 来看.
2.一个摆好的几何体的视图是唯一的,但从视图 反过来考虑几何体时,它有多种可能性.例如,正方 体的主视图是正方形,但主视图是正方形的几何体有 直三棱柱、长方体、圆柱等.
3.对于较复杂的物体,有三视图想象出物体的原 型,应搞清三个视图之间的前后、左右、上下的对 应关系.
新课讲解
由左视图 可知,物体左侧有 两个面的视图是矩形,它们的 交线是一条棱(中间的实线表 示),可见到.综合各视图可 知,物体的形状是正五棱柱.
解:物体是正五棱柱, 如图所示.
新课讲解
【例3】某工厂要加工一批密封罐,设计者给出了密 封罐的三视图(如下图),请按照三视图确定制作每 个密封罐所需钢板的面积(图中尺寸单位:mm).
人教版九年级下册第29章投影与视图29.2三视图教案

3.成果展示:每个小组将向全班展示他们的讨论成果和绘制的三视图。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“三视图在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
-掌握三视图的绘制方法:学生需要掌握如何根据几何体在三个不同视图上的投影来绘制三视图,包括投影线、隐藏线、轮廓线等的正确表达。
-能够识别和绘制简单几何体的三视图:通过实际操作,学生应能够对常见的几何体如立方体、圆柱体、圆锥体等的三视图进行识别和绘制。
2.教学难点
-空间想象能力的培养:对于一些空间想象能力较弱的学生,理解几何体与其三视图之间的对应关系是一大难点。例如,如何从二维的视图想象出三维的形状。
3.重点难点解析:在讲授过程中,我会特别强调三视图的绘制方法和视图之间的相互关系这两个重点。对于难点部分,如隐藏线和投影线的处理,我会通过实物模型和示例图来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与三视图相Байду номын сангаас的实际问题,如如何根据三视图还原一个几何体。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解三视图的基本概念。三视图是指主视图、左视图和俯视图,它们分别从不同角度展示物体的形状。三视图是工程绘图和建筑设计中不可或缺的部分,它帮助我们更直观地理解物体的三维结构。
2.案例分析:接下来,我们来看一个具体的案例。通过一个简单的立方体,演示如何绘制三视图,并讲解三视图在实际中的应用。
-实际应用中的三视图理解:将三视图的知识应用到实际问题中,如解读建筑图纸或机械图纸,对于学生来说是一个挑战,需要他们将理论知识与实践相结合。
2019版九年级数学下册 第二十九章 投影与视图 29.2 三视图(第1课时)教学课件1 新人教版

【解析】四棱锥的三视图如图
正
左
视
视
图
图
俯 视 图
【例题】 【例1】画出如图所示一些基本几何体的三视图.
圆柱 (1)
球 (2)
正三棱柱 (3)
宽相等
主视图
左视图
俯视图
宽相等:俯视图和左视图共同反映了物体前后方向的尺寸.
俯
左
球体
主
【跟踪训练】
1.下图是底面为等腰直角三角形的三棱柱的俯视图,尝
试画出它的主视图和左视图,并与同伴交流.
主视图
正面
主视图
左视图 高
长
宽
宽 俯视图
三视图位置有规定,主 视图要在左上边,它的 下方应是俯视图,左视 图坐落在右边.
主视图
左视图 高
长
宽
宽 俯视图
【跟踪训练】
下面的四组图中,是如图所示的圆柱体的三视图的是( B )
主视图
左视图
A
俯视图
主视图 左视图
B
俯视图
主视图 左视图
C
俯视图
主视图 左视图
主视图
左视图
俯视图(1)Βιβλιοθήκη 主视图俯视图(2)
左视图
2.下图是底面为等腰梯形的四棱柱的俯视图,尝试画出 它的主视图和左视图,并与同伴交流.
主视图
左视图
俯视图(3)
主视图
俯视图(4)
左视图
【例2】画出此小零件的三视图
主 视 图
左 视 图
俯 视 图
【跟踪训练】
正视图
画出此物体的三视图
侧视图
俯视图
三视图 主视图——从正面看到的图 左视图——从左面看到的图 俯视图——从上面看到的图 画物体的三视图时,要符合如下原则:
人教版九年级下册数学作业课件 第二十九章 投影与视图 三视图 第2课时 由三视图确定几何体

只给出两种视图时,往往个数不确定.
(建议用时:10 分钟)
1.若一个几何体的主视图、左视图、俯视图都是正
方形,则这个几何体是( A )
A.正方体
B.圆锥
C.圆柱
D.球
2.一个几何体的三视图如图所示,则这个几何体是
(D)
A.球体
B.圆锥
解:(1)组成这个物体的小正方体的个数可能是 4 或 5.
(2)求这个几何体的最大表面积.
解:(2)这个几何体的最大表面积是 3×2+3×2+5×2 =22.
C.棱柱
D.圆柱
3.如图是一个由 5 个相同的正方体组成的立体图形 的俯视图,方框内数字为对应位置上的小正方体的 个数,它的左视图是( A )
பைடு நூலகம்
4.一张桌子上重叠摆放了若干枚面值一元的硬币, 从三个不同方向看它得到的平面图形如图所示,那 么桌上共有 9 枚硬币.
5.如图是由若干个相同的小正方体(棱长为 1)组成 的几何体的主视图和俯视图. (1)组成这个物体的小正方体的个数可能是多少?
知识要点 由三视图确定几何体 内容
由三视图想象几何体的形状,首先,应分别根据主视图、俯视图 由三视图确
和左视图想象几何体的 前面 、 上面 和 左面 的形状, 定几何体
然后综合起来考虑整体形状. 一个摆好的几何体的三视图是唯一的,当从视图反过来考虑几何 体时,它有多种可能性.如:根据三视图确定小正方体的个数问 题.先由俯视图确定物体在平面上的形状,再根据主视图和左视 解题策略 图确定各行各列的高度.较方便的做法是在俯视图的相应位置标
29.2 三视图 初中数学人教版九年级下册精品讲义

第二十九章投影与视图29.2 三视图课程标准课标解读1.会画直棱柱、圆柱、圆锥、球的主视图、左视图、俯视图,能判断简单物体的视图,并会根据视图描述简单的几何体。
2.了解直棱柱、圆锥的侧面展开图,能根据展开图想象和制作模型。
3.通过实例,了解上述视图与展开图在现实生活中的应用。
理解和掌握三视图的基本概念,能够画出棱柱、圆柱、圆锥、球的主视图,能够正确判断简单物体的三视图。
知识点01 三视图1.三视图有关的概念(1)视图:从某一方向观察一个物体时,所看到的平面图形叫作物体的一个视图。
(2)三视图:从3个互相垂直的方向观察物体,在正面内得到的由前向后观察物体的视图,叫作主视图;在水平面内得到的由上向下观察物体的视图,叫作俯视图;在侧面内得到的由左向右观察物体的视图,叫作左视图。
【微点拨】(1)视图的本质就是正投影;物体的主视图,等同于一束平行光线自物体的前方向后方照射,在正面投影面上得到的正投影;俯视图、左视图类似。
(2)三视图中的各视图,分别从不同方向表示物体的形状,三者结合能够较全面地反映物体的形状.2. 三视图之间的关系三视图的摆放一般是,主视图在左上方,它下方应是俯视图,左视图在右边.在物体的三视图中,主视图可反映出物体的长和高,俯视图可反映出物体的长和宽,左视图可反映出物体的高和宽.【微点拨】三视图中,主视图与俯视图表示同一物体的长;主视图与左视图表示同一物体的高;左视图与俯视图表示同一物体的宽.【即学即练1】如图所示的几何体,其主视图是()A .B .C .D .【答案】A 【分析】从正面看所得到的图形即为主视图,据此求解即可.【详解】解:从正面看看到的是一个长方形,中间有两条竖着的虚线,即,故选A 知识点02 画三视图1.画几何体的三视图画一个几何体的三视图时,先观察几何体,判断出从3个方向看几何体得到的平面图形,即三视图;然后把三视图按照一定位置画出来。
画三视图时,一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,被其他部分遮挡而看不见的画成虚线,不能漏掉。
新人教版九年级数学下册第29章投影与视图29.2三视图第2课时

•
14、抱最大的希望,作最大的努力。2 021年4 月4日 星期日 上午9时 25分21 秒09:2 5:2121. 4.4
•
15、一个人炫耀什么,说明他内心缺 少什么 。。202 1年4月 上午9 时25分2 1.4.409 :25Apri l 4, 2021
•
16、业余生活要有意义,不要越轨。2 021年4 月4日 星期日9 时25分 21秒09 :25:214 April 2021
(2)从正面、侧面看立体图形,图象都是等腰三角形;ቤተ መጻሕፍቲ ባይዱ上面看, 图象是圆;可以想象出:整体是圆锥,如图所示
例5 根据物体的三视图摸索物体的现状.
分析:由主视图可知,物体正面是正五边形;由俯视图可知,由上向 下看物体是矩形的,且有饮棱(中间的实线)可见到,两条棱(虚线) 被遮挡;由左视图 可知,物体的侧面是矩形的,且有饮棱(中间的 实线)可见到.综合各视图可知,物体是五棱柱现状的.
•
17、一个人即使已登上顶峰,也仍要 自强不 息。上 午9时25 分21秒 上午9 时25分0 9:25:21 21.4.4
谢谢大家
引言
前面我们讨论了由立体图形(实物) 画出三视图,下面我们讨论由三视图 想象出立体图形(实物).
例4 根据三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和 左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑 整体图形. 解: (1)从三个方向看立体图形,图象都是矩形,可以想象出: 整体是长方体,如图所示.
解:物体是五棱柱现状的,如图所示.
练习 由三视图想象实物现状:
实
物
实
物
实
实
物
物
九年级数学下册 第二十九章 投影与视图 29.2 三视图 29.2.3 由三视图到展开图

5.一个(yī ɡè)几何体的三视图如图K-27-6所示,则该几何体的表面
积为( D )
A.4π
B.3π
C.2π+4
D.3π+4
[解析] D 观察该几何体的三视图发现(fāxiàn)其
为半圆柱,半圆柱的直径为2,故其表面积为 π×12+(π+2)×2=3π+4.故选D.
2021/12/11
第九页,共二十五页。
图K-27-6
3课时 第
(kèshí)
由三视图到展开图
6.一个长方体的三视图如图 K-27-7 所示,若其俯视图为正方
形,则这个长方体的表面积为( A )
A.66
B.48
C.48 2+36
D.57
2021/12/11
第十页,共二十五页。
图K-27-7
课时 第3
(kèshí)
由三视图到展开图
7.如图 K-27-8 是一个包装纸盒的三视图(单位:cm),则制作
2021/12/11
第十九页,共二十五页。
第3课时(kèshí) 由三视图到展开图 12.求图K-27-13中的三视图所表示(biǎoshì)的几何体的体积.
2021/12/11
图K-27-13
第二十页,共二十五页。
第3课时(kèshí) 由三视图到展开图
[解析] 由主视图和左视图的上半部分(bù fen)的矩形及俯视图中对应部分(bù fen)是圆,可以想象出该几何体的上半部分(bù fen)是一个圆柱;由主视图和左 视图的下半部分(bù fen)的矩形及俯视图相应的矩形,可以想象出该几何体的 下半部分(bù fen)是长方体,于是该几何体如图所示.
解:该几何体的体积(tǐjī)V=2×4×6+π×12×3=(48+3π)cm3.
九年级数学下册第二十九章投影与视图29.2三视图2教学课件新版新人教版

第二十九章 投影与视图
29.2 三视图(2)
一、新课引入
二、新课讲解
前面我们讨论了由立体图形(实物) 画出三视图,下面我们讨论由三视图 想象出立体图形(实物).
二、新课讲解
例1 根据三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和 左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑 整体图形. 解: (1)从三个方向看立体图形,图象都是矩形,可以想象出: 整体是长方体,如图所示.
四、强化训练
根据几何体的三视图画出它的表面展开图:
实 物
展 开 图
四、强化训练
展
开
实
图
物
四、强化训练
根据三视图描述物体的形状,试画出物体的表面展开图.
主
左
视
视
图
图
俯 视 图
实
物
展
形
开
状
图
四、强化训练
下面是一个物体的三视图,试说出它的形状
四、强化训练
用小立方块搭出符合下列三视图的几何体:
主视图
二、新课讲解
(2)从正面、侧面看立体图形,图象都是等腰三角形;从上面看, 图象是圆;可以想象出:整体是圆锥,如图所示
二、新课讲解
例2 根据物体的三视图摸索物体的现状.
分析:由主视图可知,物体正面是正五边形;由俯视图可知,由上向 下看物体是矩形的,且有一条棱(中间的实线)可见到,两条棱(虚 线)被遮挡;由左视图 可知,物体的侧面是矩形的,且有一条棱 (中间的实线)可见到.综合各视图可知,物体是五棱柱现状的.
全的人,主要是担心漏掉重要内容,影响以后的复习与思考.,这样不仅失去了做笔记的意义,也将课堂“听”与“记”的关系本末倒置了﹙太忙于记录, 便无暇紧跟老师的思路﹚。 如果只是零星记下一些突出的短语或使你感兴趣的内容,那你的笔记就可能显得有些凌乱。 做提纲式笔记因不是自始至终全都埋头做笔记,故可在听课时把时间更多地用于理解所听到的内容.事实上,理解正是做好提纲式笔记的关键。 课堂笔记要注意这五种方法:一是简明扼要,纲目清楚,首先要记下所讲章节的标题、副标题,按要点进行分段;二是要选择笔记语句,利用短语、数 字、图表、缩写或符号进行速记;三是英语、语文课的重点词汇、句型可直接记在书页边,这样便于复习时查找﹙当然也可以记在笔记本上,前提是你 能听懂﹚;四是数理化生等,主要记老师解题的新思路、补充的定义、定理、公式及例题;五是政治、历史等,着重记下老师对问题的综合阐述。
届九年级数学下册 第29章 投影与视图 29.2 三视图 画三视图课件 (新版)新人教版.ppt

数据,可以算出图1中液体的体积为
dm234.(提示:V=底面积×高)
指出正方体六个面在平面H上的正投影图形;
解:图1中,液体形状为三棱柱(填几何体的名称); 利用图2中数据,可以算出图1中液体的体积为 V液=3×4×4÷2=24(dm3). 故答案为:三棱柱,24
7
王师傅买来九块木板,要自己做一个书架.现在有两个书架的样子, 请你观察一下,再猜一猜,王师傅做的是哪个样子的书架,并说明 理由.
画三视图
2
主视图
与投影关系
正面
侧视图
左视图
侧面 水平面
3
视图与投影的关系
三视图就是物体 的三个正投影
4
画三视图
主视图
左视图 高平齐
长对正
宽相等
俯视图Leabharlann 5作三视图 6一透明的敞口正方体容器ABCD-A′B′C′D′装有一些有色液体,棱AB始终在水平桌面上,容器底部的倾斜
角为α (注:图1中∠CBE=α,图2中BQ=3dm).探究:如图1,液面刚好过棱CD,并与棱BB′交于点Q ,其三视图及尺寸如图2所示,那么:图1中,液体形状为 三棱柱 (填几何体的名称);利用图2中
人教版初中数学九年级下册第二十九章投影与视图29.2三视图第3课时由三视图到表面展开图作业设
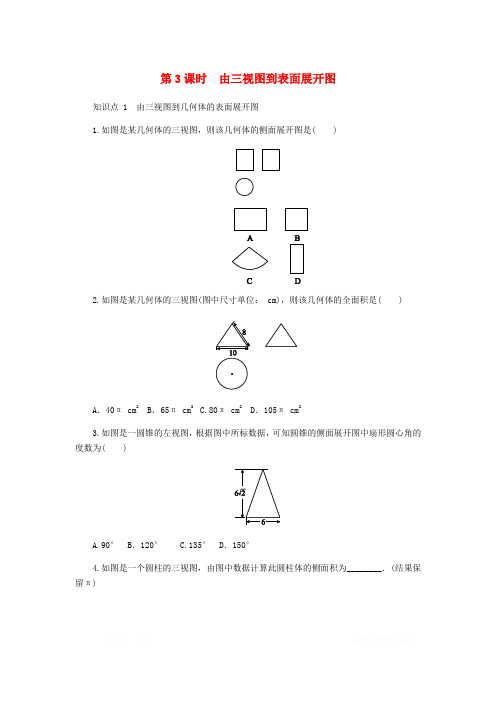
第3课时由三视图到表面展开图知识点 1 由三视图到几何体的表面展开图1.如图是某几何体的三视图,则该几何体的侧面展开图是( )2.如图是某几何体的三视图(图中尺寸单位: cm),则该几何体的全面积是( )A.40π cm2 B.65π cm2 C.80π cm2 D.105π cm23.如图是一圆锥的左视图,根据图中所标数据,可知圆锥的侧面展开图中扇形圆心角的度数为( )A.90° B.120° C.135° D.150°4.如图是一个圆柱的三视图,由图中数据计算此圆柱体的侧面积为________.(结果保留π)5.如图是三个几何体的三视图和展开图,请将同一物体的三视图和展开图搭配起来.A与______;B与______;C与______.6.根据图中的三视图画出该物体的展开图.知识点 2 由物体的展开图想象物体的三视图7.某物体的侧面展开图如图,那么它的左视图为( )8.如图是一个几何体的展开图,下面哪一个平面图形不是它的三视图中的一个视图( )9.如图是某个几何体的表面展开图,则把该几何体平放在平面上时,其俯视图为( )10.如图是某几何体的展开图.(1)这个几何体的名称是__________;(2)画出该几何体的三视图;(3)求这个几何体的体积(π取3.14).能力提升11.一个圆锥的左视图如图,则这个圆锥的侧面展开图(扇形)的弧长为( )A.2πB.4π C.6 D.6π12.一个圆柱的侧面展开图是两邻边长分别为6和8的矩形,则该圆柱的底面圆的半径是( )A.3πB.4πC.3π或4πD.6π或8π13.如图是某种型号的正六角螺母毛坯的三视图,求它的表面积.14.如图是一个几何体的三视图,若主视图的高为25,俯视图中等边三角形的边长为10,求这个几何体的表面积.15.如图是一个几何体的三视图.(1)写出这个几何体的名称;(2)根据图中所示数据计算这个几何体的全面积;(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请求出蚂蚁爬行的最短路程.参考答案1.A [解析] 由三视图可知此几何体为圆柱,它的侧面展开图为矩形,且矩形的一边为圆柱的高,另一边为圆柱的底面圆的周长.故选A.2.B [解析] 由主视图和左视图为三角形可判断出该几何体是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;根据三视图知:该圆锥的母线长为8 cm ,底面半径为10÷ 2=5(cm),故表面积为12×2πrl +πr 2=π×5×8+π×52=65π(cm 2).3.B [解析] ∵圆锥的底面直径为6,∴半径为3,圆锥的底面周长为6π.∵圆锥的高是6 2,∴圆锥的母线长为32+(6 2)2=9.设扇形的圆心角为n °,∴n π×9180=6π,解得n =120,即圆锥的侧面展开图中扇形的圆心角的度数为120°.故选B.4. 24π [解析] 由图可知,圆柱的底面直径为4,高为6,所以侧面积为4×π×6= 24π.5. c a b [解析] A 为正三棱柱,B 为圆锥,C 为正方体.6.解:展开图如图所示.7.B8.D [解析] 由几何体的展开图可知该几何体为正六棱柱,若A 项是它的俯视图,则B 项是它的主视图,C 项是它的左视图.故选D.9.B10.解:(1)圆柱. (2)三视图如图所示.(3)这个几何体的体积为πr 2h ≈3.14×52×20=1 570.11.D [解析] 根据圆锥的左视图可知底面圆的直径为6,母线长为5,∴这个圆锥的侧面展开图的弧长为πd =6π.故选D.12.C13.解:S 侧面=2×3×6=36(cm 2),S 底面=12×2×(32×2)×6=6 3(cm 2),∴S 表面=36+2×6 3=36+12 3(cm 2).14.解:根据题意可得正三角形的高为102-52=5 3,∴俯视图的面积为12×10×5 3=25 3,∴这个几何体的表面积为3×25×10+2×25 3=750+50 3.15.(1)圆锥.(2)由三视图知该圆锥底面直径为4 cm ,母线长为6 cm ,∴圆锥的侧面积S 侧=12×4π×6=12π(cm 2),底面圆的面积为π(42)2=4π(cm 2),故该几何体的全面积为12π+4π=16π(cm 2).(3)由圆锥的母线长为6 cm ,底面圆的半径为2 cm ,可得此圆锥侧面展开图扇形的圆心角为120°,半径为6 cm ,如图,连接AB ′,B ′C ,则∠B ′AC =60°,∴△AB ′C 为等边三角形,B ′D 的长为蚂蚁所爬的最短路程. ∵D 为AC 的中点, ∴B ′D ⊥AC ,∴B ′D =AB ′2-AD 2=62-32=3 3(cm), 即蚂蚁爬行的最短路程为3 3 cm.。
人教版九年级数学下册课件:29.3课题学习 制作立体模型 (共14张PPT)

二、新课讲解
(1)指出其中哪些可耀折叠成多面体、把上面的图形 描在综上,剪下来,叠一叠,验证你的答案; (2)画出由上面图形能折叠成的多面体的三视图,并 指出三视图中是怎样体现“长对正,高平齐,宽相等” 的; (3)如果上图中小三角形的边长为1,那么对应的多 面体的体积和表面积各是多少?
二、新课讲解
2.(2015黔西南州)下面几个几何体,主视图是 圆的是 (B )
A
B
C
D
五、布置作业
画出下面几何体的三视图.
六、结束语
数学是研究现实生活中数量关系 和空间形式的数学. ——恩格斯
• • • • • • • • • • • • • • • • • • • • • • •
15、如果没有人为你遮风挡雨,那就学会自己披荆斩棘,面对一切,用倔强的骄傲,活出无人能及的精彩。 16、成功的秘诀在于永不改变既定的目标。若不给自己设限,则人生中就没有限制你发挥的藩篱。幸福不会遗漏任何人,迟早有一天它会找到你。 17、一个人只要强烈地坚持不懈地追求,他就能达到目的。你在希望中享受到的乐趣,比将来实际享受的乐趣要大得多。 18、无论是对事还是对人,我们只需要做好自己的本分,不与过多人建立亲密的关系,也不要因为关系亲密便掏心掏肺,切莫交浅言深,应适可而止。 19、大家常说一句话,认真你就输了,可是不认真的话,这辈子你就废了,自己的人生都不认真面对的话,那谁要认真对待你。 20、没有收拾残局的能力,就别放纵善变的情绪。 15、所有的辉煌和伟大,一定伴随着挫折和跌倒;所有的风光背后,一定都是一串串揉和着泪水和汗水的脚印。 16、成功的反义词不是失败,而是从未行动。有一天你总会明白,遗憾比失败更让你难以面对。 17、没有一件事情可以一下子把你打垮,也不会有一件事情可以让你一步登天,慢慢走,慢慢看,生命是一个慢慢累积的过程。 18、努力也许不等于成功,可是那段追逐梦想的努力,会让你找到一个更好的自己,一个沉默努力充实安静的自己。 19、你相信梦想,梦想才会相信你。有一种落差是,你配不上自己的野心,也辜负了所受的苦难。 20、生活不会按你想要的方式进行,它会给你一段时间,让你孤独、迷茫又沉默忧郁。但如果靠这段时间跟自己独处,多看一本书,去做可以做的事,放下过去的人,等你度过低潮,那些独处的时光必定能照亮你的路,也是这些不堪陪你成熟。所以,现在没那么糟,看似生活对你的亏欠,其实都是祝愿。 5、心情就像衣服,脏了就拿去洗洗,晒晒,阳光自然就会蔓延开来。阳光那么好,何必自寻烦恼,过好每一个当下,一万个美丽的未来抵不过一个温暖的现在。 6、无论你正遭遇着什么,你都要从落魄中站起来重振旗鼓,要继续保持热忱,要继续保持微笑,就像从未受伤过一样。 7、生命的美丽,永远展现在她的进取之中 ;就像大树的美丽,是展现在它负势向上高耸入云的蓬勃生机中;像雄鹰的美丽,是展现在它搏风击雨如苍天之魂的翱翔中;像江河的美丽,是展现在它波涛汹涌一泻千里的奔流中。 8、有些事,不可避免地发生,阴晴圆缺皆有规律,我们只能坦然地接受;有些事,只要你愿意努力,矢志不渝地付出,就能慢慢改变它的轨迹。 9、与其埋怨世界,不如改变自己。管好自己的心,做好自己的事,比什么都强。人生无完美,曲折亦风景。别把失去看得过重,放弃是另一种拥有 ;不要经常艳羡他人,人做到了,心悟到了,相信属于你的风景就在下一个拐弯处。 10、有些事想开了,你就会明白,在世上,你就是你,你痛痛你自己,你累累你自己,就算有人同情你,那又怎样,最后收拾残局的还是要靠你自己。 11、人生的某些障碍,你是逃不掉的。与其费尽周折绕过去,不如勇敢地攀登,或许这会铸就你人生的高点。 12、有些压力总是得自己扛过去,说出来就成了充满负能量的抱怨。寻求安慰也无济于事,还徒增了别人的烦恼。 13、认识到我们的所见所闻都是假象,认识到此生都是虚幻,我们才能真正认识到佛法的真相。钱多了会压死你,你承受得了吗?带,带不走,放,放不下。时时刻刻发悲心,饶益众生为他人。 14、梦想总是跑在我的前面。努力追寻它们,为了那一瞬间的同步,这就是动人的生命奇迹。 15、懒惰不会让你一下子跌倒,但会在不知不觉中减少你的收获 ;勤奋也不会让你一夜成功,但会在不知不觉中积累你的成果。人生需要挑战,更需要坚持和勤奋!
2019-2020学年九年级数学下册 第29章 投影与视图 29.2 三视图(2)课件 新人教版

h
4
活动三:例题探究
例1 如图所示,分别根据三视图说出立体图形的名称.
【思考】 (1)长方体与圆锥的三视图分别是什么形状? (2)如果一个物体的三个视图均是长方形,那么这个物体是什么形状? (3)如果一个物体的主视图和左视图是等腰三角形,俯视图是带圆心的圆,那么这 个物体的形状是什么? (4)由三视图想象几何体,分别通过观察哪个视图确定几何体的前面、左面和上面?
答:由三视图描述几何体(或实物原型),一般步骤为: ① 想象:根据三视图想象从不同方向看到的几何体形状; ② 定形:综合确定几何体(或实物原型)的形状; ③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线 的位置,以及各个方向的尺寸.
2.知识拓展: (1)由一个视图不能确定物体的空间形状,根据三视图描述几何体形状或实物原型时,必 须将各视图对照起来看. (2)一个摆好的几何体的三视图是唯一的,但从视图反过来考虑几何体时,它有多种可能 性.例如,正放的正方体的主视图是正方形,但主视图是正方形的几何体还可能是长方体、 圆柱等.
29.2 三视图(2)
h
1学习Leabharlann 标1.直观想象目标:学会根据物体的三视图描述出几何体的 基本形状或实物原型,进一步发展空间想象能力.(重点) 2.数学抽象目标:通过观察探究等活动使学生能根据物体 的三视图还原出物体的形状,进一步认识立体图形与平面图 形之间的转化关系.(难点)
h
2
活动一:新课导入
h
7
活动五:检测反馈
h
8
活动五:检测反馈
h
9
活动五:检测反馈
h
10
活动五:检测反馈
h
11
解:(1)从三个方向看立体图形,视图都是矩形,可以想象出这个立体图形是长方体, 如图(1)所示. (2)从正面、侧面看立体图形,视图都是等腰三角形,从上面看,视图是带圆心的圆, 可以想象这个立体图形是圆锥,如图(2)所示.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时 由三视图想象出立体图形
葛础自我诊断
关键问答
① 如何rti 三视图判断儿何体?
② 从主视图、左视图、俯视图上分别能读出几何体的哪些量?
1. ①一个几何体的三视图如图29-2-27所示,这个几何体是() A.圆锥B.圆柱C.三棱锥D.三棱柱
2. ②某商品的外包装盒的三视图如图29-2-28所示,则这个包装盒的侧血积为(
主视图 左视图
俯视图
图 29-2-28
A. 150 兀 cm'
B. 200 兀 cm 2
C. 300 兀 cm 2
D. 400 兀 cm 2
考向提升训练
命题点1由三视图判断简单几何体[热度:97%] 3. ③某儿何体的主视图和左视图如图29-2-29所示,则该儿何体可能是() O O 主视图 左视图
图 29-2-29
A.长方体
B.圆锥
C.圆柱
D.球
解题突破
③ 熟记一些常见几何体的三视图对解决此类问题非常有帮助.
4. 下列各视图中,能组成一个立体图形的三种视图的是()
图 29-2-30
知识复习习题化
俯视图
图
29-2-27
能力备考课时化
10 cm
A.①②⑥
B.①③⑤
C.②③⑤
D.②③④
命题点2由三视图判断组合体[热度:96%]
5. ④某几何体的主视图和左视图完全一样,均如图29-2-31所示,则该几何体的俯视 图不可能是()
模型建立
④ 市两种视图确定的儿何体是不唯一的,事实上,It!三种视图确定的儿何体也可能不唯 6.
如图29-2-33所示的三视图所对应的几何体是( )
图 29-2-34
命题点3由三视图计算对应几何体的有关量[热度:94%]
7. 一个几何体的三视图如图29-2-35所示,则该几何体的表面积为(
) D n
2
主视图 左视图
图 29-2-32
主视图 左视图
俯视图
图 29-2-33
俯视图
图29-2-35
A. 4兀
B. 3n
C. 2 Ji +4
D. 3n +4
8.2017・凉山州如图29-2-36是一个儿何体的三视图,则该儿何体的侧面积是()
图 29-2-36
A. 兀
B. 10 n
C. 20 兀
D. 4 *^13
9. ⑤一个三棱锥的三视图如图29-2-37所示,这个三棱锥最长棱的长度为
方法点拨
⑤ 由三视图还原三棱锥,利用三视图,结合勾股定理分别计算各条棱长.
10. ⑥如图29-2-38是某儿何体的三视图,根据图中数据,求得该儿何体的体积为
f
10
1
< 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ■ 主视图
图 29-2-38
解题突破
⑥ 该几何体的体积为大圆柱的体积减去小圆柱的体积.
11. 己知直三棱柱的三视图如图29-2-39,在△川艸中,ZJ^V=90o , PN=L sin
, 4
z/w=-
5 ⑴求加及兀的长;
(2) 若主视图与左视图相似,求的长;
(3) 在(2)的条件下,求直三棱柱的表面积.
左视图
14-A
主视图 左视图
俯视图
主视图 1
左视图
俯视图
图 29-2-37
俯视图
图 29-2-39
命题点4由三视图推断小正方体的个数[热度:98%]
12. 如图29-2-40是由儿个大小相同的小正方体搭成的儿何体的俯视图,小正方形中 的数字表示该位置上的小正方体的个数,则该几何体的左视图是()
1
2 3
1
图 29-2-40
图 29-2-41
13. 如图29-2-42是由一些完全相同的小正方体搭成的几何体的主视图和左视图,则
图 29-2-42
A. 5
B. 6
C. 7
D. 8
14. 2017・齐齐哈尔一个几何体的主视图和俯视图如图29-2-43所示,若这个几何体 最多由臼个小正方体组成,最少由方个小正方体组成,则a+b 等于( )
组成这个儿何体的小止方体的个数最少是(
A
B D 主视图
俯视图 m
A. 10
B. 11
C. 12
D. 13
15. °如图29-2-44 由若干个相同的小立方体搭成的几何体的俯视图和左视图,则
组成这个儿何体的小立方体的个数可能是()
图 29-2-44
A.5或6
B.5或7
C.4或5或6
D. 5或6或7
方法点拨
⑦ 已知组合体的左视图、俯视图,判断组成该几何体的小正方体的数量范围的步骤:在 俯视图的方格中标上由左视图所看到的小正方体的最高层数,将这些数字填入所在横行上的 每一个方格屮,则可得到组成这个儿何体所需最多的小正方体的个数;因为由俯视图可以确 定底层小正方体的个数,所以方格中的数字最小为1,所以只要将每横行上的数字留一个不 变,英余的均改为1,就可以确定组成这个几何体所需最少的小正方体的个数.
思维拓展培优 培优找尖活动代
16. ⑧如图29-2-45是某种工件的三视图,某工厂要铸造5000件这种铁质工件,要用 去多少吨生铁?工件铸成后,表面需要涂一层防锈漆,已知1 kg 防锈漆可以涂4 nF 的 铁器面,涂完这批工件要用多少千克防锈漆?(铁的密度为7.8 g/cm\图中尺寸单位: cm)
JO. 1 1
n 1 r 1 I 主视图 左视图 -30——>
l 10J
1—^20
10
俯视图
图 29-2-45
解题突破
⑧ 先根据三视图计算工件的体积和表而积,再利用体积乘密度等于质暈,表面积(IB?)除 以4等于所需防锈漆的千克数进行汁算.
主视图 俯極图 图
29-2-43
详解详析
1. D
2. A
3. C
4. Q [解析]②③⑤能组成一个直四棱柱的三视图.
5. r
6.(7
7. D [解析]由该几何体的三视图可知其为半个圆柱,半圆柱的直径为2,高为2, 故其表面积为穴X 1~+(乃+2) X 2 = 3兀+4.
故选ZZ
8. A [解析]由三视图可知此几何体为圆锥,根据三视图的尺寸可得圆锥的底面半径 为2,高为3,・••圆锥的母线长为羽辰=莎,・・・圆锥的底面周长=圆锥的侧面展开扇形 的弧长=2疗r = 2 〃X2 = 4开,:・圆锥的侧面积=*X4 “X 寸河=2 乃.故选/.
9. 2迈 [解析]还原儿何体如图,由题意得AB=2, BC = 2, DE=BE=CE=1, BD=CD
10. 70 乃
11. 解:(1)在俯视图中过点P 作PK 丄MN 于点K,由图可知BC=MN, FG=PK.
4 、 、 PN 4
•••在 必△PMN 中,S7/?ZPMN=—=7,PN=4,
MN o
・・・MN=5, ・・・BC=5, .*.PM=^MN 2-PN 2
=3.
▼ PK 4
又 Vs7/?ZPMN=—=-,
PM o
4 12
•\PK=7X3=—
□ □
12 (2)・・•矩形ABCD 与矩形EFGH 相似,且AB=EF, ・翌=匹P 1J AB =A ••FG_EF' 1 12_
AB ・・・AB=2萌(负值已舍去).
⑶直三棱柱的表面积为*X3X4X2+(5 + 3 + 4) X2书=12 + 24书.
12. A 13. J
14. C [解析]根据主视图可知俯视图屮第一列最高有3块,第二列最高有1块, .\a = 3X2 + l = 7, b = 3+l + l = 5,
.\a + b = 7 + 5 = 12.
=谑,AD=&, AC = 2 yfi
,则 AB 2=12,
15.D[解析]由俯视图易得最底层有4个小立方体,由左视图易得第二层最多有3 个小立方体,最少有1个小立方体,那么小立方体的个数可能是5或6或7.
16.解:・・•一件工件的体积为(30X10+10X10)X20=8000(血),
・・・一件工件的质量为8000X 7. 8 = 62400 (g),
62400 尸62. 4 kg,
・•・铸造5000件这种铁质工件需生铁5000X62.4 = 312000滋=312&).
•・•一件工件的表面积为 2 X (30 X 20 + 20 X 20 + 10 X 30 + 10 X 10) =2800©/)= 0.
28 (异),
・•・涂完这批工件需要防锈漆5000X0. 284-4 = 350(^).
【关键问答】
①由三视图判断几何体,首先分别根据主视图、俯视图和左视图想象几何体的前面、上
而和左侧而,然后综合起来考虑整体图形并进行取舍.
②从主视图上能读出儿何体的长与高,从俯视图上能读出儿何体的长与宽,从左视图上
能读111几何体的宽与高.。
