人教版 八年级数学 14.2 乘法公式 课时训练(含答案)
8年级数学人教版上册同步练习14.2乘法公式(含答案解析)

14.2乘法公式专题一乘法公式1.下列各式中运算错误的是()A.a2+b2=(a+b)2-2ab B.(a-b)2=(a+b)2-4abC.(a+b)(-a+b)=-a2+b2D.(a+b)(-a-b)=-a2-b22.代数式(x+1)(x-1)(x2+1)的计算结果正确的是()A.x4-1 B.x4+1 C.(x-1)4D.(x+1)43.计算:(2x+y)(2x-y)+(x+y)2-2(2x2-xy)(其中x=2,y=3).专题二乘法公式的几何背景4.请你观察图形,依据图形面积之间的关系,不需要连其他的线,便可得到一个你非常熟悉的公式,这个公式是()A.(a+b)(a-b)=a2-b2B.(a+b)2=a2+2ab+b2C.(a-b)2=a2-2ab+b2D.(a+b)2=a2+ab+b25.如图,你能根据面积关系得到的数学公式是()A.a2-b2=(a+b)(a-b)B.(a+b)2=a2+2ab+b2C.(a-b)2=a2-2ab+b2D.a(a+b)=a2+ab6.我们在学习完全平方公式(a+b)2=a2+2ab+b2时,了解了一下它的几何背景,即通过图来说明上式成立.在习题中我们又遇到了题目“计算:(a+b+c)2”,你能将知识进行迁移,从几何背景说明(大致画出图形即可)并计算(a+b+c)2吗?状元笔记【知识要点】1.平方差公式(a+b)(a-b)=a2-b2,两个数的和与这两个数的差的积,等于这两个数的平方差.2.完全平方公式(a±b)2=a2±2ab+b2,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.【温馨提示】1.不要将平方差公式和完全平方公式相混淆,注意它们项数和符号的不同.2.完全平方公式中,中间项是左边两个数的和的2倍,注意系数的特点.【方法技巧】1.公式中的字母a、b可以是具体的数,也可以是单项式、多项式.只要符合公式的结构特征,就可以利用公式.2.有些题目往往不能直接应用公式求解,但稍做适当的变形后就可以用乘法公式求解.如:位置变化,符号变化,数字变化,系数变化,项数变化等.参考答案:1.D 解析:A中,由完全平方公式可得(a+b)2-2ab=a2+2ab+b2-2ab=a2+b2,故A正确;B中,由完全平方公式可得(a-b)2=a2-2ab+b2,(a+b)2-4ab=a2+2ab+b2-4ab=a2-2ab+b2,故B正确;C中,由平方差公式可得(a+b)(-a+b)=(a+b)(b-a)=b2-a2=-a2+b2,故C正确;D中,(a+b)(-a-b)=-(a+b)2=-a2-2ab-b2,故D错误.2.A 解析:原式=(x2-1)(x2+1)=(x2)2-1=x4-1.3.解:原式=4x2-y2+x2+2xy+y2-4x2+2xy=x2+4xy,当x=2,y=3时,原式=22+4×2×3=4+24=28.4.B 解析:这个图形的整体面积为(a+b)2;各部分的面积的和为a2+2ab+b2;所以得到公式(a+b)2=a2+2ab+b2.故选B.5.C 解析:从图中可知:阴影部分的面积是(a-b)2和b2,剩余的矩形面积是(a-b)b和(a-b)b,即大阴影部分的面积是(a-b)2,∴(a-b)2=a2-2ab+b2,故选C.6.解:(a+b+c)2的几何背景如图,整体的面积为:(a+b+c)2,用各部分的面积之和表示为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,所以(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.。
人教版 八年级上册数学 14.2 乘法公式 同步课时训练(含答案) (2)

14.2 乘法公式同步训练一、选择题1. 计算(-a-b)2的结果是()A.a2+b2B.a2+2ab+b2C.a2-b2D.a2-2ab+b22. 将202×198变形正确的是()A.2002-4 B.2022-4C.2002+2×200+4 D.2002-2×200+43. 若a2+ab+b2=(a-b)2+X,则整式X为()A.ab B.0 C.2ab D.3ab4. 化简(-2x-3)(3-2x)的结果是()A.4x2-9 B.9-4x2C.-4x2-9 D.4x2-6x+95. 若(2x+3y)(mx-ny)=9y2-4x2,则m,n的值分别为() A.2,3 B.2,-3C.-2,-3 D.-2,36. 将9.52变形正确的是()A.9.52=92+0.52 B.9.52=(10+0.5)×(10-0.5) C.9.52=92+9×0.5+0.52 D.9.52=102-2×10×0.5+0.52 7. 计算(x+1)(x2+1)·(x-1)的结果是()A.x4+1 B.(x+1)4C.x4-1 D.(x-1)48. 若(x+a)2=x2+bx+25,则()A.a=3,b=6B.a=5,b=5或a=-5,b=-10C.a=5,b=10D.a=-5,b=-10或a=5,b=109. 如图①,边长为a的大正方形中有四个边长均为b的小正方形,小华将阴影部分拼成了一个长方形(如图②),则这个长方形的面积为()A.a2-4b2B.(a+b)(a-b)C.(a+2b)(a-b)D.(a+b)(a-2b)10. 如图,阴影部分是边长为a的大正方形剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是()A .①②B .②③C .①③D .①②③二、填空题11. 如果(x +my )(x -my )=x 2-9y 2,那么m =________.12. 填空:()22121453259x y x y ⎛⎫-=- ⎪⎝⎭13. 如果(x -ay )(x +ay )=x 2-9y 2,那么a = .14. 若x -y =6,xy =7,则x 2+y 2的值等于________.15. 如图,四张全等的矩形纸片拼成的图形,请利用图中空白部分面积的不同表示方法,写出一个关于a 、b 的恒等式___________.ab ba16. 根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是____________________.三、解答题17. 计算:(41)(41)a a ---+18. 阅读材料后解决问题.小明遇到一个问题:计算(2+1)×(22+1)×(24+1)×(28+1).经过观察,小明发现将原式进行适当的变形后,可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)×(22+1)×(24+1)×(28+1)=(2-1)×(2+1)×(22+1)×(24+1)×(28+1)=(22-1)×(22+1)×(24+1)×(28+1)=(24-1)×(24+1)×(28+1)=(28-1)×(28+1)=216-1.请你根据小明解决问题的方法,试着解决下列问题:(1)计算:(2+1)×(22+1)×(24+1)×(28+1)×(216+1);(2)计算:(3+1)×(32+1)×(34+1)×(38+1)×(316+1);(3)化简:(m +n )(m 2+n 2)(m 4+n 4)(m 8+n 8)(m 16+n 16).19. 观察下列各式:(x-1)(x+1)=x2-1;(x-1)(x2+x+1)=x3-1;(x-1)(x3+x2+x+1)=x4-1;…(1)(x-1)(x4+x3+x2+x+1)=________;(2)根据规律可得:(x-1)(x n-1+…+x+1)=________(其中n为正整数);(3)计算:(3-1)(350+349+348+…+32+3+1);(4)计算:(-2)2020+(-2)2019+(-2)2018+…+(-2)3+(-2)2+(-2)+1.20. 认真阅读材料,然后回答问题:我们初中学习了多项式的运算法则,相应地,我们可以计算出多项式的展开式,如:(a+b)1=a+b,(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,….下面我们依次对(a+b)n展开式的各项系数进一步研究发现,当n取正整数时可以单独列成如图所示的形式:上面的多项式展开系数表称为“杨辉三角形”.仔细观察“杨辉三角形”,用你发现的规律回答下列问题:(1)(a+b)n展开式中共有多少项?(2)请写出多项式(a+b)5的展开式.答案一、选择题1. 【答案】B[解析] 原式=(-a)2-2·(-a)·b+b2=a2+2ab+b2.2. 【答案】A[解析] 202×198=(200+2)×(200-2)=2002-4.3. 【答案】D4. 【答案】A[解析] 原式=(-2x-3)(-2x+3)=(-2x)2-32=4x2-9.5. 【答案】C[解析] 因为(2x+3y)(mx-ny)=2mx2-2nxy+3mxy-3ny2=9y2-4x2,所以2m=-4,-3n=9,-2n+3m=0,解得m=-2,n=-3.6. 【答案】D[解析] 9.52=(10-0.5)2=102-2×10×0.5+0.52.7. 【答案】C[解析] (x+1)(x2+1)(x-1)=(x+1)(x-1)(x2+1)=(x2-1)(x2+1)=x4-1.8. 【答案】D[解析] 因为(x+a)2=x2+bx+25,所以x 2+2ax +a 2=x 2+bx +25.所以⎩⎨⎧2a =b ,a 2=25,解得⎩⎨⎧a =5,b =10或⎩⎨⎧a =-5,b =-10.9. 【答案】A [解析] 根据题意得(a +2b )(a -2b )=a 2-4b 2.10. 【答案】D [解析] 在图①中,左边的图形阴影部分的面积=a 2-b 2,右边图形的面积=(a +b )(a -b ),故可得a 2-b 2=(a +b )(a -b ),可以验证平方差公式; 在图②中,左边图形的阴影部分的面积=a 2-b 2,右边图形的面积=(2b +2a )(a -b )=(a +b )(a -b ),可得a 2-b 2=(a +b )(a -b ),可以验证平方差公式;在图③中,左边图形的阴影部分的面积=a 2-b 2,右边图形的面积=(a +b )(a -b ),可得a 2-b 2=(a +b )(a -b ),可以验证平方差公式.二、填空题11. 【答案】±3 [解析] (x +my)(x -my)=x 2-m 2y 2=x 2-9y 2,所以m 2=9.所以m =±3.12. 【答案】221212145353259x y x y x y ⎛⎫⎛⎫+-=- ⎪⎪⎝⎭⎝⎭ 【解析】221212145353259x y x y x y ⎛⎫⎛⎫+-=- ⎪⎪⎝⎭⎝⎭13. 【答案】±3 [解析] ∵(x -ay )(x +ay )=x 2-a 2y 2=x 2-9y 2,∴a 2=9,解得a =±3.14. 【答案】50 [解析] 因为x -y =6,xy =7,所以x 2+y 2=(x -y)2+2xy =62+2×7=50.15. 【答案】224()()ab a b a b =+--【解析】22()()4a b a b ab -=+-或224()()ab a b a b =+--16. 【答案】(a +b)(a -b)=a 2-b 2三、解答题17. 【答案】222(41)(41)(4)1161a a a a ---+=--=-【解析】222(41)(41)(4)1161a a a a ---+=--=-18. 【答案】解:(1)原式=(2-1)×(2+1)×(22+1)×(24+1)×(28+1)×(216+1)=232-1.(2)原式=×(3-1)×(3+1)×(32+1)×(34+1)×(38+1)×(316+1)=. (3)若m ≠n ,则原式=(m -n )(m +n )(m 2+n 2)(m 4+n 4)(m 8+n 8)(m 16+n 16)=;若m =n ,则原式=2m ·2m 2·……·2m 16=32m 31.19. 【答案】 解:(1)x 5-1(2)x n -1(3)(3-1)(350+349+348+…+32+3+1)=351-1.(4)因为(-2-1)[(-2)2020+(-2)2019+(-2)2018+…+(-2)3+(-2)2+(-2)+1]=(-2)2021-1=-22021-1,所以(-2)2020+(-2)2019+(-2)2018+…+(-2)3+(-2)2+(-2)+1=22021+13.20. 【答案】解:(1)由已知可得:(a+b)1展开式中共有2项,(a+b)2展开式中共有3项,(a+b)3展开式中共有4项,……则(a+b)n展开式中共有(n+1)项.(2)(a+b)1=a+b,(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,…则(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.。
人教版八年级数学上册同步练习14.2乘法公式(含答案解析)
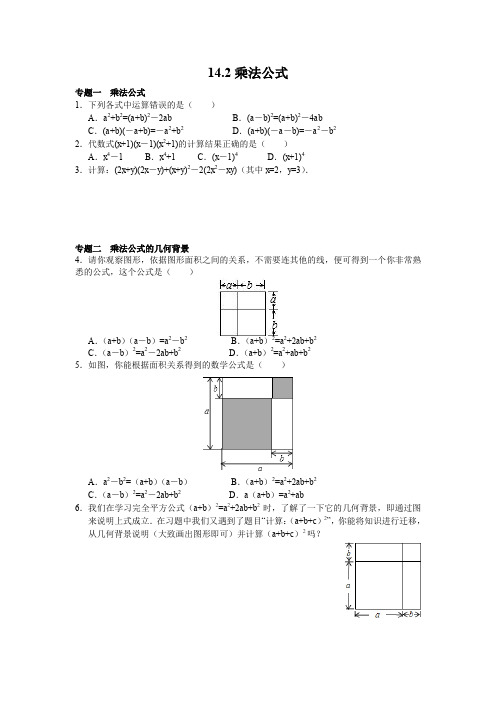
14.2乘法公式专题一乘法公式1.下列各式中运算错误的是()A.a2+b2=(a+b)2-2ab B.(a-b)2=(a+b)2-4abC.(a+b)(-a+b)=-a2+b2D.(a+b)(-a-b)=-a2-b22.代数式(x+1)(x-1)(x2+1)的计算结果正确的是()A.x4-1 B.x4+1 C.(x-1)4D.(x+1)43.计算:(2x+y)(2x-y)+(x+y)2-2(2x2-xy)(其中x=2,y=3).专题二乘法公式的几何背景4.请你观察图形,依据图形面积之间的关系,不需要连其他的线,便可得到一个你非常熟悉的公式,这个公式是()A.(a+b)(a-b)=a2-b2B.(a+b)2=a2+2ab+b2C.(a-b)2=a2-2ab+b2D.(a+b)2=a2+ab+b25.如图,你能根据面积关系得到的数学公式是()A.a2-b2=(a+b)(a-b)B.(a+b)2=a2+2ab+b2C.(a-b)2=a2-2ab+b2D.a(a+b)=a2+ab6.我们在学习完全平方公式(a+b)2=a2+2ab+b2时,了解了一下它的几何背景,即通过图来说明上式成立.在习题中我们又遇到了题目“计算:(a+b+c)2”,你能将知识进行迁移,从几何背景说明(大致画出图形即可)并计算(a+b+c)2吗?状元笔记【知识要点】1.平方差公式(a+b)(a-b)=a2-b2,两个数的和与这两个数的差的积,等于这两个数的平方差.2.完全平方公式(a±b)2=a2±2ab+b2,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.【温馨提示】1.不要将平方差公式和完全平方公式相混淆,注意它们项数和符号的不同.2.完全平方公式中,中间项是左边两个数的和的2倍,注意系数的特点.【方法技巧】1.公式中的字母a、b可以是具体的数,也可以是单项式、多项式.只要符合公式的结构特征,就可以利用公式.2.有些题目往往不能直接应用公式求解,但稍做适当的变形后就可以用乘法公式求解.如:位置变化,符号变化,数字变化,系数变化,项数变化等.参考答案:1.D 解析:A中,由完全平方公式可得(a+b)2-2ab=a2+2ab+b2-2ab=a2+b2,故A正确;B中,由完全平方公式可得(a-b)2=a2-2ab+b2,(a+b)2-4ab=a2+2ab+b2-4ab=a2-2ab+b2,故B正确;C中,由平方差公式可得(a+b)(-a+b)=(a+b)(b-a)=b2-a2=-a2+b2,故C正确;D中,(a+b)(-a-b)=-(a+b)2=-a2-2ab-b2,故D错误.2.A 解析:原式=(x2-1)(x2+1)=(x2)2-1=x4-1.3.解:原式=4x2-y2+x2+2xy+y2-4x2+2xy=x2+4xy,当x=2,y=3时,原式=22+4×2×3=4+24=28.4.B 解析:这个图形的整体面积为(a+b)2;各部分的面积的和为a2+2ab+b2;所以得到公式(a+b)2=a2+2ab+b2.故选B.5.C 解析:从图中可知:阴影部分的面积是(a-b)2和b2,剩余的矩形面积是(a-b)b和(a-b)b,即大阴影部分的面积是(a-b)2,∴(a-b)2=a2-2ab+b2,故选C.6.解:(a+b+c)2的几何背景如图,整体的面积为:(a+b+c)2,用各部分的面积之和表示为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,所以(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.。
人教版八年级数学上册14.2 乘法公式考点练习(含答案)

14.2 乘法公式考点1 平方差公式的运算1.下列各式不能用平方差公式计算的是( )A .()()11a a -+B .()()33a a +-C .(2)(2)a b a b -+-D .()()22a b a b -+--2.( -2)2020( +2)2019的值等于( )A .2B .-2C .3 -2D .2- 33.计算(x +3)(x ﹣3)的结果是( )A .x 2﹣9B .x 2﹣3C .x 2﹣6D .9﹣x 2 4.计算(x 4+1)(x 2+1)(x +1)(x ﹣1)的结果是( )A .x 8+1B .x 8﹣1C .(x +1)8D .(x ﹣1)8 5.如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”, (如8=32-12,16=52-32,则8,16均为“和谐数”),在不超过220的正整数中,所有的“和谐数”之和为( )A .3014B .3024C .3034D .3044考点2 平方差公式与几何图形6.如图,从边长为a 的大正方形中剪掉一个边长为b 的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )A.(a﹣b)2=a2﹣2ab+b2B.a(a﹣b)=a2﹣abC.(a﹣b)2=a2﹣b2D.a2﹣b2=(a+b)(a﹣b)7.在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证()A.(a+b)2=a2+2ab+b2B.(a-b)2=a2-2ab+b2C.a2-b2=(a+b)(a-b)D.(a+2b)(a-b)=a2+ab-2b28.从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为()A .()()22a b a b a b -=+-B .()2222a b a ab b +=++C .()22a b a b -=- D .()2222a b a ab b -=-+ 9.如图,在边长为a 的正方形上剪去一个边长为b 的小正方形(a >b ),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )A .(a ﹣b )2=a 2﹣2ab+b 2B .(a+b )2=a 2+2ab+b 2C .a 2﹣b 2=(a+b )(a ﹣b )D .a 2﹣ab=a (a ﹣b )10.图①②中涂色部分的面积分别为S 1,S 2,a >b >0,设k=12S S ,则有( )A .0<k <12B .12<k <1 C .1<k <2 D .k >2考点3 完全平方公式的有关计算11.计算(-x -y )2的结果正确的是( )A .x 2+y 2B .x 2-y 2C .x 2-2xy +y 2D .x 2+2xy +y 2 12.若()222ax 3y 4x 12xy by +=+-,则a b 、的值依次为( )A .29-、B .49-、C .29、D .29-、 13.下列各式,是完全平方式的是( )A .21x +B .221x x +-C .214x x -+ D .241x x -+14.若11x x -=,则221x x +的值是( )A .3B .2C .1D .415.若,则的值是( )A .1B .-1C .2D .-216.若是实数,则2(a 2+b 2)-(a+b )2的值必是( )A .正数B .负数C .非正数D .非负数 17..已知y 2+my +1是完全平方式,则m 的值是( )A .2B .±2C .1D .±1考点4 完全平方公式与几何图形18.如图,两个正方形边长分別为a ,b ,如果a +b =9,ab =12,则阴影部分的面积为()A .21.5B .22.5C .23.5D .2419.如图,能说明的公式是( )A .222()2a b a ab b +=++B .222()2a b a ab b -=-+C .22()()a b a b a b +-=-D .不能判断20.如图,将图1中阴影部分无重叠、无缝隙地拼成图2,根据两个图形中阴影部分的面积关系得到的等式是( )A .a 2-b 2=(a +b )(a -b )B .a 2+2ab +b 2=(a +b )2C .a 2-2ab +b 2=(a -b )2D .(a +b )2-(a -b )2=4ab21.如图,是一块直径为2a +2b 的圆形钢板,从中挖去直径分别为2a 、2b 的两个圆,则剩下的钢板的面积为( )A.abπB.2abπC.3abπD.4abπ答案1.C 2.D 3.A 4.B 5.B 6.D 7.C 8.A 9.C10.C 11.D 12.A 13.C 14.A 15.A 16.D 17.B 18.B 19.A 20.C 21.B。
2022-2023学年人教版八年级数学上册《14-2乘法公式》同步练习题(附答案)

2022-2023学年人教版八年级数学上册《14.2乘法公式》同步练习题(附答案)一.选择题1.下列各式计算正确的是()A.(a+b)2=a2+b2B.(a﹣b)2=a2﹣b2C.(x﹣y)2=x2﹣2xy+y2D.(x+2)(x﹣1)=x2﹣x﹣22.下列各式正确的是()A.(2a﹣1)2=4a2﹣1B.(x+)2=x2+x+C.(3m+n)2=9m2+n2D.(﹣x﹣1)2=x2﹣2x+13.下列等式成立的是()A.(2+x)(x﹣2)=x2﹣4B.(2x﹣y)(﹣2x+y)=4x2﹣y2C.(3m+2n)(3m﹣2n)=9m3﹣2n2D.(a+b)(﹣a﹣b)=a2﹣b24.若等式(3x+5)2(3x﹣5)2=81x4﹣mx2+n2成立,则()A.m=﹣30,n=5B.m=﹣30,n=﹣5或5C.m=﹣450,n=25或﹣25D.m=450,n=25或﹣255.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如4=22﹣02,12=42﹣22,20=62﹣42,因此4,12,20都是“神秘数”,则下面哪个数是“神秘数”()A.56B.60C.62D.886.若(3b+a)()=9b2﹣a2,则括号内应填的代数式是()A.﹣a﹣3b B.a+3b C.﹣3b+a D.3b﹣a7.计算20212﹣2020×2022的结果是()A.1B.﹣1C.0D.2×20212﹣1 8.式子(2+1)(22+1)(24+1)(28+1)…(21024+1)+1化简的结果为()A.21024B.21024+1C.22048D.22048+19.如图1,从边长为a的大正方形纸片中挖去一个边长为b的小正方形纸片后,将其沿实线裁成两个相同的直角梯形,然后拼成一个等腰梯形(如图2),则通过计算图形阴影部分的面积,可以验证成立的公式是()A.(a﹣b)2=a2﹣b2 B.(a﹣b)2=a2﹣2ab+b2C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)10.如图,从边长为(a+5)cm的正方形纸片中剪去一个边长为(a+2)cm的小正方形,剩余部分沿虚线剪拼成一个矩形(不重叠无缝隙),则矩形的面积为()cm2.A.a2+5a B.6a+21C.6a+14D.3a+2111.图1,是一个长为2m、宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2形式拼成一个正方形,那么中间阴影部分的面积为()A.mn B.m2﹣n2C.(m﹣n)2D.(m+n)2二.填空题12.设N=2(1﹣)(1﹣)(1﹣)……(1﹣)(1﹣),则N的值为.13.已知x2﹣y2=﹣5,则代数式(x+y)3•(x﹣y)3的值为.14.若a=20220,b=2021×2023﹣20222,c=82022×(﹣0.125)2023,则a,b,c的大小关系是(用“>”连接).15.已知4x2+mxy+16y2是完全平方式,则m=.16.若多项式4x2﹣(k﹣1)x+9可以写成一个完全平方式,则k=.三.解答题17.计算:4(x+1)2﹣(2x+5)(2x﹣5)18.计算:.19.已知,求值:(1)(2).20.对于任意四个实数a,b,c,d,可以组成两个实数对(a,b)与(c,d).我们规定:(a,b)⊗(c,d)=a2+d2﹣bc.例如:(1,2)⊗(3,4)=12+42﹣2×3=11.(1)若(3x,﹣3x)⊗(ky,y)是一个完全平方式,则常数k的值为;(2)若x+y=6,且(2x+y,x2+y2)⊗(2,x﹣2y)=60,求xy的值.21.数学活动课上,刘老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形并用A种纸片一张,B 种纸片一张,C种纸片两张拼成如图2的大正方形.由图2,可得出三个代数式:(a+b)2,a2+b2,ab之间的等量关系;(1)根据上述方法,要拼出一个面积为(a+2b)(a+b)的矩形,需要A卡片1张,B卡片2张,C卡片张.(2)根据得出的等量关系,解决如下问题:①已知:a+b=6,a2+b2=14,求ab的值;②已知(x﹣2020)2+(x﹣2022)2=10,求(x﹣2021)2的值.22.乘法公式的探究及应用.(1)如图1,可以求出阴影部分的面积是(写成两数平方差的形式);(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是,长是,面积是;(写成多项式乘法的形式)(3)比较左、右两图的阴影部分面积,可以得到乘法公式;(用式子表达)(4)运用你所得到的公式,计算下列各题:①20212﹣2020×2022;②(2m+n+p)(2m+n﹣p).参考答案一.选择题1.解:A、(a+b)2=a2+2ab+b2,故本选项不符合题意;B、(a﹣b)2=a2﹣2ab+b2,故本选项不符合题意;C、(x﹣y)2=x2﹣2xy+y2,故本选项符合题意;D、(x+2)(x﹣1)=x2+x﹣2,故本选项不符合题意.故选:C.2.解:(2a﹣1)2=4a2﹣4a+1,选项A错误;(x+)2=x2+x+,B选项正确;(3m+n)2=9m+6mn+n2,C选项错误;(﹣x﹣1)2=x2+2x+1,选项D错误.故选:B.3.解:(2+x)(x﹣2)=x2﹣4,故A成立,符合题意;(2x﹣y)(﹣2x+y)=﹣4x2+4xy﹣y2,故B不成立,不符合题意;(3m+2n)(3m﹣2n)=9m2﹣4n2,故C不成立,不符合题意;(a+b)(﹣a﹣b)=﹣a2﹣2ab﹣b2,故D不成立,不符合题意;故选:A.4.解:由于(3x+5)2(3x﹣5)2=81x4﹣mx2+n2,即[(3x+5)(3x﹣5)]2=81x4﹣mx2+n2,也就是(9x2﹣25)2=81x4﹣mx2+n2,所以81x4﹣450x2+625=81x4﹣mx2+n2,即m=450,n=±25,故选:D.5.解:∵60=162﹣142,∴60是“神秘数”,故选:B.6.解:∵9b2﹣a2=(3b+a)(3b﹣a),故选:D.7.解:原式=20212﹣(2021﹣1)×(2021+1)=20212﹣(20212﹣1)=20212﹣20212+1=1.故选:A.8.解:设S=(2+1)(22+1)(24+1)(28+1)…(21024+1)∴(2﹣1)S=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(21024+1)=(22﹣1)(22+1)(24+1)(28+1)…(21024+1)=(24﹣1)(24+1)(28+1)…(21024+1)=(21024﹣1)(21024+1)=22048﹣1,∴(2+1)(22+1)(24+1)(28+1)…(21024+1)+1=S+1=22048﹣1+1=22048.故选:C.9.解:∵图形中阴影部分的面积可表示为a2﹣b2或=(a+b)(a﹣b),∴a2﹣b2=(a+b)(a﹣b),故选:D.10.解:拼成矩形的长为a+2+a+5=2a+7,宽为a+5﹣a﹣2=3,所以面积为3(2a+7)=6a+21,故选:B.11.解:方法一:图2中四个长方形的面积的和=图1的长方形的面积=2m×2n=4mn,图2的大正方形的面积=(m+n)2,图2中阴影部分的面积=图2的大正方形的面积﹣图2中四个长方形的面积的和=(m+n)2﹣4mn=m2+2mn+n2﹣4mn=m2﹣2mn+n2=(m﹣n)2.方法二:图中阴影部分是正方形,且四个边长都是(m﹣n),∴阴影部分的面积=(m﹣n)2.故选:C.二.填空题12.解:N=2×(1﹣)×(1+)×(1﹣)×(1+)……(1﹣)×(1+)×(1﹣)×(1+)=2××××……××××=,故答案为:.13.解:∵x2﹣y2=﹣5,∴(x+y)(x﹣y)=﹣5,∴(x+y)3•(x﹣y)3=[(x+y)(x﹣y)]3=﹣125,故答案为:﹣125.14.解:a=20220=1,b=2021×2023﹣20222=(2022﹣1)(2022+1)﹣20222=20222﹣1﹣20222=﹣1,c=82022×(﹣0.125)2023=﹣0.125×(﹣0.125×8)2022=﹣0.125,∵﹣1<﹣0.125<1,∴b<c<a.故答案为:b<c<a.15.解:∵4x2+mxy+16y2是完全平方式,∴mxy=±2×2x×4y,∴m=±16.故答案为:±16.16.解:由于(2x±3)2=4x2±12x+9=4x2﹣(k﹣1)x+9,则﹣(k﹣1)=±12,解得:k=13或﹣11.故答案为:13或﹣11.三.解答题17.解:原式=4x2+8x+4﹣4x2+25=8x+29.18.解:原式=x2﹣xy+y2﹣(x2﹣y2)(4分)=﹣xy+y2.(2分)19.解:(1)∵x+﹣3=0,∴x+=3,∴=(x+)2﹣2=9﹣2=7,即=7;(2)由(1)知,=7,∴(x﹣)2=﹣2=7﹣2=5,∴x﹣=±.20.解:(1)(3x,﹣3x)⊗(ky,y)=(3x)2+y2﹣(﹣3x•ky)=9x2+3kxy+y2.∵(3x,﹣3x)⊗(ky,y)是一个完全平方式,∴3kxy=±6xy.∴k=±2.(2)∵(2x+y,x2+y2)⊗(2,x﹣2y)=60.(2x+y)2+(x﹣2y)2﹣2(x2+y2)=60.∴x2+y2=20.∵x+y=6.∴(x+y)2=36.∴x2+y2+2xy=36∴2xy=36﹣20=16.∴xy=8.21.解:(1)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张,C号卡片3张.故答案为:3.(2)①∵(a+b)2=a2+b2+2ab,∴2ab+14=36,∴ab=11;②(x﹣2020)2+(x﹣2022)2=10,∵[(x﹣2020)﹣(x﹣2022)]2=(x﹣2020)2+(x﹣2022)2﹣2(x﹣2020)(x﹣2022),∴4=10﹣2(x﹣2020)(x﹣2022),∴2(x﹣2020)(x﹣2022)=6,∵[(x﹣2020)+(x﹣2022)]2=(x﹣2020)2+(x﹣2022)2+2(x﹣2020)(x﹣2022),∴[2(x﹣2021)]2=10+6=16,即4(x﹣2021)2=16,∴(x﹣2021)2=4.22.解:(1)图1中阴影部分的面积可以看作两个正方形的面积差,即a2﹣b2,故答案为:a2﹣b2;(2)如图2,所拼成一个长方形,它的宽是a﹣b,长是a+b,面积是(a+b)(a﹣b),故答案为:a﹣b,a+b,(a+b)(a﹣b);(3)由(1)(2)可得,(a+b)(a﹣b)=a2﹣b2,故答案为:(a+b)(a﹣b)=a2﹣b2;(4)①原式=20212﹣(2021﹣1)(2021+1)=20212﹣20212+1=1;②原式=[(2m+n)+p][(2m+n)﹣p]=(2m+n)2﹣p2=4m2+4mn+n2﹣p2.。
人教版 八年级数学上册 14.2 乘法公式 同步训练(含答案)

人教版 八年级数学上册 14.2 乘法公式 同步训练一、选择题(本大题共10道小题)1. 运用乘法公式计算(a +3)(a -3)的结果是( )A .a 2-6a +9B .a 2-3a +9C .a 2-9D .a 2-6a -92. 下列各式中,运算结果是9m 2-16n 2的是 ( )A .(3m +2n )(3m -8n )B .(-4n +3m )(-4n -3m )C .(-3m +4n )(-3m -4n )D .(4n +3m )(4n -3m )3. 若(a +3b )2=(a -3b )2+A ,则A 等于( )A .6abB .12abC .-12abD .24ab 4. 如果22()()4a b a b +--=,则一定成立的是( )A .a 是b 的相反数B .a 是b -的相反数C .a 是b 的倒数D .a 是b -的倒数5. 化简(-2x -3)(3-2x )的结果是( )A .4x 2-9B .9-4x 2C .-4x 2-9D .4x 2-6x +96. 将202×198变形正确的是 ( )A .2002-4B .2022-4C .2002+2×200+4D .2002-2×200+47. 若(2x +3y )(mx -ny )=9y 2-4x 2,则m ,n 的值分别为( ) A .2,3B .2,-3C .-2,-3D .-2,38. 计算(x +1)(x 2+1)·(x -1)的结果是() A .x 4+1B .(x +1)4C .x 4-1D .(x -1)49. 设a =x -2018,b =x -2020,c =x -2019,若a 2+b 2=34,则c 2的值是( )A.16 B.12 C.8 D.410. 如图,阴影部分是边长为a的大正方形剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是()A.①②B.②③C.①③D.①②③二、填空题(本大题共6道小题)11. 如果(x-ay)(x+ay)=x2-9y2,那么a=.12. 计算:9982=________.13. 如果(x+my)(x-my)=x2-9y2,那么m=________.14. 多项式x2+1添加一个单项式后可变为完全平方式,则添加的单项式可以是________(任写一个符合条件的即可).15. 如图,四张全等的矩形纸片拼成的图形,请利用图中空白部分面积的不同表示方法,写出一个关于a、b的恒等式___________.abba16. 如图,在边长为a的正方形中剪去一个边长为b的小正方形(a b),把剩下的部分拼成一个梯形,分别计算这两个图形的面积,验证了公式_________________.。
2024年-人教版数学八年级上册14.2乘法公式同步练习(含答案)

14.2 乘法公式同步练习1.填空.2(1)_______1x x -=-2.2200720062008-⨯的计算结果是( ) A.1 B.-1 C.2 D.-23. 简便计算:10397⨯. 42(2)(2)(4)b b b +-+5. 试说明:两个连续奇数的积加上1,一定是一个偶数的平方.6. 方程22(21)(13)5(1)(1)x x x x ---=-+的解是( ) 7. 下列各式中,能用平方差公式计算的是( ) A.1122a b a b ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭B.1122a b a b ⎛⎫⎛⎫--+ ⎪⎪⎝⎭⎝⎭ C.1122a b a b ⎛⎫⎛⎫--- ⎪⎪⎝⎭⎝⎭D.1122a b a b ⎛⎫⎛⎫--+ ⎪⎪⎝⎭⎝⎭ 8. 计算:(1)()(2)a b a +-;(2)1122x x ⎛⎫⎛⎫-+ ⎪⎪⎝⎭⎝⎭;(3)()()m n m n +-;(4)(0.1)(0.1)x x -+;(5)()()x y y x +-+.9. 计算:(1)(25)(25)a a ---;(2)11113232a b a b ⎛⎫⎛⎫-+-- ⎪⎪⎝⎭⎝⎭;(3)(53)(35)ab x x ab ---;(4)11122(8)224x x x x ⎛⎫⎛⎫-+-+ ⎪⎪⎝⎭⎝⎭;(5)111()933x y x y x y x y ⎛⎫⎛⎫⎛⎫----+⎪ ⎪⎪⎝⎭⎝⎭⎝⎭.10. 利用平方差公式计算:(1)3129⨯;(2)9.910.1⨯;(3)98102⨯;(4)1003997⨯.a b11. 计算:(1)(34)(34)a b a b +-;(2)()()a b c a b c +-++;(3)112233a c b a c b ⎛⎫⎛⎫-++--+ ⎪⎪⎝⎭⎝⎭.12. 利用平方差公式计算:(1)2733⨯;(2)5.9 6.1⨯;(3)99101⨯;(4)1005995⨯.13如图是四张全等的矩形纸片拼成的图形,请利用图中空白部分面积的不同表示方法,写出一个关于a 、b 的恒等式. 14计算.2302=_________15.计算22(4)a b -=_________16. 若2154a b ab +==,,则22a b +=_________ 17. 如果226x x k ++恰好是一个整式的平方,那么常数k 的值为( ) A.3B.3-C.3±D.918.22()x y --等于( )A.222x xy y --+B.4222x x y y --+ C.4222x x y y ++D.422x xy y -- 19 计算题:(1)2(23)a b c --;(2)2(2)(2)()x y z x y z x y z +----+-.20. 已知2222263()()x y xy x y x y +==+-和,,求的值.21. 已知2(1)()5a a a b ---=,求222a b ab +-的值.22.计算2212x ⎛⎫+ ⎪⎝⎭等于( )A.42124x x ++B.4214x x -+ C.4214x x ++D.42124x x -+23. 若14a a-=,则221a a +=_________.24. 代数式26()a b -+的最大值是_______,这时a 与b 的关系为________.25. 计算:2222x y x y +-⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭.26. 已知5,6,a b ab +==-求下列各式的值. (1)22a b +;(2)22a ab b -+.27 在多项式241x +中,添加一个单项式,使其成为一个完全平方式.则添加的单项式是(只写出一个即可)28.62()()ab ab ÷=( )A.33a b B.44a b C.34a b D.43a b29.已知:如图,现有a a ⨯、b b ⨯的正方形纸片和a b ⨯的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使拼出的矩形面积为22252a ab b ++,并标出此矩形的长和宽.14.2 乘法公式同步练习1:(1)x -- 2:A a abbb3:9991 4:416b - 5:设两个连续奇数为21n -,21n +, 6.:D 7:C8:(1)222a ba a b +--;(2)214x -;(3)22m n -;(4)20.01x -;(5)22x y -.9:(1)2254a -;(2)221194a b -;(3)222925x a b -;(4)24x --;(5)21029y xy -. 10:(1)(301)(301)9001899+-=-=; (2)(100.1)(100.1)1000.0199.99-+=-=; (3)(1002)(1002)1000049996-+=-=; (4)(10003)(10003)10000009999991+-=-=.11:(1)22916a b -;(2)22()a b c +-(或2222a ab b c ++-);(3)22123a b c ⎛⎫-+- ⎪⎝⎭22214493a ab b c ⎛⎫-+- ⎪⎝⎭或.12:(1)891;(2)35.99;(3)9999;(4)999975. 13:如:22()4()a b ab a b +-=-. 14:9120415:224168a ab b -+ 16:114217:C18:C19:(1)222494612a b c ab ac bc ++--+;(2)2522y xy yz --+.20:2()32x y +=,2()20x y -=21:25222:C23:1824:6,0a b +=或a b ,互为相反数25:222x y +.26:(1)222()2251237a b a b ab +=+-=+=;(2)()()22223536251843a ab b a b ab -+=+-=-⨯-=+=.27:4x ±或1-或24x -28:B29:说明:答案不唯一,画图正确,不论画在什么位置,只要符合题意即可.不标出相应尺寸的扣2分,标错1个或少标1个扣1分. a+2b2a +b2a +ba+2b。
人教版八年级数学上册14.2 乘法公式 同步练习(Word版含简答)

2021——2022学年度人教版八年级数学上册 第十四章 整式的乘法与因式分解14.2 乘法公式 同步练习一、选择题1.下列计算正确的是( )A .(a +b )(a ﹣2b )=a 2﹣2b 2B .(a ﹣12)2=a 2﹣14C .﹣2a (3a ﹣1)=﹣6a 2+aD .(a ﹣2b )2=a 2﹣4ab +4b 22.多项式291x 加上一个单项式后﹐使它成为一个整式的完全平方,那么加上的单项式可以是( ) A .6x ± B .-1或4814x C .29x - D .6x ±或1-或29x -或4814x 3.若28x x k -+是完全平方式,则k 的值是( )A .4B .8C .16D .32 4.设, a b 是实数,定义一种新运算:()2*a b a b =-.下面有四个推断:①**a b b a =;①()222**a b a b =;①()()**a b a b -=-;①()**a b c a b a c +=+*. 其中所有正确推断的序号是( )A .①①①①B .①①①C .①①D .①①5.下列计算正确的是( )A .()222x y x y +=+B .()32626m m =C .()2224x x -=-D .()()2111x x x +-=-6.已知1x =,1y =,则代数式222x xy y ++的值为( ).A .20B .10C .D .7.若()()()248(21)2121211A =+++++,则A 的末位数字是( ) A .4 B .2 C .5 D .68.已知x +1,y ﹣1,则xy 的值为( )A .8B .48C .D .6 9.记A n =(1﹣212)(1﹣213)(1﹣214)…(1﹣21n ),其中正整数n ≥2,下列说法正确的是( ) A .A 5<A 6 B .A 52>A 4A 6C .对任意正整数n ,恒有A n <34D .存在正整数m ,使得当n >m 时,A n <10082015 10.如图:用四个全等的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用a ,b 分别表示矩形的长和宽(a b >),则下列关系中不正确的是( )A .12a b +=B .2a b -=C .35ab =D .2284a b += 二、填空题11,利用这个比例,我们规定一种“黄金算法”即:a ①b =a b ,比如1①2=×2x ①(4①8)=10,则x 的值为______.12.对于实数a ,b ,定义运算“*”:a *b =22,,a ab a b ab a a b⎧-≥⎨-<⎩,若x 1,x 2是一元二次方程x 2﹣5x +6=0的两个根,其中x 1>x 2,则x 1*x 2=____.13.已知2410x x -+=,则221x x +的值是___. 14.若8x y -=,10xy =,则22x y +=______________.15.希望小组的同学在求式子23411111 (22222)n a a a a a +++++的值(结果用n 和a 表示)时遇到了困难.经过合作探究他们想出了如图所示的图形来解释这个式子:设①ABC 的面积为a ,取BC 的中点,则有①ABD 的面积为12a ,再取AD 的中点E ,则有①ACE 的面积为212a ,再取CE 的中点F ,则有①DEF 的面积为312a ,......照此思路持续取下去.就可利用这个图形求得 23411111 (22222)n a a a a a +++++的值=___________.三、解答题16.计算(1)(2x )3(﹣5xy 2)(2)(﹣6a 2b )•(23b 2﹣13a ) (3)(3a +b )(a ﹣3b )(4)(3x +2y ﹣1)(3x ﹣2y +1)17.老师在数学课上提出这样一个问题:已知21(0)x x x +=-≠,求221x x +的值. 小明通过观察、分析、思考,形成了如下思路:先将等式两边都除以x ,得到1x x +的值,再利用完全平方公式求出221x x+. 参考小明的思路,解决下列问题:(1)已知210(0)x x x --=≠,求221x x +的值;(2)已知213(0)x x x +=≠18.一个正整数 A 若能写成A =m ²- n ²(m 、n 均为正整数,且m >n ),则称A 为“第一共同 体数”,m 、n 为A 的平方差分解数组.在A 的所有平方差分解数组中,若m - n 最大,则称m 、n 为A 的最佳平方差分解数组,此时 Q (A )= m ²+ n ².范例①:①13=7²﹣6²,①13为第一共同体数,7和6为13的平方差分解数组;范例①:32的平方差分解有两组,即 32=9²﹣7²,32=6²﹣2².① 6-2>9-7,①6和2为32的最佳平方差分解数组,Q (32)=6²+2²=40根据材料回答:(1)请模仿范例①写出两个10以内的“第一共同体数”,并写出它们的平方差分解数组;(2)判断 48 是否为第一共同体数?若不是,请说明理由,若是,请计算 Q (48)的值19.(1)对于算式()()()()()2481024212121212+1______++++=;不用计算器,你能计算出来吗?直接写出计算结果.(2)你计算结果的个位数字是________.(3)根据(1)推测()()()()()2420481111+1=_______m m m m m -+++.20.阅读下面的材料并解答后面的问题:在学了整式的乘法公式后,小明问:能求出243x x ++的最小值吗?如果能,其最小值是多少?小丽:能.求解过程如下:因为222434443(2)1x x x x x ++=++-+=+-,因为2(2)0x +≥,所以243x x ++的最小值是1-.问题:(1)小丽的求解过程正确吗?(2)你能否求出285x x -+的最小值?如果能,写出你的求解过程;(3)求265x x -+-的最大值.21.我们通常用作差法比较代数式大小.例如:已知M =2x +3,N =2x +1,比较M 和N 的大小.先求M ﹣N ,若M ﹣N >0,则M >N ;若M ﹣N <0,则M <N ;若M ﹣N =0,则M =N ,反之亦成立.本题中因为M ﹣N =2x +3﹣(2x +1)=2>0,所以M >N .(1)如图1是边长为a 的正方形,将正方形一边不变,另一边增加4,得到如图2所示的新长方形,此长方形的面积为S 1;将图1中正方形边长增加2得到如图3所示的新正方形,此正方形的面积为S 2用含a 的代数式表示S 1= ,S 2= (需要化简).然后请用作差法比较S 1与S 2大小;(2)已知A =2a 2﹣6a +1,B =a 2﹣4a ﹣1,请你用作差法比较A 与B 大小.(3)若M =(a ﹣4)2,N =16﹣(a ﹣6)2,且M =N ,求(a ﹣4)(a ﹣6)的值.22.观察:(1)如图1,已知正方形ABCD的边长为a,正方形FGCH的边长为b,长方形ABGE和长方形EFHD为阴影部分,则阴影部分的面积可表示为(写成平方差的形式);(2)将图1中的长方形ABGE和长方形EFHD剪下来,拼成如图2所示的长方形,则长方形AHDE的面积是(写成多项式相乘的形式);探究:(3)比较图1与图2的阴影部分的面积,可得等量关系;(4)若7x﹣y=5,y+7x=7,则49x2﹣y2=;应用:(5)利用公式计算:(1﹣13)(1+13)(1+213)(1+413)(1+813) (1)6413)+12813.23.(知识生成)通过不同的方法表示同一图形的面积,可以探求相应的等式,两个边长分别为a,b的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的梯形,请用两种方法计算梯形面积.(1)方法一可表示为;方法二可表示为;(2)根据方法一和方法二,你能得出a,b,c之间的数量关系是(等式的两边需写成最简形式);(3)由上可知,一直角三角形的两条直角边长为6和8,则其斜边长为.(知识迁移)通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图2是边长为a+b的正方体,被如图所示的分割线分成8块.(4)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为.(等号两边需化为最简形式)(5)已知2m﹣n=4,mn=2,利用上面的规律求8m3﹣n3的值.【参考答案】1.D 2.D 3.C 4.D 5.D 6.A 7.D 8.D 9.D 10.D11.12.3或2或313.1414.8415.12na a - 16.(1)4240-x y ;(2)23342ab a b -+;(3)22383a ab b --;(4)229441x y y -+-17.(1)221x x +=8+(2= 18.(1)7为第一共同体数,4和3为7的平方差分解数组,9为第一共同体数,5和4为9的平方差分解数组;(2)是,理由见解析,(48)50Q =19.(1)204821-;(2)5;(3)40961m -20.(1)正确;(2)能,最小值为-11,见解析;(3)4.21.(1)a 2+4a <a 2+4a +4;(2)A >B ;(3)622.(1)22a b -;(2)()()a b a b +-;(3)22()()a b a b a b -=+-;(4)35;(5)123.(1)12ab +12ab +12c 2;12(a +b )2;(2)c 2=a 2+b 2;(3)10;(4)(a +b )3=a 3+3a 2b +3ab 2+b 3;(5)8m 3﹣n 3的值为112.。
2022-2023学年人教版八年级数学上册《14-2乘法公式》同步知识点分类练习题(附答案)

2022-2023学年人教版八年级数学上册《14.2乘法公式》同步知识点分类练习题(附答案)一.完全平方公式1.下列运算正确的是()A.(m2)3=m5B.(﹣2m)2=4m2C.(m+1)2=m2+1D.m3÷m3=02.已知a+b=8,ab=12,则a2+b2的值是()A.64B.52C.58D.403.若m为任意整数,则下列对多项式(4m﹣5)2﹣9的说法正确的是()A.一定能被8整除B.一定能被8m整除C.一定能被m整除D.一定能被m﹣1整除4.计算x2﹣(x﹣1)2,正确的结果是()A.1B.2x﹣1C.﹣2x+1D.﹣2x﹣15.若实数x、y满足x﹣3=y,则代数式2x2﹣4xy+2y2的值为.6.已知x+y=,xy=﹣2,则x2+y2=.7.(1)若m2+n2=13,m+n=3,则mn=.(2)请仿照上述方法解答下列问题:若(a﹣b﹣2017)2+(2019﹣a+b)2=5,则代数式的值为.二.完全平方公式的几何背景8.如图中的两个四边形均为正方形,根据图形的面积关系,写出一个正确的等式:.9.如图,两个正方形边长分别为a,b,如果a+b=10,ab=18,则阴影部分的面积为()A.21B.22C.23D.2410.如图,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF,若这两个正方形的边长满足a+b=10,ab=20,则阴影部分的面积为.11.如图,正方形ABCD是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:(1)用两种不同的方法可以表示正方形ABCD的面积,写成一个等式为;(2)运用(1)中的等式,解决以下问题:①已知a+b=5,ab=3,求a2+b2的值;②已知x﹣y+z=11,(x﹣y)z=9,求(x﹣y)2+z2的值.12.如图①,是一个长为2m、宽为2n的长方形,用剪刀沿图中的虚线(对称轴)剪开,把它分成四个形状和大小都相同的小长方形,然后按图②那样拼成一个正方形(中间是空的).(1)图②中画有阴影的小正方形的边长为(用含m,n的式子表示);(2)观察图②,写出代数式(m+n)2,(m﹣n)2与mn之间的等量关系;(3)根据(2)中的等量关系解决下面的问题:(i)若m+n=7,mn=5,求(m﹣n)2的值;(ii)若a+=3,求a2+的值.三.完全平方式13.若x2﹣8x+m是完全平方式,则m的值为()A.4B.±4C.±16D.1614.已知关于字母x的二次三项式x2+2kx+9是完全平方式,则常数k的值为()A.3B.﹣3C.±3D.615.若多项式x2+nx+81是一个整式的平方,则n的值是()A.9B.18C.±9D.±18 16.若25x2﹣(k﹣1)x+1可以写成一个完全平方式,则k的值为.四.平方差公式17.若952+190×5+52=k+992﹣1,则k的值是()A.100B.199C.200D.299 18.下列各式不能用平方差公式计算的是()A.(﹣2a+b)(2a﹣b)B.(3+a)(a﹣3)C.(a﹣1)(a+1)D.(﹣2a+b)(﹣2a﹣b)19.下列运算中,可以运用平方差公式的是()A.(2+a)(﹣2﹣a)B.(a+)(﹣a)C.(﹣a+b)(a﹣b)D.(a2﹣b)(a+b2)20.下列计算,能用平方差公式的为()A.(a+2b)(a+2b)B.(﹣a+2b)(﹣a+2b)C.(2b﹣a)(﹣a+2b)D.(2b﹣a)(a+2b)21.用平方差公式计算:24×25=()2﹣()2=.22.计算:2020×2018﹣20192=.23.20002﹣2001×1999=.24.计算:(a+2b)(a﹣2b)=(7﹣y)2=.五.平方差公式的几何背景25.在乘法公式的学习中,我们常采用构造几何图形的方法研究问题,如图,边长为(b+2)的正方形,剪去一个边长为b的正方形之后剩余部分可剪拼成一个长方形(不重叠无缝隙),则这个长方形的长是()A.b+4B.b+2C.2b+2D.4b+426.利用图形面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.(Ⅰ)根据下列所示图形写出一个代数恒等式.(Ⅱ)已知正数a、b、c和m、n、l,满足a+m=b+n=c+l=k.试构造边长为k的正方形:,利用图形面积来说明al+bm+cn<k2并简述理由:.参考答案一.完全平方公式1.解:A、(m2)3=m6,所以A选项不符合题意;B、(﹣2m)2=(﹣2)2m2=4m2,所以B选项符合题意;C、(m+1)2=m2+2m+1,所以C选项不符合题意;D、m3÷m3=m0=1,所以D选项不符合题意.故选:B.2.解:∵a+b=8,ab=12,∴a2+b2=(a+b)2﹣2ab=82﹣2×12=40,故选:D.3.解:(4m﹣5)2﹣9=16m2﹣40m+25﹣9=16m2﹣40m+16=8(2m2﹣5m+2)=8(2m﹣1)(m﹣2),∵m为任意整数,∴2m﹣1与m﹣2都为整数,∴8(2m﹣1)(m﹣2)能被8整除,也能被2m﹣1和m﹣2整除.故选:A.4.解:x2﹣(x﹣1)2=x2﹣x2+2x﹣1=2x﹣1.故选:B.5.解:由x﹣3=y可得x﹣y=3,∴2x2﹣4xy+2y2=2(x2﹣2xy+y2)=2(x﹣y)2=2×32=2×9=18.故答案为:18.6.解:∵x+y=,xy=﹣2,∴x2+y2=(x+y)2﹣2xy=()2﹣2×(﹣2)=3+4=7.故答案为:7.7.解:(1)把m+n=3两边平方得:(m+n)2=9,即m2+n2+2mn=9,把m2+n2=13代入得:2mn=﹣4,即mn=﹣2;(2)由题意得:4=[(a﹣b﹣2017)+(2019﹣a+b)]2=(a﹣b﹣2017)2+(2019﹣a+b)2+2(a﹣b﹣2017)(2019﹣a+b),把(a﹣b﹣2017)2+(2019﹣a+b)2=5代入得:(a﹣b﹣2017)(2019﹣a+b)=﹣,则原式==﹣4038,故答案为:﹣4038二.完全平方公式的几何背景8.解:由面积法可得:(a+b)2=a2+ab+b(a+b)=a2+2ab+b2.故答案是:(a+b)2=a2+2ab+b2.9.解:S阴=a2﹣﹣=﹣+=,∵a2+b2=(a+b)2﹣2ab=102﹣2×18=64,∴S阴===24.故选:D.10.解:∵大小两个正方形边长分别为a、b,∴阴影部分的面积S=a2+b2﹣a2﹣(a+b)b=a2+b2﹣ab;∵a+b=10,ab=20,∴S=a2+b2﹣ab=(a+b)2﹣ab=×102﹣×20=20.故答案为:20.11.解:(1)正方形的面积为(a+b)2或a2+b2+2ab,∴(a+b)2=a2+b2+2ab;(2)①∵(a+b)2=a2+b2+2ab,∴a2+b2=(a+b)2﹣2ab,∵a+b=5,ab=3,∴a2+b2=(a+b)2﹣2ab=25﹣6=19;②∵(x﹣y)2+z2=(x﹣y+z)2﹣2(x﹣y)z,∵x+z﹣y=11,(x﹣y)z=9,∴(x﹣y)2+z2=(x﹣y+z)2﹣2(x﹣y)z=121﹣18=103.12.解:(1)图②中画有阴影的小正方形的边长(m﹣n);故答案为:m﹣n.(2)图②中画有阴影的小正方形的边长(m﹣n),面积为:(m﹣n)2,(图②中画有阴影的小正方形的面积还可以表示为:(m+n)2﹣4mn.∴(m﹣n)2=(m+n)2﹣4mn.(3)(i)(m﹣n)2=(m+n)2﹣4mn=49﹣20=29.(ii)a2+=﹣2=9﹣2=7.三.完全平方式13.解:∵x2﹣8x+m是完全平方式,∴m=42=16.故选:D.14.解:∵关于字母x的二次三项式x2+2kx+9=x2±2•x•3+32是完全平方式,∴k=±3,故选:C.15.解:∵多项式x2+nx+81是一个整式的平方,∴n=±18,故选:D.16.解:∵25x2﹣(k﹣1)x+1可以写成一个完全平方式,﹣(k﹣1)x=±2•5x•1,解得:k=11或﹣9,故答案为:11或﹣9.四.平方差公式17.解:∵952+190×5+52=(95+5)2=1002,∴k=1002﹣992+1=(100+99)×(100﹣99)+1=199+1=200.故选:C.18.解:根据平方差公式(a+b)(a﹣b)=a2﹣b2的特点,A不能用平方差公式.故选:A.19.解:A、只有相反项,没有相同项,不能运用平方差公式计算,故本选项错误;B、符合平方差公式的结构,可以运用平方差公式计算,故本选项正确;C、只有相反项,没有相同项,不能运用平方差公式计算,故本选项错误;D、既没有相同项,也没有相反项,不能运用平方差公式计算,故本选项错误;故选:B.20.解:A、(a+2b)(a+2b)不是平方差公式,故A选项错误;B、(﹣a+2b)(﹣a+2b)不是平方差公式,故B选项错误;C、(2b﹣a)(﹣a+2b)不是平方差公式,故C选项错误;D、(2b﹣a)(a+2b)是平方差公式,故D选项正确;故选:D.21.解:24×25=(25﹣)×(25+)=252﹣()2=625﹣=624,故答案为:25,,624.22.解:2020×2018﹣20192=(2019+1)(2019﹣1)﹣20192=20192﹣12﹣20192=﹣1故答案为:﹣1.23.解:20002﹣2001×1999=20002﹣(2000+1)×(2000﹣1)=20002﹣(20002﹣1)=20002﹣20002+1=1.故答案为:1.24.解:(a+2b)(a﹣2b)=a2﹣4b2;(7﹣y)2=49﹣14y+y2,故答案为:a2﹣4b2;49﹣14y+y2五.平方差公式的几何背景25.解:设这个大长方形的长为x,由题意得(b+2)2﹣b2=2x,解得x=2b+2,故选:C.26.解:(Ⅰ)(a+b)2﹣(a﹣b)2=4ab或(a+b)2=(a﹣b)2+4ab或(a+b)2﹣4ab=(a﹣b)2等;(Ⅱ)因为a+m=b+n=c+l=k,显然有al+bm+cn<k2。
8年级数学人教版上册同步练习14.2乘法公式(含答案解析)
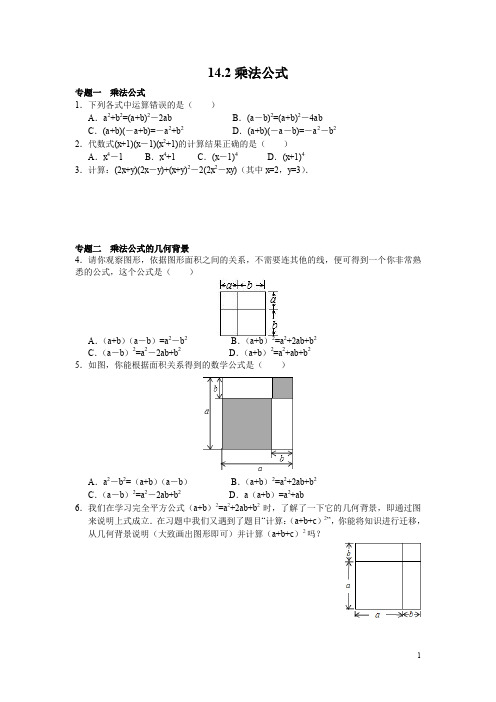
14.2乘法公式专题一乘法公式1.下列各式中运算错误的是()A.a2+b2=(a+b)2-2ab B.(a-b)2=(a+b)2-4abC.(a+b)(-a+b)=-a2+b2D.(a+b)(-a-b)=-a2-b22.代数式(x+1)(x-1)(x2+1)的计算结果正确的是()A.x4-1 B.x4+1 C.(x-1)4D.(x+1)43.计算:(2x+y)(2x-y)+(x+y)2-2(2x2-xy)(其中x=2,y=3).专题二乘法公式的几何背景4.请你观察图形,依据图形面积之间的关系,不需要连其他的线,便可得到一个你非常熟悉的公式,这个公式是()A.(a+b)(a-b)=a2-b2B.(a+b)2=a2+2ab+b2C.(a-b)2=a2-2ab+b2D.(a+b)2=a2+ab+b25.如图,你能根据面积关系得到的数学公式是()A.a2-b2=(a+b)(a-b)B.(a+b)2=a2+2ab+b2C.(a-b)2=a2-2ab+b2D.a(a+b)=a2+ab6.我们在学习完全平方公式(a+b)2=a2+2ab+b2时,了解了一下它的几何背景,即通过图来说明上式成立.在习题中我们又遇到了题目“计算:(a+b+c)2”,你能将知识进行迁移,从几何背景说明(大致画出图形即可)并计算(a+b+c)2吗?状元笔记【知识要点】1.平方差公式(a+b)(a-b)=a2-b2,两个数的和与这两个数的差的积,等于这两个数的平方差.2.完全平方公式(a±b)2=a2±2ab+b2,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.【温馨提示】1.不要将平方差公式和完全平方公式相混淆,注意它们项数和符号的不同.2.完全平方公式中,中间项是左边两个数的和的2倍,注意系数的特点.【方法技巧】1.公式中的字母a、b可以是具体的数,也可以是单项式、多项式.只要符合公式的结构特征,就可以利用公式.2.有些题目往往不能直接应用公式求解,但稍做适当的变形后就可以用乘法公式求解.如:位置变化,符号变化,数字变化,系数变化,项数变化等.参考答案:1.D 解析:A中,由完全平方公式可得(a+b)2-2ab=a2+2ab+b2-2ab=a2+b2,故A正确;B中,由完全平方公式可得(a-b)2=a2-2ab+b2,(a+b)2-4ab=a2+2ab+b2-4ab=a2-2ab+b2,故B正确;C中,由平方差公式可得(a+b)(-a+b)=(a+b)(b-a)=b2-a2=-a2+b2,故C正确;D中,(a+b)(-a-b)=-(a+b)2=-a2-2ab-b2,故D错误.2.A 解析:原式=(x2-1)(x2+1)=(x2)2-1=x4-1.3.解:原式=4x2-y2+x2+2xy+y2-4x2+2xy=x2+4xy,当x=2,y=3时,原式=22+4×2×3=4+24=28.4.B 解析:这个图形的整体面积为(a+b)2;各部分的面积的和为a2+2ab+b2;所以得到公式(a+b)2=a2+2ab+b2.故选B.5.C 解析:从图中可知:阴影部分的面积是(a-b)2和b2,剩余的矩形面积是(a-b)b和(a-b)b,即大阴影部分的面积是(a-b)2,∴(a-b)2=a2-2ab+b2,故选C.6.解:(a+b+c)2的几何背景如图,整体的面积为:(a+b+c)2,用各部分的面积之和表示为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,所以(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.。
人教版 八年级上册数学 14.2 乘法公式 同步课时训练(含答案) (2)

14.2 乘法公式同步训练一、选择题1. 计算(-a-b)2的结果是()A.a2+b2B.a2+2ab+b2C.a2-b2D.a2-2ab+b22. 将202×198变形正确的是()A.2002-4 B.2022-4C.2002+2×200+4 D.2002-2×200+43. 若a2+ab+b2=(a-b)2+X,则整式X为()A.ab B.0 C.2ab D.3ab4. 化简(-2x-3)(3-2x)的结果是()A.4x2-9 B.9-4x2C.-4x2-9 D.4x2-6x+95. 若(2x+3y)(mx-ny)=9y2-4x2,则m,n的值分别为() A.2,3 B.2,-3C.-2,-3 D.-2,36. 将9.52变形正确的是()A.9.52=92+0.52 B.9.52=(10+0.5)×(10-0.5) C.9.52=92+9×0.5+0.52 D.9.52=102-2×10×0.5+0.52 7. 计算(x+1)(x2+1)·(x-1)的结果是()A.x4+1 B.(x+1)4C.x4-1 D.(x-1)48. 若(x+a)2=x2+bx+25,则()A.a=3,b=6B.a=5,b=5或a=-5,b=-10C.a=5,b=10D.a=-5,b=-10或a=5,b=109. 如图①,边长为a的大正方形中有四个边长均为b的小正方形,小华将阴影部分拼成了一个长方形(如图②),则这个长方形的面积为()A.a2-4b2B.(a+b)(a-b)C.(a+2b)(a-b)D.(a+b)(a-2b)10. 如图,阴影部分是边长为a的大正方形剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是()A .①②B .②③C .①③D .①②③二、填空题11. 如果(x +my )(x -my )=x 2-9y 2,那么m =________.12. 填空:()22121453259x y x y ⎛⎫-=- ⎪⎝⎭13. 如果(x -ay )(x +ay )=x 2-9y 2,那么a = .14. 若x -y =6,xy =7,则x 2+y 2的值等于________.15. 如图,四张全等的矩形纸片拼成的图形,请利用图中空白部分面积的不同表示方法,写出一个关于a 、b 的恒等式___________.ab ba16. 根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是____________________.三、解答题17. 计算:(41)(41)a a ---+18. 阅读材料后解决问题.小明遇到一个问题:计算(2+1)×(22+1)×(24+1)×(28+1).经过观察,小明发现将原式进行适当的变形后,可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)×(22+1)×(24+1)×(28+1)=(2-1)×(2+1)×(22+1)×(24+1)×(28+1)=(22-1)×(22+1)×(24+1)×(28+1)=(24-1)×(24+1)×(28+1)=(28-1)×(28+1)=216-1.请你根据小明解决问题的方法,试着解决下列问题:(1)计算:(2+1)×(22+1)×(24+1)×(28+1)×(216+1);(2)计算:(3+1)×(32+1)×(34+1)×(38+1)×(316+1);(3)化简:(m +n )(m 2+n 2)(m 4+n 4)(m 8+n 8)(m 16+n 16).19. 观察下列各式:(x-1)(x+1)=x2-1;(x-1)(x2+x+1)=x3-1;(x-1)(x3+x2+x+1)=x4-1;…(1)(x-1)(x4+x3+x2+x+1)=________;(2)根据规律可得:(x-1)(x n-1+…+x+1)=________(其中n为正整数);(3)计算:(3-1)(350+349+348+…+32+3+1);(4)计算:(-2)2020+(-2)2019+(-2)2018+…+(-2)3+(-2)2+(-2)+1.20. 认真阅读材料,然后回答问题:我们初中学习了多项式的运算法则,相应地,我们可以计算出多项式的展开式,如:(a+b)1=a+b,(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,….下面我们依次对(a+b)n展开式的各项系数进一步研究发现,当n取正整数时可以单独列成如图所示的形式:上面的多项式展开系数表称为“杨辉三角形”.仔细观察“杨辉三角形”,用你发现的规律回答下列问题:(1)(a+b)n展开式中共有多少项?(2)请写出多项式(a+b)5的展开式.答案一、选择题1. 【答案】B[解析] 原式=(-a)2-2·(-a)·b+b2=a2+2ab+b2.2. 【答案】A[解析] 202×198=(200+2)×(200-2)=2002-4.3. 【答案】D4. 【答案】A[解析] 原式=(-2x-3)(-2x+3)=(-2x)2-32=4x2-9.5. 【答案】C[解析] 因为(2x+3y)(mx-ny)=2mx2-2nxy+3mxy-3ny2=9y2-4x2,所以2m=-4,-3n=9,-2n+3m=0,解得m=-2,n=-3.6. 【答案】D[解析] 9.52=(10-0.5)2=102-2×10×0.5+0.52.7. 【答案】C[解析] (x+1)(x2+1)(x-1)=(x+1)(x-1)(x2+1)=(x2-1)(x2+1)=x4-1.8. 【答案】D[解析] 因为(x+a)2=x2+bx+25,所以x 2+2ax +a 2=x 2+bx +25.所以⎩⎨⎧2a =b ,a 2=25,解得⎩⎨⎧a =5,b =10或⎩⎨⎧a =-5,b =-10.9. 【答案】A [解析] 根据题意得(a +2b )(a -2b )=a 2-4b 2.10. 【答案】D [解析] 在图①中,左边的图形阴影部分的面积=a 2-b 2,右边图形的面积=(a +b )(a -b ),故可得a 2-b 2=(a +b )(a -b ),可以验证平方差公式; 在图②中,左边图形的阴影部分的面积=a 2-b 2,右边图形的面积=(2b +2a )(a -b )=(a +b )(a -b ),可得a 2-b 2=(a +b )(a -b ),可以验证平方差公式;在图③中,左边图形的阴影部分的面积=a 2-b 2,右边图形的面积=(a +b )(a -b ),可得a 2-b 2=(a +b )(a -b ),可以验证平方差公式.二、填空题11. 【答案】±3 [解析] (x +my)(x -my)=x 2-m 2y 2=x 2-9y 2,所以m 2=9.所以m =±3.12. 【答案】221212145353259x y x y x y ⎛⎫⎛⎫+-=- ⎪⎪⎝⎭⎝⎭ 【解析】221212145353259x y x y x y ⎛⎫⎛⎫+-=- ⎪⎪⎝⎭⎝⎭13. 【答案】±3 [解析] ∵(x -ay )(x +ay )=x 2-a 2y 2=x 2-9y 2,∴a 2=9,解得a =±3.14. 【答案】50 [解析] 因为x -y =6,xy =7,所以x 2+y 2=(x -y)2+2xy =62+2×7=50.15. 【答案】224()()ab a b a b =+--【解析】22()()4a b a b ab -=+-或224()()ab a b a b =+--16. 【答案】(a +b)(a -b)=a 2-b 2三、解答题17. 【答案】222(41)(41)(4)1161a a a a ---+=--=-【解析】222(41)(41)(4)1161a a a a ---+=--=-18. 【答案】解:(1)原式=(2-1)×(2+1)×(22+1)×(24+1)×(28+1)×(216+1)=232-1.(2)原式=×(3-1)×(3+1)×(32+1)×(34+1)×(38+1)×(316+1)=. (3)若m ≠n ,则原式=(m -n )(m +n )(m 2+n 2)(m 4+n 4)(m 8+n 8)(m 16+n 16)=;若m =n ,则原式=2m ·2m 2·……·2m 16=32m 31.19. 【答案】 解:(1)x 5-1(2)x n -1(3)(3-1)(350+349+348+…+32+3+1)=351-1.(4)因为(-2-1)[(-2)2020+(-2)2019+(-2)2018+…+(-2)3+(-2)2+(-2)+1]=(-2)2021-1=-22021-1,所以(-2)2020+(-2)2019+(-2)2018+…+(-2)3+(-2)2+(-2)+1=22021+13.20. 【答案】解:(1)由已知可得:(a+b)1展开式中共有2项,(a+b)2展开式中共有3项,(a+b)3展开式中共有4项,……则(a+b)n展开式中共有(n+1)项.(2)(a+b)1=a+b,(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,…则(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.。
【推荐】人教版八年级数学上册同步练习14.2乘法公式(含答案解析).doc
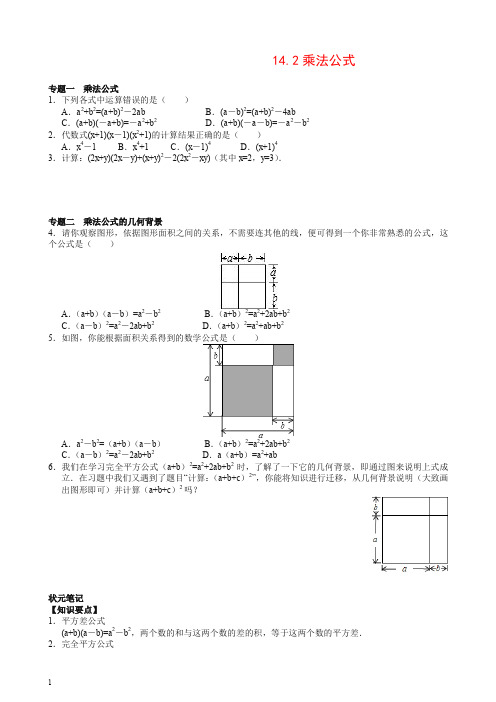
14.2乘法公式专题一乘法公式1.下列各式中运算错误的是()A.a2+b2=(a+b)2-2ab B.(a-b)2=(a+b)2-4abC.(a+b)(-a+b)=-a2+b2D.(a+b)(-a-b)=-a2-b22.代数式(x+1)(x-1)(x2+1)的计算结果正确的是()A.x4-1 B.x4+1 C.(x-1)4D.(x+1)43.计算:(2x+y)(2x-y)+(x+y)2-2(2x2-xy)(其中x=2,y=3).专题二乘法公式的几何背景4.请你观察图形,依据图形面积之间的关系,不需要连其他的线,便可得到一个你非常熟悉的公式,这个公式是()A.(a+b)(a-b)=a2-b2B.(a+b)2=a2+2ab+b2C.(a-b)2=a2-2ab+b2D.(a+b)2=a2+ab+b25.如图,你能根据面积关系得到的数学公式是()A.a2-b2=(a+b)(a-b)B.(a+b)2=a2+2ab+b2C.(a-b)2=a2-2ab+b2D.a(a+b)=a2+ab6.我们在学习完全平方公式(a+b)2=a2+2ab+b2时,了解了一下它的几何背景,即通过图来说明上式成立.在习题中我们又遇到了题目“计算:(a+b+c)2”,你能将知识进行迁移,从几何背景说明(大致画出图形即可)并计算(a+b+c)2吗?状元笔记【知识要点】1.平方差公式(a+b)(a-b)=a2-b2,两个数的和与这两个数的差的积,等于这两个数的平方差.2.完全平方公式(a±b)2=a2±2ab+b2,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.【温馨提示】1.不要将平方差公式和完全平方公式相混淆,注意它们项数和符号的不同.2.完全平方公式中,中间项是左边两个数的和的2倍,注意系数的特点.【方法技巧】1.公式中的字母a、b可以是具体的数,也可以是单项式、多项式.只要符合公式的结构特征,就可以利用公式.2.有些题目往往不能直接应用公式求解,但稍做适当的变形后就可以用乘法公式求解.如:位置变化,符号变化,数字变化,系数变化,项数变化等.参考答案:1.D 解析:A中,由完全平方公式可得(a+b)2-2ab=a2+2ab+b2-2ab=a2+b2,故A正确;B中,由完全平方公式可得(a-b)2=a2-2ab+b2,(a+b)2-4ab=a2+2ab+b2-4ab=a2-2ab+b2,故B正确;C中,由平方差公式可得(a+b)(-a+b)=(a+b)(b-a)=b2-a2=-a2+b2,故C正确;D中,(a+b)(-a-b)=-(a+b)2=-a2-2ab-b2,故D错误.2.A 解析:原式=(x2-1)(x2+1)=(x2)2-1=x4-1.3.解:原式=4x2-y2+x2+2xy+y2-4x2+2xy=x2+4xy,当x=2,y=3时,原式=22+4×2×3=4+24=28.4.B 解析:这个图形的整体面积为(a+b)2;各部分的面积的和为a2+2ab+b2;所以得到公式(a+b)2=a2+2ab+b2.故选B.5.C 解析:从图中可知:阴影部分的面积是(a-b)2和b2,剩余的矩形面积是(a-b)b和(a-b)b,即大阴影部分的面积是(a-b)2,∴(a-b)2=a2-2ab+b2,故选C.6.解:(a+b+c)2的几何背景如图,整体的面积为:(a+b+c)2,用各部分的面积之和表示为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,所以(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版八年级数学14.2 乘法公式课时训练
一、选择题(本大题共12道小题)
1. 运用乘法公式计算(a+3)(a-3)的结果是()
A.a2-6a+9
B.a2-3a+9
C.a2-9
D.a2-6a-9
2. 计算(2x+1)(2x-1)的结果为()
A.4x2-1
B.2x2-1
C.4x-1
D.4x2+1
3. 计算(x-1)2的结果是( )
A.x2-x+1 B.x2-2x+1
C.x2-1 D.2x-2
4. 运用乘法公式计算(a+3)(a-3)的结果是( )
A.a2-6a+9 B.a2-3a+9
C.a2-9 D.a2-6a-9
5. 下列整式乘法中,能运用平方差公式进行运算的是( )
A.(2a+b)(2b-a) B.(-2a-b)(2a+b)
C.(2a-b)(b-2a) D.(2a+b)(b-2a)
6. 下列各式:①(x-2y)(2y+x);②(x-2y)(-x-2y);③(-x-2y)(x+2y);④(x-2y)(-x+2y).其中能用平方差公式计算的是()
A.①②
B.①③
C.②③
D.②④
7. 若M·(2x-y2)=y4-4x2,则M应为()
A.-(2x+y2)
B.-y2+2x
C.2x+y2
D.-2x +y2
8. 将202×198变形正确的是 ( )
A.2002-4 B.2022-4
C.2002+2×200+4 D.2002-2×200+4
9. 如果,则一定成立的是( )
A.是的相反数B.是的相反数C.是的倒数D.是的倒数
10. 将9.52变形正确的是 ( )
A.9.52=92+0.52 B.9.52=(10+0.5)×(10-0.5)
C.9.52=92+9×0.5+0.52 D.9.52=102-2×10×0.5+0.52
11. 若(x+a)2=x2+bx+25,则( )
A.a=3,b=6
B.a=5,b=5或a=-5,b=-10
C.a=5,b=10
D.a=-5,b=-10或a=5,b=10
12. 如果,,是三边的长,且,那么是( )
A. 等边三角形.
B. 直角三角形.
C. 钝角三角形.
D. 形状不确定.
二、填空题(本大题共6道小题)
13. 如果(x+my)(x-my)=x2-9y2,那么m=________.
14. 填空:
15. 计算:9982=________.
16. 已知a+b=2,a2-b2=12,那么a-b=.
17.
课本上,公式(a-b)2=a2-2ab+b2是由公式(a+b)2=a2+2ab+b2推导得出的.已知(a+b)4=a4+4a3b+6a2b2+4ab3+b4,则(a-b)4=________________.
18.
根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是_______ _____________.
三、解答题(本大题共3道小题)
19.
(1)如图是用4个全等的长方形拼成的一个“回形”正方形,图中阴影部分的面积用两种方法表示可得一个等式,这个等式为________________;
(2)若(4x-y)2=9,(4x+y)2=169,求xy的值.
20. 计算
21. 如图,王大妈将一块边长为a m的正方形土地租给了邻居李大爷种植,今年,她对李大爷说:“我把你这块地的一边减少4 m,另一边增加4 m,继续租给你,你也没有吃亏,你看如何?”李大爷一听,就答应了.同学们,你认为李大爷吃亏了吗?为什么?
人教版八年级数学14.2 乘法公式课时训练-
答案
一、选择题(本大题共12道小题) 1. 【答案】C
2. 【答案】A
3. 【答案】B
4. 【答案】C
5. 【答案】D
6. 【答案】A
7. 【答案】A
[解析] M 与2x -y 2的相同项应为-y 2,相反项应为-2x 与2x ,所
以M 为-2x -y 2,即-(2x +y 2).
8. 【答案】A
[解析] 202×198=(200+2)×(200-2)=2002-4.
9. 【答案】C
【解析】将原式展开,合并后得到
,选择C .
10. 【答案】D
[解析] 9.52=(10-0.5)2=102-2×10×0.5+0.52.
11. 【答案】D
[解析] 因为(x +a)2=x 2+bx +25,
所以x 2+2ax +a 2=x 2+bx +25.
所以⎩⎪⎨⎪⎧2a =b ,a2=25,解得⎩⎪⎨⎪
⎧a =5,b =10或⎩⎪⎨⎪⎧a =-5,b =-10.
12. 【答案】A
【解析】已知关系式可化为
,即
,
所以
,故
,
,
.即.选A .
二、填空题(本大题共6道小题)
13.
【
答
案
】
±3 [解析]
(x +my)(x -my)=x 2-m 2y 2=x 2-9y 2,所以m 2=9.所以m =±3.
14. 【答案】
【解析】
15. 【答案】996004 [解析] 原式=(1000-2)2=1000000-4000+4=996004.
16. 【答案】6[解析] (a-b)(a+b)=a2-b2=2(a-b)=12,∴a-b=6.
17. 【答案】a4-4a3b+6a2b2-4ab3+b4
[解析] 因为(a+b)4=a4+4a3b+6a2b2+4ab3+b4,
所以(a-b)4=[a+(-b)]4
=a4+4a3(-b)+6a2(-b)2+4a(-b)3+(-b)4
=a4-4a3b+6a2b2-4ab3+b4.
18. 【答案】(a+b)(a-b)=a2-b2
三、解答题(本大题共3道小题)
19. 【答案】
解:(1)(b+a)2-(b-a)2=4ab
(2)因为(4x+y)2-(4x-y)2=16xy=160,所以xy=10.
20. 【答案】
【解析】原式
21. 【答案】
解:李大爷吃亏了.
理由:原来正方形土地的面积为a2m2,当一边减少4 m,另一边增加4 m时,面积为(a+4)(a-4)=(a2-16)m2.
因为a2-16<a2,
所以李大爷吃亏了.。
