质量和热量平衡式如下
工厂设计之工艺流程设计和工艺计算2

第四节 耗冷量计算
耗冷量分为工艺耗冷量和非工艺耗冷量
工艺耗冷量又包含了发酵培养基和发酵罐体的 冷却降温耗冷,生物反应放热(发酵 热)的除去等; 非工艺耗冷量则包括维护结构耗冷量、用电设 备运转放热耗冷量等。
第五节 无菌压缩空气消耗量计算(略)
第六节 抽真空量计算(略)
盲目地追求某项低的消耗定额,住住导致失衡或 产率低、分离要求太高,设备的投资费用会相应地 增加,从而致使产品成本增加。 消耗定额是工程师进行物料衡算的重要数据, 也是衡量生产技术水平的重要经济指标。
(3)转化率:是指原料通过反应器之后发生化学变 比的程度:其计算式为:
反应掉的原料量 转化率= 110% 原料投料量 投原料的总量 反应后原料的剩余量 100% 原料投料量
总平衡式
组分平衡式 元素平衡式
总质量平衡式 总摩尔平衡式 组分质量平衡式 组分摩尔平衡式 元素质量平衡式 元素摩尔平衡式
二、主要技术经济指标的确定 (一)技术经济指标确定的意义 通过生产全过程的总物料衡算、能量衡算和各 阶段的物料衡算、能量衡算,就可以求出通常构成 产品单位成本的主要部分的三项指标 : (1)生产1000kg成品或半成品的原材料消耗定额及 原料总回收率。 (2)生产1000kg成品所产生的排出物,包括副产物、 废水、废气、废渣等。
(3)生产1000kg成品的水、蒸汽、空气及冷量等消 耗定额。
(二)主要技术经济指标内容
应掌握p55上各项技术经济指标的含义和计算 方法或来源。 三、计算实例 (一)10000t/a淀粉原料酒精厂全厂总物料衡算
(二)30000t/a啤酒厂糖化车间的物料衡算
(三)3000t/a味精工厂发酵车间的物料衡算
根据实例请说明计算前所需要的基础数据有哪 些?计算得到了哪些结果?
工程热力学热力学基础知识

2、功的符号和单位
功的符号:用W表示 功的单位:1)国际单位中,J(焦耳)或kJ(千焦) 1J=1N.m 2)电力工程中常用kWh作为功的单位;
1kWh=3600kJ 装机容量为300MW的汽轮发电机组连续工作一 天的发电量是多少kWh? 比功:1kg气体与外界交换的功称为比功,用w表 示,单位用J/kg或kJ/kg。(w=W/m)
解:根据p=pb+pg,则蒸汽的绝对压力为
p=750×133.3十18.2×l06=18.3×106(Pa)=18.3MPa
说明:在火力发电厂的设备型号中,通常有表示压
力的参数;在不同设备型号中,其含义不尽相同。
18
1-3 平衡状态和热力过程
一、平衡状态、状态方程和参数坐标图
1、平衡状态
(1)定义:系统在不受外界影响的条件下,系统内 工质的宏观热力性质不随时间而变化的状态。
定其基准点和分度方法,常用的有两种温标: 摄氏温标(t,℃) : 划分100等份 纯水在1atm下,
冰点 0℃
沸点 100℃
热力学温标(绝对温标/开尔文温标)(T, K): 以水的三相点为基准点,并规定为273.16 K。
相互关系:基准点不同,但分度一样,即∆t=∆T
T= t +273.15 K
15
3.比体积(比容) 比体积v:单位质量工质所占有的体积。
v=V/m ρ=m/V
(单位: m3/kg) (单位: kg/m3)
密度ρ:单位体积内工质的质量。
相互关系:ρv=1 物理意义:二者均反映物质内部分子聚集的疏
密程度,即分子间平均距离的大小。
16
例题分析
例1-1 如图所示,用水银压力计测 量凝汽器的压力,已知测压计 读数为706mmHg,当地大气压 pb=98.07kPa,求凝汽器内蒸汽 的绝对压力。
精馏过程的数学建模

化工数学模型
SL(j)为第 j 块塔板的液相抽出量。 根据质量平衡、能量平衡等原理,其模型方程可表示为: 1. 塔板的总物料平衡式: dM(j)/dt = L(j-1)+V(j+1)-L(j)-V(j)+F(j)-SL(j)-SV(j) 2. 塔板各组分的物料平衡式: D[M(j)x(I,j)]/dt=M(j).dx(I,j)/dt+x(I,j).dM(j)/dt =L(j-1)x(I,j-1)+V(j+1)y(I,j+1)-(L(j)+SL(j))x(I,j)-(V(j)+SV(j))y(I,j)+F(j)xF(I,j) 3. 塔板的热量平衡式: D[M(j)h(j)]/dt=M(j).dh(j)/dt+h(j).dM(j)/dt =L(j-1)h(j-1)+V(j+1)H(j+1)-[(L(j)+SL(j))h(j)-[(V(j)+SV(j)).H(j)+F(j)hF (j)+Q(j) 4. 气液平衡方程: y(I,j)=K(I,j)x(I,j) 5. 归一化方程: ������(������, ������)=1 此外,我们还需要计算精馏塔的理论塔板数 N。 这里我们运用图解法计算理论塔板数,其基本过程如下: 1. 根据汽液平衡数据或汽液平衡方程绘制出汽液平衡曲线。 2. 根据精馏段操作线性方程 Yn+1=������+1xn+
3
ห้องสมุดไป่ตู้
1
化工数学模型
A
B
图1精馏过程示意图
由于实际的塔板的情况很复杂, 为了使解决问题方便, 又不失其合理性, 作了如下假设: 1. 同一塔板可按集总参数处理。 2. 和塔板上能瞬间达到气一液平衡;其过渡过程可以用补偿参数调整。 3. 塔的热损失和塔板本身的热容可以忽略不计。 4. 忽略塔板上的气相滞留量即不考虑气相流率的动态过程。 5. 塔板上液相密度近似为常数。 假设精馏塔共有n块塔板, 按惯例把塔顶称为第1块, 把塔釜称为第n块, 中间各 塔板顺次为2,3,4,5…j…n-1。 其中:M(j)为第j块塔板上的蓄液量 T(j)为第j块塔板的温度 Q(j)为第j块塔板的蓄热量∀或加热量 x(i,j)为第j块塔板的液相组成∀2 表示组分, y(i,j)为第j块塔板的气相组成) F(j)为第j块塔板的进料量) xF(i,j)为第j块塔板的进料组成) V(j+1),V(j)为第j块塔板的进、出气体量 SV(j)为第 j 块塔板的气相抽出 L(j-1),L(j)为第 j 块塔板的进、出液体量
第四章 热力学第一定律

华北科技学院化工热力学Chemical Engineering Thermodynamics第四章 热力学第一定律4.1 闭系非流动过程的能量平衡能量平衡式 体系能量的变化=体系与环境交换的净能量。
即:(能量)入 − (能量)出 = (能量)存封闭体系非流动过程的热力学第一定律:ΔU = Q + W4.2 开系通用的能量平衡方程4.3 稳流过程的能量平衡1. 开系稳流过程的能量平衡状态是稳定的 稳流过程 流动是稳定的 1)外部环境对流体提供的能量(对于1kg流体): ①外功(ws)—净功或有效功,J/kg; 规定:外界提供给流体功, ws为正; 流体传递给外界功,ws为负。
②热量(q)—获得的热量,J/kg;4.3 稳流过程的能量平衡2) 流体在流动过程中本身所具有的能量(对于1kg流体): ① 内能 U: J/kg; ② 位能: ③ 动能: ④ 静压能(压强能) m kg: 动能 = mu2/2, J 1 kg: 动能 = u2/2 , J/kg m kg: 位能 = mgZ, J 1 kg: 位能 = gZ, J/kgm kg-V m3 : 静压能 = pV , J 1V kg- m3 m:静压能=pV p = m ρ, J/kg4.3 稳流过程的能量平衡衡算范围:1-1′至2-2′截面 衡算基准:1kg不可压缩流体 基准水平面:0-0′平面流动系统依据: 输入总能量=输出总能量1 2 p1 1 2 p2 U 1 + gz1 + u1 + + we + q = U 2 + gz2 + u2 + 2 ρ 2 ρ总能量衡算式4.3 稳流过程的能量平衡1 ρ= v1 2 p1 1 2 p2 U 1 + gz1 + u1 + + ws + q = U 2 + gz2 + u2 + 2 ρ 2 ρ 1 2 1 2 U 1 + gz1 + u1 + p1v + ws + q = U 2 + gz2 + u 2 + p2 v 2 2h = U + Pv2 u12 u2 h1 + gZ1 + + ws + q = h2 + gZ 2 + 2 2P97,例4-11 2 Δh + gΔZ + Δu = ws + q 2mkg1 ΔH + mgΔZ + mΔu 2 = Ws + Q 21kg流体稳流能量衡算式mkg流体稳流能量衡算式4.3 稳流过程的能量平衡2. 稳流过程能量平衡的简化形式(1)机械能平衡方程式(柏努利方程): 流体不可压缩→ρ=常数=1/v,v△p=△p/ρ 无热、无轴功交换→q=0,ws=0 理想流体,无粘性→摩擦损耗hf=0,△U=0Δh + gΔZ + 1 2 Δu = ws + q 2条件△h=△U+v△pΔpρ+ gΔZ +1 Δu 2 = 0 24.3 稳流过程的能量平衡(2)绝热稳定流动方程式 条件:可压缩,与外界无热、无轴功交换。
传热学—第五章

第四章 对流换热在绪论中已经指出,对流换热是发生在流体和与之接触的固体壁面之间的热量传递过程,是发生在流体中的热量传递过程的特例。
由于流体系统中流体的运动,热量将主要以热传导和热对流的方式进行,这必然使热量传递过程比单纯的导热过程要复杂得多。
本章将在对换热过程进行一般性讨论的基础上,将质量守恒、动量守恒和能量守恒的基本定律应用于流体系统,导出支配流体速度场和温度场的场方程-对流换热微分方程组。
由于该方程组的复杂性,除少数简单的对流换热问题可以通过分析求解微分方程而得出相应的速度分布和温度分布之外,大多数对流换热问题的分析求解是十分困难的。
因此,在对流换热的研究中常常采用实验研究的方法来解决复杂的对流换热问题。
在这一章,我们将通过方程的无量纲化和实验研究方法的介绍而得到常用的准则及准则关系式。
讨论的重点放在工程上常用的管内流动、平行流过平板以及绕流圆管的受迫对流换热,大空间和受限空间的自然对流换热,以及蒸汽凝结与液体沸腾换热。
4-1 对流换热概述1对流换热过程对流换热是发生在流体和与之接触的固体壁面之间的热量传递过程,(直接接触是与辐射换热的区别),是宏观的热对流与微观的热传导的综合传热过程。
由于涉及流体的运动使热量的传递过程变得较为复杂,分析处理较为困难。
因此,在对流换热过程的研究和应用上,实验和数值分析的处理方法是常常采用的。
下面我们以简单的对流换热过程为例,对对流换热过程的特征进行粗略的分析。
图4-1表示一个简单的对流换热过程。
表示流体以来流速度u ∞和来流温度t ∞流过一个温度为t w 的固体壁面。
这里选取流体沿壁面流动的方向为x 坐标、垂直壁面方向为y 坐标。
由于固体壁面对流体分子的吸附作用,使得壁面上的流体是处于不流动或不滑移的状态(此论点对于极为稀薄的流体是不适用的)。
又由于流体分子相互之间的穿插扩散和(或) 相互之间的吸引造成流体之间的相互牵制。
这种相互的牵制作用就是流体的黏性力,在其作用下会使流体的速度在垂直于壁面的方向上发生改变。
热平衡方程

热平衡方程
热平衡方程是描述物体之间热量交换规律的数学表达式。
在热力学中,我们通
过热平衡方程来分析物体之间的热量转移情况,从而更好地理解热力学系统的性质。
理论基础
热平衡方程基于热动力学定律,即热量会从高温区传递到低温区,直至两者达
到热平衡。
热平衡方程通常用来描述热力学系统中各个部分之间的热量传递过程,以及系统整体的热平衡状态。
热平衡方程的一般形式
设两个物体之间的热传导面积为A,温度差为ΔT,热传导系数为k,则热平衡
方程可以表示为:
Q = k * A * ΔT
其中,Q表示单位时间内从一个物体传递到另一个物体的热量,k是热传导系数,A是热传导面积,ΔT是温度差。
实际应用
热平衡方程在工程领域有着广泛的应用。
例如,热平衡方程可用来计算建筑物
之间的热传导,帮助设计合理的供暖或制冷系统;还可以用于分析电子设备的散热效果,优化设备的工作性能。
结论
热平衡方程是热力学中一个重要的概念,它帮助我们理解热量在物体之间如何
传递,为解决工程和科学问题提供了有力的工具。
通过研究和应用热平衡方程,我们可以更好地控制和优化热力学系统,提高系统的效率和稳定性。
燃烧热的测定

应用物理2010级朱加旺一、目的要求1.明确燃烧热的定义,了解Q V与Q p的差别;2.通过萘的燃烧热的测量,了解氧弹式量热计中主要部件的作用,掌握量热计的使用技术;5.学会雷诺图解法。
二、实验原理燃烧热:1mol物质完全燃烧时所放出的热量。
恒容条件下测得的燃烧热称为恒容燃烧热(Q V),Q V=ΔU。
恒压条件下测得的燃烧热为恒压燃烧热(Q p),Q p=ΔH。
若把参加反应的气体和生成的气体作为理想气体处理,则存在如下关系式:Q p=Q V+ΔnRT。
Δn为反应产物中气体物质的总摩尔数与反应物中气体物质总摩尔数之差;R为气体常数;T为反应前后绝对温度。
本实验采用氧氮式量热计测量萘的燃烧热。
氧弹是一具特制的不锈钢容器,如图4-1所示。
为保证样品在其中迅速而完全地燃烧,需要用过量的强氧化剂,通常氧弹中充以氧气作为氧化剂。
实验时氧弹是旋转在装有一定量水的不锈钢桶中,水桶外是空气隔热层,再外面是恒定的水夹套,如图4-2所示。
引火丝及样品在体积固定的氧弹中燃烧所放出的热大部分为水桶中的水吸收;其余部分为氧弹、水桶、搅拌器及感温探头等设备吸收。
在量热计与环境没有热交换的情况下,可以写出如下热量平衡式:式中:Q V——样品的恒容燃烧热 (J·g-1);m——样品的质量 (g);C if——量热计热容,它包括氧弹、量热计及水的热容 (J·K-1);ΔT——准确温差 (K);Q丝——点火丝燃烧热。
铁丝为-6696.4 J·g-1、镍丝为-3158.9 J·g-1、Cu-Ni丝为-3136.2 J·g-1。
m丝——燃烧掉的点火丝质量(g)即原丝质量减去燃烧剩余质量;m棉—燃烧掉的棉线质量(g);Q棉—棉线燃烧热,17500J·g-1。
由(4-1)式知,要测量样品的Q V必须先知量热计的热容C if,测定的方法是用一定量已知燃烧热的标准物质(常用苯甲酸,Q V=—26477J·g-1)在相同条件下进行试验,测量其温差,经校正为真实温差后代入(4-1)式,算出值C if。
环境工程原理 第二章 质量衡算与能量衡算

第一节 常用物理量
体积分数和质量浓度之间的关系
VA A ? V
根据质量浓度的定义
mA nA M A 3 A 10 V V nA M A V 103
第二节 质量衡算
•(二)以某种元素或某种物质为衡算对象 当系统中流速、压力、密度等物理量只是位置的函数, 不随时间变化,称为稳态系统;当上述物理量不仅随位置变 化,而且随时间变化,称为非稳态系统。 稳态流动的数学特征: 对于稳态过程,内部无物料积累
0 t
m1 m2
稳态系统与非稳态系统
qm1 qm 2
第二节 质量衡算
本节的主要内容
一、衡算的基本概念 二、总质量衡算
ቤተ መጻሕፍቲ ባይዱ二节 质量衡算
一、衡算的基本概念
输入量2
分离、反应—— 分析物质流迁移转化
qV 2
某污染物
输入量1 积累量 输出量
qV 1
降解量
?
qVm
生物降解
输入量-输出量+转化量=积累量
第二节 质量衡算
一、衡算的基本概念
以某种元素或某种物质为衡算对象
(2.1.16)
混合物中惰性物质的质量
X mA xmA 1 xmA
质量比与质量分数的关系
(2.1.17)
第一节 常用物理量
3.质量比与摩尔比
(当混合物中除组分A外,其余为惰性组分时)
组分A与惰性组分的关系
nA XA n nA
组分A的摩尔比
组分A的物质的量
燃烧热的测定

实验一 燃烧热的测定(一)、实验目的1.掌握氧弹式量热计使用方法及测量物质燃烧热的技术。
2.测定萘的摩尔燃烧热。
(二)、实验原理燃烧热是指温度为T 时由物质B 与氧进行完全氧化时所放出的热。
所谓完全氧化是指C 全部生成CO 2,H 全部生成H 2O (l ),若有CO 或游离C 产生则说明氧化不完全甚至很不完全。
出现这种情况的主要原因是氧气充量不足或压力不够,为避免此种现象的发生,充氧气时一般压力在2.5~3MP a ,充气时间为60s ,这时将物质B 点燃后就能完全氧化生成CO 2和H 2O 。
在实验中用氧弹量热计进行实验时,氧弹放置在装有一定量水的铜水桶中,水桶外是空气隔热层,再外面是温度恒定的水夹套。
样品在体积固定的氧弹中燃烧放出的热、引火丝燃烧放出的热和由氧气中微量的氮气氧化成硝酸的生成热,大部分被水桶中的水吸收;另一部分则被氧弹、水桶、搅拌器及温度计等所吸收。
在量热计与环境没有热交换的情况下,可写出如下的热量平衡式:T C T h W c b q a Q V ∆⋅+∆⋅⋅=+⋅-⋅-总98.5 (1-1)式中:V Q —被测物质的定容热值,单位为J ·g -1;a —被测物质的质量,单位为g ;q —引火丝的热值,单位为J ·g -1(铁丝为-6694J ·g -1);b —烧掉的引火丝质量,单位为g ;W —水桶中水的质量单位g ;h —水的比热容单位J ·g -1·K -1;总C —氧弹、水桶等的总热容单位J ·K -1;T ∆—与环境无热交换时的真实温差。
如在实验时保持水桶中水量一定,把(1—1)式右端常数合并得到下式: T K c b q a Q V ∆⋅=+⋅-⋅-98.5 (1-2) 式中:(总C h W K +⋅=),J ·K -1;称为量热计常数。
若忽略空气中氮气氧化成硝酸时的生成热,故(1-2)式可写成:T K b q a Q V ∆⋅=⋅-⋅-则: ab q T K Q V ⋅+∆⋅-=式中:K 为量热计常数(14654 J ·K -1);q 为引火丝(镍铬丝)发热值(1400 J ·g -1) 实际上,氧弹式量热计不是严格的绝热系统,加之由于传热速度到达最高温度需要一定的时间,在这段时间里系统与环境难免发生热量交换,因此燃烧前后温度变化的测量值必须经过雷诺作图法进行校正,其校正方法如下:将燃烧前后每次观察到的温度对时间作图,取成a b c d 线[如图 1 (a) 图中b 相当于开始燃烧之点,c 为观察到最高的温度读数点,由于量热计和外界的热量交换,曲线ab 及cd 常常发生倾斜。
物理化学实验报告

《物理化学实验》标准实验报告目录实验一粘度法测定高聚物的相对摩尔质量 (3)实验二凝固点下降法测定摩尔质量 (7)实验三燃烧焓的测定 (9)实验四液体饱和蒸汽压的测定 (13)实验五碳酸钙分解压的测定 (16)实验六分光光度法测定络合物的稳定常数 (21)实验七双液系气液平衡相图的绘制 (26)实验八二组分合金相图的绘制 (29)实验九电池电动势的测定及其应用 (33)实验十碳钢在碳酸氢铵溶液中极化曲线的测定 (39)实验十一蔗糖水解速率常数的测定 (44)实验十二过氧化氢的催化分解 (49)实验十三乙酸乙酯皂化反应速率常数测定 (55)实验十四胶体电泳速度的测定 (58)实验十五溶液表面吸附作用和表面张力的测定 (62)实验十六水热法制备纳米SnO2微粉 (66)实验一 粘度法测定高聚物的相对摩尔质量一、实验目的:1、掌握乌氏粘度计测量粘度的原理和方法。
2、掌握粘度法测定聚乙烯分子量的原理、过程和数据处理方法。
二、实验原理:由于高聚物的分子质量大小不一、参差不齐,且没有一个确定的值,故实验测定某一高聚物的分子质量实际为分子质量的平均值,称为平均分子质量(即平均摩尔质量)。
根据测定原理和平均值计算方法上的不同,常分为数均分子质量、质均分子质量、Z 均分子质量和粘均分子质量。
对于同一聚合物,其测得的数均、质均、Z均或粘均分子质量在数值上往往不同。
人们常用渗透压、光散射及超离心沉降平衡等法测得分子质量的绝对值。
粘度法能测出分子质量的相对值,但因其设备简单,操作方便,并有很好的实验精度,故是人们所常用的方法之一。
粘度是液体流动时内摩擦力大小的反映。
纯溶剂粘度反映了溶剂分子间内摩擦效应之总和;而高聚物溶液粘度η是高聚物分子之间的内摩擦、高聚物分子与溶剂分子间内摩擦以及溶剂分子间内摩擦三者总和。
因此,通常高聚物溶液的粘度η大于纯溶剂粘度0η,即η>0η。
为了比较这两种粘度,引入增比粘度的概念,以sp η表示:sp η=001r ηηηη-=- (3-1) 式中r η为相对粘度,sp η表示已扣除了溶剂分子间内外摩擦效应,只留下溶剂分子与高聚物分子之间、高聚物分子相互间的内摩擦效应,其值随高聚物浓度而变。
第四章 能量衡算及热数据的估算(习题解答)
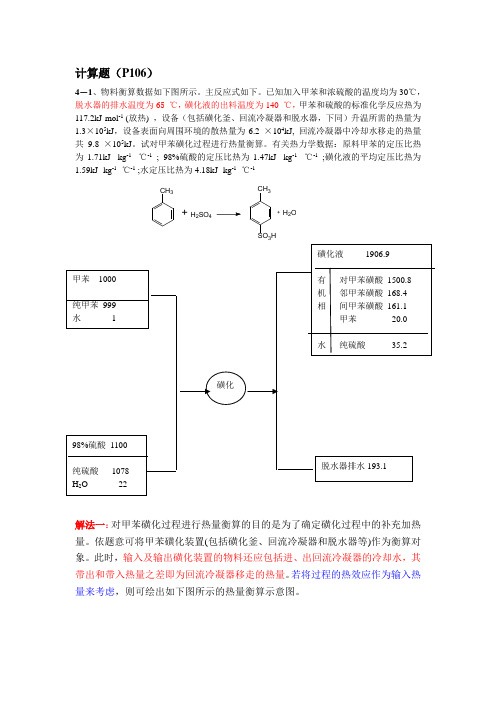
计算题(P106)4-1、物料衡算数据如下图所示。
主反应式如下。
已知加入甲苯和浓硫酸的温度均为30℃,脱水器的排水温度为65 ℃,磺化液的出料温度为140 ℃,甲苯和硫酸的标准化学反应热为117.2kJ·mol -1 (放热) ,设备(包括磺化釜、回流冷凝器和脱水器,下同)升温所需的热量为1.3×105kJ ,设备表面向周围环境的散热量为6.2 ×104kJ, 回流冷凝器中冷却水移走的热量共9.8 ×105kJ 。
试对甲苯磺化过程进行热量衡算。
有关热力学数据:原料甲苯的定压比热为1.71kJ ·kg -1 ·℃-1 ; 98%硫酸的定压比热为1.47kJ ·kg -1 ·℃-1 ;磺化液的平均定压比热为1.59kJ ·kg -1 ·℃-1 ;水定压比热为4.18kJ ·kg -1 ·℃-1解法一:对甲苯磺化过程进行热量衡算的目的是为了确定磺化过程中的补充加热量。
依题意可将甲苯磺化装置(包括磺化釜、回流冷凝器和脱水器等)作为衡算对象。
此时,输入及输出磺化装置的物料还应包括进、出回流冷凝器的冷却水,其带出和带入热量之差即为回流冷凝器移走的热量。
若将过程的热效应作为输入热量来考虑,则可绘出如下图所示的热量衡算示意图。
CH 3+H 2SO 4CH 3SO 3H+H 2O则热量平衡方程式可表示为 取热量衡算的基准温度为25o C (若取0 ℃作为基准,结果又如何?),则(1)(2)磺化过程热效应反应中共加入98%浓硫酸的质量为1100kg ,其中含水22kg 。
若以SO 3计,98%硫酸的质量分率为80%。
由式(4-44)得反应结束后,磺化液含硫酸35.2kg,水21.4kg 。
以SO 3计,硫酸的质量分率为50.8%。
则1234567Q Q Q Q Q Q Q ++=+++141000 1.71(3025)1100 1.47(3025) 1.6610Q kJ=⨯⨯-+⨯⨯-=⨯3p cQ Q Q =+1-122111 2.989(2515)110.20130.062 4773.4 kJ (kg H )s H m mm mO -∆=+--++=⋅2-122111 2.989(2515)10.50810.5080.20130.0620.5080.5081833.6 kJ (kg H )s H O ⨯-∆=+--++=⋅所以有反应消耗的甲苯量为979 kg ,则(3)反应产物(磺化液、脱水器排出的水)带走的热量Q 4 Q 4=1906.9 x 1.59 x (140-25)+193.1 x 4.18 x (65-25)=3.77 x 105 KJ (4)由题意知 Q 5=1.3 x 105 KJ Q 6=6.2 x 104 KJ Q 7=9.8 x 105 KJ 所以Q 2=Q 4+Q 5+Q 6+Q 7-Q 1-Q 3=2.12 x 105 KJ4224773.421.41833.6 6.610p Q kJ=⨯-⨯=⨯kJ1025.1 2.1179210979Q 63c ⨯=⨯⨯=kJ1032.1 1025.1106.6 Q Q Q 664cp 3⨯=⨯+⨯=+=解法二:对甲苯磺化过程进行热量衡算的目的是为了确定磺化过程中的补充加热量。
第2章发酵过程能量平衡和物质平衡

菌体生长的得率(yield)
以底物消耗为基准的菌体得率
• 微生物利用原料生长繁殖。测定生长前后 原料浓度和菌体浓度,菌体得率计算公式: • YX/S= -ΔX/ΔS (g/mol)
• 意义:原料消耗量与菌体生长量的关系; • 所消耗的原料,并非100%转变为菌体。 • YX/S与微生物,原料种类,培养条件有关。 • 同理:
菌体含碳量α2=12/(12+1.898+0.627×16+0.152×14)
×100%= 46.05%
•
碳源含碳量α1= 12/(12+4+16) ×100%=37.5%
• •可计算出菌体关于甲醇的得率是: Yx/s= Yx×(α1/α2)=0.13×0.375/0.4605 =0.106
同样,可得到产物血管生长抑制素关于甲醇的得率YP/M= 4.74×10-4 g/g。
• Yx是以元素为基准的菌体得率,与以底物消耗 为基准的菌体得率系数YX/S有如下关系: • Yx =(α2/α1)(Yx/s)
• Yx/s= Yx (α1/α2)
• Yp是以元素为基准的产物得率, 与以底物消 耗为基准的产物得率Yp/S有如下关系: • Yp =(α3/α1)(Yp/s)
• Yp/s= Yp (α1/α3)
氧的平衡式为:L+ 2b = nYX + sYp+ c + 2d
氢的平衡式为: m + 3a = gYx + rYp + 2c
2.2 物料平衡
• 例计算:
• 一株Muts(甲醇利用慢)表型的基因工程 菌巴斯德毕氏酵母,在甲醇为诱导剂诱 导下,生产“血管生长抑制素”这一产 品,生产阶段是在以甲醇为惟一碳源的 基本培养基(以NH3为氮源)中进行。 甲醇的流加通过一甲醇检测控制系统自 动进行,维持发酵液中甲醇浓度为5g/L, 在产物合成阶段,5L发酵罐中菌体生长 量为16.2g,消耗甲醇量为143g,生产 血管素为69mg,求化学平衡计量式。
萘燃烧热的测定

物理化学实验实验报告专业化学工程与工艺班级学号姓名气体常数;T 为反应时的热力学温度。
为了使被测物质能迅速而完全地燃烧,需要有强有力的氧化剂。
在实验中经常使用压力为 2.5~3MPa 的氧气作为氧化剂。
本实验所用的氧弹热量计是一种环境恒温式的热量计氧弹放置在装有一定量水的铜水桶中,水桶外是空气隔热层,再外面是温度恒定的水夹套。
样品在体积固定的氧弹中燃烧放出的热、引火丝燃烧放出的热和由氧气中微量的氮气氧化成硝酸的生成热,大部分被水桶中的水吸收,另一部分则被氧弹、水桶、搅拌器及温度计等吸收。
在量热计与环境没有热交换的情况下,可写出如下的热量平衡式: t c t Wh c qb a Q V ∆+∆=+--总98.5式中,V Q 为被测物质的定容热值;a 为被测物质的质量; q 为引火丝的热值;b 为烧掉了的引火丝的质量; 5.98 为硝酸生成热为一5983J/mol ,c 为消耗 0.0100mol/L NaOH 溶液的毫升数;W 为水桶中水的质量,h 为水的比热容;总c 为氧弹、水桶等的总比热容;t ∆为与环境无热交换时的真实温差。
如在实验时保持水桶中水量一定,把式(3)右端常数合并,得到下式:t K c qb a Q V ∆=+--98.5式中,K 称为量热计常数。
实际上,氧弹式量热计不是严格的绝热系统,加之由于传热速度的限制,燃烧后由最低温度达到最高温度需一定的时间,在这段时间里系统与环境难免发生热交换,因而从温度计上读得的温差就不是真实的温差t ∆ 。
为此,必须对读得的温差进行校正。
当热量计与周围环境存在热交换时,对温差的校正可用雷诺(Renolds )温度校正图校正。
具体方法为:称取适量待测物质,估计其燃烧后可使水温上升 1.5~2.0℃。
预先调节水温使其低于室温 1.0℃左右。
按操作步骤进行测定,将燃烧前后观察所得的一系列水温和时间关系作图。
可得如图 4-13 所示的曲线。
图中 H 点意味着燃烧开始,热量传人介质;D 点为观察到的最高温度值;从相当于室温的J 点作水平线,交曲线于I、过点作垂线ab,再将FH 线和GD 线分别延长并交ab 线于A、C 两点,其间的温度差值即为经过校正的△T。
3 回转窑系统热平衡计算

回转窑系统热平衡计算1 热平衡计算基准、范围及原始数据 1.1 热平衡计算基准物料基准:一般以1kg 熟料为基准; 温度基准:一般以0℃为基准; 1.2 热平衡范围热平衡范围必须根据回转窑系统的设计或热工测定的目的、要求来确定。
在回转窑系统设计时,其平衡范围,可以回转窑、回转窑加窑尾预热分解系统、或再加冷却机和煤磨作平衡范围。
范围选得大,则进出口物料、气体温度较低,数据易测定或取得,但往往需要的数据较多,计算也烦琐。
因此一般选回转窑加窑尾预热分解系统作为平衡范围。
1.3 原始数据根据确定的计算基准和平衡范围,取得必要的原始数据,这是一项非常重要的工作。
计算结果是否符合实际情况,主要取决于所选用的数据是否合理。
对新设计窑或改造窑来说,主要是根据同类型窑的生产资料,结合工厂具体条件和我国实际情况、合理地确定各种参数;对于生产窑来说,主要通过热工测定取得实际生产中各种参数。
若以窑加窑尾预热系统为平衡范围,一般要取得如下原始数据:生料用量、化学组成、水分、入窑温度;燃料成分、工业分析和入窑温度;一、二次空气的比例和温度;空气过剩系数、漏风系数;废气温度;飞灰量、灰温度及烧失量;收尘器收尘效率;窑体散热损失;熟料形成热等等。
熟料形成热可根据熟料形成过程中的各项物理化学热效应求得,也可用经验公式计算或直接选定。
2 物料平衡与热量平衡计算方法与步骤说明于下: 窑型:预分解窑 基准:1kg 熟料;0℃ 平衡范围:窑+预热器系统根据确定的平衡范围,绘制物料平衡图和热量平衡图,如图1和图2所示。
图1 物料平衡图 图2 热量平衡图2.1 物料平衡计算 2.1.1 收入项目 (1)燃料消耗量 m r (kg/kg 熟料)设计新窑或技术改造时,m r 是未知量,通过热平衡方程求得,已生产的窑,通过热工测定得到。
(2)入预热器物料量 ① 干生料理论消耗量sar r gsL 100100L aA m m --=式中,m gsL —干生料理论消耗量,kg/kg 熟料;A ar —燃料收到基灰分含量,%;a —燃料灰分掺入熟料中的量,%;L s —生料的烧失量,%。
热力学定律

重庆大东方学校
高二物理春周清北班 LI
3 月 23 日
布,则 A 分布更无序 C.大量分子的集合能自发地从 A 分布迚入 B 分布,则该过程是可逆的 D.大量分子的集合能自发地从 A 分布迚入 B 分布,则该过程是不可逆的 考点三:热力学第三定律 通过任何有限的步骤都不可能让系统的温度达到绝对零度。 第三定律并不像第一、二定律那样明白地告诫人们放弃制造第一种永动机和 第二种永动机的意图。而是鼓励人们想方设法尽可能接近绝对零度。现代科学可 以使用绝热去磁的方法达到 5× 10-10K,但永远达不到 0K。 考点四:永动机 第一类永动机:不用输入任何能量,却能源源不断地对外做功。因为违反能 量守恒定律而不能制成。 第二类永动机:不违反能量守恒定律,但违反热力学第二定律而不能制成。 18.如图所示为英国赛斯特城的主教约翰· 维尔金斯在 1670 年设计的一种机器, 原理是这样的:在立柱上放一个强力磁铁 A,两槽 M 和 N 靠在立柱旁。上槽 M 上端有一个小孔 C,下槽 N 弯曲。如果在 B 处放一小铁球,它就会在强磁 力作用下向上滚,滚到 C 时从小孔下落沿 N 回到 B,开始往复运动,从而迚 行“永恒的运动”。关于这种机器,下列说法正确的是( ) A.这种机器可以永恒运动,说明了永动机可以制成 B.这种机器是可以制成的,幵且小铁球在下滑时能不断对外做功 C.这种机器不能永恒运动,如果小铁球能从静止加速上升到 C,它就不可能 从 C 加速下滑到 B,幵再次从 B 回到 C D.这种机器不能永恒运动,关键是因为摩擦阻力太大,要消耗能量 考点五:能量守恒定律与能源 1.能量守恒定律 能量既不会凭空产生,也不会凭空消失,它只能从一种形 为另一种形 式, 或者从一个物体 到别的物体, 在转化或转移的过程中 保 持不变。 2.各种形式的能量间可以转化,但由于不同形式的能量有序性不一样,所以 能量转化过程中也有方向性。例如电能可以全部转化成内能,但内能却不能全部 转化成电能而不产生其他影响。 把这种特性形象地称之为各种形式的能量品质高 低不同。热能无序性最高,品质最低的一种能量。所以,虽然自然界的能量总 量不会减少,但我们依然要节约能源。 3.寻找和开发新能源,清洁能源。 19.下列关于能量耗散的说法,正确的是( ) A.能量耗散使能的总量减少,违背了能量守恒定律 B.能量耗散是指耗散在环境中的内能再也不能被人类利用 C.各种形式的能量向内能的转化,是能够自动全额发生的 D.能量耗散导致能量品质的降低 20.下列关于能源的说法中正确的是( ) A.能源是取之不尽,用之不竭的 B.能源是有限的,特别是常规能源,如煤、石油、天然气等 C.大量消耗常规能源会使环境恶化,故提倡开发利用新能源
平衡、热力学

1、理想气体状态方程将在高温低压下得到的波义耳定律、查理定理和阿佛加德罗定律合并,便可组成一个方程:pV = nRT (1-1)这就是理想气体状态方程。
式中p 是气体压力,V 是气体体积,n 是气体物质的量,T 是气体的绝对温度(热力学温度,即摄氏度数+273),R 是气体通用常数。
在国际单位制中,它们的关系如下表:(1-1)式也可以变换成下列形式:pV = MmRT (1-2) p =Vm ·M RT = M RTρ 则: ρ =RTpM(1-3) 式中m 为气体的质量,M 为气体的摩尔质量,ρ为气体的密度。
对于一定量(n 一定)的同一气体在不同条件下,则有:111T V P = 222T V P (1-4) 如果在某些特定条件下,将(1-1)、(1-2)和(1-3)式同时应用于两种不同的气体时,又可以得出一些特殊的应用。
如将(1-1)式n =RTpV,在等温、等压、等容时应用于各种气体,则可以说明阿佛加德罗定律。
因为物质的量相等的气体,含有相等的分子数。
若将(1-2)式M m = RTpV 在等温、等压和等容时应用于两种气体,则得出: 11M m = 22M m(1-5) 如果将(1-3)式ρ= RTpV,在等温等压下应用于两种气体,则有: 11ρρ = 21M m(1-6) 若令11ρρ = D ,D 为第一种气体对第二种气体得相对密度,则有: D =21M m 或 M 1 = DM 2 (1-7) 已知M 2H = 2g ·mol 1-,M空气= 29g ·mol 1-则 M 1 = 2 D 2H 或 M 1 = 29D 空气D 2H 为某气体相对H 2的密度,D 空气为某气体相对空气的密度。
2、气体分压定律和分体积定律 (1)气体分压定律当研究对象不是纯气体,而是多组分的混合气体时,由于气体具有均匀扩散而占有容器全部空间的特点,无论是对混合气,还是混合气中的每一组分,均可按照理想气体状态方程式进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质量和热量平衡式如下:
入口蒸汽量+减温水量=出口蒸汽量
减温水量=出口蒸汽流量*(入口蒸汽的焓值-出口蒸汽的焓值)/(入口蒸汽焓值-减温水的焓值)
D1 +Dj =D2
D1 h1 +Dj hj =D2 h2
式中:D1-----减温前蒸汽流量,kg/h
h1-----减温前蒸汽热焓,kJ/kg
Dj-----减温水量,kg/h
hj-----减温水热焓,kJ/kg
D2-----减温后蒸汽流量,kg/h
h2-----减温后蒸汽热焓,kJ/kg
减温水量=出口蒸汽流量*(入口蒸汽的焓值-出口蒸汽的焓值)/(入口蒸汽焓值-减温水的焓值)
入口蒸汽量+减温水量=出口蒸汽量
根据上式,可计算出在不同蒸汽温度和流量下所需要的减温水量.
D1 +Dj =D2
D1 h1 +Dj hj =D2 h2
D1h1+Djhj=(D1+Dj)h2
D1h1+Djhj= D1 h2+ Dj h2
D1h1- D1 h2= Dj h2- Djhj
Dj= D1h1- D1 h2/ h2-hj
经查询:D1:减温前蒸汽流量54000 kg/h h1:3009.27 kJ/kg (压力0.38MPa 温度272℃)
h2:减温后蒸汽热焓值(咨询值长,压力0.35MPa温度140℃)2732.37 kJ/kg,
hj:减温水热焓值:(除氧器温度88℃,查水热焓值表)369.04 kJ/kg 则:Dj=(54000 kg/h×3009.27 -54000×2732.37)÷(3009.27-369.04)=54000×276.9÷2363.33
=6326.9 kg/h
则:每班减温水量约51吨。
本厂自耗:定排、连排,合计按1.5﹪/小时计算,为54×1.5﹪=0.81,则每班为0.81×8=6.48吨。
则本厂供制盐每小时约54+6.3269=60.3269吨。
每班约:60.3269×8=483吨
本厂总耗水量每班约为:483+0.81×8=483+6.48=489.48吨(490吨)
本厂除盐水消耗量为:总耗水量-制盐回水量。
