MATLAB编写矩阵计算器
(word完整版)用MATLAB GUI设计简单计算器

摘要基于MATLAB GUI的计算器设计是利用GUIDE创建图形用户界面进行计算器设计。
设计计算器时,主要是考虑到计算器的易用性、功能的常用程度进行计算器界面与功能的设计。
通过调整控件和文本的布局及颜色,使界面简单大方、布局合理,达到界面友好的效果。
计算器设计时主要利用到get和set两个函数进行各个控件属性值的传递和设置。
计算器实现的功能有:数字0~9和小数点的输入显示,平方、开平方和对数的输入显示。
进行四则运算、正弦计算、余弦计算、正切计算和余切计算,可以求阶乘、求百分数和求倒数。
可以进行括号及变量x与变量y的输入,结合坐标轴编辑框和曲线颜色编辑框实现函数的曲线绘制。
最后运行调试,实现基于MATLAB GUI的计算器的设计。
MATLAB GUI介绍MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。
MATLAB是matrix和laboratory两个词的组合,意为矩阵工厂,主要面对科学计算、可视化以及交互式程设计的高科技计算环境。
MATLAB是将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言的编辑模式,特别是所附带的30多种面向不同领域的工具箱支持,使得它在许多科学领域中成为计算机辅助设计和分析、算法研究和应用开发的基本工具和首选平台。
MATLAB的图形用户界面(Graphical User Interface,简称GUI,又称图形用户接口)是指采用图形方式显示的计算机操作用户界面。
与早期计算机使用的命令行界面相比,图形界面对于用户来说在视觉上更易于接受。
MATLAB的图形用户界(GUI)是由光标,窗口,菜单、文字说明等对象构成一个用户界面。
matlab 矩阵代数计算

matlab 矩阵代数计算【原创版】目录一、矩阵的基本概念1.矩阵的定义2.矩阵的行和列3.矩阵的转置4.矩阵的加减法5.矩阵的乘法6.矩阵的左除7.矩阵的右除8.矩阵的点运算二、MATLAB 中的矩阵运算1.MATLAB 中如何实现矩阵的加减法2.MATLAB 中如何实现矩阵的乘法3.MATLAB 中如何实现矩阵的左除4.MATLAB 中如何实现矩阵的右除5.MATLAB 中如何实现矩阵的点运算三、如何用 MATLAB 计算一个矩阵和大量矩阵1.使用 for 循环2.使用 cellfun 函数正文一、矩阵的基本概念矩阵是数学中的一个重要概念,它由一定数量的行和列组成。
矩阵的每一个元素都可以用一个有序的二元组表示,例如:mx(m,n) 表示一个位于第 m 行第 n 列的元素。
1.矩阵的定义矩阵是一个由数字或函数组成的矩形阵列,通常用大写字母表示,如A、B 等。
矩阵的每一个元素都是一个向量,它可以是一个标量、向量或矩阵。
2.矩阵的行和列矩阵的行数和列数决定了矩阵的大小,通常用“m×n 矩阵”表示一个具有 m 行 n 列的矩阵。
3.矩阵的转置矩阵的转置是将矩阵的行和列互换,用 a"表示矩阵 a 的转置。
4.矩阵的加减法矩阵的加减法是将两个矩阵的对应元素相加或相减,结果是一个新的矩阵。
例如,ca-b 表示矩阵 c 减去矩阵 b。
5.矩阵的乘法矩阵的乘法是将两个矩阵的对应行和列元素相乘,结果是一个新的矩阵。
例如,dab 表示矩阵 a 和矩阵 b 的乘积。
6.矩阵的左除矩阵的左除是用“/”符号表示,它表示求解方程 ax=b 的解。
7.矩阵的右除矩阵的右除是用“”符号表示,它表示求解方程 xb=a 的解。
8.矩阵的点运算矩阵的点运算是对两个矩阵的对应元素进行运算,例如,ca.b 表示矩阵 c 和矩阵 b 的对应元素相乘。
二、MATLAB 中的矩阵运算MATLAB 是一种广泛使用的数学软件,它可以方便地实现矩阵的代数运算。
matlab矩阵运算

matlab矩阵运算
Matlab矩阵运算是指使用Matlab提供的矩阵相关的函数对矩阵进行
操作的一种数学运算方法。
Matlab的矩阵运算提供了一套完备的矩阵操
作工具,可以帮助用户快速而便捷的完成各种矩阵操作。
Matlab矩阵运算可以做矩阵加法、乘法、转置运算、求逆运算等,
也可以做矩阵的迹、行列式、特征分解等计算工作。
Matlab还可以用来
做矩阵的分块运算、矩阵插值、曲线拟合以及其他更复杂的矩阵操作。
此外,Matlab还提供了一组函数帮助矩阵运算,比如det()、eig()、inv()函数可以简单快速的求矩阵的行列式、特征值、逆矩阵等。
此外,Matlab还有强大的图形界面,可以帮助用户以图形的方式检查矩阵结构,方便矩阵数据的查看和分析。
matbla 矩阵运算

MATLAB 是一种广泛使用的编程语言和环境,主要用于数值计算和数据分析。
在 MATLAB 中,矩阵运算是一种常见的操作,包括矩阵的加法、减法、乘法、转置等。
以下是一些基本的矩阵运算示例:
1. 矩阵加法:
```matlab
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
B = [10, 11, 12; 13, 14, 15; 16, 17, 18];
C = A + B; % 结果为 [11, 13, 15; 17, 19, 21; 23, 25, 27]
```
2. 矩阵减法:
```matlab
C = A - B; % 结果为 [-9, -8, -7; -6, -4, -2; -6, -4, -2]
```
3. 矩阵乘法:
```matlab
D = A * B; % 结果为 [58, 64, 70; 90, 102, 114; 122, 136, 150]
```
4. 矩阵转置:
```matlab
E = A'; % 结果为 [1, 4, 7; 2, 5, 8; 3, 6, 9]
```
5. 其他操作,如矩阵的逆、行列式等,需要使用 MATLAB 内置的函数。
例如,计算矩阵的行列式:
```matlab
det_value = det(A); % det 为计算行列式的函数
```
这些是 MATLAB 中矩阵运算的一些基本操作。
实际上,MATLAB 还提供了许多其他功能和函数,可以执行更复杂的矩阵运算和操作。
MATLAB编写矩阵计算器

一、GUI开发环境简介MATLAB提供了一套可视化的创建图形窗口的工具,使用用户界面开发环境可方便的创建GUI应用程序, 它可以根据用户设计的GUI布局,自动生成M文件的框架,用户使用这一框架编制自己的应用程序。
图形用户界面(Graphical User Interfaces ,GUI)则是由窗口、光标、按键、菜单、文字说明等对象(Objects)构成的一个用户界面。
用户通过一定的方法(如鼠标或键盘)选择、激活这些图形对象,使计算机产生某种动作或变化,比如实现计算、绘图等。
二、矩阵计算器介绍2.1 程序使用的控件在矩阵计算器设计中主要用到三种控件,文本编辑框(edit text),静态文本框(Static text),命令按钮(push button),边框(panel)。
然后在通过各个按钮的回调函数,实现简单的计算功能。
2.2 程序功能介绍(1)具有用户图形界面。
实现矩阵的加、减、乘、左除、右除等简单计算。
(2)有清空键,能清除操作。
2.3 矩阵计算器界面及主要控件功能注释:text1文本编辑框控件功能:输出要计算公式。
如[12 45;78 56]+[659 238;79 56] MatA文本编辑框功能:输入参与计算矩阵AMatB文本编辑框功能:输入参与计算矩阵BMatC静态文本框功能:输出计算结果矩阵C三、部分计算操作结果(1) 加法+MatAtext1 pushbutton22pushbutton23pushbutton24pushbutton20(2)求逆(3)转置(4)群运算.*四、部分模块功能算法的实现(1)按键’加法+’响应:a=get(handles.matA,'string');textString=strcat(a,'+');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);(2)按键’转置’响应a=get(handles.matA,'string');textString=strcat(a,'''');set(handles.text1,'String',textString);(3)按键’计算’响应textString=get(handles.text1,'String');f=eval(textString);set(handles.matC,'string',num2str(f,'%15.5g'))(5)按键’清空’响应set(handles.text1,'String','')set(handles.matA,'String','[]')set(handles.matB,'String','[]')set(handles.matC,'String','')注释:其余模块功能算法与以上代码较为相似,不在一一举例。
matlab 符号矩阵运算

matlab 符号矩阵运算
在MATLAB中进行符号矩阵运算,需要使用符号计算工具箱。
以下是一些常见的符号矩阵运算:
1. 转置:符号矩阵的转置可以通过符号“ ' ”或函数transpos来实现。
例如,如果A是一个符号矩阵,则A.' 是A 的转置。
2. 乘法:两个符号矩阵的乘法可以通过函数mtimes来实现。
例如,如果A和B是两个符号矩阵,则C=A*B是A和B的乘积。
3. 加法:两个符号矩阵的加法可以通过加法运算符“+”来实现。
例如,如果A和B是两个具有相同尺寸的符号矩阵,则
C=A+B是A和B的加积。
4. 逆运算:一个方阵的逆运算可以通过函数inv来实现。
例如,如果A是一个方阵,则inv(A)是A的逆矩阵。
需要注意的是,不是所有的方阵都有逆矩阵。
5. 行列式运算:一个方阵的行列式运算可以通过函数determ或det来实现。
例如,如果A是一个方阵,则det(A)或determ(A)是A的行列式。
6. 求秩运算:一个符号矩阵的求秩运算可以通过函数rank 来实现。
例如,如果A是一个符号矩阵,则rank(A)是A的秩。
7. 特征值和特征向量运算:一个符号矩阵的特征值和特征向量运算可以通过函数eig、eigensys等来实现。
例如,如果A
是一个符号矩阵,则[V,D]=eig(A)将返回特征向量V和特征值D。
以上是一些常见的符号矩阵运算,但MATLAB符号计算工具箱还提供了许多其他函数和运算符来进行符号矩阵运算。
matlab 矩阵运算程序

matlab 矩阵运算程序摘要:一、引言二、MATLAB 简介三、MATLAB 矩阵运算1.矩阵的创建与操作2.矩阵的基本运算3.矩阵的函数处理四、MATLAB 在矩阵运算中的应用1.数据分析与处理2.图像处理与分析3.信号处理与分析五、MATLAB 与其他编程语言的矩阵运算比较六、总结正文:一、引言矩阵运算在科学计算和工程应用中有着广泛的应用,MATLAB 作为一款强大的数学软件,提供了丰富的矩阵运算功能。
本文将详细介绍MATLAB 的矩阵运算及其在各种应用场景中的应用。
二、MATLAB 简介MATLAB 是一种用于科学计算的高级编程语言,由美国MathWorks 公司开发。
它具有丰富的函数库,可以进行各种数学计算、图形绘制和数据分析等。
MATLAB 中的矩阵运算功能强大,易于使用,使得用户可以方便地进行矩阵相关的计算和处理。
三、MATLAB 矩阵运算1.矩阵的创建与操作在MATLAB 中,用户可以通过直接输入矩阵元素或者使用特定的函数创建矩阵。
例如,使用`[a,b,c]`或者`rand(m,n)`函数可以创建一个指定大小的随机矩阵。
同时,MATLAB 还提供了丰富的矩阵操作函数,如`size`、`length`、`diag`等,方便用户对矩阵进行各种操作。
2.矩阵的基本运算MATLAB 支持矩阵的加法、减法、数乘、乘法等基本运算。
同时,还提供了诸如`+`、`-`、`*`、`/`等运算符,使得矩阵运算更加直观。
此外,MATLAB 还支持诸如`inv`、`det`、`rank`等矩阵分解和性质判断函数。
3.矩阵的函数处理MATLAB 提供了丰富的矩阵函数处理函数,包括矩阵的转置、求逆、行列式、秩等。
此外,还支持诸如`sum`、`mean`、`std`等统计函数,方便用户对矩阵进行进一步的处理。
四、MATLAB 在矩阵运算中的应用1.数据分析与处理MATLAB 可以方便地进行矩阵的数据分析与处理,例如计算矩阵的行列式、秩、迹等。
MATLAB设计矩阵计算器

MATLAB程序设计语言大作业——矩阵计算器题目:矩阵计算器学号:02123010姓名:石星宇指导教师:汤建龙一、实验目的1、通过GUI(Graphical User Interface,简称GUI,图形用户界面,又称图形用户接口)设计矩阵计算器,熟悉MATLAB中GUI工具的使用和编程。
2、加深对MATLAB GUI中句柄控制变量的理解。
3、巩固线性代数中矩阵的基本运算。
二、实验内容1、利用MATLAB中的GUIDE工具箱快速生成GUI界面。
2、在生成的GUI界面中设计能够实现矩阵基本运算的矩阵计算器。
三、实验结果通过GUIDE快速生成GUI界面设计的矩阵计算器如下图所示:图1 Matrix Calculator基本界面该矩阵计算器包含四模块,分别为:输入区、输出区、功能区及其他运算区。
四、功能描述1、功能概述本矩阵计算器能够实现一些基本的矩阵运算,包括对单个矩阵的运算以及对两个矩阵的运算。
其中,对于两个矩阵的运算有:加、减、乘、除(左除、右除)、按元素乘、按元素除以及求解线性方程组;对于単个矩阵的运算有:转置(共轭与非共轭)、求逆、计算行列式、求秩、平方、立方、开方、求特征值、求2范数、LU 分解、最简阶梯阵化简等。
计算过程中,矩阵的输入方式与MATLAB 中矩阵输入方式类似。
即①矩阵行中的元素以空格或逗号间隔;②矩阵行之间以分号间隔;③整个元素列表用方括号括起来。
2、功能详细描述 2.1矩阵相加(减)输入A=[1 2 3;4 5 6;7 8 9],B=[1 4 7;2 5 8;3 6 9],按下“+”按钮,输出区显示计算结果如图2所示:输入的A 、B 矩阵必须是维数相同,否则不能实现相加运算。
如输入不同维数的矩阵且进行相加运算,则会提示出错如图3所示:两矩阵相减的运算过程与相加运算类似,在此不再赘述。
图2 矩阵相加图3 矩阵相加错误提示2.2矩阵相乘输入A=[1 2 3;4 5 6;7 8 9],B=[1 4 7;8 5 2;3 9 6],按下“*”按钮,输出区显示计算结果如图4所示:输入的A 、B 矩阵必须满足前者的列数等于后者的行数,否则不能实现矩阵的乘法运算,出现错误提示如图5所示:2.3按元素乘(除)输入同2.2。
matlab在矩阵计算中的应用

MATLAB在矩阵计算中的应用引言矩阵计算作为数学和计算机科学的重要分支,已经在很多领域中得到广泛应用。
作为一种强大的数学软件工具,M AT LA B(M at ri xL ab or at or y)在矩阵计算中功不可没。
本文将介绍M AT LA B在矩阵计算中的应用,并探讨其在科学、工程和数据处理等领域的实际应用。
矩阵基础在了解M AT LA B在矩阵计算中的应用之前,我们首先需要了解一些矩阵的基础知识。
矩阵是一个按照矩形排列的数表,由行和列组成。
在M AT LA B中,矩阵可以用一个二维数组来表示,其中每个元素都可以通过行和列的索引进行访问。
例如,一个3行2列的矩阵可以表示为:A=[1,2;3,4;5,6];矩阵运算M A TL AB提供了丰富的矩阵运算功能,可以进行矩阵的加减乘除、转置、逆矩阵等操作。
矩阵加法和减法矩阵的加法和减法是按元素进行操作的。
两个矩阵的加法可以使用M A TL AB的加法运算符`+`实现,例如:A=[1,2;3,4];B=[5,6;7,8];C=A+B;上述代码中,`A`和`B`分别表示两个2x2的矩阵,`C`表示它们的和。
矩阵乘法矩阵的乘法是按照矩阵乘法规则进行操作的。
在M AT LA B中,可以使用`*`运算符进行矩阵乘法,例如:A=[1,2;3,4];B=[5,6;7,8];C=A*B;上述代码中,`A`和`B`分别表示两个2x2的矩阵,`C`表示它们的乘积。
矩阵转置矩阵的转置是将矩阵的行和列互换得到的新矩阵。
在M AT LA B中,可以使用`'`符号进行矩阵转置,例如:A=[1,2;3,4];B=A';上述代码中,`A`表示一个2x2的矩阵,`B`表示其转置矩阵。
MATLA B应用案例M A TL AB在矩阵计算中的应用非常广泛,下面将介绍几个典型的应用案例。
线性代数线性代数是矩阵计算的重要分支之一。
在M AT LA B中,可以使用线性代数相关的函数来解决线性方程组、求解特征值和特征向量等问题。
基于MATLAB的简易矩阵计算器

《MATLAB程序设计》程序设计报告设计题目:简易矩阵计算器班级:021231******学号:********目录1.设计目标……………………2.设计内容……………………3.设计思想……………………4.设计说明……………………5.设计步骤及程序代码……………………6.运行计算器……………………7.总结…………………………1.设计目标1.熟悉MATLAB的主要控件使用方法。
2.熟悉MATLAB的GUI设计流程。
2.设计内容设计一个简易的矩阵计算器,通过对简单应用矩阵计算器的设计,编制、调试实现矩阵相加减,矩阵的转置等简单运算,以学习应用MATLAB编写程序原理,加深对MATLAB的学习及应用。
3.设计思想基于MATLAB中GUI界面的设计,通过创建类成员函数成员变量,编辑控件创建消息映射,调用信息函数完成数据的输入输出,实现计算功能。
生成简单的应用软件。
4.设计说明1)包含的功能有:加、减、乘、转置等。
2)输入的原始数据分别为A或B矩阵,分别显示在不同标签中,运算的结果则显示在输出部分。
3)计算功能基本上是用系统内部函数。
4)程序能够自动判断输入数据的正确性,如不能输入(1)。
5.设计步骤及只要代码1)打开MATLAB,点击,出现GUI的2)设计计算器版面直至3)对功能键进行设计执行A矩阵加B矩阵,其执行代码如下A = eval((get(handles.Matrix_A,'String')));B = eval((get(handles.Matrix_B,'String')));[iA jA]=size(A);[iB jB]=size(B);if iA ~= iB | jA ~= jB |(iA ~= iB & jA ~= jB) R='error.Matrix dimensions must agree.';set(handles.Answer,'string',R)guidata(hObject, handles);elseresult=A + B ;R =num2str(result);set(handles.Answer,'string',R)guidata(hObject, handles);end执行A矩阵减B矩阵,其执行代码如下A = eval((get(handles.Matrix_A,'String')));B = eval((get(handles.Matrix_B,'String')));[iA jA]=size(A);[iB jB]=size(B);if iA ~= iB | jA ~= jB |(iA ~= iB & jA ~= jB) R='error.Matrix dimensions must agree.';set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = A - B ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);end执行A矩阵与B矩阵相乘,其执行代码如下A = eval((get(handles.Matrix_A,'String')));B = eval((get(handles.Matrix_B,'String')));[iA jA]=size(A);[iB jB]=size(B);if jA~=iBR='error.Inner matrix dimensions must agree.';set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = A * B ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);end执行A右除B矩阵,其执行代码如下A = eval((get(handles.Matrix_A,'String')));B = eval((get(handles.Matrix_B,'String')));[iA jA]=size(A);[iB jB]=size(B);if iA~=iB 、R='error.Matrix dimensions must agree.';set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = A \ B ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);end执行A.*B,其执行代码如下A = eval((get(handles.Matrix_A,'String')));B = eval((get(handles.Matrix_B,'String')));result = A .* B ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);执行A./B,其执行代码如下A = eval((get(handles.Matrix_A,'String')));B = eval((get(handles.Matrix_B,'String')));result = A ./ B ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);执行A的转置,其执行代码如下A = eval((get(handles.Matrix_A,'String')));result = A' ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);执行A右除B,其执行代码如下A = eval((get(handles.Matrix_A,'String')));B = eval((get(handles.Matrix_B,'String')));[iA jA]=size(A);[iB jB]=size(B);if iA~=iB þ R='error.Matrix dimensions must agree.';set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = A / B ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);end执行求A的行列式,其执行代码如下A = eval((get(handles.Matrix_A,'String')));[iA jA]=size(A);if iA ~=jA R='error.Matrix must be square.';set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = det(A) ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);end执行求A的逆,其执行代码如下A = eval((get(handles.Matrix_A,'String')));[iA jA]=size(A);if iA ~=jAR='error.Matrix must be square.';set(handles.Answer,'String',R)guidata(hObject, handles);elseif det(A) == 0R='error.Matrix is singular to working precision.';set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = inv(A) ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);endend执行求A的非共轭转置,其执行代码如下A = eval((get(handles.Matrix_A,'String')));result = A.' ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);执行求解系数阵为方阵且非奇异的线性方程组,其执行代码如下A = eval((get(handles.Matrix_A,'String')));B = eval((get(handles.Matrix_B,'String')));[iA jA]=size(A);[iB jB]=size(B);if iA ~= iBR='error.';set(handles.Answer,'String',R)guidata(hObject, handles);elseif iA ~=jAR='error.Matrix must be square.';set(handles.Answer,'String',R)guidata(hObject, handles);elseif det(A) == 0R='error.Matrix is singular to working precision.';set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = A\B ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);endendend执行求A的秩,其执行代码如下A = eval((get(handles.Matrix_A,'String')));result = rank(A) ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);执行求A的平方,其执行代码如下A = eval((get(handles.Matrix_A,'String')));[iA jA]=size(A);if iA ~=jAR='error.Inputs must be a scalar and a square matrix.';set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = A^2 ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);end执行求A的立方,其执行代码如下A = eval((get(handles.Matrix_A,'String')));[iA jA]=size(A);if iA ~=jAR='error.Inputs must be a scalar and a square matrix.'; set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = A^3 ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);end执行求A的特征值,其执行代码如下A = eval((get(handles.Matrix_A,'String')));[iA jA]=size(A);if iA ~=jAR='error.Matrix must be square.';set(handles.Answer,'String',R)guidata(hObject, handles);elseresult = eig(A) ;R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);end执行求A开平方根,其执行代码如下A = eval(get(handles.Matrix_A,'String'));result = sqrt(A);R = num2str(result);set(handles.Answer,'String',R)执行计算矩阵范围(默认为2范数),其执行代码如下A = eval(get(handles.Matrix_A,'String'));result = norm(A);R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);执行对A的分解,其执行代码如下A = eval(get(handles.Matrix_A,'String'));[L U] = lu(A);result = [L;U];R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);执行将矩阵A化为最简阶梯矩阵,其执行代码如下A = eval(get(handles.Matrix_A,'String'));result = rref(A);R = num2str(result);set(handles.Answer,'String',R)guidata(hObject, handles);4)对输出进行设计输出框内有新添加的,使经过计算后的式子通过输出框显示。
矩阵计算器

用Matlab GUI编写一个简单的矩阵计算器摘要:矩阵是线性代数的一个主要内容,又是解决众多问题的主要工具。
而矩阵运算是矩阵理论的基本内容之一。
目前,普通的计算器只能够进行数的运算,而不能够实现矩阵的运算。
随着科技的不断发展,人们对矩阵的运用也会不断的增多。
因此,制作一个矩阵计算器对当今科技的发展有一定的推动作用。
关键字:矩阵运算、Matlab GUI、计算器正文:一、矩阵的相关知识在数学上,矩阵是指纵横排列的二维数据表格,最早来自于方程组的系数及常数所构成的方阵。
这一概念由19世纪英国数学家凯利首先提出。
矩阵,是由个数组成的一个行列的矩形表格,通常用大写字母表示,组成矩阵的每一个数,均称为矩阵的元素,通常用小写字母其元素表示,其中下标都是正整数,他们表示该元素在矩阵中的位置。
比如,或表示一个矩阵,下标表示元素位于该矩阵的第行、第列。
元素全为零的矩阵称为零矩阵。
当一个矩阵的行数与烈数相等时,该矩阵称为一个阶方阵。
对于方阵,从左上角到右下角的连线,称为主对角线;而从左下角到右上角的连线称为付对角线。
若一个阶方阵的主对角线上的元素都是,而其余元素都是零,则称为单位矩阵,记为,即:。
如一个阶方阵的主对角线上(下)方的元素都是零,则称为下(上)三角矩阵,例如,是一个阶下三角矩阵,而则是一个阶上三角矩阵。
今后我们用表示数域上的矩阵构成的集合,而用或者表示数域上的阶方阵构成的集合。
矩阵是高等代数学中的常见工具,其中的一个重要用途是解线性方程组。
线性方程组中未知量的系数可以排成一个矩阵,加上常数项,则称为增广矩阵。
另一个重要用途是表示线性变换,即是诸如f(x) 4x之类的线性函数的推广。
同时也常见于统计分析等应用数学学科中。
在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。
矩阵的运算是数值分析领域的重要问题。
将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。
如何使用Matlab进行矩阵计算

如何使用Matlab进行矩阵计算使用Matlab进行矩阵计算概述:矩阵计算在科学与工程领域中起着举足轻重的作用。
Matlab作为一种常用的科学计算软件,具备强大的矩阵计算能力。
本文将介绍如何使用Matlab进行矩阵计算,包括矩阵的创建、运算符的应用、线性方程组求解、特征值与特征向量计算以及常见的矩阵分解方法等。
一、矩阵的创建与存储在Matlab中,可以使用多种方式创建矩阵。
最简单的方式是使用方括号将元素排列起来,以分号分隔不同的行。
例如,创建一个3×3的矩阵可以使用以下代码:A = [1, 2, 3; 4, 5, 6; 7, 8, 9];Matlab还提供了一些特殊的函数来创建特定形状或者特定元素的矩阵。
例如,可以使用eye函数创建单位矩阵,zeros函数创建全零矩阵,ones函数创建全一矩阵,rand函数创建随机矩阵等。
创建好矩阵后,可以使用变量名存储矩阵。
在Matlab中,变量名是区分大小写的。
为了更好地组织代码,可以将相关的矩阵存储在不同的变量中,并且使用有意义的变量名。
二、矩阵运算符的应用Matlab中支持各种矩阵运算符的应用,包括加法、减法、数乘、矩阵乘法以及逐元素乘法等。
这些运算符可以方便地用于矩阵计算。
例如,两个矩阵相加可以使用加法运算符"+",两个矩阵相乘可以使用乘法运算符"*",数乘可以使用数值乘法运算符"*"。
需要注意的是,矩阵运算符在运算时需要满足相应的尺寸要求,否则会引发错误。
除了基本的运算符,Matlab还提供了一些特殊的运算符,例如."表示逐元素的乘法(对应位置相乘),./表示逐元素的除法,.^表示逐元素的乘方等。
三、线性方程组求解线性方程组的求解是矩阵计算的重要应用之一。
在Matlab中,可以使用“\”或者inv函数来求解线性方程组。
例如,假设有如下线性方程组 Ax = b,其中A是一个已知的矩阵,b是一个已知的列向量,x是未知的列向量。
用MATLAB做的 一个计算器

一、布局GUI。
1.打开Matlab,输入Guide 回车或者在工具栏上点击图标出现Guide 窗口:2.然后双击“Blank GUI(Default)”出现GUI窗口3.添加按钮4.根据按钮的作用及视觉效果做一定的修改把按钮的字符串大小、颜色进行设置,对按钮的位置进行排布,尽量使按钮集中在静态文本框下面。
最终设置的静态文本框为白色,其他按钮均为分红色。
5.保存、添加功能函数把做好的按钮及静态文本框保存后自动弹出Editor的M文本,对然后对相应的pushbutton添加功能函数。
以下是相应按钮的功能函数。
(1)数字按键编写。
在function pushbutton1_Callback(hObject, eventdata, handles)下输入:textString = get(handles.text1,'String');textString =strcat(textString,'0');set(handles.text1,'String',textString)这是使用句柄handles指向对象text1,并以字符串形式来存储数据文本框text1的内容,并存储数个“0”,然后由set(handles.text1,'String','textString'在text1中输出。
同理,分别在function pushbutton2~10_Callback(hObject, eventdata, handles)下给1~9数字按键下编写此类程序。
(2).符号键:function pushbutton12_Callback(hObject, eventdata, handles)textString = get(handles.text1,'String');textString =strcat(textString,'+');set(handles.text1,'String',textString)strcat的作用是将两个字符串连接起来,就是在已输入的存储数据textString 后添加“+”进行运算。
matalb矩阵计算(MATLAB矩阵计算)

matalb矩阵计算(MATLAB矩阵计算)matalb矩阵计算(MATLAB矩阵计算)4.1 array operations and matrix operationsFrom the appearance of the shape and structure of the data matrix, two-dimensional array and no difference in mathematics. However, as the embodiment of a matrix transformation or mapping operator matrix with mathematical rules, clear and strict. And array operation is defined by the software of MATLAB rules, its purpose is for data management, simple operation. The instruction form nature and perform calculations effectively. Therefore, when using MATLAB, in particular to a clear distinction between clear array operations and matrix operations. Table 4.1.1 lists the similarities and differences between the essence and connotation of two kinds of operation instruction.4.1.1 array operations and matrix operations, instruction forms and substantive meaningArray operationMatrix operationinstructionsMeaninginstructionsMeaningA.'Non conjugate transposeA'Conjugate transposeA=sAssign scalar s to each element of the array AS+BAdd scalar s to each element of the array B, respectivelyS-B, B-sThe difference between the scalar s and the elements of the array B S.*AScalar s is the product of the elements of the array A, respectively S*AThe product of the scalar s and the elements of the matrix A, respectivelyS./B, B.\sScalar s is separated by the elements of array B, respectivelyS*inv (B)Inverse multiplicative scalar B of matrix sA.^nThe N sub order of each element of the array AA^nWhen A is a square matrix, the n power of the matrix AA+BThe addition of an array corresponding elementA+Bmatrix additionA-BSubtracting elements of an arrayA-BMatrix subtractionA.*BMultiplication of an array corresponding elementA*BThe product of the same matrix NevilleA./BThe elements of A are excluded by the corresponding elements of B A/BA right, except BB.\AIt must be the sameB\AA left exceptB (usually different from right division)Exp (A)For the end to e respectively with A elements as index, exponentiationExpm (A)Matrix exponential function of ALog (A)The logarithm of the elements of ALogm (A)The matrix logarithmic function of ASqrt (A)The square root of the elements of the product of ASqrtm (A)A's square function of matricesFrom the above we can see that the array operations such as multiplication, addition, multiplication, transpose, add "points". Therefore, we should pay special attention to "multiply, divide, involution, trigonometric and exponential function", two operations are fundamentally different. In addition, in the implementation of the array and array operation when the array must be involved in computing Tongwei, the result is always with the original array array dimensions.4.2 basic operations of an arrayIn MATLAB, an array operation is a.MATLAB that uses the same calculation for multiple numbers to process arrays in a very intuitive way4.2.1 point transpose and conjugate transpose` - dot transpose. Non conjugate transpose, equivalent to conj (A') A=1:5;'b=a.'= bOneTwoThreeFourFive'c=b.'= C12345This shows that the two transpose of the row vector yields the original row vectorConjugate transpose. Transpose the vectors and conjugate each element:D=a+i*a= DColumns 1 through 31 + 1.0000i2 + 2.0000i3 + 3.0000iColumns 4 through 54 + 4.0000i5 + 5.0000iE=d'= e1 - 1.0000i2 - 2.0000i3 - 3.0000i4 - 4.0000i5 - 5.0000i4.2.2 scalar (scalar) and four operations of an arraySimple mathematical operations can be performed between scalar and array, such as addition, subtraction, multiplication, division, and mixing operations"G=[1 234"567891011 12]G=g-2= g-1 0123456789102*g-1= ans-3 -1 135791113151719Four operations between 4.2.3 arraysIn MATLAB, the array between the four operations, an array of participating in operation must have the same dimension, subtraction, multiplication, addition, operation is carried out according to the elements and elements forms. Among them, the array between the addition, subtraction and matrix addition, subtraction to the same operator, as: "+" "-". However, the array multiplication, division and matrix multiplication, division operation symbol is completely different, thereare differences, between the array multiplication and division operators: "*", "/" or ".".1. array by element add, minus"G=[1 234"567891011 12]"H=[1 111; 2222; 333; 3]"> g+h% added by element= ans23457891012131415> ans-h%, subtract by element= ans123456789 10 11 12> > > > > > > 2 g / h) 混合运算years.1 3 5 78 10 12 1415 17 19 212. 按元素乘> > > > > > > g * hyears.1 2 3 410 12 14 1627 30 33 363. 按元素除数组间的除法运算符有两个, 即左除 "/" 和右除 "." 它们之间的关系是.a /b = b.> > > > > > > g / hyears.1.00002.00003.00004.00002.50003.00004.1000 4.00003.0000 3.3333 3.66674.0000"h \ gyears.1.00002.00003.00004.00002.50003.00004.1000 4.00003.0000 3.3333 3.66674.0000幂运算.在matlab中, 数组的幂运算的运算为 "." 表示每一个元素进行幂运算. > > > > > > > (2% 数组g每个元素的平方.years.1 4 9 425, 36, 49, 6481% (144> > > > > > > g ^ (- 1)) 数组g的每个元素的倒数years.1.0000 0.5000 0.3333 0.25000.2000 0.1667 0.1429 0.12500.1111 0.1000 0.0909 0.0833> > > > > > > 2 g%, 以g的每个元素为指数对2进行乘方运算.years.2 4 8 1632, 64, 128, 256512 1024, 2048, 4096> > > > > > > "h% 以h的每个元素为指数对g中相应元素进行乘方运算.years.1 2 3 425, 36, 49, 64729 1000, 1728> > > > > > > (h - 1).years.1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 15 6 7 881% (144- 数组的指数, 对数和开方运算在matlab中, 所谓数组的运算实质是是数组内部每个元素的运算, 因此, 数组的指数, 对数和开方运算与标量的运算规则完全是一样的, 运算符函数分别为: exp () log (), () must 等.> > a = [1, 3, 4, 5, 2, 6, 3, 2, 4].> > > > > > > c = exp (a)c =2.7183 20.0855 54.59827.3891 403.4288 148.413220.0855 7.3891 54.5982> > > > > > > > > > > >数组的对数, 开方运算与数组的指数运算, 其方式完全一样, 这里不详述.向量运算.对于一行或一列的矩阵, 为向量, matlab有专门的函数来进行向量点积, 叉积和混合积的运算.the 向量的点积运算在高等数学中, 我们知道, 两向量的点积指两个向量在其中一个向量方向上的投影的乘积, 通常用来定义向量的长度.在matlab中, 向量的点积用函数 "dot"来实现, 其调用格式如下.c = dot (a, b) - 返回向量a与b的点积, 结果存放于c中.c = dot (a, b, d) - 返回向量a与b在维数为dim的点积, 结果存放于c中.> > a = [4 2 5 3 1).> > b = (3 8 10 12 13].> > > > > > > c = (a, b).c =137> > > > > > > c = dot (a, b, (4)c =32 50 36 13 6a 向量的叉积运算在高等数学中, 我们知道, 两向量的叉积返回的是与两个向量组成的平面垂直的向量.在matlab中, 向量的点积用函数 cross 来实现, 其调用格式如下.c = cross (a, b) - 返回向量a与b的叉积, 即, 结果存放于c中.c = cross (a, b, d) - 返回向量a与b在维数为dim的叉积, 结果存放于c 中.> > a = [2, 5].> > b = [3, 10].> > > > > > > c = cross (a, b)c =0 - 5 4these 向量的混合运算> > > > > > > d = dot (a, cross (b, c))d =41上例表明, 首先进行的是向量b与c的叉积运算, 然后再把叉积运算的结果与向量a进行点积运算.4.4 矩阵的基本运算如果说matlab的最大特点是强大的矩阵运算功能, 此话毫不为过.事实上, matlab中所有的计算都是以矩阵为基本单元进行的.matlab对矩阵的运算功能最全面, 也是最为强大的.矩阵在形式上与构造方面是等同于前面所述的数组的, 当其数学意义却是完全不同的.矩阵的基本运算包括矩阵的四则运算, 矩阵与标时的运算, 矩阵的幂运算, 指数运算, 对数运算, 开方运算及以矩阵的逆运算, 行列式运算等.it 矩阵的四则运算矩阵的四则运算与前面介绍的数组的四则运算基本相同.但也有一些差别.1. 矩阵的加减The addition and subtraction of a matrix is exactly the same as the addition and subtraction of an array, which requires the exact size of the two matrix to be exactly the same"A=[1 2; 35; 2; 6]";"B=[2 4; 18; 9; 0]";C=a+b= C36413116Multiplication of 2. matricesFor the multiplication of matrices, from linear algebra, we know that the two matrices required to be multiplied have the same common dimension as:"A=[1 2; 35; 2; 6]";"B=[2 41; 89, 0]";C=a*b= C182214657352622A A matrix is a matrix order, will requireB matrix multiplication and must be an order, get the matrix order. That is, only when the first matrix (left column matrix) is equal to the number of second matrices (right matrix) the number of rows, the product of two matrices is meaning.Division of 3. matricesFor the division of a matrix, there are two arithmetic symbols, namely "left" except "symbol" and "right" except "sign" / "." the right division of the matrix is slower, and the "left" operation can avoid the influence of singular matrixFor the equation, if this equation is overdetermined equation, then use division can automatically find the solution of minimizing square. If the equation is Diophantine equation, is used to solve the division operator at least at most rank (A)(rank of matrix A) non zero elements, and the solution of this type of in the solution of a minimum norm."A=[21 3420; 57820; 211417; 3431; 38]";"B=[10 2030, 40]'";X=b\a= x0.7667, 1.1867, 0.8767The above equation is overdetermined. Note that the resulting matrix X is column vector,"A=[21 34205; 78202114; 173431; 38]";"B=[10 20, 30]'";X=b\a= x1.6286, 1.2571, 1.1071, 1.0500The equation above is an indeterminate equationFour operations between 4. matrices and scalarsThe four operations and the four operations of scalar matrixand array and scalar between identical, i.e. each element in the matrix and scalar add, subtract, multiply, with the exception of the four operations. That is, when a division operation is performed, the scalar can only do the dividend.Power operation of 5. matricesThe power operation of a matrix is different from the power operation of a scalar. Using the symbol ^, it is not a power operation for each element of the matrix, but is related to some decomposition of the matrix"B=[21 3420; 782021; 1734; 31]";C=b^2= C3433207417543555376626313536231220156. matrix index, logarithmic and square root operationThe index matrix calculation, logarithmic and square root operations and an array of the corresponding operations are different. It is not a single element in the matrix operations, but for the whole matrix. These operations function as follows:Expm, expm1, expm2, expm3 - exponential arithmetic functions;Logm - logarithmic function;Sqrtm - root operation function."A=[1 34; 265; 32; 4]";> c=expm (a)= C1.0e+004 *0.4668, 0.7694, 0.92000.7919, 1.3065, 1.56130.4807, 0.7919, 0.9475> c=logm (a)= C0.5002 + 2.4406i 0.5960 - 0.6800i 0.7881 - 1.2493i0.4148 + 0.4498i 1.4660 - 0.1253i 1.0108 - 0.2302i0.5780 - 1.6143i 0.4148 + 0.4498i 1.0783 + 0.8263i> c=sqrtm (a)= C0.6190 + 0.8121i 0.8128 - 0.2263i 1.1623 - 0.4157i0.3347 + 0.1497i 2.3022 - 0.0417i 1.1475 - 0.0766i1.0271 - 0.5372i 0.3347 + 0.1497i 1.6461 + 0.2750iTranspose, inverse operation and determinant operation of 7.matricesThe transpose operator of the matrix is', 'and the inverse uses the arithmetic function: inv (), and uses the function: det () to determine the size of the determinant of the matrix"A=[1 20; 25-1; 410; -1]";C=a'= C12425100-1 -1> b=inv (a)= b52 -2-2 -1 10 -2 1> d=det (a)= DOneSpecial operations of 4.5 matricesThe special operations of matrix include matrix eigenvalue operation, conditional number operation, singular value operation, norm operation,rank operation, orthogonalization operation, trace operation, pseudo inverse operation, etc. these operations can be conveniently given by MATLABEigenvalue operations of 4.5.1 matricesIn linear algebra, it is very complicated to compute the eigenvalues of matrices. In MATLAB, the matrix eigenvalue operations are computed only by the function eig () or eigs (). The format is as follows E=eig (X) - generates a column vector consisting of the eigenvalues of the matrix X;[V, D]=eig (X) - generates two matrices V and D, where V is a matrix consisting of the eigenvectors of the matrix X as the column vectors, and D is the diagonal matrix made up of the eigenvalues of the matrix X as the main diagonal elementsThe eigs () function uses the iterative method to solve the eigenvalues and eigenvectors of the matrixD=eigs (X) - generating a column vector consisting of eigenvalues of matrix.X, X must be square, preferably large sparse matrix;[V, D]=eigs (X) - generates two matrices V and D, where V is a matrix consisting of the eigenvectors of the matrix X as the column vectors, and D is the diagonal matrix made up of the eigenvalues of the matrix X as the main diagonal elements"A=[1 20; 25-1; 410; -1]";[b, c]=eig (a)= b-0.2440 -0.9107 0.4472-0.3333 0.3333 0-0.9107 -0.2440 0.8944= C3.7321000.267901Norm operations of 4.5.2 matrices (vectors)In order to reflect the characteristics of some matrix (vector), the norm of the concept of linear algebra, it is divided into 2- norm, 1- norm, infinite norm and Frobenius norm. In MATLAB, norm (or normest)with the function () matrix (vector) norm. The format is as follows.Norm (X) -- the 2- norm of the matrix (vector) X;Norm (X, 2) - ibid;Norm (X, 1) - compute the 1- norm of the matrix (vector) X;Norm (X, INF) -- the infinite norm of the matrix (vector) X;Norm (X,'fro') - compute the Frobenius norm of the matrix (vector) X;Normest (X) -- only the 2- norm of the matrix (vector) X is computed, and the estimate of the 2- norm is applied to the computation of norm (X), which is time-consuming"X=hilb (4)"= X1, 0.5000, 0.3333, 0.25000.5000, 0.3333, 0.2500, 0.20000.3333, 0.2500, 0.2000, 0.16670.2500, 0.2000, 0.1667, 0.1429"Norm (4)"= ansFour> norm (X)= ansOne point five Zero Zero two"Norm (X, 2)= ansOne point five Zero Zero two"Norm (X, 1)= ansTwo point zero eight three three> norm (X, INF)= ansTwo point zero eight three three> norm (X,'fro')= ansOne point five zero nine seven> normest (X)= ansOne point five Zero Zero twoConditional number operation of 4.5.3 matrixThe condition number of a matrix is a quantity of the "morbid" degree of the judgement matrix. The larger the condition number of the matrix A, the more morbid the A is, and conversely, the more "good" state of the A, for example, the Hilbert matrix is a well-known ill conditioned matrixCond (X) - the condition number of the 2- norm of the return matrix X;Cond (X, P) - returns the conditional number of the P- norm of the matrix X, where P is 1,2, inf or fro;Rcond (X) - the inverse value used to compute the condition numberof a matrix. When the matrix X is ill conditioned, rcond (X) is close to 0 and X is "good", and rcond (X) is close to 1.Condest (X) - calculates the estimate of the condition number of the 1- norm of the matrix X"M=magic (3)"= M816357492"H=hilb (4)"= H1, 0.5000, 0.3333, 0.25000.5000, 0.3333, 0.2500, 0.20000.3333, 0.2500, 0.2000, 0.16670.2500, 0.2000, 0.1667, 0.1429> c1=cond (M)= C1Four point three three zero one> c2=cond (M)= C2Four point three three zero one> c3=rcond (M)= C3Zero point one eight seven five> c4=condest (M)= C4Five point three three three three > h1=cond (H)= H11.5514e+004> h2=cond (H, INF)= H22.8375e+004> h3=rcond (H)= H33.5242e-005> h4=condest (H)= H42.8375e+004From the calculation, we can see that the Rubik's cube matrix is better, and the Hilbert matrix is ill conditionedRank of 4.5.4 matrixRank is one of the important concepts in linear algebra, usually by elementary determinant or matrix can be transformed into the column transform, row echelon matrix, the number of rows and the ladder matrix contains nonzero row is a constant, the determination of the non zero line number is the rank of matrix matrix. The rank function (rank) to calculate."T=rand (6)"= T0.9501, 0.4565, 0.9218, 0.4103, 0.1389, 0.01530.2311, 0.0185, 0.7382, 0.8936, 0.2028, 0.74680.6068, 0.8214, 0.1763, 0.0579, 0.1987, 0.44510.4860, 0.4447, 0.4057, 0.3529, 0.6038, 0.93180.8913 0.6154 0.9355 0.8132 0.2722 0.46600.7621 0.7919 0.9169 0.0099 0.1988 0.4186> r =秩(t)R =六由上计算可知,矩阵T为满秩矩阵。
MATLAB矩阵及其运算

MATLAB矩阵及其运算MATLAB是一种强大的数学软件,广泛应用于科学和工程领域。
其中,矩阵及其运算是MATLAB中的重要部分,对于数据处理、线性代数和统计分析等方面都起着至关重要的作用。
本文将介绍MATLAB中矩阵的基本操作和运算,以及一些常用的矩阵函数和工具。
矩阵的创建和操作是MATLAB中的基本功能之一。
在MATLAB中,可以使用一对方括号来创建矩阵,例如:A = [1 2 3; 4 5 6; 7 8 9]这将创建一个3×3的矩阵A,其中包含1到9的数字。
此外,MATLAB还提供了一些快捷方式来创建特定类型的矩阵,比如零矩阵、单位矩阵和随机矩阵等。
例如,可以使用zeros函数创建一个全零矩阵:B = zeros(3, 4)。
这将创建一个3×4的全零矩阵B。
类似地,可以使用eye函数创建一个单位矩阵,rand函数创建一个随机矩阵等。
一旦创建了矩阵,就可以对它进行各种运算。
MATLAB中支持矩阵的加法、减法、乘法和除法运算,以及转置和逆运算等。
例如,可以使用加号和减号来进行矩阵的加法和减法运算:C = A + B。
D = A B。
这将分别计算矩阵A和B的加法和减法,并将结果分别存储在矩阵C和D中。
此外,还可以使用乘号来进行矩阵的乘法运算:E = A B。
这将计算矩阵A和B的乘法,并将结果存储在矩阵E中。
需要注意的是,在MATLAB中,矩阵的乘法运算是按照线性代数的定义进行的,即矩阵A的列数必须等于矩阵B的行数才能进行乘法运算。
除了基本的矩阵运算外,MATLAB还提供了许多内置的矩阵函数和工具,用于进行更复杂的矩阵操作。
例如,可以使用inv函数来计算矩阵的逆:F = inv(A)。
这将计算矩阵A的逆,并将结果存储在矩阵F中。
同样地,可以使用transpose 函数来计算矩阵的转置:G = transpose(A)。
这将计算矩阵A的转置,并将结果存储在矩阵G中。
此外,还可以使用eig函数来计算矩阵的特征值和特征向量,使用svd函数来进行奇异值分解,使用qr函数来进行QR分解等。
Matlab的矩阵运算范例
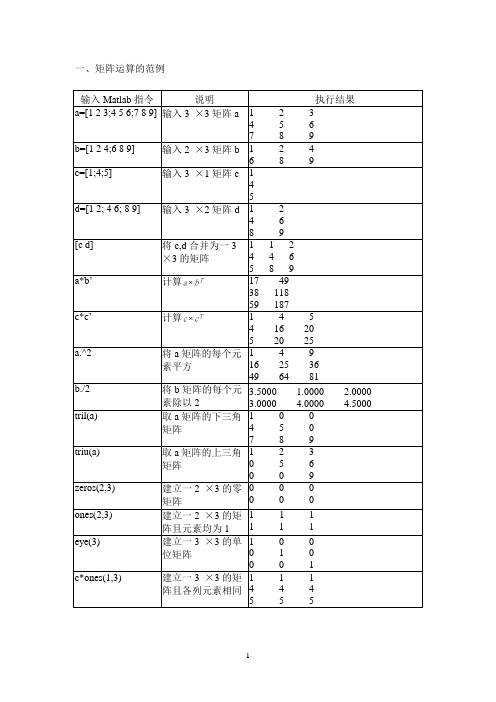
-4 -3 11
1 2 -3 0.1338 -0.0845 -0.2465
c=rref(augmtx)
0 0 1.0000 0 0 1.0000
sol=c(:,4)
方法二:以逆矩阵法求解 输入 Matlab 指令 sol=inv(a)*b 执行结果 0.1338 -0.0845 -0.2465
三、Matlab 中冒号(:)的使用范例 1. 向量的产生 输入 Matlab 指令 说明 执行结果 x=1:5 建立由 1 到 5 的列 1 2 3 4 5 向量且增量为 1 y=0:pi/4:pi 建立由 0 到π 的列 0 0.7854 1.5708 2.3562 3.1416 向量且增量为π /4 z=6:-1:1 建立由 6 到 1 的列 6 5 4 3 2 1 向量且增量为-1 a=[1 2 3];a(:) 将列向量 a 变成行 1 2 向量 3
3
cumsum(b)
prod(a) cumprod(a) prod(b)
cumprod(b)
素相加后形成的列 矩阵 2 将 b 矩阵各行的元 1 5 7 素累加后形成新的 12 15 矩阵 将 a 向量的元素相 336 乘之结果 将 a 向量的元素累 2 14 56 加后形成新的向量 80 将 b 矩阵各行的元 28 素相乘后形成的列 矩阵 将 b 矩阵各行的元 1 2 素累乘后形成新的 4 10 矩阵 28 80
1 2 3 7 8 9
1 2 3
2. 假设 a 4 5 6 ,试以 (a)上述的方法 (b)矩阵的乘法,达到换列及换行的结 4 5 6 7 8 9 1 3 2 7 9 8
果:(1) 1 2 3
(2) 4 6 5
用MATLAB制作简单计算器

用M A T L A B制作简单计算器Company number:【0089WT-8898YT-W8CCB-BUUT-202108】安阳工学院电子信息与电气工程学院《MATLAB编程与应用》课程大作业题目:用MATLAB制作简单计算器班级:电子信息工程(专升本)教师成绩由以下评分标准累计得出1、设计和仿真结果正确,分析清晰合理。
40%2、大作业报告重点突出、阐述清晰。
30%3、陈述清晰正确、有说服力,能够正确回答问题。
30%总分(上述成绩由教师填写)学生自评分值(该表格全部由学生填写)大作业总成绩(该表格“姓名”和“学号”由学生填写,“成绩”由教师填写)1.计任务: 1、熟悉MATLAB的主要控件使用方法。
2、熟悉MATLAB的GUI设计流程。
2.设计方案利用MATLAB GUI设计实现一个图形用户界面的计算器程序,要求实现:A.实现十进制数的加、减、乘、除、简单计算。
B. 科学计算函数,包括正弦、余弦、正切、(余切、开方、指数等函数运行。
C. 能够保存上次历史计算的答案,先是答案存储器中得内容。
D. 有清除键,能清除操作。
3.方案实施通过MATLAB的gui程序设计较为简单,在gui设计中主要用到两种控件,显示框用到文本编辑框(edit text),说明框用到静态文本框(Static text),数字以及运算等按钮用到命令按钮(push button)。
然后在通过各个按钮的回调函数,实现简单的计算功能。
4.方案施舍首先用MATLAB GUI功能,在绘制一个静态文本框和一个文本编辑框,以及24个命令按钮,调整好各控件大小、颜色,整体布局如图所示:图-1一、布局GUI1.打开Matlab,输入Guide 回车或者在工具栏上点击图标出现Guide 窗口:图–22.然后双击“Blank GUI(Default)”出现GUI窗口图-33.添加按钮图-44.根据按钮的作用及视觉效果做一定的修改把按钮的字符串大小、颜色进行设置,对按钮的位置进行排布,尽量使按钮集中在静态文本框下面。
MATLAB做简易计算器

MATLAB做简易计算器1、数字键的编写:textstring=get(handles.text1,'string');textstring=strcat(textstring,'0');set(handles.text1,'string',textstring);这是使用句柄handles指向对象text1,并以字符串形式来存储数据文本框text1的内容,并存储数个“0”,然后由set(handles.text1,'String','textString')在text1中输出。
同理,1~9也是这样实现。
2、符号键:textstring=get(handles.text1,'string');textstring=strcat(textstring,'+');set(handles.text1,'string',textstring);strcat的作用是将两个字符串连接起来,就是在已输入的存储数据textString后添加“+”进行运算。
然后执行set(handles.text1,'String',textString)。
符号键‘-’、‘*’、‘/’与‘+’的运算函数类似。
3、等于键:textstring=get(handles.text1,'string');s=eval(textstring);set(handles.text1,'string',s);“eval”的作用是将符号表达式转换成数值表达式。
再由set(handles.text1,'String',s)输出4、清除键:set(handles.text1,'string',' ');计算器使用:‘+’‘=’后:源程序:function varargout = jisuanqi(varargin)% JISUANQI MATLAB code for jisuanqi.fig% JISUANQI, by itself, creates a new JISUANQI or raises the existing % singleton*.%% H = JISUANQI returns the handle to a new JISUANQI or the handle to % the existing singleton*.%% JISUANQI('CALLBACK',hObject,eventData,handles,...) calls the local% function named CALLBACK in JISUANQI.M with the given input arguments.%% JISUANQI('Property','Value',...) creates a new JISUANQI or raises the% existing singleton*. Starting from the left, property value pairs are% applied to the GUI before jisuanqi_OpeningFcn gets called. An% unrecognized property name or invalid value makes propertyapplication% stop. All inputs are passed to jisuanqi_OpeningFcn via varargin. %% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one% instance to run (singleton)".%% See also: GUIDE, GUIDATA, GUIHANDLES% Edit the above text to modify the response to help jisuanqi% Last Modified by GUIDE v2.5 04-May-2015 16:44:30% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @jisuanqi_OpeningFcn, ...'gui_OutputFcn', @jisuanqi_OutputFcn, ...'gui_LayoutFcn', [] , ...'gui_Callback', []);if nargin && ischar(varargin{1})gui_State.gui_Callback = str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT% --- Executes just before jisuanqi is made visible.function jisuanqi_OpeningFcn(hObject, eventdata, handles, varargin)% This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% varargin command line arguments to jisuanqi (see VARARGIN)% Choose default command line output for jisuanqihandles.output = hObject;% Update handles structureguidata(hObject, handles);% UIWAIT makes jisuanqi wait for user response (see UIRESUME)% uiwait(handles.figure1);% --- Outputs from this function are returned to the command line. function varargout = jisuanqi_OutputFcn(hObject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT);% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Get default command line output from handles structurevarargout{1} = handles.output;% --- Executes on button press in pushbutton1.function pushbutton1_Callback(hObject, eventdata, handles)textstring=get(handles.text1,'string');textstring=strcat(textstring,'1');set(handles.text1,'string',textstring);% hObject handle to pushbutton1 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton2.function pushbutton2_Callback(hObject, eventdata, handles)textstring=get(handles.text1,'string');textstring=strcat(textstring,'2');set(handles.text1,'string',textstring);% hObject handle to pushbutton2 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton3.function pushbutton3_Callback(hObject, eventdata, handles)textstring=get(handles.text1,'string');textstring=strcat(textstring,'3');set(handles.text1,'string',textstring);% hObject handle to pushbutton3 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton4.function pushbutton4_Callback(hObject, eventdata, handles)textstring=get(handles.text1,'string');textstring=strcat(textstring,'+');set(handles.text1,'string',textstring);% hObject handle to pushbutton4 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton9.function pushbutton9_Callback(hObject, eventdata, handles)textstring=get(handles.text1,'string');textstring=strcat(textstring,'4');set(handles.text1,'string',textstring);% hObject handle to pushbutton9 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton10.function pushbutton10_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');textstring=strcat(textstring,'5');set(handles.text1,'string',textstring);% hObject handle to pushbutton10 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton11.function pushbutton11_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');textstring=strcat(textstring,'6');set(handles.text1,'string',textstring);% hObject handle to pushbutton11 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton12.function pushbutton12_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');textstring=strcat(textstring,'-');set(handles.text1,'string',textstring);% hObject handle to pushbutton12 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton13.function pushbutton13_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');textstring=strcat(textstring,'7');set(handles.text1,'string',textstring);% hObject handle to pushbutton13 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton14.function pushbutton14_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');textstring=strcat(textstring,'8');set(handles.text1,'string',textstring);% hObject handle to pushbutton14 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton15.function pushbutton15_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');textstring=strcat(textstring,'9');set(handles.text1,'string',textstring);% hObject handle to pushbutton15 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton16.function pushbutton16_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');textstring=strcat(textstring,'*');set(handles.text1,'string',textstring);% hObject handle to pushbutton16 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton17.function pushbutton17_Callback(hObject, eventdata, handles);set(handles.text1,'string',' ');% hObject handle to pushbutton17 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton18.function pushbutton18_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');textstring=strcat(textstring,'.');set(handles.text1,'string',textstring);% hObject handle to pushbutton18 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton19.function pushbutton19_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');s=eval(textstring);set(handles.text1,'string',s);% hObject handle to pushbutton19 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% --- Executes on button press in pushbutton20.function pushbutton20_Callback(hObject, eventdata, handles) textstring=get(handles.text1,'string');textstring=strcat(textstring,'/');set(handles.text1,'string',textstring);% hObject handle to pushbutton20 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)。
matlab 矩阵运算程序

matlab 矩阵运算程序MATLAB是一种强大的数学软件,主要用于数值计算、算法开发、数据可视化和数据分析等。
在MATLAB中,矩阵运算是非常常见的操作。
以下是一个简单的MATLAB矩阵运算程序示例:```matlab创建两个矩阵A和BA = [1, 2, 3;4, 5, 6;7, 8, 9];B = [9, 8, 7;6, 5, 4;3, 2, 1];矩阵加法C = A + B;disp('矩阵A和矩阵B的和:');disp(C);矩阵减法D = A - B;disp('矩阵A和矩阵B的差:'); disp(D);矩阵乘法E = A * B;disp('矩阵A和矩阵B的乘积:'); disp(E);矩阵转置T = transpose(A);disp('矩阵A的转置:');disp(T);求矩阵的行列式det_A = det(A);disp('矩阵A的行列式:');disp(det_A);求矩阵的逆矩阵inv_A = inv(A);disp('矩阵A的逆矩阵:');disp(inv_A);求矩阵的秩rank_A = rank(A);disp('矩阵A的秩:');disp(rank_A);求矩阵的特征值eig_A = eig(A);disp('矩阵A的特征值:');disp(eig_A);```以上程序演示了MATLAB中的一些基本矩阵运算,如加法、减法、乘法、转置、求行列式、求逆矩阵、求秩和求特征值等。
您可以根据实际需求修改矩阵A和B的值,然后运行该程序以观察结果。
需要注意的是,这里的矩阵运算都是在MATLAB环境下进行的。
如果要编写比MATLAB更快的矩阵运算程序,可以尝试使用如C、C++等编程语言,并链接到高性能的数学库,如Intel的Math Kernel Library(MKL)。
如何利用Matlab技术进行矩阵运算

如何利用Matlab技术进行矩阵运算矩阵运算是数学中的重要部分,可以应用于多个领域,如自然科学、工程学和经济学等。
而对于如何利用Matlab技术进行矩阵运算,是每个数学爱好者和研究者都应该掌握的技能。
本文将深入探讨如何使用Matlab进行矩阵运算,并提供一些例子和技巧供读者参考。
首先,让我们来了解一下Matlab是什么。
Matlab是一种强大的数学计算软件,被广泛应用于科学计算和工程设计中。
它不仅可以进行矩阵运算,还能进行符号计算、绘图和数据分析等任务。
Matlab具有直观友好的用户界面,使得使用者可以轻松地进行各种计算操作。
在Matlab中,可以使用一维和二维数组来表示矩阵。
一维数组称为向量,而二维数组称为矩阵。
当我们需要进行矩阵运算时,需要首先定义并初始化一个矩阵。
在Matlab中,可以通过直接输入矩阵元素的值来创建一个矩阵。
例如,我们可以使用以下命令创建一个2x2的矩阵:```MatlabA = [1 2; 3 4];```这个矩阵将被存储在变量"A"中,并且可以通过输入"A"来显示。
在进行矩阵运算前,我们需要了解一些基本的矩阵运算符。
Matlab中的加法运算使用"+"符号,减法运算使用"-"符号,乘法运算使用"*"符号。
此外,Matlab还提供了一些特殊的运算符来进行矩阵运算,如点乘运算符"."、转置运算符"'"和逆运算符"\"等。
这些运算符可以使我们更加便捷地进行矩阵计算。
接下来,让我们来探讨一些矩阵运算的实际应用。
首先,矩阵的加法和减法可以用于求解多个物理量的叠加或差值。
例如,在电路分析中,我们可以使用矩阵运算来计算电路中各个元件的电流和电压。
假设有一个电路由两个电阻和一个电源组成,我们可以使用以下命令计算电源电流I和电阻电压V:```MatlabR = [10; 20];V = 5; % 电源电压I = R \ V; % 计算电源电流V_R = R .* I; % 计算电阻电压```上述代码中,电阻值被存储在矩阵R中,电源电压被存储在变量V中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、GUI开发环境简介MATLAB提供了一套可视化的创建图形窗口的工具,使用用户界面开发环境可方便的创建GUI应用程序, 它可以根据用户设计的GUI布局,自动生成M文件的框架,用户使用这一框架编制自己的应用程序。
图形用户界面(Graphical User Interfaces ,GUI)则是由窗口、光标、按键、菜单、文字说明等对象(Objects)构成的一个用户界面。
用户通过一定的方法(如鼠标或键盘)选择、激活这些图形对象,使计算机产生某种动作或变化,比如实现计算、绘图等。
二、矩阵计算器介绍2.1 程序使用的控件在矩阵计算器设计中主要用到三种控件,文本编辑框(edit text),静态文本框(Static text),命令按钮(push button),边框(panel)。
然后在通过各个按钮的回调函数,实现简单的计算功能。
2.2 程序功能介绍(1)具有用户图形界面。
实现矩阵的加、减、乘、左除、右除等简单计算。
(2)有清空键,能清除操作。
2.3 矩阵计算器界面及主要控件功能注释:text1文本编辑框控件功能:输出要计算公式。
如[12 45;78 56]+[659 238;79 56] MatA文本编辑框功能:输入参与计算矩阵AMatB文本编辑框功能:输入参与计算矩阵BMatC静态文本框功能:输出计算结果矩阵C三、部分计算操作结果(1) 加法+MatAtext1 pushbutton22pushbutton23pushbutton24pushbutton20(2)求逆(3)转置(4)群运算.*四、部分模块功能算法的实现(1)按键’加法+’响应:a=get(handles.matA,'string');textString=strcat(a,'+');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);(2)按键’转置’响应a=get(handles.matA,'string');textString=strcat(a,'''');set(handles.text1,'String',textString);(3)按键’计算’响应textString=get(handles.text1,'String');f=eval(textString);set(handles.matC,'string',num2str(f,'%15.5g'))(5)按键’清空’响应set(handles.text1,'String','')set(handles.matA,'String','[]')set(handles.matB,'String','[]')set(handles.matC,'String','')注释:其余模块功能算法与以上代码较为相似,不在一一举例。
五、其余传参方法本程序通过文本编辑框(edit text)达到传参的目的,下面介绍两种常用的其他传参方式。
(1)运用global定义全局变量传递参数这种方法适用于gui内控件间以及不同gui间,是最简单的方式。
使用方法:gloal xxxx在每一个要到该全局变量的地方,都要添一句gloal xxxx。
缺点:全局变量破坏了程序的封装性,所以,全局变量是能少用尽量少用。
(2)运用UserData传递参数直接通过对象的userdata属性进行各个callback之间的数据存取操作。
首先必须将数据存储到一个特定的对象中,假设对象的句柄值为handles.text1,需要存储的值为value,则输入以下程序即可:set(' handles.text1,'UserData',Value);此时,value数据就存在句柄值为ui_handle的对象内,在执行的过程中若要取回变量可以通过以下方式在任意callback中获取该数据值:value=get('' handles.text1,'UserData');缺点:每个对象仅能存取一个变量值,因此当同一对象存储两次变量时,先前的变量值就会被覆盖掉,因此都用UserData存储简单与单一的数据。
六、心得这次作业在MATLAB GUI编程中是较为简单的,虽然老师当天布置的作业我当天完成,但是这期间还是遇到一些困难,比如起初我的程序计算结果矩阵C用文本编辑框(edit text),我的代码是正确的,但是却得不到结果。
最后通过上网查资料,解决了该问题。
同时我对MATLAB有了新的认识。
1、通过MATLAB矩阵计算器的设计,初步了解了关于MATLAB图形用户界面的部分控件的使用方法。
2、MATLAB的GUI提供的很多实用的控件,方便用于设计属于自己的图形界面。
3、Matlab具有强大、丰富的内置函数和工具箱,界面设计时更加简洁、快捷与直观。
七、详细代码function varargout = untitled1(varargin)gui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @untitled1_OpeningFcn, ...'gui_OutputFcn', @untitled1_OutputFcn, ...'gui_LayoutFcn', [], ...'gui_Callback', []);if nargin && ischar(varargin{1})gui_State.gui_Callback = str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:}); elsegui_mainfcn(gui_State, varargin{:});endfunction untitled1_OpeningFcn(hObject, eventdata, handles, varargin) handles.output = hObject;guidata(hObject, handles);function varargout = untitled1_OutputFcn(hObject, eventdata, handles) varargout{1} = handles.output;function calculate_Callback(hObject, eventdata, handles)textString=get(handles.text1,'String');f=eval(textString);set(handles.matC,'string',num2str(f,'%15.5g'));function button1_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'+');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);function button2_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'-');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);function button3_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'*');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);function button4_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'\');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);function button5_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'/');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);function button6_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'^-1');set(handles.text1,'String',textString);function button7_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'''');set(handles.text1,'String',textString);function matA_CreateFcn(hObject, eventdata, handles)if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction matB_CreateFcn(hObject, eventdata, handles)if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction matC_CreateFcn(hObject, eventdata, handles)if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction text10_CreateFcn(hObject, eventdata, handles)if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction text1_CreateFcn(hObject, eventdata, handles)if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction pushbutton11_Callback(hObject, eventdata, handles)set(handles.text1,'String','');set(handles.matA,'String','[]');set(handles.matB,'String','[]');set(handles.matC,'String','');function pushbutton20_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'.*');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);function pushbutton21_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'./');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);function pushbutton22_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'.\');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);function pushbutton23_Callback(hObject, eventdata, handles)a=get(handles.matA,'string');textString=strcat(a,'.^');b=get(handles.matB,'string');textString=strcat(textString,b);set(handles.text1,'String',textString);function pushbutton24_Callback(hObject, eventdata, handles) a=get(handles.matA,'string');textString=strcat(a,'.''');set(handles.text1,'String',textString);。
