第8章静电场中的导体ppt课件
合集下载
大学物理,静电场中的导体和电介质8-5 静电场的能量

取一体积元, dV 4πr 2 dr
2
R1
r
dr
Q R2 dWe wedV dr 2 8 π εr 2 2 R Q Q 1 1 2 dr We dWe ( ) 2 8 π ε R1 r 8 π ε R1 R2 9
8.5 静电场的能量
2
第8章 静电场中的导体和电介质
第8章 静电场中的导体和电介质
例:同轴电缆由内径为 R1、外径为 R2的两无限长金属圆柱 面构成,单位长度带电量分别为 +、 -,其间充有 r 电介 质。求: 1)两柱面间的场强 E;2)电势差 U;3)单位长 度电容 ;4)单位长度贮存能量。
介质中高斯定理: D dS q 0
5
8.5 静电场的能量
第8章 静电场中的导体和电介质
二、静电场的能量 能量密度 以平行板电容器为例,将电能用电场的量表示。
1 1 1 1 εS 2 2 2 2 ( Ed ) εE Sd εE V We CU 2 2 2 d 2
电场中单位体积的能量 称为电场能量密度:
d
S
εr
We we V
8.5 静电场的能量
第8章 静电场中的导体和电介质
静电场的能量 ( Electrostatic Energy ) 一个带电系统包含许多的电荷。电荷之间 存在着相互作用的电场力。 任何一个带电系统在形成的过程中,外力 必须克服电场力做功,即要消耗外界的能量。 外界对系统所做的功,应该等于系统能量 的增加。 因此,带电系统具有能量。
第8章 静电场中的导体和电介质
1 We QU 2
R1
1 λ R2 λh ln 2 2πε0 εr R1 2 λh R2 ln 4πε0 εr R1
2
R1
r
dr
Q R2 dWe wedV dr 2 8 π εr 2 2 R Q Q 1 1 2 dr We dWe ( ) 2 8 π ε R1 r 8 π ε R1 R2 9
8.5 静电场的能量
2
第8章 静电场中的导体和电介质
第8章 静电场中的导体和电介质
例:同轴电缆由内径为 R1、外径为 R2的两无限长金属圆柱 面构成,单位长度带电量分别为 +、 -,其间充有 r 电介 质。求: 1)两柱面间的场强 E;2)电势差 U;3)单位长 度电容 ;4)单位长度贮存能量。
介质中高斯定理: D dS q 0
5
8.5 静电场的能量
第8章 静电场中的导体和电介质
二、静电场的能量 能量密度 以平行板电容器为例,将电能用电场的量表示。
1 1 1 1 εS 2 2 2 2 ( Ed ) εE Sd εE V We CU 2 2 2 d 2
电场中单位体积的能量 称为电场能量密度:
d
S
εr
We we V
8.5 静电场的能量
第8章 静电场中的导体和电介质
静电场的能量 ( Electrostatic Energy ) 一个带电系统包含许多的电荷。电荷之间 存在着相互作用的电场力。 任何一个带电系统在形成的过程中,外力 必须克服电场力做功,即要消耗外界的能量。 外界对系统所做的功,应该等于系统能量 的增加。 因此,带电系统具有能量。
第8章 静电场中的导体和电介质
1 We QU 2
R1
1 λ R2 λh ln 2 2πε0 εr R1 2 λh R2 ln 4πε0 εr R1
电介质-PPT课件

导体的静电感应过程
E0
加外电场---电子在电场力作用下运动
导体的 ' 外场 E 0
导体的静电感应过程
E0
感应 E ' 外场 E 0
导体的静电感应过程
q2
+ q1
q1 + q1
q 1+ q 2
三、静电平衡导体的表面场强
. dS = E s
=
. + S d E 内
0 +
. + S d E 表
E表 S +
. S d E 侧
0
E
1
0
q
i i
1
0
S
σ
E 0
S
有导体时静电场的分析方法
导体放入静电场中:
导体的电荷 重新分布
导体上的电荷分 布影响电场分布
b a
a、b在导体内部:
b
a
U0 E 0
a、b在导体表面:
Ed l 0 即 U 0 E d l
----静电平衡的导体是等势体
静电平衡条件:
用场强来描写: 1、导体内部场强处处为零; 2、表面场强垂直于导体表面。 用电势来描写: 1、导体为一等势体; 2、导体表面是一个等势面。
E0
感应 E ' 外场 E 0
导体的静电感应过程
E0
感应 E ' 外场 E 0
导体的静电感应过程
E0 E ' E E E ' 0 0
静电场中的导体和电解质

Q + + + + ++ + + + + E= 0 S+ + + + + + + + ++
Q q + + + +++ + +-q + + - E= 0 S + 结论: 电荷分布在导体外表面, 导体 + q + + 内部和内表面没净电荷. + - - + + + + ++ 腔内有电荷q: E 0 q 0
i
结论: 电荷分布在导体内外两个表面,内表面感应电荷为-q. 外表面感应电荷为Q+q.
NIZQ
第 5页
大学物理学 静电场中的导体和电介质
结论: 在静电平衡下,导体所带的电荷只能分布在导体的 表面,导体内部没有净电荷. • 静电屏蔽 一个接地的空腔导体可以隔离内 外电场的影响. 1. 空腔导体, 腔内没有电荷 空腔导体起到屏蔽外电场的作用. 2. 空腔导体,腔内存在电荷 接地的空腔导 体可以屏蔽内、 外电场的影响.
NIZQ
第 3页
大学物理学 静电场中的导体和电介质
• 静电平衡时导体中的电场特性
E内 0
场强:
ΔVab
b
a
E dl 0
• 导体内部场强处处为零 E内 0 • 表面场强垂直于导体表面 E表面 // dS
• 导体为一等势体 V 常量 • 导体表面是一个等势面
S
0 E P dS qi
§7-6 静电场中的导体 ppt课件

内表面上有电荷吗?
PPT课件
+ + + ++ + + +
+
E0 S
10
S
E
dS
0
1
0
qi
若内表面带电
+ + + ++ + + +
+
矛
盾
U AB AB E dl 0
A
S ++
B-- E 0
导体是等势体
U AB AB E dl 0 所以内表面不带电
AB
0
+
+
A
e +
dl +
τ
+
B
PPT课件
8
二、静电平衡时导体上电荷的分布
+ + + ++ + + +
+
1. 实心导体
E0
S
E
dS
0
q
0
E0
S
q 0
结论: 导体内部无电荷
PPT课件
9
2. 有空腔导体 空腔内无电荷
S E dS 0, qi 0
电荷分布在表面上
结论: 电荷分布在外表面上(内表面无电荷)
PPT课件
11
空腔内有电荷
S1 E dS 0, qi 0
Qq
+++++++++++++++ +
PPT课件
+ + + ++ + + +
+
E0 S
10
S
E
dS
0
1
0
qi
若内表面带电
+ + + ++ + + +
+
矛
盾
U AB AB E dl 0
A
S ++
B-- E 0
导体是等势体
U AB AB E dl 0 所以内表面不带电
AB
0
+
+
A
e +
dl +
τ
+
B
PPT课件
8
二、静电平衡时导体上电荷的分布
+ + + ++ + + +
+
1. 实心导体
E0
S
E
dS
0
q
0
E0
S
q 0
结论: 导体内部无电荷
PPT课件
9
2. 有空腔导体 空腔内无电荷
S E dS 0, qi 0
电荷分布在表面上
结论: 电荷分布在外表面上(内表面无电荷)
PPT课件
11
空腔内有电荷
S1 E dS 0, qi 0
+++++++++++++++ +
大学物理静电场ppt课件

大学物理静电场ppt 课件
目录
• 静电场基本概念与性质 • 静电场中的电荷分布与电势 • 静电感应与电容器 • 静电场中的能量与动量 • 静电场与物质相互作用 • 总结回顾与拓展延伸
01
静电场基本概念与性质
电荷与电场
电荷的基本性质
同种电荷相互排斥,异种电荷相互吸引。
电场的概念
电荷周围存在的一种特殊物质,它对放入其中 的其他电荷有力的作用。
典型问题解析
电荷在电场中的受力与运动
根据库仑定律和牛顿第二定律分析电 荷在电场中的受力与运动情况。
电场强度与电势的关系
通过电场强度与电势的微分关系,分 析电场强度与电势的变化规律。
电容器与电容
分析平行板电容器、圆柱形电容器等 典型电容器的电容、电量、电压等物 理量的关系。
静电场的能量
计算静电场中电荷系统的电势能、电 场能量等物理量,分析静电场的能量 转化与守恒问题。
某些晶体在受到外力作用时,内部产生电极化现象,从而在晶体表面产生电荷的现象。 压电效应具有可逆性,即外力撤去后,晶体又恢复到不带电的状态。
热电效应
温差引起的电荷分布和电流现象。包括塞贝克效应(温差产生电压)和帕尔贴效应(电 流产生温差)。
压电效应和热电效应的应用
在传感器、换能器、制冷技术等领域有广泛应用。
静电场能量密度及总能量计算
静电场能量密度定义
01
单位体积内静电场所具有的能量。
计算公式
02
能量密度 = 1/2 * 电场强度平方 * 电介质常数。
静电场总能量计算
03
对能量密度在整个空间进行积分。
带电粒子在静电场中运动规律
运动方程
根据牛顿第二定律和库仑定律建立带电粒子在静 电场中的运动方程。
目录
• 静电场基本概念与性质 • 静电场中的电荷分布与电势 • 静电感应与电容器 • 静电场中的能量与动量 • 静电场与物质相互作用 • 总结回顾与拓展延伸
01
静电场基本概念与性质
电荷与电场
电荷的基本性质
同种电荷相互排斥,异种电荷相互吸引。
电场的概念
电荷周围存在的一种特殊物质,它对放入其中 的其他电荷有力的作用。
典型问题解析
电荷在电场中的受力与运动
根据库仑定律和牛顿第二定律分析电 荷在电场中的受力与运动情况。
电场强度与电势的关系
通过电场强度与电势的微分关系,分 析电场强度与电势的变化规律。
电容器与电容
分析平行板电容器、圆柱形电容器等 典型电容器的电容、电量、电压等物 理量的关系。
静电场的能量
计算静电场中电荷系统的电势能、电 场能量等物理量,分析静电场的能量 转化与守恒问题。
某些晶体在受到外力作用时,内部产生电极化现象,从而在晶体表面产生电荷的现象。 压电效应具有可逆性,即外力撤去后,晶体又恢复到不带电的状态。
热电效应
温差引起的电荷分布和电流现象。包括塞贝克效应(温差产生电压)和帕尔贴效应(电 流产生温差)。
压电效应和热电效应的应用
在传感器、换能器、制冷技术等领域有广泛应用。
静电场能量密度及总能量计算
静电场能量密度定义
01
单位体积内静电场所具有的能量。
计算公式
02
能量密度 = 1/2 * 电场强度平方 * 电介质常数。
静电场总能量计算
03
对能量密度在整个空间进行积分。
带电粒子在静电场中运动规律
运动方程
根据牛顿第二定律和库仑定律建立带电粒子在静 电场中的运动方程。
4静电场中的导体PPT课件

q3 q2 q
1、求电势分布(用叠加
原理)
R3
r R1
U1
q
4 0 R1
q
4 0 R2
q
4 .0 R3
q3
q2
q R1
R2
21
q (1 1 1)
40 R1 R2 R3
q3
(R1 r R2 )
U2
q
4 0 r
q
4 0 R2
q
4 0 R3
q11 1
R3
q2
q R1
R2
( )
40 r R2 R3
理论上:Q分布确定,E、U分布亦确定。 但导体上的电荷分布不是人为规定的, 如何处理有导体存在时的静电场问题?
原则:1.静电平衡的条件
E内 0
或 U const
2.静电场的基本方程
qi
S E d s
i
0
L E d l 0
3.电荷守恒定律 .
12
例: 一个金属球A,带电 qA, 同心金属球壳 B, 带电 qB, 如图,试分析它们的电荷分布。
.
28
2、腔内有电荷的 封闭导体壳:
设不带电的金属壳B内有带电体A, 在静电平衡状态下,带电情况如图。
如果要求腔内电荷不影响
腔外,可以将外壳接地。
q
–q
接地使B的外表面的
电荷全部跑光。
Q+q
.
电力线不可能到外面来, 就起到了 对外的屏蔽作用。
29
从此图可以看出, q –q
重要规律(2): 导体壳内表面上的电荷 与壳内电荷,在导体壳内 表面以外的空间的总场 强等于零。
说明:
1.这里所指的导体内部的场强是指空间中的一切电荷 (包括导体外部的电荷和导体上的电荷)在导体内部 产生的总场强。
第章静电场中的导体和电介质PPT课件

q2
EA
1 2 o
2 2 o
3 2 o
4 2 o
0
EB
1 2 O
2 2 O
3 2 o
4 2 o
0
1
23
4
由电荷守恒:
1S 2 S q1
A
B
3S 4S q2
1
4
q1 q2 2S
2
3
q1 q2 2S
20
1
4
q1 q2 2S
q1
2
3
q1 q2 2S
1
2
上述结果表明:平板相背的两面带电等
R3 R2
R3
RR11
qq1 1
RR33
问题:电势表
达式能直接写
R2 R1
q1
4 or
2
dr
R3
(q q1 )
4 or 2
dr
出来吗?
q1
4 o
1 R1
1 R2
q q1
4 o R3
V1 V2
同理,球壳的电势为:
V2
E dl
R3
R3
(q
4
q1 ) or 2
dr
q q1
2.内屏蔽
+
+
壳外表面上的电荷分布与腔内带电体的位置无关,只 取于导体外表面的形状。
若将空腔接地,则空腔外表面上的感应电荷被大地电荷 中和,腔外电场消失,腔内电荷不会对空腔外产生影响。即 接地空腔对内部电场起到了屏蔽作用,这是静电屏蔽的另外 一种——内屏蔽。
高压设备用金属导体壳接地做保护。 14
五、利用静电平衡条件和性质作定量计算
例1:半径为R和r的球形导体(R>r),用很长的细导线连 接起来,使两球带电Q、q,求两球表面的电荷面密度。
大学物理静电场课件

单位(SI): 牛 库 顿 ( 1N 仑 C 1 )米 或 ( 1V m 伏 1 )
1E 根 、式 根点据qFE 中 0库rˆ据 的 0电为 仑荷定q4指 1律定 的,,0得 向 r场有q2义 r强场 0P(当 当 的 点 呈qq球00单 时 时F对v,,EE称 位 与 与4分1rr矢 反 同布0 向 向 q)rq径 2。 ; 0 r+ˆ0q。 r-Pq rq0 PEqE0
二、电荷的守恒性
在一个孤立的带电系统中(即没有净电荷通过其界面),无 论发生怎样的物理过程,系统所具有的正负电荷电量的代数 和总是保持不变。——电荷的守恒定律 • 电荷的运动不变性 一个电荷的电量与它的运动状态无关,即 系统所带电荷与参考系的选取无关。
三、电荷的量子性 • 电量 密立根油滴实验
• 电荷的量子性
l
r
dl
2
r0
三. 计算场强 E 分布的基本方法
(3)电磁场可同时在空间叠加。
• 静电场的重要表现
(1)场中任何带电体都受电场力作用 — 动量传递 (用2)、E 带电来U体分在别电描场述中静移电动场时的,上场述对两带项电性体质做功—能量传递 (3)静电场对放在其中的导体有感应作用,对置于其中的电 介质有极化作用
二、电场强度
场源电荷:产生电场的点电荷、点电荷系、或带电体.
第八章 静止电荷的电场
相对于观察者为静止的电荷称为静电荷。它在 空间所产生的场为静电场,它是电磁场的一种特殊 状态。重点讨论真空中的静电场。
• 主要内容
• 描述静电场的两个基本物理量:电场强 度 和电势
• 静电场的两个基本定理:高斯定理和环 流定理
• 电势与电场的关系
结构框图
电相互作用
库仑定律
静电场中的导体30052
E 外
+ + + + +
+ + +
导体的静电感应过程 加上外电场后
E 外
+ + + + + +
+ + + +
导体的静电感应过程 加上外电场后
E 外
+ + + + + +
+ + + +
感应电荷
导体达到静平衡
E 感
E内 E外 E感 0
+ + + + + +E
外 + + + +
感应电荷
处于静电平衡状态的导体,导体内部电场强度处处为零,整 个导体是个等势体。表面是等势面
﹡例2.已知导体球和导体球壳的半径 R1、R2、R3、及 q、Q
Q q
求 ①电荷及场强分布;球心的电势 ②如用导线连接A、B,再作计算
解: 电荷分布 q q Q q
q q
B A R1 R2
O R3
由高斯定理得
场
0
r R1 R2 r R3
强 分 布
q
E 4 0r 2 R1 r R2
9.7 静电场中的导体
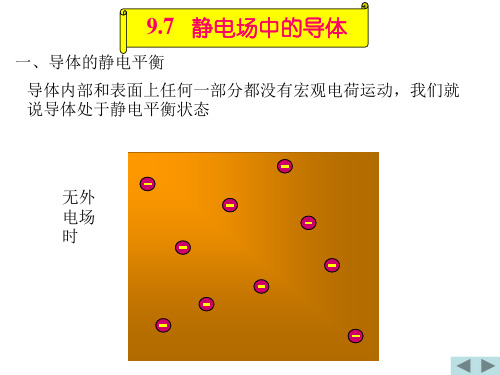
一、导体的静电平衡 导体内部和表面上任何一部分都没有宏观电荷运动,我们就 说导体处于静电平衡状态
无外 电场 时
导体的静电感应过程
E 外
加上外电场后
导体的静电感应过程
E 外
+
加上外电场后
导体的静电感应过程
E 外
+
大学物理第六版马文蔚6.1静电场中的导体课件

E 感
E内 E外 E感 0
+ + + + +
+ E外
+ + + +
感应电荷
加上外电场 E 外 E外
把金属导体置于外电场中,自由 电子将产生宏观定向运动,导体 中电荷按照外电场特性和导体形 状形成特定的分布。
在外电场作用下,引起导体中电 荷重新分布而呈现出的带电现象, 称为静电感应现象Electrostatic Induction
★★导体空腔的静电屏蔽作用:
—— 导体空腔(不论接地与否)内部电场不受腔外 电荷的影响;接地导体空腔外部的电场不受内部电场 的影响。
应用:精密测量上的仪器屏蔽罩、屏蔽室、高压带电 作业人员的屏蔽服(均压服)等。
小结: 静电平衡导体的电荷分布
Q+++q +
12、、导腔空内体腔无内导电部体荷无带:电电导荷体荷的。Q 电荷只能分布在外表++面+++。----+--Qq++++-+-=++0---q-++-
+
证明:腔体内表面所带的电量和腔内带电体所带的电量 等量异号
因为:
E内 0
故
E
dS
0
qi
0
q1
+ q1
故qi 0 (S内)
故:必存在 q1
高斯面S
(3).导体表面附近的场强:
E 面外
0
nˆ
设 P 点在表面外紧靠 ΔS 表面。 设高斯柱面如图
由
及高斯定理得
E(nˆ )
ΔS
静电场中的导体.ppt

U AB AB E dl 0
所以内表面不带电
结论 电荷分布在外表面上(内表面无电荷)
1 – 5 静电场中的导体 第一章静电场
空腔内有电荷
E dS 0, S1
qi 0
电荷分布在表面上
内表面上有电荷吗?
E dS 0, S2
qi 0
q内 q
Qq
0
导体内电场强度 外电场强度 感应电荷电场强度
1 – 5 静电场中的导体 第一章静电场
静电平衡条件
(1)导体内部任何一点处的电场强度为零;
(2)导体表面处的电场强度的方向,都与导体表面垂直.
导体表面是等势面
en
导
E dl
E
体 是 等 势 体
U E dl 0 +
E2
dl
R3
R2
R1 R2
E3
dl
R1 R1 E4 dl
VO
q
4π 0
(1 R3
1 R2
2 R1
)
2.31103 V
作钱币形高斯面 S
E
+ + +
+
+
E
++
0
+
++
小与该表面电荷面密度 +
成正比
1 – 5 静电场中的导体 第一章静电场
4 导体表面电荷分布
, E ; E
++
+ ++
++++
所以内表面不带电
结论 电荷分布在外表面上(内表面无电荷)
1 – 5 静电场中的导体 第一章静电场
空腔内有电荷
E dS 0, S1
qi 0
电荷分布在表面上
内表面上有电荷吗?
E dS 0, S2
qi 0
q内 q
0
导体内电场强度 外电场强度 感应电荷电场强度
1 – 5 静电场中的导体 第一章静电场
静电平衡条件
(1)导体内部任何一点处的电场强度为零;
(2)导体表面处的电场强度的方向,都与导体表面垂直.
导体表面是等势面
en
导
E dl
E
体 是 等 势 体
U E dl 0 +
E2
dl
R3
R2
R1 R2
E3
dl
R1 R1 E4 dl
VO
q
4π 0
(1 R3
1 R2
2 R1
)
2.31103 V
作钱币形高斯面 S
E
+ + +
+
+
E
++
0
+
++
小与该表面电荷面密度 +
成正比
1 – 5 静电场中的导体 第一章静电场
4 导体表面电荷分布
, E ; E
++
+ ++
++++
静电场中的导体PPT课件

Q q
R1
R3
法一: 由高斯定理, 得
E1 0
(r R1)
E2
q 4 π ε0r 2
(R1 r R2 )
E3 0
(R2 r R3 )
q
q
E4
Q 4π
q
ε0r 2
(r R3 )
Vo
E dl
0 R1
0
E1
dl
R2 R1
E2
dl
R1
R3
R3 R2
E3
dl
R3 E4 dl
2 R1
尖端放电现象
带电导体尖端附近的 电场特别大,可使尖端附 近的空气发生电离而成为 导体产生放电现象.
σE
< 电风实验 >
++ +++
+ +
++ +
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
19
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
1 ( q q qQ) 4 π ε0 R1 R2 R3
法二: 直接用大叠加法!
思考:1)用导线连接A,B 再作计算 Q q
连接A,B q (q) 中和
球壳外表面带电 Q q
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Q1 ? Q2 4S
?2
?
?? 3
?
Q1 ? Q2 4S
故:相对的两个板面总是带有等量异号电荷;相背的两个板面总是带有等量同号
的电荷。
.
9
8-10 如图所示,有三块互相平行的导体板,外面两块不带电, 中间一块上所带总电量为 Q,每板面积为 S,求每块板的两个
表面的电荷面密度各是多少?如果外面的两块用导线连接,再
综上,静电平衡时,导体上的电荷总量为Q,且
分布于表面。
静电平衡时,导体为等势体,也即:U 球 ? U 球心
单看球面上的电荷在球心 O 点的电势为
? ? U1 ?
dU ?
Q
dq ? Q
Q 4π?0R 4π?0R
单看点电荷 q 在球心 O 点的电势为
U2
?
q
4π?0r
由电势叠加原理:
U球
?
U .
球心
? U1 ? U2
解:空腔内表面因感应而带电 +Q, 电力线始于正电荷,指向电势降落的方向.
.
4
8-5. 如图所示,一个未带电的空腔导体球壳,内半径为R,在腔内 离球心的距离为d处(d<R),固定一电量为+q的点电荷。用导线 把球壳接地后,再把地线撤除。选无穷远处为零电势点,求球心
O处的电势。
解:依题意, 球壳带电-q , 且都分布于内表面. 于是球 外 E = 0 , 球壳上 U壳 = 0,地线撤去仍不变.
球壳单独存在时
U O球
?
?q
4?? 0 R
+q单独存在时
U Oq ?
q
4?? 0d
运用叠加原理可求 得O的电势为
U
?
q
4?? 0
(1 d
?
1) R
.
5
8求-6场一强中和性电导势体分球布壳,内并外画半出径E分-r和别为?R?1、r R曲2,线球。心放一点电荷Q,
解:依题设,易知,静电平衡时,内球壳上均匀带电-Q,外球壳
求各板面的面电荷密度。 解: (1)A、C两板不相连 导体内电场为零,由电场叠加 (取C板内不带电的外表面为球形的空腔导体A内,
放有一带电量为 +Q的带电导体B,如图所示.则比较空
腔导体A的电势UA 和导体B 的电势UB 时,可得以下 结论:[ B ]
(A) UA=UB ; (B) UA>UB ; (C) UA<UB ;
A
(D) 因空腔形状不是球形,两者无法比较.
B ?Q
Q 0r 2
R2
dr? 0dr?
R1
?
4 R2
Q 0r 2
dr ?
Q 40
(1 ? r
1 R1
?
1 )
R2
r ? R1
??
? ? ? ?
r
E? ?dr? ?
R2
0dr ?
r
? R2
Q
4??0r 2
dr
?
Q
4??0R2
? ? ?
r
E??dr? ?
? r
Q
4??0r 2
dr
?
Q
4??0r
.
R1 ? r ? R2 r ? R2 6
8-1 当一个带电导体达到静电平衡时, 下列陈述正确的是 ( C )
(A) 表面上电荷密度较大处电势较高. (B) 表面曲率较大处电势较高 (D) 导体内任一点与其表面上任一点的电势相等 (C) 导体内部的电势比导体表面的电势高
.
1
8-2 一任意形状的带电导体,其面电荷密度分布为 ? (x, y,z,)
则在导体表面外附近任意点处的电场强度的大小E(x, y, z)
= ?_(_x_, y_,_z_) ?0 ,其方向______垂直于导体表面________.
.
2
8-3 两个带电量分别为 +q、-q的两金属球,半径为R,两 球心的距离为d,且d > 2R,其间的作用力设为f1,另有两 个带电量相等的点电荷+q、-q,相距也是 d,其间作用力
高斯定理,必有: (? 2 ? ? 3)? S ? 0
? 2 ? ?? 3
(1)
显然,
?1
?
?
2
?
Q1 S
(2)
?
如图,在导体内部任取一点P,其场强是由
四个面上电荷的场强叠加而得,必有:
3?
EP
?4 ?
?
?1
Q2
S
??
2 ?? 2?0
(3)
3?
?
4
?
0
(4)
由(1)(2)(3) (4)式
?1
?
?
4
?
设为f2,可以肯定f1 > f 2 ( 填“<” , “>或”“=”.)
解:虽说两球球心的间距为R,但两球带
+q
-q
异号电荷,由于电荷间的吸引作用,两球
上的电荷在空间上会相互靠近,最终在电
荷分布达到平衡时,两球上电荷的“重心” +q
-q
间的距离实际上小于d。而一对点电荷间的
空间距离为d,由库伦定律,显然f1 > f 2
上均匀带? 电Q,4?球Q?0r壳2 e?r内Er=?0R,1 由对称性及高斯定理,得场强分布为:
E?
0 R1 ? r ? R2
Q R1
? Q ?
4??0r2 er
r ? R2
如图,选红色线为积分路径,由
?
?
?
E??dr?
R2
得电势分布为
r
? ? ?? ? ? ?? ?? ?
r
E??dr??
R1
r4
? ? U1 ?
dU ?
Q
dq
Q 4π?0R
?Q 4π? 0 R
单看点电荷 q 在球心 O 点的电势为
叠加:
Q
4π?0
R
?
q
4π?0r
?
0
U2
?
q
4π?0r
Q. ?
?
R r
q
8
8-9 两块平行放置的无限大导体平板,带电量分别为Q1、Q2, 证明其相对的两个板面总是带有等量异号电荷,相背的两个板
面总是带有等量同号的电荷,并求出各板面的电荷密度。 ? 1
解: 如图,设每个面的面积为S, 四个面上的电荷面
密度分别为? 1 、? 2、? 3及? 4 取如图所示的柱体形高斯面(底面积为 ? S)
P
?2 ?3
静电平衡时,二块导体平板内部场强均为零,则高斯面处于导体内的那部分? 4
(图中红色部分)上的电通量为零;而处于导体外的那部分(图中蓝色部分)
上,由于没有电场线穿过(场强方向垂直于导体表面),电通量也为零。则由
8-7 如图所示,一个导体球,半径为R,带电量Q,今将一点 电荷q放在球外距球心距离为r的地方,求导体球的电势。
解:导体球处在点电荷的电场中,一方面,其上 R
q
原有的电荷Q将会重新分布,另一方面,其上会 O r
有感应电荷,但因导体球绝缘孤立(即未与其他
物体相接),故其上感应电荷总量必为零。又,
静电平衡时,导体上的电荷只能分布于表面。
?
1
4??0
(Q R
?
q) r
7
8-8 如图所示,一个接地导体球,半径为R,原来不带电,今
将一点电荷q放在球外距球心距离为r的地方,求球上的感应
电荷总量。
解:导体球接地,又静电平衡时,导体为等 势体, 则
R
q
r
O
U 球心 ? U 球 ? 0
感应电荷将不均匀的分布于球面上,设总量为Q.
单看感应电荷在球心 O 点的电势为
