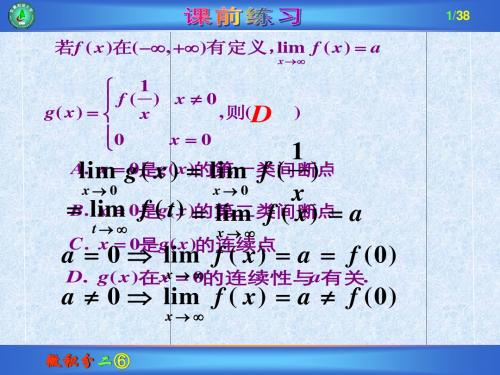
微积分:无穷小量及其比较
《微积分》讲义

《微积分》讲义第一章极限一、函数极限的概念:f=A要点:⑴x 为变量;⑵A 为一常量。
二、函数极限存在的充分必要条件:f=A f=A,f=A 例:判定是否存在?三、极限的四则运算法则⑴=f±g⑵=f·g⑶=……g≠0⑷k·f=k·f四、例:⑴⑵⑶⑷五、两个重要极限⑴=1 =1⑵=e =e ………型理论依据:⑴两边夹法则:若f≤g≤h,且limf=limh=A,则:limg=A⑵单调有界数列必有极限。
例题:⑴=⑵=⑶=⑷=⑸=六、无穷小量及其比较1、无穷小量定义:在某个变化过程中趋向于零的变量。
2、无穷大量定义:在某个变化过程中绝对值无限增大的变量。
3、高阶无穷小,低阶无穷小,同阶无穷小,等价无穷小。
4、定理:f=A f=A+a (a=0)七、函数的连续性1、定义:函数y=f在点处连续……在点处给自变量x一改变量x:⑴x0时,y0。
即:y=0⑵f=f⑶左连续:f=f右连续:f=f2、函数y=f在区间上连续。
3、连续函数的性质:⑴若函数f和g都有在点处连续,则:f±g、f·g、(g()≠0)在点处连续。
⑵若函数u=j在点处连续,而函数y=f在点=j()处连续,则复合函数f(j(x)) 在点处连续。
例:===4、函数的间断点:⑴可去间断点:f=A,但f不存在。
⑵跳跃间断点:f=A ,f=B,但A≠B。
⑶无穷间断点:函数在此区间上没有定义。
5、闭区间上连续函数的性质:若函数f在闭区间上连续,则:⑴f在闭区间上必有最大值和最小值。
⑵若f与f异号,则方程f=0 在内至少有一根。
例:证明方程式-4+1=0在区间内至少有一个根。
第二章一元函数微分学一、导数1、函数y=f在点处导数的定义:x y=f-f=A f'=A ……y',,。
2、函数y=f在区间上可导的定义:f',y',,。
3、基本初等函数的导数公式:⑴=0⑵=n·⑶=,=⑷=·lnɑ,=⑸=cosx,=-sinx=x,=-=secx·tanx,=-cscx·cotx⑹=-=-4、导数的运算:⑴、四则运算法则:=±=·g(x)+f(x)·=例:求下列函数的导数y=2-5+3x-7f(x)=+4cosx-siny=⑵、复合函数的求导法则:y u,u v,v w,w x y x'=''''例:y=lntanxy=lny=arcsin⑶、隐函数的求导法则:把y看成是x的复合函数,即遇到含有y 的式子,先对y求导,然后y再对x求导。
大学微积分无穷小量的性质与无穷小量的阶

sin
cos
1
sin(
2
)
2 sin(
)(5)
2
cos sin 1 sin( ) sin( )(6)
2
cos cos 1 cos( ) cos( )(7) sin sin 21 cos( ) cos( )(8)
2
arctan x lim x0 arcsin x
解 ∵ 当 x 0 时,
arctan x ~ x, arcsin x ~ x
lim arctanx lim x 1 x0 arcsin x x0 x
微积分(二) calculus
例8 求 lim x0
1 x sin x 1 ex2 1 x0(或
x )时,
( x )
f (x) 与 g(x)是同阶无穷小量.
特别的,当 c 1时,则称当 x x0(或 x )时,
f (x) 与 g(x)是等价无穷小量,记作
f (x) ~ g(x) x x0 或 x
注意
无穷小量阶的意义: 反映无穷小量趋于零的速度.
补充:
微积分(二) calculus
思考题:
任意两个无穷小都可以比较吗?
x 2 sin 1
lim
x0
x x2
lim sin 1 x0 x
不存在. 不可比.
作业
微积分(二) calculus
先看书 再做练习
P66 练习2.4 T1(2、3、4),T2(3、4), T5(3、4)
补充三角函数的微和积差分(化二积) 与calc积ulu化s 和差
x0
x0
x0
微积分(二) calculus
推论:有限个无穷小量的代数和还是无穷小.
无穷小量概念

无穷小量概念无穷小量是微积分中的重要概念之一,它在求解极限、微分和微分方程等方面有着广泛的应用。
本文将介绍无穷小量的定义、性质以及相关的应用。
1. 无穷小量的定义在数学中,无穷小量是指当自变量趋向于某一特定值时,函数值趋于零的量。
更加形式化地说,对于函数f(x)而言,当x趋近于x0时,若存在一个函数ε(x),满足lim(ε(x)) = 0,使得f(x) = ε(x),则称f(x)是x趋近于x0时的无穷小量。
2. 无穷小量的性质(1)线性性质:若f(x)和g(x)是x趋近于x0时的无穷小量,那么对于任意的实数a和b,af(x)+bg(x)也是x趋近于x0时的无穷小量。
(2)乘积性质:若f(x)是x趋近于x0时的无穷小量,g(x)是x趋近于x0时的有界量,则f(x)g(x)是x趋近于x0时的无穷小量。
(3)比值性质:若f(x)是x趋近于x0时的无穷小量,且g(x)是x 趋近于x0时的无穷小量,那么f(x)/g(x)的极限存在且不为零。
3. 无穷小量的应用(1)极限计算:无穷小量在极限计算中有重要作用。
通过将复杂函数转化为无穷小量之比,可以简化极限的计算过程。
(2)微分:微分的定义中包含了无穷小量的概念。
微分可以看作是函数在某一点处的局部线性近似,其中通过使用无穷小量来表示函数的变化量。
(3)微分方程:微分方程描述了自变量与函数及其导数之间的关系。
通过引入无穷小量的概念,可以将微分方程转化为更简单的形式,进而求解出函数的解。
总结:无穷小量是微积分中的重要概念,它在极限计算、微分和微分方程等方面有着重要的应用。
理解无穷小量的定义和性质对于深入理解微积分的原理和应用非常重要。
因此,在学习微积分时,我们需要充分理解无穷小量的概念,并能够熟练地运用它们解决相关问题。
3 无穷大量与无穷小量

《微积分》(第三版) 教学课件
首页 上一页 下一页 结束
(一)无穷大量与无穷小量的概念
3. 极限的充分必要条件
定理25(极限的充分必要条件) 变量y以A为极限的充分必要条件是 变量y可以
表示为A与一个无穷小量的和 即
lim yAyA 其中lim 0
《微积分》(第三版) 教学课件
《微积分》(第三版) 教学课件
首页 上一页 下一页 结束
常用的等价无穷小
当x 0时
(1) x ~sin x~ tan x~ arcsin x~ arctan x~ex 1~ ln(1 x)
(2) 1 cos x ~ x2 , n 1 x 1~ x
2
n
例7. 求 lim tan x sin x x0 sin3 x
x
因此x sin 1 仍是无穷小.lim x sin 1 0
x
x0
x
《微积分》(第三版) 教学课件
首页 上一页 下一页 结束
(二)无穷小量的比较
引例: 当x 0时, x,2x, x2 都是无穷小. x 1 0.5 0.1 0.01 0.001 … →0 2x 2 1 0.2 0.02 0. 002 … →0 x2 1 0.25 0.01 0.0001 0.000001 … →0
常用的等价无穷小
当x 0时
(1) x ~sin x~ tan x~ arcsin x~ arctan x~ex 1~ ln(1 x)
(2) 1 cos x ~ x2 , n 1 x 1~ x
2
n
例6. 求lim 3 1 xsin x 1. x0 arctan x2
解 因为 3 1 x sin x 1~~ 1 x sin x (x 0) arctan x2~x2 (x0)
微积分课间2.4 无穷大量与无穷小量

lim f ( x )不存在且 x → X 时 , f ( x ) 趋于无穷大;
(3 lim f ( x ) = ∞ ⇔ lim+ f ( x ) = ∞且 lim− f ( x ) = ∞; )
x → x0 x → x0 x → x0
lim f ( x ) = ∞ ⇔ lim f ( x ) = ∞且 lim f ( x ) = ∞ .
是无穷小 .
定义: 定义: 设 α , β是同一过程中的两个无 穷小. β (1)如 果 lim = 0, 称 β 是 比 α 高 阶 的 无 穷 小 , α 记 作 β = o (α ); β (2)如 果 lim = ∞ , 称 β 是比 α 低阶 的 无穷 小 ; α β (3)如 果 lim = C ≠ 0, 称 β 与 α 是 同 阶 的 无 穷 小 ; α β 特 殊 地 ,如 果 lim = 1, 称 β 与 α 是 等 价 的 无 穷 α 小;记 作 α ~ β . β (4)如果 lim k = C ≠ 0,k ∈ Z +,称β 是α的k阶的无穷小. ,称 α 注 若 α/β →C,则 α∼Cβ. ,
4. 无穷小量与函数极限的关系
理 lim f ( x) = A ⇔ f ( x) = A+ α( x), 定
x→x0
中 其 α(x)是 x → x0时 无 小 当 的 穷 .
意义
1.将一般极限问题转化为特殊极限问题(无穷小量); 1.将一般极限问题转化为特殊极限问题(无穷小量); 将一般极限问题转化为特殊极限问题 2.给出了函数 在 2.给出了函数f(x)在x0附近的近似表达式 f(x)≈A,误 给出了函数 ( ) , 差为α(x). 差为
x2 例如, lim 例如, ∵ = 0, x →0 3 x
2_7 无穷小量的比较
( x − 1) 2 x −1 解:1) ∵ lim = lim = 0, 2 x →1 x − 1 x →1 x + 1 1 − cos 2 x + x 3 1 − cos 2 x x3 α 2) lim = lim = lim + lim 2 2 2 x→0 β x→0 x→0 x→0 x x x 2sin 2 x = lim + lim x = 2 − 0 = 2 ≠ 1 2 x→0 x→0 x
x
x
ln(1 + x ) x ∴ lim = lim = 1 x→0 x →0 x sin x
解: ∵ x → 0 时 , e − 1 ~ x
ex −1 x ∴ lim = lim =2 x→0 1 + x − 1 x →0 1 x 2
1 1+ x −1 ~ x 2
微积分二 微积分二⑥
14/38
( x + 1)sin2x 例3 lim x→0 arcsin x 解:当x → 0时, sin2 x ~ 2 x, arcsin x ~ x.
1 1 1 2 − (cos x − 1) ⋅ x 1 2 2 2 = = lim = lim 1 1 2 x → 0+ x → 0+ 2 2 x x ( x) 2 2
微积分二 微积分二⑥
19/38
0 lim ( 型) + x→0 x(1 − cos x ) 0 (1 − cos x )(1 + cos x ) 解2:原极限= lim 原极限= x → 0+ x (1 − cos x )(1 + cos x ) 1 − cos x = lim x → 0+ x ((1 − cos x ))(1 + cos x ) 1 2 x 1 2 = lim = 2 1 x → 0+ 2 x x (1 + cos x ) 2
微积分——无穷大量与无穷小量讲解.ppt

x 因为lim lim x 0, 当x 0时,x 2比x较高阶的 x 0 x x 0 无穷小量,可以记做 x 2 o( x )
反之,当 x 0时,x是比x 2较低阶的无穷小量。
x 1 1 lim lim , 当x 0时,x与2 x是同阶的 x 0 2 x x 0 2 2 无穷小量。
练习题答案
一、1、0; 3、 ; 二、0 x
1 . 4 10 2
2、 lim f ( x ) C ;
x x
1 4、 . f ( x)
(二)无穷小量
定义2.9: 以0为极限的变量,称为无穷小量.
亦即,对于任意给定的 正数,如果在变量y的 变化过程中,总有那么 一个时刻,在那个时刻 以后,不等式 | y | 无穷小量。 例如
1 1 lim n 0, 当n 时,变量yn n 是无穷小量. n 2 2
| y | M 又因为 是无穷小量,所以,对于任意的 0,总有
那么一个时刻,在那个时刻以后,恒有
| |
M
于是,在上述两个时刻 中较晚的时刻以后,恒 有
| y || || y | M
M
成立,故 y 是无穷小量。
推论
常量与无穷小量的乘积仍是无穷小量
1 例4 求 lim x sin x 0 x 1 1 解 因为lim x=0. 而 | sin | 1,即sin 是有界变量。 x 0 x x 1 故 lim x sin =0 x 0 x
0
显然,x2比x与2x趋于0的速度快得多。 快慢是相对的,是相互比较而言。因此有
定义2.10 设,是同一过程中的两个无穷小量,
如果 lim 0, 则称是比较高阶的无穷小量, 记做 o( ) 如果 lim c 0 c为常量) ( , 则称是比是同阶的 无穷小量。特别当 c 1时,称与是等价的 无穷小量,记做 ~。 如果 lim , 则称是比较低阶的无穷小量。
微积分教学课件1-5无穷大和无穷小

注意 (1)无穷小是变量,不能与很小的数混淆;
(2)零是可以作为无穷小的唯一的数.
判断下面的函数是否为无穷小量
当x 0时, x , tan x,1 cos x
2
当x 时,
sin x x 2 ,e x
1 当n 时, n
2、定义:在某种变化趋势下,绝对值无限增大的变量 称为无穷大量.
例8、求
解
1 cos x lim x 0 1 cos x
1 cos x 1 cos x lim lim x0 1 cos x x0 (1 cos x )( cos x ) 1
lim
x 0
1 2 x 2 1 (1 cos x ) x 2
推论1、 ~ ~ ~ lim ( x) f ( x)存在, ( x) ~ ( x) lim ( x) f ( x) lim ( x) f ( x)
定理5
~ ( x) ~ ~( x) ~ ( x), ( x) ~ ( x) 推论2、 lim ~ f ( x)存在, ( x) ~ ( x) ( x) lim f ( x) lim ~ f ( x) ( x) ( x)
(4) 如果 lim k C 0, k 0, 就说 是 的 k 阶的 无穷小.
例如,
x2 lim 0, x 0 3 x
sin x lim 1, x 0 x
即 x o( 3 x ) ( x 0).
2
当 x 0 时,x 2 是比 3 x 高阶的无穷小 ;
x x0
的图形的铅直渐近线.
定义 : 如果 xlim f ( x) A 或 xlim f ( x) A ,则直线 y A 是函数 y f (x) 图形 的水平渐进近线 。
无穷小量的性质及其在微积分中的应用

无穷小量的性质及其在微积分中的应用无穷小量是微积分中的重要概念之一,它在描述变化率和极限的过程中起到了关键作用。
无穷小量可以帮助我们更好地理解函数的性质,而微积分则让我们能够推导方程、计算曲线的斜率以及求解面积和体积等问题。
本文将介绍无穷小量的基本定义和性质,并探讨它在微积分中的应用。
在微积分中,我们经常遇到那些随着自变量无限接近某一点时趋于零的量,这就是无穷小量。
无穷小量通常用符号$\delta x$或者dx来表示,其中dx表示自变量x的无穷小增量。
无穷小量有以下几个基本性质:1.乘法性质:若f(x)是一个有界函数,$\delta x$是一个无穷小量,那么f(x) * $\delta x$也是一个无穷小量。
这一性质说明了无穷小量的乘法具有自由度,可以与任何有界函数相乘。
2.加法性质:若$\delta x$和$\delta y$都是无穷小量,那么$\deltax$ + $\delta y$也是一个无穷小量。
这一性质说明了无穷小量的加法也保持了无穷小量的性质。
3.极限性质:无穷小量的极限总是为零。
当自变量趋近于某一点时,无穷小量的变化幅度趋于零,这使得我们能够更好地描述函数在某一点附近的行为。
无穷小量在微积分中的应用十分广泛。
在求导过程中,我们将差分化为无穷小量,从而能够推导出函数在某一点的斜率,即导数。
例如,对于函数$f(x)$,我们可以使用差商$\frac{f(x+\delta x)-f(x)}{\deltax}$来求解其导数。
当$\delta x$趋近于零时,此差商将近似于函数在点x处的斜率。
另一个重要的应用是在曲线的切线和法线的求解中。
通过将无穷小量引入到切线和法线的公式中,我们可以更好地理解曲线在某点的局部特征。
对于曲线$y=f(x)$,在点(x, y)处的切线方程可以表示为$y-f(x)=f'(x)(x-x_0)$,其中$f'(x)$是函数f(x)在点x处的导数,$x-x_0$表示无穷小增量。
无穷小的比较

无穷小的比较是两个数都是无穷小,可以比较相对大小。
无穷小量是数学分析中的一个概念,在经典的微积分或数学分析中,无穷小量通常以函数,序列等形式出现,无穷小量即以数0为极限的变量,无限接近于0。
确切地说,当自变量x无限接近x0或x的绝对值无限增大时,函数值fx与0无限接近,即fx,0或fx等于0,则称fx为当x,x0或x,∞时的无穷小量,特别要指出的是,切不可把很小的数与无穷小量混为一谈。
无穷小的性质无穷小量不是一个数,它是一个变量,零可以作为无穷小量的唯一一个常量,无穷小量与自变量的趋势相关,若函数在某的空心邻域内有界,则称g 为当时的有界量。
有限个无穷小量之和仍是无穷小量,有限个无穷小量之积仍是无穷小量,有界函数与无穷小量之积为无穷小量,特别地,常数和无穷小量的乘积也为无穷小量,恒不为零的无穷小量的倒数为无穷大,无穷大的倒数为无穷小。
工具/原料
笔(各种笔均可)纸(各种纸均可)
方法/步骤1 引例无穷小的多样性,如何比较? 2 回顾无穷小的定义明确多阶无穷小和等价无穷小的定义 3 学习无穷小的定理1 基于等价无穷小 4 学习无穷小的定理2 基于等价无穷小 5 由等价无穷小,简化的极限运算规则。
和差取大规则,和差替代规则 6 由等价无穷小,简化的极限运算规则。
因式替代规则7 学习例题,反复联系。
8 仔细认真,举一反三!。
2_3 无穷小量与无穷大量1

2
x
2
微积分二④
12/27
无穷大
无界
y
例如: x , x sin x ?
如图所示, x , y x sin x 是无界函数,但不是无穷大./27
2. 无穷大量的性质 1.无穷大与有界变量的代数和是无穷大 . 2.无穷大与非零常数的乘积是无穷大. 3.无穷大与无穷大的乘积是无穷大. 注:1. 无穷大与无穷大和不一定是无穷大. 两个同号的无穷大之和是同号的无穷大. 2. 无穷大与有界变量的乘积不一定是无穷大.
| y | M
成立, 则称因变量y在此变化过程中为无穷大量。 借记为
lim y
简言之: 绝对值无限增大的变量称为无穷大. 注: (1) 称一个函数是无穷大量时, 一定要明确
指出自变量的变化趋势.
微积分二④
9/27
(2) 无穷大量不是很大的数, 而是具有非正常极限的函 数,是极限不存在的一类特殊变量!!!
x
x 1
lim ln x 0, x 1, ln x为无穷小 lim sin x 0, x , sin x为无穷小
x
微积分二④
4/27
注: (1) 称一个函数是无穷小量时, 一定要明确 指出自变量的变化趋势.
(2) 无穷小量是一个变量,除 0 以外,任何 一个数无论它有多小都不是无穷小量(为什么?). 因此不要把无穷小量与一个很小的数混为一团.
练习:
2.函数 y x( x 1) x 1 当 x ____ 1 时为无穷大 x3 1
微积分二④
(3) lim f (x)= 仅仅只是一个记号,它并不代表函数 的极限值存在. 2.正负无穷大 y M y M, y M 若变量无限增大,即y M,则称为正无穷大,记作limy= 若变量无限减少即y M,则称为负无穷大,记作limy=
大学微积分上册第二章等价无穷小量的比较与应用ppt课件

2)若 lim , 则称 是比 低阶的无穷小;
3)若 lim c 0, 则称 与 是同阶无穷小;
4)若
lim
1,
பைடு நூலகம்
则称
与
是等价无穷小,
记作 ~ .
11
例3、判断下列无穷小的阶:
(1)4x3,3x2 (x 0)
(2) 1 , 1 (n ) n n2
(3)x2 16, x 4 (x 4) (4) 1 , 1 n .
例如, (1).lim sin 2x x x
lim 1 sin 2x x x
0.
(2).lim x cos 1 0.
x0
x
(3).
lim
x
arctan x2
x
lim
x
1 x2
arctanx
0.
5
例1
lim
x
3x
4x 2
4
2 x
1
2
3
sin
x
解
lim x
4x 2 3x2 4x 1
等价与相等不一样整理课件14arcsin常见的等价无穷小量有整理课件15四等价无穷小量的替换则有时的无穷小量均为注意此公式只适用于乘除此公式只适用于乘除但不适用加减但不适用加减证明
§2、5 无穷小的比较与应用
1、无穷小量 2、无穷大量 3、无穷小量的比较 4、等价无穷小量的替换
1
复习:两个重要极限
15
例5
求
lim
x0
tan x sin x x3
解 tan x ~ x sin x ~ x
原式 lim x x 0 错误 x0 x3
16
正确做法:
tan x sin x
无穷小量与无穷大量

无穷小量与无穷大量无穷小量和无穷大量是微积分中的重要概念,在研究极限和无穷时经常出现。
本文将介绍无穷小量和无穷大量的定义、性质以及它们在计算极限过程中的应用。
一、无穷小量的定义与性质无穷小量通常用符号“Δx”或者“dx”表示,表示趋于零的一个量。
严格的定义是:如果函数f(x)在某一点a处的极限为零,那么称Δx为函数f(x)在点a处的一个无穷小量。
无穷小量的性质如下:1. 有限个无穷小量的和仍然是无穷小量。
2. 有限个无穷小量的积仍然是无穷小量。
3. 无穷小量与有限数的和为无穷小量。
4. 无穷小量与有限数的积为无穷小量。
二、无穷大量的定义与性质无穷大量通常用符号“∞”表示,表示趋于无穷大的一个量。
严格的定义是:如果对于任意的正数M,总存在正数N,使得当x>N时,有|f(x)|>M,那么称f(x)为一个无穷大量。
无穷大量的性质如下:1. 有限数与无穷大量的和为无穷大量。
2. 有限数与无穷大量的差为无穷大量。
3. 有限数乘以无穷大量为无穷大量。
4. 无穷大量与零的积为无穷小量。
三、无穷小量与无穷大量的关系在极限计算中,无穷小量和无穷大量是密切相关的。
当x趋于某一特定值时,如果Δx是一个无穷小量,那么f(x)就是一个无穷大量。
根据无穷小量和无穷大量的性质,可以得到一些重要的极限计算法则。
1. 极限的四则运算法则:如果函数f(x)和g(x)在点a处的极限都存在,那么它们的和、差、积和商的极限也都存在,并且满足相应的运算规则。
2. 极限的夹逼定理:如果对于x处于某一邻域内的所有值,有f(x)≤g(x)≤h(x),且lim(f(x))=lim(h(x))=L,那么lim(g(x))也等于L。
四、无穷小量和无穷大量的应用1. 在微分学中,无穷小量被用来定义导数。
导数表示函数变化率的大小,而无穷小量则表示极小的自变量变化量,二者的关系可以通过极限的定义来推导。
2. 在积分学中,无穷小量被用来定义微积分的基本概念。
无穷小量阶的比较结论

无穷小量阶的比较结论
无穷小量阶在微积分和数学分析等学科中有广泛应用。
在无穷小量阶比较中,我们考虑两个无穷小量$a(x)$和$b(x)$,并研究它们之间的比较关系。
下面,我们将介绍无穷小量阶的比较结论。
1. 当$x\to 0$时,$ax^\alpha$的阶小于$bx^\beta$的阶
若$\alpha<\beta$,则$\lim_{x\to 0}\frac{ax^\alpha}{bx^\beta}=0$,即
$ax^\alpha$的阶小于$bx^\beta$的阶;
总结:
以上四条结论都是在特定的极限情形下成立的。
其中,前两条是在$x\to 0$或者
$x\to\infty$的极限情形下成立的,而后两条是在$x\to x_0$的极限情形下成立的。
无论是$x\to 0$、$x\to\infty$还是$x\to x_0$的极限情形,我们都可以通过求出无穷小量函数的极限值来判断其阶的大小关系。
在实际应用中,我们可以利用无穷小量阶的比较结论,研究函数的渐近性质,判断是否存在一定的增长趋势或者衰减趋势。
例如,在微积分中,我们可以利用无穷小量阶的比较关系,进行极限求解,得到导数、微分等基本概念和理论,从而能够更加深入地了解函数的特性和性质。
总之,无穷小量阶的比较关系是微积分和数学分析中的基本概念,具有非常重要的理论和实际应用价值。
通过深入理解无穷小量阶的比较结论,我们可以更好地掌握相关的数学知识,进一步提升自己的数学能力和水平。
微积分 第二章 第三节 无穷小量和无穷大量

6
ቤተ መጻሕፍቲ ባይዱ 说明:
1.称一个变量为高阶或同阶无穷小量,是没有意义
的,只有在同一个变化过程中的两个无穷小量比较时,
才能说它们阶的高低或是否同阶.
2.在同一极限过程中的两个无穷小量,并不是总能
比较阶的高低的.
3. 如果 lim x0
xk
C(C
0, k
0), 则称是x的k阶
无穷小量.
4. 利用等价无穷小量,可简化某些极限的求解过程.
M
即证得 lim f (x)g(x) 0 . x x0 3
例1 求 lim sin x . x x
解 当x 时, 1 为无穷小, x
而sin x是有界函数.
y sin x x
lim sin x 0. x x
错误解法: lim x sin 1 lim x limsin 1 0 .
3. lim f (x) A _______ f (x) A , x x0 ( 其中 lim 0 ) . x x0
4.在同一过程中,若 f (x) 是无穷大,
则 ______是无穷小.
17
二、根据定义证明:当 x 0 时,函数 y 1 2x x
是无穷大,问 x 应满足什么条件,能使 y 104 . 三、证明函数 y 1 sin 1 在区间 ( 0 , 1 ] 上无界 ,但当
13
五、小结 思考题
无穷小与无穷大是相对于过程而言的. 1. 主要内容: 三个定义;一个定理;三个性质. 2. 几点注意: (1) 无穷小( 大)是变量,不能与很小(大) 的数混淆,零是唯一的无穷小的数; (2)无穷多个无穷小的代数和(乘积)未必是 无穷小; (3) 无界变量未必是无穷大.
14
关于无穷小的若干比较方法及应用

关于无穷小的若干比较方法及应用绪玉珍(江苏师范大学科文学院㊀221000)摘㊀要:函数的极限是极限理论的一个重要组成部分ꎬ无穷小的定义与计算则是函数极限的基础.无穷小的比较问题是微积分的重要内容ꎬ为了更系统地解决此类问题ꎬ文章从无穷小比较的定义㊁等价无穷小定阶法㊁比较定阶法㊁泰勒公式定阶法㊁求导定阶法这五种方法进行了讨论ꎬ并且分别给出了对应的实例分析.灵活使用这些方法ꎬ可以做到更加有效地解决无穷小的比较问题.关键词:无穷小的比较ꎻ等价无穷小ꎻ泰勒公式ꎻ定阶法中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)03-0017-03收稿日期:2022-10-25作者简介:绪玉珍(1987-)ꎬ女ꎬ山东省邹城人ꎬ硕士ꎬ从事高等数学教学研究.基金项目:2021年江苏省高校 大学生劳动教育 基础课课程群 专项课题(2021JDKT056).㊀㊀极限理论是高等数学的基础ꎬ函数的极限是极限理论的一个重要组成部分.极限为零的变量称为无穷小量ꎬ简称 无穷小 ꎬ在函数及数列的极限㊁函数的连续性㊁微分和积分的定义中都有无穷小的应用.然而ꎬ理解清楚无穷小的概念以及运算有一定的难度.无穷小的比较问题ꎬ不仅是高等数学的重要内容ꎬ也是历年全国硕士研究生招生考试的重要考点.本文主要针对无穷小的比较给出了几种方法ꎬ有利于读者进一步理解无穷小的含义以及更加系统地掌握此类问题的解决方法.1根据定义比较无穷小定义1㊀设α及β是在同一自变量变化过程中的无穷小ꎬ且αʂ0ꎬlimβα也是在此变化过程中的极限.如果limβα=0ꎬ那么就说β是比α高阶的无穷小ꎬ记作β=oα()ꎻ如果limβα=¥ꎬ那么就说β是比α低阶的无穷小ꎻ如果limβα=cʂ0ꎬ那么就说β与α是同阶无穷小ꎻ特别地ꎬ若limβα=1ꎬ那么就说β与α是等价无穷小ꎬ记作α~βꎻ如果limβαk=cʂ0ꎬk>0ꎬ那么就说β是关于α的k阶无穷小.通过定义发现ꎬ比较两个无穷小α及βꎬ相当于求极限limβα.例1㊀当xң0时ꎬ比较2x-x2与x2-2x3的阶.解㊀因为limxң02x-x2x2-2x3=limxң02-xx-2x2=¥ꎬ所以2x-x2是比x2-2x3低阶的无穷小.注1㊀不是任意两个无穷小都可以比较ꎬ因为只有当两个无穷小量比值的极限存在或为无穷大时ꎬ才可以比较这两个无穷小.特别地ꎬxk+οxk()是x的k阶无穷小k>0().类似于这个方法ꎬ对于无穷71小的比较ꎬ除了可以使用定义ꎬ还可以通过确定每个无穷小的阶ꎬ然后比较阶的大小来比较两个无穷小.2比较无穷小的阶2.1等价无穷小定阶法定理1㊀设α~α~ꎬβ~β~ꎬ且limβ~α~存在ꎬ则limβα=limβ~α~.㊀定理1只适用于函数相乘或者相除形式的极限ꎬ加减法并不适用.例2㊀(2007年全国硕士研究生招生考试试题)当xң0+时ꎬ与x等价的无穷小量是(㊀)A.1-ex㊀㊀㊀㊀B.ln1+x1-xC.1+x-1D.1-cosx解㊀此题利用的就是等价无穷小的推广形式ꎬ当xң0+时ꎬ1-ex~-xꎬln1+x1-x~1+x1-x-1ꎬ其中1+x1-x-1=x+x1-x=xx+1()1-x~xꎬ所以ln1+x1-x~xꎬ而对于选项C㊁Dꎬ有1+x-1~12xꎬ1-cosx~12x()2=12x.故选B.2.2与(x-a)kk>0()比较定阶法由无穷小比较的定义可知:当xңa时ꎬ若φx()ң0ꎬ且limxңaφx()(x-a)k=Cʂ0ꎬk>0()ꎬ则φx()是x-a的k阶无穷小.所以xңa时ꎬ如果不能比较显然地看出一个无穷小量的阶数ꎬ则可以把此无穷小量与(x-a)k比较ꎬ通过计算来确定它是x-a的几阶无穷小.例3㊀当xң0时ꎬ比较e-ecosx与1+tanx-1+sinx的阶.解㊀因为limxң0e-ecosxxk=limxң0ecosxe1-cosx-1()xk=limxң0e1-cosx()xk=limxң0e2x2xkꎬ所以当k=2时ꎬlimxң0e-ecosxxk存在且不为0ꎬ故e-ecosx是x的2阶无穷小ꎻlimxң01+tanx-1+sinxxk=limxң0tanx-sinxxk1+tanx+1+sinx[]=limxң0tanx1-cosx()2xk=limxң01-cosx2xk-1=limxң0x24xk-1ꎬ所以当k-1=2ꎬ即k=3时ꎬlimxң01+tanx-1+sinxxk存在且不为0ꎬ故1+tanx-1+sinx是x的3阶无穷小ꎬ综上ꎬ1+tanx-1+sinx是e-ecosx的32阶无穷小.2.3泰勒公式定阶法定理2㊀如果函数fx()在x0处具有n阶导数ꎬ那么存在x0的一个邻域ꎬ对于邻域内任一xꎬ有fx()=fx0()+fᶄx0()x-x0()+fᵡx0()2!x-x0()2+ +fn()x0()n!x-x0()n+οx-x0()n()称为fx()在x0处带有佩亚诺余项的n阶泰勒公式.取x0=0ꎬ那么有带有佩亚诺余项的麦克劳林公式:fx()=f0()+fᶄ0()x+fᵡ0()2!x2+ +fn()0()n!xn+οxn()对于一些常见函数相加减的形式ꎬ用不了等价无穷小替换时ꎬ泰勒公式是个很好的选择.例4㊀当xң0时ꎬex-ax2+bx+1()是比x2高阶的无穷小ꎬ求aꎬb.解㊀因为ex的麦克劳林公式为ex=1+x+12x2+οx2()ꎬ所以ex-ax2+bx+1()=1-b()x+12-aæèçöø÷x2+οx2()ꎬ而ex-ax2+bx+1()是比x2高阶的无穷小ꎬ故1-b=012-a=0{ꎬ即a=12b=1{.81泰勒公式在求极限时使用方便ꎬ实际上利用泰勒公式还可以找一个无穷小量的等价无穷小.推论1㊀若fx()在x0处具有n阶导数ꎬ且fx0()=0ꎬfᶄx0()=0ꎬ ꎬfn-1()x0()=0ꎬfn()x0()ʂ0ꎬnȡ2()ꎬ则当xңx0时ꎬfx()~fn()x0()n!x-x0()n.特别地ꎬ若fx0()=0ꎬfᶄx0()ʂ0ꎬ则当xңx0时ꎬfx()~fᶄx0()x-x0().注2㊀在利用泰勒公式求函数相加减后的量的等价无穷小时ꎬ要将各函数展开到相同阶数ꎬ并且在加减运算完成后至少要剩余一个非零项ꎬ才可以根据推论1得到函数的等价无穷小.2.4求导定阶法定理3㊀设limxң0αx()=0ꎬ且αx()在x=0的某邻域内可导.(1)若xң0时ꎬ存在常数k>0ꎬ使得αᶄx()~xkꎬ则αx()~xk+1k+1ꎻ(2)若存在常数Cʂ0ꎬ使得limxң0αᶄx()=Cꎬ则αx()~Cx.此定理由洛必达法则容易证明.由定理3可知ꎬ比较两个无穷小α与β的阶ꎬ可以转化为比较它们各自的导函数αᶄ与βᶄ的阶数ꎬαᶄ与βᶄ阶数具有什么样的关系ꎬ则α与β阶数具有同样的关系.当前面三种定阶法都不能很好地处理无穷小比较的问题时ꎬ求导定阶法往往可以解决一定的问题.特别地ꎬ如果遇到多个无穷小是积分上限的函数ꎬ在比较这些无穷小时ꎬ求导定阶法可以快速地解决问题.例5㊀(2020年全国硕士研究生招生考试试题)当xң0+时ꎬ下列无穷小量中阶数最高的是(㊀㊀).A.ʏx0et2-1()dt㊀㊀㊀B.ʏx0ln1+t3()dtC.ʏsinx0sint2dtD.ʏ1-cosx0sin3tdt解㊀当xң0+时ꎬ由于四个选项中的无穷小都是积分上限的函数ꎬ比较它们的阶数ꎬ相当于比较它们各自的导函数的阶数.ʏx0et2-1()dt[]ᶄ=ex2-1~x2ꎻʏx0ln1+t3()dt[]ᶄ=ln1+x3()~x3ꎻʏsinx0sint2dt[]ᶄ=sinsinx()2 cosx~sinx()2~x2ꎻʏ1-cosx0sin3tdt[]ᶄ=sin31-cosx() sinx~1-cosx()32x~12æèçöø÷32x4.综上ꎬ由于ʏ1-cosx0sin3tdt的导数比其余三个函数的导数阶数高ꎬ所以ʏ1-cosx0sin3tdt是四个选项中阶数最高的ꎬ答案选D.将以上四种确定无穷小的阶数的方法灵活使用ꎬ可以更加有效地处理无穷小的比较问题.4结论本文主要从无穷小比较的定义㊁等价无穷小定阶法㊁比较定阶法㊁泰勒公式定阶法㊁求导定阶法五种方法系统地归纳了无穷小量的比较问题ꎬ并结合实例给出了分析过程ꎬ使方法可以很好地结合实例进行应用.灵活使用这些方法ꎬ可以做到更加有效地解决无穷小的比较问题.参考文献:[1]同济大学应用数学系.高等数学(7版)[M].北京:高等教育出版社ꎬ2014.[2]王莉.无穷小量定阶法及其应用[J].数学教学研究ꎬ2013ꎬ32(2):56-60.[3]华东师范大学数学系.数学分析(4版)[M].北京:高等教育出版社ꎬ2011.[4]夏滨.谈无穷小阶的比较方法[J].理科爱好者ꎬ2014ꎬ6(2):5-6.[5]许洪范ꎬ饶维亚.非标准分析中无穷小量阶的研究[J].长春大学学报ꎬ2000ꎬ10(6):26-33.[6]潘建辉ꎬ胡学刚ꎬ邓志颖.关于 无穷小的比较的教学研究[J].高等数学研究ꎬ2011ꎬ14(5):43-46.[7]方涛.关于无穷小量的几点注记[J].上海工程技术大学学报ꎬ2013ꎬ27(3):275-277.[责任编辑:李㊀璟]91。
微积分1052无穷小的比较

定义:设, 是同一过程中的两个无穷小,且 0.
(1) 如果lim 0,就说是比高阶的无穷小,
记作 o( );
(2) 如果lim C(C 0),就说与是同阶的无穷小;
特殊地 如果lim 1,则称与是等价的无穷小;
记作 ~ ;
(3)
如果
lim
k
C(C
0, k
0),就说是的k阶的
2. 等价无穷小替换定理
~ ~
18
定理. ~ 证: ~
思考题.证明下列定理.
o()
lim 1
lim( 1) 0, 即 l时, x 0 时,
~ tan x~x, 故
tan x x o(x)
19
x0
tan x
x
1
cos x2
x
)
1, 2
tan x sin x为x的三阶无穷小.
同阶
3
常见等价无穷小
lim sin x 1, 当x 0时,sin x~x; x0 x
lim tan x 1, 当x 0时,tan x~x; x0 x
lim arctan x 1, 当x 0时,arctan x~x;
lim
lim
lim .
思考:特别的,将条件修改“ ~ ” 或 ~
“
”。
9
推论 若x x0时 x与 x是等价无穷小,
且
lim
x x0
x f x A
或 .
则
lim
x x0
x
f
x
lim
x x0
x f x
A 或.
应用:用等价无穷小可给出函数的近似表达式 例如: sin x x o( x), 1 cos x 1 x2 o( x2 ). 2
微积分课件PPT06-无穷小量的比较

| sin x | 1 x (,) , ( 有界量 )
故 lim 1 sin x 0 . x x
有界量与无穷小量的乘积
例4
求
lim
x0
x3 x2
4
.
解 由于 lim x3 0 , ( 无穷小量 ) x 0
lim(x2 4) 4 ,
x 0
故
lim
x0
x3 x2
4
0
.
( 极限不为零 )
请请自自己己根根据据定定义义自自已已进进行行证证明明..
3.无穷大量的运算性质
若 lim f (x) , 则 lim | f (x) | .
无穷大量一定是同一 极限过程中的无界量.
反之不真
在某极限过程中, 无穷大量与某一有界量之和 仍是一个无穷大量.
在某极限过程中, 两个无穷大量之积 仍是一个无穷大量.
例8 两个无穷大量的和是否仍为无穷大量?
考察 {xn} : 1, 2, 3, 4, , (1)n n,
{yn} : 1, 2, 3, 4, , (1)n1n, 显然, n 时, xn , yn . 此时
{xn yn}: 0, 0,, 0,
不是无穷大量
{xn yn}: 2, 4, 6, 8,
令 (x) f (x) a , 则 (x) 0 (x x0 ) , 且
f (x) a (x) (x x0 ) .
反之亦然.
由以上的分析, 你可得出 什么结论 ?
定理
由此可看出, 寻找函数极限运算法则 可归结为寻找无穷小量的运算法则.
3.无穷小量的运算法则
同一个极限过程中的有限个 无穷小量之和仍是一个无穷小量.
x0
cos x2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x x
x
lim (1)n 0, ∴数列{(-1)n }是当n →∞时的无穷小.
n n
n
注意: 1.无穷小是变量, 不能与很小的数混淆;
2.零是可以作为无穷小的唯一的常数.
3.称一个变量是无穷小量一定要指明自变量的 极限过程。如 1 仅当 x →∞为无穷小。 x
思考题 下面说法是否正确
1、无穷小是比任何数都小的数。
二、无穷小量的比较
1、引入: 已知两个无穷小量的和、差及积仍是无穷小,
但是商呢?
思考:两个无穷小之商是否是无穷小?
x2 lim 0 x0 3x
lim sin x 1 x0 x
sin x 1
lim
x0 2x 2
3x lim x0 x 2
两个无穷小之比的极限的各种不同情况,反映了
不同的无穷小趋向零的“快慢”程度。
2、无穷小是最小的数。
3、无穷小就是 0。
4、0 是无穷小。
√
5、无穷小是(极限定义中的)ε。
无穷小与无穷大的“倒数关系”
定理
当x x0 (或x )时,若f ( x)是无穷小
(而f ( x) 0),则 1 无穷大; f (x)
反之,若f ( x)是
无穷大,则 1 是无穷小。 f (x)
2.无穷小与函数极限的关系:
无穷小.
lim x 2 0 x0 3 x
当x 0时,x2是3x的高阶无穷小。
lim sin x 1 x0 x
sin x~x ( x 0).
lim x0
1
cos x2 2
x2
1
故 x 0时,1 cos x~ x2 . 2
例1:证明 :当x 0时,4x tan 3 x为x的四阶无穷小.
三、等价无穷小替换
定理(等价无穷小替换定理)
设 ~ , ~ 且lim 存在, 则 lim lim .
证:
lim
lim( )
lim lim lim lim .
注:等价无穷小替换定理对于分子,分母的因式可用其
等价无穷小代换,选得适当可简化极限运算。
x
5.连续函数求极限的方法代入法.
lim
x x0
f (x)
f ( x0 )
( x0 连续区间)
6.等lixmx价f无[g穷( x小)]替 换f [lixmx g( x)]
(x 0
)
0
0
1.7 无穷小量及其比较
目的要求: 了解无穷小的概念与性质; 了解无穷小的阶的概念; 会用等价无穷小代换求极限。
重 点: 无穷小的概念无穷小阶的概念
难 点: 无穷小比较和等价无穷小代换
新课内容:
一、无穷小的概念与性质; 二、无穷小的比较(阶的概念) 三、等价无穷小替换
背景知识:
第二次数学危机
第二次数学危机发生在牛顿创立微积 分的十七世纪,是由牛顿学派的外部、贝 克 莱大主教提出的,是对牛顿 “无穷 小量”说法的质疑引起的。
思2考)、:有无界函限数多与无个穷无小穷的乘小积之是无和穷是小否;(还有界是积无)
穷3小)、例?常数求(与l不无im穷一x小定s的in)乘1积. 是无穷小;(常数积)
x0
x
4)、有限个无穷小的乘积是无穷小;(有限积)
5)、无穷小除以极限不为0的变量所得的商是无 穷小( 非零商) 。
思考:两个无穷小之商是否是无穷小?
定理 1 lim f ( x) A f ( x) A ( x), x x0
其中( x)是当 x x0时的无穷小.
意义:
1.将一般极限问题化为特殊极限问题(无穷小); 2.给出了函数f ( x )在x0附近的近似表达式:
f ( x ) A,误差为 ( x ).
3、定理2
1)、有限个无穷小之和是无穷小;(有限和)
解
4x tan3
lim
x0
x4
x
tan 4 lim(
x0 x
x)3
4,
故当x 0时,4x tan 3 x为x的四阶无穷小.
思考:当x 0时,求 tan x sin x关于x的阶数.
解
lim
x0
tan
x x3
sin
x
lim(
x0
tan x
x
1
cos x2
x
)
1, 2
tan x sin x为x的三阶无穷小.
2)贝克莱的发难 英国的贝克莱大主教发表文章猛烈攻 击牛顿的理论。 贝克莱问道:“无穷小”作为一个量, 究竟是不是0?
贝克莱还讽刺挖苦说:无穷小作为一 个量,既不是0,又不是非0,那它一定是 “量的鬼魂”了。
这就是著名的“贝克莱悖论”。
对牛顿微积分的这一责难并不是由数 学家提出的,但是,牛顿及他以后一百年间 的数学家,都不能有力地还击贝克莱的这种 攻击。
定义:设,是同一过程中的两个无穷小,且 0.
(1) 如果lim 0,就说是比高阶的无穷小,
记作 o();
(2) 如果 lim C(C 0), 就说与是同阶的无穷小;
特殊地 如果lim 1,则称与是等价的无穷小;
记作 ~ ;
(3) 如果lim C(C 0,k 0),就说是的k阶的 k
tan 2 x 例 lim
x0 sin 5 x x 0时,sin5 x~5 x,tan 2 x~2 x,
tan 2 x
2x 2
lim
lim .
x0 sin 5 x x0 5 x 5
例
sin x
lim
x0
x3
3x
x 0时,sin x~x, x3 3x~3x,
一、无穷小的概念与性质;
定义 若lim f(x)= 0,则称函数f(x)为当 x→x0
x → x0时(或在点x0 )的无穷小量,简称为无穷小。
注意
无穷小是极限为 0 的变量,
不是很小很小的数。
例如:
lim sin x 0, 函数sin x是当x 0时的无穷小. x0
lim 1 0, 函数 1 是当x 时的无穷小.
小结:
一、x 时函数f ( x)的极限
如何求函数极限? 1.函数极限四则运算法则
2. lim f ( x ) A lim f ( x ) A lim f ( x )
x x0
x x0
x x0
3.利用两边夹准则
4.利用重要极限 lim sin x 1 x0 x
lim(1 1 ) x e
x
总之,第二次数学危机的核心是微积 分的基础不稳固。柯西的贡献在于,将微 积分建立在极限论的基础。魏尔斯特拉斯 的贡献在于,逻辑地构造了实数系,建立 了严格的实数理论,使之成为极限理论的 基础。所以,建立数学分析(或者说微积 分)基础的“逻辑顺序”是:实数理论—极 限理论—微积分。而“历史顺序”则正好相 反。
