(大气科学基础)大气静力学方程
合集下载
气象学与气候学第四章大气运动
第四章 大气的运动
第三节 大气的水平运动和垂直运动
一、力 气压梯度力、地转偏向力、惯性离心力、摩擦力
1、气压梯度力 G ：由气压差产生的、垂直于等压面且由高
压指向低压的“力”，大小与气压梯度的数值成正比、与等压
面间距和空气密度成反比；可据等压（高）线疏密程度判断
气压梯度大小
气压梯度
水平气压梯度通常为 1～3 hPa/赤道度 垂直气压梯度通常为 11100 hPa/赤道度
1、静力学方程 垂直气压梯度或单位高度气压差 （hPa/m）
单位气压高度差 （m/hPa）
dP ＝ dZ
gP Rd T
h ＝ Rd T
gP
气压 P 相同，气温 T 越高，单位气压高度差 h 大 气温 T 相同，气压 P 越高，单位气压高度差 h 小
第四章 大气的运动
第一节 气压随高度和时间的变化 一、气压随高度变化 2、压高方程 1）通用压高方程
2、压高方程
海拔高度 （m） 30000
气压 （hPa）
12
高度
16000 11000 5500 3000 1500
0
100 250 500 700 850 1000
气压
第四章 大气的运动
第一节 气压随高度和时间的变化 二、气压随时间的变化
1、气压随时间变化的原因 ➢ 水平气流的辐合与辐散：空气是可压缩流体，密度有变化 ➢ 不同密度气团的移动 ：平流运动导致 ➢ 空气的垂直运动 ：气柱内某高度上密度变化
风向
（百帕） 1000 1005
摩擦力 R 在近地表 大气作用 高空省略
1010
（北半球）
重 力
地转偏向力 A 在高纬或大 尺度空气运
动时作用
第4章 大气静力学
z 0
重力位势： gdz ，即表示单位质量通过 任意路径由海平面上升 到某一高 度z时克服重力所做的功。 位势高度即位势米（ gpm）z g zg 1 g0 g0
g z, dz
z 0
J / kg gpm g 0 9.80665
1 zg g0 zg g 0, re z g 0 re z
似为8km。
均质大气密度不变，但温度仍随高度减小，根据静力学方程和状
态方程可知：
p RT dp T RT R dz z z T g 0 R z T g g 34.（ 2 K / km） z R Rd
34.2( K / km) 称为自动对流减温率，大气减温率超过34.2K/km，
4.1.1、大气静力学方程
大气静力学基本方程反映在重力作用下，大气处于静力平衡状态时气压随高度
的变化规律。 所谓大气静力平衡状态指大气在垂直方向上受到重力和垂直气压梯度力的作用 达平衡时状态。 对单位截面积的静止大气受力分析，具体分析见下图
单位截面积空气柱受到向上的压力为：
p p p ( p dz ) dz z z
利用大气静力学方程估计大气质量及其垂直分布 1、先求单位截面积上空气柱的质量。（空气柱的下 界面是海平面，取无限远处为大气上界）
m0 V
2、利用静力学方程 为零的条件
0
dz
dp gdz 及大气上界处气压
m0
0
p0
dp gp0 Nhomakorabea0
p0 dp g g
3、g取常数9.8 m / s 2 及海平面处p0=101325Pa
dp g 或dp gdz dz
重力位势： gdz ，即表示单位质量通过 任意路径由海平面上升 到某一高 度z时克服重力所做的功。 位势高度即位势米（ gpm）z g zg 1 g0 g0
g z, dz
z 0
J / kg gpm g 0 9.80665
1 zg g0 zg g 0, re z g 0 re z
似为8km。
均质大气密度不变，但温度仍随高度减小，根据静力学方程和状
态方程可知：
p RT dp T RT R dz z z T g 0 R z T g g 34.（ 2 K / km） z R Rd
34.2( K / km) 称为自动对流减温率，大气减温率超过34.2K/km，
4.1.1、大气静力学方程
大气静力学基本方程反映在重力作用下，大气处于静力平衡状态时气压随高度
的变化规律。 所谓大气静力平衡状态指大气在垂直方向上受到重力和垂直气压梯度力的作用 达平衡时状态。 对单位截面积的静止大气受力分析，具体分析见下图
单位截面积空气柱受到向上的压力为：
p p p ( p dz ) dz z z
利用大气静力学方程估计大气质量及其垂直分布 1、先求单位截面积上空气柱的质量。（空气柱的下 界面是海平面，取无限远处为大气上界）
m0 V
2、利用静力学方程 为零的条件
0
dz
dp gdz 及大气上界处气压
m0
0
p0
dp gp0 Nhomakorabea0
p0 dp g g
3、g取常数9.8 m / s 2 及海平面处p0=101325Pa
dp g 或dp gdz dz
《大气科学基础》课件第2章 大气动力学基础
✓ 一个名叫古斯塔·加斯佩德·科里奥利的法国人在 1835年最先用数学方法描述了这种效应，所以科学界 用他的姓氏来命名此种力。我们通常也称它为地转偏 向力。在北半球，科里奥利力使风向右偏离其原始的 路线；在南半球，这种力使风向左偏离。风速越大， 产生的偏离越大。于是，在北半球，当空气向低压中 心辐合时会向右弯曲，形成了一个逆时针方向的旋转 气流。从高压中心辐散出来的空气，则因为向右弯曲 而形成了顺时针方向的旋风。我们把逆时针旋转的叫 做气旋，把顺时针旋转的叫做反气旋。在南半球，上 述的情形正好相反。
✓ The green guy will have to run faster than the orange guy to keep up.
• 产生的原因
✓ 物体为保持水平惯性运动， 经纬网因随地球自转而产生相 对加速度。 地转偏向力向右是 在北半球，在南半球则都向左；
✓ 由于除南北两极外，各纬度 的角速度都一样，从北向南飞 的时候，南边的圈大，即越向 南纬线越长，所以线速度大， 所以在北边的时候具有的一个 小的线速度与南边的线速度相 比就显的慢了。，
like this;
Dv F Dt
“The rate of change of velocity with time is equal to the sum of the forces acting on the parcel”
Frame of Reference
• For a non-rotating Earth, these forces are:
the earth; ✓ Not a real force in the sense that it cannot cause
a motion; ✓ As an earth-bound observer, we are not aware
大气静力学
g 0 ,ϕ = F u − F c cos ϕ M 2 2 = G 2 − a Ω cos ϕ a
Gravitational field near Earth’s surface
The value of “g” depends on 1. Altitude 2. Non-uniformity of Earth’s crust 3. Non-spherical shape 4. The rotation of Earth
Dt =∑F
“The rate of change of velocity with time is equal to the sum of the forces acting on the parcel”
Frame of Reference
For a non-rotating Earth, these forces are: Pressure gradient force (Pgf) Gravitational force (ga) and Friction force (F)
惯性离心力的计算公式
Fc = Ω R = Ω a cos ϕ
2 2
=7.292E-5弧度 秒，是地球自转角速度 弧度/秒 弧度 惯性离心力的量级（ 惯性离心力的量级（0~10-2）和地心引力 相比很小!!! 相比很小
r Ω
Fc cos ϕ
惯性离心力在地心引力反方向上的投影 惯性离心力
重力
ϕ
地球的重力
Equation of Motion
We now have a new equation which states that: Dv
Dt
= Pgf + g a + F + C e + C of
02 大气静力平衡
均质层（homosphere） 或湍流层（turbosphere） 在 86km 以下，包括对流层、平流层、中 层在内，由于湍流扩散作用使大气均匀混合， 大气中各种成分所占的比例，除臭氧等可变成 分外，在垂直方向和水平方向保持不变，干空 气的平均摩尔质量d = 28.9644 kgkmol1。
2、位势高度 表示位势的大小，定义为
位势米（gpm）或位势千米（gpkm）等 1 9.80665 Jkg /gpm
实际高度与位势高度的关系
其中，
1 gpmm1。
在 100km 高度，偏差小于 1.6%。 在实际工作中，可近似认为两者数值相等。
3、流体静力平衡
气块受的地心引力与其在垂直方向的气压梯度力的分量 平衡，称流体静力假设，这种平衡关系称流体静力平衡。
(3) 中间层（mesosphere） 从平流层顶到 85km 左右称为中间层（也 称中层） ，温度随高度而下降。 中间层内水汽极少，但在高纬地区的黄昏 前后，有时在 75～90km 上空出现薄而带银白 色光亮的云，称为夜光云。
(4) 热层（thermosphere） 中间层顶以上，温度始终是增加的。 大气极稀薄，分子碰撞机会极少。热层温 度的日变化大气光学现象极光。 热层温度趋于常数的高度是热层顶。热层 顶的高度随太阳活动的强、弱而变化，高峰期 约在 500km 高度， 温度可达 2000K； 宁静期下 降到 250km 左右，温度约 500K。
，与热力学中多元过程的方程类似
压力—高度关系
或：
，
多元大气的上界（p=0）为
多元大气极限位势高度 或简称多元大气高度。
2、均质大气 34.2 ℃gpkm1，可以得到
，或
)
自动对流减温率
34.2℃gpkm
大气静力学 - 副本
CH2CH2 大气静力学方程及其应用•2.1 方程推导及适用范围•2.2 应用22•2.3 标准大气•2.4 气压场2.12.1 大气静力学方程推导及其用范围及其适用范围假定大气处于静力平衡状态，即大气相对于地面静止，达到力的平衡于地面静止，达到力的平衡。
任取一块截面积为1m2，厚度为dz的铅任取块截面积为1厚度为直气柱，对它进行受力分析当大气静止时，大气静力学方程精确成立。
当大气静时大气静力学方程精确成当大气有弱的垂直加速度时，大气静力学方程近似成立。
二、适用范围大气运动具有准水平性，即任意时刻大部分空间范围的大气以水平运动为主。
垂直加速度一般小于0.1cm/s2,比重力加速度至少小4个数量级。
个数量级大气静力学方程不仅适用于静止大气而大气静力学方程不仅适用于静止大气，而且也适用于一般大气，但不适用于有强垂直运动的大气（见图）冰雹云CH221CH2大气静力学方程及其应用•2.1 方程推导及适用范围•2.2 应用用1、平衡气压气压阶2、气压阶3、标高4、压高公式•232.3 标准大气•2.4 气压场2.2 应用1、用来定义平衡气压（大气静力学气压）对（2.1.1）式两边积分，12:;z z z →12:p p p →得2121 1.5.3z z p p gdz ρ−=−∫——（）220z p =∞=特殊地，当时，，则1.5.4gdz ∞=——（）11z p g ρ∫T h ，应用:1)天气系统垂直分布;p h 分析(天气学)2),p p临近等压面高度(大气探测)3、计算气压标高Hp标高分气压标高和密度标高，这里只介绍前者1）定义气压标高表示气压随高度的变化趋势，定义式为对于等温大气，Hp在数量上等于气压减小到起始气压的1/e所需要的高度增量。
所需要的高度增量CH221CH2大气静力学方程及其应用•2.1 方程推导及适用范围•2.2 应用用1、平衡气压气压阶2、气压阶3、标高4、压高公式•232.3 标准大气•2.4 气压场卓奥友峰8201米8000米是人类生存的极限2.3 标准大气1、定义（WMO的定义）所谓标准大气，就是能够粗略地反所谓标准大气就是能够粗略地反映出周年、中纬度状况的，得到国际上承认的，假定的大气温度、压力和密度的垂认的假定的大气温度压力和密度的垂直分布。
大气静力学方程与压高公式
Байду номын сангаас
03
大气静力学方程与压高公 式的联系
大气静力学方程与压高公式的关联性
大气静力学方程是描述大气压力和高度之间关系的方程，而压高公式则是基于大气静力学方程推导出 来的，用于计算不同高度上的气压值。
大气静力学方程和压高公式都涉及到气压和高度两个变量，它们之间存在密切的关联性，即气压随高 度的增加而减小。
THANKS
感谢观看
在天气预报中，压高公式可以用于计算和分析气压系统的发展和移动。通过分析气压的变化趋势，可 以预测未来的天气状况，如风向、降水等。
压高公式的应用
气象观测
在气象观测中，压高公式可以用于计算 和分析气压随高度的变化情况。通过对 比不同高度的气压数据，可以了解大气 的状态和垂直运动状况。
VS
数值天气预报
在数值天气预报中，压高公式是计算和分 析大气状态的重要工具之一。通过数值模 拟方法，可以预测未来一段时间内的天气 状况，为气象灾害的预警和防御提供依据 。
大气静力学方程和压高公式在气象学 中具有互补性。大气静力学方程可以 用于分析气压随高度的变化规律，而 压高公式则可以用于计算不同高度上 的气压值，为气象预报和气候分析提 供基础数据。
VS
在实际应用中，可以根据需要选择使 用大气静力学方程或压高公式，或者 将两者结合起来使用，以更好地理解 和预测大气的压力和高度变化。
实例二：某地区的气象预报
总结词
气象预报是利用大气静力学方程和压高公式 等工具，对未来天气状况进行预测。
详细描述
气象预报人员通过分析当前和历史气象数据 ，利用大气静力学方程和压高公式等工具， 预测未来一定时间内的天气状况，如温度、 降水、风向、风速等。这些预测结果对于人 们的生活和生产活动具有重要的指导意义。
03
大气静力学方程与压高公 式的联系
大气静力学方程与压高公式的关联性
大气静力学方程是描述大气压力和高度之间关系的方程，而压高公式则是基于大气静力学方程推导出 来的，用于计算不同高度上的气压值。
大气静力学方程和压高公式都涉及到气压和高度两个变量，它们之间存在密切的关联性，即气压随高 度的增加而减小。
THANKS
感谢观看
在天气预报中，压高公式可以用于计算和分析气压系统的发展和移动。通过分析气压的变化趋势，可 以预测未来的天气状况，如风向、降水等。
压高公式的应用
气象观测
在气象观测中，压高公式可以用于计算 和分析气压随高度的变化情况。通过对 比不同高度的气压数据，可以了解大气 的状态和垂直运动状况。
VS
数值天气预报
在数值天气预报中，压高公式是计算和分 析大气状态的重要工具之一。通过数值模 拟方法，可以预测未来一段时间内的天气 状况，为气象灾害的预警和防御提供依据 。
大气静力学方程和压高公式在气象学 中具有互补性。大气静力学方程可以 用于分析气压随高度的变化规律，而 压高公式则可以用于计算不同高度上 的气压值，为气象预报和气候分析提 供基础数据。
VS
在实际应用中，可以根据需要选择使 用大气静力学方程或压高公式，或者 将两者结合起来使用，以更好地理解 和预测大气的压力和高度变化。
实例二：某地区的气象预报
总结词
气象预报是利用大气静力学方程和压高公式 等工具，对未来天气状况进行预测。
详细描述
气象预报人员通过分析当前和历史气象数据 ，利用大气静力学方程和压高公式等工具， 预测未来一定时间内的天气状况，如温度、 降水、风向、风速等。这些预测结果对于人 们的生活和生产活动具有重要的指导意义。
大气科学概论课件(第五：大气压力1)
3.1.2 气压－高度公式
Gz、h只能定性判断气压的变化快慢，要 定量确定气压随高度的关系最常用压高公式。 将
dP g dZ p RdTv
由高度z1(P=P1)积分到高度z2(P=P2)：
Z 2 Z 1 Rd
P2 P1
Tv d ln P g
因为在公式中，g和T都随高度而有变 化，而且R因不同高度上空气组成的差异 也会随高度而变化，因而进行积分是困难的。
确定与气压随高度变化的定量关系，一般 是应用静力学方程和压高方程。
3.1 大气静力学方程和气压－高度公式
3.1.1 大气静力学方程
大气在垂直方向上受到重力和垂直气压梯度力的 作用达到平衡时，称为流体静力平衡状态。
通常情况下，空气的垂直加速度<10-3m/s2,比重力加速度小 一万倍。所以说，在垂直方向，实际大气可以看成处于流体静 力平衡状态，有强对流的地区除外。
dp 对 g 进行积分（0-Z，P0-P） dZ
得
p = p0 - ρgz
令p=0,则均质大气顶为 z=P0/ρg， 说明均质大气的高度是有限。
此时，均质大气的高度称大气厚度Ｈ
Ｈ≈RdT0/g0≈8000m
均质大气的密度不变，温度却是变化的， 大气的垂 直减温率Γ=3.42K/100m。均质大气是一种假设的大气 模式，在处理某些理论问题时有一定意义。
四、标准大气的压高公式（自学）
实际大气状态的空间分布是复杂的，但是人们 根据探测数据和理论计算，制定一种温度、气压、 密度等大气特性垂直分布比较接近实际大气的平 均状况的大气模式，称为标准大气。 世界气象组织（wmo）对于标准大气的定义： 所谓标准大气，就是能够粗略的反映出周年、中 纬度状况的，得到国际上承认的，假定的大气温度、 气压和密度的垂直分布。
第二章大气静力学方程及应用
T0 z p p0 ( ) T0
g Rd
——（ 1.5.11 ）
T0 c) 上界： H
3）均质大气
a) 定义：空气密度不随高度变化的 大气称为均质大气。 b) 压高公式：
p p0 gz
p0 Rd Tv 0 8km c) 上界： H g g
数值上等于低层大气的标高。
3）影响因子
T
，hp
;
应用:1)天气系统垂直分布
分析(天气学)
2)临近等压面高度 (大气探测)
p
, hp
3、计算气压标高Hp
标高分气压标高和密度标高，这里只介绍前者 1）定义 气压标高表示气压随高度的变化 趋势，定义式为
d ln p 1 H p ( ) ——（ 1.5.6） dz
2）计算式
Rd Tv p 1 Hp dp d ln p g dz dz Rd Tv ————————（ 1.5.7） g
与Tv成正比，若Tv不随高度变化， 则H p也不随高度变化。
3）等温大气的标高
对（1.5.6）式变形后两边积分，得
P2 P 1 exp(
z2 z1
卓奥友峰 8201米 8000米是 人类生存 的极限
d) 铅直温度递减率 由状态方程和大气静力学方程，求 得均质大气铅直温度递减率为： g g 34.2 K / km 34.2 K / km ? Rm Rd
对p RmT 两边关于z求导
p T RmT Rm z z z
即
整理得
或
gdz+p+dp=p
(2.1.1) dp=-gdz （ 1.5.1)
dp g dz
(2.1.2)
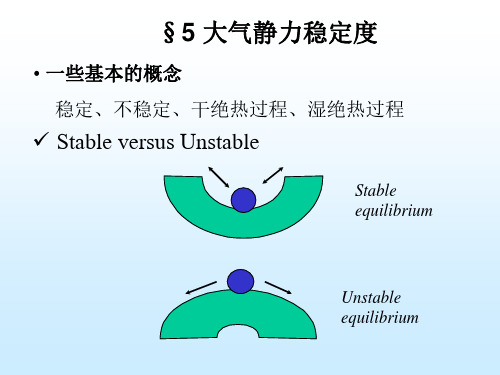
大气科学基础课件§5大气静力稳定度
对饱和湿空气而言
'
dT dz
s
静力稳度定判椐为：
>
静力不稳定
γ = γs <
静力中性 静力稳定
综合未饱和及饱和湿空气的静力稳定度判椐，有以 下3种情况：
(1) γ> γd ，对未饱和以及饱和大气，层结均不稳定 ，称为“绝对不稳定”；
(2) γ< γs ，对未饱和以及饱和大气，层结均稳定， 称为“绝对稳定”
在实际天气预报中，以下几种情况常值得注意： ✓ 在高层冷中心或冷槽与低层暖中心叠置的区域，
可能会有雷暴的发生；
✓ 冷锋过山时，若背风坡低层由暖湿空气控制，常 有雷暴的发生（夏季太行山东侧常出现此情形）
✓ 高层干平流与低层湿平流叠置的区域，常有雷暴 发生；
✓ 冷空气入侵后，如果低层有浅薄热低压接近或者 有显著的暖平流时，容易诱发雷暴发生。
• 逆温层的作用
✓ 强对流爆发前夕，在中 低层常有逆温层的存在；
✓ 阻止水汽、热量上传， 使其在低层不断积累；
✓ 一旦逆温层被破坏（通 过地面加热、整层抬升等） ，强对流天气便会发生。
思考题
1. What is “absolutely stable”? 2. What is “absolutely unstable”? 3. What is “conditionally unstable”? 4. What is “conventionally unstable”? 5. What is dry adiabatic process and moist
(1) 开始时气块的上下端 都按照干绝热上升
(2) 由于气层底部湿度较
P
大而先达到饱和状态
，按湿绝热上升，温
第四章大气压力1
2、等压线：同一水平面上（或铅直平面上）气压相等的
点所组成的曲线。 （等压线上的气压处处相等） （等压线一侧的气压高，另一侧的气压就低） 3、等高面：空间海拔高度相等的点所组成的的点所组成的曲线。
（一）图示法：绘制天气图来了解气压的时空分布。
气压的水平分布——等高面图(海平面图)
解：∵
p0 z z0 184001 tm lg pz
1 11.2 17.8 1006 .2 z 103 .0 18400 [1 ( )] lg 273 2 873 .7
∴
得：z=1291米
§2、气压场
气压的分布称为气压场，海平面上的气压分布称 为海平面气压场。气压场的空间分布（即三度空间分 布）称为空间气压场。分析气压场是天气分析的重要 内容。因此，了解表示气压场的方法和气压场的基本 型式，对于分析预报天气来说，是必须具备的基本知 识。 一、气压场的表示方法 1、等压面：空间气压相等的点组成的空中曲面。 （等压面面上的气压<等压面面下上的气压） （等压面面下的气压>等压面面上的气压）
气压（hpa） 1000
2、等高面图：空中一簇等压面，用一个等
高面来切，所得的交线投影到一个平面上 得到等高面图。
H P1 H
P3 P4 P5 P3 P2 P1 P5 P4
P2
P3
上图为地面天气图
拔海为高度=0米的等高面图
地面天气图有：02时、05时、08时、11时、14时、 17时、20时、23时
二、气压场的基本型式
气压场：等压线的各种组合型式。 1、低气压（简称低压或气旋）：由一簇闭合等压线构 成的中心气压较低。四周气压较高的区域。
1005 1000 995
气象学基础第二章
第二章大气静力学第一节大气静力学基本方程静止大气中，对每一薄层大气来说，它所受到的力有重力和垂直方向上的气体压力（气压梯度力）一、重力：是纬度的函数，随纬度增大而增大二、大气静力学方程1、大气静力学问题：大气在垂直方向上的气压分布2、公式推导（静力方程三个形式）3、物理意义：它描述了大气压力、密度和高度之间的联系。
高度差为dz的高度桑的压力差应等于两高度之间单位截面积上的空气柱所受的重力。
4、三点结论第一、气压随高度增加而减小第二、由于g随高度变化很小，所以气压随高度减小的快慢主要决定于密度。
第三、将大气静力学方程从任意高度z积分到大气上界，则（公式）表明任意高度z处的气压P等于从该高度向上到大气上界的单位截面积垂直气柱所受的重力。
三、气压垂直梯度G表示就是每升高（或降低）单位距离，气压减小（或增大）的数值，通常用z（公式）四、单位气压高度差是指垂直气柱中，没改变单位气压（通常为1百帕）所需要的上升或下降的高度。
单位气压高度差又成气压阶，用h表示，即：（公式）h的大小可以表示气压随高度变化的快慢用途：求海平面气压气压测高法第二节压高公式一、几种大气的压高公式1、均质大气假定大气密度不随高度变化，常数）（=z ρ的大气公式推导均质大气在大范围是不存在的，但在炎热的夏天中午前后，在沙漠地区，由于地面受热太甚，在某一高度之下，可以出现暂时的局部均质大气。
2、等温大气温度不随高度变化的大气公式推导等温大气的盖度是无限的。
在实际工作张，可将大气分成若干个层次，分别求各层次的平均温度，代入公式计算，然后将各层高度累加起来，就可以得到整个气层的压高关系。
3、多元大气假设在大气的垂直方向上温度的递减率为一常数，即大气温度是高度的线性函数，具有这样的大气称为多元大气。
公式推导：重点均质大气和等温大气是多元大气的两个特例4、标准大气的压高公式人们根据大量高空探测的数据和理论，规定了一种特性随高度平均分布的最接近实际大气的大气模式，称为标准大气。
第2章,大气压力
8
一 大气静力学方程
2 静力学方程的应用形式
p Rd Tv
p gdz 代入(3.1.3)式得： dp gdz Rd Tv
（3.1.4）
•
垂直气压梯度： Gz dp dz g p Rd Tv 3.42 p Tv
• 在垂直气柱中，改变单位高度(通常指100m)时所对应的气压差。
p2
Tv dp dz Rd g p
z2
z1
dz Rd (Tv g ) d ln p
p1
p2
z 2 z1 R d (Tv / g) d ln p
p1
(3.1.8)
(3.1.7)和(3.1.8)为90km以下大气压力和高度的普遍关系，称为气压
-高度公式。
虚温 Tv 和重力加速度 g 都随高度变化，通常难以求出积分数值。 为简化计算，常将 g 作为常数处理。
（3.3.5）
二、位势米（gpm ）
位势米和几何米的换算公式
Z
g z 9.8
几何 高度 位势 高度
位势米是能量单位，几何米 是长度单位。P40,表3.4
重力加 速度
三、位势高度与气压的关系
1 p2 p1 exp( Rd
p1
z2
z1
g dz) Tv
z 2 z1 R d (Tv / g) d ln p
多元大气特点：
大气上界 p2 = 0, HT = Tv0/ Γ , 多元大气有上界。
g /( Rd )
(3.2.8b) (3.2.9)
24
三、 均质大气
均质大气：大气密度不随高度变化，整层大气都保持密度的海平面值。
压高公式：（z0，p0 ~ z，p）
一 大气静力学方程
2 静力学方程的应用形式
p Rd Tv
p gdz 代入(3.1.3)式得： dp gdz Rd Tv
（3.1.4）
•
垂直气压梯度： Gz dp dz g p Rd Tv 3.42 p Tv
• 在垂直气柱中，改变单位高度(通常指100m)时所对应的气压差。
p2
Tv dp dz Rd g p
z2
z1
dz Rd (Tv g ) d ln p
p1
p2
z 2 z1 R d (Tv / g) d ln p
p1
(3.1.8)
(3.1.7)和(3.1.8)为90km以下大气压力和高度的普遍关系，称为气压
-高度公式。
虚温 Tv 和重力加速度 g 都随高度变化，通常难以求出积分数值。 为简化计算，常将 g 作为常数处理。
（3.3.5）
二、位势米（gpm ）
位势米和几何米的换算公式
Z
g z 9.8
几何 高度 位势 高度
位势米是能量单位，几何米 是长度单位。P40,表3.4
重力加 速度
三、位势高度与气压的关系
1 p2 p1 exp( Rd
p1
z2
z1
g dz) Tv
z 2 z1 R d (Tv / g) d ln p
多元大气特点：
大气上界 p2 = 0, HT = Tv0/ Γ , 多元大气有上界。
g /( Rd )
(3.2.8b) (3.2.9)
24
三、 均质大气
均质大气：大气密度不随高度变化，整层大气都保持密度的海平面值。
压高公式：（z0，p0 ~ z，p）
[理学]第五章 大气运动
![[理学]第五章 大气运动](https://img.taocdn.com/s3/m/250d7609482fb4daa58d4b87.png)
思考：
平面的变化，
从数值上看：
以上是将大气看成是静力平衡状态条件下，对一薄气柱的讨
论。如果研究的气层高度变化范围很大，气柱中上下层温度、
密度变化显著时，该式就难以直接运用，就需采用适合于较 大范围气压随高度变化的关系式，即压高方程。
(二)、压高公式
二、气压随时间的变化
（一）变化原因
水平气流的辐合与辐散； 冷暖气流水平运动； 空气垂直运动
所以高空的气压分布可用等压面上的高度分布来表示，即 用画有等高线的等压面图来表示(与地形等高线图相似)。 目前气象台所绘制的高空图，就是等压面图。常用的 等压面有：850hPa、700hpa和500hpa等。它们分别代表
1500m,3000m和5000m高度附近的水平气压场。
(四）等压面的高度单位──位势米
举例：某测站海拔高度为40米，本站气压为 1000百帕，气温为0℃，求h值，并将本站气 压订正为海平面气压。
计算结果： h=8；海平面气压为1005百帕。
Байду номын сангаас
表4· l是根据（4· 2）式计算出的不同气温和气压下的h值。
• 从表4· l中可以看出：①在同一气压下，气柱的温度愈 高，密度愈小，气压随高度递减得愈缓慢，单位气压 高度差愈大。反之，气柱温度愈低，单位气压高度差 愈小。②在同一气温下，气压值愈大的地方，空气密 度愈大，气压随高度递减得愈快，单位高度差愈小。 反之，气压愈低的地方单位气压高度差愈大。比如愈 到高空，空气愈稀薄，虽然同样取上下气压差一个百 帕，而气柱厚度却随高度而迅速增大。
称为等压线。
（二）等高线和等压面
等高线和等压面图空间气压场的情况一般用等压面图
表示。在空间的每一点都有一个气压值，如果把所有气压 相同的点连接起来，就形成一个等压面。由于同一高度上 各地的气压不等，气压在空间的分布，就象山丘一样起伏 不平。在同一高度上，气压比四周高的地方，等压面上凸，
《大气科学基础》复习大纲教学内容
《大气科学基础》复习大纲《大气科学基础》复习大纲大气动力学基础作用于空气的力：重力、气压梯度力、地转偏向力、摩擦力其中)(-k zp j y p i x p p ρρρ∂∂+∂∂+∂∂-=∇地转偏向力：V C ρρρ⨯Ω-=2科里奥利系数：φsin 2Ω=f 科里奥利力在各方向的分量：φφφφ cos u 2 z cos u 2 - y cos w 2 - sin v 2 x Ω=Ω=ΩΩ= 忽略摩擦，标准坐标系的动量方程为：g - cos u 2 z p 1 - dt dw sin u 2 - yp 1- dt dv cos w 2 - sin v 2 x p 1 - dt du φρφρφφρΩ+∂∂=Ω∂∂=ΩΩ+∂∂= 简化后：ρρρρg - p g - z p 1 - 0fu - yp 1 - dt dv fv x p 1 - dt du =∂∂∂∂=∂∂=+∂∂=z 连续方程：00)(0)(=∇+=∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂=∇+∂∂v dtd zw y v x u z w y v x u t V t ρρρρρρρρρρρ 速度散度的意义：dt d dt d v z w y v x u v ααρρ11-==∇∂∂+∂∂+∂∂=∇ρρ，ρα1=为比容单位时间质量的变化率：，流出辐散，质量减少，，流入辐合，质量增加，0000>∇<<∇>v dtd v dt d ρρρρ 单位时间体积的变化率：，缩小辐合，体积减少，，膨胀辐散，体积增加，0000<∇>>∇>v dtd v dt d ρραα 水平速度散度和垂直速度的关系： 对不可压缩大气有：0=dtd ρ，即0=∇v ρ 则：zw y v x u z w y v x u ∂∂=∂∂+∂∂=∂∂+∂∂+∂∂-0，有，加强上升运动，垂直速度随高度增大，水平辐合，，减弱上升运动，垂直速度随高度减小，水平辐散，0000>∂∂<∂∂+∂∂<∂∂>∂∂+∂∂z w y v x u z w y v x u 大气中的平衡运动：地转风：在水平气压梯度力与水平地转偏向力达到平衡的风，无加速度、无摩擦的空气水平运动梯度风是水平气压梯度力、水平地转偏向力和惯性离心力三者相平衡时的风。
大气物理学：第二章+大气压力
h dz dp
气压愈低(即高度愈高)，单位气压高度差愈大。温度愈高， 单位气压高度差亦愈大。注：可不考虑水汽的影响。
主要用于做海平面气压订正和其它一些近似估计。
例：某气象观测站的海拔高度为 64m，若某日该测站气压为 1000hPa，气温为0℃，试求海平面气压。
例：某气象观测站的海拔高度为 64m，若某日该测站气压为 1000hPa，气温为0℃，试求海平面气压。
然。
一、 大气静力学方程(5)
3、静力学方程的应用形式
代入(1)式得：
P
Rd Tv
dP gdz P gdz （1-1）
Rd Tv
一、 大气静力学方程(6)
垂直气压梯度：在垂直气柱中，每改变单位高度(通常 指100m)时所对应的气压差。
dp Gz dz
单位气压高度差，也称气压阶：在垂直气柱中，每改 变单位气压(通常指1hPa)时所对应的高度差。
二、 气压-高度公式
对 (1-1)式积分：
P
z
P
dP gdz
P0
0
Rd Tv
p
z
ln P 1 z g dz
P0
Rd 0 Tv
p0
0
二、 气压-高度公式
对 (1-1)式积分：
P
z
P
dP gdz
P0
0
Rd Tv
ln P 1 z g dz
P0
Rd 0 Tv
P
P
0
exp(
1 Rd
§2 重力位势
一、重力位势
1、重力
g
f
2
r
重力 地心引力 离心力
r
A 2r
f
§2 重力位势
R2 f f0 (R z)2
气压愈低(即高度愈高)，单位气压高度差愈大。温度愈高， 单位气压高度差亦愈大。注：可不考虑水汽的影响。
主要用于做海平面气压订正和其它一些近似估计。
例：某气象观测站的海拔高度为 64m，若某日该测站气压为 1000hPa，气温为0℃，试求海平面气压。
例：某气象观测站的海拔高度为 64m，若某日该测站气压为 1000hPa，气温为0℃，试求海平面气压。
然。
一、 大气静力学方程(5)
3、静力学方程的应用形式
代入(1)式得：
P
Rd Tv
dP gdz P gdz （1-1）
Rd Tv
一、 大气静力学方程(6)
垂直气压梯度：在垂直气柱中，每改变单位高度(通常 指100m)时所对应的气压差。
dp Gz dz
单位气压高度差，也称气压阶：在垂直气柱中，每改 变单位气压(通常指1hPa)时所对应的高度差。
二、 气压-高度公式
对 (1-1)式积分：
P
z
P
dP gdz
P0
0
Rd Tv
p
z
ln P 1 z g dz
P0
Rd 0 Tv
p0
0
二、 气压-高度公式
对 (1-1)式积分：
P
z
P
dP gdz
P0
0
Rd Tv
ln P 1 z g dz
P0
Rd 0 Tv
P
P
0
exp(
1 Rd
§2 重力位势
一、重力位势
1、重力
g
f
2
r
重力 地心引力 离心力
r
A 2r
f
§2 重力位势
R2 f f0 (R z)2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
✓ 指向赤道的分力会使地球质量向赤道方向移动， 地球形成了一个偏球面，这个偏球面就是海平面。 这时重力就与海平面垂直。
• 重力计算公式（2）
由于重力和地心引力之间的夹角很小，所以重力 的大小和方向均接近地心引力，可近似为地心引 力减去惯性离心力在地心引力反方向上的投影。 因此，地表处在纬度为φ的地点单位质量空气块所 受到的重力为：
4. 标准大气
标准大气， 垂直方向温度、气压和密度按一种假定规 律分布的大气。
如，1976年美国标准大气推广委员会所设定的标准大 气为：
✓ 空气中没有水汽； ✓ 在86千米以下大气为均匀混合物，呈静力平衡和 层状分布； ✓ 11千米以下大气温度随高度降低，平均递减率为 0.650C/100m； ✓ 11-20千米为等温大气。
• 地球的重力
Fc cos
惯性离心力在地心引力反方向上的投影
惯性离心力
重力
• 重力计算（1）
✓ 地心引力与惯性离心力之矢量和就是重力；
✓ 由上图可以看出，如果把地球表面看作球面， 则重力并不与地面垂直；
✓ 如果把惯性离心力分解成为两个分力： 一个分力与地球引力方向相反； 另一个与地面相切，指向赤道。
(equation of static equilibrium)
Form of the vertical component of the equation of motion in which all terms (including, in particular, the vertical acceleration) are considered negligible compared with the pressure and the force of gravity.
• 国际标准重力加速度
✓ 极地 g=9.832m/s2 ✓ 赤道 g=9.78m/s2 ✓ 纬度45度处 g=9.832m/s2 ✓ g随海拔高度等因子的变化也很小
因此，气象学中将g当作常数看待； 国际上规定海平面处重力加速度的标准值为：
g=9.80665m/s2
2. 静力学方程
hydrostatic equation
✓ 由上述压高公式可以看出，在均质大气中气 压随高度线性递减。
z
p p0
✓ P=0处的高度称为均质大气的上界（高度）
H
p0
0g
RdT g
✓ 均质大气是一种假设，并非实际存在；
✓ 但均质大气的某些参数在动力气象理论问题的 处理中有一定应用价值。
• 均质大气的 垂直温度梯度
A T z R 1 d P z R 1 d g R g d 3 .4C 2 /1米 0
• 静力学方程得到的推论
✓ dz>0时dp<0，说明气压随高度是下降的；
✓ 由于g随高度的变化很小，所以气压随高度下降 的快慢主要取决于密度。大气层低层密度大，气压 随高度下降快；大气层高层密度小，气压随高度下 降的慢；
✓ 将静力学方程从任意高度z积分到大气上界，得
pz
gdz
z
*表明任意高度z处的气压等于从该高度到大气上界的 单位截面积气柱所受的重力。
M
=9.81米/秒2
F G a u
2
万有引力常数G=6.672E-11牛顿.米2千克-2
地球半径a=6.371E+6米
• 离心力
由于地球自转，单位质量空气块不仅受万有引力 的作用，还要受到惯性离心力的作用
• 惯性离心力的计算公式
Fc2R2acos
Ω=7.292E-5 弧度/秒，是地球自转角速度 惯性离心力的量级（0~10-2）和地心引力 相比很小!!!
✓ 测压定高，已知不同高度两点的气压和温度，根
据压高公式可求出两点之间的高度差值。
同样，根据某测站的高度及气层的平均温度可根 据压高公式求得测站的气压；已知两点的高度及对 应的气压根据压高公式可求得气层的平均温度。
• 利用压高公式分析天气系统的垂直结构
✓ 气压场的分布与温度场密切相关；
由于温度分布不同，使气压系统随高度发生各种 不同的变化。当某地地面为高压（或低压）控制 时，到高空是否仍为高压（或低压）时系统，即 地面高低压系统垂直结构的改变是由温度场的配 置决定的。
§5 大气静力学方程
一、大气静力学基本方程 二、压高公式
什么是大气静力学？
大气静力学, 研究静止大气所受到的作用力以及 在力的作用下质量和压强分布规律的科学
一、大气静力学基本方程
1. 静止大气中的力 2. 静力学方程
• 万有引力
F
G
m1m2 d2
地球质量M=5.98E+24千克
对于地球对单 位质量空气的 吸引，万有引 力如右式
• 上述现象可以用压高公式进行解释
RT
p
p
RT m p pm
1 0
RT m pm
p
1 0
RT m pm
p
here , p p 1 p 0
温度高时，同一 等压面位势高度 增加得快
0
• 暖性高压，高温中心和高压中心相伴的高气压 • 冷性高压，低温中心和高压中心相伴的高气压
TT0 z
这样，静力学方程
dpgdz
可表示为
dp g dz
p
Rd T0 z
上式积分后, 可得
pz p0(T0T0z)Rgd
✓ 多元大气中，气压随高度变化与温度的垂直 递减率有关，温度随高度递减得快，气压随高 度递减得也快。
• 几种大气气压随高度递减情况对比
z
H p
p0
• 重力位势
将单位质量的空气块从海平面沿任意路径提升 到某一高度A时，克服重力所做的功就成为A点 的重力位势：
低压系统向冷区倾斜
高压系统向暖区倾斜
浅薄的冷高压
浅薄的热低压
气旋反气旋垂直结构示意图
g0, Fu Fc cos
G
M a2
a2
cos2
• 近地表重力场分布
The value of “g” （重力加速度）depends on：
✓ Altitude ✓ Non-uniformity of Earth’s crust ✓ Non-spherical shape ✓ The rotation of Earth
二、 压高公式
1. 均质大气的压高公式 2. 等温大气的压高公式 3. 多元大气的压高公式 4. 标准大气 5. 压高公式的应用
1. 均质大气的压高公式
均质大气，即假定大气密度不随高度变化（密 度为常数）的大气。
对静力学方程积分：
d pz p z
p0
0
0gdz
pz p0 0gz均 压质 高大 公气 式
5. 压高公式的应用
• 利用压高公式可以计算出不同高度的气压值 • 利用压高公式分析天气系统的垂直结构
• 利用压高公式可以计算出不同高度的气压值
✓ 海平面气压订正：因各气象观测站高度不同，所 测得的气压值，不能进行比较，因此必须将各站所 测得的气压值一律订正到海平面高度。
已知：海拔高度、气温和气压; 求： 海平面气压 解：首先利用温度垂直递减率求得海平面气温，然 后利用均温度值代入等温大气的压高公式中求得海 平面气压
冷高压
暖高压
冷高压和暖高压随高度变化的个例（地面）
冷高压和暖高压随高度变化的个例（925hPa）
低槽 冷高压和暖高压随高度变化的个例（700hPa）
冷高压和暖高压随高度变化的个例（500hPa）
哪种类型的气旋、反气旋能延伸到较高的高度呢？
✓ 深厚系统：暖高压、冷低压（冷涡） ✓ 浅薄系统：冷高压、热低压 ✓ 气旋中心随高度向冷区倾斜 ✓ 反气旋中心随高度向暖区倾斜
p
R0T
积分后，可得：
ln p z g z
p0
RdT
or
pz
gz
p0e RdT
z
p0e H
✓ 由上述公式可知，等温大气气压随高度按指数递 减，当z→∞时，气压为零。
z
H
p p0
3. 多元大气的压高公式
多元大气, 温度随高度线性递减的大气。 当温度的垂直递减率为
T
z
时，z高度处的温度可表示为
均质大气垂直温度梯度是个常数，而且数值 较大，若大气中的温度 梯度超过这个数值时， 则将是上层空气密度大，下层空气密度小， 大气非常不稳定，可自动上下翻转，故此温 度梯度称为自由对流梯度。
2. 等温大气的压高公式
等温大气, 气温不随高度变化的大气。
dp gdz p gdz
R0T
dp g dz
gz
重力位势的单位为焦耳/千克。实际应用中有一 个更为通俗易懂的单位来恒量重力位势，就是 位势米：
1位势米≡9.8焦耳/千克
如果高空某点A的位势为φ焦耳/千克，则用位势 米度量的位势高度为：
H gz 9.8
由于g值接近9.8，因此尽管位势高度是能量单 位，几何高度是长度单位，它们的物理意义不 同，但二者在数值上是十分接近的（可以认为 相等）。
• 重力计算公式（2）
由于重力和地心引力之间的夹角很小，所以重力 的大小和方向均接近地心引力，可近似为地心引 力减去惯性离心力在地心引力反方向上的投影。 因此，地表处在纬度为φ的地点单位质量空气块所 受到的重力为：
4. 标准大气
标准大气， 垂直方向温度、气压和密度按一种假定规 律分布的大气。
如，1976年美国标准大气推广委员会所设定的标准大 气为：
✓ 空气中没有水汽； ✓ 在86千米以下大气为均匀混合物，呈静力平衡和 层状分布； ✓ 11千米以下大气温度随高度降低，平均递减率为 0.650C/100m； ✓ 11-20千米为等温大气。
• 地球的重力
Fc cos
惯性离心力在地心引力反方向上的投影
惯性离心力
重力
• 重力计算（1）
✓ 地心引力与惯性离心力之矢量和就是重力；
✓ 由上图可以看出，如果把地球表面看作球面， 则重力并不与地面垂直；
✓ 如果把惯性离心力分解成为两个分力： 一个分力与地球引力方向相反； 另一个与地面相切，指向赤道。
(equation of static equilibrium)
Form of the vertical component of the equation of motion in which all terms (including, in particular, the vertical acceleration) are considered negligible compared with the pressure and the force of gravity.
• 国际标准重力加速度
✓ 极地 g=9.832m/s2 ✓ 赤道 g=9.78m/s2 ✓ 纬度45度处 g=9.832m/s2 ✓ g随海拔高度等因子的变化也很小
因此，气象学中将g当作常数看待； 国际上规定海平面处重力加速度的标准值为：
g=9.80665m/s2
2. 静力学方程
hydrostatic equation
✓ 由上述压高公式可以看出，在均质大气中气 压随高度线性递减。
z
p p0
✓ P=0处的高度称为均质大气的上界（高度）
H
p0
0g
RdT g
✓ 均质大气是一种假设，并非实际存在；
✓ 但均质大气的某些参数在动力气象理论问题的 处理中有一定应用价值。
• 均质大气的 垂直温度梯度
A T z R 1 d P z R 1 d g R g d 3 .4C 2 /1米 0
• 静力学方程得到的推论
✓ dz>0时dp<0，说明气压随高度是下降的；
✓ 由于g随高度的变化很小，所以气压随高度下降 的快慢主要取决于密度。大气层低层密度大，气压 随高度下降快；大气层高层密度小，气压随高度下 降的慢；
✓ 将静力学方程从任意高度z积分到大气上界，得
pz
gdz
z
*表明任意高度z处的气压等于从该高度到大气上界的 单位截面积气柱所受的重力。
M
=9.81米/秒2
F G a u
2
万有引力常数G=6.672E-11牛顿.米2千克-2
地球半径a=6.371E+6米
• 离心力
由于地球自转，单位质量空气块不仅受万有引力 的作用，还要受到惯性离心力的作用
• 惯性离心力的计算公式
Fc2R2acos
Ω=7.292E-5 弧度/秒，是地球自转角速度 惯性离心力的量级（0~10-2）和地心引力 相比很小!!!
✓ 测压定高，已知不同高度两点的气压和温度，根
据压高公式可求出两点之间的高度差值。
同样，根据某测站的高度及气层的平均温度可根 据压高公式求得测站的气压；已知两点的高度及对 应的气压根据压高公式可求得气层的平均温度。
• 利用压高公式分析天气系统的垂直结构
✓ 气压场的分布与温度场密切相关；
由于温度分布不同，使气压系统随高度发生各种 不同的变化。当某地地面为高压（或低压）控制 时，到高空是否仍为高压（或低压）时系统，即 地面高低压系统垂直结构的改变是由温度场的配 置决定的。
§5 大气静力学方程
一、大气静力学基本方程 二、压高公式
什么是大气静力学？
大气静力学, 研究静止大气所受到的作用力以及 在力的作用下质量和压强分布规律的科学
一、大气静力学基本方程
1. 静止大气中的力 2. 静力学方程
• 万有引力
F
G
m1m2 d2
地球质量M=5.98E+24千克
对于地球对单 位质量空气的 吸引，万有引 力如右式
• 上述现象可以用压高公式进行解释
RT
p
p
RT m p pm
1 0
RT m pm
p
1 0
RT m pm
p
here , p p 1 p 0
温度高时，同一 等压面位势高度 增加得快
0
• 暖性高压，高温中心和高压中心相伴的高气压 • 冷性高压，低温中心和高压中心相伴的高气压
TT0 z
这样，静力学方程
dpgdz
可表示为
dp g dz
p
Rd T0 z
上式积分后, 可得
pz p0(T0T0z)Rgd
✓ 多元大气中，气压随高度变化与温度的垂直 递减率有关，温度随高度递减得快，气压随高 度递减得也快。
• 几种大气气压随高度递减情况对比
z
H p
p0
• 重力位势
将单位质量的空气块从海平面沿任意路径提升 到某一高度A时，克服重力所做的功就成为A点 的重力位势：
低压系统向冷区倾斜
高压系统向暖区倾斜
浅薄的冷高压
浅薄的热低压
气旋反气旋垂直结构示意图
g0, Fu Fc cos
G
M a2
a2
cos2
• 近地表重力场分布
The value of “g” （重力加速度）depends on：
✓ Altitude ✓ Non-uniformity of Earth’s crust ✓ Non-spherical shape ✓ The rotation of Earth
二、 压高公式
1. 均质大气的压高公式 2. 等温大气的压高公式 3. 多元大气的压高公式 4. 标准大气 5. 压高公式的应用
1. 均质大气的压高公式
均质大气，即假定大气密度不随高度变化（密 度为常数）的大气。
对静力学方程积分：
d pz p z
p0
0
0gdz
pz p0 0gz均 压质 高大 公气 式
5. 压高公式的应用
• 利用压高公式可以计算出不同高度的气压值 • 利用压高公式分析天气系统的垂直结构
• 利用压高公式可以计算出不同高度的气压值
✓ 海平面气压订正：因各气象观测站高度不同，所 测得的气压值，不能进行比较，因此必须将各站所 测得的气压值一律订正到海平面高度。
已知：海拔高度、气温和气压; 求： 海平面气压 解：首先利用温度垂直递减率求得海平面气温，然 后利用均温度值代入等温大气的压高公式中求得海 平面气压
冷高压
暖高压
冷高压和暖高压随高度变化的个例（地面）
冷高压和暖高压随高度变化的个例（925hPa）
低槽 冷高压和暖高压随高度变化的个例（700hPa）
冷高压和暖高压随高度变化的个例（500hPa）
哪种类型的气旋、反气旋能延伸到较高的高度呢？
✓ 深厚系统：暖高压、冷低压（冷涡） ✓ 浅薄系统：冷高压、热低压 ✓ 气旋中心随高度向冷区倾斜 ✓ 反气旋中心随高度向暖区倾斜
p
R0T
积分后，可得：
ln p z g z
p0
RdT
or
pz
gz
p0e RdT
z
p0e H
✓ 由上述公式可知，等温大气气压随高度按指数递 减，当z→∞时，气压为零。
z
H
p p0
3. 多元大气的压高公式
多元大气, 温度随高度线性递减的大气。 当温度的垂直递减率为
T
z
时，z高度处的温度可表示为
均质大气垂直温度梯度是个常数，而且数值 较大，若大气中的温度 梯度超过这个数值时， 则将是上层空气密度大，下层空气密度小， 大气非常不稳定，可自动上下翻转，故此温 度梯度称为自由对流梯度。
2. 等温大气的压高公式
等温大气, 气温不随高度变化的大气。
dp gdz p gdz
R0T
dp g dz
gz
重力位势的单位为焦耳/千克。实际应用中有一 个更为通俗易懂的单位来恒量重力位势，就是 位势米：
1位势米≡9.8焦耳/千克
如果高空某点A的位势为φ焦耳/千克，则用位势 米度量的位势高度为：
H gz 9.8
由于g值接近9.8，因此尽管位势高度是能量单 位，几何高度是长度单位，它们的物理意义不 同，但二者在数值上是十分接近的（可以认为 相等）。