脑血流量
血压和脑血流量的自动调节曲线

血压和脑血流量的自动调节曲线
血压和脑血流量之间存在着自动调节机制,也被称为脑血流自动调节。
在正常情况下,脑血流量需要保持在一个相对恒定的范围内,以满足大脑的需氧供血。
血压的变化可以通过自动调节来影响脑血流量,以保持血流的稳定性。
通常情况下,当血压升高时,血管壁中的压力感受器会被激活,从而引起血管收缩,减少脑血流量,以降低血压。
反之,当血压降低时,血管壁中的压力感受器被抑制,从而引起血管扩张,增加脑血流量,以增加血压。
这种自动调节机制通常被称为脑血流压力自动调节曲线。
在这条曲线上,可以观察到当血压升高时,脑血流量随之下降,当血压降低时,脑血流量随之增加。
然而,这种自动调节系统并不是完全线性的,而是有一定的范围和限制。
当血压超过一定范围时,脑血流量的自动调节能力会受到限制,可能无法满足大脑的需氧供血。
值得注意的是,血压和脑血流量的自动调节曲线在某些疾病或情况下可能会发生改变。
例如,高血压患者可能会出现脑血管病变,导致脑血流量和自动调节能力的下降。
因此,了解血压和脑血流量的自动调节曲线对于维持大脑的正常功能和健康至关重要。
asl序列cbf计算公式

asl序列cbf计算公式
ASL(Arterial Spin Labeling)序列CBF(脑血流量)的计算
公式可以通过ASL序列的原始数据来实现。
ASL是一种用于无创测
量脑组织血流的成像技术,它利用自身血液作为内部对照,通过标
记动脉血液中的自旋来实现。
CBF是脑血流量的测量单位,通常以
ml/100g/min表示。
ASL序列CBF的计算公式涉及多个步骤,包括标记和控制图像
的获取、计算灌注信号、以及利用定量模型将信号转换为CBF值。
一般来说,ASL序列CBF的计算公式可以表示为:
CBF = λ ΔM / M0 exp(TI/T1血) (1-exp(-TI/T1组织))。
其中,CBF表示脑血流量,λ是血液的脑灌注分数(通常为
0.9ml/g)、ΔM是标记和控制图像的信号差异、M0是组织基础信号、TI是标记后的时间延迟、T1血是血液的纵向弛豫时间,T1组织是
组织的纵向弛豫时间。
这个公式涉及了ASL序列的物理原理、脑血流动力学参数以及
信号处理技术。
通过对原始ASL序列数据的处理和计算,可以得到
脑组织的血流量信息,从而在临床诊断和科研研究中发挥重要作用。
需要注意的是,ASL序列CBF的计算公式可能会因不同的研究
方法、设备厂商和成像参数而有所差异,因此在实际应用中需要结
合具体情况进行调整和修正。
脑血流量的调节

脑血流量的调节
脑血流量(CBF)主要取决于两个方面的因素:○1血管床两端之间的压力梯度,即脑灌注压(CPP);○2脑血管阻力。
任何能改变CBF的因素均通过改变脑灌注压和(或)脑血管阻力而完成。
CBF的动态调节不是单一的机制,而是许多因素共同起作用。
1.脑血流灌注压
2.脑血管阻力(由CPP和CBF的比值定量算出)
(1)静态物理因素
一般有血液的粘滞性、颅内压、血管的直径和形态三方面
(2)脑血管张力
3.脑血流量的自动调节
(1)自动调节的上下限:自动调节血压范围为平均动脉压70~180mmHg(9.3~24.0kPa)。
○1动脉血养分压(PaO2)和CO2分压(PaCO2)。
PaO2升高时,脑血管收缩,脑血流自动调节上限上移;PaO2降低时,则引起自动调节作用减弱,甚至消失。
PaCO2增高,脑血流自动调节能力减弱,PaCO2超过9.3kPa(70mmHg)时,自动调节的作用全部消失。
过度换气,降低PaCO2可使肝昏迷时丧失的自动调节恢复正常。
○2年龄
○3高血压
○4神经影响
○5药物
(2)自动调节的机制
(3)参与脑血自动调节的血管
4.脑血流量的化学调节
5.脑血流量的自动调节
(1)肾上腺素能神经对脑血流的调节
(2)胆碱能神经对脑血流的调节
(3)中区调节
(4)肽能神经对脑血流的调节
6.老年人脑血流量的变化特点
提示在老年人群中,局部脑血流量(rCBF)随着增龄而减少可用动脉粥样硬化来解释。
脑血流与脑代谢.ppt
三、动脉压与颅内压
ICP的处理临界值未清楚,大部分学 者认为20-25mmHg以上,如果CPP足够, 还可以承受更高的压力,遗憾的是压力小 于20mmHg,患者仍可形成脑疝,取决于部 位。
三、动脉压与颅内压
美国神经外科医师协会(AANS)和 脑创伤基金会对重度TBI患者处理指南建议, 在整个救治过程必须维持CPP在70mmHg以 上,一般收缩压大于110mmHg才能满足要 求。
六、麻醉药物对脑血流、脑代谢的影响
2.丙泊酚 对CMR和CBF的作用与巴比妥类似,使 两者剂量依赖性的降低。输注丙泊酚至意 识消失时,用正电子发射断层扫描测定大 脑糖代谢,全脑代谢率下降48-58%。负荷 剂量2mg/kg继以0.2mg/kg*min时CBF和 CMR分别下降51%和36%。
六、麻醉药物对脑血流、脑代谢的影响
三、补液管理与颅内压
补液总原则: 1.维持正常血容量 2.避免血清渗透压下降。
三、补液管理与颅内压
血浆渗透压295mosm/L,生理盐水略高 渗,308mosm/L,大量使用导致高氯性酸 中毒。这种酸中毒涉及细胞外液而非内液, 生理意义尚不明。
三、补液管理与颅内压
林格液低渗,273mosm/L,作为维持补 液和补充丢失液均不理想,大量输注导致 脑水肿,但它能适用多数情况,大出血或 多发伤时建议林格-生理盐水比例1:1。
一、生理学基础-脑血流 低碳酸血症对CBF的影响是不稳定的。 在过度通气初期CSF和脑组织外液PH值 均升高,而CBF急剧下降,但不会导致 长时间脑碱中毒。
一、生理学基础-脑血流
PaO2在60-300mmHg对CBF无影响,低于 60mmHg时,CBF迅速增加.
PaCO2和PaO2与CBF脑血流量的关系
ctp衍生影像指标

ctp衍生影像指标
CTP(计算机断层扫描灌注成像)是一种用于评估脑部血流动力
学的影像技术。
CTP衍生影像指标是指从CTP图像中提取的参数和
指标,用于评估脑部血流灌注情况和组织灌注状态。
这些指标包括
但不限于以下几个方面:
1. CBF(脑血流量),衡量单位时间内通过脑部血管的血液量,通常以ml/100g/min为单位。
CBF是评估脑灌注状态的重要指标,
对于脑血管疾病的诊断和治疗具有重要意义。
2. CBV(脑血容量),指单位脑组织体积中的血液容量,通常
以ml/100g为单位。
CBV反映了脑部血流量和血管扩张情况,对于
评估脑血管病变和脑组织灌注状态具有重要意义。
3. MTT(平均通过时间),指血液从动脉到静脉通过脑组织的
平均时间,通常以秒为单位。
MTT是评估脑部血流动力学变化和血
管阻力的重要指标。
4. TTP(时间至峰值),指血流灌注达到峰值的时间点,通常
以秒为单位。
TTP反映了脑部血流动力学的时间特征,对于评估脑
血管病变和缺血情况具有重要意义。
这些CTP衍生影像指标可以通过对CTP图像的分析和处理得到,通过量化分析可以帮助医生更准确地评估患者的脑血流灌注情况,
对于脑血管疾病的诊断和治疗具有重要的临床意义。
同时,这些指
标也为科研人员提供了丰富的数据,有助于深入了解脑部血流动力
学的变化规律和病理生理机制。
综上所述,CTP衍生影像指标在临
床诊断和科研领域具有重要的应用前景和意义。
大脑动脉血流最大峰值

大脑动脉血流最大峰值
大脑动脉血流最大峰值是一个可以反映大脑供血情况的指标。
一般情况下,大脑中动脉血流峰值的正常范围大约是40\~100cm/s。
如果动脉峰值流速超过100cm/s,可能说明大脑供血存在一定问题,如血管狭窄、血管痉挛等。
相反,如果低于40cm/s,也可能意味着大脑供血不足。
大脑动脉血流最大峰值通常发生在人的中年,大约在40岁左右。
此后,随着年龄的增长,大脑血流量会逐渐减少。
这一现象是由于随着年龄的增长,血管的弹性和功能会逐渐下降,导致血流量的减少。
不过,这种变化对于绝大多数人来说,不会对大脑功能产生显著的负面影响。
值得注意的是,个体差异很大,这只是一般情况下的平均趋势。
局部脑血流的测定

局部脑血流的测定一. 问题简介脑血流量是诊断和治疗脑梗塞,脑出血,动脉瘤和先天性动,静脉血管畸形等脑血管疾病的主要依据。
测定脑血流量可为研究人脑在不同的病理和生理条件下的功能提供客观指标,它对研究脑循环药物的药理作用也很有帮助。
所以人们长期致力于寻找有效地测定脑血流量的方法。
近年来出现了以放射性同位素作示踪剂测定人脑局部血流量的方法。
这种方法大致可描述如下:由受试者吸入某种放射性同位素的气体,然后将探测器置于受试者头部某固定处,定时测量该处放射性同位素的计数率(简称计数率),同时测量他呼出气的计数率。
由于动脉血将肺部的放射性同位素输送至大脑,使脑部同位素增加,而脑血流又将同位素带离,使同位素减少,实验证明由脑血流引起局部地区计数率下降的速率与当时该处的记数率成正比,其比例系数反映了该处的脑血流量,被称为脑血流量系数,只要确定该系数即可推算出脑血流量。
动脉血从肺输送同位素至大脑引起脑部计数率上升的速率与当时呼出气的计数率成正比。
试建立确定脑血流系数的数学模型并计算上述受试者的脑血流系数。
备注:该题目是上海市(1990 年)大学生数学建模竞赛A 题。
二. 模型的假定= − 1. 脑部计数率(记为 h (t ) )的上升只与肺部的放射性同位素有关,上 升速度与呼出气的记数率(记为 p (t ) )成正比,比例系数记为 k ;2. 脑部记数率 h (t ) 的下降只与该处脑血流量有关,其下降速度正比 于 h (t ) ,比例系数为脑血流系数,记为 K ,这里忽略了放射性元素的衰 变和其它因素;3. 脑血流量在测定期间恒定,心脏博动,被测试者大脑活动,情感 波动等带来的变化忽略不予考虑;4. 每次仪器测量为相互独立事件,各测量值无记忆相关;5. 放射性同位素在人体内传递是从吸入气体(含有放射物)开始的, 并假定一次吸入,因此认为同位素在肺中瞬时达到最大浓度;6. 在吸入气体瞬时,脑中放射物记数率为零;7. 脑血流量与脑血流系数 K 成单值函数关系,求得后者即可确定前 者。
脑外科麻醉基础概述

脑外科麻醉基础概述第一节脑循环的特点脑血流量(CBF)等于脑灌注压(CPP)除以脑血管阻力(CVR),其中CPP为颅内平均动脉压与平均颅内压之差,颅内平均动脉压难以测量,一般以体循环平均动脉压(MAP)代替,而CVR代表毛细血管前小动脉对压力或代谢产物浓度变化产生收缩和舒张反应的能力。
CVR的调节受内在与外来因素的影响:内在因素包括化学调节、肌源性调节(自动调节)、和血液黏度效应;外来因素在麻醉过程中包括血管活性药物和全麻药物。
一、化学调节(一)脑代谢率(CMR)大约60%的脑的能量消耗用于维持脑的电生理功能,在脑的局部CBF与CMR具有良好的匹配性,可能与神经源性的NO生成有关,而CMR则与脑的功能状态、体温和麻醉药物(包括吸入全麻药和静脉全麻药)的应用有关。
(二) 动脉血二氧化碳分压(PaCO2)由于血脑屏障(BBB)的作用,血中只有CO2能自由弥散进入脑组织细胞外液和脑脊液(H+和HCO3-则不能),故当脑代谢稳定时,细胞外液和脑脊液的pH值与PaCO2直接相关,而代谢性的酸碱变化则无此作用。
低碳酸血症导致脑组织细胞外液和脑脊液的pH 值升高,直接使脑血管收缩,CBF降低,高碳酸血症则相反。
由于CO2能快速弥散通过脑血管内皮,故此种调节的速度也很迅速。
同时,由于CSF的pH值会逐渐恢复正常,持续的过度通气尽管可以维持动脉血中升高的pH,其对CBF的作用一般在6-8小时后减弱,而这时迅速使PaCO2恢复正常会使CSF的pH值降低,导致CBF增加及可能的ICP增高(取决于之前的颅内顺应性)。
(三)动脉血氧分压(PaO2)PaO2在60-300mmHg之间变化时,CBF几乎不受影响。
低氧血症(PaO2在60 mmHg 以下)时脑血管舒张,CBF增加。
(四)脑血管自动调节机制即当MAP在50-150mmHg范围内变化时,依靠小动脉的舒缩,使CBF维持在一个恒定的水平,MAP超出此范围,CBF则随MAP的变化而增减。
脑血流量计算方法

脑血流量计算方法脑血流量是指单位时间内通过脑血管的血液量,是评估脑功能活动的重要指标之一。
脑血流量计算方法有多种,其中包括灌注加权成像、磁共振血流动力学成像、超声多普勒等。
本文将介绍这些方法的原理和应用。
1. 灌注加权成像灌注加权成像是一种使用核磁共振技术来测量脑血流量的方法。
它通过测量血流对比剂在脑组织中的分布情况来计算脑血流量。
这种方法可以提供高空间和时间分辨率的脑血流量图像,能够在短时间内获取全脑血流分布的信息。
2. 磁共振血流动力学成像磁共振血流动力学成像是一种通过测量脑血液供应和代谢的方法来计算脑血流量的技术。
它利用磁共振信号的变化来反映脑组织的代谢活动和血流供应情况,从而计算脑血流量。
这种方法可以提供脑血流量分布的空间信息,并且能够对脑功能活动进行定量评估。
3. 超声多普勒超声多普勒是一种使用超声波来测量脑血流速度和血流量的方法。
它通过测量超声波在血液中的传播速度和频率变化来计算脑血流量。
这种方法具有无创、实时和便携的特点,可以用于门诊和床边的脑血流量监测。
这些脑血流量计算方法在临床和科研中有广泛的应用。
它们可以用于评估脑血液供应不足的疾病,如脑卒中和脑缺血等。
此外,它们还可以用于研究脑功能活动的变化,如认知功能、注意力和情绪等。
通过对脑血流量的定量测量,可以更好地理解和诊断脑功能异常。
然而,这些计算方法也存在一些限制。
比如,灌注加权成像需要使用对比剂,可能对患者造成一定的风险;磁共振血流动力学成像需要复杂的数据处理和分析,对操作者的要求较高;超声多普勒对头骨的穿透能力有限,只能测量颅内血流量。
脑血流量计算方法是评估脑功能活动和脑血液供应的重要工具。
不同的方法各有优缺点,应根据具体需求选择合适的方法。
随着技术的不断发展,脑血流量计算方法将更加精确和便捷,为临床医生和科研人员提供更多有价值的信息。
血压和脑血流量的自动调节曲线

血压和脑血流量的自动调节曲线血压和脑血流量的自动调节曲线在生理学及医学领域中,血压和脑血流量的自动调节曲线是一个非常重要的主题。
它涉及到人体血液循环系统中的自动调节机制,对于维持正常的脑功能和健康至关重要。
通过深入探讨血压和脑血流量的自动调节曲线,我们可以更好地理解人体内在的自我平衡机制,以及一些疾病和症状的发生原因。
1. 脑血流量的自动调节曲线脑血流量的自动调节曲线是指在不同血压水平下,脑血管对血流量的自动调节能力。
这条曲线通常呈现为一个 U 形曲线,即在较低的血压水平时,脑血管会自动扩张以保证足够的血流量供应给脑部组织;而在较高的血压水平时,脑血管则会自动收缩,以避免过多的血流导致脑部组织的损伤。
这种自动调节能力使得脑部能够在不同情况下保持稳定的血流供应,从而维持正常的脑功能。
2. 血压的影响血压是指血液在动脉内对血管壁的压力,通常包括舒张压和收缩压两个参数。
正常情况下,血压的变化是受多种因素调节的,其中包括自主神经系统的调节和体液平衡的影响。
当血压处于较低水平时,脑部组织的血流供应会受到影响,容易导致头晕、注意力不集中甚至晕厥等症状;而当血压处于较高水平时,容易导致头痛、情绪波动甚至心脑血管疾病的风险增加。
3. 自动调节的意义了解血压和脑血流量的自动调节曲线对于人体健康具有重要意义。
它不仅有助于我们对脑部血流动力学的理解,还能指导临床治疗和药物干预。
针对一些高血压导致的脑血管病变,可以通过调节血压水平来维持正常的脑血流量,从而减少并发症的发生。
总结而言,血压和脑血流量的自动调节曲线是一个非常重要的生理学主题。
通过深入了解该曲线的形成机制和调节方式,可以帮助我们更好地理解血管自主调节的机制,从而为临床诊断和治疗提供理论基础。
加强对脑血流动力学的研究,也有助于我们更好地预防和治疗与脑血管疾病相关的病症。
个人观点和理解在我看来,血压和脑血流量的自动调节曲线是人体内一个十分精密和智能的平衡机制。
它的存在为我们提供了一个自我调节的机制,使得我们的脑部组织能够在不同情况下始终保持稳定的血流供应,从而保证脑部功能的正常运转。
脑血管血液动力学指标检测参数的参考值

脑血管血液动力学指标检测参数的参考值脑血管血液动力学指标是评估大脑血液供应和功能状态的重要指标。
这些指标可以通过各种检测方法来获取,包括超声多普勒、磁共振血流成像和脑电图等。
下面是一些常见的脑血管血液动力学指标检测参数的参考值。
1.脑血流量脑血流量是指单位时间内通过大脑的血液量。
正常成人的脑血流量范围为每分钟50-60毫升。
血液供应脑部的主要血管是颈动脉和椎动脉,因此检测脑血流量可以通过测量颈动脉和椎动脉的血流速度来确定。
2.脑血流速度脑血流速度是指血液通过脑动脉的速度。
正常成人的脑血流速度范围为每分钟50-100厘米。
通过超声多普勒技术可以非侵入性地测量脑血流速度。
3.脑血管阻力指数脑血管阻力指数是评估脑血管阻力的指标。
它是通过测量脑动脉内外径差来计算的。
正常成人的脑血管阻力指数范围为0.6-1.2。
较高的脑血管阻力指数可能表明血管狭窄或堵塞。
4.脑血管弹性脑血管弹性是指血管在血液流动时对压力的适应能力。
正常成人的脑血管弹性指数范围为2-5。
血管弹性降低可能与动脉硬化和血管损伤有关。
5.脑血氧饱和度脑血氧饱和度是指血液中氧气的含量。
正常成人的脑血氧饱和度范围为60-75%。
低脑血氧饱和度可能与缺氧和血管疾病有关。
6.脑电图脑电图是通过测量大脑电活动来评估脑功能的一种方法。
正常成人的脑电图应该有特定的频率和振幅范围。
异常的脑电图可能与癫痫、脑损伤和神经系统疾病有关。
上述的参考值是基于正常成人的范围,低于或高于这些范围可能表示不同的疾病或异常情况。
但需要注意的是,这些参考值可能因年龄、性别、体重和其他个体因素而有所不同。
因此,在进行脑血管血液动力学指标检测时,最好咨询专业医生以获得更准确的参考值。
总结起来,脑血管血液动力学指标检测参数的参考值包括脑血流量、脑血流速度、脑血管阻力指数、脑血管弹性、脑血氧饱和度和脑电图。
这些参考值可以帮助医生评估脑血液供应和功能状态,进而判断是否存在脑血管疾病或其他相关疾病。
脑血流监测与护理

血流速度
通过血管的血流量
• 在血管管径不变的情况下,血流速度与血流量成正比 • 血流速度快---血流量大 • 血流速度慢—血流量小 • 未知血管截面积的情况下,血流速度不能反应血流量
通过血管的血流量
脑血流量
一条动脉内的血流量不能代表供应该区域的脑血流量 脑血流量下降可以通过以下检查得知: CT灌注,MRI灌注,PET
脑血流监测与护理
王
丹
脑血流监测
脑血流量 血流速度 氧供情况 脑灌注压
脑血流监测
有创的: N2O饱和实验 动脉注入法133Xe清除实验 无创的: 经颅多普勒超声(TCD) 吸入法和静脉注入法133Xe清除实验
一、 脑血流监测方法
(一)经颅多普勒超声
概念:使用低频1-2MHz脉冲超声多普勒探头,通过颞骨 窗、眼眶、枕骨大孔来检测Wilis环周围脑动脉的血流速 度、方向及侧支循环状态,称为经颅多普勒超声(TCD)。
原理:是一种无创伤性颅内血流动力学方法。测定脑血 流速度,但能反映脑血流量变化,间接反映脑自动调节 能力与对CO2反应性。
正常的TCD血流频谱的形态近似直角三角形,频谱内 部分布均匀,反映血液在血管内为规则的层流状态。 层流 :正常血管中心处血流速度最快,边缘处血流 速度最慢,中心与边缘之间血流速度依次递减。
监测中保证患者处于安静平稳的状态。 如需翻身拍背,应用手轻托患者头部,保证头
部与监护探头之间不会产生移位。
临床应用: 诊断:脑血管狭窄、闭塞、畸形、痉挛;发现体外循 环下脑低灌注、血栓、气栓;
监测:颈动脉内膜剥脱术中,暂时阻断颈动脉时脑缺 血危险与评估预后;并动态反映麻醉药物、控制降压
脑血流灌注名词解释

脑血流灌注名词解释
脑血流灌注是指血液通过脑部的供应和循环过程。
它是维持脑细胞正常功能所必需的,因为脑细胞对氧气和营养物质的需求非常高。
脑血流灌注通常由以下几个方面组成:
1. 脑血流量,脑血流量是指单位时间内通过脑部的血液量。
它通常用于评估脑血管疾病或神经系统疾病的程度。
正常情况下,脑血流量应保持稳定,以确保脑细胞获得足够的氧气和营养物质。
2. 脑血流速度,脑血流速度是指血液在脑血管中流动的速度。
它可以通过超声多普勒或其他成像技术进行测量。
脑血流速度的变化可能与脑血管疾病、颅内压增高或其他神经系统疾病有关。
3. 脑血管阻力,脑血管阻力是指血液在脑血管中流动时所遇到的阻力。
脑血管阻力主要由血管的直径和血液粘度决定。
脑血管阻力的改变可能会影响脑血流灌注,导致脑部供血不足或过度供血。
4. 脑血流动力学,脑血流动力学研究血液在脑血管中的流动规
律以及与脑血流灌注相关的因素。
它包括脑血管的自动调节机制、血管舒缩功能、血液压力等。
脑血流动力学的研究有助于了解脑血流灌注的调节机制,以及一些脑血管疾病的发生机制。
总之,脑血流灌注是指血液通过脑部供应和循环的过程,它涉及到脑血流量、脑血流速度、脑血管阻力以及脑血流动力学等多个方面。
了解脑血流灌注的相关知识对于研究脑血管疾病、神经系统疾病以及脑功能的评估具有重要意义。
脑血流量的调节

脑血流量的调节1.脑血管的自身调节脑血流量取决于脑的动、静脉的压力差和脑血管的血流阻力。
在正常情况下,颈内静脉压接近于右心房压,且变化不大,故影响血流量的主要因素是颈动脉压。
政党情况下脑循环的灌注压为10.6-13.3kPa(80-100mmHg)。
平均动脉压降低或颅内压升高都可以使脑的灌注压降低。
但当平均动脉压在8.0-18.6kPa(60-140mmHg)范围内变化时,脑血管可通过自身调节的机制使脑血流量保持恒定。
平均动脉压降低到8.0kPa(60mmHg)以下时,脑血流量就会显著减少,引起脑的功能障碍。
反之,当平均动脉压超过脑血管自身调节的上限时,脑血流量显著增加。
2.CO2和O2分压对及脑血流量的影响血液CO2分压升高时,脑血管舒张,血流量增加。
CO2过多时,通过使细胞外液H+浓度升高而使脑血管舒张。
过度通气时,CO2呼出过多,动脉血CO2分压过低,脑血流量减少,可引起头晕等症状。
血液O2分压降低时,也能使脑血管舒张。
3.脑的代谢对脑血流的影响脑的各部分的血流量与该部分脑组织的代谢活动程度有关。
实验证明,在同一时间内脑的没部分的血流量是不同的,当脑的某一部分活动加强时,该部分的血流量就增多。
例如在握拳时,对侧大脑皮层运动区的血流量就增加;阅读时脑的许多区域血流量增加,特别是皮层枕叶和颞叶与语言功能有关的部分血流量增加更为明显。
代谢活动加强引起的局部脑血流量增加的机制,可能是通过代谢产物如H+离子、K+离子、腺苷,以及氧分子降低,引起脑血管舒张的。
4.神经调节颈上神经节发出的去甲云彩上腺素后纤维,其末梢分布至脑的动脉和静脉,并分布至软脑膜的血管,还有少量分布至脑实质的血管。
脑实质内的小血管有起自蓝斑去甲肾上腺素神经元的轴突末梢的分布。
副交感乙酰胆碱能神经末梢也分布至脑血管。
此外,脑血管政治家血管活性肠肽等神经肽纤维末梢分布。
神经对脑血管活动的调节作用不很明显。
刺激或切除支配脑血管的交感或副交感神经,脑血流量没有明显变化。
脑血流监测

脑血流监测目前监测脑组织血流的方法很多,临床研究中比较常用的有氢清除法、放射核素法、单光子发射计算机断层法(SPECT)和正电子发射扫描(PET)等,但以上方法较复杂,主要应用于诊断而难以用于术中监测。
在手术中和手术后使用的脑血流监测方法主要有激光多普勒血流测定法、热弥散法、经颅多普勒法等。
一、激光多普勒血流测定法激光多普勒血流测定法(laser Doppler flowmeter,LDF)是一种连续、实时、微创和敏感的微循环血流监测技术,适用于神经外科术中rCBF的监测。
1.工作原理LDF的工作原理是利用激光多普勒效应。
激光通过探头照射到脑组织内的快速运动的红细胞表面,使其波长发生改变,产生多普勒位移效应(Doppler shift)。
波长改变的程度及幅度与红细胞的数量和运动速度相关。
通过记录波长改变的幅度和强度,从而可以推测局部脑组织血流(rCBF)。
LDF的测量范围较小,在探头周围1mm3,适合检测大脑皮层的血流量,尤其使用于比较血流的相对变化。
PU值为LDF 的基本测量指标,即流动的红细胞产生多普勒位移值,是一个表示测量深度内rCBF大小的相对单位,PU值的变化反映了rCBF的改变。
2.临床应用(1)监测脑过度灌注:在脑动静脉畸形(AVM)切除前后用LDF连续监测畸形血管团周边脑组织rCBF的动态变化,可及时发现脑过度灌注,指导临床及时处理。
(2)监测局部脑灌注不足:脑动脉瘤手术中有时需暂时阻断颈总动脉或载瘤动脉,此时以LDF连续监测被阻断动脉供血区的rCBF,能准确地反映该区域脑血流的下降程度,则有助于决定动脉阻断时间,减少脑组织不可逆的缺血性损伤的可能。
动脉瘤夹闭术中LDF连续监测邻近脑组织rCBF的实时变化,以免造成夹闭血管狭窄以致出现供血区缺血,减少手术并发症的发生。
(3)观察脑血流反应:LDF持续监测重型颅脑损伤脑皮质rCBF,可了解皮层血液灌注及脑血管自动调节功能,有助于指导治疗和判断预后。
脑血流量计算公式

脑血流量计算公式
脑血流量计算公式是指根据特定的计算公式来计算人体脑部血流量的一种方法。
这种方法可以帮助医生诊断和治疗一些与脑血流量相关的疾病,例如中风、脑血管病等。
脑血流量计算公式的基本原理是根据血流速度和管道截面积来计算血流量。
脑血流量的计算需要使用超声多普勒技术测量血流速度,然后将其与管道截面积相乘即可得到血流量。
脑血流量计算公式可以使用以下公式进行计算:
血流量(ml/min)=血流速(cm/s)×截面积(cm²)×60
其中,血流速用超声多普勒仪器测量,截面积可以使用影像技术(例如MRI和CT扫描)进行测量。
脑血流量的计算公式非常重要,因为它可以帮助医生诊断和治疗一些脑部血管相关的疾病。
例如,中风是一种由于血栓或出血导致的脑血管病,可以使用脑血流量计算公式进行诊断和治疗。
此外,脑血流量计算公式也可以帮助医生评估一些慢性疾病,例如脑动脉狭窄。
总之,脑血流量计算公式是一种重要的计算方法,它可以帮助医生诊断和治疗一些与脑血流量相关的疾病。
如果您遇到脑部血管相关的问题,一定要及时咨询专业的医生,以便得到及时和有效的治疗。
脑的血流
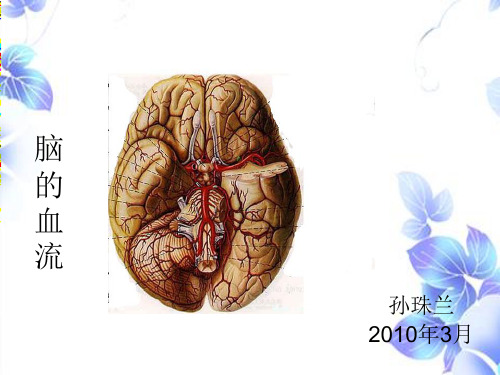
颈内动脉的主要分支
(1)眼动脉 (2)后交通动脉 (3)脉络膜前动脉 (4)大脑前动脉及前交 通动脉 (5)大脑中动脉
颈动脉解剖图
• • ⑽ 左侧颈总动脉分叉前。 ⑺ 左侧颈总动脉,直接自主动脉弓发出,在气管旁向上 走行,远端分叉为颈内动脉和颈外动脉。 ⑼ 右颈总动脉,自头臂干动脉发出,远端隐去。 ⑾ 左侧颈外动脉,除一部分进入颅内供应硬膜外,主要 分支供应头皮及颌面部等。
1.脑部代谢特点:
(2)大脑中静脉 血流丰富、无葡萄糖和糖原储备 (3)大脑下静脉
2.脑血流调节:
自动调节(Bayliss效应):60-160mmHg
(二)脑的深静脉
• (1)大脑大静脉 • (2)大脑内静脉
• (3)丘脑纹状体静脉
• (4)隔静脉 • (5)基底静脉
三、正常脑血流量
• 脑血流量是指每 100g 脑组织在单位时间内 通过的血流量 • 局部脑血流量是指单位时间内流经局部脑 组织的血流量。供应脑组织的血液约占心 排出量的14%。
• 重度颅脑损伤时 , 可使脑血流调节功能严重 紊乱,脑血流锐减,加剧脑缺血、缺氧。
•
•
•
•
⒁ 左侧大脑后动脉,主要供应左大脑后 部。
脑底动脉环(Willis环)的构成及意义
由双侧大脑前动脉、颈内动脉、大脑后动脉、前交通动 脉和后交通动脉组成。使两半球及两个供血动脉系统间
的血供相互代偿。
但脑深部穿动脉的吻合支较少,脑血流的调节和代偿作 用较差。
(一)脑的浅静脉
五、脑血液循环的生理和病理特点 (1)大脑上静脉
• •
•
⑿ 左侧颈内动脉,只供应颅内结构,自颈总动脉分出后 进入颅腔前没有分支。
⑶ 头臂干(又称无名动脉),从主动脉分出的粗短动脉 主干,分支成右锁骨下动脉和右颈总动脉等供应右上肢、 颈肩和颅脑右侧。 ⒂ 左侧眼动脉,供应眼球及眼眶内结构,供血不足时可 有黑矇等视力障碍发作。 ⒄ 左侧大脑前动脉,主要供应左侧大脑半球的前部及内 侧部分。 ⒃ 左侧大脑中动脉 ⒅ 及⒆,均为颈外动脉的远端分支,位于颅骨外。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2.14)
引入
f1 f2 k1 = , k2 = D1 D2
( 2.9) 和 ( 2.8) 可改写为
(2.10)
dQi + kiQi = f i • Wi • Ca (t ), (i = 1,2) dt
(2.11)
若这单位质量的脑组织正位于某个头部探头的探测范围, 探头就可记下闪烁计数器的计数率,设为N(t)。显然,闪烁计 数器的计数率应与探测范围中脑组织中放射性示踪剂的含量 成正比,设比例系数为γ,就有
头部清除曲线
t
3.a非线性规划方法
( 给定一组 ki , P (i = 1,2) ,可以根据测量的 C A (t ) 值用 2.20)式得 i 到理论 N (t j ) 值,它与测量值 N j 的误差平反和为
E (k1 , k 2 , P1 , P2 ) =
= ∑ N j − j = j0
(H 1)
:
此外,假设血液循环处于一种稳定平衡的状态,即:
( H 2 )流入脑组织中的动脉血和流出脑组织进入静脉的血流 量是相等的,不随时间的变化而改变。
另外还对示踪剂作如下假设和简化:
( H3 ) 133Xe 随着血液的流动而流动,与脑组织相结合而停 留在脑组织中的示踪剂的量十分微小,可以忽略不计;同时 在测量过程中,由衰变引起示踪剂放射性减少也可忽略不计。
0 t
(2.23)
它们满足微分方程的初值问题:
dN i + ki N i = PiCa (t ) (i = 1,2) dt N i (0) = 0
(2.24)
数学模型亦可归结为:已知 (2.24) 式中 C A (t ) 的 和初值问 题 ( 2.24) 解之和 N (t ) = N1 (t ) + N 2 (t ) 在 t j 的测量 值 C j 和 N j ( j = 1,• • •, n ),决定初值问题 (2.24) 中方程的系 数 k i 和 Pi (i = 1,2) 。
n
∑ [N
n j = j0
1
Q1A = f1W1∆t • Ca (t ) 由Fick原理,应有
( 2 .5 )
∆Q1 = Q1A − Q1V
即
( 2 .6 )
f1 Q1 (t + ∆t )1 − Q1 (t ) = f1 w1 ∆t • Ca (t ) − ∆tQ1 (t ) D1
(2.7)
在上式两边除以 ∆t ,然后令 微分方程
早期人们采用惰性气体来测定脑血流量,让受试者吸入惰 性气体后,在一定时间内多次采集肱动脉和颈动脉的系列血 样,分析惰性气体在这些血样的浓度,推算出脑的出血量。 这种方法需要进行动脉插管和多次采集血样,对人体会造成 一定的创伤,测量仪器也比较复杂。 近年来出现了以放射性同位素作示踪计测定人脑局部血 流量,简称rCBF(regional cerebral blood flow的缩写)的方法。 测量装置主要由安装多个(通常采用8个,16个或是32个)闪 烁计算器探头的头盔,安装一个闪烁计数器探头的头盔,安 装一个闪烁计数器的面罩,将闪烁计数器探头的面罩,将闪 烁计数器的计数转换成数字信息并输入计算机的装置,一台 电子计算机(包括外部设备)和一个废气回收装置组成。
1 2
1
2
1
现建立灰质组织中的示踪剂的平衡关系。考察时段[ t + ∆t ]中灰质组织中示踪剂含量的变化
t
,
∆Q1 = Q1 (t + ∆t ) − Q1 (t )
( 2 .1)
在1克脑组织中,灰质组织的质量为 w1 克,∆t 时间流出的 血液体积为
-
f 1 w1∆t
( 2 .2 )
灰质组织中容纳的血液中示踪剂的浓度为
t0 = 0, t j = j • δt ( j = 1,• • •, n), tn = nδt = 10
(2.21)
而 δt 为测量的时间间隔。
又由于(2.20)式中的N(t)可分解为
N (t ) = ∑ N i (t )
i =1 2
(2.22)
由于
N i (t ) = Pi ∫ e − k i ( t −τ )C A (τ )dτ (i = 1,2)
得到灰质和白质血流量。此外,我们还可以确定脑组织中 灰质与白质的百分比 wi 。利用表达式(2.18)易知
W1 P1 f 2 = W2 P2 f1
(2.26)
或
W1 − P1 f 2 W2 = 0 P2 f1
(2.27)
与
W1 + W2 = 1
(2.28)
连立,解得
P1 f 2 P1λ 2 k 2 W1 = = P2 f1 + P1 f 2 P2 λ1 k1 + P1λ 2 k 2 P2 f1 P1λ1 k1 W2 = = P2 f1 + P1 f 2 P2 λ1 k1 + P2 λ 2 k 2
(2.15)式相应地化为
N (t ) = ∑ a • f i • Wi ∫ e − ki ( t −τ ) C A (τ − θ 0 )dτ
i =1 0 2 t
(2.17)
其中α=γ/β,引入
Pi = a • f i • Wi , (i = 1,2)
(2.17)式化为
N (t ) = ∑ Pi ∫ e − ki (t −τ ) C A (τ − θ 0 )dτ
N (t ) = ∑ γ • f i • Wi ∫ e − ki ( t −τ ) Ca (τ )dτ
i =1 0 2 t
(2.15)
又设面罩中的探头测得受试者呼出气中的放射性计数率 为 C A (t ) 。由于动脉血从肺部将示踪剂带到脑部,因此呼出气中 的放射性计数率和肺动脉中示踪剂浓度成正比,比例系数 为 β 。由于动脉血从肺部流到脑部需时间 θ 0 (约为3秒钟), 就有 1 Ca (t ) = C A (t − θ 0 ) (2.16) β
用放射性同位素测定局部脑 血流量模型多媒体演示软件
一 问题的提出
在发达国家中,心脑血管疾病是威胁人们生命的最主要 疾病之一。在我国,由于人民生活的改善和健康水准的提高, 其他疾病的发病率下降,防治水平提高,心脑血管的发病率 及其导致的死亡率却相对地上升了。 脑血流量是诊断和治疗脑梗塞,脑出血,动脉瘤和先 天性动脉和静脉血管畸形等脑血管疾病的主要依据。测量 脑血流量可为研究人脑在不同的病理和生物条件下(入脑 外伤,脑循环停顿,缺氧等)的功能提供客观指标,它对 研究脑循环药物的药理作用也很有帮助。所以人们长期致 力于寻找有效地测定脑血流的方法。
∆t → 0 即得 Q (t ) 满足的
1
dQ1 f = f 1 • W1 • Ca (t ) − 1 Q1 (t ) dt D1
(2.8)
用同样的方法可得白质组织中示踪剂含量 Q2 (t ) 的方程
dQ2 f = f 2 • W2 • Ca (t ) − 2 Q2 (t ) dt D2
(2.9)
注意到初始时刻 t=0 时,灰,白质中示踪剂含量为0,有
(2.29)
由此得出单位质量脑组织的血流量为
f = f1 • W1 + f 2 • W2
(2.30)
三 参数的辨识
用上一节的数学模型解决rCBF测定问题,就要根据 N(t) 和 A (t ) C P 的离散测量值辨识 k1 , k2 , 1 ,P2 。典型的头部计数率曲线 (将测量的离散点经插值光润得到的曲线,称为头部清除曲线) 和呼出气计数率曲线分别由图2和图3所示。我们简单介绍辨识 这些参数的三种方法。
Q1 (t) /(D1 •W)
由此由静脉血从灰质带走的示踪剂量为
( 2 .3)
f1 Q = f 1 w1∆tQ1 (t ) /(D 1 • W ) = ∆tQ1 (t ) D1
v 1
( 2 .4 )
由( H 2 ),在这段时间内流入灰质的动脉血等于流出灰质 的血液量,由(2.2)式它是 f w1∆t ,又由动脉血中示踪剂浓度为 Ca(t),于是由动脉血输入的示踪剂量为
如何从测量的头部放射性计数率和面罩中的放射性计数 率确定局部脑血流量呢?要解决这个问题,首先要建立合理 的数学模型。
二 假设和建模
2.A主要假设 大脑皮层主要由灰质和白质构成。由于毛细血管分布不 同等原因,血在灰质中的流量和白质的流量是不一样的。实 验表明,血在脑灰质中流动比在脑白质中约快5-10倍,为精 确地测定脑血流量,有必要分别确定脑灰质中的血流量和脑 白质中的血流量。这两种血流量对临床诊断也是有意义的。 根据已有的实验结果,有如33 Xe 作为示踪剂,用133 Xe 作示踪剂有很多优点。首 先133 Xe 是主要随血液的流动而流动,与脑组织结合留在脑中比 例极小。其次是 133 Xe 的半衰期约为二十几个小时,对人体的危 害极小,同时不需太长时间又能进行再次测定,而且在测试 的十几分钟之内,由于衰变引起的放射性计数率的减少是相 当的。 70年代末,80年代初,这种测量rCBF 的仪器已经形成商品。 我国也进行了独立的研制。由于这种仪器能无创伤而又比较准 确地测定局部脑血流量,价格又较 CT 等有同样功能的仪器便 宜得多,因而很受医院特别是中小医院的欢迎。
Qi (0) = 0, (i = 1,2)
( 2.12 )
从(2.11), (2.12) 式立即解得
Qi (t ) = f i • Wi ∫ e − ki ( t −τ ) Ca (τ )dτ
0 t
(2.13)
于是,在时刻t,1克脑组织中示踪剂的含量应为
Q(t ) = Q1 (t ) + Q2 (t ) = ∑ f i • Wi ∫ e − ki ( t −τ ) Ca (τ ) dτ
2.b Fick原理和模型的建立 考察单位质量(1克)脑组织中的示踪剂数量,在这部分脑 组织中放射性示踪剂数量的改变应为动脉血输入的示踪剂量 与静脉血从这部分组织中携出的示踪剂量之差。这就是核医 药工程中常用的Fick原理。现在用Fick原理分别考察单位脑组 织中,灰质中的示踪剂量和白质中的示踪剂量的变化。 设单位质量灰质和白质脑流量分别为 f 和 f ,单位应 为 ml/( g •min ),即每分钟从每克脑灰质或脑白质中流出的血液 为 f 毫升或 f 毫升;又设时刻 流入脑组织的动脉血中放射性 示踪剂的浓度为Ca(t);在时刻 ,1克脑组织中灰质血液中的示 踪剂含量和白质血液中的示踪剂含量分别 Q (t) 为Q2 (t ) 和。
