轴承寿命及推力计算3.16
滚动轴承寿命计算公式

滚动轴承寿命计算公式滚动轴承寿命计算是判断滚动轴承寿命的重要方法,它是基于滚动轴承的结构及使用条件进行分析,通过考虑滚动接触应力、脂润滑条件等因素,计算出滚动轴承的寿命。
滚动轴承寿命计算公式是基于ISO标准的经验公式,其中最常使用的是基本额定寿命公式。
滚动轴承的基本额定寿命(L10)是指在相同条件下,有10%的轴承在寿命前失效。
滚动轴承寿命分为疲劳寿命和表面疲劳寿命,其中疲劳寿命是指由于滚动和滑动过程中产生的疲劳损伤导致的寿命。
表面疲劳寿命是指由外在原因(如进入外来颗粒等)引起的表面大片剥落,导致轴承失效的寿命。
滚动轴承的基本额定寿命(L10)的计算公式如下:L10 = (C/P)^3 × (1000000/60)其中,C为基本动载荷,P为等效动载荷。
基本动载荷(C)是滚动轴承能够承受的最大载荷。
它由制造商提供,根据ISO标准进行计算。
等效动载荷(P)是指滚动轴承在使用过程中的实际载荷,它考虑了滚动轴承的载荷分布及轴承的轴向受力情况。
在实际应用中,滚动轴承的使用条件可能会发生变化,例如工作温度、转速、润滑条件等。
考虑到这些因素对寿命的影响,可以使用修正系数进行修正。
其中,温度修正系数(a1)、转速修正系数(a2)和脂润滑修正系数(a3)是常见的修正系数。
它们表示滚动轴承在不同工况下寿命与基本额定寿命之间的比值。
修正后的寿命(L)可以根据以下公式计算:L = L10 × a1 × a2 × a3同时,还有其他一些公式可以用于计算滚动轴承的寿命,例如基本动载荷的计算公式和等效载荷的计算公式。
这些公式可以根据具体的应用要求和实际情况进行选择和计算。
综上所述,滚动轴承寿命计算公式是根据滚动轴承的结构和使用条件进行分析的重要方法。
通过计算基本额定寿命和修正系数,可以得到滚动轴承的寿命。
计算公式的准确性和合理性对于滚动轴承的设计和选用非常重要,可以提高轴承的使用寿命和可靠性。
轴承寿命的计算

念根据最新的滚动轴承疲劳寿命理论,一只设计优秀、材质卓越、制造精良而且安装正确的轴承,只要其承受的负荷足够轻松(不大于该轴承相应的某个持久性极限负荷值),则这个轴承的材料将永远不会产生疲劳损坏。因此,只要轴承的工作环境温度适宜而且变化幅度不大,绝对无固体尘埃、有害气体和水分侵入轴承,轴承的润滑充分而又恰到好处,润滑剂绝对纯正而无杂质,并且不会老化变质……,则这个轴承将会无限期地运转下去。这个理论的重大意义不仅在于它提供了一个比ISO寿命方程更为可靠的预测现代轴承寿命的工具,而且在于它展示了所有滚动轴承的疲劳寿命都有着可观的开发潜力,并展示了开发这种潜力的途径,因而对轴承产品的开发、质量管理和应用技术有着深远的影响。但是,轴承的无限只有在实验室的条件下才有可能“实现”,而这样的条件对于在一定工况下现场使用的轴承来说,既难办到也太昂贵。现场使用轴承,其工作负荷往往大于其相应的疲劳持久性极限负荷,在工作到一定的期限后,或晚或早总会由于本身材料达致电疲劳极限,产生疲劳剥落而无法继续使用。即使某些轴承的工作负荷低于其相应的持久性极限负荷,也会由于难以根绝的轴承污染问题而发生磨损失效。总之,现场使用中的轴承或多或少总不能充分具备上述实验室所具备的那些条件,而其中任一条件稍有不足,都会缩短轴承的可用期限,这就产生了轴承的寿命问题。一般地说,滚动轴承的寿命是指滚动轴承在实际的服务条件下(包括工作条件、环境条件和维护和保养条件等),能持续保持满足主动要求的工作性能和工作精度的特长服务期限。二、可计算的轴承寿命类别滚动轴承的失效形式多种多样,但其中多数失效形式迄今尚无可用的寿命计算方法,只有疲劳寿命、磨损寿命、润滑寿命和微动寿命可以通过计算的方法定量地加以评估。1、疲劳寿命在润滑充分而其他使用条件正常的情况下,滚动轴承常因疲劳剥落而失效,其期限疲劳寿命可以样本查得有关数据,按规定的公式和计算程序以一定的可靠性计算出来。2、磨损寿命机床主轴承取大直径以保证其高刚度,所配轴承的尺寸相应也大,在其远末达到疲劳极限之前,常因磨损而丧失要精度以致无法继续使用,对这类轴承必须用磨损寿命来徇其可能性的服务期限。实际上,现场使用的轴承大多因过度磨损而失效,所以也必须考虑磨损寿命问题。3、润滑寿命主要对于双面带密封的脂润滑轴承,一次填脂以后不再补充加脂,此时轴承有寿命便取决于滚脂的使用寿命。4、微动磨蚀寿命绞车、悬臂式起微型重机和齿轮变速箱以及汽车离合器等机构中的轴承,在其非运转状态下受到振动负荷所产生的微动磨蚀损伤。往往会发展成轴承失效的主导原因,对这类机构中的轴承,有时需要计算其微动磨蚀寿命。现将此四种寿命类别及其计算方法分别加以介绍。一、滚动轴承的疲劳寿命1、轴承疲劳寿命的基本概念一般意义的轴承疲劳寿命是指一定技术状态下(结构、工艺状态、配合、安装、游隙和润滑状态等)的滚动轴承,在主机的实际使用状态下运转,直至滚动表面发生疲劳而不能满足主机要求时的轴承内、外圈(轴、座圈)相对旋转次数的总值——总转数。当轴承转更大致恒定或为已知,疲劳寿命可用与总转数相应的运转总小时数来表示,此外,还应注意:1、影响轴承疲劳寿命的因素非常多,无法全部加以估计或通过标准试验条件而加以消除,这造成轴承实际疲劳寿命有很大的离散性,因此轴承疲劳寿命的表达参数为额定寿命L10,在ISO推荐标准R281中对L10的涵义明确规定如下:“数量上足够多的相同的一批轴承,其额定寿命L10用转数(或在转速不变时用小时数来表示,该批轴承中有90%在疲劳剥落发生前能达到或超过此转数(或小时数)”。迄今为止,世界各国都遵从上述规定。在美国等一些国家中,还用用中值寿命的概念。中值寿命LM是指一批相同轴承的中值寿命,即指其中50%的轴承在疲劳剥落前能够达到或超过总转数,或在一定转速下的工作不时数,中值寿命LM不是一批轴承寿命的算术平均值。一般中值寿命LM是额定寿命的5倍左右。2、额定寿命的概念只适用于数量足够的一批轴承,而不适用于个别轴承。例如有40套6204轴承按其使用条算得其额定寿命为1000h而不致发生疲劳破坏,其余的4套则可能不到1000h即出现疲劳失效的轴承,额定疲劳寿命的意义就代表这批轴承在正常发挥其材料潜力时可期望的寿命。因此在大多数情况下,用户在选择轴承时仍先作疲劳寿命计算,再根据实际失效类别进行校核,例如磨损寿命校核,取计算结果中的较小值为轴承计算寿命。二、轴承疲劳寿命的估计方法、轴承疲劳寿命的估计方法有计算方法和试验湛支两种。按规定公式和计算规则计算出来的轴承疲劳寿命作为计算疲劳寿命,所算出总转数值规定为内圈或轴圈转动(此时外圈或座圈为固定)时的总转数值。按照我国规定的标准试验方法(ZQ 12-94)滚动轴承疲劳寿命试验规程),在使用性能上能满足为一方法所规定各项要求的试验机,对一批轴承进行抽样疲劳寿命试验,从试验数据处理中得到的实际试验寿命,即为被试轴承所代表的该批轴承的疲劳试验寿命。滚动轴承疲劳寿命试验裨上是充分的润滑最大限度地抑制滚动轴承的磨损因素,采用强化的负荷与转速以突出轴承疲劳因素的一种强化的疲劳寿命试验方法。轴承疲劳寿命的计算法和疲劳寿命试验是相辅相成的,二者所得的结果有足够的对应性。事实上,如对每一个特定的使用场合,都抽取足够数量的轴承进行寿命试验,以验证所选轴承是否合适,这在经济上、时间上和劳动量上都是十分浩大的,所以轴承寿命的试验方法只是在十分必要或重要的情况下才使用,在绝大多数情况下,采用标准的寿命计算方法来估计轴承的使用寿命,有着足够程度的可依赖性。三、疲劳寿命的计算下述轴承疲劳寿命的计算方法是以国家标准GB6391-96《滚动轴承——-额定动负荷和额定寿命的计算方法》和国家标准ISO281/I-1997《滚动轴承——额定动负荷和额定寿命——第一部分:计算方法》为依据,此外,还介绍了瑞典SKF轴承公司新的轴承公司新的轴承疲劳寿命理论和疲劳寿命计算方法。1、疲劳寿命的基本计算公式滚动轴承疲劳寿命的基本计算公式有多种形式,以适应不同用途的需要,以下分别加以介绍。(1)基本额定寿命方程(用总转数表示)1、几个有关的基本概念,在介绍基本额定寿命方程之前,先介绍几个相关的基本概念即:单个轴承的疲劳寿命——单个轴承在其任一套圈(或垫圈)或滚动体的材料首次出现疲劳扩展之前,其中一个套圈(或垫圈)相对于另一套圈(或垫圈)转动的总转数。轴承寿命的可靠性——在同一条件下运转的一组在相同条件下运转的一组条件相同的轴承,可期望达到或超过某一规定寿命的百分率,对于单个轴承,其可靠性为该轴承能达到或超过某一规定寿命的概念。轴承的基本额定寿命——单个轴承或一组在相同条件下运转的技术条件相同的轴承,其可靠性达到90%时的寿命。3、基本额定寿命方程的计算式用总转数表示的轴承基本额定寿命方程的计算式为:L10=C/P式中L10——轴承的基本额定疲劳寿命(106r); C——对向心类轴承为径向当量动负荷(N),对推力类轴承为轴向当量动负荷(N);P——对向心类轴承为径向当量动负荷(N),对推力类轴承为轴向当量动负荷(N);ε——寿命指数,对球轴承ε=3,对滚动轴承ε=10/3。式5-1为我国国家标准和国际标准规定的滚动轴承基本额定寿命的标准计算式。轴承疲劳轴承寿命试验机的转数记录仪,可以准确地记录下轴承疲劳试验的总转数,得以方便与计算结果相对照。4、基本额定寿命方程的适用范围基本额定寿命方程5-1适用于具备以下技术条件的滚动轴承在额定疲劳寿命计算;轴承的外形尺寸选自由国家相应标准规定的轴承尺寸范围;轴承用优质淬硬钢材制造并且加工质量良好;轴承滚动接触表面的表面质量(包括几何形状精度和材质等)合乎常规标准。这些轴承必须安装正确,润滑充分,无外界杂质侵入而且不是在极端条件下运转。当不符合这些条件时,使用式5-1的计算结果便会发生偏差。为了抵消这样的偏差,就必须将按式5-1计算所得的结果乘上相应的修正系数。5、基本额定寿命方程的应用限制基本额定寿命方程5-1不适用例如有装填满的深沟球轴承,或在滚动体与套圈滚道之间的接触面积上有相当大缺口的其他种类轴承,因为这种缺口影响到接触区的承载能力。式5-1还不适用滚动体直接在轴或座孔表面上运转的场合,除非相应的轴或座孔完全按照滚动轴承承载元件的技术条件制造。当轴承在实际使用时其所承受的负荷为非正常分布(例如由于轴线不对中,外壳或轴有较大变形,滚动体的离心力作用或其他高速效应,以及向心轴承采用特别大的游隙或施加预负荷等情况造成),按式5-1计算其基本额定寿命时,就不能取得满意的结果。
轴承设计寿命计算公式

当轴承的可靠性不为90%时,应加入可靠性寿命修正系数(表7)
表7可靠性寿命修正系数a1
可靠度(%)
90
95
96
97
98
99
a1
1
0.62
0.53
0.44
0.33
0.21
(2)运转条件的寿命修正系数a3
●正常运转条件下,可取a3=1;
●润滑条件十分理想时,可取a3>1;
●润滑条件不好时,可取a3<1。
表4角接触球轴承的系数X、Y
表5其它向心轴承的系数X、Y
表6推力轴承的系数X、Y
七、成对轴承所受轴向力
计算公式:
角接触球轴承:
圆锥滚子轴承:
式中e为判断系数,可由表4查出;Y应取表5中 的数值。
??????●正排列:若
则???
若????
则???
●反排列:若
则???
若??? ?
则???
八、成对轴承当量动载荷
(3)特殊的轴承性能寿命修正系数a2
●采用夹杂物含量非常低或经过特别分析处理的钢材,可取 ;
●采用特殊的材料、工艺或设计,而润滑却不良时,a2通常不能大于1的值;
●若采用特殊的热处理造成材料硬度降低而导致轴承寿命下降,应选取相应减小的a2值。
五、载荷系数fp
当轴承承受有冲击载荷时,当量动载荷计算时,引入载荷系数(表2)
表2冲击载荷系数fp
载荷性质
fp
举 例
无冲击或轻微冲击
1.0~1.2
电机、汽轮机、通风机、水泵等
中等冲击
1.2~1.8
车辆、机床、起重机、内燃机等
强大冲击
1.8~3.0
轴承的寿命计算

一、额定寿命与额定动载荷1、轴承寿命在一定载荷作用下,轴承在出现点蚀前所经历的转数或小时数,称为轴承寿命。
由于制造精度,材料均匀程度的差异,即使是同样材料,同样尺寸的同一批轴承,在同样的工作条件下使用,其寿命长短也不相同。
若以统计寿命为1单位,最长的相对寿命为4单位,最短的为0.1-0.2单位,最长与最短寿命之比为20-40倍。
为确定轴承寿命的标准,把轴承寿命与可靠性联系起来。
2、额定寿命同样规格(型号、材料、工艺)的一批轴承,在同样的工作条件下使用,90%的轴承不产生点蚀,所经历的转数或小时数称为轴承额定寿命。
3、基本额定动载荷为比较轴承抗点蚀的承载能力,规定轴承的额定寿命为一百万转(106)时,所能承受的最大载荷为基本额定动载荷,以C表示。
也就是轴承在额定动载荷C作用下,这种轴承工作一百万转(106)而不发生点蚀失效的可靠度为90%,C越大承载能力越高。
对于基本额定动载荷(1)向心轴承是指纯径向载荷(2)推力球轴承是指纯轴向载荷(3)向心推力轴承是指产生纯径向位移得径向分量二、轴承寿命的计算公式:洛阳轴承厂以208轴承为对象,进行大量的试验研究,建立了载荷与寿命的数字关系式和曲线。
式中:L10--轴承载荷为P时,所具有的基本额定寿命(106转)C--基本额定动载荷Nε--指数对球轴承:ε=3对滚子轴承:ε=10/3P--当量动载荷(N)把在实际条件下轴承上所承受的载荷: A、R ,转化为实验条件下的载荷称为当量动载荷,对轴承元件来讲这个载荷是变动的,实验研究时,轴承寿命用106转为单位比较方便(记数器),但在实际生产中一般寿命用小时表示,为此须进行转换L10×106=Lh×60n所以滚动轴承寿命计算分为:1、已知轴承型号、载荷与轴的转速,计算Lh;2、已知载荷、转速与预期寿命,计算C ,选取轴承型号。
通常取机器的中修或大修界限为轴承的设计寿命,一般取Lh'=5000,对于高温下工作的轴承应引入温度系数ftCt=ftCt ≤120 125 150 200 300ft 1 0.95 0.90 0.80 0.60上两式变为:对于向心轴承对于推力轴承三、当量动载荷P的计算在实际生产中轴承的工作条件是多种多样的,为此,要把实际工作条件下的载荷折算为假想寿命相同的实验载荷--当量载荷。
轴承的寿命与计算

轴承的寿命轴承在随负荷旋转时,由于套圈滚道面及滚动体滚动面不断地受到交变负荷的作用,即使使用条件正常,也会因材料疲劳使滚道面及滚动面出现鱼鳞状损伤(称做剥离或剥落)。
出现这种滚动疲劳操作之前的总旋转数称做轴承的“(疲劳)寿命”。
即使是结构、尺寸、材料、加工方法等完全相同的轴承,在同样条件下旋转时,轴承的(疲劳)寿命仍会出现较大的差异。
这是因为材料疲劳本身即具有离散性,应从统计的角度来考虑。
于是就将一批相同的轴承在同样条件下分别旋转时,其中90%的轴承不出现滚动疲劳操作的总旋转数称做“轴承的基本额定寿命”(即可靠性为90%的寿命)在以固定的转速旋转时,也可用总旋转时间表示。
但在实际工作时,还会出现滚动疲劳操作以外的损伤现象(如磨损、烧伤、蠕变、磨蚀、压痕、断裂等)。
这些损伤可以通过做好轴承的选择、安装和润滑等加以避免。
轴承寿命的计算基本额定动负荷基本额定动负荷表示轴承耐滚动疲劳的能力(即负荷能力),是指大小和方向一定的纯径向负荷(对于向心轴承)或中心轴向负荷(对于推力轴承),在内圈旋转外圈固定(或内圈固定外圈旋转)的条件下,该负荷下的基本额定寿命可达100万转,向心轴承与推力抽承的基本额定动负荷分别称做径向基本定动负荷与轴向基本额定动负荷,用Cr与Ca表示,其数值载于轴承尺寸表。
基本额定寿命式(1)表示轴承的基本额定动负荷、当量动负荷及基本额定寿命之间的关系。
轴承以固定的转速旋转时,用时间表示寿命更为方便,如式(2)所示。
另外,对于铁路车辆或汽车等用行走距离(KM)表示寿命较多,如式(3)所示。
这里:L10:基本额定寿命,106转L10h:基本额定寿命,hL10s:基本额定寿命,kmP:当量动负荷,N{Kgf}厖......参照后面C:基本额定动负荷,N{Kgf}n:转速,rpmp:寿命指数球轴承..........p=3滚子轴承.......p=10/3D:车轮或轮胎直径,mm因此,作为轴承的使用条件,设当量动负荷为P,转速为n,则满足设计寿命所需要的轴承基本额定动负荷C可由式(4)计算,从轴承尺寸表中选出满足C值的轴承,即可确定轴承的尺寸。
轴承寿命计算

mm
承载中心与轴承B间距L2(附录1) L2
mm
轴承A承载负荷
F5
N
轴承B承载负荷
F6
N
30000 29509.5 27547.5 25585.5
27324
143 180 34393 7070
30000 29509.5 27547.5 25585.5 27314
143 180 34381 7067
1
计算公式: F1=F-M*0.1*9.81/Y F2=F-M*0.5*9.81/Y F3=F-M*0.9*9.81/Y F4=[(F1P*15%)+(F2P*55%)+(F3P*30%)]1/P F5=F4*L2/L1 F6=abs(F5-F4)
3、轴承寿命系数计算:
轴承 型号 转速 额定动负荷 径向负荷 可靠度系数
设计计算书
轴承寿命计算
编制: 校对: 批准: 日期:
一、计算目的:
通过轴承的承载负荷计算和轴承的寿命需求计算校核轴承寿命是否满足要求。
二、参考资料:
《机械设计手册》第3卷,P20-77至P20-86、《SKF轴承样品选型手册》
三、计算过程:
1、轴承寿命需求计算:
输入参数
载重 速度 曳引轮直径 绕绳比 使用寿命(年) 每年运行次数 平均每次运行距离(m) 输出结果:
轴承B(SKF) 6217 167 83300 7,067 0.62
3 163,320 101,259 1637.6 1015.3 127.3
7.97
计算公式: n=[60*V/(π*D/1000)]*Y Q1=[1000000/(60*n)]*(C/R)P Q2=a1*Q1 Q3=(C/R)P Q4=a1*Q3 Q5=Q*X*Z/1000000 α=Q4/Q5
轴承寿命计算公式程序

轴承寿命计算公式程序在工程领域中,轴承是一种常见的机械零件,用于支撑和减少旋转摩擦。
轴承的寿命是指在一定条件下,轴承能够正常运转的时间,通常以小时或者圈数来表示。
轴承的寿命对于机械设备的性能和可靠性具有重要的影响。
因此,准确地计算轴承的寿命对于工程设计和维护具有重要意义。
轴承的寿命计算公式是根据轴承的负荷、转速、润滑方式等因素来确定的。
一般来说,轴承的寿命可以通过以下公式来计算:L = (C/P)^p。
其中,L为轴承的寿命(小时),C为基本额定动载荷(N),P为等效动载荷(N),p为指数。
在实际应用中,轴承的寿命计算还需要考虑到轴承的使用环境、润滑方式、轴承材料等因素。
因此,轴承的寿命计算公式程序需要考虑到这些因素的影响。
首先,基本额定动载荷(C)是指在轴承额定寿命(106次转动)内,轴承能够承受的最大动载荷。
它是由轴承制造商根据轴承的材料、几何形状等因素确定的。
基本额定动载荷是轴承寿命计算的重要参数,它直接影响到轴承的寿命。
其次,等效动载荷(P)是指在实际工作条件下,轴承承受的动载荷。
由于轴承在实际工作中可能同时承受径向载荷和轴向载荷,因此需要将这两种载荷转换为等效动载荷。
等效动载荷的计算需要考虑到轴承的载荷分布、工作条件等因素。
最后,指数(p)是根据轴承的类型、润滑方式等因素确定的。
不同类型的轴承具有不同的指数,它反映了轴承在不同工作条件下的寿命特性。
综上所述,轴承的寿命计算公式程序需要考虑到轴承的基本额定动载荷、等效动载荷和指数等因素。
通过合理地计算轴承的寿命,可以帮助工程师们选择合适的轴承类型和规格,从而提高机械设备的性能和可靠性。
除了轴承的寿命计算公式程序,轴承的寿命还受到许多其他因素的影响。
例如,轴承的润滑方式对于轴承的寿命具有重要影响。
合适的润滑方式可以减少轴承的摩擦和磨损,延长轴承的寿命。
此外,轴承的安装和维护也会影响轴承的寿命。
正确的安装和定期的维护可以减少轴承的故障率,延长轴承的使用寿命。
轴承寿命计算公式

轴承寿命计算公式背景介绍轴承是机械设备中常用的零部件之一,它承受着旋转运动的负载,所以轴承的寿命对于机械设备的正常运转至关重要。
轴承寿命的计算公式是轴承设计和使用过程中的重要依据,它可以帮助工程师和用户了解轴承在不同工况下的寿命表现,并进行合理的选择和使用。
轴承寿命的影响因素轴承寿命受到多种因素的影响,包括负载、转速、润滑方式、工作温度等。
在进行轴承寿命计算时,需要考虑到这些因素的综合影响,确保计算结果的准确性。
轴承寿命计算公式简介轴承寿命计算公式的基本形式为L = (C/P)^p,其中L表示轴承的寿命,C表示基本额定动载荷,P表示等效动载荷,p表示轴承的L10寿命系数。
基本额定动载荷基本额定动载荷是指在轴承设计时,根据标准化试验条件下,轴承允许的最大动载荷。
它通常由制造商提供,并且与轴承的型号和尺寸有关。
等效动载荷等效动载荷是指在实际工况下的轴承负载,它是基于实际负载和一组修正因素计算得出的一个数值。
等效动载荷考虑到了轴承在不同方向上的负载以及负载的变化情况。
L10寿命系数L10寿命系数是根据统计学原理和实验数据推导得出的一个系数,它表示在相同工况下,90%的轴承能够运转到超过该寿命的寿命。
L10寿命系数可以根据轴承的类型、尺寸和工况条件来确定。
轴承寿命计算公式的应用轴承寿命计算公式广泛应用于轴承选择、设计和使用过程中。
通过计算公式可以得到轴承的寿命,从而进行合理的轴承选择和工程设计。
对于机械设备的用户来说,轴承寿命计算公式可以帮助他们了解设备寿命,及时进行维修和更换,减少停机时间和维修成本。
使用示例假设某机械设备的基本额定动载荷为10000N,等效动载荷为8000N,L10寿命系数为1.5。
则根据轴承寿命计算公式,可以计算出轴承的寿命为:L = (10000/8000)^1.5 = 1.32^1.5 = 2.14 × 10^7 个循环总结轴承寿命计算公式是轴承设计和使用中的重要工具,它可以帮助工程师和用户了解轴承的寿命表现,并选择合适的轴承。
轴承寿命计算
–
6005-Z 6205-Z 6305-Z
6006-Z 6206-Z 6306-Z
6007-Z 6207-Z 6307-Z
6008-Z 6208-Z 6308-Z
6009-Z 6209-Z 6309-Z
6005-2Z 6205-2Z 6305-2Z
6006-2Z 6206-2Z 6306-2Z
6007-2Z 6207-2Z 6307-2Z
速度级别 润滑 润滑脂 润滑油
重量
型号 带有一个 带有两个 防护罩 防护罩
r/min
kg
15 000 12 000 11 000
18 000 15 000 14 000
0,080 0,13 0,23
12 000 15 000 0,12 10 000 13 000 0,20 9 000 11 000 0,35
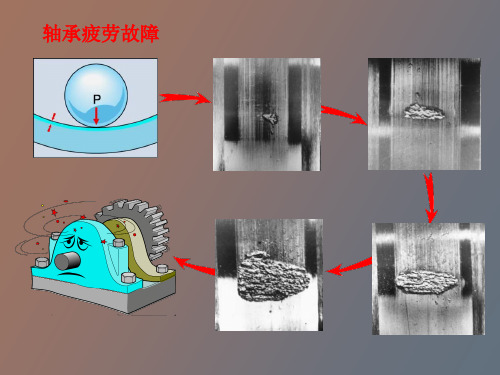
轴承疲劳故障
轴承寿命的计算准则
对一般工作条件下的回转滚动轴承——经常发生点蚀, 主要进行寿命计算,必要时进行静强度校核;
对于不转动、摆动或转速低(n≦10 r/min)的轴承,要 求控制塑性变形,只需进行静强度计算;
对于高速轴承——由于发热而造成的粘着磨损、烧伤常常 是突出的矛盾,除进行寿命计算外,还需校验极限转速。
10 000 13 000 0,16 9 000 11 000 0,29 8 500 10 000 0.46
9 500 8 500 7 500
12 000 0,19 10 000 0,37 9 000 0,63
9 000 7 500 6 700
11 000 0,25 9 000 0,41 8 000 0,83
45 75 16 85 19 100 25
动态负荷值
轴承寿命的计算.

计算轴承寿命
L10h = 1,000,000 x (C/P)p 60 x n
L10h:工作小时 n:轴承工作转速
C:额定负荷. P:当量负荷.
SKF新的寿命计算方法
• 现已被ABMA/ISO接受
Lna = a1·aSKF (C/P)p
• 新寿命方法陈述了两个基本概念
1.将疲劳负荷极限和其他几项与润滑及污染有关的因
当负荷 P0 = C0时 静态安全因素s0将为 1
正确认识额定动载荷C
额定动载荷仅是由轴承的若干基本 几 何尺寸计算而来 C ~ (la· cos)7/9· z3/4· Dw 29/27 与轴承实际制造质量和使用性能密切 相关的密切相关的很多因素, 并不能 通过C值反映: 材料质量 热处理工艺 内部结构设计 内部几何形状 制造精度 公差控制 表面硬度 滚动体与滚道的切合程度 内部摩擦
谢 谢 大 家!
其中疲劳极限pu是一个全新的概念若承受的负荷低于pu值则轴承不会产生疲劳失效损坏新寿命方法修改了调整的寿命等式以计算将理论更进一步联系实际的新发现skf与可靠性相关的寿命修正系数
轴承寿命的计算
测算轴承寿命真空吸尘器的寿命可为1000小时
典型工业应用的寿命约为40,000小时,或4-5年 左右 较昂贵的机器一般设计的使用寿命较长 –造纸机轴承设计的使用寿命为10-20万小时 (10-20年)
素也考虑其中 2.其中疲劳极限Pu是一个全新的概念,若承受的负 荷低于Pu 值,则轴承不会产生疲劳失效(损坏)
• 新寿命方法修改了调整的寿命等式以计算将理 论更进一步联系实际的新发现
调整的寿命公式中参数的选取:a1
• • • • • • • • a1 与可靠性相关的寿命调整系数. aSKF 与可靠性相关的寿命修正系数. 表现为以下相关方面: 轴承安装是否正确 轴承与相关零件选择的配合公差的选择是否合适 轴承在运行时的润滑状况 轴承在运行时的工作状态(外部的温升,振动,密封) 其他因素
(完整版)滚动轴承的寿命计算

滚动轴承的寿命计算一、基本额定寿命和基本额定动载荷1、基本额定寿命L10轴承寿命:单个滚动轴承中任一元件出现疲劳点蚀前运转的总转数或在一定转速下的工作小时数称轴承寿命。
由于材料、加工精度、热处理与装配质量不可能相同,同一批轴承在同样的工作条件下,各个轴承的寿命有很大的离散性,所以,用数理统计的办法来处理。
基本额定寿命L10——同一批轴承在相同工作条件下工作,其中90%的轴承在产生疲劳点蚀前所能运转的总转数(以106为单位)或一定转速下的工作时数。
(失效概率10%)。
2、基本额定动载荷C轴承的基本额定寿命L10=1(106转)时,轴承所能承受的载荷称基本额定动载荷C。
在基本额定动载荷作用下,轴承可以转106转而不发生点蚀失效的可靠度为90%。
基本额定动载荷C(1)向心轴承的C是纯径向载荷;(2)推力轴承的C是纯轴向载荷;(3)角接触球轴承和圆锥滚子轴承的C是指引起套圈间产生相对径向位移时载荷的径向分量。
二、滚动轴承的当量动载荷P定义:将实际载荷转换为作用效果相当并与确定基本额定动载荷的载荷条件相一致的假想载荷,该假想载荷称为当量动载荷P,在当量动载荷P作用下的轴承寿命与实际联合载荷作用下的轴承寿命相同。
1.对只能承受径向载荷R的轴承(N、滚针轴承)P=F r2.对只能承受轴向载荷A的轴承(推力球(5)和推力滚子(8))P= F a3.同时受径向载荷R和轴向载荷A的轴承P=X F r+Y F aX——径向载荷系数,Y——轴向载荷系数,X、Y——见下表。
径向动载荷系数X和轴向动载荷系数表12-3考虑冲击、振动等动载荷的影响,使轴承寿命降低,引入载荷系数fp—见下表。
载荷系数fp表12-4三、滚动轴承的寿命计算公式图12-9 载荷与寿命的关系曲线载荷与寿命的关系曲线方程为:=常数(12-3)3 球轴承ε——寿命指数10/3——滚子轴承根据定义:P=C,轴承所能承受的载荷为基本额定功载荷时,∴∴(106r) (12-2)按小时计的轴承寿命:(h)(12-3)考虑当工作t>120℃时,因金属组织硬度和润滑条件等的变化,轴承的基本额定动载荷C有所下降,∴引入温度系数f t——下表——对C修正表 12-5(106r)(12-4)(h)(12-5)当P、n已知,预期寿命为L h′,则要求选取的轴承的额定动载荷C为N ——选轴承型号和尺寸!(12-6)不同的机械上要求的轴承寿命推荐使用期见下表。
轴承设计寿命计算公式汇总

轴承设计寿命计算公式汇总
1.基本额定寿命计算公式:这是最常用的轴承寿命计算公式之一、其公式为:
L10=(C/P)^p
其中,L10为基本额定寿命(单位为小时),C为基本动态载荷(单位为牛顿),P为等效动载荷(单位为牛顿),p为寿命指数。
2.调整额定寿命计算公式:为了考虑实际工况下的不同负荷条件对轴承寿命的影响,可以采用调整额定寿命计算公式:
Lna = a1*a2*a3*a4*L10
其中,Lna为调整额定寿命,a1为轴承类型系数,a2为载荷系数,a3为调心系数,a4为润滑系数。
3.轴承磨损寿命计算公式:轴承在使用过程中会发生磨损,通过估算轴承磨损寿命可以预测轴承的使用寿命。
对于循环运动的轴承,其磨损寿命Lw可以通过以下公式计算:
Lw=Cw/F
其中,Cw为磨损因数,F为载荷。
4.疲劳寿命计算公式:轴承在高速、高负荷、长时间运行的情况下容易发生疲劳现象,疲劳寿命是指轴承在正常工作条件下能够承受的疲劳载荷循环数。
L10h=(10^6/(60*n))*((C/P)^p)
其中,L10h为疲劳寿命(单位为小时),n为转速。
5.温度因子计算公式:轴承在工作时会产生热量,可以通过计算温度因子来估算轴承的使用寿命。
温度因子aISO可以通过以下公式计算:aISO=a*〖10(ΔT/10)〗^b
其中,a、b为轴承类型参数,ΔT为温度变化。
以上是一些常用的轴承设计寿命计算公式汇总。
需要注意的是,不同类型的轴承有不同的设计寿命计算公式,具体应根据实际情况选择合适的计算方法。
此外,在进行寿命计算时还需要考虑轴承材料、润滑方式、工作温度等因素对轴承寿命的影响。
轴承设计寿命计算公式

一、滚动轴承承载能力的一般说明 滚动轴承的承载能力与轴承类型和尺寸有关。
相同外形尺寸下,滚子轴承的承载能力约为球轴承的1.5~3倍。
向心类轴承主要用于承受径向载荷,推力类轴承主要用于承受轴向载荷。
角接触轴承同时承受径向载荷和轴向载荷的联合作用,其轴向承载能力的大小随接触角α的增大而增大。
二、滚动轴承的寿命计算 轴承的寿命与载荷间的关系可表示为下列公式: 或 式中:──基本额定寿命(106转);──基本额定寿命(小时h);C──基本额定动载荷,由轴承类型、尺寸查表获得;P──当量动载荷(N),根据所受径向力、轴向力合成计算;──温度系数,由表1查得;n──轴承工作转速(r/min);──寿命指数(球轴承,滚子轴承)。
三、温度系数f t 当滚动轴承工作温度高于120℃时,需引入温度系数(表1) 当滚动轴承同时承受径向载荷和轴向载荷时,当量载荷的基本计算公式为式中:P——当量动载荷,N;——径向载荷,N;——轴向载荷,N;X——径向动载荷系数;Y——轴向动载荷系数;——负荷系数五、载荷系数f p 当轴承承受有冲击载荷时,当量动载荷计算时,引入载荷系数(表2)表2 冲击载荷系数f表3 深沟球轴承的系数X、Y表4 角接触球轴承的系数X、Y表5 其它向心轴承的系数X、Y表6 推力轴承的系数X、Y七、成对轴承所受轴向力 计算公式: 角接触球轴承: 圆锥滚子轴承:式中e为判断系数,可由表4查出;Y应取表5中的数值。
●正排列:若则 若 则 ●反排列:若则 若 则 八、成对轴承当量动载荷 根据基本公式:式中:P——当量动载荷,N;——径向载荷,N;——轴向载荷,N;X——径向动载荷系数;Y——轴向动载荷系数;——负荷系数。
九、修正额定寿命计算 对于要求不同的可靠度、特殊的轴承性能以及运转条件不属于正常情况下的轴承寿命计算时,可采用修正额定寿命计算公式:式中:──特殊的轴承性能、运转条件以及不同可靠度要求下的修正额定寿命(106转);a1──可靠度的寿命修正系数;a2──特殊的轴承性能寿命修正系数;a3──运转条件的寿命修正系数。
轴承设计寿命计算公式

一、滚动轴承承载能力的一般说明滚动轴承的承载能力与轴承类型和尺寸有关。
相同外形尺寸下,滚子轴承的承载能力约为球轴承的1.5~3倍。
向心类轴承主要用于承受径向载荷,推力类轴承主要用于承受轴向载荷。
角接触轴承同时承受径向载荷和轴向载荷的联合作用,其轴向承载能力的大小随接触角α的增大而增大。
二、滚动轴承的寿命计算轴承的寿命与载荷间的关系可表示为下列公式:或式中:──基本额定寿命(106转);──基本额定寿命(小时h);C──基本额定动载荷,由轴承类型、尺寸查表获得;P──当量动载荷(N),根据所受径向力、轴向力合成计算;──温度系数,由表1查得;n──轴承工作转速(r/min);──寿命指数(球轴承,滚子轴承)。
三、温度系数f t当滚动轴承工作温度高于120℃时,需引入温度系数(表1)表1 温度系数工作温度/℃<120 125 150 175 200 225 250 300f1.00 0.95 0.90 0.85 0.80 0.75 0.70 0.60t四、当量动载荷当滚动轴承同时承受径向载荷和轴向载荷时,当量载荷的基本计算公式为式中:P——当量动载荷,N;——径向载荷,N;——轴向载荷,N;X——径向动载荷系数;Y——轴向动载荷系数;——负荷系数五、载荷系数f p当轴承承受有冲击载荷时,当量动载荷计算时,引入载荷系数(表2)表2 冲击载荷系数f p载荷性质f p举例无冲击或轻微冲击 1.0~1.2 电机、汽轮机、通风机、水泵等中等冲击 1.2~1.8 车辆、机床、起重机、内燃机等强大冲击 1.8~3.0 破碎机、轧钢机、振动筛等六、动载荷系数X、Y表3 深沟球轴承的系数X、Y表4 角接触球轴承的系数X、Y表5 其它向心轴承的系数X、Y 表6 推力轴承的系数X、Y七、成对轴承所受轴向力计算公式:角接触球轴承:圆锥滚子轴承:式中e为判断系数,可由表4查出;Y应取表5中的数值。
●正排列:若则若则●反排列:若则若则八、成对轴承当量动载荷根据基本公式:式中:P——当量动载荷,N;——径向载荷,N;——轴向载荷,N;X——径向动载荷系数;Y——轴向动载荷系数;——负荷系数。
滚动轴承寿命计算公式

滚动轴承寿命计算公式滚动轴承是一种常见的机械元件,用于支撑和定位机器中旋转部件。
由于滚动轴承在机械运动中承受很大的力和磨损,因此其寿命是一个重要的参数。
滚动轴承的寿命计算公式是根据轴承的工作条件来确定的。
下面将详细介绍滚动轴承寿命计算的相关参考内容。
滚动轴承的寿命可以用基本额定寿命和调整因素来计算。
基本额定寿命是指在给定的负载条件下,轴承经过100万转(或行走一定的距离)后的寿命。
调整因素是考虑到轴承在实际工作条件下可能受到的额外影响。
滚动轴承的基本额定寿命可以由以下的一般计算公式得出:L10h = (C/P)^p其中,L10h是基本额定寿命,单位是小时;C 是基本动载荷额定值,单位是N;P 是相对磨损参数,通常取为3;p 是磨损指数,取决于轴承类型和使用条件。
磨损指数p的取值范围通常为3-10,具体数值需要根据具体的轴承类型和使用条件进行确定。
不同类型的轴承有不同的磨损指数。
滚动轴承的调整因素主要包括以下几个方面:1.负载系数(fT):通过考虑工作条件下的轴承负载大小和方向,计算负载系数。
一般情况下,负载系数在1以下。
2.可靠性调整因素(a1、a2、a3):根据滚动轴承的可靠性要求,计算可靠性调整因素。
这些因素通常是根据统计数据和经验值得出的。
3.寿命调整因素(aISO、aSKF):在计算基本额定寿命的基础上,根据轴承的使用条件和特殊要求进行修正。
4. 温度调整因素(aT):考虑轴承运行温度的影响,计算温度调整因素。
以上的调整因素可以通过一定的计算公式得出,具体的计算方法可以参考相关滚动轴承的手册、标准或经验数据。
除了上述计算寿命的方法外,还可以通过实际运行数据进行判断和预测轴承寿命。
例如,通过监测轴承的振动、温度等参数,结合历史数据和经验,可以进行寿命预测和故障诊断。
总结起来,滚动轴承寿命的计算公式包括基本额定寿命的公式和各种调整因素的计算。
这些公式和因素的取值需要根据具体的轴承类型和使用条件来确定。
轴承寿命及推力计算3.16

轴承使用寿命计算通用轴承寿命计算:ε⎪⎭⎫ ⎝⎛=P C n L h 6010610 (1) h L 10——基本额定寿命(h )C ——基本额定动载荷(N )P ——当量动载荷(N )N ——转速(r/min ,这里值暂取30)ε——寿命指数(球轴承取3,滚子轴承取10/3)其中当量载荷: P=X*Fr + Y*Fa (2)P 为当量动载荷Fr 轴承所受的径向载荷(N)Fa 轴承所受的轴向载荷(N)X 径向动载荷系数Y 轴向动载荷系数对悬臂轴承进行受力分析:上轴承6013-2Z 受到全部悬臂的重力以及径向力,下轴承6012-2Z 仅受到水平径向力。
根据力矩平衡,可以得出:对于6013-2Z :Fa = (∑Gi*Li)/h = 6620NFr = ∑Gi =1190N对于6012-2Z ::Fa = (∑Gi*Li)/h = 6620NFr = 0N(一)、轴承型号:GB/T 296 6013-2Z ,深沟球轴承,两侧间隙密封。
基本尺寸:基本额定静载荷:Cor = 24.8KN基本额定动载荷:Cr = 32KN查询工具书数值,带入公式计算,由Fa/Fr<e ,并根据Fa/Cor ,可以得到X 、Y 的值分别为1、0。
算出当量动载荷,带入公式: P=X*Fr + Y*Fa =0*1190+1*6620=6620Nε⎪⎭⎫ ⎝⎛=P C n L h6010610=361066203200030*6010⎪⎭⎫ ⎝⎛=h L ≈62748h(二)轴承型号:GB/T 296 6012-2Z ,深沟球轴承,两侧间隙密封。
图同上。
基本额定静载荷:Cor = 24.2KN基本额定动载荷:Cr = 31.5KN查询工具书数值,带入公式计算,由Fa/Fr>e ,并根据Fa/Cor ,可以得到X 、Y 的值分别为1、0。
算出当量动载荷,带入公式: P=X*Fr + Y*Fa =0*0+1*6620=6620Nε⎪⎭⎫ ⎝⎛=P C n L h 6010610=361066203150030*6010⎪⎭⎫ ⎝⎛=h L ≈59852h 摩擦力矩的计算:M ≈μ(d/2)F ,深沟球轴承μ值(0.0015~0.003)6013-2Z : M1=0.003*0.035*6620=0.6951NM6012-2Z : M2=0.003*0.03*6620 =0.5958NMM=M1+M2=0.6951+0.5958=1.2909NM在2400mm ,和500mm 处,推动转臂所需的力为:0.54N 、2.6N机械手受力分析一、自重夹取若四爪平衡受力,则重力有四爪平均分配。
(完整)滚动轴承的寿命计算
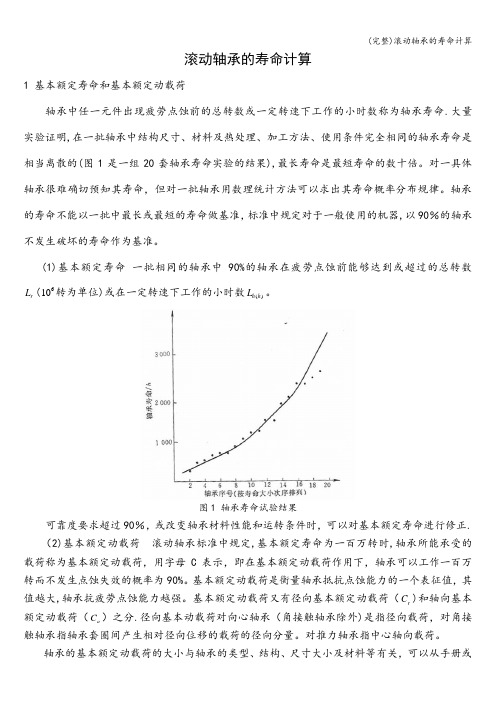
滚动轴承的寿命计算1 基本额定寿命和基本额定动载荷轴承中任一元件出现疲劳点蚀前的总转数或一定转速下工作的小时数称为轴承寿命.大量实验证明,在一批轴承中结构尺寸、材料及热处理、加工方法、使用条件完全相同的轴承寿命是相当离散的(图1是一组20套轴承寿命实验的结果),最长寿命是最短寿命的数十倍。
对一具体轴承很难确切预知其寿命,但对一批轴承用数理统计方法可以求出其寿命概率分布规律。
轴承的寿命不能以一批中最长或最短的寿命做基准,标准中规定对于一般使用的机器,以90%的轴承不发生破坏的寿命作为基准。
(1)基本额定寿命 一批相同的轴承中90%的轴承在疲劳点蚀前能够达到或超过的总转数r L (610转为单位)或在一定转速下工作的小时数()h h L 。
图1 轴承寿命试验结果可靠度要求超过90%,或改变轴承材料性能和运转条件时,可以对基本额定寿命进行修正.(2)基本额定动载荷 滚动轴承标准中规定,基本额定寿命为一百万转时,轴承所能承受的载荷称为基本额定动载荷,用字母C 表示,即在基本额定动载荷作用下,轴承可以工作一百万转而不发生点蚀失效的概率为90%。
基本额定动载荷是衡量轴承抵抗点蚀能力的一个表征值,其值越大,轴承抗疲劳点蚀能力越强。
基本额定动载荷又有径向基本额定动载荷(r C )和轴向基本额定动载荷(a C )之分.径向基本动载荷对向心轴承(角接触轴承除外)是指径向载荷,对角接触轴承指轴承套圈间产生相对径向位移的载荷的径向分量。
对推力轴承指中心轴向载荷。
轴承的基本额定动载荷的大小与轴承的类型、结构、尺寸大小及材料等有关,可以从手册或轴承产品样本中直接查出数值。
2 当量动载荷轴承的基本额定动载荷C (r C 和a C )是在一定条件下确定的。
对同时承受径向载荷和轴向载荷作用的轴承进行寿命计算时,需要把实际载荷折算为与基本额定动载荷条件相一致的一种假想载荷,此假想载荷称为当量动载荷,用字母P 表示。
当量动载荷P 的计算方法如下:同时承受径向载荷r F 和轴向载荷a F 的轴承()P r a P f XF YF =+(1)受纯径向载荷r F 的轴承(如N 、NA 类轴承)P r P f F =(2)受纯轴向载荷a F 的轴承(如5类、8类轴承)P a P f F =(3)式中:X ——径向动载荷系数,查表1; Y ——轴向动载荷系数,查表1; P f 冲击载荷系数,见表2。
轴承设计寿命计算公式

轴承设计寿命计算公式
L(寿命)=(C/P)^p
其中
L:轴承的寿命(工作时间)
C:基本动态负荷额定值(根据轴承的尺寸、材料和结构进行计算)P:轴承实际受力(根据轴承的负载情况和转速进行计算)
p:寿命指数(根据轴承的材料、制造工艺和使用环境进行选择)
轴承的基本动态负荷额定值C是指在既定的寿命要求下,能够承受的额定动态载荷。
为了能够合理地选择负荷额定值C,需要进行以下计算:
1.根据轴承的材料和制造工艺,确定基本动态载荷额定值(C0)和基本静态载荷额定值(Co);
2.根据加载情况和使用要求,计算相当负荷(P);
相当负荷是指在给定的工况下,实际受力与负荷额定值之间的比值。
为了能够准确地计算相当负荷,需要进行以下计算:
1.根据轴承受力和转速的变化情况,选择合适的负荷系数;
2.根据轴承的使用条件,考虑径向负荷和轴向负荷;
3.根据轴承的转速和运转时间,计算负荷参数。
寿命指数(p)是根据轴承材料、制造工艺和使用环境等因素考虑的一个修正系数。
为了准确地选择寿命指数,需要考虑以下因素:
1.轴承材料的强度和硬度;
2.制造工艺的精度和表面质量;
3.使用环境的温度、湿度和清洁度。
根据以上的计算和考虑因素,可以得到轴承的设计寿命(L)。
在实际设计中,通常还需要考虑其他因素,如轴承的维护和保养,以提高轴承的使用寿命。
轴承寿命的计算[1]
![轴承寿命的计算[1]](https://img.taocdn.com/s3/m/1426c1144693daef5ff73d76.png)
轴承寿命的计算1、大体额定动负荷大体额定动负荷表示轴承耐转动疲劳的能力(即负荷能力),是指大小和方向必然的纯径向负荷(关于向心轴承)或中心轴向负荷(关于推力轴承),在内圈旋转外圈固定(或内圈固定外圈旋转)的条件下,该负荷下的大体额定寿命可达100万转。
向心轴承与推力轴承的大体额定动负荷别离称做径向大体额定动负荷与轴向大体额定动负荷,用Cr与Ca表示,其数值录入轴承尺寸表。
2、大体额定寿命式1表示轴承的大体额定动负荷,当量动负荷及大体额定寿命之间的关系。
轴承以固定的转速时,用时间表示寿命更为方便,如式2所示。
另外,对于铁路车辆或汽车等用行车距离(km)表示寿命较多,如式3所示。
因此,作为轴承的使用条件,设当量动负荷为P,转速为n,则满足设计寿命所需要的轴承基本额定动负荷c可由式4计算。
从轴承表选出满足c值的轴承,即可确定轴承的尺寸。
机械要求的轴承必需寿命请参考表4。
3、依照温度进行的大体额定动负荷的修正与轴承的尺寸稳固处置轴承在高温下利历时,材料组织会发生转变、硬度降低,大体额定动负荷将比常温下利历时减小。
材料组织一旦发生转变,即便温度恢复到常温也可不能恢复。
因此,在高温下使用时,必须将轴承尺寸表的基本额定动负荷乘以表1的温度系数进行修正。
表1温度系数轴承工作温度°C 125125175200250温度系数(fT)11轴承长时刻在120摄氏度以上的工作温度下利历时,由于经一样热处置的轴承尺寸转变大,必需进行尺寸稳固处置。
尺寸稳定处理与使用温度范围如表2所示。
但经尺寸稳定处理的轴承硬度降低,有时基本额定动负荷会减小。
表2尺寸稳固处置尺寸稳定处理代号使用温度范围S0 S1 S2超过100摄氏度到150摄氏度超过150摄氏度到200摄氏度超过200摄氏度到250摄氏度4、修正额定寿命式1表示的是靠得住性90%的大体额定寿命(L10),依照用途的不同,有时也需要靠得住性高于90%的高靠得住性寿命。
轴承设计寿命计算公式

一、滚动轴承承载能力的一般说明 滚动轴承的承载能力与轴承类型和尺寸有关。
相同外形尺寸下,滚子轴承的承载能力约为球轴承的1.5~3倍。
向心类轴承主要用于承受径向载荷,推力类轴承主要用于承受轴向载荷。
角接触轴承同时承受径向载荷和轴向载荷的联合作用,其轴向承载能力的大小随接触角α的增大而增大。
二、滚动轴承的寿命计算 轴承的寿命与载荷间的关系可表示为下列公式: 或 式中:──基本额定寿命(106转);──基本额定寿命(小时h);C──基本额定动载荷,由轴承类型、尺寸查表获得;P──当量动载荷(N),根据所受径向力、轴向力合成计算;──温度系数,由表1查得;n──轴承工作转速(r/min);──寿命指数(球轴承,滚子轴承)。
三、温度系数f t 当滚动轴承工作温度高于120℃时,需引入温度系数(表1) 当滚动轴承同时承受径向载荷和轴向载荷时,当量载荷的基本计算公式为式中:P——当量动载荷,N;——径向载荷,N;——轴向载荷,N;X——径向动载荷系数;Y——轴向动载荷系数;——负荷系数五、载荷系数f p 当轴承承受有冲击载荷时,当量动载荷计算时,引入载荷系数(表2)表2 冲击载荷系数f表3 深沟球轴承的系数X、Y表4 角接触球轴承的系数X、Y表5 其它向心轴承的系数X、Y表6 推力轴承的系数X、Y七、成对轴承所受轴向力 计算公式: 角接触球轴承: 圆锥滚子轴承:式中e为判断系数,可由表4查出;Y应取表5中的数值。
●正排列:若则 若 则 ●反排列:若则 若 则 八、成对轴承当量动载荷 根据基本公式:式中:P——当量动载荷,N;——径向载荷,N;——轴向载荷,N;X——径向动载荷系数;Y——轴向动载荷系数;——负荷系数。
九、修正额定寿命计算 对于要求不同的可靠度、特殊的轴承性能以及运转条件不属于正常情况下的轴承寿命计算时,可采用修正额定寿命计算公式:式中:──特殊的轴承性能、运转条件以及不同可靠度要求下的修正额定寿命(106转);a1──可靠度的寿命修正系数;a2──特殊的轴承性能寿命修正系数;a3──运转条件的寿命修正系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴承使用寿命计算
通用轴承寿命计算:
ε⎪⎭⎫ ⎝⎛=P C n L h 6010610 (1) h L 10——基本额定寿命(h )
C ——基本额定动载荷(N )
P ——当量动载荷(N )
N ——转速(r/min ,这里值暂取30)
ε——寿命指数(球轴承取3,滚子轴承取10/3)
其中当量载荷: P=X*Fr + Y*Fa (2)
P 为当量动载荷
Fr 轴承所受的径向载荷(N)
Fa 轴承所受的轴向载荷(N)
X 径向动载荷系数
Y 轴向动载荷系数
对悬臂轴承进行受力分析:
上轴承6013-2Z 受到全部悬臂的重力以及径向力,下轴承6012-2Z 仅受到水平径向力。
根据力矩平衡,可以得出:
对于6013-2Z :Fa = (∑Gi*Li)/h = 6620N
Fr = ∑Gi =1190N
对于6012-2Z ::Fa = (∑Gi*Li)/h = 6620N
Fr = 0N
(一)、轴承型号:GB/T 296 6013-2Z ,深沟球轴承,两侧间隙密封。
基本尺寸:
基本额定静载荷:Cor = 24.8KN
基本额定动载荷:Cr = 32KN
查询工具书数值,带入公式计算,由Fa/Fr<e ,并根据Fa/Cor ,可以得到X 、Y 的值分别为1、0。
算出当量动载荷,带入公式: P=X*Fr + Y*Fa =0*1190+1*6620=6620N
ε⎪⎭⎫ ⎝⎛=P C n L h
6010610=3
61066203200030*6010⎪⎭⎫ ⎝⎛=h L ≈62748h
(二)轴承型号:GB/T 296 6012-2Z ,深沟球轴承,两侧间隙密封。
图同上。
基本额定静载荷:Cor = 24.2KN
基本额定动载荷:Cr = 31.5KN
查询工具书数值,带入公式计算,由Fa/Fr>e ,并根据Fa/Cor ,可以得到X 、Y 的值分别为1、0。
算出当量动载荷,带入公式: P=X*Fr + Y*Fa =0*0+1*6620=6620N
ε⎪⎭⎫ ⎝⎛=P C n L h 6010610=3
61066203150030*6010⎪⎭⎫ ⎝⎛=h L ≈59852h 摩擦力矩的计算:
M ≈μ(d/2)F ,深沟球轴承μ值(0.0015~0.003)
6013-2Z : M1=0.003*0.035*6620=0.6951NM
6012-2Z : M2=0.003*0.03*6620 =0.5958NM
M=M1+M2=0.6951+0.5958=1.2909NM
在2400mm ,和500mm 处,推动转臂所需的力为:0.54N 、2.6N
机械手受力分析
一、自重夹取
若四爪平衡受力,则重力有四爪平均分配。
假设机械手抓取轮毂并即将离开工作台,处于平衡状态。
设轮毂边沿与竖直方向德夹角为α,轮毂受重力为G ,机械手对轮毂的作用力为F ,摩擦力为f ,静摩擦因数为μ;机械手抓手力臂如图1上下分别为l1、l2。
对轮毂进行受力分析,在重力、抓力、静摩擦力的共同作用下稳定。
根据图有:
αcos F f μ≤ …… ①
14
22L G fl FL =- ……② 4cos sin G F F ≥
+αμα ……③ 在摩擦力不足或刚好平衡时,即αcos F f μ=,可用下式求摩擦系数范围:
[]α
ββαββαααααcos cos )15sin(sin cos )15(cos cos )21(sin 12cos sin 21sin 22H V H V l L L L l L l L +-︒--︒=+-=-++≥μ
(β为爪上杆与水平夹角,0)15sin(1)15cos(,1cos ≈-︒≈-︒≈βββ,,V 、H 分别为竖直、横杆的长度并已知,简化时可考虑采用)………④
L2、L1在系统稳定时是固定值=常数,只要 μ大于其最大值即可。
做出μ的曲线图并进行分析,找出其中几个点进行研究:
α趋向于90°时 ,这时:
, f=0 没有摩擦力
α=0°时,μ≈L2/L1。
α从0°向负90°变化时,μ值单调递增,最后趋向无穷大,趋于不稳定。
4cos sin G F F =+αμα4G F =
α变化范围在不到±45°之间,且在角在负值时,若摩擦力不够,爪会随抓取过程,打滑上移,并稳定。
变化时L2、L1变化,这个角度期间要稳定,μ值必须大于V/H ,对应爪(刹车软垫)与轮毂间的摩擦因数 ,在安全范围内(改小V/H 值)?随着爪垫磨损,摩擦系数变小,抓取位置会逐渐上升,平衡重力。
若还不能稳定,最后打滑上升,勾住轮缘。
二、若抓取时,四爪没有能平衡分配,则在起吊期间,由于相对应爪的受力不同,处理非稳定状态,配合爪脚转动副,进行自动调整,并趋于一致。
二、气缸夹取: 气缸作用面积:Mpa 5.0,20,63m m D ,4
2
2气压为其中mm d d D A ==-=π 工作压力: N P A N 33.5603105.01014.34
2063662
2=⨯⨯⨯⨯-=⨯=- αcos F f μ≤ ①
1)4
(22L N G fl FL +=- ② 4cos sin G F F ≥
+αμα ③ 在摩擦力不足或刚好平衡时,即αcos F f μ=,可用下式求摩擦系数范围:
[]αββααββα
αααααcos cos )15sin(sin 14sin cos )15(cos cos )21(sin 14sin 12cos sin 1421sin 22H V G NL H V l L G NL L L G NL l L l L +-︒---︒=+--=-+++≥μ在W AZZ-101-02004的图示状态下,F=1994N ,f 超过上限,取最大300N ,取μ=0.35,可以托起大于69.7kg 工件。
ANC 水槽夹紧装置轴承寿命
一、轴承代号:61805 轴承代号:61812。
