2.4 同轴线及其高次模解析
用二次FEM计算同轴线的高阶模截止频率

设[] F 的逆矩阵为[ ] 即[ ] [ ] 运算求出系数 c代人( ) A , A = F ~, 2 化简并令 A : 可得 X F,
u xy = F ( ,) 1 2 有 限元方 程 . () 3
波在金属波导中传播时 , 场的纵 向分量 u E 或 ) (: 应满足 H l hh 方程 : e oz m
维普资讯
第 5期
张学庆 , : 用 二次 F M计算 同轴线 的高阶模截 止频 率 等 E
・5 5・
式 中 =( ) ( ) 引入矩 阵
。 : …
:
…
,
[ ] U =
,F = []
。 : …
[ C]=
收 稿 日期 :05—1 2 20 2— 3
基金项 目: 国家 自然科学基金 (0 60 2 资助项 目、 135 0 ) 云南省 自然科学基 金 (0 4 0 2 M) 助项 目、 20 A 0 8 资 云南省 教委
自然科学基金 (3 3 1 资助项 目 0 Z 2 A) 作者 简介 : 张学庆 (9 8一) 男 , 17 , 江苏省徐 州市 人 , 硕士 , 主要 从事电磁场理论 及应用研究.
维普资讯
第2 7卷第 5 期
20 0 7年 9月
云南师 范大 学学报
J un lo n a oma Unvri o r a fYu n n N r l iest y
V0 . 7 No 5 12 .
S p.2 0 e 07
用 二 次 F M 计 算 同轴 线 的 高 阶模 截止 频 率 E
6
=
c
= y , ≤2 +f
() 1
将六 个节 点坐标 ( , 和场值 代人 ( ) Y j 1 式
同 轴 线——理论分析和特性

例题3.3-1: 同轴电缆的a=0.89mm,b=2.95mm,填充er= 2.2的介质。求最高可用频率。
圆形波导分析 4 -- 本征振方程
若为有耗介质: 为复数, 0r(1-jg/0r) = 0r(1-jtgd) 由式本征方程1.4.23可得(h1=1,h2=r)电场及 磁场纵向分量必须满足的Heimholtz方程:
1 2 1 2 2 E0 z r , f r 2 kc 0 2 2 r r r r f H 0 z r,f 3.2 3
h2r方向传播时谐变化可约去时间因子ejwt圆形波导分析圆形波导分析纵横关系纵横关系圆形波导分析圆形波导分析3纵横关系纵横关系圆形圆形波导分析波导分析本征振方程本征振方程若为有耗介质
圆形波导
Circular Waveguide 截面为圆形的波导管。 半径为a,内部充气, 只支持TE和TM模式。 特点:加工方便具有较 小的损耗,——常用于 要求双极化模的天线馈 线之中。 常用模式:TE11、TE01、和TM01
边界条件要求在r=a,b处Ez=0; 可得联立方程:
同轴线的高次模
A1 J m (kc a) A2Ym (kc a ) 0 A1 J m (kcb) A2Ym (kcb) 0 J m (kc a) Ym (kcb) = 3.3 32 J m (kc a) Ym (kcb)
此方程为超越方程,可用数值法分析。近似解:
n kc ba n 1, 2,... 2 (b a ) n 2(b a)
同轴线

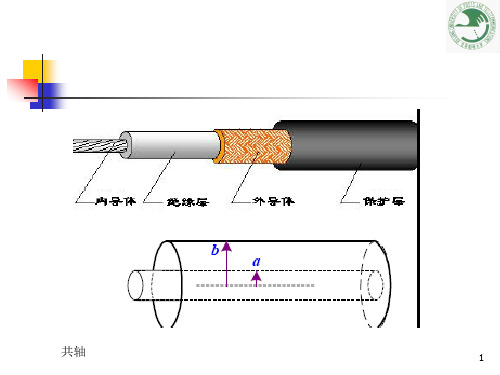
双导体传输线——宽频带微波传输线 硬同轴线:内外导体之间的介质为空气,内导 体用高频介质垫圈等支撑。 软同轴线:又称为同轴电缆,电缆的内外导体 之间填充高频介质,内导体由单根或多根导体 组成,外导体由铜线编织而成,外层再包一层 软塑料等介质。
1.8.1 同轴线中的主模— —TEM模 1.8.2 同轴线中的高次模 1.8.3 同轴线尺寸的确定
03:25:07
1 (r , ) 1 2 (r, ) (r ) 2 0 2 r r r r
同庆制作
淡 泊 以 明 志 , 宁 静 以 致 远 。
03:25:07
r dR(r ) 2 (r ) kr (r ) r R dr
1 d 2 F ( ) 2 k F ( ) d 2
n=1,2,…
cTE (a b)
11
同庆制作
同轴线尺寸的确定
淡 泊 以 明 志 , 宁 静 以 致 远 。
03:25:07
首要条件是保证同轴线只传输TEM模。由上述 分析可知,同轴线中的最低次波导模式是TE11。
min (a b)
式中λmin是最小工作波长。
Rs 1 1 ac ( ) 2 ln(b / a) a b
ac / a 0 (固定b不变)
b 3.591 a
同庆制作
淡 泊 以 明 志 , 宁 静 以 致 远 。
03:25:07
1 | V0 |2 p 2 Z0
pmax
b | U br | aEbr ln a
2 1 Vmax a 2 Ebr b ln 2 Z0 0 a
pmax / a 0
2 (b a) n
同轴线微带线
24
F<11GHz-18GHz
25
F<1GHz
26
F<18GHz-25GHz
F<50GHz
27
Summary
2 H
2Er z2
2 Er
5
同轴线的主模—TEM模
v
v
H j E
rˆ H z
ˆ Hr z
zˆ
1 r
r
(rH
)
j
rˆEr ˆE
v
v
E jH
rˆ E z
ˆ Er z
共轴
1
同轴线的主模—TEM模
y
z r
x
a0
b
2
同轴线的主模—TEM模
波导一般方程
同轴线一般方程(kc=0)
rr
2 t
2 t
E r H
kc2
E r
0
kc2H 0
r
2 t
2 t
E r H
0 0
其中,k2c=k2-β2
3
同轴线的主模—TEM模
1.TM modes
Ez
[B1 J m ( kc r )
cos m B2 N m (kcr )]sin m
e jz
边界条件要求r=a,b处,Ez=0
B1 J m (kca ) B2 N m (kca ) 0
B1
J
m
(
k
c
b
)
B2 N
m(kcb)
圆波导、同轴线、带状线、微带线简介

1、3 带状线简介
带状线的结构 带状线的结构如下图所示,由一个宽度为W, 厚度为t的中心导带和相距为d的上、下两块接地 板构成,接地板之间填充 r 的均匀介质。 带状线支持TEM波传输,这也是带状线的主 模式。同时带状线可认为是由同轴线演变而来, 故存在高次波形TE或TM模。一般可通过选择带 状线的横向尺寸来抑制高次模的出现,当取 min min b W 时可保证TEM波主模单模工 2 r 2 r 作。
2.7 10 Rs r Z 0 A 30 (b t ) c 0.16 Rs B Z 0b
r Z0 120
r Z0 120
带状线简介
Rs f / 为导体表面电阻,且 式中,
2W 1 b t 2b t A 1 ln bt bt t
同轴线简介
同轴线结构图
同轴线简介
同轴线的场方程 求解同轴线中的TEM波各场量,就是在柱坐标系 下求解横向分布函数φ所满足的拉普拉斯方程。 求得的同轴线中TEM波的横向场分量为:
E0 j z Et ar e r E0 j z HБайду номын сангаасt a e r
其中,E0是振幅常数,η =120π/ 是TEM波的 波阻抗。
圆波导
圆波导TM01场结构分布图
圆波导 线(ρ=0)附近最强。根据上述特点,它可以有 效地和轴向流动的电子流交换能量, 由此将其应 用于微波电子管中的谐振腔及直线电子加速器中 的工作模式。
1、2 同轴线简介 同轴线的概念 同轴线是一种典型的双导体传输系统, 它由内、 外同轴的两导体柱构成, 中间为支撑介质。其中, 内、 外半径分别为a和b, 填充介质的磁导率和介电常数 分别为μ 和ε。 同轴线是微波技术中最常见的TEM模传输线,它 既能支持TEM波传输,也能支持TE、TM波传播。 同时,同轴线是一种宽频带微波传输线,因此它得 到广泛的应用。其结构如下图所示。
同轴线和微带线

(3 131)
Z0
Z 01
e re
(3 132a)
由式 (3-132a) 可见,微带特征阻抗Z0旳计算归结为
求空气微带线旳特征阻抗Z01和等效相对介电常数ere。
应用保角变换拟定实际微带线旳分布电容C0和空
气微带线旳分布电容C01, 两者之比为等效相对介电常
数
e
re
C0 C01
1e
r
e
r1 110
性阻抗为
Z 01
1 v0C01
(3 132b)
当微带线v周p 围全ve0 r部, 用介质C0 (ere)填rC0充1 (如图(b))时,
则
Z0
1 v pC0
Z01
er
对于实际微带线(如图(c)),其中传播波旳相速一
定在 v0 e r vp v0 范围内, 其单位长度分布电容 一定在 C01 C0 e rC01 范围内, 故其特征阻抗一定在
rˆ m I rˆ 60 ( I )
e 2 r
er r
(3 118b)
代入(3-115)得TEM波旳行波解为
E(r , , z ; t) rˆ
60 ( I ) e j( t z)
er r
H
(r
,
,
z
;
t)
ˆ
(
I
2
r
)
e
j (
t
z)
2) TEM模旳场分布如图所示
(3 119)
2. 特征阻抗 对TEM波(无色散波),沿z向旳单一行波电流为 导体表面旳纵向电流线密度旳积分
h
1 2
2
2 w
(3 134)
也可把ere写成如下形式 e re 1 q(e r1) (3 135)
同轴线以TEM 模工作时的传输特性

2.1 相速度和波导波长
相速度是指导模等相位面移动的速度:
姨 姨 自p
越
棕 茁
越
棕 k
1
=
1-(kc /k)2
自 1-(姿/姿c )2
=
自 G
(1)
式中 自=c/着r,姿=姿c/ 姿o ,C 和 姿0 分别为 自 由空 间的 光 速和波
由公式(3)和(4),同轴线上的功率流为:
乙 乙 P=
1 2
s
E伊H*·ds=
1 2
s
Er
伊H*覬·ds=
1 2
V0 I*0
这说明传输线上的功率完全是通过导体之间的磁场和电场而不
是导体本身传输的。
由公式(3)可知,同轴线内导体附近的电场最强。由此可得击穿
前最大电压为 Vmax=Ebr1n(b/a),Ebr 是价质的击穿场强;对于空气,Ebr=
棕 姨滋着 。
横向磁场则为
H(r,覬,z)=
员 浊
z赞 伊Eot(r,覬)e-j茁z越覬赞
V0 浊r(b/a)
e-j茁z
越覬赞
Em 浊
e-j茁z
(4)
式中 浊= 姨滋/着 根据公式(3)和(4)可画出同轴线中 TEM 导模的
场结构,如图 2 所示。
从公式(3)得知同轴线内外导体之间的电位差:
乙b
Vab=自a-自b= aEr(r,覬,z)dr=Voe-j茁z r
实用科技
同轴线以 TEM 模工作时的传输特性
迪拉热窑米吉提
新疆维吾尔自治区广播电影电视局 904 台 新疆 乌鲁木齐 830049
同轴线
综合上述尺寸选择影响因素,通常采取折衷尺寸 b a ≈ 2.3 , 相应于同轴线特性阻抗为50欧。或者根据特殊要求,结合单 模传输要求,选择较大的功率容量或者较小的衰减系数。
0 l
2π
2πE0 a
η
e
− jβz
内外导体间电压:
U = ∫ Er dr = ∫
a
b
b
a
E0 a b − jβz − jβ z dre = E0 a ln e r a
特性阻抗:
U b 138 b 60 Zc = = ln = lg I εr a εr a
第2章 规则金属波导
2-6 同轴线
二、同轴线中的高次模 在同轴线中,除传输TEM主模外,还可能传输高次 模—TE模和TM模。但在实际应用中,一般不用高次模 传输功率,而采用主模TEM工作。 分析方法与圆波导类似。但由于内导体半径不为零, 圆波导分析过程中的诺依曼函数要保留。 1. TM模 TM波型
∇t2 H z (r , ϕ ) + K c2 H z (r , ϕ ) = 0
第2章 规则金属波导
2-6 同轴线
一、同轴线传输主模—TEM模 同轴线传输主模 模 (一) TEM模的场分量和场结构 一 模的场分量和场结构 同轴线传输的主模是TEM模,这种模Kc=0,λc=∞, 模 这种模K =0,λc=∞, 同轴线传输的主模是 同时E =0, =0, 同时Ez=0,Hz=0,TEM模横向场分布函数满足二维拉普拉 模横向场分布函数满足二维拉普拉 斯方程: 斯方程:
可得:
1 ∂Er β E0 a − jβz β Hϕ = = e = Er − jωµ ∂z ωµ r ωµ
第2章 规则金属波导
2-6 同轴线
《电磁场与电磁波》(第四版)习题集:第7章 导行电磁波

第7章 导行电磁波前面我们讨论了电磁波在无界空间的传播以及电磁波对平面分界面的反射与透射现象。
在这一章中我们将讨论电磁波在有界空间的传播,即导波系统中的电磁波。
所谓导波系统是指引导电磁波沿一定方向传播的装置,被引导的电磁波称为导行波。
常见的导波系统有规则金属波导(如矩形波导、圆波导)、传输线(如平行双线、同轴线)和表面波波导(如微带线),图7.0.1给出了一些常见的导波系统。
导波系统中电磁波的传输问题属于电磁场边值问题,即在给定边界条件下解电磁波动方程,这时我们可以得到导波系统中的电磁场分布和电磁波的传播特性。
在这一章中,将用该方法讨论矩形波导、圆波导和同轴线中的电磁波传播问题以及谐振腔中的场分布及相关参数。
然而,当边界比较复杂时,用这种方法得到解析解就很困难,这时如果是双导体(或多导体)导波系统且传播的电磁波频率不太高,就可以引入分布参数,用“电路”中的电压和电流等效前面波导中的电场和磁场,这种方法称为“等效传输线”法。
这一章我们还将用该方法讨论平行双线和同轴线中波的传播特性。
7.1导行电磁波概论任意截面的均匀导波系统如图7.1.1所示。
为讨论简单又不失一般性,可作如下假设: (1)波导的横截面沿z 方向是均匀的,即导波内的电场和磁场分布只与坐标x ,y 有关,与坐标z 无关。
(2)构成波导壁的导体是理想导体,即σ=∞。
(3)波导内填充的媒质为理想介质,即0σ=,且各向同性。
(4)所讨论的区域内没有源分布,即0ρ=0=J 。
a 矩形波导b 圆柱形波导c 同轴线传输线d 双线传输线e 微带线图7.0.1 常见的几种导波系统(5)波导内的电磁场是时谐场,角频率为ω。
设波导中电磁波沿+z 方向传播,对于角频率为ω的时谐场,由假设条件(1)和(2)可将其电磁场量表示为()()()(),,,,,,,z z x y z x y e x y z x y e γγ--==E E H H (7.1.1)式中γ称为传播常数,表征导波系统中电磁场的传播特性。
2章同轴高次及其它

§2.5 同轴线的高次型波
同轴线是双导体传输线, 可以传输TEM波, 但也可以传输TE, TM 波。 通常要求同轴线的工作于TEM模式. 同轴线的结构如右图所示,a为内导体外 半径,b为外导体内半径。
同轴线中的TE, TM模
当同轴线截面尺寸与信号波长可相比拟时, 同轴线内将出现高次模式-TE、TM模。
对于脊型波导来说,由于边界条件较为复杂,不便于用严格的场解法求出其中的 场分量及其截止波长,常应用简化的近似分析方法得出一些有用的结果
§2.6 脊型波导
与矩形波导相比,脊型波导有以下一些特点 : 工作带宽宽 由于凸缘的作用,相当于波导的宽边加大,因此TE10波的截止波长更 长,即大于2a;另外,当选择合适时,脊型波导中TE20波型的截止波长 可小于a,一般情况下也接近于a。因此对于脊型波导来说,TE10模单模 工作的频带范围比矩形波导宽,适用于制作宽带波导元器件; 等效阻抗低 与矩形波导TE10模式的等效阻抗Ze类似地可以定义脊形波导TE10模的 等效阻抗Z’e,计算表明,Z’e<Ze,即脊形波导的等效阻抗较低,因此易 于与低阻抗的同轴线及微带线连接。 其缺点是由于波导凸缘的存在,使导体损耗加大,而且电场的集中也降 低了功率容量。
了解高次模式的场结构,确定其截止波长,可以在给定工作频率时选择合适 的尺寸,保证同轴线中只传输TEM波 。 下面先分析TM模
同轴线的高次型波
同轴线的高次TM型波
分析同轴线中TM波的方法与分析圆波导中TM波的方法类似。对于TM波,Hz=0, Ez可表示为
cos j (t z ) Ez (r , , z, t ) [C1 J n (kc r ) C2 N n (kc r )] e sin
E Eme
同轴电缆线全解读

同轴电缆线全解读同轴线,是常见的信号传输线,中心的铜芯是传送高电平的,被绝缘材料包覆;绝缘材料外面是与铜芯共轴的筒状金属薄层,传输低电平,同时起到屏蔽作用。
目录定义同轴线的结构同轴线类型同轴电缆的主要特征鉴别同轴线的质量定义同轴线是常见的信号传输线,中心的铜芯是传送高电平的,被绝缘材料包覆;绝缘材料外面是与铜芯共轴的筒状金属薄层,传输低电平,同时起到屏蔽作用。
同轴线的结构同轴线的结构,由外向内依次是护套、外导体(屏蔽层)、绝缘介质和内导体4部分。
下面我们就分别介绍一下每一部分的作用。
护套,即最外面是一层绝缘层,起保护作用,室外电缆宜用具有优良气候特性的黑色聚乙烯,室内用户电缆从美观考虑则宜采用浅色的聚乙烯。
外导体(屏蔽层),同轴电缆的外导体有双重作用,它既作为传输回路的一根导线,传输低电平,又具有屏蔽作用,外导体通常有3种结构。
(1)金属管状。
这种结构采用铜或铝带纵包焊接,或者是无缝铜管挤包拉延而成,这种结构形式的屏蔽性能最好,但柔软性差,常用于干线电缆。
(2)铝塑料复合带纵包搭接。
这种结构有较好的屏蔽作用,且制造成本低,但由于外导体是带纵缝的圆管,电磁波会从缝隙处穿出而泄漏,应慎重使用。
(3)编织网与铝塑复合带纵包组合。
这是从单一编织网结构发展而来的,它具有柔软性好、重量轻和接头可靠等特点,实验证明,采用合理的复合结构,对屏蔽性能有很大的提高,目前这种结构形式被大量使用。
同轴线类型按照同轴线应用的位置,大致可以分为3种类型。
1、干线电缆:其绝缘外径一般为9mm以上的粗电缆,要求损耗小,柔软性要求不高。
2、支线电缆:其绝缘外径一般为7mm以上的中粗电缆,要求损耗小,同时也要一定的柔软性。
3、用户分配网电缆:其绝缘外径一般为5mm,损耗要求不是主要的,但要求良好的柔软性和室内统一直协调性。
在具体应用的时候,如果布线长度过长而导致信号衰减严重的话,选择粗一点的同轴线是个不错的主意。
总听人说-7、-5的线,你知道什么意思吗?这还要从同轴线的命名说起为了便于大家从同轴电缆的型号大致看出其结构类型,下面给出我国电缆的统一型号编制方法以及代号含义,供大家参考。
同轴线原理

同轴线原理同轴线原理是光学中的一个重要概念,它指的是两个或多个同心圆柱面之间的光学系统。
在这个原理中,光线在同轴线上传播时,会遵循一定的规律,这对于我们理解光学系统的成像和光路具有重要的意义。
本文将详细介绍同轴线原理的相关知识,希望能够帮助读者更好地理解这一概念。
首先,我们来看一下同轴线的定义。
同轴线是指通过同一点且在同一方向上的光线。
在光学系统中,同轴线可以用来描述透镜、凸透镜、凹透镜等光学元件的成像特性。
当光线沿着同轴线传播时,它们会在光学系统内部发生折射、反射等现象,从而产生不同的成像效果。
在实际的光学系统中,同轴线原理可以帮助我们更好地设计和优化光学元件。
通过合理地控制同轴线的传播路径,我们可以实现对光线的精确控制,从而达到所需的成像效果。
这在许多光学设备中都具有重要的应用,比如相机、望远镜、显微镜等。
除此之外,同轴线原理还可以帮助我们理解光学系统中的一些重要现象。
比如,当光线沿着同轴线通过透镜时,会产生不同的焦距和成像效果;当光线在反射镜上发生反射时,也会遵循同轴线原理。
因此,对同轴线原理的深入理解可以帮助我们更好地理解光学系统的工作原理。
在实际应用中,我们还可以利用同轴线原理来设计一些特殊的光学系统。
比如,利用同轴线原理可以设计出具有特定成像效果的透镜组,从而实现对光线的精确控制。
这对于一些特殊需求的光学设备来说具有重要的意义,比如激光器、光纤通信系统等。
总的来说,同轴线原理是光学中一个非常重要的概念,它对于我们理解光学系统的工作原理和优化设计具有重要的意义。
通过深入学习和理解同轴线原理,我们可以更好地应用光学知识,设计出更加高效和精确的光学系统,推动光学技术的发展和应用。
希望本文对同轴线原理有所帮助,也希望读者能够通过学习和实践,更好地理解和应用光学知识,为光学技术的发展做出贡献。
感谢阅读!。
同轴线和微带线

E(r, , z ; t ) E(r, )e j( t z)
H (r,
,
z
;
t
)
H (r,
)e
j (
t
z)
(3 115)
其中,在真空中, k 2
(3 116a)
当内、外导体间充满介质( mr、er)时
k
er
2
er
2
为在介质中的波长
er
(3 116b) (3 117 )
1) 用静态场求分布函数
rˆ m I rˆ 60 ( I )
e 2 r
er r
(3 118b)
代入(3-115)得TEM波的行波解为
E(r , , H(r , ,
z ; t) rˆ
z ; t) ˆ
60er(IFra bibliotek2( r
I) r )e
e j( t z)
j ( t z)
2) TEM模的场分布如图所示
(3 119)
一、 同轴线的TEM模
TEM模是同轴线的主模,是无色散波,其传输特
性在长线理论中已从电路的角度讨论过。下面,将从
场的角度讨论之。
1. 场分布
TEM波,Ez=Hz=0,fc = 0,分布函数应满足
TT22
E(r,
H (r,
) )
0 0
与二维静态场一致,只要用解相应二维静态场的
方法求出 E(r, )、H (r, ), 即可得沿z向传播的场量:
则
H (r
b)
I
2 b
,
H
(r
a)
I
2
a
PL
Rs 2
2
S Ht ds
35同轴线和微带线 (2)

的同轴线,习惯上采用特性阻抗为75和50两种;
75接近a 最小的要求; 50则兼顾通过功率大和 a 小这两个要求的折中考虑,此时取D/d=2.3, a 比 amin约大10%, 功率容量比最大值约小15% 。
微带线
微带线由介质基片上的导带和基片下的接地板构
成,整个微带线用薄膜工艺制作而成,其中基片采
用介电常数高、高频损耗小的陶瓷、石英或蓝宝石
等介质材料,导带材料为良导体。
微带线结构
简单、体积小、
重量轻、加工方 便,又便于与微
w
h
t
波固体器件接
成一体, 容易
微带线
实现微波电路的小型化和集成化,在微波集成电路中
获得了广泛的应用。 微带线属于半敞开式、部分填充介质的双导线传输
1.
TM
ni
c
TM
ni
2 (a i
b)
Dd i
(i 1, 2, 3, )
可见,在近似程度内,所有相同i
的
TM
ni
的c相等
而与n无关,故应避免 TM ni 模的出现。
2.
TE
ni
当 n 0、i =1 , D/d<4 时
c
TE
n1
n
(a
b)
(D
2n
d)
(n 1, 2, 3, )
同轴线所有高次模中, c最大的是 TE11 模:
E(r, , z ; t ) E(r, )e j( t z)
H (r,
,
z
;
t
)
H (r,
)e
j (
t
z)
(3 115)
同轴线

常见的信号传输线
01 基本原理
03 类型 05 鉴别方法
目录
02 结构特性 04 主要特征
同轴线(Coaxial line),是由两根同轴的圆柱导体构成的导行系统,内外导体之间填充空气或高频介质的 一种宽频带微波传输线。
基本原理
同轴线是一种屏蔽且非色散的结构,而且同轴线中导波的主模是TEM波,但同时也可传输TE模和TM模,其截 止频率为零,对应截止波长趋向于无穷大。是由同轴的两根内、外导体及中间的电介质构成的双导体传输线。一 般同轴线外导体接地,电磁场被限定在内外导体之间,所以同轴线基本没有辐射损耗,几乎不受外界信号干扰。 其工作频带比双线传输线宽,可以用于大于厘米波的波段。同轴线的原理图如图1所示。
5、检查外护层的挤包紧度,高质量的同轴电缆外护层都包得很紧,这样可缩小屏蔽层内间隙,防止空气进入 造成氧化,防止屏蔽层的相对滑动引起电性能飘移,但挤包太紧会造成剥去护层,以用力不能拉出线芯为合适。
感谢观看
3、编织与铝塑复合带纵包组合。是从单一编织结构发展而来的,它具有柔软性好、重量轻和接头可靠等特点, 采用合理的复合结构,对屏蔽性能有很大的提高,这种结构形式被大量使用。
绝缘介质,PE材质,主要是提高抗干扰性能,防止水、氧侵蚀。
内导体,铜是内导体的主要材料,可以是以下形式:退火铜线、退火铜管、铜包铝线。
2、衰减特性,同轴电缆的衰减特性通常用衰减常数来表示。衰减常数与信号的工作频率的平均方根成正比, 即频率越高,衰减常数越大,频率越低,衰减常数越小。
3、电缆的使用限期,任何电缆都有一定的寿命,电缆在使用一段时间后,由于材料老化,导体电阻变大,绝 缘介质的漏电流增加,当电缆的衰减常数比标称值增加时,该电缆就应该更新,一般电缆的寿命根据质量和使用 场合的不同在7-20年。
2.4 同轴线及其高次模解读

(2-159) 近似Kc解
数值法 解析法
确定截止波数Kc
表2.6-1给出了m取不同值时,特征 方程的第一个根和第二个根的值。
§2.4 同轴线及其中的高次波型
当m给定,方程有无穷多个根Kc;一个根对应一个波型, 第n个根对应第n个波型,用TMmn表示。 m——场量沿圆周分布的整驻波的个数,即沿角向按三 角函数分布的周期数,也就是沿波导圆周场量重复的 次数 n——场沿径向Bessel函数出现0值的数目,表示场 量沿半径分布的半个驻波的数目。
课堂练习
1. 写出矩形波导和圆波导的主模及其截止波长; 2. 画出矩形波导横截面的场结构图;
3. 圆波导中有二类简并波型,请写出所有简并波型。
§2.4 同轴线及其中的高次波型
同轴线:内、外导体构成的双导体传输线,如常见的同轴 电缆就是一种软的同轴线. 主模:TEM波 传输线理论分析 本节内容:从电磁场的角度,对TEM波、及TE波和TM波高次 波型加以讨论.
• 将同轴线应看作波导分析,采用圆柱坐标系,与圆波导相
似,满足同样的波动方程,只是边界条件不同。 • 图2-32给出了几个同轴线中的高次模 不讨论高次波型场量的表示式,只讨论它们的截止波长λc
§2.4 同轴线及其中的高次波型源自1.TM波 直接把分析圆波导时得到的纵向场分量的通解用在 这里,它也是同轴线的纵向场分量的通解: cos m jz E z B1J m K c r B2 N m K c r C e (2-157) sin m
§2.4 同轴线及其中的高次波型
令
p b/a
则上式可写为
m(m=0, 1, 2… )指 m阶Bessel函数和m阶 Neumann函数。
J m Kc a N m pKc a J m pKc a N m Kc a 0
矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2-155) (2-155)
特性阻抗:
可见Zc是唯一的,与TE或TM波不同
§2.4 同轴线及其中的高次波型
2.4.2 同轴线中的高次波型
• 用同轴线的主模TEM传输功率,不用高次模,即用单模传输;
• 为达到单模传输,就要研究高次模产生的条件;
• 当同轴线的尺寸与波长可比拟时,同轴线中出现高次模: 即E波和H波;
在内导体上
ra
I0 H J s 2a
比较得
§2.4 同轴线及其中的高次波型
aJ s C
于是
I0 C 2
I 0 j z H e 2r
I 0 j z Er H e 2r
与书中结果, 相差系数 都是由激励条件决定.
I0 E0 2a
边界条件确定
当 r=a,r=b 时,Ez=0
即
B1J m K c a B2 N m Kc a 0
B1J m Kcb B2 N m Kcb 0
消去B1和B2,可得: J m Kc a N m Kcb J m K cb N m K c a 0
课堂练习
1. 写出矩形波导和圆波导的主模及其截止波长; 2. 画出矩形波导横截面的场结构图;
3. 圆波导中有二类简并波型,请写出所有简并波型。
§2.4 同轴线及其中的高次波型
同轴线:内、外导体构成的双导体传输线,如常见的同轴 电缆就是一种软的同轴线. 主模:TEM波 传输线理论分析 本节内容:从电磁场的角度,对TEM波、及TE波和TM波高次 波型加以讨论.
轴向电流:
2 I H dl 0 H rd I 0e jz (2-154) l
内外导体间电压:
U
b a Er dr
b a
I 0 j z I 0 b j z e dr ln e 2r 2 a
Zc U 60 b 138 b ln lg I r a r a
§2.4 同轴线及其中的高次波型
场结构 纵向场 结构见 图2-31
说明
(1) 电场只有径向(r向),磁场只有角向(φ向). (2) TEM波是无色散波型,即其相速不随工作频率变化,
而且相速和群速相等,都等于波的传播速度:vp=vg=v (3) 波导波长和工作波长相等:λg=λ
§2.4 同轴线及其中的高次波型
2 1 1 t2 2 2 2 r r r r
2
§2.4 同轴线及其中的高次波型
2.4.1 同轴线中的TEM波 (Hz=0, Ez=0)
2 t E(r, ) 0 2 t H (r , ) 0
考虑到同轴线的边界条件
Eφ=Hr=0
所以,TEM波的电场只有Er ,磁场只有Hφ分量 有这么多的分量为0,那么直接用Maxwell 方程组求剩余的场分量就非常方便了
y
目的:抑制高次模
o
r
x
b
a
z
§2.4 同轴线及其中的高次波型
沿z轴传播的各种波型的电磁场满足波动方程
2 2 t H (r, ) Kc H (r, ) 0
2 2 t E(r, ) Kc E(r, ) 0
柱坐标下,电场和磁场为 ˆE (r, ) z ˆEr (r, ) E (r , ) r ˆEz (r, ) ˆH (r, ) z ˆHr (r, ) H (r , ) r ˆH z (r, ) 横向算子为
§2.4 同轴线及其中的高次波型
令
p b/a
则上式可写为
m(m=0, 1, 2… )指 m阶Bessel函数和m阶 Neumann函数。
J m Kc a N m pKc a J m pKc a N m Kc a 0
——本征方程,Kc叫本征 值。这是一个超越方程 图解法
§2.4 同轴线及其中的高次波型
教材上给出3种情况下,截止波长的计算方法: (1)Kca和Kcb较大,且a、b相差不大时:
c
2 (b a ) n
(2-161)
与m无关,就是说,在某同轴线中,如果可以传输 TM01波,那么同时也可以传输TM11、TM21波TM31等波 型。最低次TM01波的截止波长为上式n=1时。 (2) Kca和Kcb较大, 且a、b相差较大时(n=1,2; m=0, 1, 2, 3):
(2-159) 近似Kc解
数值法 解析法
确定截止波数Kc
表2.6-1给出了m取不同值时,特征 方程的第一个根和第二个根的值。
§2.4 同轴线及其中的高次波型
当m给定,方程有无穷多个根Kc;一个根对应一个波型, 第n个根对应第n个波型,用TMmn表示。 m——场量沿圆周分布的整驻波的个数,即沿角向按三 角函数分布的周期数,也就是沿波导圆周场量重复的 次数 n——场沿径向Bessel函数出现0值的数目,表示场 量沿半径分布的半个驻波的数目。
Kca/a=Kc. (3)m、n大于表中的值时:公式(2-163) 最低次TM波为 TM01:
c 2(b a)
§2.4 同轴线及其中的高次波型
• 将同轴线应看作波导分析,采用圆柱坐标系,与圆波导相
似,满足同样的波动方程,只是边界条件不同。 • 图2-32给出了几个同轴线中的高次模 不讨论高次波型场量的表示式,只讨论它们的截止波长λc
§2.4 同轴线及其中的高次波型
1.TM波 直接把分析圆波导时得到的纵向场分量的通解用在 这里,它也是同轴线的纵向场分量的通解: cos m jz E z B1J m K c r B2 N m K c r C e (2-157) sin m
§2.4 同轴线及其中的高次波型
TEM波的其余分量满足Maxwell方程组:
Er jH Er (2-148) z H jEr H (2-149) z
H Er
Er H
rH C
C为常
数,由 边界条 件决定
B (H ) 0 (2-150)
