Excel 在描述统计中的应用
浅谈Excel在统计学中的应用

浅谈Excel在统计学中的应用摘要:文章以Excel 2003为例,介绍了其在统计学方面的典型应用,即数据库统计函数与数据透视表、统计指数。
其中,在对统计指数的应用分析中还引入了典型实例,更加直观的介绍了Excel强大的统计功能。
关键词:Excel 数据库统计函数数据透视表统计指数前言:统计学是一门关于用科学的方法收集、整理、汇总、描述和分析数据资料,并在此基础上进行推断和决策的科学。
狭义的统计用来统指数据或者从数据中得到的一些数字。
从统计的定义可以看出,统计的关键在于对数据的分析与加工,而Excel强大的数据分析功能则恰恰与统计所要处理的问题相适应,因此从Excel产生之初便被广泛地应用于统计中,而专为统计分析所开发的各种宏更是使得Excel成为统计分析中一种实用而高效的工具。
虽然SPSS、SAS等专业统计软件在某些方面具有更为强大的统计分析功能,但其或者需要专业的编程,或者需要高昂的价格,因此普及性远远不如Excel。
下面以Excel 2003为例,介绍一下其在统计学方面的典型应用。
1.数据库统计函数与数据透视表Excel作为电子表格软件,其数据结构的核心是单元格和单元格区域,因此Excel同数据库软件相同都是管理处理一批有规律的数据。
基于Excel的行列结构,在工作表中按照标准的数据库规范对数据进行处理,这也被称为Excel的内部数据库技术,通过创建Excel的内部数据库,可以通过数据库函数实现对数据的统计分析。
1.1 数据库统计函数在建立内部数据库的基础上,Excel中专门包含了一组对存储在数据清单或数据库中的数据进行统计运算的工作表函数,这些函数统称为数据库函数即Dfunctions。
其中每个函数一般对应三个参数database、field和criteria,这些参数对应函数所使用的工作表区域,利用这些函数可以在日常统计工作中进行一些基本的统计运算。
Dfunctions具有相同的语法格式:Dfunctions(database,field,criteria)。
Excel软件在统计描述中的应用

课程实验报告
专业年级
课程名称
指导教师
学生姓名
学号
实验日期
实验地点实验楼
实验成绩
教务处制
二OO年月日
实验项目
名称
Excel软件在统计描握运用Excel软件来做集中趋势分析、离散程度分析、统计图及分布图绘制
实验
内容
1、统计图绘制;2、直方图分析工具运用;3、描述统计分析工具运用。
实验步骤
一、使用EXCEL进行统计图的绘制:用“插入”菜单,选择“图表”选项,输入数据即可得到结果。
二、用EXCEL进行直方图分析工具运用:先单击“工具”菜单,选择“数据分析”选项,在分析工具中选择“直方图”,在相应对话框中输入相关数据,可得到结果。
三、用EXCEL进行描述统计分析:先单击“工具”菜单,选择“数据分析”选项,在分析工具中选择“描述统计”,在相应对话框中输入相关数据,可得到结果。
实验环境
1、Windows下安装EXCEL软件完成;
2、Windows操作界面,人机对话的方式使用;
3、在“现代教育技术中心”实验楼进行教学实验。
实验结果与
分析
第1题:
根据该弹性上班制度数据可以概括出员工偏好在8:30上班。
第二题:
根据直方图数据分析得出个人计算机家庭使用3-6个小时最多。
第三题:
标准差越小的越好所以公交车1.825741858小于交通车4.642796092,公交车比较好。
统计学原理与excel的应用

统计学原理与Excel的应用1. 前言统计学是一门研究数据收集、分析和解释的学科。
它在各个领域都有广泛的应用,包括商业、医学、社会科学等等。
而Excel作为一种常用的数据处理工具,也被广泛用于统计学的应用中。
本文将介绍统计学的基本原理,并探讨如何使用Excel进行常见的统计分析。
2. 统计学基础2.1 总体与样本 - 总体:研究对象的全体。
- 样本:从总体中选取的一部分个体。
2.2 参数与统计量 - 参数:用于描述总体特征的具体数值。
- 统计量:用于描述样本特征的具体数值。
2.3 假设检验 - 假设:对总体或总体参数的某种陈述。
- 假设检验:通过收集样本数据,基于统计方法判断假设是否成立。
3. 常见统计分析方法及Excel应用3.1 描述统计学 - 描述性统计:对数据进行整理、总结和描述的方法。
- 常用描述统计方法: - 平均数:数据的算术平均值。
- 中位数:数据按大小排列后位于中间位置的值。
- 众数:数据中出现次数最多的值。
- 方差:数据与均值之间差异的平方平均值。
3.2 探索性数据分析 - 探索性数据分析:对数据进行可视化和初步分析,以发现数据的特征和规律。
- 常用探索性数据分析方法: - 直方图:展示数据的分布情况。
- 散点图:展示数据之间的关系和趋势。
- 箱线图:展示数据的中位数、四分位数和异常值。
3.3 参数估计与假设检验 - 参数估计:根据样本数据对总体参数进行估计。
- 假设检验:判断假设是否成立。
- Excel函数应用: - 参数估计:使用AVERAGE函数计算样本均值,使用STDEV函数计算样本标准差。
- 假设检验:使用T.TEST函数进行单样本或双样本t检验。
4. Excel实例演示为了更好地理解统计学原理与Excel的应用,我们将通过一个示例来演示如何使用Excel进行统计分析。
4.1 数据准备我们有一份学生的数学成绩数据,包括了学生的姓名和成绩。
我们将这些数据输入Excel表格中。
Excel在统计学分析中的应用和技巧

Excel在统计学分析中的应用和技巧Excel是一款经典的电子表格软件,在日常工作中几乎无处不在,它不仅可以处理普通的数据,同时也可以进行高级的统计数学和数据分析。
本文将介绍一些Excel在统计学分析中的应用和技巧,帮助读者更好地应用Excel进行统计学分析。
一、Excel在统计学中的应用1.统计描述Excel可以用来计算诸如平均数、中位数、标准差、方差和四分位数等统计描述性统计数据。
在数据分析中,数据的描述性统计数据有助于探索数据集的范围、分布和重要特征。
例如:在Excel中,选择数据集,使用快捷键Alt+ A+ P可打开描述性统计数据对话框,弹出描述性统计数据对话框。
在对话框上选择所需的位置,然后单击确定即可。
2.散点图和回归分析Excel中有许多类型的图表,包括散点图和回归分析表,可用于探索变量之间的关系。
散点图通常用于可见数据的统计关系,可使您通过观察数据的带状或散布情况来观察变量之间的关系。
例如,在Excel中,单击菜单栏“插入”→“散点图”,可自动创建一个简单的散点图。
3.假设检验和T检验假设检验和T检验可用于比较两个总体的均值。
检验的结果告诉我们是否有足够的证据来拒绝零假设或接受备择假设。
通常我们把P值小于等于0.05的结果认为是显著的。
在Excel中,T检验和假设检验可通过以下公式快速计算。
例如,在Excel中输入一个T检验公式= T.TEST(数组1,数组2,尾数(1,2双重尾差异/单向尾差异)(1),类型(3权,2左,1右)(1))。
二、Excel在统计学中的技巧1.条件格式化Excel中的条件格式化可使数据集中的规律和模式变得明显,提高数据集中不同信息和结果的可视化效果。
例如,在Excel中,选择所需的数据区域,并在开始菜单选项卡的样式组中单击条件格式,选择所需的条件格式规则,然后单击+按钮以添加规则。
2.筛选和排序Excel中的高级筛选和排序功能可帮助快速整理和分析大型数据集。
《应用统计学》第十章:Excel在统计分析中的应用

05
的常见问题及解决方
案
数据源问题及解决方案
解决方案
总结词:数据源问题通常涉 及数据输入错误、数据格式
不正确或数据缺失。
01
02
03
仔细检查数据输入,确保没 有遗漏或错误的数值、文本。
统一数据格式,如将日期、 数字等格式化。
04
05
使用Excel的筛选和查找功能, 查找并处理缺失值。
图表展示问题及解决方案
聚类算法
聚类算法是一种无监督学习方法,通过将相似的对象聚集在一起形 成不同的群组或簇,来发现数据的内在结构。
分类和聚类算法的应用场景
分类和聚类算法在许多领域都有广泛的应用,如市场细分、客户分 群、异常检测等。
关联规则和序列模式挖掘
关联规则挖掘
01
关联规则挖掘是发现数据集中项之间的有趣关系的过程,通常
《应用统计学》第十章 excel在统计分析中的 应用
contents
目录
• Excel在统计分析中的应用概述 • Excel在描述性统计分析中的应用 • Excel在推论性统计分析中的应用 • Excel在数据挖掘和机器学习中的应用 • Excel在统计分析中的常见问题及解决方
案
Excel在统计分析中
用于市场篮子分析、交叉销售和推荐系统等。
序列模式挖掘
02
序列模式挖掘是发现数据集中项之间时间顺序关系的过程,通
常用于时间序列分析、股票价格预测等。
关联规则和序列模式挖掘的应用场景
03
关联规则和序列模式挖掘在许多领域都有广泛的应用,如金融
欺诈检测、股票价格预测、消费者行为分析等。
Excel在统计分析中
01
02
03
Excel在统计中的应用 第3章 数据描述统计分析

3.1 集中趋势的测定与分析
3.1.1 集中趋势的测定内容 3.1.2 用Excel工作表函数描述集中趋势 3.1.3 三种平均数的特点
返回首页
3.1.1 集中趋势的测定内容
在统计研究中,需要搜集大量数据并对其进行加 工整理,对这些数据进行整理之后发现:大多数 情况下数据都会呈现出一种钟形分布,即各个变 量值与中间位置的距离越近,出现的次数越多; 与中间位置距离越远,出现的次数越少,从而形 成了一种以中间值为中心的集中趋势。这个集中 趋势是现象共性的特征,是现象规律性的数量表 现。
n2
语法:STDEVP(number1,number2,...)
例3-2 使用例3-1资料,计算各家电销售量的总 体标准差,如图3-5所示。
图3-5 计算总体标准差
例3-3 示。
两组工人生产某种零件的产量如图3-6所
图3-6 两组工人产量
图3-7 计算产量平均数
图3-8 计算两组工人产量标准差
例3-1 某商场家用电器销售情况如图3-1所示。 (1)计算各种电器的全年平均销售量,如图3-2 所示。 (2)计算各种电器销售量的中位数,如图3-3所 示。 (3)计算各种电器销售量的众数,如图3-4所示。
图3-1 某商场家用电器销售情况
图3-2 家用电器销售量平均数
图3-3 家用电器销售量中位数
图3-9 计算两组工人产量标准差系数 返回本节
3.2.3 四分位数与四分位距
四分位数是将中值的前后两部分数值再等分为二,以数值 小的一端算起,前半部的分区点称为第 1 四分位数,后半 部的分区点称为第3四分位数,而中值即为第2四分位数。 四分位数通常用于在销售额和测量值数据集中对总体进行 分组。 语法:QUARTILE(array,quart) array:需要求四分位数值的数组或数字型单元格区域。 quart:决定返回哪一个四分位值。 Quart值与QUARTILE返回值的对应关系见表3-1所示。
Excel在统计分析中的应用

使用函数向导
使用Excel帮助理解函数
3.5 常用工作表函数
自动求和按钮 SUM函数 AVERAGE函数 SQRT函数 COUNT、COUNTA和COUNTBLANK函数
COUNT函数统计数值数据的个数 COUNTA统计非空单元格的个数 COUNTBLANK统计空白单元格的数目
数据列表
大鼠生存时间(天) 剂量 1 剂量 2 剂量 3 12 20 18 13 23 19 16 26 29 19 28 31 26 31 36 35 33 42
数据排序
按单变量排序 根据某一列的数据按单一关键字对行数据进行 排序。
单击要排序的变量列中的任一单元格,再单击 常用工具栏的【升序】或【降序】按钮即可。
数据的分类与汇总
分类汇总是对数据列表按某一字段值进行分类, 将同类别数据放在一起,并分别为各类数据进行 统计汇总(求总和,平均值、最大值、最小值、 统计个数等)
操作过程:
先对数据列表依据分类字段排序
单击【数据】菜单→【分类汇总】→【分类汇 总】对话框。
三、 公式和函数
Excel在统计分析中的应用
主要内容
一、Excel基本介绍
二、数据管理功能
三、公式和函数 四、统计图的绘制 五、统计分析功能
一、Excel基本介绍
Microsoft Excel是当前功能强大、技术先进和使用
方便灵活的电子表格系统。
Excel的历史渊源
1987年10月,美国Microsoft公司推出视窗版 Excel(超越), 被公认达到软件技术的最佳专 业水平; 1993年,微软又把Word和Excel集成在Office办 公套装软件内,使其能相互共享数据。
用ECEL计算描述统计量

用ECEL计算描述统计量描述统计量是对一组数据进行概括和总结的统计指标。
通过计算描述统计量,我们可以得到数据的中心趋势、离散程度和分布情况等信息。
本文将介绍如何使用Excel计算常见的描述统计量,包括均值、中位数、众数、标准差、方差和四分位数等。
首先,我们需要准备一组数据,并将其输入到Excel的其中一列中。
以列A为例,我们在A1单元格中输入第一个数据,然后通过拖动填充手柄将数据输入到其他单元格。
下面将介绍如何计算各个描述统计量。
1.均值均值是数据的平均值,代表数据的中心趋势。
在Excel中,可以使用AVERAGE函数来计算均值。
在B1单元格中输入=AVERAGE(A:A),然后按下回车键即可得到均值。
2.中位数中位数是数据中的中间值,将数据按照大小排序后位于中间的值。
在Excel中,可以使用MEDIAN函数来计算中位数。
在B2单元格中输入=MEDIAN(A:A),然后按下回车键即可得到中位数。
3.众数众数是数据中出现频次最多的值。
在Excel中,可以使用MODE函数来计算众数。
在B3单元格中输入=MODE(A:A),然后按下回车键即可得到众数。
4.标准差标准差是衡量数据离散程度的指标,越大表示数据越分散。
在Excel 中,可以使用STDEV函数来计算标准差。
在B4单元格中输入=STDEV(A:A),然后按下回车键即可得到标准差。
5.方差方差是数据离散程度的另一种度量方式,是标准差的平方。
在Excel 中,可以使用VAR函数来计算方差。
在B5单元格中输入=VAR(A:A),然后按下回车键即可得到方差。
6.四分位数四分位数将数据分为四等份,分别是第一四分位数、中位数和第三四分位数。
在Excel中,可以使用QUARTILE函数来计算四分位数。
在B6单元格中输入=QUARTILE(A:A,1)来计算第一四分位数,输入=QUARTILE(A:A,2)来计算中位数,输入=QUARTILE(A:A,3)来计算第三四分位数。
统计学实验报告

统计学实验报告实验内容:Excel在描述统计中的应用Excel在相关与回归中的应用班级:组员:实验一、Excel在描述统计中的应用实验目的:通过实践训练,使学生能够利用“直方图”工具计算频率分布并制作直方图,利用“描述统计”工具对原始数据进行统计分析,计算分组数据的平均值和方差。
一、利用直方图工具计算频率分布并制作直方图资料:某班31名学生家庭人均纯收入与生活费支出如下:家庭人均纯收入如下:18000 2000 5000 100000 20000 7000 40000 30000 20000 9000 8000 40000 40000 30000 2500 30000 30000 30000 6000 6000 20000 7000 7000 8000 6000 36000 2500 10000 6000 7000 6000生活费支出如下:1000 500 600 1200 1000 650 1400 800 1000 800 1000 2000 2000 800 500 800 800 500 540 700 800 650 600 800 500 800 450 500 500 700 500 要求:1、以0、500、800、1000、1500为组限计算生活费支出的频数和累计频率;以0、5000、10000、20000、40000为组限计算家庭人均纯收入的频数和累计频率。
2、作出生活费支出、家庭人均纯收入的直方图3、计算生活费支出、家庭人均纯收入的平均值、中位数、方差、标准差、95%置信区间。
实验步骤:把生活费支出输入A1中,把组限输入B1中,将数据输入到表格。
1、执行菜单命令“工具”——“数据分析”2、选择“直方图”,单击“确定”按钮,弹出“数据分析”,输入区蜮:选择A1选项,按住左键不放拖到A32;接受区蜮:选择B1选项,按住左键不放拖到B6;选中“标志”复选框,选中“输出区蜮”并选择C1指定输出区蜮,选中“累计百分率”复选框和“图表输出”复选框3、单击“确定”按钮,得到各组频数和累计频率以及直方图。
excel统计应用实验小结

excel统计应用实验小结
在这个实验中,我们探索了Excel在统计数据分析方面的应用。
通过实际操作和实验,我们学习了以下几个重要的Excel统计功能:
1.数据输入与整理:我们学会了如何使用Excel表格进行数据输入和整理。
通过创建适当的列和行来组织数据,并使用合适的数据类型和格式进行输入,以确保数据的准确性和一致性。
2.数据汇总与描述统计:我们学会了如何使用Excel的函数和公式来进行数据的汇总和描述统计。
例如,我们使用SUM函数计算总和、AVERAGE函数计算平均值,以及COUNT函数计算数量等。
3.数据排序与筛选:我们学会了如何使用Excel的排序和筛选功能,对数据进行排序和筛选,以便更好地分析和理解数据的特征和趋势。
4.数据可视化与图表绘制:我们学会了如何使用Excel的图表功能,将数据可视化并绘制出各种类型的图表,如柱状图、折线图和饼图。
通过图表,我们能够更直观地观察和比较数据。
5.数据分析与推断统计:我们学会了如何使用Excel进行一些基本的推断统计分析,如t检验和相关性分析。
通过这些分析,我们能够对数据进行更深入的理解和推断。
总体而言,Excel是一个强大且灵活的工具,可以广泛应用于数据统计和分析。
通过掌握Excel的统计功能,我们可以更好地处理和分析数据,从而得出有关数据集的有意义的结论和洞察。
这些技能在实际工作和研究中都具有重要的应用价值。
1。
Excel在统计学中的应用

Excel在统计学中的应用《统计学》实验指导书前言1.实验目的《统计学》是关于数据的科学,它是论述在社会经济范围内搜集数据、整理数据、分析数据与解释数据的基本理论、基本知识、基本方法的科学,这就决定了本课程的地位——经济与管理类各专业的必修核心课,是最重要的专业基础课之一。
通过本课程的教学,能够使学生系统地掌握统计学的基本理论、基本知识与基本方法,为加强定量分析,更好地解决经济管理各专业实际问题打下良好的基础。
在上机实验的设计上,力争使每个学生都能较系统的掌握EXCEL在统计的应用,但避免枯燥的操作介绍,而是有针对性的要求学生结合问卷调查的数据与有关案例数据,运用EXCEL完成数据整理、数据分析及其结果的指标解释。
上机按照分班分期集中的形式完成相应内容的教学任务,由实验教师指导学生进行数据整理与数据分析。
⒉适用专业统计学实验适用的专业是经济与管理类各专业。
⒊先修课程概率与数理统计、统计学⒋⒌数量要求)本实验按自然班分组,每次实验指导教师指导一个实验小组,为此统计上机实验需设35个座位,实验台上配备Excel统计数据的实际案例,如教科书,教师搜集到的最新的经济管理类有关的统计数据、统计图、统计表并复印给每位学生,教授学生Excel统计功能的幻灯片及实际操作的随堂作业;××统计调查报告的范本等等。
要紧统计调查报告的制作流程图要悬挂在实验室墙壁上,便于学生参阅及按步骤有的放矢的完成调查报告,同时营造良好的实验环境。
⒍实验总体要求(1)通过统计学上机实验,进一步巩固课堂所学的理论知识。
在实验中,要将理论课所讲的内容与实际操作进行参照,弄清模拟实验资料中全部经济数据的统计处理。
(2)进行操作,提高实际工作能力。
在实验中,为学生配备了有关的经济管理类数据分析内容,比如:近几年的居民消费价格指数与分析预测内容,学生要按要求进行图表绘制并根据结果进行适当的定性分析,提高实际分析能力。
(3)通过实验,掌握统计学的基本常识,为进一步处理复杂经济现象形成的数据分析打下良好的基础。
Excel在统计学中的应用
Excel在统计学中的应用统计分析常用的软件有SAS、SPSS和Excel等,其中Excel应用较为普遍。
本附录主要介绍Excel在统计中的应用,并用实例操作的形式进行介绍。
一、用Excel作数据的频率分布表和直方图利用Excel处理数据,可以建立频率分布表和条形图。
一般统计数据有两大类,即定性数据和定量数据。
定性数据用代码转化为定量数据后再处理,这里就不涉及了,下面主要以定量数据为例来说明如何利用Excel进行分组,并作频率分布表和直方图。
[资料]现有某管理局下属40个企业产值计划完成百分比资料如下:97、123、119、112、113、117、105、107、120、107、125、142、103、115、119、88、115、158、146、126、108、110、137、136、108、127、118、87、114、105、117、124、129、138、100、103、92、95、127、104(1)据此编制分布数列(提示:产值计划完成百分比是连续变量);(2)计算向上累计频数(率);(3)画出次数分布直方图。
[步骤]第1步:打开Excel界面,输入40个企业的数据,从上到下输入A列(也可分组排列)。
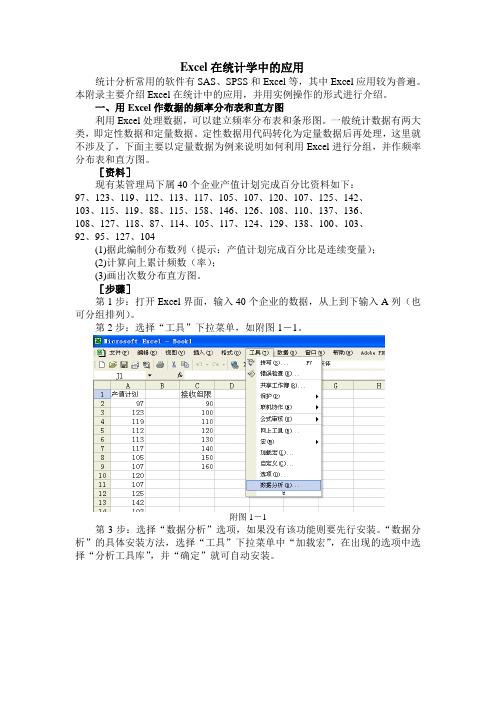
第2步:选择“工具”下拉菜单,如附图1-1。
附图1-1第3步:选择“数据分析”选项,如果没有该功能则要先行安装。
“数据分析”的具体安装方法,选择“工具”下拉菜单中“加载宏”,在出现的选项中选择“分析工具库”,并“确定”就可自动安装。
附图1-2第4步:在分析工具中选择“直方图”,如附图1-2。
附图1-3第5步:当出现“直方图”对话框时,在“输入区域”方框内键入A2:A41或$A$2:$A$41(“$”符号起到固定单元格坐标的作用,表示的是绝对地址),40个数据已输入该区域内,如果是分组排列的,就应选择整个分组区域。
在“接收区域”方框内键入C2:C9或$C$2:$C$9,所有数据分成8组(主要根据资料的特点,决定组数、组距和组限),把各组的上限输入该区域内。
实验一 数据资料的描述性统计分析(Excel应用)

2.3 图表的编辑:误差线的添加
➢ 打开数据系列格式对话框,在“误差线Y”选项卡中,选择显示 方式为“正偏差”,再选择误差量为“自定义”,单击其后数据框 右边的“折叠对话框”按钮,选择误差数据。
绘图区格式 网络线格式 图例格式 数据系列格式
叶绿素含量/%
叶绿素含量/%
图2-4 四个水稻品种类型不同时期的叶绿素含量
练习2
测定5个不同小麦品种 灌浆结实期叶片的蒸 腾速率(右图),
使用Excel软件将测定 结果绘成复式线图( 要求含误差线) 。
日期
品种
5/2 5/9 5/16 5/23 5/30
陕229
5.2 4.8 4.3
3
1
5.1
5 4.6 2.7 0.8
5.4 4.5
4 3.3 1.1
长武134 4.9 4.5 3.6 3.1 0.5
插 入 函 数
1.1 算术平均数的计算
步骤3:设置“函数参数”,在Number1后的框中选定待分析的数据
2. Excel软件的“描述统计”分析工 具
➢ 步骤1:调用菜单“工具”“数据分析”,打开“分析工
具库”对话框,选择“描述统计”工具。
2. Excel软件的“描述统计”分析工 具
➢ 步骤2:打开“描述统计”对话框,设置数据位置(输入区域)、
纸质报告和电子版文件务必在下次实验课之前 提交或发送!
练习1
使用Excel软件分别计算下面两个玉米品种的10 个果穗长度(cm)的平均数和标准差,并用柱形 图 表 示 结 果 。 ( 提 示 : 使 用 函 数 AVERAGE 和 STDEV)
品种 BS24 金皇后
果穗长度 19 21 20 20 18 19 22 21 21 19 16 21 24 15 26 18 20 19 22 19
EXCEL在统计中应用部分习题与答案

项目一 Excel在描述性统计指标中的应用(习题与答案)1.为了解某职业学院新毕业大学生的工资情况,随机抽取49人,调查得月工资如下表:实训要求:利用EXCEL计算算术平均数、标准差、标准差系数、方差、调和平均数、众数、中位数等描述统计量。
答案:2. 某学院职工相关资料如下:某学院职工按工作岗位分组资料答案:(1)条形图(2)柱形图(3)折线图(4)饼图项目二 Excel在时间数列分析中的应用(习题与答案)1.某地区2000-2003年工业总产值资料表如下:实训要求:(1)计算表中所缺数字;(2)计算平均发展速度;(3)预测2013年该地区工业总产值答案:(1)(略);(2)125%;(3)244.14亿元项目三 Excel 在指数因素分析中的应用(习题与答案)1.某市几种主要副食品调整价格前后资料如下:实训要求:(1)计算各商品零售物价和销售量的个体指数; (2)计算四种商品物价和销售量的总指数;(3)分析由于商品价格变动使该市居民增加支出的金额。
答案:(1) 各商品零售物价个体指数:%76.11180.660.7%67.10680.192.1%91.11020.244.2%33.1333.04.0014013012011============p p K p p K p p K p p K p p p p(2)(3) (万元) 即:由于商品价格变动使该市居民增加支出3.03万元。
项目四 Excel 在指数因素分析中的应用(习题与答案)1. 某工厂车间生产的100件产品重量数据统计表如下:实训要求:利用Excel 从100件产品中抽取8件进行检查分析。
答案:3.18.615.18.152.52.22.53.03.16.715.192.152.544.22.54.0I 1011P ⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯==∑∑qp q p %31.11261.2464.27==15.18.62.18.146.42.253.03.18.615.18.152.52.22.53.0I 0010⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯==∑∑qp q p q%59.11529.2161.24==03.361.2464.271011=-=-∑∑q p q p提示:利用“抽样”工具进行抽样或利用“RAND”函数进行抽样,抽样结果是可变的。
excel在数理统计中的应用

excel在数理统计中的应用Excel是一种强大的电子表格程序,可用于处理各种数学和统计问题。
在数理统计中,Excel可以用于数据分析、描述统计分析、推断统计分析、数据可视化等方面的应用。
该文将介绍Excel在数理统计中的应用。
一、数据分析Excel可用于数据的导入、存储、排序、过滤、转换、合并等操作。
数据分析通常包括数据的整理、清洗、变换、整合等步骤,Excel可轻松地完成这些过程。
Excel还提供了数据表格、散点图、线性图、饼图、柱状图等图表工具,可以帮助用户快速可视化数据,以更深入地了解其特征和关系。
例如,当开展某项调查时,需要对所收集的数据进行分析。
用户可以将数据导入Excel工作簿中,并首先运用“数据”。
数据工具的“排序”功能,按照需要的顺序排列各个变量的值。
然后可以使用“数据工具”的“筛选”功能筛选出需要的数据子集。
此外,Excel还提供了数据透视表工具,可以方便地对数据进行汇总、计算和分析。
二、描述统计分析描述统计分析主要是对数据的中心趋势、变异程度、对称性等常用统计特征进行基本统计分析。
Excel提供了多种描述性统计函数,例如求平均值、中位数、众数、分位数、方差、标准差等,并以简单和易于理解的方式汇总和呈现结果。
对于连续变量的分布,可以使用直方图和箱线图等图表工具进行展示和分析。
例如,我们可以使用Excel提供的函数,计算数据的平均值、中位数、标准差等描述性统计指标,并用直方图或箱线图来展示变量的分布特征。
这样,我们可以从多个方面对数据特征进行了解,有助于更深入地理解数据的性质。
推断统计分析主要是基于样本数据,对总体数据进行推论的方法。
Excel提供了大量的统计分析工具,帮助用户进行假设检验、置信区间估计、方差分析、回归分析等常用推断性统计分析。
例如,我们可以使用Excel进行一组样本的t检验,判断样本的均值是否显著差异。
此外,在进行回归分析时,Excel提供了多元线性回归和逐步回归分析模型,运用这些模型,可以对自变量对因变量的影响进行分析。
Excel中的描述统计分析工具

Excel中的描述统计分析工具Excel是一款常用的电子表格软件,不仅可以进行数据收集和整理,还集成了一系列的数据分析工具,其中的描述统计分析工具可以对数据进行一些基本的统计分析,帮助用户更好地理解和使用数据。
描述统计分析的定义描述统计分析,顾名思义就是对数据进行描述和总结,包括数据的集中趋势、分散程度、偏态和峰态等。
描述统计分析通常用于研究数据的一些基本特征,例如平均数、中位数、众数、标准差、变异系数等。
Excel中的描述统计分析工具均值、中位数、众数在Excel中,分别可以使用以下函数来计算数据集的均值、中位数和众数:•均值:AVERAGE(data_range),其中data_range表示数据的区间。
•中位数:MEDIAN(data_range)。
•众数:MODE.SNGL(data_range),如果数据集中有多个众数,则返回第一个。
方差、标准差和变异系数在Excel中,分别可以使用以下函数来计算数据集的方差、标准差和变异系数:•方差:VAR.P(data_range),其中data_range表示数据的区间。
注意,这里计算的是总体方差,而不是样本方差。
•标准差:STDEV.P(data_range),其中data_range表示数据的区间。
同样,这里计算的是总体标准差,而不是样本标准差。
•变异系数:STDEV.P(data_range)/AVERAGE(data_range),其中data_range表示数据的区间。
最大值、最小值、四分位数在Excel中,分别可以使用以下函数来计算数据集的最大值、最小值和四分位数:•最大值:MAX(data_range),其中data_range表示数据的区间。
•最小值:MIN(data_range),其中data_range表示数据的区间。
•四分位数:QUARTILE.EXC(data_range, quart),其中data_range 表示数据的区间,quart表示要求的四分位数,取值为1、2、3分别对应第一、二、三个四分位数。
Excel在统计分析中的应用(全113页)

单击添加章节标题内容
01
Excel在统计分析中的基础操作
02
数据输入与整理
输入数据:在Excel中输入数据可以使用键盘、复制粘贴等方式 整理数据:对输入的数据进行整理包括排序、筛选、分类等操作 数据验证:对输入的数据进行验证确保数据的准确性和完整性 数据清洗:对输入的数据进行清洗去除重复、缺失、错误等数据
Excel在统计分析中的实际案例分 析
06
市场调查数据分析
案例背景: 某公司进行 市场调查收 集了大量数 据
数据处理: 使用Excel 进行数据清 洗、整理和 格式化
数据分析: 使用Excel 进行描述性 统计分析、 交叉分析、 回归分析等
数据可视化: 使用Excel 进行数据可 视化如柱状 图、饼图、 散点图等
结论:根据 数据分析结 果提出市场 策略建议
生产质量控制分析
案例背景:某工厂生产过程中出现质量问题需要分析原因并改进
数据来源:生产记录、质量检测报告等 问题分析:使用Excel进行数据整理、清洗、可视化等操作找出质量 问题的原因 解决方案:根据分析结果制定改进措施提高产品质量
金融数据分析与应用
案例背景:某银行需要对其客户数据进行统计分析以了解客户行为和需求
常用函数: COUNT、SUM、 VERGE、MX、 MIN、STDEV、 VR等
数据处理:数据清洗、 数据转换、数据合并 等
数据可视化:利用 Excel的图表功能 如柱状图、折线图、 饼图等对数据进行 可视化展示
假设检验
假设检验的概念:检验两个或多 个总体参数是否相等
假设检验的步骤:提出假设、选 择检验方法、计算检验统计量、 确定显著性水平、做出决策
散点图:用于展示两个变量之间 的关系如身高与体重的关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节Excel 在描述统计中的应用在使用Excel 进行数据分析时,要经常使用到Excel 中一些函数和数据分析工具。
其中,函数是Excel 预定义的内置公式。
它可以接受被称为参数的特定数值,按函数的内置语法结构进行特定计算,最后返回一定的函数运算结果。
例如,SUM 函数对单元格或单元格区域执行相加运算,PMT 函数在给定的利率、贷款期限和本金数额基础上计算偿还额。
函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号。
参数可以是数字、文本、形如TRUE 或FALS E 的逻辑值、数组、形如#N/A 的错误值,或单元格引用。
给定的参数必须能产生有效的值。
参数也可以是常量、公式或其它函数。
Excel 还提供了一组数据分析工具,称为“分析工具库”,在建立复杂的统计分析时,使用现成的数据分析工具,可以节省很多时间。
只需为每一个分析工具提供必要的数据和参数,该工具就会使用适宜的统计或数学函数,在输出表格中显示相应的结果。
其中的一些工具在生成输出表格时还能同时产生图表。
如果要浏览已有的分析工具,可以单击“工具”菜单中的“数据分析”命令。
如果“数据分析”命令没有出现在“工具”菜单上,则必须运行“安装”程序来加载“分析工具库”。
安装完毕之后,必须通过“工具”菜单中的“加载宏”命令,在“加载宏”对话框中选择并启动它。
一、描述统计工具(一)简介:此分析工具用于生成对输入区域中数据的单变量分析,提供数据趋中性和易变性等有关信息。
(二)操作步骤:1.用鼠标点击工作表中待分析数据的任一单元格。
2.选择“工具”菜单的“数据分析”子菜单。
3.用鼠标双击数据分析工具中的“描述统计”选项。
4.出现“描述统计”对话框,对话框内各选项的含义如下:输入区域:在此输入待分析数据区域的单元格范围。
一般情况下Excel 会自动根据当前单元格确定待分析数据区域。
分组方式:如果需要指出输入区域中的数据是按行还是按列排列,则单击“行”或“列”。
标志位于第一行/列:如果输入区域的第一行中包含标志项(变量名),则选中“标志位于第一行”复选框;如果输入区域的第一列中包含标志项,则选中“标志位于第一列”复选框;如果输入区域没有标志项,则不选任何复选框,Excel 将在输出表中生成适宜的数据标志。
均值置信度:若需要输出由样本均值推断总体均值的置信区间,则选中此复选框,然后在右侧的编辑框中,输入所要使用的置信度。
例如,置信度95%可计算出的总体样本均值置信区间为10,则表示:在5%的显著水平下总体均值的置信区间为( X -10, X +10)。
第K 个最大/小值:如果需要在输出表的某一行中包含每个区域的数据的第k 个最大/小值,则选中此复选框。
然后在右侧的编辑框中,输入k 的数值。
输出区域:在此框中可填写输出结果表左上角单元格地址,用于控制输出结果的存放位置。
整个输出结果分为两列,左边一列包含统计标志项,右边一列包含统计值。
根据所选择的“分组方式”选项的不同,Excel 将为输入表中的每一行或每一列生成一个两列的统计表。
新工作表:单击此选项,可在当前工作簿中插入新工作表,并由新工作表的A1 单元格开始存放计算结果。
如果需要给新工作表命名,则在右侧编辑框中键入名称。
新工作簿:单击此选项,可创建一新工作簿,并在新工作簿的新工作表中存放计算结果。
汇总统计:指定输出表中生成下列统计结果,则选中此复选框。
这些统计结果有:平均值、标准误差、中值、众数、标准偏差、方差、峰值、偏斜度、极差(全距)最小值、最大值、总和、样本个数。
5.填写完“描述统计”对话框之后,按“确定”按扭即可。
(三)结果说明:描述统计工具可生成以下统计指标,按从上到下的顺序其中包括样本的平均值( X ),标准误差( n S / ),组中值(Medium),众数(Mode), 样本标准差(S),样本方差(S2), 峰度值,偏度值,极差(Max-Min), 最小值(Min),最大值(Max),样本总和,样本个数(n)和一定显著水平下总体均值的置信区间。
二.直方图工具(一)简介:直方图工具,用于在给定工作表中数据单元格区域和接收区间的情况下,计算数据的个别和累积频率,可以统计有限集中某个数值元素的出现次数。
例如,在一个有50 名学生的班级里,可以通过直方图确定考试成绩的分布情况,它会给出考分出现在指定成绩区间的学生个数,而用户必须把存放分段区间的单元地址范围填写在在直方图工具对话框中的“接收区域”框中。
(二)操作步骤:1.用鼠标点击表中待分析数据的任一单元格。
2.选择“工具”菜单的“数据分析”子菜单。
3.用鼠标双击数据分析工具中的“直方图”选项。
4.出现“直方图”对话框,对话框内主要选项的含义如下:输入区域:在此输入待分析数据区域的单元格范围。
接收区域(可选):在此输入接收区域的单元格范围,该区域应包含一组可选的用来计算频数的边界值。
这些值应当按升序排列。
只要存在的话,Excel 将统计在各个相邻边界直之间的数据出现的次数。
如果省略此处的接收区域,Excel 将在数据组的最小值和最大值之间创建一组平滑分布的接收区间。
标志:如果输入区域的第一行或第一列中包含标志项,则选中此复选框;如果输入区域没有标志项,则清除此该复选框,Excel 将在输出表中生成适宜的数据标志。
输出区域:在此输入结果输出表的左上角单元格的地址。
如果输出表将覆盖已有的数据,Excel 会自动确定输出区域的大小并显示信息。
柏拉图:选中此复选框,可以在输出表中同时显示按降序排列频率数据。
如果此复选框被清除,Excel 将只按升序来排列数据。
累积百分比:选中此复选框,可以在输出结果中添加一列累积百分比数值,并同时在直方图表中添加累积百分比折线。
如果清除此选项,则会省略以上结果。
图表输出:选中此复选框,可以在输出表中同时生成一个嵌入式直方图表。
5.按需要填写完“直方图”对话框之后,按“确定”按扭即可。
(三)结果说明:完整的结果通常包括三列和一个频率分布图,第一列是数值的区间范围,第二列是数值分布的频数,第三列是频数分布的累积百分比。
三、利用Excel 绘制散点图(一)简介:散点图是观察两个变量之间关系程度最为直观的工具之一,利用Excel 的图表向导,可以非常方便的创建并且改进一个散点图,也可以在一个图表中同时显示两个以上变量之间的散点图。
(二)操作步骤:数据如图附-3 所示,图附-3可按如下步骤建立变量x-y,x-z 的散点图:1.拖动鼠标选定数值区域A2:C12,不包括数据上面的标志项。
2.选择“插入”菜单的“图表”子菜单,进入图表向导。
3.选择“图表类型”为“散点图”,然后单击“下一步”。
4.确定用于制作图表的数据区。
Excel 将自动把你前面所选定的数据区的地址放入图表数据区的内。
5. 在此例之中,需要建立两个系列的散点图,一个是x-y 系列的散点图,一个是x-z 系列的散点图,因此,必须单击“系列”标签,确认系列1 的“X 值”方框与“数值方框”分别输入了x,y 数值的范围,在系列2 的“X 值”方框与“数值方框”分别输入了x,z 数值的范围。
在此例中,这些都是Excel 已经默认的范围,所以,可忽略第5 步,直接单击“下一步”即可。
6. 填写图表标题为“X-Y 与X-Z 散点图”,X 轴坐标名称为“X”与Y 轴坐标名称“Y/Z”,单击“下一步”。
7. 选择图表输出的位置,然后单击“完成”按扭即生成图附-4 的图表。
图附-4(三)结果说明:如图附-4 所示,Excel 中可同时生成两个序列的散点图,并分为两种颜色显示。
通过散点图可观察出两个变量的关系,为变量之间的建立模型作准备。
四、数据透视表工具(一)简介:数据透视表是Excel 中强有力的数据列表分析工具。
它不仅可以用来作单变量数据的次数分布或总和分析,还可以用来作双变量数据的交叉频数分析、总和分析和其它统计量的分析。
(二)操作步骤:如图附-5 所示,表中列出学生两门功课评定结果,图附-5可按如下步骤建立交叉频数表:1.选中图附-5 中表格中有数据的任一单元格,然后选择“数据”菜单的“数据透视表”子菜单,进入数据透视表向导。
2.选择“Microsoft Excel 数据清单或数据库”为数据源。
单击“下一步”。
3.选择待分析的数据的区域,一般情况下Excel 会自动根据当前单元格确定待分析数据区域,因此你只要直接单击“下一步”按扭即可。
4.确定数据透视表的结构,在此例中,要建立的是一个交叉频数表,分别按语文和数学的成绩对学生的人数进行交叉频数分析,因此可按图附-6将三个按扭“学号”、“语文”、“数学”分别拖放到表格的指定部位,并且双击“求和项:学号”,将其改为记数项,结果如图附-6所示,然后单击“下一步”按扭。
图附-65.选择数据透视表的显示位置之后,单击“完成按扭”,可出现如图附-7 所示的数据透视表。
图附-7(三)结果说明:如图附-7 的结果所示,数据透视表可以作为一个交叉频数分析工具。
完成数据透视表之后,可按需要修改数据表的显示格式。
例如,如果想要把表格中的频数替换成为百分比数。
可以用鼠标右击频数的任一单元格,选择“字段”子菜单,单击“选项”按扭,将“数据显示方式”替换成为“占总和的百分比”,然后单击“确定”按扭即可。
按同样方式,可将数据透视表修改成为其它不同样式。
五、排位与百分比工具(一)简介:此分析工具可以产生一个数据列表,在其中罗列给定数据集中各个数值的大小次序排位和相应的百分比排位。
用来分析数据集中各数值间的相互位置关系。
(二)操作步骤:1.用鼠标点击表中待分析数据的任一单元格。
2.选择“工具”菜单的“数据分析”子菜单。
3.用鼠标双击数据分析工具中的“排位与百分比”选项。
4.填写完“排位与百分比”对话框,单击“确定”按扭即可。
(三)结果说明:输出的结果可分为四列,第一列“点”是数值原来的存放位置,第二列是相应的数值,第三列是数值的排序号,第四列是数值的百分比排位,它的计算方法是:小于该数值的数值个数/(数值总个数-1)。
