图像放大的两种编程算法的实现

编程实现一幅图像的平移、镜像、旋转、缩小和放大。

课程设计任务书学生姓名: zhh 专业班级: 通信1002班指导教师：徐文君工作单位：信息工程学院题目: 通信工程应用技术综合训练与实习初始条件:1。

数字图像处理课程相关知识。

2。

Matlab软件的软件编程应用与仿真.要求完成的主要任务:任务:编程实现一幅图像的平移、镜像、旋转、缩小和放大.要求：1。

给出所用算法的理论依据和必要的推导过程。

2.给出原始图像和处理后的图像。

时间安排：指导教师签名：年月日系主任签名：年月日目录摘要............................................................................ Abstract (I)1 图像的几何变换 01.1图像几何变换内容 01.2 Matlab仿真使用的主要函数 02图像的平移变换 (3)2。

1图像平移变换原理 (3)2.2图像平移变换的matlab实现 (4)3图像的镜像变换 (5)3.1 图像镜像变换原理 (6)3。

2 图像镜像变换的matlab实现 (7)4图像的旋转变换 (8)4。

1图像旋转变换原理 (9)4。

2 图像旋转变换的matlab实现 (10)5图像的比例变换................................................. 错误!未定义书签。

5.1 图像比例变换原理 (13)5。

2 图像比例变换的matlab实现 (13)6 心得体会 (17)参考文献 (18)附录 (19)摘要图像是对三维实际景物的平面投影，图形图像处理主要是通过计算机对图像进行处理，从而达到预期的效果的技术.为了观测需要，常常需要进行各种不同的几何变换，主要包括图像的平移变换，图像水平、垂直镜像变换，图像旋转变换，图像比例变换。

实际上，几何变换不改变像素值，而是改变像素所在的位置。

在图像处理中,可以通过Matlab来实现图像的几何变换,此软件的语法结构简单，并且具有极强的数值计算、图形文字处理、数据分析、图形绘制及图像处理等功能。

图像放大的两种编程算法的实现

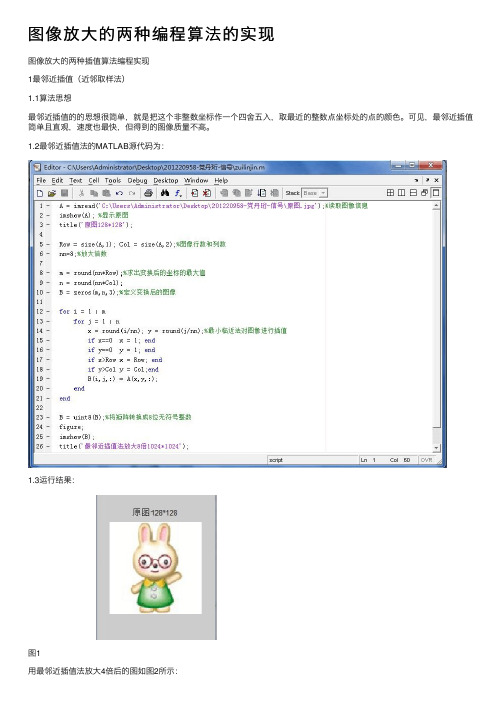
图像放⼤的两种编程算法的实现图像放⼤的两种插值算法编程实现1最邻近插值（近邻取样法）1.1算法思想最邻近插值的的思想很简单，就是把这个⾮整数坐标作⼀个四舍五⼊，取最近的整数点坐标处的点的颜⾊。

可见，最邻近插值简单且直观，速度也最快，但得到的图像质量不⾼。

1.2最邻近插值法的MATLAB源代码为：1.3运⾏结果：图1⽤最邻近插值法放⼤4倍后的图如图2所⽰：图22双线性内插值法2.1算法思想在双线性内插值法中，对于⼀个⽬的像素，设置坐标通过反向变换得到的浮点坐标为(i+u,j+v)，其中i、j均为⾮负整数，u、v为[0,1)区间的浮点数，则这个像素得值f(i+u,j+v)可由原图像中坐标为(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定，即：f(i+u,j+v)=(1-u)(1-v)f(i,j)+(1-u)vf(i,j+1)+u(1-v)f(i+1,j)+uvf(i+1,j+1)其中f(i,j)表⽰源图像(i,j)处的的像素值，以此类推。

这就是双线性内插值法。

双线性内插值法计算量⼤，但缩放后图像质量⾼，不会出现像素值不连续的的情况。

由于双线性插值具有低通滤波器的性质，使⾼频分量受损，所以可能会使图像轮廓在⼀定程度上变得模糊。

在MATLAB中，可⽤其⾃带的函数imresize()来实现双线性内插值算法。

2.2程序代码双线性内插值算法的MATLAB源代码为：2.3运⾏结果程序运⾏后，原图如图3所⽰：图3双线性内插值法放⼤8倍后的图如图4所⽰：图43结论最近邻插值运算简单快速,能够保持插值图像边缘清晰,但边缘轮廓有显著的锯齿现象,图像背景产⽣马赛克,形成伪边缘,视觉效果差,重构误差较⼤与最邻近法相⽐,双线性内插法由于考虑了待采样点周围4个直接邻点对待采样点的影响,因此基本克服了前者灰度不连续的缺点,其计算量有所增⼤。

此⽅法仅考虑4个直接邻点灰度值的影响,⽽未考虑到各邻点间灰度值变化率的影响,因此具有低通滤波器的性质,使放⼤后图像的⾼频分量受到损失,图像的轮廓变得较模。

C#实现图片放大功能的按照像素放大图像方法

C#实现图⽚放⼤功能的按照像素放⼤图像⽅法本⽂实例讲述了基于Visual C#实现的图⽚放⼤功能代码。

可以直接放⼤像素，类似photoshop的图⽚放⼤功能，可⽤于像素的定位及修改，由于使⽤了指针需要勾选允许不安全代码选项，读者可将其⽤于⾃⼰的项⽬中！关于⼏个参数说明：srcbitmap源图⽚multiple图像放⼤倍数放⼤处理后的图⽚注意：需要在头部引⽤：using System.Drawing;using System.Drawing.Imaging;⾄于命名空间读者可以⾃⼰定义。

主要功能代码如下：using System.Drawing;using System.Drawing.Imaging;public Bitmap Magnifier(Bitmap srcbitmap, int multiple){if (multiple <= 0) { multiple = 0; return srcbitmap; }Bitmap bitmap = new Bitmap(srcbitmap.Size.Width * multiple, srcbitmap.Size.Height * multiple);BitmapData srcbitmapdata = srcbitmap.LockBits(new Rectangle(new Point(0, 0), srcbitmap.Size), ImageLockMode.ReadOnly, PixelFormat.Format32bppArgb); BitmapData bitmapdata = bitmap.LockBits(new Rectangle(new Point(0, 0), bitmap.Size), ImageLockMode.ReadWrite, PixelFormat.Format32bppArgb); unsafe{byte* srcbyte = (byte*)(srcbitmapdata.Scan0.ToPointer());byte* sourcebyte = (byte*)(bitmapdata.Scan0.ToPointer());for (int y = 0; y < bitmapdata.Height; y++){for (int x = 0; x < bitmapdata.Width; x++){long index = (x / multiple) * 4 + (y / multiple) * srcbitmapdata.Stride;sourcebyte[0] = srcbyte[index];sourcebyte[1] = srcbyte[index + 1];sourcebyte[2] = srcbyte[index + 2];sourcebyte[3] = srcbyte[index + 3];sourcebyte += 4;}}}srcbitmap.UnlockBits(srcbitmapdata);bitmap.UnlockBits(bitmapdata);return bitmap;}。

c语言数字图像处理（二）：图片放大与缩小-双线性内插法

c语⾔数字图像处理（⼆）：图⽚放⼤与缩⼩-双线性内插法图像内插假设⼀幅⼤⼩为500 * 500的图像扩⼤1.5倍到750 * 750，创建⼀个750 * 750 的⽹格，使其与原图像间隔相同，然后缩⼩⾄原图⼤⼩，在原图中寻找最接近的像素（或周围的像素）进⾏赋值，最后再将结果放⼤最邻近内插法寻找最近的像素赋值双线性内插法v(x,y) = ax + by + cxy + d双线性内插法参数计算已知Q11, Q12, Q21, Q22，要插值的点为P点，⾸先在x轴上，对R1，R2两个点进⾏插值然后根据R1和R2对P点进⾏插值化简得对于边界值的处理，若x1 < 0 ,则直接令f(Q11), f(Q12) = 0处理结果原图扩⼤为6000 * 4000缩⼩为1000 * 500下⾯为代码实现的主要部分int is_in_array(short x, short y, short height, short width){if (x >= 0 && x < width && y >= 0 && y < height)return1;elsereturn0;}void bilinera_interpolation(short** in_array, short height, short width, short** out_array, short out_height, short out_width){double h_times = (double)out_height / (double)height,w_times = (double)out_width / (double)width;short x1, y1, x2, y2, f11, f12, f21, f22;double x, y;for (int i = 0; i < out_height; i++){for (int j = 0; j < out_width; j++){x = j / w_times;y = i / h_times;x1 = (short)(x - 1);x2 = (short)(x + 1);y1 = (short)(y + 1);y2 = (short)(y - 1);f11 = is_in_array(x1, y1, height, width) ? in_array[y1][x1] : 0; f12 = is_in_array(x1, y2, height, width) ? in_array[y2][x1] : 0; f21 = is_in_array(x2, y1, height, width) ? in_array[y1][x2] : 0; f22 = is_in_array(x2, y2, height, width) ? in_array[y2][x2] : 0; out_array[i][j] = (short)(((f11 * (x2 - x) * (y2 - y)) +(f21 * (x - x1) * (y2 - y)) +(f12 * (x2 - x) * (y - y1)) +(f22 * (x - x1) * (y - y1))) / ((x2 - x1) * (y2 - y1))); }}}。

编程实现一幅图像的平移、镜像、旋转、缩小和放大

课程设计任务书学生姓名：专业班级：通信1003班指导教师：郭志强工作单位：信息工程学院题目: 通信工程应用技术初始条件：（1）使用matlab软件进行操作（2）选择一个图像进行处理要求完成的主要任务:（包括课程设计工作量及其技术要求，以及说明书撰写等具体要求）（1）编程实现一幅图像的平移、镜像、旋转、缩小和放大。

（2）给出所用算法的理论依据和必要的推导过程，给出原始图像和处理后的图像。

时间安排：第15周：安排任务，布置题目；第15—18周：设计仿真，撰写报告第19周：完成设计，提交报告，答辩指导教师签名：年月日系主任（或责任教师）签名：年月日目录摘要 (I)Abstract ........................................................................................................................................................... I I 1 MA TLAB简介 .. (1)1.1 MA TLAB用途 (1)2图像选择及变换 (4)2.1 原始图像选择读取 (4)2.2 图像放大和缩小 (6)2.2.1 图像放大缩小的知识 (6)2.2.2 函数说明及参数选择 (8)2.2.3 源程序及运行结果 (8)2.3 图像任意角度的旋转 (10)2.3.1 函数说明及参数选择 (10)2.3.2 源程序及运行结果 (10)2.4 图像的平移 (12)2.4.1 函数说明及参数选择 (12)2.4.2 源程序及运行结果 (13)2.5 图像经过镜像 (13)3.5.1 函数说明及参数选择 (13)2.5.2 源程序及运行结果 (14)4 感悟体会小结 (17)5 参考文献 (18)附录 (19)全部源程序代码： (19)摘要MATLAB是—套高性能的数值计算和可视化软件，它集数值分析、矩阵运算、信号处理和图形显示于一体，构成—个方便的、界面友好的用户环境。

使用双线性插值进行图像放大的实现

使用双线性插值进行图像放大的实现一、总体设计思路Step 1：实现图像的打开、显示、保存，在打开图片之后将图片读入内存并获得了该图像除文件头以外的部分在缓存内存储的句柄，以及该图的调色板，调色板颜色种类数等等参数。

Step 2：在显示的基础上，利用代码根据放大比例重新开辟一个缓存。

将原图的BITMAPINFOHEADER拷贝过来。

并修改biHeight、biWidth、biSizeImage等参数。

Step 3：利用双线性插值算法，以原图信息为基础生成新的像素信息。

原理：双线性插值维基百科，自由的百科全书跳转到：导航, 搜索双线性插值，又称为双线性内插。

在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

红色的数据点与待插值得到的绿色点假如我们想得到未知函数在点的值，假设我们已知函数在, , , 及四个点的值。

首先在x方向进行线性插值，得到然后在y方向进行线性插值，得到这样就得到所要的结果,如果选择一个坐标系统使得的四个已知点坐标分别为(0, 0)、(0, 1)、(1, 0) 和(1, 1)，那么插值公式就可以化简为或者用矩阵运算表示为与这种插值方法名称不同的是，这种插值方法并不是线性的，它的形式是它是两个线性函数的乘积。

另外，插值也可以表示为在这两种情况下，常数的数目都对应于给定的f的数据点数目。

线性插值的结果与插值的顺序无关。

首先进行y方向的插值，然后进行x方向的插值，所得到的结果是一样的。

双线性插值的一个显然的三维空间延伸是三线性插值。

二、具体实现方案及细节1、需要改变的项：①BITMAPINFOHEADER里的biHeight、biWidth、biSizeImage。

②所有像素点信息2、具体方案的设计：①对双线性插值的理解：放大图像时，插值就是根据比例得到一个坐标(x,y)。

该坐标可分为四种情况：(1)得到的x和y都是整数且落在原图中，则直接取出该像素点的颜色信息即可。

matlab实现图像的放大及旋转

MATLAB是一个包含大量计算算法的集合。

其拥有600多个工程中要用到的数学运算函数，可以方便的实现用户所需的各种计算功能。

函数中所使用的算法都是科研和工程计算中的最新研究成果，而前经过了各种优化和容错处理。

在通常情况下，可以用它来代替底层编程语言，如C和C 。

在计算要求相同的情况下，使用MATLAB的编程工作量会大大减少。

MATLAB的这些函数集包括从最简单最基本的函数到诸如距阵，特征向量、快速傅立叶变换的复杂函数。

函数所能解决的问题其大致包括矩阵运算和线性方程组的求解、微分方程及偏微分方程的组的求解、符号运算、傅立叶变换和数据的统计分析、工程中的优化问题、稀疏矩阵运算、复数的各种运算、三角函数和其他初等数学运算、多维数组操作以及建模动态仿真等。

（4）出色的图形处理功能MATLAB自产生之日起就具有方便的数据可视化功能，以将向量和距阵用图形表现出来，并且可以对图形进行标注和打印。

高层次的作图包括二维和三维的可视化、图象处理、动画和表达式作图。

可用于科学计算和工程绘图。

新版本的MATLAB 对整个图形处理功能作了很大的改进和完善，使他不仅在一般数据可视化软件都具有的功能（例如二维曲线和三维曲面的绘制和处理等）方面更加完善，而且对于一些其他软件所没有的功能（例如图形的光照处理、色度处理以及四维数据的表现等），MATLAB 同样表现了出色的处理能力。

同时对一些特殊的可视化要求，例如图形对话等，MATLAB也有相应的功能函数，保证了用户不同层次的要求。

另外新版本的MATLAB还着重在图形用户界面（GUI）的制作上作了很大的改善，对这方面有特殊要求的用户也可以得到满足。

（5）应用广泛的模块集合工具箱MATLAB对许多专门的领域都开发了功能强大的模块集和工具箱。

一般来说，他们都是由特定领域的专家开发的，用户可以直接使用工具箱学习、应用和评估不同的方法而不需要自己编写代码。

目前，MATLAB已经把工具箱延伸到了科学研究和工程应用的诸多领域，诸如数据采集、数据库接口、概率统计、样条拟合、优化算法、偏微分方程求解、神经网络、小波分析、信号处理、图像处理、系统辨识、控制系统设计、LMI控制、鲁棒控制、模型预测、模糊逻辑、金融分析、地图工具、非线性控制设计、实时快速原型及半物理仿真、嵌入式系统开发、定点仿真、DSP 与通讯、电力系统仿真等，都在工具箱（Toolbox）家族中有了自己的一席之地。

C#编程实现图片的打开、放大、缩小

C#编程实现图片的打开、放大、缩小一、调用打开文件对话框1.选用openfiledialog1对话框控件。

2.定义一个文件名称，例如： private string FileName;3.代码调用openFileDialog1.Filter = "所有图像文件（*.bmp;*.gif.;*.jpg）|*.bmp;*.gif;*.jpg";openFileDialog1.Title = "打开文件"; //文件过滤；openFileDialog1.ShowDialog(); //打开对话框；FileName = openFileDialog1.FileName; //对fileName进行赋值；if (FileName != "") //对filename进行判断，不为空的情况下在picturebox中打开图片{FileName = openFileDialog1.FileName;Bitmap pic = new Bitmap(FileName);pictureBox1.Image = pic;}二、图片放大缩小时自动产生滚动条1.选用Panel控件，调整控件大小位置合适，并将Autoscroll属性更改为TRUE。

2.将picturebox控件拖放到panel控件上，可根据自己的需要选择picturebox的AutoMode属性。

//图片放大代码int x, y;x = pictureBox1.Location.X - 5;if (pictureBox1.Location.Y <= 0){y = 0;}else{y = pictureBox1.Location.Y - 4;}pictureBox1.Location = new Point(x, y);pictureBox1.SizeMode = PictureBoxSizeMode.StretchImage;pictureBox1.Size = new Size(pictureBox1.Width + 10, pictureBox1.Height + 14);//图片缩小代码int x, y;x = pictureBox1.Location.X + 5;if (pictureBox1.Location.X < 300){y = 0;}else{y = pictureBox1.Location.Y + 4;}pictureBox1.Location = new Point(x, y);pictureBox1.SizeMode = PictureBoxSizeMode.StretchImage;pictureBox1.Size = new Size(pictureBox1.Width - 10, pictureBox1.Height - 14);。

js、css3实现图片的放大效果

js、css3实现图⽚的放⼤效果今天看⽹易的⽹站上，当我把⿏标放上去的时候发现图⽚放⼤，移开图⽚缩⼩，于是⾃⾏尝试，结果如下。

⽅法⼀：使⽤js和css3 效果如图：这样的实现⾮常简单，就是利⽤js的mouseover和 mouseout事件，但是不知道如何使图⽚从中间放⼤，⽇后再⾏尝试吧，代码如下：<!DOCTYPE html><html><head><title>⽹易图⽚动画</title><style>div.img {width: 220px;height: 170px;margin: 200px auto;overflow: hidden;}img.bigger {width: 100%;height:100%;}@keyframes bigger {from {width: 100%;height: 100%;}to {width: 110%; height: 110%;}}@keyframes smaller {from {width: 110%;height: 110%;}to {width: 100%; height: 100%;}}</style></head><body><div class="img"><img class="bigger" src="/d9b6afa0bad743f88c1780c3a064202c20170218074455.jpeg?imageView&thumbnail=185y116&quality=85" alt=""> </div><script>var img = document.querySelector("img");img.onmouseover = function () {img.style.cssText = "animation: bigger 2s;width:110%; height:110%;";}img.onmouseout = function () {img.style.cssText = "animation: smaller 2s";}</script></body></html>⽅法⼆：使⽤css3⽅法 css3的确给我们带来了很多好处，是我们处理问题更加⽅便。

java等比缩小、放大图片尺寸

1<dependency> 2<groupId>net.coobird</groupId> 3<artifactId>thumbnailator</artifactId> 4<version>0.4.8</version> 5</dependency>
3.解决方案
代码实现：
1 /* 2 * 对图片进行等比缩小或放大 3 * @attention: 4 * Thumbnails可以将修改后的图片转换成OutputStream、BufferedImage或者File 5 * @date: 2022/2/16 18:37 6 * @param: imgInputPath 原图片路径 7 * @param: imgOutputPath 图片输出路径 8 * 可以更改原图片的格式（比如：原图片是png格式，我们可以在让其生成的时候变成非png格式） 9 * @param: scale 图片比例 10* @return: boolean 成功、失败 11*/ 12public static boolean compressPicBySize(String imgInputPath, String imgOutputPath, float scale) { 13boolean flag = false; 14String imgStatus = (scale > 1) ? "放大" : "缩小"; 15try { 16Thumbnails.of(imgInputPath).scale(scale).toFile(imgOutputPath); 17// 成功 18flag = true; ("图片{}成功", imgStatus); 20} catch (IOException e) { 21e.printStackTrace(); 22log.error("图片{}失败：{}", imgStatus, e.getMessage()); 23} 24return flag; 25}

C语言实现图片放大缩小

C语⾔实现图⽚放⼤缩⼩本⽂实例为⼤家分享了C语⾔实现图⽚放⼤缩⼩的具体代码，供⼤家参考，具体内容如下最终项⽬描述和效果⿏标按⼩图，左键图⽚缩⼩，右键图⽚放⼤。

代码如下代码⼤致的思路就是，当⿏标点击指定的地⽅时。

将图⽚的长宽，变化，在贴图。

使⽤: 将图⽚命名为1.jpg,并将其放在和.cpp⽂件同⼀⽂件夹下。

#include<stdio.h>#include<graphics.h>#include<conio.h>IMAGE maxImg;//⼤图IMAGE minImg;//⼩图struct picture{int width;//宽int langth;//长int value;//⽐率};struct picture a={400,400,2};void jia()//加载图⽚{loadimage(&maxImg,"1.jpg");loadimage(&minImg,"1.jpg",60,60);}void show_p()//显⽰图⽚{putimage(20,20,&minImg);putimage(100,0,a.width,ngth,&maxImg,0,0);}void show(){setbkcolor(WHITE);//设置窗⼝背景颜⾊cleardevice();//刷新⼀下setlinecolor(BLACK);//设置线的颜⾊setlinestyle(PS_SOLID,5);//设置线的样式//画矩形rectangle(0,0,500,400);rectangle(0,0,100,400);rectangle(0,133,100,133*2);//显⽰⽂字settextcolor(GREEN);settextstyle(20,0,"⿊体");outtextxy(10,180,"左键缩⼩");outtextxy(10,320,"右键放⼤");show_p();}void to_small(){if(ngth!=1&&a.width!=1)//不能让长宽等于1，如果等于1的话那么长宽就会变为0，再次变⼤就有问题了.{a.width/=a.value;ngth/=a.value;}loadimage(&maxImg,"1.jpg",a.width,ngth);}void to_big(){a.width*=a.value;ngth*=a.value;loadimage(&maxImg,"1.jpg",a.width,ngth);}void mouse(){MOUSEMSG m;while(1){BeginBatchDraw();//双缓存绘图，解决闪屏问题show();m=GetMouseMsg();switch(m.uMsg){case WM_LBUTTONDOWN://左键if(20<=m.x&&m.x<=80&&m.y>=20&&m.y<=80){//MessageBox(NULL,"⿏标点击图⽚","123",MB_OK);to_small();}break;case WM_RBUTTONDOWN://右键if(20<=m.x&&m.x<=80&&m.y>=20&&m.y<=80){//MessageBox(NULL,"⿏标点击图⽚","123",MB_OK);to_big();}break;}EndBatchDraw();}}int main(void){initgraph(500,400);show();jia();mouse();return 0;}以上就是本⽂的全部内容，希望对⼤家的学习有所帮助，也希望⼤家多多⽀持。

C语言图像旋转放大移动程序代码

+q*((1.0-p)*data[(m+height_xz+1)*step+channels*(n+width_xz)+2]+p*data[(m+height_xz+1)*step+channels*(n+1+width_xz)+2]));
}
else
{
R=0;
G=0;
B=0;
}
if(R<0||G<0||B<0)
data_xz[(i+height_xz)*step_xz+channels_xz*(j+width_xz)+2]=B;
}
}
cvShowImage( "现图", pImg_xz );//显示图像
cvShowImage( "原图", pImg );//显示图像
Sleep(100);
}
/////////////////////////图像处理部分///////////////////////////////////
pImg = cvLoadImage(filename, 1);//载入图像
pImg_xz = cvCreateImage(cvGetSize(pImg), IPL_DEPTH_8U,3); //创建图像
cvNamedWindow( "原图", 1 );//创建窗口
cvMoveWindow("原图",100,200);//移动窗口
data_xz = (uchar*)pImg_xz->imageData;
channels_xz = pImg_xz->nChannels;

matlab练习程序（图像放大缩小，双立方插值）

matlab练习程序（图像放⼤缩⼩，双⽴⽅插值）我主要参考了，不过他推导的系数我感觉有问题，⽤他的公式直接套⽤放⼤的图像会有⽹格，也许是我理解的有偏差。

所以我⾃⼰重新推导了这四个系数⽤这个就没问题了。

他的那些代码还是很有参考价值的。

程序代码：main.mclear all;close all;clc;w=2; %放⼤或缩⼩的宽度h=2; %放⼤或缩⼩的⾼度img=imread('lena.jpg');%imshow(img);[m n]=size(img);imgn=zeros(h*m,w*n);rot=[h 00;0 w 0;001]; %变换矩阵x=h*u,y=w*vfor i=1:h*mfor j=1:w*npix=[i j 1]/rot;float_Y=pix(1)-floor(pix(1));float_X=pix(2)-floor(pix(2));if pix(1) < 2 %边界处理,也可以⽤卷积时常⽤的边界扩展防⽌越界pix(1) = 2;endif pix(1) > m-2pix(1) = m-2;endif pix(2) < 2pix(2) =2;endif pix(2) > n-2pix(2) =n-2;endpix_up=floor(pix(1));pix_left=floor(pix(2));p=img(pix_up-1:pix_up+2,pix_left-1:pix_left+2);imgn(i,j)=bicubicInterpolate(p,float_X+1,float_Y+1);endendfigure,imshow(uint8(imgn))bicubicInterpolate.mfunction re=bicubicInterpolate(p,x,y) %先⾏插值，再列插值arr=zeros(4,1);for i=1:4arr(i)=cubicInterpolate(p(i,1:4),x);endre= cubicInterpolate(arr,y);endcubicInterpolate.mfunction re=cubicInterpolate(p,x)p=double(p);% re=p(2) + 0.5 * x*(p(3) - p(1) + x*(2.0*p(1) - 5.0*p(2) + 4.0*p(3) - p(4) + x*(3.0*(p(2) - p(3)) + p(4) - p(1))));a=(p(4)-3*p(1)+3*p(2)-p(1))/10;b=(p(3)-2*p(2)+p(1))/2-2*a;c=p(2)-p(1)-a-b;d=p(1);re=a*x^3+b*x^2+c*x+d;end效果图：原图双⽴⽅插值效果双线性插值效果区别不⼤，不过认真看双⽴⽅还是效果好些。

图像处理——插值放大(C++)

图像的2*2、4*4放大（1）双线性插值处理过程这个题目是用C++配合opencv库完成的。

首先读入图像，然后将输出图像的宽、高设置为输入图像的2（4）倍，深度、通道等信息不变。

由于双线性插值需要取插值点D邻域的四个点的信息，因此为避免出错，运算之前先将输入图像的宽、高减一。

（不减一有时候确实会出错，这里这种说法只是我的个人理解）如上图所示，我们欲求P点的RGB信息，首先取其D邻域上四个整数坐标点Q11、Q12、Q13、Q14的RGB信息，然后将RGB各通道分别计算，用公式f ( R2 ) = f ( Q12 ) + a [ f ( Q22 ) – f ( Q12 )]算出R2的RGB通道信息，其中a为R2横坐标取整后舍去的小数值。

同理可得R1的各通道灰度值，并由R1和R2的灰度值计算出P点的灰度值。

最后将我们舍掉的最后一行和最后一列加上，就完成了对图像的双线性插值放大。

处理结果2*2放大：4*4放大：程序清单#include <cv.h>#include <highgui.h>#include <iostream>using namespace std;float Abs(float f);void fun(IplImage* src, IplImage* dst);int main(){//读入图像IplImage* src = cvLoadImage("pic.png");IplImage* dst = cvCreateImage(cvSize(src->width*2,src->height*2), src->depth, src->nChannels);fun(src, dst);cvShowImage("src", src);cvShowImage("dst", dst);cvWaitKey(0);//等待用户操作cvSaveImage("pic_linear.png",dst);//存储双线性插值放大图像cvReleaseImage(&src);cvReleaseImage(&dst);return 0;}//取绝对值子函数float Abs(float f){return f>=0 ? f : -f;}//双线性插值放大函数void fun(IplImage* src, IplImage* dst){int srcWidth = src->width;int srcHeight = src->height;int dstWidth = dst->width;int dstHeight = dst->height;const float tx = (srcWidth-1.0f)/(dstWidth-1.0f);const float ty = (srcHeight-1.0f)/(dstHeight-1.0f);//源图像与目标图像的宽高比例,这里减1是为了避免报错CvPoint2D32f uv;//存储源图像的浮点坐标CvPoint3D32f f1;//存储f1点RGB各通道信息CvPoint3D32f f2;//存储f2点RGB各通道信息for (int j=0; j<dstHeight-1; j++){for (int i=0; i<dstWidth-1; i++){uv.x = i*tx;uv.y = j*ty;//对坐标取整int iu = (int)uv.x;int iv = (int)uv.y;//四个点坐标，以及插值坐标CvScalar p1, p2, p3, p4, s;p1=cvGet2D(src, iv, iu);p2=cvGet2D(src, iv, iu+1);p3=cvGet2D(src, iv+1, iu);p4=cvGet2D(src, iv+1, iu+1);//获取所需坐标RGB信息，注意这里横纵坐标是相反的//计算f1点各通道灰度f1.x = p1.val[0]*(1-Abs(uv.x-iu))+p2.val[0]*(uv.x-iu);f1.y = p1.val[1]*(1-Abs(uv.x-iu))+p2.val[1]*(uv.x-iu);f1.z = p1.val[2]*(1-Abs(uv.x-iu))+p2.val[2]*(uv.x-iu);//计算f2点各通道灰度f2.x = p3.val[0]*(1-Abs(uv.x-iu))+p4.val[0]*(uv.x-iu);f2.y = p3.val[1]*(1-Abs(uv.x-iu))+p4.val[1]*(uv.x-iu);f2.z = p3.val[2]*(1-Abs(uv.x-iu))+p4.val[2]*(uv.x-iu);//计算插值点s各通道灰度s.val[0] = f1.x*(1-Abs(uv.y-iv))+f2.x*(Abs(uv.y-iv));s.val[1] = f1.y*(1-Abs(uv.y-iv))+f2.y*(Abs(uv.y-iv));s.val[2] = f1.z*(1-Abs(uv.y-iv))+f2.z*(Abs(uv.y-iv));cvSet2D(dst, j, i, s);//插值操作，同样注意这里横纵坐标i，j是相反的}//添加上最后一列cvSet2D(dst, j, dstWidth-1, cvGet2D(dst, j, dstWidth-2));}//添加上最后一行for(int i=0; i<dstWidth; i++){cvSet2D(dst, dstHeight-1, i, cvGet2D(dst, dstHeight-2, i));}}（2）最近邻域插值这个没有找到相应的资料，最后用的opencv现成的函数做的，没啥好说的…处理结果程序清单#include <cv.h>#include <cxcore.h>#include <highgui.h>#include <cmath>using namespace std;using namespace cv;int main(int argc ,char ** argv){IplImage *scr=0;IplImage *dst=0;double scale=4;CvSize dst_cvsize;scr=cvLoadImage("C://Users/Administrator/Desktop/pic.png",-1);dst_cvsize.width=(int)(scr->width*scale);dst_cvsize.height=(int)(scr->height*scale);dst=cvCreateImage(cvSize(scr->width*4,scr->height*4),scr->depth,scr->nChannels);cvResize(scr,dst,CV_INTER_NN);/* CV_INTER_NN - 最近邻插值,CV_INTER_LINEAR - 双线性插值(缺省使用)CV_INTER_AREA - 使用象素关系重采样。

矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

matlab实现图像的放大及旋转

MATLAB是一个包含大量计算算法的集合。

其拥有600多个工程中要用到的数学运算函数，可以方便的实现用户所需的各种计算功能。

函数中所使用的算法都是科研和工程计算中的最新研究成果，而前经过了各种优化和容错处理。

在计算要求相同的情况下，使用MATLAB的编程工作量会大大减少。

MATLAB的这些函数集包括从最简单最基本的函数到诸如距阵，特征向量、快速傅立叶变换的复杂函数。

图像的几何操作一、图像的基本运算1、加法运算图像相加一般用于对同一场景的多幅图像求平均效果，以便有效地降低具有叠加性质的随机噪声。

直接采集的图像品质一般都较好，不需要进行加法运算处理，但是对于那些经过长距离模拟通信方式传送的图像（如卫星图像），这种处理是必不可少的。

在MA TLAB7.0中，如果要进行两幅图像的加法，或者给一幅图像加上一个常数，可以调用imadd函数来实现。

imadd函数将某一幅输入图像的每一个像素值与另一幅图像相应的像素值相加，返回相应的像素值之和作为输入图像。

imadd函数的调用格式可参考图像处理的工具箱。

下面的程序可将图1两幅图像叠加在一起，叠加效果如图2所示。

imshow('rice.png');imshow('cameraman.tif');I=imread('rice.png');J=imread('cameraman.tif');K=imadd(I,J,'uint16');%大小必须一样imshow(K,[])图1 图2给图像的每一个像素加上一个常数可以使图像的亮度增加。

例如以下程序示例的处理效果如图3所示。

I=imread('rice.png');J=imadd(I,50);subplot(1,2,1),imshow(I);subplot(1,2,2),imshow(J);图32、减法运算图像减法也称为差分方法，是一种常用于检测图像变化及运动物体的图像处理方法。

J2ME插值算法如何实现图片的放大缩小

J2ME插值算法如何实现图片的放大缩小J2ME插值算法如何实现图片的放大缩小//生成放大缩小后图形像素bufshort[] desBuf = new short[desW * desH];int dx = 0;int dy = 0;int sx = 0;int sy = 0;int oldy = -1;for (int i = 0; i < desH; i++) {if (oldy == tabY[i]) {System.arraycopy(desBuf, dy - desW, desBuf, dy, desW); } else {dx = 0;for (int j = 0; j < desW; j++) {desBuf[dy + dx] = srcBuf[sy + tabX[j]];dx++;}sy += (tabY[i] - oldy) * srcW;}oldy = tabY[i];dy += desW;}//生成图片desImg = Image.createImage(desW, desH); DirectUtils.getDirectGraphics(desImg.getGraphics()). drawPixels(desBuf, true, 0, desW, 0, 0, desW, desH, 0, 444); return desImg;}首先看函数的头两句，很容易，就是获取原始图片的宽度和高度int srcW = srcImg.getWidth(); //原始图像宽int srcH = srcImg.getHeight(); //原始图像高接下来一句我们要定义一个short型数组，作为获取原始图片像素信息的缓存short[] srcBuf = new short[srcW * srcH];再下来一段，有的朋友可能会有些不明白，这里要解释一下。

由于getPixels()这个函数，只能获取可变图像的像素信息，非可变图像，无法获取像素信息。

C++Builder图片放大缩小

C++Builder程序设计学号：************学生所在学院：信息工程学院****：**********教师所在学院：信息工程学院2010年1月5日2010级07班实现图像的放大、缩小、任意角度旋转功能邱剑信息工程学院摘要：当前，图形是多媒体技术中一种重要的信息媒体，数据量极大并且多种多样的存储格式，阻碍了多媒体技术的发展，为了有效地使用各类图形文件，为使多媒体技术蓬勃发展，图像的变化工作就显得极其重要。

C++Builder具有强大的更新和移植能力，应用也非常之广泛，学习C++Builder对程序设计思维能力有很好的锻炼本文主要介绍了如何利用C++程序设计实现了图像的任意倍数的放大、缩小、任意角度旋转功能。

在数字图像处理应用领域的简单运用及其重要意义，首先阐述了C++Builder软件的基本窗体结构，以及其属性，并简单的介绍图像处理软件的方法和步骤。

本设计表明，通过简单的程序设计，可以实现强大的功能。

实现功能的方式多种多样灵活多变，在日常的学习中要多注意各种函数的使用，这样才能更快的提高编写能力，实现更加强大的功能关键词：C++ 放大缩小旋转Abstract:At present, the image is one of the most important multimedia information media, data great quantity and variety of storage formats, obstruct the multimediatechnology development, in order to effectively use of various graphics files,to enable multimedia technology vigorous development, image changes jobs arevery important. C + + Builder has strong update and transplantation ability,applications are very extensive, study c + + Builder for program design thinkingability have very good exerciseThis paper mainly introduced how to use c + + programming realize image arbitrarymultiples magnification, reducing, arbitrary AngleRotating function. Indigital image processing applications, the simple use and its significance,first expounded c + + BuilderThe basic form structure, software and itsattributes, and briefly introduces image processing software methods and stepsof.This design shows that through simple programming, may realize the powerfulfunctions. Functions by many waysFlexible, in daily learning to pay moreattention to the use of various functions, such ability improved writingability,Realize more powerful functionsKeywords: C++ enlarge reduce rotationC++的简单介绍C++，这个词在中国大陆的程序员圈子中通常被读做“C加加”，而西方的程序员通常读做“C plus plus”，它是一种使用非常广泛的计算机编程语言。

C++Builder_图像的几何放大_缩小_任意角度旋转

C++Builder实现图像的放大、缩小、任意角度旋转功能学号：090081001023学生所在学院：信息工程学院学生姓名：吴静任课教师：熊邦书教师所在学院：信息工程学院2010年1月09级研8班实现图像的放大、缩小、任意角度旋转功能吴静信息工程学院摘要：本文介绍了C++程序设计在数字图像处理应用领域的简单运用及其重要意义，详细阐述了利用C++Builder设计简单的图像处理软件的方法和步骤，实现了图像的任意倍数的放大、缩小、任意角度旋转功能。

在此基础上，对数字图像处理的研究有了初步的了解，并且进一步熟悉了C++程序设计在实际应用中的一般方法和思想，为以后进一步的编程和对图像处理的研究打下了基础。

关键词：C++Builedr 放大缩小任意角度旋转Abstract:This article describes the C++ programming in digital image processing applicationsthe use and significance of a simple detailede the use of C++ Builderdesigned to be simple image processing software methods and steps to achievean arbitrary multiple of the image to enlarge,reduceany angle rotation.On thisbasis,the study of digital image processing an initial understanding ofandfurther familiar wite C++ programmers in practical appliacation of the generalmethods and ideas for future programming and further image processing to laythe foundation for the study.Keywords:C++ Builder enlarge reduce rotation at any angle1 组件介绍1.1 窗体（Form）窗体是人机交互的主要界面，窗体的界面设计是十分重要的，一个好的软件需要一个漂亮的窗体来衬托。

图像放大的两种编程算法的实现

编程实现一幅图像的平移、镜像、旋转、缩小和放大。

图像放大的两种编程算法的实现

C#实现图片放大功能的按照像素放大图像方法

c语言数字图像处理（二）：图片放大与缩小-双线性内插法

编程实现一幅图像的平移、镜像、旋转、缩小和放大

使用双线性插值进行图像放大的实现

matlab实现图像的放大及旋转

C#编程实现图片的打开、放大、缩小

js、css3实现图片的放大效果

java等比缩小、放大图片尺寸

C语言实现图片放大缩小

C语言图像旋转 放大 移动程序代码

matlab练习程序（图像放大缩小，双立方插值）

图像处理——插值放大(C++)

矿产

matlab实现图像的放大及旋转

J2ME插值算法如何实现图片的放大缩小

C++Builder图片放大缩小

C++Builder_图像的几何放大_缩小_任意角度旋转

C语言图像旋转放大移动程序代码