八上证明题
八年级上册三角形相关证明题大全(适用于复习巩固)

三角形证明题1、求证:三角形一边的中线小于其他两边和的一半。
(1)已知△ABC 中,AB=4cm ,BC=6cm ,BD 是△ABC 的中线,求BD 的取值范围. (2)在△ABC 中,AC=5,中线AD=7,则AB 边的取值范围是( ) A.1<AB<29 B.4<AB<24 C.5<AB<19 D.9<AB<19 (3)在△ABC 中,AD 是BC 上的中线,求证:A D <1/2(AB+AC )。
2、如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D 为AC 上一点,CE ⊥BD 于E . (1)若BD 平分∠ABC ,求证CE=12BD ;(2)若D 为AC 上一动点,∠AED 如何变化,若变化,求它的变化范围;若不变,求出它的度数,并说明理由。
EDC BA3、在△ABC 中,,AB=AC , 在AB 边上取点D ,在AC 延长线上了取点E ,使CE=BD , 连接DE 交BC 于点F ,求证DF=EF .B4、如图,取一张长方形纸片,用A 、B 、C 、D 表示其四个顶点,将其折叠,使点D 与点B 重合。
图中有没有全等的三角形,如果有,请先用“≌”表示出来,再说明理由。
5、如图所示,△ABC 中,∠ACB=90°,AC=BC,AE 是BC 边上的中线,过C 作CF ⊥AE, 垂足为F,过B 作BD ⊥BC 交CF 的延长线于D.求证:(1)AE=CD;(2)若AC=12cm,求BD 的长.EDCBAF6、在△ABC 中,AB=AC ,∠BAC=90°,BD 是中线,AF ⊥BD ,F 是垂足,过点C 作AB 的平行线交AF 的延长线于点E 。
求证:(1)∠ABD=∠FAD ;(2)AB=2CEF CBED7、如图所示,AB=AC ,A D ⊥BC 于D ,且AB+AC+BC=50,而AB+BD+AD=40,则AD 为多少?AD C8、如图,在△ABC 中,D 是BC 的中点,E 、F 分别是AB 、AC 上的点,且FD ⊥ED ,求证:BE+CF ﹥EFA BCDF E9、ABCD 为正方形,CE 平分∠DCF ,M 为线段BC 上的点,连接AM 、ME ,问:AM 和ME 有何大小关系?当M 点在射线BC 上运动时,AM 和ME 的大小关系改变吗?10、如图,在△ABC中,AD⊥BC ,CE⊥AB ,垂足分别为D 、E ,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是多少?为什么?HEB C11、如图, 已知△ABC中, ∠BAC=900, AB=AC, AE是过A的一条直线, 且B、C在A、E 的异侧, BD⊥AE于D, CE⊥AE于E(1)试说明: BD=DE+CE.(2) 若直线AE绕A点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD与DE、CE的关系如何? 为什么?(3) 若直线AE绕A点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD与DE、CE的关系如何? 请直接写出结果, 不需说明.12、在△ABC中∠BAC是锐角,AB=AC,AD和BE是高,它们交于点H,且AE=BE;(1)求证:AH=2BD;(2)若将∠BAC改为钝角,其余条件不变,上述的结论还成立?若成立,请证明;若不成立,请说明理由;HEAB13、如图所示,已知D是等腰△ABC底边BC上的一点,它到两腰AB、AC的距离分别为DE、DF,CM ⊥AB,垂足为M,请你探索一下线段DE、DF、CM三者之间的数量关系, 并给予证明.ED CBAMF14、在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.(1)写出点O 到△ABC的三个顶点A、B、C的距离的大小关系,并说明理由.(2)若点M、N分别是AB、AC上的点,且BM=AN,试判断△OMN形状,并证明你的结论.15、如图22⑴,AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由。
人教版八年级数学上册《第12章全等三角形证明》经典题(含答案)
∵OM=OM∴△AOM≌△BOM (AAS)∴OA=OB∵ON=ON
∴△AON≌△BON (SAS)∴∠OAB=∠OBA,∠ONA=∠ONB
∵∠ONA+∠ONB=180∴∠ONA=∠ONB=90∴OM⊥AB
15.(5分)如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.
∴∠A=∠BFE∵AB//CD∴∠A+∠D=180º∵∠BFE+∠CFE=180º
∴∠D=∠CFE又∵∠DCE=∠FCE CE平分∠BCD CE=CE
∴⊿DCE≌⊿FCE(AAS)∴CD=CF
∴BC=BF+CF=AB+CD
8.已知:AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证:∠F=∠C
∴AE垂直BD∵BE⊥AE∴点E一定在直线BD上,在等腰三角形ABD中,AB=AD,AE垂直BD∴点E也是BD的中点∴BD=2BE∵BD=CD=AC-AB∴AC-AB=2BE
12.已知,E是AB中点,AF=BD,BD=5,AC=7,求DC
∵作AG∥BD交DE延长线于G∴AGE全等BDE∴AG=BD=5∴AGF∽CDF
∵AC=AC∴△ADC≌△AFC(SAS)
∴AD=AF
∴AE=AF+FE=AD+BE
7.如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。求证:BC=AB+DC。
在BC上截取BF=AB,连接EF
人教版八年级数学上册几何证明习题集

C八年级上册几何证明题题集1、 已知:在⊿ABC 中,AB=AC ,延长AB 到D ,使AB=BD ,E 是AB 的中点。
求证:CD=2CE 。
2、 已知:在⊿ABC 中,作∠FBC=∠ECB=21∠A 。
求证:BE=CF 。
B3、 已知:在⊿ABC 中,∠A=900,AB=AC ,在BC 上任取一点P ,作PQ ∥AB 交AC 于Q ,作PR∥CA 交BA 于R ,D 是BC 的中点,求证:⊿RDQ 是等腰直角三角形。
CB4、 已知:在⊿ABC 中,∠A=900,AB=AC ,D 是AC 的中点,AE ⊥BD ,AE 延长线交BC 于F ,求证:∠ADB=∠FDC 。
ABB DCA B C DE P 图 ⑴5、如图甲,Rt ∆ABC 中,AB=AC ,点D 、E 是线段AC 上两动点,且AD=EC ,AM ⊥BD ,垂足为M ,AM 的延长线交BC 于点N ,直线BD 与直线NE 相交于点F 。
(1)试判断∆DEF 的形状,并加以证明。
(2)如图乙,若点D 、E 是直线AC 上两动点,其他条件不变,试判断∆DEF 的形状,并加以证明。
6、已知:在⊿ABC 中BD 、CE 是高,在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ,求证:MA ⊥NA 。
7、已知:如图(1),在△ABC 中,BP 、CP 分别平分∠ABC 和∠ACB ,DE 过点P 交AB 于D ,交AC 于E ,且DE ∥BC .求证:DE -DB=EC .①②③图88、△ABC为正三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,直线BN与AM相交于Q点,就下面给出的三种情况,如图8中的①②③,先用量角器分别测量∠BQM的大小,然后猜测∠BQM等于多少度.并利用图③证明你的结论.9、在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明);(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
(完整版)八年级上册——全等三角形证明题题型归类训练

(完整版)八年级上册——全等三角形证明题题型归类训练-CAL-FENGHAI.-(YICAI)-Company One1《全等三角形》证明题题型归类训练题型1:全等+等腰性质1、如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O. 求证:(1) △ABC ≌△AED ; (2) OB =OE .2、已知:如图,B 、E 、F 、C 四点在同一条直线上,AB =DC ,BE =CF ,∠B =∠C .求证:OA =OD .题型2:两次全等1、AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CFFDCBA2、已知如图,E 、F 在BD 上,且AB =CD ,BF =DE ,AE =CF ,求证:AC 与BD 互相平分O C E BDAABEO FD3、如图,在四边形ABCD 中,AD ∥BC ,∠ABC=90°DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE=AC.求证:BG=FG题型3:直角三角形全等(余角性质)1、如图,在等腰Rt △ABC 中,∠C =90°,D 是斜边上AB 上任一点,AE ⊥CD 于E ,BF ⊥CD 交CD 的延长线于F ,CH ⊥AB 于H 点,交AE 于G . 求证:BD =CG .AFC BDEG2、如图,将等腰直角三角形ABC 的直角顶点置于直线l 上,且过A ,B 两点分别作直线的垂线,垂足分别为D ,E ,请你在图中找出一对全等三角形,并写出证明它们全等的过程.3、如图,∠ABC =90°,AB =BC ,D 为AC 上一点,分别过A 、C 作BD 的垂线,垂足分别为E 、F 求证:EF =CF -AE4、在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时, 求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.ABC FD E5、如图:BE ⊥AC ,CF ⊥AB ,BM=AC ,CN=AB 。
八年级数学十二道全等几何证明题(难度适中型)

全等几何证明(1)如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°.E 为AD延长线上的一点,且CE=CA,求证:AD+CD=DE;全等几何证明(2)如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE,求证:AE=EC+CD.全等几何证明(3)已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:AD=DE.全等几何证明(4)如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD 与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E.求证:CF=CG;全等几何证明(5)如图,已知P为∠AOB的平分线OP上一点,PC⊥OA于C,PA=PB,求证AO+BO=2CO全等几何证明(6)已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC 于点F,交BC于点G,交AB的延长线于点E,且AE=AC.求证:BG=FG;全等几何证明(7)如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,求证:AC=AE+CD.全等几何证明(7)如图,AD∥BC,AE平分∠BAD,AE⊥BE;说明:AD+BC=AB.全等几何证明(8)将两个全等的直角三角形ABC和DBE如图方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.求证:AF+EF=DE全等几何证明(9)如图,在△ABC 中,AD 平分∠BAC ,AB =AC -BD,则∠B ∶∠C 的值为多少?ABCD全等几何证明(10)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.ADPCB全等几何证明(11)如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE 与CD相交于F.求证:CE=CF.AF DE CB全等几何证明(12)设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .DFE PCBA。
八年级全等三角形简单证明题及答案(15道)

如图,△ABC中,AB=AC,过点A作GE∥BC,角平 分线BD、CF相交于点H,它们的延长线分别交GE于 点E、G.试在图中找出3对全等三角形,并对其中 一对全等三角形给出证明.
:△BCF≌△CBD. △BHF≌△CHD. △BDA≌△CFA. 证明:在△BCF与△CBD中, ∵AB=AC. ∴∠ABC=∠ACB ∵BD、CF是角平分线. ∴∠BCF=1 2 ∠ACB,∠CBD=1 2 ∠ABC. ∴∠BCF=∠CBD, ∴ ∠BCF=∠CBD BC=BC ∠ABC=∠ACB 全等三角形的判定. ∴△BCF≌△CBD(ASA).
2.如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,
且DM=AC,过点M作ME∥BC交AB于点E.求证:△ABC≌△MED。
证明:∵MD⊥AB, ∴∠MDE=∠C=90°, ∵ME∥BC, ∴∠B=∠MED, 在△ABC与△MED中, ∠B=∠MED ∠C=∠EDM DM=AC , ∴△ABC≌△MED(AAS). 全等三角形的判定.
11.在△ABC中,AB=CB,∠ABC=90°,F为AB延 长线上一点,点E在BC上,且AE=CF.求证: Rt△ABE≌Rt△CBF;
(1)证明:∵∠ABC=90°, ∴∠CBF=∠ABE=90°, 在Rt△ABE和Rt△CBF中, AE=CF AB=BC , ∴Rt△ABE≌Rt△CBF(HL);
直角三角形全等的判定
如图,△ABC中,∠ABC=∠BAC=45°,点P 在AB上,AD⊥CP,BE⊥CP,垂足分别为D, E,已知DC=2,求BE的长.
∵∠ABC=∠BAC=45° ∴∠ACB=90°,AC=BC ∵∠DAC+∠ACD=90°,∠BCE+∠ACD=90° ∴∠DAC=∠BCE 又∵∠ADC=∠CEB ∴△ACD≌△CEB ∴BE=CD=2.
人教版八年级数学上册全等三角形的证明习题(大题)

全等三角形的证明1、如图,AB =AD ,∠BAD =∠CAE ,AC=AE ,求证:BC=DE2、如图,AF=DB ,BC=EF ,AC=DE ,求证:BC∠EF 。
3、已知:如图,∠ABC =∠DCB ,BD 、CA 分别是∠ABC 、∠DCB 的平分线. 求证:AB =DC .4、如图,∠DCE =90°,CD =CE ,AD∠AC ,BE∠AC ,垂足分别为A 、B . 求证:AD +AB =BE .ABCDE5、已知,AC∠CE ,AC=CE , ∠ABC=∠EDC=900,证明:BD=AB+ED 。
6、如图,在∠ABC 中,D 为BC 边的中点,过D 点分别作DE ∠AB 交AC 于点E , DF ∠AC 交AB 于点F .求证:BF=DE 。
7、如图,点E 在AB 上,AC=AD ,请你添加一个条件,使图中存在全等三角形,并给予证明。
所添条件为 ,你得到的一对全等三角形是∆ ∆≅ .证明:ABCDE8、如图,AD 平分∠BAC ,DE∠AB 于E ,DF∠AC 于F ,且DB=DC ,求证:EB=FC.9、如图,AE 是∠BAC 的平分线,AB=AC 。
若点D 是AE 上任意一点,请证明:∠ABD∠∠ACD ;10、(1)把一大一小两个等腰直角三角板(即EC=CD,AC=BC )如图1放置,点D 在BC上,连结BE ,AD ,AD 的延长线交BE 于点F . 求证:(1)ΔACD∠ΔBCE (2)AF∠BE .FE D CB AECDBABACDEFB DE A(2)把左边的小三角板逆时针旋转一定的角度如图2放置,问AF与BE是否垂直?并说明理由.图2。
八年级上册几何证明题

八年级上册几何证明题一、三角形内角和定理相关证明题。
1. 已知:在△ABC中,∠A = 50°,∠B = 60°,求证:∠C = 70°。
解析:根据三角形内角和定理,三角形内角和为180°。
在△ABC中,因为∠A+∠B +∠C=180°,已知∠A = 50°,∠B = 60°,所以∠C=180°∠A ∠B = 180°-50° 60° = 70°。
2. 如图,在△ABC中,AD是∠BAC的平分线,∠B = 70°,∠C = 30°,求∠ADC的度数。
解析:根据三角形内角和定理,在△ABC中,∠BAC=180°∠B ∠C = 180°-70° 30° = 80°。
因为AD是∠BAC的平分线,所以∠BAD = 1/2∠BAC = 40°。
在△ABD中,根据三角形外角性质,∠ADC = ∠B+∠BAD,所以∠ADC = 70°+40° = 110°。
二、等腰三角形性质证明题。
3. 已知:在等腰△ABC中,AB = AC,∠A = 80°,求∠B和∠C的度数。
解析:因为AB = AC,所以△ABC是等腰三角形,根据等腰三角形两底角相等的性质,设∠B =∠C=x。
根据三角形内角和定理,∠A+∠B +∠C = 180°,即80°+x + x = 180°,2x=180° 80°,2x = 100°,x = 50°,所以∠B =∠C = 50°。
4. 如图,在等腰三角形ABC中,AB = AC,BD⊥AC于点D,求证:∠CBD=(1)/(2)∠A。
解析:设∠A=x。
因为AB = AC,所以∠ABC =∠ACB=(1)/(2)(180° x)=90°-(x)/(2)。
八年级上册数学全等三角形证明题

八年级上册数学全等三角形证明题一、全等三角形证明题1 20题及解析。
(一)题目1。
1. 题目。
已知:如图,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE = AC,延长BE交AC于F。
求证:AF = EF。
2. 解析。
证明:延长AD到G,使DG = AD,连接BG。
因为AD是BC边上的中线,所以BD = CD。
在△BDG和△CDA中,BD = CD,∠BDG = ∠CDA(对顶角相等),DG = DA。
根据SAS(边角边)全等判定定理,可得△BDG≌△CDA。
所以BG = AC,∠G = ∠CAD。
又因为BE = AC,所以BG = BE。
所以∠G = ∠BEG。
因为∠BEG = ∠AEF(对顶角相等),所以∠AEF = ∠CAD。
所以AF = EF。
(二)题目2。
1. 题目。
如图,在△ABC和△DEF中,AB = DE,BE = CF,∠B = ∠DEF。
求证:AC = DF。
2. 解析。
因为BE = CF,所以BE + EC = CF+EC,即BC = EF。
在△ABC和△DEF中,AB = DE,∠B = ∠DEF,BC = EF。
根据SAS全等判定定理,可得△ABC≌△DEF。
所以AC = DF。
(三)题目3。
1. 题目。
已知:如图,AB = CD,AE = DF,CE = FB。
求证:AF = DE。
2. 解析。
因为CE = FB,所以CE + EF = FB + EF,即CF = BE。
在△AEB和△DFC中,AB = CD,AE = DF,BE = CF。
根据SSS(边边边)全等判定定理,可得△AEB≌△DFC。
所以∠B = ∠C。
在△ABF和△DCE中,AB = CD,∠B = ∠C,BF = CE。
根据SAS全等判定定理,可得△ABF≌△DCE。
所以AF = DE。
(四)题目4。
1. 题目。
如图,在Rt△ABC中,∠ACB = 90°,CA = CB,D是AC上一点,E在BC的延长线上,且AE = BD,BD的延长线与AE交于点F。
八年级数学几何证明题

特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解
∵△ECD为等边三角形 ∴△ECB≌△DCA( HL )
∴∠ECD=60° CD=EC ∴BC=AC
即ACB==60° ∵∠ACB=60°
—
∴△ 是等边三角形
[例2】、如图,已知BC > AB,AD=DC。BD平分∠ABC。求证:∠A+∠C=180°.
证明:在BC上截取BE=BA,连接DE, ∴∠A=∠BED AD= DE
)
∵BC = DC∴△ABD ≌ △EBD (ASA)
∠CBD=∠CDB ∴AD = DE
]
【课堂练习】
1.如图,已知AE平分∠BAC,BE上AE于E,ED∥AC,∠BAE=36°,那么∠BED=126°
延长AE交AC于F
2.如图:BE⊥AC,CF⊥AB,BM=AC,CN=AB。求证:(1)AM=AN;(2)AM⊥AN。
【变式练习】、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
证明:延长AE到点F,使得EF=AE 联结DF
—
在△ACE和△FDE中 ∴∠ADB=∠ACD+∠CDA
CE =DE ∵∠ACE=∠FDE
∠AEC=∠FED ∴∠ADB=∠ADC+∠FDE
AE=FE 即 ∠ADB = ∠ADF
在△ADC和△GDB中 ∴BG= BF
AD=GD ∴ ∠BFG=∠BGF
初中八年级数学上册的第12章全等三角形证明经典50题含答案

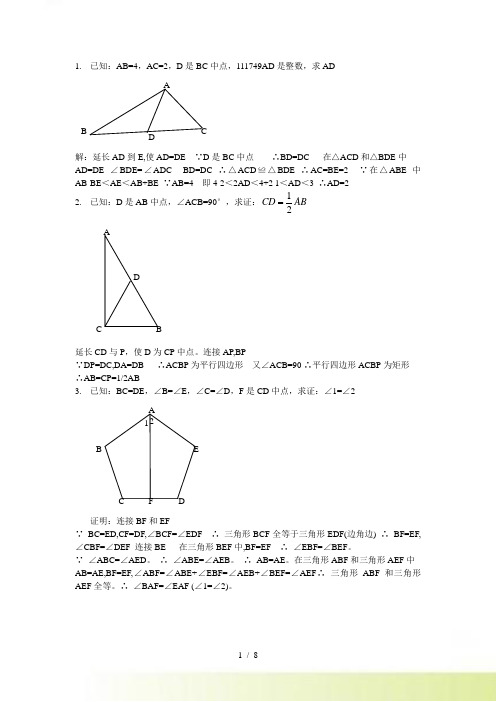
1.已知:AB=4,AC=2,D是BC中点,111749AD是整数,求ADABCD解:延伸AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=22.已知:D是AB中点,∠ACB=90°,求证:1CDAB2 ADA21EBCFD证明:连结BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连结BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF(∠1=∠2)。
4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=ACA21F∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD均分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延伸AB取点E,使AE=AC,连结DE∵AD均分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD证明:在AE上取F,使EF=EB,连结CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC均分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE7.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD ABD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:1CDAB2 ADCB解:延伸AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DEA21EBCFD证明:连结BF和EF。
人教版八年级数学上册 第12章 全等三角形证明50题(含答案)
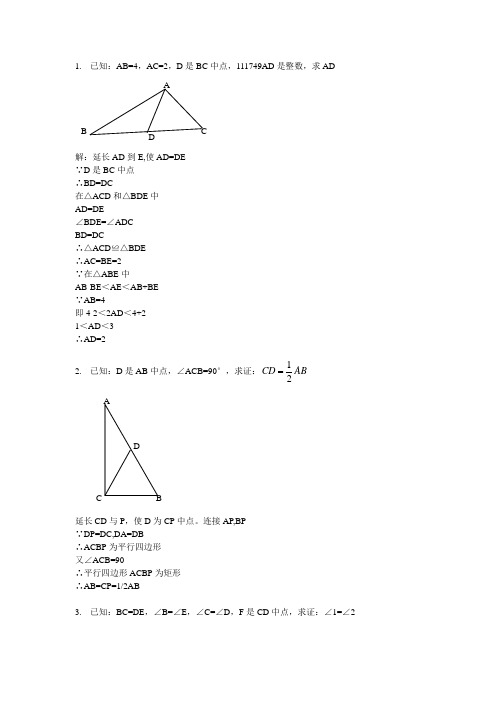
1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF (∠1=∠2)。
4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC过C作CG∥EF交AD的延长线于点GCG∥EF,可得,∠EFD=CGDDE=DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
(完整版)八年级上册几何证明题专项练习

八年级上册几何证明题专项练习1.如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.2.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.3.如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.(1)求证:AC∥DE;(2)若BF=13,EC=5,求BC的长.4.如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.5.如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB求证:AE=CE.6.如图,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC.7.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.8.如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.9.如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.10.如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.11.如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE.12.如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.13.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.(1)求证:BD=CE;(2)求证:∠M=∠N.14.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.求证:△ACD≌△CBE.15.如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=90°,且BC=CE,AB=DE.求证:△ABC≌△DEC.16.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.①求证:△ABE≌△CBD;②若∠CAE=30°,求∠BDC的度数.17.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.18.如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.(1)若△CMN的周长为15cm,求AB的长;(2)若∠MFN=70°,求∠MCN的度数.19.已知△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F.求证:∠BAF=∠ACF.20.如图所示,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F,求证:AB垂直平分DF.21.如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:(1)CF=EB.(2)AB=AF+2EB.22.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:(1)∠ECD=∠EDC;(2)OC=OD;(3)OE是线段CD的垂直平分线.23.如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:(1)AM⊥DM;(2)M为BC的中点.24.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.25.如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.26.如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O(1)求证:OB=OC;(2)若∠ABC=50°,求∠BOC的度数.27.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数.28.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.(1)求∠F的度数;(2)若CD=2,求DF的长.29.图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.30.如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.(1)图中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系,并说明理由.(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.。
初二上几何证明题100题专题训练

八年级上册几何题专题练习100题1、 已知:在⊿ABC 中,∠A=900,AB=AC,在BC 上任取一点P,作PQ ∥AB 交AC 于Q,作PR ∥CA 交BA 于R,D 是BC 的中点,求证:⊿RDQ 是等腰直角三角形.2、 已知:在⊿ABC 中,∠A=900,AB=AC,D 是AC 的中点,AE ⊥BD,AE 延伸线交BC 于F,求证:∠ADB=∠FDC.3、 已知:在⊿ABC 中BD.CE 是高,在BD.CE 或其延伸线上分离截取BM==AB,求证:MA ⊥NA.4.已知:如图(1),在△ABC 中,BP.CP 分离等分∠ABC 和∠ACB,DE 过点P 交AB 于D,交AC 于E,且DE ∥BC .求证:DE -DB=EC .5.在Rt △ABC 中,AB =AC ,∠BAC =90°,O 为BC 的中点.(1)写出点O 到△ABC 的三个极点A .B .C 的距离的大小关系(不请求证实);(2)假如点M .N 分离在线段AB .AC 上移动,在移动中保持AN =BM ,请断定△OMN 的外形,并证实你的结论.6.如图,△ABC 为等边三角形,延伸BC 到D,延伸BA 到E,AE=BD,贯穿连接EC.ED,求证:CE=DE7.如图,等腰三角形ABC 中,AB =AC,∠A =90°,BD 等分∠ABC,DE ⊥BC 且BC =10,求△DCE 的周长.8. 如图,已知△EAB ≌△DCE,AB,EC 分离是两个三角形的最长边,∠A =∠C =35°,∠CDE =100°,∠DEB =10°,求∠AEC 的度数.9. 如图,点E.A.B.F 在统一条直线上,AD 与BC 交于点O, 已知∠CAE=∠DBF,AC=BD.求证:∠C=∠D10.如图,OP 等分∠AOB,且OA=OB .(1)写出图中三对你以为全等的三角形(注:不添加任何帮助线);(2)从(1)中任选一个结论进行证实. M N DEB CA A BCO M N11. 已知:如图,AB =AC,DB =DC,AD 的延伸线交BC 于点E,求证:BE =EC.12. 如图,在△ABC 中,AB=AD=DC,∠BAD=28°,求∠B 和∠C 的度数.14. 写出下列命题的逆命题,并断定逆命题的真假.假如是真命题,请赐与证实;•假如是假命题,请举反例解释.命题:有双方上的高相等的三角形是等腰三角形.15. 如图,在△ABC 中,∠ACB=90º, D 是AC 上的一点,且AD=BC,DE AC 于D, ∠EAB=90º.求证:AB=AE .16. 如图,等边△ABC 中,点P 在△ABC 内,点Q 在△ABC 外,B ,P ,Q 三点在一条直线上,且∠ABP =∠ACQ ,BP =CQ ,问△APQ 是什么外形的三角形?试证实你的结论.17. 如图,△ABC 中,∠C=90°,AB 的中垂线DE 交AB 于E,交BC 于D,若AB=13,AC=5,则△ACD 的周长为若干?18.如图所示,AC ⊥BC,AD ⊥BD,AD =BC,CE ⊥AB,DF ⊥AB,垂足分离是E,F,求证:CE =DF.19. 如图,已知△ABC 中,∠ACB =90°,AC =BC,BE ⊥CE,垂足为E,AD ⊥CE,垂足为D.(1)断定直线BE 与AD 的地位关系是____;BE 与AD 之间的距离是线段____的长;(2)若AD =6 cm ,BE =2 cm ,求BE 与AD 之间的距离及AB 的长.20. 如图,已知 △ABC.△ADE ,点D 是BC 延伸线上一点,贯穿连接CE,求证:BD=CE 21. 如图,△ABC 中,AB =AC ,∠BAC =120°,AD AC 交BC •于点D ,求证:•BC =3AD . 13. 如图,B.D.C.E 在统一向线上,AB=AC,AD=AE,求证:BD=CE.B AE DC22. 如图,四边形ABCD 中,∠DAB=∠BCD=90°,M 为BD 中点,N 为AC 中点,求证:MN ⊥AC .23.已知:如图所示,在△ABC 中,∠ABC=45°,CD ⊥AB 于点D,BE 等分∠ABC,且BE ⊥AC 于点E,与CD 订交于点F,H 是BC 边的中点,衔接DH 与BE 订交于点G .(1)求证:BF=A C; (2)求证:DG=DF .24. 如图,点B,D 在射线AM 上,点C,E 在射线AN 上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A 的度数.25. 如图所示,在△ABC 中,AB=AC,BD ⊥AC 于点D,CE ⊥AB 于点E,BD,CE 订交于F.求证:AF 等分∠BAC.26. 如图所示,△ABC ≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求 ∠DFB 和∠DGB 的度数.27. 已知:如图,在△ABC 中,AB=AC,点D 在边BC 上,DE ⊥AB,DF ⊥AC,且DE=DF, 求证:△ABD ≌△ACD28. 如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm .现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且AC 与AE 重合,求CD 的长.29. 已知:如图,在△ABC 中,AB=AC,BD 等分∠ABC,E 是底边BC 的延伸线上的一点且CD=CE.(1)求证:△BDE 是等腰三角形(2)若 ∠A=36°,求∠ADE 的度数. 30. 如图,在△ABC 中,AB=CB,∠ABC=90°,D 为AB 延伸线上一点,点E 在BC 边上且BE=BD,贯穿连接AE.DE.DC .(1)求证:AE=CD;(2)若∠CAE=30°,求∠BDC 的度数.31. 如图,在ABC 中,点D 在AC 边上,DB=BC,点E 是CD 的中点,点F 是AB 的中点,A B C D E请解释来由.32. 已知:如图,点D为边AC上的一个动点,延伸AB至E,使BE=CD,贯穿连接DE,交BC于点P.(1)DP与PE相等吗?请解释来由.(2当DC=_________时.(不必解释来由)33. 如图,C为线段BD上一点(不与点B,D重合),在BD同侧分离作正三角形ABC 和正三角形CDE,AD与BE交于一点F,AD与CE交于点H,BE与AC交于点G.(1)求证:BE=AD;(2)求∠AFG的度数;(3)求证:CG=CH34. 已知:如图,在△ABC中,CD⊥AB,CD=BD,BF等分∠DBC,与CD,AC分离交与点E.点F,且DA=DE,H是BC边的中点,贯穿连接DH与BE订交于点G.(1)求证:△EBD≌△ACD;(2)求证:点G在∠DCB的等分线上(3)试摸索CF.GF和BG之间的等量关系,并证实你的结论.35. 如图,在在△ABC中,AB=CB,∠ABC=90°,F为AB延伸线上一单,点E在BC 上,且AE=CF.(1(2)若∠CAE=30°,求∠ACF的度数36. 如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分离交CE,AE于点G.H. 试猜测线段AE和BD数目关系,并解释来由.37. 如图,在△ABC 中,AB =AC ,AD 和BE 是高,它们订交于点H ,且AE =BE .求证:AH =2BD .38. 如图,在ABC ∆中,32B ︒∠=,48C ︒∠=,AD BC⊥于点D ,AE 等分BAC ∠交BC 于点E ,DF AE ⊥于点F ,求ADF ∠的度数.39. 如图所示,在△ABC 中,已知点D ,E ,F 分离是BC ,AD ,CE 的中点,且ABC S ∆ =4,则BEF S ∆ 的值为若干.40. 如图,ABC ∆中,90ACB ∠=,CD BA ⊥于D ,AE 等分BAC ∠交CD 于F ,交BC 于E ,求证:CEF ∆是等腰三角形.41. 如图,在四边形ABCD 中,DC ∥AB, BD 等分∠ADC, ∠ADC=60°,过点B 作BE ⊥DC,过点A 作AF ⊥BD,垂足分△BEF 的外形,并解释来由.42. 如图,已知Rt △ABC ≌Rt △ADE ,∠ABC =∠ADE =90°,BC 与DE 订交于点F ,衔接CD ,EB .(1)图中还有几对全等三角形,请你一一列举;(不必证实)(2)求证:CF =EF .43. 在ABC ∆中,BO 等分ABC ∠,点P 为直线AC 上一动点,PO BO ⊥于点O .(1)如图1,当40ABC ︒∠=,60BAC ︒∠=,点P 与点C 重应时,求APO ∠的度数;(2)如图2,当点P 在AC 延伸线时,求证:()12APO ACB BAC ∠=∠-∠; E DACF GHAE HB DC DC(3)如图3,当点P 在边AC 所示地位时,请直接写出APO ∠与ACB ∠,BAC ∠之间的数目关系式.44. 如图,在ABC ∆中,BAD DAC ∠=∠,DF AB ⊥,DM AC ⊥,AF =10cm , AC =14cm ,动点E 以2cm /s 的速度从A 点向F 点活动,动点G 以1cm /s 的速度从C 点向A 点活动,当一个点到达终点时,另一个点随之停滞活动,设活动时光为t .(1) 求证:在活动进程中,不管取何值,都有2AED DGC S S ∆∆=; (2) 当取何值时,DFE ∆与DMG ∆全等.45. 如图,在Rt △ABC 中,∠B=90°,AB=3,BC=4,将△ABC 折叠,使点B 正好落在边AC 上,与点'B 重合,AE 为折痕,求'EB 的长度46. 如图,已知ΔABC 是等腰直角三角形,∠C =90°.(1)操纵并不雅察,如图,将三角板的45°角的极点与点C 重合,使这个角落在∠ACB 的内部,双方分离与斜边AB 交于E .F 两点,然后将这个角绕着点C 在∠ACB 的内部扭转,不雅察在点E .F 的地位产生变更时,AE .EF .FB 中最长线段是否始终是EF ?写出不雅察成果.(2)摸索:AE .EF .FB 这三条线段可否构成以EF 为斜边的直角三角形?假如能,试加以证实.47. 已知BD,CE 是△ABC 的两条高,M.N 分离为BC.DE 的中点.(1)请写出线段MN 与DE 的地位有什么关系?请解释来由.(2)当∠A=45°时,请断定1△EMD 为何种三角形,并解释来由48. 如图(1),已知△ABC 中,∠BAC =90°,AB =AC,AE 是过点A 的一条直线,且点MEG F D C B AB,C 在AE 的两侧,BD ⊥AE 于点D,CE ⊥AE 于点E.(1)求证:BD =DE +CE;(2)若直线AE 绕点A 扭转到如图(2)的地位(BD <CE)时,其余前提不变,问BD 与DE,CE 的关系若何?请赐与证实;(3)若直线AE 绕点A 扭转到如图(3)的地位(BD >CE)时,其余前提不变,问BD 与DE,CE 的关系若何?请直接写出成果,不需证实.49. 如图1,两个不全等的等腰直角三角形OAB 和等腰直角三角形OCD 叠放在一路,并且有公共的直角极点O .(1)在图1中,你发明线段AC,BD 的数目关系是________________ , 直线AC,BD 订交成_________度角.(2)将图1中的△OAB 绕点O 顺时针扭转90°角,这时(1)中的两个结论是否成立?请做出断定并解释来由(3)将图1中的△OAB 绕点O 顺时针扭转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出断定并解释来由.一过离作(1)如图1,,请分离解释下列两个结论成立的来由. 结论1结论2 (2)如图2,,(写出说理进程).52. 已知两个共一个极点的等腰Rt △ABC ,Rt △CEF ,∠ABC =∠CEF =90°,衔接AF ,M 是AF 的中点,衔接MB .ME .图1 图(1)如图1,当CB 与CE 在统一向线上时,求证:MB ∥CF ;(2)如图1,若CB =a ,CE =2a ,求BM ,ME 的长;(3)如图2,当∠BCE =45°时,求证:BM =ME .53. 如图,已知ABC △中,∠B =∠C ,AB =AC=8厘米,BC =6厘米,点D 为AB 的中点.假如点P 在线段BC 上以每秒2厘米的速度由B 点向C 点活动,同时,点Q 在线段CA 上以每秒a 厘米的速度由C 点向A 点活动,设活动时光为t (秒).(1)用含t 的代数式暗示线段PC 的长度;(2)若点P .Q 的活动速度相等,经由1秒后,BPD △ 与CQP △是否全等,请解释来由;(3)若点P .Q 的活动速度不相等,当点Q 的活动速度a 为若干时,可以或许使BPD △与CQP △全等?(4)若点Q 以(3)中的活动速度从点C 动身,点P以本来的活动速度从点B 同时动身,都顺时针沿ABC △三边活动,求经由多长时光点P 与点Q 第一次在ABC △的哪条边上相遇?54. 如图,在ABC ∆中,BAD DAC ∠=∠,DF AB ⊥,DM AC ⊥,AF =10cm ,AC =14cm ,动点E 以2cm /s 的速度从A 点向F 点活动,动点G 以1cm /s 的速度从C 点向A 点活动,当一个点到达终点时,另一个点随之停滞活动,设活动时光为t .(1)求证:在活动进程中,不管t 取何值,都有2AED DGC S S ∆∆=;(2)当t 取何值时,DFE ∆与DMG ∆全等(3)在(2)的前提下,若119126BD DC =,228AED S cm ∆=,求BFD S ∆55. 已知等边△ABC 和点P,设点P 到△ABC3边的AB.AC.BC•的距离分离是h 1,h 2,h 3,△ABC 的高为h,若点P 在一边BC 上(图1),此时h=0,可得结论h 1+h 2+h 3=h,请你摸索以下问题: D B C P A Q当点P在△ABC内(图2)和点P在△ABC外(图3)这两种情形时,h1.h2.h3与h•之间有如何的关系,请写出你的猜测,并扼要解释来由.(1) (2) (3)56.如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开端,按CABC的路径活动,且速度为每秒2㎝,设活动的时光为t秒. (1)求t为何值时,CP把△ABC的周长分成相等的两部分;(2)求t为何值时,CP把△ABC的面积分成相等的两部分;并求此时CP的长;(3)求t为何值时,△BCP为等腰三角形?57. 已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A动身,沿线段AB向点B活动.(1)如图1,设点P的活动时光为t(s),那么t=(s)时,△PBC是直角三角形;(2)如图2,若另一动点Q从点B动身,沿线段BC向点C活动,假如动点P.Q都以1cm/s的速度同时动身.设活动时光为t(s),那么t为何值时,△PBQ是直角三角形?(3)如图3,若另一动点Q从点C动身,沿射线BC偏向活动.衔接PQ交AC于D.假如动点P.Q都以1cm/s的速度同时动身.设活动时光为t(s),那么t为何值时,△DCQ是等腰三角形?(4)如图4,若另一动点Q从点C动身,沿射线BC偏向活动.衔接PQ交AC于D,衔接PC.假如动点P.Q都以1cm/s的速度同时动身.请你猜测:在点P.Q的活动进程中,△PCD和△QCD的面积有什么关系?并解释来由.58.如图所示,已知AD是∠BAC的等分线,EF垂直等分AD交BC的延伸线于点F,交AD于点E,衔接AF,求证:∠B=∠CAF.59.如图所示,AD是∠BAC的等分线,DE⊥AB,DF⊥AC,垂足分离为E,F,衔接EF,EF与AD交于点G,求证:AD垂直等分EF.60.已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为_________.15.如图所示,已知点D 是等边三角形ABC 的边BC 延伸线上的一点,∠EBC=∠DAC,CE ∥AB.求证:△CDE 是等边三角形.61.如图所示,在△ABC 中,AB=AC,在AB 边上取点D,在AC 的延伸线上取点E,使得BD=CE,衔接DE 交BC 于点G,求证:DG=GE.62.一艘汽船以15海里/时的速度由南向北航行,如图,在A 处望小岛P,测得∠PAN=15°,两小时后,汽船到达B 处,测得∠PBN=30°,在小岛P 四周18海里的规模内有暗礁,若汽船持续向北航行,有无触礁安全? 63.如图,公园内两条小河MO.NO 在O 处会合,两河形成的半岛上有一处事迹P.现筹划在两条小河上各建一座小桥Q和R,并在半岛上修三段巷子,连通两座小桥和事迹.这两座小桥应建在何处,才干使修路费起码? 64. 三角形ABC 中,AB=AC,∠BAC=120°,AB 的垂直等分线EF 交AB 于E,交BC 于F .若FC=3cm,则求BF 长度65. 在Rt △ABC 中,∠ACB=90度,(1)请解释△BCD 是正三角形,(66.如图,小红用一张长方形纸片为10cm .当小红折叠时,极点D 时EC 有多长?• 67.如图一块四边形草坪ABCD,求这块草坪的面积.68. 如图,A.B 两个小集镇在河道CD 的同侧,分离到河的距离为AC=10千米,BD=30千米,且CD=30千米,如今要在河畔建一自来水厂,向A.B 两镇供水,铺设水管的费用N BA A B为每千米3万,请你在河道CD上选择水厂的地位M,使铺设水管的费用最节俭,并求出总费用是若干?69.如图,A市气候站测得台风中间在A市正东偏向300千米的B处,以/时的速度向北偏西60°的BF偏向移动,距台风中间200•千米规模内是受台风影响的区域.(1)A市是否会受到台风的影响?写出你的结论并赐与解释;(2)假如A市受此次台风影响,那么受台风影响的时光有多长?70.如图:在△ABC中,∠C=2∠B,AD是△ABC的角等分线,∠1=∠B,试解释AB=AC+CD71.如图,AD是∠BAC的角等分线,DE⊥AB垂足为E,DF⊥AC,垂足为点F,且BD=CD 求证:BE=CF72.如图,点B和点C分离为∠MAN双方上的点,AB=AC.(1)按下列语句画出图形:①AD⊥BC,垂足为D;②∠BCN的等分线CE与AD的延伸线交于点E;③贯穿连接BE;(2)在完成(1)后不添加线段和字母的情形下,请你写出除△ABD ≌△ACD外的两对全等三角形:____≌____,____≌____;(3)并选择个中的一对全等三角形予以证实.73.已知:AB=AC,AD⊥BC,CE等分∠BCN,求证:△ADB≌△ADC;△BDE≌△CDE.AB D CM NE74.如图,PB.PC分离是△ABC的外角等分线且订交于点P.求证:点P在∠A的等分线上AB CP75.如图,△ABC中,p是角等分线AD,BE的交点. 求证:点p在∠C的等分线上76.下列说法中,错误的是()A.三角形随意率性两个角的等分线的交点在三角形的内部B.三角形两个角的等分线的交点到三边的距离相等C.三角形两个角的等分线的交点在第三个角的等分线上D.三角形随意率性两个角的等分线的交点到三个极点的距离相等77.如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM等分∠BAC78.如图,AP.CP分离是△ABC外角∠MAC与∠NCA的等分线,它们订交于点P,PD⊥BM 于点D,PF⊥BN于点F.求证:BP为∠MBN的等分线.79.如图,在∠AOB的双方OA,OB上分离取OM=ON,OD=OE,DN和EM订交于点C.求证:点C在∠AOB的等分线上.80.如图,∠B=∠C=90°,M是BC的中点,DM等分∠ADC.(1)若衔接AM,则AM是否等分∠BAD?请你证实你的结论;(2)线段DM与AM有如何的地位关系?请解释来由.81.八(1)班同窗上数学活动课,应用角尺等分一个角(如图所示).设计了如下筹划:(Ⅰ)∠AOB是一个随意率性角,将角尺的直角极点P介于射线OA.OB之间,移动角尺使角尺双方雷同的刻度与M.N重合,即PM=PN,过角尺极点P的射线OP就是∠AOB 的等分线.(Ⅱ)∠AOB是一个随意率性角,在边OA.OB上分离取OM=ON,将角尺的直角极点P 介于射线OA.OB之间,移动角尺使角尺双方雷同的刻度与M.N重合,即PM=PN,过角尺极点P的射线OP就是∠AOB的等分线.(1)筹划(Ⅰ).筹划(Ⅱ)是否可行?若可行,请证实;若不成行,请解释来由;(2)在筹划(Ⅰ)PM=PN 的情形下,持续移动角尺,同时使PM ⊥OA,PN ⊥OB .此筹划是否可行?请解释来由.82.如图,P 是∠BAC 内的一点,PE ⊥AB,PF ⊥AC,垂足分离为点E,F,AE=AF. 求证:(1)PE=PF;(2)点P 在∠BAC 的角等分线上.83.如图,点D.B 分离在∠A 的双方上,C 是∠A 内一点,AB=AD,BC=CD,CE ⊥AD 于E,CF ⊥AF 于F.求证:CE=CF84.已知三角形三边长为a,b,c,且丨a+b+c 丨+丨a-b-c 丨=10,求b 的值.85.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC86.如图,△ABC 和△ADE 都是等腰直角三角形,CE 与BD订交于点M,BD 交AC 于点N,证实:(1)BD=CE.(2)BD ⊥CE.87.如图,已知AD ∥BC ,∠PAB 的等分线与∠CBA 的等分线订交于E ,CE 的连线交AP 于D .求证:AD +BC =AB 88.如图,△ABC 中BA=BC,点D 是AB 延伸线上一点,DF ⊥AC 于F 交BC 于E,求证:△DBE 是等腰三角形.89.如图,在△ABC 中,AC =BC,∠ACB=90°,D 是AC 上一点,AE ⊥BD 交BD 的延伸线于E,且.求证:BD 是∠ABC 的角等分线.90.如图,∠BAD=∠CAD,AD ⊥BC,垂足为点D,BD=CD 可知哪些线段是哪个三角形的角等分线.中线.高?91.如图所示,在△ABC 中,已知AC=8,BC=6,AD ⊥BC 于D,AD=5,BE ⊥AC 于E,求BE 的D E A B CF B A C D F 2 1 E长92.如图,AD是△ABC的角等分线,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是△DEF的角等分线吗?请解释来由.(2)若将结论与AD是∠CAB的角等分线.DE∥AB.DF∥AC中的任一前提交流,所得命题准确吗?93.如图,△ABC中,∠ABC与∠ACB的等分线交于点I,依据下列前提,求∠BIC的度数.(1)若∠ABC=70°,∠ACB=50°,则∠BIC=°(2)若∠ABC+∠ACB=120°,则∠BIC=°(3)若∠A=90°,则∠BIC=°;(4)若∠A=n°则∠BIC=°(5)从上述盘算中,我们能发明∠BIC与∠A的关系吗?AIB C94.如图,求证∠A+∠B+∠C+∠D+∠E=180°95.如图,不规矩的五角星图案,求证:∠A+∠B+∠C+∠D+∠E=180°96.D为△ABC的边AB上一点,且∠ADC=∠ACD.求证:∠ACB>∠B97.如图,D是BC延伸线上的一点,∠ABC.∠ACD的等分线交于点E,求证:∠E=1/2∠A98.如图,BE与CD订交于点A,CF为∠BCD的等分线,EF为∠BED的角等分线.(1)试求∠F与∠B,∠D的关系;(2)若∠B:∠D:∠F=2:4:x 求X的值99.如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的等分线交于点E,则∠AEC=度.100.如图,在Rt△ABC中,已知∠ACB=90°,AC=BC,D为DC的中点,CE⊥AD于E,BF∥AC交CE的延伸线于点F.求证:AB垂直等分DF.。
八年级全等三角形简单证明题及解答(5道)

汇报人:XX
目 录
• 题目一:基本的全等三角形证明 • 题目二:利用角平分线性质证明 • 题目三:通过边边边条件证明 • 题目四:结合中线性质进行证明 • 题目五:综合应用多种性质证明 • 总结与拓展
01
题目一:基本的全等三角形证明
题目描述
• 已知三角形$ABC$和三角形$DEF$,其中$AB = DE$,$AC = DF$,$\angle BAC = \angle EDF$。求证:$\triangle ABC \cong \triangle DEF$。
由第二步可知,△BDE∽△CFD。
详细解答
4. 第四步,根据相似三角形的性质,对应边成比例,所以BD/CF=DE/DF。
5. 第五步,因为BD=AD(已知),所以AD/CF=DE/DF。又因为AE/EC=DE/EF(已知), 所以AD/CF=AE/EC。
6. 第六步,交叉相乘得AD*EC=AE*CF,即AE/AD=EC/CF。又因为∠A=∠ACF(对顶角相 等),所以△ADE∽△ACF。
第三步,根据相似三 角形的性质,有 AB/AC = BD/DC。
综上,我们证明了 AB/AC = BD/DC。
03
题目三:通过边边边条件证明
题目描述
已知
△ABC和△DEF中,AB = DE,BC = EF,AC = DF。
求证
△ABC ≌ △DEF。
题目描述
【分析】
本题主要考察全等三角形的判定方法——边边边条件。根据已知条件,我们可以 直接应用边边边定理来证明两个三角形全等。
题目描述
01
【解答】
02
证明
03
04
∵ 在△ABC和△DEF中,AB = DE,BC = EF,AC = DF(已
八年级上学期证明题集锦35道基础经典
1、已知:如图,点B,E,C,F 在同一直线上,AB ∥DE,且AB=DE,BE=CF.求证:AC ∥DF .2、如图,已知: AD 是BC 上的中线 ,且DF=DE 求证:BE ∥CF .3、如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF .求证:AC=EF .FG E D C B A4 如图,ΔABC的两条高AD、BE相交于H,且AD=BD,试说明下列结论成立的理由。
(1)∠DBH=∠DAC;(2)ΔBDH≌ΔADC。
5、如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.i.求证:MB=MD,ME=MFii.当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.AB CDEH6 如图18所示,△ADF 和△BCE 中,∠A =∠B ,点D ,E ,F ,C 在同—直线上,有如下三个关系式:①AD =BC ;②DE =CF ;③BE ∥AF .(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的结论.(2)选择(1)中你写出的—个正确结论,说明它正确的理由.7两个大小不同的等腰直角三角形三角板如图20①所示放置,图20②是由它抽象出的几何图形,在同一条直线上,连结.(1)请找出图20②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);(2)试说明:.8 已知:如图,△ABC 中,∠C=90°,AD 是△ABC 的角平分线,DE ⊥AB 于E ,F 在AC 上BD=DF , 求证:CF=EB 。
B C E ,,DC DC BE D FE CB A图18 F EB D A C图20 ① ② DEA B9 已知:如图所示,点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D,E,求证:OB=OC.10 如图,在△ABC中,AD是△BAC的平分线,E,F分别为AB,AC上的点,且△EDF+△EAF=180°.求证:DE=DF.11 如图所示,在△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.12如图,AD⊥DC,BC⊥DC:,E是DC上一点,AE平分∠DAB.E是DC的中点,求证:BE平分∠ABC.13 .如图所示,在四边形ABCD中,△ADC+△ABC=180°,BC=DC,CE△AD,交AD的延长线于点E,CF△AB 于点F.求证:AC平分△BAD.14.如图所示,已知△ABC的角平分线BM,CN相交于点P,那么AP能否平分∠BAC?请说明理由.由此题你能得到一个什么结论?15 . 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求∠A的度数16如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.17、如图,已知:在等边三角形ABC 中,D 、E 分别在AB 和AC 上,且AD=CE ,BE 和CD 相交于点P 。
八年级三角形的证明题

八年级三角形的证明题一、等腰三角形性质相关证明题(8题)1. 已知:在△ABC中,AB = AC,AD是BC边上的中线。
求证:AD⊥BC。
- 证明:- 因为AB = AC,AD是BC边上的中线,所以BD = DC(中线的定义)。
- 在△ABD和△ACD中,AB = AC(已知),BD = CD(已证),AD = AD(公共边)。
- 所以△ABD≌△ACD(SSS)。
- 则∠ADB=∠ADC(全等三角形对应角相等)。
- 又因为∠ADB + ∠ADC = 180°(平角的定义),所以∠ADB = ∠ADC = 90°,即AD⊥BC。
2. 已知:在等腰△ABC中,AB = AC,∠A = 36°,求证:∠B = 72°。
- 证明:- 因为AB = AC,所以∠B = ∠C(等腰三角形两底角相等)。
- 又因为∠A+∠B + ∠C = 180°(三角形内角和定理),∠A = 36°。
- 设∠B = x,则∠C = x,可得方程36°+x + x = 180°。
- 2x=180° - 36°,2x = 144°,解得x = 72°,即∠B = 72°。
3. 已知:在△ABC中,AB = AC,D是AC上一点,且AD = BD = BC。
求∠A的度数。
- 证明:- 设∠A=x,因为AD = BD,所以∠ABD = ∠A=x(等边对等角)。
- 则∠BDC=∠A + ∠ABD = 2x(三角形外角性质)。
- 因为BD = BC,所以∠C = ∠BDC = 2x。
- 又因为AB = AC,所以∠ABC = ∠C = 2x。
- 根据三角形内角和定理,∠A+∠ABC+∠C = 180°,即x + 2x+2x = 180°。
- 5x = 180°,解得x = 36°,所以∠A = 36°。
八年级全等三角形简单证明题及答案(15道)

1.已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.证1=∠2,明:∵∠∴∠1+∠BAD=∠2+∠BAD,即:∠EAD=∠BAC,在△EAD和△BAC中∠B=∠E AB=AE ∠BAC=∠EAD ,≌(ASA),∴△ABC△AED∴BC=ED.与质.全等三角形的判定性2.如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥A B,且DM=AC,过点M作ME∥BC交AB于点E.求证:△ABC≌△MED。
证明:∵MD AB⊥,∠,∴∠MDE=C=90°∥,∵ME BC∠,∴∠B=MED∠∠∠在△ABC与△MED中, ∠B=MED C=EDMDM=AC ,≌(AAS).∴△ABC MED△全等三角形的判定.如图,E、F是四边形ABCD的对角线BD上的两点,AE∥CF,AE=CF,BE=DF.求证:△ADE≌△CBF.∥证明:∵AE CF∠,∴∠AED=CFB∵DF=BE,∴DF+EF=BE+EF,即DE=BF,在△ADE和△CBF中,∠∠AE=CF AED=CFBDE=BF ,≌△(SAS).∴△ADE CBF全等三角形的判定.5.如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.解:∵AD平分∠BAC,∴∠BAD=CAD∠.∴在△ACD和△ABD中∠∠AB=AC BAD=CADAD=AD ,△≌,∴△ACD ABD∴BD=CD,∠.∴∠DBC=DCB与质全等三角形的判定性.6.已知:如图,点E,A,C在同一直线上,AB ∥CD,AB=CE,AC=CD.求证:BC=ED.∥,证明:∵AB CD∠,∴∠BAC=ECD在△BAC和△ECD中 AB=EC∠∠,BAC=ECD AC=CD≌△(SAS),∴△BAC ECD∴CB=ED.与质全等三角形的判定性.7.如图,D、E分别是AB、AC上的点,且AB=AC,AD=AE.求证:∠B=∠C.在△ABE和△ACD中,∵ AB=AC ∠A=∠A AE=AD ,∴△ABE≌△ACD(SAS),∴∠B=∠C.与质全等三角形的判定性.8.已知AC平分∠BAD,AB=AD.求证:△ABC≌△ADC.:∵AC平分∠BAD,∠,∴∠BAC=DAC在△ABC和△ADC中,∠∠AB=AD BAC=DACAC=AC ,∴△ABC ADC≌△.全等三角形的判定.9.如图,已知点E,C在线段BF上,BE=C F,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.证明:∵AB∥DE,∴∠B=∠DEF.∵BE=CF,∴BC=EF.∵∠ACB=∠F,∴ ∠B=∠DEF BC=EF∠ACB=∠F , ∴△ABC≌△DEF.线质全等三角形的判定;平行的性.10.已知:如图,E、F在AC上,AD∥CB 且AD=CB,∠D=∠B.求证:AE=CF.证明:∵AD∥CB,∴∠A=∠C,在△ADF和△CBE中,∠A=∠C AD=CB ∠D=∠B ,∴△ADF≌△CBE(ASA),∴AF=CE,∴AF+EF=CE+EF,即AE=CF.与质全等三角形的判定性.11.在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF;(1)证明:∵∠ABC=90°,∴∠CBF=∠ABE=90°,在Rt△ABE和Rt△CBF中, AE=CFAB=BC ,∴Rt△ABE≌Rt△CBF(HL);直角三角形全等的判定如图,△ABC中,∠ABC=∠BAC=45°,点P在AB上,AD⊥CP,BE⊥CP,垂足分别为D,E,已知DC=2,求BE的长.∵∠ABC=∠BAC=45°∴∠ACB=90°,AC=BC∵∠DAC+∠ACD=90°,∠BCE+∠ACD=90°∴∠DAC=∠BCE又∵∠ADC=∠CEB∴△ACD≌△CEB∴BE=CD=2.质直角三角形全等的判定;全等三角形的性.如图,△ABC中,AB=AC,∠1=∠2,求证:AD平分∠BAC.解:∵AB=AC,∴∠ABC=∠ACB.∵∠1=∠2,∴∠ABD=∠ACD,BD=CD.∵AB=AC,BD=CD,∴△ABD≌△ACD.∴∠BAD=∠CAD.即AD平分∠BAC.与质全等三角形的判定性.如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.:△BCF≌△CBD.△BHF≌△CHD.△BDA≌△CFA.证明:在△BCF与△CBD中,∵AB=AC.∴∠ABC=∠ACB∵BD、CF是角平分线.∴∠BCF=1 2 ∠ACB,∠CBD=1 2 ∠ABC.∴∠BCF=∠CBD,∴ ∠BCF=∠CBD BC=BC ∠ABC=∠ACB∴△BCF≌△CBD(ASA).全等三角形的判定.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线.证明:∵DE⊥AB,DF⊥AC,∴Rt△BDE=Rt△DCF=90°.BD=DC BE=CF ,∴Rt△BDE≌Rt△DCF(HL),∴DE=DF,又∵DE⊥AB,DF⊥AC,∴AD是角平分线.线质与质角平分的性;全等三角形的判定性.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
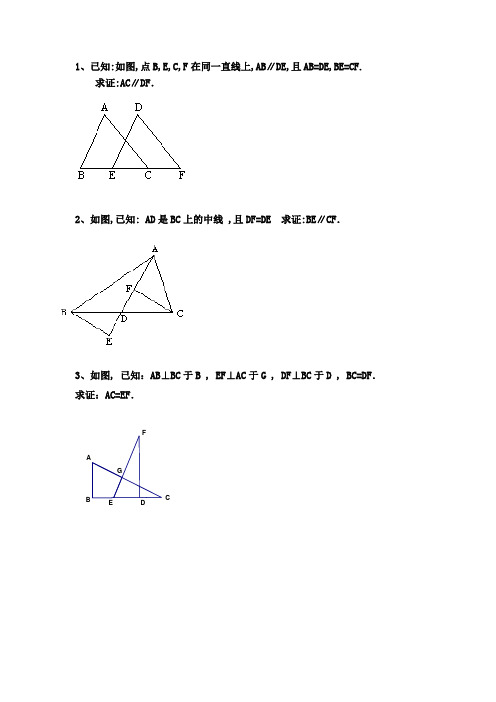
1、已知:如图,点B,E,C,F 在同一直线上,AB ∥DE,且AB=DE,BE=CF. 求证:AC ∥DF .
2、如图,已知: AD 是BC 上的中线 ,且DF=DE .
求证:BE ∥CF .
3、如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF . 求证:AC=EF .
4 如图,ΔABC 的两条高AD 、BE 相交于H ,且AD=BD ,试说明下列结论成立的理由。
(1)∠DBH=∠DAC ;
(2)ΔBDH ≌ΔADC 。
F
G
E
D
C
B
A
A B
C
D
E H
5、如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.
i.求证:MB=MD,ME=MF
ii.当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
6、如图(1),(1)已知△ABC中, ∠BAC=900, AB=AC, AE
是过A的一条直线, 且B、C在A、E的异侧, BD⊥AE于D, CE
⊥AE于E
试说明: BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD与DE、CE的关系如何? 为什么?
(3)若直线AE绕A点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD与DE、CE的关系如何? 请直接写出结果, 不需说明.
F
E
D
C B
A
7、已知:如图,CE ⊥AB 于点E ,BD ⊥AC 于点D ,BD 、CE 交于点O ,且BO=CO . 求证:O 在∠BAC 的角平分线上.
8 如图18所示,△ADF 和△BCE 中,∠A =∠B ,点D ,E ,F ,C 在同—直线上,有如下三个关系式:①AD =BC ;②DE =CF ;③BE ∥AF .
(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的结论.
(2)选择(1)中你写出的—个正确结论,说明它正确的理由.
9两个大小不同的等腰直角三角形三角板如图20①所示放置,图20②是由它抽象出的几何图形,B C E ,,在同一条直线上,连结DC .
(1)请找出图20②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母); (2)试说明:DC BE .
10如图17—①,已知等腰直角△ABC 中,BD 为斜边上的中线,E 为DC 上的一点,且AG ⊥BE 于G ,AG 交BD 于F 。
(1)求证:AF=BE
(2)如图17—②,若点E 在DC 的延长线上,其它条件不变,①的结论还能成立吗?若不能,请说明理由;若能,请予以证明。
11 如图,在△ABC 中,已知AB =AC ,∠BAC =90o ,D 是BC 上一点,EC ⊥BC ,EC =BD ,DF =FE .求证(1)△ABD ≌△ACE ;(2)AF ⊥DE .
12 如图,在Rt △ABC 中,∠ACB=45°,∠BAC=90°,AB=AC ,点D 是AB 的中点,AF ⊥CD
于H ,交BC 于F ,BE ∥AC 交AF 的延长线于E ,求证:BC 垂直且平分DE
图
20
① ②
图18
F
E B
D
A
C
13 如图,在△ABC 中,∠ACB =90°,CE ⊥AB 于点E ,AD=AC ,AF 平分∠CAB •交CE 于点F ,DF
的延长线交
AC
于点
G ,求证:(1)DF ∥BC ;(2)FG =FE
14 已知如图(1):△ABC 中,AB=AC ,∠B 、∠C 的平分线相交于点O ,过点O 作EF ∥BC 交AB 、AC 于E 、F 。
①图中有几个等腰三角形?且EF 与BE 、CF 间有怎样的关系?(不证明)
②若AB ≠AC ,其他条件不变,如图(2),图中还有等腰三角形吗?如果有,请分别指出它
们。
另第①问中EF 与BE 、CF 间的关系还存在吗?(不证明)
③若△ABC 中,AB ≠AC ,∠B 的平分线与三角形外角∠ACD 的平分线CO 交于O ,过O 点作OE ∥BC 交AB 于E ,交AC 于F 。
如图(3),这时图中还有等腰三角形吗?EF 与BE 、CF 间的关系如何?为什么(要证明你的结论)?
15 如图16,已知△ABC
为等边三角形,P 为BC 上一点,△APQ 为等边三角形。
(1)求证:AB ∥CQ ;
(2)AQ 与CQ 能否互相垂直?若能互相垂直,指出点P 在BC 上的位置,并给予证明;若AQ 与CQ 不能互相垂直,请说明理由。
(1)
C
B
F O
E
A
(2)
B
C
F O
E A
(3)
D
C O
F
A E
B
16、已知,如图,△ABC 中,AB = AC ,AD ⊥ BC 于D ,BE ⊥ AC 于E ,AD 和BE 交于H ,且BE = AE ,求证:AH = 2BD 。
A
H E
17.如图,已知点B 、C 、D 在同一条直线上,△ABC 和△CDE•都是等边三角形.BE 交AC 于F ,AD 交CE 于H ,
①求证:△BCE ≌△ACD ; ②求证:CF=CH ;
③判断△CFH•的形状并说明理由.
E
D
A
B
H
F
18、如图已知:在△ABC 中,AB = AC ,∠BAC = 120°,P 为BC 边的中点,PD ⊥AC 。
求证:CD = 3AD 。
A D
B P C
19、已知,如图,△ABC 的∠ABC 的平分线BD 与∠ACB 的外角平分线交于D 点,DE ∥BC 交AB 于E ,交AC 于F ,求证:EF = BE – CF 。
A
E F D
B C
20、如图,在Rt △ABC 中,AB = AC 。
∠A = 90°,点D 在BC 上任一点,DF ⊥AB 于F ,DE
⊥AC 于E ,M 为BC 的中点,试判断△MEF 是什么形状的三角形,并证明你的结论。
A E
F
B D M C。
