2018考研经济联考数学复习指导

合集下载

2018考研数学10-12月复习指南

2018考研数学10-12月复习指南2018考研数学的考试大纲已经公布，较往年没有变化，从2009年考研数学大纲合并后数学考试分为数一、数二、数三、数农。

2013年线性代数将克莱姆法则改成了克拉默法则。

概率论中将两个及两个以上随机变量的函数分布，改为两个及两个以上随机变量的简单函数分布，会求多个相互独立的随机变量的联合分布及函数分布改为会求多个相互独立的随机变量的联合分布及简单的函数分布，现在针对今年的考试大纲，对最后的考研复习进行说明：▶一、考试的时间：今年硕士研究生统一考试数学科目的考试时间为2018年12月27日8:30-11:30.考试时间仍为180分钟。

考研倒计时也从3位数变成了两位数，希望大家继续坚持下去!▶二、考试的性质：全国硕士研究生入学统一考试数学科考试是为招收工学、经济学、管理学硕士研究生而设置的具有常模参照性的水平考试。

水平考试是指命题不以教学基本要求和某一指定教材为依据，而以《考试大纲》为依据.对于考试大纲以外的内容大家不用涉及。

▶三、命题趋势和考点分析。

1、考研数学试题科学性和公平性原则作为公共基础课，考研数学试题以基础性，生活类试题为主尽量避免对于广大考生来说过于专业和抽象难懂的内容：为了体现不同学科专业对考生应具备数学知识和能力的不同要求.2、考研数学知识点，覆盖全面的原则考研数学的试题内容要求涵盖所有考纲要求考核的内容，尤其涵盖数一、数二、数三相区别之处(2013年数学一空间解析几何与向量代数在之前的近十年都未曾考过，13年考了一个大题一个小题共16分，那一年好多同学都是很凄惨的，所以知识点平时大家一定要无遗漏的复习，并且要抓住区别之处。

3、控制难易度的原则考研数学试题要求以中等偏上的题为主，考试及格率控制在30%—40%。

平均分稳定在75—82分。

不会出现幅度较大的变化。

4、控制题量的原则考研数学的试卷结构：可参照历年考研真题试卷。

其中客观题考查基本概念、基本理论、基本运算，解答题考查简单的分析综合及应用能力。

2018考研数学大纲权威解读及复习规划(杨超老师)

参数估计
（数一、三）
数字特征（数一）
数字特征及参数估计（数三）
参数估计
（数一、三）
数学第 15 题考什么？偏导数计算，这个属于最基本的计算，有时会考抽象的多元函数求偏导数。考了一个抽象的多元函数求偏导数的填空题。求数列求极限，K 从 1 到 N，这个题看完以后，标准的定积分定义，你可以马上写等于多少，0 到 1，这个规律永远没有改变，积分区间 0 到 1。把 N 分之 K 改成积分变量，审题很简单，这叫思维定式，用定积分的定义把它写出来，涉及到基本计算能力。18 题考了一个中值定理证明，过去在真题里面也有，19 题考了曲面积分，涉及到简单的物理应用。
数学题考什么？三种能力：
沪江网校·考研 VIP 2018 考研新大纲权威解析
第一点运算能力，这一点是我始终强调的，目前 70%、80%的同学都会遇到这个问题，觉得很慌，其实这个能力需要不断的去重复练习，一直到进入考场，这个是要一直锻炼的；
第二点，做过的题目还是不会。9 月份 10 月份会是一个关键时期，在这个阶段心态调整好，加紧复习，重复并且回忆做过的知识点和错题。三门课，以高数为例子，你重点要计算过关，可以关注我微博视频课程总结的高等数学 10 大最基本的计算。
数字特征（数三）
第 23 题混合型随（11 分）机变量
（数一、三）
二维随机变量
（数一、三）
一维随机变量及数字特征
（数一、三）
混合随机变量及期望（数一、三）
一维随机变量（数一）
二维随机变量（数三）
第 24 题（11 分）
参数估计
（数一、三）
参数估计（数一）
数字特征（数三）

2018考研数一数二数三必看重点

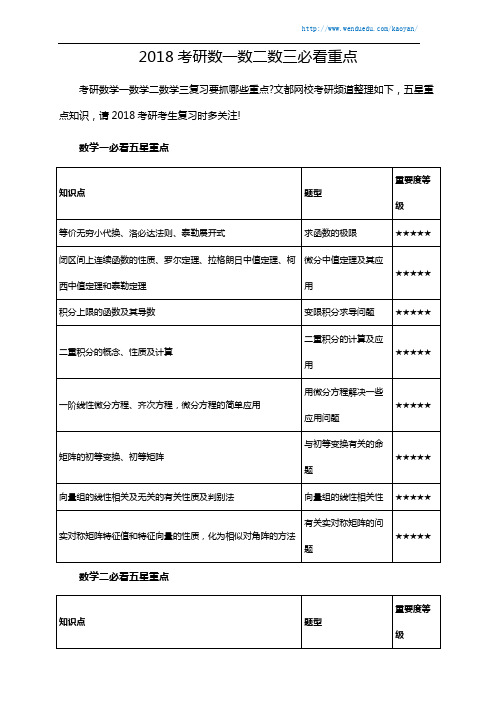
2018考研数一数二数三必看重点考研数学一数学二数学三复习要抓哪些重点?文都网校考研频道整理如下，五星重点知识，请2018考研考生复习时多关注!数学一必看五星重点知识点题型重要度等级等价无穷小代换、洛必达法则、泰勒展开式求函数的极限★★★★★闭区间上连续函数的性质、罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理微分中值定理及其应用★★★★★积分上限的函数及其导数变限积分求导问题★★★★★二重积分的概念、性质及计算二重积分的计算及应用★★★★★一阶线性微分方程、齐次方程，微分方程的简单应用用微分方程解决一些应用问题★★★★★矩阵的初等变换、初等矩阵与初等变换有关的命题★★★★★向量组的线性相关及无关的有关性质及判别法向量组的线性相关性★★★★★实对称矩阵特征值和特征向量的性质，化为相似对角阵的方法有关实对称矩阵的问题★★★★★数学二必看五星重点知识点题型重要度等级等价无穷小代换、洛必达法则、泰勒展开式求函数的极限★★★★★闭区间上连续函数的性质、罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理微分中值定理及其应用★★★★★积分上限的函数及其导数变限积分求导问题★★★★★二重积分的概念、性质及计算二重积分的计算及应用★★★★★一阶线性微分方程、齐次方程，微分方程的简单应用用微分方程解决一些应用问题★★★★★矩阵的初等变换、初等矩阵与初等变换有关的命题★★★★★向量组的线性相关及无关的有关性质及判别法向量组的线性相关性★★★★★实对称矩阵特征值和特征向量的性质，化为相似对角阵的方法有关实对称矩阵的问题★★★★★数学三必看五星重点知识点题型重要度等级等价无穷小代换、洛必达法则、泰勒展开式求函数的极限★★★★★闭区间上连续函数的性质、罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理微分中值定理及其应用★★★★★积分上限的函数及其导数变限积分求导问题★★★★★二重积分的概念、性质及计算二重积分的计算及应用★★★★★矩阵的初等变换、初等矩阵与初等变换有关的命题★★★★★向量组的线性相关及无关的有关性质及判别法向量组的线性相关性★★★★★实对称矩阵特征值和特征向量的性质，化为相似对角阵的方法有关实对称矩阵的问题★★★★★两个随机变量函数的分布二维随机变量函数的分布★★★★★随机变量的数学期望、方差、标准差及其性质，常用分布的数字特征有关数学期望与方差的计算★★★★★2018考研学子想要了解更多考研资讯、复习资料与备考经验，可以搜索文都网校进入考研频道，查看2018考研辅导课程，咨询专业老师考研相关内容。

2018经济学考研369经济类数学考点概要

2018经济学考研369经济类数学考点概要感谢凯程考研李老师对本文做出的重要贡献长期以来，经济学是考研的热门学科，由于中国入世和中外贸易的发展，经济学越来越成为广大考研学子追求的热点。

但是要注意的是很多热门专业不是因为社会的需求大产生的，通常情况下，都是广大考生盲目跟风的结果。

如果这种盲目性增大，那么热门专业读研之后，可能会带来冷就业的后果。

专业选择还是以兴趣为主，结合自身的人生规划为佳。

现凯程教育为考研考生带来重要备考信息点拨。

经济类联考中会涉及到很多方面的知识，数学、逻辑、写作都会有所涉及，数学则主要考察的数学三的知识内容，小编整理联考数学中的微积分常考知识点概念，帮助大家完成最后几天的备考。

1.若y=f(x)互为反函数，则f[g(x)]=x 若limf(x)存在，则limf(x)表示一个常数x→x0 x→x0例：已知limf(x)和limf(x)都存在，且f(x)=x^2+3xlimf(x)+2x^3limf(x)求f(x)x→1 x→2 x→1 x→2 若当x→x0时，或x→∞时，f(x)为无界变量，则当x→x0或x→∞时，f(x)必定为无穷大量(此命题是错误的)例f(x)=x x为有理数f(x)=1/x x为无理数两个无穷大量和必定为无穷大量(此命题是错误的)例x→0 (2-1/x)+(3+1/x)=55.若x→x0时，f(x)为无穷大量，则当x→x0时ef(x)必定为无穷大量。

(此命题是错误的) 当x→1时，1/(x-1)为无穷大量而lim1/(x-!)=∞lim1/(x-!)= -∞x→1+ x→1-lim e^1/(x-!)=+∞lime^1/(x-1)=0x→1+ x→1-6.若lim(un,vn)=0，则必定有lim un=0或lim vn=0n→∞n→∞n→∞(此命题是错误的)例un=1-(-1)^n vn=1+(-1)^n n=1,2….U*v=0因此lim(u,v)=0但是u,v都存在7.设对任意的x，总有Ф(x)≤f(x)≤g(x)且lim[g(x)-ф(x)]=0，则limf(x)必定x→∞x→∞存在。

2018年考研之396经济类综合联考备考策略

2018年考研之396经济类综合联考备考策略只有准备的比别人早，努力的比别人多，才有可能比别人有更多的竞争优势，而且一定要掌握好方法，才有可能考取。

考名校需要毅力和魄力，但只要付出努力一切皆有可能，一旦考取，人生命运都将因此而改变，对于2018年准备考考研的同学来说，只有准备的比别人早，努力的比别人多，才有可能比别人有更多的竞争优势，而且一定要掌握好方法，才有可能最终考取。

科目：396经济类联考：数学+逻辑+作文应试经验：396这一门课程和数三一样，虽比不上数三的难度，可是这在专硕中绝对是提分拉分重要一门，目标分数大概在120~130之间。

拿下这科其实不难，一个是要有方法，一个是要有熟练度。

先说数学，15年数学难度略有提升，但是选择题依然简单，大题的范围不超纲，需要的是能力。

主要是对数学大纲有一定的了解，避免和数三的内容重复，再一个就是记住所有的公式，之后做数学精点，这个过程要长一点，主要是提炼方法(数学精点有十套模拟题，但个别内容超纲，需注意)。

另外说一点数学中可能会出往年的数三真题，所以找来数三真题死记硬背，当然这是在清楚大纲内容的基础上，有筛选的背。

逻辑这个内容要好好说一说，很多人开始不是很适应，但是久了会发现这个内容很有意思。

逻辑也是一样会有往年的真题出现(大概3~4个，比例大于数学)。

鉴于这一点逻辑的题要多做，建议的方法是先做一遍真题详解，然后再看逻辑分册，加深印象。

因为分册排版不是很有条理，看起来很慢，没有效率。

先做真题的好处是，大家很很好的熟悉出题模式，以及答案的内容(事实上有些选项的说法，能直接看出来错误)。

做完题后看分册思路会很清楚，速度也会很快。

时间规划上，真题每天一套一小时，一个月内搞定;分册可以慢慢看，两个月内搞定。

看分册的过程很关键，还是提炼方法，总结规律。

结论题在其中是关键，从分册页数就可以看出，它的判别方法也会穿插到别的题型中。

而且在考试比例占到近四成，所以结论题的分，要拿全。

2018考研数学真题对19考生的备考指导_毙考题

2018考研数学真题对19考生的备考指导2018年考研数学已经落下帷幕。

下面我们来对今年数一数二三都出现的一道大题，就是关于数列极限的计算的大题以及变上限积分求导来进行分析以及为2019年考试复习提供建议。

2018年考研真题中，数学一、数学二和数学三都是考查了关于数列极限计算方法，数学一的第19题，数学二的第21题，数学三的第19题都是这道数列极限计算的问题。

一般这种题目数一数二考的比较多，尤其数学二，但是今年数三也考了。

数二的第16题是考察微分方程求解问题，但实际其本质还是变上限积分求导问题。

总体难度比去年有所增加。

所以通过对2018年的分析，我们发现微分方程一般不会单独出题，这个知识点只会融入到其他知识点的考核中，比如数二的第16题，它跟2016年数三考的那个大题很像。

针对2018年对极限和微分方程的考查方式，同学们在2019年考研备考中应该注意下面问题。

首先，我们必须.牢记知识体系。

极限分为函数极限和数列极限，其这章包括三个部分：首先是极限的概念以及无穷小和无穷大的介绍；然后是极限的基本性质；最后是极限的计算方法，这里既有函数极限的计算方法又有数列极限的计算方法。

大家可以把这个知识体系与前面说的2018年真题做个对照，就会发现极限的计算是重点，2018数二的第9题就是函数极限的计算题，当然数三的第15题也是函数极限的计算。

数学一的第19题，数学二的第21题，数学三的第19题都是数列极限的计算的问题。

对于变上限积分求导：一，大家要清楚基础阶段和强化阶段要复习的内容。

在基础阶段，要求知道变上限积分的定义，性质，掌握简单的变上限积分求导。

在强化阶段，大家就需要综合应用了，比如变上限积分和函数极限结合出题，2017年考研第15极限计算就是与变上限积分求导结合的题目。

还有就是这种变上限积分求导与微分方程结合的题目。

其次，.理解极限知识点内容。

在牢记知识体系之后，大家要做的就是理解知识点。

首先是极限的概念以及无穷小和无穷大的介绍。

2018年考研经济类联考数学必备知识点整理

2018年考研经济类联考数学必备知识点整理很多参加考研的考生对于数学三想必都不陌生，也了解经济类联考数学比数学三简单，但却不知道经济类联考数学考什么，所以凯程考研将经济类联考数学必考34点列举如下，供考生们参考。

正所谓知己知彼，百战不殆，在列举考点之前，同学们先看一下经济类联考数学试题特点：1、重基础：396经济类联考考题共70分，其中选择题10个，解答题10个;题目中80%的题目都是基础题，约占15个左右;所以要求考生对考研数学中的基本概念、基本理论、基本方法要非常熟悉。

2、知识面广：396经济类联考自2011年联考以来，时间不长，知识点还没有完全覆盖;所以对于考试大纲规定的考试范围内的，但试卷中还没有出现过的那部分内容，大家要尤为重视，它们可能作为未来考试中的考点出现。

3、重计算：396经济类联考的历年考试题目中还没有出现过考查证明题的，都是计算题，所以对考生的计算能力、计算的准确性、计算的方法要求较高，希望大家着重这方面的训练。

必考点：(一)微积分1、函数、极限、连续(1)求复合函数的定义域;(2)求函数表达式;(3)无穷小阶的比较;(4)利用等价无穷小替换、两个重要极限求极限;(5)求幂指函数的极限;(6)利用洛必达法则求极限;(7)分段函数在分段点处的连续性;(8)判断间断点类型;2、导数与微分(1)利用导数的四则运算法则、复合函数求导法则求导数与微分;(2)求分段函数在分段点处的导数;(3)一元函数隐函数求导;(4)一元函数的单调区间、极值、凹凸性、拐点、渐近线;(5)导数的经济应用;3、一元函数积分学(1)利用换元法与分部积分法计算不定积分;(2)利用换元法与分部积分法计算定积分;(3)变限积分求导;(4)定积分的几何应用;4、多元函数微分学(1)求二元函数的一阶偏导数;(2)求二元函数的全微分;(3)二元函数隐函数的求导。

(二)线性代数1、行列式和矩阵(1)矩阵的基本运算;(2)伴随矩阵的求法;(3)逆矩阵的求法。

2018考研数学复习：如何高效利用真题？

凯程考研辅导班，中国最权威的考研辅导机构
第 1 页共 1 页 2018考研数学复习：如何高效利用真
题？
所有考过的学长学姐都会向后辈反复强调真题的重要性，因为真题真的很重要!重要的事情要加感叹号!!!下面就简要说说如何利用真题，每个人使用真题都有自己的方法，本文的方法也只是参考。

1、不要认为真题得放到最后做，真题的利用价值堪比黄金，所以一定要充分利用才算赚到了。

基本上从强化复习开始，真题就要开始做起来了。

2、不要以为真题做了一遍答案都记住了，第二遍、第三遍再做真题时就没有效果了。

第一遍做的时候是检测自己到底有哪些知识点没有记住以及自己和考试的差距到底有多少。

做完真题要认真分析，为什么没有做对，是理解问题还是计算问题，是定义定理的概念模糊了还是根本就没有明白要考的知识点是什么。

这些都需要考生去认真分析。

只有这样才算是真正利用好了真题。

3、第二遍以及之后做真题时，你会发现你很有可能在同一个问题上犯两次甚至更多同样的错误，这个时候考生需要高度警惕，这绝对就是你复习时没有注意到的“漏洞”或者是你没有完全掌握的知识点，必须想办法(找老师或者找高手同学)解决掉，不然考试碰到此类问题你还是会失分。

4、做真题的次数多了，还可能发现一些平时容易忽略的小失误，比如第一次做对了，第二次却做错了，这些小失误也在一定程度上反映出你的知识点其实是没有完全掌握的。

5、做真题的最高境界不是全都做对了，而是把每道题都吃透了，考的是什么知识点，还有没有其他更好的解法有什么陷阱，甚至连出题人的心理都能摸索的清清楚楚。

2018考研数学必备解题思路和考点

2018考研数学必备解题思路和考点2018考研数学必备解题思路和考点考研数学做题时间180分钟，每年都有不少同学出现做不完题的情况，不是因为知识点不会，而是因为自己没有形成一个完整的思路。

今天小编给大家整理了一些2018考研数学必备解题思路知识，希望对大家有所帮助。

2018考研数学必备解题九大思路2018考研数学36个考点1.极限问题的快速分析与处理;2.巧用极限的保序性、有界性与唯一性，正确快速运用极限运算法则;3.准确快速判断分段函数特性(连续、可导与导数连续等);4.导数与微分的特别考点;5.等式与不等式证明技巧;6.处理积分计算与综合分析问题的有效方法;7.正确运用定积分性质，处理变限积分与含参积分的技巧;8.用积分表达与计算应用问题的技巧;9.级数收敛性分析与判断的快速程序化方法;10.级数展开与求和零部件组合安装法;11.“按类求解”和“观察侍定”是解微分方程的两把钥匙;12.“规律翻译”与“微量平衡分析” 是解应用题的基本方法;13.用函数观点来考察微分方程问题;14.用“多元问题”“一元化”的方法研究多元函数;15.分析“函数结构”是“抽象函数”导数的计算的关键;16.多元极(最)值问题应抓住“三个什么” “三个步骤”;17.“三定”( 坐标系、积分序和积分限 )是计算重积分的三步曲;18.灵活运用“分块积分、对称性、几何和物理意义”是计算重积分的捷径;20.掌握曲面的定向是正确利用Guass公式、Stokes公式的前提;21.将矩阵按列分块之技巧及应用;22.利用矩阵的参数的技巧;23.利用初等矩阵表示矩阵的初等变换的技巧;24.应用行列式的展开定理的技巧;25.关于向量组的线性相关与线性无关的技巧;26.利用简化行阶梯形的技巧;27.关于矩阵对角化问题的技巧;28.判断二次型正定性的技巧;29.加减求逆乘法律，全概逆概独立性，事件化简是关键，三大概型应活用;30.变量分布特征清，参数确定容易定，重要分布记背景，离散变量靠列表;31.一维连续画密度，正态计算标准化，指数分布无记忆，函数分布直接求;32.由联合分布求边缘分布的技巧，判断独立性;由联合分布求概率;33.函数期望是关键，常用分布背特征，特征性质要牢记，二维特征定相关;34.大数中心规范记，收敛方式有区别，切比雪夫估概率，近似计算用中心;35.抽样分布定义明，正态抽样四式推，矩法似然原理清，无偏有效算特征;36.区间估计靠枢轴，分位定义应明确，假设检验步骤定，两类错误会计算。

2018年考研数学备考指南【五篇】

2018年考研数学备考指南【五篇】导读：本文2018年考研数学备考指南【五篇】，仅供参考，如果觉得很不错，欢迎点评和分享。

【第一篇：做题时要不断思考、不断总结】很多同学在复习中都有这样的困惑，每天做了很多题但不会的题还是非常多，有时候明明是已经做过得，但是再刺遇到还是不会做! 这个问题很多同学存在的毛病，每次总以为不会做了，看看解题思路就会了，每次都不思考为什么不会做了?解题技巧是什么?和它同类型的题我会不会做。

其实，这些小的细节都是对考研很重要的，同学们在复习时要学会思考，最重要是学会举一反三，因为只有这样我们才能脱离题海，能够做到有效做题，高效提升! 【第二篇：注重基础，培养逆向思维】在备考时，很多同学容易陷入题海中，这也是很多考生对数学感到头痛的原因所在。

其实在前期复习知识点的时候，我们就应该把定义、定理的推导作为一个重点内容，重视推导和例题中的方法与技巧，认真分析这些方法，将它们套用到相应的练习题中，这样不仅提升了复习效率，而且还是半功倍。

同时，思维习惯影响着我们的学习效果。

当同学们进入考研数学复习备考的时候，大多数同学还是和以往的学习习惯一样复习，也就是进入了定势思维。

习惯性思考方式在一方面有优势，但这样往往会制约着我们学习成绩的提升，所以我们要做的就是打破惯性思维! 【第三篇：做题有始有终，提高计算能力】考研数学复习不等于做题，但是学好数学一定要做题，这是无可后非的问题，我们说基础的扎实巩固是根本，然后在这个基础上进行做题的练习以达到巩固的效果。

同时，需要提醒大家的是复习一定要养成一个好的习惯，拿到的数学题一定要有始有终把它算出来，这是一种计算能力的训练。

【第四篇：深入思考，并且善于总结】考研数学考试里不仅仅是考察我们基本概念、基本理论、基本方法的问题，还涉及到我们灵活运用知识的能力问题，所以仅仅是依靠教材很难把它这种考试命题的特点归纳总结出来，因此同学们要了解考试模式和考试方式等问题，历年考试的真题作为准备去参加研究生考试的同学是必备的。

2018年经济类、管理类考研数学基础班课程讲义

《附件3》----2018届管理类考研数学基础班课程讲义导论一、管理类联考数学考试大纲管理类专业学位联考(MBA,MPA,MPAc等)综合能力考试数学部分要求考生具有运用数学基础知识、基本方法分析和解决问题的能力.综合能力考试中的数学部分(75分)主要考查考生的运算能力、逻辑推理能力、空间想象能力和数据处理能力，以及分析问题和解决问题的能力，通过问题求解(15小题，每小题3分，共45分)和条件充分性判断(10小题，每小题3分，共30分)两种形式来测试.数学部分试题涉及的数学知识范围有：(一)算术1．整数(1)整数及其运算(2)整除、公倍数、公约数(3)奇数、偶数(4)质数、合数2. 分数、小数、百分数3．比与比例4．数轴与绝对值(二)代数1．整式(1)整式及其运算(2)整式的因式与因式分解2．分式及其运算3．函数(1)集合(2)一元二次函数及其图像(3)指数函数、对数函数4．代数方程(1)一元一次方程(2)一元二次方程(3)二元一次方程组5．不等式(1)不等式的性质(2)均值不等式(3)不等式求解：一元一次不等式(组)，一元二次不等式，简单绝对值不等式，简单分式不等式.6. 数列、等差数列、等比数列(三)几何1．平面图形(1)三角形(2)四边形(矩形、平行四边形、梯形) (3)圆与扇形2．空间几何体(1)长方体(2)柱体(3)球体3．平面解析几何(1)平面直角坐标系(2)直线方程与圆的方程(3)两点间距离公式与点到直线的距离公式 (四)数据分析 1. 计数原理(1)加法原理、乘法原理 (2)排列与排列数 (3)组合与组合数 2．数据描述(1)平均值 (2)方差与标准差 (3)数据的图表表示：直方图，饼图，数表 3．概率(1)事件及其简单运算 (2)加法公式 (3)乘法公式 (4)古典概型 (5)伯努利概型二、数学基础两种考查题型数学基础共25道题，满分75分,有两种考查题型：第一种是问题求解，1-15题,每道小题3分,共45分；第二种是条件充分性判断，16-20题,每道小题3分,共30分. 两种考查形式说明如下：1. 问题求解题型说明联考中的问题求解题型是我们大家非常熟悉的一般选择题，即要求考生从5个所列选项(A)、(B)、(C)、(D)、(E)中选择一个符合题干要求的选项，该题型属于单项选择题，有且只有一个正确答案.该题型有直接解法(根据题干条件推出结论)和间接解法(由结论判断题干是否成立)两种解题方法. 下面举例说明：【范例1】(200901)方程214x x -+=的根是().(A)5x =-或1x =(B)5x =或1x =-(C)3x =或53x =-(D)3x =-或53x =(E) 不存在【答案】C2. 条件充分性判断题型说明这类问题是结论明确，反问需要什么数学条件可以推出已给的结论，进一步说明：1)充分性逻辑角度:如果条件A 成立,能推出结论B 成立,即A B ⇒,称A 是B 的充分条件. 集合角度: B A ⊆ (A 是B 的子集)，则A 是B 的充分条件. 2)题目的设计：【题例】题干(结论) (1)条件一 (2)条件二 3)选项设置【考题范例1】(2012)直线b x y +=是抛物线a x y +=2的切线．(1)b x y +=与a x y +=2有且仅有一个交点．(2)).(2R x a b x x ∈-≥-【答案】A【考题范例2】(2013)某单位年终共发了100万元奖金，奖金金额分别是一等奖1.5万元、二等奖1万元、三等奖0.5万元，则该单位至少有100人．(1)得二等奖的人数最多．(2)得三等奖的人数最多．【答案】B【考题范例3】(2010) 设a 、b 为非负实数,则a b +≤54. (1)ab ≤116. (2)221a b +≤. 【答案】C【考题范例4】(2012)已知,m n 是正整数，则m 是偶数．(1)n m 23+是偶数． (2)2223n m +是偶数．【答案】D【考题范例5】(2013)1+=mq p 为质数．(1)m 为正整数，q 为质数． (2),m q 均为质数．【答案】E4)解题策略永远是从条件推结论，但可以将条件或者结论做等价化简. 解题策略1：如果条件是等号，则直接代入结论判断是否成立; 解题策略2：如果条件是范围，则看条件范围是否落入结论的范围; 解题策略3：可找特殊值证伪，一点即可说明不充分.考点精讲第一章算术第一节整数一、整数及其除法整数包括正整数、负整数和零.两个整数的和、差、积是整数，但两个整数的商不一定是整数. 1、带余除法,使得,0||r b ≤<成立,且唯一,则称为被除所得的商叫做被除所得的余数.2、整除且,使得成立,则称整除,此时称为的约数(因数),称为的倍数，记为|b a . 3、整除的性质(1)|,||c b b a c a ⇒(2)|,||(),(,)c b c a c ma nb m n Z ⇒+∀∈ 4、整数的分类由带余除法，可根据余数将整数进行分类.例如，整数被2除的余数是0,1，从而可将整数分为两类：2,21()n n n Z +∈，即偶数和奇数；类似的，整数被3除的余数是0,1,2，从而可将整数分为三类：31,31,32()n n n n Z +++∈.5、整除数的特征被2整除的数的特征：被5整除的数的特征：被4,25整除的数的特征：被8,125整除的数的特征：被3,9整除的数的特征：被6整除的数的特征：被10整除的数的特征：,,a b Z ∀∈0,b ≠,p r Z ∃∈a pb r =+,p r p a b ,r a b ,,a b Z ∀∈0,b ≠p Z ∃∈a pb =b a b a a b被12整除的数的特征：【例1】当整数n 被6除时，余数为3，则下列哪项不是6的倍数？（）A.3n -B.3n +C.2nD.3nE.4n【例2】如果是一个正整数,那么一定有约数( ).A.4B.5C.6D.8E.9【例3】有一个四位数,它被131除余13,被132除余130,则此数的各位数字和为( ).A.22B.23C.24D.25E.26 二、质数与合数 1、定义质数：一个大于1的整数，如果它的正因数只有1和它本身，则称这个数是质数（素数）. 合数：一个大于1的整数，如果除了1和它本身以外，还有别的正因数，则称这个数是合数.注：由定义知，1既不是质数也不是合数. 2、质数的性质（1）最小的质数是2；质数中只有2是偶数，其它都是奇数.（2）若p 为质数，a 是任一整数，则|p a 或a 与p 互质（a 与p 的最大公因数是1）（3）设12,,,n a a a 是n 个整数，p 为质数，若12|(,,,)n p a a a ，则p 至少能整除其中一个k a .3、质数分解定理任何一个大于1的整数，都能分解成若干个质数的乘积，且分解形式是唯一的，即12n a p p p =⋅⋅⋅，其中1a >的整数，12,,,n p p p 均为质数【例4】三名小孩中有一名学龄前儿童(年龄不足6岁)，他们的年龄都是质数(素数)，且依次相差6岁，他们的年龄之和为( )岁.A ．21B ．27C ．33D ．39E ．51n 3n n -【例5】设是小于12的不同质数(素数),且,则( ).A. 10B.12C. 14D.15E. 19 【例6】如果,,a b c 为3个连续的奇数，则30a b +=．(1)1020a b c <<<<.(2)b c ,均为质数．三、最大公因数与最小公倍数 1、定义（1）公因数、最大公因数：设,a b 是两个整数，若整数d 满足|,|d a d b ，则称d 为,a b 的一个公因数（公约数），其中最大的公因数称为,a b 的最大公因数，记为(,)a b .注：若1(,)a b =，则称,a b 是互质的.（2）公倍数、最小公倍数：设,a b 是两个整数，若整数d 满足|,|a d b d ，则称d 为,a b 的一个公倍数，其中最小的公倍数称为,a b 的最小公倍数，记为[,]a b .2、性质（1）若|,|a d b d ，则[,]|a b d . （2） (,)[,]a b a b a b ⋅=⋅（3）若|a bc ，且1(,)a b =，则|a c .【例7】3018900(,),[,]a b a b ==（1）2100270,a b ==（2）140810,a b ==【例8】两个正整数的最大公约数是6，最小公倍数是90，满足条件的正整数共有（）,,a b c 8a b b c c a -+-+-=a b c ++=对.A ．1B ．2C ．3D ．4E ．5第二节实数及其运算一、实数的分类整数有理数实数分数（有限小数、无限循环小数）无理数（无限不循环小数）1、实数的运算（1）加、减、乘、除（2）乘方运算n na a a a =⋅⋅⋅，1n n a a -=，01a = （3）开方运算n ma =1n mn maa-==2、实数的整数部分和小数部分(1) 定义：,[]x R x ∀∈表示不超过x 的最大整数，令{}[]x x x =-，称[]x 是x 的整数部分，{}x 是x 的小数部分. (2) 性质：{}[]x x x =+01{}x ≤< 3、有理数（1）整数和分数统称为有理数，任何一个有理数都可以写成0,(,,)mm n Z n n∈≠的形式.最简分数：若1(,)m n =，称mn为最简分数或既约分数. （2）有理数之间的相互转化分数小数小数分数4、无理数无限不循环小数称为无理数. （1）无理数与有理数的运算“有”＋、－、×、÷“有”= “有”＋、－“无”= “有”×、÷“无”=注：若是有理,a b 00a a b +=⇒== (2)处理无理数的方法：乘方、配方、有理化【例9】若是最简分数,其中取19~中的整数,,则( ) A. B. C. D.24E.以上结果均不正确【例10】已知为无理数,为有理数,则下列正确的有( )个. ①必为无理数. ②必为无理数.③必为有理数. ④可能为有理数. A. 0 B.1 C. 2 D.3 E. 4a b ,a b 1192b a b +=+a b=675645a (1)(3)a a ++2a 2(1)a +2(2)a +(2)(2)a a +-【例11】已知为有理数,c =则( ).A. 2B.3C. 4D.5E. 7 【例12的整数部分为,小数部分为,则( ).11第三节比和比例一、比、比例的定义若或,则和为比例外项,和为比例内项,当时,称为和的比例中项,即2b ad =.二、比例的性质 1、比例的基本性质（1）ak a b k b=⇒=⋅（2）,(0)a mam b mb =≠ （3）a cad bc b d=⇒=2、更比定理a c ab b dc d=⇒= 3、合、分比定理,,a b c 222a b c ++=αβαβ=::a b c d =a cb d=a d b c ::a b b d =b a da c a mbc md b d b na d nc++=⇒=++ 4、等比定理,(0)a c e a c e k k b d f b d f b d f++===⇒=++≠++【例13】已知非零实数,满足,则( ).A. 0B. 0或8-C. 2-或1D. 1或8-E. 8-【例14】设0a b m >>>,在有意义的条件下则的大小关系为( ).A. B. C.D. E.三、百分比问题1、定义：,即,则称为是的.2、增长率注：a 比b 大%100%%(1%)a b p p a b p b-⇔⨯=⇔=⋅+ b 比a 小%100%%(1%)a b p p b a p a-⇔⨯=⇔=⋅- 3、增加并存的恢复问题(1) 设价格为的商品,先提价,在降价后,则变化后的价格为.,,a b c b c a c a b b a c x a b c+-+-+-===3x =123,,a m a a m I I I b m b b m-+===-+321I I I <<213I I I <<123I I I <<231I I I <<132I I I <<100%%a r b⨯=%a b r =⋅a b %r 100%⨯后来值-原来值增长的百分比=原来值100%⨯原来值-后来值减少的百分比=原来值p %r %r(2) 设价格为的商品,先提价,则降价%,恢复原价.(3) 设价格为的商品,先降价,则提价%,恢复原价.【例15】某电子产品一月份按原定价的80%出售，能获利20%.二月份由于进价降低，按同样原定价的75%出售，却能获利25%，那么二月份的进价是一月份进价的（）（A ）92% （B ）90% （C ）85% （D ）80% （E ）75%【例16】企业的职工人数今年比前年增加了20℅.(1)企业的职工人数去年比前年减少了20℅.(2)企业的职工人数今年比去年增加了50℅【例17】第一季度甲公司的产值比乙公司的产值低20%；第二季度，甲公司的产值比第一季度增长了20%，乙公司的产值比第一季度增长了10%；第二季度甲、乙公司的产值之比是（）.A.96：115B.92:115C.48:55D.24:25E.10:11p %r p %r A A A【例18】甲、乙、丙三种物品，已知甲与乙的价格之和与丙的价格之比是7:2；乙与丙的价格之和与甲的价格之比为8:3，则甲与丙的价格之和与乙的价格之比是（）.A.49:50B.37:50C.37:40D.47:60E.49:60第四节绝对值一、绝对值的定义和性质1、定义和几何意义（1）定义：0||000a a a a a a >⎧⎪==⎨⎪-<⎩||0x a x a x a x a a x x a ->⎧⎪-==⎨⎪-<⎩（2）几何意义||a 表示点a 到原点的距离.||x a -表示点x 到a 的距离.2、绝对值的性质（1）非负性：||0a ≥注：非负性的和为零，则每项均为零.（2）对称性：||||,||||a a a b b a =--=- （3）自比性：||||a a a -≤≤-1010||a a a a >⎧=⎨-<⎩，20,000||||20,0a b a b ab a b a b >>⎧⎪+=<⎨⎪-<<⎩ （4）平方、开方性222||||,||a a a a ===（5）三角不等式：||||||||||||a b a b a b -≤±≤+注意：取等号的条件.||||||0a b a b ab +=+⇔≥||||||||0a b a b ab +=-⇔≤||||||0a b a b ab -=+⇔≤||||||||0a b a b ab -=-⇔≥【例19】已知2|1|(2)0x y x y -++-=，则log y x =（）A. 0B. 1C. -1D. 2E. -2【例20】(410)z x y -=(1) 实数,,x y z满足2(21)20x y x y z -+-+=(2) 实数,,x y z满足224521x xy y y +++=--【例21】若2112||33x x--=成立，则x 的取值范围是（）. A. 12x > B. 12x = C. 12x < D. 12x ≥ E.12x ≤【例22】成立.(1)(2)321x x +-+=-4.5x <-4.53x -≤≤-【例23】等式|27||2||5|m m m -=-+-成立，则实数m 的取值范围是（）A. 25m ≤≤B. 2x ≤-或5x ≥C. 25m -<<D. 2x ≤或5x ≥E. 5x ≤-或2x ≥-二、绝对值等式和不等式方法：（1）公式法；（2）零点分段讨论法；（3）平方1、绝对值等式.求解：①方程无解.②方程有唯一解.③方程有两个解.注：保证绝对值的非负性.2、绝对值不等式（1）解集为：,0,0b a b x a b b ∅≤⎧⎨-<<+>⎩(2)解集为：,0,0,0R b x a b x a b x a b b <⎧⎪≠=⎨⎪>+<->⎩或【例24】方程216x x --=的根为( ).A.或B.或73x =C.73x =或5x =-D.或E.5x =【例25】方程213x x ++-=无根.(1)1x >. (2)2x ≤-x a b -=0b <⇒0b =⇒x a =0b >⇒x a b =±x a b -<x a b ->5x =-1x =5x =3x =3x =-53x =【例26】可以确定||2x y x y+=-. (1)3x y =；（2）13x y =【例27=-x 的取值范围是（）A. 0x <B. 2x ≥-C. 20x -≤≤D. 20x -<<E. 20x -≤<【例28】方程2x x a -=有三个不同的解,则实数a 的取值范围是( ).(A) 0a = (B) 0a >或1a <- (C) 1a <- (D) 10a -<< (E) 0a >【例29】实数x 满足13||||222x x -+-<. (1)21||13x -< (2)21||11x x -≤+三、绝对值最值问题1、绝对值函数取最值的结论（1）()||||f x x a x b =-+-（2）()||||f x x a x b =---（3）()||||||f x x a x b x c =-+-+-【例30】的最小值为（）（A ）（B ）（C ）（D ）（E ）【例31】若关于x 的不等式32x x a -+-<的解集是空集,则实数a 的取值范围是( ).(A) 1a < (B) 1a ≤ (C) 1a > (D) 1a ≥ (E) 1a ≠2、含有绝对值的确定取值范围的问题（1）恒成立、无解()f x a ≥恒成立()f x a ⇔<无解min ()f x a ⇔≥()f x a ≤恒成立()f x a ⇔>无解max ()f x a ⇔≤()f x a >恒成立()f x a ⇔≤无解min ()f x a ⇔>31()||||44f x x x =---1212-0114()f x a <恒成立()f x a ⇔≥无解max ()f x a ⇔<（2）有解设()f x 是绝对值的和或差构成的函数（连续），则()f x a =有解min ()f x a ⇔≤()f x a =无解min ()f x a ⇔>【例32】方程|1||1|x x a -++=无解.(1)1a = (2)2a <【例33】不等式24x x S -+-<无解.(1)2S ≤(2)2S >【例34】方程|4||1|x x a --+=有无穷多解.(1)5a =(2)5a =-【例35】|53||32|3x x ---=的解集是空集.(1)53x >(2)7563x <<第二章代数式和函数第一节整式一、基本概念1、代数式的分类单项式整式有理式多项式代数式分式无理式2、一元n 次多项式1110()(0)n n n n n f x a x a x a x a a --=++++≠称为关于x 的一元n 次多项式.多项式相等定理：设1110()n n n n f x a x a x a x a --=++++，1110()nn n n g x b x b x b x b --=++++，则111100()(),,,n n n n f x g x a b a b a b a b --=⇔====二、整式的运算1、乘法公式①②③④⑤注：2222221[()()()]2x y z xy yz xz x y y z z x ++---=-+-+-【例1】对任意实数x ，等式450ax x b -++=恒成立，则2015()a b +=（）A.0B.1C. 1-D. 20152E. 10072222()2x y x xy y ±=±+22()()x y x y x y -=+-2222()222x y z x y z xy yz xz ++=+++++3322()()x y x y x xy y ±=±+33223()33x y x x y xy y ±=±+±【例2】已知，则（）（A ）83 （B ）84 （C ）85 （D ）86 （E ）87【例3】实数,,a b c 中至少有一个大于零.(1) ,,,x y z R ∈22,2a x y π=-+22,3b y z π=-+226c z x π=-+(2) x R ∈且1,x ≠1,a x =-1,b x =+21c x =-2、整式除法（1）竖式除法（2）带余除法任意多项式(),()(()0)f x g x g x ≠，则存在唯一的(),()p x r x ，使得()()()()f x g x p x r x =⋅+,其中()r x 的次数比()g x 的低，则称多项式()f x 除以()g x 商式为()p x ,余式为.3、整除（1）定义：当时，()()()f x g x p x =⋅，称整式()f x 能被整式()g x 整除，称()g x 为()f x 的一个因式，记为()|()g x f x .（2）性质：若,且,则.若,且,则.4、因式定理f x ()含有ax b -()因式⇔f x ()能被ax b -()整除⇔0b f a =().注：一次因式的零点恰为对应多项式方程的根.5、余式定理239x x -=433275x x x --+=()r x ()0r x =()|()h x g x ()|()g x f x ()|()h x f x ()|()h x g x ()|()h x f x ()()|()()()()h x u x f x v x g x ±多项式f x ()除以ax b -()的余式为().b r f a=【例4】若多项式3223()f x x a x x a =++-能被1x -整除，则实数a =（）A.0B. 1C. 0或1D. 2或-1E. 2或1【例5】二次三项式26x x +-是多项式43221x x ax bx a b +-+++-的一个因式. （1）16a =（2）2b =【例6】若2x x m ++被5x +除，余式为3-，则m =（）A.21B.22C.-22D.23E.-23【例7】若f x ()被1x -除，余式为9；若f x ()被2x -除，余式为16，则f x ()被12x x --()()除的余式为（）A.72x +B.73x +C.74x +D.75x +E.27x +【例8】若三次多项式g x ()满足1020324g g g g -====-()()(),()，多项式421f x x x =-+()，则34g x f x -()()被1x -除的余式为（）A.3B.5C.8D.9E.11三、整式的因式分解把一个整式化为若干个其他的整式乘积的运算称为整式的因式分解. 常用的因式分解的方法： 1、公式法2、十字相乘法3、待定系数法【例9】多项式326x ax bx ++-的两个因式是2x +和3x -，则第三个一次因式是（）A.6x -B.3x -C.1x +D.2x +E.3x +【例10】若12x y -+()是2244xy x y m ---的一个因式，则m =（）A.4B.1C.-1D.2E.0第二节分式一、分式的基本概念1、定义(1)0AB B≠()称为分式，其中A 称为分子，B 称为分母. （2）最简分式（既约分式）：分子和分母没有正次数的公因式的分式. 2、分式的基本性质（1）分子和分母同乘以（或除以）同一个不为零的式子，分式的值不变. (2)约分：把分式的分子与分母的公因式约去.(3)通分：把异分母的分式化为与原来的分式相等的同分母的分式. 3、分式的运算（1）分式的加减运算（2）分式的乘除运算（3）分式的乘方运算【例11】当20051949x y ==,时，代数式4422222x y y xx xy y x y --⋅-++的值为（）A.-3954B.3954C.-56D.56E.128【例12】已知0a b c ++=，则111111a b c b c a c a b+++++=()()()的值为（）A.0B.1C.2D.-2E.-3 二、1nnx x +类型解题方法：递推公式222112k kk k x x x x +=+-() 2112111111k k k k k k x x x x x x x x+++++=++-+()()()【例13】若2510x x -+=，则441x x+的值为（） A.527 B.257 C.526 D.256 E.356【例14】若正实数满足2421124a a a =++，则21a a a ++的值为（）A.12B.14 C.16D.112E.124三、分式方程1、分式方程0A B =的解为0A B =⎧⎨≠⎩2、增根：使得0A B =⎧⎨=⎩成立的根称为方程0A B =的增根【例15】若关于x 的方程2133m x x =---有增根，则m 的值为（） A.0 B.3 C.-1 D.-2 E.-3【例16】42233402445815x x x x x --+=-+成立.(1)x =(2)x =第三节函数一、函数的基本属性1、函数的三要素：定义域、对应法则、值域注：常用的函数定义域的基本原则（1）分母不能为零；（2）偶次根式中被开方数不能小于零；（3）对数的真数大于零，底数大于零且不等于1；（4）零指数幂的底数不等于零；（5）实际问题要考虑实际意义等 2、单调性设函数f x ()在区间a b [,]有定义，对于任意的12x x a b ∈,[,]，（1）单调增加：若12x x <，有12f x f x <()()，则称f x ()在区间a b [,]上单调增加；（2）单调减少：若12x x <，有12f x f x >()()，则称f x ()在区间a b [,]上单调减少.(3)复合函数的单调性法则：单调性相同的两个函数复合，得到的新函数是单调增加的；单调性不同的两个函数复合，得到的新函数是单调减少的. 3、奇偶性（1）偶函数：若函数f x ()在定义域上满足f x f x -=()()，则称f x ()为偶函数；（2）奇函数：若函数f x ()在定义域上满足f x f x -=-()()，则称f x ()为奇函数；（3）性质：偶函数的图像关于y 轴对称，奇函数的图像关于原点对称. 二、一元二次函数1、一元二次函数的解析式（1）一般式：20f x ax bx c a =++≠()() （2）零点式：120f x a x x x x a =--≠()()()()（3）顶点式：224024b ac b f x a x a a a-=++≠()()() 2、一元二次函数的图像及其性质（1）图像：抛物线开口判别式对称轴零点顶点（2）单调性：当0a >时，在2b a -∞-(,]上是单调减少的，在2ba -+∞[,)上是单调增加的；当0a <时，在2b a -∞-(,]上是单调增加的，在2ba-+∞[,)上是单调减少的.（3）最值：一元二次函数在对称轴处取到最值当0a >时，开口向上，有最小值；当0a <时，开口向下，有最大值.注：限定区间的最值问题，有时还需要结合单调性来求出最值. （4）零点与韦达定理设12x x ,是一元二次函数20f x ax bx c a =++≠()()与x 轴的两个交点的横坐标（称为零点），则：12b x x a +=-12c x x a⋅=【例17】函数112x y -=在定义域上的单调性为（）A ．在1-∞(,)上是增函数，在1+∞(,)上是增函数 B.减函数C ．在1-∞(,)上是减函数，在1+∞(,)上是减函数 D.增函数 E ．以上结论都不正确【例18】一元二次函数1y x x =-()的最大值是（）A.0．05B.0.1C.0.15D.0.2E.0.25【例19】设实数x y ,满足23x y +=，则222x y y ++的最小值是（）A.4B.5C.611【例20】若不等式210x ax ++≥对一切102x ∈(,)都成立，则a 的取值范围是（）A.0a ≥B.10a -<<C.512a -≤≤-D.52a ≥- E.1a ≤-三、指数函数和对数函数1、指数函数（1）定义01x y a a a =>≠,(,)，定义域为R ，值域为0+∞(,).（2）图像（3）单调性当1a >，xy a =是单调增加的；当01a <<，xy a =是单调减少的. （4）底数与图像的关系当1a >，a 值逆时针变大；当01a <<，a 值也是逆时针变大的. 2、对数函数（1）定义01a y x a a =>≠log ,(,)，定义域为0+∞(,)，值域为R .（2）图像（3）单调性当1a >，x y a =是单调增加的；当01a <<，xy a =是单调减少的. （4）对数与指数的关系：对数运算与指数运算是互逆运算ba a Nb N =⇔=log3、指数与对数的运算性质：，，，，，，，，，，，，，，，，.【例21】若，则有（）（A ）（B ）（C ）（D ）（E ）以上均不正确 b a N =01a =1a a =()nm mn a a =m n m n a a a +⋅=()nn n ab a b =⋅m n m n a a a -÷=mn a =1n na a-=log N a a N =1log 0a =log 1a a =loglog log M N M N aa a=+loglog log M M N N aa a =-log log nM Ma a n =log log logb bcaa c=1log log b a a b =log log m n b b a am n =32a -<<-13()0.32aa a >>10.3()32aa a>>1()0.332a a a>>130.3()2a aa >>【例22】744855285,,377a b c --⎛⎫⎛⎫⎛⎫===⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的大小关系是( ). (A) a b c >> (B) a c b >> (C) b a c >> (D) c a b >> (E) 以上均不正确【例23】若330m n <<log log ，则m n ,满足条件（）A.1m n >>B.1n m >>C.01m n <<<D.01n m <<<E.无法判断【例24】函数223a f x x x =+-()log ()，若20f >()，则f x ()的单调递减区间为（）A.1+∞(,)B.1-∞-(,)C.3-∞-(,)D.1-+∞(,)E.-∞+∞(,)【例25】已知函数2234x x f x +=-⨯()，且20x x -≤，则f x ()的最大值为（）A.0B.1C.2D.3E.4【例26】设164x ≤≤，函数42222812y x x x=+⋅(log )(log )log 的最大值和最小值分别是（）A.54,2B.81,9C.81,0D.54,0E.以上都不正确第三章方程和不等式函数、方程、不等式、平面解析几何等方面的问题本质上是同一个问题，只是研究的角度不同.【主要考点】1. 代数方程：一元一次方程，一元二次方程，二元一次方程组.2. 其他类型的方程：绝对值方程，分式方程，根式方程，对数方程，指数方程.3. 不等式：不等式的性质，一元一次不等式，一元二次不等式，简单的一元高次不等式.4. 不等式组：由一元一次不等式和一元二次不等式等组成的不等式组.5. 其他类型的不等式：绝对值不等式，分式不等式，根式不等式，指数不等式，对数不等式.6. 均值不等式，三角不等式.7. 线性规划问题：不等式组约束下的最值问题. 8. 应用问题.第一节方程一、基本概念1.方程、解（根）含有未知数的等式称为方程.能使方程左右两端相等的未知数的值，称为方程的解或根.考试只要求方程的实根，即方程在实数域内的解.2.方程的元和次“元”指的是方程中不同未知数的个数，“次”指的是方程中未知数的最高次数.二、一元一次方程1.方程的形式：ax b =2.解方程（1）若方程中的所有系数均为已知的实数，可利用代数式运算的法则求解方程；实例：325x +=，解得1x =.（2）若方程中含有参数，特别是未知数的系数中含有参数，通常需要分情况讨论.3.分情况讨论：①当0a ≠时，方程有唯一解b x a=； ②当0,0a b ==时，方程有无穷多解，x R ∈；③当0,0a b =≠时，方程无解.4.解析几何中的直观解释：【例 3.1】能够推出x 的方程22()0a b x a b -++=有无穷多解，下列说法中正确的个数为（）①0a b +=；②0a b +≠；③220a b -=；④0a b -=.(A)0(B)1 (C)2 (D)3(E)4【例 3.2】直线2(1)y a x a a =+-+与直线2y =-有且只有一个交点，则交点的坐标为（）(A)(1,1)a + (B)(1,2),1a a +-≠- (C)(2,1),1a a --≠-(D)(1,2)a +- (E) (2,2),1a a --≠-三、一元二次方程1.形式：20(0)ax bx c a ++=≠注：如果0a =，则退化为前一种情况.2.等价形式：220(0)0b c x x a x px q a a++=≠⇔++= 3.配方形式：222424b b ac x a a -⎛⎫+= ⎪⎝⎭ 4.一元二次方程的判别式：24b ac ∆=-5.讨论：①0∆>，方程有两个不相等的实根.②0∆=，方程有两个相等的实根.③0∆<，方程无实根.6.求根公式：1,2,02b x a-±=∆≥ 7.因式分解形式（十字相乘）：若12,x x 为方程的两个实根，则212()()0ax bx c a x x x x ++=--=.反之成立.8.韦达定理或根与系数关系：1212,b c x x x x a a+=-=. （1）为什么？（2）推广到一元三次方程20(0)ax bx c d a +++=≠，假定123,,x x x 为三个实根，则 123123,x x x x x x ++==（3）与韦达定理有关的代数式运算1211x x +=，2212x x +=3312x x +=，4412x x +=12x x -=，3312x x -= 【例 3.3】设12,x x 是方程250x px +-=的两个实根，若1211x x +的算术平均数为6，则p 的值为（）(A)50- (B)60- (C)50(D)60(E)30【例3.4】方程2780x x -+=的两个实根为121,1x x ++.（1）方程2520x x -+=的两个实根为12,x x（2）方程2520x x ++=的两个实根为12,x x【例3.5】已知方程220x ax x a +-+=有实根，则两根之积的最大值与最小值之差为（）(A)1 (B)89 (C)29 (D)19(E)无法确定【例3.6】已知一元三次方程32210x x -+=的根为1231,,x x x =，则2223x x +=（） (A)1- (B)12 (C)1 (D)2(E)3【例 3.7】设一元三次方程320x bx cx d +++=的三个实根为123,,x x x ，则22212311x x x ++=.（1）1,5,6b c d =-=-=（2）1,5,6b c d ==-=-【例3.8】方程210x ax ++=与210x x a ++-=有一公共实根.（1）2a =（2）1a =四、二元一次方程组1.形式：111222a xb yc a x b y c +=⎧⎨+=⎩ 2.求解（1）当1110a b c ≠时，几何解释 ①2211a b a b ≠，方程有唯一解. ②222111a b c a b c =≠，方程无解. ③222111a b c a b c ==，方程有无穷多组解. （2）其他情况，针对具体问题具体分析.3.重点：利用方程组解决应用问题，包括工程问题、行程问题、浓度问题、比例问题等.【例3.9】一列火车驶过铁路桥，从车头上桥到车尾离开桥公用1分25秒，随后列车又穿过一条隧道，从车头进入隧道到车尾离开隧道用了2分40秒，能确定火车的速度及车身的长度（假定火车始终匀速行驶）.（1）铁路桥长为900米.（2）隧道长为1800米.五、其他类型的方程1.分式方程（1）形式：()()f x ag x = （2）求解方法①去分母，验增根：先求方程()()0f x ag x -=的根，再验证()0g x ≠是否成立. ②()()0()()0()f x ag x f x a g x g x -=⎧=⇔⎨≠⎩【例3.10】方程213111x x x x x ++=+--的所有根之和为（） (A)1(B)1- (C)2 (D)2-(E)0【例3.11】一满桶纯酒精倒出10升后，加满水搅匀，再倒出4升后，再加满水.此时，桶中的纯酒精与水的体积之比是2:3，则桶的体积是（）升(A)15 (B)18 (C)20 (D)22(E)252.绝对值方程（1）形式：含有绝对值的方程.（2）一般形式：①直接取正负去掉绝对值，注意检验增根. 实例：1x =-②讨论范围去掉绝对值.（3）特殊形式：通常与绝对值函数有关.【例3.12】方程214x x -+=的所有根之积为（）(A)3(B)5 (C)3- (D)5-(E)6【例3.13】方程1222x x x a -+-+-=无实根.（1）1a ≤（2）0.5a =3.根式方程（1）形式：含有根式的方程.（2）求解：平方去根式，检验增根.【例3.14】2=的所有根之积为（）(A)56 (B)48 (C)36 (D)28(E)244.指数方程和对数方程（1）形式：含有指数或对数的方程.（2）求解：只考查简单的指数方程和对数方程，通常利用换元法进行化简.【例3.15】方程1332x x --=的所有根之积为（）(A)1- (B)0 (C)13 (D)1(E)3【例3.16】方程11442x x a -----⨯=有实根，则a 的取值范围是（）(A)30a -<< (B)3a ≤-或0a ≥ (C)30a -≤<(D)3a ≤-或0a > (E) 以上答案都不对第二节不等式一、基本概念1.不等号≥等价于>或=，例11≥.2.不等式的性质①a b b a >⇔<②,a b b c a c >>⇒>③,0a b c ac bc >>⇒>；,0a b c ac bc ><⇒<二、一元一次不等式1.形式：ax b >或0ax b ->2.分情况讨论：几何解释①当0a >时，b x a>； ②当0a <时，b x a <； ③当0,0a b =≥时，无解；④当0,0a b =<时，x R ∈.【例3.17】1211x -<<-. （1）0x <（2）32x >三、一元二次不等式1.形式：20ax bx c ++>或20ax bx c ++<.2.解集：注：只讨论0a >的情况.若0a <，既可不等式两边乘以1-后转化为正系数的情况，也可做类似的分析.【例3.18】已知不等式220ax bx ++>的解集为11,32⎛⎫- ⎪⎝⎭，则a b +=（） (A)12- (B)10- (C)6-(D)4-(E)6【例3.19】关于x 的不等式22(1)(1)10a x a x ----<恒成立.（1）1a ≤（2）35a >-【例3.20】若不等式2210x ax -+≥对于一切()0,1x ∈成立，则a 的取值范围是（）(A)11a -<≤ (B)2a < (C)12a -≤≤ (D)1a ≤(E)2a ≤ 四、一元高次不等式1.形式：通常为几个因式乘积的形式.2.解法：穿线法.①去掉恒正或恒负的项，调整最高次幂的系数为正，写出等价形式.②在数轴上标出零点，判断实心或空心.③从右向左依次穿线.④奇穿偶不穿.【例3.21】不等式22(28)(2)(226)0x x x x x ----->恒成立.（1）(2,1]x ∈--（2）4x >或2x <【例3.22】不等式(2)ln 0(1)(3)x e x x x x -≥--恒成立. （1）(0,1)(1,2](3,)x ∈+∞（2）[2,3)x ∈五、不等式组1.形式：若干个不等式联立组成不等式组.2.解法：取各个不等式解集的交集.【例3.23】方程2(2)0x a x a +-+=的两个实根均在(1,1)-内，则a 的取值范围是（）(A)142a -<≤+ (B)142a -≤≤- (C)142a <≤+(D)142a <≤- (E)142a <<+【例3.24】某单位年终共发50万元奖金，奖金金额分别为一等奖4万元，二等奖2万元，三等奖1万元，则该单位至少有25人.（1）得二等奖的人数最多（2）得三等奖的人数最多六、其他类型的不等式1.分式不等式：移项，通分，穿线.【例3.25】0x << （1）223211x x ->- （2）当01x <<时，223211x x ->-2.绝对值不等式：讨论法，两侧法，图像法.【例3.26】123x x +<+.（1）1x <-（2）54x >-【例3.27】2521x x x -->-（1）4x >（2）1x <-3.根式不等式：讨论法，图像法.【例3.28】x a -≥对于1x ≥恒成立. （1）34a <（2）34a =4.对数不等式和指数不等式：结合图像进行讨论.【例3.29】不等式221log ()2x x <-≤（11x ≤<-（2）2x <≤六、均值不等式和三角不等式1.均值不等式（1）2a b +≥(0,0)a b ≥≥，当且仅当a b =时等号成立. 等价表述：两个非负实数的算术平均数大于等于它们的几何平均数.两个非负实数的等差中项大于等于它们的等比中项.222a b ab +≥，当且仅当a b =时等号成立. （2）适用范围：①乘积为定值时，可求和的最小值.②和为定值时，可求乘积的最大值.（3）注意事项：一定要判断取等条件.如果不满足取等条件，则无法取得相应的最值.（4）3a b c ++≥(0,0,0)a b c ≥≥≥，当且仅当a b c ==时等号成立. 实例：对号函数1y x x =+【例3.30】已知0x >，函数223y x x=+的最小值是（）(A)((C) (D)5(E)【例3.31】若40y x x --<对一切正实数x 均成立，则y 的取值范围是（） (A)2y = (B)2y < (C)2y ≤ (D)4y ≤(E)4y <2.三角不等式（1）a b a b a b -≤+≤+，当且仅当0ab ≥时右侧的等号成立，当且仅当0ab ≤时左侧的等号成立.（2）()a b a b a b a b a b a b -≤-≤+⇔--≤+-≤+-，当且仅当0ab ≤时右侧的等号成立，当且仅当0ab ≥时左侧的等号成立.【例3.32】a b a b a b -=-=+（1）0ab ≥（2）0ab ≤七、线性规划1.解法①根据约束条件即不等式组画出可行域.②求出可行域的所有“尖点”，注意题目中是否有整数的要求.③代入目标函数，比较函数值得出结论.【例3.33】,x y 满足236x y +≤且24x y +≤，则x y +的最大值为52（1）,x y R ∈（2）,x y N ∈第一章例题答案1-5 DCDCD 6-10 EABAD 11-15 AEDAB 16-20 CCAAB 21-25 EDDEA 26-30 ECAEB 31-35 BDADE第二章例题答案1-5 CDDEE 6-10 EACCC 11-15 AEBCD 16-20 DBEAD 21-25 BADCB 26 C第三章例题答案1-5 CEDAA 6-10 EDECC 11-15 CDBBD 16-20 CDBCD 21-25 ABDEB 26-30 BADDA 31-33 ECA。

2018经济类联考数学需掌握8大知识点

2018经济类联考数学需掌握8大知识点现阶段考研复习正在火热进行中，考生要以自主学习为主，系统整理学习内容，回顾旧知识。

以下是小编搜索整理的关于2018经济类联考数学需掌握8大知识点，供参考复习，希望对大家有所帮助!想了解更多相关信息请持续关注我们()!(一)微积分1、函数、极限、连续(1)求复合函数的定义域;(2)求函数表达式;(3)无穷小阶的比较;(4)利用等价无穷小替换、两个重要极限求极限;(5)求幂指函数的极限;(6)利用洛必达法则求极限;(7)分段函数在分段点处的连续性;(8)判断间断点类型;2、导数与微分(1)利用导数的四则运算法则、复合函数求导法则求导数与微分;(2)求分段函数在分段点处的导数;(3)一元函数隐函数求导;(4)一元函数的单调区间、极值、凹凸性、拐点、渐近线;(5)导数的经济应用;3、一元函数积分学(1)利用换元法与分部积分法计算不定积分;(2)利用换元法与分部积分法计算定积分;(3)变限积分求导;(4)定积分的几何应用;4、多元函数微分学(1)求二元函数的一阶偏导数;(2)求二元函数的全微分;(3)二元函数隐函数的求导。

(二)线性代数1、行列式和矩阵(1)矩阵的基本运算;(2)伴随矩阵的求法;(3)逆矩阵的求法。

2、向量与方程组(1)向量组的线性相关性的判断;(2)向量组的线性表示;(3)求齐次方程组的通解;(4)求非齐次方程组的通解。

(三)概率论与数理统计1、随机变量及常见分布(1)利用分布函数、分布律以及概率密度函数的充分必要条件求未知参数;(2)已知分布函数求任一事件的概率;(3)常见八大分布2、随机变量的数字特征(1)利用定义或公式计算期望、方差;(2)利用性质计算期望、方差;(3)常见分布的期望与方差;(4)已知随机变量的数学期望、方差求解未知参数;。

2018考研数学：5个重点一定要搞懂

2018考研数学：5个重点一定要搞懂一、函数连续与极限极限是高数的基本工具，是三大运算之一。

求极限是考研试卷中常考的题型，是考试的重点。

要求考生对于极限的概念以及求极限的基本方法掌握到位。

在这一部分，还有两个重要的概念，即无穷小和间断点，是考试中常考的凯程，此处是我们复习的重点。

常考的题型有：无穷小阶的比较，无穷小和极限的结合，间断点类型的判断。

二、一元函数微分学求导是高数的第二大运算，要求对于各种类型函数的求导过关，也是为后面的多元函数求偏导打下基础。

这一部分需要注意两个概念：导数和微分，要求理解导数的定义以及可导的充分必要条件。

此外，还有导数的应用，这是内容比较多的一部分，是考试的重点，但不是难点，如函数的单调性、凹凸性、渐近线、拐点和方程根的判别等。

这一部分还有一个难点，就是中值定理的相关证明题，不过这部分题目解题思路不太灵活，掌握常见的技巧和方法足可应对。

三、多元函数微分学多元函数连续、可偏导及可微的定义，以及三者之间的关系要准确区分。

多元函数复合函数和隐函数求偏导和求全微分一定要过关。

这些都是考试的重点。

四、多元函数积分学数二和数三同学仅仅考查二重积分的计算，这是考试的重点，是每年必考的，常见题型有二重积分的基本计算，选择合适的坐标系法和积分次序，有必要时进行交换坐标系和积分次序等等，这些都是基本的运算。

对于数一的同学，在以上基础上，还需要学习曲线、曲面积分的计算和三重积分的计算。

尤其需要注意的是第二类曲线积分和格林公式的结合，三维曲线积分和斯托克斯公式的结合，第二类曲面积分和高斯公式的结合，这些是出大题的地方。

五、微分方程掌握考纲中要求掌握的几类方程的解法，如可分离变量方程、齐次方程、一阶线性微分方程、可降阶微分方程(数三不要求)、二阶常系数微分方程。

需要注意一下常系数线性方程的解的结构。

此外，微分方程和变上限函数、多元函数微分学或实际问题，经常会出一些综合题。

数一的个别考点伯努利方程和欧拉方程，数三的个别考点有差分方程，同学们只需要掌握一般解法即可，不需要研究太多，不是考试的重点。

2018年考研数学一精讲

2018年考研数学一精讲2018年的考研数学一科目是学生们备考的一大难关。

为了应对这个考试，很多考生选择参加培训班，从而提高自己的学习效果。

以下是对2018年考研数学一科目的一些精讲。

2018年考研数学一共有12个大题，其中包括数学分析、高等代数、概率论与数理统计、数值分析和离散数学等内容。

接下来，我们将依次对各个大题进行精讲。

第一大题是数学分析，涵盖了函数极限、连续性与间断点、一元函数的微分学和一元函数的积分学等内容。

这部分的难度主要集中在题目的变形和思维方式上，考生需要熟练掌握相关的概念和定理，并能够将其应用到实际问题中去。

第二大题是高等代数，主要包括线性方程组、矩阵与行列式、线性空间、线性变换和特征值特征向量等内容。

这部分的题目较为理论化，考生需要对相关概念有清晰的认识，并能够运用相关方法解决问题。

第三大题是概率论与数理统计，主要包括随机事件与概率、随机变量及其分布、多维随机变量及其分布、样本及抽样分布以及参数估计与假设检验等内容。

这部分的题目相对来说比较繁琐，考生需要耐心分析题目，并能够对概念的定义和定理的应用有清晰的认识。

第四大题是数值分析，主要包括插值与逼近、数值微积分、线性方程组的数值解法、非线性方程的数值解法以及常微分方程的初值问题的数值解法等内容。

这部分的题目与实际应用结合较为紧密，考生需要掌握各种数值方法的原理和算法，并能够熟练地计算。

第五大题是离散数学，主要包括命题逻辑、集合论、代数系统、图论和数论等内容。

这部分的题目相对来说较为独立，考生需要掌握各种定义和定理，并能够熟练运用它们解决问题。

总的来说，2018年考研数学一科目的难度较为适中，重点考察考生的逻辑思维能力和解题能力。

对于考生来说，除了熟练掌握相关的知识点和技巧，还需要在备考过程中注重实际操作和刷题练习。

同时，考生还需要掌握一些解题方法和技巧，例如通过画图、列式子、分析问题特点等方式。

在考试中，要保持冷静、沉着，并注意时间的合理分配。

2018考研数学高分刷题八大技巧_毙考题

2018考研数学高分刷题八大技巧2018考研复习已经进入后期，近来收到不少小伙伴吐槽说，数学刷题刷的要吐血了。

在此提醒18考研er们要刷题和技巧两结合，才能更快提高成绩哟。

(一)单选题单选题的解题方法总结一下，也就下面这几种。

1.代入法也就是说将备选的一个答案用具体的数字代入，如果与假设条件或众所周知的事实发生矛盾则予以否定。

2.演算法它适用于题干中给出的条件是解析式子。

3.图形法它适用于题干中给出的函数具有某种特性，例如奇偶性、周期性或者给出的事件是两个事件的情形，用图示法做就显得格外简单。

4.排除法排除了三个，第四个就是正确的答案，这种方法适用于题干中给出的函数是抽象函的情况。

5.反推法所谓逆推法就是假定被选的四个答案中某一个正确，然后做反推，如果得到的结果与题设条件或尽人皆知的正确结果矛盾，则否定这个备选答案。

(二)大题接下来提供给大家几个大题的答题技巧，大家认真领会方法，要做到活学活用。

6.踩点得分对于同一道题目，有的人解决得多，有的人解决得少。

为了区分这种情况，阅卷评分办法是懂多少知识就给多少分,这种方法我们叫它踩点给分.鉴于这一情况，考试中对于难度较大的题目采用一定的策略，其基本精神就是会做的题目力求不失分，部分理解的题目力争多得分。

对于会做的题目，要解决会而不对，对而不全这个老大难问题。

有的考生答案虽然对，但中间有逻辑缺陷或概念错误，或缺少关键步骤。

因此，会做的题目要特别注意表达的准确、考虑的周密、书写的规范、语言的科学，防止被分段扣点分。

对于考生会做的题目，阅卷老师则更注意找其中的合理成分，分段给点分，所以做不出来的题目得一二分易，做得出来的题目得满分难。

对绝大多数考生来说，更为重要的是如何从拿不下来的题目中得点分。

有什么样的解题策略，就有什么样的得分策略。

其实你要做的是认认真真把你解题的真实过程原原本本写出来，就是最好的得分技巧。

7.大题拿小分如果遇到一个很困难的问题，确实啃不动，一个聪明的解题策略是，将它们分解为一系列的步骤，或者是一个个小问题，先解决问题的一部分，能解决多少就解决多少，能演算几步就写几步，尚未成功不等于失败。

2018考研数学大纲发布后续复习攻略

2018考研数学大纲发布后续复习攻略2018考研数学大纲已公布，通过比对，与我们之前预测的一样，今年的数学大纲较往年相比，没有任何变化。

文都网校考研数学老师结合历年考研数学的重难点考点，带2018考生全面、深度解读数学(一)、数学(二)和数学(三)对高等数学、线性代数以及概率论与数理统计的考试要求，帮助考生在数学的复习道路上明确考试方向，少走弯路，不走偏路，直击考试重点。

下面就后续考研数学复习，给2018考生一些复习建议，帮助广大考生进行下一阶段的深度复习。

复习攻略一：明确大纲要求、把握考试重难点根据最新的数学考试大纲，要科学合理安排复习内容和复习时间。

新数学大纲没有变化，所以考生之前复习内容及复习进程都是正确的。

前面一些阶段的学习主要是以知识点为主，夯实“三基”，接下来主要是根据历年真题及考试大纲要求，将一些重难点的知识弄懂、弄透。

这样可以在数学考试中多拿一些分值。

复习攻略二：分模块、分阶段复习现在的复习阶段是处于强化、加速突破阶段，复习主要以模块、强化训练为主。

这段时间是最好的强化巩固复习时间。

暑期强化课已经结束，考试大纲也已经发布，考生应该静下心来分模块进行分析，查缺补漏。

明确自己哪一模块知识不足，着重攻克自己的难点，然后相应的做一些习题加以巩固。

复习攻略三：复习知识点以归纳总结为主这一阶段复习要注意的是，对知识点要有自己的理解，对练习题要有自己的做题思路。

这就要求考生在复习知识点的时候，要进行归纳总结。

把自己的理解和做题思路进行归纳总结。

这样子有利用明确做题思路，更加清晰的明确做题方法，提高答题速度和答题准确率，同时也有利用考生记忆。

复习攻略四：演练以真题为主考研数学要想得高分，必须做练习题。

而在后续的时间中，主要以历年真题为主。

真题具有很强的代表性，体现历年考试的重难点、考试难度等。

一般到10月份开始，考生就要着手做真题，必须按时按量的完成。

这可以帮助考生养成一个良好的习惯，调节自己的答题速度。

2018考研369经济类联考复习经典方法

2018考研369经济类联考复习经典方法
感谢凯程郑老师对本文做出的重要贡献
金融专硕是社会发展下的产物，比学术型的金融学硕士更利用就业。

金融学硕士的业务课之一考的是数学三，而金融硕士考研中业务课考的则是369经济类联考，是及数学、逻辑、写作于一体的试卷。

考研在即，369经济类联考如何完成最后几天的冲刺，小编给出以下几点建议。

一、勤练习
熟能生巧，只有多练习题目，才可以真正理解相应的知识点。

只有达到一定的熟练度之后，才可能在考场上有一定的灵活度。

二、多总结、注重整个学科框架的构建
总结包括两方面，总结解题方法以及总结知识框架。

考生们需要清楚每章的考点有哪些，对具体的某个知识点的考试要求是什么，可能的出题方向是什么，甚至典型的例题最好要做到心中有数。

三、重基础，远离偏题怪题。

以考试大纲为基础，掌握基本概念、基本理论和基本方法。

其实任何数学考试都会强调注重基础，这点对于经济类联考数学尤为如此。

比如高等数学中的积分计算，这是考试大纲中的一个考点。

我们在学习的时候，掌握常用的积分方法即可，如主要有：第一类换元积分法、第二类换元积分法和分部积分法，其中第二类换元积分法中常见的是三角代换，根据被积函数的不同形式灵活采取相应的积分方法。

如果同学们在做题的时候发现有的题目技巧性太强、复杂程度也是相当高，那这样的题目你可以果断放弃，我们应该将更多的精力放在练习基础知识、常用的解题方法上。

2018考研数学二该如何复习

2018考研数学二的复习之道
来源：智阅网
我们在复习考研数学二的时候，要注重复习方法的使用。

所以，我们就来说说冲刺复习阶段，该如何复习好考研数学二的内容。

首先，梳理、明确考试项。

从近十年考研数学真题来看，试卷中80%的题目都是基础题目，真正需要冥思苦想的偏题、难题只是少数。

这就要求同学们结合考研辅导书和大纲，先吃透基本概念、基本方法和基本定理，只有对基本概念深入理解，对基本定理和公式牢牢记住，才能找到解题的突破口和切入点。

其次，切忌各科同时推进。

建议2018届参加考研数学二的考生，高数和线性代数，最好不要放在一起复习。

高等数学最重要也是基础，而线性代数中的知识点都可以和高数联系起来出综合题，所以先复习高数，然后复习线性代数，效果会比较好。

最后，复习中，有思考也有总结。

数学就是一种思考的过程。

没有思考，一味地看，是无用功。

所以提醒考生，在学习过程中，要有思考亦有总结。

做完一道题目，把解题思路进行总结，以后遇到相同类型题目就知道从何处入手了。

再做做汤家凤老师的2018《考研数学绝对考场最后八套题》（数学二），通过试题巩固我们对于知识点的掌握，还能培养咱们的应试心理。

想买这本书的同学，还可以天猫商城北京世纪文都图书专营店、智阅网上看看，最近有很多购书优惠，买得越多，折扣越多，非常划算。

2018考研数学三143分复习经验

讲座内容概要
01 02
时间规划与安排
03 04
复习过程规划
复习资料选择
数三经验教训总结
2019/2/23
1
讲座内容概要
本人先做个自我介绍，本科毕业于湖北一所双非院校。一战对外经贸，数学三134分，总分差一分上线，义无反顾选择二战。二战数学三143分，现对外经贸金融学院金融学硕拟录取。两年的数学心路历程和学弟学妹们做个分享，希望能帮到大家。
2019/2/23 8
复习过程规划第一遍复习
直接从乐哥的全书开始做，看一章知识（知识点和例题，看完知识点独立做相应例题，不会做回过头看知识点或者翻看课本，依旧不会做，拿记号笔画记号，看例题解析搞懂，例题解析看不懂你来问我吧），全书看一章做一章配套习题（660足矣），凡遇到不懂的题目或者定理自己先尝试翻看课本知识点，先画上记号，实在不会看解析，将解析看懂（明白为什么这么做，用了哪些知识）
2019/2/23
4
复习资料选择
推荐理由：
（1）李永乐的红色全书，知识点全（二阶差分方程都有），而且例题讲解透彻，题目简单或者适中适合打基础。（2）李正元的粉红色书有点难，有些题稍带技巧（考研不会这样考，这些题不要纠结可以放过），但是知识层次和题型总结到位，适合提高用（分家后的新版线代讲义技巧性太多，所以用乐哥的线代讲义替代），所以实际上是两本全书，可做互补。（3）汤家凤的没看过听说很不错，张宇十八讲全部看过题目做的少，此书技巧性太强不适合考研
2019/2/23
6
复习资料选择视频课参考：
高数看张宇（辅之以汤家凤的中值定理和无穷级数，或者你干脆看汤家凤的），线性代数只看乐哥的配合他的线代讲义，概率论，基础好的看王式安的，个人觉得概率论太简单，概率论基础不好的看汤家凤吧，王老头的概率论讲的比较粗，他认为大家都懂。

【2018最新】2018考研数学线代复习指导-范文模板 (3页)

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==2018考研数学线代复习指导在考研数学中线代既难又简单，那么在进行线代的复习时都有哪些方法呢?下面就和小编一起来看看吧。

2018考研数学线代复习指导线性代数总共分为六章。

第一章行列式本章的考试重点是行列式的计算，考查形式有两种：一是数值型行列式的计算，二是抽象型行列式的计算。

另外数值型行列式的计算不会单独的考大题，考选择填空题较多，有时出现在大题当中的一问或者是在大题的处理其他问题需要计算行列式，题目难度不是很大。

主要方法是利用行列式的性质或者展开定理即可。

而抽象型行列式的计算主要：利用行列式的性质、利用矩阵乘法、利用特征值、直接利用公式、利用单位阵进行变形、利用相似关系。

06、08、10、12年、13年的填空题均是抽象型的行列式计算问题，14年选择考了一个数值型的矩阵行列式，15、16年的数一、三的填空题考查的是一个n行列式的计算，。

今年数一、数二、数三这块都没有涉及。

第二章矩阵本章的概念和运算较多，而且结论比较多，但是主要以填空题、选择题为主，另外也会结合其他章节的知识点考大题。

本章的重点较多，有矩阵的乘法、矩阵的秩、逆矩阵、伴随矩阵、初等变换以及初等矩阵等。

其中06、09、11、12年均考查的是初等变换与矩阵乘法之间的相互转化，10年考查的是矩阵的秩，08年考的则是抽象矩阵求逆的问题，这几年考查的形式为小题，而13年的两道大题均考查到了本章的知识点，第一道题目涉及到矩阵的运算，第二道大题则用到了矩阵的秩的相关性质。

14的第一道大题的第二问延续了13年第一道大题的思路，考查的仍然是矩阵乘法与线性方程组结合的知识，但是除了这些还涉及到了矩阵的分块。

16年只有数二了矩阵等价的判断确定参数。

第三章向量本章是线代里面的重点也是难点，抽象、概念与性质结论比较多。