中国计量大学《自动控制原理1》2017—2020年考研真题
中国计量大学821自动控制原理2 2016-2019年考研专业课真题试卷

2019年中国计量大学考研专业课初试考试真题试卷
八、(20 分) 已知一个闭环控制系统如图 5 所示,已知 T = 0.5s 。试求:
(1)判别系统的稳定性(5 分) (2)求 r(t) = t 时系统的稳态误差(5 分); (3)求单位阶跃响应序列 c(k ) ,并画出响应曲线(10 分)。
【完】
X 2 (s) X3(s)
G1(s) X1(s) G2(s) X 2(s)
H2
(s)C(s)
C(s) G4(s) X 2(s) G3(s) X3(s)
三、(20 分)
反馈系统中,前向传递函数为 G(s) k(s 40) ,反馈回路传递函数为 H (s) 1
2019年中国计量大学考研专业课初试考试真题试卷
中国计量大学 2019 年硕士研究生招生考试试题
考试科目代码:821
考试科目名称:自动控制原理 2
所有答案必须写在报考点提供的答题纸上,做在试卷 或草稿纸上无效。
一、(15 分) 求图 1 所示无源网络的传递函数。
二、(15 分)
一个单位负反馈系统的开环传递函数为
G(s)
=
(s
+
2)(s
+
K
4)(s2
+
6s
+
25)
试求闭环系统产生持续等幅振荡的 K 值和相应的振荡频率。
《自动控制原理 2》试卷 第 1 页 共 4 页
2019年中国计量大学考研专业课初试考试真题试卷
三、(20 分)
假设温度计可用传递函数 1 描述其特征,现在用温度计测量盛在容器内的水温,发
Ts +1
《自动控制原理 2》试卷 第 2 页 共 3 页
中国计量大学801自动控制原理1 17-20年真题

(1)绘制 K g 由 0 变化的根轨迹;(7 分)
(2)求系统产生持续等幅震荡时的 K g 值和振荡频率;(4 分)
(3)确定系统呈阻尼振荡动态响应的 K g 值范围。(4 分)
五、(15分)已知系统的结构如图4所示。
(1)画出系统的奈氏图(标出与实轴交点);(10 分)
(2)应用 Nyquist 稳定判据分析系统稳定时,K 的取值范围。(5 分)
三、(15 分)设单位负反馈系统的开环传递函数为:
G(s)
s(1
K 0.1s)(1
0.25s)
1. 试确定闭环系统稳定时的 K 值范围; (10 分) 2. 试确定使系统为持续等幅振荡时的 K 值。(5 分)
《自动控制原理 1》试卷 第 1 页 共 3 页
四、(15
分)设单位反馈系统开环传递函数: G(s)
(3)试在下列三种控制器结构形式中,选择一种能同时满足上述要求的 Gc (s) ,并确
定 Gc (s) 中参数的取值范围。(4 分)
① Gc (s)
K ( s 1) Ts 1
;② Gc (s)
K s
;③ Gc (s)
K ( s s
1)
四、(15分)某单位负反馈系统的开环传递函数为: G(s)
Kg
s(s 2)(s 4)
图5
七、(20 分)已知采样系统结构如图 6 所示,其中采样周期T 1。
r(t) +— T
K
1
c(t)
T
(s 1)(s 2)
图6 (1)求开环脉冲传递函数和闭环脉冲传递函数;(10 分) (2)试确定系统稳定时的 K 值范围。(10 分)
八、(20
分【完】
《自动控制原理 1》试卷 第 3 页 共 3 页
中国计量大学801自动控制原理1-2015--2017考研专业课真题

(5 分)
(2) 求相稳定裕度 γ 和剪切频率 wc ;(6 分)
(3) 判断系统的稳定性。
(4 分)
db
……
…… ………....…
26
-40
-20 20 40
w
1 2 4 wc
-40d B/dec
图3
七、(20 分)已知一采样系统如图 4 所示,其中采样时间 T=1s。试求:
(1)
开环脉冲传递函数 C(z) ; E(z)
1 T
C
0
1
0
,
U
u w
(1) 判断系统能控性;(10 分) (2) 求系统在路面 w=10cm 阶跃输入时的超调量; (5 分) (3) 求系统调整时间(稳态误差 2%)。 (5 分)
【完】
《自动控制原理 1》试卷 第 3 页 共 3 页
一、(15 分)分别用下列方法求图 1 所示系统的传递函数。 (1)结构图等效变换;(7 分) (2)梅森公式。(8 分)
R(s)
T0s +1
+-
10K1 s(s + 5)(s + 20)
N(s) + C(s) +
图3
《自动控制原理 1》试卷 第 1 页 共 3 页
四、(15 分)设单位负反馈控制系统的开环传递函数为:G(s)H (s) =
K
s(s + 2)(s + 7)
(1)绘制系统的根轨迹图;(8 分) (2)确定系统稳定时 K 的最大值;(4 分)
(2 分)
《自动控制原理 1》试卷 第 1 页 共 3 页
五、(15
分)画出
中国计量大学自动控制原理2 2015--2020年考研初试真题
ω
2
3
4
5
6
8
10
| G( jω) |
7.5
4.8
3.15
−118°
arg tgG( jω)
错误! 未找到
引用
源。
−130°
−140°
2.25 −150°
1.70 −157°
1.00 −170°
0.64 −180°
《自动控制原理 2》试卷 第 3 页 共 4 页
七、(20 分)设有单位反馈的伺服系统,其开环传递函数为
四、(20 分) 已知系统开环传递函数为:
G(s)=
s(0.2s
2
10 + 0.8s
−
1)
错误!未找到引用源。 试根据奈氏判据确定闭环系统的稳定性。
五、(20 分) 设负反馈系统如图 2,前向通道传递函数为:
G(s) = 10 s(s + 2)
若采用测速负反馈:
H (s) =1+ kss
(1)试画出以 ks 为参变量的根轨迹(10 分);
《自动控制原理 2》试卷 第 1 页 共 4 页
三、(20 分)系统的微分方程如下:
x1(t) = r(t) − c(t)
x2 (t)
=τ
dx1 (t ) dt
+
K1 x1 (t )
x3 (t) = K2 x2 (t)
x4 (t) = x3 (t) − x5 (t) − K5c(t)
dx5 (t) dt
40
−20
20
− 40 L
0.01
0.1
−20 ϕ (ω )
0o
L0 −20
0.5
− 40
自动控制原理考研真题试卷

自动控制原理考研真题试卷一、选择题(每题2分,共20分)1、在闭环控制系统中,调节器的输出信号是()A.调节器的输入信号B.调节器的输出信号C.调节器输入信号的函数D.被控对象的输出信号2、在单闭环控制系统中,如果系统开环增益无穷大,则系统可能发生()A.振荡B.失稳C.跟随误差D.超调量3、在系统设计中,为了避免积分饱和,可以采取的措施是()A.采用微分项调节器B.采用积分项调节器C.采用比例-积分-微分(PID)调节器D.采用抗积分饱和调节器4、在反馈控制系统中,如果系统存在干扰,则可以通过()来减小干扰对系统的影响。
A.增加执行机构B.增加测量元件C.增加调节器D.增加滤波器5、在连续控制系统中,如果控制器采用比例调节器,则系统的稳态误差将()A.与输入信号成正比B.与输入信号成反比C.与输入信号的平方成正比D.与输入信号的绝对值成正比6、在离散控制系统中,如果采样周期很短,则系统的稳态误差将()A.很大B.很小C.与采样周期无关D.为零7、在控制系统中,通常采用()来克服扰动对系统的影响。
A.滤波器B.放大器C.调节器D.编码器8、在控制系统设计中,通常采用()来提高系统的稳定性和响应速度。
A.串联校正B.并联校正C.反馈校正D.前馈校正9、在数字控制系统中,通常采用()来处理模拟信号。
A. A/D转换器B. D/A转换器C.模拟滤波器D.数字滤波器10、在控制系统设计中,通常采用()来提高系统的抗干扰能力。
华东师范大学是一所著名的综合性大学,其化学学科在国内具有很高的声誉。
对于想要报考华东师范大学化学专业研究生的同学来说,了解普通化学原理历年真题是非常重要的。
本文将介绍华东师范大学考研普通化学原理历年真题,帮助考生更好地备考。
一、2015年真题1、名词解释本文1)摩尔质量本文2)气体常数本文3)沉淀平衡本文4)氧化还原反应2、简答题本文1)简述拉乌尔定律和亨利定律,并说明它们在描述液体蒸气压中的应用。
2018年中国计量大学801自动控制原理1考研真题硕士研究生专业课考试试题
《自动控制原理1》试卷 第1 页 共3页
中国计量大学
2018年硕士研究生招生考试试题
考试科目代码:801 考试科目名称:自动控制原理1
所有答案必须写在报考点提供的答题纸上,做在试卷或草稿纸上无效。
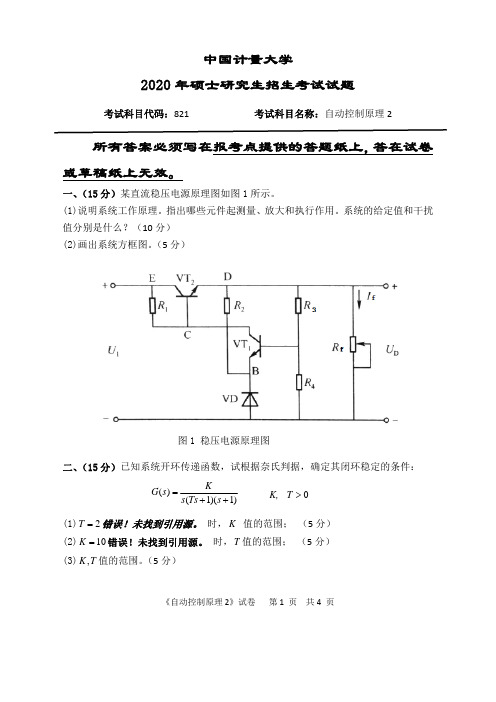
一、(15分)某系统结构图如图1所示,R(s)为输入,N(s)为扰动,C(s)为输出。
试要求:
1. 画出系统的信号流图;(5分)
2. 用梅逊公式求出其传递函数)()(s R s C ;(5分)
3. 说明在什么条件下,输出C(s)不受扰动N(s)的影响。
(5分)
图1
二、(15分)有一位置随动系统,其结构如图2所示,其中K=4,T=1。
图2
试求:
1. 该系统的无阻尼振荡频率n w 及阻尼比ς;(4分)
2. 系统的超调量%σ、调节时间s t (误差为%5±)、上升时间r t ;(6分)
3. 如果要求22=ς,在不改变时间常数T 的情况下,应怎样改变系统的开环放大系数K 。
(5分)。
中国计量大学810自动控制原理一全套考研真题(2007-2020)
【完】
《自动控制原理 1》试卷 第 4 页 共 4 页
中国计量学院 2007 年攻读硕士学位研究生入学试题
考试科目名称: 考试科目代码: 考 生 姓 名: 考 生 编 号:
自动控制原理 410
考生须知:
1、所有答案必须写在答题纸上,做在试卷 或草稿纸上无效。
2、答案必须写清题号,字迹要清楚,保持 卷面清洁。
五、(14 分)单位负反馈系统的开环传递函数为:
G(s) = 10(s +1) s(10s +1)(0.1s +1)
1.试画出开环对数幅频渐进曲线;(7 分) 2. 计算相稳定裕度。(7 分)
六、(20 分)已知离散系统的结构如下图示:
R(s)
− T = 1s
1 − e−Ts s
k
CI(s)
s(s + 1)
《自动控制原理 1》试卷 第 1 页 共 4 页
三、(15 分)系统结构图如图 3 所示,[e(t) = r(t) − b(t)] 。
图3 1. 已知 G1(s)的单位阶跃响应为1− e−2t ,试求 G1(s);(5 分) 2. 利用求出的 G1(s),当 r(t)=10·1(t)时,试求:①系统的稳态输出;②系统的超调量、 调节时间和稳态误差。(10 分)
2. 当 K=52,利用奈奎斯特稳定判据判断其闭环系统的稳定性。(5 分)
六、(15 分)已知最小相位开环系统的渐近对数幅频特性如图 5 所示,试求: 1. 系统的开环传递函数;(4 分) 2. 截止频率ωc 和相角裕量 γ ;(8 分) 3. 若使截止频率ωc = 10rad / s ,其放大倍数应取多少?(3 分)
(0.05 误差带)。
2. 求以下系统在单位斜坡输入信号作用下的稳态误差。
中国计量大学2021年硕士研究生考试试题《自动控制原理1》考试代码801

中国计量大学2021年硕士研究生招生考试试题考试科目代码:801考试科目名称:自动控制原理1所有答案必须写在报考点提供的答题纸上,做在试卷或草稿纸上无效。
一、(15分)已知系统的微分方程组如下:1521132243344()()()()()()()()()()()()()dn x t r t y t K dt x t K x t dx t K x t dt x t x t K n t dc t K x t T y t dt =-+===-=+其中()r t 、()n t 、()y t 分别为系统的给定输入、扰动输入和输出;K 1-K 5和T 均为正常数。
(1)试绘制系统的结构框图;(7分)(2)试求出系统传递函数()()Y s R s 和()()Y s N s 。
(8分)二、(15分)已知系统结构如图1所示,扰动输入()21()n t t =⨯。
(1)试求40K =时,系统在扰动作用下的稳态输出和误差;(7分)(2)试讨论在扰动作用点之前的前向通道引入积分环节1s,对结果有何影响?并计算稳态输出和误差;(4分)(3)试讨论在扰动作用点之后的前向通道引入积分环节1s,结果又如何?并计算稳态输出和误差。
(4分)图1越努力,越幸运!知识管理三、(15分)已知控制系统结构如图2所示。
11()G s K =,221()(1)T G s s T s =+,22()1r as bs G s T s+=+,其中K 1、T 1、T 2均为正值。
(1)试讨论a 和b 取值对系统稳定性的影响关系;(5分)(2)当输入为21()2r t t =时,要求系统稳态误差为零,试确定a 和b 值。
(10分)图2四、(15分)已知系统结构图3所示。
(1)绘制系统的根轨迹图;(6分)(2)试确定系统具有欠阻尼状态的开环增益*K 的取值范围;(3分)(3)试计算阻尼比为0.707时的系统的开环增益*K 值;(3分)(4)试计算开环增益6*=K 时的系统速度误差ss e 。
中国计量学院自动控制原理2005--2011年考研专业课初试真题

5
考生须知:
1、所有答案必须写在答题纸上,做在试 卷或草稿纸上无效。 2、答案必须写清题号,字迹要清楚,保 持卷面清洁。 3、试卷、草稿纸必须随答题纸一起交回 。
本试卷共 十四 大题,共 四 页码。
6
一、用运算放大器组成的有源电网络如图所示,试采用复阻抗法写出它的以
2
arctan
(1)求相位裕度为 30 o 时系统的开环传递函数; (2)在不改变截止频率 c 的前提下,试选取参数 K c 和 T ,使系统在加入串联 校正环节 Gc ( s )
K c (Ts 1) 后,系统的相位裕度提高到 60 o .(10分) s 1
8.控制系统的状态空间描述如下:
、、 计算题(10题,共96分) 1. 下图示R-LC四端网络,设信号源内阻抗为零,试求以 u i (t ) 为输入, u o (t ) 为输出的传 递函数。(9分) R1 ui
2
+
u C iL L uC R2 uo
2. 求下图示系统的开环传递函数。(9分)
R(s)
-
-
1+K1s
10/ s 5/s
4. 控制系统结构图如下图所示,其中 Gc ( s )
,要求系统的稳态误差为零,试确定参数a,b。(9分)
Gc ( s )
R(s) E(s)
-
G2
+
K1
K2 s (Ts 1)
C(s)
5.系统结构图如下图示,试绘制以 为变量的根轨迹图。(10分)
R(s)
-
1 3 s ( s 1)
C(s)
中国计量学院自动控制原理总复习.

一、系统稳定的充分与必要条件
二、劳斯稳定判据
第六节 控制系统的稳态误差分析
设 D(s)=0 控制系统的典型结构 根据终值定理得: D(s) C(s) R(s) E(s) essr=lim er(t)=lim s· Er+ (s)
t→∞ _
稳态误差 及误差系数
G1(s) s→0
G2(s)
R(s) =lim s· H(s) s →0 1+G(s)H(s) 系统误差: R(s)作用时 e(t)=r(t)-b(t) 期望值与实际值的差值。 系统给定信号作用下的稳态误差不仅与 R(s) R(s) Er(s)= = 系统的输入有关,还与系统的结构有关。 稳态误差: 1+G 1+G(s)H(s) ess=lim e(t) 进入稳态后的误差值。 1(s)G2(s)H(s)
例2 已 知 某 控 制 系 统 方 框 如 图图 所 示 ,要 求 该 系 统 的 单 位 阶跃响应 c(t)具 有 超 调 量 p 16.3%和 峰值时间 t p 1 秒, 试 确 定 前 置 放 大 器 的益 增 K及 内 反 馈 系 数 之 值.
R(s)
K
10 s ( s 1)
n
第三节 二阶系统性能分析
5. 稳态误差ess
根据稳态误差的定义和终值定理有
ess= lim e(t) = lim SE(s)
t→∞
s→0
欠阻尼二阶系统的稳态误差: 2 ωn 1 G(s)H(s)= R(s)= ζ ωn ) S(S+2 S R(s) ess= lim S =0 s→0 1+G(s)H(s)
Uc(s)
第四节 动态结构图
动态结构图的等效变换与化简
系统的动态结构图直观地反映了系统 内部各变量之间的动态关系。将复杂的动 态结构图进行化简可求出传递函数。
中国计量大学2020年《801自动控制原理1》考研专业课真题试卷
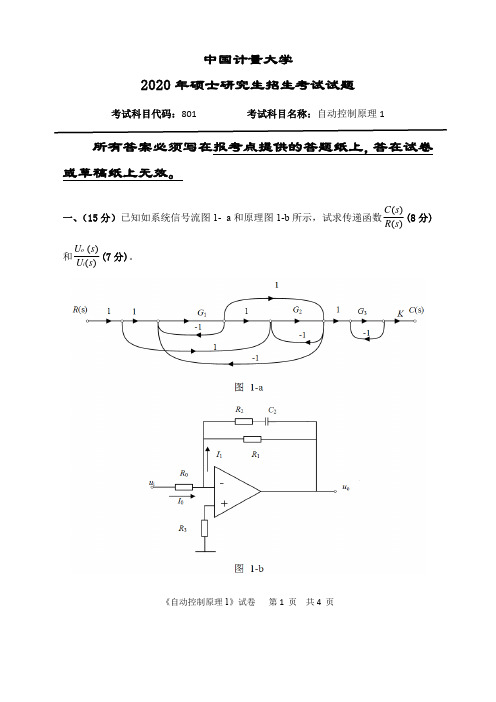
《自动控制原理 1》试卷 第 1 页 共 4 页
二、(15 分)已知控制系统结构图如图 2 所示:
(1)试分析说明内反馈 Kfs 的存在对系统稳定性的影响;(9 分) (2)计算静态加速度误差系数,分析内反馈 Kfs 的存在对系统稳态误差的影响。(6 分) 三、(15 分)有一位置随动系统,结构如图 3 所示。 K = 40 ,τ = 0.1。
中国计量大学 2020 年硕士研究生招生考试试题
考试科目代码:801
考试科目名称:自动控制原理 1
所有答案必须写在报考点提供的答题纸上,答在试卷 或草稿纸上无效。
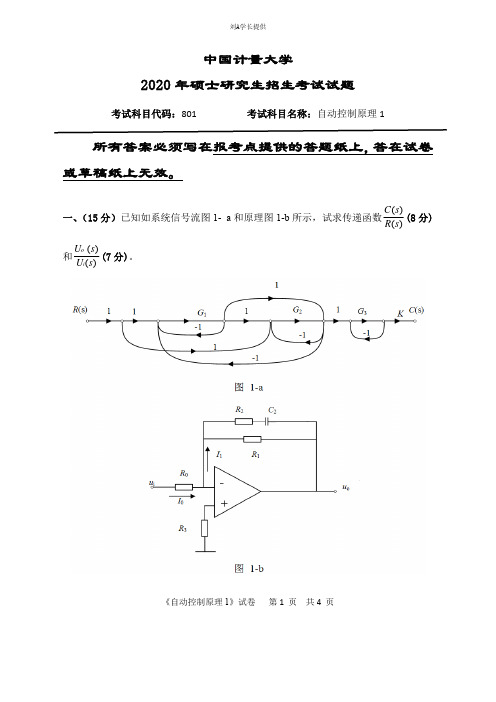
一、(15 分)已知如系统信号流图 1-
a
和原理图
1-b
所示,试求传递函数
C(s) R(s)
(8 分)
和 Uo (s) (7 分)。 Ui(s)
(1)求系统的开环和闭环极点;(5 分) (2)当输入量 R(s) 为单位阶跃函数时,求系统的自然振荡角频率 ωn ,阻尼比 ξ 和系 统的动态性能指标 tr , ts ,σ %。(10 分) 四、(15 分)已知某单位负反馈系统的开环传递函数为: G(s) = K *(s + 9)
s(s +10)2 (1)绘制当 K * 从零变化到正无穷大时,闭环系统的根轨迹图;(7 分) (2)分析该系统稳定时 K * 的取值范围;(2 分) (3)已知系统有一个闭环极点 p1 = −8.8 ,利用主导极点法近似计算此时系统单位阶跃 响应的超调量和调节时间。(6 分)
(3)求系统的传递函数Y (s) / U (s) 。(6 分)
九、(20 分)某线性定常系统的状态空间表达式如下:
⎡−1 0 2⎤ ⎡2⎤
x&
=
⎢ ⎢
2020年中国计量大学考研真题801自动控制原理1(2020年)
x&
=
Ax
(t
)
+
bu
(t
)
,
y
Hale Waihona Puke (t)=cx
(t
)
。其中,
A
=
⎡ a11
⎢ ⎣
a
21
a12 a22
⎤ ⎥ ⎦
,
b
=
⎡0⎤ ⎢⎣1⎥⎦
,
c
=
[1
1] 。已
知系统的转移矩阵为: eAT
=
⎡e−t + te−t
⎢ ⎣
−te−t
te−t e−t − te−t
⎤ ⎥ ⎦
。
(1)试求矩阵 A;(6 分)
(2)若 x (0) = [1 −1]T ,求系统单位阶跃 u (t ) = 1(t ) 作用下的响应 x (t ) ,t ≥ 0 ;(8 分)
(1)求系统的开环和闭环极点;(5 分) (2)当输入量 R(s) 为单位阶跃函数时,求系统的自然振荡角频率 ωn ,阻尼比 ξ 和系 统的动态性能指标 tr , ts ,σ %。(10 分) 四、(15 分)已知某单位负反馈系统的开环传递函数为: G(s) = K *(s + 9)
s(s +10)2 (1)绘制当 K * 从零变化到正无穷大时,闭环系统的根轨迹图;(7 分) (2)分析该系统稳定时 K * 的取值范围;(2 分) (3)已知系统有一个闭环极点 p1 = −8.8 ,利用主导极点法近似计算此时系统单位阶跃 响应的超调量和调节时间。(6 分)
(3)求系统的传递函数Y (s) / U (s) 。(6 分)
九、(20 分)某线性定常系统的状态空间表达式如下:
⎡−1 0 2⎤ ⎡2⎤
中国计量大学自动控制原理2012--2014年考研真题

0.2S + 1 B(s)
Kh
四、(15 分)
已知一单位反馈系统的开环传递函数为:G(s)
=
K0 (s + 4) s(s + 2)
。
1. 试证明该系统根轨迹的复数部分为一圆,并画出根轨迹。(8 分)
2. 分析K0从 0→∞变化时系统阻尼比的变化情况;(4 分)
3. 分析K0从 0→∞变化时系统超调量的变化情况。(3 分)
二、(15 分) 已知系统的单位脉冲响应为 g(t) = 10e−0.2t + 5e−0.5t ,
(1) 求系统的传递函数;(10 分) (2) 确定系统的单位阶跃响应达到稳态值的 95%所需的时间。(5 分)
三、(15 分)
控制系统如下图所示。若要求系统的超调量 M p = 0.25 ,峰值时间 tp = 2s 。
db
0 20
0
0.02
-20
-40
20
200
0
ω
-20
七、(20 分) 已知采样系统结构如图所示,其中采样周期 T = 0.1 s。
R(S)
-T
1-e −TS S
k
C(S)
2S +1
(1)求开环脉冲传递函数和闭环脉冲传递函数;(15 分) (2)确定闭环系统稳定的 k 值范围。(5 分)
《自动控制原理》试卷 第 2 页 共 3 页
一、(15 分) 控制系统如下图所示:
R(s)
- G1(s)
G2(s)
-
H4(s)
-
G3(s)
H2(s)
C(s)
G4(s)
-
G5(s)
G6(s)
H3(s)
H1(s)
