lec19 7.3~7.4 -8.1
2020年企业安全生产标准化第七要素2 风险和隐患辨识、评估分级(LEC法)一览表

3
8、作业人员不清楚设备内其他危害因素。
3
6
7
126
3
6、清除进出口通道障碍物。
7、分析可燃、有毒有害物质含量。
8、对企业人员讲清楚设备内其他危害因素如
9、作业现场没有监护措施。
1
3
15
45
2
序号
作业活动
危险源(危害因素)
可能的事故、后果
作业条件危险性评价(LEC)
控制措施
附件等。
9、备齐消防、救生等器材。
财产损失
3
1
3
9
1
乘座非法营运车辆
人员伤■亡
1
6
15
90
3
财产损失
1
1
3
3
1
工作地自然环境恶劣
意外伤害
1
3
15
45
2
身体素质差
生病、死亡
0.5
6
7
42
2
住宿条件差
人员伤害
3
6
3
54
2
财产损失
3
1
3
9
1
乘坐夜车
人员伤害
1
6
1
6
1
9
电脑操作
长时间使用
身体损害
1
6
1
6
1
推广工间操
电脑病毒
数据丢失、工作瘫痪
占
八、、
人员伤害
1
1
7
7
1
13
办公室工作
忘记锁门
物品丢失
3
1
3
9
1
门卫人员加强巡视
14
LEC风险评估法

LEC风险评估法
LEC法是一种常用的风险评估方法,可采取计算每一项已辨识出的危险源所带来的风险。
其风险值D由三个主要因素L、E、C的指标值的乘积表示,即D=LEC。
L——发生事故的可能性大小。
事故发生的可能性大小用概率来表示时,绝对不可能发生的事故概率为0,必然发生的事故概率为1,因此人为的将发生事故可能极小的分数定为0.1,必然要发生事故的分数可定为10,介于这两者之间的情况定为若干中间值,如下表:
E——暴露于危险环境中频繁程度。
人员出现在危险环境中的时间越多,发生危险性越大。
规定连续出现在危险环境的情况为10,而非常罕见地出现在危险环境中为0.5,介于两者之间的各种情况规定若干个中间值,如下表:
C——事故产生的后果。
事故造成人身伤害与财产损失变化范围很大,所以规定分数值在1-100之间。
轻微伤害或较小财产损失的分类规定为1,造成人员伤亡较大的可能性规定为100,其他情况的数值在1-100之间,如下表:
D——风险值。
D=L×E×C,确定D值后关键是如何确定风险级别的界限值,而这个界限值并不是长期固定不变
的;在不同时期可根据具体情况确定风险级别的界限值,以确定持续改进的措施。
如下表:。
LEC风险评价标准及风险确定准则

LEC风险评价标准及较大OHS风险确定准则1.风险评价依据1.1事故发生的可能性:发生的可能性越大,风险越高;1.2暴露于危险环境的频繁程度:暴露越频繁,风险越高;1.3事故产生的后果:后果越严重、风险越高。
2.风险评价方法风险评价采用LEC法来确定风险级别。
即:定量计算每一种危险源所带来的风险,采用以下公式: D=LEC式中: D——风险值。
L——事故发生的可能性。
E——暴露于危险环境的频繁程度。
C——发生事故产生的后果。
L、E、C各要素的参考取值范围分别见以下各表:——L―发生事故的可能性大小当事故或风险事件发生的可能性大小用概率来表示时,绝对不可能事件发生的概率为0;而必然发生的事件的概率为1,做系统安全考虑时,绝对不发生事故是不可能的,所以人为地将“发生事故可能性极小”的分数定为0.1,而必然要发生的事件的分数定为10。
介于这两种情况之间的情况指定了若干个中间值,如下表所示:事故发生的可能性(L)分数值事故发生的可能性10 完全可以预料6 相当可能3 可能,但不经常1 可能性小,完全意外0.5 很不可能,可以设想0.2 很不可能0.1 实际不可能——E-暴露于危险环境的频繁程度人员或设备出现在危险环境中的时间越多、越长,则风险性越大。
规定连续暴露在此危险环境的情况定为10,而非常罕见地出现在危险环境中定为0.5。
同样,将介于两者之间的各种情况规定若干个中间值,如下表所示:暴露于危险环境的频繁程度(E)分数值频繁程度10 连续暴露6 每天工作时间内暴露3 每周一次,或偶然暴露2 每月一次暴露1 每年几次暴露0.5 非常罕见的暴露——C―发生事故可能造成的后果事故造成的人身伤害变化范围很大,对伤亡事故来说,可从极小的轻伤至多人死亡的严重结果。
由于范围广,所以规定分数值为1~100,轻伤规定分数为1,把造成十人以上死亡的可能性分数规定为100,其它情况的数值均在1与100之间,如下表所示:发生事故产生的后果(C)分数值后果100 大灾难,许多人死亡40 灾难,数人死亡15 非常严重,一人死亡7 严重,重伤3 重大,致残1 引人注目,不利于基本的健康安全要求——D―风险分值根据公式计算作业的风险值,并参照下表评定风险级别。
LEC风险评价法

LEC风险评价法:作业条件危险性评价是一种半定量危险性评价法。
它是以与系统风险率有关的三种因素指标值之积来评价系统人员伤亡风险的大小。
其简化公式是: D=LEC---L—发生事故的可能性大小.事故或危险事件的可能性大小,当用概率来表示时,绝对不可能的事件发生的概率为0;而可能性小、完全意外发生的事件的分数值为1,在系统安全考虑时,绝对不发生事故是不可能的,所以认为地将事故实际不可能性的分数值定位0.1,而完全可能预料要发生的事件的可能性分数值定位10.介于两者之间发生事故的可能性制定了若干个中间值,如表1所示.表1 发生事故的可能性(L)人员出现在危险环境中的时间越频繁,则危险性越大.规定连续暴露在此环境的情况为10,而非常罕见地暴露在危险环境中的分数值为0.4.同样,将介于两者之间的各种为项规定若干个中间值,如表2所示.表2 暴露于危险环境的频繁程度(E)事故造成的人身伤害变化范围很大,对伤亡事故来说,可能从极小的轻伤直到多人死亡的严重结果。
由于发生事故可能产生的范围较广,所以规定分数值为1—100,轻伤规定分数为1,把发生事故造成10人以上死亡的可能性分数规定为100,其他情况的分数值均在1与100之间,如表3所示。
表3 发生事故产生的后果(C)根据公式就可以计算作业的危险程度,但关键是如何确定各个分值之积总分的评价。
依据经验,总分数值小于20被认为少有危险为1级,是低危险;如果危险分数值等于或大于70—160之间,那就是显著危险性,需要及时整改;如果危险分值等于或大于160时,其危险等级达到3-3级以上,那就表示有显著危险或高度危险性,应立即停止生产直到环境得到改善为止。
危险等级的划分是凭经验判断,难免带有局限性,不能认为是普遍适用的。
应用时需要结合实际情况予以修正。
危险性分值等级划分如表4所示。
表3 危险等级划分重大危险源的确定凡具备以下条件的均应确定为重大危险源:Ⅰ、有可能违反法律、法规及其它要求的;Ⅱ、曾经发生过群死群伤事故的;Ⅲ、直接观察到的危险,评定级别达到A、B级;Ⅳ、半定量评价(LEC法),当D≥160时评估级别3、。
LEC法取值标准对照表
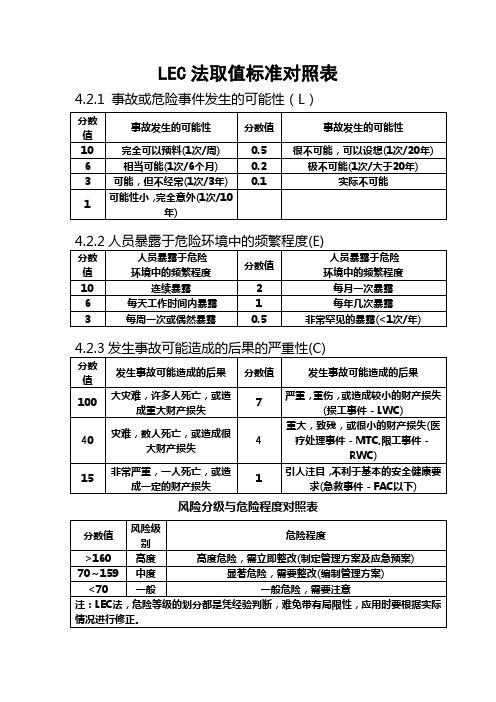
LEC法取值标准对照表4.2.1 事故或危险事件发生的可能性(L)分数值事故发生的可能性分数值事故发生的可能性10 完全可以预料(1次/周) 0.5 很不可能,可以设想(1次/20年) 6 相当可能(1次/6个月) 0.2 极不可能(1次/大于20年)3 可能,但不经常(1次/3年) 0.1 实际不可能1 可能性小,完全意外(1次/10年)4.2.2人员暴露于危险环境中的频繁程度(E)分数值人员暴露于危险环境中的频繁程度分数值人员暴露于危险环境中的频繁程度10 连续暴露 2 每月一次暴露6 每天工作时间内暴露 1 每年几次暴露3 每周一次或偶然暴露0.5 非常罕见的暴露(<1次/年)4.2.3发生事故可能造成的后果的严重性(C)分数值发生事故可能造成的后果分数值发生事故可能造成的后果100 大灾难,许多人死亡,或造成重大财产损失7严重,重伤,或造成较小的财产损失(损工事件-LWC)40 灾难,数人死亡,或造成很大财产损失4重大,致残,或很小的财产损失(医疗处理事件-MTC,限工事件-RWC)15 非常严重,一人死亡,或造成一定的财产损失1引人注目,不利于基本的安全健康要求(急救事件-FAC以下)风险分级与危险程度对照表分数值风险级别危险程度>160 高度高度危险,需立即整改(制定管理方案及应急预案) 70~159 中度显著危险,需要整改(编制管理方案)<70 一般一般危险,需要注意注:LEC法,危险等级的划分都是凭经验判断,难免带有局限性,应用时要根据实际情况进行修正。
危险源评价方法之LEC

隐患:工人戴手套操作旋转设备加工工件; 事故:工人戴着手套的手接触到了设备的旋转部位(工 件或刀具); 后果:工人受到伤害(伤害严重程度具有偶然性)。 由于对实际隐患出现的数据缺乏统计资料,所以在进行 风险评估时对“L”因子的取值极易出现因人而异的现象。 为了能够真实地评估出事故的风险状况,在风险评估前应根 据组织的安全生产管理状况对引起事故的隐患进行比较具体 的描述,进而确定事故发生可能性的分数值。根据本例,可 将戴手套操作的情景按下表的格式设定。
10个人对“L”因子取值的离散度为9.5 如此计算出的风险等级D值分别从20以下跨越 到了200以上。
例1:某单位有100名旋转设备的操作工人,平均每个工作 日加工10件工件,工人操作旋转设备、装卸工件时应戴手套 ,加工工件时禁止带手套。但是,一位工人戴着手套装上工 件以后,忘记了摘下手套便启动了旋转设备。在这种情况下 ,事故发生的可能性是什么呢?
ห้องสมุดไป่ตู้
1、重大危险源辨识
定义:长期地或临时地生产、加工、搬运、 使用或储存危险物质,且危险物质的数量等于或 超过临界量的单元。
2.重大危险源判断举例:
某生产场所有甲、乙、丙三种物质,甲
种物质的临界量和实际量分别为 5t 和 1.5t
,乙种物质的临界量和实际量分别为 2t 和
1t,丙种物质的临界量和实际量分别为 20t
这是一种简单易行的评价作业条件危险性的方法。
对于一个具有潜在危险性的作业条件,影响危险
性的主要因素有3个:事故或危险事件发生的可能性
;暴露于危险环境的情况;事故一旦发生可能产生
的后果。用公式表示为:
D=L×E×C 式中:D——作业条件的危险性; L——事故或危险事件发生的可能性; E——暴露于危险环境的频率; C——发生事故或危险的可能结果。
LEC法标准(最新整理)

《危险源辨识和风险评价表》填表说明危险源辨识和风险评价是职业健康安全管理体系建立的基础,评价出重点风险并有效控制是体系运行的关键,为此我们必须充分辨识危险源,认真填写《危险源辨识和风险评价表》。
1、设备设施/ 场所/ 岗位:根据实际确定,将所使用的设备设施或场所(填具体的设备设施名称,如果是多种设备设施,也可填场所,如锅炉房、变电站、空压张、污水站等)、人员的岗位等描述清楚。
如“拆箱机/操作工”、“制丝冷端/操作工”、“卷接包装机/操作工”、“变电站/维修电工”;“车间维修组/机修工”、、“叉车/驾驶员”、“成品库/保管员”、“分拣机/操作工”、运输车辆/司机”、“各办公室/管理和技术人员”等。
2、作业活动:该工序或工种所从事的具体作业活动。
如“卷接包装机/操作工”可能涉及到的具体作业有装卡材料、加工操作、排除故障、清理设备等;“维修电工”可能涉及到的具体作业活动有“登高作业”、“检修电气设备”等、“电焊作业”可能涉及到的具体作业活动有“开关焊机设备”、“焊接加工”等。
3、第一类危险源:该作业活动中可能接触的第一类危险源,即“存在的、可能发生意外释放的能量(能源或能量载体)或危险物质”,如带电导体、遇水自燃物质、运动的机械、奔驰的汽车、压力容器、悬吊物的势能、有毒品、烟草粉尘、机械噪声----等;一种作业活动中可能有一种或几种第一类危险源。
4、第二类危险源---危险源描述:根据第一类危险源,描述可能引发事故或伤害的人的不安全行为、物的不安全状态、作业环境的不良因素等第二类危险源及其后果,并参考《生产过程危险和有害因素分类与代码》(GB/T13861-1992)填写第二类危险源的代码;如“维修电工”在进行“检修电气设备”时,第一类危险源是“带电导体”,第二类危险源可能有“外露线路绝缘层破损”,后果是“触电”(物,代码11505)、“设备漏电”,后果是“触电”(物,代码11510)、“不按规定监控,停电检修过程中合闸通电”,后果是“触电”(人,代码515)。
LEC风险评价标准及风险确定准则

LEC风险评价标准及风险确定准则一、引言LEC(Lowest Effect Concentration)风险评价标准是一种常用的环境风险评价方法,用于评估化学物质对环境和生态系统的潜在风险。
本文将介绍LEC风险评价标准的基本原理和应用准则。
二、LEC风险评价标准的基本原理LEC风险评价标准基于化学物质对生物的毒性效应,通过确定最低影响浓度(Lowest Effect Concentration)来评估风险。
LEC是指在实验条件下,引起生物效应的最低浓度。
通常,LEC值越低,表示化学物质对生物的毒性越大。
三、LEC风险评价标准的应用准则1. 数据收集和整理:收集与评估化学物质的毒性数据,包括实验室研究、野外监测和文献回顾等。
整理数据时,应注意数据的可靠性和适用性。
2. 选择适当的生物指标:根据评估对象和环境条件,选择适当的生物指标来评估化学物质的毒性效应。
常用的生物指标包括生长抑制、繁殖受损、生存率下降等。
3. 确定LEC值:根据收集到的数据,确定LEC值。
通常使用统计方法,如NOEC(No Observed Effect Concentration)和LOEC(Lowest Observed Effect Concentration)来估算LEC值。
4. 风险等级划分:根据LEC值,将化学物质的风险等级划分为低风险、中风险和高风险。
划分标准可以根据实际情况进行调整,但应保证科学、客观和可重复。
5. 风险管理措施:根据化学物质的风险等级,制定相应的风险管理措施。
低风险化学物质可以采取监测和定期评估措施;中风险化学物质需要加强监管和限制使用;高风险化学物质应立即采取控制措施,甚至禁止使用。
6. 定期评估和修订:定期对LEC风险评价标准进行评估和修订,以适应新的科学研究和环境变化。
评估和修订应基于充分的数据和科学证据,确保标准的科学性和可靠性。
四、案例分析以某化工厂的废水排放为例,根据LEC风险评价标准,对废水中的化学物质进行风险评估。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
μ = .75, where μ is the true average inside diameter of a certain type of PVC pipe .
p < 0.10, where p is the proportion of defective circuit boards among all circuit boards produced by a certain manufacturer. μ1 – μ2 = 0, where μ1 and μ2 denote the true average breaking strengths of two different types of twine.
(n 1)S 2
2 /2,n1
2
(n 1)S 2
21 /2,n1
Proposition: A 100(1-α)% confidence interval for the variance σ2 of a normal population has lower limit
• The result of a hypothesis test is either: – The null hypothesis is rejected
• This is a strong result. It indicates that your alternative hypothesis has convincing data behind it.
2 2 n 1 s 2,n1
and upper limit
n 1 s
2
2 1 2, n1
A confidence interval for σ has lower and upper limits that are the square roots of the corresponding limits in the interval for σ2.
Tolerance Intervals(容许区间)
Let k be a number between 0 and 100. A tolerance interval for capturing at least k% of the values in a normal population distribution (which has unknown μ and σ) with a confidence level 95% has the form
16 137,324.3 16 137,324.3 , 76,172.3, 318, 064.4 28.845 6.908
Taking the square root of each endpoint yields (276.0,564.0) as the 95% CI for σ.
• Typical claims: – A new methodhe items meet (or do not meet) the specifications
– There is a difference in the average quality characteristic in the output of two processes
Example 7.15 The accompanying data on breakdown voltage of electrically stressed circuits was read from a normal probability plot. The straightness of the plot gave strong support to the assumption that breakdown voltage is approximately normally distributed . 1170 1510 1690 1740 1900 2000 2030 2100 2190 2200 2290 2380 2390 2480 2500 2580 2700 Let σ2 denote the variance of the breakdown voltage distribution and it is unknown. Determine the 95% confidence interval of σ2. Solution: The computed value of the sample variance is s2 = 137,324.3, the point estimate of σ2. With df = n-1 =16, a 95% CI require χ2.975,16 = 6.908 and χ2.025,16 = 28.845. The interval is
The CI for σ2 can be easily built from this statistic based on its distribution. The area under the χ2ν curve (v df) to the right of χ2α/2,ν is α/2, as is the area to the left of χ21-α/2,ν.Thus, the area captured between these two critical values is 1- α.
Summary of Chap. 7
• CI for μ of a normal distribution with known σ; general method for deriving CIs. • Large-sample CIs for μ and p of general distributions with known or unknown σ; one-sided CIs. • CIs for μ of a normal distribution with unknown σ (using t distribution); a PI for a single observation; • CIs for σ2 and σ of a normal distribution (using χ2 distribution).
x tolerance critical value s
Tolerance critical values for k = 90, 95, and 99 in combination with various sample sizes are given in Appendix Table A.6. This table also include critical values for a confidence level of 99%. Replacing by + gives an upper tolerance bound, and using – gives a lower tolerance bound. Critical values for obtaining these one-sided bounds also appear in Appendix Table A.6.
– The null hypothesis fails to be rejected
• This is a weak result.
• It DOES NOT imply that the null hypothesis is true. • Only that there is not a convincing amount of data to support the alternative • If you want to prove something, it should be your alternative hypothesis, not your null hypothesis.
χ2ν curve Each shaded area = α/2 1- α
2 1 /2,
2
/2,
Now ν = n -1,
2 (n 1) S 2 2 P 1 /2,n1 /2, n1 1 2
Rearrange the inequation, we obtain:
Definition
The null hypothesis ( 原 假 设 、 零 假 设 、 无 效 假 设 ) , denoted by H0, is the claim about one or more population characteristics that is initially assumed to be true (the “prior belief” claim). The alternative hypothesis(备择假设), denoted by Ha, is the assertion that is contradictory to H0. The null hypothesis will be rejected in favor of the alternative hypothesis only if sample evidence suggests that H0 is false. If the sample does not strongly contradict H0, we will continue to believe in the truth of the null hypothesis.
Chap. 8 Tests of Hypotheses Based on a Single Sample
8.1 Hypotheses and Test Procedures
A statistical hypothesis(统计假设), or hypothesis, is a claim either about the value of a single population characteristic or about the values of several population characteristics. Examples of hypotheses:
