Chap5 分析力学7
PhysicsChpt5物理双语课件

5.2 Calculate force
A tennis ball contacts the racquet for much less than one second. High-speed photographs show that the speed of the ball changes from -30 to +30 m/sec in 0.006 seconds. If the mass of the ball is 0.2 kg, how much force is applied by the racquet?
A static problem usually means there is no motion.
5.2 Calculate force
A woman is holding two dogs on a leash. If each dog pulls with a force of 80 newtons, how much force does the woman have to exert to keep the dogs from moving?
Three people are each applying 250 newtons of force to try to move a heavy cart. The people are standing on a rug. Someone nearby notices that the rug is slipping. How much force must be applied to the rug to keep it from slipping?
dynamic equilibrium
弹性力学第七章平面问题的极坐标解

第七章 平面问题的极坐标解知识点极坐标下的应力分量 极坐标下的应变分量 极坐标系的 Laplace 算符 轴对称应力分量 轴对称位移和应力表达式 曲梁纯弯曲 纯弯曲位移与平面假设 带圆孔平板拉伸问题 楔形体问题的应力函数 楔形体应力 楔形体受集中力偶作用、内容介绍在弹性力学问题的处理时,坐标系的选择从本质上讲并不影响问题的求解, 但是坐标的选取直接影响边界条件的描述形式,从而关系到问题求解的难易程 度。
对于圆形,楔形,扇形等工程构件,采用极坐标系统求解将比直角坐标系统 要方便的多。
本章的任务就是推导极坐标表示的弹性力学平面问题基本方程, 且求解一些典型问题。
极坐标平衡微分方程 几何方程的极坐标表达 应力函数 轴对称位移 厚壁圆筒作用均匀压力 曲梁弯曲应力 曲梁作用径向集中力 孔口应力 楔形体边界条件 半无限平面作用集中力二、重点1、基本未知量和基本方程的极坐标形式;2、双调和方程的极坐标形式;3、轴对称应力与厚壁圆筒应力;4、曲梁纯弯曲、楔形体和圆孔等典型问题§7.1平面问题极坐标解的基本方程学习思路:选取极坐标系处理弹性力学平面问题,首先必须将弹性力学的基本方程以及边界条件通过极坐标形式描述和表达。
本节的主要工作是介绍基本物理量,包括位移、应力和应变的极坐标形式;并且将基本方程,包括平衡微分方程、几何方程和本构关系转化为极坐标形式。
由于仍然采用应力解法,因此应力函数的极坐标表达是必要的。
应该注意的是坐标系的选取与问题求解性质无关,因此弹性力学直角坐标解的基本概念仍然适用于极坐标。
学习要点:1、极坐标下的应力分量;2、极坐标平衡微分方程;3、极坐标下的应变分量;4、几何方程的极坐标表达;5、本构方程的极坐标表达;6极坐标系的LaPIaCe算符;7、应力函数。
1、极坐标下的应力分量为了表明极坐标系统中的应力分量,从考察的平面物体中分割出微分单元体ABCD ,其由两个相距茁的圆柱面和互成d「的两个径向面构成,如图所示在极坐标系中,用二表示径向正应力,用二表示环向正应力,「,和•二:分别表示圆柱面和径向面的切应力,根据切应力互等定理,.J=.二:。
分析力学-关于作业的几点说明(精)

1.1 直角坐标系的表达式,没有写完整,需要把theta和phi用x,y,z表示出来cos(theta)=z/SQRT(x^2+y^2+z^2)cos(phi)=x/SQRT(x^2+y^2)1.15 上课时在黑板上已经推导3.6见blackboard新上传的,在部分答案那个文件夹中3.8 纯数学积分,考试不涉及4.12 ①dI的表达式的解释:I=mr2对于N各质点,公式变为I=∑miri2i=1N对于N→∞质点连续分布的情况,上述求和变为积分I=⎰mr2dr我们选取的是圆盘作为微元圆盘厚度为dh,圆盘的半径为r如答案上的图所示,r=Rh/Hdh圆盘作为微元dI=⎰dI'dI'=dmr'2dm是圆盘上一个圆环微元的质量dm=ρ(2πr'dr'dh)括号内为圆盘的体积⇒dI=⎰ρ(2πr'dr'dh)r'2ρ为体密度显然r'由0积分到rr4dI=2πρdh4再对h积分即可,积分限为0~H ②圆锥可以分解成N个微元盘绕高(此为z方向)转动的转动惯量的叠加,即为Iz=3mR2,第一问的结果10要求圆锥绕底面直径转动的转动惯量,利用平行轴定理,只需要求出每个微圆盘(质量为dmi)绕自己直径转动的转动惯量,然后加上dmi*它到底面的距离(由第一问知为H-h)的平方即可。
即可以想象成把这N个微元盘压缩在底面上,求出它们绕底面直径转动的转动惯量,然后再把它们拉到现在的位置I=⎰⎡⎣dI(绕自己直径转动)+dI(平行轴定理)⎤⎦=⎰dI(绕自己直径转动)+⎰dI(平行轴定理)=Ix(orIy)+⎰dI(平行轴定理)垂直轴定理:Iz=Ix+Iy由于圆锥绕高是轴对称,所以必然有Ix=Iy=13Iz=mR2220H12=⎰ρ(πr2dh)(H-h)=mH2010 ⎰dI(平行轴定理)=⎰dm(H-h)24.13 4.17见blackboard新上传的,在部分答案那个文件夹中。
分析力学知识点

分析力学知识点可以基于逐步思考进行学习和理解。
本文将分为以下几个部分来介绍分析力学的一些核心概念和方法。
1. 引言分析力学是力学的一个重要分支,它研究物体在受到外力作用下的运动规律。
与牛顿力学不同的是,分析力学采用了更为抽象和数学化的方法,通过建立系统的数学模型来解决运动问题。
2. 基本概念在学习分析力学之前,我们首先需要了解几个基本概念。
2.1 质点质点是分析力学研究的基本对象,它被假设为没有大小和形状的点,只有质量。
质点的位置可以用坐标来描述,通常使用笛卡尔坐标系或极坐标系。
2.2 力力是导致物体发生运动或形状改变的原因。
在分析力学中,力的大小和方向都是非常重要的。
力可以通过矢量表示,其中矢量的方向表示力的方向,矢量的大小表示力的大小。
2.3 动力学方程动力学方程是分析力学的核心内容之一。
它描述了质点在受到力作用下的运动规律。
根据牛顿第二定律,动力学方程可以表示为质点的质量乘以加速度等于受到的合力。
这个方程可以用矢量形式表示。
3. 求解方法分析力学中有多种方法可以用来求解动力学方程,下面介绍其中两种常用的方法。
3.1 拉格朗日方程拉格朗日方程是分析力学中最常用的方法之一。
它基于能量守恒原理,将系统的运动描述为质点在广义坐标下的变换。
通过建立拉格朗日函数,并利用欧拉-拉格朗日方程,可以得到描述质点运动的方程。
3.2 哈密顿方程哈密顿方程是另一种常用的方法。
它基于哈密顿函数,通过将质点的坐标和动量表示为广义坐标和广义动量的函数,可以得到描述质点运动的方程。
哈密顿方程在某些问题的求解中更为方便和有效。
4. 应用领域分析力学作为力学的一个重要分支,在很多领域都有广泛的应用。
4.1 天体力学天体力学研究天体运动的规律,包括行星、卫星等天体的运动。
分析力学提供了描述天体运动的数学方法,通过求解动力学方程,可以预测和解释天体运动的现象。
4.2 机械系统分析力学可以应用于机械系统的研究和设计。
通过建立系统的动力学模型,可以优化机械系统的结构和运动性能,提高效率和稳定性。
物理学专业英语

华中师范大学物理学院物理学专业英语仅供内部学习参考!2014一、课程的任务和教学目的通过学习《物理学专业英语》,学生将掌握物理学领域使用频率较高的专业词汇和表达方法,进而具备基本的阅读理解物理学专业文献的能力。
通过分析《物理学专业英语》课程教材中的范文,学生还将从英语角度理解物理学中个学科的研究内容和主要思想,提高学生的专业英语能力和了解物理学研究前沿的能力。
培养专业英语阅读能力,了解科技英语的特点,提高专业外语的阅读质量和阅读速度;掌握一定量的本专业英文词汇,基本达到能够独立完成一般性本专业外文资料的阅读;达到一定的笔译水平。
要求译文通顺、准确和专业化。
要求译文通顺、准确和专业化。
二、课程内容课程内容包括以下章节:物理学、经典力学、热力学、电磁学、光学、原子物理、统计力学、量子力学和狭义相对论三、基本要求1.充分利用课内时间保证充足的阅读量(约1200~1500词/学时),要求正确理解原文。
2.泛读适量课外相关英文读物,要求基本理解原文主要内容。
3.掌握基本专业词汇(不少于200词)。
4.应具有流利阅读、翻译及赏析专业英语文献,并能简单地进行写作的能力。
四、参考书目录1 Physics 物理学 (1)Introduction to physics (1)Classical and modern physics (2)Research fields (4)V ocabulary (7)2 Classical mechanics 经典力学 (10)Introduction (10)Description of classical mechanics (10)Momentum and collisions (14)Angular momentum (15)V ocabulary (16)3 Thermodynamics 热力学 (18)Introduction (18)Laws of thermodynamics (21)System models (22)Thermodynamic processes (27)Scope of thermodynamics (29)V ocabulary (30)4 Electromagnetism 电磁学 (33)Introduction (33)Electrostatics (33)Magnetostatics (35)Electromagnetic induction (40)V ocabulary (43)5 Optics 光学 (45)Introduction (45)Geometrical optics (45)Physical optics (47)Polarization (50)V ocabulary (51)6 Atomic physics 原子物理 (52)Introduction (52)Electronic configuration (52)Excitation and ionization (56)V ocabulary (59)7 Statistical mechanics 统计力学 (60)Overview (60)Fundamentals (60)Statistical ensembles (63)V ocabulary (65)8 Quantum mechanics 量子力学 (67)Introduction (67)Mathematical formulations (68)Quantization (71)Wave-particle duality (72)Quantum entanglement (75)V ocabulary (77)9 Special relativity 狭义相对论 (79)Introduction (79)Relativity of simultaneity (80)Lorentz transformations (80)Time dilation and length contraction (81)Mass-energy equivalence (82)Relativistic energy-momentum relation (86)V ocabulary (89)正文标记说明:蓝色Arial字体(例如energy):已知的专业词汇蓝色Arial字体加下划线(例如electromagnetism):新学的专业词汇黑色Times New Roman字体加下划线(例如postulate):新学的普通词汇1 Physics 物理学1 Physics 物理学Introduction to physicsPhysics is a part of natural philosophy and a natural science that involves the study of matter and its motion through space and time, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic disciplines, perhaps the oldest through its inclusion of astronomy. Over the last two millennia, physics was a part of natural philosophy along with chemistry, certain branches of mathematics, and biology, but during the Scientific Revolution in the 17th century, the natural sciences emerged as unique research programs in their own right. Physics intersects with many interdisciplinary areas of research, such as biophysics and quantum chemistry,and the boundaries of physics are not rigidly defined. New ideas in physics often explain the fundamental mechanisms of other sciences, while opening new avenues of research in areas such as mathematics and philosophy.Physics also makes significant contributions through advances in new technologies that arise from theoretical breakthroughs. For example, advances in the understanding of electromagnetism or nuclear physics led directly to the development of new products which have dramatically transformed modern-day society, such as television, computers, domestic appliances, and nuclear weapons; advances in thermodynamics led to the development of industrialization; and advances in mechanics inspired the development of calculus.Core theoriesThough physics deals with a wide variety of systems, certain theories are used by all physicists. Each of these theories were experimentally tested numerous times and found correct as an approximation of nature (within a certain domain of validity).For instance, the theory of classical mechanics accurately describes the motion of objects, provided they are much larger than atoms and moving at much less than the speed of light. These theories continue to be areas of active research, and a remarkable aspect of classical mechanics known as chaos was discovered in the 20th century, three centuries after the original formulation of classical mechanics by Isaac Newton (1642–1727) 【艾萨克·牛顿】.University PhysicsThese central theories are important tools for research into more specialized topics, and any physicist, regardless of his or her specialization, is expected to be literate in them. These include classical mechanics, quantum mechanics, thermodynamics and statistical mechanics, electromagnetism, and special relativity.Classical and modern physicsClassical mechanicsClassical physics includes the traditional branches and topics that were recognized and well-developed before the beginning of the 20th century—classical mechanics, acoustics, optics, thermodynamics, and electromagnetism.Classical mechanics is concerned with bodies acted on by forces and bodies in motion and may be divided into statics (study of the forces on a body or bodies at rest), kinematics (study of motion without regard to its causes), and dynamics (study of motion and the forces that affect it); mechanics may also be divided into solid mechanics and fluid mechanics (known together as continuum mechanics), the latter including such branches as hydrostatics, hydrodynamics, aerodynamics, and pneumatics.Acoustics is the study of how sound is produced, controlled, transmitted and received. Important modern branches of acoustics include ultrasonics, the study of sound waves of very high frequency beyond the range of human hearing; bioacoustics the physics of animal calls and hearing, and electroacoustics, the manipulation of audible sound waves using electronics.Optics, the study of light, is concerned not only with visible light but also with infrared and ultraviolet radiation, which exhibit all of the phenomena of visible light except visibility, e.g., reflection, refraction, interference, diffraction, dispersion, and polarization of light.Heat is a form of energy, the internal energy possessed by the particles of which a substance is composed; thermodynamics deals with the relationships between heat and other forms of energy.Electricity and magnetism have been studied as a single branch of physics since the intimate connection between them was discovered in the early 19th century; an electric current gives rise to a magnetic field and a changing magnetic field induces an electric current. Electrostatics deals with electric charges at rest, electrodynamics with moving charges, and magnetostatics with magnetic poles at rest.Modern PhysicsClassical physics is generally concerned with matter and energy on the normal scale of1 Physics 物理学observation, while much of modern physics is concerned with the behavior of matter and energy under extreme conditions or on the very large or very small scale.For example, atomic and nuclear physics studies matter on the smallest scale at which chemical elements can be identified.The physics of elementary particles is on an even smaller scale, as it is concerned with the most basic units of matter; this branch of physics is also known as high-energy physics because of the extremely high energies necessary to produce many types of particles in large particle accelerators. On this scale, ordinary, commonsense notions of space, time, matter, and energy are no longer valid.The two chief theories of modern physics present a different picture of the concepts of space, time, and matter from that presented by classical physics.Quantum theory is concerned with the discrete, rather than continuous, nature of many phenomena at the atomic and subatomic level, and with the complementary aspects of particles and waves in the description of such phenomena.The theory of relativity is concerned with the description of phenomena that take place in a frame of reference that is in motion with respect to an observer; the special theory of relativity is concerned with relative uniform motion in a straight line and the general theory of relativity with accelerated motion and its connection with gravitation.Both quantum theory and the theory of relativity find applications in all areas of modern physics.Difference between classical and modern physicsWhile physics aims to discover universal laws, its theories lie in explicit domains of applicability. Loosely speaking, the laws of classical physics accurately describe systems whose important length scales are greater than the atomic scale and whose motions are much slower than the speed of light. Outside of this domain, observations do not match their predictions.Albert Einstein【阿尔伯特·爱因斯坦】contributed the framework of special relativity, which replaced notions of absolute time and space with space-time and allowed an accurate description of systems whose components have speeds approaching the speed of light.Max Planck【普朗克】, Erwin Schrödinger【薛定谔】, and others introduced quantum mechanics, a probabilistic notion of particles and interactions that allowed an accurate description of atomic and subatomic scales.Later, quantum field theory unified quantum mechanics and special relativity.General relativity allowed for a dynamical, curved space-time, with which highly massiveUniversity Physicssystems and the large-scale structure of the universe can be well-described. General relativity has not yet been unified with the other fundamental descriptions; several candidate theories of quantum gravity are being developed.Research fieldsContemporary research in physics can be broadly divided into condensed matter physics; atomic, molecular, and optical physics; particle physics; astrophysics; geophysics and biophysics. Some physics departments also support research in Physics education.Since the 20th century, the individual fields of physics have become increasingly specialized, and today most physicists work in a single field for their entire careers. "Universalists" such as Albert Einstein (1879–1955) and Lev Landau (1908–1968)【列夫·朗道】, who worked in multiple fields of physics, are now very rare.Condensed matter physicsCondensed matter physics is the field of physics that deals with the macroscopic physical properties of matter. In particular, it is concerned with the "condensed" phases that appear whenever the number of particles in a system is extremely large and the interactions between them are strong.The most familiar examples of condensed phases are solids and liquids, which arise from the bonding by way of the electromagnetic force between atoms. More exotic condensed phases include the super-fluid and the Bose–Einstein condensate found in certain atomic systems at very low temperature, the superconducting phase exhibited by conduction electrons in certain materials,and the ferromagnetic and antiferromagnetic phases of spins on atomic lattices.Condensed matter physics is by far the largest field of contemporary physics.Historically, condensed matter physics grew out of solid-state physics, which is now considered one of its main subfields. The term condensed matter physics was apparently coined by Philip Anderson when he renamed his research group—previously solid-state theory—in 1967. In 1978, the Division of Solid State Physics of the American Physical Society was renamed as the Division of Condensed Matter Physics.Condensed matter physics has a large overlap with chemistry, materials science, nanotechnology and engineering.Atomic, molecular and optical physicsAtomic, molecular, and optical physics (AMO) is the study of matter–matter and light–matter interactions on the scale of single atoms and molecules.1 Physics 物理学The three areas are grouped together because of their interrelationships, the similarity of methods used, and the commonality of the energy scales that are relevant. All three areas include both classical, semi-classical and quantum treatments; they can treat their subject from a microscopic view (in contrast to a macroscopic view).Atomic physics studies the electron shells of atoms. Current research focuses on activities in quantum control, cooling and trapping of atoms and ions, low-temperature collision dynamics and the effects of electron correlation on structure and dynamics. Atomic physics is influenced by the nucleus (see, e.g., hyperfine splitting), but intra-nuclear phenomena such as fission and fusion are considered part of high-energy physics.Molecular physics focuses on multi-atomic structures and their internal and external interactions with matter and light.Optical physics is distinct from optics in that it tends to focus not on the control of classical light fields by macroscopic objects, but on the fundamental properties of optical fields and their interactions with matter in the microscopic realm.High-energy physics (particle physics) and nuclear physicsParticle physics is the study of the elementary constituents of matter and energy, and the interactions between them.In addition, particle physicists design and develop the high energy accelerators,detectors, and computer programs necessary for this research. The field is also called "high-energy physics" because many elementary particles do not occur naturally, but are created only during high-energy collisions of other particles.Currently, the interactions of elementary particles and fields are described by the Standard Model.●The model accounts for the 12 known particles of matter (quarks and leptons) thatinteract via the strong, weak, and electromagnetic fundamental forces.●Dynamics are described in terms of matter particles exchanging gauge bosons (gluons,W and Z bosons, and photons, respectively).●The Standard Model also predicts a particle known as the Higgs boson. In July 2012CERN, the European laboratory for particle physics, announced the detection of a particle consistent with the Higgs boson.Nuclear Physics is the field of physics that studies the constituents and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those in nuclear medicine and magnetic resonance imaging, ion implantation in materials engineering, and radiocarbon dating in geology and archaeology.University PhysicsAstrophysics and Physical CosmologyAstrophysics and astronomy are the application of the theories and methods of physics to the study of stellar structure, stellar evolution, the origin of the solar system, and related problems of cosmology. Because astrophysics is a broad subject, astrophysicists typically apply many disciplines of physics, including mechanics, electromagnetism, statistical mechanics, thermodynamics, quantum mechanics, relativity, nuclear and particle physics, and atomic and molecular physics.The discovery by Karl Jansky in 1931 that radio signals were emitted by celestial bodies initiated the science of radio astronomy. Most recently, the frontiers of astronomy have been expanded by space exploration. Perturbations and interference from the earth's atmosphere make space-based observations necessary for infrared, ultraviolet, gamma-ray, and X-ray astronomy.Physical cosmology is the study of the formation and evolution of the universe on its largest scales. Albert Einstein's theory of relativity plays a central role in all modern cosmological theories. In the early 20th century, Hubble's discovery that the universe was expanding, as shown by the Hubble diagram, prompted rival explanations known as the steady state universe and the Big Bang.The Big Bang was confirmed by the success of Big Bang nucleo-synthesis and the discovery of the cosmic microwave background in 1964. The Big Bang model rests on two theoretical pillars: Albert Einstein's general relativity and the cosmological principle (On a sufficiently large scale, the properties of the Universe are the same for all observers). Cosmologists have recently established the ΛCDM model (the standard model of Big Bang cosmology) of the evolution of the universe, which includes cosmic inflation, dark energy and dark matter.Current research frontiersIn condensed matter physics, an important unsolved theoretical problem is that of high-temperature superconductivity. Many condensed matter experiments are aiming to fabricate workable spintronics and quantum computers.In particle physics, the first pieces of experimental evidence for physics beyond the Standard Model have begun to appear. Foremost among these are indications that neutrinos have non-zero mass. These experimental results appear to have solved the long-standing solar neutrino problem, and the physics of massive neutrinos remains an area of active theoretical and experimental research. Particle accelerators have begun probing energy scales in the TeV range, in which experimentalists are hoping to find evidence for the super-symmetric particles, after discovery of the Higgs boson.Theoretical attempts to unify quantum mechanics and general relativity into a single theory1 Physics 物理学of quantum gravity, a program ongoing for over half a century, have not yet been decisively resolved. The current leading candidates are M-theory, superstring theory and loop quantum gravity.Many astronomical and cosmological phenomena have yet to be satisfactorily explained, including the existence of ultra-high energy cosmic rays, the baryon asymmetry, the acceleration of the universe and the anomalous rotation rates of galaxies.Although much progress has been made in high-energy, quantum, and astronomical physics, many everyday phenomena involving complexity, chaos, or turbulence are still poorly understood. Complex problems that seem like they could be solved by a clever application of dynamics and mechanics remain unsolved; examples include the formation of sand-piles, nodes in trickling water, the shape of water droplets, mechanisms of surface tension catastrophes, and self-sorting in shaken heterogeneous collections.These complex phenomena have received growing attention since the 1970s for several reasons, including the availability of modern mathematical methods and computers, which enabled complex systems to be modeled in new ways. Complex physics has become part of increasingly interdisciplinary research, as exemplified by the study of turbulence in aerodynamics and the observation of pattern formation in biological systems.Vocabulary★natural science 自然科学academic disciplines 学科astronomy 天文学in their own right 凭他们本身的实力intersects相交,交叉interdisciplinary交叉学科的,跨学科的★quantum 量子的theoretical breakthroughs 理论突破★electromagnetism 电磁学dramatically显著地★thermodynamics热力学★calculus微积分validity★classical mechanics 经典力学chaos 混沌literate 学者★quantum mechanics量子力学★thermodynamics and statistical mechanics热力学与统计物理★special relativity狭义相对论is concerned with 关注,讨论,考虑acoustics 声学★optics 光学statics静力学at rest 静息kinematics运动学★dynamics动力学ultrasonics超声学manipulation 操作,处理,使用University Physicsinfrared红外ultraviolet紫外radiation辐射reflection 反射refraction 折射★interference 干涉★diffraction 衍射dispersion散射★polarization 极化,偏振internal energy 内能Electricity电性Magnetism 磁性intimate 亲密的induces 诱导,感应scale尺度★elementary particles基本粒子★high-energy physics 高能物理particle accelerators 粒子加速器valid 有效的,正当的★discrete离散的continuous 连续的complementary 互补的★frame of reference 参照系★the special theory of relativity 狭义相对论★general theory of relativity 广义相对论gravitation 重力,万有引力explicit 详细的,清楚的★quantum field theory 量子场论★condensed matter physics凝聚态物理astrophysics天体物理geophysics地球物理Universalist博学多才者★Macroscopic宏观Exotic奇异的★Superconducting 超导Ferromagnetic铁磁质Antiferromagnetic 反铁磁质★Spin自旋Lattice 晶格,点阵,网格★Society社会,学会★microscopic微观的hyperfine splitting超精细分裂fission分裂,裂变fusion熔合,聚变constituents成分,组分accelerators加速器detectors 检测器★quarks夸克lepton 轻子gauge bosons规范玻色子gluons胶子★Higgs boson希格斯玻色子CERN欧洲核子研究中心★Magnetic Resonance Imaging磁共振成像,核磁共振ion implantation 离子注入radiocarbon dating放射性碳年代测定法geology地质学archaeology考古学stellar 恒星cosmology宇宙论celestial bodies 天体Hubble diagram 哈勃图Rival竞争的★Big Bang大爆炸nucleo-synthesis核聚合,核合成pillar支柱cosmological principle宇宙学原理ΛCDM modelΛ-冷暗物质模型cosmic inflation宇宙膨胀1 Physics 物理学fabricate制造,建造spintronics自旋电子元件,自旋电子学★neutrinos 中微子superstring 超弦baryon重子turbulence湍流,扰动,骚动catastrophes突变,灾变,灾难heterogeneous collections异质性集合pattern formation模式形成University Physics2 Classical mechanics 经典力学IntroductionIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces. The study of the motion of bodies is an ancient one, making classical mechanics one of the oldest and largest subjects in science, engineering and technology.Classical mechanics describes the motion of macroscopic objects, from projectiles to parts of machinery, as well as astronomical objects, such as spacecraft, planets, stars, and galaxies. Besides this, many specializations within the subject deal with gases, liquids, solids, and other specific sub-topics.Classical mechanics provides extremely accurate results as long as the domain of study is restricted to large objects and the speeds involved do not approach the speed of light. When the objects being dealt with become sufficiently small, it becomes necessary to introduce the other major sub-field of mechanics, quantum mechanics, which reconciles the macroscopic laws of physics with the atomic nature of matter and handles the wave–particle duality of atoms and molecules. In the case of high velocity objects approaching the speed of light, classical mechanics is enhanced by special relativity. General relativity unifies special relativity with Newton's law of universal gravitation, allowing physicists to handle gravitation at a deeper level.The initial stage in the development of classical mechanics is often referred to as Newtonian mechanics, and is associated with the physical concepts employed by and the mathematical methods invented by Newton himself, in parallel with Leibniz【莱布尼兹】, and others.Later, more abstract and general methods were developed, leading to reformulations of classical mechanics known as Lagrangian mechanics and Hamiltonian mechanics. These advances were largely made in the 18th and 19th centuries, and they extend substantially beyond Newton's work, particularly through their use of analytical mechanics. Ultimately, the mathematics developed for these were central to the creation of quantum mechanics.Description of classical mechanicsThe following introduces the basic concepts of classical mechanics. For simplicity, it often2 Classical mechanics 经典力学models real-world objects as point particles, objects with negligible size. The motion of a point particle is characterized by a small number of parameters: its position, mass, and the forces applied to it.In reality, the kind of objects that classical mechanics can describe always have a non-zero size. (The physics of very small particles, such as the electron, is more accurately described by quantum mechanics). Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom—for example, a baseball can spin while it is moving. However, the results for point particles can be used to study such objects by treating them as composite objects, made up of a large number of interacting point particles. The center of mass of a composite object behaves like a point particle.Classical mechanics uses common-sense notions of how matter and forces exist and interact. It assumes that matter and energy have definite, knowable attributes such as where an object is in space and its speed. It also assumes that objects may be directly influenced only by their immediate surroundings, known as the principle of locality.In quantum mechanics objects may have unknowable position or velocity, or instantaneously interact with other objects at a distance.Position and its derivativesThe position of a point particle is defined with respect to an arbitrary fixed reference point, O, in space, usually accompanied by a coordinate system, with the reference point located at the origin of the coordinate system. It is defined as the vector r from O to the particle.In general, the point particle need not be stationary relative to O, so r is a function of t, the time elapsed since an arbitrary initial time.In pre-Einstein relativity (known as Galilean relativity), time is considered an absolute, i.e., the time interval between any given pair of events is the same for all observers. In addition to relying on absolute time, classical mechanics assumes Euclidean geometry for the structure of space.Velocity and speedThe velocity, or the rate of change of position with time, is defined as the derivative of the position with respect to time. In classical mechanics, velocities are directly additive and subtractive as vector quantities; they must be dealt with using vector analysis.When both objects are moving in the same direction, the difference can be given in terms of speed only by ignoring direction.University PhysicsAccelerationThe acceleration , or rate of change of velocity, is the derivative of the velocity with respect to time (the second derivative of the position with respect to time).Acceleration can arise from a change with time of the magnitude of the velocity or of the direction of the velocity or both . If only the magnitude v of the velocity decreases, this is sometimes referred to as deceleration , but generally any change in the velocity with time, including deceleration, is simply referred to as acceleration.Inertial frames of referenceWhile the position and velocity and acceleration of a particle can be referred to any observer in any state of motion, classical mechanics assumes the existence of a special family of reference frames in terms of which the mechanical laws of nature take a comparatively simple form. These special reference frames are called inertial frames .An inertial frame is such that when an object without any force interactions (an idealized situation) is viewed from it, it appears either to be at rest or in a state of uniform motion in a straight line. This is the fundamental definition of an inertial frame. They are characterized by the requirement that all forces entering the observer's physical laws originate in identifiable sources (charges, gravitational bodies, and so forth).A non-inertial reference frame is one accelerating with respect to an inertial one, and in such a non-inertial frame a particle is subject to acceleration by fictitious forces that enter the equations of motion solely as a result of its accelerated motion, and do not originate in identifiable sources. These fictitious forces are in addition to the real forces recognized in an inertial frame.A key concept of inertial frames is the method for identifying them. For practical purposes, reference frames that are un-accelerated with respect to the distant stars are regarded as good approximations to inertial frames.Forces; Newton's second lawNewton was the first to mathematically express the relationship between force and momentum . Some physicists interpret Newton's second law of motion as a definition of force and mass, while others consider it a fundamental postulate, a law of nature. Either interpretation has the same mathematical consequences, historically known as "Newton's Second Law":a m t v m t p F ===d )(d d dThe quantity m v is called the (canonical ) momentum . The net force on a particle is thus equal to rate of change of momentum of the particle with time.So long as the force acting on a particle is known, Newton's second law is sufficient to。
第五章 分析力学ppt课件

或
不可解约束以等式表示,可解约束则同时以等式和 不等式表示。
5.1
约束与广义坐标
第5章 分析力
③几何约束(完整约束)与运动约束(微分约束)
某些约束仅对力学系统的空间位置加以限制,而对各质点的速
度没有限制, 这种约束称为几何约束 (geometrical constraint )。可 表示为
f r , r , r , , t 0 1 2 3
§5.0
引言
第5章 分析力
5 提出新的力学原理代替牛顿定律
牛顿力学 矢量力学 力学第一原理 拉格朗日方程 拉格朗日力学 (相当于“几何公理” ) 哈密顿力学 哈密顿原理
三者本质上相同,可以相互证明 利用无穷小计算原理对抽象数学及应用数学的应用,使用拉格 郞日和哈密顿方法给以力学问题抽象的数学处理,即把物理世 界事物属性翻译成数学关系式,中间不考虑物理意义,只在讨 论计算结果时再翻译转化到真实物理世界上去。
或
f r , r , r , , r ; r , r , r , , r 0 1 2 3 n 1 2 3 n
或
f r , r , r , , r ; r , r , r , , r , t 0 1 2 3 n 1 2 3 n f r , r , r , , r ; r , r , r , , r , t 0 1 2 3 n 1 2 3 n
或
f r , r , r , , r ; r , r , r , , r , t 0 1 2 3 n 1 2 3 n
5.1
约束与广义坐标
材料力学第五版第七节应力状态答案.doc

材料力学第五版第七节应力状态答案第七章应力状态与强度理论一、教学目标和教学内容1.教学目标通过本章学习,掌握应力状态的概念及其研究方法;会从具有受力杆件中截取单元体并标明单元体上的应力情况;会计算平面应力状态下斜截面上的应力;掌握平面应力状态和特殊空间应力状态下的主应力、主方向的计算,并会排列主应力的顺序;掌握广义胡克定律;了解复杂应力状态比能的概念;了解主应力迹线的概念。
掌握强度理论的概念。
了解材料的两种破坏形式(按破坏现象区分)。
了解常用的四个强度理论的观点、破坏条件、强度条件。
掌握常用的四个强度理论的相当应力。
了解莫尔强度理论的基本观点。
会用强度理论对一些简单的杆件结构进行强度计算。
2.教学内容应力状态的概念;平面应力状态分析;三向应力状态下的最大应力;广义胡克定律体应变;复杂应力状态的比能;⑥梁的主应力主应力迹线的概念。
讲解强度理论的概念及材料的两种破坏形式。
讲解常用的四个强度理论的基本观点,并推导其破坏条件从而建立强度计算方法。
介绍几种强度理论的应用范围和各自的优缺点。
简单介绍莫尔强度理论。
二、重点难点重点1、平面应力状态下斜截面上的应力计算,主应力及主方向的计算,最大剪应力的计算。
2、广义胡克定律及其应用。
难点1、应力状态的概念,从具体受力杆件中截面单元体并标明单元体上的应力情况。
2、斜截面上的应力计算公式中关于正负符号的约定。
3、应力主平面、主应力的概念,主应力的大小、方向的确定。
4、广义胡克定律及其应用。
5 强度理论的概念、常用的四个强度理论的观点、强度条件及其强度计算。
6 常用四个强度理论的理解。
7 危险点的确定及其强度计算。
三、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
四、建议学时10学时五、讲课提纲1、应力状态的概念所谓“应力状态”又称为一点处的应力状态(state of stresses at a given point),是指过一点不同方向面上应力的集合。
理论力学-第五章分析力学1-wcx

(1)使用范围:理想约束 (2)范围的扩展:对于有摩檫的约束,可将其视为主动力 (3)优点:去掉约束力,仅得到主动力平衡方程
局限性:无法求约束力
F Fx i Fy j Fz k 【例1】自由质点受外力作用保持平衡,所受外力为:
试由虚功原理求其平衡方程。
2、广义坐标形式的虚功原理
约束力不出现在方程中
方程形式与坐标系的选择无关
方程形式与研究对象无关
完全用数学分析的方法来处理力学问题
第一节 约束与广义坐标
一、约束 1、约束的概念:限制质点自由运动的条件 2、约束与自由度的关系:s 3n k 3、约束的分类 (1)稳定约束和非稳定约束
f ( x, y, z ) 0 稳定约束(定常约束) 约束方程 束) f ( x, y, z; t ) 0 非稳定约束(非定常约 v
a 2 sin cos l 2 a 2 sin 2
1
Q M Fa sin F
a 2 sin cos l a 何约束 f ( x, y, z; t ) 0 微分约束
, y , z ; t ) 0 f ( x, y, z; x
可以积分 不可积分
完整约束 非完整约束
可解约束
(2)完整系:只受完整约束的力学体系;
不完整系:受到不完整约束的力学体系
x
s
y
F
虚位移的大小: s l
x s cos l cos 分量形式: y s sin l sin
(2)变分运算法
先写出质点的笛卡尔坐标,找到其与广义坐标之间的关系,再 利用变分计算出对应的虚位移
周衍柏著理论力学——第五章分析力学 pdf讲义

3
不可解约束:质点始终不能脱离的约束。如质点始终被曲面 约束,即存在约束方程
f ( x, y , z ) = 0 或 f ( x, y , z , t ) = 0 (5.1.3)
约束又可分为几何约束和运动约束。 几何约束又叫做完整约束,它只限制质点在空间的位置,因 而表现为质点坐标的函数,如
f ( x, y , z ) = 0 或 f ( x, y , z , t ) = 0 (5.1.3)
dr P
δr
7
8
9
三、虚功原理 以下讨论只限于不可解约束的情况,设体系在 k 个几何约束 下处于平衡状态。由于体系处于平衡状态,所以体系中每一 个质点都处于平衡状态。 因此任一质点 Pi ,受到主动力的合力 Fi 与约束反力的合力 Ri 满足: (i = 1,2, L , n ) (5.2.3) Fi + Ri = 0 让每一质点在平衡位置发生一虚位移 δr ,则有 Fi ⋅ δr + Ri ⋅ δr = 0 (i = 1,2, L , n ) 上式对各质点求和得:
1
第一节 约束与广义坐标
一、约束的概念和分类 1、力学体系:质点的集合,且质点间存在相互作用,每一 个质点的运动都和其它质点的位置及运动有关,简称体系。 若有 n 个质点,则描述所有质点位置的坐标有 3n 个。 2、约束:限制质点自由运动的条件叫做的约束。 约束一般可表示成质点位置、速度和时间的方程。如:
理论力学第五章分析力学

P x1 , y1 1 P2 x2 , y2 B x3 , y3
1 1 Pl1 cos P2l1 cos Fl1 sin P2l2 cos Fl2 sin 0 1 2 2
ri ri q 0 Fi q mi ri q 1 i 1
s n
ri ri q 0 Fi q mi ri q 1 i 1
xi xi q1 , q2 ,...qs , t
i i
1
2
s
i 1, 2,..., n, s 3n
i
i
1
2
s
或
ri ri q1 , q2 ,...qs , t
i 1, 2,..., n, s 3n
这s个独立参数就叫广义坐标
§5.2 虚功原理
1.实位移和虚位移
第五章 分析力学
分析力学是拉格朗日等人在十八世纪在牛顿力学 基础上建立的经典力学的一个体系,因为所用的方法 完全是数学分析,称之为分析力学。建立分析力学的 目的是为了 用数学方法解决复杂的力学问题,后来的 研究发现,分析力学的体系和方法不局限于力学,对 物理学的其他领域也非常有用。其原因是将物理规律 抽象为数学原理和定理,揭示了物理规律背后更普遍 的性质,掌握这些对今后的学习很重要。 这一章的重点是拉格朗日方程,哈密顿正则方程 和正则变换在统计物理中有重要应用,泊松括号的概 念在量子力学中非常重要。
若拉氏函数不显含
王振发版-分析力学-课件-第4章-力学的变分原理

(4 - 1b)
变分的导数等于导数的变分;变分的积分等于积分 的变分.
(3)变分法 设泛函J 为定积分 J
t2 t1
, t )dt F ( q, q
现欲求通过两固定点 A (t1 , q1 ) 和 B (t 2 , q2 ) 的一条曲线 q q(t ) , 如图 实线所示,这条曲线使泛函 J 具有极 值。 为表示通过A,B两固定点的与 q (t )
非常接近的一族函数,我们将这族
函数表示为依赖于参数 当 0 时, q ( , t ) q (t ) ,就是欲求的函数 q q (t ) 。
的函数 q( , t ) q(t ) (t ) ;
因
可为不同的值,因此泛函 J 也是 ( , t ), t ]dt J ( ) F [q( , t ), q
a (1 cos )d dx 2
积分后得 由
xA 0, y A 0
a x ( sin ) C 2
得
C0 。
于是最后得
a x ( sin ) 2 a y ( cos ) 2
这是以
为参数的旋轮线的曲线方程。其中
xB, y B
给定一个由任何对象组成的集合D,这里所说的任 何对象可以是数、数组、点、线、面,也可以是函数或 某系统的状态等。设集合D中的元素用 x 表示,如果对 于集合中的每一个元素 x 对应一个数 y,则称 y 是x的泛 函,记为 y=F (x).
有时泛函可以看做是函数,函数也可看做是泛数。
譬如,如果集合D中的元素是数 x ,则泛函y=F (x)可 视为函数 y=f (x) ; 如果集合D中的元素是数组(x1, x2, …xn),则泛函 y=F (x) 可视为函数 y=f (x1, x2…xn)。
ChatGPT在科学研究中的实验设计指南

ChatGPT在科学研究中的实验设计指南概述近年来,人工智能技术的发展使得机器学习模型在各个领域得到了广泛应用。
ChatGPT作为一种基于大规模预训练模型的对话生成系统,具备了在人类水平任务上表现出色的能力。
然而,将ChatGPT应用于科学研究中的设计和实验需要一定的指导,以确保实验的可重复性、准确性和科学性。
本文将以ChatGPT在科学研究中的实验设计为主题,讨论如何设计和策划一系列科学实验,以评估ChatGPT模型的性能、鲁棒性和可解释性。
本指南将提供一些基本的方法和步骤,以帮助研究人员在实验过程中有效地利用ChatGPT。
1. 实验目的的明确化在开始实验设计之前,研究人员需要明确实验的目的和研究问题。
例如,你可能想要评估ChatGPT在特定领域任务上的表现,或者你可能想要了解ChatGPT对不同输入的鲁棒性。
明确实验目的可以指导实验设计、数据收集和结果分析。
2. 设计实验方案在设计实验方案时,需要考虑以下几个要素:2.1 实验组和对照组确定实验组和对照组,确保实验的可比性。
实验组将使用ChatGPT进行交互,而对照组则可以使用其他对话系统、或者由人类执行对话任务。
2.2 实验数据的采集考虑实验数据的来源和采集方法。
可以选择使用预设对话数据集,也可以根据实验目的设计自定义的对话数据集。
同时,也需要选择适当的对话任务来评估ChatGPT的性能。
2.3 实验设置和参数定义实验的设置和参数,例如ChatGPT的模型规模、训练轮数、批大小等。
这些参数的选择应该基于实验目的和计算资源的限制。
2.4 实验难度和变异程度实验的难度和变异程度可能会影响ChatGPT的表现。
通过合理的设计,可以确保实验结果的可解释性和可比性。
3. 实验评估指标的选择在评估ChatGPT的性能时,可以考虑以下指标:3.1 生成质量生成质量是评估ChatGPT对话回复的一项重要指标。
可以使用BLEU、ROUGE等自然语言处理指标来衡量生成质量。
ChatGPT技术在科学研究中的应用探讨

ChatGPT技术在科学研究中的应用探讨1. 引言近年来,人工智能(AI)的发展取得了突破性进展,并在各个领域产生了广泛的应用。
其中,自然语言处理(NLP)是AI中的一个重要分支,其应用已经渗透到许多领域中。
ChatGPT技术作为自然语言处理的一个重要里程碑,不仅在日常对话中有着广泛的应用,还有潜力在科学研究领域发挥重要的作用。
本文将讨论ChatGPT技术在科学研究中的应用和潜在的影响。
2. ChatGPT技术概述ChatGPT技术是OpenAI开发的一个强大的自然语言处理模型,通过预训练和微调的方式进行语言生成。
该技术通过深度学习模型对海量的数据进行学习,从而具备生成连贯、自然的对话的能力。
它可以理解人类的问题,并生成具有逻辑和连贯性的回答,从而使得对话更加自然流畅。
ChatGPT技术的开发极大地促进了人工智能在对话交互领域的发展。
3. ChatGPT在科学研究中的应用(a) 数据分析和解释:ChatGPT技术可以辅助科学家进行复杂数据的分析和解释。
科研数据通常庞大而复杂,科学家需要花费大量时间和精力才能从中挖掘出有价值的信息。
ChatGPT可以作为一个“助手”,通过自然语言对话的方式帮助科学家处理数据,回答他们的问题,提供有关数据的深入解释。
这样一来,科学家们可以更高效地利用数据,加速研究进程。
(b) 文献检索和知识综述:ChatGPT技术可以用于文献检索和知识综述的自动化。
科学研究通常需要广泛的文献调研和阅读,以确保所做的研究是建立在前人的基础上的。
ChatGPT可以通过与研究者的对话,根据特定的研究主题自动检索相关文献,并对文献进行综述和总结。
这样一来,科学家们可以节省大量的时间和努力,快速获取到领域内的最新知识,并为自己的研究提供充分的参考依据。
(c) 科学实验设计和结果分析:ChatGPT技术可以协助科学家进行实验设计和结果分析。
在科学研究中,实验设计的合理性和结果的分析方法至关重要。
《谢奇之-工程力学》基本变形强度计算

40kN
40kN
60kN
20kN
200
200
A1=200mm2
A2 =250mm2
解:轴力图如图所示
满足强度要求
添加标题
强度条件的应用:
添加标题
强度校核
添加标题
设计截面
添加标题
确定许可核载荷
添加标题
强度条件: 7-3 圆轴扭转变形强度计算
A
B
C
D
1
2
3
4
5
例3-3、图示为某组合机床主轴箱第4轴示意图。
F
F
FN(kN)
x
43kN
3、应力分析
4、强度计算
确定AC杆的直径
[s]=150MPa
斜杆的最小直径为19.1mm
例7-4:试确定气动夹具活塞杆的直径d。
D
d
p
气动夹具
工件
气缸内径D=140mm
内压p=0.6MPa
活塞杆材料为20钢
[s]=80MPa
F
F
解:
1、外力分析
2、内力分析
3、应力分析
4、强度计算
(1) 试求截面Ⅱ上距轴线40mm处的点的剪应力。
Ⅱ
Ⅱ
MA=15.9kN.m
MB=MC=
MD=
d=110mm
(2) 若已知[t]=40MPa,试校核轴的强度。
A
B
C
D
4
MA
MB
Ⅱ
Ⅱ
MC
MD
解:
1、内力分析
4.78
9.56
6.37
x
T
(kNm)
A
B
C
ChatGPT在问答系统中的性能评估方法

ChatGPT在问答系统中的性能评估方法ChatGPT是一种基于深度学习模型的语言生成模型,近年来在自然语言处理领域取得了巨大的突破。
它能够通过对话生成流畅的文本回复,极大地提升了问答系统的用户体验。
然而,对于ChatGPT这样的模型,如何评估其性能成为了一个重要的问题。
本文将探讨在问答系统中对ChatGPT的性能进行评估的方法。
1. 评估数据集的构建要对ChatGPT的性能进行评估,首先需要构建一个评估数据集。
该数据集应该包含各种类型的问题,涉及不同的领域和知识点。
同时,应该针对ChatGPT可能出现的错误进行设计,以检验其鲁棒性和泛化能力。
评估数据集的构建需要经过多轮的人工审核和改进,确保问题的质量和多样性。
2. 对话质量的评估标准ChatGPT的主要目标是生成流畅、连贯的对话。
因此,对于评估这类语言生成模型的性能,常用的指标是自动评估和人工评估相结合的方式。
其中,自动评估指标可以包括BLEU、Perplexity等。
BLEU是一种用于评估机器翻译或文本生成模型输出的相似度的指标,通过计算n-gram重叠度来度量生成的回复与标准回复之间的相似性。
Perplexity用于评估语言模型的困惑度,越低代表模型越能准确地预测下一个词。
然而,自动评估指标存在一些局限性,不能完全反映ChatGPT生成的回复是否符合人类期望。
因此,人工评估也是不可或缺的一部分。
评估人员可以基于对话的流畅性、准确性、逻辑性等方面对回复进行打分。
有时候还可以结合任务型评估,比如问答系统中回答问题的正确率等。
3. 对话一致性的评估方法ChatGPT是一个基于上下文的模型,它通过前面的对话来生成回复。
因此,对话一致性也是评估ChatGPT性能的一个重要指标。
对话一致性的评估可以通过多轮对话的测试来进行。
一种方式是随机生成一系列对话,包括上下文和回复。
然后,要求模型基于给定的上下文生成一个新的回复,评估这个回复是否与之前的回复具有一致性。
板壳力学ch5-大挠度理论

板 的函数,则 x、y 、xy 相互关联。对x 关于 y 求导两次,
理 论
对y 关于 x 求导两次,对xy 关于x、y各求导一次,得到
2 y2x 2 x2y 2 xxyy x2 w y2 2 xw 2 2 yw 2
上式为薄板大挠度弯曲中面应变协调方程,或称为 中面连续条件。
满足连续条件,中面不发生撕裂,也不发生皱褶。
Mar.2012
板壳结构
68-18
TONGJI University
由直法线假定, 得到大变形条件下, 薄板上距中面为 z
的点的应变
平
板 理 论
x (z)xz 2 xw 2 u x1 2 w x2z 2 xw 2
y (z)yz 2 yw 2 y v1 2 w y2z 2 yw 2
x (y z)x y 2 z x 2 w y u y v x w x w y 2 z x 2 w y
Mar.2012
板壳结构
68-16
(3) 总应变
TONGJI University
大变形条件下,薄板中面上的应变
平
板
理 论
x xxux12w x2
2
y yyyv12w y
几何非线性项
xyx yx y u y v x w x w y
Mar.2012
板壳结构
68-17
TONGJI University 大变形条件下,薄板上距中面为z 的点的变形 平 板 理 论
Mar.2012
板壳结构
68-28
(2) 中面内力—薄膜力
TONGJI University
平 板
根据直法线假定, 薄膜应力x、y、xy 沿板厚均匀分布,
则中面力—薄膜力—可表示为(沿板厚积分):
物理7-2
v2
v1 v2 v1
vf ( v)dv f ( v)dv
—— v1 ~ v2速率区间内 分子的平均速率
三、三种统计速率 1、最概然速率vp
f (v)的极大值对应的速率 将f (v)对v求导,并令其为零
f ( v)
d f ( v) dv
vp
vp
0
o
vp
R M k
v
2kT
2 RT RT 1.414 M M
双原子
5 RT 2
多原子
6 RT 2
m kg
m 5 RT M 2
m 6 RT M 2
例:一容器内装有某一气体(视为刚性双原子分子),其温度 为00C,压力为 1.0×10-2大气压,密度为1.24×10-2kg/m3。求: (1) 气体的摩尔质量; (2) 气体分子的平均平动动能和转动动能; (3) 容器单位体积内分子的总平动动能, (4) 若该气体有0.3 mol,求其内能。 m RT m RT 28 103 kg/mol 解: (1) pV RT M p M V p (2) t 3 r 2 i 5 2 21 3 21 kT 3.7 10 J kr kt kT 5.6 10 J 2 2 p (3) 单位体积内的分子数 n kT 3 3 kt总 n kT p 1.5 10 3 J 2 2 m i 5 (4) E RT 0.3 RT 1.7 103 J M 2 2
Z
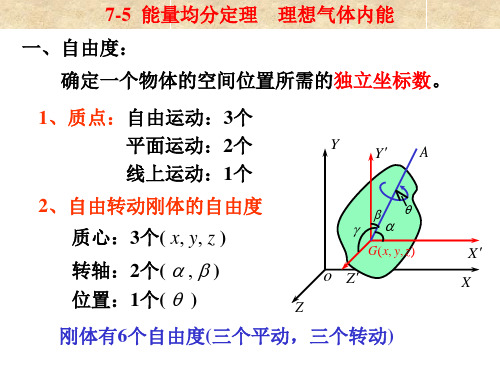
X
刚体有6个自由度(三个平动,三个转动)
3、 分子的自由度:
i :表示自由度, t :表示平动自由度, r :转动自由度,s :振动自由度。 i = t +r + s 1. 单原子分子: i = t =3 2. 双原子分子: 质心:t = 3 刚性双原子分子:i = t + r = 5 转动:r = 2 非刚性双原子分子:i =t +r + s = 7 振动:s = 2 3. 多原子分子: 刚性:i = t + r = 3 + 3 = 6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
δ ( A + B) = δA + δB δ ( AB) = AδB + BδA
以上变分运算的法则用微分运算相同
A BδA − AδB δ( ) = B B2
2、函数微分和变分(等时变分)运算可以对易(对换次序)
d δ 3、可以证明,对于等时变分, 和 dt 可对易 d x2 x2 δ 和 dx 可对易 δ ∫x F(x)dx = x δF(x)dx 积分和变分可对易 1 1
§5.7 Hamilton原理 拉格朗日方程和哈密顿正则方程; 哈密顿原理
分 式 哈 顿 理 积 形 ( 密 原 )
运用变分运算的力学原理 ⇒ 力学变分原理⇒ 微分形式(虚功原理) 实质是泛函求极值问题 一、位形空间 相空间 体系由 q } { 确定 对应
α
s 维空间(位形空间)一个“位形点”
∫
t2
t1
Ldt = s
对哈密顿原理数学表达式的说明
具有相同始点和终点众多可能运动中真实运动总是使作 用量 s的变分为零,表明哈密顿原理重要意义在于可用变分 法中求稳定值方法来挑选真实轨道 哈密顿原理的文字表述“保守的、完整的力学体系在 相同的时间内,由某一初位形转移到另一初位形的一切可 能运动中,真实运动的主函数具有稳定值,即对于真实运 动来说,主函数的变分为零。” 判断物理体系真实运动的准绳
d ∂L d ∂L ∂L d ∂L ∂L d & δqα ) − δq ( )δqα = ( δqα ) − (δqα ) = ( &α &α α &α ∂q dt ∂q dt ∂q & & dt ∂qα ∂qα dt
∫
t2 s
t1
∑{
α=1
s
d ∂L ∂L ∂L & ( δqα ) − ( δqα + δqα )}dt & & dt ∂qα ∂qα ∂qα
∫
三、Hamilton原理(力学中最重要的一条积分形式的变分原理) 运用拉氏方程导出保守力系作用下的Hamilton原理
d ∂L ∂L ( )− =0 & dt ∂qα ∂qα
d ∂L ∂L ( )− ]δqα }dt = 0 & dt ∂qα ∂qα
⇒
∫
t2 s
t1
∑{[
α=1
从 P → P2 沿可能轨道积分 1 对于等时变分
∂L = ∑∂q δqα − α=1 &α
∫∑ α
t1 =1
t2 s
(
∂L ∂L & δqα + δqα )dt = 0 & ∂qα ∂qα
t2 t1
Q δqα
t1
t2
=δqα
t2
= 0 ∴∫ δLdt = 0
又 Qδt = 0
∴δ ∫ Ldt = 0
t1
哈密顿原理数学表达式 为作用函数(主函数)
其中
⇒ “位形点”的运动表示体系的运动 位轨线
对应正则变量{qα , pα}⇒ 2s 维相空间(相宇)(相:运动状态) 体系状态改变
⇒ 相点在相空间运动 ⇒ 相轨迹
p2 x2 + ห้องสมุดไป่ตู้1 2mE 2E / k
p2 1 2 例子:谐振子 H = + kx = E 2m 2
构成相空间 x, p 中的椭圆
二、变分运算的几个法则 1、 A = A(q, p, t) B = B(q, p, t)
