找规律练习题及实用标准化问题详解
找规律的数学题一年级

找规律的数学题一年级引言数学作为一门学科,对于孩子的综合素质培养具有重要意义。
其中,找规律是培养孩子逻辑思维和数学思维的关键环节之一。
本文将介绍一些适合一年级学生的找规律数学题目,帮助孩子在学习中培养对数学的兴趣和理解能力。
问题一题目:在下面的数列中找规律,然后填空。
2, 4, 6, ,解法:这个数列中的规律是每个数都比前一个数增加2。
所以下一个数应该是8,再下一个数是10。
因此,填空处的答案是8和10。
问题二题目:下面的图形中有一个数字缺失,找出规律并填写缺失的数字。
12 34 5 67 _ 8 9解法:观察每一行的数字,我们可以发现第一行有1个数字,第二行有2个数字,第三行有3个数字,以此类推。
所以第四行应该有4个数字,而图中缺失的位置处应该填上数字10。
因此,填空处的答案是10。
问题三题目:以下是一个数表,请找出规律,在空格中填写正确的数字。
数字结果1 32 63 __4 __5 __解法:观察数字列和结果列,我们可以发现结果列中的数字是数字列中的数字乘以2得到的。
所以,对于空格处应填写的数字分别是6、8和10。
因此,填空处的答案是6、8和10。
问题四题目:数字序列2, 4, 8, 16, 32, _中的数字遵循着什么规律?找出规律并填写下一个数字。
解法:观察这个数列,可以发现每个数字都是前一个数字乘以2得到的。
所以下一个数字应该是32乘以2得到的64。
因此,下一个数字是64。
结论通过以上几个例子,我们可以看到通过找规律可以帮助孩子培养逻辑思维和数学思维能力。
在一年级学习阶段,适当引导孩子进行这样的练习,能够激发他们对数学的兴趣,提高他们的数学能力。
希望本文提供的找规律数学题目能够帮助到您和孩子们的学习。
找规律填数练习(含解析)

找规律填数练习1.找出下面数列的规律,并根据规律在横线上填上合适的数.(1)14,17,20,23,26,,(2)86,75,64,53,,(3)2,6,11,17,,(4)1,3,9,27,,2.先找出规律,再在括号里填上合适的数。
(1)18,3,15,4,12,5,,(2)1,15,3,13,5,11,,(3)1,2,3,2,4,6,3,8,9,,,3.在1、4、9、16、()36、49这个数列中,括号里应填的数是()A.30B.25C.324.先找出下列数列的排列规律,再在括号里填上合适的数。
(1)2,5,14,41,,(2)252,124,60,28,,5.下面括号里的两个数是按一定的规律组合的,在□里填适当的数。
(1)(1,24),(2,12),(3,8),(4,)(2)(64,62),(48,46),(29,27),(15,)6.找规律,填一填找规律填数-解析1.找出下面数列的规律,并根据规律在横线上填上合适的数.(1)14,17,20,23,26,,(2)86,75,64,53,,(3)2,6,11,17,,(4)1,3,9,27,,【分析】(1)17﹣14=3,20﹣17=3,23﹣20=3,26﹣23=3,依次加3即可。
(2)86﹣75=11、75﹣64=11、64﹣53=11,…,相邻两个数之间相差11,从第一个数开始,依次减11就是它后面的数。
(3)在这一组数列中每相邻两个数的差依次是4,5,6,由此可以推算出下一个加7,加8。
(4)前一个数乘3等于后一个数。
【解答】(1)26+3=29,29+3=32;(2)86,75,64,53,42,31;(3)17+7=24,24+8=32;(4)27×3=81,81×3=243;2.先找出规律,再在括号里填上合适的数。
(1)18,3,15,4,12,5,,(2)1,15,3,13,5,11,,(3)1,2,3,2,4,6,3,8,9,,,【分析】(1)观察这组数可得,每两个数为一组,其中第一个数依次减3,第二个数依次加1,据此填空即可;(2),观察这组数可得,每两个数为一组,其中第一个数依次加2,第二个数依次减2,据此填空即可;(3),观察这组数可得,每三个数为一组,其中第一个数依次加1,第二个数依次乘2,第三个数依次加3,据此填空即可。
华师版七上数学精选找规律专题18道-附答案和考点详解

华师版七上数学精选找规律专题18道一.选择题(共6小题)1.观察图中正方形四个顶点所标的数字的规律,可知数2018应标在( )A .第504个正方形的左下角B .第505个正方形的左上角C .第504个正方形的右下角D .第505个正方形的右上角2.一根1m 长的绳子,第1次剪去一半,第2次剪去剩下绳子的一半.如此剪下去,剪第8次后剩下的绳子的长度是( ) A .61()2mB .71()2mC .81()2mD .121()2m3.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形共有( )个〇.A .6055B .6056C .6057D .60584.中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )A .10B .89C .165D .2945.观察下列各式:133=,239=,3327=,4381=,53243=,63729=,⋯,你能从中发现底数为3的幂的个位数有什么规律吗?根据你发现的规律回答:20203的个位数字是()A .1B .3C .7D .96.观察式子:3211=,332212(12)3+=+=,33322123(123)6++=++=,3333221234(1234)10+++=+++=,⋯,根据你发现的规律,计算3333335678910+++++的结果是( ) A .2925B .2025C .3225D .2625二.填空题(共4小题)7.如图是一组有规律的图案,它们是由边长相同的小正方形组成,其中部分小正方形涂有阴影,依此规律,第n 个图案中有 个涂有阴影的小正方形(用含有n 的代数式表示).8.一个点从数轴上的原点开始,先向右移动1个单位长度,再向左移动2个单位长度,再向右移动3个单位长度,再向左移动4个单位长度,⋯⋯,移动2019次后,该点所对应的数是 .9.古希腊数学家把数1,3,6,10,15,21,⋯叫做三角数,它有一定的规律性.若把第一个三角数记为1a ,第二个三角数记为2a ⋯,第n 个三角数记为n a ,计算12a a +,23a a +,34a a +,⋯由此推算399400a a += .10.填在各正方形中的四个数字之间具有相同的规律,根据这种规律,m 的值应是 .三.解答题(共8小题)11.观察下列等式的规律,解答下列问题:1122()212a =+,2122()223a =+,3122()234a =+,4122()245a =+,⋯⋯. (1)第5个等式为 ;第n 个等式为 (用含n 的代数式表示,n 为正整数); (2)设112S a a =-,234S a a =-,356S a a =-,⋯⋯,100820152016S a a =-.求1231008S S S S +++⋯⋯+的值.12.如图,将连续的奇数1,3,5,7⋯按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.(1)若17x=,则a b c d+++=.(2)移动十字框,用x表示a b c d+++=.(3)设M a b c d x=++++,判断M的值能否等于2020,请说明理由.13.探索规律:观察下面由※组成的图案和算式,并解答问题21342+==213593++==21357164+++==213579255++++==(1)试猜想13579..19++++++=;试猜想13579922222++++⋯+=;(2)试猜想13579(21)(21)(23)n n n+++++⋯+-++++=;(3)写出过程,请用上述规律计算出最后数值并用科学记数法表示100110031005..19971999+++++.14.观察下面三行数:2-,4,8-,16,32-,64 ⋯①0,6,6-,18,30-,66⋯②1-,2,4-,8,16-,32⋯③(1)第①行数按什么规律排列?(2)第②③行数与第①行数有什么关系? (3)取每行数的第十个数,计算这三个数的和.15.如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推. (1)阴影部分的面积是 ; (2)如果继续分割下去,部分的面积为 ;(3)受此启发,请你求出711112482+++⋯+的值.16.探究与应用: 观察下列各式: 13+=2135++= 21357+++= 213579++++= 2⋯⋯问题:(1)在横线上填上适当的数;(2)写出一个能反映此计算一般规律的式子;(3)根据规律计算:(1)(3)(5)(7)(2019)-+-+-+-+⋯+-.(结果用科学记数法表示) 17.小学的时候我们已经学过分数的加减法法则:“同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,转化为同分母分数,再加减.”如:1132321123232323236--=-===⨯⨯⨯⨯,反之,这个式子仍然成立,即:1132321162323232323-===-=-⨯⨯⨯⨯ (1)问题发现 观察下列等式:①1212111121212122-==-=-⨯⨯⨯⨯, ②13232112323232323-==-=-⨯⨯⨯⨯, ③14343113434342334-==-=-⨯⨯⨯⨯,⋯, 猜想并写出第n 个式子的结果:1(1)n n =+ .(直接写出结果,不说明理由) (2)类比探究将(1)中的的三个等式左右两边分别相加得:1111111113111223342233444++=-+-+-=-=⨯⨯⨯,类比该问题的做法,请直接写出下列各式的结果:①111112233420192020+++⋯+=⨯⨯⨯⨯ ; ②1111122334(1)n n +++⋯+=⨯⨯⨯+ ; (3)拓展延伸 计算:1111133********+++⋯+⨯⨯⨯⨯. 18.某餐厅中,一张桌子可坐6人,有以下两种摆放方式: (1)当有n 张桌子时,两种摆放方式各能坐多少人?(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?华师版七上数学精选找规律专题18道参考答案与试题解析一.选择题(共6小题)1.观察图中正方形四个顶点所标的数字的规律,可知数2018应标在( )A .第504个正方形的左下角B .第505个正方形的左上角C .第504个正方形的右下角D .第505个正方形的右上角【分析】根据数字在图形上的变化,寻找规律即可求解. 【解答】解:观察图形的数字的变化规律,可知 (101)423+÷=⋯∴数10应标在第3个正方形的左上角;(141)433+÷=⋯∴数14应标在第4个正方形的左上角;⋯(20181)45043+÷=⋯∴数2018应标在第505个正方形的左上角;故选:B .【点评】本题考查了图形的变化规律,解决本题的关键是根据数字的变化寻找规律. 2.一根1m 长的绳子,第1次剪去一半,第2次剪去剩下绳子的一半.如此剪下去,剪第8次后剩下的绳子的长度是( ) A .61()2mB .71()2mC .81()2mD .121()2m【分析】根据题意归纳总结得到一般性规律,确定出所求即可. 【解答】解:第一次剪去全长的12,剩下全长的12, 第二次剪去剩下的12,剩下全长的2111222⨯=, 第三次再剪去剩下的12,剩下全长的23111222⨯=,如此剪下去,第8次后剩下的绳子的长为8881111()()222m ⨯==. 故选:C .【点评】此题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.3.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形共有( )个〇.A .6055B .6056C .6057D .6058【分析】设第n 个图形有n a 个〇(n 为正整数),观察图形,根据各图形中〇的个数的变化可找出“13(n a n n =+为正整数)”,再代入2019a =即可得出结论. 【解答】解:设第n 个图形有n a 个〇(n 为正整数),观察图形,可知:1131a =+⨯,2132a =+⨯,3133a =+⨯,4134a =+⨯,⋯, 13(n a n n ∴=+为正整数), 20191320196058a ∴=+⨯=.故选:D .【点评】本题考查了规律型:图形的变化类,根据各图形中〇的个数的变化找出变化规律“13(n a n n =+为正整数)”是解题的关键.4.中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )A .10B .89C .165D .294【分析】根据计数规则可知,从右边第1位的计数单位为05,右边第2位的计数单位为15,右边第3位的计数单位为25,右边第4位的计数单位为35⋯⋯依此类推,可求出结果. 【解答】解:321025153545294⨯+⨯+⨯+⨯=, 故选:D .【点评】本题考查用数字表示事件,理解“逢五进一”的计数规则是正确计算的前提. 5.观察下列各式:133=,239=,3327=,4381=,53243=,63729=,⋯,你能从中发现底数为3的幂的个位数有什么规律吗?根据你发现的规律回答:20203的个位数字是() A .1B .3C .7D .9【分析】根据题意可得出尾数每4个一循环,进而求出答案.【解答】解:133=,239=,3327=,4381=,53243=,63729=,⋯,∴尾数每4个一循环,3,9,7,1,20204505÷=,20203∴的个位数字是:1.故选:A .【点评】本题考查了规律型:数字的变化类,有理数的乘方,尾数特征,观察得到每4个数为一个循环组依次进行循环是解题的关键.6.观察式子:3211=,332212(12)3+=+=,33322123(123)6++=++=,3333221234(1234)10+++=+++=,⋯,根据你发现的规律,计算3333335678910+++++的结果是( ) A .2925B .2025C .3225D .2625【分析】根据题意找到规律:3333322(1)1234(1234)[]2n n n n ++++⋯+=++++⋯+=即可.【解答】解:3211=,332212(12)3+=+=, 33322123(123)6++=++=, 3333221234(1234)10+++=+++=,⋯,3333321234(1234)n n ∴+++⋯+=++++⋯+, 3333335678910+++++333333333(123410)(1234)=+++⋯+-+++ 22(123410)(1234)=++++⋯+-+++ 2210(101)4(41)[][]22⨯+⨯+=-225510=- 2925=.故选:A .【点评】本题考查了规律型:数字的变化类,解决本题的关键是根据数字的变化寻找规律. 二.填空题(共4小题)7.如图是一组有规律的图案,它们是由边长相同的小正方形组成,其中部分小正方形涂有阴影,依此规律,第n 个图案中有 41n + 个涂有阴影的小正方形(用含有n 的代数式表示).【分析】观察不难发现,后一个图案比前一个图案多4个涂有阴影的小正方形,然后写出第n 个图案的涂有阴影的小正方形的个数即可.【解答】解:由图可得,第1个图案涂有阴影的小正方形的个数为5, 第2个图案涂有阴影的小正方形的个数为5219⨯-=, 第3个图案涂有阴影的小正方形的个数为53213⨯-=,⋯,第n 个图案涂有阴影的小正方形的个数为5(1)41n n n --=+. 故答案为:41n +.【点评】本题是对图形变化规律的考查,观察出“后一个图案比前一个图案多4个基础图形”是解题的关键.8.一个点从数轴上的原点开始,先向右移动1个单位长度,再向左移动2个单位长度,再向右移动3个单位长度,再向左移动4个单位长度,⋯⋯,移动2019次后,该点所对应的数是 1010 .【分析】先表示出前6次移动后所对应的数,从而得出第n 次移动后,若n 为偶数,则对应的点表示的数为2n-,若n 为奇数,则对应的点表示的数为12n +,据此求解可得.【解答】解:第1次移动后对应的数为1, 第2次移动后对应的数为1-, 第3次移动后对应的数为2, 第4次移动后对应的数为2-, 第5次移动后对应的数为3, 第6次移动后对应的数为3-,⋯⋯∴第n 次移动后,若n 为偶数,则对应的点表示的数为2n -; 若n 为奇数,则对应的点表示的数为12n +, 当2019n =时,该点所对应的数为2019110102+=, 故答案为:1010.【点评】本题主要考查数字的变化规律,解题的关键是根据前几次的移动得出第n 次移动后,若n 为偶数,则对应的点表示的数为2n -,若n 为奇数,则对应的点表示的数为12n +的规律.9.古希腊数学家把数1,3,6,10,15,21,⋯叫做三角数,它有一定的规律性.若把第一个三角数记为1a ,第二个三角数记为2a ⋯,第n 个三角数记为n a ,计算12a a +,23a a +,34a a +,⋯由此推算399400a a += 51.610⨯或160000 .【分析】首先计算12a a +,23a a +,34a a +的值,然后总结规律,根据规律可以得出结论. 【解答】解:21242a a +==;2233693a a +=+==;234610164a a +=+==;⋯∴21(1)n n a a n ++=+;∴25399400400160000 1.610a a +===⨯.故答案为:51.610⨯或160000.【点评】本题考查的是规律发现,根据计算12a a +,23a a +,34a a +的值可以发现规律为21(1)n n a a n ++=+,发现规律是解决本题的关键.10.填在各正方形中的四个数字之间具有相同的规律,根据这种规律,m 的值应是 184 .【分析】正方形中的四个数字之间具有的规律是:左下方格中的数字比左上方格中的数字大2,右上方格中的数字比左上方格中的数字大4,且左下方格中的数字与右上方格中的数字的乘积等于左上方格中的数字与右下方格中数字的和.利用此规律结论可求. 【解答】解:依据正方形中的四个数字之间具有的规律,可得:131511m ⨯=+, 184m ∴=.故答案为:184.【点评】本题主要考查了数字的变化的规律,有理数的混合运算,正确发现数字的规律是解题的关键.三.解答题(共8小题)11.观察下列等式的规律,解答下列问题:1122()212a =+,2122()223a =+,3122()234a =+,4122()245a =+,⋯⋯. (1)第5个等式为122()256+ ;第n 个等式为 (用含n 的代数式表示,n 为正整数); (2)设112S a a =-,234S a a =-,356S a a =-,⋯⋯,100820152016S a a =-.求1231008S S S S +++⋯⋯+的值.【分析】(1)根据规律写出结论,再将第n 个式子化简;(2)分别计算112S a a =-,234S a a =-,356S a a =-,⋯⋯,100820152016S a a =-.再代入所求式子,可得结论.【解答】解:(1)由题意得:5122()256a =+;122()21n a n n ∴=++;故答案为:122()256+,122()21n n ++;(2)由(1)可知111n a n n =++, 1121111(1)()12233S a a ∴=-=+-+=-,234111111()()344535S a a =-=+-+=-,356111111()()566757S a a =-=+-+=-,⋯⋯⋯1008201520161111()()2015201620162017S a a =-=+-+ 1120152017=-, 1231008S S S S ∴+++⋯+,1111111(1)()()()3355720152017=-+-+-+⋯+-,112017=-, 20162017=. 【点评】此题考查数字的变化规律,利用数字之间的联系与运算的方法,得出规律,进一步利用规律,解决问题.12.如图,将连续的奇数1,3,5,7⋯按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a ,b ,c ,d ,x 表示. (1)若17x =,则a b c d +++= 68 . (2)移动十字框,用x 表示a b c d +++= .(3)设M a b c d x =++++,判断M 的值能否等于2020,请说明理由.【分析】观察图1,可知:12a x =-,2b x =-,2c x =+,12d x =+. (1)当17x =时,找出a 、b 、c 、d 的值,将其相加即可求出结论;(2)由12a x =-、2b x =-、2c x =+、12d x =+,即可求出a b c d +++的值;(3)根据2020M =,即可得出关于x 的一元一次方程,解之即可求出x 的值,由x 为偶数即可得出M 不能为2020.【解答】解:观察图1,可知:12a x =-,2b x =-,2c x =+,12d x =+. (1)当17x =时,5a =,15b =,19c =,29d =, 515192968a b c d ∴+++=+++=.故答案为:68.(2)12a x =-,2b x =-,2c x =+,12d x =+, (12)(2)(2)(12)4a b c d x x x x x ∴+++=-+-++++=.故答案为:4x .(3)M 的值不能等于2020,理由如下: 令2020M =,则42020x x +=, 解得:404x =. 404是偶数不是奇数,∴与题目x 为奇数的要求矛盾,M ∴不能为2020.【点评】本题考查了规律型中数字的变化类以及一元一次方程的应用,解题的关键是:(1)将a 、b 、c 、d 四个数相加;(2)观察图1,用含x 的代数式表示出a 、b 、c 、d ;(3)由2020M =,列出关于x 的一元一次方程.13.探索规律:观察下面由※组成的图案和算式,并解答问题 21342+== 213593++== 21357164+++== 213579255++++==(1)试猜想13579..19++++++= 100 ; 试猜想13579922222++++⋯+= ; (2)试猜想13579(21)(21)(23)n n n +++++⋯+-++++= ; (3)写出过程,请用上述规律计算出最后数值并用科学记数法表示 100110031005..19971999+++++.【分析】(1)根据题目中数字的特点,可以求得所求式子的值; (2)根据题目中式子的特点可以求得所求式子的值; (3)根据题目中的例子和式子的特点可以求得所求式子的值. 【解答】解:(1)213579..1910100++++++==,2135799135995012502222222+++⋯+++++⋯+===, 故答案为:100,1250;(2)2223113579(21)(21)(23)()(2)2n n n n n +++++++⋯+-++++==+, 故答案为:2(2)n +;(3)100110031005..19971999+++++ (1351999)(135999)=+++⋯+-+++⋯+ 22199919991()()22++=-221000500=-(1000500)(1000500)=+⨯- 1500500=⨯ 750000=57.510=⨯.【点评】本题考查数字的变化类、有理数的混合运算、科学记数法,解答本题的关键是明确题意,发现题目中数字的变化特点,求出所求式子的值. 14.观察下面三行数:2-,4,8-,16,32-,64 ⋯①0,6,6-,18,30-,66⋯②1-,2,4-,8,16-,32⋯③(1)第①行数按什么规律排列? (2)第②③行数与第①行数有什么关系?(3)取每行数的第十个数,计算这三个数的和.【分析】(1)观察可看出第一行的数分别是2-的一次方,二次方,三次方,四次方⋯且奇数项是负数,偶数项是正数,用式子表示规律为:(2)n -;(2)观察可知,第②行数比第①行相对应的数大2;第③行数是第①行相对应的数的12; (3)根据规律分别求得第10个数的值,再求其和即可. 【解答】解:(1)(2)n -;(2)第②③行数与第①行数的关系为:第②行数比第①行相对应的数大2;第③行数是第①行相对应的数的12; (3)第一行的第十个数为:1024; 第二行的第十个数为:1026; 第三行的第十个数为:512; 102410265122562++=.故这三个数的和为:2562.【点评】此题主要考查学生对规律型题的掌握情况,做此类题要求学生对给出的条件仔细观察从而找出规律.15.如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推. (1)阴影部分的面积是164; (2)如果继续分割下去,部分的面积为 ;(3)受此启发,请你求出711112482+++⋯+的值.【分析】(1)根据图形和题意,可以得到阴影部分的面积;(2)根据图形和题意,可以得到部分的面积;(3)根据图形和题目中式子的特点,可以计算出所求式子的值. 【解答】解:(1)由题意可得, 阴影部分的面积是:611()264=,故答案为:164; (2)由题意可得, 部分的面积为:1()2n ,故答案为:1()2n ;(3)711112482+++⋯+ 7112=-77212-= 1281128-=127128=. 【点评】本题考查数字的变化类、有理数的混合运算,解答本题的关键是明确题意,发现题目中数字的变化特点,求出所求式子的值. 16.探究与应用: 观察下列各式: 13+= 22135++= 21357+++= 213579++++= 2⋯⋯问题:(1)在横线上填上适当的数;(2)写出一个能反映此计算一般规律的式子;(3)根据规律计算:(1)(3)(5)(7)(2019)-+-+-+-+⋯+-.(结果用科学记数法表示) 【分析】(1)根据从1开始连续n 个奇数和等于奇数的个数n 的平方即可得;(2)根据以上所得规律列式表示即可; (3)先提取负号,再利用所的规律求解可得. 【解答】解:(1)2132+= 21353++= 213574+++= 2135795++++=⋯⋯故答案为:2、3、4、5;(2)第n 个等式为21357(21)n n ++++⋯++=; (3)原式(135792019)=-+++++⋯+ 21004=-61.00801610=-⨯.【点评】本题主要考查数字的变化规律,解题的关键是根据已知等式得出从1开始连续n 个奇数和等于奇数的个数n 的平方的规律.17.小学的时候我们已经学过分数的加减法法则:“同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,转化为同分母分数,再加减.”如:1132321123232323236--=-===⨯⨯⨯⨯,反之,这个式子仍然成立,即:1132321162323232323-===-=-⨯⨯⨯⨯ (1)问题发现 观察下列等式: ①1212111121212122-==-=-⨯⨯⨯⨯, ②13232112323232323-==-=-⨯⨯⨯⨯, ③14343113434342334-==-=-⨯⨯⨯⨯,⋯, 猜想并写出第n 个式子的结果:1(1)n n =+ 111n n -+ .(直接写出结果,不说明理由) (2)类比探究将(1)中的的三个等式左右两边分别相加得:1111111113111223342233444++=-+-+-=-=⨯⨯⨯,类比该问题的做法,请直接写出下列各式的结果:①111112233420192020+++⋯+=⨯⨯⨯⨯ ; ②1111122334(1)n n +++⋯+=⨯⨯⨯+ ; (3)拓展延伸 计算:1111133********+++⋯+⨯⨯⨯⨯. 【分析】(1)根据题目中的式子可以写出第n 个式子的结果;(2)①根据题目中的式子的特点和(1)中的结果,可以求得所求式子的值; ②根据题目中的式子的特点和(1)中的结果,可以求得所求式子的值; (3)根据题目中式子的特点,可以求得所求式子的值. 【解答】解:(1)由题目中的式子可得, 111(1)1n n n n =-++, 故答案为:111n n -+; (2)①111112233420192020+++⋯+⨯⨯⨯⨯ 111111112233420192020=-+-+-+⋯+-112020=- 20192020=, 故答案为:20192020; ②1111122334(1)n n +++⋯+⨯⨯⨯+ 11111111223341n n =-+-+-+⋯+-+ 111n =-+ 1nn =+, 故答案为:1nn +; (3)1111133********+++⋯+⨯⨯⨯⨯ 11111111(1)23355799101=⨯-+-+-+⋯+-11=⨯-(1)21011100=⨯210150=.101【点评】本题考查数字的变化类、有理数的混合运算,解答本题的关键是明确题意,发现题目中式子的变化特点,求出所求式子的值.18.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:(1)当有n张桌子时,两种摆放方式各能坐多少人?(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?【分析】能够根据桌子的摆放发现规律,然后进行计算判断.【解答】解:(1)第一种中,只有一张桌子是6人,后边多一张桌子多4人.即有n张桌子时是64(1)42+-=+.n n第二种中,有一张桌子是6人,后边多一张桌子多2人,即62(1)24n n+-=+.(2)中,分别求出两种对应的n的值,或分别求出25n=时,两种不同的摆放方式对应的人数,即可作出判断.打算用第一种摆放方式来摆放餐桌.因为,当25⨯+=>n=时,425210298当25n=时,22545498⨯+=<所以,选用第一种摆放方式.【点评】关键是通过归纳与总结,得到其中的规律.。
幼儿数学找规律练习题

幼儿数学找规律练习题在幼儿园阶段,数学教育起着至关重要的作用。
通过数学的学习,幼儿可以培养逻辑思维和解决问题的能力。
其中,找规律是数学学习中的重要一环。
通过找规律练习题,幼儿可以激发他们的思维能力和创造力。
下面,我们一起来看几道有趣的找规律练习题。
问题一:请找出下面这组数列中的规律,然后依据规律选择合适的数字填空。
1, 4, 7, 10, ___, ___思路提示:观察数字之间的变化规律,尝试找出每个数字与前一个数字之间的差异。
答案解析:观察数列中的数字,我们可以发现每个数字与前一个数字之间的差异是3。
所以,下两个数字应分别是13和16。
问题二:请在下面的括号中填上合适的数字,使得等号左边的数字和等号右边的数字之间满足相同的规律。
8 + 5 = (12 + 2)思路提示:尝试从等号左侧的数字与等号右侧的数字之间找出规律,再填入括号中。
答案解析:观察等号左侧的数字8和等号右侧的数字12,我们可以发现它们之间的差异是4。
同样地,观察等号左侧的数字5和等号右侧的数字2,我们可以发现它们之间的差异是3。
所以,合适的填入方式是(8+4) + (5-2)。
问题三:请根据以下数字序列找出规律,然后填上合适的数字。
2, 4, 16, 256, ___, ___思路提示:观察数字序列中每个数字与前一个数字之间的关系,找出规律。
答案解析:从2到4,我们可以发现乘以2的关系;从4到16,我们可以发现乘以4的关系;从16到256,我们可以发现乘以16的关系。
所以,下两个数字分别是4096和65536。
通过上面的几道找规律练习题,我们可以培养幼儿的观察力、分析解决问题的能力,同时也提升他们的创造力。
在幼儿数学教育中,找规律是锻炼孩子的数学思维和逻辑能力的重要方法之一。
然而,在数学教育中,不仅仅有找规律这一部分内容,还有很多其他的数学知识需要我们去学习和掌握。
幼儿数学教育应该贯穿于整个教育过程中,不仅仅是在幼儿园阶段进行。
十道初中数学找规律的题型及解题思路

十道初中数学找规律的题型及解题思路这里有10道初中数学找规律的题目,涵盖了常见的数列、图形等多种类型,希望能帮助学生更好地掌握找规律的技巧:数列找规律1.等差数列:1.1, 4, 7, 10, ... 下一个数是多少?2.100, 97, 94, ... 第10个数是多少?2.等比数列:1.2, 4, 8, 16, ... 第8个数是多少?2.81, 27, 9, ... 第6个数是多少?3.混合数列:1.1, 4, 9, 16, 25, ... 下一个数是多少?(提示:考虑每个数的平方)2.2, 5, 10, 17, ... 下一个数是多少?(提示:观察相邻两数的差)4.周期数列:1.1, 2, 3, 1, 2, 3, ... 第20个数是多少?2.A, B, C, A, B, C, ... 第100个数是多少?图形找规律图形的变化:1.一组图形,每个图形由小方块组成,观察图形的变化规律,画出下一个图形。
图形的旋转:1.一个图形不断旋转,观察旋转的规律,画出旋转后的图形。
图形的翻转:1.一个图形不断翻转,观察翻转的规律,画出翻转后的图形。
数字与图形结合数字与图形对应:1.一组图形,每个图形对应一个数字,找出数字与图形之间的对应关系。
图形中的数字规律:1.一个图形中包含多个数字,找出数字之间的规律。
综合题型1.数字和图形的综合:1.一组图形和数字交替出现,找出数字和图形之间的关系。
解题技巧:•观察:仔细观察数列或图形的变化规律,找出其中的共同点和差异点。
•比较:比较相邻的数或图形,找出它们的递增、递减或其他变化关系。
•联想:将题目与以前学过的知识联系起来,寻找解题思路。
•归纳:根据观察和比较的结果,归纳出一般性的规律。
•验证:将得到的规律代入后面的数或图形中进行验证,确保规律的正确性。
注意事项:•找规律题的答案可能不唯一,只要找到一种合理的规律即可。
•遇到困难时,可以尝试从不同的角度去观察和分析。
找规律填数 含答案

找规律填数小朋友们,在学习和生活中,我们经常会遇到许多按一定顺序排列起来的数。
在数学上,我们把这样的一组数叫做“数列”。
找规律填数,就是先通过对数列的观察,再经过严密的逻辑推理,然后发现数列中数的排列规律,并依据这个规律把所缺的数填写出来,从而达到解决问题的目的。
这一讲,就让我们一起来探讨数列中的奥秘吧!例1.找出下面各数的排列规律,在括号里填上合适的数。
〈1〉1,2,3,4,(),()〈2〉2,4,6,8,(),()〈3〉45,40,35,(),()点拨:〈1〉在这个数列中,通过观察可以发现,这一列数越来越大,而且后一个数都比前一个数多1,也就是说相邻两个数的差都是1,因此,括号里应按顺序填上5,6.〈2〉根据上题的方法,依次求出相邻两数的差,可以发现这列数的排列规律是:从第二个数起,后一个数都比前一个数多2,因此,括号里应按顺序填上10,12.〈3〉也可以用下面的计算过程来推算45 40 35 30 (25) (20)-5 -5 -5 -5 -5例2.找规律填数.〈1〉1,2,4,7,11,(),()〈2〉1,3,7,13.21,(),()〈3〉1,2,4,8,16,(),()点拨:〈1〉通过观察和计算我们发现,在这一列数中,数也在逐渐增加,但每次增加的数并不相同,具体变化如下:第一个数加1得到第二个数,第二个数加2得到第三个数,第三个数加3得到第四个数,第四个数加4得到第五个数,依次推算,第五个数应该加5得到第六个数是16,第六个数加6得到第七个数是22,也就是说,每次增加的数都比上次增加的数多1,也可以用下面的计算过程来推算:1 2 4 7 11 (16)(22)+1 +2 +3 +4 +5 +6〈2〉这一列数每次增加的数都比上次增加的数多2.1 3 7 13 21 (31) (43)+2 +4 +6 +8 +10 +12〈3〉这一列数每次增加的数都是它本身,第一个数是1,再加上1得到第二个数,第二个数是2,再加上2得到第三个数,第三个数是4,再加上4得到第四个数,第四个数是8,再加上8得到第五个数,依次推算,第五数是16,也应该加上16得到第六个数是32,第六个数是32,也应该加上32得到第七个数是64.可以用下面的计算过程来推算:1 2 4 8 16 (32)(64)+1 +2 +4 +8 +16 +32例3.寻找下面一列数的规律,在()填上合适的数.〈1〉1,3,1,5,1,7,(),()〈2〉17,2,14,2,11,2,(),()〈3〉25,6,20,7,15,8,(),()点拨:〈1〉通过观察可以发现,这一列数是间隔着变化的。
找规律练习题

找规律练习题1. 观察下列数列,找出规律并填写下一个数:2, 4, 8, 16, ____解析:这是一个等比数列,公比为2。
下一个数为16乘以2,即32。
2. 完成以下数列:1, 3, 6, 10, ____解析:这是一个等差数列,公差为2。
下一个数为10加2,即12。
3. 根据规律,找出下列数列的下一个数:5, 10, 20, 40, ____解析:这是一个等比数列,公比为2。
下一个数为40乘以2,即80。
4. 观察下列数列,找出规律并填写下一个数:1, 2, 4, 7, 11, ____解析:这是一个递增数列,每个数与前一个数的差分别是1, 2, 3, 4。
下一个数与前一个数的差应该是5,所以下一个数为11加5,即16。
5. 完成以下数列:2, 4, 8, 16, 32, ____解析:这是一个等比数列,公比为2。
下一个数为32乘以2,即64。
6. 根据规律,找出下列数列的下一个数:3, 6, 12, 24, 48, ____解析:这是一个等比数列,公比为2。
下一个数为48乘以2,即96。
7. 观察下列数列,找出规律并填写下一个数:1, 1, 2, 3, 5, 8,____解析:这是一个斐波那契数列,每个数是前两个数的和。
下一个数为5加8,即13。
8. 完成以下数列:2, 3, 5, 7, 11, ____解析:这是一个质数数列。
下一个质数为13。
9. 根据规律,找出下列数列的下一个数:4, 9, 16, 25, 36, ____解析:这是一个平方数列,每个数是其位置的平方。
下一个数为7的平方,即49。
10. 观察下列数列,找出规律并填写下一个数:1, 3, 6, 10, 15,____解析:这是一个等差数列,公差为2。
下一个数为15加2,即17。
11. 完成以下数列:1, 4, 9, 16, 25, ____解析:这是一个平方数列。
下一个数为6的平方,即36。
12. 根据规律,找出下列数列的下一个数:2, 5, 10, 17, 26, ____解析:这是一个递增数列,每个数与前一个数的差分别是3, 5, 7, 9。
小学生找规律数学练习题

小学生找规律数学练习题在小学数学教学中,找规律是培养学生逻辑思维和数学能力的重要方法之一。
通过找规律,学生能够培养出发现问题本质、抽象思维和解决问题的能力。
本文将为小学生提供一些有趣的找规律数学练习题,帮助他们巩固知识、开拓思维。
一、数列规律题目一:填充数列2,4,6,8,__请找出数列中缺少的数字,并写出你的思路和解法。
题目二:奇偶间隔1,4,3,8,5,__请预测并填写下一个数字,并解释你的答案。
题目三:数字交错2,4,6,3,5,__请找出数列中缺失的数字,并解释你的答案。
题目四:等差数列5,10,15,20,25,__请预测下一个数字,并列出你的理由。
二、图形规律题目五:图形填充请根据下图的规律填充最后一个图形。
★★★★★★★★★★★★★★★题目六:图形序列请找出下列图形中的规律,并填写缺少的图形。
▲ ▲▲▲▲ ▲▲ ▲▲▲▲▲▲▲▲▲三、数字运算规律题目七:数字运算200 + 100 = 300300 + 200 = 500500 + 300 = 800请预测下一个计算式,并列出你的理由。
题目八:奇数相加1 + 3 = 41 + 3 + 5 = 91 + 3 + 5 + 7 = 16请预测下一个计算式,并解释你的答案。
题目九:数字推理1 + 4 = 52 + 5 = 123 + 6 = 21请写出下一个计算式,并解释你的答案。
四、数的正负规律题目十:数的正负1,-2,3,-4,__请填写下一个数字,并解释你的答案。
题目十一:数的正负交错1,-1,2,-2,3,__请填写下一个数字,并解释你的答案。
题目十二:相邻数正负相反-1,2,-3,4,-5,__请填写下一个数字,并解释你的答案。
五、思维拓展题目十三:数的平方1,4,9,16,__请填写下一个数字,并解释你的答案。
题目十四:数的倍数2,6,12,20,__请填写下一个数字,并解释你的答案。
通过以上的练习题,小学生们可以通过分析规律来寻找数学题中的隐藏规则。
(完整版)找规律(含答案)

练习一:先找出下列各列数的排列规律,然后在括号里填上适当的数。
年级:日期:(1)2,6,10,14,(),22,26找规律(2)3,6,9,12,(),18,21专题简介:(3)33,28,23,(), 13,(),3 观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规(4)55,49,43,(), 31,(),19律,在一般情况下,我们可以从以下几个方面来找规律:(5)3,6,12,(),48,(),192 1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;(6)2,6,18,(),162,()2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;(7)128,64,32,(),8,(),23.要善于从整体上把握数据之间的联系,从而很快找出规律;(8)19,3,17,3,15,3,(),(),11,34.数之间的联系往往可以从不同的角度来理解,只要言之有理,所例 2:先找出下列数排列的规律,然后在括号里填上适当的数。
得出的规律都可以认为是正确的。
1,2,4,7,(),16,22例 1:先找出下列数排列的规律,并根据规律在括号里填上适当的数。
分析:在这列数中,前 4 个数每相邻的两个数的差依次是1,2,3。
1 ,,,,(),,19由此可以推算 7 比括号里的数少4,括号里应填: 7+4=11。
4 7 10 16分析:在这列数中,相邻的两个数的差都是 3,即每一个数加上 3 都经验证,所填的数是正确的。
等于后面的数。
根据这一规律,括号里应填的数为:应填的数为: 7+4=11 或 16-5=11 10+3=13 或 16-3=13 练习二:先找出下列数排列的规律,然后在括号里填上适当的数。
像上面按照一定的顺序排列的一串数叫做数列。
(1)10,11,13,16,20,(),31(2)1,4,9,16,25,(),49,64(3)3,2,5,2,7,2,(),(),11,2(4)53,44,36,29,(),18,(),11,9,8(5)81,64,49,36,(),16,(),4,1,0(6)28,1,26,1,24,1,(),(),20,1(7)30,2,26,2,22,2,(),(),14,2(8)1,6,4,8,7,10,(),(),13,14例 3:先找出规律,然后在括号里填上适当的数。
找规律练习题及问题详解

找规律练习题一.数字排列规律题1. 4、10、16、22、28……,求第n位数( )。
2. 2、3、5、9,17增幅为1、2、4、8. 第n位数( )3. 观察下列各式数:0,3,8,15,24,……。
试按此规律写出的第100个数是----,第n个数是---------。
4. 1,9,25,49,(),(),的第n项为(),5: 2、9、28、65.....:第n位数()6:2、4、8、16...... 第n位数. ()7:2、5、10、17、26……,第n位数. ()8 : 4,16,36,64,?,144,,…?第一百个数()9、观察下面两行数2,4,8,16,32,64,...(1)5,7,11,19,35,67...(2)根据你发现的规律,取每行第十个数,求得他们的和。
10、白黑白黑黑白黑黑黑白黑黑黑黑白黑黑黑黑黑排列的珠子,前2002个中有几个是黑的?11. =8=16=24 ……用含有N的代数式表示规律()12. 12,20,30,42,( )127,112,97,82,( )3,4,7,12,( ),2813 . 1,2,3,5,( ),1314. 0,1,1,2,4,7,13,( )15 .5,3,2,1,1,( )16. 1,4,9,16,25,( ),4917. 66,83,102,123,( ) ,18. 1,8,27,( ),12519。
3,10,29,( ),12720, 0,1,2,9,( )21;( )。
则第n项代数式为:()22 , 2/3 1/2 2/5 1/3 ( )。
则第n项代数式为()23 , 1,3,3,9,5,15,7,( )24. 2,6,12,20,( )25. 11,17,23,( ),35。
26. 2,3,10,15,26,( )。
27. : 1,8,27,64,( )28. :0,7,26,63 ,( )29. -2,-8,0,64,( )30. 1,32,81,64,25,( )31. 1,1,2,3,5,( )。
掌握找规律小学生数学练习题

掌握找规律小学生数学练习题数学作为一门重要的学科,对于小学生的学习发展至关重要。
在数学学习中,找规律是培养学生思维能力和解决问题的关键所在。
本文将介绍一些帮助小学生掌握找规律的数学练习题,旨在提高他们的数学思维能力。
第一类题目:数列找规律1. 2, 4, 6, 8, __请问下一个数是多少?解析:通过观察可以发现,每一个数都比前一个数大2。
因此,下一个数应该是10。
2. 1, 4, 9, 16, __请问下一个数是多少?解析:通过观察可以发现,每一个数都是前一个数的平方。
因此,下一个数应该是25。
3. 3, 6, 9, 12, __请问下一个数是多少?解析:通过观察可以发现,每一个数都比前一个数大3。
因此,下一个数应该是15。
通过这些例题,我们可以看出,找规律的数学题目是通过观察数列中的规律来推断下一个数的值。
这对于小学生来说是一种锻炼思维能力的好方法。
第二类题目:图形找规律1. 下面的图形中,哪一个图形是符合图形序列的规律?图1:****************图2:********************图3:******************解析:通过观察可以发现,图1和图3是符合图形序列的规律的。
图1从3角形开始,每一行增加2个星号;图3则是从4角形开始,每一行增加2个星号。
2. 下面的图形中,哪一个图形是符合图形序列的规律?图1:************************************图2:*******************************解析:通过观察可以发现,图2是符合图形序列的规律的。
图2从11个星号开始,每一行减少2个星号。
通过这些例题,我们可以看出,图形找规律的数学题目是通过观察图形的形状、大小和排列顺序来推断下一个图形的特征。
这对于小学生来说是一种培养观察力和逻辑思维的好方法。
第三类题目:等式找规律1. 4+3=7, 5+4=9, 6+5=11, __+__=13请问空白处应该填入什么数字?解析:通过观察可以发现,每一个等式都是前一个等式的结果加上1。
找规律解决问题

找规律解决问题数学是一门需要逻辑思维和抽象能力的学科,而找规律是数学中常用的解决问题的方法之一。
通过观察数列、图形或者等式中的规律,我们可以推导出一般性的结论,从而解决更复杂的问题。
在本文中,我将通过几个具体的例子,向中学生和他们的父母展示找规律解决问题的魅力和实用性。
例一:数列中的规律考虑以下数列:1, 4, 9, 16, 25, ...我们可以观察到每个数都是前一个数的平方加一。
这个规律告诉我们,第n个数可以用公式an = n^2 + 1来表示。
如果我们想知道第10个数是多少,只需要将n 替换成10,计算得到an = 10^2 + 1 = 101。
通过找到规律,我们可以轻松地解决这个问题。
例二:图形中的规律考虑以下图形序列:□□□□□□□□□□□□□□□我们可以观察到每一行的方格数目与行数相等。
根据这个规律,我们可以得到第n行的方格数目为n。
如果我们想知道第10行的方格数目,只需要将n替换成10,计算得到10。
通过找到规律,我们可以快速解决这个问题。
例三:等式中的规律考虑以下等式:1 +2 +3 + ... + n = n(n+1)/2我们可以观察到等式左边是一个数列的和,而等式右边是一个关于n的二次式。
这个规律告诉我们,任意一个正整数n的前n个正整数的和可以用公式n(n+1)/2来表示。
如果我们想知道前100个正整数的和,只需要将n替换成100,计算得到100(100+1)/2 = 5050。
通过找到规律,我们可以迅速解决这个问题。
通过上面的例子,我们可以看到找规律解决问题的方法的实用性和高效性。
不仅可以帮助我们解决数列、图形和等式中的问题,还可以在更复杂的数学问题中发挥重要作用。
除了数学领域,找规律解决问题的方法在其他学科和日常生活中也同样适用。
在科学研究中,科学家们通过观察实验数据中的规律,推导出一般性的定律和原理。
在经济学和市场分析中,人们通过观察市场趋势和数据变化的规律,做出合理的预测和决策。
一年级找规律练习题以及答案

一年级找规律练习题以及答案一年级的小朋友们,今天我们来做一些有趣的找规律练习题,锻炼我们的观察能力和逻辑思维能力。
下面是一些练习题和它们的答案,让我们一起来学习吧!练习题一:数列:2, 4, 6, 8, ( ), ( )答案:观察数列,我们发现每个数都比前一个数大2。
所以,下一个数应该是8+2=10,再下一个数应该是10+2=12。
因此,答案是10和12。
练习题二:图形序列:圆形,正方形,三角形,圆形,正方形,( ),( )答案:观察图形序列,我们发现图形是按照圆形、正方形、三角形的顺序重复出现的。
所以,下一个图形应该是三角形,再下一个图形应该是圆形。
答案是三角形和圆形。
练习题三:颜色序列:红,黄,蓝,红,黄,( ),( )答案:颜色序列是按照红、黄、蓝的顺序重复的。
所以,下一个颜色应该是蓝色,再下一个颜色应该是红色。
答案是蓝色和红色。
练习题四:数列:1, 3, 5, 7, ( ), ( )答案:这是一个奇数序列,每个数都比前一个数大2。
所以,下一个数应该是7+2=9,再下一个数应该是9+2=11。
答案是9和11。
练习题五:图形序列:大,小,大,小,( ),( )答案:图形序列是按照大、小的顺序交替出现的。
所以,下一个图形应该是大,再下一个图形应该是小。
答案是大和小。
练习题六:数列:2, 5, 9, 14, ( ), ( )答案:观察数列,我们发现相邻两个数之间的差分别是3, 4, 5。
差值每次增加1。
所以,下一个差值应该是6,因此下一个数是14+6=20,再下一个数的差值应该是7,所以是20+7=27。
答案是20和27。
结束语:小朋友们,通过这些练习题,你们是不是发现找规律其实很有趣呢?只要我们仔细观察,就能发现事物之间的规律,这能帮助我们更好地理解和解决问题。
希望你们喜欢今天的练习,下次再见啦!。
找规律试题几道经典题目(含答案)
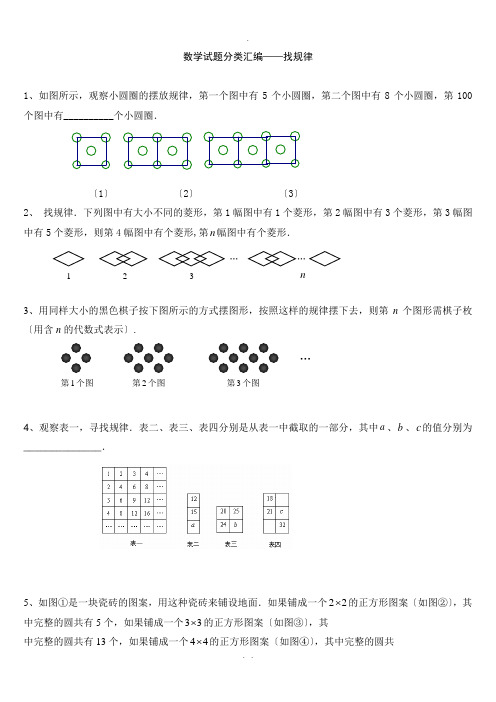
数学试题分类汇编——找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有__________个小圆圈.〔1〕 〔2〕 〔3〕2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有个菱形,第n 幅图中有个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子枚〔用含n 的代数式表示〕.4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为______________.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案〔如图②〕,其中完整的圆共有5个,如果铺成一个33⨯的正方形图案〔如图③〕,其中完整的圆共有13个,如果铺成一个44⨯的正方形图案〔如图④〕,其中完整的圆共1 2 3n … … 第1个图 第2个图 第3个图…有25个.若这样铺成一个1010 的正方形图案, 则其中完整的圆共有个.6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n 个图案需要用白色棋子枚〔用含有n 的代数式表示,并写成最简形式〕.○○○○○○○○○○○○○●●○○●●●○○●○○●●○○●●●○○○○○○○○○●●●○○○○○○7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对〔n ,m 〕表示第n 排,从左到右第m 个数,如〔4,2〕表示实数9,则表示实数17的有序实数对是. 9、如图 2 ,用n 表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n 的关系是10、观察图4的三角形数阵,则第50行的最后一个数是 〔 〕1第一排 第二排 第三排 第四排 6 ┅┅ 10 9 87 32 15 4-2 3-4 5 -67 -8 9 -10。
图形找规律专项练习60题(有标准答案解析)

图形找规律专项练习60题(有答案)1.按如下方式摆放餐桌和椅子:填表中缺少可坐人数_________;_________.2.观察表中三角形个数的变化规律:图形012…n横截线条数6??…?三角形个数若三角形的横截线有0条,则三角形的个数是6;若三角形的横截线有n条,则三角形的个数是_________(用含n的代数式表示).3.如图,在线段AB上,画1个点,可得3条线段;画2个不同点,可得6条线段;画3个不同点,可得10条线段;…照此规律,画10个不同点,可得线段_________条.4.如图是由数字组成的三角形,除最顶端的1以外,以下出现的数字都按一定的规律排列.根据它的规律,则最下排数字中x的值是_________,y的值是_________.5.下列图形都是由相同大小的单位正方形构成,依照图中规律,第六个图形中有_________个单位正方形.6.如图,用相同的火柴棒拼三角形,依此拼图规律,第7个图形中共有_________根火柴棒.7.图1是一个正方形,分别连接这个正方形的对边中点,得到图2;分别连接图2中右下角的小正方形对边中点,得到图3;再分别连接图3中右下角的小正方形对边中点,得到图4;按此方法继续下去,第n个图的所有正方形个数是_________个.8.观察下列图案:它们是按照一定规律排列的,依照此规律,第6个图案中共有_________个三角形.9.如图,依次连接一个边长为1的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第二个正方形的面积是_________;第六个正方形的面积是_________.10.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形有1个小正方形,第2个图形有3个小正方形,第3个图形有6个小正方形,第4个图形有10个小正方形…,按照这样的规律,则第10个图形有_________个小正方形.11.如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为_________.12.为庆祝“六一”儿童节,幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,则摆n条“金鱼”需用火柴棒的根数为_________.13.如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有_________个交点,二十条直线相交最多有_________个交点.14.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:图形编号(1)(2)(3)…n火柴根数从左到右依次为____________________________________.15.图(1)是一个黑色的正三角形,顺次连接三边中点,得到如图(2)所示的第2个图形(它的中间为一个白色的正三角形);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形.如此继续作下去,则在得到的第5个图形中,白色的正三角形的个数是_________.16.如图,一块圆形烙饼切一刀可以切成2块,若切两刀最多可以切成4块,切三刀最多可以切成7块…通过观察、计算填下表(其中S表示切n刀最多可以切成的块数)后,可探究一圆形烙饼切n刀最多能切成_________块(结果用n的代数式表示).n012345…nS124717.如图,是用相同的等腰梯形拼成的等腰梯形图案.第(1)个图案只有1个等腰梯形,其两腰之和为4,上下底之和为3,周长为7;第(2)个图案由3个等腰梯形拼成,其周长为13;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为_________.(用正整数n表示)18.下列各图均是用有一定规律的点组成的图案,用S表示第n个图案中点的总数,则S=_________(用含n 的式子表示).19.如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有n(n≥3)盆花,每个图案中花盆总数为S,按照图中的规律可以推断S与n(n≥3)的关系是_________.20.用火柴棍象如图这样搭图形,搭第n个图形需要_________根火柴棍.21.现有黑色三角形“”和白色三角形“”共有2011个,按照一定的规律排列如下:则黑色三角形有_________个.22.假设有足够多的黑白围棋子,按照一定的规律排成一行:○●●○○●○●●○○●○●●○○●○●●○○●…请问第2011个棋子是黑的还是白的?答:_________.23.观察下列由等腰梯形组成的图形和所给表中数据的规律后填空:梯形的个数12345…图形的周长58111417…当梯形个数为2007个时,这时图形的周长为_________24.如图,下面是一些小正方形组成的图案,第4个图案有_________个小正方形组成;第n个图案有_________个小正方形组成.25.如图所示是由火柴棒按一定规律拼出的一系列图形:依照此规律,第7个图形中火柴棒的根数是_________.26.图中的每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,每个图案的棋子总数为s,按图的排列规律推断,s与n之间的关系可用式子_________表示.27.观察下列图形,它是按一定规律排列的,那么第_________个图形中,十字星与五角星的个数和为27个.28.2条直线最多只有1个交点;3条直线最多只有3个交点;4条直线最多只有6个交点;2000条直线最多只有_________个交点.29.以下各图分别由一些边长为1的小正方形组成,请填写图2、图3中的周长,并以此推断出图10的周长为_________.30.如图所示,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么设第n个图案中有白色地面砖m块,则m与n的函数关系式是_________.31.用同样大小的黑色棋子按如图所示的规律摆放:(1)分别写出第6、7两个图形各有多少颗黑色棋子?(2)写出第n个图形黑色棋子的颗数?(3)是否存在某个图形有2012颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.32.如图,给出四个点阵,s表示每个点阵中点的个数,按照图形中的点的个数变化规律,(1)猜想第n个点阵中的点的个数s=_________.(2)若已知点阵中点的个数为37,问这个点阵是第几个?33.用棋子摆出下列一组图形:(1)填写下表:图形编号123456图中棋子数5811141720(2)照这样的方式摆下去,写出摆第n个图形所需棋子的枚数;(3)其中某一图形可能共有2011枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形.34.观察图中四个顶点的数字规律:(1)数字“30”在_________个正方形的_________;(2)请你用含有n(n≥1的整数)的式子表示正方形四个顶点的数字规律;(3)数字“2011”应标在什么位置.35.如图,各图表示若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案中花盆的总数为S.问:①当每条边有2盆花时,花盆的总数S是多少?②当每条边有3盆花时,花盆的总数S是多少?③当每条边有4盆花时,花盆的总数S是多少?④当每条边有10盆花时,花盆的总数S是多少?⑤按此规律推断,当每条边有n盆花时,花盆的总数S是多少?36.如下图是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第④、第⑤个“上”字分别需用_________和_________枚棋子;(2)第n个“上”字需用_________枚棋子;(3)七(3)班有50名同学,把每一位同学当做一枚棋子,能否让这50枚“棋子”按照以上规律恰好站成一个“上”字?若能,请计算最下一“横”的学生数;若不能,请说明理由.37.下列表格是一张对同一线段上的个数变化及线段总条数的探究统计.线段上点的个数线段的总条数11+2=31+2+3=6……(1)请你完成探究,并把探究结果填在相应的表格里;(2)若在同一线段上有10个点,则线段的总条数为_________;若在同一线段上有n个点,则有_________条线段(用含n 的式子表示)(3)若你所在的班级有60名学生,20年后参加同学聚会,见面时每两个同学之间握一次手,共握手_________次.38.如图是用棋子摆成的“H”字.(1)摆成第一个“H”字需要_________个棋子;摆第x个“H”字需要的棋子数可用含x的代数式表示为_________;(2)问第几个“H”字棋子数量正好是2012个棋子?39.我们知道,两条直线相交只有一个交点.请你探究:(1)三条直线两两相交,最多有_________个交点;(2)四条直线两两相交,最多有_________个交点;(3)n条直线两两相交,最多有_________个交点(n为正整数,且n≥2).40.如图所示,小王玩游戏:一张纸片,第一次将其撕成四小片,手中共有4张纸片,以后每次都将其中一片撕成更小的四片.如此进行下去,当小王撕到第n次时,手张共有S张纸片.根据上述情况:(1)用含n的代数式表示S;(2)当小王撕到第几次时,他手中共有70张小纸片?41.如图①是一张长方形餐桌,四周可坐6人,2张这样的桌子按图②方式拼接,四周可坐10人.现将若干张这样的餐桌按图③方式拼接起来:(1)三张餐桌按题中的拼接方式,四周可坐_________人;(2)n张餐桌按上面的方式拼接,四周可坐_________人(用含n的代数式表示).若用餐人数为26人,则这样的餐桌需要_________张.42.用棋子摆出下列一组图形:(1)填写下表:图形编号123456图形中的棋子(2)照这样的方式摆下去,写出摆第n个图形棋子的枚数;(用含n的代数式表示)(3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?43.如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,(1)第5个“广”字中的棋子个数是_________.(2)第n个“广”字需要多少枚棋子?44.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察图形并解答有关问题:(1)在第n个图中共有_________块黑瓷砖,_________块白瓷砖;(2)是否存在黑瓷砖与白瓷砖块数相等的情形?你能通过计算说明吗?45.用火柴棒按如图的方式搭三角形.照这样搭下去:(1)搭4个这样的三角形要用_________根火柴棒;13根火柴棒可以搭_________个这样的三角形;(2)搭n个这样的三角形要用_________根火柴棒(用含n的代数式表示).46.观察图中的棋子:(1)按照这样的规律摆下去,第4个图形中的棋子个数是多少?(2)用含n的代数式表示第n个图形的棋子个数;(3)求第20个图形需棋子多少个?47.如图,用正方体石墩垒石梯,下图分别表示垒到一、二、三阶梯时的情况.那么照这样垒下去,请你观察规律,并完成下列问题.(1)填出下表中未填的两个空格:阶梯级数一级二级三级四级石墩块数39(2)当垒到第n级阶梯时,共用正方体石墩多少块(用含n的代数式表示)?并求当n=100时,共用正方体石墩多少块?48.有一张厚度为0.05毫米的纸,将它对折1次后,厚度为2×0.05毫米.(1)对折3次后,厚度为多少毫米?(2)对折n次后,厚度为多少毫米?(3)对折n次后,可以得到多少条折痕?49.如图所示,用同样规格正方形瓷砖铺设矩形地面,请观察下图:按此规律,第n个图形,每一横行有_________块瓷砖,每一竖列有_________块瓷砖(用含n的代数式表示)按此规律,铺设了一矩形地面,共用瓷砖506块,请问这一矩形的每一横行有多少块瓷砖,每一竖列有多少瓷砖?50.找规律:观察下面的星阵图和相应的等式,探究其中的规律.(1)在④、⑤和⑥后面的横线上分别写出相应的等式:①1=12②1+3=22③1+3+5=32④_________;⑤_________;⑥_________;(2)通过猜想,写出第n个星阵图相对应的等式.51.将一张正方形纸片剪成四个大小一样的小正方形,然后将其中的一个正方形再剪成四个小正方形,如此循环下去,如图所示:(1)完成下表:所剪次数n12345正方形个数Sn4(2)剪n次共有S n个正方形,请用含n的代数式表示S n=_________;(3)若原正方形的边长为1,则第n次所剪得的正方形边长是_________(用含n的代数式表示).52.如图是用五角星摆成的三角形图案,每条边上有n(n>1)个点(即五角星),每个图案的总点数(即五角星总数)用S表示.(1)观察图案,当n=6时,S=_________;(2)分析上面的一些特例,你能得出怎样的规律?(用n表示S)(3)当n=2008时,求S.53.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点.观察图中每一个正方形(实线)四条边上的格点的个数,请回答下列问题:(1)由里向外第1个正方形(实线)四条边上的格点个数共有_________个;由里向外第2个正方形(实线)四条边上的格点个数共有_________个;由里向外第3个正方形(实线)四条边上的格点个数共有_________个;(2)由里向外第10个正方形(实线)四条边上的格点个数共有_________个;(3)由里向外第n个正方形(实线)四条边上的格点个数共有_________个.54.下列各图是由若干花盆组成的形如正方形的图案,每条边(包括两个顶点)有n(n>1)个花盆,每个图案花盆总数是S.(1)按要求填表:n2 3 45…S4812…(2)写出当n=10时,S=_________.(3)写出S与n的关系式:S=_________.(4)用42个花盆能摆出类似的图案吗?55.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并解答下列问题.(1)在第1个图中,共有白色瓷砖_________块.(2)在第2个图中,共有白色瓷砖_________块.(3)在第3个图中,共有白色瓷砖_________块.(4)在第10个图中,共有白色瓷砖_________块.(5)在第n个图中,共有白色瓷砖_________块.56.淮北市为创建文明城市,各种颜色的菊花摆成如下三角形的图案,每条边(包括两个顶点)上有n(n>1)盆花,每个图案花盆的总数为S,当n=2时,S=3;n=3时,S=6;n=4时,S=10.(1)当n=6时,S=_________;n=100时,S=_________.(2)你能得出怎样的规律?用n表示S.57.下面是按照一定规律画出的一系列“树枝”经观察,图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出4个“树枝”,图(4)比图(3)多出8个“树枝”,按此规律:图(5)比图(4)多出_________个树枝;图(6)比图(5)多出_________个树枝;图(8)比图(7)多出_________个树枝;…图(n+1)比图(n)多出_________个树枝.58.如图是用棋子成的“T”字图案.从图案中可以出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”图案需要11枚棋子.(1)照此规律,摆成第八个图案需要几枚棋子?(2)摆成第n个图案需要几枚棋子?(3)摆成第2010个图案需要几枚棋子?59.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:(1)当黑砖n=1时,白砖有_________块,当黑砖n=2时,白砖有_________块,当黑砖n=3时,白砖有_________块.(2)第n个图案中,白色地砖共_________块.60.下列图案是晋商大院窗格的一部分.其中,“o”代表窗纸上所贴的剪纸.探索并回答下列问题:(1)第6个图案中所贴剪纸“o”的个数是_________;(2)第n个图案中所贴剪纸“o”的个数是_________;(3)是否存在一个图案,其上所贴剪纸“o”的个数为2012个?若存在,指出是第几个;若不存在,请说明理由.图形找规律60题参考答案:1.结合图形和表格,不难发现:1张桌子座6人,多一张桌子多2人.4张桌子可以座10+2=12.即n张桌子时,共座6+2(n﹣1)=2n+4.2.当横截线有n条时,在6个的基础上多了n个6,即三角形的个数共有6+6n=6(n+1)个.故应填6(n+1)或6n+63.∵画1个点,可得3条线段,2+1=3;画2个点,可得6条线段,3+2+1=6;画3个点,可得10条线段,4+3+2+1=10;…;画n个点,则可得(1+2+3+…+n+n+1)=条线段.所以画10个点,可得=66条线段;4.根据图形可以发现,第七排的第一个数和第二数与第八排的第二个数相等,而第八排的第二个数就是x,所以x=61.另外,由图形可知,x右边的数是2×61=122,y左边的数是2×61+56=178,所以y=178+46=2245.根据题意分析可得:第1个图案中正方形的个数2个,第2个图案中正方形的个数比第1个图案中正方形的个数多4个,第3个图案中正方形的个数比第2个图案中正方形的个数多6个…,依照图中规律,第六个图形中有2+4+6+8+10+12=42个单位正方形6.图形从上到下可以分成几行,第n行中,斜放的火柴有2n根,下面横放的有n根,因而图形中有n排三角形时,火柴的根数是:斜放的是2+4+…+2n=2(1+2+…+n)横放的是:1+2+3+…+n,则每排放n根时总计有火柴数是:3(1+2+…+n)=21)nn3(把n=7代入就可以求出.故第7个图形中共有=84根火柴棒7.图1中,是1个正方形;图2中,是1+4=5个正方形;图3中,是1+4×2=9个正方形;依此类推,第n个图的所有正方形个数是1+4(n﹣1)=4n﹣3.8.∵第1个图案中有2×2+2×1=6个三角形;第2个图案中有2×3+2×2=10个三角形;第3个图案中有2×4+2×3=14个三角形;…∴第6个图案中有2×7+2×6=26个三角形.故答案为269.∵正方形的边长是1,所以它的斜边长是:=,所以第二个正方形的面积是:×=,第三个正方形的面积为=()2,以此类推,第n 个正方形的面积为()n ﹣1,所以第六个正方形的面积是()6﹣1=;故答案为:,.10.∵第一个有1个小正方形,第二个有1+2个,第三个有1+2+3个,第四个有1+2+3+4,第五个有1+2+3+4+5,∴则第10个图形有1+2+3+4+5+6+7+8+9+10=55个.故答案为:5511.依题意得:(1)摆第1个“小屋子”需要5个点;摆第2个“小屋子”需要11个点;摆第3个“小屋子”需要17个点.当n=n时,需要的点数为(6n﹣1)个.故答案为6n﹣112.由图形可知:第一个金鱼需用火柴棒的根数为:2+6=8;第二个金鱼需用火柴棒的根数为:2+2×6=14;第三个金鱼需用火柴棒的根数为:2+3×6=20;…;第n个金鱼需用火柴棒的根数为:2+n×6=2+6n.故答案为2+6n13.6条直线两两相交,最多有n (n﹣1)=×6×5=15,20条直线两两相交,最多有n(n﹣1)=×20×19=190.故答案为:15,190.14.如表格所示:图形编号(1)(2)(3)…n火柴根数71217…5n+215.设白三角形x个,黑三角形y个,则:n=1时,x=0,y=1;n=2时,x=0+1=1,y=3;n=3时,x=3+1=4,y=9;n=4时,x=4+9=13,y=27;当n=5时,x=13+27=40,所以白的正三角形个数为:40,故答案为:4016.n=1时,S=1+1=2,n=2时,S=1+1+2=4,n=3时,S=1+1+2+3=7,n=4时,S=1+1+2+3+4=11,…所以当切n刀时,S=1+1+2+3+4+…+n=1+n(n+1)=n2+n+1.故答案为n2+n+117.根据题意得:第(1)个图案只有1个等腰梯形,周长为3×1+4=7;第(2)个图案由3个等腰梯形拼成,其周长为3×3+4=13;第(3)个图案由5个等腰梯形拼成,其周长为3×5+4=19;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为3(2n﹣1)+4=6n+1;故答案为:6n+118.观察发现:第1个图形有S=9×1+1=10个点,第2个图形有S=9×2+1=19个点,第3个图形有S=9×3+1=28个点,…第n个图形有S=9n+1个点.故答案为:9n+119.n=3时,S=6=3×3﹣3=3,n=4时,S=12=4×4﹣4,n=5时,S=20=5×5﹣5,…,依此类推,边数为n数,S=n?n﹣n=n(n﹣1).故答案为:n(n﹣1).20.结合图形,发现:搭第n个三角形,需要3+2(n ﹣1)=2n+1(根).故答案为2n+121.因为2011÷6=335…1.余下的1个根据顺序应是黑色三角形,所以共有1+335×3=1006.故答案为:100622.从所给的图中可以看出,每六个棋子为一个循环,∵2011÷6=335…1,∴第2011个棋子是白的.故答案为:白23.依题意可求出梯形个数与图形周长的关系为3n+2=周长,当梯形个数为2007个时,这时图形的周长为3×2007+2=6023.故答案为:6023.24.观察图形知:第一个图形有1=12个小正方形;第二个图形有1+3=4=22个小正方形;第三个图形有1+3+5=9=32个小正方形;…第n个图形共有1+2+3+…+(2n﹣1)=n2个小正方形,当n=4时,有n2=42=16个小正方形.故答案为:16,n225.根据已知图形可以发现:第2个图形中,火柴棒的根数是7;第3个图形中,火柴棒的根数是10;第4个图形中,火柴棒的根数是13;∵每增加一个正方形火柴棒数增加3,∴第n个图形中应有的火柴棒数为:4+3(n﹣1)=3n+1.当n=7时,4+3(n﹣1)=4+3×6=22,故答案为:2226.观察图形发现:当n=2时,s=4,当n=3时,s=9,当n=4时,s=16,当n=5时,s=25,…当n=n时,s=n2,故答案为:s=n227.∵第1个图形中,十字星与五角星的个数和为3×2=6,第2个图形中,十字星与五角星的个数和为3×3=9,第3个图形中,十字星与五角星的个数和为3×4=12,…而27=3×9,∴第8个图形中,十字星与五角星的个数和=3×9=27.故答案为:828.2条直线最多的交点个数为1,3条直线最多的交点个数为1+2=3,4条直线最多的交点个数为1+2+3=6,5条直线最多的交点个数为1+2+3+4=10,…所以2000条直线最多的交点个数为1+2+3+4+…+1999==1999000.故答案为199900029.∵小正方形的边长是1,∴图1的周长是:1×4=4,图2的周长是:2×4=8,图3的周长是3×4=12,…第n个图的周长是4n,∴图10的周长是10×4=40;故答案为:8,12,4030.首先发现:第一个图案中,有白色的是6个,后边是依次多4个.所以第n个图案中,是6+4(n﹣1)=4n+2.∴m与n的函数关系式是m=4n+2.故答案为:4n+2.31.第一个图需棋子6,第二个图需棋子9,第三个图需棋子12,第四个图需棋子15,第五个图需棋子18,…第n个图需棋子3(n+1)枚.(1)当n=6时,3×(6+1)=21;当n=7时,3×(7+1)=24;(2)第n个图需棋子3(n+1)枚.(3)设第n个图形有2012颗黑色棋子,根据(1)得3(n+1)=2012解得n=,所以不存在某个图形有2012颗黑色棋子32.(1)由点阵图形可得它们的点的个数分别为:1,5,9,13,…,并得出以下规律:第一个点数:1=1+4×(1﹣1)第二个点数:5=1+4×(2﹣1)第三个点数:9=1+4×(3﹣1)第四个点数:13=1+4×(4﹣1)…因此可得:第n个点数:1+4×(n﹣1)=4n﹣3.故答案为:4n﹣3;(2)设这个点阵是x个,根据(1)得:1+4×(x﹣1)=37解得:x=10.答:这个点阵是10个33.(1)观察图形,得出枚数分别是,5,8,11,…,每个比前一个多3个,所以图形编号为5,6的棋字子数分别为17,20.故答案为:17和20.(2)由(1)得,图中棋子数是首项为5,公差为3的等差数列,所以摆第n个图形所需棋子的枚数为:5+3(n﹣1)=3n+2.(3)不可能由3n+2=2010,解得:n=669,∵n为整数,∴n=669不合题意故其中某一图形不可能共有2011枚棋子34.(1)由图可知,每个正方形标4个数字,∵30÷4=7…2,∴数字30在第8个正方形的第2个位置,即右上角;故答案为:8,右上角;(2)左下角是4的倍数,按照逆时针顺序依次减1,即正方形左下角顶点数字:4n,正方形左上角顶点数字:4n﹣1,正方形右上角顶点数字:4n﹣2,正方形右下角顶点数字:4n﹣3;(3)2011÷4=502…3,所以,数字“2011”应标第503个正方形的左上角顶点处35.依题意得:①n=2,S=3=3×2﹣3.②n=3,S=6=3×3﹣3.③n=4,S=9=3×4﹣3④n=10,S=27=3×10﹣3.…⑤按此规律推断,当每条边有n盆花时,S=3n﹣3 36.(1)第①个图形中有6个棋子;第②个图形中有6+4=10个棋子;第③个图形中有6+2×4=14个棋子;∴第⑤个图形中有6+3×4=18个棋子;第⑥个图形中有6+4×4=22个棋子.故答案为18、22;(3分)(2)第n个图形中有6+(n﹣1)×4=4n+2.故答案为4n+2.(3分)(3)4n+2=50,解得n=12.最下一横人数为2n+1=25.(4分)37.(1)5个点时,线段的条数:1+2+3+4=10,6个点时,线段的条数:1+2+3+4+5=15;(2)10个点时,线段的条数:1+2+3+4+5+6+7+8+9=45,n个点时,线段的条数:1+2+3+…+(n﹣1)=;(3)60人握手次数==1770.故答案为:(2)45,;(3)1770.38.(1)摆成第一个“H”字需要7个棋子,第二个“H”字需要棋子12个;第三个“H”字需要棋子17个;…第x个图中,有7+5(x﹣1)=5x+2(个).(2)当5x+2=2012时,解得:x=402,故第402个“H”字棋子数量正好是2012个棋子39.(1)如图(1),可得三条直线两两相交,最多有3个交点;(2)如图(2),可得三条直线两两相交,最多有6个交点;(3)由(1)得,=3,由(2)得,=6;∴可得,n 条直线两两相交,最多有个交点(n为正整数,且n≥2).故答案为3;6;.40.(1)由题目中的“每次都将其中﹣片撕成更小的四片”,可知:小王每撕一次,比上一次多增加3张小纸片.∴s=4+3(n﹣1)=3n+1;(2)当s=70时,有3n+1=70,n=23.即小王撕纸23次41.(1)结合图形,发现:每个图中,两端都是坐2人,剩下的两边则是每一张桌子是4人.则三张餐桌按题中的拼接方式,四周可坐3×4+2=14(人);(2)n张餐桌按上面的方式拼接,四周可坐(4n+2)人;若用餐人数为26人,则4n+2=26,解得n=6.故答案为:14;(4n+2),642.(1)如图所示:图形编号123456图形中的棋子6 9 12151821(2)依题意可得当摆到第n个图形时棋子的枚数应为:6+3(n﹣1)=6+3n﹣3=3n+3;(3)由上题可知此时3n+3=99,∴n=32.答:第32个图形共有99枚棋子13.由题目得:第1个“广”字中的棋子个数是7;第2个“广”字中的棋子个数是7+(2﹣1)×2=9;第3个“广”字中的棋子个数是7+(3﹣1)×2=11;第4个“广”字中的棋子个数是7+(4﹣1)×2=13;发现第5个“广”字中的棋子个数是7+(5﹣1)×2=15…进一步发现规律:第n个“广”字中的棋子个数是7+(n﹣1)×2=2n+5.故答案为:1544.(1)在第n个图形中,需用黑瓷砖4n+6块,白瓷砖n(n+1)块;(2)根据题意得n(n+1)=4n+6,n2﹣3n﹣6=0,此时没有整数解,所以不存在.故答案为:4n+6;n(n+1)45.(1)结合图形,发现:后边每多一个三角形,则需要多2根火柴.则搭4个这样的三角形要用3+2×3=9根火柴棒;13根火柴棒可以搭(13﹣3)÷2+1=6个这样的三角形;(2)根据(1)中的规律,得搭n个这样的三角形要用3+2(n﹣1)=2n+1根火柴棒.故答案为9;6;2n+146.(1)第4个图形中的棋子个数是13;(2)第n个图形的棋子个数是3n+1;(3)当n=20时,3n+1=3×20+1=61∴第20个图形需棋子61个47.(1)第一级台阶中正方体石墩的块数为:=3;第一级台阶中正方体石墩的块数为:=9;第一级台阶中正方体石墩的块数为:;…依此类推,可以发现:第几级台阶中正方体石墩的块数为:3与几的乘积乘以几加1,然后除以2.阶梯级数一级二级三级四级石墩块数391830(2)按照(1)中总结的规律可得:当垒到第n级阶梯时,共用正方体石墩块;当n=100时,∴当n=100时,共用正方体石墩15150块.答:当垒到第n级阶梯时,共用正方体石墩块;当n=100时,共用正方体石墩15150块48.由题意可知:第一次对折后,纸的厚度为2×0.05;可以得到折痕为1条;第二次对折后,纸的厚度为2×2×0.05=22×0.05;可以得到折痕为3=22﹣1条;第三次对折后,纸的厚度为2×2×2×0.05=23×0.05;可以得到折痕为7=23﹣1条;…;第n次对折后,纸的厚度为2×2×2×2× (2)0.05=2n×0.05.可以得到折痕为2n﹣1条.故:(1)对折3次后,厚度为0.4毫米;(2)对折n次后,厚度为2n×0.05毫米;(3)对折n次后,可以得到2n﹣1条折痕49.由图形我们不难看出横行砖数量为n+3,竖行砖数量为n+2,总数量为n2+5n+6;若用瓷砖506块,可以求n2+5n+6=506;所以答案为:(1)n+3,n+2;(2)每一行有23块,每一列有22块50.等号左边是从1开始,连续奇数相加,等号右边是奇数个数也就是n的平方.(1)①1+3+5+7=42;②1+3+5+7+9=52;③1+3+5+7+9+11=62.(2)1+3+5+…+(2n﹣1)=n2(n≥1的正整数)51.(1)依题意得:所剪次数n12345正方形个数Sn47101316(2)可知剪n次时,S n=3n+1.(3)n=1时,边长=;n=2时,边长=;n=3时,边长=;…;剪n次时,边长=.52.(1)S=15(2)∵n=2时,S=3×(2﹣1)=3;n=3时,S=3×(3﹣1)=6;n=4时,S=3×(4﹣1)=9;…∴S=3×(n﹣1)=3n﹣3.(3)当n=2008时,S=3×2008﹣3=6021.53.第1个正方形四条边上的格点共有4个第2个正方形四条边上的格点个数共有(4+4×1)个第3个正方形四条边上的格点个数共有(4+4×2)个…第10个正方形四条边上的格点个数共有(4+4×9)=40个第n个正方形四条边上的格点个数共有[4+4×(n﹣1)]=4n个54.由图可知,每个图形为边长是n的正方形,因此四条边的花盆数为4n,再减去重复的四个角的花盆数,即S=4n﹣4;(1)将n=5代入S=4n﹣4,得S=16;(2)将n=10入S=4n﹣4,得S=36;(3)S=4n﹣4;(4)将S=42代入S=4n﹣4得,4n﹣4=42解得n=11.5所以用42个花盆不能摆出类似的图案55.(1)在第1个图中,共有白色瓷砖1×(1+1)=2块,(2)在第2个图中,共有白色瓷砖2×(2+1)=6块,(3)在第3个图中,共有白色瓷砖3×(3+1)=12块,(4)在第10个图中,共有白色瓷砖10×(10+1)=110块,(5)在第n个图中,共有白色瓷砖n(n+1)块56.(1)由分析得:当n=6时,s=1+2+3+4+5+6=21;当n=100时,s=1+2+3+…+99+100=5050;(2)用n表示S得:S=57.(1)图(5)比图(4)多出25﹣1=16个;(2)图(6)比图(5)多出26﹣1=32个;(3)图(8)比图(7)多出28﹣1=128个;(4)图(n+1)比图(n)多出2n个.58.(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在5的基础上依次多3枚.即第n个图案需要5+3(n﹣1)=3n+2.那么当n=8时,则有26枚;故摆成第八个图案需要26枚棋子.(2)因为第①个图案有5枚棋子,第②个图案有(5+3×1)枚棋子,第③个图案有(5+3×2)枚棋子,依此规律可得第n个图案需5+3×(n﹣1)=5+3n﹣3=(3n+2)枚棋子.(3)3×2010+2=6032(枚)即第2010个图案需6032枚棋子59.(1)观察图形得:当黑砖n=1时,白砖有6块,当黑砖n=2时,白砖有10块,当黑砖n=3时,白砖有14块;(2)根据题意得:∵每个图形都比其前一个图形多4个白色地砖,∴可得规律为:第n个图形中有白色地砖6+4(n﹣1)=4n+2块.故答案为6,10,14,4n+260.第一个图案为3+2=5个窗花;第二个图案为2×3+2=8个窗花;第三个图案为3×3+2=11个窗花;…从而可以探究:第n个图案所贴窗花数为(3n+2)个.(1)20(2)3n+2(3)存在,令3n+2=2012,则3n=2010 n=670 因此是第670个。
初二函数找规律练习题

初二函数找规律练习题1. 问题描述在初二数学学习中,函数是一个重要的概念。
函数可以帮助我们在数学问题中找到规律,并运用这些规律解决问题。
下面是一些初二函数找规律的练习题,帮助学生掌握函数的应用。
2. 题目一已知函数f(x)满足f(2)=4,f(3)=6,f(4)=8,求f(1)。
解析:我们观察题目中的输入和输出,可以发现函数的关系是每个输入都比前一个大2,而输出则比前一个大2。
根据这个规律,我们可以得出函数的表达式为f(x)=2x。
因此,f(1)=2*1=2。
3. 题目二函数g(x)的表达式为g(x)=3x-1,求g(5)和g(10)。
解析:根据函数的表达式g(x)=3x-1,我们可以计算出g(5)=3*5-1=15-1=14,以及g(10)=3*10-1=30-1=29。
4. 题目三函数h(x)的图像与y=x^2的图像关于y轴对称,请根据这个特性,求出h(x)的表达式。
解析:根据题目中的条件,我们可以观察到h(x)的图像在y轴的左右两侧是对称的。
而y=x^2的图像也是对称于y轴的,因此h(x)的图像也是类似的。
由此可知,h(x)的表达式为h(x)=x^2。
5. 题目四函数k(x)满足k(x+1)=k(x)+2,已知k(1)=3,请求出k(10)。
解析:根据题目中的条件k(x+1)=k(x)+2,我们可以逐步计算出k(x)的值。
由于k(1)=3,我们可以计算出k(2)=3+2=5,k(3)=5+2=7,以此类推,我们可以计算出k(10)=3+(10-1)*2=3+18=21。
通过以上的练习题,我们可以看到函数的应用在数学中是非常重要的。
函数可以帮助我们找到规律,并解决各种数学问题。
希望同学们在解决这些题目时,能够充分理解函数的概念和应用,提高数学解题的能力。
一年级数学找规律“穿珠子”问题详解+练习

找规律“穿珠子”解决问题详细讲解
典型例题:
小红按规律穿了一串手链,但掉了2颗珠子,掉的是哪2颗?
解题分析:这类“穿珠子”问题都是运用排列规律解决实际问题的类型,解题方法一般都是:先找出事物排列的规律,再按照规律补上所缺的部分。
第一步:根据变化,找出排列规律。
根据珠子的颜色、数量、形状的变化找。
第二步:按照排列规律,补充珠子。
第三步:验证答案。
把缺少的珠子补上,围成一圈,看是否符合排列规律。
符合2颗黄珠子、1颗蓝珠子的排列规律,说明解答正确。
答:掉的是1颗黄珠子、1颗蓝珠子。
1.乐乐做了一串手链,但掉了4颗珠子,掉的是哪4颗?
2.根据规律画出被挡住的两颗珠子。
3.云云用16个海螺和扇贝,穿了一串手链,但掉了5个,掉的是哪5个?
掉了()个,()个。
4.四只小动物各穿了一串项链,这几串项链分别是谁穿的?请用线连一连。
5.找规律,接着画出5颗珠子。
1.根据规律画出箱子里的珠子。
2.东东按照规律用珠子穿成一串手链,但是掉了5颗珠子,各种颜色的珠子各掉了几颗呢?
3.猜一猜,盒子里有几颗黄珠子?几颗紫珠子?
4.花花穿的手链还缺3颗珠子,从下面圈出她需要的3颗珠子。
5.找规律,涂一涂。
初中数学找规律题及其标准答案

初中数学找规律题及其答案————————————————————————————————作者:————————————————————————————————日期:整式的加减——专题训练与提升1、根据下列5个图形及相应点的个数的变化规律,试猜测第n个图中有个点.2、找规律.下列图中有大小不同的菱形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第n幅图中共有个.3、如图,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第100个图案需棋子枚.4、观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有个.5、观察下列图形,它们是按一定规律排列的,依照此规律,第16个图形共有个★.6、如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是,第n个“广”字中的棋子个数是.7、如图1是二环三角形,可得S=∠A1+∠A2+…+∠A6=360°,下图2是二环四边形,可得S=∠A1+∠A2+…+∠A7=720°,图3是二环五边形,可得S=1080°,…聪明的同学,请你根据以上规律直接写出二环n边形(n≥3的整数)中,S= 度.(用含n的代数式表示最后结果)8、观察下列图形(每幅图中最小的三角形都是全等的),请写出第n个图中最小的三角形的个数有个.9、将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去,结果如下表.则an= .(用含n的代数式表示)所剪次数三角形个数10、用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n个图案中正三角形的个数为(用含n的代数式表示).11、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个10×10的正方形图案,则其中完整的圆共有个.12、根据下列图形的排列规律,第2008个图形是福娃(填写福娃名称即可).13、用火柴棒按照如图所示的方式摆图形,则第n个图形中,所需火柴棒的根数是.14、下列图案均是用长度相同的小木棒按一定的规律拼搭而成:拼搭第1个图案需4根小木棒,拼搭第2个图案需10根小木棒,…,依次规律,拼搭第8个图案需小木棒根.15、一张长方形桌子需配6把椅子,按如图方式将桌子拼在一起,那么8张桌子需配椅子把.16、下列每个图是由若干个圆点组成的形如四边形的图案,当每条边(包括顶点)上有n (n≥2个圆点时,图案的圆点数为S n .按此规律推断S n 关于n 的关系式为:S n = .17、如图是由火柴棒搭成的几何图案,则第n 个图案中有 根火柴棒.(用含n的代数式表示)18、观察下列图形的构成规律,根据此规律,第8个图形中有 个圆.19、观察表一,寻找规律.表二,表三分别是从表一中选取的一部分,则a+b的值为.表一:表二:表三:20、如图所示的图案是由正六边形密铺而成,黑色正六边形周围第一层有六个白色正六边形,则第n层有个白色正六边形.21、把边长为3的正三角形各边三等分,分割得到图①,图中含有1个边长是1的正六边形;把边长为4的正三角形各边四等分,分割得到图②,图中含有3个边长是1的正六边形;把边长为5的正三角形各边五等分,分割得到图③,图中含有6个边长是1的正六边形;…依此规律,把边长为7的正三角形各边七等分,并按同样的方法分割,得到的图形中含有个边长是1的正六边形.0 1 2 3 ....1 3 5 7 ....2 5 8 11 ....3 7 11 15 ....... ... ... ... ....1114a1 3722、观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆)●□☆●●□☆●□☆●●□☆●…若第一个图形是圆,则第2008个图形是(填名称).23、下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,按照图示的规律摆下去,则第n幅图中有个菱形.24、如图,观察下列图案,它们都是由边长为1cm的小正方形按一定规律拼接而成的,依此规律,则第16个图案中的小正方形有个.25、用同样大小的黑色棋子按图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需棋子枚.(用含n的代数式表示)27、如图所示是一副“三角形图”,第一行有一个三角形,第二行有2个三角形,第三行有4个三角形,第四行有8个三角形,…,你是否发现三角形的排列规律,请写出第七行有个三角形.28、如图,用3根小木棒可以摆出第(1)个正三角形,加上2根木棒可以摆出第(2)个正三角形,再加上2根木棒可以摆出第(3)个正三角形…这样继续摆下去,当摆出第(n)个正三角形时,共用了木棒根.29、观察下列图形,根据变化规律推测第100个与第个图形位置相同.30、如图,用火柴棒按以下方式搭小鱼,搭1条小鱼用8根火柴棒,搭2条小鱼用14根,…,则搭n条小鱼需要根火柴棒.(用含n的代数式表示)整式的加减——专题训练与提升参考答案1.n2-n+1 2.(2n-1)3.302 4.121 5.49 6.152n+5 7.360(n-2)8.4n-19.3n+1 10.2n+2 11.181 12.欢欢13.3n+1 14.88 15.20 16.4n-4 17.2n(n+1)18.65 19.37 20.6n 21.15 22.正方形23.(2n-1)24.136 26.3n+1 27.64 28.2n+1 29.1或4 30.6n+2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
找规律练习题一.数字排列规律题1. 4、10、16、22、28……,求第n位数( )。
2. 2、3、5、9,17增幅为1、2、4、8. 第n位数( )3. 观察下列各式数:0,3,8,15,24,……。
试按此规律写出的第100个数是----,第n个数是---------。
4. 1,9,25,49,(),(),的第n项为(),5: 2、9、28、65.....:第n位数()6:2、4、8、16...... 第n位数.()7:2、5、10、17、26……,第n位数.()8 : 4,16,36,64,?,144,196,…?第一百个数()9、观察下面两行数2,4,8,16,32,64,...(1)5,7,11,19,35,67...(2)根据你发现的规律,取每行第十个数,求得他们的和。
10、白黑白黑黑白黑黑黑白黑黑黑黑白黑黑黑黑黑排列的珠子,前2002个中有几个是黑的?11. =8=16 =24……用含有N的代数式表示规律()12. 12,20,30,42,()127,112,97,82,( )3,4,7,12,( ),2813 . 1,2,3,5,(),1314. 0,1,1,2,4,7,13,( )15 .5,3,2,1,1,( )16. 1,4,9,16,25,( ),4917. 66,83,102,123,( ) ,18. 1,8,27,( ),12519。
3,10,29,( ),12720, 0,1,2,9,()21; ()。
则第n项代数式为:()22 , 2/31/22/51/3( )。
则第n项代数式为()23 , 1,3,3,9,5,15,7,( )24. 2,6,12,20,( )25. 11,17,23,( ),35。
26. 2,3,10,15,26,( )。
27. : 1,8,27,64,( )28. :0,7,26,63 ,( )29. -2,-8,0,64,( )30. 1,32,81,64,25,( )31. 1,1,2,3,5,( )。
32. 4,5,( ),14,23,3733. 6,3,3,( ),3,-334.1,2,2,4,8,32,( )35 。
2,12,36,80,()36. 3/2, 2/3, 3/4,1/3,3/8 ( )37.观察下列各算式:1+3=4=2的平方,1+3+5=9=3的平方,1+3+5+7=16=4的平方…按此规律(1)试猜想:1+3+5+7+…+2005+2007的值?(2)推广:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少?38、下面数列后两位应该填上什么数字呢?23581217____39.请填出下面横线上的数字。
112358____ 2140、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么?41、有一串数字3610 1521 ___ 第6个是什么数?42、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2005个数是().A.1 B.2 C.3 D.443、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为 _________个.二.几何图形变化规律题44、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球个.45、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是(填图形名称).46. (2005年市中考题)在数学活动中,小明为了求的值(结果用n表示),设计如图a所示的图形。
(1)请你利用这个几何图形求的值为。
(2)请你利用图b,再设计一个能求的值的几何图形。
47.2005年省中考题)观察下面的图形(每一个正方形的边长均为1)和相应的等式,探究其中的规律:(1)写出第五个等式,并在下边给出的五个正方形上画出与之对应的图示;(2)猜想并写出与第n个图形相对应的等式。
48。
右图是一回形图,其回形通道的宽与OB的长均为1,回形线与射线OA交于点A1,A2,A3,…。
若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,……,依此类推。
则第10圈的长为。
49.瑞士中学教师巴尔末成功地从光谱数据,,,,……,中得到巴尔末公式,从而打开了光谱奥妙的大门。
请你按这种规律写出第七个数据是。
50、计算类(2005年省中考题)观察下列等式:,……则第n个等式可以表示为。
51.(2005年市中考题)观察下列各式:,,,……根据前面的规律,得:。
(其中n为正整数)52. (2005年耒阳市中考题)观察下列等式:观察下列等式:4-1=3,9-4=5,16-9=7,25-16=9,36-25=11,……这些等式反映了自然数间的某种规律,设n(n≥1)表示了自然数,用关于n的等式表示这个规律为。
53、图形类 (2005年市中考题)在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点。
观察图中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第10个正方形(实线)四条边上的整点共有个。
54、 (2005年回自治区中考题) “”代表甲种植物,“”代表乙种植物,为美化环境,采用如图所示方案种植。
按此规律,第六个图案中应种植乙种植物株。
55. (2005年呼和浩特市中考题)如图,是用积木摆放的一组图案,观察图形并探索:第五个图案中共有块积木,第n个图案中共有块积木。
56.图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面-层有一个圆圈,以下各层均比上-层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n= .如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是( );(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数-23,-22,-21,…,求图4中所有圆圈中各数的绝对值之和( ).57.例如、观察下列数表:根据数列所反映的规律,第行第列交叉点上的数应为______ .58。
要抓题目里的变量例如,用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板,则第(3)个图形中有黑色瓷砖块,第个图形中需要黑色瓷砖块(用含的代数式表示).(省2006年初中毕业升考试数学科试卷(课改区))这一题的关键是求第个图形中需要几块黑色瓷砖?59.省2006年课改实验区高中(中专)招生统一考试也出有类似的题目:“观察图(l)至(4)中小圆圈的摆放规律,并按这样的规律继续摆放,记第n个图中小圆圈的个数为m,则,m=(用含 n 的代数式表示).”60.譬如,日照市2005年中等学校招生考试数学试卷“已知下列等式:① 13=12;② 13+23=32;③ 13+23+33=62;④ 13+23+33+43=102;…………由此规律知,第⑤个等式是.”61、要善于寻找事物的循环节有譬如,市2005年中考数学试卷:“观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球个。
”62、你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示。
这样捏合到第次后可拉出64根细面条。
63.小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数的和是.–4 –3 –2 -10 1 2 4 564.现有黑色三角形“▲”和“△”共200个,按照一定规律排列如下:▲▲△△▲△▲▲△△▲△▲▲……则黑色三角形有个,白色三角形有个。
三、数、式计算规律题65、已知下列等式:①13=12;②13+23=32;③13+23+33=62;④13+23+33+43=102;由此规律知,第⑤个等式是.66、观察下面的几个算式:1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1=____.67. 观察下列算式:,,,,请你在察规律之后并用你得到的规律填空:,第n个式子呢?___________________68. 一长方形桌子可坐6人,按下列方式讲桌子拼在一起。
①2桌子拼在一起可坐______人。
3桌子拼在一起可坐____人,n桌子拼在一起可坐______人。
②一家餐厅有40这样的长方形桌子,按照上图方式每5桌子拼成1大桌子,则40桌子可拼成8大桌子,共可坐______人。
③若在②中,改成每8桌子拼成1大桌子,则共可坐_________人。
69 观察下列数据,按某种规律在横线上填上适当的数:1,,,,,,…70. 平面两两相交的6条直线,其交点个数最少为m个,最多为n个,则m+n=.71. 观察图1-27中有几个三角形?由此你发现三角形的个数有什么规律呢?一个三角形 3个三角形 ______个三角形 ______个三角形_________个三角形(n个点)归纳—猜想~~~找规律给出几个具体的、特殊的数、式或图形,要求找出其中的变化规律,从而猜想出一般性的结论.解题的思路是实施特殊向一般的简化;具体方法和步骤是(1)通过对几个特例的分析,寻找规律并且归纳;(2)猜想符合规律的一般性结论;(3)验证或证明结论是否正确,下面通过举例来说明这些问题.一、数字排列规律题1、观察下列各算式:1+3=4=2的平方,1+3+5=9=3的平方,1+3+5+7=16=4的平方…按此规律(2)试猜想:1+3+5+7+…+2005+2007的值?(3)推广:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少?2、下面数列后两位应该填上什么数字呢?23581217____3、请填出下面横线上的数字。
112358____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么?5、有一串数字3610 1521 ___ 第6个是什么数?6、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2005个数是( ). A .1 B .2C .3D .47、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为 _________个. 二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●…… 从第1个球起到第2004个球止,共有实心球个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是(填图形名称).三、数、式计算规律题 1、已知下列等式: ① 13=12; ② 13+23=32; ③ 13+23+33=62;④ 13+23+33+43=102 ; 由此规律知,第⑤个等式是 . 2、观察下面的几个算式: 1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____.3、1+2+3+…+100=?经过研究,这个问题的一般性结论是1+2+3+…+()121+=n n n ,其中n是正整数.现在我们来研究一个类似的问题:1×2+2×3+…()1+n n = ? 观察下面三个特殊的等式()2103213121⨯⨯-⨯⨯=⨯()3214323132⨯⨯-⨯⨯=⨯()4325433143⨯⨯-⨯⨯=⨯将这三个等式的两边相加,可以得到1×2+2×3+3×4=2054331=⨯⨯⨯读完这段材料,请你思考后回答: ⑴=⨯++⨯+⨯1011003221⑵()()=++++⨯⨯+⨯⨯21432321n n n ⑶()()=++++⨯⨯+⨯⨯21432321n n n 4、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+=+⨯=+b a aba b 则符合前面式子的规律,,若 (21010)参考答案:一、1、(1)1004的平方(2)n+1的平方2、2330。
