2013年中考复习分层训练21 梯形含答案
2013年中考数学复习分层训练试题(共38份,含答案)-33

第2课时等腰三角形与直角三角形一级训练1.(2011年湖南邵阳)如图4-2-31所示,在△ABC中,AB=AC,∠B=50°,则∠A=()A.40°B.50°C.80°D.100°图4-2-312.(2011年浙江舟山)如图4-2-32,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为()图4-2-32A.2 3B.3 3 C. 4 3 D. 6 33.如图4-2-33,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为()图4-2-33A.50°B.60°C.30°D.40°4.(2010年广东深圳)如图4-2-34,在△ABC中,AC=AD=BD,∠DAC=80°,则∠B 的度数是()A.40°B.35°C.25°D.20°图4-2-345.(2012年山东济宁)如图4-2-35,在平面直角坐标系中,点P的坐标为(-2,3),以点O 为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于()图4-2-35A.-4和-3之间B.3和4之间C.-5和-4之间D.4和5之间6.下列性质中,等腰三角形具有而直角三角形不一定具有的是()A.两边之和大于第三边B.有一个角的平分线垂直于这个角的对边C.有两个锐角的和等于90°D.内角和等于180°7.已知在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是()A.0<x<3 B.x>3 C.3<x<6 D.x>68.(2011年江苏无锡)如图4-2-36,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,CA的中点,若CD=5 cm,则EF=_________cm.图4-2-369.在等腰三角形ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为()A.7 B.11 C.7或11 D.7或1010.(2011年山东德州)下列命题中,其逆命题成立的是________(只填写序号).①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.11.如图4-2-37,△ABC是等边三角形,点D是BC边上的任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=2,则DE+DF=______.图4-2-3712.(2012年江苏淮安)如图4-2-38,在△ABC中,∠C=90°,点D在AC上,已知∠BDC =45°,BD=102,AB=20.求∠A的度数.图4-2-38二级训练13.若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为()A.75°或15°B.36°或60°C.75°D.30°14.(2012年贵州黔西南州)如图4-2-39,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,则四边形ACEB的周长为______.图4-2-3915.(2011年山东枣庄)如图4-2-40,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:图4-2-40(1)画线段AD∥BC且使AD=BC,连接CD;(2)线段AC的长为________,CD的长为________,AD的长为________;(3)△ACD为________三角形,四边形ABCD的面积为________;(4)若E为BC的中点,则tan∠CAE的值是______.三级训练16.如图4-2-41,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=4,则图中阴影部分的面积为________.图4-2-4117.(2011年湖北黄冈)如图4-2-42,在等腰直角三角形ABC中,∠ABC=90°,D为AC 边上的中点,过点D作DE丄DF,交AB于点E,交BC于点F,若AE=4,FC=3,求EF的长.图4-2-42。
2013—2014学年度初三数学培优班练习卷参考答案(因动点产生的梯形问题)

2013—2014学年度初三数学培优班练习卷参考答案(因动点产生的梯形问题)班级座号姓名一、选择题.1答案:B 2答案:B 3答案:C 4答案:A 5答案:B6答案:B 7故选:B 8答案:B 9答案:D 10答案:A11答案:B 12答案:A 13答案:B 14答案:C 15答案:D二、填空题.1答案:3;73 2答案:5.3答案:19.4答案:3.5答案: 6答案:7答案:66+6 8答案:4 9答案:8 10答案:11答案:233,23。
12答案:4+23。
三、计算题1、【答案】解:(1)t-2。
(2)当点N落在AB边上时,有两种情况:①如图(2)a,当点N与点D重合时,此时点P在DE上,DP=2=EC,即t-2=2,t=4。
②如图(2)b,此时点P位于线段EB上.∵DE=1 2 AC=4,∴点P在DE段的运动时间为4s,∴PE=t-6,∴PB=BE-PE=8-t,PC=PE+CE=t-4。
∵PN∥AC,∴△BNP∽△BAC。
∴PN:AC = PB:BC=2,∴PN=2PB=16-2t。
由PN=PC,得16-2t=t-4,解得t=203。
综上所述,当点N落在AB边上时,t=4或t=203。
(3)当正方形PQMN与△ABC重叠部分图形为五边形时,有两种情况:①当2<t<4时,如图(3)a所示。
DP=t-2,PQ=2,∴CQ=PE=DE-DP=4-(t-2)=6-t,AQ=AC-CQ=2+t,AM=AQ-MQ=t。
∵MN∥BC,∴△AFM∽△ABC。
∴FM:BC = AM:AC=1:2,即FM:AM=BC:AC=1:2。
∴FM=12AM=12t . ∴AMF AQPD 11S S S DP AQ PQAM FM 22∆=-=+⋅-⋅梯形()21111 [t 22t ]2t t t 2t 2224=-++⨯-⋅=-+()() 。
②当203<t <8时,如图(3)b 所示。
PE=t-6,∴PC=CM=PE+CE=t -4,AM=AC-CM=12-t ,PB=BE-PE=8-t ,∴FM=12AM=6-12t ,PG=2PB=16-2t ,∴AMF AQPD 11S S S PG AC PC AM FM 22∆=-=+⋅-⋅梯形()21115[162t 8]t 412t 6t t 22t 842224=-+⨯---⋅-=-+-()()()()。
八年级数学竞赛专题训练21 梯形(附答案)

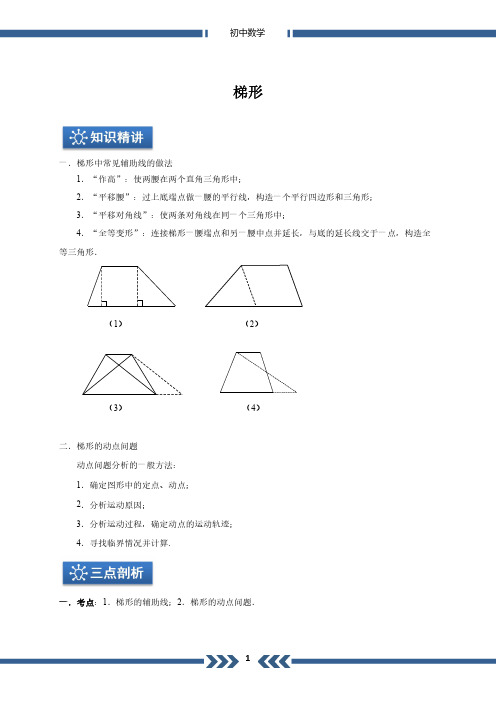
八年级数学竞赛专题训练21 梯形阅读与思考梯形是一类具有一组对边平行而另一组对边不平行的特殊四边形,梯形的主要内容是等腰梯形、直角梯形等相关概念及性质.解决梯形问题的基本思路是:通过适当添加辅助线,把梯形转化为三角形或平行四边形,常见的辅助线的方法有:(1)过一个顶点作一腰的平行线(平移腰);(2)过一个顶点作一条对角线的平行线(平移对角线);(3)过较短底的一个顶点作另一底的垂线;(4)延长两腰,使它们的延长线交于一点,将梯形还原为三角形.如图所示:例题与求解【例1】如图,在四边形ABCD中,AB//CD,∠D=2∠B,AD和CD的长度分别为a,b,那么AB的长是___________. (荆州市竞赛试题)解题思路:平移一腰,构造平行四边形、特殊三角形.AB【例2】如图1,四边形ABCD是等腰梯形,AB//CD.由四个这样的等腰梯形可以拼出图2所示的平行四边形.(1)求四边形ABCD四个内角的度数;(2)试探究四边形ABCD 四条边之间存在的等量关系,并说明理由;(3)现有图1中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图. (山东省中考试题) 解题思路:对于(1)、(2),在观察的基础上易得出结论,探寻上、下底和腰及上、下底之间的关系,从作出梯形的常见辅助线入手;对于(3),在(2)的基础上,展开想象的翅膀,就可设计出若干种图形.图2图1A【例3】如图,在等腰梯形ABCD 中,AD//BC ,AB =DC ,且AC ⊥BD ,AF 是梯形的高,梯形的面积是49cm 2,求梯形的高.(内蒙古自治区东四盟中考试题) 解题思路:由于题目条件中涉及对角线位置关系,不妨从平移对角线入手.B【例4】 如图,在等腰梯形ABCD 中,AB//DC ,AB =998,DC =1001,AD =1999,点P 在线段AD 上,问:满足条件∠BPC =900的点P 有多少个?(全国初中数学联赛试题) 解题思路:根据AB +DC =AD 这一关系,可以在AD 上取点构造等腰三角形.D【例5】如图,在等腰梯形ABCD中,CD//AB,对角线AC,BD相交于O,∠ACD=600,点S,P,Q分别为OD,OA,BC的中点.(1)求证:△PQS是等边三角形;(2)若AB=5,CD=3,求△PQS的面积;(3)若△PQS的面积与△AOD的面积的比是7:8,求梯形上、下两底的比CD:AB.(“希望杯”邀请赛试题)解题思路:多个中点给人以广泛的联想:等腰三角形性质、直角三角形斜边中线、三角形中位线等.A【例6】如图,分别以△ABC的边AC和BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到边AB的距离是AB的一半.(山东省竞赛试题)解题思路:本题考查了梯形中位线定理、全等三角形的判定与性质.关键是要构造能运用条件EP=PF的图形.EF能力训练A级1. 等腰梯形中,上底:腰:下底=1:2:3,则下底角的度数是__________.(天津市中考试题)2. 如图,直角梯形ABCD中,AB⊥BC,AD=3,BC=5,将腰DC绕点D逆时针方向旋转900至DE,连接AE,则△ADE的面积为______________. (宁波市中考试题)3.如图,在等腰梯形ABCD 中,AB//CD ,∠A =060,∠1=∠2,且梯形的周长为30cm ,则这个等腰梯形的腰长为______________.第3题图第4题图第2题图ABAB4.如图,梯形ABCD 中,AD//BC ,EF 是中位线,G 是BC 边上任一点,如果222cm S GEF =∆,那么梯形ABCD 的面积为__________. (成都市中考试题)5.等腰梯形的两条对角线互相垂直,则梯形的高h 和中位线的长m 之间的关系是 ( )A .m >hB .m =hC .m <hD .无法确定6. 梯形ABCD 中,AB//DC ,AB =5,BC =23,∠BCD =045,∠CDA =060,则DC 的长度是( )A .3327+B .8 C.219 D.38+ E. 338+(美国高中考试题)7.如图,在等腰梯形ABCD 中,AC =BC +AD ,则∠DBC 的度数是 ( )A.300B.450C.600D.900(陕西省中考试第7题图第8题图BBAC第9题图B8.如图,在直角梯形ABCD 中,AD//BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上移动,则当P A +PD 取最小值时,△APD 中边AP 上的高为( )A .17172 B .17174 C .17178 D .3 (鄂州市中考试题)9.如图,在等腰梯形ABCD 中,AD //BC ,AB =CD ,点P 为BC 边上一点,PE ⊥AB ,PF ⊥CD ,BG ⊥CD ,垂足分别为E ,F ,G .求证 :PE +PF =BG .(哈尔滨市中考试题)10. 如图,在梯形ABCD 中,AD//BC ,E ,F 分别为AB ,AC 中点,BD 与EF 相交于G .求证:)(21AD BC GF -=.BC11.如图,等腰三角形ABC 中,AB =AC ,点E 、F 分别是AB 、AC 的中点,CE ⊥BF 于点O . 求证:(1)四边形EBCF 是等腰梯形;(2)2222BE BC EF =+. (深圳市中考试题)B12.如图1,在等腰梯形ABCD 中,AD//BC ,E 是AB 的中点,过点E 作EF//BC 交CD 于点F ,AB =4,BC =6,∠B =060.(1)求点E 到BC 的距离;(2)点P 为线段EF 上的一个动点,过P 作PM ⊥EF 交BC 于点M ,过M 作MN//AB 交折线ADC 于点N ,连接PN ,设EP =x .①当点N 在线段AD 上时(如图2),△PMN 的形状是否发生改变?若不变,求出△PMN 的周长;若改变,请说明理由.②当点N 在线段DC 上时(如图3),是否存在点P ,使△PMN 为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由. (江西省中考试题)图5(备用图)图4(备用图)图2图1图3B B BC B BB 级1. 如图,在梯形ABCD 中,AB//DC ,AD =BC ,AB =10,CD =4,延长BD 到E ,使DE =DB ,作 EF ⊥AB 交BA 的延长线于点F ,则AF =__________.(山东省竞赛试题)第2题图第1题图EBF2.如图,在梯形ABCD 中,AD//BC ,AB =DC =10cm ,AC 与BD 相交于G ,且∠AGD =060,设E 为CG 中点,F 是AB 中点,则EF 长为_________.(“希望杯”邀请赛试题)3.用四条线段:7,9,13,14====d c b a 作为四条边,构成一个梯形,则在所构成的梯形中,中位线的长的最大值为_________. (湖北赛区选拔赛试题)4.如图,梯形ABCD 的两条对角线AC ,BD 相交于O 点,且AO :CO =3:2,则两条对角线将梯形分成的四个小三角形面积之比为=∆∆∆∆AOB COB DOC AOD S S S S :::_________. (安徽省中考试题)MABBC第4题图 第5题图 第6题图5.如图,在四边形ABCD 中,AD//BC ,E 是AB 的中点,若△DEC 的面积为S ,则四边形ABCD 的面积为 ( )A .S 25 B .2S C .S 47 D .S 49(重庆市竞赛试题)6.如图,在梯形ABCD 中,AD//BC ,∠B =020,∠C =070,E ,M ,F ,N 分别为AB ,BC ,CD , DA 的中点,已知BC =7,MN =3,则EF 的值为 ( )A .4B .214C .5D .6 (全国初中数学联赛试题)7.如图,梯形ABCD 中,AB//DC ,E 是AD 的中点,有以下四个命题:①若AB +DC =BC ,则∠BEC =090;②若∠BEC =090,则AB +DC =BC ;③若BE 是∠ABC 的平分线,则∠BEC =090; ④若AB +DC =BC ,则CE 是∠DCB 的平分线.其中真命题的个数是 ( )A .1个B .2个C .3个D .4个(重庆市竞赛试题)第8题图第7题图NDAC B8.如图,四边形ABCD 是一梯形,AB//CD ,∠ABC =090,AB =9cm ,BC =8cm ,CD =7cm ,M 是AD 的中点,从M 作AD 的垂线交BC 于N ,则BN 的长等于 ( )A .1cmB .1.5cmC .2cmD .2.5cm(“希望杯”邀请赛试题)9.如图,在梯形ABCD 中,AB//DC ,M 是腰BC 的中点,MN ⊥AD .求证:AD MN S ABCD ⋅=四边形(山东省竞赛试题)AB10.如图,在梯形ABCD 中,AD//BC ,分别以两腰AB ,CD 为边向两边作正方形ABGE 和正方形DCHF ,设线段AD 的垂直平分线l 交线段EF 于点M.求证:点M 为EF 的中点.(全国初中数学联赛试题)GH11.已知一个直角梯形的上底是3,下底是7,且两条对角线的长都是整数,求此直角梯形的面积.(“东方航空杯”上海市竞赛试题)12.如图1,平面直角坐标系中,反比例函数)0,0(>>=x k xky 的图象经过矩形OABD 的边BD 的三等分点(BD DF 31=)交AB 于E ,AB =12,四边形OEBF 的面积为16. (1)求k 值.(2)已知)0,13(C ,点P 从A 出发以0.5cm/s 速度沿AB 、BD 向D 运动,点Q 从C 同时出发,以1.5cm/s 的速度沿CO ,OA ,AB 向B 运动,其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,经过多少时间,四边形PQCB 为等腰梯形(如图2).(3)在(2)条件下,在梯形PQCB 内是否有一点M ,使过M 且与PB ,CQ 分别交于S ,T 的直线把PQCB 的面积分成相等的两部分,若存在,请写出点M 的坐标及CM 的长度;若不存在,请说明理由.图2图1专题21梯形例1 a +b例2⑴上底角为120°,下底角为60°;⑵梯形的上底等于下底的一半,且等于腰长; ⑶能拼出菱形,以下图形供参考:例3 7cm 提示:过A 作AE ∥BD 交CB 延长线于E ,则S △AEC =S 梯形ABCD . 例4(1)如图a ,若E 为AD 中点,则∠BEC =90°且CE,BE 分别平分∠BCD ,∠ABC ; ⑵如图b ,在BC 上取一点M ,使AB =MB ,连结AM,DM ,则∠AMD =90°; ⑶如图c ,将a ,b 组合,则四边形GEHM 为矩形.图a 图b 图c ∴当P 为AD 中点时,可以证明∠BPC =90°;在AD 上截取AP =AB ,可以证明∠BPC =90°,故满足条件∠BPC =90°的点P 有2个.例5⑴连结SC,PB .∴△OCD,△OAB 均为等边三角形,S ,P ,Q 分别为OD,OA,BC 中点, ∴SQ =12BC =12AD =SP =PQ .故△SPQ 为等边三角形.⑵∵SB =12DO +OB =132,CS =323,BC =7.∴△SPQ 的边长SQ =12BC =72.∴S △SPQ =34×(72)2=49316.(3)设CD =a ,AB =b (a <b ),BC 2=SC 2+BS 2=(32a )2+(b +a2)2=a 2+b 2+ab . ∴S △SPQ =316(a 2+ab +b 2).又S △AOD S △COD =b a ,则S △AOD =34ab . 又S △AOD S △COD =b a ,则S △AOD =34ab .∵S △PQS S △AOD =78,∴8×316 (a 2+ab +b 2)=7×34ab . 即2a 2-5ab +2b 2=0,化简得a b =12. 故CD :AB =1:2.例6如图,分别过E,F ,C,P 作AB 的垂线,垂足依次为R ,S ,T ,Q ,则PQ 就是点P 到AB 的距离,且有ER ∥PQ ∥CT ∥FS ,故四边形ERSF 为直角梯形,PQ =12(ER +FS ).易证Rt △AER ≌Rt △CAT ,Rt △BFS ≌Rt △CBT ,∴ER =AT ,FS =BT ,又AT +BT =AB =ER +FS , 故PQ =12AB .A 级1.60°2.33.6cm4.82cm 25.B6.D7.C8.C 提示:如图,作点D 关于直线BC 的对称点D ',连结DD '交BC 于E ,连结AD '交BC 于P ,过D 作DF ⊥AP 于F ,故P A +PD 此时最小.由BE =AD =2,EC =3,则可得:DE =4,∴DD '=8,则AD '=217. 又∵AD '·DF =AD ·DD ',则DF =81717.9.提示:过P 点作PQ ⊥BG 于Q ,证明PE =BQ .10.提示:连结DF 并延长交于BC 于H ,则GF =12BH ,AD =CH . 11.略12.⑴ 3⑵①当点N 在线段AD 上运动时,△PMN 形状不发生改变,其周长为3+7+4.②当点在线段DC 上运动时,△PMN 的形状发生改变,但MNC 恒为等边三角形,过E 作EG BC 于G 。
中考数学总复习 分层提分训练 梯形(以真题为例)

一级训练1.(2012年山东临沂)如图4-3-41,在等腰梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,下列结论不一定正确的是( )A.AC=BD B.OB=OC C.∠BCD=∠BDC D.∠ABD=∠ACD图4-3-41 图4-3-42 图4-3-43 2.(2012年福建漳州)如图4-3-42,在等腰梯形ABCD中,AD∥BC,AB=DC,∠B=80°,则∠D的度数是( )A.120° B.110° C.100° D.80°3.(2011年山东滨州)如图4-3-43,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )A.1 个 B.2个 C.3个 D.4个4.(2011年广西来宾)如图4-3-44,在直角梯形ABCD中,已知AB∥DC,∠DAB=90°,∠ABC=60°,EF为中位线,且BC=EF=4,那么AB=( )A.3 B.5 C.6 D.8图4-3-44 图4-3-45 图4-3-46 5.(2011年浙江台州)如图4-3-45,在梯形ABCD中,AD∥BC,∠ABC=90°,对角线BD,AC相交于点O.下列条件中,不能判断对角线互相垂直的是( )A.∠1=∠4 B. ∠1=∠3 C.∠2=∠3 D.OB2+OC2=BC26.(2012年江苏无锡)如图4-3-46,在梯形ABCD中,AD∥BC,AD=3,AB=5,BC=9,CD的垂直平分线交BC于点E,连接DE,则四边形ABED的周长等于( )A.17 B.18 C.19 D.207.等腰梯形的中位线长是15 ,一条对角线平分一个60°的底角,则梯形的周长为______.8.(2011年江苏南京)等腰梯形的腰长为5 cm,它的周长是22 cm,则它的中位线长为________cm.9.(2011年湖南邵阳)如图4-3-47,在等腰梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,∠B=60°,BC=2 cm,则上底DC的长是________cm.图4-3-47 图4-3-48 图4-3-49 10.(2011年江苏宿迁)如图4-3-48,在梯形ABCD中,AB∥DC,∠ADC的平分线与∠BCD的平分线的交点E恰在AB上.若AD=7 cm,BC=8 cm,则AB的长度是________cm.二级训练11.(2012年湖北咸宁)如图4-3-49,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC,且交CD于点E,E为CD的中点,EF∥BC交AB于点F,EG∥AB交BC于点G.当AD=2,BC=12时,四边形BGEF的周长为________.12.如图4-3-50,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC,且与AB的延长线交于点E.求证:四边形AECD是等腰梯形.图4-3-50参考答案1.C 2.C 3.C 4.B 5.B 6.A7.50 8.6 9.2 10.1511.2812.证明: ∵四边形ABCD 是菱形, ∴∠CAE =12∠DAB =30°.又∵CE ⊥AC, ∴∠E =90°-30°=60°. ∴∠E =∠DAE .∵AD ∥BC, ∴CE 不平行AD .又∵DC ∥AE, ∴四边形AECD 是等腰梯形.。
中考数学专题讲练 梯形(解析版)
2 2 =2 2 9 s 时,AP=4.5,Q 点在 EC 上 2
4.5 4 =9 2 故答案为:2;9
(2)当 5≤x≤9 时(如图 1)
y=S 梯形 ABCQ﹣S△ABP﹣S△PCQ=
1 1 1 (5+x﹣4)×4 ×5(x﹣5) (9﹣x)(x﹣4) 2 2 2
例 1.1.2 已知:如图,在梯形 ABCD 中,DC∥AB,AD=BC=2,∠A=60°,对角线 BD 平分∠ABC. (1)求对角线 BD 的长; (2)求梯形 ABCD 的面积.
【答案】 (2 ) 3 3 【解析】
(1) 2 3
(1)∵DC∥AB,AD=BC,
∴∠A=∠ABC. ∵BD 平分∠ABC,∠A=60°, ∴∠ABD=
题模一:梯形中的辅助线 例 1.1.1 梯形 ABCD 中,AD∥BC,AD=1,BC=4,∠C=70°,∠B=40°,则 AB 的长为( ) A. 2 B. 3 C. 4 D. 5 【答案】B 【解析】 作 DE∥AB 交 BC 于 E,则四边形 ABED 是平行四边形.∴BE=AD=1,∠CED=∠B=40° ∴∠CDE=70°∴AB=DE=CE=4-1=3
例 1.1.3 如图,梯形 ABCD 中,AD∥BC,点 E 在 BC 上,AE=BE,点 F 是 CD 的中点,且 AF⊥AB,若 AD=2.7,AF=4,AB=6,求 CE 的长.
【答案】 见解析 【解析】 延长 AF、BC 交于点 G.∴△AFD≌△GFC.∴AG=2AF=8,CG=AD=2.7.∵AF⊥AB,AB=6, ∴BG=10.∴BC=BG-CG=7.3.∵AE=BE,∴∠BAE=∠B.∴∠EAG=∠AGE.∴AE=GE.
(2)
2013年中考数学复习分层训练试题(共38份,含答案)-29

第三章函数第1讲函数与平面直角坐标系一级训练1.(2010年广东湛江)点P(1,2)关于x轴的对称点P1的坐标为____________.2.(2012年湖北咸宁)在函数y=1x-3中,自变量x的取值范围是__________.3.(2012年广西玉林)在平面直角坐标系中,一青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2个单位长度到点A′处,则点A′的坐标为________.4.(2012年山东荷泽)点(-2,1)在平面直角坐标系中所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限5.(2012年山东东营)将点A(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是()A.(2,3) B.(2,-1) C.(4,1) D. (0,1)6.(2010年广东河源)函数y=xx+1的自变量x的取值范围是()A.x>1 B.x≤-1 C.x≥-1 D.x>-17.(2011年山东枣庄)在平面直角坐标系中,点P(-2,x2+1)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限8.如图3-1-3,若在象棋棋盘上建立平面直角坐标系,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“兵”位于点()图3-1-3A.(-1,1) B.(-2,-1) C.(-3,1) D.(1,-2)9.(2011年内蒙古乌兰察布)在平面直角坐标系中,已知线段AB的两个端点分别是A(4,-1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为()A.(-5,4) B.(4,3) C.(-1,-2) D.(-2,-1)10.(2011年湖南衡阳)如图3-1-4,在平面直角坐标系中,菱形MNPO的顶点P坐标是(3,4),则顶点M,N的坐标分别是()图3-1-4A.M(5,0),N(8,4) B.M(4,0),N(8,4) C.M(5,0),N(7,4) D.M(4,0),N(7,4)11.(2012年山东潍坊)甲、乙两位同学用围棋子做游戏,如图3-1-5,现轮到黑棋下子,黑棋下一子后白棋下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也成轴对称图形,则下列下子方法不正确的是()图3-1-5说明:棋子的位置用数对表示,如A点在(6,3).A.黑(3,7),白(5,3) B.黑(4,7),白(6,2) C.黑(2,7),白(5,3) D.黑(3,7),白(2,6) 12.(2012年江西)某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则出发后到B地油箱中所剩油y(单位:升)与时间t(单位:小时)之间函数的大致图象是()13.(2010年广东梅州)在平面直角坐标系中,点M的坐标为(a,1-2a).(1)当a=-1时,点M在坐标系的第________象限(直接填写答案);(2)将点M向左平移2个单位长度,再向上平移1个单位长度后得到点N.当点N在第三象限时,求a的取值范围.二级训练14.王芳同学为参加学校组织的科技知识竞赛,她周末到新华书店购买资料.如图3-1-6,是王芳离家的距离与时间的函数图象.若黑点表示王芳家的位置,则王芳走的路线可能是()图3-1-6A B C D15.(2011年安徽)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图3-1-7.(1)填写下列各点的坐标:A4(_____,_____),A8(____,____),A12(____,____);(2)写出点A4n的坐标(n是正整数);(3)指出蚂蚁从点A100到点A101的移动方向.图3-1-716.(2012年山东泰安)如图3-1-8,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)……根据这个规律,第2 012个点的横坐标为________.图3-1-8三级训练17.(2012年广东梅州)如图3-1-9,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1(直接填写答案).(1)点A关于点O中心对称的点的坐标为________;(2)点A1的坐标为________;(3)在旋转过程中,点B经过的路径为弧BB1,那么弧BB1的长为________.图3-1-918.(2011年贵州贵阳)【阅读】在平面直角坐标系中,以任意两点P (x 1,y 1),Q (x 2,y 2)为端点的线段的中点坐标为⎝⎛⎭⎫x 1+x 22,y 1+y 22.【运用】(1)如图3-1-10,矩形ONEF 的对角线交于点M ,ON 、OF 分别在x 轴、y 轴上,O 为坐标原点,点E 的坐标为(4,3),则点M 的坐标为________________;(2)在平面直角坐标系中,有A (-1,2),B (3,1),C (1,4)三点,另有一点D 与点A ,B ,C 构成平行四边形的顶点,求点D 的坐标.图3-1-10。
中考数学专题二十二:梯形(含详细参考答案)

中考数学专题复习第二十二讲梯形【基础知识回顾】一、 梯形的定义、分类、和面积:1、定义:一组对边平行,而另一组对边的四边形,叫做梯形。
其中,平行的两边叫做两底间的距离叫做梯形的2、分类:梯形3、梯形的面积:梯形= (上底+下底) X 高【赵老师提醒:要判定一个四边形是梯形,除了要注明它有一组对边外,还需注明另一组对边不平行或的这组对边不相等】二、等腰梯形的性质和判定:1、性质:⑴等腰梯形的两腰相等,相等⑵等腰梯形的对角线⑶等腰梯形是对称图形一般梯形特殊梯形等腰梯形:两腰 的梯形叫做等腰梯形直角梯形:一腰与底 的梯形叫做直角梯形2、判定:⑴用定义:先证明四边形是梯形,再证明其两腰相等⑵同一底上两个角的梯形是等腰梯形⑶对角线的梯形是等腰梯形【赵老师提醒:1、梯形的性质和判定中同一底上的两个角相等“不被成”两底角相等2、等腰梯形所有的判定方法都必须先证它是梯形3、解决梯形问题的基本思路是通过做辅助线将梯形转化为形式常见的辅助线作法有要注意根据题目的特点灵活选用辅助线】【重点考点例析】考点一:梯形的基本概念和性质例1 (2012•内江)如图,四边形ABCD是梯形,BD=AC且BD⊥AC,若AB=2,CD=4,则S梯形ABCD= 9.思路分析:过点B作BE∥AC交DC的延长线于点E,过点B 作BF⊥DC于点F,判断出△BDE是等腰直角三角形,求出BF,继而利用梯形的面积公式即可求解.解答:解:过点B作BE∥AC交DC的延长线于点E,过点B 作BF⊥DC于点F,则AC=BE,DE=DC+CE=DC+AB=6,又∵BD=AC 且BD⊥AC,∴△BDE是等腰直角三角形,∴BF=DE=3,故可得梯形ABCD的面积为(AB+CD)×BF=9.故答案为:9.点评:此题考查了梯形的知识,平移一条对角线是经常用到的一种辅助线的作法,同学们要注意掌握,解答本题也要熟练等腰直角三角形的性质,难度一般.对应训练1.(2012•无锡)如图,梯形ABCD中,AD∥BC,AD=3,AB=5,BC=9,CD的垂直平分线交BC于E,连接DE,则四边形ABED 的周长等于()A.17B.18C.19D.201.考点:;.分析:由CD的垂直平分线交BC于E,根据线段垂直平分线的性质,即可得DE=CE,即可得四边形ABED的周长为AB+BC+AD,继而求得答案.解答:解:∵CD的垂直平分线交BC于E,∴DE=CE,∵AD=3,AB=5,BC=9,∴四边形ABED的周长为:AB+BE+DE+AD=AB+BE+EC+AD=AB+BC+AD=5+9+3=17.故选A.点评:此题考查了线段垂直平分线的性质.此题比较简单,注意掌握数形结合思想与转化思想的应用是解此题的关键.考点二:等腰梯形的性质例2 (2012•呼和浩特)已知:在等腰梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,则梯形的面积是()A.25B.50C.25 D.思路分析:过点D作DE∥AC交BC的延长线于点E,作DF⊥BC 于F,证平行四边形ADEC,推出AC=DE=BD,∠BDE=90°,根据等腰三角形性质推出BF=DF=EF= BE,求出DF,根据梯形的面积公式求出即可.解答:解:过点D作DE∥AC交BC的延长线于点E,∵AD∥BC (已知),即AD∥CE,∴四边形ACED是平行四边形,∴AD=CE=3,AC=DE,在等腰梯形ABCD中,AC=DB,∴DB=DE (等量代换),∵AC⊥BD,AC∥DE,∴DB⊥DE,∴△BDE是等腰直角三角形,作DF⊥BC于F,则DF=BE=5,S梯形ABCD=(AD+BC)•DF=(3+7)×5=25,故选A.点评:本题主要考查对等腰三角形性质,平行四边形的性质和判定,等腰梯形的性质,等腰直角三角形等知识点的理解和掌握,能求出高DF的长是解此题的关键.对应训练2.(2012•厦门)如图,在等腰梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,若OB=3,则OC= 3.2.3考点:.分析:先根据梯形是等腰梯形可知,AB=CD,∠BCD=∠ABC,再由全等三角形的判定定理得出△ABC≌△DCB,由全等三角形的对应角相等即可得出∠DBC=∠ACB,由等角对等边即可得出OB=OC=3.解答:解:∵梯形ABCD是等腰梯形,∴AB=CD,∠BCD=∠ABC,在△ABC与△DCB中,∵,∴△ABC≌△DCB,∴∠DBC=∠ACB,∴OB=OC=3.故答案为:3.点评:本题考查的是等腰梯形的性质及全等三角形的判定与性质,熟知在三角形中,等角对等边是解答此题的关键.考点三:等腰梯形的判定例3 (2012•襄阳)如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F.(1)求证:梯形ABCD是等腰梯形;(2)当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理由,并求出此时菱形AECD的面积.考点:;;.分析:(1)由AD∥BC,由平行线的性质,可证得∠DEC=∠EDA,∠BEA=∠EAD,又由EA=ED,由等腰三角形的性质,可得∠EAD=∠EDA,则可得∠DEC=∠AEB,继而证得△DEC≌△AEB,即可得梯形ABCD是等腰梯形;(2)由AD∥BC,BE=EC=AD,可得四边形ABED和四边形AECD均为平行四边形,又由AB⊥AC,AE=BE=EC,易证得四边形AECD是菱形;过A作AG⊥BE 于点G,易得△ABE是等边三角形,即可求得答案AG的长,继而求得菱形AECD的面积.解答:(1)证明:∵AD∥BC,∴∠DEC=∠EDA,∠BEA=∠EAD,又∵EA=ED,∴∠EAD=∠EDA,∴∠DEC=∠AEB,又∵EB=EC,∴△DEC≌△AEB,∴AB=CD,∴梯形ABCD是等腰梯形.(2)当AB⊥AC时,四边形AECD是菱形.证明:∵AD∥BC,BE=EC=AD,∴四边形ABED和四边形AECD均为平行四边形.∴AB=ED,∵AB⊥AC,∴AE=BE=EC,∴四边形AECD是菱形.过A作AG⊥BE于点G,∵AE=BE=AB=2,∴△ABE是等边三角形,∴∠AEB=60°,∴AG=,∴S菱形AECD=EC•AG=2×=2。
中考数学复习《梯形》练习题(含答案)

中考数学复习《梯形》练习题(含答案)一、选择题1.下列命题中,正确的是( )(A )对顶角相等 (B )梯形的对角线相等 (C )同位角相等 (D )平行四边形对角线相等2.如图,梯形ABCD 的对角线AC 、BD 相交于点O ,△ADO 的面积记作S 1, △BCO 的面积记作S 2,△ABO 的面积记作S 3,△CDO 的面积记作S 4,则下列关系正确是( )A. S 1= S 2B. S 1 × S 2= S 3 × S 4C. S 1 + S 2 = S 4 + S 3D. S 2= 2S 33.如图,在梯形ABCD 中,AB ∥CD ,∠A =60°, ∠B =30°, 若AD =CD =6,则AB 的长等于( ). A .9B .12C .633D .184.如图1,在直角梯形ABCD 中,∠B=90°,DC ∥AB ,动点P 从B 点出发,沿折线B →C →D →A 运动,点P 运动的速度为2个单位长度/秒,若设点P 运动的时间为x 秒,△ABP 的面积为y ,如果y 关于x 的函数图像如图2所示,则M 点的纵坐标为(▲ ) A .16 B .48C .24D .64 答案 B5. 在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,AB =BC ,E 为AB 边上一点,∠BCE =15°,且AE =AD ,连接DE 交对角线AC 于H ,连接BH .下列结论:①△ACD ≌△ACE ;②△CDE 为等边三角形;③EHBE =2;④S △EBC S △EHC =AH CH .其中结论正确的是( )A .只有①②B .只有①②④C .只有③④D .①②③④ 6.如图,,过上到点的距离分别为的点作的垂线与S 2S 3S 4S 1O DCB ADCPBA图1 ABDE H第5题相交,得到并标出一组黑色梯形,它们的面积分别为.观察图中的规律,求出第10个黑色梯形的面积( )A.32B.54C.76D.86二、填空题1.如图,在梯形ABCD 中,AD ∥BC ,点E 、F 、G 、H 是两腰上的点,AE =EF =FB ,CG =GH =HD , 且四边形EFGH 的面积为6cm 2,则梯形ABCD 的面积为 ▲ cm 2.2.如图,直角梯形ABCD 中, BA CD ,,2AB BC AB ⊥= ,将腰DA 以A 为旋转中心逆时针旋转90°至AE ,连接,,BE DE ABE ∆的面积为3,则CD 的长为 ﹡ .3.如图,在直角梯形ABCD 中,A B ⊥BC ,AD ∥BC ,EF 为中位线,若AB =2b ,EF =a ,则阴影部分的面积 .4.如图,已知梯形ABCD 中,AD ∥BC ,∠B =30°,∠C =60°,AD =4, AB =33,则下底BC 的长为 __________.D BCE F A G H (第1题图)60°30°D A5.已知等腰梯形ABCD 的中位线EF 的长为5,腰AD 的长为4,则这个等腰梯形的周长为 ;6.如图,在梯形ABCD 中,AB ∥CD ,AD =BC ,对角线AC ⊥BD ,垂足为O .若CD =3,AB =5,则AC 的长为 .7.如图,n+1个上底、两腰长皆为1,下底长为2的等腰梯形的下底均在同一直线上,设四边形P 1M 1N 1N 2面积为S 1,四边形P 2M 2N 2N 3的面积为S 2,……,四边形P n M n N n N n+1的面积记为S n ,则S n = ▲8.如图有一直角梯形零件ABCD ,AD ∥BC ,斜腰DC 的长为10cm ,∠D =120 ,则该零件另一腰AB 的长是 m.答案: 选择题 1、A 2、B 3、D 4、B 5、A 6、C填空题1、答案:182、答案:53、答案:ab4、答案:105、答案18(第6题图)CABDOA B CD第8题图67、答案:31 21 nn++8、答案:5。
(完整版)数学梯形练习题含答案

梯形练习题一.选择题 (每小题4分,共40分)1. 如果梯形中位线长20,它被一条对角线分成两段的差为5,那么两底的长分别为 A.15,30 B.25,15 C.30,20 D.以上都不对2. 等腰梯形的上底、下底、高之比为1∶3∶1,则下底角的度数是 A. 30° B. 45° C. 60° D. 75°3. 在等腰梯形ABCD 中,AD ∥BC ,AE ⊥BC 于E ,且AE=AD ,BC=3AD ,则∠B 等于 A. 30° B. 45° C. 60° D. 135°4. 等腰梯形ABCD 中,BC AD //,AC 与BD 交于O 点,图中全等三角形有 A. 两对 B. 四对 C 一对 D. 三对5. 在梯形ABCD 中,AD ∥BC ,AB=AC ,若∠D=110°,∠ACD=30°,则∠BAC 等于 A. 80° B. 90° C. 100° D. 110°6. 等腰梯形中,下列判断正确的是A. 两底相等B. 两个角相等C. 同底上两底角互补D. 对角线交点在对称轴上7. 以线段a=16,b=13为梯形的两底,c=10,d=6为腰画梯形,这样的梯形 A. 只能画出一个 B. 能画出2个 C. 能画出无数个 D. 不能画出 8. 下列命题中:①有两个角相等的梯形是等腰梯形 ②有两条边相等的梯形是等腰梯形 ③两条对角线相等的梯形是等腰梯形④等腰梯形上、下底中点连线,把梯形分成面积相等的两部分其中真命题有 A. 1个 B. 2个 C. 3个 D. 4个9. 若梯形的上底边长为4,中位线长为6,则此梯形的下底长为 A.5 B.8 C.12 D.1610. 如图,在梯形ABCD 中,边AB 与CD 平行,对角线BD 与边AD 的长相等. 若DCB ∠=110°,30=∠CBD °,那么ADB ∠等于A. 80°B. 90°C. 100°D. 110° 第Ⅱ卷(非选择题 共8道填空题8道解答题) 请将你认为正确的答案代号填在下表中 1 2 3 4 5 6 7 8 9 10 二.简答题 (每小题3分,共24分)11. 若梯形的中位线长为5,面积为20,则这个梯形的高为 . 12. 观察下列图形并填表:梯形个数 1 2 3 4 5 6 ... n周 长 5 9 13 17 ...13. 已知直角梯形的一腰与下底的夹角为60º,下底与其中的一腰都等于6,则梯形的中位线的长为14. 用下面的方法来证明:在同一底上的两个角相等的梯形是等腰梯形.(1)如图1,分别延长梯形ABCD 的腰BA ,CD ,设它们相交于点E . 通过证明△EAD 和△EBC 都是________三角形来证明.图1 图2(2)如图2,作梯形ABCD 的高AE ,DF ,通过证明Rt △ABE ≌Rt △DCF 来证明定理. 证明过程:(1)___________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ (2)_____________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ 15. 以线段16=a 、13=b 为梯形的两底,以10=c 为一腰,则另一腰长d 的范围是________;16. 在梯形中,不是同一底上的两组角的比值分别为1:3和3:7,则四个角的度数为___________________17. 如果一个直角梯形的两底长分别为7 cm ,12 cm ,斜腰长为13 cm ,那么这个梯形的面积等于_______.18. 等腰梯形的腰长为5cm ,上、下底的长分别为6cm 和12cm ,则它的面积为_______. 三.解答题 (共56分)19. 如图,在等腰梯形ABCD 中,AD ∥BC ,AB =CD .(1)利用尺规作底边AD 的中点 E.(保留作图痕迹,不写作法和证明) (2)连结EB 、EC ,求证:∠ABE=∠DCE .21. 如图,梯形ABCD 中,120AD BC AB DC ADC =∠=∥,,,对角线CA 平分DCB ∠,E 为BC 的中点,试求DCE △与四边形ABED 面积的比.C D B AAB E22. 如图,等腰梯形ABCD 中,AD ∥BC ,AB=DC ,AC ⊥BD ,过D 点作DE ∥AC 交BC 的延长线于E 点。
初中中考复习之梯形(精编含答案)

∴AE=EB=BF=FC。
在△ABF和△CBE中,∵AB=CB,∠ABF=∠CBE, BF=BE,
∴△ABF≌△CBE(SAS)。∴∠BAF=∠BCE,AF=CE。
在△AME和△CMF中,
∵∠BAF=∠BCE,∠AME=∠CMF ,AE=CF,
∴△AME≌△CMF(AAS)。∴EM=FM。
在△BEM和△BFM中,∵BE=BF,BM=BM,
点,∴BE=CE。
在△ABE和△DCE中,
∵AB=DC,∠B=∠C
,BE=CE,
∴△ABE≌△DCE(SAS)。∴AE=DE。
7、证明:∵ABCD是等腰梯形,AD∥BC,∴∠B=∠BCD, ∠BCD =∠EDC。
∴∠B=∠EDC。又∵CE=CD。∴∠EDC=∠E。∴∠B=∠E。
8、解:(1)180°-2α。
(1)∠BEF=_____(用含α的代数式表示); (2)当AB=AD时,猜想线段ED、EF的数量关系,并证明你的猜想;
(3)当AB≠AD时,将“点E在AD上”改为“点E在AD的延长线上,且 AE>AB,AB=mDE,AD=nDE”,其他条件不变(如图2),求 的值(用含m、n的代数式表示)。
9.我们知道“连接三角形两边中点的线段叫三角形的中位线”,“三角 形的中位线平行于三角形的第三边,且等于第三边的一半”.类似的, 我们把连接梯形两腰中点的线段叫做梯形的中位线.如图,在梯形ABCD 中,AD∥BC,点E,F分别是AB,CD的中点,那么EF就是梯形ABCD的中位 线.通过观察、测量,猜想EF和AD、BC有怎样的位置和数量关系?并证 明你的结论.
6.如图,在等腰梯形ABCD中,点E为底边BC的中点,连结AE、DE.求 证:AE=DE.
7.如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上的一点,且 CE=CD,求证:∠B=∠E
中考复习梯形(含答案)

梯形◆考点链接1.掌握梯形、直角梯形、等腰梯形的判定和定理,并能熟练解决实际问题.2.能用三角形的中位线定理、•梯形中位线定理来解决线段平行和线段之间的倍分问题.3.能运用一些常见的数学思想方法解题.◆典例精析【例题1】如图,在梯形ABCD 中,∠B+∠C=90°,M 、N 分别为上、下底的中点.求证:MN=12(BC-AD ). 解题思路:由∠B+∠C=90°,联想到直角三角形,从而将MN 放入直角三角形中,不采用延长两腰,因为证明很麻烦,故采用平移腰的方法.证明:如图,过M 作ME ∥AB ,MF ∥CD ,分别交BC 于E 、F ,则AM=BE ,MD=FC ,∠B=∠MEN ,∠C=∠MFN .∵M 、N 分别是AD 、BC 的中点.∴BN-BE=NC-FC ,即EN=FN .又∵∠B+∠C=90°,∴∠MEN+∠MFN=90°,∴△EMF 为直角三角形.∴MN=12EF=12(BC-AD ). 评析:在梯形这部分,除了要会应用好梯形的一些性质外,还要通过平移腰、平移对角线、延长两腰或作高等方法来转化,在解决问题时,要具体分析,灵活选择转化方法.【例题2】如图,梯形ABCD 中,AB ∥DC ,E 为AD 上一点,且BE 平分∠ABC ,CE•平分∠BCD .求证:E 为AD 的中点.解题思路:延长BE 、CD 相交于F ,证明△FED ≌△BEA .证明:延长BE ,CD 相交于F .∵CD ∥AB ,CE 平分∠BCD .∴∠F=∠1=∠2,∴CF=CB .又CE 是∠BCD 的平分线.∴E 是FB 的中点.∴∠F=∠1,FE=EB ,∠3=∠4,∴△FED ≌△BEA ,∴DE=EA ,即E 是AD 的中点.评析:梯形的性质通常与三角形的性质相结合,常将梯形的相关结论转化为三角形的相关问题.【例题3】某村计划开挖一条长1500m 的水渠,渠道的断面为等腰梯形,渠道深0.8m ,下底宽1.2m ,坡角为45°(如图),•实际开挖渠道时,•每天比原计划多挖土20m ,结果比原计划提前4天完工,求原计划每天挖土多少立方米.解题思路:过点A ,B 分别向DC 作垂线,先计算梯形的面积,进而得到所挖土的总立方数,并最终得解.解:过点A ,B 分别向DC 作垂线,P ,Q 是垂足,则AP=BQ=0.8,在Rt △APD 中,∵∠DAP=∠PDA=45°,∴DP=PA=0.8.同理CQ=0.8,∴CD=DP+PQ+QC=1.2+0.8×2=2.8,∴S 梯形ABCD =12(AB+CD )·AP=1.6(m 2). ∴挖渠道的土方数为1.6×1500=2400(m 3).设原计划每天挖土x (m 3),则实际每天挖土(x+20)m 3.∴2400240020x x++=4,即x 2+20x-12 000=0, 解得:x 1=-120,x 2=100,经检验:x 1=-120,x 2=100都是原方程的根,但挖土的体积不能为负数,故x=-120•舍去,∴x=100.答:原计划每天挖土的立方数为100m3.评析:渠道是一棱柱,其截面是图中所示的等腰梯形,故所挖土方数等于图中等腰梯形的面积乘以水渠的长度.◆探究实践【问题1】(沈阳)如图,已知梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD•相交于点O,E是BC边上一动点(点E不与B、C两点重合),EF∥BD交AC于点F,EG∥AC•交BD于点G.(1)求证:四边形EFOG的周长等于2OB;(2)请你将上述题目的条件“梯形ABCD中,AD∥BC,AB=DC•”改为另一种四边形,其他条件不变,使得结论“四边形EFOG的周长等于2OB”仍成立,•并将改编后的题目画出图形,写出已知、求证,不必证明.解题思路:(1)四边形EFOG的周长等于2OB,只要证得GE+EF=OB即可.其实只要△BOC为等腰三角形即得,因为四边形ABCD是等腰梯形,所以△BOC为等腰三角形.(2)改成的四边形只要△BOC为等腰三角形即可.故四边形改为矩形、正方形、菱形都可以.(1)证明:∵四边形ABCD是梯形,AD∥BC,AB=CD.∴∠ABC=∠DCB.又∵BC=CB,AB=DC,∴△ABC≌△DCB,∴∠DBC=∠ACB.又∵GE∥AC,∴∠BEG=∠ACB.∴∠DBC=∠BEG,∴EG=BG.∵EG∥OC,EF∥OB,∴四边形EGOF是平行四边形,∴EG=OF,EF=OG.∴四边形EGOF的周长=2(OG+GE)=2OB.(2)如图,在矩形ABCD中,对角线AC、BD相交于点O,E是BC上一个动点(•点E不与B、C两点重合),EF∥BD,交AC于点F,EG∥AC交BD于点G,求证:四边形EFOG的周长等于2OB.评析:本题是探索性题目,这类题目一定要根据已知题目找出使结论成立起决定作用的条件.【问题2】(荆州)如图,在等腰梯形ABCD中,BC∥AD,BC=8,AD=20,AB=DC=•10,点P从点A出发沿AD边向点D移动,点Q自A点出发沿A→B→C的路线移动,且PQ∥DC,•若AP=x,梯形位于线段PQ右侧部分的面积为S.(1)分别求出当点Q位于AB、BC上时,S与x之间的函数关系式,并写出自变量x•的取值范围;(2)当线段PQ将梯形ABCD分成面积相等的两部分时,x的值是多少?(3)在(2)的条件下,设线段PQ与梯形ABCD的中位线EF交于O点,那么OE与OF•的长度有什么关系?借助备用图说明理由;并进一步探究:对任何一个梯形,当一直线L•经过梯形中位线的中点并满足什么条件时,其一定平分梯形的面积?(•只要求说出条件,不需要证明).解题思路:(1)分Q在AB、BC两种情况,抓住三角形、梯形、四边形的面积关系,分别求出S与x的关系式.(2)由(1)所得关系式,求面积为梯形面积一半的x的值.(3)•梯形的面积等于中位线乘以高来分析解决.解:(1)如图,当点Q位于AB上时,PQ的右侧图形为等腰三角形AQP,底边AP=•x,过Q、B点分别作MQ⊥AD,BN⊥AD,垂足分别为M,N,又过B作BG∥DC交AD于G点,•则有AG=12,BG=DC=AB=10.在Rt△ABN中,AB=10,AN=6,∴BN=8.∵△AQP为等腰三角形,∴AM=12AP=12x . 又∵QM ⊥AD ,BN ⊥AD ,∴QM ∥BN ,∴,AM QM AM BN QM AN BN AN =∴==23x , ∴S=12AP·QM=12x·23x=13x 2, ∴当Q 在AB 上时,S=13x 2,自变量x 的取值范围是O<x≤12;当点Q 在BC 上时,PQ •右侧四边形ABQP 为梯形,则S=12(QB+AP )·BN=12 [(x-12)+x]×8=8x-48,自变量x 的取值范围是12<x<20.(2)梯形ABCD 的面积S 0=12(BC+AD )·BN=112. 当Q 在AB 移动时,△AQP 的面积最大值为 12AG ·BN=12×12×8=48<02S . 故线段PQ 等分梯形面积时,点Q 只可能在BC 上, ∴8x-48=02S =56,∴x=13. (3)如图,当PQ 等分梯形ABCD 面积时,可知S 四边形QCDP =S 四边形ABQP .又EF 是梯形的中位线.∴OE ·BN=OF ·BN .即OE=OF .探究发现:当直线L 经过梯形中位线的中点且较短的底(上底)相交时,•其一定平分梯形的面积.评析:本题探索图形之间的变换关系,并利用梯形和三角形的面积来建立函数关系式,这个题考查了三角形和梯形的有关知识,并和代数结合,它的新颖之处在于几何图形的运动和变化.◆中考演练一、填空题1.在四边形ABCD 中,AD ∥BC ,AD ≠BC ,•若使它成为等腰梯形,•则需添加的条件是________(填一个正确的条件即可).2.有一个直角梯形ABCD ,AD ∥BC ,斜腰DC 的长为10cm ,∠D=120°,如图1,•则另一腰AB 的长为_______cm .(结果不取近似值)(1) (2) (3) 3.如图2,梯形ABCD 中,AD ∥BC ,E 、F 、G 、H 分别是边DC 、BC 、AB 、DA•的中点,梯形ABCD 的边满足条件_______时,四边形EFGH 是菱形.二、选择题1.(沈阳)如图3,梯形护坡石坝的斜坡AB 的坡度i=1:3,坝高BC 为2m ,则斜坡AB 的长是( ).A ....6m2.(绍兴)如图4,M 、N 分别是直角梯形ABCD 的两腰AD 、CB 的中点,DE ⊥AB 于点E ,将△ADE 沿DE 翻折,M 与N 恰好重合,则AE :BE 等于( ).A .2:1B .1:2C .3:2D .2:3(4) (5) 3.如图5,在梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD 且AC=12,BD=9,则此梯形的中位线长是( ).A .10B .2115.22C D .12三、解答题1.(北京)如图,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,,• 求梯形的面积.2.如图,F为AB的中点,四边形CGEF为菱形,∠1=∠2=∠FCG.求证:D、F、H为线段AB的四等分点.C ◆实战模拟一、填空题1.如图6,在梯形ABCD中,AB∥CD,BC=8,,∠BCD=45°,∠BAD=120°,则梯形ABCD的面积为________.(6) (7) (8) (9)2.如图7,在梯形ABCD中,已知AB∥CD,点E为BC的中点,设△DEA的面积为S1,梯形ABCD的面积为S2,则S1与S2的关系为________.3.如图8,在梯形ABCD中,E是CD的中点,延长AE交BC于F点,已知∠B=45°,•梯形的高AH=2cm,HF=5cm,则梯形的面积等于________.二、选择题1.(天津)如图9,在梯形ABCD中,AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18cm,MN=8cm,则AB的长等于().A.10cm B.13cm C.20cm D.26cm2.(黑龙江)若等腰梯形的三边长分别为3,4,11,则这个等腰梯形的周长为().A.21 B.29 C.21或29 D.21或22或293.直角梯形的中位线长a,一腰长b,这腰和底所夹的角是30°,则它的面积为( •).A.ab B.12ab C.14ab D.18ab三、解答题1.(广东)如图,等腰梯形ABCD中,AD∥BC,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点.(1)求证:四边形MENF是菱形;(2)若四边形MENF是正方形,请探索等腰梯形ABCD的高和底边BC的数量关系,•并证明你的结论.2.(温州)如图,在ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A•出发沿AC向终点C运动,过点P分别作PM∥AB交BC于M,PN∥AD交CD于N,连结AM,设AP=x.(1)四边形PMCN的形状有可能是菱形吗?请说明理由.(2)当x为何值时,四边形PMCN的面积与△ABM的面积相等?答案:中考演练一、1.∠B=∠C或∠A=∠D,或AB=DC,或AC=BD2..AB=CD二、1.B 2.A 3.C三、1.2.∵F为AB的中点,FG∥BC,∴G为AC的中点,∵GH∥FC,∴H为AF的中点,同理D•为BF的中点,∴D、F、H为线段AB的四等分点.实战模拟一、1.16(2-3) 2.S1=12S2 3.7cm2二、1.D 2.B 3.B三、1.证EN=FN=FM=EM(2)等腰梯形ABCD的高是底边BC的一半2.(1)不可能,∵∠CMP=∠MPC=45°,PC=CM≠PM (2)x=1.。
【精品】最新中考数学总复习《第21课 梯形》精品课件

图 21-5
【精选考题 1】 (2013·浙江宁波)如图 21-6, 梯形 ABCD 5 中,AD∥BC,AB = ,BC=4,连结 BD.∠BAD 的平 2 分线交 BD 于点 E ,且 AE ∥CD,则 AD 的长为 ( ) 4 A. 3 5 C. 3 3 B. 2 D. 2
点评:(1)本题主要考查梯形的性质、等腰三角形的性质和 平行四边形的判定与性质,难度中等. (2)解决本题的关键在于准确作C∥AB ,∠A +∠B =90°.若 AB = 10, AD= 4 ,DC =5 ,则梯形 ABCD 的 面积为 .
解析:过点 C 作 CE ∥AD,如解图 6,则∠CEB =∠A , ∠CEB +∠B =∠A +∠B =90°,∴∠ECB =90°. ∵DC∥AB ,CE ∥AD,∴得□DAEC, ∴CE =AD=4,AE =DC=5, ∴EB =10-5=5, ∴Rt △ECB 中,BC= 52-42=3, 4×3 ∴S △CEB = =6,S □AECD=2S △BEC=12, 2 ∴S 梯形 ABCD=18. 答案:18
【解析】
【答案】
3 2
5. (2012·山东滨州)我们知道“连结三角形两边中点的线段叫 三角形的中位线”, “三角形的中位线平行于三角形的第 三边,且等于第三边的一半”.类似地,我们把连结梯 形两腰中点的线段叫做梯形的中位线.如图 21-4,在 梯形 ABCD 中,AD∥BC,点 E ,F 分别是 AB,CD 的 中点,那么 EF 就是梯形 ABCD 的中位线.通过观察, 测量,猜想 EF 和 AD,BC 有怎样的位置和数量关系,并证明你的结论.
2.(2013·江苏扬州 )如图 21- 1,在梯形 ABCD 中, AD ∥BC, AB =AD =CD , BC= 12, ∠ ABC =60°, 则梯形 ABCD 的周长为 .
2013年中考数学复习分层训练试题(共38份,含答案)-8

第六章 图形与变换第1讲 图形的轴对称一级训练1.(2012年广东珠海)下列图形中是轴对称图形的是( )A B C D 2.(2012年湖南益阳)下列图案中是中心对称图形,但不是轴对称图形的是( )A B C D 3.(2012年江苏扬州)下列图形中,既是轴对称图形,又是中心对称图形的是( )A .平行四边形B .等边三角形C .等腰梯形D .正方形4.反比例函数y =4x图象的对称轴的条数是( ) A .0 B .1 C .2 D .35.如图6-1-10,在△ABC 中,AB =AC =5,BC =6,点E ,F 是中线AD 上的两点,则图中阴影部分的面积是( )图6-1-10A .6B .12C .24D .306.(2011年山东济宁)如图6-1-11,△ABC 的周长为30 cm ,把△ABC 的边AC 对折,使顶点C 和点A 重合,折痕交BC 边于点D ,交AC 边于点E ,连接AD ,若AE =4 cm ,则△ABD 的周长是( )图6-1-11A .22 cmB .20 cmC .18 cmD .15 cm7.李明从镜子里看到自己身后的一个液晶屏幕上显示的数字,请问液晶屏幕上显示的数实际是( ) A. B. C. D.8.(2012年湖北黄石)如图6-1-12,在矩形纸片ABCD 中,AB =6 cm ,BC =8 cm ,现将其沿EF 对折,使得点C 与点A 重合,则AF 长为( )图6-1-12A.258cm B.254cm C.252cm D.8 cm9.(2011年湖南永州)永州市新田县的龙家大院至今已有930多年历史,因该村拥有保存完好的“三堂九井二十四巷四十八栋”明清建筑,而申报为中国历史文化名村.如图6-1-13是龙家大院的一个窗花图案,它具有很好的对称美,这个图案是由:①正六边形;②正三角形;③等腰梯形;④直角梯形等几何图形构成,在这四种几何图形中既是轴对称图形又是中心对称图形的是__________(只填序号).图6-1-1310.(2011年山东济宁)如图6-1-14,△PQR是△ABC经过某种变换后得到的图形.如果△ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标为__________________.图6-1-1411.如图6-1-15,点A,B,C的坐标分别为(0,-1),(0,2),(3,0).从下面四个点M(3,3),N(3,-3),P(-3,0),Q(-3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是________.图6-1-1512.(2011年浙江绍兴)分别按下列要求解答:(1)在图6-1-16(1)中,作出圆O关于直线l成轴对称的图形;(2)在图6-1-16(2)中,作出△ABC关于点P成中心对称的图形.图6-1-16二级训练13.(2012年四川资阳)如图6-1-17,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=2 3,则四边形MABN 的面积是()A.6 3 B.12 3 C.18 3 D.24 3图6-1-1714.如图6-1-18,AB⊥BC,AB=BC=2 cm,弧OA与弧OC关于点O中心对称,则AB,BC,弧CO,弧OA所围成图形的面积是__________cm2.图6-1-1815.如图6-1-19,在∠ABC内有一点P,问:(1)能否在BA,BC边上各找到一点M,N,使△PMN的周长最短?若能,请画图说明;若不能,请说明理由;(2)若∠ABC=40°,在(1)问的条件下,能否求出∠MPN的度数?若能,请求出它的数值;若不能,请说明理由.图6-1-19三级训练16.(2011年山东济宁)去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河同一侧的张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴,建立平面直角坐标系(如图6-1-20),两村的坐标分别为A(2,3),B(12,7).(1)若从节约经费考虑,水泵站建在距离大桥O多远的地方,可使所用输水管最短?(2)水泵站建在距离大桥O多远的地方,可使它到张村、李村的距离相等?图6-1-2017.为了美化环境,在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块:①分割后的整个图形必须是轴对称图形;②四块图形形状相同;③四块图形面积相等.现已有两种不同的分法:(1)分别作两条对角线(如图6-1-21甲);(2)过一条边的四等分点作这边的垂线段(图6-1-21乙中两个图形的分割看作同一种方法).请你按照上述三个要求,分别在下面两个正方形中给出另外两种不同的分割方法(正确画图,不写画法).图6-1-21。
2013年中考数学复习分层训练试题(共38份,含答案)-26

第3讲四边形与多边形第1课时多边形与平行四边形一级训练1.(2011年广东)正八边形的每个内角为()A.120°B.135°C.140°D.144°2.用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的正方形的个数是() A.3 B.4 C.5 D.63.(2011年湖南邵阳)如图4-3-6,▱ABCD中,对角线AC,BD相交于点O,且AB≠AD,则下列式子不正确的是()A.AC⊥BD B.AB=CD C.BO=OD D.∠BAD=∠BCD图4-3-64.如图4-3-7,在▱ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为()图4-3-7A.3 B.6 C.12 D.245.某多边形的内角和是其外角和的3倍,则此多边形的边数是()A.5 B.6 C.7 D.86.在▱ABCD中,∠A∶∠B∶∠C∶∠D的比值是()A.1∶2∶3∶4 B.1∶2∶2∶1 C.2∶2∶1∶1 D.2∶1∶2∶17.(2012年广西南宁)如图4-3-8,在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA的取值范围是()图4-3-8A.2 cm<OA<5 cm B.2 cm<OA<8 cm C.1 cm<OA<4 cm D.3 cm<OA<8 cm 8.(2011年江苏泰州)在四边形ABCD中,对角线AC,BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判定这个四边形是平行四边形的条件有()A.1组B.2组C.3组D.4组9.(2011年四川广安)若凸n边形的内角和为1 260°,则从一个顶点出发引的对角线条数是__________.10.在下列四组多边形地板砖中:①正三角形与正方形;②正三角形与正六边形;③正六边形与正方形;④正八边形与正方形. 将每组中的两种多边形结合,能密铺地面的是__________(填正确序号).11.(2011年四川宜宾)如图4-3-9,平行四边形ABCD的对角线AC,BD交于点O,E,F在AC上,G,H在BD上,AF=CE,BH=DG.求证:GF∥HE.图4-3-912.如图4-3-10,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.图4-3-10二级训练13.(2009年广东茂名)如图4-3-11,杨伯家小院子的四棵小树E,F,G,H刚好在其梯形院子ABCD各边的中点上,若在四边形EFGH种上小草,则这块草地的形状是() A.平行四边形B.矩形C.正方形D.菱形图4-3-1114.(2011年浙江金华)如图4-3-12,在▱ABCD中,AB=3,AD=4,∠ABC=60°,过BC 的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是________.图4-3-1215.(2010年广东)如图4-3-13,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.图4-3-13三级训练16.如图4-3-14,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE =DE,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为()A. 100°B.110° C. 120° D. 130°图4-3-1417.(2012年山东威海)(1)如图4-3-15(1),▱ABCD的对角线AC,BD交于点O,直线EF 过点O,分别交AD,BC于点E,F.求证:AE=CF.(2)如图4-3-15(2),将▱ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.图4-3-15。
全国各地2013年中考数学试卷分类汇编 梯形

梯形一.选择题1.(2013某某,6,3分)下列命题中是假命题的是()A.平行四边形的对边相等B.菱形的四条边相等C.矩形的对边平行且相等D.等腰梯形的对边相等考点:命题与定理;平行四边形的性质;菱形的性质;矩形的性质;等腰梯形的性质.分析:根据平行四边形、矩形、菱形、等腰梯形的判定与性质分别判断得出答案即可.解答:解:A.根据平行四边形的性质得出平行四边形的对边相等,此命题是真命题,不符合题意;B.根据菱形的性质得出菱形的四条边相等,此命题是真命题,不符合题意;C.根据矩形的性质得出矩形的对边平行且相等,此命题是真命题,不符合题意;D.根据等腰梯形的上下底边不相等,此命题是假命题,符合题意.故选:D.点评:此题主要考查了平行四边形、矩形、菱形、以及等腰梯形的判定与性质等知识,熟练掌握相关定理是解题关键.2 .(2013某某某某,6,3分)顺次连接等腰梯形四边中点所得的四边形一定是()A.矩形B.正方形C.菱形D.直角梯形考点:中点四边形.分析:根据等腰梯形的性质及中位线定理和菱形的判定,可推出四边形为菱形.解答:解:如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是各边的中点,求证:四边形EFGH是菱形.证明:连接AC、BD.∵E、F分别是AB、BC的中点,∴EF=AC.同理FG=BD,GH=AC,EH=BD,又∵四边形ABCD是等腰梯形,∴AC=BD,∴EF=FG=GH=HE,∴四边形EFGH是菱形.故选C.点评:此题主要考查了等腰梯形的性质,三角形的中位线定理和菱形的判定.用到的知识点:等腰梯形的两底角相等;三角形的中位线平行于第三边,并且等于第三边的一半;四边相等的四边形是菱形.3. (2013•某某3分)如图,梯形ABCD中,AD∥BC,AB=,B C=4,连结BD,∠BAD的平分线交BD于点E,且AE∥CD,则AD的长为()A.B.C.D.2【答案】B.【解析】延长AE交BC于F,∵AE是∠BAD的平分线,∴∠BAF=∠DAF,∵AE∥CD,∴∠DAF=∠AFB,∴∠BAF=∠AFB,∴AB=BF,∵AB=,BC=4,∴CF=4﹣=,∵AD∥BC,AE∥CD,∴四边形AFCD是平行四边形,∴AD=CF=.【方法指导】本题考查了梯形的性质,等腰三角形的性质,平行四边形的判定与性质,梯形的问题,关键在于准确作出辅助线.4.(2013某某市,6,4分)在梯形ABCD中,AD∥BC,对角线AC和BD交于点O,下列条件中,能判断梯形ABCD是等腰梯形的是()(A)∠BDC =∠BCD;(B)∠ABC =∠DAB;(C)∠ADB =∠DAC;(D)∠AOB =∠BOC.5.(2013某某某某,6,3分)如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、CD的中点且EF=6,则AD+BC的值是()A.9 B.C.12 D.15考点:梯形中位线定理.分析:根据梯形的中位线等于两底和的一半解答.解答:解:∵E和F分别是AB和CD的中点,∴EF是梯形ABCD的中位线,∴EF=(AD+BC),∵EF=6,∴AD+BC=6×2=12.故选C.点评:本题主要考查了梯形的中位线定理,熟记梯形的中位线平行于两底边并且等于两底边和的一半是解题的关键.6.(2013某某省某某市,1,3分)如图,梯形ABCD中,AD∥BC,AB=DC=3,AD=5,∠C=60°,则下底BC的长为()A.8 B.9 C.10 D.11考点:等腰梯形的性质;等边三角形的判定与性质.分析:首先构造直角三角形,进而根据等腰梯形的性质得出∠B=60°,BF=EC,AD=EF=5,求出BF即可.解答:解:过点A作AF⊥BC于点F,过点D作DE⊥BC于点E,∵梯形ABCD中,AD∥BC,AB=DC=3,AD=5,∠C=60°,∴∠B=60°,BF=EC,AD=EF=5,∴cos60°===,解得:BF=1.5,故EC=1.5,∴BC=1.5+1.5+5=8.故选:A .点评: 此题主要考查了等腰梯形的性质以及解直角三角形等知识,根据已知得出BF=EC 的长是解题关键.7.(2013某某某某,10,4分)如图5,四边形ABCD 是梯形,AD ∥BC ,CA 是∠BCD 的平分线,且AB ⊥AC ,AB=4,AD=6,则tanB=( )A .32B .22C .411D .455【答案】B .【解析】如答案图,∵CA 是∠BCD 的平分线∴∠1=∠2∵AD∥BC∴∠1=∠3从而∠3=∠2∵AD=6∴CD=AD=6作DE ⊥AC 于E可知AE=CE∵∠1=∠2,∠BAC=∠DEC∴△ABC ∽△EDC∴ACCE BC CD ∵AE=CE , CD=6∴BC=12在Rt △ABC 中,由勾股定理求得AC=82所以,tanB=22,答案选B 。
湖北省武汉市中考数学复习分层训练21 梯形

21 梯形一级训练1.(2012年山东临沂)如图4-3-41,在等腰梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,下列结论不一定正确的是( )A.AC=BD B.OB=OC C.∠BCD=∠BDC D.∠ABD=∠ACD图4-3-41 图4-3-42 图4-3-43 2.(2012年福建漳州)如图4-3-42,在等腰梯形ABCD中,AD∥BC,AB=DC,∠B=80°,则∠D的度数是( )A.120° B.110° C.100° D.80°3.(2011年山东滨州)如图4-3-43,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )A.1 个 B.2个 C.3个 D.4个4.(2011年广西来宾)如图4-3-44,在直角梯形ABCD中,已知AB∥DC,∠DAB=90°,∠ABC=60°,EF为中位线,且BC=EF=4,那么AB=( )A.3 B.5 C.6 D.8图4-3-44 图4-3-45 图4-3-46 5.(2011年浙江台州)如图4-3-45,在梯形ABCD中,AD∥BC,∠ABC=90°,对角线BD,AC相交于点O.下列条件中,不能判断对角线互相垂直的是( )A.∠1=∠4 B. ∠1=∠3 C.∠2=∠3 D.OB2+OC2=BC26.(2012年江苏无锡)如图4-3-46,在梯形ABCD中,AD∥BC,AD=3,AB=5,BC=9,CD的垂直平分线交BC于点E,连接DE,则四边形ABED的周长等于( )A.17 B.18 C.19 D.207.等腰梯形的中位线长是15 ,一条对角线平分一个60°的底角,则梯形的周长为______.8.(2011年江苏南京)等腰梯形的腰长为5 cm,它的周长是22 cm,则它的中位线长为________cm.9.(2011年湖南邵阳)如图4-3-47,在等腰梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,∠B=60°,BC=2 cm,则上底DC的长是________cm.图4-3-47 图4-3-48 图4-3-49 10.(2011年江苏宿迁)如图4-3-48,在梯形ABCD中,AB∥DC,∠ADC的平分线与∠BCD的平分线的交点E恰在AB上.若AD=7 cm,BC=8 cm,则AB的长度是________cm.二级训练11.(2012年湖北咸宁)如图4-3-49,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC,且交CD于点E,E为CD的中点,EF∥BC交AB于点F,EG∥AB交BC于点G.当AD=2,BC=12时,四边形BGEF的周长为________.12.如图4-3-50,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC,且与AB的延长线交于点E.求证:四边形AECD是等腰梯形.图4-3-50参考答案1.C 2.C 3.C 4.B 5.B 6.A7.50 8.6 9.2 10.1511.2812.证明: ∵四边形ABCD 是菱形, ∴∠CAE =12∠DAB =30°.又∵CE ⊥AC, ∴∠E =90°-30°=60°. ∴∠E =∠DAE .∵AD ∥BC, ∴CE 不平行AD .又∵DC ∥AE, ∴四边形AECD 是等腰梯形.。
梯形练习含答案
一、选择题(每小题3分,共42分)1.如图19-3-21,沿虚线EF将平行四边形ABCD剪开,则得到的四边形ABFE是()图19-3-21A.梯形B.平行四边形C.矩形D.菱形2.如图19-3-22,已知等腰梯形ABCD中,AD∥BC,∠A=110°,则∠A=()图19-3-22A.90°B.80°C.70°D.60°3.梯形ABCD中,AD∥BC,则四个角的比∠A︰∠B︰∠C︰∠D可以是()A.3︰4︰5︰6 B.6︰5︰4︰3C.3︰5︰6︰4 D.4︰5︰6︰34.如图19-3-23,在等腰梯形ABCD中,AB∥CD,AD=BC= a cm,∠A=60°,BD平分∠ABC,则这个梯形的周长是()A.4a cm B.5a cm C.6a cm D.7a cm图19-3-235.下列命题正确的有()A.等腰梯形两底角相等B.底角相等的梯形是等腰梯形C.等腰梯形对角线相等D.对角线相等的四边形不是等腰梯形6.下列结论正确的是()①梯形是轴对称图形,②等腰梯形是轴对称图形,③等腰梯形的对角线相等,④等腰梯形在同一底上的两个角相等A.①②③B.②③④C.①③④D.③④7.如果等腰梯形两底之差的一半等于它的高,那么此梯形的一个底角是()A.30° B.45°C.60°D.75°8.如图19-3-24,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,以下四个结论:①∠ABC=∠DCB,②OA=OD,③∠BCD=∠BDC,④S△AOB=S△DOC,其中正确的是()A.①②B.①④ C.②③④ D.①②④图19-3-249.梯形ABCD中,AD∥BC,AD=1,BC=4,∠C=70°,∠B=40°,则AB的长为()A.2 B.3 C.4 D.510.在梯形ABCD中,AB∥CD,∠A=60°,∠B=30°,AD=CD=6,则AB的长度为()A.9 B.12 C.18 D.11.等腰梯形ABCD中,E、F、G、H分别是各边的中点,则四边形EFGH的形状是()A.平行四边形B.矩形C.菱形D.正方形12.在等腰梯形ABCD中,AB=DC,AC、BD交于点O,则图中全等三角形共有()A.2 B.3对C.4对D.5对13.如图19-3-25,在等腰梯形ABCD中,AD∥BC,对角线AC ⊥BD于点O,AE⊥BC,DF⊥BC垂足分别为E、F,设AD=a,BC=b,则四边形AEFD的周长是()A.3a+b B.2(a+b)C.2b+a D.4a+b图19-3-2514.如图19-3-26,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A´处,若∠A´BC=20°,则∠A´BD的度数为().A.15° B.20°C.25°D.30°图19-3-26二、填空题(每空3分,共12分)15.在等腰梯形ABCD中,AD∥BC,AB=CD,∠B=40°,则∠A=_____,∠C=____,∠D=_____.16.如图19-3-27,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=3,BC=4,则梯形ABCD的面积是.图19-3-2717.在等腰梯形ABCD中,AD∥BC,AD=3cm,AB=4cm,∠B=60°,则下底BC的长为cm.18.如图19-3-28,在四边形ABCD中,已知AB与CD不平行,∠ABD=∠ACD,请你添加一个条件:,使得加上这个条件后能够推出AD∥BC且AB=CD.图19-3-28三、解答题19.(本小题满分5分)如图19-3-29:在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于O.(1)图中共有对全等三角形;(2)写出你认为全等的一对三角形,并证明.图19-3-2920.(本小题满分5分)如图19-3-30,在梯形ABCD中,AD∥BC,AB=AD=DC,AC⊥AB,将CB延长至点F,使BF=CD.(1)求∠ABC的度数;(2)求证:△CAF为等腰三角形.图19-3-3021.(本小题满分5分)如图19-3-31,在梯形ABCD中,AB∥CD,BD⊥AD,BC=CD,∠A=60°,CD=2cm.(1)求∠CBD的度数;(2)求下底AB的长.图19-3-3122.(本小题满分5分)如图19-3-32,在菱形中,°,过点作且与的延长线交于点.求证:四边形是等腰梯形.图19-3-3223.(本小题满分6分)如图19-3-33,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,求EF的长.图19-3-3324.(本小题满分6分)如图19-3-34,已知在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC.求证:AC=CE图19-3-3425.(本小题满分7分)如图19-3-35,在梯形ABCD中,AD∥BC,BD=CD,∠BDC=90°,AD=3,BC=8.求AB的长.图19-3-3526.(本小题满分7分)如图19-3-36,在梯形ABCD中,AD//BC,∠B=90°.AB=14cm,AD=15cm,BC=21cm.点M从A点开始,沿AD边向D运动,速度为厘米/秒,点N从点C开始沿CB边向点B 运动,速度为2厘米/秒,当t为何值时,(1)当为何值时,四边形MNCD是平行四边形?(2)当t为何址时,四边形MNCD是等腰梯形?图19-3-36参考答案1.A 2.C 3.D 4.B 5.C 6.B 7.B 8.D 9.B 10.C 11.C 12.B 13.A 14.C15.140°,40°,140°,16.9 17.7 18.OB=OC 19.(1)3(2)△ABC≌△DCB证明:∵四边形ABCD是等腰梯形∴AB=DC,∠ABC=∠DCB,又BC=CB,∴△ABC≌△DCB.20.(1)∵AD∥BC,∴∠DAC=∠ACB,∵AD=DC,∴∠DCA=∠DAC,∴∠DCA=∠ACB=12∠DCB,∵DC=AB,∴∠DCB=∠ABC,∴∠ACB=12∠ABC,在△ACB中,∵AC⊥AB,∴∠CAB=90°,∴∠ACB+∠ABC=90°,∴12∠ABC+∠ABC=90°,∴∠ABC=90°;(2)连接DB.∵在梯形ABCD中,AB=DC,∴AC=DB,在四边形DBF A中,DA∥BF,DA=DC=BF,∴四边形DBF A是平行四边形,∴DB=AF,∴AC=AF,即△ACF为等腰三角形.21.(1)∵∠A=60°,BD⊥AD,∴∠ABD=30°,又∵AB∥CD,∴∠CDB=∠ABD=30°,∵BC=CD,∴∠CBD=∠CDB=30°;(2)∵∠ABD=∠CBD=30°,∴∠ABC=60°=∠A,∴AD=BC=CD=2cm,在Rt△ABD中,∴AB=2AD=4cm.22.证法1:∵四边形ABCD是菱形,∴AC平分∠DAB.∵∠DAB=60°,∴∠CAE1302DAB︒=∠=.∵CE⊥AC,∴∠E= 90°-∠CAE=90°-30°=60°.∴∠DAB=∠E.∵AB//CD,∴四边形AECD是等腰梯形.图19-3-37证法2:如图19-3-37,连结BD,∵四边形ABCD是菱形,∴BD⊥AC,且AD=AB.由AD=AB,∠DAB=60°,得,△ABD是等边三角形,即BD=AD=AB.∵BD⊥AC,且CE⊥AC,∴BD∥CE.∵DC∥AB,∴四边形DBEC是平行四边形.∴BD=EC.∴AD=EC.∴四边形AECD是等腰梯形.DA B CEF图19-3-38证法3:如图19-3-38,设线段AD和EC的延长线交于点F.∵四边形ABCD 是菱形,∴AC 平分∠DAB .∵∠DAB =60°,∴∠CAE =∠CAF =12DAB ∠=30°.∵CE ⊥AC ,∴∠E =∠F =90°-30°=60°.∴△AEF 是等边三角形,且点C 是EF 的中点. ∵DC ∥AB ,∴点D 是AF 的中点. ∴1122AD AF EF EC ===.∴四边形AECD 是等腰梯形.AD B EC F G图19-3-3923.解法一:如图19-3-39,过点D 作DG ⊥BC 于点G .∵AD ∥BC ,∠B =90°,∴∠A =90°.可得四边形ABGD 为矩形.∴BG =AD =1,AB =DG .∵BC =4,∴GC =3.∵∠DGC =90°,∠C =45°,∴∠CDG =45°.∴DG =GC =3.∴AB =3.又∵E 为AB 中点, ∴1322BE AB ==. ∵EF ∥DC ,∴∠EFB =45°.在△BEF 中,∠B =90°.∴sin 45BE EF ==°.24.连结BD .∵DC ∥BE ,DC =BE ,∴四边形BECD 是平行四边形.∴DB =CE .又∵四边形ABCD 是等腰梯形,∴AC =BD .∴AC =CE .图19-3-4025.如图19-3-40,作AE ⊥BC 于E ,DF ⊥BC 于F , ∴AE ∥DF ,∠AEF =90°,∵AD ∥BC ,∴四边形AEFD 是矩形.∴EF =AD =3,AE =DF ,∵BD =CD ,DF ⊥BC ,∴DF 是△BDC 的BC 边上的中线,∵∠BDC=90°,∴142DF BC BF===,∴AE=4,BE=BF-EF=4-3=1,在Rt△ABE中,222AB AE BE=+,∴AB=.26.(1)假设当t=a时,四边形MNCD为平行四边形,根据平行四边形的判定定理有MD=NC,即:15-a=2a,解得a=5.所以当5t=秒时,四边形MNCD为平行四边形(2)假设当t=a时,四边形MNCD是等腰梯形,则CD=MN(如图19-3-41),作ME⊥BC,DF⊥BC,垂足分别是E、F,则ME=DF,NE=CF,因为CF=BC-AD=21-15=6,NF=2a-6,MN=15-a,NE=NF-MD=CF=6,所以2a-6-(15-a)=6,解得a=9.所以当t=9秒时,四边形MNCD是等腰梯形.。
武汉市中考数学复习分层训练21 梯形

21 梯形一级训练1.(2012年山东临沂)如图4-3-41,在等腰梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,下列结论不一定正确的是( )A.AC=BD B.OB=OC C.∠BCD=∠BDC D.∠ABD=∠ACD图4-3-41 图4-3-42 图4-3-43 2.(2012年福建漳州)如图4-3-42,在等腰梯形ABCD中,AD∥BC,AB=DC,∠B=80°,则∠D的度数是( )A.120° B.110° C.100° D.80°3.(2011年山东滨州)如图4-3-43,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )A.1 个 B.2个 C.3个 D.4个4.(2011年广西来宾)如图4-3-44,在直角梯形ABCD中,已知AB∥DC,∠DAB=90°,∠ABC=60°,EF为中位线,且BC=EF=4,那么AB=( )A.3 B.5 C.6 D.8图4-3-44 图4-3-45 图4-3-46 5.(2011年浙江台州)如图4-3-45,在梯形ABCD中,AD∥BC,∠ABC=90°,对角线BD,AC相交于点O.下列条件中,不能判断对角线互相垂直的是( )A.∠1=∠4 B. ∠1=∠3 C.∠2=∠3 D.OB2+OC2=BC26.(2012年江苏无锡)如图4-3-46,在梯形ABCD中,AD∥BC,AD=3,AB=5,BC=9,CD的垂直平分线交BC于点E,连接DE,则四边形ABED的周长等于( )A.17 B.18 C.19 D.207.等腰梯形的中位线长是15 ,一条对角线平分一个60°的底角,则梯形的周长为______.8.(2011年江苏南京)等腰梯形的腰长为5 cm,它的周长是22 cm,则它的中位线长为________cm.9.(2011年湖南邵阳)如图4-3-47,在等腰梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,∠B=60°,BC=2 cm,则上底DC的长是________cm.图4-3-47 图4-3-48 图4-3-49 10.(2011年江苏宿迁)如图4-3-48,在梯形ABCD中,AB∥DC,∠ADC的平分线与∠BCD的平分线的交点E恰在AB上.若AD=7 cm,BC=8 cm,则AB的长度是________cm.二级训练11.(2012年湖北咸宁)如图4-3-49,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC,且交CD于点E,E为CD的中点,EF∥BC交AB于点F,EG∥AB交BC于点G.当AD=2,BC=12时,四边形BGEF的周长为________.12.如图4-3-50,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC,且与AB的延长线交于点E.求证:四边形AECD是等腰梯形.图4-3-50参考答案1.C 2.C 3.C 4.B 5.B 6.A7.50 8.6 9.2 10.1511.2812.证明: ∵四边形ABCD 是菱形,∴∠CAE =12∠DAB =30°. 又∵CE ⊥AC, ∴∠E =90°-30°=60°. ∴∠E =∠DAE .∵AD ∥BC, ∴CE 不平行AD .又∵DC ∥AE, ∴四边形AECD 是等腰梯形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3课时梯形
一级训练
1.(2012年山东临沂)如图4-3-41,在等腰梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,下列结论不一定正确的是()
A.AC=BD B.OB=OC C.∠BCD=∠BDC D.∠ABD=∠ACD
图4-3-41 图4-3-42 图4-3-43
2.(2012年福建漳州)如图4-3-42,在等腰梯形ABCD中,AD∥BC,AB=DC,∠B=80°,则∠D的度数是()
A.120°B.110°C.100°D.80°
3.(2011年山东滨州)如图4-3-43,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为() A.1 个B.2个C.3个D.4个
4.(2011年广西来宾)如图4-3-44,在直角梯形ABCD中,已知AB∥DC,∠DAB=90°,∠ABC=60°,EF为中位线,且BC=EF=4,那么AB=()
A.3 B.5 C.6 D.8
图4-3-44 图4-3-45 图4-3-46
5.(2011年浙江台州)如图4-3-45,在梯形ABCD中,AD∥BC,∠ABC=90°,对角线BD,AC相交于点O.下列条件中,不能判断对角线互相垂直的是()
A.∠1=∠4 B. ∠1=∠3 C.∠2=∠3D.OB2+OC2=BC2
6.(2012年江苏无锡)如图4-3-46,在梯形ABCD中,AD∥BC,AD=3,AB=5,BC=9,CD的垂直平分线交BC于点E,连接DE,则四边形ABED的周长等于()
A.17 B.18 C.19 D.20
7.等腰梯形的中位线长是15 ,一条对角线平分一个60°的底角,则梯形的周长为______.8.(2011年江苏南京)等腰梯形的腰长为5 cm,它的周长是22 cm,则它的中位线长为________cm.
9.(2011年湖南邵阳)如图4-3-47,在等腰梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,∠B=60°,BC=2 cm,则上底DC的长是________cm.
图4-3-47 图4-3-48 图4-3-49 10.(2011年江苏宿迁)如图4-3-48,在梯形ABCD中,AB∥DC,∠ADC的平分线与∠BCD 的平分线的交点E恰在AB上.若AD=7 cm,BC=8 cm,则AB的长度是________cm.
二级训练
11.(2012年湖北咸宁)如图4-3-49,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC,且交CD于点E,E为CD的中点,EF∥BC交AB于点F,EG∥AB交BC于点G.
当AD=2,BC=12时,四边形BGEF的周长为________.
12.如图4-3-50,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC,且与AB的延长线交于点E.求证:四边形AECD是等腰梯形.
图4-3-50
参考答案
1.C 2.C 3.C 4.B 5.B 6.A 7.508.69.210.15
11.28
12.证明:∵四边形ABCD是菱形,
∴∠CAE=1
2∠DAB=30°.
又∵CE⊥AC, ∴∠E=90°-30°=60°.
∴∠E=∠DAE.
∵AD∥BC, ∴CE不平行AD.
又∵DC∥AE, ∴四边形AECD是等腰梯形.。
