2017-2018学年北京市海淀区九上期中数学试卷
2018北京市海淀区初三(上)期中数学

18.(1)问题发现:如图 1,如果△ACB 和△CDE 均为等边三角形,点 A、D、E 在同一直线上,连接 BE.则 AD 与 BE
的数量关系为
;∠AEB 的度数为
度.
(2)拓展探究:如图 2,如果△ACB 和△CDE 均为等腰三角形,∠ACB=∠DCE=90°,点 A、D、E 在同一直线上,连
接 BE,判断线段 AE 与 BE 的位置关系,并说明理由.
∴S= BQ·BP=
=-t2+3t(0≤t≤3),
观察只有 C 选项符合, 故选 C. 【点睛】本题考查了二次函数的应用,动点问题的函数图象,熟练掌握二次函数的图象及性质是解题的关键. 二.填空题(共 8 小题,满分 24 分,每小题 3 分) 9. 【答案】(﹣1,2). 【解析】 试题分析:根据“平面直角坐标系中任意一点 P(x,y),关于原点的对称点是(﹣x,﹣y),即关于原点的对称点, 横纵坐标都变成相反数”解答. 解:根据关于原点对称的点的坐标的特点, ∴点(1,﹣2)关于原点过对称的点的坐标是(﹣1,2). 故答案为:(﹣1,2). 考点:关于原点对称的点的坐标. 10. 【答案】y=﹣x2+4.
= (x2﹣12x)+21
= [(x﹣6)2﹣36]+21
= (x﹣6)2+3,
故 y= (x﹣6)2+3,向左平移 2 个单位后,
得到新抛物线的解析式为:y= (x﹣4)2+3. 故选 D. 【点睛】本题考查了二次函数图象与几何变换,熟记函数图象平移的规律并正确配方将原式变形是解题关 键. 3. 【答案】D 【解析】
3 / 23
22.已知关于 x 的方程 x2﹣2x+m=0 有两个不相等的实数根 x1、x2 (1)求实数 m 的取值范围; (2)若 x1﹣x2=2,求实数 m 的值. 23.解方程:x2+6x﹣2=0. 24.在平面直角坐标系中,平行四边形 ABOC 如图放置,点 A、C 的坐标分别是(0,4),(﹣1,0),将此平行四边形 绕点 O 顺时针旋转 90°,得到平行四边形 A′B′C′D′. (1)若抛物线经过点 C、A、A′,求此抛物线的解析式; (2)点 M 是第一象限内抛物线上的一动点,为点 M 在何处时,△AMA′的面积最大?最大面积是多少?并求出此到 点 M 的坐标.
2018北京海淀初三(上)期中数学

∴∠1=∠2,CD=BD.
∵CD=BF,
∴BF=BD.
∴∠3=∠F.
∴∠4=∠3 ∠F=2∠3.
(1)求证:DE 与⊙O 相切;
(2)若 CD=BF, AE=3,求 DF 的长.
25.有这样一个问题:探究函数 y=|������−3|+������+3的图象与性质.
2
小东根据学习函数的经验,对函数 y=|������−3|+������+3的图象与性质进行了探究.
2
下面是小东的探究过程,请补充完成:
(1)化简函数解析式,当 x≥3 时,y=
,当 x<3 时,y=
;
(2)根据(1)中的结果,请在所给坐标系中画出函数 y=|������−3|+������+3的图象;
2
(3)结合画出的函数图象,解决问题:若关于 x 的方程 ax+1=只有一个实数|������−3|+������+3根,直接写出实数 a 的取值范
D. (������ + 1)2=3
5.如图,以 O 为圆心的两个同心圆中,大圆的弦 AB 是小圆的切线,点 P 为切点.若大圆半径为 2,小圆半径为 1,则 AB 的长为
A. 2√3
B. 2√2
C. √5
D. 2
6.将抛物线 y=(������ + 1)2-2 向上平移 a 个单位后得到的抛物线恰好与 x 轴有一个交点,则 a 的值为
同理∠AOD=120°,
∴∠COD=∠AOC=∠AOD=120°
∴AC=CD=AD(
)(填推理的依据).
∴∠ACD 是等边三角形.
20.已知-1 是方程������2+ax-b=0 的一个根,求������2+������2+2b 的值
北京市海淀区2017-2018学年度第一学期初三第一学期期中学业水平调研试题及答案

初三第一学期期中学业水平调研英语2017.11学校_______________ 姓名_______________ 准考证号_________________听力理解(共30)一、听后选择(共12分,每小题1.5分)听对话或独白,根据对话或独白的内容,从下面各题所给的A、B、C三个选项中选择最佳选项。
每段对话或独白你将听两遍。
请听一段对话,完成第1至第2小题。
1 . What does the man want to buy?A.A scarfB. A sweaterC. A skirt2 . How much does the man pay at last ?A. 30 dollarsB. 40 dollarsC.6 0 dollars请听一段对话,完成第3至第4小题。
3 . What’s the matter with the boy ?A.He has a bad coldB. He lets his parents downC. He worries about a test.4 . What does the girl advise Jim to do ?A. Go to the doctor’sB. Study with friendsC. Take some exercise.请听一段对话,完成第5至第6小题。
5 . Where is the woman going?A.To the libraryB. To the museumC. To the hospital.6 . How long will it take the woman to get there by subway ?A . About 10 minutes B. About 20 minutes C.About 30 minutes请听一段对话,完成第7至第8小题。
7 . Who will take you to the airport ?A. A guideB. A pilotC.A teacher .8 . What is the speech mainly about?A. What to do on the plane.B. When to fly to another city.C. How to deal with fears of flying.二、听后回答(共10分,每小题2分)听对话,根据对话内容笔头回答问题。
2018年-2018年学年北京市海淀区九上期中数学试题整理

2017-2018学年北京市海淀区九上期中数学试卷一、选择题(共8小题;共40分)1. 一元二次方程的二次项系数、一次项系数、常数项分别是A. ,,B. ,,C. ,,D. ,,2. 把抛物线向上平移个单位长度得到的抛物线的表达式为A. B. C. D.3. 如图,,,是上的三个点.若,则的大小为A. B. C. D.4. 下列手机手势解锁图案中,是中心对称图形的是A. B.C. D.5. 用配方法解方程,下列配方正确的是A. B.C. D.6. 风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转后能与原来的图案重合,那么的值可能是A. B. C. D.7. 二次函数与一次函数的图象如图所示,则满足的的取值范围是A. B. 或C. 或D.8. 如图,动点从格点出发,在网格平面内运动,设点走过的路程为,点到直线的距离为.已知与的关系如图所示.下列选项中,可能是点的运动路线的是A. B.C. D.二、填空题(共8小题;共40分)9. 点关于原点的对称点的坐标为.10. 写出一个图象开口向上,过点的二次函数的表达式:.11. 如图,四边形内接于,为的延长线上一点.若,则的大小为.12. 抛物线与轴的公共点的个数是.13. 如图,在平面直角坐标系中,点,点的坐标分别为,,将线段绕点顺时针旋转,若点的对应点的坐标为,则点的对应点的坐标为.14. 已知抛物线经过点,,则(填“”,“”,或“”).15. 如图,的半径与弦交于点,若,,,则的长为.16. 下面是“作已知三角形的高”的尺规作图过程.已知:.求作:边上的高.作法:如图,()分别以点和点为圆心,大于的长为半径作弧,两弧相交于,两点;()作直线,交于点;()以为圆心,为半径作,与的延长线交于点,连接.线段即为所作的高.请回答:该尺规作图的依据是.三、解答题(共12小题;共156分)17. 解方程:.18. 如图,等边三角形的边长为,是线段上的点,,以为边作等边三角形,连接.求的长.19. 已知是方程的一个根,求的值.20. 如图,在中,.求证:.21. 如图,是一块边长为米的正方形苗圃,园林部门拟将其改造为矩形的形状,其中点在边上,点在的延长线上,.设的长为米,改造后苗圃的面积为平方米.(1)与之间的函数关系式为(不需写自变量的取值范围);(2)根据改造方案,改造后的矩形苗圃的面积与原正方形苗圃的面积相等,请问此时的长为多少米?22. 关于的一元二次方程有两个不相等的实数根,.(1)求实数的取值范围;(2)是否存在实数,使得成立?如果存在,求出的值;如果不存在,请说明理由.23. 古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家——“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”.以为例,花拉子米的几何解法如下:如图,在边长为的正方形的两个相邻边上作边长分别为和的矩形,再补上一个边长为的小正方形,最终把图形补成一个大正方形.通过不同的方式来表示大正方形的面积,可以将原方程化为,从而得到此方程的正根是.24. 如图,在平面直角坐标系中,点的坐标为,点的横坐标为,将点绕点旋转,使它的对应点恰好落在轴上(不与点重合);再将点绕点逆时针旋转得到点.(1)直接写出点和点的坐标;(2)求经过,,三点的抛物线的表达式.25. 如图,为的直径,点在上,过点作交于点,交于点,.(1)求证:为的中点;(2)若,求四边形的面积.26. 在平面直角坐标系中,已知抛物线和直线.(1)抛物线的顶点的坐标为;(2)请判断点是否在直线上,并说明理由;(3)记函数的图象为,,过点垂直于轴的直线与图象交于,.当时,若存在使得成立,结合图象,求的取值范围.27. 对于平面直角坐标系中的点,给出如下定义:记点到轴的距离为,到轴的距离为,若,则称为点的“引力值”;若,则称为点的“引力值”.特别地,若点在坐标轴上,则点的“引力值”为.例如,到轴的距离为,到轴的距离为,因为,所以点的“引力值”为.(1)① 的“引力值”为;②若的“引力值”为,则的值为;(2)若点在直线上,且点的“引力值”为,求点的坐标;(3)已知是以为圆心,半径为的圆上的一个动点,那么点的“引力值”的取值范围是.28. 在中,斜边的中点关于的对称点为点,将绕点顺时针旋转至,连接,,如图所示.(1)在① ,② ,中,等于旋转角的是(填出满足条件的的角的序号);(2)若,求的大小(用含的式子表示);(3)是的中点,连接,用等式表示线段与之间的数量关系,并证明.答案第一部分1. D2. A3. D4. B5. A6. D7. A8. D第二部分9.10. 答案不唯一,例如11.12.13.14.15.. ①到线段两端点距离相等的点在线段的垂直平分线上;②直径所对的圆周角是直角; 两点确定一条直线第三部分17.所以或所以18. 如图,是等边三角形,,..是等边三角形,,...在和中..,,..19. 是方程的一个根,..原式20. 在中,,.,,在中,,在中,..21. (1)(或)(2)由题意,原正方形苗圃的面积为平方米,得解得:不合题意舍去答:此时的长为米.22. (1)因为方程有两个不相等的实数根,所以,所以.(2)存在实数使得.,即是说是原方程的一个根,则.解得:或.当时,方程为,有两个相等的实数根,与题意不符,舍去.所以.23. ;;【解析】通过不同的方式来表示大正方形的面积,可以将原方程化为,从而得到此方程的正根是.24. (1)点的坐标为,点的坐标为.(2)方法:设抛物线的解析式为.因为它经过,,,则解得所以经过,,三点的抛物线的表达式为.【解析】方法:抛物线经过,,故可设其表达式为.因为在抛物线上,所以,得.所以经过,,三点的抛物线的表达式为.方法:抛物线经过,,则其对称轴为直线.设抛物线的表达式为.将,代入,得解得所以经过,,三点的抛物线的表达式为.25. (1)在中,于点,,,,在和中,,,为的中点.(2)连接,如图.是的直径,,,,,,四边形是平行四边形,是的中点,,,,,是等边三角形,,,在中,,,,,,,,.四边形26. (1)(2)点在直线上,理由如下:直线的表达式为,当时,,在直线上.(3)如图,不妨设点在点左侧.由题意知:要使得成立,即是要求点与点关于直线对称.又函数的图象关于直线对称,当时,若存在使得成立,即要求点在的图象上.根据图象,临界位置为射线过与的交点处,以及射线过与的交点处.此时以及,故的取值范围是.27. (1);(2)设点的坐标为,由于点的“引力值”为,则或,即或,当时,,此时点的“引力值”为,舍去;当时,,此时点坐标为;当时,,解得,此时点的“引力值”为,舍去,当时,,,此时点坐标为;综上所述,点的坐标为或.(3)28. (1)(2)连接,,,,如图,中,,为的中点,..,.点和点关于直线对称,.,点,,在以为圆心,为半径的圆上..(3),证明如下:连接并延长到点,使,连接,如图,,,..,.,.,....,,.,.四边形是平行四边形..,,..。
2017-2018学年北京市海淀区九年级上期中数学试题含答案

第 1 页 共 14 页初三第一学期期中学业水平调研数学2017.11学校班级___________姓名成绩 一、选择题(本题共24分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的.请将正确选项前的字母填在表格中相应的位置.1.一元二次方程3610x x --=的二次项系数、一次项系数、常数项分别是 A .3,6,1B .3,6,1-C .3,6-,1D .3,6-,1-2.把抛物线2y x =向上平移1个单位长度得到的抛物线的表达式为 A .21y x =+ B .21y x =- C .21y x =-+D .21y x =--3.如图,A ,B ,C 是⊙O 上的三个点. 若∠C =35°,则∠AOB 的 大小为 A .35° B .55° C .65° D .70° 4.下列手机手势解锁图案中,是中心对称图形的是A B C D 5.用配方法解方程2420x x -+=,配方正确的是 A .()222x -= B.()222x +=C .()222x -=-D .()226x -=6.风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n °后能与原来的图案重合,那么n 的值可能是A .45B .60C .90D .120第 1 页 共 14 页7.二次函数21y ax bx c =++与一次函数2y mx n =+2ax bx c mx n ++>+的x 的取值范围是A .30x -<<B .3x <-或0x >C .3x <-或1x >D .03x <<8.如图1,动点P 从格点A 出发,在网格平面内运动,设点P 走过的路程为s ,点P 到直线l 的距离为d . 已知d 与s 的关系如图2所示.下列选项中,可能是点P 的运动路线的是A B C D二、填空题(本题共24分,每小题3分)9.点P (1-,2)关于原点的对称点的坐标为________. 10.写出一个图象开口向上,过点(0,0)的二次函数的表达式:________.11.如图,四边形ABCD 内接于⊙O ,E 为CD 的延长线上一点. 若∠B =110°,则∠ADE 的大小为________. 12.抛物线21y x x =--与x 轴的公共点的个数是________. 13.如图,在平面直角坐标系xOy 中,点A ,点B 的坐标分别 为(0,2),(1-,0),将线段AB 绕点O 顺时针旋转,若点A 的对应点A '的坐标为(2,0),则点B 的对应点B '的 坐标为________.14.已知抛物线22y x x =+经过点1(4)y -,,2(1)y ,,则1y ________2y (填“>”,“=”,或“<”).15.如图,⊙O 的半径OA 与弦BC 交于点D ,若OD =3,AD =2, BD =CD ,则BC 的长为________.lllll。
北京市海淀区 九年级数学上册 期中试题含答案【精品】

初三第一学期期中学业水平调研数学2017.11学校班级___________姓名成绩 一、选择题(本题共24分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的.请将正确选项前的字母填在表格中相应的位置.1.一元二次方程23610x x --=的二次项系数、一次项系数、常数项分别是 A .3,6,1B .3,6,1-C .3,6-,1D .3,6-,1-2.把抛物线2y x =向上平移1个单位长度得到的抛物线的表达式为 A .21y x =+B .21y x =- C .21y x =-+D .21y x =--3.如图,A ,B ,C 是⊙O 上的三个点. 若∠C =35°,则∠AOB 的大小为 A .35°B .55°C .65°D .70°4.下列手机手势解锁图案中,是中心对称图形的是A B C D 5.用配方法解方程2420xx -+=,配方正确的是 A .()222x -= B .()222x +=C .()222x -=-D .()226x -=6.风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n °后能与原的图案重合,那么n 的值可能是A .45B .60C .90D .1207.二次函数21y ax bx c =++与一次函数2y mx n =+的图象如图所示,则满足2ax bx c mx n ++>+的的取值范围是A .30x -<<B .3x <-或0x >C .3x <-或1x >D .03x <<8.如图1,动点P 从格点A 出发,在网格平面内运动,设点P 走过的路程为s ,点P 到直线l 的距离为d . 已知d 与s 的关系如图2所示.下列选项中,可能是点P 的运动路线的是A B C D二、填空题(本题共24分,每小题3分)9.点P (1-,2)关于原点的对称点的坐标为________. 10.写出一个图象开口向上,过点(0,0)的二次函数的 表达式:________.l l ll l11.如图,四边形ABCD 内接于⊙O ,E 为CD 的延长线上一点. 若∠B =110°,则∠ADE 的大小为________.12.抛物线21y x x =--与轴的公共点的个数是________. 13.如图,在平面直角坐标系Oy 中,点A ,点B 的坐标分别 为(0,2),(1-,0),将线段AB 绕点O 顺时针旋转,若 点A 的对应点A '的坐标为(2,0),则点B 的对应点B '的 坐标为________.14.已知抛物线22y x x =+经过点1(4)y -,,2(1)y ,,则1y ________2y (填“>”,“=”,或“<”).15.如图,⊙O 的半径OA 与弦BC 交于点D ,若OD =3,AD =2,BD =CD ,则BC 的长为________.16.下面是“作已知三角形的高”的尺规作图过程.请回答:该尺规作图的依据是_______________________________________________.三、解答题(本题共72分,第17题4分,第18~23题,每小题5分,第24~25题,每小题7分,第26~ 28题,每小题8分) 17.解方程:2430x x -+=.18.如图,等边三角形ABC 的边长为3,点D 是线段BC 上的点,CD =2,以AD 为边作等边三角形ADE ,连接CE .求CE 的长.19.已知m 是方程2310x x -+=的一个根,求()()()2322m m m -++-的值.20.如图,在⊙O 中,»»AB CD =.求证:∠B =∠C .21.如图,ABCD 是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E 在AB 边上,点G 在AD 的延长线上,DG =2BE .设BE 的长为米,改造后苗圃AEFG 的面积为y 平方米.(1)y 与之间的函数关系式为_____________________(不需写自变量的取值范围); (2)根据改造方案,改造后的矩形苗圃AEFG 的面积与原正方形苗圃ABCD 的面积相等,请问此时BE 的长为多少米?EB D CAE22.关于x 的一元二次方程()222110x m x m +-+-=有两个不相等的实数根12,x x .(1)求实数m 的取值范围;(2)是否存在实数m ,使得120x x =成立?如果存在,求出m 的值;如果不存在,请说明理由.23.古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家——“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式证明曾用数字解释过的问题的正确性”. 以21039x x +=为例,花拉子米的几何解法如下: 如图,在边长为x 的正方形的两个相邻边上作边长分别为x 和5的矩形,再补上一个边长为5的小正方形,最终把图形补 成一个大正方形.通过不同的方式表示大正方形的面积,可以将原方程化为()2________39x +=+,从而得到此方程的正根是________.24.如图,在平面直角坐标系Oy 中,点A 的坐标为(1,0),点P 的横坐标为2,将点A 绕点P 旋转,使它的对应点B 恰好落在轴上(不与合);再将点B 绕点O 逆时针旋转90°得到点C . (1)直接写出点B 和点C 的坐标;(2)求经过A ,B ,C 三点的抛物线的表达式.55 5x x xx 525.如图,AB 为⊙O 的直径,点C 在⊙O 上,过点O 作OD ⊥BC 交BC 于点E ,交⊙O于点D ,CD ∥AB .(1)求证:E 为OD 的中点;(2)若CB =6,求四边形CAOD 的面积.26.在平面直角坐标系xOy 中,已知抛物线C :244y x x =-+和直线l :2(0)y kx k k =->.(1)抛物线C 的顶点D 的坐标为________; (2)请判断点D 是否在直线l 上,并说明理由;(3)记函数2442,22x x x y kx k x ⎧-+≤=⎨->⎩,,的图象为G ,点(0,)M t ,过点M 垂直于y 轴的直线与图象G 交于点11()P x y ,,22()Q x y ,.当13t <<时,若存在t 使得124x x =+成立,结合图象,求k 的取值范围.27.对于平面直角坐标系Oy 中的点P ,给出如下定义:记点P 到轴的距离为1d ,到y 轴的距离为2d ,若12d d ≤,则称1d 为点P 的“引力值”;若12d d >,则称2d 为点P 的“引力值”.特别地,若点P 在坐标轴上,则点P 的“引力值”为0.例如,点P (2-,3)到轴的距离为3,到y 轴的距离为2,因为23<,所以点P 的“引力值”为2.(1)①点A (1,4-)的“引力值”为________;②若点B (a ,3)的“引力值”为2,则a 的值为________;(2)若点C 在直线24y x =-+上,且点C 的“引力值”为2,求点C 的坐标;(3)已知点M是以D(3,4)为圆心,半径为2的圆上的一个动点,那么点M的“引力值”d的取值范围是.28.在Rt△ABC中,斜边AC的中点M关于BC的对称点为点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,如图所示.(1)在①∠BOE,②∠ACD,③∠COE中,等于旋转角的是________(填出满足条件的的角的序号);(2)若∠A=α,求∠BEC的大小(用含α的式子表示);(3)点N是BD的中点,连接MN,用等式表示线段MN与BE之间的数量关系,并证明.初三第一学期期中学业水平调研数学参考答案2017.11一、选择题(本题共24分,每小题3分)9.(1,2-) 10.答案不唯一,例如2y x = 11.110° 12.2 13.(0,1)14.>15.816.①到线段两端点距离相等的点在线段的垂直平分线上;②直径所对的圆周角是直角;③两点确定一条直线.(注:写出前两个即可给3分,写出前两个中的一个得2分,其余正确的理由得1分) 三、解答题(本题共72分) 17.解法一:解:2441x x -+=,()221x -=,………………2分21x -=±,11x =,23x =.………………4分解法二:解:()()130x x --=,………………2分 10x -=或30x -=,11x =,23x =.………………4分 18.解:∵△ABC 是等边三角形, ∴AB =BC =AC ,∠BAC =60°. ∴∠1+∠3=60°.………………1分 ∵△ADE 是等边三角形, ∴AD =AE ,∠DAE =60°.∴∠2+∠3=60°.………………2分 ∴∠1=∠2.在△ABD 与△ACE 中12AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△ACE (SAS ). ∴CE =BD .………………4分 ∵BC =3,CD =2,321EDCBA∴BD =BC -CD =1.∴CE =1.………………5分19.解:∵m 是方程2310x x -+=的一个根,∴2310m m -+=.………………2分 ∴231m m -=-.∴原式22694m m m =-++-………………4分()2235m m =-+3=.………………5分20.方法1:证明:∵在⊙O 中,»»AB CD =, ∴∠AOB =∠COD .………………2分 ∵OA =OB ,OC =OD ,∴在△AOB 中,1902B AOB ∠=︒-∠,在△COD 中,1902C COD ∠=︒-∠.………………4分 ∴∠B =∠C .………………5分方法2:证明:∵在⊙O 中,»»AB CD =, ∴AB =CD .………………2分 ∵OA =OB ,OC =OD ,∴△AOB ≌△COD (SSS ).………………4分 ∴∠B =∠C .………………5分21.解:(1)22416y x x =-++(或()()442y x x =-+)………………3分(2)由题意,原正方形苗圃的面积为16平方米,得2241616x x -++=. 解得:12x =,20x =(不合题意,舍去).………………5分 答:此时BE 的长为2米. 22.解:(1)∵方程()222110xm x m +-+-=有两个不相等的实数根,∴()()224141880m m m ∆=---=-+>,∴1m <.………………2分(2)存在实数m 使得120x x =.120x x =,即是说0是原方程的一个根,则210m -= (3)分解得:1m =-或1m =.………………4分当1m =时,方程为20x =,有两个相等的实数根,与题意不符,舍去. ∴1m =-.………………5分23.通过不同的方式表示大正方形的面积,可以将原方程化为()25 x +………………1分39 25 =+………………3分从而得到此方程的正根是 3 .………………5分24.(1)点B 的坐标为(3,0),点C 的坐标为(0,3);………………2分 (2)方法1:设抛物线的解析式为2y ax bx c =++. 因为它经过A (1,0),B (3,0),C (0,3),则0,930,3.a b c a b c c ++=⎧⎪++=⎨⎪=⎩………………4分 解得1,4,3.a b c =⎧⎪=-⎨⎪=⎩………………6分∴ 经过,,A B C 三点的抛物线的表达式为243y x x =-+.………………7分 方法2:抛物线经过点A (1,0),B (3,0),故可设其表达式为(1)(3)(0)y a x x a =--≠. ………………4分因为点C (0,3)在抛物线上,所以()()01033a --=,得1a =.………………6分∴经过,,A B C 三点的抛物线的表达式为243y x x =-+.………………7分 方法3:抛物线经过点A (1,0),B (3,0),则其对称轴为2x =. 设抛物线的表达式为()22y a x k =-+.………………4分将A (1,0),C (0,3)代入,得0,4 3.a k a k +=⎧⎨+=⎩解得1,1.a k =⎧⎨=-⎩………………6分∴经过,,A B C 三点的抛物线的表达式为243y x x =-+.………………7分25.(1)证明:∵在⊙O 中,OD ⊥BC 于E , ∴CE =BE .………………1分 ∵CD ∥AB ,∴∠DCE =∠B .………………2分 在△DCE 与△OBE 中,,.DCE B CE BE CED BEO ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△DCE ≌△OBE (ASA ). ∴DE =OE .∴E 为OD 的中点.………………4分(2)解: 连接OC .∵AB 是⊙O 的直径, ∴∠ACB =90°. ∵OD ⊥BC , ∴∠CED =90°=∠ACB . ∴AC ∥OD .………………5分 ∵CD ∥AB ,∴四边形CAOD 是平行四边形. ∵E 是OD 的中点,CE ⊥OD , ∴OC =CD . ∵OC =OD , ∴OC =OD =CD .∴△OCD 是等边三角形. ∴∠D =60°.………………6分 ∴∠DCE =90°-∠D =30°. ∴在Rt △CDE 中,CD =2DE . ∵BC =6, ∴CE =BE =3.∵22224CE DE CD DE +==,∴DE =CD =∴OD CD ==AAB∴CAOD S OD CE =⋅=四边形………………7分26.(1)(2,0);………………2分 (2)点D 在直线l 上,理由如下: 直线l 的表达式为2(0)y kx k k =->,∵当2x =时,220y k k =-=,………………3分 ∴点D (2,0)在直线l 上.………………4分 注:如果只有结论正确,给1分.(3)如图,不妨设点P 在点Q 左侧.由题意知:要使得124x x =+成立,即是要求点P 与点Q 关于直线2x =对称.又因为函数244y x x =-+的图象关于直线2x =对称,所以当13t <<时,若存在t 使得124x x =+成立,即要求点Q在244(2,13)y x x x y =-+><<的图象上.………………6分根据图象,临界位置为射线2(0,2)y kx k k x =->>过244(2)y x x x =-+>与1y =的交点(3,1)A 处,以及射线2(0,2)y kx k k x =->>过244(2)y x x x =-+>与3y =的交点(2B 处.此时1k =以及k =1k <<………………8分27.(1)①1,②2±;………………2分 注:错一个得1分.(2)解:设点C 的坐标为(,y ).由于点C 的“引力值”为2,则2x =或2y =,即2x =±,或2y =±. 当2x =时,240y x =-+=,此时点C 的“引力值”为0,舍去; 当2x =-时,248y x =-+=,此时C 点坐标为(-2,8);当2y =时,242x -+=,解得1x =,此时点C 的“引力值”为1,舍去; 当2y =-时,242x -+=-,3x =,此时C 点坐标为(3,-2); 综上所述,点C 的坐标为(2-,8)或(3,2-).………………5分 注:得出一个正确答案得2分. (3)712d +≤≤.………………8分 注:答对一边给2分;两端数值正确,少等号给2分;一端数值正确且少等号给1分.28.(1)③;………………1分(2)连接BM,OB,OC,OE.∵Rt△ABC中,∠ABC=90°,M为AC的中点,∴MA=MB=MC=12 AC.………………2分∴∠A=∠ABM.∵∠A=α,∴∠BMC=∠A+∠ABM=2α.∵点M和点O关于直线BC对称,∴∠BOC=∠BMC=2α.………………3分∵OC=OB=OE,∴点C,B,E在以O为圆心,OB为半径的圆上.∴12BEC BOCα∠=∠=.………………4分(3)12MN BE=,证明如下:连接BM并延长到点F,使BM=MF,连接FD. ∵∠A=α,∠ABC=90°,∴∠ACB=90°-∠A=90°-α.∴∠DEC=∠ACB=90°-α.∵∠BEC=α,∴∠BED=∠BEC+∠DEC=90°.∵BC=CE,∴∠CBE=∠CEB=α.∵MB=MC,∴∠MBC=∠ACB=90°-α.∴∠MBE=∠MBC+∠CBE=90°.∴∠MBE+∠BED=180°.∴BF∥DE.………………6分∵BF=2BM,AC=2BM,∴BF=AC.∵AC=DE,∴BF=DE.∴四边形BFDE是平行四边形.………………7分OMNABDCEBD∴DF=BE.∵BM=MF,BN=ND,∴MN=12 DF.∴MN =12 BE.………………8分注:如果只有结论正确,给1分.解答题解法不唯一,如有其它解法相应给分.。
2017年-2018北京市海淀区初三年级第一学期期中数学试题(附答案解析)

2017年-2018北京市海淀区初三年级第⼀学期期中数学试题(附答案解析)AOA '海淀区九年级第⼀学期期中练习数学 2016.11学校姓名学号⼀、选择题(本题共30分,每⼩题3分)下⾯各题均有四个选项,其中只有⼀个..是符合题意的.请将正确选项前的字母填在表格中相应的位置.题号 1 2 3 4 5 6 7 8 9 10 答案1.⼀元⼆次⽅程2320x x --=的⼆次项系数、⼀次项系数、常数项分别是 A .3,1-,2- B .3,1,2- C .3,1-,2 D .3,1,22.⾥约奥运会后,受到奥运健⼉的感召,群众参与体育运动的热度不减,全民健⾝再次成为了⼀种时尚,球场上也出现了更多年轻⼈的⾝影.请问下⾯四幅球类的平⾯图案中,是中⼼对称图形的是A B C D3.⽤配⽅法解⽅程2620x x ++=,配⽅正确的是A .()239x += B .()239x -= C .()236x += D .()237x +=4.如图,⼩林坐在秋千上,秋千旋转了80°,⼩林的位置也从 A 点运动到了A '点,则'OAA ∠的度数为 A .40° B .50° C .70° D .80°5.将抛物线22y x =平移后得到抛物线221y x =+,则平移⽅式为 A .向左平移1个单位B .向右平移1个单位C .向上平移1个单位D .向下平移1个单位6.在△ABC 中,90C ?∠=,以点B 为圆⼼,以BC 长为半径作圆,点A 与该圆的位置关系为 A .点A 在圆外 B .点A 在圆内C .点A 在圆上 D .⽆法确定 7.若扇形的圆⼼⾓为60°,半径为6,则该扇形的弧长为C .3πD .4π 8.已知2是关于x 的⽅程230x ax a +-=的根,则a 的值为A .4-B .4C .2D .459.给出⼀种运算:对于函数nx y =,规定1-='n nx y .例如:若函数41y x =,则有314y x '=.函数32y x =,则⽅程212y '=的解是A .14x =,24x =-B .123x =,223x =-C .0==x xD .2x =,2x =-10.太阳影⼦定位技术是通过分析视频中物体的太阳影⼦变化,确定视频拍摄地点的⼀种⽅法.为了确定视频拍摄地的经度,我们需要对⽐视频中影⼦最短的时刻与同⼀天东经120度影⼦最短的时刻.在⼀定条件下,直杆的太阳影⼦长度l (单位:⽶)与时刻t (单位:时)的关系满⾜函数关系2l at bt c =++(a ,b ,c 是常数),如图记录了三个时刻的数据,根据上述函数模型和记录的数据,则该地影⼦最短时,最接近的时刻t 是A .12.75B .13C .13.33D .13.5⼆、填空题(本题共18分,每⼩题3分) 11.⽅程02=-x x 的解为.12.请写出⼀个对称轴为3x =的抛物线的解析式.13.如图,⽤直⾓曲尺检查半圆形的⼯件,其中合格的是图(填“甲”、“⼄”或“丙”),你的根据是_____________________________________________________________________________________________.14.若关于x 的⽅程220x x k --=有两个相等的实数根,则k 的值是.15.如图,△ABC 内接于⊙O ,∠C =45°,半径OB 的长为3,则AB 的长为.丙1413120.350.40.6Ol (⽶)t (时)CBAOyxO –1–2–3123–1–2–312316.CPI 指居民消费价格指数,反映居民家庭购买消费商品及服务的价格⽔平的变动情况.CPI 的涨跌率在⼀定程度受到季节性因素和天⽓因素的影响.根据北京市2015年与2016年CPI 涨跌率的统计图中的信息,请判断2015年1~8⽉份与2016年1~8⽉份,同⽉份⽐较CPI 涨跌率下降最多的⽉份是⽉;请根据图中提供的信息,预估北京市2016年第四季度CPI 涨跌率变化趋势是,你的预估理由是.三、解答题(本题共72分,第17~26题,每⼩题5分,第27题7分,第28题7分,第29题8分) 17.解⽅程:246x x +=.18.求抛物线22y x x =-的对称轴和顶点坐标,并画出图象.19.如图,A ,D 是半圆上的两点,O 为圆⼼,BC 是直径,∠D =35°,求∠OAC 的度数.D B O C A图220.已知:2230m m +-=.求证:关于x 的⽅程2220x mx m --=有两个不相等的实数根.21.如图,在等边△ABC 中,点D 是 AB 边上⼀点,连接CD ,将线段CD 绕点C 按顺时针⽅向旋转60°后得到CE ,连接AE .求证:AE ∥BC .22.如图1,在线段AB 上找⼀点C ,C 把AB 分为AC 和CB 两段,其中BC 是较⼩的⼀段,如果2BC AB AC ?=,那么称线段AB 被点C 黄⾦分割.⾦分割,已知太和殿到内⾦⽔桥的距离约为100丈,求太和门到太和殿之间的距离(5的近似值取2.2).A C B图1B CDA EDOMB EC FA23.如图1是某公园⼀块草坪上的⾃动旋转喷⽔装置,这种旋转喷⽔装置的旋转⾓度为240°,它的喷灌区是⼀个扇形.⼩涛同学想了解这种装置能够喷灌的草坪⾯积,他测量出了相关数据,并画出了⽰意图.如图2,A ,B 两点的距离为18⽶,求这种装置能够喷灌的草坪⾯积.24.下表是⼆次函数2y ax bx c =++的部分x ,y 的对应值:x… 1-12-12 132 252 3 … y…m141-74- 2-74- 1-142…(1)⼆次函数图象的开⼝向,顶点坐标是,m 的值为;(2)当0x >时,y 的取值范围是;(3)当抛物线2y ax bx c =++的顶点在直线y x n =+的下⽅时,n 的取值范围是.25.如图,在△ABC 中,AB =BC ,以AB 为直径的⊙O 分别交AC ,BC 于点D ,E ,过点A 作⊙O 的切线交BC的延长线于点F ,连接AE .(1)求证:∠ABC =2∠CAF ;(2)过点C 作CM ⊥AF 于M 点,若CM = 4,BE = 6,求AE 的长.图1OA B240°图2xy–1–2–3–4–512345–1–2–3–4–512345O 26.⼩华在研究函数1y x =与22y x =图象关系时发现:如图所⽰,当1x =时,11y =,22y =;当2x =时,12y =,24y =;…;当x a =时,1y a =,22y a =.他得出如果将函数1y x =图象上各点的横坐标不变,纵坐标变为原来的2倍,就可以得到函数22y x =的图象.类⽐⼩华的研究⽅法,解决下列问题:(1)如果函数3y x =图象上各点横坐标不变,纵坐标变为原来的3倍,得到的函数图象的表达式为;(2)①将函数2y x =图象上各点的横坐标不变,纵坐标变为原来的倍,得到函数24y x =的图象;②将函数2y x =图象上各点的纵坐标不变,横坐标变为原来的2倍,得到图象的函数表达式为.(2)若抛物线与y 轴正半轴交于点A ,其对称轴与x 轴交于点B ,当△OAB 是等腰直⾓三⾓形时,求n 的值;(3)点C 的坐标为(3,0),若该抛物线与线段OC 有且只有⼀个交点,求n 的取值范围. xyy 2=2xOy 1=x–1–2–31234567–11234528.在菱形ABCD 中,∠BAD =α,E 为对⾓线AC 上的⼀点(不与A ,C 重合),将射线EB 绕点E 顺时针旋转β⾓之后,所得射线与直线AD 交于F 点.试探究线段EB 与EF 的数量关系.⼩宇发现点E 的位置,α和β的⼤⼩都不确定,于是他从特殊情况开始进⾏探究.(1)如图1,当α=β=90°时,菱形ABCD 是正⽅形.⼩宇发现,在正⽅形中,AC 平分∠BAD ,作EM ⊥AD 于M ,EN ⊥AB 于N .由⾓平分线的性质可知EM =EN ,进⽽可得EMF ENB △≌△,并由全等三⾓形的性质得到EB 与EF 的数量关系为.(2)如图2,当α=60°,β=120°时,①依题意补②请帮⼩宇继续探究(1)的结论是否成⽴.若成⽴,请给出证明;若不成⽴,请举出反例说明;(3)⼩宇在利⽤特殊图形得到了⼀些结论之后,在此基础上对⼀般的图形进⾏了探究,设∠ABE =γ,若旋转后所得的线段EF 与EB 的数量关系满⾜(1)中的结论,请直接写出⾓α,β,γ满⾜的关系:.FD CA BEM CD A N B E图1 图2长度为点P 到AOB ∠的距离,记为()d P AOB ∠,.特别的,当点P 在AOB ∠的边上时,()0d P AOB ∠=,.在平⾯直⾓坐标系xOy 中,A ()40,.(1)如图1,若M (0,2),N (1-,0),则()d M AOB ∠=,,()d N AOB ∠=,;(2)在正⽅形OABC 中,点B (4,4).①如图2,若点P 在直线34y x =+上,且()22d P AOB ∠=,,求点P 的坐标;②如图3,若点P 在抛物线24y x =-上,满⾜()22d P AOB ∠=,的点P 有个,请你画出⽰意图,并标出点P .图2xyy=3x+4CBA–1–2–3123456–1–2–3123456O21y xBAO 60°-12图3xyOCBA–1–2–3–4–512345–1–2–3–4–5123456789数学答案 2016.11⼀、选择题(本题共30分,每⼩题3分)题号 1 2 3 4 5 6 7 8 9 10 答案ACDBCA⼆、填空题(本题共18分,每⼩题3分)11.1201x x ==,; 12.()23y x =-(答案不唯⼀);13.⼄,90°的圆周⾓所对的弦是直径; 14.1-; 15.32;16.8,第⼆空填“上涨”、“下降”、“先减后增”等,第三空要能⽀持第⼆空的合理性即可.三、解答题(本题共72分,第17~26题,每⼩题5分,第27题7分,第28题7分,第29题8分) 17.解法⼀:解:24410x x ++=, ----------------------------------------------------------------------------------1分 ()2210x +=, -------------------------------------------------------------------------------------3分210x =-±,1210x =-+,2210x =--. -------------------------------------------------------------5分解法⼆:解:2460x x +-=, ----------------------------------------------------------------------------------1分()2244416-4221b ac b x a-±-??-±-==, ----------------------------------------------------3分210x =-±,1210x =-+,2210x =--. -------------------------------------------------------------5分18.解:()211y x =--, -----------------------------------------------------------------------------------1分顶点为()11-,. ----------------------------------------------------------------------------------3分yxO –1–2–31223----------------------------------------------------------------------------5分19.解法⼀:解:∵35D ∠=°,∴35B D ∠=∠=°. ---------------------------------------------1分∵BC 是直径,∴90BAC ∠=°.∴90ACB ∠=°55ABC -∠=°. -------------------------------3分∵OA OC =,∴55OAC OCA ∠=∠=°. --------------------------------------5分解法⼆:解:∵35D ∠=°,∴270AOC D ∠=∠=°. ---------------------------------------------------------------------1分∵OA OC =,∴OAC OCA ∠=∠, ----------------------------------------------------------------------------3分∵180OAC OCA AOC ∠+∠+∠=°,∴55OAC ∠=°. ---------------------------------------------------------------------------------5分20.解:∵2230m m +-=,∴223m m +=. ---------------------------------------------------------------------------------1分∴248m m ?=+ -----------------------------------------------------------------------------------2分 ()242120m m =+=>, ------------------------------------------------------------------4分∴原⽅程有两个不相等的实数根. -------------------------------------------------------------5分21.解:∵等边ABC △,∴AC BC =,60B ACB ∠=∠=°.DB O CAA E∵线段CD 绕点C 顺时针旋转60°得到CE ,∴CD CE =,60DCE ∠=°.∴DCE ACB ∠=∠.------------------------------------------------1分即1223∠+∠=∠+∠.∴13∠=∠. -----------------------------------------------------------------------------------------2分在BCD △与ACE △中,13BC AC CD CE =??∠=∠??=?,∴EAC ACB ∠=∠.--------------------------------------------------------------------------------4分∴AE BC ∥. --------------------------------------------------------------------------------------5分22.解:设太和门到太和殿的距离为x 丈, -----------------------------------------------------------1分由题意可得,()2100100x x =-. ----------------------------------------------------------------------------3分150505x =-+,250505x =--(舍). --------------------------------------------4分 5050 2.260x ≈-+?=.答:太和门到太和殿的距离为60丈. ------------------------------------------------------------5分 23.解:过点O 作OC AB ⊥于C 点.∵OC AB ⊥,18AB =,∴192AC AB ==. ---------------------------------------1分∵OA OB =,360AOB ∠=°240-°120=°,∴1602AOC AOB ∠=∠=°. ---------------------------2分在Rt OAC △中,222OA OC AC =+,⼜∵12OC OA =,∴63r OA ==. -----------------------------------------4分∴240360S =πr 2=72π(m 2).----------------------------------5分24.(1)上;()12-,;2;(说明:每空1分) ------------------------------------------------------3分 240°A C BO(3)3n >-. -------------------------------------------------------------------------------------------5分 25.(1)连接BD ,∵AB 是直径,∴90ADB ∠=°. --------------------------1分∵AF 是⊙O 的切线,∴90BAF ∠=°.∴1290BAC BAC ∠+∠=∠+∠=°.∴12∠=∠. ∵AB=BC ,∴2122ABC ∠=∠=∠. ---------------------------------------------------------------------2分(2)∵12334∠=∠=∠∠=∠,,∴24∠=∠.∵AB 是直径,∴CE ⊥AE .--------------------------------------------------------------------------------------------3分∵CM ⊥AF ,CM =4,∴CE =CM =4. --------------------------------------------------------------------------------------4分∵BE =6,∴AB =BC =BE +EC =10.在Rt △ABE 中,22221068AE AB BE =-=-=. ----------------------------------------------------5分26.(1)9y x =; -------------------------------------------------------------------------------------------1分(2)①4; ----------------------------------------------------------------------------------------------3分②214y x =. --------------------------------------------------------------------------------------5分27.(1)4-. ----------------------------------------------------------------------------------------------1分(2)241y x x n =-+-,4321AB EC FMOD()01A n -,,()20B , , ------------------------------------------------------------------2分 12n -=,3n =. --------------------------------------------------------------------------------------------3分(3)如图1,当抛物线顶点在x 轴上时,5n =,------------------------------------------------4分如图2,当抛物线过点C (3,0)时,4n =,--------------------------------------------------5分如图3,当抛物线过原点时,1n =, ---------------------------------------------------------6分结合图象可得,14n ≤<或5n =.------------------------------------------------------------7分–1–2–3123–1–2–3123O xyC –1–2–3123–1–2–3123y xO C –1–212345–1–2–3–412O xy C 28.(1)EB=EF ; ------------------------------------------------------------------------------------------1分(2)①;A BCDEF ---------------------------------------------------------------------2分②结论依然成⽴EB =EF . -----------------------------------3分证法1:过点E 作EM ⊥AF 于M ,EN ⊥AB 于N .∵四边形ABCD 为菱形,∴12∠=∠.∵EM ⊥AF ,EN ⊥AB .∴=90FME N ∠=∠°,EM=EN . -------------------4分∵60BAD ∠=°,120BEF ∠=°,∴3360F ∠+∠=°180BAD BEF -∠-∠=°.∵3180EBN ∠+∠=°,∴F EBN ∠=∠.------------------------------------------------------------------------------5分在△EFM 与△EBN 中,F EBN FME N EM EN ∠=∠??∠=∠??=?,,,∴△EFM ≌△EBN .321NM F EDC图2 图3证法2:连接ED∵四边形ABCD 是菱形,∴AD =AB ,∠DAC =∠BAE .⼜∵AE =AE , ∴△ADE ≌△ABE .∴ED =EB ,∠ADE =∠ABE . ------------------------4分⼜∵∠DAB =60°,∠BEF =120°.∴∠F +∠ABE =180°.⼜∵∠ADE +∠FDE =180°, --------------------------5分∴∠F =∠FDE .∴EF =ED .∴EF =EB . -------------------------------------------------------------------------------------6分(3)+=180αβ°或++=18022αβγ°. ------------------------------------------------------7分29.(1)1;1.(说明:每空1分) --------------------------------------------------------------------2分(2)①如图,点P 在EF 上时,OP =22,设P (x ,3x +4),()22348x x ++=,12225x x =-=-,(舍),P ()22--,, --------------------------------4分点P 在射线FG 上时,P 到射线OB 的距离为22,点P 与点C 重合,P ()04,, -------------------------------------5分∴P ()22--,,()04,.②4. -------------------------------------------------------------------------------------------------6分F E D CB A y xGFE–1–2–312345–1–2–3–4–51BCxy CBAO –1–2–312345–1–2–3–4–512345P 4P 2P 1P 3-------------------------------------------------------------8分(说明:每标对两个点得1分)1、发⽣以下情形,本协议即终⽌:(1)、公司因客观原因未能设⽴;(2)、公司营业执照被依法吊销;(3)、公司被依法宣告破产;(4)、甲⼄丙三⽅⼀致同意解除本协议。
2017-2018学年北京市海淀区九年级上期中数学试题含答案
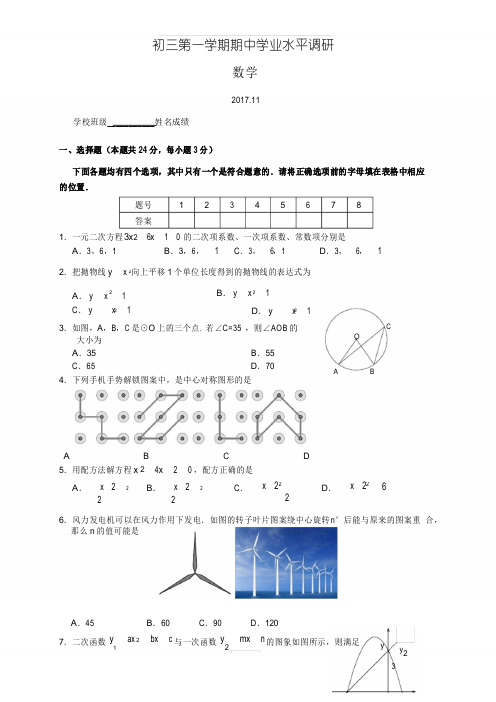
初三第一学期期中学业水平调研数学2017.11学校班级___________姓名成绩一、选择题(本题共 24 分,每小题 3 分)下面各题均有四个选项,其中只有一个是符合题意的.请将正确选项前的字母填在表格中相应 的位置.题号 答案12 3 4 5 6 7 81.一元二次方程 3x 2 6 x 1 0的二次项系数、一次项系数、常数项分别是A .3,6,1B .3,6,1C .3, 6,1D .3, 6,12.把抛物线 y x 向上平移 1 个单位长度得到的抛物线的表达式为A . y x 1C . yx 1B . y x 1D . yx 13.如图,A ,B ,C 是⊙O 上的三个点. 若∠C =35°,则∠AOB 的C大小为 A .35° B .55° C .65° D .70° 4.下列手机手势解锁图案中,是中心对称图形的是OA BAB C D5.用配方法解方程 x 2 4 x 2 0 ,配方正确的是A .x 222B .x 222C .x 22D .x 266.风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n °后能与原来的图案重 合,那么 n 的值可能是A .45B .60C .90D .1207.二次函数yax 2 bx c与一次函数y mx n的图象如图所示,则满足.. 2 222 2 22ax2bx c mx n的x的取值范围是A.3x 0C.x 3或x 1 8.如图1,动点P从格点AB.x 3或x 0D.0x 3出发,在网格平面内运动,设点P走过的路程为s,点P到直线l的距离为d.已知d与s的关系如图2所示.下列选项中,可能是点P的运动路线的是l d43A21 l l l lO图1A A A AA B C D二、填空题(本题共24分,每小题3分)9.点P(1,2)关于原点的对称点的坐标为________.12345图2s10.写出一个图象开口向上,过点(0,0)的二次函数的表达式:________.A B11.如图,四边形ABCD内接于⊙O,E为CD的延长线上一点.若∠B=110°,则∠ADE的大小为________.OE D C12.抛物线y x2x 1与x轴的公共点的个数是________.13.如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(1,0),将线段AB绕点O顺时针旋转,若y A点A的对应点A的坐标为(2,0),则点B的对应点B 的坐标为________.BO A'x14.已知抛物线y x22x经过点(4,y ),(1,y )12,则y 1________y(填“>”,“=”,或“<”).215.如图,⊙O的半径OA与弦BC交于点D,若OD=3,AD=2,BD=CD,则BC的长为________.OB DAC16.下面是“作已知三角形的高”的尺规作图过程.已知△:ABC.AB C 求作:BC边上的高AD.作法:如图,1(1)分别以点A和点C为圆心,大于AC的2长为半径作弧,两弧相交于P,Q两点;A POD Q B C(2)作直线PQ,交AC于点O;(3)以O为圆心,OA为半径作⊙O,与CB的延长线交于点D,连接AD.线段AD即为所作的高.请回答:该尺规作图的依据是_______________________________________________.三、解答题(本题共72分,第17题4分,第18~23题,每小题5分,第24~25题,每小题7分,第26~ 28题,每小题8分)17.解方程:x24x 30.18.如图,等边三角形ABC的边长为3,点D是线段BC上的点,CD=2,以AD 为边作等边三角形ADE,连接CE.求CE的长.AEB D C19.已知m 是方程x23x 10的一个根,求m 32m 2m 2的值.20.如图,在⊙O中,AB CD.求证:∠B=∠C.BO C A D21.如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形A EFG的形状,其中点E在AB边上,点G在AD的延长线上,DG=2BE.设BE的长为x米,改造后苗圃A EFG的面积为y平方米.(1)y与x之间的函数关系式为_____________________(不需写自变量的取值范围);(2)根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米?A D GEH FB C22.关于x的一元二次方程x22m 1x m210有两个不相等的实数根x,x12.(1)求实数m的取值范围;(2)是否存在实数m,使得x x 012由.成立?如果存在,求出m的值;如果不存在,请说明理23.古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家——“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”.»»以x210x 39为例,花拉子米的几何解法如下:如图,在边长为x的正方形的两个相邻边上作边长分别为x和x55的矩形,再补上一个边长为5的小正方形,最终把图形补成一个大正方形.通过不同的方式来表示大正方形的面积,可以将原方程化为x xx55x ____239____,从而得到此方程的正根是________.524.如图,在平面直角坐标系xOy中,点A的坐标为(1,0),点P 的横坐标为2,将点A绕点P旋转,使它的对应点B恰好落在x轴上(不与A点重合);再B绕点O逆时针旋转90°得到点C.(1)直接写出点B和点C的坐标;(2)求经过A,B,C三点的抛物线的表达式.yPO A x将点25.如图,AB为⊙O的直径,点C在⊙O上,过点O作OD⊥BC交BC于点E,交⊙O于点D,CD∥AB.(1)求证:E为OD的中点;(2)若CB=6,求四边形CAOD的面积.C DEA O B26.在平面直角坐标系xOy中,已知抛物线C:y x24x 4和直线l:y kx 2k(k 0).(1)抛物线C的顶点D的坐标为________;(2)请判断点D是否在直线l上,并说明理由;x 2 4x 4,x 2,(3)记函数ykx 2k,x 2的图象为G,点M(0,t),过点M垂直于y轴的直线与图象G交于点P(x,y )11,Q(x,y)22.当1t 3时,若存在t使得x x124成立,结合图象,求k的取值范围.y6543x27.对于平面直角坐标系xOy中的点P,给出如下定义:记点P到x轴的距离为d,到y轴的距1离为d2,若d d12,则称d1为点P的“引力值”;若d d12,则称d2为点P的“引力值”.特别地,若点P在坐标轴上,则点P的“引力值”为0.例如,点P(2力值”为2.,3)到x 轴的距离为3,到y轴的距离为2,因为23,所以点P的“引(1)①点A(1,4)的“引力值”为________;②若点B(a,3)的“引力值”为2,则a的值为________;(2)若点C在直线y 2x 4y8765432上,且点C的“引力值”为2,求点C的坐标;1–4 –3–2–1O–1–2–3–412345678xy8765(3)已知点M是以D(3,4)为圆心,半径为2上的一个动点,那么点M的“引力值”d 4321的圆的取值范围是.–4 –3–2–1O–112345678x–2–3–428.在△R t ABC中,斜边AC的中点M关于BC的对称点为点O,△将ABC绕点O 顺时针旋转至△DCE,连接BD,BE,如图所示.(1)在①∠BOE,②∠ACD,③∠COE中,等于旋转角的是________(填出满足条件的的角的序号);(2)若∠A=α,求∠BEC 的大小(用含 α 的式子表示);(3)点 N 是 BD 的中点,连接 MN ,用等式表示线段 MN 与 BE 之间的数量关系,并证明.ADMNBCEO初三第一学期期中学业水平调研数学参考答案一、选择题(本题共 24 分,每小题 3 分)2017.11题号答案1D 2A 3D 4B 5A 6D 7A 8D二、填空题(本题共 24 分,每小题 3 分)9.(1,2 )10.答案不唯一,例如yx211.110°12.213.(0,1)14.>15.816.①到线段两端点距离相等的点在线段的垂直平分线上;②直径所对的圆周角是直角;③两点 确定一条直线.(注:写出前两个即可给 3 分,写出前两个中的一个得 2 分,其余正确的理由得 1 分)三、解答题(本题共 72 分)17.解法一:解: x2 4 x 4 1,x 221,………………2 分x 21,x11,x3 2.………………4 分解法二:解:x 1x 3,………………2 分x 10或 x 3 0,18.解:∵△ABC是等边三角形,∴AB =BC =AC ,∠BAC =60°. ∴∠1+∠3=60°.………………1 分 ∵△ADE 是等边三角形,A1 3 2∴AD =AE ,∠DAE =60°.∴∠2+∠3=60°.………………2 分E∴∠1=∠2.在△ABD 与△ACE 中AB AC12 ,BDCAD AE ∴△ABD ≌△ACE (SAS ). ∴CE =BD .………………4 分 ∵BC =3,CD =2, ∴BD =BC -CD =1.∴CE =1.………………5 分 19.解:∵m 是方程 x 3 x 1 0的一个根,∴ m 23m 1 0.………………2 分∴ m 2 3m1 .∴原式m 2 6m 9 m 2m 23m 53 .………………5 分24………………4 分20.方法 1:AB CD ,证明:∵在⊙O 中,∴∠AOB =∠COD .………………2 分 ∵OA =OB ,OC =OD , 1∴在△AOB 中, B 90 AOB , 21在△COD 中, C 90COD .………………4 分 2BOCAD∴∠B =∠C .………………5 分方法 2:证明:∵在⊙O 中, AB CD,∴AB =CD .………………2 分 ∵OA =OB ,OC =OD ,∴△AOB ≌△COD (SSS ).………………4 分 ∴∠B =∠C .………………5 分2» »» »)………………3分21.解:(1)y 2x24x 16(或y4x 42x(2)由题意,原正方形苗圃的面积为16平方米,得2x24x 1616.解得:x 2,x 0(不合题意,舍去).………………5分12答:此时BE的长为2米.有两个不相等的实数根,22.解:(1)∵方程x22m 1x m 210∴4,m 124m 218m 80∴m 1.………………2分0.(2)存在实数m使得x x12x x 0,即是说0是原方程的一个根,则m210.………………3分12解得:m 1或m 1.………………4分当m 1时,方程为x20,有两个相等的实数根,与题意不符,舍去.∴m.………………5分123.通过不同的方式来表示大正方形的面积,可以将原方程化为x 5………………1分23925………………3分从而得到此方程的正根是3.………………5分24.(1)点B的坐标为(3,0),点C 的坐标为(0,3);………………2分(2)方法1:设抛物线的解析式为y ax2bx c. 因为它经过A(1,0),B(3,0),C(0,3),a b c 0,则9a 3b c 0,………………4分c 3.a 1,解得b 4,………………6分c 3.方法2:抛物线经过点A(1,0),B(3,0),故可设其表达式为………………4分因为点C(0,3)在抛物线上,a 01033,得a1.………………6分所以y a(x 1)(x 3)(a 0).∴经过A,B,C三点的抛物线的表达式为y x24x 3.………………7分方法3:抛物线经过点A(1,0),B(3,0),则其对称轴为x 2.设抛物线的表达式为y a x 22k.………………4分将A(1,0),C(0,3)代入,得a k 0, 4a k 3.解得a 1,k 1.………………6分∴经过A,B,C三点的抛物线的表达式为y x24x 3.………………7分25.(1)证明:∵在⊙O中,OD⊥BC于E,∴CE=BE.………………1分∵CD∥AB,∴∠DCE=∠B.………………2分AC DEO B在△DCE与△OBE 中DCE B,CE BE,CED BEO.∴△DCE≌△OBE(ASA).∴DE=OE.∴E为OD 的中点.………………4分(2)解:连接OC.∵AB 是⊙O 的直径,∴∠ACB=90°.∵OD⊥BC,∴∠CED=90°=∠ACB.∴AC∥OD.………………5分AC DEO B∵CD∥AB,∴四边形CAOD 是平行四边形.∵E是OD 的中点,CE⊥OD,∴OC=CD.∵OC=OD,∴OC=OD=CD.∴△OCD是等边三角形.∴∠D=60°.………………6分∴∠DCE=90°-∠D=30°. ∴在△R t CDE中,CD=2DE.∵BC=6,∴CE=BE=3.∵C E2DE2CD24D E2,∴DE 3,C D 23.∴O D CD 23.∴S四边形C AODOD CE 63.………………7分26.(1)(2,0);………………2分(2)点D 在直线l上,理由如下:直线l 的表达式为y kx 2k(k 0),∵当x 2时,y 2k 2k 0,………………3分∴点D(2,0)在直线l 上.………………4分注:如果只有结论正确,给1分.(3)如图,不妨设点P在点Q左侧.由题意知:要使得x x 4成立,即是要求点P 与12y 6 5点Q 关于直线x 2对称.又因为函数y x24x 4的图象关于直线x 2对称,所以当1t 3时,若存在t使得x x 4 成立,即要求点Q12在y x24x 4(x 2,1y 3)的图象–2–14321OBP QA123456x上.………………6分根据图象,临界位置为射线y kx 2k(k 0,x 2)过–1–2y x24x 4(x 2)与y 1的交点A(3,1)处,以及射线y kx 2k(k 0,x 2)过y x24x 4(x 2)与y 3的交点B(23,3)处.此时k 1以及k 3,故k的取值范围是1k 3.………………8分27.(1)①1,②2;………………2分注:错一个得1分.(2)解:设点C的坐标为(x,y).由于点C 的“引力值”为2,则x 2或y 2,即x 2,或y 2.当x 2时,y 2x 40,此时点C的“引力值”为0,舍去;当x2时,y 2x 48,此时C 点坐标为(-2,8);当y 2时,2x 42,解得x 1,此时点C 的“引力值”为1,舍去;当y 2时,2x 42,x 3,此时C 点坐标为(3,-2);综上所述,点C的坐标为(2,8)或(3,2).………………5分注:得出一个正确答案得2 分.(3)1d 772.………………8分注:答对一边给2分;两端数值正确,少等号给2分;一端数值正确且少等号给1分.28.(1)③;………………1分(2)连接BM,OB,OC,OE.∵△R t ABC中,∠ABC=90°,M为AC的中点,1∴MA=MB=MC=AC.………………2分2∴∠A=∠ABM.∵∠A=α,∴∠BMC=∠A+∠ABM=2α.∵点M 和点O关于直线BC对称,AMNB CD∴∠BOC=∠BMC=2α.………………3分E ∵OC=OB=OE,∴点C,B,E 在以O 为圆心,OB为半径的圆上.O1∴BEC BOC2.………………4分(3)MN 12BE,证明如下:连接BM并延长到点F,使BM=MF,连接FD.∵∠A=α,∠ABC=90°,∴∠ACB=90°-∠A=90°-α.∴∠DEC=∠ACB=90°-α.A F∵∠BEC=α,D∴∠BED=∠BEC+∠DEC=90°.∵BC=CE,∴∠CBE=∠CEB=α.MN∵MB=MC,B C∴∠MBC=∠ACB=90°-α.∴∠MBE=∠MBC+∠CBE=90°.E ∴∠MBE+∠BED=180°.∴BF∥DE.………………6分∵BF=2BM,AC=2BM,∴BF=AC.∵AC=DE,∴BF=DE.∴四边形BFDE是平行四边形.………………7分∴DF=BE.∵BM=MF,BN=ND,1∴MN=DF.21∴MN=BE.………………8分2O注:如果只有结论正确,给1分.解答题解法不唯一,如有其它解法相应给分.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年北京市海淀区九上期中数学试卷一、选择题(共8小题;共40分)1. 一元二次方程3x2−6x−1=0的二次项系数、一次项系数、常数项分别是( )A. 3,6,1B. 3,6,−1C. 3,−6,1D. 3,−6,−12. 把抛物线y=x2向上平移1个单位长度得到的抛物线的表达式为( )A. y=x2+1B. y=x2−1C. y=−x2+1D. y=−x2−13. 如图,A,B,C是⊙O上的三个点.若∠C=35∘,则∠AOB的大小为( )A. 35∘B. 55∘C. 65∘D. 70∘4. 下列手机手势解锁图案中,是中心对称图形的是( )A. B.C. D.5. 用配方法解方程x2−4x+2=0,下列配方正确的是( )A. (x−2)2=2B. (x+2)2=2C. (x−2)2=−2D. (x−2)2=66. 风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n∘后能与原来的图案重合,那么n的值可能是( )A. 45B. 60C. 90D. 1207. 二次函数y1=ax2+bx+c与一次函数y2=mx+n的图象如图所示,则满足ax2+bx+c>mx+n的x的取值范围是( )A. −3<x<0B. x<−3或x>0C. x<−3或x>1D. 0<x<38. 如图1,动点P从格点A出发,在网格平面内运动,设点P走过的路程为s,点P到直线l的距离为d.已知d与s的关系如图2所示.下列选项中,可能是点P的运动路线的是( )A. B.C. D.二、填空题(共8小题;共40分)9. 点P(−1,2)关于原点的对称点的坐标为.10. 写出一个图象开口向上,过点(0,0)的二次函数的表达式:.11. 如图,四边形ABCD内接于⊙O,E为CD的延长线上一点.若∠B=110∘,则∠ADE的大小为.12. 抛物线y=x2−x−1与x轴的公共点的个数是.13. 如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(−1,0),将线段AB绕点O顺时针旋转,若点A的对应点Aʹ的坐标为(2,0),则点B的对应点Bʹ的坐标为.14. 已知抛物线y=x2+2x经过点(−4,y1),(1,y2),则y1y2(填“>”,“=”,或“<”).15. 如图,⊙O的半径OA与弦BC交于点D,若OD=3,AD=2,BD=CD,则BC的长为.16. 下面是“作已知三角形的高”的尺规作图过程.已知:△ABC.求作:BC边上的高AD.作法:如图,AC的长为半径作弧,两弧相交于P,Q两点;(1)分别以点A和点C为圆心,大于12(2)作直线PQ,交AC于点O;(3)以O为圆心,OA为半径作⊙O,与CB的延长线交于点D,连接AD.线段AD即为所作的高.请回答:该尺规作图的依据是.三、解答题(共12小题;共156分)17. 解方程:x2−4x+3=0.18. 如图,等边三角形ABC的边长为3,D是线段BC上的点,CD=2,以AD为边作等边三角形ADE,连接CE.求CE的长.19. 已知m是方程x2−3x+1=0的一个根,求(m−3)2+(m+2)(m−2)的值.20. 如图,在⊙O中,AB=CD.求证:∠B=∠C.21. 如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在AD的延长线上,DG=2BE.设BE的长为x米,改造后苗圃AEFG的面积为y平方米.(1)y与x之间的函数关系式为(不需写自变量的取值范围);(2)根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米?22. 关于x的一元二次方程x2+2(m−1)x+m2−1=0有两个不相等的实数根x=x1,x=x2.(1)求实数m的取值范围;(2)是否存在实数m,使得x1x2=0成立?如果存在,求出m的值;如果不存在,请说明理由.23. 古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家——“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”.以x2+10x=39为例,花拉子米的几何解法如下:如图,在边长为x的正方形的两个相邻边上作边长分别为x和5的矩形,再补上一个边长为5的小正方形,最终把图形补成一个大正方形.通过不同的方式来表示大正方形的面积,可以将原方程化为(x+ )2=39+ ,从而得到此方程的正根是.24. 如图,在平面直角坐标系xOy中,点A的坐标为(1,0),点P的横坐标为2,将点A绕点P旋转,使它的对应点B恰好落在x轴上(不与A点重合);再将点B绕点O逆时针旋转90∘得到点C.(1)直接写出点B和点C的坐标;(2)求经过A,B,C三点的抛物线的表达式.25. 如图,AB为⊙O的直径,点C在⊙O上,过点O作OD⊥BC交BC于点E,交⊙O于点D,CD∥AB.(1)求证:E为OD的中点;(2)若CB=6,求四边形CAOD的面积.26. 在平面直角坐标系xOy中,已知抛物线C:y=x2−4x+4和直线l:y=kx−2k(k>0).(1)抛物线C的顶点D的坐标为;(2)请判断点D是否在直线l上,并说明理由;(3)记函数 y ={x 2−4x +4,x ≤2kx −2k,x >2的图象为 G ,M (0,t ),过点 M 垂直于 y 轴的直线与图象 G 交于 P (x 1,y 1),Q (x 2,y 2).当 1<t <3 时,若存在 t 使得 x 1+x 2=4 成立,结合图象,求 k 的取值范围.27. 对于平面直角坐标系 xOy 中的点 P ,给出如下定义:记点 P 到 x 轴的距离为 d 1,到 y 轴的距离为 d 2,若 d 1≤d 2,则称 d 1 为点 P 的“引力值”;若 d 1>d 2,则称 d 2 为点 P 的“引力值”.特别地,若点 P 在坐标轴上,则点 P 的“引力值”为 0.例如,P (−2,3) 到 x 轴的距离为 3,到 y 轴的距离为 2,因为 2<3,所以点 P 的“引力值”为 2.(1)① A (1,−4) 的“引力值”为 ;②若 B (a,3) 的“引力值”为 2,则 a 的值为 ;(2)若点 C 在直线 y =−2x +4 上,且点 C 的“引力值”为 2,求点 C 的坐标;(3)已知 M 是以 D (3,4) 为圆心,半径为 2 的圆上的一个动点,那么点 M 的“引力值”d 的取值范围是 .28. 在 Rt △ABC 中,斜边 AC 的中点 M 关于 BC 的对称点为点 O ,将 △ABC 绕点 O 顺时针旋转至△DCE ,连接 BD ,BE ,如图所示.(1)在 ①∠BOE ,②∠ACD ,③∠COE 中,等于旋转角的是 (填出满足条件的的角的序号);(2)若 ∠A =α,求 ∠BEC 的大小(用含 α 的式子表示);(3)N 是 BD 的中点,连接 MN ,用等式表示线段 MN 与 BE 之间的数量关系,并证明.答案第一部分1. D2. A3. D4. B5. A6. D7. A8. D第二部分9. (1,−2)10. 答案不唯一,例如y=x211. 110∘12. 213. (0,1)14. >15. 816. ①到线段两端点距离相等的点在线段的垂直平分线上;②直径所对的圆周角是直角;③两点确定一条直线第三部分17.(x−1)⋅(x−3)=0,所以x−1=0或x−3=0.所以x1=1,x2=3.18. 如图,∵△ABC是等边三角形,∴AB=BC=AC,∠BAC=60∘.∴∠1+∠3=60∘.∵△ADE是等边三角形,∴AD=AE,∠DAE=60∘.∴∠2+∠3=60∘.∴∠1=∠2.在△ABD和△ACE中{AB=AC,∠1=∠2, AD=AE.∴△ABD≌△ACE(SAS).∴CE=BD.∵BC=3,CD=2,∴BD=BC−CD=1.∴CE=1.19. ∵m是方程x2−3x+1=0的一个根,∴m2−3m+1=0.∴m2−3m=−1.∴原式=m2−6m+9+m2−4=2(m2−3m)+5=3.20. ∵在⊙O中,AB=CD,∴∠AOB=∠COD.∵OA=OB,OC=OD,∴在△AOB中,∠B=90∘−12∠AOB,在△COD中,∠C=90∘−12∠COD.∴∠B=∠C.21. (1)y=−2x2+4x+16(或y=(4−x)(4+2x))(2)由题意,原正方形苗圃的面积为16平方米,得−2x2+4x+16=16.解得:x1=2,x2=0(不合题意,舍去),答:此时BE的长为2米.22. (1)因为方程x2+2(m−1)x+m2−1=0有两个不相等的实数根,所以Δ=4(m−1)2−4(m2−1)=−8m+8>0,所以m<1.(2)存在实数m使得x1x2=0.x1x2=0,即是说x=0是原方程的一个根,则m2−1=0.解得:m=−1或m=1.当 m =1 时,方程为 x 2=0,有两个相等的实数根,与题意不符,舍去. 所以 m =−1.23. 5;25;3【解析】通过不同的方式来表示大正方形的面积,可以将原方程化为 (x +5)2=39+25, 从而得到此方程的正根是 3.24. (1) 点 B 的坐标为 (3,0),点 C 的坐标为 (0,3).(2) 方法 1:设抛物线的解析式为 y =ax 2+bx +c .因为它经过 A (1,0),B (3,0),C (0,3),则 {a +b +c =0,9a +3b +c =0,c =3, 解得 {a =1,b =−4,c =3.所以经过 A ,B ,C 三点的抛物线的表达式为 y =x 2−4x +3.【解析】方法 2:抛物线经过 A (1,0),B (3,0),故可设其表达式为 y =a (x −1)(x −3)(a ≠0). 因为 C (0,3) 在抛物线上,所以 a (0−1)(0−3)=3,得 a =1.所以经过 A ,B ,C 三点的抛物线的表达式为 y =x 2−4x +3.方法 3:抛物线经过 A (1,0),B (3,0),则其对称轴为直线 x =2.设抛物线的表达式为 y =a (x −2)2+k .将 A (1,0),C (0,3) 代入,得 {a +k =0,4a +k =3, 解得 {a =1,k =−1.所以经过 A ,B ,C 三点的抛物线的表达式为 y =x 2−4x +3.25. (1) ∵ 在 ⊙O 中,OD ⊥BC 于点 E ,∴CE =BE ,∵CD ∥AB ,∴∠DCE =∠B ,在 △DCE 和 △OBE 中,{∠DCE =∠B,CE =BE,∠CED =∠BEO.∴△DCE ≌△OBE ,∴DE =OE ,∴E 为 OD 的中点.(2) 连接 OC ,如图.∵AB是⊙O的直径,∴∠ACB=90∘,∵OD⊥BC,∴∠CED=90∘=∠ACB,∴AC∥OD,∵CD∥AB,∴四边形CAOD是平行四边形,∵E是OD的中点,CE⊥OD,∴OC=CD,∵OC=OD,∴OC=OD=CD,∴△OCD是等边三角形,∴∠D=60∘,∴∠DCE=90∘−∠D=30∘,∴在Rt△CDE中,CD=2DE,∵BC=6,∴CE=BE=3,∵CE2+DE2=CD2=4DE2,∴DE=√3,CD=2√3,∴OD=CD=2√3,=OD⋅CE=6√3.∴S四边形CAOD26. (1)(2,0)(2)点D在直线l上,理由如下:直线l的表达式为y=kx−2k(k>0),∵当x=2时,y=2k−2k=0,∴D(2,0)在直线l上.(3)如图,不妨设点P在点Q左侧.由题意知:要使得x1+x2=4成立,即是要求点P与点Q关于直线x=2对称.又∵函数y=x2−4x+4的图象关于直线x=2对称,∴当1<t<3时,若存在t使得x1+x2=4成立,即要求点Q在y=x2−4x+4(x>2,1<y<3)的图象上.根据图象,临界位置为射线y=kx−2k(k>0,x>2)过y=x2−4x+4(x>2)与y=1的交点A(3,1)处,以及射线y=kx−2k(k>0,x>2)过y=x2−4x+4(x>2)与y=3的交点B(2+√3,3)处.此时k=1以及k=√3,故k的取值范围是1<k<√3.27. (1)1;±2(2)设点C的坐标为(x,y),由于点C的“引力值”为2,则∣x∣=2或∣y∣=2,即x=±2或y=±2,当x=2时,y=−2x+4=0,此时点C的“引力值”为0,舍去;当x=−2时,y=−2x+4=8,此时C点坐标为(−2,8);当y=2时,−2x+4=2,解得x=1,此时点C的“引力值”为1,舍去,当y=−2时,−2x+4=−2,x=3,此时C点坐标为(3,−2);综上所述,点C的坐标为(−2,8)或(3,−2).(3)1≤d≤7+√7228. (1)③(2)连接BM,OB,OC,OE,如图1,∵Rt△ABC中,∠ABC=90∘,M为AC的中点,∴MA=MB=MC=12AC.第11页(共13 页)∴∠A=∠ABM.∵∠A=α,∴∠BMC=∠A+∠ABM=2α.∵点M和点O关于直线BC对称,∴∠BOC=∠BMC=2α.∵OC=OB=OE,∴点C,B,E在以O为圆心,OB为半径的圆上.∠BOC=α.∴∠BEC=12BE,证明如下:(3)MN=12连接BM并延长到点F,使BM=MF,连接FD,如图2,∵∠A=α,∠ABC=90∘,∴∠ACB=90∘−∠A=90∘−α.∴∠DEC=∠ACB=90∘−α.∵∠BEC=α,∴∠BED=∠BEC+∠DEC=90∘.∵BC=CE,∴∠CBE=∠CEB=α.∵MB=MC,∴∠MBC=∠ACB=90∘−α.∴∠MBE=∠MBC+∠CBE=90∘.∴∠MBE+∠BED=180∘.∴BF∥DE.∵BF=2BM,AC=2BM,∴BF=AC.∵AC=DE,∴BF=DE.∴四边形BFDE是平行四边形.∴DF=BE.∵BM=MF,BN=ND,DF.∴MN=12第12页(共13 页)BE.∴MN=12第13页(共13 页)。
