2018考前三个月高考数学理科(江苏专用)总复习训练题:小题满分练8 (word版含答案)
2018考前三个月高考数学理科(江苏专用)总复习训练题:——解答题滚动练5

解答题滚动练51.已知α∈(0,π),且sin ⎝⎛⎭⎪⎫α+π3=6-24. (1)求sin ⎝⎛⎭⎪⎫α-π4的值; (2)求cos ⎝⎛⎭⎪⎫2α-π3的值. 解 方法一 联立⎩⎪⎨⎪⎧ sin ⎝⎛⎭⎪⎫α+π3=6-24,sin 2α+cos 2α=1.⇒4sin 2α-(6-2)sin α-(1+3)=0,解得sin α=6+24或sin α=-22, 因为α∈(0,π),所以sin α=6+24, 所以cos α=2-64. (1)sin ⎝⎛⎭⎪⎫α-π4=sin αcos π4-cos αsin π4=6+24×22-2-64×22=62×22=32. (2)sin2α=2sin αcos α=2×6+24×2-64=-12,cos2α=1-2sin 2α=-32. cos ⎝⎛⎭⎪⎫2α-π3=cos2αcos π3+sin2αsin π3=-32. 方法二 因为α∈(0,π),sin ⎝⎛⎭⎪⎫α+π3=6-24<12,所以5π6<α+π3<4π3, sin 11π12=sin ⎝ ⎛⎭⎪⎫π4-π6=sin π4cos π6-cos π4sin π6=6-24, 所以α+π3=11π12,所以α=7π12. (1)sin ⎝ ⎛⎭⎪⎫α-π4=sin ⎝ ⎛⎭⎪⎫7π12-π4 =sin π3=32.(2)cos ⎝ ⎛⎭⎪⎫2α-π3=cos ⎝⎛⎭⎪⎫2×7π12-π3=cos 5π6=-32. 2.如图,在四棱锥P -ABCD 中,△ACD 是正三角形,BD 垂直平分AC ,垂足为M ,∠ABC =120°,PA =AB =1,PD =2,N 为PD 的中点.(1)求证:AD ⊥平面PAB ;(2)求证:CN ∥平面PAB .证明 (1)因为BD 垂直平分AC ,所以BA =BC ,在△ABC 中,因为∠ABC =120°,所以∠BAC =30°.因为△ACD 是正三角形,所以∠DAC =60°,所以∠BAD =90°,即AD ⊥AB .因为AB =1,∠ABC =120°,所以AD =AC =3,又因为PA =1,PD =2,由PA 2+AD 2=PD 2,知∠PAD =90°,即AD ⊥AP .因为AB ,AP ⊂平面PAB ,AB ∩AP =A ,所以AD ⊥平面PAB .(2)方法一 取AD 的中点H ,连结CH ,NH .因为N 为PD 的中点,所以HN ∥PA ,因为PA ⊂平面PAB ,HN ⊄平面PAB ,所以HN ∥平面PAB .由△ACD 是正三角形,H 为AD 的中点,所以CH ⊥AD .由(1)知,BA ⊥AD ,所以CH ∥BA ,因为BA ⊂平面PAB ,CH ⊄平面PAB ,所以CH ∥平面PAB .因为CH ,HN ⊂平面CNH ,CH ∩HN =H ,所以平面CNH ∥平面PAB .因为CN ⊂平面CNH ,所以CN ∥平面PAB .方法二 取PA 的中点S ,过C 作CT ∥AD 交AB 的延长线于T ,连结ST ,SN .因为N 为PD 的中点,所以SN ∥AD ,且SN =12AD , 因为CT ∥AD ,所以CT ∥SN .由(1)知,AB ⊥AD ,所以CT ⊥AT ,在Rt △CBT 中,BC =1,∠CBT =60°,得CT =32. 由(1)知,AD =3,所以CT =12AD , 所以CT =SN .所以四边形SNCT 是平行四边形,所以CN ∥TS .因为TS ⊂平面PAB ,CN ⊄平面PAB ,所以CN ∥平面PAB .3.已知圆O :x 2+y 2=4,两个定点A (a,2),B (m,1),其中a ∈R ,m >0.P 为圆O 上任意一点,且PA PB=k (k 为常数).(1)求常数k 的值;(2)过点E (a ,t )作直线l 与圆C :x 2+y 2=m 交于M ,N 两点,若M 点恰好是线段NE 的中点,求实数t 的取值范围.解 (1)设点P (x ,y ),x 2+y 2=4, PA =(x -a )2+(y -2)2,PB =(x -m )2+(y -1)2, 因为PA PB =k ,所以(x -a )2+(y -2)2=k 2[(x -m )2+(y -1)2],又x 2+y 2=4,化简得2ax +4y -a 2-8=k 2(2mx +2y -m 2-5),因为P 为圆O 上任意一点,所以⎩⎪⎨⎪⎧ 2a =2mk 2,4=2k 2,a 2+8=k 2(m 2+5),又m >0,k >0,解得⎩⎨⎧ k =2,a =2,m =1,所以常数k = 2. (2)方法一 设M (x 0,y 0),M 是线段NE 的中点,N (2x 0-2,2y 0-t ),又点M ,N 在圆C 上,即关于x ,y 的方程组⎩⎪⎨⎪⎧ x 20+y 20=1,(2x 0-2)2+(2y 0-t )2=1有解, 化简得⎩⎪⎨⎪⎧ x 20+y 20=1,8x 0+4ty 0-t 2-7=0有解, 即直线n :8x +4ty -t 2-7=0与圆C :x 2+y 2=1有交点,则点(0,0)到直线n 的距离d =|t 2+7|64+16t 2≤1,化简得,t 4-2t 2-15≤0, 解得t ∈[-5,5].方法二 设过E 的切线与圆C 切于切点F ,EF 2=EM ·EN ,又M 是线段NE 的中点,所以EN =2MN ,EM =MN ,所以EF 2=2MN 2,又EF 2=EC 2-CF 2=22+t 2-1=t 2+3,MN ≤2,所以t 2+3≤8,所以t ∈[-5,5].4.已知函数f (x )=-x 2-(2a +1)x +ln x ,且该函数在x =1处取得极值.(1)求实数a 的值,并求出函数的单调区间;(2)若函数g (x )=f (x )-b +5x 2在区间(0,2018)上只有一个零点,求实数b 的值. 解 (1)由已知,得f ′(x )=-2x -2a -1+1x, 据题意,f ′(1)=0,得到a =-1,所以f (x )=-x 2+x +ln x , f ′(x )=-2x +1+1x =(2x +1)(-x +1)x. 由x >0,令f ′(x )>0,得0<x <1,令f ′(x )<0,得x >1,所以函数f (x )在x =1处取得极值,所以a =-1, f (x )的单调增区间为(0,1),f (x )的单调减区间为(1,+∞).(2)g (x )=f (x )-b +5x 2=-x 2+7x 2+ln x -b ,x ∈(0,2018). 则g ′(x )=-2x +72+1x, 令g ′(x )=0, 得x =2,负值舍去.当0<x <2时,g ′(x )>0,g (x )的单调增区间为(0,2),当2<x <2018时,g ′(x )<0,g (x )的单调减区间为(2,2018).所以函数g (x )=f (x )-b +5x 2在区间(0,2018)上只有一个零点,等价于g (2)=0, 解得b =ln2+3.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——小题满分练9 含答案

小题满分练91.(2017·苏北四市期末)已知集合A ={-2,0},B ={-2,3},则A ∪B =________. 答案 {-2,0,3}2.已知i 为虚数单位,则复数2i1+i =________.答案 1+i3.(2017·南通、扬州、泰州、淮安三调)某人随机播放甲、乙、丙、丁4首歌曲中的2首,则甲、乙2首歌曲至少有1首被播放的概率是________. 答案 56解析 从甲、乙、丙、丁4首歌曲中随机抽取2首播放,因为播放是有顺序的,所以所有的基本事件有:(甲,乙),(乙,甲),(甲,丙),(丙,甲),(甲,丁),(丁,甲),(乙,丙),(丙,乙),(乙,丁),(丁,乙),(丙,丁),(丁,丙),共12个,而甲、乙2首歌曲至少有1首被播放的事件所包含的基本事件有:(甲,乙),(乙,甲),(甲,丙),(丙,甲),(甲,丁),(丁,甲),(乙,丙),(丙,乙),(乙,丁),(丁,乙),共10个,故所求事件的概率为P =1012=56.4.(2017·常州期末)双曲线x 24-y 212=1的右焦点与左准线之间的距离是________.答案 5解析 因为a 2=4,b 2=12,所以c 2=16,即右焦点为(4,0),又左准线为x =-a 2c=-1,故右焦点到左准线的距离为5.5.已知命题p :“∀x ∈[1,2],x 2-a ≥0”,命题q :“∃x ∈R ,使x 2+2ax +2-a =0”,若命题“p 且q ”是真命题,则实数a 的取值范围是______________. 答案 {a |a ≤-2或a =1}解析 p 为真,则x 2≥a ,所以a ≤1;q 为真,则Δ=(2a )2-4(2-a )≥0,解得a ≥1或a ≤-2.命题“p 且q ”为真命题, 则a 的取值范围为a ≤-2或a =1.6.(2017·苏州期末)阅读下面的流程图,如果输出的函数f (x )的值在区间⎣⎢⎡⎦⎥⎤14,12内,那么输入的实数x 的取值范围是________.答案 [-2,-1]解析 流程图表示输出分段函数f (x )=⎩⎪⎨⎪⎧2x,x ∈[-2,2],2,x ∉[-2,2]的值.令f (x )∈⎣⎢⎡⎦⎥⎤14,12,得⎩⎪⎨⎪⎧-2≤x ≤2,14≤2x ≤12,解得-2≤x ≤-1.7.已知圆锥的母线长为10cm ,侧面积为60πcm 2,则此圆锥的体积为________cm 3. 答案 96π解析 设圆锥的底面半径为r cm ,高为h cm ,则12·2πr ·10=60π,所以r =6cm ,从而高h=8cm ,此圆锥的体积V =13×36π×8=96π(cm 3).8.(2017·广东佛山检测)所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数(也称为完备数、完美数).如:6=1+2+3;28=1+2+4+7+14;496=1+2+4+8+16+31+62+124+248.此外,它们都可以表示为2的一些连续正整数次幂之和.如6=21+22,28=22+23+24,…,按此规律,8128可表示为________. 答案 26+27+…+212解析 因为8 128=26×127, 又由1-2n1-2=127,解得n =7.所以8 128=26×(1+2+…+26) =26+27+ (212)9.(2017·常州期末)设S n 为等差数列{a n }的前n 项和,若a 3=4,S 9-S 6=27,则S 10=__________. 答案 65解析 因为S 9-S 6=a 7+a 8+a 9=3a 8=27,所以a 8=9,即S 10=10(a 1+a 10)2=5(a 3+a 8)=65.10.(2017届苏北四市一模)若tan β=2tan α,且cos αsin β=23,则sin(α-β)的值为________. 答案 -13解析 因为tan β=2tan α,所以sin βcos β=2sin αcos α,即cos αsin β=2sin αcos β.又因为cos αsin β=23,所以sin αcos β=13,从而sin(α-β)=sin αcos β-cos αsin β=13-23=-13.11.函数f (x )的图象关于y 轴对称,且对任意x ∈R 都有f (x -3)=-f (x ),若当x ∈⎝ ⎛⎭⎪⎫32,52时,f (x )=⎝ ⎛⎭⎪⎫12x,则f (2017)=________.答案 -14解析 因为函数f (x )对任意x ∈R 都有f (x -3)=-f (x ), 所以f (x -6)=-f (x -3)=f (x ), 函数f (x )是周期为6的函数,f (2017)=f (336×6+1)=f (1),由f (x -3)=-f (x )可得f (-2-3)=-f (-2)=f (1), 因为函数f (x )的图象关于y 轴对称, 所以函数f (x )是偶函数,f (-2)=f (2)=⎝ ⎛⎭⎪⎫122=14,所以f (2017)=f (1)=-f (-2)=-14.12.(2017·南京三模)如图,在直三棱柱ABC -A 1B 1C 1中,AB =1,BC =2,BB 1=3,∠ABC =90°,点D 为侧棱BB 1上的动点.当AD +DC 1最小时,三棱锥D -ABC 1的体积为________.答案 13解析 将侧面展开如图,所以由平面几何性质可得:AD +DC 1≥AC 1,当且仅当A ,D ,C 1三点共线时取等号.此时BD =1,所以S △ABD =12×AB ×BD =12.在直三棱柱ABC-A 1B 1C 1中有BB 1⊥CB ,又AB ⊥CB ,易得CB ⊥平面ABD ,所以C 1B 1⊥平面ABD ,即C 1B 1是三棱锥C 1-ABD 的高,所以11D ABC C ABD V V --==13×C 1B 1×S △ABD =13×2×12=13.13.(2017届苏北四市一模)已知正数a ,b 满足1a +9b=ab -5,则ab 的最小值为________.答案 36解析 因为正数a ,b 满足1a +9b =ab -5,所以ab -5≥29ab,当且仅当9a =b 时等号成立,即ab -5ab -6≥0,解得ab ≥6或ab ≤-1(舍去),因此ab ≥36,从而(ab )min =36.14.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若△ABC 为锐角三角形,且满足b 2-a 2=ac ,则1tan A -1tan B的取值范围是__________.答案 ⎝⎛⎭⎪⎫1,233解析 方法一 原式可化为1tan A -1tan B =cos A sin A -cos B sin B =sin B cos A -cos B sin A sin A sin B =sin (B -A )sin A sin B.由b 2-a 2=ac ,得b 2=a 2+ac =a 2+c 2-2ac cos B ,即a =c -2a cos B ,也就是sin A =sin C -2sin A ·cos B ,即sin A =sin(A +B )-2sin A cos B =sin(B -A ),由于△ABC 为锐角三角形,所以有A =B -A ,即B =2A ,故1tan A -1tan B =1sin B ,在锐角三角形ABC 中易知,π3<B <π2,32<sin B <1,故1tan A -1tan B ∈⎝ ⎛⎭⎪⎫1,233.方法二 根据题意,作CD ⊥AB ,垂足为点D ,画出示意图.因为b 2-a2=AD 2-BD 2=(AD +BD )(AD -BD )=c (AD -BD )=ac ,所以AD -BD =a ,而AD +BD =c ,所以BD =c -a 2,则c >a ,即c a>1,在锐角三角形ABC 中有b2+a 2>c 2,则a 2+a 2+ac >c 2,即⎝ ⎛⎭⎪⎫c a 2-c a -2<0,解得-1<c a <2,因此,1<c a <2.而1tan A -1tan B =AD -BDCD=a a 2-⎝⎛⎭⎪⎫c -a 22=11-14⎝ ⎛⎭⎪⎫c a -12∈⎝ ⎛⎭⎪⎫1,233.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——考前回扣6 Word版含答案
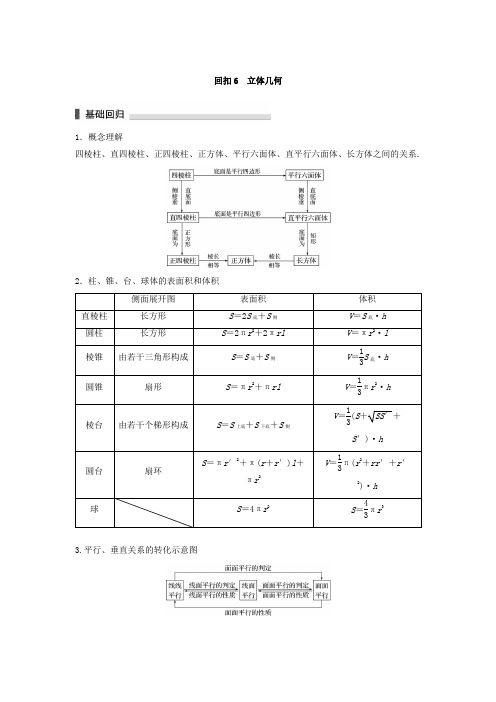
回扣6 立体几何1.概念理解四棱柱、直四棱柱、正四棱柱、正方体、平行六面体、直平行六面体、长方体之间的关系.2.柱、锥、台、球体的表面积和体积3.平行、垂直关系的转化示意图1.易混淆几何体的表面积与侧面积的区别,几何体的表面积是几何体的侧面积与所有底面面积之和,不能漏掉几何体的底面积;求锥体体积时,易漏掉体积公式中的系数13.2.不清楚空间线面平行与垂直关系中的判定定理和性质定理,忽视判定定理和性质定理中的条件,导致判断出错.如由α⊥β,α∩β=l ,m ⊥l ,易误得出m ⊥β的结论,就是因为忽视面面垂直的性质定理中m ⊂α的限制条件.3.注意图形的翻折与展开前后变与不变的量以及位置关系.对照前后图形,弄清楚变与不变的元素后,再立足于不变的元素的位置关系与数量关系去探求变化后的元素在空间中的位置与数量关系.1.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是________. 答案 2π解析 几何体的底面圆半径为1,高为1,则侧面积S =2πrh =2π×1×1=2π. 2.用平面α截球O 所得截面圆的半径为3,球心O 到平面α的距离为4,则此球的表面积为__________. 答案 100π解析 依题意,设球的半径为R ,满足R 2=32+42=25, ∴S 球=4πR 2=100π.3.(2017·南京高淳区质检)若正四棱锥的底面边长为22,体积为8,则其侧面积为__________. 答案 422解析 因为V =13×(22)2h =8,所以h =3,所以斜高h ′=32+(2)2=11.所以其侧面积为S 侧=4×⎝ ⎛⎭⎪⎫12×22×11=422. 4.设m ,n 是不同的直线,α,β,γ是不同的平面,有以下四个命题:①⎩⎪⎨⎪⎧ α∥β,α∥γ⇒β∥γ;②⎩⎪⎨⎪⎧α⊥β,m ∥α⇒m ⊥β;③⎩⎪⎨⎪⎧m ⊥α,m ∥β⇒α⊥β;④⎩⎪⎨⎪⎧m ∥n ,n ⊂α⇒m ∥α.其中正确的命题是________.(填序号) 答案 ①③解析 ①中平行于同一平面的两平面平行是正确的;②中m ,β可能平行,相交或直线在平面内;③中由面面垂直的判定定理可知结论正确;④中m ,α可能平行或线在面内. 5.在三棱锥S -ABC 中,底面ABC 是边长为3的等边三角形,SA ⊥SC ,SB ⊥SC ,SA =SB =2,则该三棱锥的体积为________. 答案354解析 如图,∵SA ⊥SC ,SB ⊥SC ,且SA ∩SB =S , ∴SC ⊥平面SAB ,在Rt △BSC 中,由SB =2,BC =3,得SC = 5.在△SAB 中,取AB 中点D ,连结SD ,则SD ⊥AB ,且BD =32,∴SD =22-⎝ ⎛⎭⎪⎫322=72,∴V =13×12×3×72×5=354.6.已知m ,n 为不同直线,α,β为不同平面,给出下列命题: ①若m ⊥α,m ⊥n ,则n ∥α; ②若m ⊥β,n ⊥β,则m ∥n ; ③若m ⊥α,m ⊥β,则α∥β; ④若m ⊂α,n ⊂β,α∥β,则n ∥m ;⑤若α⊥β,α∩β=m ,n ⊂α,m ⊥n ,则n ⊥β. 其中正确的命题是________.(填写所有正确命题的序号) 答案 ②③⑤解析 命题①,若m ⊥α,m ⊥n ,则n ∥α或n ⊂α,故不正确;命题②,若m ⊥β,n ⊥β,则m ∥n ,由线面垂直的性质定理易知正确;命题③,由线面垂直的性质定理易知正确;命题④,若m ⊂α,n ⊂β,α∥β,则n ∥m 或m ,n 异面,所以不正确;命题⑤是面面垂直的性质定理,所以是正确命题.故答案为②③⑤.7.如图,三棱锥A -BCD 的棱长全相等,点E 为AD 的中点,则直线CE 与BD 所成角的余弦值为__________.答案36解析 方法一 取AB 的中点G ,连结EG ,CG . ∵E 为AD 的中点,∴EG ∥BD .∴∠GEC 为CE 与BD 所成的角.设AB =1, 则EG =12BD =12,CE =CG =32,∴cos ∠GEC =EG 2+EC 2-GC 22×EG ×EC=⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫322-⎝ ⎛⎭⎪⎫3222×12×32=36. 方法二 设AB =1,则CE →·BD →=(AE →-AC →)·(AD →-AB →)=⎝ ⎛⎭⎪⎫12AD →-AC →·(AD →-AB →)=12AD →2-12AD →·AB →-AC →·AD →+AC →·AB →=12-12cos60°-cos60°+cos60°=14. ∴cos 〈CE→,BD →〉=CE →·BD →|CE →||BD →|=1432=36.8.如图所示,在边长为5+2的正方形ABCD 中,以A 为圆心画一个扇形,以O 为圆心画一个圆,M ,N ,K 为切点,以扇形为圆锥的侧面,以圆O 为圆锥底面,围成一个圆锥,则圆锥的全面积S =________. 答案 10π 解析设圆锥的母线长为l ,底面半径为r ,由已知条件得⎩⎪⎨⎪⎧l +r +2r =(5+2)×2,2πr l=π2,解得r =2,l =42,则S =πrl +πr 2=10π.9.如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,PD ⊥BC ,G 为PA 上一点. (1)求证:平面PCD ⊥平面ABCD ;(2)若PC ∥平面BDG ,求证:G 为PA 的中点.证明 (1)∵底面ABCD 为矩形,∴BC ⊥CD , 又∵PD ⊥BC ,PD ∩CD =D ,CD ,PD ⊂平面PCD , ∴BC ⊥平面PCD .又∵BC ⊂平面ABCD ,∴平面ABCD ⊥平面PCD .(2)连结AC 交BD 于点O ,连结GO ,∵PC ∥平面BDG , 平面PCA ∩平面BDG =GO , ∴PC ∥GO , ∴PG GA =COOA.∵底面ABCD 为矩形, ∴O 是AC 的中点,即CO =OA , ∴PG =GA ,∴G 为PA 的中点.10.在正四棱锥S -ABCD 中,底面边长为a ,侧棱长为2a ,P 为侧棱SD 上的一点. (1)当四面体ACPS 的体积为6a 318时,求SP PD的值;(2)在(1)的条件下,若E 是SC 的中点,求证:BE ∥平面APC .(1)解 设PD =x ,连结BD ,AC ,交点为O .过P 作PH ⊥BD 于点H ,∵平面SBD ⊥平面ABCD 且BD 为交线,则PH ⊥平面ABCD ,又SO ⊥平面ABCD , ∴PH ∥SO .在Rt △SOB 中,SO =SB 2-BO 2=62a , ∵PH SO =PD SD,∴PH =PD ·SOSD=x ·62a 2a=32x , ∴V SPAC =V S -ACD -V P -ACD=13×⎝ ⎛⎭⎪⎫12×a ×a ⎝ ⎛⎭⎪⎫62a -32x =618a 3, 解得x =23a , ∴SP PD =21=2.(2)证明 取SP 的中点Q ,连结QE ,BQ , 则EQ ∥PC ,EQ ⊄平面PAC ,PC ⊂平面PAC , ∴EQ ∥平面PAC .∵P 为QD 的中点,O 为BD 的中点, ∴BQ ∥PO ,又BQ ⊄平面PAC ,PO ⊂平面PAC , ∴BQ ∥平面PAC ,而EQ 与BQ 为平面BEQ 内的两条相交直线, ∴平面BEQ ∥平面PAC ,而BE ⊂平面BEQ ,∴BE ∥平面APC .。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——考前回扣3 含答案

;回扣3 三角函数与平面向量;;1.准确记忆六组诱导公式;; 对于“k π2±α,k ∈Z ”的三角函数值与α角的三角函数值的关系口诀:奇变偶不变,符号看象限.;2.三角函数恒等变换“四大策略”;;(1)常值代换:特别是“1”的代换,1=sin 2θ+cos 2θ=tan45°等. (2)降次与升次:正用二倍角公式升次,逆用二倍角公式降次. (3)弦、切互化:一般是切化弦.;;(4)灵活运用辅助角公式a sin α+b cos α=a 2+b 2sin(α+φ)⎝ ⎛⎭⎪⎫其中tan φ=b a .3.三种三角函数的性质;;4.函数y =A sin(ωx +φ)(ω>0,A >0)的图象 (1)“五点法”作图设z =ωx +φ,令z =0,π2,π,3π2,2π,求出相应的x 的值与y 的值,描点、连线可得.(2)由三角函数的图象确定解析式时,一般利用五点中的零点或最值点作为解题突破口. (3)图象变换y =sin x ―――――――――→向左(φ>0)或向右(φ<0)平移|φ|个单位长度y =sin(x +φ) ――――――――――――→横坐标变为原来的1ω(ω>0)倍纵坐标不变y =sin(ωx +φ) ―――――――――――→纵坐标变为原来的A (A >0)倍横坐标不变y =A sin(ωx +φ). 5.正弦定理及其变形asin A=b sin B =csin C=2R (2R 为△ABC 外接圆的直径).变形:a =2R sin A ,b =2R sin B ,c =2R sin C . sin A =a 2R ,sin B =b 2R ,sin C =c2R.a ∶b ∶c =sin A ∶sin B ∶sin C .6.余弦定理及其推论、变形a 2=b 2+c 2-2bc cos A ,b 2=a 2+c 2-2ac cos B , c 2=a 2+b 2-2ab cos C .推论:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.变形:b 2+c 2-a 2=2bc cos A ,a 2+c 2-b 2=2ac cos B ,a 2+b 2-c 2=2ab cos C .7.面积公式S △ABC =12bc sin A =12ac sin B =12ab sin C .8.平面向量的数量积(1)若a ,b 为非零向量,夹角为θ,则a·b =|a||b |cos θ. (2)设a =(x 1,y 1),b =(x 2,y 2),则a·b =x 1x 2+y 1y 2. 9.两个非零向量平行、垂直的充要条件 若a =(x 1,y 1),b =(x 2,y 2),则 (1)a ∥b ⇔a =λb (b ≠0)⇔x 1y 2-x 2y 1=0. (2)a ⊥b ⇔a·b =0⇔x 1x 2+y 1y 2=0. 10.利用数量积求长度(1)若a =(x ,y ),则|a |=a·a =x 2+y 2. (2)若A (x 1,y 1),B (x 2,y 2),则 |AB →|=(x 2-x 1)2+(y 2-y 1)2.11.利用数量积求夹角若a =(x 1,y 1),b =(x 2,y 2),θ为a 与b 的夹角, 则cos θ=a·b |a||b |=x 1x 2+y 1y 2x 21+y 21 x 22+y 22. 12.三角形“四心”向量形式的充要条件设O 为△ABC 所在平面上一点,角A ,B ,C 所对的边长分别为a ,b ,c ,则(1)O 为△ABC 的外心⇔|OA →|=|OB →|=|OC →|=a 2sin A.(2)O 为△ABC 的重心⇔OA →+OB →+OC →=0.(3)O 为△ABC 的垂心⇔OA →·OB →=OB →·OC →=OC →·OA →. (4)O 为△ABC 的内心⇔aOA →+bOB →+cOC →=0.1.利用同角三角函数的平方关系式求值时,不要忽视角的范围,要先判断函数值的符号. 2.在求三角函数的值域(或最值)时,不要忽略x 的取值范围.3.求函数f (x )=A sin(ωx +φ)的单调区间时,要注意A 与ω的符号,当ω<0时,需把ω的符号化为正值后求解.4.三角函数图象变换中,注意由y =sin ωx 的图象变换得y =sin(ωx +φ)时,平移量为⎪⎪⎪⎪⎪⎪φω,而不是φ. 5.在已知两边和其中一边的对角时,要注意检验解是否满足“大边对大角”,避免增解. 6.要特别注意零向量带来的问题:0的模是0,方向任意,并不是没有方向;0与任意非零向量平行.7.a·b >0是〈a ,b 〉为锐角的必要不充分条件;a·b <0是〈a ,b 〉为钝角的必要不充分条件.1.2sin45°cos15°-sin30°的值=________. 答案32解析 2sin45°cos15°-sin30°=2sin45°cos15°-sin(45°-15°)=2sin45°cos15°-(sin45°cos15°-cos45°sin15°)=sin45°cos15°+cos45°sin15°=sin60°=32. 2.(1+tan18°)(1+tan27°)的值是________. 答案 2解析 由题意得tan(18°+27°)=tan18°+tan27°1-tan18°tan27°,即tan18°+tan27°1-tan18°tan27°=1, 所以tan18°+tan27°=1-tan18°tan27°,所以(1+tan18°)(1+tan27°)=1+tan18°+tan27°+tan18°tan27°=2.3.(2017·江苏泰州中学期中)向量a =(cos10°,sin10°),b =(cos70°,sin70°),|a -2b |=________. 答案3解析 a ·b =cos70°cos10°+sin70°sin10°=cos60°=12,|a |=|b |=1,所以|a -2b |=a 2+4b 2-4a ·b =1+4-2= 3.4.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC 的面积是________. 答案332解析 c 2=(a -b )2+6,即c 2=a 2+b 2-2ab +6,① ∵C =π3,由余弦定理得c 2=a 2+b 2-ab ,②由①和②得ab =6,∴S △ABC =12ab sin C =12×6×32=332.5.已知两点A (1,0),B (1,1),O 为坐标原点,点C 在第二象限,且∠AOC =135°,设OC →=-OA →+λOB →(λ∈R ),则λ的值为__________. 答案 12解析 由∠AOC =135°知,点C 在射线y =-x (x <0)上,设点C 的坐标为(a ,-a ),a <0,则有(a ,-a )=(-1+λ,λ),得a =-1+λ,-a =λ,消去a 得λ=12.6.已知a ,b 为同一平面内的两个向量,且a =(1,2),|b |=12|a |,若a +2b 与2a -b 垂直,则a 与b 的夹角为________. 答案 π解析 |b |=12|a |=52,而(a +2b )·(2a -b )=0,即2a 2-2b 2+3a·b =0,所以a·b =-52,从而cos 〈a ,b 〉=a·b|a||b |=-1,所以〈a ,b 〉=π.7.已知函数f (x )=3sin ⎝⎛⎭⎪⎫ωx -π6(ω>0)和g (x )=3cos(2x +φ)的图象的对称中心完全相同,若x ∈⎣⎢⎡⎦⎥⎤0,π2,则f (x )的取值范围是________.答案 ⎣⎢⎡⎦⎥⎤-32,3解析 由两个三角函数图象的对称中心完全相同可知,两函数的周期相同,故ω=2, 所以f (x )=3sin ⎝⎛⎭⎪⎫2x -π6, 那么当x ∈⎣⎢⎡⎦⎥⎤0,π2时,-π6≤2x -π6≤5π6, 所以-12≤sin ⎝ ⎛⎭⎪⎫2x -π6≤1,故f (x )∈⎣⎢⎡⎦⎥⎤-32,3.8.在等腰梯形ABCD 中,已知AB ∥DC ,AB =2,BC =1,∠ABC =60°,动点E 和F 分别在线段BC 和DC 上,且BE →=λBC →,DF →=19λDC →,则AE →·AF →的最小值为__________.答案2918解析 方法一 在梯形ABCD 中,AB =2,BC =1,∠ABC =60°,可得DC =1,AE →=AB →+λBC →,AF →=AD →+19λDC →(λ>0),∴AE →·AF →=(AB →+λBC →)·⎝ ⎛⎭⎪⎫AD →+19λDC →=AB →·AD →+AB →·19λDC→+λBC →·AD →+λBC →·19λDC →=2×1×cos60°+2×1×19λ+λ×1×1×cos60°+λ×19λ×1×1×cos120°=29λ+λ2+1718≥229λ·λ2+1718=2918,当且仅当29λ=λ2,即λ=23时,取得最小值为2918. 方法二 以点A 为坐标原点,AB 所在的直线为x 轴建立平面直角坐标系,则B (2,0),C ⎝ ⎛⎭⎪⎫32,32,D ⎝ ⎛⎭⎪⎫12,32.又BE →=λBC →,DF →=19λDC →,则E ⎝ ⎛⎭⎪⎫2-12λ,32λ,F ⎝ ⎛⎭⎪⎫12+19λ,32,λ>0,∴AE →·AF →=⎝ ⎛⎭⎪⎫2-12λ⎝ ⎛⎭⎪⎫12+19λ+34λ=1718+29λ+12λ≥1718+229λ·12λ=2918,λ>0,当且仅当29λ=12λ,即λ=23时取等号,故AE →·AF →的最小值为2918.9.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3-3sin ⎝ ⎛⎭⎪⎫2x -π6. (1)求函数f (x )的最小正周期和单调增区间;(2)当x ∈⎣⎢⎡⎦⎥⎤-π6,π3时,试求f (x )的最值,并写出取得最值时自变量x 的值.解 (1)由题意知,f (x )=-sin2x +3cos2x =2sin ⎝⎛⎭⎪⎫2x +2π3, 所以f (x )的最小正周期为T =2π2=π.当-π2+2k π≤2x +2π3≤π2+2k π(k ∈Z )时,f (x )单调递增,解得x ∈⎣⎢⎡⎦⎥⎤-7π12+k π,-π12+k π(k ∈Z ), 所以f (x )的单调增区间为⎣⎢⎡⎦⎥⎤-7π12+k π,-π12+k π(k ∈Z ). (2)因为x ∈⎣⎢⎡⎦⎥⎤-π6,π3,所以π3≤2x +2π3≤4π3,当2x +2π3=π2,即x =-π12时,f (x )取得最大值2,当2x +2π3=4π3,即x =π3时,f (x )取得最小值- 3.10.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知cos C +(cos A -3sin A )cos B =0.(1)求角B 的大小;(2)若a =2,b =7,求△ABC 的面积. 解 (1)由已知得-cos(A +B )+cos A cos B -3sin A cos B =0, 即sin A sin B -3sin A cos B =0, 因为sin A ≠0, 所以sin B -3cos B =0,又cos B ≠0,所以tan B =3, 又0<B <π,所以B =π3.(2)因为sin B =32,cos B =12, 所以a sin A =b sin B =732=2213,又a =2, 所以sin A =321=217, 因为a <b , 所以cos A =277.所以sin C =sin(A +B )=sin A cos B +cos A sin B =32114,所以S =12ab sin C =332.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——小题满分练3 Word版含答案

小题满分练31.(2017·南京三模)已知全集U ={1,2,3,4},集合A ={1,4},B ={3,4},则∁U (A ∪B )=__________.答案 {2}解析 由题意可得A ∪B ={1,3,4},故∁U (A ∪B )={2}.2.(2017届苏北四市一模)已知复数z 满足z (1-i)=2,其中i 为虚数单位,则z 的实部为________.答案 1解析 因为z (1-i)=2,所以z =21-i=1+i ,故实部为1. 3.某工厂生产A ,B ,C ,D 四种不同型号的产品,产品数量之比依次为2∶3∶5∶1.现用分层抽样方法抽出一个容量为n 的样本,若样本中A 种型号有16件,那么此样本的容量n 为________.答案 88解析 根据分层抽样的特点,样本中A 种型号产品应是样本容量的22+3+5+1=211,所以样本的容量n =16÷211=88. 4.函数y =ln ⎝ ⎛⎭⎪⎫1+1x +1-x 2的定义域为________. 答案 (0,1]解析 根据题意可知,⎩⎪⎨⎪⎧ 1+1x>0,x ≠0,1-x 2≥0⇒⎩⎪⎨⎪⎧ x +1x >0,-1≤x ≤1⇒0<x ≤1,故定义域为(0,1].5.(2017届苏北四市一模)若随机地从1,2,3,4,5五个数中选出两个数,则这两个数恰好为一奇一偶的概率为__________.答案 35解析 从1,2,3,4,5五个数中选出两个数的所有基本事件为(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10个,其中一奇一偶的基本事件有6个,故所求事件的概率为P =610=35.6.(2017届南京、盐城一模)如图是一个算法流程图,则输出的x 的值是________.答案 9解析 经过第一次循环后得x =1+4=5,y =9-2=7,此时x <y ,进行第二次循环;经过第二次循环后得x =5+4=9,y =7-2=5,此时x >y ,退出循环,故输出的x =9.7.在△ABC 中,∠BAC =120°,AC =4,BC =27,则△ABC 的面积为________. 答案 2 3解析 由题意知,在△ABC 中,已知A =120°,b =4,a =27,由余弦定理得cos A =42+c 2-(27)22×4×c =-12, 解得c =2或c =-6(舍去),则S △ABC =12bc sin A =12×4×2×32=2 3. 8.(2017·南京学情调研)在平面直角坐标系xOy 中,双曲线C :x 2a 2-y 24=1(a >0)的一条渐近线与直线y =2x +1平行,则实数a 的值是________.答案 1解析 由双曲线的方程可知其渐近线方程为y =±2ax .因为一条渐近线与直线y =2x +1平行,所以2a=2,解得a =1. 9.(2017·南通、扬州、淮安、宿迁、泰州、徐州六市调研)已知{a n }是公差不为0的等差数列,S n 是其前n 项和.若a 2a 3=a 4a 5,S 9=27,则a 1的值是________.答案 -5解析 首先由S 9=9a 5=27,得a 5=3.设公差为d (d ≠0),则(3-3d )(3-2d )=3(3-d ),即d 2-2d =0,从而得d =2.所以a 1=a 5-4d =3-8=-5.10.(2017·苏州暑假测试)已知α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫π2,π,cos α=13,sin(α+β)=-35,则cos β=________. 答案 -4+6215解析 因为α∈⎝ ⎛⎭⎪⎫0,π2,cos α=13,所以sin α=223.又α+β∈⎝ ⎛⎭⎪⎫π2,3π2,sin(α+β)=-35<0,所以α+β∈⎝⎛⎭⎪⎫π,3π2,故cos(α+β)=-45,从而cos β=cos(α+β-α)=cos(α+β)cos α+sin(α+β)sin α=-45×13-35×223=-4+6215. 11.(2017·南通、扬州、淮安、宿迁、泰州、徐州六市调研)如图,在平面四边形ABCD 中,O 为BD 的中点,且OA =3,OC =5.若AB →·AD →=-7,则BC →·DC →的值是__________.答案 9解析 BC →·DC →=(OC →-OB →)·(OC →-OD →)=(OC →+OD →)·(OC →-OD →)=OC 2-OD 2,类似AB →·AD →=AO2-OD 2=-7,所以BC →·DC →=OC 2-OD 2=OC 2-AO 2-7=9.12.将矩形ABCD 绕边AB 旋转一周得到一个圆柱,AB =3,BC =2,圆柱上底面圆心为O ,△EFG 为下底面圆的一个内接直角三角形,则三棱锥O -EFG 体积的最大值是________. 答案 4解析 设Rt △EFG 的两条直角边分别为a ,b ,则a 2+b 2=16,三棱锥O -EFG 的高为3,从而V O -EFG =13S △EFG ·3=12ab ≤a 2+b 24=4,当且仅当a =b =22时等号成立,故三棱锥O -EFG 的体积的最大值为4.13.(2017届南京、盐城一模)如图,在平面直角坐标系中,分别在x 轴与直线y =33(x +1)上从左向右依次取点A k ,B k ,k =1,2,…,其中A 1是坐标原点,使△A k B k A k +1都是等边三角形,则△A 10B 10A 11的边长是________.答案 512解析 设第n 个正三角形的边长为a n ,则点B 1⎝ ⎛⎭⎪⎫12a 1,32a 1在直线y =33(x +1)上, 从而32a 1=33⎝ ⎛⎭⎪⎫12a 1+1,解得a 1=1, 当n ≥2时,B n ⎝⎛⎭⎪⎫a 1+a 2+…+a n -1+12a n ,32a n . 因为B n 在直线y =33(x +1)上, 所以32a n =33⎝ ⎛⎭⎪⎫a 1+a 2+…+a n -1+12a n +1, 即a n =a 1+a 2+…+a n -1+1,从而a n +1=a 1+a 2+…+a n +1,两式相减得a n +1=2a n (n ≥2),又a 2=a 1+1=2,故{a n }是以a 1=1为首项,q =2为公比的等比数列,从而△A 10B 10A 11的边长为a 10=29=512.14.已知函数f (x )=(x -1)e x +12ax 2+1(其中a ∈R )有两个零点,则a 的取值范围是____________________.答案 (-∞,-1)∪(-1,0)解析 由题意,f ′(x )=x (e x +a ),其中f (0)=0,故函数还有一个不为零的零点,分类讨论:(1)当a ≥0时,由f ′(x )<0,得x <0,由f ′(x )>0,得x >0,此时函数仅有一个零点;(2)当a <0时,由f ′(x )=0可得,x 1=0,x 2=ln(-a ),①当ln(-a )<0,即-1<a <0时,当x ∈(-∞,ln(-a ))∪(0,+∞)时,f ′(x )>0,当x ∈(-ln(-a ),0)时,f ′(x )<0,所以当x =ln(-a )时,f (x )取得极大值,当x =0时,函数取得极小值,而f (ln(-a ))>f (0)可知函数有两个零点,此时满足条件.②当ln(-a )=0,即a =-1时,当x∈(-∞,0)∪(0,+∞)时,f′(x)>0,函数单调递增,函数只有一个零点,不满足条件.③当ln(-a)>0,即a<-1时,当x∈(-∞,0)∪(ln(-a),+∞)时,f′(x)>0,当x∈(0,ln(-a))时,f′(x)<0,所以当x=ln(-a)时,f(x)取得极小值,当x=0时,函数取得极大值,由f(ln(-a))<f(0)可知函数有两个零点,此时满足条件.综上可得,a的取值范围是(-∞,-1)∪(-1,0).。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——小题满分练8 Word版含答案

小题满分练81.(2017·扬州期末)已知集合A ={x |x ≤0},B ={-1,0,1,2},则A ∩B =________. 答案 {-1,0}解析 根据交集的定义,A ∩B ={x |x ≤0}∩{-1,0,1,2}={-1,0}. 2.双曲线x 24-y 25=1的离心率为________.答案 32解析 因为a 2=4,b 2=5,所以c 2=a 2+b 2=9,离心率e =c a =32.3.从某班抽取5名学生测量身高(单位:cm),得到的数据为160,162,159,160,159,则该组数据的方差s 2=________. 答案 65解析 由题干条件可得x =160+162+159+160+1595=160,所以s 2=15(4+1+1)=65.4.(2017·苏州期末)一架飞机向目标投弹,击毁目标的概率为0.2,目标未受损的概率为0.4,则目标受损但未完全击毁的概率为________. 答案 0.4解析 设“目标受损但未完全击毁”为事件A ,则其对立事件A 是“目标未受损或击毁目标”.P (A )=1-P (A )=1-(0.4+0.2)=0.4. 5.如图所示,该伪代码运行的结果为__________.S ←0 i ←1While S ≤20S ←S +i i ←i +2End While Print i 答案 11解析 第一次循环,S =1,i =3;第二次循环,S =1+3=4,i =5;第三次循环,S =4+5=9,i =7;第四次循环,S =9+7=16,i =9;第五次循环,S =16+9=25,i =11,此时S >20,故输出i =11.6.已知平面向量a ,b 满足(a +b )·(2a -b )=-4,且|a |=2,|b |=4,则a 与b 的夹角为________. 答案π3解析 由题意可得(a +b )·(2a -b )=2a 2-b 2+a ·b =8-16+a ·b =-4,解得a ·b =4,所以cos θ=a ·b |a ||b |=12,又因为θ∈[0,π],所以θ=π3.7.已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=1-log 2x ,则不等式f (x )<0的解集是________. 答案 (-2,0)∪(2,+∞)解析 当x <0时,f (x )=-f (-x )=log 2(-x )-1,f (x )<0,即log 2(-x )-1<0,解得-2<x <0;当x >0时,f (x )=1-log 2x ,f (x )<0,即1-log 2x <0,解得x >2.综上,不等式f (x )<0的解集是(-2,0)∪(2,+∞).8.已知正五棱锥底面边长为2,底面正五边形中心到侧面斜高距离为3,斜高长为4,则此正五棱锥体积为________. 答案 20解析 设正五棱锥高为h ,底面正五边形的角为108°, 底面正五边形中心到边距离为tan54°,h =12tan54°,则此正五棱锥体积为13×5×12×2×tan54°×12tan54°=20.9.设△ABC 是等腰三角形,∠ABC =120°,则以A ,B 为焦点且过点C 的双曲线的离心率为________. 答案3+12解析 设AB =BC =2c ,则由余弦定理可得CA =AB 2+BC 2-2AB ×BC co s120°=23c .根据双曲线的定义可得CA -CB =2a ,即23c -2c =2a ,所以(3-1)c =a ,故双曲线的离心率e =c a =3+12. 10.若数列{a n }满足a 1+3a 2+32a 3+…+3n -1a n =n2,其前n 项和为S n ,则S n =________.答案 34⎝⎛⎭⎪⎫1-13n解析 因为a 1+3a 2+32a 3+…+3n -1a n =n 2,所以当n ≥2时有a 1+3a 2+32a 3+…+3n -2a n -1=n -12,两式作差得3n -1a n =12,所以a n =12·13n -1,又因为当n =1时,a 1=12适合此式,所以数列{}a n 的通项公式为a n =12·13n -1,所以S n =12⎝ ⎛⎭⎪⎫1-13n 1-13=34⎝ ⎛⎭⎪⎫1-13n .11.已知sin ⎝ ⎛⎭⎪⎫x +π6=13,则sin ⎝ ⎛⎭⎪⎫x -5π6+sin 2⎝ ⎛⎭⎪⎫π3-x 的值为________.答案 59解析 sin ⎝ ⎛⎭⎪⎫x -5π6=sin ⎝ ⎛⎭⎪⎫x +π6-π=-sin ⎝ ⎛⎭⎪⎫x +π6=-13,sin 2⎝ ⎛⎭⎪⎫π3-x =cos 2⎝ ⎛⎭⎪⎫x +π6=1-sin 2⎝ ⎛⎭⎪⎫x +π6=1-19=89,所以sin ⎝ ⎛⎭⎪⎫x -5π6+sin 2⎝ ⎛⎭⎪⎫π3-x =-13+89=59.12.已知点P 是△ABC 内一点(不包括边界),且AP →=mAB →+nAC →,m ,n ∈R ,则(m -2)2+(n -2)2的取值范围是________.答案 ⎝ ⎛⎭⎪⎫92,8 解析 因为点P 是△ABC 内一点(不包括边界),且AP →=mAB →+nAC →,所以m ,n 满足条件⎩⎪⎨⎪⎧m >0,n >0,m +n <1,作出不等式组表示的平面区域如图所示.因为(m -2)2+(n -2)2表示的是区域内的动点(m ,n )到点A (2,2)的距离的平方.因为点A 到直线m +n =1的距离为|2+2-1|2=32,故⎝ ⎛⎭⎪⎫322<(m -2)2+(n -2)2<OA 2,即(m -2)2+(n -2)2的取值范围是⎝ ⎛⎭⎪⎫92,8.13.椭圆x 24+y 23=1的左、右焦点分别为F 1,F 2,过椭圆的右焦点F 2作一条直线l 交椭圆于P ,Q 两点,则△F 1PQ 的内切圆面积的最大值是________.答案9π16解析 令直线l :x =my +1,与椭圆方程联立消去x ,得()3m 2+4y 2+6my -9=0,可设P ()x 1,y 1,Q ()x 2,y 2, 则y 1+y 2=-6m 3m 2+4,y 1y 2=-93m 2+4.可知1F PQS =12F 1F 2||y 1-y 2 =()y 1+y 22-4y 1y 2=12m 2+1()3m 2+42,又m 2+1()3m 2+42=19()m 2+1+1m 2+1+6≤116, 故1F PQS≤3.三角形的周长与三角形内切圆的半径的积是三角形面积的二倍, 则内切圆半径r =12F PQS8≤34,其面积的最大值为9π16. 14.已知函数f (x )的定义域为R ,若存在常数k ,使|f (x )|≤k2017|x |对所有实数都成立,则称函数f (x )为“期望函数”,给出下列函数: ①f (x )=x 2;②f (x )=x e x;③f (x )=xx 2-x +1;④f (x )=xe x +1.其中函数f (x )为“期望函数”的是________.(写出所有符合条件的函数序号) 答案 ③④解析 ①假设函数f (x )=x 2为“期望函数”,则|f (x )|=|x 2|≤k2017|x |,当x ≠0时,k ≥2017|x |,因此不存在k ,因此假设错误,即函数f (x )=x 2不是“期望函数”;②假设函数f (x )=x e x 为“期望函数”,则|f (x )|=|x e x |≤k2017|x |,当x ≠0时,k ≥2017e x,因此不存在k ,因此假设错误;③假设函数f (x )=xx 2-x +1为“期望函数”,|f (x )|=|x |⎝ ⎛⎭⎪⎫x -122+34≤43|x |,当x ≠0时,对任意的k 2017≥43,都有|f (x )|≤k 2017|x |成立,故正确;④假设函数f (x )=xe x+1为“期望函数”,|f (x )|=|x |e x +1≤k2017|x |对所有实数都成立,故正确.故答案为③④.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——附加题高分练5套集合((含答案)18页

2018考前三个月高考数学理科(江苏专用)总复习训练题:——附加题高分练5套集合((含答案)附加题高分练 1.矩阵与变换1.(2017·常州期末)已知矩阵A =⎣⎡⎦⎤2 13 2,列向量X =⎣⎡⎦⎤x y ,B =⎣⎡⎦⎤47,若AX =B ,直接写出A -1,并求出X .解 由A =⎣⎡⎦⎤2 13 2,得到A -1=⎣⎡⎦⎤ 2 -1-3 2.由AX =B ,得到X =A -1B =⎣⎡⎦⎤ 2 -1-3 2⎣⎡⎦⎤47=⎣⎡⎦⎤12.也可由AX =B 得到⎣⎡⎦⎤2 13 2⎣⎡⎦⎤x y =⎣⎡⎦⎤47,即⎩⎪⎨⎪⎧2x +y =4,3x +2y =7,解得⎩⎪⎨⎪⎧x =1,y =2,所以X =⎣⎡⎦⎤12.2.(2017·江苏淮阴中学调研)已知矩阵A =⎣⎡⎦⎤3 3c d ,若矩阵A 属于特征值6的一个特征向量为α1=⎣⎡⎦⎤11,属于特征值1的一个特征向量α2=⎣⎡⎦⎤ 3-2.求矩阵A ,并写出A 的逆矩阵.解 由矩阵A 属于特征值6的一个特征向量α1=⎣⎡⎦⎤11可得,⎣⎡⎦⎤33cd ⎣⎡⎦⎤11=6⎣⎡⎦⎤11,即c +d =6;由矩阵A 属于特征值1的一个特征向量α2=⎣⎡⎦⎤ 3-2,可得⎣⎡⎦⎤3 3c d ⎣⎡⎦⎤ 3-2=⎣⎡⎦⎤3-2,即3c -2d =-2,解得⎩⎪⎨⎪⎧c =2,d =4.即A =⎣⎡⎦⎤3 32 4,A 的逆矩阵是⎣⎢⎡⎦⎥⎤23 -12-13 123.(2017·江苏建湖中学月考)曲线x 2+4xy +2y 2=1在二阶矩阵M =⎣⎡⎦⎤1 a b 1的作用下变换为曲线x 2-2y 2=1. (1)求实数a ,b 的值; (2)求M 的逆矩阵M -1.解 (1)设P (x ,y )为曲线x 2-2y 2=1上任意一点,P ′(x ′,y ′)为曲线x 2+4xy +2y 2=1上与P 对应的点,则⎣⎡⎦⎤1 a b 1⎣⎡⎦⎤x ′y ′=⎣⎡⎦⎤x y ,即⎩⎪⎨⎪⎧x =x ′+ay ′,y =bx ′+y ′,代入x 2-2y 2=1得(x ′+ay ′)2-2(bx ′+y ′)2=1得(1-2b 2)x ′2+(2a -4b )x ′y ′+(a 2-2)y ′2=1,及方程x 2+4xy +2y 2=1,从而⎩⎪⎨⎪⎧1-2b 2=1,2a -4b =4,a 2-2=2,解得a =2,b =0. (2)因为M =⎪⎪⎪⎪1 20 1=1≠0,故M-1=⎣⎢⎡⎦⎥⎤11 -210111=⎣⎡⎦⎤1 -20 1. 4.已知曲线C :y 2=12x ,在矩阵M =⎣⎢⎡⎦⎥⎤1 00 -2对应的变换作用下得到曲线C 1,C 1在矩阵N =⎣⎢⎡⎦⎥⎤0 11 0对应的变换作用下得到曲线C 2,求曲线C 2的方程. 解 设A =NM ,则A =⎣⎢⎡⎦⎥⎤0 11 0⎣⎢⎡⎦⎥⎤1 00 -2=⎣⎢⎡⎦⎥⎤0 -21 0, 设P (x ′,y ′)是曲线C 上任一点,在两次变换下,在曲线C 2上对应的点为P (x ,y ), 则⎣⎢⎡⎦⎥⎤x y =⎣⎢⎡⎦⎥⎤0 -21 0⎣⎢⎡⎦⎥⎤x ′y ′=⎣⎢⎡⎦⎥⎤-2y ′ x ′,即⎩⎪⎨⎪⎧x =-2y ′,y =x ′,∴⎩⎪⎨⎪⎧x ′=y ,y ′=-12x .又点P (x ′,y ′)在曲线C :y 2=12x 上,∴⎝ ⎛⎭⎪⎫-12x 2=12y ,即x 2=2y .3.曲线与方程、抛物线1.(2017·江苏南通天星湖中学质检)已知点A (1,2)在抛物线F :y 2=2px 上.(1)若△ABC 的三个顶点都在抛物线F 上,记三边AB ,BC ,CA 所在直线的斜率分别为k 1,k 2,k 3, 求1k 1-1k 2+1k 3的值;(2)若四边形ABCD 的四个顶点都在抛物线F 上,记四边AB ,BC ,CD ,DA 所在直线的斜率分别为k 1,k 2,k 3,k 4,求1k 1-1k 2+1k 3-1k 4的值.解 (1)由点A (1,2)在抛物线F 上,得p =2,∴抛物线F :y 2=4x ,设B ⎝ ⎛⎭⎪⎫y 214,y 1,C ⎝ ⎛⎭⎪⎫y 224,y 2, ∴1k 1-1k 2+1k 3=y 214-1y 1-2-y 224-y 214y 2-y 1+1-y 2242-y 2=y 1+24-y 2+y 14+2+y 24=1. (2)另设D ⎝ ⎛⎭⎪⎫y 234,y 3,则1k 1-1k 2+1k 3-1k 4=y 1+24-y 2+y 14+y 3+y 24-2+y 34=0.2.(2017·江苏赣榆中学月考)抛物线关于x 轴对称,它的顶点在坐标原点,点P (1,2),A (x 1,y 1),B (x 2,y 2)均在抛物线上.(1)写出该抛物线的方程及其准线方程;(2)当PA 与PB 的斜率存在且倾斜角互补时,求y 1+y 2的值及直线AB 的斜率. 解 (1)由已知条件,可设抛物线的方程为y 2=2px . ∵点P (1,2)在抛物线上, ∴22=2p ×1,得p =2,故所求抛物线的方程是y 2=4x ,准线方程是x =-1. (2)设直线PA 的斜率为k PA ,直线PB 的斜率为k PB , 则k PA =y 1-2x 1-1(x 1≠1),k PB =y 2-2x 2-1(x 2≠1). ∵PA 与PB 的斜率存在且倾斜角互补, ∴k PA =-k PB ,由A (x 1,y 1),B (x 2,y 2)在抛物线上,得y 21=4x 1,① y 22=4x 2,②∴y 1-214y 21-1=-y 2-214y 22-1, ∴y 1+2=-(y 2+2),∴y 1+y 2=-4,由①-②得直线AB 的斜率k AB =y 2-y 1x 2-x 1=4y 1+y 2=-44=-1(x 1≠x 2).3.(2017·江苏常州中学质检)已知点A (-1,0),F (1,0),动点P 满足AP →·AF →=2||FP →. (1)求动点P 的轨迹C 的方程;(2)在直线l :y =2x +2上取一点Q ,过点Q 作轨迹C 的两条切线,切点分别为M ,N .问:是否存在点Q ,使得直线MN ∥l ?若存在,求出点Q 的坐标;若不存在,请说明理由. 解 (1)设P (x ,y ),则AP →=(x +1,y ),FP →=(x -1,y ),AF →=(2,0), 由AP →·AF →=2|FP →|,得2(x +1)=2(x -1)2+y 2,化简得y 2=4x . 故动点P 的轨迹C 的方程为y 2=4x .(2)直线l 方程为y =2(x +1),设Q (x 0,y 0),M (x 1,y 1),N (x 2,y 2).设过点M 的切线方程为x -x 1=m (y -y 1),代入y 2=4x ,得y 2-4my +4my 1-y 21=0, 由Δ=16m 2-16my 1+4y 21=0,得m =y 12,所以过点M 的切线方程为y 1y =2(x +x 1),同理过点N 的切线方程为y 2y =2(x +x 2).所以直线MN 的方程为y 0y =2(x 0+x ),又MN ∥l ,所以2y 0=2,得y 0=1,而y 0=2(x 0+1),故点Q 的坐标为⎝ ⎛⎭⎪⎫-12,1. 4.(2017·江苏宝应中学质检)如图,已知抛物线C :y 2=4x 的焦点为F ,过F 的直线l 与抛物线C 交于A (x 1,y 1)(y 1>0),B (x 2,y 2)两点,T 为抛物线的准线与x 轴的交点.(1)若TA →·TB →=1,求直线l 的斜率; (2)求∠ATF 的最大值.解 (1)因为抛物线y 2=4x 焦点为F (1,0),T (-1,0).当l ⊥x 轴时,A (1,2),B (1,-2),此时TA →·TB →=0,与TA →·TB →=1矛盾, 所以设直线l 的方程为y =k (x -1),代入y 2=4x ,得k 2x 2-(2k 2+4)x +k 2=0, 则x 1+x 2=2k 2+4k2,x 1x 2=1,①所以y 21y 22=16x 1x 2=16,所以y 1y 2=-4,② 因为TA →·TB →=1,所以(x 1+1)(x 2+1)+y 1y 2=1, 将①②代入并整理得,k 2=4,所以k =±2. (2)因为y 1>0,所以tan ∠ATF =y 1x 1+1=y 1y 14+1=1y 14+1y 1≤1,当且仅当y 14=1y 1,即y 1=2时,取等号,所以∠ATF ≤π4,所以∠ATF 的最大值为π4.4.空间向量与立体几何1.(2017·苏锡常镇调研)如图,已知正四棱锥P -ABCD 中,PA =AB =2,点M ,N 分别在PA ,BD 上,且PM PA =BN BD =13.(1)求异面直线MN 与PC 所成角的大小; (2)求二面角N -PC -B 的余弦值.解 (1)设AC ,BD 交于点O ,在正四棱锥P -ABCD 中,OP ⊥平面ABCD ,又PA =AB =2,所以OP = 2.以O 为坐标原点,DA →,AB →,OP →方向分别为x 轴,y 轴,z 轴正方向,建立空间直角坐标系O -xyz ,如图.则A (1,-1,0),B (1,1,0),C (-1,1,0),D (-1,-1,0),P (0,0,2),AP →=(-1,1,2).故OM →=OA →+AM →=OA →+23AP →=⎝ ⎛⎭⎪⎫13,-13,223,ON →=13OB →=⎝ ⎛⎭⎪⎫13,13,0,所以MN →=⎝ ⎛⎭⎪⎫0,23,-223,PC →=(-1,1,-2),所以cos 〈MN →,PC →〉=MN →·PC →|MN →||PC →|=32,所以异面直线MN 与PC 所成角的大小为π6.(2)由(1)知PC →=(-1,1,-2),CB →=(2,0,0),NC →=⎝ ⎛⎭⎪⎫-43,23,0.设m =(x ,y ,z )是平面PCB 的法向量,则m ·PC →=0,m ·CB →=0,可得⎩⎨⎧-x +y -2z =0,x =0,令y =2,则z =1,即m =(0,2,1).设n =(x 1,y 1,z 1)是平面PCN 的法向量,则n ·PC →=0,n ·CN →=0,可得⎩⎨⎧-x 1+y 1-2z 1=0,-2x 1+y 1=0,令x 1=2,则y 1=4,z 1=2,即n =(2,4,2),所以cos 〈m ,n 〉=m·n |m||n|=523×22=53333,则二面角N -PC -B 的余弦值为53333.2.(2017·常州期末)如图,以正四棱锥V -ABCD 的底面中心O 为坐标原点建立空间直角坐标系O -xyz ,其中Ox ∥BC ,Oy ∥AB ,E 为VC 的中点.正四棱锥的底面边长为2a ,高为h ,且有cos 〈BE →,DE →〉=-1549.(1)求h a的值;(2)求二面角B -VC -D 的余弦值.解 (1)根据条件,可得B (a ,a,0),C (-a ,a,0),D (-a ,-a,0),V (0,0,h ),E ⎝ ⎛⎭⎪⎫-a 2,a 2,h 2,所以BE →=⎝ ⎛⎭⎪⎫-32a ,-a 2,h 2,DE →=⎝ ⎛⎭⎪⎫a 2,32a ,h 2,故cos 〈BE →,DE →〉=h 2-6a 2h 2+10a 2.又cos 〈BE →,DE →〉=-1549,则h 2-6a 2h 2+10a 2=-1549,解得h a =32.(2)由h a =32,得BE →=⎝ ⎛⎭⎪⎫-32a ,-a 2,34a ,DE →=⎝ ⎛⎭⎪⎫a 2,32a ,34a ,且容易得到,CB →=(2a,0,0),DC →=(0,2a,0). 设平面BVC 的法向量为n 1=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧n 1·BE →=0,n 1·CB →=0.即⎩⎪⎨⎪⎧-32ax 1-a 2y 1+34az 1=0,2ax 1=0,则⎩⎪⎨⎪⎧x 1=0,2y 1=3z 1,取y 1=3,z 1=2,则n 1=(0,3,2).同理可得平面DVC 的一个法向量为n 2=(-3,0,2). cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=0×(-3)+3×0+2×213×13=413,结合图形,可以知道二面角B -VC -D 的余弦值为-413.3.(2017·南京学情调研)如图,在底面为正方形的四棱锥P -ABCD 中,侧棱PD ⊥底面ABCD ,PD =DC ,E 是线段PC 的中点.(1)求异面直线AP 与BE 所成角的大小;(2)若点F 在线段PB 上,且使得二面角F -DE -B 的正弦值为33,求PFPB的值.解 (1)在四棱锥P -ABCD 中,底面ABCD 为正方形,侧棱PD ⊥底面ABCD ,所以DA ,DC ,DP 两两垂直,故以{DA →,DC →,DP →}为正交基底,建立空间直角坐标系D -xyz .因为PD =DC ,所以DA =DC =DP , 不妨设DA =DC =DP =2,则D (0,0,0),A (2,0,0),C (0,2,0),P (0,0,2),B (2,2,0). 因为E 是PC 的中点,所以E (0,1,1), 所以AP →=(-2,0,2),BE →=(-2,-1,1), 所以cos 〈AP →,BE →〉=AP →·BE →|AP →||BE →|=32,从而〈AP →,BE →〉=π6.因此异面直线AP 与BE 所成角的大小为π6.(2)由(1)可知,DE →=(0,1,1),DB →=(2,2,0),PB →=(2,2,-2). 设PF →=λPB →,则PF →=(2λ,2λ,-2λ),从而DF →=DP →+PF →=(2λ,2λ,2-2λ). 设m =(x 1,y 1,z 1)为平面DEF 的法向量, 则⎩⎪⎨⎪⎧ m ·DF →=0,m ·DE →=0,即⎩⎪⎨⎪⎧λx 1+λy 1+(1-λ)z 1=0,y 1+z 1=0,取z 1=λ,则y 1=-λ,x 1=2λ-1.故m =(2λ-1,-λ,λ)为平面DEF 的一个法向量, 设n =(x 2,y 2,z 2)为平面DEB 的法向量. 则⎩⎪⎨⎪⎧n ·DB →=0,n ·DE →=0,即⎩⎪⎨⎪⎧2x 2+2y 2=0,y 2+z 2=0,取x 2=1,则y 2=-1,z 2=1.所以n =(1,-1,1)为平面BDE 的一个法向量. 因为二面角F -DE -B 的余弦值的绝对值为63, 即|cos 〈m ,n 〉|=|m·n ||m||n|=|4λ-1|3·(2λ-1)2+2λ2=63, 化简得4λ2=1.因为点F 在线段PB 上,所以0≤λ≤1, 所以λ=12,即PF PB =12.4.(2017·苏北四市一模)如图,在四棱锥P -ABCD 中,PA ⊥平面ABCD ,∠ABC =∠BAD =90°,AD =AP =4,AB =BC =2,M 为PC 的中点. (1)求异面直线AP ,BM 所成角的余弦值;(2)点N 在线段AD 上,且AN =λ,若直线MN 与平面PBC 所成角的正弦值为45,求λ的值.解 (1)因为PA ⊥平面ABCD ,且AB ,AD ⊂平面ABCD ,所以PA ⊥AB ,PA ⊥AD . 又因为∠BAD =90°,所以PA ,AB ,AD 两两互相垂直.分别以AB ,AD ,AP 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示,则由AD =2AB =2BC =4,PA =4可得A (0,0,0),B (2,0,0),C (2,2,0),D (0,4,0),P (0,0,4).又因为M 为PC 的中点,所以M (1,1,2). 所以BM →=(-1,1,2),AP →=(0,0,4), 所以cos 〈AP →,BM →〉=AP →·BM →|AP →||BM →|=0×(-1)+0×1+4×24×6=63,所以异面直线AP ,BM 所成角的余弦值为63. (2)因为AN =λ,所以N (0,λ,0)(0≤λ≤4),则MN →=(-1,λ-1,-2),BC →=(0,2,0),PB →=(2,0,-4).设平面PBC 的法向量为m =(x ,y ,z ), 则⎩⎪⎨⎪⎧m ·BC →=0,m ·PB →=0,即⎩⎪⎨⎪⎧2y =0,2x -4z =0.令x =2,解得y =0,z =1,所以m =(2,0,1)是平面PBC 的一个法向量.因为直线MN 与平面PBC 所成角的正弦值为45,所以|cos 〈MN →,m 〉|=|MN →·m ||MN →||m |=|-2-2|5+(λ-1)2·5=45,解得λ=1∈[0,4],所以λ的值为1.5.离散型随机变量的概率分布1.(2017·南京、盐城一模)某年级星期一至星期五每天下午排3节课,每天下午随机选择1节作为综合实践课(上午不排该课程),张老师与王老师分别任教甲、乙两个班的综合实践课程.(1)求这两个班“在星期一不同时上综合实践课”的概率;(2)设这两个班“在一周中同时上综合实践课的节数”为X ,求X 的概率分布与数学期望E (X ). 解 (1)这两个班“在星期一不同时上综合实践课”的概率为P =1-33×3=23.(2)由题意得X ~B ⎝ ⎛⎭⎪⎫5,13,P (X =k )=C k 5⎝ ⎛⎭⎪⎫13k·⎝ ⎛⎭⎪⎫235-k ,k =0,1,2,3,4,5.所以X 的概率分布为所以X 的数学期望为E (X )=5×13=53.2.一位网民在网上光顾某网店,经过一番浏览后,对该店铺中的A ,B ,C 三种商品有购买意向.已知该网民购买A 种商品的概率为34,购买B 种商品的概率为23,购买C 种商品的概率为12.假设该网民是否购买这三种商品相互独立. (1)求该网民至少购买2种商品的概率;(2)用随机变量η表示该网民购买商品的种数,求η的概率分布和数学期望. 解 (1)该网民恰好购买2种商品的概率为P (AB C )+P (A B C )+P (A BC )=34×23×12+34×13×12+14×23×12=1124;该网民恰好购买3种商品的概率为P (ABC )=34×23×12=14,所以P =1124+14=1724.故该网民至少购买2种商品的概率为1724.(2)随机变量η的可能取值为0,1,2,3,由(1)知,P (η=2)=1124,P (η=3)=14,而P (η=0)=P (A B C )=14×13×12=124,所以P (η=1)=1-P (η=0)-P (η=2)-P (η=3)=14.随机变量η的概率分布为所以随机变量η的数学期望E (η)=0×124+1×14+2×1124+3×14=2312.3.(2017·南京学情调研)甲、乙两人轮流投篮,每人每次投一次篮,先投中者获胜,投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为25,乙每次投篮命中的概率为23,且各次投篮互不影响.现由甲先投.(1)求甲获胜的概率;(2)求投篮结束时甲的投篮次数X 的概率分布与数学期望.解 (1)设甲第i 次投中获胜的事件为A 1(i =1,2,3),则A 1,A 2,A 3彼此互斥. 甲获胜的事件为A 1+A 2+A 3.P (A 1)=25,P (A 2)=35×13×25=225, P (A 3)=⎝ ⎛⎭⎪⎫352×⎝ ⎛⎭⎪⎫132×25=2125. 所以P (A 1+A 2+A 3)=P (A 1)+P (A 2)+P (A 3)=25+225+2125=62125.(2)X 的所有可能取值为1,2,3. 则P (X =1)=25+35×23=45,P (X =2)=225+35×13×35×23=425, P (X =3)=⎝ ⎛⎭⎪⎫352×⎝ ⎛⎭⎪⎫132×1=125.即X 的概率分布为所以数学期望E (X )=1×45+2×425+3×125=3125.4.为了提高学生学习数学的兴趣,某校决定在每周的同一时间开设《数学史》、《生活中的数学》、《数学与哲学》、《数学建模》四门校本选修课程,甲、乙、丙三位同学每人均在四门校本课程中随机选一门进行学习,假设三人选择课程时互不影响,且每人选择每一课程都是等可能的.(1)求甲、乙、丙三人选择的课程互不相同的概率;(2)设X 为甲、乙、丙三人中选修《数学史》的人数,求X 的概率分布和数学期望E (X ). 解 (1)甲、乙、丙三人从四门课程中各任选一门,共有43=64种不同的选法,记“甲、乙、丙三人选择的课程互不相同”为事件M ,事件M 共包含A 34=24个基本事件,则P (M )=2464=38,所以甲、乙、丙三人选择的课程互不相同的概率为38.(2)方法一 X 可能的取值为0,1,2,3. P (X =0)=3343=2764,P (X =1)=C 13×3243=2764,P (X =2)=C 23×343=964,P (X =3)=C 3343=164.所以X 的概率分布为所以E (X )=0×2764+1×2764+2×964+3×164=34.方法二 甲、乙、丙三人从四门课程中任选一门,可以看成三次独立重复试验,X 为甲、乙、丙三人中选修《数学史》的人数,则X ~B ⎝ ⎛⎭⎪⎫3,14,所以P (X =k )=C k 3⎝ ⎛⎭⎪⎫14k ⎝ ⎛⎭⎪⎫343-k,k =0,1,2,3,所以X 的概率分布为所以X 的数学期望E (X )=3×14=34.6.计数原理、二项式定理和数学归纳法1.已知等式(1+x )2n -1=(1+x )n -1(1+x )n.(1)求(1+x )2n -1的展开式中含x n 的项的系数,并化简:C 0n -1C n n +C 1n -1C n -1n +…+C n -1n -1C 1n ;(2)证明:(C 1n )2+2(C 2n )2+…+n (C n n )2=n C n2n -1. (1)解 (1+x )2n -1的展开式中含x n 的项的系数为C n2n -1,由(1+x )n -1(1+x )n=(C 0n -1+C 1n -1x +…+C n -1n -1xn -1)(C 0n +C 1n x +…+C n n x n )可知,(1+x )n -1(1+x )n的展开式中含x n的项的系数为C 0n -1C n n +C 1n -1C n -1n +…+C n -1n -1C 1n . 所以C 0n -1C n n +C 1n -1C n -1n +…+C n -1n -1C 1n =C n2n -1. (2)证明 当k ∈N *时,k C kn =k ·n !k !(n -k )!=n !(k -1)!(n -k )!=n ·(n -1)!(k -1)!(n -k )!=n C k -1n -1,所以(C 1n )2+2(C 2n )2+…+n (C n n)2=∑k =1n[k (C k n )2]=k =1n (k C k n C k n )=k =1n (n C k -1n -1C k n )=n k =1n (C k -1n -1C kn )=n k =1n (C n -k n -1C kn ).由(1)知C 0n -1C n n +C 1n -1C n -1n +…+C n -1n -1C 1n =C n2n -1, 即k =1n (C n -k n -1C k n )=C n2n -1,所以(C 1n )2+2(C 2n )2+…+n (C n n )2=n C n2n -1.2.(2017·江苏泰州中学调研)在平面直角坐标系xOy 中,点P (x 0,y 0)在曲线y =x 2(x >0)上.已知点A (0,-1),P n (x n0,y n0),n ∈N *.记直线AP n 的斜率为k n . (1)若k 1=2,求P 1的坐标; (2)若k 1为偶数,求证:k n 为偶数.(1)解 因为k 1=2,所以y 0+1x 0=x 20+1x 0=2,解得x 0=1,y 0=1,所以P 1的坐标为(1,1).(2)证明 方法一 设k 1=2p (p ∈N *),即y 0+1x 0=x 20+1x 0=2p .所以x 20-2px 0+1=0,所以x 0=p ±p 2-1.因为y 0=x 2,所以k n =y n 0+1x n 0=x 2n0+1x n 0=x n0+1x n 0,所以当x 0=p +p 2-1时,k n =(p +p 2-1)n+⎝ ⎛⎭⎪⎫1p +p 2-1n =(p +p 2-1)n +(p -p 2-1)n. 同理,当x 0=p -p 2-1时,k n =(p +p 2-1)n +(p -p 2-1)n.①当n =2m (m ∈N *)时,k n =2∑k =0mC 2k n pn -2k(p 2-1)k,所以k n 为偶数.②当n =2m +1(m ∈N )时,k n =2∑k =0mC 2k n pn -2k(p 2-1)k,所以k n 为偶数.综上,k n 为偶数.方法二 因为⎝⎛⎭⎪⎫x 0+1x 0⎝⎛⎭⎪⎫x n +10+1xn +10=x n +20+1x n +20+x n0+1x n 0,所以k n +2=k 1k n +1-k n .k 2=x 20+1x 20=⎝⎛⎭⎪⎫x 0+1x 02-2=k 21-2. 设命题p (n ):k n ,k n +1均为偶数.以下用数学归纳法证明“命题p (n )是真命题”.①因为k 1是偶数,所以k 2=k 21-2也是偶数.当n =1时,p (n )是真命题;②假设当n =m (m ∈N *)时,p (n )是真命题,即k m ,k m +1均为偶数,则k m +2=k 1k m +1-k m 也是偶数,即当n =m +1时,p (n )也是真命题.由①②可知,对n ∈N *,p (n )均是真命题,从而k n 是偶数.3.(2017·江苏扬州中学模拟)在数列{a n }中,a n =cos π3×2n -2(n ∈N *)(1)试将a n +1表示为a n 的函数关系式; (2)若数列{b n }满足b n =1-2n ·n !(n ∈N *),猜想a n 与b n 的大小关系,并证明你的结论. 解 (1)a n =cos π3×2n -2=cos 2π3×2n -1=2⎝⎛⎭⎪⎫cosπ3×2n -12-1, ∴a n =2a 2n +1-1, ∴a n +1=±a n +12,又n ∈N *,n +1≥2,a n +1>0, ∴a n +1=a n +12.(2)当n =1时,a 1=-12,b 1=1-2=-1,∴a 1>b 1,当n =2时,a 2=12,b 2=1-12=12,∴a 2=b 2, 当n =3时,a 3=32,b 3=1-19=89,∴a 3<b 3, 猜想:当n ≥3时,a n <b n ,下面用数学归纳法证明. ①当n =3时,由上知,a 3<b 3,结论成立. ②假设当n =k ,k ≥3,n ∈N *时,a k <b k 成立, 即a k <1-2k ·k !, 则当n =k +1时,a k +1=a k +12<2-2k ·k !2=1-1k ·k !, b k +1=1-2(k +1)·(k +1)!,要证a k +1<b k +1,即证明⎝⎛⎭⎪⎫1-1k ·k !2<⎝ ⎛⎭⎪⎫1-2(k +1)·(k +1)!2,即证明1-1k ·k !<1-4(k +1)·(k +1)!+⎝ ⎛⎭⎪⎫2(k +1)·(k +1)!2,即证明1k ·k !-4(k +1)·(k +1)!+⎝ ⎛⎭⎪⎫2(k +1)·(k +1)!2>0, 即证明(k -1)2k (k +1)·(k +1)!+⎝ ⎛⎭⎪⎫2(k +1)·(k +1)!2>0,显然成立.∴n =k +1时,结论也成立.综合①②可知:当n ≥3时,a n <b n 成立.综上可得:当n =1时,a 1>b 1;当n =2时,a 2=b 2, 当n ≥3,n ∈N *时,a n <b n .4.已知f n (x )=C 0n x n-C 1n (x -1)n +…+(-1)k C k n (x -k )n +…+(-1)n C n n (x -n )n,其中x ∈R ,n ∈N *,k ∈N ,k ≤n .(1)试求f 1(x ),f 2(x ),f 3(x )的值;(2)试猜测f n (x )关于n 的表达式,并证明你的结论. 解 (1)f 1(x )=C 01x -C 11(x -1)=1,f 2(x )=C 02x 2-C 12(x -1)2+C 22(x -2)2=x 2-2(x -1)2+(x -2)2=2,f 3(x )=C 03x 3-C 13(x -1)3+C 23(x -2)3-C 33(x -3)3=x 3-3(x -1)3+3(x -2)3-(x -3)3=6.(2)猜测f n (x )=n !,n ∈N *. 以下用数学归纳法证明.①当n =1时,f 1(x )=1,等式成立.②假设当n =m 时,等式成立,即f m (x )=k =0m (-1)k C k m (x -k )m =m !. 当n =m +1时,则f m +1(x )=k =0m +1(-1)k C k m +1·(x -k )m +1.因为C k m +1=C k m +C k -1m ,k C k m +1=(m +1)·C k -1m ,其中k =1,2,…,m , 且C 0m +1=C 0m ,C m +1m +1=C mm ,所以f m +1(x )=k =0m +1(-1)k C k m +1(x -k )m +1=x k =0m +1(-1)k C k m +1(x -k )m -k =0m +1(-1)k k C km +1(x -k )m=x k =0m(-1)k C k m(x -k )m+x ∑k =1m +1·(-1)k Ck -1m(x -k )m-(m +1)∑k =1m +1·(-1)k C k -1m (x -k )m=x ·m !+(-x +m +1)k =0m (-1)k C km ·[(x -1)-k ]m=x ·m !+(-x +m +1)·m! =(m +1)·m !=(m +1)!. 即n =m +1时,等式也成立.由①②可知,对n ∈N *,均有f n (x )=n !.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——解答题滚动练8套集合((含答案)35页

2018考前三个月高考数学理科(江苏专用)总复习训练题: ——解答题滚动练8套集合((含答案)解答题滚动练11.(2017·盐城三模)设△ABC 面积的大小为S ,且3AB →·AC →=2S . (1)求sin A 的值;(2)若C =π4,AB →·AC →=16,求AC .解 (1)设△ABC 的内角A ,B ,C 所对边的边长分别为a ,b ,c ,由3AB →·AC →=2S , 得3bc cos A =2×12bc sin A ,得sin A =3cos A .即sin 2A =9cos 2A =9(1-sin 2A ),所以sin 2A =910.又A ∈(0,π),所以sin A >0,故sin A =31010.(2)由sin A =3cos A 和sin A =31010,得cos A =1010,又AB →·AC →=16,所以bc ·cos A =16,得bc =1610① 又C =π4,所以sin B =sin(A +C )=sin A cos C +cos A sin C=31010×22+1010×22=255.在△ABC 中,由正弦定理,得b sin B =csin C ,即b 255=c 22,得c =104b ,②联立①②,解得b =8,即AC =8.2.(2017·江苏泰兴中学质检)如图,在正三棱柱ABC -A 1B 1C 1中,E 是侧面AA 1B 1B 对角线的交点,F 是侧面AA 1C 1C 对角线的交点,D 是棱BC 的中点.求证:(1)EF ∥平面ABC ; (2)平面AEF ⊥平面A 1AD . 证明 (1)连结A 1B 和A 1C .因为E ,F 分别是侧面AA 1B 1B 和侧面AA 1C 1C 的对角线的交点, 所以E ,F 分别是A 1B 和A 1C 的中点,所以EF ∥BC . 又BC ⊂平面ABC ,EF ⊄平面ABC , 故EF ∥平面ABC .(2)因为三棱柱ABC -A 1B 1C 1为正三棱柱, 所以A 1A ⊥平面ABC , 所以BC ⊥A 1A .故由EF ∥BC ,得EF ⊥A 1A .又因为D 是棱BC 的中点,且△ABC 为正三角形,所以BC ⊥AD . 故由EF ∥BC ,得EF ⊥AD .而A 1A ∩AD =A ,A 1A ,AD ⊂平面A 1AD , 所以EF ⊥平面A 1AD .又EF ⊂平面AEF ,故平面AEF ⊥平面A 1AD .3.如图,在平面直角坐标系xOy 中,设椭圆C :x 2a2+y 2=1(a >1).(1)若椭圆C 的焦距为2,求a 的值;(2)求直线y =kx +1被椭圆C 截得的线段长(用a ,k 表示);(3)若以A (0,1)为圆心的圆与椭圆C 总有4个公共点,求椭圆C 的离心率e 的取值范围.解 (1)由椭圆C :x 2a2+y 2=1(a >1)知,焦距为2a 2-1=2,解得a =±2,因为a >1,所以a = 2. (2)设直线y =kx +1被椭圆截得的线段长为AP ,由⎩⎪⎨⎪⎧y =kx +1,x 2a2+y 2=1,得(1+a 2k 2)x 2+2a 2kx =0,解得x 1=0,x 2=-2a 2k 1+a 2k2.因此AP =1+k 2|x 1-x 2|=2a 2|k |1+a 2k2·1+k 2. (3)因为圆与椭圆的公共点有4个,由对称性可设y 轴左侧的椭圆上有2个不同的公共点为P ,Q ,满足AP =AQ .记直线AP ,AQ 的斜率分别为k 1,k 2,k 1和k 2一正一负,且k 21≠k 22.由(2)知,AP =2a 2|k 1|1+k 211+a 2k 21,AQ =2a 2|k 2|1+k 221+a 2k 22,则2a 2|k 1|1+k 211+a 2k 21=2a 2|k 2|1+k 221+a 2k 22, 所以(k 21-k 22)[1+k 21+k 22+a 2(2-a 2)k 21k 22]=0, 因为k 21≠k 22,所以1+k 21+k 22+a 2(2-a 2)k 21k 22=0,变形得,⎝ ⎛⎭⎪⎫1k 21+1⎝ ⎛⎭⎪⎫1k 22+1=1+a 2(a 2-2),从而1+a 2(a 2-2)>1, 解得a >2,则e =c a=1-1a 2∈⎝ ⎛⎭⎪⎫22,1.4.已知数列{a n }是等差数列,{b n }是等比数列且满足a 1+a 2+a 3=9,b 1b 2b 3=27. (1)若a 4=b 3,b 4-b 3=m .①当m =18时,求数列{a n }和{b n }的通项公式; ②若数列{b n }是唯一的,求m 的值;(2)若a 1+b 1,a 2+b 2,a 3+b 3均为正整数,且成等比数列,求数列{a n }的公差d 的最大值. 解 (1)①由数列{a n }是等差数列及a 1+a 2+a 3=9,得a 2=3, 由数列{b n }是等比数列及b 1b 2b 3=27,得b 2=3. 设数列{a n }的公差为d ,数列{b n }的公比为q ,若m =18,则有⎩⎪⎨⎪⎧3+2d =3q ,3q 2-3q =18,解得⎩⎪⎨⎪⎧d =3,q =3或⎩⎪⎨⎪⎧d =-92,q =-2.所以{a n }和{b n }的通项公式为⎩⎪⎨⎪⎧a n =3n -3,b n =3n -1或⎩⎪⎨⎪⎧a n =-92n +12,b n =3(-2)n -2.②由题设b 4-b 3=m ,得3q 2-3q =m ,即3q 2-3q -m =0,(*) 因为数列{b n }是唯一的,所以若q =0,则m =0,检验知,当m =0时,q =1或0(舍去),满足题意; 若q ≠0,则Δ=(-3)2+12m =0,解得m =-34,代入(*)式,解得q =12,又b 2=3,所以{b n }是唯一的等比数列,符合题意. 所以m =0或-34.(2)依题意,36=(a 1+b 1)(a 3+b 3),设{b n }公比为q ,则有36=⎝ ⎛⎭⎪⎫3-d +3q (3+d +3q ),(**)记s =3-d +3q,t =3+d +3q ,则st =36.将(**)中的q 消去,整理得d 2+(s -t )d +3(s +t )-36=0,d 的大根为t -s +(s -t )2-12(s +t )+1442=t -s +(s +t -6)2-362,而s ,t ∈N *,所以(s ,t )的所有可能取值为:(1,36),(2,18),(3,12),(4,9),(6,6),(9,4),(12,3),(18,2),(36,1). 所以当s =1,t =36时,d 的最大值为35+5372.解答题滚动练21.(2017·南京、盐城二模)如图,在△ABC 中,D 为边BC 上一点,AD =6,BD =3,DC =2. (1)如图1,若AD ⊥BC ,求∠BAC 的大小; (2)如图2,若∠ABC =π4,求△ADC 的面积.解 (1) 由已知,得tan ∠BAD =36=12,tan ∠CAD =26=13,所以tan ∠BAC =tan(∠BAD +∠CAD )=12+131-12×13=1.因为∠BAC ∈(0,π),所以∠BAC =π4.(2) 以B 为原点,BC 所在直线为x 轴建立平面直角坐标系,则B (0,0),D (3,0),C (5,0). 因为∠ABC =π4,所以设A (a ,a ),其中a >0.由AD =6,BD =3,得(a -3)2+a 2=62,即2a 2-6a -27=0,解得a =32(1+7).所以S △ADC =12DC ·a =32(1+7).2.如图,ABCD 是一块边长为100米的正方形地皮,其中ATPS 是一半径为90米的底面为扇形小山(P 为圆弧TS 上的点),其余部分为平地.今有开发商想在平地上建一个两边落在BC 及CD 上的长方形停车场PQCR.(1)设∠PAB =θ,试将矩形PQCR 面积表示为θ的函数; (2)求停车场PQCR 面积的最大值及最小值.解 (1)S PQCR =f (θ)=(100-90cos θ)(100-90sin θ)=8100sin θcos θ-9000(sin θ+cos θ)+10000 , θ∈⎣⎢⎡⎦⎥⎤0,π2.(2)由(1)知S PQCR =f (θ)=8100sin θcos θ-9000(sin θ+cos θ)+10000,θ∈⎣⎢⎡⎦⎥⎤0,π2.令sin θ+cos θ=t ,则t =2sin ⎝ ⎛⎭⎪⎫θ+π4∈[1,2].∴S PQCR =81002t 2-9000t +10000-81002,当t =109时,S PQCR 取得最小值950(m 2),当t =2时,S PQCR 取得最大值14050-90002(m 2).答 停车场面积的最大值和最小值分别为14050-90002(m 2)和950(m 2).3.如图,点A (1,3)为椭圆x 22+y 2n=1上一定点,过点A 引两直线与椭圆分别交于B ,C 两点.(1)求椭圆方程;(2)若直线AB ,AC 与x 轴围成的是以点A 为顶点的等腰三角形. ①求直线BC 的斜率;②求△ABC 的面积的最大值,并求出此时直线BC 的方程.解 (1)把点A (1,3)代入x 22+y 2n =1得n =6,故椭圆方程为x 22+y 26=1.(2)①显然题中等腰三角形腰所在的直线不可能与x 轴垂直. 因此其斜率必存在,设两腰的斜率分别为k 1,k 2,由⎩⎪⎨⎪⎧y -3=k 1(x -1),x 22+y 26=1,消去y ,得(3+k 21)x 2+2k 1(3-k 1)x +(3-k 1)2-6=0,∴点B 的横坐标为x =1-6+23k 1k 21+3(x =1为点A 的横坐标),∴点B 的纵坐标为y =3-23k 21+6k 1k 21+3,即B ⎝ ⎛⎭⎪⎫1-6+23k 1k 21+3,3-23k 21+6k 1k 21+3.∵k 1+k 2=0,∴直线BC 的斜率为k BC = 3.②设B (x 1,y 1),C (x 2,y 2),直线BC 的方程为y =3x +m ,代入方程x 22+y 26=1得6x 2+23mx+m 2-6=0,∴x 1+x 2=-33m ,x 1x 2=m 2-66,∴BC =1+(3)2·|x 1-x 2| =2·(x 1+x 2)2-4x 1x 2 =23312-m 2,又点A 到直线BC 的距离为d =|m |2,∴S △ABC =12BC ·d =36m 2(12-m 2)=36-(m 2-6)2+36, ∴当m 2=6,即m =6或m =-6时,△ABC 面积取得最大值 3. 此时,直线BC 的方程为y =3x ± 6.4.已知函数f (x )=2x 3+ax 2+bx +c (a ,b ,c ∈R ).(1)若函数f (x )为奇函数,且图象过点(-1,2),求f (x )的解析式; (2)若x =1和x =2是函数f (x )的两个极值点. ①求a ,b 的值;②求函数f (x )在区间[0,3]上的零点个数. 解 (1)因为函数f (x )为奇函数,所以f (-x )=-f (x ),即2(-x )3+a (-x )2+b (-x )+c =-2x 3-ax 2-bx -c , 整理得,ax 2+c =0,所以a =c =0,从而f (x )=2x 3+bx , 又函数f (x )图象过点(-1,2),所以b =-4. 从而f (x )=2x 3-4x .(2)①f (x )=2x 3+ax 2+bx +c (a ,b ,c ∈R )的导函数f ′(x )=6x 2+2ax +b . 因为f (x )在x =1和x =2处取得极值, 所以f ′(1)=0,f ′(2)=0,即⎩⎪⎨⎪⎧6+2a +b =0,24+4a +b =0,解得a =-9,b =12.②由①得f(x)=2x3-9x2+12x+c(c∈R),f′(x)=6(x-1)(x-2).列表:显然,函数f(x)在[0,3]上的图象是一条不间断的曲线.由表知,函数f(x)在[0,3]上的最小值为f(0)=c,最大值为f(3)=9+c.所以当c>0或9+c<0(即c<-9)时,函数f(x)在区间[0,3]上的零点个数为0.当-5<c<0时,因为f(0)f(1)=c(5+c)<0,且函数f(x)在(0,1)上是单调增函数,所以函数f(x)在(0,1)上有1个零点.当-5<c<-4时,因为f(1)f(2)=(5+c)(4+c)<0,且f(x)在(1,2)上是单调减函数,所以函数f(x)在(1,2)上有1个零点.当-9<c<-4时,因为f(2)f(3)=(4+c)(9+c)<0,且f(x)在(2,3)上是单调增函数,所以函数f(x)在(2,3)上有1个零点.综上,当c>0或c<-9时,函数f(x)在区间[0,3]上的零点个数为0;当-9≤c<-5或-4<c≤0时,零点个数为1;当c=-4或c=-5时,零点个数为2;当-5<c<-4时,零点个数3.解答题滚动练31.(2017·镇江期末)已知向量m =(cos α,-1),n =(2,sin α),其中α∈⎝⎛⎭⎪⎫0,π2,且m ⊥n .(1)求cos2α的值; (2)若sin(α-β)=1010,且β∈⎝⎛⎭⎪⎫0,π2,求角β的大小.解 方法一 (1)由m ⊥n ,得2cos α-sin α=0,所以sin α=2cos α,代入cos 2α+sin 2α=1,得5cos 2α=1,且α∈⎝⎛⎭⎪⎫0,π2,则cos α=55,sin α=255, 则cos2α=2cos 2α-1=2×⎝⎛⎭⎪⎫552-1=-35. (2)由α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫0,π2,得α-β∈⎝ ⎛⎭⎪⎫-π2,π2.又sin(α-β)=1010,则cos(α-β)=31010. 则sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β)=255×31010-55×1010=22. 因为β∈⎝⎛⎭⎪⎫0,π2,所以β=π4.方法二 (1)由m ⊥n ,得2cos α-sin α=0,tan α=2,故cos2α=cos 2α-sin 2α=cos 2α-sin 2αcos 2α+sin 2α=1-tan 2α1+tan 2α=1-41+4=-35. (2)由(1)知,2cos α-sin α=0,且cos 2α+sin 2α=1,α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝⎛⎭⎪⎫0,π2,则sin α=255,cos α=55,以下同方法一(2).2.如图,在四棱锥P -ABCD 中,AB ⊥平面PAD ,DC ∥AB ,DC =2AB ,E 为棱PA 上一点. (1)设O 为AC 与BD 的交点,若PE =2AE ,求证:OE ∥平面PBC ; (2)若DE ⊥AP ,求证:PB ⊥DE .证明 (1)在△AOB 与△COD 中, 因为DC ∥AB ,DC =2AB ,所以AO CO =AB CD =12, 又因为PE =2AE ,所以在△APC 中,有AO CO =AE PE =12,则OE ∥PC . 又因为OE ⊄平面PBC ,PC ⊂平面PBC ,所以OE ∥平面PBC . (2)因为AB ⊥平面PAD ,DE ⊂平面PAD , 所以AB ⊥DE .又因为AP ⊥DE ,AB ⊂平面PAB ,AP ⊂平面PAB ,AP ∩AB =A , 所以DE ⊥平面PAB ,又PB ⊂平面PAB ,所以DE ⊥PB .3.已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为1.8元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下:7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.(1)当9天购买一次配料时,求该厂用于配料的保管费用P 是多少元?(2)设该厂x 天购买一次配料,求该厂在这x 天中用于配料的总费用y (元)关于x 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?解 (1)当9天购买一次时,该厂用于配料的保管费用P =70+0.03×200×(1+2)=88(元). (2)①当0<x ≤7时,y =360x +10x +236=370x +236, ②当x >7时,y =360x +236+70+6[(x -7)+(x -8)+…+2+1]=3x 2+321x +432∴y =⎩⎪⎨⎪⎧370x +236,0<x ≤7,3x 2+321x +432,x >7.∴设该厂x 天购买一次配料平均每天支付的费用为f (x )元. f (x )=⎩⎪⎨⎪⎧370x +236x ,0<x ≤7,3x 2+321x +432x,x >7.当0<x ≤7时,f (x )=370+236x ,当且仅当x =7时f (x )有最小值28267≈404(元),当x >7时,f (x )=3x 2+321x +432x=3⎝ ⎛⎭⎪⎫x +144x +321≥393,当且仅当x =12时取等号.∵393<404,∴当x =12时f (x )有最小值393元.4.已知函数f (x )=2ln x -x 2+ax (a ∈R ).(1)当a =2时,求f (x )的图象在x =1处的切线方程;(2)若函数g (x )=f (x )-ax +m 在⎣⎢⎡⎦⎥⎤1e ,e 上有两个零点,求实数m 的取值范围;(3)若函数f (x )的图象与x 轴有两个不同的交点A (x 1,0),B (x 2,0),且0<x 1<x 2,求证:f ′⎝ ⎛⎭⎪⎫x 1+x 22<0(其中f ′(x )是f (x )的导函数). (1)解 当a =2时,f (x )=2ln x -x 2+2x ,f ′(x )=2x-2x +2,切点坐标为(1,1),切线的斜率k =f ′(1)=2,则切线方程为y -1=2(x -1),即y =2x -1. (2)解 g (x )=2ln x -x 2+m ,则g ′(x )=2x -2x =-2(x +1)(x -1)x,∵x ∈⎣⎢⎡⎦⎥⎤1e ,e ,故g ′(x )=0时,x =1.当1e <x <1时,g ′(x )>0;当1<x <e 时,g ′(x )<0.故g (x )在x =1处取得极大值g (1)=m -1.又g ⎝ ⎛⎭⎪⎫1e =m -2-1e 2,g (e)=m +2-e 2,g (e)-g ⎝ ⎛⎭⎪⎫1e =4-e 2+1e 2<0,则g (e)<g ⎝ ⎛⎭⎪⎫1e ,所以g (x )在⎣⎢⎡⎦⎥⎤1e ,e 上的最小值为g (e). g (x )在⎣⎢⎡⎦⎥⎤1e ,e 上有两个零点的条件是⎩⎪⎨⎪⎧g (1)=m -1>0,g ⎝ ⎛⎭⎪⎫1e =m -2-1e 2≤0,解得1<m ≤2+1e 2,所以实数m 的取值范围是⎝⎛⎦⎥⎤1,2+1e 2.(3)证明 因为f (x )的图象与x 轴交于两个不同的点A (x 1,0),B (x 2,0),所以方程2ln x -x 2+ax =0的两个根为x 1,x 2,则⎩⎪⎨⎪⎧2ln x 1-x 21+ax 1=0,2ln x 2-x 22+ax 2=0,两式相减得a =(x 1+x 2)-2(ln x 1-ln x 2)x 1-x 2,又f (x )=2ln x -x 2+ax ,f ′(x )=2x -2x +a ,则f ′⎝ ⎛⎭⎪⎫x 1+x 22=4x 1+x 2-(x 1+x 2)+a =4x 1+x 2-2(ln x 1-ln x 2)x 1-x 2.下证4x 1+x 2-2(ln x 1-ln x 2)x 1-x 2<0,即证明2(x 2-x 1)x 1+x 2+ln x 1x 2<0,令t =x 1x 2. 因为0<x 1<x 2,所以0<t <1,即证明u (t )=2(1-t )t +1+ln t <0在0<t <1上恒成立.因为u ′(t )=-2(t +1)-2(1-t )(t +1)2+1t =1t -4(t +1)2=(t -1)2t (t +1)2,又0<t <1,所以u ′(t )>0, 所以u (t )在(0,1)上是增函数,则u (t )<u (1)=0,从而知2(x 2-x 1)x 1+x 2+ln x 1x 2<0,故4x 1+x 2-2(ln x 1-ln x 2)x 1-x 2<0,即f ′⎝ ⎛⎭⎪⎫x 1+x 22<0成立.解答题滚动练41.如图,在四棱锥P -ABCD 中,已知底面ABCD 为矩形,且AB =2,BC =1,E ,F 分别是AB ,PC 的中点,PA ⊥DE .(1)求证:EF ∥平面PAD ; (2)求证:平面PAC ⊥平面PDE .证明 (1)方法一 取线段PD 的中点M ,连结FM ,AM . 因为F 为PC 的中点,所以FM ∥CD ,且FM =12CD .因为四边形ABCD 为矩形,E 为AB 的中点, 所以EA ∥CD ,且EA =12CD .所以FM ∥EA ,且FM =EA .所以四边形AEFM 为平行四边形,所以EF ∥AM . 又AM ⊂平面PAD ,EF ⊄平面PAD , 所以EF ∥平面PAD .方法二 连结CE 并延长交DA 的延长线于N ,连结PN .因为四边形ABCD 为矩形,所以AD ∥BC , 所以∠BCE =∠ANE ,∠CBE =∠NAE . 又AE =EB ,所以△CEB ≌△NEA . 所以CE =NE .又F 为PC 的中点,所以EF ∥NP . 又NP ⊂平面PAD ,EF ⊄平面PAD , 所以EF ∥平面PAD .方法三 取CD 的中点Q ,连结FQ ,EQ .在矩形ABCD 中,E 为AB 的中点, 所以AE =DQ ,且AE ∥DQ . 所以四边形AEQD 为平行四边形, 所以EQ ∥AD .又AD ⊂平面PAD ,EQ ⊄平面PAD , 所以EQ ∥平面PAD .因为Q ,F 分别为CD ,CP 的中点, 所以FQ ∥PD .又PD ⊂平面PAD ,FQ ⊄平面PAD , 所以FQ ∥平面PAD .又FQ ,EQ ⊂平面EQF ,FQ ∩EQ =Q ,所以平面EQF ∥平面PAD . 因为EF ⊂平面EQF ,所以EF ∥平面PAD .(2)设AC ,DE 相交于G . 在矩形ABCD 中, 因为AB =2BC ,E 为AB 的中点,所以DA AE =CDDA= 2.又∠DAE =∠CDA ,所以△DAE ∽△CDA , 所以∠ADE =∠DCA .又∠ADE +∠CDE =∠ADC =90°, 所以∠DCA +∠CDE =90°.由△DGC 的内角和为180°,得∠DGC =90°. 即DE ⊥AC . 又PA ⊥DE ,PA ∩AC =A ,PA ,AC ⊂平面PAC ,所以DE ⊥平面PAC ,又DE ⊂平面PDE ,所以平面PAC ⊥平面PDE .2.如图所示,A ,B 是两个垃圾中转站,B 在A 的正东方向16km 处,AB 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在AB 的北面建一个垃圾发电厂P .垃圾发电厂P 的选址拟满足以下两个要求(A ,B ,P 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点P 到直线AB 的距离要尽可能大).现估测得A ,B 两个中转站每天集中的生活垃圾量分别约为30吨和50吨,问垃圾发电厂该如何选址才能同时满足上述要求?解 方法一 由条件①,得PA PB =5030=53. 设PA =5x ,PB =3x ,则cos ∠PAB =(5x )2+162-(3x )22×16×5x =x 10+85x ,所以点P 到直线AB 的距离h =PA sin ∠PAB =5x1-⎝ ⎛⎭⎪⎫x 10+85x 2=-14x 4+17x 2-64 =-14(x 2-34)2+225, 所以当x 2=34,即x =34时,h 取得最大值15km. 即选址应满足PA =534km ,PB =334km.方法二 以AB 所在直线为x 轴,线段AB 的中垂线为y 轴,建立如图所示的平面直角坐标系, 则A (-8,0),B (8,0).由条件①,得PA PB =5030=53.设P (x ,y )(y >0),则3(x +8)2+y 2=5(x -8)2+y 2, 化简得(x -17)2+y 2=152(y >0),即点P 的轨迹是以点(17,0)为圆心、15为半径的圆位于x 轴上方的部分. 则当x =17时,点P 到直线AB 的距离最大,最大值为15km. 所以点P 的选址应满足在上述坐标系中坐标为(17,15)即可.方法三 由条件①,得PA PB =5030=53.过点P 作PD 垂直于AB ,设PD =h ,AD =x ,则DB =|16-x |, 3x 2+h 2=5h 2+(16-x )2,h 2=-(x -25)2+225.所以当x =25时,h 取得最大值15. 答 选址应满足PA =534km ,PB =334km. 3.已知数列{a n }满足a n +a n +1=2n -3,n ∈N *. (1)若数列{a n }为等差数列,求a 1;(2)设a 1=a (a >0),∀n ∈N *,n ≥2,不等式a 2n +a 2n +1a n +a n +1≥3成立,求实数a 的最小值.解 (1)设数列{a n }公差为d ,则2n -3=a n +a n +1=a 1+(n -1)d +a 1+nd =2dn +(2a 1-d )对∀n ∈N *成立,所以⎩⎪⎨⎪⎧2d =2,2a 1-d =-3,故d =1,a 1=-1.(2)由a n +a n +1=2n -3,知{a n -(n -2)}为等比数列,公比q =-1, 所以a n -(n -2)=(a +1)(-1)n -1,故a n =(n -2)+(a +1)(-1)n -1.①当n 为不小于3的奇数时,由a 2n +a 2n +1a n +a n +1≥3,得(n -1+a )2+(n -2-a )22n -3≥3,化简得a 2+a ≥-(n -3)2+2恒成立,所以a 2+a ≥2,解得a ≥1. ②n 为不小于2的偶数时,同理有a 2+3a ≥-(n -3)2恒成立,因为a >0,显然恒成立.所以a >0.由①②得a ≥1,故a 的最小值为1.4.已知椭圆C 的方程为x 2a 2+y 2b2=1(a >b >0),点A ,B 分别为其左、右顶点,点F 1,F 2分别为其左、右焦点,以点A 为圆心、AF 1为半径作圆A ,以点B 为圆心、OB 为半径作圆B .若直线l :y =-33x 被圆A 和圆B 截得的弦长之比为15∶6. (1)求椭圆C 的离心率;(2)已知a =7,问在x 轴上是否存在点P ,使得过点P 有无数条直线被圆A 和圆B 截得的弦长之比为3∶4,若存在,请求出所有点P 的坐标;若不存在,请说明理由.解 (1)分别过点A ,B 作直线l 的垂线,垂足为A 1,B 1, 由题意得AA 1=BB 1,由点到直线距离公式得AA 1=BB 1=a2,因为圆A 以AF 1为半径,所以半径为a -c ,被直线l 截得的弦长为2(a -c )2-⎝ ⎛⎭⎪⎫a 22,因为圆B 以OB 为半径,所以半径为a ,被直线l 截得的弦长为2a 2-⎝ ⎛⎭⎪⎫a 22. 因为直线l :y =-33x 被圆A 和圆B 截得的弦长之比为15∶6,化简得7a 2-32ac +16c 2=0,两边同时除以a 2,得16e 2-32e +7=0, 解得e =14或e =74(舍去).所以所求的离心率为14.(2)存在点P ,使得过点P 有无数条直线被圆A 和圆B 截得的弦长之比为3∶4, 设点P (x 0,0),由题意可得直线方程为y =k (x -x 0), 则直线截圆A 所得的弦长为2(a -c )2-⎝⎛⎭⎪⎫|k (-7-x 0)|1+k 22, 直线截圆B 所得的弦长为2a 2-⎝⎛⎭⎪⎫|k (7-x 0)|1+k 22,2(a -c )2-⎝ ⎛⎭⎪⎫k (7+x 0)1+k 222a 2-⎝ ⎛⎭⎪⎫k (7-x 0)1+k 22=34, 即有16⎣⎢⎡⎦⎥⎤(a -c )2-⎝ ⎛⎭⎪⎫7k +kx 01+k 22=9⎣⎢⎡⎦⎥⎤a 2-⎝ ⎛⎭⎪⎫7k -kx 01+k 22,其中a =7,c =74,a -c =214,上式整理得,16(7k +kx 0)21+k 2=9(7k -kx 0)21+k 2,关于k 的方程有无穷多解, 故有7x 20+350x 0+343=0, 解得x 0=-1或x 0=-49,故存在2个点P ,使得过点P 有无数条直线被圆A 和圆B 截得的弦长之比为3∶4,P 点坐标为(-1,0)或(-49,0).解答题滚动练51.已知α∈(0,π),且sin ⎝ ⎛⎭⎪⎫α+π3=6-24. (1)求sin ⎝ ⎛⎭⎪⎫α-π4的值;(2)求cos ⎝⎛⎭⎪⎫2α-π3的值. 解 方法一 联立⎩⎪⎨⎪⎧sin ⎝⎛⎭⎪⎫α+π3=6-24,sin 2α+cos 2α=1.⇒4sin 2α-(6-2)sin α-(1+3)=0, 解得sin α=6+24或sin α=-22, 因为α∈(0,π),所以sin α=6+24, 所以cos α=2-64. (1)sin ⎝ ⎛⎭⎪⎫α-π4=sin αcos π4-cos αsin π4=6+24×22-2-64×22=62×22=32. (2)sin2α=2sin αcos α=2×6+24×2-64=-12,cos2α=1-2sin 2α=-32. cos ⎝⎛⎭⎪⎫2α-π3=cos2αcos π3+sin2αsin π3=-32.方法二 因为α∈(0,π),sin ⎝ ⎛⎭⎪⎫α+π3=6-24<12,所以5π6<α+π3<4π3,sin 11π12=sin ⎝ ⎛⎭⎪⎫π4-π6=sin π4cos π6-cos π4sin π6=6-24,所以α+π3=11π12,所以α=7π12.(1)sin ⎝ ⎛⎭⎪⎫α-π4=sin ⎝ ⎛⎭⎪⎫7π12-π4=sin π3=32.(2)cos ⎝ ⎛⎭⎪⎫2α-π3=cos ⎝⎛⎭⎪⎫2×7π12-π3=cos 5π6=-32.2.如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.(1)求证:AD⊥平面PAB;(2)求证:CN∥平面PAB.证明(1)因为BD垂直平分AC,所以BA=BC,在△ABC中,因为∠ABC=120°,所以∠BAC=30°.因为△ACD是正三角形,所以∠DAC=60°,所以∠BAD=90°,即AD⊥AB.因为AB=1,∠ABC=120°,所以AD=AC=3,又因为PA=1,PD=2,由PA2+AD2=PD2,知∠PAD=90°,即AD⊥AP.因为AB,AP⊂平面PAB,AB∩AP=A,所以AD⊥平面PAB.(2)方法一取AD的中点H,连结CH,NH.因为N为PD的中点,所以HN∥PA,因为PA⊂平面PAB,HN⊄平面PAB,所以HN∥平面PAB.由△ACD是正三角形,H为AD的中点,所以CH⊥AD.由(1)知,BA⊥AD,所以CH∥BA,因为BA⊂平面PAB,CH⊄平面PAB,所以CH∥平面PAB.因为CH,HN⊂平面CNH,CH∩HN=H,所以平面CNH∥平面PAB.因为CN⊂平面CNH,所以CN∥平面PAB.方法二取PA的中点S,过C作CT∥AD交AB的延长线于T,连结ST,SN.因为N 为PD 的中点,所以SN ∥AD ,且SN =12AD ,因为CT ∥AD ,所以CT ∥SN . 由(1)知,AB ⊥AD ,所以CT ⊥AT , 在Rt △CBT 中,BC =1,∠CBT =60°, 得CT =32. 由(1)知,AD =3,所以CT =12AD ,所以CT =SN .所以四边形SNCT 是平行四边形, 所以CN ∥TS .因为TS ⊂平面PAB ,CN ⊄平面PAB , 所以CN ∥平面PAB .3.已知圆O :x 2+y 2=4,两个定点A (a,2),B (m,1),其中a ∈R ,m >0.P 为圆O 上任意一点,且PA PB=k (k 为常数). (1)求常数k 的值;(2)过点E (a ,t )作直线l 与圆C :x 2+y 2=m 交于M ,N 两点,若M 点恰好是线段NE 的中点,求实数t 的取值范围.解 (1)设点P (x ,y ),x 2+y 2=4,PA =(x -a )2+(y -2)2,PB =(x -m )2+(y -1)2,因为PAPB=k ,所以(x -a )2+(y -2)2=k 2[(x -m )2+(y -1)2], 又x 2+y 2=4,化简得2ax +4y -a 2-8=k 2(2mx +2y -m 2-5), 因为P 为圆O 上任意一点,所以⎩⎪⎨⎪⎧2a =2mk 2,4=2k 2,a 2+8=k 2(m 2+5),又m >0,k >0,解得⎩⎨⎧k =2,a =2,m =1,所以常数k = 2.(2)方法一 设M (x 0,y 0),M 是线段NE 的中点,N (2x 0-2,2y 0-t ),又点M ,N 在圆C 上,即关于x ,y 的方程组⎩⎪⎨⎪⎧x 20+y 20=1,(2x 0-2)2+(2y 0-t )2=1有解,化简得⎩⎪⎨⎪⎧x 20+y 20=1,8x 0+4ty 0-t 2-7=0有解,即直线n :8x +4ty -t 2-7=0与圆C :x 2+y 2=1有交点, 则点(0,0)到直线n 的距离d =|t 2+7|64+16t2≤1,化简得,t 4-2t 2-15≤0, 解得t ∈[-5,5].方法二 设过E 的切线与圆C 切于切点F ,EF 2=EM ·EN , 又M 是线段NE 的中点,所以EN =2MN ,EM =MN ,所以EF 2=2MN 2, 又EF 2=EC 2-CF 2=22+t 2-1=t 2+3,MN ≤2, 所以t 2+3≤8, 所以t ∈[-5,5].4.已知函数f (x )=-x 2-(2a +1)x +ln x ,且该函数在x =1处取得极值. (1)求实数a 的值,并求出函数的单调区间; (2)若函数g (x )=f (x )-b +5x2在区间(0,2018)上只有一个零点,求实数b 的值. 解 (1)由已知,得f ′(x )=-2x -2a -1+1x,据题意,f ′(1)=0,得到a =-1, 所以f (x )=-x 2+x +ln x ,f ′(x )=-2x +1+1x=(2x +1)(-x +1)x.由x >0,令f ′(x )>0,得0<x <1,令f ′(x )<0,得x >1,所以函数f (x )在x =1处取得极值,所以a =-1,f (x )的单调增区间为(0,1),f (x )的单调减区间为(1,+∞).(2)g (x )=f (x )-b +5x 2=-x 2+7x 2+ln x -b ,x ∈(0,2018).则g ′(x )=-2x +72+1x,令g ′(x )=0, 得x =2,负值舍去.当0<x <2时,g ′(x )>0,g (x )的单调增区间为(0,2), 当2<x <2018时,g ′(x )<0,g (x )的单调减区间为(2,2018). 所以函数g (x )=f (x )-b +5x2在区间(0,2018)上只有一个零点,等价于g (2)=0, 解得b =ln2+3.解答题滚动练61.在△ABC 中,三个内角分别为A ,B ,C ,已知sin ⎝⎛⎭⎪⎫A +π6=2cos A .(1)若cos C =63,求证:2a -3c =0; (2)若B ∈⎝⎛⎭⎪⎫0,π3,且cos(A -B )=45,求sin B .(1)证明 因为sin ⎝ ⎛⎭⎪⎫A +π6=2cos A ,得32sin A +12cos A =2cos A ,即sin A =3cos A ,因为A ∈(0,π),且cos A ≠0, 所以tan A =3,所以A =π3.因为sin 2C +cos 2C =1,cos C =63,C ∈(0,π), 所以sin C =33, 由正弦定理知a sin A =c sin C ,即a c =sin A sin C =3233=32,即2a -3c =0.(2)解 因为B ∈⎝ ⎛⎭⎪⎫0,π3,所以A -B =π3-B ∈⎝ ⎛⎭⎪⎫0,π3,因为sin 2(A -B )+cos 2(A -B )=1, 所以sin(A -B )=35,所以sin B =sin(A -(A -B ))=sin A cos(A -B )-cos A ·sin(A -B )=43-310.2.已知函数f (x )=ax 3-2x -ln x ,a ∈R .(1)若曲线y =f (x )在x =1处的切线方程为y =b ,求a +b 的值; (2)在(1)的条件下,求函数f (x )零点的个数. 解 (1)f ′(x )=3ax 2-2-1x,由题意,f ′(1)=0,f (1)=b ,解得,a =1,b =-1, 所以a +b =0.(2)由(1)知,f (x )=x 3-2x -ln x ,f ′(x )=3x 2-2-1x=3x 3-2x -1x=(x -1)(3x 2+3x +1)x,令f ′(x )=0,得x =1,且当0<x <1时,f ′(x )<0;当x >1时,f ′(x )>0, 所以函数f (x )在(0,1)上单调递减,在(1,+∞)上单调递增.因为f (1)=-1<0,f ⎝ ⎛⎭⎪⎫1e =1e -2e +1>0,f (e)=e 3-2e -1>0,函数f (x )在区间⎣⎢⎡⎦⎥⎤1e ,1和[1,e]上的图象是一条不间断的曲线,由零点存在性定理,知函数f (x )有两个零点. 3.已知圆M :x 2+(y -4)2=4,点P 是直线l :x -2y =0上的一动点,过点P 作圆M 的切线PA ,PB ,切点为A ,B .(1)当切线PA 的长度为23时,求点P 的坐标;(2)若△PAM 的外接圆为圆N ,试问:当P 运动时,圆N 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由; (3)求线段AB 长度的最小值.解 (1)由题意可知,圆M 的半径r =2,设P (2b ,b ), 因为PA 是圆M 的一条切线,A 为切点, 所以∠MAP =90°,所以MP =(0-2b )2+(4-b )2=AM 2+AP 2=4, 解得b =0或b =85,所以P (0,0)或P ⎝⎛⎭⎪⎫165,85.(2)设P (2b ,b ),因为∠MAP =90°,所以经过A ,P ,M 三点的圆N 以MP 为直径,其方程为(x -b )2+⎝⎛⎭⎪⎫y -b +422=4b 2+(b -4)24,即(2x +y -4)b -(x 2+y 2-4y )=0.由⎩⎪⎨⎪⎧2x +y -4=0,x 2+y 2-4y =0,解得⎩⎨⎧x =0,y =4,或⎩⎪⎨⎪⎧x =85,y =45,所以圆过定点(0,4),⎝ ⎛⎭⎪⎫85,45.(3)因为圆N 方程为(x -b )2+⎝ ⎛⎭⎪⎫y -b +422=4b 2+(b -4)24,即x 2+y 2-2bx -(b +4)y +4b =0.①圆M :x 2+(y -4)2=4,即x 2+y 2-8y +12=0.② ②-①得圆M 与圆N 的相交弦AB 所在直线方程为 2bx +(b -4)y +12-4b =0, 点M 到直线AB 的距离d =45b 2-8b +16, 相交弦长AB =24-d 2=41-45b 2-8b +16 =41-45⎝ ⎛⎭⎪⎫b -452+645.当b =45时,AB 有最小值11.4.如图是一“T ”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m ,东西向渠宽2m(从拐角处,即图中A ,B 处开始).假定渠内的水面始终保持水平位置(即无高度差).(1)在水平面内,过点A 的一条直线与水渠的内壁交于P ,Q 两点,且与水渠的一边的夹角为θ⎝⎛⎭⎪⎫0<θ<π2,将线段PQ的长度l 表示为θ的函数;(2)若从南面漂来一根长为7m 的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?请说明理由.解 (1)由题意,PA =2sin θ,QA =4cos θ,所以l =PA +QA =2sin θ+4cos θ⎝ ⎛⎭⎪⎫0<θ<π2. (2)设f (θ)=2sin θ+4cos θ,θ∈⎝⎛⎭⎪⎫0,π2.由f ′(θ)=-2cos θsin 2θ+4sin θcos 2θ=2(22sin 3θ-cos 3θ)sin 2θcos 2θ, 令f ′(θ)=0,得tan θ0=22. 且当θ∈(0,θ0),f ′(θ)<0;当θ∈⎝ ⎛⎭⎪⎫θ0,π2,f ′(θ)>0,所以f (θ)在(0,θ0)上单调递减,在⎝⎛⎭⎪⎫θ0,π2上单调递增,所以当θ=θ0时,f (θ)取得极小值,即为最小值.即这根竹竿能通过拐角处的长度的最大值为36m.因为36>7,所以这根竹竿能从拐角处一直漂向东西向的水渠.解答题滚动练71.如图,在三棱柱ABC -A 1B 1C 1中,所有棱长都相等,且∠ABB 1=60°,D 为AC 的中点,求证:(1)B 1C ∥平面A 1BD ; (2)AB ⊥B 1C .证明 (1)连结AB 1交A 1B 于点E ,连结DE .因为D ,E 分别为AC ,AB 1的中点,所以DE ∥B 1C . 因为DE ⊂平面A 1BD ,B 1C ⊄平面A 1BD , 所以B 1C ∥平面A 1BD .(2)取AB 的中点O ,连结OC ,OB 1.因为BA =BB 1,且∠ABB 1=60°,所以△ABB 1为正三角形,而O 为AB 的中点,所以OB 1⊥AB . 在正三角形ABC 中,O 为AB 中点,所以OC ⊥AB . 因为OB 1∩OC =O ,且OB 1⊂平面OB 1C ,OC ⊂平面OB 1C , 所以AB ⊥平面OB 1C .又因为B 1C ⊂平面OB 1C ,所以AB ⊥B 1C .2.已知数列{a n }的前n 项和S n 满足:S n =t (S n -a n +1)(t 为常数,且t ≠0,t ≠1). (1)证明:{a n }成等比数列;(2)设b n =a 2n +S n ·a n ,若数列{b n }为等比数列,求t 的值. (1)证明 当n =1时,S 1=t (S 1-a 1+1),得a 1=t ,当n ≥2时,S n =t (S n -a n +1),即(1-t )S n =-ta n +t ,(1-t )S n -1=-ta n -1+t , 所以a n =ta n -1,故{a n }成等比数列.(2)解 由(1)知{a n }成等比数列且公比是t ,∴a n =t n,故b n =(t n )2+t (1-t n )1-t ·t n ,即b n =t 2n +t n +1-2t 2n +11-t.若数列{b n }是等比数列,则有b 22=b 1·b 3,而b 1=2t 2,b 2=t 3(2t +1),b 3=t 4(2t 2+t +1), 故[t 3(2t +1)]2=(2t 2)·t 4(2t 2+t +1),解得t =12,再将t =12代入b n 得b n =⎝ ⎛⎭⎪⎫12n ,由b n +1b n =12知{b n }为等比数列,所以t =12. 3.图1是一段半圆柱形水渠的直观图,其横断面如图2所示,其中C 为半圆弧ACB 的中点,渠宽AB 为2m.(1)当渠中水深CD 为0.4m 时,求水面的宽度;(2)若把这条水渠改挖(不准填土)成横断面为等腰梯形的水渠,且使渠的底面与地面平行,则当改挖后的水渠底宽为多少时,所挖出的土量最少?解 (1) 如图,以AB 所在直线为x 轴,AB 的垂直平分线为y 轴,以1m 为单位长度,建立平面直角坐标系xOy .半圆弧ACB 的方程为x 2+y 2=1(y ≤0),A (-1,0),B (1,0),C (0,-1),D (0,-0.6).直线y =-0.6与半圆弧的交点为(±0.8,-0.6). 答 所求的水面宽度为1.6 m.(2)要使得所挖出的土量最少,则等腰梯形的两腰及下底与半圆弧ACB 相切.设等腰梯形的右腰与半圆弧ACB 相切于点T (cos θ,sin θ)⎝ ⎛⎭⎪⎫-π2<θ<0,则切线EF 的方程为x cos θ+y sin θ=1. 令y =0,得E ⎝⎛⎭⎪⎫1cos θ,0,令y =-1,得F ⎝⎛⎭⎪⎫1+sin θcos θ,-1,设梯形OCFE 的面积为S ,则S =12(CF +OE )·OC=12⎝ ⎛⎭⎪⎫1cos θ+1+sin θcos θ×1=2+sin θ2cos θ, S ′=2cos 2θ-(2+sin θ)·(-2sin θ)4cos 2θ=1+2sin θ2cos 2θ, 令S ′=0,得θ=-π6.当θ=-π6时,S 取得最小值,最小值为32,此时CF =1+sin ⎝ ⎛⎭⎪⎫-π6cos ⎝ ⎛⎭⎪⎫-π6=33.答 当改挖后的水渠底宽为233m 时,所挖出的土量最少. 4.函数f (x )=1+ln x -k (x -2)x,其中k 为常数. (1)若k =0,求曲线y =f (x )在点(1,f (1))处的切线方程; (2)若k =5,求证:f (x )有且仅有两个零点;(3)若k 为整数,且当x >2时,f (x )>0恒成立,求k 的最大值. (1)解 当k =0时,f (x )=1+ln x . 因为f ′(x )=1x,从而f ′(1)=1.又f (1)=1,所以曲线y =f (x )在点(1,f (1))处的切线方程为y -1=x -1, 即x -y =0.(2)证明 当k =5时,f (x )=ln x +10x-4.因为f ′(x )=x -10x 2,从而当x ∈(0,10)时,f ′(x )<0,f (x )单调递减;当x ∈(10,+∞)时,f ′(x )>0,f (x )单调递增. 所以当x =10时,f (x )有极小值. 因为f (10)=ln10-3<0,f (1)=6>0, 所以f (x )在(1,10)之间有一个零点. 因为f (e 4)=4+10e4-4>0,所以f (x )在(10,e 4)之间有一个零点. 从而f (x )有两个不同的零点. (3)解 方法一 由题意知,1+ln x -k (x -2)x>0在(2,+∞)上恒成立, 即k <x +x ln xx -2在(2,+∞)上恒成立. 令h (x )=x +x ln x x -2,则h ′(x )=x -2ln x -4(x -2)2. 设ν(x )=x -2ln x -4,则ν′(x )=x -2x. 当x ∈(2,+∞)时,ν′(x )>0,所以ν(x )在(2,+∞)上为增函数.因为ν(8)=8-2ln8-4=4-2ln8<0,ν(9)=5-2ln9>0, 所以存在x 0∈(8,9),ν(x 0)=0,即x 0-2ln x 0-4=0.当x ∈(2,x 0)时,h ′(x )<0,h (x )单调递减,当x ∈(x 0,+∞)时,h ′(x )>0,h (x )单调递增.所以当x =x 0时,h (x )的最小值为h (x 0)=x 0+x 0ln x 0x 0-2.因为ln x 0=x 0-42,所以h (x 0)=x 02∈(4,4.5). 故所求的整数k 的最大值为4. 方法二 由题意知,1+ln x -k (x -2)x>0在(2,+∞)上恒成立. f (x )=1+ln x -k (x -2)x ,f ′(x )=x -2kx2.①当2k ≤2,即k ≤1时,f ′(x )>0在(2,+∞)上恒成立, 所以f (x )在(2,+∞)上单调递增. 而f (2)=1+ln2>0成立,所以满足要求. ②当2k >2,即k >1时,当x ∈(2,2k )时,f ′(x )<0,f (x )单调递减,当x ∈(2k ,+∞)时,f ′(x )>0,f (x )单调递增.所以当x =2k 时,f (x )有最小值f (2k )=2+ln2k -k . 从而f (x )>0在(2,+∞)上恒成立等价于2+ln2k -k >0.令g (k )=2+ln2k -k ,则g ′(k )=1-kk<0,从而g (k )在(1,+∞)为减函数.因为g (4)=ln8-2>0,g (5)=ln10-3<0, 所以使2+ln2k -k >0成立的最大正整数k =4. 综合①②,知所求的整数k 的最大值为4.解答题滚动练81.(2017·江苏溧阳中学模拟)在三棱锥S -ABC 中,SA ⊥平面ABC ,SA =AB =AC =33BC ,点D 是BC 边的中点,点E 是线段AD 上一点,且AE =4DE ,点M 是线段SD 上一点.(1)求证:BC ⊥AM ;(2)若AM ⊥平面SBC ,求证:EM ∥平面ABS . 证明 (1)∵AB =AC ,D 是BC 的中点,∴AD ⊥BC , ∵SA ⊥平面ABC ,BC ⊂平面ABC , ∴SA ⊥BC ,又AD ∩SA =A ,AD ,SA ⊂平面SAD , ∴BC ⊥平面SAD ,又AM ⊂平面SAD ,∴BC ⊥AM .(2)∵AM ⊥平面SBC ,SD ⊂平面SBC ,∴AM ⊥SD .设SA =1,则AD =12,SD =52,AM =55,SM =255,MD =510.∴SM =4MD . 又AE =4DE , ∴ME ∥SA ,又ME ⊄平面ABS ,SA ⊂平面ABS , ∴EM ∥平面ABS .2.(2017·江苏郑集高级中学质检)在△ABC 中,已知(sin A +sin B +sin C )(sin B +sin C -sin A )=3sin B sin C . (1)求角A 的值;(2)求3sin B -cos C 的最大值.解 (1)因为(sin A +sin B +sin C )(sin B +sin C -sin A )=3sin B sin C , 由正弦定理,得(a +b +c )(b +c -a )=3bc ,所以b 2+c 2-a 2=bc ,所以cos A =b 2+c 2-a 22bc =12,因为A ∈(0,π),所以A =π3. (2)由A =π3,得B +C =2π3,所以3sin B -cos C =3sin B -cos ⎝ ⎛⎭⎪⎫2π3-B=3sin B -⎝ ⎛⎭⎪⎫-12cos B +32sin B =sin ⎝ ⎛⎭⎪⎫B +π6,因为0<B <2π3,所以π6<B +π6<5π6,当B +π6=π2,即B =π3时,3sin B -cos C 取最大值1.3.(2017·南通、扬州、淮安、宿迁、泰州、徐州六市二调)一缉私艇巡航至距领海边界线l (一条南北方向的直线)3.8海里的A 处,发现在其北偏东30°方向相距4海里的B 处有一走私船正欲逃跑,缉私艇立即追击.已知缉私艇的最大航速是走私船最大航速的3倍.假设缉私艇和走私船均按直线方向以最大航速航行.(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;(参考数据:sin17°=36,33≈5.7446); (2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.解 (1)如图甲,设缉私艇在点C 处拦截到走私船. 在△ABC 中,B =120°,AB =4,设BC =a ,AC =3a . 由正弦定理,得sin A a =sin120°3a ,所以sin A =36.因为B =120°,所以A 为锐角,从而A =17°. 由余弦定理,得(3a )2=42+a 2-2×4a cos120°, 即2a 2-a -4=0,解得a =1+334≈1.7. 点B 到l 的距离为3.8-2=1.8,而a <1.8,所以点C 在领海内. 答 缉私艇的追击方向应为北偏东47°.(2)如图乙,以A 为原点,正北方向为y 轴正方向,1海里为1个单位长度,建立平面直角坐标系xAy ,则A (0,0),B (2,23),直线l 的方程为x =3.8. 设缉私艇在点P (x ,y )处拦截到走私船.由AP =3BP ,得x 2+y 2=9[(x -2)2+(y -23)2].整理,得⎝ ⎛⎭⎪⎫x -942+⎝ ⎛⎭⎪⎫y -9342=94.点P 的轨迹是以M ⎝ ⎛⎭⎪⎫94,934为圆心,半径r =32的圆.圆心M 到直线l 的距离d =3.8-94=1.55>r ,所以直线l 与圆M 外离,即点P 总在领海内.答 无论走私船沿何方向逃跑,缉私艇总能在领海内成功拦截.4.如图,在平面直角坐标系xOy 中,已知圆O :x 2+y 2=4,椭圆C :x 24+y 2=1,A 为椭圆右顶点.过原点O 且异于坐标轴的直线与椭圆C 交于B ,C 两点,直线AB 与圆O 的另一交点为P ,直线PD 与圆O 的另一交点为Q ,其中D ⎝ ⎛⎭⎪⎫-65,0.设直线AB ,AC 的斜率分别为k 1,k 2.(1)求k 1k 2的值;(2)记直线PQ ,BC 的斜率分别为k PQ ,k BC ,是否存在常数λ,使得k PQ =λk BC ?若存在,求λ值;若不存在,说明理由; (3)求证:直线AC 必过点Q .(1)解 设B (x 0,y 0),则C (-x 0,-y 0),x 204+y 20=1,所以k 1k 2=y 0x 0-2·y 0x 0+2=y 20x 20-4=1-14x 20x 20-4=-14.(2)解 由题意得直线AP 的方程为y =k 1(x -2),联立⎩⎪⎨⎪⎧y =k 1(x -2),x 2+y 2=4,得(1+k 21)x 2-4k 21x+4(k 21-1)=0, 设P (x p ,y p ),解得x p =2(k 21-1)1+k 21,y p =k 1(x p -2)=-4k 11+k 21,联立⎩⎪⎨⎪⎧y =k 1(x -2),x 24+y 2=1,得(1+4k 21)x 2-16k 21x +4(4k 21-1)=0,设B (x B ,y B ),解得x B =2(4k 21-1)1+4k 21,y B =k 1(x B -2)=-4k 11+4k 21,所以k BC =y B x B =-2k 14k 21-1,k PQ =y p x p +65=-4k 11+k 212(k 21-1)1+k 21+65=-5k 14k 21-1,所以k PQ =52k BC ,故存在常数λ=52,使得k PQ =52k BC ,(3)证明 当直线PQ 与x 轴垂直时,Q ⎝ ⎛⎭⎪⎫-65,-85,则k AQ =852+65=12=k 2,所以直线AC 必过点Q .当直线PQ 与x 轴不垂直时,直线PQ 方程为y =-5k 14k 21-1⎝ ⎛⎭⎪⎫x +65, 联立⎩⎪⎨⎪⎧y =-5k 14k 21-1⎝ ⎛⎭⎪⎫x +65x 2+y 2=4,,解得x Q =-2(16k 21-1)16k 21+1,y Q =16k 116k 21+1, 所以k AQ =16k 116k 21+1-2(16k 21-1)16k 21+1-2=-14k 1=k 2, 故直线AC 必过点Q .。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——解答题滚动练3 含答案

解答题滚动练31.(2017·镇江期末)已知向量m =(cos α,-1),n =(2,sin α),其中α∈⎝⎛⎭⎪⎫0,π2,且m ⊥n .(1)求cos2α的值; (2)若sin(α-β)=1010,且β∈⎝⎛⎭⎪⎫0,π2,求角β的大小.解 方法一 (1)由m ⊥n ,得2cos α-sin α=0,所以sin α=2cos α,代入cos 2α+sin 2α=1,得5cos 2α=1,且α∈⎝⎛⎭⎪⎫0,π2,则cos α=55,sin α=255, 则cos2α=2cos 2α-1=2×⎝⎛⎭⎪⎫552-1=-35. (2)由α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫0,π2,得α-β∈⎝ ⎛⎭⎪⎫-π2,π2.又sin(α-β)=1010,则cos(α-β)=31010. 则sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β)=255×31010-55×1010=22. 因为β∈⎝⎛⎭⎪⎫0,π2,所以β=π4.方法二 (1)由m ⊥n ,得2cos α-sin α=0,tan α=2,故cos2α=cos 2α-sin 2α=cos 2α-sin 2αcos 2α+sin 2α=1-tan 2α1+tan 2α=1-41+4=-35. (2)由(1)知,2cos α-sin α=0,且cos 2α+sin 2α=1,α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝⎛⎭⎪⎫0,π2,则sin α=255,cos α=55,以下同方法一(2).2.如图,在四棱锥P -ABCD 中,AB ⊥平面PAD ,DC ∥AB ,DC =2AB ,E 为棱PA 上一点. (1)设O 为AC 与BD 的交点,若PE =2AE ,求证:OE ∥平面PBC ; (2)若DE ⊥AP ,求证:PB ⊥DE .证明 (1)在△AOB 与△COD 中, 因为DC ∥AB ,DC =2AB ,所以AO CO =AB CD =12, 又因为PE =2AE ,所以在△APC 中,有AO CO =AE PE =12,则OE ∥PC . 又因为OE ⊄平面PBC ,PC ⊂平面PBC ,所以OE ∥平面PBC . (2)因为AB ⊥平面PAD ,DE ⊂平面PAD , 所以AB ⊥DE .又因为AP ⊥DE ,AB ⊂平面PAB ,AP ⊂平面PAB ,AP ∩AB =A , 所以DE ⊥平面PAB ,又PB ⊂平面PAB ,所以DE ⊥PB .3.已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为1.8元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下:7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.(1)当9天购买一次配料时,求该厂用于配料的保管费用P 是多少元?(2)设该厂x 天购买一次配料,求该厂在这x 天中用于配料的总费用y (元)关于x 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?解 (1)当9天购买一次时,该厂用于配料的保管费用P =70+0.03×200×(1+2)=88(元). (2)①当0<x ≤7时,y =360x +10x +236=370x +236, ②当x >7时,y =360x +236+70+6[(x -7)+(x -8)+…+2+1]=3x 2+321x +432∴y =⎩⎪⎨⎪⎧370x +236,0<x ≤7,3x 2+321x +432,x >7.∴设该厂x 天购买一次配料平均每天支付的费用为f (x )元. f (x )=⎩⎪⎨⎪⎧370x +236x ,0<x ≤7,3x 2+321x +432x,x >7.当0<x ≤7时,f (x )=370+236x ,当且仅当x =7时f (x )有最小值28267≈404(元), 当x >7时,f (x )=3x 2+321x +432x=3⎝ ⎛⎭⎪⎫x +144x +321≥393,当且仅当x =12时取等号.∵393<404,∴当x =12时f (x )有最小值393元.4.已知函数f (x )=2ln x -x 2+ax (a ∈R ).(1)当a =2时,求f (x )的图象在x =1处的切线方程;(2)若函数g (x )=f (x )-ax +m 在⎣⎢⎡⎦⎥⎤1e ,e 上有两个零点,求实数m 的取值范围; (3)若函数f (x )的图象与x 轴有两个不同的交点A (x 1,0),B (x 2,0),且0<x 1<x 2,求证:f ′⎝ ⎛⎭⎪⎫x 1+x 22<0(其中f ′(x )是f (x )的导函数). (1)解 当a =2时,f (x )=2ln x -x 2+2x ,f ′(x )=2x-2x +2,切点坐标为(1,1),切线的斜率k =f ′(1)=2,则切线方程为y -1=2(x -1),即y =2x -1. (2)解 g (x )=2ln x -x 2+m ,则g ′(x )=2x -2x =-2(x +1)(x -1)x,∵x ∈⎣⎢⎡⎦⎥⎤1e ,e ,故g ′(x )=0时,x =1.当1e <x <1时,g ′(x )>0;当1<x <e 时,g ′(x )<0.故g (x )在x =1处取得极大值g (1)=m -1.又g ⎝ ⎛⎭⎪⎫1e =m -2-1e 2,g (e)=m +2-e 2,g (e)-g ⎝ ⎛⎭⎪⎫1e =4-e 2+1e 2<0,则g (e)<g ⎝ ⎛⎭⎪⎫1e ,所以g (x )在⎣⎢⎡⎦⎥⎤1e ,e 上的最小值为g (e). g (x )在⎣⎢⎡⎦⎥⎤1e ,e 上有两个零点的条件是⎩⎪⎨⎪⎧g (1)=m -1>0,g ⎝ ⎛⎭⎪⎫1e =m -2-1e 2≤0,解得1<m ≤2+1e 2,所以实数m 的取值范围是⎝⎛⎦⎥⎤1,2+1e 2.(3)证明 因为f (x )的图象与x 轴交于两个不同的点A (x 1,0),B (x 2,0),所以方程2ln x -x 2+ax =0的两个根为x 1,x 2,则⎩⎪⎨⎪⎧2ln x 1-x 21+ax 1=0,2ln x 2-x 22+ax 2=0,两式相减得a =(x 1+x 2)-2(ln x 1-ln x 2)x 1-x 2,又f (x )=2ln x -x 2+ax ,f ′(x )=2x -2x +a ,则f ′⎝ ⎛⎭⎪⎫x 1+x 22=4x 1+x 2-(x 1+x 2)+a =4x 1+x 2-2(ln x 1-ln x 2)x 1-x 2. 下证4x 1+x 2-2(ln x 1-ln x 2)x 1-x 2<0,即证明2(x 2-x 1)x 1+x 2+ln x 1x 2<0,令t =x 1x 2. 因为0<x 1<x 2,所以0<t <1,即证明u (t )=2(1-t )t +1+ln t <0在0<t <1上恒成立.因为u ′(t )=-2(t +1)-2(1-t )(t +1)2+1t =1t -4(t +1)2=(t -1)2t (t +1)2,又0<t <1,所以u ′(t )>0, 所以u (t )在(0,1)上是增函数,则u (t )<u (1)=0,从而知2(x 2-x 1)x 1+x 2+ln x 1x 2<0,故4x 1+x 2-2(ln x 1-ln x 2)x 1-x 2<0,即f ′⎝ ⎛⎭⎪⎫x 1+x 22<0成立.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——考前回扣3 Word版含答案

回扣3 三角函数与平面向量1.准确记忆六组诱导公式 对于“k π2±α,k ∈Z ”的三角函数值与α角的三角函数值的关系口诀:奇变偶不变,符号看象限.2.三角函数恒等变换“四大策略”(1)常值代换:特别是“1”的代换,1=sin 2θ+cos 2θ=tan45°等. (2)降次与升次:正用二倍角公式升次,逆用二倍角公式降次. (3)弦、切互化:一般是切化弦.(4)灵活运用辅助角公式a sin α+b cos α=a 2+b 2sin(α+φ)⎝ ⎛⎭⎪⎫其中tan φ=b a .3.三种三角函数的性质4.函数y =A sin(ωx +φ)(ω>0,A >0)的图象 (1)“五点法”作图设z =ωx +φ,令z =0,π2,π,3π2,2π,求出相应的x 的值与y 的值,描点、连线可得.(2)由三角函数的图象确定解析式时,一般利用五点中的零点或最值点作为解题突破口. (3)图象变换y =sin x ―――――――――→向左(φ>0)或向右(φ<0)平移|φ|个单位长度y =sin(x +φ) ――――――――――――→横坐标变为原来的1ω(ω>0)倍纵坐标不变y =sin(ωx +φ) ―――――――――――→纵坐标变为原来的A (A >0)倍横坐标不变y =A sin(ωx +φ). 5.正弦定理及其变形asin A=b sin B =csin C=2R (2R 为△ABC 外接圆的直径).变形:a =2R sin A ,b =2R sin B ,c =2R sin C . sin A =a 2R ,sin B =b 2R ,sin C =c2R.a ∶b ∶c =sin A ∶sin B ∶sin C .6.余弦定理及其推论、变形a 2=b 2+c 2-2bc cos A ,b 2=a 2+c 2-2ac cos B , c 2=a 2+b 2-2ab cos C .推论:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.变形:b 2+c 2-a 2=2bc cos A ,a 2+c 2-b 2=2ac cos B ,a 2+b 2-c 2=2ab cos C .7.面积公式S △ABC =12bc sin A =12ac sin B =12ab sin C .8.平面向量的数量积(1)若a ,b 为非零向量,夹角为θ,则a·b =|a||b |cos θ. (2)设a =(x 1,y 1),b =(x 2,y 2),则a·b =x 1x 2+y 1y 2. 9.两个非零向量平行、垂直的充要条件 若a =(x 1,y 1),b =(x 2,y 2),则 (1)a ∥b ⇔a =λb (b ≠0)⇔x 1y 2-x 2y 1=0. (2)a ⊥b ⇔a·b =0⇔x 1x 2+y 1y 2=0. 10.利用数量积求长度(1)若a =(x ,y ),则|a |=a·a =x 2+y 2. (2)若A (x 1,y 1),B (x 2,y 2),则 |AB →|=(x 2-x 1)2+(y 2-y 1)2.11.利用数量积求夹角若a =(x 1,y 1),b =(x 2,y 2),θ为a 与b 的夹角, 则cos θ=a·b |a||b |=x 1x 2+y 1y 2x 21+y 21 x 22+y 22. 12.三角形“四心”向量形式的充要条件设O 为△ABC 所在平面上一点,角A ,B ,C 所对的边长分别为a ,b ,c ,则(1)O 为△ABC 的外心⇔|OA →|=|OB →|=|OC →|=a 2sin A.(2)O 为△ABC 的重心⇔OA →+OB →+OC →=0.(3)O 为△ABC 的垂心⇔OA →·OB →=OB →·OC →=OC →·OA →. (4)O 为△ABC 的内心⇔aOA →+bOB →+cOC →=0.1.利用同角三角函数的平方关系式求值时,不要忽视角的范围,要先判断函数值的符号. 2.在求三角函数的值域(或最值)时,不要忽略x 的取值范围.3.求函数f (x )=A sin(ωx +φ)的单调区间时,要注意A 与ω的符号,当ω<0时,需把ω的符号化为正值后求解.4.三角函数图象变换中,注意由y =sin ωx 的图象变换得y =sin(ωx +φ)时,平移量为⎪⎪⎪⎪⎪⎪φω,而不是φ. 5.在已知两边和其中一边的对角时,要注意检验解是否满足“大边对大角”,避免增解. 6.要特别注意零向量带来的问题:0的模是0,方向任意,并不是没有方向;0与任意非零向量平行.7.a·b >0是〈a ,b 〉为锐角的必要不充分条件;a·b <0是〈a ,b 〉为钝角的必要不充分条件.1.2sin45°cos15°-sin30°的值=________. 答案32解析 2sin45°cos15°-sin30°=2sin45°cos15°-sin(45°-15°)=2sin45°cos15°-(sin45°cos15°-cos45°sin15°)=sin45°cos15°+cos45°sin15°=sin60°=32. 2.(1+tan18°)(1+tan27°)的值是________. 答案 2解析 由题意得tan(18°+27°)=tan18°+tan27°1-tan18°tan27°,即tan18°+tan27°1-tan18°tan27°=1, 所以tan18°+tan27°=1-tan18°tan27°,所以(1+tan18°)(1+tan27°)=1+tan18°+tan27°+tan18°tan27°=2.3.(2017·江苏泰州中学期中)向量a =(cos10°,sin10°),b =(cos70°,sin70°),|a -2b |=________. 答案3解析 a ·b =cos70°cos10°+sin70°sin10°=cos60°=12,|a |=|b |=1,所以|a -2b |=a 2+4b 2-4a ·b =1+4-2= 3.4.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC 的面积是________. 答案332解析 c 2=(a -b )2+6,即c 2=a 2+b 2-2ab +6,① ∵C =π3,由余弦定理得c 2=a 2+b 2-ab ,②由①和②得ab =6,∴S △ABC =12ab sin C =12×6×32=332.5.已知两点A (1,0),B (1,1),O 为坐标原点,点C 在第二象限,且∠AOC =135°,设OC →=-OA →+λOB →(λ∈R ),则λ的值为__________. 答案 12解析 由∠AOC =135°知,点C 在射线y =-x (x <0)上,设点C 的坐标为(a ,-a ),a <0,则有(a ,-a )=(-1+λ,λ),得a =-1+λ,-a =λ,消去a 得λ=12.6.已知a ,b 为同一平面内的两个向量,且a =(1,2),|b |=12|a |,若a +2b 与2a -b 垂直,则a 与b 的夹角为________. 答案 π解析 |b |=12|a |=52,而(a +2b )·(2a -b )=0,即2a 2-2b 2+3a·b =0,所以a·b =-52,从而cos 〈a ,b 〉=a·b|a||b |=-1,所以〈a ,b 〉=π.7.已知函数f (x )=3sin ⎝⎛⎭⎪⎫ωx -π6(ω>0)和g (x )=3cos(2x +φ)的图象的对称中心完全相同,若x ∈⎣⎢⎡⎦⎥⎤0,π2,则f (x )的取值范围是________.答案 ⎣⎢⎡⎦⎥⎤-32,3解析 由两个三角函数图象的对称中心完全相同可知,两函数的周期相同,故ω=2, 所以f (x )=3sin ⎝⎛⎭⎪⎫2x -π6, 那么当x ∈⎣⎢⎡⎦⎥⎤0,π2时,-π6≤2x -π6≤5π6, 所以-12≤sin ⎝ ⎛⎭⎪⎫2x -π6≤1,故f (x )∈⎣⎢⎡⎦⎥⎤-32,3.8.在等腰梯形ABCD 中,已知AB ∥DC ,AB =2,BC =1,∠ABC =60°,动点E 和F 分别在线段BC 和DC 上,且BE →=λBC →,DF →=19λDC →,则AE →·AF →的最小值为__________.答案2918解析 方法一 在梯形ABCD 中,AB =2,BC =1,∠ABC =60°,可得DC =1,AE →=AB →+λBC →,AF →=AD →+19λDC →(λ>0),∴AE →·AF →=(AB →+λBC →)·⎝ ⎛⎭⎪⎫AD →+19λDC →=AB →·AD →+AB →·19λDC→+λBC →·AD →+λBC →·19λDC →=2×1×cos60°+2×1×19λ+λ×1×1×cos60°+λ×19λ×1×1×cos120°=29λ+λ2+1718≥229λ·λ2+1718=2918,当且仅当29λ=λ2,即λ=23时,取得最小值为2918. 方法二 以点A 为坐标原点,AB 所在的直线为x 轴建立平面直角坐标系,则B (2,0),C ⎝ ⎛⎭⎪⎫32,32,D ⎝ ⎛⎭⎪⎫12,32.又BE →=λBC →,DF →=19λDC →,则E ⎝ ⎛⎭⎪⎫2-12λ,32λ,F ⎝ ⎛⎭⎪⎫12+19λ,32,λ>0,∴AE →·AF →=⎝ ⎛⎭⎪⎫2-12λ⎝ ⎛⎭⎪⎫12+19λ+34λ=1718+29λ+12λ≥1718+229λ·12λ=2918,λ>0,当且仅当29λ=12λ,即λ=23时取等号,故AE →·AF →的最小值为2918.9.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3-3sin ⎝ ⎛⎭⎪⎫2x -π6. (1)求函数f (x )的最小正周期和单调增区间;(2)当x ∈⎣⎢⎡⎦⎥⎤-π6,π3时,试求f (x )的最值,并写出取得最值时自变量x 的值.解 (1)由题意知,f (x )=-sin2x +3cos2x =2sin ⎝⎛⎭⎪⎫2x +2π3, 所以f (x )的最小正周期为T =2π2=π.当-π2+2k π≤2x +2π3≤π2+2k π(k ∈Z )时,f (x )单调递增,解得x ∈⎣⎢⎡⎦⎥⎤-7π12+k π,-π12+k π(k ∈Z ), 所以f (x )的单调增区间为⎣⎢⎡⎦⎥⎤-7π12+k π,-π12+k π(k ∈Z ). (2)因为x ∈⎣⎢⎡⎦⎥⎤-π6,π3,所以π3≤2x +2π3≤4π3,当2x +2π3=π2,即x =-π12时,f (x )取得最大值2,当2x +2π3=4π3,即x =π3时,f (x )取得最小值- 3.10.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知cos C +(cos A -3sin A )cos B =0.(1)求角B 的大小;(2)若a =2,b =7,求△ABC 的面积. 解 (1)由已知得-cos(A +B )+cos A cos B -3sin A cos B =0, 即sin A sin B -3sin A cos B =0, 因为sin A ≠0, 所以sin B -3cos B =0,又cos B ≠0,所以tan B =3, 又0<B <π,所以B =π3.(2)因为sin B =32,cos B =12, 所以a sin A =b sin B =732=2213,又a =2, 所以sin A =321=217, 因为a <b , 所以cos A =277.所以sin C =sin(A +B )=sin A cos B +cos A sin B =32114,所以S =12ab sin C =332.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——考前回扣4

回扣4 数列1.牢记概念与公式等差数列、等比数列2.活用定理与结论(1)等差、等比数列{a n}的常用性质(2)判断等差数列的常用方法①定义法a n+1-a n=d(常数)(n∈N*)⇔{a n}是等差数列.②通项公式法a n=pn+q(p,q为常数,n∈N*)⇔{a n}是等差数列.③中项公式法2a n+1=a n+a n+2 (n∈N*)⇔{a n}是等差数列.④前n项和公式法S n=An2+Bn(A,B为常数,n∈N*)⇔{a n}是等差数列.(3)判断等比数列的常用方法①定义法a n+1=q (q是不为0的常数,n∈N*)⇔{a n}是等比数列.a n②通项公式法a n =cq n (c ,q 均是不为0的常数,n ∈N *)⇔{a n }是等比数列.③中项公式法a 2n +1=a n ·a n +2(a n ·a n +1·a n +2≠0,n ∈N *)⇔{a n }是等比数列.3.数列求和的常用方法(1)等差数列或等比数列的求和,直接利用公式求和.(2)形如{a n ·b n }(其中{a n }为等差数列,{b n }为等比数列)的数列,利用错位相减法求和. (3)通项公式形如a n =c(an +b 1)(an +b 2)(其中a ,b 1,b 2,c 为常数)用裂项相消法求和.(4)通项公式形如a n =(-1)n·n 或a n =a ·(-1)n(其中a 为常数,n ∈N *)等正负项交叉的数列求和一般用并项法.并项时应注意分n 为奇数、偶数两种情况讨论.(5)分组求和法:分组求和法是解决通项公式可以写成c n =a n +b n 形式的数列求和问题的方法,其中{a n }与{b n }是等差(比)数列或一些可以直接求和的数列. (6)并项求和法:先将某些项放在一起求和,然后再求S n .1.已知数列的前n 项和求a n ,易忽视n =1的情形,直接用S n -S n -1表示.事实上,当n =1时,a 1=S 1;当n ≥2时,a n =S n -S n -1.2.易混淆几何平均数与等比中项,正数a ,b 的等比中项是±ab .3.等差数列中不能熟练利用数列的性质转化已知条件,灵活整体代换进行基本运算.如等差数列{a n }与{b n }的前n 项和分别为S n 和T n ,已知S n T n =n +12n +3,求a nb n时,无法正确赋值求解.4.易忽视等比数列中公比q ≠0导致增解,易忽视等比数列的奇数项或偶数项符号相同造成增解.5.运用等比数列的前n 项和公式时,易忘记分类讨论.一定分q =1和q ≠1两种情况进行讨论.6.利用错位相减法求和时,要注意寻找规律,不要漏掉第一项和最后一项. 7.裂项相消法求和时,分裂前后的值要相等, 如1n (n +2)≠1n -1n +2,而是1n (n +2)=12⎝ ⎛⎭⎪⎫1n -1n +2.8.通项中含有(-1)n的数列求和时,要把结果写成n 为奇数和n 为偶数两种情况的分段形式.1.在等差数列{a n }中,已知a 3+a 8=10,则3a 5+a 7=________.答案 20解析 设公差为d ,则a 3+a 8=2a 1+9d =10, 3a 5+a 7=3(a 1+4d )+(a 1+6d )=4a 1+18d =2×10=20.2.(2017·南京、盐城一模)设{a n }是等差数列,若a 4+a 5+a 6=21,则S 9=____________. 答案 63解析 ∵a 4+a 5+a 6=21,∴3a 5=21,可得a 5=7, ∴S 9=9×(a 1+a 9)2=9×(2a 5)2=9a 5=63.3.已知数列{a n }的前n 项和为S n ,若S n =2a n -4(n ∈N *),则a n 的通项公式为________. 答案 2n +1解析 a n +1=S n +1-S n =2a n +1-4-(2a n -4)⇒a n +1=2a n ,再令n =1,∴S 1=2a 1-4,解得a 1=4,∴数列{a n }是以4为首项,2为公比的等比数列,∴a n =4·2n -1=2n +1.4.(2017·南京高淳区质检)若S n 为等差数列{a n }的前n 项和,S 9=-36,S 13=-104,则a 5与a 7的等比中项为__________. 答案 ±4 2解析 由S 9=-36,S 13=-104,可解得a 1=4,d =-2,所以a 5=-4,a 7=-8. 设a 5与a 7的等比中项为x ,则x 2=a 5a 7=32, 所以x =±4 2.5.若等比数列{a n }的各项均为正数,且a 10a 11+a 9a 12=2e 5,则ln a 1+ln a 2+…+ln a 20=________. 答案 50解析 ∵数列{a n }为等比数列,且a 10a 11+a 9a 12=2e 5, ∴a 10a 11+a 9a 12=2a 10a 11=2e 5, ∴a 10a 11=e 5,∴ln a 1+ln a 2+…+ln a 20=ln(a 1a 2…a 20) =ln(a 10a 11)10=ln(e 5)10=lne 50=50.6.已知等比数列{a n }的前n 项和为S n ,a 1+a 3=52,且a 2+a 4=54,则S nan =________.答案 2n-1解析 设等比数列{a n }的公比为q , 则⎩⎪⎨⎪⎧a 1(1+q 2)=52,a 1q (1+q 2)=54,解得⎩⎪⎨⎪⎧a 1=2,q =12,∴S n a n =a 1(1-q n)1-q a 1q n -1=2×⎝ ⎛⎭⎪⎫1-12n 1-122×⎝ ⎛⎭⎪⎫12n -1=2n-1. 7.若数列{a n }满足a 2-a 1>a 3-a 2>a 4-a 3>…>a n +1-a n >…,则称数列{a n }为“差递减”数列.若数列{a n }是“差递减”数列,且其通项a n 与其前n 项和S n ()n ∈N *满足2S n =3a n +2λ-1()n ∈N *,则实数λ的取值范围是________.答案 ⎝ ⎛⎭⎪⎫12,+∞解析 当n =1时,2a 1=3a 1+2λ-1,a 1=1-2λ,当n >1时,2S n -1=3a n -1+2λ-1,所以2a n =3a n -3a n -1,a n =3a n -1,所以a n =()1-2λ3n -1,a n -a n -1=()1-2λ3n -1-()1-2λ3n -2=()2-4λ3n -2,依题意()2-4λ3n -2是一个减数列,所以2-4λ<0,λ>12.8.已知等差数列{a n }的公差d ≠0,且a 1,a 3,a 13成等比数列,若a 1=1,S n 是数列{a n }前n 项的和,则2S n +16a n +3(n ∈N *)的最小值为________.答案 4解析 据题意由a 1,a 3,a 13成等比数列,可得(1+2d )2=1+12d ,解得d =2,故a n =2n -1,S n =n 2,因此2S n +16a n +3=2n 2+162n +2=n 2+8n +1=(n +1)2-2(n +1)+9n +1=(n +1)+9n +1-2,据基本不等式知2S n +16a n +3=(n +1)+9n +1-2≥2(n +1)×9n +1-2=4,当n =2时取得最小值4. 9.已知首项都是1的两个数列{a n },{b n }(b n ≠0,n ∈N *)满足a n b n +1-a n +1b n +2b n +1b n =0. (1)令c n =a n b n,求数列{c n }的通项公式; (2)在(1)的条件下,若b n =3n -1,求数列{a n }的前n 项和S n .解 (1)因为a n b n +1-a n +1b n +2b n +1b n =0,b n ≠0(n ∈N *),所以a n +1b n +1-a nb n=2,即c n +1-c n =2.所以数列{}c n 是首项c 1=1,公差d =2的等差数列,故c n =2n -1. (2)由b n =3n -1知,a n =c n b n =(2n -1)3n -1,于是数列{a n }的前n 项和S n =1×30+3×31+5×32+…+(2n -1)×3n -1,3S n =1×31+3×32+…+(2n -3)×3n -1+(2n -1)×3n,两式相减得-2S n =1+2×(31+32+…+3n -1)-(2n -1)×3n =-2-(2n -2)3n,所以S n =(n -1)3n+1.10.(2017·江苏南师附中质检)已知数列{a n }和{b n }满足a 1a 2a 3…a n =n b(n ∈N *).若{a n }为等比数列,且a 1=2,b 3=6+b 2. (1)求{a n }和{b n }的通项公式;(2)设c n =1a n -1b n(n ∈N *),记数列{c n }的前n 项和为S n .(i)求S n ;(ii)求正整数k ,使得对任意n ∈N *均有S k ≥S n . 解 (1)∵a 1a 2a 3…a n =(2)b n (n ∈N *),①当n ≥2,n ∈N *时,a 1a 2a 3…a n -1=1n b -,②由①②知a n =1n n b b --,令n =3,则有a 3=32b b -.∵b 3=6+b 2, ∴a 3=8.∵{a n }为等比数列,且a 1=2,设{a n }的公比为q , ∴则q 2=a 3a 1=4,由题意知a n >0,∴q >0,∴q =2. ∴a n =2n (n ∈N *).又由a 1a 2a 3…a n =n b(n ∈N *),得21×22×23…×2n =n b,即(1)22,n n n b +=∴b n =n (n +1)(n ∈N *). (2)(i)∵c n =1a n -1b n =12n -1n (n +1)=12n -⎝ ⎛⎭⎪⎫1n -1n +1, ∴S n =c 1+c 2+c 3+…+c n=12-⎝ ⎛⎭⎪⎫11-12+122-⎝ ⎛⎭⎪⎫12-13+…+12n -⎝ ⎛⎭⎪⎫1n -1n +1 =12+122+…+12n -⎝ ⎛⎭⎪⎫1-1n +1 =1-12n -1+1n +1=1n +1-12n .(ii)∵c 1=0,c 2>0,c 3>0,c 4>0, 当n ≥5时,c n =1n (n +1)⎣⎢⎡⎦⎥⎤n (n +1)2n-1, 而n (n +1)2n-(n +1)(n +2)2n +1=(n +1)(n -2)2n +1>0,得n (n +1)2n≤5×(5+1)25<1,∴当n ≥5时,c n <0.综上,对任意的n ∈N *恒有S 4≥S n ,故k =4.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——考前回扣10套集合((含答案)62页

2018考前三个月高考数学理科(江苏专用) 总复习训练题:——考前回扣10集合(含答案)回扣1 函数的图象与性质1.函数的定义域和值域(1)求函数定义域的类型和相应方法①若已知函数的解析式,则函数的定义域是使解析式有意义的自变量的取值范围; ②若已知f (x )的定义域为[a ,b ],则f (g (x ))的定义域为不等式a ≤g (x )≤b 的解集;反之,已知f (g (x ))的定义域为[a ,b ],则f (x )的定义域为函数y =g (x )(x ∈[a ,b ])的值域. (2)常见函数的值域①一次函数y =kx +b (k ≠0)的值域为R ;②二次函数y =ax 2+bx +c (a ≠0):当a >0时,值域为⎣⎢⎡⎭⎪⎫4ac -b 24a ,+∞,当a <0时,值域为⎝ ⎛⎦⎥⎤-∞,4ac -b 24a ;③反比例函数y =kx(k ≠0)的值域为{y ∈R |y ≠0}. 2.函数的奇偶性、周期性(1)奇偶性是函数在其定义域上的整体性质,对于定义域内的任意x (定义域关于原点对称),都有f (-x )=-f (x )成立,则f (x )为奇函数(都有f (-x )=f (x )成立,则f (x )为偶函数). (2)周期性是函数在其定义域上的整体性质,一般地,对于函数f (x ),如果对于定义域内的任意一个x 的值,若f (x +T )=f (x )(T ≠0),则f (x )是周期函数,T 是它的一个周期. 3.关于函数周期性、对称性的结论 (1)函数的周期性①若函数f (x )满足f (x +a )=f (x -a ),则f (x )是周期函数,2a 是它的一个周期; ②设f (x )是R 上的偶函数,且图象关于直线x =a (a ≠0)对称,则f (x )是周期函数,2a 是它的一个周期;③设f (x )是R 上的奇函数,且图象关于直线x =a (a ≠0)对称,则f (x )是周期函数,4a 是它的一个周期. (2)函数图象的对称性①若函数y =f (x )满足f (a +x )=f (a -x ), 即f (x )=f (2a -x ),则f (x )的图象关于直线x =a 对称;②若函数y =f (x )满足f (a +x )=-f (a -x ), 即f (x )=-f (2a -x ),则f (x )的图象关于点(a,0)对称;③若函数y =f (x )满足f (a +x )=f (b -x ), 则函数f (x )的图象关于直线x =a +b2对称.4.函数的单调性函数的单调性是函数在其定义域上的局部性质. ①单调性的定义的等价形式:设x 1,x 2∈[a ,b ], 那么(x 1-x 2)[f (x 1)-f (x 2)]>0⇔f (x 1)-f (x 2)x 1-x 2>0⇔f (x )在[a ,b ]上是增函数;(x 1-x 2)[f (x 1)-f (x 2)]<0⇔f (x 1)-f (x 2)x 1-x 2<0⇔f (x )在[a ,b ]上是减函数.②若函数f (x )和g (x )都是减函数,则在公共定义域内,f (x )+g (x )是减函数;若函数f (x )和g (x )都是增函数,则在公共定义域内,f (x )+g (x )是增函数;根据同增异减判断复合函数y =f (g (x ))的单调性. 5.函数图象的基本变换 (1)平移变换y =f (x )――――→h >0,右移h <0,左移y =f (x -h ), y =f (x )――――→k >0,上移k <0,下移y =f (x )+k . (2)伸缩变换y =f (x )――――→0<ω<1,伸ω>1,缩y =f (ωx ), y =f (x )――――→0<A <1,缩A >1,伸y =Af (x ). (3)对称变换y =f (x )――→x 轴y =-f (x ), y =f (x )――→y 轴y =f (-x ), y =f (x )――→原点y =-f (-x ).6.准确记忆指数函数与对数函数的基本性质 (1)定点:y =a x(a >0,且a ≠1)恒过(0,1)点;y =log a x (a >0,且a ≠1)恒过(1,0)点.(2)单调性:当a >1时,y =a x在R 上单调递增;y =log a x 在(0,+∞)上单调递增;当0<a <1时,y =a x在R 上单调递减;y =log a x 在(0,+∞)上单调递减. 7.函数与方程(1)零点定义:x 0为函数f (x )的零点⇔f (x 0)=0⇔(x 0,0)为f (x )的图象与x 轴的交点. (2)确定函数零点的三种常用方法 ①解方程判定法:解方程f (x )=0;②零点定理法:根据连续函数y =f (x )满足f (a )f (b )<0,判断函数在区间(a ,b )内存在零点; ③数形结合法:尤其是方程两端对应的函数类型不同时多用此法求解.1.解决函数问题时要注意函数的定义域,要树立定义域优先原则. 2.解决分段函数问题时,要注意与解析式对应的自变量的取值范围.3.求函数单调区间时,多个单调区间之间不能用符号“∪”和“或”连接,可用“及”连接或用“,”隔开.单调区间必须是“区间”,而不能用集合或不等式代替.4.判断函数的奇偶性,要注意定义域必须关于原点对称,有时还要对函数式化简整理,但必须注意使定义域不受影响.5.准确理解基本初等函数的定义和性质.如函数y =a x(a >0,且a ≠1)的单调性容易忽视字母a 的取值讨论,忽视a x>0;对数函数y =log a x (a >0,且a ≠1)容易忽视真数与底数的限制条件.6.易混淆函数的零点和函数图象与x 轴的交点,不能把函数零点、方程的解、不等式解集的端点值进行准确互化.1.若函数f (x )=⎩⎪⎨⎪⎧2x +2,x ≤0,2x-4,x >0,则f (f (1))=________.答案 -2解析 f (f (1))=f (21-4)=f (-2)=2³(-2)+2=-2.2.函数f (x )=x 2-2ax +2在区间(-∞,1]上递减,则a 的取值范围是________. 答案 [1,+∞)解析 函数f (x )=x 2-2ax +2=x 2-2ax +a 2-a 2+2=(x -a )2-a 2+2, ∵二次函数图象开口向上,对称轴为直线x =a ,且在区间(-∞,1]上递减, ∴a 的取值范围是[1,+∞).3.(2017²江苏南通天星湖中学质检)若函数f (x )=⎩⎪⎨⎪⎧x (x -b ),x ≥0,ax (x +2),x <0(a ,b ∈R )为奇函数,则f (a +b )的值为________. 答案 -1解析 因为函数f (x )为奇函数,所以f (-1)=-f (1),f (-2)=-f (2),即⎩⎪⎨⎪⎧a (-1+2)=1(1-b ),2a (-2+2)=2(2-b ),解得a =-1,b =2.经验证a =-1,b =2满足题设条件, 所以f (a +b )=f (1)=-1.4.(2017²江苏如东中学质检)设函数f (x )=ax 2-2x +2,对于满足1<x <4的一切x 值都有f (x )>0,则实数a 的取值范围为________.答案 ⎝ ⎛⎭⎪⎫12,+∞解析 由题意得a >2x -2x2对1<x <4恒成立,又2x -2x 2=-2⎝ ⎛⎭⎪⎫1x -122+12,14<1x <1, ∴⎝ ⎛⎭⎪⎫2x -2x 2max =12,∴a >12.5.已知函数f (x )=||x +2||x ,且满足f (a -1)<f (2),则实数a 的取值范围是________. 答案 (-1,3)解析 因为f (-x )=f (x ),所以函数f (x )是偶函数,当x ≥0时,f (x )=x +2x是单调增函数,故由偶函数的性质及f (a -1)<f (2)可得|a -1|<2,即-2<a -1<2, 即-1<a <3.6.已知定义在R 上的奇函数f (x )满足f (x +2)=-f (x ),且f (-1)=2,则f (2017)=________. 答案 -2解析 由题意得f (x +4)=-f (x +2)=f (x ),所以函数是以4为周期的周期函数,所以f (2017)=f (1)=-f (-1)=-2.7.已知函数f (x )为奇函数,且在[0,2]上单调递增,若f (log 2m )<f (log 4(m +2))成立,则实数m 的取值范围是________________.答案 ⎣⎢⎡⎭⎪⎫14,2 解析 因为函数f (x )是奇函数,且在[0,2]上单调递增,所以函数f (x )在[-2,2]上单调递增.故由f (log 2m )<f (log 4(m +2)),可得⎩⎪⎨⎪⎧-2≤log 2m ≤2,-2≤log 4(m +2)≤2,log 2m <log 4(m +2),m >0,m +2>0,故有⎩⎪⎨⎪⎧14≤m ≤4,116≤m +2≤16,m 2<m +2,m >0,m +2>0,解得14≤m <2.综上可知,m 的取值范围是⎣⎢⎡⎭⎪⎫14,2. 8.定义在R 上的函数f (x )满足f (-x )=-f (x ),f (x -2)=f (x +2),且当x ∈(-1,0)时,f (x )=2x +15,则f (log 220)=__________.答案 -1解析 由f (x -2)=f (x +2)⇒f (x )=f (x +4), 因为4<log 220<5,所以0<log 220-4<1, -1<4-log 220<0.又因为f (-x )=-f (x ),所以f (log 220)=f (log 220-4)=-f (4-log 220)=-f ⎝ ⎛⎭⎪⎫log 245=-1.9.若函数f (x )=⎩⎪⎨⎪⎧(3-a )x -3,x ≤7,a x -6,x >7单调递增,则实数a 的取值范围是________.答案 ⎝ ⎛⎭⎪⎫94,3解析 因为函数f (x )=⎩⎪⎨⎪⎧(3-a )x -3,x ≤7,a x -6,x >7单调递增,所以1<a <3.又由题意得7(3-a )-3<a ,解得a >94,所以实数a 的取值范围是⎝ ⎛⎭⎪⎫94,3.10.已知函数f (x )=⎩⎪⎨⎪⎧2-|x |,x ≤2,(x -2)2,x >2,函数g (x )=3-f (2-x ),则函数y =f (x )-g (x )的零点个数为__________. 答案 2解析 当x >2时,g (x )=x -1,f (x )=(x -2)2; 当0≤x ≤2时,g (x )=3-x ,f (x )=2-x ; 当x <0时,g (x )=3-x 2,f (x )=2+x .由于函数y =f (x )-g (x )的零点个数就是方程f (x )-g (x )=0的根的个数.当x >2时,方程f (x )-g (x )=0可化为x 2-5x +5=0,其根为x =5+52或x =5-52(舍去);当0≤x ≤2时,方程f (x )-g (x )=0可化为2-x =3-x ,无解;当x <0时,方程f (x )-g (x )=0可化为x 2+x -1=0,其根为x =-1-52或x =-1+52(舍去).所以函数y =f (x )-g (x )的零点个数为2.11.设函数f (x )=⎩⎪⎨⎪⎧x 2-6x +6,x ≥0,3x +4,x <0,若互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3),则x 1+x 2+x 3的取值范围是____________. 答案 ⎝⎛⎭⎪⎫113,6 解析 由题意可得函数f (x )的图象如图所示,若存在互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3)=k ,则k ∈(-3,4),不妨令x 1<x 2<x 3,则x 1∈⎝ ⎛⎭⎪⎫-73,0,x 2+x 3=6,故x 1+x 2+x 3∈⎝ ⎛⎭⎪⎫113,6.12.定义在R 上的函数f (x )满足f (x +2)=2f (x )-2,当x ∈(0,2]时,f (x )=⎩⎪⎨⎪⎧x 2-x ,x ∈(0,1),1x,x ∈[1,2],若当x ∈(0,4]时,t 2-7t 2≤f (x )≤3-t 恒成立,则实数t 的取值范围是______________. 答案 [1,2]解析 当x ∈(0,1)时,f (x )=x 2-x ,函数无最大值,最小值为-14;当x ∈[1,2]时,f (x )=1x ,函数最大值为1,最小值为12;当x ∈(2,3)时,f (x )=2f (x -2)-2=2x 2-10x +10,函数值满足-52≤f (x )<-2;当x ∈[3,4]时,f (x )=2f (x -2)-2=2x -2-2,函数值满足-1≤f (x )≤0.综上,当x ∈(0,4]时,函数f (x )的最小值为-52,最大值为1.由t 2-7t 2≤f (x )≤3-t 恒成立,得⎩⎪⎨⎪⎧t 2-7t 2≤-52,3-t ≥1,∴⎩⎪⎨⎪⎧1≤t ≤52,t ≤2,∴1≤t ≤2.回扣2 导数1.导数的几何意义(1)f′(x0)的几何意义:曲线y=f(x)在点(x0,f(x0))处的切线的斜率,该切线的方程为y -f(x0)=f′(x0)²(x-x0).(2)切点的两大特征:①在曲线y=f(x)上;②在切线上.2.利用导数研究函数的单调性(1)求可导函数单调区间的一般步骤①求函数f(x)的定义域;②求导函数f′(x);③由f′(x)>0的解集确定函数f(x)的单调增区间,由f′(x)<0的解集确定函数f(x)的单调减区间.(2)由函数的单调性求参数的取值范围①若可导函数f(x)在区间M上单调递增,则f′(x)≥0(x∈M)恒成立;若可导函数f(x)在区间M上单调递减,则f′(x)≤0(x∈M)恒成立;②若可导函数在某区间上存在单调递增(减)区间,f′(x)>0(或f′(x)<0)在该区间上存在解集;③若已知f(x)在区间I上的单调性,区间I中含有参数时,可先求出f(x)的单调区间,则I是其单调区间的子集.3.利用导数研究函数的极值与最值(1)求函数的极值的一般步骤①确定函数的定义域;②解方程f′(x)=0;③判断f′(x)在方程f′(x)=0的根x0两侧的符号变化:若左正右负,则x0为极大值点;若左负右正,则x0为极小值点;若不变号,则x0不是极值点.(2)求函数f(x)在区间[a,b]上的最值的一般步骤①求函数y=f(x)在[a,b]内的极值;②比较函数y=f(x)的各极值与端点处的函数值f(a),f(b)的大小,最大的一个是最大值,最小的一个是最小值.1.已知可导函数f (x )在(a ,b )上单调递增(减),则f ′(x )≥0(≤0)对∀x ∈(a ,b )恒成立,不能漏掉“=”,且需验证“=”不能恒成立;已知可导函数f (x )的单调递增(减)区间为(a ,b ),则f ′(x )>0(<0)的解集为(a ,b ).2.f ′(x )=0的解不一定是函数f (x )的极值点.一定要检验在x =x 0的两侧f ′(x )的符号是否发生变化,若变化,则为极值点;若不变化,则不是极值点.1.曲线y =f (x )=xx 2+1在点(1,f (1))处的切线方程是____________.答案 y =12解析 ∵f (x )=xx 2+1的导数f ′(x )=1-x2(1+x 2)2,∴曲线在点(1,f (1))处的切线斜率k =0,∵切点为⎝ ⎛⎭⎪⎫1,12, ∴曲线在点(1,f (1))处的切线方程为y =12.2.(2016²四川)已知a 为函数f (x )=x 3-12x 的极小值点,则a =__________. 答案 2解析 ∵f (x )=x 3-12x ,∴f ′(x )=3x 2-12, 令f ′(x )=0,则x 1=-2,x 2=2.当x ∈(-∞,-2),(2,+∞)时,f ′(x )>0,f (x )单调递增; 当x ∈(-2,2)时,f ′(x )<0,f (x )单调递减, ∴f (x )的极小值点为a =2.3.f (x )=x 2+3xf ′(2),则1+f ′(1)=________. 答案 -3解析 由f (x )=x 2+3xf ′(2),求导可得f ′(x )=2x +3f ′(2),f ′(2)=4+3f ′(2),f ′(2)=-2,则f ′(x )=2x -6,f ′(1)=2-6=-4,所以1+f ′(1)=-3.4.设曲线f (x )=-e x-x (e 为自然对数的底数)上任意一点处的切线为l 1,总存在曲线g (x )=3ax +2cos x 上某点处的切线l 2,使得l 1⊥l 2,则实数a 的取值范围为____________.答案 ⎣⎢⎡⎦⎥⎤-13,23解析 由f (x )=-e x -x ,得f ′(x )=-e x-1, 因为e x+1>1,所以1e x +1∈(0,1),由g (x )=3ax +2cos x ,得g ′(x )=3a -2sin x , 又-2sin x ∈[-2,2],所以3a -2sin x ∈[-2+3a,2+3a ],要使过曲线f (x )=-e x-x 上任意一点的切线l 1, 总存在过曲线g (x )=3ax +2cos x 上一点处的切线l 2,使得l 1⊥l 2,则⎩⎪⎨⎪⎧-2+3a ≤0,2+3a ≥1,解得-13≤a ≤23.5.函数f (x )=x 3+ax 2+bx +a 2在x =1处有极小值10,则a +b 的值为________. 答案 -7解析 ∵f ′(x )=3x 2+2ax +b ,由已知可得⎩⎪⎨⎪⎧f ′(1)=3+2a +b =0,f (1)=1+a +b +a 2=10,解得a =4,b =-11或a =-3,b =3, 经验证,a =4,b =-11符合题意, 故a +b =-7.6.若函数f (x )=x 2-12ln x +1在其定义域内的一个子区间(k -1,k +1)内不是单调函数,则实数k 的取值范围是______________.答案 ⎣⎢⎡⎭⎪⎫1,32 解析 因为f (x )的定义域为(0,+∞),f ′(x )=2x -12x ,由f ′(x )=0,得x =12.利用图象可得 ⎩⎪⎨⎪⎧k -1<12<k +1,k -1≥0,解得1≤k <32.7.已知奇函数f (x )是定义在R 上的可导函数,其导函数为f ′(x ),当x >0时,有2f (x )+xf ′(x )>x 2,则不等式(x +2018)2f (x +2018)+4f (-2)<0的解集为____________. 答案 (-∞,-2016)解析 由题观察联想可设g (x )=x 2f (x ),g ′(x )=2xf (x )+x 2f ′(x ),结合条件x >0,2f (x )+xf ′(x )>x 2,得g ′(x )=2xf (x )+x 2f ′(x )>0,g (x )=x 2f (x )在(0,+∞)上为增函数.又f (x )为R 上的奇函数,所以g (x )为奇函数,所以g (x )在(-∞,0)上为增函数. 由(x +2018)2f (x +2018)+4f (-2)<0, 可得(x +2018)2f (x +2018)<4f (2), 即g (x +2018)<g (2),所以x +2018<2,故x <-2016. 8.若函数f (x )=⎩⎪⎨⎪⎧12x -1,x <1,ln xx 2,x ≥1,则函数y =|f (x )|-18的零点个数为________.答案 4解析 当x <1时,f (x )=12x -1单调递减,且f (x )>-12;当x ≥1时,f (x )=ln xx 2,则f ′(x )=1-2ln xx3,令f ′(x )=0,得x =e ,当∈[1,e)时,f ′(x )>0,f (x )单调递增,当x ∈(e ,+∞)时,f ′(x )<0,f (x )单调递减,所以f (x )max =f (e)=12e >18,且f (x )≥0,当x 趋近于+∞时,f (x )趋近于0.作出函数y =|f (x )|的大致图象如图所示,由图可知,函数y =|f (x )|-18的零点个数为4.9.已知函数f (x )=x +1ex(e 为自然对数的底数).(1)求函数f (x )的单调区间;(2)设函数φ(x )=xf (x )+tf ′(x )+1e x ,存在实数x 1,x 2∈[0,1],使得2φ(x 1)<φ(x 2)成立,求实数t 的取值范围.解 (1)∵函数的定义域为R ,f ′(x )=-xe x ,∴当x <0时,f ′(x )>0,当x >0时,f ′(x )<0, ∴f (x )在(-∞,0)上单调递增,在(0,+∞)上单调递减. ∴f (x )的单调增区间为(-∞,0), 单调减区间为(0,+∞).(2)存在x 1,x 2∈[0,1],使得2φ(x 1)<φ(x 2)成立, 则2[φ(x )]min <[φ(x )]max . ∵φ(x )=xf (x )+tf ′(x )+e -x=x 2+(1-t )x +1ex,∴φ′(x )=-x 2+(1+t )x -t e x =-(x -t )(x -1)e x. ①当t ≥1时,φ′(x )≤0,φ(x )在[0,1]上单调递减, ∴2φ(1)<φ(0),即t >3-e2>1;②当t ≤0时,φ′(x )≥0,φ(x )在[0,1]上单调递增, ∴2φ(0)<φ(1),即t <3-2e <0;③当0<t <1时,若x ∈[0,t ),φ′(x )<0,φ(x )在[0,t )上单调递减, 若x ∈(t,1],φ′(x )≥0,φ(x )在(t,1]上单调递增, ∴2φ(t )<max{φ(0),φ(1)}, 即2t +1e t<max ⎩⎨⎧⎭⎬⎫1,3-t e .(*) 由(1)知,g (t )=2²t +1et在[0,1]上单调递减,故4e ≤2t +1e t ≤2,而2e ≤3-t e ≤3e , ∴不等式(*)无解.综上所述,存在t ∈(-∞,3-2e)∪⎝ ⎛⎭⎪⎫3-e 2,+∞,使得命题成立.10.(2017²山东)已知函数f (x )=13x 3-12ax 2,a ∈R .(1)当a =2时,求曲线y =f (x )在点(3,f (3))处的切线方程;(2)设函数g (x )=f (x )+(x -a )cos x -sin x ,讨论g (x )的单调性并判断有无极值,有极值时求出极值.解 (1)由题意f ′(x )=x 2-ax ,所以当a =2时,f (3)=0,f ′(x )=x 2-2x , 所以f ′(3)=3,因此曲线y =f (x )在点(3,f (3))处的切线方程是y =3(x -3),即3x -y -9=0.(2)因为g (x )=f (x )+(x -a )cos x -sin x ,所以g ′(x )=f ′(x )+cos x -(x -a )sin x -cos x =x (x -a )-(x -a )sin x =(x -a )(x -sin x ). 令h (x )=x -sin x , 则h ′(x )=1-cos x ≥0, 所以h (x )在R 上单调递增.因为h (0)=0,所以当x >0时,h (x )>0; 当x <0时,h (x )<0.①当a <0时,g ′(x )=(x -a )(x -sin x ),当x ∈(-∞,a )时,x -a <0,g ′(x )>0,g (x )单调递增; 当x ∈(a,0)时,x -a >0,g ′(x )<0,g (x )单调递减; 当x ∈(0,+∞)时,x -a >0,g ′(x )>0,g (x )单调递增. 所以当x =a 时,g (x )取到极大值, 极大值是g (a )=-16a 3-sin a ;当x =0时,g (x )取到极小值,极小值是g (0)=-a . ②当a =0时,g ′(x )=x (x -sin x ),当x ∈(-∞,+∞)时,g ′(x )≥0,g (x )单调递增;所以g (x )在(-∞,+∞)上单调递增,g (x )无极大值也无极小值; ③当a >0时,g ′(x )=(x -a )(x -sin x ),当x ∈(-∞,0)时,x -a <0,g ′(x )>0,g (x )单调递增; 当x ∈(0,a )时,x -a <0,g ′(x )<0,g (x )单调递减; 当x ∈(a ,+∞)时,x -a >0,g ′(x )>0,g (x )单调递增. 所以当x =0时,g (x )取到极大值, 极大值是g (0)=-a ; 当x =a 时,g (x )取到极小值, 极小值是g (a )=-16a 3-sin a .综上所述,当a <0时,函数g (x )在(-∞,a )和(0,+∞)上单调递增,在(a,0)上单调递减,函数既有极大值,又有极小值,极大值是g (a )=-16a 3-sin a ,极小值是g (0)=-a ;当a =0时,函数g (x )在(-∞,+∞)上单调递增,无极值;当a >0时,函数g (x )在(-∞,0)和(a ,+∞)上单调递增,在(0,a )上单调递减,函数既有极大值,又有极小值,极大值是g (0)=-a ,极小值是g (a )=-16a 3-sin a .回扣3 三角函数与平面向量1.准确记忆六组诱导公式 对于“k π2±α,k ∈Z ”的三角函数值与α角的三角函数值的关系口诀:奇变偶不变,符号看象限.2.三角函数恒等变换“四大策略”(1)常值代换:特别是“1”的代换,1=sin 2θ+cos 2θ=tan45°等. (2)降次与升次:正用二倍角公式升次,逆用二倍角公式降次. (3)弦、切互化:一般是切化弦.(4)灵活运用辅助角公式a sin α+b cos α=a 2+b 2sin(α+φ)⎝⎛⎭⎪⎫其中tan φ=ba.3.三种三角函数的性质4.函数y =A sin(ωx +φ)(ω>0,A >0)的图象 (1)“五点法”作图设z =ωx +φ,令z =0,π2,π,3π2,2π,求出相应的x 的值与y 的值,描点、连线可得.(2)由三角函数的图象确定解析式时,一般利用五点中的零点或最值点作为解题突破口. (3)图象变换y =sin x ―――――――――→向左(φ>0)或向右(φ<0)平移|φ|个单位长度y =sin(x +φ) ――――――――――――→横坐标变为原来的1ω(ω>0)倍纵坐标不变y =sin(ωx +φ) ―――――――――――→纵坐标变为原来的A (A >0)倍横坐标不变y =A sin(ωx +φ). 5.正弦定理及其变形asin A=b sin B =csin C=2R (2R 为△ABC 外接圆的直径).变形:a =2R sin A ,b =2R sin B ,c =2R sin C . sin A =a 2R ,sin B =b 2R ,sin C =c2R.a ∶b ∶c =sin A ∶sin B ∶sin C .6.余弦定理及其推论、变形a 2=b 2+c 2-2bc cos A ,b 2=a 2+c 2-2ac cos B , c 2=a 2+b 2-2ab cos C .推论:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.变形:b 2+c 2-a 2=2bc cos A ,a 2+c 2-b 2=2ac cos B ,a 2+b 2-c 2=2ab cos C .7.面积公式S △ABC =12bc sin A =12ac sin B =12ab sin C .8.平面向量的数量积(1)若a ,b 为非零向量,夹角为θ,则a²b =|a||b |cos θ. (2)设a =(x 1,y 1),b =(x 2,y 2),则a²b =x 1x 2+y 1y 2. 9.两个非零向量平行、垂直的充要条件 若a =(x 1,y 1),b =(x 2,y 2),则 (1)a ∥b ⇔a =λb (b ≠0)⇔x 1y 2-x 2y 1=0. (2)a ⊥b ⇔a²b =0⇔x 1x 2+y 1y 2=0. 10.利用数量积求长度(1)若a =(x ,y ),则|a |=a²a =x 2+y 2. (2)若A (x 1,y 1),B (x 2,y 2),则|AB →|=(x 2-x 1)2+(y 2-y 1)2.11.利用数量积求夹角若a =(x 1,y 1),b =(x 2,y 2),θ为a 与b 的夹角, 则cos θ=a²b |a||b |=x 1x 2+y 1y 2x 21+y 21 x 22+y 22. 12.三角形“四心”向量形式的充要条件设O 为△ABC 所在平面上一点,角A ,B ,C 所对的边长分别为a ,b ,c ,则(1)O 为△ABC 的外心⇔|OA →|=|OB →|=|OC →|=a 2sin A.(2)O 为△ABC 的重心⇔OA →+OB →+OC →=0.(3)O 为△ABC 的垂心⇔OA →²OB →=OB →²OC →=OC →²OA →. (4)O 为△ABC 的内心⇔aOA →+bOB →+cOC →=0.1.利用同角三角函数的平方关系式求值时,不要忽视角的范围,要先判断函数值的符号. 2.在求三角函数的值域(或最值)时,不要忽略x 的取值范围.3.求函数f (x )=A sin(ωx +φ)的单调区间时,要注意A 与ω的符号,当ω<0时,需把ω的符号化为正值后求解.4.三角函数图象变换中,注意由y =sin ωx 的图象变换得y =sin(ωx +φ)时,平移量为⎪⎪⎪⎪⎪⎪φω,而不是φ. 5.在已知两边和其中一边的对角时,要注意检验解是否满足“大边对大角”,避免增解. 6.要特别注意零向量带来的问题:0的模是0,方向任意,并不是没有方向;0与任意非零向量平行.7.a²b >0是〈a ,b 〉为锐角的必要不充分条件;a²b <0是〈a ,b 〉为钝角的必要不充分条件.1.2sin45°cos15°-sin30°的值=________. 答案32解析2sin45°cos15°-sin30°=2sin45°cos15°-sin(45°-15°)=2sin45°cos15°-(sin45°cos15°-cos45°sin15°)=sin45°cos15°+2.(1+tan18°)(1+tan27°)的值是________. 答案 2解析 由题意得tan(18°+27°)=tan18°+tan27°1-tan18°tan27°,即tan18°+tan27°1-tan18°tan27°=1, 所以tan18°+tan27°=1-tan18°tan27°,所以(1+tan18°)(1+tan27°)=1+tan18°+tan27°+tan18°tan27°=2.3.(2017²江苏泰州中学期中)向量a =(cos10°,sin10°),b =(cos70°,sin70°),|a -2b |=________. 答案3解析 a ²b =cos70°cos10°+sin70°sin10°=cos60°=12,|a |=|b |=1,所以|a -2b |=a 2+4b 2-4a ²b =1+4-2= 3.4.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC 的面积是________. 答案332解析 c 2=(a -b )2+6,即c 2=a 2+b 2-2ab +6,① ∵C =π3,由余弦定理得c 2=a 2+b 2-ab ,②由①和②得ab =6,∴S △ABC =12ab sin C =12³6³32=332.5.已知两点A (1,0),B (1,1),O 为坐标原点,点C 在第二象限,且∠AOC =135°,设OC →=-OA →+λOB →(λ∈R ),则λ的值为__________. 答案 12解析 由∠AOC =135°知,点C 在射线y =-x (x <0)上,设点C 的坐标为(a ,-a ),a <0,则有(a ,-a )=(-1+λ,λ),得a =-1+λ,-a =λ,消去a 得λ=12.6.已知a ,b 为同一平面内的两个向量,且a =(1,2),|b |=12|a |,若a +2b 与2a -b 垂直,则a 与b 的夹角为________.答案 π解析 |b |=12|a |=52,而(a +2b )²(2a -b )=0,即2a 2-2b 2+3a²b =0,所以a²b =-52,从而cos 〈a ,b 〉=a²b|a||b |=-1,所以〈a ,b 〉=π.7.已知函数f (x )=3sin ⎝⎛⎭⎪⎫ωx -π6(ω>0)和g (x )=3cos(2x +φ)的图象的对称中心完全相同,若x ∈⎣⎢⎡⎦⎥⎤0,π2,则f (x )的取值范围是________.答案 ⎣⎢⎡⎦⎥⎤-32,3解析 由两个三角函数图象的对称中心完全相同可知,两函数的周期相同,故ω=2, 所以f (x )=3sin ⎝⎛⎭⎪⎫2x -π6, 那么当x ∈⎣⎢⎡⎦⎥⎤0,π2时,-π6≤2x -π6≤5π6, 所以-12≤sin ⎝ ⎛⎭⎪⎫2x -π6≤1,故f (x )∈⎣⎢⎡⎦⎥⎤-32,3.8.在等腰梯形ABCD 中,已知AB ∥DC ,AB =2,BC =1,∠ABC =60°,动点E 和F 分别在线段BC 和DC 上,且BE →=λBC →,DF →=19λDC →,则AE →²AF →的最小值为__________.答案2918解析 方法一 在梯形ABCD 中,AB =2,BC =1,∠ABC =60°,可得DC =1,AE →=AB →+λBC →,AF →=AD →+19λDC →(λ>0),∴AE →²AF →=(AB →+λBC →)²⎝ ⎛⎭⎪⎫AD →+19λDC →=AB →²AD →+AB →²19λDC→+λBC →²AD →+λBC →²19λDC →=2³1³cos60°+2³1³19λ+λ³1³1³cos60°+λ³19λ³1³1³cos120°=29λ+λ2+1718≥229λ²λ2+1718=2918,当且仅当29λ=λ2,即λ=23时,取得最小值为2918. 方法二 以点A 为坐标原点,AB 所在的直线为x 轴建立平面直角坐标系,则B (2,0),C ⎝ ⎛⎭⎪⎫32,32,D ⎝ ⎛⎭⎪⎫12,32. 又BE →=λBC →,DF →=19λDC →,则E ⎝ ⎛⎭⎪⎫2-12λ,32λ,F ⎝ ⎛⎭⎪⎫12+19λ,32,λ>0,仅当29λ=12λ,即λ=23时取等号,故AE →²AF →的最小值为2918.9.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3-3sin ⎝ ⎛⎭⎪⎫2x -π6. (1)求函数f (x )的最小正周期和单调增区间;(2)当x ∈⎣⎢⎡⎦⎥⎤-π6,π3时,试求f (x )的最值,并写出取得最值时自变量x 的值.解 (1)由题意知,f (x )=-sin2x +3cos2x =2sin ⎝⎛⎭⎪⎫2x +2π3, 所以f (x )的最小正周期为T =2π2=π.当-π2+2k π≤2x +2π3≤π2+2k π(k ∈Z )时,f (x )单调递增,解得x ∈⎣⎢⎡⎦⎥⎤-7π12+k π,-π12+k π(k ∈Z ), 所以f (x )的单调增区间为⎣⎢⎡⎦⎥⎤-7π12+k π,-π12+k π(k ∈Z ). (2)因为x ∈⎣⎢⎡⎦⎥⎤-π6,π3,所以π3≤2x +2π3≤4π3,当2x +2π3=π2,即x =-π12时,f (x )取得最大值2,当2x +2π3=4π3,即x =π3时,f (x )取得最小值- 3.10.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知cos C +(cos A -3sin A )cos B =0.(1)求角B 的大小;(2)若a =2,b =7,求△ABC 的面积. 解 (1)由已知得-cos(A +B )+cos A cos B -3sin A cos B =0, 即sin A sin B -3sin A cos B =0, 因为sin A ≠0,又0<B <π,所以B =π3.(2)因为sin B =32,cos B =12, 所以a sin A =b sin B =732=2213,又a =2, 所以sin A =321=217, 因为a <b , 所以cos A =277.所以sin C =sin(A +B )=sin A cos B +cos A sin B =32114,所以S =12ab sin C =332.回扣4 数列1.牢记概念与公式等差数列、等比数列2.活用定理与结论(1)等差、等比数列{a n}的常用性质(2)判断等差数列的常用方法①定义法a n+1-a n=d(常数)(n∈N*)⇔{a n}是等差数列.②通项公式法a n=pn+q(p,q为常数,n∈N*)⇔{a n}是等差数列.③中项公式法2a n+1=a n+a n+2 (n∈N*)⇔{a n}是等差数列.④前n项和公式法S n=An2+Bn(A,B为常数,n∈N*)⇔{a n}是等差数列.(3)判断等比数列的常用方法①定义法a n+1=q (q是不为0的常数,n∈N*)⇔{a n}是等比数列.a n②通项公式法a n =cq n (c ,q 均是不为0的常数,n ∈N *)⇔{a n }是等比数列.③中项公式法a 2n +1=a n ²a n +2(a n ²a n +1²a n +2≠0,n ∈N *)⇔{a n }是等比数列.3.数列求和的常用方法(1)等差数列或等比数列的求和,直接利用公式求和.(2)形如{a n ²b n }(其中{a n }为等差数列,{b n }为等比数列)的数列,利用错位相减法求和. (3)通项公式形如a n =c(an +b 1)(an +b 2)(其中a ,b 1,b 2,c 为常数)用裂项相消法求和.(4)通项公式形如a n =(-1)n²n 或a n =a ²(-1)n(其中a 为常数,n ∈N *)等正负项交叉的数列求和一般用并项法.并项时应注意分n 为奇数、偶数两种情况讨论.(5)分组求和法:分组求和法是解决通项公式可以写成c n =a n +b n 形式的数列求和问题的方法,其中{a n }与{b n }是等差(比)数列或一些可以直接求和的数列. (6)并项求和法:先将某些项放在一起求和,然后再求S n .1.已知数列的前n 项和求a n ,易忽视n =1的情形,直接用S n -S n -1表示.事实上,当n =1时,a 1=S 1;当n ≥2时,a n =S n -S n -1.2.易混淆几何平均数与等比中项,正数a ,b 的等比中项是±ab .3.等差数列中不能熟练利用数列的性质转化已知条件,灵活整体代换进行基本运算.如等差数列{a n }与{b n }的前n 项和分别为S n 和T n ,已知S n T n =n +12n +3,求a nb n时,无法正确赋值求解.4.易忽视等比数列中公比q ≠0导致增解,易忽视等比数列的奇数项或偶数项符号相同造成增解.5.运用等比数列的前n 项和公式时,易忘记分类讨论.一定分q =1和q ≠1两种情况进行讨论.6.利用错位相减法求和时,要注意寻找规律,不要漏掉第一项和最后一项. 7.裂项相消法求和时,分裂前后的值要相等, 如1n (n +2)≠1n -1n +2,而是1n (n +2)=12⎝ ⎛⎭⎪⎫1n -1n +2.8.通项中含有(-1)n的数列求和时,要把结果写成n 为奇数和n 为偶数两种情况的分段形式.1.在等差数列{a n }中,已知a 3+a 8=10,则3a 5+a 7=________. 答案 20解析 设公差为d ,则a 3+a 8=2a 1+9d =10,3a 5+a 7=3(a 1+4d )+(a 1+6d )=4a 1+18d =2³10=20.2.(2017²南京、盐城一模)设{a n }是等差数列,若a 4+a 5+a 6=21,则S 9=____________. 答案 63解析 ∵a 4+a 5+a 6=21,∴3a 5=21,可得a 5=7, ∴S 9=9³(a 1+a 9)2=9³(2a 5)2=9a 5=63.3.已知数列{a n }的前n 项和为S n ,若S n =2a n -4(n ∈N *),则a n 的通项公式为________. 答案 2n +1解析 a n +1=S n +1-S n =2a n +1-4-(2a n -4)⇒a n +1=2a n ,再令n =1,∴S 1=2a 1-4,解得a 1=4,∴数列{a n }是以4为首项,2为公比的等比数列,∴a n =4²2n -1=2n +1.4.(2017²南京高淳区质检)若S n 为等差数列{a n }的前n 项和,S 9=-36,S 13=-104,则a 5与a 7的等比中项为__________. 答案 ±4 2解析 由S 9=-36,S 13=-104,可解得a 1=4,d =-2,所以a 5=-4,a 7=-8. 设a 5与a 7的等比中项为x ,则x 2=a 5a 7=32, 所以x =±4 2.5.若等比数列{a n }的各项均为正数,且a 10a 11+a 9a 12=2e 5,则ln a 1+ln a 2+…+ln a 20=________. 答案 50解析 ∵数列{a n }为等比数列,且a 10a 11+a 9a 12=2e 5, ∴a 10a 11+a 9a 12=2a 10a 11=2e 5, ∴a 10a 11=e 5,∴ln a 1+ln a 2+…+ln a 20=ln(a 1a 2…a 20) =ln(a 10a 11)10=ln(e 5)10=lne 50=50.6.已知等比数列{a n }的前n 项和为S n ,a 1+a 3=52,且a 2+a 4=54,则S nan =________.答案 2n-1解析 设等比数列{a n }的公比为q ,则⎩⎪⎨⎪⎧a 1(1+q 2)=52,a 1q (1+q 2)=54,解得⎩⎪⎨⎪⎧a 1=2,q =12,∴S n a n =a 1(1-q n )1-q a 1q n -1=2³⎝ ⎛⎭⎪⎫1-12n 1-122³⎝ ⎛⎭⎪⎫12n -1=2n-1. 7.若数列{a n }满足a 2-a 1>a 3-a 2>a 4-a 3>…>a n +1-a n >…,则称数列{a n }为“差递减”数列.若数列{a n }是“差递减”数列,且其通项a n 与其前n 项和S n ()n ∈N *满足2S n =3a n +2λ-1()n ∈N *,则实数λ的取值范围是________.答案 ⎝ ⎛⎭⎪⎫12,+∞解析 当n =1时,2a 1=3a 1+2λ-1,a 1=1-2λ,当n >1时,2S n -1=3a n -1+2λ-1,所以2a n =3a n -3a n -1,a n =3a n -1,所以a n =()1-2λ3n -1,a n -a n -1=()1-2λ3n -1-()1-2λ3n -2=()2-4λ3n -2,依题意()2-4λ3n -2是一个减数列,所以2-4λ<0,λ>12.8.已知等差数列{a n }的公差d ≠0,且a 1,a 3,a 13成等比数列,若a 1=1,S n 是数列{a n }前n 项的和,则2S n +16a n +3(n ∈N *)的最小值为________.答案 4解析 据题意由a 1,a 3,a 13成等比数列,可得(1+2d )2=1+12d ,解得d =2,故a n =2n -1,S n =n 2,因此2S n +16a n +3=2n 2+162n +2=n 2+8n +1=(n +1)2-2(n +1)+9n +1=(n +1)+9n +1-2,据基本不等式知2S n +16a n +3=(n +1)+9n +1-2≥2(n +1)³9n +1-2=4,当n =2时取得最小值4. 9.已知首项都是1的两个数列{a n },{b n }(b n ≠0,n ∈N *)满足a n b n +1-a n +1b n +2b n +1b n =0. (1)令c n =a n b n,求数列{c n }的通项公式; (2)在(1)的条件下,若b n =3n -1,求数列{a n }的前n 项和S n .解 (1)因为a n b n +1-a n +1b n +2b n +1b n =0,b n ≠0(n ∈N *),所以a n +1b n +1-a nb n=2,即c n +1-c n =2.所以数列{}c n 是首项c 1=1,公差d =2的等差数列,故c n =2n -1. (2)由b n =3n -1知,a n =c n b n =(2n -1)3n -1,于是数列{a n }的前n 项和S n =1³30+3³31+5³32+…+(2n -1)³3n -1,3S n =1³31+3³32+…+(2n -3)³3n -1+(2n -1)³3n,两式相减得-2S n =1+2³(31+32+…+3n -1)-(2n -1)³3n =-2-(2n -2)3n,所以S n =(n -1)3n+1.10.(2017²江苏南师附中质检)已知数列{a n }和{b n }满足a 1a 2a 3…a n =n b(n ∈N *).若{a n }为等比数列,且a 1=2,b 3=6+b 2. (1)求{a n }和{b n }的通项公式;(2)设c n =1a n -1b n(n ∈N *),记数列{c n }的前n 项和为S n .(i)求S n ;(ii)求正整数k ,使得对任意n ∈N *均有S k ≥S n . 解 (1)∵a 1a 2a 3…a n =(2)b n (n ∈N *),①当n ≥2,n ∈N *时,a 1a 2a 3…a n -1=1n b-,②由①②知a n =1nn b b --,令n =3,则有a 3=32b b -.∵b 3=6+b 2, ∴a 3=8.∵{a n }为等比数列,且a 1=2,设{a n }的公比为q , ∴则q 2=a 3a 1=4,由题意知a n >0,∴q >0,∴q =2. ∴a n =2n (n ∈N *).又由a 1a 2a 3…a n =n b(n ∈N *),得21³22³23…³2n =n b,即(1)22,n n n b +=∴b n =n (n +1)(n ∈N *). (2)(i)∵c n =1a n -1b n =12n -1n (n +1)=12n -⎝ ⎛⎭⎪⎫1n -1n +1, ∴S n =c 1+c 2+c 3+…+c n=12-⎝ ⎛⎭⎪⎫11-12+122-⎝ ⎛⎭⎪⎫12-13+…+12n -⎝ ⎛⎭⎪⎫1n -1n +1 =12+122+…+12n -⎝ ⎛⎭⎪⎫1-1n +1 =1-12n -1+1n +1=1n +1-12n . (ii)∵c 1=0,c 2>0,c 3>0,c 4>0,当n ≥5时,c n =1n (n +1)⎣⎢⎡⎦⎥⎤n (n +1)2n-1, 而n (n +1)2n-(n +1)(n +2)2n +1=(n +1)(n -2)2n +1>0,得n (n +1)2n≤5³(5+1)25<1,∴当n ≥5时,c n <0.综上,对任意的n ∈N *恒有S 4≥S n ,故k =4.回扣5 不等式1.一元二次不等式的解法解一元二次不等式的步骤:一化(将二次项系数化为正数);二判(判断Δ的符号);三解(解对应的一元二次方程);四写(大于取两边,小于取中间).解含有参数的一元二次不等式一般要分类讨论,往往从以下几个方面来考虑:①二次项系数,它决定二次函数的开口方向;②判别式Δ,它决定根的情形,一般分Δ>0,Δ=0,Δ<0三种情况;③在有根的条件下,要比较两根的大小. 2.一元二次不等式的恒成立问题(1)ax 2+bx +c >0(a ≠0)恒成立的条件是⎩⎪⎨⎪⎧ a >0,Δ<0.(2)ax 2+bx +c <0(a ≠0)恒成立的条件是⎩⎪⎨⎪⎧a <0,Δ<0.3.分式不等式f (x )g (x )>0(<0)⇔f (x )g (x )>0(<0); f (x )g (x )≥0(≤0)⇔⎩⎪⎨⎪⎧f (x )g (x )≥0(≤0),g (x )≠0.4.基本不等式 (1)a +b2≥ab (a ,b ∈(0,+∞)),当且仅当a =b 时取等号.(2)在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,满足基本不等式中“正”“定”“等”的条件. 5.线性规划(1)可行域的确定,“线定界,点定域”.(2)线性目标函数的最大值、最小值一般在可行域的顶点处取得.(3)线性目标函数的最值也可在可行域的边界上取得,这时满足条件的最优解有无数多个.1.不等式两端同时乘以一个数或同时除以一个数,不讨论这个数的正负,从而出错. 2.解形如一元二次不等式ax 2+bx +c >0时,易忽视系数a 的讨论导致漏解或错解,要注意分a >0,a <0进行讨论.3.应注意求解分式不等式时正确进行同解变形,不能把f (x )g (x )≤0直接转化为f (x )²g (x )≤0,而忽视g (x )≠0.4.容易忽视使用基本不等式求最值的条件,即“一正、二定、三相等”导致错解,如求函数f (x )=x 2+2+1x 2+2的最值,就不能利用基本不等式求最值;求解函数y =x +3x(x <0)时应先转化为正数再求解.5.解线性规划问题,要注意边界的虚实;注意目标函数中y 的系数的正负;注意最优整数解.6.求解线性规划问题时,不能准确把握目标函数的几何意义导致错解,如y -2x +2是指已知区域内的点(x ,y )与点(-2,2)连线的斜率,而(x -1)2+(y -1)2是指已知区域内的点(x ,y )到点(1,1)的距离的平方等.1.(2017²泰州二中调研)函数y =3-2x -x 2的定义域是________. 答案 [-3,1]解析 由3-2x -x 2≥0,得x 2+2x -3≤0, 解得x ∈[-3,1].2.若不等式2kx 2+kx -38≥0的解集为空集,则实数k 的取值范围是____________.答案 (-3,0]解析 由题意可知,2kx 2+kx -38<0恒成立,当k =0时成立,当k ≠0时需满足⎩⎪⎨⎪⎧k <0,Δ<0,代入求得-3<k <0,所以实数k 的取值范围是(-3,0].3.二次不等式ax 2+bx +c <0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <13或x >12,则关于x 的不等式cx 2-bx +a >0的解集为________. 答案 {x |-3<x <-2}解析 由已知,-b a =56,c a =16,且a <0,则b =-56a ,c =16a ,故不等式cx 2-bx +a >0可化为x 2+5x +6<0,解得-3<x <-2.4.(2016²上海)若x ,y 满足⎩⎪⎨⎪⎧x ≥0,y ≥0,y ≥x +1,则x -2y 的最大值为________.答案 -2解析 令z =x -2y ,则y =12x -z2.当在y 轴上截距最小时,z 最大.即过点(0,1)时,z 取最大值,z =0-2³1=-2.5.要制作一个容积为4m 3,高为1m 的无盖长方体容器.已知该容器的底面造价是20元/m 2,侧面造价是10元/m 2,则该容器的最低总造价是________元. 答案 160解析 由题意知,体积V =4m 3,高h =1m ,所以底面积S =4m 2,设底面矩形的一条边长是x m ,则另一条边长是4xm ,又设总造价是y 元,则y =20³4+10³⎝ ⎛⎭⎪⎫2x +8x ≥80+202x ²8x =160,当且仅当2x =8x,即x =2时取得等号.6.(2017²江苏南京高淳区质检)设P 是函数y =x (x +1)图象上异于原点的动点,且该图象的点P 处的切线的倾斜角为θ,则θ的取值范围是________. 答案 ⎣⎢⎡⎭⎪⎫π3,π2解析 因为y ′=12x(x +1)+x =3x +12x =32x +12x(x >0)≥23x 2²12x=3,当且仅当x =13时取等,所以k =tan θ≥3,又θ∈[0,π),所以θ∈⎣⎢⎡⎭⎪⎫π3,π2.7.若不等式tt 2+9≤a ≤t +2t2在t ∈(0,2]上恒成立,则a 的取值范围是______________. 答案 ⎣⎢⎡⎦⎥⎤213,1 解析 ∵tt 2+9=1t +9t ,而t +9t 在区间(0,2]上单调递减,∴t +9t ≥2+92=132,t t 2+9=1t +9t≤213(当且仅当t =2时等号成立),又t +2t 2=1t +2t 2=2⎝ ⎛⎭⎪⎫1t +142-18, ∵1t ≥12,∴2⎝ ⎛⎭⎪⎫1t +142-18≥1(当且仅当t =2时等号成立),故a 的取值范围是⎣⎢⎡⎦⎥⎤213,1. 8.若a ,b 均为非负实数,且a +b =1,则1a +2b +42a +b的最小值为________. 答案 3解析 方法一 令a +2b =s,2a +b =t ,则1a +2b +42a +b =1s +4t.由题意知,s ≥0,t ≥0,且s +t =3(a +b )=3,所以1s +4t =s +t 3⎝ ⎛⎭⎪⎫1s +4t =13⎝ ⎛⎭⎪⎫5+t s +4s t ≥13³9=3,当且仅当s =1,t=2时等号成立.所以1a +2b +42a +b的最小值为3.方法二 因为a +b =1,所以1a +2b +42a +b =11+b +41+a, 令1+b =s ,a +1=t ,则11+b +41+a =1s +4t ,由题意知,s ≥1,t ≥1,且s +t =3,所以1s +4t =s +t 3⎝ ⎛⎭⎪⎫1s +4t =13⎝ ⎛⎭⎪⎫5+t s +4s t ≥13³9=3,当且仅当s =1,t =2时等号成立.所以1a +2b +42a +b的最小值为3. 9.解关于x 的不等式x 2+ax -2x -1≤x +1.解 原不等式可化为x 2+ax -2x -1-(x +1)≤0,即ax -1x -1≤0, 当a =0时,有-1x -1≤0,所以x >1, 当a ≠0时,①当a <0时,有x -1ax -1≥0,且1a <1,所以x ≤1a或x >1; ②当0<a <1时,有x -1a x -1≤0,且1a >1,所以1<x ≤1a;③当a =1时,有x -1x -1≤0,所以x ∈∅, ④当a >1时,有x -1ax -1≤0,且1a <1,所以1a≤x <1, 综上,当a <0时,原不等式的解集为⎝ ⎛⎦⎥⎤-∞,1a ∪(1,+∞),当a =0时,原不等式的解集为(1,+∞),当0<a <1时,原不等式的解集为⎝⎛⎦⎥⎤1,1a ,当a =1时,原不等式的解集为∅, 当a >1时,原不等式的解集为⎣⎢⎡⎭⎪⎫1a ,1.10.(2017²江苏苏州期中)如图,有一块平行四边形绿地ABCD ,经测量BC =2百米,CD =1百米,∠BCD =120°,拟过线段BC 上一点E 设计一条直路EF (点F 在四边形ABCD 的边上,不计路的宽度),将绿地分为面积之比为1∶3的左右两部分,分别种植不同的花卉,设EC。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——压轴大题突破练1 Word版含答案

压轴大题突破练1.函数与导数1.设函数f (x )=x ln x +ax ,a ∈R .(1)当a =1时,求曲线y =f (x )在点(1,f (1))处的切线方程;(2)求函数y =f (x )在⎣⎢⎡⎦⎥⎤1e ,e 上的最小值; (3)若g (x )=f (x )+12ax 2-(2a +1)x ,求证:a ≥0是函数y =g (x )在x ∈(1,2)时单调递增的充分不必要条件.(1)解 由f (x )=x ln x +ax ,得f ′(x )=ln x +a +1.当a =1时,f ′(x )=ln x +2,f (1)=1,f ′(1)=2,求得切线方程为y =2x -1.(2)解 令f ′(x )=0,得x =e-(a +1). ∴当e -(a +1)≤1e ,即a ≥0时,x ∈⎣⎢⎡⎦⎥⎤1e ,e 时f ′(x )≥0恒成立,f (x )单调递增, 此时f (x )min =f ⎝ ⎛⎭⎪⎫1e =a -1e . 当e -(a +1)≥e ,即a ≤-2时,x ∈⎣⎢⎡⎦⎥⎤1e ,e 时f ′(x )≤0恒成立,f (x )单调递减,此时f (x )min =f (e)=a e +e.当1e <e -(a +1)<e ,即-2<a <0时,x ∈⎣⎢⎡⎭⎪⎫1e ,e -(a +1)时f ′(x )<0,f (x )单调递减;当x ∈(e -(a +1),e)时,f ′(x )>0,f (x )单调递增,此时f (x )min =f (e-(a +1))=-e -(a +1).(3)证明 g ′(x )=f ′(x )+ax -(2a +1)=ln x +ax -a =ln x +a (x -1),∴当a ≥0时,x ∈(1,2)时,ln x >0,a (x -1)≥0, g ′(x )>0恒成立,函数y =g (x )在x ∈(1,2)时单调递增,充分条件成立;又当a =-12时,代入g ′(x )=ln x +a (x -1) =ln x -12x +12. 设h (x )=g ′(x )=ln x -12x +12,x ∈(1,2),则h ′(x )=1x -12=2-x 2x>0恒成立, ∴当x ∈(1,2)时,h (x )单调递增.又h (1)=0,∴当x ∈(1,2)时,h (x )>0恒成立.而h (x )=g ′(x ),∴当x ∈(1,2)时,g ′(x )>0恒成立,函数y =g (x )单调递增,∴必要条件不成立.综上,a ≥0是函数y =g (x )在x ∈(1,2)时单调递增的充分不必要条件.2.设函数f (x )=e x -|x -a |,其中a 是实数.(1)若f (x )在R 上单调递增,求实数a 的取值范围;(2)若函数有极大值点x 2和极小值点x 1,且f (x 2)-f (x 1)≥k (x 2-x 1)恒成立,求实数k 的取值范围.解 (1)因为f (x )=e x -|x -a |=⎩⎪⎨⎪⎧ e x -x +a ,x ≥a ,e x +x -a ,x <a ,则f ′(x )=⎩⎪⎨⎪⎧ e x -1,x ≥a ,e x +1,x <a ,因为f (x )在R 上单调递增,所以f ′(x )≥0恒成立,当x <a 时,f ′(x )=e x +1≥1>0恒成立,当x ≥a 时,f ′(x )=e x-1≥0恒成立, 故应f ′(a )≥0,即a ≥0.(2)由(1)知当a ≥0时,f (x )在R 上单调递增,不符合题意,所以有a <0.此时,当x <a 时,f ′(x )=e x +1≥1>0,f (x )单调递增,当x ≥a 时,f ′(x )=e x -1,令f ′(x )=0,得x =0,所以f ′(x )<0在(a,0)上恒成立,f (x )在(a,0)上单调递减,f ′(x )>0在(0,+∞)上恒成立,f (x )在(0,+∞)上单调递增,所以f (x )极大=f (a )=e a ,f (x )极小=f (0)=1+a ,即a <0符合题意.由f (x 2)-f (x 1)≥k (x 2-x 1)恒成立,可得e a -a -1≥ka 对任意a <0恒成立,设g (a )=e a -(k +1)a -1,求导,得g ′(a )=e a -(k +1),①当k ≤-1时,g ′(a )>0恒成立,g (a )在(-∞,0)上单调递增,又因为g (-1)=1e+k <0,与g (a )>0矛盾;②当k ≥0时,g ′(a )<0在(-∞,0)上恒成立,g (a )在(-∞,0)上单调递减, 又因为g (0)=0,所以此时g (a )≥0恒成立,符合题意;③当-1<k <0时,g ′(a )>0在(-∞,0)上的解集为(ln(k +1),0),即g (a )在(ln(k +1),0)上单调递增,又因为g (0)=0,所以g (ln (k +1))<0不符合题意. 综上,实数k 的取值范围为[0,+∞).3.(2017·江苏泰兴中学质检)已知函数f (x )=13x 3-mx 2-x +13m ,其中m ∈R . (1)求函数y =f (x )的单调区间;(2)若对任意的x 1,x 2∈[-1,1],都有|f ′(x 1)-f ′(x 2)|≤4,求实数m 的取值范围;(3)求函数f (x )的零点个数.解 (1)f ′(x )=x 2-2mx -1,由f ′(x )≥0,得x ≤m -m 2+1或x ≥m +m 2+1;故函数f (x )的单调增区间为(-∞,m -m 2+1),(m +m 2+1,+∞),由f ′(x )<0,得m -m 2-1<x <m +m 2+1,故函数f (x )的单调减区间为(m -m 2+1,m +m 2+1).(2)“对任意的x 1,x 2∈[-1,1],都有|f ′(x 1)-f ′(x 2)|≤4”等价于“函数y =f ′(x ),x ∈[-1,1]的最大值与最小值的差小于等于4”.对于f ′(x )=x 2-2mx -1,对称轴x =m .①当m <-1时,f ′(x )的最大值为f ′(1),最小值为f ′(-1),由f ′(1)-f ′(-1)≤4,即-4m ≤4,解得m ≥-1,舍去;②当-1≤m ≤1时,f ′(x )的最大值为f ′(1)或f ′(-1),最小值为f ′(m ),由⎩⎪⎨⎪⎧ f ′(1)-f ′(m )≤4,f ′(-1)-f ′(m )≤4,即⎩⎪⎨⎪⎧ m 2-2m -3≤0,m 2+2m -3≤0,解得-1≤m ≤1;③当m >1时,f ′(x )的最大值为f ′(-1),最小值为f ′(1),由f ′(-1)-f ′(1)≤4,即4m ≤4,解得m ≤1,舍去.综上,实数m 的取值范围是[-1,1].(3)由f ′(x )=0,得x 2-2mx -1=0,因为Δ=4m 2+4>0,所以y =f (x )既有极大值也有极小值.设f ′(x 0)=0,即x 20-2mx 0-1=0,x 20=2mx 0+1,则f (x 0)=13x 30-mx 20-x 0+13m =-13mx 20-23x 0+13m =-23x 0(m 2+1), 所以极大值f (m -m 2+1)=-23(m -m 2+1)(m 2+1)>0, 极小值f (m +m 2+1)=-23(m +m 2+1)(m 2+1)<0, 故函数f (x )有三个零点.4.已知函数f (x )=x 3+ax 2-a 2x +2,a ∈R .(1)若a <0,试求函数y =f (x )的单调递减区间;(2)若a =0,且曲线y =f (x )在点A ,B (A ,B 不重合)处切线的交点位于直线x =2上,证明:A ,B 两点的横坐标之和小于4;(3)如果对于一切x 1,x 2,x 3∈[0,1],总存在以f (x 1),f (x 2),f (x 3)为三边长的三角形,试求正实数a 的取值范围.(1)解 函数f (x )的导函数f ′(x )=3x 2+2ax -a 2=3(x +a )⎝ ⎛⎭⎪⎫x -a 3. 因为a <0,由f ′(x )<0,解得a 3<x <-a . 所以函数y =f (x )的单调递减区间为⎝ ⎛⎭⎪⎫a 3,-a . (2)证明 当a =0时,f (x )=x 3+2.设在点A (x 1,x 31+2),B (x 2,x 32+2)处的切线交于直线x =2上一点P (2,t ).因为y ′=3x 2,所以曲线y =f (x )在点A 处的切线斜率为k =3x 21,所以在点A 处的切线方程为y -(x 31+2)=3x 21(x -x 1).因为切线过点P ,所以t -(x 31+2)=3x 21(2-x 1),即2x 31-6x 21+(t -2)=0.同理可得2x 32-6x 22+(t -2)=0,两式相减得2(x 31-x 32)-6(x 21-x 22)=0,即(x 1-x 2)(x 21+x 1x 2+x 22)-3(x 1-x 2)(x 1+x 2)=0,因为x 1-x 2≠0,所以x 21+x 1x 2+x 22-3(x 1+x 2)=0,即(x 1+x 2)2-x 1x 2-3(x 1+x 2)=0. 因为x 1x 2≤⎝ ⎛⎭⎪⎫x 1+x 222,且x 1≠x 2, 所以x 1x 2<⎝ ⎛⎭⎪⎫x 1+x 222. 从而上式可以化为(x 1+x 2)2-⎝ ⎛⎭⎪⎫x 1+x 222-3(x 1+x 2)<0,即(x 1+x 2)(x 1+x 2-4)<0. 解得0<x 1+x 2<4,即A ,B 两点的横坐标之和小于4.(3)解 由题设知,f (0)<f (1)+f (1),即2<2(-a 2+a +3),解得-1<a <2.又因为a >0,所以0<a <2.因为f ′(x )=3(x +a )⎝ ⎛⎭⎪⎫x -a 3, 所以当x ∈⎝ ⎛⎭⎪⎫0,a 3时,f ′(x )<0,f (x )单调递减,当x ∈⎝ ⎛⎭⎪⎫a 3,1时,f ′(x )>0,f (x )单调递增. 所以当x =a 3时,f (x )有最小值f ⎝ ⎛⎭⎪⎫a 3=-527a 3+2. 从而条件转化为⎩⎪⎨⎪⎧ f ⎝ ⎛⎭⎪⎫a 3=-527a 3+2>0, ①f (0)<2⎝ ⎛⎭⎪⎫-527a 3+2, ②f (1)<2⎝ ⎛⎭⎪⎫-527a 3+2. ③由①得a <33235;由②得a <335,再根据0<a <2,得0<a <335.不等式③化为1027a 3-a 2+a -1<0. 令g (a )=1027a 3-a 2+a -1,则g ′(a )=109a 2-2a +1>0,所以g (a )为增函数. 又g (2)=-127<0,所以当a ∈⎝ ⎛⎭⎪⎪⎫0,335时,g (a )<0恒成立,即③成立. 所以a 的取值范围为⎝⎛⎭⎪⎪⎫0,335.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——解答题滚动练2 Word版含答案

解答题滚动练21.(2017·南京、盐城二模)如图,在△ABC 中,D 为边BC 上一点,AD =6,BD =3,DC =2. (1)如图1,若AD ⊥BC ,求∠BAC 的大小; (2)如图2,若∠ABC =π4,求△ADC 的面积.解 (1) 由已知,得tan ∠BAD =36=12,tan ∠CAD =26=13,所以tan ∠BAC =tan(∠BAD +∠CAD )=12+131-12×13=1.因为∠BAC ∈(0,π),所以∠BAC =π4.(2) 以B 为原点,BC 所在直线为x 轴建立平面直角坐标系,则B (0,0),D (3,0),C (5,0). 因为∠ABC =π4,所以设A (a ,a ),其中a >0.由AD =6,BD =3,得(a -3)2+a 2=62,即2a 2-6a -27=0,解得a =32(1+7).所以S △ADC =12DC ·a =32(1+7).2.如图,ABCD 是一块边长为100米的正方形地皮,其中ATPS 是一半径为90米的底面为扇形小山(P 为圆弧TS 上的点),其余部分为平地.今有开发商想在平地上建一个两边落在BC 及CD 上的长方形停车场PQCR.(1)设∠PAB =θ,试将矩形PQCR 面积表示为θ的函数; (2)求停车场PQCR 面积的最大值及最小值.解 (1)S PQCR =f (θ)=(100-90cos θ)(100-90sin θ)=8100sin θcos θ-9000(sin θ+cos θ)+10000 , θ∈⎣⎢⎡⎦⎥⎤0,π2.(2)由(1)知S PQCR =f (θ)=8100sin θcos θ-9000(sin θ+cos θ)+10000,θ∈⎣⎢⎡⎦⎥⎤0,π2.令sin θ+cos θ=t ,则t =2sin ⎝ ⎛⎭⎪⎫θ+π4∈[1,2].∴S PQCR =81002t 2-9000t +10000-81002,当t =109时,S PQCR 取得最小值950(m 2),当t =2时,S PQCR 取得最大值14050-90002(m 2).答 停车场面积的最大值和最小值分别为14050-90002(m 2)和950(m 2).3.如图,点A (1,3)为椭圆x 22+y 2n=1上一定点,过点A 引两直线与椭圆分别交于B ,C 两点.(1)求椭圆方程;(2)若直线AB ,AC 与x 轴围成的是以点A 为顶点的等腰三角形. ①求直线BC 的斜率;②求△ABC 的面积的最大值,并求出此时直线BC 的方程.解 (1)把点A (1,3)代入x 22+y 2n =1得n =6,故椭圆方程为x 22+y 26=1.(2)①显然题中等腰三角形腰所在的直线不可能与x 轴垂直. 因此其斜率必存在,设两腰的斜率分别为k 1,k 2,由⎩⎪⎨⎪⎧y -3=k 1(x -1),x 22+y 26=1,消去y ,得(3+k 21)x 2+2k 1(3-k 1)x +(3-k 1)2-6=0,∴点B 的横坐标为x =1-6+23k 1k 21+3(x =1为点A 的横坐标),∴点B 的纵坐标为y =3-23k 21+6k 1k 21+3,即B ⎝ ⎛⎭⎪⎫1-6+23k 1k 21+3,3-23k 21+6k 1k 21+3.同理可得点C 的坐标为C ⎝ ⎛⎭⎪⎫1-6+23k 2k 22+3,3-23k 22+6k 2k 22+3.∵k 1+k 2=0,∴直线BC 的斜率为k BC = 3.②设B (x 1,y 1),C (x 2,y 2),直线BC 的方程为y =3x +m ,代入方程x 22+y 26=1得6x 2+23mx+m 2-6=0,∴x 1+x 2=-33m ,x 1x 2=m 2-66,∴BC =1+(3)2·|x 1-x 2| =2·(x 1+x 2)2-4x 1x 2 =23312-m 2,又点A 到直线BC 的距离为d =|m |2,∴S △ABC =12BC ·d =36m 2(12-m 2)=36-(m 2-6)2+36, ∴当m 2=6,即m =6或m =-6时,△ABC 面积取得最大值 3. 此时,直线BC 的方程为y =3x ± 6.4.已知函数f (x )=2x 3+ax 2+bx +c (a ,b ,c ∈R ).(1)若函数f (x )为奇函数,且图象过点(-1,2),求f (x )的解析式; (2)若x =1和x =2是函数f (x )的两个极值点. ①求a ,b 的值;②求函数f (x )在区间[0,3]上的零点个数. 解 (1)因为函数f (x )为奇函数,所以f (-x )=-f (x ),即2(-x )3+a (-x )2+b (-x )+c =-2x 3-ax 2-bx -c , 整理得,ax 2+c =0,所以a =c =0,从而f (x )=2x 3+bx , 又函数f (x )图象过点(-1,2),所以b =-4. 从而f (x )=2x 3-4x .(2)①f (x )=2x 3+ax 2+bx +c (a ,b ,c ∈R )的导函数f ′(x )=6x 2+2ax +b . 因为f (x )在x =1和x =2处取得极值,所以f ′(1)=0,f ′(2)=0,即⎩⎪⎨⎪⎧6+2a +b =0,24+4a +b =0,解得a =-9,b =12.②由①得f (x )=2x 3-9x 2+12x +c (c ∈R ),f ′(x )=6(x -1)(x -2).列表:显然,函数f (x )在[0,3]上的图象是一条不间断的曲线.由表知,函数f (x )在[0,3]上的最小值为f (0)=c ,最大值为f (3)=9+c . 所以当c >0或9+c <0(即c <-9)时,函数f (x )在区间[0,3]上的零点个数为0. 当-5<c <0时,因为f (0)f (1)=c (5+c )<0,且函数f (x )在(0,1)上是单调增函数, 所以函数f (x )在(0,1)上有1个零点.当-5<c <-4时,因为f (1)f (2)=(5+c )(4+c )<0,且f (x )在(1,2)上是单调减函数, 所以函数f (x )在(1,2)上有1个零点.当-9<c <-4时,因为f (2)f (3)=(4+c )(9+c )<0,且f (x )在(2,3)上是单调增函数, 所以函数f (x )在(2,3)上有1个零点.综上,当c >0或c <-9时,函数f (x )在区间[0,3]上的零点个数为0; 当-9≤c <-5或-4<c ≤0时,零点个数为1; 当c =-4或c =-5时,零点个数为2; 当-5<c <-4时,零点个数3.。
江苏专用2018届高考数学总复习考前三个月小题满分练1理

小题满分练11.设全集U=R,A={x|x2-2x≤0},B={y|y=cos x,x∈R},则图中阴影部分表示的区间是________.答案(-∞,-1)∪(2,+∞)解析因为A={x|0≤x≤2}=[0,2],B={y|-1≤y≤1}=[-1,1],所以A∪B=[-1,2],所以∁R(A∪B)=(-∞,-1)∪(2,+∞).2.(2017·苏州暑假测试)命题“∃x>1,x2≥2”的否定是________.答案∀x>1,x2<2解析根据存在性命题的否定规则得“∃x>1,x2≥2”的否定是“∀x>1,x2<2”.3.若复数z满足z i=1+2i,则z的共轭复数是________.答案2+i解析∵z i=1+2i,∴z=1+2ii=2-i,∴z=2+i.4.(2017·徐州、连云港、宿迁三检)已知一组数据3,6,9,8,4,则该组数据的方差是________.答案265(或5.2)解析这组数据的平均数x=15(3+6+9+8+4)=6,方差s2=15(9+0+9+4+4)=265.5.若流程图如图所示,则该程序运行后输出的值是________.答案10000解析i=0,S=0⇒i=1,S=1⇒i=2,S=4⇒i=3,S=9…,由此可知S =i 2,所以当i =100时,S =10000.6.(2017·常州期末)满足等式cos2x -1=3cos x (x ∈[0,π])的x 的值为________. 答案2π3解析 由题意可得,2cos 2x -3cos x -2=0,解得cos x =-12或cos x =2(舍去).又x ∈[0,π],故x =2π3.7.(2017·河北衡水中学模拟)已知{}a n 为等差数列,S n 为其前n 项和,公差为d ,若S 20172017-S 1717=100,则d 的值为________.答案110解析 因为S n n=na 1+n (n -1)2dn=a 1+(n -1)2d ,所以S 2 0172 017-S 1717=a 1+2 017-12d -⎝ ⎛⎭⎪⎫a 1+17-12d =1 000d =100,所以d =110.8.(2017·常州期末)以一个圆柱的下底面为底面,并以圆柱的上底面圆心为顶点作圆锥,若所得的圆锥底面半径等于圆锥的高,则圆锥的侧面积与圆柱的侧面积之比为________. 答案2∶2解析 如图,由题意可得圆柱的侧面积为S 1=2πrh =2πr 2.圆锥的母线l =h 2+r 2=2r ,故圆锥的侧面积为S 2=12×2πr ×l =2πr 2,所以S 2∶S 1=2∶2.9.(2017·无锡期末)设不等式组⎩⎪⎨⎪⎧x ≥1,x -y ≤0,x +y ≤4表示的平面区域为M ,若直线y =kx -2上存在M 内的点,则实数k 的取值范围为________. 答案 [2,5]解析 直线y =kx -2上存在M 内的点,即直线与平面区域M 有公共点,作出平面区域M ,注意到直线y =kx -2经过定点P (0,-2),求得直线l 1:x -y =0和l 2:x +y =4的交点A (2,2)及l 2和l 3:x =1的交点B (1,3),则k PA =2,k PB =5,由题意可得k 的取值范围是[2,5].10.已知f (x )是定义在R 上的偶函数,且对于任意的x ∈[0,+∞),满足f (x +2)=f (x ).若当x ∈[0,2)时,f (x )=|x 2-x -1|,则函数y =f (x )-1在区间[-2,4]上的零点个数为________. 答案 7解析 作出函数f (x )的图象(如图),则它与直线y =1在[-2,4]上的交点的个数,即为函数y =f (x )-1在[-2,4]上的零点的个数,由图象观察知共有7个交点,从而函数y =f (x )-1在[-2,4]上的零点有7个. 11.(2017·无锡期末)设点P 是有公共焦点F 1,F 2的椭圆C 1与双曲线C 2的一个交点,且PF 1⊥PF 2,椭圆C 1的离心率为e 1,双曲线C 2的离心率为e 2,若e 2=3e 1,则e 1=________. 答案53解析 不妨设F 1,F 2分别是左、右焦点,椭圆的长半轴长为a 1,双曲线的实半轴长为a 2,P为椭圆与双曲线在第一象限内的交点,则根据椭圆和双曲线的定义可得⎩⎪⎨⎪⎧PF 1+PF 2=2a 1,PF 1-PF 2=2a 2,解得⎩⎪⎨⎪⎧PF 1=a 1+a 2,PF 2=a 1-a 2.因为PF 1⊥PF 2,所以PF 21+PF 22=F 1F 22,即(a 1+a 2)2+(a 1-a 2)2=(2c )2,化简得a 21+a 22=2c 2,所以⎝ ⎛⎭⎪⎫a 1c 2+⎝ ⎛⎭⎪⎫a 2c 2=2,即1e 21+1e 22=2,又因为e 2=3e 1,所以e 21=59,故e 1=53. 12.如图,在平行四边形ABCD 中,E 为DC 的中点,AE 与BD 交于点M ,AB =2,AD =1,且MA →·MB →=-16,则AB →·AD →=________.答案 34解析 因为MA →·MB →=(MD →+DA →)·23DB →=⎝ ⎛⎭⎪⎫13BD →+DA →·23DB →=⎝ ⎛⎭⎪⎫13AD →-13AB →+DA →·⎝ ⎛⎭⎪⎫23AB →-23AD →=⎝ ⎛⎭⎪⎫-23AD →-13AB →·⎝ ⎛⎭⎪⎫23AB →-23AD →=49AD →2-29AB →2-29AB →·AD →=-29AB →·AD →=-16,所以AB →·AD →=34.13.(2017·南通一调)已知函数f (x )=|x |+|x -4|,则不等式f (x 2+2)>f (x )的解集用区间表示为________.答案 (-∞,-2)∪(2,+∞)解析 函数f (x )的图象如图,可知图象关于直线x =2对称. 因为x 2+2>0且f (x 2+2)>f (x ),则必有⎩⎪⎨⎪⎧x 2+2>4,x 2+2>x ,4<(x 2+2)+x ,即⎩⎪⎨⎪⎧x 2>2,x 2-x +2>0,x 2+x -2>0,解得x ∈(-∞,-2)∪(2,+∞).14.(2017·无锡期末)已知a >0,b >0,c >2,且a +b =2,则ac b +c ab -c 2+5c -2的最小值为________. 答案10+ 5解析 因为a >0,b >0,所以a b +1ab -12=a b +(a +b )24ab -12=a b +a 2+2ab +b 24ab -12=5a 4b +b 4a ≥52,当且仅当b =5a 时等号成立.又因为c >2,由不等式的性质可得ac b +c ab -c 2+5c -2=c ·⎝ ⎛⎭⎪⎫a b +1ab -12+5c -2≥52c +5c -2. 又因为52c +5c -2=52(c -2)+5c -2+5≥10+5,当且仅当c =2+2时等号成立. 所以ac b +c ab -c 2+5c -2的最小值为10+ 5.。
2018年考前三个月高考数学理科(江苏专用)总复习——考前回扣8 Word版 含答案

回扣8 算法、复数、概率统计1.复数的相关概念及运算法则(1)复数z =a +b i(a ,b ∈R )的分类①z 是实数⇔b =0;②z 是虚数⇔b ≠0;③z 是纯虚数⇔a =0且b ≠0.(2)共轭复数复数z =a +b i 的共轭复数z =a -b i.(3)复数的模复数z =a +b i 的模|z |=a 2+b 2.(4)复数相等的充要条件 a +b i =c +d i ⇔a =c 且b =d (a ,b ,c ,d ∈R ).特别地,a +b i =0⇔a =0且b =0(a ,b ∈R ).(5)复数的运算法则加减法:(a +b i)±(c +d i)=(a ±c )+(b ±d )i ;乘法:(a +b i)(c +d i)=(ac -bd )+(ad +bc )i ;除法:(a +b i)÷(c +d i)=ac +bd c 2+d 2+bc -ad c 2+d 2i ()其中a ,b ,c ,d ∈R .2.复数的几个常见结论(1)(1±i)2=±2i.(2)1+i 1-i =i ,1-i 1+i=-i. (3)i 4n =1,i 4n +1=i ,i 4n +2=-1,i 4n +3=-i ,i 4n +i 4n +1+i 4n +2+i 4n +3=0(n ∈Z ).(4)ω=-12±32i ,且ω0=1,ω2=ω,ω3=1,1+ω+ω2=0. 3.程序框图的三种基本逻辑结构(1)顺序结构:如图(1)所示.(2)条件结构:如图(2)和图(3)所示.(3)循环结构:如图(4)和图(5)所示.4.牢记概念与公式(1)概率的计算公式①古典概型的概率计算公式P (A )=事件A 包含的基本事件数m 基本事件总数n; ②互斥事件的概率计算公式P (A +B )=P (A )+P (B );③对立事件的概率计算公式P (A )=1-P (A );④几何概型的概率计算公式P (A )=构成事件A 的区域长度(面积或体积)试验的全部结果所构成的区域长度(面积或体积). (2)抽样方法简单随机抽样、分层抽样、系统抽样.①从容量为N 的总体中抽取容量为n 的样本,则每个个体被抽到的概率都为n N ;②分层抽样实际上就是按比例抽样,即按各层个体数占总体的比确定各层应抽取的样本容量.(3)统计中四个数据特征①众数:在样本数据中,出现次数最多的那个数据;②中位数:在样本数据中,将数据按大小排列,位于最中间的数据.如果数据的个数为偶数,就取中间两个数据的平均数作为中位数;③平均数:样本数据的算术平均数,即x =1n(x 1+x 2+…x n ); ④方差与标准差方差:s 2=1n[(x 1-x )2+(x 2-x )2+…+(x n -x )2];s =1n [(x 1-x )2+(x 2-x )2+…+(x n -x )2].1.应用互斥事件的概率加法公式,一定要注意首先确定各事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.2.正确区别互斥事件与对立事件的关系:对立事件是互斥事件,是互斥中的特殊情况,但互斥事件不一定是对立事件,“互斥”是“对立”的必要不充分条件.3.混淆频率分布条形图和频率分布直方图,误把频率分布直方图纵轴的几何意义当成频率,导致样本数据的频率求错.4.要注意概率P (A |B )与P (AB )的区别(1)在P (A |B )中,事件A ,B 发生有时间上的差异,B 先A 后;在P (AB )中,事件A ,B 同时发生.(2)样本空间不同,在P (A |B )中,事件B 成为样本空间;在P (AB )中,样本空间仍为Ω,因而有P (A |B )≥P (AB ).5.复数z 为纯虚数的充要条件是a =0且b ≠0(z =a +b i ,a ,b ∈R ).还要注意巧妙运用参数问题和合理消参的技巧.6.在解决含有循环结构的框图时,要弄清停止循环的条件.注意理解循环条件中“≥”与“>”的区别.7.在循环结构中,易错误判定循环体结束的条件,导致错求输出的结果.1.(2017·江苏南京高淳区质检)若a +i 1-i(i 是虚数单位)是实数,则实数a 的值是________. 答案 -1解析 因为a +i 1-i =(a +i )(1+i )(1-i )(1+i )=a -1+(a +1)i 2是实数,所以a +1=0,所以a =-1. 2.(2017·江苏南京溧水中学质检)某算法的伪代码如图所示,该算法输出的结果是________.I ←1S ←1While S ≤24S ←S ×II ←I +1Print I答案 6解析 该算法经过五次循环:经过第一次循环,因为S =1<24,所以得到新的S =1,I =2; 然后经过第二次循环,因为S =1<24,所以得到新的S =2,I =3;然后经过第三次循环,因为S =2<24,所以得到新的S =6,I =4;然后经过第四次循环,因为S =6<24,所以得到新的S =24,I =5;然后经过第五次循环,因为S =24,所以得到新的S =120,I =6;所以结束循环体并输出最后的I .综上所述,可得最后输出的结果是6.3.甲、乙两同学用茎叶图记录高三前5次数学测试的成绩,如图所示,他们在分析对比成绩变化时,发现乙同学成绩的一个数字看不清楚了,若已知乙的平均成绩低于甲的平均成绩,则看不清楚的数字为________.答案 0解析 设看不清的数字为x ,甲的平均成绩为99+100+101+102+1035=101, 所以93+94+97+110+(110+x )5<101,解得x <1, 所以x =0.4.样本容量为1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为________.答案 680解析 根据给定的频率分布直方图可知,4×(0.02+0.08+x +0.03+0.03)=1⇒x =0.09,则在[6,14)之间的频率为4×(0.08+0.09)=0.68,所以在[6,14)之间的频数为1000×0.68=680.5.已知样本9,10,11,x ,y 的平均数是10,标准差是2,则xy =________.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——考前回扣2 Word版含答案

回扣2 导数1.导数的几何意义(1)f′(x0)的几何意义:曲线y=f(x)在点(x0,f(x0))处的切线的斜率,该切线的方程为y -f(x0)=f′(x0)·(x-x0).(2)切点的两大特征:①在曲线y=f(x)上;②在切线上.2.利用导数研究函数的单调性(1)求可导函数单调区间的一般步骤①求函数f(x)的定义域;②求导函数f′(x);③由f′(x)>0的解集确定函数f(x)的单调增区间,由f′(x)<0的解集确定函数f(x)的单调减区间.(2)由函数的单调性求参数的取值范围①若可导函数f(x)在区间M上单调递增,则f′(x)≥0(x∈M)恒成立;若可导函数f(x)在区间M上单调递减,则f′(x)≤0(x∈M)恒成立;②若可导函数在某区间上存在单调递增(减)区间,f′(x)>0(或f′(x)<0)在该区间上存在解集;③若已知f(x)在区间I上的单调性,区间I中含有参数时,可先求出f(x)的单调区间,则I是其单调区间的子集.3.利用导数研究函数的极值与最值(1)求函数的极值的一般步骤①确定函数的定义域;②解方程f′(x)=0;③判断f′(x)在方程f′(x)=0的根x0两侧的符号变化:若左正右负,则x0为极大值点;若左负右正,则x0为极小值点;若不变号,则x0不是极值点.(2)求函数f(x)在区间[a,b]上的最值的一般步骤①求函数y=f(x)在[a,b]内的极值;②比较函数y=f(x)的各极值与端点处的函数值f(a),f(b)的大小,最大的一个是最大值,最小的一个是最小值.1.已知可导函数f (x )在(a ,b )上单调递增(减),则f ′(x )≥0(≤0)对∀x ∈(a ,b )恒成立,不能漏掉“=”,且需验证“=”不能恒成立;已知可导函数f (x )的单调递增(减)区间为(a ,b ),则f ′(x )>0(<0)的解集为(a ,b ).2.f ′(x )=0的解不一定是函数f (x )的极值点.一定要检验在x =x 0的两侧f ′(x )的符号是否发生变化,若变化,则为极值点;若不变化,则不是极值点.1.曲线y =f (x )=x x 2+1在点(1,f (1))处的切线方程是____________. 答案 y =12解析 ∵f (x )=x x 2+1的导数f ′(x )=1-x 2(1+x 2)2, ∴曲线在点(1,f (1))处的切线斜率k =0, ∵切点为⎝ ⎛⎭⎪⎫1,12, ∴曲线在点(1,f (1))处的切线方程为y =12. 2.(2016·四川)已知a 为函数f (x )=x 3-12x 的极小值点,则a =__________.答案 2解析 ∵f (x )=x 3-12x ,∴f ′(x )=3x 2-12,令f ′(x )=0,则x 1=-2,x 2=2.当x ∈(-∞,-2),(2,+∞)时,f ′(x )>0,f (x )单调递增;当x ∈(-2,2)时,f ′(x )<0,f (x )单调递减,∴f (x )的极小值点为a =2.3.f (x )=x 2+3xf ′(2),则1+f ′(1)=________.答案 -3解析 由f (x )=x 2+3xf ′(2),求导可得f ′(x )=2x +3f ′(2),f ′(2)=4+3f ′(2), f ′(2)=-2,则f ′(x )=2x -6,f ′(1)=2-6=-4,所以1+f ′(1)=-3.4.设曲线f (x )=-e x-x (e 为自然对数的底数)上任意一点处的切线为l 1,总存在曲线g (x )=3ax +2cos x 上某点处的切线l 2,使得l 1⊥l 2,则实数a 的取值范围为____________.答案 ⎣⎢⎡⎦⎥⎤-13,23 解析 由f (x )=-e x -x ,得f ′(x )=-e x -1,因为e x +1>1,所以1e x +1∈(0,1), 由g (x )=3ax +2cos x ,得g ′(x )=3a -2sin x ,又-2sin x ∈[-2,2],所以3a -2sin x ∈[-2+3a,2+3a ],要使过曲线f (x )=-e x -x 上任意一点的切线l 1,总存在过曲线g (x )=3ax +2cos x 上一点处的切线l 2,使得l 1⊥l 2,则⎩⎪⎨⎪⎧-2+3a ≤0,2+3a ≥1, 解得-13≤a ≤23. 5.函数f (x )=x 3+ax 2+bx +a 2在x =1处有极小值10,则a +b 的值为________.答案 -7解析 ∵f ′(x )=3x 2+2ax +b ,由已知可得⎩⎪⎨⎪⎧ f ′(1)=3+2a +b =0,f (1)=1+a +b +a 2=10,解得a =4,b =-11或a =-3,b =3,经验证,a =4,b =-11符合题意,故a +b =-7.6.若函数f (x )=x 2-12ln x +1在其定义域内的一个子区间(k -1,k +1)内不是单调函数,则实数k 的取值范围是______________.答案 ⎣⎢⎡⎭⎪⎫1,32 解析 因为f (x )的定义域为(0,+∞),f ′(x )=2x -12x, 由f ′(x )=0,得x =12. 利用图象可得⎩⎪⎨⎪⎧ k -1<12<k +1,k -1≥0,解得1≤k <32. 7.已知奇函数f (x )是定义在R 上的可导函数,其导函数为f ′(x ),当x >0时,有2f (x )+xf ′(x )>x 2,则不等式(x +2018)2f (x +2018)+4f (-2)<0的解集为____________. 答案 (-∞,-2016)解析 由题观察联想可设g (x )=x 2f (x ),g ′(x )=2xf (x )+x 2f ′(x ),结合条件x >0,2f (x )+xf ′(x )>x 2,得 g ′(x )=2xf (x )+x 2f ′(x )>0,g (x )=x 2f (x )在(0,+∞)上为增函数.又f (x )为R 上的奇函数,所以g (x )为奇函数,所以g (x )在(-∞,0)上为增函数. 由(x +2018)2f (x +2018)+4f (-2)<0,可得(x +2018)2f (x +2018)<4f (2),即g (x +2018)<g (2),所以x +2018<2,故x <-2016.8.若函数f (x )=⎩⎪⎨⎪⎧ 12x -1,x <1,ln x x 2,x ≥1,则函数y =|f (x )|-18的零点个数为________. 答案 4解析 当x <1时,f (x )=12x -1单调递减,且f (x )>-12;当x ≥1时,f (x )=ln x x 2,则f ′(x )=1-2ln x x 3,令f ′(x )=0,得x =e ,当∈[1,e)时,f ′(x )>0,f (x )单调递增,当x ∈(e ,+∞)时,f ′(x )<0,f (x )单调递减,所以f (x )max =f (e)=12e >18,且f (x )≥0,当x 趋近于+∞时,f (x )趋近于0.作出函数y =|f (x )|的大致图象如图所示,由图可知,函数y =|f (x )|-18的零点个数为4.9.已知函数f (x )=x +1e x (e 为自然对数的底数).(1)求函数f (x )的单调区间;(2)设函数φ(x )=xf (x )+tf ′(x )+1e x ,存在实数x 1,x 2∈[0,1],使得2φ(x 1)<φ(x 2)成立,求实数t 的取值范围.解 (1)∵函数的定义域为R ,f ′(x )=-xe x ,∴当x <0时,f ′(x )>0,当x >0时,f ′(x )<0,∴f (x )在(-∞,0)上单调递增,在(0,+∞)上单调递减.∴f (x )的单调增区间为(-∞,0),单调减区间为(0,+∞).(2)存在x 1,x 2∈[0,1],使得2φ(x 1)<φ(x 2)成立,则2[φ(x )]min <[φ(x )]max .∵φ(x )=xf (x )+tf ′(x )+e -x =x 2+(1-t )x +1e x , ∴φ′(x )=-x 2+(1+t )x -t e x =-(x -t )(x -1)e x . ①当t ≥1时,φ′(x )≤0,φ(x )在[0,1]上单调递减,∴2φ(1)<φ(0),即t >3-e 2>1; ②当t ≤0时,φ′(x )≥0,φ(x )在[0,1]上单调递增,∴2φ(0)<φ(1),即t <3-2e <0;③当0<t <1时,若x ∈[0,t ),φ′(x )<0,φ(x )在[0,t )上单调递减,若x ∈(t,1],φ′(x )≥0,φ(x )在(t,1]上单调递增,∴2φ(t )<max{φ(0),φ(1)},即2t +1e t <max ⎩⎨⎧⎭⎬⎫1,3-t e .(*) 由(1)知,g (t )=2·t +1e t 在[0,1]上单调递减,故4e ≤2t +1e t ≤2,而2e ≤3-t e ≤3e, ∴不等式(*)无解.综上所述,存在t ∈(-∞,3-2e)∪⎝ ⎛⎭⎪⎫3-e 2,+∞,使得命题成立. 10.(2017·山东)已知函数f (x )=13x 3-12ax 2,a ∈R . (1)当a =2时,求曲线y =f (x )在点(3,f (3))处的切线方程;(2)设函数g (x )=f (x )+(x -a )cos x -sin x ,讨论g (x )的单调性并判断有无极值,有极值时求出极值.解 (1)由题意f ′(x )=x 2-ax ,所以当a =2时,f (3)=0,f ′(x )=x 2-2x ,所以f ′(3)=3,因此曲线y =f (x )在点(3,f (3))处的切线方程是y =3(x -3),即3x -y -9=0.(2)因为g (x )=f (x )+(x -a )cos x -sin x ,所以g ′(x )=f ′(x )+cos x -(x -a )sin x -cos x=x (x -a )-(x -a )sin x =(x -a )(x -sin x ).令h (x )=x -sin x ,则h ′(x )=1-cos x ≥0,所以h (x )在R 上单调递增.因为h (0)=0,所以当x >0时,h (x )>0;当x <0时,h (x )<0.①当a <0时,g ′(x )=(x -a )(x -sin x ),当x ∈(-∞,a )时,x -a <0,g ′(x )>0,g (x )单调递增;当x ∈(a,0)时,x -a >0,g ′(x )<0,g (x )单调递减;当x ∈(0,+∞)时,x -a >0,g ′(x )>0,g (x )单调递增.所以当x =a 时,g (x )取到极大值,极大值是g (a )=-16a 3-sin a ; 当x =0时,g (x )取到极小值,极小值是g (0)=-a .②当a =0时,g ′(x )=x (x -sin x ),当x ∈(-∞,+∞)时,g ′(x )≥0,g (x )单调递增;所以g (x )在(-∞,+∞)上单调递增,g (x )无极大值也无极小值;③当a >0时,g ′(x )=(x -a )(x -sin x ),当x ∈(-∞,0)时,x -a <0,g ′(x )>0,g (x )单调递增;当x ∈(0,a )时,x -a <0,g ′(x )<0,g (x )单调递减;当x ∈(a ,+∞)时,x -a >0,g ′(x )>0,g (x )单调递增.所以当x =0时,g (x )取到极大值,极大值是g (0)=-a ;当x =a 时,g (x )取到极小值,极小值是g (a )=-16a 3-sin a . 综上所述,当a <0时,函数g (x )在(-∞,a )和(0,+∞)上单调递增,在(a,0)上单调递减,函数既有极大值,又有极小值,极大值是g (a )=-16a 3-sin a ,极小值是g (0)=-a ; 当a =0时,函数g (x )在(-∞,+∞)上单调递增,无极值;当a >0时,函数g (x )在(-∞,0)和(a ,+∞)上单调递增,在(0,a )上单调递减,函数既有极大值,又有极小值,极大值是g (0)=-a ,极小值是g (a )=-16a 3-sin a .。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——解答题滚动练5 含答案

解答题滚动练51.已知α∈(0,π),且sin ⎝⎛⎭⎪⎫α+π3=6-24. (1)求sin ⎝⎛⎭⎪⎫α-π4的值; (2)求cos ⎝⎛⎭⎪⎫2α-π3的值. 解 方法一 联立⎩⎪⎨⎪⎧ sin ⎝ ⎛⎭⎪⎫α+π3=6-24,sin 2α+cos 2α=1.⇒4sin 2α-(6-2)sin α-(1+3)=0,解得sin α=6+24或sin α=-22, 因为α∈(0,π),所以sin α=6+24, 所以cos α=2-64. (1)sin ⎝⎛⎭⎪⎫α-π4=sin αcos π4-cos αsin π4=6+24×22-2-64×22=62×22=32. (2)sin2α=2sin αcos α=2×6+24×2-64=-12,cos2α=1-2sin 2α=-32. cos ⎝⎛⎭⎪⎫2α-π3=cos2αcos π3+sin2αsin π3=-32. 方法二 因为α∈(0,π),sin ⎝⎛⎭⎪⎫α+π3=6-24<12,所以5π6<α+π3<4π3, sin 11π12=sin ⎝ ⎛⎭⎪⎫π4-π6=sin π4cos π6-cos π4sin π6=6-24, 所以α+π3=11π12,所以α=7π12. (1)sin ⎝ ⎛⎭⎪⎫α-π4=sin ⎝ ⎛⎭⎪⎫7π12-π4 =sin π3=32. (2)cos ⎝ ⎛⎭⎪⎫2α-π3=cos ⎝⎛⎭⎪⎫2×7π12-π3=cos 5π6=-32.2.如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.(1)求证:AD⊥平面PAB;(2)求证:CN∥平面PAB.证明(1)因为BD垂直平分AC,所以BA=BC,在△ABC中,因为∠ABC=120°,所以∠BAC=30°.因为△ACD是正三角形,所以∠DAC=60°,所以∠BAD=90°,即AD⊥AB.因为AB=1,∠ABC=120°,所以AD=AC=3,又因为PA=1,PD=2,由PA2+AD2=PD2,知∠PAD=90°,即AD⊥AP.因为AB,AP⊂平面PAB,AB∩AP=A,所以AD⊥平面PAB.(2)方法一取AD的中点H,连结CH,NH.因为N为PD的中点,所以HN∥PA,因为PA⊂平面PAB,HN⊄平面PAB,所以HN∥平面PAB.由△ACD是正三角形,H为AD的中点,所以CH⊥AD.由(1)知,BA⊥AD,所以CH∥BA,因为BA⊂平面PAB,CH⊄平面PAB,所以CH∥平面PAB.因为CH,HN⊂平面CNH,CH∩HN=H,所以平面CNH∥平面PAB.因为CN⊂平面CNH,所以CN∥平面PAB.方法二取PA的中点S,过C作CT∥AD交AB的延长线于T,连结ST,SN.因为N 为PD 的中点,所以SN ∥AD ,且SN =12AD , 因为CT ∥AD ,所以CT ∥SN .由(1)知,AB ⊥AD ,所以CT ⊥AT ,在Rt △CBT 中,BC =1,∠CBT =60°,得CT =32. 由(1)知,AD =3,所以CT =12AD , 所以CT =SN .所以四边形SNCT 是平行四边形,所以CN ∥TS .因为TS ⊂平面PAB ,CN ⊄平面PAB ,所以CN ∥平面PAB .3.已知圆O :x 2+y 2=4,两个定点A (a,2),B (m,1),其中a ∈R ,m >0.P 为圆O 上任意一点,且PA PB=k (k 为常数).(1)求常数k 的值;(2)过点E (a ,t )作直线l 与圆C :x 2+y 2=m 交于M ,N 两点,若M 点恰好是线段NE 的中点,求实数t 的取值范围.解 (1)设点P (x ,y ),x 2+y 2=4, PA =(x -a )2+(y -2)2,PB =(x -m )2+(y -1)2, 因为PA PB =k ,所以(x -a )2+(y -2)2=k 2[(x -m )2+(y -1)2],又x 2+y 2=4,化简得2ax +4y -a 2-8=k 2(2mx +2y -m 2-5),因为P 为圆O 上任意一点,所以⎩⎪⎨⎪⎧ 2a =2mk 2,4=2k 2,a 2+8=k 2(m 2+5),又m >0,k >0,解得⎩⎨⎧ k =2,a =2,m =1,所以常数k = 2. (2)方法一 设M (x 0,y 0),M 是线段NE 的中点,N (2x 0-2,2y 0-t ),又点M ,N 在圆C 上,即关于x ,y 的方程组⎩⎪⎨⎪⎧ x 20+y 20=1,(2x 0-2)2+(2y 0-t )2=1有解,化简得⎩⎪⎨⎪⎧x 20+y 20=1,8x 0+4ty 0-t 2-7=0有解, 即直线n :8x +4ty -t 2-7=0与圆C :x 2+y 2=1有交点,则点(0,0)到直线n 的距离d =|t 2+7|64+16t 2≤1,化简得,t 4-2t 2-15≤0, 解得t ∈[-5,5].方法二 设过E 的切线与圆C 切于切点F ,EF 2=EM ·EN ,又M 是线段NE 的中点,所以EN =2MN ,EM =MN ,所以EF 2=2MN 2,又EF 2=EC 2-CF 2=22+t 2-1=t 2+3,MN ≤2,所以t 2+3≤8,所以t ∈[-5,5].4.已知函数f (x )=-x 2-(2a +1)x +ln x ,且该函数在x =1处取得极值.(1)求实数a 的值,并求出函数的单调区间;(2)若函数g (x )=f (x )-b +5x 2在区间(0,2018)上只有一个零点,求实数b 的值. 解 (1)由已知,得f ′(x )=-2x -2a -1+1x, 据题意,f ′(1)=0,得到a =-1,所以f (x )=-x 2+x +ln x , f ′(x )=-2x +1+1x =(2x +1)(-x +1)x. 由x >0,令f ′(x )>0,得0<x <1,令f ′(x )<0,得x >1,所以函数f (x )在x =1处取得极值,所以a =-1, f (x )的单调增区间为(0,1),f (x )的单调减区间为(1,+∞).(2)g (x )=f (x )-b +5x 2=-x 2+7x 2+ln x -b ,x ∈(0,2018). 则g ′(x )=-2x +72+1x, 令g ′(x )=0, 得x =2,负值舍去.当0<x <2时,g ′(x )>0,g (x )的单调增区间为(0,2),当2<x <2018时,g ′(x )<0,g (x )的单调减区间为(2,2018).所以函数g (x )=f (x )-b +5x 2在区间(0,2018)上只有一个零点,等价于g (2)=0, 解得b =ln2+3.。
江苏专用2018届高考数学总复习考前三个月小题满分练4理20180123139

小题满分练41.(2017届南京、盐城一模)已知集合A={-1,0,1},B=(-∞,0),则A∩B=________.答案{-1}解析因为A={-1,0,1},B=(-∞,0),所以A∩B={-1}.52.复数的共轭复数是________.3+4i3 4答案+i5 53.(2017届南京、盐城一模)从数字1,2,3,4中随机选两个数字,则选中的数字中至少有一个是偶数的概率为________.5答案6解析从数字1,2,3,4中随机选两个数字的所有基本事件有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),共6个基本事件,其中一个偶数都没有的基本事件有1个,所以至少有一个是1 5偶数的概率为1-=.6 64.采用随机模拟的方法估计某运动员射击击中目标的概率.先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了如下20组随机数:7527029371409857034743738636694714174698 0371623326168045601136619597742476104281根据以上数据估计该运动员射击4次至少击中3次的概率为________.答案0.4解析由题意可得,符合题意的模拟数据有:752798578636694746988045959774248共8组,由古典概型公式可得该运动员射击4次至少击中3次的概率为P==0.4.205.运行如图所示的伪代码,其结果为________.S←1For I From 1 To 7 Step2S←S+IEnd ForPrint S1答案17解析本算法的功能是求和S=1+1+3+5+7=17.6.(2017届苏北四市一模)设实数x,y满足Error!则3x+2y的最大值为________.答案 33 z解析作出不等式组所表示的平面区域(如图),令z=3x+2y,则y=-x+,故当目标函数2 2经过点C(1,0)时,取得最大值,故z max=3.17.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=2,cos C=-,3sin A=2sin B,4则c=________.答案 4解析由正弦定理得,3a=2b,b=3.a2+b2-c2 4+9-c2 1由余弦定理,得cos C===-,解得c=4.2ab 2 × 2 × 3 48.(2017·无锡期末)已知f(x)=Error!是奇函数,则f(g(-2))=________.答案 1解析因为f(x)是奇函数,所以g(-2)=f(-2)=-f(2)=-1,从而f(g(-2))=f(-1)=-f(1)=1.9.已知直三棱柱ABC-A1B1C1的各棱长均为2,E为棱CC1的中点,则三棱锥A1-B1C1E的体积为__________.答案3 3解析根据等体积变换思想-=-,因为直三棱柱ABC-A1B1C1的各棱长均为2,EV VA B C E E A B C111111为棱CC 1的中点,所以三棱锥E-A1B1C1的底面是边长为2的正三角形,高EC1=1,因此VE-A B C1111 1 3 3= 3SA·EC1=××1=,故三棱锥A1-B1C1E的体积为.3 3 3 3A B C111π 3 π10.(2017·南京、盐城二模)若sin(α-6)=5,α∈(0,2),则cosα的值为________.4 3-3答案102π 3 4 π解析令α-=β,由已知得β是锐角,且sinβ=,cosβ=,所以cosα=cos6 5)5 (β=cosβcos -sinβ·sin=×-×=.6 6 5 2 5 2 10111.已知a>b>1且2log a b+3log b a=7,则a+的最小值为________.b2-1答案 31 解析因为2log a b+3log b a=7,所以2(log a b)2-7log a b+3=0,解得log a b=或log a b=3,21 1 1因为a>b>1,所以log a b∈(0,1),故log a b=,从而b=,因此a+=a+=(a-1)a2 b2-1 a-11++1≥3,当且仅当a=2时等号成立.a-1→→12.在正方形ABCD中,AB=AD=2,M,N分别是边BC,CD上的动点,当AM·AN=4时,MN的取值范围为________.答案[2,2]解析如图所示,以点A为坐标原点建立平面直角坐标系,设M(2,y),N(x,2 )(0 ≤x≤2,0 ≤y≤2),→→则AM·AN=2x+2y=4,∴x+y=2,MN=(x-2 )2+(y-2 )2,可以看做线段x+y=2(0 ≤x≤2,0 ≤y≤2)上的点到定点(2,2 )的距离,其最小值为2,最大值为2,故MN的取值范围为[2,2].y2 x213.(2017·常州期末)已知抛物线x2=2py(p>0)的焦点F是椭圆+=1(a>b>0)的一个a2 b2焦点,若P,Q是椭圆与抛物线的公共点,且直线PQ经过焦点F,则该椭圆的离心率为__________.答案2-1p 解析方法一由抛物线方程可得,焦点为F(0,2 );由椭圆方程可得,上焦点为(0,c).故p b2 2b2=c,将y=c代入椭圆方程可得x=±.又抛物线通径为2p,所以2p==4c,所以b2=a22 a a-c2=2ac,即e2+2e-1=0,解得e=2-1.3p p p 方法二由抛物线方程以及直线y=可得,Q.又=c,即Q(2c c,),2 (p,2 )2c2 4c2代入椭圆方程可得+=1化,简可得e4-6e2+1=0解,得e2=3-2 2e,2=3a2 b2+2 2>1(舍去)即,e=3-2 2=2-1(负值舍去).14.(2017·南通一调)在平面直角坐标系xOy中,已知B,C为圆x2+y2=4上两点,点A(1,1),且AB⊥AC,则线段BC的长的取值范围为________.答案[ 6-2,6+2]解析方法一设BC的中点为M(x,y).因为OB2=OM2+BM2=OM2+AM2,所以4=x2+y2+(x-1)2+(y-1)2,1 1 3化简得(x-2 )2+(y-2 )2=, 21 1 6所以点M的轨迹是以(,为圆心,为半径的圆,2 )2 26-2 6+2所以AM的取值范围是[ 2 ],,2所以BC的取值范围是[ 6-2,6+2].方法二设BC的中点为M,设AM=x,OM=y.因为OC2=OM2+CM2=OM2+AM2,所以x2+y2=4. 因为OA=2,所以x+y≥2,x+2≥y,y+2≥x.如图所示,6-2 6+2可得x∈[ 2 ],,2所以BC的取值范围是[ 6-2,6+2].4。
江苏专用2018届高考数学总复习考前三个月小题满分练3理

小题满分练31.(2017·南京三模)已知全集U ={1,2,3,4},集合A ={1,4},B ={3,4},则∁U (A ∪B )=__________.答案 {2}解析 由题意可得A ∪B ={1,3,4},故∁U (A ∪B )={2}.2.(2017届苏北四市一模)已知复数z 满足z (1-i)=2,其中i 为虚数单位,则z 的实部为________.答案 1解析 因为z (1-i)=2,所以z =21-i=1+i ,故实部为1. 3.某工厂生产A ,B ,C ,D 四种不同型号的产品,产品数量之比依次为2∶3∶5∶1.现用分层抽样方法抽出一个容量为n 的样本,若样本中A 种型号有16件,那么此样本的容量n 为________.答案 88解析 根据分层抽样的特点,样本中A 种型号产品应是样本容量的22+3+5+1=211,所以样本的容量n =16÷211=88. 4.函数y =ln ⎝ ⎛⎭⎪⎫1+1x +1-x 2的定义域为________. 答案 (0,1]解析 根据题意可知,⎩⎪⎨⎪⎧ 1+1x>0,x ≠0,1-x 2≥0⇒⎩⎪⎨⎪⎧ x +1x >0,-1≤x ≤1⇒0<x ≤1,故定义域为(0,1].5.(2017届苏北四市一模)若随机地从1,2,3,4,5五个数中选出两个数,则这两个数恰好为一奇一偶的概率为__________.答案 35解析 从1,2,3,4,5五个数中选出两个数的所有基本事件为(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10个,其中一奇一偶的基本事件有6个,故所求事件的概率为P =610=35.6.(2017届南京、盐城一模)如图是一个算法流程图,则输出的x 的值是________.答案 9解析 经过第一次循环后得x =1+4=5,y =9-2=7,此时x <y ,进行第二次循环;经过第二次循环后得x =5+4=9,y =7-2=5,此时x >y ,退出循环,故输出的x =9.7.在△ABC 中,∠BAC =120°,AC =4,BC =27,则△ABC 的面积为________. 答案 2 3解析 由题意知,在△ABC 中,已知A =120°,b =4,a =27,由余弦定理得cos A =42+c 2-(27)22×4×c =-12, 解得c =2或c =-6(舍去),则S △ABC =12bc sin A =12×4×2×32=2 3. 8.(2017·南京学情调研)在平面直角坐标系xOy 中,双曲线C :x 2a 2-y 24=1(a >0)的一条渐近线与直线y =2x +1平行,则实数a 的值是________.答案 1解析 由双曲线的方程可知其渐近线方程为y =±2ax .因为一条渐近线与直线y =2x +1平行,所以2a=2,解得a =1. 9.(2017·南通、扬州、淮安、宿迁、泰州、徐州六市调研)已知{a n }是公差不为0的等差数列,S n 是其前n 项和.若a 2a 3=a 4a 5,S 9=27,则a 1的值是________.答案 -5解析 首先由S 9=9a 5=27,得a 5=3.设公差为d (d ≠0),则(3-3d )(3-2d )=3(3-d ),即d 2-2d =0,从而得d =2.所以a 1=a 5-4d =3-8=-5.10.(2017·苏州暑假测试)已知α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫π2,π,cos α=13,sin(α+β)=-35,则cos β=________. 答案 -4+6215解析 因为α∈⎝ ⎛⎭⎪⎫0,π2,cos α=13,所以sin α=223.又α+β∈⎝ ⎛⎭⎪⎫π2,3π2,sin(α+β)=-35<0,所以α+β∈⎝⎛⎭⎪⎫π,3π2,故cos(α+β)=-45,从而cos β=cos(α+β-α)=cos(α+β)cos α+sin(α+β)sin α=-45×13-35×223=-4+6215. 11.(2017·南通、扬州、淮安、宿迁、泰州、徐州六市调研)如图,在平面四边形ABCD 中,O 为BD 的中点,且OA =3,OC =5.若AB →·AD →=-7,则BC →·DC →的值是__________.答案 9解析 BC →·DC →=(OC →-OB →)·(OC →-OD →)=(OC →+OD →)·(OC →-OD →)=OC 2-OD 2,类似AB →·AD →=AO2-OD 2=-7,所以BC →·DC →=OC 2-OD 2=OC 2-AO 2-7=9.12.将矩形ABCD 绕边AB 旋转一周得到一个圆柱,AB =3,BC =2,圆柱上底面圆心为O ,△EFG 为下底面圆的一个内接直角三角形,则三棱锥O -EFG 体积的最大值是________. 答案 4解析 设Rt △EFG 的两条直角边分别为a ,b ,则a 2+b 2=16,三棱锥O -EFG 的高为3,从而V O -EFG =13S △EFG ·3=12ab ≤a 2+b 24=4,当且仅当a =b =22时等号成立,故三棱锥O -EFG 的体积的最大值为4.13.(2017届南京、盐城一模)如图,在平面直角坐标系中,分别在x 轴与直线y =33(x +1)上从左向右依次取点A k ,B k ,k =1,2,…,其中A 1是坐标原点,使△A k B k A k +1都是等边三角形,则△A 10B 10A 11的边长是________.答案 512解析 设第n 个正三角形的边长为a n ,则点B 1⎝ ⎛⎭⎪⎫12a 1,32a 1在直线y =33(x +1)上, 从而32a 1=33⎝ ⎛⎭⎪⎫12a 1+1,解得a 1=1, 当n ≥2时,B n ⎝⎛⎭⎪⎫a 1+a 2+…+a n -1+12a n ,32a n . 因为B n 在直线y =33(x +1)上, 所以32a n =33⎝ ⎛⎭⎪⎫a 1+a 2+…+a n -1+12a n +1, 即a n =a 1+a 2+…+a n -1+1,从而a n +1=a 1+a 2+…+a n +1,两式相减得a n +1=2a n (n ≥2),又a 2=a 1+1=2,故{a n }是以a 1=1为首项,q =2为公比的等比数列,从而△A 10B 10A 11的边长为a 10=29=512.14.已知函数f (x )=(x -1)e x +12ax 2+1(其中a ∈R )有两个零点,则a 的取值范围是____________________.答案 (-∞,-1)∪(-1,0)解析 由题意,f ′(x )=x (e x +a ),其中f (0)=0,故函数还有一个不为零的零点,分类讨论:(1)当a ≥0时,由f ′(x )<0,得x <0,由f ′(x )>0,得x >0,此时函数仅有一个零点;(2)当a <0时,由f ′(x )=0可得,x 1=0,x 2=ln(-a ),①当ln(-a )<0,即-1<a <0时,当x ∈(-∞,ln(-a ))∪(0,+∞)时,f ′(x )>0,当x ∈(-ln(-a ),0)时,f ′(x )<0,所以当x =ln(-a )时,f (x )取得极大值,当x =0时,函数取得极小值,而f (ln(-a ))>f (0)可知函数有两个零点,此时满足条件.②当ln(-a )=0,即a =-1时,当x∈(-∞,0)∪(0,+∞)时,f′(x)>0,函数单调递增,函数只有一个零点,不满足条件.③当ln(-a)>0,即a<-1时,当x∈(-∞,0)∪(ln(-a),+∞)时,f′(x)>0,当x∈(0,ln(-a))时,f′(x)<0,所以当x=ln(-a)时,f(x)取得极小值,当x=0时,函数取得极大值,由f(ln(-a))<f(0)可知函数有两个零点,此时满足条件.综上可得,a的取值范围是(-∞,-1)∪(-1,0).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小题满分练8
1.(2017·扬州期末)已知集合A ={x |x ≤0},B ={-1,0,1,2},则A ∩B =________. 答案 {-1,0}
解析 根据交集的定义,A ∩B ={x |x ≤0}∩{-1,0,1,2}={-1,0}. 2.双曲线x 24-y 2
5=1的离心率为________.
答案 32
解析 因为a 2=4,b 2=5,所以c 2=a 2+b 2
=9,离心率e =c a =32
.
3.从某班抽取5名学生测量身高(单位:cm),得到的数据为160,162,159,160,159,则该组数据的方差s 2
=________. 答案 65
解析 由题干条件可得x =
160+162+159+160+1595=160,所以s 2
=15(4+1+1)=65
.
4.(2017·苏州期末)一架飞机向目标投弹,击毁目标的概率为0.2,目标未受损的概率为0.4,则目标受损但未完全击毁的概率为________. 答案 0.4
解析 设“目标受损但未完全击毁”为事件A ,则其对立事件A 是“目标未受损或击毁目标”.P (A )=1-P (A )=1-(0.4+0.2)=0.4. 5.如图所示,该伪代码运行的结果为__________.
S ←0 i ←1
While S ≤20
S ←S +i i ←i +2
End While Print i 答案 11
解析 第一次循环,S =1,i =3;第二次循环,S =1+3=4,i =5;第三次循环,S =4+5=9,i =7;第四次循环,S =9+7=16,i =9;第五次循环,S =16+9=25,i =11,此时
S >20,故输出i =11.
6.已知平面向量a ,b 满足(a +b )·(2a -b )=-4,且|a |=2,|b |=4,则a 与b 的夹角为________. 答案
π3
解析 由题意可得(a +b )·(2a -b )=2a 2
-b 2
+a ·b =8-16+a ·b =-4,解得a ·b =4,
所以cos θ=a ·b |a ||b |=12,又因为θ∈[0,π],所以θ=π
3
.
7.已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=1-log 2x ,则不等式f (x )<0的解集是________. 答案 (-2,0)∪(2,+∞)
解析 当x <0时,f (x )=-f (-x )=log 2(-x )-1,f (x )<0,即log 2(-x )-1<0,解得-2<x <0;当x >0时,f (x )=1-log 2x ,f (x )<0,即1-log 2x <0,解得x >2.综上,不等式f (x )<0的解集是
(-2,0)∪(2,+∞).
8.已知正五棱锥底面边长为2,底面正五边形中心到侧面斜高距离为3,斜高长为4,则此正五棱锥体积为________. 答案 20
解析 设正五棱锥高为h ,底面正五边形的角为108°, 底面正五边形中心到边距离为tan54°,
h =
12tan54°,则此正五棱锥体积为13×5×12×2×tan54°×12tan54°
=20.
9.设△ABC 是等腰三角形,∠ABC =120°,则以A ,B 为焦点且过点C 的双曲线的离心率为________. 答案
3+1
2
解析 设AB =BC =2c ,则由余弦定理可得CA =AB 2
+BC 2
-2AB ×BC c os120°=23c .根据双曲线的定义可得CA -CB =2a ,即23c -2c =2a ,所以(3-1)c =a ,故双曲线的离心率
e =c a =3+12
. 10.若数列{a n }满足a 1+3a 2+32
a 3+…+3n -1
a n =n
2
,其前n 项和为S n ,则S n =________.
答案 34⎝
⎛
⎭⎪⎫1-13n
解析 因为a 1+3a 2+32
a 3+…+3
n -1
a n =n 2
,
所以当n ≥2时有a 1+3a 2+32a 3+…+3n -2
a n -1=n -12
,
两式作差得3
n -1
a n =1
2
,
所以a n =12·1
3
n -1,
又因为当n =1时,a 1=1
2适合此式,
所以数列{}a n 的通项公式为a n =12·1
3n -1,
所以S n =12⎝ ⎛
⎭⎪⎫1-131-13
=34⎝ ⎛⎭⎪⎫
1-13.
11.已知sin ⎝ ⎛⎭⎪⎫x +π6=13,则sin ⎝ ⎛⎭⎪⎫x -5π6+sin 2⎝ ⎛⎭
⎪⎫π
3-x 的值为________.
答案 5
9
解析 sin ⎝ ⎛⎭⎪⎫x -5π6=sin ⎝ ⎛⎭⎪⎫x +π6-π=-sin ⎝ ⎛⎭⎪⎫x +π6=-13,sin 2⎝ ⎛⎭⎪⎫π3-x =cos 2⎝ ⎛⎭⎪⎫x +π6=1
-sin 2⎝ ⎛⎭⎪⎫x +π6=1-19=89,所以sin ⎝ ⎛⎭⎪⎫x -5π6+sin 2⎝ ⎛⎭
⎪⎫π
3-x =-13+89=59.
12.已知点P 是△ABC 内一点(不包括边界),且AP →=mAB →+nAC →,m ,n ∈R ,则(m -2)2
+(n -2)2
的取值范围是________.
答案 ⎝ ⎛⎭
⎪⎫92,8 解析 因为点P 是△ABC 内一点(不包括边界),且AP →=mAB →+nAC →
,所以
m ,n 满足条件⎩⎪⎨⎪
⎧
m >0,n >0,
m +n <1,
作出不等式组表示的平面区域如图所
示.因为(m -2)2
+(n -2)2
表示的是区域内的动点(m ,n )到点A (2,2)的距离的平方.因为点A 到直线m +n =1的距离为|2+2-1|2=32
,故⎝ ⎛⎭⎪⎫322<(m -2)2+(n -2)2<OA 2,即(m -2)
2
+(n -2)2
的取值范围是⎝ ⎛⎭
⎪⎫92,8.
13.椭圆x 24+y 2
3
=1的左、右焦点分别为F 1,F 2,过椭圆的右焦点F 2作一条直线l 交椭圆于
P ,
Q 两点,则△F 1PQ 的内切圆面积的最大值是________.
答案
9π16
解析 令直线l :x =my +1,
与椭圆方程联立消去x ,得()3m 2
+4y 2
+6my -9=0,
可设P ()x 1,y 1,Q ()x 2,y 2, 则y 1+y 2=-6m 3m 2+4,y 1y 2=-9
3m 2+4.
可知1F PQ S =1
2F 1F 2||y 1-y 2
=
()y 1+y 22-4y 1y 2
=12
m 2+1
()3m 2+42
,
又m 2+1()3m 2+42
=1
9()m 2
+1+
1
m 2
+1
+6≤116
, 故1F PQ S ≤3.
三角形的周长与三角形内切圆的半径的积是三角形面积的二倍, 则内切圆半径r =
12F PQ
S 8
≤34,其面积的最大值为9π16
. 14.已知函数f (x )的定义域为R ,若存在常数k ,使|f (x )|≤k
2017|x |对所有实数都成立,
则称函数f (x )为“期望函数”,给出下列函数: ①f (x )=x 2
;②f (x )=x e x
;③f (x )=x
x 2
-x +1
;
④f (x )=x
e x +1
.
其中函数f (x )为“期望函数”的是________.(写出所有符合条件的函数序号) 答案 ③④
解析 ①假设函数f (x )=x 2
为“期望函数”,则|f (x )|=|x 2
|≤k
2017|x |,当x ≠0时,k ≥
2017|x |,因此不存在k ,因此假设错误,即函数f (x )=x 2
不是“期望函数”;②假设函数
f (x )=x e x 为“期望函数”,则|f (x )|=|x e x |≤
k
2017
|x |,当x ≠0时,k ≥2017e x
,因此不存在k ,因此假设错误;③假设函数f (x )=
x
x 2-x +1为“期望函数”,|f (x )|=
|x |⎝ ⎛
⎭
⎪⎫x -122+34≤4
3|x |,
当x ≠0时,对任意的k 2017≥43,都有|f (x )|≤k 2017|x |成立,故正确;④假设函数f (x )=x
e x
+1
为“期望函数”,|f (x )|=|x |e x +1≤k
2017|x |对所有实数都成立,故正确.故答案为③④.。
