1[1].4.3正切函数的性质与图象(好好)
必修四1.4.3正切函数的性质与图象

3 (1) 2 4 (1)
(2)2
(2)
题型三
【例 3】 求下列函数的最小正周期: ( 1) y=- tan x 3 ;
求周期
ቤተ መጻሕፍቲ ባይዱ
3
5
( 2) y=| tan x| . 分析: ( 1) 利用 T= 求解; ( 2) 画出函数图象利用图象法求解.
|ω|
解: ( 1) ∵ ω= , ∴ 最小正周期 T= = 3.
内都是增函数。
kπ , ( ,0) k Z 2
对称轴呢?
典型例题
例1.求函数y= tan(
2
x
3
)的定义域、周期和单调区间。
5 定义域: x x 2k , k 3
周期:T 2
5 1 单调增区间: +2k , 2k , k 3 3
y tan x
正切函数的图象
3 2
0
y
3 2
2
3 2
o
x
问题4、正切函数 y
= tanx 的单调性。
2 k ,
正切函数在开区间(问题5、正切函数 y
= tanx
2 的值域。
k ), k 内都是增函数.
值域为R
正 切 函 数 图 像
性质 :
预习自测 1 (1) x k x k , k (2) x x k , k 2 (3) x k x k , k 2 k 2 x x , k 3 6
x k x k , k 2
1.4.3正切函数的图像和性质(1)

1 π 解: f (x) = 3tan( x + ) ∵ 2 4
1 π x + ); 2 4
= f (x + ) 2 π ∴ 周期T = 2
= 3 tan[2(x + ) + ] π 2 4
1 π = 3 tan( x + + π ) 2 4 1 π = 3 tan[ ( x + 2π ) + ]
3π (2kπ ,2kπ + ) 2 2
1 π x + )的单调递减区间为 : 2 4
π
例4 求下列函数的周期 求下列函数的周期:
解 :∵ f ( x) = 3 tan(2 x + ) π 4
(1) y = 3 tan(2x + ); 4 π
π
( 2 )变题 y = 3 tan(
= 3tan( x + +π) 2 4
解: (1) ∵ 90 < 167 < 173 < 180 上是增函数 ∵ y = tan x, 在 (900 ,2700 ) 又
3π 3π ∴ tan( ) < tan( ) 4 5
即
11 π 13 π tan( ) < tan( ) 4 5
解 : 因为原函数可化为 y = 3 tan( ); : 2 4 ∵ u = x + 为增函数; 且y = tan u的单调区间为 : x π 2 4 令u = ; 所以y = tan u的单调递增区间为 : π π
解 : (1)令u = x + , 则y = 3 tan u 2 4 1 π
1 π (1) y = 3 tan( x + ); 2 4 1 π
1.4.3正切函数的性质和图象课件.ppt

y
的终边 的终边
y
y
y
的终边
的终边
复习回顾 问题:正弦曲线是怎样画的?
练习:画出下列各角的正切线:
y
的终边 的终边
y
y
y
的终边
的终边
复习回顾 问题:正弦曲线是怎样画的?
练习:画出下列各角的正切线:
y
的终边 的终边
y
y
y
的终边
的终边
复习回顾 问题:正弦曲线是怎样画的?
3
2
2k
]
减函数
奇函数
2
对称轴: x
2
k
,k
Z
对称中心: (k , 0) k Z
y=cosx
y
1
0
2
3 2
2
5 2
x
-1
xR
y [1,1]
x 2k 时, ymax 1 x 2k 时,ymin 1
x[ 2k , 2k ] 增函数
2
值域: R
y y tan x
周期性: 正切函数是周期函数,
周期是
2
2
o 2
x 2
奇偶性: 奇函数
单调性: 在 ( k , k ) k Z
2
2
内是增函数
对称性: 对称中心是(k , 0), k Z
2
对称轴呢?
例1.观察图象,写出满足下列条件的x值的范围:
解:
y
3
0 x
1.4.3 正切函数的性质与图象 课件

-
-
P1
6
o1
M-11 A
y
1p1/
作法: (1) 等分 (2) 作正弦线 (3) 平移 (4) 连线
o
6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
-1 -
1、用平移正弦线得y sin x, x [0,2 ]图象.
2、再利用周期性把该段图象向左、右扩展得到.
§
正切函数的性质
周期性
由诱导公式得 tan(x ) tan x, x R,x k, k Z
2
所以,正切函数是周期函数,周期是 .
奇偶性
由诱导公式得 tan(x) tan x, x R,x k, k Z
2
所以正切函数是奇函数.
单调性
所以,函2数的3定义2域是x
x
2k
3
,
k
Z.3
由于f+x
2
kT<
2
txan
32<2x
Tk,k3Z,
tan
2
x
3
2
T
解得
ta2nk23x<x<3 2k
f (3x,)k,
Z .
2
T
即T
2
因此,函数的单调递增区间是:
2k
,2k 3
3
, k Z. 2
周期T
另解:周期T
正切函数的图像和性质 (精致版)
2 对称轴: x k , k Z
2 对称中心: (k ,0) k Z
2
对称轴: x k , k Z 对称中心:( k , 0) k Z
2
探索一 你可以从一个新的角度来研究正 切函数的性质吗?
正弦函数 正切函数
定义+三角函数线
三角函数图象
课后练习
作业:
P45.2、3、4
课后思考
思考1:我们分别从什么角度讨论了正切函数 的性质?这两种讨论方法分别有什么特点? 思考2:你能用同样的方法去讨论正、余弦 函数的性质吗?
想一想? 得到y tan x最小正周期为__ ____
由y tan x最小正周期为
反馈练习:求下列函数的周期:
x (1) y 5 tan 2
2
(2) y tan(4 x ) 3
4
巩固练习 1、比较下列每组数的大小。
13π 11π tan() 与 tan() (2) 4 5
正切函数的对称中心
正 切 函 数 图 像
性质 :
渐 进 线
渐 进 线
⑴ ⑵ ⑶ ⑷
定义域: {x | x k, k Z} 2 值域: R 周期性: 奇偶性: 奇函数,图象关于原点对称。
⑸ 单调性: 在每一个开区间 ( k , k ) , k Z 内都是增函数。 2 2 kZ x k , (7)对称中心 (6)渐近线方程: 2
kπ ( ,0) 2
问题:
(1)正切函数是整个定义域上的增函数吗?为什么?
(2)正切函数会不会在某一区间内是减函数?为什么?
A
B
1.4.3正切函数的性质与图象

B
)
π 2.y=tanx(x≠kπ+ ,k∈Z)在定义域上的单调性为( 2 A.在整个定义域上为增函数 B.在整个定义域上为减函数
C
)
π π C.在每一个区间- +kπ, +kπ (k∈Z)上为增函数 2 2 π π D.在每一个区间- +2kπ, +2kπ (k∈Z)上为增函数 2 2
(2)∵tan496°=tan136°,
y=tanx 在(90°,270°)上是增函数,270°>136°>126
°>90°,∴tan136°>tan126°,即 tan496°>tan126°.
不求值, 比较下列每组中两个正切值的大小, 用不等号 “<” 、 “>”连接起来.
< (1)tan32°________tan215 °.
O 6
4 3 2
x
正切函数的性质 :
定义域: x x k , k Z 2 值域: R
周期性:
k 对称中心是 ( , 0), k Z 2
T
奇偶性: 奇函数
单调性: 在开区间 2 k , 2 k k Z 内递增
cosx 是偶函数,∴(4)对. 因此,正确的命题的序号是(1)(4).
解:令 z x
例1.求函数 y tan (x )的定义域 . 4
z z k , k z 2 由x z k , 4 2 可得 x k k 2 4 4
y A tan( x ) T y tan x T π
2、奇偶性 π tan( x ) tan x , x R, x kπ , k Z 2 正切函数是奇函数
1.4.3-正切函数的性质与图像

答案:
1、定义域 2、值域
3、单调性
4、奇偶性 5、周期性
x
x
|
x
R且x
1 3
k
5
18
,k
Z
yR
在x
1 3
k
18
,
1 3
k
5
18
上是增函数;
非奇非偶函数
最小正周期是
3
四、小结:正切函数的图像和性质
1、 正 切 曲 线 是 先 利 用移平正 切 线 得y tan x, x ( , )的 图 象 , 22
思考 3、正切函数 y tan x 是否具有奇偶性?
由诱导公式知
f x tan x tan x f x, x R, x k , k Z
2
正切函数是奇函数.
思考
4、能否由正切线的变化规律及正切函数周期性来讨论它的单调性?
y
y
T
x
o x (1,0) A
o x x (1,0) A
1、利用正切函数的定义,说出正切函数的定义域;
tan y x 0 的终边不在y轴上
x
k
(k
z)
2
思考
2、正切函数 y tan x 是否为周期函数?
由诱导公式知
f x tanx tan x f x, x R, x k , k Z
2 ∴ y tan x是周期函数, 是它的一个周期.
24
令t x ;所以y tan t的单调递增区间为:
24
k t k , k Z
2
2
由t 1 x 得 :
24
k 1 x k
22 4
2
y
3 tan(
1 2
1.4.3正切函数的图像和性质

单调性及值域
渐近 线
正切曲线是被相互平行的直线 x
2
k , k Z
kZ
所隔开的无穷多支曲线组成的
单调递增区间: k , k 2 2
值域:R
思考:
(1)正切函数是整个定义域上的增函数吗?为什么?
(2)正切函数会不会在某一区间内是减函数?
tan1670 tan1730
y tan x在 , 上是增函数, 2
167 173 180
0
13π 11π tan() 与 tan() (2) 4 5
0
11 13 tan( ) tan( ). 4 5
比较大小:
(1) tan138
2 T 2
T
( 结论:f ( x ) A tan x ) (A 0, 0)的周期 T
正切函数的基本性质
奇偶性
f ( x ) sin x , x R 为奇函数 f ( x ) cos x , x R 为偶函数
f ( x) tan x,x k ,k Z 2
定义域
y tan x
终边不能落在y轴上
定义域: { x | x
2
k , k Z}
例1
求函数
y tan x 的定义域。 3 2
解:函数y tan x 的自变量应该满足 3 2 x k , k 2 3 2 1 函数的定义域为 x x 2k , k . 3
三角函数
1.4.3正切函数的性质与图象
复习回顾
1.如下图,利用三角函数线表示出角α 的正弦、 余弦、正切值?
1.4.3正切函数的图像与性质

课堂展示
探究1
展示:1组
独立思考, 独立审题 1.结合批阅情况,改正错误,找准错因。
探究2、3、4 展示:6组
2.明确自己的疑问,以备小组合作讨论解决。
3.学有余力的同学力争做好“拓展提升”。 要求:思维敏捷,手、脑、眼并用。
例1 展示:5组
例2 展示:2组
例3 展示:3组
激情点评
探究1
点评:9组 探究2、3、4 点评:8组
思考:在整个定义域内是增函数么?
正切函数的性质与图像
(五)定义域、值域:
k (六)关于对称点对称轴:从图象可以看出:无对称轴。 ( , 0) 直线 为渐近线,对称点为零点及函数值不存在的点,即 2 x k k Z 2
应用提升
• 例1
求函数y tan x 的定义域,值域,并指出它的周期性, 3 2 奇偶性,单调性,对称中心,作出它的大致草图
复习回顾
y 1 -6 -5 -4 -3 -2 - o -1 y 1 -6 -5 -4 -3 -2 - -1 2 3 4 5 6 x
y=sinx
y=cosx
2 3 4 5 6 x
六.对称轴和对称点:
y sin x的对称轴:x k
2
, 对称点: ( k ,0);
学习目标:
1.会画出的 y tan x 图像; 2.掌握正切函数 y tan x 的性质;并能够熟练的应用。
[重点]: 画正切函数的图像,理解正切函数的性质。
[难点]:正切函数的性质及其应用。
合作学习:重点讨论:
探究1. 借助正切线,做出正切函数y=tanx的图像。 探究2.由正切函数的图像得到正切函数的定义域与值域。 探究3.由正切函数的图像得到正切函数的周期性、奇偶性。
19-20版 第1章 1.4 1.4.3 正切函数的性质与图象

1.4.3 正切函数的性质与图象正切函数的图象与性质思考:正切函数图象的对称中心都在正切函数图象上吗?[提示] 不是,在⎝ ⎛⎭⎪⎫k π2,0中,当k 为偶数时,在函数图象上,当k 为奇数时,不在函数图象上.1.函数f (x )=tan ⎝ ⎛⎭⎪⎫x +π4的单调增区间为( )A .⎝ ⎛⎭⎪⎫k π-π2,k π+π2,k ∈Z B .()k π,k π+π,k ∈ZC .⎝ ⎛⎭⎪⎫k π-3π4,k π+π4,k ∈ZD .⎝ ⎛⎭⎪⎫k π-π4,k π+3π4,k ∈ZC [令k π-π2<x +π4<k π+π2(k ∈Z )得k π-3π4<x <k π+π4(k ∈Z ),故单调增区间为⎝ ⎛⎭⎪⎫k π-3π4,k π+π4(k ∈Z ).]2.函数y =tan ⎝ ⎛⎭⎪⎫2x -π6的定义域为________.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π2+π3,k ∈Z[因为2x -π6≠k π+π2,k ∈Z ,所以x ≠k π2+π3,k ∈Z ,所以函数y =tan ⎝ ⎛⎭⎪⎫2x -π6的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π2+π3,k ∈Z .]3.函数y =tan 3x 的最小正周期是________. π3 [函数y =tan 3x 的最小正周期是π3.] 4.函数y =tan ⎝ ⎛⎭⎪⎫x -π5的对称中心是________.⎝ ⎛⎭⎪⎫k π2+π5,0(k ∈Z ) [令x -π5=k π2(k ∈Z )得x =k π2+π5(k ∈Z ),∴对称中心为⎝ ⎛⎭⎪⎫k π2+π5,0(k ∈Z ).]【例1】 (1)函数y =1tan x ⎝ ⎛⎭⎪-4<x <4,且x ≠0的值域是( )A .(-1,1)B .(-∞,-1)∪(1,+∞)C .(-∞,1)D .(-1,+∞)(2)求下列函数的定义域: ①y =11+tan x;②y =lg(3-tan x ).思路点拨:(1)由x 范围求出tan x 的范围→求1tan x 的范围 (2)①中注意分母不为零且y =tan x 本身的定义域; ②中注意对数大于零⇒从而得到定义域.(1)B [当-π4<x <0时,-1<tan x <0,∴1tan x <-1; 当0<x <π4时,0<tan x <1,∴1tan x >1.即当x ∈⎝ ⎛⎭⎪⎫-π4,0∪⎝ ⎛⎭⎪⎫0,π4时,函数y =1tan x 的值域是(-∞,-1)∪(1,+∞).](2)[解] ①要使函数y =11+tan x有意义,需使⎩⎨⎧1+tan x ≠0,x ≠k π+π2(k ∈Z ),所以函数的定义域为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫k ∈R 且x ≠k π-π4,x ≠k π+π2,k ∈Z .②因为3-tan x >0,所以tan x < 3. 又因为tan x =3时,x =π3+k π(k ∈Z ),根据正切函数图象,得k π-π2<x <k π+π3(k ∈Z ),所以函数的定义域是⎩⎨⎧x ⎪⎪⎪⎭⎬⎫k π-π2<x <k π+π3,k ∈Z .1.求正切函数定义域的方法(1)求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y =tan x 有意义,即x ≠π2+k π,k ∈Z .(2)求正切型函数y =A tan(ωx +φ)(A ≠0,ω>0)的定义域时,要将“ωx +φ”视为一个“整体”.令ωx +φ≠k π+π2,k ∈Z ,解得x .2.解形如tan x >a 的不等式的步骤提醒:求定义域时,要注意正切函数自身的限制条件.1.求函数y =tan x +1+lg(1-tan x )的定义域. [解] 要使函数y =tan x +1+lg(1-tan x )有意义,则⎩⎪⎨⎪⎧tan x +1≥0,1-tan x >0,即-1≤tan x <1.当x ∈⎝ ⎛⎭⎪⎫-π2,π2上满足上述不等式的x 的取值范围是⎣⎢⎡⎭⎪⎫-π4,π4.又因为y =tan x 的周期为π,所以所求x 的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪-π4+k π≤x <π4+k π,k ∈Z .【例2】 (1)函数f (x )=tan⎝ ⎛⎭⎪⎫2x +π3的周期为________.(2)已知函数y =tan ⎝ ⎛⎭⎪⎫x -π3,则该函数图象的对称中心坐标为________.(3)判断下列函数的奇偶性:①y =3x tan 2x -2x 4;②y =cos ⎝ ⎛⎭⎪⎫π2-x +tan x .思路点拨:(1)形如y =A tan(ωx +φ)(Aω≠0)的周期T =π|ω|,也可以用定义法求周期.(2)形如y =A tan(ωx +φ)(Aω≠0)的对称中心横坐标可由ωx +φ=k π2,k ∈Z 求出.(3)先求定义域,看是否关于原点对称,若对称再判断f (-x )与f (x )的关系. (1)π2 (2)⎝ ⎛⎭⎪⎫k π2+π3,0(k ∈Z ) [(1)法一:(定义法)∵tan ⎝ ⎛⎭⎪⎫2x +π3+π=tan ⎝ ⎛⎭⎪⎫2x +π3,即tan ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x +π2+π3=tan ⎝ ⎛⎭⎪⎫2x +π3, ∴f (x )=tan ⎝ ⎛⎭⎪⎫2x +π3的周期是π2.法二:(公式法)f (x )=tan ⎝ ⎛⎭⎪⎫2x +π3的周期T =π2.(2)由x -π3=k π2(k ∈Z )得x =k π2+π3(k ∈Z ),所以图象的对称中心坐标为⎝ ⎛⎭⎪⎫k π2+π3,0,k ∈Z .] (3)[解] ①定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π2+π4,k ∈Z ,关于原点对称,又f (-x )=3(-x )tan 2(-x )-2(-x )4=3x tan 2x -2x 4=f (x ),所以它是偶函数.②定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π+π2,k ∈Z ,关于原点对称,y =cos ⎝ ⎛⎭⎪⎫π2-x +tan x =sin x +tan x ,又f (-x )=sin(-x )+tan(-x )=-sin x -tan x =-f (x ),所以它是奇函数.1.函数f (x )=A tan(ωx +φ)周期的求解方法. (1)定义法.(2)公式法:对于函数f (x )=A tan(ωx +φ)的最小正周期T =π|ω|.(3)观察法(或图象法):观察函数的图象,看自变量间隔多少,函数值重复出现.2.判定与正切函数有关的函数奇偶性的方法.先求函数的定义域,看其定义域是否关于原点对称,若其不关于原点对称,则该函数为非奇非偶函数;若其关于原点对称,再看f (-x )与f (x )的关系.提醒:y =tan x ,x ≠k π+π2(k ∈Z )的对称中心坐标为⎝ ⎛⎭⎪⎫k π2,0,k ∈Z .2.判断下列函数的奇偶性: (1)f (x )=tan 2x -tan xtan x -1;(2)f (x )=tan ⎝ ⎛⎭⎪⎫x -π4+tan ⎝ ⎛⎭⎪⎫x +π4.[解](1)由⎩⎨⎧x ≠k π+π2,k ∈Z ,tan x ≠1,得f (x )的定义域为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ≠k π+π2且x ≠k π+π4,k ∈Z , 不关于原点对称,所以函数f (x )既不是偶函数,也不是奇函数.(2)函数定义域为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ≠k π-π4且x ≠k π+π4,k ∈Z ,关于原点对称,又f (-x )=tan ⎝ ⎛⎭⎪⎫-x -π4+tan ⎝ ⎛⎭⎪⎫-x +π4 =-tan ⎝ ⎛⎭⎪⎫x +π4-tan ⎝ ⎛⎭⎪⎫x -π4=-f (x ), 所以函数是奇函数.1.正切函数y =tan x 在其定义域内是否为增函数?提示:不是.正切函数的图象被直线x =k π+π2(k ∈Z )隔开,所以它的单调区间只在⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )内,而不能说它在定义域内是增函数.假设x 1=π4,x 2=54π,x 1<x 2,但tan x 1=tan x 2.2.如果让你比较tan ⎝ ⎛⎭⎪⎫-4π3与tan ⎝ ⎛⎭⎪⎫-11π5的大小,你应该怎样做?提示:先根据正切函数的周期性把两角化到同一单调区间内,再由正切函数的单调性进行比较.【例3】 (1)不通过求值,比较下列各组中两个三角函数值的大小: ①tan 13π4与tan 17π5; ②tan ⎝ ⎛⎭⎪⎫-13π4与tan ⎝ ⎛⎭⎪⎫-16π5.(2)求函数y =3tan ⎝ ⎛⎭⎪⎫π4-2x 的单调区间.思路点拨:(1)把角化成同一单调区间上 →根据正切函数单调性比较出大小(2)化为y =-3tan ⎝ ⎛⎭⎪⎫2x -π4→解-π2+k π<2x -π4<k π+π2,k ∈Z →求出单调区间[解] (1)①因为tan 13π4=tan π4,tan 17π5=tan 2π5, 又0<π4<2π5<π2,y =tan x 在⎣⎢⎡⎭⎪⎫0,π2内单调递增,所以tan π4<tan 2π5,即tan 13π4<tan 17π5. ②因为tan ⎝ ⎛⎭⎪⎫-13π4=-tan π4,tan ⎝ ⎛⎭⎪⎫-16π5=-tan π5, 又0<π5<π4<π2,y =tan x 在⎣⎢⎡⎭⎪⎫0,π2内单调递增,所以tan π4>tan π5, 所以-tan π4<-tan π5, 即tan ⎝ ⎛⎭⎪⎫-13π4<tan ⎝ ⎛⎭⎪⎫-16π5.(2)y =3tan ⎝ ⎛⎭⎪⎫π4-2x =-3tan ⎝ ⎛⎭⎪⎫2x -π4,由-π2+k π<2x -π4<π2+k π,k ∈Z 得,-π8+k 2π<x <3π8+k2π,k ∈Z ,所以y =3tan ⎝ ⎛⎭⎪⎫π4-2x 的减区间为⎝ ⎛⎭⎪⎫-π8+k2π,3π8+k 2π,k ∈Z .1.将本例(2)中的函数改为“y =3tan ⎝ ⎛⎭⎪⎫12x -π4”,结果又如何?[解] 由k π-π2<12x -π4<k π+π2(k ∈Z ), 得2k π-π2<x <2k π+32π(k ∈Z ),∴函数y =3tan ⎝ ⎛⎭⎪⎫12x -π4的单调递增区间是⎝ ⎛⎭⎪⎫2k π-π2,2k π+32π(k ∈Z ).2.将本例(2)中函数改为“y =lg tan ⎝ ⎛⎭⎪⎫2x -π4”结果又如何?[解] 因为函数y =lg x 在(0,+∞)上为增函数,所以函数y =lg tan x 的单调递增区间就是函数y =tan x (tan x >0)的单调递增区间,令k π<2x -π4<k π+π2(k ∈Z ),得k π2+π8<x <k π2+3π8(k ∈Z ), 故y =lg tan ⎝ ⎛⎭⎪⎫2x -π4的增区间为⎝ ⎛⎭⎪⎫k π2+π8,k π2+3π8,k ∈Z .1.求函数y =A tan(ωx +φ)(A >0,ω≠0,且A ,ω,φ都是常数)的单调区间的方法.(1)若ω>0,由于y =tan x 在每一个单调区间上都是增函数,故可用“整体代换”的思想,令k π-π2<ωx +φ<k π+π2,k ∈Z ,解得x 的范围即可.(2)若ω<0,可利用诱导公式先把y =A tan(ωx +φ)转化为y =A tan[-(-ωx -φ)]=-A tan(-ωx -φ),即把x 的系数化为正值,再利用“整体代换”的思想,求得x 的范围即可.2.运用正切函数单调性比较大小的步骤.(1)运用函数的周期性或诱导公式将角化到同一单调区间内. (2)运用单调性比较大小关系.提醒:y =A tan(ωx +φ)(A >0,ω>0)只有增区间;y =A tan(ωx +φ)(A <0,ω>0)只有减区间.1.正切函数在整个定义域上的图象叫正切曲线.正切曲线是由相互平行的直线x =k π+π2(k ∈Z )所隔开的无穷多支曲线组成,每支曲线向上、向下无限接近相应的两条直线,且每支曲线都是单调递增的.2.正切函数的性质 (1)正切函数y =tan x的定义域是⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ≠k π+π2,k ∈Z ,值域是R .(2)正切函数y =tan x 的最小正周期是π,函数y =A tan(ωx +φ)(Aω≠0)的周期为T =π|ω|.(3)正切函数在⎝ ⎛⎭⎪⎫-π2+k π,π2+k π(k ∈Z )上递增,不能写成闭区间.正切函数无单调减区间.1.下列说法正确的是( ) A .正切函数的定义域和值域都是R B .正切函数在其定义域内是单调增函数 C .函数y =|tan x |与y =tan x 的周期都是π D .函数y =tan|x |的最小正周期是π2C [y =tan x 的定义域为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ≠k π+π2(k ∈Z ),所以A 错;由正切函数图象可知B 错;画出y =tan x ,y =|tan x |和y =tan|x |的图象可知C 正确,D 错误,因为y =tan|x |不是周期函数.]2.在下列函数中同时满足:①在⎝ ⎛⎭⎪⎫0,π2上递增;②以2π为周期;③是奇函数的是( )A .y =tan xB .y =cos xC .y =tan x 2D .y =-tan xC [A ,D 的周期为π,B 中函数在⎝ ⎛⎭⎪⎫0,π2上递减,故选C.] 3.函数y =|tan x |在⎝ ⎛⎭⎪⎫-π2,3π2上的单调减区间为________. ⎝ ⎛⎦⎥⎤-π2,0和⎝ ⎛⎦⎥⎤π2,π [如图,观察图象可知,y =|tan x |在⎝ ⎛⎭⎪⎫-π2,3π2上的单调减区间为⎝ ⎛⎦⎥⎤-π2,0和⎝ ⎛⎦⎥⎤π2,π.]4.求函数y =tan ⎝ ⎛⎭⎪⎫x 2-π3的定义域、最小正周期、单调区间及其图象的对称中心.[解] ①由x 2-π3≠k π+π2,k ∈Z ,得x ≠2k π+5π3,k ∈Z ,∴函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠2k π+53π,k ∈Z . ②T =π12=2π,∴函数的最小正周期为2π.③由k π-π2<x 2-π3<k π+π2,k ∈Z ,得2k π-π3<x <2k π+5π3,k ∈Z ,∴函数的单调递增区间为⎝ ⎛⎭⎪⎫2k π-π3,2k π+5π3, k ∈Z . ④由x 2-π3=k π2,k ∈Z ,得x =k π+2π3,k ∈Z ,∴函数图象的对称中心是⎝ ⎛⎭⎪⎫k π+2π3,0,k ∈Z .。
1.4.3 正切函数的性质与图象

2
k , k Z
y A tan( x )
2.奇偶性
tan( x) tan x, x
T
2
k , k Z
正切函数是奇函数
练习:求下列函数的最小正周期: 1 π (1)y=tan(- x);(2)y=tan(2x+ ). 2 12
T 2 1 2
[规律方法] 对于形如y=tan(ωx+φ)(ω、φ为 非零常数)的函数性质和图象的研究,应以正 切函数的性质与图象为基础,运用整体思想和 换元法求解.如果ω<0,一般先利用诱导公式 将x的系数化为正数,再进行求解.
例 4 利用正切函数的单调性比较下列两个 函数值的大小: 6 13 (1)tan-5π与 tan- 7 π; (2)tan 2 与 tan 9.
T
2
利用正切线画出函数在 , 的图象 2 2
y
O1
3 4 6 2
O 6
4 3 2
x
图
y
象
3 2
2
2
3 2
x
特征
三点两 线
2
由直线 x 1.有无穷多支曲线组成,
k , k Z隔开
2.在每个分支里是单调递增的 3.有渐近线 x
无减区间 在每一个开区间内都是单调增函数.能不能说
正切函数在整个定义域上单调递增?
例 1 求函数 y= tan x+1+lg(1-tan x)的 定义域.
变式训练 求下列函数的定义域: 1 (1)y= ;(2)y=lg( 3-tan x). 1+tan x
课件2:1.4.3 正切函数的性质与图象

(3)由 k x k , k Z 解得
2
2
3 2
5
1
2k x 2k , k Z
3
3
5
1
所以,函数的单调增区间为:( 2k , 2k ), k Z
3
3
典型例题
1 π
求函数 y=tan( x- )的定义域、周期及单调区间.
x , , 的图像?
2 2
( ,
tan )
3
A
0
3
3
X
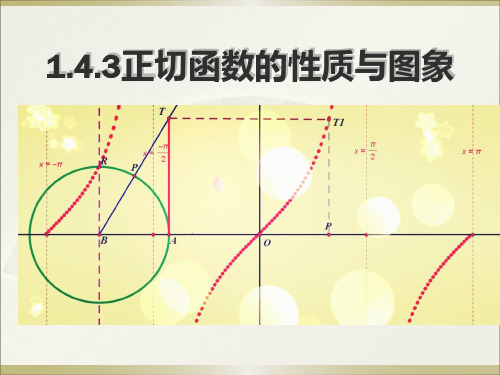
作法: (1) 等分:把单位圆右半圆分成8等份。
3
3
(2) 作正切线
, , , , ,
8
8
4
8
8Hale Waihona Puke 4(3) 平移(4) 连线
o
3 0
2
8
4
8
8
4
3
8
2
想一想
正切函数在整个定义域内是增函数吗?
2
解析:(1)函数的自变量x应满足
x k , k Z
2
3 2
即
1
x 2k , k Z
3
1
所以,函数的定义域为:
x
/
x
2
k
,
k
Z
3
(2)周期 T 2
2
典型例题
求函数 y tan( x ) 的定义域、周期和单调区间.
1[1].4.3_正切函数的图象和性质课件(上课)
![1[1].4.3_正切函数的图象和性质课件(上课)](https://img.taocdn.com/s3/m/fe18e981bceb19e8b8f6bad3.png)
2
1
2
Байду номын сангаасo
4
2
2
x
练习: 1) tan x 0
2) tan x 0
例1、求函数
y tan( x ) 2 3
的定义域、周期、单调区间
变式1:求函数 的定义域 变式2:求函数单调 区间;
例2、 比较下列各组中两个正切函数值的大小 0 0 (1) 与 tan 143
正切函数的性质和图象
回顾: 1.如何作正弦函数的图像? 2.如何研究正弦函数,余弦函数的性质? y y=sinx
1 -6 -5 -4 -3 -2 - -1 y 1 -6 -5 -4 -3 -2 - -1 o 2 3 4 5 6 x
y=cosx
2 3 4 5 6 x
3
4
6
3 3 tan tan tan 4 4 4 3 tan tan tan tan 6 4 即
2
叫做正切曲线.
2
k , (k Z )的图象 , 并把它
y
3 2
2
0
2
3 2
x
思考:如何作正切函数的简图?
正切函数 y tan x 的性质和图像:
{ 1.定义域: x | x
2值域:
2
k , k Z }
y
y tan x
R
3周期性: 正切函数是周期函数, 周期是
3.诱导公式:奇变偶不变符号看象限
1.4.3 正切函数的性质和图像

B
(2)我们怎么做出正切函数 在 - , 内的简图 2 2
一点两线
三点两线
(3)直线y=a与y=tanx的两个相邻的交点间的距离是多少? (4)正切函数具有怎样的对称性?
x 1 变式 : y 3 tan( ) (1) y 3 tan( x ); 2 4 2 4 1 解 : 原函数可化为 : y 3 tan( x ); 解:令 k x k 2 4 2 2 4 2 1 3 令k x k 2k x 2k 2 2 4 2 2 2
1 y 3 tan( x )递增区间为 : 2 4
数学应用 例3 求下列的单调区间:
1 y 3 tan( x )递减区间为 : 2 4
总结:对于函数 y A t an( x )的单调区间的求解, 应注意哪些方面?
3 ,k z 2k , 2k 2 2
x
2
3
由图可知:x k , 2 x
6
)
3
2求函数y tan x 1 1 tan x的定义域
y
令k
3
2x
6
k
2
,k z
-
1
2
k k x 2 4 2 3 k k 解集为x / x ,k z 2 4 2 3
5 2
关于原点对称
5 2
3 2
-
O 2 2
3 2
X
f(-x)=tan(-x)=-tanx=-f(x)
正切函数是奇函数
思考 4 :结合正切函数的周期性,正切函数的单 调性如何?
课件6:1.4.3 正切函数的性质与图象

所以函数的定义域为xx∈R且x≠kπ-π4,x≠kπ+π2,k∈Z.
(2)因为 3-tan x>0,所以 tan x< 3. 又因为 tan x= 3时,x=π3+kπ(k∈Z), 根据正切函数图象(图略),得 kπ-2π<x<kπ+3π(k∈Z), 所以函数的定义域是xkπ-π2<x<kπ+π3,k∈Z.
谢谢观看!
[达标·检测]
1.函数 y=tan x-π4≤x≤π4且x≠0的值域是(
)
A.[-1,1]
B.[-1,0)∪(0,1]
C.(-∞,1]
D.[-1,+∞)
【解析】 根据函数的单调性可得.
【答案】 B
2.函数 f(x)=tanx+6π的定义域是________,f6π=________. 【解析】 由题意知 x+6π≠kπ+π2(k∈Z),即 x≠3π+kπ(k∈Z). 故定义域为xx≠kπ+π3,k∈Z,且 f6π=tan6π+π6= 3. 【答案】 xx≠kπ+π3,k∈Z 3
是增函数
π 2.函数 y=tan ωx(ω≠0)的最小正周期是______|ω__| ___.
[题型·探究] 类型 1 正切函数的定义域、值域问题
例 1 (1)函数 y= tan x+1+lg(1-tan x)的定义域是________. (2)函数 y=tan(sin x)的值域为________. 【自主解答】 (1)要使函数 y= tan x+1+lg(1-tan x)有意义, 则t1a-n xta+n 1x≥>00,,即-1≤tan x<1. 在-π2,π2上满足上述不等式的 x 的取值范围是-π4,π4. 又因为 y=tan x 的周期为 π, 所以所求 x 的定义域为x-π4+kπ≤x<π4+kπ,k∈Z.
课件4:1.4.3 正切函数的性质与图象

1.正切函数的图象
课后小结
正切函数有无数多条渐近线,渐近线方程为 x=kπ+2π,k∈Z,相邻
两条渐近线之间都有一支正切曲线,且单调递增.
2.正切函数的性质 (1)正切函数 y=tan x 的定义域是x|x≠kπ+2π,k∈Z,值域是 R. (2)正切函数 y=tan x 的最小正周期是 π,函数 y=Atan(ωx+φ) (Aω≠0) 的周期为|ωπ |.
(3)正切函数在-π2+kπ,π2+kπ(k∈Z)上单调递增,正切函数无单调函数 y=3tan(2x+π4)的定义域是( C ) A.{x|x≠kπ+π2,k∈Z} B.{x|x≠2kπ-38π,k∈Z} C.{x|x≠2kπ+π8,k∈Z} D.{x|x≠2kπ,k∈Z}
2.函数 f(x)=tan(x+π4)的单调增区间为 ( C ) A.(kπ-π2,kπ+π2),k∈Z B.(kπ,(k+1)π),k∈Z C.(kπ-34π,kπ+π4),k∈Z D.(kπ-π4,kπ+34π),k∈Z
第一章 三角函数
1.4 三角函数的图象与性质
1.4.3 正切函数的性质与图象
正切函数 y=tan x 的性质与图象
y=tan x
图象
定义域
{x|x∈R,且 x≠kπ+π2,k∈Z}
值域 周期 奇偶性 单调性
R 最小正周期为 π
奇函数 在开区间 kπ-π2,kπ+2π (k∈Z)
内递增
例 1 求函数 y= tan x+1+lg(1-tan x)的定义域. 解:由题意得t1a-n xta+n 1x≥>00 ,即-1≤tan x<1. 在-π2,π2内,满足上述不等式的 x 的取值范围是-π4,π4, 又 y=tan x 的周期为 π, 所以所求 x 的范围是kπ-π4,kπ+π4 (k∈Z). 即函数的定义域为kπ-π4,kπ+4π (k∈Z).
1.4.3正切函数的性质与图像

例:求函数 y tan( x ) 的定义域、 2
单调区间和最小正周期.
小结:
1、正切函数的性质和图象
2、数形结合的思想方法 作业:
1、课本第46页习题 6、7、8、9 2、(选作)由周期函数定义推导出函数 y tan( x ), ( 0) 的最小正周期
再 见
2
o
2
3 0 2 8 4 8
8
4
3 8
2
三 点 两 线 法
-
x , 的简图 想一想:如何快速画出正切函数 y=tanx 2 2
想一想:结合正切函数的周期性 , 如何画出正切函数在整 个定义域内的图象?
正切函数的图象(正切曲线)是被互相平行的直线所 隔开的无穷多支相同形状的曲线组成的。 想一想:正切函数在整个定义域内是增函数吗? 正切函数会不会在某一区间内是减函数?
思考2:正切函数是周期函数吗?最小正周期 T=_______
正切函数是周期函数,周期是 k(k Z,k 0) 思考3:正切函数具有奇偶性吗? 正切函数是奇函数
思考4:当角x在 ( 2 , 2 )
内增加时,正切值发生什 么变化?正切函数的单调性如何?
正切函数在开区间 ( k k 内都是增函数 2
高中数学必修4 1.4.3 正切函数的性质与图象
闫丽丽
嘉峪关市一中
y 正切函数的定义: tan x
正切函数的几何意义:
k , k Z 2
tan AT
y
α的终边
有向线段AT——正切线
1
T
P( x, y)
A( 1,0)
§1.4.3正切函数的性质和图象

整体代换
2 函数的对称中心为 ( k ,0), k Z 3
函数y A tan(wx )( A 0, w 0)性质归纳
1.定义域: 整体代换
把wx 视为一个整体 整体 , 令wx
y
y tan x
3 2
2
o
2
3 2
x
正切曲线是由被相互平行的的直线 x k ( k Z ) 2 所隔开的无穷多支曲线组成的
正切函数y=tanx 的性质总结: 1.定义域:
{x | x
y
y tan x
2
k , k Z }
2.值域:R 3.周期性: 最小正周期
k y A tan( x )为奇函数 ,k Z 2 y A tan( x )不可能成为偶函数
例1.求函数y tan( x )的定义域, 周期和单调区间 2 3 和对称中心坐标
定义域求法:
整体代换
1 由 x k解得 x 2k , k Z 2 3 2 3 1 函数定义域为 { x | x 2k , k Z } 3 周期求法:
公式法
T 2 函数的周期为 2
, )的图象? 2 2
利用单位圆中的正切线 作出y tan x , x (
作法: (1) 等分 (2) 作正切线 (3) 平移 (4) 连线
o1
y
, )的图象 2 2
1
1[1].4.3正切函数的性质和图象
![1[1].4.3正切函数的性质和图象](https://img.taocdn.com/s3/m/86799fd15fbfc77da269b1ab.png)
x
奇偶性: 奇函数 tan(-x)=-tanx
单调性: 在 (
2 2 内是增函数 k 对称性: 对称中心是 ( , 0), k Z 2
k ,
k ) k Z
对称轴呢?
3、 求函数y=sin -3x 的单调递增区间。 4 2k 2k 7 k为整数 + , + 3 4 3 12
课堂练习
1.给出四个函数: (A)y=cos(2x+π/6) (B)y=sin(2x+π/6)
(C)y=sin(x/2+π/6)
(D)y=tan(x+π/6)
则同时具有以下两个性质的函数是( ①最小正周期是π 称.
A
)
②图象关于点(π/6,0)对
例1.观察图象,写出满足下列条件的x值的范围:
2
对称轴: 对称中心:(
x k , k Z
2
k , 0) k Z
1.正切函数 y tan x 的性质:
定义域: {x | x 值域:
y
y tan x
2
k , k Z }
R
周期性: 正切函数是周期函数, 周期是
2 2Fra biblioteko 2
2
(1)tan x 0; (2)tan x 0; (3)tan x 0
解:
y
(1) x (k ,
2
y tan x
k )
k Z
(2) x k
(3) x (
k Z
k , k ) k Z
2
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f ( x ) ta n (
f ( x ) A tan ( x ) ) 2 x 3
2) a n[ x At tan ( ( x( ) ) 2 3
Aa nn ( xx + ) ) t ta ( 2 3
T
(4)利用单位圆中的正切线研究值域;
由正切线可以看到,
y ta n x 在 (
y
2
,
2
)
内可以取任意实数,但没 有最大值、最小值 因此,正切函数的值域是 实数集R
O
x
人人都是人才,人人都可成才
合作探究一
1.画一个周期内正切函数图像 (1)选择一个周期 ( 把单位圆右半圆分成8等份。 (2)利用单位圆作正切线 (3)平移正切线 (4)用光滑的曲线 连接正切线的交叉点 A
上是增函数
人人都是人才,人人都可成才
合作探究二
y
(4) 周期性: T
(5) 奇偶性: 奇函数, 图象关于原点对称。 (6) 对称性: 对称中心:
3 2
P(x,y)
·
2
0
2
3 2
x
不一定在正切曲线上
对称轴: 无
P′ (-x,-y )
·
人人都是人才,人人都可成才
练习提高
由 k x k , k Z
2 2 3 2
解得
5 1 2k x 2k , k Z x 3 3
所以原函数的单调递增区间是
( 5 1 2 k , 2 k ), k Z 3 3
整体思想
人人都是人才,人人都可成才
反思提升
变式:求使不等式 ta n (
(2)从数的角度研究奇偶性;
ta n ( x ) ta n x
ቤተ መጻሕፍቲ ባይዱ
x | x k , k Z 2
人人都是人才,人人都可成才
合作探究一
y
(3)利用单位圆中的正切线研究单调性; y
T
x
O
A
O
A
x
y
T
几 何 画 板 演 示
y
T
O
A
x
A
O
x
T
人人都是人才,人人都可成才
整体思想
1 2k , k Z }. 3
所以,原函数的定义域是 { x | x
人人都是人才,人人都可成才
典型例题 例题反思
例2.求函数 y ta n (
解: (周期)
2
x
3
)
的定义域、周期和单调区间。
的周期是
f ( x ) A ta n ( x )( 0 )
0
上是增函数,
0
13 5
) ta n
2 5
tan 167 tan 173
又 0<
ta n ( 11 4
4
<
2 5
<
2
13 5
) ta n (
)
说明:比较两个正切值大小,关键是把相应的角化到 y=tanx的同一单调区间内,再利用y=tanx的单调递增性 解决。
例1. 比较下列每组数的大小.
(1)tan167 与tan173 (2)tan(o o
11 4
)与 tan(
11 4
13 5
)
解: 90 167 173 180
0 0 0
0
解 : ta n (
ta n (
) ta n
4
y tan x在 , 2
课堂小结
三、课堂小结
一类图像: y ta n x 两种思想:①整体思想 六个性质:
周期性 单调性 奇偶性 对称性
②数形结合思想
四“信”
定义域
值域
二“誉”
人人都是人才,人人都可成才
课后作业
课后练习:
完成学案中的课后作业
人人都是人才,人人都可成才
, ) 2 2
T
2
3 8
, 4 ,8 ,8 , ,8 4
3
人人都是人才,人人都可成才
合作探究二
2.向左向右扩展得到正切函数图象
3 2
2
3 2
人人都是人才,人人都可成才
合作探究二
4.正切函数y=tanx的性质 3.图象特征
y
(1)间断性: 正切曲线是被相互平行的直线 ⑴ 定义域:
2 2 3 2
解得
5 1 2k x 2k , k Z 3 3
所以原函数的单调递增区间是
( 5 1 2 k , 2 k ), k Z 3 3
人人都是人才,人人都可成才
例题反思
例1.求函数 y ta n (
解: (单调区间)
2
x
3
)
的定义域、周期和单调区间。
.
有时数学也要 大胆猜想
]
(x ff ( x 2 ) )
所以原函数的周期是2.
人人都是人才,人人都可成才
练习提高
练习2:求下列函数 的周期.
(1) y tan 1 2 (2) y 5 tan( 1 2 x,x 2 k , k Z
T 2
x+
人人都是人才,人人都可成才
复习回顾
2.我们是怎样研究正、余弦函数的性质的? 图象 性质 3.如何作出正弦函数图像的?
B
y 1
O1
A O
-1
3
2 3
4 3
5 3
2
x
y=sinx x[0,2] y=sinx xR
y
1 -4 -3 -2 -
o
-1
2
3
4
5
6 x
人人都是人才,人人都可成才
3
), 2 k x
5 3
, k Z
T 2
说明:正切函数的周期仅与自变量的系数有关。
人人都是人才,人人都可成才
典型例题
例2.求函数 y ta n (
解: (单调区间)
2
x
3
)
的定义域、周期和单调区间。
由 k x k , k Z
人人都是人才,人人都可成才
练 习 1 : ta n
7 8
与 ta n
6
有时也可看图像
人人都是人才,人人都可成才
典型例题
例2.求函数 y ta n (
(定义域) 解: 自变量x应满足 即
x
2
x
3
3
)
2
的定义域、周期和单调区间。
k , k Z
2
x
1 2k , k Z 3
x 2 k , k Z
{ x | x k , k Z } 2 所隔开的无穷多支曲线组成的。
渐近线
(2)趋势:
3 2
2
0
2
3 2
x (2) 值域: R 在每个开区间上成上升趋势
(3)单调性: 在每一个开区间
(
2
k ,
2
k ), k z
合作探究一
从新的角度看:
(1)从数的角度研究周期性;
(2)从数的角度研究奇偶性; (3)利用单位圆中的正切线研究单调性; (4)利用单位圆中的正切线研究值域;
人人都是人才,人人都可成才
合作探究一
(1)从数的角度研究周期性;
ta n ( x ) ta n x
x | x k , k Z 2
解: 由
k
2 3
2
x
3
) 0 成立x
的值的范围。
2
x
3
2
k , k Z
解得
2k x
1 2k , k Z 3
整体思想 数形结合
所以使不等式成立 x 的值的范围是
2 1 2k , 2k , k Z 3 3
人人都是人才,人人都可成才
合作探究一
2
(3)利用单位圆中的正切线研究单调性(结论);
( ,
2
) 是 y ta n 的 一个单调递增区间。
2
又周期为 所以 y ta n 在每一个开区间 单调递增, 无单调递减区间。
(
k ,
2
k ), k Z
人人都是人才,人人都可成才
合作探究一
太湖高级中学
蒋萍莉
人人都是人才,人人都可成才
复习回顾
1.正切函数的定义
y
的终边
P(x,y)
定义域:
x | x k , k Z 2
M
x
正切函数是以角为自变量,以角的终边上的点 的比值为函数值的函数,即
ta n y x x 0
的 终 边 不 在 y轴 上
