Bootstrap方法在经济计量领域的应用
stata bootstrap解读

Stata是一种统计分析软件,广泛用于各种社会科学、经济学、生物学等领域的数据分析。
Bootstrap是一种增广样本统计方法,用于解决小样本问题,提供了一种非参数统计中估计统计量方差进而进行区间估计的统计方法。
在Stata中应用Bootstrap的基本步骤如下:采用有放回抽样方法从原始样本中抽取一定数量的子样本。
根据抽出的样本计算想要的统计量。
重复前两步K次,得到K个统计量的估计值。
根据K个估计值获得统计量的分布,并计算置信区间。
在解读Stata的Bootstrap结果时,需要注意以下几点:置信区间的范围:Bootstrap通过重复抽样生成多个样本,并计算每个样本的统计量,然后根据这些统计量生成一个置信区间。
因此,置信区间的范围反映了估计的精确度。
如果置信区间很窄,说明估计很精确;如果置信区间很宽,说明估计的精确度较低。
样本大小的影响:Bootstrap方法依赖于样本大小,因此样本大小会影响Bootstrap结果的准确性和可靠性。
如果样本大小较小,那么置信区间的范围可能会更宽,降低了估计的精确度。
因此,在解读Bootstrap结果时,需要考虑样本大小的影响。
异常值的影响:在Bootstrap过程中,异常值可能会对结果产生较大的影响。
如果原始样本中存在异常值,那么这些异常值可能会在重复抽样过程中被重复抽中,从而影响Bootstrap结果的准确性。
因此,在解读Bootstrap结果时,需要考虑异常值的影响。
假设检验的结果:在Bootstrap过程中,也可以进行假设检验。
通过比较观察到的统计量和假设的临界值,可以判断一个假设是否成立。
在解读Bootstrap 结果时,需要关注假设检验的结果。
几类线性模型中的Bootstrap方法及其应用

几类线性模型中的Bootstrap方法及其应用引言:线性模型被广泛应用于各个领域,如经济学、统计学和机器学习等。
为了提高线性模型的准确性和稳定性,研究人员发展了一种称为Bootstrap方法的统计学技术。
Bootstrap方法通过从原始数据集中重复抽样来生成多个虚拟数据集,并基于这些虚拟数据集进行统计分析。
本文将介绍几类常见的线性模型以及Bootstrap 方法在这些模型中的应用。
一、简单线性回归模型简单线性回归模型是最简单的线性模型之一,用于建立一个自变量和一个因变量之间的线性关系。
Bootstrap方法可以用于计算回归系数的置信区间,通过重复抽样计算得到多个回归系数,然后利用这些回归系数的分布进行置信区间估计。
二、多元线性回归模型多元线性回归模型是简单线性回归模型的扩展,其中包含多个自变量和一个因变量之间的线性关系。
Bootstrap方法可以用于估计回归系数的标准误差,通过重复抽样计算得到多个回归系数的标准误差,然后利用这些标准误差的分布进行估计。
三、逻辑回归模型逻辑回归模型是一种广义线性模型,用于建立一个二分类因变量与多个自变量之间的关系。
Bootstrap方法可以用于计算模型的预测准确率的置信区间,通过重复抽样计算得到多个模型的预测准确率,然后利用这些准确率的分布进行置信区间估计。
四、岭回归模型岭回归模型是一种正则化线性模型,用于解决多重共线性问题。
Bootstrap方法可以用于选择最佳的正则化参数,通过重复抽样计算得到多个模型的正则化参数,然后选择使得模型性能最好的参数。
结论:Bootstrap方法在几类线性模型中有广泛的应用,可以用于估计回归系数的置信区间、标准误差的估计、模型预测准确率的置信区间和正则化参数的选择。
通过Bootstrap方法,我们可以提高线性模型的准确性和稳定性,从而更好地应用于实际问题中。
newey-west估计法stata boostrap -回复

newey-west估计法stata boostrap -回复新哈维-韦斯特估计法(Newey-West estimator)是一种用于计量经济学中的假设检验和置信区间构造的方法,特别适用于时间序列数据。
它克服了传统OLS(Ordinary Least Squares)估计法在面对自相关或异方差时的缺陷,提供了更加准确和稳健的估计结果。
本文将一步一步介绍如何使用Stata进行Newey-West估计和Bootstrap方法。
首先,我们需要了解Newey-West估计方法的理论基础。
在时间序列数据分析中,时间上的自相关会导致OLS估计的标准误增大,从而估计结果不准确。
Newey-West估计法通过引入自相关项的权重矩阵,对标准权值进行调整,从而得到更准确的估计结果。
同时,Newey-West估计法还可以考虑异方差的问题,通过加权协方差矩阵的方法,进一步提高了估计的准确性和稳健性。
接下来,我们将介绍如何在Stata中使用Newey-West估计方法。
首先,我们需要加载Stata软件,并导入用于分析的数据集。
假设我们的数据集为"data.dta"文件。
stata导入数据use "data.dta", clear然后,我们可以使用Stata中的`newey`命令来进行Newey-West估计。
`newey`命令的使用方法如下:stata进行Newey-West估计newey dependent_var independent_vars, lag(lag_order)在上述命令中,`dependent_var`代表因变量,`independent_vars`代表自变量,`lag_order`代表滞后阶数。
通过制定滞后阶数,我们可以考虑时间序列数据的自相关性。
除了默认的Newey-West估计方法外,Stata还提供了一些选项供我们进行进一步设置。
例如,我们可以使用`standard`选项来计算标准误:stata使用standard选项计算标准误newey dependent_var independent_vars, lag(lag_order) standard 此外,我们还可以使用`vce(robust)`选项来进行异方差-稳健的Newey-West估计:stata进行异方差-稳健的Newey-West估计newey dependent_var independent_vars, lag(lag_order)vce(robust)通过上述步骤,我们可以获得经过Newey-West估计的OLS回归结果,从而得到更准确和稳健的估计结果。
bootstrap法

bootstrap法Bootstrap法是一种常用的统计学方法,它可以用来评估统计学中的参数估计和假设检验的准确性。
Bootstrap法最初由布拉德利·埃夫隆和皮特·哈尔在1979年提出,并在之后的几十年里得到了广泛的应用。
本文将介绍Bootstrap法的基本原理、应用场景以及实现方法。
一、Bootstrap法的原理Bootstrap法的基本思想是通过从样本中重复抽取数据来估计统计量的分布。
具体而言,Bootstrap法包括以下步骤:1. 从原始数据样本中随机抽取一个固定数量的样本(通常与原始样本大小相同),并将其作为一个新的样本。
2. 重复步骤1多次,通常是1000次或更多次。
3. 对每个新样本计算统计量(如均值、方差、中位数等)。
4. 将所有计算出的统计量按升序排列。
5. 根据需要计算出置信区间和标准误等统计量。
Bootstrap法的核心在于重复抽样。
通过从原始数据样本中重复随机抽样,我们可以获得更准确的统计量估计和假设检验结果。
在某些情况下,原始数据可能不符合正态分布或其他假设检验的前提条件。
Bootstrap法可以通过生成新的样本来解决这些问题。
二、Bootstrap法的应用场景Bootstrap法可以用于各种统计学应用中,包括参数估计、假设检验、回归分析、时间序列分析等。
以下是Bootstrap法的一些常见应用场景:1. 参数估计:Bootstrap法可以用来估计统计量的标准误和置信区间,如均值、中位数、方差、相关系数等。
2. 假设检验:Bootstrap法可以用来检验假设检验的显著性,如两个总体均值是否相等、回归系数是否显著等。
3. 回归分析:Bootstrap法可以用来估计回归系数的标准误和置信区间,以及模型的预测误差等。
4. 时间序列分析:Bootstrap法可以用来估计时间序列模型的参数和预测误差,以及分析时间序列的置信区间和假设检验结果等。
三、Bootstrap法的实现方法Bootstrap法的实现方法相对简单,可以使用各种编程语言和软件包来实现。
数量经济学欧变玲空间经济计量模型Moran检验的Bootstrap渐近改进

简言之,当模型误差服从正态独立同分布时,利用 Bootstrap方法构建统计量,进行空间相关性Moran’s I 检验,收敛速度提高,空间经济计量模型Moran检验 获得Bootstrap渐近改进。Bootstrap Moran检验具有 更好的有限样本性质。
16
数理推导结论
3 当模型误差满足常见空间相关性检验Moran’s I统计 量渐近分布的经典假设,存在异方差,Bootstrap Moran检 验则能够有效地进行空间相关性检验。
17
概言之,当有限样本或模型误差不满足Moran’s I统计量 渐近分布的经典假设条件时,数理推导结果显示: Bootstrap Moran检验能够更有效地检验模型OLS估计 残差间的空间相关性。
18
19
利用统计量分布函数的Edgeworth展开研究Bootstrap方法有 效性颇具代表性,本文基于此展开数理证明工作。
14
数理推导结论
1 当模型误差满足常见空间相关性检验Moran’s I统计量 渐近分布的经典假设时,渐近检验的收敛速度 。 O(N 1/2 )
2 当模型误差满足常见空间相关性检验Moran’s I统计量 渐近分布的经典假设时,Bootstrap Moran检验的收敛速 度 O ( N 。1 )
大样本 误差服从独立同分布
有限样本
误差不服从独立同分 布
7
缘生
在有限样本或模型误差不满足Moran检验的经典 假设,存在异方差或分布未知情况下,如何检验 研究对象间的空间关系?
8
通过文献研究,本文尝试利用Bootstrap方法构造空 间相关检验统计量,解决有限样本或模型误差不服 从正态独立同分布情况下的空间相关性检验难题。
2SLS或GMM方法
bootstrap 回归系数计算

bootstrap 回归系数计算摘要::1.回归系数计算方法2.Bootstrap方法概述3.Bootstrap回归系数计算步骤4.优点与局限性5.实际应用案例正文:一、回归系数计算方法回归分析是研究自变量与依变量之间相依程度的一种统计方法。
在回归分析中,回归系数是度量自变量对依变量影响的指标,它反映当自变量每变化一个单位时,依变量所期望的变化量。
常见的回归系数计算方法有最小二乘法、极大似然估计等。
二、Bootstrap方法概述Bootstrap是一种基于抽样的统计分析方法。
它通过从原始数据中随机抽取一定数量的样本,构建若干个样本数据集,然后对每个数据集进行回归分析,从而得到回归系数的分布。
Bootstrap方法可以用来估计回归系数的置信区间,检验回归关系的显著性等。
三、Bootstrap回归系数计算步骤1.从原始数据中随机抽取一定数量的样本(通常为n/b,其中n为原始数据个数,b为bootstrap重复次数)。
2.对每个抽取的样本数据进行回归分析,计算回归系数。
3.重复步骤1和2,得到一系列回归系数。
4.分析这些回归系数的分布,得出回归系数的置信区间或显著性检验结果。
四、优点与局限性Bootstrap方法的优点在于其简单、易实施,可以有效地估计回归系数的置信区间和显著性。
同时,Bootstrap方法具有较强的抗噪声能力,能够在一定程度上克服异常值对回归分析的影响。
然而,Bootstrap方法也存在局限性。
由于Bootstrap是基于抽样的方法,其结果受到抽样数量和抽样方式的影响。
另外,Bootstrap方法无法解决多元线性回归中的多重共线性问题。
五、实际应用案例在金融领域,Bootstrap回归系数计算方法可以用于估算股票价格与宏观经济变量之间的关系,为企业投资决策提供依据。
在医学领域,Bootstrap方法可以用于评估某种治疗方案的有效性,为临床决策提供参考。
此外,Bootstrap方法还在教育、社会科学等领域具有广泛的应用。
空间经济计量滞后模型Bootstrap Moran检验功效的模拟分析

i c ss f ma a pea d Q e ns a a w i t a i. n ae l sm l n u e p t l e h m tx os l i g r
K e o d S a ile o m erc a o e r svem o es;Bo tta o a e t Po r y w r s: p ta c no ti utr gesi d l osrp M rn ts ; we ;M o t ro n e Ca l
中图 分 类 号 : 2 2 0 1 文 献 标 识 码 : A 文 章 编 号 :0 2— 5 5 2 l ) 9— 0 1— 6 10 4 6 ( 0 O 0 0 9 0
S m ul to i a i n Ana y i o we f Bo t t a o a a no tc Te t l ss f r Po r o o s r p M r n Di g s i s s i pa i lEc n m e r c Au 0 e r s i e M o l n S ta o o t i t r g e sV de s
Ou Bi n i g Lo g Z he L n Gu n p n a ln n hi i a g ig
Absr c Th a y t a t: e s mpttc iti u in f oi dsrb to o M o a ’ I ttsi c nt fe tv l t t p ta c rea in mo 2SL r nS saitc a ’ e fc iey es s ai l o r lto a ng S r sd a si p ta c n me rc a o e rs i e mo l t h i .d. er r I t s pa r we a p y wo r sd a — a e e i u l n s aile o o ti utr g e sv des wih t e .i ro . n hi pe , p l t e i u lb s d Bo tta t o sfrdig o tct si pailc rea in i paile o m erc a tr g e sv o e . I o o sr p me h d o a n si e tngs ta o r lto n as ta c no ti uo e r s iem d 1 n c mpa io t rs n wi h t h o ei a s m po i e t u x e ie Mo t ro sm u ain i diae ha n ve o o rwh t rte e rr r he te r tc la y ttc t s ,o re tnsv n e Ca l i lto n c ts t ti iw fp we ehe h ros a e i i d o o , b o sr p t s r hi mo e s up ro iie a pe prpete .. rn t o tta e tf t s o d lha s e ir fn t s m l o ris, a c n nd a mo e fe tv l he k pail r ef cie y c c s ta d pe e c h n t s mp oi e t Es cal e nd n e t a he a y t tct s. pe ily,t we fBo tta e ti r e r a l h n t a fa y hepo ro osrp t s smo e r ma k b et a h to s mpttc ts o i e t
蒙特卡洛和bootstrap 等概率方法

蒙特卡洛和bootstrap 等概率方法全文共四篇示例,供读者参考第一篇示例:蒙特卡洛和bootstrap是常用的概率方法,它们在统计学和金融等领域有着广泛的应用。
在这篇文章中,我们将介绍蒙特卡洛方法和bootstrap方法的基本概念、原理及其在实际中的应用。
蒙特卡洛方法是一种基于随机抽样的统计模拟方法,通过生成大量随机数来近似求解复杂的数学问题。
蒙特卡洛方法通常用于求解无法通过解析方法获得精确解的概率分布或数值问题。
它的核心思想是通过生成大量的随机样本,通过样本的统计特性来估计目标量。
蒙特卡洛方法在金融风险管理、物理学、生物学等领域中有着广泛的应用。
在金融领域,蒙特卡洛方法被广泛应用于风险管理、期权定价等问题。
通过蒙特卡洛模拟可以估计不同投资组合的风险暴露度,制定有效的风险控制措施。
蒙特卡洛方法还可以用于股票价格模拟、利率建模等问题。
与蒙特卡洛方法类似,bootstrap方法也是一种基于数据的统计方法,它通过重复抽样的方式来估计统计量的分布。
bootstrap方法的主要思想是通过自助法(bootstrap)生成大量的重复样本,用这些样本来计算目标量的统计特性。
bootstrap方法在参数估计、假设检验、置信区间估计等问题中有着广泛的应用。
在金融领域,bootstrap方法常用于估计参数的置信区间、模型选择、风险度量等问题。
通过bootstrap方法可以对回归模型进行检验和验证,评估模型的拟合度和预测能力。
bootstrap方法还可以用于人口统计学、市场营销等领域。
第二篇示例:蒙特卡洛方法和bootstrap方法是统计学中常用的概率方法,它们通过模拟随机事件来估计各种参数和进行推断。
在实际应用中,这两种方法常常被用于数据分析、风险管理、金融建模等领域。
本文将分别介绍蒙特卡洛方法和bootstrap方法的原理和应用,并比较它们的优缺点。
蒙特卡洛方法是一种通过重复随机抽样的方法来估计不确定性的统计方法。
非参数统计中的Bootstrap方法详解(五)

在统计学中,Bootstrap方法是一种用于估计统计量的非参数统计方法。
它的提出和发展为统计学领域带来了重大的影响,成为了一种常用的统计分析工具。
本文将详细介绍Bootstrap方法的原理、应用和相关概念,以及在实际问题中的应用。
Bootstrap方法最早由Bradley Efron于1979年提出,它的核心思想是通过对样本数据的重抽样,来估计总体的分布以及统计量的性质。
这种方法的优势在于不需要对总体分布做出假设,尤其适用于小样本情况下的统计推断。
通过不断地重抽样和计算得到的统计量,可以得到统计量的抽样分布,从而对总体分布和统计量进行估计和推断。
在Bootstrap方法中,首先需要从原始样本中进行有放回的重抽样,得到和原始样本大小相同的重抽样集合。
然后利用这些重抽样数据集合来估计统计量,例如均值、方差等。
通过重复这一过程,可以得到大量的估计值,从而得到统计量的抽样分布。
最终可以利用这些抽样分布对总体分布的性质进行估计,以及对统计量的置信区间和假设检验进行推断。
Bootstrap方法在实际应用中有着广泛的应用。
例如在金融领域,利用Bootstrap方法可以对股票收益率的分布进行估计,从而对风险进行评估。
在医学研究中,Bootstrap方法可以用来对患者的生存时间进行推断。
在工程领域,Bootstrap方法可以用来对数据的不确定性进行分析。
总之,Bootstrap方法在各个领域都有着重要的应用价值,成为了一种强大的统计分析工具。
除了介绍Bootstrap方法的原理和应用,我们还需要了解一些相关的概念。
首先是自助样本(bootstrap sample),即通过有放回的重抽样得到的新样本。
其次是统计量(statistic),即对样本数据进行运算得到的数值,例如样本均值、样本方差等。
另外还有抽样分布(sampling distribution),即统计量在不同抽样情况下的分布。
了解这些相关概念,对深入理解Bootstrap方法的原理与应用至关重要。
bootstrap方法

bootstrap方法Bootstrap方法。
Bootstrap方法是一种统计学上的重要技术,它可以用来估计统计量的抽样分布,计算置信区间和假设检验的p值。
Bootstrap方法的基本思想是通过对原始数据的重抽样来模拟总体分布,从而进行统计推断。
本文将介绍Bootstrap方法的基本原理、应用领域以及实际操作步骤。
Bootstrap方法的基本原理是利用样本数据来模拟总体分布,通过对原始数据的重抽样来构建多个虚拟样本,进而估计统计量的抽样分布。
在实际应用中,我们通常会进行大量的重抽样,比如重复抽取1000次或更多次,以获得统计量的抽样分布。
通过这种方法,我们可以获得统计量的置信区间,评估参数的不确定性,以及进行假设检验。
Bootstrap方法在实际应用中有着广泛的应用领域,比如金融、医学、生态学、工程等领域。
在金融领域,Bootstrap方法常常用于风险管理和金融衍生品定价;在医学领域,Bootstrap方法可以用于估计参数的置信区间和进行假设检验;在生态学领域,Bootstrap方法可以用于估计物种丰富度和多样性指数;在工程领域,Bootstrap方法可以用于估计工程参数的不确定性。
实际操作Bootstrap方法时,首先需要从原始数据中进行重抽样,构建多个虚拟样本。
然后针对每个虚拟样本计算统计量的值,比如均值、中位数、方差等。
通过对这些统计量的分布进行分析,我们可以得到统计量的抽样分布,从而获得置信区间和假设检验的p值。
总之,Bootstrap方法是一种强大的统计学技术,它可以在不知道总体分布的情况下进行统计推断,适用于各种领域的数据分析和统计推断。
通过对原始数据的重抽样,Bootstrap方法可以帮助我们更准确地估计参数的不确定性,评估统计量的置信区间,以及进行假设检验。
因此,掌握Bootstrap方法对于数据分析和统计推断是非常重要的。
空间经济计量模型Bootstrap检验的水平扭曲

空间经济计量模型Bootstrap检验的水平扭曲龙志和1 欧变玲1 林光平2(1 华南理工大学经济与贸易学院;2 美国波特兰州立大学)摘要本文使用回归残差的Boo tstrap方法,对线性模型空间相关性进行检验。
基于空间相关性检验统计量Mo ran s I,在不同Bootstrap样本数及不同空间衔接结构下,研究并比较Bootstr ap和渐近检验方法。
通过M onte Car lo实验揭示了当空间经济计量模型中残差不满足经典正态假定条件时,空间相关性的渐近检验理论不再有效。
本文把Boo tstrap方法用于空间相关性检验,对水平扭曲进行了分析校正。
研究同时发现,从水平扭曲角度来看,无论残差是否满足经典正态假定条件,空间经济计量模型Bootstrap检验通常都很有效。
关键词 水平扭曲 Bo otstrap检验 M oran s I指数中图分类号 F224 0 文献标识码 ASize Distortion of Bootstrap Tests for SpatialEconometric ModelAbstract:In this paper,w e intr oduce the residual based bo otstrap m ethods for hy pothesis testing of spatial correlation in a linear reg ressio n mo del Based on Mor an s I test statistic for spatial cor relation,the size disto rtio n o f bootstr ap and asym ptotic tests are evaluated and com pared for different sample size and fo r vari o us str uctures of spatial co ntiguous w eig ht matr ix By considering the mo re realis tic heterog eneous non norm al distribution assumption,the applicability of the as y mpto tic test is invalid Instead,the residual based boo tstrap tests have dem onstra ted the superior ity in smaller size disto rtio n in comparison w ith asym ptotic tests Our ex tensiv e Mo nte Carlo simulatio n indicates that spatial boo tstrap test is an ef fective alternative to the theo retical asy mpto tic approach w hen the classical distri引 言近年来,空间经济计量已逐渐成为经济管理研究工具箱中重要的分析技术。
非参数统计中的Bootstrap方法详解(十)

Bootstrap方法是一种用于估计统计量抽样分布的非参数统计方法。
它是由Bradley Efron在1979年提出的,被广泛应用在统计学、计量经济学、金融学等领域。
Bootstrap方法的原理和应用十分复杂,本文将对Bootstrap方法进行详细的解析。
Bootstrap方法的基本原理是通过重抽样的方法来估计统计量的抽样分布。
传统的统计方法通常基于对总体分布的假设,如正态分布、均匀分布等,然后利用这个假设对抽样分布进行估计。
而Bootstrap方法则不依赖于总体分布的假设,而是直接利用样本数据进行分析。
在Bootstrap方法中,我们首先从原始样本数据中随机抽取一定数量的样本,然后对这些抽样数据进行统计量的计算。
这个过程被称为“重抽样”。
重抽样的次数通常大于等于1000次,以确保估计的准确性。
通过对重抽样得到的统计量进行排序,我们可以得到统计量的抽样分布,从而进行置信区间估计、假设检验等统计推断。
Bootstrap方法的一个重要特点是对原始样本数据的利用效率非常高。
传统的参数统计方法通常需要对总体分布作出假设,并且需要满足一定的分布形式和参数条件。
而Bootstrap方法则可以直接利用样本数据进行分析,不需要对总体分布作出过多的假设。
另一个重要特点是Bootstrap方法对于各种统计量的估计都是一致的。
无论是均值、方差、中位数、相关系数等统计量,都可以通过Bootstrap方法进行估计。
这使得Bootstrap方法在实际应用中具有非常广泛的适用性。
除了对统计量的估计,Bootstrap方法还可以用于模型选择、预测等领域。
在模型选择中,我们可以通过Bootstrap方法对不同模型的性能进行比较,从而选择最优的模型。
在预测中,Bootstrap方法可以通过对样本数据的重抽样来估计预测误差的分布,从而提高预测的准确性。
然而,虽然Bootstrap方法具有诸多优点,但也存在一定的局限性。
首先,在样本量较小的情况下,Bootstrap方法的估计可能不够稳健。
bootstrap法

bootstrap法Bootstrap法,也称为自助法,是一种统计学方法,用于估计样本数据的统计量和置信区间。
它的主要思想是通过从样本中重复抽取数据来创建新的样本集,从而获得对总体的估计。
Bootstrap法最早由布莱曼(Bradley Efron)在1979年提出,是一种非参数统计方法。
它的优点是可以用于任何类型的数据,包括连续型、离散型、偏态分布等。
由于它的普适性和易于实现,Bootstrap 法已经成为了统计学中常用的方法之一。
Bootstrap法的基本思想是:根据已有的样本数据,进行有放回的抽样,得到与原始样本数据大小相等的新样本。
这个过程重复进行n次,得到n个新样本。
对于每个新样本,我们可以计算出所关心的统计量(如均值、方差、中位数等)的值,从而得到n个统计量。
这些统计量的分布就是原始样本数据中该统计量的抽样分布,可以用于估计总体的统计量。
Bootstrap法的具体步骤如下:1. 从原始样本中有放回地抽取n个样本,得到新样本集。
2. 对新样本集进行统计分析,得到所关心的统计量的值。
3. 重复步骤1和2,得到n个统计量的值。
4. 根据n个统计量的值,计算出该统计量的抽样分布,从而得到估计值和置信区间。
Bootstrap法的优点在于,它不需要假设数据服从特定的分布,也不需要对数据进行任何假设检验。
它可以处理大部分数据类型,包括缺失数据和异常值。
此外,Bootstrap法还可以用于估计参数的标准误差、评估模型的预测误差等。
但是,Bootstrap法也存在一些限制。
由于需要进行大量的重复抽样,计算量较大,需要较长的计算时间。
此外,当样本数据较少时,Bootstrap法可能会出现样本抽取中的偏差,导致估计结果不准确。
总之,Bootstrap法是一种简单、直观、普适性强的统计学方法,可以用于估计总体的各种统计量,并提供置信区间。
在实际应用中,Bootstrap法已经被广泛应用于生物统计、金融风险管理、质量控制等领域。
计量经济学协整检验方法

计量经济学协整检验方法协整检验(cointegration test)是计量经济学中用于检验变量之间是否存在长期稳定的均衡关系的方法。
它的主要目的是确定变量之间的长期关系,即是否存在一个稳定的均衡关系,从而可以进行有效的经济分析和预测。
本文将介绍几种常用的协整检验方法。
1. 单位根检验方法(Unit root test)单位根检验用于检验时间序列数据是否具有非平稳性。
一般来说,如果变量是非平稳的,那么它们之间就不可能存在长期稳定的均衡关系。
常用的单位根检验方法有ADF检验(Augmented Dickey-Fuller test)和KPSS检验(Kwiatkowski–Phillips–Schmidt–Shin test)等。
ADF检验是一种参数统计方法,可以用来检验变量是否是单位根过程,从而判断是否存在协整关系;KPSS检验则是一种非参数统计方法,用于检验变量是否是平稳的。
2. Johansen协整检验方法(Johansen cointegration test)Johansen协整检验方法是一种常用的多变量协整检验方法,可以同时检验多个变量之间的协整关系。
该方法基于向量自回归模型(vector autoregressive model,VAR),通过对向量误差修正模型(vectorerror correction model,VECM)的估计,检验向量自回归参数的协整关系。
Johansen协整检验方法具有较强的参数估计效率和较好的统计性质,被广泛应用于实证研究中。
3. Engle-Granger两步法(Engle-Granger two-step method)Engle-Granger两步法是一种常用的两步骤协整检验方法。
首先,通过对变量进行单位根检验,确定哪些变量是非平稳的;然后,对非平稳变量进行协整关系的估计和检验。
该方法的优点是简单易行,适用于小样本情况,但它的估计效率相对较低。
4. 引导回归法(Bootstrap method)引导回归法是一种非参数的协整检验方法,用于解决传统统计方法在小样本情况下可能存在的偏误和低功效问题。
中介效应bootstrap法

中介效应bootstrap法中介效应是指在一个因果关系中,中介变量在解释因果关系时所起到的作用。
中介效应bootstrap法是一种用于估计中介效应和其置信区间的统计方法。
本文将介绍中介效应bootstrap法的基本原理、步骤和应用。
中介效应bootstrap法的基本原理是基于自助法(bootstrap method)的思想。
自助法是一种用于估计参数统计量的非参数方法,它通过从原始样本中重复有放回地抽取样本,构建多个重复样本,并基于这些重复样本来估计参数统计量的分布。
中介效应bootstrap法利用自助法的思想,通过构建多个重复样本来估计中介效应及其置信区间。
中介效应bootstrap法的步骤如下:1. 收集数据:首先需要收集相关的数据,包括自变量、中介变量和因变量的测量数据。
2. 确定中介效应模型:根据研究问题和理论假设,建立中介效应模型。
中介效应模型通常由自变量对中介变量的回归方程、中介变量对因变量的回归方程和自变量对因变量的回归方程组成。
3. 进行自助抽样:利用自助法的思想,从原始样本中有放回地抽取样本,构建多个重复样本。
通常建议进行1000次以上的自助抽样。
4. 估计中介效应:对于每个重复样本,根据中介效应模型的回归系数估计中介效应的值。
可以使用回归系数乘积法、差异法或比率法来估计中介效应。
5. 构建置信区间:利用重复样本得到的中介效应估计值,可以计算中介效应的置信区间。
常见的方法包括基于百分位数的置信区间和基于标准误差的置信区间。
中介效应bootstrap法的应用非常广泛,特别适用于中介效应的检验和估计。
它可以用于社会科学、医学、心理学等领域的研究,帮助研究者了解中介变量在因果关系中的作用机制。
中介效应bootstrap法是一种用于估计中介效应和其置信区间的统计方法。
通过构建多个重复样本,利用自助法的思想,可以对中介效应进行估计和推断。
中介效应bootstrap法在研究中介效应的检验和估计中发挥着重要的作用,为我们理解因果关系提供了有效的工具。
如何进行计量经济模型的稳健性检验与处理

如何进行计量经济模型的稳健性检验与处理在计量经济学领域,稳健性检验和处理是保证经济模型分析和研究结果可靠性的重要步骤。
稳健性检验和处理能够帮助研究者排除可能的偏误和外生影响,从而得到更准确和可靠的结果。
本文将介绍稳健性检验和处理的基本概念、方法和步骤,并提供一些常用的稳健性检验和处理技巧。
一、稳健性检验的基本概念稳健性检验是指通过改变模型的设定或方法来检验研究结果的鲁棒性。
在计量经济学中,常见的稳健性检验包括变量选择的稳健性检验、函数形式的稳健性检验、异方差性的稳健性检验等。
稳健性检验的目的是验证模型结果的稳定性,即在不同的假设设定或方法选择下,结果是否仍然可靠。
二、稳健性处理的基本步骤稳健性处理是在进行稳健性检验的基础上,对可能的偏误和外生影响进行修正或调整,以得到更准确和可靠的结果。
稳健性处理的基本步骤如下:1. 多种方法比较:对同一问题采用多种方法进行分析和计算,比较不同方法的结果。
这样可以验证结果的一致性和稳健性。
2. 异常值处理:对于可能造成偏误的异常值,可以进行修正或剔除。
常用的处理方法包括Winsorize方法和Trim方法等。
3. 非参数方法:非参数方法不对数据分布做出任何假设,可以有效避免模型设定的偏误。
非参数方法适用于数据分布不确定或偏斜的情况。
4. 机器学习方法:机器学习方法可以通过自动建模和数据驱动的方式提供更加准确和稳健的结果。
常用的机器学习方法包括决策树、随机森林和神经网络等。
5. 鲁棒标准误差:鲁棒标准误差可以有效衡量模型结果的稳定性。
相比于传统的标准误差,鲁棒标准误差对异常值更为敏感,能够更好地反映数据的真实情况。
三、常用的稳健性检验和处理技巧除了上述的基本步骤,下面介绍一些常用的稳健性检验和处理技巧:1. Bootstrap方法:Bootstrap方法通过重复抽取样本,并基于重复样本计算统计指标,来估计参数的分布。
Bootstrap方法可以有效处理样本量小、数据非正态分布等问题。
基于Bootstrap方法的FDI与GDP因果关系的检验
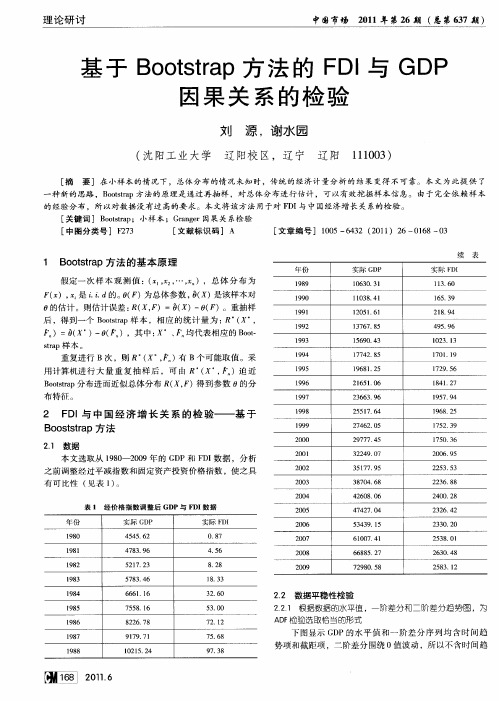
年 份
1 9 98 l9 9 0 1 91 9 19 9 2
的经验 分布 ,所 以对数据 没有 过 高的要 求。本 文将该 方 法用 于对 F I 中国经济增 长 关 系的检 验 。 D与
1 B osrp方 法 的基 本原 理 o tt a
假 定一 次 样 本 观 测 值 :(。 :… , ),总 体 分 布 为 ,, F x 是 ii 的 。 ( ) ( ), .d . 0 F 为总体 参数 , ) ( 是该 样本 对
l5 . 6 7 0 3 2 0 . 0 6 95
B o t p分 布进 而近似 总体 分布 R X, )得 到参数 0的分 o tr sa ( F
2 F I 中 国 经 济 增 长 关 系 的 检 验— — 基 于 D 与 B o tt p方法 o ssr a
2 1 数据 . 本 文选取从 18 - 2 0 9 0 0 9年 的 G P和 F I D D 数据 ,分析 之前 调整 经过 平减指 数 和固定 资产投 资价 格指数 ,使 之具
61 O . 1 0 7 4
2 5 . 3 2 3 5 2 3 . 8 2 6 8 2 0 . 8 4 0 2 22 . 2 3 6 4 23 . 0 3 0 2
2 38 0l 5 .
实际 G P D
44 6 5 5. 2 4 8 .6 7 39 5 1 2 2 7. 3 5 8 .6 7 34
[ 摘
一
要 ]在 小样本 的情 况下 ,总体 分布 的情况 未知 时 ,传 统 的经济 计量 分析 的 结果 变得 不 可 靠。 本 文为此 提 供 了
种新 的思路 ,B o t p方法 的原理 是通过 再抽 样 ,对 总体 分布 进行 估计 ,可 以有效 挖掘样 本信 息 。 由于 完全依 赖 样 本 ot r sa [ 关键词 ]B o t p otr ;小样 本 ;G a gr因果关 系检 验 sa rn e [ 图分类号 ]F 7 中 23 [ 文献 标识码 ]A [ 文章编 号 ] 10 0 5—6 3 (0 1 6— 1 8—0 4 2 2 1 )2 0 6 3
Bootstrap方法在空间计量模型检验中的应用

研究领域:数理经济与计量经济学Bootstrap方法在空间经济计量模型检验中的应用林光平龙志和吴梅[内容提要]:本文采用Bootstrap方法对空间经济计量模型的残差分布进行Moran’s指数I模拟检验,可用于空间计量模型的(事先)确定及(事后)验证。
通过两个实例表明,在回归误差服从独立分布的假设之下,有别于依据大样本理论分布的经典检定法,Bootstrap 方法能有效的解决空间经济计量模型残差分布不确定时,模型中变量间空间相关性的检验问题。
关键词: Bootstrap Moran’s指数空间相关性Abstract: We apply a method of residual bootstrapping for testing spatial correlation in a linear regression model. Based on the Moran’s index I, the bootstrap procedure can be used for model identification (pre-test) and diagnostic checking (post-test) of a spatial econometric model. With two empirical examples, under the assumption of independent distribution of the model errors, the bootstrap method is proven to be an effective alternative to the theoretical asymptotic approach when the classical distributional assumption is violated.Keyword: Bootstrap, Moran’s index, spatial correlation.一、引言空间经济计量学是经济计量研究近十来年发展起来的一个重要分支。
kleibergen-paap rk lm 统计量临界值

kleibergen-paap rk lm 统计量临界值1. 引言1.1 概述在经济学、金融学和统计学等领域,研究人员常常需要进行模型检验和估计。
而针对这些模型的检验中,如何确定临界值是一个重要的问题。
本文讨论了一种常用的统计量——Kleibergen-Paap RK LM统计量及其临界值的确定方法。
1.2 文章结构本文将围绕Kleibergen-Paap RK LM统计量展开讨论。
首先介绍了该统计量的定义与原理,并探讨了它的应用领域以及其特点与优势。
接着,我们将重点关注临界值的确定方法,包括Monte Carlo模拟法、多重比较法(Bootstrap)以及基于中心极限定理法(Asymptotic)。
然后,在实例分析与应用场景讨论部分,我们将通过具体案例来解析数据并提供相应结果和解释。
最后,在结论与展望部分,总结研究发现并探讨了研究局限性以及未来发展方向。
1.3 目的本文的目的是介绍和阐述Kleibergen-Paap RK LM统计量及其临界值确定方法。
通过深入剖析该统计量的定义、原理和应用领域,我们希望能够帮助读者更好地理解该统计量的作用和意义。
同时,通过介绍临界值的确定方法,我们将为研究人员提供一些实用的方法和技巧。
最后,在实例分析与应用场景讨论部分,我们将通过具体案例来验证该统计量在实际问题中的应用价值,并对未来可能的研究方向进行展望。
2. Kleibergen-Paap RK LM统计量:2.1 定义与原理:Kleibergen-Paap RK LM统计量是一种基于Lagrange Multiplier (LM)方法的检验统计量,用于验证经济计量模型的有效性和一致性。
该统计量由Erik H. Kleibergen和Richard Paap在2006年提出,被广泛应用于多元线性回归模型中存在内生性问题的情况。
在传统的OLS(Ordinary Least Squares)估计方法中,当使用含有内生变量的模型时,OLS估计结果将产生偏误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( l otr ,参数 Bo tp Wi Bo t p d sa otr ,非参数 Bo t p sa otr 等方法) sa ,
所 抽 取 的样 本 数 等 于 原 始 样 本 的大 小 ;同 时 , 为 了 减 小
第 2卷 7
28 第月期 0 年77 0
工 业 技 术 经 济
V17 N. 总_ o 02 7 第. .
17期 7
B o t p方 法 在 经 济计 量 领域 的应用 otr sa
龙 志和 欧 变玲 5 04 ) 16 0
( 南理工 大学 ,广州 华
[ 摘
要 ] 作 为 一种 数 据 挖 掘 方 法 ,Bosa 法 为 解 决误 差 项 分 布 未知 时 经 济 计 量 模 型 问题 提 otrp方 t
r
该方法在理 论 和应用 研 究方 面,尤其 是在 医学 、军事 、 金融 、经济学等领域得到广泛发展 ( ai o n aKn Dv snadM c i d — nn 02等【 。) o ,20 ]。根据 截面数据 、时 问序列 数据 和面 板数据的特征 ,目前 已经 出现了相应 的 B o t p otr 抽样 方 sa
适 用范 围和 实现 步骤 , 总结 B o t p 法 在 经 济 计 量领 域 的研 究现 状 ,并 在 此基 础 上 指 出 Bo t p方 法 otr 方 sa otr sa
可 能 的 发展 趋 势 。
[ 关键词 ] B ot p方法 otr saFra bibliotek经济计量
综述
空 间相 关性检验
[ 中图分类号 ]F2 . [ 240 文献标识码 ]A
sa 方 法 。第 四 部 分 ,分 析 Bo tp方 法 经 济 计 领 r tp otr sa 域 的研 究 现 状 和 发 展趋 势 。
2 B os a, 法 的 基 本 思 想 o tt l方 r:
学者的研究角度 不同 ,对 Bo tp方 法的 定亦 有 ott sa
所 不 同 (e rH l 92 _ 根 据 闻 渎 的 闻 『 文 献 资 Pt a ,19 )1 e l 。 J 、 J 料 驯 ,可 把 Bos p方 法 界 定 为 :基 于 原 数 据 现 洲 ” otr t a 值 ,对 所 研 究 问 题 韵 相 应 项 目 进 行 有 放 回 地 随 机 拙 样
法 ,例 如 :可 处 理 截 面 数 据 中 异 方 差 问 题 的 Wi ot l Bo d —
sa ( , 18 ;D v o . n .l hi ,20 ) t p Wu 96 ai nR adE F eae 0 1 ,适 用 r s a r
实的参数值,比如: = { ̄F() 如 ldox} o ,F 为未知总体分
l 弓 言 l
“ otrp [o t ”法 尚 没 有 通 行 的 中 文 译 名 ,文 献 中 有 :  ̄ sa “ 攀法” “ 靴 , 自助 法 ” “ 、 自举 法 ” 和 “ 自助 法 回 归 ” 等 。
B )t p 法 足 美 国 斯 坦 福 大 学 Ef 教 授 (99年 ) ttr 方  ̄sa fr o t 17 …
布函数 。根据 中心极 限定 理 ,可利用从样 本获得 的经验 分布 估计 总体分布 F,进而得到 %的 Bo t p 0 otr 估计为 : sa
r
供 了一 种 有 效 的研 究途 径 。本 文 在 界 定 Bo t p方 法 的 概 念 、基 本 思 想 基 础 上 ,梳 理 经 济计 量 领 域 常 见 otr sa 的 四 种 Bosa 法 :残 差 Bo t p otr t p方 otr ,参 数 Bo t p sa otr ,Wi otrp Pi otr sa l Bo t 和 a s o t p等 的 简单 发 展 历 史 、 d sa r B sa
本信息 ,对总体的分布特性 进行统计推 断的一种 非参 数
统 计方 法 。在 经 济 计 量 模 型 中 ,为 便 于 计 算 ,通 常 假 定 差 项 服 从 正 态 分 布 。 然 而 ,现 实 世 界 中 ,误 差 项 的 分 布通 常 是 末 知 的 , Bo t p 法 为 解 决 误 差 项 分 布 未 知 otr 方 sa 【经 济 计 量 模 型 问 题 提 供 了 一 种 有 效 的 研 究 途 径 。 { . j 1 v snadMaKm o (99 o6 ) i o n c il 19 ,2o )等 J 研 究 发 现 ad n 。 的 Bo t p 法 优 于 基 于 大 样本 的渐 近 理 论 。 otr 方 sa Iosa 方 法 的 出 现 ,在 一 定 程 度 上 解 决 了 无 法 获 k trp  ̄t
J f 纳前 人 研 究 成 果 的 基 础 上 ,提 出 的 根 据 给 定 的 原 始 _ ]
样本 复制 观 测 信 息 ,不 需 要 进 行 分 布 似 设 或 增 加 新 的样
究 ,结构如下。第二部分 ,在 Bo tp 法界定基础 上, otr 方 sa
阐述 Bo t p方 法 的 基 本 思 想 。第 三 部 分 , 从 Bosa otr sa otr tp 方 法 适 用 范 围 、执 行 步 骤 等 方 面 介 绍 五 种 常 见 的 Bo ot
功效 损 失 ,所 选 取 的 Bo t p重 抽 样 次 数 一 般 为 9 , otr sa 9
19 9 ,99等 ,保 证 d* ( 9 ,49 9 B+1 为 整 数 。其 中 。是 ) 名 义 显 著性 水 平 ,B是 Bo tp重抽 样 次 数 。 otr sa Bo t p 法 的 基 本 思 想 是 :假 设 0 =0 ( ) 为 真 ot a 方 s r o
