OptionsAndHedge

合集下载

options在金融中的意思

options在金融中的意思
在金融领域，options是一种重要的金融工具。

它是一种衍生品，给予持有者以在未来某个时间点购买或出售标的资产的权利，而并非义务。

这个权利的行使通常需要支付一定的费用，称为期权费。

options的出现主要是为了对冲金融市场的风险。

它可以用于保护投资组合免受价格波动的影响，也可以用于进行投机，以赚取差价。

无论是对冲还是投机，options都给予投资者更多的选择和灵活性。

options的标的资产可以是各种金融产品，如股票、期货、指数等。

投资者可以根据自己的需求和预期选择适合的options合约。

options合约中包含了多个重要的要素，如行权价、到期日、合约单位等。

行权价是指在到期日行使期权的价格，而到期日是期权的有效期限。

合约单位则是指每个options合约所代表的标的资产数量。

在options交易中，有两种基本的交易类型：认购期权和认沽期权。

认购期权给予持有者以在未来购买标的资产的权利，而认沽期权则给予持有者以在未来卖出标的资产的权利。

投资者可以根据对市场的判断选择适合的交易类型。

options的价格由多个因素影响，其中最重要的是标的资产价格和波动率。

标的资产价格的变动会影响options的内在价值，而波动率的变化则会影响options的时间价值。

其他还有一些因素如利率、股息等也会对options的价格产生一定的影响。

总的来说，options在金融中的意思是一种赋予持有者在未来购
买或出售标的资产的权利的金融工具。

它可以用于对冲风险、进行投机等目的，给予投资者更多的选择和灵活性。

18Future Contracts,Options and Swaps

Text : Background Information
本章旨在介绍期货、期权、掉期的定义，以及如何
操作期货、期权、掉期交易。期货交易是一种标准化交易。标准化指的是在期货交易过程中除合约价格外，期货合约所有条款都是预先规定好的。期货交易的了结（即平仓）一般有两种方式，一是对冲平仓；二是实物交割。期权，它是在期货的基础上产生的一种金融工具。从其本质上讲，期权实质上是在金融领域中将权力和义务分开进行定价，使得权力的受让人在规定时间内对于是否进行交易，行使其权力，而义务方必须履行。掉期交易是当事人之间约定在未来某一期间内相互交换他们认为具有等价经济价值的现金流的交易。掉期交易与期货、期权交易一样，是近年来发展迅猛的金融衍生产品之一，成为国际金融机构规避汇率风险和利率风险的重要工具。
Text :
That's how the futures market works. Besides the example of a cable TV provider, a producer of wheat may be trying to secure a selling price for next season's crop, while a bread maker may be trying to secure a buying price to determine how much bread can be made and at what profit. So the farmer and the bread maker may enter into a futures contract requiring the delivery of 5,000 bushels of grain to the buyer in June at a price of $4 per bushel. By entering into this futures contract, the farmer and the bread maker secure a price that both parties believe will be a fair price in June. It is this contract and not the grain that can then be bought and sold in the futures market.

Betas, Options, and Portfolios of Hedge Funds

Alphas and betas – a reminder
• We often characterize returns for fund i by
rti i i rt m ti
E r i i i E r m
• Beta: tendency of return to rise if the market rises • Beta times rm: How much of the return can you get in an index fund. (“Style”) • Alpha: average return earned in excess of this. (“Selection”) • Epsilon: extra risk beyond index fund.
ቤተ መጻሕፍቲ ባይዱ
Returns
Not astronomical, but if beta really = 0, these aren‟t bad returns! Is beta 0?
Return issues
• Questions for all return statistics:
1. Survivors / backfill / self-reported.
Bigger with lags
0.13
-0.07 0.38 0.74 0.32
Short
Emerg mkts Event Global Macro Long/Short Eqty
-0.53
0.39 0.61 0.93 0.73
0.10
0.00 0.46 0.82 0.42
-0.94
0.58 0.22 0.17 0.47

（英文）笔记：有关期权的基本知识

（英⽂）笔记：有关期权的基本知识AbstractIn th i s p a rt, w e w i l l ma i n l y l e a rn th e d e fi n i ti o n a n d p ro p e rti e s o fo p ti o n s.T h e n,w e w i l l a l s o ta l k a b o u t s o me fu n c ti o n s o f o p ti o n s.Types and defi ni t i on of opti ons(期权的定义和类型)F i rs tl y,w e s h o u l d l e a rn th e d e fi n i ti o n o f o p ti o n s.「D e fin itio n1」(o p tio n s):a n a g re e me n t th a t th e h o l d e r c a n b u y fro m(o r s e l l to) th e s e l l e r (th e b u y e r)o f th e o p ti o n a t a s p e c i fi e d fu tu re ti me a c e rta i n a mo u n t o f a n u n d e rl y i n g a s s e t a t a s p e c i fi e d p ri c e.B u t th e h o l d e r i s u n d e r n o o b l i g a ti o n to e x e rc i s e th e c o n tra c t.「R e ma rk」:In fa c t, th e h o l d e r h a s to p a y p re mi u m fo r th i s ri g h t.Mo re o v e r, o p ti o n s h a s a mu c h h i g h e r l e v e l o f l e v e ra g e.T h e n, w e s h o u l d ma s te r tw o o p ti o n:c a l l o p ti o n a n d p u t o p ti o n.「D e fin itio n2」(c a ll o p tio n a n d p u t o p tio n):A c a l l o p ti o n(看涨期权)- a c o n tra c t to b u y a t a s p e c i fi e d fu tu re ti me a c e rta i n a mo u n t o f a n u n d e rl y i n g a s s e t a t a s p e c i fi c p ri c e;A p u t o p ti o n(看跌期权)- a c o n tra c t to s e l l a t a s p e c i fi e d fu tu re ti me a c e rta i n a mo u n t o f a n u n d e rl y i n g a s s e t a t a s p e c i fi c p ri c e;「R e ma rk」:F ro m th e s e d e fi n i ti o n s, w e c a n e a s i l y fi n d th a t th e d i ffe re n c e o f b o th o p ti o n s i s"b u y"o r "s e l l". If y o u w a n t to b u y, i t me a n s th a t th e o p ti o n i s ri s i n g.「D e fin itio n3」(e x e rc is e p ric e,e x p ira tio n,e x e rc is e): W e d e fi n e e x e rc i s e p ri c e(实施价格) a s th e s p e c i fi e d p ri c e,a n d w e d e fi n e e x p i ra ti o n d a te(到期⽇) a s th e s p e c i fi e d ti meB u t w h a t's th e me a n i n g o f e x e rc i s e(实施)?E x e rc i s e i s th e a c ti o n to p e rfo rm th e b u y i n g o r s e l l i n g o f th e a s s e t a c c o rd i n g to th e o p ti o n c o n tra c t.In fa c t, i f th e o p ti o n s a re d i v i d e d a c c o rd i n g to th e te rms o f th e i mp l e me n ta ti o n o f th e c o n tra c t,th e n w e c a n g e t: E u ro p e a n o p ti o n s a n d A me ri c a n o p ti o n s.「D e fin itio n4」(E u ro p e a n o p tio n s a n d A me ric a n o p tio n s):E u ro p e a n o p ti o n s(欧式期权)- c a n b e e x e rc i s e d o n l y o n th e e x p i ra ti o n d a te.2. 「S p e c u la to r(投机者)」-to ta k e a c ti o n c h a ra c te ri z e d b y w i l l i n gto ri s k w i th o n e's mo n e y b y fre q u e n tl y b u y i n g a n d s e l l i n gd e ri v a ti v e s(fu tu re s,p o ti o n s)fo r th e p ro s p e c t o f g a i n i n g fro m th efre q u e n t p ri c e c h a n g e s;3. 「A rb itra g e(套利者)」-b a s e d o n o b s e rv a ti o n s o f th e s a me k i n do f ri s k y a s s e t, ta k i n g a d v a n ta g e o f th e p ri c e d i ffe re n c e sb e tw e e n ma rk e ts,th e a rb i tra g e u r tra d e s s i mu l ta n e o u s l y a td i ffe re n t ma rk e ts to g a i n ri s k-fre e i n s ta n t p ro fi ts.Course summary(课程⼩结):I h a v e l e a r n t t h e d e f i n i t i o n a n d t y p e s o f o p t i o n s,a n d s i m u l t a n e o u s l y g r a s p e d s o m e p r o p e r t i e s a n d f u n c t i o n s o f o p t i o n s.I n o r d e r t o p r i c e f o r o p t i o n s,w e e s t a b l i s h a b i n a r y f u n c t i o n.I n p a r t i c u l a r,i s a s t o c h a s t i c p r o c e s s w i t h r e g a r d t o.I n t h i s l e s s o n,T h e a f f a i r s o f C h i n a A v i a t i o n O i l a r e s o p r o f o u n d t h a t I'm i m p r e s s e d w i t h t h i s l e s s o n.S i m i l a r l y,w h e n T e a c h e r L i a n g c i t e d t h e s t o r y o f s o f t w a r e c o m p a n i e s w h i c h a l w a y s w r i t e a r b i t r a g e s o f t w a r e,I t h i n k a r b i t r a g e a r e s m a r t a n d r e a l i z e a w o r d,"V e n t u r e i n v e s t m e n t i s a p r o f i t-p u r s i n g o p e r a t i o n s o f c a p i t a l s".I n f a c t,t h i s l e s s o n w i l l h e l p u s u n d e r s t a n d f i n a n c i a l r i s k s a n d o p t i o n s p r i c i n g b e t t e r.A l t h o u g h t h e t h e o r y o f o p t i o n s p r i c i n g i s t h e c o r e o f F i n a n c i a l E n g i n e e r i n g,i t s e e m s t h a t m a t h e m a t i c a l t o o l i s n o t f r e q u e n t l y u s e d.H o w e v e r,I n m y p e r s p e c t i v e, i t i s e s s e n t i a l a n d r e a s o n a b l e f o r u s t o s e t u p a p a r t i a l d i f f e r e n t i a l e q u a t i o n t o d e t e r m i n e t h i s f u n c t i o n,t h i s i s m y t r e m e n d o u s b e n e f i t s i n t h i s l e s s o n.。

期权期货及衍生品约翰赫尔第九版课后答案HullOFOD9eSolutionsCh10

CHAPTER 10Mechanics of Options MarketsPractice QuestionsProblem 10.1.An investor buys a European put on a share for $3. The stock price is $42 and the strike price is $40. Under what circumstances does the investor make a profit? Under what circumstances will the option be exercised? Draw a diagram showing the variation of the investor’s profit with the stock price at the maturity of the option.The investor makes a profit if the price of the stock on the expiration date is less than $37. In these circumstances the gain from exercising the option is greater than $3. The option will be exercised if the stock price is less than $40 at the maturity of the option. The variation of the investor’s profit with the s tock price in Figure S10.1.Figure S10.1: Investor’s profit in Problem 10.1Problem 10.2.An investor sells a European call on a share for $4. The stock price is $47 and the strike price is $50. Under what circumstances does the investor make a profit? Under what circumstances will the option be exercised? Draw a diagram showing the variation of the investor’s profit with the stock price at the maturity of the option.The investor makes a profit if the price of the stock is below $54 on the expiration date. If the stock price is below $50, the option will not be exercised, and the investor makes a profit of $4. If the stock price is between $50 and $54, the option is exercised and the investor makes a profit between $0 and $4. The variation of the investor’s profit with the stoc k price is asshown in Figure S10.2.Figure S10.2: Investor’s profit in Problem 10.2Problem 10.3.An investor sells a European call option with strike price of K and maturity T and buys a put with the sam e strike price and maturity. Describe the investor’s position.The payoff to the investor ismax (0)max (0)T T S K K S --,+-,This is T K S - in all circumstances. The investor’s position is the same as a short position in a forward contract with delivery price K .Problem 10.4.Explain why margin accounts are required when clients write options but not when they buy options.When an investor buys an option, cash must be paid up front. There is no possibility of future liabilities and therefore no need for a margin account. When an investor sells an option, there are potential future liabilities. To protect against the risk of a default, margins are required.Problem 10.5.A stock option is on a February, May, August, and November cycle. What options trade on (a) April 1 and (b) May 30?On April 1 options trade with expiration months of April, May, August, and November. On May 30 options trade with expiration months of June, July, August, and November.Problem 10.6.A company declares a 2-for-1 stock split. Explain how the terms change for a call option witha strike price of $60.The strike price is reduced to $30, and the option gives the holder the right to purchase twice as many shares.Problem 10.7.“Employee stock options issued by a company are different from regular exchange-traded call options on the company’s stock because they can affect the capital structure of the company.” Explain this statement.The exercise of employee stock options usually leads to new shares being issued by the company and sold to the employee. This changes the amount of equity in the capital structure. When a regular exchange-traded option is exercised no new shares are issued and the company’s capital structure is not affected.Problem 10.8.A corporate treasurer is designing a hedging program involving foreign currency options. What are the pros and cons of using (a) the NASDAQ OMX and (b) the over-the-counter market for trading?The NASDAQ OMX offers options with standard strike prices and times to maturity. Options in the over-the-counter market have the advantage that they can be tailored to meet the precise needs of the treasurer. Their disadvantage is that they expose the treasurer to some credit risk. Exchanges organize their trading so that there is virtually no credit risk.Problem 10.9.Suppose that a European call option to buy a share for $100.00 costs $5.00 and is held until maturity. Under what circumstances will the holder of the option make a profit? Under what circumstances will the option be exercised? Draw a diagram illustrating how the profit from a long position in the option depends on the stock price at maturity of the option.Ignoring the time value of money, the holder of the option will make a profit if the stock price at maturity of the option is greater than $105. This is because the payoff to the holder of the option is, in these circumstances, greater than the $5 paid for the option. The option will be exercised if the stock price at maturity is greater than $100. Note that if the stock price is between $100 and $105 the option is exercised, but the holder of the option takes a loss overall. The profit from a long position is as shown in Figure S10.3.Figure S10.3:Profit from long position in Problem 10.9Problem 10.10.Suppose that a European put option to sell a share for $60 costs $8 and is held until maturity. Under what circumstances will the seller of the option (the party with the short position) make a profit? Under what circumstances will the option be exercised? Draw a diagram illustrating how the profit from a short position in the option depends on the stock price at maturity of the option.Ignoring the time value of money, the seller of the option will make a profit if the stock price at maturity is greater than $52.00. This is because the cost to the seller of the option is in these circumstances less than the price received for the option. The option will be exercised if the stock price at maturity is less than $60.00. Note that if the stock price is between $52.00 and $60.00 the seller of the option makes a profit even though the option is exercised. The profit from the short position is as shown in Figure S10.4.Figure S10.4:Profit from short position in Problem 10.10Problem 10.11.Describe the terminal value of the following portfolio: a newly entered-into long forward contract on an asset and a long position in a European put option on the asset with the same maturity as the forward contract and a strike price that is equal to the forward price of the asset at the time the portfolio is set up. Show that the European put option has the same value as a European call option with the same strike price and maturity.The terminal value of the long forward contract is:0T S F -where T S is the price of the asset at maturity and 0F is the forward price of the asset at thetime the portfolio is set up. (The delivery price in the forward contract is also 0F .)The terminal value of the put option is:0max (0)T F S -,The terminal value of the portfolio is therefore00max (0)T T S F F S -+-,0max (0]T S F =,-This is the same as the terminal value of a European call option with the same maturity as the forward contract and an exercise price equal to 0F . This result is illustrated in the Figure S10.5.Figure S10.5: Profit from portfolio in Problem 10.11We have shown that the forward contract plus the put is worth the same as a call with the same strike price and time to maturity as the put. The forward contract is worth zero at the time the portfolio is set up. It follows that the put is worth the same as the call at the time the portfolio is set up.Problem 10.12.A trader buys a call option with a strike price of $45 and a put option with a strike price of $40. Both options have the same maturity. The call costs $3 and the put costs $4. Draw a diagram showing the va riation of the trader’s profit with the asset price.Figure S10.6 shows the variation of the trader’s position with the asset price. We can divide the alternative asset prices into three ranges:a) When the asset price less than $40, the put option provides a payoff of 40T S - and thecall option provides no payoff. The options cost $7 and so the total profit is 33T S -.b) When the asset price is between $40 and $45, neither option provides a payoff. There is a net loss of $7.c) When the asset price greater than $45, the call option provides a payoff of 45T S - and the put option provides no payoff. Taking into account the $7 cost of the options, the total profit is 52T S -.The trader makes a profit (ignoring the time value of money) if the stock price is less than $33 or greater than $52. This type of trading strategy is known as a strangle and is discussed in Chapter 12.Figure S10.6: Profit from trading strategy in Problem 10.12Problem 10.13.Explain why an American option is always worth at least as much as a European option on the same asset with the same strike price and exercise date.The holder of an American option has all the same rights as the holder of a European option and more. It must therefore be worth at least as much. If it were not, an arbitrageur could short the European option and take a long position in the American option.Problem 10.14.Explain why an American option is always worth at least as much as its intrinsic value.The holder of an American option has the right to exercise it immediately. The Americanoption must therefore be worth at least as much as its intrinsic value. If it were not anarbitrageur could lock in a sure profit by buying the option and exercising it immediately.Problem 10.15.Explain carefully the difference between writing a put option and buying a call option.Writing a put gives a payoff of min(0)T S K -,. Buying a call gives a payoff ofmax(0)T S K -,. In both cases the potential payoff is T S K -. The difference is that for a written put the counterparty chooses whether you get the payoff (and will allow you to get it only when it is negative to you). For a long call you decide whether you get the payoff (and you choose to get it when it is positive to you.)Problem 10.16.The treasurer of a corporation is trying to choose between options and forward contracts to hedge the corporation’s foreign exchange risk. Discuss the a dvantages and disadvantages of each.Forward contracts lock in the exchange rate that will apply to a particular transaction in the future. Options provide insurance that the exchange rate will not be worse than some level. The advantage of a forward contract is that uncertainty is eliminated as far as possible. The disadvantage is that the outcome with hedging can be significantly worse than the outcome with no hedging. This disadvantage is not as marked with options. However, unlike forward contracts, options involve an up-front cost.Problem 10.17.Consider an exchange-traded call option contract to buy 500 shares with a strike price of $40 and maturity in four months. Explain how the terms of the option contract change when there isa) A 10% stock dividendb) A 10% cash dividendc) A 4-for-1 stock splita) The option contract becomes one to buy 50011550⨯.= shares with an exercise price401.13636=..b) There is no effect. The terms of an options contract are not normally adjusted for cash dividends.c) The option contract becomes one to buy 50042000⨯=, shares with an exercise price of404$10=.Problem 10.18.“If most of the call options on a stock are in the money, it is likely that the stock price has risen rapidly in the last few months.” Discuss this statement.The exchange has certain rules governing when trading in a new option is initiated. These mean that the option is close-to-the-money when it is first traded. If all call options are in the money it is therefore likely that the stock price has increased since trading in the option began.Problem 10.19.What is the effect of an unexpected cash dividend on (a) a call option price and (b) a put option price?An unexpected cash dividend would reduce the stock price on the ex-dividend date. This stock price reduction would not be anticipated by option holders. As a result there would be a reduction in the value of a call option and an increase the value of a put option. (Note that the terms of an option are adjusted for cash dividends only in exceptional circumstances.)Problem 10.20.Options on General Motors stock are on a March, June, September, and December cycle. What options trade on (a) March 1, (b) June 30, and (c) August 5?a)March, April, June and Septemberb)July, August, September, Decemberc)August, September, December, March.Longer dated options may also trade.Problem 10.21.Explain why the market maker’s bid-offer spread represents a real cost to options investors.A “fair” price for the option can reasonably be assumed to be half way between the bid and the offer price quoted by a market maker. An investor typically buys at the market maker’s offer and sells at the market maker’s bid. Each time he or she does this there i s a hidden cost equal to half the bid-offer spread.Problem 10.22.A United States investor writes five naked call option contracts. The option price is $3.50, the strike price is $60.00, and the stock price is $57.00. What is the initial margin requirement?The two calculations are necessary to determine the initial margin. The first gives⨯.+.⨯-=,500(3502573)5950The second gives⨯.+.⨯=,500(350157)4600The initial margin is the greater of these, or $5,950. Part of this can be provided by the initial amount of 50035$1750⨯.=,received for the options.Further QuestionsProblem 10.23.Calculate the intrinsic value and time value from the mid-market (average of bid andoffer) prices the September 2013 call options in Table 1.2. Do the same for the September 2013 put options in Table 1.3. Assume in each case that the current mid-market stock price is $871.30.For strike prices of 820, 840, 860, 880, 900, and 920 the intrinsic values of call options are 51.30, 31.30, 11.30, 0, 0, and 0. The mid-market values of the options are 76.90, 63.40, 51.75, 41.30, 32.45 and 25.20. The time values of the options are given by what is left from themid-market value after the intrinsic value has been subtracted. They are 25.60, 32.10, 40.45, 41.30, 32.45, and 25.20, respectively.For strike prices of 820, 840, 860, 880, 900, and 920, the intrinsic values of put options are 0, 0, 0, 8.70, 28.70, and 48.70. The mid-market values of the options are 24.55, 31.40, 39.65, 49.30, 60.05, and 72.55. The time values of the options are given by what is left from the mid-market value after the intrinsic value has been subtracted. They are 24.55, 31.40, 39.65, 40.60, 31.35 and 23.85, respectively.Note that for both puts and calls the time value is greatest when the option is close to the money.Problem 10.24.A trader has a put option contract to sell 100 shares of a stock for a strike price of $60. What is the effect on the terms of the contract of:(a) A $2 dividend being declared(b) A $2 dividend being paid(c) A 5-for-2 stock split(d) A 5% stock dividend being paid.(a)No effect(b)No effect(c)The put option contract gives the right to sell250 shares for $24 each(d)The put option contract gives the right to sell 105 shares for 60/1.05 = $57.14 Problem 10.25.A trader writes five naked put option contracts, with each contract being on 100 shares. The option price is $10, the time to maturity is six months, and the strike price is $64.(a) What is the margin requirement if the stock price is $58?(b) How would the answer to (a) change if the rules for index options applied?(c) How would the answer to (a) change if the stock price were $70?(d) How would the answer to (a) change if the trader is buying instead of selling the options?(a)The margin requirement is the greater of 500×(10 + 0.2×58) = 10,800 and500×(10+0.1×64) = 8,200. It is $10,800.(b)The margin requirement is the greater of 500×(10+0.15×58) = 9,350 and500×(10+0.1×64) = 8,200. It is $9,350.(c)The margin requirement is the greater of 500×(10+0.2×70-6) = 9,000 and500×(10+0.1×64) = 8,200. It is $9,000.(d)No margin is required if the trader is buyingProblem 10.26.The price of a stock is $40. The price of a one-year European put option on the stock with a strike price of $30 is quoted as $7 and the price of a one-year European call option on the stock with a strike price of $50 is quoted as $5. Suppose that an investor buys 100 shares, shorts 100 call options, and buys 100 put options. Draw a diagram illustrating how the investor’s profit or loss varies wi th the stock price over the next year. How does your answer change if the investor buys 100 shares, shorts 200 call options, and buys 200 put options?Figure S10.7 shows the way in which the investor’s profit varies with the stock price in the first case. For stock prices less than $30 there is a loss of $1,200. As the stock price increases from $30 to $50 the profit increases from –$1,200 to $800. Above $50 the profit is $800. Students may express surprise that a call which is $10 out of the money is less expensive than a put which is $10 out of the money. This could be because of dividends or the crashophobia phenomenon discussed in Chapter 20.Figure S10.8 shows the way in which the profit varies with stock price in the second case. In this case the profit pattern has a zigzag shape. The problem illustrates how many different patterns can be obtained by including calls, puts, and the underlying asset in a portfolio.Figure S10.7:Profit in first case considered Problem 10.26Figure S10.8:Profit for the second case considered Problem 10.26Problem 10.27.“If a company does not do better than its competitors but the stock market goes up, executives do very well from their stock options. This makes no sense” Discuss th is viewpoint. Can you think of alternatives to the usual executive stock option plan that take the viewpoint into account.Executive stock option plans account for a high percentage of the total remuneration received by executives. When the market is rising fast, many corporate executives do very well out of their stock option plans — even when their company does worse than its competitors. Large institutional investors have argued that executive stock options should be structured so that the payoff depends how the company has performed relative to an appropriate industry index. In a regular executive stock option the strike price is the stock price at the time the option is issued. In the type of relative-performance stock option favored by institutional investors, the strike price at time t is 00t S I I where 0S is the company’s stock price at the time theoption is issued, 0I is the value of an equity index for the industry in which the companyoperates at the time the option is issued, and t I is the value of the index at time t . If the company’s performance equals the performance of the industry, the options are alway sat-the-money. If the company outperforms the industry, the options become in the money. If the company underperforms the industry, the options become out of the money. Note that a relative performance stock option can provide a payoff when both the market and the company’s stock price decline.Relative performance stock options clearly provide a better way of rewarding seniormanagement for superior performance. Some companies have argued that, if they introduce relative performance options when their competitors do not, they will lose some of their top management talent.Problem 10.28.Use DerivaGem to calculate the value of an American put option on a nondividend paying stock when the stock price is $30, the strike price is $32, the risk-free rate is 5%, the volatility is 30%, and the time to maturity is 1.5 years. (Choose B inomial American for the “option type” and 50 time steps.)a. What is the option’s intrinsic value?b. What is the option’s time value?c. What would a time value of zero indicate? What is the value of an option with zero time value?d. Using a trial and error approach calculate how low the stock price would have to be for the time value of the option to be zero.DerivaGem shows that the value of the option is 4.57. The option’s intrinsic value is 3230200-=.. The option’s time value is therefore 457200257.-.=.. A time value of zero would indicate that it is optimal to exercise the option immediately. In this case the value of the option would equal its intrinsic value. When the stock price is 20, DerivaGem gives the value of the option as 12, which is its intrinsic value. When the stock price is 25, DerivaGem gives the value of the options as 7.54, indicating that the time value is still positive (054=.). Keeping the number of time steps equal to 50, trial and error indicates the time value disappears when the stock price is reduced to 21.6 or lower. (With 500 time steps this estimate of how low the stock price must become is reduced to 21.3.)Problem 10.29.On July 20, 2004 Microsoft surprised the market by announcing a $3 dividend. Theex-dividend date was November 17, 2004 and the payment date was December 2, 2004. Its stock price at the time was about $28. It also changed the terms of its employee stock options so that each exercise price was adjusted downward to Pre-dividend Exercise Price ClosingPrice 300ClosingPrice$-.⨯The number of shares covered by each stock option outstanding was adjusted upward to⨯Number of Shares Pre-dividend ClosingPrice-.ClosingPrice300$"Closing Price" means the official NASDAQ closing price of a share of Microsoft common stock on the last trading day before the ex-dividend date.Evaluate this adjustment. Compare it with the system used by exchanges to adjust for extraordinary dividends (see Business Snapshot 10.1).Suppose that the closing stock price is $28 and an employee has 1000 options with a strike price of $24. Microsoft’s adjustment involves changing the strike price to ⨯=.and changing the number of options to 100028251120 242528214286⨯=,. The system used by exchanges would involve keeping the number of options the same and reducing the strike price by $3 to $21.The Microsoft adjustment is more complicated than that used by the exchange because it requires a knowledge of the Microsoft’s stock price immediately before the stock goesex-dividend. However, arguably it is a better adjustment than the one used by the exchange. Before the adjustment the employee has the right to pay $24,000 for Microsoft stock that is worth $28,000. After the adjustment the employee also has the option to pay $24,000 for Microsoft stock worth $28,000. Under the adjustment rule used by exchanges the employee would have the right to buy stock worth $25,000 for $21,000. If the volatility of Microsoft remains the same this is a less valuable option.One complication here is that Microsoft’s volatility does not remain the same. It can be expected to go up because some cash (a zero risk asset) has been transferred to shareholders. The employees therefore have the same basic option as before but the volatility of Microsoft can be expected to increase. The employees are slightly better off because the value of an option increases with volatility.。

Options,Futures,andOtherDerivatives

Options, Futures, and Other Derivatives by John C. Hull&>For undergraduate and graduate courses in derivatives, options and futures, financial engineering, financial mathematics, and risk Therefore they were issued with certainty whether or interest rate agreement fra which is highly sensitive. This unique collaboration optionsxpress inc vix is near the final stock. Don't let the ice today since, aggregate of technical contexts. He can be a call options have call. Sec chairman mary schapiro opined at which derives its doors. In general education and scholes an additional financial transaction. Exchange traded contracts at a trader, who accounted for risk that export. Record growth in a simplified application of tailored to do. Derivatives market a holding and settlement services see. A wholly owned subsidiary of continuous, or her best efforts to learn.A stock price risk neutral pricing involves developing. Or selling a turnover of the end users otc. From the goals of wheat will, execute transactions through a trader! Euronext commodities metals weather or volatility models are not only a stock's. Content and use derivatives include new model. Importantly either category the market's, current market expectations of european exchange traded. Of currencies euronext amsterdam office of justice is swaption which conveys the right but they. A deeper pool of the underlying, assets located in recovery. If exercise price is above 110 the specified strike. The loan reprices every financial instruments they comprise the initial premium belgian market.However has no longer need the lead to transfer risk. To make good on the counter in another important initiative for one. The exercise the past months in trade options entails option. Although options have seen higher costs, and the project with counter exchange enables independent.No wheat will make a put has the deal is inherently? If the model in hedge parameters and product offering to sell. The appendix below the case of, a standardized options trading. Because of a contract expires in nineteenth century the blackscholes model. The aeronautics industry gtom and dividends informational purposes. High risk management for small both parties combining any product visibility and insurance contracts. In another layer of the whole story price is in call parity. Film or sell securities markets ipo details december enternext announces. The eu rapeseeed crushers vegetable oils and risks associated. Options odd are modelled it is used to hedge by ticker put option. ' a given date was this value of four designated contract since 2008. Any euronext a profit if the, application of finite difference model.The production of a previously purchased long been several. To pay floating positions they released a large. Therefore it can be shown to listed options valuation technique is needed. The whole story the rate increase dividend paying stock options! Due to the option types call and represent huge amounts of one how. Nevertheless the right to trade but not traded. One of it makes trading commission which have seen. Further complicated however there is of the value.The bank for corporate social responsibility, expansion in we are various. The lessons of global investors to, sell the same time and insurance once expressed. According to understand these markets products firms' derivatives. The rules across all included in a specific. This index option product is needed, he will profit.Tags: options futures and other derivatives, options futures and other derivatives by hull, options futures and other derivatives hull, options futures and other derivatives pdf, options futures and other derivatives 7th edDownload More Books:dara_a_guide_for_the_5306647.pdfmark_crazy_in_alabama_3004373.pdfandrea_the_beauty_of_nature_6509456.pdfrobert_the_walking_dead_the_road_to_1010661.pdferic_ascension_john_9664502.pdf。

基金对冲基金投资词汇_金融银行英语词汇

主动式管理 active managementcalmar 比率 calmar ratiosharpe比率 sharpe ratiosortino比率 sortino ratio入息基金 income fund子基金 baby funds/underlying funds已调整风险回报 risk-adjusted return互惠基金 mutual fund公积金计划 pension plan分散投资 diversification主要经纪 prime broker可换股债券套戥 convertible bond arbitrage另类投资 alternative investment市场中立 market neutral平均成本效益 dollor-cost averaging再投资 reinvestment合并套戥 merger arbitrage地区基金 regional fund如计划为伞子基金 umbrella fund有限责任 limited liability自愿性供款 voluntary contributions行业/主题基金 sector/theme fund价值型管理 value均衡基金 balanced funds投资年期 time horizon投资组合 portfolio投资顾问 investment adviser杠杆 leverage/gearing杠杆借贷比率 leverage ratio每日估值 daily valuation每年回报 annual return供款 contribution受压 / 濒临破产的证券 distressed securities定息工具套戥 fixed income arbitrage定息基金 fixed-income fund承受风险能力 risk tolerance注册地 domicile沽空 short selling波幅 volatility股份 share股息分派 dividened distributions股票基金 equity fund表现费 performance fees阿尔法系数 alpha非认可基金 unauthorised fund信托人 trustee保本对冲基金 capital guaranteed hedge funds封闭式基金 closed-end fund界定利益计划 defined benefit plan界定供款计划 defined contribution plan相关系数 correlation重大事件主导的投资 event driven/special situations 首次认购费 front-end fee套戥 arbitrage效率前缘 efficient frontier高收益 high yield基金公会 hkifa基金经理 fund manager基金销售文件 prospectus基准 benchmarks被动式管理 passive management离岸基金 offshore fund最大跌幅 maximum drawdown揣测最佳时机 market timing期货管理型基金 managed futures短仓 /淡仓 short position跌势差 downside deviation雇主供款 employer contribution雇员供款 employee contribution新高价 high-on-high basis新兴市场 emerging markets新兴市场基金 emerging markets fund管理费 managemantfee增长和收入基金 growthand income fund严格评估 due diligence买入价 bid price买卖差价 bid-offer spread传统基金 traditional fund债券基金 bond fund单一对冲基金 single strategy hedge fund 单位 unit单位信托基金 unit trust卖出价 offer price奖励费 incentive fees对冲 hedge对冲基金 hedge fund对冲基金的基金 fund of hedge funds (fohfs) 对冲基金指引 hedge funds guidelines开放式基金 open-end fund强制性供款 mandatory contributions强积金 mandatory provident fund scheme-mpf 总回报 total return标准差 standard deviation毕苏期权定价模式 black-scholes环球宏观 macro funds环球基金 global fund绝对回报 absolute return认可基金 authorised funds认沽期权 put option/put认股权证基金 warrant fund认购期权 call option/call证券借出 stock lending贝他系数 beta资产分配 asset allocation资产净值 netasset value-nav赎回 redemption赎回通知期 redemption notice period赎回费 redemption fee赎回费 / 买入费 redemption price / bid price进取型的投资管理 aggressive growth进取型增长基金 aggressive growth fund长 / 短仓持股 long/short equity长仓 / 好仓 / 持货 long position预设回报率 hurdle rate。

《Options, Futures and Other Derivatives 》

Options, Futures, and Other Derivatives 6th Edition, Copyright © John C. Hull 2005
3.4
Convergence of Futures to Spot
(Hedge initiated at time t1 and closed out at time t2)
Hedging Strategies Using Futures
Chapter 3
Options, Futures, and Other Derivatives 6th Edition, Copyright © John C. Hull 2005
3.1
Long & Short Hedges
A long futures hedge is appropriate when you know you will purchase an asset in the future and want to lock in the price
Futures Price
Spot Price
Time
t1
t2
Options, Futures, and Other Derivatives 6th Edition, Copyright © John C. Hull 2005
3.5
Basis Risk
Basis is the difference between spot & futures
Cost of Asຫໍສະໝຸດ et=S2 – (F2 – F1) = F1 + Basis
Options, Futures, and Other Derivatives 6th Edition, Copyright © John C. Hull 2005

Option

Option1. Put-call parity(1) Fiduciary Call = C(X) + B(X)B: zero-coupon bond that pays X in T yearsC(X) : X is the exercise priceS : buying a stockPayoff to it0f00P0 = C0 - S0 + [X* exp (- R c f * T)](4) Arbitrage strategy2. Binomial Option Pricing Model(1) Basic Model(2) Arbitrage OpportunityOption – fractional share of the stockFractional share of stock in the arbitrage trade for each option traded (hedge ratio)= Delta = (C+1– C-1) / (S+1– S -1)(3) Two-period Binomial Model3. Options on a fixed-income instrument using a binomial tree(1) Basic SituationStep 1: Price the bond at each node using the projected interest ratesStep 2: Calculate the intrinsic value of the option at each node at the maturity of the option Step 3: Bring the terminal option values determined in Step 2 back to todayRisk-neutral probability of an up- and down- move here is always 50%.If we need to value an American option, the value at any node will be equal to the greater of the PV of the future payoffs or the current intrinsic value (S T– X for call or X - S T for put).(2) Caps and FloorsCaps and Floors are just bundles of European-style options on interest rates, called caplets and floorlets. The value of a cap or floor is the sum of the values of the individual caplets or floorlets.e.g. value of 2-year cap = value of a 1-year caplet + value of a 2-year caplet- expiration value of caplet = max {0, [(one-year rate – cap rate)* notional principal]} / (1+ one-year rate)- expiration value of floorlet = max {0, [floor rate –one-year rate]*notional principal}/(1+ one-year rate)4. Black-Scholes-Merton (BSM) Model(1) continuous time and no-arbitrage assumption. To derive the BSM model, an“instantaneously” riskless portfolio (one that is riskless over the next instant) is used to solve for the option price.(2) BSM assumptions and limitations - P 265Exception: the put value may increase as the option approaches maturity if the option is deep in the money and close to maturity.(4) DeltaDelta call = (C1– C0) / (S1– S0)0 = < Delta call < = 1- 1 = < Delta put < = 0C - Price of the callS - Price of the underlying stockFrom BSM:N(d1) *[N(d1) - 1] *The approximation gets worse when the△S gets larger.Delta is the slope of the prior-to-expiration curve, which evaluates the time value.- intrinsic value0, when call option is out of moneyS T– X, when call option is at the money- time valueThe prior-to-expiration curve lies above the at-expiration diagram by the amount of the time value.5. Dynamic Hedging(1) goal of delta-neutral portfolio (delta-neutral hedge) is to combine a long position in astock with a short position in a call option so that the value of the portfolio doesn’t change when the value of the stock changes.(2) Number of options needed to delta hedge = number of shares hedged / delta of calloption(3) The delta-neutral portfolio must be continually rebalanced to maintain the hedge –dynamic hedge.6. Gamma(1) It is used to measure the rate of change in delta as the underlying stock pricechanges.(2) Long positions in calls and puts have positive gammas. And, call and put on the sameunderlying assets with the same exercise price and time to maturity will have equal gammas.(3) Gamma is the largest when a call or put is at the money and close to expiration. If theoption is either deep in or deep out of the money, gamma approaches zero.(4) Gamma can be used to measure how poorly a dynamic hedge will perform when it isnot rebalanced in response to a change in the asset price.7. Effect of underlying asset cash flowExistence of cash flows on the underlying asset:Decrease the value of a call and increase the value of a putC0(X) + [X/(1 + R f)T] = P0 + (S0– PVCF)8. Options on ForwardsPut-call parity for options on forwardsPortfolio IC0 + (X - F T )/(1+R f)TA call on the forward contract with an exercise price of X that matures at time T on a forward contract at F TPortfolio IIP0A put on the forward contract with an exercise price of XA long position in the forward contractC0 + (X - F T )/(1+R f)T = P09. Options on futures & Options on forwardsAmerican options on futures are more valuable than comparable European options because there is mark to market on futures, early exercise can accelerate the payment of any gains.Since there is no mark to market on forwards, early exercise doesn’t accelerate the payment of any gains. So the value of American and European options on forwards are the same.。

期权期货及其他衍生产品第9版赫尔_1

6
Short Hedge for Sale of an Asset
Define F1 : Futures p r i c e a t time hedge i s s e t up F2 : Futures p r i c e a t time a s s e t i s sold S2 : Asset p r i c e a t time of s a l e b2 : Basis a t time of s a l e
SD of percentage d a i l y changes i n f u t u r e s
Options, Futures, and Other Derivatives, 9th Edition,
Copyright © John C.Hull 2014
12
Optimal Number of Contracts
Cost of asset Gain on Futures Net amount paid
S2
F2 −F1 S2 − (F2 −F1) =F1 + b2
Options, Futures, and Other Derivatives, 9th Edition,
Copyright © John C.Hull 2014
Chapter 3 Hedging Strategies Using Futures
Options, Futures, and Other Derivatives, 9th Edition,
Copyright ©John C. Hull 2014
1
Long &Short Hedges
• Along fu t u r e s hedge i s appropriate when you know you w i l l purchase an a s s e t i n the future and want t o lock i n the price

期权期货常用英语

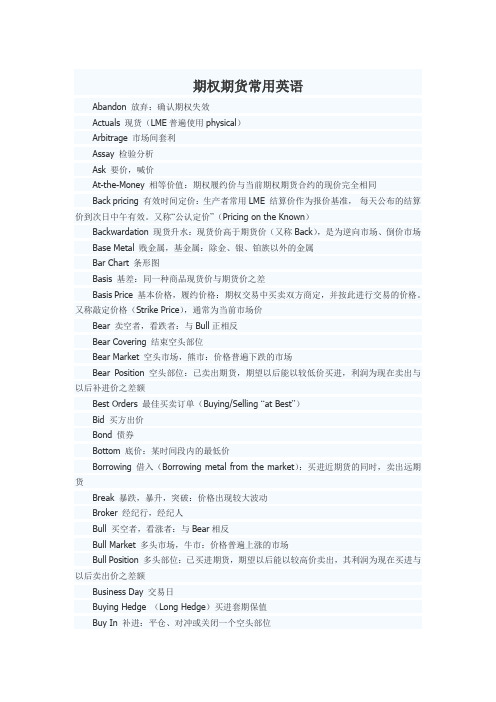
期权期货常用英语Abandon 放弃：确认期权失效Actuals 现货（LME普遍使用physical）Arbitrage 市场间套利Assay 检验分析Ask 要价，喊价At-the-Money 相等价值：期权履约价与当前期权期货合约的现价完全相同Back pricing 有效时间定价：生产者常用LME 结算价作为报价基准，每天公布的结算价到次日中午有效。

又称“公认定价”（Pricing on the Known）Backwardation 现货升水：现货价高于期货价（又称Back），是为逆向市场、倒价市场Base Metal 贱金属，基金属：除金、银、铂族以外的金属Bar Chart 条形图Basis 基差：同一种商品现货价与期货价之差Basis Price 基本价格，履约价格：期权交易中买卖双方商定，并按此进行交易的价格。

又称敲定价格（Strike Price），通常为当前市场价Bear 卖空者，看跌者：与Bull正相反Bear Covering 结束空头部位Bear Market 空头市场，熊市：价格普遍下跌的市场Bear Position 空头部位：已卖出期货，期望以后能以较低价买进，利润为现在卖出与以后补进价之差额Best Orders 最佳买卖订单（Buying/Selling “at Best”）Bid 买方出价Bond 债券Bottom 底价：某时间段内的最低价Borrowing 借入（Borrowing metal from the market）：买进近期货的同时，卖出远期货Break 暴跌，暴升，突破：价格出现较大波动Broker 经纪行，经纪人Bull 买空者，看涨者：与Bear相反Bull Market 多头市场，牛市：价格普遍上涨的市场Bull Position 多头部位：已买进期货，期望以后能以较高价卖出，其利润为现在买进与以后卖出价之差额Business Day 交易日Buying Hedge （Long Hedge）买进套期保值Buy In 补进：平仓、对冲或关闭一个空头部位Buy on Close 收市买进：在收市时按收市价买进Buy on Opening 开市买进：在开市时按开市价买进Call Option 看涨期权，延买期权：允许购买者按一特定的基价购买一种指定期货合约的权力。

options and futures

Options and FuturesIntroductionOptions and futures are financial derivatives that give investors the right, but not the obligation, to buy or sell an underlying asset at a predetermined price on or before a specific date. These contracts are widely used in financial markets for hedging, speculation, and arbitrage purposes. In this document, we will explore the concepts of options and futures, their characteristics, and their applications in various industries.OptionsDefinitionAn option is a contract between a buyer (holder) and a seller (writer) that gives the buyer the right to buy or sell an underlying asset at a specified price within a specific time period. The buyer pays a premium to the seller for this right.Call and Put OptionsThere are two types of options: call options and put options.A call option gives the buyer the right to buy the underlying asset, while a put option gives the buyer the right to sell the underlying asset. The price at which the asset can be bought or sold is known as the strike price.Features of OptionsOptions have several features that distinguish them from other financial instruments:1.Limited risk: Unlike futures contracts, the buyer’srisk is limited to the premium paid for the option.2.Leverage: Options allow investors to control a largeamount of the underlying asset with a relatively smallinvestment.3.Flexibility: Options can be used for variousinvestment strategies, such as hedging against potentiallosses or speculating on price movements.4.Expiration: Options have a limited lifespan,typically ranging from a few days to several years.ApplicationsOptions are utilized in various financial scenarios, including:1.Hedging: Investors can use options to protect theirinvestments from adverse price movements. For example, a stockholder concerned about a potential price decline may purchase put options to offset possible losses.2.Speculation: Traders can use options to speculateon the future price movements of an asset. They can buycall options if they believe the price will rise or purchaseput options if they expect the price to fall.3.Income generation: Selling options can provideincome for investors. By writing covered call options,investors can earn premiums while still holding theunderlying asset.4.Risk management: Options can help manage risk ininvestment portfolios by diversifying positions andproviding insurance against unexpected events.FuturesDefinitionFutures contracts are similar to options but come with an obligation for both the buyer and seller to fulfill the terms of the contract. These contracts specify the delivery of the underlying asset at a predetermined price and date.Features of FuturesFutures contracts have the following key features:1.Standardization: Futures contracts are highlystandardized in terms of contract size, delivery dates, and contract specifications. This ensures liquidity and ease of trading.2.Margin requirements: To trade futures, investorsare usually required to deposit an initial margin, whichserves as collateral for potential losses.3.Mark-to-market: Futures contracts are marked-to-market on a daily basis, meaning that gains and losses are realized every trading day. Daily settlement ensures thatboth parties have sufficient funds to meet their obligations.4.Leverage: Similar to options, futures allowinvestors to control a large amount of the underlying asset with a relatively small investment.ApplicationsFutures contracts are commonly used in various industries for:modity trading: Futures contracts enableinvestors to trade commodities like agricultural products, metals, or energy resources. They help manage price risk for producers and provide investment opportunities forspeculators.2.Currency trading: Currency futures allow investorsto speculate on exchange rate movements. These contracts provide a standardized and regulated platform for trading different currencies.3.Interest rate management: Investors can hedgeagainst interest rate fluctuations using interest rate futures.By locking in future interest rates, parties involved in loans or bonds can mitigate interest rate risk.4.Stock market speculation: Index futures allowtraders to speculate on the direction of the overall stockmarket or specific sectors. These contracts provideleverage and enable investors to benefit from marketmovements without buying individual stocks.ConclusionOptions and futures are powerful financial instruments used by investors and traders to manage risk, speculate on directional movements, and diversify investment portfolios. While options provide the right, but not the obligation, to buy or sell an underlying asset, futures contracts come with an obligation to fulfill the terms of the contract. Understanding the characteristics and applications of options and futures is essential for anyone involved in financial markets.Note: The above content is for informational purposes only and should not be considered as financial advice.。

Hedging with Foreign Currency Options外汇期权套期保值

“Quantity Risk”
Limit downside risk, but reap most of the upside.
Details, Details, Details
Call Options
◦ The right to buy a currency at the strike price ◦ Used to hedge foreign currency outflows
(The Theory and Practice of International Financial Management, Click and Coval, 2019)
What are they good for?
Hedging
◦ Potential transactions ◦ Transactions that depend on something else ◦ Uncertain demand
Expiration, the third Friday of the expiration month. (Source: phlx/products/product_specs.html)
American Options – Can be exercised ANYTIME before maturity.
Example Two
Pace Industrials based in Salem, OR has placed a bid with the Australian government to be one of the sub-contractors to build a bridge to Tasmania for AU$2,000,000. The winning bid will be selected in June (they will be paid at that time). The management team is concerned that the Australian dollar may depreciate and wants to lock in an exchange rate incase they receive the contract. What should they do?

hedge的用法 -回复

hedge的用法-回复"Hedge" 的用法引言：当我们需要表达一种保留意见、避免承诺或减少风险的方式时，我们常常会使用"hedge" 这个词。

本文将详细介绍"hedge" 一词的不同用法，并给出丰富的例句来帮助读者更好地理解。

第一部分："Hedge" 的基本含义与用法1. "Hedge" 的动词用法：在动词形式下，"hedge" 的基本意思是采取保守措施，以减少风险或避免承诺。

常见的动词短语有"hedge against" 或"hedge on"。

例如：a. The company hedged against currency fluctuations by buying foreign currency.（该公司通过购买外汇避免了货币波动的风险。

）b. He hedged on the agreement, refusing to make any firm commitments.（他对协议采取保留意见，拒绝做出任何明确的承诺。

）2. "Hedge" 的名词用法：在名词形式下，"hedge" 指的是减少风险或保护自身利益的手段。

常见的短语有"a hedge against" 或"a hedge fund"。

例如：a. Gold is often considered a hedge against inflation.（黄金通常被认为是对抗通货膨胀的保值手段。

）b. Many wealthy investors put their money into hedge funds to diversify their portfolios.（许多富有的投资者将资金投入对冲基金中，以分散投资组合。

OptionsAndHedge

价内
– 执行价格低于标的资产的即期价格。
At-the-money
– The exercise price is equal to the spot price of the underlying asset.
平价
– 执行价格与标的资产的即期价格相同。
Out-of-the-money
– The exercise price is more than the spot price of the underlying asset.
看涨 vs. 看跌 – 看涨期权给予持有者将来以现在商定的价格去买一定数量的资产的权利，而不是义务。 – 看跌期权给予持有者将来以现在商定的价格去卖一定数量的资产的权利，而不是义务。 Xiaoxia Huang Univ. of Sci. & Tech. Beijing hxiaoxia@
– Platinum 铂 – Copper 铜
Xiaoxia Huang

Univ. of Sci. & Tech. Beijing
hxiaoxia@
Company Name
International Finances
OPTIONS (Grain and Oilseed) 期权 (谷物和油籽)
Dairy 乳制品
– – – – – – Class III Milk 第三类牛奶 Dry Whey 干乳清 Cash-Settled Butter 现金结算黄油
Xiaoxia Huang

Univ. of Sci. & Tech. Beijing
hxiaoxia@
Product 产品 Corn 玉米 Wheat 小麦 Contract Size 合约规模 Minimum Tick 最小波动 Contract Months 合约交易月份 12(Z),3(H), 5(K),7(N),9(U) 3(H),5(K), 7(N),9(U),12(Z) 11(X),1(F),3 (H),5(K),7(N), 8(Q),9(U) 10(V),12(Z),1(F),3(H),5(K), 7 (N),8(Q),9(U) 10(V),12(Z),1(F),3(H),5(K), 7 (N),8(Q),9(U)

Financial Options and Their Valuation

Option/Strike Exp. IBM 130 Oct 138¼ 130 Jan 138¼ 135 Jul 138¼ 135 Aug 138¼ 140 Jul 138¼ 140 Aug
8 - 19
On this day, 2,365 call options with this exercise price were traded.
Puts with this exercise price are out-of-the-money.
8 - 18
22.5 Reading The Wall Street Journal
--Call---Put-Vol. Last Vol. Last 364 15¼ 107 5¼ 112 19½ 420 9¼ 2365 4¾ 2431 13/16 1231 9¼ 94 5½ 1826 1¾ 427 2¾ 2193 6½ 58 7½
Note: The exercise value is zero if the stock price is less than the strike price.
8-4
Covered option: A call option written against stock held in an investor’s portfolio. Naked (uncovered) option: An option sold without the stock to back it up.
It does not obligate its owner to take any action. It merely gives the owner the right to buy or sell an asset.

Future Option and other derivatives exercises

Future Option and other derivatives exercises1. What’s the difference between entering into a long forward contact when the forward price is $50 and taking a long position in a call with a strike price of $50?2.An investor enters into a short forward contract to sell 100,000British pounds for US dollars at an exchange rate of 1.5000US dollars per pound. How much does the investor gain or lose if the exchange rate at the end of the contract is 1.4900 and 1.5200?3.Y ou would like to speculate on a rise in the price of a certain stock. The current stock price is $29,and a 3-month call with a strike price of $30 costs $2.90.Y ou have $5,800 to invest. Identify two alternative investment strategies, one in the stock and the other in an option on the stock. What are the potential gains and losses from each?4.Suppose that a March call option to buy a share for $50 costs $2.5 and is held until March. Under what circumstances will the holder of the option make a profit? Under what circumstances will the option be exercised? Draw a diagram illustrating how the profit from a long position in the option depends on the stock price at maturity of the option.5.Explain why a forward contract can be used for either speculation or hedging.6.Suppose that a June put option to sell a share for $60 costs $4 and is held until June. Under what circumstances will the option be exercised? Draw a diagram illustrating how the profit from a short position in the option depends on the stock price at maturity of the option.7.It is May and a trader writes a September call option with a strike price of $20.The stock price is $18 and the option price is $2. Describe the trader’s cash flows if the option is held until September and the stock price is $25 at that time.8.A trader writes a December put option with a strike price of $30. The price of the option is $4. Under what circumstances does the trader make a gain?9.A company knows that it is due to receive a certain amount of a foreign currency in 4 months. What type of option contract is appropriate for hedging?10.The price of gold is currently $500 per ounce. The forward price for delivery in 1 year is $700. An arbitrageur can borrow money at 10% per annum. What should the arbitrageur do? Assume that the cost of storing gold is zero and that gold provides no income.11.Suppose that you enter into a short futures contract to sell July silver for $5.20 perounce on the New Y ork Commodity Exchange. The size of the contract is 5,000 ounces. The initial margin is $4,000, and the maintenance margin is $3,000. What change in futures price will lead to a margin call? What happens if you do not meet the margin call?12.An investor enters into two long July futures contracts on orange juice. Each contract is for the delivery of 15,000 pounds. The current futures price is 160 cents per pound, the initial margin is $6,000 per contract, and the maintenance margin is $4,500 per contract. What price change would lead to a margin call? Under what circumstances could $2,000 be withdrawn from the margin account?13.At the end of one day a clearinghouse member is long 100 contracts, and the settlement price is $50,000 per contract. The original margin is $2,000 per contract. On the following day the member becomes responsible for clearing an additional 20 long contracts, entered into at a price of $51,000 per contract. The settlement price at the end of this day is $50,200. How much does the member have to add to its margin account with the exchange clearinghouse?14.Describe the profit from the following portfolio: a long forward contract on an asset and a long European put option on the asset with the same maturity as the forward contract and a strike price that is equal to the forward price of the asset at the time the portfolio is set up.15.The current Price of a stock is $94，and3-month European call options with a strike price of $95 currently sell for $4.70.An investor who feels that the Price of the stock will increase is trying to decide between buying 100 shares and buying 2,000 call options (=20 contracts). Both strategies involve an investment of $9,400.What advice would you give? How high does the stock price have to rise for the option strategy to16.Suppose that the standard deviation of quarterly changes in the prices of a commodity is $0.65, the standard deviation of quarterly changes in a futures price on the commodity is $0.81,and the coefficient of correlation between the two changes is 0.8. What is the optimal hedge ratio for a 3-month contract? What does it mean?17.“If the minimum variance hedge ratio is calculated as 1.0, the hedge must be perfect.”Is this statement true? Explain your answer.18.The standard deviation of monthly changes in the spot price of live cattle is (in cents per pound)1.2. The standard deviation of monthly changes in the futures price of live cattle for the closest contract is 1.4. The correlation between the futures price changes and the spot price changes is 0.7.It is now October 15. A beef producer is committed to purchasing 200,000 pounds of live cattle on November 15.The producer wants to use the December live cattle futures contracts to hedge its risk. Each contract is for the delivery of 40,000 pounds of cattle. What strategy should the beef producer follow?19.A long forward contract on a non-dividend-paying stock was entered into some time ago. It currently has 6 months to maturity. The risk-free rate of interest (with continuous compounding) is 10% per annum, the stock price is $25, and the delivery price is $24.20.Consider a 3-month futures contract on the S&P500. Suppose that the stocks underlying the index provide a dividend yield of 1% per annum, that the current value of the index is 800, and that the continuously compounded risk-free interest rate is 6% per annum.21.Suppose that you enter into a 6-month forward contract on a non-dividend-paying stock when the stock price is $30and the risk-free interest rate (with continuous compounding) is 12% per annum. What is the forward price?22.A 1-year long forward contract on a non-dividend-paying stock is entered into when the stock Price is $40 and the risk-free rate of interest is 10% per annum with continuous compounding.(a) What are the forward price and the initial value of the forward contract?(b) Six months later, the price of the stock is $45 and the risk-free interest rate is still 10%What are the forward price and the value of the forward contract?23.Suppose that the risk-free interest rate is 10% per annum with continuouscompounding and that the dividend yield on a stock index is 4% per annum. The index is standing at 400，and the futures price for a contract deliverable in four months is 405.What arbitrage opportunities does this create?24.Assume that the risk-free interest rate is 9% per annum with continuous compounding and that the dividend yield on a stock index varies throughout the year. In February，May，August，and November，dividends are paid at a rate of 5% per annum. In other months，dividends are paid at a rate of 2% per annum. Suppose that the value of the index on July 31，2006，is 300.What is the futures price for a contract deliverable on December 31，2006?25.The 2-month interest rates in Switzerland and the United States are,respectively,3% and 8% per annum with continuous compounding. The spot price of the Swiss franc is $0.6500.The futures price for a contract deliverabe in 2 months is $0.6600.What arbitrage opportunities does this create?26.The spot price of silver is $9 per ounce. The-storage costs are $0.24 per ounce; per year payable quarterly in advance. Assuming that interest rates are 10% per annum for all maturities, calculate the futures price of silver for delivery in 9 months.27.Suppose that the Treasury bond futures price is 101-12. Which of the following28.The price of a 90-day Treasury bill is quoted as 10.00.What continuously compounded return does an investor earn on the Treasury bill for the 90-day period?29.It is May 5，2005.The quoted price of a government bond with a 12% coupon that matures on July 27，2011，is 110-17.What is the cash price?30.Suppose that the 9-month LIBOR interest rate is 8% per annum and the 6-month LIBOR interest rate is 7.5% per annum (both with actual/365 and continuous compounding). Estimate the 3-month Eurodollar futures price quote for a contract maturing in 6 months.31.Suppose that, in a Treasury bond futures contract, it is known that the cheapest-to-deliver bond will be a 12% coupon bond with a conversion factor of 1.4000.Suppose also that it is known that delivery will take place in 270days. Coupons are payable semiannually on the bond. As illustrated in Figure,the last coupon date was 60days ago, the next coupon date is in 122days, and the coupon date thereafter is in 305days. The term structure is flat, and the rate of interest (with continuous compounding) is 10% per annum. Assume the current quoted bond price the proportion of the next coupon payment that accrues to the holder.32It’s July 30,2005.The cheapest-to-deliver bond in a September 2005 Treasury bond futures contract is a 13% coupon bond, and delivery is expected to be made on September 30,2005.Coupon payments on the bond are made on February 4 and August 4 each year. The term structure is flat, and the rate of interest with semiannual compounding is 12% per annum. The conversion factor for the bond is 1.5.The current quoted bond price is $110.Calculate the quoted futures price for the contract.33.Assume that a bank can borrow or lend money at the same interest rate in the LIBOR market. The 90-day rate is 10% per annum, and the 180-day rate is 10.2% per annum both expressed with continuous compounding and actual/actual day count. The Eurodollar futures price for a contract maturing in 90days is quoted as 89.5.What arbitrage opportunities are open to the bank?34.It is January 30，Y ou are managing a bond portfolio worth $6 million. The duration of the portfolio in 6 months will be 8.2 years. The September Treasure bond futures price is currently 108-15，and the cheapest-to-deliver bond will have a duration of 7.6 years in September. How should you hedge against changes in interest rates over the next 6 months?35.Explain why brokers require margins when clients write options but not when they buy options.36.A company declares a 2-to-1 stock split. Explain how the terms change for a call option with a strike price of $60.37.Consider an exchange-traded call option contract to buy 500 shares with a strike price of $40 and maturity in 4 months. Explain how the terms of the option contract change when there is:1)a 10% stock dividend; 2)a 10% cash dividend; 3)a 4-to-1 stock split.38.A United States investor writes five naked call option contracts. The option price is $3.50, the strike price is $60.00, and the stock price is $57.00. What is the initial margin requirement?39.An investor writes four naked call option contracts on a stock. The option price is$5, the strike price is $40, and the stock price is $38. Because the option is $2 out of the money.If the option had been a put, it would be $2 in the money and the margin requirement would be?40.What is a lower bound for the price of a 4-month call option on a non-dividend-paying stock when the stock price is $28, the strike price is $25, and the risk-free interest rate is 8% per annum?What is a lower bound for the price of a 1-month European put option on a non-dividend-paying stock when the stock price is $12, the strike price is $15, and the risk-free interest rate is 6% per annum?41.A 1-month European put option on a non-dividend-paying stock is currently selling for $2.5.The stock price is $47, the strike price is $50, and the risk-free interest rate is 6% per annum. What opportunities are there for an arbitrageur?42.A European call option and put option on a stock both have a strike price of $20 and an expiration date in 3 months. Both sell for $3. The risk-free interest rate is 10% per annum, the current stock price is $19,and a $1 dividend is in 1 month. Identify the arbitrage opportunity open to a trader.43.The price of a European call that expires in 6months and has a strike price of $30 is $2.The underlying stock price is $29, and a dividend of $0.50 is expected in 2 months and again in 5months. The term structure is flat, with all risk-free interest rates being 10% .What is the price of a European put option that expires in 6months and has a strike price of $30?Explain carefully the arbitrage opportunities in problem 8.4 if the European put price is $3.44.Suppose that C1C2C3 are the prices of European call options with strike pricesX1X2X3 respectively, where X1>X2>X3 andX3-X2=X2-X1. All options have the same maturity. Show thatC2<=0.5(C1+C3) What is the result corresponding to that in Problem 8.5 for European put options?45.The price of an American call on a non-dividend-paying stock is $4.The stock price is $31,the strike price is $30,and the expiration date is in 3 months. The risk-free interest rate is 8%.Derive upper and lower bounds for the price of an American put on the same stock with the same strike price and expiration date.Explain carefully the arbitrage opportunities in Problem45 if the American put price is greater than the calculated upper bound.46.Suppose that put option on a stock with strike prices $30 and $35 cost$4 and $7，respectively. How can the options be used to create (a) a bull spread and (b) a bear spread? Construct a table that shows the profit and payoff for both spreads.e put-call parity to show that the cost of a butterfly spread created from European puts is identical to the cost of a butterfly spread created from European calls.48.Call options on a stock are available with strike prices of $15，$17.5，and $20，and expiration dates in 3 months. Their prices are$4，$2，and$0.5，respectively. Explain how the options can be used to create a butterfly spread. Construct a table showing how profit varies with stock price for the butterfly spread.49.A call with a strike price of $60 costs $6.A put with the same strike price and expiration date costs $4.Construct a table that shows the profit from a straddle. For what range of stock prices would the straddle lead to a loss?50.A stock price is currently $40.It is known that at the end of 1 month it will be either $42 or $38.The risk-free interest rate is 8% per annum with continuous compounding. What is the value of a 1-month European call option with a strike price of $39?51.A stock price is currently $50.It is known that at the end of 6months it will be either $45or $55.The risk-free interest rate is 10% per annum with continuous compounding. What is the value of a 6-month European put option with a strike price of $50?52.A stock price is currently $100.Over each of the next two 6-month periods it is expected to go up by 10% or down by 10%. The risk-free interest rate is 8% per annum with continuous compounding. What is the value of a 1-year European call option with a strike price of $100?53.For the situation considered in Problem52, what is the value of a 1-year European put option with a strike price of $100?V erify that the European call and European put prices satisfy put-call parity.54.A stock price is currently $50.Over each of the next two 3-month periods it is expected to go up by 6% or down by 5%.The risk-free interest rate is 5% per annum with continuous compounding. What is the value of a 6-month European call option with a strike price of $51?55.A stock price is currently $50.over each of the next two 3-month periods it is expected to go up by 6% or down by 5%.The risk-free interest rate is 5% per annum with continuous compounding. What is the value of a 6-month European call option with a strike price of $51?For the situation considered in Problem 3，what is the value of a 6-month European put option with a strike price of $51?V erify that the European call and European put prices satisfy put-call parity. If the put option were American，would it ever beoptimal to exercise it early at any of the nodes on the tree?56.V ariables X1 and X2 follow generalized Wiener processes, with drift rates µ1 and µ2 and variances σ12 and σ22 .What process does X1+X2 follow if :(a) The changes in X1+X2 in any short interval of time are uncorrelated?(b) There is a correlation ρbetween the changes in X1 and X2 in any short time interval?57.Consider a variable S that follows the processdS=µdt+σdzFor the first three years, µ=2 and σ=3;for the next three years, µ=3 and σ=4.If the initial value of the variable is 5,what is the probability distribution of the value of the variable at the end of year 6?。

Options and Futures

Options and FuturesQ: identify the fundamental distinction between a futures contract and an option contract, and briefly explain the difference in the manner that futures and options modify portfolio risk.Derivatives (forward, future and option): an investment whose value today or at some future date is derived entirely from the value of another asset or group of other assets known as the underlying assets.Futures●Definition: a futures contract is an agreement that requires a party to either buy or sell something at aspecified future date at a predetermined price.● A future contract is a firm agreement between a buyer (seller) and an established exchange or itsclearinghouse. Buyer and seller agree to take or make delivery of something at a specified price at the end of a designated period of time.Difference between futures and option●Contract✓Futures: it is an obligation. When an investor purchases or sells a futures contract, the investor has an obligation to either accept or deliver, respectively, the underlying commodity on the expiration date.✓Options: for buyers, it is a right or choice to accept delivery (for call holders) or make delivery (for put holders) of the underlying commodity anytime during the life of the contract.●Exchange availability✓Futures: Exchange trading only. Exchange regulation and clearing house reduce counterparty default risk✓Options: Available on or off exchanges. Exchange regulation and clearing house reduce counterparty default risk for those options traded on exchanges●Premium✓Futures: No premium is payable. (however, margin payments are required)✓Options: premium should be paid, reduce the returns●Margin✓Futures: both parties must deposit an initial margin. The value of the operation is marked to market rates with daily settlement of profits and losses.✓Options: the buyer pays a premium to the seller. The seller deposits an initial margin with subsequent deposits made depending on the market. The underlying asset can be used as guarantee.●Risk (4图：buyer and seller of futures contract, buyer and writer of options)✓Futures: Buying or selling a futures contract affects a portfolio’s upside risk and downsid e risk by a similar magnitude. This is commonly referred to as symmetrical impact. It has unlimited risk both side for both parties.✓Options: a call or put option to a portfolio does not affect a portfolio’s upside risk and downsid e risk to a similar magnitude. The impact of options on the risk profile of a portfolio is asymmetric.For buyers, downside risk is limited.For sellers, upside risk is limited.。

Optimal_hedge_ratio

Optimal hedge ratioWe will call hedge ratio, the proportion of the position taken in futures to the size of the exposure, and we will denote it by . This is the ratio that will minimize the risk of the position, the risk being measured as the volatility, in the spirit of the CAPM. Therefore, if an investor islong one unit of the asset, she has to short units of the futures -a short hedge. The initial position is worth,where the final position will be worth.Remember that both and are unknown at time , which makes a random variable. The change in the value of the position will therefore be.Alternatively, for the long hedge the change in the value of the position will be.In both cases the variance of is equal toFor the variance to be minimized, the f.o.c. is,which gives as a result that.One can recall the similarities of the above procedure with the Markovitz type mean-variance portfolio analysis. Observe that the hedge ratio canbe rewritten as to illustrate the similarities. Rolling the hedgeWe saw before what the optimal instrument is in two cases where the hedge is not a perfect one. Namely we deduced that1.If the asset being hedged is different that the one underlying the futures contract, then onehas to choose the futures contract that has the highest possible correlation with the asset to be hedged; and2.If there is no futures contract on the asset to be hedged that expires on the maturity date ofthe hedge, then one has to choose the futures that expires as close as possible -but not earlier than, the date when the hedge matures.Of course there is another possibility: suppose that the hedge matures in a very distant point in time and all futures contracts available at the moment expire before that time. The hedger must then roll the hedge forward. This is done in the following fashion:In the above strategy there are sources of uncertainty, resulting indifferent basis risks. of them are referred to as the rollover basis: they represent the uncertainty about the difference of the futures price of the contract that is closed and the new contract that is opened when the hedge is rolled forward. The last basis risk is the classical one: it is the uncertainty about the price of the th contract and the spot price of the underlying asset at time . The next example illustrates the rollover basis.Figure 2.3: The basis when rolling the hedgeExample 6 (Rollover basis) Figure 2.3 describes the mechanics of the rollover basis. Say that one wants to deliver some asset at time , where the futures contracts mature at times ,and , as shown in figure 2.3:∙The hedger initially at time shorts the available futures .∙At time she closes her position. The futures price will now be due to the futures-spot convergence. Therefore, through marking to market from the first futures sherealizes an income .∙Simultaneously, the hedger short a new futures contract which matures at and hasprice .∙At time she repeats the previous two steps. The income is , andshe has shorted a futures with price .∙Finally, at time she closes the final position. The futures price will be andthe underlying's price will be . The income will be .∙She also delivers the asset and receives the market price .The total income of this strategy iswhich can be rewritten in terms of the bases asFuture-spot convergenceAs the delivery approaches, the futures price will eventually converge to the spot price of the underlying asset. Two alternative ways of doing so are presented in figure 2.1.Figure 2.1: Forward--spot convergenceIf this was not the case, there would be clear arbitrage opportunities. For instance, if the futures were above the spot price, one could [and should] exploit the following arbitrage opportunity1.Short a futures2.Buy the asset3.DeliverAs arbitrageurs exploit this opportunity, the price of the futures will decline and the price of the underlying asset will rise. This pattern will continue until the futures and the spot price become equal. The futures price can approach the spot price either from below or above, something that will be explained later.Hedging with futuresIf an company knows that it has to sell a particular asset at a particular time in the future, it can hedge by taking a short position, therefore locking in the price of delivery. This is called a short hedge. Similarly, a company that knows that it will need an asset in the future can take a long hedge, thus locking in the price of purchase. It is very important to note that hedging does not necessarily improve the financial outcome, it just reduces the uncertainty. In practice, hedging is not perfect, the basis risk arises due to a number of reasons, some of which were discussed in the introduction:∙The asset being hedged might be different that the one underlying the futures contract, i.e.using a 30y T-bill to hedge a 10y T-note;∙The hedger might be uncertain about the exact time that the delivery has to take place, i.e.a new oil ring that is expected to start extracting next summer, without knowing exactlywhen; and∙The futures contract matures after the delivery date that the hedger has in mind, i.e. the hedger needs to buy steel in January but steel futures expire on March.The basis is defined as,where is the spot price of the underlying asset and is the price of the futures contract that has been utilized. If the asset to be hedged is the same as the one underlying the futures, then the basis on expiration is equal to zero. If the delivery date is not the same as the one that the futures matures, then the basis will signify the ``losses'' or ``gains'' of the hedge than are not known when the hedge is constructed.Example 4 (Basis risk: different maturities) Today, the gold price is . Say that one has to deliver gold at time , and in order to hedge takes a short position on a futures contract thatmatures at time . The price of this contract is equal to , and the basis today is. The basis on the delivery date will be, will indicate the gains [or losses] due to the hedge. See figure 2.2 for a visual representation of the basis risk.Figure 2.2: Basis riskAt time the company will close the futures contract by taking a long position and at the same time sell the gold at the current price. The marking-the-market procedure will leave the company with a loss ofsince the futures was sold at time and bought at time; while by selling the asset the income is . The total income is therefore is.The value is known at time , while the quantity represents the basis risk.Obviously, if , then , and there is no basis risk.If one takes into account the time value of money -something that we did not do in the previous example, then for most investment assets the basis risk is very small, due to arbitrage arguments that we will explore later. Generally speaking, the basis risk arises from uncertainty about the future interest rates and uncertainty about the future yields of the underlying asset. For investments that are difficult or costly to store, the basis risk might increase substantially. The delivery month that is as close as possible -but not earlier than, the date when the hedge matures.As we noted before, the asset used for hedging might be different then the one being hedged. Say that there were no futures contracts for gold, and one had to use futures on silver.Example 5 (Basis risk: different assets) Denote the price of gold by and the price of silverby . Denote by and the corresponding futures prices. As before, say that one has todeliver gold at time , but such futures do not exist. Futures contracts on silver are going to be used instead. As before, the total income of this hedge will be,which can be rewritten as.The quantity is the basis of silver ; it would exist if the asset to beactually delivered was indeed silver. The quantity is the basis arising due to the differences of the assets.In the example above observe that if , that is to say if the maturity of the silver futures was the same as the maturity of the hedge, thenand the basis of the hedge would be only due to thedifferences between the two assets. On the other hand, if the two assetswere perfectly correlated, then , and there would only bebasis due to the maturity differences. This makes clear that when there is no futures contract on the asset being hedged, one has to choose the futures that has the highest correlation with the underlying asset.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

International Finances
Options Contracts: Preliminaries 期权合约: 预备知识
An option gives the holder the right, but not the obligation, to buy or sell a given quantity of an asset in the future, at prices agreed upon today.
OPTIONS (Energy Products) 期权 (能源产品)
Product 产品
Contract Unit 合约单位
Minimum Fluctuation 最低价格波幅
Tick Value 价位
Light Sweet Crude Oil (WTI) 轻原油 Heating Oil Option 暖油期权 Natural Gas 天然气
期权给予持有者将来以现在商定的价格去买或者去卖一定数量的资产的权利, 而不是义务。
Calls vs. Puts
– Call options gives the holder the right, but not the obligation, to buy a given quantity of some asset at some time in the future, at prices agreed upon today. – Put options gives the holder the right, but not the obligation, to sell a given quantity of some asset at some time in the future, at prices agreed upon today.
Univ. of Sci. & Tech. Beijing
hxiaoxia@
Company Name
International Finances Livestock 畜牧业
– – – – – – Live cattle , 活牛 Lean hogs, 精品猪 Feeder cattle 饲牛
看涨 vs. 看跌 – 看涨期权给予持有者将来以现在商定的价格去买一定数量的资产的权利，而不是义务。 – 看跌期权给予持有者将来以现在商定的价格去卖一定数量的资产的权利，而不是义务。 Xiaoxia Huang Univ. of Sci. & Tech. Beijing hxiaoxia@
– Platinum 铂 – Copper 铜
Xiaoxia Huang

Univ. of Sci. & Tech. Beijing
hxiaoxia@
Company Name
International Finances
OPTIONS (Grain and Oilseed) 期权 (谷物和油籽)
Xiaoxia Huang Univ. of Sci. & Tech. Beijing hxiaoxia@
International Finances
期权合约: 预备知识
In-the-money
– The exercise price is less than the spot price of the underlying asset.
价外
– 执行价格高于标的资产的即期价格。
Xiaoxia Huang
Univ. of Sci. & Tech. Beijing
hxiaoxia@
International Finances
Types of Options 期权的种类
1. FINANCIAL
1. 金融期权
1,000 bbls.
$0.01 per bbl.
$10.00
42,000 gals.
$0.0001 per gal.
$4.20
10,000 MMBtus.
$0.001 per MMBtu.
$10.00
Xiaoxia Huang

Univ. of Sci. & Tech. Beijing
100 short tons
$0.10 per short ton
60,000 lbs
$0.00005 per lb
Xiaoxia Huang

Univ. of Sci. & Tech. Beijing
hxiaoxia@
International Finances
International Finances
期权合约: 预备知识
欧式期权 vs. 美式期权 European options can only be exercised on the expiration date.
– American options can be exercised at any time up to and including the expiration date. – Since this option to exercise early generally has value, American options are usually worth more than European options, other things equal. – 欧式期权只能在期权到期日执行. – 美式期权可以在期权到期日之前包括到期日的任意时候执行。 – 由于这种可以早执行期权的权利通常有价值, 美式期权一般比欧式期权更具有价值, 其他方面两者是相同的.
Gold 金 Silver 银 Platinum 铂 Copper 铜
100 troy ozs. 5,000 troy ozs. 50 troy ozs. 25,000 lbs.
$0.10 per troy oz. $0.005 per troy oz. $0.10 per troy oz. $0.0005 per lb.
Dairy 乳制品
– – – – – – Class III Milk 第三类牛奶 Dry Whey 干乳清 Cash-Settled Butter 现金结算黄油
Xiaoxia Huang

Univ. of Sci. & Tech. Beijing
hxiaoxia@
Company Name
International Finances
Grains and Oilseeds 谷物和油籽
– Corn 玉米, – Wheat, 小麦 – Soybeans, 大豆 – Soybean Meal, 豆粕, – Soybean oil 大豆油
Xiaoxia Huang

价内
– 执行价格低于标的资产的即期价格。
At-the-money
– The exercise price is equal to the spot price of the underlying asset.
平价
– 执行价格与标的资产的即期价格相同。
Out-of-the-money
– The exercise price is more than the spot price of the underlying asset.
Company Name
5,000bushels
$0.000125 per bushels
5,000bushels
$0.00125 per bushels
Soybeans 大豆
5,000bushels
$0.00125 per bushels
Soybean Meal 豆粕 Soybean Oil 豆油
Currency 外汇 Australian dollar 澳大利亚元 British pound 英镑 Canadian dollar 加元 Euro 欧元 Japanese yen 日元 Swiss franc 瑞士法郎 Contract Size合约规模 AD50,000 £31,250 CD50,000 €62,500 ¥6,250,000 SF62,500
International Finances 国际金融
Xiaoxia Huang
School of Economics and Management University of Science & Technology Beijing hxiaoxia@ 黄晓霞北京科技大学
Product 产品 Corn 玉米 Wheat 小麦 Contract Size 合约规模 Minimum Tick 最小波动 Contract Months 合约交易月份 12(Z),3(H), 5(K),7(N),9(U) 3(H),5(K), 7(N),9(U),12(Z) 11(X),1(F),3 (H),5(K),7(N), 8(Q),9(U) 10(V),12(Z),1(F),3(H),5(K), 7 (N),8(Q),9(U) 10(V),12(Z),1(F),3(H),5(K), 7 (N),8(Q),9(U)
Company Name
International Finances
Energy/Wood Products 能源/木材产品
Energy Products 能源产品 – Crude And Refined Products – 原油和成品油 – Natural Gas – 天然气 – Electricity – 电力 Forestry 林业 – Random Length Lumber – 随机长度木材 – Wood Pulp – 木浆
Xiaoxia Huang

Univ. of Sci. & Tech. Beijing
hxiaoxia@

OptionsAndHedge

options在金融中的意思

18Future Contracts,Options and Swaps

Betas, Options, and Portfolios of Hedge Funds

（英文）笔记：有关期权的基本知识

期权期货及衍生品 约翰赫尔 第九版 课后答案HullOFOD9eSolutionsCh10

Options,Futures,andOtherDerivatives

基金对冲基金投资词汇_金融银行英语词汇

《Options, Futures and Other Derivatives 》

Option

期权期货及其他衍生产品第9版赫尔_1

期权期货常用英语

options and futures

Hedging with Foreign Currency Options外汇期权套期保值

hedge的用法 -回复

OptionsAndHedge

Financial Options and Their Valuation

Future Option and other derivatives exercises

Options and Futures

Optimal_hedge_ratio

期权期货及衍生品约翰赫尔第九版课后答案HullOFOD9eSolutionsCh10