流水线车间调度问题matlab源程序
单目标调度优化问题及matlab实现

标题:深度解析单目标调度优化问题及Matlab实现在现代社会中,调度优化问题一直是一个备受关注的领域。
单目标调度优化问题,作为其中的一个重要分支,涉及了工业生产、交通运输、资源分配等诸多领域,其优化方案的设计与实现对于提高效率、降低成本、优化资源配置等方面具有重要意义。
本文将深入剖析单目标调度优化问题,并结合Matlab实现,带领读者深入探讨这一激动人心的领域。
一、单目标调度优化问题概述单目标调度优化问题是指在满足一定约束条件的前提下,通过合理的调度安排,使得某一特定目标函数最优化。
这一类问题的特点是具有明确的优化目标,例如最小化生产时间、最大化资源利用率等。
在实际应用中,针对不同的领域和具体问题,单目标调度优化问题有着丰富的表现形式和具体求解方法。
针对单目标调度优化问题,首先需要明确问题的具体场景和约束条件,以确定目标函数的形式。
在生产调度中,可以以最小化生产总时间为目标函数;在交通运输调度中,可以以最小化运输成本为目标函数。
需要建立相应的数学模型,以便将问题具体化为数学表达式。
通过合适的优化算法对模型进行求解,得到最优化的调度方案。
在实际求解过程中,常用的算法包括遗传算法、模拟退火算法、粒子群算法等。
二、单目标调度优化问题的具体应用举例单目标调度优化问题具有广泛的应用领域,下面将对几个具体的应用场景进行举例说明。
1. 生产调度问题在制造业中,生产调度问题是一个典型的单目标调度优化问题。
通过合理的生产调度安排,可以最大限度地提高生产效率,降低成本,缩短生产周期,实现资源的最优配置。
对于机器作业调度,可以通过合理安排机器的工作顺序和时间,最小化总的生产时间,提高作业效率。
2. 交通运输调度问题在物流行业中,交通运输调度问题是一个常见的单目标调度优化问题。
通过合理的运输调度安排,可以降低运输成本,提高运输效率,优化货物配送路径。
对于货车的路线规划和货物的装载顺序,可以通过优化算法得到最优的调度方案,以最小化运输成本。
Matlab/Visual C++混合编程求解单件车间调度问题

m e n ta r
y
,
o
f
the
he d u lin g
the
y , bu t
tc
ha
c
gre
a
in f l
.
m o
r
de
r n
iz
a
g
e m e n s c
t in
e n
te
p is
it h
a n c o m v e
in g le
it e
tin
m
v a r
ie ty
p
r o
du d
c
ts
o n
,
,
则 约束条件为 :
,
工
任 务 所 需 的 各 种 约 束 ( 加 工 次 序 所 需 机 器 ) 使所 有 的
、
,
( 1 ) 每 个 工 件 的 各 道 工 序 的 加 工 顺 序 预 先 确 定 且 保持 有
任 务 能尽 量 如期 完 成 就 成 为 十 分 现 实 和 迫 切 的 问 题 这
, ,
s m a e
ll ba
n c
h p r o du
n c
t io
to
u
m o
s o
de
e
T his p a p e
p
r e s e n
ts
a n n
im p r
the the
e
d
he du lin g
s w e r e
lg o r it hm
o
d
dj u
e
s
g
a
lg o r ith m
matlab车辆调度优化算法

车辆调度优化算法在现代物流和运输领域中扮演着重要的角色。
随着城市化进程的加快和人们对快速高效货运的需求不断增加,车辆调度优化算法的研究和应用变得尤为重要。
其中,matlab作为一种强大的计算工具,被广泛应用于车辆调度优化算法的研究和实践中。
本文将从以下几个方面对matlab车辆调度优化算法进行探讨。
一、matlab在车辆调度优化算法中的应用概述1. Matlab在数学建模方面的优势Matlab作为一种强大的数学软件工具,拥有丰富的数学函数库和强大的矩阵运算能力,能够快速高效地进行数学建模和优化计算。
在车辆调度优化算法中,这种优势使得Matlab成为一种理想的工具。
2. Matlab在算法研究和实现中的应用Matlab提供了丰富的算法工具箱,包括遗传算法、模拟退火算法、粒子裙优化算法等常用的优化算法,这些算法的灵活性和易用性使得Matlab成为车辆调度优化算法研究和实现的理想选择。
二、matlab在车辆路径规划中的应用1. 车辆路径规划的基本问题和挑战车辆路径规划是车辆调度优化算法中的重要问题之一,它涉及到如何合理安排车辆的行驶路线,以最大限度地减少行驶距离和时间。
这是一个 NP 难题,需要运用各种优化算法来求解。
2. Matlab在车辆路径规划中的具体应用Matlab提供了丰富的优化算法工具箱,可以很方便地用来解决车辆路径规划中的优化问题。
可以利用遗传算法来对车辆路径进行优化,或者利用模拟退火算法来寻找最优路径。
三、matlab在车辆调度问题中的应用实例1. 基于Matlab的车辆调度优化算法研究以某物流公司的货物配送路线为例,通过Matlab对车辆调度优化算法进行研究和实现,能够有效降低运输成本,提高运输效率。
2. 基于Matlab的算法实现与性能评测通过实际案例,可以用Matlab对车辆调度优化算法进行实现,并进行性能评测,评估算法的优劣,为实际应用提供参考。
matlab在车辆调度优化算法中具有重要的应用价值,并且在实际的研究和实践中得到了广泛的应用。
求解置换流水车间调度问题的一种混合算法

求解置换流水车间调度问题的一种混合算法0. 前言置换流水车间调度问题(PFSP是对经典的流水车间调度问题进行简化后得到的一类子问题,最早在石化工业中得到应用,随后扩展到制造系统、生产线组装和信息设备服务上[1] 。
该问题一般可以描述为,n个待加工工件需要在m台机器上进行加工。
问题的目标是求出这n 个工件在每台机器上的加工顺序,从而使得某个调度指标达到最优,最常用的指标为工件的总完工时间(makespar)最短。
PFSP最早由Johnson于1954年进行研究[2],具有NP难性质[3] 。
求解方法主要有数学规划,启发式方法和基于人工智能的元启发式算法[4] 。
数学规划等适用于小规模问题,启发式方法计算便捷,却又无法保证解的质量。
随着计算智能的发展,基于人工智能的元启发式优化算法成为研究的重点。
遗传算法(GA是研究与应用得最为广泛的智能优化算法,利用遗传算法求解PFSP问题的研究也有很多。
遗传算法具有操作简单、容易实现的优点,且求解时不受约束条件限制。
然而,遗传算法通常存在着过早收敛,容易陷入局部最优的现象。
导致这一现象的原因在于遗传算法的交叉、变异操作具有一定的随机性,在求解PFSP问题的过程中往往会破坏构造块,产生所谓的连锁问题。
为了克服遗传算法的缺陷,研究人员提出了一种不进行遗传操作的分布估计算法[5] (EDA。
EDA是一种运用统计学习的新型优化算法。
相比GA EDA在全局搜索上有较大的优势,而局部搜索能力不足,同样会导致局部最优[6][7] 。
以混合优化为思路,本文将设计一种EDA与GA吉合的混合算法来求解PFSP 问题,混合算法通过EDA的概率模型和GA的交叉变异操作两种方式来生成个体,并引入模糊控制理论[8] 来自适应调节两种算法生成个体的比例。
1. 置换流水车间调度问题PFSP问题通常假设:(1)n台工件在m台机器上加工。
(2)每个工件以相同的顺序在m台机器上加工。
(3)每个工件在每台机器上的加工时间是预先确定的。
遗传算法应用实例及matlab程序

遗传算法应用实例及matlab程序遗传算法是一种模拟自然进化过程的优化算法,在多个领域都有广泛的应用。
下面将以一个经典的实例,车间调度问题,来说明遗传算法在实际问题中的应用,并给出一个基于MATLAB的实现。
车间调度问题是一个经典的组合优化问题,它是指在给定一系列任务和一台机器的情况下,如何安排任务的执行顺序,以便最小化任务的完成时间或最大化任务的完成效率。
这个问题通常是NP困难问题,因此传统的优化算法往往难以找到全局最优解。
遗传算法能够解决车间调度问题,其基本思想是通过模拟生物进化的过程,不断演化和改进任务的调度顺序,以找到最优解。
具体步骤如下:1. 初始种群的生成:生成一批初始调度方案,每个方案都表示为一个染色体,一般采用随机生成的方式。
2. 个体适应度的计算:根据染色体中任务的执行顺序,计算每个调度方案的适应度值,一般使用任务完成时间作为适应度度量。
3. 选择操作:根据个体的适应度,采用选择策略选择一部分优秀个体作为父代。
4. 交叉操作:对选中的个体进行交叉操作,生成新的子代个体。
5. 变异操作:对子代个体进行变异操作,引入随机性,增加搜索空间的广度。
6. 替换操作:用新的个体替换原来的个体,形成新一代的种群。
7. 迭代过程:重复执行选择、交叉、变异和替换操作,直到达到预定的终止条件。
下面给出基于MATLAB的实现示例:matlabfunction [best_solution, best_fitness] =genetic_algorithm(num_generations, population_size) % 初始化种群population = generate_population(population_size);for generation = 1:num_generations% 计算适应度fitness = calculate_fitness(population);% 选择操作selected_population = selection(population, fitness);% 交叉操作crossed_population = crossover(selected_population);% 变异操作mutated_population = mutation(crossed_population);% 替换操作population = replace(population, selected_population, mutated_population);end% 找到最优解[~, index] = max(fitness);best_solution = population(index,:);best_fitness = fitness(index);endfunction population = generate_population(population_size) % 根据问题的具体要求,生成初始种群population = randi([1, num_tasks], [population_size, num_tasks]); endfunction fitness = calculate_fitness(population)% 根据任务执行顺序,计算每个调度方案的适应度% 这里以任务完成时间作为适应度度量fitness = zeros(size(population, 1), 1);for i = 1:size(population, 1)solution = population(i,:);% 计算任务完成时间completion_time = calculate_completion_time(solution);% 适应度为任务完成时间的倒数fitness(i) = 1 / completion_time;endendfunction selected_population = selection(population, fitness) % 根据适应度值选择父代个体% 这里采用轮盘赌选择策略selected_population = zeros(size(population));for i = 1:size(population, 1)% 计算选择概率prob = fitness / sum(fitness);% 轮盘赌选择selected_population(i,:) = population(find(rand <= cumsum(prob), 1),:);endendfunction crossed_population = crossover(selected_population) % 对选中的个体进行交叉操作% 这里采用单点交叉crossed_population = zeros(size(selected_population));for i = 1:size(selected_population, 1) / 2parent1 = selected_population(2*i-1,:);parent2 = selected_population(2*i,:);% 随机选择交叉点crossover_point = randi([1, size(parent1,2)]);% 交叉操作crossed_population(2*i-1,:) = [parent1(1:crossover_point), parent2(crossover_point+1:end)];crossed_population(2*i,:) = [parent2(1:crossover_point), parent1(crossover_point+1:end)];endendfunction mutated_population = mutation(crossed_population) % 对子代个体进行变异操作% 这里采用单点变异mutated_population = crossed_population;for i = 1:size(mutated_population, 1)individual = mutated_population(i,:);% 随机选择变异点mutation_point = randi([1, size(individual,2)]);% 变异操作mutated_population(i,mutation_point) = randi([1, num_tasks]);endendfunction new_population = replace(population, selected_population, mutated_population)% 根据选择、交叉和变异得到的个体替换原来的个体new_population = mutated_population;for i = 1:size(population, 1)if ismember(population(i,:), selected_population, 'rows')% 保留选择得到的个体continue;else% 随机选择一个父代个体进行替换index = randi([1, size(selected_population,1)]);new_population(i,:) = selected_population(index,:);endendend该示例代码实现了车间调度问题的遗传算法求解过程,具体实现了种群的初始化、适应度计算、选择、交叉、变异和替换等操作。
VB与Matlab集成求解车间调度优化问题

t e 技 术动态数 据交 换 ( D ) i X、 v D E 技术 、 态连接库 ( L )Ma 动 D L、 —
tx B C M 组 件 技 术 等 。前 两 种 方 法 最 大 的缺 点 是 不 能 脱 离 rV 、O i
Maa tb工作环境。D L技术是应用 Ma T os 司的 MieaT l L t ol公 h d v
求解 问题 时间复杂度 、 空间复杂度 的扩 大 , 组合优化 问题 的搜 索空间呈几何级数 急剧扩大 ,以目前一般计算机的处理能力 , 用枚举 法有时很难或者甚至不可能得到其精确最优解 。 对于这
来越 高 , 简单 的、 局部 的、 规的控 制和仅 凭经验 的管理 已经 常
不 能满足现代生产的要求 。构建 高效 的调度方案与优 化技术 已成为提 高制造系统性能的主导 因素 ,车间调度 问题应运 而 生 。车间调度问题具有建模 / 计算复 杂性 、 动态随机性 、 多约 束性 、 目标性 等特点 , 多 因此 在其应 用软件 的实现上 , 一方 面 要求具有 良好 的人 机交互和动态显示性 能 ,另一方面要考 虑 其数值计算能力。
具 软 件 ,借 用 c +编 译 器 将 Maa + tb的 M 函数 文件 转 换 为 l
D L在 V L , B中加载该 D L 但这种方法需要单独开发可执行文 L。 件。 a iV M tx B是 M tWo r a h r k针对 V B提供 的一个 Ma a , l fb库 它提
内容包括分配决策( 工件的加工顺 序 ) 和时间决策( 工件各工序
Mi oo i a B s c sfV s l ai 由微 软 公 司开 发 的 优 秀 的 程 序 可 r t u c是 视 化 设计 语 言 之 一 , 在 数 据 处 理 方 面 却 非 常 繁 琐 , 码 冗 长 但 代
置换流水车间调度问题的MATLAB求解

置换流⽔车间调度问题的MATLAB求解物流运筹实务课程设计题⽬:置换流⽔车间调度问题的MATLAB求解置换流⽔车间调度问题的MATLAB求解⽬录⼀、前⾔ (5)⼆、问题描述 (6)三、算法设计 (7)四、实验结果 (15)摘要⾃从Johnson 1954年发表第⼀篇关于流⽔车间调度问题的⽂章以来.流⽔车间调度问题引起了许多学者的关注。
安排合理有效的⽣产调度是⽣产活动能井然有序开展,⽣产资源得到最佳配置,运作过程简明流畅的有⼒保证。
流⽔车间调度问题是许多实际流⽔线⽣产调度问题的简化模型。
它⽆论是在离散制造⼯业还是在流程⼯业中都具有⼴泛的应⽤。
因此,对进⾏研究具有重要的理论意义和⼯程价值。
流⽔线调度问题中⼀个⾮常典型的问题,⽽置换流⽔线调度问题作为FSP 问题的⼦问题,是⼀个著名的组合优化问题。
该问题是⼀个典型的NP难问题,也是⽣产管理的核⼼内容。
随着⽣产规模的扩⼤,流⽔线调度问题的优化对提⾼资源利⽤率的作⽤越来越⼤,因此对其研究具有重要的理论和现实意义。
关键字:流⽔车间,单件⼩批量⽣产,jsp模型,Matlab前⾔企业资源的合理配置和优化利⽤很⼤程度上体现在车间⼀层的⽣产活动中,所以加强车间层的⽣产计划与控制⼀直在企业⽣产经营活动中占有⼗分重要的地位。
车间⽣产计划与控制的核⼼理论是调度理论。
车间调度问题是⼀类重要的组合优化问题。
为适应订货式、多品种、⼩批量⽣产的需要,引进了置换流⽔车间调度概念。
在置换流⽔车间调度优化后,可以避免或⼤⼤减少流程⼯作时间、提⾼⽣产效率。
因此,研究成组技术下车间调度问题是很有必要的。
⽣产调度,即对⽣产过程进⾏作业计划,是整个个先进⽣产制造系统实现管理技术、优化技术、⽩动化与计算机技术发展的核⼼。
置换流⽔车间调度问题是许多实际⽣产调度问题的简化模型。
⽣产计划与调度直接关系着企业的产出效率和⽣产成本,有效的计划与调度算法能最⼤限度地提⾼企业的效益。
调度问题是组合优化问题,属于NP问题,难以⽤常规⼒⼀法求解。
基于MATLAB-GUI的生产车间调度系统设计

第2期(总第225期)2021年4月No2Apr机械工程与自动化MECHANICAL ENGINEERING & AUTOMATION文章编号=672-6413(2021)02-0119-02基于MATLAB-GUI 的生产车间调度系统设计^王 辉,张嘉薇,罗萌萌,何浩浩,吐列克•杰恩斯别克,戴 敏(扬州大学机械工程学院,江苏扬州225127)摘要:物联智能制造是未来工业发展的趋势,针对的是传统的生产调度管理模式效率低、成本高、安全性低等问题。
为提高企业在同一行业的竞争力,利用MATLAB 的图形用户界面(GraphicalUserInterfaces ,GUI )设计了一种生产车间调度管理系统,为车间生产决策与企业管理提供了辅助工具。
关键词:调度系统设计;MATLAB-GUI ;生产车间中图分类号:TP391.9:TP278 文献标识码:A0引言随着工业物联网与智能制造的飞速发展,科技辅助 使人类制造能力越来越强大[]。
据统计,截止2019年, 全球制造业引领的物联网投资支出高达一千八百亿美 元,这表明工业物联网和智能制造是未来制造企业发 展方向⑵。
许多中小型企业为了提高市场竞争水平, 逐渐从传统的管理和生产模式向基于物联网的智能管 理和智能控制模式转变。
目前,工程科技的发展不断创新,自Mathworks 公司于1984年开发MATLAB 软件,无数的研究者们 利用其进行科学仿真和算法开发并广泛应用于电子信 息、航空航天等领域34]。
其中MATLAB 中的图形用 户界面模块为系统设计提供了便捷高效的开发环 境[]。
本文针对某企业具体生产情况,基于MATLAB 图形用户界面设计了企业生产车间调度系统,以实现 车间调度的仿真(如甘特图等)o 1生产车间调度系统功能本系统主要分为四个功能模块,分别为账户管理、 基础数据、系统仿真和结果展示模块。
具体的车间调 度系统功能模块如图1 所示。
1. 1 账户管理模块功能账户管理模块的主要功能为防护系统的安全。
车间生产计划与调度实验

实验二车间生产计划与调度实验一、实验目的1.加深对作业计划与调度概念的理解;2.通过对实际柔性制造教学系统的分析,熟练掌握车间层调度模型建立、掌握车间调度方法;3.通过不同排序算法的应用以及完工时间的分析,掌握各种算法的调度可行解产生过程、特点,体会可行解与最优解的区别;4.让学生了解本实验系统所使用的MATLAB软件并使用此软件编写程序实现车间层生产计划调度问题。
二、实验器材1.柔性制造教学实验系统2.PC机一台;3.Matlab软件一套;三、实验原理车间生产作业计划,就是把加工的零件进行排序,确定工件加工的先后顺序。
对于某一工作地,在给定的一段时间内,顺次决定下一个被加工的工件。
一般说来,一个工作地可选择的下一个工件会有很多种,因此,按什么样的准则来选择,对排序方案的优劣有很大的影响。
为了得到所希望的排序方案,需要借助一些优先顺序规则。
当几项工作在一个工作地等待时,运用这些有限规则可以决定下一项应进行的工作。
这种调度方法,就是运用若干预先规定的优先顺序规则,顺次决定下一个应被加工的工件的排序方法。
本实验系统采用以下具有代表性的车间作业计划模型:有m 台不同的机器和n 个不同的工件,并假设:①一个工件不能同时两次访问同一机器;②任何一个工件的前一道工序加工完成后,方能进行后一道工序的加工;③在同一台机器上一个加工任务完成后,方能开始另一个加工任务;④不同工件的工序之间没有先后约束;⑤一个工件仅同时在一台机床上加工,一台机器仅能同时加工一个工件;⑥每个工件的每道工序的开工时间一定大于等于零;⑦工序应尽量使用负荷低、空闲的设备;⑧工件数、机器数和加工时间已知,加工时间与加工顺序无关。
依据所考察的目标函数不同,采用的作业计划和生产调度的规则也各异,人们既可以把作业处理时间的长短、作业的优先等级作为生产调度的规则来计划作业,也可以某台设备的效率或整个系统的生产率的高低作为生产调度的规则来计划作业。
因此,生产系统的调度规则种类很多,其中,主要由SPT、FCFS、EDD、SS、DS 等。
202306 粒子群算法PSO求解混合流水车间调度问题Matlab编程教学视频配套资料

202306 粒子群算法PSO求解混合流水车间调度问题Matlab编程教学视频配套资料简介在现代生产中的许多制造业领域,混合流水车间调度问题是一个重要而复杂的问题。
该问题的目标是在满足约束条件的前提下,使得整个车间的流程最优化。
为了解决这个问题,我们将会介绍粒子群算法(PSO)及其在混合流水车间调度问题中的应用。
本文档是相关视频教学的配套资料,提供了Matlab编程教学视频的辅助材料。
内容本文档的内容将分为以下几个部分:1.混合流水车间调度问题概述首先,我们将介绍什么是混合流水车间调度问题以及该问题的重要性。
我们将讨论具体的问题定义和目标,并解释约束条件。
2.粒子群算法(PSO)简介接下来,我们将对粒子群算法进行介绍。
我们将解释PSO的基本原理、工作方式和核心思想。
同时,我们还将部分讨论PSO的优点和局限性。
3.混合流水车间调度问题的模型构建在本部分,我们将详细描述如何将混合流水车间调度问题建模为一个数学模型。
我们将阐述各个因素和变量,并给出相应的数学表达式。
4.使用Matlab进行PSO编程这是本文档的核心部分,我们将教授如何使用Matlab编写粒子群算法以求解混合流水车间调度问题。
我们将逐步讲解核心代码片段,并解释每个步骤的原理和实现。
5.案例分析与实例演示最后,我们将通过一个案例对混合流水车间调度问题进行实例演示。
我们将提供相应的示例数据,并使用前面介绍的Matlab代码进行求解。
我们将演示代码运行的结果,并进行相应的分析和讨论。
学习目标通过学习本教学视频配套资料,您将能够:•了解混合流水车间调度问题的定义和目标;•理解粒子群算法的基本原理和工作方式;•学会使用Matlab编程解决混合流水车间调度问题;•掌握如何实际应用PSO算法去优化车间调度;•能够通过案例分析和实例演示加深对混合流水车间调度问题和PSO算法的理解。
预备知识为了更好地理解本教学视频,我们建议您具备一些基本的数学和编程知识。
02流水线车间生产调度的遗传算法MATLAB源代码

流水线车间生产调度的遗传算法MATLAB源代码n个任务在流水线上进行m个阶段的加工,每一阶段至少有一台机器且至少有一个阶段存在多台机器,并且同一阶段上各机器的处理性能相同,在每一阶段各任务均要完成一道工序,各任务的每道工序可以在相应阶段上的任意一台机器上加工,已知任务各道工序的处理时间,要求确定所有任务的排序以及每一阶段上机器的分配情况,使得调度指标(一般求Makespan)最小。
function [Zp,Y1p,Y2p,Y3p,Xp,LC1,LC2]=JSPGA(M,N,Pm,T,P)%--------------------------------------------------------------------------% JSPGA.m% 流水线型车间作业调度遗传算法% GreenSim团队——专业级算法设计&代写程序% 欢迎访问GreenSim团队主页→/greensim%--------------------------------------------------------------------------% 输入参数列表% M 遗传进化迭代次数% N 种群规模(取偶数)% Pm 变异概率% T m×n的矩阵,存储m个工件n个工序的加工时间% P 1×n的向量,n个工序中,每一个工序所具有的机床数目% 输出参数列表% Zp 最优的Makespan值% Y1p 最优方案中,各工件各工序的开始时刻,可根据它绘出甘特图% Y2p 最优方案中,各工件各工序的结束时刻,可根据它绘出甘特图% Y3p 最优方案中,各工件各工序使用的机器编号% Xp 最优决策变量的值,决策变量是一个实数编码的m×n矩阵% LC1 收敛曲线1,各代最优个体适应值的记录% LC2 收敛曲线2,各代群体平均适应值的记录% 最后,程序还将绘出三副图片:两条收敛曲线图和甘特图(各工件的调度时序图)%第一步:变量初始化[m,n]=size(T);%m是总工件数,n是总工序数Xp=zeros(m,n);%最优决策变量LC1=zeros(1,M);%收敛曲线1LC2=zeros(1,N);%收敛曲线2%第二步:随机产生初始种群farm=cell(1,N);%采用细胞结构存储种群for k=1:NX=zeros(m,n);for j=1:nfor i=1:mX(i,j)=1+(P(j)-eps)*rand;endfarm{k}=X;endcounter=0;%设置迭代计数器while counter<M%停止条件为达到最大迭代次数%第三步:交叉newfarm=cell(1,N);%交叉产生的新种群存在其中Ser=randperm(N);for i=1:2:(N-1)A=farm{Ser(i)};%父代个体Manner=unidrnd(2);%随机选择交叉方式if Manner==1cp=unidrnd(m-1);%随机选择交叉点%双亲双子单点交叉a=[A(1:cp,:);B((cp+1):m,:)];%子代个体b=[B(1:cp,:);A((cp+1):m,:)];elsecp=unidrnd(n-1);%随机选择交叉点b=[B(:,1:cp),A(:,(cp+1):n)];endnewfarm{i}=a;%交叉后的子代存入newfarmnewfarm{i+1}=b;end%新旧种群合并FARM=[farm,newfarm];%第四步:选择复制FITNESS=zeros(1,2*N);fitness=zeros(1,N);plotif=0;for i=1:(2*N)X=FARM{i};Z=COST(X,T,P,plotif);%调用计算费用的子函数FITNESS(i)=Z;end%选择复制采取两两随机配对竞争的方式,具有保留最优个体的能力 Ser=randperm(2*N);for i=1:Nf2=FITNESS(Ser(2*i));if f1<=f2farm{i}=FARM{Ser(2*i-1)};fitness(i)=FITNESS(Ser(2*i-1));elsefarm{i}=FARM{Ser(2*i)};end%记录最佳个体和收敛曲线minfitness=min(fitness)meanfitness=mean(fitness)LC1(counter+1)=minfitness;%收敛曲线1,各代最优个体适应值的记录 LC2(counter+1)=meanfitness;%收敛曲线2,各代群体平均适应值的记录 pos=find(fitness==minfitness);Xp=farm{pos(1)};%第五步:变异for i=1:Nif Pm>rand;%变异概率为PmX=farm{i};I=unidrnd(m);J=unidrnd(n);X(I,J)=1+(P(J)-eps)*rand;farm{i}=X;endendfarm{pos(1)}=Xp;counter=counter+1end%输出结果并绘图figure(1);plotif=1;X=Xp;[Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif);figure(2);plot(LC1);figure(3);plot(LC2);function [Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif)% JSPGA的内联子函数,用于求调度方案的Makespan值% 输入参数列表% X 调度方案的编码矩阵,是一个实数编码的m×n矩阵% T m×n的矩阵,存储m个工件n个工序的加工时间% P 1×n的向量,n个工序中,每一个工序所具有的机床数目% plotif 是否绘甘特图的控制参数% 输出参数列表% Zp 最优的Makespan值% Y1p 最优方案中,各工件各工序的开始时刻% Y2p 最优方案中,各工件各工序的结束时刻% Y3p 最优方案中,各工件各工序使用的机器编号%第一步:变量初始化[m,n]=size(X);Y1p=zeros(m,n);Y2p=zeros(m,n);Y3p=zeros(m,n);%第二步:计算第一道工序的安排Q1=zeros(m,1);Q2=zeros(m,1);R=X(:,1);%取出第一道工序Q3=floor(R);%向下取整即得到各工件在第一道工序使用的机器的编号%下面计算各工件第一道工序的开始时刻和结束时刻for i=1:P(1)%取出机器编号pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号lenpos=length(pos);if lenpos>=1Q1(pos(1))=0;if lenpos>=2for j=2:lenposQ1(pos(j))=Q2(pos(j-1));Q2(pos(j))=Q2(pos(j-1))+T(pos(j),1);endendendendY1p(:,1)=Q1;Y3p(:,1)=Q3;%第三步:计算剩余工序的安排for k=2:nR=X(:,k);%取出第k道工序Q3=floor(R);%向下取整即得到各工件在第k道工序使用的机器的编号%下面计算各工件第k道工序的开始时刻和结束时刻for i=1:P(k)%取出机器编号pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号lenpos=length(pos);if lenpos>=1EndTime=Y2p(pos,k-1);%取出这些机器在上一个工序中的结束时刻POS=zeros(1,lenpos);%上一个工序完成时间由早到晚的排序for jj=1:lenposPOS(jj)=ppp(1);EndTime(ppp(1))=Inf;end%根据上一个工序完成时刻的早晚,计算各工件第k道工序的开始时刻和结束时刻Q1(pos(POS(1)))=Y2p(pos(POS(1)),k-1);Q2(pos(POS(1)))=Q1(pos(POS(1)))+T(pos(POS(1)),k);%前一个工件的结束时刻if lenpos>=2for j=2:lenposQ1(pos(POS(j)))=Y2p(pos(POS(j)),k-1);%预定的开始时刻为上一个工序的结束时刻if Q1(pos(POS(j)))<Q2(pos(POS(j-1)))%如果比前面的工件的结束时刻还早Q1(pos(POS(j)))=Q2(pos(POS(j-1)));endendendendendY1p(:,k)=Q1;Y2p(:,k)=Q2;Y3p(:,k)=Q3;end%第四步:计算最优的Makespan值Y2m=Y2p(:,n);Zp=max(Y2m);%第五步:绘甘特图if plotiffor i=1:mfor j=1:nmPoint1=Y1p(i,j);mPoint2=Y2p(i,j);mText=m+1-i;PlotRec(mPoint1,mPoint2,mText);Word=num2str(Y3p(i,j));%text(0.5*mPoint1+0.5*mPoint2,mText-0.5,Word);hold onx1=mPoint1;y1=mText-1;x2=mPoint2;y2=mText-1;x4=mPoint1;y4=mText;%fill([x1,x2,x3,x4],[y1,y2,y3,y4],'r');fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,0.5,1]);text(0.5*mPoint1+0.5*mPoint2,mText-0.5,Word);endendendfunction PlotRec(mPoint1,mPoint2,mText)% 此函数画出小矩形% 输入:% mPoint1 输入点1,较小,横坐标% mPoint2 输入点2,较大,横坐标% mText 输入的文本,序号,纵坐标vPoint = zeros(4,2) ;vPoint(1,:) = [mPoint1,mText-1];vPoint(2,:) = [mPoint2,mText-1];vPoint(3,:) = [mPoint1,mText];vPoint(4,:) = [mPoint2,mText];plot([vPoint(1,1),vPoint(2,1)],[vPoint(1,2),vPoint(2,2)]); hold on ;plot([vPoint(1,1),vPoint(3,1)],[vPoint(1,2),vPoint(3,2)]); plot([vPoint(2,1),vPoint(4,1)],[vPoint(2,2),vPoint(4,2)]); plot([vPoint(3,1),vPoint(4,1)],[vPoint(3,2),vPoint(4,2)]);。
带多处理器的混合流水车间调度matlab程序

function [Zp,Y1p,Y2p,Y3p,Xp,LC1,LC2]=JSPGA(M,N,Pm,T,P)T=[8 90 0 0 0 0 0 0 0 0;0 0 99 62 0 0 0 0 0 0;0 0 0 0 76 94 0 0 0 0;0 0 0 0 0 0 14 68 0 0;0 0 0 0 0 0 0 0 88 27];P=[2;1;4;2;4;1;1;2;4;2];N=100;M=400;Pm=0.75;%--------------------------------------------------------------------------% JSPGA.m% 流水线型车间作业调度遗传算法% 输入参数列表% M 遗传进化迭代次数% N 种群规模(取偶数)% Pm 变异概率% T m×n的矩阵,存储m个工件n个工序的加工时间% P 1×n的向量,n个工序中,每一个工序所具有的机床数目% 输出参数列表% Zp 最优的Makespan值% Y1p 最优方案中,各工件各工序的开始时刻,可根据它绘出甘特图% Y2p 最优方案中,各工件各工序的结束时刻,可根据它绘出甘特图% Y3p 最优方案中,各工件各工序使用的机器编号% Xp 最优决策变量的值,决策变量是一个实数编码的m×n矩阵% LC1 收敛曲线1,各代最优个体适应值的记录% LC2 收敛曲线2,各代群体平均适应值的记录% 最后,程序还将绘出三副图片:两条收敛曲线图和甘特图(各工件的调度时序图)%第一步:变量初始化[m,n]=size(T);%m是总工件数,n是总工序数Xp=zeros(m,n);%最优决策变量LC1=zeros(1,M);%收敛曲线1LC2=zeros(1,N);%收敛曲线2%第二步:随机产生初始种群farm=cell(1,N);%采用细胞结构存储种群for k=1:NX=zeros(m,n);for j=1:nfor i=1:mX(i,j)=1+(P(j)-eps)*rand;endendfarm{k}=X;endcounter=0;%设置迭代计数器while counter<M%停止条件为达到最大迭代次数%第三步:交叉newfarm=cell(1,N);%交叉产生的新种群存在其中Ser=randperm(N);for i=1:2:(N-1)A=farm{Ser(i)};%父代个体B=farm{Ser(i+1)};%父代相邻个体Manner=unidrnd(2);%随机选择交叉方式if Manner==1cp=unidrnd(m-1);%随机选择交叉点%双亲双子单点交叉a=[A(1:cp,:);B((cp+1):m,:)];%子代个体b=[B(1:cp,:);A((cp+1):m,:)];elsecp=unidrnd(n-1);%随机选择交叉点a=[A(:,1:cp),B(:,(cp+1):n)];%双亲双子单点交叉 b=[B(:,1:cp),A(:,(cp+1):n)];endnewfarm{i}=a;%交叉后的子代存入newfarmnewfarm{i+1}=b;end%新旧种群合并FARM=[farm,newfarm];%第四步:选择复制FITNESS=zeros(1,2*N);fitness=zeros(1,N);plotif=0;for i=1:(2*N)X=FARM{i};Z=COST(X,T,P,plotif);%调用计算费用的子函数FITNESS(i)=Z;end%选择复制采取两两随机配对竞争的方式,具有保留最优个体的能力 Ser=randperm(2*N);for i=1:Nf1=FITNESS(Ser(2*i-1));f2=FITNESS(Ser(2*i));if f1<=f2farm{i}=FARM{Ser(2*i-1)};fitness(i)=FITNESS(Ser(2*i-1));elsefarm{i}=FARM{Ser(2*i)};fitness(i)=FITNESS(Ser(2*i));endend%记录最佳个体和收敛曲线minfitness=min(fitness);meanfitness=mean(fitness);LC1(counter+1)=minfitness;%收敛曲线1,各代最优个体适应值的记录 LC2(counter+1)=meanfitness;%收敛曲线2,各代群体平均适应值的记录 pos=find(fitness==minfitness);Xp=farm{pos(1)};%第五步:变异for i=1:Nif Pm>rand;%变异概率为PmX=farm{i};I=unidrnd(m);J=unidrnd(n);X(I,J)=1+(P(J)-eps)*rand;farm{i}=X;endendfarm{pos(1)}=Xp;counter=counter+1;end%输出结果并绘图figure(1);plotif=1;X=Xp;[Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif);figure(2);plot(LC1);figure(3);plot(LC2);function [Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif)% JSPGA的内联子函数,用于求调度方案的Makespan值% 输入参数列表% X 调度方案的编码矩阵,是一个实数编码的m×n矩阵% T m×n的矩阵,存储m个工件n个工序的加工时间% P 1×n的向量,n个工序中,每一个工序所具有的机床数目% plotif 是否绘甘特图的控制参数% 输出参数列表% Zp 最优的Makespan值% Y1p 最优方案中,各工件各工序的开始时刻% Y2p 最优方案中,各工件各工序的结束时刻% Y3p 最优方案中,各工件各工序使用的机器编号%第一步:变量初始化[m,n]=size(X);Y1p=zeros(m,n);Y2p=zeros(m,n);Y3p=zeros(m,n);%第二步:计算第一道工序的安排Q1=zeros(m,1);Q2=zeros(m,1);R=X(:,1);%取出第一道工序Q3=floor(R);%向下取整即得到各工件在第一道工序使用的机器的编号%下面计算各工件第一道工序的开始时刻和结束时刻for i=1:P(1)%取出机器编号pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号lenpos=length(pos);if lenpos>=1Q1(pos(1))=0;if lenpos>=2for j=2:lenposQ1(pos(j))=Q2(pos(j-1));Q2(pos(j))=Q2(pos(j-1))+T(pos(j),1);endendendendY1p(:,1)=Q1;Y3p(:,1)=Q3;%第三步:计算剩余工序的安排for k=2:nR=X(:,k);%取出第k道工序Q3=floor(R);%向下取整即得到各工件在第k道工序使用的机器的编号%下面计算各工件第k道工序的开始时刻和结束时刻for i=1:P(k)%取出机器编号pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号lenpos=length(pos);if lenpos>=1EndTime=Y2p(pos,k-1);%取出这些机器在上一个工序中的结束时刻POS=zeros(1,lenpos);%上一个工序完成时间由早到晚的排序for jj=1:lenposPOS(jj)=ppp(1);EndTime(ppp(1))=Inf;end%根据上一个工序完成时刻的早晚,计算各工件第k道工序的开始时刻和结束时刻Q1(pos(POS(1)))=Y2p(pos(POS(1)),k-1);Q2(pos(POS(1)))=Q1(pos(POS(1)))+T(pos(POS(1)),k);%前一个工件的结束时刻if lenpos>=2for j=2:lenposQ1(pos(POS(j)))=Y2p(pos(POS(j)),k-1);%预定的开始时刻为上一个工序的结束时刻if Q1(pos(POS(j)))<Q2(pos(POS(j-1)))%如果比前面的工件的结束时刻还早Q1(pos(POS(j)))=Q2(pos(POS(j-1)));endendendendendY1p(:,k)=Q1;Y2p(:,k)=Q2;Y3p(:,k)=Q3;end%第四步:计算最优的Makespan值Y2m=Y2p(:,n);Zp=max(Y2m);%第五步:绘甘特图if plotiffor i=1:mfor j=1:nmPoint1=Y1p(i,j);mPoint2=Y2p(i,j);mText=m+1-i;PlotRec(mPoint1,mPoint2,mText);Word=num2str(Y3p(i,j));%text(0.5*mPoint1+0.5*mPoint2,mText-0.5,Word);hold onx1=mPoint1;y1=mText-1;x2=mPoint2;y2=mText-1;x4=mPoint1;y4=mText;%fill([x1,x2,x3,x4],[y1,y2,y3,y4],'r');fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,0.5,1]);text(0.5*mPoint1+0.5*mPoint2,mText-0.5,Word);endendendfunction PlotRec(mPoint1,mPoint2,mText)% 此函数画出小矩形% 输入:% mPoint1 输入点1,较小,横坐标% mPoint2 输入点2,较大,横坐标% mText 输入的文本,序号,纵坐标vPoint = zeros(4,2) ;vPoint(1,:) = [mPoint1,mText-1];vPoint(2,:) = [mPoint2,mText-1];vPoint(3,:) = [mPoint1,mText];vPoint(4,:) = [mPoint2,mText];plot([vPoint(1,1),vPoint(2,1)],[vPoint(1,2),vPoint(2,2)]); hold on ;plot([vPoint(1,1),vPoint(3,1)],[vPoint(1,2),vPoint(3,2)]); plot([vPoint(2,1),vPoint(4,1)],[vPoint(2,2),vPoint(4,2)]); plot([vPoint(3,1),vPoint(4,1)],[vPoint(3,2),vPoint(4,2)]);。
matlab模拟退火算法单约束车间流水线调度解决实现及示例
matlab模拟退⽕算法单约束车间流⽔线调度解决实现及⽰例⽬录⼀、车间调度简介1 车间调度定义2 传统作业车间调度3 柔性作业车间调度⼆、模拟退⽕算法简介三、部分源代码四、运⾏结果五、matlab版本及参考⽂献⼀、车间调度简介1 车间调度定义车间调度是指根据产品制造的合理需求分配加⼯车间顺序,从⽽达到合理利⽤产品制造资源、提⾼企业经济效益的⽬的。
车间调度问题从数学上可以描述为有n个待加⼯的零件要在m台机器上加⼯。
问题需要满⾜的条件包括每个零件的各道⼯序使⽤每台机器不多于1次,每个零件都按照⼀定的顺序进⾏加⼯。
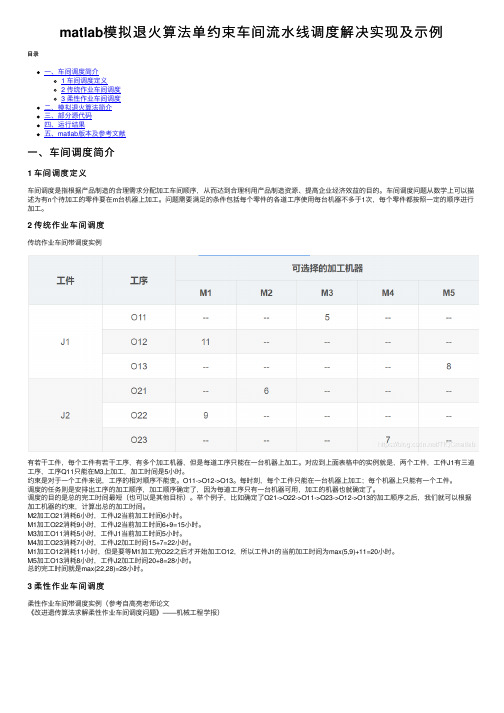
2 传统作业车间调度传统作业车间带调度实例有若⼲⼯件,每个⼯件有若⼲⼯序,有多个加⼯机器,但是每道⼯序只能在⼀台机器上加⼯。
对应到上⾯表格中的实例就是,两个⼯件,⼯件J1有三道⼯序,⼯序Q11只能在M3上加⼯,加⼯时间是5⼩时。
约束是对于⼀个⼯件来说,⼯序的相对顺序不能变。
O11->O12->O13。
每时刻,每个⼯件只能在⼀台机器上加⼯;每个机器上只能有⼀个⼯件。
调度的任务则是安排出⼯序的加⼯顺序,加⼯顺序确定了,因为每道⼯序只有⼀台机器可⽤,加⼯的机器也就确定了。
调度的⽬的是总的完⼯时间最短(也可以是其他⽬标)。
举个例⼦,⽐如确定了O21->O22->O11->O23->O12->O13的加⼯顺序之后,我们就可以根据加⼯机器的约束,计算出总的加⼯时间。
M2加⼯O21消耗6⼩时,⼯件J2当前加⼯时间6⼩时。
M1加⼯O22消耗9⼩时,⼯件J2当前加⼯时间6+9=15⼩时。
M3加⼯O11消耗5⼩时,⼯件J1当前加⼯时间5⼩时。
M4加⼯O23消耗7⼩时,⼯件J2加⼯时间15+7=22⼩时。
M1加⼯O12消耗11⼩时,但是要等M1加⼯完O22之后才开始加⼯O12,所以⼯件J1的当前加⼯时间为max(5,9)+11=20⼩时。
M5加⼯O13消耗8⼩时,⼯件J2加⼯时间20+8=28⼩时。
Matlab优化算法在生产调度中的应用

Matlab优化算法在生产调度中的应用在现代制造业中,生产调度是企业保证生产效率、提高产品质量的重要环节。
为了能够更好地进行生产调度,优化算法被广泛应用于解决各种工程问题。
其中,Matlab优化算法以其强大的数学计算和优化能力深受生产调度领域的青睐。
本文将探讨Matlab优化算法在生产调度中的应用。
1. 生产调度的挑战随着全球化经济的快速发展,企业面临着越来越复杂的生产调度问题。
生产调度需要在有限的资源下,有效地组织生产活动,最大化利用资源,同时满足客户需求和市场变化。
然而,生产调度问题存在着很多挑战,比如任务分配、机器工序顺序、作业优化等。
这些问题需要高效的算法来求解,并且要在短时间内给出最优解。
2. Matlab优化算法概述Matlab是一种广泛应用于科学计算和工程领域的高级计算机语言和环境。
Matlab提供了许多优化函数和工具箱,能够快速实现各种优化算法。
其中,常见的优化算法包括遗传算法、粒子群算法、模拟退火算法等。
这些算法能够在多个目标函数和约束条件下找到最优解。
3. Matlab优化算法在生产调度中的应用案例为了更好地理解Matlab优化算法在生产调度中的应用,下面将介绍两个实际案例。
3.1. 任务分配问题在一个工厂中,有多个任务需要被分配给多个机器进行加工。
每个任务有不同的工艺流程和时间要求,而每个机器也有不同的加工能力和可用时间。
如何通过合理的任务分配,使得生产效率最大化成为了一道亟待解决的难题。
通过借助Matlab优化算法,可以建立一个数学模型来解决任务分配问题。
首先,将任务和机器分别表示成变量,然后设置各种限制条件,如时间限制、机器容量等。
接下来,通过设置目标函数,例如最小化加工时间或最大化机器利用率,利用Matlab优化算法求解该数学模型,找到最优的任务分配方案。
这样,在有限的资源下,能够最大程度地提高生产效率。
3.2. 机器工序顺序问题在一家汽车制造企业中,生产线上存在多个机器按照顺序进行工序加工。
matlab车间调度的书籍

matlab车间调度的书籍
车间调度问题是一个经典的组合优化问题,涉及工件在机器上的加工顺序,以最小化某些代价函数,如总完工时间。
使用MATLAB解决此类问题时,可以参考以下书籍:
1. 《MATLAB智能算法30个案例分析》:这本书详细介绍了如何使用MATLAB实现各种智能算法,包括遗传算法、免疫算法、退火算法、粒子群算法、鱼群算法、蚁群算法和神经网络算法等。
其中,第11章专门介绍了基于多层编码遗传算法的车间调度算法。
2. 《智能优化算法及其MATLAB实例(第2版)》:这本书对智能优化算法进行了全面介绍,包括遗传算法、粒子群算法、蚁群算法、模拟退火算法等,并提供了丰富的MATLAB实例。
3. 《MATLAB优化算法源代码》:这本书主要介绍如何使用MATLAB实现各种经典优化算法,包括梯度下降法、牛顿法、遗传算法等。
对于车间调度问题,可以使用其中的遗传算法或模拟退火算法等启发式方法进行求解。
此外,还可以查阅一些关于车间调度问题的学术论文,了解最新的研究进展和算法应用。
总之,通过阅读这些书籍和论文,可以深入了解如何使用MATLAB解决车间调度问题,并掌握相关的优化算法和实现技巧。
matlab生产调度问题及其优化算法

生产调度问题及其优化算法(采用遗传算法与MATLAB编程)信息014 孙卓明二零零三年八月十四日生产调度问题及其优化算法背景及摘要这是一个典型的Job-Shop动态排序问题。
目前调度问题的理论研究成果主要集中在以Job-Shop问题为代表的基于最小化完工时间的调度问题上。
一个复杂的制造系统不仅可能涉及到成千上万道车间调度工序,而且工序的变更又可能导致相当大的调度规模。
解空间容量巨大,N个工件、M台机器的问题包含M(N)!种排列。
由于问题的连环嵌套性,使得用图解方法也变得不切实际。
传统的运筹学方法,即便在单目标优化的静态调度问题中也难以有效应用。
本文给出三个模型。
首先通过贪婪法手工求得本问题最优解,既而通过编解码程序随机模拟优化方案得出最优解。
最后采用现代进化算法中有代表性发展优势的遗传算法。
文章有针对性地选取遗传算法关键环节的适宜方法,采用MATLAB 软件实现算法模拟,得出优化方案,并与计算机随机模拟结果加以比较显示出遗传算法之优化效果。
对车间调度系列问题的有效解决具有一定参考和借鉴价值。
一.问题重述某重型机械厂产品都是单件性的,其中有一车间共有A,B,C,D四种不同设备,现接受6件产品的加工任务,每件产品接受的程序在指定的设备上加工,条件:1、每件产品必须按规定的工序加工,不得颠倒;2、每台设备在同一时间只能担任一项任务。
(每件产品的每个工序为一个任务)问题:做出生产安排,希望在尽可能短的时间里,完成所接受的全部任务。
要求:给出每台设备承担任务的时间表。
注:在上面,机器 A,B,C,D 即为机器 1,2,3,4,程序中以数字1,2,3,4表示,说明时则用A,B,C,D二.模型假设1.每一时刻,每台机器只能加工一个工件,且每个工件只能被一台机器所加工 ,同时加工过程为不间断; 2.所有机器均同时开工,且工件从机器I 到机器J 的转移过程时间损耗不计; 3.各工件必须按工艺路线以指定的次序在机器上加工多次; 4.操作允许等待,即前一操作未完成,则后面的操作需要等待,可用资源有限。
生产调度matlab

function [Zp,Y1p,Y2p,Y3p,Xp,LC1,LC2]=JSPGA(M,N,Pm,T,P)%greemsim原创--------------------------------------------------------------------------% JSPGA.m% 输入参数列表% M 遗传进化迭代次数% N 种群规模(取偶数)% Pm 变异概率% T m×n的矩阵,存储m个工件n个工序的加工时间% P 1×n的向量,n个工序中,每一个工序所具有的机床数目% 输出参数列表% Zp 最优的Makespan值% Y1p 最优方案中,各工件各工序的开始时刻,可根据它绘出甘特图% Y2p 最优方案中,各工件各工序的结束时刻,可根据它绘出甘特图% Y3p 最优方案中,各工件各工序使用的机器编号% Xp 最优决策变量的值,决策变量是一个实数编码的m×n矩阵% LC1 收敛曲线1,各代最优个体适应值的记录% LC2 收敛曲线2,各代群体平均适应值的记录% 最后,程序还将绘出三副图片:两条收敛曲线图和甘特图(各工件的调度时序图)%第一步:变量初始化[m,n]=size(T);%m是总工件数,n是总工序数Xp=zeros(m,n);%最优决策变量LC1=zeros(1,M);%收敛曲线1LC2=zeros(1,N);%收敛曲线2%第二步:随机产生初始种群farm=cell(1,N);%采用细胞结构存储种群for k=1:NX=zeros(m,n);for j=1:nfor i=1:mX(i,j)=1+(P(j)-eps)*rand;endendfarm{k}=X;endcounter=0;%设置迭代计数器while counter<M%停止条件为达到最大迭代次数%第三步:交叉newfarm=cell(1,N);%交叉产生的新种群存在其中Ser=randperm(N);for i=1:2:(N-1)A=farm{Ser(i)}; %父代个体B=farm{Ser(i+1)};Manner=unidrnd(2);%随机选择交叉方式if Manner==1cp=unidrnd(m-1);%随机选择交叉点%双亲双子单点交叉a=[A(1:cp,:);B((cp+1):m,:)];%子代个体b=[B(1:cp,:);A((cp+1):m,:)];elsecp=unidrnd(n-1);%随机选择交叉点a=[A(:,1:cp),B(:,(cp+1):n)];b=[B(:,1:cp),A(:,(cp+1):n)];endnewfarm{i}=a;%交叉后的子代存入newfarm newfarm{i+1}=b;end%新旧种群合并FARM=[farm,newfarm];%第四步:选择复制FITNESS=zeros(1,2*N);fitness=zeros(1,N);plotif=0;for i=1:(2*N)X=FARM{i};Z=COST(X,T,P,plotif);%调用计算费用的子函数FITNESS(i)=Z;end%选择复制采取两两随机配对竞争的方式,具有保留最优个体的能力Ser=randperm(2*N);for i=1:Nf1=FITNESS(Ser(2*i-1));f2=FITNESS(Ser(2*i));if f1<=f2farm{i}=FARM{Ser(2*i-1)};fitness(i)=FITNESS(Ser(2*i-1));elsefarm{i}=FARM{Ser(2*i)};fitness(i)=FITNESS(Ser(2*i));endend%记录最佳个体和收敛曲线minfitness=min(fitness)meanfitness=mean(fitness)LC1(counter+1)=minfitness;%收敛曲线1,各代最优个体适应值的记录LC2(counter+1)=meanfitness;%收敛曲线2,各代群体平均适应值的记录pos=find(fitness==minfitness);Xp=farm{pos(1)};%第五步:变异for i=1:Nif Pm>rand;%变异概率为PmX=farm{i};I=unidrnd(m);J=unidrnd(n);X(I,J)=1+(P(J)-eps)*rand;farm{i}=X;endendfarm{pos(1)}=Xp;counter=counter+1end%输出结果并绘图figure(1);plotif=1;X=Xp;[Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif); figure(2);plot(LC1);figure(3);plot(LC2);function [Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif)% JSPGA的内联子函数,用于求调度方案的Makespan值% 输入参数列表% X 调度方案的编码矩阵,是一个实数编码的m×n矩阵% T m×n的矩阵,存储m个工件n个工序的加工时间% P 1×n的向量,n个工序中,每一个工序所具有的机床数目% plotif 是否绘甘特图的控制参数% 输出参数列表% Zp 最优的Makespan值% Y1p 最优方案中,各工件各工序的开始时刻% Y2p 最优方案中,各工件各工序的结束时刻% Y3p 最优方案中,各工件各工序使用的机器编号%第一步:变量初始化[m,n]=size(X);Y1p=zeros(m,n);Y2p=zeros(m,n);Y3p=zeros(m,n);%第二步:计算第一道工序的安排Q1=zeros(m,1);Q2=zeros(m,1);R=X(:,1);%取出第一道工序Q3=floor(R);%向下取整即得到各工件在第一道工序使用的机器的编号%下面计算各工件第一道工序的开始时刻和结束时刻for i=1:P(1)%取出机器编号pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号lenpos=length(pos);if lenpos>=1Q1(pos(1))=0;Q2(pos(1))=T(pos(1),1);if lenpos>=2for j=2:lenposQ1(pos(j))=Q2(pos(j-1));Q2(pos(j))=Q2(pos(j-1))+T(pos(j),1);endendendendY1p(:,1)=Q1;Y2p(:,1)=Q2;Y3p(:,1)=Q3;%第三步:计算剩余工序的安排for k=2:nR=X(:,k);%取出第k道工序Q3=floor(R);%向下取整即得到各工件在第k道工序使用的机器的编号%下面计算各工件第k道工序的开始时刻和结束时刻for i=1:P(k)%取出机器编号pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号lenpos=length(pos);if lenpos>=1EndTime=Y2p(pos,k-1);%取出这些机器在上一个工序中的结束时刻POS=zeros(1,lenpos);%上一个工序完成时间由早到晚的排序for jj=1:lenposMinEndTime=min(EndTime);ppp=find(EndTime==MinEndTime);POS(jj)=ppp(1);EndTime(ppp(1))=Inf;end%根据上一个工序完成时刻的早晚,计算各工件第k道工序的开始时刻和结束时刻Q1(pos(POS(1)))=Y2p(pos(POS(1)),k-1);Q2(pos(POS(1)))=Q1(pos(POS(1)))+T(pos(POS(1)),k);%前一个工件的结束时刻if lenpos>=2for j=2:lenposQ1(pos(POS(j)))=Y2p(pos(POS(j)),k-1);%预定的开始时刻为上一个工序的结束时刻if Q1(pos(POS(j)))<Q2(pos(POS(j-1)))%如果比前面的工件的结束时刻还早Q1(pos(POS(j)))=Q2(pos(POS(j-1)));endendendendendY1p(:,k)=Q1;Y2p(:,k)=Q2;Y3p(:,k)=Q3;end%第四步:计算最优的Makespan值Y2m=Y2p(:,n);Zp=max(Y2m);%第五步:绘甘特图if plotiffor i=1:mfor j=1:nmPoint1=Y1p(i,j);mPoint2=Y2p(i,j);mText=m+1-i;PlotRec(mPoint1,mPoint2,mText);Word=num2str(Y3p(i,j));text(0.5*mPoint1+0.5*mPoint2,mText-0.5,Word); hold onx1=mPoint1;y1=mText-1;x2=mPoint2;y2=mText-1;x3=mPoint2;y3=mText;x4=mPoint1;y4=mText;fill([x1,x2,x3,x4],[y1,y2,y3,y4],'r');fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,0.5,1]); text(0.5*mPoint1+0.5*mPoint2,mText-0.5,Word); endendendfunction PlotRec(mPoint1,mPoint2,mText)% 此函数画出小矩形% 输入:% mPoint1 输入点1,较小,横坐标% mPoint2 输入点2,较大,横坐标标准文案% mText 输入的文本,序号,纵坐标vPoint = zeros(4,2) ;vPoint(1,:) = [mPoint1,mText-1];vPoint(2,:) = [mPoint2,mText-1];vPoint(3,:) = [mPoint1,mText];vPoint(4,:) = [mPoint2,mText];plot([vPoint(1,1),vPoint(2,1)],[vPoint(1,2),vPoint(2,2)]); hold on ;plot([vPoint(1,1),vPoint(3,1)],[vPoint(1,2),vPoint(3,2)]); plot([vPoint(2,1),vPoint(4,1)],[vPoint(2,2),vPoint(4,2)]); plot([vPoint(3,1),vPoint(4,1)],[vPoint(3,2),vPoint(4,2)]);大全。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%新旧种群合并
FARM=[farm,newfarm];
%第四步:选择复制
FITNESS=zeros(1,2*N);
fitness=zeros(1,N);
plotif=0;
for i=1:(2*N)
X=FARM{i};
end
%输出结果并绘图
figure(1);
plotif=1;
X=Xp;
[Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif);
figure(2);
plot(LC1);
figure(3);
plot(LC2);
function [Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif)
X=zeros(m,n);
for j=1:n
for i=1:m
X(i,j)=1+(P(j)-eps)*rand;
end
end
farm{k}=X;
end
counter=0;%设置迭代计数器
while counter<M%停止条件为达到最大迭代次数
%根据上一个工序完成时刻的早晚,计算各工件第k道工序的开始时刻和结束时刻
Q1(pos(POS(1)))=Y2p(pos(POS(1)),k-1);
Q2(pos(POS(1)))=Q1(pos(POS(1)))+T(pos(POS(1)),k);%前一个工件的结束时刻
% JSPGA的内联子函数,用于求调度方案的Makespan值
% 输入参数列表
% X 调度方案的编码矩阵,是一个实数编码的m×n矩阵
% T m×n的矩阵,存储m个工件n个工序的加工时间
% P 1×n的向量,n个工序中,每一个工序所具有的机床数目
Y2p(:,k)=Q2;
Y3p(:,k)=Q3;
end
%第四步:计算最优的Makespan值
Y2m=Y2p(:,n);
Zp=max(Y2m);
Z=COST(X,T,P,plotif);%调用计算费用的子函数
FITNESS(i)=Z;
end
%选择复制采取两两随机配对竞争的方式,具有保留最优个体的能力
Ser=randperm(2*N);
for i=1:N
f2=FITNESS(Ser(2*i));
else
cp=unidrnd(n-1);%随机选择交叉点
b=[B(:,1:cp),A(:,(cp+1):n)];
end
newfarm{i}=a;%交叉后的子代存入newfarm
newfarm{i+1}=b;
J=unidrnd(n);
X(I,J)=1+(P(J)-eps)*rand;
farm{i}=X;
end
end
farm{pos(1)}=Xp;
counter=counter+1
Q1(pos(POS(j)))=Q2(pos(POS(j-1)));
end
end
end
end
end
Y1p(:,k)=Q1;
%--------------------------------------------------------------------------
% 输入参数列表
% M 遗传进化迭代次数
% N 种群规模(取偶数)
% Pm 变异概率
% T m×n的矩阵,存储m个工件n个工序的加工时间
流水线型车间作业调度问题遗传算法Matlab源码
流水线型车间作业调度问题可以描述如下:n个任务在流水线上进行m个阶段的加工,每一阶段至少有一台机器且至少有一个阶段存在多台机器,并且同一阶段上各机器的处理性能相同,在每一阶段各任务均要完成一道工序,各任务的每道工序可以在相应阶段上的任意一台机器上加工,已知任务各道工序的处理时间,要求确定所有任务的排序以及每一阶段上机器的分配情况,使得调度指标(一般求Makespan)最小。下面的源码是求解流水线型车间作业调度问题的遗传算法通用MATLAB源码,属于GreenSim团队原创作品,转载请注明。
% plotif 是否绘甘特图的控制参数
% 输出参数列表
% Zp 最优的Makespan值
% Y1p 最优方案中,各工件各工序的开始时刻
% Y2p 最优方案中,各工件各工序的结束时刻
% Y3p 最优方案中,各工件各工序使用的机器编号
%第一步:变量初始化
%下面计算各工件第一道工序的开始时刻和结束时刻
for i=1:P(1)%取出机器编号
pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号
lenpos=length(pos);
if lenpos>=1
Q1(pos(1))=0;
POS=zeros(1,lenpos);%上一个工序完成时间由早到晚的排序
for jj=1:lenpos
POS(jj)=ppp(1);
EndTime(ppp(1))=Inf;
end
if lenpos>=2
for j=2:lenpos
Q1(pos(POS(j)))=Y2p(pos(POS(j)),k-1);%预定的开始时刻为上一个工序的结束时刻
if Q1(pos(POS(j)))<Q2(pos(POS(j-1)))%如果比前面的工件的结束时刻还早
% P 1×n的向量,n个工序中,每一个工序所具有的机床数目
% 输出参数列表
% Zp 最优的Makespan值
% Y1p 最优方案中,各工件各工序的开始时刻,可根据它绘出甘特图
% Y2p 最优方案中,各工件各工序的结束时刻,可根据它绘出甘特图
end
%记录最佳个体和收敛曲线
minfitness=min(fitness)
meanfitness=mean(fitness)
LC1(counter+1)=minfitness;%收敛曲线1,各代最优个体适应值的记录
LC2(counter+1)=meanfitness;%收敛曲线2,各代群体平均适应值的记录
function [Zp,Y1p,Y2p,Y3p,Xp,LC1,LC2]=JSPGA(M,N,Pm,T,P)
%--------------------------------------------------------------------------
% JSPGA.m
% 流水线型车间作业调度遗传算法
for i=1:P(k)%取出机器编号
pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号
lenpos=length(pos);
if lenpos>=1
EndTime=Y2p(pos,k-1);%取出这些机器在上一个工farm=cell(1,N);%交叉产生的新种群存在其中
Ser=randperm(N);
for i=1:2:(N-1)
A=farm{Ser(i)};%父代个体
Manner=unidrnd(2);%随机选择交叉方式
if f1<=f2
farm{i}=FARM{Ser(2*i-1)};
fitness(i)=FITNESS(Ser(2*i-1));
else
farm{i}=FARM{Ser(2*i)};
end
% GreenSim团队原创作品,转载请注明
% Email:greensim@
% GreenSim团队主页:/greensim
% 欢迎访问GreenSim——算法仿真团队→/greensim
% Y3p 最优方案中,各工件各工序使用的机器编号
% Xp 最优决策变量的值,决策变量是一个实数编码的m×n矩阵
% LC1 收敛曲线1,各代最优个体适应值的记录
% LC2 收敛曲线2,各代群体平均适应值的记录
% 最后,程序还将绘出三副图片:两条收敛曲线图和甘特图(各工件的调度时序图)
[m,n]=size(X);
Y1p=zeros(m,n);
Y2p=zeros(m,n);
Y3p=zeros(m,n);
%第二步:计算第一道工序的安排
Q1=zeros(m,1);
Q2=zeros(m,1);
R=X(:,1);%取出第一道工序
Q3=floor(R);%向下取整即得到各工件在第一道工序使用的机器的编号
end
end
end
Y1p(:,1)=Q1;
Y3p(:,1)=Q3;
%第三步:计算剩余工序的安排
for k=2:n
R=X(:,k);%取出第k道工序
Q3=floor(R);%向下取整即得到各工件在第k道工序使用的机器的编号
%下面计算各工件第k道工序的开始时刻和结束时刻
%第一步:变量初始化
[m,n]=size(T);%m是总工件数,n是总工序数
Xp=zeros(m,n);%最优决策变量
LC1=zeros(1,M);%收敛曲线1
LC2=zeros(1,N);%收敛曲线2
%第二步:随机产生初始种群
farm=cell(1,N);%采用细胞结构存储种群
for k=1:N
pos=find(fitness==minfitness);
Xp=farm{pos(1)};
%第五步:变异
for i=1:N
if Pm>rand;%变异概率为Pm
