江苏省泰兴中学高一数学苏教版必修2教学案:第1章13平面与平面的位置关系(2)
苏教版高中数学必修2教案汇编

苏教版高中数学必修2教案汇编目录平面的基本性质(第1课时)教案 (1)平面的基本性质(第2课时)教案 (3)平面与平面的位置关系(第1课时)教案 (5)平面与平面的位置关系(第2课时)教案 (7)平面与平面的位置关系(第3课时)教案 (9)直观图画法教案 (11)直线与平面的位置关系(第1课时)教案 (13)直线与平面的位置关系(第2课时)教案 (15)直线与平面的位置关系(第3课时)教案 (17)空间两直线的位置关系(第1课时)教案 (19)空间两直线的位置关系(第2课时)教案 (21)中心投影和平行投影教案 (23)棱柱、棱锥和棱台教案 (25)空间几何体的表面积教案 (27)空间几何体的体积(第1课时)教案 (29)空间几何体的体积(第2课时)教案 (31)立体几何复习(第1课时)教案 (33)立体几何复习(第2课时)教案 (38)立体几何复习(第3课时)教案 (43)平面的基本性质(第1课时)教案教学目标:理解平面的概念。
了解平面的基本性质,能正确使用集合符号表示有关点、线、面的位置关系。
能正确地运用平面的基本性质解决一些简单的问题。
教学重点:平面的基本性质教学难点:平面基本性质的掌握与运用教学过程:一、问题情境:问题1:生活中常见的黑板、平整的操场、桌面、平静的湖面等等,都给我们以平面的印象,你们能举出更多例子吗?它们有何共同特征?二、学生活动:共同探讨上述问题:三、知识建构:1、平面:(1)几何特征:(2)从平移角度:(3)从集合角度:2、平面表示:(1)图形语言:(2)符号语言:思考:一个平面将空间分成几个部分?两个平面呢?3、平面的基本性质:公理1:符号表示:说明:公理2:符号表示:说明:公理3:符号表示:说明:四、知识运用:例1、在长方体ABCD-A ’B ’C ’D ’中,下列命题是否正确?为什么?(1)AC ’在平面CC ’B ’B 内;(2)O ,O ’是平面ABCD ,A ’B ’C ’D ’的中心,则平面AA ’C ’C 与平面B ’BDD ’交线为OO ’;(3)点A 、O 、C 可确定平面;(4)设l ⊆面AC ,直线m ⊆平面D'C ,若l 与m 相交,则交点在直线CD 上。
江苏省泰兴中学高中数学 第1章 立体几何初步 4 平面的基本性质(2)教学案(无答案)苏教版必修2

江苏省泰兴中学高一数学教学案(121)必修 2 平面的基本性质(2)班级 姓名目标要求1、了解公理3及推论1、推论2、推论3,并能运用推论解释生活中的一些现象; 2、初步学习立体几何中的证明.重点难点 公理3及三个推论的理解和运用. 典例剖析例1、已知:,,,A l B l C l D l ∈∈∈∉,(如图),求证:直线,,AD BD CD 共面.例2、求证:两两相交且不过同一点的三条直线在同一个平面内.例3、 如图,在棱长为a 的正方体1111ABCD A B C D -中,M 、N 分别为1AA 、11C D 的中点,过D 、M 、N 三点的平面与直线11A B 交于点P ,求线段1PB 的长.αlC BAD例4、如图,正方体1111ABCD A B C D 中,P ,,M N 分别为CD ,111,A B CC 的中点。
(1)求作直线PN 与平面1111A B C D 交点;(2)过三点P 、M 、N 的平面与平面1111A B C D 交线. 学习反思1、公理3: ; 推论1______________________________________________________; 推论2: ; 推论3:2、证明点线共面问题的基本方法是:由公理3及三个推论直接得出其中一部分点线确定一个平面,由公理1证明其余的点线也在该平面内.3、平面是立体几何中的基本要素之一,公理3及三个推论是判断平面存在性和唯一性的方法. 课堂练习1、 指出下列说法是否正确,并说明理由.(1)四条线段顺次首尾相连接,所得的图形是平面图形;NM1B 1C 1(2)空间三个点确定一个平面;(3)平面α和平面β若有公共点,就不止一个;(4)因为平面型斜屋面不与地面相交,所以屋面所在的平面与地面不相交.2、下列判断中,正确的是 . A 、四边形是平面图形 B 、两个平面有三个公共点,它们必然重合 C 、三条直线两两相交,它们必在同一平面内D 、一条直线与两条平行直线相交,这三条直线必定在同一个平面内3、空间三条直线交于同一点,它们确定平面的个数为n ,则n 的可能取值为 .4、画一个"三个平面两两相交"的直观图.江苏省泰兴中学高一数学作业(121)班级 姓名 得分1、 已知,,A B C 表示不同的点,,,a l m 表示不同的直线,,αβ表示不同的平面,下面推理不正确的是 . A 、若A l ∈,A α∈,B l ∈,B α∈,则l α⊂ B 、若A α∈,A β∈,B α∈,B β∈,则AB αβ=I C 、若,,a l m 两两相交,则,,a l m 一定在同一平面内D 、若,,A B C α∈,,,A B C β∈,且,,A B C 不共线,则,αβ重合2、下列判断中不正确的是 . A 、经过空间任意三点有且只有一个平面 B 、过两条相交直线的平面有且只有一个 C 、若两个平面相交,则它们有且只有一条公共直线 D 、过两条平行直线的平面有且只有一个3、在正方体1111ABCD A B C D -中有下列两个判断:(1)由11A C B 、、确定DOABC的平面是11ADC B ;(2)由11A C B 、、确定的平面与由1A C D 、、确定平面是同一平面.其中 .A 、(1)正确 (2)正确B 、(1)正确 (2)错误C 、(1)错误 (2)正确D 、(1)错误 (2)错误4、已知正方体1111ABCD A B C D -中,,,P Q R 分别是11,,AB AD B C 的中点,那么正方体的过,,P Q R 的截面图形是 .5、给出下列四个命题:(1)圆心和圆上两点可确定一个平面;(2)经过一点的三条直线可以确定一个平面;(3)点A 在平面α内,也在直线a 上,则直线a 在平面α内;(4)平面α与平面β有不在同一条直线上的三个公共点,则平面α与平面β重合;其中正确的序号是 .6、如图,若直线l 与四边形ABCD 的三条边,,AB AD CD 分别交于点,,E F G ,求证ABCD 为平面四边形.7、证明空间无三线共点且两两相交的四条直线在同一平面内.8、如图,正方体1111ABCD A B C D -中,,M N 分别为111,A B CC 的中点,画出过,,D M N 三DFG ACEBl点的平面与平面1BC ,平面1AB 的交线.9、已知直线////a b c ,直线d 与a,b,c 分别相交于点A,B,C,求证:,,,a b c d 四条直线共面.CB A cb ad。
高中数学1.2.4平面与平面的位置关系(2)教案苏教版必修2

124 平面与平面的位置关系(2)教学目标:1.理解和掌握二面角及二面角的平面角;2•理解和掌握直二面角的概念;3.会求二面角的大小;4.理解和掌握面面垂直的判定和性质定理.教材分析及教材内容的定位:空间问题平面化是立体几何的核心思想之一,而这个思想的形成需要一个过程,本节课需要对此进行渗透.因此本节课具有承上启下的作用.教学重点:二面角及二面角的平面角的概念及求法.面面垂直的判定和性质定理.教学难点:如何度量二面角的大小.教学方法:通过直观观察,猜想,研究面面垂直的判定和性质定理,培养学生的自主学习能力,发展学生的合情推理能力及逻辑论证能力.教学过程:一、问题情境1.复习两平面平行的定义、判定、性质;2.复习两平行平面间的距离;3.情境问题:两平面相交也是生产和生活中常见的现象,如发射人造地球卫星时,要使卫星的轨道平面和地球赤道平面形成一定的角度. 笔记本电脑使用时,也需要展开一定的角度等等,那么我们如何来刻画这种两个平面所成的“角”呢?二、学生活动自由发言,通过回忆(异面直线所成的角,直线和平面所成的角),思考类比.三、建构数学1.二面角:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱.每个半平面叫做二面角的面.二面角的表示:一l —.2.二面角的平面角以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.二面角的平面角的三个特征:1.点在棱上;2.线在面内;3.与棱垂直.二面角的平面角的范围:0 < < 180 (平面角是直角的二面角叫作直二面角)二面角的平面角的作法:1.定义法;2.作垂面.3.两平面垂直定义一般地,如果两个平面所成的二面角是直二面角,我们就说这两个平面互相垂直. 记作:为什么教室的门转到任何位置时,门所在平面都与地面垂直?如何判断两个平面垂直?4.两平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直.符号语言:i 图形语言简记为:线面垂直面面垂直四、数学运用1.例题.例1 如图所示:在正方体ABC DAB GD中:(1)求二面角D-ABD的大小;(2)求二面角A-ABD的大小.例2如图,将等腰直角△ ABC沿中线AD折成二面角B—AD- C,使BC= AB求二面角B- AD- C的大小.例3 在正方体ABCDA B i CD中,求证:平面AQ CAL平面B i D DB分析:根据两个平面垂直的判定定理,要证平面ACCAL平面BiDDB只需在其中的一个平面内找一条直线垂直于另一个平面即可.练习:1.判断下列说法是否正确:(1)过平面外一条直线一定可以做一个平面与已知平面平行;(2)过平面外一条直线一定可以做一个平面与已知平面垂直;(3)两平面平行,其中一个平面内的任意一条直线平行于另一个平面;(4)两平面垂直,其中一个平面内的任意一条直线垂直于另一个平面.2•判断下列命题是否正确,并说明理由:(1)若丄,丄,则// .(2)若丄,丄,则丄.(3)若 // i, // 1,丄,贝U i 丄1.五、要点归纳与方法小结本节课学习了以下内容:1.判断两平面垂直的方法有哪些?(1)定义:两平面所成的二面角是直二面角;(2)判定定理:线面垂直面面垂直;2•解题时要注重线线、线面、面面垂直的相互关系;3.理解数学的化归思想.。
苏教版高中学案数学必修第二册课件 第13章 立体几何初步 平面与平面的位置关系 第2课时 两平面垂直

跟踪训练1如图,在三棱锥中,侧棱,,求证:平面平面.
跟踪训练2如图,已知是所在平面外的一点,且平面,平面平面,求证:.
证明如图,在平面内作于点,
平面平面,平面,且,平面.又平面,.平面,平面,.,平面,又平面,.
【题型三】线面垂直、面面垂直的综合问题
例3如图1,在平面四边形中,,,,将沿边折起如图2,使________,,分别为,的中点.在题目横线上选择下述其中一个条件,然后解答此题.①;②平面平面.
续表
跟踪训练4[2023泰州期中]如图,在直棱柱中,,,则二面角的平面角的正弦值为___.
[解析]过作,交于,过作,交于,连接,如图.
因为三棱柱为直三棱柱,故,所以平面.又,平面,所以,.又,所以平面,又平面,所以,故是二面角的平面角的补角.因为,,所以,,.在直角三角形中,.
作垂直于直线的射线,,则射线和构成的叫作二面角的平面角.平面角是直角的二面角叫作直二面角.
知识点2. 平面与平面垂直的定义与判定
1.平面与平面垂直定义定义:两个平面相交,如果它们所成的二面角是直二面角,那么就说这两个平面垂直.表示方法:平面与垂直,记作.画法:两个互相垂直的平面通常把直立平面的竖边画成与水平平面的横边垂直.如图:
【课标要求】1.理解二面角及其平面角的概念.2.掌握两个平面互相垂直的定义和画法.3.理解并掌握两个平面垂直的判定定理和性质定理,并能解决有关面面垂直的问题.
1
要点深化·核心知识提炼
高中数学新苏教版精品教案《苏教版高中数学必修2 1.2.4 平面与平面的位置关系》2

平面与平面的平行〔一〕
教学目标
1、理解并掌握两个平面平行、两个平面相交的定义;
2、掌握两个平面平行的判定和性质定理,并能运用其解决一些具体问题;
3、理解面面垂直的性质定理,能用面面垂直的性质定理证明空间中线面的垂直关系;
4、理解线线平行、线面平行、面面平行;线线垂直、线面垂直、面面垂直内在联系
教学重点平面与平面平行、垂直的判定定理和性质定理
教学难点平行的相互转化,垂直的相互转化
教学过程
1、观察书上第43页图1—2—40,面ABCD与面位置关系是;
面ABCD与面位置关系是;
2、两平面平行定义:;
3、两个平面相交定义:;
4、空间两平面位置关系:
5、两个平面平行的判定定理:
;图:
符号表示: ;
6、设E,F,E 1,F 1分别是长方体ABCD -A 1B 1C 1D 1的棱AB,CD,A 1B 1,C 1D 1的中点, 那么平面ED 与平面的位置关系为 ;
探究一:
●如图, 在正方体ABCD -A 1B 1C 1D 1中,求证: 平面A 1BD
探究二:
●正方体ABCD -A 1B 1C 1D 1中,点F 为A 1D 的中点. 〔1〕求证:A 1B ∥平面AFC ;
〔2〕求证:平面A 1B C 1∥平面AFC .
探究三:
●,垂足为A ,,垂足为B ,求证
回忆反思:
1、平面与平面平行、垂直的判定和性质定理。
B A
C
D B 1
C 1
D 1
A 1 F
2、线线平行、线面平行、面面平行如何相互转化?
3、线线垂直、线面垂直、面面垂直如何相互转化?。
高中数学新苏教版精品教案《苏教版高中数学必修2 1.2.4 平面与平面的位置关系》

教学设计说明---------平面与平面平行的判定一教材内容解析本节课是平面与平面位置关系的第一课时,主要内容是两个平面平行的判定定理及其应用,它是在学生学习了空间两直线位置关系、空间直线和平面位置关系之后,又一种图形直角的位置关系的研究,为后面学习两个平面平行的性质以及将来研究多面体奠定了基础。
本节把面面位置关系与线面位置关系类比,把面面平行的判定与线面平行的判定类比,渗透类比的数学方法。
定理的证明和应用体现了线线平行、线面平行到面面平行的转化,体现了转化的数学思想。
二教学目标设置1、知识与技能:理解平面与平面平行的判定定理,并会初步运用。
转化与化归思想在解决问题中的运用。
通过问题解决,进一步培养学生观察、发现的能力和空间想像能力。
2、过程与方法启发式。
以实际情景(三角板实验),启发、引导学生逐步经历定理的直观感知过程。
指导学生进行合情推理。
对于立体几何的学习,学生已初步入门,让学生自己主动地去获取知识、发现问题、教师予以指导,帮助学生合情推理、澄清概念、加深认识、正确运用。
3、情感态度与价值观让学生在发现中学习,增强学习的积极性;培养学生主动探究知识、合作交流的意识,在体验数学美的过程中激发学生的学习兴趣,从而培养学生勤于动手、勤于思考的良好习惯。
三学生学情分析立体几何的学习,学生已初步入门,上一届线面平行的判定为学生学习本节的内容打下良好的基础。
高一学生已经有了自己的判断,合作,交流的能力,但是课堂的活动性不强,基于此现象,老师应充分利用自己的教学智慧和课堂组织能力积极调动学生的积极性,让学生积极参与到课堂的教学中来。
基于以上情况,本人选择了自主探究,合作交流,让学生通过自己的实践和思考去发现问题,解决问题。
四教学策略本节课本着“教师为主导,学生为主体,课本为主线”的原则进行设计,教师的主导作用,在于激发学生的求知欲。
通过实际情境,让学生主动参与探究过程,激发学生的学习兴趣,而后的层层设问,引导学生步入问题情境,师生共同推进课堂教学活动。
苏教版江苏省泰兴中学高一数学必修2教学案:第1章4平面的基本性质(2)
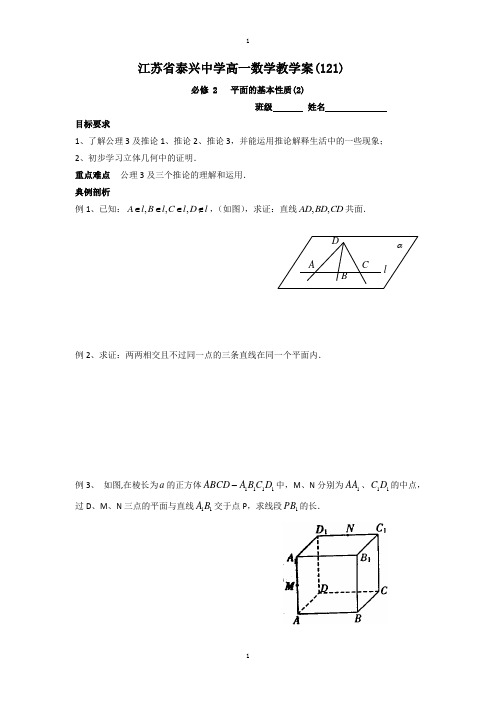
江苏省泰兴中学高一数学教学案(121)必修 2 平面的基本性质(2)班级 姓名目标要求1、了解公理3及推论1、推论2、推论3,并能运用推论解释生活中的一些现象; 2、初步学习立体几何中的证明.重点难点 公理3及三个推论的理解和运用. 典例剖析例1、已知:,,,A l B l C l D l ∈∈∈∉,(如图),求证:直线,,AD BD CD 共面.例2、求证:两两相交且不过同一点的三条直线在同一个平面内.例3、 如图,在棱长为a 的正方体1111ABCD A B C D -中,M 、N 分别为1AA 、11C D 的中点,过D 、M 、N 三点的平面与直线11A B 交于点P ,求线段1PB 的长.例4、如图,正方体1111ABCD A B C D -中,P ,,M N 分别为CD ,111,A B CC 的中点。
(1)求作直线PN 与平面1111A B C D 交点;(2)过三点P 、M 、N 的平面与平面1111A B C D 交线.学习反思1、公理3: ; 推论1______________________________________________________; 推论2: ; 推论3:2、证明点线共面问题的基本方法是:由公理3及三个推论直接得出其中一部分点线确定一个平面,由公理1证明其余的点线也在该平面内.3、平面是立体几何中的基本要素之一,公理3及三个推论是判断平面存在性和唯一性的方法. 课堂练习1、 指出下列说法是否正确,并说明理由.(1)四条线段顺次首尾相连接,所得的图形是平面图形; (2)空间三个点确定一个平面;(3)平面α和平面β若有公共点,就不止一个;(4)因为平面型斜屋面不与地面相交,所以屋面所在的平面与地面不相交.2、下列判断中,正确的是 . A 、四边形是平面图形 B 、两个平面有三个公共点,它们必然重合 C 、三条直线两两相交,它们必在同一平面内D 、一条直线与两条平行直线相交,这三条直线必定在同一个平面内3、空间三条直线交于同一点,它们确定平面的个数为n ,则n 的可能取值为 .4、画一个"三个平面两两相交"的直观图.NM1B 1C 1江苏省泰兴中学高一数学作业(121)班级 姓名 得分1、 已知,,A B C 表示不同的点,,,a l m 表示不同的直线,,αβ表示不同的平面,下面推理不正确的是 . A 、若A l ∈,A α∈,B l ∈,B α∈,则l α⊂ B 、若A α∈,A β∈,B α∈,B β∈,则AB αβ=C 、若,,a l m 两两相交,则,,a l m 一定在同一平面内D 、若,,A B C α∈,,,A B C β∈,且,,A B C 不共线,则,αβ重合2、下列判断中不正确的是 . A 、经过空间任意三点有且只有一个平面 B 、过两条相交直线的平面有且只有一个 C 、若两个平面相交,则它们有且只有一条公共直线 D 、过两条平行直线的平面有且只有一个3、在正方体1111ABCD A B C D -中有下列两个判断:(1)由11A C B 、、确定的平面是11ADC B ;(2)由11A C B 、、确定的平面与由1A C D 、、确定平面是同一平面.其中 .A 、(1)正确 (2)正确B 、(1)正确 (2)错误C 、(1)错误 (2)正确D 、(1)错误 (2)错误4、已知正方体1111ABCD A B C D -中,,,P Q R 分别是11,,AB AD B C 的中点,那么正方体的过,,P Q R 的截面图形是 .5、给出下列四个命题:(1)圆心和圆上两点可确定一个平面;(2)经过一点的三条直线可以确定一个平面;(3)点A 在平面α内,也在直线a 上,则直线a 在平面α内;(4)平面α与平面β有不在同一条直线上的三个公共点,则平面α与平面β重合;其中正确的序号是 .6、如图,若直线l 与四边形ABCD 的三条边,,AB AD CD 分别交于点,,E F G ,求证ABCD 为平面四边形.D GCBlDO 1OD 1C 1B 1ABCA 17、证明空间无三线共点且两两相交的四条直线在同一平面内.8、如图,正方体1111ABCD A B C D 中,,M N 分别为111,A B CC 的中点,画出过,,D M N 三点的平面与平面1BC ,平面1AB 的交线.9、已知直线////a b c ,直线d 与a,b,c 分别相交于点A,B,C,求证:,,,a b c d 四条直线共面.C B Ac ba dNM11C 1。
江苏省泰兴中学高一数学苏教版必修2教学案:第1章8直线与平面的位置关系(2)
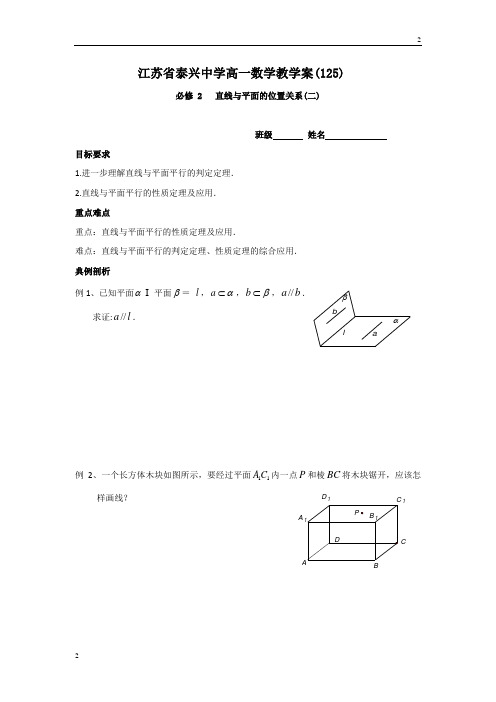
江苏省泰兴中学高一数学教学案(125)必修 2 直线与平面的位置关系(二)班级 姓名目标要求1.进一步理解直线与平面平行的判定定理.2.直线与平面平行的性质定理及应用. 重点难点重点:直线与平面平行的性质定理及应用.难点:直线与平面平行的判定定理、性质定理的综合应用. 典例剖析 例1、已知平面α平面β= l ,a α⊂,b β⊂,//a b .求证://a l .例2、一个长方体木块如图所示,要经过平面11A C 内一点P 和棱BC 将木块锯开,应该怎样画线?albβαBCA D 11例3、如图,CD αβ=,EF αγ=,AB βγ=,//AB α.求证://CD EF .例4、求证:如果一条直线和两个相交平面均平行,那么这条直线就和它们的交线平行. 学习反思直线与平面平行的判定定理 ________________________________________;γβFEDCBAα直线与平面平行的性质定理是 . 两定理说明了 和 可以相互转化.课堂练习1、判断命题的真假(1)若直线//a 平面α,则//a α内任意直线; ( ) (2)若直线//a 平面α,则//a α内无数条直线; ( ) (3)若直线//a 平面α内无数条直线,则//a α; ( ) (4)若,a b 异面,则过不在,a b 上的任一点o 总有一个平面与,a b 都平行.( )2、如图,//,//,,AB AC BD C D ααα∈∈. 求证:AC BD =.3、在正方体1AC 中,分别作出符合下列条件的截面:(不需要写作法) (1)过正方体三个顶点且与直线AC 平行; (2)过BD 且与1A C 平行.DCBAα1A 1C1A 1C江苏省泰兴中学高一数学作业(125)班级 姓名 得分1、已知直线//a b ,且a 与平面α相交,则b 与α的位置关系是 .2、过平面外一点与已知平面平行的直线有 条.3、a ,b 是两条不重合的直线,给出以下四个命题:①若||,,||a b b a αα⊂则 ②若||,,||a b a b αα⊂平面则 ③若||,a b ||,a α平面则||b α ④若||,||,||a b a b αα平面平面则 其中真命题的序号是_________________. 4、下面给出了四个命题①如果a 、b 是两条直线,且a||b ,那么a 平行于经过b 的任何一个平面 ②如果直线a 和平面α满足a||α,那么a 与α内的任何直线平行 ③如果直线a 、b 满足a||α,b||α,则直线a||b④如果直线a ,b 和平面α满足a||b ,a||α,b α⊄,那么b||α 其中正确的序号是_______________. 5、如图,在三棱柱111ABC A B C -中,111,,//E B C F B C E F C C ∈∈,点M ∈侧面 11AA B B , 点,,M E F 确定平面γ.试作出平面γ与三棱柱111ABC A B C -表面的交线,并写出作法.1A C6、如图,四边形EFGH 为空间四边形ABCD 的一个截面,若截面为平行四边形。
江苏省泰兴中学高一数学苏教版必修2教学案:第1章13平面与平面的位置关系(2)

江苏省泰兴中学高一数学教学案(130)必修 2 平面与平面的位置关系(2)班级 姓名目标要求1、进一步掌握两平面平行的判定定理及其应用;2、理解两平面平行的性质定理及其应用;3、理解两个平行平面间的距离. 重点难点重点:两平面平行的性质定理及其应用; 难点:线线、线面、面面平行之间的相互转化. 典例剖析例1、求证:如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.例2、已知平面//α平面β,且,αβ之间的距离为12,过点P (P 在,αβ的外侧)的直线交,αβ于点,A B ,且2PA PB =,求点P 到平面α的距离.例3、已知平面α//平面β,,AB CD 是夹在这两个平面之间的线段,且,,AE EB CG GD ==AB 、CD 异面. 求证: //EG 平面β.学习反思1、两平面平行的性质定理是 , 其实质是 .2、根据所给图形,写出两个正确的命题:(1)(2) 3、领悟转化思想:线//线线//面面//面课堂练习1、下列命题中,正确命题的序号是__________________.(1)、一条直线在两个平行平面中的一个平面内,则在另一个平面内必有一条直线与这条直线平行 (2)、两条平行线中的一条垂直于两个平行平面中的一个平面,则另一条一定垂直于另一个平面 (3)、有两边平行,另两边分别在两平行平面内的四边形是平行四边形 (4)、若两平面平行,则分别在这两个平面内的两条直线互相平行2、已知平面α//平面β,则下列四个命题正确命题的序号是_________________. (1)、平面α内的一条直线可以和平面β内的无数条直线平行 (2)、平面α内至少有两条直线与平面β平行 (3)、平面α内的直线不可能与平面β内的直线垂直 (4)、平面α内的直线与平面β内的直线不可能相交3、下列命题正确的序号是 _______________.(1)、夹在两个平行平面间的平行线段相等,平行线段的长度叫做两个平行平面间的距离 (2)、两个平行平面间的公垂线段长度相等且互相平行,公垂线段的长度叫做两个平行平面间的距离lαβ(3)、夹在两平行平面间的两线段相等,则这两条线段所在直线平行 (4)、平面α平面βa =,平面α平面γb =,//a b ,那么β//γ4、夹在平行平面,αβ间的线段8AB =,AB 与α成45角,则,αβ间的距离为5、求证:夹在两个平行平面间的平行线段相等.江苏省泰兴中学高一数学作业(130)班级 姓名 得分1、若平面//α平面β,直线a α⊂,点B β∈,则在平面β内过点B 的所有直线中( ) A 、不一定存在与a 平行的直线 B 、只有两条与a 平行的直线 C 、存在无数多条与a 平行的直线 D 、存在唯一的一条与a 平行的直线2、下列命题中, 正确命题的序号的是__________________. (1)、平面//α平面β,则平面α内任一直线//a β (2)、直线//a α,直线,b a ⊥则b α⊥ (3)、若直线m,n 都平行于平面α,则//m n(4)、平面α内的两条直线平行于β,则平面//α平面β3、给出下列命题:①若平面α内有无数个点到平面β的距离相等,则//αβ;②若平面α内有不共线三点到平面β的距离相等,则//αβ;③平行于同一条直线的两个平面平行;④垂直于同一条直线的两个平面平行;⑤与同一条直线成等角的两个平面平行;⑥若在空间内两条异面直线同时平行于两个平面,则这两个平面平行.其中所有正确命题的序号为_____________.4、如右图,直线,AC DF 被三个平行平面,,αβγ所截,若AC 与α成30,4,12,10AB BC DF ===,则平面,βγ之间的距离为 ,DE = ,EF = .5、如图,有一块长方体的木料,经过木料表面1111A B C D 内的一点P , 在这个面内画线段,使其与木料表面ABCD 的线段EF 平行, 应该怎样画?6、已知两平行平面,αβ,点P 到α的距离为2cm ,P 到β的距离为3cm ,过P 点的直线与,αβ 分别交于,A B 两点,且8AB cm =,求直线AB 与α所成角的正弦值.7、如图,正方体1111ABCD A B C D -中,点N 在BD 上,点M 在1B C 上,且CM DN =. 求证://MN 平面11AA B B .A 1CABMD 1C 1B 1A 18、四棱柱1111ABCD A B C D 的相对侧面分别平行,过它的一个顶点A 的一个平面截它的 四个侧面得四边形AMFN . 求证:四边形AMFN 是平行四边形.。
苏教版江苏省泰兴中学高一数学必修2教学案:第1章15平面与平面的位置关系(4)
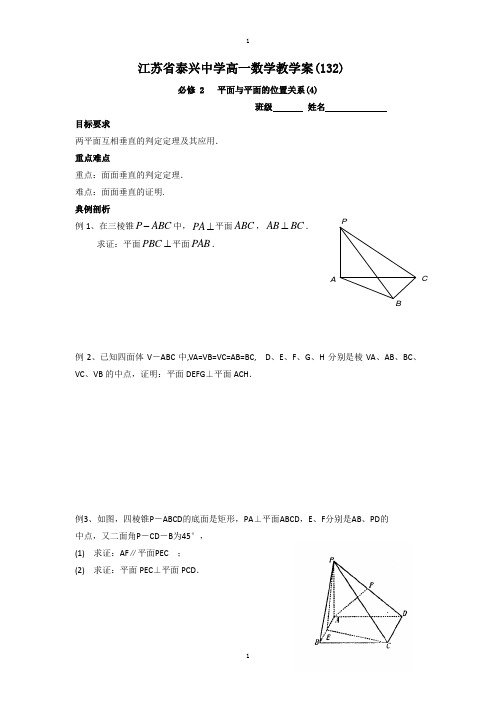
江苏省泰兴中学高一数学教学案(132)必修 2 平面与平面的位置关系(4)班级 姓名目标要求两平面互相垂直的判定定理及其应用. 重点难点重点:面面垂直的判定定理. 难点:面面垂直的证明. 典例剖析例1、在三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥. 求证:平面PBC ⊥平面PAB .例2、已知四面体V -ABC 中,VA=VB=VC=AB=BC, D 、E 、F 、G 、H 分别是棱VA 、AB 、BC 、VC 、VB 的中点,证明:平面DEFG ⊥平面ACH .例3、如图,四棱锥P -ABCD 的底面是矩形,PA ⊥平面ABCD ,E 、F 分别是AB 、PD 的 中点,又二面角P -CD -B 为45°, (1) 求证:AF ∥平面PEC ; (2) 求证:平面PEC ⊥平面PCD .PABC课堂练习1、设直线,m n 和平面,αβ,则下列命题中正确的序号是_______________ . (1)、若m n ⊥,,m α⊂n β⊂,则αβ⊥ (2)、若//m n ,n β⊥,,m α⊂则αβ⊥ (3)、若//m n ,m α⊥,n β⊥,则αβ⊥ (4)、若m n ⊥,m αβ⋂=,n α⊂,则αβ⊥2、已知PA 垂直于正方形ABCD 所在的平面,连结PB 、PD 、AC 、PC ,则图中与平面ABCD 垂直的平面是_________________ .3、已知,αβ是两个平面,直线,l l αβ⊄⊄,设(1)l α⊥,(2)//l β,(3)αβ⊥,若以其中两个作为条件,另一个作为结论,写出一个正确命题_____________ .4、在四棱锥P ABCD -中,若PA ⊥平面ABCD ,且ABCD 是菱形.求证:平面PAC ⊥平面PBD .江苏省泰兴中学高一数学作业(132)班级 姓名 得分1、如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,底面各边 都相等,M 是PC 上的一动点,当M 满足 时, 平面MBD ⊥平面PCD .2、将边长为1的正方形ABCD 沿对角线BD 折叠成直二面角后, AC 的长为______________.3、已知E 是菱形ABCD 所在平面外一点, 且ED=EB . 求证:平面EBD ⊥平面AEC .PA BCDMCPABD4、如图, 在正方体ABCD—A1B1C1D1中, E为CC1的中点, O为底面中心, 求证:(1)A1O⊥面BED;(2)平面BDE⊥平面A1ACC1.5、如图P是Rt∆ABC外一点, 且PA = PB = PC, ∠A CB = 90︒,求证:平面PAB⊥平面ABC.6、S 是ΔABC 所在平面外一点, SA=SB=SC ,90,60ASC ASB BSC ∠=︒∠=∠=︒. 求证:平面ASC ⊥平面ABC .7、如图,已知AB 是平面α的垂线,AC 是平面α的斜线,CD α⊂,CD AC ⊥.求证:平面ABC ⊥平面ACD .αABC D。
江苏省泰兴中学高一数学苏教版必修2教学案:第1章6空间两条直线的位置关系(2)

江苏省泰兴中学高一数学教学案(123)必修 2 空间两条直线的位置关系(2)班级 姓名目标要求1、 理解异面直线的定义,异面直线所成角的定义、两条异面直线垂直的定义;2、 理解异面直线判定的方法,并会求简单的异面直线所成角;3、体会空间问题化归为平面问题求解的策略. 重点难点重点:异面直线的判定及异面直线所成角的定义; 难点:异面直线所成角的定义和范围. 典例剖析例1、(1)在空间四边形ABCD 中,直线AB 与CD 位置关系是_______________.(2)下列命题中①已知a,b,c三条直线,其中a,b异面,若a||c,则b与c异面②若a与b异面,b与c异面,则a与c异面 ③分别在两个平面内的直线一定是异面直线 ④既不平行也不相交的两条直线是异面直线 正确命题的序号是_____________.例2、如图,已知,a b 是异面直线,,,a b l αβαβ⊂⊂=,求证:直线,a b 中至少有一条与直线l 相交.abβα例3、如图,已知不共面的直线,,a b c 相交于O 点,M,P 是直线a 上两点,N,Q 分别是,b c 上一点.求证:MN,PQ 是异面直线.例4、如图,已知1111ABCD A B C D -是棱长为a 的正方体(1) 正方体的哪些棱所在的直线与直线1BC 是异面直 线? (2) 求异面直线1AA 与BC 所成的角;(3) 求异面直线1BC 和AC 所成的角.1A a bcNQP MOα学习反思1、反证法的一般步骤是 ;2、求异面直线所成角的关键是____________,如何作出异面直线所成角?______________ 课堂练习1、给出下列命题(1),,a b αβ⊂⊂则a 和b 是异面直线 (2)a 与b 异面,b 与c 异面,则a 与c 异面 (3)a,b 不同在一个平面内,则a 与b 异面 (4)a,b 不同在一个任何平面内,则a 、b 异面 正确命题的序号是______________.2、设两条异面直线所成角为θ,则角θ的范围是 ______________.3、在棱长为a 的正方体1111ABCD A B C D -中,则11A C 与1B C 成角为____________.4、在两个相交的平面内各画一条直线,使它们成:(1)平行直线; (2)相交直线; (3)异面直线.江苏省泰兴中学高一数学作业(123)班级 姓名 得分1、一条直线和两条异面直线的一条平行,则它与另一条的位置关系是 ___________2、已知四棱柱1111ABCD A B C D -,与棱AA 1异面的棱有_______________.3、下列命题中,正确的命题序号是________________. ①ABC θ∠=,直线//,//a AB b BC ,则a b 与所成的角为θ; ②若直线//a b ,且b c 与所成的角为θ,则a c 与所成的角也为θ; ③若直线,a b 与直线c 所成的角相等,则//a b ; ④若直线,a b 与直线c 所成的角不相等,则a b 与不平行.4、若120AOB ∠=︒,直线a OA ,a 和OB 异面,则a 和OB 所成的角为_____________.5、正方体ABCD-A 1B 1C 1D 1的棱长为a,那么(1)哪些棱所在的直线与直线BA 1成异面直线 . (2)直线BA 1与CC 1所成角的大小为 . (3)直线BA 1与B 1C 所成角的大小 .6、正方体1111ABCD A B C D -中,E 、F 分别是棱AD 、CC 1的中点,则A 1E 与BF 所成的角为 .7、分别和两条异面直线,a b 都相交的两直线,c d 的位置关系是 . 8、,a b 是异面直线,A ,B ,C ,D 是四个不同的点,且,,,A C a B D b ∈∈ 求证:AB 与CD 是异面直线.9、如图,空间四边形ABCD中,F,G分别是边BC、DA的中点,空间四边形的两条对角线AC、BD的长均为2,(1)若,求两条对角线AC、BD所成的角的大小.(2) 若,求两条对角线AC、BD所成的角的余弦值.10、如图,在正方体1111ABCD A B C D -中,1AA a =,E 、F 分别是BC 、CD 的中点,求异面直线1AD 与EF 所成角的大小.1A。
2021年高中苏教版数学必修二名师导学:第1章 第13课时 平面与平面的位置关系(2)

第13课时平面与平面的位置关系(2)教学过程一、问题情境幻灯片呈现人造卫星轨道平面及赤道平面的图片,让同学观看.二、数学建构(一)生成概念问题1缓慢打开教室的门,问“门面与墙面之间的角度有什么变动?”(引导同学用平面角来刻画)问题2“人造地球卫星绕地球旋转,卫星的轨道平面和地球赤道平面的角度有什么变化?”(引导同学用平面角来刻画)问题3实际上在我们的日常生活中有很多问题与两个平面相交所成的角有关.比如修筑水坝时,为了使水坝坚固耐久,必需使水坝面和水平面成适当的角度,如何用数学语言刻画两个平面所形成的这种“角”呢?(引导同学通过这几个例子归纳)通过争辩,给出二面角的有关概念.1.二面角的有关概念:(1)二面角的概念:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线动身的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面.(2)二面角的图形表示与符号表示:图形表示:(图2)符号表示:①若棱为l,两个面分别为α,β的二面角记为α-l-β;②若棱为AB,面为α,β的二面角,记作二面角α-AB-β或者P-AB-Q,其中P∈α,Q∈β.(3)二面角的平面角的定义及作法:(图3)以二面角的棱上任意一点O为端点,在两个半平面内分别作棱的两条垂线OA,OB,则∠AOB叫做二面角α-l-β的平面角.思考二面角α-l-β的平面角∠AOB的大小与点O的位置有关吗?依据“等角定理”,二面角α-l-β的平面角∠AOB的大小与点O在棱上的位置无关,而这一结论正是用平面角来度量二面角大小的理论基础.(二)理解概念(1)二面角的定义满足:①角的顶点在棱上;②角的两边分别在两个半平面内;③角的两边分别垂直于棱.(2)用二面角的平面角表示二面角的大小,二面角的平面角是多少度,二面角就是多少度.(3)二面角的平面角的范围是[0,π].(4)二面角的平面角是90°时,则称为直二面角,此时组成直二面角的两个平面相互垂直.2.两个平面垂直的定义:假如两个平面所成的二面角是直二面角,那么就说这两个平面相互垂直.(图4)记作α⊥β.(三)巩固概念问题为什么教室的门转到任何位置时,门所在的平面都与地面垂直?通过观看可以发觉,门在转动的过程中,门轴始终与地面垂直.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省泰兴中学高一数学教学案(130)
必修 2 平面与平面的位置关系(2)
班级 姓名
目标要求
1、进一步掌握两平面平行的判定定理及其应用;
2、理解两平面平行的性质定理及其应用;
3、理解两个平行平面间的距离.重点难点
重点:两平面平行的性质定理及其应用;难点:线线、线面、面面平行之间的相互转化.典例剖析
例1、求证:如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.
例2、已知平面平面,且之间的距离为12,过点
//αβ,αβ 于点,且,求点到平面,αβ,A B 2PA PB =P α
例3、已知平面//平面,是夹在这两个平面之间的线段,
αβ,AB CD 且AB 、CD 异面. 求证: 平面.
,,AE EB CG GD ==//EG β 学习反思
1、两平面平行的性质定理是 ,其实质是 .
2、根据所给图形,写出两个正确的命题:(1) (2)
3、领悟转化思想:线//线线//面面//面A A 课堂练习
1、下列命题中,正确命题的序号是__________________.
(1)、一条直线在两个平行平面中的一个平面内,则在另一个平面内必有一条直线与这条直线平行
(2)、两条平行线中的一条垂直于两个平行平面中的一个平面,则另一条一定垂直于另一个平面(3)、有两边平行,另两边分别在两平行平面内的四边形是平行四边形 (4)、若两平面平行,则分别在这两个平面内的两条直线互相平行
2、已知平面//平面,则下列四个命题正确命题的序号是_________________. αβ(1)、平面内的一条直线可以和平面内的无数条直线平行αβ(2)、平面内至少有两条直线与平面平行 αβ(3)、平面内的直线不可能与平面内的直线垂直
αβl
αβ
(4)、平面内的直线与平面内的直线不可能相交αβ3、下列命题正确的序号是 _______________.
(1)、夹在两个平行平面间的平行线段相等,平行线段的长度叫做两个平行平面间的距离(2)、两个平行平面间的公垂线段长度相等且互相平行,公垂线段的长度叫做两个平行平面
间的距离
(3)、夹在两平行平面间的两线段相等,则这两条线段所在直线平行 (4)、平面平面,平面平面,,那么//α βa =α γb =//a b βγ
4、夹在平行平面间的线段,与成45角,则间的距离为 ,αβ8AB =AB α ,αβ
5、求证:夹在两个平行平面间的平行线段相等.
江苏省泰兴中学高一数学作业(130)
班级 姓名 得分
1、若平面平面,直线,点,则在平面内过点B 的所有直线中(
//αβa α⊂B β∈β)
A 、不一定存在与平行的直线 a
B 、只有两条与a 平行的直线
C 、存在无数多条与a 平行的直线
D 、存在唯一的一条与a 平行的直线
2、下列命题中, 正确命题的序号的是__________________.(1)、平面平面,则平面内任一直线//αβα//a β(2)、直线,直线则 //a α,b a ⊥b α⊥(3)、若直线m,n 都平行于平面,则α//m n
(4)、平面内的两条直线平行于,则平面平面αβ//αβ
3、给出下列命题:①若平面内有无数个点到平面的距离相等,则;②若平面
αβ//αβ内有不共线三点到平面的距离相等,则;③平行于同一条直线的两个平面平行;
αβ//αβ④垂直于同一条直线的两个平面平行;⑤与同一条直线成等角的两个平面平行;⑥若在空间内两条异面直线同时平行于两个平面,则这两个平面平行.其中所有正确命题的序号为_____________.
4、如右图,直线被三个平行平面所截,若与
,AC DF ,,αβγAC 成,,则平面之间的距离为
α30 4,12,10AB BC DF ===,βγ, ,
.
DE
=EF =5、如图,有一块长方体的木料,经过木料表面内的一点, 1111A B C D P 在这个面内画线段,使其与木料表面ABCD 的线段EF 平行,应该怎样画?
6、已知两平行平面,点到的距离为,到的距离为,过点的直线,αβP α2cm P β3cm P 与 分别交于两点,且,求直线AB 与所成角的正弦值.
,αβ,A B 8AB cm =α
C A C
A
B
7、如图,正方体中,点在上,点在上,且.1111ABCD A B C D -N BD M 1B C CM DN =求证:平面.
//MN 11AA B B 8、四棱柱的相对侧面分别平行,过它的一个顶点A 的一个平面截它的1111ABCD A B C D -四个侧面得四边形AMFN . 求证:四边形AMFN 是平行四边形.
M
N
D 1
C 1
B 1
A 1
D
C
B
A。
