2015年秋季新版苏科版九年级数学上学期2.2、圆的对称性课件8
合集下载
苏教版九年级数学上册第2章对称图形——圆最新PPT课件

法一:连接 OA
A
B
O
法二:延长 CO交⊙O于D,连
接DA
D
A
B
O
C
C
『要点』通过辅助线的添加,建立同弧所对的
圆周角及圆心角或直径所对的圆周角,实现所
求对象的转换。
2.如图2,在⊙O中,弦AB=1.8cm,圆周角 ∠ACB=30°,则⊙O的直径等于__3_._6__cm。
连接AO,并延长交⊙O于D, A 连接BD,
∵OC⊥AB,
O
∴在△AOC中,AO2-OC2=AC2,
∴S圆环面积=π(AO2-OC2)=πAC2,A C B
『要点』遇到相切问题经常需要作出过切点 的半径,垂径定理往往需要建立的直角三角 形,并利用勾股定理求解三边。
5.如图,过圆外一点O作⊙O′的两条切线OA、
OB,A、B是切点,且OO' 圆O半径长两倍,则 ∠AOB=__6_0__°_
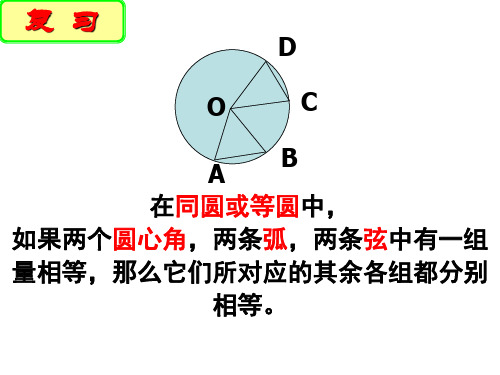
在同圆或等圆中,如果两
个圆心角,两条 弧,两条 弦, 中有一组量 相等 ,那么它们 B′ 所对应的其余各组量都分 别 相等 .
A′ B
·
O
A
圆周角定理
同弧或等弧所对的圆周角 相等 ,都等于 它所对弧的圆心角 度数的一半 。
直径所对的圆周角是 直角 ,90°所对 的弦是 直径 。
C
·
O
C 2
C1
C
3
∵l是⊙O的切线, 切点为A,OA是⊙O的直径, ∴OA⊥l
·O
A
l
圆的切线的判定
·O
经过 半径 的外端,并且 垂直于A这条 l 半径 的直线是圆的切线。
∵OA是⊙O的半径,l⊥OA于A, ∴l是⊙O的切线。
切线长定理
2.2 圆的对称性 苏科版九年级数学上册课件

又因为O'A'=OA,
O'B'=OB,所以点A'与点A
重合,点B'与点B重合(如图
2-10(2))
这样,A'B'与AB重合,A'B'与AB重合,即AB=AB AB =A'B'
上面的结论,在同圆中也成立
在同圆或等圆中,相等的圆心角所对的弧相等,所对的
弦相等.
思考与探索
在同圆或等圆中,如果圆心角所对的弧相等,那么它们
所对的弦相等吗?
这两个圆心角相等吗?
为什么?
如果圆心角所对的弦相等呢?
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中
有一组量相等,那么它们所对应的其余各组量都分别相
等。
我们知道,将顶点在圆心的周角等分成360份,每一份
圆心角是1°的角。因为同圆中相等的圆心角所对的弧
相等,所以整个圆也被等分
成360份,我们把1°的圆心
∴∠ABC=∠BAC
练习
1如图,在⊙O中,AC=BD、∠AOB-50求∠COD的度数
解:∵AC=BD,
∴AC-BC=BD-BC
∴AB=CD
∴∠AOB=∠COD.
又∵∠AOB=50°
∴∠COD=50°
练习
2如图,在⊙O中,AB=AC,∠A-40°求∠ABC的度数。
解:∵AB=AC ∴AB-AC,
∴∠ABC=∠ACB,
变)时,图形具有怎样的对称性?
当图①中的弦AB 为直径(AB 与CD 相互垂直的条件不变)
时,它既是轴对称图形,又是中心对称图形.
练习
(3)当图②中的点B在⊙O上运动到什么位置时,图形成
为轴对称图形?
当图②中的点 B 在⊙O 上运动到使弦AB 等于弦AC 时,
O'B'=OB,所以点A'与点A
重合,点B'与点B重合(如图
2-10(2))
这样,A'B'与AB重合,A'B'与AB重合,即AB=AB AB =A'B'
上面的结论,在同圆中也成立
在同圆或等圆中,相等的圆心角所对的弧相等,所对的
弦相等.
思考与探索
在同圆或等圆中,如果圆心角所对的弧相等,那么它们
所对的弦相等吗?
这两个圆心角相等吗?
为什么?
如果圆心角所对的弦相等呢?
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中
有一组量相等,那么它们所对应的其余各组量都分别相
等。
我们知道,将顶点在圆心的周角等分成360份,每一份
圆心角是1°的角。因为同圆中相等的圆心角所对的弧
相等,所以整个圆也被等分
成360份,我们把1°的圆心
∴∠ABC=∠BAC
练习
1如图,在⊙O中,AC=BD、∠AOB-50求∠COD的度数
解:∵AC=BD,
∴AC-BC=BD-BC
∴AB=CD
∴∠AOB=∠COD.
又∵∠AOB=50°
∴∠COD=50°
练习
2如图,在⊙O中,AB=AC,∠A-40°求∠ABC的度数。
解:∵AB=AC ∴AB-AC,
∴∠ABC=∠ACB,
变)时,图形具有怎样的对称性?
当图①中的弦AB 为直径(AB 与CD 相互垂直的条件不变)
时,它既是轴对称图形,又是中心对称图形.
练习
(3)当图②中的点B在⊙O上运动到什么位置时,图形成
为轴对称图形?
当图②中的点 B 在⊙O 上运动到使弦AB 等于弦AC 时,
苏科版初三课件2.2 圆的对称性 (2)

2.2 圆的对称性(2)
知识应用
1. 如图,CD为⊙O的直径,弦AB⊥CD于点 E,CE=1,AB=10,求CD的长.
2.2 圆的对称性(2)
拓展延伸
如图,AB、CD是⊙O的两条弦,AB∥CD, 弧 AC与弧BD相等吗?为什么?
2.2 圆的对称性(2)
变式一
若⊙O的直径是50cm,弦AB∥CD,且AB =48 cm,CD=40 cm,求AB、CD之间的距 离.
结论:AM=BM A⌒D=B⌒D A⌒C=⌒BC
2.2 圆的对称性(2)
典型例题
例1.如图,以点O为圆心的两个同心圆 中,大圆的弦AB交小圆于点C、D.AC与BD 相等吗?为什么?
AC
O
P
DB
2.2 圆的对称性(2)
典型例题
例2. 如图,已知在⊙O中,弦AB的长 为8厘米,圆心O到AB的距离为直径是50cm,弦AB∥CD,且AB=48 cm, CD=40 cm,求AB、CD之间的距离.
如图,在半径为5的扇形AOB中,∠AOB=90°, 点C是弧AB上的一个动点(不与点A、B重合) OD⊥BC,OE⊥AC,垂足分别为D、E. (1)当BC=6时,求线段OD的长; (2)在△DOE中是否存在长度保持不变的边?如
果存在,请指出并求其长度,如果不存在,请说 明理由;
2.2 圆的对称性(2)
课堂总结
通过本节课的学习,你对圆的对称性有哪些认识?
2.2 圆的对称性(2)
课后作业
课本P49 的5,6,7, 8.
2.2 圆的对称性(2)
初中数学 九年级(上册)
2.2 圆的对称性 (2)
初三数学组
2.2 圆的对称性(2)
操作一
在纸上画⊙O,并画出它的任意一条直径, 将⊙O沿这条直径折叠,折痕两旁的部分重合 吗?
【最新苏科版精选】苏科初中数学九上《2.0第2章 对称图形——圆》PPT课件.ppt

5. 边长分别为3,4,5的三角形的内切圆半径与外接圆 半径的比为( ) A.1∶5 B.2∶5 C.3∶5 D.4∶5
6.已知△ABC,AC=12,BC=5,AB=13。
则△ABC的外接圆半径为
。
7. 正三角形的边长为a,它的内切圆和外接圆
的半径分别是____, ____
8.如图,直角坐标系中一条圆弧经过网格点
5.锐角三角形的外心在三角形__内__,直角三角
形的外心在三角形__在_斜边的中点上 _,钝角
三角形的外心在三角形__外__。
3. Rt△ ABC三边的长为a、b、c,则内切圆的半 径是r=______________
4.外心到___________________的距离相等, 是________________________的交点; 内心到______________________的距离相 等,是_______________________的交点;
(2)AB、AD
C
E·
A
二、过三点的圆及外接圆
1.过一点的圆有___无__数___个 2.过两点的圆有___无___数___个,这些圆的圆心
的都在_连__结__着__两_点__的__线__段_ 的垂直平分线 上.
3.过______________可以确定一个圆
4.如何作过不在同一直线上的三点的圆(或三 角形的外接圆、找外心、破镜重圆、到三个村 庄距离相等)
例1.如图,⊙O为△ABC的外接圆, AB为直径,AC=BC, 则∠A的 度数为( )
A.30° B.40° C.45° D.60° 例2. 在⊙O中,弦AB所对的圆心角∠AOB=100°, 则弦AB所对的圆周角为____________.
练习
6.已知△ABC,AC=12,BC=5,AB=13。
则△ABC的外接圆半径为
。
7. 正三角形的边长为a,它的内切圆和外接圆
的半径分别是____, ____
8.如图,直角坐标系中一条圆弧经过网格点
5.锐角三角形的外心在三角形__内__,直角三角
形的外心在三角形__在_斜边的中点上 _,钝角
三角形的外心在三角形__外__。
3. Rt△ ABC三边的长为a、b、c,则内切圆的半 径是r=______________
4.外心到___________________的距离相等, 是________________________的交点; 内心到______________________的距离相 等,是_______________________的交点;
(2)AB、AD
C
E·
A
二、过三点的圆及外接圆
1.过一点的圆有___无__数___个 2.过两点的圆有___无___数___个,这些圆的圆心
的都在_连__结__着__两_点__的__线__段_ 的垂直平分线 上.
3.过______________可以确定一个圆
4.如何作过不在同一直线上的三点的圆(或三 角形的外接圆、找外心、破镜重圆、到三个村 庄距离相等)
例1.如图,⊙O为△ABC的外接圆, AB为直径,AC=BC, 则∠A的 度数为( )
A.30° B.40° C.45° D.60° 例2. 在⊙O中,弦AB所对的圆心角∠AOB=100°, 则弦AB所对的圆周角为____________.
练习
九年级数学上册第2章对称图形_圆2.2圆的对称性(2)课件(新版)苏科版

圆有无数条对称轴.
做一做: 剪一个圆形纸片,在圆形纸片上任意画一条垂直
于直径CD的弦AB,垂足为P,再将纸片沿着直径CD对着,
比较AP与PB,A⌒C与C⌒B,你能发现什么结论?
·O
AP
B
D
线段: AP=BP
弧:
⌒⌒
AC=BC,
⌒⌒
AD=BD
C
理由如下:
把圆沿着直径CD折叠时,CD两侧的两
·O
个半圆重合,点A与点B重合,AP与BP
试一试
你能利用垂径定理解决求赵州桥主桥拱半径的问题吗?
解:如图,用AB表示主桥拱,
设AB所在圆的圆心为O,半径
为R.
经过圆心O作弦AB的垂线OC垂
足为D,与弧AB交于点C,则D
A 是AB的中点,C是弧AB的中点, CD就是拱高.
C
D
B
∴ AB=37m,CD=7.23m.
∴ AD= AB=18.5m,OD=OC-CD=R-7.23.
出反例.
C
特别说明:
A
圆的两条直径是互相平分的.
·O B
D
【例题讲解】
例1 如图,OE⊥AB于E,若☉O的半径为10cm,OE=6cm, 则AB= 16 cm.
解析:连接OA,∵ OE⊥AB,
∴ AE OA2 OE2 102 62 8 cm.
∴ AB=2AE=16cm.
AEB O·
O
∵ OA2 AD2 OD2
R2=18.52+(R-7.23)2 解得R≈27.3(m). 即主桥拱半径约为27.3m.
练一练
如图a、b,一弓形弦长为 4 6 cm,弓形所在的圆的半径
为7cm,则弓形的高为_2c_m_或_1_2_c_m_.
做一做: 剪一个圆形纸片,在圆形纸片上任意画一条垂直
于直径CD的弦AB,垂足为P,再将纸片沿着直径CD对着,
比较AP与PB,A⌒C与C⌒B,你能发现什么结论?
·O
AP
B
D
线段: AP=BP
弧:
⌒⌒
AC=BC,
⌒⌒
AD=BD
C
理由如下:
把圆沿着直径CD折叠时,CD两侧的两
·O
个半圆重合,点A与点B重合,AP与BP
试一试
你能利用垂径定理解决求赵州桥主桥拱半径的问题吗?
解:如图,用AB表示主桥拱,
设AB所在圆的圆心为O,半径
为R.
经过圆心O作弦AB的垂线OC垂
足为D,与弧AB交于点C,则D
A 是AB的中点,C是弧AB的中点, CD就是拱高.
C
D
B
∴ AB=37m,CD=7.23m.
∴ AD= AB=18.5m,OD=OC-CD=R-7.23.
出反例.
C
特别说明:
A
圆的两条直径是互相平分的.
·O B
D
【例题讲解】
例1 如图,OE⊥AB于E,若☉O的半径为10cm,OE=6cm, 则AB= 16 cm.
解析:连接OA,∵ OE⊥AB,
∴ AE OA2 OE2 102 62 8 cm.
∴ AB=2AE=16cm.
AEB O·
O
∵ OA2 AD2 OD2
R2=18.52+(R-7.23)2 解得R≈27.3(m). 即主桥拱半径约为27.3m.
练一练
如图a、b,一弓形弦长为 4 6 cm,弓形所在的圆的半径
为7cm,则弓形的高为_2c_m_或_1_2_c_m_.
苏科版九上数学课件2-2圆的对称性(2)

O
求半径OC的长。
A
D
B
练习2:在圆O中,直径CE⊥AB于 D,OD=4㎝,弦AC=㎝, 10 求圆O的半径。
C E O
A
D
B
C
挑战自我画一画
如图,M为⊙O内的一点,利用尺规作一条弦AB, 使AB过点M.并且AM=BM.
A
●M B
●O
小结:
1:圆是轴对称图形
2:垂径定理及其运用
思考题:如图,CD为圆O的直径,弦 AB交CD于E,∠CEB=30°, DE=9㎝,CE=3㎝,求弦AB的长。
初中数学课件
金戈铁骑整理制作
九年级数学(上)第五章 圆
•5.2.圆的对称性(2)
学习目标:
1:理解圆是轴对称图形。
2:掌握垂径定理,并能灵活运用。
复习
如图,如AB=CD则()如
⌒⌒
AB=CD
则()
如∠AOB=∠COD则()
D
O
C
A
B
基本图形:
C
A
B
M└
●O
D
例1已知:如图,在以O 为圆心的两个同心圆中, 大圆的弦AB交小圆于C, D两点,AC与BD相等吗? 为什么?
A
D
E C
O
B
O.
A C 弦AB的长为8㎝, 圆心O到AB的距离为3㎝,求圆O的半径。
AE
B
O
变式1:在半径为5㎝的圆O中,有长8㎝的 弦AB,求点O与AB的距离。
2:在半径为5㎝的圆O中,圆心O到弦AB的距离 为3㎝,求AB的长。
E
练1:如图,
圆O的弦AB=8㎝,
DC=2㎝,直径CE⊥AB于D,
苏科版-数学-九年级上册- 圆的对称性 参考课件

3.连接AE、BE;
4.作AE、BE的垂直平分线m、n,与交⌒AE、⌒BE与点F、G;
∴点E、F、G就是所求A⌒B的四等分点.
๔ 拓展& 提高 ☞
变式二:你能确定弧AB所在圆的圆心吗? 方法:只要在圆弧
上任意取三点,连
a
C
b
结两条弦,画这两
条弦的垂直平分线,A
B
交点即为圆弧所在
O
圆的圆心.
๔ 例题& 讲解 ☞
在白纸上任意作一个圆和这个圆的任意一条直径CD, 然后沿着直径所在的直线把纸折叠,你发现了什么?
C
O
D
问:(1)圆是轴对称图形吗? (2)它的对称轴是什么?你能找到多少条对称轴?
结论:
圆是轴对称图形,每一条直径所在的直线都是对称轴.
๔ 操作& 思考 ☞
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB, 垂足为M,将圆形纸片沿直径CD折叠,你能发现图中有 哪些等量关系?与同伴说说你的想法和理由.
例4.如图,一条排水管的截面。已知排水管的半径 OB=10,水面宽AB=16.求截面圆心O到水面的距离.
解:作OC⊥AB,垂足为点C,与 AB 相交于点D.
∴AC=BC=1
AB=
1
×16=8
在Rt△BOC中 2
2
10 C
OC OB2 BC2 102 82 6
8
8
答:截面圆心O到水面的距离为6.
C
A M└
B 通过折叠可以发现:
●O
AM=BM,AC=BC ,AD=BD
如何证明上述的结论呢?
D
๔ 探索& 交流 ☞
已知:如图, CD是⊙O的直径,CD⊥AB,垂足为M.
4.作AE、BE的垂直平分线m、n,与交⌒AE、⌒BE与点F、G;
∴点E、F、G就是所求A⌒B的四等分点.
๔ 拓展& 提高 ☞
变式二:你能确定弧AB所在圆的圆心吗? 方法:只要在圆弧
上任意取三点,连
a
C
b
结两条弦,画这两
条弦的垂直平分线,A
B
交点即为圆弧所在
O
圆的圆心.
๔ 例题& 讲解 ☞
在白纸上任意作一个圆和这个圆的任意一条直径CD, 然后沿着直径所在的直线把纸折叠,你发现了什么?
C
O
D
问:(1)圆是轴对称图形吗? (2)它的对称轴是什么?你能找到多少条对称轴?
结论:
圆是轴对称图形,每一条直径所在的直线都是对称轴.
๔ 操作& 思考 ☞
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB, 垂足为M,将圆形纸片沿直径CD折叠,你能发现图中有 哪些等量关系?与同伴说说你的想法和理由.
例4.如图,一条排水管的截面。已知排水管的半径 OB=10,水面宽AB=16.求截面圆心O到水面的距离.
解:作OC⊥AB,垂足为点C,与 AB 相交于点D.
∴AC=BC=1
AB=
1
×16=8
在Rt△BOC中 2
2
10 C
OC OB2 BC2 102 82 6
8
8
答:截面圆心O到水面的距离为6.
C
A M└
B 通过折叠可以发现:
●O
AM=BM,AC=BC ,AD=BD
如何证明上述的结论呢?
D
๔ 探索& 交流 ☞
已知:如图, CD是⊙O的直径,CD⊥AB,垂足为M.
2.2 圆的对称性 课件 苏科版数学九年级上册(40张PPT)

解:如图2.2-9,连接OC. ∵ CD⊥AB,
感悟新知
∴ CH=DH=12CD=12×8=4(垂直于弦的直径平分弦). 又∵ OC=12AB=12×10=5, ∴在Rt△OCH中,利用勾股定理,得 OH= OC2-CH2= 52-42=3.
方法提醒
感悟新知
利用垂径定理求线段的长的方法: 垂径定理是解决圆中的计算、证明问题常用 的知识, 求线段长时,一般利用半径、圆心到 弦的垂线段、弦的一半构造直角三角形,运用 勾股定理求解,即用“垂径定理+勾股定理” 求解.
感悟新知
例 3 [模拟·武汉] 如图2.2-5,A、B、C、D是⊙O上四点, 且AB=CD. 求证:AD=BC. 解题秘方:由圆心角、弧、弦之间的 关系定理的推论证明 A⌒D=B⌒C即可解决 问题.
感悟新知
证明:∵ AB=CD,∴ A⌒B=C⌒D . ∴ A⌒C+B⌒C =A⌒C+A⌒D . ∴ A⌒D=B⌒C . ∴ AD=BC.
解题秘方:紧扣圆的旋转不变性,结合旋转中心O确定 旋转角.
解:因为圆心O为旋转中心,旋转后的图形与原图形重 合,所以∠AOB=∠BOC=∠AOC=360°÷3= 120°.所以旋转角可以为120°. 答案:D
感悟新知
特别提醒
在圆的许多性质中,圆的对称性(轴对称、 中心对称及旋转不变性)是最基本的性质.此题 利用性质时要结合图形,易误得旋转角度是 60°.
感悟新知
例 6 [模拟·泰州] 如图2.2-10, 在△ABC中,AB=5, AC=4,BC=2,以点A为圆心,AB 长为半径作 ⊙A,延长BC交⊙A于点D, 则CD 的长为( ) A. 5 B. 4
C.
9 2
D. 2 5
感悟新知
解题秘方:连接AD,过点A作AE⊥BD于E,利用同圆 的半径相等可得AD=AB=5,利用垂径定理可知DE= BE,得CE=DE-2,再利用勾股定理构建方程可求DE 的长,进而可得CD的长.
苏科版数学九年级上册《圆的对称性》教学课件
●O
交流
• 圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无
数条对称轴. 可利用折叠的方法即可解决上述问题.
●O
探索
• AB是⊙O的一条弦. 作直径CD,使CD⊥AB,垂足为M.
下图是轴对称图形吗?如果是,其对称轴是什么?
• 你能发现图中有哪些等量关系?与同伴说说你的想法 和理由.
B
M
A O
4.过⊙O内一点M的最长弦长为10cm,最短弦 长为8cm,那么OM长为____.
B
M
A O
5、如图,⊙O的直径是10,弦AB的长为8, P是AB上的一个动点, ①则OP的取值范围是 3≤OP≤5。
②使线段OP的长度为整数值的P点
位置有___5_____个。
注意圆的轴对称性
O
A p1P C p2 B
7、如图,已知圆O的直径AB与弦CD相交于G, AE⊥CD于E,BF⊥CD于F,且圆O的半径为10㎝, CD=16 ㎝,求AE-BF的长。
C
E
A
G B
O
F
D
4.在直径为650mm的圆柱形油槽内装入一些 油后,截面如图,若油面宽AB=600mm,求油的 最大深度。
A
B
ф650mm
600mm
Hale Waihona Puke O∟ADB
6.如图,矩形ABCD与⊙O交于点A、 B、E、F,DE=1,EF=3,则AB=___.
DE A
FC
G
H
B
O
7试、说如明图:,(在1圆)OO中C=,OD已(知2A)C=A︵BED=,︵BF
O
C A
E
D B
F
一、圆是轴对称图形,其对称轴是 任意一 条过圆心的直线(或直径所在直线.)
交流
• 圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无
数条对称轴. 可利用折叠的方法即可解决上述问题.
●O
探索
• AB是⊙O的一条弦. 作直径CD,使CD⊥AB,垂足为M.
下图是轴对称图形吗?如果是,其对称轴是什么?
• 你能发现图中有哪些等量关系?与同伴说说你的想法 和理由.
B
M
A O
4.过⊙O内一点M的最长弦长为10cm,最短弦 长为8cm,那么OM长为____.
B
M
A O
5、如图,⊙O的直径是10,弦AB的长为8, P是AB上的一个动点, ①则OP的取值范围是 3≤OP≤5。
②使线段OP的长度为整数值的P点
位置有___5_____个。
注意圆的轴对称性
O
A p1P C p2 B
7、如图,已知圆O的直径AB与弦CD相交于G, AE⊥CD于E,BF⊥CD于F,且圆O的半径为10㎝, CD=16 ㎝,求AE-BF的长。
C
E
A
G B
O
F
D
4.在直径为650mm的圆柱形油槽内装入一些 油后,截面如图,若油面宽AB=600mm,求油的 最大深度。
A
B
ф650mm
600mm
Hale Waihona Puke O∟ADB
6.如图,矩形ABCD与⊙O交于点A、 B、E、F,DE=1,EF=3,则AB=___.
DE A
FC
G
H
B
O
7试、说如明图:,(在1圆)OO中C=,OD已(知2A)C=A︵BED=,︵BF
O
C A
E
D B
F
一、圆是轴对称图形,其对称轴是 任意一 条过圆心的直线(或直径所在直线.)
苏科版数学九年级上册2.2圆的对称性 课件(共17张PPT)

所对的弦相等.
2.2 圆的对称性(1)
议一议
在同圆或等圆中,如果圆心角所对的弧相等,那么
它们所对的弦相等吗?这两个圆心角相等吗?为什么?
B
B′
A O
A′ O′
AB=A′B′
AB=A′B′
∠AOB =∠ A′O ′B ′
2.2 圆的对称性(1)
议一议
在同圆或等圆中,如果圆心角所对的弦相等,那
么圆心角所对的弧相等吗?它们圆心角相等吗?为
九年级(上册)
2.2 圆的对称性 (1)
2.2 圆的对称性(1)
看一看
你知道车轮为什么设计成圆形?设计成三角 形、四边形又会怎样?从中你发现了什么?
2.2 圆的对称性(1)
想一想
圆绕着圆心 旋转任何角度后, 都能与自身重合.
圆是中心对称图形,圆心是它的对称中心.
2.2 圆的对称性(1)
想一想
(1)在两张透明纸片上,分别作半径相等的⊙O和⊙O′. (2)在⊙O和⊙O′中,分别作相等的圆心角∠AOB ,
什么?
B
B′
A O
A′ O′
AB=A′B′
AB= A′B′
∠AOB =∠ A′O ′ B ′
2.2 圆的对称性(1)
议一议
在同圆或等圆中,如果两个圆心角,两条弧,两条
弦中有一组量相等,那么它们所对应的其余各组都分
别相等.
B
B′
O
A
O′
A′
1.因为∠AOB=∠ A′O ′B ′,所以 AB=A′B′; AB=A′B′. 2.因为AB=A′B′,所以 AB=A′B′; ∠AOB=∠ A′O′ B′.
2.2 圆的对称性(1)
作业
圆的对称性课件苏科版九年级数学上册(完整版)2

·O
即△AOB是等腰三角形.
∵P是AB的中点,即AP=BP, ∴AB⊥CD.
A
P C
B
∵ CD是直径,CD⊥AB,
∴ A⌒C
=B⌒C,
⌒ AD
=B⌒D(. 垂径定理)
2.已知:在☉O中,CD是直径,AB是弦,A⌒C =B⌒C,
求证:CD垂直平分AB.
证明:连接OA、OB、CA、CB,则OA=OB.
系是否依然成立?为什么?
A
B
C
D
O·
O ·′
通过平移和旋转将两个等圆变成同一个圆,我们发现:如 果∠AOB=∠COD,那么,AB⌒=C⌒D,弦AB=弦CD.
弧、弦与圆心角的关系定理
1.在同圆或等圆中,相等的圆心角所对的弧相等,所
对的弦也相等.
①∠AOB=∠COD CB
②A⌒B=C⌒D ③AB=CD
由此易得 A⌒D =B⌒D.
垂径定理
垂直于弦的直径平分弦以及弦所对的两条弧.
C
推导格式:
∵ CD是直径,CD⊥AB,
∴ AP=BP,
A⌒C =B⌒C,
⌒⌒ AD =BD.
·O
AP B D
下列图形是否具备垂径定理的条件?如果不是,请说明为 什么?
C
A O
A
EB
D
C B
O A
是
不是,因为
没有垂直
O
E
BA
C O
EB D
是
不是,因为CD
没有过圆心
➢垂径定理的几个基本图形:
C A
O
O
A
EB
D
A
DB
E
B D O
A C
O CB
数学九年级上苏科版52圆的对称性课件

圆心与垂足之间的
距离(如线段OD).
D
实验:将图形1中的扇形AOB绕点O
图1
逆时针旋转某个角度,得到图2中
的图形,同学们可以通过比较前后
两个图形,发现∠AOB与∠A’OB’、
AB与AB’、
有何关系?
图2
B
A O
若∠AOB=∠AOB 则AB=AB AB=AB
在同圆 或等圆 B 中,相 等的圆 心角所 对的弧 A相所等对的, 弦相等。
∴∠AOB=∠BOC=∠AOC
• 如图,MN为半圆O的直径,半径OA⊥MN, D 为OA的中点,过点D作BC//MN,
• 求证:( 1 ) 四边形ABOC为菱形; (2)∠MNB=∠BAC.
如图,点O是∠EPF的平分线上一点,以O为圆心的圆和角的两 边所在的直线分别交于点A、B和C、D,求证:AB=CD.
B E
O
C
D A
圆心角、弧、弦、弦心距之间的关系
B
C
如果 AB = CD ,
则图中有哪些弧等?
A⌒B = C⌒D
A
O
D⌒ AB +
⌒⌒
AC = BD
B⌒C =
⌒ CD
? +
⌒ BC
A⌒C = B⌒D
AC = BD ?
n°弧
∵把圆心角等分成360份,则每一份的
圆心角是1º.同时整个圆也被分成了 360份.
3,如图:在圆O中,已知AC=BD,
试说明:(1)OC=OD
(2)A︵E=
︵
BF
O
C A
E
D B
F
A
如图1,在⊙O中,弧AB=弧AC,
∠ACB=60°,
O
2.2圆的对称性(2)-苏科版九年级数学上册课件

CD过圆心O CD⊥AB
AC=BC
AD=BD
A
两个条件缺一不可
判断:
1.经过圆心的直线平分弦. ( ×) 2.垂直于弦的直线平分弦 .( ×)
C
O
E
B
D CC
AA┏EE OO DD
BB
例1.已知:如图,在以O为圆心的两个同 心圆中,大圆的弦AB交小圆于C、D两 点.AC与BD相等吗?为什么?
O
AC E DB
A
AE=BE, AC=BC AD=BD
O
E
B
D
将一圆形纸片对折后,你发现了什么结论?
圆是轴对称图形, 经过圆心的任意一 条直线都是它的对称轴.
当弦AB垂直于直径 CD时,将纸片沿CD对 折,你发现了什么?
AE=BE, AC=BC AD=BD
A
C
O
E
B
D
已知: 在⊙O中,CD是直径,
C
AB是弦,CD⊥AB于E.
②
O
求证: AE=BE,AC=BC
AD=BD
垂径定理:
A
E
B
D
垂直于弦的直径平分这条弦,并且平分弦
所对的两条弧.
垂直于弦的直径 C
符号语言:
AE=BE
CD是过直圆径心O
O
CD⊥AB于E
AC=BC
AD=BD A
E
B
D
垂径定理:
垂直于弦的直径平分这条弦,并且平分弦 所对的两条弧.
符号语言:
AE=BE
例2.如图,已知:在⊙O中,弦AB的 长为8cm,圆心O到AB的距离为3cm. 求⊙O的半径.
O 53 A 4E B
常用辅助线:过圆心作弦的垂线段
九年级数学上册 2.2 圆的对称性 苏科版

教师寄语 新知的生成常得益于思维的碰撞; 思维的碰撞常发生于语言的交流。
歌唱生活,享受数学
整理课件
2.2 圆的对称性(1)
整理课件
复习回忆
1、什么是中心对称图形?
把一个图形绕着某一个点旋转180∘,如果旋转后的图形
能够和原来的图形互相重合,那么这个图形叫做中心
对称图形。这个点叫做它的对称中心。
2、我们采用什么方法研究中心对称图形?
那么它们所对的弦相等吗?
这两个圆心角相等吗?
A
A’
O
B
O’
B’
AB = A’B’
AB=A’B’
AOB= A’O’B’
整理课件
讨论交流
在同圆或等圆中,如果圆心角所对的弦相等, 那么圆心角所对的弧相等吗?它们圆心角相等吗?
A
A’
O
B
O’
B’
AB=A’B’
AB = A’B’
AOB= A’O’B’
O
解:在⊙O中,∵
,
∴∠AOC=∠BOD( )
B ∴∠AOC-∠BOC=∠BOD-∠BOC( )
A 即∠AOB=∠COD
又∠AOB=50°,∴∠COD=50°,
即
的度数为50°
整理课件
回顾总结
通过本节课的学习,你有什么收获?
1.圆是中心对称图形,圆心是它的对称中心。
2.在同圆或等圆中, 如果两个圆心角,两条弧,两条弦中有一组量相等, 那么它们所对应的其余各组都分别相等。 3. 圆心角的度数与它所对的弧的度数相等。
AB =A’B’ AO整B理课=件A’O’B’
运用新知,解决问题
解:相等;
理由:在⊙O中,
O
∵∠AOC=∠BOC,
歌唱生活,享受数学
整理课件
2.2 圆的对称性(1)
整理课件
复习回忆
1、什么是中心对称图形?
把一个图形绕着某一个点旋转180∘,如果旋转后的图形
能够和原来的图形互相重合,那么这个图形叫做中心
对称图形。这个点叫做它的对称中心。
2、我们采用什么方法研究中心对称图形?
那么它们所对的弦相等吗?
这两个圆心角相等吗?
A
A’
O
B
O’
B’
AB = A’B’
AB=A’B’
AOB= A’O’B’
整理课件
讨论交流
在同圆或等圆中,如果圆心角所对的弦相等, 那么圆心角所对的弧相等吗?它们圆心角相等吗?
A
A’
O
B
O’
B’
AB=A’B’
AB = A’B’
AOB= A’O’B’
O
解:在⊙O中,∵
,
∴∠AOC=∠BOD( )
B ∴∠AOC-∠BOC=∠BOD-∠BOC( )
A 即∠AOB=∠COD
又∠AOB=50°,∴∠COD=50°,
即
的度数为50°
整理课件
回顾总结
通过本节课的学习,你有什么收获?
1.圆是中心对称图形,圆心是它的对称中心。
2.在同圆或等圆中, 如果两个圆心角,两条弧,两条弦中有一组量相等, 那么它们所对应的其余各组都分别相等。 3. 圆心角的度数与它所对的弧的度数相等。
AB =A’B’ AO整B理课=件A’O’B’
运用新知,解决问题
解:相等;
理由:在⊙O中,
O
∵∠AOC=∠BOC,
苏科版九年级数学上册《22 圆的对称性》(2)课件

O
∴AE=BE=
1 AB 1 8 4
2
2
OA OE2 AE2 32 42 5 答: ⊙O的半径为5cm
变式:在半径为5 ㎝的圆O中,圆心O到弦AB的 距离为3 ㎝,求AB的长。
挑战自我画一画
• 如图,M为⊙O内的一点,利用尺规作一条弦AB, 使AB过点M.并且AM=BM.
A
●M B
●O
B
垂径定理:垂直于弦的直径
平分弦及弦所对的两条弧.
证∴∵已CCO明知DPC::是==连在弦DO接你定,⊙PDOOA能理,,C中B∠O、证吗B,⊥PO明?OCA⊥DCDBC.=于是D∠P直,B。径O,D. A
∵∠求BO证C:=P∠CB=OPDD,,
∴∴∠AB⌒CO=CB⌒ B⌒D=C;∠=A⌒ABC⌒DO=A,⌒DA⌒DC.=A⌒D
O
C
P
D
B
总结归纳
定理 垂直于弦的直径平分 弦及弦所对的两条弧.
推导格式:
C
A M└
B
●O
如图∵ CD是直径,
CD⊥AB,
∴AM=BM,
A⌒C =B⌒C,
⌒⌒ AD =BD.
D
定理分析:若是一条经过圆心的直线或 线段垂直于弦平分弦吗?
例题
例1 已知:如图,在以O为圆心的两个同心 圆中,大圆的弦AB交小圆于C,D两点,AC 与BD相等吗?为什么?
●O
圆的对称性
• 圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无 数条对称轴.
利用折叠的方法即可发现上述结论.
●O
如图,CD是⊙O的弦,画直 径AB⊥CD,垂足为P。图中有哪些 相等的线段、相等的弧?为什么?
A
A
苏科版九上数学课件2-2-2圆的对称性(1)

3.
回顾总结
通过本课的学习,你又有 什么收获?
O与 O重合。
B
B'
A
A'
O
O'
探索
A
O
B
A’
O’
B’
AA B =’B’
AB=A’B
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
讨论交流
在同圆或等圆中,如果圆心角所对的弧相等,
那么它们所对的弦相等吗?这两个圆心角相等吗?
为什么?
A
A’
O
B
O’
B’
AB=A’B
AA B =’ B’
讨论交流
初中数学课件
金戈铁骑整理制作
初中数学九年级上册 (苏科版)
2.2圆的对称性(一)
2、圆是中心对称图形,圆心是它的 对称中心。
尝试
1.在两张透明纸O 片 和 O 上 ’ ,
2.在 O和 O’中,分 别 AO 作 A B 相 ’, O ,连接AB,A’B’ 。
3.将两张透明纸片叠在一起,使
在同圆或等圆中,如果圆心角所对的弦相等,
那么圆心角所对的弧相等吗?它们圆心角相等吗?
为什么?
A
A’
O
B
O’
B’
AB= AA ’B A B =’’B’
在同圆或等圆中, 如果两个圆心角,两条弧,两条弦中有一组量相等, 那么它们所对应的其余各组都分别相等。
AB=
1. A A O ’O B’ = B
A A B = ’B
AB
2. A A = B ’ B
A A O ’
A A = B ’B
3. A B =
A A O ’O
回顾总结
通过本课的学习,你又有 什么收获?
O与 O重合。
B
B'
A
A'
O
O'
探索
A
O
B
A’
O’
B’
AA B =’B’
AB=A’B
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
讨论交流
在同圆或等圆中,如果圆心角所对的弧相等,
那么它们所对的弦相等吗?这两个圆心角相等吗?
为什么?
A
A’
O
B
O’
B’
AB=A’B
AA B =’ B’
讨论交流
初中数学课件
金戈铁骑整理制作
初中数学九年级上册 (苏科版)
2.2圆的对称性(一)
2、圆是中心对称图形,圆心是它的 对称中心。
尝试
1.在两张透明纸O 片 和 O 上 ’ ,
2.在 O和 O’中,分 别 AO 作 A B 相 ’, O ,连接AB,A’B’ 。
3.将两张透明纸片叠在一起,使
在同圆或等圆中,如果圆心角所对的弦相等,
那么圆心角所对的弧相等吗?它们圆心角相等吗?
为什么?
A
A’
O
B
O’
B’
AB= AA ’B A B =’’B’
在同圆或等圆中, 如果两个圆心角,两条弧,两条弦中有一组量相等, 那么它们所对应的其余各组都分别相等。
AB=
1. A A O ’O B’ = B
A A B = ’B
AB
2. A A = B ’ B
A A O ’
A A = B ’B
3. A B =
A A O ’O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
O
D
课后小结:
1.圆是中心对称图形,圆心是它的对称中心。
2.在同圆或等圆中, 如果两个圆心角,两条弧,两条弦中有一组量相等, 那么它们所对应的其余各组都分别相等。
3. 圆心角的度数与它所对的弧的度数相等。
A C
B
O
D
1的圆心角
C D
1的弧
O
n的圆心角
B A
n的弧
n的圆心角对着 n的弧, n的弧对着 n的圆心角。
圆心角的度数与它所对的弧的度数相等。
例 1:如图在 ABC 中, C=90, B=28,以 C为圆心, 以 CA为半径的圆交 AB于点 D,交 BC于点 E , 求 AD, DE的度数。
3.将两张透明纸片叠在一起,使 O与
B
O重合。
B'
A
O
O'
A'
A
A’
O
B
O’
B’
AOB= A’O’B’
AB Leabharlann A’B’AB=A’B’在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
思考与探索:
在同圆或等圆中,如果圆心角所对的弧相等, 那么它们所对的弦相等吗?这两个圆心角相等吗? 为什么? A
1.
AOB= A’O’B’
AB=A’B’ AB = A’B’
2.
AB = A’B’
AB=A’B’ AOB= A’O’B’
AB = A’B’ AOB= A’O’B’
3.
AB=A’B’
练习:
1.如图,在 O中,AC =BD , AOB=50,求 COD的度数。 A
C D O B A
B
D
E
A
C
例 2:如图 ,AB,AC,BC 都是 O的弦, AOC= BOC, ABC与 BAC相等吗?为什么?
解: ABC= BAC
∵ AOC= BOC
O
AC=BC
ABC= BAC
A C B
书本
P115页
E
第 2题
D
F
2 3
1
O
C
O
A
B
书本
P115页
第 3题
B
C
O B C
2.如图,在 O中,AB =AC, A=40,求 ABC的度数。
3.如图,在同圆中,若 AOB=2 COD,则AB与 2CD的大小关系是( ( A)AB > 2CD (B) AB < 2CD (C) AB= 2CD (D) 不能确定
C)
A
C O D
B
4.在同圆中,若AB=2CD,则 AB与 2CD的大小关系是( B ) ( A) AB> 2CD (B)AB < 2CD (C) AB = 2CD (D) 不能确定
复习提问:
1、什么是中心对称图形?。举例说明
把一个图形绕着某一个点旋转180∘,如果旋转后的图形能够
和原来的图形互相重合,那么这个图形叫做中心对称图形。
平行四边形、矩形、菱形、正方形
圆是中心对称图形,圆心是它的对称中心。
尝试与交流
1.在两张透明纸片上,分别作半径相等的 O和 O’
2.在 O和 O’中,分别作相等的圆心角 AOB, A’O’B’ ,连接 AB, A’B’ 。
A’ O B O’ B’
AB = A’B’
AB=A’B’
AOB= A’O’B’
思考与探索:
在同圆或等圆中,如果圆心角所对的弦相等,
那么圆心角所对的弧相等吗?它们圆心角相等吗?
为什么?
O
A
A’
B
O’
B’
AB=A’B’
AB = A’B’
AOB= A’O’B’
在同圆或等圆中, 如果两个圆心角,两条弧,两条弦中有一组量相等, 那么它们所对应的其余各组都分别相等。
