第1章习题参考答案 men
大学高数高数第一章(终)课后参考答案及知识总结

第一章函数、极限与连续内容概要课后习题全解习题1-1★1.求下列函数的定义域:知识点:自然定义域指实数范围内使函数表达式有意义的自变量x 的取值的集合; 思路:常见的表达式有 ① a log □,( □0>) ② /N □, ( □0≠) ③(0)≥W④ arcsin W (W[]1,1-∈)等解:(1)[)(]1,00,11100101122⋃-∈⇒⎩⎨⎧≤≤-≠⇒⎩⎨⎧≥-≠⇒--=x x x x x x x y ;(2)31121121arcsin≤≤-⇒≤-≤-⇒-=x x x y ; (3)()()3,00,030031arctan 3⋃∞-∈⇒⎩⎨⎧≠≤⇒⎩⎨⎧≠≥-⇒+-=x x x x x x x y ;(4)()()3,11,1,,1310301lg 3⋃-∞-∈⇒⎩⎨⎧-<<<⇒⎩⎨⎧-<-<⇒-=-x x or x x x x x y x;(5)()()4,22,11601110)16(log 221⋃∈⇒⎪⎩⎪⎨⎧-<-≠-<⇒-=-x x x x x y x ; ★ 2.下列各题中,函数是否相同?为什么?(1)2lg )(x x f =与x x g lg 2)(=;(2)12+=x y 与12+=y x知识点:函数相等的条件;思路:函数的两个要素是f (作用法则)及定义域D (作用范围),当两个函数作用法则f 相同(化简后代数表达式相同)且定义域相同时,两函数相同;解:(1)2lg )(x x f =的定义域D={}R x x x ∈≠,0,x x g lg )(=的定义域{},0R x x x D ∈>=,虽然作用法则相同x x lg 2lg 2=,但显然两者定义域不同,故不是同一函数;(2)12+=x y ,以x 为自变量,显然定义域为实数R ;12+=y x ,以x 为自变量,显然定义域也为实数R ;两者作用法则相同“2□1+”与自变量用何记号表示无关,故两者为同一函数;★ 3.设⎪⎪⎩⎪⎪⎨⎧≥<=3,03,sin )(ππϕx x x x ,求)2()4()4()6(--ϕπϕπϕπϕ,,,,并做出函数)(x y ϕ=的图形知识点:分段函数;思路:注意自变量的不同范围; 解:216sin)6(==ππϕ,224sin 4==⎪⎭⎫⎝⎛ππϕ,224sin 4=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-ππϕ()02=-ϕ;如图:★ 4.试证下列各函数在指定区间内的单调性 :(1)()1,1∞--=xxy (2)x x y ln 2+=,()+∞,0 知识点:单调性定义。
第一章课后习题及答案

第一章1.(Q1) What is the difference between a host and an end system List the types of endsystems. Is a Web server an end systemAnswer: There is no difference. Throughout this text, the words “host” and “end system” are used interchangeably. End systems include PCs, workstations, Web servers, mail servers, Internet-connected PDAs, WebTVs, etc.2.(Q2) The word protocol is often used to describe diplomatic relations. Give an example of adiplomatic protocol.Answer: Suppose Alice, an ambassador of country A wants to invite Bob, an ambassador of country B, over for dinner. Alice doesn’t simply just call Bob on the phone and say, come to our dinner table now”. Instead, she calls Bob and suggests a date and time. Bob may respond by saying he’s not available that p articular date, but he is available another date. Alice and Bob continue to send “messages” back and forth until they agree on a date and time. Bob then shows up at the embassy on the agreed date, hopefully not more than 15 minutes before or after the agreed time. Diplomatic protocols also allow for either Alice or Bob to politely cancel the engagement if they have reasonable excuses.3.(Q3) What is a client program What is a server program Does a server program request andreceive services from a client programAnswer: A networking program usually has two programs, each running on a different host, communicating with each other. The program that initiates the communication is the client.Typically, the client program requests and receives services from the server program.4.(Q4) List six access technologies. Classify each one as residential access, company access, ormobile access.Answer:1. Dial-up modem over telephone line: residential; 2. DSL over telephone line: residential or small office; 3. Cable to HFC: residential; 4. 100 Mbps switched Etherent: company; 5. Wireless LAN: mobile; 6. Cellular mobile access (for example, 3G/4G): mobile5.(Q5) List the available residential access technologies in your city. For each type of access,provide the advertised downstream rate, upstream rate, and monthly price.Answer: Current possibilities include: dial-up (up to 56kbps); DSL (up to 1 Mbps upstream, up to 8 Mbps downstream); cable modem (up to 30Mbps downstream, 2 Mbps upstream.6.(Q7) What are some of the physical media that Ethernet can run overAnswer: Ethernet most commonly runs over twisted-pair copper wire and “thin” coaxial cable. It also can run over fibers optic links and thick coaxial cable.7.(Q8) Dial-up modems, HFC, and DSL are all used for residential access. For each of theseaccess technologies, provide a range of transmission rates and comment on whether the transmission rate is shared or dedicated.Answer:Dial up modems: up to 56 Kbps, bandwidth is dedicated; ISDN: up to 128 kbps, bandwidth is dedicated; ADSL: downstream channel is .5-8 Mbps, upstream channel is up to1 Mbps, bandwidth is dedicated; HFC, downstream channel is 10-30 Mbps and upstreamchannel is usually less than a few Mbps, bandwidth is shared.8.(Q13) Why is it said that packet switching employs statistical multiplexing Contraststatistical multiplexing with the multiplexing that takes place in TDM.Answer: In a packet switched network, the packets from different sources flowing on a link do not follow any fixed, pre-defined pattern. In TDM circuit switching, each host gets the same slot in a revolving TDM frame.9.(Q14) Suppose users share a 2Mbps link. Also suppose each user requires 1Mbps whentransmitting, but each user transmits only 20 percent of the time. (See the discussion of statistical multiplexing in Section .)a.When circuit switching is used, how many users can be supportedb.For the remainder of this problem, suppose packet switching is used. Why will there beessentially no queuing delay before the link if two or fewer users transmit at the same time Why will there be a queuing delay if three users transmit at the same timec.Find the probability that a given user is transmitting.d.Suppose now there are three users. Find the probability that at any given time, allthree users are transmitting simultaneously. Find the fraction of time during which the queue grows.Answer:a. 2 users can be supported because each user requires half of the link bandwidth.b.Since each user requires 1Mbps when transmitting, if two or fewer users transmitsimultaneously, a maximum of 2Mbps will be required. Since the available bandwidth of the shared link is 2Mbps, there will be no queuing delay before the link. Whereas, if three users transmit simultaneously, the bandwidth required will be 3Mbps which is more than the available bandwidth of the shared link. In this case, there will be queuing delay before the link.c.Probability that a given user is transmitting =d.Probability that all three users are transmittingsimultaneously. Since the queue grows when all the usersare transmitting, the fraction of time during which the queue grows (which is equal to the probability that all three users are transmitting simultaneously) is .10.(Q16) Consider sending a packet from a source host to a destination host over a fixed route.List the delay components in the end-to-end delay. Which of these delays are constant and which are variableAnswer:The delay components are processing delays, transmission delays, propagation delays, and queuing delays. All of these delays are fixed, except for the queuing delays, which are variable.11.(Q19) Suppose Host A wants to send a large file to Host B. The path from Host A to Host Bhas three links, of rates R1 = 250 kbps, R2 = 500 kbps, and R3 = 1 Mbps.a.Assuming no other traffic in the network, what is the throughput for the file transfer.b.Suppose the file is 2 million bytes. Roughly, how long will it take to transfer the file toHost Bc.Repeat (a) and (b), but now with R2 reduced to 200 kbps.Answer:a.250 kbpsb.64 secondsc.200 kbps; 80 seconds12.(P2) Consider the circuit-switched network in Figure . Recall that there are n circuits oneach link.a.What is the maximum number of simultaneous connections that can be in progress atany one time in this networkb.Suppose that all connections are between the switch in the upper-left-hand cornerand the switch in the lower-right-hand corner. What is the maximum number ofsimultaneous connections that can be in progressAnswer:a.We can n connections between each of the four pairs of adjacent switches. This gives amaximum of 4n connections.b.We can n connections passing through the switch in the upper-right-hand corner andanother n connections passing through the switch in the lower-left-hand corner, giving a total of 2n connections.13.(P4) Review the car-caravan analogy in Section . Assume a propagation speed of 50km/hour.a.Suppose the caravan travels 150 km, beginning in front of one tollbooth, passingthrough a second tollbooth, and finishing just before a third tollbooth. What is theend-to-end delayb.Repeat (a), now assuming that there are five cars in the caravan instead of ten.Answer: Tollbooths are 150 km apart, and the cars propagate at 50 km/hr, A tollbooth services a car at a rate of one car every 12 seconds.a.There are ten cars. It takes 120 seconds, or two minutes, for the first tollbooth to servicethe 10 cars. Each of these cars has a propagation delay of 180 minutes before arriving at the second tollbooth. Thus, all the cars are lined up before the second tollbooth after 182 minutes. The whole process repeats itself for traveling between the second and third tollbooths. Thus the total delay is 364 minutes.b.Delay between tollbooths is 5*12 seconds plus 180 minutes, ., 181minutes. The totaldelay is twice this amount, ., 362 minutes.14.(P5) This elementary problem begins to explore propagation delay and transmission delay,two central concepts in data networking. Consider two hosts, A and B, connected by a single link of rate R bps. Suppose that the two hosts are separated by m meters, and suppose the propagation speed along the link is s meters/sec. Host A is to send a packet of size L bits to Host B.a.Express the propagation delay, d prop , in terms of m and s.b.Determine the transmission time of the packet, d trans , in terms of L and R.c.Ignoring processing and queuing delays, obtain an expression for the end-to-enddelay.d.Suppose Host A begins to transmit the packet at time t = 0. At time t = d trans , where isthe last bit of the packete.Suppose d prop is greater than d trans . At time t = d trans , where is the first bit of thepacketf.Suppose d prop is less than d trans . At time t = d trans , where is the first bit of the packetg.Suppose s = *108, L = 100bits, and R = 28kbps. Find the distance m so that d prop equalsd trans .Answer:a. d prop = m/s seconds.b. d trans = L/R seconds.c. d end-to-end = (m/s + L/R) seconds.d.The bit is just leaving Host A.e.The first bit is in the link and has not reached Host B.f.The first bit has reached Host B.g.Want15.(P6) In this problem we consider sending real-time voice from Host A to Host B over apacket-switched network (VoIP). Host A converts analog voice to a digital 64 kbps bit stream on the fly. Host A then groups the bits into 56-Byte packets. There is one linkbetween Host A and B; its transmission rate is 500 kbps and its propagation delay is 2 msec.As soon as Host A gathers a packet, it sends it to Host B. As soon as Host B receives an entire packet, it converts the packet’s bits to an analog signal. How much time elapses from the time a bit is created (from the original analog signal at Host A) until the bit is decoded (as part of the analog signal at Host B)Answer: Consider the first bit in a packet. Before this bit can be transmitted, all of the bits in the packet must be generated. This requiresThe time required to transmit the packet isPropagation delay = 2 msec.The delay until decoding is7msec + 896μsec + 2msec = msecA similar analysis shows that all bits experience a delay of msec.16.(P9) Consider a packet of length L which begins at end system A, travels over one link to apacket switch, and travels from the packet switch over a second link to a destination end system. Let d i, s i, and R i denote the length, propagation speed, and the transmission rate of link i, for i= 1, 2. The packet switch delays each packet by d proc. Assuming no queuing delays, in terms of d i, s i, R i, (i= 1, 2), and L, what is the total end-to-end delay for the packet Suppose now the packet Length is 1,000 bytes, the propagation speed on both links is * 108 m/s, the transmission rates of both links is 1 Mbps, the packet switch processing delay is 2 msec, the length of the first link is 6,000 km, and the length of the last link is 3,000 km. For these values, what is the end-to-end delayAnswer: The first end system requires L/R1to transmit the packet onto the first link; the packet propagates over the first link in d1/s1; the packet switch adds a processing delay ofd proc; after receiving the entire packet, the packet switch requires L/R2to transmit the packetonto the second link; the packet propagates over the second link in d2/s2. Adding these five delays givesd end-end = L/R1 + L/R2 + d1/s1 + d2/s2 + d procTo answer the second question, we simply plug the values into the equation to get 8 + 8 +24 + 12 + 2 = 54 msec.17.(P10) In the above problem, suppose R1 = R2 = R and d proc= 0. Further suppose the packetswitch does not store-and-forward packets but instead immediately transmits each bit it receivers before waiting for the packet to arrive. What is the end-to-end delayAnswer: Because bits are immediately transmitted, the packet switch does not introduce any delay; in particular, it does not introduce a transmission delay. Thus,d end-end = L/R + d1/s1 + d2/s2For the values in Problem 9, we get 8 + 24 + 12 = 44 msec.18.(P11) Suppose N packets arrive simultaneously to a link at which no packets are currentlybeing transmitted or queued. Each packet is of length L and the link has transmission rate R.What is the average queuing delay for the N packetsAnswer:The queuing delay is 0 for the first transmitted packet, L/R for the second transmitted packet, and generally, (n-1)L/R for the nth transmitted packet. Thus, the average delay for the N packets is(L/R + 2L/R + ....... + (N-1)L/R)/N = L/RN(1 + 2 + ..... + (N-1)) = LN(N-1)/(2RN) = (N-1)L/(2R) Note that here we used the well-known fact that1 +2 + ....... + N = N(N+1)/219.(P14) Consider the queuing delay in a router buffer. Let I denote traffic intensity; that is, I =La/R. Suppose that the queuing delay takes the form IL/R (1-I) for I<1.a.Provide a formula for the total delay, that is, the queuing delay plus the transmissiondelay.b.Plot the total delay as a function of L/R.Answer:a.The transmission delay is L / R . The total delay isb.Let x = L / R.20.(P16) Perform a Traceroute between source and destination on the same continent at threedifferent hours of the day.a.Find the average and standard deviation of the round-trip delays at each of the threehours.b.Find the number of routers in the path at each of the three hours. Did the pathschange during any of the hoursc.Try to identify the number of ISP networks that the Traceroute packets pass throughfrom source to destination. Routers with similar names and/or similar IP addresses should be considered as part of the same ISP. In your experiments, do the largest delays occur at the peering interfaces between adjacent ISPsd.Repeat the above for a source and destination on different continents. Compare theintra-continent and inter-continent results.Answer: Experiments.21.(P18) Suppose two hosts, A and B, are separated by 10,000 kilometers and are connectedby a direct link of R = 2 Mbps. Suppose the propagation speed over the link is 108 meters/sec.a.Calculate the bandwidth-delay product, R d prop.b.Consider sending a file of 400,000 bits from Host A to Host B. Suppose the file is sentcontinuously as one large message. What is the maximum number of bits that will be in the link at any given timec.Provide an interpretation of the bandwidth-delay product.d.What is the width (in meters) of a bit in the link Is it longer than a football fielde.Derive a general expression for the width of a bit in terms of the propagation speed s,the transmission rate R, and the length of the link m.Answer:a.d prop = 107 / 108 = sec; so R d prop = 80,000bitsb.80,000bitsc.The bandwidth-delay product of a link is the maximum number of bits that can be in thelink.d. 1 bit is 125 meters long, which is longer than a football fielde.m / (R d prop ) = m / (R * m / s) = s/R22.(P20) Consider problem P18 but now with a link of R = 1 Gbps.a.Calculate the bandwidth-delay product, R·d prop .b.Consider sending a file of 400,000 bits from Host A to Host B. Suppose the file is sentcontinuously as one big message. What is the maximum number of bits that will be inthe link at any given timec.What is the width (in meters) of a bit in the linkAnswer:a.40,000,000 bits.b.400,000 bits.c.meters.23.(P21) Refer again to problem P18.a.How long does it take to send the file, assuming it is sent continuouslyb.Suppose now the file is broken up into 10 packet is acknowledged by the receiver andthe transmission time of an acknowledgment packet is negligible. Finally, assumethat the sender cannot send a packet until the preceding one is acknowledged. Howlong does it take to send the filepare the results from (a) and (b).Answer:a. d trans + d prop = 200 msec + 40 msec = 240 msecb.10 * (t trans + 2 t prop ) = 10 * (20 msec + 80 msec) = sec。
第1章习题答案

AB
i
eiT ( AB) (eiT A)B eiT A
A
i
AB i
A
iB
1-2
1
1
12 1
1. aT a 1, 2, 1 2 6, aaT 2 1, 2, 1 2 4 2
1
1
1 21
12 1 (aaT )100 (aT a)99 aaT 699 2 4 2 .
1 21
2.
Am 1 (aaT )(aaT ) (aaT ) (aT a)m (aaT ) k m A
1-1
1.
( A B)2 A2 AB BA B2 , AB
BA .
2.
( A E)2 A2 AE EA E, AE EA .
3.
( A E)( A E) A2 AE EA E A2 E,
( A E)( A E) A2 E .
4.
( AB)2 A2B2
AB BA .
11
5.
A
11
10
6.
A
00
10
7.
123 1
3.
abT 1 2 3 1 1, 2, 3
123 1
1
111
1
baT 2 1,1,1 2 2 2 , bTa 1, 2, 3 1 6.
3
333
1
AB (E aaT )(E 3aaT ) E 2aaT 3(aaT )(aaT )
E 2aaT 3a(aT a)aT E (2 3k)aaT
AB=E a 0 aaT O
1 00
1 00 2 1 0 3 r2 101
4. A 3 2
A B r3 2r1
c1
c2 C,
经济学原理 曼昆课后答案 chapter 1

Problems and Applications1. a. A family deciding whether to buy a new car faces a tradeoff between the costof the car and other things they might want to buy. For example, buying thecar might mean they must give up going on vacation for the next two years.So the real cost of the car is the family's opportunity cost in terms of what theymust give up.b. For a member of Congress deciding whether to increase spending on nationalparks, the tradeoff is between parks and other spending items or tax cuts. Ifmore money goes into the park system, that may mean less spending onnational defense or on the police force. Or, instead of spending more moneyon the park system, taxes could be reduced.c. When a company president decides whether to open a new factory, thedecision is based on whether the new factory will increase the firm's profitscompared to other alternatives. For example, the company could upgradeexisting equipment or expand existing factories. The bottom line is: Whichmethod of expanding production will increase profit the most?d. In deciding how much to prepare for class, a professor faces a tradeoffbetween the value of improving the quality of the lecture compared to otherthings she could do with her time, such as working on additional research.2. When the benefits of something are psychological, such as going on a vacation, it isn'teasy to compare benefits to costs to determine if it's worth doing. But there are two ways to think about the benefits. One is to compare the vacation with what youwould do in its place. If you didn't go on vacation, would you buy something like anew set of golf clubs? Then you can decide if you'd rather have the new clubs or the vacation. A second way is to think about how much work you had to do to earn the money to pay for the vacation; then you can decide if the psychological benefits of the vacation were worth the psychological cost of working.3. If you are thinking of going skiing instead of working at your part-time job, the cost ofskiing includes its monetary and time costs, plus the opportunity cost of the wagesyou're giving up by not working. If the choice is between skiing and going to thelibrary to study, then the cost of skiing is its monetary and time costs plus the cost to you of getting a lower grade in your course.4. If you spend $100 now instead of investing it for a year and earning 5 percent interest,you are giving up the opportunity to spend $105 a year from now. The idea thatmoney has a time value is the basis for the field of finance, the subfield of economics that has to do with prices of financial instruments like stocks and bonds.5. The fact that you've already sunk $5 million isn't relevant to your decision anymore,since that money is gone. What matters now is the chance to earn profits at themargin. If you spend another $1 million and can generate sales of $3 million, you'llearn $2 million in marginal profit, so you should do so. You are right to think that the project has lost a total of $3 million ($6 million in costs and only $3 million in revenue) and you shouldn't have started it. That's true, but if you don't spend the additional $1 million, you won't have any sales and your losses will be $5 million. So what matters is not the total profit, but the profit you can earn at the margin. In fact, you'd pay up to $3 million to complete development; any more than that, and you won't beincreasing profit at the margin.6. Harry suggests looking at whether productivity would rise or fall. Productivity iscertainly important, since the more productive workers are, the lower the cost pergallon of potion. Harry wants to look at average cost. But both Harry and Ron are missing the other side of the equation−revenue. A firm wants to maximize its profits, so it needs to examine both costs and revenues. Thus, Hermione is right−it’s best to examine whether the extra revenue would exceed the extra costs. In addition,Hermione is the only one who’s thinking at the margin.7. a. Since a person gets fewer after-tax Social Security benefits the greater is his orher income, there's an incentive not to save for retirement. If you save a lot,your income will be higher, and you won't get as much after-tax Social Securityincome as someone who didn't save as much. The unintended consequenceof the taxation of Social Security benefits is to reduce saving; yet the SocialSecurity system arose because of worries that people wouldn’t save enoughfor retirement.b. For the same reason, you'll tend not to work (or not work as much) after age65. The more you work, the lower your after-tax Social Security benefits willbe. Thus the taxation of Social Security benefits discourages work effort afterage 65.8. a. When welfare recipients who are able to work have their benefits cut off aftertwo years, they have greater incentive to find jobs than if their benefits were tolast forever.b. The loss of benefits means that someone who can't find a job will get noincome at all, so the distribution of income will become less equal. But theeconomy will be more efficient, since welfare recipients have a greaterincentive to find jobs. Thus the change in the law is one that increasesefficiency but reduces equity.9. By specializing in each task, you and your roommate can finish the chores more quickly.If you divided each task equally, it would take you more time to cook than it would takeyour roommate, and it would take him more time to clean than it would take you. By specializing, you reduce the total time spent on chores.Similarly, countries can specialize and trade, making both better off. For example,suppose it takes Spanish workers less time to make clothes than French workers, and French workers can make wine more efficiently than Spanish workers. Then Spainand France can both benefit if Spanish workers produce all the clothes and Frenchworkers produce all the wine, and they exchange some wine for some clothes.10. a. Being a central planner is tough! To produce the right number of CDs by theright artists and deliver them to the right people requires an enormous amountof information. You need to know about production techniques and costs inthe CD industry. You need to know each person's musical tastes and whichartists they want to hear. If you make the wrong decisions, you'll beproducing too many CDs by artists that people don't want to hear, and notenough by others.b. Your decisions about how many CDs to produce carry over to other decisions.You have to make the right number of CD players for people to use. If youmake too many CDs and not enough cassette tapes, people with cassetteplayers will be stuck with CDs they can't play. The probability of makingmistakes is very high. You will also be faced with tough choices about themusic industry compared to other parts of the economy. If you produce moresports equipment, you'll have fewer resources for making CDs. So alldecisions about the economy influence your decisions about CD production.11. a. Efficiency: The market failure comes from the monopoly by the cable TVfirm.b. Equityc. Efficiency: An externality arises because secondhand smoke harmsnonsmokers.d. Efficiency: The market failure occurs because of Standard Oil's monopolypower.e. Equityf. Efficiency: There's an externality because of accidents caused by drunkdrivers.12. a. If everyone were guaranteed the best health care possible, much more of ournation's output would be devoted to medical care than is now the case.Would that be efficient? If you think that currently doctors form a monopolyand restrict health care to keep their incomes high, you might think efficiencywould increase by providing more health care. But more likely, if thegovernment mandated increased spending on health care, the economy wouldbe less efficient because it would give people more health care than theywould choose to pay for. From the point of view of equity, if poor people areless likely to have adequate health care, providing more health care wouldrepresent an improvement. Each person would have a more even slice of theeconomic pie, though the pie would consist of more health care and less ofother goods.b. When workers are laid off, equity considerations argue for the unemploymentbenefits system to provide them with some income until they can find new jobs.After all, no one plans to be laid off, so unemployment benefits are a form ofinsurance. But there’s an efficiency problem why work if you can getincome for doing nothing? The economy isn’t operating e fficiently if peopleremain unemployed for a long time, and unemployment benefits encourageunemployment. Thus, there’s a tradeoff between equity and efficiency. Themore generous are unemployment benefits, the less income is lost by anunemployed person, but the more that person is encouraged to remainunemployed. So greater equity reduces efficiency.13. Since average income in the United States has roughly doubled every 35 years, we arelikely to have a better standard of living than our parents, and a much better standard of living than our grandparents. This is mainly the result of increased productivity, so that an hour of work produces more goods and services than it used to. Thusincomes have continuously risen over time, as has the standard of living.14. If Americans save more and it leads to more spending on factories, there will be anincrease in production and productivity, since the same number of workers will havemore equipment to work with. The benefits from higher productivity will go to boththe workers, who will get paid more since they're producing more, and the factoryowners, who will get a return on their investments. There's no such thing as a freelunch, though, because when people save more, they're giving up spending. They get higher incomes at the cost of buying fewer goods.15. a. If people have more money, they're probably going to spend more on goodsand services.b. If prices are sticky, and people spend more on goods and services, then outputmay increase, as producers increase output to meet the higher demand ratherthan raising prices.c. If prices can adjust, then people's higher spending will be matched withincreased prices, and output won't rise.16. To make an intelligent decision about whether to reduce inflation, a policymaker wouldneed to know what causes inflation and unemployment, as well as what determines the tradeoff between them. Because prices are sticky, an attempt to reduce inflation willlead to higher unemployment. A policymaker thus faces a tradeoff between the benefits of lower inflation compared to the cost of higher unemployment.。
第1章课后题标准答案

第1章课后题答案————————————————————————————————作者:————————————————————————————————日期:2一、判断题1、数据库就是大量数据的集合(F)2、在Visual FoxPro 6.0中,数组的每个元素的数据类型必须一致。
(F)3、函数自变量类型和函数值的类型肯定一致。
(F)4、数据库中,各条记录的同一个字段可以有不同的值。
(T)5、不论表文件是否打开,同名的字段变量的优先级高于内存变量。
(F)6、内存变量的数据类型一经确定,就不能再改变了。
(F)7、同一表达式中的每一项类型可以不同。
(T)8、宏代换函数可以改变数据类型。
(T)9、NULL是指没有任何值,与0、空字符串或空格串具有相同的意义。
(F)10、内存变量和字段变量可以取同名,引用内存变量的正确方法是M->变量名。
(T)11、Visual Foxpro 的命令窗口,可以输入命令,但不能改变命令的字体、字型等各项编辑工作(F)。
12、备注型字段一般用于存放图片,电子表格,声音,设计分析图等数据,而通用型字段则用于保存大量的文本信息,源程序代码等多种信息。
(F)13、在使用VAL函数时,要转换的字符必须全部由数字字符组成,否则将无法转换。
(F)14、项目管理器连编的可执行文件可以在脱离VFP的环境运行。
(T)15、STORE和“=”命令具有相同功能,它们都可以在一条命令中给多个变量赋值。
(F)二、单选题1、数据库DB、数据库系统DBS、数据库管理系统DBMS三者之间的关系是:(A)(A)DBS包括DB和DBMS (B)DBMS包括DB和DBS(C)DB包括DBS和DBMS (D)DBS就是DB,也就是DBMS2、Visual FoxPro 6.0数据库系统是(C)型数据库系统。
(A)网络(B)层次(C)关系(D)链状3、设A=”123”,B=”234”,表达式(C)的值为假(.F.)。
经济学原理 曼昆课后答案 chapter 1

Problems and Applicat ions1. a. A family deciding whether to buy a new car faces a tradeoff between the costof the car and other things they might want to buy. For example, buying thecar might mean they must give up going on vacation for the next two years.So the real cost of the car is the family's opportunity cost in terms of what theymust give up.b. For a member of Congress deciding whether to increase spending on nationalparks, the tradeoff is between parks and other spending items or tax cuts. Ifmore money goes into the park system, that may mean less spending onnational defense or on the police force. Or, instead of spending more moneyon the park system, taxes could be reduced.c. When a company president decides whether to open a new factory, thedecision is based on whether the new factory will increase the firm's profitscompared to other alternatives. For example, the company could upgradeexisting equipment or expand existing factories. The bottom line is: Whichmethod of expanding production will increase profit the most?d. In deciding how much to prepare for class, a professor faces a tradeoffbetween the value of improving the quality of the lecture compared to otherthings she could do with her time, such as working on additional research.2. When the benefits of something are psychological, such as going on a vacation, it isn'teasy to compare benefits to costs to determine if it's worth doing. But there are two ways to think about the benefits. One is to compare the vaca tion with what youwould do in its place. If you didn't go on vacation, would you buy something like anew set of golf clubs? Then you can decide if you'd rather have the new clubs or the vacation. A second way is to think about how much work you had to do to earn the money to pay for the vacation; then you can decide if the psychological benefits of the vacation were worth the psychological cost of working.3. If you are thinking of going skiing instead of working at your part-time job, the cost ofskiing includes its monetary and time costs, plus the opportunity cost of the wagesyou're giving up by not working. If the choice is between skiing and going to thelibrary to study, then the cost of skiing is its monetary and time costs plus the cost to you of getting a lower grade in your course.4. If you spend $100 now instead of investing it for a year and earning 5 percent interest,you are giving up the opportunity to spend $105 a year from now. The idea thatmoney has a time value is the basis for the field of finance, the subfield of economics that has to do with prices of financial instruments like stocks and bonds.5. The fact that you've already sunk $5 million isn't relevant to your decision anymore,since that money is gone. What matters now is the chance to earn profits at themargin. If you spend another $1 million and can generate sales of $3 million, you'llearn $2 million in marginal profit, so you should do so. You are right to think that the project has lost a total of $3 million ($6 million in costs and only $3 million in revenue) and you shouldn't have started it. That's true, but if you don't spend the additional $1 million, you won't have any sales and your losses will be $5 million. So what matters is not the total profit, but the profit you can earn at the margin. In fact, you'd pay up to $3 million to complete development; any more than that, and you won't beincreasing profit at the margin.6. Harry suggests looking at whether productivity would rise or fall. Productivity iscertainly important, since the more productive workers are, the lower the cost pergallon of potion. Harry wants to look at average cost. But both Harry and Ron aremissing the other side of the equation−revenue. A firm wants to maximize its profits, so it needs to examine both costs and revenues. Thus, Hermione is right−it’s best to examine whether the extra revenue would exceed the extra costs. In addition,Hermione is the only one who’s thinking at the margin.7. a. Since a person gets fewer after-tax Social Security benefits the greater is his orher income, there's an incentive not to save for retirement. If you save a lot,your income will be higher, and you won't get as much after-tax Social Securityincome as someone who didn't save as much. The unintended consequenceof the taxation of Social Security benefits is to reduce saving; yet the SocialSecurity system arose because of worries that people wouldn’t save enoughfor retirement.b. For the same reason, you'll tend not to work (or not work as much) after age65. The more you work, the lower your after-tax Social Security benefits willbe. Thus the taxation of Social Security benefits discourages work effort afterage 65.8. a. When welfare recipients who are able to work have their benefits cut off aftertwo years, they have greater incentive to find jobs than if their benefits were tolast forever.b. The loss of benefits means that someone who can't find a job will get noincome at all, so the distribution of income will become less equal. But theeconomy will be more efficient, since welfare recipients have a greaterincentive to find jobs. Thus the change in the law is one that increasesefficiency but reduces equity.9. By specializing in each task, you and your roommate can finish the chores more quickly.If you divided each task equally, it would take you more time to cook than it would takeyour roommate, and it would take him more time to clean than it would take you. By specializing, you reduce the total time spent on chores.Similarly, countries can specialize and trade, making both better off. For example,suppose it takes Spanish workers less time to make clothes than French workers, and French workers can make wine more efficiently than Spanish workers. Then Spainand France can both benefit if Spanish workers produce all the clothes and Frenchworkers produce all the wine, and they exchange some wine for some clothes.10. a. Being a central planner is tough! To produce the right number of CDs by theright artists and deliver them to the right people requires an enormous amountof information. You need to know about production techniques and costs inthe CD industry. You need to know each person's musical tastes and whichartists they want to hear. If you make the wrong decisions, you'll beproducing too many CDs by artists that people don't want to hear, and notenough by others.b. Your decisions about how many CDs to produce carry over to other decisions.You have to make the right number of CD players for people to use. If youmake too many CDs and not enough cassette tapes, people with cassetteplayers will be stuck with CDs they can't play. The probability of makingmistakes is very high. You will also be faced with tough choices about themusic industry compared to other parts of the economy. If you produce moresports equipment, you'll have fewer resources for making CDs. So alldecisions about the economy influence your decisions about CD production.11. a. Efficiency: The market failure comes from the monopoly by the cable TVfirm.b. Equityc. Efficiency: An externality arises because secondhand smoke harmsnonsmokers.d. Efficiency: The market failure occurs because of Standard Oil's monopolypower.e. Equityf. Efficiency: There's an externality because of accidents caused by drunkdrivers.12. a. If everyone were guaranteed the best health care possible, much more of ournation's output would be devoted to medical care than is now the case.Would that be efficient? If you think that currently doctors form a monopolyand restrict health care to keep their incomes high, you might think efficiencywould increase by providing more health care. But more likely, if thegovernment mandated increased spending on health care, the economy wouldbe less efficient because it would give people more health care than theywould choose to pay for. From the point of view of equity, if poor people areless likely to have adequate health care, providing more health care wouldrepresent an improvement. Each person would have a more even slice of theeconomic pie, though the pie would consist of more health care and less ofother goods.b. When workers are laid off, equity considerations argue for the unemploymentbenefits system to provide them with some income until they can find new jobs.After all, no one plans to be laid off, so unemployment benefits are a form ofinsurance. But there’s an efficiency problem why work if you can getincome for doing nothing? The economy isn’t operating e fficiently if peopleremain unemployed for a long time, and unemployment benefits encourageunemployment. Thus, there’s a tradeoff between equity and efficiency. Themore generous are unemployment benefits, the less income is lost by anunemployed person, but the more that person is encouraged to remainunemployed. So greater equity reduces efficiency.13. Since average income in the United States has roughly doubled every 35 years, we arelikely to have a better standard of living than our parents, and a much better standard of living than our grandparents. This is mainly the result of increased productivity, so that an hour of work produces more goods and services than it used to. Thusincomes have continuously risen over time, as has the standard of living.14. If Americans save more and it leads to more spending on factories, there will be anincrease in production and productivity, since the same number of workers will havemore equipment to work with. The benefits from higher productivity will g o to boththe workers, who will get paid more since they're producing more, and the factoryowners, who will get a return on their investments. There's no such thing as a freelunch, though, because when people save more, they're giving up spending. They get higher incomes at the cost of buying fewer goods.15. a. If people have more money, they're probably going to spend more on goodsand services.b. If prices are sticky, and people spend more on goods and services, then outputmay increase, as producers increase output to meet the higher demand ratherthan raising prices.c. If prices can adjust, then people's higher spending will be matched withincreased prices, and output won't rise.16. To make an intelligent decision about whether to reduce inflation, a policymaker wouldneed to know what causes inflation and unemployment, as well as what determines the tradeoff between them. Because prices are sticky, an attempt to reduce inflation willlead to higher unemployment. A policymaker thus faces a tradeoff between the benefits of lower inflation compared to the cost of higher unemployment.。
高等数学课后习题及参考答案(第一章)

高等数学课后习题及参考答案(第一章)习题1-11. 设A =(-∞, -5)⋃(5, +∞), B =[-10, 3), 写出A ⋃B , A ⋂B , A \B 及A \(A \B )的表达式.解 A ⋃B =(-∞, 3)⋃(5, +∞),A ⋂B =[-10, -5),A \B =(-∞, -10)⋃(5, +∞),A \(A \B )=[-10, -5).2. 设A 、B 是任意两个集合, 证明对偶律: (A ⋂B )C =A C ⋃B C .证明 因为x ∈(A ⋂B )C ⇔x ∉A ⋂B ⇔ x ∉A 或x ∉B ⇔ x ∈A C 或x ∈B C ⇔ x ∈A C ⋃B C , 所以 (A ⋂B )C =A C ⋃B C .3. 设映射f : X →Y , A ⊂X , B ⊂X . 证明(1)f (A ⋃B )=f (A )⋃f (B );(2)f (A ⋂B )⊂f (A )⋂f (B ).证明 因为y ∈f (A ⋃B )⇔∃x ∈A ⋃B , 使f (x )=y⇔(因为x ∈A 或x ∈B ) y ∈f (A )或y ∈f (B )⇔ y ∈f (A )⋃f (B ),所以 f (A ⋃B )=f (A )⋃f (B ).(2)因为y ∈f (A ⋂B )⇒∃x ∈A ⋂B , 使f (x )=y ⇔(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )⇒ y ∈ f (A )⋂f (B ),所以 f (A ⋂B )⊂f (A )⋂f (B ).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.证明 因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射.又因为对于任意的x 1≠x 2, 必有f (x 1)≠f (x 2), 否则若f (x 1)=f (x 2)⇒g [ f (x 1)]=g [f (x 2)] ⇒ x 1=x 2.因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y →X , 因为对每个y ∈Y , 有g (y )=x ∈X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X →Y , A ⊂X . 证明:(1)f -1(f (A ))⊃A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x ∈A ⇒ f (x )=y ∈f (A ) ⇒ f -1(y )=x ∈f -1(f (A )),所以 f -1(f (A ))⊃A .(2)由(1)知f -1(f (A ))⊃A .另一方面, 对于任意的x ∈f -1(f (A ))⇒存在y ∈f (A ), 使f -1(y )=x ⇒f (x )=y . 因为y ∈f (A )且f 是单射, 所以x ∈A . 这就证明了f -1(f (A ))⊂A . 因此f -1(f (A ))=A . 6. 求下列函数的自然定义域:(1)23+=x y ;解 由3x +2≥0得32->x . 函数的定义域为) ,32[∞+-. (2)211xy -=; 解 由1-x 2≠0得x ≠±1. 函数的定义域为(-∞, -1)⋃(-1, 1)⋃(1, +∞).(3)211x xy --=; 解 由x ≠0且1-x 2≥0得函数的定义域D =[-1, 0)⋃(0, 1].(4)241x y -=; 解 由4-x 2>0得 |x |<2. 函数的定义域为(-2, 2).(5)x y sin =;解 由x ≥0得函数的定义D =[0, +∞).(6) y =tan(x +1);解 由21π≠+x (k =0, ±1, ±2, ⋅ ⋅ ⋅)得函数的定义域为 12-+≠ππk x (k =0, ±1, ±2, ⋅ ⋅ ⋅).(7) y =arcsin(x -3);解 由|x -3|≤1得函数的定义域D =[2, 4].(8)xx y 1arctan 3+-=; 解 由3-x ≥0且x ≠0得函数的定义域D =(-∞, 0)⋃(0, 3).(9) y =ln(x +1);解 由x +1>0得函数的定义域D =(-1, +∞).(10)x e y 1=.解 由x ≠0得函数的定义域D =(-∞, 0)⋃(0, +∞).7. 下列各题中, 函数f (x )和g (x )是否相同?为什么?(1)f (x )=lg x 2, g (x )=2lg x ;(2) f (x )=x , g (x )=2x ;(3)334)(x x x f -=,31)(-=x x x g .(4)f (x )=1, g (x )=sec 2x -tan 2x .解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x <0时, g (x )=-x .(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, ϕ(-2), 并作出函数y =ϕ(x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ. 9. 试证下列函数在指定区间内的单调性:(1)xx y -=1, (-∞, 1); (2)y =x +ln x , (0, +∞).证明 (1)对于任意的x 1, x 2∈(-∞, 1), 有1-x 1>0, 1-x 2>0. 因为当x 1<x 2时, 0)1)(1(112121221121<---=---=-x x x x x x x x y y ,所以函数xx y -=1在区间(-∞, 1)内是单调增加的. (2)对于任意的x 1, x 2∈(0, +∞), 当x 1<x 2时, 有0ln )()ln ()ln (2121221121<+-=+-+=-x x x x x x x x y y , 所以函数y =x +ln x 在区间(0, +∞)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明 对于∀x 1, x 2∈(-l , 0)且x 1<x 2, 有-x 1, -x 2∈(0, l )且-x 1>-x 2.因为f (x )在(0, l )内单调增加且为奇函数, 所以f (-x 2)<f (-x 1), -f (x 2)<-f (x 1), f (x 2)>f (x 1),这就证明了对于∀x 1, x 2∈(-l , 0), 有f (x 1)< f (x 2), 所以f (x )在(-l , 0)内也单调增加. 11. 设下面所考虑的函数都是定义在对称区间(-l , l )上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明 (1)设F (x )=f (x )+g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )+g (-x )=f (x )+g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的和是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )+g (-x )=-f (x )-g (x )=-F (x ),所以F (x )为奇函数, 即两个奇函数的和是奇函数.(2)设F (x )=f (x )⋅g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )⋅g (-x )=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的积是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )⋅g (-x )=[-f (x )][-g (x )]=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个奇函数的积是偶函数.如果f (x )是偶函数, 而g (x )是奇函数, 则F (-x )=f (-x )⋅g (-x )=f (x )[-g (x )]=-f (x )⋅g (x )=-F (x ),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y =x 2(1-x 2);(2)y =3x 2-x 3;(3)2211x x y +-=; (4)y =x (x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x a a y -+=. 解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数.(2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数.(5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=-----, 所以f (x )是偶函数. 13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期:(1)y =cos(x -2);解 是周期函数, 周期为l =2π.(2)y =cos 4x ;解 是周期函数, 周期为2π=l . (3)y =1+sin πx ;解 是周期函数, 周期为l =2.(4)y =x cos x ;解 不是周期函数.(5)y =sin 2x .解 是周期函数, 周期为l =π.14. 求下列函数的反函数:(1)31+=x y ;解 由31+=x y 得x =y 3-1, 所以31+=x y 的反函数为y =x 3-1.(2)xx y +-=11; 解 由x x y +-=11得y y x +-=11, 所以x x y +-=11的反函数为xx y +-=11. (3)dcx b ax y ++=(ad -bc ≠0); 解 由d cx b ax y ++=得a cy b dy x -+-=, 所以d cx b ax y ++=的反函数为acx b dx y -+-=. (4) y =2sin3x ;解 由y =2sin 3x 得2arcsin 31y x =, 所以y =2sin3x 的反函数为2arcsin 31x y =. (5) y =1+ln(x +2);解 由y =1+ln(x +2)得x =e y -1-2, 所以y =1+ln(x +2)的反函数为y =e x -1-2.(6)122+=x x y . 解 由122+=x x y 得y y x -=1log 2, 所以122+=x x y 的反函数为x x y -=1log 2. 15. 设函数f (x )在数集X 上有定义, 试证: 函数f (x )在X 上有界的充分必要条件是它在X 上既有上界又有下界.证明 先证必要性. 设函数f (x )在X 上有界, 则存在正数M , 使|f (x )|≤M , 即-M ≤f (x )≤M . 这就证明了f (x )在X 上有下界-M 和上界M .再证充分性. 设函数f (x )在X 上有下界K 1和上界K 2, 即K 1≤f (x )≤ K 2 . 取M =max{|K 1|, |K 2|}, 则 -M ≤ K 1≤f (x )≤ K 2≤M ,即 |f (x )|≤M .这就证明了f (x )在X 上有界.16. 在下列各题中, 求由所给函数复合而成的函数, 并求这函数分别对应于给定自变量值x 1和x 2的函数值:(1) y =u 2, u =sin x , 61π=x , 32π=x ; 解 y =sin 2x , 41)21(6sin 221===πy ,43)23(3sin 222===πy . (2) y =sin u , u =2x , 81π=x ,42π=x ; 解 y =sin2x , 224sin )82sin(1==⋅=ππy ,12sin )42sin(2==⋅=ππy .(3)u y =, u =1+x 2, x 1=1, x 2= 2;解 21x y +=, 21121=+=y , 52122=+=y .(4) y =e u , u =x 2, x 1 =0, x 2=1;解 2x e y =, 1201==e y , e e y ==212.(5) y =u 2 , u =e x , x 1=1, x 2=-1.解 y =e 2x , y 1=e 2⋅1=e 2, y 2=e 2⋅(-1)=e -2.17. 设f (x )的定义域D =[0, 1], 求下列各函数的定义域:(1) f (x 2);解 由0≤x 2≤1得|x |≤1, 所以函数f (x 2)的定义域为[-1, 1].(2) f (sin x );解 由0≤sin x ≤1得2n π≤x ≤(2n +1)π (n =0, ±1, ±2⋅ ⋅ ⋅), 所以函数f (sin x )的定义域为[2n π, (2n +1)π] (n =0, ±1, ±2⋅ ⋅ ⋅) .(3) f (x +a )(a >0);解 由0≤x +a ≤1得-a ≤x ≤1-a , 所以函数f (x +a )的定义域为[-a , 1-a ].(4) f (x +a )+f (x -a )(a >0).解 由0≤x +a ≤1且0≤x -a ≤1得: 当210≤<a 时, a ≤x ≤1-a ; 当21>a 时, 无解. 因此当210≤<a 时函数的定义域为[a , 1-a ], 当21>a 时函数无意义. 18. 设⎪⎩⎪⎨⎧>-=<=1|| 11||01|| 1)(x x x x f , g (x )=e x , 求f [g (x )]和g [f (x )], 并作出这两个函数的图形.解 ⎪⎩⎪⎨⎧>-=<=1|| 11||01|| 1)]([x x x e e e x g f , 即⎪⎩⎪⎨⎧>-=<=0 10 00 1)]([x x x x g f . ⎪⎩⎪⎨⎧>=<==-1|| 1||e 1|| )]([101)(x e x x e e xfg x f , 即⎪⎩⎪⎨⎧>=<=-1|| 1|| 11|| )]([1x e x x e x f g .19. 已知水渠的横断面为等腰梯形, 斜角ϕ=40︒(图1-37). 当过水断面ABCD 的面积为定值S 0时, 求湿周L (L =AB +BC +CD )与水深h 之间的函数关系式, 并指明其定义域.图1-37解 40sin h DC AB ==, 又从0)]40cot 2([21S h BC BC h =⋅++ 得h hS BC ⋅-= 40cot 0, 所以 h h S L40sin 40cos 20-+=. 自变量h 的取值范围应由不等式组h >0, 040cot 0>⋅-h hS 确定, 定义域为40cot 00S h <<.20. 收敛音机每台售价为90元, 成本为60元. 厂方为鼓励销售商大量采购, 决定凡是订购量超过100台以上的, 每多订购1台, 售价就降低1分, 但最低价为每台75元.(1)将每台的实际售价p 表示为订购量x 的函数;(2)将厂方所获的利润P 表示成订购量x 的函数;(3)某一商行订购了1000台, 厂方可获利润多少?解 (1)当0≤x ≤100时, p =90.令0.01(x 0-100)=90-75, 得x 0=1600. 因此当x ≥1600时, p =75.当100<x <1600时,p =90-(x -100)⨯0.01=91-0. 01x .综合上述结果得到⎪⎩⎪⎨⎧≥<<-≤≤=1600 75160010001.0911000 90x x x x p . (2)⎪⎩⎪⎨⎧≥<<-≤≤=-=1600 151600100 01.0311000 30)60(2x x x x x x x x p P .(3) P =31⨯1000-0.01⨯10002=21000(元).习题1-21. 观察一般项x n 如下的数列{x n }的变化趋势, 写出它们的极限:(1)nn x 21=; 解 当n →∞时, nn x 21=→0, 021lim =∞→n n . (2)nx n n 1)1(-=; 解 当n →∞时, n x n n 1)1(-=→0, 01)1(lim =-∞→nn n . (3)212nx n +=; 解 当n →∞时, 212n x n +=→2, 2)12(lim 2=+∞→nn . (4)11+-=n n x n ; 解 当n →∞时, 12111+-=+-=n n n x n →0, 111lim =+-∞→n n n . (5) x n =n (-1)n .解 当n →∞时, x n =n (-1)n 没有极限.2. 设数列{x n }的一般项nn x n 2cos π=. 问n n x ∞→lim =? 求出N , 使当n >N 时, x n 与其极限之差的绝对值小于正数ε , 当ε =0.001时, 求出数N .解 0lim =∞→n n x . n n n x n 1|2cos ||0|≤=-π. ∀ε >0, 要使|x n -0|<ε , 只要ε<n 1, 也就是ε1>n . 取]1[ε=N , 则∀n >N , 有|x n -0|<ε .当ε =0.001时, ]1[ε=N =1000. 3. 根据数列极限的定义证明:(1)01lim 2=∞→n n ;分析 要使ε<=-221|01|n n , 只须ε12>n , 即ε1>n . 证明 因为∀ε>0, ∃]1[ε=N , 当n >N 时, 有ε<-|01|2n , 所以01lim 2=∞→n n . (2)231213lim =++∞→n n n ; 分析 要使ε<<+=-++n n n n 41)12(21|231213|, 只须ε<n41, 即ε41>n . 证明 因为∀ε>0, ∃]41[ε=N , 当n >N 时, 有ε<-++|231213|n n , 所以231213lim =++∞→n n n . (3)1lim 22=+∞→na n n ; 分析 要使ε<<++=-+=-+na n a n n a n n a n n a n 22222222)(|1|, 只须ε2a n >. 证明 因为∀ε>0, ∃][2εa N =, 当∀n >N 时, 有ε<-+|1|22n a n , 所以1lim 22=+∞→na n n . (4)19 999.0lim =⋅⋅⋅∞→个n n . 分析 要使|0.99 ⋅ ⋅ ⋅ 9-1|ε<=-1101n , 只须1101-n <ε , 即ε1lg 1+>n . 证明 因为∀ε>0, ∃]1lg 1[ε+=N , 当∀n >N 时, 有|0.99 ⋅ ⋅ ⋅ 9-1|<ε , 所以19 999.0lim =⋅⋅⋅∞→个n n . 4. a u n n =∞→lim , 证明||||lim a u n n =∞→. 并举例说明: 如果数列{|x n |}有极限, 但数列{x n }未必有极限.证明 因为a u n n =∞→lim , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有ε<-||a u n , 从而 ||u n |-|a ||≤|u n -a |<ε .这就证明了||||lim a u n n =∞→.数列{|x n |}有极限, 但数列{x n }未必有极限. 例如1|)1(|lim =-∞→n n , 但n n )1(lim -∞→不存在.5. 设数列{x n }有界, 又0lim =∞→n n y , 证明: 0lim =∞→n n n y x .证明 因为数列{x n }有界, 所以存在M , 使∀n ∈Z , 有|x n |≤M .又0lim =∞→n n y , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有M y n ε<||. 从而当n >N 时, 有εε=⋅<≤=-M M y M y x y x n n n n n |||||0|,所以0lim =∞→n n n y x .6. 对于数列{x n }, 若x 2k -1→a (k →∞), x 2k →a (k →∞), 证明: x n →a (n →∞).证明 因为x 2k -1→a (k →∞), x 2k →a (k →∞), 所以∀ε>0, ∃K 1, 当2k -1>2K 1-1时, 有| x 2k -1-a |<ε ; ∃K 2, 当2k >2K 2时, 有|x 2k -a |<ε .取N =max{2K 1-1, 2K 2}, 只要n >N , 就有|x n -a |<ε . 因此x n →a (n →∞).习题1-31. 根据函数极限的定义证明: (1)8)13(lim 3=-→x x ;分析 因为|(3x -1)-8|=|3x -9|=3|x -3|, 所以要使|(3x -1)-8|<ε , 只须ε31|3|<-x .证明 因为∀ε>0, ∃εδ31=, 当0<|x -3|<δ时, 有|(3x -1)-8|<ε , 所以8)13(lim 3=-→x x .(2)12)25(lim 2=+→x x ;分析 因为|(5x +2)-12|=|5x -10|=5|x -2|, 所以要使|(5x +2)-12|<ε , 只须ε51|2|<-x .证明 因为∀ε >0, ∃εδ51=, 当0<|x -2|<δ时, 有 |(5x +2)-12|<ε , 所以12)25(lim 2=+→x x .(3)424lim 22-=+--→x x x ;分析 因为|)2(||2|244)4(2422--=+=+++=--+-x x x x x x x , 所以要使ε<--+-)4(242x x , 只须ε<--|)2(|x . 证明 因为∀ε >0, ∃εδ=, 当0<|x -(-2)|<δ时, 有ε<--+-)4(242x x , 所以424lim22-=+--→x x x .(4)21241lim 321=+--→x x x . 分析 因为|)21(|2|221|212413--=--=-+-x x x x , 所以要使ε<-+-212413x x , 只须ε21|)21(|<--x .证明 因为∀ε >0, ∃εδ21=, 当δ<--<|)21(|0x 时, 有ε<-+-212413x x , 所以21241lim 321=+--→x x x . 2. 根据函数极限的定义证明:(1)2121lim 33=+∞→x x x ; 分析 因为333333||21212121x x x x x x =-+=-+, 所以要使ε<-+212133x x , 只须ε<3||21x , 即321||ε>x . 证明 因为∀ε >0, ∃321ε=X , 当|x |>X 时, 有ε<-+212133x x , 所以2121lim 33=+∞→x x x . (2)0sin lim =+∞→xx x .分析 因为xx x x x 1|sin |0sin ≤=-. 所以要使ε<-0sin x x , 只须ε<x1, 即21ε>x .证明 因为∀ε>0, ∃21ε=X , 当x >X 时, 有ε<-0sin xx ,所以0sin lim =+∞→xx x .3. 当x →2时, y =x 2→4. 问δ等于多少, 使当|x -2|<δ时, |y -4|<0.001? 解 由于当x →2时, |x -2|→0, 故可设|x -2|<1, 即1<x <3. 要使|x 2-4|=|x +2||x -2|<5|x -2|<0.001, 只要0002.05001.0|2|=<-x .取δ=0.0002, 则当0<|x -2|<δ时, 就有|x 2-4|<0. 001.4. 当x →∞时, 13122→+-=x x y , 问X 等于多少, 使当|x |>X 时, |y -1|<0.01?解 要使01.034131222<+=-+-x x x , 只要397301.04||=->x , 故397=X .5. 证明函数f (x )=|x |当x →0时极限为零.证明 因为|f (x )-0|=||x |-0|=|x |=|x -0|, 所以要使|f (x )-0|<ε, 只须|x |<ε.因为对∀ε>0, ∃δ=ε, 使当0<|x -0|<δ, 时有 |f (x )-0|=||x |-0|<ε, 所以0||lim 0=→x x .6. 求,)(xx x f = x x x ||)(=ϕ当x →0时的左﹑右极限, 并说明它们在x →0时的极限是否存在. 证明 因为11lim lim )(lim 000===---→→→x x x x x x f ,11lim lim )(lim 000===+++→→→x x x x x x f ,)(lim )(lim 0x f x f x x +→→=-,所以极限)(lim 0x f x →存在.因为1lim ||lim )(lim 000-=-==---→→→xx x x x x x x ϕ,1lim ||lim )(lim 000===+++→→→x x x x x x x x ϕ,)(lim )(lim 0x x x x ϕϕ+→→≠-,所以极限)(lim 0x x ϕ→不存在.7. 证明: 若x →+∞及x →-∞时, 函数f (x )的极限都存在且都等于A , 则A x f x =∞→)(lim .证明 因为A x f x =-∞→)(lim , A x f x =+∞→)(lim , 所以∀ε>0, ∃X 1>0, 使当x <-X 1时, 有|f (x )-A |<ε ;∃X 2>0, 使当x >X 2时, 有|f (x )-A |<ε .取X =max{X 1, X 2}, 则当|x |>X 时, 有|f (x )-A |<ε , 即A x f x =∞→)(lim .8. 根据极限的定义证明: 函数f (x )当x →x 0 时极限存在的充分必要条件是左极限、右极限各自存在并且相等.证明 先证明必要性. 设f (x )→A (x →x 0), 则∀ε>0, ∃δ>0, 使当0<|x -x 0|<δ 时, 有|f (x )-A |<ε .因此当x 0-δ<x <x 0和x 0<x <x 0+δ 时都有 |f (x )-A |<ε .这说明f (x )当x →x 0时左右极限都存在并且都等于A . 再证明充分性. 设f (x 0-0)=f (x 0+0)=A , 则∀ε>0, ∃δ1>0, 使当x 0-δ1<x <x 0时, 有| f (x )-A <ε ; ∃δ2>0, 使当x 0<x <x 0+δ2时, 有| f (x )-A |<ε .取δ=min{δ1, δ2}, 则当0<|x -x 0|<δ 时, 有x 0-δ1<x <x 0及x 0<x <x 0+δ2 , 从而有 | f (x )-A |<ε ,即f (x )→A (x →x 0).9. 试给出x →∞时函数极限的局部有界性的定理, 并加以证明.解 x →∞时函数极限的局部有界性的定理: 如果f (x )当x →∞时的极限存在, 则存在X >0及M >0, 使当|x |>X 时, |f (x )|<M .证明 设f (x )→A (x →∞), 则对于ε =1, ∃X >0, 当|x |>X 时, 有|f (x )-A |<ε =1. 所以 |f (x )|=|f (x )-A +A |≤|f (x )-A |+|A |<1+|A |.这就是说存在X >0及M >0, 使当|x |>X 时, |f (x )|<M , 其中M =1+|A |. 习题1-41. 两个无穷小的商是否一定是无穷小?举例说明之. 解 不一定.例如, 当x →0时, α(x )=2x , β(x )=3x 都是无穷小, 但32)()(lim0=→x x x βα, )()(x x βα不是无穷小.2. 根据定义证明:(1)392+-=x x y 当x →3时为无穷小; (2)xx y 1sin =当x →0时为无穷小.证明 (1)当x ≠3时|3|39||2-=+-=x x x y . 因为∀ε>0, ∃δ=ε , 当0<|x -3|<δ时, 有εδ=<-=+-=|3|39||2x x x y ,所以当x →3时392+-=x x y 为无穷小. (2)当x ≠0时|0||1sin |||||-≤=x xx y . 因为∀ε>0, ∃δ=ε , 当0<|x -0|<δ时, 有εδ=<-≤=|0||1sin |||||x xx y ,所以当x →0时xx y 1sin =为无穷小.3. 根据定义证明: 函数xx y 21+=为当x →0时的无穷大. 问x 应满足什么条件,能使|y |>104?证明 分析2||11221||-≥+=+=x x x x y , 要使|y |>M , 只须M x >-2||1, 即21||+<M x .证明 因为∀M >0, ∃21+=M δ, 使当0<|x -0|<δ时, 有M x x >+21,所以当x →0时, 函数xx y 21+=是无穷大.取M =104, 则21014+=δ. 当2101|0|04+<-<x 时, |y |>104. 4. 求下列极限并说明理由: (1)xx x 12lim +∞→;(2)xx x --→11lim 20.解 (1)因为xx x 1212+=+, 而当x →∞ 时x 1是无穷小, 所以212lim =+∞→x x x .(2)因为x xx +=--1112(x ≠1), 而当x →0时x 为无穷小, 所以111lim 20=--→x x x .6. 函数y =x cos x 在(-∞, +∞)内是否有界?这个函数是否为当x →+∞ 时的无穷大?为什么?解 函数y =x cos x 在(-∞, +∞)内无界.这是因为∀M >0, 在(-∞, +∞)内总能找到这样的x , 使得|y (x )|>M . 例如y (2k π)=2k π cos2k π=2k π (k =0, 1, 2, ⋅ ⋅ ⋅),当k 充分大时, 就有| y (2k π)|>M .当x →+∞ 时, 函数y =x cos x 不是无穷大.这是因为∀M >0, 找不到这样一个时刻N , 使对一切大于N 的x , 都有|y (x )|>M . 例如0)22cos()22()22(=++=+ππππππk k k y (k =0, 1, 2, ⋅ ⋅ ⋅),对任何大的N , 当k 充分大时, 总有N k x >+=22ππ, 但|y (x )|=0<M .7. 证明: 函数xx y 1sin 1=在区间(0, 1]上无界, 但这函数不是当x →0+时的无穷大.证明 函数xx y 1sin 1=在区间(0, 1]上无界. 这是因为∀M >0, 在(0, 1]中总可以找到点x k , 使y (x k )>M . 例如当221ππ+=k x k (k =0, 1, 2, ⋅ ⋅ ⋅)时, 有22)(ππ+=k x y k ,当k 充分大时, y (x k )>M .当x →0+ 时, 函数xx y 1sin 1=不是无穷大. 这是因为∀M >0, 对所有的δ>0, 总可以找到这样的点x k , 使0<x k <δ, 但y (x k )<M . 例如可取πk x k 21=(k =0, 1, 2, ⋅ ⋅ ⋅),当k 充分大时, x k <δ, 但y (x k )=2k πsin2k π=0<M .习题1-51. 计算下列极限:(1)35lim 22-+→x x x ; 解 9325235lim 222-=-+=-+→x x x .(2)13lim 223+-→x x x ; 解 01)3(3)3(13lim 22223=+-=+-→x x x . (3)112lim 221-+-→x x x x ;解 02011lim )1)(1()1(lim 112lim 121221==+-=+--=-+-→→→x x x x x x x x x x x . (4)xx x x x x 2324lim2230++-→; 解 2123124lim 2324lim 202230=++-=++-→→x x x x x x x x x x . (5)hx h x h 220)(lim -+→;解 x h x hx h hx x h x h x h h h 2)2(lim 2lim )(lim 02220220=+=-++=-+→→→. (6))112(lim 2xx x +-∞→; 解 21lim 1lim2)112(lim 22=+-=+-∞→∞→∞→x x x x x x x . (7)121lim 22---∞→x x x x ; 解 2111211lim 121lim 2222=---=---∞→∞→xx x x x xx x . (8)13lim 242--+∞→x x x x x ; 解 013lim 242=--+∞→x x x x x (分子次数低于分母次数, 极限为零). 或 012111lim 13lim 4232242=--+=--+∞→∞→x x x x x x x x x x . (9)4586lim 224+-+-→x x x x x ; 解 32142412lim )4)(1()4)(2(lim 4586lim 44224=--=--=----=+-+-→→→x x x x x x x x x x x x x .(10))12)(11(lim 2x x x -+∞→;解 221)12(lim )11(lim )12)(11(lim 22=⨯=-⋅+=-+∞→∞→∞→x x x x x x x . (11))21 41211(lim n n +⋅⋅⋅+++∞→;解 2211)21(1lim )21 41211(lim 1=--=+⋅⋅⋅++++∞→∞→n n n n . (12)2)1( 321limnn n -+⋅⋅⋅+++∞→; 解 211lim 212)1(lim )1( 321lim 22=-=-=-+⋅⋅⋅+++∞→∞→∞→n n n nn n n n n n . (13)35)3)(2)(1(limn n n n n +++∞→;解 515)3)(2)(1(lim 3=+++∞→nn n n n (分子与分母的次数相同, 极限为 最高次项系数之比).或 51)31)(21)(11(lim 515)3)(2)(1(lim 3=+++=+++∞→∞→n n n n n n n n n . (14))1311(lim 31x x x ---→;解 )1)(1()2)(1(lim )1)(1(31lim )1311(lim 2122131x x x x x x x x x x x x x x x ++-+--=++--++=---→→→ 112lim21-=+++-=→x x x x . 2. 计算下列极限: (1)2232)2(2lim -+→x x x x ; 解 因为01602)2(lim 2322==+-→x x x x , 所以∞=-+→2232)2(2lim x x x x . (2)12lim 2+∞→x x x ;解 ∞=+∞→12lim 2x x x (因为分子次数高于分母次数).(3))12(lim 3+-∞→x x x .解 ∞=+-∞→)12(lim 3x x x (因为分子次数高于分母次数).3. 计算下列极限: (1)xx x 1sin lim 20→;解 01sin lim 20=→xx x (当x →0时, x 2是无穷小, 而x 1sin 是有界变量).(2)xx x arctan lim ∞→.解 0arctan 1lim arctan lim =⋅=∞→∞→x x xx x x (当x →∞时, x 1是无穷小,而arctan x 是有界变量).4. 证明本节定理3中的(2).习题1-61. 计算下列极限: (1)xx x ωsin lim 0→;解 ωωωωω==→→x x xx x x sin lim sin lim 00.(2)xx x 3tan lim 0→;解 33cos 133sin lim 33tan lim 00=⋅=→→xx x x x x x .(3)xx x 5sin 2sin lim 0→;解 52525sin 522sin lim 5sin 2sin lim 00=⋅⋅=→→x x x x x x x x .(4)x x x cot lim 0→;解 1cos lim sin lim cos sin lim cot lim 0000=⋅=⋅=→→→→x x x x x x x x x x x x .(5)xx x x sin 2cos 1lim 0-→;解 2)sin (lim 2sin 2lim 2cos 1lim sin 2cos 1lim 20220200===-=-→→→→x x x x x x x x x x x x x . 或 2sin lim 2sin sin 2lim sin 2cos 1lim 0200===-→→→xx x x x x x x x x x . (6)n n n x 2sin 2lim ∞→(x 为不等于零的常数). 解 x x xx x nn n n nn =⋅=∞→∞→22sin lim2sin 2lim . 2. 计算下列极限:(1)x x x 1)1(lim -→; 解 11)(1)1()(101})](1[lim {)](1[lim )1(lim ---→--→→=-+=-+=-e x x x x x x x x x .(2)x x x 1)21(lim +→;解 2221221010])21(lim [)21(lim )21(lim e x x x x x x x x x =+=+=+→⋅→→.(3)x x xx 2)1(lim +∞→; 解 222])11(lim [)1(lim e xx x x x x x =+=+∞→∞→.(4)kx x x)11(lim -∞→(k 为正整数).解 k k x x kx x e xx ---∞→∞→=-+=-))(()11(lim )11(lim .3. 根据函数极限的定义, 证明极限存在的准则I '. 证明 仅对x →x 0的情形加以证明.设ε为任一给定的正数, 由于A x g x x =→)(lim 0, 故由定义知, 对ε>0, 存在δ1>0, 使得当0<|x -x 0|<δ1时, 恒有|g (x )-A |<ε, 即A -ε<g (x )<A +ε.由于A x h x x =→)(lim 0, 故由定义知, 对ε>0, 存在δ2>0, 使得当0<|x -x 0|<δ2时, 恒有|h (x )-A |<ε, 即A -ε<h (x )<A +ε.取δ=min{δ1, δ2}, 则当0<|x -x 0|<δ时, A -ε<g (x )<A +ε与A -ε<h (x )<A +ε 同时成立, 又因为g (x )≤f (x )≤h (x ), 所以 A -ε<f (x )<A +ε, 即 |f (x )-A |<ε, 因此A x f x x =→)(lim 0.证明 仅对x →x 0的情形加以证明. 因为A x g x x =→)(lim 0, A x h x x =→)(lim 0,所以对任一给定的ε>0, 存在δ>0, 使得当0<|x -x 0|<δ时, 恒有 |g (x )-A |<ε及|h (x )-A |<ε,即 A -ε<g (x )<A +ε及A -ε<h (x )<A +ε.又因为 g (x )≤f (x )≤h (x ), 所以 A -ε<f (x )<A +ε, 即 |f (x )-A |<ε, 因此A x f x x =→)(lim 0.4. 利用极限存在准则证明: (1)111lim =+∞→nn ;证明 因为n n 11111+<+<,而 11lim =∞→n 且1)11(lim =+∞→n n ,由极限存在准则I , 111lim =+∞→nn .(2)1)1 211(lim 222=++⋅⋅⋅++++∞→πππn n n n n n ;证明 因为πππππ+<++⋅⋅⋅++++<+2222222)1 211(n n n n n n n n n n , 而 1lim 22=+∞→πn n n n , 1lim 22=+∞→πn n n , 所以 1)1 211(lim 222=++⋅⋅⋅++++∞→πππn n n n n n .(3)数列2,22+, 222++, ⋅ ⋅ ⋅ 的极限存在;证明 21=x , n n x x +=+21(n =1, 2, 3, ⋅ ⋅ ⋅). 先证明数列{x n }有界.当n =1时221<=x , 假定n =k 时x k <2, 则当n =k +1时, 22221=+<+=+k k x x , 所以x n <2(n =1, 2, 3, ⋅ ⋅ ⋅), 即数列{x n }有界.再证明数列单调增. 因为nn n n n n n n n n n n x x x x x x x x x x x x +++--=++-+=-+=-+2)1)(2(22221, 而x n -2<0, x n +1>0, 所以x n +1-x n >0, 即数列{x n }单调增.因为数列{x n }单调增加有上界, 所以此数列是有极限的. (4)11lim 0=+→n x x ;证明 当|x |≤1时, 则有 1+x ≤1+|x |≤(1+|x |)n , 1+x ≥1-|x |≥(1-|x |)n , 从而有 ||11||1x x x n +≤+≤-. 因为 1|)|1(lim |)|1(lim 0=+=-→→x x x x ,根据夹逼准则, 有 11lim 0=+→n x x .(5)1]1[lim 0=+→xx x .证明 因为x x x 1]1[11≤<-, 所以1]1[1≤<-xx x .又因为11lim )1(lim 00==-++→→x x x , 根据夹逼准则, 有1]1[lim 0=+→xx x .习题 1-71. 当x →0时, 2x -x 2 与x 2-x 3相比, 哪一个是高阶无穷小?解 因为02lim 2lim 202320=--=--→→xx x x x x x x x ,所以当x →0时, x 2-x 3是高阶无穷小, 即x 2-x 3=o (2x -x 2).2. 当x →1时, 无穷小1-x 和(1)1-x 3, (2))1(212x -是否同阶?是否等价?解 (1)因为3)1(lim 1)1)(1(lim 11lim 212131=++=-++-=--→→→x x xx x x x x x x x , 所以当x →1时, 1-x 和1-x 3是同阶的无穷小, 但不是等价无穷小.(2)因为1)1(lim 211)1(21lim 121=+=--→→x x x x x , 所以当x →1时, 1-x 和)1(212x -是同阶的无穷小, 而且是等价无穷小.3. 证明: 当x →0时, 有: (1) arctan x ~x ;(2)2~1sec 2x x -. 证明 (1)因为1tan limarctan lim 00==→→y yxx y x (提示: 令y =arctan x , 则当x →0时, y →0),所以当x →0时, arctan x ~x .(2)因为1)22sin 2(lim 22sin 2lim cos cos 1lim 2211sec lim 202202020===-=-→→→→x xx x x x x xx x x x x , 所以当x →0时, 2~1sec 2x x -. 4. 利用等价无穷小的性质, 求下列极限: (1)xx x 23tan lim 0→;(2)mn x x x )(sin )sin(lim 0→(n , m 为正整数);(3)x x x x 30sin sin tan lim -→; (4))1sin 1)(11(tan sin lim320-+-+-→x x x x x .解 (1)2323lim 23tan lim 00==→→x x x x x x .(2)⎪⎩⎪⎨⎧<∞>===→→mn m n m n x x x x mn x m n x 0 1lim )(sin )sin(lim00. (3)21cos 21lim sin cos cos 1lim sin )1cos 1(sin lim sin sin tan lim 220203030==-=-=-→→→→x x x x x x xx x x x x x x x x . (4)因为32221)2(2~2sin tan 2)1(cos tan tan sin x x x x x x x x x -=⋅--=-=-(x →0),23232223231~11)1(11x x x x x ++++=-+(x →0), x x x x x ~sin ~1sin 1sin 1sin 1++=-+(x →0), 所以 33121lim )1sin 1)(11(tan sin lim 230320-=⋅-=-+-+-→→x x x x x x x x x .5. 证明无穷小的等价关系具有下列性质: (1) α ~α (自反性);(2) 若α ~β, 则β~α(对称性); (3)若α ~β, β~γ, 则α~γ(传递性). 证明 (1)1lim =αα, 所以α ~α ;(2) 若α ~β, 则1lim =βα, 从而1lim=αβ. 因此β~α ;(3) 若α ~β, β~γ, 1lim limlim =⋅=βαγβγα. 因此α~γ. 习题1-81. 研究下列函数的连续性, 并画出函数的图形:(1)⎩⎨⎧≤<-≤≤=21 210 )(2x x x x x f ;解 已知多项式函数是连续函数, 所以函数f (x )在[0, 1)和(1, 2]内是连续的. 在x =1处, 因为f (1)=1, 并且1lim )(lim 211==--→→x x f x x , 1)2(lim )(lim 11=-=++→→x x f x x .所以1)(lim 1=→x f x , 从而函数f (x )在x =1处是连续的.综上所述,函数f (x )在[0, 2]上是连续函数.(2)⎩⎨⎧>≤≤-=1|| 111 )(x x x x f .解 只需考察函数在x =-1和x =1处的连续性. 在x =-1处, 因为f (-1)=-1, 并且)1(11lim )(lim 11-≠==---→-→f x f x x ,)1(1lim )(lim 11-=-==++-→-→f x x f x x ,所以函数在x =-1处间断, 但右连续. 在x =1处, 因为f (1)=1, 并且1lim )(lim 11==--→→x x f x x =f (1), 11lim )(lim 11==++→→x x x f =f (1),所以函数在x =1处连续.综合上述讨论, 函数在(-∞, -1)和(-1, +∞)内连续, 在x =-1处间断, 但右连续. 2. 下列函数在指出的点处间断, 说明这些间断点属于哪一类, 如果是可去间断点, 则补充或改变函数的定义使它连续:(1)23122+--=x x x y , x =1, x =2;解 )1)(2()1)(1(23122---+=+--=x x x x x x x y . 因为函数在x =2和x =1处无定义, 所以x =2和x =1是函数的间断点.因为∞=+--=→→231lim lim 2222x x x y x x , 所以x =2是函数的第二类间断点;因为2)2()1(limlim 11-=-+=→→x x y x x , 所以x =1是函数的第一类间断点, 并且是可去间断点. 在x =1处, 令y =-2, 则函数在x =1处成为连续的. (2)x x y tan =, x =k , 2ππ+=k x (k =0, ±1, ±2, ⋅ ⋅ ⋅);解 函数在点x =k π(k ∈Z)和2ππ+=k x (k ∈Z)处无定义, 因而这些点都是函数的间断点.因∞=→x x k x tan lim π(k ≠0), 故x =k π(k ≠0)是第二类间断点;因为1tan lim0=→xx x , 0tan lim2=+→x x k x ππ(k ∈Z), 所以x =0和2ππ+=k x (k ∈Z) 是第一类间断点且是可去间断点.令y |x =0=1, 则函数在x =0处成为连续的;令2 ππ+=k x 时, y =0, 则函数在2ππ+=k x 处成为连续的.(3)xy 1cos 2=, x =0;解 因为函数x y 1cos 2=在x =0处无定义, 所以x =0是函数xy 1cos 2=的间断点.又因为xx 1cos lim 20→不存在, 所以x =0是函数的第二类间断点.(4)⎩⎨⎧>-≤-=1 311x x x x y , x =1.解 因为0)1(lim )(lim 11=-=--→→x x f x x 2)3(lim )(lim 11=-=++→→x x f x x , 所以x =1是函数的第一类不可去间断点.3. 讨论函数x x x x f nnn 2211lim )(+-=∞→的连续性, 若有间断点, 判别其类型. 解 ⎪⎩⎪⎨⎧<=>-=+-=∞→1||1|| 01|| 11lim)(22x x x x x x x x x f nn n .在分段点x =-1处, 因为1)(lim )(lim 11=-=---→-→x x f x x , 1lim )(lim 11-==++-→-→x x f x x , 所以x =-1为函数的第一类不可去间断点.在分段点x =1处, 因为1lim )(lim 11==--→→x x f x x , 1)(lim )(lim 11-=-=++→→x x f x x , 所以x =1为函数的第一类不可去间断点.4. 证明: 若函数f (x )在点x 0连续且f (x 0)≠0, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.证明 不妨设f (x 0)>0. 因为f (x )在x 0连续, 所以0)()(lim 00>=→x f x f x x , 由极限的局部保号性定理, 存在x 0的某一去心邻域)(0x U , 使当x ∈)(0x U时f (x )>0, 从而当x ∈U (x 0)时, f (x )>0. 这就是说, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0. 5. 试分别举出具有以下性质的函数f (x )的例子:(1)x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅是f (x )的所有间断点, 且它们都是无穷间断点;解 函数x x x f ππcsc )csc()(+=在点x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅处是间断的且这些点是函数的无穷间断点.(2)f (x )在R 上处处不连续, 但|f (x )|在R 上处处连续;解 函数⎩⎨⎧∉∈-=QQx x x f 1 1)(在R 上处处不连续, 但|f (x )|=1在R 上处处连续.(3)f (x )在R 上处处有定义, 但仅在一点连续.解 函数⎩⎨⎧∉-∈=Q Qx x x x x f )(在R 上处处有定义, 它只在x =0处连续.习题1-91. 求函数633)(223-+--+=x x x x x x f 的连续区间, 并求极限)(lim 0x f x →, )(lim 3x f x -→及)(lim 2x f x →.解 )2)(3()1)(1)(3(633)(223-++-+=-+--+=x x x x x x x x x x x f , 函数在(-∞, +∞)内除点x =2和x =-3外是连续的, 所以函数f (x )的连续区间为(-∞, -3)、(-3, 2)、(2, +∞). 在函数的连续点x =0处, 21)0()(lim 0==→f x f x .在函数的间断点x =2和x =-3处, ∞=-++-+=→→)2)(3()1)(1)(3(lim)(lim 22x x x x x x f x x , 582)1)(1(lim )(lim 33-=-+-=-→-→x x x x f x x .2. 设函数f (x )与g (x )在点x 0连续, 证明函数ϕ(x )=max{f (x ), g (x )}, ψ(x )=min{f (x ), g (x )} 在点x 0也连续.证明 已知)()(lim 00x f x f x x =→, )()(lim 00x g x g x x =→.可以验证] |)()(|)()([21)(x g x f x g x f x -++=ϕ,] |)()(|)()([21)(x g x f x g x f x --+=ψ.因此 ] |)()(|)()([21)(00000x g x f x g x f x -++=ϕ,] |)()(|)()([21)(00000x g x f x g x f x --+=ψ.因为] |)()(|)()([21lim )(lim 00x g x f x g x f x x x x x -++=→→ϕ] |)(lim )(lim |)(lim )(lim [210000x g x f x g x f x x x x x x x x →→→→-++=] |)()(|)()([210000x g x f x g x f -++==ϕ(x 0),所以ϕ(x )在点x 0也连续.同理可证明ψ(x )在点x 0也连续.3. 求下列极限: (1)52lim 20+-→x x x ;(2)34)2(sin lim x x π→;(3))2cos 2ln(lim 6x x π→;(4)xx x 11lim 0-+→;(5)145lim 1---→x x x x ;(6)a x a x a x --→sin sin lim ;(7))(lim 22x x x x x --++∞→.解 (1)因为函数52)(2+-=x x x f 是初等函数, f (x )在点x =0有定义, 所以 55020)0(52lim 220=+⋅-==+-→f x x x .(2)因为函数f (x )=(sin 2x )3是初等函数, f (x )在点4π=x 有定义, 所以1)42(sin )4()2(sin lim 334=⋅==→πππf x x .(3)因为函数f (x )=ln(2cos2x )是初等函数, f (x )在点6π=x 有定义, 所以0)62cos 2ln()6()2cos 2ln(lim 6=⋅==→πππf x x .(4))11(lim)11()11)(11(lim 11lim 000++=++++-+=-+→→→x x x x x x x x x x x x 211101111lim=++=++=→x x .(5))45)(1()45)(45(lim 145lim 11x x x x x x x x x x x x +--+---=---→→)45)(1(44lim 1x x x x x +---=→214154454lim 1=+-⋅=+-=→x x x .。
高等数学 复旦大学出版 第一章习题解答

1.1-1.3练习参考答案()()()()()()()()124313242134112233441122344311223344122133442143122134431.11111D a a a a a a a a a a a a a a a a a a a a abcd ab ad cd ττττ=+-+-+-+-=++++二、1.4练习参考答案21313243414223340001.02324320020020364106303730c c c c c c c c c c c c a b cd a b c d a b c d a a b a b c a a b a b c a a b a b c D aa ab a bc a a b a a b aa ba b caa ba------+++++++++====+++++++++二、()()()12213231223323n nn 111,11,i 2i 21,12320001000n n n ni n i i i n n n nna x a a a a a x a a x a x x x a a x x x x x +--==------==--=--∏∏按第一列展开n .从第一行开始,前一行减去后一行D ()112131212231321n3233211,i 21,n 0000n n n n ni i n n n nx a a a x a a a a a x a a a x x a x a -=------==--∏按第一列展开n 或从第行开始,后一行减去前一行D ()()()()()211111111111111*********1101110111001110111111111111011101111101110111011r x r n n n n n n x xx x x x x x x x xxx x x x x --++--++-=-=-----=-=----按第一列展开3.从第一行开始,前一行减去后一行011101-D=1-()()()11113222111111111111111011111011n n n n n n n xxx xxx xx-+++-----=-==-=----按第一列展开331axay az by bz bx x y z y z xayaz ax bz bx by a y z x b z x y azaxaybxbybz zxyxyz=+=+=三、.左边右边 ()()()()()()()()222222221233231233232.0123323123323aa a ab b b bc c c c ddd d ++++++==++++++3-24-1c c c c 左边=右边()()()()()()()11222121121121211.D 111111n n n n n n n n n n n n n na a x a xx a x x a xa xa x a +-+--------=--+--++--++=+++++ 二、按最后一行展开112212111111111101+1110012.011+1001011112,3,),nn n i i nn n i ia a D a a a a a a a a i n a =+-⎛⎫==-=+⎪⎝⎭+-=∑加边11注意:这里简写了步骤,鸡爪型行列式要经过列变(C +C ,变成三角形行列式才写出结果。
1.-第一章课后习题及答案

1.-第一章课后习题及答案第一章1.(Q1) What is the difference between a host and an end system? List the types of end systems. Is a Web server an end system?Answer: There is no difference. Throughout this text, the words “host” and “end system” are used interchangeably. End systems include PCs, workstations, Web servers, mail servers, Internet-connected PDAs, WebTVs, etc.2.(Q2) The word protocol is often used to describe diplomatic relations. Give an example of a diplomatic protocol.Answer: Suppose Alice, an ambassador of country A wants to invite Bob, an ambassador of country B, over for dinner. Alice doesn’t simply just call Bob on the phone and say, come to our dinner table n ow”. Instead, she calls Bob and suggestsa date and time. Bob may respond by saying he’s not available that particular date, but he is available another date. Alice and Bob continue to send “messages” back and forth until they agree on a date and time. Bob then shows up at the embassy on the agreed date, hopefully not more than 15 minutes before or after the agreed time. Diplomatic protocols also allow for either Alice or Bob to politely cancel the engagement if they have reasonable excuses.3.(Q3) What is a client program? What is a server program? Does a server program request and receive services from a client program?Answer: A networking program usually has two programs, each running on a different host, communicating with each other. The program that initiates the communicationAnswer: Current possibilities include: dial-up (up to 56kbps); DSL (up to 1 Mbps upstream, up to 8 Mbps downstream); cable modem (up to 30Mbps downstream, 2 Mbps upstream.4.(Q7) What are some of the physical media that Ethernet can run over?Answer: Ethernet most commonly runs over twisted-pair copper wire and “thin” coaxial cable. It also can run over fibers optic links and thick coaxial cable.5.(Q8) Dial-up modems, HFC, and DSL are all used for residential access. For each of these access technologies, provide a range of transmission rates and comment on whether the transmission rate is shared or dedicated.Answer: Dial up modems: up to 56 Kbps, bandwidth is dedicated; ISDN: up to 128 kbps, bandwidth is dedicated; ADSL: downstream channel is .5-8 Mbps, upstream channel is up to 1 Mbps, bandwidth is dedicated; HFC, downstream channel is 10-30 Mbps and upstream channel is usually less than a few Mbps, bandwidth is shared.6.(Q13) Why is it said that packet switching employs statistical multiplexing? Contrast statistical multiplexing with the multiplexing that takes place in TDM.Answer: In a packet switched network, the packets from different sources flowing on a link do not follow any fixed, pre-defined pattern. In TDM circuit switching, each host gets the same slot in a revolving TDM frame.7.(Q14) Suppose users share a 2Mbps link. Also suppose each user requires 1Mbps when transmitting, but each user transmits only 20 percent of the time. (See the discussion of statistical multiplexing in Section 1.3.)a.When circuit switching is used, how many users can be supported?b.For the remainder of this problem, suppose packet switching is used. Why will there be essentially no queuing delay before the link if two or fewer users transmit at the same time? Why will there be a queuing delay if three users transmit at the same time?c.Find the probability that a given user is transmitting.d.Suppose now there are three users. Find the probability that at any given time, all three users are transmitting simultaneously. Find the fraction oftime during which the queue grows.Answer:a.2 users can be supported because each user requires half of the link bandwidth.b.Since each user requires 1Mbps when transmitting, if two or fewer users transmit simultaneously, a maximum of 2Mbps will be required. Since the available bandwidth of the shared link is 2Mbps, there will be no queuing delay before the link. Whereas, if three users transmit simultaneously, the bandwidth required will be 3Mbps which is more than the available bandwidth of the shared link. In this case, there will be queuing delay before the link.c.Probability that a given user is transmitting = 0.2d.Probability that all three users are transmitting simultaneously=(3)p3(1−p)0=0.23=0.008. Since the 3queue grows when all the users are transmitting, the fraction of time during which the queue grows (which is equal to the probability that all three users are transmitting simultaneously) is 0.008.8.(Q16) Consider sending a packet froma source host to a destination host over a fixed route. List the delay components in the end-to-end delay. Which of these delays are constant and which are variable?Answer: The delay components are processing delays, transmission delays, propagation delays, and queuing delays. All of these delays are fixed, except for the queuing delays, which are variable.9.(Q19) Suppose Host A wants to send a large file to Host B. The path from Host A to Host B has three links, of rates R1= 250 kbps, R2 = 500 kbps, and R3= 1 Mbps.a.Assuming no other traffic in the network, what is the throughput for the file transfer.b.Suppose the file is 2 million bytes. Roughly, how long will it take to transfer the file to Host B?c.Repeat (a) and (b), but now with R2 reduced to 200 kbps.Answer:a.250 kbpsb.64 secondsc.200 kbps; 80 seconds10.(P2) Consider the circuit-switched network in Figure 1.8. Recall that there are n circuits on each link.a.W hat is the maximum number ofsimultaneous connections that can be in progress at any one time in this network?b.S uppose that all connections arebetween the switch in the upper-left-hand corner and the switch in the lower-right-hand corner. What is the maximum number of simultaneous connections that can be in progress?Answer:a.We can n connections between eachof the four pairs of adjacent switches.This gives a maximum of 4n connections.b.We can n connections passingthrough the switch in the upper-right-hand corner and another n connections passing through the switch in the lower-left-hand corner, giving a total of 2n connections.11.(P4) Review the car-caravan analogy in Section 1.4. Assume a propagation speed of 50 km/hour.a.S uppose the caravan travels 150 km,beginning in front of one tollbooth, passing through a second tollbooth, and finishing just before a third tollbooth.What is the end-to-end delay?b.R epeat (a), now assuming that thereare five cars in the caravan instead of ten.Answer: Tollbooths are 150 km apart, and the cars propagate at 50 km/hr, A tollbooth services a car at a rate of one car every 12 seconds.a.There are ten cars. It takes 120seconds, or two minutes, for the first tollbooth to service the 10 cars. Each of these cars has a propagation delay of 180 minutes before arriving at the second tollbooth. Thus, all the cars arelined up before the second tollbooth after 182 minutes. The whole process repeats itself for traveling between the second and third tollbooths. Thus the total delay is 364 minutes.b.Delay between tollbooths is 5*12seconds plus 180 minutes, i.e., 181minutes. The total delay is twice this amount, i.e., 362 minutes.12.(P5) This elementary problem begins to explore propagation delay and transmission delay, two central concepts in data networking. Consider two hosts, A and B, connected by a single link of rate R bps. Suppose that the two hosts are separated by m meters, and suppose the propagation speed along the link is s meters/sec. Host A is to send a packet of size L bits to Host B.a.E xpress the propagation delay, d prop ,in terms of m and s.b.D etermine the transmission time ofthe packet, d trans , in terms of L and R.c.I gnoring processing and queuingdelays, obtain an expression for the end-to-end delay.d.S uppose Host A begins to transmitthe packet at time t = 0. At time t =d trans , where is the last bit of the packet?e.S uppose d prop is greater than d trans . Attime t = d trans , where is the first bit of the packet?f.S uppose d prop is less than d trans . At timet = d trans , where is the first bit of the packet?g.S uppose s = 2.5*108, L = 100bits, and R= 28kbps. Find the distance m so thatd prop equals d trans .Answer:a.d prop = m/s seconds.b.d trans = L/R seconds.c.d end-to-end = (m/s + L/R) seconds.d.T he bit is just leaving Host A.e.T he first bit is in the link and has notreached Host B.f.T he first bit has reached Host B.g.W antm=LS=1003(2.5∗108) =893 km.13.(P6) In this problem we consider sending real-time voice from Host A to Host B over a packet-switched network (VoIP). Host A converts analog voice to a digital 64 kbps bit stream on the fly. Host A then groups the bits into 56-Byte packets. There is one link between Host A and B; its transmission rate is 500 kbps and its propagation delay is 2 msec. As soon as Host A gathers a packet, it sends it to Host B. As soon as Host B receivesan entire packet, it converts the packet’s bits to an analog signal. How much time elapses from the time a bit is created (from the original analog signal at Host A) until the bit is decoded (as part of the analog signal at Host B)?Answer: Consider the first bit in a packet. Before this bit can be transmitted, all of the bits in the packet must be generated. This requires56∗8sec=7 msec3The time required to transmit the packet is56∗8sec=896 μsec3Propagation delay = 2 msec.The delay until decoding is7msec + 896μsec + 2msec = 9.896 msecA similar analysis shows that all bits experience a delay of 9.896 msec.14.(P9) Consider a packet of length Lwhich begins at end system A, travels overone link to a packet switch, and travelsfrom the packet switch over a second linkto a destination end system. Let d i, s i, and Rdenote the length, propagation speed, iand the transmission rate of link i, for i = 1, 2. The packet switch delays each packet by d proc. Assuming no queuing delays, in terms of d i, s i, R i, (i = 1, 2), and L, what is the total end-to-end delay for the packet? Suppose now the packet Length is 1,000 bytes, the propagation speed on both links is 2.5 * 108 m/s, the transmission rates of both links is 1 Mbps, the packet switch processing delay is 2 msec, the length of the first link is 6,000 km, and the length of the last link is 3,000 km. For these values, what is the end-to-end delay?Answer: The first end system requires L/R1to transmit the packet onto the first link; the packet propagates over the first link in d1/s1; the packet switch adds a processing delay of d proc; after receiving the entire packet, the packet switch requires L/R2to transmit the packet onto the second link; the packet propagates over the second link in d2/s2. Adding these five delays givesdend-end = L/R1+ L/R2+ d1/s1+ d2/s2+ dprocTo answer the second question, we simply plug the values into the equation to get 8 + 8 + 24 + 12 + 2 = 54 msec.15.(P10) In the above problem, supposeR 1= R2= R and dproc= 0. Further suppose thepacket switch does not store-and-forward packets but instead immediately transmits each bit it receivers before waiting for the packet to arrive. What is the end-to-end delay?Answer: Because bits are immediately transmitted, the packet switch does not introduce any delay; in particular, it does not introduce a transmission delay. Thus,dend-end = L/R + d1/s1+ d2/s2For the values in Problem 9, we get 8 + 24 + 12 = 44 msec.16.(P11) Suppose N packets arrive simultaneously to a link at which no packets are currently being transmitted or queued. Each packet is of length L and the link has transmission rate R. What is the average queuing delay for the N packets?Answer: The queuing delay is 0 for the first transmitted packet, L/R for the second transmitted packet, and generally,(n-1)L/R for the nth transmitted packet. Thus, the average delay for the N packets is(L/R + 2L/R + ....... + (N-1)L/R)/N = L/RN(1 + 2 + ..... + (N-1)) = LN(N-1)/(2RN) = (N-1)L/(2R)Note that here we used the well-known fact that1 +2 + ....... + N = N(N+1)/217.(P14) Consider the queuing delay ina router buffer. Let I denote traffic intensity; that is, I = La/R. Suppose that the queuing delay takes the form IL/R (1-I) for I<1.a.Provide a formula for the total delay, that is, the queuing delay plus the transmission delay.b.Plot the total delay as a function of L/R.Answer:a.The transmission delay is L / R .The total delay isIL+ L=L/Rb.Let x = L / R.Total delay=x18.(P16) Perform a Traceroute between source and destination on the same continent at three different hours of the day.a.Find the average and standard deviation of the round-trip delays at each of the three hours.b.Find the number of routers in the path at each of the three hours. Did the paths change during any of the hours?c.Try to identify the number of ISP networks that the Traceroute packetspass through from source to destination. Routers with similar names and/or similar IP addresses should be considered as part of the same ISP. In your experiments, do the largest delays occur at the peering interfaces between adjacent ISPs?d.Repeat the above for a source and destination on different continents. Compare the intra-continent and inter-continent results.Answer: Experiments.19.(P18) Suppose two hosts, A and B, are separated by 10,000 kilometers and are connected by a direct link of R = 2 Mbps. Suppose the propagation speed over the link is 2.5•108 meters/sec.a.Calculate the bandwidth-delay product, R •d prop.b.Consider sending a file of 400,000 bits from Host A to Host B. Suppose the file is sent continuously as one large message. What is the maximum number of bits that will be in the link at any given time?c.Provide an interpretation of the bandwidth-delay product.d.What is the width (in meters) of a bit in the link? Is it longer than a football field?e.Derive a general expression for the width of a bit in terms of the propagation speed s, the transmission rate R, and the length of the link m.Answer:a.d prop = 107 / 2.5•108 = 0.04 sec; so R •d prop = 80,000bitsb.80,000bitsc.The bandwidth-delay product of alink is the maximum number of bits thatcan be in the link.d.1 bit is 125 meters long, which islonger than a football field) = m / (R * m / s) =e.m / (R • dprops/R20.(P20) Consider problem P18 but now with a link of R = 1 Gbps.a.C alculate the bandwidth-delayproduct, R·d prop .b.C onsider sending a file of 400,000bits from Host A to Host B. Suppose the file is sent continuously as one big message. What is the maximum number of bits that will be in the link at any given time?c.W hat is the width (in meters) of abit in the link?Answer:a.40,000,000 bits.b.400,000 bits.c.0.25 meters.21.(P21) Refer again to problem P18.a.H ow long does it take to send the file,assuming it is sent continuously?b.S uppose now the file is broken up into10 packet is acknowledged by thereceiver and the transmission time of an acknowledgment packet is negligible.Finally, assume that the sender cannot send a packet until the preceding one is acknowledged. How long does it take to send the file?c.C ompare the results from (a) and (b).Answer:a.d trans + d prop = 200 msec + 40 msec = 240msecb.10 * (t trans + 2 t prop ) = 10 * (20 msec +80 msec) = 1.0 sec。
《高等数学一》第一章-函数--课后习题(含答案解析)

第一章函数历年试题模拟试题课后习题(含答案解析)[单选题]1、设函数,则f(x)=()A、x(x+1)B、x(x-1)C、(x+1)(x-2)D、(x-1)(x+2)【正确答案】B【答案解析】本题考察函数解析式求解.,故[单选题]2、已知函数f(x)的定义域为[0,4],函数g(x)=f(x+1)+f(x-1)的定义域是().A、[1,3]B、[-1,5]C、[-1,3]D、[1,5]【正确答案】A【答案解析】x是函数g(x)中的定义域中的点,当且仅当x满足0≤x+1≤4且0≤x-1≤4即-1≤x≤3且1≤x≤5也即1≤x≤3,由此可知函数g(x)的定义域D(g)={x|1≤x≤3}=[1,3]. [单选题]3、设函数f(x)的定义域为[0,4],则函数f(x2)的定义域为().A、[0,2]B、[0,16]C、[-16,16]D、[-2,2]【正确答案】D【答案解析】根据f(x)的定义域,可知中应该满足:[单选题]4、函数的定义域为().A、[-1,1]B、[-1,3]C、(-1,1)D、(-1,3)【正确答案】B【答案解析】根据根号函数的性质,应该满足:即[单选题]写出函数的定义域及函数值().A、B、C、D、【正确答案】C【答案解析】分段函数的定义域为各个分段区间定义域的并集,故D=(-∞,-1]∪(-1,+∞).[单选题]6、设函数,则对所有的x,则f(-x)=().A、B、C、D、【正确答案】A【答案解析】本题考察三角函数公式。
.[单选题]7、设则=().A、B、C、D、【正确答案】B【答案解析】令则,故[单选题]8、则().A、B、C、D、【正确答案】D【答案解析】[单选题]9、在R上,下列函数中为有界函数的是().xA、eB、1+sin xC、ln x【正确答案】B【答案解析】由函数图像不难看出在R上e x,lnx,tanx都是无界的,只有1+sinx可能有界,由于|sinx|≤1,|1+sinx|≤1+|sinx|≤2所以有界.[单选题]10、不等式的解集为().A、B、C、D、【正确答案】D【答案解析】[单选题]11、().A、B、C、D、【正确答案】A【答案解析】根据二角和公式,[单选题]12、函数的反函数是().A、B、C、D、【正确答案】A【答案解析】由所以,故.[单选题]13、已知则().A、B、C、D、【正确答案】C【答案解析】[单选题]14、已知为等差数列,,则().A、-2B、1C、3D、7【正确答案】A因为同理可得:故d=a4-a3=-2.[单选题]15、计算().A、B、C、D、【正确答案】A【答案解析】根据偶次根式函数的意义,可知,故[单选题]16、计算().A、0B、1C、2D、4【正确答案】C【答案解析】原式=[单选题]将函数|表示为分段函数时,=().A、B、C、D、【正确答案】B【答案解析】由条件[单选题]18、函数f(x)=是().A、奇函数B、偶函数C、有界函数D、周期函数【正确答案】C【答案解析】易知不是周期函数,,即不等于,也不等于,故为非奇、非偶函数.,故为有界函数.[单选题]19、函数,则的定义域为().A、[1,5]C、(1,5]D、[1,5)【正确答案】A【答案解析】由反正切函数的定义域知:,故定义域为[1,5].[单选题]20、下列等式成立的是()A、B、C、D、【正确答案】B【答案解析】A中(e x)2=,C中,D中[单选题]21、下列函数为偶函数的是()A、y=xsinxB、y=xcosxC、y=sinx+cosxD、y=x(sinx+cosx)【正确答案】A【答案解析】sinx是奇函数,cosx是偶函数。
1.-第一章课后习题及答案

1.-第一章课后习题及答案第一章1.(Q1) What is the difference between a host and an end system? List the types of end systems. Is a Web server an end system?Answer: There is no difference. Throughout this text, the words “host” and “end system” are used interchangeably. End systems include PCs, workstations, Web servers, mail servers, Internet-connected PDAs, WebTVs, etc.2.(Q2) The word protocol is often used to describe diplomatic relations. Give an example of a diplomatic protocol.Answer: Suppose Alice, an ambassador of country A wants to invite Bob, an ambassador of country B, over for dinner. Alice doesn’t simply just call Bob on the phone and say, come to our dinner table now”. Instead, she calls Bob and suggestsa date and time. Bob may respond by saying he’s not available that particular date, but he is available another date. Alice and Bob continue to send “messages” back and forth until they agree on a date and time. Bob then shows up at the embassy on the agreed date, hopefully not more than 15 minutes before or after the agreed time. Diplomatic protocols also allow for either Alice or Bob to politely cancel the engagement if they have reasonable excuses.3.(Q3) What is a client program? What is a server program? Does a server program request and receive services from a client program?Answer: A networking program usually has two programs, each running on a different host, communicating with each other. The program that initiates the communicationAnswer: Current possibilities include: dial-up (up to 56kbps); DSL (up to 1 Mbps upstream, up to 8 Mbps downstream); cable modem (up to 30Mbps downstream, 2 Mbps upstream.4.(Q7) What are some of the physical media that Ethernet can run over?Answer: Ethernet most commonly runs over twisted-pair copper wire and “thin” coaxial cable. It also can run over fibers optic links and thick coaxial cable.5.(Q8) Dial-up modems, HFC, and DSL are all used for residential access. For each of these access technologies, provide a range of transmission rates and comment on whether the transmission rate is shared or dedicated.Answer: Dial up modems: up to 56 Kbps, bandwidth is dedicated; ISDN: up to 128 kbps, bandwidth is dedicated; ADSL: downstream channel is .5-8 Mbps, upstream channel is up to 1 Mbps, bandwidth is dedicated; HFC, downstream channel is 10-30 Mbps and upstream channel is usually less than a few Mbps, bandwidth is shared.6.(Q13) Why is it said that packet switching employs statistical multiplexing? Contrast statistical multiplexing with the multiplexing that takes place in TDM.Answer: In a packet switched network, the packets from different sources flowing on a link do not follow any fixed, pre-defined pattern. In TDM circuit switching, each host gets the same slot in a revolving TDM frame.7.(Q14) Suppose users share a 2Mbps link. Also suppose each user requires 1Mbps when transmitting, but each user transmits only 20 percent of the time. (See the discussion of statistical multiplexing in Section 1.3.)a.When circuit switching is used, how many users can be supported?b.For the remainder of this problem, suppose packet switching is used. Why will there be essentially no queuing delay before the link if two or fewer users transmit at the same time? Why will there be a queuing delay if three users transmit at the same time?c.Find the probability that a given user is transmitting.d.Suppose now there are three users. Find the probability that at any given time, all three users are transmitting simultaneously. Find the fraction oftime during which the queue grows.Answer:a.2 users can be supported because each user requires half of the link bandwidth.b.Since each user requires 1Mbps when transmitting, if two or fewer users transmit simultaneously, a maximum of 2Mbps will be required. Since the available bandwidth of the shared link is 2Mbps, there will be no queuing delay before the link. Whereas, if three users transmit simultaneously, the bandwidth required will be 3Mbps which is more than the available bandwidth of the shared link. In this case, there will be queuing delay before the link.c.Probability that a given user is transmitting = 0.2d.Probability that all three users are transmitting simultaneously=(3)p3(1−p)0=0.23=0.008. Since the 3queue grows when all the users are transmitting, the fraction of time during which the queue grows (which is equal to the probability that all three users are transmitting simultaneously) is 0.008.8.(Q16) Consider sending a packet froma source host to a destination host over a fixed route. List the delay components in the end-to-end delay. Which of these delays are constant and which are variable?Answer: The delay components are processing delays, transmission delays, propagation delays, and queuing delays. All of these delays are fixed, except for the queuing delays, which are variable.9.(Q19) Suppose Host A wants to send a large file to Host B. The path from Host A to Host B has three links, of rates R1= 250 kbps, R2 = 500 kbps, and R3= 1 Mbps.a.Assuming no other traffic in the network, what is the throughput for the file transfer.b.Suppose the file is 2 million bytes. Roughly, how long will it take to transfer the file to Host B?c.Repeat (a) and (b), but now with R2 reduced to 200 kbps.Answer:a.250 kbpsb.64 secondsc.200 kbps; 80 seconds10.(P2) Consider the circuit-switched network in Figure 1.8. Recall that there are n circuits on each link.a.W hat is the maximum number ofsimultaneous connections that can be in progress at any one time in this network?b.S uppose that all connections arebetween the switch in the upper-left-hand corner and the switch in the lower-right-hand corner. What is the maximum number of simultaneous connections that can be in progress?Answer:a.We can n connections between eachof the four pairs of adjacent switches.This gives a maximum of 4n connections.b.We can n connections passingthrough the switch in the upper-right-hand corner and another n connections passing through the switch in the lower-left-hand corner, giving a total of 2n connections.11.(P4) Review the car-caravan analogy in Section 1.4. Assume a propagation speed of 50 km/hour.a.S uppose the caravan travels 150 km,beginning in front of one tollbooth, passing through a second tollbooth, and finishing just before a third tollbooth.What is the end-to-end delay?b.R epeat (a), now assuming that thereare five cars in the caravan instead of ten.Answer: Tollbooths are 150 km apart, and the cars propagate at 50 km/hr, A tollbooth services a car at a rate of one car every 12 seconds.a.There are ten cars. It takes 120seconds, or two minutes, for the first tollbooth to service the 10 cars. Each of these cars has a propagation delay of 180 minutes before arriving at the second tollbooth. Thus, all the cars arelined up before the second tollbooth after 182 minutes. The whole process repeats itself for traveling between the second and third tollbooths. Thus the total delay is 364 minutes.b.Delay between tollbooths is 5*12seconds plus 180 minutes, i.e., 181minutes. The total delay is twice this amount, i.e., 362 minutes.12.(P5) This elementary problem begins to explore propagation delay and transmission delay, two central concepts in data networking. Consider two hosts, A and B, connected by a single link of rate R bps. Suppose that the two hosts are separated by m meters, and suppose the propagation speed along the link is s meters/sec. Host A is to send a packet of size L bits to Host B.a.E xpress the propagation delay, d prop ,in terms of m and s.b.D etermine the transmission time ofthe packet, d trans , in terms of L and R.c.I gnoring processing and queuingdelays, obtain an expression for the end-to-end delay.d.S uppose Host A begins to transmitthe packet at time t = 0. At time t =d trans , where is the last bit of the packet?e.S uppose d prop is greater than d trans . Attime t = d trans , where is the first bit of the packet?f.S uppose d prop is less than d trans . At timet = d trans , where is the first bit of the packet?g.S uppose s = 2.5*108, L = 100bits, and R= 28kbps. Find the distance m so thatd prop equals d trans .Answer:a.d prop = m/s seconds.b.d trans = L/R seconds.c.d end-to-end = (m/s + L/R) seconds.d.T he bit is just leaving Host A.e.T he first bit is in the link and has notreached Host B.f.T he first bit has reached Host B.g.W antm=LS=1003(2.5∗108) =893 km.13.(P6) In this problem we consider sending real-time voice from Host A to Host B over a packet-switched network (VoIP). Host A converts analog voice to a digital 64 kbps bit stream on the fly. Host A then groups the bits into 56-Byte packets. There is one link between Host A and B; its transmission rate is 500 kbps and its propagation delay is 2 msec. As soon as Host A gathers a packet, it sends it to Host B. As soon as Host B receivesan entire packet, it converts the packet’s bits to an analog signal. How much time elapses from the time a bit is created (from the original analog signal at Host A) until the bit is decoded (as part of the analog signal at Host B)?Answer: Consider the first bit in a packet. Before this bit can be transmitted, all of the bits in the packet must be generated. This requires56∗8sec=7 msec3The time required to transmit the packet is56∗8sec=896 μsec3Propagation delay = 2 msec.The delay until decoding is7msec + 896μsec + 2msec = 9.896 msecA similar analysis shows that all bits experience a delay of 9.896 msec.14.(P9) Consider a packet of length Lwhich begins at end system A, travels overone link to a packet switch, and travelsfrom the packet switch over a second linkto a destination end system. Let d i, s i, and Rdenote the length, propagation speed, iand the transmission rate of link i, for i = 1, 2. The packet switch delays each packet by d proc. Assuming no queuing delays, in terms of d i, s i, R i, (i = 1, 2), and L, what is the total end-to-end delay for the packet? Suppose now the packet Length is 1,000 bytes, the propagation speed on both links is 2.5 * 108 m/s, the transmission rates of both links is 1 Mbps, the packet switch processing delay is 2 msec, the length of the first link is 6,000 km, and the length of the last link is 3,000 km. For these values, what is the end-to-end delay?Answer: The first end system requires L/R1to transmit the packet onto the first link; the packet propagates over the first link in d1/s1; the packet switch adds a processing delay of d proc; after receiving the entire packet, the packet switch requires L/R2to transmit the packet onto the second link; the packet propagates over the second link in d2/s2. Adding these five delays givesdend-end = L/R1+ L/R2+ d1/s1+ d2/s2+ dprocTo answer the second question, we simply plug the values into the equation to get 8 + 8 + 24 + 12 + 2 = 54 msec.15.(P10) In the above problem, supposeR 1= R2= R and dproc= 0. Further suppose thepacket switch does not store-and-forward packets but instead immediately transmits each bit it receivers before waiting for the packet to arrive. What is the end-to-end delay?Answer: Because bits are immediately transmitted, the packet switch does not introduce any delay; in particular, it does not introduce a transmission delay. Thus,dend-end = L/R + d1/s1+ d2/s2For the values in Problem 9, we get 8 + 24 + 12 = 44 msec.16.(P11) Suppose N packets arrive simultaneously to a link at which no packets are currently being transmitted or queued. Each packet is of length L and the link has transmission rate R. What is the average queuing delay for the N packets?Answer: The queuing delay is 0 for the first transmitted packet, L/R for the second transmitted packet, and generally,(n-1)L/R for the nth transmitted packet. Thus, the average delay for the N packets is(L/R + 2L/R + ....... + (N-1)L/R)/N = L/RN(1 + 2 + ..... + (N-1)) = LN(N-1)/(2RN) = (N-1)L/(2R)Note that here we used the well-known fact that1 +2 + ....... + N = N(N+1)/217.(P14) Consider the queuing delay ina router buffer. Let I denote traffic intensity; that is, I = La/R. Suppose that the queuing delay takes the form IL/R (1-I) for I<1.a.Provide a formula for the total delay, that is, the queuing delay plus the transmission delay.b.Plot the total delay as a function of L/R.Answer:a.The transmission delay is L / R .The total delay isIL+ L=L/Rb.Let x = L / R.Total delay=x18.(P16) Perform a Traceroute between source and destination on the same continent at three different hours of the day.a.Find the average and standard deviation of the round-trip delays at each of the three hours.b.Find the number of routers in the path at each of the three hours. Did the paths change during any of the hours?c.Try to identify the number of ISP networks that the Traceroute packetspass through from source to destination. Routers with similar names and/or similar IP addresses should be considered as part of the same ISP. In your experiments, do the largest delays occur at the peering interfaces between adjacent ISPs?d.Repeat the above for a source and destination on different continents. Compare the intra-continent and inter-continent results.Answer: Experiments.19.(P18) Suppose two hosts, A and B, are separated by 10,000 kilometers and are connected by a direct link of R = 2 Mbps. Suppose the propagation speed over the link is 2.5•108 meters/sec.a.Calculate the bandwidth-delay product, R •d prop.b.Consider sending a file of 400,000 bits from Host A to Host B. Suppose the file is sent continuously as one large message. What is the maximum number of bits that will be in the link at any given time?c.Provide an interpretation of the bandwidth-delay product.d.What is the width (in meters) of a bit in the link? Is it longer than a football field?e.Derive a general expression for the width of a bit in terms of the propagation speed s, the transmission rate R, and the length of the link m.Answer:a.d prop = 107 / 2.5•108 = 0.04 sec; so R •d prop = 80,000bitsb.80,000bitsc.The bandwidth-delay product of alink is the maximum number of bits thatcan be in the link.d.1 bit is 125 meters long, which islonger than a football field) = m / (R * m / s) =e.m / (R • dprops/R20.(P20) Consider problem P18 but now with a link of R = 1 Gbps.a.C alculate the bandwidth-delayproduct, R·d prop .b.C onsider sending a file of 400,000bits from Host A to Host B. Suppose the file is sent continuously as one big message. What is the maximum number of bits that will be in the link at any given time?c.W hat is the width (in meters) of abit in the link?Answer:a.40,000,000 bits.b.400,000 bits.c.0.25 meters.21.(P21) Refer again to problem P18.a.H ow long does it take to send the file,assuming it is sent continuously?b.S uppose now the file is broken up into10 packet is acknowledged by thereceiver and the transmission time of an acknowledgment packet is negligible.Finally, assume that the sender cannot send a packet until the preceding one is acknowledged. How long does it take to send the file?c.C ompare the results from (a) and (b).Answer:a.d trans + d prop = 200 msec + 40 msec = 240msecb.10 * (t trans + 2 t prop ) = 10 * (20 msec +80 msec) = 1.0 sec。
第1章习题答案

(一)单项选择题 1.B 2.D 3.A 4.B S.C 6.B 7.B 8.C 9.A 10.C
11.C 12. D 13. D14.A 15.C 16.B 17.C 18.A 19.C 20.B 21.C 22. D 23. B 24. D 25. D26.A 27.D 28.C 29.C 30.D 31.D 32.B 33.A 34.A 35.D 36. C 37.B38.D 39.B 40.B 41.A 42. B 43. B 44.D
上一页 下一页 返回
第1章习题答案
(3)西方国家工人大量失业都发生在经济严重萧条、衰退时 期,是资本主义各种危机因素长期积累、总体爆发的结果, 因此资本主义制度不可能根本解决失业问题。我国目前国有 企业职工下岗分流出现在我国经济快速发展时期,是党和国 家为实现经济体制和经济增长方式两个根本转变(由计划经济 向市场经济转变、粗放型经济增长方式向集约型转变)而主动 采取的重大措施,尽管短期内给我国带来了社会问题,但从 长远的发展看,我们可以通过下岗再就业、职工培训和社会 保障等来逐步解决失业问题。
上一页 下一页 返回
第1章习题答案
(2)消费方式健康,摒弃落后的生活习惯,提高消费的科学 性。
首先,通过教育、宣传,使人们树立科学的价值观和消费观。 其次,不断提高消费者的素质。再次,净化消费环境。最后, 从可持续发展的战略高度,提倡进行绿色消费。
(3)结构合理,物质消费和精神消费要协调发展。 消费结构合理是指消费结构在一定的生产发展阶段由非科学
上一页 下一页 返回
第1章习题答案
(五)简答题 1.答案要点: 树立积极合理的消费观就要做到水平适度、结构合理、方式
健康,具体体现在: (1)家庭生活消费必须与国情及家庭收入相适应,提倡适度
第一章章末练习 - 解析版
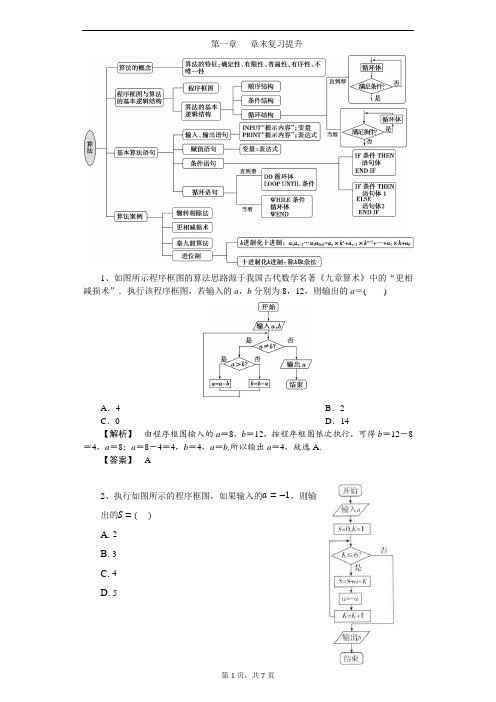
第一章章末复习提升1、如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为8,12,则输出的a=()A.4 B.2C.0 D.14【解析】由程序框图输入的a=8,b=12,按程序框图依次执行,可得b=12-8=4,a=8;a=8-4=4,b=4,a=b.所以输出a=4,故选A.【答案】 A2、执行如图所示的程序框图,如果输入的a=−1,则输出的S=()A. 2B. 3C. 4D. 5【答案】B解:根据程序框图执行的过程如下:第一次:是,S=0+(−1)×1=−1,a=1,K=2;第二次:是,S=−1+1×2=1,a=−1,K=3;第三次:是,S=1+(−1)×3=−2,a=1,K=4;第四次:是,S=−2+1×4=2,a=−1,K=5;第五次:是,S=2+(−1)×5=−3,a=1,K=6;第六次:是,S=−3+1×6=3,a=−1,K=7;第七次:否,输出S=3.故选B.3、计算12+22+32+…+1002的程序框图如图,则该框图的判断框中应填的条件为()A.i<100?B.i>100?C.i≤100?D.i≥100?【解析】根据算法程序框图知选B.【答案】 B4、执行如图所示的程序框图,输出的S值为()A. 2B. 32C. 53D. 85【答案】C解:当k=0时,满足进行循环的条件,执行完循环体后,k=1,S=2,当k=1时,满足进行循环的条件,执行完循环体后,k=2,S=32,当k=2时,满足进行循环的条件,执行完循环体后,k=3,S=53,当k=3时,不满足进行循环的条件,故输出结果为:53,故选:C.5、执行如图所示的程序框图,输出的s的值为()A. 53B. 85C. 138D. 2113【答案】C解:该程序框图的执行过程为:i=0,s=1,i≤4成立,i=1,s=2;i≤4成立,i=2,s=32;;i≤4成立,i=3,s=53;i≤4成立,i=4,s=85;i≤4成立,i=5,s=138i>4,输出s.,故s=138故选C.6、如图程序框图是为了求出满足3n−2n>1000的最小偶数n,那么在◇和□两个空白框中,可以分别填入()A. A>1000和n=n+1B. A>1000和n=n+2C. A≤1000和n=n+1D. A≤1000和n=n+2【答案】D解:∵要求A>1000时输出,且框图中在“否”时输出,∴“◇”内要填写“A≤1000”,∵要求n为偶数,且n的初始值为0,∴“□”中n依次加2可保证其为偶数,∴D选项满足要求,故选D.7、执行下面的程序框图,输入的x=0,y=1,n=1,则输出x,y的值满足()A. y=2xB. y=3xC. y=4xD. y=5x【答案】D解:执行题中的程序框图,知=0,y=1×1=1,x2+y2<36;第一次进入循环体:x=0+1−12=1,第二次执行循环体:n=1+2=3,x=0+3−12y=3×1=3,x2+y2<36;=3,第三次执行循环体:n=3+2=5,x=1+5−12y=5×3=15,x2+y2>36,满足x2+y2≥36,故退出循环,输出x=3,y=15,满足y=5x.故选D.8、执行下图所示的程序框图,输出S的值为()A. 25B. 24C. 21D. 9【答案】A解:初始值S=0,i=9;第一步,S=0+9=9,T=9+9−2=16,此时S<T,故i=9−2=7;第二步:S=9+7=16,T=16+7−2=21,此时S<T,故i=7−2=5;第三步:S=16+5=21,T=21+5−2=24,此时S<T,故i=5−2=3;第四步:S=21+3=24,T=24+3−2=25,此时S<T,故i=3−2=1;第五步:S=24+1=25,T=25+1−2=24,此时S>T,故输出S=25;故选:A.9、执行如图所示的程序框图,如果输入的t∈[−2,2],则输出的S属于()A. [−6,−2]B. [−5,−1]C. [−4,5]D. [−3,6]【答案】D解:当t∈[0,2]时,S=[−3,−1];当t∈[−2,0)时,2t2+1∈(1,9],∴S∈(−2,6].综上所述,S∈[−3,6].故选D.10、执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是()A. s>12B. s>75C. s>710D. s>45【答案】C解:由程序框图知执行一次循环结构s=1×99+1=910,k=9−1=8,再执行一次循环结构s=910×89=810,k=7,接着再执行一次循环结构s=810×78=710,k=6,∵输出的k=6,∴s=710,∴判断框的条件是s>710.故选C.11、执行如图的程序框图,如果输入的ɛ为0.01,则输出s的值等于()A. 2−124B. 2−125C. 2−126D. 2−127【答案】C解:第一次执行循环体后,s=1,x=12,不满足退出循环的条件x<0.01;再次执行循环体后,s=1+12,x=122,不满足退出循环的条件x<0.01;再次执行循环体后,s=1+12+122,x=123,不满足退出循环的条件x<0.01;…由于126>0.01,而127<0.01,可得:当s=1+12+122++⋯126,x=127,此时,满足退出循环的条件x<0.01,输出s=1+12+122+⋯126=2−126.故选C.。
第1章的参考答案.doc

1.什么是计算机语言?答:计算机语言是人机交流的语言,也称为程序设计语言。
人们通过给计算机一系列命令,让计算机按给定的命令一步步地工作来实现计算机控制。
2.机器语言、汇编语言和高级语言分别有什么特点?答:(1)机器语言是最底层的计算机语言。
在用机器语言编写的程序中,每一条机器指令都是二进制形式的代码,即由一连串的二进制数符。
和1组合起来的编码。
程序中的每一条指令规定了计算机要完成的一个操作。
在指令代码中,一般包括操作码和地址码,其中操作码告诉计算机做何种操作,即“干什么”,地址码则指出被操作的对象存放在什么位置。
用机器语言编写的程序,计算机硬件可以直接识别。
由于机器语言程序是由二进制数符0和1组成的系列,所以用它编写的程序直接针对计算机硬件,执行效率高,能充分发挥计算机的速度和性能,这也是机器语言的优点。
但是由于二进制数序列“难学、难记、难写、难检查、难调试”,编写起来非常繁琐,而且用机器语言编写的程序完全依赖于机器,程序的可移植性差,所以一般不用机器语言编写程序。
(2)汇编语言:人们用一些容易记忆和辨别的有意义的符号来表示机器指令,如用指令助记符表示机器语言指令代码中的操作码,用地址符号表示地址码。
这样用一些符号表示机器指令的语言就是汇编语言,也称为符号语言。
汇编语言与机器语言一一对应,依赖于机器硬件,移植性不好,但执行效率比较高。
针对计算机特定硬件而编制的汇编语言程序,能准确发挥计•算机硬件的功能和特长,程序精练而质量高,所以至今仍是一种常用而强有力的软件开发工具。
(3)高级语言高级语言是一种更接近于自然语言的计算机语言,包括Fortran. Basic、Pascak Cobol 及C 语言等。
高级语言源程序主要由语句(statements)构成,语句是要计算机完成指定任务的命令。
高级语言有各自的语法,独立于具体机器,移植性好。
为了使高级语言编写的程序能够在不同的计算机系统上运行,首先必须将程序翻译成运行程序的计算机特有的机器语言。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 0 r 2
1 4 0
q
q 2 4 0 r rl cos 1
Eθ Er- θ2 r+ r θ O q
θ1
Er
P
-q
E E E Er E r Er E E E
其中——
q 4 0 q 4 0
(
cos cos 2ql cos 2 p cos ) 2 2 3 4 0 r 4 0 r 3 r r sin sin ql sin p sin 2 ) 2 3 4 0 r 4 0 r 3 r r
(1) F (2)a
q1 q 2 7.64 10 2 N (排斥力) 4 0 r 2 1 F 1.14 10 29 m / s m
1.1-10 两小球质量都是 m,都用长为 l 的细线挂在同一点,若它们带上相同的电量,平衡时 两线夹角为 2θ。设小球的半径都可以略去不计,求每个小球上的电量。 解: 小球静止时, 作用其上的库仑力和重力在垂直于悬线方向上 的分量必定相等。
(1) Fe
e2 8.22 10 8 N (吸引力) 2 4 0 r 1 m1 m2 3.63 10 47 N (吸引力) Fe / Fg 2.26 10 39 r2 e2 2.19 10 6 m / s 4 0 mr 1
(2) Fg G (3)m
v2 1 e2 v r 4 0 r 2
由此可知, 在原子范围内, 与库仑力相比, 万有引力完全可以略去不计
1.1-5 卢瑟福实验证明:当两个原子核之间的距离小到 10-15 米时,它们之间的排斥力仍遵守 库仑定律。金的原子核中有 79 个质子,氦的原子核(即α粒子)中有 2 个质子。已知每个 质子带电 e=1.6× 10-19 C,α粒子的质量为 6.68× 10-27 kg.。当α粒子与金核相距为 6.9× 10-15m 时(设这时它们仍都可当作点电荷) 。求(1)α粒子所受的力; (2)α粒子的加速度。 解:
dq 4 0 ( x 2 2rdr e 4 0 ( x 2 dE E dE
0 R
x r2) x r2)
3 2 3 2
R
x dr e 2 0 ( x 2 r 2 ) 3 2
r O
P x
e x (1 ) 2 2 0 x R2
(2)保持σe 不变时,
距离为 x. x q Q 2q
F
Qq 2Qq 1 0 2 4 0 x 4 0 (l x) 2 1
x ( 2 1)l
1.2-3 在早期(1911 年)的一连串实验中,密立根在不同时刻观察单个油滴上呈现的电荷, 其测量结果(绝对值)如下: 6.568×10-19 库仑 13.13×10-19 库仑 19.71×10-19 库仑 8.204×10-19 库仑 16.48×10-19 库仑 22.89×10-19 库仑 -19 -19 11.50×10 库仑 18.08×10 库仑 26.13×10-19 库仑 根据这些数据,可以推得基本电荷 e 的数值为多少? 解 : 油 滴 所 带 电 荷 为 基 本 电 荷 的 整 数 倍 。 则 各 实 验 数 据 可 表 示 为 k ie 。 取 各 项 之 差
E dS E ds a 2 E
S S
1.3-3※ 如附图所示, 在半径为R1和R2的两个同心球面上, 分别均匀地分布着电荷Q1和Q2, 求: (1)Ⅰ、Ⅱ、Ⅲ三个区域内的场强分布; (2)若Q1=-Q2,情况如何?画出此情形的E-r 曲线。 解: (1)应用高斯定理 Q2 Q1 R1 O R2
R 0时, E 0; R 时, E
e 2 0
(3)保持总电量不变时,
E
e Q x x (1 ) (1 ) 2 2 0 2 0 R x2 R2 x2 R2
Q 4 0 x 2 ; R 时, E 0
R 0时, E
1.3-2 均匀电场与半径为 a 的半球面的轴线平行,试用面积分计算通过此半球面的电通量。 解:通过半球面的电通量与通过半球面在垂直于场强方向上的投影面积的电通量相等。
3 2
0
R/√2
R
x
3q 18 0 R 2
d 2E 3qx 3R 2 2 x 2 d 2E 当 r R / 2 时 0 4 0 ( x 2 R 2 ) 7 2 dx 2 dx 2
E m为极大值
1.2-13 半径为 R 的圆面上均匀带电,电荷面密度为σe, (1)求轴线上离圆心的坐标为 x 处 的场强; (2)在保持σe 不变的情况下,当 R→0 和 R→∞时结果各如何?(3)在保持总电 荷 Q=πR2σe 不变的情况下,当 R→0 和 R→∞时结果各如何? 解: (1)由对称性可知,场强 E 沿轴线方向 利用上题结果
dE
dq 4 0 r (l z ) 2
2
1
r A r -l 0 l-z +l z
dE z dE cos dE r dE sin 1 1 ( ) 2 8 0 l r r 4l 2 l q 1 E r dE r l 2 4 0 r r 4l 2 E z dE z
2q l2 3Q 当r l时E 3 2 (Q 2ql 2 ) 2 4 4 0 r r 4 0 r
四极子可看成两个偶极子组成,它们在 P 点所产生的场强分别为
P 点的场强为
1.2-9 附图中所示为另一种电四极子,设 q 和 l 都已知,图中 P 点到电四极子中心 O 的距离 为 x.PO 与正方形的一对边平行。求 P 点的电场强度 E。当 x>>l 时,E=?
(
cos 1
r
l
2
cos
r r l
2 cos
l sin sin 1 2 r l sin 2 sin 2 r
cos 2
r
1.2- 8 附图中所示是一种电四极子,它由两个相同的电偶极子 P=ql 组成,这两偶极子在一 直线上,但方向相反,它们的负电荷重合在一起。证明:在它们的延长线上离中心为 r 处,
(k 2 k1 )e 1.636 10 19 C (k 3 k 2 )e 3.296 10 19 C (k 4 k 3 )e 1.630 10 19 C (k 5 k 4 )e 3.350 10 19 C (k 6 k 5 )e 1.60 10 19 C (k 7 k 6 )e 3.18 10 19 C (k 8 k 7 )e 3.18 10 19 C (k 9 k 8 )e 3.24 10 19 C ek的最小值接近1.60 10 19 C , 没有理由认为e 1.60 10 19 C 所以只能有k 2 k1 k 4 k 3 k 6 k 5 1, k3 k 2 k5 k 4 k 7 k 6 k8 k k9 k8 2 e的数值有1.636,1.675,1.59,1.648,1.60,1.62,1.63,1.63(10 19 C ), 取平均值e (1.629 0.046) 10 19 C
Fe cos Fg sin Fe Fg tan 1 4 0 q2 mg tan (2l sin ) 2 4 0 mg tan
l
θ θ
l
q 2l sin
1.1-7 两个点电荷带电 2q 和 q,相距 l,第三个点电荷放在何处所受的合力为零? 解:设所放的点电荷电量为 Q。若 Q 与 q 同号,则三者互相排斥,不可能达到平衡; 故 Q 只能与 q 异号。当 Q 在 2q 和 q 联线之外的任何地方,也不可能达到平衡。由此可 知,只有 Q 与 q 异号,且处于两点荷之间的联线上,才有可能达到平衡。设 Q 到 q 的
l l
q
(2)延长线上任一点 B 处
dE z
dq 4 0 ( z l ) 2
l l
1
E z dE z
1 4 0 z l 2
2
q
1.2-12 如图所示,一半径为 R 的均匀带电圆环,电荷总量为 q。 (1)求轴线上离环中心 O 为 x 处的场强 E; (2)画出 E—x 曲线; (3)轴线上什么地方场强最大?其值是多少? 解: (1)由对称性可知,所求场强 E 的方向平行于圆环的轴线
3 2
-q
O +q
r
P
本题中的四极子可看成左右一对竖直反向偶极子组成, 它们在 P 点所产生的场强分别为
P 点的场强为
1.2-10※均匀带电细棒(1)在通过自身端点的垂直面上和(2)在自身的延长线上的场强分 布,设棒长为 2l,带电总量为 q . 解: (1)一端的垂直面上任一点 A 处
dE
dq 1 q 1 2 dl 2 2 2 4 0 x R 8 0 R x R 2 1 8 0 R x R 2
2 2 3 2
E dE cos q
2
q
x
x
8 0 R ( x 2 R 2 )
2R
0
dl
x2 R2 q x
dl
S
E dS
1
0 i 1
