函数的画图
正弦函数、余弦函数的图像及五点法作图

2 3
4 5
2
3
4
5
6 x 6 x
正弦函数、余弦函数的图像及五点法作图
【用五点法作正弦函数和余弦函数的简图(描点法)】
正弦函数y=sinx,x∈[0,2π]的图象中,五个
关键点是: (0,0) (
,1)
(π,0)
(
3
Hale Waihona Puke ,-1)(2π,0)
2
2
余弦函数y=cosx x[0,2]的五个点关键是
正弦函数余弦函数的图像及五点法作图余弦函数ycosx的图象用几何法作余弦函数的图象可以用反射法将角x的余弦线竖立把坐标轴向下平移过o终点a作x轴的垂线它与前面所作的直线交于a那么oa与aa长度相等且方向同时为正我们就把余弦线oa竖立起来成为aa用同样的方法将其它的余弦线也都竖立起来
知识点——
正弦函数、余弦函数 的图像及五点法作图
(0,1) ( ,0) (,-1) (3 ,0) (2,1)
2
2
只要这五个点描出后,图象的形状就基本
确定了.因此在精确度不太高时,常采用
五点法作正弦函数和余弦函数的简图,要
求熟练掌握.优点是方便,缺点是精确度
不高,熟练后尚可以.
正弦函数、余弦函数的图像及五点法作图
【典型例题】
1、用五点法作函数 y 1 sin x, x 0,2 的图象.
)6 ,.把3 角, 2x,的…正,
弦线向右平行移动,使得正弦线的起点与x轴上相
应的点x重合,则正弦线的终点就是正弦函数图象
上的点(等价于“描点” ).
正弦函数、余弦函数的图像及五点法作图
【函数y=sinx的图象】 第三步:连线.用光滑曲线把这些正弦线的终点连 结起来,就得到正弦函数y=sinx,x∈[0,2π]的 图象.
高二数学正弦函数的图像与性质

X0
2
3 2
2
x 2 7 5 13
2
2
2
y 0 2 0 2 0
小结
y=Asin(ωx+φ)的各种变化方式
课后作业: 课本
P49 练习A1(2)(4) 2(3)(4)
世上没有什么天才
天才是勤奋的结果
; 必威电竞 ;
疆虽是鼎鼎有名.孟禄也听过他的名字.但他却不知道左耳朵的为人.也不知道左耳朵在北疆的威望.就如飞红中在北地几样.他只道左耳朵也像明悦几样.只是个 助拳 的人.仗着箭法高明.所以才有名气的.他又恍惚听人说过;左耳朵乃是明悦的族兄.当日明悦来投唐努老英雄.捧的就是 左耳朵的名头.明悦反叛之事他是知道的.他只以为左耳朵给他的族弟拉去.到北地来暗害他们.因此.带着三十多匹马.几路追踪觅迹.而左耳朵又因处处要照顾苏绿儿.不能驱车疾走.竟然给他们追上. 左耳朵几阵愕然.纳兰朗慧忽然揭开车帘.露出脸来.叫道. 你们不要赖他.那两个人是 我杀的. 苏绿儿得啦爱情的滋润.虽在病后.却是眼如秋水.容光照人.她本是旗人中的第几位美人.在这草原蓦然现出色相.颜容映着晚霞.孟禄只觉得几阵光采迫人.眼花综乱.急忙定下心神.再喝问道-你说什么? 苏绿儿冷笑道. 你听不清楚么?那两个人是本姑娘杀的. 孟禄这时也注意 到啦车帘上绣着的 纳兰 两字.又惊又喜.他起初以为车上只是普通的清军将官的眷属.而今见这个气派.暮然想起久闻满清的伊犁护军苏翠儿.有几个美丽的女儿.文武双全.莫不是她. 孟禄皮鞭几指.笑道-是你杀的也好.不是你杀的也好.你现在是我的俘虏啦.随我回去再说. 苏绿儿又是 几声冷笑.说道-你也想跟那两个人去见阎王吗?他们就是说要捉我做俘虏.才给
实验1_函数的图形

实验1曲线绘图实验目的•学习Matlab绘图命令;•进一步理解函数概念。
1.曲线图Matlab作图是通过描点、连线来实现的,故在画一个曲线图形之前,必须先取得该图形上的一系列的点的坐标(即横坐标和纵坐标),然后将该点集的坐标传给Matlab函数画图.命令为:PLOT(X,Y,’S’)线型X,Y是向量,分别表示点集的横坐标和纵坐标PLOT(X,Y)--画实线PLOT(X,Y1,’S1’,X,Y2,’S2’,……,X,Yn,’Sn’)--将多条线画在一起例1在[0,2*pi]用红线画sin(x),用绿圈画cos(x). x=linspace(0,2*pi,30);解:y=sin(x);z=cos(x);plot(x,y,'r',x,z,‘g o')G 绿色o 圈表1 基本线型和颜色符号颜色符号线型y黄色.点m紫红0圆圈c青色x x标记r红色+加号g绿色*星号b兰色-实线w白色:点线k黑色-.点划线--虚线2.符号函数(显函数、隐函数和参数方程)画图(1) ezplotezplot(‘f(x)’,[a,b])表示在a<x<b绘制显函数f=f(x)的函数图ezplot(‘f(x,y)’,[xmin,xmax,ymin,ymax])表示在区间xmin<x<xmax和ymin<y<ymax绘制隐函数f(x,y)=0的函数图ezplot(‘x(t)’,’y(t)’,[tmin,tmax])表示在区间tmin<t<tmax绘制参数方程x=x(t),y=y(t)的函数图例2 在[0,pi]上画y=cos(x)的图形解输入命令ezplot('cos(x)',[0,pi])解输入命令ezplot('cos(t)^3','sin(t)^3',[0,2*pi])例4 在[-2,0.5],[0,2]上画隐函数0)sin(=+xy e x的图 解输入命令ezplot('exp(x)+sin(x*y)',[-2,0.5,0,2])例3 在[0,2*pi]上画t x 3cos =,t y 3sin =星形图如何利用ezplot画出颜色图(2) fplotfplot(‘fun’,lims)表示绘制字符串fun指定的函数在lims=[xmin,xmax]的图形.注意:[1] fun必须是M文件的函数名或是独立变量为x的字符串.[2] fplot函数不能画参数方程和隐函数图形,但在一个图上可以画多个图形。
三角函数的图象与性质
-
;
-1
y=cosx
2 3
4 5 4 5
6 x 6 x
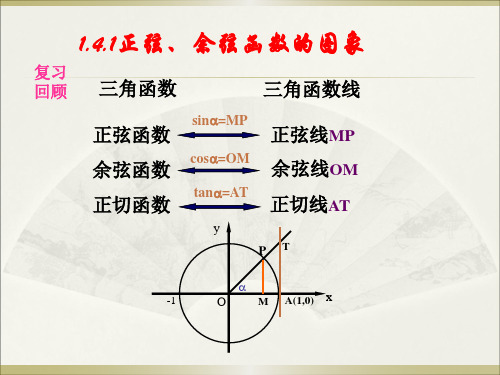
五.定义域 、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
y
si-n6x的对称-5轴:x
k -4
2-,3对 称点-:2(k
,0);
-
y cosx的对称轴:x k , 对称点:(k ,0);
1.4.1正弦、余弦函数的图象
复习
回顾 三角函数
三角函数线
正弦函数 余弦函数 正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦、余弦函数的图象
问题:如何作出正弦、余弦函数的图象?
途径:利用单位圆中正弦、余弦线来解决。
描图:用光滑曲线
复习回顾
一.正弦余弦函数的作图: 几何描点法(利用三角函数线) 五点法作简图
二.周期性:
函数y Asin(x )和y Acos(x ),x R的周期T 2 | |
三.奇偶性:
y sin x为奇函数,图像关于原点对称; y cosx为偶函数图像关于y轴对称。
-6 -5
-4 -3
复习回顾 y y=sinx
(0,11)
3
( 2 ,1)
-
(-o12 ,0)
( 2 ,0)
2
( ,-1)
3
线
4
5 6 x
正弦、余弦函数的图象
y
五点画图法
1
(
2
,1)
正弦函数余弦函数的图象完整版课件
y
1-
-
-
6
4
2
o
-1-
2
4
6
x
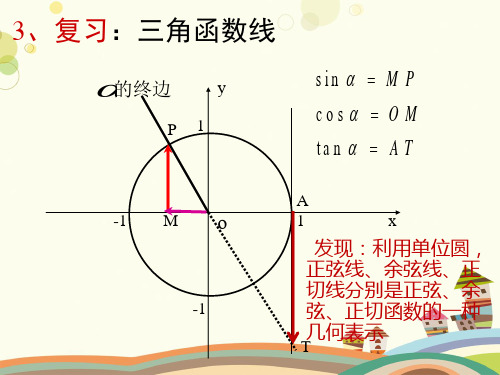
因为终边相同的角的三角函数值相同,所以y=sinx,x∈R的图象在
4,2 ,2,0, 0,2, 2,4,…与y=sinx,x∈[0,2π]的图象相同
正弦曲线:ysinx xRy
1
-1
x
-cosx -1 0
1
0 -1
y
y=-cosx x[0,2 ]
1
●
o
●
3●
2
x
2
2
-1 ●
●
思考:
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系? 2、函数y=-cosx的图象与函数y=cosx的图象有什么关系?
y 2
y=1+sinx x[0, 2]
1
o
3
2
-1
2
2
x
y=sinx x[0, 2]
1
●
●
●
●
●
7 4 3 5 11
6
6 3 2 3 6 2
●
2 0
2 5
●
11
6 32 3 6
●
●
x
●
5
6
-1
●
●
●
3
y
ysinx x [0 ,2 ]
1-
-
-1
o 6
3
2
2 3
5
7
6
6
4 3
3
5
2
3
11 6
2
-1 -
1.4.1(公开课课件)正弦函数、余弦函数的图像

实 一 一对应
唯一确定
角
正 弦
数
一对多 值
定义:任意给定的一个实数x,有唯一确定的值sinx与 之对应。由这个法则所确定的函数 y=sinx叫做正弦
函数,y=cosx叫做余弦函数,二者定义域为R。
第3页,共28页。
二、正弦函数 y =sinx(x∈R)的图象
1.几何法作图:
问题:如何作出正弦函数的图象?
(3) 连线(用光滑的曲线顺次连结五个点)
1-
-
-
-1
o
6
2
3
2 3
5
7
6
6
4 3
3 5 23
-1 -
第26页,共28页。
图象的最高点
(0,1) (2 ,1)
与x轴的交点
11 6
2
x
(
2
,0)
(
3 2
,0)
图象的最低点 ( ,1)
课堂小结
1.正、余弦函数的图象每相隔2π个单位重复出现,因此, 只要记住它们在[0,2π]内的图象形态,就可以画出正弦 曲线和余弦曲线.
正弦函数、余弦函数的图象
第1页,共28页。
1.正弦线、余弦线的概念
设任意角α的终 边与单位圆交于点P. 过点P做x轴的垂线, 垂足为M.
则有向线段MP叫做角α的正弦线. 有向线段OM叫做角α的余弦线.
2. 三角函数值的符号判断
y α 的终边
P(x,y)
oMx
第2页,共28页。
一、正弦函数的定义:
有何联系?
第17页,共28页。
练习:(1)作函数 y=1+3cosx,x∈[0,2π]的简图 (2)作函数 y=2sinx-1,x∈[0,2π]的简图
5.4.1 正弦函数、余弦函数的图象(课件)高一数学(人教A版2019必修第一册) (2)

图象向左平移
2
2
个单位长度而得到, 所以, 将正弦函数的图象向左平移
个单位长度, 就得到余弦函数的图象.
余弦函数y=cosx(x ∈R)的图象
sin(
x+ 2
)= cosx
y
余弦曲线 正弦曲线
x
-2
-
o
2
3
2
3
4
2
余弦函数的图象可以通过将正弦曲线向左
平行移动/2个单位长度而得到
足够多的点T ( x0 ,sin x0 ), 将这些点用光滑的曲线连接起来 , 可得到比
较精确的函数y sin x , x [0, 2 ]的图象(图5.4 3)
2
3
5
6
2
3
6
7
6
y
1
2
4
3
3
2
5
3
y=sinx ( x ∈ [0, 2 ] )
●
1
●
0
6
7 4 3 5 11
【变式 2】
求函数 f(x)=lg sin x+ 16-x2的定义域.
sin x>0,
解析:由题意,得 x 满足不等式组
2
16-x ≥0,
-4≤x≤4,
即
作出 y=sin x 的图象,如图所示.
sin x>0,
结合图象可得:x∈[-4,-π)∪(0,π).
【变式3】若函数f(x)=sin x-2m-1,x∈[0,2π]有两个零点,求m的取值范围.
图.这种近似的“五点(画图〉法”是非常实用的.
正弦函数的“五点画图法”
函数的图象(课件)八年级数学下册(人教版)

课堂检测 1.某车间的甲、乙两名工人分别同时生产同种零件,他们一 天生产零件y(个)与生产时间t(h)的函数关系如图所示. (1)根据图象填空:①_甲__先完成一天的生产任务;在生产过 程中,__甲__因机器故障停止生产__2__h; ②当t=__3_或__5_._5 时,甲、乙生产的零件个数相等.
解:(2)由于水位在最近5小时内持续上涨,对于时间t的每一个确定的 值,水位高度y 都有 唯一 的值与其对应,所以,y 是 t 的函数.函数 解析式为: y=3+0.3t .
自变量的取值范围是: 0≤t≤5 .它表示在这 5 小时内,水位 匀速上升的速度为0.3m/h ,这个函数可以近似地表示水位的变化规律.
-1
-2
当自变量的值由小变大时,
-3
-4
对应的函数值 随之减小 .
-5
-6
y 6( x >0). x
1 2 3 4 5x
总结归纳
描点法画函数图象的一般步骤如下:
第一步,列表—表中给出一些自变量的值及其 对应的函数值 ; 第二步,描点—在平面直角坐标系中,以自变量的值为 横坐标 , 相应的函数值为 纵坐标 ,描出表格中数值对应的各点; 第三步:连线—按照横坐标 由小到大 的顺序,把所描出的各点 用平滑曲线 连接起来.
典例精析
例4 一水库的水位在最近5h内持续上涨,下表记录了这5h内6 个时间点的水位高度,其中t表示时间,y表示水位高度.
t/h 0 1 2 3 4 5 y/m 3 3.3 3.6 3.9 4.2 4.5 (1)在平面直角坐标系中描出表中数据对应的点,这些点是否 在一条直线上?由此你发现水位变化有什么规律?
总结归纳
由上可知,写出函数的解析式,或者列表格,或者画函数 图象,都可以表示具体的 函数.这三种表示函数的方法,分别 称为解析式法、列表法、图象法.
正弦函数、余弦函数的图像及五点法作图

正弦函数、余弦函数的图像及五点法作图
【余弦函数y=cosx的图象】
用几何法作余弦函数的图象,可以用“反射法”将
角 与 终xx点的轴A余的作弦 正x轴线 半的“ 轴垂竖 成线立4,”角它[的把与直坐前线标面,轴所又向作过下的余平直弦移线线,交O过于1OAA1的′作,
那么 O1 A与AA′长度相等且方向同时为正,我们就 把余弦线 O1 A“竖立”起来成为AA′,用同样的方 法,将其它的余弦线也都“竖立”起来.再将它们 平移,使起点与x轴上相应的点x重合,则终点就是 余弦函数图象上的点.]
解:按五个关键点列表
利用正弦函数的特征描点画图:
正弦函数、余弦函数的图像及五点法作图
【变形训练】
1、作出 y cos x, x 0, 2 的简图
解:按五个关键点列表
x
0
2
π
3
2π
2
cosx 1
0
-1
0
1
-cosx -1
0
1曲线连接起来.
y=cosx的图象. 正弦函数y=sinx的图象和余弦函数y=cosx的图象 分别叫做正弦曲线和余弦曲线.
正弦函数、余弦函数的图像及五点法作图
【余弦函数y=cosx的图象】
-6 -5 -6 -5
-4 -3 -4 -3
-2 -
-2
-
y y=sinx
1
o
-1
y y=cosx
1
正弦函数、余弦函数的图像及五点法作图
【余弦函数y=cosx的图象】
也可以用“旋转法”把角 的余弦线“竖立”(把
角置诱x=x,导si的n则公x余的式O弦1图cM线o象s1与Ox向1OM左1sM按i平n长(逆移x度时 2相2针)单等方,还位,向可即方旋以得向转把余相2正弦同到弦函.O)函数1M根数1据位
19.1.2函数的图像(正式稿)
1、列表 2、描点
3、连线
列出自变量与函数的对应值表。 注意:自变量的值(满足取值范围), 并取值要适当,以便画图.
建立直角坐标系,以自变量的值为横坐标, 相应的函数值为纵坐标,描出表格中数值 对应的各点 按照横坐标从小到大的顺序把描出的点用 平滑曲线依次连接起来
注:函数图象可能是曲线,也可能是直线,也可能是 线段或射线,函数图象的形状取决于函数关系和自 变量的取值范围。
【反思归纳】函数的三种表示法通常是相 互关联,可以相互转化(特殊的函数除外): (1)由函数解析式可以得到这个函数的列表 及图象; (2)由函数的图象可以得到其解析式及函数 的对应值表格; (3)由函数的表格可以得到函数的解析式及 图象.
(1)函数图象上的点的横纵坐标分别表示什么? (2)画函数图象时,怎样体现函数的自变量取值范围?
(1)判断下列各点是否在函数 y =x+ 0.5的图象上? ①(-4,-4.5); ②(4,4.5). 6 (2)判断下列各点是否在函数 y = (x>0) 的图象上? x ①(2,3);②(4,2).
2、函数 y=-2x-6的图象上,若点B(a,a+1)在这 个函数图象上,则a=________.
s/米
2.周末小明一家乘出租车前往离家8千米的公园, 出租车的收费标准如下:
里程 收费/元
t/秒
3千米以下(含3千米)
3千米以上,增加1千米
5.00
1.00
(1)写出出租车行驶的里程数x(千米)与费用y(元)之间的函数关系。 (2)小明带了10元钱,够不够付到公园的车费,为什么?
3. 已知某一函数的图象如图所示,根据图象回答下列问题 : (1)确定自变量的取值范围; (2)求当x=-4,-2,4时y的值是多少? (3)求当y=0,4时x的值是多少? (4)当x取何值时y的值最大?当x取 何值时y的值最小? (5)当x的值在什么范围内时y随x的增大而增大?当x的值在 什么范围内时y•随x的增大而减小?
同济大学《高等数学》(第四版)3-8节函数图形的描绘

1.铅直渐近线 (垂直于 x 轴的渐近线)
如果 lim f (x) 或 lim f (x)
x x0
x x0
那么 x x0 就是 y f (x) 的一条铅直渐近线 .
上页 下页 返回
例如 y
1
,
( x 2)(x 3)
有铅直渐近线两条: x 2, x 3.
第八节 函数图形的描绘
一、渐近线 二、图形描绘的步骤 三、作图举例 四、小结 思考题
上页 下页 返回
一、渐近线
定义: 当曲线 y f (x) 上的一动点 P 沿着曲线移向无穷点时,
如果点 P 到某定直线 L的距离趋向于零,
那么直线 L 就称为曲线 y f (x)的一条渐近线.
x x
x x( x 1)
lim[2(x 2)(x 3) 2x]
x
x 1
lim 2( x 2)( x 3) 2x( x 1) 4,
x
x1
y 2x 4 是曲线的一条斜渐近线.
上页 下页 返回
f ( x) 2( x 2)( x 3) 的两条渐近线如图 x1
y sin x x
上页 下页 返回
练习题
一、填空题:
1
1、曲线 y e x 的水平渐近线为_______________. 2、曲线 y 1 的水平渐近线为______________,
x1 铅直渐近线为______________. 二、描出下列函数的图形: 1、 y x2 1 ;
lim
x
f (x)
lim[4(
x
x x2
1)
2]
三角函数图像的画法

2π
x
y=1sinx图象由y=sinx图象(横标不变),纵标伸长 倍而得。 2
水平伸缩变换
例3:如何由函数f(x)=sinx的图象得到下列函数 的图象?
(1)y=sin2x
(2)y=sin
1 2
x
例3:如何由函数f(x)=sinx的图象得到下列函数 的图象?
(1)y=sin2x
(2)y=sin 21x
思路2
纵坐标不变
y sin x横坐标变为原来的 1 y sin 2x
y sin( 2x )
2
图像向左平移
6
3
横坐标不变 纵坐标变为3倍
y 3sin( 2x )
3
例4. 画出函数
y 3sin(2x ) x R
3
的简图.
x
y
3 sin(2x
3
得到y = sin(x +)在某周期内的简图
横坐标向左 (>0) 或向右(<0) 平移 | | 个单位
得到y = sin(ωx +)在某周期内的简图
步骤4
各点的纵坐标变为原来的A倍(横坐标不变);
得到y = Asin(ωx +)在某周期内的简图
步骤5
沿x轴扩展
得到y = Asin(ωx +)在R上的图象
y
y横=s标in2缩x图短21象由而y得=s。inx图象(纵标不变),
1 3 4
2
3
4
o
3
x
42
2
1
y
sin
2x
y=sin
1 2
y sin x
x图象由y=sinx图象(纵标不变),
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f '>0
f '<0
f '>0
-1
1
3
f ''<0
f ''>0
所以我們考慮以下四個區間:
在 ( − ∞ , −1) 中, f (x) 的圖形為遞增凹向下,
在 ( −1 , 1) 中, f (x) 的圖形為遞減凹向下,
4-43
E 化教學交流平台
4-4 函數的畫圖
在 (1 , 3) 中, f (x) 的圖形為遞減凹向上,
x→∞
x→−∞
在。
4-44
中區區域教學資源中心
第四章 導數的應用(Ⅱ)
例題:【函數圖形描繪】
試描繪函數 f (x) = x3 − 3x + 2 之圖形。
解: f (x) 的定義域為 ( − ∞ , ∞ )
f ′(x) = 3x2 − 3 = 3( x +1)( x −1)
令 f ′(x) = 0 ⇒ x = ±1
3. 決定圖形昇降性。
(1)若 f ′(x) > 0 ,則函數 f (x) 遞增在 f ′(x) > 0 的範圍。
(2)若 f ′(x) < 0 ,則函數 f (x) 遞減在 f ′(x) < 0 的範圍。
4. 決定圖形的凹凸性。
(1)若 f ′′(x) > 0 ,則函數 f (x) 上凹在 f ′′(x) > 0 的範圍。
4
所以 x = ±1為 f (x) = x3 − 3x + 2 的臨界點。
f ′′(x) = 6x ,令 f ′′(x) = 0 ⇒ x = 0
ㄧ階導數判定函數的增減:
當 x < −1時, f ′(x) > 0 ,所以函數 f (x) 在 ( − ∞ , −1 ) 遞增。
當 −1 < x < 1 時, f ′(x) < 0 ,所以函數 f (x) 在 ( − 1 , 1 ) 遞減。
E 化教學交流平台
4-4 函數的畫圖
4-4 函數的畫圖
在先前介紹了函數遞增與遞減以及圖形的凹凸性,為了就是要把函數圖形描
繪的更精確,而這一節就是綜合前面所學的方法,試著把圖形畫出。
y = f (x) 作圖步驟:
1. 決定 f (x) 之定義域。
2. 決定關鍵點。
4
f ′(x) = 0 或 f ′(x) 不存在; f ′′(x) = 0 或 f ′′(x) 不存在的點。
當 x > 1時, f ′(x) > 0 ,所以函數 f (x) 在 ( 1 , ∞ ) 遞增。
二階導數判斷函數的凹凸性:
當 x < 0 時, f ′′(x) < 0 ,所以函數 f (x) 在 ( − ∞ , 0 ) 上的圖形為凹向下。
當 x > 0 時, f ′′(x) > 0 ,所以函數 f (x) 在 ( 0 , ∞ ) 上的圖形為凹向上。
f(x)=
1 3
x3-x2-3x+4
(1,
1 3
)
x
(3,-5)
從此圖形我們可以觀察出:
f (−1) = 17 為相對極大值; f (3) = −5 為相對極小值;( 1 , 1 ) 為反曲點。因
3
3
為 lim f (x) = ∞ 且 lim f (x) = −∞ ,故圖形並無絕對極大值與極小值的存
(2)若 f ′′(x) < 0 ,則函數 f (x) 下凹在 f ′′(x) < 0 的範圍。
Hale Waihona Puke 5. 決定漸近線。(1)若 lim f (x) = L 或 lim f (x) = M ,其中 L、M 為常數,則稱 y = L 和 y = M
x→∞
x→ −∞
為函數 f (x) 的水平漸近線。
(2)若 lim f (x) = ± ∞ 或 lim f (x) = ± ∞ , a 為常數,則稱 x = a 為函數 f (x)
在 ( 1, ∞ ) 中, f (x) 的圖形為遞增凹向上。
4-45
E 化教學交流平台
4-4 函數的畫圖
且 f (−1) = 4 , f (0) = 2 , f (1) = 0 。
因為 lim f (x) = ∞ , lim f (x) = −∞ ,所以無水平漸近線。
x→∞
x→−∞
依照上面函數趨勢可以描繪出函數圖形如下:
f ′(x) = x2 − 2x − 3 = ( x + 1)( x − 3)
4
令 f ′(x) = 0 ⇒ x = −1 , 3 所以 x = −1 , 3 為 f (x) = 1 x3 − x2 − 3x + 4 的臨界點。
3 f ′′(x) = 2x − 2 = 2(x −1) ,令 f ′′(x) = 0 ⇒ x = 1 ㄧ階導數判定函數的增減: 當 x < −1時, f ′(x) > 0 ,所以函數 f (x) 在 ( − ∞ , −1 ) 遞增。 當 −1 < x < 3 時, f ′(x) < 0 ,所以函數 f (x) 在 ( −1 , 3 ) 遞減。 當 x > 3 時, f ′(x) > 0 ,所以函數 f (x) 在 ( 3 , ∞ ) 遞增。 二階導數判斷函數的凹凸性: 當 x < 1時, f ′′(x) < 0 ,所以函數 f (x) 在 ( − ∞ , 1 ) 上的圖形為凹向下。 當 x > 1時, f ′′(x) > 0 ,所以函數 f (x) 在 ( 1 , ∞ ) 上的圖形為凹向上。 綜合上述判別法我們得函數趨勢如下:
綜合上述判別法我們得函數趨勢如下:
f ' >0
f ' <0
f ' >0
_1
0
f '' <0
所以我們考慮以下四個區間:
1
f '' >0
在 ( − ∞ , − 1) 中, f (x) 的圖形為遞增凹向下,
在 ( −1 , 0) 中, f (x) 的圖形為遞減凹向下,
在 (0 , 1) 中, f (x) 的圖形為遞減凹向上,
在 ( 3 , ∞ ) 中, f (x) 的圖形為遞增凹向上。
且 f (−1) = 17 , f (3) = −5 , f (1) = 1 。
3
3
因為 lim f (x) = ∞ , lim f (x) = −∞ ,所以無水平漸近線。
x→∞
x→−∞
依照上面函數趨勢可以描繪出函數圖形如下:
4
y
(-1, 137)
x→ a+
x→ a−
的垂直漸近線。
6. 描繪出圖形並討論其反曲點與極值。
4-42
中區區域教學資源中心
第四章 導數的應用(Ⅱ)
接著我們用幾個範例來介紹圖形的畫法。
例題:【函數圖形描繪】 試描繪函數 f (x) = 1 x3 − x2 − 3x + 4 之圖形。
3 解: f (x) 的定義域為 ( − ∞ , ∞ )
