最新3层合板的刚度与强1度汇总
合集下载
8.第八次课——一般层合板的刚度+层合板的强度(讲课用)
* 12
3.2.4 几种典型对称层合板的面内刚度
正交对称层合板的相关特性
特性（2）：正则化面内刚度系数A*12、A*66不随着单层组体积含量v0和v90变化， 是一个常量。 其中，根据正则化面内刚度系数A*12、A*66的定义式，面内泊松耦合刚度系数A*12 和剪切刚度系数A*66是两个由原材料性质确定的常数。
m4 2m 2 n 2 4m 2 n 2 Q 11 m2 n2 m4 n4 4m 2 n 2 Q 22 2 2 2 2 2 2 2 mn 2m n m n Q12 3 3 3 3 3 Q mn mn m n 2 mn m n 66 m3n m3n mn3 2 m3n mn3 n4 2m 2 n 2 4m 2 n 2 m cos n sin
* 12
3.2.4 几种典型对称层合板的面内刚度
对于正交层合板，根据偏轴模量和正轴模量之间的转换关系式：
4 Q11 m n4 Q 22 2 2 m n Q12 2 2 Q m n 66 3 Q16 m n Q mn3 26
特性一
这是因为上述正则化面内刚度系数与偏轴角的正负无关，不论是 正偏轴角还是负偏轴角，在x或者y方向所提供的刚度是相等的。
3.2.4 几种典型对称层合板的面内刚度
* A11 U 1Q U 2Q cos 2 U 3Q cos 4 * A22 U1Q U 2Q cos 2 U 3Q cos 4 * A12 U 4Q U 3Q cos 4
2 1 * * A16 V3 AU 2Q V4*AU 3Q 0 2 1 * A26 V3*AU 2Q V4*AU 3Q 0 2
3.2.4 几种典型对称层合板的面内刚度
正交对称层合板的相关特性
特性（2）：正则化面内刚度系数A*12、A*66不随着单层组体积含量v0和v90变化， 是一个常量。 其中，根据正则化面内刚度系数A*12、A*66的定义式，面内泊松耦合刚度系数A*12 和剪切刚度系数A*66是两个由原材料性质确定的常数。
m4 2m 2 n 2 4m 2 n 2 Q 11 m2 n2 m4 n4 4m 2 n 2 Q 22 2 2 2 2 2 2 2 mn 2m n m n Q12 3 3 3 3 3 Q mn mn m n 2 mn m n 66 m3n m3n mn3 2 m3n mn3 n4 2m 2 n 2 4m 2 n 2 m cos n sin
* 12
3.2.4 几种典型对称层合板的面内刚度
对于正交层合板，根据偏轴模量和正轴模量之间的转换关系式：
4 Q11 m n4 Q 22 2 2 m n Q12 2 2 Q m n 66 3 Q16 m n Q mn3 26
特性一
这是因为上述正则化面内刚度系数与偏轴角的正负无关，不论是 正偏轴角还是负偏轴角，在x或者y方向所提供的刚度是相等的。
3.2.4 几种典型对称层合板的面内刚度
* A11 U 1Q U 2Q cos 2 U 3Q cos 4 * A22 U1Q U 2Q cos 2 U 3Q cos 4 * A12 U 4Q U 3Q cos 4
2 1 * * A16 V3 AU 2Q V4*AU 3Q 0 2 1 * A26 V3*AU 2Q V4*AU 3Q 0 2
3层合板刚度与强度讲诉课件
[0/90]3 有编织物铺层
0, 90 ±45
[(±45)/(0, 90)]
混杂纤维层合板
90G 45K 0C
[0C/45K/90G]
夹层板
0 90 C5 90 0
[0/90/C5]
C：碳纤维 Carbon
K：芳纶纤维 Kevlar
G：玻璃纤维 Glass
B：硼纤维 Boron
实例
-h/2
h/2
[03/902/45/-453]S
V1*A V (0) V (90) V2*A 1 V3*A V4*A 0
A1*6 A2*6 0
N
* x
[Q11
(Q11
Q22 )V
] (90) 0 x
Q12
0 y
N
* y
Q12
0 x
[Q22
(Q11
Q22
)V
(90)
]
0 y
N
* xy
Q66
0 xy
无拉剪/剪拉耦合效应
2、斜交铺设对称层合板
二.基本假设
层合板的各单层间粘接牢固，不滑移、不脱离，有共同变形； ε(1) =ε(2) =……=ε(n)
各单层板近似处于平面应力状态； σz = 0，τyz =τzx = 0
直线法假设：弯曲前垂直于中面的直线段，弯曲变形后仍为 直线，并垂直于变形后的中面，且长度不变.
上表面 中面 下表面
γzx =γyz = 0 εz = 0
I. 层合板概述
一.层合板的特点
层合板 由两层或两层以上的单层板叠合而成的整体结构单元.
层合板的特点：
厚度方向非均匀，因此会产生耦合效应，使变形情况复杂； 各向异性（某些结构具有一定对称性）； 铺层情况多样，整体未必有确定的弹性主方向； 力学性质不仅取决于铺层的力学性质和厚度，也取决于铺层
0, 90 ±45
[(±45)/(0, 90)]
混杂纤维层合板
90G 45K 0C
[0C/45K/90G]
夹层板
0 90 C5 90 0
[0/90/C5]
C：碳纤维 Carbon
K：芳纶纤维 Kevlar
G：玻璃纤维 Glass
B：硼纤维 Boron
实例
-h/2
h/2
[03/902/45/-453]S
V1*A V (0) V (90) V2*A 1 V3*A V4*A 0
A1*6 A2*6 0
N
* x
[Q11
(Q11
Q22 )V
] (90) 0 x
Q12
0 y
N
* y
Q12
0 x
[Q22
(Q11
Q22
)V
(90)
]
0 y
N
* xy
Q66
0 xy
无拉剪/剪拉耦合效应
2、斜交铺设对称层合板
二.基本假设
层合板的各单层间粘接牢固，不滑移、不脱离，有共同变形； ε(1) =ε(2) =……=ε(n)
各单层板近似处于平面应力状态； σz = 0，τyz =τzx = 0
直线法假设：弯曲前垂直于中面的直线段，弯曲变形后仍为 直线，并垂直于变形后的中面，且长度不变.
上表面 中面 下表面
γzx =γyz = 0 εz = 0
I. 层合板概述
一.层合板的特点
层合板 由两层或两层以上的单层板叠合而成的整体结构单元.
层合板的特点：
厚度方向非均匀，因此会产生耦合效应，使变形情况复杂； 各向异性（某些结构具有一定对称性）； 铺层情况多样，整体未必有确定的弹性主方向； 力学性质不仅取决于铺层的力学性质和厚度，也取决于铺层
层合板强度计算 例1
例三层正交铺设层合板如图所示。
外层厚度为t 1, 内层为t 2＝10t 1, 总厚度为t , 各铺层均为玻璃、环氧树脂，力学性能如表。
板承受面内拉力N x , 分析层合板的强度。
1. 计算层合板首层破坏的强度(1) 计算各铺层的刚度计算材料主方向的刚度系数ij Q :1221122112212221112666611212122112212211/,1,1,,,E E S S S S G S Q E S S Q E S S Q E S S Q ννννν=-=∆-===∆=-=∆==∆==得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=62.800033.1858.4058.492.54][Q GPa计算各铺层在整体坐标系xy 下的刚度ij Q422411111266222244121122661242242211126622331611126612226626111266cos 2(2)sin cos sin (4)sin cos (sin cos )sin 2(2)sin cos cos (2)sin cos (2)sin cos (2)Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q θθθθθθθθθθθθθθθθ=+++=+-++=+++=--+-+=--331222662244661122126666sin cos (2)sin cos (22)sin cos (sin cos )Q Q Q Q Q Q Q Q Q θθθθθθθθ⎧⎪⎪⎪⎪⎨⎪⎪+-+⎪⎪=+--++⎩ 由于是正交铺设，于是有3,13162.800033.1858.4058.492.54][][⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==Q Q GPa2262.800092.5458.4058.433.18][⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Q GPa(2) 计算层合板的刚度层合板的合力与合力矩为与层合板中面变形的关系为⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧k εD B B A M N 0 ⎪⎪⎪⎩⎪⎪⎪⎨⎧+=-==-==-=∑∑∑∑∑∑==-==-==-N k N k k k k k k ij kNk k N k k k ij Nk kN k k k ij h z h z z D z h z z B h z z A 1132k ij 313k ij 1k ij 1212k ij 1k ij 11k ij )121()Q ()()Q (31)Q ()()Q (21)Q ()()Q ( 拉伸刚度为2213,1)(2)(t Q t Q A ij ij ij +=，11212,10t t t t ==，计算得到t A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=62.800082.4858.4058.442.24][GPa耦合刚度为0=ij B ，弯扭刚度为ij D (此例中无弯扭载荷，不用计算)。
复合材料层合板的刚度与强度分析
经典层合板理论
上式中的 Aij,Bij,Dij 依次称为拉伸刚度，耦合 刚度及弯曲刚度
由于耦合刚度 B i j 的存在，层合板面内内力 会引起弯曲变形（弯曲和扭曲），而弯曲 内力（弯矩和扭矩）会引起面内变形，此 现象被称为拉弯耦合效应
经典层合板理论
层合板的合力及合力矩可用块矩阵表达：
N A B0
经典层合板理论
由于每个单层的刚度矩阵在单层内不变，因 此可以从每一层的积分号中提出：
Nx
Ny
N
Q Q1121
Nxy k1Q16
Q12 Q22 Q26
Q Q Q162666
zk zk1
xy00 x0y
dz
zk zk1
kx
ky zdz
kxy
Mx
My
N
Q11 Q12
Mxy k1Q16
A1 1 A1 2 0
A1 2 A22 0
0 0 A66
0 x
0 y
0 xy
M
x
M y
D11
D1
2
D12 D22
0 0
k k
x y
M
xy
0
0
D66
k
xy
对称层合板的刚度分析
（2）特殊正交各向异性层组成的对称层合板 这种层合板由材料主向与坐标轴一致的正交
0 x
0 y
0 xy
x
aa
v0 y
u
0
v0
y x
中面的曲率为：
k
x
ky
k
x
y
a
a
2w x2 2w y2
2w
2
x y
其中 k x y 为中面扭曲率
层合板面内刚度N解剖
k
k 1
Zk1 )
2 h
n/2
Q(k ij
)
(
Z
k
k 1
Zk1 )
各层厚度相同时，简化成
Ai*j
2h0 h
n/2
Q(k) ij
k 1
2 n
n/2
Q(k) ij
k 1
偏轴模量分量求平均值
与铺层顺序关系？
多向层合的结果总是使得多向层合板各向异性系数较铺层的小。
正则化几何因子法
A* 11
＝ ［02/902 / 02 / 902 /902 / 02/902 / 02 ] ［0/ 90]s ＝ ［0/90/0] 奇数层
［0C/45K/90G] C-碳纤维，K－Kevlar，G－玻纤 ［02/902/C4]s ＝ ［02/902/C4/902/02] C的下标 4－夹芯厚度毫米数
二、面内力与面内应变关系
本科生课程
复合材料力学与结构设计
第 三 章 层合板的刚度与强度
经典层合板理论：各单层之间完全紧密粘接的，忽 略层间的影响，且限于线弹性、小变形情况下研究 层合板的刚度与强度。
面内刚度 对称层合板的刚度
弯曲刚度 一般层合板的刚度（面内、弯曲、耦合刚度）
层合板的强度
3.1对称层合板的面内刚度
对称层合板：指单层的方向和铺设顺序相对于几何中面镜 面对称。一般单层的材料和厚度也是相同的，不同单层材料 构成的层合板(如混杂复合材料)，要求材料相对几何中面也 是镜面对称的。
如［-φ/φ]s ，指 -φ和φ 铺层含量相同
A Q *
( )
11
11
A2*2
Q( ) 22
A Q *
三、对称层合板面内工程弹性常数
第04章 层合板的刚度和强度
§4.2.2（2-2）
• 层合板的刚度
A
n
Q k dz Q k zk zk 1 k 1 z k 1
n zk n
k 1
1 n B Q k zdz Q 2 k 1 k 1 z k 1
n zk
zk
z
k k
2
k
z2 k 1
D16 k x D26 k y k D66 xy
0 D11 B16 x 0 B26 y D12 0 D B66 xy 16
§4.2.2（3-1）
• 层合板的弹性特性
第四章 层合板的刚度 和强度
§4.1 §4.2 §4.3 §4.4 §4.5 §4.6 层合板的特点 层合板的刚度和柔度 层合板的柔度 不同层合板刚度计算 层合板刚度的实验验证 层合板强度
回总目录
§4.1
这一章的内容包括书上的第五章和第六章， 是本课程的重点。
§4.1
层合板的特点
1∘经典层合板理论的 基本假设 2∘层合板的特点 3∘层合板的表示方法
3
k
n 1 D Q k z 2 dz Q 3 k 1 k 1 z k 1
z
z3 k 1
§4.2.2（2-2）
• 层合板的刚度
N x A11 N y A12 N A xy 16
M x B11 M y B12 M B xy 16
§4.2.2（1-3）
t Mx 2 x x n zk M y y zdz y zdz k 1 zk 1 M t xy 2 xy xy k
第三讲：复合材料层合板的刚度与强度分析
0 xy
k
xy
等号右边第一项表示层合板中面应变 等号右边第二项表示层合板中面曲率
经典层合板理论
中面的应变为：
aa
u0
0 x
0 y
0 xy
x
aa
v0 y
u0
v0
dz
k 1
zk zk 1
x
y
xy
dz
M
x
M y
M
xy
h
2
x
N
h
2
y xy
zdz
k 1
zk zk 1
x
y
xy
zdz
经典层合板理论
经典层合板理论
经典层合板理论-层合板的合力
层合板上的合力 Nx, Ny , 及Nxy合力矩 是指单位长度上的力或力矩）
（都 M x , M y , M xy
经典层合板理论
合力及合力矩的定义式为：
N
x
Ny
N
xy
h
2
x
N
h
2
y xy
y)
z
w( x, x
y)
v
v0
(
x,
y)
z
w( x, y
y)
式中的 u0,v0,表w 示中面的位移分量，并且只是 坐标 的x,函y 数，其中 为挠w 度函数
第三讲：复合材料层合板的刚度与强度分析优秀课件
z
w z
0
zx
u z
w x
0
zy
v z
w y
0
经典层合板理论
将上面三式分别对 z 积分得到：
w w(x, y)
u
u0
(x,
y)
z
w( x, x
y)
v
v0
(
x,
y)
z
w( x, y
y)
式中的 u0,v0, w 表示中面的位移分量，并且只 是坐标 x, y的函数，其中 w 为挠度函数
经典层合板理论
经典层合板理论的基本假设 层合板的应力和应变关系 层合板的合力及合力矩
层合板的限制条件
层合板为薄板 层合板各单层粘接良好，变形连续 整个层合板等厚度
经典层合板的基本假设
直法线假设： yz 0, zx 0
等法线假设： z 0 平面应力假设： z 0； xz =0； yz =0 忽略正应力假设： z 0
面值，因此可以从求和记号中移出得到：
N
x
Ny
A11
A12
A12 A22
A16 A26
0 x
0 y
B11 B12
B12 B22
B16 B26
kx ky
N
xy
A16
A26
A66
0 xy
B16
B26
B66
kxy
M M M
x y xy
B11 B12 B16
经典层合板理论
中面的应变为：
aa
u0
0 x
0 y
0 xy
x
aa
v0 y
u0
v0
y x
中面的曲率为：
3_层合板的刚度与强1度
a
62
a
22
(310)
同理，仅受xy方向剪 切应力时，
Nx y0,Nx Ny 0,
9/13/2019
面内剪切弹性模量 G
0 xy
1
a
66
面内剪拉耦合系数
0 x , xy
a
16
a
66
(311)
面内剪拉耦合系数
0 y , xy
由正则化面内刚度系数矩阵求逆，可得正则化面内柔
度系数矩阵为： aa1211
a61
a12 a22 a62
aaa162666AA1*1*1A1A2*2*A 202A2*1*(22(AA1*1*2)2)22
a
26
a
66
weizhou@
14
3.1.3 对称层合板的面内工程弹性常数
当层合板具有正交各向异性的性能，且参考轴也正好
与正交各向异性的主方向重合时，A16 A26 0，
则(3-9)~(3-11)可表示为如下形式：
Ex0
A11 m0
x0
A21 A22
Ny z
x
Nxy
Nx
定义任意一个单层k的应力为
(
, (k)
x
, (k)
y
) (k)
xy
此单层的厚度为dz
则k单层x方向的面内力为 Nx(k) x(k)dz
将每一个单层的面内力叠加，得到厚度为h的层合板在
x方向的面内力为：
Nx
dz h 2 (k)
h 2 x
9/13/2019
复合材料层合板的刚度与强度分析
Nx Ny
A11 A12
A12 A22
A16 A26
0 x
0 y
B11 B12
B12 B22
B16 B26
kx ky
Nxy
A16
A26
A66
0 xy
B16
B26
B66
k
x
z ky
xy
0 xy
k
xy
等号右边第一项表示层合板中面应变 等号右边第二项表示层合板中面曲率
经典层合板理论
中面的应变为：
a
a
u
0
0
x
0 y
0 x y
x
u x
u0 x
z
2w x2
y
v y
v0 y
z
2w y 2
xy
u y
v x
( u0 y
v0 x
)
2z
2w xy
经典层合板理论
上式可以用矩阵形式来表达：
x
y
0 x
0 y
aaaA
1
Et
几种典型层合板的刚度
(3.3.58)
可见，面内剪切或扭转变形时均不与其它变形耦合。
3.3.4 两种非对称层合板的刚度
4.规则反对称层合板 讨论按如下规则铺设得到的层合板：[-φ8/ φ 8]T，[φ 4/ φ 4]2T ，[-φ 2/ φ 2]4T ，[-φ / φ]8T，它们的单层组数分 别为m=2,4,8 。
cos 2 cos 2 0 0 3 sin 2 2m 3 sin 2 2m
cos 4 cos 4 1 cos 4 (Q ) cos 4 U 2 3 sin 4 (Q ) m U 3 3 sin 4 m
A11 U1(Q ) V1A V2A 1 (Q ) V1 A V2 A A22 U1 (Q ) A U 0 V 12 4 2 A (Q ) U (Q ) 2 0 V2 A A66 U 5 0 V 2 V A16 (Q ) 3A 4A U 3 A26 0 V3 A 2 V4 A
1D
(3.3.39)*
①按式（3.3.20）*和式(3.2.19)计算Aij*
( 90 ) 1 (0) A (Q ij Q ij ) 2 ij
(3.3.50)
②按式(3-64)和式(3.3.38)计算Dij*
( 90 ) 1 (0) D (Q ij Q ij ) 2 ij
n 2
（3.3.39）
* V1* cos 2 V D 2 D cos 4 3 3 * * V3 D sin 2 V4 D sin 4 m m
层合板的刚度与强度.
0
x
11 x
12
y
16
xy
a N a N a N 0
y
21
x
22
y
26
xy
（3－4）
a N a N a N 0
xy
61
x
62
y
66
xy
很明显，aij*=aijh，称为对称层合板的正则化面内柔度系数。 aij*的意义是，当对称层合板为单向层合板时，
a s ij
ij 即单向层合板的正则化面内柔度系数就是柔量分量。
称为层合板的面内刚度系数。面内刚度系数也象模量分量一
样，具有对称性。即Aij=Aji
为了使本章讨论对称层合板的刚度与以前讨论单向层合 板的刚度相关联。因此，将面内力与面内刚度系数进行正则 化，即设
N
x
Nx h
N
y
Ny h
N
xy
N xy
h
A
ij
Aij h
Nx*、Ny*、Nxy*称为层合板的正则化面内力，单位是Pa或N/m2， 它们实际上表示了层合板的平均应力，又称层合板应力。 Aij* 称为层合板的正则化面内刚度系数，单位是Pa或N/m2， 与模量分量的量纲一样。
在面内变形下，由于层合板各铺层是紧密粘接
的，因而可认为位移是一致的，即层合板厚度方向 上坐标为Z的任一点的面内位移就等于中面的位移， 即
u(z)=u0
v(z)=v0
这在层合板的厚度与长度、宽度相比为很小时
是合理的。
所以沿层合板厚度上各点的应变是一样的。
εx(z)=εx˚ εy (z)=εy˚ γxy(z)=γxy˚
或【05/902/45/-456/45/902/05】T 另外，总数为奇数层的对称层合板往往采用T的标记法。 例如：【05/903/05】T
3层合板的刚度与强1度
a
62
a
22
(310)
同理，仅受xy方向剪 切应力时，
Nx y0,Nx Ny 0,
7/16/2019
面内剪切弹性模量 G
0 xy
1
a
66
面内剪拉耦合系数
0 x , xy
a
16
a
66
(311)
面内剪拉耦合系数
0 y , xy
7/16/2019
weizhou@
3
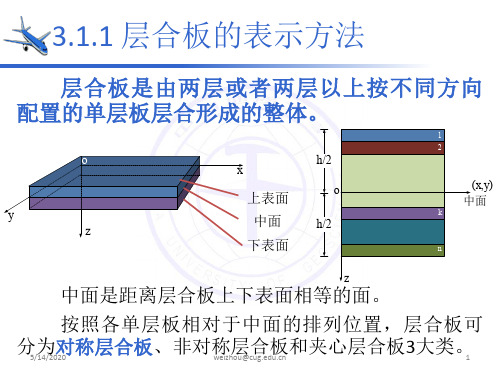
3.1.1 层合板的表示方法
7/16/2019
weizhou@
4
3.1.1 层合板的表示方法
7/16/2019
weizhou@
5
3.1.1 层合板的表示方法
7/16/2019
weizhou@
weizhou@
16)
式中 V i
ni n
为某一定
向层的体积含量，ni
为某一定向层的层
数，l为定向数。
18
3.1.5 几种典型对称层合板的面内刚度
1) 正交铺设对称层合板
各个单层只按0 o和90 o方向铺设的对称层合板称为正交 铺设对称层合板。
由式(3-16)可得：
V 1 A V ( 0 ) V ( 9 )0 V 2 A 1V 3 A V 4 A 0
Ey0
A22 m0
y0
A12 A11
Gx0y A66
(39a)
式中
m0 (1 (AA111A2)222)1
(3-10a)
此时
x 0,y xx 0,yx 0 ,xy y 0,xy 0
3 层合板的刚度与强度
3 层合板的刚度与强度
层合板的刚度与强度的分析是建立在已知单 层刚度与强度的基础上。 假设层合板为连续、均匀、正交各向异性的 单层构成的一种连续性材料，并假设各单层 之间是完全紧密粘接，且限于线弹性、小变 形情况下研究层合板的刚度与强度，这种层 合理论称为经典层合理论。 本章是利用经典层合理论来讨论层合板的刚 度与强度。
nx0nynxy0利用公式34得an?exxx????11001aa?xyx????????11210??aaxxyxxy??????11610???同理an?eyyy????22001aa?yxy????????22120??aayxyyxy??????22620???面内剪切弹性模量agxy??6601aaxyxxyx??????66610???aaxyyxyy??????66620???面内泊松耦合系数aax????11210?aay????22120?拉剪耦合系数aaxxy???11610?aayxy???22620?剪拉耦合系数aaxyx???66160?aaxyy???66260?314面内刚度系数的计算?由于面内刚度系数与构成对称层合板的各铺层模量有简单的积分关系式而且各铺层可以有不同的偏轴模量所以正则化面内刚度系数可改写成求和的形式进行计算
0 0 x 11 x 12 y 16
0 0 y 21 x 22 y 26 0 0 xy 61 x 62 y 66
ቤተ መጻሕፍቲ ባይዱ
0 xy
0 xy 0 xy
（3－2）
上式为对称层合板的正则化面内力——面内应变关系式， 实质上就是对称层合板的平均应力（称层合板应力）和面内应 变的关系式。 我们将面内力——面内应变的关系式作逆变换，可得面内 应变与面内力的关系式。
层合板的刚度与强度的分析是建立在已知单 层刚度与强度的基础上。 假设层合板为连续、均匀、正交各向异性的 单层构成的一种连续性材料，并假设各单层 之间是完全紧密粘接，且限于线弹性、小变 形情况下研究层合板的刚度与强度，这种层 合理论称为经典层合理论。 本章是利用经典层合理论来讨论层合板的刚 度与强度。
nx0nynxy0利用公式34得an?exxx????11001aa?xyx????????11210??aaxxyxxy??????11610???同理an?eyyy????22001aa?yxy????????22120??aayxyyxy??????22620???面内剪切弹性模量agxy??6601aaxyxxyx??????66610???aaxyyxyy??????66620???面内泊松耦合系数aax????11210?aay????22120?拉剪耦合系数aaxxy???11610?aayxy???22620?剪拉耦合系数aaxyx???66160?aaxyy???66260?314面内刚度系数的计算?由于面内刚度系数与构成对称层合板的各铺层模量有简单的积分关系式而且各铺层可以有不同的偏轴模量所以正则化面内刚度系数可改写成求和的形式进行计算
0 0 x 11 x 12 y 16
0 0 y 21 x 22 y 26 0 0 xy 61 x 62 y 66
ቤተ መጻሕፍቲ ባይዱ
0 xy
0 xy 0 xy
（3－2）
上式为对称层合板的正则化面内力——面内应变关系式， 实质上就是对称层合板的平均应力（称层合板应力）和面内应 变的关系式。 我们将面内力——面内应变的关系式作逆变换，可得面内 应变与面内力的关系式。
层汇总板三层钢筋算量
钢筋根数=(1-0.1)/0.15+1=7(四舍五入)
钢筋长度=3.15=3.15
钢筋重量=7*3.15*0.3935856[钢筋比重]=8.679
1
A8@150 :板底筋从⑧～⑨ 范围⑨～⑨
钢筋根数=(1-0.1)/0.15+1=7(四舍五入)
钢筋长度=8.4+2*6.25*0.008[弯钩]=8.5
钢筋重量=2.57*0.61654[钢筋比重]=1.585
1
L10@110 :板面筋从(41.47,244.48)～(39.07,244.48) 范围(39.07,244.98)～(39.07,243.98)
钢筋根数=(0-0.1)/0.11+1=1(四舍五入)
钢筋长度=2.4+0.1[板厚]+0.1[板厚]-2*0.015=2.57
钢筋重量=7*4.041*0.61654[钢筋比重]=17.44
1
L10@150 :板底筋从①～(11.07,234.03) 范围(11.07,233.53)～(11.07,234.53)
钢筋根数=(1-0.1)/0.15+1=7(四舍五入)
钢筋长度=4.041=4.041
钢筋重量=7*4.041*0.61654[钢筋比重]=17.44
钢筋重量=2.57*0.61654[钢筋比重]=1.585
1
L10@110 :板面筋从(37.27,244.48)～(34.87,244.48) 范围(34.87,244.98)～(34.87,243.98)
钢筋根数=(0-0.1)/0.11+1=1(四舍五入)
钢筋长度=2.4+0.1[板厚]+0.1[板厚]-2*0.015=2.57
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
9
3.1.2 面内力与面内应变的关系
为了使层合板的面内刚度能直接和单层的模量相比较
，将层合板的面内刚度系数作正则化处理，将式(3-4)两
端同时除以h：
AijAij h aijaijh
NxNx h Ny Ny h NxyNxyh
(3-6)
式(3-4)和(3-5)可分别变形为：
NNxy AA1211
A12 A22
3层合板的刚度与强1度
3.1.1 层合板的表示方法
层合板的简明标记方法：
1) 偶数层对称层合板：对称铺层只写出一半， 括号外加写下标“s”表示对称。
2) 奇数层对称层合板：在对称中面上的铺层用 顶标“－”表示。
3) 非对称层合板，必须在标记中标明全部铺层 组的铺设顺序。例如：[05/902/45/90/03]。这 种层合板标记，仅表明由底面向上至顶面的 铺设顺序，而不能相反。
5
3.1.2 面内力与面内应变的关系
层合板面内刚度的基
本假设： o
1)层合板只承受面内力作
用，只引起面内形变， y
不引起弯曲形变；
Ny z
x
Nxy
Nx
2) 层合板为薄板，即板的厚度远远小于长度和宽度；
3) 层合板各单层粘接牢固，具有相同的变形。层合板
厚度方向上坐标为z的任一点的应变都等于中面的
应变。
weizhou@
8
3.1.2 面内力与面内应变的关系
求得：
NNxy AA1211
A12 A22
AA1266xy00
(3-4)
Nxy A61 A62 A66x0y
式中
h2 (k)
Aijh2Qij dz(i,j1,2,6)
且有Aij=Aji
(34a)
Aij称为层合板的面内刚度系数 将式(3-4)作逆变换，得到面内应变与面内力的关系：
AA1266xy00
Nxy A61 A62 A66x0y
xy00 aa1211
a12 a22
aa1266NNxy
x0y a61 a62 a66Nxy
8/11/2020
(3-7)
weizhou@
(3-8)
10
3.1.2 面内力与面内应变的关系
上一页中：
A
ij
为正则化面内刚度系数
面内拉压弹性模量
E
0 y
1
a
22
面内泊松耦合系数
0 y
a
12
a
22
面内拉剪耦合系数
0 xy
,y
a
62
a
22
(310)
同理，仅受xy方向剪 切应力时，
Nx y0,Nx Ny 0,
8/11/2020
面内剪切弹性模量 G
0 xy
1
a
66
面内剪拉耦合系数
0 x , xy
a
16
8/11/2020
weizhou@
2
3.1.1 层合板的表示方法
8/11/2020
weizhou@
3
3.1.1 层合板的表示方法
8/11/2020
weizhou@
4
3.1.1 层合板的表示方法
8/11/2020
weizhou@
a
ij
为正则化面内柔度系数
Nx,Ny,Nxy 为正则化面内力，实质上就是对称层合
板的平均应力，简称层合板应力，量纲
为应力量纲(Pa或N/m2)。
当对称层合板为单向层合板时，正则化面 内刚(柔)度系数变为单层的模(柔)量分量
。
8/11/2020
weizhou@
11
3.1.3 对称层合板的面内工程弹性常数
Nx
定义任意一个单层k的应力为
(
, (k)
x
, (k)
y
) (k)
xy
此单层的厚度为dz
则k单层x方向的面内力为 Nx(k) x(k)dz
将每一个单层的面内力叠加，得到厚度为h的层合板在
x方向的面内力为：
Nx
dz h 2 (k)
h 2 x
8/11/2020
weizhou@
0(x) x
1
a
11
0 x
0(x) y
0(x) x
a
21
a
11
0 xy , x
0(x) xy
0(x) x
a
61
a
11
(3-9)
8/11/2020
weizhou@
12
3.1.3 对称层合板的面内工程弹性常数
同理，仅受y方向单向 拉伸(压缩)时，
Ny 0,Nx Nx y0,
x(z)x 0 ,y(z)y 0 ,x(y z)x 0y
(3-2)
8/11/2020
weizhou@
6
3.1.2 面内力与面内应变的关系
图中的Nx, Ny, Nxy为面内
o
力，即层合板内单位宽度
上的内力。单位为帕米
(Pa ·m)或牛顿/米(N/m)。 y
Ny z
x
Nxy
Ex0
A11 m0
x0
A21 A22
Ey0
A22 m0
y0
A12 A11
Gx0y A66
(39a)
式中
m0 (1 (AA111A2)222)1
(3-10a)
此时
x 0,y xx 0,yx 0 ,xy y 0,xy 0
xy00 aa1211
a12 a22
aa1266NNxy
(3-5)
x0y a61 a62 a66Nxy
a 称为层合板的面内柔度系数 8/11i/j2020
weizhou@
式中
a11 a12 a16 A11 A12 A161 a21 a22 a26A21 A22 A26 a61 a62 a66 A61 A62 A66
7
3.1.2 面内力与面内应变的关系
同理，可求出Ny和Nxy，即：
N xdz
N y N xy
h2
h 2
( y
k
)
dz
dz h 2 ( k )
h 2 xy
(3-3)
将式(2-9)代入式(3-3)，并考虑式(3-2)，可求出面内力和 面内应变的关系。
8/11/2020
当对称板仅受x方向单向拉伸(压缩)时，Nx 0,Ny Nx y0,
式(3-8)变为：
x 0 (x ) a 1 N 1 x , y 0 (x ) a 2 N 1 x , x 0 (x ) y a 6 N 1 x
定义： 面内拉压弹性模量 面内泊松耦合系数 面内拉剪耦合系数
E
0 x
N
x
a
66
(311)
面内剪拉耦合系数
0 y , xy
a
26
a
66
weizhou@
13
3.1.3 对称层合板的面内工程弹性常数
当层合板具有正交各向异性的性能，且参考轴也正好
与正交各向异性的主方向重合时，A16 A26 0，
则(3-9)~(3-11)可表示为如下形式：
3.1.2 面内力与面内应变的关系
为了使层合板的面内刚度能直接和单层的模量相比较
，将层合板的面内刚度系数作正则化处理，将式(3-4)两
端同时除以h：
AijAij h aijaijh
NxNx h Ny Ny h NxyNxyh
(3-6)
式(3-4)和(3-5)可分别变形为：
NNxy AA1211
A12 A22
3层合板的刚度与强1度
3.1.1 层合板的表示方法
层合板的简明标记方法：
1) 偶数层对称层合板：对称铺层只写出一半， 括号外加写下标“s”表示对称。
2) 奇数层对称层合板：在对称中面上的铺层用 顶标“－”表示。
3) 非对称层合板，必须在标记中标明全部铺层 组的铺设顺序。例如：[05/902/45/90/03]。这 种层合板标记，仅表明由底面向上至顶面的 铺设顺序，而不能相反。
5
3.1.2 面内力与面内应变的关系
层合板面内刚度的基
本假设： o
1)层合板只承受面内力作
用，只引起面内形变， y
不引起弯曲形变；
Ny z
x
Nxy
Nx
2) 层合板为薄板，即板的厚度远远小于长度和宽度；
3) 层合板各单层粘接牢固，具有相同的变形。层合板
厚度方向上坐标为z的任一点的应变都等于中面的
应变。
weizhou@
8
3.1.2 面内力与面内应变的关系
求得：
NNxy AA1211
A12 A22
AA1266xy00
(3-4)
Nxy A61 A62 A66x0y
式中
h2 (k)
Aijh2Qij dz(i,j1,2,6)
且有Aij=Aji
(34a)
Aij称为层合板的面内刚度系数 将式(3-4)作逆变换，得到面内应变与面内力的关系：
AA1266xy00
Nxy A61 A62 A66x0y
xy00 aa1211
a12 a22
aa1266NNxy
x0y a61 a62 a66Nxy
8/11/2020
(3-7)
weizhou@
(3-8)
10
3.1.2 面内力与面内应变的关系
上一页中：
A
ij
为正则化面内刚度系数
面内拉压弹性模量
E
0 y
1
a
22
面内泊松耦合系数
0 y
a
12
a
22
面内拉剪耦合系数
0 xy
,y
a
62
a
22
(310)
同理，仅受xy方向剪 切应力时，
Nx y0,Nx Ny 0,
8/11/2020
面内剪切弹性模量 G
0 xy
1
a
66
面内剪拉耦合系数
0 x , xy
a
16
8/11/2020
weizhou@
2
3.1.1 层合板的表示方法
8/11/2020
weizhou@
3
3.1.1 层合板的表示方法
8/11/2020
weizhou@
4
3.1.1 层合板的表示方法
8/11/2020
weizhou@
a
ij
为正则化面内柔度系数
Nx,Ny,Nxy 为正则化面内力，实质上就是对称层合
板的平均应力，简称层合板应力，量纲
为应力量纲(Pa或N/m2)。
当对称层合板为单向层合板时，正则化面 内刚(柔)度系数变为单层的模(柔)量分量
。
8/11/2020
weizhou@
11
3.1.3 对称层合板的面内工程弹性常数
Nx
定义任意一个单层k的应力为
(
, (k)
x
, (k)
y
) (k)
xy
此单层的厚度为dz
则k单层x方向的面内力为 Nx(k) x(k)dz
将每一个单层的面内力叠加，得到厚度为h的层合板在
x方向的面内力为：
Nx
dz h 2 (k)
h 2 x
8/11/2020
weizhou@
0(x) x
1
a
11
0 x
0(x) y
0(x) x
a
21
a
11
0 xy , x
0(x) xy
0(x) x
a
61
a
11
(3-9)
8/11/2020
weizhou@
12
3.1.3 对称层合板的面内工程弹性常数
同理，仅受y方向单向 拉伸(压缩)时，
Ny 0,Nx Nx y0,
x(z)x 0 ,y(z)y 0 ,x(y z)x 0y
(3-2)
8/11/2020
weizhou@
6
3.1.2 面内力与面内应变的关系
图中的Nx, Ny, Nxy为面内
o
力，即层合板内单位宽度
上的内力。单位为帕米
(Pa ·m)或牛顿/米(N/m)。 y
Ny z
x
Nxy
Ex0
A11 m0
x0
A21 A22
Ey0
A22 m0
y0
A12 A11
Gx0y A66
(39a)
式中
m0 (1 (AA111A2)222)1
(3-10a)
此时
x 0,y xx 0,yx 0 ,xy y 0,xy 0
xy00 aa1211
a12 a22
aa1266NNxy
(3-5)
x0y a61 a62 a66Nxy
a 称为层合板的面内柔度系数 8/11i/j2020
weizhou@
式中
a11 a12 a16 A11 A12 A161 a21 a22 a26A21 A22 A26 a61 a62 a66 A61 A62 A66
7
3.1.2 面内力与面内应变的关系
同理，可求出Ny和Nxy，即：
N xdz
N y N xy
h2
h 2
( y
k
)
dz
dz h 2 ( k )
h 2 xy
(3-3)
将式(2-9)代入式(3-3)，并考虑式(3-2)，可求出面内力和 面内应变的关系。
8/11/2020
当对称板仅受x方向单向拉伸(压缩)时，Nx 0,Ny Nx y0,
式(3-8)变为：
x 0 (x ) a 1 N 1 x , y 0 (x ) a 2 N 1 x , x 0 (x ) y a 6 N 1 x
定义： 面内拉压弹性模量 面内泊松耦合系数 面内拉剪耦合系数
E
0 x
N
x
a
66
(311)
面内剪拉耦合系数
0 y , xy
a
26
a
66
weizhou@
13
3.1.3 对称层合板的面内工程弹性常数
当层合板具有正交各向异性的性能，且参考轴也正好
与正交各向异性的主方向重合时，A16 A26 0，
则(3-9)~(3-11)可表示为如下形式：