统计建模与R软件课后答案
统计建模与R软件习题仅供参考

原假设:油漆工人的血小板计数与正常成年男子无差异。
备择假设:油漆工人的血小板计数与正常成年男子有差异。
因为p值小于,拒绝原假设,则认为油漆工人的血小板计数与正常成年男子有差异。
由程序结果可知,x<=1000的概率为,所以x大于1000的概率为.P值为,大于,接受原假设,则两种方法治疗后患者血红蛋白无差异。
(1)以上检验中p值均大于,接受原假设,数据来自正态分布。
(2)三种检验的结果都显示两组数据均值无差异。
(3)因为p值为,大于,所以接受原假设,两组数据方差相同。
(1)因为两组数据p值都大于,所以均接受原假设,两组数据都服从正态分布。
(2)P=>,接受原假设,可认为两组样本方差相同。
(3)P值小于,拒绝原假设,两组有差别。
P 值>,故接受原假设,表示调查结果支持该市老年人口的看法。
不能认为这种处理能增加母鸡的比例。
接受原假设,符合自由组合定律。
因为p值大于,接受原假设,可以认为X服从poission分布。
因为p大于,接受原假设,所以两样本来自同一总体。
因为p值小于,拒绝原假设,有影响。
因为P 值< ,所以拒绝原假设,B与C不独立。
由于p值大于,故两变量独立,两种工艺对产品的质量没有影响。
因为p值大于,接受原假设,可以认定两种方法测定结果相同。
(1)p<,拒绝原假设,中位数小于(2)p<,所以拒绝原假设,中位数小于(1)p值大于,接受原假设,无差别。
(2)p=<,拒绝原假设,有差别。
(3)p=<,拒绝原假设,有差别。
(4)可认为两组数据方差相同。
综上,该数据可做t检验,p值小于,拒绝原假设,有差别。
(5)综上所述,Wilcoxon符号秩检验的差异检出能力最强,符号检验的差异检出最弱。
(6)P值均小于,接受原假设,二者有关系,呈正相关。
因为p值大于,接受原假设,尚不能认为新方法的疗效显着优于原疗法。
(完整版)统计建模与R软件课后答案

第二章2.1> x<-c(1,2,3);y<-c(4,5,6)> e<-c(1,1,1)> z<-2*x+y+e;z[1] 7 10 13> z1<-crossprod(x,y);z1[,1][1,] 32> z2<-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 8 10 12[3,] 12 15 182.2(1)> A<-matrix(1:20,nrow=4);B<-matrix(1:20,nrow=4,byrow=T) > C<-A+B;C(2)> D<-A%*%B;D(3)> E<-A*B;E(4)> F<-A[1:3,1:3](5)> G<-B[,-3]> x<-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x2.4> H<-matrix(nrow=5,ncol=5)> for (i in 1:5)+ for(j in 1:5)+ H[i,j]<-1/(i+j-1)(1)> det(H)(2)> solve(H)(3)> eigen(H)2.5> studentdata<-data.frame(姓名=c('张三','李四','王五','赵六','丁一')+ ,性别=c('女','男','女','男','女'),年龄=c('14','15','16','14','15'),+ 身高=c('156','165','157','162','159'),体重=c('42','49','41.5','52','45.5')) 2.6> write.table(studentdata,file='student.txt')> write.csv(studentdata,file='student.csv')2.7count<-function(n){if (n<=0)print('要求输入一个正整数')repeat{if (n%%2==0)n<-n/2elsen<-(3*n+1)if(n==1)break}print('运算成功')}}第三章3.1首先将数据录入为x。
统计建模与R软件课后参考答案(可编辑修改word版)

第二章2.1> x<-c(1,2,3);y<-c(4,5,6)> e<-c(1,1,1)> z<-2*x+y+e;z[1] 7 10 13>z1<-crossprod(x,y);z1[,1][1,] 32>z2<-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 8 10 12[3,] 12 15 182.2(1) > A<-matrix(1:20,nrow=4);B<-matrix(1:20,nrow=4,byrow=T) >C<-A+B;C(2) > D<-A%*%B;D(3) > E<-A*B;E(4) > F<-A[1:3,1:3](5) > G<-B[,-3]2.3>x<-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x2.4>H<-matrix(nrow=5,ncol=5)>for (i in 1:5)+ for(j in 1:5)+ H[i,j]<-1/(i+j-1)(1)> det(H)(2)> solve(H)(3)> eigen(H)2.5>studentdata<-data.frame(姓名=c('张三','李四','王五','赵六','丁一') + ,性别=c('女','男','女','男','女'),年龄=c('14','15','16','14','15'),+ 身高=c('156','165','157','162','159'),体重=c('42','49','41.5','52','45.5')) 2.6>write.table(studentdata,file='student.txt')>write.csv(studentdata,file='student.csv')2.7count<-function(n){if (n<=0)print('要求输入一个正整数')else{ repeat{if (n%%2==0)n<-n/2elsen<-(3*n+1)if(n==1)break}print('运算成功')}}第三章3.1首先将数据录入为x。
统计建模与R语言习题6.6答案

统计建模与R语言习题6.6答案Homework6.6 P333解:设抗生素为x1(有用抗生素为1,没有为0)危险因子为x2(有危险因子为1,没有为0)计划为x3(事先有计划为1,临时决定为0)感染为Y整个R语言计算过程:doc<-data.frame(x1<-c(1,1,1,1,0,0,0,0),x2<-c(1,1,0,0,1,1,0,0),x3<-c(1,0,1,0,1,0,1,0) ,success<-c(1,11,0,0,28,23,8,0),fail<-c(17,87,2,0,30,3,32,9))doc$Ymat<-cbind(doc$success,doc$fail)glm.sol<-glm(Ymat~x1+x2+x3,family=binomial,data=doc) summary(glm.sol)pre<-predict(glm.sol,data.frame(x1=1,x2=1,x3=0))p<-exp(pre)/(1+exp(pre));ppre<-predict(glm.sol,data.frame(x1=1,x2=1,x3=1))p<-exp(pre)/(1+exp(pre));ppre<-predict(glm.sol,data.frame(x1=0,x2=1,x3=1))p<-exp(pre)/(1+exp(pre));ppre<-predict(glm.sol,data.frame(x1=1,x2=0,x3=1))p<-exp(pre)/(1+exp(pre));p回归模型输出结果如下:Call:glm(formula = Ymat ~ x1 + x2 + x3, family = binomial, data = doc)Deviance Residuals:1 2 3 4 5 6 7 8 0.26470 -0.07162 -0.15231 0.00000 -0.785201.49623 1.21563 -2.56229 Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -0.8207 0.4947 -1.659 0.0971 .x1 -3.2544 0.4813 -6.761 1.37e-11 ***x2 2.0299 0.4553 4.459 8.25e-06 ***x3 -1.0720 0.4254 -2.520 0.0117 *---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 83.491 on 6 degrees of freedomResidual deviance: 10.997 on 3 degrees of freedomAIC: 36.178Number of Fisher Scoring iterations: 5从上述结果即有常数项以及x项的系数β分别为-0.8207,-3.2544, 2.0299,-1.0720,并且回归方程通过检验得到回归模型:P=exp(-0.8207-3.2544x1+2.0299x2-1.0720x3)/(1+exp(-0.8207-3.2544x1+2.0299x2-1.0720x3))假设医生需要对一产妇进行剖腹手术,令x1=1,x2=1,x3=0即在手术中是用抗生素且有危险因子和临时决定进行手术,那么pre<-predict(glm.sol,data.frame(x1=1,x2=1,x3=0))p<-exp(pre)/(1+exp(pre));p10.1145421即11.4521%,也就是说在临时决定进行手术的感染率为11.4521% 那么当x3=1时pre<-predict(glm.sol,data.frame(x1=1,x2=1,x3=1))> p<-exp(pre)/(1+exp(pre));p10.04240619即4.240619%,也就是说在事先有计划进行手术的感染率为4.240619%。
统计建模与R软件(薛毅)第九章答案
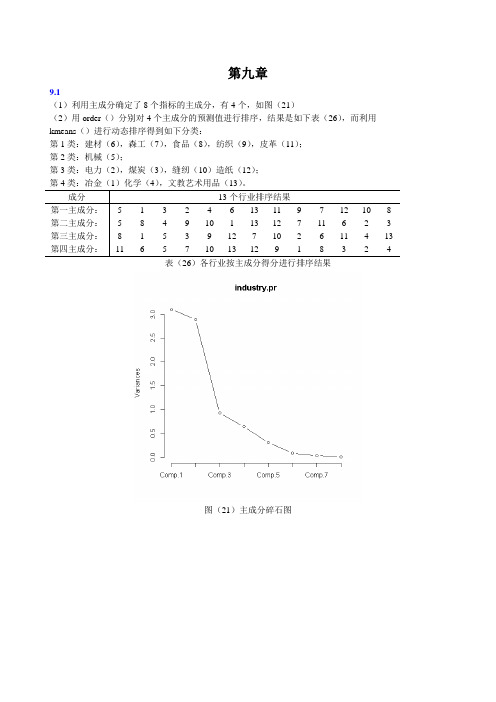
第九章9.1(1)利用主成分确定了8个指标的主成分,有4个,如图(21)(2)用order()分别对4个主成分的预测值进行排序,结果是如下表(26),而利用kmeans()进行动态排序得到如下分类:第1类:建材(6),森工(7),食品(8),纺织(9),皮革(11);第2类:机械(5);第3类:电力(2),煤炭(3),缝纫(10)造纸(12);第4类:冶金(1)化学(4),文教艺术用品(13)。
成分13个行业排序结果第一主成分: 5 1 3 2 4 6 13 11 9 7 12 10 8 第二主成分: 5 8 4 9 10 1 13 12 7 11 6 2 3 第三主成分:8 1 5 3 9 12 7 10 2 6 11 4 13 第四主成分:11 6 5 7 10 13 12 9 1 8 3 2 4表(26)各行业按主成分得分进行排序结果图(21)主成分碎石图图(22)第一主成分与第二主成分下的散点图习题程序与结论:> industry<-data.frame(+X1=c(90342,4903,6735,49454,139190,12215,2372,11062,17111,1206,2150,5251,14341),+X2=c(52455,1973,21139,36241,203505,16219,6572,23078,23907,3930,5704,6155,13203),+X3=c(101091,2035,3767,81557,215898,10351,8103,54935,52108,6126,6200,10383,19396),+X4=c(19272,10313,1780,22504,10609,6382,12329,23804,21796,15586,10870,16875,14691),+ X5=c(82.0,34.2,36.1,98.1,93.2,62.5,184.4,370.4,221.5,330.4,184.2,146.4,94.6),+ X6=c(16.1,7.1,8.2,25.9,12.6,8.7,22.2,41.0,21.5,29.5,12.0,27.5,17.8),+X7=c(197435,592077,726396,348226,139572,145818,20921,65486,63806,1840,8913,78796,6354), +X8=c(0.172,0.003,0.003,0.985,0.628,0.066,0.152,0.263,0.276,0.437,0.274,0.151,1.574) )> industry.pr<-princomp(industry,cor=T)> summary(industry.pr) ####做主成分分析,得到4个主成分,累积贡献率达94.68% Importance of components:Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Standard deviation 1.7620762 1.7021873 0.9644768 0.80132532 0.55143824Proportion of Variance 0.3881141 0.3621802 0.1162769 0.08026528 0.03801052Cumulative Proportion 0.3881141 0.7502943 0.8665712 0.94683649 0.98484701Comp.6 Comp.7 Comp.8Standard deviation 0.29427497 0.179400062 0.0494143207Proportion of Variance 0.01082472 0.004023048 0.0003052219Cumulative Proportion 0.99567173 0.999694778 1.0000000000> load<-loadings(industry.pr) ####求出载荷矩阵> loadLoadings:Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8X1 -0.477 -0.296 -0.104 0.184 0.758 0.245X2 -0.473 -0.278 -0.163 -0.174 -0.305 -0.518 0.527X3 -0.424 -0.378 -0.156 -0.174 -0.781X4 0.213 -0.451 0.516 0.539 0.288 -0.249 0.220X5 0.388 -0.331 -0.321 -0.199 -0.450 0.582 0.233X6 0.352 -0.403 -0.145 0.279 -0.317 -0.714X7 -0.215 0.377 -0.140 0.758 -0.418 0.194X8 -0.273 0.891 -0.322 0.122Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8SS loadings 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000Proportion Var 0.125 0.125 0.125 0.125 0.125 0.125 0.125 0.125Cumulative Var 0.125 0.250 0.375 0.500 0.625 0.750 0.875 1.000> plot(load[,1:2])> text(load[,1],load[,2],adj=c(-0.4,-0.3))> screeplot(industry.pr,npcs=4,type="lines") ####得出主成分的碎石图> biplot(industry.pr) ####得出在第一,第二主成分之下的散点图> p<-predict(industry.pr) ####预测数据,讲预测值放入p中> order(p[,1]);order(p[,2]);order(p[,3]);order(p[,4]);####将预测值分别以第一,第二,第三,第四主成分进行排序[1] 5 1 3 2 4 6 13 11 9 7 12 10 8[1] 5 8 4 9 10 1 13 12 7 11 6 2 3[1] 8 1 5 3 9 12 7 10 2 6 11 4 13[1] 11 6 5 7 10 13 12 9 1 8 3 2 4> kmeans(scale(p),4) ####将预测值进行标准化,并分为4类K-means clustering with 4 clusters of sizes 5, 1, 4, 3Cluster means:Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.61 0.5132590 -0.03438438 -0.3405983 -0.5130031 0.2355151 0.224410402 -2.5699693 -1.32913757 -0.4848689 -0.9460127 -0.9000187 -0.064979503 0.2381581 0.72871986 -0.2995918 0.3126036 -0.4744091 -0.197097104 -0.3163193 -0.47127333 1.1287426 0.7535380 0.5400265 -0.08956137Comp.7 Comp.81 -0.38197798 -0.74748552 -0.67500209 0.45695483 0.09063069 0.98269154 0.74078975 -0.2167643Clustering vector:[1] 4 3 3 4 2 1 1 1 1 3 1 3 4Within cluster sum of squares by cluster:[1] 19.41137 0.00000 24.49504 16.61172(between_SS / total_SS = 37.0 %)Available components:[1] "cluster" "centers" "totss" "withinss" "tot.withinss"[6] "betweenss" "size"9.2####用数据框的形式输入数据####用数据框的形式输入数据sale<-data.frame(X1=c(82.9,88.0,99.9,105.3,117.7,131.0,148.2,161.8,174.2,184.7),X2=c(92,93,96,94,100,101,105,112,112,112),X3=c(17.1,21.3,25.1,29.0,34.0,40.0,44.0,49.0,51.0,53.0),X4=c(94,96,97,97,100,101,104,109,111,111),Y=c(8.4,9.6,10.4,11.4,12.2,14.2,15.8,17.9,19.6,20.8))####作线性回归lm.sol<-lm(Y~X1+X2+X3+X4,data=sale)summary(lm.sol)显示结果Call:lm(formula = Y ~ X1 + X2 + X3 + X4, data = sale)Residuals:1 2 3 4 5 6 70.024803 0.079476 0.012381 -0.007025 -0.288345 0.216090 -0.1420858 9 100.158360 -0.135964 0.082310Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) -17.66768 5.94360 -2.973 0.03107 *X1 0.09006 0.02095 4.298 0.00773 **X2 -0.23132 0.07132 -3.243 0.02287 *X3 0.01806 0.03907 0.462 0.66328X4 0.42075 0.11847 3.552 0.01636 *---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.2037 on 5 degrees of freedomMultiple R-squared: 0.9988, Adjusted R-squared: 0.9978F-statistic: 1021 on 4 and 5 DF, p-value: 1.827e-07模型通过t检验和F检验,因此回归方程为:Y=-17.66768+0.09006X1-0.23132X2+0.01806X3+0.42075X4 Y 是销售量,X1是居民可支配收入X2是该类消费品平均价格指数,X1和X2越高Y越高这与实际情况不符,原因是4个变量存在多重共线性,对变量作主成分回归,先作主成分分析。
统计建模与R软件假设检验习题答案

04 习题答案解析
习题一答案解析
答案:D
解析:根据题目描述,A、B、C三个选项都是描述数据特征的,而D选项是描述数据来源的,与题目 要求的“数据特征”不符。
习题二答案解析
答案:B
解析:根据题目要求,需要选择一个假设检验的方法。A选项是参数检验,适用于总体分布已知的情况;B选项是非参数检验 ,适用于总体分布未知或不符合正态分布的情况;C选项是回归分析,用于研究变量之间的关系;D选项是聚类分析,用于数 据的分类。根据题目描述,由于总体分布未知且不符合正态分布,所以选择B选项。
模型评估
01
02
03
交叉验证
将数据集分成训练集和测 试集,使用训练集训练模 型,在测试集上评估模型 的性能。
均方误差
衡量预测值与实际值之间 的误差,越小越好。
准确率
衡量分类模型正确预测的 比例,越高越好。
02 R软件基础
R软件介绍
总结词
R软件是一种开源的统计计算和图形绘制软件,广泛应用于数据分析和统计建模 。
解析:根据题目要求,需要选择一个统计量 来描述数据的集中趋势。A选项是平均数, 是最常用的描述集中趋势的统计量;B选项 是中位数,描述数据的中位数位置;C选项 是众数,描述数据中出现次数最多的数;D 选项是标准差,描述数据的离散程度。根据
题目要求,选择A选项。
习题五答案解析
答案:C
解析:根据题目要求,需要选择一个统计量来检验两 个样本是否来自同一个总体。A选项是t检验,适用于 两个正态分布的总体;B选项是卡方检验,适用于分 类数据的比较;C选项是F检验,适用于两个总体方差 的比较;D选项是z检验,适用于总体比例的比较。根 据题目要求,选择C选项。
假设检验的优缺点
统计建模与R软件课后答案

第二章2.1> x<-c(1,2,3);y<-c(4,5,6)> e<-c(1,1,1)> z<-2*x+y+e;z[1] 7 10 13> z1<-crossprod(x,y);z1[,1][1,] 32> z2<-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 8 10 12[3,] 12 15 182.2(1) >A<-matrix(1:20,nrow=4);B<-matrix(1:20,nrow=4,byrow=T) > C<-A+B;C(2)> D<-A%*%B;D(3)> E<-A*B;E(4)> F<-A[1:3,1:3](5)> G<-B[,-3]2.3> x<-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x2.4> H<-matrix(nrow=5,ncol=5)> for (i in 1:5)+ for(j in 1:5)+ H[i,j]<-1/(i+j-1)(1)> det(H)(2)> solve(H)(3)> eigen(H)2.5> studentdata<-data.frame(姓名=c('张三','李四','王五','赵六','丁一')+ ,性别=c('女','男','女','男','女'),年龄=c('14','15','16','14','15'),+ 身高=c('156','165','157','162','159'),体重=c('42','49','41.5','52','45.5'))2.6> write.table(studentdata,file='student.txt')> write.csv(studentdata,file='student.csv')2.7count<-function(n){if (n<=0)print('要求输入一个正整数')else{repeat{if (n%%2==0)n<-n/2elsen<-(3*n+1)if(n==1)break}print('运算成功')}}第三章3.1首先将数据录入为x。
统计建模与r软件 课后习题答案

统计建模与r软件课后习题答案统计建模与R软件课后习题答案在统计建模与R软件课程中,学生们经常需要完成一系列的习题来巩固所学知识。
这些习题涉及到统计建模的理论和实践,以及如何使用R软件来进行数据分析和建模。
在本文中,我们将给出一些常见的统计建模与R软件课后习题的答案,希望能够帮助学生更好地理解课程内容。
1. 线性回归模型习题:使用R软件对给定数据集进行线性回归分析,并给出回归方程和相关系数。
答案:在R软件中,可以使用lm()函数来进行线性回归分析。
例如,对于数据集data,可以使用以下代码进行线性回归分析:```model <- lm(y ~ x, data=data)summary(model)```其中,y和x分别表示因变量和自变量。
通过summary()函数可以得到回归方程和相关系数等信息。
2. 逻辑回归模型习题:使用R软件对给定数据集进行逻辑回归分析,并给出回归方程和模型拟合度。
答案:逻辑回归分析可以使用glm()函数来进行。
例如,对于数据集data,可以使用以下代码进行逻辑回归分析:```model <- glm(y ~ x, data=data, family=binomial)summary(model)```其中,y和x分别表示因变量和自变量,family=binomial表示使用二项分布进行逻辑回归分析。
通过summary()函数可以得到回归方程和模型拟合度等信息。
3. 方差分析习题:使用R软件对给定数据集进行方差分析,并给出各组之间的差异是否显著。
答案:在R软件中,可以使用aov()函数来进行方差分析。
例如,对于数据集data,可以使用以下代码进行方差分析:```model <- aov(y ~ group, data=data)summary(model)```其中,y和group分别表示因变量和自变量。
通过summary()函数可以得到各组之间的差异是否显著等信息。
统计建模与R软件第七章习题答案

统计建模与R软件第七章习题答案统计建模与R软件第七章习题答案(方差分析)Ex7.1(1)>lamp<-data.frame(X=c(115,116,98,83,103,107,118,116,73,89,85,97),A=f a ctor(rep(1:3,c(4,4,4))))> lamp.aov<-aov(X~A,data=lamp);summary(lamp.aov)Df Sum Sq Mean Sq F value Pr(>F)A 2 1304 652.0 4.923 0.0359 *Residuals 9 1192 132.4P值小于0.05,有显著差异。
(2)对甲的区间估计:> a<-c(115,116,98,83)> t.test(a)One Sample t-testdata: at = 13.1341, df = 3, p-value = 0.0009534alternative hypothesis: true mean is not equal to 095 percent confidence interval:78.04264 127.95736sample estimates:mean of x103或者用这个命令更简单:>attach(lamp)> t.test(X[A==1])乙的均值估计为111,95%置信区间为99.59932, 122.40068。
丙的均值估计为86,95%置信区间为70.08777, 101.91223。
(3)多重检验:> attach(lamp)P值不做调整:> pairwise.t.test(X,A,p.adjust.method = "none")Pairwise comparisons using t tests with pooled SDdata: X and A1 22 0.351 -3 0.066 0.013P值进行Holm调整:P value adjustment method: none> pairwise.t.test(X,A,p.adjust.method = "holm",data)Pairwise comparisons using t tests with pooled SDdata: X and A1 22 0.35 -3 0.13 0.04P value adjustment method: holm不论采取哪种方法,都可看出乙和丙有显著差异。
统计建模与R软件课后答案修订稿

统计建模与R软件课后答案文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]第二章> x<-c(1,2,3);y<-c(4,5,6)> e<-c(1,1,1)> z<-2*x+y+e;z[1] 7 10 13> z1<-crossprod(x,y);z1[,1][1,] 32> z2<-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 8 10 12[3,] 12 15 18(1) > A<-matrix(1:20,nrow=4);B<-matrix(1:20,nrow=4,byrow=T) > C<-A+B;C(2)> D<-A%*%B;D(3)> E<-A*B;E(4)> F<-A[1:3,1:3](5)> G<-B[,-3]> x<-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x> H<-matrix(nrow=5,ncol=5)> for (i in 1:5)+ for(j in 1:5)+ H[i,j]<-1/(i+j-1)(1)> det(H)(2)> solve(H)(3)> eigen(H)> studentdata<(姓名=c('张三','李四','王五','赵六','丁一')+ ,性别=c('女','男','女','男','女'),年龄=c('14','15','16','14','15'), + 身高=c('156','165','157','162','159'),体重=c('42','49','','52',''))> (studentdata,file='')> (studentdata,file='')count<-function(n){if (n<=0)print('要求输入一个正整数')else{repeat{if (n%%2==0)n<-n/2elsen<-(3*n+1)if(n==1)break}print('运算成功')}}第三章首先将数据录入为x。
统计建模与R软件课后参考答案

第二章2.1> x<-c(1,2,3);y<-c(4,5,6)> e<-c(1,1,1)> z<-2*x+y+e;z[1] 7 10 13> z1<-crossprod(x,y);z1[,1][1,] 32> z2<-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 8 10 12[3,] 12 15 182.2(1) > A<-matrix(1:20,nrow=4);B<-matrix(1:20,nrow=4,byrow=T) > C<-A+B;C(2)> D<-A%*%B;D(3)> E<-A*B;E(4)> F<-A[1:3,1:3](5)> G<-B[,-3]> x<-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x2.4> H<-matrix(nrow=5,ncol=5)> for (i in 1:5)+ for(j in 1:5)+ H[i,j]<-1/(i+j-1)(1)> det(H)(2)> solve(H)(3)> eigen(H)2.5> studentdata<-data.frame(姓名=c('张三','李四','王五','赵六','丁一')+ ,性别=c('女','男','女','男','女'),年龄=c('14','15','16','14','15'),+ 身高=c('156','165','157','162','159'),体重=c('42','49','41.5','52','45.5')) 2.6> write.table(studentdata,file='student.txt')> write.csv(studentdata,file='student.csv')2.7count<-function(n){if (n<=0)print('要求输入一个正整数')repeat{if (n%%2==0)n<-n/2elsen<-(3*n+1)if(n==1)break}print('运算成功')}}第三章3.1首先将数据录入为x。
统计建模与R软件课后答案

第二章2.1> x<-c(1,2,3);y<-c(4,5,6)> e<-c(1,1,1)> z<-2*x+y+e;z[1] 7 10 13> z1<-crossprod(x,y);z1[,1][1,] 32> z2<-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 8 10 12[3,] 12 15 182.2(1) > A<-matrix(1:20,nrow=4);B<-matrix(1:20,nrow=4,byrow=T) > C<-A+B;C(2) > D<-A%*%B;D(3) > E<-A*B;E(4) > F<-A[1:3,1:3](5) > G<-B[,-3]2.3> x<-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x> H<-matrix(nrow=5,ncol=5)> for (i in 1:5)+ for(j in 1:5)+ H[i,j]<-1/(i+j-1)(1)> det(H)(2)> solve(H)(3)> eigen(H)2.5> studentdata<-data.frame(姓名=c('张三','李四','王五','赵六','丁一')+ ,性别=c('女','男','女','男','女'),年龄=c('14','15','16','14','15'),+ 身高=c('156','165','157','162','159'),体重=c('42','49','41.5','52','45.5')) 2.6> write.table(studentdata,file='student.txt')> write.csv(studentdata,file='student.csv')2.7count<-function(n){if (n<=0)print('要求输入一个正整数')else{repeat{if (n%%2==0)n<-n/2n<-(3*n+1)if(n==1)break}print('运算成功')}}第三章3.1首先将数据录入为x。
统计建模与R软件 习题6.4 答案

Homework6.4 P332解:这个过程中回归R语言计算过程如下:toothpaste<-data.frame(X1<-c(-0.05,0.25,0.60,0,0.25,0.2,0.15,0.05,-0.15,0.15,0.2,0.1,0.4,0.45,0.35,0.3,0.5,0.5,0.4,-0.05,-0 .05,-0.1,0.2,0.1,0.5,0.6,-0.05,0,0.05,0.55),X2<-c(5.5,6.75,7.25,5.5,7,6.5,6.75,5.25,5.25,6,6.5,6.25,7,6.9,6.8,6.8,7.1,7,6.8,6.5,6.25,6,6.5,7,6.8, 6.8,6.5,5.75,5.8,6.8),Y<-c(7.38,8.51,9.52,7.5,9.33,8.28,8.75,7.87,7.1,8,7.89,8.15,9.1,8.86,8.9,8.87,9.26,9,8.75,7.95,7.6 5,7.27,8,8.5,8.75,9.21,8.27,7.67,7.93,9.26))lm.sol<-lm(Y~X1+X2,data=toothpaste);summary(lm.sol)influence.measures(lm.sol)回归结果输出如下:Call:lm(formula = Y ~ X1 + X2, data = toothpaste)Residuals:Min 1Q Median 3Q Max-0.49779 -0.12031 -0.00867 0.11084 0.58106Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 4.4075 0.7223 6.102 1.62e-06 ***X1 1.5883 0.2994 5.304 1.35e-05 ***X2 0.5635 0.1191 4.733 6.25e-05 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 0.2383 on 27 degrees of freedomMultiple R-squared: 0.886, Adjusted R-squared: 0.8776F-statistic: 105 on 2 and 27 DF, p-value: 1.845e-13从上述输出的结果知道,模型通过t检验和F检验,因此可以得到回归模型:.4XXY++=407556352.015883.1回归诊断结果如下:Influence measures oflm(formula = Y ~ X1 + X2, data = toothpaste) :dfb.1_ dfb.X1 dfb.X2 dffit cov.r cook.d hat inf1 -0.05536 -6.96e-03 0.050306 -0.0807 1.281 2.25e-03 0.13012 0.04401 2.83e-02 -0.048123 -0.0922 1.152 2.92e-03 0.04703 -0.01269 6.49e-02 0.010195 0.1295 1.277 5.78e-03 0.13394 -0.00929 -2.98e-03 0.008653 -0.0118 1.299 4.81e-05 0.13805 -0.68922 -4.88e-01 0.719765 0.9115 0.536 2.18e-01 0.0909 *6 0.01121 1.59e-02 -0.016637 -0.0860 1.133 2.54e-03 0.03487 -0.26976 -2.67e-01 0.290196 0.3922 0.997 4.98e-02 0.07968 1.17309 6.39e-01 -1.129656 1.2670 0.895 4.69e-01 0.2493 *9 -0.03920 -5.27e-05 0.035418 -0.0601 1.373 1.25e-03 0.1860 *10 -0.02101 -1.08e-02 0.019442 -0.0295 1.194 3.02e-04 0.063611 0.05653 8.02e-02 -0.083875 -0.4338 0.670 5.42e-02 0.034812 0.00259 -1.74e-02 0.001766 0.0546 1.160 1.03e-03 0.041913 -0.04609 1.35e-02 0.047372 0.1279 1.167 5.61e-03 0.065614 -0.00181 -8.57e-02 0.001894 -0.1784 1.149 1.08e-02 0.070715 -0.01729 1.83e-02 0.019442 0.0994 1.149 3.39e-03 0.047616 -0.05590 -1.53e-02 0.060772 0.1449 1.118 7.15e-03 0.046517 -0.01349 3.00e-02 0.012894 0.0786 1.223 2.13e-03 0.090618 0.00123 -1.01e-01 0.000402 -0.1972 1.173 1.33e-02 0.088119 -0.00397 -5.62e-02 0.002754 -0.1299 1.149 5.78e-03 0.056620 0.04972 6.92e-02 -0.054542 -0.0782 1.320 2.11e-03 0.155121 0.11714 2.36e-01 -0.139343 -0.2970 1.142 2.97e-02 0.102022 0.08114 3.85e-01 -0.126203 -0.5601 0.929 9.84e-02 0.104123 0.04240 6.02e-02 -0.062902 -0.3253 0.841 3.29e-02 0.034824 0.01971 1.90e-02 -0.020667 -0.0235 1.378 1.90e-04 0.1873 *25 -0.13024 -3.05e-01 0.133977 -0.4177 1.038 5.69e-02 0.098226 0.01670 3.14e-02 -0.017393 0.0367 1.351 4.67e-04 0.1714 *27 -0.35156 -4.89e-01 0.385694 0.5528 1.100 9.94e-02 0.155128 0.01703 -1.01e-04 -0.014952 0.0296 1.223 3.03e-04 0.085529 0.14921 3.39e-02 -0.134903 0.2241 1.140 1.70e-02 0.080230 0.10055 2.05e-01 -0.104290 0.2545 1.227 2.21e-02 0.1309从上面诊断输出结果可以得到对回归模型存在影响的有样本点5、8、9、24、26,从dfb.1_角度看,点8对响应变量影响最大,从dffit cov.r 角度看,点24、26对自变量影响最大,那么考虑去掉样本点8、24、26除去影响点后整个R语言的计算过程如下:toothpaste<-data.frame( X1=c(-0.05,0.25,0.60,0,0.20,0.15,-0.15,0.15,0.10,0.40,0.45,0.35,0.30,0.5 0,0.50,0.40,-0.05,-0.05,-0.10,0.20,0.10,0.50,0.60,-0.05,0,0.05,0.55),X2=c(5.50,6.75,7.25,5.50,6.50,6.75,5.25,6.00,6.25,7.00,6.90,6.80,6.80,7.10,7.00,6.80,6.50,6.25,6. 00,6.50,7.00,6.80,6.80,6.50,5.75,5.80,6.80),Y=c(7.38,8.51,9.52,7.50,8.28,8.75,7.10,8.00,8.15,9.10,8.86,8.90,8.87,9.26,9.00,8.75,7.95,7.65,7.27,8.00,8.50,8.75,9.21,8.27,7.67,7.93,9.26))lm.sol<-lm(Y~X1+X2,data=toothpaste);summary(lm.sol)回归输出结果如下:Call:lm(formula = Y ~ X1 + X2, data = toothpaste)Residuals:Min 1Q Median 3Q Max-0.37130 -0.10114 0.03066 0.10016 0.30162Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 4.0759 0.6267 6.504 1.00e-06 ***X1 1.5276 0.2354 6.489 1.04e-06 ***X2 0.6138 0.1027 5.974 3.63e-06 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 0.1767 on 24 degrees of freedomMultiple R-squared: 0.9378, Adjusted R-squared: 0.9327F-statistic: 181 on 2 and 24 DF, p-value: 3.33e-15模型通过t 检验和F 检验,因此回归模型为:26138.015276.10759.4X X Y ++=∧。
统计建模与R软件薛毅第六章答案
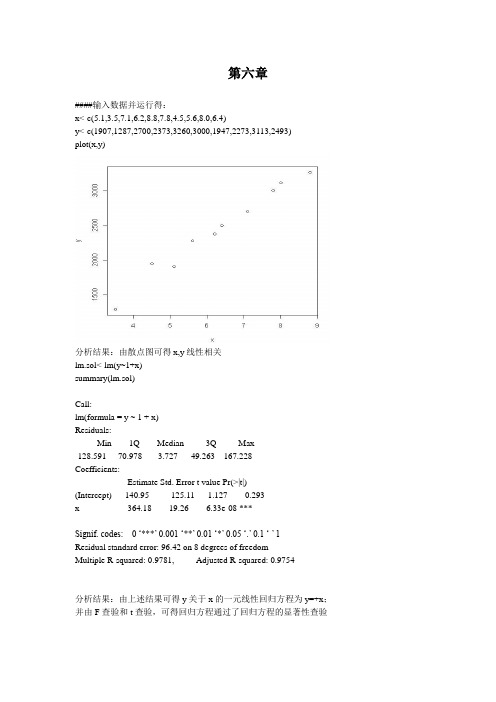
第六章####输入数据并运行得:x<-c(5.1,3.5,7.1,6.2,8.8,7.8,4.5,5.6,8.0,6.4)y<-c(1907,1287,2700,2373,3260,3000,1947,2273,3113,2493)plot(x,y)分析结果:由散点图可得x,y线性相关lm.sol<-lm(y~1+x)summary(lm.sol)Call:lm(formula = y ~ 1 + x)Residuals:Min 1Q Median 3Q Max-128.591 -70.978 -3.727 49.263 167.228Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 140.95 125.11 1.127 0.293x 364.18 19.26 6.33e-08 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 96.42 on 8 degrees of freedomMultiple R-squared: 0.9781, Adjusted R-squared: 0.9754分析结果:由上述结果可得y关于x的一元线性回归方程为y=+x;并由F查验和t查验,可得回归方程通过了回归方程的显著性查验####对数据进行预测,而且给相应的区间估量new<-data.frame(x=7)lm.pred<-predict(lm.sol,new,interval="prediction",level=0.95)fit lwr upr分析结果:预测值为,估量区间为[2454.971 ,]####输入数据并运行x1<-c(0.4,0.4,3.1,0.6,4.7,1.7,9.4,10.1,11.6,12.6,10.9,23.1,23.1,21.6,23.1,1.9,26.8,29.9)x2<-c(52,23,19,34,24,65,44,31,29,58,37,46,50,44,56,36,58,51)x3<-c(158,163,37,157,59,123,46,117,173,112,111,114,134,73,168,143,202,124)y<-c(64,60,71,61,54,77,81,93,93,51,76,96,77,93,95,54,168,99)lm.sol<-lm(y~x1+x2+x3)summary(lm.sol)Call:lm(formula = y ~ x1 + x2 + x3)Residuals:Min 1Q Median 3Q Max-11.383 -2.659 12.095 48.807Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 43.65007 18.05442 2.418 0.02984 *x1 1.78534 0.53977 3.308 0.00518 **x2 -0.08329 0.42037 -0.198 0.84579x3 0.16102 0.11158 1.443 0.17098---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 19.97 on 14 degrees of freedomMultiple R-squared: 0.5493, Adjusted R-squared: 0.4527F-statistic: 5.688 on 3 and 14 DF, p-value: 0.009227分析结果:由上述结果可得y关于x1,x2,x3的多元线性回归方程为y=+x1-x2+x3;通过F查验,但回归方程的t查验并非显著。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章2.1> x<(1,2,3)<(4,5,6)> e<(1,1,1)> z<-2*[1] 7 10 13> z1<()1[,1][1,] 32> z2<()2[,1] [,2] [,3] [1,] 4 5 6 [2,] 8 10 12 [3,] 12 15 182.2(1) > A<(1:204)<(1:204) > C<(2) > D<*(3) > E<*(4) > F<[1:3,1:3](5) > G<[3]2.3> x<((1,5)(2,3)(3,4)(4,2))2.4> H<(55)> (i 1:5)+ (j 1:5)+ H[]<-1/(1)(1)> (H)(2)> (H)(3)> (H)2.5> <(姓名('张三','李四','王五','赵六','丁一')+ ,性别('女','男','女','男','女'),年龄('14','15','16','14','15'),+ 身高('156','165','157','162','159'),体重('42','49','41.5','52','45.5'))2.6> ('')> ('')2.7<(n){(n<=0)('要求输入一个正整数'){{(20)n<2n<-(3*1)(1)}('运算成功')}}第三章3.1首先将数据录入为x。
利用函数。
如下> (x)3.2> ()> ((x)'')> y<(x)(x)> ((y,73.668,3.9389)'')> ((x))> ((y,73.668,3.9389))> (x)> (x)3.3> (x)> (x)> (x)3.4> (x)> (x,'',73.668,3.9389): xD = 0.073, = 0.6611::(x, "", 73.668, 3.9389) :这里出现警告信息是因为检验要求样本数据是连续的,不允许出现重复值3.5>x1<(2,4,3,2,4,7,7,2,2,5,4)2<(5,6,8,5,10,7,12,12,6,6)3< (7,11,6,6,7,9,5,5,10,6,3,10)> (x123('x1','x2','x3')(2,3,4))>()>((c((1(x1))(2(x2))(3(x3))))(x123))3.6> <(x1(65,70,70,69,66,67,68,72,66,68),2(45,45,48,46,50,46,47,43,47,48)3(27.6,30.7,31.8,32.6,3 1.0,31.3,37.0,33.6,33.1,34.2))> ()具体有相关关系的两个变量的散点图要么是从左下角到右上角(正相关),要么是从左上角到右下角(负相关)。
从上图可知所有的图中偶读没有这样的趋势,故均不相关。
3.7(1)> <('3.7')> ()> (体重~身高)(2)> (体重~身高|性别)(3)> (体重~身高|年龄)(4)> (体重~身高|年龄+性别)只列出(4)的结果,如下图3.8> x<(-2,3,0.5)<(-1,7,0.5)> f<()+ x^4-2*x^2*^2-2*x*2*y^2+9*2-4*4> z<()>((0,1,2,3,4,5,10,15,20,30,40,50,60,80,100)'') > ()> (30300.7'')3.9> (身高,体重)根据得出的结果看是相关的。
具体结果不再列出3.10> <('48名求职者得分')> ()然后按照G的标准来画出星图> ()> $G1<-()/7> $G2<-()/3> $G3<-()/3> $G4<> $G5<> a<([,17:21])> (a)这里从17开始取,是因为在中将也作为了一列3.11使用P159已经编好的函数,接着上题,直接有> (a)第四章4.1 (1)先求矩估计。
总体的期望为1112()a a ax dx a +∞+-∞++=+⎰。
因此我们有12()a E x a +=+。
可解得(2*E (x̅)-1)/(1(x̅)).因此我们用样本的均值来估计a 即可。
在R 中实现如下> x<(0.1,0.2,0.9,0.8,0.7,0.7)> (2*(x)-1)/(1(x))[1] 0.3076923(2)采用极大似然估计首先求出极大似然函数为L (a;x )=∏(a +1)x i a =(a +1)n ∏x i a ni=1n i=1再取对数为ln L (a;x )=nln (a +1)+aln(∏x i ni=1最后求导ðlnL(a;x)ða =n a +1+ln ∏x i ni=1 好了下面开始用R 编程求解,注意此题中6.方法一、使用函数> f<(a) 6/(1)((x))> ((0,1))方法二、使用函数> g<(a) 6*(1)*((x))> ((0,1))4.2用极大似然估计得出λ=n/∑x i n i=1.现用R 求解如下>x<((5,365)(15,245)(25,150)(35,100)(45,70)(55,45)(65,25))> 1000(x)4.3换句话讲,就是用该样本来估计泊松分布中的参数,然后求出该分布的均值。
我们知道泊松分布中的参数λ,既是均值又是方差。
因此我们只需要用样本均值作矩估计即可在R 中实现如下> x<((0,17)(1,20)(2,10)(3,2)(4,1))> (x)[1] 14.4> f<(x) {<(-13[1]+((5[2])*x[2]-2)*x[2],(-29[1]+((x[2]+1)*x[2]-14 )*x[2]))+ (^2)}> ((0.52))4.5在矩估计中,正态分布总体的均值用样本的均值估计。
故在R中实现如下> x<(54,67,68,78,70,66,67,70,65,69)> (x)[1] 67.4然后用作区间估计,如下> (x)> ('')> ('')此时我们只需要区间估计的结果,所以我们只看中的关于置信区间的输出即可。
同时也给出均值检验的结果,但是默认0并不是我们想要的。
下面我们来做是否低于72的均值假设检验。
如下> (''72): xt = -2.4534, = 9, = 0.9817: 7295 :63.96295:x67.4结果说明:我们的备择假设是比72要大,但是p值为0.9817,所以我们不接受备择假设,接受原假设比72小。
因此这10名患者的平均脉搏次数比正常人要小。
4.6我们可以用两种方式来做一做> x<(140,137,136,140,145,148,140,135,144,141)> y<(135,118,115,140,128,131,130,115,131,125)> ()> ()结果不再列出,但是可以发现用均值差估计和配对数据估计的结果的数值有一点小小的差别。
但得出的结论是不影响的(他们的期望差别很大)4.7> A<(0.143,0.142,0.143,0.137)> B<(0.140,0.142,0.136,0.138,0.140)> ()4.8> x<(140,137,136,140,145,148,140,135,144,141)> y<(135,118,115,140,128,131,130,115,131,125)> ()> ()4.9泊松分布的参数就等于它的均值也等于方差。
我们直接用样本均值来估计参数即可,然后作样本均值0.95的置信区间即可。
> x<((0,7)(1,10)(2,12)(3,8)(4,3)(5,2))> (x)[1] 1.904762> (x)4.10正态总体均值用样本均值来估计。
故如下> x<(1067,919,1196,785,1126,936,918,1156,920,948)> ('')注意才是求区间下限的(都比它大的意思嘛)第五章5.1这是一个假设检验问题,即检验油漆作业工人的血小板的均值是否为225.在R中实现如下> x<()1: 220 188 162 230 145 160 238 188 247 11311: 126 245 164 231 256 183 190 158 224 17521:20> (225)5.2考察正态密度函数的概率在R中的计算。
首先我们要把该正态分布的均值和方差给估计出来,这个就利用样本即可。
然后用函数来计算大于1000的概率。
如下> x<(1067,919,1196,785,1126,936,918,1156,920,948)> (1000(x)(x))[1] 0.5087941> 1-0.5087941[1] 0.49120595.3这是检验两个总体是否存在差异的问题。
可用符号检验和秩检验。
两种方法实现如下> x<(113,120,138,120,100,118,138,123)> y<(138,116,125,136,110,132,130,110)> ((x<y)(x))= 1> ()= 0.792可见无论哪种方法P值都大于0.05,故接受原假设,他们无差异5.4(1)采用w检验法>x<(-0.75.6,2,2.8,0.7,3.5,4,5.8,7.10.5,2.51.6,1.7,3,0.4 ,4.5,4.6,2.5,61.4)>y<(3.7,6.5,5,5.2,0.8,0.2,0.6,3.4,6.61.1,6,3.8,2,1.6,2, 2.2,1.2,3.1,1.72)> (x)> (y)采用检验法> (x,''(x)(x))> (y,''(y)(y))采用拟合优度法对x进行检验> A<(((-2,0,2,4,6,8)))> A(-2,0] (0,2] (2,4] (4,6] (6,8]4 4 6 4 1发现A中有频数小于5,故应该重新调整分组> A<(((-2,2,4,8)))> A(-2,2] (2,4] (4,8]8 6 5然后再计算理论分布> p<(c(-2,2,4,8)(x)(x))> p<(p[2][3][2],1[3])最后检验> ()采用拟合优度法对y进行检验> B<(((-2.1,1,2,4,7)))> B(-2.1,1] (1,2] (2,4] (4,7]5 5 5 5> p<(c(1,2,4)(y)(y))> p<(p[1][2][1][3][2],1[3])> ()以上的所有结果都不再列出,结论是试验组和对照组都是来自正态分布。
