基于并行遗传算法的网格资源分配方法

合集下载

并行遗传算法

谢谢大家！！
主从式并行计算
□ 在这种并行方式中，一个主过程调节若干个仆过程。其中主过程控制选择、交叉和变异，仆过程仅执行适配值的计算。 □ 缺点：1、各仆过程计算适应度值的时间存在明显差异时，将会照成整个系统长时间的等待；2、整个系统可靠性较差，对主过程状况的依赖性较大。
□ □ □ □ 伪代码： Begin (1)产生一个初始群体 (2)while running do (2.1)for =1 to s do 计算个体i的适应度值(并行部分) （2.2）选择、交叉、变异操作，产生子代（2.3）子代取代父代，形成新一代个体 End while End
隐含并行性
□ 设ε为一小正数，L< ε(l-1)+1,N=2l,2，则遗传算法一次处理的存活概率不小于1- ε且定义长度不大于L的模式数位O（N3）. □ 遗传算法表面上仅对每代的N个个体作处理，但实际上并行处理了大约O（N3）个模式，并且无额外的存储，这正是遗传算法具有高校搜索能力的原因，这就是遗传算法的隐含并行。
并行遗传算法
□ 传统的遗传算法出现的问题：局部搜索性能较差，对某些分布变化缓慢，面对大型计算问题速度难以达到要求 □ 并行遗传算法提出：在遗传算法并行运算的基础上，通过多种群并行进化和引入迁移算子进行进行种群之间的信息交流，实现多种群的协同进化。通过人工选择系数对每个种群最优化个体保存，通过对协调种群间的信息交换策略得到最好的进化效果。 □ 遗传算法的并行化实现就是将进化过程划分到不同的计算节点上，进行分布式进化，并通过一定的种群间信息交换策略实现优良基因的转换。
ቤተ መጻሕፍቲ ባይዱ
细粒度并行算法
□ 如果并行系统中有足够多的处理器，那么系统可以为每个个体分配一个处理器，让它们相互独立的并行执行进程，这样就能获得并行遗传算法的最大可能的并发性。 □ 代码： □ Begin (1)产生一个初始群体并将它分配到P=N个处理器上； (2)For=1 to N do while running do (2.1)do step (a) and (b) in parallel (a)接收迁入个体 (b)发送本个体 (2.2)对迁入个体进行适应度评估 (2.3)从迁入的个体中选择对象 (2.4)交叉操作 (2.5)子代变异 (2.6)评估本个体及其后代 (2.7)用后代取代本个体 end while End for End

ei收录的计算机类核心源计算机研究与发展计算机学报软件学

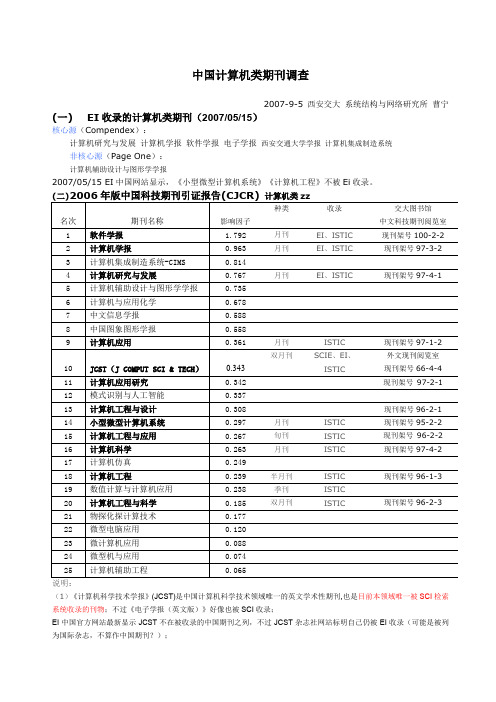
中国计算机类期刊调查2007-9-5 西安交大系统结构与网络研究所曹宁(一)EI收录的计算机类期刊（2007/05/15）核心源（Compendex）：计算机研究与发展计算机学报软件学报电子学报西安交通大学学报计算机集成制造系统非核心源（Page One）：计算机辅助设计与图形学学报2007/05/15 EI中国网站显示，《小型微型计算机系统》《计算机工程》不被Ei收录。

说明：（1）《计算机科学技术学报》(JCST)是中国计算机科学技术领域唯一的英文学术性期刊,也是目前本领域唯一被SCI检索系统收录的刊物；不过《电子学报（英文版）》好像也被SCI收录；EI中国官方网站最新显示JCST不在被收录的中国期刊之列，不过JCST杂志社网站标明自己仍被EI收录（可能是被列为国际杂志，不算作中国期刊？）；（2）ISTIC就是中国科技期刊引证报告统计源期刊，也就是所谓的核心期刊。

不过不同的学校和专业有不同的认定，要以学校的具体规定为准。

(三)EI核心源期刊调查（原创）（1）计算机研究与发展（EI核心源，中文核心）I.官方网站投稿指南学术论文：有创新学术见解的研究成果的完整论述，对该学术领域的发展有积极意义。

字数不超过8,000字。

技术报告：面向国民经济和社会发展的、先进实用的开发成果的技术总结。

字数不超过8,000字。

短文：创新的学术研究成果或阶段性成果的简要论述。

字数不超过5,000字。

简报：先进、实用的技术开发成果的简要报导。

字数不超过3,000字。

综述：对新兴的、活跃的学术研究领域或技术开发领域的评述。

字数不超过10,000字。

研究热点论文：对目前国内外计算机前沿热点研究领域的介绍文章。

字数不超过8000字。

注意：本刊优先刊登有以下基金项目资助的论文：1.国家基金项目（如国家自然科学基金项目、“八六三”、“九七三”等）。

2. 省部级基金项目。

II.个人调查结论（浏览已出版的文章）1.每篇文章至少有一项国家基金支持，大多有两三项（国家自然科学基金，863,973）；2.大部分文章与算法相关；3.基本每篇都有实验仿真及数据分析，看来比较注重此项；4.中科院下属各研究所文章占据绝大部分（本杂志由中国科学院计算技术研究所与中国计算机学会联合主办）；5.第一作者至少是博士研究生；6.网格方面的文章数较多，但逐年递减；7.Web服务和QoS方面的文章一直很少；III.数据统计1.07年前72.063.04（4.5.04-07年与（2）电子学报（I.官方网站投稿指南1.投稿需另行寄出稿件评审费(中文150元；英文180元）。

移动网格计算中的任务调度与资源管理方法研究

移动网格计算中的任务调度与资源管理方法研究随着移动终端设备和无线通信技术的快速发展，移动网格计算作为一种新兴的计算模式，正在得到越来越广泛的应用。

在移动网格计算环境中，任务调度和资源管理是关键的技术问题，直接影响到计算性能和资源利用率。

本文将重点研究移动网格计算中的任务调度与资源管理方法，并探讨其相关的技术挑战和解决方案。

一、任务调度方法研究在移动网格计算中，任务调度是指将各个参与计算的终端设备上的任务分配到合适的计算节点上执行的过程。

合理的任务调度可以提高计算效率、减少计算时间，并降低能耗。

目前主要的任务调度方法有下面几种：1. 贪心算法贪心算法是一种简单而有效的任务调度方法。

在贪心算法中，根据预先设置的任务优先级和计算节点的状态信息，将任务分配给第一个满足条件的计算节点。

贪心算法具有低计算复杂度和实时性好的特点，但对资源的利用率并不高。

2. 遗传算法遗传算法是一种通过模拟生物进化过程来优化任务调度问题的算法。

在遗传算法中，通过不断地交叉、变异和选择等操作，逐步演化出适应度高的任务调度方案。

遗传算法具有较强的全局搜索能力，可以在复杂的问题中找到较好的解，但计算复杂度较高，不适合实时任务调度。

3. 蚁群算法蚁群算法是一种模拟蚂蚁觅食行为的优化算法。

在蚁群算法中，每个蚂蚁代表一个任务，通过信息素释放和感知信息来选择下一个计算节点。

蚁群算法具有较好的全局搜索能力和适应性，能够找到较优的任务调度方案，但对参数的选择敏感，调参较为困难。

二、资源管理方法研究资源管理是指如何有效地利用移动网格计算环境中的有限资源，包括计算资源、存储资源和网络带宽等。

合理的资源管理可以提高系统的稳定性和性能。

目前主要的资源管理方法有下面几种：1. 资源预测与分配资源预测是指通过对历史数据和当前状态的分析，预测未来一段时间内资源的使用情况。

基于资源预测的资源分配方法可以根据预测结果，动态地分配资源给不同的任务，以满足任务的需求，提高资源利用率。

基于遗传算法的网格服务工作流调度的研究

Ｊｎ０６ａ．２０
基于遗传算法的网格服务工作流调度的研究
郭文彩，杨扬
（北京科技大学信息工程学院，京１０８）北００３
（ｅｇｏａｏ．Ｏｃ）ｗ — ｕ＠ｙｈｏＣＢ．ｎ摘要：网格服务的提出为网格工作流的研究提供了新的契机与挑战，网格服务组成的工作流由
ｄｓｒｉｅｓｈｄｌｇｉｉｃｌｔｏｖｙｍｅｎｆｃａｓｃａｇｒｔｍｓＦａｕｅｎｓａｃｉｇｃｎｕｒｎｌｎｌｂｌ，ｅｖｃｃｅｕｉｓｄｆｕｔｏｓｌｅｂａｓｏｌｓｉｌｏｈ．ｅｔｒｄｉｅｒｈｎｏｃｒｅｔａｄｇｏａｙｎｉｆｉｙｌｇｎｔｇｒｈＣｅａｂ￣ｒｏｔｎｆｒｓｌｉｇＧＳｃｅｕｉｇｐｏｌｍ．ｅｅｏｅａＧＡ－ａｅｄｓｒｉｅｓｈｄｌｇｅｅｃａｏｔｍａｂｅｅｐｉｏｏｖｎＦｓｈｄｌｒｂｅＴｒｆｒ，ｉｌｉｎｏｎｈｂｄｓｅｖｃｃｅｕｉｎｌｏｔｍ，ＧＳＧＡ，ｗｓｐｏｉｅｒｂａｎｎｅｂｓＧＳｓａｃｉｈｈｇｅｔｔｅｓＥｐｒｍｅｔｒｓｌｒｖｔｖｉｂｅａｇｒｈｉＦａｒｖｄｄｆｔｉｉｇｔｅｔＦｉｔｅｗｔｉｈｓｆｎｓｘｅｏｏｈｎｎｉｉｎｅｕｔｐｏｅｉａａｌｌｓａａｄｂｔｒｔａｏｒｄｔｎｇｒｈ．Ａｏｃｕｉｎｈｕｔｅｏｋｗ８ｌｏｐｉｔｄｏｔｎｅｔｎｓｍｅｔｉｏａａｏｉｍｓｓａｃｎｌｓ．ｔｅｆｒｒｗｒｓａｓｏｎｅｕ．ｅｈａｉｌｌｔｏｈＫｅｒｓｙｗｏｄ：ｄｓｒｉｅｏｋｌｗ；ｓｈｄｉｇｅｅｉｇｒｈｅｃ；ｗｒｉｖｏｃｅｕｎ；ｇｎｔａｏｔｍｌｃｌｉ

基于网格法的遗传算法及其应用

式中，表一种策略；剐弋ｓ表示计算精度；表示将Ｐ中的不同元素按从小到大的顺序排列得到的集合；表示统计频率；表示ｒ集合中的个
数．
有的位．这样产生的个体具有较好的多样性，但遍历性稍差，不能充满整个搜索空间，这将会降低遗传算子的搜索效率．均匀设计法可以均匀布点整个初始群体，群体中的个体有较好的遍历性和多样性，产生初始点时，了达到 “ 但为均
它有一个缺点，是相邻整数的二进制编码可就
以下公式中参数的含义请详细参阅文献【．８］平均截止代数的公式为：
Ｓ＝∑ ・Ｐ（）１
能有较大的ｒｍｎ距离，ｌｍｉａｇ这就是所谓的Ｈｍａ－
ｍｉｇ崖，如１和１的二进制表示为叭１１ｎ悬例５６１和１００算法要从１改进到ｌ必需改变所００，５６则
２３丽格法优化效率的定量评价．
Ⅳｓ）（来评价网格法的优化效率，现采用如下函数优化为例：
ｍａｘ一２＝１０一一５，）０一ｘ）
２＜ｘ＿８２．＜
（）３
ｓｔ一３ｔ３．．：
这２种方法都采用实数编码、最优个体保留、赌轮比例选择、一点交叉、均匀变异的方式，控制参数为：群体规模＝０计算精度ｅ１一阈３；＝０；值代数＝０５；终止代数＝０５；交叉概率ｐ＝００）５变异概率ｐ＝．４．所不同的只有．－．；６４８０１）．－３初始群体的产生方式不同．在交叉概率和变异概率的取值范围中，网格法和随机法各独立运行２０，０次获得的平均截止代数和截止代数分布熵如图２所示．图２中可以看出，从网格法的优化效率要稍好于随机法．

网格资源分配算法的研究

Ｅ— ａｌｙｙｑ＠１．ｏｌｍｉ：ｄｐｈ６３ｃｎ
ＹＡＮＤａｐｎ．－ｅｇＤＵｅｄｎ．ｇｒｔｍｅｅｒｈｆｒｓｕｃｌｃｔｎｎｇｉｅｖｒｎｅｔＣｏｕｅＥｎｉｅｒｎｎＸｕ－ｏｇＡｌｏｉｈｒｓａｃｏｅｏｒｅａｌａｉｉｒｄｎｉｏｍｎ・ｍｐｔｒｏｏｇｎｅｉｇａｄ
Ａｐｌａｉｎ．０８．４２）１５１７ｐｉｔｓ２０４（９：３ — ３．ｃｏ
Ａｂｔａｔｓｒｃ：Ａｓｒｓｕｃｌｃｔｎｅｏｓａｍａｎｐｏｌｍｎｒｄｏｕｉｇａｅ，ｔｐｅｅｔｒｓａｃｏｏｏｕａｉｎｌｉ — ｅｏｒｅａｌａｉｂｃｍｅｉｒｂｅｉｇｃｍｐｔｒａａｒｓｎ，ｅｅｒｈｆｓｍｅｃｍｐｔｔａｎｏｏｉｎｏ
ｐｏｅｎｇｎｒｔｄｅｕｔｙｌｒｉｅｅａｅｒｓｌｂｍａｉｇｕｅｏｎｏｏ）ｌｏｉｍ．ｈｅｕｔｏｈｉｍｌｔｎｈｗｓｈｔｈｒｐｓｄａｇｒｈｓｋｎｓｆａｔｃｌｎ＂ａｇｒｈＴｅｒｓｌｆｔｅｓｎａｉｓｏｔａｔｏｔｅｐｏｏｅｌｏｔｍｉ
在满足用户需求的前提下，效地提高了网格资源利用率。有
关键词：网格；资源分配；传算法；群算法遗蚁Ｄ：０７８．ｓ．０ — ３１０８９３文章编号：０２８３（０８２ — １５０文献标识码：中图分类号：Ｐ９ＯＩ１．７／ｉｎ１２８３．０．．８３ｊｓ０２２０１０ — ３１２０）９０３— ３ＡＴ３３

基于并行遗传算法的微电网控制方法研究

摘要：微电网快速普及背景下，如何对微电网进行高效控制成为电力从业人员重点关注的问题。

鉴于此，引入并行遗传算法技术，构建微电网最优控制模型，确定微电网控制约束条件，并以此为基础设计微电网最优控制软件，借助该软件实现对于微电网的有效控制。

关键词：并行遗传算法；微电网；并行性0 引言作为一种全新的发电、供电方法，微电网在保障电力供应稳定性、提高电力输送效率等方面发挥了重要作用。

为确保微电网能够稳定、持续运行，相关研究人员积极尝试将并行遗传算法引入微电网控制工作中，对最优控制遗传算法变量进行优化，明确并行遗传算法计算流程，基于MATLAB开发环境设计微电网最优控制软件系统，通过这种方式达到“环境最优化”与“经济最优化”双重目标。

1 遗传算法并行性及分类1.1 遗传算法固有的并行性实际生活中，不同的物种在同一时刻以“相互独立”的状态进行进化，从宏观层面来看，物种的进化即并行化过程。

研究人员将物种的进化过程引入机器人深度学习领域，以遗传算法为核心模拟物种进化过程，利用选择操作模拟物种进化过程中的自然选择，利用变异操作模拟物种进化过程中的基因突变。

因此，遗传算法的基础运行逻辑中继承了物种进化的并行性。

使用遗传算法处理数据信息时，其数量级为O（n3），这代表遗传算法对N个染色体进行遗传操作，其内部遗传信息的数量级为O（n3），研究人员将其称为“隐含并行性”。

1.2 并行遗传算法分类1.2.1 全局并行全局并行作为一种直接并行化模式，主要应用于串行遗传算法领域。

全局并行模式的特点在于仅有一个群体，在该群体中，每一个个体可以自由匹配，基于群体适应度调整个体适应度，无论是遗传匹配操作还是遗传选择操作，均具有全局性。

该模式下，个体之间相互独立，无须进行信息交互，针对个体的评价主要由主/从进程负责。

该模式通常采用同步通信技术，个体适应数据被发送给主进程之后，主进程开始计算个体绝对适应值并根据计算结果进行选择操作，通过这种方式提高遗传算法计算性能。

基于遗传算法的网格任务调度方法研究

取低分辨率，以简化运算数据，提高速度。而在形变完成后，由于没有形变计算，全体数据即可采用高分辨率显示，以体现效果。我们利用、Ｉ中抽取点的方法，ｒｒ ’ Ｋ以完成数据的变换。手术模拟流程在ＶｓａＣ＋＋．ｅ２０ｉｌｕｎｔ０３实现，使之与ＶＫ显并Ｔ示实时结合。
，
图１手术模拟流程
［］ＳｅｈｎＳＨＮＥＫｖｎＭＯＴＯＲ６ｔｐｅＣＥＤＬ，ｅｉＮＧＭＥＹ，ｅａ．Ａｓｒｃｌｔ１ｕｇａｉｓｕａｏｒｐａｎｎｎｅｆｍｎｐｉｏｌｆｌｓＪ．ｉｌｔｆｌｉｇａｄｐｒｒｉｇｒａｒｆｃｅｉ［］ｍｒｏｎｏｅｔｐ
ＢｏｄｃｏｕｉｇＶＣ）１９，（８８：７５４ｉｍｅｉａＣｍｐｔ（Ｂ，９２９１０）５４— ８．ｌｎ
［］ｏｒｎＲａＴｍｆＴｓｅｎｒｃｒＳｕｔｎＤ．５ＪｅＢｗ．ｅ —ｉｅｏｉｕｄｔｔｉｌｉ［］ｌｏｌＳｔｓａＳｕｕｍａｏｅ
ＰＤ．Ｄｉｓｒａｉｎ，ＣａｉｒｉＤｅｒｍｅｔｆＣｏｕｅＳｉｈ．ｓｅｔｔｏｌｏａ：ｆｎｐａｔｎｏｍｐｔｒｃ — ｅｃｎｅ，Ｓａｆｒｉｅｓｔ２０１ｔｎｏｄＵｎｖｒｉｙ，０３，１—１．３
仪器仪表用户
常慎微，以达到稳定。此处的平方根起补偿作用，Ｅｎ很小当（）时起到放大的作用，避免调节的过早饱和。同时对惯量因以子也作了自适应调节，调节机制更为简洁，／通常取０９ｏ。．。这种对＂和ｏ不断地渐增和适时地抑制相互作用的机制ｔ可使迭代过程较快逃离局部极小状态和走出“ 台 ” 加快收平，敛速度，并且对参数的敏感性小，有较好的鲁棒性。具

一种基于遗传一蚁群算法的网格任务调度策略

ｏｅｅｉｃｅｕｉｇａｇｒｈ，ｎｖｉｅｉｅｆｉｎｙｐｏｌｍｆｎｃｅｕｉｇａｇｒｈａｓｉｉａｓａｃｉｇｓａｅ，ｉｆｎｔｓｈｄｌｌｏｔｍａｄａｏｄｔｎｆｃｅｃｒｂｅｏｔｓｈｄｌｌｏｔｍｔｔｔｌｅｒｈｎｔｇｔｓｇｃｎｉｈｉａｎｉｉｎｉｈ
ｐｐｒｐｏｏｅｒｄｔｓｃｅｕｉｇｓｒｔｇａｅｎｔｅｇｎｔ－ｎｌｏｔｍ，ｉｈｉｔｇａｅｈｌｂｌｓａｃａａｉｔａｅｒｐｓｄａｇｉｋｓｈｄｌｔａｅｙｂｓｄｏｈｅｅｉａｔｇｒｈｗｈｃｎｅｒｔｄｔｅｇｏａｅｒｈｃｐｂｌｙａｎｃａｉｉｏｅｅｉｌｏｔｍｎｈｏｕｉｎｐｅｉｉｎｏｎｇｒｈ，ｎｏｓｓｅｈｄａｔｇｓｏｅｅｔｏａｇｒｈ．ｈｅｔｆｇｎｔａｇｒｈａｄｔｅｓｌｔｒｃｓｏｆａｔａｏｉｍａｄｐｓｅｓｄｔｅａｖｎａｅｆｈｓｗｏｉｍｓＴｅｔｓｃｉｏｌｔｔｌｔｒｓｌｎｓｍｕａｉｎｅｐｒｍｅｔｓｏｈｔｈｒｐｓｄｍｅｈｄｏｔｅｆｒｈｅｅｉａｇｒｔｍｎｈｎｌｏｉｍａｅｕｔｏｉｌｔｘｅｓｏｉｎｓｈｗｔａｅｐｏｏｅｔｏｕｐｒｏｍｓｔｅｇｎｔｏｉｔｃｌｈａｄｔｅａｔａｇｒｔｓａｈｗｏｅｎａｅｏｖｏｓｓｈｄｌｇｅｃｅｃｄａｔｇｈｎｔｅｓｈｄｌｇｓｚｆｇｉａｋｉａｇｎｕｈｈｌ，ａｄｈｓｔｂｉｕｃｅｕｉｆｉｎｙａｖｎａｅｗｅｈｃｅｕｉｉｏｄｔｓＳｌｒｅｅｏｇ．ｈｎｉｎｅｒ

基于遗传神经网络的网格资源预测模型

传神经网络的网格资源预测模型。利用ＧＡ对Ｂ神经网络Ｐ
的连接权值和阈值进行优化，弥补ＢＰ神经网络收敛慢缺陷，
．．．．— —
２４３．— ．．． —
同时发挥ＢＰ神经网络的优异非线性预测能力，后采用该最
型训练误差平方和作为个体的适应度值，即有：
（）５
∑
其中，Ｐ表示种群中个体的数目表示适应度值倒数。５交叉操作。由于本文采用实数编码方式，）其交叉方式相应采用实数交叉法，两条染色体进行交叉如下：
统，然后采用ＢＰ神经网络进行预测Ｊ。设网络资源时间序
列为：，，｝采用相空间重构可以得到某一点状态 …，，矢量的重构序列：
ＮｅｗｏｋＢａｅｎＧｅｅｉｇｒｔｍｔｒｓｄｏｎｔＡｌｏｉｃｈ
ＹＡＮＧｉＢａ
（ｕｕｂｉｏｅｅｕｎｅｒｅｅｇｕ０１０，ｈｎ）Ｈｌｎｅｒｌｇ，Ｈｌｂｉｉｎｇ２０８ＣｉａｅｃｌｕｅＮｍ
＝
｛，ｆ，，ｆ１｝ｆ＋ … ＋一（）
（）１
其中，＝１２ … ，，表示相点个数，ｉ，，ｍ为嵌入维数，ｒ表
示延迟时间。
ｆ茸（一）６＝６＋
Ｌ＝ Ⅱ １一ｂＨ（）＋Ｗｂ日
（６）
（
６变异操作。具体变异方式为：）
（一一）ｇ，）
：
采用ＢＰ神经网络层对重构后的网格资源时间序列进行预测，输入层节点数为嵌入维数（，出层节点数为１其ｍ）输，设隐层节点为Ｐ，么基于Ｂ那ｐ神经网络的网格源源预测模

基于改进遗传算法的网格资源调度策略算法研究

其中Ｍ口（＋２…Ｍｎｎ＝Ｍ１＋＝Ｍ）；／Ｒ（＋Ｒ３３Ｒ＋Ｉ／）
３１遗传算法简介．
作者简介：王猛，吉林省吉林市人，男，本科，究方向：电子信息科学与技术。研
一
３ — ５
好的性状的染色体更有几率产生优良的后代，由于本算
美国密西根大学教授Ｊｏ．ＨｏｌａｈｎＨ．ｌｄ为遗传算法创始ｎ
１引言．
人，ｌａＨｏｌｄ认为，可用一组二进制串来模拟一组计算机程ｎ序，并且定义了一个衡量每个“ 程序 ” 的正确性的度量：应适
网格计算技术是一种先进的资源共享模型，是连接网
Ｔ｝Ｔ为第ｉｎ；ｉ个任务。资源集ＲＲｌＩ ……ｇ｝Ｒ＝ｆ，，ｎ；ｉ
为第ｉ个资源。为完成第ｉＭｉ个任务所需要的时间。ｒ为第Ｒｉ
ｉ资源与执行单位资源所需要时间的比率。个
在举例中假设子任务分别为Ｔ１Ｔ；资源分别为Ｒ１～７，Ｒ，３２Ｒ；资源完成时间与执行所需要的单位时间比率Ｒｌｒ．，Ｒ２Ｒ３完成标准资源所需要的时间Ｍ１Ｍ７分。可以用一ｒ，ｒ；－个ＤＡＧ图来表示这个问题，以图１为例。由ＤＡＧ图，可得一种编码方案ＴＴＴＴＴＴＴ。３１４５６７２按照这样的顺序随机最先完成任务可以生成一个任务分配序列。
（每个子任务在标准资源上运行所需要的时间已知，３）且
资源每一资源的处理速度相对的计算速度的比例关系已知；

并行计算、分布式计算、集群计算和网格计算的介绍和区别？

并⾏计算、分布式计算、集群计算和⽹格计算的介绍和区别？并⾏计算（Parallel Computing）并⾏计算或称平⾏计算是相对于串⾏计算来说的。

并⾏计算（Parallel Computing）是指同时使⽤多种计算资源解决计算问题的过程。

为执⾏并⾏计算，计算资源应包括⼀台配有多处理机（并⾏处理）的计算机、⼀个与⽹络相连的计算机专有编号，或者两者结合使⽤。

并⾏计算的主要⽬的是快速解决⼤型且复杂的计算问题。

并⾏计算可以划分成时间并⾏和空间并⾏。

时间并⾏即流⽔线技术，空间并⾏使⽤多个处理器执⾏并发计算，当前研究的主要是空间的并⾏问题。

以程序和算法设计⼈员的⾓度看，并⾏计算⼜可分为数据并⾏和任务并⾏。

数据并⾏把⼤的任务化解成若⼲个相同的⼦任务，处理起来⽐任务并⾏简单。

空间上的并⾏导致两类并⾏机的产⽣，按照Michael Flynn（费林分类法）的说法分为单指令流多数据流（SIMD）和多指令流多数据流（MIMD），⽽常⽤的串⾏机也称为单指令流单数据流（SISD）。

MIMD类的机器⼜可分为常见的五类：并⾏向量处理机（PVP）、对称多处理机（SMP）、⼤规模并⾏处理机（MPP）、⼯作站机群（COW）、分布式共享存储处理机（DSM）。

2. 分布式计算（Distributed Computing）分布式计算这个研究领域，主要研究分散系统（Distributed system）如何进⾏计算。

分散系统是⼀组计算机，通过计算机⽹络相互链接与通信后形成的系统。

把需要进⾏⼤量计算的⼯程数据分区成⼩块，由多台计算机分别计算，在上传运算结果后，将结果统⼀合并得出数据结论的科学。

⽬前常见的分布式计算项⽬通常使⽤世界各地上千万志愿者计算机的闲置计算能⼒，通过互联⽹进⾏数据传输。

如分析计算蛋⽩质的内部结构和相关药物的Folding@home项⽬，该项⽬结构庞⼤，需要惊⼈的计算量，由⼀台电脑计算是不可能完成的。

即使现在有了计算能⼒超强的超级电脑，但是⼀些科研机构的经费却⼜⼗分有限。

基于改进遗传算法的知识网格资源调度研究

任务分配至合适的知识网格资源，协同完成计算任务。资源的分配必须满足使用者成本，时间，资源质量上的偏好。当前的研究中，于资源的分配多考虑以时间对或成本最小化作为目标函数，以时间或成本的预算并
个子目标，通过单个最优解的集成来满足整体目标的约束Ｈ．】但是并列式选择方法是对子目标的平均分配．并不能够满足知识网格中求解问题过程所需要的按一定顺序和优先级调度资源这一要求本文将对知识网格资源调度的多目标约束进行详细的分析，对并列式
第２９卷第１１期２１００年１１月
情
报
杂
志
ＪＯＵＲＮＡＬＯＦＩＮＴＥＩＬＬＧＥＮＣＥ
Ｖ０．９ＮＯ．１１２１ＮＯ２０Ｖ．０１
基于改进遗传算法的知识网格资源调度研究术
ＲｅｅｒｈｎＫｎｗｌｄｇｉｓｕｃｈｄｕｉｓｄｏｍｐｏｅｎｔｃＡｌｏｉｈｓａｃｏｏｅｅＧｒｄＲｅｏｒｅＳｃｅｌｎｇＢａｅｎＩｒｖｄＧｅｅｉｇｒｔｍ
束．将结果集合在一起来满足整体目标，经过交叉和变异计算来生成新的种群。提高了算法搜索能力和收敛速并再
度。能更有效地解决多目标约束的知识网格资源调度问题
关键词知识网格资源调度遗传算法
李广明
（海金融学院信息管理学院上上海２１０）０２９
摘
要
传统的遗传算法比较适用于解决单一目标问题。在知识网格中，务和资源的调度问题是十分复杂的，任往

基于一种自适应并行遗传算法的网格资源选择策略

ｉｄｃｔｓｔａｈｇｒｔｍａｆｃｉｅｙｓｌｅｔｅｐｏｌｍｆｐｍａｕｏｖｒｅｃｎｉａｅｈｔｔｅａｏｉｌｈｃｎｅｆｔｌｏｖｈｒｂｅｏｒｅｖｅｔｒｃｎｅｇｎｅ，ａｄｐｏｕｅｒｓｈｅｎｒｄｃｕｓｅ
维普资讯
第１３卷第５期
２００７年１０月
上海大学学报（自然科学版）
ＪＵＮＬＯＨＮＨＩＮＶＲＩＹ（ＡＵＡＣＥＣ）ＯＲＡＦＳＡＧＡＩ Байду номын сангаас ＳＴＮＴＲＬＳＩＮＥＵ
ｐａｌｌｍｏｅｉｌｔｎｏｅｒａｌｅｄｌｓｍｕａｉｆｔｏｈｄｅｏｒｅｅｅｔｎｔａｅｙｏＣ＋ＭＰＩｐａｏｍｓｍａｅ．Ｔｈｒｓｌｒｓｕｓｓｌｃｉｓｒｔｇｎｃｏｌｔｒｉｄｆｅｅｕｔ
摘要：格是在某一单一时间，网络中众多的计算机资源集中起来共同处理某个单一问题的．如何有效地从众网将而多的资源中选出多个较优秀的资源是一个ＮＰ问题．文提出一种新的自适应的并行遗传算法（ＡＧ，对网格该ＮＰＡ）并资源的选择策略在ｃ＋ＭＩ台上进行了并行模拟．果表明，算法不仅有效地避免了过早收敛的现象，且取Ｐ平结该而得了比改进型的并行遗传算法（ＩＧ）优的搜索结果．后对遗传算法的搜索和收敛规律进行了一些讨论．ＮＰＡ更最

基于遗传算法的航天测控网资源分配模型与仿真

了一种航天测控网资源分配模型。该模型立足于航天测控网现有的硬件资源，在不增加测控网建设成本的基础上，引入效益因子，既优先满足测控级别较高的卫星的测控需求，又充分考虑接受测控任务时各个测控站的时延和带宽
等实际因素，通过分配不同的权重，实现现有测控资源利用率的最大化，并采用遗传算法（ＧＡ）对该模型进行求解。通过仿真实验表明，与传统的资源分配方法相比，该模型的任务完成率提高了２３％，测控资源利用效率为传统方法的２倍以上，而算法的运行时间与传统的方法相当。因此，在多窗口多星同时测控的条件下，该模型更能合理ａｎｇ。
（ＳｃｈｏｏｌｏｆＡｕｔｏｍｏｔｉｖｅａｎｄＥｌｅｃｔｒｏｎｉｃＥｎｇｉｎｅｅｒｉｎｇ，ＸｃｈｉａｎｇＣｏｌｌｅｇｅ，ＸｃｉｈａｎｇＳｃｉｈｕａｎ６１５０１３，Ｃｈｉｎａ）Ａｂｓｔｒａｃｔ：Ｔｏｒｅｓｏｌｖｅｔｈｅｒｅｓｏｕｒｃｅｐｒｅｓｓｕｒｅｏｆｍｕｌｔｉ．ｓａｔｅｌｌｉｔｅｏｎｏｒｂｉｔ．ｔｅｌｅｍｅｔｒｙｉｎＴｒ＆ＣｆＴｒａｃｋｉｎｇ，Ｔｅｌｅｍｅｔｒｙａｎｄ
ＪｏｕｒｎａｌｏｆＣｏｍｐｕｔｅｒＡｐｐｌｉｃａｔｉｏｎｓ

基于遗传算法的网格简化研究

储、传输、编辑以及实时绘制等带来的困难有着重
要的意义。

本文针对最常见、应用最广泛的三角网格进
行研究，通过网格部分删除与重构，达到三角网格简化与曲面形状匹配的最优化目标，实验表明，ｉ
Ｅ－ｉ：ｃｅｈｉ＠ｓｉ．ｏｃｍａｌｈｎｕｑｚｉ１ｍ．ｎｔ２，
第４期
陈慧群，Ｊ吉，张斌：皋于遗传算法的网格简化研究ｊ亮
４７
索到的当前网格，角网格ｉ＝，… １，）ｉ（ｌｉ２ｉ为其包１ ≠６
角形折叠、顶点聚类和网格重新划分等简化算法上，采用以下两种方式来实现简化设计：
］
。
文献提出的改进型边折叠算法，在Ｇｒｎ算ａｌｄａ
１、利用数量比例权重来选择所要删除的三角
第８第４卷期
２１年１月００２
深圳信息职业技术学院学报
ＪｕｎｌｆｈｎｈｎＩｓｉｔｆｎｏｍａｉｎＴｅｈｏｏｙｏｒａｅｚｅｎｔｕｅｏｆｒｔｃｎｌｇｏＳｔＩｏ
Ｖ０１．Ｎｏ．８４
化算法，在该方法重建出的多分辨率模型表面上，
【收稿日期］０００ —１２１— ９
分析基础上，验证本文方法的可行性及准确性。
【基金项目】深圳信息职业技术学院青年自然科学基金资助项目（Ｎ００３Ｑ一８１）【作者简介］陈慧群（９２１８一），男，江西高安人，讲师、硕士，主要研究方向为计算机图形学、Ａ／Ａ技术。ＣＤＣＭ

基于遗传算法的网格资源分配与调度研究

ａｌｃｔｎａｄｓｈｄｉｇｉｄ．ｌｏａｉｎｃｅｕｌｎｎｏ
Ｋｅｒｓｄ；ｇｎｔｌｏｔｍ；ｔｓｌｃｔｎａｄｓｈｄｌｇｙｗｏｄ：ｅｅｉａｇｒｈｃｉａｋａｌａｉｎｃｅｕｉｏｏｎ
ＲｅｅｒｈｏｓｌｃｔｏｎｄＳｈｅｌｎｇｉＧｒｄＢａｅｎＧｅｅｉｇｒｔｍｓａｃｎＴａｋＡｌａｉｎａｃｄｕｉｎｉｓｄｏｎｔｃＡｌｏｉｈｏ
ＹＥＪｎ，ＸＩｉｃｎｉｇＥＬ－ｏｇ
ｌｔｎ’ ｏｖｒｅｃｎｎｒａｅｈｆｃｅｃｆｌｃｎｌｂｌｅｃａａｉｔ．ＳｍｕａｉｎｒｓｌｓｓｏｈｔｈｓａｇｒｈａｉＳｃｎｅｇｎｅａｄｉｃｅｓｓｔｅｅｉｎｙｏｔａｉｌｏｔｍｏｉｏｌｓｒｉｏｔｉ
ｉｍｏｅｅｅｔｅｆｒｔｅａｌａｉｎｏｓｕｃｓｃｍｐｒｄｗｔｔｅｌｏｔｍ，ｉｃｎｂｕｃｓｆｌｐｌｄｔｎｅｅｄｎａｋｓｒｆｃｉｏｈｌｔｆｒｏｒｅｏａｅｈｏｈｒａｇｒｈｖｃｏｏｅｉｉｔａｅｓｃｅｓｕｌａｐｉｉｄｐｎｅｔｓｙｅｏｔ
ｉｌｉｐｒｌｌｓａｅｓａｃａａｉｔｄｌｓｄｔｏｖａｋａｌｃｔｎａｄｓｈｄｌｇｐｏｌｍｓｍｐｉｔａａｌｐｃｅｒｈｃｐｂｌｙｉｗｉｅｙｕｅＯｓｌｅｔｓｌａｉｎｃｅｕｉｒｂｅ．Ｂａｅｎｔｅｒｓａｃｎｃｅｉｓｏｏｎｓｄｏｅｅｒｈｏｈ

高性能并行计算中的任务调度与资源分配策略

高性能并行计算中的任务调度与资源分配策略在高性能并行计算领域，任务调度和资源分配策略是至关重要的环节。

通过合理的任务调度和资源分配策略，可以最大程度地提升并行计算系统的性能和效率。

本文将围绕该主题展开，介绍高性能并行计算中的任务调度和资源分配策略的基本原理、方法和挑战，并提出一些解决方案。

任务调度是指根据任务特性和系统状态，将任务分配给合适的处理单元（如多核、多节点等），使得系统的性能得到最大化。

在任务调度中，需考虑任务的计算量、通信量以及可执行性等因素。

一种常用的任务调度方法是静态任务调度，即在任务开始前确定每个任务的执行顺序和分配策略。

另一种常见的任务调度方法是动态任务调度，即根据任务的运行状态和系统的负载情况，实时调整任务的优先级和分配策略。

资源分配策略是指将计算资源（如CPU、内存、网络带宽等）合理地分配给任务，以最大限度地提高并行计算系统的利用率。

资源分配策略应根据任务的需求和系统的特点进行优化，以满足任务的计算需求和实现资源的均衡利用。

一种常用的资源分配策略是静态资源分配，即在任务开始前确定每个任务需要的资源量，并进行相应的分配。

另一种常见的资源分配策略是动态资源分配，即根据任务执行的实时情况和系统负载的变化，动态分配资源以最优化任务的执行效率。

在任务调度和资源分配中，面临着一些挑战和困难。

首先，任务调度和资源分配需要在不同任务之间、不同节点之间、不同通信机制之间进行协调与决策，这增加了复杂性。

其次，系统中存在着不同类型的任务和不同类型的资源，如何选择合适的任务调度策略和资源分配策略也是一个难题。

此外，任务调度和资源分配需要考虑任务的实时性和响应性，以避免任务等待时间过长。

针对上述挑战和困难，研究者们提出了一些解决方案。

一种解决方案是采用智能算法进行任务调度和资源分配。

智能算法（如遗传算法、模糊算法等）可以根据任务的特性和系统的状态进行学习和优化，以求得较优的调度和分配方案。

另一种解决方案是采用预测模型进行任务调度和资源分配。

SPH方法并行化解决方案

SPH方法并行化解决方案背景介绍：SPH（Smoothed Particle Hydrodynamics）方法是一种基于粒子的数值摹拟方法，广泛应用于流体力学、固体力学、天体物理学等领域。

然而，由于SPH方法的计算复杂度较高，对大规模问题的求解效率较低。

因此，为了提高SPH方法的计算效率，需要将其并行化处理。

解决方案：SPH方法的并行化解决方案可以分为以下几个步骤：1. 网格划分：将计算域划分为多个网格，每一个网格负责一部份粒子的计算。

网格划分可以采用空间划分方法，如二叉树划分、四叉树划分等。

划分后，每一个网格内的粒子可以并行计算。

2. 粒子排序：对每一个网格内的粒子进行排序，使得相邻的粒子在内存中连续存储。

这样可以提高访问内存的效率，减少数据的读取时间。

3. 粒子间相互作用计算：根据SPH方法的核函数，计算每一个粒子与其相邻粒子之间的相互作用力。

由于每一个粒子的相互作用力只与其相邻粒子有关，因此可以将计算任务划分为多个子任务，每一个子任务负责计算一部份粒子的相互作用力。

这样可以实现粒子间的并行计算。

4. 数据通信：由于粒子的相互作用力需要考虑相邻粒子的影响，因此需要进行数据通信。

可以采用消息传递接口（MPI）等并行编程工具，将每一个网格内的粒子信息传递给相邻网格。

5. 结果合并：将各个网格内的计算结果进行合并，得到整体的SPH方法求解结果。

优势和效果评估：通过将SPH方法并行化处理，可以显著提高计算效率，缩短计算时间。

并行化处理可以充分利用多核处理器和分布式计算资源，使得大规模问题的求解成为可能。

此外，由于并行化处理可以减少数据的读取时间和通信开消，还可以降低计算资源的消耗。

为了评估并行化解决方案的效果，可以进行以下实验和测试：1. 对照串行计算和并行计算的计算时间，以评估并行化处理的加速比。

2. 针对不同规模的问题，比较并行化处理的计算时间和计算资源的消耗情况。

3. 分析并行化处理中数据通信的开消，以评估并行化方案的可扩展性。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

计算资源上执行的调度串７孓幽，它是任务ＤＡＧ图的一个拓扑排序．是将ＤＡＧ中所有任务顶点排
成一个线性序列，使得图中任意一对顶点ｆ．和ｏ，若存在边（‘，ｆ，）．则，Ⅳ在线性序列巾出现在，，
之前。乃曲仍为一个Ｊ维整数向量，其中ｍ＾（七）＝ｊ表示任务ｆ』是调度串中的第足个任务，该串
主要表一：分配到同一个计算资源的任务的执行顺序。下面给出图ｌ中ＤＡＧ的一个染色体的例子（如图２所乃÷），图ｌ中任务集为７＇＝（，ｏ，ｆＩ，，２，＾，ｆ．），令计算资源集合为Ｃ＝‰，ｃＩ，巳｝，非计算资源
（１）
网格资源匹配到任务的目标是使得任务的整体调度执行时间（ｍａｋｅｓｐａｎ）最短。假设ｆ个任务映射到一个计算资源ｑｔ其中首先开始执行的任务为，』，最后执行的任务为７』，那么ｑ上任务的整
体执行时间为ｃＤ叩（ｏ，ｃ，）一跏一（ｆｆ，ｃ，）。系统中共有以个计算资源，令最大时间跨度为：
‰＝ｍ舣｛（ｃＤ叩（ｏ，ｃＪ）一＆酬（‘，ｃ，）），，＝１’２，…，刀｝
Ａｃｙｃｌｉｃ
Ｇｒ印ｈ，ＤＡＧ）来模拟（如图ｌ所
嘲Ｉ任务的ＤＡＧ
示），其中节点表示任务，边ｈ，ｆ．１表示执行先后关系，边上的值表示数据传
输。另外。称，．为，．的直接前驱任务，称ｆ，为，ｉ的直接后继任务。用一个矩阵以ｊ・疗）来表示任务在每个计算资源上的估计执行时间，资源问的通讯代价用矩阵ｃ（门・（，，＋脚））米表示。另外，这里规定任务的执行是一个原子事件，即一个任务在得到了它所需的全部资源后才开始执行。下面定义一些文中需要用的参数。
（两个串的分法相同），再从三段中随机地选取一段在两个串之间进行交换，形成新踟口ｆ串
（尺＿『，ｌ口ｒ串）。调度串的交叉是这样操作的：对于两个任务调度串随机选择一个分割点（对两个串是相同的）将两个串分成前后两部分，然后将后面部分中的任务重新排序，使得一个调度串中重排序的任务是这些任务在另一个串中的原始排列（如图３所示）。这样做的目的是保证调度串的合法性，使它仍为任务ＤＡＧ的一个拓扑排序。
最优适应度
６．７５．９６．９
并行出现的代数时间ຫໍສະໝຸດ 分）４０＿一５
４５。一６
５０６
＿——
６结束语
网格资源分配是网格中间件需要解决的关键问题，随着资源与任务数量的增加，问题的规模将以指数级增长，因此需要研究更为高效的资源分配算法。本文提出了一种基于并行遗传算法的资源分配算法，通过实验证明该并行的方法极大地提高了算法求解的质量与速度，是一种有效的网格资源分配方法，有利于提高网格的服务质量．
集合为尺＝｛％，‘，厂’，气｝。
Ｉ１２
一－熙黼
３．２适应度计算
跏帆
，—１嚣：ｌ
ｐｎｂｍ吣坛
剐删删
叫瑟赫善
圈２圉ｌ中ＤＡＧ的三个染色体
用（１）式中ｋ的倒数ｚ＝％ｍ作为染色体的适应度，这样‰越小适应度越大，所对应解，‘Ｍ‘、’，
的质量越高。为了避免适应度值太小而不容易比较，将其扩大１００倍．得到ｚ＝ｌｏ％，，、。／’Ⅻ、’，
１引言
目前．网格计算（ＧｒｉｄＣｏｍｐｕｔｉｎｇ）已成为高性能计算发展的主要趋势。由于网格中集成资源的异构性、分布性和自治性等特点，需要网格中间件来屏蔽这些特性，从而为人们提供透明的服务。其中，首要解决的关键问题就是资源分配问题。简单地说．网格资源分配就是将力个独立的任务映射到历个异构的可用资源上，使得任务完成的总时间最小并使资源的利用率最高。很显然．将在空间大小为２。的资源集合上寻找满足目标的最优资源集合，因此这是一个ＮＰ问题。人们通常利用启发式算法来简化问题并寻求问题的最优解，但多数这类算法通常都难以避免局部最小值问题。遗传算法作为一种最有效的启发式全局随机搜索算法，对于ＮＰ问题能够得到满意的结果。
ａ
ＮｅｗＣｏｍｐｕｔｉｎｇＩｎｆｈｓｔｒｕｃｔｕ他．Ｍｏｒｇ柚Ｋａｕｆｍ锄ｎ．Ｓ锄
现。
３．１染色体的设计在遗传算法的应用中。首要工作是设计问题解的编码方式，即染色体表示。可以用二：迸制、整数和实数变量等表示问题的编码，文中采用整数形式。在文中，任务和资源都用他们的序号来
表示，染色体采用与文献【５】相类似的方法，包括三部分。一部分是计算资源匹配串锄口，，这是
一个５维整数向量，其中ｃｍ口ｆ（ｆ）＝＿，表示为任务，』分配计算资源ｃ，：第二部分是非计算资源的匹配串尺研讲．同样为５维整数向量，尺所口ｆ（ｆ）＝－，表示为任务‘分配计算资源‘；第三部分是任务在
图４并行遗传算法的执行流程
５实验结果
为了评估该并行遗传算法的性能．本文在由８台微机（Ｐｅｎｄｉｕｍ１．７Ｇ）构成的集群上实现了该并行遗传算法和柏应的串行遗传算法。并对不同规模资源与任务的情况进行了测试，计算结果如表ｌ所示．其巾ＩＣ删、ＩＭ孙Ｉ和ｌ７１分别表示计算资源的数目、非计算资源的数目和任务数目。从比较结果可以看出，在得到相同质量的解的情况下，并行算法比串行算法大大减少了寻优时间，特别足
１１４
在问题规模很大时。相对于串行算法．在进化同样的代数时，并行算法能够抉得质景更高的解。这些主要得益于并行算法子种群问的相互隔离保持了算法的多样性，算法的迁移增强了子种群的适应能力，所以使其具有出色的效率。
竺竺二卫垂［二二星墨＆．．竺竺二二！二二兰兰茎主
表１实验计算结果
。４，
。
串行拦筹｝｝—等
３．３遗传算子
本文采用赌轮选择机制，令∑彳表示群体的适应度值之总和，Ｚ表示种群中第ｆ个染色
体的适应度值，它产生后代的能力正好为其适应度值所占份额馁，。，厶Ｊｔ
交叉操作采取两种策略；即对于资源分配串（ｏ打口ｒ和胁口ｆ）和任务调度串（乃拍）交叉是不同
的。对于资源匹配串交叉操作这样进行：将两个被选出的Ｃ珈ｃｌｆ串（尺掰厦串），都随机地分成三段
在参考文献［５】中将遗传算法应用于异质计算环境中的任务匹配和调度，但采用串行的方法。考虑
到遗传算法的天然并行性，并结合网格资源分配的特点，本文提出了基于并行遗传算法的网格资源分配方法。通过实验表明，本文提出的方法是可行的，提高了资源分配速度和求解的质量。
２问题定义
这里讨论的资源分配是静态的．即网格中资源和任务的信息是事先已知的，。而且提交到叫格中的应用己被分解成多个任务。本文将网格系统中的资源分为两组：计算资源和非计算资源。计算资源如高性能计算平台、工作站、ＰＣ机等；非计算资源如分布式并行存储服务器、数据仓库、文件服务器等。用集合Ｃ＝｛ｃＩ，ｃ２．．．．，乞｝表示丹个计算资源．用尺＝“，乞，．．．，‘）表示历个非计算资源，现有的ｓ个任务用７’＝“，ｒ２，．．．，ｆ．｝来表示，任务之间存在执行顺序关系和数据传输，这可以用有向无环图（Ｄｉｒｅｃｔｅｄ
４并行遗传算法的设计
并行遗传算法可以克服经典遗传算法的不足，从而提高遗传算法的求解速度和质景。目前。并行遗传算法主要存在主从式、粗粒度和细粒度的并行化模型。粗粒度模犁又称分布式模型（ＤｉｓｔｒｉｂｕｔｅｄＳｔｙｌｅ）或孤岛模型（ＩｓＩａｎｄ－ｂａｓｅｄＭｏｄｅｌ）．是适应性最强和应用最Ｊ“的遗传算法并行化模型。粗粒度模犁足将随机生成的初始群体依处理器个数分割成若干个子群体。各个子群体在不同的处理器上柏互独立的并发执行。每经过～定的进化代，各子群体刚会交换若干个体以引入其他
参考文献：
【１１【２】【３】Ｉ锄Ｆｏｓｔｅｒ＇Ｃ州Ｋｅｓｓｅｌｍ卸．Ｔｈｃ
Ｆ甩ｎｃｉｓｃｏ．１９９９ＳｉｈＧＣ，Ｌ＿ｅｅＥＡ．Ａｃｏｍｐｉｌｅ．ｔｉｍｅｓｃｈｅｄｕｌｉｎｇｈ叫ｒｉｓｔｉｃｆｏｒｉｎｔｅｒｃｏ仰ｅｃｔｉｏｎ－ｃｏｎｓｔｒａｉｎｅｄｈｅｔｅｍｇ∞ｅｏｕｓｐｒｏｃｅｓｓｏｒ盯ｃｈｉｔｅｃｔｕｒｅｓ．ＩＥＥＥＴｒａｎｓａｃｔｉｏｎｓｏｎＰ赳－ａｌｌｅＩ柚ｄＤｉｓ仃ｉｂｕｔｅｄＳｙｓｔｅｍｓ。１９９３。４（２】：１７５．１８７ＨＪ．Ａｄｙｎａｆｎｉｃｍａｔｃｈｉｎｇ柚ｄ∞ｈｅｄｕｌｉｎｇａｌｇｏｒｉｔｈｍｆｏｒｈｅｔｅｒｏｇｅｎｅｏｕｓｃｏｍｐｕｔｉｎｇｓｙｓｔｅｍｓ．Ｉｎ：ＪｏｈｎＫ，ｅｄ．Ａｎｔｏｎｌｏ．７ｔｈＩＥＥＥＨｅｔｅｍｇｅｎｅ叫ｓＣｏｍＤｕｔｉｎ２Ｗｏｒｌｃｓｈｏｐ（ＨＣＷ’９８）．ＬｏｓＣａＩｉｆｏｍｉａ：ＩＥＥＥＣｏｍｐｕｔｃｒＳｏｃｉｅｔｙＰｒｅｓｓ．１９９８：５７．６９ＡｌｈｕｓａｉｎｉＧｒｉｄ：Ｂｌｕｅｐｒｉｎｔｆｏｒ
【乃幽２：目炒）｛篡鹭毡蓦一｛焉搦粥
前部后部
图３任务调度串交又操作的例子
‘ｌ乃幽２：｛２，ｏ，ｌ，４，３）
变异操作对资源分配串（Ｃ所口，和尺用口ｆ）和任务调度串（拈幽）也是不同的。对于资源分配串变异操作较简单，即从选择的资源分配串中随机地选取一个资源，然后变成任意一个同类型的其他资源。调度串的变异操作首先随机地选择一个任务，然后确定该任务的合法变化范围。这里合法变化范围指的是在拓扑排序中该任务的所有直接前趋任务之后和所有直接后继任务之前的位置。经过变异操作，该任务被随机地移动到合法范围内的其他位置。当然对于染色体的交叉操作和变异操作是以一定概率进行的，本文的算法中交叉概率取０．６。变异概率取０．２，可以得到较好的性能。
・￡（ｆｊ，ｃ，）：任务‘在计算资源ｑ上的估计执行时间。
Ｅｆ‘，ｃ．）的值被定义为无穷大．・＆口厂，（‘，ｃ．）：任务‘在计算资源ｃ，上的最早开始时间。
如果任务‘不能在ｃ，上执行．
・ｃＤ唧Ｉ‘，ｃ．）：任务‘在计算资源ｃ，上的最早完成时间。它被定义为：
ｃＤ，，妒“，勺）＝＆口，ｆ＠，巳）＋Ｅ“，巳）
因此目标函数为ｍｉｎ｛‰）・
３染色体及遗传算子的设计
‘２’
遗传算法是一个很有价值随机优化的搜索算法．它从一组初始解出发，除了目标函数值，在不需要其他信息的情况下就可以实现对可行域的全局高效搜索，这种良好的特性使遗传算法成为组合优化和函数优化的有效工具。遗传算法操作的是一群编码化的可行解，称为种群。它通过种群的更新与迭代来搜索全局最优解，而迭代由选择、交叉和变异等具有生物意义的遗传算子来实