北师大版九年级数学上册第一章测试题及答案证明(二)(B).doc

合集下载

北师大版数学九年级上册课本答案

北师大版数学九年级上册课本答案【篇一：北师版九年级数学上册第一章测试卷(含答案)】卷满分120分考试时间120分钟）一、选择题（共10小题，每小题3分，计30分）1、下列各组图形中，是全等三角形的一组是（）a.底边长都为15cm的两个等腰三角形b.腰长都为15cm的两个等腰三角形d.边长为12cm的两个等边三角形2、等腰三角形的周长为13，其中一边长为3，则该等腰三角形的底边长为（）a.7b.3c.7或3d.53、一个三角形如果有两边的垂直平分线的交点在第三边上，那么这个三角形是（）a.等腰三角形b.等边三角形c.直角三角形d.等腰直角三角形4、用反证法证明命题“一个三角形中不能有两个角是直角”，应先假设这个三角形中（）a.有两个角是直角b.有两个角是钝角c.有两个角是锐角d.一个角是钝角，一个角是直角6、如图1-2，在一次强台风中一棵大树在离地面5m处折断倒下，倒a.10mb.15mc.25md.30mcba d 图1-1图1-27、下列命题①对顶角相等②如果三角形中有一个角是钝角，那么另外两个角是锐角③若两直线平行，则内错角相等④三边都相等的三角形是等边三角形。

其中逆命题正确的有（）a.①③b.②④c.①②d.③④8、如图1-3（1）在△abc中，d、e分别是ab,ac的中点，将△ade沿线段de向下折叠，得到图形1-3（2），下列关于图（2）的四个结论中，一定不成立的是（）c.△dba是等腰三角形d.de∥bce c 图1-3 b c （2）（1） aa.1b.2c.3d.4be aa c图1-4图1-5二、填空题（共6小题，每小题3分，计18分）11、已知三条不同的直线a,b,c在同一平面内，下列四个命题：①如果③如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c 其中属于真命题的是（填写所有真命题的序号）12、一个三角形三边之比为2:5:3，这个三角形的形状是13、把“同角的余交相等”改写成“如果??，那么??”的形式为cd=3，则ab的长度为15、如图1-7，p是正方形abcd内一点，将△abp绕点b顺时针方向旋转能与△cbp?重合，若pb=3，则pp?的长度为a p dbd b cc n c a b ?图1-6 图1-7图1-8三、解答题（共6小题，计72分，解答应写过程）ad图1-918、（10分）已知：如图1-10，de为△abc的边ab的垂直平分线，m d cd为△abc的外角平分线，与de交于点d，dm⊥bc的延长线于点m，dn⊥ac于点n，求证：an=bm。

第一章特殊的平行四边形复习测试 2021-2022学年北师大版九年级数学上册(word含答案)

北师大版九年级数学上册第一章特殊的平行四边形复习测试一．选择题1．对角线互相垂直平分的四边形是（）A．平行四边形B．菱形C．矩形D．任意四边形2．如图，剪两张对边平行且宽度相同的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（）A．∠ABC＝∠ADC，∠BAD＝∠BCD B．AB＝BCC．AB＝CD，AD＝BC D．∠DAB+∠BCD＝180°3．下列关于∠ABCD的叙述，正确的是（）A．若AB∠BC，则∠ABCD是菱形B．若AC＝BD，则∠ABCD是矩形C．若AC平分∠BAD，则∠ABCD是正方形D．若AC∠BD，则∠ABCD是正方形4．如图，四边形ABCD为平行四边形，延长AD到E，使DE＝AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）A．AB＝BE B．CE∠DE C．∠ADB＝90°D．BE∠DC5．如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′与DC相交于点E，则下列结论一定正确的是（）A．∠DAB′＝∠CAB′ B．∠ACD＝∠B′CD C．AD＝AE D．AE＝CE 6．菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF＝，BD＝2，则菱形ABCD的面积为（）A．2B．C．6D．87．如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠CBF为（）A．75°B．60°C．55°D．45°8．如图，在菱形ABCD中，AC＝8，BD＝6，则∠ABC的周长是（）A．14B．16C．18D．209．若顺次连接四边形ABCD四边的中点，得到的图形是一个矩形，则四边形ABCD 一定是（）A．矩形B．菱形C．对角线相等的四边形D．对角线互相垂直的四边形10．如图，在正方形ABCD中，∠ABE和∠CDF为直角三角形，∠AEB＝∠CFD ＝90°，AE＝CF＝5，BE＝DF＝12，则EF的长是（）A．7B．8C．7D．711．如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，连接OE．若OE＝3，则菱形ABCD的周长是（）A．6B．12C．18D．2412．如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE∠BD，垂足为点E，若∠EAC＝2∠CAD，则∠BAE＝（）A．60°B．45°C．30°D．22.5°二．填空题13．如图，在Rt∠ABC中，E是斜边AB的中点，若AC＝8，BC＝6，则CE＝．14．如图，在平行四边形ABCD中，延长AD到点E，使DE＝AD，连接EB，EC，DB请你添加一个条件，使四边形DBCE是矩形．15．如图，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD 上移动，则PE+PC的最小值是．16．如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF ＝20°，则∠AED等于度．17．如图，在四边形ABCD中，AC=BD=6，E，F，G，H分别为AB，BC，CD，DA的中点，连接EG，HF交于点O．则EG2+FH2=．18．已知，如图，∠MON＝45°，OA1＝1，作正方形A1B1C1A2，周长记作C1；再作第二个正方形A2B2C2A3，周长记作C2；继续作第三个正方形A3B3C3A4，周长记作C3；点A1、A2、A3、A4…在射线ON上，点B1、B2、B3、B4…在射线OM上，…依此类推，则第n个正方形的周长Cn＝___ ．三．解答题19．如图，在菱形ABCD中，CE＝CF．求证：AE＝AF．20．如图，将∠ABCD的边AB延长至点E，使AB＝BE，连接DE，EC，DE交BC于点O．（1）求证：∠ABD∠∠BEC；（2）连接BD，若∠BOD＝2∠A，求证：四边形BECD是矩形．21．已知：如图，在∠ABCD中，E，F分别是边AD，BC上的点，且AE＝CF，直线EF分别交BA的延长线、DC的延长线于点G，H，交BD于点O．（1）求证：∠ABE∠∠CDF；（2）连接DG，若DG＝BG，则四边形BEDF是什么特殊四边形？请说明理由．22．如图，在菱形ABCD中，对角线AC与BD相交于点O，MN过点O且与边AD、BC分别交于点M和点N．（1）请你判断OM和ON的数量关系，并说明理由；（2）过点D作DE∠AC交BC的延长线于点E，当AB＝6，AC＝8时，求∠BDE 的周长．23．如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF＝45°，将∠ADF绕点A顺时针旋转90°后，得到∠ABQ，连接EQ，求证：（1）EA是∠QED的平分线；（2）EF2＝BE2+DF2．24．如图，平行四边形ABCD中，AB＝3cm，BC＝5cm，∠B＝60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．（1）求证：四边形CEDF是平行四边形；（2）∠当AE＝cm时，四边形CEDF是矩形；∠当AE＝cm时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）25．在正方形ABCD中，E是边CD上一点（点E不与点C、D重合），连接BE．【感知】如图∠，过点A作AF∠BE交BC于点F．易证∠ABF∠∠BCE．（不需要证明）【探究】如图∠，取BE的中点M，过点M作FG∠BE交BC于点F，交AD于点G．（1）求证：BE＝FG．（2）连接CM，若CM＝1，则FG的长为．【应用】如图∠，取BE的中点M，连接CM．过点C作CG∠BE交AD于点G，连接EG、MG．若CM＝3，则四边形GMCE的面积为．北师大版九年级数学上册第一章特殊的平行四边形复习测试答案提示一．选择题1．对角线互相垂直平分的四边形是（）选：B．A．平行四边形B．菱形C．矩形D．任意四边形2．如图，剪两张对边平行且宽度相同的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（）选：D．A．∠ABC＝∠ADC，∠BAD＝∠BCD B．AB＝BCC．AB＝CD，AD＝BC D．∠DAB+∠BCD＝180°3．下列关于∠ABCD的叙述，正确的是（）选：B．A．若AB∠BC，则∠ABCD是菱形B．若AC＝BD，则∠ABCD是矩形C．若AC平分∠BAD，则∠ABCD是正方形D．若AC∠BD，则∠ABCD是正方形4．如图，四边形ABCD为平行四边形，延长AD到E，使DE＝AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）选：D．A．AB＝BE B．CE∠DE C．∠ADB＝90°D．BE∠DC5．如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′与DC相交于点E，则下列结论一定正确的是（）选：D．A．∠DAB′＝∠CAB′B．∠ACD＝∠B′CDC．AD＝AE D．AE＝CE6．菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF＝，BD＝2，则菱形ABCD的面积为（）选：A．A．2B．C．6D．87．如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠CBF为（）选：A．A．75°B．60°C．55°D．45°8．如图，在菱形ABCD中，AC＝8，BD＝6，则∠ABC的周长是（）选：C．A．14B．16C．18D．209．若顺次连接四边形ABCD四边的中点，得到的图形是一个矩形，则四边形ABCD 一定是（）选：D．A．矩形B．菱形C．对角线相等的四边形D．对角线互相垂直的四边形10．如图，在正方形ABCD中，∠ABE和∠CDF为直角三角形，∠AEB＝∠CFD ＝90°，AE＝CF＝5，BE＝DF＝12，则EF的长是（）选：C．A．7B．8C．7D．7解：如图所示：∠四边形ABCD是正方形，∠∠BAD＝∠ABC＝∠BCD＝∠ADC＝90°，AB＝BC＝CD＝AD，∠∠BAE+∠DAG＝90°，在∠ABE和∠CDF中，，∠∠ABE∠∠CDF（SSS），∠∠ABE＝∠CDF，∠∠AEB＝∠CFD＝90°，∠∠ABE+∠BAE＝90°，∠∠ABE＝∠DAG＝∠CDF，同理：∠ABE＝∠DAG＝∠CDF＝∠BCH，∠∠DAG+∠ADG＝∠CDF+∠ADG＝90°，即∠DGA＝90°，同理：∠CHB＝90°，在∠ABE和∠ADG中，，∠∠ABE∠∠ADG（AAS），∠AE＝DG，BE＝AG，同理：AE＝DG＝CF＝BH＝5，BE＝AG＝DF＝CH＝12，∠EG＝GF＝FH＝EF＝12﹣5＝7，∠∠GEH＝180°﹣90°＝90°，∠四边形EGFH是正方形，∠EF＝EG＝7；11．如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，连接OE．若OE＝3，则菱形ABCD的周长是（）选：D．A．6B．12C．18D．2412．如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE∠BD，垂足为点E，若∠EAC＝2∠CAD，则∠BAE＝（）选：D．A．60°B．45°C．30°D．22.5°二．填空题13．如图，在Rt∠ABC中，E是斜边AB的中点，若AC＝8，BC＝6，则CE＝5．14．如图，在平行四边形ABCD中，延长AD到点E，使DE＝AD，连接EB，EC，DB请你添加一个条件EB＝DC，使四边形DBCE是矩形．15．如图，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD 上移动，则PE+PC的最小值是．16．如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF ＝20°，则∠AED等于65度．17．如图，在四边形ABCD中，AC=BD=6，E，F，G，H分别为AB，BC，CD，DA的中点，连接EG，HF交于点O．则EG2+FH2=．答案36解析连接EF，FG，GH，HE，∠点E，F，G，H分别是AB，BC，CD，DA的中点，AC=3，∠EF∠AC∠GH，EF=GH=12BD=3，EH∠BD∠FG，EH=FG=12∠EF=FG=GH=EH，∠四边形EFGH是菱形．∠EG∠FH，OE=OG，OH=OF．∠EG2+FH2=(2OE)2+(2OH)2=4OE2+4OH2=4(OE2+OH2)=4EH2=36．18．已知，如图，∠MON＝45°，OA1＝1，作正方形A1B1C1A2，周长记作C1；再作第二个正方形A2B2C2A3，周长记作C2；继续作第三个正方形A3B3C3A4，周长记作C3；点A1、A2、A3、A4…在射线ON上，点B1、B2、B3、B4…在射线OM上，…依此类推，则第n个正方形的周长Cn＝__2n＋1__．三．解答题19．如图，在菱形ABCD中，CE＝CF．求证：AE＝AF．证明：如图，连接AC，∠四边形ABCD是菱形，∠∠BCA＝∠DCA，∠CE＝CF，AC＝AC，∠∠ECA∠∠FCA（SAS），∠AE＝AF．20．如图，将∠ABCD的边AB延长至点E，使AB＝BE，连接DE，EC，DE交BC于点O．（1）求证：∠ABD∠∠BEC；（2）连接BD，若∠BOD＝2∠A，求证：四边形BECD是矩形．证明：（1）在平行四边形ABCD中，AD＝BC，AB＝CD，AB∠CD，则BE∠CD．又∠AB＝BE，∠BE＝DC，∠四边形BECD为平行四边形，∠BD＝EC．∠在∠ABD与∠BEC中，，∠∠ABD∠∠BEC（SSS）；（2）由（1）知，四边形BECD为平行四边形，则OD＝OE，OC＝OB．∠四边形ABCD为平行四边形，∠∠A＝∠BCD，即∠A＝∠OCD．又∠∠BOD＝2∠A，∠BOD＝∠OCD+∠ODC，∠∠OCD＝∠ODC，∠OC＝OD，∠OC+OB＝OD+OE，即BC＝ED，∠平行四边形BECD为矩形．21．已知：如图，在∠ABCD中，E，F分别是边AD，BC上的点，且AE＝CF，直线EF分别交BA的延长线、DC的延长线于点G，H，交BD于点O．（1）求证：∠ABE∠∠CDF；（2）连接DG，若DG＝BG，则四边形BEDF是什么特殊四边形？请说明理由．（1）证明：∠四边形ABCD是平行四边形，∠AB＝CD，∠BAE＝∠DCF，在∠ABE和∠CDF中，，∠∠ABE∠∠CDF（SAS）；（2）解：四边形BEDF是菱形；理由如下：如图所示：∠四边形ABCD是平行四边形，∠AD∠BC，AD＝BC，∠AE＝CF，∠DE＝BF，∠四边形BEDF是平行四边形，∠OB＝OD，∠DG＝BG，∠EF∠BD，∠四边形BEDF是菱形．22．如图，在菱形ABCD中，对角线AC与BD相交于点O，MN过点O且与边AD、BC分别交于点M和点N．（1）请你判断OM和ON的数量关系，并说明理由；（2）过点D作DE∠AC交BC的延长线于点E，当AB＝6，AC＝8时，求∠BDE 的周长．解：（1）∠四边形ABCD是菱形，∠AD∠BC，AO＝OC，∠，∠OM＝ON．（2）∠四边形ABCD是菱形，∠AC∠BD，AD＝BC＝AB＝6，∠BO＝＝2，∠，∠DE∠AC，AD∠CE，∠四边形ACED是平行四边形，∠DE＝AC＝8，∠∠BDE的周长是：BD+DE+BE＝BD+AC+（BC+CE）＝4+8+（6+6）＝20即∠BDE的周长是20．23．如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF＝45°，将∠ADF绕点A顺时针旋转90°后，得到∠ABQ，连接EQ，求证：（1）EA是∠QED的平分线；（2）EF2＝BE2+DF2．证明：（1）∠将∠ADF绕点A顺时针旋转90°后，得到∠ABQ，∠QB＝DF，AQ＝AF，∠BAQ＝∠DAF，∠∠EAF＝45°，∠∠DAF+∠BAE＝45°，∠∠QAE＝45°，∠∠QAE＝∠F AE，在∠AQE和∠AFE中，∠∠AQE∠∠AFE（SAS），∠∠AEQ＝∠AEF，∠EA是∠QED的平分线；（2）由（1）得∠AQE∠∠AFE，∠QE＝EF，由旋转的性质，得∠ABQ＝∠ADF，∠ADF+∠ABD＝90°，则∠QBE＝∠ABQ+∠ABD＝90°，在Rt∠QBE中，QB2+BE2＝QE2，又∠QB＝DF，∠EF2＝BE2+DF2．24．如图，平行四边形ABCD中，AB＝3cm，BC＝5cm，∠B＝60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．（1）求证：四边形CEDF是平行四边形；（2）∠当AE＝ 3.5cm时，四边形CEDF是矩形；∠当AE＝2cm时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）（1）证明：∠四边形ABCD是平行四边形，∠CF∠ED，∠∠FCG＝∠EDG，∠G是CD的中点，∠CG＝DG，在∠FCG和∠EDG中，，∠∠FCG∠∠EDG（ASA）∠FG＝EG，∠CG＝DG，∠四边形CEDF是平行四边形；（2）∠解：当AE＝3.5时，平行四边形CEDF是矩形，理由是：过A作AM∠BC于M，∠∠B＝60°，AB＝3，∠BM＝1.5，∠四边形ABCD是平行四边形，∠∠CDA＝∠B＝60°，DC＝AB＝3，BC＝AD＝5，∠AE＝3.5，∠DE＝1.5＝BM，在∠MBA和∠EDC中，，∠∠MBA∠∠EDC（SAS），∠∠CED＝∠AMB＝90°，∠四边形CEDF是平行四边形，∠四边形CEDF是矩形，故答案为：3.5；∠当AE＝2时，四边形CEDF是菱形，理由是：∠AD＝5，AE＝2，∠DE＝3，∠CD＝3，∠CDE＝60°，∠∠CDE是等边三角形，∠CE＝DE，∠四边形CEDF是平行四边形，∠四边形CEDF是菱形，故答案为：2．25．在正方形ABCD中，E是边CD上一点（点E不与点C、D重合），连接BE．【感知】如图∠，过点A作AF∠BE交BC于点F．易证∠ABF∠∠BCE．（不需要证明）【探究】如图∠，取BE的中点M，过点M作FG∠BE交BC于点F，交AD于点G．（1）求证：BE＝FG．（2）连接CM，若CM＝1，则FG的长为2．【应用】如图∠，取BE的中点M，连接CM．过点C作CG∠BE交AD于点G，连接EG、MG．若CM＝3，则四边形GMCE的面积为9．解：感知：∠四边形ABCD是正方形，∠AB＝BC，∠BCE＝∠ABC＝90°，∠∠ABE+∠CBE＝90°，∠AF∠BE，∠∠ABE+∠BAF＝90°，∠∠BAF＝∠CBE，在∠ABF和∠BCE中，，∠∠ABF∠∠BCE（ASA）；探究：（1）如图∠，过点G作GP∠BC于P，∠四边形ABCD是正方形，∠AB＝BC，∠A＝∠ABC＝90°，∠四边形ABPG是矩形，∠PG＝AB，∠PG＝BC，同感知的方法得，∠PGF＝∠CBE，在∠PGF和∠CBE中，，∠∠PGF∠∠CBE（ASA），∠BE＝FG，（2）由（1）知，FG＝BE，连接CM，∠∠BCE＝90°，点M是BE的中点，∠BE＝2CM＝2，∠FG＝2，故答案为：2．应用：同探究（2）得，BE＝2ME＝2CM＝6，∠ME＝3，同探究（1）得，CG＝BE＝6，∠BE∠CG，∠S四边形CEGM＝CG×ME＝×6×3＝9，故答案为9．。

北师大版九年级数学上册-第一章-特殊的平行四边形-单元测试题(有答案)

九年级数学上册第一章特殊的平行四边形单元测试题班级：姓名：成绩：一．选择题（共10小题，每小题3分，共30分）1．下列属于菱形性质的是（）A．对角线相等 B．对角线互相垂直C．对角互补 D．四个角都是直角2．如图，AC＝AD，BC＝BD，则正确的结论是（）A．AB 垂直平分CD B．CD垂直平分ABC．AB与CD互相垂直平分D．四边形ABCD是菱形3．如图，四边形ABCD的对角线相交于点O，且点O是BD的中点，若AB＝AD＝5，BD＝8，∠ABD＝∠CDB，则四边形ABCD的面积为（）A．40 B．24 C．20 D．154．如图，O为矩形ABCD的对角线AC的中点，过点O作AC的垂线EF分别交AD、BC于点E、F，连结CE．若该矩形的周长为20，则△CDE的周长为（）A．10 B．9 C．8 D．55．如图，在▱ABCD中，对角线AC与BD 交于点O，添加下列条件不能判定▱ABCD为矩形的只有（）A．AC＝BD B．AB＝6，BC＝8，AC＝10 C．AC⊥BD D．∠1＝∠26．如图，在▱ABCD中，对角线AC、BD相交于点O，且OA＝OD，∠OAD＝55°，则∠OAB的度数为（）A．35°B．40°C．45°D．50°7．如图，在正方形ABCD中，分别以点B，C为圆心，BC长为半径画弧，两弧相交于点E，连接AE，BE得到△ABE，则△ABE与正方形ABCD的面积比为（）A．1：2 B．1：3 C．1：4 D．8．已知四边形ABCD中，∠A＝∠B＝∠C＝90°，如添加一个条件，使得该四边形成为正方形，那么所添加的这个条件可以是（）A．∠D＝90°B．AB＝CD C．AB＝BC D．AC＝BD9．如图，在平面直角坐标系中，菱形ABCD的边长为6，它的一边AB在x轴上，且AB的中点是坐标原点，点D在y轴正半轴上，则点C的坐标为（）A．（3，3）B．（3，3）C．（6，3）D．（6，3）二．填空题（共8小题，每小题3分，共24分）10．矩形（非正方形）四个内角的平分线围成的四边形是形．（填特殊四边形）11．如图，E是菱形ABCD的对角线BD上一点，过点E作EF⊥BC于点F．若EF ＝4，则点E到边AB的距离为．12．在菱形ABCD中，AC＝12cm，若菱形ABCD的面积是96cm2，则AB＝．13．如图，矩形ABCD的对角线AC与BD相交点O，∠AOB＝60°，AB＝10，E、F 分别为AO、AD的中点，则EF的长是．14．如图，四边形ABCD是正方形，延长AB到点E，使AE＝AC，则∠BCE的度数是．15．如图，菱形ABCD的周长是20，对角线AC、BD相交于点O．若BO＝3，则菱形ABCD的面积为．16．已知：如图，在长方形ABCD中，AB＝2，AD＝3．延长BC到点E，使CE＝1，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为时，△ABP和△DCE全等．17．如图，在正方形ABCD和正方形CEFG中，BC＝1，CE＝3，点D是CG边上一点，H是AF 的中点，那么CH的长是．三．解答题（共7小题，共66分）18．已知：如图所示，菱形ABCD中，DE⊥AB于点E，且E为AB的中点，已知BD＝4，求菱形ABCD的周长和面积．19．如图，已知四边形ABCD是平行四边形，AE⊥BC，AF⊥DC，垂足分别是E，F，并且BE ＝DF．求证；四边形ABCD是菱形．20．如图，在矩形ABCD中，AE⊥BD于点E，∠DAE＝2∠BAE，求∠EAC的度数．21．如图，在四边形ABCD中，AD∥BC，∠D＝90°，E为边BC上一点，且EC＝AD，连结AC．（1）求证：四边形AECD是矩形；（2）若AC平分∠DAB，AB＝5，EC＝2，求AE的长，22．如图，在边长12的正方形ABCD中，点E是CD的中点，点F在边AD上，且AF＝3DF，连接BE，BF，EF，请判断△BEF的形状，并说明理由．23．如图，正方形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC．（1）求证：四边形OCED是正方形．（2）若AC ＝，则点E到边AB 的距离为．24．如图，已知四边形ABCD为正方形，AB＝4，点E为对角线AC上一动点，连接DE、过点E作EF⊥DE．交BC点F，以DE、EF为邻边作矩形DEFC，连接CG．（1）求证：矩形DEFG是正方形；（2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．参考答案一．选择题1．解：A、菱形的对角线互相垂直，但不一定相等，故原命题错误，不符合题意；B、菱形的对角线互相垂直，故原命题正确，符合题意；C、菱形的对角相等，故原命题错误，不符合题意；D、矩形的四个角都是直角，菱形不一定是，故原命题错误，不符合题意，故选：B．2．解：∵AC＝AD，BC＝BD，∴AB垂直平分CD，故选：A．3．解：∵AB＝AD，点O是BD的中点，∴AC⊥BD，∠BAO＝∠DAO，∵∠ABD＝∠CDB，∴AB∥CD，∴∠BAC＝∠ACD，∴∠DAC＝∠ACD，∴AD＝CD，∴AB＝CD，∴四边形ABCD是菱形，∵AB＝5，BO ＝BD＝4，∴AO＝3，∴AC＝2AO＝6，∴四边形ABCD 的面积＝×6×8＝24，故选：B．4．解：∵O为矩形ABCD的对角线AC的中点，∴AO＝OC，∵过点O作AC的垂线EF分别交AD、BC于点E、F，∴AE＝CE，∵矩形的周长为20，∴AD+DC＝AB+BC＝10，∴△CDE的周长为CD+DE+CE＝CD+DE+AE＝CD+AD＝10，故选：A．5．解：A、正确．对角线相等的平行四边形是矩形．B、正确．∵AB＝6，BC＝8，AC＝10，∴AB2+BC2＝62+82＝102，∴∠ABC＝90°，∴平行四边形ABCD为矩形．C、错误．对角线垂直的平行四边形是菱形，D、正确，∵∠1＝∠2，∴AO＝BO，∴AC＝BD，∴平行四边形ABCD是矩形．故选：C．6．解：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∵OA＝OD，∴AC＝BD，∴四边形ABCD是矩形，∴∠DAB＝90°，∵∠OAD＝55°，∴∠OAB＝∠DAB﹣∠OAD＝35°故选：A．7．解：过E作EF⊥AB于F，由题意得，△BCE是等边三角形，∴∠EBC＝60°，∵四边形ABCD是正方形，∴∠ABC＝90°，∴∠ABE＝30°，∴EF ＝BE，设正方形的边长为a，则AB＝BE＝BC＝a，∴EF ＝a，∴S△ABE ＝AB•EF ＝•a a ＝a，S正方形ABCD＝a2，∴△ABE与正方形ABCD的面积比为1：4，故选：C．8．解：由∠A＝∠B＝∠C＝90°可判定四边形ABCD为矩形，因此再添加条件：一组邻边相等，即可判定四边形ABCD为正方形，故选：C．9．解：过点D作BC的垂线，交BC的延长线于F，∵∠ADC＝∠ABC＝90°，∴∠A+∠BCD＝180°，∵∠FCD+∠BCD＝180°，∴∠A＝∠FCD，又∠AED＝∠F＝90°，AD＝DC，∴△ADE≌△CDF，∴DE＝DF，S四边形ABCD＝S正方形DEBF＝16，∴DE＝4．故选：C．10．解：∵四边形ABCD是菱形∴AB＝AD＝CD＝6，AB∥CD∵AB的中点是坐标原点，∴AO＝BO＝3，∴DO ＝＝3∴点C坐标（6，3）故选：D．二．填空题11．解：∵AF，BE是矩形的内角平分线．∴∠ABF＝∠BAF﹣90°．故∠1＝∠2＝90°．同理可证四边形GMON四个内角都是90°，则四边形GMON为矩形．又∵有矩形ABCD且AF、BE、DK、CJ为矩形ABCD四角的平分线，∴有等腰直角△DOC，等腰直角△AMD，等腰直角△BNC，AD＝BC．∴OD＝OC，△AMD≌△BNC，∴NC＝DM，∴NC﹣OC＝DM﹣OD，即OM＝ON，∴矩形GMON为正方形，故答案为：正方．12．解：∵四边形ABCD为菱形，∴BD平分∠ABC，∵E为BD上的一点，EF＝4，∴点E到AB的距离＝EF＝4，故答案为：4．13．解：如图，∵四边形ABCD是菱形∴AO＝CO＝6cm，BO＝DO，AC⊥BD ∵S菱形ABCD ＝×AC×BD＝96∴BD＝16cm∴BO＝DO＝8cm∴AB ＝＝10cm故答案为：10cm14．解：∵四边形ABCD是矩形，∴AO＝OC，DO＝BO，AC＝BD，∴DO＝CO＝AO＝BO，∵∠AOB＝60°，∴△AOB是等边三角形，∵AB＝10，∴AO＝OB＝DO＝10，∵E、F分别为AO、AD的中点，∴EF ＝DO ＝＝5，故答案为：5．15．解：∵四边形ABCD是正方形，∴∠CAE＝45°＝∠ACB．∵AE＝AC，∴∠ACE＝（180°﹣45°）÷2＝67.5°．∴∠BCE＝∠ACE﹣∠ACB＝67.5°﹣45°＝22.5°．故答案为22.5°．16．解：∵菱形ABCD的周长是20，∴AB＝5，AC⊥BD，AO＝CO，BO＝DO＝3，∴AO ＝＝4∴AC＝8，BD＝6∴菱形ABCD 的面积＝AC×BD＝24，故答案为：2417．解：因为AB＝CD，若∠ABP＝∠DCE＝90°，BP＝CE＝1，根据SAS证得△ABP≌△DCE，由题意得：BP＝2t＝1，所以t＝0.5，因为AB＝CD，若∠BAP＝∠DCE＝90°，AP＝CE＝1，根据SAS证得△BAP≌△DCE，由题意得：AP＝8﹣2t＝1，解得t＝3.5．所以，当t的值为0.5或3.5秒时．△ABP和△DCE全等．故答案为：0.5秒或3.5秒．18．解：∵四边形ABCD和四边形CEFG都是正方形，∴∠ACD＝45°，∠FCG＝45°，AC ＝BC ＝，CF ＝CE＝3，∴∠ACF＝45°+45°＝90°，在Rt△ACF中，由勾股定理得：AF ＝＝＝2，∵H是AF的中点，∴CH ＝AF ＝．故答案为：．三．解答题19．解：∵DE⊥AB于E，且E为AB的中点，∴AD＝BD，∵四边形ABCD是菱形，∴AD＝BA，∴AB＝AD＝BD，∴△ABD是等边三角形，∴∠DAB＝60°；∵BD＝4，∴DO＝2，AD＝4，∴AO ＝＝2，∴AC＝4；∴AB ＝＝＝4，∴菱形ABCD的周长为4×4＝16；菱形ABCD 的面积为：BD•AC ＝×4×4＝8．20．证明：∵四边形ABCD是平行四边形，∴∠B＝∠D，∵AE⊥BC，AF⊥DC∴∠AEB＝∠AFD＝90°．又∵BE＝DF，∴△ABE≌△ADF（AAS）∴DA＝AB，∴平行四边形ABCD是菱形．21．解：∵四边形ABCD是矩形，∴AC＝BD，AO＝OC，OD＝OB，∠BAD＝90°，∴OA＝OB，∵∠BAD＝90°，∠DAE＝2∠BAE，∴∠BAE＝30°，∵AE⊥BD，∴∠AEB＝90°，∴∠ABO＝90°﹣30°＝60°，∵OA＝OB，∴△OAB是等边三角形，∴∠BAO＝60°，∴∠EAC＝∠BAO﹣∠BAE＝60°﹣30°＝30°．22．解：（1）证明：∵AD∥BC，EC＝AD，∴四边形AECD是平行四边形．又∵∠D＝90°，∴四边形AECD是矩形．（2）∵AC平分∠DAB．∴∠BAC＝∠DAC．∵AD∥BC，∴∠DAC＝∠ACB．∴∠BAC＝∠ACB．∴BA＝BC＝5．∵EC＝2，∴BE＝3．∴在Rt△ABE中，AE ＝＝＝4．23．解：△BEF是直角三角形，理由如下：∵四边形ABCD是正方形，∴∠A＝∠C＝∠D＝90°．∵点E是CD的中点，∴DE＝CE ＝CD＝6．∵AF＝3DF，∴DF ＝AD＝3．∴AF＝3DF＝9．在Rt△ABF中，由勾股定理可得BF2＝AB2+AF2＝144+81＝225，在Rt△BCE中，由勾股定理可得BE2＝CB2+CE2＝144+36＝180，在Rt△DEF中，由勾股定理可得EF2＝DF2+DE2＝9+36＝45，∵BE2+EF2＝180+45＝225，BF2＝225，∴BE2+EF2＝BF2．∴△BEF是直角三角形．24．（1）证明：∵CE∥BD，DE∥AC，∴四边形OCED是平行四边形，在正方形ABCD中，AC⊥BD，OD＝OC，∴∠COD＝90°，∴四边形OCED是正方形．（2）解：如图，连接EO并延长，交AB于G，交CD于H，由（1）知：四边形OCED是正方形，∴CD⊥OE，∵四边形ABCD是正方形，∴AB∥CD，∴EG⊥AB，∵AC ＝，∴AB＝BC＝1＝GH，Rt△DCE中，∵DE＝CE，EH⊥CD，∴DH＝CH，∴EH ＝CD＝0.5，∴EG＝1+0.5＝1.5，∴点E到边AB的距离为1.5；故答案为：1.5．25．解：（1）如图所示，过E作EM⊥BC于M点，过E作EN⊥CD于N点，∵正方形ABCD，∴∠BCD＝90°，∠ECN＝45°，∴∠EMC＝∠ENC＝∠BCD＝90°，且NE＝NC，∴四边形EMCN为正方形，∵四边形DEFG是矩形，∴EM＝EN，∠DEN+∠NEF＝∠MEF+∠NEF＝90°，∴∠DEN＝∠MEF，又∠DNE＝∠FME＝90°，在△DEN和△FEM中，，∴△DEN≌△FEM（ASA），∴ED＝EF，∴矩形DEFG为正方形，（2）CE+CG的值为定值，理由如下：∵矩形DEFG为正方形，∴DE＝DG，∠EDC+∠CDG＝90°，∵四边形ABCD是正方形，∵AD＝DC，∠ADE+∠EDC＝90°，∴∠ADE＝∠CDG，在△ADE和△CDG中，，∴△ADE≌△CDG（SAS），∴AE＝CG，∴AC＝AE+CE＝AB＝×4＝8，∴CE+CG＝8是定值．。

北师大版九年级数学上册第一章同步测试题及答案

北师大版九年级数学上册第一章同步测试题及答案1.1菱形的性质与判定一、选择题1. 如图，在菱形ABCD 中，AB =4，∠B =60°，AE ⊥BC ，AF ⊥CD ，垂足分别为E ，F ，连接EF ，则的△AEF 的面积是（）A. 4√3B. 3√3C. 2√3D. √32. 如图，在菱形ABCD 中，AB =8，点E ，F 分别在AB ，AD 上，且AE =AF ，过点E 作EG ∥AD 交CD 于点G ，过点F 作FH ∥AB 交BC 于点H ，EG 与FH 交于点O ．当四边形AEOF 与四边形CGOH 的周长之差为12时，AE 的值为（）A. 6.5B. 6C. 5.5D. 53. 如图，BD 是菱形ABCD 的对角线，CE ⊥AB 交于点E ，交BD 于点F ，且点E 是AB 中点，则tan ∠BFE 的值是（）A. 12B. 2C. √33D. √3 4. 如图，在菱形中，对角线AC 、BD 交于点O ，E 为AD 边中点，菱形ABCD 的周长为28，则OE 的长等于（） A. 3.5 B. 4 C. 7 D. 145. 如图，在菱形ABCD中，AB=6，∠ABD=30°，则菱形ABCD的面积是（）A. 18B. 18√3C. 36D. 36√36. 如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60°，则花坛对角线AC的长等于（）A. 6√3米B. 6米C. 3√3米D. 3米（x 7. 如图，O是坐标原点，菱形OABC的顶点A的坐标为（-3，4），顶点C在x轴的负半轴上，函数y=kx＜0）的图象经过顶点B，则k的值为（）A. -12B. -27C. -32D. -368. 如图，菱形ABCD的对角线AC，BD相交于O点，E，F分别是AB，BC边上的中点，连接EF．若EF=√3，BD=4，则菱形ABCD的周长为（）A. 4B. 4√3C. 4√7D. 289. 菱形具有而平行四边形不具有的性质是（）A. 两组对边分别平行B. 两组对角分别相等C. 对角线互相平分D. 对角线互相垂直10. 某校的校园内有一个由两个相同的正六边形（边长为2.5m）围成的花坛，如图中的阴影部分所示，校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示，并在新扩充的部分种上草坪，则扩建后菱形区域的周长为（）A. 20mB. 25mC. 30mD. 35m11. 如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB 的度数是（）A. 108°B. 72°C. 90°D. 100°12. 在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E、F分别为BC、CD的中点，则∠EAF等于（）A. 60°B. 55°C. 45°D. 30°13. 菱形的两条对角线长分别为6和8，则菱形的面积是（）A. 10B. 20C. 24D. 4814. 在菱形ABCD中，下列结论错误的是（）A. BO=DOB. ∠DAC=∠BACC. AC⊥BDD. AO=DO15. 如图，在菱形ABCD中，P、Q分别是AD、AC的中点，如果PQ=3，那么菱形ABCD的周长是（）A. 30B. 24C. 18D. 6二、填空题（共5题）16. 如图，AD是△ABC的高，DE∥AC，DF∥AB，则△ABC满足条件________时，四边形AEDF是菱形．17. 如图，在△ABC中，已知E、F、D分别是AB、AC、BC上的点，且DE∥AC，DF∥AB，要使四边形AEDF 是菱形，在不改变图形的前提下，你需添加的一个条件是________就可以证明这个多边形是菱形18. 如图，四边形ABCD的对角线AC、BD相交于点O，且OA=OC，OB=OD．请你添加一个适当的条件：_________，使四边形ABCD成为菱形．AB的长为半19. 如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于12径画弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是_________20. 如图，四边形ABCD是平行四边形，AC与BD相交于点O，添加一个条件：________ ，可使它成为菱形.三、解答题（共5题）21. 如图，已知在△ABC中，∠ACB=90°，CE是中线，△ACD与△ACE关于直线AC对称．（1）求证：四边形ADCE是菱形；（2）求证：BC=ED．22. 如图，△ABC与△CDE都是等边三角形，点E、F分别为AC、BC的中点．（1）求证：四边形EFCD是菱形；（2）如果AB=8，求D、F两点间的距离．23. 如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．（1）求证：四边形AECD是菱形；（2）若点E是AB的中点，试判断△ABC的形状，并说明理由．24. 如图，四边形ABCD中，AB∥CD，CE∥AD交AB于E，AE=AD．求证：四边形AECD是菱形25. 如图，由两个等宽的矩形叠合而得到四边形ABCD．试判断四边形ABCD的形状并证明答案一、选择题1.【答案】B【解析】∵四边形ABCD是菱形，∴BC=CD，∠B=∠D=60°，∵AE⊥BC，AF⊥CD，∴BC×AE=CD×AF，∠BAE=∠DAF=30°，∴AE=AF，∵∠B=60°，∴∠BAD=120°，∴∠EAF=120°-30°-30°=60°，∴△AEF 是等边三角形，∴AE=EF，∠AEF=60°，∵AB=4，∴AE=AB×sin60°=2√3∴EF=AE=2√3∴AM=AE•sin60°=3，∴△AEF的面积是：12EF•AM=12×2√3×3=3√3.故选:B.2.【答案】C【解析】根据题意可得四边形AEOF和四边形CGOH为菱形，且OH=EB，设AE=x，则BE=8－x，根据菱形的周长之差为12，可得两个菱形的边长之差为3，即x－（8－x）=3，解得：x=5．5考点：菱形的性质3. 【答案】D【解析】根据菱形的性质，在菱形ABCD中，AB=BC，E为AB的中点，因此可知BE=12BC，又由CE⊥AB，可知△BCA为直角三角形，∠BCE=30°，∠EBC=60°，再由菱形的对角线平分每一组对角，可得∠EBF=12∠EBC=30°，因此可求∠BFE=60°，进而可得tan∠BFE=√3．故选D考点：菱形的性质，解直角三角形4. 【答案】A【解析】根据菱形的四条边都相等求出AB，再根据菱形的对角线互相平分可得OB=OD，然后判断出OE是△ABD的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半求解即可．∵菱形ABCD的周长为28，∴AB=28÷4=7，OB=OD，∵E为AD边中点，∴OE是△ABD的中位线，∴OE=AB=×7=3.5．故选A．点评：本题考查了菱形的性质，三角形的中位线平行于第三边并且等于第三边的一半，熟记性质与定理是解题的关键．5. 【答案】B【解析】过点A作AE⊥BC于E，如图，∵在菱形ABCD中，AB=6，∠ABD=30°，∴∠BAE=30°，∵AE⊥BC，∴AE=3√3，∴菱形ABCD的面积是6×3√3=18√3，故选B．考点：菱形的性质．6. 【答案】A【解析】本题考查的是菱形的性质，直角三角形的性质解决即可.因为菱形周长为24米，所以边长为6米，因为∠BAD=60°，所以∠BAO=30°，∴OA=3√3米,∴AC=6√3米. 故选A.7. 【答案】C【解析】∵A（﹣3，4），∴OA==5，∵四边形OABC 是菱形，∴AO=CB=OC=AB=5，则点B 的横坐标为﹣3﹣5=﹣8，故B 的坐标为：（﹣8，4），将点B 的坐标代入得，4=，解得：k=﹣32．故选C ． 8. 【答案】C【解析】∵E ，F 分别是AB ，BC 边上的中点，∴EF 是△ABC 的中位线，∴AC=2EF=2√3.∵菱形ABCD 的对角线AC ，BD 相交于O 点，∴∠AOB=90°，AO=12AC=√3，BO=12BD=2.∴AB=√A02+BO 2=√7，∴C 菱形ABCD=4AB=4√7.故选C.9. 【答案】D【解析】A 、不正确，两组对边分别平行；B 、不正确，两组对角分别相等，两者均有此性质正确；C 、不正确，对角线互相平分，两者均具有此性质；D 、菱形的对角线互相垂直但平行四边形却无此性质．故选D ．10. 【答案】C【解析】如图，∵花坛是由两个相同的正六边形围成，∴∠FGM=∠GMN=120°，GM=GF=EF,∴∠BMG= ∠BGM=60°，∴△BMG 是等边三角形，∴BG=GM=2.5（m ），同理可证：AF=EF=2.5（m ）∴AB=BG+GF +AF=2.5×3=7.5（m ），∴扩建后菱形区域的周长为7.5×4=30（m ），故选C ．考点：菱形的性质．11. 【答案】B【解析】如图，连接AP ，∵在菱形ABCD 中，∠ADC=72°，BD 为菱形ABCD 的对角线，∴∠ADP=∠CDP=12 ∠ADC=36°.∵AD 的垂直平分线交对角线BD 于点P ，垂足为E ，∴PA=PD.∴∠DAP=∠ADP=36°.∴∠APB= ∠DAP+∠ADP=72°.又∵菱形ABCD 是关于对角线BD 对称的，∴∠CPB=∠APB=72°.故选B.点睛：连接AP ，利用线段垂直平分线的性质和菱形的性质求得∠APB 的度数是解本题的基础，而利用通常容易忽略的“菱形是关于对称轴所在直线对称的”，由轴对称的性质得到∠CPB=∠APB 才是解决本题的关键.12. 【答案】A【解析】如图，连接AC ，∵AE ⊥BC 于点E ，AF ⊥CD 于点F ，且E 、F 分别为BC 、CD 的中点，∴AB= AC ，AD=AC.又∵在菱形ABCD 中，AB=BC=CD=AD ，∴AB=BC=CD=AD=AC.∴△ABC 和△ADC 都是等边三角形.∴∠BAC=∠DAC=60°，∴∠EAC=12∠BAC=30°，∠FA C=12∠DAC=30°，∴∠EAF=∠EAC+∠FAC=60°.故选A.13.【答案】C【解析】由菱形的两条对角线的长分别是6和8，根据菱形的面积等于对角线积的一半，即可求得答案．∵菱形的两条对角线的长分别是6和8，∴这个菱形的面积是：×6×8=24．故选C ．考点：菱形的性质．14. 【答案】D【解析】根据菱形的性质：“菱形的对角线互相垂直平分，每一条对角线平分一组对角”可知：选项A 、B 、C 的结论都是正确的，只有选项D 的结论不一定成立.故选D.15. 【答案】B【解析】∵P ，Q 分别是AD ，AC 的中点，∴PQ 是△ADC的中位线，∴DC=2PQ=6.又∵在菱形ABCD 中，AB=BC=AD=CD ，∴C 菱形ABCD =6+6+6+6=24.故选B.二、填空题（共5题）16. 【答案】AB=AC 或∠B=∠C【解析】∵DE ∥AC ，DF ∥AB ，∴四边形AEDF 是平行四边形.所以当四边形AEDF 中有一组邻边相等时，它就是菱形了.由此在△ABC 中可添加条件：（1）AB=AC 或（2）∠B=∠C.（1）当添加条件“AB=AC ”时， ∵AD 是△ABC 的高，AB=AC ，∴点D 是BC 边的中点，又∵DE ∥AC ，DF ∥AB ，∴点E 、F 分别是AB 、AC 的中点，∴AE=12AB ，AF=12AC ，∴AE=AF，∴平行四边形AEDF 是菱形.（2）当添加条件“∠B=∠C”时，则由∠B=∠C 可得AB=AC ，同（1）的方法可证得：AE=AF ，∴平行四边形AEDF 是菱形.17. 【答案】AB=AC ，答案不唯一【解析】根据DE∥AC，DF∥AB，可直接判断出四边形AEDF 是平行四边形，要使其变为菱形，只要邻边相等即可，从而可以得出．条件AE=AF （或AD 平分角BAC ，等）∵DE∥AC，DF∥AB，∴四边形AEDF 是平行四边形，又AE=AF ，∴四边形AEDF 是菱形．考点: 菱形的判定.18. 【答案】AB=AD ，答案不唯一【解析】由已知条件可证四边形ABCD是平行四边形，而要使平行四边形是菱形，根据菱形的判定方法可添加：（1）四边形ABCD中，有一组邻边相等；（2）四边形ABCD的对角线互相垂直；因此，本题的答案不唯一，如可添加：AB=AD，证明如下：∵四边形ABCD的对角线AC、BD相交于点O，且OA=OC，OB=OD．∴四边形ABCD是平行四边形.又∵AB=AD，∴平行四边形ABCD是菱形.点睛：本题方法不唯一，由已知条件可证得四边形ABCD是平行四边形，结合菱形判定方法中的：①有一组邻边相等的平行四边形是菱形；②对角线相等的平行四边形是菱形；就可得到本题添加条件的方法有3种：（1）直接添加四组邻边中的任意一组相等；（2）直接添加对角线AC⊥BD；（3）在题中添加能够证明（1）或（2）的其它条件.19. 【答案】菱形【解析】∵分别以A和B为圆心，大于1AB的长为半径画弧，两弧相交于C、D，∴AC=AD=BD=BC，∴四边2形ADBC是菱形．故答案为：菱形．20. 【答案】AB=BC或AC⊥BD等【解析】有一组领边相等的平行四边形为菱形，对角线互相垂直的平行四边形为菱形．本题的答案有很多种，只要写出符合条件的即可．考点：菱形的性质．三、解答题（共5题）21. 【答案】（1）证明见解析；（2）证明见解析.【解析】（1）由△ABC中，∠ACB=90°，CE是中线，可证得：CE=AE，再由△ACD与△ACE关于直线AC对称，可得AD=AE=CE=CD，从而可得四边形ADCE是菱形；（2）由（1）可得DC∥BE，DC=AE=BE，从而可证得：四边形BCDE是平行四边形，就可得到：BC=DE.（1）证明：∵∠C=90°，点E为AB的中点，∴EA=EC.∵△ACD与△ACE关于直线AC对称．∴△ACD≌△ACE，∴EA=EC=DA=DC，∴四边形ADCE是菱形；（2）∵四边形ADCE是菱形，∴CD∥AE且CD=AE，∵AE=EB，∴CD∥EB且CD=EB∴四边形BCDE为平行四边形，∴DE=BC．22. 【答案】（1）证明见解析；（2）4√3【解析】（1）由△ABC是等边三角形，点E、F分别为AC、BC的中点可证得：EF=EC=FC；由△DEC是等边三角形可得：DE=DC=EC，从而可得EF=FC=CD=DE，由此可得：四边形EFCD是菱形；（2）连接DF交AC于点G，由已知易证EF=EC=4，再由菱形的对角线互相垂直平分，可得EG=2，再由勾股定理可得：FG=2√3，从而可得DF=4√3.解：（1）∵△ABC 与△CDE 都是等边三角形∴AB=AC=BC，ED=DC=EC∵点E 、F 分别为AC 、BC 的中点∴EF=12AB ，EC=12AC ，FC=12BC∴EF=EC=FC，∴EF=FC=ED=DC，∴四边形EFCD 是菱形．（2）连接DF ，与EC 相交于点G ，∵四边形EFCD 是菱形，∴DF⊥EC，垂足为G ，EG=12EC ，∴∠EGF=90°，又∵AB=8， EF=12AB ，EC=12AC ，∴EF=4，EC=4，EG=2，∴GF=√EF 2−EG 2=2√3，∴DF=2GF=4√3.23. 【答案】（1）证明见解析；（2）直角三角形．解：（1）四边形ABCD 中，AB∥CD，过C 作CE∥AD 交AB 于E ，则四边形AECD 是平行四边形（两组对边分别平行的四边形是平行四边形），因为AB∥CD，所以∠EAC =∠ACD ；AC 平分∠BAD，所以∠EAC =∠CAD ，因此∠ACD =∠CAD ，所以AD=CD ，所以四边形AECD 是菱形.（2）由（1）知四边形AECD 是菱形，所以AE=CE ；点E 是AB 的中点，AE=BE ，所以CE=AE=BE ，所以△ABC 是直角三角形（斜边上的中线等于斜边的一半是直角三角形）考点：平行四边形，菱形，直角三角形点评：本题考查平行四边形，菱形，直角三角形，要求考生掌握平行四边形的判定方法，菱形的判定方法和性质，直角三角形的性质24.【答案】证明见解析.【解析】由AB∥CD，CE∥AD可证得：四边形AECD是平行四边形，再由AE=AD即可证得平行四边形AECD 是菱形.解：∵AB∥CD，CE∥AD，∴四边形AECD是平行四边形，∵AE=AD，∴四边形AECD是菱形.25. 【答案】四边形ABCD是菱形．证明见解析.【解析】过点A作AR⊥BC于点R，AS⊥CD于点S，由已知可得：AD∥BC，AB∥CD，从而得到四边形ABCD 是平行四边形；由矩形纸条等宽可得AR=AS，由面积法可证得：BC=DC，从而可得：平行四边形ABCD是菱形.解：四边形ABCD是菱形．理由如下：作AR⊥BC于R，AS⊥CD于S，由题意知：AD∥BC，AB∥CD，∴四边形ABCD是平行四边形，∵两个矩形等宽，∴AR=AS，∵S平行四边形ABCD=AR•BC=AS•CD，∴BC=CD，∴平行四边形ABCD是菱形.点睛：本题第一步容易证得四边形ABCD是平行四边形；第二步抓住题中条件“等宽的矩形”通过作辅助线AR⊥BC，AS⊥CD，就可得AR=AS，再用“面积法”证得：BC=CD是解决本题的关键.1.2矩形的性质与判定一、选择题1. 如图，小贤为了体验四边形的不稳定性，将四根木条用钉子钉成一个矩形框架ABCD，B与D两点之间用一根橡皮筋拉直固定，然后向右扭动框架，观察所得四边形的变化，下列判断错误的是（）A. 四边形ABCD由矩形变为平行四边形B. BD的长度增大C. 四边形ABCD的面积不变D. 四边形ABCD的周长不变2. 如图，在矩形ABCD中，对角线AC、BD交于点O，以下说法错误的是（）A. ∠ABC=90°B. AC=BDC. OA=OBD. OA=AD3. 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=5，AD=12，则四边形ABOM的周长为（）A. 17B. 18C. 19D. 204. 如图，矩形的两条对角线的一个交角为60°，两条对角线的长度的和为20cm，则这个矩形的一条较短边的长度为（）A. 10cmB. 8cmC. 6cmD. 5cm5. 如图，矩形ABCD的两条对角线交于点O，若∠AOD=120°，AB=6，则AC等于（）A. 8B. 10C. 12D. 186. 如图，在矩形ABCD中，对角线AC、BD相交于点O，若∠ACB=30°，AB=2，则BD的长为（）A. 4B. 3C. 2D. 17. 一个矩形被分成不同的4个三角形，其中绿色三角形的面积占矩形面积的15%，黄色的三角形的面积是212，则该矩形的面积为（）A. 602B. 702C. 1202D. 14028. 如图，矩形ABCD中，AC交BD于点O，∠AOD=60°，OE⊥AC．若AD=√3，则OE=（）A. 1B. 2C. 3D. 49. 矩形的一内角平分线把矩形的一条边分成3和5两部分，则该矩形的周长是（）A. 16B. 22或16C. 26D. 22或2610. 矩形具有而菱形不具有的性质是（）A. 对角线相等B. 两组对边分别平行C. 对角线互相平分D. 两组对角分别相等11. 矩形的一内角平分线把矩形的一条边分成3cm和5cm的两部分，则此矩形的周长为（）A. 16cmB. 22cmC. 26cmD. 22cm或26cm12. 矩形的对角线所成的角之一是65°，则对角线与各边所成的角度是（）A. 57.5°B. 32.5°C. 57.5°，23.5°D. 57.5°，32.5°13. 矩形具有而菱形不具有的性质是（）A. 对角线相等B. 对角线平分一组对角C. 对角线互相平分D. 对角线互相垂直14. 过四边形的各个顶点分别作对角线的平行线，若这四条平行线围成一个矩形，则原四边形一定是（）A. 对角线相等的四边形B. 对角线垂直的四边形C. 对角线互相平分且相等的四边形D. 对角线互相垂直平分的四边形15. 若矩形的一条对角线与一边的夹角是40°，则两条对角线所夹的锐角的度数为（）A. 80°B. 60°C. 45°D. 40°二、填空题16. 如图，平行四边形ABCD的对角线相交于点O，请你添加一个条件__________（只添一个即可），使平行四边形ABCD是矩形．17. 平行四边形ABCD的对角线相交于点O，分别添加下列条件：①∠ABC=90°；②AC⊥BD；③AB=BC；④AC 平分∠BAD；⑤AO=DO．使得四边形ABCD是矩形的条件有________18. 如图，要使平行四边形ABCD是矩形，则应添加的条件是________（只填一个）．19. 如图，在四边形ABCD中，对角线AC，BD相交于点O，且AO=CO，BO=DO，在不添加任何辅助线的前提下，要想该四边形成为矩形，只需再加上一个条件是________（填上你认为正确的一个答案即可）20. 木工做一个长方形桌面，量得桌面的长为15cm，宽为8cm，对角线为17cm，这个桌面_________（填”合格”或”不合格”）三、解答题21. 如图，平行四边形ABCD中，点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG，AH=CF．（1）求证：四边形EFGH是平行四边形；（2）如果AB=AD，且AH=AE，求证：四边形EFGH是矩形22. 如图，在△ABC中，AB=AC=5，BC=6，AD为BC边上的高，过点A作AE∥BC，过点D作DE∥AC，AE与DE交于点E，AB与DE交于点F，连结BE．求四边形AEBD的面积23. 如图，在平行四边形ABCD中，∠BAD的平分线交CD于点E，交BC的延长线于点F，连接BE，∠F=45°．求证：四边形ABCD是矩形24. 有一块形状如图所示的玻璃，不小心把DEF部分打碎，现在只测得AB=60cm，BC=80cm，∠A=120°，∠B=60°，∠C=150°，你能设计一个方案，根据测得的数据求出AD的长吗？25. 如图，△ABC中，AB=AC，AD、AE分别是∠BAC与∠BAC的外角的平分线，BE⊥AE．求证：AB=DE答案一、选择题1. 【答案】C【解析】由题意可知，当向右扭动框架时，BD 可伸长，故BD 的长度变大，四边形ABCD 由矩形变为平行四边形，因为四条边的长度不变，所以四边形ABCD 的周长不变.原来矩形ABCD 的面积等于BC 乘以AB ，变化后平行四边形ABCD 的面积等于底乘以高，即BC 乘以BC 边上的高，BC 边上的高小于AB ，所以四边形ABCD 的面积变小了，故A,B,D 说法正确，C 说法错误.故正确的选项是C.考点：1.四边形面积计算；2.四边形的不稳定性.2. 【答案】D【解析】本题考查了矩形的性质；熟练掌握矩形的性质是解决问题的关键．矩形的性质：四个角都是直角，对角线互相平分且相等；由矩形的性质容易得出结论．∵四边形ABCD 是矩形，∴∠ABC=∠BCD=∠CDA =∠BAD=90°，AC=BD ，OA=AC ，OB=BD ，∴OA=OB，∴A、B 、C 正确，D 错误考点：矩形的性质3. 【答案】D【解析】∵O 是矩形ABCD 的对角线AC 的中点，M 是AD 的中点，∴∠ABC=∠D=90°，CD=AB=5，BC=AD=12，OA=OB ，OM 为△ACD 的中位线，∴OM=12CD=2.5，AC=√52+122=13，∵O 是矩形ABCD 的对角线AC 的中点，∴BO=12AC=6.5,∴四边形ABOM 的周长为AB+AM+BO+OM=5+6+6.5+2.5=20，故选D ．考点：矩形的性质．4. 【答案】D【解析】∵四边形ABCD 是矩形，∴OA=OC=12AC ，OD=OB=12BD ，AC=BD ，∴OA=OB，∵AC+BD=20，∴AC=BD=10cm，∴OA=OB=5cm，∵OA=OB，∠AOB=60°，∴△OAB 是等边三角形，∴AB=OA=5cm，故选D ．考点：1．矩形的性质；2．等边三角形的判定与性质．5. 【答案】C【解析】根据∠AOD=120°可得∠AOB=60°，根据矩形的性质可得AO=BO ，则△AOB 是正三角形，则AO=AB=6，则AC=2AO=12．考点：矩形的性质．6. 【答案】A【解析】在矩形ABCD 中，∠ABC =90°，∵∠ACB =30°，AB =2，∴AC =2AB =2×2=4，∵四边形ABCD 是矩形，∴BD =AC =4．故选A ．7. 【答案】A【解析】黄色三角形与绿色三角形面积之和是矩形面积的50%，而绿色三角形面积占矩形面积的15%，所以黄色三角形面积占矩形面积的（50%-15%）=35%，已知黄色三角形面积是21平方厘米，故矩形的面积=21÷（50%-15%）=21÷35%=60（cm 2）．故选A ．考点：矩形的性质．8.【答案】A【解析】∵四边形ABCD是矩形，∠AOD=60°，∴△ADO是等边三角形，∴OA=√3，∠OAD=60°，∴∠OAE= 30°，∵OE⊥AC，∴△OAE是一个含30°的直角三角形，∴OE=1，故选A．9.【答案】D【解析】∵四边形ABCD是矩形，∴AD=BC，AB=CD，AD∥BC，∴∠AEB=∠EBC，∵BE平分∠ABC，∴∠ABE=∠EBC，∴∠AEB=∠ABE，∴AE=AB，①当AE=3，DE=5时，AD=BC=3+5=8，AB=CD=AE=3，即矩形ABCD的周长是AD+AB+BC+CD=8+3+8+3=22；②当AE=5，DE=3时，AD=BC=3+5=8，AB=CD=AE=5，即矩形ABCD的周长是AD+AB+BC+CD=8+5+8+5=26；即矩形的周长是22或26，故选D．考点：矩形的性质.10.【答案】A【解析】∵矩形具有的性质是：对角线相等且互相平分，两组对边分别平行，两组对角分别相等；菱形具有的性质是：两组对边分别平行，对角线互相平分，两组对角分别相等；∴矩形具有而菱形不具有的性质是：对角线相等．故选A．11. 【答案】D【解析】∵四边形ABCD是矩形，∴AD=BC，AB=CD，AD∥BC，∴∠AEB=∠CBE，∵BE平分∠ABC，∴∠ABE=∠CBE，∴∠AEB=∠ABE，∴AB=AE，当AE=3cm时，AB=AE=3=CD，AD=3cm+5cm=8cm=BC，∴此时矩形ABCD的周长是AB+BC+CD+AD=3cm+8cm+3cm+8cm=22cm；当AE=5cm时，AB=AE=5cm=CD，AD=3cm+5cm=8cm=BC，∴此时矩形ABCD的周长是AB+BC+CD+AD=5cm+8cm+5cm+8cm=26cm；故选D．考点：矩形的性质．12. 【答案】D【解析】∵四边形ABCD是矩形，∴∠ABC=90°，AD∥BC，AB∥CD，AC=BD，AO=OC，OB=OD，∴OB=OA=OC=OD，∠OAB=∠OCD，∠DAO=∠OCB，∴∠OAD=∠ODA，∠OCB=∠OBC，∠ODC=∠OCD，∠OAB=∠OBA=1×2×（180°﹣65°）=57.5°，∵∠ABC=90°，∴∠ACB=90°﹣57.5°=32.5°，即（180°﹣∠AOB）=12∠OAD=∠ODA=∠OBC=∠OCB=32.5°，∠OAB=∠OBA=∠ODC=∠OCD=57.5°，对角线与各边所成的角度是57.5°和32.5°，故选D．点睛：本题考查了矩形的性质，三角形的内角和定理，等腰三角形的性质的应用，能正确运用矩形的性质进行推理是解此题的关键，注意：矩形的对角线相等且互相平分．13. 【答案】A【解析】菱形的对角线互相平分、垂直、对角线平分一组对角，矩形的对角线互相平分、相等，∴矩形具有而菱形不具有的性质是对角线相等，故选A．考点：1．菱形的性质；2．矩形的性质．14. 【答案】B【解析】∵四边形EFGH是矩形，∴∠E=90°，∵EF∥AC，EH∥BD，∴∠E+∠EAG=180°，∠E+∠EBO=180°，∴∠EAO=∠E BO=90°，∴四边形AEBO是矩形，∴∠AOB=90°，∴AC⊥BD，故选B．15. 【答案】A【解析】如图,根据题意可得：∠1=40°，∵四边形ABCD是矩形，∴OB=OC，∴∠OBC=∠1=40°，则∠AOB=2∠1=80°．故选A．考点：矩形的性质．二、填空题16. 【答案】AC=BD．答案不唯一【解析】添加的条件是AC=BD，理由是：∵AC=BD，四边形ABCD是平行四边形，∴平行四边形ABCD是矩形，故答案为：AC=BD．答案不唯一．点睛：本题考查了矩形的判定定理的应用，注意：对角线相等的平行四边形是矩形，此题是一道开放型的题目，答案不唯一．17.【答案】①⑤【解析】要使得平行四边形ABCD为矩形添加：①∠ABC=90°；⑤AO=DO2个即可；故答案为：①⑤．18. 【答案】∠ABC=90°或AC=BD（不唯一）【解析】本题考查了平行四边形的性质、矩形的判定．根据对角线相等的平行四边形是矩形，填空即可∵四边形ABCD是平行四边形，AC=BD，∴平行四边形ABCD是矩形，故答案为AC=BD．19. 【答案】∠DAB=90°【解析】可以添加条件∠DAB=90°.∵AO=CO，BO=DO，∴四边形ABCD是平行四边形.∵∠DAB=90°，∴四边形ABCD是矩形.故答案为：∠DAB=90°.20. 【答案】合格【解析】勾股定理的逆定理：若一个三角形的两边长的平方和等于第三边的平方，则这个三角形的直角三角形.∵∴这个桌面合格.考点：勾股定理的逆定理点评：本题属于基础应用题，只需学生熟练掌握勾股定理的逆定理，即可完成.三、解答题21. 【答案】（1）证明见解析；（2）证明见解析.【解析】（1）易证得△AEH≌△CGF，从而证得BE=DG，DH=BF．故有，△BEF≌△DGH，根据两组对边分别相等的四边形是平行四边形而得证．（2）由题意知，平行四边形ABCD是菱形，连接AC，BD，则有AC⊥BD，由AB=AD，且AH=AE可证得HE∥BD，同理可得到HG∥AC，故HG⊥HE，又由（1）知四边形HGFE是平行四边形，故四边形HGFE是矩形．证明：（1）在平行四边形ABCD中，∠A=∠C，又∵AE=CG，AH=CF，∴△AEH≌△CGF．∴EH=GF．在平行四边形ABCD中，AB=CD，AD=BC，∴AB-AE=CD-CG，AD-AH=BC-CF，即BE=DG，DH=BF．又∵在平行四边形ABCD中，∠B=∠D，∴△BEF≌△DGH．∴GH=EF．∴四边形EFGH是平行四边形．（2）在平行四边形ABCD中，AB∥CD，AB=CD．设∠A=α，则∠D=180°-α．∵AE=AH，∴∠AHE=∠AEH=180°−a2=90°−a2．∵AD=AB=CD，AH=AE=CG，∴AD-AH=CD-CG，即DH=DG．∴∠DHG=∠DGH=180°−(180−a)2=a2．∴∠EHG=180°-∠DHG-∠AHE=90°．又∵四边形EFGH是平行四边形，∴四边形EFGH是矩形．考点：1.矩形的判定与性质；2.全等三角形的判定与性质；3.平行四边形的判定与性质．22. 【答案】12.【解析】利用平行四边形的性质和矩形的判定定理推知平行四边形AEBD是矩形．在Rt△ADC中，由勾股定理可以求得AD的长度，由等腰三角形的性质求得CD（或BD）的长度，则矩形的面积=长×宽=AD•BD=AD•CD．解：∵AE∥BC，BE∥AC，∴四边形AEDC是平行四边形，∴AE=CD．在△ABC中，AB=AC，AD为BC边上的高，∴∠ADB=90°，BD=CD，∴BD=AE，∴平行四边形AEBD是矩形．BC=3，∴AD=√52−32=4，在Rt△ADC中，∠ADB=90°，AC=5，CD=12∴四边形AEBD的面积为：BD•AD=CD•AD=3×4=12．点睛：本题考查了矩形的判定与性质和勾股定理，根据“等腰三角形的性质和有一内角为直角的平行四边形为矩形”推知平行四边形AEBD是矩形是解题的难点．23. 【答案】证明见解析.【解析】欲证明四边形ABCD是矩形，只需推知∠DAB是直角．证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAF=∠F.∵∠F=45°，∴∠DAE=45°．∵AF是∠BAD的平分线，∴∠EAB=∠DAE=45°，∴∠DAB=90°．又∵四边形ABCD是平行四边形，∴四边形ABCD是矩形．24. 【答案】AD＝140cm．【解析】过C作CM∥AB，交AD于M，推出平行四边形ABCM，推出AM=BC=80cm，AB=CM=60cm，∠B=∠AMC，求出∠D=∠MCD，求出CM=DM=60cm，代入AD=AM+DM求出即可．解：过C作CM∥AB，交AD于M，∵∠A=120°，∠B=60°，∴∠A+∠B=180°，∴AM∥BC，∵AB∥CM，∴四边形ABCM是平行四边形，∴AB=CM=60cm，BC=AM=80cm，∠B=∠AMC=60°，∵AD∥BC，∠C=150°，∴∠D=180°﹣150°=30°，∴∠MCD=60°﹣30°=30°=∠D，∴CM=DM=60cm，∴AD=60cm+80cm=140cm．25. 【答案】证明见解析.【解析】先由角平分线和等腰三角形的性质证明AE∥BD，再由AD、AE分别是∠BAC与∠BAC的外角的平分线可证得DA⊥AE，可得AD∥BE，可证得四边形ADBE为矩形，可得结论．（∠BAC+∠FAB）=90°，证明：∵AD、AE分别是∠BAC与∠BAC的外角的平分线，∴∠BAD+∠EAB=12∵BE⊥AE，∴DA∥BE，∵AB=AC，∴∠ABC=∠ACB，∵∠FAB=∠ABC+∠ACB=2∠ABC，且∠FAB=2∠EAB，∴∠ABC=∠EAB，∴AE∥BD，∴四边形AEBD为平行四边形，且∠BEA=90°，∴四边形AEBD为矩形，∴AB=DE．点睛：本题主要考查矩形的判定和性质，由角平分线及等腰三角形的性质证明AE∥BD是解题的关键．1.3正方形的性质与判定一、选择题（2）如果a≥0，那么（1）若直角三角形的两条边长为5和12，则第三边长是13；1. 下列五个命题：=a;（3）若点P（a，b）在第三象限，则点P（﹣a，﹣b+1）在第一象限；（4）对角线互相垂直且相等的四边形是正方形；（5）两边及第三边上的中线对应相等的两个三角形全等．其中不正确命题的个数是（）A. 2个B. 3个C. 4个D. 5个2. 下列命题中，正确命题是（）A. 两条对角线相等的四边形是平行四边形B. 两条对角线相等的四边形是矩形C. 两条对角线互相垂直平分的四边边是菱形D. 两条对角线平分且相等的四边形是正方形3. 下列命题中，真命题是（）A. 两条对角线垂直的四边形是菱形B. 对角线垂直且相等的四边形是正方形C. 两条对角线相等的四边形是矩形D. 两条对角线相等的平行四边形是矩形4. 下列说法中错误的是（）A. 两条对角线互相平分的四边形是平行四边形B. 两条对角线相等的四边形是矩形C. 两条对角线互相垂直的矩形是正方形D. 两条对角线相等的菱形是正方形5. 下列说法中，不正确的是（）A. 有三个角是直角的四边形是矩形B. 对角线相等的四边形是矩形C. 对角线互相垂直的矩形是正方形D. 对角线互相垂直的平行四边形是菱形6. 如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD=CE．连接DE，DF，EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CDFE不可能为正方形；③DE长度的最小值为4；④四边形CDFE的面积保持不变；⑤△CDE面积的最大值为8．其中正确的结论是（）A. ①②③B. ①④⑤C. ①③④D. ③④⑤7. 如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）A. 当AB=BC时，它是菱形B. 当AC⊥BD时，它是菱形C. 当∠ABC=90°时，它是矩形D. 当AC=BD时，它是正方形8. 下列命题中正确的是（）A. 两条对角线互相平分的四边形是平行四边形B. 两条对角线相等的四边形是矩形C. 两条对角线互相垂直的四边形是菱形D. 两条对角线互相垂直且平分的四边形是正方形9. 已知四边形ABCD中，∠A=∠B=∠C=90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（）A. ∠D=90°B. AB=CDC. AD=BCD. BC=CD10. 如图，将一张长方形纸片对折两次，然后剪下一个角，打开．如果要剪出一个正方形，那么剪口线与折痕成（）A. 22.5°角B. 30°角C. 45°角D. 60°角11. 在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是（）A. AC=BD，AB∥CD，AB=CDB. AD∥BC，∠A=∠CC. AO=BO=CO=DO，AC⊥BDD. AO=CO，BO=DO，AB=BC12. 用两个全等的直角三角形拼下列图形：（1）平行四边形（不包含菱形、矩形、正方形）；（2）矩形；（3）菱形；（4）正方形；（5）等腰三角形，一定可以拼成的图形是（）A. （1）（2）（5）B. （2）（3）（5）C. （1）（4）（5）D. （1）（2）（3）13. 下列说法中，错误的是（）A. 一组对边平行且相等的四边形是平行四边形B. 两条对角线互相垂直且平分的四边形是菱形C. 四个角都相等的四边形是矩形。

北师大版九年级数学上册第一章特殊的平行四边形综合练习题（含答案,教师版）

北师大版九年级数学上册第一章特殊的平行四边形综合练习题（含答案,教师版）北师大版九年级数学上册第一章特殊的平行四边形综合练习题1.如图，以正方形ABCD的顶点A为坐标原点，直线AB为x轴建立平面直角坐标系，对角线AC与BD相交于点E，P为BC上一点，点P坐标为(a，b)，则点P绕点E顺时针旋转90°得到的对应点P′的坐标是(D)A．(a－b，a) B．(b，a) C．(a－b，0) D．(b，0)2.如图，菱形ABCD边长为6，∠BAD＝120°，点E，F分别在AB，AD上且BE＝AF，则EF的最小值为(A)．A．B．．D3.如图，在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C4.如图，在边长为1的菱形ABCD中，∠ABC＝60°，将△ABD沿射线BD的方向平移得到△A′B′D′，分别连接A′C，A′D，B′C，则A′C＋B′C5.菱形OBCD在平面直角坐标系中的位置如图所示，顶点B(2，0)，∠DOB＝60°，点P是对角线OC上一个动点，E(0，－1)，当EP＋BP最短时，点P6.如图，在平面直角坐标系中，矩形OABC 的两边OA ，OC 分别在x 轴和y 轴上，并且OA ＝5，OC ＝3.若把矩形OABC 绕着点O 逆时针旋转，使点A 恰好落在BC 边上的A 1处，则点C 的对应点C 1的坐标为(－95，125)．7.如图，∠MON ＝90°，矩形ABCD 的顶点A ，B 分别在边OM ，ON 上，当B 在边ON 上运动时，A 随之在边OM 上运动，矩形ABCD 的形状保持不变，其中AB ＝4，BC ＝1，在运动过程中，点D 到点O8.如图，在矩形纸片ABCD 中，AB ＝8，BC ＝6，点E 是AD 的中点，点F 是AB 上一动点．将△AEF 沿直线EF 折叠，点A 落在点A ′处．在EF 上任取一点G ，连接GC ，GA ′，CA ′，则△CGA ′周长的最小值为9.如图，在△ABC 中，∠ABC ＝90°，BD 为AC 的中线，过点C 作CE ⊥BD 于点E ，过点A 作BD 的平行线，交CE 的延长线于点F ，在AF 的延长线上截取FG ＝BD ，连接BG ，DF.(1)求证：四边形BDFG 为菱形；(2)若AG ＝13，CF ＝6，则四边形BDFG 的周长为20．证明：∵∠ABC ＝90°，BD 为AC 的中线，∴BD ＝12AC.∵AG ∥BD ，BD ＝FG ，∴四边形BDFG 是平行四边形．∵CF ⊥BD ，∴CF ⊥AG.又∵点D 是AC 中点，∴DF ＝12AC.∴BD ＝DF.∴四边形BDFG 是菱形．10.如图，E ，F 分别是矩形ABCD 的边AD ，AB 上的点，EF ＝EC ，且EF ⊥EC. (1)求证：AE ＝DC ； (2)若DC ＝2，则BE ＝2．证明：在矩形ABCD 中，∠A ＝∠D ＝90°，∴∠EFA ＋∠AEF ＝90°. ∵EF ⊥EC ，∴∠FEC ＝90°. ∴∠AEF ＋∠CED ＝90°. ∴∠EFA ＝∠CED. 在△AEF 和△DCE 中，∠A ＝∠D ，∠EFA ＝∠CED ，EF ＝CE ，∴△AEF ≌△DCE(AAS)．∴AE ＝DC.11.已知：在矩形ABCD 中，BD 是对角线，AE ⊥BD 于点E ，CF ⊥BD 于点F. (1)如图1，求证：AE ＝CF ；(2)如图2，当∠ADB ＝30°时，连接AF ，CE ，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于矩形ABCD 面积的18.解：(1)证明：∵四边形ABCD 是矩形，∴AB ＝CD ，AB ∥CD ，AD ∥BC. ∴∠ABE ＝∠CDF. ∵AE ⊥BD ，CF ⊥BD ，∴∠AEB ＝∠CFD ＝90°.在△ABE 和△CDF 中，∠ABE ＝∠CDF ，∠AEB ＝∠CFD ，AB ＝CD ，∴△ABE ≌△CDF(AAS)．∴AE ＝CF. (2)S △ABE ＝S △CDF ＝S △BCE ＝S △ADF ＝18S 矩形ABCD .12.如图，在四边形ABCD 中，BC ∥AD ，BC ＝12AD ，点E 为AD 的中点，点F 为AE 的中点，AC⊥CD ，连接BE ，CE ，CF.(1)判断四边形ABCE 的形状，并说明理由；(2)如果AB ＝4，∠D ＝30°，点P 为BE 上的动点，求△PAF 周长的最小值．解：(1)四边形ABCE 是菱形，理由如下：∵点E 是AD 的中点，∴AE ＝12AD.∵BC ＝12AD ，∴AE ＝BC.∵BC ∥AD ，∴四边形ABCE 是平行四边形．∵AC ⊥CD ，点E 是AD 的中点，∴CE ＝AE ＝DE. ∴四边形ABCE 是菱形．(2)∵四边形ABCE 是菱形．∴AE ＝EC ＝AB ＝4，点A ，C 关于BE 对称．2AE＝2.∴当PA＋PF最小时，△PAF的周长最小，即点P为CF与BE的交点时，△PAF的周长最小．此时△PAF的周长为PA＋PF＋AF＝CF＋AF.∵CE＝DE，∴∠ECD＝∠D＝30°，∠ACE＝90°－30°＝60°.∴△ACE是等边三角形．∴AC＝AE＝CE＝4.∵AF＝EF，∴CF⊥AE.∴CF＝AC2－AF2＝2 3.△PAF周长的最小值为CF＋AF＝23＋2.13.如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D 作DE⊥BC，垂足为F，交直线MN于点E，连接CD，BE.(1)求证：CE＝AD；(2)当D为AB的中点时，四边形CDBE是什么特殊四边形？说明你的理由；(3)若D为AB的中点，则当∠A的大小满足什么条件时，四边形CDBE是正方形？请说明你的理由．解：(1)证明：∵DE⊥BC，∴∠DFB＝90°.∵∠ACB＝90°，∴∠ACB＝∠DFB.∴AC∥DE.∵MN∥AB，即CE∥AD，∴四边形ADEC是平行四边形．∴CE＝AD.(2)四边形CDBE是菱形．理由：∵CE＝AD，∴BD＝CE.∵BD∥CE，∴四边形CDBE是平行四边形．∵∠ACB＝90°，D为AB的中点，∴CD＝BD.∴四边形CDBE是菱形．(3)当∠A＝45°时，四边形CDBE是正方形．理由：∵∠ACB＝90°，∠A＝45°，∴∠ABC＝∠A＝45°.∴AC＝BC.∵D为AB的中点，∴CD⊥AB.∴∠CDB＝90°.又∵四边形CDBE是菱形，∴四边形CDBE是正方形．14.如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连接EC，连接AP并延长交CD于点F，连接BP，交CE于点H.(1)若∠PBA∶∠PBC＝1∶2，判断△PBC的形状，并说明理由；(2)求证：四边形AECF为平行四边形．解：(1)△PBC是等边三角形，理由如下：在矩形ABCD中，∠ABC＝90°，∵∠PBA∶∠PBC＝1∶2，∴∠PBC＝60°.由折叠的性质，得PC＝BC.∴△PBC是等边三角形．(2)证明：由折叠的性质，得△EBC≌△EPC.∴BE＝PE.∴∠EBP＝∠EPB.∵E为AB的中点，∴BE＝AE.∴AE＝PE.∴∠EPA＝∠EAP.∵∠EBP ＋∠EPB ＋∠EPA ＋∠EAP ＝180°，∴∠EPB ＋∠EPA ＝90°. ∴∠BPA ＝90°，即BP ⊥AF.由折叠的性质，得BP ⊥CE ，∴AF ∥CE. ∵四边形ABCD 是矩形，∴AE ∥CF. ∴四边形AECF 为平行四边形．15.如图，将一张矩形纸片ABCD 沿直线MN 折叠，使点C 落在点A 处，点D 落在点E 处，直线MN 交BC 于点M ，交AD 于点N.(1)求证：CM ＝CN ；(2)若△CMN 的面积与△CDN 的面积比为3∶1，求MNDN的值．解：(1)证明：由折叠的性质，得∠ENM ＝∠DNM ，又∵∠ANE ＝∠CND ，∴∠ANM ＝∠CNM. ∵四边形ABCD 是矩形，∴AD ∥BC. ∴∠ANM ＝∠CMN. ∴∠CMN ＝∠CNM. ∴CM ＝CN.(2)过点N 作NH ⊥BC 于点H ，则四边形NHCD 是矩形，∴HC ＝DN ，NH ＝DC. ∵S △CMN S △CDN ＝12MC ·NH12ND ·NH ＝MC ND＝3，∴MC ＝3ND ＝3HC.∴MH ＝2HC.设DN ＝x ，则HC ＝x ，MH ＝2x. ∴CM ＝CN ＝3x.在Rt △CDN 中，DC ＝CN 2－DN 2＝22x. 在Rt △MNH 中，MN ＝MH 2＋HN 2＝23x. ∴MN DN ＝23x x＝2 3. 16.在正方形ABCD 中，点E ，F 分别在边BC ，AD 上，DE ＝EF ，过点D 作DG ⊥EF 于点H ，交AB 边于点G.(1)如图1，求证：DE ＝DG ；(2)如图2，将EF 绕点E 逆时针旋转90°得到EK ，点F 对应点K ，连接KG ，EG.若H 为DG 的中点，在不添加任何辅助线及字母的情况下，请直接写出图中所有与EG 长度相等的线段(不包括EG)．解：(1)证明：∵四边形ABCD 是正方形，∴AD ＝DC ，AD ∥BC ，∠DAG ＝∠DCE ＝90°. ∴∠DEC ＝∠EDF.∵DE ＝EF ，∴∠EFD ＝∠EDF. ∴∠EFD ＝∠DEC.∵DG ⊥EF ，∴∠GHF ＝90°. ∴∠DGA ＋∠AFH ＝180°. ∵∠AFH ＋∠EFD ＝180°，∴∠DGA ＝∠EFD ＝∠DEC. 在△DAG 和△DCE 中，∠DGA ＝∠DEC ，∠DAG ＝∠DCE ，DA ＝DC ，∴△DAG ≌△DCE(AAS)．∴DG ＝DE.(2)与线段EG 相等的线段有：DE ，DG ，GK ，KE ，EF.17.如图，BD 是正方形ABCD 的对角线，线段BC 在其所在的直线上平移，将平移得到的线段记为PQ ，连接PA ，过点Q 作QO ⊥BD ，垂足为O ，连接OA ，OP.(1)如图1所示，求证：AP ＝2OA ；(2)如图2所示，PQ 在BC 的延长线上，如图3所示，PQ 在BC 的反向延长线上，猜想线段AP ，OA 之间有怎样的数量关系？请直接写出你的猜想，不需证明．解：(1)证明：∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABD ＝∠CBD ＝45°. ∵QO ⊥BD ，∴∠BOQ ＝90°. ∴∠BQO ＝∠CBD ＝45°.∴OB ＝OQ. ∵PQ ＝BC ，∴AB ＝PQ.在△ABO 和△PQO 中，OB ＝OQ ，∠ABO ＝∠PQO ，AB ＝PQ ，∴△ABO ≌△PQO(SAS)．∴OA ＝OP ，∠AOB ＝∠POQ. ∵∠BOP ＋∠POQ ＝90°，∴∠BOP ＋∠AOB ＝90，即∠AOP ＝90°. ∴△AOP 是等腰直角三角形．∴AP ＝2OA.(2)当PQ 在BC 的延长线上时，线段AP ，OA 之间的数量关系为AP ＝2OA ；当PQ 在BC 的反向延长线上时，线段AP ，OA 之间的数量关系为AP ＝2OA.。

2020秋北师大版九年级数学上第一、二章检测题含答案

单元测试(一) 特殊平行四边形(满分：150分，考试用时120分钟)一、选择题(本大题共15个小题，每小题3分，共45分)1.如图，在Rt△ABC中，CD是斜边AB上的中线，若AB＝8，则CD的长是( )A．6 B．5 C．4 D．32．如图，矩形ABCD中，对角线AC、BD相交于点O，若∠OAD＝40°，则∠COD＝( )A．20° B．40° C．80° D．100°3．如图，在菱形ABCD中，对角线AC、BD交于点O，下列说法错误的是( )A．AB∥DC B．AC＝BD C．AC⊥BD D．OA＝OC4．如图，在矩形ABCD中，对角线AC、BD相交于点O，若OA＝2，则BD的长为( )A．4 B．3 C．2 D．15．如果要证明ABCD为正方形，那么我们需要在四边形ABCD是平行四边形的基础上，进一步证明( )A．AB＝AD且AC⊥BD B．AB＝AD且AC＝BDC．∠A＝∠B且AC＝BD D．AC和BD互相垂直平分6．菱形的两条对角线长分别是6和8，则此菱形的边长是( )A．10 B．8 C．6 D．57．在正方形ABCD中，AB＝12，对角线AC，BD相交于点O，则△ABO的周长是( )A．12＋12 2 B．2＋6 2C．12＋ 2 D．24＋6 28．如图，在菱形ABCD中，对角线AC、BD相交于点O，E为AB的中点，且OE＝a，则菱形ABCD的周长为( ) A．16a B．12aC．8a D．4a9．正方形的一条对角线长为4，则这个正方形面积是( )A．8 B．4 2C．8 2 D．1610．下列命题中，错误的是( )A．平行四边形的对角线互相平分B．菱形的对角线互相垂直平分C．矩形的对角线相等且互相垂直平分D．角平分线上的点到角两边的距离相等11．如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件中能够判定四边形ACED为菱形的是( )A．AB＝BC B．AC＝BCC．∠B＝60° D．∠ACB＝60°12．如图，E是矩形ABCD中BC边的中点，将△ABE沿AE折叠到△AFE，F在矩形ABCD内部，延长AF交DC于G点，若∠AEB＝55°，则∠DAF＝( )A．40° B．35°C．20° D．15°13．如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为( )A．75° B．60° C．55° D．45°14．将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当∠B＝90°时，如图1，测得AC＝2，当∠B＝60°时，如图2，AC＝( )A. 2 B．2 C. 6 D．2 215．如图，四边形ABCD为平行四边形，延长AD到E，使DE＝AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是( )A．AB＝BE B．DE⊥DCC．∠ADB＝90° D．CE⊥DE二、填空题(本大题共5个小题，每小题5分，共25分)16．如图，菱形ABCD的一条对角线的中点O到AB的距离为2，那么O点到另一边的距离为________．17．如图，在矩形ABCD中，对角线AC、BD相交于点O，∠ACB＝30°，则∠AOB的大小为________度．18．如图所示，已知ABCD，下列条件：①AC＝BD，②AB＝AD，③∠1＝∠2，④AB⊥BC中，能说明ABCD是矩形的有________(填写序号)．19．如图，在四边形ABCD中，AB＝BC＝CD＝DA，对角线AC与BD相交于点O，若不增加任何字母与辅助线，要使四边形ABCD是正方形，则还需增加一个条件是________________．20．已知E是正方形ABCD的对角线AC上一点，AE＝AD，过点E作AC的垂线，交边CD于点F，那么∠FAD＝________度．三、解答题(本大题共7个小题，各题分值见题号后，共80分)21．(8分)如图，矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86 cm，对角线长是13 cm，那么矩形的周长是多少？22．(8分)如图，四边形ABCD中，AB＝CD，∠BAD＋∠ADC＝180°，AC与BD相交于点O，△AOB是等边三角形，求证：四边形ABCD是矩形．23．(10分)如图，已知正方形ABCD，延长AB到E，使AE＝AC，以AE为一边作菱形AEFC，若菱形的面积为92，求正方形的边长．24.(12分)如图，在菱形ABCD中，∠A＝60°，AB＝4，O为对角线BD的中点，过O点作OE⊥AB，垂足为E.(1)求∠ABD的度数；(2)求线段BE的长．25．(12分)如图，在正方形ABCD中，点E，F分别在边AB，BC上，AF＝DE，AF和DE相交于点G.(1)观察图形，写出图中所有与∠AED相等的角；(2)选择图中与∠AED相等的任意一个角，并加以证明．26．(14分)以边长为2的正方形的中心O为端点，引两条相互垂直的射线，分别与正方形的边交于A、B两点，求线段AB的最小值．27．(16分)已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．(1)求证：△ABM≌△DCM；(2)判断四边形MENF是什么特殊四边形，并证明你的结论；(3)当AD∶AB＝________时，四边形MENF是正方形．参考答案1.C2.C3.B4.A5.B6.D7.A8.C9.A 10.C 11.B 12.C 13.B 14.A 15.B 16.2 17.60 18.①④ 19.AC ＝BD 或AB ⊥BC 20.22.521.∵△AOB 、△BOC 、△COD 和△AOD 四个小三角形的周长和为86 cm ，且AC ＝BD ＝13 cm ， ∴AB ＋BC ＋CD ＋DA ＝86－2(AC ＋BD)＝86－4×13＝34(cm)，即矩形ABCD 的周长是34 cm.22.证明：∵∠BAD ＋∠ADC ＝180°， ∴AB ∥CD.又∵AB ＝CD ，∴四边形ABCD 是平行四边形． ∵△AOB 是等边三角形， ∴AO ＝BO.∴2AO ＝2BO ，即AC ＝BD. ∴四边形ABCD 是矩形． 2 23.设正方形的边长为x ，∵AC 为正方形ABCD 的对角线，∴AC ＝2x.∴S 菱形AEFC ＝AE ·CB ＝2x ·x ＝2x 2.∴2x 2＝9 2. ∴x 2＝9.∴x ＝±3.舍去x ＝－3. ∴正方形边长为3.24.(1)在菱形ABCD 中，AB ＝AD ，∠A ＝60°， ∴△ABD 为等边三角形． ∴∠ABD ＝60°.(2)由(1)可知BD ＝AB ＝4，又∵O 为BD 的中点， ∴OB ＝2.又∵OE ⊥AB ，∠ABD ＝60°， ∴∠BOE ＝30°. ∴BE ＝12OB ＝1.25.(1)由图可知，∠DAG ，∠AFB ，∠CDE 与∠AED 相等． (2)选择∠AFB ＝∠AED ，证明如下： ∵四边形ABCD 是正方形，∴∠DAB ＝∠B ＝90°，AB ＝AD.在Rt △BAF 和Rt △ADE 中，⎩⎪⎨⎪⎧BA ＝AD ，AF ＝DE ，∴Rt △BAF ≌Rt △ADE(HL)．∴∠AFB ＝∠AED.26.∵四边形CDEF 是正方形，∴∠OCD ＝∠ODB ＝45°，∠COD ＝90°，OC ＝OD. ∵AO ⊥OB ， ∴∠AOB ＝90°.∴∠AOC ＋∠AOD ＝90°，∠AOD ＋∠BOD ＝90°. ∴∠AOC ＝∠BOD.∵在△COA 和△DOB 中，⎩⎪⎨⎪⎧∠OCA ＝∠ODB ，OC ＝OD ，∠AOC ＝∠BOD ，∴△COA ≌△DOB.∴OA ＝OB.∵∠AOB ＝90°，∴△AOB 是等腰直角三角形．由勾股定理得AB ＝OA 2＋OB 2＝2OA ，要使AB 最小，只要OA 取最小值即可，根据垂线段最短，OA ⊥CD 时，OA 最小， ∵四边形CDEF 是正方形， ∴FC ⊥CD ，OD ＝OF ＝OC. ∴CA ＝DA. ∴OA ＝12CF ＝1.∴AB ＝ 2.∴AB 的最小值为 2.27.(1)证明：∵四边形ABCD 是矩形， ∴AB ＝CD ，∠A ＝∠D ＝90°. 又∵M 是AD 的中点， ∴AM ＝DM.在△ABM 和△DCM 中，⎩⎪⎨⎪⎧AB ＝CD ，∠A ＝∠D ，AM ＝DM ，∴△ABM ≌△DCM(SAS)．（2）四边形MENF 是菱形．证明：∵E ，F ，N 分别是BM ，CM ，CB 的中点， ∴NE ∥MF ，NE ＝MF.∴四边形MENF 是平行四边形．由(1)，得BM ＝CM ， ∴ME ＝MF.∴四边形MENF 是菱形．（3）当AD ∶AB ＝2∶1时，四边形MENF 是正方形．理由： ∵M 为AD 中点， ∴AD ＝2AM.∵AD ∶AB ＝2∶1， ∴AM ＝AB. ∵∠A ＝90°，∴∠ABM ＝∠AMB ＝45°. 同理：∠DMC ＝45°.∴∠EMF ＝180°－45°－45°＝90°. ∵四边形MENF 是菱形， ∴四边形MENF 是正方形．故答案为2∶1.单元测试(二) 一元二次方程(满分：150分，考试用时120分钟)一、选择题(本大题共15个小题，每小题3分，共45分) 1.下列方程中，关于x 的一元二次方程是( )A ．x 2＋2y ＝1 B.1x 2＋1x－2＝0C ．ax 2＋bx ＋c ＝0 D ．x 2＋2x ＝12．用公式法解一元二次方程3x 2－2x ＋3＝0时，首先要确定a ，b ，c 的值，下列叙述正确的是( )A ．a ＝3，b ＝2，c ＝3B ．a ＝－3，b ＝2，c ＝3C ．a ＝3，b ＝2，c ＝－3D ．a ＝3，b ＝－2，c ＝33．若关于x 的方程2x m －1＋x －m ＝0是一元二次方程，则m 为( )A ．1B ．2C ．3D ．04．一元二次方程x 2－2x －1＝0的根的情况是( )A ．有两个相等的实数根B ．有两个不相等的实数根C ．只有一个实数根D ．没有实数根5．一元二次方程x 2＋4x －3＝0的两根为x 1，x 2，则x 1·x 2的值是( )A ．4B ．－4C ．3D ．－3 6．方程x(x ＋2)＝0的根是( )A ．x ＝2B ．x ＝0C ．x 1＝0，x 2＝－2D ．x 1＝0，x 2＝27．用配方法解方程x 2－2x －5＝0时，原方程应变形为( )A ．(x ＋1)2＝6B ．(x －1)2＝6C ．(x ＋2)2＝9D ．(x －2)2＝9 8．根据下面表格中的对应值：判断方程ax 2＋bx ＋c ＝A ．3＜x ＜3.23 B ．3.23＜x ＜3.24 C ．3.24＜x ＜3.25 D ．3.25＜x ＜3.26 9．解方程(x ＋1)(x ＋3)＝5较为合适的方法是( )A ．直接开平方法B ．配方法C ．公式法或配方法D ．分解因式法10．已知x ＝1是一元二次方程x 2＋mx ＋n ＝0的一个根，则m 2＋2mn ＋n 2的值为( )A ．0B ．1C ．2D ．411．三角形两边长分别为3和6，第三边是方程x 2－6x ＋8＝0的根，则三角形的周长为( )A ．11B ．13C ．15D ．11或13 12．下列说法不正确的是( )A ．方程x 2＝x 有一根为0B ．方程x 2－1＝0的两根互为相反数C ．方程(x －1)2－1＝0的两根互为相反数D ．方程x 2－x ＋2＝0无实数根13．对二次三项式x 2－10x ＋36，小聪同学认为：无论x 取什么实数，它的值都不可能等于11；小颖同学认为：可以取两个不同的值，使它的值等于11.你认为( )A．小聪对，小颖错 B．小聪错，小颖对C．他们两人都对 D．他们两人都错14．如图，在长为100米，宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7 644平方米，则道路的宽应为多少米？设道路的宽为x米，则可列方程为( )A．100×80－100x－80x＝7 644B．(100－x)(80－x)＋x2＝7 644C．(100－x)(80－x)＝7 644D．100x＋80x＝35615．若关于x的一元二次方程x2－2x＋kb＋1＝0有两个不相等的实数根，则一次函数y＝kx＋b的大致图象可能是( )二、填空题(本大题共5小题，每小题5分，共25分)16．将方程3x(x－1)＝5化为ax2＋bx＋c＝0的形式为____________．17．若x＝1是一元二次方程x2＋2x＋m＝0的一个根，则m的值为________．18．若(m＋n)(m＋n＋5)＝6，则m＋n的值是________．19．一件工艺品进价100元，标价135元售出，每天可售出100件，根据销售统计，一件工艺品每降低1元出售，则每天可多售出4件，要使顾客尽量得到优惠，且每天获得的利润为3 596，每件工艺品需降价________元．20．已知关于x的方程x2－(a＋b)x＋ab－1＝0，x1、x2是此方程的两个实数根，现给出三个结论：①x1≠x2；②x1x2<ab；③x21＋x22<a2＋b2.则正确结论的序号是________．(填上你认为正确的所有序号)三、解答题(本大题共7个小题，各题分值见题号后，共80分)21．(8分)选择适当的方法解下列方程：(1)(x－3)2＝4；(2)x2－5x＋1＝0.22．(8分)已知m，n是关于x的一元二次方程x2－3x＋a＝0的两个解，若mn＋m＋n＝2，求a的值．23．(10分)随着市民环保意识的增强，烟花爆竹销售量逐年下降．咸宁市2013年销售烟花爆竹20万箱，到2015年烟花爆竹销售量为9.8万箱．求咸宁市2013年到2015年烟花爆竹年销售量的平均下降率．24.(12分)小林准备进行如下操作实验：把一根长为40 cm的铁丝剪成两段，并把每一段各围成一个正方形．(1)要使这两个正方形的面积之和等于58 cm2，小林该怎么剪？(2)小峰对小林说：“这两个正方形的面积之和不可能等于48 cm2.”他的说法对吗？请说明理由．25．(12分)已知：关于x的方程x2＋2mx＋m2－1＝0.(1)不解方程，判别方程的根的情况；(2)若方程有一个根为3，求m的值．26.(14分)观察下列一元二次方程，并回答问题：第1个方程：x2＋x＝0；第2个方程：x2－1＝0；第3个方程：x2－x－2＝0；第4个方程：x2－2x－3＝0；…(1)第2 016个方程是____________________；(2)直接写出第n个方程，并求出第n个方程的解；(3)说出这列一元二次方程的解的一个共同特点．27．(16分)已知关于x的一元二次方程(a＋c)x2＋2bx＋(a－c)＝0，其中a，b，c分别为△ABC三边的长．(1)如果x＝－1是方程的根，试判断△ABC的形状，并说明理由；(2)如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；(3)如果△ABC是等边三角形，试求这个一元二次方程的根．参考答案1．D 2.D 3.C 4.B 5.D 6.C 7.B 8.C 9.C 10.B 11.B 12.C 13.D 14.C 15.B 16.3x 2－3x －5＝0 17.－3 18.－6或1 19.6 20.①② 21.(1)x 1＝1，x 2＝5. (2)x 1＝5＋212，x 2＝5－212.22.∵m ，n 是关于x 的一元二次方程x 2－3x ＋a ＝0的两个解，∴m ＋n ＝3，mn ＝a. ∵mn ＋m ＋n ＝2，∴a ＋3＝2.解得a ＝－1.23.设年销售量的平均下降率为x ，依题意，得20(1－x)2＝9.8. 解这个方程，得x 1＝0.3，x 2＝1.7. ∵x 2＝1.7不符合题意， ∴x ＝0.3＝30%.答：咸宁市2013年到2015年烟花爆竹年销售量的平均下降率为30%.24.(1)设其中一个正方形的边长为x cm ，则另一个正方形的边长为(10－x)cm.由题意，得x 2＋(10－x)2＝58.解得x 1＝3，x 2＝7.4×3＝12，4×7＝28.答：小林把绳子剪成12 cm 和28 cm 的两段．(2)假设能围成．由(1)得x 2＋(10－x)2＝48.化简得x 2－10x ＋26＝0. ∵b 2－4ac ＝(－10)2－4×1×26＝－4<0， ∴此方程没有实数根． ∴小峰的说法是对的．25.(1)∵b 2－4ac ＝(2m)2－4×1×(m 2－1)＝4＞0， ∴方程有两个不相等的实数根．(2)将x ＝3代入原方程，得9＋6m ＋m 2－1＝0.解得m 1＝－2，m 2＝－4.26.(1)x 2－2 014x －2 015＝0(2)第n 个方程是x 2－(n －2)x －(n －1)＝0，解得x 1＝－1，x 2＝n －1.(3)这列一元二次方程的解的一个共同特点：有一根是－1. 27.(1)△ABC 是等腰三角形．理由： ∵x ＝－1是方程的根，∴(a ＋c)×(－1)2－2b ＋(a －c)＝0. ∴a ＋c －2b ＋a －c ＝0. ∴a －b ＝0. ∴a ＝b.∴△ABC 是等腰三角形．(2)∵方程有两个相等的实数根，∴(2b)2－4(a ＋c)(a －c)＝0.∴4b 2－4a 2＋4c 2＝0. ∴a 2＝b 2＋c 2.∴△ABC 是直角三角形． (3)∵△ABC 是等边三角形，∴(a ＋c)x 2＋2bx ＋(a －c)＝0可整理为2ax 2＋2ax ＝0. ∴x 2＋x ＝0.解得x 1＝0，x 2＝－1.。

北师大版数学九年级上册课本答案.doc

北师大版数学九年级上册课本答案【篇一：北师版九年级数学上册第一章测试卷(含答案)】卷满分120 分考试时间120 分钟）一、选择题（共10 小题，每小题 3 分，计30 分）1、下列各组图形中，是全等三角形的一组是（）a.底边长都为15cm 的两个等腰三角形b.腰长都为15cm 的两个等腰三角形d.边长为12cm 的两个等边三角形2、等腰三角形的周长为13，其中一边长为3，则该等腰三角形的底边长为（）a.7b.3c.7 或3d.53、一个三角形如果有两边的垂直平分线的交点在第三边上，那么这个三角形是（）a.等腰三角形b.等边三角形c. 直角三角形d.等腰直角三角形4、用反证法证明命题“一个三角形中不能有两个角是直角”，应先假设这个三角形中（）a.有两个角是直角b.有两个角是钝角c. 有两个角是锐角d.一个角是钝角，一个角是直角6、如图1-2，在一次强台风中一棵大树在离地面5m 处折断倒下，倒a.10mb.15mc.25md.30m c ba d 图1-1 图1-27、下列命题①对顶角相等②如果三角形中有一个角是钝角，那么另外两个角是锐角③若两直线平行，则内错角相等④三边都相等的三角形是等边三角形。

其中逆命题正确的有（）a.①③b. ②④c.①②d.③④8、如图1-3（1）在△abc 中，d、e 分别是ab,ac 的中点，将△ade 沿线段de 向下折叠，得到图形1-3（2），下列关于图（2）的四个结论中，一定不成立的是（）c. △dba 是等腰三角形d.de ∥bce c 图1-3 b c （2）（1）aa.1b.2c.3d.4be aa c图1-4 图1-5二、填空题（共 6 小题，每小题 3 分，计18 分）11、已知三条不同的直线a,b,c 在同一平面内，下列四个命题：①如果③如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c 其中属于真命题的是（填写所有真命题的序号）12、一个三角形三边之比为2:5:3 ，这个三角形的形状是13、把“同角的余交相等”改写成“如果?? ，那么??”的形式为cd=3 ，则ab 的长度为15、如图1-7，p 是正方形abcd 内一点，将△abp 绕点b 顺时针方向旋转能与△cbp? 重合，若pb=3 ，则pp? 的长度为a p d bd b cc n c a b ?图1-6 图1-7 图1-8三、解答题（共 6 小题，计72 分，解答应写过程）ad 图1-918、（10 分）已知：如图1-10 ，de 为△abc 的边ab 的垂直平分线，m d cd 为△abc 的外角平分线，与de 交于点d，dm ⊥bc 的延长线于点m，dn ⊥ac 于点n，求证：an=bm 。

北师大版九年级数学上册第一单元测试题含答案

北师大版九年级数学上册第一章测试题及答案一、选择题(每题3分，共30分)1．菱形、矩形、正方形都具有的性质是()A．四条边相等，四个角相等B．对角线相等C．对角线互相垂直D．对角线互相平分2．如图，在菱形ABCD中，AB＝5，∠BCD＝120°，则△ABC的周长等于() A．20 B．15 C．10 D．53．如图，EF过矩形ABCD对角线的交点O，且分别交AB，CD于点E，F，那么阴影部分的面积是矩形ABCD面积的()A．15B．14C．13D．3104．如图，菱形ABCD的周长为24 cm，对角线AC，BD相交于点O，点E是AD 的中点，连接OE，则线段OE的长等于()A．3 cm B．4 cm C．2.5 cm D．2 cm5．如图，在矩形ABCD中，AB＝3，对角线AC，BD相交于点O，AE垂直平分OB于点E，则AD的长为()A．3 B．2 2 C. 6 D．3 36．顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是()A．菱形B．对角线互相垂直的四边形C．矩形D．对角线相等的四边形7．如图，把一张长方形纸片对折两次，然后剪下一个角，为了得到一个钝角为120°的菱形，剪口与第二次折痕所成角的度数应为()A．15°或30°B．30°或45°C．45°或60°D．30°或60°8．如图，在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E，F分别为BC，CD的中点，则∠EAF等于()A．75°B．45°C．60°D．30°9．如图，在矩形纸片ABCD中，AB＝4，BC＝8，将纸片沿EF折叠，使点C与点A重合，则下列结论错误的是()A．AF＝AEB．△ABE≌△AGFC．EF＝2 5D．AF＝EF10．如图，在正方形ABCD中，点E，F分别在BC，CD上，△AEF是等边三角形，连接AC交EF于点G，下列结论：①BE＝DF；②∠DAF＝15°；③AC 垂直平分EF；④BE＋DF＝EF；⑤S△CEF＝2S△ABE.其中正确结论有() A．2个B．3个C．4个D．5个二、填空题(每题3分，共24分)11．如图是一个平行四边形的活动框架，对角线是两根橡皮筋．若改变框架的形状，则∠α也随之变化，两条对角线长度也在发生改变．当∠α的度数为________时，两条对角线长度相等．12．如图，在菱形ABCD中，∠B＝60°，AB＝4，则以AC为边的正方形ACEF 的周长为________．13．如图，在矩形ABCD中，对角线AC，BD相交于点O，DE⊥AC于点E，∠EDC∶∠EDA＝1∶2，且AC＝10，则EC的长度是________．14．如图，点E在正方形ABCD的边CD上，若△ABE的面积为18，CE＝4，则线段BE的长为________．15．菱形ABCD在直角坐标系中的位置如图所示，其中点A的坐标为(1，0)，点B的坐标为(0，3)，动点P从点A出发，沿A→B→C→D→A→B→……的路径，在菱形的边上以每秒0.5个单位长度的速度移动，移动到第2 019 s时，点P的坐标为________．16．如图，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF＝4.设AB＝x，AD＝y，则x2＋(y－4)2的值为________．17．如图，在矩形ABCD中，AB＝3，BC＝2，点E为AD的中点，点F为BC 边上任一点，过点F分别作EB，EC的垂线，垂足分别为点G，H，则FG ＋FH＝________.18．如图，在Rt△ABC中，∠ACB＝90°，以斜边AB为边向外作正方形ABDE，且正方形的对角线交于点O，连接OC.已知AC＝5，OC＝62，则另一直角边BC的长为________．三、解答题(19，20题每题9分，21题10分，22，23题每题12分，24题14分，共66分)19．如图，四边形ABCD是菱形，DE⊥AB交BA的延长线于点E，DF⊥BC交BC的延长线于点F.求证：DE＝DF.20．如图，点O是菱形ABCD对角线的交点，过点C作CE∥OD，过点D作DE∥AC，CE与DE相交于点E.(1)求证：四边形OCED是矩形．(2)若AB＝4，∠ABC＝60°，求矩形OCED的面积．21．如图，矩形ABCD的对角线AC，BD相交于点O，过点B作AC的平行线交DC的延长线于点E.(1)求证：BD＝BE.(2)若BE＝10，CE＝6，连接OE，求△ODE的面积．22．如图，将矩形纸片ABCD沿对角线BD折叠，使点A落在平面上的F点处，DF交BC于点E.(1)求证：△DCE≌△BFE.(2)若CD＝2，∠ADB＝30°，求BE的长．23．如图，在菱形ABCD中，AB＝4，∠BAD＝120°，以点A为顶点的一个60°的∠EAF绕点A旋转，∠EAF的两边分别交BC，CD于点E，F，且E，F 不与B，C，D重合，连接EF.(1)求证：BE＝CF.(2)在∠EAF绕点A旋转的过程中，四边形AECF的面积是否发生变化？如果不变，求出其定值；如果变化，请说明理由．24．在正方形ABCD的外侧作直线AP，点B关于直线AP的对称点为E，连接BE，DE，其中DE交直线AP于点F.(1)依题意补全图①；(2)若∠P AB＝20°，求∠ADF的度数；(3)如图②，若45°＜∠P AB＜90°，用等式表示线段AB，EF，FD之间的数量关系，并给出证明．答案一、1．D2．B3．B4．A解析：∵菱形ABCD的周长为24 cm，∴AB＝24÷4＝6 (cm)，OB＝OD.又∵E为AD边的中点，∴OE是△ABD的中位线．∴OE＝12AB＝12×6＝3 (cm)．故选A.5．D6．D7．D8．C9．D解析：如图，由折叠的性质得∠1＝∠2.∵AD∥BC，∴∠3＝∠1.∴∠2＝∠3.∴AE＝AF.故选项A正确．由折叠的性质得CD＝AG，∠D＝∠G＝90°.∵AB＝CD，∴AB＝AG.又∵AE＝AF，∠B＝90°，∴Rt△ABE≌Rt△AGF(HL)．故选项B正确．设DF＝x，则GF＝x，AF＝8－x.又∵AG＝AB＝4，∴在Rt△AGF中，根据勾股定理得(8－x)2＝42＋x2.解得x＝3.∴AF＝8－x＝5.则AE＝AF＝5，∴BE＝AE2－AB2＝52－42＝3.过点F作FM⊥BC于点M，则FM＝4，EM＝5－3＝2.在Rt△EFM中，根据勾股定理得EF＝EM2＋FM2＝22＋42＝20＝25，则选项C正确．∵AF＝5，EF＝25，∴AF≠EF.故选项D错误．10．C 解析：∵四边形ABCD 是正方形，∴AB ＝BC ＝CD ＝AD ，∠B ＝∠BCD ＝∠D ＝∠BAD ＝90°. ∵△AEF 是等边三角形， ∴AE ＝EF ＝AF ，∠EAF ＝60°. ∴∠BAE ＋∠DAF ＝30°. 在Rt △ABE 和Rt △ADF 中，∴Rt △ABE ≌Rt △ADF (HL)． ∴BE ＝DF (故①正确)， ∠BAE ＝∠DAF .∴∠DAF ＋∠DAF ＝30°，即∠DAF ＝15°(故②正确)． ∵BC ＝CD ，∴BC －BE ＝CD －DF ，即CE ＝CF ，又∵AE ＝AF ，∴AC 垂直平分EF (故③正确)．设EC ＝x ，由勾股定理，得EF ＝AE ＝2x ，∴EG ＝CG ＝22x . ∴AG ＝62x . ∴AC ＝6x ＋2x2.∴AB ＝BC ＝3x ＋x 2.∴BE ＝3x ＋x 2－x ＝3x －x2.∴BE ＋DF ＝3x －x ≠2x (故④错误)．易知S △CEF ＝x 22，S △ABE ＝3x －x 2·3x ＋x22＝x 24，∴2S △ABE ＝x 22＝S △CEF (故⑤正确)．综上所述，正确的有4个．二、11．90° 12．16 13．2.514．213 解析：设正方形的边长为a ，∵S △ABE ＝18，∴S 正方形ABCD ＝2S △ABE ＝36， ∴a 2＝36.∵a ＞0，∴a ＝6. 在Rt △BCE 中，∵BC ＝6，CE ＝4，∠C ＝90°， ∴BE ＝BC 2＋CE 2＝62＋42＝213. 15．⎝ ⎛⎭⎪⎫14，334 16．16 解析：∵四边形ABCD 是矩形，AB ＝x ，AD ＝y ，∴CD ＝AB ＝x ，BC ＝AD ＝y ，∠BCD ＝90°.又∵BD ⊥DE ，点F 是BE 的中点，DF ＝4，∴BF ＝DF ＝EF ＝4，∴CF ＝4－BC ＝4－y.在Rt △DCF 中，DC 2＋CF 2＝DF 2，即x 2＋(4－y )2＝42＝16.∴x 2＋(y －4)2＝16. 17．3105 解析：如图，连接EF ，∵四边形ABCD 是矩形，∴CD ＝AB ＝3，AD ＝BC ＝2，∠A ＝∠D ＝90°. ∵点E 为AD 的中点，∴AE ＝DE ＝1，∴BE ＝AE 2＋AB 2＝12＋32＝10，CE ＝DE 2＋DC 2＝12＋32＝10， ∴CE ＝BE .∵S △BCE ＝S △BEF ＋S △CEF ，∴12BC ·AB ＝12BE ·FG ＋12CE ·FH ，∴BC ·AB ＝BE (FG ＋FH )，即2×3＝10(FG ＋FH )，解得FG ＋FH ＝3105.18．7 解析：如图，过点O 作OM ⊥CA ，交CA 的延长线于点M ，过点O作ON ⊥BC 于点N ，易证△OMA ≌△ONB ，CN ＝OM ，∴OM ＝ON ，MA ＝N B.又∵∠ACB ＝90°，∠OMA ＝∠ONB ＝90°，OM ＝ON ， ∴四边形OMCN 是正方形． ∴△OCM 为等腰直角三角形． ∵OC ＝62，∴CM ＝OM ＝6.∴MA＝CM－AC＝6－5＝1.∴BC＝CN＋NB＝OM＋MA＝6＋1＝7. 故答案为7.三、19．证明：连接DB.∵四边形ABCD是菱形，∴BD平分∠ABC.又∵DE⊥AB，DF⊥BC，∴DE＝DF.20．(1)证明：∵CE∥OD，DE∥AC，∴四边形OCED是平行四边形．又∵四边形ABCD是菱形，∴AC⊥BD，即∠COD＝90°，∴四边形OCED是矩形．(2)解：∵在菱形ABCD中，AB＝4，∴AB＝BC＝CD＝4.又∵∠ABC＝60°，∴△ABC是等边三角形，∴AC＝4，∴OC＝12AC＝2，∴OD＝42－22＝23，∴矩形OCED的面积是23×2＝4 3.21．(1)证明：∵四边形ABCD是矩形，∴AC＝BD，AB∥CD.又∵BE∥AC，E在DC的延长线上．∴四边形ABEC是平行四边形，∴AC＝BE，∴BD＝BE.(2)解：如图，过点O作OF⊥CD于点F.∵四边形ABCD是矩形，∴∠BCD＝90°，∴∠BCE＝90°.在Rt△BCE中，根据勾股定理可得BC＝8.∵BE＝BD，∴CD＝CE＝6，∴DE＝12.∵OD＝OC，∴CF＝DF，又OB＝OD，∴OF为△BCD的中位线，∴OF＝12BC＝4，∴S△ODE＝12DE·OF＝12×12×4＝24.22．(1)证明：∵在矩形ABCD中，AD∥BC，∠A＝∠C＝90°，∴∠ADB＝∠DBC.根据折叠的性质得∠ADB＝∠FDB，∠F＝∠A＝90°，∴∠DBC＝∠FDB，∠C＝∠F.∴BE＝DE.在△DCE和△BFE中，∴△DCE≌△BFE.(2)解：在Rt△BCD中，∵CD＝2，∠DBC＝∠ADB＝30°，∴BD＝4.∴BC＝2 3.在Rt△ECD中，易得∠EDC＝30°.∴DE＝2EC.∴(2EC)2－EC2＝CD2.又∵CD＝2，∴CE＝23 3.∴BE＝BC－EC＝43 3.23．(1)证明：如图，连接AC.∵四边形ABCD为菱形，∠BAD＝120°，∴AB＝BC＝CD＝DA，∴∠BAC＝∠DAC＝60°，∴△ABC 和△ADC都是等边三角形，∴∠ABE＝∠ACF＝60°，∠1＋∠2＝60°.∵∠3＋∠2＝∠EAF＝60°，∴∠1＝∠3.∵∠ABC＝60°，AB＝BC，∴△ABC 为等边三角形．∴AB ＝AC .∴△ABE ≌△ACF .∴BE ＝CF .(2)解：四边形AECF 的面积不变．由(1)知△ABE ≌△ACF ，则S △ABE ＝S △ACF ，故S 四边形AECF ＝S △AEC ＋S △ACF ＝S △AEC ＋S △ABE ＝S △ABC .如图，过点A 作AM ⊥BC 于点M ，则BM ＝MC ＝2，∴AM ＝AB 2－BM 2＝42－22＝2 3.∴S △ABC ＝12BC ·AM ＝12×4×23＝4 3.故S 四边形AECF ＝4 3.24．解：(1)如图①.(2)如图②，连接AE ，∵点E 是点B 关于直线AP 的对称点，∴∠P AE ＝∠P AB ＝20°，AE ＝AB.∵四边形ABCD 是正方形，∴AE ＝AB ＝AD ，∠BAD ＝90°.∴∠AED ＝∠ADE ，∠EAD ＝∠DAB ＋∠BAP ＋∠P AE ＝130°.∴∠ADF ＝180°－130°2＝25°. (3)EF 2＋FD 2＝2AB 2.证明如下：如图③，连接AE ，BF ，BD ，由轴对称和正方形的性质可得，EF ＝BF ，AE ＝AB ＝AD ，易得∠ABF ＝∠AEF ＝∠ADF .∵∠BAD ＝90°， ∴∠ABF ＋∠FBD ＋∠ADB ＝90°.∴∠ADF ＋∠ADB ＋∠F BD ＝90°.∴∠BFD ＝90°.在Rt △BFD 中，由勾股定理得BF 2＋FD 2＝BD 2.在Rt △ABD 中，由勾股定理得BD 2＝AB 2＋AD 2＝2AB 2，∴EF 2＋FD 2＝2AB 2.。

北师大版九年级数学上册第一章特殊平行四边形单元测试卷-(含答案及解析)

北师大版九年级数学上册单元测试卷第一章特殊平行四边形1．下列说法正确的是A ．对角线垂直的四边形是菱形B ．对角线互相平分的四边形是菱形C ．菱形的对角线相等且互相平分D ．菱形的对角线互相垂直且平分 2．下列说法中，你认为正确的是（）A ．四边形具有稳定性B ．等边三角形是中心对称图形C ．任意多边形的外角和是360D ．矩形的对角线一定互相垂直 3．已知下列命题：①矩形是轴对称图形，且有两条对称轴；①两条对角线相等的四边形是矩形；①有两个角相等的平行四边形是矩形；①两条对角线相等且互相平分的四边形是矩形．其中正确的有（）A ．4个B ．3个C ．2个D ．1个 4．如图，下列条件中①AC BD ⊥①BAD 90∠=①AB BC =①AC BD =，能使平行四边形ABCD 是菱形的是（）A ．①①B ．①①C ．①①D ．①①① 5．已知菱形ABCD ，对角线5AC =，12BD =，则菱形的面积为（）A ．60B ．50C ．40D ．30 6．在数学活动课上，为探究四边形瓷砖是否为菱形，以下拟定的测量方案，正确的是（）A ．测量一组对边是否平行且相等B ．测量四个内角是否相等C ．测量两条对角线是否互相垂直D ．测量四条边是否相等一、单选题（共30分，每小题3分）7．如图，把长方形ABCD 沿对角线BD 折叠，下列结论：①①ABD 与△EDB 全等；①①ABF 与△EDF 全等；①AF EF =；①①BDF 是等腰三角形．其中正确的有（）A ．1个B ．2个C ．3个D ．4个 8．如图，在正方形ABCD 中，E 为对角线BD 上一点，CE 交AD 于点F ，连接AE ．若①AEC=140︒，则①DFC 等于（）A ．55°B ．60°C ．65°D ．70°9．如图，在四边形ABCD 中，对角线AC 与BD 相交于点O ，,AO CO BO DO ==.添加下列条件，可以判定四边形ABCD 是矩形的是（）A ．AB AD =B ．AC BD =C ．AC BD ⊥ D ．ABO CBO ∠=∠ 10．如图，已知四边形ABCD 是平行四边形，下列结论中不正确的是（）A ．当AB BC =时，它是菱形 B ．当AC BD ⊥时，它是菱形C ．当90ABC ∠=︒时，它是矩形D ．当AC BD =时，它是正方形二、填空题（共30分，每小题3分） 11．矩形的两条对角线的夹角为60，较短的边长为12cm ，则对角线长为________cm ． 12．已知菱形的周长为20，一条对角线长为8，则菱形的面积为________．13．如图所示，已知ABCD 中，下列条件：①AC =BD ；①AB =AD ；①①1=①2；①AB ①BC 中，能说明ABCD 是矩形的有______________（填写序号）14．如图，已知菱形ABCD 的对角线AC ，BD 的长分别为6，4，则AB 长为__．15．如图，平行四边形ABCD 是对角线互相垂直的四边形，请你添加一个适当的条件________，使ABCD 成为正方形（只需添加一个即可）．16．如图，在矩形ABCD 中，边AB 的长为3，点E ，F 分别在AD ，BC 上，连接BE ，DF ，EF ，BD ．若四边形BEDF 是菱形，且EF =AE +FC ，则边BC 的长为____________．17．如图，将两张长为16cm ，宽为4cm 的矩形纸条交叉，使重叠部分是一个菱形，那么菱形周长的最大值与最小值的和是________．18．如图，矩形ABCD 的对角线相交于点O ，DE ①AC ，CE ①BD ，已知AB =6cm ，BC =8cm ，则四边形ODEC 的周长为______cm ．19．如图，菱形ABCD 的对角线AC ，BD 相交于O 点，E ，F 分别是AB ，BC 边上的中点，连接EF ，若EF =4BD =，则菱形ABCD 的面积为________．20．如图，将平行四边形ABCD 的边DC 延长到E ，使CE CD =，连接AE 交BC 于F ，AFC n D ∠∠=，当n =______时，四边形ABEC 是矩形．三、解答题（共60分） 21．矩形ABCD 中68AB cm BC cm AE ==，，平分BAC ∠交BC 于E CF ，平分ACD ∠交AD 于F ．（共8分）（1）说明四边形AECF 为平行四边形；（2）求四边形AECF 的面积．22．如图，在矩形ABCD中，对角线AC与BD交于点O，且①ADO为等边三角形，过点A 作AE①BD于点E.（共8分）(1)求①ABD的度数；(2)若BD＝10，求AE的长．23．已知如图，两个长为8，宽为2的矩形纸条倾斜地重叠着．（共10分）()1求证：两矩形重叠部分为菱形；()2求菱形面积最大和最小值．24．如图，在ABC 中，5AB AC ==，6BC =，AD 为BC 边上的高，过点A 作//AE BC ，过点D 作//DE AC ，AE 与DE 交于点E ，AB 与DE 交于点F ，连结BE ．（共10分）()1求证：四边形AEBD 是矩形；()2求四边形AEBD 的面积．25．如图，正方形ABCD中，E、F分别在BC、DC上，且45.∠=试说明：EAF+=．（共12分）BE DF EF26．如图，菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA 上，连接CF．（共12分）()1求证：HEA CGF∠=∠；()2当AH DG=时，求证：菱形EFGH为正方形．参考答案：1．D 2．C 3．C 4．A 5．D 6．D 7．D 8．C 9．B 10．D11．24 12．24 13．①① 1415．90ABC∠=16．17．4018．20 19．20．221．（1）见解析；（2）30cm2（1）①四边形ABCD是矩形，①AD①BC（即AF①CE），AB①CD，①①BAC=①ACD，又①AE平分①BAC，CF平分①ACD，①①EAC=①FCA，①AE①CF，①四边形AECF是平行四边形；（2）过点E作EO①AC于点O，①①B=90°，AE平分①BAC，①EO=BO，①AE=AE，①Rt①ABE①Rt①AOE，①AO=AB=6，①在Rt①ABC，10,①OC=AC-AO=4（cm）,设CE=x，则EO=BE=BC-CE=8-x，①在Rt①OEC中由勾股定理可得：222-+=，解得：58(x x4)x=，①EC=5，①S四边形AECF=CE·AB=5×6=30（cm2）.22．(1)①ABD＝30°；(2)AE(1)①四边形ABCD是矩形，①①DAB＝90°，①①ADO为等边三角形，①①ADB＝60°，①①ABD＝180°－①DAB－①ADB＝30°；(2)①BD＝10，①BAD＝90°，①ABD＝30°，①AD＝12BD＝5，①①ADO为等边三角形，①AD＝AO＝DO＝5，①AE①DO，①DE＝EO＝12DO＝2.5，在Rt①AED中，由勾股定理得AE23．（1）详见解析；（2）菱形面积最大和最小值分别是172、4．()1根据题意得：AD//BC，AB//CD，①四边形ABCD是平行四边形．如图1，分别作CD，BC边上的高为AE，AF，①两纸条宽度相同，①AE AF=．①平行四边形ABCD的面积为AE CD BC AF⨯=⨯，①CD BC=．①平行四边形ABCD为菱形；()2如图2，此时菱形ABCD的面积最大．设AB x =，EB 8x =-，AE 2=，则由勾股定理得到：2222(8x)x +-=，解得 17x 4=， 1717S 242=⨯=最大；如图3，此时菱形ABCD 的面积最小．S 224=⨯=最小．综上所述，菱形面积最大和最小值分别是172、4． 24．（1）详见解析；（2）12. ()1①AE //BC ，BE //AC ，①四边形AEDC 是平行四边形． ①AE CD =．在ABC 中，AB AC =，AD 为BC 边上的高， ①ADB 90∠=，BD CD =．①BD AE =．①四边形AEBD 是矩形．()2在Rt ADC 中，ADB 90∠=，AC 5=，1BD CD BC 32===，①AD 4=．①四边形AEBD 的面积BD AD 3412=⋅=⨯=． 25．证明见解析.①四边形ABCD 为正方形①AB=AD,①BAD=①B=①ADF=90°如图，把△ABE 逆时针旋转90°得到△ADG ，①BE =GD ，AE =AG ．①ADG=①ABE=90°，①GAD=①BAE ①①ADG+①ADF=180°①G 、D 、F 在同一条直线上.①①EAF =45°，①①F AG =①GAD+①DAF=①BAE+①DAF=①BAD-①EAF=90°﹣45°=45°， ①①EAF =①F AG ．在△AEF 和△AGF 中，①AE AG EAF FAG AF AF =⎧⎪∠=∠⎨⎪=⎩，①①AEF ①①AGF （SAS ），①EF =GF ，即EF =GD +DF ，①BE +DF =EF ．26．（1）详见解析；（2）详见解析.（1）连接GE ，①AB//CD ，①AEG CGE ∠∠=，①GF//HE ，①HEG FGE ∠∠=，①HEA CGF ∠∠=；()2①四边形ABCD 是正方形， ①D A 90∠∠==， ①四边形EFGH 是菱形， ①HG HE =，在Rt HAE 和Rt GDH 中， AH DG HE HG =⎧⎨=⎩， ①()Rt HAE Rt GDH HL ≅， ①AHE DGH ∠∠=，又DHG DGH 90∠∠+=， ①DHG AHE 90∠∠+=， ①GHE 90∠=， ①菱形EFGH 为正方形；。

北师大版九年级数学上册第一章特殊平行四边形单元综合测试题及答案

第一章：特殊的平行四边形单元测试卷（典型题汇总）一、选择题(本大题共6小题，共24分)1．下列关于▱ABCD的叙述中，正确的是( )A．若AB⊥BC，则▱ABCD是菱形B．若AC⊥BD，则▱ABCD是正方形C．若AC＝BD，则▱ABCD是矩形D．若AB＝AD，则▱ABCD是正方形2．如图1，在△ABC中，D是边BC上的点(与B，C两点不重合)，过点D作DE∥AC，DF ∥AB，分别交AB，AC于E，F两点，下列说法正确的是( )A．若AD⊥BC，则四边形AEDF是矩形B．若AD垂直平分BC，则四边形AEDF是矩形C．若BD＝CD，则四边形AEDF是菱形D．若AD平分∠BAC，则四边形AEDF是菱形123．如图2，在菱形ABCD中，对角线AC，BD相交于点O，作OE⊥AB，垂足为E，若∠ADC ＝130°，则∠AOE的度数为( )A．75° B．65° C．55° D．50°4．如图3，P是矩形ABCD的边AD上的一个动点，矩形的两条边AB，BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是( )A.125B.65C.245 D．不确定345．如图4，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是( )A．2.5 B.5 C.322 D．26．如图5，在平面直角坐标系中，四边形OABC是正方形，点A的坐标是(4，0)，P为边AB上一点，∠CPB＝60°，沿CP折叠正方形OABC，折叠后，点B落在平面内的点B′处，则点B′的坐标为( )图5A．(2，2 3) B．(32，2－3)C．(2，4－2 3) D．(32，4－2 3)二、填空题(本大题共6小题，共30分)7．已知菱形的边长为6，一个内角为60°，则菱形的较短对角线的长是________．8．如图6所示，在矩形纸片ABCD中，AB＝2 cm，点E在BC上，且AE＝EC.若将纸片沿AE折叠，点B恰好与AC上的点B′重合，则AC＝________ cm.679．如图7所示，若菱形ABCD的边长为2，∠ABC＝45°，则点D的坐标为________．10．如图8，在正方形ABCD的外侧作等边三角形ADE，则∠BED的度数是________．8911．如图9所示，在四边形ABCD中，对角线AC⊥BD，垂足为O，E，F，G，H分别为AD，AB，BC，CD的中点．若AC＝8，BD＝6，则四边形EFGH的面积为________．图1012．如图10，在矩形ABCD中，已知AB＝6，BC＝8，BD的垂直平分线交AD于点E，交BC于点F，则△BOF的面积为________．三、解答题(共46分)13．(10分)如图11，E，F是正方形ABCD的对角线AC上的两点，且AE＝CF.(1)求证：四边形BEDF是菱形；(2)若正方形ABCD的边长为4，AE＝2，求菱形BEDF的面积．图1114．(10分)如图12，已知平行四边形ABCD的对角线AC，BD相交于点O，AC＝20 cm，BD＝12 cm，两动点E，F同时以2 cm/s的速度分别从点A，C出发在线段AC上相对运动，点E到点C，点F到点A时停止运动．(1)求证：当点E，F在运动过程中不与点O重合时，以点B，E，D，F为顶点的四边形为平行四边形；(2)当点E，F的运动时间t为何值时，四边形BEDF为矩形？图1215．(12分)如图13，△ABC是以BC为底的等腰三角形，AD是边BC上的高，E，F分别是AB，AC的中点．(1)求证：四边形AEDF是菱形；(2)如果四边形AEDF的周长为12，两条对角线的和等于7，求四边形AEDF的面积S.图1316．(14分)如图14，四边形ABCD是正方形，E是直线CD上的点，将△ADE沿AE对折得到△AFE，直线EF交边BC于点G，连接AG.(1)求证：△ABG≌△AFG；(2)当DE是线段CD的一半时，请你在备用图中利用尺规作图画出符合题意的图形(保留作图痕迹，不写作法)；(3)在(2)的条件下，求∠EAG的度数．图141．C 2.D 3.B 4.A5．B ．6．C7．6 .8．49．(2＋2，2)10．45°.11．12 12.75813．解：(1)证明：连接BD交AC于点O，∵四边形ABCD为正方形，∴BD⊥AC，OD＝OB＝OA＝OC.∵AE＝CF，∴OA－AE＝OC－CF，即OE＝OF，∴四边形BEDF为平行四边形，且BD⊥EF，∴四边形BEDF为菱形．(2)∵正方形ABCD的边长为4，∴BD＝AC＝4 2.∵AE＝CF＝2，∴EF＝AC－2 2＝2 2，∴S菱形BEDF＝12BD·EF＝12×4 2×2 2＝8.14．解：(1)证明：连接DE，EB，BF，FD.∵两动点E，F同时以2 cm/s的速度分别从点A，C出发在线段AC上相对运动，∴AE＝CF.∵平行四边形ABCD的对角线AC，BD相交于点O，∴OD＝OB，OA＝OC(平行四边形的对角线互相平分)，∴OA－AE＝OC－CF或AE－OA＝CF－OC，即OE＝OF，∴四边形BEDF为平行四边形(对角线互相平分的四边形是平行四边形)，即以点B，E，D，F为顶点的四边形是平行四边形．(2)当点E在OA上，点F在OC上，EF＝BD＝12 cm时，四边形BEDF为矩形．∵运动时间为t，∴AE＝CF＝2t，∴EF＝20－4t＝12，∴t＝2；当点E在OC上，点F在OA上时，EF＝BD＝12 cm，EF＝4t－20＝12，∴t＝8.因此，当点E，F的运动时间t为2 s或8 s时，四边形BEDF为矩形．15．解：(1)证明：∵AD⊥BC，E，F分别是AB，AC的中点，∴在Rt△ABD中，DE＝12AB＝AE，在Rt△ACD中，DF＝12AC＝AF.又∵AB＝AC，∴AE＝AF＝DE＝DF，∴四边形AEDF是菱形．(2)如图，∵菱形AEDF的周长为12，∴AE＝3.设EF＝x，AD＝y，则x＋y＝7，∴x2＋2xy＋y2＝49.①由四边形AEDF是菱形得AD⊥EF，∴在Rt△AOE中，AO2＋EO2＝AE2，∴(12y)2＋(12x)2＝32，即x2＋y2＝36.②把②代入①，可得2xy＝13，∴xy＝132，∴菱形AEDF的面积S＝12xy＝134.16．解：(1)证明：∵四边形ABCD为正方形，∴AB＝AD，∠B＝∠D＝90°.∵将△ADE沿AE对折得到△AFE，∴AF＝AD＝AB，∠AFE＝∠D＝90°.在Rt△ABG和Rt△AFG中，AB＝AF，AG＝AG，)∴Rt△ABG≌Rt△AFG(HL)．(2)如图所示：(3)∵△AFE≌△ADE，△ABG≌△AFG，∴∠EAF＝∠EAD，∠GAF＝∠GAB.∵在正方形ABCD中，∠BAD＝90°，∴∠EAG＝∠EAF＋∠GAF＝12×90°＝45°.第一章：特殊的平行四边形单元测试卷（典型题汇总）（100分钟，120分）一、选择题1．下列给出的条件中，不能判断四边形ABCD是平行四边形的是（）A．AB∥CD，AD=BC B．∠A=∠C，∠B=∠D C．AB∥CD，AD∥BC D．AB=CD，AD=BC 2．如图，在平行四边形ABCD中，对角线AC、BD相交于点O，若BD、AC的和为18cm，CD：DA=2：3，△AOB的周长为13cm，那么BC的长是（）A．6cm B．9cm C．3cm D．12cm3．如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′等于（）A．50° B．55° C．60° D．65°4．给出以下三个命题：①对角线相等的四边形是矩形；②对角线互相垂直的四边形是菱形；③对角线互相垂直的矩形是正方形；④菱形对角线的平方和等于边长平方的4倍．其中真命题的是（）A．③B．①② C．②③D．③④5．如图，矩形ABCD中，E在AD上，且EF⊥EC，EF=EC，DE=2，矩形的周长为16，则AE的长是（）A．3B．4 C．5 D．76．已知一矩形的两边长分别为10cm和15cm，其中一个内角的平分线分长边为两部分，这两部分的长为（）A．6 cm和9 cm B．5 cm和10 cm C．4 cm和11 cm D．7 cm和8 cm7．如图，四边形ABCD的对角线互相平分，要使它成为矩形，那么需要添加的条件是（）A．AB=CD B．AD=BC C．AB=BC D．AC=BD8．如图为菱形ABCD与△ABE的重叠情形，其中D在BE上．若AB=17，BD=16，AE=25，则DE的长度为何？（）A．8 B．9 C．11 D．129．如图，边长为1的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′，边B′C′与DC交于点O，则四边形AB′OD的周长是（）A．2B．3 C．D．1+10．如图，正方形ABCD的面积为4，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（）A．2B．3 C．D．二、填空题11．等边三角形、平行四边形、矩形、正方形四个图形中，既是轴对称图形又是中心对称图形的是矩形、正方形．12．已知菱形的两条对角线长分别为2cm，3cm，则它的面积是3cm2．【解答】解：∵菱形的两条对角线长分别为2cm，3cm，∴它的面积是：×2×3=3（cm2）．13．如图，在正方形ABCD的外侧，作等边△ADE，则∠BED的度数是45°．【解答】解：∵四边形ABCD是正方形，∴AB=AD，∠BAD=90°．∵等边三角形ADE，∴AD=AE，∠DAE=∠AED=60°．∠BAE=∠BAD+∠DAE=90°+60°=150°，AB=AE，∠AEB=∠ABE=（180°﹣∠BAE）÷2=15°，∠BED=∠DAE﹣∠AEB=60°﹣15°=45°，故答案为：45°．14．如图，在菱形ABCD中，对角线AC、BD相交于点O，H为AD边中点，菱形ABCD的周长为28，则OH的长等于 3.5 ．【解答】解：∵四边形ABCD是菱形，∴AB=BC=CD=DA，AC⊥BD，∴∠AOD=90°，∵AB+BC+CD+DA=28，∴AD=7，∵H为AD边中点，∴OH=AD=3.5；15．如图，点E在正方形ABCD的边CD上．若△ABE的面积为8，CE=3，则线段BE的长为5．【解答】解：过E作EM⊥AB于M，∵四边形ABCD是正方形，∴AD=BC=CD=AB，∴EM=AD，BM=CE，∵△ABE的面积为8，∴×AB×EM=8，解得：EM=4，即AD=DC=BC=AB=4，∵CE=3，由勾股定理得：BE===5，三、解答题（15题12分，16题12分，17题16分）16．如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，求△AEF的周长。

数学九年级上册第一单元测试题

北师大版数学九年级上册第一单元测试题一．选择题（共10小题）1．菱形具有而一般平行四边形不具有的性质是（）A．对边相等B．对角相等C．对角线互相平分 D．对角线互相垂直2．如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（）A．B．C．5 D．43．菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF=，BD=2，则菱形ABCD的面积为（）A．2 B．C．6 D．84．如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）A．△AFD≌△DCE B．AF=AD C．AB=AF D．BE=AD﹣DF5．如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是（）A．3 B．4 C．5 D．66．下列命题中，真命题是（）A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形7．如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（）A．1 B．2 C．3 D．48．如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD需满足的条件是（）A．AB=AD B．AC=BD C．AD=BC D．AB=CD9．如图，在正方形ABCD中，H是BC延长线上一点，使CE=CH，连接DH，延长BE交DH于G，则下面结论错误的是（）A．BE=DH B．∠H+∠BEC=90°C．BG⊥DH D．∠HDC+∠ABE=90°10．如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF；⑤S△CEF=2S△ABE，其中正确结论有（）A．2个 B．3个 C．4个 D．5个二．填空题（共10小题）11．如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=．12．如图，菱形ABCD的对角线AC、BD相交于点O，E为AD的中点，若OE=3，则菱形ABCD的周长为．13．如图，将正方形纸片按如图折叠，AM为折痕，点B落在对角线AC上的点E 处，则∠CME=．14．如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则的值等于．15．菱形的两条对角线长分别为16和12，则它的面积为．16．如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC．若AC=4，则四边形CODE的周长是．17．如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为．18．如图，在矩形ABCD中，AD=9cm，AB=3cm，将其折叠，使点D与点B重合，则重叠部分（△BEF）的面积为．19．如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=6，AD=8，则四边形ABOM的周长为．20．矩形ABCD中，AB=5，BC=4，将矩形折叠，使得点B落在线段CD的点F处，则线段BE的长为．三．解答题（共10小题）21．如图，在▱ABCD中，BC=2AB=4，点E、F分别是BC、AD的中点．（1）求证：△ABE≌△CDF；（2）当四边形AECF为菱形时，求出该菱形的面积．22．如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD 的垂线交BA的延长线于点E．（1）证明：四边形ACDE是平行四边形；（2）若AC=8，BD=6，求△ADE的周长．23．如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．（1）求证：四边形AECF是菱形；（2）若AB=，∠DCF=30°，求四边形AECF的面积．（结果保留根号）24．如图，菱形ABCD的对角线AC，BD相交于点O，且DE∥AC，AE∥BD．求证：四边形AODE是矩形．25．如图，四边形ABCD是正方形，点E是BC的中点，∠AEF=90°，EF交正方形外角的平分线CF于F．求证：AE=EF．26．已知，如图，正方形ABCD中，E为BC边上一点，F为BA延长线上一点，且CE=AF．连接DE、DF．求证：DE=DF．27．如图，在正方形ABCD中，E是边AB的中点，F是边BC的中点，连结CE、DF．求证：CE=DF．28．如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连结CE，若∠E=50°，求∠BAO的大小．29．如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF=CE．（1）求证：四边形ACEF是平行四边形；（2）当∠B满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．30．如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于N，连接BM，DN．（1）求证：四边形BMDN是菱形；（2）若AB=2，AD=4，求MD的长．01月18日dxzxshuxue的初中数学组卷参考答案与试题解析一．选择题（共10小题）1．（2016•莆田）菱形具有而一般平行四边形不具有的性质是（）A．对边相等B．对角相等C．对角线互相平分 D．对角线互相垂直【分析】由菱形的性质可得：菱形的对角线互相平分且垂直；而平行四边形的对角线互相平分；则可求得答案．【解答】解：∵菱形具有的性质：对边相等，对角相等，对角线互相平分，对角线互相垂直；平行四边形具有的性质：对边相等，对角相等，对角线互相平分；∴菱形具有而一般平行四边形不具有的性质是：对角线互相垂直．故选D．【点评】此题考查了菱形的性质以及平行四边形的性质．注意菱形的对角线互相平分且垂直．2．（2016•枣庄）如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（）A．B．C．5 D．4【分析】根据菱形性质求出AO=4，OB=3，∠AOB=90°，根据勾股定理求出AB，再根据菱形的面积公式求出即可．【解答】解：∵四边形ABCD是菱形，∴AO=OC，BO=OD，AC⊥BD，∵AC=8，DB=6，∴AO=4，OB=3，∠AOB=90°，由勾股定理得：AB==5，∵S=，菱形ABCD∴，∴DH=，故选A．【点评】本题考查了勾股定理和菱形的性质的应用，能根据菱形的性质得出S菱=是解此题的关键．形ABCD3．（2016•宁夏）菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD 边上的中点，连接EF．若EF=，BD=2，则菱形ABCD的面积为（）A．2 B．C．6 D．8【分析】根据中位线定理可得对角线AC的长，再由菱形面积等于对角线乘积的一半可得答案．【解答】解：∵E，F分别是AD，CD边上的中点，EF=，∴AC=2EF=2，又∵BD=2，∴菱形ABCD的面积S=×AC×BD=×2×2=2，故选：A．【点评】本题主要考查菱形的性质与中位线定理，熟练掌握中位线定理和菱形面积公式是关键．4．（2016•荆门）如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）A．△AFD≌△DCE B．AF=AD C．AB=AF D．BE=AD﹣DF【分析】先根据已知条件判定△AFD≌△DCE（AAS），再根据矩形的对边相等，以及全等三角形的对应边相等进行判断即可．【解答】解：（A）由矩形ABCD，AF⊥DE可得∠C=∠AFD=90°，AD∥BC，∴∠ADF=∠DEC．又∵DE=AD，∴△AFD≌△DCE（AAS），故（A）正确；（B）∵∠ADF不一定等于30°，∴直角三角形ADF中，AF不一定等于AD的一半，故（B）错误；（C）由△AFD≌△DCE，可得AF=CD，由矩形ABCD，可得AB=CD，∴AB=AF，故（C）正确；（D）由△AFD≌△DCE，可得CE=DF，由矩形ABCD，可得BC=AD，又∵BE=BC﹣EC，∴BE=AD﹣DF，故（D）正确；故选B．【点评】本题主要考查了矩形和全等三角形，解决问题的关键是掌握矩形的性质：矩形的四个角都是直角，矩形的对边相等．解题时注意：在直角三角形中，若有一个锐角等于30°，则这个锐角所对的直角边等于斜边的一半．5．（2016•毕节市）如图，正方形ABCD的边长为9，将正方形折叠，使顶点D 落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是（）A．3 B．4 C．5 D．6【分析】根据折叠可得DH=EH，在直角△CEH中，设CH=x，则DH=EH=9﹣x，根据BE：EC=2：1可得CE=3，可以根据勾股定理列出方程，从而解出CH的长．【解答】解：设CH=x，则DH=EH=9﹣x，∵BE：EC=2：1，BC=9，∴CE=BC=3，∴在Rt△ECH中，EH2=EC2+CH2，即（9﹣x）2=32+x2，解得：x=4，即CH=4．故选（B）．【点评】本题主要考查正方形的性质以及翻折变换，折叠问题其实质是轴对称变换．在直角三角形中，利用勾股定理列出方程进行求解是解决本题的关键．6．（2016•内江）下列命题中，真命题是（）A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形【分析】A、根据矩形的定义作出判断；B、根据菱形的性质作出判断；C、根据平行四边形的判定定理作出判断；D、根据正方形的判定定理作出判断．【解答】解：A、两条对角线相等且相互平分的四边形为矩形；故本选项错误；B、对角线互相垂直的平行四边形是菱形；故本选项错误；C、对角线互相平分的四边形是平行四边形；故本选项正确；D、对角线互相垂直平分且相等的四边形是正方形；故本选项错误；故选C．【点评】本题综合考查了正方形、矩形、菱形及平行四边形的判定．解答此题时，必须理清矩形、正方形、菱形与平行四边形间的关系．7．（2016•龙岩模拟）如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（）A．1 B．2 C．3 D．4【分析】作F点关于BD的对称点F′，则PF=PF′，由两点之间线段最短可知当E、P、F′在一条直线上时，EP+FP有最小值，然后求得EF′的长度即可．【解答】解：作F点关于BD的对称点F′，则PF=PF′，连接EF′交BD于点P．∴EP+FP=EP+F′P．由两点之间线段最短可知：当E、P、F′在一条直线上时，EP+FP的值最小，此时EP+FP=EP+F′P=EF′．∵四边形ABCD为菱形，周长为12，∴AB=BC=CD=DA=3，AB∥CD，∵AF=2，AE=1，∴DF=AE=1，∴四边形AEF′D是平行四边形，∴EF′=AD=3．∴EP+FP的最小值为3．故选：C．【点评】本题主要考查的是菱形的性质、轴对称﹣﹣路径最短问题，明确当E、P、F′在一条直线上时EP+FP有最小值是解题的关键．8．（2016•蜀山区二模）如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD 需满足的条件是（）A．AB=AD B．AC=BD C．AD=BC D．AB=CD【分析】由点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，根据三角形中位线的性质，可得EF=GH=AB，EH=FG=CD，又由当EF=FG=GH=EH时，四边形EFGH是菱形，即可求得答案．【解答】解：∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，∴EF=GH=AB，EH=FG=CD，∵当EF=FG=GH=EH时，四边形EFGH是菱形，∴当AB=CD时，四边形EFGH是菱形．故选：D．【点评】此题考查了中点四边形的性质、菱形的判定以及三角形中位线的性质．此题难度适中，注意掌握数形结合思想的应用．9．（2016•曹县校级模拟）如图，在正方形ABCD中，H是BC延长线上一点，使CE=CH，连接DH，延长BE交DH于G，则下面结论错误的是（）A．BE=DH B．∠H+∠BEC=90°C．BG⊥DH D．∠HDC+∠ABE=90°【分析】根据正方形的四条边都相等，角都是直角，先证明△BCE和△DCH全等，再根据全等三角形对应边相等，全等三角对应角相等，对各选项分析判断后利用排除法．【解答】解：在正方形ABCD中，BC=CD，∠BCD=∠DCH=90°，在△BCE和△DCH中，，∴△BCE≌△DCH（SAS），∴BE=DH，故A选项正确；∠H=∠BEC，故B选项错误；∠EBC=∠HDC，∴∠EBC+BEC=∠HDC+DEG，∵BCD=90°，∴∠EBC+BEC=90°，∴∠HDC+DEG=90°，∴BG⊥DH，故C选项正确；∵∠ABE+∠EBC=90°，∴∠HDC+∠ABE=90°，故D选项正确．故选B．【点评】本题主要利用正方形的和三角形全等的性质求解，熟练掌握性质是解题的关键．10．（2016•新华区一模）如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF；⑤S△CEF=2S△ABE，其中正确结论有（）A．2个 B．3个 C．4个 D．5个【分析】通过条件可以得出△ABE≌△ADF，从而得出∠BAE=∠DAF，BE=DF，由正方形的性质就可以得出EC=FC，就可以得出AC垂直平分EF，设EC=x，BE=y，由勾股定理就可以得出x与y的关系，表示出BE与EF，利用三角形的面积公式分别表示出S△CEF 和2S△ABE，再通过比较大小就可以得出结论．【解答】解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=∠BCD=∠D=∠BAD=90°．∵△AEF等边三角形，∴AE=EF=AF，∠EAF=60°．∴∠BAE+∠DAF=30°．在Rt△ABE和Rt△ADF中，，Rt△ABE≌Rt△ADF（HL），∴BE=DF（故①正确）．∠BAE=∠DAF，∴∠DAF+∠DAF=30°，即∠DAF=15°（故②正确），∵BC=CD，∴BC﹣BE=CD﹣DF，即CE=CF，∵AE=AF，∴AC垂直平分EF．（故③正确）．设EC=x，由勾股定理，得EF=x，CG=x，AG=AEsin60°=EFsin60°=2×CGsin60°=x，∴AC=，∴AB=，∴BE=﹣x=，∴BE+DF=x﹣x≠x，（故④错误），=x2，∵S△CEFS△ABE=x2，∴2S=x2=S△CEF，（故⑤正确）．△ABE综上所述，正确的有4个，故选：C．【点评】本题考查了正方形的性质的运用，全等三角形的判定及性质的运用，勾股定理的运用，等边三角形的性质的运用，三角形的面积公式的运用，解答本题时运用勾股定理的性质解题时关键．二．填空题（共10小题）11．（2016•内江）如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=．【分析】先根据菱形的性质得AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，再在Rt△OBC中利用勾股定理计算出BC=5，然后利用面积法计算OE的长．【解答】解：∵四边形ABCD为菱形，∴AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，在Rt△OBC中，∵OB=3，OC=4，∴BC==5，∵OE⊥BC，∴OE•BC=OB•OC，∴OE==．故答案为．【点评】本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．也考查了勾股定理和三角形面积公式．12．（2016•扬州）如图，菱形ABCD的对角线AC、BD相交于点O，E为AD的中点，若OE=3，则菱形ABCD的周长为24．【分析】由菱形的性质可得出AC⊥BD，AB=BC=CD=DA，再根据直角三角形斜边上的中线等于斜边的一半得出AD的长，结合菱形的周长公式即可得出结论．【解答】解：∵四边形ABCD为菱形，∴AC⊥BD，AB=BC=CD=DA，∴△AOD为直角三角形．∵OE=3，且点E为线段AD的中点，∴AD=2OE=6．C菱形ABCD=4AD=4×6=24．故答案为：24．【点评】本题考查了菱形的性质以及直角三角形的性质，解题的关键是求出AD=6．本题属于基础题，难度不大，解决该题型题目时，根据菱形的性质找出对角线互相垂直，再通过直角三角形的性质找出菱形的一条变成是关键．13．（2016•龙岩）如图，将正方形纸片按如图折叠，AM为折痕，点B落在对角线AC上的点E处，则∠CME=45°．【分析】由正方形的性质和折叠的性质即可得出结果．【解答】解：∵四边形ABCD是正方形，∴∠B=90°，∠ACB=45°，由折叠的性质得：∠AEM=∠B=90°，∴∠CEM=90°，∴∠CME=90°﹣45°=45°；故答案为：45°．【点评】本题考查了正方形的性质、折叠的性质；熟练掌握正方形和折叠的性质是解决问题的关键．14．（2016•天津）如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则的值等于．【分析】根据辅助线的性质得到∠ABD=∠CBD=45°，四边形MNPQ和AEFG均为正方形，推出△BEF与△BMN是等腰直角三角形，于是得到FE=BE=AE=AB，BM=MN=QM，同理DQ=MQ，即可得到结论．【解答】解：在正方形ABCD中，∵∠ABD=∠CBD=45°，∵四边形MNPQ和AEFG均为正方形，∴∠BEF=∠AEF=90°，∠BMN=∠QMN=90°，∴△BEF与△BMN是等腰直角三角形，∴FE=BE=AE=AB，BM=MN=QM，同理DQ=MQ，∴MN=BD=AB，∴==，故答案为：．【点评】本题考查了正方形的性质，等腰直角三角形的性质，正方形的面积的计算，熟练掌握等腰直角三角形的性质是解题的关键．15．（2016•白云区校级二模）菱形的两条对角线长分别为16和12，则它的面积为96．【分析】由菱形的两条对角线长分别为16和12，根据菱形的面积等于对角线积的一半，即可求得答案．【解答】解：∵菱形的两条对角线长分别为16和12，∴它的面积为：×16×12=96．故答案为：96．【点评】此题考查了菱形的性质．注意菱形的面积等于对角线积的一半．16．（2016•河源校级一模）如图，矩形ABCD的对角线AC，BD相交于点O，CE ∥BD，DE∥AC．若AC=4，则四边形CODE的周长是8．【分析】先证明四边形CODE是平行四边形，再根据矩形的性质得出OC=OD，然后证明四边形CODE是菱形，即可求出周长．【解答】解：∵CE∥BD，DE∥AC，∴四边形CODE是平行四边形，∵四边形ABCD是矩形，∴OC=AC=2，OD=BD，AC=BD，∴OC=OD=2，∴四边形CODE是菱形，∴DE=CEOC=OD=2，∴四边形CODE的周长=2×4=8；故答案为：8．【点评】本题考查了菱形的判定与性质以及矩形的性质；证明四边形是菱形是解决问题的关键．17．（2016•临沭县校级一模）如图，在矩形ABCD中，AB=2，BC=4，对角线AC 的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为．【分析】由矩形的性质得出CD=AB=2，AD=BC=4，∠D=90°，由线段垂直平分线的性质得出CE=AE，设CE=AE=x，则DE=4﹣x，由勾股定理得出方程，解方程即可．【解答】解：∵四边形ABCD是矩形，∴CD=AB=2，AD=BC=4，∠D=90°，∵EF是AC的垂直平分线，∴CE=AE，设CE=AE=x，则DE=4﹣x，在Rt△CDE中，由勾股定理得：CD2+DE2=CE2，即22+（4﹣x）2=x2，解得：x=，∴CE=；故答案为：．【点评】本题考查了矩形的性质、线段垂直平分线的性质、勾股定理；熟练掌握矩形的性质，并能进行推理计算是解决问题的关键．18．（2016•抚顺模拟）如图，在矩形ABCD中，AD=9cm，AB=3cm，将其折叠，使点D与点B重合，则重叠部分（△BEF）的面积为7.5cm2．【分析】设DE=xcm，由翻折的性质可知DE=EB=x，则AE=（9﹣x）cm，在Rt△ABE中，由勾股定理求得ED的长；由翻折的性质可知∠DEF=∠BEF，由矩形的性质可知BC∥AD，从而得到∠BFE=∠DEF，故此可知∠BFE=∠FEB，得出FB=BE，最后根据三角形的面积公式求解即可．【解答】解：设DE=xcm．由翻折的性质可知DE=EB=x，∠DEF=∠BEF，则AE=（9﹣x）cm．在Rt△ABE中，由勾股定理得；BE2=EA2+AB2，即x2=（9﹣x）2+32．解得：x=5．∴DE=5cm．∵四边形ABCD为矩形，∴BC∥AD．∴∠BFE=∠DEF．∴∠BFE=∠FEB．∴FB=BE=5cm．∴△BEF的面积=BF•AB=×3×5=7.5（cm2）；故答案为：7.5cm2．【点评】本题主要考查的是翻折的性质、勾股定理的应用，等腰三角形的判定、三角形的面积公式，证得△BEF为等腰三角形，从而得到FB的长是解题的关键．19．（2016•苏州校级二模）如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=6，AD=8，则四边形ABOM的周长为18．【分析】根据矩形的性质，直角三角形斜边中线性质，三角形中位线性质求出BO、OM、AM即可解决问题．【解答】解：∵四边形ABCD是矩形，∴AD=BC=8，AB=CD=6，∠ABC=90°，∴AC==10，∵AO=OC，∴BO=AC=5，∵AO=OC，AM=MD=4，∴OM=CD=3，∴四边形ABOM的周长为AB+OB+OM+AM=6+5+3+4=18．故答案为18．【点评】本题看成矩形的性质、三角形中位线定理、直角三角形斜边中线性质等知识，解题的关键是灵活应用中线知识解决问题，属于中考常考题型．20．（2016•天桥区三模）矩形ABCD中，AB=5，BC=4，将矩形折叠，使得点B 落在线段CD的点F处，则线段BE的长为 2.5．【分析】根据翻转前后，图形的对应边和对应角相等，可知EF=BF，AB=AE，故可求出DE的长，然后设出FC的长，则EF=4﹣FC，再根据勾股定理的知识，即可求出BF的长．【解答】解：∵四边形ABCD是矩形，∴∠B=∠D=90°，∵将矩形折叠，使得点B落在线段CD的点F处，∴AE=AB=5，AD=BC=4，EF=BF，在Rt△ADE中，由勾股定理，得DE=3．在矩形ABCD中，DC=AB=5．∴CE=DC﹣DE=2．设FC=x，则EF=4﹣x．在Rt△CEF中，x2+22=（4﹣x）2．解得x=1.5．∴BF=BC﹣CF=4﹣1.5=2.5，故答案为：2.5．【点评】本题考查了矩形的性质、勾股定理的运用以及翻转变换的知识，属于基础题，注意掌握图形翻转前后对应边和对应角相等是解题关键．三．解答题（共10小题）21．（2016•安顺）如图，在▱ABCD中，BC=2AB=4，点E、F分别是BC、AD的中点．（1）求证：△ABE≌△CDF；（2）当四边形AECF为菱形时，求出该菱形的面积．【分析】第（1）问要证明三角形全等，由平行四边形的性质，很容易用SAS证全等．第（2）要求菱形的面积，在第（1）问的基础上很快知道△ABE为等边三角形．这样菱形的高就可求了，用面积公式可求得．【解答】（1）证明：∵在▱ABCD中，AB=CD，∴BC=AD，∠ABC=∠CDA．又∵BE=EC=BC，AF=DF=AD，∴BE=DF．∴△ABE≌△CDF．（2）解：∵四边形AECF为菱形，∴AE=EC．又∵点E是边BC的中点，∴BE=EC，即BE=AE．又BC=2AB=4，∴AB=BC=BE，∴AB=BE=AE，即△ABE为等边三角形，▱ABCD的BC边上的高为2×sin60°=，∴菱形AECF的面积为2．【点评】考查了全等三角形，四边形的知识以及逻辑推理能力．（1）用SAS证全等；（2）若四边形AECF为菱形，则AE=EC=BE=AB，所以△ABE为等边三角形．22．（2016•苏州）如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D 作对角线BD的垂线交BA的延长线于点E．（1）证明：四边形ACDE是平行四边形；（2）若AC=8，BD=6，求△ADE的周长．【分析】（1）根据平行四边形的判定证明即可；（2）利用平行四边形的性质得出平行四边形的周长即可．【解答】（1）证明：∵四边形ABCD是菱形，∴AB∥CD，AC⊥BD，∴AE∥CD，∠AOB=90°，∵DE⊥BD，即∠EDB=90°，∴∠AOB=∠EDB，∴DE∥AC，∴四边形ACDE是平行四边形；（2）解：∵四边形ABCD是菱形，AC=8，BD=6，∴AO=4，DO=3，AD=CD=5，∵四边形ACDE是平行四边形，∴AE=CD=5，DE=AC=8，∴△ADE的周长为AD+AE+DE=5+5+8=18．【点评】此题考查平行四边形的性质和判定问题，关键是根据平行四边形的判定解答即可．23．（2016•贺州）如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．（1）求证：四边形AECF是菱形；（2）若AB=，∠DCF=30°，求四边形AECF的面积．（结果保留根号）【分析】（1）由过AC的中点O作EF⊥AC，根据线段垂直平分线的性质，可得AF=CF，AE=CE，OA=OC，然后由四边形ABCD是矩形，易证得△AOF≌△COE，则可得AF=CE，继而证得结论；（2）由四边形ABCD是矩形，易求得CD的长，然后利用三角函数求得CF的长，继而求得答案．【解答】（1）证明：∵O是AC的中点，且EF⊥AC，∴AF=CF，AE=CE，OA=OC，∵四边形ABCD是矩形，∴AD∥BC，∴∠AFO=∠CEO，在△AOF和△COE中，，∴△AOF≌△COE（AAS），∴AF=CE，∴AF=CF=CE=AE，∴四边形AECF是菱形；（2）解：∵四边形ABCD是矩形，∴CD=AB=，在Rt△CDF中，cos∠DCF=，∠DCF=30°，∴CF==2，∵四边形AECF是菱形，∴CE=CF=2，∴四边形AECF是的面积为：EC•AB=2．【点评】此题考查了矩形的性质、菱形的判定与性质以及三角函数等知识．注意证得△AOF≌△COE是关键．24．（2016•吉林）如图，菱形ABCD的对角线AC，BD相交于点O，且DE∥AC，AE∥BD．求证：四边形AODE是矩形．【分析】根据菱形的性质得出AC⊥BD，再根据平行四边形的判定定理得四边形AODE为平行四边形，由矩形的判定定理得出四边形AODE是矩形．【解答】证明：∵四边形ABCD为菱形，∴AC⊥BD，∴∠AOD=90°，∵DE∥AC，AE∥BD，∴四边形AODE为平行四边形，∴四边形AODE是矩形．【点评】本题考查了矩形的判定以及菱形的性质，还考查了平行四边形的判定，掌握平行四边形的判定方法是解题的关键．25．（2016•通辽）如图，四边形ABCD是正方形，点E是BC的中点，∠AEF=90°，EF交正方形外角的平分线CF于F．求证：AE=EF．【分析】先取AB的中点H，连接EH，根据∠AEF=90°和ABCD是正方形，得出∠1=∠2，再根据E是BC的中点，H是AB的中点，得出BH=BE，AH=CE，最后根据CF是∠DCG的角平分线，得出∠AHE=∠ECF=135°，从而证出△AHE≌△ECF，即可得出AE=EF．【解答】证明：取AB的中点H，连接EH；∵∠AEF=90°，∴∠2+∠AEB=90°，∵四边形ABCD是正方形，∴∠1+∠AEB=90°，∴∠1=∠2，∵E是BC的中点，H是AB的中点，∴BH=BE，AH=CE，∴∠BHE=45°，∵CF是∠DCG的角平分线，∴∠FCG=45°，∴∠AHE=∠ECF=135°，在△AHE和△ECF中，，∴△AHE≌△ECF（ASA），∴AE=EF．【点评】此题考查了正方形的性质和全等三角形的判定与性质，解题的关键是取AB的中点H，得出AH=EC，再根据全等三角形的判定得出△AHE≌△ECF．26．（2016•无锡）已知，如图，正方形ABCD中，E为BC边上一点，F为BA延长线上一点，且CE=AF．连接DE、DF．求证：DE=DF．【分析】根据正方形的性质可得AD=CD，∠C=∠DAF=90°，然后利用“边角边”证明△DCE和△DAF全等，再根据全等三角形对应边相等证明即可．【解答】证明：∵四边形ABCD是正方形，∴AD=CD，∠DAB=∠C=90°，∴∠FAD=180°﹣∠DAB=90°．在△DCE和△DAF中，，∴△DCE≌△DAF（SAS），∴DE=DF．【点评】本题考查了正方形的性质，全等三角形的判定与性质，利用全等三角形对应边相等证明线段相等是常用的方法之一，一定要熟练掌握并灵活运用．27．（2016•乐山）如图，在正方形ABCD中，E是边AB的中点，F是边BC的中点，连结CE、DF．求证：CE=DF．【分析】欲证明CE=DF，只要证明△CEB≌△DFC即可．【解答】证明：∵ABCD是正方形，∴AB=BC=CD，∠EBC=∠FCD=90°，又∵E、F分别是AB、BC的中点，∴BE=CF，在△CEB和△DFC中，，∴△CEB≌△DFC，∴CE=DF．【点评】本题考查正方形的性质、全等三角形的判定和性质，解题的关键是熟练掌握正方形的性质以及全等三角形的判定和性质，属于基础题，中考常考题型．28．（2016•长春二模）如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连结CE，若∠E=50°，求∠BAO的大小．【分析】根据菱形的四条边都相等可得AB=BC，从而得到BC=BE，再根据等腰三角形的性质求出∠CBE，然后根据两直线平行，同位角相等可得∠BAD=∠CBE，再根据菱形的对角线平分一组对角线可得∠BAO=∠BAD，问题得解．【解答】解：菱形ABCD中，AB=BC，∵BE=AB，∴BC=BE，∴∠BCE=∠E=50°，∴∠CBE=180°﹣50°×2=80°，∵AD∥BC，∴∠BAD=∠CBE=80°，∴∠BAO=∠BAD=×80°=40°．【点评】本题考查了菱形的性质，等腰三角形的性质，平行线的性质，熟记各性质并准确识图是解题的关键．29．（2016•哈尔滨模拟）如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE 交BC于D，交AB于E，F在DE上，并且AF=CE．（1）求证：四边形ACEF是平行四边形；（2）当∠B满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．【分析】（1）ED是BC的垂直平分线，根据中垂线的性质：中垂线上的点线段两个端点的距离相等，则EB=EC，故有∠3=∠4，在直角三角形ACB中，∠2与∠4互余，∠1与∠3互余，则可得到AE=CE，从而证得△ACE和△EFA都是等腰三角形，又因为FD⊥BC，AC⊥BC，所以AC∥FE，再根据内错角相等得到AF∥CE，故四边形ACEF是平行四边形；（2）由于△ACE是等腰三角形，当∠1=60°时△ACE是等边三角形，有AC=EC，有平行四边形ACEF是菱形．【解答】解：（1）∵ED是BC的垂直平分线∴EB=EC，ED⊥BC，∴∠3=∠4，∵∠ACB=90°，∴FE∥AC，∴∠1=∠5，∵∠2与∠4互余，∠1与∠3互余∴∠1=∠2，∴AE=CE，又∵AF=CE，∴△ACE和△EFA都是等腰三角形，∴∠5=∠F，∴∠2=∠F，∴在△EFA和△ACE中∵，∴△EFA≌△ACE（AAS），∴∠AEC=∠EAF∴AF∥CE∴四边形ACEF是平行四边形；（2）当∠B=30°时，四边形ACEF是菱形．证明如下：∵∠B=30°，∠ACB=90°∴∠1=∠2=60°∴∠AEC=60°∴AC=EC∴平行四边形ACEF是菱形．【点评】本题综合利用了中垂线的性质、等边对等角和等角对等边、直角三角形的性质、平行四边形和判定和性质、菱形的判定求解，有利于学生思维能力的训练．涉及的知识点有：有一组邻边相等的平行四边形是菱形．30．（2016•会宁县一模）如图，在矩形ABCD中，对角线BD的垂直平分线MN 与AD相交于点M，与BD相交于点O，与BC相交于N，连接BM，DN．（1）求证：四边形BMDN是菱形；（2）若AB=2，AD=4，求MD的长．【分析】（1）根据矩形性质求出AD∥BC，推出∠MDO=∠NBO，∠DMO=∠BNO，证△DMO≌△BNO，推出OM=ON，得出平行四边形BMDN，推出菱形BMDN；（2）根据菱形性质求出DM=BM，在Rt△AMB中，根据勾股定理得出BM2=AM2+AB2，即可列方程求得．【解答】（1）证明：∵四边形ABCD是矩形∴AD∥BC，∠A=90°，∴∠MDO=∠NBO，∠DMO=∠BNO，∵在△DMO和△BNO中∴△DMO≌△BNO（ASA），∴OM=ON，∵OB=OD，∴四边形BMDN是平行四边形，∵MN⊥BD，∴平行四边形BMDN是菱形．（2）解：∵四边形BMDN是菱形，∴MB=MD，设MD长为x，则MB=DM=x，在Rt△AMB中，BM2=AM2+AB2即x2=（4﹣x）2+22，解得：x=，答：MD长为．【点评】本题考查了矩形性质，平行四边形的判定，菱形的判定和性质，勾股定理等知识点的应用，对角线互相平分的四边形是平行四边形，对角线互相垂直的平行四边形是菱形．。

北师大版数学九年级上册第一章特殊平行四边形单元检测(2)

设，则，
在中，，即，
解得；
（2）如图，当点在的延长线时，
设，则，
在中，，即，
解得；
综上，的长为2或18，
故选：B．
【点睛】本题考查了长方形的性质、勾股定理、轴对称，正确分两种情况讨论是解题关键．
7．C
【分析】连接BD，证明△FOB≌△EOC，同理得到△HOD≌△GOC，即可得到答案．
(1)经过思考小明想到如下方法：
以BC为边作正方形BCMN，将四边形ABCD绕着正方形BCMN的中心按顺时针方向旋转90°，180°，270°，而分别得到四边形FNBA，EMNF，DCME，则四边形ADEF是________．（填一种特殊的平行四边形）
∴S四边形ABCD＝________．
(2)解决问题：如图③，在四边形ABCD中，∠BAD＝140°，∠CDA＝160°，AB＝CD，AD＝6，BC＝12，则四边形ABCD的面积为多少？
5．C
【分析】根据直角三角形的斜边上的中线的性质，即可得到△CDF是等边三角形，进而得到∠ACD=60°，根据∠BCD和∠BDC的角平分线相交于点E，即可得出∠CED=115°，即可得到∠ACD+∠CED=60°+115°=175°．
【详解】如图：
∵CD⊥AB，F为边AC的中点，
∴DF= AC=CF，
故B选项正确；
当时，利用对角线互相垂直的平行四边形是菱形，可知四边形ABCD是菱形，
故C选项正确
当时，利用有一个角是直角的平行四边形是矩形，可知四边形ABCD是矩形，
故D选项错误；
故选：D．
【点睛】此题考查平行四边形的性质，正方形的判定、矩形的判定和菱形的判定，掌握正方形的判定、矩形的判定和菱形的判定定理是解题关键．

北师大版九年级数学上册《第一章特殊平行四边形》单元测试卷(带答案)

北师大版九年级数学上册《第一章特殊平行四边形》单元测试卷(带答案)一、选择题1．菱形的周长为20cm，一条对角线长为8cm，则菱形的面积为（）2cm．A．48B．24C．12D．202．菱形具有而矩形不一定具有的性质是（）A．对角线相等B．对角线互相垂直C．对角相等D．对边平行3．要检验一个四边形画框是否为矩形，可行的测量方法是（）A．测量四边形画框的两个角是否为90︒B．测量四边形画框的对角线是否相等且互相平分C．测量四边形画框的一组对边是否平行且相等D．测量四边形画框的四边是否相等4．如图，在矩形ABCD中，已知AE BD⊥于E，∠BDC=60°，BE=1，则AB的长为（）A．3B．2C．3D35．下列条件中，能判定四边形是正方形的是（）A．对角线相等的平行四边形B．对角线互相平分且垂直的四边形C．对角线互相垂直且相等的四边形D．对角线相等且互相垂直的平行四边形6．如图，将图1的正方形剪成四块，恰能拼成图2的矩形，则ba=（）A 51-B 53+C 51+D 217．如图，在菱形ABCD 中 50ABC ∠=︒ ，对角线AC ，BD 交于点O ，E 为CD 的中点，连接OE ，则 AOE ∠ 的度数是（）A ．110°B ．112°C ．115°D ．120°8．如图，在四边形ABCD 中，AB ＝1，BC ＝4，CD ＝6，∠A ＝90°，∠B ＝∠C ＝120°，则AD 的长度为（）A ．3B ．3C ．3D ．3+39．如图，点E 、F 在矩形ABCD 的对角线BD 所在的直线上，BE =DF ，则四边形AECF 是( )A ．平行四边形B ．矩形C ．菱形D ．正方形10．如图，在边长为2的正方形ABCD 中，点E ，F 分别是边BC ，CD 上的动点，且BE CF =，连接BF ，DE ，则BF DE +的最小值为（）A 3B 5C ．3D ．512．如图，将四根长度相等的细木条首尾相连，用钉子钉成四边形ABCD ，∠A ＝120°，则A ．13．如图，在矩形ABCD 中，E 是BC 边上一点90AED ∠=︒，∠EAD=30°，F 是AD 边的中点2cm EF =则BE = cm ．14．如图，在边长为4的正方形ABCD 中，E 是AB 边上的一点，且AE=3，点Q 为对角线AC 上的动点，则∠BEQ 周长的最小值为．三、解答题15．如图，在矩形ABCD 中，AC ，BD 相交于点O ，AE//BD ，BE//AC ．（1）求证：四边形AEBO 是菱形；（2）若2AB =，OB=3，求AD 的长及四边形AEBO 的面积．16．如图，平行四边形ABCD 中，AC=6，BD=8，点P 从点A 出发以每秒1cm 的速度沿射线AC 移动，点Q 从点C 出发以每秒1cm 的速度沿射线CA 移动．（1）经过几秒，以P ，Q ，B ，D 为顶点的四边形为矩形？（2）若BC∠AC 垂足为C ，求（1）中矩形边BQ 的长．17．如图，在正方形ABCD 中，点E 、F 分别在边BC 、CD 上，且∠EAF =45°，分别连接EF 、BD ，BD 与AF 、AE 分别相交于点M 、N.（1）求证：EF =BE +DF .为了证明“EF =BE +DF ”，小明延长CB 至点G ，使BG =DF ，连接AG ，请画出辅助线并按小明的思路写出证明过程. （2）若正方形ABCD 的边长为6，BE =2，求DF 的长.18．已知：如图，在 Rt ABC 中 90ACB ∠=︒ ， CD 是 ABC 的角平分线，DE ⊥BC ，DF ⊥AC ，垂足分別为E 、F.求证：四边形 CEDF 是正方形.四、综合题19．如图，在ABC 中，AB=AC=2，∠BAC=45°，AEF 是由ABC 绕点A 按逆时针方向旋转得到的，连接BE ，CF 相交于点D .（1）求证：BE CF =；（2）当四边形ABDF 为菱形时，求CD 的长.20．如图，菱形ABCD 的对角线AC 、BD 相交于点O ，过点D 作DE∠AC ，且12DE AC =，连接CE（1）求证：四边形OCED为矩形；（2）连接AE，若DB=6，AC=8，求AE的长.21．已知正方形ABCD和正方形AEFG有一个公共点A，点G、E分别在线段AD、AB上.（1）如图1，连接DF、BF，若将正方形AEFG绕点A按顺时针方向旋转，判断∠“在旋转的过程中线段DF与BF的长始终相等.”是否正确，若正确请说明理由，若不正确请举反例说明；（2）若将正方形AEFG绕点A按顺时针方向旋转，连结DG，在旋转的过程中，你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.22．已知，矩形ABCD中，AB＝4cm，BC＝8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．（1）如图（1），连接AF、CE．①四边形AFCE是什么特殊四边形？说明理由；②求AF的长；（2）如图（2），动点P、Q分别从A、C两点同时出发，沿∠AFB和∠CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，已知点P的速度为每秒5cm，点Q 的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．答案解析部分1．【答案】B【解析】【解答】解：∵菱形周长为20cm∴一条边的边长a=5cm又∵一条对角线长为8cm根据勾股定理可得另一条对角线长的一半22543 b-=∴另一条对角线长为6cm∴2186242m=⨯⨯=菱形的面积故答案为：B.【分析】本题考查菱形的性质、菱形的面积公式以及勾股定理，首先根据菱形的四边相等可知边长为5，又因为菱形的对角线垂直，所以结合一条已知的对角线求出另一条对角线的长度为6，两条对角线长度已知即可求出菱形的面积.2．【答案】B【解析】【解答】矩形的对角线相等，菱形的对角线不一定相等，故A不符合题意；矩形的对角线互相不垂直，菱形的对角线互相垂直，故B符合题意；因为矩形与菱形都是特殊的平行四边形，所以矩形与菱形的对角都相等，故C不符合题意；因为矩形与菱形都是特殊的平行四边形，所以矩形与菱形的对边都平行，故D不符合题意；故答案为：B．【分析】菱形和矩形具有平行四边形的一切性质，菱形特有：四条边都相等，对角线互相垂直且平分一组对角，矩形特有：四个角都是直角，对角线相等，据此逐一判断即可.3．【答案】B【解析】【解答】解：A、测量四边形画框的两个角是否为90°，不能判定为矩形，故选项A不符合题意；B、测量四边形画框的对角线是否相等且互相平分，能判定为矩形，故选项B符合题意；C、测量四边形画框的一组对边是否平行且相等，能判定为平行四边形，不能判定是否为矩形，故选项C 不符合题意；D、测量四边形画框的四边是否相等，能判断四边形是菱形，故选项D不符合题意.【分析】一组对边平行且相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形；对角线相等的平行四边形是矩形；有一个角是直角的平行四边形是矩形；四边相等的四边形是菱形，据此一一判断得出答案.4．【答案】B【解析】【解答】解：四边形ABCD 为矩形60BDC ∠=︒=60ABD ∴∠︒AE BD ⊥30BAE ∴∠=︒AB 2∴=故答案为：B ．【分析】由矩形的性质求出∠ABD=90°，利用三角形内角和求出∠BAE=30°，再根据含30°角的直角三角形的性质即可求解.5．【答案】D【解析】【解答】解：A 、对角线相等的平行四边形是矩形，故此选项不符合题意；B 、对角线互相平分且垂直的四边形是菱形，故此选项不符合题意；C 、对角线相等且互相垂直的平行四边形是正方形，故C 选项不符合题意，D 选项符合题意.故答案为：D.【分析】利用对角线互相平分，垂直且相等的四边形是正方形；对角线相等且互相垂直的平行四边形是正方形，一一判断可得答案.6．【答案】C【解析】【解答】解：依题意得()2()a b b b a b +=++整理得：22222a b ab b ab ++=+则220a b ab -+= 方程两边同时除以2a 2()10b b a a --=152b a +∴=（负值已经舍去）【分析】根据左图可以知道图形是一个正方形，边长为（a＋b），右图是一个长方形，长宽分别为（b＋a＋b）、b，并且它们的面积相等，由此即可列出等式（a＋b）2＝b（b＋a＋b），解方程即可求出ba的值.7．【答案】C【解析】【解答】解：∵四边形ABCD是菱形∴AC∠BD，∠CDO= 12∠ADC=12∠ABC=25°∴∠DOC=90°∵点E是CD的中点∴OE=DE= 12CD∴∠DOE=∠CDO=25°∴∠AOE=∠AOD+∠DOE=90°+25°=115°故答案为：C.【分析】根据菱形的性质得出AC∠BD，∠CDO=25°，然后根据直角三角形斜边中线的性质求出OE=DE，则由等腰三角形的性质求出∠DOE=25°，最后根据角的和差关系求∠AOE的度数即可. 8．【答案】A【解析】【解答】解：延长DC、AB，DC、AB的延长线相交于点E∵∠ABC=∠BCD=120°∴∠EBC=∠ECB=60°∴∠BCE是等边三角形∵BC=4，∴EC=BE=BC=4∵AB=1，CD=6∴AE=1+4=5，DE=CD+CE=4+6=10∵∠A=90°∴22221057553DE AE-=-=故答案为：53.【分析】延长DC、AB，DC、AB的延长线相交于点E，结合已知易得∠BCE是等边三角形，由等边三角形的性质可得EC=BE=BC，由线段的构成可求出AE、DE的值，然后在直角三角形ADE中，用勾股定理可求得AD的值.9．【答案】A∴AO=CO BO=DO又BE=DF∴ BO+BE=DO+DF即EO=FO∴ 四边形AECF 是平行四边（对角线互相平分的四边形是平行四边形）故选：A【分析】根据矩形性质得到平行四边形的判定条件。

北师大版九年级数学上册第一单元测试题含答案

北师大版九年级数学上册第一单元测试题含答案北师大版九年级数学上册第一章测试题及答案一、选择题(每题3分，共30分)1.菱形、矩形、正方形都具有的性质是()A．四条边相等，四个角相等B．对角线相等C．对角线互相垂直D．对角线互相平分2.如图，在菱形ABCD中，AB=5，∠BCD=120°，则△ABC的周长等于()A．20B．15C．10D．53.如图，EF过矩形ABCD对角线的交点O，且分别交AB，CD于点E，F，那么阴影部分的面积是矩形ABCD面积的() A．1/5B．1/4C．1/3D．1/104.如图，菱形ABCD的周长为24 cm，对角线AC，BD相交于点O，点E是AD的中点，连接OE，则线段OE的长等于()A．3 cmB．4 cmC．2.5 cmD．2 cm5.如图，在矩形ABCD中，AB=3，对角线AC，BD相交于点O，AE垂直平分OB于点E，则AD的长为()A．3B．2√2C．6D．3√26.顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是()A．菱形B．对角线互相垂直的四边形C．矩形D．对角线相等的四边形7.如图，把一张长方形纸片对折两次，然后剪下一个角，为了得到一个钝角为120°的菱形，剪口与第二次折痕所成角的度数应为()A．15°或30°B．30°或45°C．45°或60°D．30°或60°8.如图，在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E，F分别为BC，CD的中点，则∠EAF等于() A．75°B．45°C．60°D．30°9.如图，在矩形纸片ABCD中，AB=4，BC=8，将纸片沿EF折叠，使点C与点A重合，则下列结论错误的是() A．AF=AEB．△ABE≌△AGFC．EF=25D．AF=EF10.如图，在正方形ABCD中，点E，F分别在BC，CD 上，△AEF是等边三角形，连接XXX于点G，下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF；⑤S△CEF=2S△ABE。

九年级数学上册《第一章矩形的性质与判定》同步练习题及答案(北师大版)

九年级数学上册《第一章矩形的性质与判定》同步练习题及答案（北师大版）1．如图，点E为矩形ABCD内一点，且EA＝EB．求证：∠ECD＝∠EDC．2．如图，在矩形ABCD中，点M在CD上，AM＝AB，BN⊥AM，垂足为N．（1）求证：△ABN≌△MAD；（2）若AD＝3，MN＝1，求AB的长．3．如图，在矩形ABCD中，O是对角线AC的中点，过点O作EF⊥AC分别交AD，BC于点E，F．（1）求证：△AOE≌△COF；（2）若AB＝8，BC＝16，求CF的长．4．如图，在平行四边形ABCD中，过点D作DE⊥AB于点E，点F在边CD上，且FC＝AE，连接AF、BF．（1）求证：四边形DEBF是矩形；（2）若AF平分∠DAB，FC＝3，DF＝5，求BF的长．5．如图，在平行四边形ABCD中，CE⊥AD于点E，延长DA至点F，使得EF＝DA，连接BF，CF．（1）求证：四边形BCEF是矩形；（2）若AB＝3，CF＝4，DF＝5，求EF的长．6．如图，在▱ABCD中，点E、F在AD边上，且BF＝CE，AE＝DF．（1）求证：△ABF≌△DCE；（2）求证：四边形ABCD是矩形．7．已知：如图，四边形ABCD是平行四边形，CE∥BD交AD的延长线于点E，CE＝AC．（1）求证：四边形ABCD是矩形；（2）若AB＝4，AD＝3，求四边形BCED的周长．8．如图，在四边形ABCD中，AD∥BC，∠ABC＝∠ADC＝90°，对角线AC，BD交于点O，DE平分∠ADC 交BC于点E，连接OE．（1）求证：四边形ABCD是矩形；（2）若∠BDE＝15°，求∠DOE；（3）在（2）的条件下，若AB＝2，求△BOE的面积．9．如图，在四边形ABCD中，AC、BD相交于点O，AD∥BC，∠ADC＝∠ABC，OA＝OB．（1）如图1，求证：四边形ABCD为矩形；（2）如图2，P是AD边上任意一点，PE⊥BD，PF⊥AC，E、F分别是垂足，若AD＝12，AB＝5，求PE+PF的值．10．如图，在矩形ABCD中，E为DC边的中点，连接AB，AE的延长线和BC的延长线相交于点F．（1）求证：△ADE≌△FCE；（2）连接AC，与BE相交于点G，若△GEC的面积为2，求矩形ABCD的面积．11．如图，在矩形ABCD中，O为对角线BD的中点，过点O作直线分别与矩形的边AB，CD交于E，F 两点，连接BF，DE．（1）求证：四边形BEDF为平行四边形；（2）若AD＝1，AB＝3，且EF⊥BD，求AE的长．12．已知：如图，平行四边形ABCD中，M、N分别为AB和CD的中点．（1）求证：四边形AMCN是平行四边形；（2）当△ABC的边AC、BC满足什么数量关系时，四边形AMCN是矩形，请说明理由．13．如图，过△ABC边AC的中点O，作OE⊥AC，交AB于点E，过点A作AD∥BC，与BO的延长线交于点D，连接CD，CE，若CE平分∠ACB，CE⊥BO于点F．（1）求证：OC＝BC．（2）四边形ABCD是矩形．14．已知，在四边形ABCD中，AD∥BC，点E为BC的中点，连接AC，DE交于点F，AB＝AC，AF＝CF．（1）如图1，求证：四边形AECD是矩形；（2）如图2，连接BF，在不添加任何辅助线的情况下，请直接写出图2中与△BEF面积相等的三角形．15．如图，AD是▱ABDE的对角线，∠ADE＝90°，延长ED至点C，使DC＝ED，连接AC交BD于点O，连接BC．（1）求证：四边形ABCD是矩形；（2）连接OE，若AD＝4，AB＝2，求OE的长．16．如图，矩形ABCD中，AB＝2，BC＝5，E、P分别在AD、BC上，且DE＝BP＝1（1）判断△BEC的形状，并说明理由；（2）求证：四边形EFPH是矩形．17．如图△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．（1）求证：OE＝OF；（2）若CE＝4，CF＝3，求OC的长；（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．18．如图，在平行四边形ABCD中，已知对角线AC、BD相交于点O，若E、F是AC上两动点，分别从A、C两点以相同的速度1cm/s向点O运动．（1）当E与F不重合时，四边形DEBF是否是平行四边形？请说明理由；（2）若AC＝16cm，BD＝12cm，点E，F在运动过程中，四边形DEBF能否为矩形？如能，求出此时的运动时间t的值，如不能，请说明理由．19．如图，在矩形ABCD中，AB＝5，AD＝3，点P是AB边上一点（不与A，B重合），连接CP，过点P 作PQ⊥CP交AD边于点Q，连接CQ．（1）当△CDQ≌△CPQ时，求AQ的长；（2）取CQ的中点M，连接MD，MP，MD⊥MP，求AQ的长．20．如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至G，使EG＝AE，连接CG．（1）求证：△ABE≌△CDF；（2）当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．21．如图，在长方形ABCD中，BC＝20cm，P、Q、M、N分别从A、B、C、D出发沿AD、BC、CB、DA 方向在长方形的边上同时运动，当有一个点先到达所在运动边的另一个端点时即停止，已知在相同时间内，若BQ＝xcm（x≠0），则AP＝2xcm，CM＝3xcm，DN＝x2cm．（1）当x为何值时，点的运动停止？（2）点P与点N可能相遇吗？点Q与点M呢？请通过计算说明理由．（3）当x为何值时，以P、Q、M、N为顶点的四边形是平行四边形？22．如图，AC为矩形ABCD的对角线，BE⊥AC于点E，DF⊥AC于点F．（1）求证：△ABE≌△CDF．（2）求证：四边形BFDE是平行四边形．23．如图，矩形ABCD中，AB＝4cm，BC＝8cm，动点M从点D出发，按折线D→C→B→A→D方向以2cm/s 的速度运动，动点N从点D出发，按折线DABCD方向以1cm/s的速度运动．（1）若动点M、N同时出发，经过几秒钟两点相遇？（2）若点E在线段BC上，且BE＝3cm，若动点M、N同时出发，相遇时停止运动，经过几秒钟，点A、E、M、N组成平行四边形？24．如图，长方形ABCD中，AB＝4cm，BC＝6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A﹣B﹣C﹣D回到点A，设点P运动的时间为t秒．（1）当t＝3秒时，求△ABP的面积；（2）当t为何值时，点P与点A的距离为5cm？（3）当t为何值时（2＜t＜5），以线段AD、CP、AP的长度为三边长的三角形是直角三角形，且AP是斜边．参考答案1．证明：∵EA＝EB∴∠EAB＝∠EBA在矩形ABCD中，∠DAB＝∠CBA＝90°，AD＝BC ∴∠DAB﹣∠EAB＝∠CBA﹣∠EBA即∠EAD＝∠EBC在△ADE和△BCE中{AD=BC∠DAE=∠CBE EA=EB∴△ADE≌△BCE（SAS）．∴ED＝EC∴∠ECD＝∠EDC．2．（1）证明：在矩形ABCD中，∠D＝90°，DC∥AB ∴∠BAN＝∠AMD∵BN⊥AM∴∠BNA＝90°在△ABN和△MAD中{∠BAN=∠AMD ∠BNA=∠D=90°AB=AM∴△ABN≌△MAD（AAS）；（2）解：∵△ABN≌△MAD∴BN＝AD＝3∵AB2＝AN2+BN2∴AB2＝（AB﹣1）2+9∴AB＝53．（1）证明：∵四边形ABCD是矩形∴AD∥BC∴∠DAC＝∠BCA∵点O是AC的中点∴AO＝CO在△AEO和△CFO中{∠DAC=∠ACB AO=CO∠AOE=∠COF∴△AEO≌△CFO（ASA）；（2）解：如图，连接AF∵AO＝CO，EF⊥AC∴AF＝FC∵AF2＝AB2+BF2∴CF2＝（16﹣CF）2+64∴CF＝10．4．（1）证明：∵四边形ABCD是平行四边形∴DC∥AB，DC＝AB∵FC＝AE∴CD﹣FC＝AB﹣AE即DF＝BE∴四边形DEBF是平行四边形又∵DE⊥AB∴∠DEB＝90°∴平行四边形DEBF是矩形；（2）解：∵AF平分∠DAB∴∠DAF＝∠BAF∵DC∥AB∴∠DF A＝∠BAF∴∠DF A＝∠DAF∴AD＝DF＝5在Rt△AED中，由勾股定理得：DE=√AD2−AE2=√52−32=4由（1）得：四边形DEBF是矩形∴BF＝DE＝4．5．（1）证明：∵四边形ABCD是平行四边形∴AD∥BC，AD＝BC∵EF＝DA∴EF＝BC，EF∥BC∴四边形BCEF是平行四边形又∵CE⊥AD∴∠CEF＝90°∴平行四边形BCEF是矩形；（2）解：∵四边形ABCD是平行四边形∴CD＝AB＝3∵CF＝4，DF＝5∴CD2+CF2＝DF2∴△CDF是直角三角形，∠DCF＝90°∴△CDF的面积=12DF×CE=12CF×CD∴CE=CF×CDDF=4×35=125由（1）得：EF＝BC，四边形BCEF是矩形∴∠FBC＝90°，BF＝CE=12 5∴BC=√CF2−BF2=√42−(125)2=165∴EF=16 5．6．证明：（1）∵四边形ABCD是平行四边形∴AB＝CD，AB∥CD∵AE＝FD∴AE+EF＝FD+EF即AF＝DE在△ABF和△DCE中{AB=CD BF=CE AF=DE∴△ABF≌△DCE（SSS）；（2）由（1）可知：△ABF≌△DCE∴∠A＝∠D∵AB∥CD∴∠A+∠D＝180°∴2∠A＝180°∴∠A＝90°∴▱ABCD为矩形．7．（1）证明：∵四边形ABCD是平行四边形∴AE∥BC∵CE∥BD∴四边形BCED是平行四边形∴CE＝BD．∵CE＝AC∴AC＝BD．∴▱ABCD是矩形；（2）解：∵AB＝4，AD＝3，∠DAB＝90°∴BD=√AB2+AD2=√42+32=5．∵四边形BCED是平行四边形∴四边形BCED的周长为2（BC+BD）＝2×（3+5）＝16．8．（1）证明：∵AD∥BC∴∠ABC+∠BAD＝180°∵∠ABC＝90°∴∠BAD＝90°∴∠BAD＝∠ABC＝∠ADC＝90°∴四边形ABCD是矩形；（2）解：∵四边形ABCD是矩形，DE平分∠ADC∴∠CDE＝∠CED＝45°∴EC＝DC又∵∠BDE＝15°∴∠CDO＝60°又∵矩形的对角线互相平分且相等∴OD＝OC∴△OCD是等边三角形∴∠DOC＝∠OCD＝60°∴∠OCB＝90°﹣∠DCO＝30°∵CO＝CE∴∠COE＝（180°﹣30°）÷2＝75°∴∠DOE＝∠DOC+∠COE＝60°+75°＝135°；（3）解：作OF⊥BC于F．∵四边形ABCD是矩形∴CD＝AB＝2，∠BCD＝90°，AO＝CO，BO＝DO，AC＝BD ∴AO＝BO＝CO＝DO∴BF＝FC∴OF=12CD＝1∵∠OCB＝30°，AB＝2∴BC＝2√3∵DE平分∠ADC，∠ADC＝90°∴∠EDC＝45°在Rt△EDC中，EC＝CD＝2∴△BOE的面积=12•EB•OF=12×（2√3−2）×1=√3−1．9．证明：（1）∵AD∥BC∴∠ABC+∠BAD＝180°，∠ADC+∠BCD＝180°∵∠ABC ＝∠ADC∴∠BAD ＝∠BCD∴四边形ABCD 是平行四边形∴OA ＝OC =12AC ，OB ＝OD =12BD∵OA ＝OB∴AC ＝BD∴四边形ABCD 是矩形；（2）如图，连接OP∵AD ＝12，AB ＝5∴BD =√AB 2+AD 2=√144+25=13∴BO ＝OD ＝AO ＝CO =132 ∵S △AOD =14S 矩形ABCD =14×12×5＝15∴S △AOP +S △POD ＝15∴12×132×FP +12×132×EP ＝15 ∴PE +PF =6013．10．（1）证明：∵四边形ABCD 是矩形∴AD ∥CB ，AD ＝BC∴∠D ＝∠FCE ；∵E 为DC 中点∴ED ＝EC在△ADE 与△FCE 中{∠D =∠FCE DE =CE ∠AED =∠FEC∴△ADE ≌△FCE （ASA ）；（2）解：∵四边形ABCD 是矩形∴AB ∥CD ，AB ＝DC∴AB EC =BG EG ，S △ABGS △CEG =（AB EC ）2∵DE ＝CE∴AB ＝2CE∴BG EG =2，S △ABGS △CEG =（AB EC ）2＝4∵△GEC 的面积为2∴S △BGC ＝2S △CEG ＝4，S △ABG ＝4S △CEG ＝8∴S △ABC ＝S △BGC +S △ABG ＝4+8＝12∴矩形ABCD 的面积＝2S △ABC ＝24．11．（1）证明：∵四边形ABCD 是矩形∴AB ∥CD∴∠OBE ＝∠ODF∵O 为对角线BD 的中点∴OB ＝OD在△OBE 和△ODF 中{∠OBE =∠ODF OB =OD ∠BOE =∠DOF∴△OBE ≌△ODF （ASA ）∴BE ＝DF又∵BE ∥DF∴四边形BEDF 为平行四边形；（2）解：∵四边形ABCD 是矩形∴∠A ＝90°由（1）得：四边形BEDF 为平行四边形∵EF ⊥BD∴平行四边形BEDF 为菱形∴BE ＝DE设AE ＝x ，则DE ＝BE ＝3﹣x在Rt △ADE 中，由勾股定理得：AD 2+AE 2＝DE 2即12+x 2＝（3﹣x ）2解得：x =43即AE 的长为43． 12．（1）证明∵四边形ABCD 是平行四边形∴AB ＝CD ，AB ∥CD∵M ，N 分别为AB 和CD 的中点∴AM =12AB ，CN =12CD∴AM ＝CN∵AB ∥CD∴四边形AMCN 是平行四边形；（2）解：AC ＝BC 时，四边形AMCN 是矩形证明∵AC ＝BC ，且M 是BC 的中点∴CM ⊥AB即∠AMC ＝90°∴四边形AMCN 是矩形．13．证明：（1）∵CE 平分∠ACB∴∠OCE ＝∠BCE∵BO ⊥CE∴∠CFO ＝∠CFB ＝90°在△OCF 与△BCF 中{∠OCE =∠BCE CF =CF ∠CFO =∠CFB△OCF ≌△BCF （ASA ）∴OC ＝BC ；（2）∵点O 是AC 的中点∴OA ＝OC∵AD ∥BC∴∠DAO ＝∠BCO ，∠ADO ＝∠CBO在△OAD 与△OCB 中{∠DAO =∠BCO OA =OC ∠ADO =∠CBO∴△OAD ≌△OCB （ASA ）∴AD ＝BC∵AD ∥BC∴四边形ABCD 是平行四边形∵OE ⊥AC∴∠EOC ＝90°在△OCE 与△BCE 中{CE =CE ∠OCE =∠BEC OC =BC∴△OCE ≌△BCE （SAS ）∴∠EBC ＝∠EOC ＝90°∴四边形ABCD 是矩形．14．（1）证明：∵AD ∥BC∴∠F AD ＝∠FCE ，∠FDA ＝∠FEC在△ADF 和△CEF 中{∠FAD =∠FCE ∠FDA =∠FEC AF =CF∴△ADF ≌△CEF （AAS ）∴AD ＝CE∵AD ∥CE∴四边形AECD 为平行四边形∵AB ＝AC ，点E 为BC 的中点∴AE ⊥BC∴∠AEC ＝90°∴平行四边形AECD 为矩形；（2）解：图2中与△BEF 面积相等的三角形为△AEF ，△ADF ，△CDF ，△CEF ．理由如下：∵点E为BC的中点∴S△CEF＝S△BEF∵AF＝CF∴S△AEF＝S△CEF，S△ADF＝S△CDF由（1）可知，四边形AECD是矩形∴EF＝DF∴S△AEF＝S△ADF∴S△CEF＝S△BEF＝S△AEF＝S△ADF＝S△CDF即与△BEF面积相等的三角形为△AEF，△ADF，△CDF，△CEF．15．（1）证明：∵四边形ABDE是平行四边形∴AB∥DE，AB＝ED∵DC＝ED∴DC＝AB，DC∥AB∴四边形ABCD是平行四边形∵DE⊥AD∴∠ADC＝90°∴四边形ABCD是矩形；（2）解：过O作OF⊥CD于F∵四边形ABCD是矩形，AD＝4，AB＝2∴DE＝CD＝AB＝2，AD＝BC＝4，AC＝BD，AO＝OC，BO＝DO ∴OD＝OC∵OF⊥CD∴DF＝CF=12CD=12×2=1∴OF=12BC=12×4=2，EF＝DE+DF＝2+1＝3∴OE=√EF2+OF2=√32+22=√13．16．解：（1）△BEC是直角三角形：理由是：∵矩形ABCD∴∠ADC＝∠ABP＝90°，AD＝BC＝5，AB＝CD＝2由勾股定理得：CE=√CD2+DE2=√22+12=√5同理BE＝2√5∴CE2+BE2＝5+20＝25∵BC2＝52＝25∴BE2+CE2＝BC2∴∠BEC＝90°∴△BEC是直角三角形．（2）∵矩形ABCD∴AD＝BC，AD∥BC∵DE＝BP∴四边形DEBP是平行四边形∴BE∥DP∵AD＝BC，AD∥BC，DE＝BP∴AE＝CP∴四边形AECP是平行四边形∴AP∥CE∴四边形EFPH是平行四边形∵∠BEC＝90°∴平行四边形EFPH是矩形．17．（1）证明：∵MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F ∴∠2＝∠5，∠4＝∠6∵MN∥BC∴∠1＝∠5，∠3＝∠6∴∠1＝∠2，∠3＝∠4∴EO＝CO，FO＝CO∴OE＝OF；（2）解：∵∠2＝∠5，∠4＝∠6∴∠2+∠4＝∠5+∠6＝90°∵CE＝4，CF＝3∴EF=√42+32=5∴OC=12EF=52；（3）当点O在边AC上运动到AC中点时，四边形AECF是矩形．证明：当O为AC的中点时，AO＝CO∵EO＝FO∴四边形AECF是平行四边形∵∠ECF＝90°∴平行四边形AECF是矩形．18．解：（1）当E与F不重合时，四边形DEBF是平行四边形．理由：∵四边形ABCD是平行四边形∴OA＝OC，OB＝OD；∵E、F两动点，分别从A、C两点以相同的速度向点O运动∴AE＝CF；∴OE＝OF；∴BD、EF互相平分；∴四边形DEBF是平行四边形；（2）四边形DEBF能是矩形．理由：∵四边形DEBF是平行四边形∴当BD＝EF时，四边形DEBF是矩形；∵BD＝12cm∴EF＝12cm；∴OE＝OF＝6cm；∵AC＝16cm；∴OA＝OC＝8cm；∴AE＝2cm由于动点的速度都是1cm/s所以t＝2（s）故当运动时间t＝2s时，以D、E、B、F为顶点的四边形是矩形．19．解：（1）∵△CDQ≌△CPQ∴DQ＝PQ，PC＝DC∵AB＝DC＝5，AD＝BC＝3∴PC＝5在Rt△PBC中，PB=√PC2−BC2=4∴P A＝AB﹣PB＝5﹣4＝1设AQ＝x，则DQ＝PQ＝3﹣x在Rt△P AQ中，（3﹣x）2＝x2+12解得x=4 3∴AQ=4 3．（2）方法1，如图2，过M作EF⊥CD于F，则EF⊥AB ∵MD⊥MP∴∠PMD＝90°∴∠PME+∠DMF＝90°∵∠FDM+∠DMF＝90°∴∠MDF＝∠PME∵M是QC的中点∴DM=12QC，PM=12QC∴DM＝PM在△MDF和△PME中{∠MDF=∠PME ∠DFM=∠MEP DM=PM∴△MDF≌△PME（AAS）∴ME＝DF，PE＝MF∵EF⊥CD，AD⊥CD∴EF∥AD∵QM＝MC∴DF＝CF=12DC=52∴ME=5 2∵ME是梯形ABCQ的中位线∴2ME＝AQ+BC，即5＝AQ+3∴AQ＝2．方法2、∵点M是Rt△CDQ的斜边CQ中点∴DM＝CM∴∠DMQ＝2∠DCQ∵点M是Rt△CPQ的斜边的中点∴MP＝CM∴∠PMQ＝2∠PCQ∵∠DMP＝90°∴2∠DCQ+2∠PCQ＝90°∴∠PCD＝45°，°∠BCP＝90°﹣45°＝45°∴∠BPC＝45°＝∠BCP，∴BP＝BC＝3∵∠CPQ＝90°∴∠APQ＝180°﹣90°﹣45°＝45°∴∠AQP＝90°﹣45°＝45°＝∠APQ∴AQ＝AP＝2．20．（1）证明：∵四边形ABCD是平行四边形∴AB＝CD，AB∥CD，OB＝OD，OA＝OC∴∠ABE＝∠CDF∵点E，F分别为OB，OD的中点∴BE=12OB，DF=12OD∴BE＝DF在△ABE和△CDF中{AB=CD∠ABE=∠CDF BE=DF∴△ABE≌△CDF（SAS）；（2）解：当AC＝2AB时，四边形EGCF是矩形；理由如下：∵AC＝2OA，AC＝2AB∴AB＝OA∵E是OB的中点∴AG⊥OB∴∠OEG＝90°同理：CF⊥OD∴AG∥CF∴EG∥CF由（1）得：△ABE≌△CDF∴AE＝CF∵EG＝AE∴EG＝CF∴四边形EGCF是平行四边形∵∠OEG＝90°∴四边形EGCF是矩形．21．解：（1）由题意得x2＝20∴x＝2√5∴当x为2√5时，点的运动停止；（2）当点P与点N相遇时，2x+x2＝20解得x＝2√21−1或﹣1﹣2√21（舍去）当点Q与点M相遇时，x+3x＝20解得x＝5当x＝5时，x2＝25＞20∴点Q与点M不能相遇；（3）∵当点N到达A点时，x2＝20∴x＝2√5∴BQ＝2√5cm，CM＝6√5cm∵BQ+CM＝8√5＜20∴此时M点与Q点还未相遇∴点Q只能在点M的左侧①如图，当点P在点N的左侧时20﹣（x+3x）＝20﹣（2x+x2）解得x＝0（舍去）或x＝2∴当x＝2时，以P、Q、M、N为顶点的四边形是平行四边形；②如图，当点P在点N的右侧时20﹣（x+3x）＝（2x+x2）﹣20解得x＝4或﹣10（舍去）∴当x＝4时，以P、Q、M、N为顶点的四边形是平行四边形综上，当x＝2或4时，以P、Q、M、N为顶点的四边形是平行四边形．22．证明：（1）∵四边形ABCD是矩形∴AB＝CD，AB∥CD∴∠BAE＝∠DCF又∵BE⊥AC，DF⊥AC∴∠AEB＝∠CFD＝90°在△ABE和△CDF中{∠AEB=∠CFD ∠BAE=∠DCF AB=CD∴△ABE≌△CDF（AAS）；（2）由（1）得：△ABE≌△CDF∴BE＝DF又∵BE⊥AC，DF⊥AC∴BE∥DF∴四边形BFDE是平行四边形．23．解：（1）设t秒时两点相遇根据题意得，t+2t＝2（4+8）解得t＝8答：经过8秒两点相遇；（2）观察图象可知，点M不可能在AB或DC上．①如图1，点M在E点右侧时，当AN＝ME时，四边形AEMN为平行四边形得：8﹣t＝9﹣2t解得t＝1∵t ＝1时，点M 还在DC 上∴t ＝1舍去；②如图2，点M 在E 点左侧时，当AN ＝ME 时，四边形AEMN 为平行四边形得：8﹣t ＝2t ﹣9解得t =173．所以，经过173秒钟，点A 、E 、M 、N 组成平行四边形．24．解：（1）当t ＝3时，点P 的路程为2×3＝6cm∵AB ＝4cm ，BC ＝6cm∴点P 在BC 上∴S △ABP =12AB ⋅BP =4（cm 2）．（2）（Ⅰ）若点P 在BC 上∵在Rt △ABP 中，AP ＝5，AB ＝4∴BP ＝2t ﹣4＝3∴t =72；（Ⅱ）若点P 在DC 上则在Rt △ADP 中，AP 是斜边∵AD ＝6∴AP ＞6∴AP ≠5；（Ⅲ）若点P 在AD 上AP ＝5则点P 的路程为20﹣5＝15∴t=15 2综上，当t=72秒或t=152时，AP＝5cm．（3）当2＜t＜5时，点P在BC边上∵BP＝2t﹣4，CP＝10﹣2t∴AP2＝AB2+BP2＝42+（2t﹣4）2由题意，有AD2+CP2＝AP2∴62+（10﹣2t）2＝42+（2t﹣4）2∴t=133＜5即t=13 3．。

北师大版九年级数学上册第1章达标测试卷附答案

北师大版九年级数学上册第一章达标测试卷一、选择题(每题3分，共30分)1．如图，已知菱形ABCD 的边长等于2，∠DAB ＝60°，则对角线BD 的长为( )A ．1B. 3C ．2D ．2 3(第1题) (第3题) (第4题) (第6题) 2．已知正方形的面积为36，则其对角线的长为( )A ．6B ．6 2C ．9D ．9 23．如图，矩形ABCD 的对角线AC ＝8 cm ，∠AOD ＝120°，则AB 的长为( )A. 3 cmB ．2 cmC ．2 3 cmD ．4 cm4．如图，菱形ABCD 的对角线AC ，BD 的长分别为6 cm ，8 cm ，则这个菱形的周长为( )A ．5 cmB ．10 cmC ．14 cmD ．20 cm5．下列命题中，真命题是( )A ．对角线相等的四边形是矩形B ．对角线互相垂直的四边形是菱形C ．对角线互相平分的四边形是平行四边形D ．对角线互相垂直平分的四边形是正方形6．如图，EF 过矩形ABCD 对角线的交点O ，分别交AB ，CD 于点E ，F ，那么阴影部分的面积是矩形ABCD 的面积的( ) A.15B.14C.13D.3107．如图，在△ABC 中，AB ＝AC ，四边形ADEF 为菱形，S △ABC ＝83，则S 菱形ADEF 等于( )A ．4B ．4 6C ．4 3D ．28(第7题) (第9题) (第10题)8．在四边形ABCD中，点O是对角线的交点，能判定这个四边形是正方形的条件是() A．AC＝BD，AB∥CD，AB＝CD B．AD∥BC，∠BAD＝∠BCDC．AO＝BO＝CO＝DO，AC⊥BD D．AO＝CO，BO＝DO，AB＝BC9．如图，四边形ABCD中，∠BAD＝∠C＝90°，AB＝AD，AE⊥BC于点E，若线段AE＝6，则四边形ABCD的面积是()A．3 B．4 C．2 6 D．610．如图，把矩形OABC放入平面直角坐标系中，点B的坐标为(10，8)，点D是OC上一点，将△BCD沿BD折叠，点C恰好落在OA上的点E处，则点D的坐标是() A．(0，4) B．(0，5) C．(0，3) D．(0，2)二、填空题(每题3分，共30分)11．在Rt△ABC中，如果斜边上的中线CD＝4 cm，那么斜边AB＝________．12．已知菱形的两条对角线长分别为2 cm，3 cm，则它的面积是________．13．如图，一活动菱形衣架中，菱形的边长均为16 cm，若墙上钉子间的距离AB＝BC＝16 cm，则∠1＝________．(第13题)(第16题)(第17题)14．已知矩形ABCD的对角线AC，BD相交于点O，当添加条件__________时，矩形ABCD 是正方形(只填一个即可)．15．矩形的对角线相交所成的角中，有一个角是60°，这个角所对的边长为1 cm，则其对角线长为________，矩形的面积为________．16．如图，菱形ABCD的顶点A在x轴上，点B的坐标为(8，2)，点D的坐标为(0，2)，则点C的坐标为________．17．如图，在正方形ABCD的外侧作等边三角形ADE，则∠BED＝________．18．如图，四边形ABCD是菱形，AC＝24，BD＝10，DH⊥AB于点H，则线段BH的长为________．(第18题)(第19题)(第20题)19．如图，已知正方形ABCD的边长为1，连接AC，BD，CE平分∠ACD交BD于点E，则DE＝________．20．如图，在正方形ABCD中，点E，F分别在BC，CD上，△AEF是等边三角形，连接AC交EF于点G.下列结论：①BE＝DF；②∠DAF＝15°；③AC垂直平分EF；④BE＋DF＝EF；⑤S△CEF＝2S△ABE.其中正确结论的序号为__________．三、解答题(21题8分，26题12分，其余每题10分，共60分)21．如图，在矩形ABCD中，AC与BD交于点O，BE⊥AC，CF⊥BD，垂足分别为E，F.求证：BE＝CF.22.如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE＝AB，连接CE.(1)求证：BD＝EC；(2)若∠E＝50°，求∠BAO的大小．23．如图，点E是正方形ABCD内一点，△CDE是等边三角形，连接EB，EA，延长BE交AD于点F.(1)求证：△ADE≌△BCE；(2)求∠AFB的度数．24．如图，在正方形ABCD中，E是AB上一点，BE＝2，AE＝3BE，P是AC上一动点，连接PE，PB.(1)在AC上找一点P，使△BPE的周长最小(作图说明)；(2)求出△BPE周长的最小值．25．如图，在等腰三角形ABC中，AB＝AC，AH⊥BC于点H，点E是AH上一点，延长AH 至点F，使FH＝EH，连接BE，CE，BF，CF.(1)求证：四边形EBFC是菱形；(2)如果∠BAC＝∠ECF，求证：AC⊥CF.26．在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD于点F，取FD的中点G，连接EG，CG，如图①，易证EG＝CG且EG⊥CG.(1)将△BEF绕点B逆时针旋转90°，如图②，则线段EG和CG有怎样的数量关系和位置关系？请直接写出你的猜想．(2)将△BEF绕点B逆时针旋转180°，如图③，则线段EG和CG又有怎样的数量关系和位置关系？请写出你的猜想，并加以证明．答案一、1.C 2.B 3.D 4.D 5.C 6.B7．C8.C9.D10.C二、11.8 cm12.3 cm213.120°14．AC⊥BD(答案不唯一)15．2 cm； 3 cm216.(4，4)17.45°18.501319.2－120.①②③⑤三、21.证明：∵四边形ABCD为矩形，∴OA＝OC，OB＝OD，AC＝BD.∴BO＝CO.∵BE⊥AC于点E，CF⊥BD于点F，∴∠BEO＝∠CFO＝90°.又∵∠BOE＝∠COF，∴△BOE≌△COF(AAS)．∴BE＝CF.22．(1)证明：∵四边形ABCD是菱形，∴AB∥CD，AB＝CD.又∵E在AB的延长线上，且BE＝AB，∴BE∥CD，BE＝CD.∴四边形BECD是平行四边形．∴BD＝EC.(2)解：∵四边形BECD是平行四边形，∴BD∥CE.∴∠ABO＝∠E＝50°.又∵四边形ABCD是菱形，∴AC⊥BD.∴∠BAO＝90°－∠ABO＝40°.23．(1)证明：∵四边形ABCD是正方形，∴∠DAB＝∠ADC＝∠BCD＝90°，AD＝BC.∵△CDE 是等边三角形，∴∠CDE ＝∠DCE ＝60°，DE ＝CE . ∴∠ADE ＝∠BCE ＝30°. 在△ADE 和△BCE 中，⎩⎨⎧AD ＝BC ，∠ADE ＝∠BCE ，DE ＝CE ，∴△ADE ≌△BCE (SAS)． (2)解：∵△ADE ≌△BCE ， ∴AE ＝BE . ∴∠BAE ＝∠ABE .又∵∠BAE ＋∠DAE ＝90°， ∠ABE ＋∠AFB ＝90°， ∴∠DAE ＝∠AFB .∵∠ADE ＝30°，DE ＝DC ＝DA ， ∴∠DAE ＝75°. ∴∠AFB ＝75°.24．解：(1)如图，连接DE ，交AC 于点P ′，连接BP ′，则此时P ′B ＋P ′E 的值最小，即当点P 在点P ′处时，△BPE 的周长最小．(2)∵四边形ABCD 是正方形， ∴B ，D 关于AC 对称． ∴P ′B ＝P ′D . ∴P ′B ＋P ′E ＝DE . ∵BE ＝2，AE ＝3BE ， ∴AE ＝6.∴AD ＝AB ＝8. ∴DE ＝62＋82＝10. ∴PB ＋PE 的最小值是10.∴△BPE的周长的最小值为10＋BE＝10＋2＝12. 25．证明：(1)∵AB＝AC，AH⊥BC，∴BH＝CH.又∵FH＝EH，∴四边形EBFC是平行四边形.又∵EF⊥BC，∴四边形EBFC是菱形．(2)如图所示．∵四边形EBFC是菱形，∴∠2＝∠3＝12∠ECF.∵AB＝AC，AH⊥BC，∴∠4＝12∠BAC.又∵∠BAC＝∠ECF，∴∠4＝∠3.∵∠4＋∠1＋∠2＝90°，∴∠3＋∠1＋∠2＝90°，即AC⊥CF.26．解：(1)EG＝CG，EG⊥CG.(2)EG＝CG，EG⊥CG.证明如下：延长FE交DC的延长线于点M，连接MG，如图所示．易得∠AEM＝90°，∠EBC＝90°，∠BCM＝90°，∴四边形BEMC 是矩形．∴BE ＝CM ，BC ＝EM ，∠EMC ＝90°. 易知∠ABD ＝45°， ∴∠EBF ＝45°. 又∵∠BEF ＝90°，∴△BEF 为等腰直角三角形． ∴BE ＝EF ，∠F ＝45°. ∴EF ＝CM .∵∠EMC ＝90°，FG ＝DG ， ∴MG ＝12FD ＝FG . ∵BC ＝EM ，BC ＝CD ， ∴EM ＝CD . ∵EF ＝CM ， ∴FM ＝DM . 又∵FG ＝DG ，∴∠CMG ＝12∠EMC ＝45°. ∴∠F ＝∠CMG . 在△GFE 和△GMC 中，⎩⎨⎧FG ＝MG ，∠F ＝∠GMC ，EF ＝CM ，∴△GFE ≌△GMC (SAS)． ∴EG ＝CG ，∠FGE ＝∠MGC . ∵MF ＝MD ，FG ＝DG ， ∴MG ⊥FD .∴∠FGE ＋∠EGM ＝90°. ∴∠MGC ＋∠EGM ＝90°，即∠EGC ＝90°. ∴EG ⊥CG .九年级数学上册期末达标检测卷一、选择题(每题4分，共40分)1．已知a，d，c，b是成比例线段，其中a＝3 cm，b＝2 cm，c＝6 cm，则d的长度为()A．4 cm B．1 cm C．9 cm D．5 cm2．在反比例函数y＝k－1x图象的每一支曲线上，y都随x的增大而减小，则k的取值范围是()A．k＜0 B．k＞0 C．k＜1 D．k＞13．对于抛物线y＝－12(x＋2)2＋3，有下列结论：①抛物线的开口向下；②对称轴为直线x＝2；③顶点坐标为(－2，3)；④当x＞2时，y随x的增大而减小．其中正确结论的个数为()A．1 B．2 C．3 D．44．如图，在▱ABCD中，E是AD边的中点，连接BE并延长交CD的延长线于点F，则△EDF与△BCF的周长之比是()A．1：2 B．1：3 C．1：4 D．1：55．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，若AC＝5，BC ＝2，则sin∠ACD的值为()A.52 B.2 55 C.53 D.236．如图，P为线段AB上一点，AD与BC相交于点E，∠CPD＝∠A＝∠B，BC 交PD于点F，AD交PC于点G，则图中相似三角形有()A．1对B．2对C．3对D．4对7．如图，在直角平面坐标系中，△OAB 的顶点为O (0，0)，A (4，3)，B (3，0)．以点O 为位似中心，在第三象限内作与△OAB 的相似比为13的位似图形△OCD ，则点C 的坐标为( )A ．(－1，－1) B.⎝ ⎛⎭⎪⎫－43，－1 C.⎝ ⎛⎭⎪⎫－1，－43 D ．(－2，－1) 8．如图，在笔直的海岸线l 上有A ，B 两个观测站，且AB ＝2 km.从A 站测得船C 在北偏东45°方向，从B 站测得船C 在北偏东22.5°方向，且tan 22.5°＝2－1，则船C 离海岸线l 的距离(即CD 的长)为( ) A ．4 kmB ．(2＋2)kmC ．2 2 kmD ．(4－2)km9．如图，已知边长为4的正方形EFCD 截去一角成为五边形ABCDE ，其中AF＝2，BF ＝1.在AB 上找一点P ，使得矩形PNDM 有最大面积，则矩形PNDM 面积的最大值为( ) A ．8B ．12C.252D ．1410．如图，在平面直角坐标系中，抛物线y ＝－x 2＋2 3x 的顶点为A ，且与x轴的正半轴交于点B ，点P 为该抛物线对称轴上一点，则OP ＋12AP 的最小值为( ) A.3＋2214B.3＋232C ．3D ．2 3二、填空题(每题5分，共20分)11．如图，在由边长相同的小正方形组成的网格中，点A ，B ，C ，D 都在这些小正方形的顶点上，AB ，CD 相交于点P ，则tan ∠APD 的值是________．12．如图，点P 是反比例函数y ＝43x (x >0)图象上一动点，在y 轴上取点Q ，使得以P ，Q ，O 为顶点的三角形是含有30°角的直角三角形，则符合条件的点Q 的坐标是________________．13．如图是二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象，其与x 轴的交点的横坐标分别为x 1，x 2，其中－2＜x 1＜－1，0＜x 2＜1，下列结论：①abc ＞0；②4a －2b ＋c ＜0；③2a －b ＜0.其中正确的有____________(填序号)．14．如图，在矩形纸片ABCD 中，AB ＝6，BC ＝10，点E 在CD 上，将△BCE 沿BE 折叠，使点C 恰好落在边AD 上的点F 处；点G 在AF 上，将△ABG 沿BG 折叠，使点A 恰好落在线段BF 上的点H 处，有下列结论：①∠EBG ＝45°；②△DEF ∽△ABG ；③S △ABG ＝32S △FGH ；④AG ＋DF ＝FG .其中正确的有____________(填序号)．三、解答题(15～18题每题8分；19，20题每题10分；21，22题每题12分；23题14分，共90分)15．计算：(－1)2 022－6tan30°＋⎝ ⎛⎭⎪⎫12－2＋|1－3|.16．已知抛物线y ＝12x 2－4x ＋7与直线y ＝12x 交于A ，B 两点(点A 在点B 左侧)．(1)求A ，B 两点的坐标；(2)求抛物线顶点C 的坐标，并求△ABC 的面积．17．如图，在△ABC中，AB＝43，AC＝10，∠B＝60°，求△ABC的面积．18．如图，△ABC三个顶点的坐标分别为A(1，2)，B(3，1)，C(2，3)，以原点O 为位似中心，将△ABC放大为原来的2倍得到△A′B′C′.(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法)；(2)计算△A′B′C′的面积．19．如图，已知在正方形ABCD中，BE平分∠DBC，交CD边于点E，将△BCE 绕点C顺时针旋转到△DCF的位置，并延长BE交DF于点G.(1)求证：△BDG∽△DEG；(2)若EG·BG＝4，求BE的长．20．设P(x，0)是x轴上的一个动点，它与原点的距离为y1.(1)求y1关于x的函数表达式，并画出这个函数的图象；(2)若反比例函数y2＝kx的图象与函数y1的图象相交于点A，且点A的纵坐标为2.①求k的值；②结合图象，当y1＞y2时，写出x的取值范围．21．如图，某大楼DE的顶部竖有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°，沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i＝1：3，AB＝8米，AE＝12米．(1)求点B距水平面AE的高度BH；(2)求广告牌CD的高度．(测角器的高度忽略不计，结果精确到0.1米，参考数据：2≈1.414，3≈1.732)22．某公司经销一种绿茶，每千克成本为50元．经市场调查发现，在一段时间内，销售量w(千克)随销售单价x(元/千克)的变化而变化，具体表达式为w＝－2x＋240.设这种绿茶在这段时间内的销售利润为y元，解答下列问题：(1)求y与x的函数表达式；(2)当x取何值时，y的值最大？(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克，公司想要在这段时间内获得2 250元的销售利润，销售单价应定为多少？23．矩形ABCD的一条边AD＝8，将矩形ABCD折叠，使得点B落在CD边上的点P处．(1)如图①，已知折痕与边BC交于点O.①求证：△OCP∽△PDA；②若△OCP与△PDA的面积比为1：4，求边AB的长；(2)如图②，在(1)的条件下，擦去AO和OP，连接BP.动点M在线段AP上(不与点P，A重合)，动点N在线段AB的延长线上，且BN＝PM，连接MN交PB于点F，作ME⊥BP于点E.试问动点M，N在移动的过程中，线段EF的长度是否发生变化？若不变，求出线段EF的长度；若变化，说明理由．答案一、1.B 2.D3．C【点拨】∵a＜0，∴抛物线的开口向下，①正确；抛物线y＝－12(x＋2)2＋3的对称轴为直线x＝－2，②错误；顶点坐标为(－2，3)，③正确；④抛物线开口向下，当x＞2时，图象是下降趋势，y随x的增大而减小，④正确．故选C.4．A【点拨】在▱ABCD中，AD＝BC，AD∥BC，∵E是AD的中点，∴DE＝12AD＝12BC.由AD∥BC可得，△EDF∽△BCF.它们的周长比等于相似比，∴周长比等于ED BC＝12BC：BC＝1：2.故选A.5．C【点拨】∵在Rt△ABC中，∠ACB＝90°，AC＝5，BC＝2，∴AB ＝AC 2＋BC 2＝（5）2＋22＝3. ∵∠ACB ＝90°，CD ⊥AB ， ∴∠ACD ＋∠BCD ＝90°，∠B ＋∠BCD ＝90°，∴∠ACD ＝∠B ， ∴sin ∠ACD ＝sin B ＝AC AB ＝53. 故选C.6．C 【点拨】∵∠CPD ＝∠A ，∠D ＝∠D ，∴△ADP ∽△PDG ，∴∠APD ＝∠PGD ，∴∠FPB ＝∠AGP .∵∠CPF ＝∠B ，∠C ＝∠C ，∴△CPF ∽△CBP ，∴∠CFP ＝∠CPB ，∴∠PFB ＝∠APG ；在△AGP 和△BPF 中，∠AGP ＝∠BPF ，∠APG ＝∠BFP ，∴△AGP ∽△BPF .故选C. 7．B 8.B9．B 【点拨】延长NP 交EF 于点G ，设PG ＝x ，则PN ＝4－x . ∵PG ∥BF ，∴△APG ∽△ABF ， ∴AG AF ＝PG BF ，即AG 2＝x 1，解得AG ＝2x ，∴PM ＝EG ＝EA ＋AG ＝2＋2x ，∴S 矩形PNDM ＝PM ·PN ＝(2＋2x )(4－x )＝－2x 2＋6x ＋8＝－2⎝ ⎛⎭⎪⎫x －322＋252(0≤x ≤1)，当x ＝1时，矩形PNDM 的面积最大，最大值为12.故选B .10．C 【点拨】连接AB ，过点P 作PC ⊥AB 于点C .设抛物线的对称轴与x 轴的交点为点D .易求出抛物线的对称轴为直线x ＝3，顶点A (3，3)，故BD ＝OD ＝3，AD ＝3，在Rt △ABD 中，tan ∠BAD ＝BD AD ＝33，∴∠BAD ＝30°，∴PC ＝12AP .当O ，P ，C 三点共线时，OP ＋PC 的长最短，最短距离为sin ∠OBC ·OB ＝sin 60°×2 3＝3.∴OP ＋12AP 的最小值为3.故选C.二、11.212．(0，23)或(0，2)或⎝ ⎛⎭⎪⎫0，833或(0，8) 13．①②③ 【点拨】①∵图象开口向下， ∴a ＜0，∵图象的对称轴在y 轴左侧， ∴－b2a ＜0，而a ＜0，∴b ＜0， ∵图象与y 轴的交点在正半轴上， ∴c ＞0，∴abc ＞0，故结论正确． ②∵－2＜x 1＜－1，∴当x ＝－2时，y ＝4a －2b ＋c ＜0，故结论正确． ③∵－2＜x 1＜－1，0＜x 2＜1， ∴－b2a ＞－1，∵a ＜0， ∴2a －b ＜0，故结论正确．故正确的结论有①②③.14．①③④ 【点拨】∵△BCE 沿BE 折叠，点C 恰好落在边AD 上的点F 处， ∴∠1＝∠2，CE ＝FE ，BF ＝BC ＝10.在Rt △ABF 中，∵AB ＝6，BF ＝10， ∴AF ＝102－62＝8，∴DF ＝AD －AF ＝10－8＝2.设EF ＝x ，则CE ＝x ，DE ＝CD －CE ＝6－x .在Rt △DEF 中，∵DE 2＋DF 2＝EF 2，∴(6－x )2＋22＝x 2，解得x ＝103，∴DE ＝83.∵△ABG 沿BG 折叠，点A 恰好落在线段BF 上的点H 处，∴∠3＝∠4，BH ＝BA ＝6，AG ＝HG ，∴∠EBG ＝∠2＋∠3＝12∠ABC ＝45°，∴①正确．HF ＝BF －BH ＝10－6＝4，设AG ＝y ，则GH ＝y ，GF ＝8－y .在Rt △HGF 中，∵GH 2＋HF 2＝GF 2，∴y 2＋42＝(8－y )2，解得y ＝3，∴AG ＝GH ＝3，GF ＝5.∵∠A ＝∠D ，AB DE ＝94，AG DF ＝32，∴AB DE ≠AGDF ，∴△ABG 与△DEF 不相似，∴②错误．∵S △ABG ＝12AB ·AG ＝12×6×3＝9，S △FGH ＝12GH ·HF ＝12×3×4＝6，∴S △ABG ＝32S △FGH ，∴③正确．∵AG ＋DF ＝3＋2＝5，而FG ＝5，∴AG ＋DF ＝FG ，∴④正确．三、15.解：原式＝1－6×33＋4＋3－1＝4－ 3.16．解：(1)联立⎩⎪⎨⎪⎧y ＝12x 2－4x ＋7，y ＝12x ，解得⎩⎨⎧x ＝2，y ＝1或⎩⎪⎨⎪⎧x ＝7，y ＝72.∴A (2，1)，B ⎝ ⎛⎭⎪⎫7，72.(2)∵y ＝12x 2－4x ＋7＝12(x －4)2－1， ∴顶点C 的坐标为(4，－1)．过顶点C 作CD ∥x 轴交直线y ＝12x 于点D ，如图．在y ＝12x 中，令y ＝－1，得12x ＝－1，解得x ＝－2，∴CD ＝6，∴S △ABC ＝S △BCD －S △ACD ＝12×6×⎝ ⎛⎭⎪⎫72＋1－12×6×(1＋1)＝7.5.17．解：过点A 作AD ⊥BC 于点D .在Rt △ABD 中，AD ＝AB ·sin B ＝4 3×32＝6，BD ＝AB ·cos B ＝4 3×12＝2 3.在Rt △ACD 中，CD ＝AC 2－AD 2＝102－62＝8， ∴BC ＝BD ＋CD ＝2 3＋8.∴S △ABC ＝12BC ·AD ＝12×(23＋8)×6＝63＋24. 18．解：(1)如图．(2)S △A ′B ′C ′＝4×4－12×2×2－12×2×4－12×2×4＝6.19．(1)证明：∵BE 平分∠DBC ， ∴∠DBG ＝∠CBE ，根据旋转的性质，得∠EDG ＝∠CBE ， ∴∠DBG ＝∠EDG ，又∵∠DGB ＝∠EGD ， ∴△BDG ∽△DEG .(2)解：由(1)知△BDG ∽△DEG ， ∴BG DG ＝DGEG ，∴DG 2＝EG ·BG . ∵EG ·BG ＝4，∴DG 2＝4， ∴DG ＝2(负值舍去)．∵∠EDG ＝∠CBE ，∠DEG ＝∠BEC ， ∴∠BGD ＝∠BCE ＝90°. ∴∠BGF ＝∠BGD ＝90°.又∵BG ＝BG ，∠DBG ＝∠FBG ， ∴△DBG ≌△FBG .∴DG ＝FG ，∴DF ＝2DG ＝4，由题意可知，BE ＝DF ， ∴BE ＝4.20．解：(1)由题意得，y 1＝||x ，即y 1＝||x ＝⎩⎨⎧x ，x ≥0，－x ，x ＜0.函数图象如图所示．(2)①∵点A的纵坐标为2，点A在函数y1的图象上，∴||x＝2，即x＝±2.∴点A 的坐标为(2，2)或(－2，2)．∴k＝±4.②当k＝4时，图象如图①，当y1>y2时，x的取值范围为x＜0或x＞2；当k＝－4时，图象如图②，当y1>y2时，x的取值范围为x＜－2或x＞0. 21．解：(1)过点B作BG⊥DE于点G，如图．在Rt△ABH中，tan ∠BAH＝13＝33，∴∠BAH＝30°，∴BH＝12AB＝4(米)．∴点B距水平面AE的高度BH为4米．(2)由(1)知BH＝4(米)，∴GE＝BH＝4(米)，AH＝4 3(米)．∴BG＝HE＝AH＋AE＝(4 3＋12)米．在Rt△BGC中，∠CBG＝45°，∴CG＝BG＝(4 3＋12)米．在Rt△ADE中，∠DAE＝60°，AE＝12米，∴DE＝AE·tan ∠DAE＝12·tan 60°＝12 3(米)．∴CD＝CG＋GE－DE＝4 3＋12＋4－12 3＝16－8 3≈16－8×1.732≈2.1(米)．∴广告牌CD的高度约为2.1米．22．解：(1)由题意得y＝(x－50)·w＝(x－50)·(－2x＋240)＝－2x2＋340x－12 000，∴y与x的函数表达式为y＝－2x2＋340x－12 000.(2)y＝－2x2＋340x－12 000＝－2(x－85)2＋2 450，∴当x＝85时，y的值最大．(3)当y＝2 250时，可得－2(x－85)2＋2 450＝2 250，解这个方程，得x1＝75，x2＝95，根据题意知，x＝95不合题意，故舍去，∴销售单价应定为75元/千克．23．(1)①证明：如图，∵四边形ABCD 是矩形，∴∠C ＝∠D ＝∠B ＝90°，∴∠1＋∠3＝90°.由折叠可得∠APO ＝∠B ＝90°，∴∠1＋∠2＝90°.∴∠3＝∠2.又∵∠C ＝∠D ，∴△OCP ∽△PDA .②解：∵△OCP 与△PDA 的面积比为1：4，且△OCP ∽△PDA ， ∴OP P A ＝CP DA ＝12.∴CP ＝12AD ＝4，AP ＝2OP .设OP ＝x ，则易得CO ＝8－x .在Rt △PCO 中，∠C ＝90°，由勾股定理得 x 2＝(8－x )2＋42.解得x ＝5.∴AB ＝AP ＝2OP ＝10.(2)解：线段EF 的长度不变．作MQ ∥AN ，交PB 于点Q ，如图．∵AP ＝AB ，MQ ∥AN ，∴∠APB＝∠ABP＝∠MQP.∴MP＝MQ.又∵BN＝PM，∴BN＝QM.∵MQ∥AN，∴∠QMF＝∠BNF，∠MQF＝∠FBN，∴△MFQ≌△NFB.∴QF＝FB.∴QF＝12QB.∵MP＝MQ，ME⊥PQ，∴EQ＝12PQ.∴EF＝EQ＋QF＝12PQ＋12QB＝12PB.∵PC＝4，BC＝8，∠C＝90°. ∴PB＝82＋42＝4 5，∴EF＝12PB＝2 5.∴动点M，N在移动的过程中，线段EF的长度不变，恒为2 5.。

北师大版九年级数学上册第一章证明二__试题大全

北师大版数学九年级上册第一章证明二（一）选择题：1. 设M 表示直角三角形，N 表示等腰三角形，P 表示等边三角形，Q 表示等腰直角三角形，则下列四个图中，能表示他们之间关系的是（）2. 具有下列条件的两个等腰三角形，不能判断它们全等的是（） A. 顶角、一腰对应相等 B. 底边、一腰对应相等 C. 两腰对应相等 D. 一底角、底边对应相等3. △ABC 中，∠A ：∠B ：∠C=1：2：3，CD ⊥AB 于点D ，若BC=a ，则AD 等于（）A aB aC aD a....12323234. 下列命题的逆命题是真命题的是（）A. 对顶角相等B. 若a=b ，则|a|=|b|C. 末位是零的整数能被5整除D. 直角三角形的两个锐角互余 5. 如图，△ABC 中，AB=AC ，点D 在AC 边上，且BD=BC=AD ，则∠A 的度数为（）A. 30°B. 36°C. 45°D. 70° 6. 下列说法错误的是（）A. 任何命题都有逆命题B. 定理都有逆定理C. 命题的逆命题不一定是正确的D. 定理的逆定理一定是正确的（二）填空题：1. 如果等腰三角形的一个角是80°，那么另外两个角是____________度。

2. 等腰三角形底角15°，则等腰三角形的顶角、腰上的高与底边的夹角分别是__________。

3. 在△ABC 和△ADC 中，下列论断：①AB=AD ；②∠BAC=∠DAC ；③BC=DC ，把其中两个论断作为条件，另一个论断作为结论，写出一个真命题：____________。

4. 如图，折叠长方形的一边AD ，点D 落在BC 边的点F 处，已知：AB=8cm ，BC=10cm ，则△EFC 的周长=____________cm 。

（三）作图题：已知：如图，△ABC 中，AB=AC 。

（1）按照下列要求画出图形：①作∠BAC 的平分线交BC 于点D ； ②过D 作DE ⊥AB ，垂足为点E ； ③过D 作DF ⊥AC ，垂足为点F 。

北师大版九年级数学上册第一章证明(二)测试题及答案(B)

九年级数学上册第一单元测试题

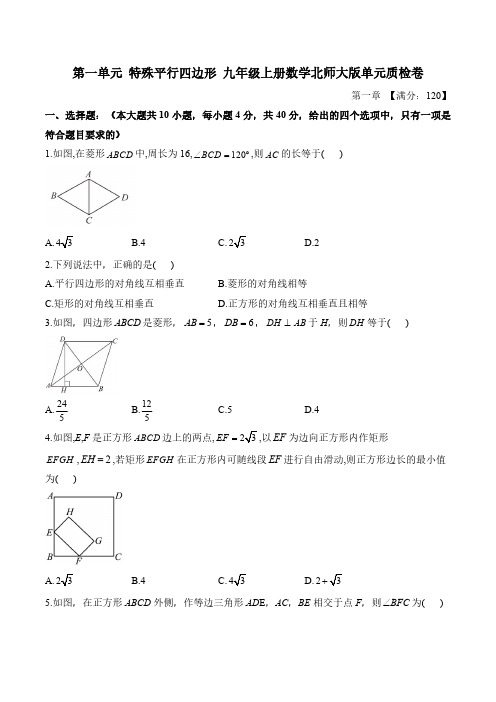
第一单元特殊平行四边形九年级上册数学北师大版单元质检卷第一章【满分：120】一、选择题：（本大题共10小题，每小题4分，共40分，给出的四个选项中，只有一项是符合题目要求的）1.如图,在菱形ABCD 中,周长为16,120BCD ∠=︒,则AC 的长等于()A. B.4 C. D.22.下列说法中，正确的是()A.平行四边形的对角线互相垂直B.菱形的对角线相等C.矩形的对角线互相垂直D.正方形的对角线互相垂直且相等3.如图，四边形ABCD 是菱形，5AB =，6DB =，DH AB ⊥于H ，则DH 等于()A.245 B.125 C.5 D.44.如图,E ,F 是正方形ABCD 边上的两点,EF =,以EF 为边向正方形内作矩形EFGH ,2EH =,若矩形EFGH 在正方形内可随线段EF 进行自由滑动,则正方形边长的最小值为()A. B.4 C. D.25.如图，在正方形ABCD 外侧，作等边三角形AD E ，AC ，BE 相交于点F ，则BFC ∠为()A.75°B.60°C.55°D.45°6.现有一矩形ABCD,借助此矩形作菱形,两位同学提供了如下方案：方案Ⅰ：分别取边AB,BC,CD,DA的中点E,F,G,H,顺次连接这四点,围成的四边形EFGH即为所求.方案Ⅱ：连接AC,作AC的垂直平分线分别交AD,BC于点F,E,连接AE,CF,四边形AECF即为所求.对于方案Ⅰ,Ⅱ,说法正确的是()A.Ⅰ可行、Ⅱ不可行B.Ⅰ不可行、Ⅱ可行C.Ⅰ,Ⅱ都可行D.Ⅰ,Ⅱ都不可行7.如图所示，正方形ABCD的面积为12，ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD PE+的和最小，则这个最小值为()A.43B.3638.如图,在菱形纸片ABCD中,2AB=,60A∠=︒,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为()A.74 B.95 C.19107369.如图,菱形ABCD ,点A 、B 、C 、D 均在坐标轴上,120ABC ∠=︒,点()30A -,,点E 是CD 的中点,点P 是OC 上的一动点,则PD PE +的最小值是()A.3B.5C.2233210.如图,正方形ABCD 的边长为4,G 是对角线BD 上一动点,GE CD ⊥于点E ,GF BC ⊥于点F ,连接EF ,给出四种情况：①若G 为BD 的中点,则四边形CEGF 是正方形；②若G 为BD 上任意一点,则AG EF =；③点G 在运动过程中,GE GF +的值为定值4；③点G 在运动过程中,线段EF 的最小值为22正确的有()A.①②③③B.①②③C.①②③D.①③③二、填空题（每小题4分，共20分）11.如图,点E 是正方形ABCD 的边DC 上一点,把ADE △绕点A 顺时针旋转90°到ABF △的位置,若四边形AECF 的面积为25,2DE =,则AE 的长为______.12.如图菱形ABCD 中,70B ∠=︒,AB 的垂直平分线交对角线AC 于点E ,连接DE ,则ADE ∠的度数是______.13.如图，菱形ABCD 中，108A ∠=︒，AD 的垂直平分线交对角线BD 于点P ，垂足为N ，连结CP ，则BPC ∠=_____度.14.如图,在矩形ABCD 中,3AB =,4BC =,BCD ∠的平分线交边AD 于点E ,M ,N 分别是边AB ,BC 上的动点,且BM BN =,P 是线段CE 上的动点,连接PM ,PN .当BN =______时,PM PN +的值最小.15.如图，将一张长方形纸片ABCD 沿着对角线BD 向下折叠，顶点A 落在点A '处，A D '交BC 于点E ，BC 的垂直平分线分别交BD ，BC ，BA '点F ，G ，H ，连接CF ，CH 若8AD =，6AB =，则GH 的长为________.三、解答题（本大题共6小题，共计60分，解答题应写出演算步骤或证明过程）16.（8分）如图,四边形ABCD 是菱形,点E ,F 分别在AB 和AD 上,且BE DF =.点G ,H 分别在CD 和BC 上,且//EG AD ,//FH AB ,EG 与FH 交于点M .求证：四边形AEMF 为菱形.17.（8分）在学习矩形的过程中,小明发现将矩形ABCD 折叠,使得点B 与点D 重合,所得折痕在BD 的垂直平分线上,折痕平分矩形的面积.他想对此折痕平分矩形的面积进行证明.他的思路是首先作出线段BD 的垂直平分线,通过三角形全等的证明,将折痕左侧的四边形的面积转化为三角形的面积,使问题得到解决.请根据小明的思路完成下面的作图与填空：用直尺和圆规,作BD 的垂直平分线MN ,MN 交AD 于点M ,交BC 于点N ,垂足为点O .∵四边形ABCD 是矩形,∴①,∴ADB CBD ∠=∠,DMO BNO ∠=∠,∵②,∴③,∴()AAS BON DOM ≌△△,BON BON ABNM ABOM S S S S =++四边形四边形△△,DOM ABOM S S =+四边形△,ABD S =△,又∵12ABD ABCDS S =矩形△,∴④,即MN 平分矩形ABCD 的面积.18.（10分）已知：如图，在ABC △中，90ACB ∠=︒，D 点是AB 的中点，DE 、DF 分别是BDC △、ADC △的角平分线.(1)请直接写出AD 、BD 、CD 之间的数量关系：；(2)求证：四边形DECF 是矩形；(3)当ABC △满足条件时，四边形DECF 是正方形.(直接填空即可)19.（10分）已知：如图1，四边形ABCD 四条边上的中点分别为E 、F 、G 、H ，顺次连接EF 、FG 、GH 、HE ，得到四边形EFGH (即四边形ABCD 的中点四边形).(1)四边形EFGH 的形状是__________，证明你的结论.(2)如图2，请连接四边形ABCD 的对角线AC 与BD ，当AC 与BD 满足__________条件时，四边形EFGH 是正方形，证明你的结论.20.（12分）(1)【操作与探究】如图1,正方形ABCD 中,点E 、F 分别是BC ,CD 上一点45EAF ∠=︒.延长CB 至点Q ,使得BQ DF =,连接AQ ,EF ,请根据题意画出图形.①求证：BE DF EF +=；②若3BE =,4CF =,求正方形的边长AB .(2)[迁移与应用]如图2,正方形ABCD 中,点E 在AB 边上(不与端点重合),F 、G 分别是CD ,BC 上一点,EF 交AG 于点M ,45FMG ∠=︒,若2GC BG =,直接写出EF AG的值：______.21.（12分）在矩形ABCD 中，6AB =，8BC =，E 、F 是对角线AC 上的两个动点，分别从A 、C 同时出发相向而行，速度均为每秒1个单位长度，运动时间为t 秒，其中010t ≤≤.(1)若G ，H 分别是AD ，BC 中点，则四边形EGFH 一定是怎样的四边形(E 、F 相遇时除外)？解：________(直接填空，不用说理)(2)在(1)条件下，若四边形EGFH 为矩形，求t 的值；答案以及解析1.答案：B解析：在菱形ABCD 中,1602ACB BCD ∠=∠=︒,AB BC =,∴ABC △是等边三角形,∵菱形ABCD 的周长为16,∴4AB BC ==,∴4AC =故选B.2.答案：D解析：A 、平行四边形的对角线互相平分，此选项错误，不合题意；B 、菱形的对角线互相垂直，此选项错误，不合题意；C 、矩形的对角线相等，此选项错误，不合题意；D 、正方形的对角线一定互相垂直且相等，此选项正确，符合题意.故选D.3.答案：A解析：如图所示，设菱形的对角线交于O ，四边形ABCD 是菱形6DB =，∴132OB BD ==，AC BD ⊥∴4OA ==，∴28AC OA == 12ABCD S AB DH AC BD =⋅=⋅菱形，∴2425AC BD DH AB ⋅==，故选：A.4.答案：B解析：连接HF ,如图,∵四边形EFGH 是矩形,∴90HEF ∠=︒,∴4HF ==,过点H 作HM AB ⊥于点M ,则MB HF ≤,∴4MB ≤,根据题意,AB MB ≥,∴正方形边长的最小值为4.故选：B.5.答案：B解析：∵四边形ABCD 是正方形，90BAD ∴∠=︒，AB AD =，45BAF ∠=︒，ADE △是等边三角形，60DAE ∴∠=︒，AD AE =，9060150BAE ∴∠=︒︒=︒＋，AB AE=18011()25015ABE AEB ∴∠=∠=︒-︒=︒，451560BFC BAF ABE ∴∠=∠+∠=︒+︒=︒；故选：B.6.答案：C解析：方案I, 四边形ABCD 为矩形,AB CD ∴=,AD BC =,90A B C D ∠=∠=∠=∠=︒ 点E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,AE BE CG DG ∴===,AH BF CF DH ===,(SAS)AEH BEF CGF DGH ∴≌≌≌△△△△,EG EF GF GH ∴===,∴四边形EFGH 为菱形;方案1, 四边形ABCD为矩形,∴,AD BC//∴∠=∠,FAC ECA垂直平分AC,EF∴=,AE CE=,AF CF∴∠=∠,EAC ECA∠=∠FAC FCA∴∠=∠,EACA FCA∴,//AE CF=,,AF CFAF CE//∴四边形AECF为菱形.∴方案I、II都可行,故选:C.7.答案：B解析：连接BD，PB，如图所示：∵四边形ABCD为正方形，∴点B与D关于AC对称，∴PD PB=，∴PD PE PB PE BE+=+≥，∴PD PE+最小值为BE的长，∵正方形ABCD的面积为12，∴AB==又∵ABE是等边三角形，∴BE AB==，∴PD PE+最小值为B正确.故选：B.8.答案：A解析：连接BE ,BD ,如图,∵四边形ABCD 为菱形,60A ∠=︒,∴BDC △为等边三角形,60C A ∠=∠=︒,∴906030CBE ∠=︒-︒=︒.∵E 点为CD 的中点,∴1CE DE ==,BE CD ⊥.在Rt BCE △中,22BC CE ==,BE ==.∵//AB CD ,∴BE AB ⊥.∵菱形纸片翻折,使点A 落在CD 的中点E 处,∴EF AF =.设EF AF x ==,则2BF x =-,在Rt BEF △中,()2222x x -+=,解得74x =.故选A.9.答案：A解析：如图：连接BE ,,∵菱形ABCD ,∴B 、D 关于直线AC 对称,∵直线AC 上的动点P 到E 、D 两定点距离之和最小∴根据“将军饮马”模型可知BE 长度即是PD PE +的最小值.,∵菱形ABCD ,120ABC ∠=︒,点()30A -,,∴60CDB ∠=︒,30DAO ∠=︒,3OA =,∴3OD =3AD DC CB ===∴CDB △是等边三角形∴23BD =∵点E 是CD 的中点,∴132DE CD ==,且BE CD ⊥,∴223BE BD DE =-=故选：A.10.答案：A解析：四边形ABCD 是正方形,90C ∴∠=︒,AD DC =,45CBG CDG ADG ∠=∠=∠=︒,GE CD ⊥ 于点E ,GF BC ⊥于点F ,90GEC GFC ∴∠=∠=︒,∴四边形GFCE 是矩形,45EGD EDG ∠=∠=︒,45FGB CBG ∠=∠=︒,∴2DG GE =,2BG GF =,∵G 为BD 的中点,∴DG BG=∴GE GF=∴四边形GFCE 是正方形,故①正确；连接GC,∵四边形GFCE 是矩形,∴EF GC =,在ADG △与CDG △中,AD CD ADG CDG DG DG =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADG CDG ∴≌△△,AG GC ∴=,AG EF ∴=,故②正确；∵45EGD EDG ∠=∠=︒∴GE ED =,∵四边形GFCE 是矩形,∴GF CE=∴4GE GF ED CE CD +=+==,即GE GF +的值为定值4,故③正确；∵EF GC =,∴当CG 最小时,EF 最小,∴当CG BD ⊥时,CG 最小,在Rt BCD △中,BD ==,∵1122BCD S BD CG BC CD =⋅=⋅△∴44=⨯∴CG =∴线段EF 的最小值为,故③正确；∴正确的有①②③③.故选：A.11.解析：∵把ADE △顺时针旋转ABF △的位置,∴四边形AECF 的面积等于正方形ABCD 的面积等于25,∴5AD DC ==,∵2DE =,∴Rt ADE △中,AE ==.12.答案：55︒/55度解析：如图,连接BE ,∵菱形ABCD 中,70ABC ∠=︒,∴//AD BC ,DAC BAC ∠=∠,∴18070110DAB ∠=︒-︒=︒,55DAC BAC ∠=∠=︒,∵AB 的垂直平分线交对角线AC 于点E ,∴EA EB =,∴55EAB EBA ∠=∠=︒,∴由菱形的轴对称的性质可得：55ADE ABE ∠=∠=︒,故答案为：55︒.13.答案：72解析：如图，连接AP ，在菱形ABCD 中，72ADC ∠=︒，11270326ADP ADC ∴∠=∠=⨯︒=︒， NP 是AB 的垂直平分线，AP CP ∴=，36ADP DAP ∴∠=∠=︒，363672APB ADP DAP ∴∠=∠+∠=︒+︒=︒，由菱形的对称性得，72CPB APB ∠=∠=︒.故答案为：72.14.答案：2解析：∵矩形ABCD ,∴90BCD D ∠=∠=︒,∵BCD ∠的平分线交边AD 于点E ,∴45BCE DCE ∠=∠=︒,∴CDE △为等腰直角三角形,作点N 关于EC 的对称点N ',则N '在直线CD 上,连接PN ',∴PM PN PM PN MN ''+=+≥,∵垂线段最短,∴MN AB '⊥时,PM PN +的值最小,如图：此时：四边形BCN M ',四边形BNPM ,四边形PNCN '均为矩形,∴4MN BC '==,∵BM BN =,∴四边形BNPM 为正方形,∴12BN NP PM PN MN ''====,∴2BN =；故答案为：2.15.答案：76解析：由题可知6A B AB CD '===，A BD ABD CDB ∠=∠=∠'，BEA DEC ∠=∠'90A DCE ∠=∠='︒，∴A BE CDE '≌△△，∴A E CE '=，BE DE=设CE t =，则8BE t DE =-=，在Rt DCE △中，222CE CD DE +=，∴()22268t t +=-，解得74t =，∴74A E CE ='=， HF 是BC 的垂直平分线，∴4BG CG ==，∴79444GE CG CE =-=-=，连接EH .设A H x '=，则6BH x =-，在Rt BGH △中，()2222616GH BH BG x =-=--，在Rt A EH '△中，22224916EH A E A H x =+'+'=在Rt EGH △中，222GH GE EH +=，即：()2281496161616x x --+=+解得116x =，∴76GH ==，故答案为：76.16.答案：证明见解析解析：证明：//EG AD ,//FH AB ,∴四边形AEMF 为平行四边形,四边形ABCD 是菱形.AB AD ∴=.BE DF = ,AB BE AD DF ∴-=-,即AE AF =,∴四边形AEMF 为菱形.17.答案：//AD BC ,MN 垂直平分线段BD ,DO BO =,12ABNM ABCD S S =四边形矩形解析：图形如图所示：四边形ABCD 是矩形,∴①//AD BC ,ADB CBD ∴∠=∠,DMO BNO ∠=∠,②MN 垂直平分线段BD ,∴③DO BO =,()AAS BON DOM ∴≌△△,BONABNM ABOM S S S =+四边形四边形△DOMABOM S S =+四边形△ABD S =△,又12ABD ABCDS S =矩形△,∴④12ABNM ABCD S S =四边形矩形,即MN 平分矩形ABCD 的面积.故答案为：//AD BC ,MN 垂直平分线段BD ,DO BO =,12ABNM ABCDS S =四边形矩形.18.答案：(1)CD AD BD==(2)证明见解析(3)AC BC =(答案不唯一)解析：(1)∵在ABC △中，90ACB ∠=︒，D 点是AB 的中点，∴12CD AD BD AB ===，故答案为：CD AD BD ==；(2)证明：∵CD AD BD ==，DE 、DF 分别是BDC △、ADC △的角平分线，∴DF AC ⊥，DE BC⊥又∵90ACB ∠=︒，∴四边形DECF 是矩形；(3)当ABC △满足条件AC BC =时，四边形DECF 是正方形，理由如下：∵CD AD BD ==，DE 、DF 分别是BDC △、ADC △的角平分线，∴12CF AC =，12CE BC =∵AC BC =，∴CF CE =，∴矩形DECF 是正方形，故答案为：AC BC =(答案不唯一)；19.答案：(1)平行四边形，证明见解析(2)互相垂直且相等(AC BD ⊥且AC BD =)，证明见解析解析：(1)证明：四边形EFGH 是平行四边形，证明如下；如图1，连接BD ，点E 、H 分别是AB 、AD 中点，∴//EH BD ，12EH BD =，同理，//FG BD ，12FG BD =，∴//EH FG ，EH FG =，∴四边形EFGH 是平行四边形；(2)互相垂直且相等(AC BD ⊥且AC BD =)，证明如下；如图2，连结AC ，BD同理(1)可知，四边形EFGH 是平行四边形，∵AC BD ⊥，∴EH HG ⊥，∴平行四边形EFGH 是矩形，∵AC BD =，∴EH HG =，∴四边形EFGH 是正方形.20.答案：(1)①证明见解析②6(2)324解析：画图如图所示,①证明：∵正方形ABCD ,∴AD AB =,90ABQ D ∠=∠=︒,∵BQ DF =,∴QAB FAD ≌△△,∴QAB DAF ∠=∠,QA AF =,∵45EAF ∠=︒,90BAD ∠=︒,∴45QAB BAE DAF BAE ∠+∠=∠+∠=︒,∴QAE FAE ∠=∠,∵AE AE =,∴QAE FAE ≌△△,∴QE EF =,∴EF BE BQ BE DF =+=+；②设正方形边长为x ,∵3BE =,4CF =,∴3CE x =-,4DF x =-,由①得1EF BE DF x =+=-,根据勾股定理得,222(3)4(1)x x -+=-,解得6x =,正方形的边长6AB =.(2)作//AN EF ,连接GN ,设正方形的边长为6a ,DN m =,∴45FMG NAG ∠=∠=︒,四边形AEFN 是平行四边形,∴EF AN =,∵2GC BG =,∴24GC BG a ==,6CN a m =-,2GN a m =+,根据勾股定理得,222(4)(6)(2)a a m a m +-=+,解得,3m a =,则AN ==,AG ==,324EF AN AG AG ===.21.答案：(1)四边形EGFH 是平行四边形(2)2t =或8t =解析：(1)∵四边形ABCD 是矩形，∴AD BC =，//AD BC ，∴GAE HCF ∠=∠，∵G ，H 分别是AD ，BC 中点，∴12AG AD =，12CH BC =，∴AG CH =，∵点E ，F 的运动速度相同，∴AE CF =，∴()SAS AGE CHF ≌△△，∴GE FH =，AEG CFH ∠=∠，∴180180AEG CFH ︒-∠=︒-∠，即GEF HFE ∠=∠，∴//GE FH ，∴四边形EGFH 是平行四边形.故答案为：四边形EGFH 是平行四边形(2)如图1，连接GH ，∵G ，H 分别是AD ，BC 中点，∴12AG AD =，12BH BC =，∴AG BH =，∵AD BC =，∵在矩形ABCD 中，//AD BC ，90B ∠=︒，∴四边形ABHG 是矩形，∴6GH AB ==，(1)如图1，当四边形EGFH 是矩形时，6EF GH ==，∵6AB =，8BC =∴10AC =，AE CF t == ，1026EF t ∴=-=，2t ∴=；(2)如图2，当四边形EGFH 是矩形时，同理6EF GH ==，AE CF t ==102106EF t t t ∴=+-=-=，8t ∴=；综上所述，四边形EGFH 为矩形时，2t =或8t =.。

北师大版九年级上册数学第一章测试题(附答案)

北师大版九年级上册数学第一章测试题(附答案)北师大版九年级上册数学第一章测试题（附答案）一、单选题（共12题；共24分）1.已知四边形ABCD中，对角线AC，BD相交于点O。

下列结论一定成立的是（）A.对角线相等B.四边形是矩形C.四边形是平行四边形D.对角线互相平分2.矩形、菱形、正方形都一定具有的性质是（）A.邻边相等B.四个角都是直角C.对角线相等D.对角线互相平分3.如图，CD于E，F，PD．点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，连接PB，若AE=2，PF=8，则图中阴影部分的面积为（）A.10B.12C.16D.184.如图，将两根相同的矩形木条沿虚线剪开得到四根完全一样的木条，然后重新围城一个矩形画，则围城的矩形画框的内框的面积为（）A.48B.64C.72D.965.如图，在矩形ABCD中，E为BC边的中点，∠AEC的平分线交AD边于点F，若AB=3，AD=8，则FD的长度为（）A.1B.2C.3D.46.在四张边长都是10厘米的正方形纸板上，分别剪下一个长5厘米，宽3厘米的长方形，剩下图形周长最长的是（）A.一个等腰直角三角形B.一个等腰非直角三角形C.一个矩形D.一个等边三角形7.在直角坐标系中，A，B，C，D四个点的坐标依次为（-1，y），（x，y），（-1，5），（-5，z），若这四个点构成的四边形是菱形，则满足条件的z的值有（）A.1个B.3个C.4个D.5个8.下列命题正确的是（）A.对角线相等的四边形是矩形B.对角线互相垂直且相等的四边形是正方形C.对角线互相垂直的四边形是菱形D.两组对角线分别相等的四边形是平行四边形9.四边形ABCD的对角线AC=BD，AC⊥BD，分别过A、B、C、D作对角线的平行线，所成的四边形EFMN是（）A.正方形B.菱形C.矩形D.任意四边形10.若正方形的周长为40，则其对角线长为（）A.20B.25C.30D.35答案：1.A2.C3.B4.C5.B6.C7.B8.B9.B 10.DA。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

北九上第一章证明（二）水平测试（B ）一、选择题（本大题有10小题，每小题3分，共30分．请选出每小题中一个符合题意的正确选项，不选、多选、错选，均不给分）1.两个直角三角形全等的条件是（）（A ）一锐角对应相等；（B ）两锐角对应相等；（C ）一条边对应相等；（D ）两条边对应相等.2.到ABC ∆的三个顶点距离相等的点是ABC ∆的（）.（A ）三边垂直平分线的交点；（B ）三条角平分线的交点；（C ）三条高的交点；（D ）三边中线的交点. 3.如图，由21∠=∠，DC BC =，EC AC =，得A B C ∆≌EDC∆的根据是（）（A ）SAS （B ）ASA （C ）AAS （D ）SSS4.ABC ∆中，AC AB =，BD 平分ABC ∠交AC 边于点D ， 75=∠BDC ，则A ∠的度数为（）（A ）35° （B ）40° （C ）70° （D ）110°5.下列两个三角形中，一定全等的是（）（A ）有一个角是40°，腰相等的两个等腰三角形；（B ）两个等边三角形；（C ）有一个角是100°，底相等的两个等腰三角形；（D ）有一条边相等，有一个内角相等的两个等腰三角形.6.适合条件A ∠=B ∠ =C ∠31的三角形一定是（）（A ）锐角三角形；（B ）钝角三角形；（C ）直角三角形；（D ）任意三角形.7.有一块边长为24米的正方形绿地，如图所示，在绿地旁边B 处有健身器材，由于居住在A 处的居民践踏了绿地，小明想在A 处树立一个标牌“少走▇米，踏之何忍？”请你计算后帮小明在标牌的“▇”填上适当的数字是（）.（A ）3米（B ）4米（C ）5米（D ）6米8. 一个三角形如果有两边的垂直平分线的交点在第三边上，那么这个三角形是（）.（A ）等腰三角形; （B ）等边三角形; （C ）直角三角形; （D ）等腰直角三角形.9.如图，已知AC 平分PAQ ∠，点B 、B '分别在边AP 、AQ 上，如果添加一个条件，即可推出AB =B A '，那么该条件不可以是（）(A)AC B B ⊥' (B)C B BC '=(C)ACB ∠=B AC '∠ (D)ABC ∠ =C B A '∠10.如图，AO FD ⊥于D ，BO FE ⊥于E ，下列条件：①OF 是AOB ∠的平分线；②EF DF =；③EO DO =；④OFD ∠=OFE ∠.其中能够证明DOF ∆≌EOF ∆的条件的个数有（）(A)1个 (B)2个 (C)3个 (D)4个A B 24 7 （第7题）（第9题）(第10题) （第3题）二、填空题(本大题有10小题，每小题3分，共30分．将答案填在题中横线上)11.在ABC ∆中，边AB 、BC 、AC 的垂直平分线相交于P ，则PA 、PB 、PC 的大小关系是 .12.如果等腰三角形的一个角是80°，那么顶角是度.13.若等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的底角为 .14. ABC ∆中， 90=∠C ，AD 平分BAC ∠，交BC 于点D ,若7=DC ，则D 到AB 的距离是 .15.如图，ABC ∠＝DCB ∠，需要补充一个直接条件才能使ABC ∆≌DCB ∆．甲、乙、丙、丁四位同学填写的条件分别是：甲“DC AB =”；乙“DB AC =”；丙“D A ∠=∠”；丁“ACB ∠＝DBC ∠”．那么这四位同学填写错误的是 .16. 用反证法证明 “三角形中至少有一个角不小于60°时，假设“ ”，则与“ ”矛盾，所以原命题正确．17.补全“求作AOB ∠的平分线”的作法：①在OA 和OB 上分别截取OD 、OE ，使OD =OE .②分别以D 、E 为圆心，以为半径画弧，两弧在AOB ∠内交于点C .③作射线OC 即为AOB ∠的平分线.18.一轮船以每小时20海里的速度沿正东方向航行.上午8时，该船在A处测得某灯塔位于它的北偏东30°的B 处(如图)，上午9时行到C 处，测得灯塔恰好在它的正北方向，此时它与灯塔的距离是海里(结果保留根号).19.在ABC ∆中，A ∠＝90°，AC AB =，BD 平分B ∠交AC 于D ，BC DE ⊥于E ，若10=BC ，则DEC ∆的周长是 .20.如图是2002年8月在北京召开的第24届国际数学家大会的会标，它是由4个相同的直角三角形拼和而成.若图中大小正方形的面积分别为522cm 和42cm ，则直角三角形的两条直角边的和是 cm .三、解答题(本大题有6小题，共60分．解答需写出必要的文字说明、演算步骤或证明过程)21.（8分）已知：如图，A ∠= 90=∠D ，BD AC =.求证：OC OB =.A BC D （第15题）(第18题)(第20题)22.（8分）如图，OCB OBC ∠=∠，AOC AOB ∠=∠，请你写一个能用全部已知条件才能推出的结论，并证明你的结论.23.（10分）已知：如图，在等边三角形ABC 的AC 边上取中点D ，BC 的延长线上取一点E ，使 CE ＝CD ．求证：BD ＝DE .24.（10分）已知：如图，ABC ∆中，AC AB =，120=∠A .(1)用直尺和圆规作AB 的垂直平分线，分别交BC 、AB 于点M 、N (保留作图痕迹，不写作法).(2)猜想CM 与BM 之间有何数量关系，并证明你的猜想.A B CO A B C25. （本题满分12分）阅读下面的题目及分析过程，并按要求进行证明．已知：如图，E 是BC 的中点，点A 在DE 上，且CDE BAE ∠=∠．求证：CD AB =. 分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等．因此，要证CD AB =，必须添加适当的辅助线，构造全等三角形或等腰三角形．现给出如下三种添加辅助线的方法，请任意选择其中一种，对原题进行证明．AB C DE F A B C D E EF =DE （3） F G A B C D E （1） AB C D E CF ∥AB （2） F26．（12分）已知：如图，点C 为线段AB 上一点，ACM ∆、CBN ∆是等边三角形，可以说明：ACN ∆≌MCB ∆，从而得到结论：BM AN =．现要求：（1）将ACM ∆绕C 点按逆时针方向旋转180°，使A 点落在CB 上．请对照原题图在下图中画出符合要求的图形（不写作法，保留作图痕迹）．（2）在（1）所得到的图形中，结论“BM AN =”是否还成立？若成立，请给予证明；若不成立，请说明理由．（3）在（1）所得到的图形中，设MA 的延长线与BN 相交于D 点，请你判断△ABD 与四边形MDNC 的形状，并说明你的结论的正确性．A BC MNB CN参考答案一、DAABCDDCBD二、11.PC PB PA ==； 12. 80或 20； 13. 75； 14.7； 15.乙；16.三角形的三个内角都小于 60，三角形的内角和是 180；17.大于DE 21的长为半径；18. 320；19.10；20. 10.三、21由A ∠= 90=∠D ，BD AC =，BC BC =知BAC ∆≌CDB ∆，因此有DC AB =.又DOC AOB ∠=∠（对顶角），A ∠= 90=∠D ，所以BAC ∆≌CDB ∆，所以OD AO =.又BD AC =，所以BO BD AO AC -=-，即OC OB =.22.∵ ∠OBC =∠OCB ，∴ OB =OC .又∵ ∠AOB =∠AOC ，OA =OA ， ∴ △AOB ≌△AOC ，∴AB =AC .23. BD 是正三角形ABC 的AC 边的中线得AC BD ⊥，BD 平分ABC ∠， 30=∠DBE .由CE CD =知∠CDE ＝∠E .由∠ACE ＝ 120°，得∠CDE ＋∠E ＝60°，所以∠CDE ＝∠E ＝300，则有BD ＝ DE ．24.（1）作图略；（2）连接AM ，则BM =AM .∵ AB =AC ，∠BAC =120°，∴ ∠B =∠C =30°于是 ∠MAB =∠B =30°，∠MAC =90°.∴ .21CM AM =故CM BM 21=，即CM =2BM .25.方法一：作BF ⊥DE 于点F ，CG ⊥DE 于点G . ∴ ∠F =∠CGE =90°.又∵ ∠BEF =∠CEG ，BE =CE ，∴ △BFE ≌△CGE .∴ BF =CG .在△ABF 和△DCG 中，∵ ∠F =∠DGC =90°，∠BAE =∠CDE ，BF =CG ，∴ △ABF ≌△DCG .∴ AB =CD .方法二：作CF ∥AB ，交DE 的延长线于点F .∴ ∠F =∠BAE .又∵ ∠ABE =∠D ，∴ ∠F =∠D .∴ CF =CD .∵ ∠F =∠BAE ，∠AEB =∠FEC ，BE =C E ，∴ △ABE ≌△FCE .∴ AB =CF . ∴ AB =CD .方法三：延长DE 至点F ，使EF =DE .又∵ BE =CE ，∠BEF =∠CED ，∴ △BEF ≌△CED . ∴ B F=CD ，∠D =∠F . 又∵ ∠BAE =∠D ，∴ ∠BAE =∠F . ∴ AB =BF .∴ AB =CD .26.（1）作图略.（2）结论“AN =BM ”还成立.证明：∵ CN =CB ，∠ACN =∠MCB =60°，CA =CM ，∴ △ACN ≌△MCB .∴ AN =BM .（3）△ABD 是等边三角形，四边形MDNC 是平行四边形.证明： ∵ ∠DAB =∠MAC =60°，∠DBA =60°∴ ∠ADB =60°.∴ △ABD 是等边三角形.∵ ∠ADB =∠AMC =60°，∴ ND ∥CM .∵ ∠ADB =∠BNC =60°，∴ MD ∥CN .∴ 四边形MDNC 是平行四边形.。

北师大版九年级数学上册第一章测试题及答案证明(二)(B).doc

北师大版数学九年级上册课本答案

第一章特殊的平行四边形 复习测试 2021-2022学年北师大版九年级数学上册(word含答案)

北师大版九年级数学上册-第一章-特殊的平行四边形-单元测试题(有答案)

北师大版九年级数学上册第一章同步测试题及答案

北师大版九年级数学上册第一章特殊的平行四边形综合练习题（含答案,教师版）

2020秋北师大版九年级数学上第一、二章检测题含答案

北师大版数学九年级上册课本答案.doc

北师大版九年级数学上册第一单元测试题含答案

北师大版九年级数学上册第一章特殊平行四边形单元测试卷-(含答案及解析)

北师大版九年级数学上册第一章特殊平行四边形单元综合测试题及答案

数学九年级上册第一单元测试题

北师大版数学九年级上册第一章特殊平行四边形单元检测(2)

北师大版九年级数学上册《第一章特殊平行四边形》单元测试卷(带答案)

北师大版九年级数学上册第一单元测试题含答案

九年级数学上册《第一章 矩形的性质与判定》同步练习题及答案(北师大版)

北师大版九年级数学上册第1章达标测试卷附答案

北师大版九年级数学上册__第一章__证明二__试题大全

北师大版九年级数学上册第一章证明(二)测试题及答案(B)

九年级数学上册第一单元测试题

北师大版九年级上册数学第一章测试题(附答案)

第一章特殊的平行四边形复习测试 2021-2022学年北师大版九年级数学上册(word含答案)

九年级数学上册《第一章矩形的性质与判定》同步练习题及答案(北师大版)

北师大版九年级数学上册第一章证明二__试题大全