江苏省淮安市2015届高三上学期期中模拟数学试卷Word版含答案
淮安市、宿迁市2014-2015学年度高三第一学期期中联考

淮安市、宿迁市2014-2015学年度高三第一学期期中联考物理试题一、单项选择题:本题共6小题,每小题3分共计18分,每小题只有一个选项符合题意。
1.物块A 置于倾角为30°的斜面上,用轻弹簧、细绳跨过定滑轮与物块B 相连,弹簧轴线与斜面平行,它们均处于静止状态,如图所示。
A 、B 重力分别为10N 和4N ,不计滑轮与细线间的摩擦,则A .弹簧对A 的拉力大小为6NB .弹簧对A 的拉力大小为10NC .斜面对A 的摩擦力大小为1ND .斜面对A 的摩擦力大小为6N2.地球赤道上的物体随地球自转的向心加速度为a ;假设月球绕地球作匀速圆周运动,轨道半径为r 1,向心加速度为a 1。
已知万有引力常量为G ,地球半径为R 。
下列说法中正确的是A .地球质量M =Gr a 211B .地球质量M =G aR 2C .地球赤道表面处重力加速度g = aD .加速度之比a a 1=221R r3.如图所示,半径为R 的均匀带正电薄球壳,壳内的电场强度处处为零,其球心位于坐标原点O , 一带正电的试探电荷靠近球壳表面处由静止释放沿坐标轴向右运动。
下列关于坐标轴上某点电势ϕ、试探电荷在该点的动能k E 与离球心距离x 的关系图线,可能正确的是4.如图甲所示,电源的电动势为E ,内阻为r ,R 为电阻箱,○A 为理想电流表。
图乙为电源的输出功率P 与电流表示数I 的关系图象,其中功率P 0分别对应电流I 1、I 2,外电阻R 1、R 2。
下列说法中正确的是A .12EI I r +>B .12EI I r+=C .12R r r R >D .12R rr R <甲乙P 30°A B C D5.如图所示,质量均为m 的A 、B 两物块置于水平地面上,物块与地面间的动摩擦因数均为μ,物块间用一水平轻绳相连,绳中无拉力。
现用水平力F 向右拉物块A ,假设最大静摩擦力等于滑动摩擦力。
江苏省淮安市重点中学高三上学期10月联合质量检测 数学

江苏省淮安市重点中学2015届高三联合质量检测数学试卷考试时间:2014.10考生注意:1.本试卷包括填空题(第1题—第14题)、解答题(第15题—第20题),本试卷满分160分,考试时间120分钟。
2.答题前,请您务必将自己的姓名、班级、准考证号用0.5毫米黑色字迹的签字笔填写在答题卡的指定位置。
3.作答各题时,必须用书写黑色字迹的0.5毫米签字笔写在答题卡的指定位置,在其它位置作答一律无效.一、填空题:(本大题共14小题,每小题5分,共70分。
请将答案填入答题纸填空题的相应答题线上)1.命题“”的否定是 。
2.已知i 为虚数单位,若12(,)1i a bi a b R i+=+∈+,则a +b 的值是 。
3.为了调查城市PM2. 5的情况,按地域把48个城市分成大型、中型、小型三组,对应的城市数分别为8, 16, 24。
.若用分层抽样的方法抽取12个城市,则中型组中应抽取的城市数为 。
4.在大小相同的4个球中,红球2个,白球2个。
若从中任意选取2个球,则所选的2个球恰好不同色的概率是 。
5.若集合{{}2|,|2A x y B y y x ====+,则= 。
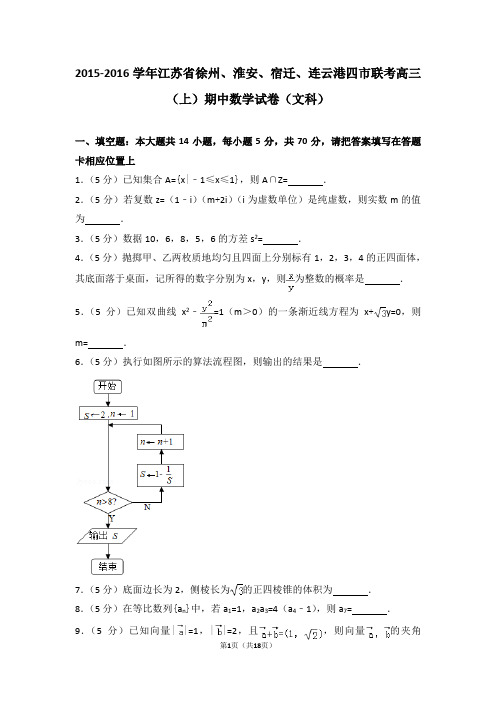
6.如图所示的流程图中,输出的结果是 。
7.若x >-3,则的最小值为 。
8.已知函数()2sin()(0)f x x ωϕω=+>的部分图象如图所示,则 。
9.已知双曲线 (a>0,b>0)的焦点到一条渐近线的距离等于实轴长,那么该双曲线的离心率为 。
10.数列{}的前n 项和为,且,则{}的通项公式= 。
11.在直角三角形ABC 中,ABAC, AB = AC=1,,则的值等于 。
12.直线的倾斜角为,则的值为 。
13.己知是定义在R 上的奇函数.,且当x0时,,则此函数的值域为 。
14.图为函数的图象,其在点M(t, f (t))处的切线为l ,切线l 与Y 轴和直线y=1分别交于点P, Q ,点N (0,1) ,若△PQN 的面积为b 时的点M 恰好有两个,则b 的取值范围为 。
2015-2016学年江苏省徐州、淮安、宿迁、连云港四市联考高三(上)期中数学试卷和答案(文科)
2015-2016学年江苏省徐州、淮安、宿迁、连云港四市联考高三(上)期中数学试卷(文科)一、填空题:本大题共14小题,每小题5分,共70分,请把答案填写在答题卡相应位置上1.(5分)已知集合A={x|﹣1≤x≤1},则A∩Z=.2.(5分)若复数z=(1﹣i)(m+2i)(i为虚数单位)是纯虚数,则实数m的值为.3.(5分)数据10,6,8,5,6的方差s2=.4.(5分)抛掷甲、乙两枚质地均匀且四面上分别标有1,2,3,4的正四面体,其底面落于桌面,记所得的数字分别为x,y,则为整数的概率是.5.(5分)已知双曲线x2﹣=1(m>0)的一条渐近线方程为x+y=0,则m=.6.(5分)执行如图所示的算法流程图,则输出的结果是.7.(5分)底面边长为2,侧棱长为的正四棱锥的体积为.8.(5分)在等比数列{a n}中,若a1=1,a2a3=4(a4﹣1),则a7=.9.(5分)已知向量||=1,||=2,且,则向量的夹角为.10.(5分)直线ax+y+1=0被圆x2+y2﹣2ax+a=0截得的弦长为2,则实数a的值是.11.(5分)已知函数f(x)=﹣x2+2x.则不等式f(log2x)<f(2)的解集为.12.(5分)将函数y=sin2x的图象向左平移φ(φ>0)个单位,若所得的图象过点(,),则φ的最小值为.13.(5分)在△ABC中,AB=2,AC=3,∠A的平分线于AB边上的中线交于点O,若=x+y(x,y∈R),则x+y的值为.14.(5分)已知函数f(x)=e x﹣1+x﹣2(e为自然对数的底数).g(x)=x2﹣ax ﹣a+3.若存在实数x1,x2,使得f(x1)=g(x2)=0.且|x1﹣x2|≤1,则实数a 的取值范围是.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或计算步骤15.(14分)在锐角ABC中,角A、B、C所对的边分别为a,b,c,b=4,c=6,且asinB=2.(1)求角A的大小;(2)若D为BC的中点,求线段AD的长.16.(14分)如图,在四棱锥P﹣ABCD中,AB∥CD,AC⊥BD,AC与BD交于点O,且平面PAC⊥底面ABCD,E为棱PA上一点.(1)求证:BD⊥OE;(2)若AB=2CD,AE=2EP,求证:EO∥平面PBC.17.(14分)已知数列{a n}满足2a n+1=a n+a n+2+k(n∈N*,k∈R),且a1=2,a3+a5=﹣4.(1)若k=0,求数列{a n}的前n项和S n;(2)若a4=﹣1,求数列{a n}的通项公式a n.18.(16分)如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠AC B=θ.(1)若a=1.5,问:观察者离墙多远时,视角θ最大?(2)若tanθ=,当a变化时,求x的取值范围.19.(16分)如图,椭圆C:+=1(a>b>0)的上、下顶点分别为A,B,右焦点为F,点P在椭圆C上,且OP⊥AF.(1)若点P坐标为(,1),求椭圆C的方程;(2)延长AF交椭圆C于点Q,若直线OP的斜率是直线BQ的斜率的2倍,求椭圆C的离心率;(3)求证:存在椭圆C,使直线AF平分线段OP.20.(16分)已知函数f(x)=cosx+ax2﹣1,a∈R.(1)求证:函数f(x)是偶函数;(2)当a=1时,求函数f(x)在[﹣π,π]上的最大值及最小值;(3)若对于任意的实数x恒有f(x)≥0,求实数a的取值范围.2015-2016学年江苏省徐州、淮安、宿迁、连云港四市联考高三(上)期中数学试卷(文科)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分,请把答案填写在答题卡相应位置上1.(5分)已知集合A={x|﹣1≤x≤1},则A∩Z={﹣1,0,1} .【解答】解:∵集合A={x|﹣1≤x≤1},则A∩Z={﹣1,0,1},故答案为:{﹣1,0,1}.2.(5分)若复数z=(1﹣i)(m+2i)(i为虚数单位)是纯虚数,则实数m的值为﹣2.【解答】解:∵复数z=(1﹣i)(m+2i)=m+2+(2﹣m)i是纯虚数,∴,解得m=﹣2.故答案为:﹣2.3.(5分)数据10,6,8,5,6的方差s2=.【解答】解:这组数据的平均数为(10+6+8+5+6)÷5=7方差S2=[(10﹣7)2+(6﹣7)2+(8﹣7)2+(5﹣7)2+(6﹣7)2]=,故答案为:.4.(5分)抛掷甲、乙两枚质地均匀且四面上分别标有1,2,3,4的正四面体,其底面落于桌面,记所得的数字分别为x,y,则为整数的概率是.【解答】解:由题意知本题是一个古典概型,∵试验发生包含的事件是抛掷甲、乙两枚质地均匀的正四面体,记所得的数字分别为x,y,共有4×4=16种结果,满足条件的事件是为整数,包括当y=1时,有4种结果,当y=2时,有2种结果,当y=3时,有1种结果,当y=4时,有1种结果,共有4+2+1+1=8种结果,∴根据古典概型概率公式得到P==,故答案为:5.(5分)已知双曲线x2﹣=1(m>0)的一条渐近线方程为x+y=0,则m=.【解答】解:∵双曲线x2﹣=1(m>0)的一条渐近线方程为x+y=0,∴m=,故答案为:.6.(5分)执行如图所示的算法流程图,则输出的结果是﹣1.【解答】解:当n=1时,不满足退出循环的条件:S=,n=2;当n=2时,不满足退出循环的条件:S=﹣1,n=3;当n=3时,不满足退出循环的条件:S=2,n=4;当n=4时,不满足退出循环的条件:S=,n=5;当n=5时,不满足退出循环的条件:S=﹣1,n=6;当n=6时,不满足退出循环的条件:S=2,n=7;当n=7时,不满足退出循环的条件:S=,n=8;当n=8时,不满足退出循环的条件:S=﹣1,n=9;当n=9时,满足退出循环的条件,故输出的S值为:﹣1,故答案为:﹣17.(5分)底面边长为2,侧棱长为的正四棱锥的体积为.【解答】解:取底面中心O,过O作OE⊥AB,垂足为E,连接SO,AO,∵四棱锥S﹣ABCD为正四棱锥,∴SO⊥平面ABCD,∵AO⊂平面ABCD,∴SO⊥AO.∵四边形ABCD是边长为2的正方形,∴AE=AB=1,∠OAE=∠BAD=45°,∴OE=AE=1,∵OE2+AE2=AO2,∴AO=,∵SA=,∴SO==1.V=•S ABCD•SO=•22•1=.故答案为.8.(5分)在等比数列{a n}中,若a1=1,a2a3=4(a4﹣1),则a7=.【解答】解:设等比数列{a n}中,∵a1=1,a2a3=4(a4﹣1),∴q3=4(q3﹣1),解得q3=.则a7==.故答案为:.9.(5分)已知向量||=1,||=2,且,则向量的夹角为.【解答】解:+=(1,),可得|+|=,即有2+2+2•=3,即为1+4+2•=3,即有•=﹣1,则cos<,>==﹣,由0≤<,>≤π,可得<,>=.故答案为:.10.(5分)直线ax+y+1=0被圆x2+y2﹣2ax+a=0截得的弦长为2,则实数a的值是﹣2.【解答】解:圆x2+y2﹣2ax+a=0可化为(x﹣a)2+y2=a2﹣a∴圆心为:(a,0),半径为:圆心到直线的距离为:d==.∵直线ax+y+1=0被圆x2+y2﹣2ax+a=0截得的弦长为2,∴a2+1+1=a2﹣a,∴a=﹣2.故答案为:﹣2.11.(5分)已知函数f(x)=﹣x2+2x.则不等式f(log2x)<f(2)的解集为(4,+∞)∪(0,1).【解答】解:函数f(x)=﹣x2+2x=﹣(x﹣1)2+1 的图象关于直线x=1对称,且开口向下,则由不等式f(log2x)<f(2),可得|2﹣1|<|log2x﹣1|,即|log2x﹣1|>1,得log2x﹣1>1,或log2x﹣1<﹣1.解得x>4,或0<x<1,故答案为:(4,+∞)∪(0,1).12.(5分)将函数y=sin2x的图象向左平移φ(φ>0)个单位,若所得的图象过点(,),则φ的最小值为.【解答】解:函数y=sin2x的图象向左平移φ(φ>0)个单位,若所得的图象对应的函数解析式为y=sin2(x+φ),再根据所得函数的图象过点(,),可得sin2(+φ)=,则φ的最小值满足2φ+=,求得φ的最小值为,故答案为:.13.(5分)在△ABC中,AB=2,AC=3,∠A的平分线于AB边上的中线交于点O,若=x+y(x,y∈R),则x+y的值为.【解答】解:如图,设AB中点D;∵AO在∠BAC的平分线上,AB=2,AC=3;∴存在k,使;∵D,O,C三点共线,D是AB中点;∴=;∴由平面向量基本定理得;解得;∴;又;∴.故答案为:.14.(5分)已知函数f(x)=e x﹣1+x﹣2(e为自然对数的底数).g(x)=x2﹣ax ﹣a+3.若存在实数x1,x2,使得f(x1)=g(x2)=0.且|x1﹣x2|≤1,则实数a 的取值范围是[2,3] .【解答】解:函数f(x)=e x﹣1+x﹣2的导数为f′(x)=e x﹣1+1>0,f(x)在R上递增,由f(1)=0,可得f(x1)=0,解得x1=1,存在实数x1,x2,使得f(x1)=g(x2)=0.且|x1﹣x2|≤1,即为g(x2)=0且|1﹣x2|≤1,即x2﹣ax﹣a+3=0在0≤x≤2有解,即有a==(x+1)+﹣2在0≤x≤2有解,令t=x+1(1≤t≤3),则t+﹣2在[1,2]递减,[2,3]递增,可得最小值为2,最大值为3,则a的取值范围是[2,3].故答案为:[2,3].二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或计算步骤15.(14分)在锐角ABC中,角A、B、C所对的边分别为a,b,c,b=4,c=6,且asinB=2.(1)求角A的大小;(2)若D为BC的中点,求线段AD的长.【解答】解:(1)根据正弦定理得,,所以,asinB=bsinA=2,因为,b=4,所以,sinA=,且三角形为锐角三角形,所以,A=;(2)由(1)得,cosA=,根据余弦定理,a2=b2+c2﹣2bccosA,所以,a2=42+62﹣2×4×6×=28,解得a=2,因为D为BC的中点,则AD为BC边的中线,因此,根据三角形中线长公式:|AD|=m a==,即线段AD的长度为.16.(14分)如图,在四棱锥P﹣ABCD中,AB∥CD,AC⊥BD,AC与BD交于点O,且平面PAC⊥底面ABCD,E为棱PA上一点.(1)求证:BD⊥OE;(2)若AB=2CD,AE=2EP,求证:EO∥平面PBC.【解答】(1)证明:在四棱锥P﹣ABCD中,∵AC⊥BD,且平面PAC⊥底面ABCD,BD∩AC=O,∴BD⊥平面PAC,∵OE⊂平面PAC,∴BD⊥OE.(2)证明:∵AB=2CD,AE=2EP,∴=2,∵AB∥CD,AC与BD交于点O,∴△AOB∽△COD,∴,∴,∴OE∥PC,∵EO⊄平面PBC,PC⊂平面PBC,∴EO∥平面PBC.17.(14分)已知数列{a n}满足2a n+1=a n+a n+2+k(n∈N*,k∈R),且a1=2,a3+a5=﹣4.(1)若k=0,求数列{a n}的前n项和S n;(2)若a4=﹣1,求数列{a n}的通项公式a n.【解答】解:(1)若k=0,则数列{a n}满足2a n+1=a n+a n+2(n∈N*,k∈R),∴数列{a n}是等差数列,设公差为d,∵a1=2,a3+a5=﹣4.∴2×2+6d=﹣4,解得d=.∴S n=2n×=.(2)2a n+1=a n+a n+2+k(n∈N*,k∈R),a3+a5=﹣4,a4=﹣1,则2a4=a3+a5+k,﹣2=﹣4+k,解得k=2.数列{a n}满足2a n+1=a n+a n+2+2,当n≥2时,2a n=a n﹣1+a n+1+2,相减可得:2(a n+1﹣a n)=(a n﹣a n﹣1)+(a n+2﹣a n+1),令b n=a n+1﹣a n,则2b n=b n﹣1+b n+1.∴数列{b n}是等差数列,公差=b4﹣b3=(a5﹣a4)﹣(a4﹣a3)=﹣2.首项为b1=a2﹣a1,b2=a3﹣a2,b3=a4﹣a3,由2b2=b1+b3,可得2(a3﹣a2)=a2﹣2﹣1﹣a3,解得3(a3﹣a2)=﹣3,b2=a3﹣a2=﹣1.∴b n=b2+(n﹣2)(﹣2)=﹣2n+3.∴a n﹣a n=﹣2n+3.+1∴a n=(a n﹣a n﹣1)+(a n﹣1﹣a n﹣2)+…+(a2﹣a1)+a1=[﹣2(n﹣1)+3]+[﹣2(n﹣2)+3]+…+(﹣2+3)+2=+2=﹣n2+4n﹣1.18.(16分)如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.(1)若a=1.5,问:观察者离墙多远时,视角θ最大?(2)若tanθ=,当a变化时,求x的取值范围.【解答】解:(1)如图,作CD⊥AF于D,则CD=EF,设∠A CD=α,∠BCD=β,CD=x,则θ=α﹣β,在Rt△ACD和Rt△BCD中,tanα=,tanβ=,则tanθ=tan(α﹣β)==(x>0),令u=,则ux2﹣2x+1.25u=0,∵上述方程有大于0的实数根,∴△≥0,即4﹣4×1.25u2≥0,∴u≤,即(tanθ)max=,∵正切函数y=tanx在(0,)上是增函数,∴视角θ同时取得最大值,此时,x==,∴观察者离墙米远时,视角θ最大;(2)由(1)可知,tanθ===,即x2﹣4x+4=﹣a2+6a﹣4,∴(x﹣2)2=﹣(a﹣3)2+5,∵1≤a≤2,∴1≤(x﹣2)2≤4,化简得:0≤x≤1或3≤x≤4,又∵x>1,∴3≤x≤4.19.(16分)如图,椭圆C:+=1(a>b>0)的上、下顶点分别为A,B,右焦点为F,点P在椭圆C上,且OP⊥AF.(1)若点P坐标为(,1),求椭圆C的方程;(2)延长AF交椭圆C于点Q,若直线OP的斜率是直线BQ的斜率的2倍,求椭圆C的离心率;(3)求证:存在椭圆C,使直线AF平分线段OP.【解答】解:(1)由题意可知,A(0,b),F(c,0),所以,k AF=﹣,再由P(,1),OP⊥AF,所以,k OP•k AF=﹣1,k OP=得k AF=﹣,即=,联立方程,解得a2=,b2=,所以,椭圆的方程为;(2)由题意知,直线AF:即y=﹣x+b,联立椭圆方程,解得Q(,+b),由OP⊥AF得k OP=,而k BQ=k OP=,即=,解得a2=2b2,故e=;(3)假设存在椭圆C使得直线AF平分线段OP,则线段OP的中点必在直线AF 上,因此,直线AF与椭圆C必有两个不同的交点(其中一个交点为A,另一个为交点Q),只需证明存在这样的点Q使得其纵坐标y Q≥﹣b即可,不妨设P(x,y),则OP的中点为M(,),将M代入直线AF的方程得,再联立方程消去x并化简得,(c2+1)y2﹣4bc2y+4b2c2﹣b2=0,△=16b2c4﹣4(c2+1)(4b2c2﹣b2)>0,解得c2<,而y1+y2=,其中y1=b,则y2=•b=(3﹣)b∈(﹣b,0),即证.20.(16分)已知函数f(x)=cosx+ax2﹣1,a∈R.(1)求证:函数f(x)是偶函数;(2)当a=1时,求函数f(x)在[﹣π,π]上的最大值及最小值;(3)若对于任意的实数x恒有f(x)≥0,求实数a的取值范围.【解答】解:(1)证明:函数f(x)=cosx+ax2﹣1,定义域为R,f(﹣x)=cos(﹣x)+a(﹣x)2﹣1=cosx+ax2﹣1=f(x),则f(x)为偶函数;(2)当a=1时,函数f(x)在[﹣π,π]上的最大值及最小值,即为f(x)在[0,π]上的最大值及最小值,此时f(x)=cosx+x2﹣1,导数为f′(x)=2x﹣sinx,0≤x≤π,令g(x)=2x﹣sinx,导数为2﹣cosx>0,即g(x)递增,即有g(x)≥g(0)=0,则f′(x)≥0,即f(x)在[0,π]递增,x=0时,取得最小值0,x=π时,取得最大值π2﹣2,则有函数f(x)在[﹣π,π]上的最大值π2﹣2,最小值为0;(3)对于任意的实数x恒有f(x)≥0,即有cosx+ax2﹣1≥0,即ax2≥1﹣cosx≥0,显然a≥0,x=0时,显然成立;由偶函数的性质,只要考虑x>0的情况.当x>0时,a≥=,即为2a≥()2,由x>0,则=t>0,考虑sint﹣t的导数为cost﹣1≤0,即sint﹣t递减,即有sint﹣t<0,即sint<t,则有<1,故()2<1,即有2a≥1,解得a≥.则实数a的取值范围为[,+∞).。
江苏省淮安市淮海中学2015届高三10月月考 数学试卷

淮安市淮海中学2015届高三月考数 学 试 题 2014.10一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题纸上.1.若集合}2,1{-=m A ,且{2}A B =I ,则实数m 的值为 ▲ .2.已知i 为虚数单位,若12(,)1ia bi ab R i+=+∈+,则a b +的值是 ▲ . 3.某校高一、高二、高三分别有学生1600名、1200名、800名,为了解该校高中学生的牙齿健康状况,按各年级的学生数进行分层抽样,若高三抽取20名学生,则高一、高二共抽取的学生数为 ▲ .4.从1,2,3,4,5这5个数中一次随机地取2个数,则所取2个数的和为5的概率是 ▲ .5. 右图是一个算法的流程图,最后输出的k = ▲ .6.已知1sin 3θ=-,则cos(2)πθ+的值等于 ▲ .7. 已知公差不为0的等差数列{}n a 的前n 项和为n S ,且523a a =,若65S a λ=,则λ= ▲ .8.如图,在棱长为2的正方体ABCD —A 1B 1C 1D 1中,E ,F分别是棱AB ,BC 中点,则三棱锥A 1—B 1EF 的体积为 ▲ .9. 在直角三角形ABC 中,1,1,2AB AC AB AC BD DC ⊥===,则AD CD ⋅uuu r uu u r的值等于___▲_____.10.直线1y kx =+与圆22(3)(2)9x y -+-=相交于A B 、两点,若4AB >,则k 的取值范围是 ___▲_____.11.已知f (x )是定义在R 上的奇函数,当x ≥0时,f (x )=x 2+2x ,若f (2-a 2)>f (a ),则实数a 的取值范围是___▲_____.12.已知数列{}n a 的通项公式为n c a n n=+,若对任意*n N ∈,都有3n a a ≥,则实数c 的取值范围是___▲_____ .13.已知函数,1,log 31,3)(3⎩⎨⎧≥-<=x x x x f x 若方程|f(x)|=a 有三个零点,则实数a 的取值范围是▲ .(第5题)EADCFP 14.若ABC ∆的内角A 、B ,满足sin 2cos()sin BA B A=+,则tan B 的最大值为 ▲ . 二、解答题:本大题共6小题,共计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题卡的指定区域内.15.(本小题满分14分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若4b =,8BA BC ⋅=. (1)求22a c +的值;(2)求函数2()cos cos f B B B B +的值域. 16.(本小题满分14分)如图,在三棱锥P —ABC 中,平面P AC ⊥平面ABC ,60BAC ∠=,E ,F 分别是AP ,AC 的中点,点D 在棱AB 上,且AD AC =.求证:(1)//EF 平面PBC ;(2)平面DEF ⊥平面P AC .17、(本小题满分14分)某园林公司计划在一块以O 为圆心,R (R 为常数,单位为米)为半径的半圆形地上种植花草树木,其中阴影部分区域为观赏样板地,△OCD 区域用于种植花木出售,其余区域用于种植草皮出售.如图所示.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.(1)设∠COD =θ(单位:弧度),用θ表示阴影部分的面积 S 阴影=f (θ);(2)园林公司应该怎样规划这块土地,才能使总利润最大?并求相对应的θ.18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆22221(0)y x a b a b+=>> 的离心率为12,过椭圆右焦点F 作两条互相垂直的弦AB 与CD .当直线AB 斜率为0时,7AB CD +=. (1)求椭圆的方程;(2)求AB CD +的取值范围.19.(本题满分16分)(第18题)已知等比数列{}n a 的公比1q >,前n 项和为3123,7,3,3,4n S S a a a =++成等差数列,数列{}n b 的前n 项和为,6(31)2n n n T T n b =++,其中*n N ∈。
淮安市2015—2016学年度高三年级信息卷数学试卷
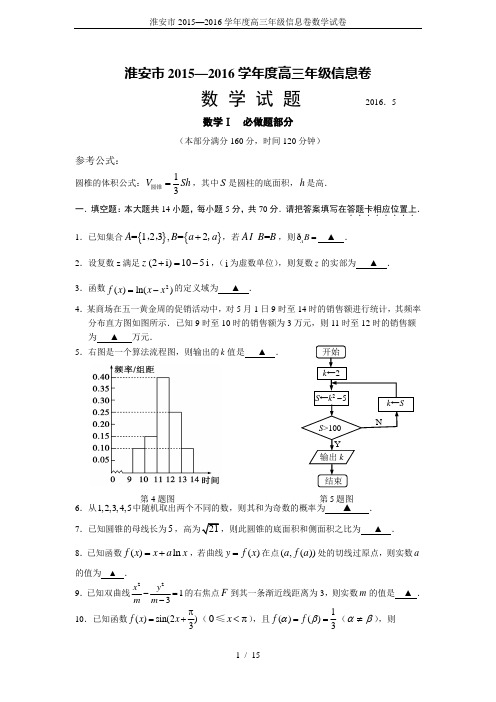
第4题图第5题图淮安市2015—2016学年度高三年级信息卷数 学 试 题 2016.5数学Ⅰ 必做题部分(本部分满分160分,时间120分钟)参考公式:圆椎的体积公式:13V Sh =圆锥,其中S 是圆柱的底面积,h 是高. 一.填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡...相应位置....上.. 1.已知集合{}{}=123,=2A B a a +,,,,若=AB B ,则A B =ð ▲ .2.设复数z 满足(2i)105i z +=-,(i 为虚数单位),则复数z 的实部为 ▲ . 3.函数2()ln()f x x x =-的定义域为 ▲ .4.某商场在五一黄金周的促销活动中,对5月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额 为 ▲ 万元.5.右图是一个算法流程图,则输出的k值是 ▲ .6.从1,2,3,4,5中随机取出两个不同的数,则其和为奇数的概率为 ▲ . 7.已知圆锥的母线长为5,则此圆锥的底面积和侧面积之比为 ▲ . 8.已知函数()ln f x x a x =+,若曲线()y f x =在点(,())a f a 处的切线过原点,则实数a的值为 ▲ .9.已知双曲线2213x y m m -=-的右焦点F 到其一条渐近线距离为3,则实数m 的值是 ▲ .10.已知函数()sin(2)3f x x π=+(0x <π≤),且1()()3f f αβ==(βα≠),则DP第14题图=+βα ▲ .11.设,x y 满足约束条件0,0,210,x x y x y ⎧⎪-⎨⎪-+⎩≤≤≥则目标函数z xy =的取值范围为 ▲ .12.已知等差数列{}n a 的首项为a ,公差为4-,其前n 项和为n S .若存在m N +∈,使得36m S =,则实数a 的最小值为 ▲ .13.在区间(,]t -∞上存在x ,使得不等式240x x t -+≤成立,则实数t 的取值范围是 ▲ . 14.如图,在等腰梯形ABCD 中,2AB =,4CD =,BC = 点E ,F 分别为AD ,BC 的中点.如果对于常数λ,在A B C D 的四条边上,有且只有8个不同的点P 使得λ=⋅成 立,那么实数λ的取值范围为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分) 已知()()()cos ,sin ,3,1,0,m n ααα==-∈π.(1)若m n ⊥,求角α的值; (2)求||m n +的最小值.在三棱锥P -ABC 中,D 为AB 的中点.(1)若与BC 平行的平面PDE 交AC 于点E ,求证:点E 为AC 的中点;(2)若P A =PB ,且△PCD 为锐角三角形,又平面PCD ⊥平面ABC ,求证:AB ⊥PC .17.(本小题满分14分)某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,,A B 两点为喷泉,圆心O 为AB 的中点,其中OA OB a ==米,半径10OC =米,市民可位于水池边缘任意一点C 处观赏.(1)若当3OBC 2π∠=时,sin 3BCO 1∠=,求此时a(2)设22y CA CB =+,且22232CA CB +≤.(i )试将y 表示为a 的函数,并求出a 的取值范围;(ii )若同时要求市民在水池边缘任意一点C 观赏角度ACB ∠的最大值不小于6π,试求,A B 两处喷泉间距离的最小值.第17题图 第16题图已知椭圆C :22221x y a b+=(0a b >>)的离心率为2,椭圆C 与y 轴交于,A B 两点,且2AB =. (1)求椭圆C 的方程;(2)设点P 是椭圆C 上的一个动点,且点P 在y 轴的右侧,直线,PA PB 与直线4x =交于,M N 两点,若以MN 为直径的圆与x 轴交于,E F ,求点P 横坐标的取值范围及EF 的最大值.19.(本小题满分16分)已知数列{}n a ,其前n 项和为n S .(1)若{}n a 是公差为d )0(>d 的等差数列,且也是公差为d 的等差数列,求数列{}n a 的通项公式;(2)若数列{}n a 对任意m n ∈*N ,,且m n ≠,都有2m n mnm n S a a a a m n m n+-=+++-,求证: 数列{}n a 是等差数列.20.(本小题满分16分)已知函数2()e x ax f x =,直线1ey x =为曲线()y f x =的切线.e 为自然对数的底数.(1)求实数a 的值;(2)用min{,}m n 表示,m n 中的最小值,设函数1()min{(),}(0)g x f x x x x=->,若函数2()()h x g x cx =-为增函数,求实数c 的取值范围.第21A 图淮安市2015—2016学年度高三年级信息卷数 学 试 题 2016.5数学Ⅱ 附加题部分21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两小题,并在相应的答题区域内作....................答.,若多做,则按作答的前两小题评分。
徐州、淮安、宿迁、连云港四市2015届高三第一次模拟考试数学试卷(纯word)

徐州、淮安、宿迁、连云港四市2015届高三第一次模拟考试数学试卷一、填空题:本大题共14小题,每小题5分,共计70分.不需写出解题过程,请把答案直接填写在答题卡相应位置上,1.己知集合{}{}0,1,2,3,2,3,4,5A B ==,则 AB 中元素的个数为_______.2.设复数z 满足 (4)32i z i -=+(i 是虚数单位),则z 的虚部为_______. 3.如图,茎叶图记录了甲、乙两组各3名同学在期末考试中的数学成绩, 则方差较小的那组同学成绩的方差为_______.4.某用人单位从甲、乙、丙、丁4名应聘者中招聘2人,若每名应聘者被录用的机会均等,则甲、乙2人中至少有1入被录用的概率为_______. 5.如图是一个算法的流程图,若输入x 的值为2,则输出y 的值为_____. 6. 已知圆锥的轴截面是边长为2的正三角形,则该圆锥的体积为 ______. 7. 已知 ()f x 是定义在R 上的奇函数,当 0x <时,2()log (2)f x x =-, 则(0)(2)f f +的值为_____.8. 在等差数列{}n a 中,已知2811a a +=,则3113a a +的值为______. 9. 若实数,x y 满足40x y +-≥,则226210z x y x y =++-+的最小值为_____.10. 已知椭圆22221(0)x y a b a b+=>>,点12,,,A B B F 依次为其左顶点、下顶点、上顶点和右焦点,若直线 2AB 与直线 1B F 的交点恰在椭圆的右准线上,则椭圆的离心率为______. 11.将函数2sin()(0)4y x πωω=->的图象分别向左、向右各平移4π个单位长度后,所得的两个图象对称轴重合,则ω的最小值为______.12.己知a ,b 为正数,且直线 60ax by +-=与直线 2(3)50x b y +-+=互相平行,则2a +3b 的最小值为________.13.已知函数 22,0,()2,0x x f x x x x +⎧-≥⎪=⎨<⎪⎩,则不等式 (())3f f x ≤的解集为______.14.在△ABC 中,己知 3,45AC A =∠=,点D 满足 2CD BD =,且 AD =则BC 的长为_______ .二、解答题:本大题共6小题.15~17每小题14分,18~20每小题16分,共计90分.请在答题卡指定的区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分) 己知向量(1,2sin ),(sin(),1)3a b πθθ==+,R θ∈.(1)若a b ⊥,求tan θ的值: (2)若//a b ,且(0,)2πθ∈,求θ的值.16.(本小题满分14分)如图,在三棱锥P - ABC 中,已知平面PBC ⊥平面ABC . (1)若AB ⊥BC ,CD ⊥PB ,求证:CP ⊥P A :(2)若过点A 作直线l 上平面ABC ,求证:l //平面PBC .17.(本小题满分14分)在平面直角坐标系xOy 中,己知点(3,4),(9,0)A B -,C ,D 分别为线段OA ,OB 上的动点,且满足AC =BD .(1)若AC =4,求直线CD 的方程;(2)证明:∆OCD 的外接圈恒过定点(异于原点O ).18.(本小题满分16分)如图,有一个长方形地块ABCD ,边AB 为2km ,AD 为4 km.,地块的一角是湿地(图中阴影部分),其边缘线AC 是以直线AD 为对称轴,以A 为顶点的抛物线的一部分.现要铺设一条过边缘线AC 上一点P 的直线型隔离带EF ,E ,F 分别在边AB ,BC 上(隔离带不能穿越湿地,且占地面积忽略不计).设点P 到边AD 的距离为t (单位:km),△BEF 的面积为S (单位: 2km ).(I)求S 关于t 的函数解析式,并指出该函数的定义域;(2)是否存在点P ,使隔离出的△BEF 面积S 超过32km ?并说明理由.19.(本小题满分16分)在数列{}n a 中,已知12211,2,n n n a a a a a n N λ*++==+=+∈,λ为常数.(1)证明: 14,5,a a a 成等差数列; (2)设22n na a n c +-=,求数列 的前n 项和 n S ;(3)当0λ≠时,数列 {}1n a -中是否存在三项1111,1,1s t p a a a +++---成等比数列,且,,s t p 也成等比数列?若存在,求出,,s t p 的值;若不存在,说明理由.20.(本小题满分16分)己知函数21()ln ,2f x x ax x a R =-+∈ (1)若(1)0f =,求函数 ()f x 的单调递减区间;(2)若关于x 的不等式()1f x ax ≤-恒成立,求整数 a 的最小值:(3)若 2a =-,正实数 12,x x 满足 1212()()0f x f x x x ++=,证明: 12x x +≥附加题部分21.【选做题】本题包括A, B, C, D 四小题,请选定其中两题,并在相应的答题区域内作答.解答时应写出文字说明、证明过程或演算步骤.A 选修4-1:几何证明选讲(本小题满分10分)如图,O 是△ABC 的外接圆,AB = AC ,延长BC 到点D ,使得CD = AC ,连结AD 交O 于点E .求证:BE 平分∠ABC .B.选修4-2:矩阵与变换(本小题满分10分)已知,a b R ∈,矩阵 1 3a A b -⎡⎤=⎢⎥⎣⎦所对应的变换A T 将直线 10x y --=变换为自身,求a ,b 的值。
2015年江苏省淮安市淮海中学高考一模数学试卷【解析版】

2015年江苏省淮安市淮海中学高考数学一模试卷一、填空题:本大题共14小题,每小题5分,共计70分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.1.(5分)若集合A={0,1,2,4},B={1,2,3},则A∩B=.2.(5分)复数(i为虚数单位)的实部等于.3.(5分)如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为.4.(5分)若双曲线的离心率为2,则a等于.5.(5分)抛掷一粒骰子,观察掷出的点数,设事件A为出现奇数,事件B为出现2点,已知P(A)=,P(B)=,则出现奇数点或2点的概率是.6.(5分)根据如图所示的伪代码,当输入a的值为3时,最后输出的S的值为.7.(5分)已知数列{a n}为等比数列,a4+a7=2,a5•a6=﹣8,则a1+a10的值为.8.(5分)已知sin(+θ)=,θ∈(0,π),则cos(﹣θ)=.9.(5分)已知函数f(x)=x2+abx+a+2b.若f(0)=4,则f(1)的最大值为.10.(5分)如图所示,已知三棱柱ABCA1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1ABC1的体积为.11.(5分)已知存在实数a,满足对任意的实数b,直线y=﹣x+b都不是曲线y =x3﹣3ax的切线,则实数a的取值范围是.12.(5分)如图,在△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且=+λ(λ∈R),则AD的长为.13.(5分)已知A(﹣2,0),B(2,0),点P在圆(x﹣3)2+(y﹣4)2=r2(r >0)上,满足P A2+PB2=40,若这样的点P有两个,则r的取值范围是.14.(5分)已知函数f(x)=,若f(f(x))=t有3个零点,则t的取值范围是.二、解答题:本大题共10小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知=,=(cos A,﹣2cos A),=﹣1.(1)求∠A的大小;(2)若,c=2,求△ABC的面积.16.(14分)如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,平面P AB⊥平面ABCD,P A⊥PB,BP=BC,E为PC的中点.(1)求证:AP∥平面BDE;(2)求证:BE⊥平面P AC.17.(14分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.(1)设∠PBO=α,把y表示成α的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?18.(16分)如图,椭圆C:经过点P(1,),离心率e =,直线l的方程为x=4.(1)求椭圆C的方程;(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记P A,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由.19.(16分)已知数列{a n}是等差数列,{b n}是等比数列,且满足a1+a2+a3=9,b1b2b3=27.(1)若a4=b3,b4﹣b3=m.①当m=18时,求数列{a n}和{b n}的通项公式;②若数列{b n}是唯一的,求m的值;(2)若a1+b1,a2+b2,a3+b3均为正整数,且成等比数列,求数列{a n}的公差d 的最大值.20.(16分)已知函数f(x)=x•lnx,g(x)=ax3﹣.(1)求f(x)的单调增区间和最小值;(2)若函数y=f(x)与函数y=g(x)在交点处存在公共切线,求实数a的值;(3)若x∈(0,e2]时,函数y=f(x)的图象恰好位于两条平行直线l1:y=kx;l2:y=kx+m之间,当l1与l2间的距离最小时,求实数m的值.21.(10分)(选修4﹣2:矩阵与变换)已知矩阵A=,若矩阵A属于特征值6的一个特征向量为=,属于特征值1的一个特征向量为=.求矩阵A,并写出A的逆矩阵.22.(10分)在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,求线段AB的最小值.23.(10分)如图,已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,AA1=AB=AC =1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足.(1)证明:PN⊥AM;(2)若平面PMN与平面ABC所成的角为45°,试确定点P的位置.24.(10分)已知数列{a n}满足:.(1)若a=﹣1,求数列{a n}的通项公式;(2)若a=3,试证明:对∀n∈N*,a n是4的倍数.2015年江苏省淮安市淮海中学高考数学一模试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共计70分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.1.(5分)若集合A={0,1,2,4},B={1,2,3},则A∩B={1,2}.【解答】解:∵A={0,1,2,4},B={1,2,3},则A∩B={0,1,2,4}∩{1,2,3}={1,2}.故答案为:{1,2}.2.(5分)复数(i为虚数单位)的实部等于﹣3.【解答】解:∵=.∴复数(i为虚数单位)的实部等于﹣3.故答案为:﹣3.3.(5分)如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为 6.8.【解答】解:∵根据茎叶图可知这组数据是8,9,10,13,15这组数据的平均数是=11∴这组数据的方差是[(8﹣11)2+(9﹣11)2+(10﹣11)2+(13﹣11)2+(15﹣11)2]=[9+4+1+4+16]=6.8故答案为:6.8.4.(5分)若双曲线的离心率为2,则a等于1.【解答】解:由=1可知虚轴b=,而离心率e=,解得a=1.故答案:1.5.(5分)抛掷一粒骰子,观察掷出的点数,设事件A为出现奇数,事件B为出现2点,已知P(A)=,P(B)=,则出现奇数点或2点的概率是.【解答】解:由题意知抛掷一粒骰子出现奇数和出现2点是互斥事件,∵P(A)=,P(B)=,∴出现奇数点或2点的概率根据互斥事件的概率公式得到P=P(A)+P(B)=+=,故答案为:6.(5分)根据如图所示的伪代码,当输入a的值为3时,最后输出的S的值为21.【解答】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加,当不满足条件i≤3时推出循环.此时S=3+6+12=21,故输出的S值为21.故答案为:21.7.(5分)已知数列{a n}为等比数列,a4+a7=2,a5•a6=﹣8,则a1+a10的值为﹣7.【解答】解:a4+a7=2,a5•a6=﹣8,由等比数列的性质可知a5•a6=a4•a7∴a4•a7=﹣8,a4+a7=2,∴a4=﹣2,a7=4或a4=4,a7=﹣2,∴a1=1,q3=﹣2或a1=﹣8,q3=﹣,∴a1+a10=﹣7.故答案为:﹣7.8.(5分)已知sin(+θ)=,θ∈(0,π),则cos(﹣θ)=.【解答】解:∵sin(+θ)=,θ∈(0,π),∴可得cosθ=,sinθ==,∴cos(﹣θ)=cos[π﹣()]=﹣cos()=﹣(cos cosθ﹣sinsinθ)=.故答案为:.9.(5分)已知函数f(x)=x2+abx+a+2b.若f(0)=4,则f(1)的最大值为7.【解答】解:由若f(0)=4得,a+2b=4,则f(1)=1+ab+a+2b=5+ab=5+(4﹣2b)b=﹣2b2+4b+5=﹣2(b﹣1)2+7≤7,当且仅当b=1时,f(1)取最大值为7;故选答案为7.10.(5分)如图所示,已知三棱柱ABCA1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1ABC1的体积为.【解答】解:∵三棱柱ABC﹣A1B1C1的所有棱长均为1,且AA1⊥底面ABC,∴===,点A到平面BB1C1的距离h==,∴三棱锥B1ABC1的体积:V===.故答案为:.11.(5分)已知存在实数a,满足对任意的实数b,直线y=﹣x+b都不是曲线y=x3﹣3ax的切线,则实数a的取值范围是.【解答】解:设f(x)=x3﹣3ax,求导函数,可得f′(x)=3x2﹣3a∈[﹣3a,+∞),∵存在实数a,满足对任意的实数b,直线y=﹣x+b都不是曲线y=x3﹣3ax的切线,∴﹣1∉[﹣3a,+∞),∴﹣3a>﹣1,即实数a的取值范围为故答案为:12.(5分)如图,在△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且=+λ(λ∈R),则AD的长为3.【解答】解:因为B,D,C三点共线,所以有+λ=1,解得λ=,如图,过点D分别作AC,AB的平行线交AB,AC于点M,N,则=,=,∵△ABC中,∠A=60°,∠A的平分线交BC于D,∴AMDN是菱形,∵AB=4,∴AN=AM=3,∴AD=3.故答案为:3.13.(5分)已知A(﹣2,0),B(2,0),点P在圆(x﹣3)2+(y﹣4)2=r2(r >0)上,满足P A2+PB2=40,若这样的点P有两个,则r的取值范围是(1,9).【解答】解:设P(x,y),∵A(﹣2,0),B(2,0),P A2+PB2=40,∴(x+2)2+y2+(x﹣2)2+y2=40,整理,得x2+y2=16,又∵点P在圆(x﹣3)2+(y﹣4)2=r2(r>0)上,这样的点P有两个,∵圆(x﹣3)2+(y﹣4)2=r2(r>0)的圆心M(3,4),半径为r,x2+y2=16的圆心O(0,0),半径为4,∴|OM|==5,∵满足条件的点P有两个,∴两圆x2+y2=16和(x﹣3)2+(y﹣4)2=r2(r>0)相交,∴|r﹣4|<|OM|=5<|r+4|,解得1<r<9.故答案为:(1,9).14.(5分)已知函数f(x)=,若f(f(x))=t有3个零点,则t的取值范围是1≤t<3.【解答】解:易得函数f(x)=在[0,1]上单调递增,在(1,3]上单调递减,∴函数的最大值为f(1)=3,f(0)=1,f(3)=0,∴当t=3时,f(m)=t只有一个根m=1,而当m=1时方程f(x)=m有两解,不合题意;当t=1时,f(m)=t只有两个根m=0,此时对应x一解,或x=,此时对应x两解,符合题意;∴当1≤t<3时,原方程有三解.故答案为:1≤t<3二、解答题:本大题共10小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知=,=(cos A,﹣2cos A),=﹣1.(1)求∠A的大小;(2)若,c=2,求△ABC的面积.【解答】解:(1)由于=,=(cos A,﹣2cos A),则=,∴,即∴,即.∵0<A<π,∴,∴,解得.(2)由正弦定理可知,∴,又∵∴,.则△ABC的面积为.16.(14分)如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,平面P AB⊥平面ABCD,P A⊥PB,BP=BC,E为PC的中点.(1)求证:AP∥平面BDE;(2)求证:BE⊥平面P AC.【解答】证明:(1)设AC∩BD=O,连结OE.∵四边形ABCD为矩形,∴O是AC的中点.∵E是PC中点,∴OE∥AP.∵AP⊄平面BDE,OE⊂平面BDE,∴AP∥平面BDE.(2)∵平面P AB⊥平面ABCD,BC⊥AB,平面P AB∩平面ABCD=AB,∴BC⊥平面P AB.∵AP⊂平面P AB,∴BC⊥P A.∵PB⊥P A,BC∩PB=B,BC,PB⊂平面PBC,∴P A⊥平面PBC.∵BE⊂平面PBC,∴P A⊥BE.∵BP=PC,且E为PC中点,∴BE⊥PC.∵P A∩PC=P,P A,PC⊂平面P AC,∴BE⊥平面P AC.17.(14分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.(1)设∠PBO=α,把y表示成α的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?【解答】解:(1)∵在Rt△AOB中,AB=6,∴OB=OA=.∴由题意知.∴点P到A、B、C的距离之和为.∴所求函数关系式为.(2)由(1)得,令y′=0即,又,从而当时,y′<0;当时,y′>0.∴当时,取得最小值,此时(km),即点P在OA上距O点km处.即变电站建于距O点km处时,它到三个小区的距离之和最小.18.(16分)如图,椭圆C:经过点P(1,),离心率e =,直线l的方程为x=4.(1)求椭圆C的方程;(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记P A,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由.【解答】解:(1)椭圆C:经过点P(1,),可得①由离心率e=得=,即a=2c,则b2=3c2②,代入①解得c=1,a=2,b =故椭圆的方程为(2)方法一:由题意可设AB的斜率为k,则直线AB的方程为y=k(x﹣1)③代入椭圆方程并整理得(4k2+3)x2﹣8k2x+4k2﹣12=0设A(x1,y1),B(x2,y2),x1+x2=,④在方程③中,令x=4得,M的坐标为(4,3k),从而,,=k﹣注意到A,F,B共线,则有k=k AF=k BF,即有==k所以k1+k2=+=+﹣(+)=2k﹣×⑤④代入⑤得k1+k2=2k﹣×=2k﹣1又k3=k﹣,所以k1+k2=2k3故存在常数λ=2符合题意方法二:设B(x0,y0)(x0≠1),则直线FB的方程为令x=4,求得M(4,)从而直线PM的斜率为k3=,联立,得A(,),则直线P A的斜率k1=,直线PB的斜率为k2=所以k1+k2=+=2×=2k3,故存在常数λ=2符合题意19.(16分)已知数列{a n}是等差数列,{b n}是等比数列,且满足a1+a2+a3=9,b1b2b3=27.(1)若a4=b3,b4﹣b3=m.①当m=18时,求数列{a n}和{b n}的通项公式;②若数列{b n}是唯一的,求m的值;(2)若a1+b1,a2+b2,a3+b3均为正整数,且成等比数列,求数列{a n}的公差d 的最大值.【解答】解:(1)①由数列{a n}是等差数列及a1+a2+a3=9,得a2=3,由数列{b n}是等比数列及b1b2b3=27,得b2=3.…(2分)设数列{a n}的公差为d,数列{b n}的公比为q,若m=18,则有解得或,所以,{a n}和{b n}的通项公式为a n=3n﹣3,b n=3n﹣1或a n=﹣n+12,b n=3•(﹣2)n﹣2…(4分)②由题设b4﹣b3=m,得3q2﹣3q=m,即3q2﹣3q﹣m=0(*).因为数列{b n}是唯一的,所以若q=0,则m=0,检验知,当m=0时,q=1或0(舍去),满足题意;若q≠0,则(﹣3)2+12m=0,解得m=﹣,代入(*)式,解得q=,又b2=3,所以{b n}是唯一的等比数列,符合题意.所以,m=0或﹣.…(8分)(2)依题意,36=(a1+b1)(a3+b3),设{b n}公比为q,则有36=(3﹣d+)(3+d+3q),(**)记m=3﹣d+,n=3+d+3q,则mn=36.将(**)中的q消去,整理得:d2+(m﹣n)d+3(m+n)﹣36=0 …(10分)d的大根为=而m,n∈N*,所以(m,n)的可能取值为:(1,36),(2,18),(3,12),(4,9),(6,6),(9,4),(12,3),(18,2),(36,1).所以,当m=1,n=36时,d的最大值为.…(16分)20.(16分)已知函数f(x)=x•lnx,g(x)=ax3﹣.(1)求f(x)的单调增区间和最小值;(2)若函数y=f(x)与函数y=g(x)在交点处存在公共切线,求实数a的值;(3)若x∈(0,e2]时,函数y=f(x)的图象恰好位于两条平行直线l1:y=kx;l2:y=kx+m之间,当l1与l2间的距离最小时,求实数m的值.【解答】解:(1)因为f'(x)=lnx+1,由f'(x)>0,得,所以f(x)的单调增区间为,又当时,f'(x)<0,则f(x)在上单调减,当时,f'(x)>0,则f(x)在上单调增,所以f(x)的最小值为.(2)因为f'(x)=lnx+1,,设公切点处的横坐标为x°,则与f(x)相切的直线方程为:y=(lnx°+1)x﹣x°,与g(x)相切的直线方程为:,所以,解之得,由(1)知,所以.(3)若直线l1过(e2,2e2),则k=2,此时有lnx°+1=2(x°为切点处的横坐标),所以x°=e,m=﹣e,当k>2时,有l2:y=(lnx°+1)x﹣x°,l1:y=(lnx°+1)x,且x°>2,所以两平行线间的距离,令h(x)=xlnx﹣(lnx°+1)x+x°,因为h'(x)=lnx+1﹣lnx°﹣1=lnx﹣lnx°,所以当x<x°时,h'(x)<0,则h(x)在(0,x°)上单调减;当x>x°时,h'(x)>0,则h(x)在上单调增,所以h(x)有最小值h(x°)=0,即函数f(x)的图象均在l2的上方,令,则,所以当x>x°时,t(x)>t(x°),所以当d最小时,x°=e,m=﹣e.21.(10分)(选修4﹣2:矩阵与变换)已知矩阵A=,若矩阵A属于特征值6的一个特征向量为=,属于特征值1的一个特征向量为=.求矩阵A,并写出A的逆矩阵.【解答】解:由矩阵A属于特征值6的一个特征向量为α1=可得=6,即c+d=6;…(3分)由矩阵A属于特征值1的一个特征向量为α2=,可得=,即3c﹣2d=﹣2,…(6分)解得即A=,…(8分)∴A逆矩阵是A﹣1==.22.(10分)在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,求线段AB的最小值.【解答】解:将曲线C1的参数θ消去可得(x﹣3)2+(y﹣4)2=1.将曲线C2:ρ=1化为直角坐标方程为x2+y2=1.曲线C1是以(3,4)为圆心,1为半径的圆;曲线C2是以(0,0)为圆心,1为半径的圆,求得两圆圆心距为=5,可得AB的最小值为5﹣1﹣1=3.23.(10分)如图,已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,AA1=AB=AC =1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足.(1)证明:PN⊥AM;(2)若平面PMN与平面ABC所成的角为45°,试确定点P的位置.【解答】解:(1)证明:如图,以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A﹣xyz.则P(λ,0,1),N(,,0),M(0,1,),从而=(﹣λ,,﹣1),=(0,1,),=(﹣λ)×0+×1﹣1×=0,所以PN⊥AM.(2)平面ABC的一个法向量为==(0,0,1).设平面PMN的一个法向量为=(x,y,z),由(1)得=(λ,﹣1,).由解得∵平面PMN与平面ABC所成的二面角为45°,∴|cos<,>|=||==,解得λ=﹣.(11分)故点P在B1A1的延长线上,且|A1P|=.(12分)24.(10分)已知数列{a n}满足:.(1)若a=﹣1,求数列{a n}的通项公式;(2)若a=3,试证明:对∀n∈N*,a n是4的倍数.【解答】(1)解:a=﹣1时,令b n=a n﹣1,则∵b1=﹣5为奇数,b n也是奇数且只能为﹣1∴,即;(2)证明:a=3时,①n=1时,a1=﹣4,命题成立;②设n=k时,命题成立,则存在t∈N*,使得a k=4t∴=34t﹣1+1=27•(4﹣1)4(t﹣1)+1∵(4﹣1)4(t﹣1)=+…+4+1=4m+1,m∈Z ∴=27•(4m+1)+1=4(27m+7)∴n=k+1时,命题成立由①②可知,对∀n∈N*,a n是4的倍数.第21页(共21页)。
江苏省淮阴市2015届高三数学上学期期中调研测试试题苏教版

淮阴区期中调研测试数学试题一、选择题(本大题满分70分,每小题5分)1、 设集合}|{},1|{a x x B x x A <=>=,若R B A =⋃,则实数a 的取值范围为2、 复数i i z +-=2)21(的实部为3、某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4∶5∶5∶6,则应从一年级本科生中抽取________名学生.4、从1、2、3、4这4个数中一次性随机地取两个数,则所取两个数的和为5的概率为5、函数)62sin(2π-=x y 的图像中,离坐标原点最近的一条对称轴的方程为6、阅读如图11所示的程序框图,运行相应的程序,则程序运行后输出的结果为图117、等比数列}{n a 的公比大于1,6,152415=-=-a a a a ,则=3a8、一个圆柱和一个圆锥同底等高,若圆锥的侧面积是其底面积的2倍,则圆柱的侧面积是其底面积的 倍。
9、在平面直角坐标系中,直线0323=+-y x 被圆422=+y x截得的弦长为10、设函数1sin )1()(22+++=x xx x x f 的最大值为M ,最小值为m ,则=+m M 11、已知点),1(m P 是函数xax y 2+=图像上的点,直线b y x =+是该函数图像在P 点处的切线,则=-+m b a12、设P 为ABC ∆中线AD 的中点,D 为边BC 中点,且2=AD ,若3-=•PC PB ,则=•AC AB13、若存在正数x 使1)(<-a x e x成立,则a 的取值范围是 14、已知0,0,1≠>=+x y y x ,则1||||21++y x x 的最小值为二、解答题(本大题共6小题,共90分。
解答应写出文字说明、证明过程或演算步骤) 15、(本题满分14分)已知2tan ),,2(-=∈αππα(1)求)4sin(απ+的值;(2)求)232cos(απ-的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015届高三数学期中模拟(二)一、填空题:(本大题共14小题,每小题5分,共70分.)1.设集合{2,3,4}A =,{2,4,6}B =,若x A ∈且x B ∉,则x 等于____________. 2. 写出命题:“若x =3,则x 2-2x -3=0”的否命题: 。
3. 已知角α终边上一点P 的坐标是)3cos 2,3sin 2(-,则=αsin 。
4.运已知i i z 2)1(2=+,则z = 。
5.若命题“,R x ∈∃使得012≤++ax ax ”为假命题,则实数a 的取值范围为6.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =__________.7.如图,菱形ABCD 的边长为2,60A ∠=︒,M 为DC 的中点,若N 为菱形内任意一点(含边界),则AM AN ⋅的最大值为____________.8.各项均为正偶数的数列1a ,2a ,3a ,4a 中,前三项依次成公差为(0)d d >的等差数列,后三项依次成公比为q 的等比数列.若4188a a -=,则q 的所有可能的值构成的集合为__________.9.函数|cos |sin cos |sin |)(x x x x x f ⋅+⋅=的值域为 。
10.方程s i n 3c o s 0x x a +=在(0,2)π内有相异两解,αβ,则αβ+= 。
11.已知函数22log (1) (0)()2 (0)x x f x x x x +>⎧=⎨--≤⎩,,若函数()()g x f x m =-有3个零点,则实数m 的取值范围是 。
12.已知锐角B A ,满足A B A tan 2)tan(=+,则B tan 的最大值是 。
13.已知函数1)12(31)(223+-+-++=a a x a x x x f 若函数)(x f 在(]31,上存在唯一的极值点.则实数a 的取值范围为14.已知函数m x m x x f -+-+-=2)2()(2,且|)(|x f y =在[]0,1-上为单调减函数,则实数m 的取值范围为二、解答题:(本大题共6小题,共90分.) 15.(本小题满分14分)如图,在ABC ∆中,45=∠C ,D 为BC 中点,2=BC ,记锐角α=∠ADB .且满足2572cos -=α. (1)求CAD ∠cos ;(2)求BC 边上的高h 的值.16、(本小题满分14分)已知二次函数2()f x ax bx =+,(1)f x +为偶函数,函数()f x 的图象与直线y x =相切.(Ⅰ)求()f x 的解析式;(Ⅱ)设集合{|()0}A x f x =>,{||1|}B x x m =-<,若集合B 是集合A 的子集,求实数m 的取值范围.CBD A17. (本小题满分14分)设命题:p 函数)161lg()(2a x ax x f +-=的定义域为R ,命题:q 不等式ax x +<+112对一切的正实数均成立.如果命题""q p 或为真命题,命题”且q p "为假命题,求实数a 的取值范围。
18.(本小题满分16分)为丰富农村业余文化生活,决定在N B A ,,三个村子的中间地带建造文化中心。
通过测量,发现三个村子分别位于矩形ABCD 的两个顶点B A ,和以边AB 的中心M 为圆心,以MC 长为半径的圆弧的中心N 处,且km BC km AB 24,8==。
经协商,文化服务中心拟建在与B A ,等距离的O 处,并建造三条道路NO BO AO ,,与各村通达。
若道路建设成本BO AO ,段为每公里a 2万元,NO 段为每公里a 万元,建设总费用为w 万元。
(1)若三条道路建设的费用相同,求该文化中心离N 村的距离; (2)若建设总费用最少,求该文化中心离N 村的距离。
19.(本小题满分16分)已知等比数列{}n a 满足*12111()2n n a a a a n N ++++=-∈。
(1)求数列{}n a 的通项公式;(2)在n a 与1n a +之间插入1n -个数组成一个公差为n d 的等差数列。
①设1n nb d =,求数列{}n b 的前n 项和n T ; ②在数列{}n d 中是否存在三项,,m k p d d d (其中,,m k p 成等差数列)成等比数列?求出这样的三项;若不存在,说明理由。
20、(本小题满分16分)已知函数1()2ln f x a x x x=-+(a R ∈且0a ≠),2()2gxx x =--+()b R ∈.(Ⅰ)若()f x 在定义域上有极值,求实数a 的取值范围;(Ⅱ)当a =[]11,x e ∀∈,总[]21,x e ∃∈,使得12()()f x g x <,求实数b 的取值范围;(其中e 为自然对数的底数)(Ⅲ)对n N ∀∈,且2n ≥,证明: 4ln(!)(1)(2)n n n <-+.一、填空题:(本大题共14小题,每小题5分,共70分.)1.设集合{2,3,4}A =,{2,4,6}B =,若x A ∈且x B ∉,则x 等于____________.3 2. 写出命题:“若x =3,则x 2-2x -3=0”的否命题: 。
“若3x ≠则2230x x --≠”3. 已知角α终边上一点P 的坐标是)3cos 2,3sin 2(-,则=αsin 。
cos3-4. 已知i i z 2)1(2=+,则z = 。
15.若命题“,R x ∈∃使得012≤++ax ax ”为假命题,则实数a 的取值范围为[)40,6.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =__________.-27.如图,菱形ABCD 的边长为2,60A ∠=︒,M 为DC 的中点,若N 为菱形内任意一点(含边界),则AM AN ⋅的最大值为____________.98.各项均为正偶数的数列1a ,2a ,3a ,4a 中,前三项依次成公差为(0)d d >的等差数列,后三项依次成公比为q 的等比数列.若4188a a -=,则q 的所有可能的值构成的集合为__________.答案:58,37⎧⎫⎨⎬⎩⎭.解:由题意,可设1a ,1a d +,12a d +,188a +,其中1a ,d 均为正偶数,则2111(2)()(88)a d a d a +=++, 整理得14(22)0388d d a d -=>-(注意体会这里用“10a >”而不用“12a ≥”的好处),所以 (22)(388)0d d --<,即88223d <<,所以d 的所有可能值为24,26,28.当24d =时,112a =,53q =;当26d =时,12085a =(舍去);当28d =时,1168a =,87q =.所以q 的所有可能的值构成的集合为58,37⎧⎫⎨⎬⎩⎭.9.函数|cos |sin cos |sin |)(x x x x x f ⋅+⋅=的值域为 。
[]1,1-10.方程s i n 3c o s 0x x a +=在(0,2)π内有相异两解,αβ,则αβ+= 。
3π,37π(图1)11.已知函数22log (1) (0)()2 (0)x x f x x x x +>⎧=⎨--≤⎩,,若函数()()g x f x m =-有3个零点,则实数m的取值范围是 。
(0,1)12.已知锐角B A ,满足A B A tan 2)tan(=+,则B tan 的最大值是 。
413.已知函数1)12(31)(223+-+-++=a a x a x x x f 若函数)(x f 在(]31,上存在唯一的极值点.则实数a 的取值范围为 [)1-7-,14.已知函数m x m x x f -+-+-=2)2()(2,且|)(|x f y =在[]0,1-上为单调减函数,则实数m 的取值范围为 20≥≤m m 或 14.解:判别式()()281226m m m m ∆=-+=--,① 当0∆≤时,即26m ≤≤时,函数()f x ≤0恒成立, 所以2()()(2)2f x f x x m x m =-=--+-, 对称轴方程为22m x -=,所以当20 22m m -≥,即≥时符合题意(如图1),此时26m ≤≤;②当0∆>时,即26m m <>或时,方程()0f x =的两个实根为1 2x =,, 不妨设12x x<,由题意及图象得 10x ≥或221 20 m x -⎧-⎪⎨⎪⎩≤,≥,即2m -2)或21,220m m -⎧-⎪⎨⎪-⎩≤解得2 0m m ≥,或≤,此时0 6m m >≤,或, 综上得m 的取值范围是0 2m m ≤,或≥.二、解答题:(本大题共6小题,共90分.) 15.(本小题满分14分)如图,在ABC ∆中,45=∠C ,D 为BC 中点,2=BC ,记锐角α=∠ADB .且满足2572cos -=α. (1)求CAD ∠cos ;(2)求BC 边上的高h 的值.CBD A15.解(1)∵27cos 22cos 125αα=-=-,∴29cos 25α=,∵(0,)2πα∈,∴3cos 5α=,4sin 5α=,…………………3分 45CAD α∠=-︒,∴())cos cos 45cos sin 2CAD ααα∠=-︒=+10=.……………7分 (2)由(1)得,∴sin sin()sin cos cos sin 44410CAD πππααα∠=-=-=,……9分在ACD ∆中,由正弦定理得:sin sin CD AD CAD C =∠∠,1sin 5sin 10CD C AD CAD ⨯⋅∠===∠, 则高4sin 545h AD ADB =⋅∠=⨯=.…14分16、(本小题满分14分)已知二次函数2()f x ax bx =+,(1)f x +为偶函数,函数()f x 的图象与直线y x =相切.(Ⅰ)求()f x 的解析式;(Ⅱ)设集合{|()0}A x f x =>,{||1|}B x x m =-<,若集合B 是集合A 的子集,求实数m 的取值范围.16、解:(Ⅰ)∵22(1)(1)(1)(2)()f x a x b x ax a b x a b +=+++=++++为偶函数, ∴202a b b a +=⇒=- …………2分2()2f x ax ax =- ()22f x ax a '=- 设()f x 与y x =相切于00(,)P x x ,则0200001221220ax a a ax ax x x ⎧-=⎧=-⎪⎪⇒⎨⎨-=⎪⎩⎪=⎩ ∴21()2f x x x =-+. ……………6分(运用判别式处理同样给分)(Ⅱ){|()0}{|02}A x f x x x =>=<< {||1|}B x x m =-< ∵B A ⊆∴①当0m ≤时,有B =∅,满足B A ⊆ ………………10分 ②当0m >时,{|11}B x m x m =-<<+ 要使B A ⊆,则0100112m m m m >⎧⎪-≥⇒<≤⎨⎪+≤⎩综合① ②,要使B A ⊆,实数m 的取值范围为(,1]-∞. ……14分17. (本小题满分14分)设命题:p 函数)161lg()(2a x ax x f +-=的定义域为R ,命题:q 不等式ax x +<+112对一切的正实数均成立.如果命题""q p 或为真命题,命题”且q p "为假命题,求实数a 的取值范围。
