完整word版,自动控制原理期末试卷及答案,推荐文档
自动控制原理期末考试卷与答案

自动控制原理期末考试卷与答案一、填空题(每空 1 分,共20分)1、对自动控制系统的基本要求可以概括为三个方面,即: 稳定性 、快速性和 准确性 。
2、控制系统的 输出拉氏变换与输入拉氏变换在零初始条件下的比值 称为传递函数。
3、在经典控制理论中,可采用 劳斯判据(或:时域分析法)、根轨迹法或奈奎斯特判据(或:频域分析法) 等方法判断线性控制系统稳定性。
4、控制系统的数学模型,取决于系统 结构 和 参数, 与外作用及初始条件无关。
5、线性系统的对数幅频特性,纵坐标取值为20lg ()A ω(或:()L ω),横坐标为lg ω 。
6、奈奎斯特稳定判据中,Z = P - R ,其中P 是指 开环传函中具有正实部的极点的个数,Z 是指 闭环传函中具有正实部的极点的个数,R 指 奈氏曲线逆时针方向包围 (-1, j0 )整圈数。
7、在二阶系统的单位阶跃响应图中,s t 定义为 调整时间 。
%σ是超调量 。
8、设系统的开环传递函数为12(1)(1)K s T s T s ++,则其开环幅频特性为2212()()1()1KA T T ωωωω=+⋅+,相频特性为01112()90()()tg T tg T ϕωωω--=---。
9、反馈控制又称偏差控制,其控制作用是通过 给定值 与反馈量的差值进行的。
10、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为1050.20.5s s s s+++。
11、自动控制系统有两种基本控制方式,当控制装置与受控对象之间只有顺向作用而无反向联系时,称为 开环控制系统;当控制装置与受控对象之间不但有顺向作用而且还有反向联系时,称为 闭环控制系统;含有测速发电机的电动机速度控制系统,属于 闭环控制系统。
12、根轨迹起始于开环极点,终止于开环零点。
13、稳定是对控制系统最基本的要求,若一个控制系统的响应曲线为衰减振荡,则该系统 稳定。
期末考试试题集-自动控制原理(含完整答案)

期末考试-复习重点自动控制原理1. 2. 一、单项选择题(每小题 1分,共20分) 系统和输入已知,求输出并对动态特性进行研究,称为( A.系统综合 B.系统辨识 惯性环节和积分环节的频率特性在(A.幅频特性的斜率B.最小幅值C.系统分析 )上相等。
C.相位变化率 )D.系统设计 D.穿越频率 通过测量输出量,产生一个与输出信号存在确定函数比例关系值的元件称为( A.比较元件 B.给定元件 C.反馈元件 o 从0变化到+8时,延迟环节频率特性极坐标图为( A.圆 B.半圆 C.椭圆 5.当忽略电动机的电枢电感后, 以电动机的转速为输出变量, 个()A.比例环节 3. 4.B.微分环节C.积分环节 6.若系统的开环传递函数为10 s(5s 2) ,则它的开环增益为 7.8. 9. A.1 B.2 C.5 D.放大元件 ) D.双曲线 电枢电压为输入变量时, 电动机可看作一D.惯性环节 D.10 5 s 2+2s +5 B.欠阻尼系统 C.过阻尼系统 Z 不变,提高o n ,则可以() B. 减少上升时间和峰值时间 D.减少上升时间和超调量 1一阶微分环节G (s ) =1 Ts ,当频率 时,则相频特性• G (j ・)为()T C. 90 °)B.稳定裕量越大D. 稳态误差越小二阶系统的传递函数 G(s) ,则该系统是(A.临界阻尼系统 若保持二阶系统的 A.提高上升时间和峰值时间 C.提高上升时间和调整时间 A.45 °B.-45 ° 10.最小相位系统的开环增益越大,其( A.振荡次数越多 C.相位变化越小 con ,11.设系统的特征方程为 D s 二s 4 8s 3 17s 2 16s 5 =0 , A.稳定 B.临界稳定 C.不稳定D.零阻尼系统 D.-90 °则此系统 () D.稳定性不确定。
12.某单位反馈系统的开环传递函数为: G^s(s 1)(s 5),当k=()时,闭环系统临界稳定。
完整word版,《自动控制原理》试卷及答案(英文10套),推荐文档

AUTOMATIC CONTROL THEOREM (1)⒈ Derive the transfer function and the differential equation of the electric network⒉ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . (12%) ⒊ The characteristic equation is given 010)6(5)(123=++++=+K S K S S S GH . Discuss the distribution of the closed-loop poles. (16%)① There are 3 roots on the LHP ② There are 2 roots on the LHP② There are 1 roots on the LHP ④ There are no roots on the LHP . K=?⒋ Consider a unity-feedback control system whose open-loop transfer function is )6.0(14.0)(++=S S S S G . Obtain the response to a unit-step input. What is the rise time for this system? What is the maximum overshoot? (10%)Fig.15. Sketch the root-locus plot for the system )1()(+=S S K S GH . ( The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis.③ Discuss the stability. (12%)6. The system block diagram is shown Fig.3. Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤e . (12%)Fig.37. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (12%)8. Sketch the Bode diagram of the system shown in Fig.4. (14%)⒈212121121212)()()(C C S C C R R C S C C R S V S V ++++=⒉ 2423241321121413211)()(H G H G G G G G G G H G G G G G G G S R S C ++++++=⒊ ① 0<K<6 ② K ≤0 ③ K ≥6 ④ no answer⒋⒌①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2③⒍5.75.3≤≤K⒎ )154.82)(181.34)(1481.3)(1316.0()11.0(62.31)(+++++=S S S S S S GHAUTOMATIC CONTROL THEOREM (2)⒈Derive the transfer function and the differential equation of the electric network⒉ Consider the equation group shown in Equation.1. Draw block diagram and obtain the closed-loop transfer function )()(S R S C . (16% ) Equation.1 ⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111S X S G S C S G S G S C S X S X S X S G S X S G S X S C S G S G S G S R S G S X⒊ Use Routh ’s criterion to determine the number of roots in the right-half S plane for the equation 0400600226283)(12345=+++++=+S S S S S S GH . Analyze stability.(12% )⒋ Determine the range of K value ,when )1(2t t r ++=, 5.0≤SS e . (12% )Fig.1⒌Fig.3 shows a unity-feedback control system. By sketching the Nyquist diagram of the system, determine the maximum value of K consistent with stability, and check the result using Routh ’s criterion. Sketch the root-locus for the system (20%)(18% )⒎ Determine the transfer function. Assume a minimum-phase transfer function.(10% )⒈1)(1)()(2122112221112++++=S C R C R C R S C R C R S V S V⒉ )(1)()(8743215436324321G G G G G G G G G G G G G G G G S R S C -+++=⒊ There are 4 roots in the left-half S plane, 2 roots on the imaginary axes, 0 root in the RSP. The system is unstable.⒋ 208<≤K⒌ K=20⒍⒎ )154.82)(181.34)(1481.3)(1316.0()11.0(62.31)(+++++=S S S S S S GHAUTOMATIC CONTROL THEOREM (3)⒈List the major advantages and disadvantages of open-loop control systems. (12% )⒉Derive the transfer function and the differential equation of the electric network⒊ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E , )()(S P S C . (12%)⒋ The characteristic equation is given 02023)(123=+++=+S S S S GH . Discuss the distribution of the closed-loop poles. (16%)5. Sketch the root-locus plot for the system )1()(+=S S K S GH . (The gain K is assumed to be positive.)④ Determine the breakaway point and K value.⑤ Determine the value of K at which root loci cross the imaginary axis. ⑥ Discuss the stability. (14%)6. The system block diagram is shown Fig.3. 21+=S K G , )3(42+=S S G . Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤SS e . (15%)7. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (15%)⒈ Solution: The advantages of open-loop control systems are as follows: ① Simple construction and ease of maintenance② Less expensive than a corresponding closed-loop system③ There is no stability problem④ Convenient when output is hard to measure or economically not feasible. (For example, it would be quite expensive to provide a device to measure the quality of the output of a toaster.)The disadvantages of open-loop control systems are as follows:① Disturbances and changes in calibration cause errors, and the output may be different from what is desired.② To maintain the required quality in the output, recalibration is necessary from time to time.⒉ 1)(1)()()(2122112221122112221112+++++++=S C R C R C R S C R C R S C R C R S C R C R S U S U ⒊351343212321215143211)()(H G G H G G G G H G G H G G G G G G G G S R S C +++++= 35134321232121253121431)1()()(H G G H G G G G H G G H G G H G G H G G G G S P S C ++++-+=⒋ R=2, L=1⒌ S:①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2⒍5.75.3≤≤KAUTOMATIC CONTROL THEOREM (4)⒈ Find the poles of the following )(s F :se s F --=11)( (12%)⒉Consider the system shown in Fig.1,where 6.0=ξ and 5=n ωrad/sec. Obtain the rise time r t , peak time p t , maximum overshoot P M , and settling time s t when the system is subjected to a unit-step input. (10%)⒊ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E , )()(S P S C . (12%)⒋ The characteristic equation is given 02023)(123=+++=+S S S S GH . Discuss the distribution of the closed-loop poles. (16%)5. Sketch the root-locus plot for the system )1()(+=S S K S GH . (The gain K is assumed to be positive.)⑦ Determine the breakaway point and K value.⑧ Determine the value of K at which root loci cross the imaginary axis.⑨ Discuss the stability. (12%)6. The system block diagram is shown Fig.3. 21+=S K G , )3(42+=S S G . Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤SS e . (12%)7. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (12%)8. Sketch the Bode diagram of the system shown in Fig.4. (14%)⒈ Solution: The poles are found from 1=-s e or 1)sin (cos )(=-=-+-ωωσωσj e e j From this it follows that πωσn 2,0±== ),2,1,0(K =n . Thus, the poles are located at πn j s 2±=⒉Solution: rise time sec 55.0=r t , peak time sec 785.0=p t ,maximum overshoot 095.0=P M ,and settling time sec 33.1=s t for the %2 criterion, settling time sec 1=s t for the %5 criterion.⒊ 351343212321215143211)()(H G G H G G G G H G G H G G G G G G G G S R S C +++++= 35134321232121253121431)1()()(H G G H G G G G H G G H G G H G G H G G G G S P S C ++++-+=⒋R=2, L=15. S:①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2⒍5.75.3≤≤KAUTOMATIC CONTROL THEOREM (5)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function )()(S R S C , )()(S R S E . (18%)⒉ The characteristic equation is given 0483224123)(12345=+++++=+S S S S S S GH . Discuss the distribution of the closed-loop poles. (16%)⒊ Sketch the root-locus plot for the system )15.0)(1()(++=S S S K S GH . (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (18%)⒋ The system block diagram is shown Fig.2. 1111+=S T K G , 1222+=S T K G . ①Suppose 0=r , 1=n . Determine the value of SS e . ②Suppose 1=r , 1=n . Determine the value of SS e . (14%)⒌ Sketch the Bode diagram for the following transfer function. )1()(Ts s K s GH +=, 7=K , 087.0=T . (10%)⒍ A system with the open-loop transfer function )1()(2+=TS s K S GH is inherently unstable. This system can be stabilized by adding derivative control. Sketch the polar plots for the open-loop transfer function with and without derivative control. (14%)⒎ Draw the block diagram and determine the transfer function. (10%)⒈∆=321)()(G G G S R S C ⒉R=0, L=3,I=2⒋①2121K K K e ss +-=②21211K K K e ss +-= ⒎11)()(12+=RCs s U s UAUTOMATIC CONTROL THEOREM (6)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function )()(S R S C , )()(S R S E . (18%)⒉The characteristic equation is given 012012212010525)(12345=+++++=+S S S S S S GH . Discuss thedistribution of the closed-loop poles. (12%)⒊ Sketch the root-locus plot for the system )3()1()(-+=S S S K S GH . (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (15%)⒋ The system block diagram is shown Fig.2. SG 11=, )125.0(102+=S S G . Suppose t r +=1, 1.0=n . Determine the value of SS e . (12%)⒌ Calculate the transfer function for the following Bode diagram of the minimum phase. (15%)⒍ For the system show as follows, )5(4)(+=s s s G ,1)(=s H , (16%) ① Determine the system output )(t c to a unit step, ramp input.② Determine the coefficient P K , V K and the steady state error to t t r 2)(=.⒎ Plot the Bode diagram of the system described by the open-loop transfer function elements )5.01()1(10)(s s s s G ++=, 1)(=s H . (12%)w⒈32221212321221122211)1()()(H H G H H G G H H G G H G H G H G G G S R S C +-++-+-+= ⒉R=0, L=5 ⒌)1611()14)(1)(110(05.0)(2s s s s s s G ++++= ⒍t t e e t c 431341)(--+-= t t e e t t c 41213445)(---+-= ∞=P K , 8.0=V K , 5.2=ss eAUTOMATIC CONTROL THEOREM (7)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . (16%)⒉ The characteristic equation is given 01087444)(123456=+--+-+=+S S S S S S S GH . Discuss the distribution of the closed-loop poles. (10%)⒊ Sketch the root-locus plot for the system 3)1()(S S K S GH +=. (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (15%)⒋ Show that the steady-state error in the response to ramp inputs can be made zero, if the closed-loop transfer function is given by:nn n n n n a s a s a s a s a s R s C +++++=---1111)()(Λ ;1)(=s H (12%)⒌ Calculate the transfer function for the following Bode diagram of the minimum phase.(15%)w⒍ Sketch the Nyquist diagram (Polar plot) for the system described by the open-loop transfer function )12.0(11.0)(++=s s s S GH , and find the frequency and phase such that magnitude is unity. (16%)⒎ The stability of a closed-loop system with the following open-loop transfer function )1()1()(122++=s T s s T K S GH depends on the relative magnitudes of 1T and 2T . Draw Nyquist diagram and determine the stability of the system.(16%) ( 00021>>>T T K )⒈3213221132112)()(G G G G G G G G G G G G S R S C ++-++=⒉R=2, I=2,L=2 ⒌)1()1()(32122++=ωωωs s s s G⒍o s rad 5.95/986.0-=Φ=ωAUTOMATIC CONTROL THEOREM (8)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . (16%)⒉ The characteristic equation is given 04)2(3)(123=++++=+S K KS S S GH . Discuss the condition of stability. (12%)⒊ Draw the root-locus plot for the system 22)4()1()(++=S S KS GH ;1)(=s H .Observe that values of K the system is overdamped and values of K it is underdamped. (16%)⒋ The system transfer function is )1)(21()5.01()(s s s s K s G +++=,1)(=s H . Determine thesteady-state error SS e when input is unit impulse )(t δ、unit step )(1t 、unit ramp t and unit parabolic function221t . (16%)⒌ ① Calculate the transfer function (minimum phase);② Draw the phase-angle versus ω (12%) w⒍ Draw the root locus for the system with open-loop transfer function.)3)(2()1()(+++=s s s s K s GH (14%)⒎ )1()(3+=Ts s Ks GH Draw the polar plot and determine the stability of system. (14%)⒈43214321432143211)()(G G G G G G G G G G G G G G G G S R S C -+--+= ⒉∞ππK 528.0⒊S:0<K<0.0718 or K>14 overdamped ;0.0718<K<14 underdamped⒋S: )(t δ 0=ss e ; )(1t 0=ss e ; t K e ss 1=; 221t ∞=ss e⒌S:21ωω=K ; )1()1()(32121++=ωωωωs s ss GAUTOMATIC CONTROL THEOREM (9)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)(S C , )(S E . (12%)⒉ The characteristic equation is given0750075005.34)(123=+++=+K S S S S GH . Discuss the condition of stability. (16%)⒊ Sketch the root-locus plot for the system )1(4)()(2++=s s a s S GH . (The gain a isassumed to be positive.)① Determine the breakaway point and a value.② Determine the value of a at which root loci cross the imaginary axis. ③ Discuss the stability. (12%)⒋ Consider the system shown in Fig.2. 1)(1+=s K s G i , )1()(2+=Ts s Ks G . Assumethat the input is a ramp input, or at t r =)( where a is an arbitrary constant. Show that by properly adjusting the value of i K , the steady-state error SS e in the response to ramp inputs can be made zero. (15%)⒌ Consider the closed-loop system having the following open-loop transfer function:)1()(-=TS S KS GH . ① Sketch the polar plot ( Nyquist diagram). ② Determine thestability of the closed-loop system. (12%)⒍Sketch the root-locus plot. (18%)⒎Obtain the closed-loop transfer function )()(S R S C . (15%)⒈354211335421243212321313542143211)1()()(H G G G G H G H G G G G H G G G G H G G H G H G G G G G G G G G S R S C --++++-= 354211335421243212321335422341)()(H G G G G H G H G G G G H G G G G H G G H G H G G G H H G S N S E --+++--= ⒉45.30ππK⒌S: N=1 P=1 Z=0; the closed-loop system is stable ⒎2423241321121413211)()(H G H G G G G G G G H G G G G G G G S R S C ++++++=AUTOMATIC CONTROL THEOREM (10)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C ,⒉ The characteristic equation is given01510520)(1234=++++=+S S KS S S GH . Discuss the condition of stability. (14%)⒊ Consider a unity-feedback control system whose open-loop transfer function is)6.0(14.0)(++=S S S S G . Obtain the response to a unit-step input. What is the rise time forthis system? What is the maximum overshoot? (10%)⒋ Sketch the root-locus plot for the system )25.01()5.01()(s S s K S GH +-=. (The gain K isassumed to be positive.)③ Determine the breakaway point and K value.④ Determine the value of K at which root loci cross the imaginary axis. Discuss the stability. (15%)⒌ The system transfer function is )5(4)(+=s s s G ,1)(=s H . ①Determine thesteady-state output )(t c when input is unit step )(1t 、unit ramp t . ②Determine theP K 、V K and a K , obtain the steady-state error SS e when input is t t r 2)(=. (12%)⒍ Consider the closed-loop system whose open-loop transfer function is given by:①TS K S GH +=1)(; ②TS K S GH -=1)(; ③1)(-=TS KS GH . Examine the stabilityof the system. (15%)⒎ Sketch the root-locus plot 。
自动控制原理期末考试卷与答案

自动控制原理期末考试卷与答案一、填空题(每空 1 分,共20分)1、对自动控制系统的基本要求可以概括为三个方面,即: 稳定性 、快速性和 准确性 。
2、控制系统的 输出拉氏变换与输入拉氏变换在零初始条件下的比值 称为传递函数。
3、在经典控制理论中,可采用 劳斯判据(或:时域分析法)、根轨迹法或奈奎斯特判据(或:频域分析法) 等方法判断线性控制系统稳定性。
4、控制系统的数学模型,取决于系统 结构 和 参数, 与外作用及初始条件无关。
5、线性系统的对数幅频特性,纵坐标取值为20lg ()A ω(或:()L ω),横坐标为lg ω. 6、奈奎斯特稳定判据中,Z = P — R ,其中P 是指 开环传函中具有正实部的极点的个数,Z 是指 闭环传函中具有正实部的极点的个数,R 指 奈氏曲线逆时针方向包围 (-1, j0 )整圈数。
7、在二阶系统的单位阶跃响应图中,定义为 调整时间 。
%σ是超调量 。
8、设系统的开环传递函数为12(1)(1)Ks T s T s ++,则其开环幅频特性为2212()()1()1KA T T ωωωω=+⋅+,相频特性为01112()90()()tg T tg T ϕωωω--=---。
9、反馈控制又称偏差控制,其控制作用是通过给定值 与反馈量的差值进行的。
10、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s )为1050.20.5s s s s+++。
11、自动控制系统有两种基本控制方式,当控制装置与受控对象之间只有顺向作用而无反向联系时,称为 开环控制系统;当控制装置与受控对象之间不但有顺向作用而且还有反向联系时,称为 闭环控制系统;含有测速发电机的电动机速度控制系统,属于 闭环控制系统。
12、根轨迹起始于开环极点,终止于开环零点。
13、稳定是对控制系统最基本的要求,若一个控制系统的响应曲线为衰减振荡,则该系统 稳定。
自动控制原理期末考试卷含答案

自动控制原理期末考试卷与答案一、填空题〔每空 1 分,共20分〕1、对自动控制系统的根本要求可以概括为三个方面,即: 稳定性 、快速性和 准确性 。
2、控制系统的 输出拉氏变换与输入拉氏变换在零初始条件下的比值 称为传递函数。
3、在经典控制理论中,可采用 劳斯判据(或:时域分析法)、根轨迹法或奈奎斯特判据(或:频域分析法) 等方法判断线性控制系统稳定性。
4、控制系统的数学模型,取决于系统 结构 和 参数, 与外作用及初始条件无关。
5、线性系统的对数幅频特性,纵坐标取值为20lg ()A ω(或:()L ω),横坐标为lg ω 。
6、奈奎斯特稳定判据中,Z = P - R ,其中P 是指 开环传函中具有正实部的极点的个数,Z 是指 闭环传函中具有正实部的极点的个数,R 指 奈氏曲线逆时针方向包围 (-1, j0 )整圈数。
7、在二阶系统的单位阶跃响应图中,s t 定义为 调整时间 。
%σ是超调量 。
8、设系统的开环传递函数为12(1)(1)Ks T s T s ++,那么其开环幅频特性为2212()()1()1KA T T ωωωω=+⋅+,相频特性为01112()90()()tg T tg T ϕωωω--=---。
9、反应控制又称偏差控制,其控制作用是通过 给定值 与反应量的差值进行的。
10、假设某系统的单位脉冲响应为0.20.5()105tt g t ee --=+,那么该系统的传递函数G(s)为1050.20.5s s s s+++。
11、自动控制系统有两种根本控制方式,当控制装置与受控对象之间只有顺向作用而无反向联系时,称为 开环控制系统;当控制装置与受控对象之间不但有顺向作用而且还有反向联系时,称为 闭环控制系统;含有测速发电机的电动机速度控制系统,属于 闭环控制系统。
12、根轨迹起始于开环极点,终止于开环零点。
13、稳定是对控制系统最根本的要求,假设一个控制系统的响应曲线为衰减振荡,那么该系统 稳定。
自动控制原理期末试卷及答案
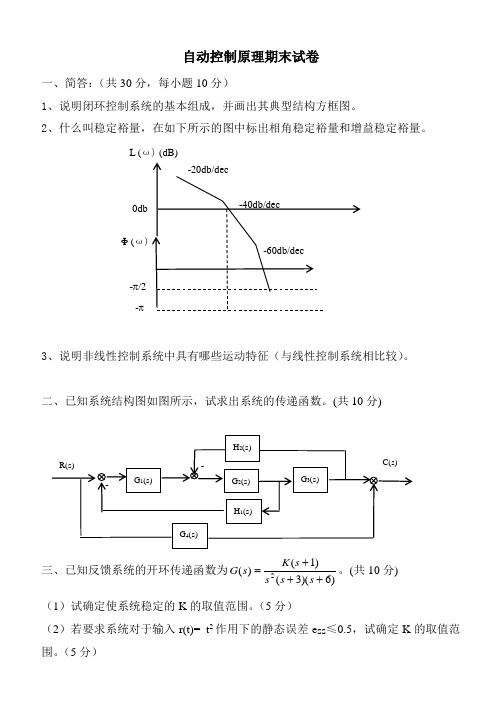
自动控制原理期末试卷一、简答:(共30分,每小题10分)1、说明闭环控制系统的基本组成,并画出其典型结构方框图。
2、什么叫稳定裕量,在如下所示的图中标出相角稳定裕量和增益稳定裕量。
3、说明非线性控制系统中具有哪些运动特征(与线性控制系统相比较)。
二、已知系统结构图如图所示,试求出系统的传递函数。
(共10分)三、已知反馈系统的开环传递函数为)6)(3()1()(2+++=s s s s K s G 。
(共10分) (1)试确定使系统稳定的K 的取值范围。
(5分)(2)若要求系统对于输入r(t)= t 2作用下的静态误差e SS ≤0.5,试确定K 的取值范围。
(5分)四、已知最小相位系统开环对数幅頻特性图如图所示,写出相应的传递函数。
(共10分)五、已知单位负反馈系统的开环传递函数为 )1)(1()(21++=s T s T s Ks G 。
(共10分)(1)试概略画出G (s )对应的Nyquist 图。
(5分) (2)由Nyquist 稳定判据给出闭环系统稳定的条件。
(5分) 六、已知系统的开环传递函数为)1()3(2)(+++=s s s s K s G )(绘制负反馈的根轨迹图,并确定使系统处于欠阻尼的K 值范围。
(共15分) 七、某采样控制系统的结构如图所示,已知τ=1,求: (1)求系统的脉冲传递函数。
(10分) (2)求系统稳定的K 值范围。
(5分)答案一、 简答:(共30分,每小题10分)1、答案:闭环控制系统的基本组成:检测元件、比较元件、放大元件、执行元件、给定元件、校正元件及被控对象。
(共6分,除被控对象外,每一个元件给1分)典型结构方框图(4分,可以没有局部反馈)2、答案:稳定裕量是系统距离稳定 的边界所具有的余量(5分)。
相角稳定裕量(3分)。
增益稳定裕量(2分)。
3、答案:与线性控制系统相比非线性控制系统表现出如下的特征: (1)非线性控制系统的运动不满足态的迭加原理。
自动控制原理期末试题3套及答案一套

⾃动控制原理期末试题3套及答案⼀套⾃动控制理论(A/B 卷闭卷)⼀、填空题(每空 1 分,共15分)1、反馈控制⼜称偏差控制,其控制作⽤是通过与反馈量的差值进⾏的。
2、复合控制有两种基本形式:即按的前馈复合控制和按的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联⽅式连接,其等效传递函数为()G s ,则G(s)为(⽤G 1(s)与G 2(s) 表⽰)。
4、典型⼆阶系统极点分布如图1所⽰,则⽆阻尼⾃然频率=n ω,阻尼⽐=ξ,该系统的特征⽅程为,该系统的单位阶跃响应曲线为。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为。
6、根轨迹起始于,终⽌于。
7、设某最⼩相位系统的相频特性为101()()90()tg tg T ?ωτωω--=--,则该系统的开环传递函数为。
8、PI 控制器的输⼊-输出关系的时域表达式是,其相应的传递函数为,由于积分环节的引⼊,可以改善系统的性能。
⼆、选择题(每题 2 分,共20分)1、采⽤负反馈形式连接后,则 ( )A 、⼀定能使闭环系统稳定;B 、系统动态性能⼀定会提⾼;C 、⼀定能使⼲扰引起的误差逐渐减⼩,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提⾼系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引⼊串联超前校正装置。
3、系统特征⽅程为 0632)(23=+++=s s s s D ,则系统 ( )A 、稳定;B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平⾯闭环极点数2=Z 。
4、系统在2)(t t r =作⽤下的稳态误差∞=ss e ,说明 ( )A 、型别2B 、系统不稳定;C 、输⼊幅值过⼤;D 、闭环传递函数中有⼀个积分环节。
5、对于以下情况应绘制0°根轨迹的是( )A 、主反馈⼝符号为“-” ;B 、除r K 外的其他参数变化时;C 、⾮单位反馈系统;D 、根轨迹⽅程(标准形式)为1)()(+=s H s G 。
自动控制原理-期末试卷及答案

自动控制原理-期末试卷及答案-CAL-FENGHAI.-(YICAI)-Company One1课程名称: 自动控制理论 (A/B 卷 闭卷) 考试时间 100分钟考生注意事项:1、本试卷共 2 页,试卷如有缺页或破损,请立即举手报告以便更换。
2、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。
3、答案请写在答题纸之密封线内和纸卷正面,否则不记分。
一、填空题(每空 1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 的前馈复合控制和按 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示, 则无阻尼自然频率=n ω , 阻尼比=ξ ,该系统的特征方程为 , 该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+, 则该系统的传递函数G(s)为 。
6、根轨迹起始于 ,终止于 。
7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 , 其相应的传递函数为 ,由于积分环节的引入,可以改善系统的 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( ) A 、稳定; B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平面闭环极点数2=Z 。
期末考试试题集-自动控制原理(含完整答案)

1 ,则该环节是( 5s 1
A. 比例环节
B. 积分环节
C. 惯性环节
D. 放大元件 )
D. 微分环节
6. 已知系统的微分方程为 3 x 0 t 6 x0 t 2 x 0 t 2 xi t ,则系统的传递函数是(
)
2 A.
3s2 6 s 2 2
C. 2 s2 6 s 3
1 B.
3s 2 6s 2 1
)
K
A.
Ts 1
sd
B.
s(s a)(s b)
K
C.
s( s a)
K D. s2 (s a)
15.
单位反馈系统开环传递函数为
Gs
4 s2 (s2 3s
,当输入为单位斜坡时,其加速度误差 2)
为( )
A.0
B.0.25
C.4
D.
16. 若已知某串联校正装置的传递函数为 A. 相位超前校正 B. 相位滞后校正
就可以判断其稳定性。
26. 一般讲系统的位置误差指输入是
所引起的输出位置上的误差。
27. 超前校正是由于正相移的作用,使截止频率附近的
明显上升,从而具有较大
的稳定裕度。
28. 二阶系统当共轭复数极点位于
线上时,对应的阻尼比为 0.707 。
29.PID 调节中的“P”指的是
控制器。
30. 若要求系统的快速性好,则闭环极点应距虚轴越
一个( )
A. 比例环节
B. 微分环节
C. 积分环节
D. 惯性环节
10
6. 若系统的开环传 递函数为
,则它的开环增益为( )
s(5s 2)
A.1
B.2
C.5
D.10
自动控制原理-期末试卷及答案

课程名称: 自动控制理论 (A/B 卷 闭卷) 考试时间 100分钟考生注意事项:1、本试卷共 2 页,试卷如有缺页或破损,请立即举手报告以便更换。
2、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。
3、答案请写在答题纸之密封线内和纸卷正面,否则不记分。
一、填空题(每空 1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 的前馈复合控制和按 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示, 则无阻尼自然频率=n ω , 阻尼比=ξ ,该系统的特征方程为 , 该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+, 则该系统的传递函数G(s)为 。
6、根轨迹起始于 ,终止于 。
7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 ,其相应的传递函数为 ,由于积分环节的引入,可以改善系统的 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( )A 、稳定;B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平面闭环极点数2=Z 。
(完整word版)自动控制原理试卷包含答案

自动控制原理试卷一. 是非题(5分):(1)系统的稳态误差有系统的开环放大倍数k 和类型决定的( );(2)系统的频率特性是系统输入为正弦信号时的输出( );(3)开环传递函数为)0(2>k s k 的单位负反馈系统能跟深速度输入信号( );(4)传递函数中的是有量纲的,其单位为 ( );(5)闭环系统的极点均为稳定的实极点,则阶跃响应是无 调的( );二. 是非题(5分):(1)为了使系统的过度过程比较平稳要求系统的相角裕量大于零( );(2)Bode 图的横坐标是按角频率均匀分度的,按其对数值标产生的( );(3)对于最小相位系统,根据对数幅频特性就能画出相频特性( );(4)单位闭环负反馈系统的开环传递函数为)()()(s D s N s G =,劳斯稳定判据是根据)(s D 的系数判闭环 系统的稳定性( );奈奎斯特稳定判据是根据)(s G 的幅相频率特性曲线判闭环系统的稳定性 ( )。
三. 填空计算题(15分):(1)如图所示:RC 网络,其输出)(t u c 与输入)(t u r 的微分方程描述为 ,假定在零初始条件下,系统的传递函数)(s φ= ,该系统在)(1)(t t u r =作用时,有)(t u c = 。
(2)系统结构如图,该系统是 反馈系统,是 阶系统,是 型系统,若要使系统的放大系数为1,调节时间为0.1秒(取%σ的误差带),0k 应为 ,t k 应为 。
(3)如果单位负反馈系统的开环传递函数是))(()()(b s a s c s k s G +++=,该系统是 阶系统,是 型系统,该系统的稳态位置误差系数为 ,稳态速度误差系数为 ,稳态加速度误差系数为速度误差系数为 。
四. 是非简答题(5分):(1)已知某系统的开环传递函数在右半s 平面的极点数为,试叙述Nyquist 稳定判据的结论。
(2)试叙述系统稳定的充分必要条件。
(3)系统的稳定性不仅与系统结构有关,而且与输入信号有关,该结论是否正确。
自动控制原理_期末试卷及答案

一、填空题(每空 1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过 给定值 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 输入 的前馈复合控制和按 扰动 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示, 则无阻尼自然频率=n ω ,阻尼比=ξ,该系统的特征方程为 , 该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105tt g t ee --=+,则该系统的传递函数G(s)为 。
6、根轨迹起始于 ,终止于 。
7、设某最小相位系统的相频特性为11()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 ,其相应的传递函数为 ,由于积分环节的引入,可以改善系统的稳态 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( )A 、稳定;B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平面闭环极点数2=Z 。
4、系统在2)(t t r =作用下的稳态误差∞=ss e ,说明 ( )A 、 型别2<v ;B 、系统不稳定;C 、 输入幅值过大;D 、闭环传递函数中有一个积分环节。
5、对于以下情况应绘制0°根轨迹的是( )A 、主反馈口符号为“-” ;B 、除r K 外的其他参数变化时;C 、非单位反馈系统;D 、根轨迹方程(标准形式)为1)()(+=s H s G 。
期末考试试卷试题集自动控制原理含完整包括答案.docx

WORD格式.期末考试 - 复习重点自动控制原理1一、单项选择题(每小题 1 分,共20 分)1.系统和输入已知,求输出并对动态特性进行研究,称为()A. 系统综合B. 系统辨识C. 系统分析D. 系统设计2.惯性环节和积分环节的频率特性在()上相等。
A. 幅频特性的斜率B. 最小幅值C. 相位变化率D. 穿越频率3. 通过测量输出量,产生一个与输出信号存在确定函数比例关系值的元件称为()A. 比较元件B.给定元件C. 反馈元件D. 放大元件ω从 0变化到 + ∞时,延迟环节频率特性极坐标图为4. ()A. 圆B.半C. 椭圆D. 双曲线圆5.当忽略电动机的电枢电感后,以电动机的转速为输出变量,电枢电压为输入变量时,电动机可看作一个()A. 比例环节B. 微分环节C. 积分环节D. 惯性环节10,则它的开环增益为6. 若系统的开环传递函数为()s(5s2)A.1B.2C.5D.1057. 二阶系统的传递函数G ( s),则该系统是()A. 临界阻尼系s22s 5D. 零阻尼系B. 欠阻尼系统 C. 过阻尼系统统统8.若保持二阶系统的ζ 不变,提高ω n,则可以()A. 提高上升时间和峰值时间B. 减少上升时间和峰值时间C. 提高上升时间和调整时间D. 减少上升时间和超调量9. 一阶微分环节 G1(s) 1 Ts ,当频率时,则相频特性 G ( j) 为()TA.45 °B. -45 °C.90 °D. -90°专业资料整理WORD格式.....专业资料整理WORD格式.10.最小相位系统的开环增益越大,其()B.稳定裕量越A. 振荡次数越多大D.稳态误差越C. 相位变化越小小11. 设系统的特征方程D ss48s3 17s 20 ,则此系统为16 s 5 ()A. 稳定B.临界稳C. 不稳定D. 稳定性不确定。
定k)时,闭环系统临界稳12. 某单位反馈系统的开环传递函数为:G s,当 k= (定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称: 自动控制理论 (A/B 卷 闭卷) 考试时间 100分钟考生注意事项:1、本试卷共 2 页,试卷如有缺页或破损,请立即举手报告以便更换。
2、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。
3、答案请写在答题纸之密封线内和纸卷正面,否则不记分。
一、填空题(每空 1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 的前馈复合控制和按 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示, 则无阻尼自然频率=n ω , 阻尼比=ξ ,该系统的特征方程为 , 该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+, 则该系统的传递函数G(s)为 。
6、根轨迹起始于 ,终止于 。
7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 , 其相应的传递函数为 ,由于积分环节的引入,可以改善系统的 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( ) A 、稳定; B 、单位阶跃响应曲线为单调指数上升; C 、临界稳定; D 、右半平面闭环极点数2=Z 。
4、系统在2)(t t r =作用下的稳态误差∞=ss e ,说明 ( )A 、 型别2<v ;B 、系统不稳定;C 、 输入幅值过大;D 、闭环传递函数中有一个积分环节。
5、对于以下情况应绘制0°根轨迹的是( )A 、主反馈口符号为“-” ;B 、除r K 外的其他参数变化时;C 、非单位反馈系统;D 、根轨迹方程(标准形式)为1)()(+=s H s G 。
6、开环频域性能指标中的相角裕度γ对应时域性能指标( ) 。
A 、超调%σB 、稳态误差ss eC 、调整时间s tD 、峰值时间p t 7、已知开环幅频特性如图2所示, 则图中不稳定的系统是( )。
系统① 系统② 系统③图2A 、系统①B 、系统②C 、系统③D 、都不稳定8、若某最小相位系统的相角裕度0γ>o,则下列说法正确的是 ( )。
A 、不稳定;B 、只有当幅值裕度1g k >时才稳定;C 、稳定;D 、不能判用相角裕度判断系统的稳定性。
9、若某串联校正装置的传递函数为101 1001ss++,则该校正装置属于( )。
A、超前校正B、滞后校正C、滞后-超前校正D、不能判断10、下列串联校正装置的传递函数中,能在1cω=处提供最大相位超前角的是:A、1011ss++B、1010.11ss++C、210.51ss++D、0.11101ss++三、(8分)试建立如图3所示电路的动态微分方程,并求传递函数。
图3四、(共20分)系统结构图如图4所示:1、写出闭环传递函数()()()C ssR sΦ=表达式;(4分)2、要使系统满足条件:707.0=ξ,2=nω,试确定相应的参数K和β;(4分)3、求此时系统的动态性能指标st,σ;(4分)4、ttr2)(=时,求系统由()r t产生的稳态误差sse;(4分)5、确定)(sGn,使干扰)(tn对系统输出)(tc无影响。
(4分)五、(共15分)已知某单位反馈系统的开环传递函数为2()(3)rKG ss s=+:1、绘制该系统以根轨迹增益K r为变量的根轨迹(求出:渐近线、分离点、图4与虚轴的交点等);(8分)2、确定使系统满足10<<ξ的开环增益K 的取值范围。
(7分)六、(共22分)某最小相位系统的开环对数幅频特性曲线0()L ω如图5所示:1、写出该系统的开环传递函数)(0s G ;(8分)2、写出该系统的开环频率特性、开环幅频特性及开环相频特性。
(3分)3、求系统的相角裕度γ。
(7分)4、若系统的稳定裕度不够大,可以采用什么措施提高系统的稳定裕度?(4分)试题一答案一、填空题(每题1分,共15分)1、给定值2、输入;扰动;3、G 1(s)+G 2(s);4、2;20.707=;2220s s ++=;衰减振荡 5、1050.20.5s s s s+++;6、开环极点;开环零点7、(1)(1)K s s Ts τ++8、1()[()()]p u t K e t e t dt T =+⎰;1[1]p K Ts+; 稳态性能二、判断选择题(每题2分,共 20分)1、D2、A3、C4、A5、D6、A7、B8、C9、B 10、B三、(8分)建立电路的动态微分方程,并求传递函数。
解:1、建立电路的动态微分方程 根据KCL有200i 10i )t (u )]t (u )t (d[u )t (u )t (u R dt C R =-+-(2分)即 )t (u )t (du )t (u )()t (du i 2i 21021021R dtC R R R R dt C R R +=++ (2分)2、求传递函数对微分方程进行拉氏变换得)(U )(U )(U )()(U i 2i 21021021s R s Cs R R s R R s Cs R R +=++ (2分)得传递函数 2121221i 0)(U )(U )(R R Cs R R R Cs R R s s s G +++==(2分)四、(共20分)解:1、(4分) 22222221)()()(n n n s s K s K s K sK s K s Ks R s C s ωξωωββ++=++=++==Φ 2、(4分) ⎩⎨⎧=====2224222n n K K ξωβω ⎩⎨⎧==707.04βK3、(4分) 0010032.42==--ξξπσe83.2244===ns t ξω4、(4分) )1(1)(1)(2+=+=+=s s K s s K sK s K s G βββ ⎩⎨⎧==11v K K β414.12===βKss K Ae 5、(4分)令:0)()(11)()()(=s s G ss K s N s C s n n ∆-⎪⎭⎫ ⎝⎛+==Φβ 得:βK s s G n +=)(五、(共15分)1、绘制根轨迹 (8分)(1)系统有有3个开环极点(起点):0、-3、-3,无开环零点(有限终点);(1分)(2)实轴上的轨迹:(-∞,-3)及(-3,0); (1分)(3) 3条渐近线: ⎪⎩⎪⎨⎧︒︒±-=--=180,602333a σ (2分) (4) 分离点: 0321=++d d 得: 1-=d (2分)432=+⋅=d d K r (5)与虚轴交点:096)(23=+++=r K s s s s D[][]⎩⎨⎧=+-==+-=06)(Re 09)(Im 23r K j D j D ωωωωω ⎩⎨⎧==543r K ω (2分) 绘制根轨迹如右图所示。
2、(7分)开环增益K 与根轨迹增益K r 的关系:⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+=139)3()(22s s K s s K s G rr 得9rK K = (1分)系统稳定时根轨迹增益K r 的取值范围:54<r K , (2分)系统稳定且为欠阻尼状态时根轨迹增益K r 的取值范围:544<<r K , (3分)系统稳定且为欠阻尼状态时开环增益K 的取值范围:694<<K (1分) 六、(共22分)解:1、从开环波特图可知,原系统具有比例环节、一个积分环节、两个惯性环节。
故其开环传函应有以下形式 12()11(1)(1)KG s s s s ωω=++ (2分)由图可知:1ω=处的纵坐标为40dB, 则(1)20lg 40L K ==, 得100K = (2分)1210ωω=和=100 (2分)故系统的开环传函为 ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=1100110100)(0s s s s G (2分)2、写出该系统的开环频率特性、开环幅频特性及开环相频特性: 开环频率特性 0100()1110100G j j j j ωωωω=⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭(1分)开环幅频特性0()A ω=(1分)开环相频特性: 110()900.10.01s tg tg ϕωω--=---o (1分)3、求系统的相角裕度γ:求幅值穿越频率,令0()1A ω== 得31.6/c rad s ω≈(3分)11110()900.10.0190 3.160.316180c c c tg tg tg tg ϕωωω----=---=---≈-o o o (2分) 0180()1801800c γϕω=+=-=o o o (2分)对最小相位系统0γ=o临界稳定4、(4分)可以采用以下措施提高系统的稳定裕度:增加串联超前校正装置;增加串联滞后校正装置;增加串联滞后-超前校正装置;增加开环零点;增加PI 或PD 或PID 控制器;在积分环节外加单位负反馈。
