一种简易的方法求解流量有上下界的网络中网络流问题

合集下载

最大流在信息学竞赛中应用的一个模型--江涛

最大流在信息学竞赛中应用的一个模型江涛关键字：网络可行流最大流附加网络无源汇必要弧流的分离有上下界的最大流建模引言：最大流类的模型在当今信息学比赛中有相当广泛的应用。

但在教学中，发现很多同学对流模型的原理和变形并不掌握，只是记下经典的算法和题目，以便比赛中套用。

这当然有很大的局限性，也不是学习之正道。

本讲想通过对最大流模型，特别是附加网络的一些分析、讨论，达到抛砖引玉目的。

一、网络与流的概念一个实例：运输网络图1.1网络定义：●一个有向图G=(V，E)；●有两个特别的点：源点s、汇点t；●图中每条边(u,v)∈E，有一个非负值的容量C(u,v)记为G=(V，E，C)网络三要素：点、边、容量可行流定义：是网络G上的一个“流”，即每条边上有个“流量”P(u,v)，要满足下面两个条件：流的容量限制---弧：),(),(0vuCvuP≤≤对任意弧(u,v)---有向边流的平衡---点：除源点和汇点，对任意中间点有：流入u的“流量”与流出u的“流量”相等。

即：},{t sVu-∈∀有∑∑∈∈=-VxVxx u PuxP0),(),(网络的流量：源点的净流出“流量” 或汇点的净流入“流量”。

即：∑∑∑∑∈∈∈∈-=-Vx Vx Vx Vx x t P t x P s x P x s P ),(),(),(),(注意，我们这里说的流量是一种速率，而不是指总量。

联系上面所说的实例，下面是一个流量为1的可行流：图1.2标准图示法：图1.3例1.1有一个n*m的国际棋盘，上面有一些格子被挖掉，即不能放棋子，现求最多能放多少个棋子“车”，并保证它们不互相攻击(即：不在同一行，也不在同一列)？分析：1)行、列限制---最多只能一个车控制；2)车对行、列的影响---一个车控制一个行和边；例子：图1.4图1.5显然，我们要求车最多，也就是求流量最大---最大流问题。

下面是一个解：图1.6即(1,3)、(2,1)、(3,2)格上各放一个车，可得到一个最优方案。

有上下界网络最大流与最小截问题

（．Ｄｐｒｎｏ１ｅａｔｔｆＭａｈｍｔｓＮｎｈｎｎｖｒｔ，ａｃａｇ３０３，ｈｎ；．ＩｔｕｅｏＳｓｍｅｔｅａｉ，ａｃａｇＵｉｓｙＮｎｈｎ３０１Ｃｉ２ｎｉｔｆｙ— ｃｅｉａｓｔ
ｔｎｉｅｒｇＮｎｈｎｎｅｉ，ａｃａｇ３０３，ｈｎ）ｅＥｇｎｅｎ，ａｃａｇＵｉｒｔＮｎｈｎ３０Ｃｉａｎｒｉｖｓｙ１
ＡｂｔａｔＦｒｃｎｅｉｎｅｔｕｌｅｉｉｎｓｐｏｙｔｍｅａｉｅｔｈｒｂｅｏｘｍｕｆｗ＆ｍｉｍｕｓｒｃ：ｏｏｖｎｅｃｏｂｉｄｃｓｏｕｐｒｓｓｅｒｌｔｖｏｔｅｐｏｌｍｆｍａｉｍｏｄｔｌｎｉｍ
ＰｒｂｅｏｘｍｕＦｏ＆ＭｉｉｕＣｕｔｏｏｌｍｆＭａｉｍｌｗｎｍｍｔＳｅｆＮｅｗｏｋｗｉｏｒ＆ＵｐｅｃＣａａｉｅｔｒｔＬｗｅｈｐｒＡｒｐｃｔｓｉ
ＸＩａ．ｏｇＥＦｎｒｎ，ＪＡｎ．ｎＩＲｅａ
关键词：筹学；策支持系统；运决数值实验；上下界网络；大流；小截；小饱和流有最最最
中图分类号：９５２４Ｎ４；０２
文章标识码：Ａ
文章编号：０７３２（０８０．０４０１０．ｏｅｗｈｌｅｓｂｅｓｌｔｎｅｉｔ，ａｄｈｓｇｏｅｏｍａｃｎｔｅｓｎｅｏｅｎｍｐｅｎｅｎｉｎｔｈｒｂｌｍｉｅａｆａｉｌｏｕｉｘｓｓｎａｏｄｐｒｒｎｅｉｈｅｓｆｂｉｇｉｌｍｅｔｄｏｏｆ

网络流问题及其求解方法

网络流问题及其求解方法网络流问题是指在一个有向图中，给定网络的容量限制，找到从源点到汇点的最大流量。

这个问题在实际生活中有着广泛的应用，比如在运输、通信、电力等领域。

本文将介绍网络流问题以及几种常见的求解方法。

1. 网络流问题的定义网络流问题可以用有向图来表示。

图中的每条边具有一个容量，表示该边能够通过的最大流量。

同时，图中有一个源点，表示流量的起点，以及一个汇点，表示流量的终点。

问题的目标是找到从源点到汇点的最大流量。

2. 求解方法一：最短增广路径算法最短增广路径算法是一种基于广度优先搜索的方法。

算法的思想是在图中不断寻找增广路径，即从源点到汇点且每条边的流量都满足容量限制的路径。

然后通过增加路径上的流量来更新网络的流量，并继续寻找下一个增广路径。

直到找不到增广路径为止，即可得到最大流量。

3. 求解方法二：最大流-最小割定理最大流-最小割定理是网络流问题的一个重要性质。

该定理指出，网络的最大流量等于它的最小割。

最小割是指将网络分成两个部分，一部分包含源点，另一部分包含汇点，并且割边的总容量最小。

根据该定理，可以通过寻找最小割来求解网络流问题。

4. 求解方法三：Ford-Fulkerson算法Ford-Fulkerson算法是一种经典的求解网络流问题的方法。

该算法通过不断寻找增广路径来更新网络的流量，直到无法再找到增广路径为止。

算法的关键在于如何选择增广路径，一种常见的选择策略是使用深度优先搜索。

Ford-Fulkerson算法的时间复杂度与最大流的大小有关，一般情况下为O(fE)，其中f为最大流量，E为图中边的数量。

总结：网络流问题是一个重要的优化问题，在实际应用中具有广泛的应用。

本文介绍了网络流问题的定义以及几种常见的求解方法，包括最短增广路径算法、最大流-最小割定理和Ford-Fulkerson算法。

这些算法都可以有效地求解网络流问题，并在实践中得到广泛应用。

通过研究网络流问题及其求解方法，可以为实际问题的建模和解决提供有力的工具。

网络流算法的实现与应用

网络流算法的实现与应用网络流算法是图论中的一类重要算法，通过对网络中流的分配与调度来解决相关问题。

本文将探讨网络流算法的实现原理与应用场景。

一、网络流算法概述网络流算法主要处理的是“网络流”问题，即在一个图论模型中，寻找一种边的流动方式，使得源点到汇点的流量最大化或者达到某种要求。

常见的网络流算法包括最大流算法、最小割算法和最大权闭合子图算法等。

二、网络流算法的实现1. 最大流算法最大流算法旨在寻找网络中从源点到汇点的最大流量。

其中，最常用的算法是Edmonds-Karp算法，它是基于BFS（广度优先搜索）的增广路径寻找。

在实现过程中，可以使用图的邻接矩阵或邻接表来表示网络，利用算法的迭代思想不断寻找增广路径，并同时更新网络中的流量与残余容量，直到无法找到增广路径为止。

2. 最小割算法最小割算法用于求解网络中的最小割问题，即将网络分割为两个部分，使得切开的边的权值之和最小。

其中，Ford-Fulkerson算法是经典的最小割算法之一。

在实现过程中，可以通过DFS（深度优先搜索）或BFS寻找增广路径，并不断更新割与割集，直到最小割的权值无法再减小。

3. 最大权闭合子图算法最大权闭合子图算法用于求解有向图中的最大权闭合子图问题，其中闭合子图是指若干个节点的集合，对于任意一对节点u和v，如果存在一条从u到v的有向边，则u必定属于闭合子图中。

在实现过程中，可以使用Bellman-Ford算法来寻找最短路径，并通过路径上的正权重进行子图的扩展，最终得到最大权闭合子图。

三、网络流算法的应用网络流算法具有广泛的应用场景，以下介绍几个常见的应用领域：1. 传输网络规划网络流算法可以用于解决最大流问题，从而优化传输网络的规划。

例如，在通信网络中，可以通过最大流算法来确定最大传输容量，从而提高网络的传输效率。

2. 作业调度网络流算法可以用于解决作业调度问题，例如在工业生产中，通过最大流算法来确定最大的作业处理能力，从而提高生产效率。

最大流算法解决最小割问题及网络流问题

最大流算法解决最小割问题及网络流问题最大流算法（maximum flow algorithm）是解决网络流问题的一种常用方法。

网络流问题是指在一个有向图中，每条边都有一个容量限制，要求在源点和汇点之间找到一条路径，使得路径上每条边的流量都不超过其容量限制，同时保证从源点流出的总流量最大。

最小割问题（minimum cut problem）是网络流问题的一个相关概念。

在一个有向图中，边上的容量表示其最大流量限制，我们需要找到一条割（cut），将图分为两个部分，并使得割的容量最小。

割的容量是指割中每条边的容量之和。

最大流算法可以解决最小割问题。

常用的最大流算法包括Ford-Fulkerson算法和Edmonds-Karp算法。

Ford-Fulkerson算法是一种经典的最大流算法。

它通过不断寻找增广路径来更新流的值，直到无法找到增广路径为止。

增广路径是一条从源点到汇点的路径，其上每条边的剩余容量都大于0，并且路径上的流量不超过容量限制。

Edmonds-Karp算法是基于Ford-Fulkerson算法的一种优化方法。

它使用广度优先搜索（BFS）来寻找增广路径，可以保证在每次寻找增广路径时更新的流量最小。

最大流算法的应用非常广泛。

例如，可以使用最大流算法来优化交通流量，解决作业分配问题，以及在计算机网络中进行路由和流量控制等。

总结起来，最大流算法是解决最小割问题和网络流问题的一种常用方法。

通过寻找增广路径来更新流的值，最大流算法可以在保证路径上每条边的流量不超过容量限制的前提下，使得从源点流出的总流量最大化。

局域网网络流量分析方法

局域网网络流量分析方法在当今互联网发展迅猛的时代，局域网已经成为公司、学校及家庭之间进行信息共享和通信的重要工具。

然而，对于网络管理员来说，了解和分析局域网的网络流量是非常重要的，因为它可以提供有价值的数据用于网络优化、故障排除和安全监控。

因此，本文将介绍几种常用的局域网网络流量分析方法。

一、抓包分析抓包分析是最常见也是最直接的方法之一，它通过截获和分析传输在局域网上的数据包来获取流量信息。

网络管理员可以使用抓包工具，如Wireshark或tcpdump，在局域网上进行数据包捕捉，并对数据包进行解析和分析。

抓包分析可以提供详细的数据包信息，包括源IP地址、目标IP地址、协议类型、数据包大小、传输时间等，这些信息可以帮助管理员了解局域网上的流量分布和流量使用情况。

二、流量监测工具除了抓包分析外，流量监测工具也是一种常用的网络流量分析方法。

流量监测工具可以实时监测和记录局域网上的网络流量数据，并提供可视化的图表和统计信息。

通过使用流量监测工具，管理员可以轻松地查看和分析局域网上的流量趋势、流量峰值和流量来源，以便更好地规划和优化网络资源。

三、流量分析算法除了使用工具进行抓包和监测之外，还可以使用流量分析算法来对局域网的网络流量进行统计和分析。

例如，常用的流量分析算法有：1. 度数中心性算法：通过统计节点的连接数量来衡量其在网络流量中的重要性，进而确定网络中的关键节点；2. PageRank算法：基于链接分析的方法，根据节点之间的链接关系和流量流动情况，评估节点的重要性；3. 聚类分析算法：通过将节点划分为不同的群组来分析网络流量的结构和特征。

这些流量分析算法可以帮助管理员深入理解局域网的流量特征和流量分布，为网络优化和规划提供决策支持。

综上所述，局域网网络流量分析是网络管理员必备的技能之一。

通过抓包分析、流量监测工具和流量分析算法等方法，管理员可以全面了解局域网上的流量情况，促进网络优化和故障排除。

网络流算法

最大流算法

第1步，令x=(xij)是任意整数可行流，可能是零流，给s一个永久标号(-, ∞)。第2步(找增广路)，如果所有标号都已经被检查，转到第4步。找到一个标号但未检查的点i, 并做如下检查，

对每一个弧(i,j),如果xij<Cij, 且j未标号,则给j一个标号(+i, δ(j) ),其中， δ(j)=min{Cij-xij , δ(i) } 对每一个弧(j, i),如果xji>0,且j未标号，则给j一个标号(-i, δ(j) ),其中， δ(j)=min{xji , δ(i) }
定理1：对于已知的网络流图，设任意一可行流为f，任意一割切为(U, W)，必有：V(f) ≤ C(U, W)。定理2：可行流f是最大流的充分必要条件是：f中不存在可改进路。定理3：整流定理。如果网络中所有的弧的容量是整数，则存在整数值的最大流。定理4：最大流最小割定理。最大流等于最小割，即max V(f) = min C(U, W)。
剩余图(残余网络)

剩余图G’=(V,E’) 流量网络G=(V,E)中，对于任意一条边(a,b)，若 flow(a,b)<capacity(a,b) or 则(a,b)∈ E’ flow(b,a)>0
可以沿着a--->b 方向增广
剩余图的权值代表能沿边增广的大小
有向图剩余图

DINIC算法演示：
3 源点 4 2 2
找到增广路路线， 2 （红色路线）汇点 5
对增广路进行增广，增广后退回到源点 3 2 汇点
找到增广路路线，（红色路线） 3 2 3 2 对增广路进行增广，增广后退回到源点，再无增广路线汇点 1 汇点

有上下界网络流问题

有上下界网络流问题1.无源汇最大流2.有源汇最大流3.有源汇最小流1.无源汇最大流问题sgu194题意：给n个点，及m根pipe，每根pipe用来流躺液体的，单向的，每时每刻每根pipe 流进来的物质要等于流出去的物质，要使得m条pipe组成一个循环体，里面流躺物质。

并且满足每根pipe一定的流量限制，范围为[Li,Ri].即要满足每时刻流进来的不能超过Ri(最大流问题)，同时最小不能低于Li。

例如：46(4个点，6个pipe)12 1 3 (1->2上界为3，下界为1)23 1 33 4 1 34 1 1 31 3 1 34 2 1 3可行流：再如：所有pipe的上界为2下界为1的话，就不能得到一种可行流。

题解：上界用ci表示，下界用bi表示。

下界是必须流满的，那么对于每一条边，去掉下界后，其自由流为ci– bi。

主要思想：每一个点流进来的流=流出去的流对于每一个点i，令Mi= sum(i点所有流进来的下界流)– sum(i点所有流出去的下界流)如果Mi大于0，代表此点必须还要流出去Mi的自由流，那么我们从源点连一条Mi 的边到该点。

如果Mi小于0，代表此点必须还要流进来Mi的自由流，那么我们从该点连一条Mi 的边到汇点。

如果求S->T的最大流，看是否满流(S的相邻边都流满)。

满流则有解，否则无解。

2.有源汇最大流zoj3229题意：经过构图之后得到这样的问题，源点s，汇点t，有些边有上下界[Li,Ri].求s->t 的最大流。

题解：满足所有下界的情况下，判断是否存在可行流，方法可以转化成上面无源汇上下界判断方法。

只要连一条T→S的边，流量为无穷，没有下界，那么原图就得到一个无源汇的循环流图。

接下来的事情一样：原图中的边的流量设成自由流量ci– bi。

新建源点SS 汇点TT，求Mi，连边。

然后求SS→TT最大流，判是否满流。

判定有解之后然后求最大流，信息都在上面求得的残留网络里面。

几种限流算法及实现方式

几种限流算法及实现方式
常见的限流算法包括计数器算法、漏桶算法、令牌桶算法、固定窗口算法、滑动窗口算法。

1、计数器算法：这是一种简单且容易实现的限流算法。

通过在系统内设置每N秒的访问量，超过这个访问量的访问直接丢弃，从而实现限流访问。

具体实现时，可以将时间划分为固定的窗口大小，例如1秒，在窗口时间段内，每来一个请求就对计数器加1，当计数器达到设定的时间限制之后，则抛弃超出的请求。

2、漏桶算法：漏桶算法是一种流量控制算法，用于控制流入网络的数据速率，以防止网络拥塞。

它的思想是将数据包看作是水滴，漏桶看作是一个固定容量的容器，水流进桶的速度可以是随机的，但是水流出桶的速度是恒定的。

当水流进桶的速度较慢，桶不会被填满，请求就可以被处理。

当水流进桶的速度过快时，桶会逐渐被填满，当水超过桶的容量就会溢出，即被丢弃。

3、令牌桶算法：令牌桶算法是网络流量整形（Traffic Shaping）和速率限制（Rate Limiting）中最常使用的一种算法。

它通过生成令牌来控制数据包的发送速率，令牌桶算法允许系统在一定时间内处理超出正常速率的数据包，从而实现平滑的流量控制。

4、固定窗口算法：这种算法通过维护一个计数器，在单位时间内记录该窗口接受请求的次数。

当次数少于限流阈值时，就允许访问，并且计数器加1；当次数大于限流阈值时，就拒绝访问。

当前的时间窗口过去之后，计数器清零。

5、滑动窗口算法：滑动窗口算法通过维护一个时间窗口来控制单位时间内请求的数量。

它统计时间窗口内的请求次数，并根据预设的阈值来决定是否允许新的请求通过。

这种方式没有了时间窗口突变的问题，限流比较准确。

如何使用网络流量分析技术解决网络拥堵症结(八)

网络拥堵是我们在日常使用互联网时经常遇到的问题。

当我们打开网页或下载文件时，经常会遇到网速慢、加载缓慢的情况。

而作为一名网络技术人员，我们可以借助网络流量分析技术来解决这一问题。

网络流量分析技术是一种通过监控和分析网络流量来获取关于网络活动的信息的技术。

通过对网络数据包进行分析，可以了解网络中存在的拥堵症结，并制定相应的解决方案。

下面将介绍如何使用网络流量分析技术来解决网络拥堵的问题。

首先，我们可以通过网络流量分析来确定网络拥堵的原因。

网络拥堵的原因有很多，可能是网络带宽不足，也可能是网络设备负载过高，还可能是网络协议存在问题等。

通过对网络流量进行分析，我们可以追踪到具体的拥堵点，找出造成网络拥堵的具体原因。

其次，我们可以通过网络流量分析来优化网络拓扑结构。

网络拓扑结构决定了网络中各个节点之间的连接方式。

通过网络流量分析，我们可以了解到哪些节点之间存在高负载、数据传输较慢等问题，然后可以选择合适的调整方案，例如增加带宽、优化路由等，以提高网络的性能和效率。

此外，网络流量分析也可以帮助我们发现网络中可能存在的安全威胁。

通过对网络流量进行监控和分析，可以检测到异常流量或恶意攻击，如DDoS攻击、网络钓鱼等。

及早发现并采取相应的防护措施，可以保护网络的安全和稳定。

除了以上几点，网络流量分析还可以帮助我们进行容量规划。

通过对网络流量的监控和分析，我们可以获得网络使用情况的历史数据和趋势，从而可以预测未来的网络需求，并做出相应的容量规划。

这样可以避免网络持续发生拥堵问题，保障网络的稳定性和可扩展性。

然而，要想充分发挥网络流量分析技术的作用，我们也需要一些前提条件。

首先，网络流量监测设备是必需的，如流量监测器、数据包捕获器等。

其次，我们需要分析这些数据所需的工具和技术，如网络流量分析软件、统计学方法等。

最后，专业的网络技术人员和团队是必不可少的，他们需要具备一定的网络知识和技能，才能准确分析和解决网络拥堵问题。

如何使用二进制搜索算法解决网络流问题

如何使用二进制搜索算法解决网络流问题网络流问题是计算机科学中的一个重要问题，它在各个领域都有广泛的应用。

解决网络流问题的算法有很多种，其中二进制搜索算法是一种高效且常用的方法。

本文将介绍二进制搜索算法的原理和应用，以及如何使用它来解决网络流问题。

一、二进制搜索算法的原理二进制搜索算法是一种分而治之的思想，在解决网络流问题中具有很大的优势。

它的基本原理是将问题的解空间划分为若干个子空间，并通过二进制搜索的方式逐步缩小解空间，最终找到问题的解。

具体来说，二进制搜索算法的步骤如下：1. 确定问题的解空间。

网络流问题的解空间通常是一个有界的整数区间，比如某个网络中的最大流量限制。

2. 将解空间划分为两个子空间。

根据问题的特点，可以选择合适的划分方式，比如将解空间一分为二。

3. 判断问题的解是否在某个子空间中。

通过对子空间中的解进行检验，可以确定问题的解是否在该子空间中。

4. 缩小解空间。

根据判断结果，可以舍弃某个子空间，从而缩小解空间。

5. 重复步骤2-4，直到找到问题的解。

二、二进制搜索算法在网络流问题中的应用二进制搜索算法在网络流问题中有广泛的应用，其中最常见的是在最大流问题中的应用。

最大流问题是指在一个网络中找到从源点到汇点的最大流量。

使用二进制搜索算法解决最大流问题的步骤如下：1. 确定最大流量的上下界。

最大流量的上界通常是网络中的最大容量，下界可以根据实际情况确定。

2. 将最大流量的上下界进行二进制搜索。

假设当前搜索的最大流量为x，通过网络流算法计算出该最大流量下的网络流。

3. 判断最大流量是否达到上界。

如果达到上界，则缩小最大流量的上界，否则增大最大流量的下界。

4. 重复步骤2-3，直到找到最大流量。

三、使用二进制搜索算法解决网络流问题的优势二进制搜索算法在解决网络流问题中具有以下优势：1. 高效性。

二进制搜索算法通过逐步缩小解空间，能够快速找到问题的解。

2. 精确性。

二进制搜索算法能够精确地找到问题的解，不会出现遗漏或错误的情况。

如何使用网络流量分析技术解决网络拥堵症结

网络拥堵症结是当前互联网发展中的一个严峻问题。

随着人们对互联网的依赖度越来越高，网络带宽的需求也与日俱增。

然而，互联网的基础设施并没有跟上这一步伐，导致网络拥堵问题日益突出。

在这种背景下，网络流量分析技术的应用成为解决网络拥堵症结的有效途径。

首先，网络流量分析技术能够帮助我们识别网络拥堵的源头。

通过对网络中的数据流进行监测和分析，可以准确地定位网络拥堵所在。

通过这种方式，网络运营商和网络管理员能够及时采取相应的措施，来解决网络拥堵问题。

例如，他们可以调整网络设备的配置，增加网络带宽，或者优化路由算法，以提高网络的传输效率。

其次，网络流量分析技术还可以帮助我们优化网络资源的分配。

通过分析网络流量，我们可以了解网络中不同应用程序或服务的使用情况，以及用户的使用习惯。

在此基础上，网络运营商和服务提供商可以根据不同应用的需求，合理分配网络资源。

例如，他们可以将更多的带宽分配给热门应用或者高价值用户，以提高用户体验和满足用户需求。

此外，网络流量分析技术还可以帮助我们发现网络中的异常流量和网络攻击。

通过对网络流量进行实时监测和分析，可以及时发现网络中的异常行为。

这些异常行为可能是网络攻击的迹象，如DDoS攻击、流量劫持等。

通过分析异常流量的特征和行为模式，网络管理员可以采取相应的防御措施，保护网络安全，维护网络正常运行。

此外，网络流量分析技术的应用还可以帮助我们对网络拥堵问题进行预测和预防。

通过对历史流量数据的分析，我们可以发现网络流量的增长趋势，以及网络拥堵的诱因。

在此基础上，网络运营商和服务提供商可以做出相应的规划和调整，以应对未来的网络拥堵问题。

例如，他们可以提前增加网络带宽，优化网络拓扑结构，或者引入新的网络技术和协议，以提升网络的容量和稳定性。

总之，网络流量分析技术是解决网络拥堵症结的有力工具。

通过对网络中的流量进行监测、分析和优化，我们可以准确地识别网络拥堵的源头，优化网络资源的分配，发现和应对网络攻击，预测和预防网络拥堵问题。

如何使用网络流量分析技术解决网络拥堵问题(五)

网络流量分析技术在解决网络拥堵问题中扮演着重要角色。

随着互联网的快速发展，网络拥堵问题愈发突出，我们需要借助先进的技术手段来解决这一挑战。

本文将深入探讨如何使用网络流量分析技术来缓解网络拥堵问题，并介绍其原理、方法和应用。

一、网络流量分析技术的原理网络流量分析技术是通过对网络流量数据进行监测、收集、分析和处理，以获得对网络流量特征的认识和理解的一种技术手段。

它主要基于网络流量数据包的抓取和分析，通过对网络流量的监测和分析，获取网络流量的实时状态、流量分布特征、流量类型等信息，从而为网络拥堵问题提供解决方案。

二、网络流量分析技术的方法1. 数据包捕获和分析网络流量分析的基础是对网络数据包的捕获和分析。

通过使用网络流量分析工具，可以实时抓取网络数据包，并对其进行深入分析，包括解析数据包的协议信息、源IP地址和目的IP地址、数据包大小等。

通过对数据包的分析，可以获得网络的流量分布情况和流量特征，从而为后续的网络优化提供参考依据。

2. 流量监测和识别为了解决网络拥堵问题，需要对网络流量进行实时的监测和识别。

流量监测可以通过部署流量监测设备或使用网络流量分析工具来实现。

通过监测网络流量，可以了解网络流量的变化趋势和峰值，从而及时发现网络拥堵问题，并进行相应的优化调整。

3. 流量调度和优化通过对网络流量进行分析，可以了解网络流量的分布情况和瓶颈节点，从而进行流量调度和优化。

流量调度可以通过调整网络路由、负载均衡等手段来实现，以实现流量的均衡分配和优化路由选择。

同时，还可以通过网络带宽的扩容、网络设备的升级等措施，提升网络的吞吐量和处理能力。

三、网络流量分析技术的应用1. 网络安全网络流量分析技术可以帮助识别网络攻击行为和异常流量，并进行相应的安全策略调整。

通过对网络流量的实时监测和分析，可以提前发现潜在的网络攻击，并采取相应的措施进行应对。

2. 网络性能优化通过网络流量分析，可以了解网络的瓶颈节点和负载情况，从而进行性能优化。

网络架构中的网络流量分析工具与方法介绍(四)

网络架构中的网络流量分析工具与方法介绍随着互联网的快速发展，网络架构中的网络流量分析工具与方法变得越来越重要。

在如今的数字化时代，网络流量分析既是确保网络安全的必备手段，也是优化网络性能的重要工具。

本文将介绍几种常用的网络流量分析工具与方法。

一、数据包分析工具数据包分析工具是最基础的网络流量分析工具，它能够捕获和解码网络中的数据包，从而帮助我们深入了解网络流量的特征和行为。

其中最常用的工具之一是Wireshark，它是一个免费的开源软件，支持多种操作系统平台。

它提供了丰富的过滤和显示功能，可以捕获和分析各种协议的数据包，使我们能够深入了解网络通信的细节。

除了Wireshark之外，还有其他一些数据包分析工具可供选择。

例如，TCPDump是一个命令行工具，适用于Unix和Linux系统。

它可以实时捕获和保存网络流量，并提供强大的过滤功能。

另外，Tshark是Wireshark的命令行版本，它可以通过脚本和命令行进行自动化操作。

这些工具的使用都需要一定的技术基础，但能够提供准确而详尽的网络流量信息。

二、流量分析方法除了数据包分析工具，流量分析方法也是网络流量分析的重要组成部分。

其中，流量分析主要可以分为统计分析和行为分析两种方法。

统计分析方法是对网络流量的数量和特征进行统计和整理。

通过统计分析，我们可以了解网络流量的规模、流量分布、流量峰值等信息。

统计分析方法可以帮助我们发现潜在的网络瓶颈，优化网络性能。

例如，我们可以利用网络流量统计数据，确定是否需要扩容网络带宽或调整网络拓扑结构。

行为分析方法则侧重于对网络流量的行为和模式进行分析。

它可以通过分析网络流量的源地址、目的地址、协议类型、端口号等特征，识别和分析网络中的异常行为和安全威胁。

例如，通过行为分析，我们可以检测到DDoS攻击、恶意软件传播等网络安全事故，并采取相应措施进行应对和防范。

对于流量分析方法，我们还可以借助一些特定的工具和技术来进行更深入的分析。

如何使用超级计算技术进行网络流量分析

如何使用超级计算技术进行网络流量分析网络流量分析是一项重要的技术，它通过监视和分析网络传输的数据流，以获得关于网络活动和通信模式的深入洞察。

超级计算技术提供了一种强大的工具，可以帮助我们更加准确和高效地进行网络流量分析。

本文将介绍如何利用超级计算技术进行网络流量分析，并提供一些实用的技巧和建议。

首先，在进行网络流量分析之前，我们需要在超级计算机上设置合适的环境。

这包括安装和配置必要的软件和工具，例如Wireshark、Bro、Snort等。

另外，还需要准备足够的存储空间来存储捕获到的网络流量数据，以便后续的分析和处理。

一旦环境准备就绪，我们可以开始进行网络流量分析。

以下是一些常用的方法和技巧：1. 数据捕获：使用适当的工具在超级计算机上捕获网络流量数据。

这些工具可以监视整个网络或特定的网络接口，以便获取所需的数据。

在捕获期间，建议将捕获的数据写入磁盘，以确保不会丢失任何重要的信息。

2. 数据清洗和过滤：网络流量数据通常很庞大，包含大量的无关信息。

在进行进一步分析之前，我们需要对数据进行清洗和过滤。

这包括删除重复数据、过滤无关流量（如广告、垃圾邮件等）和识别感兴趣的数据流。

3. 数据解析和提取：网络流量数据通常以二进制格式存储，需要进行解析和提取才能得到有用的信息。

超级计算技术可以加速这个过程，提高解析和提取的效率。

例如，我们可以使用并行计算和分布式处理来处理大规模的网络流量数据集。

4. 数据分析和可视化：一旦数据被解析和提取，我们可以进行各种分析和可视化操作，以获得关于网络活动和通信模式的洞察。

超级计算技术可以加速这些操作，使得分析结果更加准确和高效。

例如，我们可以使用并行计算来提高分析和可视化的速度。

5. 异常检测和安全分析：网络流量分析还可以用于检测异常和进行安全分析。

通过分析网络流量数据中的异常模式和行为，我们可以及时发现潜在的网络攻击和安全威胁。

超级计算技术可以帮助我们处理大规模的网络流量数据，提高异常检测和安全分析的准确性和效率。

有上下界网络流地初步思考

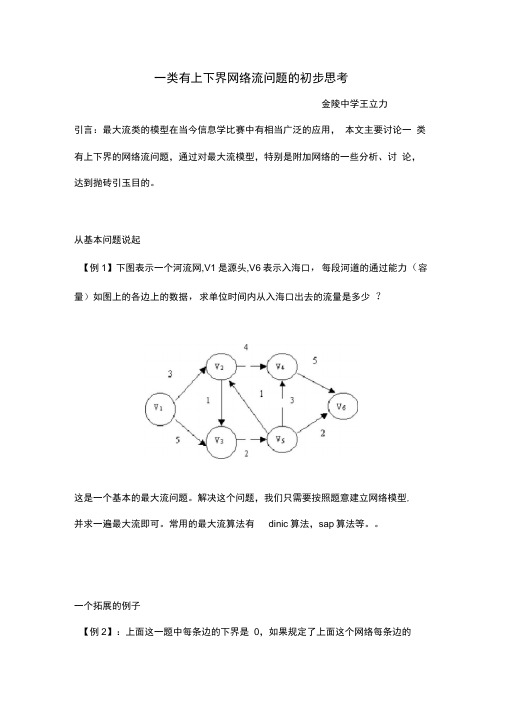
一类有上下界网络流问题的初步思考金陵中学王立力引言：最大流类的模型在当今信息学比赛中有相当广泛的应用，本文主要讨论一类有上下界的网络流问题，通过对最大流模型，特别是附加网络的一些分析、讨论，达到抛砖引玉目的。

从基本问题说起【例1】下图表示一个河流网,V1是源头,V6表示入海口，每段河道的通过能力（容量）如图上的各边上的数据，求单位时间内从入海口出去的流量是多少？这是一个基本的最大流问题。

解决这个问题，我们只需要按照题意建立网络模型,并求一遍最大流即可。

常用的最大流算法有dinic算法，sap算法等。

一个拓展的例子【例2】：上面这一题中每条边的下界是0，如果规定了上面这个网络每条边的一个自然数下界，即最小的流量，那么这题应该怎么做呢？为了最终能够解决问题，不妨来看一个简化版的问题：在一个有上下界的流网络G中，不设源和汇，但要求任意一个点i都满足流量平衡条件：f(u,i) f(i,v)(u,i) E (i,v) E且每条边(u , v)都满足容量限制B(u, v)<f(u, v)<C(u, v)的条件下，寻找一个可行流f，或指出这样的可行流不存在。

不妨称这个问题为无源汇的可行流。

首先很显然的，我们可以想到，如果把所有边的下界都一定要取到，所以把它们都从上界中减去，然后再在剩下来的网络中求一个可行流。

那么它是原来网络中的可行流吗？这样的转化是不对的，因为它并不满足流量守恒这一个条件。

为了弥补这一不足，我们可以给这个转化过的网络附加上一个源和汇。

如果设：M(i) B(u,i) B(i,v)(u,i) E (i,v) E即M(i)为流入结点i的下界总和减去流出i的下界总和。

如果M (i)是正数设一附加源S o,则可以令C' (S o, i) = M(i)。

否则设一附加汇T o,令C' (i, T o) = - M(i)。

如果所有从源点流出的弧和流入汇点的弧都满载，那么该网络存在一个可行流现在我们回到原问题：我们从汇点到源点添加一条上界为无穷大，下界为a的边，那么如果这个网络中存在可行流，则原网络中满足上下界的最大流流量>=a。

上下界网络流

有上下界的网络流即对边的流量有限制，必须在[down,up]的范围内。

其实普通的网络流也是一种特殊的有上下界的网络流，只是每条边的流量限制为[0,cap]。

分类有上下界的网络流分为两种：∙有源汇所有点都要求满足流量平衡∙无源汇除了源点汇点都要满足流量平衡（源点只有流出，汇点只有流入）无源汇可行流from 《图论原理胡伯涛》因此，对于一条边u->v，我们在新图中连三条边：∙u->v cap=up−down∙S->v cap=down∙u->T cap=down对于这个图求最大流，然后判断最大流是否等于∑down i，如果等于就是可行流，否则没有可行流。

∙例题SGU 194*注:由于是无源汇的，所以并没有最大流最小流之说。

int n,m;int id[200*200];int ans[200*200];int main(){scanf("%d%d",&n,&m);int u,v,l,r,st,ed;int sum=0;st=0,ed=n+1;rep(i,1,m) {scanf("%d%d%d%d",&u,&v,&l,&r);ac.AddEdge(u,v,r-l);id[i]=ac.m-2;sum+=l;ac.AddEdge(st,v,l);ac.AddEdge(u,ed,l);ans[i]=l;}if(ac.Maxflow(st,ed)!=sum) {puts("NO");}else {puts("YES");for(int i = 1; i <= m; ++i) {printf("%d\n",ac.edges[id[i]].flow+ans[i]);}}return 0;}有源汇可行流我们连一条t->s,流量限制为[0,inf]的边，有源汇就变成了无源汇，像上面一样求解即可。