奥数试卷11
【奥数卷】精编小学六年级奥数典型题测试卷(十一)含答案与解析

精编小学六年级奥数典型题测试卷(十一)估算(考试时间:100分钟试卷满分:100分)班级___________ 姓名___________ 学号____________ 分数____________一.选择题(共4小题,满分16分,每小题4分)1.(4分)在所有分母小于10的最简分数中,最接近20.14的分数是()A.B.C.D.2.(4分)把自己的一只拳头伸进装满水的脸盆中,估计溢出来的水的体积()A.大于1毫升,小于1升B.大于1升,小于1立方米C.大约1升D.大约1毫升3.(4分)估计一下,海安实小校园的总面积约为()公顷.A.1B.20C.5D.1004.(4分)班级教室铺地砖,用这张数学考试卷一样大的地砖铺,大约要()块.A.100B.1000C.10000D.100000评卷人得分二.填空题(共10小题,满分40分,每小题4分)5.(4分)估算:1+++…+2(比较大小).6.(4分)8.01×1.24+8.02×1.23+8.03×1.22的整数部分是.7.(4分)如果224<□×5<226,那么□中可填的自然数是.8.(4分)若将算式﹣+﹣+…+的值化为小数,则小数点后第1个数字是.9.(4分)将宽2米的一些汽车停在长度为30米的末划停车格的路边,如图,在随意停靠汽车的情况下,最多总可以停部.10.(4分)一本书如果每天读40页,8天读不完,9天又有余;如果每天读50页,7天读不完,8天又有余;如果每天读n(n是自然数)页,恰好用9天读完.这本书共有页.11.(4分)有24个偶数的平均数,如果保留一位小数的得数是15.9,那么保留两位小数的得数是.12.(4分)王亮从1月5日开始读一部小说.如果他每天读80页,到1月9日读完;如果他每天读90页,到1月8日读完.为了不影响正常学习,王亮准备减少每天的阅读量,并决定分a天读完,这样,每天都读a页便刚好全部读完.这部小说共有页.13.(4分)在横线上分别填入两个相邻的整数,使不等式成立.<<.14.(4分)满足下式的n最小等于.>.评卷人得分三.解答题(共8小题,满分44分)15.(5分)居民区捐助“环保工程”,48户居民共捐款2378.45元,请你估算一下平均每户捐款多少元?16.(5分)求算式+++++++++的整数部分.17.(5分)有17个自然数,它们的平均值精确到小数点后一位数是21.3,那么精确到小数点后三位数是多少?18.(5分)货轮上卸下若干只箱子,总重量为10吨,每只箱子的重量不超过1吨,为了保证能把这些箱子一次运走,问至少需要多少辆载重3吨的汽车?19.(6分)已知,那么S的整数部分是多少?20.(6分)计算下式的精确到小数点后三位数的近似值:1357902468÷8642097531.21.(6分)已知,则与A最接近的整数是.22.(6分)估算一下“0.896×30.01﹣×40.1”的结果大约是多少?参考答案一.选择题(共4小题,满分16分,每小题4分)1.(4分)在所有分母小于10的最简分数中,最接近20.14的分数是()A.B.C.D.【分析】把选中的各个数都化为小数,再同20.14进行比较,差最小的最接近20.14,据此解答.【解答】解:A.=20.2,20.2﹣20.14=0.06B.≈20.14,20.14﹣20.14=0C.≈20.11,20.14﹣20.11=0.03D.=20.125,20.14﹣20.125=0.015故选:B.2.(4分)把自己的一只拳头伸进装满水的脸盆中,估计溢出来的水的体积()A.大于1毫升,小于1升B.大于1升,小于1立方米C.大约1升D.大约1毫升【分析】1毫升=1立方厘米,1升=1立方分米,边长是1厘米的正方体的体积是1立方厘米,边长是1分米的正方体的体积是1立方分米,据此分析解答即可.【解答】解:1毫升=1立方厘米,1升=1立方分米,边长是1厘米的正方体的体积是1立方厘米,边长是1分米的正方体的体积是1立方分米故选:A.3.(4分)估计一下,海安实小校园的总面积约为()公顷.A.1B.20C.5D.100【分析】因为1公顷=10000平方米,即相当于边长为1000米的正方形的面积,所以1公顷稍小,5公顷比较符合实际情况.【解答】解:估计一下,海安实小校园的总面积约为20公顷.故选:C.4.(4分)班级教室铺地砖,用这张数学考试卷一样大的地砖铺,大约要()块.A.100B.1000C.10000D.100000【分析】一张数学考试卷的面积约是0.1平方米,即一样大的地砖的面积约是0.1平方米,教室的面积大约是100平方米,然后求出100里面有几个0.1即可.【解答】解:一张数学考试卷的面积约是0.1平方米,教室的面积大约是100平方米,100÷0.1=1000(块)答:大约要1000块.故选:B.二.填空题(共10小题,满分40分,每小题4分)5.(4分)估算:1+++…+<2(比较大小).【分析】先将1+++…+扩大为1+++×7,再把求得的结果与2进行比较即可求解.【解答】解:1+++…+<1+++×7=1+++=1<2故答案为:<.6.(4分)8.01×1.24+8.02×1.23+8.03×1.22的整数部分是29.【分析】根据题意,将算式中的8.01,8.02,8.03利用四舍五入法取整数8,然后再利用乘法分配律进行计算即可得到答案.【解答】解:8.01×1.24+8.02×1.23+8.03×1.22≈8×(1.24+1.23+1.22),=8×3.69,=29.52,答:8.01×1.24+8.02×1.23+8.03×1.22的整数部分是29.故答案为:29.7.(4分)如果224<□×5<226,那么□中可填的自然数是45.【分析】因为□×5这个数大于224,小于226,所以□×5=225,然后根据“积÷一个因数=另一个因数”即可得出答案.【解答】解:225÷5=45故答案为:45.8.(4分)若将算式﹣+﹣+…+的值化为小数,则小数点后第1个数字是4.【分析】根据分数数列运算符号的加减周期性,将分数数列分组求近似值,进行估算.【解答】解:﹣≈0.41﹣≈0.01548﹣≈0.00﹣≈0.00133﹣≈0.00063…推理后面每两个分数之差更接近0,而且是有限个求和,所以小数点后第一位为4.故答案为:4.9.(4分)将宽2米的一些汽车停在长度为30米的末划停车格的路边,如图,在随意停靠汽车的情况下,最多总可以停6部.【分析】此题应根据一辆车所占的比例进行估测,一辆车所占的长度大约是这个停车格的,由此可以估测,在随意停靠汽车的情况下,最大可以停6部;由此解答即可.【解答】解:将宽2米的一些汽车停在长度为30米的末划停车格的路边,如图,在随意停靠汽车的情况下,最多总可以停6部;故答案为:6.10.(4分)一本书如果每天读40页,8天读不完,9天又有余;如果每天读50页,7天读不完,8天又有余;如果每天读n(n是自然数)页,恰好用9天读完.这本书共有351页.【分析】“每天读40页,8天读不完,9天又有余”说明页数在320﹣360之间;“要是每天读50页,7天读不完,8天又有余”,说明页数在350﹣400之间;恰好用9天读完,说明页数是9的倍数;在320﹣360和350﹣400之间,是9的倍数的只有351,解决问题.【解答】解:由每天读40页可知,这本书的页数应该在320和360之间;由每天读50页可知,这本书在350和400页之间;因此,此书的页数是350到360页之间;9天恰好读完,则页数是9的倍数,在350到360间只有351是9的倍数.所以这本书共有351页.答:这本书共有351页.故答案为:351.11.(4分)有24个偶数的平均数,如果保留一位小数的得数是15.9,那么保留两位小数的得数是15.92.【分析】因为计算它们的平均数时,得数保留一位小数的得数是15.9,所以它们的平均数不小于15.85,小于15.95;所以它们的和不小于15.85×24=380.4,小于15.95×24=382.8.所以它们的和最大值是382,计算它们的平均数时,得数保留二位小数,最大是15.92.【解答】解:设这24个偶数之和为S.由S>15.85×24=380.4和S<15.95×24=382.8,以及S是偶数,推知S=382,所求数为382÷24≈15.92.答:保留两位小数的得数是15.92.故答案为:15.92.12.(4分)王亮从1月5日开始读一部小说.如果他每天读80页,到1月9日读完;如果他每天读90页,到1月8日读完.为了不影响正常学习,王亮准备减少每天的阅读量,并决定分a天读完,这样,每天都读a页便刚好全部读完.这部小说共有324页.【分析】1月5日到1月9日共有5天,他最少有4天是读80页,即这本书不少于320页;1月5日到1月9日,共4天,他读90页的时间最多有4天,这本书不多于360页;a天读a页,这本书共有:a2页,在这个范围内找出一个自然数的平方.【解答】解:80×(5﹣1)=320(页),90×4=360(页),这本书的页数就再320﹣360页之间,因为18×18=324,320<324<360;所以这本书有324页;故答案为:324.13.(4分)在横线上分别填入两个相邻的整数,使不等式成立.9<<10.【分析】此题用扩展法进行解答,为了方便,我们把中间的式子假设为A,则A=10﹣(+++…++),因为<+++…+<,所以,9<10﹣<A<9.5<10,进而得出结论.【解答】解:我们把中间的式子假设为A,则;A=(1﹣)+(1﹣)+(1﹣)+…+(1﹣)+(1﹣),=10﹣(+++…++),因为<+++…+<,所以,9<10﹣<A<9.5<10;故答案为:9,10.14.(4分)满足下式的n最小等于40.>.【分析】根据分数的巧算,利用分数的拆项原理和拆项方法进行解答.【解答】解:原式左端等于,可得不等式,所以,解得,故n最小等于40.故答案为:40.三.解答题(共8小题,满分44分)15.(5分)居民区捐助“环保工程”,48户居民共捐款2378.45元,请你估算一下平均每户捐款多少元?【分析】根据平均分除法的意义,用2378.45元除以48即可求出平均每户捐款多少元,然后把2378.45看作2400,48看作50估算即可.【解答】解:2378.45÷48≈2400÷50=48(元)答:平均每户大约捐款48元.16.(5分)求算式+++++++++的整数部分.【分析】这个算式中有10个数字,最大的是,最小的是,所以×10<+++++++++<×10,<+++++++++<2,据此解答即可.【解答】解:因为:×10<+++++++++<×10所以:<+++++++++<2故此算式+++++++++的整数部分是1.答:算式+++++++++的整数部分是1.17.(5分)有17个自然数,它们的平均值精确到小数点后一位数是21.3,那么精确到小数点后三位数是多少?【分析】保留一位小数是21.3,则原来的两位小数最小是21.25,最大是21.34,由此可以求出这17个数的和的范围,据此解答即可.【解答】解:21.25×17=361.25,21.34×17=362.78则361.25≤17个数之和<362.78,所以这17个数的和是362.362÷17≈21.294答:精确到小数点后三位数是21.294.18.(5分)货轮上卸下若干只箱子,总重量为10吨,每只箱子的重量不超过1吨,为了保证能把这些箱子一次运走,问至少需要多少辆载重3吨的汽车?【分析】因为每一只箱子的重量不超过1吨,所以每一辆汽车可运走的箱子重量不会少于2吨,否则可以再放一只箱子.所以,5辆汽车本是足够的,但是4辆汽车并不一定能把箱子全部运走.例如,设有13只箱子,所以每辆汽车只能运走3只箱子,13只箱子用4辆汽车一次运不走.因此,为了保证能一次把箱子全部运走,至少需要5辆汽车.【解答】解:每辆汽车至少可以运2吨,所以5辆汽车一定能把这些货物都运走.但箱子总数为13,14时,4辆汽车一次不能运完,所以至少需要5辆汽车.答:至少需要5辆载重3吨的汽车.19.(6分)已知,那么S的整数部分是多少?【分析】根据,算出S的取值范围,进而得出结论.【解答】解:因为,即201<S<201.9,所以S的整数部分是201;答:S的整数部分是201.20.(6分)计算下式的精确到小数点后三位数的近似值:1357902468÷8642097531.【分析】本题考查估算.【解答】解:因为1357÷8643≈0.15701358÷8642≈0.1571所以:1357902468÷8642097531≈0.15721.(6分)已知,则与A最接近的整数是143.【分析】将父母扩大与缩小,利用极限思想,即可得出结论.【解答】解:由题意,>≈142.5,<≈143.4,所以与A最接近的整数是143,故答案为143.22.(6分)估算一下“0.896×30.01﹣×40.1”的结果大约是多少?【分析】把算式“0.896×30.01﹣×40.1”中的0.896看作0.9、30.01看作30、40.1看作40,然后根据混合运算的计算法则计算即可.【解答】解:0.896×30.01﹣×40.1≈0.9×30﹣×40=27﹣8=19。
奥数考试真题试卷电子版

奥数考试真题试卷电子版一、奥数真题试卷(20题)(一)填空题(1 - 10题)1. 题目:计算1 + 2 + 3 + … + 100。
- 解析:这是一个等差数列求和问题,根据等差数列求和公式S = (n(a_1 +a_n))/(2),其中n = 100(项数),a_1=1(首项),a_n = 100(末项)。
则S=(100×(1 + 100))/(2)=5050。
2. 题目:一个数除以5余3,除以6余4,除以7余5,这个数最小是多少?- 解析:这个数加上2就能被5、6、7整除。
5、6、7的最小公倍数是5×6×7 = 210,所以这个数最小是210 - 2=208。
3. 题目:在1 - 100中,能被3或5整除的数有多少个?- 解析:能被3整除的数有100÷3 = 33·s·s1,即33个;能被5整除的数有100÷5 = 20个;能被3和5整除(即能被15整除)的数有100÷15 = 6·s·s10,即6个。
根据容斥原理,能被3或5整除的数有33+20 - 6 = 47个。
4. 题目:把1/7化成小数,小数点后面第100位数字是多少?- 解析:1÷7 = 0.142857142857·s,循环节是142857,共6位。
100÷6 = 16·s·s4,所以第100位数字是8。
5. 题目:有一个长方体,长、宽、高分别是3、4、5厘米,在这个长方体中挖去一个最大的正方体,剩下部分的体积是多少?- 解析:长方体体积为3×4×5 = 60立方厘米,能挖去的最大正方体棱长为3厘米,其体积为3×3×3 = 27立方厘米,剩下部分体积为60 - 27 = 33立方厘米。
6. 题目:甲、乙两人分别从A、B两地同时出发相向而行,甲的速度是每小时5千米,乙的速度是每小时4千米,两人相遇后继续前行,甲到达B地后立即返回,乙到达A地后也立即返回,两人第二次相遇的地点距离A地3千米,求A、B两地的距离。
小学五年级奥数竞赛试卷1-12

小学五年级奥数测试题1、计算4。
75–9。
63+(8。
25-1.37)17。
48×37—174。
8×2.72、在算式□×5÷3×9+11=1991中,□里应填入的数字是( )。
3、一个自然数与它本身相加、相减、相除所得的和、差、商再相加,结果是1991,那么原来的自然数是( )4、某同学在计算一道除法题时,误将除数32写成23,所得的商是32余数是11,正确的商与余数的和是()5、亮亮从家步行去学校,每小时走5千米。
回家时骑自行车,每小时走13千米。
骑自行车比步行的时间少4小时,亮亮家到学校的距离是( )千米。
6、一个两位数,个位数字是十位数字的3倍,如果这个数加上60,则两个数字相等,这个两位数是( )。
7、两个自然数的和是286,其中一个数的末位数是0,如果把这个零去掉,所得的数与另一个数相同,那么原来两位数的积是( )8、下图中,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的长的2倍,那么三角形CDE的面积是()平方厘米.9、甲乙丙丁四个人共买了10个面包平均分着吃,甲拿出6个面包的钱,乙和丙都只拿出2个面包的钱,丁没带钱。
吃完后一算,丁应该拿出1.25元,甲应收回( )元。
10、在200位学生中,至少有( )人在同一个月过生日。
11、暑假小明去游园,遇到了甲、乙、丙、丁四位同学,小明和四位同学都握了手,甲和3个人握了手,乙和2个人握了手,丙和1个人握了手,那么丁和()个人握了手。
12、有一个长方形,它的长和宽各增加8厘米,这个长方形的面积就增加了208平方厘米,原来长方形的周长是( )厘米。
13、甲乙二人环绕周长是400米的跑道跑步,如果两人从同一地点出发背向而行,那么经过2分钟两人相遇;如果两人从同一地点出发同向而行,那么经过20分钟两人相遇,已知甲的速度比乙的速度快,甲每分钟跑()米。
14、甲对乙说:“当我的岁数是你现在的岁数时,你才4岁."乙对甲说:“当我的岁数是你现在的岁数时,你已经61岁了。
小学奥数五六年级经典难度试题11题详细解析分享

小学奥数五六年级经典难度试题11题详细解析分享1、若4 个连续正整数的乘积是358800,则这4 个数的和是__________。
方法1:分解质因数,再凑成4个连续的自然数的乘积。
方法2:根据题目的特别性进行估算。
末尾2个0,说明这个数是25的倍数,四个连续的自然数最多几个数含有质因数5?答:1个数含有质因数5即是5的倍数。
说明5的倍数的数在这里是25的倍数。
25的倍数有哪些?25、50、75、100……如果说是50,那么四个数最小为50、49、48、47,乘积50×49×48×47>40×40×40×40=2560000>358800,所以四个自然数其中一个是25。
22、23、24、25;23、24、25、2624、25、26、2725、26、27、28分析:如果含有27则是9的倍数,但是358800不是9的倍数,所以不含有27 。
因为358800不是11的倍数,所以不含有22 。
所以只能是23、24、25、26,四个数之和:(23+26)×4÷2=98 。
2、 4个连续整数的和是 5 的倍数。
下列论述中一定正确的序号是__________。
①4 个整数的和的最后一位数是 5;②最大的一个整数的最后一位数是 9;③最小的一个整数是奇数;④没有任何一个数是 5 的倍数;⑤有一个数的最后一位数是 3。
分析:等差数列和=(首项+末项)×项数÷2末项=首项+(项数-1)×公差假设第一个自然数为x,那么最后一个为X+1×(4-1)=X+3 。
四个自然数的和=(X+X+3)×4÷2=(2X+3)×2=5的倍数。
(2X+3)×2=5的倍数,(2X+3)×2一定是偶数,所以四个自然数的和的个位一定是0 。
∴①是错的。
分析②:和是(2X+3)×2是5的倍数,其中2和5互质,所以2X+3一定是5的倍数,且2X是偶数,所以2X+3是奇数,所以2X+3个位是5,所以2X个位是2,所以X个位是1或者6 ,所以个位可以是:1、2、3、4或者6、7、8、9,所以②不一定是9,所以不成立。
四年级下册数学试题-奥数专题讲练:11 数学游戏 提高篇(解析版)全国通用

第十一讲 数学游戏在今天这节课中,我们来研究数学游戏中的必胜策略.由于策略的制定是没有固定模式的,教师在本节课中要引导学生通过具体问题具体分析,不断积累经验,以提高观察和分析问题的能力. 知识点:1、取火柴以及与其同类型的游戏中的策略2、其他游戏中的取胜策略.分析:同同应先报1,那么不管琪琪接下来报什么数(11或11以下的数),同同都可以说12.同理同同可以说出23、34、45、67、78、89、100.分析可知,如果同同想先到达100,他必须先到达89,如果同同说的和与100相差11,那么不管琪琪加什么数,同同都可以找到一个数,加在琪琪说出的和上,从而使总和为100.同理要先到达89,必须使琪琪与89相差11,也就是要先报出78.继续如此推下去,同同必须先报67、56、45、34、23、12和1,所以他应先报1.我们在进行竞赛与竞争时,往往要认真分析情况,制定出好的方案,使自己获胜,这种方案就是对策.在小学数学竞赛中,常有与智力游戏相结合而提出的一些简单的对策问题,它所涉及的数学知识都比较简单.但这类题的解答对我们的智力将是一种很有益的锻炼.这类问题也属于我们所说的“博弈问题”.在数学游戏中有一类取火柴游戏,它有很多种玩法,由于游戏的规则不同,取胜的方法也就不同.但不论哪种玩法,要想取胜,一定离不开用数学思想去推算.其核心思想有:逆推和对称分组.(一) 智取火柴以及同类型的游戏 专题精讲 教学目标想 挑 战吗?同同和琪琪玩游戏,同同说了任意一个从1到10的自然数,琪琪在同同说出的数上加上一个不能超过10的自然数,然后说出它们的和.接下来同同再在琪琪说出的和上加上一个不超过10的任意自然数,并说出新的和.琪琪接着再在新的和上加上一个不超过10的数,这样一个个接着相加,一直到最后的和是100为止.例如同同说9,琪琪说19,同同说28等等,谁第一个得到100,谁就获胜.如果同同先报数,他用什么方法可以取胜?【例1】桌子上放着60根火柴,甲、乙二人轮流每次取走1~3根.规定谁取走最后一根火柴谁获胜.如果双方都采用最佳方法,甲先取,那么谁将获胜?分析:我们采用逆推法分析这道题.获胜方在最后一次取走最后一根;往前逆推,在倒数第二次取时,必须留给对方4根,此时无论对方取1,2或3根,获胜方都可以取走最后一根;再往前逆推,获胜方要想留给对方4根,在倒数第三次取时,必须留给对方8根……由此可知,获胜方只要每次留给对方的都是4的倍数根,则必胜.现在桌上有60根火柴,甲先取,不可能留给乙4的倍数根,而甲每次取完后,乙再取都可以留给甲4的倍数根,所以在双方都采用最佳策略的情况下,乙必胜.同学们再想一想为什么一定要留给对方4的倍数根,而不是5的倍数根或其它倍数根呢?提问:(1)甲取几根,乙取3减几根可以吗?不可以,那样的话,甲取3根,乙就没法取了.(2)甲取几根,乙取5减几根可以吗?不可以,那样的话甲取1根,乙就没法取了.所以关键在于规定每次只能取1~3根,1+3=4,在两人紧接着的两次取火柴中,后取的总能保证两人取的总数是4.利用这一特点,就能分析出谁采用最佳方法必胜,最佳方法是什么.由此出发,对于例题的各种变化,都能分析出谁能获胜及获胜的方法.[前铺]桌子上放着10根火柴,甲、乙二人轮流每次取走1~2根.规定谁取走最后一根火柴谁获胜.如果双方都采用最佳方法,甲先取,那么谁将获胜?分析:如果获胜方在最后取得最后一根火柴,那么在倒数第二次取时,必须留给对方3根,要想留给对方3根,倒数第三次取时,必须留给对方6根.要想留给对方6根,倒数第四次取时必须留给对方9根,而甲每次取完都能留给乙3的倍数根,所以在双方都采用最佳策略的情况下,甲必胜.[拓展一]在例1中将“每次取走1~3根”改为“每次取走1~6根”,其余不变,情形会怎样?分析:由例1的分析知,只要始终留给对方(1+6=)7的倍数根火柴,就一定获胜.因为60÷7=8……4,所以只要甲第一次取走4根,剩下56根火柴是7的倍数,以后总留给乙7的倍数根火柴,甲必胜.由此看出,在每次取1~n根火柴,取到最后一根火柴者获胜的规定下,谁能做到总给对方留下(1+n)的倍数根火柴,谁将获胜.[拓展二]将例1中“谁取走最后一根火柴谁获胜”改为“谁取走最后一根火柴谁输”,其余不变,情形又将如何?分析:最后留给对方1根火柴者必胜,按照例1中的逆推的方法分析,只要每次留给对方4的倍数加1根火柴必胜.甲先取,只要第一次取3根,剩下57根(57除以4余1),以后每次都将除以4余1的根数留给乙,甲必胜.由此看出,在每次取1~n根火柴,取到最后一根火柴者为负的规定下,谁能做到总给对方留下(1+n)的倍数加1根火柴,谁将获胜.[小结]我们可以把解决这类问题的一般方法总结为余数问题.,即如果有余数,则先取者胜,且取余数根数;如果没有余数,则后取者胜,每“回合”共取N+1根.【例2】今有两堆火柴,一堆35根,另一堆24根.两人轮流在其中任一堆中拿取,取的根数不限,但不能不取.规定取得最后一根者为赢.问:先取者有何策略能获胜?分析:本题虽然也是取火柴问题,但由于火柴的堆数多于一堆,故本题的获胜策略与前面的例题完全不同.先取者在35根一堆火柴中取11根火柴,使得取后剩下两堆的火柴数相同.以后无论对手在某一堆取几根火柴,你只须在另一堆也取同样多根火柴.只要对手有火柴可取,你也有火柴可取,也就是说,最后一根火柴总会被你拿到.这样先取者总可获胜.请同学们想一想,如果在上面玩法中,两堆火柴数目一开始就相同,例如两堆都是35根火柴,那么先取者还能获胜吗?[拓展一]甲、乙两人轮流往一张圆桌面上放同样大小的硬币,规定每人每次只能放一枚,硬币平放且不能有重叠部分,放好的硬币不再移动.谁放了最后一枚,使得对方再也找不到地方放下一枚硬币的时候就赢了.说明放第一枚硬币的甲百战百胜的策略.分析:采用“对称”思想.设想圆桌面只有一枚硬币那么大,当然甲一定获胜.对于一般的较大的圆桌面,由于圆是中心对称的,甲可以先把硬币放在桌面中心,然后,乙在某个位置放一枚硬币,甲就在与之中心对称的位置放一枚硬币.按此方法,只要乙能找到位置放一枚硬币,根据圆的中心对称性,甲定能找到与这一位置中心对称的地方放上一枚硬币.由于圆桌面的面积是有限的,最后,乙找不到放硬币的地方,于是甲获胜.[拓展二]有3堆火柴,分别有1根、2根与3根火柴.甲先乙后轮流从任意一堆里取火柴,取的根数不限,规定谁能取到最后一根或最后几根火柴就获胜.如果采用最佳方法,那么谁将获胜?分析:根据上一例题的解法,谁在某次取过火柴之后,恰好留下两堆数目相等的火柴,谁就能取胜.甲先取,共有六种取法:从第1堆里取1根,从第2堆里取1根或2根;第3堆里取1根、2根或3根.无论哪种取法,乙采取正确的取法,都可以留下两堆数目相等的火柴(同学们不妨自己试试),所以乙采用最佳方法一定获胜.【例3】甲、乙二人轮流报数,必须报不大于6的自然数,把两人报出的数依次加起来,谁报数后加起来的数是2000,谁就获胜.如果甲要取胜,是先报还是后报?报几?以后怎样报?分析:采用倒推法(倒推法是解决这类问题一种常用的数学方法).由于每次报的数是1~6的自然数,2000-1=1999,2000-6=1994,甲要获胜,必须使乙最后一次报数加起来的和的范围是1994~1999,由于1994-1=1993(或1999-6=1993),因此,甲倒数第二次报数后加起来的和必须是1993.同样,由于1993-1=1992,1993-6=1987,所以要使乙倒数第二次报数后加起来的和的范围是1987~1992,甲倒数第三次报数后加起来的和必须是1986.同样,由于1986-1=1985,1986-6=1980,所以要使乙倒数第三次报数后加起来的和的范围是1980~1985,甲倒数第四次报数后加起来的和必须是1979,….把甲报完数后加起来必须得到的和从后往前进行排列:2000、1993、1986、1979、….观察这一数列,发现这是一等差数列,且公差d=7,这些数被7除都余5.因此这一数列的最后三项为:19、12、5.所以甲要获胜,必须先报,报5.因为12-5=7,所以以后乙报几,甲就报7减几,例如乙报3,甲就接着报4(=7-3).所以甲要获胜必须先报,甲先报5;以后,乙报几甲就接着报7减几.[说明]如果对方一定要先报数,那么你可以利用对方不懂得这个秘诀的条件,去占领下一个“制高点”,从而确保获胜.[拓展]如果游戏的规则改为“先达到2000者输”,应如何制定“作战”方针呢?分析:显然此时要想获胜,必须先达到1999,重复上面的分析,不难得到每次应占领的“制高点”是:1999,1993,1986,1979,……,19,12,5.因此获胜的策略是:(1)让自己先报4;(2)每次对方报a(1≤a≤6),你就是报7-a.这样,最终的胜利一定是属于你的.【例4】有一种“抢某个数字”的游戏,是两个人从自然数1开始轮流报数,规定每次至少报几个数与至多报几个数(都是自然数),最后谁报到规定的“某个数字”为胜.如“抢50”游戏,规定每次必须报1.2个自然数,从1开始,谁抢报到50为胜.例如甲先报l,乙就可接着报2或2,3;若乙报2,甲就可接着报3或3,4;若乙报2,3;甲就可接着报4或4,5.依次下去,谁能报到50为胜.如果你是甲,并且先报数,有没有必胜的策略?分析:由于每次必须报1~2个自然数,那么甲先报1次后,就可保证每次与乙刚报的数字数目之和为3.如乙报1个数,甲就接着报2个数;若乙报2个数,甲就接着报1个数.因此,甲若想必胜,报完第一次数剩下的数的个数必须是3个倍数才可以.而50=3×16+2,因此甲有必胜的策略:甲先报1,2,然后,乙若报1个数,甲就报2个数;乙若报2个数,甲就报1个数.[拓展]若是抢别的数字,规定每次必须报别的一定数目的自然数,先报数的人还有没有必胜的策略?分析:借鉴前面经验,若是“抢40”游戏,规定每次必须报1~3个自然数,从1开始轮流往后报数.若甲先乙后,则乙有必胜的策略.因为乙可以保证每次与甲刚报完的数字数目之和为4,而40=4×10刚好是4的倍数.推广开来,若是“抢数字a”游戏,每次必须报1~n个自然数,从1开始轮流往后报数,且甲先乙后,那么会有两种情况:情况1:若a是(1+n)的整数倍,则后报数的乙有必胜的策略;情况2:若a不是(1+n)的整数倍,则先报数的甲有必胜的策略,且甲先报的数字个数必须是数字.除以(1+n)的余数.说明:“抢数字”游戏还有很多与之类似的变形游戏.如果你对“抢数字”游戏的规则与玩法非常熟悉的话,那么类似的变形游戏就会“如鱼得水”.不费功夫了.[小笑话]某天军训中,教练对同学说:“第一排报数!”小明惊讶的看着教练.教练很奇怪的又说了一遍:“第一排报数!”小明还是很无奈很惊讶的看着教练.教练又大声说了一遍:“第一排报数!”于是小明极其不情愿的走到大树前抱着树.(二)其它游戏中的取胜策略【例5】有100个人站成一排,从左到右依次进行1,2报数,凡是报1的人离开队伍,剩下的人继续从左到右进行1,2报数,最后留在队伍中的人获胜,如此下去,要想获胜,应站在队列中的第几个位置?分析:将这100个人从左到右依次编号为1,2,3,…,98,99,100.第一次报完后.剩下的是2的倍数, 2,4,6,8,10,…,96,98,100.第二次报完后,剩下的是4的倍数,4,8,12,16,…,92,96,100.第三次报完后,剩下的是8的倍数,8,16,24,…,80,88,96.第四次报完后,剩下的是16的倍数,16,32,48,64,80,96.第五次报完后,剩下的是32的倍数,32,64,96.第六次报完后,还剩下一人,也就是第64人.所以要想获胜,应站在队伍中的第64个位置.[数学趣题]神父的诡计一艘不大的船只在海上遇到了风暴,摆在船上25位乘客面前的路只有两条:要么全部乘客与船只同归于尽;要么牺牲一部分人的生命,把他们抛进大海,减轻船的载重量,船及其他人还有得救的可能,但是这样做至少得把一半以上的人抛进海里.大家都同意走第二条路,然而谁也不愿意自动跳进海里.乘客里有11个基督徒,其中一个是神父,于是大家就公推神父出个主意.奸诈的神父想了一下,就让大家坐成一个环形,并且从他依序报数,“1,2,3”,规定报到“3”的人就被抛进海里,下一个继续由“1”报起,同时声称这是上帝的旨意,大家的命运都由上帝来安排,不得抗拒.结果有14个人被抛进海里,而剩下的11个人全部都是基督徒.大难不死的其它10个基督徒突然醒悟过来,原来神父是用诡计救了他们.请你想想,这11个人应在什么位置,才可以避免被抛进海里去呢?分析:神父只要让11个基督徒占领1、4、5、8、10、13、14、17、19、22、23这11个位置,就可以保证他们不被抛进海里.【例6】 在一个6×5的棋盘上,甲、乙二人轮流往棋盘的方格内放棋子.甲先放第一枚棋子,乙只能在与这枚棋子所在格相邻的格内放棋子(相邻格指有公共边的两个格).甲再放时又必须放在乙刚放的棋子的相邻格内,以后照此规则放.谁无法放棋子时谁失败.那么谁会有必胜的策略呢?分析:若甲有必胜的策略,则在甲放入第一枚棋子后,只要乙能放,那么甲就能放;反之,若乙有必胜的策略,则只要甲能放,乙就能放.因本题中给出的是6×5的棋盘,可分成15个1×2的小块,如下图,有AA ,BB 两种,无论甲放入哪里的A 或B 方格中,乙都放在同一小块的A 或B 方格内.所以乙有必胜的策略. B B B BB B B B B B BB B B A A A A A A AA A A A A A AA A[拓展]若本题中给出的是5×5的棋盘,则甲有必胜的策略.推广一下,若给的是奇数×奇数的棋盘,则先放棋子的有必胜的策略.否则,后放棋子的有必胜的策略.【例7】 右图是一种“红黑棋”,甲、乙两人玩棋,分别取红、黑两方.规黑黑黑黑黑黑红红红红红红定:下棋时,每人每次只能走任意一枚棋,每枚棋子每次可以走一格或几格.红棋从左向右走,黑棋从右向左走,但不能跳过对方棋子走,也不能重叠在对方有棋子的格中.一直到谁无法走棋时,谁就失败.甲先乙后走棋,问甲有没有必胜的策略?分析:甲若想必胜,那么甲走一次棋后,“乙能走甲就能走”,观察棋盘,第二、三行都有9个空格,第四、五行都有5个空格,而第一行只有1个空格,第六行有3个空格,因此甲第1次只要将第六行也变为1个空格,那么就形成一种对称局面,“乙能走甲就能走”.因此甲有必胜的策略:甲先把第六行的红棋向右走两格,使中间只有一个空格.以后乙走第一行,甲就相应地走第六行;乙走第二行,甲就相应地走第三行;乙走第三行;甲就相应地走第二行;乙走第四行,甲就相应地走第五行,乙走第五行,甲就相应地走第四行;乙走第六行,甲就相应地走第一行.且每次甲与乙走的格数要相同,那么最后肯定是乙无法走棋失败,甲必胜.【例8】 右图是一张3×3的方格纸,甲、乙两人轮流在方格中写下2,4,5,6,7,8,9,10,11九个数字中的一个,数字不能重复.最后,甲的得分是上、下两行六个数之和,乙的得分是左、右两列六个数之和,得分多者为胜.如果甲先乙后,那么甲有没有必胜的策略?分析:观察右图,图中四个角的数是甲、乙两人所共有的,所以胜负只与放在A 、B 、C 、D 四个格内的数字有关.甲若想获胜,必须让A ,C 两格内的数字之和大于B ,D 两格内的数字之和.观察所给的九个数字,2+1l<4+10.因此,只要甲将2填入B 或D 方格中,以后无论乙怎样填,甲第二次只要把10或1l 填人A 或C ,甲就必胜.所以甲有必胜的策略:甲先把2填入B 格,若乙将1 1填入D ,甲就将10填入A ;若乙将4填入A ,甲就将11或10填入C ,这样甲就必胜.【例9】 两个人进行如下游戏,即两个人轮流从数列1,2,3,…,100,101中删去9个数,经过这样的11次删除后,还剩下两个数,如果这两个数的差是55,这时判第一个删数的人获胜,问谁能获胜?分析:按照题目中的要求,剩下两个数的差是55,就判第一个勾数的人获胜,那么我们就把差是55的数分组(1,56),(2,57),(3,58),(4,59),(5,60),…,(45,100),(46,101),还剩下47,48,49,50,51,52,53,54,55没有分组,即第一次若把这九个数去掉,剩下的数正好两个一组,每组数的差为55,剩下的工作就是要如何保证剩下的都是成组的数,若对手接下来删去的9个数是每组一个,那么甲就把每个数成组的另一个数删去即可,剩下的还是成组的数,若对手删去的是一个组的两个数,外加7个单独的,那么甲便把这7个数成组的另外一个删去,再删去一组数,还可以保证剩下的都是成组的数;若对手删去的是2个组的4个数,外加5个单独的,我们便也用同样的方式,……不论对手怎样删,我们都能保证剩下的为成组的数,一共删了(101-2)÷9=11次,即可保证最后两个数的差为55,从而判第一个删数的人获胜.【例10】 桌子上有8颗瓜子,甲、乙两人轮流拿瓜子,他们规定,假如甲先拿(当然,乙也可以先拿),甲可拿任意颗瓜子,但不能拿光,接着乙拿,乙可以拿不多于甲所拿瓜子的2倍,又轮到甲拿,甲可以拿不多于乙拿瓜子的2倍,这样交替进行,谁最后把瓜子拿光就算胜利.D B A C分析:假如甲先拿,且拿3颗以上,则剩下的瓜子可由乙一次拿走,于是乙胜,甲输;甲为了不让乙胜,显然不能拿多于3颗的瓜子数,而只能拿2或1颗.若甲决定拿2颗,乙就可以拿1(或2、3、4)颗,如乙拿2或3或4都将认输,故乙只能拿1颗.现在桌子上只剩下5颗瓜子,且又轮到甲拿瓜子,因刚才乙只拿了一颗,故甲可拿1或2颗瓜子,如拿2颗,乙就能把剩下的瓜子拿光而获胜.所以甲只能拿1颗,接着拿瓜子的乙也可拿1或2颗,为保证胜利,乙也拿1颗,这样桌子上只剩下3颗瓜子,仍轮到甲拿瓜子,且只能拿1颗或2颗,不管怎样拿,甲都是输定了.若甲决定拿1颗,则乙就拿2颗,此时桌上只剩下5颗且甲拿,情形和以上一样.故无论何种取法甲必输.这个数字游戏和斐波那契数列:1,1,2,3,5,8,13,21,…有关.8为该数列中的一项.事实上是:如果甲、乙两人都清楚这个游戏的“窍门”,那么如瓜子数是该数列的某一项,则先拿者输,如瓜子数不是该数列的某一项,则先拿者赢.专题展望本讲主要讲了游戏中的取胜策略问题,希望同学们通过本讲的学习掌握在游戏中取胜的数学思想方法,在游戏中学到知识,请同学们再接再厉,加油!练习十一1.(例1)桌上放着40根火柴,甲、乙二人轮流取,每次可取1到3根,规定谁取到最后一根谁获胜.假设甲先取,那么谁一定获胜,如何获胜?分析:乙一定获胜.每次可取1~3根,则甲、乙每轮所取的火柴之和总可以凑成4,例如,甲取1根,乙就取3根;甲取2根,乙就取2根;甲取3根,乙就取1根,因为40是4的倍数,无论甲如何取,乙总有相应的取法使得这一轮里火柴共被取走4根,因此,乙必定可以取走最后一根火柴.2.(例2)有两堆枚数相等的棋子,甲、乙两人轮流在其中任意一堆里取,取的枚数不限,但不能不取,谁取到最后一枚棋子谁获胜.如果甲后取,那么他一定能获胜吗?分析:甲必胜.3.(例3)两人轮流报数,但报出的数只能是1至10的自然数.同时把所报数一一累加起来,谁先使这个累加和达到100,谁就获胜.问怎样才能确保获胜?分析:这个问题可以倒着想,要想使总和先达到100,应该最后给对方留下多少个数呢?由于每个人报的数最大是10,最小是1,因此对方最后一次报完数后,总和最大是99,最小是90,所以最后一次应该给对方留下11个数,也就是说要先达到100,就必须先达到89.如何抢到89这个数呢?采用同样的分析方法可知,应先达到78.依此类推,可以得到每次报数应占领的“制高点”是:100,89,78,67,56,45,34,23,12,1.所以获胜的策略是:(1)先报1;(2)每次对方报a(1≤a≤10),你就报11-a.这样,每次你都能占领一个“制高点”,以确保获胜..4.(例7)下图是一副“1999”棋,甲、乙两人玩棋,分别取红、黑两方分析:甲胜.利用对称性,甲先走第二行的8步.此时,前两行相同,后两行相同.以后,当乙走某行的a步时,甲就走对应行的a步,总保持前两行相同,后两行相同.只要乙能走棋,甲必能走棋,所以乙先无棋可走,甲胜.5.(例9)黑板上写着一排相连的自然数1,2,3,…,51.甲、乙两人轮流划掉连续的3个数.规定在谁划过之后另一人再也划不成了,谁就算取胜.问:甲有必胜的策略吗?分析:甲先划,把中间25,26,27这三个数划去,就将1到51这51个数分成了两组,每组有24个数.这样,只要乙在某一组里有数字可划,那么甲在另一组里相对称的位置上就总有数字可划.因此,若甲先划,且按上述策略去进行,则甲必能获胜.数学故事大海盗雷斯家族世代都是海盗头子,到十六世纪中叶时,更是盛况空前,希尔顿·雷斯和艾登·雷斯兄弟各自拥有自己强大的海盗军队,在地中海一带不可一世.终于有一天两兄弟闹不和,都想掌握整个家族,享用家族世代积攒的财宝.但是他们又都不敢跟对方开战,因为他们都没有必胜的把握,而且就算战胜了对方自己的军队也必定伤亡惨重,也许从此就一蹶不振,所以双方一直僵持不下,难以解决.他们的父亲眼见分裂之势已成,无法挽回,又不忍见两个儿子自相残杀,于是想了一个办法,以使事情顺利解决.于是他找了一天把两个儿子召集在一起,说道:“我知道要你们像以前一样相处是不可能了,但你们要是自相残杀岂不是让我们的敌人占了便宜,或许我们的家族也会有灭亡的危险,所以我想了一个办法,能令你们和平地分成两个强大的海盗军团,但你们要答应我遵守我所说的规则!”两兄弟见父亲说的有理便答应了.于是老人接着说:“是这样的,我相信你的军队实力足以自立当世.你们惟一想争的只是家族的财宝,我把财宝中最贵重的部分装在一个箱子中,其余的分别平均装在99个箱子中,你们两个轮流来我这里取箱子,每次取1到lO箱都可以,不能少取也不能多取,我会把最贵重的一箱放在最后,你们取到的箱子都归自己所有,谁取到最贵重的一箱谁就继续留在这里,而另一方必须离开地中海到别处发展,以免互相之间产生摩擦,手足相残.”两兄弟均觉依照这个办法虽然自己有可能被赶出家门,但机会是平等的,还算公平,便答应了.等父亲把财宝准备好,又出现了一个问题:谁先取呢?于是讨论决定:双方划拳,胜者决定先取还是后取.划拳的结果是希尔顿.雷斯赢了,他想了一下决定先取.于是两兄弟轮流到父亲处取财宝,几轮下来最后一箱贵重的财宝被希尔顿·雷斯取走了.艾登·雷斯依照约定离开了地中海,再也没有回来.父亲虽然眼见家族分裂老怀伤感,但见两兄弟相安无事也心怀安慰.几十年后,雷斯家族日趋没落,雷斯兄弟也各自在战斗中被西班牙皇家海军击败,他们逃出来后流落异乡,从此一蹶不振.一日,他们在某个小镇碰见,十分高兴,于是来到酒吧喝酒,后来聊到当年的分裂,艾登·雷斯说:“唉,当初运气不佳,被你碰巧取到了大财宝,我才被迫背井离乡!”那知希尔顿·雷斯哈哈一笑,说到:“我决定先取的时候就知道我赢定了!”艾登·雷斯非常诧异,问道:“怎么会?你怎么能知道我每次会取几箱呢?”希尔顿·雷斯回答道:“不用知道,我先取一箱,以后每次所取的箱数都与你取的凑够1l箱,这样我就赢定了.”艾登·雷斯想了一下顿时恍然大悟,后悔当时没有明白.。
小学三年级奥数试卷--经典

小学三年级奥数试卷经典(考试时间:90分钟,满分:100分)一、选择题(每题2分,共30分)1. ()1+2+3+4+5+6+7+8+9+10 的和是多少?A. 55B. 45C. 65D. 752. ()一个长方形的长是10厘米,宽是5厘米,它的面积是多少平方厘米?A. 50B. 60C. 70D. 803. ()小华有10个苹果,他给了小红3个,小华还剩几个苹果?A. 7B. 8C. 9D. 10A. 16B. 18C. 20D. 225. ()小刚有5个球,小明有8个球,他们一共有多少个球?A. 12B. 13C. 14D. 15二、判断题(每题1分,共20分)6. ()1千克等于1000克。
()7. ()一个正方形的四条边长度相等。
()8. ()6的倍数都是偶数。
()9. ()小猫有4条腿,小狗有3条腿。
()10. ()3+3+3+3+3 等于3×5。
()三、填空题(每空1分,共10分)11. ()一个长方形的长是8厘米,宽是4厘米,它的面积是()平方厘米。
12. ()9+7=(),7+9=()。
13. ()小丽有15个糖果,她吃掉了(),还剩下()个糖果。
14. ()一个正方形的边长是5厘米,它的周长是()厘米。
15. ()小华有20元钱,他买了一本书花了8元,他还剩下()元。
四、简答题(每题10分,共10分)16. 请写出3个3的倍数,并说明为什么它们是3的倍数。
17. 请计算1+2+3+4+5+6+7+8+9+10 的和。
五、综合题(1和2两题7分,3和4两题8分,共30分)18. ()小华有10个苹果,他先给了小红3个,然后又给了小明2个,他还剩几个苹果?(7分)19. ()一个长方形的长是12厘米,宽是5厘米,求它的面积和周长。
(7分)20. ()小刚有20元钱,他买了一支铅笔花了2元,又买了一本书花了15元,他还剩下多少钱?如果他要把剩下的钱全部用来买糖果,每颗糖果5角,他最多可以买几颗糖果?(8分)21. ()一个正方形的边长是6厘米,求它的面积和周长。
小学五年级奥数第11课抽屉原理的一般表达试题附答案-精品
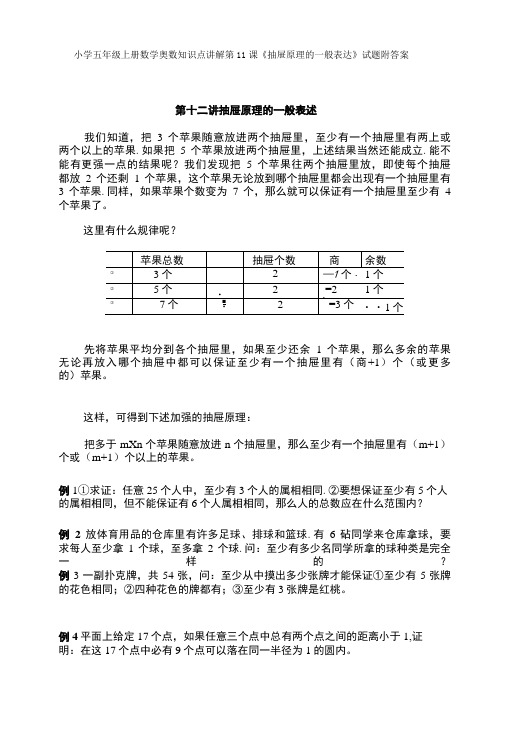
小学五年级上册数学奥数知识点讲解第11课《抽屉原理的一般表达》试题附答案第十二讲抽屉原理的一般表述我们知道,把3个苹果随意放进两个抽屉里,至少有一个抽屉里有两上或两个以上的苹果.如果把5个苹果放进两个抽屉里,上述结果当然还能成立.能不能有更强一点的结果呢?我们发现把5个苹果往两个抽屉里放,即使每个抽屉都放2个还剩1个苹果,这个苹果无论放到哪个抽屉里都会出现有一个抽屉里有3个苹果.同样,如果苹果个数变为7个,那么就可以保证有一个抽屉里至少有4 个苹果了。
这里有什么规律呢?先将苹果平均分到各个抽屉里,如果至少还余1个苹果,那么多余的苹果无论再放入哪个抽屉中都可以保证至少有一个抽屉里有(商+1)个(或更多的)苹果。
这样,可得到下述加强的抽屉原理:把多于mXn个苹果随意放进n个抽屉里,那么至少有一个抽屉里有(m+1)个或(m+1)个以上的苹果。
例1①求证:任意25个人中,至少有3个人的属相相同.②要想保证至少有5个人的属相相同,但不能保证有6个人属相相同,那么人的总数应在什么范围内?例2放体育用品的仓库里有许多足球、排球和篮球.有6砧同学来仓库拿球,要求每人至少拿1个球,至多拿2个球.问:至少有多少名同学所拿的球种类是完全一样的?例3一副扑克牌,共54张,问:至少从中摸出多少张牌才能保证①至少有5张牌的花色相同;②四种花色的牌都有;③至少有3张牌是红桃。
例4平面上给定17个点,如果任意三个点中总有两个点之间的距离小于1,证明:在这17个点中必有9个点可以落在同一半径为1的圆内。
例5把1、2、3、…、10这十个数按任意顺序排成一圈,求证在这一圈数中一定有相邻的三个数之和不小于17o例6在边长为3米的正方形内,任意放入28个点,求证:必有4个点,以它们为顶点的四边形的面积不超过1平方米。
分析与解答根据题目的结论,考虑把这个大正方形分割成面积为1平方米的9个小正方形(如右图)。
答案例1①求证:任意25个人中,至少有3个人的属相相同.②要想保证至少有5个人的属相相同,但不能保证有6个人属相相同,那么人的总数应在什么范围内?分析与解答①把12种属相看作12个抽屉。
二年级奥数题 (11)

二年级奥数题(二)1、湖里有一只船,船上坐着穿红色、黄色、绿色衣服的人。
小刚把穿三种颜色的人数相加,小红把他们的人数相乘,得数都一样,船上有几人?2、小猴要爬上6米高的大树,可是每次他爬上4米后,他又掉下2米,小猴第几次才能爬上树顶?3、傍晚,小明开灯做作业,本来拉一次开关,灯就亮了。
但是他连拉了七次开关,灯都没亮,后来,才知道停电。
你知道来电时,灯亮的还是不亮的?4、一根绳子长6米,对折以后再对折,每折长几米?5、有一根绳子,连续对折3次,量得每折长4米,这根绳子长几米?6、口袋里有红球、黄球、和白球若干个,冬冬闭着眼睛每次从袋中摸一个球。
现在,他至少要摸几次,才能保证能摸出两个颜色相同的球?7、把16只鸡分别装进5个笼子里,怎样才能使每个笼子里的鸡只数不同?8、有5条交叉的路,要把10盏灯安装在路上,使每条路上安装4盏灯,该怎样安装?画图试一试。
9、烙熟一块饼需要4分钟,每面2分钟。
一只锅只能同时烙2块饼,要烙3块饼,至少需要几分钟?烙7块呢?10、有四枚五分的硬币,国徽面全部朝上放在桌子上,每次翻3枚,至少要翻几次,才能使这4枚硬币的国徽面全部朝下?11、10加上3,减去5,再加上3,再减去5……这样连续几次,做多少次结果为0?12、24减去4,加上1,再减去4,加上1,……这样连续几次,结果为0?13、8个同学参加打乒乓球比赛。
比赛采用淘汰制,每场比赛淘汰1人。
到决出冠军时,要多少场?14、红黄两盒小棒,红盒里比蓝盒里多5根,从红盒子里拿出1根放进蓝盒子里后,红盒子里的小棒比蓝盒子里的多几根?15、爸爸买回3个球,两红一黄,哥妹两人抢着要,爸爸叫他们背对背坐着,爸爸给哥哥塞个红球,给妹妹塞个黄球。
把剩下的藏在自己背后。
爸爸让他们猜他手里是什么球,谁猜队就给谁。
那么,谁一定猜对呢?16、甲乙丙丁各自参加篮球、排球、足球和象棋。
现在知道:(1)甲的身材比排球运动员高。
(2)几年前,丁由于事故,失去了双腿。
一年级奥数训练题11套

一年级奥数训练题11.楼层小宏与爸爸一起上楼,小宏走得慢,爸爸走得快,小宏上了1层时,爸爸已上了2层,问小宏上到3楼时,爸爸上到几楼?2.分水果一个小组有10个人,7个人爱吃香蕉,5个人爱吃苹果,问既爱吃香蕉又爱吃苹果的有几个人?3.小鸭子说稀奇,道稀奇,鸭子队里有只鸡,正着数,它第6,倒着数,它第7,小鸭一共有几只?4. 找规律填数:① 5、7、9、11、13、()②0、1、1、2、3、5、8、()5. 按要求填数:36、12、45、7、35、23、60、55()>()>()>()>()>()>()>()13、24、15、7、61、25、14、8()<()<()<()<()<()<()<()6、有一个两位数,个为是9十位是4,这个两位数是()7、有14小朋友排成一队,从左往右数红红排在第4位,从右向左数明明也是排在第4位,那么红红和明明两人之间有多少人?8、最小三位数的是()最大的三位数是()。
9、用5、7、4三个数可以排成()个不相同的三位数。
分别写出来。
10、要把一根木棒锯成5段需要4分钟,要是想锯成7段需要多少分钟?11、计算:3+5+7+9+11+13+15+17+19+21=5+10+15+20+25+30=12、有14个小朋友在玩捉迷藏的游戏,有6个小朋友被捉住了,还有多少个小朋友没被捉住啊?13、、有一个个位数,在它的右边加上一个零,构成一个两位数,这个两位比原来的数要大36,则原来的各位数是()。
14、按要求填补算式完整:9+()=21 21-()=1921-()=18 24+()=4315、老师让小朋友们植树,先植了10棵桃树,然后老师让同学们在每两棵桃树间植一棵梨树,那么一共还可以植多少棵梨树?16.分糖块三个小朋友分5块糖。
要求每人都分到糖,但每人分到的糖块数不能一样多,你能分吗?17.树的年龄公园里有三棵树,它们的树龄分别由1、2、3、4、5、6这六个数字中的不同的两个数字组成,而其中一棵的树龄正好是其他两棵树龄和的一半,你知道这三棵树各是多少岁吗?18.奇偶问题①把10个球分成三组,要求每组球的个数都是奇数,怎样分?②②把11个苹果分给三个小朋友,要求每个小朋友分得偶数个苹果,怎样分?19:春游 45个小朋友排成一队去春游。
小学四年级奥数第11课《填横式1》试题附答案

小学四年级上册数学奥数知识点讲解第11课《填横式1》试题附答案第十三讲填横式(一)整数可以分为奇数和偶数两类.我们把1,3,5,7,9和个位数字是1,3,5,7,9的数叫奇数.把0,2,4,6,8和个位数是0,2,4,6,8的数叫偶数.①整数的加法有以下性质:奇数+奇数二偶数;奇数+偶数二奇数;偶数+偶数二偶数.②整数的减法有以下性质:奇数稳数二偶数;奇数T禺数二奇数;偶数希数二奇数;偶数稳数二奇数;偶数T禺数二偶数.③整数的乘法有以下性质:奇数X奇数二奇数;奇数X偶数二偶数;偶数X偶数二偶数.@奇数/偶数.利用上面的性质住住可以巧妙地解出一些数字问题,请看下面的例题.例1把1~8这八个数字写成两个四位数字,使它们的差等于III1即:例2将1〜9这九个数字分别填入下面算式的九个口中,使每个算式都成立.'□+口=□<□一□=□□×□=□例3将1~9分别填入下面算式的中,使每个算式都成立,其中1,2,5已填出.∫□×□=5∏I四+□=□+□例4将1~8这八个数字分别填入下面算式的口中,使每个算式都成立.∫□×□=□□t□×□+9=□□答案例1把1~8这八个数字写成两个四位数字,使它们的差等于II11即:□□□□-□□□□=1111分析注意到两个四位数字的差是1111,也就是要求被减数上的每一位数,都要比减数上相对应的位上的数大1而所给的八个数字最小的是1,是奇数,所以被减数各位上的数字都应是偶数,而减数的每一位,都是比被减数上相对应的位上的数小1的奇数.这样就可以得到答案.解:本题的答案不惟一,下面是其中的三个.则亚E-EHiEniii;EE囱回-回回亚I=I1I1;回回回回也回回m=1111补充说明:这道题的答案共有24个.同学们可以试着写出其他的解.例2将1-9这九个数字分别填入下面算式的九个口中,使每个算式都成立.□÷□=□□×□≡□分析①审题.在题目的三个算式中,乘法运算要求比较高,它要求在从1~9这九个数字中选出两个,使它们的积是一位数,且三个数字不能重复.②选择解题的突破口.由①的分析可知,填出第三个乘法算式是解题的关键.③确定各空格中的数字.由前面的分析,满足乘法算式的只有2X3=6和2X4=8.如果第三式填2X3=6.则剩下的数是1,4,5,7,8,9,共两个偶数,四个奇数.由整数的运算性质知,两个偶数必定是前两个式中各填一个试一试,可以这样填:(答案不是惟一的,这里只填出一个).如果第三式填2X4=8,则剩下的数是1,3,5,6,7,9.其中只有一个偶数和五个奇数,由整数的运算性质知,无论怎样组合都不能填出前两个算式.解:本题的一个答案是:例3将1~9分别填入下面算式的中,使每个算式都成立,其中1,2,5已填出.∫□×□≡5∏‘回+□=□÷□分析①审题.本题由两个算式构成,题目中给了三个数字.由题目可见,第一个算式的要求比较高.②选择解题的突破口.填出第一式是解决这道题的关键.③确定各口中的数字,观察题目发现,满足第一个算式的只有7X8=56和6X9=54.如果第一式填7X8=56,则剩下的数是3,4,9.无论怎样把它们填入第二式,都不能满足.所以这种填法不行.如果第一式填6X9=54,则剩下的数是3,7,8.可以这样填入第二式,即:12+回二团+回解:本题的答案是:(O<[2>50112÷[U=[2]÷0补充说明:形如例2、例3这样的多个算式填数的问题,在解决时,常常把填出要求比较高的算式(如乘法算式)作为解题的突破口,然后再考虑其他算式,得出答案.有时,答案是不惟一的,在解题时,只要写出一个正确的答案就可以了.例4将1~8这八个数字分别填入下面算式的口中,使每个算式都成立.∫□×□≡□□∖□×□+9=□□分析①审题.题目中的□比较多,且两个算式要求都比较高.如果硬猜会很难,为叙述方便,我们将各空格中填上字母如下:‘国X回=回叵]‘叵IX国+9=国国②选择解题的突破口.由于要填的数字中没有0,而所有的数字不能重复.所以,第一式的A、B、D不能填5.且第二式的E、F中,只能有一个填5,不妨设可填在E上,这样,5只能填在C、E、G、H四个空格之一.这就是解决本题的突破口.③确定各口中的数字.⑴若C=5,则第一式为:阿X回二回回,空格A、B只能填7和8,此时D=6.即:回二EE.此时,剩下数字1,2,3,4去填第二式.在用它们去填E、F时,有如下几种情况:1X2,1×3,1×4,2×3,2×4,3X4.(注意:在讨论中,应该把各种可能性不重、不漏地考虑到.这样从小到大,循序渐进的方法很重要).把每一种情况都试验结果知,只有E、F填3和4时,可以满足第二个等式,此时,囱X@+9二日[斗这就找到了一个解.(ii)若E=5,则第二个算式为:回X®+9=回回,F不能填偶数,否则结果中的H=9,重复.F只能填奇数1,3,7.若F=I,则G=I,出现重复数字,不行,若F=3,则第二式为:E1XB]+9二回回,剩下数字1,6,7,8,无论怎样,都无法满足第一式,不行;若F=7.则网昨44,出现重复数字.也不行,所以,E所在空格不能填5.Gii)若G=5,则第二个算式为回X回+9二回回.这时,E、F可以填6、7或6、8.如果E、F填6、7,则有向Xm+9=∣苑],H=I.下面用剩下的数字2,3,4,8填第一式.分析第一式,可以得到两个解为:∫0×国=国区]∫0Xri1=5∏^1⅛□÷94∏ΓΓ痼X0÷9=0□如果E、F填6、8,则有网x[i]+9胴同,H=T.下面用剩下的数字1,2,3,4填第一式,分析第一式,可以这样填:0×0=0∣2∣∙GV)若H=5,则第二个算式为:回X回+9二回回,这时回XM的个位必须等于6.EXF 可以是IX6,2×3,2×8,7×8.如果E、F填1和6,则G=I,重复,不行.如果E、F填2和3,则囱X回+9=/回,剩下的数字为:4、6、7、8,不论怎样填,都不能满足第一式,所以E、F不能填2和3.如果E、F填2和8,则G=2,重复.不行.如果E、F填7和8,则第二式为团乂回+9二回回.剩下的数字是1,2,3,4.用它们填第一式,可以是:m×g=∣τ]∣2].解:H×[I]=□□./团义国=国©∖□×0÷9=[D[1]∣0×□÷9=[J]∏]5X叵]=囱0,O×0=[T][Γ]:国xE+9=国Ijj国乂国+9=囱区IJEXH=∣T∣[Γ](0×回+9=回£]补充说明:这道题应用乘法的交换律还可以写出一些解答的形式.习题十三1.把1~8这八个数字分别填入下面的口中,使算式成立.□□□□+□□□□=99992 .把O〜9这十个数字分别填入下面的口中,使各算式都成立.(□÷□=□<□-口=□1□×□=□□3 .把2~9这个八个数字分别填入下面的口中,使各算式都成立(□+□^□=□1□×□≡□□4 .把1-9这九个数字分别填入下面的口中,使各算式都成立.'□+□=□四年级奥数上册: 第十三讲填横式(一)习题解答习题十三解答1 ,0000+IU00®=9999(解不惟-,有384种不同的填法).2 .解不惟一,第一、二式可有不同填法.[国+团・国国0・臼∣0×□=[i]03•解不惟一,第一式可有不同填法.∫□÷U]-[4]=0 /团+m-叵]=团(叵|X回=回回驮∣0×H]=Ξ0回+回=叵]f0+国=回②1叵]@x 国=团叵]回[[1][∑]×□=囱回回f0÷[U=ΞΜ但+B=□P□×E=[I][I]0[[∑EM1]=回③国/©+国=团」口+回=国 ΘPE×□=[2J[I]□⑧[回回Xm=回国国但+②=团 JE+*回⑨[叵][∑]X[I]=国回国(EΞ×0≡ΞEH]附:奥数技巧分享分享四个奥数小技巧。
奥数11

1、甲乙丙三人共有人民币168元,第一次甲拿出与乙相同的钱给乙;第二次乙拿出与丙相同的钱给丙;第三次丙拿出与这时甲相同的钱给甲。
这样,甲乙丙三人的钱数相同,原来甲比乙多多少钱?2、甲乙两个仓库各有粮食若干吨,从甲仓库运出1/4到乙仓库,又从乙仓库运出1/4到甲仓库,这时两仓库储量相等。
原来甲仓库粮食是乙仓库的几分之几?3、一天,一个财迷在一座桥上碰到一个老人,老人对他说:“你要走过这座桥再回来,你身上的钱就会增加1倍,但是作为报酬,你每走一个来回要给我32个铜板。
”财迷觉得挺合算就同意了。
他在桥上走一个来回钱果然增加1倍,他很高兴的给了老人32个铜板。
可是当他走完5个来回后,身上的最后32个铜板都给了老人。
你知道财迷有多少个铜板吗?4、三棵树上落着若干只小鸟。
第一棵树上飞10只到第二棵树上,第二棵树上飞5只到第三棵树上,第三棵树上飞4只到第一棵树上,这时三棵树上都正好事20只。
原来每棵树上各有多少只小鸟?5、乐乐在计算两个数相加时,把一个加数个位上的1错看成了7,把另一个加数十位上的8错看成了3,所得和是2955,求原来的正确答案是多少?6、某班一次语文和数学考试,语文得100的有7人,数学得100的有13人,上课了,老师说全班得100分的同学站起来。
你想一想,人数最多有几个?最少有几个?7、实验小学53名同学参加跳绳比赛,有37名同学踢毽子比赛,有24名同学参加游泳比赛,每人最多参加两项比赛,参加比赛的最多有多少人?参加两项比赛的最多有多少人?8、某班共有36名同学,在一次测验中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人,两题都没答对的有多少人?9、有50个学生,他们穿的裤子是白色或黑色,上衣是兰色或红色。
若有14人穿的是兰上衣白裤子,31人穿黑裤子,18人穿红上衣,求穿红上衣黑裤子的学生是多少?10、五十名学生面向老师站成一排,按老师口令从左到右一次报数:1、2、…..50,报完后,老师让所有报数是4的倍数的同学向后转,接着又让所有报数是6的倍数的同学向后转,问现在还有多少同学面向老师?11、某班的全体同学参加了思维训练、天文兴趣和蝴蝶工艺三个项目的测试,有4名同学在三个项目上都未达到优秀,其余每人至少有一个项目达到优秀,达到优秀的人数如下表,求这个班的学生数。
小学奥数第11周 假设法解题

6
4
年的年龄各是多少岁?
3
1
2. 小红今年的年龄是妈妈的 ,10 年后小红的年龄是妈妈的 ,小红今年多少岁?
8
2
5 3. 甲书架上的书是乙书架上的 ,甲、乙两个书架上各增加 90 本后,甲书架上的书是
7
4 乙书架上的 ,甲、乙两各书架原来各有多少本书?
5
例题 4。
4 王芳原有的图书本数是李卫的 ,两人各捐给“希望工程”10 本后,则王芳的图书的
加 400 棵,则中学是小学的 2 倍。求中、小学原来各植树多少棵? 3. 两堆煤,第一堆是第二堆的 2 倍,第一堆用去 8 吨,第二堆用去 11 吨,第一堆剩下的
重量是第二堆的 4 倍。求第二堆煤原来是多少吨?
例题 2。 王明平时积蓄下来的零花钱比陈刚的 3 倍多 6.40 元,若两个人各买了一本 4.40 元的故
5 5 10
4 30× =24(本)
5
答:李卫原有图书 30 本,王芳原有图书 24 本。
练习 4
4 1. 甲书架上的书是乙书架上的 ,从这两个书架上各借出 112 本后,甲书架上书架上各有多少本书?
7
6
4
2. 小明今年的年龄是爸爸的 ,10 年前小明的年龄是爸爸的 ,小明和爸爸今年各多
事书后,王明的钱就是陈刚的 8 倍,陈刚原来有零花钱多少元? 【思路导航】假设仍然保持王明的钱比陈刚的 3 倍多 6.40 元,则王明要相应地花去 4.40×3
=13.20 元,但王明只花去了 4.40 元,比 13.20 元少 13.20-4.40=8.80 元,那 么王明买书后的钱比陈刚买书后的钱的 3 倍多 6.40+8.80=15.20 元,而题中已 告诉:买书后王明的钱是陈刚的 8 倍,所以,15.20 元就对应着陈刚花钱后剩 下钱的 8-3=5 倍。 【6.40+(4.40×3-4.40】÷(8-3)+4.40=7.44(元)
2022年小学四年级奥数典型题测试卷(全国通用)11《周期问题》(解析版)

【四年级奥数举一反三—全国通用】测评卷11《周期问题》试卷满分:100分考试时间:100分钟姓名:_________班级:_________得分:_________一.选择题(共7小题,满分21分,每小题3分)1.(2016•创新杯)将某数的3倍减5,计算出答案:将这个答案的3倍减5,计算出答案;⋯;这样反复4次,最后得出的结果是1177,那么原数是()A.14 B.15 C.16 D.17【解答】解:第四次计算后的结果为1177,第三次计算后的结果为:(11775)3394+÷=,第二次计算后的结果为:(3945)3133+÷=,第一次计算后的结果为(1335)346+÷=,原数为:(465)317+÷==.故选:D。
2.(2012•华罗庚金杯)在2012年,1月1日是星期日,并且()A.1月份有5个星期三,2月份只有4个星期三B.1月份有5个星期三,2月份也有5个星期三C.1月份有4个星期三,2月份也有4个星期三D.1月份有4个星期三,2月份有5个星期三【解答】解:因为2012年1月有31天,2月有29天,⋯(天),÷=(星期)33174⋯(天),÷=(星期)12974所以1月份有4个星期三,2月份有5个星期三.故选:D。
3.(2011•其他模拟)鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪12种动物依次代表各年的年号,如果公元1年是鸡年,那么公元2005年是()年.A.鸡B.牛C.虎D.兔【解答】解:2005121671÷=⋯,所以,以鸡开始循环的第1种动物是鸡,由此得出,公元2005年是鸡年,故选:A。
4.(2014•迎春杯)为了减少城市交通拥堵的情况,某城市拟定从2014年1月1日起开始试行新的限行规则,规定尾号为1、6的车辆周一、周二限行,尾号2、7的车辆周二、周三限行,尾号3、8的车辆周三、周四限行,尾号4、9的车辆周四、周五限行,尾号5、0的车辆周五、周一限行,周六、周日不限行.由于1月31日是春节,因此,1月30日和1月31日两天不限行.已知2014年1月1日是周三并且限行,那么2014年1月份()组尾号可出行的天数最少.A.1、6 B.2、7 C.4、9 D.5、0【解答】解:依题意可知:1月份共31天,由于1月1日是周三,所以1月份周三、周四、周五共5天,周一、周二共4天.其中1月30日周四、1月31日周五.所以只看周三即可.周三2、7以及3、8限行.故选:B。
小学五年级奥数竞赛试卷1-12

小学五年级奥数竞赛试卷1-121、计算4.75–9.63+(8.25-1.37) 17.48×37-174.8×2.72、在算式□×5÷3×9+11=1991中;□里应填入的数字是( ).3、一个自然数与它本身相加、相减、相除所得的和、差、商再相加;结果是1991;那么原来的自然数是( )4、某同学在计算一道除法题时;误将除数32写成23;所得的商是32余数是11;正确的商与余数的和是( )5、亮亮从家步行去学校;每小时走5千米.回家时骑自行车;每小时走13千米.骑自行车比步行的时间少4小时;亮亮家到学校的距离是( )千米.6、一个两位数;个位数字是十位数字的3倍;如果这个数加上60;则两个数字相等;这个两位数是( ).7、两个自然数的和是286;其中一个数的末位数是0;如果把这个零去掉;所得的数与另一个数相同;那么原来两位数的积是( )8、下图中;三角形ABC的面积是30平方厘米;D是BC的中点;AE的长是ED的长的2倍;那么三角形CDE的面积是( )平方厘米.9、甲乙丙丁四个人共买了10个面包平均分着吃;甲拿出6个面包的钱;乙和丙都只拿出2个面包的钱;丁没带钱.吃完后一算;丁应该拿出1.25元;甲应收回( )元.10、在200位学生中;至少有( )人在同一个月过生日.11、暑假小明去游园;遇到了甲、乙、丙、丁四位同学;小明和四位同学都握了手;甲和3个人握了手;乙和2个人握了手;丙和1个人握了手;那么丁和( )个人握了手.12、有一个长方形;它的长和宽各增加8厘米;这个长方形的面积就增加了208平方厘米;原来长方形的周长是( )厘米.13、甲乙二人环绕周长是400米的跑道跑步;如果两人从同一地点出发背向而行;那么经过2分钟两人相遇;如果两人从同一地点出发同向而行;那么经过20分钟两人相遇;已知甲的速度比乙的速度快;甲每分钟跑( )米.14、甲对乙说:“当我的岁数是你现在的岁数时;你才4岁.”乙对甲说:“当我的岁数是你现在的岁数时;你已经61岁了.”现在甲( )岁.15、王刚有红、蓝、黑三种铅笔共20支;其中黑铅笔的支数比红铅笔的一半多1支;蓝铅笔的支数比黑铅笔的一半多1支.王刚有蓝铅笔( )支.16、为了维护少年儿童的交通安全;一年级四个班购买了一批小黄帽.四个班出的钱一样多.分帽子时;一班比其他三个班少拿8顶;因而二、三、四班分别给一班6.2元.那么每顶小黄帽( )元.17、小明从家到学校的路程是540米;小明上学要走9分钟;回家时比上学少用3分钟.那么小明往返一趟平均每分钟走( )米.18、水果店运来西瓜的个数是白兰瓜个数的2倍.如果每天卖白兰瓜40个;西瓜50个;若干天后卖完了白兰瓜;西瓜还剩360个.水果店运来的西瓜和白兰瓜共( )个.19、用3个大瓶和5个小瓶可装墨水5.6千克;用1个大瓶和3个小瓶可装墨水2.4千克.那么用2个大瓶和1个小瓶可装墨水( )千克.20、小明从家到学校上课;开始时以每分钟50米的速度走了2分钟;这时他想:若根据以往上学的经验;再按这个速度走下去;肯定要迟到8分钟.于是他立即加快速度;每分钟多走10米;结果小明早到了5分钟.小明家到学校的路程是( )米.五年级奥数试卷一2(每题6分;共120分) 班级:姓名:一、填空(每题5分)1、 1+1.2+1.4+1.6+……+10=_____2、 0.45-[10-(0.2+6.37÷0.7)] ×0.5=____3、 3+4-9+5+6-10+……101+102-58=___4、在下面等式中适当地添上+、-、÷、×;使等式成立.1 2 3 4 5 6 7 8 9=19956、一堆苹果;三个分成一份;最后剩下1个;五个分成一份;最后剩下2个;七个分成一份;最后剩下3个.这堆苹果至少有___个.7、把4-10这七个数填入六边形的中心及顶足上的圆圈内;使在每条直线上的三个数之和均为21.8、规定:a※b=(b+a)×b;那么(2※3)※5=__.9、 10辆大卡车和15辆小卡车去运贷物64吨;每辆大卡车比每辆小卡车多运1.9吨;那么每辆大卡车运__吨;每辆小卡车运___吨.10、ABC三只桶;A容量10升;B7升;C3升;现在A中装满水;利用这三只水桶把A桶中的水平均分成两份;至少要操作___次.二、解答题(每题10分)1、有甲、乙、丙三个数;从甲数中取出17加到乙数;从丙数中取19加到甲数;从乙数中取20加到丙数;这时三个数都是200.那么甲、乙、丙三个数原来各是多少?2、某校有100名同学参加数学竞赛;平均分是63分;其中男生平均是60分;女生平均分是70分.男生比女生多几人?3、五年级一班开学第一天;每两位同学见面握一次手;全班40人共要握多少次手?4、甲、乙两人骑车分别从AB两地同时出发相向而行;甲每小时行11千米;乙每小时行15千米;两人相遇后又继续前进.已知出发4小时两人相距30千米.求两地相距多少千米?5、父亲今年50岁;儿子今年14岁;几年前父亲的年龄是儿子的5倍?6、某人驾驶汽车;要行35000千米的路程(路面相同);汽车共六个轮胎;甲装上六只轮胎;车上又带上1只备用轮胎;为了使七个轮胎磨损相同;司机有规律地把七只轮胎轮换使用;到达终点时;每只轮胎行驶多少千米?7、列车通过250米长的隧道用25秒;通过210米长的隧道用了23秒.又知列车的前方有一辆与它行驶方向相同的货车;货车车身长320米;速度为每秒17米;列车与货车从相遇到离开需要多少秒?8、李叔叔下午要到工厂上3点的班;他估计快到上班时间了;到屋里看钟;可是钟早在12点10分就停了;他上足发条后忘了拔针;匆匆离家到工厂一看;离上班时间还有10分钟.8小时工作后夜里11点下班;李9、龟兔赛跑;全程5.2千米.兔子每小时跑20千米;乌龟每小时跑了800米.乌龟不停地跑;兔子边跑边玩;它先跑1分钟;然后玩6分钟;又跑2分钟;又玩12分钟;再跑3分钟;然后又玩18分钟……这样如此继续;问谁先到达终点?早到几分钟?小学五年级奥数试卷3一、仔细分析;认真填写.1、找规律填空.(1) 4、9、16、25、()、()、()……(2) 1、3、6、10、()、()、()2、有三个质数;他们的乘积是1001;这三个质数各是()、()().3、小明从家到学校的路程是540米;小明上学要走9分钟;回家时比上学少用3分钟;那么小明往返一趟平均每分钟走()米.4、五年级开展数学竞赛;一共20题;答对一题得7分;答错一题扣4分;王磊得74分;他答对了()题.5、在计算30.6除于一个数时;由于小数点向右点错了一位;结果得204;正确答案应该是().6、有数字卡片3、5、6、0各一张;可以组成()个不同的三位数;结果按从小到大的顺序排列;第七个数是().7、甲、乙两数是互质数;且最小公倍数是156;那么甲、乙两数可能是()和().8、箱子里有同样多的红球和黄球;每次取出5个红球和3个黄球;取得若干次;红球还剩2个;黄球还剩14个;那么箱子里原来有红球()个.9、一个三位数;它能被2整除;又有约数5;百位上的数是最小的质数;十位上的数是百位上的数的倍数;这个三位数可能是().10、有三根小棒;分别长12厘米、44厘米、56厘米.要把他们都截成同样长的小棒;不许剩余;每根小棒最长能有()厘米.11、用2100个棱长1厘米的正方体堆成一个长方体;它的高是1分米;长和宽都大于高.它的长是()厘米;宽是()厘米.12、把右图的木块平均分成三块后;木块的表面积增加()平方厘米.14、一个自然数被3除余1;被5除余2;被7除余3;这个自然数最小是().15、36的约数有()个;这些约数的和是().16、用一根长38厘米的铁丝围长方形;使他们的长和宽都是整厘米数;可以有()种围法.17、便民冷饮店每3个空汽水瓶可以换1瓶汽水;小东在暑假里买了99瓶汽水;喝完后又用空瓶换汽水;那么她最多能喝到()瓶汽水.18、已知:(■+▲)×0.3=4.2;而且▲÷0.4=12.算一算:▲=();■=().二、仔细观察;认真计算.① 49.84-(51.17-12.56)÷27② 2.5×32×1.25③ 38.4×187-15.4×384+3.3×16④(1+3+5+7+……+97+99)÷17三、请你设计方案.50个同学去划船;每条大船可以坐6人;租金10元;每条小船可以坐4人;租金8元.(1)请你至少写出两种租船方案.(2)怎样租船最省钱;最少要花多少钱?四、应用与实践.(1)东风汽车厂原计划制造一批高级轿车;每天制造18辆;要30天完成;如果每天多制造2辆;可以提前几天完成?(2)一个化肥厂原计划14天完成一项任务;由于每天多生产化肥3.5吨;结果9天就完成了任务;原计划每天生产化肥多少吨?(3)一个林场用喷雾器给树喷药;2台喷雾器4小时喷了200棵;照这样计算;6台喷雾器5小时可以(4)两座大楼相距300米.甲、乙两人各从一座大楼门口同时向相反的方向走去;7分钟后两人相距860米;甲每分钟走37米;乙每分钟走多少米?(5)买足球3个;排球5个;需要228元;买足球6个;排球2个;需要312元.现在体育组买了11个足球;9个排球;共需要多少元?六、附加题.(1)一次比赛;共5名评委参加评分;选手丁哈哈得分情况是:如果去掉一个最高分和一个最低分;平均分是9.58分;如果去掉一个最高分;平均分是9.4分;如果去掉一个最低分;平均分是9.66分.如果5个分都保留算平均分;他应该得多少分?(2)盒装“酸牛奶”的形状是长6厘米、宽4厘米、高10厘米的长方体;请你为酸牛奶加工厂设计一种包装箱;要求每箱装12盒;要既省材料又便于搬运.画一画、想一想、试一试;你设计的包装箱的长、宽、高各是多少?小学五年级奥数试卷41.有一数列: 1 、 2 、 4 、 7 、 11 、 16 、……这列数列第 16 个数是().2.一只蜗牛掉在 12 米深的井里;它白天向上爬 5 米;夜间向下滑 3 米;这只蜗牛()天就能爬出井口.3.有数组{1;2;3;4};{2;4;6;8};{3;6;9;12};……那么第100个数组的四个数的和是().4.由 1 、 2 、 0 、 4 、3 五个数字可以组成()个三位数.5.某数加上 5;乘以5;减去5;再除以5;结果等于5;这个数是().6.两数相除;商 7 余 3 ;如果被除数、除数、商及余数相加和是 53 ;被除数是();除数是().7.东方小学五年级举行数学竞赛;10 个赛题每做对一题得8分;错一题倒扣5分;张华全解答;但只得41分;他做对( )题.8.一个口袋里有四种不同颜色的小球;每次摸出2个;要保证有10次所摸的结果是一样的;至少要摸()次9.王飞每小时40千米的速度行了240千米;按原路返回每小时行60千米;王飞往返平均速度是每小时行()千米.10.松鼠妈妈采松子;晴天每天可采24个;雨天每天可采16个;他一连几天一共采了168个松子;平均每天采21个;这几天当中一共有()天晴天.11.甲汽车每小时行驶 40千米;乙汽车每小时行驶 45千米;两汽车同时从同一地点向同一方向行驶;1小时后;乙汽车回原地取东西;并在原地停留半小时后追甲汽车;问距原地( )千米处追上甲车.12.某班统计数学成绩;得平均分为87.13;经复查;发现将吴江的98分误作89分;再计算;平均分为87.31求这个班有学生()人.13.“IMO”是国际数学奥林匹克竞赛的缩写;把这三个字母写成三种不同的颜色;现有五种不同的颜色;按上述要求可以写出()中不同颜色搭配的“IMO”.14.六年级有 43 人;比五年级少 33 人;五年级男生比女生多 8 人;五年级有女生()人.男生()人.15.在1、2、3、…… 99、100中;数字2在一共出现了()次.16.甲乙丙三人到银行储蓄;如果甲给乙200元;则甲乙钱数同样多;如果乙给丙150元;丙就比乙多300元;甲和乙哪个人存款多?();多存()元.17.张彬买了3斤鸭和4斤鸡;共付出9元6角;李杰买了3斤鸡和 4斤鸭;付出 9 元 3 角;每斤鸡比每斤鸭少()元.18.学校有一批图书分给几个班;如果每班分10本;则余48本;如果每班分13本;则不足24本;问每班分()本刚好分完19.一天; A,B,C 三人去郊外钓鱼;已知 A 比 B 多钓 6 条; C 钓的鱼的条数是 A 的 2 倍;比 B 多钓 22 条;他们一共钓了()条鱼.20.在一座铁路桥全长1200米;一列火车开过大桥需要75秒;火车开过路旁的电线杆只需15秒;那么火车全长是()米.小学数学五年级竞赛试题51、小华有2枚5分硬币;5枚2分硬币;10枚1分硬币;他要取出1角钱;共有()种不同的取法.2、一个质数的3倍与另一个质数的2倍之和为100;这两个质数之和是().3、在1~600这600个自然数中;能被3或5整除的数有()个.4、有42个苹果34个梨;平均分给若干人;结果多出4个梨;少3个苹果;则最多可以分给()个人.5、甲、乙两人同时从A点背向出发沿400米环行跑道行走,甲每分钟走80米,乙每分钟走50米;这二人最少用()分钟再在A点相遇.6、11时15分;时针和分针所夹的钝角是()度.7、一个涂满颜色的正方体;每面等距离切若干刀后;切成若干小正方体块;其中两面涂色的有60块;那么一面涂色的有()块.8、六一儿童节游艺活动中;老师让每位同学从一个装有许多玻璃球的口袋中摸两个球;这些球给人的手感相同;只有红、黄、白、蓝、绿五色之分(摸时看不到颜色);结果发现总有两个人取的球相同;由此可知;参加取球的至少有()人.9、自然数A的所有约数两两求和;又得到若干个自然数.在这些和中;最小的是4;最大的是500;那么A =()10、李然从常熟虞山下的言子墓以每分12米的速度跑上祖师山;然后以每分24米的速度原路返回;他往返平均每分行()米.用淘汰赛;共要进行()场比赛.12、甲、乙、丙三人各拿出同样多的钱合买一种英语本;买回后甲和乙都比丙多要6本;因此;甲、乙分别给丙1.5元钱;每本英语本()元.13、一个表面都涂上红色的正方体,最少要切()刀,才能得到100个各面都不是红色的正方体.14、五(1)班全班45人选中队长;每人投一票;现已统计到李辰已得票16票;王莹得票18票;王莹至少再得()票就能保证当选(得票多者当选)15、在一次晚会上男宾与每一个人握手(但他的妻子除外),女宾不与女宾握手,如果有8对夫妻参加晚会,那么这16人共握手()次.16、甲、乙、丙三个电台;分别有4、4、3人;新年中彼此祝贺;每两个电台的人都彼此一一通话;那么他们一共要通话()次.17、如果把1到999这些自然数按照从小到大的顺序排成一排;这样就组成了一个多位数:12345678910111213…996997998999.那么在这个数里;从左到右的第2000个数字是( ).18、、一个正方体;它的表面积是20平方厘米;现在把它切割成8个完全相同的小正方体.这些小正方体的表面积之和是().小学数学五年级竞赛试题61、六(1)班男生是女生人数的 2倍.体育课上;老师按每4个男生、3个女生分成一组进行游戏.这样;当女生分完时男生还剩8人.求这个班女生一共有多少人?2、常熟市举行小学生“百科知识竞赛”;大约有381~450名学生参加;测试结果是全体学生的平均分是76分;男生平均分是79分;女生平均分是71分.求参加测试的男生和女生至少各有多少人.3、小明从家到学校有两条一样长的路;一条是平路;另一条的一半是上坡路;一半是下坡路.小明上学两条路所用的时间一样;已知下坡的速度是平路的1.5倍;那么上坡的速度是平路速度的几分之几?4、在AB一段公路上;甲骑自行车从A往B;乙骑摩托车从B往A;他们同时出发;经过80分钟两人相遇;乙到A后马上折回;在第一次相遇后40分钟追上甲;乙到B地后马上返回;再过多少时间甲与乙再相遇?5、两辆汽车从甲乙两地同时相向而行;在距乙地95千米处相遇;相遇后两车又继续前进;它们各自到达6、百货公司委托运输公司运送1000只花瓶;双方商定每只的运费为1.5元;如打破一只;这只花瓶不但不计运费;还要赔偿9.5元.结果运输公司共得到了1456元运费.问运输过程中打破了几只花瓶?7、用长72米的篱笆靠墙围成一个长方形.长和宽各多少时围成的面积最大?面积是多少?8、某地收取电费的标准是:每月用电不超过50度;每度收5角;如果超过50度,超出部分按每度8角收费.某月甲用户比乙用户多交3元3角电费;这个月甲、乙各用了多少度电?9、小轿车、面包车和大客车的速度分别为60千米/小时、48千米/小时和42千米/小时;小轿车和大客车从甲地、面包车从乙地同时相向出发;面包车遇到小轿车后30分钟又遇到大客车.甲、乙两地相距多远?10、某班学习小组有12人;一次数学测验只有10人参加;平均分是81.5分.后来;缺考的李明和张红进行了补考;李明补考成绩比原10人平均分少1.5分;而张红的补考成绩却比12人的平均分多12.5分;张红考了多少分?11、某风景区门票的票价如下:50人以下每张12元;51-100人每张10元;100人以上每张8元.现在有甲、乙两个旅游团;若分开购票;两个旅游团总共需门票费1142元;若两个旅游团合在一起作为一个团体购票;总共只需付门票864元.这两个旅游团各有多少人?12、有两条纸带;一条长21厘米;一条长13厘米;把两条纸带都剪下同样的一段后;发现长纸带剩下的长度是短纸带剩下的长度的2倍.请问:剪下的一段有多长?13、小星有48块巧克力;小强有36块巧克力.如果每次小星给小强8块;同时小强又给小星4块;经过多少次这样的交换后;小强的块数是小星的2倍?14、袋里有若干个球;小明每次拿出其中的一半再放回一个球;这样共操作了3次;袋中还有6个球.请问:袋中原有多少个球?15、有一根长180厘米的绳子;从一端开始;每3厘米作一个记号;每4厘米也作一记号.然后将标有记号16、某班学生排队;如果每排3人;就多1人;如果每排5人;就多3人;如果每排7人;就多2人;这个班级至少有多少人?17、甲、乙两车往返于相距270千米的A、B两地;甲车先从A地出发;12分钟后;乙车也从A地出发;并在距A地90千米的C地追上甲车.乙车到B地后立即按原速返回;甲车到B地休息5分钟后加快速度;向A地返回;在C地又将乙车追上.最后甲车比乙车早几分钟到达A地?18、甲乙两人分别从相距130千米的AB两地同时沿笔直的公路乘车相向而行;各自前往B地、A地.甲每小时行28千米;乙每小时行32千米.甲乙各有一个对讲机;当他们之间的距离不大于10千米时;两人可用对讲机联络.问:(1)两人出发后多久可以用对讲机联络?(2)他们能用对讲机联络多长时间?小学五年级奥数竞赛试卷71. 简算:15.48×35-154.8×1.9+15.48×842.解方程.5×(2x+7)-30=3×(2x+7) x=3.循环小数0.37 205 小数点右面第106位上的数字是 .4. 一排电线杆;原来两根之间的距离是35米;现改为45米;如果起点的一根位置不移动;至少米又有一根电线杆不需要移动.5.一船在静水中每小时18千米;在一条顺水用4小时行了80千米;这条河的水流速度是 .6.同学们去春游;带水壶的有78 人;带水果的有77 人;既带水壶又带水果的有48 人.参加春游的同学共有人.7.在做一道两位数乘以两位数的乘法题时;小马虎把一个乘数中的数字5看成了8;由此得乘积为1872.那么原来的乘积是________.8. 同时被3、4、5整除的最小四位数是 .9. 某个游戏;满分为100分;每人可以做4次;以平均分为游戏的成绩.小王的平均分为85分;那么;他任何一次游戏的得分都不能低于分.10. 五年级数学竞赛;小明获得的名次与他的年龄和竞赛的成绩相乘之积是2134;小明获得的名次名;成绩是分.11.有一个六位数□2002□能被88整除;这个六位数是 .12.用5、5、5、1四个数字组成一个算式;使其结果为24.算式是 .13. 五年级有六个班;每班人数相等.从每班选16人参加少先队活动;剩下的同学相当于原来4个班的人数;原来每班人.14.连续5个奇数的和是95;其中最大的是;最小的是 .15.1+2+3+4+5……+2007+2008的和是 .(奇数或偶数)16.在八个房间里;有七个房间开着灯;如果每次同时拨动四个房间的开关;(能或不能)把全部房间的灯关上;每次拨动5个房间的开关;(能或不能)把全部房间的灯关上.17.大年三十彩灯悬,彩灯齐明光灿灿,三三数时能数尽,五五数时剩一盏,七七数时刚刚好,八八数时还缺三.请你自己猜一猜;彩灯至少有盏18.甲、乙、丙、丁四位同学在篮球比赛中犯规的次数各不相同;A、B、C、D四位裁判有一段对话:A 说:“甲犯规4次;乙犯规3次.”B说:“丙犯规4次;乙犯规2次.”C说:“丁犯规2次;丙犯规3次.”D 说:“丁犯规1次;乙犯规3次.”记录员说:“A、B、C、D四位裁判每人只说对了一半.”甲犯规次.19.甲、乙、丙分别在南京、苏州、西安工作;他们的职业分别是工人;农民和教师.已知⑴甲不在南京工作;⑵乙不在苏州工作;⑶在苏州工作的是工人;⑷在南京工作的不是教师;⑸乙不是农民.那么;甲是;在工作.小学五年级奥数测试题81、计算:0.9999×0.7+0.1111×2.72、找规律填数(1) 1、4、7、10、( )、16、19(2) 2、6、18、54、( )、486、14583、小红步行上学;每分钟走60米;离家11分钟后;妈妈发现小红的数学书忘在家中;立即带着数学书以每分钟280米的速度去追小红;妈妈出发( )分钟后追上小红.4、三辆汽车共运输货物910吨;第一辆汽车比第二辆汽车多运30吨;第三辆汽车比第二辆汽车少运20吨;第一辆汽车运货物( )吨.5、小红、小张、小李三人在一起;其中一位是工人;一位是战士;一位是大学生.现在知道:小李比战士年龄大;小红和大学生不同岁;大学生比小张年龄小;他们三人中;( )是工人.6、一个长方形;如果长增加6厘米或者宽增加4厘米;面积都比原来增加48平方厘米;这个长方形原来的面积是( )平方厘米.7、等腰直角三角形斜边长为8厘米;则此三角形的面积是( )平方厘米.8、有50位同学植树;男同学每人植树5棵;女同学每人植树4棵;共植树230.男同学有( )人;女同学有( )人.9、人民商场以每只13元的价格购进一批茶杯;以每只14.8元的价格卖出.卖到还剩下5只时;除去购进这批茶杯的成本外;还获得88元利润.这批茶杯有( )只.10、把盒中200只红球进行调换.每次调换必须首先从盒中取出3只红球;然后再放入2只白球;那么;在最后一次调换之前盒中的球数是( )只.11、有一个正方形的花池;周围边长为25厘米的方砖铺了一条宽1.5米的小路;用去方砖1776块;花池的面积是( )平方米.12、甲乙丙三个工人搬运一批物资;共得劳务费384元;甲得的2倍等于乙得的3倍;乙得的2倍等于丙的4倍;乙得( )元;丙得( )元.13、自动扶梯以均匀的速度由下往上行驶;两个小孩嫌电梯太慢;急着从扶梯上楼;甲小孩每分钟走26级;乙小孩每分钟走14级;结果甲小孩用4分钟到达楼上;乙小孩用6分钟到达楼上;该扶梯共有( )级.14、甲乙丙三人同时从400米的环形跑道的同一地点出发;丙与甲乙方向相反.已知甲速度每秒6米;乙速度每秒5米;丙速度每秒4.5米;他们出发后( )秒;丙第一次位于甲;乙的正中间.15、对一个两位数进行一次操作是指:将它的两个数字相乘;如果得到一个一位数;则将它写两遍.例如对39进行5次操作依次得到39—27—14一44—16—66.那么经过4次操作变为88的两位数有( )个. 16、将长、宽、高分别为11、10、8的长方体的三个面染上红色;另一个面染上黄色;然后切成棱长为1的单位小正方体;那么只染了一种颜色的小正方体最多有( )个.17、五个裁判员给一名体操运动员评分;去掉一个最高分和一个最低分;平均得9.58分;去掉一个最高分平均得9.46分;去掉一个最低分平均得9.66分.这个运动员的最高分和最低分相差( )分.18、某人驾驶一辆小轿车要作32000千米的长途旅行;除了车上装着四只轮胎;只带了一只备用胎;为了使五只轮胎磨损程度相同;司机有规律地把五只轮胎轮换使用;到达终点时.每只轮胎行驶了( )千米.19、甲、乙、丙三人的平均年龄为42岁;若将甲的岁数增加7岁;乙的岁数增大2倍;丙的年龄缩小2倍;则三人岁数相等;丙的年龄是( )岁.20、幼儿园给大班、小班分水果;大班每人分得3个苹果和1个梨;小班每人分得5个苹果和2个梨;结果发现小班比大班少分得24个苹果.(1)如果两个班分得的梨一样多;那么小班有( )人.(2)如果小班比大班多分得2个梨;那么小班有( )人.小学五年级奥数测试题9一、填空题:1、如果六位数1992□□能被105整除,那么它的最后两位数是_____.2、从1至100以内所有同时不能被3和5整除的自然数的和是_____.3、把分数化成小数后;小数点第110位上的数字是_____.4、一筐苹果,如果按5个一堆放,最后多出3个.如果按6个一堆放,最后多出4个.如果按7个一堆放,还多出1个.这筐苹果至少有_____个.5、狗追狐狸;狗跳一次前进1.8米,狐狸跳一次前进1.1米.狗每跳两次时狐狸恰好跳3次.如果开始时狗离狐狸有30米,那么狗跑米才能追上狐狸.6、某班有59名小学生,他们都订阅了《小朋友》、《儿童时代》、《少年报》中的一种或几种,那么其中至少有名学生订的报刊种类完全相同.7、某班共有30名男生,其中20人参加足球队,12人参加蓝球队,10人参加排球队.已知没有一个人同时参加3个队,且每人至少参加一个队,有6人既参加足球队又参加蓝球队,有2人既参加蓝球队又参加排球队,那么既参加足球队又参加排球队的有人.8、用60元钱可以买一级茶叶144克;或买二级茶叶180克;或买三级茶叶240克.现将这三种茶叶分别按整克数装袋;要求每袋的价格都相等;那么每袋的价格最低是_______元钱.二、计算题:1、一本书的页码从1至62、即共有62页.在把这本书的各页的页码累加起来时;有一个页码被错误地多加了一次.结果;得到的和数为2000.问:这个被多加了一次的页码是几?2、对两个自然数a和b;它们的最小公倍数与最大公约数的差;定义为a☆b;即a☆b=[a;b]-(a;b). 比如;10和14的最小公倍数是70;最大公约数是2;那么10☆14=70-2=68.(1)求12☆21的值;(2)已知6☆x=27;求x的值.3、要砌一个面积为72平方米的长方形猪圈;长方形的边长以米为单位都是自然数;这个猪圈的围墙最少长多少米?。
小学一年级数学奥数题试卷

一、选择题(每题5分,共20分)1. 小明有5个苹果,妈妈又给了他3个苹果,小明现在有多少个苹果?A. 8个B. 10个C. 12个2. 小红有3个橘子,小华有2个橘子,他们两个人一共有多少个橘子?A. 5个B. 6个C. 7个3. 小刚用15个巧克力换来了5个棒棒糖,每个棒棒糖多少个巧克力换来的?A. 2个B. 3个C. 4个4. 小明、小红和小丽三个人一共做了8个纸飞机,小明做了3个,小红做了2个,那么小丽做了多少个?A. 1个B. 2个C. 3个5. 下列哪个不是偶数?A. 2B. 3C. 4二、填空题(每题5分,共25分)6. 6个苹果加上4个苹果等于多少个苹果?________7. 9减去3等于多少?________8. 7加上5等于多少?________9. 10减去6等于多少?________10. 8加上2等于多少?________11. 小明有5个球,小华有3个球,他们两个人一共有多少个球?________12. 下列哪个数是3的倍数?________13. 下列哪个数是4的倍数?________14. 下列哪个数是5的倍数?________15. 下列哪个数是6的倍数?________三、应用题(每题10分,共30分)16. 小花有12个气球,她给了小明3个,又给了小丽2个,小花还剩多少个气球?17. 小明有8块巧克力,他每天吃2块,吃了几天后,小明还剩多少块巧克力?18. 小红有7个铅笔,她用掉了3个,还剩多少个铅笔?四、拓展题(每题15分,共30分)19. 小猫有4个鱼缸,每个鱼缸里有5条金鱼,一共有多少条金鱼?20. 小狗有6个骨头,小猫有4个骨头,它们一共有多少个骨头?答案:一、选择题1. A2. A3. B4. C5. B二、填空题6. 107. 68. 129. 410. 1011. 1012. 613. 814. 1015. 12三、应用题16. 5个17. 3天后,小明还剩1块巧克力。
三年级奥数学练习试卷思维培训资料 (11)

第一讲 速算与巧算同学们,我们又在奥数网见面了!一提到“数学”,大家第一个想到的大多都会是计算。
计算是数学的“地基”,只有打牢这个“地基”,我们的数学大厦才能建高、建好!在数学计算中有许多好的方法技巧和规律,我们如果能理解掌握、灵活运用,“数学大厦”的地基就会为你的成长提供最好的帮助!呵呵!下面就让我们一起来看看吧!加减法中的巧算小朋友们,你知道“凑整”的思想么?在速算、巧算中我们常常为了方便计算而采用“凑整”的思想,它大大加快了我们的计算速度和正确率 。
【例1】 用你的好办法算出下式结果: (1)1350+49+68+51+32+1650(2)33+105+18+95+57+56+12+114 (3)378+26+609 (4)66+218+79+87分析:(1)先观察算式,找能凑整的数,一般找能凑整的数看个位就可以了。
如右图,我们可以先把能凑整的数标出来,能“凑整”的先算,写成算式时一定要看清是不是每个数都写进去了,故有:(1)式=(1350+1650)+(49+51)+(68+32)=3000+100+100=3200(2)式 =(33+57)+(105+95)+(18+12)+(56+114)= 90+200+30+170 = 290+200 = 490分析:在许多情况下,我们没有如例1那么理想的“凑整”状态,这个时候我们可以自己创造条件,变成理想的“凑整”状态,而后进行计算。
(3)原式=(378+22)+(609+1)+(26-22-1)=400+610+3=1013或,原式=(378+2)+(26+4)+(609-2-4)=380+30+603=410+603=1013(4)原式=(66+4)+(218+2)+(87+3)+(79-4-2-3) =70+220+90+70=450方法不唯一,以上仅供参考!可鼓励学生多方位凑整求和。
【例2】 用你的好办法算出下式结果: (1)356+(84-36) (2)376-(87-24) (3)1000-90-80-20-10 (4)178-33-16-29 去括号和添括号的法则:在只有加减运算的算式里,如果括号前面是“+”号,则不论去掉括号或添上括号,括号里面的运算符号都不变;如果括号前面是“-”号,则不论去掉括号或添上括号,括号里面的运算符号都要改变,“+”变“-”,“-”变“+”,即: a +(b +c +d )= a +b +c +d a -(b +a +d )= a -b -c -d a -(b -c )= a -b +c分析:(1)原式=356+84-36=356-36+84=320+84=404注意:在加减运算中,改变运算顺序时要带着符号搬家。
小学二年级下册数学奥数知识点讲解第11课《找规律法》试题附答案

小学二年级下册数学奥数知识点讲解第 11课《找规律法》试题附答案笫十一讲找规律祛观察、搜集己知事矢 从甲发现具有规律性的线索,用以探焉未知事件的 奥秘,是人类智力活动的主要內容.数学上有很多材料可用以来模拟这种活銳培养学注这方面的能力. 例1观察数列的前面几项,找岀规律,写岀该数列的第100项来?12345, 23451, 3951N 45123, ■-例2把写上1?1|100£100个号码的牌子,偉卩面那祥依次分发给四个人.你 知這第『珂牌子会落到谁的手里字小明小英小方小军例3四个小功物换开始小乩 小魏 小兔和小猫分别坐在1、2、3, 4 号位子上(如下圏所示)•第一次它们上下两制啓仏 第二次左右换位.第三次 又上下交换.第四次左右交换•这样一6交换下去,问十次换包扁 小兔坐在第 几号座位上7例4从1开始,每隔两个数写岀一个数,得到一列数,求这列数前第100个数是多少令L 4 7, 10. 13,…例5茴图游戏先画第一代,一个再画第二代.左△下面画出两条銭 段*左一条钱段的末罐又画一个△,左另一条的末端蔺一人6 商第三代,在 笫二代的△下面文画岀两条线段,一条末端茴△・另一条末端画6 而在笫二 代的。
的下面画一条线.线的末端再画一个…一直煦此画下去(见下 图)-问第十次的△和O 共有多少个?S E E3EQO 00002 3ft---- 3-答案第十一讲找规律法观察.搜集己知事实.从中岌现具有规律性的銭報 用以探需未知事件的 奥秘,是人类智力活动的主要内容.数学上有很多材料可用以来模拟这种活动、培界学生这方面的能力. 例1观察数列的前面几项,找岀规律,与出该数列的第100项来?12345, 234B1, 34512> 45123,…解’为了寻找规律.再多写岀几项出来。
并给以编号’1 2 3 4 5 612345, 23451, 34512, 45123, 51234, 12345, 7 8 9 10 U 12 2345L 34512, 45123, 51234, 12345, 2345L廿細巩察,可发现该数列的第电项同第1项,•第7项同兼项"第倾同第3 项•…也就是说该数列各项的出现具有周期性,他们是循环出现的,一个循环 节包含100-5=20.可见第100项与勲项.第10项一拝(项数都能被遵除),即第100项是 51234. 例2把写上1到10哒血个号码的牌子,像下面那样依次分发给四个人,你 知置第73号牌子会落到谁的手里?解;仔细观察,你会发现;分给」卜明的牌子号码是匚齡乞13,…,号码除以4余1,00 0 y m国回分给小英的牌子号码是2, 6, 10, 14,…,号码除以4余2; 分给小方的牌子号码是3, 7, 11,…,号码除以4余3,分给小军的牌子号码是4, 8, 12,…,号码除以4余0 (整除)・ 因此,试用4除73看看余几?73*4=18 •余 1可见73号牌会落到小明的手里. 这就是运用了如下的规律:小明小英小芳小军用这种规律预测第几号牌子发给谁,是很容易的,请同学们自己再试一试. 例3四个小动物换位,开始水鼠、小猴、小兔和小猫分别坐在1、2、3、4 号位子上(如下图所示).第一次它们上下两排换位,第二次左右换位,第三次 又上下交换,第四次左右交换.这样一直交换下去,问十次换位后,小兔坐在第 几号座位上?解;为了能找出变化规律,再接着写岀几次换位情况,见下图.肝住小兔的位置进行观察:叫2猴兔L 2貓鼠彳*很1 2鼠4兔开始第一汝交换它到了第1号位;它到了第2号位; 它到了第4号位' 它到了第3号位, 它又到了第1号位 可以岌现,每经过四次换位后,小兔又回到了原未的位置,利用这个规律 以及10-4二2・・・余2,可知:第十次换位后,小兔的座位同第二次换位后的位置一样,即左第二号位. 如果再仔细地把换位图连续起来研究研究,可以发现,随着一次次地交 换, 小兔的座位按顺时针旋转, 小鼠的座位按逆时针旋转,<1、寮的座位按顺时针旋转,小猫的座位按逆时针旋转,按这个规律也可以预测任何小动物在交换几次后的座位•例4从1开始,每隔两个数写岀一个数,得到一列数,求这列数的第100个 数是多少?1, 4, 7, 10, 13,…解:不难看岀,这是一个等差数列,它的后一项都比相邻的前一项大3,即 公差二3,还可臥发现:笫2项等于第1项加1个公差即4=1+1X3.第一次换位后, 笫二次换位后, 第三次换位后, 第四次换位后, 第五次换位后第3项等于第1项加2个公差即7=1+2 X 3.第4项等于第1项加3个公差即10二1+3X3.第5项等于第1项加4个公差即13二1+4X3.可见笫"项等于笫1项加(n-1)个公差,即|第口项=笫1项十Gl) X公差按这个规律,可求出:第10035=1+ c 100-1) x 3=1+99X3=238.例5画图游戏先画第一代,一个△,再画笫二代,在△下面画岀两条线段,在一条线段的末端又画一个厶,在另一条的末端画一个O;画第三代,在第二代的△下面又画出两条线段,1条末端画4,另1条耒端画O;而在第二代的0的下面画一条线,线的末端再画一个△;…一直照此画下去(见下图),问第十次的△和O共有多少个?—第一代—第二代—第三代解:按着画图规则继续画出几代,以便于观察,以期从中找岀图形的生成规律,见下图.第一代△第三代7 △第五代貝P △ Vb △ 6 第^AOAZXOZXOA AO A Z O数一数,各代的图形(包括△利0)的个数列成下表;第几代 — 二 三 四 五 六 • • • 图形个数 1 2 3 5 8 12• • •可以发现各代图形个数组成一个数列,这个数列的生成规律是,从第三项 起每一项都是前面两项之和.援此规律接着把数列写下去,可得出第十代的△和 O 共有別个(见下表):第几项 —— 二 三 四 五 六 七 A 九 十 十一 十二 • •• 图形个数 1 2 3 5 8 13 21 34 55 89 144 233• • •这就是著名的裴波那契数列•裴波那契是意大利的数学家,他生活在距今大 约七百多年以前的时代.例6如下图所示,5个大小不等的中心有孔的圜盘,按大的在下、小的在上 的次序套在木桩上构成了一座圆盘塔.现在要把这座圆盘塔移到另一个木桩上. 规定移动时妾遵守一个条件,每搬一次只许拿一个圆盘而且任何吋侯大圆盘都 不能压住小圆盘•假如还有第三个木桩可作临时存放圆盘之用•问把这5个圆盘全 部移到另一个木桩上至少需要搬动多少次?(下图所示)第二代 第四代 △△O解:先从最简单情形试起.①当仅有一个圆盘时,显然只需搬动一次(见下贝图)•②当有两个圆盘时,只需搬动3次(见下图).(0)③当有三个圆盘时,总结.找规律,①当仅有一个圆盘时,只需搬1次.③ 当有三个圆盘时,必须先妄把上面的两个小的圆盘搬到临时桩上,见上 图中的(1) ~(3)•由前面可知,这需要搬动3次,然后把最下层的最大圆盘搬 一次到中间桩上,见图(4),之后再扌巴上面的两个搬到中间桩上,这又需搬3 次,见图中(5)~⑺.所以共搬动2X3+1 h 次.⑥推论,当有4个圆盘时,就需要先扌巴上面的3个圆盘搬到临吋桩上,需要7 次,然后把下面的大圆盘搬到中间桩上(1次),之后再把临时桩上的3个圆盘 搬到中间桩上,这又需妄了次,所以共需搬动2XM 二15次.⑤可见当有5个圆盘时,要把它按规定搬到中间桩上去共需要:2X15+1=31 次.这样也可以与岀一个一股的魯式(叫递推公式)20Xtij 一种情况的搬动次数+1=后一种情况的赧动次数对于有更多圆盘的情况可由这个公式算岀来.国盘个数 1 2 34567 8 9 10搬动次数 137 15 31 63 127 255 511 1023• • •逬一步进行考察,并联想到另一个数列2n 1 23 4 5 6 78 9 102n148163264128 256 512 1024当圆到©-小m-羊后<5>若把n个圆盘搬动的次数写成g 把两个表对照后可得出进行蠡r如接把圆酬代入计算就行了’祕再松松式那样习题十11.先计算下面的前几个算式,找出规律,再继续往下写出一些算式,① IX 9+2二② 9X9+7=12X9+3二98X9+6二123X9+4= 987X9+5 二1234* 9+5= 9876X 9+4=• I •• • •Z先计算下面的奇妙算式,找岀规律,再继续写岀一些算式’19+9X9二118+98X9二1117+987X3=11116+9876X9=111115+98765X9=• • •3•先计算下面的前几个算式,找岀规律,再继续写岀一些算式:1X1=lixu=111X111=1111X1111=11111X11111=• • •4•有一列数是2、9、8、2、…,从第三个数起:每一个数都是它前面的两个数相乘积的个位数字(比如第三个数蹴是2X9=8的个位数字).问这一列数的第1Q0个数是几?5.如杲全体自然数按下表逬行排列,那么数1000应在哪个字母下面?6.如果自然数如下图所示排成四列,问101在哪个字母下面?7.3X3的末位数字是9, 3X3X3的末位数是7, 3X 3X3X3的末位数字是L. 求35个羿目乘的结杲的耒位数字是几?二年级奥数下册:第十一讲找规律法习题解答习题十一解答1.① 1X9^2=11L2X 9+3=111123X9^4=1111L234X 9+5^1111112345X94-6=111111123456X9+7=11111111234567X^+8=1111111.112345678 X9+9=L1U11.11L②9 X 9+7=8898X9+6=888ggyx g+5=gg889876X2+0=8888898765X9+3=888888987654X9+2=88888889876543X9+1=88888888・2.19+9X9=100118+98X^10001117+987X9=1000011116+9876X9=100000111115+98765 xg 二100000011111141-987654X9=1000000011111113+9876543X^=100000000111111112+98765432x9=10000000001111111111+987654321X9= 10000000000.3.1X1=111X11=121111X111=123211111X1111=123432111111X11111=123454321111111X111111=123456543211111111x1111111=123456765432111111111X11111111=123456787654321111111111X111111111=123456789876543214.解:按数列的生成规律再多写岀一些数来,再仔细观察,找出规律:2、9、& 2、6、2、2^ 4、8^ 2、6、2^ 2、4. 8、2、6、2、2、4、…可见,除最前面的两个数2和9以外,*、2、6、2、2、4这六个数依次重复岀现.因此可利用这个规律,按下面的方法找岀第100个数岀来:100-2=98,98* 6=16—2.即笫100个数与这六个数的第2个数相同,即笫100个数是2.5.解:不难发现,每个字母下面的数除以7的亲数都是相同的•如第1列的三个数1、8和15,除以7时的余数都是h第2列的三个数2、9和16,除以T时的余数都是2;第3列的三个数3. 10和17,除以7的余数都是3;…•利用这个规律,可求出第1000个自然数在哪个字母下面:1000-7=142'-6所以1000在字母F 的下面.6. 解:可以这样找出排列的规律性:全体自然数依次循环排列在A 、B 、C 、 D 、D 、C 、B 、21个字母的下面,且卩依上题解题方法:101-8=12*-5.可知101与5均排在同一字母下面,即在D 的下面.7•解;从简单情况做起,列表找规律;仔细观察可发现,乘积的末位数字的岀现有周期性的规律:看相乘的3的个 数除以4的余数,余1.时,积的末位数字是3,畲2吋,积的末位数字是9,余3时,积的末位数字是7,整除时,积的末位数字是1,35-4=8-3所以这个积的末位数字是7・。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
32是4的倍数,那么□里能填的最小数是观察下图,?代表的数是
小丽将一些巧克力装入大,小两种礼盒中的一种礼盒内,如果每个小礼盒装
果每个大礼盒装8块巧克力,那么少
从甲地到乙地,小张走完全程要用
后来,在某一时刻,小张未走的路程恰好是小李未走的路程的
从1分,2分,5分硬币各有5枚的一堆硬币中取出一些,合成1角钱,共有不同的取法_____
如图5,5个等腰直角三角形叠放在一起,他们的斜边都在一条直线上厘米,其余4个等腰直角三角形的斜边长依次多。
