卡方检验计算表格-a
卡方检验

• (2)分析过程说明 • ①表6-1的资料是经过人为汇总得到的,即是采用频数表 格式来记录的的资料,同组分别有两种互不相容的结果— —杀灭或未杀灭,两组各自的结果互不影响,即相互独立。 对于这种频数表格资料,在卡方检验之前须用Weight Cases命令对频数变量进行预先统计处理,操作如下:单 击Data-Weight Cases命令,则弹出如图6-3所示对话框, 选中Weight cases by,按三角按钮将变量“计数”置入 Frequency Variable框内,定义“计数”为权数,按OK 。 • ②单击主菜单Analyze-Descriptive Statistics-Crosstabs, 则弹出对话框,按三角按钮将行变量“治疗方法” 置入 Row框内,将列变量“治疗效果” 置入Column框内,如 图6-4。 • ③按Stastics按钮,弹出“选择统计方法”对话框(见图 6-5),选中Chi-square,按Continue,返回图6-4,点OK, 输出表6-2、表 6-3。
x 2 1.428, p 0.839 0.05
,差异不显著,可以认为不同的治疗方法与治疗效果无关,即三 种治疗方法对治疗效果的影响差异不显著。
下表为不同灌溉方式下水稻叶片衰老情况的资料,试测验 稻叶衰老的情况是否与灌溉方式有关?
灌溉方式 深水 浅水 湿润 总计 绿叶数 146 183 152 481 黄叶数 7 9 14 30 枯叶数 7 13 16 36
第五章 卡方检验
一、2X2列联表的独立性检验 (一)计算公式
(二)例题及统计分析
例6.1 分别用灭螨A和灭螨B杀灭害虫,结果如表6-1, 问两种灭螨剂的效果差异是否显著? 表6-1 灭螨A和B杀灭害虫试验结果
组别 灭螨A 灭螨B 未杀灭数C1 12 22 TC1=34 杀灭数C2 32 14 TC2=46 TR1=44 TR2=36 T=80
卡方检验

第二节
行×列表资料的 检验
2
行×列表资料
① 两个样本率比较时,基本数据有4个,排成2行 2列,称为2 ×2表,即四格表; ② 多个样本率或构成比比较时,基本数据超过2 行2列,有R行C列,称R×C表或行列表。
检验统计量(通用公式)
A n( 1) nR nC
2
2
(行数 1)(列数 1)
【
2
2 χ 基本公式】
2
( AT ) , (行数-1)(列数 1) T
T为理论频数(theoretical frequency)
式中,A为实际频数(actual frequency)
nR nC TRC n
【 χ2检验的基本原理】
若H0:π1=π2=π0成立,
四个格子的实际频数A与理论频数T相差不应该很大,即统计
度函数可给出不同自由度的一簇分布曲线。
2分布的形状依赖于自由度的大小;当自由
度趋向于无穷大时, 2分布趋向正态分布。
χ2分布特点
χ2分布是一组曲线。 χ2分布与自由度有关 自由度一定时, χ2值越大,P值越小;反之亦然。 =1时, P=0.05, x2 =3.84 P=0.01, x2 =6.63
三、配对四格表资料的 检验
2
也称McNemar检验(McNemar's test)
例6.3 某研究室用甲、乙两种血清学方法检查410 例确诊的鼻咽癌患者,得到结果如表6.4 ,问两 种方法检出率有无差别?
表6.4 两种血清学检验结果
甲法 + - 合计 乙法 + 261(a) 8(c) 269 - 110(b) 31(d) 141 合计 371 39 410
表中,a, d 为两法观察结果一致, b, c 为两法观察结果不一致。
卡方检验

表7-1 两种疗法疗效的比较的四格表(four-fold table)
分组
试验组 对照组 合计
疗效
有效 无效
99
5
75
21
174
26
合计
104 96 200
有效率
95.20% 78.13% 87.00%
πA = πB
pA ≠ pB
pA = pB?
πA ≠ πB ?
表7-1 两种疗法疗效的比较的四格表(four-fold table)
1+ 2-
4
-
+
3+
3+
…
…
…
…
…
n
-
+
n1 + n2 +
配对四格表的χ2检验(McNemar's test)
例7-3 分析目的:两法有无差别 假设(+,-)与(-,+)两格子理
论频数相等均为:
Q. McNemar 1900-1986 美国心理学家 统计学家
配对四格表的χ 2检验
HH01α: :=BB0.= ≠0C5C。或或两两种种方方法法检检出出率率不相同同 b+c≥40:
2. Scheffè可信区间法 3. Bonferroni法:调整检验水准
– k=R(R-1)/2,α’=α/k
– 例7-9: α’=0.05 / 3=0.0167 – 结果保守 4. SNK检验:参照定量资料的原理
χ2检验的其它应用
拟合优度检验(goodness of fit)
– 判断实际频数与理论频数的吻合程度 – 应用:
是否为小概率事件,以判断假设检验是否成 立。
χ2分布(chi-square distribution)
第二节 普通四格表χ 2检验与专用公式
第十二章 卡方检验

2
χ2 检验:检验观测次数与理论次数是否
一致的统计方法。
(二)χ2的特性
• 可加性 偏离度
2
f0 fe
fe
2
0
2
f 0 f e时,
χ 2值永为正值
主要适用于计数资料
(三) χ2分布及其特点
• χ 2分布:由 许多χ 2值组 df=1 df=4 df=10 df=20
X Y SSR b XY n
Y SS Y n
2 t
b t SEb
3、预测
2
SSe 2 SEYX SY 1 r n2
SSe SSt SSR
ˆ 1.96 SE D .95, Y Y YX
例12-3:随机抽取84名中学生做取消快 慢 班的民意调查。赞成者42,不赞成21,不 表 例12-8:甲、乙两校高中毕业生参加高 态21。试问能否说明在总体中有不同意见? 校统 一考试,结果甲校90名毕业生,录取了67 名, 乙校105名毕业生录取了65名,问两校录取
1、方程建立
XY X Y n SY b r X X n S X Y b X a Y bX
2 2
SSR F SSe n 2
SEb MSe
回归 小结
n
2 S 1 r Y 2 X 2 SX n 2 X n
2、方程检验
f0 fe (f0-fe)2 (f0例12-6:某班50 fe)2/fe 名学生的品行评定结 优 8 3.5 20.25 5.79 2.25 0.10 果是:优8名、良20 良 20 21.5 0.57 名,中18名,差4名。中 18 21.5 12.25 差 4 3.5 0.25 0.07 试检验其评定的分布 ∑ 50 50 — 6.53 与正态分布所期待的 2(3)0.05=7.81 结果有无显著差别?
卡方检验卡方检验公式简易卡方检验计算器卡方公式统计学必备

卡方检验卡方检验公式简易卡方检验计算器卡方公式统计学必备卡方检验(Chi-square test)是一种常用的统计方法,用于检验两个分类变量之间是否存在相关性。
它的原理是比较实际观察到的分布和理论推断的分布之间的差异。
卡方检验的原假设是:两个变量之间不存在相关性,即观察到的分布和理论推断的分布没有显著差异。
如果卡方检验的计算结果显示观察到的分布与理论推断的分布存在显著差异,则可以拒绝原假设,即两个变量之间存在相关性。
卡方检验的计算公式如下:卡方值(Chi-square value)= Σ((观察值-理论值)^2 / 理论值)其中,Σ表示对所有观察值进行求和,观察值是实际观察到的频数,理论值是根据原假设推断出的期望频数。
为了计算卡方值,首先需要根据原假设推断出理论频数分布。
然后计算每个格子中的观察值与理论值的差异,并将差异平方后除以理论值。
最后将所有格子的差异平方和进行求和,得到卡方值。
简易卡方检验计算器可以帮助我们快速计算卡方值和对应的P值。
P值表示观察到的数据在原假设成立的情况下发生的概率。
如果P值小于设定的显著性水平(通常是0.05),则可以拒绝原假设。
卡方检验在统计学中被广泛应用,特别是在分析两个分类变量之间的相关性时。
它可以用于研究医学、社会科学、市场研究等领域中的问题。
对卡方检验的详细解释超过了1200字,在这里无法全部展开。
然而,我们可以总结一些关键要点:1.卡方检验适用于两个分类变量之间的相关性研究。
2.原假设是两个变量之间不存在相关性。
3.可以使用卡方检验公式计算卡方值。
4.简易卡方检验计算器可以帮助我们快速计算卡方值和P值。
5.如果P值小于设定的显著性水平,可以拒绝原假设。
6.卡方检验在统计学中有广泛应用,特别是在社会科学和医学研究中。
卡方检验是一种强有力的统计方法,可以帮助我们理解两个分类变量之间的关系。
通过对卡方检验的学习和应用,我们可以更好地分析和解释各种数据。
卡方检验

浙江大学医学院流行病与卫生统计学教研室
沈毅
卡方检验基础
2值的计算:
( A E) E
供了完整的支持,此处只涉及两分类变量间关联程度的指
标,更系统的相关程度指标见相关与回归一章。
浙江大学医学院流行病与卫生统计学教研室
沈毅
两分类变量间关联程度的度量
相对危险度RR:是一个概率的比值,指试验组人群反应阳性概率 与对照组人群反应阳性概率的比值。数值为1,表明试验因素与
反应阳性无关联;小于1时,表明试验因素导致反应阳性的发生
小 结
3.Kappa一致性检验对两种方法结果的一致
程度进行评价;配对检验则用于分析两种
分类方法的分类结果是否有差异。
浙江大学医学院流行病与卫生统计学教研室
沈毅
小 结 4.分层卡方检验是把研究对象分解成不同层次,按 各层对象来进行行变量与列变量的独立性研究。可 在去除分层因素下更准确地对行列变量的独立性进
浙江大学医学院流行病与卫生统计学教研室 沈毅
小 结
2.关联程度的测量:卡方检验从定性的角度分析是否存在 相关,而各种关联指标从定量的角度分析相关的程度大小。 不同的指标适合不同类型的变量。 RR值是一个概率的比值,是指试验组人群反应阳性概率与 对照组人群反应概率的比值。用于反映试验因素与反应阳 性的关联程度。 OR值是比值的比。是反应阳性人群中试验因素有无的比例 与反应阴性人群中试验因素有无的比例之比。在下列两个 条件均满足时,可用于估计RR值:①所关注的事件发生概 率比较小(<0.1),②所设计的研究是病例对照研究。 浙江大学医学院流行病与卫生统计学教研室 沈毅
医学统计方法之卡方检验

合计
145 109 254 57.09
1.建立检验假设并确定检验水准
H0:三种治疗方案的有效率相同 H1 :三种治疗方案的有效率不全相同
α=0.05
2.计算检验统计量 22 5 4( 5 1 2 4 92 3 5 2 4 52 5 92 1 52 1 )
1 0 0 1 4 51 0 0 1 0 98 0 1 4 58 0 1 0 97 4 1 4 57 4 1 0 9 2 5 4(0 .1 7 9 40 .2 2 0 30 .1 0 5 60 .2 3 2 20 .3 2 4 40 .0 2 7 9 1 ) 2 2 .8 1
完整版课件
21
若不采用校正公式:
2 (29265)242 5.49
(25)(269)(226)(59)
在α=0.05水准下,χ2> χ2 0.05(1),则P<0.05。
完整版课件
back
22
表8-16 配对四格表基本结构的
甲种属性
乙种属性
+
-
合计
+ 合计
a
b
a+c
c
d
c+d
a+c
b+d n=a+b+c+d
T
bc
1
式中,a, d 为两法观察结果一致的两种情况,
b, c为两法观察结果不一致的两种情况。
配对卡方检验公式使用条件:
b+c>40, 2 (b c)2 , 1
bc
b+c≤40,
2 c
( b c 1)2 bc
,
=1
例8.4 现有198份痰标本,每份标本分别用A、B两种 培养基培养结核菌,结果如下表,A培养基的阳性培 养率为36.36%,B培养基的阳性培养率为34.34%,试 问A、B两种培养基的阳性培养率是否相等?
快速学会卡方检验

分层卡方检验结果,即考虑了年龄分层因素的影响以后,对饮酒与食管
癌检验结果,共给出CMH2检验和MH 2检验两种结果,前者是后者的改进,
可见P 值均小于0.05,即可认为饮酒与食管癌有关。
调整年龄混杂后OR的估计值
结果分析
结果显示,去除了年龄混杂效应以后饮酒与不饮酒优势比
ORMH 值为5.205,95%CI:3.593-7.541。
小 结
3.Kappa一致性检验对两种方法结果的一致
程度进行评价;配对检验则用于分析两种
分类方法的分类结果是否有差异。
小 结 4.分层卡方检验是把研究对象分解成不同层次,按 各层对象来进行行变量与列变量的独立性研究。可
在去除分层因素下更准确地对行列变量的独立性进
行研究。在SPSS中,Crosstab过程的Statistics子
结果分析
表示药物加化疗与单用药物治疗某种癌症的疗效比较的行 ×列表,除了观察值以外,还有期望值和有效率。
四格表卡方检验
结果分析
此为四格表2检验的结果,2=6.508,P=0.011,差异有统计学 意义,即药物加化疗与单用药物治疗癌症的疗效有统计学差异。
对频数变量加权
(或选择工具栏中的天枰)
一致性检验
注意:
Kappa检验会利用列联表的全部信息,而McNemar 检 验只会利用非主对角线单元格上的信息。因此,对于 一致性较好,即绝大多数数据都在主对角线的大样本
列联表,McNemar检验可能会失去实用价值。
两分类变量间关联程度的度量
2检验可以从定性的角度说明两个变量是否存在关联,当
拒绝原假设时,在统计上有把握认为两个变量存在相关。 但接下来的问题是,如果两变量之间存在相关性,它们之 间的关联程度有多大?针对不同的变量类型,在SPSS中可 以计算各种各样的相关指标,而且Crosstabs过程也对此提
统计学-四格表资料分析卡方检验

方法原理
• 从卡方的计算公式可见,当观察频数与期望频数完全 一致时,卡方值为0;
• 观察频数与期望频数越接近,两者之间的差异越小, 卡方值越小;
• 反之,观察频数与期望频数差别越大,两者之间的差 异越大,卡方值越大。
• 当然,卡方值的大小也和自由度有关。
方法原理
卡方分布
显然,卡方值的大小不仅与A、E之差有关,还 与单.1元2 格数(自由度)有关
方法原理
根据 H0 得 b、c 两格的理论数均为 Tb = Tc = (b+c)/2,对 应的配对检验统计量为:
2 (b c)2 ,
bc
1
一般在 b + c < 40 时,采用确切概率法。
注意事项
McNemar检验(配对卡方检验)只会利用非主对角线 单元格上的信息,即它只关心两者不一致的评价 情况,用于比较两个评价者间存在怎样的倾向。 因此,对于一致性较好的大样本数据(a,d较大且 b,c较小时),McNemar检验可能会失去实用价值。 例如对1万个案例进行一致性评价,9995个都是 完全一致的,在主对角线上,另有5个分布在左 下的三角区,显然,此时一致性相当的好。但 如果使用McNemar检验,此时反而会得出两种评 价有差异的结论来。
Pearson’s 卡方检验
2 P
k i 1
( Ai
Ti )2 Ti
A: 实际頻数 (actual frequency) T: 理论頻数 (theoretical frequency)
Chi-squared distribution
概述
卡方检验是以卡方分布为基础的一种常用假设检 验方法,主要用于分类变量,它基本的无效假设 是(不包括配对资料):
Poisson分布资料是离散型资料,但不具有分类特征,故 视为计量资料。
多元统计 卡方检验

在遗传学中,我们研究某一性状是否受一对等位基 因的控制,该性状在后代的分离比例是否符合某 种规律
例1 孟德尔的豌豆花试验(红花 705 朵、白花 224朵):这一分离是否符合他自己提出的 3:1 的分离比例的假设?
如果这一 3:1 的理论比例是正确的,那么这一试 验所出现的红花和白花的理论比例应当是:
1477
493
446
143
现假定控制翅膀长度和身体颜色的两对基因是相互 独立的,且都是显隐性关系,则四种类型的果蝇 其比例应当是 9:3:3:1
现需验证这次试验的结果是否符合这一分离比例
首先求:1477 + 493 + 446 + 143 = 2559
2559
?
9 16
?
1439.44
2559
?
3 16
我们以例 3 来说明适合性检验的一般步骤
设立无效假设,H0 :果蝇的分类观测值与理论值相符 vs H A : 两者不符
计算 ? 2值,前面已经得到 ? 2 ? 5.519
df = 4-1 = 3
查 ? 2值表,得
?2 0.05,3
?
7.815
?
2
?
5.519 ?
?2 0.05,3
?
7.815
? p ? 0.05
150
50
50
?
0.107 ? 0.98 ? 0.18 ? 1.267 ?
?2 0.05,2
? 5.991
? p ? 0.05
接受无效假设,即这三部分资料的实际观测值符合
9:3:3 的理论比例
再检查余下的 aabb与这三部分之和是否符合 1:15
前三部分之和(理论值): 240 aabb :16
卡方检验及校正卡方检验的计算

2X 检验或卡方检验和校正卡方检验的计算私立广厦学校 郭捷思在教育学量的研究中,各种各样的统计方法已经被广泛的应用,特别是由于统计软件(如:SPSS )的不断成熟,给教育研究者提供了多种量的研究方法。
但是,这并不是无论什么量的研究都要通过统计软件来实现,也不是所有量的研究一定要运用统计软件才能快捷,简便的实现。
本文将教给大家几种简便的方法来实现卡方检验。
2X 检验(chi-square test )或称卡方检验方法可以根据样本数据,推断总体分布与期望分布或某一理论分布是否存在显著差异,是一种吻合性检验,通常适于对有多项分类值的总体分布的分析。
它的零假设是样本来自的总体分布与期望分布或某一理论分布无显著差异。
根据卡方检验基本思想的理论依据,对变量总体分布的检验就可以从对各个观察频数的分析入手。
为检验实际分布与理论分布(期望分布)之间是否存在显著差异,可采用卡方检验统计量。
典型的卡方统计量是pearson 卡方,其基本公式为:∑=-=ki o i e i o i f f f X 12)( 式中k 为子集个数,o f 为观察频数,e f 为期望频数,2X 服从k —1个自由度的卡方分布。
如果2X 值较大,则说明观测频数分布与期望频数分布差距较大;反之,如果2X 值较小,则说明观测频数分布与期望频数分布较接近。
我们将通过代入数据运算这条公式,计算出2X统计量的观测值,并依据卡方分布表计算观测值对应的概率p值。
下面,将通过几个实际例子来探究如何进行卡方检验。
一、四格表资料的卡方检验例1:某学校分别运用传统教学和多媒体教学在两个平行班的数学课上进行试验,目的为了检测两种教学方法对学生的成绩影响是否有差异。
本实验把学生的成绩划分为优秀人数(80分以上)和非优秀人数。
表1:两种教学方法学生成绩优秀率的比较表内这四个数据(斜体)是整个表中的基本资料,其余数据均由此推算出来;这四格资料表就专称四格表(fourfold table),或称2行2列表(2×2 contingency table)从该资料算出的;两种教学的优秀率分别为40%和68.6%,两者的差别可能是抽样误差所致,亦可能是两种教学效果确有所不同。
卡方检验——精选推荐
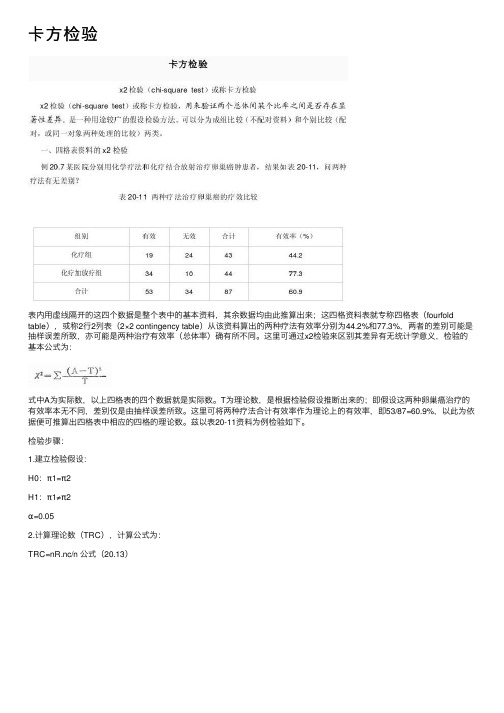
卡⽅检验表内⽤虚线隔开的这四个数据是整个表中的基本资料,其余数据均由此推算出来;这四格资料表就专称四格表(fourfold table),或称2⾏2列表(2×2 contingency table)从该资料算出的两种疗法有效率分别为44.2%和77.3%,两者的差别可能是抽样误差所致,亦可能是两种治疗有效率(总体率)确有所不同。
这⾥可通过x2检验来区别其差异有⽆统计学意义,检验的基本公式为:式中A为实际数,以上四格表的四个数据就是实际数。
T为理论数,是根据检验假设推断出来的;即假设这两种卵巢癌治疗的有效率本⽆不同,差别仅是由抽样误差所致。
这⾥可将两种疗法合计有效率作为理论上的有效率,即53/87=60.9%,以此为依据便可推算出四格表中相应的四格的理论数。
兹以表20-11资料为例检验如下。
检验步骤:1.建⽴检验假设:H0:π1=π2H1:π1≠π2α=0.052.计算理论数(TRC),计算公式为:TRC=nR.nc/n 公式(20.13)因为上表每⾏和每列合计数都是固定的,所以只要⽤TRC式求得其中⼀项理论数(例如T1. 1=26.2),则其余三项理论数都可⽤同⾏或同列合计数相减,直接求出,⽰范如下:T1.1=26.2T1.2=43-26.2=16.8T2.1=53-26.2=26.8T2.2=44-26.2=17.23.计算x2值按公式20.12代⼊4.查x2值表求P值在查表之前应知本题⾃由度。
按x2检验的⾃由度v=(⾏数-1)(列数-1),则该题的⾃由度v=(2-1)(2-1)=1,查x2界值表(附表20-1),找到x20.001(1)=6.63,⽽本题x2=10.0 1即x2>x20.001(1),P<0.01,差异有⾼度统计学意义,按α=0.05⽔准,拒绝H0,可以认为采⽤化疗加放疗治疗卵巢癌的疗效⽐单⽤化疗佳。
通过实例计算,读者对卡⽅的基本公式有如下理解:若各理论数与相应实际数相差越⼩,x2值越⼩;如两者相同,则x2值必为零,⽽x2永远为正值。
卡方检验

综合结果表明:西药组与中药组有效率无差别;中西医结合组有效率高于单纯西药组和 单纯中药组。
步骤 分割 三种方案治疗病毒性肝炎疗效比较的χ 2 分割计算表 处理组 有效人数 无效人数 合计 有效率(%) χ2 西药组 51 49 100 51.00 0.936 中药组 35 45 80 43.75 合计 86 94 180 西药组+中药组 86 94 180 47.78 21.854 中西医结合组 59 15 74 79.73 合计 145 109 254 22.790 ν 1 P >0.05
四.配对计数资料的卡方检验
例5 有50份咽喉涂抹标本,每份按同
样的条件分别接种于甲乙两种培
养基中,观察结核杆菌生长情况,
比较两种培养基的效果(如下表5)
表5两种培养基培养白喉杆菌的比较 乙
甲 + + 23(a) - 12(b) 合 计 35
-
合 计
7(c)
30
8(d)
20
15
50
配对计数资料的计算公式:
即假设两疗法无差别,生存率都是 等于合计的54.81%,那么
甲疗法治疗46人,则理论上有 46 ╳ 54.81%=25.21人生存 乙疗法治疗58人,则理论生有 58 ╳ 54.81%=31.79人生存, 故每个实际数所对应的理论数 算法是,该实际数对应的行和乘 列和再除以总的N样本含量。 即 TRC=nR nC / n
0.05(1)
= 3.84,
P >0.05,差异无统计学意义, 按 α=0.05水准,不拒绝H0,
认为两种疗效没有差异。
注意:当n<40或出现T<1时,校 正法也不行,要用精确检验法直
接计算概率。
excel数据表计算卡方检验的p值【范本模板】

(二)用EXCEL的统计函数进行统计卡方检验(χ2)卡方(χ2)常用以检验两个或两个以上样本率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
卡方检验常采用四格表,如图5-4-18所示,比较的A、B两组数据分别用a、b、c、d表示,a为A组的阳性例数,b 为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5—4-18所示。
(1)比较的A、B两组数据分别用a、b、c、d表示。
a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论值T11、T12、、T21和T22.将实际值和理论值分别输入如图所示的四个单元格(图5-4-19).选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“fx”处,鼠标器左键点击工具栏的“fx”快捷键,打开函数选择框。
(2)在函数选择框的“函数分类”栏选择“统计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
(3)在“Actual_range"项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:"分隔(图5—4—20)。
在数据输入完毕后,p值的计算结果立即显示。
用鼠标器点击“确定”按钮,观察计算结果。
图5-4—18 四格表图5—4—19 四格表数据输入图5-4—20 计算选择框图5-4—21 p值计算结果4.在表存放概率p 值的空白单元格处显示p 值的计算结果。
在“编辑”栏处显示χ2检验的函数“CHITEST"及两组比较数据的起始与结束单元格的行列号(图5-4—21).。
统计方法卡方检验

卡方检验用途:可以对两个率或构成比以及多个率或构成比间的差异做统计学检验第一节. 四格表资料的χ2检验例8.1 为了解铅中毒病人是否有尿棕色素增加现象,分别对病人组和对照组的尿液作尿棕色素定性检查,结果见表8.1,问铅中毒病人和对照人群的尿棕色素阳性率有无差别?表8.1 两组人群尿棕色素阳性率比较组别阳性数阴性数合计阳性率%病人29(18.74) 7(17.26) 36 80.56对照9(19.26)28(17.74) 37 24.32合计38 35 73 52.05卡方检验的基本思想表1中29、7、9、28是构成四格表资料的四个基本格子的数字,其余行合计和列合计以及总的合计都可以根据该四个数字推算出来,故该类资料被称为四格表资料四格表卡方检验的步骤以例8.1为例1.建立假设:H0:π1 = π2H1:π1≠π2α=0.05四格表的四格子里的数字是实际数,在表1中四个数字旁边括号中的四个数字为理论数,其含义是当无效假设成立的时候,理论上两组人群各有多少阳性和阴性的人数。
若H0:π1=π2成立→p1=p2=p即假设两组间阳性率无差别,阳性率都是等于合计的52.05%,那么铅中毒病人36人,则理论上有36 ╳52.05%=18.74人为阳性;对照组37人,则理论上有37 ╳52.05%=19.26人为阳性。
故每个实际数所对应的理论数算法是,该实际数对应的行和乘列和再除以总的N样本含量。
即TRC=nR nC / n2.计算理论数第1行1列: T11=36×38/73= 18.74依次类推T12 = 17.26T21 = 19.26T22 = 17.74四格表中理论数的两大特征:(1)理论频数表的构成相同,即不但各行构成比相同,而且各列构成比也相同;(2)各个基本格子实际数与理论数的差别(绝对值)相同。
一、卡方检验基本公式A: 实际数 T: 理论数卡方检验的基本思想是看理论数与实际数的吻合程度上述公式中卡方统计量的大小取决于实际数和理论数的相差大小情况,如果无效假设成立的话,那么实际数和理论数不应该相差过大,所以卡方统计量应该较小,而如果卡方统计量越大,则越有可能推翻无效假设而得出有统计差异的结论。
