二次函数动点问题典型例题

合集下载

二次函数动点问题

5.如图，等腰直角三角形ABC以2m/s的速度沿直线L向正方形移动，直到AB与CD重合。设xs时，三角形与正方形重叠部分的面积为ym² 。（1）写出y与x的函数关系式；（2）当x=2,3.5时，y分别是多少？
（3）当重叠部分的面积是正方形的面积的一半时，三角形移动了多长时间？
动面问题
6.如图（1）等腰直角三角形ABC以2m/s的速度沿矩形 DEFG的GF边向右移动，直到BC与GF重合。已知 BC=GF=12m,EF=6m,设xs时，三角形与矩形重叠部分的面积为ym² (1)参考图②，图③写出y与x之间的关系式；（2）当x1=2.5，x2=5时，y分别是多少？ 7 （3)当重叠部分的面积为矩形面积的时，三角形 18 移动了多长时间？
图（1）
图（2）
图（3）
P
B
Q
C
3.在梯形ABCD，AD∥BC,AB=BC=10cm,CD=6cm ∠c=90°，点P从A点出发沿线段AB以每秒Icm/s的速度向终B点运动；动点Q同时从B点出发沿线段BC以每秒2cm/s的速度向终点C运动．设运动的时间为t秒 (0<t<5)．（1）求AD的长．（2）t为何值时,△PBQ为直角三角形．（3）设△PBQ的面积为y，求y与t之间的函数关系式（4）是否存在某一时刻t，使△PБайду номын сангаасQ面积等于梯形形 ABCD面积的2/5？若存在，求出此时的t值；若不存在，说明理由；
A
P BP=12-2t，BQ=4t △PBQ的面积: S=1/2(12-2t) •4t B 即S=- 4t² +24t=- 4(t-3)² +36
Q
C
2.已知：如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、 BC方向匀速移动，它们的速度都是1cm/s，当点 P到达点B时，P、Q两点停止运动．设点P的运动时间为t（s），（1）当t为何值时，△PBQ是直角三角形? （2）设四边形APQC的面积为y（cm2），求y与t 的关系式；（3）是否存在某一时刻t，使四边形APQC的面积是△ABC面积的三分之二？若存在求出t的值，若不存在说明理由 A

二次函数动点专项练习30题(有答案)

二次函数动点专项练习30题（有答案）1．在平面直角坐标系xOy中，二次函数y=﹣x2+x+2的图象与x轴交于点A，B（点B在点A的左侧），与y 轴交于点C．过动点H（0，m）作平行于x轴的直线l，直线l与二次函数y=﹣x2+x+2的图象相交于点D，E．（1）写出点A，点B的坐标；（2）若m＞0，以DE为直径作⊙Q，当⊙Q与x轴相切时，求m的值；（3）直线l上是否存在一点F，使得△ACF是等腰直角三角形？若存在，求m的值；若不存在，请说明理由．2．如图，已知抛物线y=﹣+bx+c图象经过A（﹣1，0），B（4，0）两点．（1）求抛物线的解析式；（2）若C（m，m﹣1）是抛物线上位于第一象限内的点，D是线段AB上的一个动点（不与A、B重合），过点D 分别作DE∥BC交AC于E，DF∥AC交BC于F．①求证：四边形DECF是矩形；②连接EF，线段EF的长是否存在最小值？若存在，求出EF的最小值；若不存在，请说明理由．3．如图，抛物线y=（x﹣3）2﹣1与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D．（1）求点A，B，D的坐标；（2）连接CD，过原点O作OE⊥CD，垂足为H，OE与抛物线的对称轴交于点E，连接AE，AD，求证：∠AEO=∠ADC；（3）以（2）中的点E为圆心，1为半径画圆，在对称轴右侧的抛物线上有一动点P，过点P作⊙E的切线，切点为Q，当PQ的长最小时，求点P的坐标，并直接写出点Q的坐标．4．如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点．（1）求这条抛物线的解析式；（2）E为抛物线上一动点，是否存在点E使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；（3）若将直线BC平移，使其经过点A，且与抛物线相交于点D，连接BD，试求出∠BDA的度数．5．如图，已知二次函数图象的顶点坐标为M（2，0），直线y=x+2与该二次函数的图象交于A、B两点，其中点A 在y轴上，P为线段AB上一动点（除A，B两端点外），过P作x轴的垂线与二次函数的图象交于点Q设线段PQ 的长为l，点P的横坐标为x．（1）求二次函数的解析式；（2）求l与x之间的函数关系式，并求出l的取值范围；（3）线段AB上是否存在一点P，使四边形PQMA为梯形？若存在，求出点P的坐标；若不存在，请说明理由．6．如图，已知抛物线经过原点O和x轴上另一点A，它的对称轴x=2 与x轴交于点C，直线y=﹣2x+7经过抛物线上一点B（5，m），且与直线x=2交于点E．（1）求m的值及该抛物线的函数关系式；（2）若点D是x轴上一动点，当△DCB∽△ECB时，求点D的坐标；（3）若P（x，y）是该抛物线上的一个动点，是否存在这样的点P，使得PB=PC？若存在，试求出所有符合条件的点P的坐标；若不存在，请说明理由．7．矩形OABC在平面直角坐标系中的位置如图所示，其中OA=5，AB=2，抛物线y=﹣x 2+3x的图象与BC交于D、E两点．（1）求DE的长_________；（2）M是BC上的动点，若OM⊥AM，求点M的坐标；（3）在抛物线上是否存在点Q，使以D、O、Q、M为顶点的四边形是平行四边形？若存在，求出点Q的坐标；若不存在，请说明理由．8．如图，已知抛物线与x轴交于A（﹣4，0）和B（1，0）两点，与y轴交于C（0，﹣2）点．（1）求此抛物线的解析式；（2）设G是线段BC上的动点，作GH∥AC交AB于H，连接CH，当△BGH的面积是△CGH面积的3倍时，求H点的坐标；（3）若M为抛物线上A、C两点间的一个动点，过M作y轴的平行线，交AC于N，当M点运动到什么位置时，线段MN的值最大，并求此时M点的坐标．9．如图，抛物线y=ax 2+bx+3（a≠0）的图象经过A（3，0），B（4，1）两点，且与y轴交于点C．（1）直接写出点C的坐标；（2）试求抛物线y=ax2+bx+3（a≠0）的函数关系式；（3）连接AC，点E为线段AC上的动点（不与A、C重合），经过A、E、O三点的圆交直线AB于点F．当△OEF 的面积取得最小值时，请求出点E的坐标．10．抛物线y=a（x+6）2﹣3与x轴相交于A，B两点，与y轴相交于C，D为抛物线的顶点，直线DE⊥x轴，垂足为E，AE2=3DE．（1）求这个抛物线的解析式；（2）P为直线DE上的一动点，以PC为斜边构造直角三角形，使直角顶点落在x轴上．若在x轴上的直角顶点只有一个时，求点P的坐标；（3）M为抛物线上的一动点，过M作直线MN⊥DM，交直线DE于N，当M点在抛物线的第二象限的部分上运动时，是否存在使点E三等分线段DN的情况？若存在，请求出所有符合条件的M的坐标；若不存在，请说明理由．11．如图，已知抛物线y=ax 2+bx+c经过点A（2，3），B（6，1），C（0，﹣2）．（1）求此抛物线的解析式，并用配方法把解析式化为顶点式；（2）点P是抛物线对称轴上的动点，当AP⊥CP时，求点P的坐标；（3）设直线BC与x轴交于点D，点H是抛物线与x轴的一个交点，点E（t，n）是抛物线上的动点，四边形OEDC 的面积为S．当S取何值时，满足条件的点E只有一个？当S取何值时，满足条件的点E有两个？12．如图，抛物线的对称轴是直线x=1，它与x轴交于A、B两点，与y轴交于C点，点A、C的坐标分别是（﹣1，0）、（0，3）（1）求此抛物线对应的函数解析式；（2）若点P是抛物线上位于x轴上方的一个动点，求△ABP面积的最大值；（3）若过点A（﹣1，0）的直线AD与抛物线的对称轴和x轴围成的三角形的面积为6，求此直线的解析式．13．已知抛物线y=ax 2+bx+c的对称轴为直线x=2，且与x轴交于A、B两点，与y轴交于点C，其中A（1，0），C（0，﹣3）．（1）求抛物线的解析式；（2）若点P在抛物线上运动（点P异于点A）．①如图1．当△PBC面积与△ABC面积相等时．求点P的坐标；②如图2．当∠PCB=∠BCA时，求直线CP的解析式．14．如图，平面直角坐标系xOy中，点A的坐标为（﹣2，2），点B的坐标为（6，6），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点E．（1）求点E的坐标；（2）求抛物线的函数解析式；（3）点F为线段OB上的一个动点（不与点O、B重合），直线EF与抛物线交于M、N两点（点N在y轴右侧），连接ON、BN，当点F在线段OB上运动时，求△BON面积的最大值，并求出此时点N的坐标；（4）连接AN，当△BON面积最大时，在坐标平面内求使得△BOP与△OAN相似（点B、O、P分别与点O、A、N对应）的点P的坐标．15．如图，抛物线y=ax2+bx+（a≠0）经过A（﹣3，0）、C（5，0）两点，点B为抛物线的顶点，抛物线的对称轴与x轴交于点D．（1）求此抛物线的解析式；（2）动点P从点B出发，沿线段BD向终点D作匀速运动，速度为每秒1个单位长度，运动时间为ts，过点P作PM⊥BD交BC于点M，过点M作MN∥BD，交抛物线于点N．①当t为何值时，线段MN最长；②在点P运动的过程中，是否有某一时刻，使得以O、P、M、C为顶点的四边形为等腰梯形？若存在，求出此刻的t值；若不存在，请说明理由．参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标是．16．如图，抛物线y=ax2+2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A（﹣4，0）和B．（1）求该抛物线的解析式；（2）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CEQ的面积最大时，求点Q 的坐标；（3）平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（﹣2，0）．问是否有直线l，使△ODF是等腰三角形？若存在，请求出点F的坐标；若不存在，请说明理由．17．在平面直角坐标系xOy中，抛物线y=ax2++c与x轴交于点（﹣1，0）和点B，与y轴交于点C（0，4）．（1）求抛物线的解析式；（2）若P是抛物线上一点，且△ABP的面积是，求P点的坐标；（3）若D是线段BC上的一个动点，过点D作DE⊥BC，交OC于E点．设CD的长为t，四边形DEOB的周长为l，求l与t之间的函数关系式，并写出t的取值范围．18．（2011?宝安区三模）如图，在直角坐标系中，点A（2，0），点B（0，4），AB的垂直平分线交AB于C，交x 轴于D，（1）求点C、D的坐标；（2）求过点B、C、D的抛物线的解析式；（3）点P为CD间的抛物线上一点，求当点P在何处时，以P，C，D，B为顶点的四边形的面积最大？19．（2010?菏泽）如图所示，抛物线y=ax2+bx+c经过原点O，与x轴交于另一点N，直线y=kx+4与两坐标轴分别交于A、D两点，与抛物线交于B（1，m）、C（2，2）两点．（1）求直线与抛物线的解析式；（2）若抛物线在x轴上方的部分有一动点P（x，y），设∠PON=α，求当△PON的面积最大时tanα的值；（3）若动点P保持（2）中的运动路线，问是否存在点P，使得△POA的面积等于△PON面积的？若存在，请求出点P的坐标；若不存在，请说明理由．20．已知抛物线y=ax 2+bx+c的顶点为A（3，﹣3），与x轴的一个交点为B（1，0）．（1）求抛物线的解析式．（2）P是y轴上一个动点，求使P到A、B两点的距离之和最小的点P0的坐标．（3）设抛物线与x轴的另一个交点为C．在抛物线上是否存在点M，使得△MBC的面积等于以点A、P0、B、C 为顶点的四边形面积的三分之一？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．21．如图，已知抛物线y=+bx+c与y轴相交于C，与x轴相交于A、B，点A的坐标为（2，0），点C的坐标为（0，﹣1）．（1）求抛物线的解析式；（2）点E是线段AC上一动点，过点E作DE⊥x轴于点D，连接DC，当△DCE的面积最大时，求点D的坐标；（3）在直线BC上是否存在一点P，使△ACP为等腰三角形？若存在，求点P的坐标；若不存在，说明理由．22．如图，已知抛物线y=ax 2+bx+c（a≠0）的顶点坐标为Q（2，﹣1），且与y轴交于点C（0，3），与x轴交于A，B两点（点A在点B的右侧），点P是该抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交AC于点D．（1）求该抛物线的函数关系式；（2）当△ADP是直角三角形时，求点P的坐标；（3）在题（2）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．23．如图，在直角坐标系xOy中，正方形OCBA的顶点A，C分别在y轴，x轴上，点B坐标为（6，6），抛物线y=ax2+bx+c经过点A，B两点，且3a﹣b=﹣1．（1）求a，b，c的值；（2）如果动点E，F同时分别从点A，点B出发，分别沿A→B，B→C运动，速度都是每秒1个单位长度，当点E 到达终点B时，点E，F随之停止运动，设运动时间为t秒，△EBF的面积为S．①试求出S与t之间的函数关系式，并求出S的最大值；②当S取得最大值时，在抛物线上是否存在点R，使得以E，B，R，F为顶点的四边形是平行四边形？如果存在，求出点R的坐标；如果不存在，请说明理由．24．如图，抛物线经过A（4，0），B（1，0），C（0，﹣2）三点．（1）求出抛物线的解析式；（2）P是（1）中抛物线AB段上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△ACO相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；（3）在直线AC上方的抛物线上有一点D，使得△DCA的面积最大，求出点D的坐标．25．在平面直角坐标系中，已知抛物线经过A（﹣4，0），B（0，﹣4），C（2，0）三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．26．如图1，在平面直角坐标系xOy中，已知A、B两点的坐标分别为（4，0）、（0，2），将△OAB绕点O逆时针旋转90°后得到△OCD，抛物线y=ax2﹣2ax+4经过点A．（1）求抛物线的函数表达式，并判断点D是否在该抛物线上；（2）如图2，若点P是抛物线对称轴上的一个动点，求使|PC﹣PD|的值最大时点P的坐标；（3）设抛物线上是否存在点E，使△CDE是以CD为直角边的直角三角形？若存在，请求出所有点E的坐标；若不存在，请说明理由．27．已知抛物线y=x2+bx+1的顶点在x轴上，且与y轴交于A点．直线y=kx+m经过A、B两点，点B的坐标为（3，4）．（1）求抛物线的解析式，并判断点B是否在抛物线上；（2）如果点B在抛物线上，P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于点E，设线段PE的长h，点P的横坐标为x，当x为何值时，h取得最大值，求出这时的h值．28．如图，已知直线y=x+1与y轴交于点A，与x轴交于点D，抛物线y=x2+bx+c与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）．（1）求该抛物线的解析式；（2）动点P在x轴上移动，当△PAE是直角三角形时，求点P的坐标P；（3）在抛物线的对称轴上找一点M，使|AM﹣MC|的值最大，求出点M的坐标．29．阅读材料：如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”．我们可得出一种计算三角形面积的新方法：S△ABC=ah，即三角形面积等于水平宽与铅垂高乘积的一半．解答下列问题：如图2，抛物线顶点坐标为点C（1，4），交x轴于点A（3，0），交y轴于点B．（1）求抛物线和直线AB的解析式；（2）点P是抛物线（在第一象限内）上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S△CAB；（3）是否存在抛物线上一点P，使S△PAB=S△CAB？若存在，求出P点的坐标；若不存在，请说明理由．30．如图，抛物线与x轴交于A（x1，0），B（x2，0）两点，且x1＞x2，与y轴交于点C（0，4），其中x1，x2是方程x2﹣2x﹣8=0的两个根．（1）求这条抛物线的解析式；（2）点P是线段AB上的动点，过点P作PE∥AC，交BC于点E，连接CP，当△CPE的面积最大时，求点P的坐标；（3）探究：若点Q是抛物线对称轴上的点，是否存在这样的点Q，使△QBC成为等腰三角形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．二次函数动点30题参考答案：1．解：（1）当y=0时，有，解得：x1=4，x2=﹣1，∴A、B两点的坐标分别为（4，0）和（﹣1，0）．（2）∵⊙Q与x轴相切，且与交于D、E两点，∴圆心Q位于直线与抛物线对称轴的交点处，∵抛物线的对称轴为，⊙Q的半径为H点的纵坐标m（m＞0），∴D、E两点的坐标分别为：（﹣m，m），（+m，m）∵E点在二次函数的图象上，∴，解得或（不合题意，舍去）．（3）存在．①如图1，当∠ACF=90°，AC=FC时，过点F作FG⊥y轴于G，∴∠AOC=∠CGF=90°，∵∠ACO+∠FCG=90°，∠GFC+∠FCG=90°，∴∠ACO=∠CFG，∴△ACO≌△CFG，∴CG=AO=4，∵CO=2，∴m=OG=2+4=6；反向延长FC，使得CF=CF′，此时△ACF′亦为等腰直角三角形，易得y C﹣y F′=CG=4，∴m=CO﹣4=2﹣4=﹣2．②如图2，当∠CAF=90°，AC=AF时，过点F作FP⊥x轴于P，∵∠AOC=∠APF=90°，∠ACO+∠OAC=90°，∠FAP+∠OAC=90°，∴∠ACO=∠FAP，∴△ACO≌△∠FAP，∴FP=AO=4，∴m=FP=4；反向延长FA，使得AF=AF′，此时△ACF’亦为等腰直角三角形，易得y A﹣y F′=FP=4，∴m=0﹣4=﹣4．③如图3，当∠AFC=90°，FA=FC时，则F点一定在AC的中垂线上，此时存在两个点分别记为F，F′，分别过F，F′两点作x轴、y轴的垂线，分别交于E，G，D，H．∵∠DFC+∠CFE=∠CFE+∠EFA=90°，∴∠DFC=∠EFA，∵∠CDF=∠AEF，CF=AF，∴△CDF≌△AEF，∴CD=AE，DF=EF，∴四边形OEFD为正方形，∴OA=OE+AE=OD+AE=OC+CD+AE=OC+2CD，∴4=2+2?CD，∴CD=1，∴m=OC+CD=2+1=3．∵∠HF′C+∠CGF′=∠CF′G+∠GF′A，∴∠HF′C=∠GF′A，∵∠HF′C=∠GF′A，CF′=AF′，∴△HF′C≌△GF′A，∴HF′=GF′，CH=AG，∴四边形OHF′G为正方形，∴OH=CH﹣CO=AG﹣CO=AO﹣OG﹣CO=AO﹣OH﹣CO=4﹣OH﹣2，∴OH=1，∴m=﹣1．∵y=﹣x2+x+2=﹣（x﹣）2+，∴y的最大值为．∵直线l与抛物线有两个交点，∴m＜．∴m可取值为：﹣4、﹣2、﹣1或3．综上所述，直线l上存在一点F，使得△ACF是等腰直角三角形，m的值为﹣4、﹣2、﹣1或3 2．（1）∵抛物线y=﹣+bx+c图象经过A（﹣1，0），B（4，0）两点，∴根据题意，得，解得，所以抛物线的解析式为：；（2）①证明：∵把C（m，m﹣1）代入得∴，解得：m=3或m=﹣2，∵C（m，m﹣1）位于第一象限，∴，∴m＞1，∴m=﹣2舍去，∴m=3，∴点C坐标为（3，2），过C点作CH⊥AB，垂足为H，则∠AHC=∠BHC=90°，由A（﹣1，0）、B（4，0）、C（3，2）得AH=4，CH=2，BH=1，AB=5∵，∠AHC=∠BHC=90°∴△AHC∽△CHB，∴∠ACH=∠CBH，∵∠CBH+∠BCH=90°∴∠ACH+∠BCH=90°∴∠ACB=90°，∵DE∥BC，DF∥AC，∴四边形DECF是平行四边形，∴?DECF是矩形；②存在；连接CD∵四边形DECF是矩形，∴EF=CD，当CD⊥AB时，CD的值最小，∵C（3，2），∴DC的最小值是2，∴EF的最小值是2；3. （1）解：顶点D的坐标为（3，﹣1）．令y=0，得（x﹣3）2﹣1=0，解得：x1=3+，x2=3﹣，∵点A在点B的左侧，∴A（3﹣，0），B（3+，0）．（2）证明：如答图1，过顶点D作DG⊥y轴于点G，则G（0，﹣1），GD=3．令x=0，得y=，∴C（0，）．∴CG=OC+OG=+1=，∴tan∠DCG=．设对称轴交x轴于点M，则OM=3，DM=1，AM=3﹣（3﹣）=．由OE⊥CD，易知∠EOM=∠DCG．∴tan∠EOM=tan∠DCG==，解得EM=2，∴DE=EM+DM=3．在Rt△AEM中，AM=，EM=2，由勾股定理得：AE=；在Rt△ADM中，AM=，DM=1，由勾股定理得：AD=．∵AE2+AD2=6+3=9=DE2，∴△ADE为直角三角形，∠EAD=90°．设AE交CD于点F，∵∠AEO+∠EFH=90°，∠ADC+AFD=90°，∠EFH=∠AFD（对顶角相等），∴∠AEO=∠ADC．（3）解：依题意画出图形，如答图2所示：由⊙E的半径为1，根据切线性质及勾股定理，得PQ2=EP2﹣1，要使切线长PQ最小，只需EP长最小，即EP2最小．设点P坐标为（x，y），由勾股定理得：EP2=（x﹣3）2+（y﹣2）2．∵y=（x﹣3）2﹣1，∴（x﹣3）2=2y+2．∴EP2=2y+2+（y﹣2）2=（y﹣1）2+5当y=1时，EP2有最小值，最小值为5．将y=1代入y=（x﹣3）2﹣1，得（x﹣3）2﹣1=1，解得：x1=1，x2=5．又∵点P在对称轴右侧的抛物线上，∴x1=1舍去．∴P（5，1）．此时点Q坐标为（3，1）或（，）4.解：（1）∵该抛物线过点C（0，2），∴可设该抛物线的解析式为y=ax2+bx+2．将A（﹣1，0），B（4，0）代入，得，解得，∴抛物线的解析式为：y=﹣x2+x+2．（2）存在．由图象可知，以A、B为直角顶点的△ABE不存在，所以△ABE只可能是以点E为直角顶点的三角形．在Rt△BOC中，OC=2，OB=4，∴BC==．在Rt△BOC中，设BC边上的高为h，则×h=×2×4，∴h=．∵△BEA∽△COB，设E点坐标为（x，y），∴=，∴y=±2将y=2代入抛物线y=﹣x2+x+2，得x1=0，x2=3．当y=﹣2时，不合题意舍去．∴E点坐标为（0，2），（3，2）．（3）如图2，连结AC，作DE⊥x轴于点E，作BF⊥AD于点F，∴∠BED=∠BFD=∠AFB=90°．设BC的解析式为y=kx+b，由图象，得，∴，y BC=﹣x+2．由BC∥AD，设AD的解析式为y=﹣x+n，由图象，得0=﹣×（﹣1）+n∴n=﹣，y AD=﹣x﹣．∴﹣x2+x+2=﹣x﹣，解得：x1=﹣1，x2=5∴D（﹣1，0）与A重合，舍去；∴D（5，﹣3）．∵DE⊥x轴，∴DE=3，OE=5．由勾股定理，得BD=．∵A（﹣1，0），B（4，0），C（0，2），∴OA=1，OB=4，OC=2．∴AB=5在Rt△AOC中，Rt△BOC中，由勾股定理，得AC=，BC=2，∴AC2=5，BC2=20，AB2=25，∴AC2+BC2=AB2∴△ACB是直角三角形，∴∠ACB=90°．∵BC∥AD，∴∠CAF+∠ACB=180°，∴∠CAF=90°．∴∠CAF=∠ACB=∠AFB=90°，∴四边形ACBF是矩形，∴AC=BF=，在Rt△BFD中，由勾股定理，得DF=，∴DF=BF，∴∠ADB=45°5．解：（1）依题意，设二次函数的解析式为y=a（x﹣2）2，由于直线y=x+2与y轴交于（0，2），∴x=0，y=2满足y=a（x﹣2）2，于是求得a=，二次函数的解析式为y=（x﹣2）2；（2）∵PQ⊥x轴且横坐标为x，∴l=（x+2）﹣（x﹣2）2=﹣x2+3x，由得点B的坐标为B（6，8），∵点p在线段AB上运动，∴0＜x＜6．∵，∴当x=3时，．∴0＜l＜；（3）作MQ∥AP．过M作MD∥PQ，MD交AB于N，则四边形PQMD为平行四边形．∴MD=PQ，∵M（2，0），∴D（2，4），∴MD=4．∴．∴x2﹣6x+8=0，∴x1=2，x2=4．∵2＜x＜6，∴x=4．∴P（4，6），Q（4，2）．即P点的坐标为：（4，6）6．：（1）∵点B（5，m）在直线y=﹣2x+7上，∴m=﹣5×2+7=﹣3，∴B（5，﹣3），∵抛物线经过原点O和点A，对称轴为x=2，∴点A的坐标为（4，0）设所求的抛物线对应函数关系式为y=a（x﹣0）（x﹣4），将点B（5，﹣3）代入上式，得﹣3=a（5﹣0）（5﹣4），∴a=﹣，∴所求的抛物线对应的函数关系式为y=﹣x（x﹣4），即y=﹣x2+x．（2）∵点A（4，0），B（5，﹣3），C（2，0），∴AC=4﹣2=2，BC==3，当点D在直线x=2的右侧时，当△DCB∽△ECB，∴=，即=，解得：CD=9，∴点D的坐标为：（11，0），当点D在直线x=2的左侧时，∵∠ACB=∠CDB+∠CBA，且∠ACB＜∠DCB，∴在△DCB中不可能存在与∠DCB相等的角，即此时不存在点使三角形相似；综上所述，存在点D的坐标是（11，0），使三角形相似；（3）存在符合条件的点P使PB=PC，∵C（2，0），B（5，﹣3），∴∠ACB=45°，BC垂直平分线的解析式为：y=x﹣5，∴，∴解得：，，∴符合条件的点P的坐标为（，）或（，）．7．解：（1）由图知：点D、E的纵坐标为2，依题意，有：﹣x2+3x=2，解得：x1=1、x2=2∴D（1，2）、E（2，2），DE=1．（2）如右图；矩形OABC中，∠OMA=90°，∴∠CMO=∠MAB=90°﹣∠AMB，又∠OCM=∠MBA=90°，∴△OCM∽△MBA，有：=设点M（m，2），则：CM=m，BM=5﹣m∴=，解得m1=1，m2=4∴点M的坐标为（1，2）或（4，2）．（3）若以D、O、Q、M为顶点的四边形是平行四边形，那么点D、M不共点，所以点M取（4，2）；①当DM为平行四边形的对角线时，点O、Q关于DM的中点对称，即点Q的纵坐标为4，由图知，点Q必不在抛物线图象上，不合题意；②当DM为平行四边形的边时，OM∥OQ，且OM=OQ；∵D（1，2）、M（4，2）∴OQ=DM=3，即Q（﹣3，0）或（3，0）；经验证，点（﹣3，0）不在抛物线图象上；点（3，0）在抛物线图象上；综上，存在符合条件的点Q，且坐标为（3，0）8. 解：（1）设抛物线的解析式：y=a（x+4）（x﹣1），代入C（0，﹣2），得：﹣2=a（0+4）（0﹣1），解得：a=故抛物线的解析式：y=（x+4）（x﹣1）=x2+x﹣2．（2）∵当△BGH的面积是△CGH面积的3倍，∴BG：CG=3：1，即BG：BC=3：4；∵GH∥AC，∴==；易知：BA=OB+OA=5，则BH=AB=，∴OH=BH﹣OB=﹣1=，即H（﹣，0）．（3）设直线AC：y=kx+b，代入A（﹣4，0）、C（0，﹣2），得：，解得故直线AC：y=﹣x﹣2；设M（x，x2+x﹣2），则N（x，﹣x﹣2），则：MN=（﹣x﹣2）﹣（x2+x﹣2）=﹣x2﹣2x=﹣（x+2）2+2因此当M运动到OA的中垂线上，即M（﹣2，﹣3）时，线段MN的长最大．9．（1）令x=0，可得y=3，故点C的坐标为（0，3）；（2）将点A（3，0），B（4，1）代入可得：，解得：，故函数解析式为y=x2﹣x+3；（3）如图，∵点A（3，0），点B（4，1），∴直线AB的解析式为：y=x﹣3，∵A（3，0），C（0，3），∴OA=3，OC=3，∴tan∠OAC===1，∴∠OAC=45°，∴∠OAC=∠OAF=45°，∵∠OEF=∠OAF=45°，∠OFE=∠OAE=45°，∴OE=OF，∠EOF=180°﹣45°×2=90°，∴△OEF是等腰直角三角形，∴S△OEF=×OE×OF=OE2，当OE最小时，S△FEO最小，根据等腰直角三角形的性质，当OE⊥AC时，OE最小，此时点E为AC的中点，故点E的坐标为（，）．10.解：（1）易知抛物线的顶点D（﹣6，﹣3），则DE=3，OE=6；∵AE2=3DE=9，∴AE=3，即A（﹣3，0）；将A点坐标代入抛物线的解析式中，得：a（﹣3+6）2﹣3=0，即a=，即抛物线的解析式为：y=（x+6）2﹣3=x2+4x+9．（2）设点P（﹣6，t），易知C（0，9）；则PC的中点Q（﹣3，）；易知：PC=；若以PC为斜边构造直角三角形，在x轴上的直角顶点只有一个时，以PC为直径的圆与x轴相切，即：||=，解得t=1，故点P（﹣6，1），当点P与点E重合时，由抛物线的解析式可知，A（﹣3，0），B（﹣9，0）．所以P（﹣6，0），故点P的坐标为（﹣6，1）或（﹣6，0），（3）设点M（a，b）（a＜0，b＞0），分两种情况讨论：①当NE=2DE时，NE=6，即N（﹣6，6），已知D（﹣6，﹣3），则有：直线MN的斜率：k1=，直线MD的斜率：k2=；由于MN⊥DM，则k1?k2==﹣1，整理得：a2+b2+12a﹣3b+18=0…（△），由抛物线的解析式得：a2+4a+9=b，整理得：a2+12a﹣3b+27=0…（□）；（△）﹣（□）得：b2=9，即b=3（负值舍去），将b=3代入（□）得：a=﹣6+3，a=﹣6﹣3，故点M（﹣6+3，3）或（﹣6﹣3，3）；②当2NE=DE时，NE=，即N（﹣6，），已知D（﹣6，﹣3），则有：直线MN的斜率：k1=，直线DM的斜率：k2=；由题意得：k1?k2==﹣1，整理得：a2+b2+b+12a+=0，而a2+12a﹣3b+27=0；两式相减，得：2b2+9b+9=0，解得b=﹣2，b=﹣，（均不符合题意，舍去）；综上可知：存在符合条件的M点，且坐标为：M（﹣6+3，3）或（﹣6﹣3，3）．11．（1）将A，B，C三点坐标代入y=ax2+bx+c中，得，解得，∴y=﹣x2+x﹣2=﹣（x﹣）2+；（2）设点P（，m），分别过A、C两点作对称轴的垂线，垂足为A′，C′，∵AP⊥CP，∴△AA′P∽△PC′C，可得=，即=，解得m1=，m2=﹣，∴P（，）或（，﹣）；（3）①由B（6，1），C（0，﹣2），得直线BC的解析式为y=x﹣2，∴D（4，0），当E点为抛物线顶点时，满足条件的点E只有一个，此时S=×4×2+×4×=，∵S△BOC=×2×6=6，∴当6≤S＜时，满足条件的点E有两个．②当4＜S＜6时，﹣x2+x﹣2=0的△＞0，方程有两个不相等的实数根，此时0＜n＜1，需满足的条件点E只能在点H与点B之间的抛物线上，故此时满足条件的点E只有一个．12. 解：（1）∵抛物线的对称轴是直线x=1，设抛物线的解析式是y=a（x﹣1）2+k，∴解得：，∴y=﹣（x﹣1）2+4即y=﹣x2+2x+3（2）∵y=﹣x2+2x+3，当y=0时，∴x2﹣2x﹣3=0，解得：x1=﹣1，x2=3，∴B（3，0），A（﹣1，0）∴AB=4．设P（a，﹣a2+2a+3）∴S△ABP==﹣2（a﹣1）2+8，∴△ABP面积的最大值为8（3）设D的坐标为（1，b），∴=6，∴b=±6，∴D（1，6）或（1，﹣6），设AD的解析式为y=kx+b，得或解得：或∴直线AD的解析式为：y=3x+3或y=﹣3x﹣313. 解：（1）由题意，得，解得∴抛物线的解析式为y=﹣x2+4x﹣3；（2）①令﹣x2+4x﹣3=0，解得x1=1，x2=3，∴B（3，0），当点P在x轴上方时，如图1，过点A作直线BC的平行线交抛物线于点P，易求直线BC的解析式为y=x﹣3，∴设直线AP的解析式为y=x+n，∵直线AP过点A（1，0），代入求得n=﹣1．∴直线AP的解析式为y=x﹣1解方程组，得，∴点P1（2，1）当点P在x轴下方时，如图1：设直线AP1交y轴于点E（0，﹣1），把直线BC向下平移2个单位，交抛物线于点P2，P3，得直线P2P3的解析式为y=x﹣5，解方程组，得，∴P2（，），P3（，），综上所述，点P的坐标为：P1（2，1），P2（，），P3（，），②∵B（3，0），C（0，﹣3）∴OB=OC，∴∠OCB=∠OBC=45°设直线CP的解析式为y=kx﹣3如图2，延长CP交x轴于点Q，设∠OCA=α，则∠ACB=45°﹣α，∵∠PCB=∠BCA，∴∠PCB=45°﹣α，∴∠OQC=∠OBC﹣∠PCB=45°﹣（45°﹣α）=α，∴∠OCA=∠OQC又∵∠AOC=∠COQ=90°∴Rt△AOC∽Rt△COQ∴，∴，∴OQ=9，∴Q（9，0）∵直线CP过点Q（9，0），∴9k﹣3=0∴∴直线CP的解析式为．其它方法略．114．解：（1）设直线AB解析式为y=kx+b，将A（﹣2，2），B（6，6）代入，得，解得，∴y=x+3，令x=0，∴E（0，3）；（2）设抛物线解析式为y=ax2+bx+c，将A（﹣2，2），B（6，6），O（0，0）三点坐标代入，得，解得，∴y=x2﹣x（3）依题意，得直线OB的解析式为y=x，设过N点且与直线OB平行的直线解析式为y=x+m，联立，得x2﹣6x﹣4m=0，当△=36+16m=0时，过N点与OB平行的直线与抛物线有唯一的公共点，则点N到BO的距离最大，所以△BON面积最大，解得m=﹣，x=3，y=，即N（3，）；此时△BON面积=×6×6﹣（+6）×3﹣××3=；（4）过点A作AS⊥GQ于S，∵A（﹣2，2），B（6，6），N（3，），∵∠AOE=∠OAS=∠BOH=45°，OG=3，NG=，NS=，AS=5，在Rt△SAN和Rt△NOG中，∴tan∠SAN=tan∠NOG=，∴∠SAN=∠NOG，∴∠OAS﹣∠SAN=∠BOG﹣∠NOG，∴∠OAN=∠NOB，∴ON的延长线上存在一点P，使得△BOP∽△OAN，∵A（﹣2，2），N（3，），∵△BOP与△OAN相似（点B、O、P分别与点O、A、N对应），即△BOP∽△OAN，∴BO：OA=OP：AN=BP：ON又∵A（﹣2，2），N（3，），B（6，6），∴BO=6，OA=2，AN=，ON=，∴OP=，BP=，设P点坐标为（4x，x），∴16x2+x2=（）2，解得x=，4x=15，∵P、P′关于直线y=x轴对称，∴P点坐标为（15，）或（，15）．15.解：（1）∵抛物线y=ax2+bx+与x轴交于点A（﹣3，0），C（5，0）∴解得．∴抛物线的函数关系式为y=﹣x2+x+．（2）①延长NM 交AC 于E ，∵B 为抛物线y=﹣x 2+x+的顶点，∴B （1，8）．（5分）∴BD=8，OD=1．∵C （5，0），∴CD=4．∵PM ⊥BD ，BD ⊥AC ，∴PM ∥AC ．∴∠BPM=∠BDC=90°，∠BMP=∠BCD ．∴△BPM ∽△BDC ．∴=．根据题意可得BP=t ，∴=．∴PM=t ．∵MN ∥BD ，PM ∥AC ，∠BDC=90°，∴四边形PMED 为矩形．∴DE=PM=t ．∴OE=OD+DE=1+t ．∴E （1+t ，0）．∵点N 在抛物线上，横坐标为1+t ，∴点N 的纵坐标为﹣（1+t ）2+（1+t ）+．∴NE=﹣（1+t ）2+（1+t ）+=﹣t 2+8．∵PB=t ，PD=ME ，∴EM=8﹣t ．∴MN=NE ﹣EM=﹣t 2+8﹣（8﹣t ）=﹣（t ﹣4）2+2．当t=4时，MN 最大=2．②存在符合条件的t 值．连接OP ，如图（2）．若四边形OPMC 是等腰梯形，只需OD=EC ．∵OD=1，DE=PM=t ，∴EC=5﹣（t+1）．∴5﹣（t+1）=1．解得t=6．∴当t=6时，四边形OPMC是等腰梯形16．（1）由题意，得：，解得：，∴所求抛物线的解析式为：y=﹣x2﹣x+4．（2）设点Q的坐标为（m，0），过点E作EG⊥x轴于点G．由﹣x2﹣x+4=0，得x1=2，x2=﹣4，∴点B的坐标为（2，0），∴AB=6，BQ=2﹣m，∵QE∥AC，∴△BQE∽△BAC，∴，即，∴EG=（2﹣m），∴S△CQE=S△CBQ﹣S△EBQ=BQ?CO﹣BQ?EG=（2﹣m）[4﹣（2﹣m）]=﹣（m+1）2+3又∵﹣4≤m≤2，∴当m=﹣1时，S△CQE有最大值3，此时Q（﹣1，0）．（3）存在．在△ODF中．（ⅰ）若DO=DF，∵A（﹣4，0），D（﹣2，0）∴AD=OD=DF=2，又在Rt△AOC中，OA=OC=4，∴∠OAC=45°，∴∠DFA=∠OAC=45°，∴∠ADF=90°．此时，点F的坐标为（﹣2，2）（ⅱ）若FO=FD，过点F作FM⊥x轴于点M由等腰三角形的性质得：OM=MD=1，∴AM=3，∴在等腰直角△AMF中，MF=AM=3，∴F（﹣1，3）；（ⅲ）若OD=OF，∵OA=OC=4，且∠AOC=90°，∴AC=4，∴点O到AC的距离为2，而OF=OD=2＜2，∴此时不存在这样的直线l，使得△ODF是等腰三角形，综上所述，存在这样的直线l，使得△ODF是等腰三角形，所求点F的坐标为：F（﹣2，2）或（﹣1，3）．17.解：（1）∵抛物线y=ax2++c与x轴交于点（﹣1，0）和点B，与y轴交于点C（0，4）．∴，解得：，∴y=﹣x2++4；（2）令y=0，可得x1=﹣1，x2=3，∴B点坐标为：（3，0），设P点坐标为（x，y），依据题意得出：×4×|y|=，∴|y|=，∵y=﹣x2++4；=﹣（x﹣1）2+，∴抛物线开口向下，顶点坐标为（1，），∴纵坐标最大值为：，∴y=﹣，∴﹣=﹣x2++4；解得：x1=﹣2，x2=4，∴P点的坐标为：（4，﹣），（﹣2，﹣）；（3）如图所示：在△ABC中，OB=3，CO=4，∠BOC=90°，由勾股定理得BC=5，∵DE⊥BC，∴∠EDC=∠BOC=90°，∵∠DCE=∠OCB，∴△DCE∽△OCB，∴==，∵CD=t，∴==，∴CE=t，DE=t，∴四边形DEOB的周长为l=EO+BO+DB+DE=4﹣t+3+t+5﹣t=12﹣t，t的取值范围是：0＜t＜．18．：（1）过C作CD⊥x轴于G，∵点C为线段AB的中点，∴CG是△OAB的中位线，∴点C的坐标是（1，2），┅┅┅┅┅┅┅┅（1分）又∵OA=2，OB=4，∴AB=，AC=，显然△ABO∽△ADC，∴，即，┅┅┅┅┅┅┅┅┅┅┅（2分）∴AD=5OD=AD﹣OA=3，∴点D的坐标是（﹣3，0）；┅┅┅┅┅┅┅┅┅（3分）（2）解：设过B（0，4），C（1，2），D（﹣3，0）的抛物线的关系式为y=ax2+bx+c，∴，┅┅┅┅┅┅（4分）解得：，┅┅┅┅┅┅┅┅┅┅┅┅（5分）∴抛物线的关系式为；┅┅┅┅┅┅┅┅┅（6分）（3）解：设点P的坐标为（x，y）连BD，过点P作PH⊥x轴于H，交BD于E，S四边形PBCD=S△BCD+S△PBD，∵S△BCD=S△ACD为定值，∴要使四边形PBCD的面积最大就是使△PBD的面积最大，①当P在BD间的抛物线上时，即﹣3＜x＜0，S△PBD=S△PBE+S△PED=PE×DH+PE×OH=PE×OD=PE，∵PE=PH﹣EH=y P﹣y E，┅┅┅┅┅┅┅┅（7分）直线BD的关系式为y=，∴PE=，=，当x=时，PE最大为，∴点P的坐标（，），┅┅┅┅┅┅┅┅┅┅（8分）②当P在BC间的抛物线上时，即0＜x＜1，同理可求出四边形PBCD的面积，很显然，此时四边形PBCD的面积要小于点P在BD间的抛物线上时的四边形PBCD的面积，故P点的坐标是（，）．┅┅┅┅┅┅┅┅┅（9分）19.解：（1）将点C（2，2）代入直线y=kx+4，可得k=﹣1所以直线的解析式为y=﹣x+4当x=1时，y=3，所以B点的坐标为（1，3）将B、C、O三点的坐标分别代入抛物线y=ax2+bx+c，可得解得，所以所求的抛物线为y=﹣2x2+5x．（2）因为ON的长是一定值，所以当点P为抛物线的顶点时，△PON的面积最大，又该抛物线的顶点坐标为（），此时tan∠PON=．（3）存在；把x=0代入直线y=﹣x+4得y=4，所以点A（0，4）把y=0代入抛物线y=﹣2x2+5x得x=0或x=，所以点N（，0）设动点P坐标为（x，y），其中y=﹣2x2+5x （0＜x＜）则得：S△OAP=|OA|?x=2xS△ONP=|ON|?y=?（﹣2x2+5x）=（﹣2x2+5x）由S△OAP=S△ONP，即2x=?（﹣2x2+5x）解得x=0或x=1，舍去x=0得x=1，由此得y=3所以得点P存在，其坐标为（1，3）20.解：（1）设抛物线的解析式为：y=a（x﹣3）2﹣3，依题意有：a（1﹣3）2﹣3=0，a=，∴该抛物线的解析式为：y=（x﹣3）2﹣3=x2﹣x+．（2）设B点关于y轴的对称点为B′，则B′（﹣1，0）；设直线AB′的解析式为y=kx+b，则有：，解得；∴y=﹣x﹣；故P0（0，﹣）．（3）由（1）的抛物线知：y=x 2﹣x+=（x﹣1）（x﹣5），故C（5，0）；∵S四边形AP0BC=S△AB′C﹣S△BB′P0=×6×3﹣×2×=；∴S△BCM=S四边形AP0BC=；易知BC=4，则|y M|=；当M的纵坐标为时，x2﹣x+=，解得x=3+，x=3﹣；当M的纵坐标为﹣时，x2﹣x+=﹣，解得x=3+，x=3﹣；故符合条件的M点有四个，它们的坐标分别是：M1（3+，），M2（3﹣，），M3（3+，﹣），M4（3﹣，﹣）．21．：（1）由于抛物线经过A（2，0），C（0，﹣1），则有：，解得；∴抛物线的解析式为：y=﹣x﹣1．（2）∵A（2，0），C（0，﹣1），∴直线AC：y=x﹣1；设D（x，0），则E（x，x﹣1），故DE=0﹣（x﹣1）=1﹣x；∴△DCE的面积：S=DE×|x D|=×（1﹣x）×x=﹣x2+x=﹣（x﹣1）2+，因此当x=1，即D（1，0）时，△DCE的面积最大，且最大值为．（3）由（1）的抛物线解析式易知：B（﹣1，0），可求得直线BC的解析式为：y=﹣x﹣1；设P（x，﹣x﹣1），因为A（2，0），C（0，﹣1），则有：AP2=（x﹣2）2+（﹣x﹣1）2=2x2﹣2x+5，AC2=5，CP2=x2+（﹣x﹣1+1）2=2x2；①当AP=CP时，AP2=CP2，有：2x2﹣2x+5=2x2，解得x=2.5，∴P1（2.5，﹣3.5）；②当AP=AC时，AP2=AC2，有：2x2﹣2x+5=5，解得x=0（舍去），x=1，∴P2（1，﹣2）；③当CP=AC时，CP2=AC2，有：2x2=5，解得x=±，∴P3（，﹣﹣1），P4（﹣，﹣1）；综上所述，存在符合条件的P点，且P点坐标为：P1（2.5，﹣3.5）、P2（1，﹣2）、P3（，﹣﹣1）、P4（﹣，﹣1）．22．解：（1）∵抛物线的顶点为Q（2，﹣1），∴设抛物线的解析式为y=a（x﹣2）2﹣1，将C（0，3）代入上式，得：3=a（0﹣2）2﹣1，a=1；∴y=（x﹣2）2﹣1，即y=x2﹣4x+3；（2）分两种情况：①当点P1为直角顶点时，点P1与点B重合；令y=0，得x2﹣4x+3=0，解得x1=1，x2=3；∵点A在点B的右边，∴B（1，0），A（3，0）；∴P1（1，0）；②当点A为△AP2D2的直角顶点时；∵OA=OC，∠AOC=90°，∴∠OAD2=45°；当∠D2AP2=90°时，∠OAP2=45°，∴AO平分∠D2AP2；又∵P2D2∥y轴，∴P2D2⊥AO，∴P2、D2关于x轴对称；设直线AC的函数关系式为y=kx+b（k≠0）．将A（3，0），C（0，3）代入上式得：，解得；∴y=﹣x+3；设D2（x，﹣x+3），P2（x，x2﹣4x+3），则有：（﹣x+3）+（x2﹣4x+3）=0，即x2﹣5x+6=0；解得x1=2，x2=3（舍去）；∴当x=2时，y=x2﹣4x+3=22﹣4×2+3=﹣1；∴P2的坐标为P2（2，﹣1）（即为抛物线顶点）．∴P点坐标为P1（1，0），P2（2，﹣1）；（3）由（2）知，当P点的坐标为P1（1，0）时，不能构成平行四边形；当点P的坐标为P2（2，﹣1）（即顶点Q）时，平移直线AP交x轴于点E，交抛物线于F；∵P（2，﹣1），∴可设F（x，1）；∴x2﹣4x+3=1，解得x1=2﹣，x2=2+；∴符合条件的F点有两个，即F1（2﹣，1），F2（2+，1）．23．解：（1）由已知A（0，6），B（6，6）在抛物线上，得方程组，（1分）解得．（3分）（2）①运动开始t秒时，EB=6﹣t，BF=t，S=EB?BF=（6﹣t）t=﹣t2+3t，（4分）以为S=﹣t2+3t=﹣（t﹣3）2+，所以当t=3时，S有最大值．（5分）②当S取得最大值时，∵由①知t=3，∴BF=3，CF=3，EB=6﹣3=3，若存在某点R，使得以E，B，R，F为顶点的四边形是平行四边形，则FR1=EB且FR1∥EB，。

(二次函数的应用)30道中考动点压轴题和函数压轴题

（二次函数）二次函数30道中考动点压轴题和函数压轴题1如图1，在直角坐标系中，已知△AOC的两个顶点坐标分别为A（2，0），C（0，2）．（1）请你以AC的中点为对称中心，画出△AOC的中心对称图形△ABC，此图与原图组成的四边形OABC的形状是，请说明理由；（2）如图2，已知D（12-，0），过A，C，D的抛物线与（1）所得的四边形OABC的边BC交于点E，求抛物线的解析式及点E的坐标；（3）在问题（2）的图形中，一动点P由抛物线上的点A开始，沿四边形OABC的边从A ﹣B﹣C向终点C运动，连接OP交AC于N，若P运动所经过的路程为x，试问：当x为何值时，△AON为等腰三角形（只写出判断的条件与对应的结果）？2如图，在平面直角坐标系中，直线1y=x+12与抛物线2y=ax+bx3-交于A，B两点，点A在x轴上，点B的纵坐标为3。

点P是直线AB下方的抛物线上一动点（不与A，B重合），过点P作x轴的垂线交直线AB与点C，作PD⊥AB于点D（1）求a，b及sin ACP∠的值（2）设点P的横坐标为m①用含m的代数式表示线段PD的长，并求出线段PD长的最大值；②连接PB，线段PC把△PDB分成两个三角形，是否存在适合的m值，使这两个三角形的面积之比为9：10？若存在，直接写出m值；若不存在，说明理由.3．已知直线y＝kx＋3（k＜0）分别交x轴、y轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作x轴的垂线交直线AB于点C，设运动时间为t秒．（1）当k＝－1时，线段OA上另有一动点Q由点A向点O运动，它与点P以相同速度同时出发，当点P到达点A时两点同时停止运动（如图1）．①直接写出t＝1秒时C、Q两点的坐标；②若以Q、C、A为顶点的三角形与△AOB相似，求t的值．（2）当k ＝－34时，设以C 为顶点的抛物线y ＝(x ＋m)2＋n 与直线AB 的另一交点为D （如图2）．① 求CD 的长；② 设△COD 的OC 边上的高为h ，当t 为何值时，h 的值最大？4．已知二次函数的图象经过A （2，0）、C （0，12）两点，与x 轴的另一交点为点B ，且对称轴为直线x ＝4，设顶点为点D ．（1）求二次函数的解析式及顶点D 的坐标；（2）如图1，在直线y ＝2x 上是否存在点E ，使四边形ODBE 为等腰梯形？若存在，求出点E 的坐标；若不存在，请说明理由；（3）如图2，点P 是线段OD 上的一个动点（不与O 、D 重合），以每秒 2 个单位长度的速度由点D 向点O 运动，过点P 作直线PQ ∥x 轴，交BD 于点Q ，将△DPQ 沿直线PQ 对折，得到△D 1PQ ．在点P 运动的过程中，设△D 1PQ 与梯形OPQB 的重叠部分的面积为S ，运动时间为t 秒，求S 关于t 的函数关系式．5．A 、C 上，抛物线y ＝－2 3）．（1）求抛物线的表达式；（2）如果点P 由点A 出发，沿AB 边以2cm /s 的速度向点B 运动，同时点Q 由点B 出发，沿BC 边以1cm /s 的速度向点C 运动，当其中一点到达终点时，另一点也随之停止运动．设S ＝PQ2（cm 2）．①试求出S 与运动时间t 之间的函数关系式，并写出t 的取值范围；②当S 取54时，在抛物线上是否存在点R ，使得以点P 、B 、Q 、R 为顶点的四边形是平行图1图2图2 图1四边形？如果存在，求出R 点的坐标；如果不存在，请说明理由；（3）在抛物线的对称轴上求点M ，使得M 到D 、A 的距离之差最大，求出点M 的坐标．6．在梯形OABC 中，CB ∥OA ，∠AOC ＝60°，∠OAB ＝90°，OC ＝2，BC ＝4，以O 点为原点，OA 所在的直线为x 轴，建立平面直角坐标系，另有一边长为2的等边△DEF ，DE 在x 轴上（如图1），如果让△DEF 以每秒1个单位的速度向左作匀速直线运动，开始时点D 与点A 重合，当点D 到达坐标原点时运动停止．（1）设△DEF 运动时间为t ，△DEF 与梯形OABC 重叠部分的面积为S ，求S 关于t 的函数关系式；（2）探究：在△DEF 运动过程中，如果射线DF 交经过O 、C 、B 三点的抛物线于点G ，是否存在这样的时刻t ，使得△OAG 的面积与梯形OABC 的面积相等？若存在，求出t 的值；若不存在，请说明理由．7．已知二次函数y ＝ax2＋bx －2的图象与x 轴交于A 、B 两点，与y 轴交于点C ，点A 的坐标为（4，0），且当x ＝－2和x ＝5时二次函数的函数值y 相等．（1）求实数a 、b 的值；（2）如图1，动点E 、F 同时从A 点出发，其中点E 以每秒2个单位长度的速度沿AB 边向终点B 运动，点F 以每秒 5个单位长度的速度沿射线AC 方向运动．当点E 停止运动时，点F 随之停止运动．设运动时间为t 秒．连接EF ，将△AEF 沿EF 翻折，使点A 落在点D 处，得到△DEF ．①当t 为何值时，线段DF 平分△ABC 的面积？②是否存在某一时刻t ，使得△DCF 为直角三角形？若存在，求出t 的值；若不存在，请说明理由．③设△DEF 与△ABC 重叠部分的面积为S ，求S 关于t 的函数关系式；（3）如图2，点P 在二次函数图象上运动，点Q 在二次函数图象的对称轴上运动，四边形PQBC 能否成为以PQ 为底的等腰梯形？如果能，直接写出P 、Q 两点的坐标；如果不能，请说明理由．8．如图，直线y＝－43x＋4与x轴交于点B，与y轴交于点C，二次函数的图象经过A（－1，0）、B、C三点．（1）求二次函数的表达式；（2）设二次函数图象的顶点为D，求四边形OCDB的面积；（3）若动点E、F同时从O点出发，其中点E以每秒32个单位长度的速度沿折线OBC按O→B→C的路线运动，点F以每秒4个单位长度的速度沿折线OCB按O→C→B的路线运动，当E、F两点相遇时，整个运动随之结束．设运动时间为t（秒），△OEF的面积为S（平方单位）．①在E、F两点运动过程中，是否存在EF∥OC？若存在，求出此时t的值；若不存在，请说明理由；②求S关于t的函数关系式，并求S的最大值．9．已知抛物线y＝4，0）点B作BC∥x轴交抛物线于点C．动点E、F分别从O、A两点同时出发，其中点E沿线段OA以每秒1个单位长度的速度向A点运动，点F沿折线A→B→C以每秒1个单位长度的速度向C点运动．设动点运动的时间为t（秒）．（1）求抛物线的解析式；（2）记△EF A的面积为S，求S关于t的函数关系式，并求S的最大值，指出此时△EF A的形状；（3）是否存在这样的t值，使△EF A、F两点的坐标；若不存在，请说明理由．10．如图，抛物线y＝ax2＋bx＋4与x轴交于A（－2，0）、B（4，0）两点，与y轴交于C 点．（1）求抛物线的解析式；（2）T是抛物线对称轴上的一点，且△ATC是以AC为底的等腰三角形，求点T的坐标；（3）M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行，当点M 到达原点时，点Q 立刻掉头并以每秒32个单位长度的速度向点B 方向移动，当点M 到达抛物线的对称轴时，两点停止运动．过点M 的直线l ⊥x 轴交AC 或BC 于点P ．求点M 的运动时间t 与△APQ 面积S 的函数关系式，并求出S 的最大值．11．如图，对称轴为直线x ＝－1的抛物线经过点A （－3，0）和点C （0，3），与x 轴的另一交点为B ．点P 、Q 同时从B 点出发，均以每秒1个单位长度的速度分别沿BA 、BC 边运动，其中一个点到达终点时，另一点也随之停止运动．设运动时间为t （秒）．（1）求抛物线的解析式；（2）连接PQ ，将△BPQ 沿PQ 翻折，所得的△B ′PQ 与△ABC 重叠部分的面积记为S ，求S 与t 之间的函数关系式，并求S 的最大值；（3）若点D 的坐标为（－4，3），当点B ′ 恰好落在抛物线上时，在抛物线的对称轴时是否存在点M ，使四边形MADB ′的周长最小，若存在，求出这个最小值；若不存在，请说明理由．12．如图，抛物线y ＝ax2＋bx ＋152（a ≠0）经过A （－3，0）、C （5，0）两点，点B 为抛物线的顶点，抛物线的对称轴与x 轴交于点D ．（1）求此抛物线的解析式；（2）动点P 从点B 出发，沿线段BD 向终点D 作匀速运动，速度为每秒1个单位长度，运动时间为t s ，过点P 作PM ⊥BD 交BC 于点M ，过点M 作MN ∥BD ，交抛物线于点N ． ①当t 为何值时，线段MN 最长；②在点P 运动的过程中，是否有某一时刻，使得以O 、P 、形？若存在，求出此刻的t 值；若不存在，请说明理由．13．如图，抛物线y ＝－x2－2x ＋3与x 轴相交于点A 、B （A 在B 的左侧），与y 轴交于点C ．（1）求线段AC 所在直线的解析式；（2）点M 是第二象限内抛物线上的一点，且S △MAC＝12S △MAB，求点M 的坐标；（3）点P 以每秒1个单位长度的速度，沿线段BA 由B 向A 运动，同时，点Q 以每秒2个单位长度的速度，从A 开始沿射线AC 运动，当P 到达A 时，整个运动随即结束．设运动的时间为t 秒．①求△APQ 的面积S 与t 的函数关系式，并求当t 为何值时，△APQ 的面积最大，最大面积是多少？②在整个运动过程中，以PQ 为直径的圆能否与直线BC 相切？若能，请直接写出相应的t 值；若不能，请说明理由；③直接写出线段PQ 的中点在整个运动过程中所经过路径的长．14．如图，二次函数c x y +-=221的图象经过点D ⎪⎭⎫ ⎝⎛-29,3，与x 轴交于A 、B 两点． ⑴求c 的值；⑵如图①，设点C 为该二次函数的图象在x 轴上方的一点，直线AC 将四边形ABCD 的面积二等分，试证明线段BD 被直线AC 平分，并求此时直线AC 的函数解析式； ⑶设点P 、Q 为该二次函数的图象在x 轴上方的两个动点，试猜想：是否存在这样的点P 、Q ，使△AQP ≌△ABP ？如果存在，请举例验证你的猜想；如果不存在，请说明理由．（图②供选用）15．（2010福建福州）如图，在△ABC 中，∠C ＝45°，BC ＝10，高AD ＝8，矩形EFPQ 的一边QP 在BC 边上，E 、F 两点分别在AB 、AC 上，AD 交EF 于点H ．（1）求证：AH AD ＝EFBC；（2）设EF ＝x ，当x 为何值时，矩形EFPQ 的面积最大?并求其最大值；（3）当矩形EFPQ 的面积最大时，该矩形EFPQ 以每秒1个单位的速度沿射线QC 匀速运动(当点Q 与点C 重合时停止运动)，设运动时间为t 秒，矩形EFFQ 与△ABC 重叠部分的面积为S ，求S 与t 的函数关系式．16．（2010福建福州）如图1，在平面直角坐标系中，点B 在直线y ＝2x 上，过点B 作x 轴的垂线，垂足为A ，OA ＝5．若抛物线y ＝16x 2＋bx ＋c 过O 、A 两点．（1）求该抛物线的解析式；（2）若A 点关于直线y ＝2x 的对称点为C ，判断点C 是否在该抛物线上，并说明理由；（3）如图2，在（2）的条件下，⊙O 1是以BC 为直径的圆．过原点O 作⊙O 1的切线OP ，P 为切点(点P 与点C 不重合)．抛物线上是否存在点Q ，使得以PQ 为直径的圆与⊙O 1相切?若存在，求出点Q 的横坐标；若不存在，请说明理由17．（2010江苏无锡）如图，矩形ABCD 的顶点A 、B 的坐标分别为（-4，0）和（2，0），BC=设直线AC 与直线x =4交于点E ．（1）求以直线x =4为对称轴，且过C 与原点O 的抛物线的函数关系式，并说明此抛物线一定过点E ；（2）设（1）中的抛物线与x 轴的另一个交点为N ，M 是该抛物线上位于C 、N 之间的一动点，求△CMN 面积的最大值．(第2题)(图1) (图2)18．（2010湖南邵阳）如图，抛物线y ＝2134x x -++与x 轴交于点A 、B ，与y 轴相交于点C ，顶点为点D ，对称轴l 与直线BC 相交于点E ，与x 轴交于点F 。

二次函数—动点产生的线段最值问题典型例题

二次函数——动点产生的线段最值问题【例1】如图，在直角坐标系中，点A,B,C 的坐标分别为（-1，0），（3，0），（0，3），过A,B,C 三点的抛物线的对称轴为直线l ．（1）求抛物线的解析式及顶点D 的坐标；（2）点E 是抛物线的对称轴上的一个动点，求当AE+CE 最小时点E 的坐标；（3）点P 是x 轴上的一个动点，求当PD+PC 最小时点P 的坐标；（4）点Q 是抛物线的对称轴上的一个动点，当点Q 在什么位置时有QB QC-最大？并求出最大值．解：（1）设抛物线的解析式为：y=ax 2+bx+c ，∵抛物线经过A 、B 、C 三点， ∴09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得：123a b c =-⎧⎪=⎨⎪=⎩，∴抛物线的解析式为：y=-x 2+2x+3．∵y=-x 2+2x+3= 2(1)4x --+， ∴该抛物线的对称轴为直线x=1，顶点D 的坐标为（1，4）．（2）∵点A 关于抛物线的对称轴的对称点为B ，则AE=BE ，要使AE+CE 最小，即BE+CE 最小,则B 、E 、C 三点共线如图，连接BC 交抛物线的对称轴于点E ，解法一：设直线BC 的解析式为y=kx+n ，则303k n n +=⎧⎨=⎩,解得13k n =-⎧⎨=⎩∴3y x =-+．当x=1时，3132x -+=-+=，∴点E 的坐标为（1，2）解法二：设抛物线的对称轴交x 轴于点F ．∵E F ∥y 轴，∴∠BEF =∠BCO ，∠BFE =∠BOC∴△BFE ∽△BOC ∴BF EF BO CO=， ∴3133EF -=, ∴2EF = ∴点E 的坐标为（1，2）（3）作出点C 关于x 轴的对称点为C′，则C′（0，-3），OC′=3，如图，连接C′D 交x 轴于点P ，∵点C 关于x 轴的对称点为C′，则PC=P C′，F E要使PD+PC 最小，即PD+P C′最小,则D 、P 、C′三点共线设直线C′D 的解析式为y=kx+n ，则43k n n +=⎧⎨=-⎩,解得73k n =⎧⎨=⎩∴73y x =-．当y=0时，073x =-，∴37x =∴点P 的坐标为（37，0）（4）∵点A 关于抛物线的对称轴的对称点为B ，则QB=QA ，要使QB QC -最大，即QA QC -最大,则A 、C 、Q 三点共线如图，连接AC 交抛物线的对称轴于点Q ，解法一：设直线AC 的解析式为y=kx+n ，则03k n n -+=⎧⎨=⎩,解得33k n =⎧⎨=⎩∴33y x =+．当x=1时，333136x +=⨯+=，∴点Q 的坐标为（1，6）解法二：设抛物线的对称轴交x 轴于点F ．∵QF ∥y 轴，∴∠ACO =∠AQF ，∠AOC =∠AFQ∴△AOC ∽△AFQ ∴AO CO AF QF=， ∴1311QF=+, ∴6QF = ∴点Q 的坐标为（1，6）∴QB QC QA QC AC -=-===即当点Q 的坐标为（1，6）时，QB QC-【作业1】（2011菏泽）如图，抛物线y=21x 2+bx ﹣2与x 轴交于A ，B 两点，与y 轴交于C 点，且A （-1，0）．（1）求抛物线的解析式及顶点D 的坐标；（2）判断△ABC 的形状，证明你的结论；（3）点M （m ，0）是x 轴上的一个动点，当MC+MD 的值最小时，求m 的值．解：（1）∵点A （﹣1，0）在抛物线y=21x 2+bx ﹣2上， ∴21×（﹣1 ）2+b×（﹣1）﹣2=0，解得b=-23 ∴抛物线的解析式为y=21x 2﹣23x ﹣2． QF -- C ′Py=21x 2﹣23x ﹣2=21（ x 2﹣3x ﹣4 ）=21（x ﹣23）2﹣825， ∴顶点D 的坐标为（23，﹣825）．（2）当x=0时y=﹣2，∴C（0，﹣2），OC=2．当y=0时，21x 2﹣23x ﹣2=0，∴x 1=﹣1，x 2=4，∴B （4，0） ∴OA=1，OB=4，AB=5． ∵AB 2=25，AC 2=OA 2+OC 2=5，BC 2=OC 2+OB 2=20，∴AC 2+BC 2=AB 2．∴△ABC 是直角三角形．（3）作出点C 关于x 轴的对称点C′，则C′（0，2），OC′=2，连接C′D 交x 轴于点M ，根据轴对称性及两点之间线段最短可知，MC+MD 的值最小．解法一：设抛物线的对称轴交x 轴于点E ．∵ED∥y 轴，∴∠OC′M=∠EDM，∠C′OM=∠DEM∴△C′OM∽△DEM． ∴ED C O EM OM '=，∴825223=-m m , ∴m=4124 解法二：设直线C′D 的解析式为y=kx+n ，则⎪⎩⎪⎨⎧-=+=825232n k n ,解得n=2，1241-=k ∴21241+-=x y ． ∴当y=0时，-4124,4124,021241=∴==+m x x 【作业2】2011四川广安）如图所示，在平面直角坐标系中，四边形ABCD 是直角梯形，BC ∥AD ，∠BAD ＝ 90°，BC 与y 轴相交于点M ，且M 是BC 的中点，A 、B 、D 三点的坐标分别是A （－1，0），B ( －1，2)，D ( 3，0)，连接DM ，并把线段DM 沿DA 方向平移到ON ，若抛物线y ＝ax 2＋bx ＋c 经过点D 、M 、N ．（1）求抛物线的解析式．（2）抛物线上是否存在点P ．使得PA ＝PC ．若存在，求出点P 的坐标；若不存在．请说明理由．（3）设抛物线与x 轴的另—个交点为E ．点Q 是抛物线的对称轴上的一个动点，当点Q 在什么位置时有QE QC -最大？并求出最大值．解：（1）由题意可得M （0，2），N （－3，2）， ∴ 2,293,093.c a b c a b c =⎧⎪=-+⎨⎪=++⎩ 解得：1,91,32.a b c ⎧=-⎪⎪⎪=-⎨⎪=⎪⎪⎩E∴211293y x x =--+（2）∵PA ＝PC ， ∴P 为AC 的垂直平分线上，依题意，AC 的垂直平分线经过（－1，2）、（1，0），其所在的直线为y ＝－x ＋1．根据题意可列方程组21,11 2.93y x y x x =-+⎧⎪⎨=--+⎪⎩解得：1132x y ⎧=+⎪⎨=--⎪⎩2232x y ⎧=-⎪⎨=-+⎪⎩∴P 1（32+--）、P 2（32--+）．（3）如图所示，延长DC 交抛物线的对称轴于点Q ，根据题意可知此时点Q 满足条件．由题意可知C （1，2），D （3，0），可求得CD 所在的直线的解析式为3y x =-+．抛物线211293y x x =--+的对称轴为直线 1.5x =-． ∵点Q 在直线x ＝－1.5上，又在直线3y x =-+上． ∴Q （－1 .5，4.5），QE ＝QD ． ∴QE QC QD QC CD -=-===．即当点Q 的坐标为（－1.5，4.5）时，QE QC -有最大值，最大值为。

二次函数动点问题专题

二次函数动点问题专题一、因动点产生的面积问题1、如图，抛物线与x轴交与A(1,0),B(- 3，0)两点，（1）求该抛物线的解析式；（2）设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由. （3）在（1）中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？，若存在，求出点P的坐标及△PBC的面积最大值.若没有，请说明理由.cbxxy++-=2ABC2、如图，抛物线y=12x2+b x-2与x轴交于A、B两点，与y轴交于C点，且A（-1,0）。

（1）求抛物线的解析式及顶点D的坐标；（2）判断△ABC的形状，证明你的结论；（3）点M（m，0）是x轴上一个动点，当CM+DM的值最小时，求m的值；（4）点P为直线BC下方抛物线上一动点，问当P在什么位置时，四边形ACPB 的面积最大，求出此时的P点坐标及最大面积。

3．如图，在平面直角坐标系中，二次函数y＝x2＋bx＋c的图象与x轴交于A、B 两点，B点的坐标为（3，0），与y轴交于C（0，－3）点，点P是直线BC下方抛物线上的动点．（1）求这个二次函数表达式；（2）连接PO、PC，并将△POC沿y轴对折，得到四边形POP′C，那么是否存在点P，使得四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由；（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．4、（2015中大附中一模）如图，已知抛物线c bx ax y ++=2过点A （6，0），B （－2，0），C （0，－3）．（1）求此抛物线的解析式；（2）若点H 是该抛物线第四象限的任意一点，求四边形OCHA 的最大面积；（3）若点Q 在y 轴上，点G 为该抛物线的顶点，且∠GQA =45º，求点Q 的坐标．5、（2016•越秀区一模）如图，已知抛物线y=x 2﹣（m +3）x +9的顶点C 在x 轴正半轴上，一次函数y=x +3与抛物线交于A 、B 两点，与x 、y 轴分别交于D 、E 两点．（1）求m 的值；（2）求A 、B 两点的坐标；（3）当﹣3＜x ＜1时，在抛物线上是否存在一点P ，使得△PAB 的面积是△ABC 面积的2倍？若存在，请求出点P 的坐标；若不存在，请说明理由．二、因动点产生的等腰三角形存在性问题1、已知：如图抛物线a x x y +-=421过点A （0,3），抛物线1y 与抛物线2y 关于y 轴对称，抛物线2y 的对称轴交x 轴于点B ，点P 是x 轴上的一个动点，点Q 是第四象限内抛物线1y 上的一点。

专题：二次函数中的动点问题(平行四边形存在性问题)

二次函数中的动点问题（二）平行四边形的存在性问题一.技巧提炼如图1,点人（召,开）、3（忑,儿）、C（X3Os）是坐标平面内不在同一直线上的三点。

平面直角坐标系中是否存在点D,使得以A、B、C、D四点为顶点的四边形为平行四边形，如果存在，请求出点D的坐标。

如图2,过A、B、C分别作BC、AC、AB的平行线，则以不在同一直线上的三点为顶点的平行四边形有三个。

由已知的三点坐标可根据图形平移的坐标性质，直接写出第四个顶点的坐标。

3、平面直角坐标系中直线和直线12:当h时k尸k2；当h丄I2时ki-k2=-14、二次函数中平行四边形的存在性问题：解题思路：（1）先分类（2）再画图（3）后计算二、精讲精练1、已知抛物线y=ax-+bx+c与x轴相交于A、E两点（A、B分别在原点的左右两侧），与y轴正半轴相交于C点，且OA：OB：OC=1：3：3,AABC的面积为6,（如图1）（1）求抛物线的解析式：（2）坐标平面内是否存在点M,使得以点M、A、B、C为顶点四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由；（3）如图2,在直线BC±方的抛物线上是否存在一动点P,ABCP面枳最大？如果存在，求出最人面积,2、如图，己知抛物线经过A(-2,0),B(・3,3)及原点6顶点为C(1)求抛物线的函数解析式：(2)设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标。

【变式练习】7如图，对称轴为直线x二一的抛物线经过点A(6,0)和B(0,4)・2(1)求抛物线解析式及顶点坐标；(2)设点E(x,y)是抛物线上一动点，且位于第四彖限，四边形0EAF是以0A为对角线的平行四边形, 求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；①当平行四边形OEAF的面积为24时，请判断平行四边形0EAF是否为菱形？②是否存在点E,使平行四边形0EAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由.、方法规律1、平行四边形模型探究如图1，点&（內,开）、3（七,儿）、C（X3，”）是坐标平面内不在同一直线上的三点。

二次函数动点及最值问题

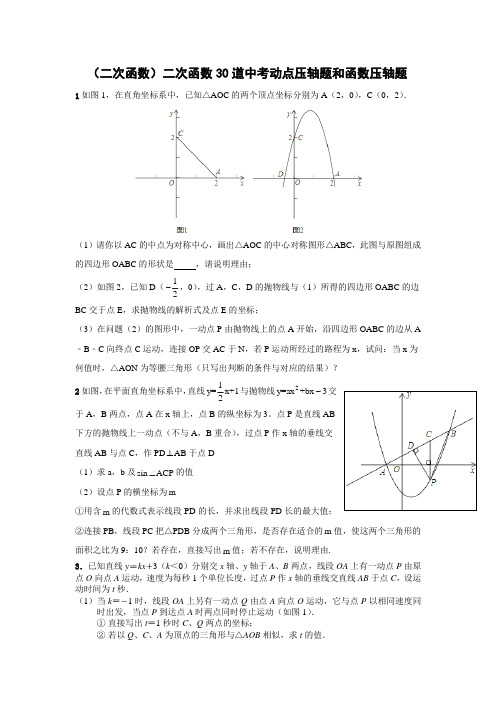
一、二次函数中的最值问题：例1：在平面直角坐标系中，全等的两个三角形Rt⊿AOB与Rt A’OC’如图放置，点B、C’的坐标分别为（1，3），（0，1），BO 与A’ C’相交于D,若⊿A’OC’绕点O旋转90°至⊿AOC，如图所示（1）若抛物线过C、A、A’，求此抛物线的解析式及对称轴；∴y=-x2+2x+3（2）、若点P是第一象限内抛物线线上的一动点，问P在何处时△AP A’的面积最大？最大面积是多少？并求出此时的点P的坐标。

（3）、设抛物线的顶点为N,在抛物线上是否存在点P,使△A’AN与△A’AP的面积相等?,若存在,请求出此时点P的坐标，若不存在，请说明理由。

例2、（2012攀枝花）如图，在平面直角坐标系xOy中，四边形ABCD是菱形，顶点A．C．D均在坐标轴上，且AB=5，sinB=．（1）求过A．C．D三点的抛物线的解析式；（2）记直线AB的解析式为y1=mx+n，（1）中抛物线的解析式为y2=ax2+bx+c，求当y1＜y2时，自变量x的取值范围；（3）设直线AB与（1）中抛物线的另一个交点为E，P点为抛物线上A．E两点之间的一个动点，当P点在何处时，△PAE的面积最大？并求出面积的最大值．解答：解：（1）∵四边形ABCD是菱形，∴AB=AD=CD=BC=5，sinB=sinD=；Rt△OCD中，OC=CD•sinD=4，OD=3；OA=AD﹣OD=2，即：A（﹣2，0）、B（﹣5，4）、C（0，4）、D（3，0）；设抛物线的解析式为：y=a（x+2）（x﹣3），得：2×（﹣3）a=4，a=﹣；∴抛物线：y=﹣x2+x+4．（2）由A（﹣2，0）、B（﹣5，4）得直线AB：y1=﹣x﹣；由（1）得：y2=﹣x2+x+4，则：，解得：，；由图可知：当y1＜y2时，﹣2＜x＜5．（3）∵S△APE=AE•h，∴当P到直线AB的距离最远时，S△ABC最大；若设直线L∥AB，则直线L与抛物线有且只有一个交点时，该交点为点P；设直线L：y=﹣x+b，当直线L与抛物线有且只有一个交点时，﹣x+b=﹣x2+x+4，且△=0；求得：b=，即直线L：y=﹣x+；可得点P（，）．由（2）得：E（5，﹣），则直线PE：y=﹣x+9；新课标第一网则点F（，0），AF=OA+OF=；∴△PAE的最大值：S△PAE=S△PAF+S△AEF=××（+）=．综上所述，当P（，）时，△PAE的面积最大，为．针对训练：1、（2013宜宾）如图，抛物线y1=x2﹣1交x轴的正半轴于点A，交y轴于点B，将此抛物线向右平移4个单位得抛物线y2，两条抛物线相交于点C．（1）请直接写出抛物线y2的解析式；（2）若点P是x轴上一动点，且满足∠CPA=∠OBA，求出所有满足条件的P点坐标；（3）在第四象限内抛物线y2上，是否存在点Q，使得△QOC中OC边上的高h有最大值？若存在，请求出点Q的坐标及h的最大值；若不存在，请说明理由．解答：解：（1）抛物线y1=x﹣1向右平移4个单位的顶点坐标为（4，﹣1），所以，抛物线y2的解析式为y2=（x﹣4）2﹣1；（2）x=0时，y=﹣1，y=0时，x2﹣1=0，解得x1=1，x2=﹣1，所以，点A（1，0），B（0，﹣1），∴∠OBA=45°，联立，解得，∴点C的坐标为（2，3），∵∠CPA=∠OBA，∴点P在点A的左边时，坐标为（﹣1，0），在点A的右边时，坐标为（5，0），所以，点P的坐标为（﹣1，0）或（5，0）；（3）存在．∵点C（2，3），∴直线OC的解析式为y=x，设与OC平行的直线y=x+b，联立，消掉y得，2x2﹣19x+30﹣2b=0，当△=0，方程有两个相等的实数根时，△QOC中OC边上的高h有最大值，此时x1=x2=×（﹣）=，此时y=（﹣4）2﹣1=﹣，∴存在第四象限的点Q（，﹣），使得△QOC中OC边上的高h有最大值，此时△=192﹣4×2×（30﹣2b）=0，解得b=﹣，∴过点Q与OC平行的直线解析式为y=x﹣，令y=0，则x﹣=0，解得x=，设直线与x轴的交点为E，则E（，0），过点C作CD⊥x轴于D，根据勾股定理，OC==，则sin ∠COD==，解得h 最大=×=．2、如图，抛物线)0(2232≠--=a x ax y 的图象与x 轴交于A 、B 两点，与y 轴交于C 点，已知B 点坐标为()0,4.（1）求抛物线的解析式；（2）试探究ABC ∆的外接圆的圆心位置，并求出圆心坐标；（3）若点M 是线段BC 下方的抛物线上一点，求MBC ∆的面积的最大值，并类型一、最值问题：类型一、最值问题：（2013•泸州）如图，在直角坐标系中，点A 的坐标为（﹣2，0），点B 的坐标为（1，﹣），已知抛物线y=ax 2+bx+c （a ≠0）经过三点A 、B 、O （O 为原点）．（1）求抛物线的解析式；（2）在该抛物线的对称轴上，是否存在点C ，使△BOC 的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由；（3）如果点P 是该抛物线上x 轴上方的一个动点，那么△PAB 是否有最大面积？若有，求出此时P 点的坐标及△PAB 的最大面积；若没有，请说明理由．（注意：本题中的结果均保留根号）），﹣﹣（+，解得：﹣，﹣，﹣﹣x（PE（+y）﹣y）﹣（（y+（﹣x+x x+（）﹣的面积最大，最大值为××，，类型二、探索三角形的存在性。

二次函数动点问题压轴题专题汇编(含答案)

二次函数动点问题压轴题专题汇编(含答案)二次函数的动态问题（动点）正方形ABCD的顶点A，B的坐标分别为(0,10)，(8,4)，顶点C，D在第一象限。

点P从点A出发，沿正方形按逆时针方向匀速运动，同时，点Q从点E(4,0)出发，沿x轴正方向以相同速度运动。

当点P到达点C时，P，Q两点同时停止运动，设运动的时间为t秒。

1) 求正方形ABCD的边长。

解：作BF⊥y轴于F。

则FB=8，FA=6，AB=10.2) 当点P在AB边上运动时，△OPQ的面积S（平方单位）与时间t（秒）之间的函数图象为抛物线的一部分。

求P，Q两点的运动速度。

解：由图可知，点P从点A运动到点B用了10秒。

又AB=10，故P，Q两点的运动速度均为每秒1个单位。

3) 求(2)中面积S（平方单位）与时间t（秒）的函数关系式及面积S取最大值时点P的坐标。

解：方法一：作PG⊥y轴于G，则PG∥BF。

由相似三角形可得：GA/AP=FA/AB，即6/10=t/AP，故GA=3/5t。

又OG=10-3/5t，OQ=4+t。

则S=1/2×OQ×OG=1/2×(t+4)×(10-3/5t)=-3/10t²+19/5t+20.对XXX求导得：S'=(-6/5)t+19/5，令其为0，解得t=19/3.此时S有最大值。

此时GP=76/15，OG=31/5，P的坐标为(76/15,31/5)。

方法二：当t=5时，OG=7，OQ=9，S=63/2.设所求函数关系式为S=at²+bt+20.抛物线过点(5,63/2)，则a=-3/10，b=19/2.代入可得S=-3/10t²+19/2t+20.同样可得最大值时t=19/3，P的坐标为(76/15,31/5)。

4) 若点P，Q保持(2)中的速度不变，则点P沿着AB边运动时，∠XXX的大小随着时间t的增大而增大；沿着BC边运动时，∠XXX的大小随着时间t的增大而减小。

初中数学二次函数动点问题

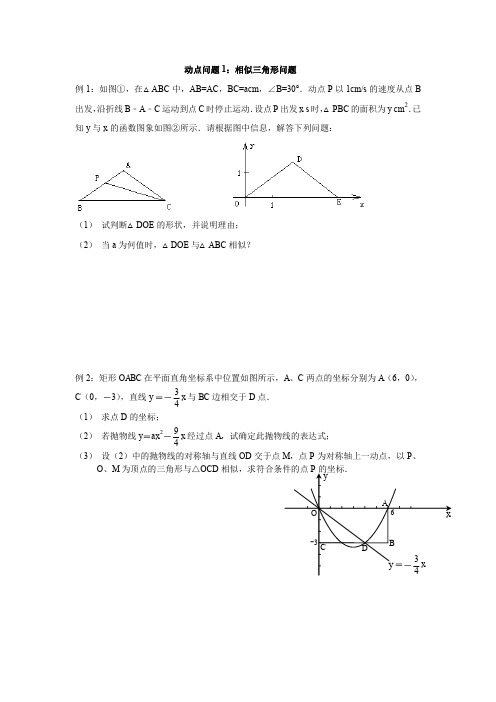
动点问题1：相似三角形问题例1：如图①，在△ABC 中，AB=AC ，BC=acm ，∠B=30°．动点P 以1cm/s 的速度从点B 出发，沿折线B ﹣A ﹣C 运动到点C 时停止运动．设点P 出发x s 时，△PBC 的面积为y cm 2．已知y 与x 的函数图象如图②所示．请根据图中信息，解答下列问题：（1）试判断△DOE 的形状，并说明理由；（2）当a 为何值时，△DOE 与△ABC 相似？例2：矩形OABC 在平面直角坐标系中位置如图所示，A 、C 两点的坐标分别为A （6，0），C （0，－3），直线y ＝－43x 与BC 边相交于D 点．（1）求点D 的坐标；（2）若抛物线y ＝ax 2－49x 经过点A ，试确定此抛物线的表达式；（3）设（2）中的抛物线的对称轴与直线OD 交于点M ，点P 为对称轴上一动点，以P 、O 、M 为顶点的三角形与△OCD例3.如图，抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．（1）求抛物线的解析式；（2）在抛物线上求点M，使△MOB的面积是△AOB面积的3倍；（3）连结OA，AB，在x轴下方的抛物线上是否存在点N，使△OBN与△OAB相似？若存在，求出N点的坐标作业1.如图，已知抛物线y ＝x 2－1与x 轴交于A 、B 两点，与y 轴交于点C ．（1）求A 、B 、C 三点的坐标．（2）过点A 作AP ∥CB 交抛物线于点P ，求四边形ACBP 的面积．（3）在x 轴上方的抛物线上是否存在一点M ，过M 作MG ⊥x 轴于点G ，使以A 、M 、G 三点为顶点的三角形与△PCA 相似？若存在，请求出M 点的坐标；否则，请说明理由．2.如图，已知抛物线y ＝43x 2＋bx ＋c 与坐标轴交于A 、B 、C 三点，A 点的坐标为（－1，0），过点C 的直线y ＝t43x －3与x 轴交于点Q ，点P 是线段BC 上的一个动点，过P 作PH ⊥OB 于点H ．若PB ＝5t ，且0＜t ＜1．（1）填空：点C 的坐标是___________，b ＝_______，c ＝_______；（2）求线段QH 的长（用含t 的式子表示）；（3）依点P 的变化，是否存在t 的值，使以P 、H 、Q 为顶点的三角形与△COQ 相似？若存在，求出所有t3.已知，如图1，过点B (0，－1)作平行于x 轴的直线l ，抛物线y ＝41x2上的两点A 、B 的横坐标分别为－1和4，直线AB 交y 轴于点F ，过点A 、B 分别作直线l 的垂线，垂足分别为点C 、D ，连接CF 、DF ．（1）求点A 、B 、F 的坐标；（2）求证：CF ⊥DF ；（3）点P 是抛物线y ＝41x 2对称轴右侧图象上的一动点，过点P 作PQ ⊥OP 交x 轴于点Q ，是否存在点P 使得△OPQ 与△CDF 相似？若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．(备用图)(图1)。

(完整版)二次函数和动点(带详细答案)

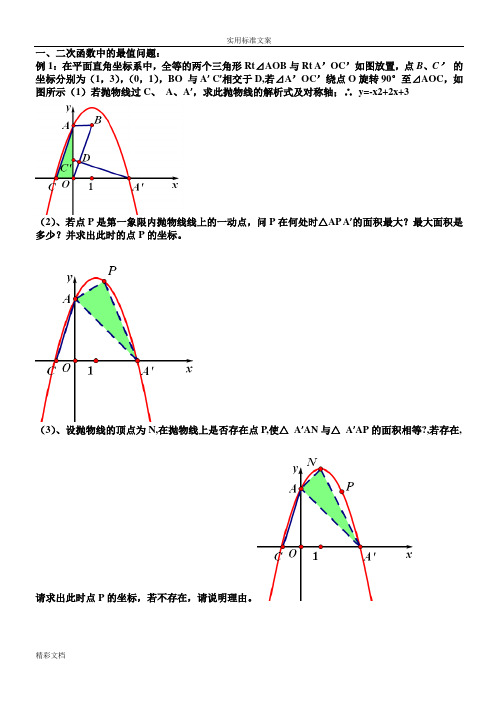
二次函数和动点综合题型一．解答题（共30小题）1．（2015•滨州模拟）如图所示，在平面直角坐标系中，以点M（2，3）为圆心，5为半径的圆交x轴于A，B两点，过点M作x轴的垂线，垂足为D；过点B作⊙M的切线，与直线MD交于N点．（1）求点B、点N的坐标以及直线BN的解析式；（2）求过A、N、B、三点（对称轴与y轴平行）的抛物线的解析式；（3）设（2）中的抛物线与y轴交于点P，以点D，B，P三点为顶点作平行四边形，请你求出第四个顶点Q的坐标，并判断Q是否在（2）中的抛物线上．2．（2015•湖州模拟）如图①，Rt△ABC中，∠B=90°∠CAB=30°，AC⊥x轴．它的顶点A的坐标为（10，0），顶点B的坐标为，点P从点A出发，沿A→B→C的方向匀速运动，同时点Q从点D（0，2）出发，沿y轴正方向以相同速度运动，当点P到达点C时，两点同时停止运动，设运动的时间为t秒．（1）求∠BAO的度数．（直接写出结果）（2）当点P在AB上运动时，△OPQ的面积S与时间t（秒）之间的函数图象为抛物线的一部分（如图②），求点P的运动速度．（3）求题（2）中面积S与时间之间的函数关系式，及面积S取最大值时点P的坐标．（4）如果点P，Q保持题（2）中的速度不变，当t取何值时，PO=PQ，请说明理由．3．（2015•贵港一模）如图，二次函数的图象经过点A（4，0），B（﹣4，﹣4），且与y轴交于点C．（1）试求此二次函数的解析式；（2）试证明：∠BAO=∠CAO（其中O是原点）；（3）若P是线段AB上的一个动点（不与A、B重合），过P作y轴的平行线，分别交此二次函数图象及x轴于Q、H两点，试问：是否存在这样的点P，使PH=2QH？若存在，请求出点P的坐标；若不存在，请说明理由．4．（2015•深圳模拟）已知正方形OABC中，O为坐标原点，点A在y轴的正半轴上，点C在x轴的正半轴上，点B（4，4）．二次函数y=﹣x2+bx+c的图象经过点A、B．点P（t，0）是x轴上一动点，连接AP．（1）求此二次函数的解析式；（2）如图①，过点P作AP的垂线与线段BC交于点G，当点P在线段OC（点P不与点C、O重合）上运动至何处时，线段GC的长有最大值，求出这个最大值；（3）如图②，过点O作AP的垂线与直线BC交于点D，二次函数y=﹣x2+bx+c的图象上是否存在点Q，使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形？若存在，求出t的值；若不存在，请说明理由．5．（2014•泰安）二次函数y=ax2+bx+c的图象经过点（﹣1，4），且与直线y=﹣x+1相交于A、B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（﹣3，0）．（1）求二次函数的表达式；。

(word完整版)初中数学二次函数动点问题

函数性问题专题—动点问题函数及其图象是初中数学中的主要内容之一，也是初中数学与高中数学相联系的纽带．它与代数、几何、三角函数等知识有着密切联系，中考命题中既重点考查函数及其图象的有关基础知识，同时以函数为背景的综合性问题也是命题热点之一，多数省市作压轴题．因此，在中考复习中，关注这一热点显得十分重要．以函数为背景的综合性问题往往都可归结为动点性问题，我们把它归纳为以下七种题型（附例题）一、因动点而产生的面积问题例1：如图10，已知抛物线P：y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：x …-3 -2 1 2 …y …-52-4 -520 …(1) 求A、B、C三点的坐标；(2) 若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；(3) 当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=k·DF，若点M不在抛物线P上，求k的取值范围.若因为时间不够等方面的原因，经过探索、思考仍无法圆满解答本题，请不要轻易放弃，试试将上述(2)、(3)小题换为下列问题解答(已知条件及第(1)小题与上相同，完全正确解答只能得到5分)：(2) 若点D的坐标为(1，0)，求矩形DEFG的面积.例2：如图1，已知直线12y x=-与抛物线2164y x=-+交于A B，两点．（1）求A B，两点的坐标；（2）求线段AB的垂直平分线的解析式；（3）如图2，取与线段AB等长的一根橡皮筋，端点分别固定在A B，两处．用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动，动点P将与A B，构成无数个三角形，这些三角求出最大面积，并指出此时P点的坐标；如果不存在，请简要说明理由．yxOyxOPA图2图1BBA图10例3：如图1，矩形ODEF 的一边落在矩形ABCO 的一边上，并且矩形ODE F ∽矩形ABCO ，其相似比为1 : 4，矩形ABCO 的边AB=4,BC=43．(1)求矩形ODEF 的面积； (2）将图l 中的矩形ODEF 绕点O 逆时针旋转 900，若旋转过程中OF 与OA 的夹角（图2中的∠FOA ）的正切的值为x ，两个矩形重叠部分的面积为y ，求 y 与 x 的函数关系式；(3)将图1中的矩形ODEF 绕点O 逆时针旋转一周，连结EC 、EA ，△ACE 的面积是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，请说明理由。

二次函数动点问题典型例题

二次函数动点问题典型例题等腰三角形问题1.如图，在平面直角坐标系中，已知抛物线y=ax2+bx的对称轴为x=1,且经过点A (2, 1), 点P是抛物线上的动点，P的横坐标为m (0<m<2),过点P作PB±x轴，垂足为B, PB 交OA于点C,点O关于直线PB的对称点为D,连接CD, AD,过点A作AE±x轴，垂足为E.(1)求抛物线的解析式；(2)填空：①用含m的式子表示点C, D的坐标：C (, ),D (, )；②当m=一时，^ACD的周长最小；(3)若4ACD为等腰三角形，求出所有符合条件的点P的坐标.面积最大1.如图，抛物线丫=-3x2+mx+n与x轴交于A、B两点，与y轴交于点C,抛物线的对称轴交x轴于点口，已知A (- 1, 0), C (0, 2).(1)求抛物线的表达式；(2)在抛物线的对称轴上是否存在点P,使4PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；(3)点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标.2 .已知：如图，直线y=3x+3与x 轴交于C 点，与y 轴交于A 点，B 点在x 轴上，△OAB 是等腰直角三角形.（1）求过A 、B 、C 三点的抛物线的解析式；（2）若直线CDMB 交抛物线于D 点，求D 点的坐标;（3）若P 点是抛物线上的动点，且在第一象限，那么0PAB 是否有最大面积？若有，求出此时P 点的坐标和^PAB 的最大面积；若没有，请说明理由.3 . （2015•黔西南州）（第26题）如图，在平面直角坐标系中，平行四边形ABOC 如图放置，将此平行四边形绕点O 顺时针旋转90°得到平行四边形A'B'OC'.抛物线y= - x 2+2x+3经过点A 、C 、A'三点.求平行四边形ABOC 和平行四边形A‘B‘OC'重叠部分400口的面积;(1) 求A 、A’、C 三点的坐标;(2) (3)点M是第一象限内抛物线上的一动点，问点M在何处时，^AMA’的面积最大？最大最短路径1.(2014绵阳)3口图，抛物线y=ax2+bx+c (a/0)的图象过点M (-2, \月)，顶点坐标为N (-1, W),且与x轴交于A、B两点，与y轴交于C点.(1)求抛物线的解析式；(2)点P为抛物线对称轴上的动点，当△PBC为等腰三角形时，求点P的坐标；(3)在直线AC上是否存在一点Q,使4QBM的周长最小？若存在，求出Q点坐标；若不存在，请说明理由.2.(2014•泸州)如图，已知一次函数y1=1x+b的图象l与二次函数y2=-x2+mx+b的图象C' 都经过点B (0, 1)和点C,且图象C’过点A (2-.：亏0).(1)求二次函数的最大值；(2)设使y2>y1成立的x取值的所有整数和为s,若s是关于x的方程(1+■上)篁上邑=0的根，求a的值；_(3)若点F、G在图象C'上，长度为巧的线段DE在线段BC上移动，EF与DG始终平行于y 面积是多少？并写出此时M的坐标.轴，当四边形DEFG的面积最大时，在x轴上求点P,使PD+PE最小，求出点P的坐标.平行四边形1.(2015•贵州省贵阳，第24题9分)如图，经过点C (0, -4)的抛物线y=ax2+bx+c (aN0) 与x轴相交于A (-2, 0), B两点.(1) a > 0, b2-4ac > 0 (填“>”或“<”)；(2)若该抛物线关于直线x=2对称，求抛物线的函数表达式；(3)在(2)的条件下，连接AC, E是抛物线上一动点，过点E作AC的平行线交x轴于点F.是否存在这样的点E,使得以A, C, E, F为顶点所组成的四边形是平行四边形？若存在，2.(14分)(2015•葫芦岛)(第26题)如图，直线y=-^ x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+^x+c经过B、C两点.(1)求抛物线的解析式；(2)如图，点E是直线BC上方抛物线上的一动点，当^BEC面积最大时，请求出点E的坐标和4BEC面积的最大值？(3)在(2)的结论下，过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点，在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由.管用图3.(2015•辽宁抚顺)(第26题，14分))已知，△ABC在平面直角坐标系中的位置如图①所示，A点坐标为(-6, 0), B点坐标为(4, 0),点D为BC的中点，点E为线段AB上一动点，连接DE经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.(1)求抛物线的解析式；(2)如图①，将4BDE以DE为轴翻折，点B的对称点为点G,当点G恰好落在抛物线的对称轴上时，求G点的坐标；(3)如图②，当点E在线段AB上运动时，抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形？若存在，请直接写出点F的坐标；若不存在，请说明理由.图①图②4.(2015•梧州，第26题12分)如图，抛物线y=ax2+bx+2与坐标轴交于A、B、C三点，其中B (4, 0)、C (- 2, 0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE±x轴，垂足为E,交AB于点F.(1)求此抛物线的解析式；(2)在DE上作点G,使G点与D点关于F点对称，以G为圆心，GD为半径作圆，当。

二次函数典型例题——动点

二次函数典型例题——动点在平面直角坐标系xOy 中，抛物线22y mx nx =+-与直线y =x －1交于A （－1，a ）、B （b ，０）两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）求△ABC 的面积；（3）点(t,0)P 是x 轴上的一个动点．过点P 作x 轴的垂线交直线AB 于点M ，交抛物线于点N ．当点M 位于点N 的上方时，直接写出t 的取值范围．C B AyxO解：（1）∵ 抛物线过原点和A (23,0-)，∴ 抛物线对称轴为3-=x . ∴ B (3,3-).设抛物线的解析式为2+33y a x =+（）.∵ 抛物线经过(0, 0), ∴ 0=3a +3. ∴ a =-1.∴3)3(2++-=x y ……………………………………………1分 =.322x x --∵ C 为AB 的中点, A (23,0-)、B (3,3-)，可得 C (333,22-) . 可得直线OC 的解析式为x y 33-=. ……………………………………………2分（2）连结OB . 依题意点E 为抛物线x x y 322--=与直线x y 33-=的交点（点E 与点O 不重合）.由23323,y x y x x ⎧=-⎪⎨⎪=--⎩，解得 53,35,3x y ⎧=-⎪⎪⎨⎪=⎪⎩或0,0.x y =⎧⎨=⎩（不合题意，舍）.∴ E （535,33-） …………………………3分过E 作EF ⊥y 轴于F , 可得OF =53，∵ OE =DE ，EF ⊥y 轴， ∴ OF=DF . ∴ DO =2OF =103. ∴ D (0,10)3. ………………………………………………………………………4分 ∴ BD =2210233733-+-=（）（）. ……………………………………………5分（3）E 点的坐标为(333,22-)或(31,22-). ……………………………………………8分已知：抛物线1C ：622-+-=bx x y 与抛物线2C 关于原点对称，抛物线1C 与x 轴分别交于A （1,0），B （m,0）,顶点为M ，抛物线2C 与x 轴分别交于C ，D 两点（点C 在点D 的左侧），顶点为N ．（1）求m 的值；（2）求抛物线2C 的解析式；（3）若抛物线1C 与抛物线2C 同时以每秒1个单位的速度沿x 轴方向分别向左、向右运动，此时记A ，B ，C ，D ，M ，N 在某一时刻的新位置分别为'''''',,,,,N M D C B A ，当点'A 与点'D 重合时运动停止．在运动过程中，四边形''''N C M B 能否形成矩形？若能，求出此时运动时间t （秒）的值，若不能，说明理由．（1）∵抛物线622-+-=bx x y 过点 A （1,0）∴620-+-=b …………………………………1分∴8=b∴抛物线1C 的解析式为 2)2(268222+--=-+-=x x x y ∴)2,2(M令0=y ，则06822=-+-x x 解这个方程，得3,121==x x∴3=m ……………………………………2分F CD E B AyxO（2）由题意，抛物线2C 过点C （-3,0）,D （-1,0）,N （-2，-2）∴抛物线2C 的解析式为 6822)2(222++=-+=x x x y …………3分（3）过点'M 作H M '⊥x 轴于点H ， …………………………………4分若四边形''''N C M B 是矩形，则''OM OB =由题意，设'M )2,2(t -，'B )0,3(t -，则H )0,2(t - ………………5分在Rt △OH M '中，2222'''OB OM H M OH ==+∴222)3(2)2(-=+-t t …………………………………6分解得21=t ∴21=t 秒时，四边形''''N C M B 是矩形．………………………………7分如图，在矩形ABCO 中，AO=3，tan ∠ACB=34，以O 为坐标原点，OC 为x 轴，OA 为y 轴建立平面直角坐标系。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

二次函数动点问题典型例题
一、等腰三角形问题
1. 如图，在平面直角坐标系中，已知抛物线y=ax2+bx的对称轴为x=，且经过点A（2，1），点P是抛物线上的动点，P的横坐标为m（0＜m＜2），过点P作PB⊥x轴，垂足为B，PB 交OA于点C，点O关于直线PB的对称点为D，连接CD，AD，过点A作AE⊥x轴，垂足为E．
（1）求抛物线的解析式；
（2）填空：
①用含m的式子表示点C，D的坐标：
C（，），D（，）；
②当m= 时，△ACD的周长最小；
（3）若△ACD为等腰三角形，求出所有符合条件的点P的坐标．
二、面积最大
1. 如图，抛物线y=﹣x2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．
（1）求抛物线的表达式；
（2）在抛物线的对称轴上是否存有点P，使△PCD是以CD为腰的等腰三角形？如果存有，直接写出P点的坐标；如果不存有，请说明理由；
（3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．
2．已知：如图，直线y=3x+3与x轴交于C点，与y轴交于A点，B点在x轴上，△OAB是等腰直角三角形．
（1）求过A、B、C三点的抛物线的解析式；
（2）若直线CD∥AB交抛物线于D点，求D点的坐标；
（3）若P点是抛物线上的动点，且在第一象限，那么△PAB是否有最大面积？若有，求出此时P点的坐标和△PAB的最大面积；若没有，请说明理由．。