八年级数学竞赛例题专题讲解：多边形的边与角
初中数学竞赛多边形(含答案)
多边形在同一平面内，由一些线段首尾顺次相接组成的图形叫做多边形。
如果延长多边形的任一条边，整个多边形都在这条延长边的一侧，那么这样的多边形就叫做凸多边形。
下面所说的多边形均指凸多边形。
它的重要性质是：几边形的内角和是，由于这个结论与边数有关，所以这不是对多边形的最本质的刻划。
更加本质的是它的推论：任意多边形的外角和等于。
多边形中通过连结对角线中把多边形就分割为若干个三角形，这就把研究多边形的问题转化为研究三角形的问题，这是一种重要的研究思路，请读者在下面的解题过程中认真体会这种思路。
例1已知多边形的内角和是外角和的3倍，求这个多边形的边数。
思路设多边数的边数为n，然后通过已知条件列出n的方程，再求出n值。
解设这个多边形的边数为n，根据题意得解之得 n=8答：这个多边形的边数为8说明本题通过设边数为n，然后依题意列出n的方程，再求出n值。
这是运用方程的思想解几何题。
这种思想方法今后还会经常用到。
例2一个多边形的每个内角都等于，求这个多边形的边数。
思路1 利用多边形的内角和定理。
解法1 设这个多边形的边数为n，根据题意得解之得n=10思路2 利用多边形的外角和定理。
解法 2 因为这个多边形的每个内角都等于，所以每个外角都等于，而多边形的外角和是，所以这个多边形的边数是.说明当你们学习了解法1和解法2后，你们心里产生了怎样的想法呢？显然，解法1比较传统，解法2则标新立异，这就启发我们解题时选择恰当的出发点是多么重要。
例3一个多边形除了一个内角之外的所有内角和等于，求这个多边形的边数和这个内角的度数。
思路利用多边形的内角和定理。
解设这个多边形的边数为n，这个内角的度数为X，根据题意有.又解之得又由n是正整数得n=14说明在解题中要重视对题目隐含条件的发掘和利用。
如本题中的x取值范围是。
n是正整数等。
例4 求证：n边形的内角中，最多有3个锐角。
思路1 用反证法.证法1 假设n边形至少有4个锐角，取出4个锐角之后剩下的角记为，，，则有，得那么，，中至少有一个大于，而这与，，中的每一个都小于180矛盾。
八年级数学竞赛例题专题讲解14：多边形的边与角 含答案
专题14 多边形的边与角阅读与思考主要是指多边形的边、内外角、对角线、凸多边形、凹多边形等基本概念和多边形内角和定理、外角和定理，其中多边形内、外角和定理是解有关多边形问题的基础．多边形的许多性质与问题往往可以利用三角形来说明、解决，将多边形问题转化为三角形问题是解多边形问.题的基本策略，转化的方法是连对角线或向外补形．多边形的内角和是随着多边形的边数变化而变化的，但外角和却总是不变的，所以，我们常以外角和的“不变”来制约内角和的“变”，把内角问题转化为外角问题来处理，这是解多边形相关问题的常用技巧．例题与求解【例1】两个凸多边形，它们的边长之和为12，对角线的条数之和为19，那么这两个多边形的边数分别是＿＿＿＿和＿＿＿＿．（“希望杯”邀请赛试题）解题思路：设两个凸多边形分别有m，n条边，分别引出(3)2m m-，(3)2n n-条对角线，由此得m，n方程组．【例2】凸边形有且只有3个钝角，那么n的最大值是（）A．5 B．6 C．7 D．8解题思路：运用钝角、锐角概念，建立关于n的不等式，通过求解不等式逼近求解．【例3】凸n边形除去一个内角外，其余内角和为2570°，求n的值．（山东省竞赛试题）解题思路：利用n边形内角和公式，以及边数n为大于等于3的自然数这一要求，推出该角大小，进而求出n的值．录入：王云峰【例4】如图，凸八边形ABCDEFGH 的八个内角都相等，边AB ，BC ，CD ，DE ，EF ，FG 的长分为7，4，2，5，6，2，求该八边形的周长． （全国通讯赛试题）解题思路：该八边形每一内角均为135°，每一外角为45°，可将八边形问题转化为特殊三角形解决、特殊四边形加以解决．【例5】如图所示，小华从M 点出发，沿直线前进10米后，向左转20°，再沿直线前进10米后，又向左转20°，…这样走下去，他第一次回到出发地M 时，行走了多少米？解题思路：试着将图形画完，你也许就知道答案了．能力训练A 级1．如图，凸四边形有＿＿＿个；∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝＿＿＿．（重庆市竞赛试题）A DE FG HM2．如图，凸四边形ABCD 的四边AB ，BC ，CD 和DA 的长分别为3，4，12和13，∠ABC ＝90°，则四边形ABCD 的面积为＿＿＿．3．如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝＿＿＿．4．如图，ABCD 是凸四边形，则x 的取值范围是＿＿＿．.5．一个凸多边形的每一内角都等于140°，那么，从这个多边形的一个顶点出发的对角线的条数是（ ）A ．9条B ．8条C ．7条D ．6条（“祖冲之杯”邀请赛试题）6．—个凸n 边形的内角和小于1999°，那么n 的最大值是（ ）（全国初中联赛试题）A ．11B ．12C ．13D ．147．如图，是一个正方形桌面，如果把桌面砍下一个角后，桌面还剩（ ）个角．A ．5个B ．5个或3个C ．5个或3个或4个D ．4个 8．—个凸n 边形，除一个内角外，其余1n 个内角的和为2400°，则n 的值是（ ）A ．15B ．16C ．17D ．不能确定9．如图，在四边形ABCD 中，AB ＝AD ＝8，∠A ＝60°，∠D ＝150°，四边形周长为32，求BC 和DC 的长．A BCD EFG 第1题 A BC D 第2题 AB D EFG 第3题 A B C D24x 第4题 第7题 AB CD10．—个凸n边形的最小内角为95°，其他内角依次增加10°，求n的值．（“希望杯”邀请赛试题）11．平面上有A，B，C，D四点，其中任何三点都不在一直线上，求证：在△ABC，△ABD，△ACD，△BDC中至少有—个三角形的内角不超过45°．（江苏省竞赛试题）12．我们常见到如图那样图案的地面，它们分别是全用正方形或全用正六边形形状的材料铺成的，这样形状的材料能铺成平整的、无空隙的地面．问：（1）像上面那样铺地面，能否全用正五边形的材料，为什么？（2）你能不能另外想出一个用一种多边形（不一定是正多边形）的材料铺地的方案？把你想到的方案画成草图．（3）请你再画出一个用两种不同的正多边形材料铺地的草图．（安徽省中考试题）B级1．一个正m边形恰好被正n边形围住（无重叠、无间隙，如图所示是m＝4，n＝8的情况），若m ＝10，则n＝＿＿＿＿．2．如图，六边形ABCDEF 中，∠A ＝∠B ＝∠C ＝∠D ＝∠E ＝∠F ，且AB ＋BC ＝11，F A -CD ＝3，则BC ＋DE ＝＿＿＿＿．（北京市竞赛试题）3．如图，延长凸五边形A 1A 2A 3A 4A 5的各边相交得到五个角：∠B 1，∠B 2，∠B 3，∠B 4，∠B 5，它们的和等于＿＿＿．若延长凸n 边形（n ≥5）的各边相交，则得到的n 个角的和等于＿＿＿＿．（第十二届“希望杯”邀请赛试题）4．如图，在四边形ABCD 中，AB＝4BC ＝1，CD ＝3，∠B ＝135°，∠C ＝90°，则∠D ＝（ ）A ．60°B ．67.5°C ．75°D ．不能确定（重庆市竞赛试题）5．如图，已知O 是四边形ABCD 内一点，OA ＝OB ＝OC ，∠ABC ＝∠ADC ＝70°，则∠DAO ＋∠DCO 的大小是（ ）A ．70°B ．110°C ．140°D ．150°6．在一个多边形中，除了两个内角外，其余内角之和为2002°，则这个多边形的边数为（ ）A ．12B ．12或13C ．14D ．14或15（江苏省竞赛试题）7．一个凸十一边形由若干个边长为1的正方形或正三角形无重叠、无间隙地拼成，求此凸十一边形各个内角大小，并画出这样的凸十一边形的草图．（全国通讯赛试题）第1题 ABC D EF 第2题 1A 1B 2A 2B 3B 4B 5B 3A 4A 5A 第3题 AB CD 第4题 O ABC D 第5题8．一块地能被n 块相同的正方形地砖所覆盖，如果使用较小的相同正方形地砖，那么需n ＋76块这样的地砖才能覆盖该块地，已知n 及地砖的边长都是整数，求n 的值．（上海市竞赛试题）9．设有一个边长为1的正三角形，记作A 1如下左图，将A 1的每条边三等分，在中间的线段上各向形外作正三角形，去掉中间的线段后得到的图形记作A 2（如下中图）；将A 2的每条边三等分，并重复上述过程，所得到的图形记作A 3（如下右图）；再将A 3的每条边三等分，并重复上述过程，所得到的图形记作 A 4，求A 4的周长．（全国初中数学联赛试题）10．在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫作平面镶嵌），这显然与正多边形的内角大小有关，当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．（1）请根据下列图形，填写表中空格：1A 2A 3A（3）从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形．说明你的理由．（陕西省中考试题）。
人教版 八年级上册数学 竞赛专题：多边形的边和角(含答案)
人教版 八年级数学 竞赛专题：多边形的边与角（含答案）【例1】两个凸多边形，它们的边长之和为12，对角线的条数之和为19，那么这两个多边形的边数分别是＿＿＿＿和＿＿＿＿．【例2】凸边形有且只有3个钝角，那么n 的最大值是（ ） A ．5B ．6C ．7D ．8【例3】凸n 边形除去一个内角外，其余内角和为2570°，求n 的值．【例4】如图，凸八边形ABCDEFGH 的八个内角都相等，边AB ，BC ，CD ，DE ，EF ，FG 的长分为7，4，2，5，6，2，求该八边形的周长．【例5】如图所示，小华从M 点出发，沿直线前进10米后，向左转20°，再沿直线前进10米后，又向左转20°，…这样走下去，他第一次回到出发地M 时，行走了多少米？M D EF GH能力训练A 级1．如图，凸四边形有＿＿＿个；∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝＿＿＿．2．如图，凸四边形ABCD 的四边AB ，BC ，CD 和DA 的长分别为3，4，12和13，∠ABC ＝90°，则四边形ABCD 的面积为＿＿＿．3．如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝＿＿＿．4．如图，ABCD 是凸四边形，则x 的取值范围是＿＿＿．.5．一个凸多边形的每一内角都等于140°，那么，从这个多边形的一个顶点出发的对角线的条数是（ ）A ．9条B ．8条C ．7条D ．6条6．—个凸n 边形的内角和小于1999°，那么n 的最大值是（ ） A ．11B ．12C ．13D ．147．如图，是一个正方形桌面，如果把桌面砍下一个角后，桌面还剩（ ）个角． A ．5个B ．5个或3个C ．5个或3个或4个D ．4个8．—个凸n 边形，除一个内角外，其余1n 个内角的和为2400°，则n 的值是（ ） A ．15B ．16C ．17D ．不能确定9．如图，在四边形ABCD 中，AB ＝AD ＝8，∠A ＝60°，∠D ＝150°，四边形周长为32，求BC 和DC 的长．AB CDA BDEF G第3题AB CD24x第4题第7题A B CD E FG第1题ABCD第2题10．—个凸n 边形的最小内角为95°，其他内角依次增加10°，求n 的值．11．平面上有A ，B ，C ，D 四点，其中任何三点都不在一直线上，求证：在△ABC ，△ABD ，△ACD ，△BDC 中至少有—个三角形的内角不超过45°．12．我们常见到如图那样图案的地面，它们分别是全用正方形或全用正六边形形状的材料铺成的，这样形状的材料能铺成平整的、无空隙的地面．问：（1）像上面那样铺地面，能否全用正五边形的材料，为什么？（2）你能不能另外想出一个用一种多边形（不一定是正多边形）的材料铺地的方案？把你想到的方案画成草图．（3）请你再画出一个用两种不同的正多边形材料铺地的草图．B 级1．一个正m 边形恰好被正n 边形围住（无重叠、无间隙，如图所示是m ＝4，n ＝8的情况），若m ＝10，则n ＝＿＿＿＿．第1题A BCD EF 第2题1A 1B 2A 2B 3B 45B 3A 4A 5A 第3题2．如图，六边形ABCDEF 中，∠A ＝∠B ＝∠C ＝∠D ＝∠E ＝∠F ，且AB ＋BC ＝11，F A -CD ＝3，则BC ＋DE ＝＿＿＿＿．3．如图，延长凸五边形A 1A 2A 3A 4A 5的各边相交得到五个角：∠B 1，∠B 2，∠B 3，∠B 4，∠B 5，它们的和等于＿＿＿．若延长凸n 边形（n ≥5）的各边相交，则得到的n 个角的和等于＿＿＿＿．4．如图，在四边形ABCD 中，AB＝4BC ＝1，CD ＝3，∠B ＝135°，∠C ＝90°，则∠D ＝（ ） A ．60°B ．67.5°C ．75°D ．不能确定5．如图，已知O 是四边形ABCD 内一点，OA ＝OB ＝OC ，∠ABC ＝∠ADC ＝70°，则∠DAO ＋∠DCO 的大小是（ ）A ．70°B ．110°C ．140°D ．150°6．在一个多边形中，除了两个内角外，其余内角之和为2002°，则这个多边形的边数为（ ） A ．12B ．12或13C ．14D ．14或157．一个凸十一边形由若干个边长为1的正方形或正三角形无重叠、无间隙地拼成，求此凸十一边形各个内角大小，并画出这样的凸十一边形的草图．8．一块地能被n 块相同的正方形地砖所覆盖，如果使用较小的相同正方形地砖，那么需n ＋76块这样的地砖才能覆盖该块地，已知n 及地砖的边长都是整数，求n 的值．ABCD第4题OABCD第5题9．设有一个边长为1的正三角形，记作A 1如下左图，将A 1的每条边三等分，在中间的线段上各向形外作正三角形，去掉中间的线段后得到的图形记作A 2（如下中图）；将A 2的每条边三等分，并重复上述过程，所得到的图形记作A 3（如下右图）；再将A 3的每条边三等分，并重复上述过程，所得到的图形记作A 4，求A 4的周长．10．在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫作平面镶嵌），这显然与正多边形的内角大小有关，当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．（1）请根据下列图形，填写表中空格：（3）从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形．说明你的理由．参考答案例1 5 7 例2 B例3 n ＝17 提示：设此角为x ，则（n －2）×180°＝x ＋2570°，得2570360180x n +︒+︒=︒，x ＝130°，此时n ＝17.例4 双向延长AB ，CD ，EF ，GH 得四边形MNPQ ，如图，原八边形的内角都相等，其每一内角均为1A 2A 3A(82)1801358-⨯︒=︒，每一外角均为45°，因此MNPQ 为长方形，△BPC ，△DQE ，△FMG ，△ANH都是等腰直角三角形.设GH ＝x ，HA ＝y ，由MQ ＝NP ，得MF ＋FE ＋EQ ＝NA ＋AB ＋BP ，∴67y +=++，∴3y =∵MN ＝QP ，∴x ＝3＋7＋4＋2＋5＋6＋2＋3＋3＝32.例5 将整个图形画完，就知道是一个边长为10米的正多边形，且每个外角的大小都是20°，由多边形的外角和等于360°知这是一个18边形，所以小华第一次回到M 点时走的总路程是180米.A 级1. 7；540°2. 363. 540°4. 1＜x ＜135. D6. C7. C8.A9. BC ＝10，DC ＝6 10. n ＝611. 提示：分构成凸四边形和凹四边形两种情况讨论，并用反证法加以证明推出矛盾.12.(1)所用材料的形状不能是正五边形,因为,正五边形的每个内角都是108°,要铺成平整的,无空隙的地面, 必须使若干个正五边形拼成一个周角，但找不到符合条件的以n ×108°=360°的n 值,故不能用形状是正五边形的材料铺地面. ⑵⑶略. B 级1.52.143.180°;(n －4)180°4.B5.D 由OA=OB=OC 得∠BAO=∠ABO,∠BCO=∠OBC,所以∠DAO+∠DCO=360°－3×70°=150°6.D7.提示：因凸十一边形由正方形或正三角形拼成，故其内角的大小只能是60°,90°,120°,\ 150°四种可能,设这些角的个数分别为x ,y ,z ,w ,则116090120150(112)180x y z w x y z w +++=⎧⎨+++=-⨯⎩解得x =y =0,z =1,w =10.说明这个十一边形一个内角为120°,由两个正三角形的内角拼成，其余10个角均为150°,由一个正三角形内角与一个正方形内角拼成,图略. 8.n =324 9.649提示：从A 1开始,每进行一次操作,所得到的图形的周长是原来图形周长的43倍.10.(1)108°;120°;()02180n n-⨯ (2)正三角形、正四边形(或正方形)正六边形.假定在接合处一共有k 块正边形地砖，由于正n边形的所有内角都相等，则()02180360nkn-⨯=g即24222nkn n==+--.因k为整数，故n－2|4，n—2=1，2，4，得n=3,4 或6，由此可见，只有三种正多边形的瓷砖，可以按要求铺地，即正三角形、正方形和正六边形.(3)如:正方形和正八边形，草图如下，设在一个顶点周围有m个正方形的角，n个正八边形的角，那么，m，n应是方程m·90°+n·135°=360°的整数解.即2m+3n=8的整数解.∵这个方程的整数解只有12mn=⎧⎨=⎩一组∴符合条件的图形只有一种.。
中考体系-73.多边形的边和角(最全,含答案)
多边形的边和角一、多边形的边二、多边形的角三、多边形的对角线四、镶嵌五、多边形综合一、多边形的边已知内角和求边数1.【易】（2012年海淀二模）若一个多边形的内角和等于540︒，则这个多边形的边数是___________．【答案】52.【易】（河南省实验中学2011年内部中考数学第一轮复习资料4）若一个多边形的内角和等于720︒，则这个多边形的边数是（）A．5 B．6 C．7 D．8【答案】B3.【易】（2012福建泉州中考）n边形的内角和为900︒，则n=__________．【答案】74.【易】（2012南外初二期末）一个多边形的内角和等于1080︒，则这个多边形为_____边形．【答案】八5.【易】（天津市河西区2011年初中毕业生学业考试模拟试卷（二）数学）一个多边形的内角和等于1260︒，则它是（）A．五边形B．七边形C．九边形D．十边形【答案】C已知一个内角求边数6.【易】（2012师达中学初一下期中）一个多边形的每一个内角都是108︒，它是_______边形．【答案】五7.【易】（丰台区2011学年度第二学期期末练习）若一个正多边形的每个内角等于120︒，则这个正多边形的边数是（）A．8 B．7 C．6 D．5【答案】C8.【易】（2009年武昌水果湖第二中学初一下期末）一个多边形的每一个内角都是135︒，则这个多边形是（）A．七边形B．八边形C．九边形D．十边形【答案】B9.【易】（2010北京22中初一下期中）若一个正多边形的一个内角是140︒，则这个正多边形的边数是（）A．10 B．9 C．8 D．7【答案】B10.【易】（北京市西城区2010年抽样测试）若一个正多边形的一个内角是144︒，则这个多边形的边数为（）A．12 B．11 C．10 D．9【答案】C11.【易】（东城2011二模）若一个正多边形的一个内角等于150︒，则这个正多边形的边数是（）A．9 B．10 C．11 D．12【答案】D12.【易】（2012年铁二中初一下期中）已知正多边形的每一个内角都是160︒，则正多边形的边数为______．【答案】18已知一个外角求边数13.【易】（2010年朝阳二模）若一个多边形的每一个外角都是36︒，则这个多边形的边数是（）A．6 B．8 C．9 D．10【答案】D14.【易】（2011年莆田中考）若一个正多边形的一个外角等于40︒，则这个多边形是_________边形．【答案】九15.【易】（2011年山西省初中毕业生学业考试）一个正多边形，它的每一个外角都等于45︒，则该正多边形是（）A．正六边形B．正七边形C．正八边形D．正九边形【答案】C16.【易】（北京市东城区2010学年度初三年级综合练习）若一个正多边形的一个外角是60︒，则这个正多边形的边数是（ ） A ．5 B ．6 C ．7 D ．8 【答案】B17. 【易】（河南省实验中学2011年内部中考数学第一轮复习资料4）一个正多边形的每一个外角都等于72︒，则这个多边形的边数是_________． 【答案】518. 【易】（2012初二深圳罗湖统考）如图，小明从点O 出发，每前进10米后向右转20︒，再前进10米又向右转20︒，……，这样一直走下去，当小明第一次回到出发点O 时，他一共走了（ ）米A ．190B ．180C ．170D ．160【答案】B19. 【易】（2010初一下期中）某科技小组制作了一个机器人，它能根据指令要求进行行走和旋转．某一指令规定：机器人先向前行走1米，然后左转45︒，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了________米．（n 边形的内角和是()2180n -︒）【答案】8已知内外角关系求边数20. 【易】（2011年来宾市初中毕业升学统一考试试题）如果一个多边形的内角和是其外角和的一半，那么这个多边形是（ ） A ．六边形 B ．五边形 C ．四边形 D ．三角形 【答案】D21. 【易】（2009年怀柔一模）若一个多边形的内角和等于它外角和的1.5倍，则这个多边形的边数是（ ） A ．4 B ．5 C ．6 D ．7 【答案】B22. 【易】（巴中市2013年高中阶段教育学校招生考试数学试卷）若一个多边形的内角和与外角和相等，则这个多边形是_______边形.20°20°O23.【易】(娄度市2013年初中毕业学业考试数学试题卷)（西城2011二模）一个多边形的内角和是它的外角和的2倍，则这个多边形的边数为_______．【答案】624.【易】（2013年长沙市初中毕业学业水平考试数学试卷）下列多边形中，内角和与外角和相等的是（）A．四边形B．五边形C．六边形D．八边形【答案】A25.【易】（2013宣武外国语实验学校第二学期期中考试）一个多边形的内角和是外角和的3倍，则这个多边形的边数是___________【答案】826.【易】一个多边形的内角和等于十边形的外角和的3倍，则这个多边形是________边形【答案】八27.【易】（天津市红桥区2011七年级第二学期期中考试数学）一个多边形的内角和是外角和的倍，则这个多边形是（）边形．4A．六B．八C．十D．十二【答案】C28.【易】（河南省实验中学2011年内部中考数学第一轮复习资料4）已知多边形的内角和为其外角和的5倍，则这个多边形的边数为_________．【答案】1229.【易】（武汉二中广雅中学七年级（下）数学期中）已知一个多边形的每一个内角都相等，且一个内角等于它相邻外角的9倍，则这个多边形的边数是（）A．9 B．12 C．18 D．20【答案】D30.【易】（2012陈经纶中学七年级下期中）一个n边形的内角和比它的外角和的2倍还大180︒，则边数n为_________．【答案】731.【易】（2010年北京师大附中期中）某多边形的内角与外角和共1080︒，则这个多边形的边数为_________【答案】632.【易】（沈阳）若一个多边形的所有内角与某一外角的和为1350︒，那么这个多边形是（）A．七边形B．八边形C．九边形D．十边形33.【易】（初一数学下期末复习）若一个多边形的内角和与外角和等于1440︒，则这个多边形的边数是__________．【答案】834.【易】（天津市南开区2010学年度第二学期期中质量检测七年级数学试卷）一个多边形的内角和与外角和的比为5:2，则这个多边形是_________【答案】七边形35.【易】（2012育鸿中学初一下期中）一个多边形的内角和与外角和之比是7:2，则这个多边形是_________边形．【答案】九36.【易】（2010年21中初一下期中）n边形的内角和与外角和之比为4:1，则边数为__________ ．【答案】1037.【易】（2010年房山区初三年级统一练习）如果正n边形的一个外角与和它相邻的内角之比是1:3，那么n的值是（）A．5 B．6 C．7 D．8【答案】D38.【易】（2012人大附初一上期中）若一个正多边形的每一个外角都是相邻内角的14，则这个正多边形为（）A．正八边形B．正九边形C．正十边形D．正十二边形【答案】C39.【易】（2012首师大附中初一下期中）一个正多边形，它的一个外角等于与它相邻的内角的15，则这个多边形是____边形．【答案】十二40.【中】（河南省实验中学2011年内部中考数学第一轮复习资料4）一个多边形的内角和与它的一个外角的和为570︒，那么这个多边形的边数为________ 【答案】541.【中】（耀华嘉诚2008学年第一学期九年级第二次月考）外角大于内角的正多边形是正_______边形，外角等于内角的正多边形是正_____边形，外角等于内角的23的正多边形是正_________边形．【答案】三，四，五42. 【中】（2012年度初一第二学期期末模拟）一个多边形截去一个角后所形成的多边形的内角和是1260︒，那么原多边形的边数不可能是（ ） A ．8 B ．9 C ．10 D ．11 【答案】D截去一个角，会有这么几个变化：1、内角增加了一个，那么原来边数是：1260180218︒︒+-=÷2、内角减少了一个，那么原来边数是：12601802110︒︒++=÷3、内角不变，那么原来边数是：126018029︒︒+=÷43. 【中】（2012重庆綦江区三江初一下期中）一个多边形截去一个内角后，形成另一个多边形，它的内角和为2520︒，则原来多边形的边数不可能是（ ） A ．15条 B ．16条 C ．17条 D ．18条 【答案】D截去一个角，会有这么几个变化：1、内角增加了一个，那么原来边数是：25201802115︒︒+-=÷2、内角减少了一个，那么原来边数是：25201802117︒︒++=÷3、内角不变，那么原来边数是：2520180216︒︒+=÷44. 【中】（清华附初一下期中）在一个多边形中，除了两个内角外，其余内角和为2010度，则这个多边形的边数为_____________． 【答案】14或1545. 【中】（南省实验中学2011年内部中考数学第一轮复习资料4）一个多边形少一个内角的度数和为2300︒． ⑴求它的边数；⑵求少的那个内角的度数． 【答案】⑴ 15⑵ 40︒46. 【中】（沈阳）一个多边形恰有5个钝角，则此多边形的边数最多是______________．【答案】8设这个凸多边形的边数为n ，其中5个内角为钝角，()5n -个内角为直角或锐角．()()2180180590n n ∴-⋅︒⋅︒+-⋅︒＜5 n ∴＜9，取8n =.47. 【中】（天津竞赛题）如果一个凸n 边形恰有4个内角是钝角，那么，这个多边形的边数n 最多为___________ 【答案】7因为凸n 边形恰有4个内角是钝角，所以这4个内角之和大于360︒，且小于720︒，而另外的()4n -个内角是直角或锐角，则这()4n -个内角之和不大于()490n-⨯︒，且大于0︒，于是，有不等式()()︒+︒-⨯︒︒+-⨯︒＜＜，解得48n n36002180720490＜＜，故边数n最多为7n二、多边形的角多边形内外角和48.【易】（百色市2011年初中毕业暨升学考试）五边形的外角和等于（）A．180︒B．360︒C．540︒D．720︒【答案】B49.【易】（河南省实验中学2011年内部中考数学第一轮复习资料4）四边形的内角和等于__________．【答案】360︒50.【易】（天津市河西区2010学年度第二学期七年级期中阶段性质量调查数学试卷）如图，已知长边形ABCD，若沿图中虚线减去B∠，则剩下的多边形AEFCD的内角和为______．【答案】540︒51.【易】（2012年北京十二中第二学期期中考试试卷）六边形的内角和是__________【答案】720︒52.【易】（2009年北京55中初一下期中）一个八边形的内角和为________︒．【答案】1080n+时，它的内角和增加（）53.【易】（沈阳）当多边形的边数由n增加到1A．180︒B．270︒C．360︒D．120︒【答案】A54.【易】（2009年北京65中初一下期中）一个多边形的边数每增加一条，这个多边形的（）A．内角和增加360度B．外角和增加360度C．对角线增加一条D．内角和增加180度【答案】D55.【易】（河南省实验中学2011年内部中考数学第一轮复习资料4）下面各角能成为某多边形的内角的和的是（）A．430︒B．4343︒C．4320︒D．4360︒【答案】C56. 【易】（2010中大附中期末考试）九边形中有一个内角等于120︒，则其它内角的和为___________． 【答案】1140︒57. 【易】（2012年中关村中学初一下期中）一个多边形的每一个内角都是144︒，则它的内角和等于（ ） A ．1260︒ B ．1440︒ C ．1620︒ D ．1800︒【答案】B58. 【易】（2012北大附初一下期中）若一个多边形的每个外角都等于30︒，则它的内角和等于_________． 【答案】1800︒59. 【易】（2012年铁二中初一下期中）(北大附中2013学年度第二学期期末考试初一年级数学试卷)一个多边形的每一个外角都等于40︒，那么这个多边形的内角和为（ ） A ．1260︒ B ．900︒ C ．1620︒ D ．360︒ 【答案】A60. 【易】（2010武汉市新洲区初一下期末）已知多边形的每一个外角都是72︒，则该多边形的内角和是（ ） A ．700︒ B ．720︒ C ．540︒ D ．1080︒ 【答案】C∵多边形的每一个外角都是72︒，∴多边形的边数为：360572=， ∴该多边形的内角和为：()52180540-︒=︒×．61. 【易】（2012人大附初一上期中）若从一个多边形的一个顶点出发，可以引3条对角线，则这个多边形的内角和为___________． 【答案】720︒62. 【易】（2010年湖北武汉华一寄宿学校）从n 边形的一个顶点出发一共可引6条对角线，则这个n 边形的内角和等于（ ） A ．1260︒ B ．1440︒ C ．1620︒ D ．1800︒ 【答案】A63. 【易】（2011年松江区初中毕业生学业模拟考试）从多边形一个顶点可作9条对角线，则这个多边形内角和为________度． 【答案】180064.【易】（2013年福建省泉州市初中毕业、升学考试）九边形的外角和为_________．【答案】360︒65.【中】（天津市河西区2011学年度第二学期七年级期中质量调查）动脑筋完成下表：四边形五边形六边形边形1 2 3四边形五边形六边形n边形多边形内外角66.【易】（2012年铁二中初一下期中）正n边形的每一个内角的度数为________，每一个外角的度数为________．【答案】()1802nn-度，360n度.67.【易】（2011年无锡市中考）正五边形的每一个内角都等于________︒．【答案】10868.【易】（2013年晋江市初中学业升学考试）正六边形的每个内角的度数为______．【答案】120︒69.【易】（2011年广东省初中毕业生学业考试）正八边形的每个内角为（）A．120︒B．135︒C．140︒D．144︒【答案】B70.【易】（2011年上海静安区九年级二模）正五边形每个外角的度数是_________．【答案】72︒71.【易】（2012北京中考）正十边形的每个外角等于（）A．18︒B．36︒C．45︒D．60︒【答案】B72.【中】（武汉二中广雅中学七年级（下）数学月考（四））n>），锐角最多有（）个一个n边形中（4n-A．3 B．4 C．5 D．()3【答案】A73.【中】（耀华嘉诚2009学年第一学期九年级第二次月考）正多边形的一个中心角与该正多边形的一个外角的关系是（）A．互余B．互补C．相等D．互余或互补【答案】C74.【中】（2010年武珞路中学七年级下期中）一个多边形除了一个内角外，其余各内角的度数和为2550︒，则这个内角的度数为（）A．30︒B．60︒C．120︒D．150︒【答案】D75.【中】（2010湖北武汉武昌初一下期末）小明在计算一个多边形的内角和时，由于粗心少计算了一个内角，结果得1345°，则未计算的内角的大小为（）A．80︒B．85︒C．95︒D．100︒【答案】C76.【中】（2009武汉二中初一下期中）下列命题中：①如果四边形一组对角互补，那么另一组对角也互补．②一个多边形的内角中最多只能有3个锐角．③三角形的中线把三角形分成面积相等的两部分．④有公共端点，有一条公共边且和为180°的两个角是邻补角．其中正确的有（）A．1个B．2个C．3个D．4个【答案】C77.【中】（2009⑴ 内角和为2005︒，小明为什么说不可能？ ⑵ 小华求的是几边形的内角和？⑶ 错把外角当内角的那个外角的度数你能求吗？是多少度呢？ 【答案】⑴ 因为2005︒不是180︒的整数倍，所以小明说不可能；⑵ 依题意有()21802005x -⋅=， 解得2513180x =． 因而多边形的边数是13，该多边形为十三边形．⑶ 13边形的内角和是()1321801980-=×度，则错把外角当内角的那个外角的度数是2005198025-=︒．78. 【难】（天津竞赛题）如果一个凸n 边形的一个顶点引出的所有对角线把这个凸n 边形分成了m 个小三角形，若m 等于这个凸n 边形对角线条数的49，那么此n 边形的内角和为___________ 【答案】720︒综合求角度79. 【易】（2009年浙江省宁波市中考数学试题及答案）如图，1∠、2∠、3∠、4∠是五边形ABCD 的外角，且123470∠=∠=∠=∠=︒，则AED ∠的度数是（ ）2431E DC BAA ．110︒B ．108︒C ．105︒D ．100︒ 【答案】D80. 【易】（2013年河北省初中毕业生升学文化课数学试卷）如图11，四边形ABCD 中，点M ，N 分别在AB ，BC 上，将BMN △沿MN 翻折，得FMN △，若MF AD ∥，FN DC ∥，则B ∠=_________．【答案】95︒81. 【易】（2013年湖北省咸宁市中考数学试卷）如图，过正五边形ABCDE 的顶点A 作直线l BE ∥，则1∠的度数为（ ） A ．30︒ B ．36︒ C ．38︒ D ．45︒【答案】B82. 【易】（北京市西城区（南区）2012学年度第一学期期末）如图，六边形ABCDEP 是轴对称图形，CP 所在的直线是它的对称轴，若150APC BCP ∠+∠=︒，则APE BCD ∠+∠的大小是（ ）A ．B ．C ．D ．【答案】B83. 【易】（南京市2013年初中毕业生学业考试数学试题）P BCDEA150︒300︒210︒330︒如图将矩形ABCD 绕点A 顺时针旋转到AB C D '''的位置，旋转角090αα︒︒（＜＜）．若1110∠=︒，则α∠=____________︒．【答案】2084. 【易】（乐山市2013年高中阶段教育学校招生统一考试数学）如图7，在四边形ABCD 中，45A =∠°，直线l 与边AB AD 、分别相交于点M N 、，则12+=∠∠_______.【答案】225︒85. 【中】（河南省实验中学2011年内部中考数学第一轮复习资料4）求下图中x 的值．【答案】60︒86. 【易】（天津市红桥区2011七年级第二学期期中考试数学）用一条宽度相同的足够长的线条，打一个结，如图所示，然后轻轻拉紧、压平就可以得到如图所示的正五边形ABCDE （五个角、五条边相等），其中BAC ∠的度数为__________度．1C′D′B′DCBAED CBAx °150°120°2x°1287. 【中】（河南省实验中学2011年内部中考数学第一轮复习资料4）如图，在正五边形ABCDE 中，连结AC ，AD ，则CAD ∠的度数是__________︒．【答案】3688. 【中】（福建宁德中考）图⑴表示一个正五棱柱形状的高大建筑物，图⑵是它的俯视图．小健站在地面观察该建筑物，当他在图⑵中的阴影部分所表示的区域活动时，能同时看到建筑物的三个侧面，图中MPN ∠的度数为___________【答案】36︒89. 【中】（2012育鸿中学初一下期中）如图，在四边形ABCD 中，点E 在BC 上，180A ADE ∠+∠=︒，78B ∠=︒，60C ∠=︒，求EDC ∠的度数．【答案】42︒90. 【中】（2012年铁二中初一下期中）已知：如图，DC AB ∥，BAE BCD ∠=∠，AE DE ⊥，130D ∠=︒，求B ∠的度数．图（2）图（1）91. 【中】（2012年铁二中初一下期中）如图，四边形ABCD 中，40B ∠=︒，沿直线MN 剪去B ∠，则所得五边形AEFCD 中，12∠+∠=___________．【答案】220︒92. 【中】（2011年南京）如图，过正五边形ABCDE 的顶点A 作直线l CD ∥，则1∠=________．【答案】36︒93. 【中】（长春中考题）在平面内，有一条公共边的正六边形和正方形如图放置，则∠α等于_______度【答案】150︒94. 【难】（希望杯竞赛题）如图，延长凸五边形12345A A A A A 的各边相交得到5个角，即1B ∠，2B ∠，3B ∠，4B ∠，5B ∠，它们的和等于________；若延长凸n 边形()5n ≥的各边相交，则得到的n 个角的和等于_________1EC DBAlα【答案】180︒，()4180n -︒三、 多边形对角线95. 【易】（2012北京十一中学七年级下期中）若一个多边形从任一个顶点，只可以引三条对角线，则它是（ ）边形 A ．四 B ．五 C ．六 D ．七 【答案】C96. 【易】（河南省实验中学2011年内部中考数学第一轮复习资料4）在凸多边形中，四边形有2条对角线，五边形有5条对角线，经过观察、探索、归纳，你认为凸八边形的对角线条数应该是多少条？简单扼要地写出你的思考过程． 【答案】2097. 【易】（山西省太原市初中数学竞赛试卷）在凸多边形中，四边形有两条对角线，五边形有5条对角线．观察探索凸十边形有（ ）条对角线． A ．29 B ．32 C ．35 D ．38 【答案】C98. 【易】（北京171初一下期中）若多边形每个角都是150︒，则从此多边形的一个顶点出发的对角线条数为（ ） A ．7 B ．8 C ．9 D ．10 【答案】C99. 【中】（2011年四川省广安市中考数学试卷）若凸n 边形的内角和为1260︒，则从一个顶点出发引的对角线条数是___________. 【答案】6100. 【中】（2011年广东省河源市初中毕业生学业水平考试与高中阶段学校招生考试）凸n边形的对角线的条数记作()4n a n ≥，例如：42a =，那么：①5a =______________；②65a a -=___________；③1n n a a +-=_________．（4n ≥，用n 含的代数式表示） 【答案】5；4；1n -B 5B 4B 3B 2B 1A 5A 4A 3A 2A 1101. 【中】（2011深圳中学初二上期末）已知正n 边形共有3n +条对角线，其周长为x ，对角线长度之和为y ，试求yx的值． 【答案】6n =，y x =四、 平面镶嵌102. 【易】（2012教师进修初一下期中）只用下列正多边形，不能进行平面镶嵌的是（ ） A ．正三角形 B ．正四边形 C ．正六边形 D ．正八边形【答案】D103. 【易】（2012初一下检测）某市为了让居民有更多休闲和娱乐的地方，政府新建了几处广场，工人师傅在铺设地面时，准备选用同一种正多边形地砖．现有下面几种形状的正多边形地砖，其中不能进行平面镶嵌的是（ ） A ．正三角形 B ．正方形 C ．正五边形 D ．正六边形 【答案】C104. 【易】（广州）只用下列正多边形地砖中的一种，能够铺满地面的是（ ）A ．正十边形B ．正八边形C ．正六边形D ．正五边形 【答案】C105. 【易】（2010中大附中期末考试）在海珠广场修建的工程中，计划采用同一种正多边形地板铺设地面，在下面的地板砖：①正方形 ②正五边形 ③正六边形 ④正八边形 中能够铺满地面的地板砖的种数有（ ） A ．1种 B ．2种 C ．3种 D ．4种 【答案】B106. 【易】（2012首师大附中初一下期中）商店出售下列形状的地砖：⑴正方形；⑵长方形；⑶正五边形；⑷正六边形；若只选购其中一种地砖镶嵌地面，则可供选择的地砖共有（ ） A ．1种 B ．2种 C ．3种 D ．4种 【答案】C107. 【易】（武汉二中广雅中学2011下学期期末七年级数学）能与正六边形同时进行平面镶嵌的是（ ） A ．正方形 B ．正八边形 C ．正五边形 D ．正三角形 【答案】D108. 【易】（2012陈经纶中学七年级下期中）如果在一个顶点周围用两个正方形和个正三角形恰好可以进行平面镶嵌，则的值是（ ） A ．3 B ．4 C ．5 D ．6n n【答案】A109. 【易】（2012学年度第二学期河南省实验中学期中试卷）用两个正三角形与下面的（ ）若干个可以形成平面镶嵌 A ．正方形 B ．正六边形 C ．正八边形 D ．正十二边形 【答案】B110. 【易】（2012师达中学初一下期中）用正三角形和正六边形镶嵌平面，若每一个顶点处有2个正三角形，则有________个正六边形． 【答案】2111. 【易】（2012北大附初一下期中） 用边长相等的正三角形和正六边形镶嵌平面，若正三角形的个数为m 个，正六边形的个数为n 个，那么m 、n 满足的关系是________． 【答案】26m n +=112. 【易】（2012育鸿中学初一下期中）一幅美丽的图案，在其顶点处由四个正多边形镶嵌而成，其中三个分别为正三角形、正四边形、正六边形，则第四个为（ ） A ．正三边形 B ．正四边形 C ．正五边形 D ．正六边形 【答案】B113. 【易】（2012年中关村中学初一下期中）一幅美丽的图案，在某个顶点处由三个边长相等的正多边形镶嵌而成，其中两个分别为正十二边形、正四边形，则另一个为（ ）A ．正三角形B ．正四边形C ．正五边形D ．正六边形 【答案】D114. 【易】（河南省实验中学2011年内部中考数学第一轮复习资料4）一幅图案．在某个顶点处由三个边长相等的正多边形镶嵌而成．其中的两个分别是正方形和正六边形，则第三个正多边形的边数是______________． 【答案】12115. 【易】（清华附中初一下期中）在下列四组多边形地板砖中，①正三角形与正方形；②正三角形与正六边形；③正六边形与正方形；④正八边形与正方形．将每组中的两种多边形结合，能密铺地面的是（ ）A ．①③④B ．②③④C ．①②③D ．①②④ 【答案】D116. 【易】（武汉二中初一下期中）装修房子铺地板，有下列规格的地板砖供挑选：①正方形②正三角形③正五边形④正六边形，若所有地砖的边长相等，使用其中的一种或两种规格的地砖，选择方案有（ ） A ．5种 B ．6种 C ．7种 D ．8种 【答案】B117. 【易】（2010武汉洪山去初一下期末）用三块正多边形的木板铺地，拼在一起并相交于一点的各边完全吻合，其中两块木板的边数都是8，则第三块木板的边数应是（ ） A ．4 B ．5 C ．6 D ．8 【答案】A正八边形的每个内角为：1803608135︒-︒=︒÷，两个正八边形在一个顶点处的内角和为：2135270︒=︒×， 那么另一个多边形的内角度数为：36027090︒-︒=︒， ∵正方形的每个内角和为90︒， ∴另一个是正方形．118. 【易】（2010年初二第二学期综合考试）如图所示，已知等边三角形ABC 的边长为1，按图中所示的规律，用2008个这样的三角形镶嵌而成的四边形的周长是（ ）A ．2008B ．2009C ．2010D ．2011【答案】C119. 【易】（河南省实验中学2011年内部中考数学第一轮复习资料4）请你用正三角形、正方形、正六边形三种图形设计一个能铺满整个地面的美丽图案． 【答案】120. 【易】（浙江省2009年初中毕业生学业考试（丽水市卷））下述美妙的图案中，是由正三角形、正方形、正六边形、正八边形中的三种镶嵌而成的为（ ）【答案】D121. 【中】（天津市初中毕业生学业考试试卷）如图，是由12个边长相等的正三角形镶嵌而成的平面图形，则图中的平行四边形共有_______个．ABCD【答案】21122. 【中】（2010年河北省中考题）如图，两个正六边形的边长均为1，其中一个正六边形的一边恰在另一个正六边形的对角线上，则这个图形（阴影部分）外轮廓线的周长是（ ）A ．7B ．8C ．9D ．10【答案】B123. 【中】（沈阳初二）如图，用4个全等的直角三角形与1个小正方形镶嵌而成的的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x ，y 表示直角三角形的两直边（>x y ），下列四个说法：①2249+=x y ，②2-=x y ，③2449+=xy ，④9+=x y ．其中说法正确的是（ ）A ．①②B ．①②③C ．①②④D ．①②③④【答案】B124. 【中】（浙江省2009年初中毕业生学业考试（衢州卷））陈老师要为他家的长方形餐厅（如图）选择一张餐桌，并且想按如下要求摆放：餐桌一侧靠墙，靠墙对面的桌边留出宽度不小于80cm 的通道，另两边各留出宽度不小于60cm 的通道．那么在下面四张餐桌中，其大小规格符合要求的餐桌编号是_____________（把符合要求的编号都写上）．x yG FHEDCBA【答案】①②③④125.【中】（漳州中考题）我们知道形状为正五边形的地砖不能铺满地面，但某公园的一段路面是用型号相同的特殊的五边形地砖铺成的．如图，是拼铺图案的一部分，其中每个五边形有3个内角相等，那么这3个内角都等于________度【答案】120五、多边形综合中心角、边心距、外接/内切圆126.【易】（奉贤区调研测试）如果正多边形的中心角等于30︒，那么它的每个内角为_________度；【答案】150127.【易】（上海普陀区初三下质量调研）中心角是40︒的正多边形的边数是_____________【答案】9128.【易】（2013年天津市初中毕业生学业数学考试试卷）正六边形的边心距与边长之比为（）A3B2C．1:2D2CDEBA（第15题）桌面是边长为80cm的正方形桌面是长、宽分别为100cm和64cm的长方形桌面是半径为45cm的圆桌面的中间是边长为60cm的正方形，两头均为半圆【答案】B129.【中】（肇庆市2011年初中毕业生学业考试数学试题））A．6 B．12 C．D．【答案】B130.【中】（2011年上海金山区初三二模）已知正多边形的半径与边长相等，那么正多边形的边数是（）A．4 B．5 C．6 D．8【答案】C131.【中】（学年第一学期南汇区九年级数学期末质量抽查试卷）正六边形的边心距为3，则它的半径长为_________，面积为_________．【答案】，132.【中】（莆田市毕业考试）一个圆内接正六边形的边长为2，那么这个正六边形的边心距为_________．133.【中】（天津市初中毕业生学业考试试卷）边长为的正六边形的内切圆的半径为（）A．2a B．a CD．12a【答案】C134.【中】（台州市初中学业水平考试）如图，O的内接多边形周长为3，O的外切多边形周长为3.4，则下列各数中与此圆的周长最接近的是（）ABaCD【答案】C圆外切多边形的周长大于圆周长，圆内接多边形的周长小于圆周长．圆的内接多边形周长为3，外切多边形周长为3.4，所以圆周长在3与3.4之间．只有C选项满足条件．135.【中】（2009年安徽省芜湖市中考）小赵对芜湖科技馆富有创意的科学方舟形象设计很有兴趣，他回家后将一正五边形纸片沿其对称轴对折．旋转放置，做成科学方舟模型．如图所示，该正五边形的边心距OBAC为科学方舟船头A到船底的距离，请你计算12AC AB+=______________．（不能用三角函数表达式表示）136.【中】（杭州市各类高中招生文化考试）如图，有一个圆O和两个正六边形1T，2T．1T的6个顶点都在圆周上，2T的6条边都和圆O相切（我们称1T，2T分别为圆O的内接正六边形和外切正六边形）．⑴设1T，2T的边长分别为a，b，圆O的半径为r，求:r a及:r b的值；⑵求正六边形1T，2T的面积比12:S S的值．【答案】⑴连接圆心O和1T的6个顶点可得6个全等的正三角形．所以:1:1r a=；连接圆心O和2T相邻的两个顶点，得以圆O半径为高的正三角形，所以:2r b=；B门。
初中八年级数学竞赛培优讲义全套专题14 多边形的边与角_答案[精品]
![初中八年级数学竞赛培优讲义全套专题14 多边形的边与角_答案[精品]](https://img.taocdn.com/s3/m/3c1500b34b35eefdc9d3335f.png)
专题14 多边形的边与角例1 5 7 例2 B例3 n ＝17 提示：设此角为，则（n －2）×180°＝＋2570°，得2570360180x n +︒+︒=︒，＝130°，此时n ＝17.例4 双向延长AB ，CD ，EF ，GH 得四边形MNPQ ，如图，原八边形的内角都相等，其每一内角均为(82)1801358-⨯︒=︒，每一外角均为45°，因此MNPQ 为长方形，△BPC ，△DQE ，△FMG ，△ANH 都是等腰直角三角形.设GH ＝，HA ＝y ，由MQ ＝NP ，得MF ＋FE ＋EQ ＝NA ＋AB ＋BP ，∴6722y +=++3y =∵MN ＝QP ，∴＝3＋，∴周长＝7＋4＋2＋5＋6＋2＋3＋＋332.例5 将整个图形画完，就知道是一个边长为10米的正多边形，且每个外角的大小都是20°，由多边形的外角和等于360°知这是一个18边形，所以小华第一次回到M 点时走的总路程是180米.A 级1. 7；540°2. 363. 540°4. 1＜＜135. D6. C7. C8.A9. BC ＝10，DC ＝6 10. n ＝611. 提示：分构成凸四边形和凹四边形两种情况讨论，并用反证法加以证明推出矛盾.12.(1)所用材料的形状不能是正五边形,因为,正五边形的每个内角都是108°,要铺成平整的,无空隙的地面, 必须使若干个正五边形拼成一个周角，但找不到符合条件的以n ×108°=360°的n 值,故不能用形状是正五边形的材料铺地面.⑵⑶略.B 级1.52.143.180°;(n －4)180°4.B5.D 由OA=OB=OC 得∠BAO=∠ABO,∠BCO=∠OBC,所以∠DAO+∠DCO=360°－3×70°=150°6.D7.提示：因凸十一边形由正方形或正三角形拼成，故其内角的大小只能是60°,90°,120°,\ 150°四种可能,设这些角的个数分别为,y ,,w ,则116090120150(112)180x y z w x y z w +++=⎧⎨+++=-⨯⎩解得=y=0,=1,w=10.说明这个十一边形一个内角为120°,由两个正三角形的内角拼成，其余10个角均为150°,由一个正三角形内角与一个正方形内角拼成,图略.8.n=3249.649提示：从A1开始,每进行一次操作,所得到的图形的周长是原图形周长的43倍.10.(1)108°;120°; ()02180nn-⨯(2)正三角形、正四边形(或正方形)正六边形.假定在接合处一共有块正边形地砖，由于正n边形的所有内角都相等，则()02180360nkn-⨯=g即24222nkn n==+--.因为整数，故n－2|4，n—2=1，2，4，得 n=3,4 或6，由此可见，只有三种正多边形的瓷砖，可以按要求铺地，即正三角形、正方形和正六边形.(3)如正方形和正八边形，草图如下，设在一个顶点周围有m个正方形的角，n个正八边形的角，那么，m，n应是方程m·90°+n·135°=360°的整数解.即2m+3n=8的整数解.∵这个方程的整数解只有12mn=⎧⎨=⎩一组∴符合条件的图形只有一种.。
初中数学：多边形的内角和与外角和题型总结
1、多边形的内角和等于（n-2）180˚，n是多边形的边数。
2、多边形的外角和等于360˚。
这两个结论的证明也比较简单，在这里简单说明一下。
1、一个多边形，边数为n，将一个顶点与其它顶点相连，可以把这个多边形分割成（n-2）个三角形，每个三角形的内角和是360˚，所以多边形的内角和就是（n-2）180˚。
2、一个多边形，边数为n，每一个内角和它相邻的外角构成一个平角，n条边就构成n 个平角。
外角和就等于n个平角减去多边形的内角和，也就是360˚。
这两个知识在考查时，主要有四种类型，我们来看一下。
1、考查多边形边数和内角和的关系。
这类型题主要是知道边数求出内角和，或者知道内角和求出边数。
第（1）题，知道边数，求内角和。
第（2）题，知道内角和，求边数。
第（3）题，稍微复杂，两个多边形，知道边数之比和内角和之比，列方程求出边数。
第（4）、（5）、（6）题，稍为复杂，知道边数，先求出内角和，再去求多边形中的某个内角。
这些题型都比较简单。
这里还有一道题比较复杂一点，同学们可以尝试做一下。
2、外角和与内角和相结合这类型的关键点是，要知道多边形的内角和是隐藏的已知量，它等于360˚。
这类题型都是根据多边形内角和与外角和的关系，列一个方程，求出边数。
3、多边形，少一个角，其余内角和是一定值。
这种题型，运用到了不等式，是一个难点和重点。
它的运用的知识是，多边形的一个内角，它的取值范围是大于0，小于180。
除去的这个角的度数等于内角和减去其余内角和，据此，可以列一个不等式组，进行求解。
下面有练习，大家可以试一下。
4、正多数形正多边形的内角相等，边相等。
考查类型，1、知道边数，求内角；2、知道内角，求边数；3、知道外角，求边数。
在考试中，经常考察的方式是这样的。
八年级数学竞赛讲座多边形的边角与对角线附答案
第十四讲多边形的边角与对角线边、角、对角线是多边形中最基本的概念，求多边形的边数、内外角度数、对角线条数是解与多边形相关的基本问题，常用到三角形内角和、多边形内、外角和定理、不等式、方程等知识.多边形的内角和定理反映出一定的规律性：（n —2）X 180°随n的变化而变化；而多边形的外角和定理反映出更本质的规律；360。
是一个常数，把内角问题转化为外角问题，以静制动是解多边形有关问题的常用技巧.将多边形问题转化为三角形问题来处理是解多边形问题的基本策略，连对角线或向外补形、对内分割是转化的常用方法，从凸n边形的一个顶点引出的对角线把凸n边形分成（n_2）个多角形，凸n边形一共可引出n（n—3）对角线.2例题求解【例1】在一个多边形中，除了两个内角外，其余内角之和为2002° ,则这个多边形的边数是______________ （江苏省竞赛题）思路点拨设除去的角为。
，y°,多边形的边数为n，可建立关于x、y的不定方程；又0° <x<180° , 0°<y<180。
，又可得到关于n的不等式•故有两种解题途径，注意n为自然数的隐含条件.链接世界上的万事万物是一个不断地聚合和分裂的过程，点是几何学最原始的概念，点生线、线生面、面生体，几何元素的聚合不断产生新的图形，另一方面，不断地分割已有的图形可得到新的几何图形，发现新的几何性质，多边形可分成三角形，三角形可以合成其他一些几何图形.【例2】在凸10边形的所有内角中，锐角的个数最多是（）A . 0B . 1C . 3D . 5（全国初中数学竞赛题）思路点拨多边形的内角和是随着多边形的边数变化而变化的，而外角和却总是不变的，因此，可把内角为锐角的个数讨论转化为外角为钝角的个数的探讨.【例3】如图，已知在厶ABC中，AB= AC AD丄BC于D,且AD=BC=4若将此三角形沿AD剪开成为两个三角形，在平面上把这两个三角形拼成一个四边形，你能拼出所有的不同形状的四边形吗？画出所拼四边形的示意图（标出图中直角），并分别写出所拼四边形的对角线的长.（乌鲁木齐市中考题）A思路点拨把动手操作与合情想象相结合，解题的关键是能注意到重合的边作为四边形对角线有不同情形.注教学建模是当今教学教育、考试改革最热门的一个话题，简单地说，“数学建模”就是通过数学化（引元、画图等）把实际问题特化为一个数学问题，再运用相应的数学知识方法（模型）解决问题.本例通过设元，把“没有重叠、没有空隙”转译成等式，通过不定方程求解.【例4】在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫做平面镶嵌），这显然与正多边形的内角大小有关，当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360 ° ）时，就拼成了一个平面图形.（1）请根据下列图形，填写表中空格：（2）如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？（3）从正三角形、正四边形，正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由.（陕西省中考题）止多边形边数3 \—1 —5 6 ]…- --- -------- - -- - ------ U --- ----- ----- i ----------思路点拨本例主要研究两个问题：①如果限用一种正多边形镶嵌，可选哪些正多边形；②选用两种正多边形镶嵌，既具有开放性，又具有探索性•假定正n边形满足铺砌要求，那么在它的顶点接合的地方，n 个内角的和为360 °，这样，将问题的讨论转化为求不定方程的正整数解.【例5】如图，五边形ABCDE的每条边所在直线沿该边垂直方向向外平移4个单位，得到新的五边形A'B'C'D'E'（1）图中5块阴影部分即四边形AHA'G BFB'P、COC'N DMD'L EKE'I能拼成一个五边形吗？说明理由.（2）证明五边形A'B'C'D'E'的周长比五边形ABCD正的周长至少增加25个单位.（江苏省竞赛题）学力训练1 •如图，用硬纸片剪一个长为16cm 宽为12cm 的长方形，再沿对角线把它分成两个三角形，用这两个三角形可拼出各种三角形和四边形来，其中周长最大的是 __________ cm,周长最小的是cm•（ 选6《荚国中小学数学课程标准》）2. ______________________________________ 如图，/ 1 + Z 2+Z 3+Z 4+Z 5+Z 6=3. _____________________________________________________________________ 如图，ABCD 是凸四边形，AB=2, BC=4 CD=7则线段AD 的取值范围是 ___________________________________ 4•用黑白两种颜色的正六边形地面砖按如下所示的规律，拼成若干个图案： （1） 第4个图案中有白色地面砖 _______ 块； （2） 第n 个图案中有白色地面砖 _______ 块. （江西省中考题）思路点拨（1）5 块阴影部分要能拼成一个五边形须满足条件: ,A'GB' ； B'PC' ； C'ND' ； D'LE' ； E'lA'点分别共线； /1+ / 2+ / 3+ / 4+ / 5=360；（2）增加的周长等于A'H+A'G+B'F+B'P+C'0+C'N+D'M+D'L+E'K+E'l ，用圆的周长逼近估算.A . 4笹V 命C . 6 个7第3个（“希望杯”邀请赛试题）6. —个凸多边 形的每一内角都等于 140°,那么，从这个多边形的一个顶点出发的对角线的条数是 （）A. 9条 B . 8条 C . 7条 D . 6条7 •有一个边长为 4m 的正六边形客厅，用边长为 50cm 的正三角形瓷砖铺满，则需要这种瓷砖（）A . 216 块B . 288 块C . 384 块D . 512 块 （“希望杯”邀请赛试题）&已知△ ABC 是边长为2的等边三角形，△ ACD 是一个含有30°角的直角三角形，现将△ ABC 和△ ACD 拼 成一个凸四边形 ABCD （1））画出四边形ABCD⑵ 求出四边形 ABCD 的对角线BD 的长.（上海市闵行区中考题）9 .如图，四边形 ABCD 中, AB= BC = CD / ABC=90，/ BCD= 150°,求/ BAD 的度数. （北京市竞赛题）10. 如图，在五边形 A 1A 2AAA 中，B 是A 的对边AA 4的中点，连结 A 1B 1,我们称 A 1B 1是这个五边形的一条 中对线，如果五边形的每条中对线都将五边形的面积分成相等的两部分，求证：五边形的每条边都有一条11. _______________________ 如图，凸四边形有 _________________________ 个；/ A+Z B+Z C+Z D+Z E+Z F+Z G ___________________（重庆市竞赛题）12. ________________________________________________________________________________________ 如对角线和它平行.（安徽省中考|第勺魁）(% 11题」【第12题》图，延长凸五边形A1AAA4A的各边相交得到5个角，Z B,Z B, Z B3, Z B,Z B s,它们的和等于___________________若延长凸n 边形（n > 5）的各边相交，则得到的 n 个角的和等于 ________ . （“希望杯”邀请赛试题）13•设有一个边长为1的正三角形，记作 A （图a ），将每条边三等分，在中间的线段上向外作正三角形， 去掉中间的线段后所得到的图形记作A 2（图b ），再将每条边三等分，并重复上述过程，所得到的图形记作A 3（图C ）;再将每条边三 等分，并重复上述过程，所得到的图形记作A 4,那么，A 的周长是 _________ ； A 这个多边形的面积是原三角形面积的 __________ 倍. （全国初中数学联赛题）14 .如图，六边形 ABCDEF 中, Z A=Z B=Z C=Z D=Z E=Z F,且 AB+BC=11FA — CD=3 贝U BC+DC __ •（ 北 京市竞赛题）15.在一个n 边形中，除了一个内角外，其余 （n 一 1）个内角的和为2750°，则这个内角的度数为（）A . 130°D . 140°C . 105 °D . 120°16.如图，四边形 ABCD 中,Z BAD=90 , AB=BC=23 , AC=6 AD=3,贝U CD 的长为() A. 4 B . 4、2 C . 3 .2 D . 3注 按题中的方法’不断地做下去，就会成为下图那样的图形，它的边界有一个美丽的名称一一雪花曲 线或科克曲线（瑞典数学家），这类图形称为“分形”，大量的物理、生物与数学现象都导致分形，分形是 新兴学科“混沌”的重要分支.17.如图，设Z CGE a ，则Z A+Z B+Z C+Z D+Z C+Z F=()l 第 \3.3（江苏省竞赛题）D AH（第20题」ACA. 360° 一 a B . 270° — a C. 180 ° +a D . 2a （山东省竞赛题） 18.平面上有 A 、B, C D 四点，其中任何三点都不在一直线上，求证：在△ 中至少有一个三角形的内角不超过 45 °.19. 一块地能被n 块相同的正方形地砖所覆盖，如果用较小的相同正方形地砖，那么需 n+76块这样的地砖才能覆盖该块地，已知 n 及地砖的边长都是整数，求n .（上海市竞赛题）20. 如图，凸八边形 ABCDEFG 的8个内角都相等，边 AB BC CD DE EF 、FG 的长分别为7, 4, 2, 5, 6, 2，求该八边形的周长.21•如图I 是一张可折叠的钢丝床的示意图，这是展开后支撑起来放在地面上的情况，如果折叠起来，床 头部分被折到了床面之下（这里的A B C 、D 各点都是活动的），活动床头是根据三角形的稳定性和四边 形的不稳定性设计而成的，其折叠过程可由图2的变换反映出来.如果已知四边形 ABCD 中, AB=6, CD=15那么BC AD 取多长时，才能实现上述的折叠变化 ?的大小，并画出这样的凸 n 边形的草图.ABC △ ABD △ ACD △ BDC（淄博市中考题）22.—个凸n 边形由若干个边长为1的正方形或正三角形无重叠、无间隙地拼成，求此凸 n 边形各个内角C A S09 14-1ns raM的边角馬对角ti【例IE求解】fl 1 "或脂由逢伽2002*<(B-2>X180*<2Q02' + 360MJW 13«2 3C外幣中範懈的个疲不舗超过3忙•又内划与内掛中盥驚羅多不16亀it 3牛+优3屋过适当携合可以组戍以下网种不同理弑的囚边離*时角拔民井JH为K *72*2和2 帀4巽和”芈+4)正三用需、正四边厢I或正方幣)、正珀边幣、假定在樓合处一冀有*块正”边序地砖.由于正n边曙的所有肉希那相誓禺―初X180■羽°JTW 人・；^ = 2 +不±・S 故<-2|4t rt-2-U2,4 碍用=氛4 販6曲此可S1.只有三ff正参边形的瓷砖■可戲檢豪束傭地、暫正三曲幣、正方腦《1圧六边麻一(3>如1正方砸稍iEA边旌■覃圈如右「设在一牛IB点周屈有抽亍正方带的用f d正人边形的魁，犀幺，叭”扈是方程曲・M'4-n • 135*-360-的畫数11.即2m + 3ii-8的整敢歸.f m" 1 •「这牛方程的BftHRW“一胡・・=杆舍条件的ffiJBR有「种.I 片■-£9fS(D ffl中5块祈番部舟电拼虐一牛水五边彰BF-»AG-^H-E/-£K»DL-=DM-CN^<；O«flP=4ZBF/T « Z AGA'^ZCTX* - Z.BPH'匸£DMIY^^CNC■/£!<『■£ DLD* = “ HA r -ZEf^-90*A(ZA +ZB J+ ZC + Zi/■+*Zf/)+ <Zl + Z2 + Z3±Z4 + Z5) = 5X 180', lffJZA H+ ziB，+ZC/+Z£X+ZE'=(5-2)Xiao*-3X 180" A Zl+Z2 + Z3+Z4 + Z5-360D⑵爹边带増加的腾长等于A'H + A^ + B'F + B'P + ro+rt + DM+^L^^K+n.Xffllfr^ffl中阴童，但草构戍的五边矗的隔长"谨五边弼存在一个tS* i的最大囿•其周KS>MfllK#«.S>Bx>aX3J J4-25. 12>25.【学力训练】1.72.56 2- 360* J.设AD-<r.J|i| 7-(4+2)<j<7 + 4 + 2t得］Vi<13 4. (DlBi(2)4ff+2.窕ii |•边理外拒申3个角为惋盘"即内桶申星多碑3牛下是|ft命+褂M€3+2N5t. D 7. C»>■取儿為的中点Bt'ft為曲人為Si A, 4A* •因力AjBy-BtA^SfU ■釦,・片・又因为四边曲為冷儿& 与四边昭4民儿息的面积相积所以鬼屮幵=S A7入.同理艮内“丹-S^y 所以亀**九=3厶22，所以厶為乩儿与△凡九久的益其边A.A,上的髙相算俪联几凡"A.A”同理可证五边带.4//］儿起的邯条边分閘与一斎対角线平行.11* 7,540" 13+180*T(w —2) * IfiO*—n * 180*+(jf —2) * 180*=(w —4) * 180"IX (D3X (-^- J1=^ I(t)S+3X yS+ax 4 X ^S+31X4X ^S-M. 14向外补幣得正三祐坯IS. A 16. D HD作DE丄于E 17. D1乩假谡从四点中(fiS出的三点构赋的三竟幣的三牛内瀚AH大于45J当九BCD构成&四边形时*可碍各角和大于前丁・舟四<1 )108* *120", “一^小単*«. ttl图，可井和得BD“7冶皿・2拧». 75*11边誓内坤*1为閔3矛盾1肖4BCD 构虚凹四边梅时+可側各坤和大于18^,与三输带内角和为180D Jffi.1・ 设丈小正方序边悅分别为才寸.则"P = J + 76〉*，若(x.y) = J,记j- = dxi ・_/・曲必*5 ,y t )=1*则JIJ -? = (M + 76)^I解榕 (Ji + >i )<j| '->])«* 76j^ 3! X 19 X .20.取向延长AB.CD.EF.GH 暂呼边MNPQ,原人边形内谢祁相爭.英邯一牛內角为n 損阳.毎一个外爲为45".因此MNP Q 为快方形，△HPC\ADQE,AFMG* iANHfl 是等眾直命三肃惑.设GH=r.HA = y ・由MQ-NP,得MF+FE+EQ-M4 +AB+BP,即血+6 + 滲 =%十7 + 2応解得$ = 3亠庄•同理由MN^QP.m 工=3十2 72.^BEA 边带周怏为32+A21.由图2的第一舎图形得MO+CD 4 H AD 2.即W + + W = ①又由图2的第三和第0M 个图旳得AB+AD=CD+BC,即6+AD=lS+BC ②解由①、③联立的方程堀得BC-30,AD=39.tt BC\AD^»j^ 30和39时"才能賓现上述的折畏蜚代.12,因为凸十一边矗是由正三储舷和正方幣擠嵐的，所以.各内轴的大小只可能是60\90M2Q*,l50*.设这4牛角个敷分别为 J j ■十 _y+z+ u*・]13\$、*、越■剧 I,\60x+90>+ 120r+ l50ui= (11 -2) X 180化简冉3z 十2y+w ・l*正豐数解为x = ^=0,s=l.w-10,ii 说明.所求凸十一边形一个角毘120笃它由两牛正三您形 的内角拼琥•其余10个角都是150*,*由一牛iE 三m 矗的内帝和i 片正方形的内角携成.草用略.j-t = 10>! =94* J -324. (8-2) X 1B0'。
与多边形有关的竞赛题
（ 本讲 适合初 中）
边形 ， 以 ， 内角 和为 所 其
３ ４×（ ２— ）×１０ ＝３ ６ ６ ２ ８ 。 ４× ０×１０ ， ８。
近 年来 的初 中数 学竞 赛经 常涉及 与 多边 形 的角 度运算 、 长度运算 、 几何证 明 等知识 点
有 关 的题 目． 文列举 几 例 ， 过割 与补 的基 本 通 本 思路 ， 多 边形 转 化 为 三角 形 或 四 边形 予 将
再各 剪 ５ ８刀 得 ３ ４个 六 十 二 边 形 和 ３ ３×５ ８
个 三角形 ．
于是 ， 共剪 了
５ ３ ３ ８＋ ３＋ ３×５ ８＝２０ ５ 刀 ） ０ （ ．
（０６， 国初 中数 学竞 赛 ） ２０ 全
（ ２０ ４ Ａ） ０
（ ） ０ Ｃ ２０ ６
（ ２０ ５ Ｂ） ０
．大六角星形：ｓ ｓ ｜六个小六角星形 ＝２： ． ３
通 过割 与补将 问题转化 为 三角形 或 四边
形 的面积 ， 利用 面积 法 的技 巧 进行求 解 ．
例 ３ 如 图 ２， 个 大 的六 角 星 形 （ 实 一 粗
线） 的顶点 是周 围六个 全等 的 阴影 小 六 角 星
形 的中心 ， 相邻 的两 个 小 六 角 星形 各 有 一 个
＋
＝
＋ Ｃ＋／ Ｄ ＋ Ｅ＋／ Ｆ＋／ Ｇ
●
所 以 ， 六角 星形 的面 积是 大
＝
５ ４０。 ．
１ ２ｘ
×
学口
（） ３ 由题设 条 件知 ， 大六 角星形 的顶 点 Ａ 到其 中心 Ｏ 的距 离 为 ２ ． 此 ， 六 角 星 形 口因 大 的面积 是一个 小 六角 星形 的面积 的 ４倍 ． 则
初中数学竞赛公式及定理精简版
一般定理与公式1、多边形内角和定理n边形的内角的和等于（n-2）×180°2、推论任意多边的外角和等于360°3、等腰梯形性质定理等腰梯形在同一底上的两个角相等4、等腰梯形的两条对角线相等5、等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形6、梯形中位线定理梯形的中位线平行于两底，并且等于两底和的一半L=（a+b）÷2 S=L×h7、比例的基本性质如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d8、合比性质如果a／b=c／d,那么(a±b)／b=(c±d)／d9、等比性质如果a／b=c／d=…=m／n(b+d+…+n≠0),那么(a+c+…+m)／(b+d+…+n)=a10、任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值11、任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值12、相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等13、如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项14、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项15、从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等16、如果两个圆相切，那么切点一定在连心线上17、①两圆外离d＞R+r ②两圆外切d=R+r③两圆相交R-r＜d＜R+r(R＞r)④两圆内切d=R-r(R＞r) ⑤两圆内含d＜R-r(R＞r)18、相交两圆的连心线垂直平分两圆的公共弦19、定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形20、正三角形面积√3a／4 ，a表示边长21、弧长计算公式：L=nπR／18022、扇形面积公式：S扇形=nπR2／360=LR／223、内公切线长= d-(R-r) 外公切线长= d-(R+r)三角函数定理与公式两角和公式sin(A+B)=sin A·cos B+cos A·sin Bsin(A-B)=sin A·cos B-sin B·cos Acos(A+B)=cos A·cos B-sin A·sin Bcos(A-B)=cos A·cos B+sin A·sin Btan(A+B)=(tan A+tanB)/(1-tanAtanB) tan(A-B)=(tan A-tan B)/(1+tan A·tan B) cot(A+B)=(cotA·cotB-1)/(cot B+cot A) cot(A-B)=(cot A·cot B+1)/(cot B-cot A)倍角公式tan2A=2·tanA/(1-tan2A)cot 2A=(cot 2A-1)/2·cotAcos2a=cos2a-sin2a=2·cos2a-1=1-2·sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cos A)/2) cos(A/2)=-√((1+cos A)/2)tan(A/2)=√(((1-cosA)/(1+cos A)) tan(A/2)=-√((1-cosA)/(1+cosA))cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinA·cosB=sin(A+B)+sin(A-B) 2cosA·sinB=sin(A+B)-sin(A-B)2cosA·cosB=cos(A+B)-sin(A-B) -2sinA·sinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)·sin((A-B)/2) tanA+tanB=sin(A+B)/cosA·cosB tanA-tanB=sin(A-B)/cosA·cosBcot A+cot B·sin(A+B)/sinA·sinB -cot A+cot B·sin(A+B)/sinA·sinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3一些平面几何的著名定理1、勾股定理（毕达哥拉斯定理）2、射影定理（欧几里得定理）3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
北京市八年级数学下册 多边形及其角度计算专题讲解 (新版)北师大版
多边形及其角度计算专题讲解重难点易错点解析题一题面：题面：已知，一个凸多边形的每一个内角都是140°，那么这个多边形的边数是多少？内角和是多少？外角和是多少？每一个顶点出发有多少条对角线？共有多少条对角线？n边形：内角和=180°(n2)外角和=360°每一个顶点出发的对角线=n 3对角线总条数=()32n n-正多边形：边长相等、内角相等金题精讲题一题面：现有边长相同的正三角形、正方形和正六边形纸片若干张，下列拼法中不能镶嵌成一个平面图案的是（）A．正方形和正六边形B．正三角形和正方形C．正三角形和正六边形D．正三角形、正方形和正六边形镶嵌问题题二题面：下图是为某机器人编制的一段程序，如果机器人在平地上按图所示的步骤行走，那么该机器人所走的总路程为 m.多边形外角和题三题面：(1)一个多边形对角线的条数等于边数的5倍，则这个多边形的内角和是 .(2)一个多边形的每一个内角都等于150°，那么这个多边形的对角线数目是 .(3)过m边形的一个顶点有4条对角线，n边形没有对角线，p边形有p条对角线，则边数为(m+n p)的正多边形每一个内角的度数是 .根据公式，列方程解决问题题四题面：如图，在四边形ABCD 中，∠B =∠D =90°，AE 、CF 分别平分∠BAD 和∠BCD ，那么AE 和CF 的位置关系是什么？并说明.F ECA BD多边形内角和在几何题目中的综合应用思维拓展题一题面：在凸十边形的所有内角中，锐角的个数最多是 .内角问题转化为外角讲义参考答案重难点易错点解析题一答案：9 1260° 360° 6 27金题精讲题一答案： A题二答案：12题三答案：(1)1980° (2)54 (3)108°题四答案：AE∥CF思维拓展答案：3。
八年级数学竞赛例题专题讲解： 多边形的边与角
八年级数学竞赛例题专题讲解：多边形的边与角阅读与思考两个几何图形的全等是指两个图形之间的一种关系,其中最基本的关系是两个图形的点的对应关系,以及对应边之间、对应角之间的相等关系．全等三角形是研究三角形、四边形等图形性质的主要工具,是解决有关线段、角等问题的一个出发点,证明线段相等、线段和差相等、角相等、两直线位置关系等问题总要直接或间接用到全等三角形,我们把这种应用全等三角形来解决问题的方法称为全等三角形法．我们实际遇到的图形,两个全等三角形并不重合在一起,而是处于各种不同的位置,但其中一个是由另一个经过平移、翻折、旋转等变换而成的．了解全等变换的这几种形式,有助于发现全等三角形、确定对应元素．善于在复杂的图形中发现、分解、构造基本的全等三角形是解题的关键,应熟悉涉及有关会共边、公共角的以下两类基本图形：例题与求解【例1】考查下列命题：①全等三角形的对应边上的中线、高、角平分线对应相等；②两边和其中一边上的中线（或第三边上的中线）对应相等的两个三角形全等；③两角和其中一角的角平分线（或第三角的角平分线）对应相等的两个三角形全等；④两边和其中一边上的高（或第三边上高）对应相等的两个三角形全等．其中正确命题的个数有（）A．4个B．3个C．2个D．1个（山东省竞赛试题）解题思路：真命题给出证明,假命题举出一个反例．【例2】如图,已知BD 、CE 是△ABC 的高,点P 在BD 的延长线上,BP ＝AC ,点Q 在CE 上,CQ ＝AB ．求证：（1）AP ＝AQ ；（2）AP ⊥AQ ．（第十六届江苏省竞赛试题）解题思路：（1）证明对应的两个三角形全等；（2）证明∠P AQ ＝90°．【例3】如图,已知为AD 为△ABC 的中线,求证：AD ＜1()2AB AC ．（陕西省中考试题）解题思路：三角形三边关系定理是证明线段不等关系的基本工具,关键是设法将AB ,AC ,AD 集中到同一个三角形中,从构造2AD 入手．【例4】如图,已知AC ∥BD ,EA 、EB 分别平分∠CAB 、∠DBA ,CD 过点E ． 求证：AB ＝AC ＋BD ．（“希望杯”邀请赛试题）解题思路：本例是线段和差问题的证明,截长法（或补短法）是证明这类问题的基本方法,即在AB 上截取AF ,使AF ＝AC ,以下只要证明FB ＝BD 即可,于是将问题转化为证明两线段相等．QABC DEOPABCD【例5】如图1,CD 是经过∠BCA 顶点C 的一条直线,CA ＝CB ,E ,F 分别是直线CD 上两点,且∠BEC ＝∠CF A ＝∠α．（1）若直线CD 经过∠BCA 内部,且E ,F 在射线CD 上,请解决下面两个问题：①如图2,若∠BCA ＝90°,∠α＝90°,则BE ＿＿＿＿CF ,EF ＿＿＿＿BE AF -（填“＞”、“＜”或“＝”）；②如图3,若0°＜∠BCA ＜180°,请添加一个关于∠α与∠BCA 关系的条件＿＿＿＿,使①中的两个结论仍然成立,并证明这两个结论；（2）如图4,若直线CD 经过∠BCA 的外部,∠α＝∠BCA ,请提出EF ,BE 、AF 三条线段数量关系的合理猜想（不要求证明）．（台州市中考试题）解题思路：对于②,可用①进行逆推,寻找△BCE ≌△CAF 应满足的条件．对于（2）可用归纳类比方法提出猜想．BCDEFαα图1ABCDEF 图2 ABCE F图3D ABCDEF图4A BCDE【例6】如图,在四边形ABCD 中,∠ACB ＝∠BAD ＝105°,∠ABC ＝∠ADC ＝45°． 求证：CD ＝AB ．（天津市竞赛试题）解题思路：由已知易得∠CAB ＝30°,∠GAC ＝75°,∠DCA ＝60°,∠ACB ＋∠DAC ＝180°,由特殊度数可联想到特殊三角形、共线点等．能力训练A 级1．如图,在△ABC 中,∠C ＝90°,BC ＝40,AD 是∠BAC 的平分线交BC 于D ,且DC ︰DB ＝3︰5,则点D 到AB 的距离是＿＿＿＿．2．如图,在Rt △ABC 中,∠BAC ＝90°,AB ＝AC ,分别过B ,C 作经过点A 的直线的垂线BD ,CE ,若BD ＝3cm,CE ＝4cm,则DE ＝＿＿＿＿．3．如图,△ABE 和△ACF 分别是以△ABC 的边AB 、AC 为边的形外的等腰直角三角形,CE 和BF 相交于O,则∠EOB ＝＿＿＿＿．4．如图,四边形ABCD 中,对角线AC 与BD 相交于点E ,若AC 平分∠DAB ,且AB ＝AE ,AC ＝AD ．有如下四个结论：①AC ⊥BD ；②BC ＝DE ；③∠DBC ＝12∠DAB ；④△ABE 是等边三角形．请写出正确结论的序号＿＿＿＿．（把你认为正确结论的序号都填上）（天津市中考试题）ABCD 第1题AD E第2题ABCEFO第3题ABCDE第4题AB CD5．如图,点E 在△ABC 外部,点D 在BC 边上,DE 交AC 于F ,若∠1＝∠2＝∠3,AC ＝AE ,则（ ）A ．△ABD ≌△AFDB ．△AFE ≌△ADCC ．△AFE ≌△DFCD ．△ABC ≌△ADE6．如图,△ABC 中,∠C ＝90°,AC ＝BC ,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E ．若AB ＝6cm,则△DEB 的周长为（ ）A ．5cmB ．6cmC ．7cmD ．8cm7．如图,从下列四个条件：①BC ＝B 'C ；②AC ＝A ′C ；③∠A ′CA ＝∠B ′CB ；④AB ＝A ′B ′中,任取三个为题设,余下的一个为结论,则最多可以构成的正确命题的个数是（ ）A ．1个B ．2个C ．3个D ．4个（北京市东城区中考试题）8．如图1,在锐角△ABC 中,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 交于F ,且BF ＝AC ． （1）求证：ED 平分∠FEC ；（2）如图2,若△ABC 中,∠C 为钝角,其他条件不变,（1）中结论是否仍然成立？若不成立,请说明理由；若成立,请给予证明．9．在等腰Rt △AOB 和等腰Rt △DOC 中,∠AOB ＝∠DOC ＝90°,连AD ,M 为AD 中点,连OM ． （1）如图1,请写出OM 与BC 的关系,并说明理由；（2）将图1中的△COD 旋转至图2的位置,其他条件不变,（1）中结论是否成立？请说明理由．第5题ABCDE F 321ABCDE第6题ABCB 'A '第7题A BCDE F图1ABD EFC图210．如图,已知∠1＝∠2,EF ⊥AD 于P ,交BC 延长线于M ．求证：∠M ＝1()2ACB B ∠-∠． （天津市竞赛试题）11．如图,已知△ABC 中,∠A ＝60°,BE ,CD 分别平分∠ABC ,∠ACB ,P 为BE ,CD 的交点． 求证：BD ＋CE ＝BC ．12．如图,已知点D 为等腰直角△ABC 内一点,∠CAD ＝∠CBD ＝15°,E 为AD 延长线上的一点,且CE ＝CA ．ABCDM O图1ABCDM O图2A BC DE PABCDEF MP21（1）求证：DE 平分∠BDC ；（2）若点M 在DE 上,且DC ＝DM ,求证：ME ＝BD ．（日照市中考试题）B 级1．在△ABC 中,高AD 和BE 交于H 点,且BH ＝AC ,则∠ABC ＝＿＿＿＿．（武汉市竞赛试题）2．在△ABC 中,AD 为BC 边上的中线,若AB ＝5,AC ＝3,则AD 的取值范围是＿＿＿＿．（“希望杯”竞赛试题）3．如图,在△ABC 中,AB ＞AC ,AD 是角平分线,P 是AD 上任意一点,在AB -AC 与BP -PC 两式中,较大的一个是＿＿＿＿．4．如图,已知AB ∥CD ,AC ∥DB ,AD 与BC 交于O ,AE ⊥BC 于E ,DF ⊥BC 于F ,那么图中全等的三角形有（ ）A ．5对B ．6对C ．7对D ．8对5．如图,AD 是△ABC 的中线,E ,F 分别在AB ,AC 上,且DE ⊥DF ,则（ ） A ．BE ＋CF ＞EF B ．BE ＋CF ＝EFC ．BE ＋CF ＜EFD ．BE ＋CF 与的大小关系不确定（第十五届江苏省竞赛试题）6．如果两个三角形的两条边和其中一边上的高分别对应相等,那么这两个三角形的第三边所对的角（ ）A ．相等B ．不相等C ．互余D.互补或相等 （北京市竞赛试题）ABC 第2题DA BC PD第3题A BCD E FO 第4题第5题A BCDEF A7．如图,在△ABE 和△ACD 中,给出以下四个论断：①AB ＝AC ；②AD ＝AE ；③AM ＝AN ；④AD ⊥DC ,AE ⊥BE ．以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中,使之组成一个真命题,并写出证明过程．已知：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿． 求证：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿．（荆州市中考试题）8．如图,在四边形ABCD 中,AC 平分∠BAD ,过C 作CE ⊥AB 于E ,并且AE ＝1()2AB AD ,求∠ABC ＋∠ADC 的度数． （上海市竞赛试题）9．在四边形ABCD 中,已知AB ＝a ,AD ＝6,且BC ＝DC ,对角线AC 平分∠BAD ,问a 与b 的大小符合什么条件时,有∠B ＋∠D ＝180°,请画出图形并证明你的结论．（河北省竞赛试题）10．如图,在△ABC 中,∠ABC ＝60°,AD ,CE ：分别平分∠BAC ,∠ACB ．求证：AC ＝AE ＋CD ．（武汉市选拔赛试题）ABC DEM NABCDE11．如图,在Rt △ABC 中,∠B ＝90°,AP ,CQ 分别平分∠BAC ,∠BCA ．AP 交CQ 于I ,连PQ ． 求证：IAC ACPQS S ∆四边形为定值．12．在△ABC 中,∠ACB ＝90°,AC ＝BC ,直线MN 经过点C ,且AD 丄MN 于O ,BE ⊥MN 于E ．（1）当直线MN 绕点C 旋转到图1的位置时,求证：DE ＝AD ＋BE ； （2）当直线MN 绕点C 旋转到图2的位置时,求证：DE ＝AD -BE ；（3）当直线MN 绕点C 旋转到图3的位置时,试问：DE ,AD ,BE 有怎样的等量关系？请写出这个等量关系,并加以证明． （海口市中考试题）ABCDEMN图1CMN图3DEB CMN图2DEQAB CIPA BCDEO13．CD 是经过∠BCA 顶点C 的一条直线,CA ＝CB ,E ,F 分别是直线CD 上两点,且∠BEC ＝∠CF A ＝∠α．（1）若直线CD 经过∠BCA 内部,且E ,F 在射线CD 上,请解决下面两个问题：①如图1,若∠BCA ＝90°,∠α＝90°,则BE ＿＿＿＿CF ,EF ＿＿＿＿BE AF -（填“＞”、“＜”或“＝”）；②如图2,若0°＜∠BCA ＜180°,请添加一个关于∠α与∠BCA 关系的条件＿＿＿＿,使①中的两个结论仍然成立,并证明这两个结论；（2）如图3,若直线CD 经过∠BCA 的外部,∠α＝∠BCA ,请提出EF ,BE 、AF 三条线段数量关系的合理猜想（不要求证明）．（台州市中考试题）ABCDEF 图1ABCEF图2DABCDEF图3。
八年级数学竞赛专题训练14 多边形的边与角(附答案)
八年级数学竞赛专题训练14 多边形的边与角阅读与思考主要是指多边形的边、内外角、对角线、凸多边形、凹多边形等基本概念和多边形内角和定理、外角和定理，其中多边形内、外角和定理是解有关多边形问题的基础．多边形的许多性质与问题往往可以利用三角形来说明、解决，将多边形问题转化为三角形问题是解多边形问.题的基本策略，转化的方法是连对角线或向外补形．多边形的内角和是随着多边形的边数变化而变化的，但外角和却总是不变的，所以，我们常以外角和的“不变”来制约内角和的“变”，把内角问题转化为外角问题来处理，这是解多边形相关问题的常用技巧．例题与求解【例1】两个凸多边形，它们的边长之和为12，对角线的条数之和为19，那么这两个多边形的边数分别是＿＿＿＿和＿＿＿＿．（“希望杯”邀请赛试题）解题思路：设两个凸多边形分别有m，n条边，分别引出(3)2m m-，(3)2n n-条对角线，由此得m，n方程组．【例2】凸边形有且只有3个钝角，那么n的最大值是（）A．5 B．6 C．7 D．8解题思路：运用钝角、锐角概念，建立关于n的不等式，通过求解不等式逼近求解．【例3】凸n边形除去一个内角外，其余内角和为2570°，求n的值．（山东省竞赛试题）解题思路：利用n边形内角和公式，以及边数n为大于等于3的自然数这一要求，推出该角大小，进而求出n的值．【例4】如图，凸八边形ABCDEFGH 的八个内角都相等，边AB ，BC ，CD ，DE ，EF ，FG 的长分为7，4，2，5，6，2，求该八边形的周长． （全国通讯赛试题）解题思路：该八边形每一内角均为135°，每一外角为45°，可将八边形问题转化为特殊三角形解决、特殊四边形加以解决．【例5】如图所示，小华从M 点出发，沿直线前进10米后，向左转20°，再沿直线前进10米后，又向左转20°，…这样走下去，他第一次回到出发地M 时，行走了多少米？解题思路：试着将图形画完，你也许就知道答案了．能力训练A 级1．如图，凸四边形有＿＿＿个；∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝＿＿＿．（重庆市竞赛试题）2．如图，凸四边形ABCD 的四边AB ，BC ，CD 和DA 的长分别为3，4，12和13，∠ABC ＝90°，则A B CD E FG第1题ABCD第2题M A BD EF GH四边形ABCD 的面积为＿＿＿．3．如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝＿＿＿．4．如图，ABCD 是凸四边形，则x 的取值范围是＿＿＿．.5．一个凸多边形的每一内角都等于140°，那么，从这个多边形的一个顶点出发的对角线的条数是（ ）A ．9条B ．8条C ．7条D ．6条（“祖冲之杯”邀请赛试题）6．—个凸n 边形的内角和小于1999°，那么n 的最大值是（ ）（全国初中联赛试题）A ．11B ．12C ．13D ．147．如图，是一个正方形桌面，如果把桌面砍下一个角后，桌面还剩（ ）个角． A ．5个B ．5个或3个C ．5个或3个或4个D ．4个8．—个凸n 边形，除一个内角外，其余1n 个内角的和为2400°，则n 的值是（ ） A ．15B ．16C ．17D ．不能确定9．如图，在四边形ABCD 中，AB ＝AD ＝8，∠A ＝60°，∠D ＝150°，四边形周长为32，求BC 和DC 的长．10．—个凸n 边形的最小内角为95°，其他内角依次增加10°，求n 的值．（“希望杯”邀请赛试题）A BDE F G第3题AB CD24x第4题第7题AB CD11．平面上有A ，B ，C ，D 四点，其中任何三点都不在一直线上，求证：在△ABC ，△ABD ，△ACD ，△BDC 中至少有—个三角形的内角不超过45°．（江苏省竞赛试题）12．我们常见到如图那样图案的地面，它们分别是全用正方形或全用正六边形形状的材料铺成的，这样形状的材料能铺成平整的、无空隙的地面．问：（1）像上面那样铺地面，能否全用正五边形的材料，为什么？（2）你能不能另外想出一个用一种多边形（不一定是正多边形）的材料铺地的方案？把你想到的方案画成草图．（3）请你再画出一个用两种不同的正多边形材料铺地的草图．（安徽省中考试题）B 级1．一个正m 边形恰好被正n 边形围住（无重叠、无间隙，如图所示是m ＝4，n ＝8的情况），若m ＝10，则n ＝＿＿＿＿．2．如图，六边形ABCDEF 中，∠A ＝∠B ＝∠C ＝∠D ＝∠E ＝∠F ，且AB ＋BC ＝11，FA CD ＝3，则BC ＋DE ＝＿＿＿＿．（北京市竞赛试题）第1题A BCD EF 第2题1A 1B 2A 2B 3B 45B 3A 4A 5A 第3题3．如图，延长凸五边形A 1A 2A 3A 4A 5的各边相交得到五个角：∠B 1，∠B 2，∠B 3，∠B 4，∠B 5，它们的和等于＿＿＿．若延长凸n 边形（n ≥5）的各边相交，则得到的n 个角的和等于＿＿＿＿．（第十二届“希望杯”邀请赛试题）4．如图，在四边形ABCD 中，AB＝4，BC ＝1，CD ＝3，∠B ＝135°，∠C ＝90°，则∠D ＝（ ） A ．60°B ．67.5°C ．75°D ．不能确定（重庆市竞赛试题）5．如图，已知O 是四边形ABCD 内一点，OA ＝OB ＝OC ，∠ABC ＝∠ADC ＝70°，则∠DAO ＋∠DCO 的大小是（ ）A ．70°B ．110°C ．140°D ．150°6．在一个多边形中，除了两个内角外，其余内角之和为2002°，则这个多边形的边数为（ ） A ．12B ．12或13C ．14D ．14或15（江苏省竞赛试题）7．一个凸十一边形由若干个边长为1的正方形或正三角形无重叠、无间隙地拼成，求此凸十一边形各个内角大小，并画出这样的凸十一边形的草图．（全国通讯赛试题）8．一块地能被n 块相同的正方形地砖所覆盖，如果使用较小的相同正方形地砖，那么需n ＋76块这样的地砖才能覆盖该块地，已知n 及地砖的边长都是整数，求n 的值．（上海市竞赛试题）ABCD第4题OABCD第5题9．设有一个边长为1的正三角形，记作A 1如下左图，将A 1的每条边三等分，在中间的线段上各向形外作正三角形，去掉中间的线段后得到的图形记作A 2（如下中图）；将A 2的每条边三等分，并重复上述过程，所得到的图形记作A 3（如下右图）；再将A 3的每条边三等分，并重复上述过程，所得到的图形记作 A 4，求A 4的周长．（全国初中数学联赛试题）10．在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫作平面镶嵌），这显然与正多边形的内角大小有关，当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．（1）请根据下列图形，填写表中空格：（3）从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形．说明你的理由．（陕西省中考试题）1A 2A 3A专题14 多边形的边与角例1 5 7 例2 B例3 n ＝17 提示：设此角为x ，则（n －2）×180°＝x ＋2570°，得2570360180x n +︒+︒=︒，x ＝130°，此时n ＝17.例4 双向延长AB ，CD ，EF ，GH 得四边形MNPQ ，如图，原八边形的内角都相等，其每一内角均为(82)1801358-⨯︒=︒，每一外角均为45°，因此MNPQ 为长方形，△BPC ，△DQE ，△FMG ，△ANH都是等腰直角三角形.设GH ＝x ，HA ＝y ，由MQ ＝NP ，得MF ＋FE ＋EQ ＝NA ＋AB ＋BP ，∴5222672222y ++=++，∴32y =-. ∵MN ＝QP ，∴x ＝3＋22，∴周长＝7＋4＋2＋5＋6＋2＋3＋22＋3－2＝32＋2.例5 将整个图形画完，就知道是一个边长为10米的正多边形，且每个外角的大小都是20°，由多边形的外角和等于360°知这是一个18边形，所以小华第一次回到M 点时走的总路程是180米.A 级1. 7；540°2. 363. 540°4. 1＜x ＜135. D6. C7. C8.A9. BC ＝10，DC ＝6 10. n ＝611. 提示：分构成凸四边形和凹四边形两种情况讨论，并用反证法加以证明推出矛盾.12.(1)所用材料的形状不能是正五边形,因为,正五边形的每个内角都是108°,要铺成平整的,无空隙的地面, 必须使若干个正五边形拼成一个周角，但找不到符合条件的以n ×108°=360°的n 值,故不能用形状是正五边形的材料铺地面. ⑵⑶略. B 级1.52.143.180°;(n －4)180°4.B5.D 由OA=OB=OC 得∠BAO=∠ABO,∠BCO=∠OBC,所以∠DAO+∠DCO=360°－3×70°=150°6.D7.提示：因凸十一边形由正方形或正三角形拼成，故其内角的大小只能是60°,90°,120°,\ 150°四种可能,设这些角的个数分别为x,y,z,w,则11 6090120150(112)180x y z wx y z w+++=⎧⎨+++=-⨯⎩解得x=y=0,z=1,w=10.说明这个十一边形一个内角为120°,由两个正三角形的内角拼成，其余10个角均为150°,由一个正三角形内角与一个正方形内角拼成,图略.8.n=3249.649提示：从A1开始,每进行一次操作,所得到的图形的周长是原来图形周长的43倍.10.(1)108°;120°; ()02180nn-⨯(2)正三角形、正四边形(或正方形)正六边形.假定在接合处一共有k块正边形地砖，由于正n边形的所有内角都相等，则()02180360nkn-⨯=即24222nkn n==+--.因k为整数，故n－2|4，n—2=1，2，4，得n=3,4 或6，由此可见，只有三种正多边形的瓷砖，可以按要求铺地，即正三角形、正方形和正六边形.(3)如:正方形和正八边形，草图如下，设在一个顶点周围有m个正方形的角，n个正八边形的角，那么，m，n应是方程m·90°+n·135°=360°的整数解.即2m+3n=8的整数解.∵这个方程的整数解只有12mn=⎧⎨=⎩一组∴符合条件的图形只有一种.。
八年级数学几何图形第4讲 探求多边形边数及角度问题(学生版)
第4讲探求多边形边数及角度问题（原卷版）第一部分典例剖析+针对训练类型一剪去一个角问题典例1（2021秋•余干县月考）如图，将六边形纸片ABCDEF沿虚线剪去一个角（∠BCD）后，得到∠1+∠2+∠3+∠4+∠5＝460°．（1）求六边形ABCDEF的内角和；（2）求∠BGD的度数．典例2 （2021春•江都区期中）【课本引申】我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？【尝试探究】（1）如图1，∠DBC与∠ECB分别为△ABC的两个外角，试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系？为什么？【拓展运用】（2）如图2，在△ABC纸片中剪去△CED，得到四边形ABDE，若∠1+∠2＝230°，则剪掉的∠C＝；（3）小明联想到了曾经解决的一个问题：如图3，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有何数量关系？请直接写出答案．（4）如图4，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，∠P与∠A、∠D有何数量关系？为什么？（若需要利用上面的结论说明，可直接使用，不需说明理由）针对训练11．（2021秋•韶关期末）探索归纳：（1）如图1，已知△ABC为直角三角形，∠A＝90°，若沿图中虚线剪去∠A，则∠1+∠2＝．（2）如图2，已知△ABC中，∠A＝40°，剪去∠A后成四边形，则∠1+∠2＝．（3）如图2，根据（1）与（2）的求解过程，你归纳猜想∠1+∠2与∠A的关系是．（4）如图3，若没有剪掉∠A，而是把它折成如图3形状，试探究∠1+∠2与∠A的关系，并说明理由．2．（2020春•淮阳区期末）将一个凸n边形剪去一个角得到一个新的多边形，其内角和为1620°，求n的值．类型二多算、漏算、错算一个角问题典例3 （2022春•宝应县校级月考）小马虎同学在计算某个多边形的内角和时得到1840°，老师说他算错了，于是小马虎认真地检查了一遍（1）若他检查发现其中一个内角多算了一次，求这个多边形的边数是多少？（2）若他检查发现漏算了一个内角，求漏算的那个内角是多少度？这个多边形是几边形？典例4（2022•石家庄模拟）看图回答问题：（1）内角和为2014°，小明为什么说不可能？（2）小华求的是几边形的内角和？针对训练23．（2021秋•海阳市期末）小东在计算多边形的内角和时不小心多计算一个内角，得到的和为1350°，则这个多边形的边数是（）A．7B．8C．9D．104．（2021秋•通山县校级月考）某同学在计算多边形的内角和时，得到的答案是1125°，老师指出他少加了一个内角的度数，你知道这个同学计算的是几边形的内角和吗？他少加的那个内角的度数是多少？本号资料@皆@来源于微信公众号：数学#第六感第二部分专题提优训练1．（2022•河北）如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为α，β，则正确的是（）A．α﹣β＝0B．α﹣β＜0C．α﹣β＞0D．无法比较α与β的大小2．（2021秋•寻乌县期末）将一个四边形ABCD的纸片剪去一个三角形，则剩下图形的内角和为（）A．180°B．180°或360°C．360°或540°D．180°或360°或540°3．（2021秋•黄石期末）将一长方形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和之和不可能是（）A．360°B．540°C．720°D．730°4．（2021秋•通道县期中）如图，已知△ABC中，∠C＝90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）A．135°B．270°C．300°D．315°5．（2021春•兴化市期中）将一个五边形沿着某条直线剪开，得到两个新多边形，如果两个新多边形的内角和分别为α，β，那么α+β＝°．6．（2021秋•交城县期中）已知一个包装盒的底面是内角和为720°的多边形，它是由另一个多边形纸片剪掉一个角以后得到的，则原多边形是边形．本号资料*皆来源于微信公众号：数@*学第六感7．（2021春•常熟市期中）如图，四边形ABCD中，AD∥BC，∠C＝120°，若沿图中虚线剪去∠D，则∠1+∠2＝°．8．（2021春•嵩县期末）如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2340°。
初中数学竞赛 知识点和真题 第17讲 多边形的概念及内角和w
第17讲 多边形的概念知识方法扫描在同一平面内，由一些线段首尾顺次相接组成的图形叫做多边形。
如果延长多边形的任一条边，整个多边形都在这条延长边的一侧，那么这样的多边形就叫做凸多边形。
下面所说的多边形一般指凸多边形。
n 边形的内角和是（n-2）·180，任意多边形的外角和等于360°。
n 边形的两个不相邻的顶点的连线叫做n 边形的对角线，n 边形有21n(n-3)条对角线.经典例题解析例1（1986年北京市初中数学竞赛试题） 长为4的线段分成4小线段，以这四小线段为边可以作成一个四边形，则其中每一小段必须满足的条件是（A ）不大于1 （B ） 大于21或小于1 （C ） 小于2 （D ）大于21且小于1解 设x 为四小线段中的任意一段，则为4-x 其余三段之和， 由于两点之间，线段最短，有4-x>x ， 解得：x<2, 故应选C例2 （第13届“五羊杯”初中数学邀请赛试题）一个多边形一共有14条对角线，则它的内角和为________.解 一个n 边形，从一个顶点出发，有(n-3)条对角线，共有21n(n-3)条对角线(因为每条对角线被计算了两次)，于是有21n(n-3)=14，从而n(n-3)=28，因为 7×4=28， 故n=7.所以，这个三角形的内角和为 (7-2)·180°=900°.例3． （2001年山东省初中数学竞赛试题） 在凸n 边形中，小于108°的角最多可以有（ ）(A) 3个 (B) 4个 (C ) 5个 (D) 6个 解：设凸n 边形中，小于108°的角有x 个。
当多边形的一个内角小于108°时，它的外角大于72°，而任意多边形的外角和等于360°， 故有72x<360,解得 x<5, 故小于108°的角最多可以有4个。
故选B 。
评注 利用多边形外角和为360°的结论来解题，是处理与多边形有关的问题的常用的思路和方法。
八年级数学三角形考点专题训练(三)---多边形及其内角和
三角形第三部分：多边形及其内角和一、学习目标1．知道多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念．2．知道多边形的内角和与外角和定理；运用多边形内角和与外角和定理进行有关的计算．二、知识精讲知识点1：基本概念（1）在平面内，由一些线段相接组成的叫做多边形。
（2）多边形组成的角叫做多边形的内角。
（3）多边形的边与它的的邻边的组成的角叫做多边形的外角。
（4）连接多边形的两个顶点的线段叫做多边形的对角线。
（5）都相等，都相等的多边形叫做正多边形。
【例1】探究：画出下列多边形的对角线．回答问题：（1）从四边形的一个顶点出发可以画条对角线，把四边形分成了个三角形；四边形共有条对角线．（2）从五边形的一个顶点出发可以画条对角线，把五边形分成了个三角形；五边形共有条对角线．（3）从六边形的一个顶点出发可以画条对角线，把六边形分成了个三角形；六边形共有条对角线．（4）猜想：①从100 边形的一个顶点出发可以画条对角线，把100 边形分成了个三角形；100 边形共有条对角线．②从n边形的一个顶点出发可以画条对角线，把n分成了个三角形；n 边形共有条对角线．【题组训练】：1.从n边形的一个顶点出发可作条对角线，从n边形n个顶点出发可作条对角线，除去重复作的对角线，则n边形的对角线的总数为条．2.过m边形的一个顶点有7条对角线，n 边形没有对角线，k 边形有2条对角线，则（m-k）= ．3.过十边形的一个顶点可作出条对角线，把十边形分成了个三角形。
4.十二边形共有条对角线，过一个顶点可作条对角线，可把十二边形分成个三角形。
5.过n边形的一个顶点的所有对角线，把多边形分成8个三角形，则这个多边形的边数是。
6.一个多边形的对角线的条数等于它的边数的4倍，这个多边形的边数是。
7.下列图形中，是正多边形的是（）A.直角三角形B.等腰三角形C.长方形D.正方形8.九边形的对角线有（）A.25 条B.31 条C.27 条D.30 条知识点2：多边形的内角和与外角和n 边形的内角和= ;任意多边形的外角和都为 .【例1】探索规律：【例2】一个多边形的内角和为1980°，求多边形的边数。
第三节 多边形的边与角(含答案)...八年级数学 学而思
第三节 多边形的边与角1.多边形(1)多边形的概念：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形． (2)正多边形的概念：各个角都相等，各条边都相等的多边形叫做正多边形． 注：①多边形可分为凸多边形和凹多边形，②在没有特殊说明的情况下，我们所说的多边形是凸多边形．画出多边形的任何一条边所在的直线，整个图形都在这条直线的同一侧，这样的图形叫凸多边形，2. 多边形的对角线多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线． 3. 多边形内角与外角(1)多边形内角和定理：,3(180)2≥⋅-n n ο（且n 为整数）．(2)多边形的外角和等于.360ο注：①多边形的外角和指每个顶点处取一个外角，则n 边形取n 个外角，无论边数是几，其外角和永远为.360ο②借助内角和和邻补角概念共同推出以上结论：外角和为.360ο4.平面镶嵌 （密铺）平面图形镶嵌的定义：用形状，大小完全相同的一种或几种平面图形进行拼接．彼此之间不留空隙，不重叠地铺成一片，这就是平面图形的镶嵌， 注：正多边形镶嵌有三个条件限制：①边长相等；②顶点公共；③在一个顶点处各正多边形的内角之和为.360ο1.辨别凸多边形可用两种方法(1)画多边形任何一边所在的直线整个多边形都在此直线的同一侧． (2)每个内角的度数均小于,180ο通常所说的多边形指凸多边形 2.对多边形对角线条数公式2)3(n -n 的理解 n 边形的一个顶点不能与它本身及左右两个邻点相连成对角线，故可连出)3(-n 条．共有n 个顶点，应为n)3(-n 条，这样算出的数，正好多出了一倍，所以再除以2．利用以上公式，求对角线条数时，直接代入边数n 的值计算，而计算边数时，需利用方程思想， 解方程求，n3.判断一种或几种图形是否能够镶嵌只要看一看拼在同一顶点处的几个角能否构成周角，若能构成,360ο则说明能够进行平面镶嵌，反之则不能， 总结：①单一正多边形的镶嵌：正三角形，正四边形，正六边形．②两种正多边形的镶嵌：3个正三角形和2个正方形、四个正三角形和1个正六边形、2个正三角形和2个正六边形、1个正三角形和2个正十二边形、1个正方形和2个正八边形等． ③用任意的同一种三角形或四边形能镶嵌成一个平面图案．例1．把一个多边形纸片沿一条直线剪下一个三角形后，变成一个18边形，则原多边形纸片的边数不可能是( )16.A 17.B 18.C 19.D检测1．把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是( )A.六边形 B ．五边形 C ．四边形 D ．三角形例2．一个机器人从点0出发，每前进1米，就向右转体),1801(<<a a 照这样走下去，如果他恰好能回到O 点，且所走过的路程最短，则a 的值等于检测2．某科技小组制作了一个机器人，它能根据指令要求进行行走和旋转．某一指令规定：机器人先向前行走1米，然后左转,45ο若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了 米，例3．小张由于粗心，计算一个多边形的内角和少加了一个内角的度数，得到2009度，那么他少加的内角是检测3．（衡阳县校级期末）已知在一个n 边形中，)1(-n 个内角的和是,1290ο那么这个n 边形的另一个内角的度数是( )ο30.A ο90.B ο120.C ο150.D例4．（江苏吴中区校级期末）如果多边形的每个内角都比它相邻的外角的4倍多,30ο求这个多边形的内角和及对角线的总条数，检测4．（山东高密市期末）一个多边形，它的内角和比外角和的4倍多,180ο则这个多边形的边数及内角和度数分别为 例5．用三种边长相等的正多边形地砖铺地，其顶点拼在一起，刚好能完全铺满地面．已知正多边形的边数为,,,z y x则zy x 111++的值为( ) 1.A 32.B 21.C 31.D检测5．用正三角形和正六边形铺成一个平面，则在同一个顶点处，正三角形和正六边形的个数之比为( )1:4.A 1:1.B 4:1.C 1:11:4.或D第三节 多边形及其内角和(建议用时 35分钟)实战演练1．下列图中不是凸多边形的是( )2．下列图形中，是正多边形的是( )A 直角三角形B ．等腰三角形C ．长方形D ．正方形3．一名模型赛车手遥控一辆赛车．先前进1m ．然后原地逆时针方向旋转角)1800(οο<<αa 被称为一次操作．若五次操作后，发现赛车回到出发点，则角α为( )ο72.A o o B 44108.或 o C 144. ο4472.或oD4．下列关于多边形的说法不正确的是( )A.内角和与外角和相等的多边形是四边形 B 十边形的内角和为ο1440C 多边形的内角中最多有四个直角D 十边形共有40条对角线 5．下列正多边形的组合中，能够铺满地面的是( )A.正三角形和正五边形B.正六边形和正方形C.正八边形和正方形D.正五边形和正八边形 6．一个正多边形的周长是100，边长为10，则正多边形的边数=n 7．正六边形的每一个内角都等于 度．8．一个凸多边形的内角中，最多有 个锐角．9．如果一个多边形的内角与外角和的差是,1440ο那么这个多边形是 边形．10．将一个正六边形纸片对折，并完全重合，那么得到的图形是 边形．11.如图1-3-1所示，①中多边形（边数为12）是由正三角形“扩展”而来的，②中多边形是由正方形“扩展”而来的……依此类推，则由正n 边形“扩展”而来的多边形的边数为131--12．我们知道各边都相等，各角都相等的多边形是正多边形，小明却说各边都相等的多边形就是正多边形，各角都相等的多边形也是正多边形，他的说法对吗？如果不对，你能举反例（画出相应图形）说明吗？ 13.（山东历下期末）一个多边形的内角和比四边形的内角和多,720ο并且这个多边形的各内角都相等，这个多边形的每个内角是多少度．14．（河北中考）已知n 边形的内角和.180)2(ο⨯-=n θ(1)甲同学说，θ能取;360ο而乙同学说，θ也能取.630ο甲、乙的说法对吗？若对，求出边数n ．若不对，说明理由；(2)若n 边形变为)(x n +边形，发现内角和增加了,360ο用列方程的方法确定． 15.已知正n 边形的周长为60．边长为a ． (1)当3=n 时，请直接写出a 的值；(2)把正n 边形的周长与边数同时增加7后，假设得到的仍是正多边形，它的边数为,7+n 周长为67，边长为6．有人分别取n 等于,120,20,3再求出相应的以与6，然后断言：“无论”取任何大干2的正整数，a 与b 一定不相等，”你认为这种说法对吗？若不对，请求出不符合这一说法的n 的值．16.如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫作正多边形，如图1-3-2所示，就是一组正多边形，观察每个正多边形中/a 的变化情况，解答下列问题：231--(2)根据规律，是否存在一个正多边形，其中的?20ο=∠α若存在，请求出咒的值，若不存在，请说明理由． 17.在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形铺砌成美丽的图案，也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫作平面镶嵌）．这显然与正多边形的内角大小有关．当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角)360(ο时，就拼成了一个平面图形．331--(1)请根据图1-3-3所示，填写表中空格：(2)如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形；(3)正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由．18．如图1-3-4所示．(1)已知：如图①所示，在△ADC 中，CP DP ,分别平分ADC ∠和,ACD ∠试探究P ∠与A ∠的数量关系（直接写出结论）；(2)已知：如图②所示，在四边形ABCD 中，DP ，CP 分别平分ADC ∠和,BCD ∠试利用上述结论探究B A P ∠+∠∠与的数量关系（写出说理过程）；(3)若将(2)中的四边形ABCD 改为六边形ABCDEF （如图③），请直接写出+∠∠A P 与F E B ∠+∠+∠的数量关系：431--19.如图1-3-5所示，已知凸四边形ABCD 中，.90C oA =∠=∠(1)如图①，若DE 平分,ADC ∠BF 平分ABC ∠的邻补角，判断DE 与BF 位置关系并证明； (2)如图②，若BF ，DE 分别平分ADC ABC ∠∠,的邻补角，判断DE 与BF 位置关系并证明．531--拓展创新 20.看图回答问题：内角和为,2014ο小明为什么说不可能？ 拓展1．在20题的条件下，小华求的是几边形的内角和，拓展2．在20题的条件下，错把外角当内角的那个外角的度数你能求出来吗？它是多少度．极限挑战21.把一个多边形沿着几条直线剪开，分割成若干个多边形．分割后的多边形的边数总和比原多边形的边数多13条，内角和是原多边形内角和的1.3倍．求：原来的多边形是几边形？把原来的多边形分割成了多少个多边形．答案。
八年级数学上册：多边形的边与角
八年级数学上册：多边形的边与角知识导航1.多边形的边与角的关系；2.多边形中角度计算.【板块一】多边形的边角的关系方法技巧熟记n 边形内角和外角和以及正多边形边角的关系，直接运用公式计算.题型一求多边形边数【例1】若一个多边形的内角和是外角和的3倍，求这个多边形的边数.题型二求多边形对角线条数【例2】一个多边形的内角和为1800°，则这个多边形的对角线共有______条.题型三探究多边形边角变化规律【例3】一个多边形的边数每增加一条，这个多边形的()A.内角和增加180°B.外角和增加360°C.对角线增加一条D.内角和增加360°题型四正多边形内外角与边数关系【例4】如果一个正多边形的内角和等于外角和的2倍，求每一个内角的度数.针对练习11.如图，如果边长相等的正五边形和正方形的一边重合，则∠1的度数是_________.2.一个多边形截去一个角后，形成另一个多边形的内角和为2520°，求原多边形的边数.1【板块二】多边形中角度计算方法技巧1.直接运用公式计算；2.运用转化思想，整体思想，设参计算等解决多边形中角度问题.题型一正多边形组合求角【例5】有公共顶点A ，B 的正五边形和正六边形按如图所示位置摆放，连接AC 交正六边形于点D ，求∠ADE 的度数.ED C BA题型二多边形多角求和(转化思想＋整体思想)【例6】“转化思想”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题.(1)请你根据已经学过的知识求出下面星形图1中∠A ＋∠B ＋∠C ＋∠D ＋∠E 的度数；(2)若对图1中星形截去一个角，如图2，请你求出∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F 的度数；(3)若再对图2中的角进一步截去，你能由(1)(2)所得的方法或规律，猜想图3中的∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＋∠H ＋∠M ＋∠N 的度数吗?(只要写出结论，不需要写出解题过程)图1图2图3E A BCD 2211N M GF E D C B A F E DC B A题型3多边形与角平分线夹角【例7】(2018济宁)如图，在五边形ABCDE 中，∠A ＋∠B ＋∠E ＝300°，DP ，CP 分别平分∠EDC ，∠BCD ，求∠P 的度数.PEABC【例8】如图1，四边形ABCD 中，设∠A ＝α，∠D ＝β，∠P 为四边形ABCD 的内角∠ABC 与外角∠DCE 的平分线所在直线相交而形成的锐角.(1)如图1，若α＋β＞180°，求∠P 的度数(用含α，β的代数式表示)；(2)如图2，若α＋β＜180°，请在图2中画出∠P ，并直接写出∠P 的度数(用含α，β的代数式表示).图1图2A B C D EABC D E针对练习21.如图，以正六边形ADHGFE 的一边AD 为边向外作正方形ABCD ，求∠BED 的度数.AB C DEF G2.如图1所示，△ABO 与△CDO 称为“对顶三角形”，其中∠A ＋∠B ＝∠C ＋∠D.利用这个结论，在图2中，求∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G 的度数.图1图2ACD EF G O D CBA3.如图，P 是四边形ABCD 的外角∠EBC 与∠BCF 的平分线BP 和CP 的交点，设∠A ＋∠D ＝α.(1)求∠BPC 与α之间的数量关系；(2)根据α的值的情况，判断△BPC 的形状(按角分类).ABC D EFP4.动手操作，探究:探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系已知:如图1，在△ADC 中，DP ，CP 分别平分∠ADC 和ACD ，试探究∠P 与∠A 的数量关系并说明理由；探究二:若将△ADC 改为任意四边形ABCD 呢?已知:如图2，在四边形ABCD 中，DP ，CP 分别平分∠ADC 和∠BCD ，请你利用上述结论探究∠P 与∠A ＋∠B 的数量关系，并说明理由；探究三:若将上题中的四边形ABCD 改为六边形ABCDEF ，如图3所示，请你直接写出∠P 与∠A ＋∠B ＋∠E ＋∠F 的数量关系.图3图2P P P A B C DE F AB C 图1AC D。
专题__多边形的角与对角线[1]
![专题__多边形的角与对角线[1]](https://img.taocdn.com/s3/m/606ff6c26f1aff00bed51e93.png)
初中数学竞赛辅导专题讲座多边形的角与对角线1. ⑴n 边形的内角和是()02180n -⨯，外角和是0360(定值)。
⑵正n 边形的每个内角的度数都是()02180n n -⨯，每个外角的度数都是0360n。
⑶多边形的内角和一定能被0180整除, 且边数每增加一条,内角和就增加0180.2. 任意凸多边形的所有内(外)角中最多有3个角是锐(钝)角。
3. 过n 边形一个顶点有()3n -条对角线，这些对角线将三角形分成了()2n -个三角形，在n 边形中共有()32n n -条对角线。
4. 一般地，多边形能镶嵌平面需要满足两个条件：⑴拼接在同一个点的各个角的和恰好等于0360（周角）；⑵相邻的多边形有公共边。
例1（2003年“TRULY ®信利杯”全国初中数学竞赛试题）如图所示，∠A +∠B +∠C +∠D +∠E +∠F +∠G =（ ） (A)360° (B) 450°(C) 540° (D) 720°例2（1988年“辽教杯”上海市初中数学竞赛）一个凸n 边形中，除了一个内角外, 其余各内角的和为3290︒,则这个内角的度数是( ) (A)140° (B) 130° (C) 120° (D) 110°例3（1985年上海市初中数学竞赛）以三角形的三个顶点和它内部的7个点，共10 个点为顶点，能把原三角形分割成小三角形的个数是（ ） (A)11 (B) 15 (C) 19 (D) 不能确定例4（1988年上海市初三数学竞赛）（“希望杯”邀请赛培训题）若凸4n+2边形A 1A 2……A 4n+2(n 为自然数)的每个内角都是30°的整数倍，且∠A 1=∠A 2=∠A 3=90°，则n 的所有可能值是多少?例5 (1995年湖北省黄冈地区初中数学竞赛)⑴计算凸九边形所有对角线的条数,以及以凸十边形顶点为顶点的三角形的个数.⑵在凸九边形每个顶点处任意写一个自然数,在⑴中的三角形中,若三个顶点所标三数之和为奇数,则称该三角形为奇三角形; 若三数之和为偶数,则称为偶三角形.试证明: 奇三角形个数必为偶数.例6 (第七届日本数学奥林匹克竞赛试题)把一个多边形沿着几条直线剪开，分割成若干个多边形。
初二年级奥数多边形的内角和试题及答案
【导语】奥林匹克数学竞赛或数学奥林匹克竞赛，简称奥数。
奥数对青少年的脑⼒锻炼有着⼀定的作⽤，可以通过奥数对思维和逻辑进⾏锻炼，对学⽣起到的并不仅仅是数学⽅⾯的作⽤，通常⽐普通数学要深奥⼀些。
下⾯是⽆忧考为⼤家带来的初⼆年级奥数多边形的内⾓和试题及答案，欢迎⼤家阅读。
1 n边形的内⾓和等于_____. 1-1 五边形的内⾓和等于____. 2 多边形的外⾓和等于____. 2-1 ⼀个⼗边形的外⾓和等于____. 1.⼀个六边形的内⾓和等于( )A.180°B.360°C.540°D.720° 2.⼀个多边形的内⾓和是900°，这个多边形的边数是( )A.4B.5C.6D.7 3.四边形A BCD中，若∠A+∠C+∠D=280°，则∠B的度数为( ) A .80° B.90° C .170° D.20° 4.正六边形的每⼀个内⾓为 ____，每⼀个外⾓为____. 5.在四边形ABCD中，若∠A∶∠B∶∠C∶∠D=3∶1∶2∶3，则该四边形中的⾓的度数是____. 6.求如图所⽰的图形中x的值： 7.已知两个多边形的内⾓和为1 800°,且两多边形的边数之⽐为2∶5,求这两个多边形的边数. 知识点2 多边形的外⾓和 8.七边形外⾓和为( )A.180°B.360°C.900°D.1 260° 9.⼀个正多边形的每个外⾓都等于36°，那么它是( )A.正六边形B.正⼋边形C.正⼗边形D.正⼗⼆边形 10.不能作为正多边形的内⾓的度数的是( )A.120°B.108°C.144°D.145° 11.如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外⾓，则∠1+∠2+∠3等于( )A.90°B.180°C.210°D.270° 12.⼀个多边形的边数每增加1条,其内⾓和就增加____,其外⾓和____. 13.若⼀个多边形每个外⾓都等于它相邻的内⾓的12,求这个多边形的边数. 14.四边形的四个内⾓( )A.可以都是锐⾓B.可以都是钝⾓C.可以都是直⾓D.必须有两个锐⾓ 15.多边形的每个内⾓都等于150°，则从此多边形的⼀个顶点出发可作的对⾓线共有( )A.8条B.9条C.10条D.11条 16.如图，⼀个多边形纸⽚按图⽰的剪法剪去⼀个内⾓后，得到⼀个内⾓和为2 340°的新多边形，则原多边形的边数为( )A.13B.14 C .15 D.16 17.⼀个多边形的内⾓和⽐外⾓和的3倍多180°，则它的边数是____. 18.如图，正六边形ABCDEF，P是BC边上⼀动点，过P作PM∥AB交AF于M，作PN∥CD交DE于N.则∠MPN=____. 19.求下图中∠α的度数. 20.多边形的内⾓和与某⼀个外⾓的度数总和为1 350°，求多边形的边数. 21.四边形ABCD中，∠A=140°，∠D=80°. (1)如图1，若∠B=∠C，试求出∠C的度数； (2)如图2，若∠ABC的⾓平分线BE交DC于点E，且BE∥AD，试求出∠C的度数. 22.(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系； (2)如果我们把∠1、∠2称为四边形的外⾓,那么请你⽤⽂字描述上述的关系式; (3)⽤你发现的结论解决下列问题: 如图,AE、DE分别是四边形ABCD的外⾓∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数. 参考答案 1 (n-2)×180° 1-1 540° 2 360° 2-1 360°1.D2.D3.A4.120°60°5.120°6.(1)根据图形可知：x=360-150-90-70=50.(2)根据图形可知：x=180-[360-(90+73+82)]=65.(3)根据图形可知：x+x+30+60+x+x-10=540.解得x=115. 7.设两多边形的边数分别为2n和5n,则它们的内⾓和分别为(2n-2)×18 0°和(5n-2)×180°,则(2n-2)×180°+(5n-2)×180°=1 800°,解得n=2,2n=4,5n=10.答：这两个多边形分别为四边形和⼗边形. 8.B 9.C 10.D 11.B 12.180°不变 13.设这个多边形的每个外⾓为x°,则它相邻的每个内⾓为(2x)°,∴x+2x=180.解得x=60.360°÷60°=6.即这个多边形的边数为六边形. 14.C 15.B 16.B 17.9 18.60° 19.根据图中的数据可知：第⼀个图：α=360°-65°-70°-(180°-40°)=85°；第⼆个图：α=180°-(360°-90°-90°-40°)=40°. 20.设这个外⾓度数为x°，由题意，得(n-2)×180+x=1 350.解得x=1 710-180n.∵0＜x＜180，∴0＜1 710-180n＜180.解得8.5＜n＜9.5.⼜∵n为正整数，∴n=9.故多边形的边数是9. 21.(1)∵∠A+∠B+∠C+∠D=360°，∠B=∠C，∴∠C= ＝70°.(2)∵BE∥AD，∴∠BEC=∠D=80°，∠ABE=180°-∠A=180°-140°=40°.⼜∵BE平分∠ABC，∴∠EBC=∠ABE=40°.∴∠C=180°-∠EBC-∠BEC=60°. 22.(1)∵∠3、∠4、∠5、∠6是四边形的四个内⾓，∴∠3+∠4+∠5+∠6=360°.∴∠3+∠4=360°-(∠5+∠6).∵∠1+∠5=180°，∠2+∠6=180°，∴∠1+∠2=360°-(∠5+∠6).∴∠1+∠2=∠3+∠4.(2)四边形的任意两个外⾓的和等于与它们不相邻的两个内⾓的和.(3)∵∠B+∠C=240°，∴∠MDA+∠NAD=240°.∵AE、DE分别是∠NAD、∠MDA的平分线，∴∠ADE= ∠MDA，∠DAE= ∠NAD.∴∠ADE+∠DAE= (∠MDA+∠NAD)=120°.∴∠E=180°-(∠ADE+∠DAE)=60°.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
八年级数学竞赛例题专题讲解：多边形的边与角
阅读与思考
主要是指多边形的边、内外角、对角线、凸多边形、凹多边形等基本概念和多边形内角和定理、外角和定理,其中多边形内、外角和定理是解有关多边形问题的基础．
多边形的许多性质与问题往往可以利用三角形来说明、解决,将多边形问题转化为三角形问题是解多边形问.题的基本策略,转化的方法是连对角线或向外补形．
多边形的内角和是随着多边形的边数变化而变化的,但外角和却总是不变的,所以,我们常以外角和的“不变”来制约内角和的“变”,把内角问题转化为外角问题来处理,这是解多边形相关问题的常用技巧． 例题与求解
【例1】两个凸多边形,它们的边长之和为12,对角线的条数之和为19,那么这两个多边形的边数分别是＿＿＿＿和＿＿＿＿．
（“希望杯”邀请赛试题）
解题思路：设两个凸多边形分别有m ,n 条边,分别引出
(3)2
m m -,(3)2n n -条对角线,由此得
m ,n 方程组．
【例2】凸边形有且只有3个钝角,那么n 的最大值是（ ） A ．5
B ．6
C ．7
D ．8
解题思路：运用钝角、锐角概念,建立关于n 的不等式,通过求解不等式逼近求解．
【例3】凸n 边形除去一个内角外,其余内角和为2570°,求n 的值．
（山东省竞赛试题）
解题思路：利用n 边形内角和公式,以及边数n 为大于等于3的自然数这一要求,推出该角大小,进而求出n 的值．
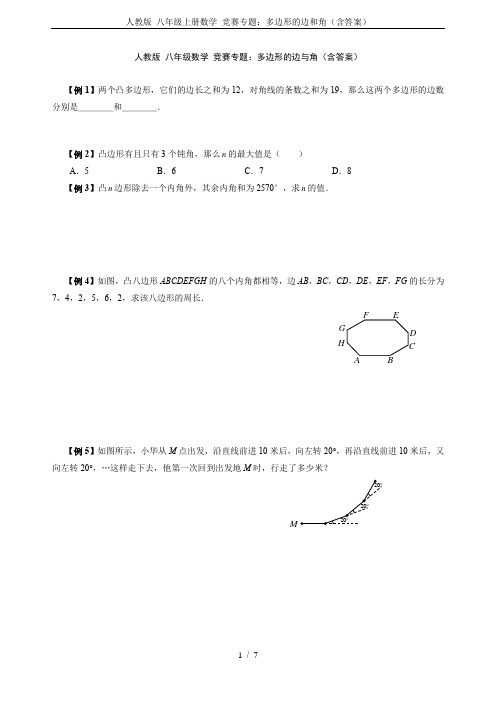
【例4】如图,凸八边形ABCDEFGH 的八个内角都相等,边AB ,BC ,CD ,DE ,EF ,FG 的长分为7,4,2,5,6,2,求该八边形的周长． （全国通讯赛试题）
解题思路：该八边形每一内角均为135°,每一外角为45°,可将八边形问题转化为特殊三角形解决、特殊四边形加以解决．
【例5】如图所示,小华从M 点出发,沿直线前进10米后,向左转20°,再沿直线前进10米后,又向左转20°,…这样走下去,他第一次回到出发地M 时,行走了多少米？
解题思路：试着将图形画完,你也许就知道答案了．
能力训练
A 级
1．如图,凸四边形有＿＿＿个；∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝＿＿＿．
C
D E
F G
H
M
（重庆市竞赛试题）
2．如图,凸四边形ABCD 的四边AB ,BC ,CD 和DA 的长分别为3,4,12和13,∠ABC ＝90°,则四边形ABCD 的面积为＿＿＿．
3．如图,∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝＿＿＿．
4．如图,ABCD 是凸四边形,则x 的取值范围是＿＿＿．.
5．一个凸多边形的每一内角都等于140°,那么,从这个多边形的一个顶点出发的对角线的条数是（ ）
A ．9条
B ．8条
C ．7条
D ．6条
（“祖冲之杯”邀请赛试题）
6．—个凸n 边形的内角和小于1999°,那么n 的最大值是（ ）
（全国初中联赛试题）
A ．11
B ．12
C ．13
D ．14
7．如图,是一个正方形桌面,如果把桌面砍下一个角后,桌面还剩（ ）个角． A ．5个
B ．5个或3个
C ．5个或3个或4个
D ．4个
8．—个凸n 边形,除一个内角外,其余1n 个内角的和为2400°,则n 的值是（ ） A ．15
B ．16
C ．17
D ．不能确定
9．如图,在四边形ABCD 中,AB ＝AD ＝8,∠A ＝60°,∠D ＝150°,四边形周长为32,求BC 和DC 的长．
A B C
D E F
G
第1题
A
B
C
D
第2题
A B
D
E
F G
第3题
A
B
C
D
24x
第4题
第7题
10．—个凸n 边形的最小内角为95°,其他内角依次增加10°,求n 的值．
（“希望杯”邀请赛试题）
11．平面上有A ,B ,C ,D 四点,其中任何三点都不在一直线上,求证：在△ABC ,△ABD ,△ACD ,△BDC 中至少有—个三角形的内角不超过45°．
（江苏省竞赛试题）
12．我们常见到如图那样图案的地面,它们分别是全用正方形或全用正六边形形状的材料铺成的,这样形状的材料能铺成平整的、无空隙的地面．问：
（1）像上面那样铺地面,能否全用正五边形的材料,为什么？
（2）你能不能另外想出一个用一种多边形（不一定是正多边形）的材料铺地的方案？把你想到的方案画成草图．
（3）请你再画出一个用两种不同的正多边形材料铺地的草图．
（安徽省中考试题）
A
B C
D
B 级
1．一个正m 边形恰好被正n 边形围住（无重叠、无间隙,如图所示是m ＝4,n ＝8的情况）,若m ＝10,则n ＝＿＿＿＿．
2．如图,六边形ABCDEF 中,∠A ＝∠B ＝∠C ＝∠D ＝∠E ＝∠F ,且AB ＋BC ＝11,F A -CD ＝3,则BC ＋DE ＝＿＿＿＿．
（北京市竞赛试题）
3．如图,延长凸五边形A 1A 2A 3A 4A 5的各边相交得到五个角：∠B 1,∠B 2,∠B 3,∠B 4,∠B 5,它们的和等于＿＿＿．若延长凸n 边形（n ≥5）的各边相交,则得到的n 个角的和等于＿＿＿＿．
（第十二届“希望杯”邀请赛试题）
4．如图,在四边形ABCD 中,AB
＝4BC ＝1,CD ＝3,∠B ＝135°,∠C ＝90°,则∠D ＝（ ） A ．60°
B ．67.5°
C ．75°
D ．不能确定
（重庆市竞赛试题）
5．如图,已知O 是四边形ABCD 内一点,OA ＝OB ＝OC ,∠ABC ＝∠ADC ＝70°,则∠DAO ＋∠DCO 的大小是（ ）
A ．70°
B ．110°
C ．140°
D ．150°
6．在一个多边形中,除了两个内角外,其余内角之和为2002°,则这个多边形的边数为（ ）
第1题
A B
C
D E
F 第2题
1A 1
B 2
A 2
B 3
B 4
5
B 3
A 4
A 5A 第3题
A
B
C
D
第4题
O
A
B
C
D
第5题
A．12 B．12或13 C．14 D．14或15
（江苏省竞赛试题）7．一个凸十一边形由若干个边长为1的正方形或正三角形无重叠、无间隙地拼成,求此凸十一边形各个内角大小,并画出这样的凸十一边形的草图．
（全国通讯赛试题）
8．一块地能被n块相同的正方形地砖所覆盖,如果使用较小的相同正方形地砖,那么需n＋76块这样的地砖才能覆盖该块地,已知n及地砖的边长都是整数,求n的值．
（上海市竞赛试题）
9．设有一个边长为1的正三角形,记作A1如下左图,将A1的每条边三等分,在中间的线段上各向形外作正三角形,去掉中间的线段后得到的图形记作A2（如下中图）；将A2的每条边三等分,并重复上述过程,所得到的图形记作A3（如下右图）；再将A3的每条边三等分,并重复上述过程,
所得到的图形记作A4,求A4的周长．
（全国初中数学联赛试题）
10．在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠（在几何里叫作平面镶嵌）,这显然与正多边形的内角大小有关,当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时,就拼成了一个平面图形．
（1）请根据下列图形,填写表中空格：
（3）从正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形．说明你的理由．
（陕西省中考试题）
1
A 2A 3
A。