10-4 惠更斯原理 波的衍射波的干涉
惠更斯原理可以用来解释波的衍射现象

惠更斯原理可以用来解释波的衍射现象什么是“波的衍射”?波的衍射是指在一定环境中,波的传播过程中,由于物体的形状、大小以及空间的设置而导致的波的反射和折射现象。
衍射的原理被英国物理学家威廉惠更斯(William Henry Fox Talbot)在19世纪提出,即“波的衍射现象可以用惠更斯原理来解释”。
惠更斯原理是一种物理原理,它认为波的传播过程中,由于空气的反射和折射,波的衍射现象会发生,这就是惠更斯原理的基本概念。
根据惠更斯原理,当一个可以发出的波被一个物体阻挡时,波会反射、折射和衍射这三种现象,这三种现象都是由波的波长、波的频率等特征决定的。
首先,当一个物体阻挡了发出的波,这个波会反射回去。
这就是折射现象,因为当发出的波穿过物体时,波的频率和波长会发生变化,从而使波发生变化,最终形成反射波。
其次,当发出的波穿过一个物体且与物体表面的角度相差不大时,波会发生折射现象,即波从一个介质向另一个介质的转折。
这是因为当波穿过物体时,波的方向会发生变化,由于介质的不同,波的频率会发生变化,从而导致波发生折射现象。
最后,当发出的波穿过物体或者是遇到两个物体时,波会发生衍射现象。
衍射是指在一定环境中,由于物体的形状、大小而导致的波的反射以及折射现象。
如果在一条两头封闭的弯管中放入一个波,这个波会在管道内形成一个圆环,从而产生衍射现象。
总的来说,惠更斯原理可以用来解释波的衍射,当发出的波在一定环境中穿越物体时,会发生反射、折射和衍射现象,这一切都是由波的波长、波的频率、物体的形状以及大小等特征决定的。
惠更斯原理通过描述波在物体和介质之间的传播过程,使人们理解了波的衍射现象,可以说,这一原理对物理学的发展具有重要性。
随着科技发展,对惠更斯原理的了解也越来越深入。
如今,物理学家们不仅可以用此原理来解释波的衍射现象,而且还可以用它来探究很多其他物理现象,比如微粒衍射、波的干涉和共振等,从而有助于我们更深入地理解物理学。
惠更斯原理、衍射现象讲解

对此类现象进行大量的总结后,荷兰物理学家惠更斯在1679年指出,介质中传播的 波传播到各个点时,每个点都可以看成是发射子波的波源,所有子波形成的包络面 就是新的波前,这就是惠更斯原理;不管是机械波还是电磁波,惠更斯原理都是适 用的;
图2所示的平面波中,根据惠更斯原理,波面S1上的各个点都可以看作是新的波源, 所有波源的包络面S2就是新的波前,当然S1与S2之间的距离就要由波长决定。
比如人在室内时能够听到室外的声音,就是声波绕过门、窗或者缝继续传播的现象。 生活中不只是机械波才存在衍射现象,电磁波 也会存在衍射现象,衍射现象是波动的一个特征之一。
下一章《大型交响乐队演奏中的物理学原理,波的干涉现象》讲解波的干涉现象。
当波在向前传播时,难免会遇到障碍物,于是把波遇到障碍物时,绕过障碍物边缘 继续向前传播的现象叫做衍射;解释衍射现象最好的理论就是惠更斯原理,
图3所示的三幅图中,小孔的尺寸分别是1/10λ、λ、10λ,可以看出小孔的尺寸越 小,小孔处子波的包络面越接近于圆形,也就是说进入图中阴影部分的波前越多, 绕过障碍物传播的现象越明显,当小孔的直径很大时,大部分的波前保持原来的方 向,只有很小一部分波前进入阴影部分。
《从惠更斯原理看,我们知道了波在介质中传播时,实际上就是每个质 点重复上一个质点的运动状态,于是介质中的每个质点都可以看作是一个新的波源, 因为它包含了起始波源的所有信息,
比如图1所示的水面波在传播时,当小孔的大小和波长差不多时,其他位置的质点 在振动时被障碍物挡住,不能继续向前传播,而处于小孔位置的质点就可以以自身 为波源,带动周围的质点继续振动,于是就出现了圆形波。
惠更斯原理与波的衍射

非相干叠加.swf
例 如图所示, A、B两点为同一介质的两相干波源,其
振幅皆为A=5 cm, 频率皆为100 Hz, 但当点A为波峰时,
点B适为波谷。设波速为10 m/s, (A、B两波源的振动垂
直于平面),试写出由A、B发出的两列波传到P点时干涉
的结果。
图示两列振动方向相同得同方向传播得波动得叠加:
同频率不同振幅的两个波的叠加
频率比为2:1的两个等幅波的叠加
一个高频波和一个低频波的叠加
频率相近的两列等幅波的叠加
叠加原理在物理上得重要性还在于可将一列复杂得 波分解为简谐波得组合。
二、波得干涉
干涉现象就是波动形式所独具得重要特征之 讨一论。两列频率相同,振动方向相同,相位相同或相位 差恒定得简谐波得叠加———一种最简单也就是最重 要得波得叠加情况。这两列波叠加后得图像稳定,不 随时间而变化。
Q
解:(1)取坐标如图所示,由题知:= 2 m
两波在S 1 左侧得任一点P得相位差:
P
2
1
2
r2
r1
2 20.5 21
2
2
Ⅰ区处处干涉相消
Ⅰ
Ⅱ
Ⅲ
S1
S2
x
P 0R
Q
两波在S 2 右侧得任一点Q得相位差:
Q
2
1
2
r2
r1
2
2
20.5 2
20
Ⅱ区处处干涉加强
Q
2 [
2
(20.5 x)
o
Hale Waihona Puke xu驻波有一定得波形,此波形不移动,各点以各自确定得 振幅在各自得平衡位置附近振动,没有振动状态或相位得 传播、因此驻波就是一种特殊得振动状态,不就是波,她 不具备波得特性。
波的衍射和干涉(含多个演示动画)课件

衍射类型 衍射公式
干涉动画
干涉现象
展示两列波相遇时产生干涉的现 象,说明干涉是波的叠加产生加
强或减弱的现象。
干涉类型
介绍不同类型的干涉,如驻波和 行波干涉,并解释它们在实验中
的应用。
干涉公式
介绍干涉的定量公式,如波动方 程和干涉相长公式,并解释其在
理论分析中的作用。
综合演示动画
综合演示 实验分析 应用实例
CATALOGUE
结论与总结
结论
衍射是波绕过障碍物继续传播 的现象,是波特有的性质。
干涉是两列频率相同的波相互 叠加,形成稳定的强弱分布的 现象。
衍射和干涉是波动性质的重要 表现,在生产和生活实际中有 广泛的应用。
总结
本课件介绍了波的衍射和干涉的 基本概念、产生条件、现象和应
用。
通过动画演示和实验视频,帮助 学生深入理解衍射和干涉的原理
当两列或多列波相遇时,它们相互叠 加形成干涉现象。
反射
当波遇到较大的障碍物时,波会被反 射回来,形成反射现象。
CATALOGUE
波的干涉
干涉现象
干涉现象定义 干涉现象的实例 干涉现象的特点
干涉原理
干涉原理概述
1
干涉原理的数学描述
2
干涉原理的应用
3
干涉分 类
CATALOGUE
演示动画
衍射动画
CATALOGUE
实验操作
衍射实验
准备实验器材
包括光源、狭缝、屏幕等。
操作步骤
调整光源和狭缝的位置,观察衍射现象,记录实验数据。
数据分析
分析衍射图像,计算衍射角、衍射强度等参数,并与理论值进行 比较。
干涉实验
准备实验器材
波的衍射和干涉

λ
s1 s2
y1 r 1
y2
*
P
r2
λ r2 y2 P = A2 cos(ωt + ϕ2 − 2 π ) λ y p = y p1 + y p 2 ?
y p = y p1 + y p 2
7
λ r2 y2P = A2 cos( t +ϕ2 −2π ) = A2 cos( t +ϕ2p ) ω ω λ yP = y1P + y2 P = A cos(ωt + ϕ ) p16
(λ ,ν , T , A)
3
1 波的叠加原理 (线 叠加原理) 叠加原理) 波的叠加性:在相遇区, 波的叠加性:在相遇区,任一质点的振动为 合成。 二波单独在该点引起的振动的合成 (线性叠加) 二波单独在该点引起的振动的合成。 线性叠加)
强振动,非线性介质中传播不成立。 强振动,非线性介质中传播不成立。
ϕ1 = ϕ 2
(k = 0,1,2,3...)
(2) δ = r2 − r = ±kλ ) 1
Amax = A + A2 1
δ = r2 − r1 = ±(2k +1)
λ
2
Amin = A − A2 1
15
11
例 如图所示,A、B 两点为同一介质中两相 如图所示, 、 干波源.其振幅皆为5cm,频率皆为 干波源.其振幅皆为 ,频率皆为100Hz, , 为波峰时, 恰为波谷.设波速 但当点 A 为波峰时,点B 恰为波谷 设波速 1 试写出由A、 发出的两列波 发出的两列波传到 为 10m ⋅ s −,试写出由 、B发出的两列波传到 时干涉的结果. 点P 时干涉的结果
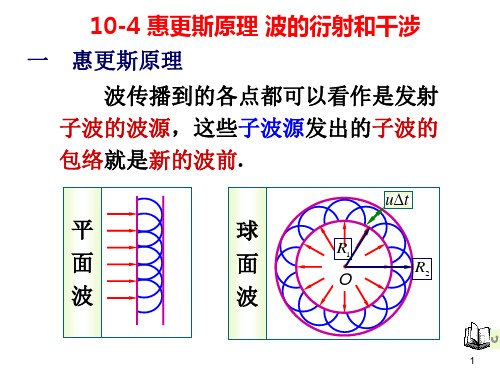
1010-4 惠更斯原理 波的衍射和干涉 一 惠更斯原理 波传播到的各点都可以看作是发射 子波的波源,这些子波源发出的子波的 子波源发出的 子波的波源,这些子波源发出的子波的 包络就是新的波前. 就是新的波前 包络就是新的波前 平 面 波 球 面 波
惠更斯原理与干涉

y y1 y2
A cos(t )
S2 ●
其中 A A12 A22 2 A1 A2 cos[( 20 10 ) 2 ( r2 r1 )]
合振动振幅
2、干涉现象的强度分布规律
y y1 y2 A cos(t )
合振动振幅 A
波阵面
. r . . . .. S.. . .. S
1
. . .. .
Δr ut t t
● ●
t
2
●
2. 应用 :
惠更斯原理对任何波动过程都是适用的 不论是机械波还是电磁波,只要知道某一 时刻的波阵面,由这一原理用作图方法就可以 确定任一时刻的波阵面,从而较直观地解决了 波的的传播问题。 用惠更斯原理,用作图法能简捷地说明波在传播 过程中发生的衍射、散射、反射和折射等现象。
波阵面
t 时刻波阵面上各点均可 看成是发射子波的点波源
●
惠更斯原理解决 波的传播问题
波的传 播方向
ut
以 t 时刻的波阵面上各点为中心、以 u⊿t 为半径, 画出许多球形子波,这些子波在波线方向的包迹就 是 t+⊿t 时刻的新的波阵面。 根据:波的传播方向 波阵面 波的传播方向
●
ut
t+⊿t 时刻
A A12 A22 2 A1 A2 cos
相干项
I I 1 I 2 2 I 1 I 2 cos
r1
S1 ●
P
●
2 ( 20 10 ) ( r2 r1 ) S ● ( 对给定的两波源,20 10 )是一定的, 因此, 取决于波程差 r2 r1
三、用惠更斯原理解释波的反射和折射现象 波动从一种介质传到另一种介质时,在两种 介质的分界面上,传播方向要发生变化,产生反 射和折射现象。 大量实验表明: 机械波和光波遵循反射定律和折射定律 下面由惠更斯原理用作图法 求出波的传播方向,并证明折射定律。 1、波的反射(Reflection) (自学)
球面波平面波.
(k 0,1,2,3,)
11
例 如图所示,A、B 两点为同一介质中两相 干波源.其振幅皆为5cm,频率皆为100Hz, 但当点 A 为波峰时,点B 恰为波谷.设波速 为10ms,1 试写出由A、B发出的两列波传到 点P 时干涉的结果.
P
A B π u /
15m
rA Ap rB BP
缝宽比波长大的多,衍射不明显
缝宽与波长差不多,衍射比较明显
缝宽小于波长,衍射更明显 2
三 波的干涉
1 波的叠加原理 波在相遇区域,任一质点的振动为二
波单独在该点引起的振动的合成.
叠加性:在相遇区合振动为分振动的合成
独立性: 相遇时直接合成,分开后传 播情况与未相遇时相同,互不干扰.
比 粒子相遇 碰撞,各自运动状态改变 较 波相遇 相遇区域合成,然后保持各自特征继续传播
s1
(1) 2k 1π Amin A1 A2 s2
k 0,1,2,3...
1 2
(2) r2 r1 k Amax A1 A2
r2
r1
(2k
1)
2
Amin A1 A2
r1 *P r2
15
9
位相差
2
1
2π
r2 r1
如果2 1即相干波源S1、S2同位相
s1
则
2π
r2
r1
2π
s2
r1 *P r2
r2 r1 称为波程差(波走过的路程之差)
2π
物理原理波的干涉与衍射

物理原理波的干涉与衍射物理原理:波的干涉与衍射一、引言波动理论是物理学中重要的研究领域,涉及各种波的行为和性质。
其中,波的干涉和衍射是波动理论中的两个重要现象。
本文将着重介绍波的干涉和衍射的基本原理及其应用。
二、波的干涉1. 干涉现象的定义干涉是指两个或多个波在特定条件下相遇时发生相互作用的现象。
干涉的结果取决于波的干涉相位差。
2. 干涉的分类干涉分为等厚干涉和等倾干涉两种类型。
等厚干涉是指波通过等厚介质产生的干涉现象,如牛顿环。
等倾干涉是指波通过等倾介质产生的干涉现象,如双缝干涉。
3. 干涉的原理干涉原理基于波的叠加原理,即波的合成等于各个波的矢量和。
干涉现象的出现是因为波的相位差引起的干涉条件改变。
4. 干涉的应用(1)干涉仪:干涉仪是利用波的干涉现象测量光的性质和物体的参数的仪器。
常见的干涉仪有迈克尔逊干涉仪和杨氏双缝干涉仪。
(2)涂膜技术:干涉技术可以应用于薄膜的制备和检测,用于提高光学元件的性能。
(3)干涉图案:干涉现象产生的干涉图案可以用于制作光栅、干涉滤波器等。
三、波的衍射1. 衍射现象的定义衍射是指波通过障碍物边缘或在有限孔径中传播时,波的传播方向和波前面发生弯曲和变形的现象。
2. 衍射的原理衍射原理基于海耶-菲涅尔原理,即波传播时,每个波前上的每个点都可以看作是波源,它们产生的次波相互叠加形成新的波前。
3. 衍射的特点(1)衍射现象的出现与波的波长和传播环境有关,有利于波的传播方向的弯曲。
(2)衍射现象在光学中明显,但也存在于其他波动现象中,如声波和水波。
4. 衍射的应用(1)光学衍射:衍射可以用于测量光的波长、制备光栅、研究光学仪器的分辨率等。
(2)声学衍射:衍射可以用于声学测量、超声波成像、喇叭和扩音器的设计等。
(3)电磁波衍射:衍射在天线设计、射频识别技术等方面有重要应用。
四、干涉与衍射的区别干涉和衍射是波的两种重要现象,它们之间存在一些区别:(1)干涉是在波的传播方向上相交的两个或多个波相互作用,衍射是波通过障碍物边缘或有限孔径时发生的波的弯曲与变形。
参考资料用惠更斯原理解释波的衍射现象

参考资料●用惠更斯原理解释波的衍射现象
从波源发出的波经过同一传播时间到达的各点所组成的面,叫做波面〔或波
前〕.荷兰物理学家惠更斯经过长期研究,于1690年提出了一条关于波的传播
的重要原理,叫做惠更斯原理,这一原理是:波面上的各点可以看做是新的波源,叫做子波源.从这些子波源发出的子波所形成的包面〔或包迹〕,就是下一时刻的新的波面.
用惠更斯原理很容易说明水波通过障碍物的缝时的衍射现象.如图5-41所示,设波阵面为直线形的水波,到达障碍物的缝时,缝上各点成为新的子波源.以这些子波源为中心作半径为vt〔v为波速〕的半圆面,再作与半圆面相切的包面,这个包面就是波通过缝后在时刻t的波面.从图中可以看出,直线形水波通过缝
后,除与缝的宽度相等局部的波面仍为直线外,在缝的边缘处,波面的相当大的一局部发生了弯曲,传播到了障碍物的后面,这就是衍射现象.
当缝的大小〔或障碍物的大小〕跟波长相差不多时就发生明显的衍射现象.如果缝很宽,其宽度远大于波长,那么波通过缝后根本上是沿直线传播的,衍射现象就很不明显了.
用惠更斯原理虽然能定性地解释衍射现象,但不能对衍射现象作出定量的分析.19世纪初法国物理学家菲涅耳补充了惠更斯原理,他认为任一时刻的波面并不是简单地由子波的包迹形成的,而是它们互相干预的结果.经过这样补充的惠更斯-菲涅耳原理,能够确切地解释波的衍射现象.。
惠更斯原理(波的反射和折射)

一.惠更斯原理
引言:
波在各向同性的均匀介质中传播时,波速、波 振面形状、波的传播方向等均保持不变。但是,如 果波在传播过程中遇到障碍物或传到不同介质的界 面时,则波速、波振面形状、以及波的传播方向等 都要发生变化,产生反射、折射、衍射、散射等现 象。在这种情况下,要通过求解波动方程来预言波 的行为就比较复杂了。惠更斯原理提供了一种定性 的几何作图方法,在很广泛的范围内解决了波的传 播方向等问题。
2015-6-19
三、用惠更斯原理解释波的反射现象
入射波的波面
入射波的波线
反射波的波线
反射波的波面
波的反射定律: 当波传到两种介质交界面发生反射时
(1)入射线、法线、反射线在同一平面内;
(2)入射线与反射线分居法线两侧; (3)反射角等于入射角; (4)反射波的波长、频率、波速与入射波相同。
即时应用
甲、乙两人平行站在一堵墙前面,两人相距 2a, 距离墙均为 3a,当甲开了一枪后,乙在时间 t 后 听到第一声枪响,则乙听到第二声枪响的时间为 ( C ) A.听不到 B.甲开枪 3t 后 3+ 7 C.甲开枪 2t 后 D.甲开枪 t后 2
2015-6-19
三、用惠更斯原理解释波的折射现象
1. 折射现象
:
波在传播过程中,从一种介质进入另一种 介质时,波的传播方向发生偏折的现象。
2. 发生折射的原因: 不同介质中波的传播速度不同。
i A i
C
入射波的波面
r
折射波的波面
B
r
D
3. 折射定律:
(1)入射线、法线、折射线在同 一平面内; (2)入射线与折射线分居法线两 侧; (3)入射角正弦与折射角正弦之比等于波在第一种介质中传
用惠更斯原理解释波的传播规律

用惠更斯原理解释波的传播规律
根据惠更斯原理,波在传播过程中通过衍射和干涉现象展现出特定的传播规律。
惠更
斯原理是由法国物理学家惠更斯在18世纪提出的。
惠更斯原理认为,波在传播过程中会扩展成以波前为起点的大量次级波。
这些次级波
会沿着最短路径传播,即光在传播过程中会沿直线传播。
这样波就可以沿着传播路径传送
能量。
当波前遇到一个障碍物时,波会弯曲沿着边缘传播。
这种现象称为衍射。
衍射使得波
能够围绕障碍物传播,从而达到空间中其他区域。
在波的传播过程中,当两个或多个波相交时,它们会相互干涉。
根据干涉现象的性质,有可能会加强或削弱波的振幅,形成波纹或波峰的叠加。
惠更斯原理可以解释光的传播,特别是光的衍射和干涉。
它提供了一种理论基础,以
解释波如何在空间中展开,并影响光在传播过程中的行为。
利用惠更斯原理可以解释波的传播规律,包括直线传播、衍射和干涉现象。
这个原理
为我们理解波的传播提供了重要的理论基础。
惠更斯原理 波的反射、折射及衍射

对于光波:
u1 u2
c c
u2 u1
n2 n1
B
i
i
A i D
C u1 u2
sin i
sin
n2 n1
(
折射率:n
c u
)
·7 ·
Chapter 14. 波的传播与叠加 §14. 4 惠更斯原理 波的反射、折射及衍射
四、透镜的折射
空气中薄透镜的焦距:
f
1 n1
F
R2 R1 R1R2
f
·8 ·
Chapter 14. 波的传播与叠加 §14. 4 惠更斯原理 波的反射、折射及衍射
一、惠更斯原理
1. 媒质中波动各点皆可当作球面子波的新波源; 2. 任意时刻各子波源所发出子波的包迹即为新波阵面。
惠更斯(Christiaan Huygens,1629~1695)荷
兰物理学家、天文学家、数学家、他是 介于伽利略与牛顿之间一位重要的物理 学先驱。他最早取得成果的是数学,他 研究过包络线、二次曲线、曲线求长法, 他发现悬链线《摆线》与抛物线的区别, 他是概率论的创始人。
·4 ·
Chapter 14. 波的传播与叠加 §14. 4 惠更斯原理 波的反射、折射及衍射
二、波的衍射现象
当障碍物的宽度 >> 波长时, 衍射现象不明显。当障碍物 的宽度 ~波长时,衍射现象 较明显。
·5 ·
Chapter 14. 波的传播与叠加 §14. 4 惠更斯原理 波的反射、折射及衍射
Chapter 14. 波的传播与叠加 §14. 4 惠更斯原理 波的反射、折射及衍射
§14.4 惠更斯原理
波的反射、折射及衍射
·1 ·
Chapter 14. 波的传播与叠加 §14. 4 惠更斯原理 波的反射、折射及衍射
波的衍射现象及其特点分析

波的衍射现象及其特点分析波的衍射是一种波动现象,它描述了当波通过障碍物或开口时,波的传播方向会发生偏折、扩散和干涉等现象。
波的衍射是波动光学中的重要概念,不仅在科学研究中有广泛应用,也在日常生活中频繁出现。
本文将对波的衍射现象及其特点进行分析。
一、波的衍射现象衍射现象最早被荷兰科学家惠更斯研究并提出衍射原理。
当波遇到一个障碍物或经过一个开口时,波会朝着障碍物或开口的周围扩散,形成新的波前。
这种扩散导致波在物体后方形成衍射图样,即波的干涉和掠过障碍物的波绕射。
这种波的传播方式与直线传播相比,具有更广泛的倾斜角度和更大的扩散带宽。
波的衍射可分为几种主要类型:边缘衍射、孔衍射和屏障衍射。
边缘衍射发生在波通过边缘或障碍物的细小孔隙时,例如当光通过尺寸与波长相当的狭缝时,会出现明暗相间的衍射条纹。
孔衍射指的是波通过较大开口时,例如光通过一个小孔,会产生出射光的圆形扩散图案。
屏障衍射发生在波通过一个具有一定宽度的障碍物时,例如水波通过一个挡板时,会产生波前扩散和干涉的现象。
二、波的衍射特点1. 衍射角度与波长的关系。
根据惠更斯原理,波的衍射角度与波长成反比关系。
衍射角度越大,波长越短,波的扩散现象越显著。
这意味着不同波长的波在通过障碍物或开口时会发生不同程度的偏折和扩散。
2. 衍射带宽与波的宽度关系。
衍射带宽代表在波传播过程中,波的干涉和扩散所覆盖的范围。
衍射带宽与波的宽度成正比关系,波的宽度越大,衍射带宽越宽。
这意味着波在传播过程中会更加扩散,导致衍射图样的清晰度下降。
3. 衍射图样的特征。
不同类型的波通过障碍物或开口时,产生的衍射图样也具有不同的特征。
例如,边缘衍射的图样通常呈现出明暗相间的条纹,孔衍射的图样呈现出圆形扩散,屏障衍射的图样则是在屏障周围形成波前扩散的效果。
4. 波的衍射与干涉的关系。
波的衍射和波的干涉是密不可分的。
在波通过一个障碍物或开口时,波前扩散会导致干涉现象,即不同波的叠加和形成干涉条纹。
惠更斯原理 波的衍射、反射和折射

t x 驻波方程 y = 2 A cos 2π cos 2π A合 = 2 A cos 2π λ T λ 2.波节与波腹
﹙1﹚波节: 当2π ﹚波节: .波节位置 波节位置 0.
x
x = (2k +1)
= (2k + 1) 时 A合=0 -- 波节 λ 2
x
π
λ
t
波节
4
(k = 0,±1,±2L)
x
∆ϕ = ϕ2 − ϕ1 −
2π
干涉静止: 干涉静止:A合
= A2 − A = 0 ∆ϕ = (2k +1)π 1 ∴ x = 2k + 15(m ) ( k = 0 , ± 1, ± 2 L ± 7 )
即
λ 2π = π − [(30 − x) − x] = π − π [15 − x] = ( x − 14 )π 4
t 时刻波面 t+∆t时刻波面
波传播方向
t+ ∆t
t
u∆ t 平面波
球面波
二、波的衍射
波在传播过程中, 波在传播过程中, 遇到障碍物时 其传播方向发生改变, 其传播方向发生改变, 绕过障碍物 波的衍射. 波的衍射 的边缘继续传播 ---波的衍射. 利用惠更斯原理可解释衍射: 利用惠更斯原理可解释衍射: 波到达狭缝处, 波到达狭缝处, 缝上各点都可看作 得到新的 作子波源, 作子波源, 作出子波包络, 作出子波包络, 在缝的边缘, 在缝的边缘, 波的传播方向 波面。 波面。 发生改变。 发生改变。 当狭缝缩小,与波长相近时, 当狭缝缩小,与波长相近时, 衍射效果显著。 衍射效果显著。 衍射现象是波动特征之一。 衍射现象是波动特征之一。
加 强 减 弱
x
x
惠更斯原理解释波的衍射

惠更斯原理解释波的衍射
惠更斯原理是一种波动理论,它假定光波是由相互独立的粒子所组成的,当粒子通过介质时,粒子会受到介质中粒子的相互作用,从而使光波发生方向改变。
根据惠更斯原理,当光线从一种介质传播到另一种介质时,光线方向发生改变的原因是,光线在不同介质中的粒子相互作用不同,从而导致光线的传播方向发生改变。
惠更斯原理可以解释许多光学现象,如折射、反射、干涉和衍射等。
在反射过程中,惠更斯原理假定光线的反射是由于入射光线和反射光线在界面处发生相互作用,从而导致光线的方向发生改变。
在折射过程中,惠更斯原理假定光线从一种介质传播到另一种介质时,光线的方向发生改变是由于光线在不同介质中的粒子相互作用不同。
惠更斯原理还可以解释光的双折射现象。
光的双折射是指光线通过某些介质时,会发生两个相互垂直的折射光线。
惠更斯原理认为,这是由于介质的折射率随着光线的方向不同而发生变化,从而导致光线在通过介质时发生两个相互垂直的折射。
虽然惠更斯原理是一种有效的光学理论,但是它也有一些限制和注意事项。
首先,惠更斯原理假定光波是由相互独立的粒子所组成的,这个假定并不总是成立的。
其次,惠更斯原理不能解释光的所有现象,如光电效应和康普顿效应等。
此外,惠更斯原理也不能解释一些量子光学现象,如自发辐射和受激发射等。
总之,惠更斯原理是解释反射折射现象的一个重要原理,它假定光波是由相互独立的粒子所组成的,当光线从一种介质传播到另一种
介质时,光线的方向发生改变是由于光线在不同介质中的粒子相互作用不同。
虽然惠更斯原理不能解释所有的光学现象,但是它仍然是一个非常有用的光学理论,在许多光学现象的解释中都有广泛的应用。
惠更斯原理知识要点归纳

惠更斯原理知识要点归纳1.惠更斯原理的提出-惠更斯原理是由法国科学家惠更斯在17世纪末提出的,他认为光的传播是沿着波前传播的。
-波前是指在其中一时刻上,波动现象的波面所构成的空间形状,可理解为光波前沿。
2.波前的传播-根据惠更斯原理,光波的传播是沿着波前进行的,每个波前上的每一点都是次波的波源。
-这意味着波在传播过程中,每个波前上的每个波源都会向各个方向发射次波。
3.次波的传播-次波是指波的振动模式,它在波源附近的传播是球面波,也就是说次波沿着波源周围的球面向外传播。
-波源附近的球面波传播到远离波源很远的地方时,可以看作是平面波。
4.波的衍射-根据惠更斯原理,波在经过一个障碍物的时候会发生衍射现象。
这是因为每个波前上的每个波源都会向障碍物后方发射次波。
-这些次波在障碍物后方重新叠加形成新的波前,这种现象就是波的衍射。
5.波的折射-当波由一种介质传播到另一种介质时,会发生波的折射现象。
根据惠更斯原理,波通过介质界面上的每个点时,都会发射次波。
-这些次波在另一种介质中传播并重新叠加,形成新的波前。
折射的角度取决于两种介质的光密度比。
6.杨氏实验-杨氏实验是惠更斯原理的重要实验证据。
实验中,光通过一个狭缝后,形成衍射图案。
-这说明光波在通过狭缝时,会发生衍射现象,波前上的每个波源都会发射次波。
7.波的干涉-根据惠更斯原理,波在两个波面相交时会发生干涉现象。
在干涉现象中,两个波面上的每个波源都会向各个方向发射次波。
-这些次波在相交区域内重新叠加形成新的波前,干涉现象的结果可以是加强或者抵消。
8.波的衍射和干涉的应用-波的衍射和干涉是光的特性,也是光学研究和应用中的重要现象。
-在光学仪器中,可以利用波的衍射和干涉原理来进行测量、成像和分析等应用。
总结:惠更斯原理是关于光波传播的重要原理,它强调了波面上的每个点都是波源,波的传播是波阵面的传播,通过波的次波的叠加来形成新的波阵面。
根据惠更斯原理,可以解释波的衍射和干涉现象,这些现象在光学研究和应用中起着重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12-4 惠更斯原理波的衍射和干涉
1、了解惠更斯原理和波的叠加原理;
2、理解波的相干条件,能应用相位差和波程差分析、确定相干波叠加后振幅加强
和减弱的条件。
重点:惠更斯原理,波的干涉;
难点:相干波叠加后振幅强弱条件的分析
课堂讲授(MCAI教学)
1个学时
一、波的几何描述
波线:沿波的传播方向画的带箭头的线叫波线。
波面:振动相位相同的点组成的曲面。
波前(波阵面):波源最初振动状态传到的点连成的面曲。
在各向同性媒质中,波线与波面垂直。
二、惠更斯原理
1、原理:
媒质中波传到的各点,都可看作开始发射子波的子波源
(点波源)。
在以后的任一时刻,这些子波面的包络面就是
实际的波在该时刻的波前。
2、应用:
t时刻波面→ t+∆t时刻波面→波的传播方向能
正确解释波的衍射、波的反射、波的折射等。
三、波的衍射
1、现象
波传播过程中当遇到障碍物时,能绕过障碍物的边
缘而传播的现象。
2、作图
可用惠更斯原理作图
四、波的叠加原理
1、波传播的独立性:
媒质中同时有几列波时,每列波都将保持自己原有的特性(传播方向、振动方向、频率等),不受其它波的影响。
2、叠加原理:
在几列波相遇而互相交叠的区域中,某点的振动是各列波单独传播时在该点引起的振动的矢量和。
叠加原理是一个重要的物理规律满足叠加原理的物理系统为线性系统。
3、波动方程的线性决定了波服从叠加原理
(1) 波的强度过大→非线性波→叠加原理不成立
(2) 光波在媒质中传播时
弱光:媒质可看作线性媒质。
强光:媒质非线性,波的叠加原理不成立。
五、波的干涉
1、干涉现象
波叠加时在空间出现稳定的振动加强和减弱的分布
2、相干条件
(1) 频率相同
(2) 有恒定的相位差
(3) 振动方向相同
3、波场的强度分布
(1) 波场中任一点的合振动
设S 1、S 2为相干波源,它们在同一均匀媒质中传播,在P 点相遇。
振动方向垂直纸面
S 1 :y 10 = A 1cos(ω t+ϕ 1)
S 2 :y 20 = A 2cos(ω t +ϕ 2)
p 点两分振动
y 1 = A 1cos(ω t +ϕ 1 - kr 1)
y 2 = A 2cos(ω t +ϕ 2 - kr 2) 相位差:2πλ=k
∆ϕ = (ϕ 2 - ϕ 1) - k (r 2-r 1)
p 点合振动12cos()ωϕ=+=+y y y A t
合振动的初相
111222111222sin()sin()tg cos()cos()
ϕϕϕϕϕ-+-=-+-A kr A kr A kr A kr 合振幅
A = (A 12+A 22 +2A 1A 2cos ∆ϕ )1/2
强度12ϕ=++∆I I I
( I ∝A 2 )
(2) 加强、减弱条件
加强条件(相长干涉)
∆ϕ = ( ϕ 2-ϕ 1) - k (r 2-r 1) =±2m π (m =0,1,2,…)
合振幅最大A = A 1+A 2
max 12=++I I I
若 A 1 = A 2 , 则I max = 4 I 1
减弱条件(相干相消)
∆ϕ = (ϕ 2-ϕ 1) - k (r 2-r 1) = ±(2m+1)π (m =0,1,2,…)
合振幅最小A = | A 1 - A 2
|
min 12=+-I I I
若 A 1 = A 2 ,则 I min = 0
一般情况
| A 1 - A 2| < A < (A 1+A 2)
(3)加强减弱条件的另一种表述
设φ2 =φ1 ,取δ= r 2-r 1 为波程差
212()π
ϕδλ∆=-=k r r
加强条件 δ = r 2-r 1 = ± m λ m = 0,1,2,…
减弱条件
δ = r 2-r 1 = ±(2m+1)λ/2 m = 0,1,2,…
[例题1] 如图所示,A 、B 两点为处于同一媒质中,且相距20m 的两个波源,它们作同频率,同方向的振动。
设它们激起的平面简谐波振幅相同,波速均为200m/s ,频率为100Hz ,且A 点出现波峰时,B 点出现波谷。
求A 、B 连线上因干涉而静止的各点的位置。
解:已知u =200m/s ,ν=100Hz 以A 为坐标原点 cos(2)πν=AO y A t
则B 点振源的振动为cos(2)πνπ=+BO y A t
A 点激发右行波
cos 2()πνλ
=-A x y A t B 点激发左行波
cos 2πνπλ⎡⎤⎛⎫=++ ⎪⎢⎥⎝
⎭⎣⎦B x y A t 原点从B 移至A 点
20cos 2πνπλ⎡-⎤⎛⎫=-+ ⎪⎢⎥⎝
⎭⎣⎦A x y A t 在C 点相遇而静止(合振幅为零
) 2m λν=
=u
2022(21)ϕπνππνπλλ⎡-⎤⎛⎫⎛⎫∴∆=-+--=±+ ⎪ ⎪⎢⎥⎝
⎭⎝⎭⎣⎦x x t t m 2(20)2(21)ππππλλ
--++=±+x x m 即:2x = ±mλ+ 20
当 λ= 2时,x = 10 ± m m = 0, 1, 2,… 即x = 0,1,2,…,19,20米处为静止。
