AMC8 2006年
AMC8(美国数学邀请赛)

AMC8(美国数学邀请赛)AMC8(美国数学邀请赛)AMC8(American Mathematics Competition8)AMC8是美国初中数学竞赛,是针对八年级以下学生的数学科测试,有些小学四~六年级的优秀学生也可以参加,该竞赛开始于1985年,于每年11月中旬的一个星期二举行。
AMC8竞赛内容与美国7、8年级数学大纲相对应,包括(但不局限于)整数、分数、小数、百分数、比例、数论、日常的几何、面积、体积、概率及统计、逻辑推理等。
美国数学协会(MAA)组织AMC8竞赛的目的是通过这样一种对学生有吸引力的考试,增加学生在数学方面的兴趣及学习数学的热情,促进学生学习中学数学必修课程之外的数学内容,增强问题解决的能力,该考试给参加者提供了应用初中所学概念处理由易到难,并包含广泛应用的问题的机会,以使他们得到在初中数学课堂中所不能得到的解决问题的经验,获得高分的部分学生将受邀参加美国高中数学竞赛AMC10。
题数︰25题时间︰40分钟题型︰选择题满分︰25分成绩处理︰AMC总部计分方式︰答对一题一分,答错不倒扣美国数学竞赛amc8的常用数学英语单词美国数学竞赛amc8的常用数学英语单词数学mathematics, maths(BrE), math(AmE)被除数dividend除数divisor 商quotient 等于equals, is equal to, is equivalent to 大于is greater than小于is lesser than大于等于is equal or greater than小于等于is equal or lesser than运算符operator数字digit数number自然数natural number公理axiom定理theorem计算calculation运算operation证明prove假设hypothesis, hypotheses(pl.)命题proposition算术arithmetic加plus(prep.), add(v.), addition(n.)被加数augend, summand加数addend和sum减minus(prep.), subtract(v.), subtraction(n.)被减数minuend减数subtrahend差remainder乘times(prep.), multiply(v.), multiplication(n.)被乘数multiplicand, faciend乘数multiplicator积product除divided by(prep.), divide(v.), division(n.)整数integer小数decimal小数点decimal point分数fraction分子numerator分母denominator比ratio正positive负negative零null, zero, nought, nil十进制decimal system二进制binary system十六进制hexadecimal system权weight, significance进位carry截尾truncation四舍五入round下舍入round down上舍入round up有效数字significant digit无效数字insignificant digit代数algebra公式formula, formulae(pl.)单项式monomial多项式polynomial, multinomial系数coefficient未知数unknown, x-factor, y-factor, z-factor 等式,方程式equation一次方程simple equation二次方程quadratic equation三次方程cubic equation四次方程quartic equation不等式inequation阶乘factorial对数logarithm指数,幂exponent乘方power二次方,平方square三次方,立方cube四次方the power of four, the fourth power n次方the power of n, the nth power开方evolution, extraction二次方根,平方根square root三次方根,立方根cube root四次方根the root of four, the fourth root n次方根the root of n, the nth root集合aggregate元素element空集void子集subset交集intersection并集union补集complement映射mapping函数function定义域domain, field of definition值域range常量constant变量variable单调性monotonicity奇偶性parity周期性periodicity图象image数列,级数series微积分calculus微分differential导数derivative极限limit无穷大infinite(a.)infinity(n.)无穷小infinitesimal积分integral定积分definite integral不定积分indefinite integral有理数rational number无理数irrational number实数real number虚数imaginary number复数complex number矩阵matrix行列式determinant几何geometry点point线line面plane体solid线段segment射线radial平行parallel相交intersect角angle角度degree弧度radian锐角acute angle直角right angle钝角obtuse angle平角straight angle周角perigon底base边side高height三角形triangle锐角三角形acute triangle直角三角形right triangle直角边leg斜边hypotenuse勾股定理Pythagorean theorem钝角三角形obtuse triangle不等边三角形scalene triangle等腰三角形isosceles triangle等边三角形equilateral triangle四边形quadrilateral平行四边形parallelogram矩形rectangle长length宽width菱形rhomb, rhombus, rhombi(pl.), diamond 正方形square 梯形trapezoid直角梯形right trapezoid等腰梯形isosceles trapezoid五边形pentagon六边形hexagon七边形heptagon八边形octagon九边形enneagon十边形decagon十一边形hendecagon十二边形dodecagon多边形polygon正多边形equilateral polygon圆circle圆心centre(BrE), center(AmE)半径radius 直径diameter圆周率pi弧arc半圆semicircle扇形sector环ring椭圆ellipse圆周circumference周长perimeter面积area轨迹locus, loca(pl.)相似similar全等congruent四面体tetrahedron五面体pentahedron六面体hexahedron平行六面体parallelepiped立方体cube七面体heptahedron八面体octahedron九面体enneahedron十面体decahedron十一面体hendecahedron 十二面体dodecahedron 二十面体icosahedron多面体polyhedron棱锥pyramid棱柱prism棱台frustum of a prism 旋转rotation轴axis圆锥cone圆柱cylinder圆台frustum of a cone球sphere半球hemisphere底面undersurface表面积surface area体积volume空间space坐标系coordinates坐标轴x-axis, y-axis, z-axis 横坐标x-coordinate纵坐标y-coordinate原点origin双曲线hyperbola抛物线parabola三角trigonometry正弦sine余弦cosine正切tangent余切cotangent正割secant余割cosecant反正弦arc sine反余弦arc cosine反正切arc tangent反余切arc cotangent反正割arc secant反余割arc cosecant相位phase周期period振幅amplitude内心incentre(BrE), incenter(AmE)外心excentre(BrE), excenter(AmE)旁心escentre(BrE), escenter(AmE)垂心orthocentre(BrE), orthocenter(AmE)重心barycentre(BrE), barycenter(AmE)内切圆inscribed circle 外切圆circumcircle统计statistics平均数average加权平均数weighted average方差variance标准差root-mean-square deviation, standard deviation 比例propotion百分比percent百分点percentage百分位数percentile排列permutation组合combination概率,或然率probability分布distribution正态分布normal distribution非正态分布abnormal distribution 图表graph条形统计图bar graph柱形统计图histogram折线统计图broken line graph曲线统计图curve diagram扇形统计图pie diagram。
美国数学竞赛AMC8 -- 2010年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 -- 2010年真题解析(英文解析+中文解析)Problem 1Answer: CSolution:Given that these are the only math teachers at Euclid Middle School and we are told how many from each class are taking the AMC 8, we simply add the three numbers to find the total.11+8+9=28.中文解析:参加竞赛的学生总人数是:11+8+9=28. 答案是C。
Problem 2Answer: DSolution:Substitute a=5, b=10 into the expression for a@b to get: 5@10=(5*10)/(5+10)=50/15=10/3.中文解析:(5*10)/(5+10)=50/15=10/3. 答案是D。
Problem 3Answer: CSolution:The highest price was in Month 1, which was $17. The lowest price was in Month 3, which was $10. 17 is 17/10 =170% of 10, and is 170-100=70% more than 10. Therefore, the answer is 70. 中文解析:最高价是1月,17美元。
最低价格是3月10美元。
最高价比最低价多:(17-10)/10=70%。
答案是C。
Problem 4Answer: CSolution:Putting the numbers in numerical order we get the list 0,0,1,2,3,3,3,4 The mode is 3, The median is (2+3)/2=2.5. The average is 2. is The sum of all three is 3+2.5+2=7.5.中文解析:这组数按照从小到大的顺序排列是:0,0,1,2,3,3,3,4. 中位数Median是2.5;mode 是3,mean是16/8=2. 因此mean,median,mode的和是: 2.5+3+2=7.5. 答案是C。
2006AMC试题 B

AMC 10 2006 B1 What is (−1)1+ (−1)2+ · · · + (−1)2006?(A) − 2006 (B) − 1 (C) 0 (D) 1 (E) 20062 For real numbers x and y, define x⊕y = (x + y)(x − y). What is 3⊕(4⊕5)?(A) − 72 (B) − 27 (C) − 24 (D) 24 (E) 723 A football game was played between two teams, the Cougars and the Panthers. The two teams scored a total of 34 points, and the Cougars won by a margin of 14 points. How many points did the Panthers score?(A) 10 (B) 14 (C) 17 (D) 20 (E) 244 Circles of diameter 1 inch and 3 inches have the same center. The smaller circle is painted red, and the portion outside the smaller circle and inside the larger circle is painted blue. What is the ratio of the blue-painted area to the red-painted area?(A) 2 (B) 3 (C) 6 (D) 8 (E) 95 A 2 x 3 rectangle and a 3 x 4 rectangle are contained within a square without overlapping at any interior point, and the sides of the square are parallel to the sides of the two given rectangles. What is the smallest possible area of the square?(A) 16 (B) 25 (C) 36 (D) 49 (E) 646 A region is bounded by semicircular arcs constructed on the side of a square whose sides measure 2/π, as shown. What is the perimeter of this region?(A)4/π(B) 2 (C)8/π(D) 4 (E)16/π7 Which of the following is equivalent to when x < 0?(A) −8 A square of area 40 is inscribed in a semicircle as shown. What is the area of the semicircle?(A) 20π(B) 25π(C) 30π(D) 40π(E) 50π9 Francesca uses 100 grams of lemon juice, 100 grams of sugar, and 400 grams of water to make lemonade. There are 25 calories in 100 grams of lemon juice and 386 calories in 100 grams of sugar. Water contains no calories. How many calories are in 200 grams of her lemonade.(A) 129 (B) 137 (C) 174 (D) 223 (E) 41110 In a triangle with integer side lengths, one side is three times as long as a second side, and the length of the third side is 15. What is the greatest possible perimeter of the triangle?(A) 43 (B) 44 (C) 45 (D) 46 (E) 4711 What is the tens digit in the sum 7! + 8! + 9! + · · · + 2006!?(A) 1 (B) 3 (C) 4 (D) 6 (E) 912 The lines x =14y + a and y =14x + b intersect at the point (1, 2). What is a + b?(A) 0 (B)3/4(C) 1 (D) 2 (E)9/413 Joe and JoAnn each bought 12 ounces of coffee in a 16-ounce cup. Joe drank 2 ounces of his coffee and then added 2 ounces of cream. JoAnn added 2 ounces of cream, stirred the coffee well, and then drank 2 ounces. What is the resulting ratio of the amount of cream inJoe’s coffee to that in JoAnn’s coffee?(A)6/7(B)13/14(C) 1 (D)14/13(E)7/614 Let a and b be the roots of the equation x2− mx + 2 = 0. Suppose that a + (1/b) and b +(1/a)are the roots of the equation x2− px + q = 0. What is q?(A)5/2(B)7/2(C) 4 (D)9/2(E) 815 Rhombus ABCD is similar to rhombus BFDE. The area of rhombus ABCD is 24, and\BAD =60_. What is the area of rhombus BFDE?16 Leap Day, February 29, 2004, occurred on a Sunday. On what day of the week will Leap Day,February 29, 2020, occur?(A) Tuesday (B) Wednesday (C) Thursday (D) Friday (E) Saturday17 Bob and Alice each have a bag that contains one ball of each of the colors blue, green, orange, red, and violet. Alice randomly selects one ball from her bag and puts it into Bob’s bag. Bob then randomly selects one ball from his bag and puts it into Alice’s bag. What is the probability that after this process, the contents of the two bags are the same?(A)1/10(B)1/6(C)1/5(D)1/3(E)1/218 Let a1, a2, ... be a sequence for which a1= 2 a2= 3 and a n=( a n−1)/(a n−2)for each positive integer n≥3.What is a2006?(A)1/2(B)2/3(C)3/2(D) 2 (E) 319 A circle of radius 2 is centered at O. Square OABC has side length 1. Sides AB and CB are extended past b to meet the circle at D and E, respectively. What is the area of the shaded region in the figure, which is bounded by BD, BE, and the minor arc connecting D and E?(A)π/3+1(B)π(2 )/2_(C) π(2 π− 1)/2(E)π/3−20 In rectangle ABCD, we have A = (6,−22), B = (2006, 178), and D = (8, y), for some integer y.What is the area of rectangle ABCD?(A) 4000 (B) 4040 (C) 4400 (D) 40, 000 (E) 40, 40021 For a particular peculiar pair of dice, the probabilities of rolling 1, 2, 3, 4, 5 and 6 on each die are in the ratio 1 : 2 : 3 : 4 : 5 : 6. What is the probability of rolling a total of 7 on the two dice?(A)4/63(B)1/8(C)8/63(D)1/6(E)2/722 Elmo makes N sandwiches for a fundraiser. For each sandwich he uses B globs of peanut butter at 4 cents per glob and J blobs of jam at 5 cents per glob. The cost of the peanut butter and jam to make all the sandwiches is $2.53. Assume that B, J, and N are all positive integers with N > 1.What is the cost of the jam Elmo uses to make the sandwiches?(A) $1.05 (B) $1.25 (C) $1.45 (D) $1.65 (E) $1.8523 A triangle is partitioned into three triangles and a quadrilateral by drawing two lines from vertices to their opposite sides. The areas of the three triangles are 3, 7, and 7, as shown. What is the area of the shaded quadrilateral?(A) 15 (B) 17 (C)352(D) 18 (E)55/324 Circles with centers O and P have radii 2 and 4, respectively, and are externally tangent. Points A and B are on the circle centered at O, and points C and D are on the circle centered at P, such that AD and BC are common external tangents to the circles. What is the area of hexagon AOBCPD?25 Mr. Jones has eight children of different ages. On a family trip his olderst child, who is 9, spots a license plate with a 4-digit number in which each of two digitrs appears two times. “Look, daddy!” she excl aims. “That number is evenly divisible by the age of each of us kids!” “That’s right,” replies Mr. Jones, “and the last two digits just happen to be my age.” Which of the following is not the age of one of Mr. Jones’s children?(A) 4 (B) 5 (C) 6 (D) 7 (E) 8。
2001-2006-AMC8-中文试题和答案

2001 年美国AMC8 (2001年月日时间40分钟)1. 卡西的商店正在制作一个高尔夫球奖品。
他必须给一颗高尔夫球面上的300个小凹洞着色,如果他每着色一个小凹洞需要2秒钟,试问共需多分钟才能完成他的工作。
(A) 4 (B) 6 (C) 8 (D) 10 (E) 12 。
2. 我正在思考两个正整数,它们的乘积是24且它们的和是11,试问这两个数中较大的数是什么。
(A) 3 (B) 4 (C) 6 (D) 8 (E) 12 。
3. 史密斯有63元,艾伯特比安加多2元,而安加所有的钱是史密斯的三分之一,试问艾伯特有元。
(A) 17 (B) 18 (C) 19 (D) 21 (E) 23 。
4. 在每个数字只能使用一次的情形下,将1,2,3,4及9作成最小的五位数,且此五位数为偶数,则其十位数字为。
(A) 1 (B) 2 (C) 3 (D) 4 (E) 9 。
5. 在一个暴风雨的黑夜里,史努比突然看见一道闪光。
10秒钟后,他听到打雷声音。
声音的速率是每秒1088呎,但1哩是5280呎。
若以哩为单位的条件下,估计史努比离闪电处的距离最接近下列何者。
(A) 1 (B) 1 (C) 2 (D) 2 (E) 3 。
6. 在一笔直道路的一旁有等间隔的6棵树。
第1棵树与第4棵树之间的距离是60呎。
试问第1棵树到最后一棵树之间的距离是呎。
(A) 90 (B) 100 (C) 105 (D) 120 (E) 140 。
问题7、8、9请参考下列叙述:主题:竞赛场所上的风筝展览7. 葛妮芙为提升她的学校年度风筝奥林匹亚竞赛的质量,制作了一个小风筝与一个大风筝,并陈列在公告栏展览,这两个风筝都如同图中的形状,葛妮芙将小风筝张贴在单位长为一吋(即每两点距离一吋)的格子板上,并将大风筝张贴在单位长三吋(即每两点距离三吋)的格子板上。
试问小风筝的面积是平方吋。
(A) 21 (B) 22 (C) 23 (D) 24 (E) 25。
2006年AMC8试题及答案

Copyright © 2016 Art of Problem Solving Mindy made three purchases for dollars, dollars, and dollars. What was her total, tothe nearest dollar?The three prices round to , , and , which has a sum of2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byFirstQuestion Followed by Problem 21 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and Solutions The problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_1&oldid=55964"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingOn the AMC 8 contest Billy answers 13 questions correctly, answers 7 questions incorrectly and doesn'tanswer the last 5. What is his score?As the AMC 8 only rewards 1 point for each correct answer, everything is irrelevant except the number Billy answered correctly, .2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 1Followed by Problem 31 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and Solutions The problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_2&oldid=55965"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingElisa swims laps in the pool. When she first started, she completed 10 laps in 25 minutes. Now, she canfinish 12 laps in 24 minutes. By how many minutes has she improved her lap time?When Elisa started, she finished a lap in minutes. Now, she finishes a lap is minutes.The difference is .2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 2Followed by Problem 41 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and Solutions The problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_3&oldid=55966"SolutionSee AlsoCopyright © 2016 Art of Problem Solving Initially, a spinner points west. Chenille moves it clockwise revolutions and then counterclockwiserevolutions. In what direction does the spinner point after the two moves?If the spinner goes clockwise revolutions and then counterclockwise revolutions, it ultimately goes counterclockwise which brings the spinner pointing.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 3Followed by Problem 51 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and Solutions The problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_4&oldid=55967"SolutionSee AlsoPoints and are midpoints of the sides of the larger square. If the larger square has area 60, what is the area of the smaller square?Drawing segments and , the number of triangles outside square is the same as the number of triangles inside the square. Thus areas must be equal so the area of is half the area of thelarger square which is .If the side length of the larger square is , the side length of the smaller square is . Therefore the area of the smaller square is , half of the larger square's area, .Thus, the area of the smaller square in the picture is .Copyright © 2016 Art of Problem Solving The letter T is formed by placing twoinch rectangles next to each other, as shown. What is theperimeter of the T, in inches?If the two rectangles were seperate, the perimeter would be . It easy to see that their connection erases 2 from each of the rectangles, so the final perimeter is .2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 5Followed by Problem 71 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'s American Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_6&oldid=55969"SolutionSee AlsoCopyright © 2016 Art of Problem Solving Circle has a radius of . Circle has a circumference of . Circle has an area of . List thecircles in order from smallest to largest ing the formulas of circles, and , we find that circle has a radius of and circle has a radius of . Thus, the order from smallest to largest radius is.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 6Followed by Problem 81 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21• 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'s American Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_7&oldid=55970"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingThe table shows some of the results of a survey by radiostation KAMC. What percentage of the males surveyedlisten to the station?Filling out the chart, it becomes Thus, the percentage of males surveyed that listen to the station is .2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 7Followed by Problem 91 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and Solutions The problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_8&oldid=55971"SolutionSee AlsoCopyright © 2016 Art of Problem Solving What is the product of?By telescoping, it's easy to see the sum becomes .2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 8Followed by Problem 101 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and Solutions The problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_9&oldid=55972"SolutionSee AlsoJorge's teacher asks him to plot all the ordered pairs of positive integers for which is the width and is the length of a rectangle with area 12. What should his graph look like?Copyright © 2016 Art of Problem SolvingThe length of the rectangle will relate invertly to the width, specifically using the theorem . Theonly graph that could represent a inverted relationship is . (The rest are linear graphs thatrepresent direct relationships)2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded by Problem 9Followed by Problem 111 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_10&oldid=55973"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingHow many two-digit numbers have digits whose sum is a perfect square?There is integer whose digits sum to : .There are integers whose digits sum to : .There are integers whose digits sum to : .There are integers whose digits sum to :.Two digits cannot sum toor any greater square since the greatest sum of digits of a two-digit number is.Thus, the answer is.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded by Problem 10Followed by Problem 121 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_11&oldid=80944"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingAntonette gets on a 10-problem test, on a 20-problem test and on a 30-problem test. Ifthe three tests are combined into one 60-problem test, which percent is closest to her overall score?Adding them up gets. The overall percentage correct would be.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded by Problem 11Followed by Problem 131 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_12&oldid=55975"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingCassie leaves Escanaba at 8:30 AM heading for Marquette on her bike. She bikes at a uniform rate of 12 miles per hour. Brian leaves Marquette at 9:00 AM heading for Escanaba on his bike. He bikes at a uniform rate of 16 miles per hour. They both bike on the same 62-mile route between Escanaba and Marquette. At what time inthe morning do they meet?If Cassie leavesan hour earlier then Brian, when Brian starts, the distance between them will be. Every hour, they will getmiles closer., so 2 hours from 9:00AM is when they meet, which is.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded by Problem 12Followed by Problem 141 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_13&oldid=55976"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingProblems 14, 15 and 16 involve Mrs. Reed's English assignment.A Novel AssignmentThe students in Mrs. Reed's English class are reading the same -page novel. Three friends, Alice, Bob and Chandra, are in the class. Alice reads a page in 20 seconds, Bob reads a page in seconds and Chandra reads a page inseconds.If Bob and Chandra both read the whole book, Bob will spend how many more seconds reading than Chandra?The information is the same for Problems 14,15, and 16. Therefore, we shall only use the information we need. All we need for this problem is that there's 760 pages, Bob reads a page in 45 seconds and Chandrareads a page in 30 seconds. A lot of people will find how long it takes Bob to read the book, how long it takes Chandra to read the book, and then find the seconds. However, if we just set up the expression, we can find an easier way.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded by Problem 13Followed by Problem 151 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_14&oldid=55977"SolutionSee AlsoLet be the number of pages that Chandra reads.Distribute theAdd to both sidesDivide both sides by to make it easier to solveDivide both sides bySolution 2Bob and Chandra read at a rate of seconds per page, respectively. Simplifying that gets us Bob reads pages for every pages that Chandra reads. Therefore Chandra should read of the book. =$\boxed{\textbf{(C)} 456}See AlsoCopyright © 2016 Art of Problem SolvingProblems 14, 15 and 16 involve Mrs. Reed's English assignment.A Novel AssignmentThe students in Mrs. Reed's English class are reading the same 760-page novel. Three friends, Alice, Bob and Chandra, are in the class. Alice reads a page in 20 seconds, Bob reads a page in 45 seconds and Chandra reads a page in 30 seconds.Before Chandra and Bob start reading, Alice says she would like to team read with them. If they divide the book into three sections so that each reads for the same length of time, how many seconds will each have toread?The amount of pages Bob, Chandra, and Alice would read is in the ratio 4:6:9. Therefore, Bob, Chandra, and Alice read 160, 240, and 360 pages respectively. They would also be reading in the same amount of time because the ratio of pages read was based on the time it takes each of them to read a page. Therefore, the amount of seconds each person reads is.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded by Problem 15Followed by Problem 171 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_16&oldid=55979"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingJeff rotates spinners ,andand adds the resulting numbers. What is the probability that his sum isan odd number?In order for Jeff to have an odd number sum, the numbers must either be Odd + Odd + Odd or Even + Even +Odd. We easily notice that we cannot obtain Odd + Odd + Odd because spinner contains only even numbers.Therefore we must work with Even + Even + Odd and spinner will give us one of our even numbers. We also see that spinner only contains odd, so spinner must give us our odd nmber. We still need one evennumber from spinner . There is only 1 even number: . Since spinning the required numbers are automatic onthe other spinners, we only have to find the probability of spinning a in spinner , which clearly is2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded by Problem 16Followed by Problem 181 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24• 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_17&oldid=55980"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingA cube with 3-inch edges is made using 27 cubes with 1-inch edges. Nineteen of the smaller cubes are white and eight are black. If the eight black cubes are placed at the corners of the larger cube, what fraction of the surface area of the larger cube is white?The surface area of the cube is . Each of the eight black cubes has 3 faces on the outside,making black faces. Therefore there are white faces. To find the probability,we evaluate.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded by Problem 17Followed by Problem 191 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 •25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_18&oldid=55981"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingTriangleis an isosceles triangle with . Pointis the midpoint of bothand, and is 11 units long. Triangleis congruent to triangle . What is the length of?Since triangleis congruent to triangleand ,. Since,. Because pointis the midpoint of,.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded by Problem 18Followed by Problem 201 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19• 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_19&oldid=55982"SolutionSee AlsoA singles tournament had six players. Each player played every other player only once, with no ties. If Helen won 4 games, Ines won 3 games, Janet won 2 games, Kendra won 2 games and Lara won 2 games, how manygames did Monica win?Since there are 6 players, a total ofgames are played. So far,games finished (one person won from each game), so Monica needs to win.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 19Followed byProblem 211 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 •20• 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'sAmerican Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_20&oldid=81054"SolutionSee AlsoCopyright © 2016 Art of Problem SolvingCopyright © 2016 Art of Problem Solving An aquarium has a rectangular base that measures cm by cm and has a height ofcm. The aquarium is filled with water to a depth of cm. A rock with volume is then placed in the aquarium and completely submerged. By how many centimeters does the water level rise?The water level will rise cm for every . Since is of , the waterwill rise 2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 20Followed by Problem 221 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22• 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'s American Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_21&oldid=55984"SolutionSee AlsoThree different one-digit positive integers are placed in the bottom row of cells. Numbers in adjacent cells are added and the sum is placed in the cell above them. In the second row, continue the same process toobtain a number in the top cell. What is the difference between the largest and smallest numbers possible inthe top cell?If the lower cells contain and , then the second row will contain and , and the top cell will contain . To obtain the smallest sum, place in the center cell and and in the outer ones. The top number will be . For the largest sum, place in the center cell and and in the outer ones. This top number will be . The difference is .2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 21Followed by Problem 231 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 •22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'s American Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_22&oldid=55985"SolutionSee AlsoThe counting numbers that leave a remainder of 4 when divided by 6 are The counting numbers that leave a remainder of 3 when divided by 5 are So 28 isthe smallest possible number of coins that meets both conditions. Because , there areIf there were two more coins in the box, the number of coins would be divisible by both 6 and 5. The smallest number that is divisible by 6 and 5 is , so the smallest possible number of coins in the box isand the remainder when divided by 7 is .The problems on this page are copyrighted by the Mathematical Association of America ()'s American Mathematics Competitions ().Copyright © 2016 Art of Problem Solving In the multiplication problem below , , , and are different digits. What is?, so . Therefore, and , so.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 23Followed by Problem 251 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 •24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'s American Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_24&oldid=68712"SolutionSee AlsoCopyright © 2016 Art of Problem Solving Barry wrote 6 different numbers, one on each side of 3 cards, and laid the cards on a table, as shown. The sums of the two numbers on each of the three cards are equal. The three numbers on the hidden sides areprime numbers. What is the average of the hidden prime numbers?Notice that 44 and 38 are both even, while 59 is odd. If any odd prime is added to 59, an even number will be obtained. However, the only way to obtain this even number would be to add another even number to 44, and a different one to 38. Since there is only one even prime (2), the middle card's hidden number cannot be anodd prime, and so must be even. Therefore, the middle card's hidden number must be 2, so the constant sum is . Thus, the first card's hidden number is , and the last card's hidden number is .Since the sum of the hidden primes is, the average of the primes is.2006 AMC 8 (Problems • Answer Key • Resources(/Forum/resources.php?c=182&cid=42&year=2006))Preceded byProblem 24Followed by Last Problem1 •2 •3 •4 •5 •6 •7 •8 •9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 •19 • 20 • 21 • 22 • 23 • 24 • 25All AJHSME/AMC 8 Problems and SolutionsThe problems on this page are copyrighted by the Mathematical Association of America ()'s American Mathematics Competitions ().Retrieved from "/wiki/index.php?title=2006_AMC_8_Problems/Problem_25&oldid=55988"SolutionSee Also。
2006年AMC8试题答案

This Solutions Pamphlet gives at least one solution for each problem on this year’s exam and shows that all the problems can be solved using material normally as-sociated with the mathematics curriculum for students in eighth grade or below. These solutions are by no means the only ones possible, nor are they necessarily superior to others the reader may devise.We hope that teachers will share these solutions with their students. However, the publication, reproduction, or communication of the problems or solutions of the AMC 8 during the period when students are eligible to participate seriously jeopardizes the integrity of the results. Dissemination at any time via copier, telephone, e-mail, World Wide Web or media of any type is a violation of the competition rules.Correspondence about the problems and solutions should be addressed to:Ms. Bonnie Leitch , AMC 8 Chair / bleitch@548 Hill Avenue, New Braunfels, TX 78130Orders for prior year Exam questions and Solutions Pamphlets should be addressed to:Attn: Publications American Mathematics Competitions University of Nebraska-Lincoln P .O. Box 81606Lincoln, NE 68501-1606Copyright © 2006, The Mathematical Association of AmericaT he M aTheMaTical a ssociaTion of a MericaAmerican Mathematics Competitions 22nd AnnualAMC 8(American Mathematics Contest 8)Solutions PamphletTuesday, NOVEMBER 14, 20061.(D)Mindy’s total was approximately 2+5+10=$17.2.(C)On the AMC 8a student’s score is the number of problems answered cor-rectly.So Billy’s score is 13.Because there is no penalty for guessing,if he wants to increase his score,he probably should fill in the last five answers.3.(A)When Elisa started,she completed a lap in 2510=2.5minutes.Now she cancomplete a lap in 2412=2minutes.She has improved her lap time by 2.5−2=0.5or 12minute.4.(B)Ignore the number of complete revolutions because they do not affect direc-tion.One-fourth of the distance around the circle clockwise from west is north.Three-fourths of the distance counterclockwise around the circle from north is east.Chenille’s spinner points east.5.(D)Divide the larger square into 8congruent triangles,as shown,4of which make up the smaller square.ABD The area of the smaller square is 48or 12of the area of the larger square,so thearea of the smaller square is equal to 30.6.(C)11422442The perimeter is 4+2+1+4+2+4+1+2=20inches.OREach rectangle has perimeter =2l +2w =2(4)+2(2)=8+4=12inches.When the two rectangles are positioned to form the T,a two-inch segment of each rectangle is inside the T and is not on the perimeter of the T.So the perimeter of the T is 2(12)−2(2)=24−4=20inches.7.(B)Because circumference C =2πr and circle Y has circumference 8π,itsradius is 8π2π=4.Because area A =πr 2and circle Z has area 9π,its radius is √9=3.Ordering the radii gives 3<π<4,so the circles in ascending order ofradii length are Z ,X and Y .8.(E)Because 200−96=104of those surveyed were male,104−26=78of those surveyed are male listeners.Listen Don’t Listen Total Male7826104Female583896Total 13664200The percentage of males surveyed who listen to KAMC is 78104×100%=75%.9.(C)Note that in each fraction,the numerator is the same as the denominatorin the next fraction,so they divide.The product of ¡32ס4¡3ס5¡4×...×2006$$$2005=20062=1003.10.(A)When the area of a rectangle is 12square units and the sides are integers,the factors of 12are the possible lengths of the sides.In point form,the side lengths could be (1,12),(2,6),(3,4),(4,3),(6,2)and (12,1).Only graph A fits these points.11.(C)The sum of the digits of a two-digit number is at most 9+9=18.Thismeans the only possible perfect square sums are 1,4,9and 16.Each square has the following two-digit possibilities:1:104:40,31,22,139:90,81,72,63,54,45,36,27,1816:97,88,79There are 17two-digit numbers in all.12.(D)Note that 70%of 10is 7,80%of 20is 16and 90%of 30is 27.Antonetteanswers 7+16+27=50problems correctly out of 60problems in all.Her overall score is 5060or 83.3%.13.(D)Between 8:30and 9:00AM Cassie travels 6miles.At 9:00Cassie and Brianare only 56miles apart.After 9:00,because they are both biking towards each other,the distance between them decreases at the rate of 12+16=28miles per hour.At that rate,it will take them 5628=2hours to meet.So they will meetat 11:00AM.14.(B)Bob takes 45−30=15more seconds per page than Chandra.So thedifference in their total reading times is 760·15=11,400seconds.Bob will spend 11,400more seconds reading than Chandra.15.(C)The ratio of time it takes Bob to read a page to the time it takes Chandrato read a page is45:30or3:2,so Bob should read23of the number of pagesthat Chandra reads.Divide the book into5parts,each with7605=152pages.Chandra will read thefirst3·152=456pages,while Bob reads the last2·152= 304pages.ORIf Chandra reads x pages,she will read for30x seconds.Bob has to read760−x pages,and this takes him45(760−x)seconds.Because Chandra and Bob read the same amount of time,30x=45(760−x).Solving for x,30x=45·760−45x,75x=45·760,x=45·76075=456.So Chandra will read thefirst456pages.16.(E)The least common multiple of20,45and30is22·32·5=ing theLCM,in180seconds Alice reads18020=9pages,Chandra reads18030=6pagesand Bob reads18045=4pages.Together they read a total of19pages in180seconds.The total number of seconds each reads is76019·180=7200.17.(B)Because the sum of a number from spinner Q and a number from spinner Ris always odd,the sum of the numbers on the three spinners will be odd exactly when the number from spinner P is even.Because2is the only even number onspinner P,the probability of getting an odd sum is13.18.(D)Four black andfive white squares are visible on each of the six faces of thecube.So59of the surface will be white.19.(D)Because triangles ABD and ECD are congruent and triangle ABC isisosceles,EC=AB=BC=11.That means BD=112or5.5.20.(C)Each of the six players played5games,and each game involved two players.So there were6·52=15games.Helen,Ines,Janet,Kendra and Lara won a totalof4+3+2+2+2=13games,so Monica won15−13=2games.21.(A)Using the volume formula lwh=V,the volume of water in the aquariumis100×40×37=148,000cm3.When the rock is put in,the water and the rock will occupy a box-shaped region with volume148,000+1000=149,000cm3.The volume of the water and the rock is100×40×h,where h is the new height of the water.The new volume=4000h=149,000cm3,so the new height ish=1490004000=37.25cm.After adding the rock,the water rises37.25−37=0.25cm.ORBecause the shape of the rock is irrelevant,we may assume that the rock is shaped like a rectangular box with base measuring100cm×40cm and height hing the volume formula,100×40×h=1000,so h=1000100×40=0.25cm.When the rock is put into the aquarium,the water level will rise by0.25cm.22.(D)If the lower cells contain A,B and C,then the second row will containA+B and B+C,and the top cell will contain A+2B+C.To obtain the smallest sum,place1in the center cell and2and3in the outer ones.The top number will be7.For the largest sum,place9in the center cell and7and8in the outer ones.This top number will be33.The difference is33−7=26. 23.(A)The counting numbers that leave a remainder of4when divided by6are4,10,16,22,28,34,....The counting numbers that leave a remainder of3when divided by5are3,8,13,18,23,28,33,....So28is the smallest possible number of coins that meets both conditions.Because4×7=28,there are no coins left when they are divided among seven people.ORIf there were two more coins in the box,the number of coins would be divisible by both6and5.The smallest number that is divisible by6and5is30,so the smallest possible number of coins in the box is28.24.(A)We can decompose CDCD into CD×100+CD=CD(101).That meansthat A=1and B=0.The sum is1+0=1.25.(B)There are one odd and two even numbers showing.Because all primesother than2are odd and the sum of an even number and an odd number is odd,the common sum must be odd.That means2must be opposite59and the common sum is2+59=61.The other two hidden numbers are61−44=17and61−38=23.The average of2,17and23is2+17+233=423=14.TheAmerican Mathematics Competitionsare Sponsored byThe Mathematical Association of AmericaThe Akamai FoundationContributorsAmerican Mathematical Association of Two Year CollegesAmerican Mathematical SocietyAmerican Society of Pension ActuariesAmerican Statistical AssociationArt of Problem SolvingCanada/USA MathcampCanada/USA MathpathCasualty Actuarial SocietyClay Mathematics InstituteConsortium for Mathematics & its ApplicationsInstitute for Operations Research and the Management SciencesL. G. Balfour CompanyMu Alpha ThetaNational Council of Teachers of MathematicsNational Assessment & TestingPedagoguery Software Inc.Pi Mu EpsilonSociety of ActuariesU.S.A. Math Talent SearchW. H. Freeman and CompanyWolfram Research Inc.。
全国中学生生物学联赛试题及答案及美国数学竞赛8年级(AMC8)真题(附答案)(电脑版)

全国中学生生物学联赛试题注意事项:1.所有试题使用2B铅笔在机读卡上作答;2.试题按学科分类,单选和多选题混排,多选题答案完全正确才可得分3.纸质试卷72题,电子试卷48题,共计l20题;4.答题时间120分钟。
一、细胞生物学、生物化学、微生物学16题1.癌细胞与正常细胞的不同之处在于A.癌细胞不能合成DNA B.癌细胞被锁定在细胞周期中的S期C.癌细胞能持续分裂尽管彼此紧密相接D.癌细胞始终处于细胞周期中的分裂期2.人的肌肉组织分为快缩纤维和慢缩纤维两种,快缩纤维负责剧烈运动如举重,短跑,易产生酸痛感觉;慢缩纤维负责慢跑,游泳等有氧运动。
以下关于慢缩纤维和快缩纤维的描述,哪个是正确的A.快缩纤维含有的线粒体多,有氧呼吸能产生大量乳酸和ATP供能B.慢缩纤维含有的线粒体多,有氧呼吸不产生乳酸,产生的ATP也少C.快缩纤维含有的线粒体少,主要依靠糖酵解产生ATP供能,因此产生大量乳酸D.慢缩纤维含有的线粒体多,主要依靠糖酵解产生ATP供能3.在光合作用中参与电子传递的载体是A.叶绿素B.磷酸烯醇式丙酮酸C.NADH D.NADPH4.肽链生物合成时,信号肽A.是线粒体的定位信号B.将新生肽链导入内质网C.控制蛋白质分子的最终构象D.处于肽链的C末端5.原核细胞的特征包括A.无核糖体B.无转录后修饰C.无有氧呼吸D.无染色体6.以下糖类中属于寡糖的有(多选2分)A.甘露糖B.麦芽糖C.半乳糖D.蔗糖E.糖原7.以下关于蛋白质变性后所产生现象的描述不正确的是:A.溶解度降低B.疏水侧链基团被包裹在分子内部C.形成沉淀D.失去结晶能力8.真菌中的半知菌是指。
A.没有光合作用B.菌丝没有横隔C.没有发现有性生殖阶段D.不能运动。
9.关于维生素A的生理功能,下面的描述中哪个是错误的?A.抑制胆碱酯酶活性B.构成视觉细胞感光物质的成分C.参与上皮组织细胞膜糖蛋白合成D.严重缺乏时导致夜盲症10.磷酸戊糖途径的发生部位在A.细胞质B.线粒体C.叶绿体D.细胞膜11.在C4植物循环中,CO2进入叶肉细胞被固定的最初产物是A.甘油酸-3-磷酸B.苹果酸C.草酰乙酸D.丙酮酸12.在等电聚焦电泳过程中,随着蛋白质样品的迁移,电流的变化为A.越变越大,当样品到达其等电点位置时,电流达到最大值B.越变越小,当样品到达其等电点位置时,电流达到最小值,接近于零C.基本不变,为一恒定值D.不确定13.利用酵母菌进行乙醇发酵时若通入氧气,会导致菌株对葡萄糖利用速度降低,甚至停止生成乙醇,这种现象称为A.呼吸抑制效应B.巴斯德效应C.分子氧效应D.葡萄糖效应14.巴斯德设计的曲颈瓶实验,可以(单选1分)A.证明酒是酵母菌发酵获得B.否定自然发生学说的论点C.说明培养基灭菌后的作用D.验证某细菌是不能培养的15.营养缺陷型菌株是指(单选1分)A.不需要添加生长因子可在基础培养基上生长的菌株B.不需要添加生长因子可在丰富培养基上生长的菌株C.因突变需提供某种营养才能在基础培养基上生长的菌株D.因自发或诱发突变而导致的可抵抗环境不良因素的菌株16.以下哪类化合物属于微生物的次生代谢产物(多选2分)A.脂肪B.色素C.抗生素D.蛋白质E.毒素二、植物和动物的解剖、生理、组织和器官18题17.草履虫、水螅、乌贼、蟾蜍受到刺激后,均可从体内发出一些物质以攻击或防御敌害,在他们身体上,发出这些物质的结构是A.刺丝泡、刺细胞、墨囊、耳后腺B.刺丝泡、刺丝囊、外套腔、唾液腺C.表膜泡、刺丝囊、墨囊、唾液腺D.表膜泡、刺细胞、外套腔、耳后腺18.在动物卵裂时期,由于不同动物受精卵内卵黄多少及其在卵内分布的不同,卵裂方式也有很大差异,海胆、沙蚕、昆虫、乌贼的卵裂方式依次分别为(单选1分) A.完全均等卵裂(等裂)、表面卵裂、螺旋形卵裂、盘裂B.螺旋形卵裂、完全均等卵裂(等裂)、盘裂、表面卵裂C.螺旋形卵裂、完全均等卵裂(等裂)、表面卵裂、盘裂D.完全均等卵裂(等裂)、螺旋形卵裂、表面卵裂、盘裂19.不同动物类群具有独特的特征,现存棘皮动物、海绵动物、哺乳动物、鸟类所特有的特征依次为A.水管系、水沟系、下颌为单一齿骨、羽毛B.后口、水沟系、胎生、飞翔C.后口、骨针、胎生、羽毛D.水管系、骨针、下颌为单一齿骨、飞翔20.节肢动物类群很多,不同类群的排泄器官亦有差异,节肢动物门甲壳纲动物的排泄器官有(多选l分)A.基节腺B.触角腺C.颚腺D.马氏管21.家鸽的一侧体动脉弓退化,雌家鸽的一侧卵巢和输卵管也退化了,退化的这些器官是(单选1分)A.左体动脉弓和右侧的卵巢、输卵管B.左体动脉弓和左侧的卵巢、输卵管C.右体动脉弓和左侧的卵巢、输卵管D.右体动脉弓和右侧的卵巢、输卵管22.在海滨潮间带经常可以见到石鳖和沙蚕,以下不属于它们共同特征的是A.以裂体腔法形成真体腔B.后肾型排泄系统C.具有担轮幼虫期D.开管式循环系统23.以下哪项不是文昌鱼的特征A.具有脊索,背神经管,鳃裂B.有分节的肌肉,有哈氏窝C.有头,有心脏D.有特化的口器24.一家饭店涉嫌出售野生鸟类,检查人员在检查时发现了一种鸟类的足,三趾向前一趾向后,后趾与前面三趾在同一平面上,趾长,基部有蹼相连,这种鸟类是A.鹈形目B.鹳形目C.雁形目D.鹤形目25.以下哪组元素在植物体内参与氧化还原反应(单选2分)A.钼镍铜铁B.铁铜镁钼C.钙镁镍铜D.锰镍镁铜26.盐胁迫条件下,较耐盐的禾本科植物大麦可以通过将盐分局域于以下部位来缓解盐分对植物生长造成的危害(多选l分)A.根系B.幼叶C.叶鞘D.老叶27.关于植物的种子,下列描述正确的是(多选2分)A.种子由胚珠发育而来B.种子表面均有种孔、种脐和种脊的结构C.种子中的胚乳多来源于受精后的中央细胞,也有来自于雌配子体的细胞D.胚是休眠的幼小孢子体E.无胚乳种子在发育过程中没有胚乳形成28.有关被子植物花的叙述,下列哪一个是错误的(单选2分)A.花是适应于繁殖功能的变态短枝B.花托、花萼和花冠被认为是叶的变态C.雄蕊和雌蕊也被认为是叶的变态D.花托、花被、雄蕊和雌蕊均有茎的顶端分生组织产生29.玉米干旱缺水时叶片的内卷主要是失水造成的A.叶肉细胞B.叶表皮的毛状体C.位于上表皮的泡状(运动)细胞D.位于下表皮的泡状(运动)细胞30.有关C4植物,以下说法中正确的是(多选2分)A.叶解剖结构中可观察到“花环结构”B.光合作用CO2的初步固定和同化在不同细胞中进行C.光合作用CO2的初步固定和同化在同一细胞中进行D.在一定范围的强光、高温条件下光合效率高31.心肌细胞有效不应期的长短主要取决于A.静息电位水平B.0期去极化的速度C.阈电位水平D.平台期的长短32.血液中CO2分压升高使呼吸运动加强的最主要途径是(单选2分)A.直接刺激脑桥的呼吸相关神经元B.直接刺激延髓呼吸中枢的神经元C.刺激中枢化学感受器D.刺激颈动脉体和主动脉体感受器33.当去甲肾上腺素与β受体结合时,下列哪一种肌肉收缩或收缩加强(单选1分) A.心室肌B.子宫平滑肌C.小肠平滑肌D.血管平滑肌E.支气管平滑肌34.下列哪种因素可引起人尿量的明显增加的(多选2分)A.献血200ml后B.饮用清水1000ml后C.静脉注射神经垂体激素D.饮用生理盐水100ml后三、动物行为学、生态学15题35.如果一项研究,专注于了解不同生态因子对生物的影响,及生物对它们的耐受,那么这个研究属于哪一层次上的研究A.个体生态学B.种群生态学C.群落生态学D.生态系统生态学36.关于高等动物种群中性别比例,下面论述中错误的是A.大多数种群倾向于使出生性比趋近于l:1 B.老年组往往雌性多于雄性C.出生的时候,往往雄性多于雌性D.种群性比与世代长度直接相关37.社会性寄生是指A.寄生在动物社会中是普遍现象B.寄生只发生在特定社会等级的动物中C.社会性昆虫中发生的寄生行为D.强迫寄主动物为其提供食物或其他利益38.关于外来物种,以下论述错误的是A.所有的外来物种都是入侵种,都是有害的B.外来物种可以依靠风、鸟、昆虫等自然因素入侵C.有些外来物种是人类有意引入的D.入侵物种可能对生态系统造成长久的破坏39.适合度是指A.动物单一行为的适应性B.动物调整自己的行为以适合于生活在当时的环境C.动物的总体繁殖成功性D.最适合动物生活习性、满足营养需求的食物40.以下哪种情况不属于动物的行为节律A.候鸟随季节的迁徙B.哺乳动物晨昏活动习性C.细菌生长速度随营养物浓度起落而快慢变化D.招潮蟹的活动随潮汐变化而变化41.动物的生长和发育是需要一定温度的,下列哪个说法是正确的(单选2分) A.外界温度的高低直接决定了动物机体的体温,进而影响其生长发育B.当外界温度低于某一温度时,昆虫就停止生长发育,这一温度阈值称为发育起点温度C.动物的发育速度总是随环境温度的增高而加快的D.昆虫发育的有效积温是发育历期乘以发育期的平均温度,然后求和42.下列有关水生群落演替的说法中哪个是错误的A.水生群落的演替一般会依次经历裸底期、浮水植物期、沉水植物期、挺水植物期、湿生草本植物期等阶段B.在这一演替过程中池底逐渐变浅,最终向陆地变化C.挺水植物根系往往较发达,可以使水底迅速增高D.浮水植物的叶子漂浮在水面,影响到水下光照,不利于沉水植物生长43.关于固定行为型,下述论述正确的是(多选2分)A.固定行为型被特定的外部刺激所释放B.每一个物种都有物种特异的固定行为型C.固定行为型一旦释放就会持续到底D.固定行为型是一种先天行为44.在动物行为学研究中,严格定义行为类型是研究工作的基础。
美国数学竞赛AMC8 -- 2008年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2008年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:50-12-24=14中文解析:总共花的钱是:12+12*2=36元。
剩余50-36=14元。
答案是BProblem 2Answer: ASolution:We can derive that c=8,L=6, U=7,and E=1. Therefore, the answer is 8671.中文解析:这10个字母的对应关系是: B -0;E-1; S-2; ......K -9. 按照这个对应关系:C-8,L-6,U-7,E-1. 即8671. 答案是A。
Problem 3Answer: ASolution:We can go backwards by days, but we can also backwards by weeks. If we go backwards by weeks, we see that February 6 is a Friday. If we now go backwards by days, February 1 is a Sunday.中文解析:13日是周五,则13-7=6,即6日也是周五,则倒推2月1日是周日。
答案是A。
Problem 4Answer: CSolution:The area outside the small triangle but inside the large triangle is 16-1=15. This is equally distributed between the three trapezoids. Each trapezoid has an area of 15/3=5.中文解析:大三角形的面积等于小的等边三角形的面积加上3个梯形的面积。
据此,三个梯形的面积是16-1=15. 每个梯形的面积是15/3=5. 答案是C。
2006年AMC8试题

(A) 12 (B) 16 (C) 20 (D) 22 (E) 24
7 Circle X has a radius of π. Circle Y has a circumference of 8π. Circle Z has an area of 9π. List the circles in order from smallest to largest radius.
(A) 425 (B) 444 (C) 456 (D) 484 (E) 506
16 Problems 14, 15 and 16 involve Mrs. Reed’s English assignment.
A Novel Assignment
The students in Mrs. Reed’s English class are reading the same 760-page novel. Three friends, Alice, Bob and Chandra, are in the class. Alice reads a page in 20 seconds, Bob reads a page in 45 seconds and Chandra reads a page in 30 seconds.
USA
AMC 8 2006
1 Mindy made three purchases for $1.98, $5.04 and $9.89. What was her total, to the nearest dollar?
(A) $10 (B) $15 (C) $16 (D) $17 (E) $18
3 Elisa swims laps in the pool. When she first started, she completed 10 laps in 25 minutes.
2007-2012 AMC8 中文试题和答案

卤味面 起司肉燥面水饭 意大利面 人 數 A3BCD E3 62007年 美国AMC8 (2007年11月 日 时间40分钟)1. 如果希瑞莎能够持续6周,平均每周花10小时帮忙照顾房子,她的父母就帮她买她喜爱乐 团的入场券。
在前五周她分别花了8、11、7、12及10小时照顾房子。
在最后一周,她必须 要花多少小时去照顾房子才能获得入场券?(A) 9 (B) 10 (C) 11 (D) 12 (E) 13 。
2. 调查650位学生对面食种类的偏好。
选项包含:卤味面、起司 肉燥面、水饺、意大利面,调查结果如长条图所示。
试问偏好 意大利面的学生数与偏好起司肉燥面的学生数之比值为多少? (A)52 (B) 21 (C) 45 (D) 35 (E) 25。
3. 250的最小两个质因子之和为多少?(A) 2 (B) 5 (C) 7 (D) 10 (E) 12 。
4. 某间鬼屋有六个窗子。
小精灵乔治从一个窗子进入屋内,而从不同的另一个窗子出来的方法 共有多少种?(A) 12 (B) 15 (C) 18 (D) 30 (E) 36 。
5. 姜德想买一辆价值美金500元的越野脚踏车。
在他生日时,祖父母给他美金50元,姑姑给 他美金35元,表哥给他美金15元。
他送报纸每周可赚美金16元。
若用他生日得到的所有礼 金及送报纸所有赚得的钱去买越野脚踏车,他需要送几周的报纸才能有足够的钱? (A) 24 (B) 25 (C) 26 (D) 27 (E) 28 。
6. 在1985年美国的长途电话费是每分钟41分钱,在2005年的长途电话费是每分钟7分钱。
试求每分钟长途电话费下降的百分率最接近下列哪一项? (A) 7 (B) 17 (C) 34 (D) 41 (E) 80 。
7. 房间内5个人的平均年龄为30岁。
若其中一位18岁的人离开了房间,则剩下四个人的平均 年龄是几岁? (A) 25 (B) 26 (C) 29 (D) 33 (E) 36 。
2006年AMC8试题

INSTRUCTIONS1. DO NOT OPEN THIS BOOKLET UNTIL YOUR PROCTOR TELLS YOU.2. This is a twenty-five question multiple choice test. Each question is followed by answers marked A, B, C, D and E. Only one of these is correct.3. Mark your answer to each problem on the AMC 8 Answer Form with a #2 pencil. Check the blackened circles for accuracy and erase errors and stray marks completely. Only answers properly marked on the answer form will be graded.4. There is no penalty for guessing. Your score on this test is the number of correct answers.5. No aids are permitted other than scratch paper, graph paper, rulers, erasers, and cal-culators that are accepted for use on the SAT. No problems on the test will require the use of a calculator.6.Figures are not necessarily drawn to scale.7. Before beginning the test, your proctor will ask you to record certain information on the answer form.8. When your proctor gives the signal, begin working on the problems. You will have 40 minutes to complete the test.9. When you finish the exam, sign your name in the space provided on the Answer Form.The Committee on the American Mathematics Competitions reserves the right to re-examine students before deciding whether to grant official status to their scores. The Committee also reserves the right to disqualify all scores from a school if it determines that the required security procedures were not followed.The publication, reproduction or communication of the problems or solutions of the AMC 8 during the period when students are eligible to participate seriously jeopardizes the integrity of the results. Dissemination via copier, telephone, e-mail, World Wide Web or media of any type during this period is a violation of the competition rules. After the contest period, permission to make copies of individual problems in paper or electronic form including posting on web-pages for educational use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear the copyright notice.Cop yright © 2006, The Mathematical Association of AmericaT he M aTheMaTical a ssociaTion of a MericaAmerican Mathematics Competitions 22nd AnnualAMC 8(American Mathematics Contest 8)T uesday, NOVEMBER 14, 20061.Mindy made three purchases for $1.98,$5.04and $9.89.What was her total,to the nearest dollar?(A)$10(B)$15(C)$16(D)$17(E)$182.On the AMC 8contest Billy answers 13questions correctly,answers 7questions incorrectly and doesn’t answer the last 5.What is his score?(A)1(B)6(C)13(D)19(E)263.Elisa swims laps in the pool.When she first started,shecompleted 10laps in 25minutes.Now she can finish 12lapsin 24minutes.By how many minutes has she improved herlap time?(A)12(B)34(C)1(D)2(E)34.Initially,a spinner points west.Chenille moves it clockwise214revolutions and then counterclockwise 334revolutions.In what direction does the spinner point after the twomoves?(A)north (B)east (C)south (D)west (E)northwest 5.Points A ,B ,C and D are midpoints of the sides of the larger square.If the larger square has area 60,what is the area of the smaller square?ABCD (A)15(B)20(C)24(D)30(E)406.The letter T is formed by placing two2inch×4inch rectangles next to eachother,as shown.What is the perimeter of the T,in inches?(A)12(B)16(C)20(D)22(E)247.Circle X has a radius ofπ.Circle Y has a circumference of8π.Circle Z has anarea of9π.List the circles in order from smallest to largest radius.(A)X,Y,Z(B)Z,X,Y(C)Y,X,Z(D)Z,Y,X(E)X,Z,Y8.The table shows some of the results of a survey by radiostation KAMC.What percentage of the males surveyedlisten to the station?Listen Don’t Listen TotalMale?26?Female58?96Total13664200(A)39(B)48(C)52(D)55(E)759.What is the product of32×43×54...×20062005?(A)1(B)1002(C)1003(D)2005(E)200610.Jorge’s teacher asks him to plot all the ordered pairs(w,l)of positive integersfor which w is the width and l is the length of a rectangle with area12.What should his graph look like?(A)(B)(C)(D)(E)11.How many two-digit numbers have digits whose sum is a perfect square?(A)13(B)16(C)17(D)18(E)1912.Antonette gets70%on a10-problem test,80%on a20-problem test and90%on a30-problem test.If the three tests are combined into one60-problem test, which percent is closest to her overall score?(A)40(B)77(C)80(D)83(E)8713.Cassie leaves Escanaba at8:30AM heading for Marquette on her bike.Shebikes at a uniform rate of12miles per hour.Brian leaves Marquette at9:00 AM heading for Escanaba on his bike.He bikes at a uniform rate of16miles per hour.They both bike on the same62-mile route between Escanaba and Marquette.At what time in the morning do they meet?(A)10:00(B)10:15(C)10:30(D)11:00(E)11:30Problems14,15and16involve Mrs.Reed’s English assignment.A Novel AssignmentThe students in Mrs.Reed’s English class are reading the same760-page novel.Three friends,Alice,Bob and Chandra,are in the class.Alice reads a page in 20seconds,Bob reads a page in45seconds and Chandra reads a page in30 seconds.14.If Bob and Chandra both read the whole book,Bob willspend how many more seconds reading than Chandra?(A)7,600(B)11,400(C)12,500(D)15,200(E)22,80015.Chandra and Bob,who each have a copy of the book,decide that they can savetime by“team reading”the novel.In this scheme,Chandra will read from page 1to a certain page and Bob will read from the next page through page760,finishing the book.When they are through they will tell each other about the part they read.What is the last page that Chandra should read so that she and Bob spend the same amount of time reading the novel?(A)425(B)444(C)456(D)484(E)50616.Before Chandra and Bob start reading,Alice says she would like to team readwith them.If they divide the book into three sections so that each reads for the same length of time,how many seconds will each have to read?(A)6400(B)6600(C)6800(D)7000(E)720017.Jeffrotates spinners P,Q and R and adds the resulting numbers.What is theprobability that his sum is an odd number?P Q R(A)14(B)13(C)12(D)23(E)3418.A cube with3-inch edges is made using27cubes with1-inch edges.Nineteenof the smaller cubes are white and eight are black.If the eight black cubes are placed at the corners of the larger cube,what fraction of the surface area of the larger cube is white?(A)19(B)14(C)49(D)59(E)192719.Triangle ABC is an isosceles triangle with AB=BC.Point D is the midpointof both BC and AE,and CE is11units long.Triangle ABD is congruent to triangle ECD.What is the length of BD?A BDCE(A)4(B)4.5(C)5(D)5.5(E)620.A singles tournament had six players.Each player played every other playeronly once,with no ties.If Helen won4games,Ines won3games,Janet won 2games,Kendra won2games and Lara won2games,how many games did Monica win?(A)0(B)1(C)2(D)3(E)421.An aquarium has a rectangular base that measures100cm by40cm and has aheight of50cm.The aquarium isfilled with water to a depth of37cm.A rock with volume1000cm3is then placed in the aquarium and completely submerged.By how many centimeters does the water level rise?(A)0.25(B)0.5(C)1(D)1.25(E)2.522.Three different one-digit positive integers are placed in the bottom row of cells.Numbers in adjacent cells are added and the sum is placed in the cell above them.In the second row,continue the same process to obtain a number in the top cell.What is the difference between the largest and smallest numbers possible in the top cell?(A)16(B)24(C)25(D)26(E)3523.A box contains gold coins.If the coins are equally divided amongsix people,four coins are left over.If the coins are equally dividedamongfive people,three coins are left over.If the box holds thesmallest number of coins that meets these two conditions,howmany coins are left when equally divided among seven people?(A)0(B)1(C)2(D)3(E)524.In the multiplication problem below,A,B,C and D are different digits.Whatis A+B?ABA×CDCDCD(A)1(B)2(C)3(D)4(E)925.Barry wrote6different numbers,one on each side of3cards,and laid the cardson a table,as shown.The sums of the two numbers on each of the three cards are equal.The three numbers on the hidden sides are prime numbers.What is the average of the hidden prime numbers?445938(A)13(B)14(C)15(D)16(E)17SOLUTIONSYour School Manager has been sent at least one copy of the 2006 AMC 8 Solutions Pamphlet. It is meant to be loaned to students (but not duplicated).WRITE TO USComments about the problems and solutions for this AMC 8 should be addressed to:Ms. Bonnie Leitch, AMC 8 Chair / bleitch@548 Hill Avenue, New Braunfels, TX 78130Comments about administrative arrangements should be addressed to:MAA American Mathematics Competitions / amcinfo@American Mathematics Competitions, University of Nebraska-LincolnP.O. Box 880658, Lincoln, NE 68588-0658AMC 10 & AMC 12The AMC 10 and AMC 12 are 25-question, 75-minute contests with 5 choices of answers for each problem (A through E). Schools with high scoring students on the AMC 8 will receive an Invitation Brochure for the 2007 AMC 10. The best way to prepare for these upper level contests is to study exams from previous years. Orders for all publications listed below should be addressed to:American Mathematics CompetitionsATTN: PublicationsP.O. Box 81606Lincoln, NE 68501-1606PUBLICATIONSA complete listing of current publications, with ordering instructions, is at our web site:/amc.**Administration On An Earlier Date Will Disqualify Your School’s Results**1. All information (Rules and Instructions) needed to administer this exam is contained in the TEACHERS’ MANUAL, which is outside of this package. PLEASE READ THE MANUAL BEFORE NOVEMBER 14, 2006. Noth-ing is needed from inside this package until November 14.2. Your PRINCIPAL or VICE-PRINCIPAL must verify on the AMC 8 CER-TIFICATION FORM that you followed all rules associated with the conduct of the exam.3. The Answer Forms must be mailed First Class to the AMC office no later than 24 hours following the exam.4. THE AMC 8 IS TO BE ADMINISTERED DURING A CONVENIENT 40 MINUTE PERIOD. THE EXAM MAY BE GIVEN DURING A REGULAR MATH CLASS.5. The publication, reproduction or communication of the problems or solutions of this test during the period when students are eligible to participate seriously jeopardizes the integrity of the results. Dissemination at any time via copier, telephone, e-mail, World Wide Web or media of any type is a violation of the competition rules.The American Mathematics Competitionsare Sponsored by The Mathematical Association of America –– MAA /The Akamai Foundation – /Contributors American Mathematical Association of Two Year Colleges ...................................................... /American Mathematical Society ........................................................................................... /American Society of Pension Actuaries ............................................................................... /American Statistical Association ....................................................................................... /Art of Problem Solving /Canada/USA Mathpath /Canada/USA Mathcamp /Casualty Actuarial Society ................................................................................................ /Clay Mathematics Institute ........................................................................................... /Consortium for Mathematics & its Applications /Institute for Operations Research and the Management Sciences .................................................. /L. G. Balfour Company /Mu Alpha Theta .................................................................................................... /National Assessment & Testing ................................................................../National Council of Teachers of Mathematics ...................................................................... /Pedagoguery Software Inc. /Pi Mu Epsilon ............................................................................................................. /Society of Actuaries .............................................................................................................. /U. S. A. Math Talent Search ............................................................................................ /W. H. Freeman and Company .................................................................................www. /Wolfram Research Inc. /2006AMC 8DO NOT OPEN UNTIL TUESDAY, NOVEMBER 14, 2006。
2006amc8解析

2006amc8解析
2006年AMC 8是一场备受期待的数学竞赛。
作为一名参赛者,我充满了紧张和兴奋。
我坐在考场上,紧握着铅笔,等待着考题的出现。
第一道题目出现在试卷上,题目要求计算一个数字的平方根。
我仔细思考了一下,然后用笔在答题卡上写下了我的解答。
接着,我继续阅读下一道题目。
第二道题目是一道几何题。
题目描述了一个矩形和一个三角形的关系,要求计算两者的面积比。
这个题目对我来说稍微有一些难度,但我努力思考并找到了解题思路。
我将我的答案写在了答题卡上,继续前进。
第三道题目是一道关于数字模式的题目。
题目给出了一系列数字,要求我们找出规律并计算下一个数字是多少。
这个题目需要一些耐心和逻辑思维,但我成功地解决了它。
我继续解答剩下的题目,每一道题目都有着自己的难度和挑战。
有些题目需要运用数学知识,有些题目则需要灵活运用思维。
我努力思考每一个问题,并尽力给出最准确的答案。
时间到了,我交卷离开了考场。
虽然我不知道自己的得分情况,但我知道我尽力了。
这次竞赛对我来说是一次宝贵的学习经验,我学到了很多新的数学概念和解题技巧。
参加AMC 8是一种挑战,但也是一种乐趣。
这次竞赛让我更加热爱数学,并激发了我对数学的探索欲望。
我期待着未来的数学竞赛,希望能够在其中继续成长和进步。
总的来说,2006年AMC 8是一次令人难忘的竞赛经历。
通过这次竞赛,我不仅提高了自己的数学水平,还培养了解决问题的能力和团队合作精神。
这次经历让我更加热爱数学,并愿意迎接更多的数学挑战。
AMC8(美国数学竞赛)历年真题、答案及中英文解析

AMC8(美国数学竞赛)历年真题、答案及中英文解析艾蕾特教育的AMC8 美国数学竞赛考试历年真题、答案及中英文解析:AMC8-2020年:真题 --- 答案---解析(英文解析+中文解析)AMC8 - 2019年:真题----答案----解析(英文解析+中文解析)AMC8 - 2018年:真题----答案----解析(英文解析+中文解析)AMC8 - 2017年:真题----答案----解析(英文解析+中文解析)AMC8 - 2016年:真题----答案----解析(英文解析+中文解析)AMC8 - 2015年:真题----答案----解析(英文解析+中文解析)AMC8 - 2014年:真题----答案----解析(英文解析+中文解析)AMC8 - 2013年:真题----答案----解析(英文解析+中文解析)AMC8 - 2012年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 2010年:真题----答案----解析(英文解析+中文解析)AMC8 - 2009年:真题----答案----解析(英文解析+中文解析)AMC8 - 2008年:真题----答案----解析(英文解析+中文解析)AMC8 - 2007年:真题----答案----解析(英文解析+中文解析)AMC8 - 2006年:真题----答案----解析(英文解析+中文解析)AMC8 - 2005年:真题----答案----解析(英文解析+中文解析)AMC8 - 2004年:真题----答案----解析(英文解析+中文解析)AMC8 - 2003年:真题----答案----解析(英文解析+中文解析)AMC8 - 2002年:真题----答案----解析(英文解析+中文解析)AMC8 - 2001年:真题----答案----解析(英文解析+中文解析)AMC8 - 2000年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1998年:真题----答案----解析(英文解析+中文解析)AMC8 - 1997年:真题----答案----解析(英文解析+中文解析)AMC8 - 1996年:真题----答案----解析(英文解析+中文解析)AMC8 - 1995年:真题----答案----解析(英文解析+中文解析)AMC8 - 1994年:真题----答案----解析(英文解析+中文解析)AMC8 - 1993年:真题----答案----解析(英文解析+中文解析)AMC8 - 1992年:真题----答案----解析(英文解析+中文解析)AMC8 - 1991年:真题----答案----解析(英文解析+中文解析)AMC8 - 1990年:真题----答案----解析(英文解析+中文解析)AMC8 - 1989年:真题----答案----解析(英文解析+中文解析)AMC8 - 1988年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1986年:真题----答案----解析(英文解析+中文解析)AMC8 - 1985年:真题----答案----解析(英文解析+中文解析)◆AMC介绍◆AMC(American Mathematics Competitions) 由美国数学协会(MAA)组织的数学竞赛,分为 AMC8 、 AMC10、 AMC12 。
2006AMC试题 A

AMC 10 2006 A1 Sandwiches at Joe’s Fast Food cost $3 each and sodas cost $2 each. How many dollars will it cost to purchase 5 sandwiches and 8 sodas?(A) 31 (B) 32 (C) 33 (D) 34 (E) 352 Define x⊕y = x3− y. What is h⊕(h⊕h)?(A) − h (B) 0 (C) h (D) 2h (E) h33 The ratio of Mary’s age to Alice’s age is 3 : 5. Alice is 30 years old. How old is Mary?(A) 15 (B) 18 (C) 20 (D) 24 (E) 504 A digital watch displays hours and minutes with AM and PM. What is the largest possible sum of the digits in the display?(A) 17 (B) 19 (C) 21 (D) 22 (E) 235 Doug and Dave shared a pizza with 8 equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half the pizza. The cost of a plain pizza was $8, and there wasan additional cost of $2 for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each paid for what he had eaten. How many more dollars did Dave pay than Doug?(A) 1 (B) 2 (C) 3 (D) 4 (E) 56 What non-zero real value for x satisfies (7x)14= (14x)7?(A)1/7 (B)2/7 (C) 1 (D) 7 (E) 147 The 8 × 18 rectangle ABCD is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is y?(A)6 (B) 7 (C) 8 (D) 9 (E) 108 A parabola with equation y = x2+ bx + c passes through the points (2, 3) and (4, 3). What is c?(A) 2 (B) 5 (C) 7 (D) 10 (E) 119 How many sets of two or more consecutive positive integers have a sum of 15?(A) 1 (B) 2 (C) 3 (D) 4 (E) 510 For how many real values of x is an integer?(A) 3 (B) 6 (C) 9 (D) 10 (E) 1111 Which of the following describes the graph of the equation (x + y)2= x2+ y2?(A) the empty set (B) one point (C) two lines (D) a circle (E) the entire plane12 Rolly wishes to secure his dog with an 8-foot rope to a square shed that is 16 feet on each side. His preliminary drawings are shown.(A) I, by 8π(B) I, by 6π(C) II, by 4π(D) II, by 8π(E) II, by 10π13 A player pays $5 to play a game. A die is rolled. If the number on the die is odd, the game is lost. If the number on the die is even, the die is rolled again. In this case the player wins if the second number matches the first and loses otherwise. How much should the player win if the game is fair? (In a fair game the probability of winning times the amount won is what the player should pay.)(A) $12 (B) $30 (C) $50 (D) $60 (E) $10014 A number of linked rings, each 1 cm thick, are hanging on a peg. The top ring has an outside diameter of 20 cm. The outside diameter of each of the outer rings is 1 cm less than that of the ring above it. The bottom ring has an outside diameter of 3 cm. What is the distance, in cm, from the top of the top ring to the bottom of the bottom ring?(A) 171 (B) 173 (C) 182 (D) 188 (E) 21015 Odell and Kershaw run for 30 minutes on a circular track. Odell runs clockwise at 250m/min and uses the inner lane with a radius of 50 meters. Kershaw runs counterclockwise at 300 m/min and uses the outer lane with a radius of 60 meters, starting on the same radial line as Odell. How many times after the start do they pass each other?(A) 29 (B) 42 (C) 45 (D) 47 (E) 5016 A circle of radius 1 is tangent to a circle of radius 2. The sides of 4ABC are tangent to the circles as shown, and the sides AB and AC are congruent. What is the area of 4ABC?(E) 2417 In rectangle ADEH, points B and C trisect AD, and points G and F trisect HE. In addition, AH = AC = 2. What is the area of quadrilateral WXY Z shown in the figure?(A)1/2(B)18 A license plate in a certain state consists of 4 digits, not necessarily distinct, and 2 letters, also not necessarily distinct. These six characters may appear in any order, except that the two letters must appear next to each other. How many distinct license plates are possible?(A) 104 · 262(B) 103· 263(C) 5 · 104· 262(D) 102· 264(E) 5 · 103· 26319 How many non-similar triangle have angles whose degree measures are distinct positive integers in arithmetic progression?(A) 0 (B) 1 (C) 59 (D) 89 (E) 17820 Six distinct positive integers are randomly chosen between 1 and 2006, inclusive. What is the probability that some pair of these integers has a difference that is a multiple of 5?(A)1/2(B)3/5(C)2/3(D)4/5(E) 121 How many four-digit positive integers have at least one digit that is a 2 or a 3?(A) 2439 (B) 4096 (C) 4903 (D) 4904 (E) 541622 Two farmers agree that pigs are worth $300 and that goats are worth $210. When one farmer owes the other money, he pays the debt in pigs or goats, with “change” received in the form of goats or pigs as necessary. (For example, a $390 debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way?(A) $5 (B) $10 (C) $30 (D) $90 (E) $21023 Circles with centers A and B have radii 3 and 8, respectively. A common internal tangent intersects the circles at C and D, respectively. Lines AB and CD intersect at E, and AE = 5. What is CD?(E)55/324 Centers of adjacent faces of a unit cube are joined to form a regular octahedron. What is the volume of this octahedron?(A)1/8(B)1/6(C)1/4(D)1/3(E)1/225 A bug starts at one vertex of a cube and moves along the edges of the cube according to the following rule. At each vertex the bug will choose to travel along one of the three edges emanating from that vertex. Each edge has equal probability of being chosen, and all choices are independent. What is the probability that after seven moves the bug will have visited every vertex exactly once?(A)1/2187(B)1/729(C)2/243(D)1/81(E)5/243。
AMC_2006
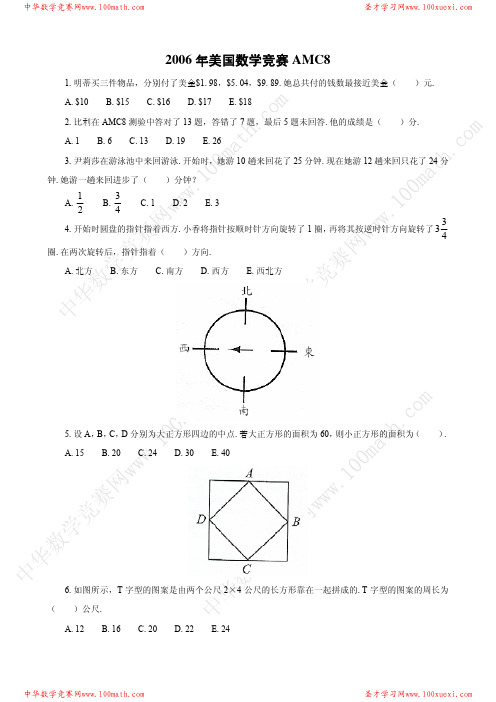
有 30 道题目的测验卷答对了 90%.若将这三份试卷合成一份有 60 道题目的测验卷,他的答对率最接近百
分之( ).
om A.49 B.77 C.80 D.83 E.87 h.c m 13.小明早上 8:30 从甲地骑脚踏車向乙地出发,他的速率是每小时 12 公里.小华早上 9:00 从乙地骑 at .co 脚踏車向甲地出发,他的速率是每小时 16 公里.他们两人骑車在連接两地长 62 公里的同一条路径上.他们 00m th 在早上( )相遇. .1 0ma A.10:00 B.10:15 C.10:30 D.11:00 E.11:30 www .10 下列第 14 题,第 15 题及第 16 题是关于锐德老师所规定的英文作业.
圣才学习网
7.圆 X 的半径为 π,圆 Y 的周长为 8π,圆 Z 的面积为 9π,则三个圆依半径由小到大排列的顺序为( ). ww 100 A.X,Y,Z B.Z,X,Y C.Y,X,Z D.Z,Y,X E.X,Z,Y 网w w. 8.下表为 KAMC 广播电台收听率调查的一些结果.在受调查的男性中有收听的占百分之( ).
25.贝克将六个相异的数分别写在三张卡片的两面上,并将卡片放在桌上,如图所示.如果每张卡片两 .10 ma 面上的数之和都相等,且被盖住的三个数都是质数,则被盖住的三个质数的平均值是( ).
中华数学竞赛网www 华数学竞赛网www.100 A.13 B.14 C.15 D.16 E.17 中
中华数学竞赛网
圣才学习网
中华数学竞赛网
圣才学习网
A.0 B.1 C.2 D.3 E.5 24.在下面的直式乘法运算中 A,B,C,D 为相异的数字.之值是( ). A.1 B.2 C.3 D.4 E.9
美国数学竞赛AMC8 -- 2006年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2006年真题解析(英文解析+中文解析) \Problem 1Answer: DSolution:The three prices round to $2, $5, and $10, which has a sum of 17.中文解析:三件商品价格先近似取整,然后求和:2+5+10=17. 答案是D。
Problem 2Answer: CSolution:As the AMC 8 only rewards 1 point for each correct answer, everything is irrelevant except the number Billy answered correctly,13.中文解析:正确的题目每题1分,错误或没做的题目都是0分,做对13题的得分应该是13. 答案是C。
Problem 3Answer: ASolution:When Elisa started, she finished a lap in 25/10=2.5 minutes. Now, she finishes a lap is 24/12=2 minutes. The difference is 2.5-2=0.5中文解析:开始25分钟游10圈,平均2.5分钟游1圈。
后来24分钟游12圈,平均2分钟游1圈。
速度从2.5分钟提高到2分钟,提高了0.5分钟,即1/2 分钟。
答案是A。
Problem 4Answer: BSolution:If the spinner goes clockwise 2+1/4 revolutions and then counterclockwise 3+3/4 revolutions, it ultimately goes counterclockwise 1+1/2 which brings the spinner pointing east.中文解析:最初方向指向西,转整数圈不改变指针方向。
2006AMC试题 B

AMC 10 2006 B1 What is (−1)1+ (−1)2+ · · · + (−1)2006?(A) − 2006 (B) − 1 (C) 0 (D) 1 (E) 20062 For real numbers x and y, define x⊕y = (x + y)(x − y). What is 3⊕(4⊕5)?(A) − 72 (B) − 27 (C) − 24 (D) 24 (E) 723 A football game was played between two teams, the Cougars and the Panthers. The two teams scored a total of 34 points, and the Cougars won by a margin of 14 points. How many points did the Panthers score?(A) 10 (B) 14 (C) 17 (D) 20 (E) 244 Circles of diameter 1 inch and 3 inches have the same center. The smaller circle is painted red, and the portion outside the smaller circle and inside the larger circle is painted blue. What is the ratio of the blue-painted area to the red-painted area?(A) 2 (B) 3 (C) 6 (D) 8 (E) 95 A 2 x 3 rectangle and a 3 x 4 rectangle are contained within a square without overlapping at any interior point, and the sides of the square are parallel to the sides of the two given rectangles. What is the smallest possible area of the square?(A) 16 (B) 25 (C) 36 (D) 49 (E) 646 A region is bounded by semicircular arcs constructed on the side of a square whose sides measure 2/π, as shown. What is the perimeter of this region?(A)4/π(B) 2 (C)8/π(D) 4 (E)16/π7 Which of the following is equivalent to when x < 0?(A) −8 A square of area 40 is inscribed in a semicircle as shown. What is the area of the semicircle?(A) 20π(B) 25π(C) 30π(D) 40π(E) 50π9 Francesca uses 100 grams of lemon juice, 100 grams of sugar, and 400 grams of water to make lemonade. There are 25 calories in 100 grams of lemon juice and 386 calories in 100 grams of sugar. Water contains no calories. How many calories are in 200 grams of her lemonade.(A) 129 (B) 137 (C) 174 (D) 223 (E) 41110 In a triangle with integer side lengths, one side is three times as long as a second side, and the length of the third side is 15. What is the greatest possible perimeter of the triangle?(A) 43 (B) 44 (C) 45 (D) 46 (E) 4711 What is the tens digit in the sum 7! + 8! + 9! + · · · + 2006!?(A) 1 (B) 3 (C) 4 (D) 6 (E) 912 The lines x =14y + a and y =14x + b intersect at the point (1, 2). What is a + b?(A) 0 (B)3/4(C) 1 (D) 2 (E)9/413 Joe and JoAnn each bought 12 ounces of coffee in a 16-ounce cup. Joe drank 2 ounces of his coffee and then added 2 ounces of cream. JoAnn added 2 ounces of cream, stirred the coffee well, and then drank 2 ounces. What is the resulting ratio of the amount of cream inJoe’s coffee to that in JoAnn’s coffee?(A)6/7(B)13/14(C) 1 (D)14/13(E)7/614 Let a and b be the roots of the equation x2− mx + 2 = 0. Suppose that a + (1/b) and b +(1/a)are the roots of the equation x2− px + q = 0. What is q?(A)5/2(B)7/2(C) 4 (D)9/2(E) 815 Rhombus ABCD is similar to rhombus BFDE. The area of rhombus ABCD is 24, and\BAD =60_. What is the area of rhombus BFDE?16 Leap Day, February 29, 2004, occurred on a Sunday. On what day of the week will Leap Day,February 29, 2020, occur?(A) Tuesday (B) Wednesday (C) Thursday (D) Friday (E) Saturday17 Bob and Alice each have a bag that contains one ball of each of the colors blue, green, orange, red, and violet. Alice randomly selects one ball from her bag and puts it into Bob’s bag. Bob then randomly selects one ball from his bag and puts it into Alice’s bag. What is the probability that after this process, the contents of the two bags are the same?(A)1/10(B)1/6(C)1/5(D)1/3(E)1/218 Let a1, a2, ... be a sequence for which a1= 2 a2= 3 and a n=( a n−1)/(a n−2)for each positive integer n≥3.What is a2006?(A)1/2(B)2/3(C)3/2(D) 2 (E) 319 A circle of radius 2 is centered at O. Square OABC has side length 1. Sides AB and CB are extended past b to meet the circle at D and E, respectively. What is the area of the shaded region in the figure, which is bounded by BD, BE, and the minor arc connecting D and E?(A)π/3+1(B)π(2 )/2_(C) π(2 π− 1)/2(E)π/3−20 In rectangle ABCD, we have A = (6,−22), B = (2006, 178), and D = (8, y), for some integer y.What is the area of rectangle ABCD?(A) 4000 (B) 4040 (C) 4400 (D) 40, 000 (E) 40, 40021 For a particular peculiar pair of dice, the probabilities of rolling 1, 2, 3, 4, 5 and 6 on each die are in the ratio 1 : 2 : 3 : 4 : 5 : 6. What is the probability of rolling a total of 7 on the two dice?(A)4/63(B)1/8(C)8/63(D)1/6(E)2/722 Elmo makes N sandwiches for a fundraiser. For each sandwich he uses B globs of peanut butter at 4 cents per glob and J blobs of jam at 5 cents per glob. The cost of the peanut butter and jam to make all the sandwiches is $2.53. Assume that B, J, and N are all positive integers with N > 1.What is the cost of the jam Elmo uses to make the sandwiches?(A) $1.05 (B) $1.25 (C) $1.45 (D) $1.65 (E) $1.8523 A triangle is partitioned into three triangles and a quadrilateral by drawing two lines from vertices to their opposite sides. The areas of the three triangles are 3, 7, and 7, as shown. What is the area of the shaded quadrilateral?(A) 15 (B) 17 (C)352(D) 18 (E)55/324 Circles with centers O and P have radii 2 and 4, respectively, and are externally tangent. Points A and B are on the circle centered at O, and points C and D are on the circle centered at P, such that AD and BC are common external tangents to the circles. What is the area of hexagon AOBCPD?25 Mr. Jones has eight children of different ages. On a family trip his olderst child, who is 9, spots a license plate with a 4-digit number in which each of two digitrs appears two times. “Look, daddy!” she excl aims. “That number is evenly divisible by the age of each of us kids!” “That’s right,” replies Mr. Jones, “and the last two digits just happen to be my age.” Which of the following is not the age of one of Mr. Jones’s children?(A) 4 (B) 5 (C) 6 (D) 7 (E) 8。
美国数学竞赛AMC8 -- 2005年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2005年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:If x is the number, then 2x=60 and x=30. Dividing the number by 2 yields 15.中文解析:按照Connie的计算,这个数乘以2是60,可知这个数是30. 应该做的计算是30除以2,因而正确答案应该是15. 答案是B。
Problem 2Answer: CSolution:Karl paid 5*2.5=$12.5. 20% of this cost that he saved is 12.5*0.2=$2.5.中文解析:Karl按原价买了5个文件夹,支付的费用是:2.5*5=12.5. 折扣价是:1.25*0.8=10。
如果Karl 等一天,可以省2.5元。
答案是C.Problem 3Answer: DSolution:Rotating square ABCD counterclockwise 45° so that the line of symmetry BD is a vertical line makes it easier to see that 4 squares need to be colored to match its corresponding square.中文解析:如上图所示,以BD为对称轴,标蓝色的方块需要涂黑。
共4块,答案是D。
Problem 4Answer: CSolution:The perimeter of the triangle is 6.1+8.2+9.7=24cm. A square's perimeter is four times its side length, since all its side lengths are equal. If the square's perimeter is 24, the side length is24/4=6, and the area is 6*6=36.中文解析:三角形的周长是:6.1+8.2+9.7=24. 正方形的周长和三角形相等,也是24,则其边长是24/4=6. 其面积是:6*6=36. 答案是C。
