C数学建模实验二
数学建模实验报告

湖南城市学院数学与计算科学学院《数学建模》实验报告专业:学号:姓名:指导教师:成绩:年月日目录实验一 初等模型........................................................................ 错误!未定义书签。
实验二 优化模型........................................................................ 错误!未定义书签。
实验三 微分方程模型................................................................ 错误!未定义书签。
实验四 稳定性模型.................................................................... 错误!未定义书签。
实验五 差分方程模型................................................................ 错误!未定义书签。
实验六 离散模型........................................................................ 错误!未定义书签。
实验七 数据处理........................................................................ 错误!未定义书签。
实验八 回归分析模型................................................................ 错误!未定义书签。
实验一 初等模型实验目的:掌握数学建模的基本步骤,会用初等数学知识分析和解决实际问题。
实验内容:A 、B 两题选作一题,撰写实验报告,包括问题分析、模型假设、模型构建、模型求解和结果分析与解释五个步骤。
数学建模基础实验报告(3篇)

第1篇一、实验目的本次实验旨在让学生掌握数学建模的基本步骤,学会运用数学知识分析和解决实际问题。
通过本次实验,培养学生主动探索、努力进取的学风,增强学生的应用意识和创新能力,为今后从事科研工作打下初步的基础。
二、实验内容本次实验选取了一道实际问题进行建模与分析,具体如下:题目:某公司想用全行业的销售额作为自变量来预测公司的销售量。
表中给出了1977—1981年公司的销售额和行业销售额的分季度数据(单位:百万元)。
1. 数据准备:将数据整理成表格形式,并输入到计算机中。
2. 数据分析:观察数据分布情况,初步判断是否适合使用线性回归模型进行拟合。
3. 模型建立:利用统计软件(如MATLAB、SPSS等)进行线性回归分析,建立公司销售额对全行业的回归模型。
4. 模型检验:对模型进行检验,包括残差分析、DW检验等,以判断模型的拟合效果。
5. 结果分析:分析模型的拟合效果,并对公司销售量的预测进行评估。
三、实验步骤1. 数据准备将数据整理成表格形式,包括年份、季度、公司销售额和行业销售额。
将数据输入到计算机中,为后续分析做准备。
2. 数据分析观察数据分布情况,绘制散点图,初步判断是否适合使用线性回归模型进行拟合。
3. 模型建立利用统计软件进行线性回归分析,建立公司销售额对全行业的回归模型。
具体步骤如下:(1)选择合适的统计软件,如MATLAB。
(2)输入数据,进行数据预处理。
(3)编写线性回归分析程序,计算回归系数。
(4)输出回归系数、截距等参数。
4. 模型检验对模型进行检验,包括残差分析、DW检验等。
(1)残差分析:计算残差,绘制残差图,观察残差的分布情况。
(2)DW检验:计算DW值,判断随机误差项是否存在自相关性。
5. 结果分析分析模型的拟合效果,并对公司销售量的预测进行评估。
四、实验结果与分析1. 数据分析通过绘制散点图,观察数据分布情况,初步判断数据适合使用线性回归模型进行拟合。
2. 模型建立利用MATLAB进行线性回归分析,得到回归模型如下:公司销售额 = 0.9656 行业销售额 + 0.01143. 模型检验(1)残差分析:绘制残差图,观察残差的分布情况,发现残差基本呈随机分布,说明模型拟合效果较好。
数学建模题目c (2)
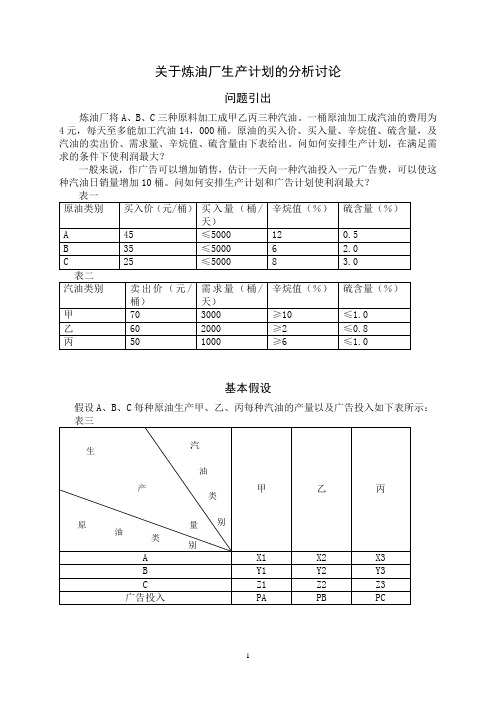
关于炼油厂生产计划的分析讨论问题引出炼油厂将A、B、C三种原料加工成甲乙丙三种汽油。
一桶原油加工成汽油的费用为4元,每天至多能加工汽油14,000桶。
原油的买入价、买入量、辛烷值、硫含量,及汽油的卖出价、需求量、辛烷值、硫含量由下表给出。
问如何安排生产计划,在满足需求的条件下使利润最大?一般来说,作广告可以增加销售,估计一天向一种汽油投入一元广告费,可以使这种汽油日销量增加10桶。
问如何安排生产计划和广告计划使利润最大?基本假设假设A、B、C每种原油生产甲、乙、丙每种汽油的产量以及广告投入如下表所示:建立模型及求解一、不考虑广告投入时的模型求解:由以上述条件可知:PA=PB=PC=0;总利润为:70*3000+60*2000+50*1000-45*(X1+X2+X3)-35*(Y1+Y2+Y3)-25*(Z1+Z2+Z3)-4*(X1+X2+ X3+Y1+Y2+Y3+Z1+Z2+Z3)针对买入量与总产量得条件①:X1+X2+X3+Y1+Y2+Y3+Z1+Z2+Z3≤14000;X1+X2+X3≤5000;Y1+Y2+Y3≤5000;Z1+Z2+Z3≤5000;针对需求量得条件②:X1+Y1+Z1≥3000;X2+Y2+Z2≥2000;X3+Y3+Z3≥1000;针对辛烷值得条件③:12%*X1+6%*Y1+8%*Z1≥10%*(X1+Y1+Z1);12%*X2+6%*Y2+8%*Z2≥2%*(X2+Y2+Z2);12%*X3+6%*Y3+8%*Z3≥6%*(X3+Y3+Z3);针对硫含量得条件④:0.5%*X1+2.0%*Y1+3.0%*Z1≤1.0%*(X1+Y1+Z1);0.5%*X2+2.0%*Y2+3.0%*Z2≤0.8%*(X2+Y2+Z2);0.5%*X3+2.0%*Y3+3.0%*Z3≤1.0%*(X3+Y3+Z3);X1,X2,X3,Y1,Y2,Y3,Z1,Z2,Z3均为非负整数;结果分析与检验利用LING0 9.0求解在上述四条件下利润的最大值得(LINGO程序见附录一):当X1=2400,X2=1600, X3=800,Z1=600,Z2=400,Z3=200,其余变量值为0;即用A类原油生产2400桶甲类汽油,生产1600桶乙类石油,生产800桶丙类石油,用C类原油生产600桶甲类汽油,用C类原油生产400桶乙类汽油,用C类原油生产200桶丙类汽油时,总利润达到最大值为110000元。
2021数学建模c题第二问模型

2021数学建模c题第二问模型摘要:1.问题背景及分析2.数学建模方法3.模型求解步骤4.模型检验与优化5.结论与启示正文:一、问题背景及分析随着我国科技发展的日益加快,数学建模在各个领域的应用越来越广泛。
以2021年数学建模C题第二问为例,题目要求针对某一实际问题,建立数学模型并进行求解。
本题的关键在于深入分析问题背景,找到合适的数学建模方法。
二、数学建模方法在分析问题后,我们可以选择适当的数学建模方法。
常用的数学建模方法有:微分方程模型、概率论模型、线性规划模型、神经网络模型等。
针对本题,我们可以选择以下方法:1.微分方程模型:根据问题中的动态关系,建立微分方程描述系统的行为。
2.概率论模型:分析问题中的不确定性因素,利用概率论方法描述随机过程。
3.线性规划模型:优化问题求解,合理安排资源分配等。
4.神经网络模型:模拟人脑神经网络,进行模式识别和预测。
三、模型求解步骤1.针对问题背景,选择合适的数学模型。
2.建立数学模型,包括相应的方程、边界条件等。
3.选择合适的求解方法,如数值方法、解析方法等。
4.编写程序或使用数学软件求解模型。
5.分析模型结果,检验模型的有效性。
四、模型检验与优化1.检验模型是否符合实际问题的背景和条件。
2.检验模型求解结果的合理性和可靠性。
3.对比不同模型的优缺点,选择合适的模型。
4.针对模型存在的问题,进行优化和改进。
五、结论与启示通过对2021年数学建模C题第二问的分析和解答,我们可以得出以下结论:1.数学建模是一项实践性较强的任务,需要结合问题背景选择合适的建模方法。
2.建立数学模型时,要注重模型的实际意义和可行性。
3.模型求解过程中,要熟练掌握各种求解方法,并灵活运用数学软件。
4.模型检验与优化是数学建模的重要环节,关系到模型的实用价值。
本次数学建模C题的解答过程给我们带来了许多启示,如面对复杂问题时,要学会分析问题背景、寻找关键因素,并灵活运用所学知识。
数学建模实验报告2

aij >0,
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
数学建模实验二:微分方程模型Matlab求解与分析

实验二: 微分方程模型Matlab 求解与分析一、实验目的[1] 掌握解析、数值解法,并学会用图形观察解的形态和进行解的定性分析; [2] 熟悉MATLAB 软件关于微分方程求解的各种命令;[3] 通过范例学习建立微分方程方面的数学模型以及求解全过程; [4] 熟悉离散 Logistic 模型的求解与混沌的产生过程。
二、实验原理1. 微分方程模型与MATLAB 求解解析解用MATLAB 命令dsolve(‘eqn1’,’eqn2’, ...) 求常微分方程(组)的解析解。
其中‘eqni'表示第i 个微分方程,Dny 表示y 的n 阶导数,默认的自变量为t 。
(1) 微分方程 例1 求解一阶微分方程 21y dxdy+= (1) 求通解 输入:dsolve('Dy=1+y^2')输出:ans =tan(t+C1)(2)求特解 输入:dsolve('Dy=1+y^2','y(0)=1','x')指定初值为1,自变量为x 输出:ans =tan(x+1/4*pi)例2 求解二阶微分方程 221()04(/2)2(/2)2/x y xy x y y y πππ'''++-=='=-原方程两边都除以2x ,得211(1)04y y y x x'''++-= 输入:dsolve('D2y+(1/x)*Dy+(1-1/4/x^2)*y=0','y(pi/2)=2,Dy(pi/2)=-2/pi','x')ans =- (exp(x*i)*(pi/2)^(1/2)*i)/x^(1/2) +(exp(x*i)*exp(-x*2*i)*(pi/2)^(3/2)*2*i)/(pi*x^(1/2))试试能不用用simplify 函数化简 输入: simplify(ans)ans =2^(1/2)*pi^(1/2)/x^(1/2)*sin(x) (2)微分方程组例3 求解 d f /d x =3f +4g ; d g /d x =-4f +3g 。
数学实验与数学建模 实验二

数学实验与数学建模实验二2.圆钢原材料每根长5.5米,现需要A,B,C三种圆钢材料,长度分别为3.1m,2.1m,1.2m,数量分别为100根,200根,400根,试安排下料方式,使所需圆钢原材料的总数最少。
约束条件为:目标函数:则列lingo程序如下:min=x1+x2+x3+x4+x5;x1+x2>=100;x1+x3+2*x4>=200;2*x2+2*x3+x4+4*x5>=400;@gin(x1);@gin(x2);@gin(x3);@gin(x4);@gin(x5);End运行结果如下:结合lingo数据得出结论:方案一和三没有采用,方案二和四用去100跟原材料,方案五用去25跟原材料,一共用去225根原材料,即为最优。
3.住宅小区服务中心选址:某地新建一个生活住宅区,共有20栋住宅楼,小区内所有道路都是东西或南北走向,开发商拟在小区内修建一个服务中心,地址选在离所有楼房的总路程最小的地方。
为保证建筑物之间有足够的空间,服务中心的位置与其他楼房位置之间的距离不能少于30米(已经考虑了所有建筑的占地面积),请你确定服务中心的位置。
设初始点X0=[20,20],设(ai,bi)(i=1,......,20)为第i栋住宅楼的坐标:a=[29.74 4.9 69.32 65.0 98.3 55.27 40.0 19.8 62.5 73.3 37.58 0.98 41.98 75.37 79.38 92.0 84.47 36.77 62.08 73.13],b=[19.39 90.48 56,92 63.18 23.44 54.88 93.16 33.5 65.5 39.19 62.73 69.9 39.72 41.37 65.52 43.5 34.6 75.2 12.32 86.7]。
约束条件:目标函数:解:列出lingo式子如下:model:sets:zl/1..20/:x,y,e;endsetsdata:x=29.74,4.9,69.32,65.0,98.3,55.27,40.0,19.8,62.5,73.3,37.58,0.98,41.98,75.37,79.38,92.0,84.47,36.77,62.08,7 3.13;y=19.39,90.48,56.92,63.18,23.44,54.88,93.16,33.5,65.5,39.19,62.73,69.9,39.72,41.37,65.52,43.5,34.6,75.2,12.32,86.7;e=20,20;enddatamin=@sum(zl(i):(((x(i)-px)^2)^(1/2)+((y(i)-py)^2)^(1/2)));@for(zl(i):(x(i)-px)^2+(y(i)-py)^2>=900);end运行结果如下:得出结论为:当服务中心的坐标为[1.281228,9.897984]时,离所有的楼房的总路程最小。
数学建模实验

数学建模实验项目一梯子问题一、实验目的与意义:1、进一步熟悉数学建模步骤;2、练习Matlab优化工具箱函数;3、进一步熟悉最优化模型的求解过程。
二、实验要求:1、较能熟练应用Matlab工具箱去求解常规的最优化模型;2、注重问题分析与模型建立,熟悉建模小论文的写作过程;3、提高Matlab的编程应用技能。
三、实验学时数:2学时四、实验类别:综合性五、实验内容与步骤:一幢楼房的后面是一个很大的花园。
在花园中紧靠着楼房建有一个温室,温室高10英尺,延伸进花园7英尺。
清洁工要打扫温室上方的楼房的窗户。
他只有借助于梯子,一头放在花园中,一头靠在楼房的墙上,攀援上去进行工作。
他只有一架20米长的梯子,你认为他能否成功?能满足要求的梯子的最小长度是多少?步骤:1.先进行问题分析,明确问题;2.建立模型,并运用Matlab函数求解;3.对结果进行分析说明;4.设计程序画出图形,对问题进行直观的分析和了解(主要用画线函数plot,line)5.写一篇建模小论文。
数学建模实验项目二养老基金问题一、实验目的与意义:1、练习初等问题的建模过程;2、练习Matlab基本编程命令;二、实验要求:3、较能熟练应用Matlab基本命令和函数;4、注重问题分析与模型建立,了解建模小论文的写作过程;5、提高Matlab的编程应用技能。
三、实验学时数:1学时四、实验类别:综合性五、实验内容与步骤:某大学青年教师从31岁开始建立自己的养老基金,他把已有的积蓄10000元也一次性地存入,已知月利率为0.001(以复利计),每月存入700元,试问当他60岁退休时,他的退休基金有多少?又若,他退休后每月要从银行提取1000元,试问多少年后他的基金将用完?微分方程实验项目一狐狸与野兔问题一、实验目的与意义:1、认识微分方程的建模过程;2、认识微分方程的数值解法。
二、实验要求:1、熟练应用Matlab 的符号求解工具箱求解常微分方程;2、掌握机理分析建立微分方程的方法和步骤;3、提高Matlab 的编程应用技能。
数学建模的实验报告

数学建模实验报告姓名:学院:专业班级:学号:数学建模实验报告(一)——用最小二乘法进行数据拟合一.实验目的:1.学会用最小二乘法进行数据拟合。
2.熟悉掌握matlab软件的文件操作和命令环境。
3.掌握数据可视化的基本操作步骤。
4.通过matlab绘制二维图形以及三维图形。
二.实验任务:来自课本64页习题:用最小二乘法求一形如y=a+b x2的多项式,使之与下列数据拟合:三.实验过程:1.实验方法:用最小二乘法解决实际问题包含两个基本环节:先根据所给出数据点的变化趋势与问题的实际背景确定函数类;然后按照最小二乘法原则求最小二乘解来确定系数。
即要求出二次多项式: y=a+b x2的系数。
2.程序:x=[19 25 31 38 44]y=[19.0 32.3 49.0 73.3 97.8]ab=y/[ones(size(x));x.^2];a=ab(1),b=ab(2)xx=19:44;plot(xx,a+b*xx.^2,x,y,'.')3.上机调试得到结果如下:x = 19 25 31 38 44y=19.0000 32.3000 49.0000 73.3000 97.8000a = 0.9726b = 0.0500图形:四.心得体会通过本次的数学模型的建立与处理,我们学习并掌握了用最小二乘法进行数据拟合,及多项式数据拟合的方法,进一步学会了使用matlab软件,加深了我们的数学知识,提高了我们解决实际问题的能力,为以后深入学习数学建模打下了坚实的基础。
数学建模实验报告(二)——用Newton法求方程的解一.实验目的1.掌握Newton法求方程的解的原理和方法。
2.利用Matlab进行编程求近似解。
二.实验任务来自课本109页习题4-2:用Newton法求f(x)=x-cosx=0的近似解三.实验过程1.实验原理:把f(x)在x0点附近展开成泰勒级数f(x) = f(x0)+(x-x0)f'(x0)+(x-x0)^2*f''(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f'(x0)(x-x0)=0 设f'(x0)≠0则其解为x1=x0-f(x0)/f'(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f'(x(n))。
数学建模实验报告

内江师范学院中学数学建模实验报告册编制数学建模组审定牟廉明专业:班级:级班学号:姓名:数学与信息科学学院2016年3月说明1.学生在做实验之前必须要准备实验,主要包括预习与本次实验相关的理论知识,熟练与本次实验相关的软件操作,收集整理相关的实验参考资料,要求学生在做实验时能带上充足的参考资料;若准备不充分,则学生不得参加本次实验,不得书写实验报告;2.要求学生要认真做实验,主要是指不得迟到、早退和旷课,在做实验过程中要严格遵守实验室规章制度,认真完成实验内容,极积主动地向实验教师提问等;若学生无故旷课,则本次实验成绩不合格;3.学生要认真工整地书写实验报告,实验报告的内容要紧扣实验的要求和目的,不得抄袭他人的实验报告;4.实验成绩评定分为优秀、合格、不合格,实验只是对学生的动手能力进行考核,跟据所做的的情况酌情给分。
根据实验准备、实验态度、实验报告的书写、实验报告的内容进行综合评定。
实验名称:数学规划模型(实验一)指导教师:实验时数: 4 实验设备:安装了VC++、mathematica、matlab的计算机实验日期:年月日实验地点:实验目的:掌握优化问题的建模思想和方法,熟悉优化问题的软件实现。
实验准备:1.在开始本实验之前,请回顾教科书的相关内容;2.需要一台准备安装Windows XP Professional操作系统和装有数学软件的计算机。
实验内容及要求原料钢管每根17米,客户需求4米50根,6米20根,8米15根,如何下料最节省?若客户增加需求:5米10根,由于采用不同切割模式太多,会增加生产和管理成本,规定切割模式不能超过3种,如何下料最节省?实验过程:摘要:生活中我们常常遇到对原材料进行加工、切割、裁剪的问题,将原材料加工成所需大小的过程,称为原料下料问题。
按工艺要求,确定下料方案,使用料最省,或利润最大是典型的优化问题。
以此次钢管下料问题我们采用数学中的线性规划模型.对模型进行了合理的理论证明和推导,然后借助于解决线性规划的专业软件Lingo 对题目所提供的数据进行计算从而得出最优解。
数学建模-数学实验2

实验5 定积分的近似计算一、问题求定积分的近似值。
二、实验目的了解定积分计算的梯形法与抛物线法;会用Mathematica语言编写求定积分近似值的程序;会用Mathematica中的系统算符求定积分。
三、预备知识根据牛顿-莱布尼兹公式,定积分的值可以通过求原函数而计算出来,但在工程技术与科学实验中,有些定积分的被积函数的原函数可能求不出来,即使求出,计算也可能很复杂;特别地,当被积函数是用图形或表格给出时,更不能用牛顿-莱布尼兹公式计算。
因此必需寻求定积分的近似计算方法,根据定积分的几何意义就是曲线,直线,及轴所围的面积,因此有下述近似计算方法。
1.梯形法梯形法就是把曲边梯形分成若干窄小曲边梯形,然后用相应的窄小梯形来近似代替窄小曲边梯形,以窄小梯形的面积之和作为曲边梯形的近似值。
具体做法如下:用分点将区间 [,] 分成个等长的小区间,每个小区间的长度记为,设函数y =f (x) 对应于各分点的函数值为 y0 , y1 , y2 ,… yn ,如右图所示,每一个窄小梯形的面积为:==(i =1,2,…n)从而有= (1)(1)式称为梯形法公式。
若时存在且,可以证明梯形法的误差为|-|对于较复杂函数f(x),估计的上限往往比计算定积分本身更复杂,与实验四的牛顿迭代法的误差估计类似,在编程计算定积分时可采用如下方法估计误差。
记=,误差限为,逐步计算,若则以A(n+1)作为的近似值,实现该方法的Mathematica程序如下。
f[x_]:=以x为自变量的函数表达式;er=误差限a=积分下限; b=积分上限;n=4;(*从4等分开始计算*)A[t_]:=((b-a)/t)*((f[a]+f[b])/2+Sum[f[a+i*(b-a)/t],{i,1,t-1}]); (*梯形法公式*) While[Abs[N[A[n+1]-A[n]]]>er,n=n+1];N[A[n]] (*输出定积分的近似值*)n (*输出计算停止时对[a,b]的等分数*)上述程序的效率并不高,因为在计算A(n+1)时没有利用到A(n)的信息,这里我们可以采用步长加倍法,即第二次计算时等分数加倍,A(2n)与A(n)的关系为A(2n)==A(n)+误差估计用,上述方法的Mathematica程序请读者自行考虑。
[数学建模]自选实验题二 汉诺塔游戏的解法演示
![[数学建模]自选实验题二 汉诺塔游戏的解法演示](https://img.taocdn.com/s3/m/505e153f5727a5e9856a6117.png)
汉诺塔游戏的解法演示问题背景汉诺塔是源自印度神话里的玩具。
上帝创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上安大小顺序摞着64片黄金圆盘。
上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
有预言说,这件事完成时宇宙会在一瞬间闪电式毁灭。
也有人相信婆罗门至今还在一刻不停地搬动着圆盘。
数学模型现在有三根相邻的柱子,标号为A,B,C,A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘,现在把所有盘子一个一个移动到柱子B上,并且每次移动同一根柱子上都不能出现大盘子在小盘子上方,请问至少需要多少次移动,设移动次数为H(n)。
首先我们肯定是把上面n-1个盘子移动到柱子C上,然后把最大的一块放在B上,最后把C上的所有盘子移动到B上,由此我们得出表达式:H(1) = 1H(n) = 2*H(n-1)+1 (n>1)那么我们很快就能得到H(n)的一般式:H(n) = 2^n - 1 (n>0)并且这种方法的确是最少次数的,证明非常简单,可以尝试从2个盘子的移动开始证。
下面利用这种思想,给出一个用Mathematica软件模拟出的解法演示。
解析方法利用Mathematica,程序如下:(*一.输入变量区域*)(*输入圆环总数:如果总数在11以内还是可以很快出结果的*)zongshu = 11;(*从位置1移动到位置2则输入1->2,从位置1移动到位置3则输入1->3*)weizhi = "1->3";(*二.计算结果区域*)(*下面这三行是赋初值*)a = Table[ii, {ii, zongshu, 1, -1}];arr1 = {a, {}, {}};arr2 = {arr1};(*下面这两个二级嵌套的If语句用来判断最小圆环的移动方向*)If[weizhi == "1->3" || weizhi == "1→3",mowei = 3;If[Mod[zongshu, 2] == 0,fangx = 1,fangx = -1];];If[weizhi == "1->2" || weizhi == "1→2",mowei = 2;If[Mod[zongshu, 2] == 1,fangx = 1,fangx = -1];];For[ii = 1; jj = 1, ii < 2^(zongshu - 1) + 1, ii++,kk = arr1[[jj]][[-1]];arr1[[jj]] = Delete[arr1[[jj]], -1];jj = Mod[jj + fangx + 2, 3] + 1;arr1[[jj]] = Append[arr1[[jj]], kk];arr2 = Append[arr2, arr1];(*下面这两个If语句用来判断移动是否已经完成*)If[mowei == 2 && arr1[[1]] == {} && arr1[[3]] == {}, Break[];];If[mowei == 3 && arr1[[1]] == {} && arr1[[2]] == {}, Break[];];(*下面这一个三级嵌套的If语句判断除了最小圆环以外的圆环的移动方向*)If[arr1[[Mod[jj + 1, 3] + 1]] == {},xuanze = 1,If[arr1[[Mod[jj, 3] + 1]] == {},xuanze = 2,If[arr1[[Mod[jj, 3] + 1]][[-1]] < arr1[[Mod[jj + 1, 3] + 1]][[-1]],xuanze = 1,xuanze = 2;];];];(*下面这一个If语句用来接受上面的判断结果,然后移动圆环,也可以和上面的判断语句合并在一起写*)If[xuanze == 1,kk = arr1[[Mod[jj, 3] + 1]][[-1]];arr1[[Mod[jj, 3] + 1]] = Delete[arr1[[Mod[jj, 3] + 1]], -1];arr1[[Mod[jj + 1, 3] + 1]] = Append[arr1[[Mod[jj + 1, 3] + 1]], kk],kk = arr1[[Mod[jj + 1, 3] + 1]][[-1]];arr1[[Mod[jj + 1, 3] + 1]] = Delete[arr1[[Mod[jj + 1, 3] + 1]], -1];arr1[[Mod[jj, 3] + 1]] = Append[arr1[[Mod[jj, 3] + 1]], kk];];(*下面的arr2用来记录每一步的移动结果*)arr2 = Append[arr2, arr1];];(*下面的arr2是记录的完整的每一步移动结果,但是此处选择了不显示该结果,若要显示该结果,去掉arr2后的分号即可*)arr2;(*三.制作动画区域*)(*下面的tu[0]只是一个空的框架,防止动画过程中比例的变化*)tu[0] = Graphics3D[{Opacity[0], EdgeForm[None],Cuboid[{-zongshu, zongshu, 0}, {zongshu, 7*zongshu, zongshu + 2}]}, Boxed -> False, ViewPoint -> Right];For[zhen = 1; mm = 1, zhen <= Length[arr2], zhen++,For[ii = 1; kk1 = 1, ii <= 3, ii++,For[jj = 1, jj <= Length[arr2[[zhen]][[ii]]], jj++,(*下面的tu[kk1]用来记录每一步的圆环的位置*)tu[kk1] =Cylinder[{{0, 2*ii*zongshu, jj - 1}, {0, 2*ii*zongshu, jj}},arr2[[zhen]][[ii]][[jj]]];kk1++;];];(*下面的tu[zongshu+1]是三个杆*)tu[zongshu + 1] =Table[{Y ellow, Cylinder[{{0, 2*ii*zongshu, 0}, {0, 2*ii*zongshu, zongshu + 1}}, 0.3]}, {ii, 1, 3}];(*下面的zongtu[mm]用来记录整个动画过程*)zongtu[mm] =Graphics3D[Table[tu[kk2], {kk2, 1, zongshu + 1}],V iewPoint -> Right, Boxed -> False,PlotLabel -> Style[StringJoin["第", ToString[mm - 1], "步"], 16, Blue, FontWeight -> Bold, FontFamily -> "宋体"]];mm++;];(*下面的Animate命令为显示整个移动圆环的过程*)Animate[DynamicModule[{}, Show[zongtu[bushu], tu[0]]], {bushu, 1, Length[arr2], 1}, DisplayAllSteps -> True,AnimationRate -> 1,AnimationRepetitions -> 2, AnimationRunning -> False,BaseStyle -> Blue]。
数学建模计算实验2
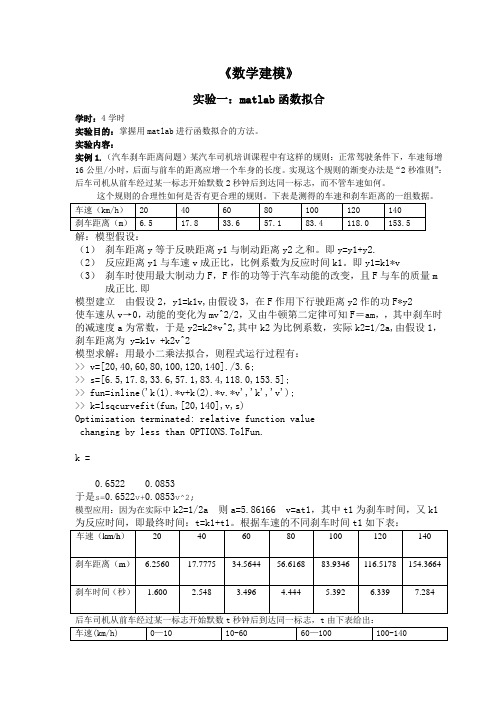
《数学建模》实验一:matlab函数拟合学时:4学时实验目的:掌握用matlab进行函数拟合的方法。
实验内容:实例1.(汽车刹车距离问题)某汽车司机培训课程中有这样的规则:正常驾驶条件下,车速每增16公里/小时,后面与前车的距离应增一个车身的长度。
实现这个规则的渐变办法是“2秒准则”:后车司机从前车经过某一标志开始默数2秒钟后到达同一标志,而不管车速如何。
这个规则的合理性如何是否有更合理的规则。
下表是测得的车速和刹车距离的一组数据。
车速(km/h)20 40 60 80 100 120 140刹车距离(m) 6.5 17.8 33.6 57.1 83.4 118.0 153.5解:模型假设:(1)刹车距离y等于反映距离y1与制动距离y2之和。
即y=y1+y2.(2)反应距离y1与车速v成正比,比例系数为反应时间k1。
即y1=k1*v(3)刹车时使用最大制动力F,F作的功等于汽车动能的改变,且F与车的质量m 成正比.即模型建立由假设2,y1=k1v,由假设3,在F作用下行驶距离y2作的功F*y2使车速从v→0,动能的变化为mv^2/2,又由牛顿第二定律可知F=am,,其中刹车时的减速度a为常数,于是y2=k2*v^2,其中k2为比例系数,实际k2=1/2a,由假设1,刹车距离为 y=k1v +k2v^2模型求解:用最小二乘法拟合,则程式运行过程有:>> v=[20,40,60,80,100,120,140]./3.6;>> s=[6.5,17.8,33.6,57.1,83.4,118.0,153.5];>> fun=inline('k(1).*v+k(2).*v.*v','k','v');>> k=lsqcurvefit(fun,[20,140],v,s)Optimization terminated: relative function valuechanging by less than OPTIONS.TolFun.k =0.6522 0.0853于是s=0.6522v+0.0853v^2;模型应用:因为在实际中k2=1/2a 则a=5.86166 v=at1,其中t1为刹车时间,又k1为反应时间,即最终时间:t=k1+t1。
数学建模实验2

《数学建模与数学实验》实验报告实验二水道测量专业、班级信息1002 学号201010010213 姓名兰雪娇课程编号81010240 实验类型验证性学时 2实验(上机)地点教七楼数学实验中心完成时间2012-6-7任课教师谷根代评分一、实验目的及要求1.掌握数学软件Matlab的基本用法和一些常用的规则,能用该软件进行编程;2.能够借助数学软件进行二维和三维网格化数据绘图;3.理解数据生成的基本方法。
二、借助数学软件,研究、解答以下问题(一)依题“水道测量”所给数据和要求,讨论在下面假设情况下的模型。
假设:(1)海底光滑,无暗礁(因浅水海域);(2)每个给定的数据点对未知点的影响与它们之间距离的平方成反比。
【解】:由于是在考察水域内随机测量有限个数据点,因此所得的数据是散乱的,这就必须对这些散乱数据进行规则化处理。
散乱数据规则化处理的一般流程是:散乱数据的三角剖分→三角网格优化→构造插值曲面→生成规则网格数据1.1 三角剖分一般地,如果一组三维散乱数据点能够有效地投影到某个平面,就可以把空间三角剖分简化为平面问题处理。
曲面较为平坦时,用这样的方法处理效果比较好。
水道的水底面起伏较大,若将三维散乱数据投影到平面上进行三角剖分将明显改变相邻三角形之间的内角关系,也无法真实反映其空间的角度关系,从而影响剖分效果。
因此,这里采用曲面上散乱数据三角剖分的Choi算法。
1.2 三角网格优化这里采用光顺准则对三角网格进行优化,即当空间四边形严格凸时,选择一条对角线(即一对三角形)使得该四边形四条边上的两共边三角形(面)之间的最小夹角最大。
如图2所示,设空间中一个严格凸的四边形ABCD ,四边形由四边e 1,e 2,e 3,e 4界定。
该四边形可看作三角网格中的一个局部区域,我们的目标是利用光顺准则使该局部区域与周围的三角网格光滑的相连接,即对该四边形选择一种三角剖分,使得四条边上两条边三角形(面)之间的最小夹角最大。
数学建模实验二

基本实验1.微分方程稳定性分析绘出下列自治系统相应的轨线,并标出随t 增加的运动方向,确定平衡点,并按稳定的、渐近稳定的、或不稳定的进行分类:解答:(1)由平衡点的定义可得,f(x)=x=0,f(y)=y=0,因此平衡点为(0,0),系统的线性近似方程的系数矩阵为⎥⎦⎤⎢⎣⎡=1001A ,解得其特征值121==λλ.()0221<-=+-=λλp ,0121>=⋅=λλq .对照稳定性的情况表,可知平衡点(0, 0)是不稳定的。
自治系统相应轨线为:(2)由平衡点的定义可得,f(x)=-x=0,f(y)=2y=0,因此平衡点为(0,0),系统的线性近似方程的系数矩阵为⎥⎦⎤⎢⎣⎡-=2001A ,解得其特征值2;121=-=λλ.()0121<-=+-=λλp ,0221<-=⋅=λλq .对照稳定性的情况表,可知平衡点(0, 0)是不稳定的。
自治系统相应轨线为:(3)由平衡点的定义可得,f(x)=y=0,f(y)=-2x=0,因此平衡点为(0,0),系统的线性近似方程的系数矩阵为⎥⎦⎤⎢⎣⎡-=0210A ,解得其特征值i i 2;221-==λλ.()021=+-=λλp ,0221>=⋅=λλq .对照稳定性的情况表,可知平衡点(0, 0)是不稳定的。
自治系统相应轨线为:(4)由平衡点的定义可得,f(x)=-x=0,f(y)=-2y=0,因此平衡点为(0,0),系统的线性近似方程的系数矩阵为⎥⎦⎤⎢⎣⎡--=2001A ,解得其特征值2;121-=-=λλ.()0321>=+-=λλp ,0221>=⋅=λλq .对照稳定性的情况表,可知平衡点(0, 0)是稳定的。
自治系统相应轨线为:2.营养平衡问题营养以每单位时间R 个分子的常速流入一个细胞,并且以其内营养浓度成比例的速度离开,比例常数为K ,设N 为t 时刻的浓度,则上述营养变化速度的数学描述为:KN R dtdN-= 即N 的变化速度等于营养进入细胞的速度减去它们离开的速度,营养的浓度会达到平衡吗?如果能,平衡解是什么?它是稳定的吗?试用这个方程解的图示解释之。
2021数学建模国赛c题第二问模型

2021数学建模国赛c题第二问模型1. 前言2021年数学建模国赛c题第二问是一个涉及“研究城市人口流动和疫情传播的模型”题目。
这是一个具有挑战性的问题,需要我们综合运用数学建模、统计、计算机编程等知识,来解决一个实际且紧迫的社会问题。
2. 评估题目需求我们需要全面评估题目的需求,明确题目背后需要解决的具体问题。
该题目涉及到城市人口流动和疫情传播的模型,需要我们研究城市间的人口迁移规律、疫情的传播特点,以及如何通过合理的措施来阻断疫情传播。
在文章中,我们需要深入探讨城市间的人口迁移模型、疫情传播的规律,并结合实际案例进行分析和建模。
3. 写作思路针对该题目,我们可以从简单到复杂的方式来详细阐述。
从城市间的人口迁移规律开始,介绍人口迁移的影响因素、模型的构建以及现实中的应用。
紧可以探讨疫情传播的规律,包括传染病的基本属性、传播途径和数学模型的建立。
结合城市人口流动和疫情传播的模型,提出预防和控制疫情传播的对策。
4. 撰写文章在文章中,我们将详细介绍城市人口迁移模型的建立,分析疫情传播的特点,并提出应对疫情传播的策略。
我们将从人口迁移的影响因素入手,逐步扩展到人口迁移模型的构建,探讨不同模型在实际中的应用,特别是在疫情传播方面的影响。
我们将深入探讨传染病的基本属性、传播途径和数学模型的建立,探索疫情传播规律的数学描述和预测。
我们将结合人口迁移和疫情传播的模型,提出有效的防控策略,并对未来的研究方向进行展望。
5. 个人观点和理解从我个人的角度来看,城市人口流动和疫情传播的模型研究具有重要的实践意义。
通过深入研究题目涉及的内容,可以更好地了解人口迁移和疫情传播的规律,并为实际防疫工作提供科学的依据。
在当前疫情下,这一话题更显得尤为重要,因此我们必须深入研究、切实解决。
6. 总结和回顾在本文中,我们对2021数学建模国赛c题第二问的城市人口流动和疫情传播的模型进行了深入的研究和探讨。
我们从人口迁移模型、疫情传播规律以及防控策略等方面进行了详细的论述,旨在为读者提供全面、深刻且灵活的理解。
数学建模 -实验报告2

output =
iterations: 11 funcCount: 12 algorithm: 'golden section search, parabolic interpolation'
message: 'Optimization terminated: the current x satisfies the term...'
度AB,但是,当病床的长度一定时,要计算病床的宽度就比较麻烦,因此我们从定宽变长的角度来考虑
问题。这样就得到了这个问题的模型二。
假设:1、在转弯过程中我们的策略是转动与推进相结合;
2、在转弯的过程中,病床的宽度 h w 保持不变(显然 0 1 )。
记当病床的AB边与水平走廊的夹角为 时,恰好与走廊相抵的病床长度AB为 L( , w, ) (参看
的充分必要条件是:病床长度 L Lmin (w, ) 。因此,问题归结为求函数 L( , w, ) 关于变量 的最小值
Lmin (w, ) 。
令 t sin cos 得:1 t
2
, sin
cos
t2
1
,代入(6)式得
2
L( , w, ) f (t, w, )
图2
只要
L 2 h2 w2 2
0hw
化简得: L 2 w2 h2
0hw
(1)
即:当病床的长度 L 不超过走廊宽度 w 与病床宽度 h 的平方差的平方根
倍时,我们就可以把病床平推转过走廊拐角。 到此,我们似乎已经完全解决了这个问题。在下结论之前,我们来
Q B
O
F
D
the current x satisfies the term...' 即最小值在 x=0.2176 附近,为-1.1312。
《数学建模》实验报告二

《数学建模》实验报告二院系专业学号姓名指导教师二O一五年四月十六日第一部分:数学建模论文P135:11题有4名同学到一家公司参加三个阶段的面试:公司要求每个同学都必须首先找公司秘书初试,然后到部门主管处复试,最后到经理处参加面试,并且不允许插队(即在任何一个阶段4名同学的顺序是一样的),由于4名同学的专业背景不同,所以每人在三个阶段的面试时间也不同,如表1所示。
这4名同学约定他们全部面试完以后一起离开公司,假定现在时间是早晨8:00,请问他们最早何时能离开公司?表1 面试时间要求单位:min一:问题的提出本题问题是要合理安排4名同学的面试顺序,使完成全部面试所花费的时间最少。
二:模型假设定义数学符号如下tij:第i名同学参加第j阶段面试需要的时间;xij:第i名同学参加第j阶段面试的开始时刻(记早上8:00面试开始为0时刻)(i=1, 2, 3, 4;j=1, 2, 3);T:完成全部面试所花费的最少时间。
三:模型建立目标函数:Min T={Max i{xi3+ti3}}模型约束条件:①每个人只有参加完前一阶段的面试后才能进入下一个阶段,则xij+tij<=x(i,j+1) (i=1, 2, 3, 4,j=1, 2);②每个阶段j在同一时间只能面试1名同学,所以用0-1变量yik表示第k名同学是否排在第i名同学前面(1表示是,0表示否),则xij+ tij–xkj<=Tyik (i, k=1, 2, 3, 4; j=1, 2, 3; i<k)xkj+ tkj–xij<=T(1–yik) (i, k=1, 2, 3, 4; j=1, 2, 3; i<k) 线性优化目标:Min Ts.t. T >=x13+ t13T >=x23+ t23T >=x33+ t33T >=x43+ t43xij+ tij <=x(i, j+1) (i=1, 2, 3, 4;j=1, 2)xij+ tij–xkj<=Tyik (i, k=1, 2, 3, 4; j=1, 2, 3; i<k)xkj+ tkj–xij<=T(1–yik)(i, k=1, 2, 3, 4; j=1, 2, 3; i<k)xi3+ ti3<=T (i=1, 2, 3, 4)四:模型解法与结果程序:Model:min =T;T >= x13+ t13;T >= x23+ t23;T >= x33+ t33;T >= x43+ t43;x11+ t11 <= x12;x12+ t12 <= x13;x21+ t21 <= x22;x22+ t22 <= x23;x31+ t31 <= x32;x32+ t32 <= x33;x41+ t41 <= x42;x42+ t42 <= x43;x11+ t11 - x21<= T*y12;x21+ t21 - x11<= T*(1-y12); x12+ t12 - x22<= T*y12;x22+ t22 - x12<= T*(1-y12); x13+ t13 - x23<= T*y12;x23+ t23 - x13<= T*(1-y12); x11+ t11 - x31<= T*y13;x31+ t31 - x11<= T*(1-y13); x12+ t12 - x32<= T*y13;x32+ t32 - x12<= T*(1-y13); x13+ t13 - x33<= T*y13;x33+ t33 - x13<= T*(1-y13); x11+ t11 - x41<= T*y14;x41+ t41 - x11<= T*(1-y14); x12+ t12 - x42<= T*y14;x42+ t42 - x12<= T*(1-y14); x13+ t13 - x43<= T*y14;x43+ t43 - x13<= T*(1-y14); x21+ t21 - x31<= T*y23;x31+ t31 - x21<= T*(1-y23); x22+ t22 - x32<= T*y23;x32+ t32 - x32<= T*(1-y23); x23+ t23 - x33<= T*y23;x33+ t33 - x23<= T*(1-y23); x21+ t21 - x41<= T*y24;x41+ t41 - x21<= T*(1-y24);x22+ t22 - x42<= T*y24;x42+ t42 - x22<= T*(1-y24);x23+ t23 - x43<= T*y24;x43+ t43 - x23<= T*(1-y24);x31+ t31 - x41<= T*y34;x41+ t41 - x31<= T*(1-y34);x32+ t32 - x42<= T*y34;x42+ t42 - x32<= T*(1-y34);x33+ t33 - x43<= T*y34;x43+ t43 - x33<= T*(1-y34);t11=13;t12=15;t13=20;t21=10;t22=20;t23=18;t31=20;t32=16;t33=10;t41=8;t42=10;t43=15;@bin(y12);@bin(y13);@bin(y14);@bin(y23);@bin(y24);@bin(y34);End运行结果:Local optimal solution found.Objective value: 84.00000Extended solver steps: 35Total solver iterations: 975Variable Value Reduced Cost T 84.00000 0.000000 X13 36.00000 0.000000 T13 20.00000 0.000000 X23 56.00000 0.000000 T23 18.00000 0.000000X33 74.00000 0.000000T33 10.00000 0.000000X43 18.00000 0.000000T43 15.00000 0.000000X11 8.000000 0.000000T11 13.00000 0.000000X12 21.00000 0.000000T12 15.00000 0.000000X21 21.00000 0.000000T21 10.00000 0.000000X22 36.00000 0.000000T22 20.00000 0.000000X31 31.00000 0.000000T31 20.00000 0.000000X32 56.40000 0.000000T32 16.00000 0.000000X41 0.000000 0.9999970T41 8.000000 0.000000X42 8.000000 0.000000T42 10.00000 0.000000Y12 0.000000 -83.99950Y13 0.000000 0.000000Y14 1.000000 83.99950Y23 0.000000 -83.99950Y24 1.000000 0.000000Y34 1.000000 0.000000五:模型结果的分析所有面试完成至少需要84分钟,其面试顺序为4-1-2-3 (即丁-甲-乙-丙)。
全国研究生数学建模竞赛C题二有关小麦和风级的一些知识

附件二有关小麦和风级的一些知识一、结构分蘖是小麦从根部发育出来的侧枝(见图1),早期生出的能抽穗结实的分蘖称为有效分蘖,晚期生出的不能抽穗或抽穗而不结实的称为无效分蘖。
有效分蘖与单位面积的穗数直接有关。
采集数据时对小麦去除叶片、叶鞘(见图2)。
如果考虑叶片叶鞘以及降雨对抗倒的影响,据田间经验在灌浆期这几个因素与小麦植株本身自重有关。
图1 成株期小麦单株照片图2 小麦茎秆结构图图3 成熟期小麦单株照片(叶片、叶鞘已脱落)二、生长周期(一)生育期:小麦从种子萌发、出苗、生根、长叶、拔节、孕穗、抽穗、开花、结实,经过一系列生长发育过程,到产生新的种子,叫小麦的一生。
从播种到成熟需要的天数叫生育期。
小麦的生育期一般在230—270天。
(二)生育时期:生产上根据小麦不同生长发育阶段,为了便于栽培管理,又把小麦的一生主要划分为出苗期、分蘖期、越冬期、返青期、拔节期、孕穗期、抽穗期、开花期、灌浆期、成熟期。
其中灌浆期又可分为籽粒形成期、乳熟期、腊熟期、完熟期。
(三)生长阶段:根据小麦器官形成的特点,可将几个连续的生育时期合并为某一生长阶段。
一般可分为三个生长阶段。
1.苗期阶段:从出苗到起身期。
主要进行营养生长,即以长根、长叶和分蘖为主。
2.中期阶段:从起身至开花期。
这是营养生长与生殖生长并进阶段,既有根、茎、叶的生长,又有麦穗分化发育。
3.后期阶段从开花至成熟期。
也称子粒形成阶段,以生殖生长为主。
三、描述材料力学性能的几个物理量1、弹性模量(elastic modulus):弹性模量指的是与材料有关的比例常数。
即材料在弹性变形阶段内,正应力和对应的正应变的比值。
(1)弹性变形(elastic deformation):材料在外力作用下产生变形,当外力取消后,材料变形即可消失并能完全恢复原来形状的性质称为弹性。
这种可恢复的变形称为弹性变形。
(2)、应力(stress):受力物体截面上内力的集度。
2、应变:对一根细杆施加一个拉力F,这个拉力除以杆的截面积S,称为“线应力”,杆的伸长量dL除以原长L,称为“线应变”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二逻辑运算和判断选取控制
一.目的要求
1.了解C语言表示逻辑量的方法(以0代表”假”,以1代表”真”);
2.学会正确使用逻辑运算符和逻辑表达式;
3.熟练掌握if语句和switch语句。
二.实验内容
先编写以下程序,解决以下问题,然后上机调试运行程序。
1.有一函数
y={x (x<1)
2x-1 (1<=x<10)
3x-11 (x>=10)
用scanf函数输入x的值(分别为x<1,1-10,x>=10三种情况),求y值。
2.给出一个百分制成绩,要求输出成绩等级’A’、’B’、’C’、’D’、’E’。
90分以上为’A’,
81-89分为’B’,70-79分为’C’,60-69分为’D’,60分以下为’E’。
3.给一个不多于5位的正整数,要求:
(1)求出它是几位数;
(2)分别打印出每一位数字;
(3)按逆序打印出各位数字,例如原数为123,应输出321。
