运筹学课件 单纯形法的计算步骤
合集下载
运筹学课件1-4单纯形法计算步骤

b 21 4
9 4
3 x1 1 -1 3 4 -1 12
9 x2 3 1 9 0 1 0
0 x3 1 0 0 1 0 0
0 x4 0 1 0 -3 1 -9
θ 7 4
9/4 -
所以把x3换出为非基变量,x1为换入变量即新的基变量。
第20页
cj
CB 0 0
0 9 3
XB x3 x4 cj-zj x3 x2 cj-zj x1
cj-zj
x3 x1 x5 cj-zj
6
0 1 0
5
5/2 1/2 1
0
1 0 0
0
-1/2 1/2 -1
0
0 0 1
75 5
0
2
0
-3
0
5
x2
5
0
1
0
-1
1
第10页
cj CB 0 0 0 0 6 0 XB x3 x4 x5 b 90 75 80 105/2 75/2 5
6 x1 1 2 2
5 x2 3 1 2
9/4
-
3 9
9/4 25/4
1 0 0
25
第24页
cj CB 0 0 XB x3 x4 cj-zj b 21 4
3 x1 1 -1 3
9 x2 3 1 9
0 x3 1 0 0
0 x4 0 1 0 θ 7 4
0
9
x3
x2 cj-zj x1 x2 cj-zj
9
4
4
-1 12
0
1 0 0 1 0
1
0 0 1/4 1/4 -3
i 1
第1页
单纯形表求解线性规划问题
第四节 单纯形法的计算步骤

上表中由于所有σ 上表中由于所有 j>0 ,表明已求得最优解 x1=4, x2=2, x3=0, x4=0, x5=0, x6=4, , , , , , , Z=14。 。 当确定x 为换入变量计算θ值时 值时, ◆当确定 6为换入变量计算 值时,有两个相 同的最小值: 同的最小值:2/0.5=4,8/2=4。任选其中一 , 。 个作为换出变量时, 个作为换出变量时,则下面表中另一基变 量的值将等于0,这种现象称为退化 退化。 量的值将等于 ,这种现象称为退化。含有 一个或多个基变量为0的基可行解称为 的基可行解称为退化 一个或多个基变量为 的基可行解称为退化 的基可行解。 的基可行解。
18
迭代
xB
次数
cB
x1
x2
x3
x4
x5 bi
θi
50
x1
100
0
0
0
50 0 100
1 0 0
0
0 0 1
0
1 -2 0
- 50
0 1 0
0
-1 1 1
- 50
50 50 250 -27500
2
x4 x2
σj
2010年8月
管理工程学院
18
《运筹学》 运筹学》
19
所有的检验数 σ j ≤ 0, 此基本可行解: 此基本可行解:
2010年8月
管理工程学院
5
《运筹学》 运筹学》
6
c1 … cl b b1´
⋮
c j→ cB c1
⋮
… cm … xm …0 …⋮ 0 …1 …
⋮
…cj …xj …a1j´ …⋮ a2j´ …⋮ amj´
… ck … cn … xk …xn …0 …⋮ 1 …0
单纯形法的计算步骤

运筹学基础及应用
解:化标准型
max
z 2 x1 x2 0 x3 0 x4 0 x5 5 x2 x3 15 6 x 2 x x4 24 1 2 x5 5 x1 x2 x1 , , x5 0
运筹学基础及应用
表1:列初始单纯形表 (单位矩阵对应的变量为基变量)
运筹学基础及应用
单纯形表
- Z x1基变量 x 2 ... xm XB 0 1 1E 0 单位阵 ....... 0 1 1 c c 0... c 1 2 m xm xNn 非基变量 1 .... X a1m 1 ...a1n a 2 m 1N...a 2 n
非基阵 ......
在上一节单纯形法迭代原理中可 知,每一次迭代计算只要表示出当前的约 束方程组及目标函数即可。
a1m 1 xm 1 ..... a1n xn b1 x1 x a2 m 1 xm 1 ..... a2 n xn b2 2 .......... .......... .......... ..... xm amm 1 xm 1 ..... amn xn bm Z c1 x1 ... cm xm cm 1 xm 1 ... cn xn 0
3
0 1 5/4 -15/2 1*3/2 0 0 1/4 -1/2 +0*15/2 检验数<=0 1 0 -1/4 3/2
cj z j
8.5
0
0
-1/4
-1/2
最优解为X=(7/2,3/2,15/2,0,0) 目标函数值Z=8.5
cj
CB
0 0 0
2
1
0最小的值对应 0 0
1.4单纯形法计算步骤

的基可行解就是最优解。
第三步:从一个基可行解转换另一个目标函 数值更大的基可行解,列出新表。
▪ (1)确定换入基变量
只要有检验数 j 0,
对应变量x
可作为换入基的变量,
j
当有一个以上检验数大于零时,
一般从中选取一个最大的
。
k
k max{ j j 0}
对应的变量xk作为换入基的变量 (简称入基变量)
§4 单纯形法 的计算步骤
单纯形法计算步骤:
▪ 第一步:求出线性规划的初始基可行解,列出 初始单纯形表。 对于会有明显可行基的线性规划问题LP,直接 作出其单纯形表,得到第一个基可行解,单纯 形方法是与单纯形表相互对应的。
如果线性规划问题:
max z c1x1 c2 x2 cm xm cm1xm1 cn xn
▪ 有可能发生循环的情况,诶了避免循环, 人们选择了一种Bland方法,这是有效的避 免循环的方法。但同学照样可以使用本教材 中所介绍的方法,因为事实上出现循环的情 况是不多见的,而个别出现循环的情况都是 人为的构造的。
)0
当 当aaiikk
0,显然成立 z0
bl
k )
alk
z0 bl
k
alk
0
故目标函数值单调不减,
我们一定可以在有限步内求得
最优解或者判定LP无有界的最优解。
例:max z 3x1 5x2
x1
8
s.t
3x1
2x2 4x2
12 36
alk 到第i行上去,使新表中第k列除主元素 变为1以外,其余元素全化为零。
通过这样换基迭代, 一定可以做到以下两点:
▪ (1)从可行基迭代到可行基; ▪ (2)使目标函数值不断增加。
第三步:从一个基可行解转换另一个目标函 数值更大的基可行解,列出新表。
▪ (1)确定换入基变量
只要有检验数 j 0,
对应变量x
可作为换入基的变量,
j
当有一个以上检验数大于零时,
一般从中选取一个最大的
。
k
k max{ j j 0}
对应的变量xk作为换入基的变量 (简称入基变量)
§4 单纯形法 的计算步骤
单纯形法计算步骤:
▪ 第一步:求出线性规划的初始基可行解,列出 初始单纯形表。 对于会有明显可行基的线性规划问题LP,直接 作出其单纯形表,得到第一个基可行解,单纯 形方法是与单纯形表相互对应的。
如果线性规划问题:
max z c1x1 c2 x2 cm xm cm1xm1 cn xn
▪ 有可能发生循环的情况,诶了避免循环, 人们选择了一种Bland方法,这是有效的避 免循环的方法。但同学照样可以使用本教材 中所介绍的方法,因为事实上出现循环的情 况是不多见的,而个别出现循环的情况都是 人为的构造的。
)0
当 当aaiikk
0,显然成立 z0
bl
k )
alk
z0 bl
k
alk
0
故目标函数值单调不减,
我们一定可以在有限步内求得
最优解或者判定LP无有界的最优解。
例:max z 3x1 5x2
x1
8
s.t
3x1
2x2 4x2
12 36
alk 到第i行上去,使新表中第k列除主元素 变为1以外,其余元素全化为零。
通过这样换基迭代, 一定可以做到以下两点:
▪ (1)从可行基迭代到可行基; ▪ (2)使目标函数值不断增加。
运筹学-第1章 3-单纯形法

解: 1 2 3 0 A p1 p 2 p3 p 4 , 则 B p1 p 4 0 3 1 1
选 XB = (x1 x4)T 令x2 = x3 = 0 则 初始基可行解:X = (3
0
0
4)T
5
(2)人工变量法(大M法) 若给定问题标准化后,系数矩阵中不存在m个线性无关的单
以alk为主 元进行初 等行变换
xm a mm 1 x m 1 amk x k a mn x n bm xj 0 j 1,2, , n
0 0 0 a1m1 a1k a1n b1 1 1 0 0 a2m1 a2k a2n b2 0 A 0 0 1 0 alm 1 alk aln bl 0 0 0 1 amm 1 amk amn bm
解就是原问题的最优解
若变化后的问题中含有非零的人工变量则元问题无可行
解
7
2.最优性检验和解的判别
x i bi a im 1 x m 1 , ,a in x n i 1, , m代入目标函数 Z
c1 x1 c2 x 2 c n x n c1 (b1 a1m 1 x m 1 a1n x n ) c2 (b2 a 2 m 1 x m 1 a 2 n x n ) cm (bm a mm 1 x m 1 a mn x n ) c m 1 x m 1 c n x n ci bi
(1)因为所有 Xj ≥0,当所有σ j<0 时,则 Z≤Z0,则该基可行解 对应最优解; (2)因为所有 Xj ≥ 0 ,当 σ j≤ 0 且存在 σ j =0 ( j=m+1,„,n) 时,则该线性规划问题有无穷多最优解; ( 3 )对基可行解 X0, 若存在某个 σ k>0, 且所有 aik≤0(Pj≤0), i=1,2,„,m,则该问题无界(无界解); (4)因为所有Xj≥0,当存在σ j>0时,则该基可行解不是最优 解,需要寻找另一个基可行解;
选 XB = (x1 x4)T 令x2 = x3 = 0 则 初始基可行解:X = (3
0
0
4)T
5
(2)人工变量法(大M法) 若给定问题标准化后,系数矩阵中不存在m个线性无关的单
以alk为主 元进行初 等行变换
xm a mm 1 x m 1 amk x k a mn x n bm xj 0 j 1,2, , n
0 0 0 a1m1 a1k a1n b1 1 1 0 0 a2m1 a2k a2n b2 0 A 0 0 1 0 alm 1 alk aln bl 0 0 0 1 amm 1 amk amn bm
解就是原问题的最优解
若变化后的问题中含有非零的人工变量则元问题无可行
解
7
2.最优性检验和解的判别
x i bi a im 1 x m 1 , ,a in x n i 1, , m代入目标函数 Z
c1 x1 c2 x 2 c n x n c1 (b1 a1m 1 x m 1 a1n x n ) c2 (b2 a 2 m 1 x m 1 a 2 n x n ) cm (bm a mm 1 x m 1 a mn x n ) c m 1 x m 1 c n x n ci bi
(1)因为所有 Xj ≥0,当所有σ j<0 时,则 Z≤Z0,则该基可行解 对应最优解; (2)因为所有 Xj ≥ 0 ,当 σ j≤ 0 且存在 σ j =0 ( j=m+1,„,n) 时,则该线性规划问题有无穷多最优解; ( 3 )对基可行解 X0, 若存在某个 σ k>0, 且所有 aik≤0(Pj≤0), i=1,2,„,m,则该问题无界(无界解); (4)因为所有Xj≥0,当存在σ j>0时,则该基可行解不是最优 解,需要寻找另一个基可行解;
运筹学单纯形法ppt课件

• 当第一阶段中目标函数的最优值=0,即人工变量=0, 则转入第二阶段;若第一阶段中目标函数的最优值不等于 0,即人工变量不等于0,则判断原问题为无解。
• 第二阶段:将第一阶段计算所得的单纯形表划去人工变量 所在的列,并将目标函数换为原问题的目标函数作为第二 阶段的初始单纯形表,进行进一步的求解。
14
s.t.
32x1x133xx2 22
x3 x3
100 120
x1, x2 , x3 0
cj
40 45 25 0 0
CB XB bi x1 x2 x3 x4 x5 θ
0 x4 100 2 [ 3 ] 1
1
0
100/3
0 x5 120 3 3 2 0 1
40
σj
40 45 25
两阶段法的算法流程图
MaxZ=-3x1+x3 x1+ x2+ x3≤4
-2x1+ x2- x3≥1 3x2+x3=9
xi ≥0,j=1,2,3
求解辅助问题,得到辅助 问题的最优解
引进人工变量x6,x7,构造辅助 问题,辅助问题的目标函数为
所有人工变量之和的极小化
Max W= -x6 - x7
x1+ x2+ x3+x4
取值
xj无约束 令xj = xj′- xj″
xj ≤ 0 令 xj′= - xj
xj′ ≥0 xj″ ≥0
右端项
bi < 0
约束条 件两端 同乘以
-1
等式或不等式
≤
=
≥
加松 弛变 量xs
加入 人工 变量
xa
减去 剩余 变量xs
加入 人工 变量xa
• 第二阶段:将第一阶段计算所得的单纯形表划去人工变量 所在的列,并将目标函数换为原问题的目标函数作为第二 阶段的初始单纯形表,进行进一步的求解。
14
s.t.
32x1x133xx2 22
x3 x3
100 120
x1, x2 , x3 0
cj
40 45 25 0 0
CB XB bi x1 x2 x3 x4 x5 θ
0 x4 100 2 [ 3 ] 1
1
0
100/3
0 x5 120 3 3 2 0 1
40
σj
40 45 25
两阶段法的算法流程图
MaxZ=-3x1+x3 x1+ x2+ x3≤4
-2x1+ x2- x3≥1 3x2+x3=9
xi ≥0,j=1,2,3
求解辅助问题,得到辅助 问题的最优解
引进人工变量x6,x7,构造辅助 问题,辅助问题的目标函数为
所有人工变量之和的极小化
Max W= -x6 - x7
x1+ x2+ x3+x4
取值
xj无约束 令xj = xj′- xj″
xj ≤ 0 令 xj′= - xj
xj′ ≥0 xj″ ≥0
右端项
bi < 0
约束条 件两端 同乘以
-1
等式或不等式
≤
=
≥
加松 弛变 量xs
加入 人工 变量
xa
减去 剩余 变量xs
加入 人工 变量xa
运筹学课件1-3单纯形法原理

§1.3 单纯形法原理
理论方法 算法步骤 单纯形表
算例
第1页
一、基本概念
考虑线性规划标准形式 max z CX s .t . AX b X 0 :
其中A为m×n阶矩阵
可行解:满足AX=b,且X≥0的解称为可行解。 可行域:全部可行解的集合称为可行域。 最优解:使目标函数达到最大值的可行解称为最 优解。 基:设B是系数矩阵A的一个m×n阶的满秩子矩阵, 称B是(LP)的一个基。
-5 0 0
2.5 0 4 4 0 3
1.5 17.5 22 19
-3 0 0 0
问:基解中零的个数至少有多少个? 至少n-m个
例3
x1=0, x3=0 x2=3, x4=-2 是基解,但不 是可行解
D
max z=x1+2x2 s.t. x1+x23 x2 1 x1, x2 0
max z=x1+2x2 s.t. x1+x2+ x3 =3 x2 +x4=1 x1, x2 ,x3, x40
第12页
三、几个基本定理
引理 线性规划问题的可行解为基可行解的充要条件 是它的正分量所对应的系数列向量线性无关。
证: (2)充分性
若向量 P1 , P2 , , Pk 线性无关,
则必有 k m
T
当 k m 时, P1 , P2 , , Pm 构成基
从而 X ( x1 , , x m , 0 , , 0 ) 为相应的基可行解
若X
(X
(0)
(0)
证。
(0)
不是基可行解
(0)
,由定理 2 知 X
到通过 X
) CX ) CX
理论方法 算法步骤 单纯形表
算例
第1页
一、基本概念
考虑线性规划标准形式 max z CX s .t . AX b X 0 :
其中A为m×n阶矩阵
可行解:满足AX=b,且X≥0的解称为可行解。 可行域:全部可行解的集合称为可行域。 最优解:使目标函数达到最大值的可行解称为最 优解。 基:设B是系数矩阵A的一个m×n阶的满秩子矩阵, 称B是(LP)的一个基。
-5 0 0
2.5 0 4 4 0 3
1.5 17.5 22 19
-3 0 0 0
问:基解中零的个数至少有多少个? 至少n-m个
例3
x1=0, x3=0 x2=3, x4=-2 是基解,但不 是可行解
D
max z=x1+2x2 s.t. x1+x23 x2 1 x1, x2 0
max z=x1+2x2 s.t. x1+x2+ x3 =3 x2 +x4=1 x1, x2 ,x3, x40
第12页
三、几个基本定理
引理 线性规划问题的可行解为基可行解的充要条件 是它的正分量所对应的系数列向量线性无关。
证: (2)充分性
若向量 P1 , P2 , , Pk 线性无关,
则必有 k m
T
当 k m 时, P1 , P2 , , Pm 构成基
从而 X ( x1 , , x m , 0 , , 0 ) 为相应的基可行解
若X
(X
(0)
(0)
证。
(0)
不是基可行解
(0)
,由定理 2 知 X
到通过 X
) CX ) CX
运筹学1-4单纯型法的计算步骤

2 X1 1 3 X2 2
Z8
1 0 -1 4/3 -1/3 0 1 2 -1/3 1/3 0 0 -1 -5/3 -1/3
从最优表可知: 该LP的
最优解是X*=(1, 2, 0, 0, 0)T 相应的目标函数最优值是Zmax=8
表格单纯形法求解步骤
第一步:将LP化为标准型,并加以整理。
引入适当的松驰变量、剩余变量和人工变量 ,使约束条件化为等式,并且约束方程组的系数 阵中有一个单位阵。
(这一步计算机可自动完成)
确定初始可行基,写出初始基本可行解
第二步:最优性检验
计算检验数,检查: 所有检验数是否≤ 0?
是——结束,写出最优解和目标函数最优值; 还有正检验数——检查相应系数列≤ 0?
是——结束,该LP无“有限最优解”! 不属于上述两种情况,转入下一步—基变换。
确定是停止迭代还是转入基变换?
0 1 0
0
0
1
0
0
0
1 c1 c2
0 a1,m1 a1,m2 0 a2,m1 a2,m2
1 a a m,m1 m,m2 cm cm1 cm2
a1,n b1
a2,n
b2
am,n bm
cn 0
-Z,x1,…,xm所对应的系数 列向量构成一个基
用矩阵的初等行变换将该基变成单位阵,这时
c1, c2 , , cm 变成0,相应的增广矩
第四步:判断检验数、入基、出基变量。 …….
三、表格单纯形法:
1、 初始单纯形表的建立 (1)表格结构:
Cj 2 3 3 0 0
CB
XB
b xj
x1 x2 x3 x4 x5
j
0 X4
3
《单纯形法计算步骤》课件

《单纯形法计算步骤》 PPT课件
单纯形法是一种常用的线性规划求解方法。
算法简介
单纯形法通过逐步迭代的方式逐步化问题的解。 它能够解决满足线性可行性和有解性条件的线性规划问题。
计算步骤
1
步骤一
对原问题进行初等变换化简,转化为标准
步骤二
形式。
构造初始可行基解系统。
3
步骤三
判断当前基解系统是否为最优解,若是则
当问题有多个最优解时,需 比较确定最终的最优解。
结论
强有力的求解方法
单纯形法是一种强有力的线性 规划求解方法。
相对简单易实现
它的计算步骤相对简单,容易 实现和应用。
计算复杂度
随问题规模增大,计算复杂度 也会增加,需考虑其他高效的 求解方法。
步骤四
4
输出。
找到目标函数最优化的进入变量。
5
步骤五
找到最优组合约束的离开变量。
步骤六
6
对基向量进行初等变换,更新基变量和非
基变量。
7
步骤七
重复步骤三到步骤六,直到找到最优解或 问题无解。
注意事项
1 维护线性可行性
2 选择变量
3 多个最优解
在每一步计算中,需要保持 线性可行性和有解性条件。
选择进入变量和离开变量时, 需要经过计算和判断。
单纯形法是一种常用的线性规划求解方法。
算法简介
单纯形法通过逐步迭代的方式逐步化问题的解。 它能够解决满足线性可行性和有解性条件的线性规划问题。
计算步骤
1
步骤一
对原问题进行初等变换化简,转化为标准
步骤二
形式。
构造初始可行基解系统。
3
步骤三
判断当前基解系统是否为最优解,若是则
当问题有多个最优解时,需 比较确定最终的最优解。
结论
强有力的求解方法
单纯形法是一种强有力的线性 规划求解方法。
相对简单易实现
它的计算步骤相对简单,容易 实现和应用。
计算复杂度
随问题规模增大,计算复杂度 也会增加,需考虑其他高效的 求解方法。
步骤四
4
输出。
找到目标函数最优化的进入变量。
5
步骤五
找到最优组合约束的离开变量。
步骤六
6
对基向量进行初等变换,更新基变量和非
基变量。
7
步骤七
重复步骤三到步骤六,直到找到最优解或 问题无解。
注意事项
1 维护线性可行性
2 选择变量
3 多个最优解
在每一步计算中,需要保持 线性可行性和有解性条件。
选择进入变量和离开变量时, 需要经过计算和判断。
运筹学之单纯形法.ppt

x1 ,x2 ,… ,xn ≥ 0
2.基本过程:
1)加入人工变量;
2)通过单纯形法的迭带,将虚拟的人 工变量从原来的基变量中替换出去, 变成非基变量,使每一个人工变量都 等于0.反之,如果不能都变为非基变 量,表明原问题无可行解.
(一)、大M法:
2.4 单纯形法补遗
2.4.1 进基变量的相持及其突破
Y
结束
N
沿边界找新
的基本可行解
2.1 单纯形法的基本思想
单纯形法的三种形式:1)方程组形式; 2)表格形式;3)矩阵形式。
2.1.1 方程组形式的单纯形法
maxZ=3X1 +5X2
X1
+X3
=8
2X2 +X4 =12
3X1+4X2
+X5 =36
X1 … X5 0
解:(1)、确定初始可行解
B=(a3 a4 a5)=I Z -3X1-5X2 =0 X3 =8- X1 X4=12-2X2
此时可以确定X5为离基变量
Z
+1/2X4 +X5 =42
X3 +2/3X4 -1/3X5 =4
X2 +1/2X4 =6
X1 -2/3X4+1/3X5=4
令X4 =X5 =0
X =(4, 6, 4, 0, 0)T Z =42
。此时4=1/2, 5=1, Z值不
再增大了,X值是最优基本解
即:X*=(4,6)T,Z*=42
X6
X7
CB XB -36 M -M -6 -M -4 0
0
M
0
0
0
X3 100
2
3
1
00
0
2.基本过程:
1)加入人工变量;
2)通过单纯形法的迭带,将虚拟的人 工变量从原来的基变量中替换出去, 变成非基变量,使每一个人工变量都 等于0.反之,如果不能都变为非基变 量,表明原问题无可行解.
(一)、大M法:
2.4 单纯形法补遗
2.4.1 进基变量的相持及其突破
Y
结束
N
沿边界找新
的基本可行解
2.1 单纯形法的基本思想
单纯形法的三种形式:1)方程组形式; 2)表格形式;3)矩阵形式。
2.1.1 方程组形式的单纯形法
maxZ=3X1 +5X2
X1
+X3
=8
2X2 +X4 =12
3X1+4X2
+X5 =36
X1 … X5 0
解:(1)、确定初始可行解
B=(a3 a4 a5)=I Z -3X1-5X2 =0 X3 =8- X1 X4=12-2X2
此时可以确定X5为离基变量
Z
+1/2X4 +X5 =42
X3 +2/3X4 -1/3X5 =4
X2 +1/2X4 =6
X1 -2/3X4+1/3X5=4
令X4 =X5 =0
X =(4, 6, 4, 0, 0)T Z =42
。此时4=1/2, 5=1, Z值不
再增大了,X值是最优基本解
即:X*=(4,6)T,Z*=42
X6
X7
CB XB -36 M -M -6 -M -4 0
0
M
0
0
0
X3 100
2
3
1
00
0
单纯形法求解过程

单纯形法求解过程
单纯形法是用于线性规划问题的求解方法,其基本思想是通过在可行域上面不断切换对偶约束条件,直到得到最优解。
下面是单纯形法的求解过程:
1. 把线性规划问题转化为标准形式。
即使问题没有等式限制,也应该加入冗余变量,将问题转化为等式约束形式。
2. 建立初始单纯形表。
即为原问题中的等式约束形式添加一个松弛变量,得到一个标准单纯形表。
3. 选择入基变量和出基变量。
在单纯形表中,选取一个非基变量作为入基变量,并且选取一个基变量作为出基变量。
选择的原则是:使目标函数值趋近最优,并且不破坏约束条件。
选择的方法是使用规则最优法或是人工选择。
4. 计算新的单纯形表。
用选定的入基变量和出基变量来更新单纯形表。
通过新单纯形表,进一步判断问题是否已经达到最优解,如果不是,则回到第3步。
5. 如果最后的单纯形表为最优解,则停止计算,并得到最优解。
否则,该问题可能是无限制的或是无可行解的。
运筹学01.10单纯形法的算法步骤

2011-3-10
3
运筹学
Operations Research
∴ ( LP)的最优解为(50,250,0,50,0)T ,最优值为27500. 故原线性规划问题的最优解为(50,250)T ,最优值为27500. ▌
2011-3-10
4
运筹学
Operations Research
例2 利用单纯形法求解线性规划问题:
2011-3-10
16
运筹学
Operations Research
解:(1)(2)
(3) max z = 5 x + 3x 1 2
s. t. 1 4 8 x2 ≤ − x1 − 5 25 5 4 x1 + x 2 ≤ 2 5 x1 , x 8
故 [ x , x ]都是原规划的最优解.▐
2011-3-10
运筹学
Operations Research
∃rk = 0(xk为非基变量),
注:(1)在最终的单纯形表中,若
则只需以第k列为枢轴列,仍按最小比原则选择枢轴行,转 轴后即可得线性规划问题的另一最优解. (2)图解法:
基本最优解
2011-3-10
2011-3-10
2
运筹学
Operations Research
例1 利用单纯形法求解线性规划问题:
max z = 50 x1 + 100 x2 s. t. x1 + x2 ≤ 300 2 x1 + x2 ≤ 400 x2 ≤ 250 x1 , x2 ≥ 0
解:将所给线性规划问题化为标准形
取初始可行基 B = ( P3 , P4 , P5 ) = I 3
2011-3-10
3
运筹学
Operations Research
∴ ( LP)的最优解为(50,250,0,50,0)T ,最优值为27500. 故原线性规划问题的最优解为(50,250)T ,最优值为27500. ▌
2011-3-10
4
运筹学
Operations Research
例2 利用单纯形法求解线性规划问题:
2011-3-10
16
运筹学
Operations Research
解:(1)(2)
(3) max z = 5 x + 3x 1 2
s. t. 1 4 8 x2 ≤ − x1 − 5 25 5 4 x1 + x 2 ≤ 2 5 x1 , x 8
故 [ x , x ]都是原规划的最优解.▐
2011-3-10
运筹学
Operations Research
∃rk = 0(xk为非基变量),
注:(1)在最终的单纯形表中,若
则只需以第k列为枢轴列,仍按最小比原则选择枢轴行,转 轴后即可得线性规划问题的另一最优解. (2)图解法:
基本最优解
2011-3-10
2011-3-10
2
运筹学
Operations Research
例1 利用单纯形法求解线性规划问题:
max z = 50 x1 + 100 x2 s. t. x1 + x2 ≤ 300 2 x1 + x2 ≤ 400 x2 ≤ 250 x1 , x2 ≥ 0
解:将所给线性规划问题化为标准形
取初始可行基 B = ( P3 , P4 , P5 ) = I 3
2011-3-10
运筹学单纯形法计算步骤

检验数>0
确定主行
确定主列 21
表3:基变换
(初等行变换,主列化为单位向量,主元为1)
2 1 000
0
15/2 0 0 1 5/4 -15/2
2 1
7/2 3/2
1 0
0 1
0 0
1/4 -1/4
-31/检/22 验数<=0
0 0 0 -1/4 -1/2
22
思考:
一般主列选择正检验数中最大者对应的 列,也可选择其它正检验数的列.以第2列
Page 34
单纯形法的解的情况
单纯形法求解线性规划问题,解的情况也 有四种:
唯一最优解:上面的情况,所有的检验数都小 于等于0,并且非基变量的检验数都小于零
无穷多解:所有的检验数都小于等于0,至少 有一个非基变量的检验数为0
无界解:如果某imp>0,而且对应列中所有的 系数都小于等于0,这时,变量可以增长到无 穷大,线性规划问题有无界解
230 0 0
最小的值对应 的行为主行
0
8
1 21 0 0 4
0
16 4 0 0 1 0 —
0
12 0 4 0 0 1 3
23
正检验数中最大者对 应的列为主位向量 换出 换入
表2:基变换
(初等行变换,主列化为单位向量,主元为1)
2
0
2
1
0
16 4
3
3
0
2
正检验数中最大者对 应的列为主列
单纯形表结构
2
主元
1 C0 0 0
— 24/6 5/1
检验数
10
用单纯形表求解例1
第一章 线性规划与单纯形法
11
14单纯形法计算步骤
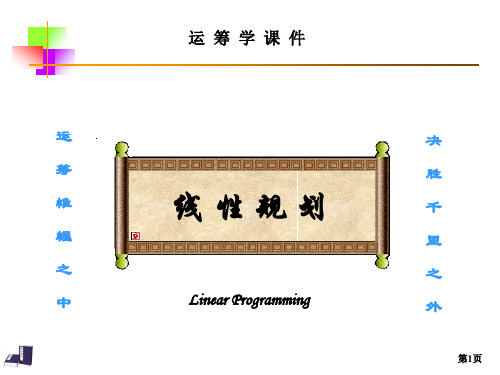
-1/20
1/40 1/40
3/20
X*=(0.5,0,0.15,0,0)T, z=2×1/2+3×3/20=1.45
第13页
练 习
用单纯形法求解问题 1、
m inz x 2 2 x 3 x1 2 x 2 x 3 2 x2 3 x3 x4 1 s.t . x2 x3 x5 2 x j 0; j 1,2,...,5
第14页
练 习
2.
min z 8 3x1 5 x2 8 s.t. x1 2 x2 x3 4 x1 x4 16 4 x2 x5 12 x j 0( j 1, 2,3, 4,5)
第15页
练 习
3.
min z 8 3x1 5 x2 8 s.t. x1 2 x2 x3 4 x1 x4 16 4 x2 x5 12 x j 0( j 1, 2,3, 4,5)
CB XB
2 1
1 1
x3 x2
σj x1 x2 σj
1 0
1 1
[1] -1
0 1 0 0
0 1
0 0 1 0
1 0
0 1 1 0
-1 2
-1 -1 1 -1
第10页
关于单纯形法的补充说明
无最优解(无界解)的判定
若对基可行解X1,存在非基变量xk的检验数 σk>0,但aik≤0,i=1,2,…,m即xk的系数列 向量无正分量,则问题无最优解。
a1m+1 a2m+1 amm+1
m i 1
… …
…
a1k a2k amk
m i 1
1/40 1/40
3/20
X*=(0.5,0,0.15,0,0)T, z=2×1/2+3×3/20=1.45
第13页
练 习
用单纯形法求解问题 1、
m inz x 2 2 x 3 x1 2 x 2 x 3 2 x2 3 x3 x4 1 s.t . x2 x3 x5 2 x j 0; j 1,2,...,5
第14页
练 习
2.
min z 8 3x1 5 x2 8 s.t. x1 2 x2 x3 4 x1 x4 16 4 x2 x5 12 x j 0( j 1, 2,3, 4,5)
第15页
练 习
3.
min z 8 3x1 5 x2 8 s.t. x1 2 x2 x3 4 x1 x4 16 4 x2 x5 12 x j 0( j 1, 2,3, 4,5)
CB XB
2 1
1 1
x3 x2
σj x1 x2 σj
1 0
1 1
[1] -1
0 1 0 0
0 1
0 0 1 0
1 0
0 1 1 0
-1 2
-1 -1 1 -1
第10页
关于单纯形法的补充说明
无最优解(无界解)的判定
若对基可行解X1,存在非基变量xk的检验数 σk>0,但aik≤0,i=1,2,…,m即xk的系数列 向量无正分量,则问题无最优解。
a1m+1 a2m+1 amm+1
m i 1
… …
…
a1k a2k amk
m i 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二阶段:以第一阶段的最优解(不含人工变量)为初 始解,以原目标函数为目标函数。
例8 试用两阶段法求解线性规划问题
min z =-3x1+x2+x3
x1 2 x2 x3 11
s.t.
4 x1 2 x1
x2
2x3 3 x3 1
x1 , x2 , x3 0
0 0 -1 0 0
x2
3 5 11/5
Z0=0
Z1=15
x1
如果将x1换入基底,得 另一解,由可行域凸性 易知,有两个最优解必 有无穷多组最优解 当非基底变量的检验数 中有取零值,或检验数 中零的个数大于基变量 个数时,有无穷多解。
四、无(有)界解
max z=x1+x2 -2x1+x2 4 x1- x2 2 -3x1+x23 x1 ,x2 0
反之,若加了人工变量的问题解后最优解中仍含人工变量为 基变量,便说明原问题无可行解。例3的单纯形表格为:
Cj
3
-1
-1
0
0
-M
CB XB b
x1
x2
x3
x4
x5
x6
0 x4 1
1
-2
1
1
0
0
-M x6 13 -4
1
2
0
-1
1
-M x7 1 -2
0
[1] 0
0
0
j
3-6M M-1 3M-1 0
-M
x1 2 x2 x3 x4
11
4 2
x1 x1
x2
2
x3 x3
x5 x6 3 x7 1
x1 , , x7 0
这时,初始基和初始基可行解很明显。X(0)=(0,0,0, 11,0,3,1)T不满足原来的约束条件。如何使得可从 X(0)开始,经迭代逐步得到x6=0,x7=0 的基可行解,从 而求得问题的最优解,有两种方法:
0
σj
-1
0
-3 x1 4
1
0
1 x2 1
0
1
0 x3 9
0
0
σj
20
0
1
00
x3
x4
x5
0
1 -2 4
0
0 -1 —
1
0 0—
0
01
0 1/3 -2/3
0
0 -1
1 2/3 -4/3
0 1/3 1/3
5. 2 线性规划问题解的讨论
一、无可行解
max z=2x1+4x2 x1 +x2 10 2x1 +x2 40 x1 ,x2 0
0 x4 16
4
0
0
10
4
3 x2 3
0 1 0 0 1/4 -
-z
-9
2 0 0 0 -3/4
X(1)=(0,3,2,16,0)T, z1 =9
cj
2 30 0 0
CB XB
b
x1
x2
x3
x4
x5
2 x1 2 0 x4 8 3 x2 3
1
0
1
0 -1/2 -
0 0 -4 1 2
4
0 1 0 0 1/4 12
x2
2 x3 x3
3 1
x1 , x2 ,x 3 0
标准型:
max z’ =3x1-x2-x3
x1 2 x2 x3 x4 11
s.t.
4 2
x1 x1
x2 2x3 x3
x5 3 1
x1 , , x5 0
其中第2、3个约束方程中无明显基变量,分别加上人工变x6, x7
4 x2 20 0
1 0 1/3
3 x1 20 1
0 0 1/3
cj- zj
0 0 0 -7/3
x2
x1
此题初始解是退化的。 最优解也是退化解。 退化解迭代中,当换入 变量取零值时目标函数 值没有改进,
三、 有无穷多最优解的情况
最优解中有非基变量的检验数等于零的 情况。以这种非基变量作为换入变量,迭代可 求得另一基最优解。
例8 min z =-3x1+x2+x3
x1 2 x2 x3 11
s.t.
4x1 2 x1
x2
2
x3 x3
3 1
x1 , x2 ,x3 0
例8 s.t.
min z =-3x1+x2+x3
x1 2 x2 x3 11
4 x1 2 x1
3 40
x1 x2 x3 1 11 2 10 [1] -1 0
3+M 4-M 0
0 [2] 1 0 30 1 -1 0
0 70 0 1 1/2 0 0 -3/2 1 0 1/2
0 -M
θ x4 x5
00 1 -1 01
00
0 1 0
0 0 1 0
cj- zj
0 0 -3.5 0
0 x3 0 0
0 1 -1/3
X* = (4,1,9,0,0), z* = 2
0 -1
0 -M
-2 -1
0 -1
-2/3 -1
-4/3 -1/3
0
-1
1
-2
1
0
1
0 -3M+1
4
2.两阶段法
第一阶段:以人工变量之和最小化为目标函数 min = x6+x7
只要原问题有可行解,该最小化问题的最优目标函数值就 是 0,解得的最优解 x6=0,x7=0,对应原问题一个基可行解。 反之若该问题的最优解目标函数值大于零,则说明原问题无可 行解。
检验数 中零的 个数多 于基变 量的个 数
检验数大 于零,但 对应列元 素小于等 于零,无 换出变量
单纯形法小结
根据实际问题给出数学模型,列出初始单纯形表,进行标准化,见表
xj≥0 变 xj≤0 量 xj 无约束
约 b>0
不需要处理
令 xj′=-xj; xj′≥0 令 xj=xj′-xj″;xj′,xj″≥0 不需要处理
CB XB
b
x1
x2
x3
x4
x5
2 x1 4 0 x5 4 3 x2 2
1 0 0 1/4 0 0 0 -2 1/2 1 0 1 1/2 -1/8 0
-z
-14
0
0 -1.5 -1/8 0
X(3)=(4,2,0,4,0)T, z3 =14
§5 单纯形法的进一步讨论
5.1 人工变量法
解决初始基可行解的问题。当某个约束方 程中没有明 显的基变量时,在该方程中加上 人工变量。
0
-M
x7
0
11
0 3/2
1
1
0
0 x4 10 3
-2
0
1
-M x6 1
0
[1]
0
0
-1 x3 1 -2
0
1
0
1 -1+M 0
0
0 x4 12 [3]
0
-1 x2 1 0
1
-1 x3 1 -2
0
1
0
0
1
0
0
1
0
0
0
3 x1 4
1
0
0
1/3
-1 x2 1
0
1
0
0
-1 x3 9
0
0
0
0
1
2/3
0 -1/3
向量Pk 0,则此问题是无界解,停止计算。否则,转入下一步 。
(4).根据max(j > 0) =k,确定xk为换入变量,按 规则计算 =min{bi/aik\aik>0}
可确定第l行的基变量为换出变量。转入下一步。 (5).以 alk 为主元素进行迭代(即用高斯消去法或称为旋转变 换),把 xk 所对应的列向量变换为(0,0,…,1,…,0)T,将
勃兰特规则(P35)可避免死循环。
例:
max z=3x1+4x2 x1 +x2 40
2x1+x260 x1-x2 =0 x1 ,x2 0
cj →
CB XB b 0 x3 40 0 x4 60 -M x5 0
cj- zj
0 x3 40 0 x4 60 3 x1 0
cj- zj 4 x2 20 0 x4 0 3 x1 20
任一最优解可表示为所有基最优解的凸 组合。
例 max z=3x1+5x2 3x1 +5x2 15 2x1 + x2 5 2x1+2x2 11 x1 ,x2 0
CB XB b
0 x3 15
0 x4 5
0 x5 11
cj-zj
5 x2 3
0 x4 2
0 x5
5
cj-zj
3 50 00 x1 x2 x3 x4 x5 3 [5] 1 0 0 2 1010 2 2001 3 5000 3/5 1 1/5 0 0 7/5 0 -1/5 1 0 4/5 0 -2/5 0 1
-z
-13
0
0 -2
0 1/4
cj
2 30 0 0
CB XB
b
x1
x2
x3
x4
x5
2 x1 2 0 x4 8 3 x2 3
1
0
1
0 -1/2 -
0 0 -4 1 (2 ) 4
例8 试用两阶段法求解线性规划问题
min z =-3x1+x2+x3
x1 2 x2 x3 11
s.t.
4 x1 2 x1
x2
2x3 3 x3 1
x1 , x2 , x3 0
0 0 -1 0 0
x2
3 5 11/5
Z0=0
Z1=15
x1
如果将x1换入基底,得 另一解,由可行域凸性 易知,有两个最优解必 有无穷多组最优解 当非基底变量的检验数 中有取零值,或检验数 中零的个数大于基变量 个数时,有无穷多解。
四、无(有)界解
max z=x1+x2 -2x1+x2 4 x1- x2 2 -3x1+x23 x1 ,x2 0
反之,若加了人工变量的问题解后最优解中仍含人工变量为 基变量,便说明原问题无可行解。例3的单纯形表格为:
Cj
3
-1
-1
0
0
-M
CB XB b
x1
x2
x3
x4
x5
x6
0 x4 1
1
-2
1
1
0
0
-M x6 13 -4
1
2
0
-1
1
-M x7 1 -2
0
[1] 0
0
0
j
3-6M M-1 3M-1 0
-M
x1 2 x2 x3 x4
11
4 2
x1 x1
x2
2
x3 x3
x5 x6 3 x7 1
x1 , , x7 0
这时,初始基和初始基可行解很明显。X(0)=(0,0,0, 11,0,3,1)T不满足原来的约束条件。如何使得可从 X(0)开始,经迭代逐步得到x6=0,x7=0 的基可行解,从 而求得问题的最优解,有两种方法:
0
σj
-1
0
-3 x1 4
1
0
1 x2 1
0
1
0 x3 9
0
0
σj
20
0
1
00
x3
x4
x5
0
1 -2 4
0
0 -1 —
1
0 0—
0
01
0 1/3 -2/3
0
0 -1
1 2/3 -4/3
0 1/3 1/3
5. 2 线性规划问题解的讨论
一、无可行解
max z=2x1+4x2 x1 +x2 10 2x1 +x2 40 x1 ,x2 0
0 x4 16
4
0
0
10
4
3 x2 3
0 1 0 0 1/4 -
-z
-9
2 0 0 0 -3/4
X(1)=(0,3,2,16,0)T, z1 =9
cj
2 30 0 0
CB XB
b
x1
x2
x3
x4
x5
2 x1 2 0 x4 8 3 x2 3
1
0
1
0 -1/2 -
0 0 -4 1 2
4
0 1 0 0 1/4 12
x2
2 x3 x3
3 1
x1 , x2 ,x 3 0
标准型:
max z’ =3x1-x2-x3
x1 2 x2 x3 x4 11
s.t.
4 2
x1 x1
x2 2x3 x3
x5 3 1
x1 , , x5 0
其中第2、3个约束方程中无明显基变量,分别加上人工变x6, x7
4 x2 20 0
1 0 1/3
3 x1 20 1
0 0 1/3
cj- zj
0 0 0 -7/3
x2
x1
此题初始解是退化的。 最优解也是退化解。 退化解迭代中,当换入 变量取零值时目标函数 值没有改进,
三、 有无穷多最优解的情况
最优解中有非基变量的检验数等于零的 情况。以这种非基变量作为换入变量,迭代可 求得另一基最优解。
例8 min z =-3x1+x2+x3
x1 2 x2 x3 11
s.t.
4x1 2 x1
x2
2
x3 x3
3 1
x1 , x2 ,x3 0
例8 s.t.
min z =-3x1+x2+x3
x1 2 x2 x3 11
4 x1 2 x1
3 40
x1 x2 x3 1 11 2 10 [1] -1 0
3+M 4-M 0
0 [2] 1 0 30 1 -1 0
0 70 0 1 1/2 0 0 -3/2 1 0 1/2
0 -M
θ x4 x5
00 1 -1 01
00
0 1 0
0 0 1 0
cj- zj
0 0 -3.5 0
0 x3 0 0
0 1 -1/3
X* = (4,1,9,0,0), z* = 2
0 -1
0 -M
-2 -1
0 -1
-2/3 -1
-4/3 -1/3
0
-1
1
-2
1
0
1
0 -3M+1
4
2.两阶段法
第一阶段:以人工变量之和最小化为目标函数 min = x6+x7
只要原问题有可行解,该最小化问题的最优目标函数值就 是 0,解得的最优解 x6=0,x7=0,对应原问题一个基可行解。 反之若该问题的最优解目标函数值大于零,则说明原问题无可 行解。
检验数 中零的 个数多 于基变 量的个 数
检验数大 于零,但 对应列元 素小于等 于零,无 换出变量
单纯形法小结
根据实际问题给出数学模型,列出初始单纯形表,进行标准化,见表
xj≥0 变 xj≤0 量 xj 无约束
约 b>0
不需要处理
令 xj′=-xj; xj′≥0 令 xj=xj′-xj″;xj′,xj″≥0 不需要处理
CB XB
b
x1
x2
x3
x4
x5
2 x1 4 0 x5 4 3 x2 2
1 0 0 1/4 0 0 0 -2 1/2 1 0 1 1/2 -1/8 0
-z
-14
0
0 -1.5 -1/8 0
X(3)=(4,2,0,4,0)T, z3 =14
§5 单纯形法的进一步讨论
5.1 人工变量法
解决初始基可行解的问题。当某个约束方 程中没有明 显的基变量时,在该方程中加上 人工变量。
0
-M
x7
0
11
0 3/2
1
1
0
0 x4 10 3
-2
0
1
-M x6 1
0
[1]
0
0
-1 x3 1 -2
0
1
0
1 -1+M 0
0
0 x4 12 [3]
0
-1 x2 1 0
1
-1 x3 1 -2
0
1
0
0
1
0
0
1
0
0
0
3 x1 4
1
0
0
1/3
-1 x2 1
0
1
0
0
-1 x3 9
0
0
0
0
1
2/3
0 -1/3
向量Pk 0,则此问题是无界解,停止计算。否则,转入下一步 。
(4).根据max(j > 0) =k,确定xk为换入变量,按 规则计算 =min{bi/aik\aik>0}
可确定第l行的基变量为换出变量。转入下一步。 (5).以 alk 为主元素进行迭代(即用高斯消去法或称为旋转变 换),把 xk 所对应的列向量变换为(0,0,…,1,…,0)T,将
勃兰特规则(P35)可避免死循环。
例:
max z=3x1+4x2 x1 +x2 40
2x1+x260 x1-x2 =0 x1 ,x2 0
cj →
CB XB b 0 x3 40 0 x4 60 -M x5 0
cj- zj
0 x3 40 0 x4 60 3 x1 0
cj- zj 4 x2 20 0 x4 0 3 x1 20
任一最优解可表示为所有基最优解的凸 组合。
例 max z=3x1+5x2 3x1 +5x2 15 2x1 + x2 5 2x1+2x2 11 x1 ,x2 0
CB XB b
0 x3 15
0 x4 5
0 x5 11
cj-zj
5 x2 3
0 x4 2
0 x5
5
cj-zj
3 50 00 x1 x2 x3 x4 x5 3 [5] 1 0 0 2 1010 2 2001 3 5000 3/5 1 1/5 0 0 7/5 0 -1/5 1 0 4/5 0 -2/5 0 1
-z
-13
0
0 -2
0 1/4
cj
2 30 0 0
CB XB
b
x1
x2
x3
x4
x5
2 x1 2 0 x4 8 3 x2 3
1
0
1
0 -1/2 -
0 0 -4 1 (2 ) 4
