(完整版)七年级数学下册相交线和平行线拔高训练

合集下载

(完整版)平行线与相交线提高训练

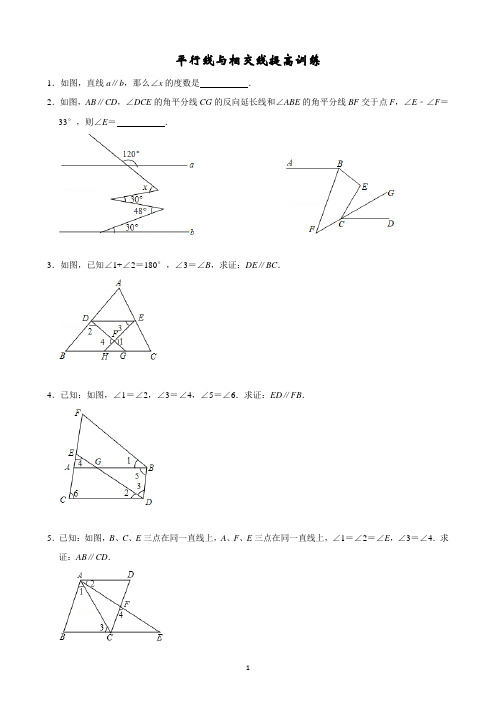
平行线与相交线提高训练1．如图，直线a∥b，那么∠x的度数是．2．如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F＝33°，则∠E＝．3．如图，已知∠1+∠2＝180°，∠3＝∠B，求证：DE∥BC．4．已知：如图，∠1＝∠2，∠3＝∠4，∠5＝∠6．求证：ED∥FB．5．已知：如图，B、C、E三点在同一直线上，A、F、E三点在同一直线上，∠1＝∠2＝∠E，∠3＝∠4．求证：AB∥CD．6．已知，如图，AE∥BD，∠1＝3∠2，∠2＝26°，求∠C．7．直线l1∥l2，∠A＝125°，∠B＝105°，求∠1+∠2的度数（提示：要作辅助线哟！）8．已知：射线OP∥AE（1）如图1，∠AOP的角平分线交射线AE与点B，若∠BOP＝58°，求∠A的度数．（2）如图2，若点C在射线AE上，OB平分∠AOC交AE于点B，OD平分∠COP交AE于点D，∠ADO＝39°，求∠ABO﹣∠AOB的度数．（3）如图3，若∠A＝m，依次作出∠AOP的角平分线OB，∠BOP的角平分线OB1，∠B1OP的角平分线OB2，∠B n﹣1OP的角平分线OB n，其中点B，B1，B2，…，B n﹣1，B n都在射线AE上，试求∠AB n O 的度数．9．数学思考：（1）如图1，已知AB∥CD，探究下面图形中∠APC和∠P AB、∠PCD的关系，并证明你的结论推广延伸：（2）①如图2，已知AA1∥BA1，请你猜想∠A1，∠B1，∠B2，∠A2、∠A3的关系，并证明你的猜想；②如图3，已知AA1∥BA n，直接写出∠A1，∠B1，∠B2，∠A2、…∠B n﹣1、∠A n的关系拓展应用：（3）①如图4所示，若AB∥EF，用含α，β，γ的式子表示x，应为A.180°+α+β﹣γB.180°﹣α﹣γ+βC．β+γ﹣αD．α+β+γ②如图5，AB∥CD，且∠AFE＝40°，∠FGH＝90°，∠HMN＝30°，∠CNP＝50°，请你根据上述结论直接写出∠GHM的度数是．10．已知，直线AB∥DC，点P为平面上一点，连接AP与CP．（1）如图1，点P在直线AB、CD之间，当∠BAP＝60°，∠DCP＝20°时，求∠APC．（2）如图2，点P在直线AB、CD之间，∠BAP与∠DCP的角平分线相交于点K，写出∠AKC与∠APC 之间的数量关系，并说明理由．（3）如图3，点P落在CD外，∠BAP与∠DCP的角平分线相交于点K，∠AKC与∠APC有何数量关系？并说明理由．11．如图，已知AM∥BN，∠A＝80°，点P是射线AM上动点（与A不重合），BC、BD分别平分∠ABP 和∠PBN，交射线AM于C、D．（1）求∠CBD的度数；（2）当点P运动时，那么∠APB：∠ADB的度数比值是否随之发生变化？若不变，请求出这个比值；若变化，请找出变化规律；（3）当点P运动到使∠ACB＝∠ABD时，求∠ABC的度数．12．如图1，AB∥CD，直线EF交AB于点E，交CD于点F，点G在CD上，点P在直线EF左侧、且在直线AB和CD之间，连接PE、PG．（1）求证：∠EPG＝∠AEP+∠PGC；（2）连接EG，若EG平分∠PEF，∠AEP+∠PGE＝110°，∠PGC＝∠EFC，求∠AEP的度数；（3）如图2，若EF平分∠PEB，∠PGC的平分线所在的直线与EF相交于点H，则∠EPG与∠EHG 之间的数量关系为．13．已知E、D分别在∠AOB的边OA、OB上，C为平面内一点，DE、DF分别是∠CDO、∠CDB的平分线．（1）如图1，若点C在OA上，且FD∥AO，求证：DE⊥AO；（2）如图2，若点C在∠AOB的内部，且∠DEO＝∠DEC，请猜想∠DCE、∠AEC、∠CDB之间的数量关系，并证明；（3）若点C在∠AOB的外部，且∠DEO＝∠DEC，请根据图3、图4分别写出∠DCE、∠AEC、∠CDB 之间的数量关系（不需证明）．14．已知，AB∥CD，点E为射线FG上一点．（1）如图1，若∠EAF＝30°，∠EDG＝40°，则∠AED＝°；（2）如图2，当点E在FG延长线上时，此时CD与AE交于点H，则∠AED、∠EAF、∠EDG之间满足怎样的关系，请说明你的结论；（3）如图3，DI平分∠EDC，交AE于点K，交AI于点I，且∠EAI：∠BAI＝1：2，∠AED＝22°，∠I＝20°，求∠EKD的度数．15．长江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图，灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是a°/秒，灯B转动的速度是b°/秒，且a、b满足|a﹣3b|+（a+b﹣4）2＝0．假定这一带长江两岸河堤是平行的，即PQ∥MN，且∠BAN＝45°（1）求a、b的值；（2）若灯B射线先转动20秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？（3）如图，两灯同时转动，在灯A射线到达AN之前．若射出的光束交于点C，过C作CD⊥AC交PQ 于点D，则在转动过程中，∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请求出其取值范围．16．已知如图，∠COD＝90°，直线AB与OC交于点B，与OD交于点A，射线OE与射线AF交于点G．（1）若OE平分∠BOA，AF平分∠BAD，∠OBA＝42°，则∠OGA＝；（2）若∠GOA＝∠BOA，∠GAD＝∠BAD，∠OBA＝42°，则∠OGA＝；（3）将（2）中的“∠OBA＝42°”改为“∠OBA＝α”，其它条件不变，求∠OGA的度数．（用含α的代数式表示）（4）若OE将∠BOA分成1：2两部分，AF平分∠BAD，∠ABO＝α（30°＜α＜90°），求∠OGA的度数．（用含α的代数式表示）17．已知直线AB∥CD，E是直线AB的上方一点，连接AE、EC（1）如图1，求证：∠AEC+∠EAB＝∠ECD（2）如图2，AF平分∠BAE，CF平分∠DCE，且∠AFC比∠AEC的倍少40°，直接写出∠AEC的度数18．直线MN与直线PQ相交于O，点A在射线OP上运动，点B在射线OM上运动．（1）如图1，若∠AOB＝80°，已知AE、BE分别是∠BAO和∠ABO的角平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．（2）如图2，若∠AOB＝80°，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，AD、BC的延长线交于点F，点A、B在运动的过程中，∠F＝；DE、CE又分别是∠ADC和∠BCD 的角平分线，点A、B在运动的过程中，∠CED的大小也不发生变化，其大小为：∠CED＝．（3）如图3，若∠AOB＝90°，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F，则∠EAF＝；（4）如图3，若AF，AE分别是∠GAO，∠BAO的角平分线，∠AOB＝90°，在△AEF中，如果有一个角是另一个角的4倍，则∠ABO的度数＝．20．如图，点D、点E分别在△ABC边AB，AC上，∠CBD＝∠CDB，DE∥BC，∠CDE的平分线交AC 于F点．（1）求证：∠DBF+∠DFB＝90°；（2）如图②，如果∠ACD的平分线与AB交于G点，∠BGC＝50°，求∠DEC的度数．（3）如图③，如果H点是BC边上的一个动点（不与B、C重合），AH交DC于M点，∠CAH的平分线AI交DF于N点，当H点在BC上运动时，的值是否发生变化？如果变化，说明理由；如果不变，试求出其值．。

初一数学下册相交线与平行线专项提升训练(含答案详解)

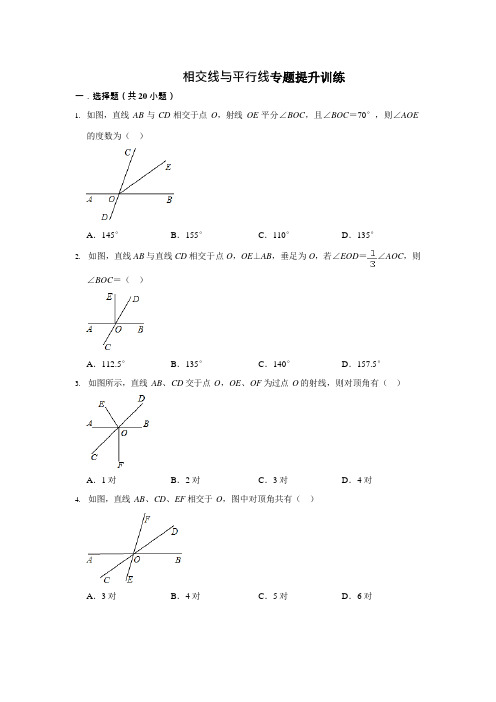
一．选择题（共20 小题）相交线与平行线专题提升训练1.如图，直线AB 与CD 相交于点O，射线OE 平分∠BOC，且∠BOC＝70°，则∠AOE的度数为（）A．145°B．155°C．110°D．135°2.如图，直线AB 与直线CD 相交于点O，OE⊥AB，垂足为O，若∠EOD＝∠AOC，则∠BOC＝（）A．112.5°B．135°C．140°D．157.5°3.如图所示，直线AB、CD 交于点O，OE、OF 为过点O 的射线，则对顶角有（）A．1 对B．2 对C．3 对D．4 对4.如图，直线AB、CD、EF 相交于O，图中对顶角共有（）A．3 对B．4 对C．5 对D．6 对5．4 条直线交于一点，则对顶角有（）A．4 对B．6 对C．8 对D．12 对6.如图所示，直线AB，CD，EF，MN，GH 相交于点O，则图中对顶角共有（）A.3对B．6 对C．12 对D．20 对7.如图，直线AB、CD 相交于点O，作射线OE，则图中邻补角有（）A.4对B．6 对C．7 对D．8 对8.某城市有四条直线型主干道分别为l1，l2，l3，l4，l3 和l4 相交，l1 和l2 相互平行且与l3、l4 相交成如图所示的图形，则共可得同旁内角（）对．A．4 B．8 C．12 D．169.如图，下列四个条件中，能判断DE∥AC 的是（）A．∠2＝∠4 B．∠3＝∠4 C．∠AFE＝∠ACB D．∠BED＝∠C10.如图，若∠3＝∠4，则下列条件中，不能判定AB∥CD 的是（）A．∠1＝∠2 B．∠1＝∠3 且∠2＝∠4C．∠1+∠3＝90°且∠2+∠4＝90°D．∠1+∠2＝90°11.如图，能够证明a∥b 的是（）A．∠1＝∠2 B．∠4＝∠5 C．∠4＝∠3 D．∠1＝∠5 12．如图，已知：∠1＝∠2，∠3＝∠4，那么下列结论成立的是（）A．∠l＝∠3 B．∠2＝∠3 C．AB∥CD D．AE∥DF 13．如图，∠1 与∠2 互补，∠2 与∠3 互补，那么（）A．L1∥L2 B．L1⊥L5 C．L3∥L4 D．L3∥L514.将AD 与BC 两边平行的纸条ABCD 按如图所示折叠，则∠1 的度数为（）A．72°B．45°C．56°D．60°15.如图，把三角尺的直角顶点放在直尺的一边上，若∠1＝32°，则∠2 的度数为（）A．68°B．58°C．48°D．32°16.如图，把一张长方形的纸片ABCD沿EF折叠，若∠AED'＝40°，则∠EFB的度数为（）A．40°B．50°C．60°D．70°17.如图，将一张矩形纸片折叠，若∠1＝80°，则∠2 的度数是（）A．50°B．60°C．70°D．80°18.如图，将长方形纸条ABCD 沿EF 折叠后，ED 与BF 交于G 点，若∠EFC＝130°，则∠AED 的度数为（）A．55°B．70°C．75°D．80°19.如图，将一张对边互相平行的纸条沿EF 折叠，若∠EFB＝32°，则①∠C′EF＝32°；②∠AEC＝148°；③∠BGE＝64°；④∠BFD＝116°，则下列结论正确的有（）11.1个B．2 个C．3 个D．4 个20.如图，将矩形ABCD 沿EF 折叠，点C 落在点H 处，点D 落在AB 边上的点G 处，若∠AEG＝30°，则∠EFC 等于（）A．115°B．75°C．105°D．150°二．填空题（共13 小题）21.如图，P 是直线l 外一点，从点P 向直线l 引PA，PB，PC，PD 几条线段，其中只有PA 与l 垂直．这几条线段中，最短的是，依据是．22.如图，为了把河中的水引到C 处，可过点C 作CD⊥AB 于D，然后沿CD 开渠，这样做可使所开的渠道最短，这种设计的依据是．23.如图，将直尺一边与量角器的零刻度线对齐，则图中线段OA，OB、OC 中最短的线段是，你的依据是和．24．（1）两条直线相交于一点有2组不同的对顶角；（2）三条直线相交于一点有6 组不同的对顶角；（3）四条直线相交于一点有12 组不同的对顶角；（4）n条直线相交于同一点有组不同对顶角．（如图所示）25.如图，直线l1、l2、l3 相交于一点O，对顶角一共有对．26.如图，直线a，b，c 两两相交于A，B，C 三点，则图中有对对顶角；有对同位角；有对内错角；有对同旁内角．27.图中，与∠1 成同位角的角的个数是．28.四条直线，每一条都与另外三条相交，且四条直线不相交于同一点，每条直线交另外两条直线，都能组成组同位角，这个图形中共有组同位角．29.平面内5 条直线两两相交，且没有3 条直线交于一点，那么图中共有对同旁内角．30.如图，将一张长方形纸条沿某条直线折叠，若∠1＝116°，则∠2 等于．31.有一条长方形纸带，按如图所示沿AB 折叠，若∠1＝40°，则纸带重叠部分中∠CAB＝°．32.如图（1）是长方形纸条，∠DEF＝20°，将纸条沿EF折叠成如图（2），则图（2）中的∠CFG 的度数是．33.将一条两边互相平行的纸带沿EF折叠，如图（1），AD∥BC，ED'∥FC'，设∠AED'＝x°（1）∠EFB＝．（用含x的代数式表示）（2）若将图1继续沿BF折叠成图（2），∠EFC″＝．（用含x的代数式表示）．三．解答题（共10 小题）34.如图，直线AB、CD 相交于O，OE⊥CD，且∠BOD 的度数是∠AOD 的5倍．求：（1）∠AOD、∠BOD的度数；（2）∠BOE 的度数．35.如图，直线AB 和CD 相交于点O，OE 把∠AOC 分成两部分，且∠AOE：∠EOC＝2：5（1）如图1，若∠BOD＝70°，求∠BOE；（2）如图2，若OF 平分∠BOE，∠BOF＝∠AOC+10°，求∠EOF．36.如图，直线AB、CD 相交于点O，OE 平分∠BOC，∠COF＝90°．（1）若∠AOF＝70°，求∠BOE 的度数；（2）若∠BOE：∠BOD＝3：2，求∠AOF 的度数．37.如图，已知∠A＝∠C，∠1+∠2＝180°，试猜想AB 与CD 之间有怎样的位置关系？并说明理由．38．（1）如图，已知∠ABC，画一个角∠DEF，使DE∥AB，EF∥BC，且DE交BC于点P．探究：∠ABC 与∠DEF 分别有怎样的数量关系？并选择一种情况说明理由．图1 中∠ABC 与∠DEF 数量关系为；图2 中∠ABC 与∠DEF 数量关系为．选择一种情况说明理由：（2）由（1）你得出的结论是．（3）若两个角的两边互相平行，且一个角比另一个角的2 倍少30°，直接写出这两个角的度数．39.如图，已知∠AED＝∠ACB，CD⊥AB，HF⊥AB，猜想∠1 与∠2 的数量关系并说明的理由．40．如图，AB∥DG，∠1+∠2＝180°，（1）求证：AD∥EF；（2）若DG 是∠ADC 的平分线，∠2＝150°，求∠B 的度数．41.如图，已知∠1+∠2＝180°，∠DEF＝∠A，试判断∠ACB 与∠DEB 的大小关系，并证明．42.如图，在△ABC 中，CD⊥AB，垂足为D，点E 在BC 上，EF⊥AB，垂足为F．∠1＝∠2，试判断DG 与BC 的位置关系，并说明理由．43.综合与探究如图，已知AM∥BN，∠A＝60°，点P是射线AM上一动点（与点A不重合）．BC，BD 别平分∠ABP 和∠PBN，分别交射线AM 于点C，D．（1）求∠ABN、∠CBD 的度数；根据下列求解过程填空．解：∵AM∥BN，∴∠ABN+∠A＝180°∵∠A＝60°，∴∠ABN＝，∴∠ABP+∠PBN＝120°，∵BC 平分∠ABP，BD 平分∠PBN，∴∠ABP＝2∠CBP、∠PBN＝，（）∴2∠CBP+2∠DBP＝120°，∴∠CBD＝∠CBP+∠DBP＝．（2）当点P 运动时，∠APB 与∠ADB 之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．（3）当点P 运动到使∠ACB＝∠ABD 时，直接写出∠ABC 的度数．相交线与平行线必备参考答案与试卷解析一．选择题（共20 小题）1.如图，直线AB 与CD 相交于点O，射线OE 平分∠BOC，且∠BOC＝70°，则∠AOE的度数为（）A．145°B．155°C．110°D．135°【分析】依据∠BOC＝70°，OE 平分∠BOC，即可得到∠COE＝35°，∠AOC＝180°﹣70°＝110°，进而得出∠AOE 的度数．【解答】解：∵∠BOC＝70°，OE 平分∠BOC，∴∠COE＝35°，∠AOC＝180°﹣70°＝110°，∴∠AOE＝∠AOC+∠COE＝110°+35°＝145°．故选：A．【点评】本题主要考查了对顶角与邻补角，解题时注意：对顶角相等，邻补角互补，即和为180°．2.如图，直线AB 与直线CD 相交于点O，OE⊥AB，垂足为O，若∠EOD＝∠AOC，则∠BOC＝（）A．112.5°B．135°C．140°D．157.5°【分析】根据平角、直角及角的和差关系可求出∠AOC+∠EOD＝90°，再与已知∠EOD ＝∠AOC 联立，求出∠AOC，利用互补关系求∠BOC．【解答】解：∵∠COD＝180°，OE⊥AB，∴∠AOC+∠AOE+∠EOD＝180°，∠AOE＝90°，∴∠AOC+∠EOD＝90°，①又∵∠EOD＝∠AOC，②由①、②得，∠AOC＝67.5°，∵∠BOC 与∠AOC 是邻补角，∴∠BOC＝180°﹣∠AOC＝112.5°．故选：A．【点评】此题主要考查了对顶角、余角、补角的关系．解题时注意运用邻补角的性质：邻补角互补，即和为180°．3.如图所示，直线AB、CD 交于点O，OE、OF 为过点O 的射线，则对顶角有（）A．1 对B．2 对C．3 对D．4 对【分析】据对顶角的定义对各图形判断即可．【解答】解：图中的对顶角有：∠AOC 与∠BOD，∠AOD 与∠BOC 共2对．故选：B．【点评】本题考查了对顶角的定义，是基础题，熟记概念并准确识图是解题的关键．4.如图，直线AB、CD、EF 相交于O，图中对顶角共有（）A．3 对B．4 对C．5 对D．6 对【分析】根据对顶角的定义，对顶角的两边互为反向延长线，可以判断．【解答】解：图中对顶角有：∠AOF 与∠BOE、∠AOD 与∠BOC、∠FOD 与∠EOC、∠FOB 与∠AOE、∠DOB 与∠AOC、∠DOE 与∠COF，共6对．故选：D．【点评】本题考查了对顶角的定义，注意对顶角是两条直线相交而成的四个角中，没有公共边的两个角．5．4 条直线交于一点，则对顶角有（）A．4 对B．6 对C．8 对D．12 对【分析】每两条直线交于一点，形成两对对顶角，4 条直线交于一点，则有6 条直线形成两对对顶角，那么对顶角的个数有12 对．【解答】解：根据对顶角的定义可知：4 条直线交于一点，则对顶角有12 对．故选D．【点评】本题考查对顶角的概念，两直线相交形成两对对顶角．6.如图所示，直线AB，CD，EF，MN，GH 相交于点O，则图中对顶角共有（）A.3对B．6 对C．12 对D．20 对【分析】n 条不同直线相交于一点，可以得到n（n﹣1）对对顶角，依据规律可得结果．【解答】解：2 条直线交于一点，对顶角有 2 对，2＝2×1；3条直线交于一点，对顶角有6 对，6＝3×2；4条直线交于一点，对顶角有12 对，12＝4×3；由规律可得，n 条不同直线相交于一点，可以得到n（n﹣1）对对顶角，∴直线AB，CD，EF，MN，GH 相交于点O，对顶角共有5×4＝20 对，故选：D．【点评】本题考查了对顶角的定义，注意对顶角是两条直线相交而成的四个角中，没有公共边的两个角．7.如图，直线AB、CD 相交于点O，作射线OE，则图中邻补角有（）A.4对B．6 对C．7 对D．8 对【分析】根据邻补角定义，两个角的和等于180°，并且有一条边是公共边的两个角互为邻补角，进行解答．【解答】解：如图，邻补角有：∠AOC 与∠AOD，∠AOD 与∠BOD，∠BOD 与∠BOC，∠BOE 与∠AOE，∠BOC 与∠AOC，∠COE 与∠DOE．所以共 6 对．故选：B．【点评】本题主要考查邻补角的定义，注意按一定顺序寻找方能做到不重不漏．8.某城市有四条直线型主干道分别为l1，l2，l3，l4，l3 和l4 相交，l1 和l2 相互平行且与l3、l4 相交成如图所示的图形，则共可得同旁内角（）对．A．4 B．8 C．12 D．16【分析】观察图形，确定不同的截线分类讨论，如分l1、l2 被l3 所截，l1、l2 被l4 所截，l1、l3 被l4 所截，l2、l3 被l4 所截，l3、l4 被l1 所截，l3、l4 被l2 所截l1、l4 被l3 所截、l2、l4 被l3 所截来讨论．【解答】解：l1、l2 被l3 所截，有两对同旁内角，其它同理，故一共有同旁内角2×8＝16 对．故选：D．【点评】在较复杂图形中确定“三线八角”可从截线入手，分类讨论，做到不重复不遗漏．9.如图，下列四个条件中，能判断DE∥AC 的是（）A．∠2＝∠4 B．∠3＝∠4 C．∠AFE＝∠ACB D．∠BED＝∠C 【分析】根据平行线的判定方法一一判断即可．【解答】解：∵∠3＝∠4，∴DE∥AC，故选：B．【点评】本题考查平行线的判定，解题的关键是熟练掌握基本知识，属于中考常考题型．10.如图，若∠3＝∠4，则下列条件中，不能判定AB∥CD 的是（）A．∠1＝∠2 B．∠1＝∠3 且∠2＝∠4C．∠1+∠3＝90°且∠2+∠4＝90°D．∠1+∠2＝90°【分析】利用平行线的判定方法一一判断即可．【解答】解：A、由∠1＝∠2，∠3＝∠4，可以推出∠ABC＝∠DCB，推出AB∥CD，故本选项不符合题意．B、由∠1＝∠3，∠2＝∠4，可以推出∠ABC＝∠DCB，推出AB∥CD，故本选项不符合题意．C、由∠1+∠3＝90°，∠2+∠4＝90°，可以推出∠ABC＝∠DCB，推出AB∥CD，故本选项不符合题意．D、由∠1+∠2＝90°无法推出∠ABC＝∠DCB，故本选项符合题意．故选：D．【点评】本题考查平行线的判定，解题的关键是熟练掌握基本知识，属于中考常考题型．11.如图，能够证明a∥b 的是（）第18 页（共41 页）A．∠1＝∠2 B．∠4＝∠5 C．∠4＝∠3 D．∠1＝∠5【分析】根据平行线的判定一一判断即可．【解答】解：∵∠4＝∠5，∴a∥b（内错角相等两直线平行）．故选：B．【点评】本题考查平行线的判定，解题的关键是熟练掌握基本知识，属于中考常考题型．12．如图，已知：∠1＝∠2，∠3＝∠4，那么下列结论成立的是（）A．∠l＝∠3 B．∠2＝∠3 C．AB∥CD D．AE∥DF【分析】证明∠BAD＝∠CDA 即可判断．【解答】解：∵∠1＝∠2，∠3＝∠4，∴∠BAD＝∠CDA，∴AB∥CD，故选：C．【点评】本题考查平行线的判定，解题的关键是熟练掌握基本知识，属于中考常考题型．13．如图，∠1 与∠2 互补，∠2 与∠3 互补，那么（）A．L1∥L2 B．L1⊥L5 C．L3∥L4 D．L3∥L5【分析】因为∠1 与∠2 互补，∠2 与∠3 互补，根据同一个角的补角相等，得∠1＝∠3；所以根据内错角相等，两直线平行，可知L3∥L5．【解答】解：∵∠1 与∠2 互补，∠2 与∠3 互补，∴∠1＝∠3（同角的补角相等）．∴L3∥L5（内错角相等，两直线平行）．故选：D．【点评】本题要会运用补角的性质：“同一个角的补角相等”，找到内错角的相等关系，从而证明出两直线平行．14.将AD 与BC 两边平行的纸条ABCD 按如图所示折叠，则∠1 的度数为（）A．72°B．45°C．56°D．60°【分析】根据折叠的性质得出∠C'EF＝62°，利用平行线的性质进行解答即可．【解答】解：∵一张长方形纸条ABCD 折叠，∴∠C'EF＝∠FEC＝62°，∵AD∥BC，∴∠1＝∠C'FB＝180°﹣62°﹣62°＝56°，故选：C．【点评】本题考查了平行线的性质、翻折变换（折叠问题）．正确观察图形，熟练掌握平行线的性质是解题的关键．15.如图，把三角尺的直角顶点放在直尺的一边上，若∠1＝32°，则∠2 的度数为（）A．68°B．58°C．48°D．32°【分析】因直尺和三角板得AD∥FE，∠BAC＝90°；再由AD∥FE 得∠2＝∠3；平角构建∠1+∠BAC+∠3＝180°得∠1+∠3＝90°，已知∠1＝32°可求出∠3＝58°，即∠2＝58°．【解答】解：如图所示：∵AD∥FE，∴∠2＝∠3，又∵∠1+∠BAC+∠3＝180°，∠BAC＝90°，∴∠1+∠3＝90°，又∵∠1＝32°，∴∠3＝58°，∴∠2＝58°，故选：B．【点评】本题综合考查了平行线的性质，直角，平角和角的和差相关知识的应用，重点是平行线的性质．16.如图，把一张长方形的纸片ABCD沿EF折叠，若∠AED'＝40°，则∠EFB的度数为（）A．40°B．50°C．60°D．70°【分析】根据折叠性质得出∠DED′＝2∠DEF，根据∠AED′的度数求出∠DED′，即可求出∠DEF 的度数，进而得到答案．【解答】解：由翻折的性质得：∠DED′＝2∠DEF，∵∠AED′＝40°，∴∠DED′＝180°﹣∠AED′＝140°，∴∠DEF＝70°，又∵AD∥BC，∴∠EFB＝∠DEF＝70°．故选：D．【点评】本题考查平行线的性质，三角形的内角和定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．17.如图，将一张矩形纸片折叠，若∠1＝80°，则∠2 的度数是（）A．50°B．60°C．70°D．80°【分析】利用平行线的性质解决问题即可．【解答】解：∵a∥b，∴∠1＝∠3＝80°，由翻折不变性可知：∠2＝∠4＝（180°﹣80°）＝50°，故选：A．【点评】本题考查平行线的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．18.如图，将长方形纸条ABCD 沿EF 折叠后，ED 与BF 交于G 点，若∠EFC＝130°，则∠AED 的度数为（）A．55°B．70°C．75°D．80°【分析】求出∠DEF，根据∠AED＝180°﹣2∠AED 即可解决问题．【解答】解：∵DE∥CF，∴∠EFC+∠DEF＝180°，∵∠EFC＝130°，∴∠DEF＝50°，∴∠AED＝180°﹣2×50°＝80°，故选：D．【点评】本题考查平行线的判定和性质，解题的关键是熟练掌握基本知识，属于中考常考题型．19.如图，将一张对边互相平行的纸条沿EF 折叠，若∠EFB＝32°，则①∠C′EF＝32°；②∠AEC＝148°；③∠BGE＝64°；④∠BFD＝116°，则下列结论正确的有（）11.1个B．2 个C．3 个D．4 个【分析】根据平行线的性质及翻折变换的性质对各小题进行逐一分析即可．【解答】解：①∵AE∥BG，∠EFB＝32°，∴∠C′EF＝∠EFB＝32°，故本小题正确；②∵AE∥BG，∠EFB＝32°，∴∠AEF＝180°﹣∠EFB＝180°﹣32°＝148°，∵∠AEF＝∠AEC+∠GEF，∴∠AEC＜148°，故本小题错误；③∵∠C′EF＝32°，∴∠GEF＝∠C′EF＝32°，∴∠C′EG＝∠C′EF+∠GEF＝32°+32°＝64°，∵AC′∥BD′，∴∠BGE＝∠C′EG＝64°，故本小题正确；④∵∠BGE＝64°，∴∠CGF＝∠BGE＝64°，∵DF∥CG，∴∠BFD＝180°﹣∠CGF＝180°﹣64°＝116°，故本小题正确．故选：C．【点评】本题考查的是平行线的性质及翻折变换的性质，熟知图形翻折不变性的性质是解答此题的关键．20.如图，将矩形ABCD 沿EF 折叠，点C 落在点H 处，点D 落在AB 边上的点G 处，若∠AEG＝30°，则∠EFC 等于（）A．115°B．75°C．105°D．150°【分析】利用翻折变换的性质求出∠DEF，再利用平行线的性质解决问题即可．【解答】解：∵∠AEG＝30°，∴∠DEG＝150°，由翻折的性质可知：∠DEF＝∠FEG＝∠DEG＝75°，∵AD∥BC，∴∠DEF+∠EFC＝180°，∴∠EFC＝105°，故选：C．【点评】本题考查平行线的性质，翻折变换等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．二．填空题（共13 小题）21.如图，P 是直线l 外一点，从点P 向直线l 引PA，PB，PC，PD 几条线段，其中只有PA 与l 垂直．这几条线段中，最短的是PA ，依据是垂线段最短．【分析】根据“直线外一点到直线上各点的所有线中，垂线段最短”进行解答．【解答】解：直线外一点与直线上各点连接的所有线段中，最短的是PA，依据是垂线段最短，故答案为：PA，垂线段最短．【点评】本题主要考查了垂线段最短的性质，熟记性质是解题的关键．22.如图，为了把河中的水引到C 处，可过点C 作CD⊥AB 于D，然后沿CD 开渠，这样做可使所开的渠道最短，这种设计的依据是垂线段最短．【分析】过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短．据此作答．【解答】解：过D 点引CD⊥AB 于D，然后沿CD 开渠，可使所开渠道最短，这种设计的依据是垂线段最短．故答案为：垂线段最短．【点评】本题考查了垂线的性质在实际生活中的运用，属于基础题．23.如图，将直尺一边与量角器的零刻度线对齐，则图中线段OA，OB、OC 中最短的线段是OB ，你的依据是垂线段最短和平行线的性质．【分析】依据垂线段最短，即可得到图中线段OA，OB、OC 中最短的线段；依据平行线的性质，即可得到∠OBC＝90°，进而得出OB⊥AC．【解答】解：由题可得，图中线段OA，OB、OC 中最短的线段是OB，依据为垂线段最短和平行线的性质．故答案为：OB，垂线段最短，平行线的性质．【点评】本题主要考查了垂线段最短，垂线段最短指的是从直线外一点到这条直线所作的垂线段最短．它是相对于这点与直线上其他各点的连线而言．24．（1）两条直线相交于一点有2组不同的对顶角；（2）三条直线相交于一点有6 组不同的对顶角；（3）四条直线相交于一点有12 组不同的对顶角；（4）n条直线相交于同一点有n（n﹣1）组不同对顶角．（如图所示）【分析】根据（1）（2）（3）得出规律，可求n条直线相交于同一点有多少组不同对顶角．【解答】解：观察图形可知，n 条直线相交于同一点有（1+2+…+n﹣1）×2＝×2＝n（n﹣1）组不同对顶角．故答案为：n（n﹣1）．【点评】考查了对顶角的定义，关键是熟悉对顶角：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角．25.如图，直线l1、l2、l3 相交于一点O，对顶角一共有6 对．【分析】识别图中的对顶角应从这个较复杂的图形中分解出三个基本图形（即定义图形）即直线AB、CD 相交于O；直线AB，EF 相交于O；直线CD，EF 相交于O．由于两条直线相交组成对顶角，所以上述图中共有6 对对顶角．【解答】解：如图，图中共有 6 对对顶角：∠AOC 和∠BOD，∠AOD 和∠BOC；∠AOF 和∠BOE，∠AOE 和∠BOF；∠COF 和∠DOE，∠COE 和∠DOF．故答案为：6【点评】本题考查了对顶角的定义，有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角．26.如图，直线a，b，c 两两相交于A，B，C 三点，则图中有 6 对对顶角；有12 对同位角；有6 对内错角；有6 对同旁内角．【分析】根据3 条直线两两相交，共有3 个点，每个点有两对对顶角，得出对顶角、内错角、同旁内角的对数．【解答】解：3 条直线两两相交，共有3 个点，每个点有两对对顶角，任意两条直接被第三条截有12 对同位角，6 对内错角，6 对同旁内角，所以对顶角有6 对，12 对同位角，6 对内错角，6 对同旁内角；故答案为：6 12 6 6【点评】本题考查了同位角、内错角、同旁内角的定义．注意在截线的同旁找同位角，在被截直线之间找内错角、同旁内角．要结合图形，熟记同位角、内错角、同旁内角的位置特点．两条直线被第三条直线所截所形成的八个角中，有4 组同位角．27.图中，与∠1 成同位角的角的个数是3 ．【分析】据五条直线相交关系分别讨论：l1、l2 被b 所截，与∠1 成同位角的角的有1 个；a、b 被l2 所截，与∠1 成同位角的角的有1 个；c、b 被l2 所截，与∠1 成同位角的角的有1 个．共计3 个．【解答】解：据同位角定义，l1l2 被 b 所截，与∠1 成同位角的角的有 1 个；a、b 被l2 所截，与∠1 成同位角的角的有1 个；c、b 被l2 所截，与∠1 成同位角的角的有1 个．一共有3 个，故填3．【点评】本题考查了同位角的定义，注意不要漏解．28.四条直线，每一条都与另外三条相交，且四条直线不相交于同一点，每条直线交另外两条直线，都能组成4 组同位角，这个图形中共有48 组同位角．【分析】每条直线都与另3 条直线相交，有3 个交点．每2 个交点决定一条线段，共有3条线段.4 条直线两两相交且无三线共点，共有3×4＝12 条线段．每条线段各有4 组同位角，可知同位角的总组数．【解答】解：∵平面上4 条直线两两相交且无三线共点，∴共有3×4＝12 条线段．又∵每条线段各有 4 组同位角，∴共有同位角12×4＝48 组．故每条直线交另外两条直线，都能组成4 组同位角．这个图形中共有48 组同位角．故答案为：4，48．【点评】本题考查了同位角的定义．注意在截线的同旁找同位角．要结合图形，熟记同位角的位置特点．两条直线被第三条直线所截所形成的八个角中，有4 组同位角．29.平面内5 条直线两两相交，且没有3 条直线交于一点，那么图中共有60 对同旁内角．【分析】每条直线都与另4 条直线相交，且没有3 条直线交于一点，共有30 条线段．每条线段两侧各有一对同旁内角内角，可知同旁内角的总对数．【解答】解：如图所示：∵平面上5 条直线两两相交且无三线共点，∴共有30 条线段．又∵每条线段两侧各有一对同旁内角，∴共有同旁内角30×2＝60对．故答案为：60．【点评】本题考查了同旁内角的定义．注意在截线的同旁找同旁内角．要结合图形，熟记同旁内角的位置特点．两条直线被第三条直线所截所形成的八个角中，有两对同旁内角．注意按顺序一个点一个点的数，不要重复也不要遗漏．30.如图，将一张长方形纸条沿某条直线折叠，若∠1＝116°，则∠2 等于58°．【分析】依据平行线的性质以及折叠的性质，即可得到∠2 的度数．【解答】解：如图，∵AB∥CD，∴∠1＝∠BAC＝116°，由折叠可得，∠BAD＝∠BAC＝58°，∵AB∥CD，∴∠2＝∠BAD＝58°，故答案为：58°．【点评】本题考查平行线的性质，翻折变换知识，解题的关键是熟练掌握基本知识，属于中考常考题型．31.有一条长方形纸带，按如图所示沿AB 折叠，若∠1＝40°，则纸带重叠部分中∠CAB＝70 °．【分析】可利用平行线的性质求出∠FAC 的大小，进而可求∠CAB 的大小．【解答】解：∵长方形纸带，∴BE∥AF，∴∠1＝∠CAF＝40°，由于折叠可得：∠CAB＝，故答案为：70【点评】此题考查平行线的性质，熟练掌握平行线的性质，会求解一些简单的计算问题．32.如图（1）是长方形纸条，∠DEF＝20°，将纸条沿EF折叠成如图（2），则图（2）中的∠CFG 的度数是140°．【分析】先根据平行线的性质得出∠DEF＝∠EFB，根据图形折叠的性质得出∠EFC 的度数，进而得出∠CFG 即可．【解答】解：∵AD∥BC，∴∠DEF＝∠EFB＝20°，由折叠可得：∠EFC＝180°﹣20°＝160°，∴∠CFG＝160°﹣20°＝140°，故答案为：140°．【点评】本题考查了平行线的性质，图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．33.将一条两边互相平行的纸带沿EF折叠，如图（1），AD∥BC，ED'∥FC'，设∠AED'＝x°（1）∠EFB＝90°﹣x° ．（用含x的代数式表示）（2）若将图1继续沿BF折叠成图（2），∠EFC″＝﹣90° ．（用含x的代数式表示）．【分析】（1）由平行线的性质得∠DEF＝∠EFB，∠AEH+∠EHB＝180°，折叠和三角形的外角得∠D'EF＝∠EFB，∠EFB＝∠EHB，最后计算出∠EFB＝90°﹣x°；（2）由折叠和平角的定义求出∠EFC'＝90°+ ，再次折叠经计算求出∠EFC''＝．【解答】解：（1）如图1所示：∵AD∥BC，∴∠DEF＝∠EFB，∠AEH+∠EHB＝180°，又∵∠DEF＝∠D'EF，∴∠D'EF＝∠EFB，又∵∠EHB＝∠D'EF+∠EFB，∴∠EFB＝∠EHB，又∵∠AED'＝x°，∴∠EHB＝180°﹣x°∴∠EFB＝＝90°﹣x°（2）如图2 所示：∵∠EFB+∠EFC'＝180°，∴∠EFC'＝180°﹣（90°﹣°）＝90°+ ，又∵∠EFC'＝2∠EFB+∠EFC''，∴∠EFC''＝∠EFC'﹣2∠EFB＝90°+ ﹣2（90°﹣°）＝，故答案为．【点评】本题综合考查了平行线的性质，折叠问题，等腰三角形的性质，三角形的外角定理，平角的定义和角的和差等相关知识，重点掌握平行线的性质，难点是折叠前后的变及不变的问题，二次折叠角的前后大小等量关系．三．解答题（共10 小题）34.如图，直线AB、CD 相交于O，OE⊥CD，且∠BOD 的度数是∠AOD 的5倍．求：（1）∠AOD、∠BOD的度数；（2）∠BOE 的度数．【分析】（1）根据∠BOD+∠AOD＝180°和∠BOD＝5∠AOD 求出即可；（2）求出∠BOC，∠EOC，代入∠BOE＝∠EOC﹣∠BOC 求出即可．【解答】解：（1）∵AB是直线（已知），∴∠BOD+∠AOD＝180°，∵∠BOD 的度数是∠AOD 的 5 倍，∴∠AOD＝×180°＝30°，∠BOD＝×180°＝150°．（2）∵∠BOC＝∠AOD＝30°，OE⊥DC，∴∠EOC＝90°，∴∠BOE＝∠EOC﹣∠BOC＝90°﹣30°＝60°．【点评】本题考查了垂直定义，邻补角，对顶角，角的有关计算的应用，主要考查学生的计算能力．35.如图，直线AB 和CD 相交于点O，OE 把∠AOC 分成两部分，且∠AOE：∠EOC＝2：5（1）如图1，若∠BOD＝70°，求∠BOE；（2）如图2，若OF 平分∠BOE，∠BOF＝∠AOC+10°，求∠EOF．【分析】（1）依据对顶角相等以及邻补角，即可得到∠AOC＝70°，∠BOC＝110°，再根据∠AOE：∠EOC＝2：5，即可得到∠COE 的度数，进而得出∠BOE 的度数；（2）设∠AOE＝2α，∠EOC＝5α，则∠BOF＝7α+10°，∠BOF＝∠BOE＝（180°﹣∠AOE）＝（180°﹣2α），根据7α+10°＝（180°﹣2α），即可得到α的值，进而得到∠EOF 的度数．【解答】解：（1）∵∠BOD＝70°，直线AB和CD相交于点O，∴∠AOC＝70°，∠BOC＝110°，又∵∠AOE：∠EOC＝2：5，∴∠COE＝70°×＝50°，∴∠BOE＝50°+110°＝160°；（2）设∠AOE＝2α，∠EOC＝5α，则∠BOF＝7α+10°，∵OF 平分∠BOE，∴∠BOF＝∠BOE＝（180°﹣∠AOE）＝（180°﹣2α），∴7α+10°＝（180°﹣2α），解得α＝10°，∴∠EOF＝∠BOF＝70°+10°＝80°．【点评】本题考查了对顶角、邻补角以及角平分线的定义，解决问题的关键是利用了对顶角相等，邻补角互补的关系．36.如图，直线AB、CD 相交于点O，OE 平分∠BOC，∠COF＝90°．（1）若∠AOF＝70°，求∠BOE 的度数；（2）若∠BOE：∠BOD＝3：2，求∠AOF 的度数．【分析】（1）先根据余角的概念求出∠AOC 的度数，再根据邻补角的性质求出∠BOC 的度数，最后根据角平分线的定义计算即可；（2）根据角平分线的定义和邻补角的性质计算即可．【解答】解：（1）∵∠COF＝90°，∠AOF＝70°，∴∠AOC＝90°﹣70°＝20°，∴∠BOC＝180°﹣20°＝160°，∵OE 平分∠BOC，∴∠BOE＝∠BOC＝80°；（2）∵∠BOE：∠BOD＝3：2，OE 平分∠BOC，∴∠EOC：∠BOE：∠BOD＝3：3：2，∵∠EOC+∠BOE+∠BOD＝180°，∴∠BOD＝45°，∴∠AOC＝∠BOD＝45°，又∵∠COF＝90°，∴∠AOF＝90°﹣45°＝45°．【点评】本题考查的是对顶角、邻补角的性质以及角平分线的定义，掌握对顶角相等、邻补角之和等于180°是解题的关键．37.如图，已知∠A＝∠C，∠1+∠2＝180°，试猜想AB 与CD 之间有怎样的位置关系？并说明理由．【分析】由∠1+∠2＝180°可证得AD∥BC，得∠ADE＝∠C，已知∠A＝∠C，等量代换后可得∠ADE＝∠A，即AB、CD 被直线AD 所截形成的内错角相等，由此可证得AB 与CD 平行．【解答】证明：AB∥CD，理由如下：∵∠1+∠2＝180°（已知）∴AD∥BC（同旁内角互补，两直线平行）（2分）∴∠EDA＝∠C（两直线平行，同位角相等）（3分）又∵∠A＝∠C（已知）∴∠A＝∠EDA（等量代换）（5分）∴AB∥CD．（内错角相等，两直线平行）（6分）【点评】此题主要考查平行线的判定和性质．正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键．38．（1）如图，已知∠ABC，画一个角∠DEF，使DE∥AB，EF∥BC，且DE交BC于点P．探究：∠ABC 与∠DEF 分别有怎样的数量关系？并选择一种情况说明理由．图1 中∠ABC 与∠DEF 数量关系为∠ABC+∠DEF＝180°；图2 中∠ABC 与∠DEF 数量关系为∠ABC＝∠DEF ．选择一种情况说明理由：（2）由（1）你得出的结论是如果两个角的两边互相平行，那么这两个角相等或互补．（3）若两个角的两边互相平行，且一个角比另一个角的2 倍少30°，直接写出这两个角的度数．【分析】（1）利用平行线的性质即可判断．（2）根据平行线的性质解决问题即可．（3）设两个角分别为x 和2x﹣30°，由题意x＝2x﹣30°或x+2x﹣30°＝180°，解方程即可解决问题．【解答】解：（1）如图1中，∠ABC+∠DEF＝180°．如图2中，∠ABC＝∠DEF，故答案为∠ABC+∠DEF＝180°，∠ABC＝∠DEF．理由：①如图1 中，∵BC∥EF，∴∠DPB＝∠DEF，∵AB∥DE，∴∠ABC+∠DPB＝180°，∴∠ABC+∠DEF＝180°．②如图2 中，∵BC∥EF，∴∠DPC＝∠DEF，∵AB∥DE，∴∠ABC＝∠DPC，∴∠ABC＝∠DEF．（2）结论：如果两个角的两边互相平行，那么这两个角相等或互补．故答案为如果两个角的两边互相平行，那么这两个角相等或互补．（3）设两个角分别为x 和2x﹣30°，由题意x＝2x﹣30°或x+2x﹣30°＝180°，解得x＝30°或x＝70°，∴这两个角的度数为30°，30°或70°和110°．【点评】本题考查平行线的判定和性质，一元一次方程的应用等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．39.如图，已知∠AED＝∠ACB，CD⊥AB，HF⊥AB，猜想∠1 与∠2 的数量关系并说明的理由．。

人教版七年级下册数学第五章相交线与平行线含答案(步步高升)

人教版七年级下册数学第五章相交线与平行线含答案一、单选题(共15题，共计45分)1、如图，直线a、b被直线c所截，若a∥b，∠1=130°，则∠2等于（）A.30°B.40°C.50°D.60°2、下列说法中正确的是（）A.若a⊥b，b⊥c，则a⊥cB.在同一平面内，不相交的两条线段必平行 C.两条直线被第三条直线所截，所得的同位角相等 D.两条平行线被第三条直线所截，一对内错角的角平分线互相平行3、下列图形中，由AB∥CD，能得到∠1=∠2的是A. B. C.D.4、如图，和都是等腰直角三角形，且，，O为AC中点若点D在直线BC上运动，连接OE，则在点D运动过程中，线段OE的最小值为A. B.1 C. D.25、下列说法中，错误的有（）A.过两点有且只有一条直线B.直线外一点到这条线段的垂线段叫点到直线的距离C.两点之间，线段最短D.垂线段最短6、如图，在⊙O中，AB∥CD，∠BCD=100°，E为上的任意一点，A、B、C、D是⊙O上的四个点，则∠AEC的角度为（）A.110°B.70°C.80°D.100°7、如图，直线AB交CD于O，OE⊥AB，且∠DOE=50°，则∠AOC等于（）A.40°B.45°C.50°D.60°8、如图，直线a∥b，将一个直角三角尺按如图所示的位置摆放，若∠1＝52°，则∠2的度数为（）A.38°B.52°C.48°D.62°9、在同一平面内，有三条直线a、b、c，下列说法：①若a与b相交，b与c 相交，则a与c相交；②若a∥b，b与c相交（不重合），则a与c相交；③若a⊥b，b⊥c，则a⊥c，④若a∥b，b∥c，则a∥c，其中正确的结论的个数为（）A.1个B.2个C.3个D.4个10、如图，直线l1∥l2，直线l3与l1， l2分别交于A，B两点，点C是直线l2上一点，且AC⊥AB，若∠1=42°，则∠2的度数是（）A.142°B.138°C.132°D.48°11、如图形中，周长最长的是（）A. B. C.D.12、下列命题中的假命题是（）A.两直线平行，内错角相等B.同位角相等，两直线平行C.两直线平行，同旁内角相等D.平行于同一条直线的两直线平行13、如图，AD是∠EAC的平分线，AD∥BC，∠B＝30°，则∠C为（）A.30°B.60°C.80°D.120°14、如图，AB//CD，∠CDE=140°，则∠A的度数为（）A.140 0°B.60°C.50°D.40°15、如图，在点B处测得A处的俯角是（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，过点C(3,4)的直线交轴于点A，∠ABC=90°，AB=CB，曲线过点B，将点A沿轴正方向平移个单位长度恰好落在该曲线上，则的值为________.17、如图，已知∠B=∠1，CD是△ABC的角平分线，求证：∠5=2∠4．请在下面横线上填出推理的依据：证明：∵∠B=∠1，（已知）∴DE∥BC．（________）∴∠2=∠3．（________）∵CD是△ABC的角平分线，（________）∴∠3=∠4．（________）∴∠4=∠2．（________）∵∠5=∠2+∠4，（________）∴∠5=2∠4．（________）18、如图，∠ACD=110°，再需要添加一个条件：________ ，就可确定AB∥ED．19、如图，已知直线a∥b，△ABC的顶点B在直线b上，∠C=90°，∠1=36°，则∠2的度数是________．20、如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为________．21、如图所示，在三角形ABC中，∠A=90°，则A到BC的垂线段为________，C到AB的距离为________．22、如图，已知，，则________.23、如图，AB∥CD，∠B=160°，∠D=120°，则∠E=________24、已知：直线l1∥l2，一块含30°角的直角三角板如图所示放置，∠1＝25°，则∠2等于________.25、如图，已知AD∥BC，∠B=36°，BD平分∠ADE，则∠DEC=________.三、解答题(共6题，共计25分)26、一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10，试求CD的长．27、如图，在平面直角坐标系中，点P的坐标为（﹣4，0），⊙P的半径为2，．将⊙P沿x轴向右平移4个单位长度得⊙P1；①画出⊙P1与x轴正半轴，y轴正半轴的交点分别为A，B，求劣弧AB与弦AB围②设⊙P1成的图形的面积（结果保留π）．28、如图，在△ 中，，的平分线交于；若，点为边上的动点，求长度的最小值．29、填写下列空格完成证明：如图，EF∥AD ，∠1 = ∠2 ，∠BAC =70° ，求∠AGD .解：∵ EF∥AD ，∴ ∠2 = ▲ .（）∵ ∠1 = ∠2 ，∴ ∠1 = ∠3.（）∴▲ ∥▲ .（）∴ ∠BAC + ▲ = 180° .（）∵ ∠BAC = 70° ，∴ ∠AGD =▲ ° .30、如图：点、、、在一条直线上，、，，求证：．参考答案一、单选题(共15题，共计45分)1、C2、D3、B4、B5、B6、D7、A9、B10、C11、A12、C13、A14、D15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共6题，共计25分)26、27、29、。

北师大数学七年级下册第二章相交线与平行线拔高题(附答案详解)

北师大数学七年级下第二章拔高题一．选择题（共7小题）1．如图，AB∥CD，BF平分∠ABE，且BF∥DE，则∠ABE与∠D的关系是（）A．∠ABE＝3∠D B．∠ABE+∠D＝90°C．∠ABE+3∠D＝180°D．∠ABE＝2∠D2．如图，将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上，已知∠A＝30°，∠1＝40°，则∠2的度数为（）A．55°B．60°C．65°D．70°3．如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1＝2∠2，则∠AEF的度数为（）A．60°B．65°C．72°D．75°5．下列生活实例中，数学原理解释错误的一项是（）A．从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线B．两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短C．把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线D．从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短6．如图，已知AB∥DE，∠ABC＝80°，∠CDE＝150°，则∠BCD＝（）A．30°B．40°C．50°D．60°7．如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，则图2中∠AEF的度数为（）A．120°B．108°C．126°D．114°二．填空题（共8小题）8．将一块60°的直角三角板DEF放置在45°的直角三角板ABC上，移动三角板DEF使两条直角边DE、DF恰分别经过B、C两点，若EF∥BC，则∠ABD＝°．9．如图，将一张矩形纸片ABCD沿EF折叠后，点C落在AB边上的点G处，点D落在点H处．若∠1＝62°，则图中∠BEG的度数为．10．如图，已知DE∥BC，2∠D＝3∠DBC，∠1＝∠2．则∠DEB＝度．11．如图，已知AE∥BD，∠1＝130°，∠2＝28°，则∠C的度数为．12．如图，BE∥CF，则∠A+∠B+∠C+∠D＝度．第9题第10题第11题第12题13．如图，若OP∥QR∥ST，则∠1，∠2，∠3的数量关系是：．14．如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是．15．如图，∠AOB的一边OA为平面镜，∠AOB＝37°，在OB上有一点E，从E点射出一束光线经OA上一点D反射，此时∠ODE＝∠ADC，且反射光线DC恰好与OB平行，则∠DEB的度数是．第13题第14题第15题三．解答题（共11小题）16．如图，AB∥CD，直线EF与AB，CD交于点G，H，GM⊥GE，∠BGM＝20°，HN 平分∠CHE，求∠NHD的度数．17．如图，直线AB∥CD，并且被直线MN所截，MN分别交AB和CD于点E、F，点Q在PM 上，且∠AEP＝∠CFQ．求证：∠EPM＝∠FQM．18．如图，已知AB∥CD，∠A＝40°．点P是射线AB上一动点（与点A不重合），CE、CF 分别平分∠ACP和∠DCP交射线AB于点E、F．（1）求∠ECF的度数；（2）随着点P的运动，∠APC与∠AFC之间的数量关系是否改变？若不改变，请求出此数量关系；若改变，请说明理由；（3）当∠AEC＝∠ACF时，求∠APC的度数．19．【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．（1）若∠AFH＝60°，∠CHF＝50°，则∠EOF＝度，∠FOH＝度．（2）若∠AFH+∠CHF＝100°，求∠FOH的度数．【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF＝α，直接写出∠FOH的度数．（用含a的代数式表示）20．如图，AB∥CD，∠ABD和∠BDC的平分线交于点E，BE交CD于点F．（1）求证：∠1+∠2＝90°；（2）如果∠EDF＝36°，那么∠BFC等于多少度？21．如图，AB∥CD，点E在线段AB上，连接EC、ED、AD，且ED平分∠CEB，AD⊥EF，若∠ADC＝42°，∠A﹣∠B＝8°，求∠BDE的度数．22．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．23．已知AB∥CD，点E为平面内一点，BE⊥CE于E．（1）如图1，请直接写出∠ABE和∠DCE之间的数量关系；（2）如图2，过点E作EF⊥CD，垂足为F，求证：∠CEF＝∠ABE；（3）如图3，在（2）的条件下，作EG平分∠CEF，交DF于点G，作ED平分∠BEF，交CD 于D，连接BD，若∠DBE+∠ABD＝180°，且∠BDE＝3∠GEF，求∠BEG的度数．24．（1）如图①，若AB∥CD，求∠B+∠D+∠E1的度数？（2）如图②，若AB∥CD，求∠B+∠D+∠E1+∠E2的度数？（3）如图③，若AB∥CD，求∠B+∠D+∠E1+∠E2+∠E3的度数？（4）如图④，若AB∥CD，猜想∠B+∠D+∠E1+∠E2+…+∠E n的度数？25．如图，已知直线l1∥l2，点A、B分别在l1与l2上．直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠P AC，∠APB，∠PBD之间的关系又是如何？26．如图，已知∠ABC＝∠ACB，BD平分∠ABC，CE平分∠ACB，F是BC延长线上一点，且∠DBC ＝∠F，求证：EC∥DF．一．选择题（共7小题）1．如图，AB∥CD，BF平分∠ABE，且BF∥DE，则∠ABE与∠D的关系是（）A．∠ABE＝3∠D B．∠ABE+∠D＝90°C．∠ABE+3∠D＝180°D．∠ABE＝2∠D【解答】证明：如图，延长DE交AB的延长线于G，∵AB∥CD，∴∠D＝∠G，∵BF∥DE，∴∠G＝∠ABF，∴∠D＝∠ABF，∵BF平分∠ABE，∴∠ABE＝2∠ABF＝2∠D，即∠ABE＝2∠D．故选：D．2．如图，将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上，已知∠A＝30°，∠1＝40°，则∠2的度数为（）A．55°B．60°C．65°D．70°【解答】解：∵EF∥MN，∠1＝40°，∴∠1＝∠3＝40°，∵∠A＝30°，∴∠2＝∠A+∠3＝70°，故选：D．3．如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1＝2∠2，则∠AEF的度数为（）A．60°B．65°C．72°D．75°【解答】解：由翻折的性质可知：∠AEF＝∠FEA′，∵AB∥CD，∴∠AEF＝∠1，∵∠1＝2∠2，设∠2＝x，则∠AEF＝∠1＝∠FEA′＝2x，∴5x＝180°，∴x＝36°，∴∠AEF＝2x＝72°，故选：C．4．在下列图形中，由∠1＝∠2一定能得到AB∥CD的是（）A．B．C．D．【解答】解：如下图，∵∠1＝∠2，∴AB∥CD，故选：A．5．下列生活实例中，数学原理解释错误的一项是（）A．从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线B．两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短C．把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线D．从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短【解答】解：A、从一条河向一个村庄引一条最短的水渠，其中数学原理是：垂线段最短，故原命题错误；B、两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短，正确；C、一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线，正确；D、从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短，正确．故选：A．6．如图，已知AB∥DE，∠ABC＝80°，∠CDE＝150°，则∠BCD＝（）A．30°B．40°C．50°D．60°【解答】解：反向延长DE交BC于M，∵AB∥DE，∴∠BMD＝∠ABC＝80°，∴∠CMD＝180°﹣∠BMD＝100°；又∵∠CDE＝∠CMD+∠BCD，∴∠BCD＝∠CDE﹣∠CMD＝150°﹣100°＝50°．故选：C．7．如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，则图2中∠AEF的度数为（）A．120°B．108°C．126°D．114°【解答】解：如图，设∠B′FE＝x，∵纸条沿EF折叠，∴∠BFE＝∠B′FE＝x，∠AEF＝∠A′EF，∴∠BFC＝∠BFE﹣∠CFE＝x﹣18°，∵纸条沿BF折叠，∴∠C′FB＝∠BFC＝x﹣18°，而∠B′FE+∠BFE+∠C′FE＝180°，∴x+x+x﹣18°＝180°，解得x＝66°，∵A′D′∥B′C′，∴∠A′EF＝180°﹣∠B′FE＝180°﹣66°＝114°，∴∠AEF＝114°．故选：D．二．填空题（共8小题）8．将一块60°的直角三角板DEF放置在45°的直角三角板ABC上，移动三角板DEF使两条直角边DE、DF恰分别经过B、C两点，若EF∥BC，则∠ABD＝15°．【解答】解：∵将一块60°的直角三角板DEF放置在45°的直角三角板ABC上，∴∠E＝30°，∠ABC＝45°，∵EF∥BC，∴∠DBC＝∠E＝30°，∴∠ABD＝45°﹣30°＝15°，故答案为：159．如图，将一张矩形纸片ABCD沿EF折叠后，点C落在AB边上的点G处，点D落在点H处．若∠1＝62°，则图中∠BEG的度数为56°．【解答】解：∵AD∥BC，∴∠1＝∠FEC＝62°，由翻折可得：∠FEG＝∠FEC＝62°，∴∠BEG＝180°﹣62°﹣62°＝56°，故答案为：56°10．如图，已知DE∥BC，2∠D＝3∠DBC，∠1＝∠2．则∠DEB＝36度．【解答】解：∵DE∥BC，∴∠E＝∠1，∵∠1＝∠2，∴∠1＝∠2＝∠B，设∠1＝∠2＝∠B＝x，∵2∠D＝3∠DBC，∴∠D＝3x，∴5x＝180°，∴x＝36°故答案为36．11．如图，已知AE∥BD，∠1＝130°，∠2＝28°，则∠C的度数为22°．【解答】解：∵AE∥BD，∠1＝130°，∠2＝28°，∴∠CBD＝∠1＝130°，∠CDB＝∠2＝28°，∴∠C＝180°﹣∠CBD﹣∠CDB＝180°﹣130°﹣28°＝22°．故答案为：22°12．如图，BE∥CF，则∠A+∠B+∠C+∠D＝180度．【解答】解：如图所示，由图知∠A+∠B＝∠BPD，∵BE∥CF，∴∠CQD＝∠BPD＝∠A+∠B，又∵∠CQD+∠C+∠D＝180°，∴∠A+∠B+∠C+∠D＝180°，故答案为：180．13．如图，若OP∥QR∥ST，则∠1，∠2，∠3的数量关系是：∠2+∠3﹣∠1＝180°．【解答】解：如图，延长TS，∵OP∥QR∥ST，∴∠2＝∠4，∵∠3与∠ESR互补，∴∠ESR＝180°﹣∠3，∵∠4是△FSR的外角，∴∠FSR+∠1＝∠4，即180°﹣∠3+∠1＝∠2，∴∠2+∠3﹣∠1＝180°．故答案为：∠2+∠3﹣∠1＝180°．14．如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是∠α﹣∠β＝90°．【解答】解：过C作CF∥AB，∵AB∥DE，∴AB∥DE∥CF，∴∠1＝∠β，∠α＝180°﹣∠2，∴∠α﹣∠β＝180°﹣∠2﹣∠1＝180°﹣∠BCD＝90°，故答案为∠α﹣∠β＝90°．15．如图，∠AOB的一边OA为平面镜，∠AOB＝37°，在OB上有一点E，从E点射出一束光线经OA上一点D反射，此时∠ODE＝∠ADC，且反射光线DC恰好与OB平行，则∠DEB的度数是74°．【解答】解：过点D作DF⊥AO交OB于点F．∵入射角等于反射角，∴∠1＝∠3，∵CD∥OB，∴∠1＝∠2（两直线平行，内错角相等）；∴∠2＝∠3（等量代换）；在Rt△DOF中，∠ODF＝90°，∠AOB＝37°，∴∠2＝90°﹣37°＝53°；∴在△DEF中，∠DEB＝180°﹣2∠2＝74°．故答案为：74°．三．解答题（共11小题）16．如图，AB∥CD，直线EF与AB，CD交于点G，H，GM⊥GE，∠BGM＝20°，HN平分∠CHE，求∠NHD的度数．【解答】解：∵GM⊥GE∴∠EGM＝90°∵∠BGM＝20°∴∠EGB＝∠EGM﹣∠BGM＝70°∴∠AGH＝∠EGB＝70°∵AB∥CD∴∠AGH+∠CHG＝180°∴∠CHG＝110°∵HN平分∠CHE∴∠NHC＝∠CHG＝×110°＝55°∴∠NHD＝180°﹣∠CHN＝180°﹣55°＝125°17．如图，直线AB∥CD，并且被直线MN所截，MN分别交AB和CD于点E、F，点Q在PM上，且∠AEP＝∠CFQ．求证：∠EPM＝∠FQM．【解答】解：∵AB∥CD∴∠AEM＝∠CFM，∵∠AEP＝∠CFQ，∴∠MEP＝∠MFQ，∴EP∥FQ，∴∠EPM＝∠FQM．18．如图，已知AB∥CD，∠A＝40°．点P是射线AB上一动点（与点A不重合），CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F．（1）求∠ECF的度数；（2）随着点P的运动，∠APC与∠AFC之间的数量关系是否改变？若不改变，请求出此数量关系；若改变，请说明理由；（3）当∠AEC＝∠ACF时，求∠APC的度数．【解答】解：（1）∵AB∥CD，∴∠A+∠ACD＝180°，∴∠ACD＝180°﹣40°＝140°，∵CE平分∠ACP，CF平分∠DCP，∴∠ACP＝2∠ECP，∠DCP＝2∠PCF，∴∠ECF＝∠ACD＝70°；（2）不变．数量关系为：∠APC＝2∠AFC．∵AB∥CD，∴∠AFC＝∠DCF，∠APC＝∠DCP，∵CF平分∠DCP，∴∠DCP＝2∠DCF，∴∠APC＝2∠AFC；（3）∵AB∥CD，∴∠AEC＝∠ECD，当∠AEC＝∠ACF时，则有∠ECD＝∠ACF，∴∠ACE＝∠DCF，∴∠PCD＝∠ACD＝70°，∴∠APC＝∠PCD＝70°．19．【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．（1）若∠AFH＝60°，∠CHF＝50°，则∠EOF＝30度，∠FOH＝125度．（2）若∠AFH+∠CHF＝100°，求∠FOH的度数．【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF＝α，直接写出∠FOH的度数．（用含a的代数式表示）【解答】解：【探究】（1）∵∠AFH＝60°，OF平分∠AFH，∴∠OFH＝30°，又∵EG∥FH，∴∠EOF＝∠OFH＝30°；∵∠CHF＝50°，OH平分∠CHF，∴∠FHO＝25°，∴△FOH中，∠FOH＝180°﹣∠OFH﹣∠OHF＝125°；故答案为：30，125；（2）∵FO平分∠AFH，HO平分∠CHF，∴∠OFH＝∠AFH，∠OHF＝∠CHF．∵∠AFH+∠CHF＝100°，∴∠OFH+∠OHF＝（∠AFH+∠CHF）＝×100°＝50°．∵EG∥FH，∴∠EOF＝∠OFH，∠GOH＝∠OHF．∴∠EOF+∠GOH＝∠OFH+∠OHF＝50°．∵∠EOF+∠GOH+∠FOH＝180°，∴∠FOH＝180°﹣（∠EOF+∠GOH）＝180°﹣50°＝130°．【拓展】∵∠AFH和∠CHI的平分线交于点O，∴∠OFH＝∠AFH，∠OHI＝∠CHI，∴∠FOH＝∠OHI﹣∠OFH＝（∠CHI﹣∠AFH）＝（180°﹣∠CHF﹣∠AFH）＝（180°﹣α）＝90°﹣α．20．如图，AB∥CD，∠ABD和∠BDC的平分线交于点E，BE交CD于点F．（1）求证：∠1+∠2＝90°；（2）如果∠EDF＝36°，那么∠BFC等于多少度？【解答】解：（1）∵AB∥CD，∴∠ABD+∠BDC＝180°，∵BE、DE平分∠ABD、∠BDC，∴∠1＝∠ABD，∠2＝∠BDC，∴∠1+∠2＝（∠ABD+∠BDC）＝90°，（2）∵DE平分∠BDC，∴∠2＝∠EDF＝36°，又∵∠1+∠2＝90°，∴∠1＝54°，又∵AB∥CD，∴∠BFC＝180°﹣∠1＝180°﹣54°＝126°．21．如图，AB∥CD，点E在线段AB上，连接EC、ED、AD，且ED平分∠CEB，AD⊥EF，若∠ADC＝42°，∠A﹣∠B＝8°，求∠BDE的度数．【解答】解：∵AB∥CD，∴∠ADC＝∠A＝42°，∵∠A﹣∠B＝8°，∴∠B＝34°，∵AD⊥EF，∴∠AFE＝90°，∴∠AEF＝48°，∴∠BEC＝132°，∵DE平分∠BEC，∴∠BED＝∠BEC＝66°，∴∠BDE＝180°﹣66°﹣34°＝80°．22．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．【解答】解：（1）证明：如图，过点E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠3＝∠1，∠4＝∠2，∴∠3+∠4＝∠1+∠2，即∠BED＝∠1+∠2；（2）∠1+∠EGH＝∠2+∠BEG，理由如下：如图，分别过点E、G作EF∥AB，GH∥AB，∵AB∥CD，∴AB∥EF∥GH∥CD，∴∠1＝∠3，∠4＝∠5，∠6＝∠2，∴∠1+∠5+∠6＝∠3+∠4+∠2，即∠1+∠EGH＝∠2+∠BEG；（3）由题可得，向左的角度数之和与向右的角度数之和相等，∴∠1、∠3、∠5与∠2、∠4、∠6之间的关系为：∠1+∠3+∠5＝∠2+∠4+∠6．23．已知AB∥CD，点E为平面内一点，BE⊥CE于E．（1）如图1，请直接写出∠ABE和∠DCE之间的数量关系；（2）如图2，过点E作EF⊥CD，垂足为F，求证：∠CEF＝∠ABE；（3）如图3，在（2）的条件下，作EG平分∠CEF，交DF于点G，作ED平分∠BEF，交CD 于D，连接BD，若∠DBE+∠ABD＝180°，且∠BDE＝3∠GEF，求∠BEG的度数．【解答】解：（1）结论：∠ECD＝90°+∠ABE．理由：如图1中，从BE交DC的延长线于H．∵AB∥CH，∴∠ABE＝∠H，∵BE⊥CE，∴∠CEH＝90°，∴∠ECD＝∠H+∠CEH＝90°+∠H，∴∠ECD＝90°+∠ABE．（2）如图2中，作EM∥CD，∵EM∥CD，CD∥AB，∴AB∥CD∥EM，∴∠BEM＝∠ABE，∠F+∠FEM＝180°，∵EF⊥CD，∴∠F＝90°，∴∠FEM＝90°，∴∠CEF与∠CEM互余，∵BE⊥CE，∴∠BEC＝90°，∴∠BEM与∠CEM互余，∴∠CEF＝∠BEM，∴∠CEF＝∠ABE．（3）如图3中，设∠GEF＝α，∠EDF＝β．∴∠BDE＝3∠GEF＝3α，∵EG平分∠CEF，∴∠CEF＝2∠FEG＝2α，∴∠ABE＝∠CEF＝2α，∵AB∥CD∥EM，∴∠MED＝∠EDF＝β，∠KBD＝∠BDF＝3α+β，∠ABD+∠BDF＝180°，∴∠BED＝∠BEM+∠MED＝2α+β，∵ED平分∠BEF，∴∠BED＝∠FED＝2α+β，∴∠DEC＝β，∵∠BEC＝90°，∴2α+2β＝90°，∵∠DBE+∠ABD＝180°，∠ABD+∠BDF＝180°，∴∠DBE＝∠BDF＝∠BDE+∠EDF＝3α+β，∵∠ABK＝180°，∴∠ABE+∠B＝DBE+∠KBD＝180°，即2α+（3α+β）+（3α+β）＝180°，∴6α+（2α+2β）＝180°，∴α＝15°，∴∠BEG＝∠BEC+∠CEG＝90°+15°＝105°．24．（1）如图①，若AB∥CD，求∠B+∠D+∠E1的度数？（2）如图②，若AB∥CD，求∠B+∠D+∠E1+∠E2的度数？（3）如图③，若AB∥CD，求∠B+∠D+∠E1+∠E2+∠E3的度数？（4）如图④，若AB∥CD，猜想∠B+∠D+∠E1+∠E2+…+∠E n的度数？【解答】解：（1）如图①，过E1作E1F∥AB，则E1F∥CD，∴∠B+∠1＝180°①，∠D+∠1＝180°②，①+②得∠B+∠1+∠D+∠2＝360°，即∠B+∠D+∠E1＝360°；（2）如图②，分别过E1，E2作E1F∥AB，E2G∥AB，则E1F∥E2G∥CD，∴∠1+∠B＝∠2+∠3＝∠4+∠D＝180°，∴∠B+∠D+∠E1+∠E2＝∠1+∠B+∠2+∠3+∠4+∠D＝540°＝3×180°；（3）如图③，分别过E1，E2，E3作E1F1∥E2F2∥E3F3∥AB，则E1F1∥E2F2∥E3F3∥CD，∴∠B+∠BE1E2＝180°，∠E2E1F1+∠E1E2F2＝180°，∠E3E2F2+∠E2E3F3＝180°，∠DE3F3+∠D＝180°，∴∠B+∠D+∠E1+∠E2+∠E3＝720°；（4）由（1）（2）（3）知，拐点的个数n与角的和之间的关系是（n+1）?180°，∴∠B+∠D+∠E1+∠E2+…+∠E n＝（n+1）?180°．25．如图，已知直线l1∥l2，点A、B分别在l1与l2上．直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠P AC，∠APB，∠PBD之间的关系又是如何？【解答】解：（1）如图，当P点在C、D之间运动时，则有∠APB＝∠PAC+∠PBD．理由如下：过点P作PE∥l1，∵l1∥l2，∴PE∥l2∥l1，∴∠P AC＝∠1，∠PBD＝∠2，∴∠APB＝∠1+∠2＝∠P AC+∠PBD；（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），则有两种情形：①如图，当点P在在l2下方时，有结论：∠APB＝∠P AC﹣∠PBD．理由是：过点P作PE∥l1，则∠APE＝∠PAC，又∵l1∥l2，∴PE∥l2，∴∠BPE＝∠PBD，∵∠APE＝∠APB+∠BPE，∴∠P AC＝∠APB+∠PBD，∴∠APB＝∠PAC﹣∠PBD；②如图，当点P在l1上方时，有结论：∠APB＝∠PBD﹣∠P AC．理由是：过点P作PE∥l2，则∠BPE＝∠PBD，又∵l1∥l2，∴PE∥l1，∴∠APE＝∠PAC，∵∠BPE＝∠APE+∠APB，∴∠PBD＝∠P AC+∠APB，∴∠APB＝∠PBD﹣∠P AC．26．如图，已知∠ABC＝∠ACB，BD平分∠ABC，CE平分∠ACB，F是BC延长线上一点，且∠DBC ＝∠F，求证：EC∥DF．【解答】证明：∵∠ABC＝∠ACB，BD平分∠ABC，CE平分∠ACB，∴∠DBC＝∠ABC，∠ECB＝∠ACB，∴∠DBC＝∠ECB．∵∠DBC＝∠F，∴∠ECB＝∠F，∴EC∥DF．。

(完整word版)七年级数学初一数学相交线与平行线基础题拔高题汇总(超经典超详细)

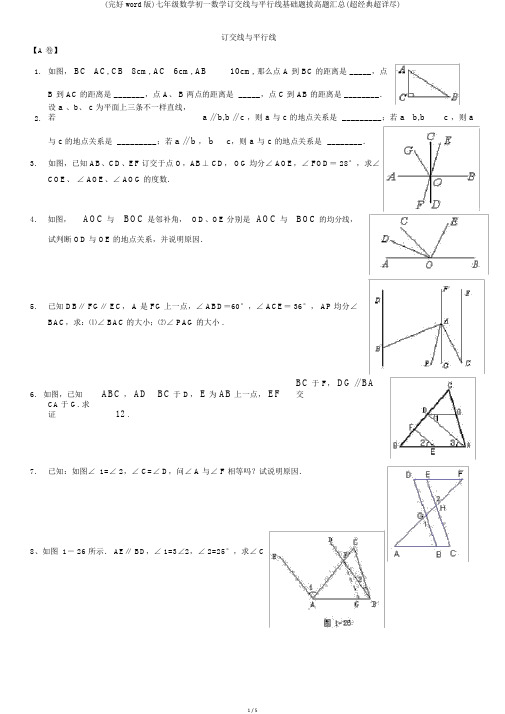
订交线与平行线【A 卷】1. 如图， BC AC, CB 8cm, AC 6cm, AB 10cm, 那么点A到BC的距离是_____，点B 到 AC的距离是_______，点 A、 B两点的距离是_____，点 C到 AB的距离是________．2. 设 a 、b、c为平面上三条不一样直线，若 a // b,b // c ，则a与c的地点关系是_________；若 a b,b c ，则a 与 c 的地点关系是_________；若a // b，b c，则a与c的地点关系是________．3.如图，已知 AB、CD、EF订交于点 O，AB⊥ CD， OG均分∠ AOE，∠ FOD＝28°，求∠COE、∠ AOE、∠ AOG的度数．4.如图，AOC 与BOC 是邻补角，OD、OE分别是AOC 与BOC 的均分线，试判断 OD与 OE的地点关系，并说明原因．5.已知 DB∥ FG∥ EC， A 是 FG上一点，∠ ABD＝60°，∠ ACE＝36°， AP均分∠BAC，求：⑴∠ BAC的大小；⑵∠ PAG的大小.6. 如图，已知ABC ， AD BC于D， E为 AB上一点， EF BC 于F， DG // BA 交CA于G. 求证12 .7.已知：如图∠ 1=∠ 2，∠C=∠D，问∠A与∠F相等吗？试说明原因．8、如图 1－ 26 所示． AE∥ BD，∠ 1=3∠2，∠ 2=25°，求∠ C【B 卷】1、如图，∠１＋∠２＝∠BCD ，求证 AB ∥ DE 。

2、已知：∠Ｂ＋∠Ｄ＋∠Ｆ＝360o.求证： AB ∥ EF。

3、如图把长方形纸片沿EF 折叠，使 D ，C分别落在 D ，C的地点，若∠EFB 65o，则∠ AED 等于（）Ａ． 50o Ｂ． 55o Ｃ． 60o Ｄ． 65o4、如图， AB ∥ CD ，那么∠ A ，∠ P，∠ C 的数目关系是 ()A. ∠ A+ ∠P+∠ C=90°B.∠ A+ ∠ P+∠C=180 °C.∠A+ ∠P+∠ C=360°D. ∠P+∠ C=∠ A5、已知：如图， AB//CD ，则图中、、三个角之间的数目关系为（） .A 、 + + =360 B、++ =180C、 + - =180D、--=906、如图，把三角形纸片沿DE 折叠，当点 A 落在四边形 BCED 内部时，则∠ A 与∠ 1+∠2 之间有一种数目关系一直保持不变．请试着找一找这个规律，你发现的规律是( )．(A) ∠ A ＝∠ 1+∠ 2 (B)2 ∠ A＝∠ 1+∠2 (C)3∠A ＝ 2∠ 1+∠ 2 (D)3 ∠ A=2( ∠ 1 十∠ 2)7、如图：已知ABC与 DEF 是一副三角板的拼图，A,E,C, D在同一条线上.A（ 1）、求证EF // BC ；（ 2）、求1与 2 的度数E P F1 O28、如图，直线 AB、CD 被直线 EF 所截，∠AEF+∠ CFE=180 °，∠1=∠ 2，则图中的∠ H C 与Q BD1E∠ G 相等吗？说明你的原因。

(完整版)北师大数学七年级下册第二章相交线与平行线拔高题

北师大数学七年级下第二章拔高题一．选择题（共7小题）1．如图，AB∥CD，BF平分∠ABE，且BF∥DE，则∠ABE与∠D的关系是（）A．∠ABE＝3∠D B．∠ABE+∠D＝90°C．∠ABE+3∠D＝180°D．∠ABE＝2∠D2．如图，将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上，已知∠A＝30°，∠1＝40°，则∠2的度数为（）A．55°B．60°C．65°D．70°3．如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1＝2∠2，则∠AEF的度数为（）A．60°B．65°C．72°D．75°5．下列生活实例中，数学原理解释错误的一项是（）A．从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线B．两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短C．把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线D．从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短6．如图，已知AB∥DE，∠ABC＝80°，∠CDE＝150°，则∠BCD＝（）A．30°B．40°C．50°D．60°7．如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，则图2中∠AEF的度数为（）A．120°B．108°C．126°D．114°二．填空题（共8小题）8．将一块60°的直角三角板DEF放置在45°的直角三角板ABC上，移动三角板DEF使两条直角边DE、DF恰分别经过B、C两点，若EF∥BC，则∠ABD＝°．9．如图，将一张矩形纸片ABCD沿EF折叠后，点C落在AB边上的点G处，点D落在点H处．若∠1＝62°，则图中∠BEG的度数为．10．如图，已知DE∥BC，2∠D＝3∠DBC，∠1＝∠2．则∠DEB＝度．11．如图，已知AE∥BD，∠1＝130°，∠2＝28°，则∠C的度数为．12．如图，BE∥CF，则∠A+∠B+∠C+∠D＝度．第9题第10题第11题第12题13．如图，若OP∥QR∥ST，则∠1，∠2，∠3的数量关系是：．14．如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是．15．如图，∠AOB的一边OA为平面镜，∠AOB＝37°，在OB上有一点E，从E点射出一束光线经OA上一点D反射，此时∠ODE＝∠ADC，且反射光线DC恰好与OB平行，则∠DEB的度数是．第13题第14题第15题三．解答题（共11小题）16．如图，AB∥CD，直线EF与AB，CD交于点G，H，GM⊥GE，∠BGM＝20°，HN 平分∠CHE，求∠NHD的度数．17．如图，直线AB∥CD，并且被直线MN所截，MN分别交AB和CD于点E、F，点Q在PM 上，且∠AEP＝∠CFQ．求证：∠EPM＝∠FQM．18．如图，已知AB∥CD，∠A＝40°．点P是射线AB上一动点（与点A不重合），CE、CF 分别平分∠ACP和∠DCP交射线AB于点E、F．（1）求∠ECF的度数；（2）随着点P的运动，∠APC与∠AFC之间的数量关系是否改变？若不改变，请求出此数量关系；若改变，请说明理由；（3）当∠AEC＝∠ACF时，求∠APC的度数．19．【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．（1）若∠AFH＝60°，∠CHF＝50°，则∠EOF＝度，∠FOH＝度．（2）若∠AFH+∠CHF＝100°，求∠FOH的度数．【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF＝α，直接写出∠FOH的度数．（用含a的代数式表示）20．如图，AB∥CD，∠ABD和∠BDC的平分线交于点E，BE交CD于点F．（1）求证：∠1+∠2＝90°；（2）如果∠EDF＝36°，那么∠BFC等于多少度？21．如图，AB∥CD，点E在线段AB上，连接EC、ED、AD，且ED平分∠CEB，AD⊥EF，若∠ADC＝42°，∠A﹣∠B＝8°，求∠BDE的度数．22．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．23．已知AB∥CD，点E为平面内一点，BE⊥CE于E．（1）如图1，请直接写出∠ABE和∠DCE之间的数量关系；（2）如图2，过点E作EF⊥CD，垂足为F，求证：∠CEF＝∠ABE；（3）如图3，在（2）的条件下，作EG平分∠CEF，交DF于点G，作ED平分∠BEF，交CD 于D，连接BD，若∠DBE+∠ABD＝180°，且∠BDE＝3∠GEF，求∠BEG的度数．24．（1）如图①，若AB∥CD，求∠B+∠D+∠E1的度数？（2）如图②，若AB∥CD，求∠B+∠D+∠E1+∠E2的度数？（3）如图③，若AB∥CD，求∠B+∠D+∠E1+∠E2+∠E3的度数？（4）如图④，若AB∥CD，猜想∠B+∠D+∠E1+∠E2+⋯+∠E n的度数？25．如图，已知直线l1∥l2，点A、B分别在l1与l2上．直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？26．如图，已知∠ABC＝∠ACB，BD平分∠ABC，CE平分∠ACB，F是BC延长线上一点，且∠DBC ＝∠F，求证：EC∥DF．一．选择题（共7小题）1．如图，AB∥CD，BF平分∠ABE，且BF∥DE，则∠ABE与∠D的关系是（）A．∠ABE＝3∠D B．∠ABE+∠D＝90°C．∠ABE+3∠D＝180°D．∠ABE＝2∠D【解答】证明：如图，延长DE交AB的延长线于G，∵AB∥CD，∴∠D＝∠G，∵BF∥DE，∴∠G＝∠ABF，∴∠D＝∠ABF，∵BF平分∠ABE，∴∠ABE＝2∠ABF＝2∠D，即∠ABE＝2∠D．故选：D．2．如图，将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上，已知∠A＝30°，∠1＝40°，则∠2的度数为（）A．55°B．60°C．65°D．70°【解答】解：∵EF∥MN，∠1＝40°，∴∠1＝∠3＝40°，∵∠A＝30°，∴∠2＝∠A+∠3＝70°，故选：D．3．如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1＝2∠2，则∠AEF的度数为（）A．60°B．65°C．72°D．75°【解答】解：由翻折的性质可知：∠AEF＝∠FEA′，∵AB∥CD，∴∠AEF＝∠1，∵∠1＝2∠2，设∠2＝x，则∠AEF＝∠1＝∠FEA′＝2x，∴5x＝180°，∴x＝36°，∴∠AEF＝2x＝72°，故选：C．4．在下列图形中，由∠1＝∠2一定能得到AB∥CD的是（）A．B．C．D．【解答】解：如下图，∵∠1＝∠2，∴AB∥CD，故选：A．5．下列生活实例中，数学原理解释错误的一项是（）A．从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线B．两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短C．把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线D．从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短【解答】解：A、从一条河向一个村庄引一条最短的水渠，其中数学原理是：垂线段最短，故原命题错误；B、两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短，正确；C、一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线，正确；D、从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短，正确．故选：A．6．如图，已知AB∥DE，∠ABC＝80°，∠CDE＝150°，则∠BCD＝（）A．30°B．40°C．50°D．60°【解答】解：反向延长DE交BC于M，∵AB∥DE，∴∠BMD＝∠ABC＝80°，∴∠CMD＝180°﹣∠BMD＝100°；又∵∠CDE＝∠CMD+∠BCD，∴∠BCD＝∠CDE﹣∠CMD＝150°﹣100°＝50°．故选：C．7．如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，则图2中∠AEF的度数为（）A．120°B．108°C．126°D．114°【解答】解：如图，设∠B′FE＝x，∵纸条沿EF折叠，∴∠BFE＝∠B′FE＝x，∠AEF＝∠A′EF，∴∠BFC＝∠BFE﹣∠CFE＝x﹣18°，∵纸条沿BF折叠，∴∠C′FB＝∠BFC＝x﹣18°，而∠B′FE+∠BFE+∠C′FE＝180°，∴x+x+x﹣18°＝180°，解得x＝66°，∵A′D′∥B′C′，∴∠A′EF＝180°﹣∠B′FE＝180°﹣66°＝114°，∴∠AEF＝114°．故选：D．二．填空题（共8小题）8．将一块60°的直角三角板DEF放置在45°的直角三角板ABC上，移动三角板DEF使两条直角边DE、DF恰分别经过B、C两点，若EF∥BC，则∠ABD＝15°．【解答】解：∵将一块60°的直角三角板DEF放置在45°的直角三角板ABC上，∴∠E＝30°，∠ABC＝45°，∵EF∥BC，∴∠DBC＝∠E＝30°，∴∠ABD＝45°﹣30°＝15°，故答案为：159．如图，将一张矩形纸片ABCD沿EF折叠后，点C落在AB边上的点G处，点D落在点H处．若∠1＝62°，则图中∠BEG的度数为56°．【解答】解：∵AD∥BC，∴∠1＝∠FEC＝62°，由翻折可得：∠FEG＝∠FEC＝62°，∴∠BEG＝180°﹣62°﹣62°＝56°，故答案为：56°10．如图，已知DE∥BC，2∠D＝3∠DBC，∠1＝∠2．则∠DEB＝36度．【解答】解：∵DE∥BC，∴∠E＝∠1，∵∠1＝∠2，∴∠1＝∠2＝∠B，设∠1＝∠2＝∠B＝x，∵2∠D＝3∠DBC，∴∠D＝3x，∴5x＝180°，∴x＝36°故答案为36．11．如图，已知AE∥BD，∠1＝130°，∠2＝28°，则∠C的度数为22°．【解答】解：∵AE∥BD，∠1＝130°，∠2＝28°，∴∠CBD＝∠1＝130°，∠CDB＝∠2＝28°，∴∠C＝180°﹣∠CBD﹣∠CDB＝180°﹣130°﹣28°＝22°．故答案为：22°12．如图，BE∥CF，则∠A+∠B+∠C+∠D＝180度．【解答】解：如图所示，由图知∠A+∠B＝∠BPD，∵BE∥CF，∴∠CQD＝∠BPD＝∠A+∠B，又∵∠CQD+∠C+∠D＝180°，∴∠A+∠B+∠C+∠D＝180°，故答案为：180．13．如图，若OP∥QR∥ST，则∠1，∠2，∠3的数量关系是：∠2+∠3﹣∠1＝180°．【解答】解：如图，延长TS，∵OP∥QR∥ST，∴∠2＝∠4，∵∠3与∠ESR互补，∴∠ESR＝180°﹣∠3，∵∠4是△FSR的外角，∴∠FSR+∠1＝∠4，即180°﹣∠3+∠1＝∠2，∴∠2+∠3﹣∠1＝180°．故答案为：∠2+∠3﹣∠1＝180°．14．如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是∠α﹣∠β＝90°．【解答】解：过C作CF∥AB，∵AB∥DE，∴AB∥DE∥CF，∴∠1＝∠β，∠α＝180°﹣∠2，∴∠α﹣∠β＝180°﹣∠2﹣∠1＝180°﹣∠BCD＝90°，故答案为∠α﹣∠β＝90°．15．如图，∠AOB的一边OA为平面镜，∠AOB＝37°，在OB上有一点E，从E点射出一束光线经OA上一点D反射，此时∠ODE＝∠ADC，且反射光线DC恰好与OB平行，则∠DEB的度数是74°．【解答】解：过点D作DF⊥AO交OB于点F．∵入射角等于反射角，∴∠1＝∠3，∵CD∥OB，∴∠1＝∠2（两直线平行，内错角相等）；∴∠2＝∠3（等量代换）；在Rt△DOF中，∠ODF＝90°，∠AOB＝37°，∴∠2＝90°﹣37°＝53°；∴在△DEF中，∠DEB＝180°﹣2∠2＝74°．故答案为：74°．三．解答题（共11小题）16．如图，AB∥CD，直线EF与AB，CD交于点G，H，GM⊥GE，∠BGM＝20°，HN平分∠CHE，求∠NHD的度数．【解答】解：∵GM⊥GE∴∠EGM＝90°∵∠BGM＝20°∴∠EGB＝∠EGM﹣∠BGM＝70°∴∠AGH＝∠EGB＝70°∵AB∥CD∴∠AGH+∠CHG＝180°∴∠CHG＝110°∵HN平分∠CHE∴∠NHC＝∠CHG＝×110°＝55°∴∠NHD＝180°﹣∠CHN＝180°﹣55°＝125°17．如图，直线AB∥CD，并且被直线MN所截，MN分别交AB和CD于点E、F，点Q在PM上，且∠AEP＝∠CFQ．求证：∠EPM＝∠FQM．【解答】解：∵AB∥CD∴∠AEM＝∠CFM，∵∠AEP＝∠CFQ，∴∠MEP＝∠MFQ，∴EP∥FQ，∴∠EPM＝∠FQM．18．如图，已知AB∥CD，∠A＝40°．点P是射线AB上一动点（与点A不重合），CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F．（1）求∠ECF的度数；（2）随着点P的运动，∠APC与∠AFC之间的数量关系是否改变？若不改变，请求出此数量关系；若改变，请说明理由；（3）当∠AEC＝∠ACF时，求∠APC的度数．【解答】解：（1）∵AB∥CD，∴∠A+∠ACD＝180°，∴∠ACD＝180°﹣40°＝140°，∵CE平分∠ACP，CF平分∠DCP，∴∠ACP＝2∠ECP，∠DCP＝2∠PCF，∴∠ECF＝∠ACD＝70°；（2）不变．数量关系为：∠APC＝2∠AFC．∵AB∥CD，∴∠AFC＝∠DCF，∠APC＝∠DCP，∵CF平分∠DCP，∴∠DCP＝2∠DCF，∴∠APC＝2∠AFC；（3）∵AB∥CD，∴∠AEC＝∠ECD，当∠AEC＝∠ACF时，则有∠ECD＝∠ACF，∴∠ACE＝∠DCF，∴∠PCD＝∠ACD＝70°，∴∠APC＝∠PCD＝70°．19．【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．（1）若∠AFH＝60°，∠CHF＝50°，则∠EOF＝30度，∠FOH＝125度．（2）若∠AFH+∠CHF＝100°，求∠FOH的度数．【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF＝α，直接写出∠FOH的度数．（用含a的代数式表示）【解答】解：【探究】（1）∵∠AFH＝60°，OF平分∠AFH，∴∠OFH＝30°，又∵EG∥FH，∴∠EOF＝∠OFH＝30°；∵∠CHF＝50°，OH平分∠CHF，∴∠FHO＝25°，∴△FOH中，∠FOH＝180°﹣∠OFH﹣∠OHF＝125°；故答案为：30，125；（2）∵FO平分∠AFH，HO平分∠CHF，∴∠OFH＝∠AFH，∠OHF＝∠CHF．∵∠AFH+∠CHF＝100°，∴∠OFH+∠OHF＝（∠AFH+∠CHF）＝×100°＝50°．∵EG∥FH，∴∠EOF＝∠OFH，∠GOH＝∠OHF．∴∠EOF+∠GOH＝∠OFH+∠OHF＝50°．∵∠EOF+∠GOH+∠FOH＝180°，∴∠FOH＝180°﹣（∠EOF+∠GOH）＝180°﹣50°＝130°．【拓展】∵∠AFH和∠CHI的平分线交于点O，∴∠OFH＝∠AFH，∠OHI＝∠CHI，∴∠FOH＝∠OHI﹣∠OFH＝（∠CHI﹣∠AFH）＝（180°﹣∠CHF﹣∠AFH）＝（180°﹣α）＝90°﹣α．20．如图，AB∥CD，∠ABD和∠BDC的平分线交于点E，BE交CD于点F．（1）求证：∠1+∠2＝90°；（2）如果∠EDF＝36°，那么∠BFC等于多少度？【解答】解：（1）∵AB∥CD，∴∠ABD+∠BDC＝180°，∵BE、DE平分∠ABD、∠BDC，∴∠1＝∠ABD，∠2＝∠BDC，∴∠1+∠2＝（∠ABD+∠BDC）＝90°，（2）∵DE平分∠BDC，∴∠2＝∠EDF＝36°，又∵∠1+∠2＝90°，∴∠1＝54°，又∵AB∥CD，∴∠BFC＝180°﹣∠1＝180°﹣54°＝126°．21．如图，AB∥CD，点E在线段AB上，连接EC、ED、AD，且ED平分∠CEB，AD⊥EF，若∠ADC＝42°，∠A﹣∠B＝8°，求∠BDE的度数．【解答】解：∵AB∥CD，∴∠ADC＝∠A＝42°，∵∠A﹣∠B＝8°，∴∠B＝34°，∵AD⊥EF，∴∠AFE＝90°，∴∠AEF＝48°，∴∠BEC＝132°，∵DE平分∠BEC，∴∠BED＝∠BEC＝66°，∴∠BDE＝180°﹣66°﹣34°＝80°．22．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．【解答】解：（1）证明：如图，过点E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠3＝∠1，∠4＝∠2，∴∠3+∠4＝∠1+∠2，即∠BED＝∠1+∠2；（2）∠1+∠EGH＝∠2+∠BEG，理由如下：如图，分别过点E、G作EF∥AB，GH∥AB，∵AB∥CD，∴AB∥EF∥GH∥CD，∴∠1＝∠3，∠4＝∠5，∠6＝∠2，∴∠1+∠5+∠6＝∠3+∠4+∠2，即∠1+∠EGH＝∠2+∠BEG；（3）由题可得，向左的角度数之和与向右的角度数之和相等，∴∠1、∠3、∠5与∠2、∠4、∠6之间的关系为：∠1+∠3+∠5＝∠2+∠4+∠6．23．已知AB∥CD，点E为平面内一点，BE⊥CE于E．（1）如图1，请直接写出∠ABE和∠DCE之间的数量关系；（2）如图2，过点E作EF⊥CD，垂足为F，求证：∠CEF＝∠ABE；（3）如图3，在（2）的条件下，作EG平分∠CEF，交DF于点G，作ED平分∠BEF，交CD 于D，连接BD，若∠DBE+∠ABD＝180°，且∠BDE＝3∠GEF，求∠BEG的度数．【解答】解：（1）结论：∠ECD＝90°+∠ABE．理由：如图1中，从BE交DC的延长线于H．∵AB∥CH，∴∠ABE＝∠H，∵BE⊥CE，∴∠CEH＝90°，∴∠ECD＝∠H+∠CEH＝90°+∠H，∴∠ECD＝90°+∠ABE．（2）如图2中，作EM∥CD，∵EM∥CD，CD∥AB，∴AB∥CD∥EM，∴∠BEM＝∠ABE，∠F+∠FEM＝180°，∵EF⊥CD，∴∠F＝90°，∴∠FEM＝90°，∴∠CEF与∠CEM互余，∵BE⊥CE，∴∠BEC＝90°，∴∠BEM与∠CEM互余，∴∠CEF＝∠BEM，∴∠CEF＝∠ABE．（3）如图3中，设∠GEF＝α，∠EDF＝β．∴∠BDE＝3∠GEF＝3α，∵EG平分∠CEF，∴∠CEF＝2∠FEG＝2α，∴∠ABE＝∠CEF＝2α，∵AB∥CD∥EM，∴∠MED＝∠EDF＝β，∠KBD＝∠BDF＝3α+β，∠ABD+∠BDF＝180°，∴∠BED＝∠BEM+∠MED＝2α+β，∵ED平分∠BEF，∴∠BED＝∠FED＝2α+β，∴∠DEC＝β，∵∠BEC＝90°，∴2α+2β＝90°，∵∠DBE+∠ABD＝180°，∠ABD+∠BDF＝180°，∴∠DBE＝∠BDF＝∠BDE+∠EDF＝3α+β，∵∠ABK＝180°，∴∠ABE+∠B＝DBE+∠KBD＝180°，即2α+（3α+β）+（3α+β）＝180°，∴6α+（2α+2β）＝180°，∴α＝15°，∴∠BEG＝∠BEC+∠CEG＝90°+15°＝105°．24．（1）如图①，若AB∥CD，求∠B+∠D+∠E1的度数？（2）如图②，若AB∥CD，求∠B+∠D+∠E1+∠E2的度数？（3）如图③，若AB∥CD，求∠B+∠D+∠E1+∠E2+∠E3的度数？（4）如图④，若AB∥CD，猜想∠B+∠D+∠E1+∠E2+⋯+∠E n的度数？①，过E1作E1F∥AB，则E1F∥CD，【解答】解：（1）如图∴∠B+∠1＝180°①，∠D+∠1＝180°②，①+②得∠B+∠1+∠D+∠2＝360°，即∠B+∠D+∠E1＝360°；过E1，E2作E1F∥AB，E2G∥AB，则E1F∥E2G∥CD，（2）如图②，分别∴∠1+∠B＝∠2+∠3＝∠4+∠D＝180°，∴∠B+∠D+∠E1+∠E2＝∠1+∠B+∠2+∠3+∠4+∠D＝540°＝3×180°；过E1，E2，E3作E1F1∥E2F2∥E3F3∥AB，则E1F1∥E2F2∥E3F3∥CD，（3）如图③，分别∴∠B+∠BE1E2＝180°，∠E2E1F1+∠E1E2F2＝180°，∠E3E2F2+∠E2E3F3＝180°，∠DE3F3+∠D＝180°，∴∠B+∠D+∠E1+∠E2+∠E3＝720°；（4）由（1）（2）（3）知，拐点的个数n与角的和之间的关系是（n+1）?180°，∴∠B+∠D+∠E1+∠E2+⋯+∠E n＝（n+1）?180°．25．如图，已知直线l1∥l2，点A、B分别在l1与l2上．直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？P点在C、D之间运动时，则有∠APB＝∠PAC+∠PBD．理由如下：【解答】解：（1）如图，当过点P作PE∥l1，∵l1∥l2，∴PE∥l2∥l1，∴∠PAC＝∠1，∠PBD＝∠2，∴∠APB＝∠1+∠2＝∠PAC+∠PBD；（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），则有两种情形：①如图，当点P在在l2下方时，有结论：∠APB＝∠PAC﹣∠PBD．理由是：过点P作PE∥l1，则∠APE＝∠PAC，又∵l1∥l2，∴PE∥l2，∴∠BPE＝∠PBD，∵∠APE＝∠APB+∠BPE，∴∠PAC＝∠APB+∠PBD，∴∠APB＝∠PAC﹣∠PBD；②如图，当点P在l1上方时，有结论：∠APB＝∠PBD﹣∠PAC．理由是：过点P作PE∥l2，则∠BPE＝∠PBD，又∵l1∥l2，∴PE∥l1，∴∠APE＝∠PAC，∵∠BPE＝∠APE+∠APB，∴∠PBD＝∠PAC+∠APB，∴∠APB＝∠PBD﹣∠PAC．26．如图，已知∠ABC＝∠ACB，BD平分∠ABC，CE平分∠ACB，F是BC延长线上一点，且∠DBC ＝∠F，求证：EC∥DF．【解答】证明：∵∠ABC＝∠ACB，BD平分∠ABC，CE平分∠ACB，∴∠DBC＝∠ABC，∠ECB＝∠ACB，∴∠DBC＝∠ECB．∵∠DBC＝∠F，∴∠ECB＝∠F，∴EC∥DF．。

精品七年级数学下册相交线与平行线综合提高题

相交线与平行线综合提高题1.若∠α与∠β是同旁内角，∠α=500,则∠β的度数是（）A.50°B.130°C.50°或130°D.不能确定2.已知线段AB的长为10cm,点A、B到直线L的距离分别为6cm和4cm,符合条件的L的条数为（）A.1B.2C.3D.43.如图，能与∠α构成同旁内角的角有（）A.5个B.4个C.3个D.2个4.如图，直线m平行直线n，∠1=1050，∠2=1400，则∠3等于（）A.550B.600C.650D.7005.如图,AB∥DE,那么∠BCD于（）A.∠2-∠1B.∠1+∠2C.1800+∠1-∠2D.1800+∠2-2∠16.如图，OP∥QR∥ST，则下列各式中正确的是（）A.∠1+∠2+∠3=180°B.∠1+∠2-∠3=90°C.∠1-∠2+∠3=90°D.∠2+∠3-∠1=180°7.如图,AD∥BC,点O在AD上,BO、CO分别平分∠ABC、∠DCB,若∠A+∠D=m0,则∠BOC=______．8.如图,在平面内,两条直线l1，l2相交于点O，对于平面内任意一点M,若p、q分别是点M到直线l1，l2的距离，则称(p，q)为点M的“距离坐标”．根据上述规定，“距离坐标”是(2，1)的点共有个．9.如图,AF∥CD,∠ABC=1000,∠BAF=1400,∠BCD=∠DEF,∠CDE=1460,则∠F=10.如图,AB∥CD,∠D的度数是∠E度数的2倍,∠B度数是∠D度数的四分之三，则∠E的度数为11.如图，AB∥CD∥EF，∠D=300，∠BED=800，BE平分∠BEG,则∠BEG=12.如图(1),直线m//n,则∠A+∠B+∠C= ;如图(2),直线m//n,则∠A+∠B+∠C+∠D= ;如图(n),直线m//n,则∠A+∠B+∠C+...= ;图 (1) 图(2) 图(n)13.如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140º，求∠BFD的度数。

人教版七年级数学下册《第五章相交线与平行线》能力提升卷-附答案

人教版七年级数学下册《第五章相交线与平行线》能力提升卷-附答案班级：___________________ 姓名：_________________ 得分：_______________注意事项：本试卷满分120分试题共23题其中选择10道、填空6道、解答7道．答卷前考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题每小题3分共30分）在每小题所给出的四个选项中只有一项是符合题目要求的．1．（2022秋•唐河县期末）如图下列图形中的∠1和∠2不是同位角的是（）A．B．C．D．【分析】根据同位角的意义逐项进行判断即可．【解答】解：选项A中的∠1与∠2 是直线AB、BC被直线EF所截的同位角因此选项A不符合题意；选项B中的∠1与∠2 是直线AB、MG被直线EM所截的同位角因此选项B不符合题意；选项C中的∠1与∠2 没有公共的截线因此不是同位角所以选项C符合题意；选项D中的∠1与∠2 是直线CD、EF被直线AB所截的同位角因此选项D不符合题意；故选：C．2．（2022秋•长春期末）如图测量运动员跳远成绩选取的是AB的长度其依据是（）A．两点确定一条直线B．两点之间直线最短C．两点之间线段最短D．垂线段最短【分析】利用垂线段最短求解．【解答】解：该运动员跳远成绩的依据是：垂线段最短；故选：D．3．（2020秋•射洪市期末）如图所示下列结论中正确的是（）A．∠1和∠2是同位角B．∠2和∠3是同旁内角C．∠1和∠4是内错角D．∠3和∠4是对顶角【分析】根据同位角内错角同旁内角以及对顶角的定义进行解答．【解答】解：A、∠1和∠2是同旁内角故本选项错误；B、∠2和∠3是同旁内角故本选项正确；C、∠1和∠4是同位角故本选项错误；D、∠3和∠4是邻补角故本选项错误；故选：B．4．（2018秋•龙岗区期末）下列四个命题中真命题是（）A．两条直线被第三条直线所截内错角相等B．如果∠1和∠2是对顶角那么∠1＝∠2C．三角形的一个外角大于任何一个内角D．如果x2＞0 那么x＞0【分析】利用平行线的性质、对顶角的性质、三角形的外角的性质分别判断后即可确定正确的选项．【解答】解：A、两条直线被第三条直线所截内错角相等错误为假命题；B、如果∠1和∠2是对顶角那么∠1＝∠2 正确为真命题；C、三角形的一个外角大于任何一个内角错误为假命题；D、如果x2＞0 那么x＞0 错误为假命题故选：B．5．（2022秋•玉泉区期末）如图直线AB、CD相交于点O OA平分∠EOC∠EOC：∠EOD＝1：2 则∠BOD等于（）A．30°B．36°C．45°D．72°【分析】根据邻补角的定义求出∠EOC再根据角平分线的定义求出∠AOC然后根据对顶角相等解答．【解答】解：∵∠EOC：∠EOD＝1：2∴∠EOC＝180°×＝60°∵OA平分∠EOC∴∠AOC＝∠EOC＝×60°＝30°∴∠BOD＝∠AOC＝30°．故选：A．6．（2022秋•宛城区期末）如图下列能判定AB∥CD的条件有（）个（1）∠1＝∠2；（2）∠3＝∠4；（3）∠B＝∠5；（4）∠B+∠BCD＝180°．A．1B．2C．3D．4【分析】根据平行线的判定方法对四个条件分别进行判断即可．【解答】解：（1）∵∠1＝∠2∴AD∥BC；（2）∵∠3＝∠4∴AB∥CD；（3）∵∠B＝∠5∴AB∥CD；（4）∵∠B+∠BCD＝180°∴AB∥CD．故选：C．7．（2022秋•卧龙区校级期末）如图所示下列推理正确的个数有（）①若∠1＝∠2 则AB∥CD②若AD∥BC则∠3+∠A＝180°③若∠C+∠CDA＝180°则AD∥BC④若AB∥CD则∠3＝∠4．A．0个B．1个C．2个D．3个【分析】根据平行线的判定（内错角相等两直线平行同位角相等两直线平行同旁内角互补两直线平行）和平行线的性质（两直线平行内错角相等两直线平行同位角相等两直线平行同旁内角互补）判断即可．【解答】解：∵∠1＝∠2∴AB∥DC∴①正确；∵AD∥BC∴∠CBA+∠A＝180°∠3+∠A＜180°∴②错误；∵∠C+∠CDA＝180°∴AD∥BC∴③正确；由AD∥BC才能推出∠3＝∠4 而由AB∥CD不能推出∠3＝∠4 ∴④错误；正确的个数有2个故选：C．8．（2022秋•市中区校级期末）如图在下列给出的条件中不能判定AB∥CD的是（）A．∠BAD+∠ADC＝180°B．∠ABD＝∠BDCC．∠ADB＝∠DBC D．∠ABE＝∠DCE【分析】在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角被判断平行的两直线是否由“三线八角”而产生的被截直线．【解答】解：A、正确∵∠BAD+∠ADC＝180°∴AB∥CD（同旁内角互补两直线平行）；B、正确∵∠ABD＝∠BDC∴AB∥CD（内错角相等两直线平行）；C、∠ADB＝∠DBC判定的是AD∥BC所以不符合要求；D、正确∵∠ABE＝∠DCE∴AB∥CD（同位角相等两直线平行）；故选：C．9．（2022秋•兴宁区校级期中）如图某校区2号楼楼梯的示意图现在要在楼梯上铺一条地毯如果楼梯的宽度是1.8米那么地毯的面积为（）A．（a+1.8）h m2B．（h+1.8）a m2C．1.8（h+a）m2D．1.8ah m2【分析】根据图形可得地毯长度为（a+h）米再根据长方形的面积公式解答即可．【解答】解：由题意得地毯的长度为（a+h）米故地毯的面积为：1.8（h+a）m2．故选：C．10．（2022秋•南岗区校级期中）如图AB∥CD∥EF则下列各式中正确的是（）A．∠1+∠2+∠3＝180°B．∠1+∠2＝180°+∠3C．∠1+∠3＝180°+∠2D．∠2+∠3＝180°+∠1【分析】根据两直线平行同旁内角互补可得∠2+∠BDC＝180°再根据两直线平行内错角相等可得∠3＝∠CDE而∠CDE＝∠1+∠BDC整理可得∠2+∠3﹣∠1＝180°．【解答】解：∵AB∥CD∥EF∴∠2+∠BDC＝180°∠3＝∠CDE又∠BDC＝∠CDE﹣∠1∴∠2+∠3﹣∠1＝180°．故选：D．二、填空题（本大题共6小题每小题4分共24分）请把答案直接填写在横线上11．（2022•东阳市校级开学）如图所示图中用数字标出的角中∠2的内错角是∠6．【分析】两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线（截线）的两旁则这样一对角叫做内错角由此即可判断．【解答】解：图中用数字标出的角中∠2的内错角是∠6．故答案为：∠6．12．（2022秋•姜堰区期中）如图△ABC经过平移得到△A'B'C' 连接BB'、CC' 若BB'＝1.2cm则CC'＝ 1.2cm．【分析】根据平移的性质即可得到结论．【解答】解：∵△ABC经过平移得到△A'B'C' 连接BB'、CC' BB'＝1.2cm∴CC'＝BB′＝1.2cm故答案为：1.2．13．（2022春•和平区校级月考）如图CD⊥AD BE⊥AC AF⊥CF CD＝2cm BE＝1.5cm AF＝4cm则点A到直线BC的距离是4cm点B到直线AC的距离是 1.5cm点C到直线AB的距离是2 cm．【分析】根据点到直线的距离：直线外一点到直线的垂线段的长度叫做点到直线的距离解答即可．【解答】解：∵CD⊥AD BE⊥AC AF⊥CF CD＝2cm BE＝1.5cm AF＝4cm∴点A到直线BC的距离是4cm点B到直线AC的距离是1.5cm点C到直线AB的距离是2cm．故答案为：4、1.5、2．14．（2022春•新乐市校级月考）如图直线EF CD相交于点O OA⊥OB垂足为O且OC平分∠AOF．（1）若∠AOE＝40°则∠DOE的度数为70°；（2）∠AOE与∠BOD的数量关系为∠AOE＝2∠BOD．【分析】（1）利用邻补角的定义进行计算即可；（2）利用第一步的步骤和思路推理即可．【解答】解：（1）∵OA⊥OB∴∠AOB＝90°∵∠AOF+∠AOE＝180°∠AOE＝40°∴∠AOF＝140°∵OC平分∠AOF∴∠AOC＝∠COF＝70°∵∠BOD+∠AOB+∠AOC＝180°∴∠DOE＝∠COF＝70°．故答案为：70°；（2）∵∠AOE+∠AOF＝180°∠AOC＝∠COF∴∠AOC＝（180°﹣∠AOE）＝90°﹣∠AOE∵∠BOD+∠AOB+∠AOC＝180°∴∠BOD＝180°﹣90°﹣∠AOC＝90°﹣（90°﹣∠AOE）＝﹣∠AOE∴∠AOE＝2∠BOD．故答案为：∠AOE＝2∠BOD．15．（2022秋•南岗区校级期中）已知两个角的两边分别互相平行其中一个角的度数比另一个角度数的多15°则这个角为20°或48°．【分析】由两个角的两边都平行可得此两角互补或相等然后设其中一个角为x°分别从两角相等或互补去分析由其中一个角的度数是另一个角的3倍少20°列方程求解即可求得答案．【解答】解：∵两个角的两边都平行∴此两角互补或相等设其中一个角为x°∵其中一个角的度数比另一个角度数的多15°∴①若两角相等则x＝x+15 解得：x＝20②若两角互补则x＝（180﹣x）+15 解得：x＝48∴两个角的度数分别是20°或48°．故答案为：20°或48．16．（2022秋•香坊区校级期中）如图已知AB∥CD∠P AQ＝2∠BAQ∠PCD＝3∠QCD∠P＝75°则∠AQC＝95°．【分析】先根据平行线的性质求出∠APC+∠P AB+∠PCD＝360°由∠APC＝75°求出∠P AB+∠PCD＝285°根据∠P AQ＝2∠BAQ可得∠P AB＝3∠BAQ由∠PCD＝3∠QCD可得∠BAQ+∠QCD＝95°最后证∠AQC＝∠BAQ+∠QCD即可得出答案．【解答】解：过点P作PE∥AB过点Q作QF∥AB如图：∵AB∥CD QF∥AB∴AB∥QF∥CD∴∠BAQ＝∠AQF∠QCD＝∠CQF∴∠BAQ+∠QCD＝∠AQF+∠CQF即∠BAQ+∠QCD＝∠AQC∵AB∥CD PE∥AB∴AB∥PE∥CD∴∠APE+∠P AB＝180°∠CPE+∠PCD＝180°∴∠APE+∠CPE+∠P AB+∠PCD＝360°即∠APC+∠P AB+∠PCD＝360°∵∠APC＝75°∴∠P AB+∠PCD＝285°∵∠P AQ＝2∠BAQ∴∠P AB＝3∠BAQ∵∠PCD＝3∠QCD∴3∠BAQ+3∠QCD＝285°∴∠BAQ+∠QCD＝95°∴∠AQC＝95°．故答案为：95°．三、解答题（本大题共7小题共66分．解答时应写出文字说明、证明过程或演算步骤）17．（2022春•金东区期末）如图△ABC△A1B1C1的顶点都在边长为1个单位长度的小正方形组成的网格线交点上．（1）将△ABC向右平移4个单位得到△A2B2C2请画出△A2B2C2．（2）试描述△A1B1C1经过怎样的平移可得到△A2B2C2．【分析】（1）利用平移的性质可画出△A2B2C2；（2）根据平移的特征可得答案．【解答】解：（1）如图△A2B2C2即为所求；（2）将△A1B1C1向左平移2个单位再向下平移4个单位可得到△A2B2C2．18．（2021春•新市区校级期末）如图点G在CD上已知∠BAG+∠AGD＝180°EA平分∠BAG FG 平分∠AGC请说明AE∥GF的理由．解：因为∠BAG+∠AGD＝180°（已知）∠AGC+∠AGD＝180°（邻补角的定义）所以∠BAG＝∠AGC（同角的补角相等）．因为EA平分∠BAG所以∠1＝∠BAG（角平分线的定义）．因为FG平分∠AGC所以∠2＝∠AGC得∠1＝∠2（等量代换）所以AE∥GF（内错角相等两直线平行）．【分析】根据邻补角的定义及题意得出∠BAG＝∠AGC再根据角平分线的定义得到∠1＝∠2 即可判定AE∥GF．【解答】解：因为∠BAG+∠AGD＝180°（已知）∠AGC+∠AGD＝180°（邻补角的定义）所以∠BAG＝∠AGC（同角的补角相等）因为EA平分∠BAG所以∠1＝∠BAG（角平分线的定义）因为FG平分∠AGC所以∠2＝∠AGC得∠1＝∠2（等量代换）所以AE∥GF（内错角相等两直线平行）．故答案为：已知；邻补角的定义；同角的补角相等；∠BAG；角平分线的定义；∠AGC；等量代换；内错角相等两直线平行．19．判断下列命题是真命题还是假命题；如果是假命题举一个反例．（1）同旁内角互补；（2）如果a＞b那么ac＞bc；（3）两个锐角的和是钝角．【分析】（1）根据平行线的性质判断即可；（2）根据不等式的性质判断即可；（3）根据角的分类判断即可．【解答】解：（1）同旁内角互补是假命题如两直线不平行同旁内角不能互补；（2）如果a＞b那么ac＞bc是假命题如c＝0时ac＝bc；（3）两个锐角的和是钝角是假命题如30°+30°＝60°．20．（2022秋•中山市期末）如图已知直线AB CD相交于点O OE平分∠BOD OF平分∠COB∠BOE ＝36°求∠AOF的度数．【分析】根据角平分线可得∠BOE＝∠DOE根据邻补角可得∠BOC的度数根据角平分线的定义可得∠COF再根据对顶角及角的和差可得答案．【解答】解：∵直线AB CD相交于点O OE平分∠BOD OF平分∠COB∴∠BOE＝∠DOE＝36°∠BOF＝∠COF∴∠BOD＝∠AOC＝2∠BOE＝72°∴∠BOC＝180°﹣∠BOD＝108°∴∠COF＝＝54°∴∠AOF＝∠AOC+∠COF＝72°+54°＝126°．21．（2022秋•皇姑区校级期末）如图已知直线AB∥DF∠D+∠B＝180°．（1）求证：DE∥BC；（2）如果∠AMD＝70°求∠AGC的度数．【分析】（1）根据平行线的性质得出∠D+∠BHD＝180°求出∠B＝∠DHB根据平行线的判定得出即可；（2）根据平行线的性质求出∠AGB＝∠AMD＝75°根据邻补角的定义求出即可．【解答】（1）证明：∵AB∥DF∴∠D+∠BHD＝180°∵∠D+∠B＝180°∴∠B＝∠DHB∴DE∥BC；（2）解：∵DE∥BC∠AMD＝70°∴∠AGB＝∠AMD＝70°∴∠AGC＝180°﹣∠AGB＝180°﹣70°＝110°．22．（2022秋•二道区校级期末）如图点O在直线AB上OC⊥OD∠D与∠1互余．（1）求证：ED∥AB；（2）OF平分∠AOD交DE于点F若∠OFD＝65°补全图形并求∠1的度数．【分析】（1）根据垂直的定义、余角的概念推出∠D＝∠DOB即可判定ED∥AB；（2）根据平行线的性质、角平分线的定义求出∠AOD＝2∠AOF＝130°根据角的和差即可求解．【解答】（1）证明：∵OC⊥OD∴∠COD＝90°∴∠1+∠DOB＝90°∵∠D与∠1互余∴∠D+∠1＝90°∴∠D＝∠DOB∴ED∥AB；（2）解：如图∵ED∥AB∠OFD＝65°∴∠AOF＝∠OFD＝65°∵OF平分∠AOD∴∠AOD＝2∠AOF＝130°∵∠COD＝90°∠AOD＝∠1+∠COD∴∠1＝40°．23．（2022秋•朝阳区校级期末）（1）问题发现：如图①直线AB∥CD连接BE CE可以发现∠B+∠C ＝∠BEC．请把下面的证明过程补充完整：证明：过点E作EF∥AB∵AB∥DC（已知）EF∥AB（辅助线的作法）∴EF∥DC（平行于同一直线的两直线平行）．∴∠C＝∠CEF．（两直线平行内错角相等）．∵EF∥AB∴∠B＝∠BEF（同理）．∴∠B+∠C＝∠BEF+∠CEF．即∠B+∠C＝∠BEC．（2）拓展探究：如果点E运动到图②所示的位置其他条件不变说明：∠B+∠BEC+∠C＝360°．（3）解决问题：如图③AB∥DC E、F、G是AB与CD之间的点直接写出∠1 ∠2 ∠3 ∠4 ∠5之间的数量关系∠1+∠3+∠5＝∠2+∠4．【分析】（1）过点E作EF∥AB根据平行线的性质及角的和差求解即可；（2）过点E作EF∥AB根据平行线的性质及角的和差求解即可；（3）过点F作FM∥AB根据（1）求解即可．【解答】（1）证明：如图①过点E作EF∥AB∵AB∥DC（已知）EF∥AB（辅助线的作法）∴EF∥DC（平行于同一直线的两直线平行）∴∠C＝∠CEF（两直线平行内错角相等）∵EF∥AB∴∠B＝∠BEF（同理）∴∠B+∠C＝∠BEF+∠CEF（等量代换）即∠B+∠C＝∠BEC故答案为：平行于同一直线的两直线平行；两直线平行内错角相等；∠BEF+∠CEF；（2）解：如图②过点E作EF∥AB∵AB∥CD EF∥AB∴EF∥CD∴∠C+∠CEF＝180°∠B+∠BEF＝180°∴∠B+∠C+∠AEC＝360°∴∠B+∠C＝360°﹣（∠BEF+∠CEF）即∠B+∠C＝360°﹣∠BEC；∠B+∠BEC+∠C＝360°．（3）解：∠1+∠3+∠5＝∠2+∠4 理由如下：如图过点F作FM∥AB则AB∥FM∥CD由（1）得∠1+∠3+∠5＝∠2+∠4．故答案为：∠1+∠3+∠5＝∠2+∠4．。

人教版初中七年级数学下册第五章《相交线与平行线》提高卷(含答案解析)(1)

一、选择题1．如图，若1234//,//l l l l ，则图中与1 互补的角有（）A ．1个B ．2个C ．3个D ．4个D解析：D【分析】直接利用平行线的性质得出相等的角以及互补的角进而得出答案．【详解】解：解：∵1234//,//l l l l ，∴∠1+∠2=180°，∠2=∠4，∵∠4=∠5，∠2=∠3，∴图中与∠1互补的角有：∠2，∠3，∠4，∠5共4个．故选：D ．【点睛】本题主要考查了平行线的性质，注意不要漏角是解题的关键．2．在下列命题中，为真命题的是（）A ．相等的角是对顶角B ．平行于同一条直线的两条直线互相平行C ．同旁内角互补D ．垂直于同一条直线的两条直线互相平行B解析：B【分析】根据对顶角、平行公理的推论、平行线的判定、同旁内角逐项判断即可得．【详解】A 、相等的角不一定是对顶角，此项是假命题；B 、平行于同一条直线的两条直线互相平行，此项是真命题；C 、两直线平行，同旁内角互补，此项是假命题；D 、在同一平面内，垂直于同一条直线的两条直线互相平行，此项是假命题；故选：B ．【点睛】本题考查了命题与定理、平行线的判定与性质等知识点，熟练掌握平行线的判定与性质是解题关键．3．下列语句中不是命题的有（）（1）两点之间，线段最短；（2）连接A、B两点；（3）鸟是动物；（4）不相交的两条直线叫做平行线；（5）无论a为怎样的有理数，式子a2+1的值都是正数吗？A．1个B．2个C．3个D．4个C解析：C【分析】根据命题的定义对各语句进行判断．【详解】两点之间，线段最短，所以（1）为命题；连接A、B两点，它为描述性语言，所以（2）不是命题；鸟是动物，所以（3）为命题；不相交的两条直线叫做平行线，所以（4）为命题；无论a为怎样的有理数，式子a2+1的值都是正数吗？它为疑问句，所以（5）不是命题．故选：C．【点睛】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．4．如图，将周长为7的△ABC沿BC方向向右平移2个单位得到△DEF，则四边形ABFD的周长为（）A．8 B．9 C．10 D．11D解析：D【分析】根据平移的基本性质，得出四边形ABFD的周长=AD+AB+BF+DF=2+AB+BC+2+AC即可得出答案．【详解】解：根据题意，将周长为7的△ABC沿BC方向向右平移2个单位得到△DEF，∴AD=2，BF=BC+CF=BC+2，DF=AC；又∵AB+BC+AC=7，∴四边形ABFD 的周长=AD+AB+BF+DF=2+AB+BC+2+AC=11．故选：D ．【点睛】本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．得到CF=AD ，DF=AC 是解题的关键．5．对于命题“如果∠1+∠2＝90°，那么∠1≠∠2”，能说明它是假命题的反例是（） A ．∠1＝50°，∠2＝40°B ．∠1＝50°，∠2＝50°C ．∠1＝∠2＝45°D ．∠1＝40°，∠2＝40°C 解析：C【分析】能说明是假命题的反例就是能满足已知条件，但不满足结论的例子．【详解】A 、满足条件∠1＋∠2＝90°，也满足结论∠1≠∠2，故A 选项错误；B 、不满足条件，故B 选项错误；C 、满足条件，不满足结论，故C 选项正确；D 、不满足条件，也不满足结论，故D 选项错误．故选：C ．【点睛】此题考查了命题与定理的知识，理解能说明它是假命题的反例的含义是解决本题的关键． 6．下列命题中，属于真命题的是（）A ．相等的角是对顶角B ．一个角的补角大于这个角C ．绝对值最小的数是0D ．如果a b =，那么a=b C 解析：C【分析】根据对顶角、补角、绝对值的定义与性质逐项判断即可得．【详解】A 、相等的角不一定是对顶角，此项是假命题；B 、一个角的补角不一定大于这个角，如这个角为130︒，其补角为50︒，小于这个角，此项是假命题；C 、由绝对值的非负性得：绝对值最小的数是0，此项是真命题；D 、如果a b =，那么a b =或=-a b ，此项是假命题；故选：C ．【点睛】本题考查了对顶角、补角、绝对值、真命题与假命题，熟练掌握各定义与性质是解题关键．7．如图，A 是直线l 外一点，过点A 作AB l ⊥于点B ，在直线l 上取一点C ，连接AC ，使2AC AB =，P 在线段BC 上，连接AP ．若3AB =，则线段AP 的长不可能是（）A ．4B ．5C ．2D ．5.5C解析：C【分析】根据题意计算出AC 的长度，由垂线段最短得出AP 的范围，选出AP 的长度不可能的选项即可．【详解】3AB =，26AC AB cm ∴==，结合垂线段最短，得：36AP ≤≤．故选：C ．【点睛】本题主要考查直线外一点与直线上各点连接的所有线段中，垂线段最短，熟记概念并求出对应线段的范围是解题关键．8．如图，给出下列条件：①∠1＝∠2：②∠3＝∠4：③AB ∥CE ，且∠ADC ＝∠B ：④AB ∥CE ，且∠BCD ＝∠BAD ．其中能推出BC ∥AD 的条件为（）A ．①②B ．②④C ．②③D ．②③④D解析：D【分析】根据平行线的判定条件，逐一判断，排除错误答案．【详解】解：①∵∠1＝∠2，∴AB ∥CD ，不符合题意；②∵∠3＝∠4，∴BC ∥AD ，符合题意；③∵AB ∥CD ，∴∠B+∠BCD ＝180°，∵∠ADC＝∠B，∴∠ADC+∠BCD＝180°，由同旁内角互补，两直线平行可得BC∥AD，故符合题意；④∵AB∥CE，∴∠B+∠BCD＝180°，∵∠BCD＝∠BAD，∴∠B+∠BAD＝180°，由同旁内角互补，两直线平行可得BC∥AD，故符合题意；故能推出BC∥AD的条件为②③④．故选：D．【点睛】本题考查了平行线的判定，关键是掌握判定定理：同位角相等，两直线平行．内错角相等，两直线平行．同旁内角互补，两直线平行．9．如图，△ABC经平移得到△EFB，则下列说法正确的有（）①线段AC的对应线段是线段EB；②点C的对应点是点B；③AC∥EB；④平移的距离等于线段BF的长度．A．1 B．2 C．3 D．4D解析：D【分析】根据平移的特点分别判断各选项即可．【详解】∵△ABC经平移得到△EFB∴点A、B、C的对应点分别为E、F、B，②正确∴BE是AC的对应线段，①正确∴AC∥EB，③正确平移距离为对应点连线的长度，即BF的长度，④正确故选：D【点睛】本题考查平移的特点，注意，在平移过程中，一定要把握住对应点，仅对应点的连线之间才有平行、相等的一些关系．10．如图是郝老师的某次行车路线，总共拐了三次弯，最后行车路线与开始的路线是平行的，已知第一次转过的角度120︒，第三次转过的角度135︒，则第二次拐弯的角度是（）A．75︒B．120︒C．135︒D．无法确定A解析：A【解析】分析：根据两直线平行，内错角相等，得到∠BFD的度数，进而得出∠CFD的度数，再由三角形外角的性质即可得到结论．详解：如图，延长ED交BC于F．∵DE∥AB，∴∠DFB=∠ABF=120°，∴∠CFD=60°．∵∠CDE=∠C+∠CFD，∴∠C=∠CDE-∠CFD=135°－60°=75°．故选A．点睛：本题考查了平行线的性质及三角形外角的性质．解题的关键是理解题意，灵活应用平行线的性质解决问题，属于中考常考题型．二、填空题11．如图，点A在直线m上，点B在直线l上，点A到直线l的距离为a，点B到直线m 的距离为b，线段AB的长度为c，通过测量等方法可以判断在a，b，c三个数据中，最大的是_____________．【分析】过点A作AD垂直于垂足为D过点B作BH垂直于垂足为H连接AB根据点到直线垂线段最短可知AB ＞ADAB＞BH可得最大【详解】过点A作AD垂直于垂足为D过点B作BH垂直于垂足为H连接AB由题意得解析：c【分析】过点A作AD垂直于l垂足为D，过点B作BH垂直于m垂足为H,连接AB，根据点到直线垂线段最短，可知AB＞AD，AB＞BH，可得c最大．【详解】过点A作AD垂直于l垂足为D，过点B作BH垂直于m垂足为H,连接AB，由题意得：AD=a， BH=b，AB=c；根据点到直线垂线段最短，可知AB＞AD，AB＞BH∴c＞a，c＞b；∴c最大故答案：c【点睛】本题主要考查了垂线段最短的性质，熟记性质是解题的关键．∠=∠=∠=︒，则∠4的度数是___________．12．已知：如图，12354126°【分析】由∠1=∠2及对顶角相等可得出∠1=∠5利用同位角相等两直线平行可得出l1∥l2利用两直线平行同旁内角互补可求出∠6的度数再利用对顶角相等可得出∠4的度数【详解】解：给各角标上序号如解析：126°．【分析】由∠1=∠2及对顶角相等可得出∠1=∠5，利用“同位角相等，两直线平行”可得出l1∥l2，利用“两直线平行，同旁内角互补”可求出∠6的度数，再利用对顶角相等可得出∠4的度数．【详解】解：给各角标上序号，如图所示．∵∠1=∠2，∠2=∠5，∴∠1=∠5，∴l1∥l2，∴∠3+∠6=180°．∵∠3=54°，∴∠6=180°-54°=126°，∴∠4=∠6=126°．故答案为：126°．【点睛】本题考查了平行线的判定与性质，牢记平行线的各判定与性质定理是解题的关键．13．阅读下面材料：在数学课上，老师提出如下问题：如图，需要在A、B两地和公路l之间修地下管道．请你设计一种最节省材料的修路方案：小丽设计的方案如下：如图，（1）连接AB；（2）过点A画线段AC⊥直线l于点C，所以线段BA和线段AC即为所求．老师说：“小丽的画法正确”请回答：小丽的画图依据是___．两点之间线段最短；直线外一点到这条直线上所有点连结的线段中垂线段最短（或垂线段最短）【分析】根据线段的概念和垂线的性质即可求解【详解】由垂线段最短可知点A到直线l的最短距离为AC由两点之间线段最短可解析：两点之间线段最短；直线外一点到这条直线上所有点连结的线段中，垂线段最短（或垂线段最短）【分析】根据线段的概念和垂线的性质即可求解．【详解】由垂线段最短可知，点A 到直线l 的最短距离为AC ，由两点之间线段最短可知，点B 到点A 的最短距离为AB ．故答案为：两点之间线段最短；直线外一点到这条直线上所有点连结的线段中，垂线段最短（或垂线段最短）；【点睛】本题考察线段的概念和垂线的性质，熟练掌握其概念和性质是解题的关键．14．如图，长8米宽6米的草坪上有一条弯折的小路（小路进出口的宽度相等，且每段小路均为平行四边形），小路进出口的宽度均为1米，则绿地的面积为__平方米．42【分析】利用平移表示出草坪的长和宽然后根据长方形的面积公式列式计算即可得解【详解】解：由平移的性质得:草坪的长为8﹣1＝7（米）宽为6米草坪的面积＝7×6＝42（平方米）故答案为：42【点睛】本解析：42【分析】利用平移表示出草坪的长和宽，然后根据长方形的面积公式列式计算即可得解．【详解】解：由平移的性质，得:草坪的长为8﹣1＝7（米），宽为6米，草坪的面积＝7×6＝42（平方米）．故答案为：42．【点睛】本题考查了平移的性质，熟记性质并理解求出与草坪的面积相当的长方形的长和宽是解题的关键．15．如图，把直角梯形ABCD 沿AD 方向平移到梯形EFGH ，28HG cm =，5MG cm =，4MC cm =，则阴影部分的面积是___ 130cm2【分析】根据平移的性质可知梯形EFGH ≌梯形ABCD 那么GH=CDBC=FG 观察可知梯形EFMD 是两个梯形的公共部分那么阴影部分的面积就等于梯形MGHD 再根据梯形的面积计算公式计算即可【解析：130cm 2．【分析】根据平移的性质可知梯形EFGH≌梯形ABCD，那么GH=CD，BC=FG，观察可知梯形EFMD 是两个梯形的公共部分，那么阴影部分的面积就等于梯形MGHD，再根据梯形的面积计算公式计算即可．【详解】解：∵直角梯形EFGH是由直角梯形ABCD平移得到的，∴梯形EFGH≌梯形ABCD，∴GH=CD，BC=FG，∵梯形EFMD是两个梯形的公共部分，∴S梯形ABCD-S梯形EFMD=S梯形EFGH-S梯形EFMD，∴S阴影=S梯形MGHD=12（DM+GH）•GM=12（28-4+28）×5=130（cm2）．故答案是130cm2．【点睛】本题考查了图形的平移，解题的关键是知道平移前后的两个图形全等．16．把命题“等角的余角相等”改写成“如果…，那么…”的形式为______．如果两个角相等那么这两个角的余角相等【分析】把命题的题设写在如果的后面把命题的结论部分写在那么的后面即可【详解】解：命题等角的余角相等写成如果…那么…的形式为：如果两个角是相等角的余角那么这两个角相解析：如果两个角相等，那么这两个角的余角相等【分析】把命题的题设写在如果的后面，把命题的结论部分写在那么的后面即可．【详解】解：命题“等角的余角相等”写成“如果…，那么…．”的形式为：如果两个角是相等角的余角，那么这两个角相等．故答案为：如果两个角是相等角的余角，那么这两个角相等．【点睛】本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．17．用反证法证明“三角形中至少有一个内角不大于60°，应先假设这个三角形中____________________．三角形的三个内角都大于60°【分析】根据反证法的步骤先假设结论不成立即否定命题即可【详解】根据反证法的步骤第一步应假设结论的反面成立即三角形的三个内角都大于60°故答案为：三角形的三个内角都大于60解析：三角形的三个内角都大于60°【分析】根据反证法的步骤，先假设结论不成立，即否定命题即可．【详解】根据反证法的步骤，第一步应假设结论的反面成立，即三角形的三个内角都大于60°．故答案为：三角形的三个内角都大于60°．【点睛】本题考查了反证法的知识，掌握反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立是解题的关键．18．如图是某公园里一处矩形风景欣赏区ABCD ，长AB=50米，宽BC=30米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那么小明沿着小路的中间出口A 到出口B 所走的路线（图中虚线）长为______米．98【解析】∵利用已知可以得出此图形可以分为横向与纵向分析水平距离等于AB 铅直距离等于（AD-1）×2又∵长AB=50米宽BC=25米∴小明沿着小路的中间出口A 到出口B 所走的路线（图中虚线）长为50解析：98【解析】∵利用已知可以得出此图形可以分为横向与纵向分析，水平距离等于AB ，铅直距离等于（AD -1）×2，又∵长AB =50米，宽BC =25米，∴小明沿着小路的中间出口A 到出口B 所走的路线（图中虚线）长为50+（25-1）×2=98米，故答案为98．19．如图，AD 平分,34BDF ∠∠=∠，若150,2130∠=︒∠=︒，则CBD ∠=________︒．65【分析】利用平行线的判定定理和性质定理等量代换可得∠CBD=∠EBC 可得结果【详解】∵∠1=50°∴∠DBE=180°-∠1=180°-50°=130°∵∠2=130°∴∠DBE=∠2∴AE ∥C解析：65【分析】利用平行线的判定定理和性质定理，等量代换可得∠CBD=∠EBC ，可得结果．【详解】∵∠1=50°，∴∠DBE=180°-∠1=180°-50°=130°，∵∠2=130°，∴∠DBE=∠2，∴AE∥CF，∴∠4=∠ADF，∵∠3=∠4，∴∠EBC=∠4，∴AD∥BC，∵AD平分∠BDF，∴∠ADB=∠ADF，∵AD∥BC，∴∠ADB=∠CBD，∴∠4=∠CBD，∴∠CBD=∠EBC=12∠DBE=12×130°=65°．故答案为：65．【点睛】本题主要考查了平行线的判定定理和性质定理，角平分线的定义等，熟练掌握定理是解答此题的关键．20．如图，两个大小一样的直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置，AB=10，DH=4，平移距离为8，则阴影部分的面积是_______________．64【分析】根据平移变化只改变图形的位置不改变图形的形状可得出两个三角形大小一样阴影部分面积等于梯形ABEH的面积；DE=AB根据线段的和差关系可求出HE的长度再根据梯形的面积公式即可得答案【详解】解析：64【分析】根据平移变化只改变图形的位置，不改变图形的形状，可得出两个三角形大小一样，阴影部分面积等于梯形ABEH的面积；DE=AB，根据线段的和差关系可求出HE的长度，再根据梯形的面积公式即可得答案．【详解】∵两个三角形大小一样，∴S△ABC=S△DEF，∴S△ABC-S△HEC=S△DEF-S△HEC，∴S阴影=S梯形ABEH，∵其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置，AB=10，∴DE=AB=10，∵DH=4，∴HE=DE-DH=6，∵平移距离是8，∴BE=8，∴S阴影=S梯形ABEH=12（HE+AB）·BE=12×（10+6）×8=64，故答案为：64【点睛】本题主要考查了平移的性质，通过观察图形把阴影部分的面积转化为熟知图形的面积是关键的一步．三、解答题21．在一张地图上有、、A B C三地，但地图被墨迹污染，C地具体位置看不清楚，但知道C地在A地的北偏东30°方向，在B地南偏东45°方向．（1）根据以上条件，在地图上画出C地的位置；（2）直接写出ACB的度数．解析：（1）见详解；（2）105°．【分析】（1）过点A、B作正北方向，再据方位角的含义画射线BX和AY，两射线之交点即是C 地；（2）记过点A的正北方向线与射线BX之交点为D，先求得∠CDA的度数，最后由三角形内角和为180°计算得∠ACB的度数．【详解】（1）如下图，第一步过B作m的平行线BS，以B为顶点作射线BX，使∠SBX=45°；第二步过A作m的平行线AN交BX于点D，以A为顶点作射线AY，使∠NAY=30°；则射线BX与射线AY的交点就是C地．（2）如上图，由C 地在B 地南偏东45°方向得∠SBX=45°∵SB ∥m ，AN ∥m∴SB ∥AN∴∠ADC=∠SBX=45°由C 地在A 地的北偏东30°方向得∠NAY=30°，∴∠ACB=180°-∠ADC-∠NAY=180°-45°-30°=105°．【点睛】此题考查方位角、平行线等知识，其中理解方位角正确画出图形是关键．22．如图，有三个论断：①12∠=∠；②B C ∠=∠；③A D ∠=∠，请你从中任选两个作为条件，另一个作为结论构成一个命题，并证明该命题的正确性．解析：答案见解析【分析】先从①②③中任选两个作为条件，另一个作为结论构成一个命题，然后根据平行线的判定和性质及对顶角相等进行证明即可．【详解】已知：12∠=∠，B C ∠=∠求证：A D ∠=∠证明：如图：13∠=∠ 又12∠=∠32∴∠=∠//EC BF ∴AEC B ∴∠=∠又B C ∠=∠AEC C ∴∠=∠//AB CD ∴A D ∴∠=∠．【点睛】本题主要考查了平行线的判定与性质以及命题与定理的证明问题，证明的一般步骤包括写出已知、求证、画出图形和证明．23．如图，DE 平分∠ADF ，DF ∥BC ，点E ，F 在线段AC 上，点A ，D ，B 在一直线上，连接BF ．（1）若∠ADF ＝70°，∠ABF ＝25°，求∠CBF 的度数；（2）若BF 平分∠ABC 时，求证：BF ∥DE ．解析：（1）∠CBF ＝45°；（2）见解析．【分析】（1）根据平行线的性质和已知条件即可求出∠CBF 的度数；（2）根据平行线的性质可得∠ABC ＝∠ADF ，再根据BF 平分∠ABC ，DE 平分∠ADF ，可得∠ADE ＝∠ABF ，再根据同位角相等，两直线平行即可证明BF ∥DE ．【详解】解：（1）∵DF ∥BC ，∴∠ABC ＝∠ADF ＝70°，∵∠ABF ＝25°，∴∠CBF ＝70°﹣25°＝45°；（2）证明：∵DF ∥BC ，∴∠ABC ＝∠ADF ，∵BF 平分∠ABC ，DE 平分∠ADF ，∴∠ADE 12=∠ADF ，∠ABF 12=∠ABC ， ∴∠ADE ＝∠ABF ，∴BF ∥DE ．【点睛】本题考查了平行线的判定与性质，解决本题的关键是掌握平行线的判定与性质．24．如图，//,//DE BC EF AB ，图中与∠BFE 互补的角有几个，请分别写出来．解析：∠EFC 、∠DEF 、∠ADE 、∠B ．【分析】根据平行的性质得EFC DEF ADE B ∠=∠=∠=∠，由180BFE EFC ∠+∠=︒，可知这些角与BFE ∠都互补．【详解】解：180BFE EFC ∠+∠=︒，∵//DE BC ，∴DEF EFC ∠=∠，∴180BFE DEF ∠+∠=︒，∵//EF AB ，∴DEF ADE ∠=∠，∴180BFE ADE ∠+∠=︒，∵//DE BC ，∴ADE B ∠=∠，∴180BFE B ∠+∠=︒，与∠BFE 互补的角有4个，分别为：∠EFC 、∠DEF 、∠ADE 、∠B ．【点睛】本题考查平行线的性质，解题的关键利用平行线的性质找相等的角．25．如图，在△ABC 中，CD ⊥AB ，垂足为D ，点E 在BC 上，EF ⊥AB ，垂足为F ．（1）CD 与EF 平行吗？为什么？（2）如果∠1=∠2，且∠3=115°，∠A=30°，求∠B 的度数．解析：（1）CD 与EF 平行．理由见解析；（2）∠B=35°【分析】（1）先根据垂直的定义得到∠CDB=∠EFB=90°，然后根据同位角相等，两直线平行可判断EF ∥CD ；（2）由EF ∥CD ，根据平行线的性质得∠2=∠BCD ，而∠1=∠2，所以∠1=∠BCD ，根据内错角相等，两直线平行得到DG ∥BC ，所以∠ACB=∠3=115°，根据三角形的内角和即可得到结论．【详解】（1）CD 与EF 平行．理由如下：∵CD ⊥AB ，EF ⊥AB ，∴∠CDB=∠EFB=90°，∴EF ∥CD ；（2）∵EF ∥CD ，∴∠2=∠BCD ，∵∠1=∠2，∴∠1=∠BCD ，∴DG ∥BC ，∴∠ACB=∠3=115°，∵∠A=30°，∴∠B=35°．【点评】本题考查了平行线的判定与性质，注意：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，同位角相等．26．把一块含60°角的直角三角尺()0090,60EFG EFG EGF ∠=∠=放在两条平行线,AB CD 之间．（1）如图1，若三角形的60°角的顶点G 放在CD 上，且221∠=∠，求1∠的度数；（2）如图2，若把三角尺的两个锐角的顶点,E G 分别放在AB 和CD 上，请你探索并说明AEF ∠与FGC ∠间的数量关系；（3）如图3，若把三角尺的直角顶点F 放在CD 上，30°角的顶点E 落在AB 上，请直接写出AEG ∠与CFG ∠的数量关系．解析：（1）40°；（2）∠AEF+∠FGC=90°；（3）AEG ∠+CFG ∠=300°【分析】（1）根据平行线的性质得：1=∠EGD ，结合∠2=2∠1和平角的定义，即可求解；（2）过点F 作FP ∥AB ，根据平行线的性质和直角的意义，即可求解；（3）根据平行线的性质得∠AEF+∠CFE=180°，结合条件，即可求解．【详解】(1)∵AB ∥CD ，∴∠1=∠EGD ，∵∠2+∠FGE+∠EGD=180°，∠2=2∠1，∴2∠1+60°+∠1=180°，解得∠1=40°；(2)如图,过点F 作FP ∥AB ，∵CD ∥AB ，∴FP ∥AB ∥CD ，∴∠AEF=∠EFP ，∠FGC=∠GFP .∴∠AEF+∠FGC=∠EFP+∠GFP=∠EFG ，∵∠EFG=90°，∴∠AEF+∠FGC=90°；(3) AEG ∠+CFG ∠=300°，理由如下：∵AB ∥CD ，∴∠AEF+∠CFE=180°，即AEG ∠−30°+CFG ∠−90°=180°，整理得：AEG ∠+CFG ∠=300°．【点睛】本题主要考查平行线的性质，添加辅助线，构造相等的角，是解题的关键27．如图所示，在平面直角坐标系中，已知A （0，1）、B （2，0）、C （4，3）．（1）在平面直角坐标系中画出△ABC ，作出△ABC 向下平移3格后的△A 1B 1C 1；（2）求△ABC 的面积；（3）已知点Q 为y 轴上一点，若△ACQ 的面积为8，求点Q 的坐标．解析：（1）见解析；（2）4；（3）（0，5）或（0，-3）．【分析】（1）先在平面直角坐标系中描点，再连接，然后分别作出平移后的对应点，再顺次连接即可得；（2）利用割补法求解可得；（3）根据三角形面积公式求出AQ 的长，即可确定点Q 的坐标．【详解】解：（1）如图所示，（2）△ABC 的面积=111342421234222⨯-⨯⨯-⨯⨯-⨯⨯= （3）∵Q 为y 轴上一点，△ACQ 的面积为8， ∴1||482AQ ⨯⨯=， ∴AQ=4 ∴点Q 的纵坐标为：4+1=5或1-4=-3，故Q 点坐标为：（0，5）或（0，-3）．【点睛】本题主要考查的是作图-平移变换、点的坐标与图形的性质，明确△ABC 的面积=四边形的面积-3个直角三角形的面积是解题的关键．28．如图，直线AB ，CD 相交于点O ，OE 平分∠BOC ，FO ⊥CD 于点O ，若∠BOD ∶∠EOB=2∶3，求∠AOF 的度数．解析：45︒．【分析】设2BOD x ∠=，从而可得3EOB x ∠=，先根据角平分线的定义3EOC EOB x ∠=∠=，再根据平角的定义可得求出x 的值，然后根据垂直的定义可得90DOF ∠=︒，最后根据平角的定义即可得．【详解】设2BOD x ∠=，则3EOB x ∠=，∵OE 平分BOC ∠，∴3EOC EOB x ∠=∠=，180BOD EOB EOC ∠+∠+∠=︒，233180x x x ∴++=︒，解得22.5x =︒，45BOD ∴∠=︒，FO CD ⊥，90DOF ∴∠=︒，又180BOD DOF AOF ∠+∠+∠=︒，4590180AOF ∴︒+︒+∠=︒，解得45AOF ∠=︒．【点睛】本题考查了角平分线的定义、平角的定义、垂直的定义等知识点，熟练掌握并理解各定义是解题关键．。

(完整版)七年级数学下册相交线与平行线测试题

七年级下册相交线与平行线测试题一、选择题1. 下列正确说法的个数是（）①同位角相等②对顶角相等③等角的补角相等④两直线平行，同旁内角相等A . 1， B。

2， C. 3， D。

42。

下列说法正确的是（）A.两点之间，直线最短;B。

过一点有一条直线平行于已知直线；C。

和已知直线垂直的直线有且只有一条；D.在平面内过一点有且只有一条直线垂直于已知直线。

3. 下列图中∠1和∠2是同位角的是（）A. ⑴、⑵、⑶， B。

⑵、⑶、⑷, C. ⑶、⑷、⑸， D。

⑴、⑵、⑸4. 如果一个角的补角是150°，那么这个角的余角的度数是 ( ）A。

30° B。

60° C.90° D.120°5。

下列语句中，是对顶角的语句为 ( )A.有公共顶点并且相等的两个角B。

两条直线相交，有公共顶点的两个角C。

顶点相对的两个角D.两条直线相交，有公共顶点没有公共边的两个角6。

下列命题正确的是 ( )A。

内错角相等B.相等的角是对顶角C。

三条直线相交 ,必产生同位角、内错角、同旁内角D。

同位角相等，两直线平行7。

两平行直线被第三条直线所截,同旁内角的平分线（） A.互相重合B。

互相平行 C.互相垂直 D。

无法确定8。

在平面内,将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转。

下列图案中，不能由一个图形通过旋转而构成的是（）A B C D9。

三条直线相交于一点，构成的对顶角共有（ )A、3对B、4对C、5对D、6对10. 如图,已知AB∥CD∥EF,BC∥AD，AC平分∠BAD，那么图中与∠AGE相等的角有 ( ）A。

5个B。

4个 C.3个D。

2个11。

如图6，BO平分∠ABC,CO平分∠ACB，且MN∥BC，设AB＝12，BC＝24,AC＝18，则△AMN的周长为（ )。

A、30B、36C、42D、1812。

如图,若AB∥CD，则∠A、∠E、∠D之间的关系是 ( )A。

北师大数学七年级下册第二章相交线与平行线拔高题(附答案详解)

北师大数学七年级下第二章拔高题一．选择题（共7小题）1．如图，AB∥CD，BF平分∠ABE，且BF∥DE，则∠ABE与∠D的关系是（）A．∠ABE＝3∠D B．∠ABE+∠D＝90°C．∠ABE+3∠D＝180°D．∠ABE＝2∠D2．如图，将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上，已知∠A＝30°，∠1＝40°，则∠2的度数为（）A．55°B．60°C．65°D．70°3．如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1＝2∠2，则∠AEF的度数为（）A．60°B．65°C．72°D．75°5．下列生活实例中，数学原理解释错误的一项是（）A．从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线B．两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短C．把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线D．从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短6．如图，已知AB∥DE，∠ABC＝80°，∠CDE＝150°，则∠BCD＝（）A．30°B．40°C．50°D．60°7．如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，则图2中∠AEF的度数为（）A．120°B．108°C．126°D．114°二．填空题（共8小题）8．将一块60°的直角三角板DEF放置在45°的直角三角板ABC上，移动三角板DEF使两条直角边DE、DF恰分别经过B、C两点，若EF∥BC，则∠ABD＝°．9．如图，将一张矩形纸片ABCD沿EF折叠后，点C落在AB边上的点G处，点D落在点H处．若∠1＝62°，则图中∠BEG的度数为．10．如图，已知DE∥BC，2∠D＝3∠DBC，∠1＝∠2．则∠DEB＝度．11．如图，已知AE∥BD，∠1＝130°，∠2＝28°，则∠C的度数为．12．如图，BE∥CF，则∠A+∠B+∠C+∠D＝度．第9题第10题第11题第12题13．如图，若OP∥QR∥ST，则∠1，∠2，∠3的数量关系是：．14．如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是．15．如图，∠AOB的一边OA为平面镜，∠AOB＝37°，在OB上有一点E，从E点射出一束光线经OA上一点D反射，此时∠ODE＝∠ADC，且反射光线DC恰好与OB平行，则∠DEB的度数是．第13题第14题第15题三．解答题（共11小题）16．如图，AB∥CD，直线EF与AB，CD交于点G，H，GM⊥GE，∠BGM＝20°，HN 平分∠CHE，求∠NHD的度数．17．如图，直线AB∥CD，并且被直线MN所截，MN分别交AB和CD于点E、F，点Q在PM 上，且∠AEP＝∠CFQ．求证：∠EPM＝∠FQM．18．如图，已知AB∥CD，∠A＝40°．点P是射线AB上一动点（与点A不重合），CE、CF 分别平分∠ACP和∠DCP交射线AB于点E、F．（1）求∠ECF的度数；（2）随着点P的运动，∠APC与∠AFC之间的数量关系是否改变？若不改变，请求出此数量关系；若改变，请说明理由；（3）当∠AEC＝∠ACF时，求∠APC的度数．19．【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．（1）若∠AFH＝60°，∠CHF＝50°，则∠EOF＝度，∠FOH＝度．（2）若∠AFH+∠CHF＝100°，求∠FOH的度数．【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF＝α，直接写出∠FOH的度数．（用含a的代数式表示）20．如图，AB∥CD，∠ABD和∠BDC的平分线交于点E，BE交CD于点F．（1）求证：∠1+∠2＝90°；（2）如果∠EDF＝36°，那么∠BFC等于多少度？21．如图，AB∥CD，点E在线段AB上，连接EC、ED、AD，且ED平分∠CEB，AD⊥EF，若∠ADC＝42°，∠A﹣∠B＝8°，求∠BDE的度数．22．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．23．已知AB∥CD，点E为平面内一点，BE⊥CE于E．（1）如图1，请直接写出∠ABE和∠DCE之间的数量关系；（2）如图2，过点E作EF⊥CD，垂足为F，求证：∠CEF＝∠ABE；（3）如图3，在（2）的条件下，作EG平分∠CEF，交DF于点G，作ED平分∠BEF，交CD 于D，连接BD，若∠DBE+∠ABD＝180°，且∠BDE＝3∠GEF，求∠BEG的度数．24．（1）如图①，若AB∥CD，求∠B+∠D+∠E1的度数？（2）如图②，若AB∥CD，求∠B+∠D+∠E1+∠E2的度数？（3）如图③，若AB∥CD，求∠B+∠D+∠E1+∠E2+∠E3的度数？（4）如图④，若AB∥CD，猜想∠B+∠D+∠E1+∠E2+…+∠E n的度数？25．如图，已知直线l1∥l2，点A、B分别在l1与l2上．直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．（1）如果P点在C、D之间运动时，问∠P AC，∠APB，∠PBD有怎样的数量关系？请说明理由．（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠P AC，∠APB，∠PBD之间的关系又是如何？26．如图，已知∠ABC＝∠ACB，BD平分∠ABC，CE平分∠ACB，F是BC延长线上一点，且∠DBC ＝∠F，求证：EC∥DF．一．选择题（共7小题）1．如图，AB∥CD，BF平分∠ABE，且BF∥DE，则∠ABE与∠D的关系是（）A．∠ABE＝3∠D B．∠ABE+∠D＝90°C．∠ABE+3∠D＝180°D．∠ABE＝2∠D【解答】证明：如图，延长DE交AB的延长线于G，∵AB∥CD，∴∠D＝∠G，∵BF∥DE，∴∠G＝∠ABF，∴∠D＝∠ABF，∵BF平分∠ABE，∴∠ABE＝2∠ABF＝2∠D，即∠ABE＝2∠D．故选：D．2．如图，将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上，已知∠A＝30°，∠1＝40°，则∠2的度数为（）A．55°B．60°C．65°D．70°【解答】解：∵EF∥MN，∠1＝40°，∴∠1＝∠3＝40°，∵∠A＝30°，∴∠2＝∠A+∠3＝70°，故选：D．3．如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1＝2∠2，则∠AEF的度数为（）A．60°B．65°C．72°D．75°【解答】解：由翻折的性质可知：∠AEF＝∠FEA′，∵AB∥CD，∴∠AEF＝∠1，∵∠1＝2∠2，设∠2＝x，则∠AEF＝∠1＝∠FEA′＝2x，∴5x＝180°，∴x＝36°，∴∠AEF＝2x＝72°，故选：C．4．在下列图形中，由∠1＝∠2一定能得到AB∥CD的是（）A．B．C．D．【解答】解：如下图，∵∠1＝∠2，∴AB∥CD，故选：A．5．下列生活实例中，数学原理解释错误的一项是（）A．从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线B．两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短C．把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线D．从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短【解答】解：A、从一条河向一个村庄引一条最短的水渠，其中数学原理是：垂线段最短，故原命题错误；B、两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短，正确；C、一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线，正确；D、从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短，正确．故选：A．6．如图，已知AB∥DE，∠ABC＝80°，∠CDE＝150°，则∠BCD＝（）A．30°B．40°C．50°D．60°【解答】解：反向延长DE交BC于M，∵AB∥DE，∴∠BMD＝∠ABC＝80°，∴∠CMD＝180°﹣∠BMD＝100°；又∵∠CDE＝∠CMD+∠BCD，∴∠BCD＝∠CDE﹣∠CMD＝150°﹣100°＝50°．故选：C．7．如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，则图2中∠AEF的度数为（）A．120°B．108°C．126°D．114°【解答】解：如图，设∠B′FE＝x，∵纸条沿EF折叠，∴∠BFE＝∠B′FE＝x，∠AEF＝∠A′EF，∴∠BFC＝∠BFE﹣∠CFE＝x﹣18°，∵纸条沿BF折叠，∴∠C′FB＝∠BFC＝x﹣18°，而∠B′FE+∠BFE+∠C′FE＝180°，∴x+x+x﹣18°＝180°，解得x＝66°，∵A′D′∥B′C′，∴∠A′EF＝180°﹣∠B′FE＝180°﹣66°＝114°，∴∠AEF＝114°．故选：D．二．填空题（共8小题）8．将一块60°的直角三角板DEF放置在45°的直角三角板ABC上，移动三角板DEF使两条直角边DE、DF恰分别经过B、C两点，若EF∥BC，则∠ABD＝15°．【解答】解：∵将一块60°的直角三角板DEF放置在45°的直角三角板ABC上，∴∠E＝30°，∠ABC＝45°，∵EF∥BC，∴∠DBC＝∠E＝30°，∴∠ABD＝45°﹣30°＝15°，故答案为：159．如图，将一张矩形纸片ABCD沿EF折叠后，点C落在AB边上的点G处，点D落在点H处．若∠1＝62°，则图中∠BEG的度数为56°．【解答】解：∵AD∥BC，∴∠1＝∠FEC＝62°，由翻折可得：∠FEG＝∠FEC＝62°，∴∠BEG＝180°﹣62°﹣62°＝56°，故答案为：56°10．如图，已知DE∥BC，2∠D＝3∠DBC，∠1＝∠2．则∠DEB＝36度．【解答】解：∵DE∥BC，∴∠E＝∠1，∵∠1＝∠2，∴∠1＝∠2＝∠B，设∠1＝∠2＝∠B＝x，∵2∠D＝3∠DBC，∴∠D＝3x，∴5x＝180°，∴x＝36°故答案为36．11．如图，已知AE∥BD，∠1＝130°，∠2＝28°，则∠C的度数为22°．【解答】解：∵AE∥BD，∠1＝130°，∠2＝28°，∴∠CBD＝∠1＝130°，∠CDB＝∠2＝28°，∴∠C＝180°﹣∠CBD﹣∠CDB＝180°﹣130°﹣28°＝22°．故答案为：22°12．如图，BE∥CF，则∠A+∠B+∠C+∠D＝180度．【解答】解：如图所示，由图知∠A+∠B＝∠BPD，∵BE∥CF，∴∠CQD＝∠BPD＝∠A+∠B，又∵∠CQD+∠C+∠D＝180°，∴∠A+∠B+∠C+∠D＝180°，故答案为：180．13．如图，若OP∥QR∥ST，则∠1，∠2，∠3的数量关系是：∠2+∠3﹣∠1＝180°．【解答】解：如图，延长TS，∵OP∥QR∥ST，∴∠2＝∠4，∵∠3与∠ESR互补，∴∠ESR＝180°﹣∠3，∵∠4是△FSR的外角，∴∠FSR+∠1＝∠4，即180°﹣∠3+∠1＝∠2，∴∠2+∠3﹣∠1＝180°．故答案为：∠2+∠3﹣∠1＝180°．14．如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是∠α﹣∠β＝90°．【解答】解：过C作CF∥AB，∵AB∥DE，∴AB∥DE∥CF，∴∠1＝∠β，∠α＝180°﹣∠2，∴∠α﹣∠β＝180°﹣∠2﹣∠1＝180°﹣∠BCD＝90°，故答案为∠α﹣∠β＝90°．15．如图，∠AOB的一边OA为平面镜，∠AOB＝37°，在OB上有一点E，从E点射出一束光线经OA上一点D反射，此时∠ODE＝∠ADC，且反射光线DC恰好与OB平行，则∠DEB的度数是74°．【解答】解：过点D作DF⊥AO交OB于点F．∵入射角等于反射角，∴∠1＝∠3，∵CD∥OB，∴∠1＝∠2（两直线平行，内错角相等）；∴∠2＝∠3（等量代换）；在Rt△DOF中，∠ODF＝90°，∠AOB＝37°，∴∠2＝90°﹣37°＝53°；∴在△DEF中，∠DEB＝180°﹣2∠2＝74°．故答案为：74°．三．解答题（共11小题）16．如图，AB∥CD，直线EF与AB，CD交于点G，H，GM⊥GE，∠BGM＝20°，HN平分∠CHE，求∠NHD的度数．【解答】解：∵GM⊥GE∴∠EGM＝90°∵∠BGM＝20°∴∠EGB＝∠EGM﹣∠BGM＝70°∴∠AGH＝∠EGB＝70°∵AB∥CD∴∠AGH+∠CHG＝180°∴∠CHG＝110°∵HN平分∠CHE∴∠NHC＝∠CHG＝×110°＝55°∴∠NHD＝180°﹣∠CHN＝180°﹣55°＝125°17．如图，直线AB∥CD，并且被直线MN所截，MN分别交AB和CD于点E、F，点Q在PM上，且∠AEP＝∠CFQ．求证：∠EPM＝∠FQM．【解答】解：∵AB∥CD∴∠AEM＝∠CFM，∵∠AEP＝∠CFQ，∴∠MEP＝∠MFQ，∴EP∥FQ，∴∠EPM＝∠FQM．18．如图，已知AB∥CD，∠A＝40°．点P是射线AB上一动点（与点A不重合），CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F．（1）求∠ECF的度数；（2）随着点P的运动，∠APC与∠AFC之间的数量关系是否改变？若不改变，请求出此数量关系；若改变，请说明理由；（3）当∠AEC＝∠ACF时，求∠APC的度数．【解答】解：（1）∵AB∥CD，∴∠A+∠ACD＝180°，∴∠ACD＝180°﹣40°＝140°，∵CE平分∠ACP，CF平分∠DCP，∴∠ACP＝2∠ECP，∠DCP＝2∠PCF，∴∠ECF＝∠ACD＝70°；（2）不变．数量关系为：∠APC＝2∠AFC．∵AB∥CD，∴∠AFC＝∠DCF，∠APC＝∠DCP，∵CF平分∠DCP，∴∠DCP＝2∠DCF，∴∠APC＝2∠AFC；（3）∵AB∥CD，∴∠AEC＝∠ECD，当∠AEC＝∠ACF时，则有∠ECD＝∠ACF，∴∠ACE＝∠DCF，∴∠PCD＝∠ACD＝70°，∴∠APC＝∠PCD＝70°．19．【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．（1）若∠AFH＝60°，∠CHF＝50°，则∠EOF＝30度，∠FOH＝125度．（2）若∠AFH+∠CHF＝100°，求∠FOH的度数．【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF＝α，直接写出∠FOH的度数．（用含a的代数式表示）【解答】解：【探究】（1）∵∠AFH＝60°，OF平分∠AFH，∴∠OFH＝30°，又∵EG∥FH，∴∠EOF＝∠OFH＝30°；∵∠CHF＝50°，OH平分∠CHF，∴∠FHO＝25°，∴△FOH中，∠FOH＝180°﹣∠OFH﹣∠OHF＝125°；故答案为：30，125；（2）∵FO平分∠AFH，HO平分∠CHF，∴∠OFH＝∠AFH，∠OHF＝∠CHF．∵∠AFH+∠CHF＝100°，∴∠OFH+∠OHF＝（∠AFH+∠CHF）＝×100°＝50°．∵EG∥FH，∴∠EOF＝∠OFH，∠GOH＝∠OHF．∴∠EOF+∠GOH＝∠OFH+∠OHF＝50°．∵∠EOF+∠GOH+∠FOH＝180°，∴∠FOH＝180°﹣（∠EOF+∠GOH）＝180°﹣50°＝130°．【拓展】∵∠AFH和∠CHI的平分线交于点O，∴∠OFH＝∠AFH，∠OHI＝∠CHI，∴∠FOH＝∠OHI﹣∠OFH＝（∠CHI﹣∠AFH）＝（180°﹣∠CHF﹣∠AFH）＝（180°﹣α）＝90°﹣α．20．如图，AB∥CD，∠ABD和∠BDC的平分线交于点E，BE交CD于点F．（1）求证：∠1+∠2＝90°；（2）如果∠EDF＝36°，那么∠BFC等于多少度？【解答】解：（1）∵AB∥CD，∴∠ABD+∠BDC＝180°，∵BE、DE平分∠ABD、∠BDC，∴∠1＝∠ABD，∠2＝∠BDC，∴∠1+∠2＝（∠ABD+∠BDC）＝90°，（2）∵DE平分∠BDC，∴∠2＝∠EDF＝36°，又∵∠1+∠2＝90°，∴∠1＝54°，又∵AB∥CD，∴∠BFC＝180°﹣∠1＝180°﹣54°＝126°．21．如图，AB∥CD，点E在线段AB上，连接EC、ED、AD，且ED平分∠CEB，AD⊥EF，若∠ADC＝42°，∠A﹣∠B＝8°，求∠BDE的度数．【解答】解：∵AB∥CD，∴∠ADC＝∠A＝42°，∵∠A﹣∠B＝8°，∴∠B＝34°，∵AD⊥EF，∴∠AFE＝90°，∴∠AEF＝48°，∴∠BEC＝132°，∵DE平分∠BEC，∴∠BED＝∠BEC＝66°，∴∠BDE＝180°﹣66°﹣34°＝80°．22．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．【解答】解：（1）证明：如图，过点E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠3＝∠1，∠4＝∠2，∴∠3+∠4＝∠1+∠2，即∠BED＝∠1+∠2；（2）∠1+∠EGH＝∠2+∠BEG，理由如下：如图，分别过点E、G作EF∥AB，GH∥AB，∵AB∥CD，∴AB∥EF∥GH∥CD，∴∠1＝∠3，∠4＝∠5，∠6＝∠2，∴∠1+∠5+∠6＝∠3+∠4+∠2，即∠1+∠EGH＝∠2+∠BEG；（3）由题可得，向左的角度数之和与向右的角度数之和相等，∴∠1、∠3、∠5与∠2、∠4、∠6之间的关系为：∠1+∠3+∠5＝∠2+∠4+∠6．23．已知AB∥CD，点E为平面内一点，BE⊥CE于E．（1）如图1，请直接写出∠ABE和∠DCE之间的数量关系；（2）如图2，过点E作EF⊥CD，垂足为F，求证：∠CEF＝∠ABE；（3）如图3，在（2）的条件下，作EG平分∠CEF，交DF于点G，作ED平分∠BEF，交CD 于D，连接BD，若∠DBE+∠ABD＝180°，且∠BDE＝3∠GEF，求∠BEG的度数．【解答】解：（1）结论：∠ECD＝90°+∠ABE．理由：如图1中，从BE交DC的延长线于H．∵AB∥CH，∴∠ABE＝∠H，∵BE⊥CE，∴∠CEH＝90°，∴∠ECD＝∠H+∠CEH＝90°+∠H，∴∠ECD＝90°+∠ABE．（2）如图2中，作EM∥CD，∵EM∥CD，CD∥AB，∴AB∥CD∥EM，∴∠BEM＝∠ABE，∠F+∠FEM＝180°，∵EF⊥CD，∴∠F＝90°，∴∠FEM＝90°，∴∠CEF与∠CEM互余，∵BE⊥CE，∴∠BEC＝90°，∴∠BEM与∠CEM互余，∴∠CEF＝∠BEM，∴∠CEF＝∠ABE．（3）如图3中，设∠GEF＝α，∠EDF＝β．∴∠BDE＝3∠GEF＝3α，∵EG平分∠CEF，∴∠CEF＝2∠FEG＝2α，∴∠ABE＝∠CEF＝2α，∵AB∥CD∥EM，∴∠MED＝∠EDF＝β，∠KBD＝∠BDF＝3α+β，∠ABD+∠BDF＝180°，∴∠BED＝∠BEM+∠MED＝2α+β，∵ED平分∠BEF，∴∠BED＝∠FED＝2α+β，∴∠DEC＝β，∵∠BEC＝90°，∴2α+2β＝90°，∵∠DBE+∠ABD＝180°，∠ABD+∠BDF＝180°，∴∠DBE＝∠BDF＝∠BDE+∠EDF＝3α+β，∵∠ABK＝180°，∴∠ABE+∠B＝DBE+∠KBD＝180°，即2α+（3α+β）+（3α+β）＝180°，∴6α+（2α+2β）＝180°，∴α＝15°，∴∠BEG＝∠BEC+∠CEG＝90°+15°＝105°．24．（1）如图①，若AB∥CD，求∠B+∠D+∠E1的度数？（2）如图②，若AB∥CD，求∠B+∠D+∠E1+∠E2的度数？（3）如图③，若AB∥CD，求∠B+∠D+∠E1+∠E2+∠E3的度数？（4）如图④，若AB∥CD，猜想∠B+∠D+∠E1+∠E2+…+∠E n的度数？【解答】解：（1）如图①，过E1作E1F∥AB，则E1F∥CD，∴∠B+∠1＝180°①，∠D+∠1＝180°②，①+②得∠B+∠1+∠D+∠2＝360°，即∠B+∠D+∠E1＝360°；（2）如图②，分别过E1，E2作E1F∥AB，E2G∥AB，则E1F∥E2G∥CD，∴∠1+∠B＝∠2+∠3＝∠4+∠D＝180°，∴∠B+∠D+∠E1+∠E2＝∠1+∠B+∠2+∠3+∠4+∠D＝540°＝3×180°；（3）如图③，分别过E1，E2，E3作E1F1∥E2F2∥E3F3∥AB，则E1F1∥E2F2∥E3F3∥CD，∴∠B+∠BE1E2＝180°，∠E2E1F1+∠E1E2F2＝180°，∠E3E2F2+∠E2E3F3＝180°，∠DE3F3+∠D＝180°，∴∠B+∠D+∠E1+∠E2+∠E3＝720°；（4）由（1）（2）（3）知，拐点的个数n与角的和之间的关系是（n+1）•180°，∴∠B+∠D+∠E1+∠E2+…+∠E n＝（n+1）•180°．25．如图，已知直线l1∥l2，点A、B分别在l1与l2上．直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．（1）如果P点在C、D之间运动时，问∠P AC，∠APB，∠PBD有怎样的数量关系？请说明理由．（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠P AC，∠APB，∠PBD之间的关系又是如何？【解答】解：（1）如图，当P点在C、D之间运动时，则有∠APB＝∠P AC+∠PBD．理由如下：过点P作PE∥l1，∵l1∥l2，∴PE∥l2∥l1，∴∠P AC＝∠1，∠PBD＝∠2，∴∠APB＝∠1+∠2＝∠P AC+∠PBD；（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），则有两种情形：①如图，当点P在在l2下方时，有结论：∠APB＝∠P AC﹣∠PBD．理由是：过点P作PE∥l1，则∠APE＝∠P AC，又∵l1∥l2，∴PE∥l2，∴∠BPE＝∠PBD，∵∠APE＝∠APB+∠BPE，∴∠P AC＝∠APB+∠PBD，∴∠APB＝∠P AC﹣∠PBD；②如图，当点P在l1上方时，有结论：∠APB＝∠PBD﹣∠P AC．理由是：过点P作PE∥l2，则∠BPE＝∠PBD，又∵l1∥l2，∴PE∥l1，∴∠APE＝∠P AC，∵∠BPE＝∠APE+∠APB，∴∠PBD＝∠P AC+∠APB，∴∠APB＝∠PBD﹣∠P AC．26．如图，已知∠ABC＝∠ACB，BD平分∠ABC，CE平分∠ACB，F是BC延长线上一点，且∠DBC ＝∠F，求证：EC∥DF．【解答】证明：∵∠ABC＝∠ACB，BD平分∠ABC，CE平分∠ACB，∴∠DBC＝∠ABC，∠ECB＝∠ACB，∴∠DBC＝∠ECB．∵∠DBC＝∠F，∴∠ECB＝∠F，∴EC∥DF．。

2022年人教版七年级数学下册第五章相交线与平行线章节训练试卷(含答案详解)

七年级数学下册第五章相交线与平行线章节训练（2021-2022学年考试时间：90分钟，总分100分）班级：__________ 姓名：__________ 总分：__________一、单选题（10小题，每小题3分，共计30分）1、下列说法中，真命题的个数为（）①两条平行线被第三条直线所截，同位角相等；②在同一平面内，如果两条直线都与第三条直线垂直，那么这两条直线互相平行；③过一点有且只有一条直线与这条直线平行；④点到直线的距离是这一点到直线的垂线段；A．1个B．2个C．3个D．4个2、如图，△ABC沿直线BC向右平移得到△DEF，己知EC=2，BF=8，则CF的长为（）A．3 B．4 C．5 D．63、如图，∠1＝35°，∠AOC＝90°，点B，O，D在同一条直线上，则∠2的度数为（）A．125°B．115°C．105°D．95°4、如图，直线AB ，CD 相交于点O ，90AOE ∠=︒，90DOF ∠=︒，OB 平分DOG ∠，给出下列结论：①当50AOF ∠=︒时，50DOE ∠=︒；②OD 为EOG ∠的平分线；③若150AOD ∠=︒时，30EOF ∠=︒；④BOG EOF ∠=∠．其中正确的结论有（）A ．4个B ．3个C ．2个D ．1个5、下列语句中，正确的有（）①一条直线的垂线只有一条；②在同一平面内，过直线上一点有且仅有一条直线与已知直线垂直；③两直线相交，则交点叫垂足；④互相垂直的两条直线形成的四个角一定都是直角．A ．0个B ．1个C ．2个D ．3个6、如图，直线b 、c 被直线a 所截，则1∠与2∠是（）A ．对顶角B ．同位角C ．内错角D ．同旁内角7、 “小小竹排江中游，巍巍青山两岸走”，所描绘的图形变换主要是（）A ．平移变换B ．翻折变换C ．旋转变换D ．以上都不对8、直线AB 、BC 、CD 、EG 如图所示．若∠1=∠2，则下列结论错误的是（）A．AB∥CD B．∠EFB=∠3C．∠4=∠5D．∠3=∠5 9、以下命题是假命题的是（）A 2B．有两边相等的三角形是等腰三角形C．三角形三个内角的和等于180°D．过直线外一点有且只有一条直线与已知直线平行10、下列命题中是假命题的是（）A．实数与数轴上的点一一对应B．内错角相等，两直线平行C．平行于同一条直线的两条直线互相平行D．如果一个角的两边分别平行于另一个角的两边，那么这两个角相等二、填空题（5小题，每小题4分，共计20分）1、如图，AB∥CD，∠EGB＝50°，则∠CHG的大小为 _____．2、如图，AC平分∠DAB，∠1＝∠2，试说明AB CD∥．证明：∵AC平分∠DAB___( )___，∴∠1＝∠__________( )____，又∵∠1＝∠2____( )____，∴∠2＝∠__________( )____，∴AB∥__________( )____．3、如图，在直线AB上有一点O，OC⊥OD，OE是∠DOB的角平分线，当∠DOE＝20°时，∠AOC＝___°．4、将命题“直角三角形斜边上的中线等于斜边的一半”改写成“如果…那么…”的形式_________．5、如图，直线AB、CD相交于点O，∠AOD＋∠BOC＝240°，则∠BOC的度数为__________°．三、解答题（5小题，每小题10分，共计50分）1、如图，将长为5cm，宽为3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A B C D，则阴影部分的面积为多少2''''cm．2、在如图所示55⨯的网格中，每个正方形的边长都是1，横纵线段的交点叫做格点，线段AB的两个端点都在格点上，点P也在格点上；（1）在图①中过点P作AB的平行线；（2）在图②中过点P作PQ⊥AB，垂足为Q；连接AP和BP，则三角形ABP的面积是．3、已知点O为直线AB上一点，将直角三角板MON按如图所示放置，且直角顶点在O处，在MON∠内部作射线OC，且OC恰好平分BOM∠．（1）若24∠=︒，求AOM∠的度数；CON（2）若2∠的度数．∠=∠，求AOMBON CON4、如图，①过点Q作QD⊥AB，垂足为点D；②过点P作PE⊥AB，垂足为点E；③过点Q作QF⊥AC，垂足为点F；④连P，Q两点；⑤P，Q两点间的距离是线段______的长度；⑥点Q到直线AB的距离是线段______的长度；⑦点Q到直线AC的距离是线段______的长度；⑧点P到直线AB的距离是线段______的长度．5、读下列语句，用直尺和三角尺画出图形．（1）点P是直线AB外的一点，直线CD经过点P，且CD与AB平行；（2）直线AB与CD相交于点O，点P是AB、CD外的一点，直线EF经过点P，且EF∥AB，与直线CD相交于点E．---------参考答案-----------一、单选题1、B【分析】根据平行线的性质与判定，点到直线的距离的定义逐项分析判断即可【详解】①两条平行线被第三条直线所截，同位角相等，故①是真命题；②在同一平面内，如果两条直线都与第三条直线垂直，那么这两条直线互相平行，故②是真命题；③在同一平面内，过直线外一点有且只有一条直线与这条直线平行，故③不是真命题，④点到直线的距离是这一点到直线的垂线段的长度，故④不是真命题，故真命题是①②，故选B【点睛】本题考查了判断真假命题，平行线的性质与判定，点到直线的距离的定义，掌握相关性质定理是解题的关键．2、A【分析】证明BE=CF即可解决问题．【详解】解：由平移的性质可知，BC=EF，∴BE=CF，∵BF=8，EC=2，∴BE+CF=8-2=6，∴CF=BE=3，故选：A．【点睛】本题考查平移变换，解题的关键是熟练掌握平移的性质．平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．3、A【分析】利用互余角的概念与邻补角的概念解答即可．【详解】解：∵∠1＝35°，∠AOC＝90°，∴∠BOC＝∠AOC−∠1＝55°．∵点B，O，D在同一条直线上，∴∠2＝180°−∠BOC＝125°．故选：A．【点睛】本题主要考查了角的和差运算，互余角的关系以及邻补角的关系．准确使用邻补角的关系是解题的关键．4、B【分析】由邻补角，角平分线的定义，余角的性质进行依次判断即可．【详解】解：∵∠AOE=90°，∠DOF=90°，∴∠BOE=90°=∠AOE=∠DOF，∴∠AOF+∠EOF=90°，∠EOF+∠EOD=90°，∠EOD+∠BOD=90°，∴∠EOF=∠BOD，∠AOF=∠DOE，∴当∠AOF=50°时，∠DOE=50°；故①正确；∵OB平分∠DOG，∴∠BOD=∠BOG，∴∠BOD=∠BOG=∠EOF=∠AOC，故④正确；∵150∠=︒，AOD∴∠BOD=180°-150°=30°，∴30∠=︒EOF故③正确；若OD为EOG∠的平分线，则∠DOE=∠DOG，∴∠BOG+∠BOD=90°-∠EOE，∴∠EOF=30°，而无法确定30∠=︒，EOF∴无法说明②的正确性；故选：B．【点睛】本题考查了邻补角，角平分线的定义，余角的性质，数形结合是解决本题的关键．5、C【分析】根据垂线的性质和定义进行分析即可．【详解】解：①一条直线的垂线只有一条，说法错误；②在同一平面内，过直线上一点有且仅有一条直线与已知直线垂直，说法正确；③两条直线相交，则交点叫垂足，说法错误；④互相垂直的两条直线形成的四个角一定是直角，说法正确．正确的共有2个；故选：C．【点睛】此题主要考查垂线的性质和定义以及真假命题的判断．6、B【分析】根据对顶角、同位角、内错角、同旁内角的特征去判断即可．【详解】∠1与∠2是同位角故选：B【点睛】本题考查了同位角的含义，理解同位角的含义并正确判断同位角是关键．7、A【分析】根据平移是图形沿某一直线方向移动一定的距离，可得答案．【详解】解：“小小竹排水中游，巍巍青山两岸走”所描绘的图形变换主要是平移变换，故选：A．【点睛】本题考查了平移变换，利用了平移的定义．8、D【分析】根据平行线的判定与性质、对顶角相等逐项判断即可．【详解】解：∵∠1=∠2，∴AB∥CD，故A正确，不符合题意；∴∠4=∠5，故C正确，不符合题意；∵∠EFB与∠3是对顶角，∴∠EFB=∠3，故B正确，无法判断∠3=∠5，故D错误，符合题意，故选：D．【点睛】本题考查平行线的判定与性质、对顶角相等，熟练掌握平行线的判定与性质是解答的关键．9、A【分析】分别利用算术平方根、等腰三角形的判定、三角形内角和公式、平行的相关内容，进行分析判断即可．【详解】解：A A是假命题，B、有两边相等的三角形是等腰三角形，B是真命题，C、三角形三个内角的和等于180°，C是真命题，D、过直线外一点有且只有一条直线与已知直线平行，D是真命题，故选：A．【点睛】本题主要是考查了真假命题，正确的命题为真命题，错误的命题为假命题，根据所学知识，对各个命题的正确与否进行分析，这是解决该题的关键．10、D【分析】根据题意利用实数的性质、平行线的判定等知识分别判断后即可得出正确选项．【详解】解：A、实数与数轴上的点一一对应，正确，是真命题，不符合题意；B、内错角相等，两直线平行，正确，是真命题，不符合题意；C、平行于同一直线的两条直线平行，正确，是真命题，不符合题意；D、如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补，故原命题错误，是假命题，符合题意．故选：D．【点睛】本题考查命题与定理的知识，解题的关键是了解实数的性质、平行线的判定等知识．二、填空题1、130°【解析】【分析】根据平行线的性质可得∠EHD＝∠EGB＝50°，再利用邻补角的性质可求解．【详解】解：∵AB∥CD，∠EGB＝50°，∴∠EHD＝∠EGB＝50°，∴∠CHG＝180°﹣∠EHD＝130°．故答案为：130°．【点睛】本题主要考查平行线的性质，邻补角，属于基础题．2、已知 3 角平分线的定义已知 3 等量代换CD内错角相等，两直线平行【解析】【分析】根据平行线证明对书写过程的要求和格式填写即可.【详解】证明：∵AC平分∠DAB(已知)，∴∠1＝∠ 3 (角平分线的定义)，又∵∠1＝∠2(已知)，∴∠2＝∠ 3 (等量代换)，∴AB∥CD (内错角相等，两直线平行)．故答案为：已知；3；角平分线的定义；已知；3；等量代换；CD；内错角相等，两直线平行【点睛】本题主要考查平行线证明的书写，正确的逻辑推理和书写格式是解题的关键.3、50【解析】【分析】先求出∠BOD，根据平角的性质即可求出∠AOC．【详解】∵OE是∠DOB的角平分线，当∠DOE＝20°∴∠BOD=2∠DOE＝40°∵OC⊥OD，∴∠AOC=180°-90°-∠BOD=50°故答案为：50．【点睛】此题主要考查角度求解，解题的关键是熟知角平分线的性质、直角的性质．4、如果一个三角形是直角三角形，那么它斜边上的中线等于斜边的一半【解析】【分析】由题意将命题的条件改成如果的内容，将命题的结论改为那么的内容进行分析即可．【详解】解：将命题“直角三角形斜边上的中线等于斜边的一半”改写成“如果…那么…”的形式为：如果一个三角形是直角三角形，那么它斜边上的中线等于斜边的一半．故答案为：如果一个三角形是直角三角形，那么它斜边上的中线等于斜边的一半．【点睛】本题主要考查命题与定理，理解“如果…那么…”的意义并找到命题的条件和结论是解题的关键．5、120【解析】【分析】由题意根据对顶角相等得出∠BOC=∠AOD进而结合∠AOD＋∠BOC＝240°即可求出∠BOC的度数．【详解】解：∵∠AOD＋∠BOC＝240°，∠BOC=∠AOD，∴∠BOC =120°．故答案为：120．【点睛】本题考查的是对顶角的性质，熟练掌握对顶角相等是解题的关键．三、解答题1、18【分析】利用平移的性质求出空白部分矩形的长，宽即可解决；【详解】由题意可得，空白部分是矩形，长为()523cm cm -=，宽为()312cm cm -=，∴阴影部分的面积253223218cm =⨯⨯-⨯⨯=；【点睛】本题主要考查了矩形的性质，平移的性质，准确计算是解题的关键．2、（1）见解析；（2）见解析，5．【分析】（1）根据平行线的画法即可得；（2）根据垂线的画法即可得，再利用1个长方形的面积减去3个直角三角形的面积即可得．【详解】解：（1）如图①，PC 即为所求．（2）如图②，PQ即为所求．三角形ABP的面积为111 343131425 222⨯-⨯⨯-⨯⨯-⨯⨯=，故答案为：5．【点睛】本题考查了平行线和垂线的画法等知识点，熟练掌握平行线和垂线的画法是解题关键．3、（1）48°；（2）45°．【分析】（1）先根据余角的定义求出∠MOC，再根据角平分线的定义求出∠BOM，然后根据∠AOM=180°-∠BOM 计算即可；（2）根据角的倍分关系以及角平分线的定义即可求解；【详解】解：（1）∵∠MON=90°，∠CON=24°，∴∠MOC=90°-∠CON=66°，∵OC平分∠MOB，∴∠BOM=2∠MOC=132°，∴∠AOM=180°-∠BOM=48°；（2）∵∠BON=2∠NOC，OC平分∠MOB，∴∠MOC=∠BOC=3∠NOC，∵∠MOC+∠NOC=∠MON=90°，∴3∠NOC+∠NOC=90°，∴4∠NOC=90°，∴∠BON=2∠NOC=45°，∴∠AOM=180°-∠MON-∠BON=180°-90°-45°=45°；【点睛】本题考查了角平分线的意义、互补、互余的意义，正确表示各个角，理清各个角之间的关系是得出正确结论的关键．4、①②③④作图见解析；⑤PQ；⑥QD；⑦QF；⑧PE【分析】由题意①②③④根据题目要求即可作出图示，⑤⑥⑦⑧根据两点之间距离及点到直线的距离的定义即可得出答案．【详解】①②③④作图如图所示；⑤根据两点之间距离即可得出P，Q两点间的距离是线段PQ的长度；⑥根据点到直线的距离可得出点Q到直线AB的距离是线段QD的长度；⑦根据点到直线的距离可得出点Q到直线AC的距离是线段QF的长度；⑧根据点到直线的距离可得出点P到直线AB的距离是线段PE的长度.【点睛】本题主要考查基本作图和两点之间距离及点到直线的距离，熟练掌握相关概念与作图方法是解题的关键．5、（1）见解析；（2）见解析【分析】（1）过直线AB外的点P作CD//AB即可；（2）先画两条相交直线AB与CD交于点O，再过直线AB、CD外的一点P作AB的平行线EF且交直线CD于点E．【详解】解： (1)如图所示：(1)如图所示：【点睛】本题主要考查了相交线与平行线的作图，培养学生的理解能力和动手操作能力以及数形结合思想成为解答本题的关键．。

七年级数学下册相交线和平行线拔高训练

4.2 相交线和平行线典型例题及强化训练课标要求①了解对顶角，知道对项角相等。

②了解垂线、垂线段等概念，了解垂线段最短的性质，体会点到直线距离的意义。

③知道过一点有且仅有一条直线垂直干已知直线，会用三角尺或量角器过一点画一条直线的垂线。

④知道两直线平行同位角相等，进一步探索平行线的性质⑤知道过直线外一点有且仅有一条直线平行于已知直线，会用角尺和直尺过已知直线外一点画这条直线的平行线。

⑥体会两条平行线之间距离的意义，会度量两条平行线之间的距离。

典型例题1.判定与性质例1 判断题：1)不相交的两条直线叫做平行线。

( )2)过一点有且只有一条直线与已知直线平行。

( )3)两直线平行，同旁内角相等。

( )4)两条直线被第三条直线所截，同位角相等。

( )答案：(1)错，应为“在同一平面内，不相交的两条直线叫做平行线”。

(2)错，应为“过直线外一点，有且只有一条直线与已知直线平行”。

(3)错，应为“两直线平行，同旁内角互补”。

(4)错，应为“两条平行线被第三条直线所截，同位角相等”。

例2 已知：如图，AB∥CD，求证：∠B+∠D=∠BED。

分析：可以考虑把∠BED变成两个角的和。

如图5，过E点引一条直线EF∥AB，则有∠B=∠1，再设法证明∠D=∠2，需证EF∥CD，这可通过已知AB∥CD和EF∥AB得到。

证明：过点E作EF∥AB，则∠B=∠1（两直线平行，内错角相等）。

∵AB∥CD（已知），又∵EF∥AB（已作），∴EF∥CD（平行于同一直线的两条直线互相平行）。

∴∠D=∠2（两直线平行，内错角相等）。

又∵∠BED=∠1+∠2，∴∠BED=∠B+∠D（等量代换）。

变式1已知：如图6，AB∥CD，求证：∠BED=360°-（∠B+∠D）。

分析：此题与例1的区别在于E点的位置及结论。

我们通常所说的∠BED都是指小于平角的角，如果把∠BED看成是大于平角的角，可以认为此题的结论与例1的结论是一致的。

因此，我们模仿例1作辅助线，不难解决此题。

人教版七年级数学下册《平行线》拔高练习

《平行线》拔高练习一、选择题（本大题共5小题，共25.0分）1．（5分）下列说法：①用两根钉子固定一根木条，体现数学事实是两点之间线段最短；②射线AB与射线BA表示同一条射线；③若AB＝BC，则B为线段AC的中点；④不相交的两条直线叫做平行线；⑤过一点有且只有一条直线与已知直线垂直，其中正确的有（）A．0个B．1个C．2个D．3个2．（5分）给出下列判断：①两条不相交的直线叫做平行线；②不相等的两个角一定不是对顶角；③若两个角的一边在同一直线上，另一对边互相平行，则这两个角相等；④如果两个角是邻补角，那么这两个角的平分线组成的图形是直角，其中正确的有（）A．1个B．2个C．3个D．4个3．（5分）下列说法中，正确的是（）A．两条不相交的直线叫做平行线B．一条直线的平行线有且只有一条C．在同一平面内，若直线a∥b，a∥c，则b∥cD．若两条线段不相交，则它们互相平行4．（5分）下列说法正确的有（）①两点之间的所有连线中，线段最短；②相等的角叫对顶角；③过一点有且只有一条直线与已知直线平行；④过一点有且只有一条直线与已知直线垂直；⑤两点之间的距离是两点间的线段；⑥在同一平面内的两直线位置关系只有两种：平行或相交．A．1个B．2个C．3个D．4个5．（5分）下列说法正确的是（）A．不相交的两条线段是平行线B．不相交的两条直线是平行线C．不相交的两条射线是平行线D．在同一平面内，不相交的两条直线是平行线二、填空题（本大题共5小题，共25.0分）6．（5分）下列说法中：①棱柱的上、下底面的形状相同；②若AB＝BC，则点B为线段AC的中点；③相等的两个角一定是对顶角；④在同一平面内，不相交的两条直线叫做平行线；⑤直线外一点与直线上各点连接的所有线段中，垂线段最短．正确的有．（只填序号）7．（5分）在同一平面内有三条直线，如果使其中有且只有两条直线平行，那么这三条直线有且只有个交点．8．（5分）在同一平面内，两条直线的位置关系只有两种，．9．（5分）下列说法：①两条不相交的直线叫平行线；②两条不相交的线段，在同一平面内必平行；③经过直线外一点有且只有一条直线与这条直线平行；④若直线a∥b，a∥c，那么b∥c，其中错误的是（只填序号）10．（5分）若直线a∥b，a∥c，则直线b与c的位置关系是．三、解答题（本大题共5小题，共50.0分）11．（10分）（1）画线段AC＝30mm（点A在左侧）；（2）以C为顶点，CA为一边，画∠ACM＝90°；（3）以A为顶点，AC为一边，在∠ACM的同侧画∠CAN＝60°，AN与CM相交于点B；量得AB＝mm；（4）画出AB中点D，连接DC，此时量得DC＝mm；请你猜想AB与DC的数量关系是：AB＝DC（5）作点D到直线BC的距离DE，且量得DE＝mm，请你猜想DE与AC的数量关系是：DE＝AC，位置关系是．12．（10分）画图题：（1）在如图所示的方格纸中，经过线段AB外一点C，不用量角器与三角尺，仅用直尺，画线段AB的垂线EF和平行线GH．（2）判断EF、GH的位置关系是．（3）连接AC和BC，则三角形ABC的面积是．13．（10分）利用直尺画图（1）利用图1中的网格，过P点画直线AB的平行线和垂线．（2）把图（2）网格中的三条线段通过平移使三条线段AB、CD、EF首尾顺次相接组成一个三角形．（3）在图（3）的网格中画一个三角形：满足①是直角三角形；②任意两个顶点都不在同一条网格线上；③三角形的顶点都在格点上（即在网格线的交点上）．14．（10分）把图中的互相平行的线写出来，互相垂直的线写出来：15．（10分）如图，AB∥CD，E为AC的中点，（1）请过E作线段EF，且使EF∥AB，EF与BD相交于F；（2）请回答：EF与CD平行吗？为什么？《平行线》拔高练习参考答案与试题解析一、选择题（本大题共5小题，共25.0分）1．（5分）下列说法：①用两根钉子固定一根木条，体现数学事实是两点之间线段最短；②射线AB与射线BA表示同一条射线；③若AB＝BC，则B为线段AC的中点；④不相交的两条直线叫做平行线；⑤过一点有且只有一条直线与已知直线垂直，其中正确的有（）A．0个B．1个C．2个D．3个【分析】根据平行线、相交线等相关知识解答．【解答】解：①用两根钉子固定一根木条，体现数学事实是两点确定一条直线，此结论错误；②射线AB与射线BA的起点不同、方向不同，不是同一射线，此结论错误；③若AB＝BC，则B不一定是线段AC的中点，此结论错误；④同一平面内不相交的两条直线叫做平行线，此结论错误；⑤同一平面内，过一点有且只有一条直线与已知直线垂直，此结论错误；故选：A．【点评】本题主要考查了射线，垂线与平行线，解题的关键是熟记平行线与射线的定义及垂线的性质．2．（5分）给出下列判断：①两条不相交的直线叫做平行线；②不相等的两个角一定不是对顶角；③若两个角的一边在同一直线上，另一对边互相平行，则这两个角相等；④如果两个角是邻补角，那么这两个角的平分线组成的图形是直角，其中正确的有（）A．1个B．2个C．3个D．4个【分析】根据平行线的定义、对顶角相等、邻补角的定义和角平分线的定义逐个判断即可．【解答】解：在同一平面内，两条不相交的直线叫做平行线，故①错误；不相等的两个角一定不是对顶角，故②正确；若两个角的一边在同一直线上，另一对边互相平行，则这两个角相等或互补，故③错误；∵∠AOC和∠BOC是邻补角，∴∠AOC+∠BOC＝180°，∵OD平分∠AOC，OE平分∠BOC，∴∠DOC＝∠AOC，∠EOC＝BOC，∴∠DOE＝∠DOC+∠EOC＝×180°＝90°，即∠DOE是直角，故④正确；即正确的个数是2个，故选：B．【点评】本题考查了平行线的定义、对顶角相等、邻补角的定义和角平分线的定义等知识点，能熟记知识点的内容是解此题的关键．3．（5分）下列说法中，正确的是（）A．两条不相交的直线叫做平行线B．一条直线的平行线有且只有一条C．在同一平面内，若直线a∥b，a∥c，则b∥cD．若两条线段不相交，则它们互相平行【分析】根据平行线的定义、性质、判定方法判断，排除错误答案．【解答】解：A、平行线的定义：在同一平面内，两条不相交的直线叫做平行线．故错误；B、过直线外一点，有且只有一条直线与已知直线平行．故错误；C、在同一平面内，平行于同一直线的两条直线平行．故正确；D、根据平行线的定义知是错误的．故选：C．【点评】本题考查平行线的定义、性质及平行公理，熟练掌握公理和概念是解决本题的关键．4．（5分）下列说法正确的有（）①两点之间的所有连线中，线段最短；②相等的角叫对顶角；③过一点有且只有一条直线与已知直线平行；④过一点有且只有一条直线与已知直线垂直；⑤两点之间的距离是两点间的线段；⑥在同一平面内的两直线位置关系只有两种：平行或相交．A．1个B．2个C．3个D．4个【分析】①根据两点之间线段最短判断．②对顶角：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角．③根据平行公理进行判断．④根据垂线的性质进行判断．⑤距离是指的长度．⑥根据在同一平面内，两条不重合的直线的位置关系．【解答】解：①两点之间的所有连线中，线段最短，故①正确．②相等的角不一定是对顶角，故②错误．③经过直线外一点有且只有一条直线与已知直线平行，故③错误．④平面内过一点有且只有一条直线与已知直线垂直，故④错误．⑤两点之间的距离是两点间的线段的长度，故⑤错误．⑥在同一平面内，两直线的位置关系只有两种：相交和平行，故⑥正确．综上所述，正确的结论有2个．故选：B．【点评】本题主要考查对平行线的定义，两点间的距离，相交线等知识点的理解和掌握，能熟练地运用性质进行说理是解此题的关键．5．（5分）下列说法正确的是（）A．不相交的两条线段是平行线B．不相交的两条直线是平行线C．不相交的两条射线是平行线D．在同一平面内，不相交的两条直线是平行线【分析】根据平行线的定义，即可解答．【解答】解：根据平行线的定义：在同一平面内，不相交的两条直线是平行线．A，B，C错误；D正确；故选：D．【点评】本题考查了平行线的定义，解决本题的关键是熟记平行线的定义．二、填空题（本大题共5小题，共25.0分）6．（5分）下列说法中：①棱柱的上、下底面的形状相同；②若AB＝BC，则点B为线段AC的中点；③相等的两个角一定是对顶角；④在同一平面内，不相交的两条直线叫做平行线；⑤直线外一点与直线上各点连接的所有线段中，垂线段最短．正确的有①④⑤．（只填序号）【分析】分别根据棱柱的特征以及对顶角和垂线段的性质得出答案即可．【解答】解：①棱柱的上、下底面的形状相同，正确；②若AB＝BC，则点B为线段AC的中点，A，B，C不一定在一条直线上，故错误；③相等的两个角一定是对顶角，角的顶点不一定在一个位置，故此选项错误；④在同一平面内，不相交的两条直线叫做平行线，正确；⑤直线外一点与直线上各点连接的所有线段中，垂线段最短，正确．故答案为：①④⑤．【点评】此题主要考查了命题与定理等知识，熟练掌握相关定理是解题关键．7．（5分）在同一平面内有三条直线，如果使其中有且只有两条直线平行，那么这三条直线有且只有2个交点．【分析】根据同一平面内直线的位置关系得到第三条直线与另两平行直线相交，再根据直线平行和直线相交的定义即可得到交点的个数．【解答】解：∵在同一平面内有三条直线，如果其中有两条且只有两条相互平行，∴第三条直线与另两平行直线相交，∴它们共有2个交点．故答案为2．【点评】本题考查了直线平行的定义：没有公共点的两条直线是平行直线．也考查了同一平面内两直线的位置关系有：平行，相交．8．（5分）在同一平面内，两条直线的位置关系只有两种相交，平行．【分析】在同一平面内，两条直线的位置关系只有两种：平行或相交．【解答】解：在同一平面内，两条直线的位置关系只有两种：相交，平行．故答案为：平行，相交【点评】本题考查了在同一平面内两条直线的位置关系．9．（5分）下列说法：①两条不相交的直线叫平行线；②两条不相交的线段，在同一平面内必平行；③经过直线外一点有且只有一条直线与这条直线平行；④若直线a∥b，a∥c，那么b∥c，其中错误的是①②（只填序号）【分析】根据平行线的定义，平行公理即其推论进行判定即可．【解答】解：①在同一平面内，两条不相交的直线叫平行线；故错误；②两条不相交的线段，在同一平面内不一定平行；故错误；③经过直线外一点有且只有一条直线与这条直线平行；故正确；④若直线a∥b，a∥c，那么b∥c，故正确；其中错误的是①②，故答案为：①②．【点评】本题考查了平行线的定义，平行公理即其推论，熟练掌握公理和概念是解决本题的关键．10．（5分）若直线a∥b，a∥c，则直线b与c的位置关系是平行．【分析】根据平行于同一条直线的两条直线互相平行，可得答案．【解答】解：若直线a∥b，a∥c，则直线b与c的位置关系是平行，故答案为：平行．【点评】本题考查了平行公理及推论，利用了平行推论：平行于同一条直线的两条直线互相平行．三、解答题（本大题共5小题，共50.0分）11．（10分）（1）画线段AC＝30mm（点A在左侧）；（2）以C为顶点，CA为一边，画∠ACM＝90°；（3）以A为顶点，AC为一边，在∠ACM的同侧画∠CAN＝60°，AN与CM相交于点B；量得AB＝60mm；（4）画出AB中点D，连接DC，此时量得DC＝30mm；请你猜想AB与DC的数量关系是：AB＝2DC（5）作点D到直线BC的距离DE，且量得DE＝15mm，请你猜想DE与AC的数量关系是：DE＝AC，位置关系是平行．【分析】（1）借助直尺作图；（2）利用量角器作图；（3）利用量角器测得∠CAN＝60°，然后根据三角函数求得AB的长度；（4）利用直尺测出AB的中点D，然后在直角三角形ABC中求斜边AB上的中线CD的长度及斜边AB与斜边上中线CD的关系；（5）过点D作AC的平行线DE，然后根据平行线的性质（两直线平行，对应线段成比例）来求DE的长度．【解答】（1）作法：①作射线AO；②在射线AO上截取线段AC＝30mm；（2）作法：以C为顶点，利用量角器测得∠ACM＝90°；（3）作法：以A为顶点，利用量角器测得∠CAN＝60°；在直角三角形ABC中，∠CAB＝60°，AC＝30mm，∴AB＝AC÷cos∠CAB＝60mm；（4）作法：利用直尺，以A点为起点，量得AD＝30mm，点D即为所求；在直角三角形ABC中，CD为斜边AB上的中线，∴CD＝AB＝30mm；∴AB＝2DC；（5）作法：过点D作DE∥AC交CM于点E，DE即为所求；∵DE⊥BC，AC⊥BC，∵DE∥AC，∴DE：AC＝BD：AC＝1：2，∴DE＝AC＝15mm．故答案为：（3）60；（4）30、2；（5）15、、平行．【点评】本题综合考查了角的画法、线段的画法及平行线的性质与直角三角形的性质．这是一道比较容易的题目，只要多一份细心，就会多一分收获的．12．（10分）画图题：（1）在如图所示的方格纸中，经过线段AB外一点C，不用量角器与三角尺，仅用直尺，画线段AB的垂线EF和平行线GH．（2）判断EF、GH的位置关系是垂直．（3）连接AC和BC，则三角形ABC的面积是10．【分析】（1）过点C作5×1的矩形的对角线所在的直线，可得AB的垂线和平行线；（2）易得EF与GH的位置关系是：垂直；（3）根据三角形的面积公式解答．【解答】解：（1）如图（2）EF与GH的位置关系是：垂直；（3）设小方格的边长是1，则AB＝2，CH＝2，＝×2×2＝10．∴S△ABC【点评】此题灵活考查了过直线外一点作它的平行线、垂线，以及学生的观察、总结能力．13．（10分）利用直尺画图（1）利用图1中的网格，过P点画直线AB的平行线和垂线．（2）把图（2）网格中的三条线段通过平移使三条线段AB、CD、EF首尾顺次相接组成一个三角形．（3）在图（3）的网格中画一个三角形：满足①是直角三角形；②任意两个顶点都不在同一条网格线上；③三角形的顶点都在格点上（即在网格线的交点上）．【分析】（1）根据网格结构的特点，利用直线与网格的夹角的关系找出与AB平行的格点以及垂直的格点作出即可；（2）根据网格结构的特点，过点E找出与AB、CD位置相同的线段，过点F找出与AB、CD位置相同的线段，作出即可；（3）根据网格结构以及勾股定理逆定理找出符合的线段，作出即可．【解答】解：如图（1），CD∥AB，PQ⊥AB；如图（2），△EFG或△EFH都是所求作的三角形；如图（3），△ABC是符合条件的直角三角形．【点评】本题考查了平行线的作法，垂线的作法，以及线段的平移，掌握网格结构的特点并熟练应用是解题的关键．14．（10分）把图中的互相平行的线写出来，互相垂直的线写出来：【分析】根据平行线和垂直的定义即可解答．【解答】解：AB∥CD，MN∥OP，EF∥GH；AB⊥GH，AB⊥EF，CD⊥MN，CD⊥EF，CD⊥GH．【点评】本题考查了平行线和垂直的定义，理解定义是关键．15．（10分）如图，AB∥CD，E为AC的中点，（1）请过E作线段EF，且使EF∥AB，EF与BD相交于F；（2）请回答：EF与CD平行吗？为什么？【考点】J8：平行公理及推论；N2：作图—基本作图．【分析】（1）利用作一角等于已知角作法，作∠CEF＝∠A，利用同位角相等两直线平行得出即可；（2）利用如果两条直线都与第三条直线平行，那么这两条直线也互相平行，得出答案即可．【解答】解：（1）如图所示：①以点A为圆心，任意长为半径．即AW为半径画弧，交于AB于点M，②以AW为半径，以点E为圆心画弧，③以R为圆心，WM为半径画弧，交于点N，即作出了∠CEF＝∠A，延长EN交于BD于点F，∵∠FEC＝∠A，∴EF∥AB（同位角相等，两直线平行）；（2）EF∥CD，∵EF∥AB，AB∥CD，∴EF∥CD（如果两条直线都与第三条直线平行，那么这两条直线也互相平行）．【点评】此题主要考查了平行公理的推论以及作一条直线平行于已知直线，正确作出∠CEF＝∠A是解题关键．。

(完整word版)七年级数学下册相交线和平行线拔高训练

4.2 相交线和平行线典型例题及强化训练课标要求①了解对顶角，知道对项角相等。

②了解垂线、垂线段等概念，了解垂线段最短的性质，体会点到直线距离的意义。

③知道过一点有且仅有一条直线垂直干已知直线，会用三角尺或量角器过一点画一条直线的垂线。

⑥体会两条平行线之间距离的意义，会度量两条平行线之间的距离。

典型例题 1.判定与性质例1 判断题：1)不相交的两条直线叫做平行线。

( ) 2)过一点有且只有一条直线与已知直线平行。

( ) 3)两直线平行，同旁内角相等。

( ) 4)两条直线被第三条直线所截，同位角相等。

( ) 答案：(1)错，应为“在同一平面内，不相交的两条直线叫做平行线”。

(2)错，应为“过直线外一点，有且只有一条直线与已知直线平行”。

(3)错，应为“两直线平行，同旁内角互补 ”。

(4)错，应为“两条平行线被第三条直线所截，同位角相等”。

例2 已知：如图，AB ∥CD ，求证：∠B+∠D=∠BED 。

分析：可以考虑把∠BED 变成两个角的和。

如图5，过E 点引一条直线EF ∥AB ，则有∠B=∠1，再设法证明∠D=∠2，需证EF ∥CD ，这可通过已知AB ∥CD 和EF ∥AB 得到。

证明：过点E 作EF ∥AB ，则∠B=∠1（两直线平行，内错角相等）。

∵AB ∥CD （已知），又∵EF ∥AB （已作），∴EF ∥CD （平行于同一直线的两条直线互相平行）。

∴∠D=∠2（两直线平行，内错角相等）。

又∵∠BED=∠1+∠2，∴∠BED=∠B+∠D （等量代换）。

变式1已知：如图6，AB ∥CD ，求证：∠BED=360°-（∠B+∠D ）。

分析：此题与例1的区别在于E 点的位置及结论。

我们通常所说的∠BED 都是指小于平角的角，如果把∠BED 看成是大于平角的角，可以认为此题的结论与例1的结论是一致的。

(整理)七级数学相交线与平行线拔高练习

（一）安全预评价依据
除了房地产市场外，在不同职业和地点的工资差别中也可以发现类似的情形。
3.建设项目环境影响评价文件的审查要求
2.环境影响评价的概念
（2）生产、储存危险化学品（包括使用长输管道输送危险化学品）的建设项目；
2.环境影响评价工程师职业资格制度
本章中环境影响评价制度，2010年的真题中全部集中在环境影响评价这一节。环境保护的对象，环境影响评价制度，环境影响评价文件的组成、文件的报批等是历的适当性；
（2）疾病成本法与人力资本法
分）4（、请简要分析小说中“她”这个人物形象。17山东威海：分）31现代文阅读（一、分）19（题。14~19（一）阅读下文，完成评卷人得分享受高考蒋子龙年夏天漫长而奇热，我想跟社会爆炒高考有关。1994离高考还有一个多月哪，社会就已经把高考的气氛造得十足了，学校召开家长会，报纸、电视、广播等各种传媒天天是高考、高考，开讲座，设专栏，将学生该怎样复习，怎样应考，怎样调节自己的心理。对考生家长讲的就更多了，要照顾好考生，给他们做好处的，增加营养，又不要让孩子感到是专为他们做的，以免增加他们的心理负担。千万不要给考生施加压力，家长不得老谈高考的事，要劝孩子多休息，多陪他们外出散步，缓解紧张情绪。社会把高考]学科网:来源[锣鼓敲得惊地动天。这一年我们家是“高考户”??日，真正意义上的高考开始了，考生们必须自己上阵，别人无法替代。老天可怜，从前一天晚上开始变阴，稍微凉快一些了。学校嘱7月7很快就到了咐过，不能让考试吃得太饱，喝水太多，以免考试中途去厕所。早饭要精致，营养丰富，水分还要少，这并不难做到。考场离我的家甚远，骑自相车大约要半小时，我提出要送女儿去考场，在家长会上她的老师也是这样要求家长的，怕自行车万一出点问题，耽误考试。女儿起初不同意，我平时上学比去考场更远，您为什么不送？为什么不担心我的自行车出问题？这就不怕增加我的心理负担？我说，你心里无负担，我给增加一点也无妨。她笑了，笑得很甜，很可爱。我检查了她的准考证、文具盒，没有准考证是不准入考场的。我和女儿穿好雨衣，用塑料袋把她的准考证和文具盒裹好。刚出家门天上就开始掉雨点，好像我们的脚蹬子连接着播雨机，越往前蹬，雨点越大，越蹬得快，雨点越密。行至中途，已是倾盆一般，许多骑自行车的人都下车躲到商店廊下去避雨。我和女儿仍旧骑在车上，且有点兴致勃勃。我问她感觉怎么样？她说棒极了！预示着你的高考必定顺利，旗开得胜。你敢不极了，你属龙，我也属龙，两条龙一起出动奔考场，就该有大雨相随，这叫雨从龙。好兆头，对，的确棒敢大声说三句：我一定能够考好！女儿说这有什么不敢，果然大喊三声。我哈哈大笑，周围一片哗哗的雨声。我觉得心里轻松多了，我想女儿也是如此。这大雨还真有点专门护送我们爷俩的意思，到了考场雨就变得小些了。我原以为我们来得够早的，想不到考场外已经站满了家长，我估计里面有多少学生，外面就有多少家长。学生进了考场，大部分家长并不离去，还站在雨里等着，他们担心自己的孩子在考试中出问题，比如：晕场了、生病了、忘记带什么东西了。我对女儿有信心，就说，我先回家，两个小时以后再来接你。放心大胆地考，考砸了也没关系！上午的考试快结束的时候，我从冰箱里拿了一瓶矿泉水，又回到考场外面等候女儿，在考场的大门外面家长们排成两行长长的厚厚的人墙，等待着自己的孩子从考场内出来。家长们此时的心情格外敏感，看到最前面出来的考生脸色沉重，有位家长禁不住说，看来题够难的，孩子们没有考好。其实每个人心一出考场她就对姐姐说，里都在紧张地根据考生的脸色猜测题目的难易程度，猜测自己的孩子能考得怎么样。有个女孩阴沉着脸，来接她的可能是她的姐姐，你安慰安慰我吧??不等另一个姑娘说出安慰的话，她竟呜呜地哭起来了。我的女儿出来了，她也看见了我，远远地向我招了招手，笑了。女儿的笑清纯而灿烂，令我们夫妻百看不厌，她平时的一笑都能解我的心头百愁，此时这一笑，不管她实际考得怎么样，我的心里立刻也阳光灿烂起来。竞争是激烈而残酷的，哭和闹都没有用，就应该咬牙坚持下去。我的女儿在考后能有这样美丽的笑容，即使她考不上大学，我也是满意的。我拧开矿泉水的瓶塞，让她喝个够，她此时需要补充水分。看着她喝水的样子，我有一种幸福感。沉浸在上午考试的兴奋里，赶紧让脑子进入下一门要考得功课。在回家的路上我告诉她，无论上午考好了，还是考得不太理想，都忘记它，不能就这样我每天往返考场四次，把女儿送进考场，她出考场后把她接回家，她不再拒绝，反而觉得这样很方便，我成了她的同伴，她的管家，她的保镖。平时我们各忙各的，虽然父女关系也算亲密，但不像这样同甘苦共患难，有一种父女加战友的情谊。加上口试三天半的时间很快就过去了，一切又恢复了正常。（有删改）我很怀恋女儿高考的这段时间，因为，我享受了平时享受不到的许多快乐。分）4（，请具体说说作者享受到哪些快乐。作者在最后说“享受了平时享受不到的许多快乐”14.分）2（（用文中的词语或句子回答），请解释“爆炒”一词在文中的意思。文章开头说“我想跟社会爆炒高考有关”15.月7“很快就到了16.分）2”作者为什么说“真正意义”上的高考开始了？（日，真正意义上的高考开始了。7，作用是文中画线段落采用的主要表达方式是17.分）3（文章倒数第四段作者为什么详写了女儿的笑，请谈谈你的理解。18.分）4（针对社会、学校、家长的这些做法，任选一角度，谈谈你的看法。19.分）①女儿更加成熟，更理解父母的良苦用心，能从容乐观地面对高考；②父女关系更加亲密；③家庭生活更加温馨和谐；④拥有了宝贵的经历4（共14.分，答三点满分）1（每点和丰富的人生体验。分）把高考的气氛造得十足（或者把高考锣鼓敲得惊地动天）2（共15.日才是学生正式参加考试，才是高考真正的开始。7月7分）因为之前是社会、学校、家庭为高考作准备，2（共16. 1分）描写（4（共17. 1（每点。写出了家长们紧张焦灼的心理、小女孩的难过脆弱，侧面写出了“我”的紧张、担忧，反衬出女儿坦然乐观的心态。分）分）分）女儿的笑饱含着对父亲的理解、体贴、安慰，也张扬着自信和坦然，缓解了我紧张、担忧的心情，让我拥有幸福感，享受到了女儿高考带给3（共18.（意思对即可）我的快乐。“要保持良好的心态”等方面回答，言之成理即可。“高考只是一次人生经历”分）围绕“社会、学校、家庭给学生造成的压力”4（共19.（二）三、山东济宁如果你足够优秀周海亮多年前的一个夏天，我报考美术师专。复试在县城的美专进行，参加复试的头—天，父亲问我：“需要我陪你去吗?”我说，不用。父亲说：“那你一个人去好了。我去了也帮不上你什么忙。”第二天早晨，我一个人挤上了通往县城的汽车。我结结巴巴的跟服务员要房间。然后找到了考场。考场设在美术岁。下了汽车，按照父亲的嘱咐，我找了一家旅店。17那是我第一次出远门。那年我师专的一间教室里。在那里，我第—次见到那么多的画夹画板，第一次见到石膏模型。我兴奋得浑身战栗，能在这样的教室里画画，我愿意拿所有的代价交换。当天我彻夜未眠。躺在陌生的旅店，兴奋与紧张将我裹挟。我想明天假如我发挥得好，就将实现画一辈子画的梦想；假如发挥得不好，极有可能我会和父辈们一样，将自己的一生消耗在地头田畔。那天我发挥得糟透了。我想即使我发挥得再好也没用，等待进考场时，我听到一些考生的风言风语。他们说考试只是一种形式，人选其实早已内定。他们的话似乎有道理，我看到校门口的轿车排成一排，一些可疑的人在鬼鬼祟祟地交头接耳。我我第一次感到世界是可怕的，原来还有另一种力量可以操纵一件事情，并轻易埋葬一个人的梦想。识的人都知道，过多用橡皮是素描中的大忌。我稀里糊涂考场上我告诉自己不要紧张，可是我做不到。手心全是汗，我不停的用着橡皮——稍有素描常地交了考卷，垂头丧气地回到家。父亲在村口接我。他给我讲两天来村子里发生的事。他做了一桌菜，他第一次把我当成男人，在我的酒杯里倒满了酒。那天我和父亲说了很多话，唯独没有谈起考试的事。用不着问，父亲能从我的眼神里读到一切。两个多月后，录取通知书仍然没有盼来，我考上美专的希望彻底破灭。我终于跟父亲讲起那天的事，我告诉他被录取的人员可能内定得差不多了。为证明我的话是正确的，我给父亲举了很多例子。父亲听后，看了我很久。他说我相信你说的那些都是真的。可是，如果你足够优秀，那么他们就没有不录取你的道理。你被淘汰的理由只有一个一一你还不够优秀。”暗，我们不喜欢这—切，可是我们无法改变，然而我们可以改变自己。我们可以努力把自己变得非常优秀。你世上的确有龌龊、阴有时候就是这样。这变得足够优秀，你才有战胜这些龌龊和阴暗的可能。当你的才华光芒四射，任何龌龊和阴暗，都不能将其遮挡。当然，很有可能，你一辈子都达不到足够优秀。可是你应该有吧自己变得足够优秀的想法，并将其变成为自己的行动。假如你只为”变得足够优秀“而活，首先，你不会变得龌龊和阴暗，其次，你会快乐，第三，你极有可能变得足够优秀。多年来我—直相信父亲的话：只要你没有成功，被别人击败，就证明你还不够优秀，怨天怨地，都是悲观和毫无作用的。你必须让自己变得更加优秀。这不是对龌龊和阴暗的妥协，而是一种乐观的人生态度。页19第

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4.2 相交线和平行线典型例题及强化训练课标要求①了解对顶角，知道对项角相等。

②了解垂线、垂线段等概念，了解垂线段最短的性质，体会点到直线距离的意义。

③知道过一点有且仅有一条直线垂直干已知直线，会用三角尺或量角器过一点画一条直线的垂线。

⑥体会两条平行线之间距离的意义，会度量两条平行线之间的距离。

典型例题 1.判定与性质例1 判断题：1)不相交的两条直线叫做平行线。

( ) 2)过一点有且只有一条直线与已知直线平行。

( ) 3)两直线平行，同旁内角相等。

( ) 4)两条直线被第三条直线所截，同位角相等。

( ) 答案：(1)错，应为“在同一平面内，不相交的两条直线叫做平行线”。

(2)错，应为“过直线外一点，有且只有一条直线与已知直线平行”。

(3)错，应为“两直线平行，同旁内角互补 ”。

(4)错，应为“两条平行线被第三条直线所截，同位角相等”。

例2 已知：如图，AB ∥CD ，求证：∠B+∠D=∠BED 。

分析：可以考虑把∠BED 变成两个角的和。

如图5，过E 点引一条直线EF ∥AB ，则有∠B=∠1，再设法证明∠D=∠2，需证EF ∥CD ，这可通过已知AB ∥CD 和EF ∥AB 得到。

证明：过点E 作EF ∥AB ，则∠B=∠1（两直线平行，内错角相等）。

∵AB ∥CD （已知），又∵EF ∥AB （已作），∴EF ∥CD （平行于同一直线的两条直线互相平行）。

∴∠D=∠2（两直线平行，内错角相等）。

又∵∠BED=∠1+∠2，∴∠BED=∠B+∠D （等量代换）。

变式1已知：如图6，AB ∥CD ，求证：∠BED=360°-（∠B+∠D ）。

分析：此题与例1的区别在于E 点的位置及结论。

我们通常所说的∠BED 都是指小于平角的角，如果把∠BED 看成是大于平角的角，可以认为此题的结论与例1的结论是一致的。

因此，我们模仿例1作辅助线，不难解决此题。

证明：过点E 作EF ∥AB ，则∠B+∠1=180°（两直线平行，同旁内角互补）。

∵AB ∥CD （已知），又∵EF ∥AB （已作），∴EF ∥CD （平行于同一直线的两条直线互相平行）。

∴∠D+∠2=180°（两直线平行，同旁内角互补）。

∴∠B+∠1+∠D+∠2=180°+180°（等式的性质）。

又∵∠BED=∠1+∠2，∴∠B+∠D+∠BED=360°（等量代换）。

∴∠BED==360°-（∠B+∠D ）（等式的性质）。

变式2已知：如图7，AB ∥CD ，求证：∠BED=∠D-∠B 。

分析：此题与例1的区别在于E 点的位置不同，从而结论也不同。

模仿例1A BEDF与变式1作辅助线的方法，可以解决此题。

证明：过点E作EF∥AB，则∠FEB=∠B（两直线平行，内错角相等）。

∵AB∥CD（已知），又∵EF∥AB（已作），∴EF∥CD（平行于同一直线的两条直线互相平行）。

∴∠FED=∠D（两直线平行，内错角相等）。

∵∠BED=∠FED-∠FEB，∴∠BED=∠D-∠B（等量代换）。

变式3已知：如图8，AB∥CD，求证：∠BED=∠B-∠D。

分析：此题与变式2类似，只是∠B、∠D的大小发生了变化。

证明：过点E作EF∥AB，则∠1+∠B=180°（两直线平行，同旁内角互补）。

∵AB∥CD（已知），又∵EF∥AB（已作），∴EF∥CD（平行于同一直线的两条直线互相平行）。

∴∠FED+∠D=180°（两直线平行，同旁内角互补）。

∴∠1+∠2+∠D=180°。

∴∠1+∠2+∠D-（∠1+∠B）=180°-180°（等式的性质）。

∴∠2=∠B-∠D（等式的性质）。

即∠BED=∠B-∠D。

例3 已知：如图9，AB∥CD，∠ABF=∠DCE。

求证：∠BFE=∠FEC。

证法一：过F点作FG∥AB ，则∠ABF=∠1（两直线平行，内错角相等）。

过E点作EH∥CD ，则∠DCE=∠4（两直线平行，内错角相等）。

∵FG∥AB（已作），AB∥CD（已知），∴FG∥CD（平行于同一直线的两条直线互相平行）。

又∵EH∥CD （已知），∴FG∥EH（平行于同一直线的两条直线互相平行）。

∴∠2=∠3（两直线平行，内错角相等）。

∴∠1+∠2=∠3+∠4（等式的性质）即∠BFE=∠FEC。

证法二：如图10，延长BF、DC相交于G点。

∵AB∥CD（已知），∴∠1=∠ABF（两直线平行，内错角相等）。

又∵∠ABF=∠DCE（已知），∴∠1=∠DCE（等量代换）。

∴BG∥EC（同位角相等，两直线平行）。

∴∠BFE=∠FEC（两直线平行，内错角相等）。

如果延长CE、AB相交于H点（如图11），也可用同样的方法证明（过程略）。

证法三：（如图12）连结BC。

∵AB∥CD（已知），∴∠ABC=∠BCD（两直线平行，内错角相等）。

又∵∠ABF=∠DCE（已知），∴∠ABC-∠ABF =∠BCD-∠DCE（等式的性质）。

即∠FBC=∠BCE。

∴BF∥EC（内错角相等，两直线平行）。

∴∠BFE=∠FEC（两直线平行，内错角相等）。

强化训练一.填空1.完成下列推理过程①∵∠3= ∠4（已知）， __∥___（） ②∵∠5= ∠DAB （已知），∴____∥______（）③∵∠CDA + =180°（已知）， ∴AD ∥BC （）2. 如图,已知DE ∥BC,BD 是∠ABC 的平分线，∠EDC ＝109°， ∠ABC ＝50°则∠A 度，∠BDC ＝度。

3. 如图，AB ∥CD,BE,CE 分别平分∠ABC ，∠BCD, 则∠AEB ＋∠CED= 。

4、将点P(-3，y)向下平移3个单位，向左平移2个单位后得到点Q(x ，-1)，则xy=___________ 。

5、已知：如图，直线AB 和CD 相交于O ，OE 平分∠BOC ，且∠AOC=68°，则∠BOE= 二.选择题1.在海上，灯塔位于一艘船的北偏东40度方向，那么这艘船位于这个灯塔的（）A 南偏西50度方向；B 南偏西40度方向；C 北偏东50度方向；D 北偏东40度方向2.如图,AB ∥EF ∥DC ，EG ∥BD, 则图中与∠1相等的角共有( )个 A 6个 B .5个 C .4个 D.2个3、同一平面内的四条直线若满足a ⊥b,b ⊥c,c ⊥d,则下列式子成立的是（）A 、 a ∥dB 、b ⊥dC 、a ⊥dD 、b ∥c4、如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( ) A. 50° B. 60° C.70° D.80° 5.已知：AB ∥CD ，且∠ABC=20°，∠CFE=30°, 则∠BCF 的度数是 ( )A. 160°B.150°C.70°D.50°6（2003南通市）判断题已知，如图，下列条件中不能判断直线l 1∥l 2的是（）（A ）∠1＝∠3 （B ）∠2＝∠3（C ）∠4＝∠5 （D ）∠2＋∠4＝180°7.（北京市海淀区2003年）. 如图，直线c 与直线a 、b 相交，且a//b ，则下列结论：(1)21∠=∠；(2)31∠=∠；(3)23∠=∠中正确的个数为（）A. 0B. 1C. 2D. 38.（2004年浙江省富阳市）下列命题正确的是（）A 、两直线与第三条直线相交，同位角相等；B 、两线与第三线相交，内错角相等；C 、两直线平行，内错角相等；D 、两直线平行，同旁内角相等。

ABCDEFGH1ABEDC543CD AC A BED 9.（2003年安徽省）如图，AB ∥CD ，AC ⊥BC ，图中与∠CAB 互余的角有……（） A.1个 B.2个 C.3个 D.4个10.( 日照市2004年)如图，已知直线AB ∥CD ，当点E 直线AB 与CD 之间时，有∠BED ＝∠ABE ＋∠CDE 成立；而当点E 在直线AB 与CD 之外时，下列关系式成立的是（） A ∠BED ＝∠ABE ＋∠CDE 或∠BED ＝∠ABE －∠CDE; B ∠BED ＝∠ABE －∠CDEC ∠BED ＝∠CDE －∠ABE 或∠BED ＝∠ABE －∠CDE; D ∠BED ＝∠CDE －∠ABE三.解下列各题：1.如图，已知OA ⊥OC ，OB ⊥OD ，∠3=26°，求∠1、∠2的度数。

2、已知AD ∥BC ，∠A= ∠C ，求证：AB ∥CD 。

3.如图,AB ∥CD,求∠BAE ＋∠AEF ＋∠EFC ＋∠FCD 的度数.4.已知,如图AC ⊥BC,HF ⊥AB,CD ⊥AB, ∠EDC 与∠CHF 互补, 求证：DE ⊥AC.5.如图，已知AB ∥ED ，∠ABC=135°,∠BCD=80°，求∠CDE 的度数。

6.已知：如图，AD ⊥BC 于D ，EG ⊥BC 于G ，AE =AF.求证：AD 平分∠BAC 。

四、如图A 、B 是两块麦地，P 是一个水库，A 、B 之间有一条水渠，现在要将水库中的水引到A 、B 两地浇灌小麦，你认为怎样修水渠省时省料经济合算？请说出你的设计方案，并说明理由。

A B E F 第3题D CA B 321DB C第1题第2题 3 2 1F DEA C G E F DB A H A BC DE 第4题第5题第6题相交线与平行线2.1略；121°，84°；3. 90°；4.-10；5。

56°三.1.解：∵OA⊥OC，OB⊥OD∴∠1+∠2 =90°，∠3+∠2 =90°∴∠1=∠3=26°∴∠2=64°2证明：∵AD∥BC，∴∠A+∠B=180°∵∠A= ∠C，∴∠C+∠B=180°∴AB∥CD.2.解：连结AC.∵AB∥DC∴∠CAB+∠ACD=180°∵∠CAE+∠ACF+∠E+∠F =360°∴∠CAB+∠ACD=180°∴∠BAE＋∠AEF＋∠EFC＋∠FCD=540°4. 证明：∵HF⊥AB，AB⊥CD∴CD∥HF，∴∠CHF+∠HCD=180°∵∠EDC与∠CHF互补,∴∠EDC =∠HCD，∴ED∥CB∴∠AED=∠ACB ∵∠ACB=90°∴∠AED=90°∴DE⊥AC.5.解：延长BC交 DE于F.由∠ABC=135°易得∠BFD=45°, 又∠BCD=80°，得∠CDE=35°6.证明：∵AD⊥BC于D，EG⊥BC于G ∴AD∥EG，∴∠2=∠3, ∠1=∠E,∵AE =AF∴∠E = ∠3，∴∠1 = ∠2，∴AD平分∠BAC。

(完整版)七年级数学下册相交线和平行线拔高训练

(完整版)平行线与相交线提高训练

初一数学下册相交线与平行线专项提升训练(含答案详解)

最新七级数学相交线与平行线拔高练习

人教版七年级下册数学第五章相交线与平行线含答案(步步高升)

北师大数学七年级下册第二章相交线与平行线拔高题(附答案详解)

(完整word版)七年级数学初一数学相交线与平行线基础题拔高题汇总(超经典超详细)

(完整版)北师大数学七年级下册第二章相交线与平行线拔高题

精品七年级数学下册相交线与平行线综合提高题

人教版七年级数学下册《第五章相交线与平行线》能力提升卷-附答案

人教版初中七年级数学下册第五章《相交线与平行线》提高卷(含答案解析)(1)

(完整版)七年级数学下册相交线与平行线测试题

北师大数学七年级下册第二章相交线与平行线拔高题(附答案详解)

2022年人教版七年级数学下册第五章相交线与平行线章节训练试卷(含答案详解)

七年级数学下册相交线和平行线拔高训练

人教版七年级数学下册《平行线》拔高练习

最新北师大七年级下册数学平行线与相交线单元测试拔高

(完整word版)七年级数学下册相交线和平行线拔高训练

(整理)七级数学相交线与平行线拔高练习

(完整版)七年级数学下册相交线和平行线拔高训练

(完整版)平行线与相交线提高训练

初一数学下册相交线与平行线专项提升训练(含答案详解)

最新七级数学相交线与平行线拔高练习

人教版七年级下册数学第五章 相交线与平行线含答案(步步高升)

北师大数学七年级下册第二章相交线与平行线拔高题(附答案详解)

(完整word版)七年级数学初一数学相交线与平行线基础题拔高题汇总(超经典超详细)

(完整版)北师大数学七年级下册第二章相交线与平行线拔高题

精品七年级数学下册 相交线与平行线综合提高题

人教版七年级数学下册《第五章相交线与平行线》能力提升卷-附答案

人教版初中七年级数学下册第五章《相交线与平行线》提高卷(含答案解析)(1)

(完整版)七年级数学下册相交线与平行线测试题

北师大数学七年级下册第二章相交线与平行线拔高题(附答案详解)

2022年人教版七年级数学下册第五章相交线与平行线章节训练试卷(含答案详解)

七年级数学下册相交线和平行线拔高训练

人教版七年级数学下册《平行线》拔高练习

最新北师大七年级下册数学平行线与相交线单元测试拔高

(完整word版)七年级数学下册相交线和平行线拔高训练

(整理)七级数学相交线与平行线拔高练习

人教版七年级下册数学第五章相交线与平行线含答案(步步高升)

精品七年级数学下册相交线与平行线综合提高题