2019届九年级数学下册 第二十九章 投影与视图 29.2 三视图(3)课件 新人教版
合集下载
人教版九年级数学下册第二十九章《29.2_三视图(第1课时)》优质课课件
A
B
C
D
正面
6
3、长方体的主视图、俯视图如 图3所示（单位：m）正↗面，2 第2则题图 其左
视图面积是( D )
图3
A．4 B．12 C．1 D．3
4、下图是由7个完全相同的小立方块搭成的几何体，那么这个几何体的
左视图是（ A ）
A
B
C
D
5、如图所示几何体的主视图是（ D ）
↗ 正面 2
第2题图
回顾 思考
在水平面内得到的由上向下观察物体的视图，叫做俯视图
在侧面内得到由左向右观察物体的视图，叫做左视图．
主视图
投影面
左视图
正面
俯视图
侧面 水平面
三视图中，主视图与俯视图表示同一物体的长，主视图与左视图表示 同一物体的高，左视图与俯视图表示同一物体的宽，因此三个视图的大 小是互相联系的，画三视图时，三个视图要放在正确的位置
例3 图是一根钢管的直观图，画出它的三视图．
分析：钢管有内外壁，从一定角度看它时，看不见内壁，为全面地反 映立体图形的现状，画图时规定：
看得见部分的轮廓线画成实线，因被其他部分遮挡而看不见部分 的轮廓线画成虚线．
解：图是钢管的三视图，其中的虚线表示钢管的内壁．
主
左
视
视
图
图
俯 视 图
练
习
1. 画出如图所示的三棱柱的三视图（这个三柱上下底 面是正三角形）．
柱
俯 视 图
主
左
视
三图
视 图
棱
柱
俯 视 图
主 视
四图 棱 锥
俯 视 图
左
主
左
视
视
视
图
人教版九年级数学下册第29章教学课件
ABCD ）放在三个不同位置:
D
C
D
D
A
B
A
C
A
B C
D'
A'
Q
C'
D'
C'
B' A'
B'
B D（' C'）
A（' B' ）
（1）纸板平 （2）纸板倾斜 （3）纸板垂直 行于投影面； 于投影面； 于投影面．
三种情形下纸板的正投影的形状、大小如何？
通过观察，我们可以发现：
（1）当P 平行于投影面 Q 时，P的正投影与 P的 _形__状__、__大__小__一__样__；
知识点2 平行投影
由平行光线形成的投影叫做平行投影.
探照灯发出的光线形成的投影是平行投影.
太阳光照射形成的投影也是平行投影.
因为太阳距离我们很远，射到地面的太阳 光可以看成一组互相平行的射线.
知识点3 中心投影
由同一点（点光源）发出的光线形成的投 影叫做中心投影.
物体在灯泡发出的光线照射下形成的影子 就是中心投影.
例2 确定图中路灯灯泡的位置，并画出小赵 在灯光下的影子．
解：因为灯泡为点光源，所以光线相交的位置即 为灯泡所在的位置；小赵在灯下的影子即如图所示.
随堂演练
基础巩固
1. 把下列物体与它们的投影用线连接起来.
2. 下面两幅图表示两根标杆在同一时刻 的投影.请在图中画出形成投影的光线.它们 是平行投影还是中心投影？并说明理由.
解：第（1）幅图为平行投影，因为其 投影线互相平行；第（2）幅图为中心投影， 因为其投影线集中于一点.
3. 小华拿一个矩形木框在阳光下玩，矩 形木框在地面上形成的投影不可能是（ A ）.
29.2 第1课时 三视图 课件PPT 《全品学练考》九年级下数学
第二十九章 投影与视图
第1课时 三视图及其画法
这首诗教会了我们怎样观察物体（横看、侧看、近看、身处其 中看），这类似于本节课所研究的内容——三视图.
第1课时 三视图及其画法
1.观察体验
下图表示从不同方向看到一架飞机的图形：
对于同一物体，如果从不同角度观察，所得到的视图可 能是不同的.
第1课时 三视图及其画法
球
俯
视
图
谢 谢 观 看！
第1课时 三视图及其画法 支架的三视图
主视图
左视图
俯视图
第1课时 三视图及其画法
练习 （1） 画出如图所示的正三棱柱的三视图.
正
主
左
三
视
视
棱
图
图
柱 俯
视
图
第1课时 三视图及其画法
(2) 画出圆锥的三视图．
主
左
视
视
圆
图
图
锥
俯
视·
图
第1课时 三视图及其画法
(3) 画出半球的三视图．
主
左
视
视
半图
图
这些图形的投影面分别在什么位置？
从上面看
第1课时 三视图及其画法
2.观察探究 把物体放在三个
互相垂直的平面的空 间：从投影的角度认 识三视图
主视图
正面
左视图
俯视图
侧面 水平面
第1课时 三视图及其画法
用投影的方法 画三视图：左视图、 右视图各是什么形状？
主视图
正面
左视图
俯视图
侧面 水平面
第1课时 三视图及其画法 主视图 左视图
长对正，高平齐，宽相等.
第1课时 三视图及其画法 3.应用 例1 画出下图所示的一些几何体的三视图.
第1课时 三视图及其画法
这首诗教会了我们怎样观察物体（横看、侧看、近看、身处其 中看），这类似于本节课所研究的内容——三视图.
第1课时 三视图及其画法
1.观察体验
下图表示从不同方向看到一架飞机的图形：
对于同一物体，如果从不同角度观察，所得到的视图可 能是不同的.
第1课时 三视图及其画法
球
俯
视
图
谢 谢 观 看！
第1课时 三视图及其画法 支架的三视图
主视图
左视图
俯视图
第1课时 三视图及其画法
练习 （1） 画出如图所示的正三棱柱的三视图.
正
主
左
三
视
视
棱
图
图
柱 俯
视
图
第1课时 三视图及其画法
(2) 画出圆锥的三视图．
主
左
视
视
圆
图
图
锥
俯
视·
图
第1课时 三视图及其画法
(3) 画出半球的三视图．
主
左
视
视
半图
图
这些图形的投影面分别在什么位置？
从上面看
第1课时 三视图及其画法
2.观察探究 把物体放在三个
互相垂直的平面的空 间：从投影的角度认 识三视图
主视图
正面
左视图
俯视图
侧面 水平面
第1课时 三视图及其画法
用投影的方法 画三视图：左视图、 右视图各是什么形状？
主视图
正面
左视图
俯视图
侧面 水平面
第1课时 三视图及其画法 主视图 左视图
长对正，高平齐，宽相等.
第1课时 三视图及其画法 3.应用 例1 画出下图所示的一些几何体的三视图.
2019版九年级数学下册 第二十九章 投影与视图 29.2 三视图(第1课时)教学课件1 新人教版
【解析】四棱锥的三视图如图
正
左
视
视
图
图
俯 视 图
【例题】 【例1】画出如图所示一些基本几何体的三视图.
圆柱 （1）
球 （2）
正三棱柱 （3）
宽相等
主视图
左视图
俯视图
宽相等:俯视图和左视图共同反映了物体前后方向的尺寸.
俯
左
球体
主
【跟踪训练】
1.下图是底面为等腰直角三角形的三棱柱的俯视图,尝
试画出它的主视图和左视图,并与同伴交流.
主视图
正面
主视图
左视图 高
长
宽
宽 俯视图
三视图位置有规定，主 视图要在左上边，它的 下方应是俯视图，左视 图坐落在右边.
主视图
左视图 高
长
宽
宽 俯视图
【跟踪训练】
下面的四组图中，是如图所示的圆柱体的三视图的是（ B ）
主视图
左视图
A
俯视图
主视图 左视图
B
俯视图
主视图 左视图
C
俯视图
主视图 左视图
主视图
左视图
俯视图(1)Βιβλιοθήκη 主视图俯视图(2)
左视图
2.下图是底面为等腰梯形的四棱柱的俯视图,尝试画出 它的主视图和左视图,并与同伴交流.
主视图
左视图
俯视图(3)
主视图
俯视图(4)
左视图
【例2】画出此小零件的三视图
主 视 图
左 视 图
俯 视 图
【跟踪训练】
正视图
画出此物体的三视图
侧视图
俯视图
三视图 主视图——从正面看到的图 左视图——从左面看到的图 俯视图——从上面看到的图 画物体的三视图时,要符合如下原则:
人教版数学九年级下示范课件：第29章摄影与视图
中心 投影
平行的投射线 从一点出发的投射 线
放大 (位似变换)
都是物体在光线 的照射下，在某 个平面内形成的 影子.(即都是投 影)
29.1
投影
第2课时
1、能根据正投影的性质画出简单的平面图形的正投影；
2、培养动手实践能力，发展空间想象能力.
1.什么叫投影? 一般地,用 光线 照射物体,在 的影子叫做物体的投影.
思考:平行投影和中心投影有什么区别和联系呢?
把下列物体与它们的投影用线连接起来：
变式训练：1、如图是一根电线杆在一天中不同时 刻的影长图，试按其一天中时间先后顺序排列，正 确的是（ ） C
北 北 北 北
① （A）①②③④ （C）④①③②
①
东
②
② ③ （B）④②③① （D）④③②①
③
东
东
④
④
东
【例1】（1）它们 是太阳的光线还是 灯光的光线? 它们是灯光的光线！
知 识 点 一 投 影
物体在日光或灯光的照射下，会在地面、墙壁等处 形成影子，影子与物体的形状有密切的关系。
2、一般地，用光线照射物体，在某个平面（地板、 __ _________ 墙壁等）上得到的 影子 叫做物体的投影. ___ _____叫做投影线，投影所在的 平面 叫做 照射光线 投影面.
三、研读课文 练一练
不同 位置 物体 线段 面
物体平行于 投影面
形状、大小不 变（全等） 形状、大小不 变（全等）
物体倾斜于 投影面
大小变化 形状、大小均 变化
物体垂直于 投影面 点 线
当物体的某个面平行于投影面时，这个面的正 投影与这个面的形状、大小完全相同.
【例】画出如图摆放的正方体在投影面P上的正投影. （1）正方体的一个面ABCD平行于投影面P； （2）正方体的一个面ABCD倾斜于投影面P，上底面ADEF垂直 于投影面P,并且对角线AE垂直于投影面P.
平行的投射线 从一点出发的投射 线
放大 (位似变换)
都是物体在光线 的照射下，在某 个平面内形成的 影子.(即都是投 影)
29.1
投影
第2课时
1、能根据正投影的性质画出简单的平面图形的正投影；
2、培养动手实践能力，发展空间想象能力.
1.什么叫投影? 一般地,用 光线 照射物体,在 的影子叫做物体的投影.
思考:平行投影和中心投影有什么区别和联系呢?
把下列物体与它们的投影用线连接起来：
变式训练：1、如图是一根电线杆在一天中不同时 刻的影长图，试按其一天中时间先后顺序排列，正 确的是（ ） C
北 北 北 北
① （A）①②③④ （C）④①③②
①
东
②
② ③ （B）④②③① （D）④③②①
③
东
东
④
④
东
【例1】（1）它们 是太阳的光线还是 灯光的光线? 它们是灯光的光线！
知 识 点 一 投 影
物体在日光或灯光的照射下，会在地面、墙壁等处 形成影子，影子与物体的形状有密切的关系。
2、一般地，用光线照射物体，在某个平面（地板、 __ _________ 墙壁等）上得到的 影子 叫做物体的投影. ___ _____叫做投影线，投影所在的 平面 叫做 照射光线 投影面.
三、研读课文 练一练
不同 位置 物体 线段 面
物体平行于 投影面
形状、大小不 变（全等） 形状、大小不 变（全等）
物体倾斜于 投影面
大小变化 形状、大小均 变化
物体垂直于 投影面 点 线
当物体的某个面平行于投影面时，这个面的正 投影与这个面的形状、大小完全相同.
【例】画出如图摆放的正方体在投影面P上的正投影. （1）正方体的一个面ABCD平行于投影面P； （2）正方体的一个面ABCD倾斜于投影面P，上底面ADEF垂直 于投影面P,并且对角线AE垂直于投影面P.
九年级数学下册29.2三视图课件新版新人教版
尖子生好方法:听课时应该始终跟着老师的节奏，要善于抓住老师讲解中的关键词，构建自己的知识结构。利用老师讲课的间隙，猜想老师还会讲什么，会怎样讲， 怎样讲会更好，如果让我来讲，我会怎样讲。这种方法适合于听课容易分心的同学。
2019/7/7
精选最新中小学教学课件
30
thank
you!
2019/7/7
主
左
三 棱
视 图
视 图
柱
俯 视 图
主
左
主
左
视
四
图
棱
视
视
图
球图
视 图
锥
俯
俯
视
视
图
图
例2 画出如图所示的支架（一 种小零件）的三视图．
分析：支架的现状：由两个大小不等的长方体构成的组合体， 画三视图时要注意这两个长方体的上下、前后位置关系．
解：如图是支架的三视图．
正面
主
左
视
视
图
图
俯 视 图
例3:如图是一根钢管的直观图，画出它的三视图．
例 5某工厂要加工一批密封罐，设计者给出了密封
罐的三视图，请你按照三视图确定制作每个密封罐 所需钢板的面积．
50
50
100
100
分析：对于某些立体图形，沿着其中一些线（例如棱柱的棱） 剪开，可以把立体图形的表面展开成一个平面图形——展开 图．在实际的生产中，三视图和展开图往往结合在一起使 用．解决本题的思路是，由三视图想象出密封罐的立体形状， 再进一步画出展开图，从而计算面积．
分析：钢管有内外壁，从一定角度看它时，看不见内壁，为全面地反 映立体图形的现状，画图时规定：
看得见部分的轮廓线画成实线，因被其他部分遮挡而看不见部分的轮 廓线画成虚线．
2019/7/7
精选最新中小学教学课件
30
thank
you!
2019/7/7
主
左
三 棱
视 图
视 图
柱
俯 视 图
主
左
主
左
视
四
图
棱
视
视
图
球图
视 图
锥
俯
俯
视
视
图
图
例2 画出如图所示的支架（一 种小零件）的三视图．
分析：支架的现状：由两个大小不等的长方体构成的组合体， 画三视图时要注意这两个长方体的上下、前后位置关系．
解：如图是支架的三视图．
正面
主
左
视
视
图
图
俯 视 图
例3:如图是一根钢管的直观图，画出它的三视图．
例 5某工厂要加工一批密封罐，设计者给出了密封
罐的三视图，请你按照三视图确定制作每个密封罐 所需钢板的面积．
50
50
100
100
分析：对于某些立体图形，沿着其中一些线（例如棱柱的棱） 剪开，可以把立体图形的表面展开成一个平面图形——展开 图．在实际的生产中，三视图和展开图往往结合在一起使 用．解决本题的思路是，由三视图想象出密封罐的立体形状， 再进一步画出展开图，从而计算面积．
分析：钢管有内外壁，从一定角度看它时，看不见内壁，为全面地反 映立体图形的现状，画图时规定：
看得见部分的轮廓线画成实线，因被其他部分遮挡而看不见部分的轮 廓线画成虚线．
九年级数学下册 第二十九章 投影与视图 29.2 三视图(2)课件下册数学课件
两个(liǎnɡ ɡè)大小不等的长方体构成
（2）画组合体的三视图时，构成组合 体的各个部分的视图也要注意
长对正 高平齐 宽相等
12/10/2021
第五页，共十七页。
二、新课讲解(jiǎngjiě)
知 （3）请你画出它的三视图. 识 点 一
主视图
左视图(shìtú)
12/10/2021
俯视图
第六页，共十七页。
二、新课讲解(jiǎngjiě)
例2 右图是一根钢管的直观图，画出
它的三视图.
知
（1）钢管有内外壁，从一定(yīdìng)角度看它
识
时，看不见内壁.为全面地反映立体图
点
形的形状，画图时我们需要怎样的处理？
一
看得见部分的轮廓线画 成实线，看不见部分的
轮廓线画成虚线
12/10/2021
第七页，共十七页。
点 一
所以内壁 画为虚线.图中虚线与相邻 实线的距离即钢管 壁厚 ，它等于(děngyú)左视图
中两圆 半径之差 .
12/10/2021
第九页，共十七页。
三、归纳(guīnà)小结
1、画组合体的三视图时，构成组 合体(hé tǐ)的各个部分的视图也要注意
“长对正 ，高平齐 ， 宽相等 .”
2、学习反思：________________ __________________________.
时，构成组合体的各个部分的视图也要注意。例2 右图是一根钢管的直观图，画出。形的形状，画图时 我们需要怎样的处理。合体的各个部分的视图也要注意
Image
12/10/2021
第十七页，共十七页。
二、新课讲解( jiǎngjiě)
解：虚线表示钢管(gāngguǎn)的内 壁，三视图如下：
（2）画组合体的三视图时，构成组合 体的各个部分的视图也要注意
长对正 高平齐 宽相等
12/10/2021
第五页，共十七页。
二、新课讲解(jiǎngjiě)
知 （3）请你画出它的三视图. 识 点 一
主视图
左视图(shìtú)
12/10/2021
俯视图
第六页，共十七页。
二、新课讲解(jiǎngjiě)
例2 右图是一根钢管的直观图，画出
它的三视图.
知
（1）钢管有内外壁，从一定(yīdìng)角度看它
识
时，看不见内壁.为全面地反映立体图
点
形的形状，画图时我们需要怎样的处理？
一
看得见部分的轮廓线画 成实线，看不见部分的
轮廓线画成虚线
12/10/2021
第七页，共十七页。
点 一
所以内壁 画为虚线.图中虚线与相邻 实线的距离即钢管 壁厚 ，它等于(děngyú)左视图
中两圆 半径之差 .
12/10/2021
第九页，共十七页。
三、归纳(guīnà)小结
1、画组合体的三视图时，构成组 合体(hé tǐ)的各个部分的视图也要注意
“长对正 ，高平齐 ， 宽相等 .”
2、学习反思：________________ __________________________.
时，构成组合体的各个部分的视图也要注意。例2 右图是一根钢管的直观图，画出。形的形状，画图时 我们需要怎样的处理。合体的各个部分的视图也要注意
Image
12/10/2021
第十七页，共十七页。
二、新课讲解( jiǎngjiě)
解：虚线表示钢管(gāngguǎn)的内 壁，三视图如下：
九年级数学下册第二十九章投影与视图29.2三视图(第一课时认识几何体的三视图)课件(新版)新人教版
2. 常见的几何体的三视图：
几何体
主视图
左视图
俯视图
例1 如图所示的几何体的左视图是( C )
导引：左视图是从物体的左面看到的视图，从圆柱的左 边向右边看，看到的是一个矩形，故选C.
总结
单个几何体的三视图直接根据常见的几何体三 视图中识别．
1 把图中的几何体与它们对应的三视图用线连接起来.
2 (2015·资阳)如图是一个圆台，它的主视图是( )
三视图的画法：画三视图时，三个视图要放在正确的 位置，并且使主视图与俯视图的长对正；主视图与左 视图的高平齐；左 视图与俯视图的宽 相等． 如图(2)为图(1)按 1∶1的比例画出 的三视图．
例2 画出图中基本几何体的三视图
分析：画这些基本几何体的三视图时，要注意 从三个方面观
察它们.具体方法为：
1. 视图的相关概念： (1)视图：当我们从某一方向观察一个物体时，所看到
的平面图形叫做物体的一个视图，视图可以看作物 体在某一方向光线下的正投影． (2)三视图：一个物体在三个投影面内进行正投影，在 正面内得到的由前向后观察物体的视图，叫做主视 图；在水平面内得到的由上向下观察物体的视图， 叫做俯视图；在侧面内得到的由左向右观察物体的 视图，叫做左视图．
(1) 确定主视图的位置，画出主视图；
(2) 在主视图正下方画出俯视图，注意与主 视图“长对
正”；
(3) 在主视图正右方画出左视图，注意与主 视图“高平
齐”，与俯视图“宽相等”；
(4) 为表示圆柱、圆锥等的对称轴，规定在视图中加画
点划线（
）表示对称轴.
解： 如图所示.
总结
不论是画单个几何体的三视图还是组合几何体的 三视图，都必须注意两点：一是遵循“长对正，高平 齐，宽相等”的原则；二是看得见的轮廓线画成实线， 看不见的轮廓线画成虚线．
人教版初中数学九年级下册第二十九章投影与视图29.2三视图第3课时由三视图到表面展开图作业设
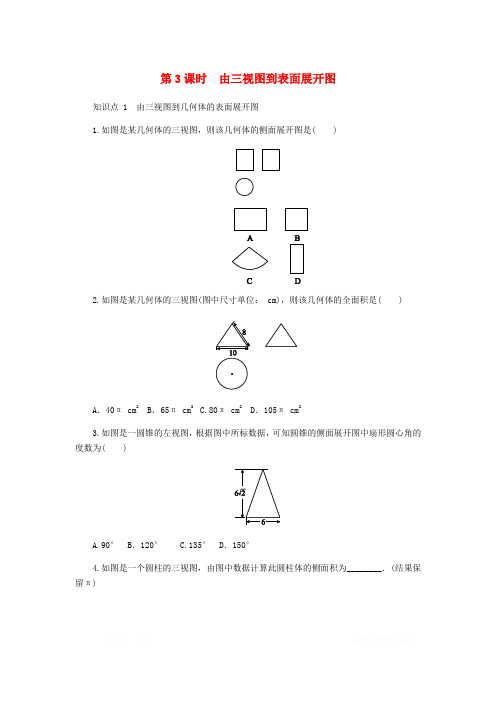
第3课时由三视图到表面展开图知识点 1 由三视图到几何体的表面展开图1.如图是某几何体的三视图，则该几何体的侧面展开图是( )2.如图是某几何体的三视图(图中尺寸单位： cm)，则该几何体的全面积是( )A．40π cm2 B．65π cm2 C.80π cm2 D．105π cm23.如图是一圆锥的左视图，根据图中所标数据，可知圆锥的侧面展开图中扇形圆心角的度数为( )A.90° B．120° C.135° D．150°4.如图是一个圆柱的三视图，由图中数据计算此圆柱体的侧面积为________．(结果保留π)5.如图是三个几何体的三视图和展开图，请将同一物体的三视图和展开图搭配起来．A与______；B与______；C与______．6.根据图中的三视图画出该物体的展开图．知识点 2 由物体的展开图想象物体的三视图7.某物体的侧面展开图如图，那么它的左视图为( )8.如图是一个几何体的展开图，下面哪一个平面图形不是它的三视图中的一个视图( )9．如图是某个几何体的表面展开图，则把该几何体平放在平面上时，其俯视图为( )10.如图是某几何体的展开图．(1)这个几何体的名称是__________；(2)画出该几何体的三视图；(3)求这个几何体的体积(π取3.14)．能力提升11．一个圆锥的左视图如图，则这个圆锥的侧面展开图(扇形)的弧长为( )A.2πB．4π C.6 D．6π12.一个圆柱的侧面展开图是两邻边长分别为6和8的矩形，则该圆柱的底面圆的半径是( )A.3πB.4πC.3π或4πD.6π或8π13.如图是某种型号的正六角螺母毛坯的三视图，求它的表面积．14.如图是一个几何体的三视图，若主视图的高为25，俯视图中等边三角形的边长为10，求这个几何体的表面积．15.如图是一个几何体的三视图．(1)写出这个几何体的名称；(2)根据图中所示数据计算这个几何体的全面积；(3)如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC的中点D，请求出蚂蚁爬行的最短路程．参考答案1．A [解析] 由三视图可知此几何体为圆柱，它的侧面展开图为矩形，且矩形的一边为圆柱的高，另一边为圆柱的底面圆的周长．故选A.2.B [解析] 由主视图和左视图为三角形可判断出该几何体是锥体，由俯视图是圆形可判断出这个几何体应该是圆锥；根据三视图知：该圆锥的母线长为8 cm ，底面半径为10÷ 2＝5(cm)，故表面积为12×2πrl ＋πr 2＝π×5×8＋π×52＝65π(cm 2)．3.B [解析] ∵圆锥的底面直径为6，∴半径为3，圆锥的底面周长为6π.∵圆锥的高是6 2，∴圆锥的母线长为32＋（6 2）2＝9.设扇形的圆心角为n °，∴n π×9180＝6π，解得n ＝120，即圆锥的侧面展开图中扇形的圆心角的度数为120°.故选B.4. 24π [解析] 由图可知，圆柱的底面直径为4，高为6，所以侧面积为4×π×6＝ 24π.5. c a b [解析] A 为正三棱柱，B 为圆锥，C 为正方体．6.解：展开图如图所示.7.B8.D [解析] 由几何体的展开图可知该几何体为正六棱柱，若A 项是它的俯视图，则B 项是它的主视图，C 项是它的左视图．故选D.9.B10.解：(1)圆柱. (2)三视图如图所示.(3)这个几何体的体积为πr 2h ≈3.14×52×20＝1 570.11.D [解析] 根据圆锥的左视图可知底面圆的直径为6，母线长为5，∴这个圆锥的侧面展开图的弧长为πd ＝6π.故选D.12.C13.解：S 侧面＝2×3×6＝36(cm 2)，S 底面＝12×2×(32×2)×6＝6 3(cm 2)，∴S 表面＝36＋2×6 3＝36＋12 3(cm 2).14.解：根据题意可得正三角形的高为102－52＝5 3，∴俯视图的面积为12×10×5 3＝25 3，∴这个几何体的表面积为3×25×10＋2×25 3＝750＋50 3.15.(1)圆锥．(2)由三视图知该圆锥底面直径为4 cm ，母线长为6 cm ，∴圆锥的侧面积S 侧＝12×4π×6＝12π(cm 2)，底面圆的面积为π(42)2＝4π(cm 2)，故该几何体的全面积为12π＋4π＝16π(cm 2)．(3)由圆锥的母线长为6 cm ，底面圆的半径为2 cm ，可得此圆锥侧面展开图扇形的圆心角为120°，半径为6 cm ，如图，连接AB ′，B ′C ，则∠B ′AC ＝60°，∴△AB ′C 为等边三角形，B ′D 的长为蚂蚁所爬的最短路程． ∵D 为AC 的中点， ∴B ′D ⊥AC ，∴B ′D ＝AB ′2－AD 2＝62－32＝3 3(cm)， 即蚂蚁爬行的最短路程为3 3 cm.。
人教版九年级数学下册第二十九章《29.2 三视图》优质课课件
图 图时，构成组合体的各
个部分的视图也要注意
“长对正 ，高平齐 ，宽相等 .”
三、研读课文
知 （3）请你画出它的三视图. 识 点 一
主视图
左视图
俯视图
三、研读课文
例3 右图是一根钢管的直观图，画出
它的三视图.
知 识 点 一
（1）钢管有内外壁，从一定角度看它 时，看不见内壁.为全面地反映立体图 形的形状，画图时我们需要怎样的处理？
三、研读课文
认真阅读课本本节的内容， 完成下面练习并体验知识点 的形成过程.
三、研读课文
例2 画出如图所示的支架（一种小零件）
的三视图，支架的两个台阶的高度和宽
知 度都是同一长度.
识 点 一
组 合 体 的 三
（1）这个小零件支 架是由几个什么基 本几何体构成的？ 两个大小不等的长方体构成
视 （2）画研读课文
画出图中的几何体的三视图.
四、归纳小结
1、三视图位置有规定，主视图要在左上边，它
下方应是 俯视图 ，左视图坐落在 右上边 .
2、画三视图时，三个视图要放在正确的位置，并
且使主视图与俯视图的 长对正 ，主视图与左
视图的 高平齐 ，左视图与俯视图
从正面看 从左面看 从上面看
三
视
图
的
知位
识 点
置 关 系
二和
大
小
关
系
三、研读课文
3、如图， 三视图中各视图的大小也有 关系.主视图与俯视图表示 同一物体的 长 ，主视图与 左视图表示同一的 高 ， 左视图与俯视图表示同一物 体的 宽 .因此三视图的大 小是互相联系的.画三视图 时，三个视图要放在正确的 位置，并且使主视图与俯视 图的长对正，主视图与左视 图的高平齐，左视图与俯视 图的宽相等 .
人教版九年级数学下册第二十九章投影与视图PPT教学课件
新课讲解
问题1 观察日晷、皮影戏的图片，你能解释其中的道理吗？
新课讲解
北京故宫中的日晷闻名世界，是我国 光辉灿烂的文化瑰宝．它是我国古代利用 日影测定时刻的仪器，它由“晷面”与“ 晷针”组成，当太阳光照在日晷中轴上产 生投影，晷针的影子就会投向晷面，随着 时间的推移，晷针的影子长度发生变化， 晷针的影子在晷面上慢慢移动，聪明的古 人以此来显示时刻．
问题5 如图，把一根直的细铁丝（记为线段AB）放在 三个不同位置： （1）铁丝平行于投影面；（2）铁丝倾斜于投影面； （3）铁丝垂直于投影面． 三种情况下铁丝的正投影的形状、大小如何？
新课讲解
解：（1）当线段AB平行于投影面时，它的正投影是 线段A1B1，它们的大小关系为AB=A1B1； （2）当线段AB倾斜于投影面时，它的正投影是线段 A2B2，它们的大小关系为AB＞A2B2； （3）当线段AB垂直于投影面时，它的正投影是一个 点A3．
新课讲解
问题4 下图中三角尺的投影各是什么投影？它们 的投影线与投影面的位置关系有什么区别？
新课讲解
答：两幅图中的投影都是平行投影．从左边数第一幅 图中投影线斜着照射投影面，第二幅图中投影线垂直 照射投影面（即投影线正对着投影面）． 像第二幅图这样，投影线垂直于投影面产生的投影叫 做正投影．
新课讲解
新课讲解
分析：（1）当正方体在如图(1)的位置时，正方 体的一个面ABCD及与其相对的另一面与投影面平 行，这两个面的正投影是与正方体的一个面的形状、 大小完全相同的正方形A'B'C'D'．正方形A'B'C'D'的 四条边分别是正方体其余四个面（这些面垂直于投影 面）的投影．因此，正方体的正投影是一个正方形．
九年级数学下册 第二十九章 投影与视图 29.2 三视图教学
你能画出几何体的三视图吗？
第三页，共二十页。
主视图
左视图(shìtú)
请画出这个(zhège)几何体的三视图
2021/12/11
第四页，共二十页。
俯视图
2021/12/11
第五页，共二十页。
画一个(yī ɡè)物体的 三视图时,主视图、
左视图、俯视图所画
的位置如图,且要符合
如下原则:
长对正,
高平齐,
2021/12/11
第十六页，共二十页。
由三视图想象实物(shíwù)形状：
实 物
(sh íwù)
2021/12/11
实 物
(sh íwù)
第十七页，共二十页。
实 物
(sh íwù)
2021/12/11
实 物
(sh íwù)
第十八页，共二十页。
本课小 结
通过本节课的学习(xuéxí)你有什么收获和体会？你 还有什么困惑？
宽相等(xiāngděng).
圆 柱
(yuánzh
ù)和 圆 锥 三 视 图
圆柱
圆锥
2021/12/11
主视图
左视图
(shìtú)
主视图
左视图
(shìtú)
第六页，共二十页。
俯视图
·
俯视图
球的三视图
主视图
左视图
(shìtú)
2021/12/11
俯视图
第七页，共二十页。
下图是一个蒙古包的照片.小明认为这个蒙古包可以看成如图的几何体,请 画出这个几何体的三种视图(shìtú).你与小明的做法相同吗?
俯视图(2)
俯视图(3) 俯视图(4)
2021/12/11
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二十九章 投影与视 图
29.2 三视图（3）
ppt课件
1
一、新课引入
一个物体的俯视图是圆，则该物体有
可能是 圆柱、球 (写两个即可)．
ppt课件
2
一、新课引入
1 能熟练地画出物体的三视图； 2 能够由三视图想像出物体的
形状，提高空间想象能力.
ppt课件
3
二、新课讲解
根
知据
识 点 一
三 视 图 说
出
立
体
图
形
图3
ppt课件
图4
7
二、新课讲解
根
知 识
据 三 视
点图
二描
述
物
体
的
形
状
例2 根据物体的三视图描述物体的形状. （1）根据主视图该物体与什么几何体有关？ （2）请同学们再结合左视图与俯视图，试判
断下立体图形的名称.
解：
（1）由主视图可知，物体 的正面是正五边形。
（2）由左视图可知，物体 的侧面是矩形，且有一条棱； 由俯视图可知，由上向下看 物体是矩形，且有一条棱。 所以物体是五棱柱形状。
根
知 据 (2)从正面、侧面看立体图形，图象都是
识 点 一
三 视 图 说
等腰三角形；从上面看，图象是圆；可以
想象出:整体是 圆锥 ，如图(2)所示.
出 立
根据“长对正，高平齐，宽相等”的关系，
体 试下画出它们的立体图形.
图 形 解:如图
ppt课件
(1)
5
(2)
二、新课讲解
练一练
根 1、如下图为一个几何体的三视图，那
2、学习反思： __________________________.
ppt课件
10
四、强化训练 1. 圆柱对应的主视图是（ A ）.
A.
B.
C.
D.
ppt课件
11
四、强化训练
2.如果用 □ 表示1个立方体，用 表 示两个立方体叠加，用 ■ 表示三个 立方体叠加，那么下图由6个立方体
叠成的几何体的主视图是 ( B )
ppt课件
8
二、新课讲解
根
知 识
据 三 视
点图
二描
述
物
体
的
形
状
（3）若物体为五棱柱，应该是怎样摆 放的？你能根据“长对正，高平齐，宽 相等”的关系，确定轮廓线的位置，以 及各个方向的尺寸吗？
解：①物体如图所示摆放；
②可以
ppt课件
9
三、归纳小结
1、由三视图想象立体图形时，要先分 别根据主视图、俯视图和左视图想象立 体图形的前面、上面和左侧面，然后再 综合起来考虑整体图形.
ppt课件
12
四、强化训练
3.一个几何体的三视图如图所示（其中 标注的a、b、c为相应的边长），则这 个几何体的体积是 a·b·c .
ppt课件
13
五、布置作业
根据下面的三视图说出这个几何体是 怎样由四个正方体组合而成的.
解：如图，这个几何 体是由前面3个正方 体，后面1 个正方体 组合而成的。
知据
识 点 一
三 视 图 说
么这个几何体是___圆__锥_______．
出
立
体
图
形
ppt课件
6
二、新课讲解
练一练
根 2、根据下列物体的三视图，填出几何体的名称：
知据
识 点 所示的几何体是____________；
六棱柱 （2）如图8所示的几何体是___圆__台_______.
ppt课件
14
六、结束语
我之所以比笛卡儿看得远些， 是 因为我站在巨人的肩上.
——牛顿
ppt课件
15
出
立
体
图
形
例1 根据三视图说出立体图形的名称.
（1）
（2）
分析:由三视图想象立体图形时，要先分别根
据主视图、俯视图和左视图想象立体图形的前
面、上面和左侧面，然后再综合起来考虑整体
ppt课件 图形.
4
二、新课讲解
(1)从三个方向看立体图形，图象都是矩形， 可以想象出:整体是长方体 ，如图(1)所示；
29.2 三视图（3）
ppt课件
1
一、新课引入
一个物体的俯视图是圆，则该物体有
可能是 圆柱、球 (写两个即可)．
ppt课件
2
一、新课引入
1 能熟练地画出物体的三视图； 2 能够由三视图想像出物体的
形状，提高空间想象能力.
ppt课件
3
二、新课讲解
根
知据
识 点 一
三 视 图 说
出
立
体
图
形
图3
ppt课件
图4
7
二、新课讲解
根
知 识
据 三 视
点图
二描
述
物
体
的
形
状
例2 根据物体的三视图描述物体的形状. （1）根据主视图该物体与什么几何体有关？ （2）请同学们再结合左视图与俯视图，试判
断下立体图形的名称.
解：
（1）由主视图可知，物体 的正面是正五边形。
（2）由左视图可知，物体 的侧面是矩形，且有一条棱； 由俯视图可知，由上向下看 物体是矩形，且有一条棱。 所以物体是五棱柱形状。
根
知 据 (2)从正面、侧面看立体图形，图象都是
识 点 一
三 视 图 说
等腰三角形；从上面看，图象是圆；可以
想象出:整体是 圆锥 ，如图(2)所示.
出 立
根据“长对正，高平齐，宽相等”的关系，
体 试下画出它们的立体图形.
图 形 解:如图
ppt课件
(1)
5
(2)
二、新课讲解
练一练
根 1、如下图为一个几何体的三视图，那
2、学习反思： __________________________.
ppt课件
10
四、强化训练 1. 圆柱对应的主视图是（ A ）.
A.
B.
C.
D.
ppt课件
11
四、强化训练
2.如果用 □ 表示1个立方体，用 表 示两个立方体叠加，用 ■ 表示三个 立方体叠加，那么下图由6个立方体
叠成的几何体的主视图是 ( B )
ppt课件
8
二、新课讲解
根
知 识
据 三 视
点图
二描
述
物
体
的
形
状
（3）若物体为五棱柱，应该是怎样摆 放的？你能根据“长对正，高平齐，宽 相等”的关系，确定轮廓线的位置，以 及各个方向的尺寸吗？
解：①物体如图所示摆放；
②可以
ppt课件
9
三、归纳小结
1、由三视图想象立体图形时，要先分 别根据主视图、俯视图和左视图想象立 体图形的前面、上面和左侧面，然后再 综合起来考虑整体图形.
ppt课件
12
四、强化训练
3.一个几何体的三视图如图所示（其中 标注的a、b、c为相应的边长），则这 个几何体的体积是 a·b·c .
ppt课件
13
五、布置作业
根据下面的三视图说出这个几何体是 怎样由四个正方体组合而成的.
解：如图，这个几何 体是由前面3个正方 体，后面1 个正方体 组合而成的。
知据
识 点 一
三 视 图 说
么这个几何体是___圆__锥_______．
出
立
体
图
形
ppt课件
6
二、新课讲解
练一练
根 2、根据下列物体的三视图，填出几何体的名称：
知据
识 点 所示的几何体是____________；
六棱柱 （2）如图8所示的几何体是___圆__台_______.
ppt课件
14
六、结束语
我之所以比笛卡儿看得远些， 是 因为我站在巨人的肩上.
——牛顿
ppt课件
15
出
立
体
图
形
例1 根据三视图说出立体图形的名称.
（1）
（2）
分析:由三视图想象立体图形时，要先分别根
据主视图、俯视图和左视图想象立体图形的前
面、上面和左侧面，然后再综合起来考虑整体
ppt课件 图形.
4
二、新课讲解
(1)从三个方向看立体图形，图象都是矩形， 可以想象出:整体是长方体 ，如图(1)所示；